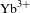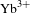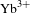1 Introduction
High-power
![]() $\text{Yb}^{3+}$
doped fiber lasers have experienced an impressive progress in the last few decades. The maximum output power for multimode regime from a single fiber laser has reached hundreds of kilowatts[Reference Snitzer1] for continuum regime (Figure 1). Actually, in the first operation of a fiber laser, in the early 1960s, not
$\text{Yb}^{3+}$
doped fiber lasers have experienced an impressive progress in the last few decades. The maximum output power for multimode regime from a single fiber laser has reached hundreds of kilowatts[Reference Snitzer1] for continuum regime (Figure 1). Actually, in the first operation of a fiber laser, in the early 1960s, not
![]() $\text{Yb}^{3+}$
doped but
$\text{Yb}^{3+}$
doped but
![]() $\text{Nd}^{3+}$
doped fiber was used as the gain medium[Reference Snitzer2–Reference O’Connor, Gapontsev, Fomin, Abramov and Ferin4]. Years later,
$\text{Nd}^{3+}$
doped fiber was used as the gain medium[Reference Snitzer2–Reference O’Connor, Gapontsev, Fomin, Abramov and Ferin4]. Years later,
![]() $\text{Er}^{3+}$
doped fiber was widely used in the communication area due to its special emission wavelength, which locates in the communication window. Until now, a great attention is still paid to
$\text{Er}^{3+}$
doped fiber was widely used in the communication area due to its special emission wavelength, which locates in the communication window. Until now, a great attention is still paid to
![]() $\text{Er}^{3+}$
doped fiber, while the
$\text{Er}^{3+}$
doped fiber, while the
![]() $\text{Nd}^{3+}$
doped fiber disappears gradually because of an excellent alternate in
$\text{Nd}^{3+}$
doped fiber disappears gradually because of an excellent alternate in
![]() $1~\unicode[STIX]{x03BC}\text{m}$
regime, which is
$1~\unicode[STIX]{x03BC}\text{m}$
regime, which is
![]() $\text{Yb}^{3+}$
doped fiber. Compared to
$\text{Yb}^{3+}$
doped fiber. Compared to
![]() $\text{Nd}^{3+}$
doped fibers,
$\text{Nd}^{3+}$
doped fibers,
![]() $\text{Yb}^{3+}$
doped fibers take advantage of wider gain bandwidth, long fluorescence lifetime of upper level, lower quantum defect and higher quench-free concentration, which result in the scaling of the output power of fiber lasers.
$\text{Yb}^{3+}$
doped fibers take advantage of wider gain bandwidth, long fluorescence lifetime of upper level, lower quantum defect and higher quench-free concentration, which result in the scaling of the output power of fiber lasers.
As the key component of the fiber laser,
![]() $\text{Yb}^{3+}$
doped fiber has experienced innovations both in the theoretical and technical aspects. Double-cladding fiber (DCF) structure[Reference Snitzer, Po, Hakimi, Tumminelli and McCollum5] is absolutely one of them. This structure separates the waveguides of signal and pump light, leading to a large increase of the tolerable power. Based on DCF, asymmetrical inner cladding substantially improved core absorption efficiency, increasing the output power further. Dominic et al.
[Reference Dominic, MacCormack, Waarts, Sanders, Bickness, Dohle, Wolak, Yeh and Zucker6] demonstrated the first single-mode
$\text{Yb}^{3+}$
doped fiber has experienced innovations both in the theoretical and technical aspects. Double-cladding fiber (DCF) structure[Reference Snitzer, Po, Hakimi, Tumminelli and McCollum5] is absolutely one of them. This structure separates the waveguides of signal and pump light, leading to a large increase of the tolerable power. Based on DCF, asymmetrical inner cladding substantially improved core absorption efficiency, increasing the output power further. Dominic et al.
[Reference Dominic, MacCormack, Waarts, Sanders, Bickness, Dohle, Wolak, Yeh and Zucker6] demonstrated the first single-mode
![]() $\text{Yb}^{3+}$
doped fiber laser with an output power of over 100 W. A rectangular inner cladding was used and the conversion efficiency was 58%. Five years later, in 2004, Jeong et al.
[Reference Jeong, Sahu, Payne and Nilsson7] improved the output power to 1.36 kW at
$\text{Yb}^{3+}$
doped fiber laser with an output power of over 100 W. A rectangular inner cladding was used and the conversion efficiency was 58%. Five years later, in 2004, Jeong et al.
[Reference Jeong, Sahu, Payne and Nilsson7] improved the output power to 1.36 kW at
![]() $1.1~\unicode[STIX]{x03BC}\text{m}$
with 83% slope efficiency, which generated, by D-shape inner cladding, Yb-doped fiber with an NA below 0.05. In 2009, IPG Photonics Corporation issued a product of high-power fiber laser with a 10 kW single-mode output at 1070 nm[Reference Snitzer1] and an excellent stability simultaneously. This work increased the single-mode output to a higher level, driving us to optimize the fabrication techniques further to achieve a higher output power.
$1.1~\unicode[STIX]{x03BC}\text{m}$
with 83% slope efficiency, which generated, by D-shape inner cladding, Yb-doped fiber with an NA below 0.05. In 2009, IPG Photonics Corporation issued a product of high-power fiber laser with a 10 kW single-mode output at 1070 nm[Reference Snitzer1] and an excellent stability simultaneously. This work increased the single-mode output to a higher level, driving us to optimize the fabrication techniques further to achieve a higher output power.
This paper reviews the efforts made by researchers to optimize the fiber fabrication technology at the beginning. Then methods to overcome the challenges, on the way of pursuing higher power and applying high-power lasers, will be demonstrated. Firstly, this paper discusses the research state of rare-earth doped fiber fabrication technology and analyzes its development trend. Secondly, stability of the fiber laser limits the practical performance seriously. For the stability of power, photo-darkening (PD) effect decreases the output power of
![]() $\text{Yb}^{3+}$
doped fiber lasers when operating for a long time Thirdly, high beam quality is required for most applications of high-power fiber lasers such as welding, cutting, and weapon. Thus, appropriate designing of
$\text{Yb}^{3+}$
doped fiber lasers when operating for a long time Thirdly, high beam quality is required for most applications of high-power fiber lasers such as welding, cutting, and weapon. Thus, appropriate designing of
![]() $\text{Yb}^{3+}$
doped fibers to achieve a single-mode operation in high-power fiber lasers is of much importance. In addition, the beam quality will degrade when the power reaches a certain value, which is called mode instability (MI) effect. To conclude, we present that future
$\text{Yb}^{3+}$
doped fibers to achieve a single-mode operation in high-power fiber lasers is of much importance. In addition, the beam quality will degrade when the power reaches a certain value, which is called mode instability (MI) effect. To conclude, we present that future
![]() $\text{Yb}^{3+}$
doped fiber fabrication needs overall consideration to mitigate PD effect, enlarge MI threshold and improve the output beam quality simultaneously.
$\text{Yb}^{3+}$
doped fiber fabrication needs overall consideration to mitigate PD effect, enlarge MI threshold and improve the output beam quality simultaneously.

Figure 1. Impressive progress of fiber lasers output in the last few decades.
2 Fabrication technology of
 $\text{Yb}^{3+}$
doped fibers
$\text{Yb}^{3+}$
doped fibers
For an ultra-high-power fiber laser, a large core size helps to eliminate nonlinearity and increase the damage threshold; it is a challenge to obtain a large size core for MCVD techniques. Generally, several soot layers need to be deposited and parameters of each deposition should be controlled precisely. Besides, impurities could be introduced when unloading the substrate tube and soaking it with
![]() $\text{Yb}^{3+}$
solution, which is fatal for high-power fiber lasers. To overcome this, in situ solution doping technique was proposed[Reference Webb, Boyland, Standish, Lin, Alam and Sahu8], which eliminated the need to remove the tube and significantly reduced the processing time. While for solution doping technique, it is difficult to control the refractive index profile precisely. So, researchers tried to find an approach to deposit
$\text{Yb}^{3+}$
solution, which is fatal for high-power fiber lasers. To overcome this, in situ solution doping technique was proposed[Reference Webb, Boyland, Standish, Lin, Alam and Sahu8], which eliminated the need to remove the tube and significantly reduced the processing time. While for solution doping technique, it is difficult to control the refractive index profile precisely. So, researchers tried to find an approach to deposit
![]() $\text{Yb}_{2}\text{O}_{3}$
just like
$\text{Yb}_{2}\text{O}_{3}$
just like
![]() $\text{SiO}_{2}$
and
$\text{SiO}_{2}$
and
![]() $\text{GeO}_{2}$
. As the development of material science, an organic Yb compound called
$\text{GeO}_{2}$
. As the development of material science, an organic Yb compound called
![]() $\text{Yb(DPM)}_{3}$
(DPM
$\text{Yb(DPM)}_{3}$
(DPM
![]() $=$
dipivaloymethanate ligand
$=$
dipivaloymethanate ligand
![]() $(\text{C}_{11}\text{H}_{19}\text{O}_{2})$
)[Reference Sekiya, Barua, Saito and Ikushima9] was chosen because it is volatile when being heated above
$(\text{C}_{11}\text{H}_{19}\text{O}_{2})$
)[Reference Sekiya, Barua, Saito and Ikushima9] was chosen because it is volatile when being heated above
![]() $200\,^{\circ }\text{C}$
. Sekiya et al. set two furnaces for
$200\,^{\circ }\text{C}$
. Sekiya et al. set two furnaces for
![]() $\text{Yb(DPM)}_{3}$
and
$\text{Yb(DPM)}_{3}$
and
![]() $\text{AlCl}_{3}$
. High purity of He went through the furnace to carry
$\text{AlCl}_{3}$
. High purity of He went through the furnace to carry
![]() $\text{Yb(DPM)}_{3}$
and
$\text{Yb(DPM)}_{3}$
and
![]() $\text{AlCl}_{3}$
, which were in gas phase, into the substrate tube. A core larger than 5 mm could be obtained, via adjusting the Yb and Al concentrations. This technology makes it possible to adjust the deposition parameter of every single pass, leading to a homogeneous refraction index profile (shown as Figure 2). However, this technique requires more about the equipment over the traditional MCVD system. Because
$\text{AlCl}_{3}$
, which were in gas phase, into the substrate tube. A core larger than 5 mm could be obtained, via adjusting the Yb and Al concentrations. This technology makes it possible to adjust the deposition parameter of every single pass, leading to a homogeneous refraction index profile (shown as Figure 2). However, this technique requires more about the equipment over the traditional MCVD system. Because
![]() $\text{Yb(DPM)}_{3}$
is volatile only when heated above
$\text{Yb(DPM)}_{3}$
is volatile only when heated above
![]() $200\,^{\circ }\text{C}$
, the
$200\,^{\circ }\text{C}$
, the
![]() $\text{Yb(DPM)}_{3}$
raw material pipeline before the substrate tube should always be heated up to
$\text{Yb(DPM)}_{3}$
raw material pipeline before the substrate tube should always be heated up to
![]() $200\,^{\circ }\text{C}$
. Besides, the mixture of gases with highly different temperatures influences the uniformity along the preform. These years, porous glass technology was adopted again to fabricate active fibers. Porous glass was first developed to prepare communications fibers[Reference Simmons, Mohr, Tran, Macedo and Litovitz10], and now important advances have been made in the preparation of active optical fibers. Porous glasses can be understood as the leaching products of phase-separated sodium borosilicate glasses[Reference Yang, Yamashita and Akai11]. A
$200\,^{\circ }\text{C}$
. Besides, the mixture of gases with highly different temperatures influences the uniformity along the preform. These years, porous glass technology was adopted again to fabricate active fibers. Porous glass was first developed to prepare communications fibers[Reference Simmons, Mohr, Tran, Macedo and Litovitz10], and now important advances have been made in the preparation of active optical fibers. Porous glasses can be understood as the leaching products of phase-separated sodium borosilicate glasses[Reference Yang, Yamashita and Akai11]. A
![]() $\text{Yb}^{3+}$
doped large-core double-cladding silica fiber with the active core prepared from nanoporous silica rod by the glass phase-separation technology was reported[Reference Chu, Ma, Yang, Liao, Wang, Hu, Peng, Li, Dai, Li and Yang12]. The measurements show that the fiber has a
$\text{Yb}^{3+}$
doped large-core double-cladding silica fiber with the active core prepared from nanoporous silica rod by the glass phase-separation technology was reported[Reference Chu, Ma, Yang, Liao, Wang, Hu, Peng, Li, Dai, Li and Yang12]. The measurements show that the fiber has a
![]() $\text{Yb}^{3+}$
concentration of 9811 ppm by weight, a low background attenuation of
$\text{Yb}^{3+}$
concentration of 9811 ppm by weight, a low background attenuation of
![]() $0.02~\text{dB}/\text{m}$
and absorption from
$0.02~\text{dB}/\text{m}$
and absorption from
![]() $\text{Yb}^{3+}$
about
$\text{Yb}^{3+}$
about
![]() $5.5~\text{dB}/\text{m}$
at 976 nm. The laser performance presents a high-slope efficiency of 72.8% for laser emission at 1071 nm and a low laser threshold of 3 W within only 2.3 m fiber length. Benefiting from uniformly distributed nanoscale pores, nanoporous silica glass exhibits remarkable advantages in its doping level, core diameter, refractive index engineering and optical homogeneity[Reference Yang, Dai, Liu, Jiang, Peng, Li, Yamashita, Akai and Li13]. There are other technologies such as direct nanoparticle deposition (DND) technology, powder in tube direct drawing fiber technology and REPUSIL technology. These methods are difficult to reduce the impurity when fabricating the preform. Up to now, though MCVD process together with solution doping is the most mature technology, another better method is urgent, and the gas phase deposition is a candidate after realizing a high uniformity along the preform.
$5.5~\text{dB}/\text{m}$
at 976 nm. The laser performance presents a high-slope efficiency of 72.8% for laser emission at 1071 nm and a low laser threshold of 3 W within only 2.3 m fiber length. Benefiting from uniformly distributed nanoscale pores, nanoporous silica glass exhibits remarkable advantages in its doping level, core diameter, refractive index engineering and optical homogeneity[Reference Yang, Dai, Liu, Jiang, Peng, Li, Yamashita, Akai and Li13]. There are other technologies such as direct nanoparticle deposition (DND) technology, powder in tube direct drawing fiber technology and REPUSIL technology. These methods are difficult to reduce the impurity when fabricating the preform. Up to now, though MCVD process together with solution doping is the most mature technology, another better method is urgent, and the gas phase deposition is a candidate after realizing a high uniformity along the preform.

Figure 2. Profile of refractive index for gas phase doping technology.
3 Photo-darkening effect
PD effect was first discovered by researchers from University of Southampton in 1997[Reference Paschotta, Nilsson, Barber, Caplen, Tropper and Hanna14]. Researchers found the lifetime quenching in Yb-doped fibers, which led to a strong unbleachable loss. They assumed this unexpected behavior to be caused by some unidentified impurity or structural defect. Generally, the PD effect introduces background loss at visible wavelengths and the loss extends to the near-infrared range, covering the pumping and lasing wavelengths[Reference Manek-H, Boullet, Cardinal, Guillen, Ermeneux, Podgorski, Doua and Salin15], therefore deteriorating the fiber laser property. The PD effect reduces the efficiency and the lifetime of
![]() $\text{Yb}^{3+}$
doped fiber lasers, leads to instability of the system and finally greatly limits the applications and development of fiber lasers. It has been convinced to be one of the main bottlenecks of increasing laser power.
$\text{Yb}^{3+}$
doped fiber lasers, leads to instability of the system and finally greatly limits the applications and development of fiber lasers. It has been convinced to be one of the main bottlenecks of increasing laser power.
To measure the PD-induced excess loss, Koponen et al. proposed to observe the transmission changes at visible wavelengths and therefore predict the PD at signal wavelengths. Furthermore, they found the loss at 633 nm has a near linear correlation with that at signal wavelength, which is about 71 times[Reference Koponen, Söderlund, Hoffman and Tammela16]. Besides, the equilibrium state of PD loss depends on the pump power level, as reported by Jetschke et al. [Reference Jetschke, Unger, Röpke and Kirchhof17].
The mechanism of PD effect is still under exploration. Color centers in Yb-doped fibers are considered to be the reason to induce PD effect. In 2007, Yoo et al. proposed the 220 nm absorption peak in
![]() $\text{Yb}/\text{Al}$
doped fiber to be related to Yb-associated oxygen deficiency centers (ODCs) and act as a precursor of the PD[Reference Yoo, Basu, Boyland, Sones, Nilsson, Sahu and Payne18]. Engholm et al. explained that the absorption band near 230 nm is a charge transfer (CT) band and further induces PD loss[Reference Engholm, Norin and Åberg19]. In 2010, a new mechanism was reported by Peretti et al.
[Reference Peretti, Jurdyc, Jacquier, Gonnet, Pastouret, Burov and Cavani20]. They attributed the formation of color centers to Tm impurities in Yb-doped fibers, where Tm ions absorb energy from Yb ions, cascade up to higher energy levels and then emit UV and visible light.
$\text{Yb}/\text{Al}$
doped fiber to be related to Yb-associated oxygen deficiency centers (ODCs) and act as a precursor of the PD[Reference Yoo, Basu, Boyland, Sones, Nilsson, Sahu and Payne18]. Engholm et al. explained that the absorption band near 230 nm is a charge transfer (CT) band and further induces PD loss[Reference Engholm, Norin and Åberg19]. In 2010, a new mechanism was reported by Peretti et al.
[Reference Peretti, Jurdyc, Jacquier, Gonnet, Pastouret, Burov and Cavani20]. They attributed the formation of color centers to Tm impurities in Yb-doped fibers, where Tm ions absorb energy from Yb ions, cascade up to higher energy levels and then emit UV and visible light.
To overcome the PD effect, various methods including post-treatment and fiber designing have been proposed. Post-treatment of fiber includes photo-bleaching, thermal-bleaching and
![]() $\text{H}_{2}$
or
$\text{H}_{2}$
or
![]() $\text{O}_{2}$
loading. Fiber designing includes co-doping with other ions and optimizing the
$\text{O}_{2}$
loading. Fiber designing includes co-doping with other ions and optimizing the
![]() $\text{Yb}^{3+}$
distribution. The existed PD loss can be bleached with certain wavelengths (405 nm[Reference Piccoli, Gebavi, Lablonde, Cadier, Robin, Monteville, Le Goffic, Landais, Méchin and Milanese21], 543 nm[Reference Guzman Chávez, Kir’yanov, Barmenkov and Il’Ichev22], 550 nm[Reference Piccoli, Robin, Brand, Klotzbach and Taccheo23], 633 nm[Reference Gebavi, Taccheo, Lablonde, Cadier, Robin, Méchin and Tregoat24] and 793 nm[Reference Zhao, Xing, Li, Liao, Wang, Peng, Yang, Dai, Li and Li25]) pumping. However, these studies were taken at a low output power level. So bleaching the existed PD loss is doubtful for high-power fiber lasers. The existed PD loss will also be mitigated when heating the photo-darkened fiber over
$\text{Yb}^{3+}$
distribution. The existed PD loss can be bleached with certain wavelengths (405 nm[Reference Piccoli, Gebavi, Lablonde, Cadier, Robin, Monteville, Le Goffic, Landais, Méchin and Milanese21], 543 nm[Reference Guzman Chávez, Kir’yanov, Barmenkov and Il’Ichev22], 550 nm[Reference Piccoli, Robin, Brand, Klotzbach and Taccheo23], 633 nm[Reference Gebavi, Taccheo, Lablonde, Cadier, Robin, Méchin and Tregoat24] and 793 nm[Reference Zhao, Xing, Li, Liao, Wang, Peng, Yang, Dai, Li and Li25]) pumping. However, these studies were taken at a low output power level. So bleaching the existed PD loss is doubtful for high-power fiber lasers. The existed PD loss will also be mitigated when heating the photo-darkened fiber over
![]() $300\,^{\circ }\text{C}$
[Reference Jasapara, Andrejco, DiGiovanni and Windeler26], but high temperature leads to fiber properties degradation.
$300\,^{\circ }\text{C}$
[Reference Jasapara, Andrejco, DiGiovanni and Windeler26], but high temperature leads to fiber properties degradation.
![]() $\text{H}_{2}$
[Reference Jasapara, Andrejco, DiGiovanni and Windeler26] or
$\text{H}_{2}$
[Reference Jasapara, Andrejco, DiGiovanni and Windeler26] or
![]() $\text{O}_{2}$
[Reference Yoo, Basu, Boyland, Sones, Nilsson, Sahu and Payne18] loading method also reduces the PD effectively, which needs complex vacuum high pressure operation. From the fiber fabrication technique, co-doping with other ions is a primary method to overcome PD effect. Aluminum[Reference Kitabayashi, Ikeda, Nakai, Sakai, Himeno and Ohashi27], phosphorus[Reference Lee, Sinha, Digonnet, Byer and Jiang28], cerium[Reference Engholm, Jelger, Laurell and Norin29], alkaline earth metals[Reference Sakaguchi, Fujimoto, Masuda, Miyanaga and Nakano30] as well as sodium ions[Reference Zhao, Liu, Li, Li, Peng, Yang, Dai, Li and Li31] have been selected as co-dopants during fiber fabrication process. This method is widely used in commercial fiber production while the changes of NA, background loss and laser efficiency induced by co-dopants still need to be overcome[Reference Mel’kumov, Bufetov, Kravtsov, Shubin and Dianov32, Reference Unger, Schwuchow, Jetschke, Reichel, Scheffel and Kirchhof33]. Figure 3 shows the relationship between the excess loss @702 nm and operation time of
$\text{O}_{2}$
[Reference Yoo, Basu, Boyland, Sones, Nilsson, Sahu and Payne18] loading method also reduces the PD effectively, which needs complex vacuum high pressure operation. From the fiber fabrication technique, co-doping with other ions is a primary method to overcome PD effect. Aluminum[Reference Kitabayashi, Ikeda, Nakai, Sakai, Himeno and Ohashi27], phosphorus[Reference Lee, Sinha, Digonnet, Byer and Jiang28], cerium[Reference Engholm, Jelger, Laurell and Norin29], alkaline earth metals[Reference Sakaguchi, Fujimoto, Masuda, Miyanaga and Nakano30] as well as sodium ions[Reference Zhao, Liu, Li, Li, Peng, Yang, Dai, Li and Li31] have been selected as co-dopants during fiber fabrication process. This method is widely used in commercial fiber production while the changes of NA, background loss and laser efficiency induced by co-dopants still need to be overcome[Reference Mel’kumov, Bufetov, Kravtsov, Shubin and Dianov32, Reference Unger, Schwuchow, Jetschke, Reichel, Scheffel and Kirchhof33]. Figure 3 shows the relationship between the excess loss @702 nm and operation time of
![]() $\text{Yb}^{3+}$
fibers with different co-dopants. This indicates that Na, Ce and P can suppress the PD effect. In addition, PD effect is related with the population of up-conversion in the
$\text{Yb}^{3+}$
fibers with different co-dopants. This indicates that Na, Ce and P can suppress the PD effect. In addition, PD effect is related with the population of up-conversion in the
![]() $\text{Yb}^{3+}$
fiber. The distribution of up-conversion is determined by the distribution of laser power. The laser power is lower in the edge area of the core, where the up-conversion rate is high, leading to a more severe PD effect. So fibers with confined
$\text{Yb}^{3+}$
fiber. The distribution of up-conversion is determined by the distribution of laser power. The laser power is lower in the edge area of the core, where the up-conversion rate is high, leading to a more severe PD effect. So fibers with confined
![]() $\text{Yb}^{3+}$
doping area make all the
$\text{Yb}^{3+}$
doping area make all the
![]() $\text{Yb}^{3+}$
keep a state of low up-conversion, which reduces the PD effect partly.
$\text{Yb}^{3+}$
keep a state of low up-conversion, which reduces the PD effect partly.
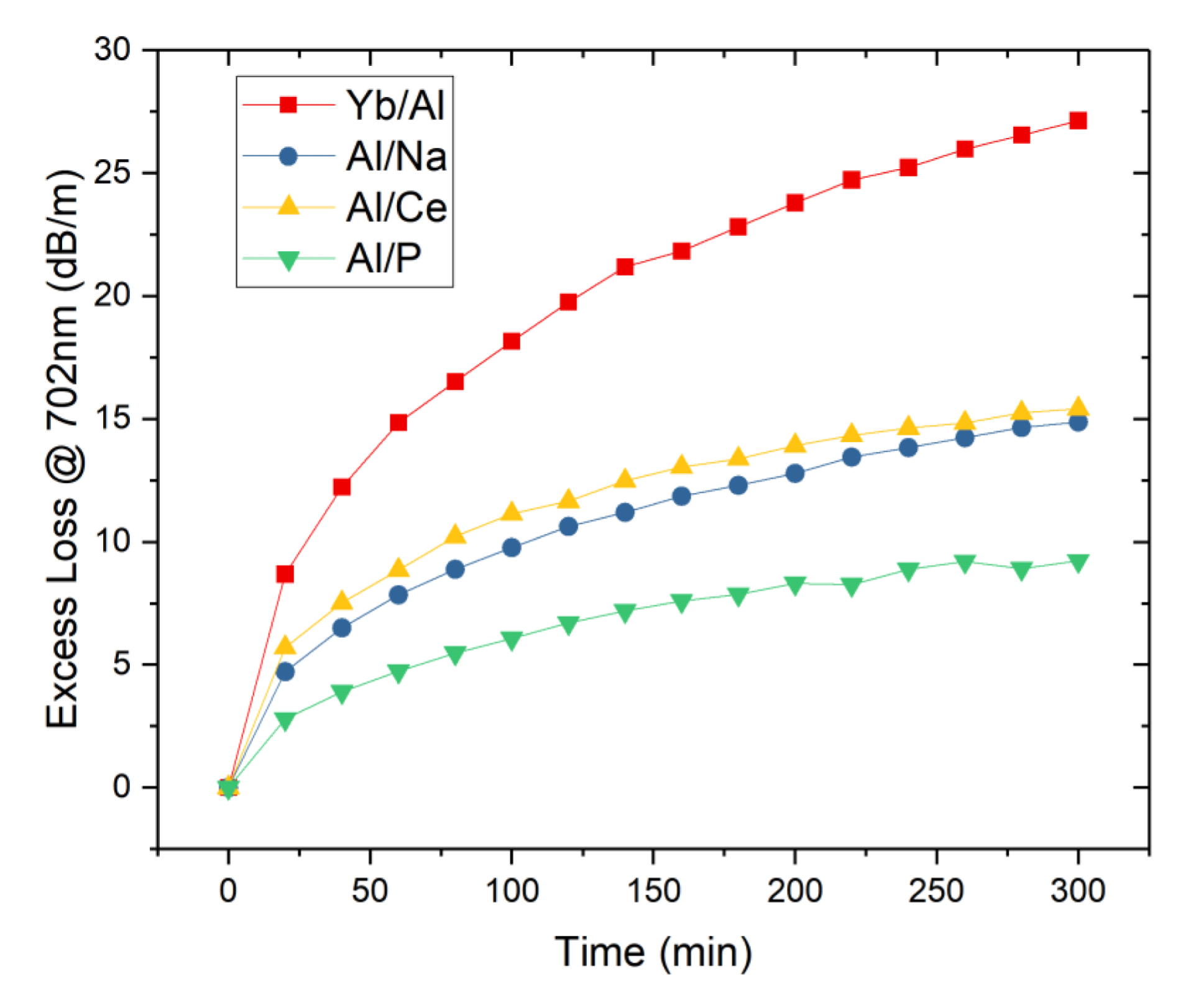
Figure 3. Relationship between the excess loss @702 nm and operation time of
![]() $\text{Yb}^{3+}$
fibers with different co-dopants.
$\text{Yb}^{3+}$
fibers with different co-dopants.
Until now, researchers have made much effort to reveal the PD mechanism and mitigate the loss in
![]() $\text{Yb}^{3+}$
doped fibers. However, there are still lots of works to be investigated about PD effect. First, it is necessary to develop PD measurement setup for large mode area fibers, which is significant in high-power levels. Besides, the relationship between PD and MI as well as the influence of thermal effect from PD on fiber index are also hot research topics in laser areas. These research works might help us to understand the PD mechanism, fabricate fibers with better properties and make them more stable in applications.
$\text{Yb}^{3+}$
doped fibers. However, there are still lots of works to be investigated about PD effect. First, it is necessary to develop PD measurement setup for large mode area fibers, which is significant in high-power levels. Besides, the relationship between PD and MI as well as the influence of thermal effect from PD on fiber index are also hot research topics in laser areas. These research works might help us to understand the PD mechanism, fabricate fibers with better properties and make them more stable in applications.
4 Mode instability
Researchers from Jena University discovered MI first[Reference Eidam, Hanf, Seise, Andersen, Gabler, Wirth, Schreiber, Limpert and Tünnermann34], from that on, researchers across the globe have devoted much interest to it and carried out a vast amount of investigations on it. The phenomenon MI can be defined as: when output power of a fiber laser exceeded a certain threshold power level, output beam profile would fluctuate randomly and beam quality would deteriorate[Reference Eidam, Wirth, Jauregui, Stutzki, Jansen, Otto, Schmidt, Schreiber, Limpert and Tünnermann35]. MI is becoming the most limiting factor for further power scaling of high-power fiber laser and its applications; thus it is meaningful to deeply investigate its exact physical origin and finally mitigate, even completely, solve it.
MI in high-power fiber lasers has been widely recognized as a kind of thermal effect. It was suggested[Reference Jauregui, Eidam, Limpert and Tünnermann36] that long period grating caused by heat deposition in the fiber core could be the possible reason. However, it was pointed out that energy transferring between fundamental mode and high-order modes only takes place when a phase shift exists between the interference intensity pattern and thermal induced index grating. So far, thermal induced index grating is acknowledged by scientific community as the main reason for MI in high-power fiber lasers, but the origin of this phase shift is still under discussion. As has been suggested in Ref. [Reference Mith and Smith37], one possible source of the phase shift could be the small frequency difference between two modes. Such a small frequency difference will cause a moving interference pattern. Due to the limited thermal response of a fiber, thermal induced index grating will have a time delay with respect to the optical intensity pattern. Thus, the phase shift appears.
The dissenting view[Reference Ward, Robin and Dajani38] on the origin of the phase shift suggests that such a frequency difference is not necessary. The numerical simulation by beam propagation method (BPM) shows that monochromatic input beams can also cause MI. However, up to now, no particular process responsible for this ‘monochromatic’ MI.
Recent researches reveal more details about MI. Thresholds of MI were observed to degrade with operation time in several reports[Reference Johansen, Laurila, Maack, Noordegraaf, Jakobsen, Alkeskjold and Lægsgaard39–Reference Otto, Modsching, Jauregui, Limpert and Tünnermann41], and this kind of degradation of MI threshold can be reversed by thermally post-processing the active fiber. These experimental results strongly suggest that, besides quantum defect, PD in the fiber lasers plays an important role in the determination of MI threshold. What is more, in the quasi-static degradation (or quasi-static MI) of fiber lasers, the PD has been seen as the main heat source. In the modeling by Ward[Reference Ward42], there is a phase-shifted index grating written by a modal interference pattern that transfers fundamental mode into high-order mode. The origin of this phase shift is the PD-induced warmup process of the fiber. As the fiber is warming up, the interference patterns caused by fundamental mode and high-order modes should move since they have a different overlap with the core and different changes in effective index, while heat deposition induced by time-dependent PD does not instantaneously follow the optical intensity. Then the phase shift occurs, leading to a slow energy transferring from fundamental mode to high-order modes.
There are also some reports about low-threshold MI in few-mode fibers, especially when backward reflection exists. Researchers find that MI thresholds decrease dramatically in the presence of a backward reflection of signal from the output fiber end or an external counter-propagating beam. As thermal grating is recognized as the main mechanism of MI in large-mode area fibers, the population (electronic) grating[Reference Antipov, Kuznetsov, Tyrtyshnyy, Alekseev and Vershinin43] could be the dominant mechanism for the low-threshold MI effect in the few-mode fibers.
For MI mitigation strategy, it can be categorized as two counterparts: intrinsic mitigation and extrinsic mitigation[Reference Jauregui, Otto, Stutzki, Jansen, Limpert and Tünnermann44]. Intrinsic mitigation can be expressed as: from active fiber itself to mitigate MI. Similarly, extrinsic mitigation can be defined as: from fiber laser to mitigate MI.
4.1 Intrinsic mitigation
4.1.1 Fiber structure parameter optimization
The essence of MI is the strong dynamic mode coupling between fundamental mode (FM) and higher-order mode (HOM); thus any fiber design which suppresses HOM will be beneficial for MI mitigation and threshold power level increase. Hansen and his colleagues from Technical University of Denmark acquired a correlation between
![]() $\text{LP}_{01}$
and
$\text{LP}_{01}$
and
![]() $\text{LP}_{11}$
nonlinear coupling coefficient and mode frequency difference under the condition, fiber core radius is constant and normalized frequency and doping radius are varying according to their thermally induced mode coupling model[Reference Hansen, Alkeskjold, Broeng and Lægsgaard45]. According to their simulation, several conclusions are drawn.
$\text{LP}_{11}$
nonlinear coupling coefficient and mode frequency difference under the condition, fiber core radius is constant and normalized frequency and doping radius are varying according to their thermally induced mode coupling model[Reference Hansen, Alkeskjold, Broeng and Lægsgaard45]. According to their simulation, several conclusions are drawn.
(1) Maximum value of nonlinear coupling coefficient is insensitive to varying fiber core diameter if cladding diameter and normalized frequency is constant.
(2) Correlation between nonlinear coupling coefficient and normalized frequency is positive if core diameter is constant, that is to say, correlation between MI threshold and normalized frequency is negative.
(3) Correlation between nonlinear coupling coefficient and doped radius is positive if core diameter and normalized frequency are constant, that is to say, correlation between MI threshold and doping radius is negative.
4.1.2 Photo-darkening mitigation
As mentioned before, Otto et al. from Jena University found that PD effect is closely linked to MI in their experiment[Reference Otto, Modsching, Jauregui, Limpert and Tünnermann46]. Against their expectations, the trend between MI threshold and signal wavelength does not monotonically decrease, which indicates that quantum defect may not be only heat source in active fiber, and PD induced extra loss is most possible secondary heat source in active fiber. Based on this assumption, they simulated thermal load and output power under the condition taking PD into consideration or not, it is found that even though PD induced a little power loss, but heat load PD contributed is comparable to quantum defects induced heating.
In order to investigate connection between MI and PD more deeply, Otto et al. conducted an experiment to compare MI properties of pre-darkened fiber and pristine fiber. For pristine fiber, as test process pushes forward, MI threshold is initially high and decreases continually as number of measurement increases; conversely, for pre-darkened fiber, MI threshold is initially low and increases continually as number of measurement increases.
4.2 Extrinsic mitigation
4.2.1 Optimizing pumping scheme
Yang et al. constructed a high-power all-fiber laser oscillator to investigate extrinsic mitigation of MI[Reference Yang, Zhang, Shi, Wang, Zhou, Xu, Chen, Liu and Lu47]. For co-pumping configuration, max output power is about 1.6 kW, further power scaling is limited by onset of MI, MI threshold is raised to above 2.5 kW by changing co-pump scheme to bidirectional pumping, further power amplification is limited by pump power restriction, which proves bidirectional pump scheme beneficial to MI suppression.
4.2.2 Varying coiling method
Tao et al. employed a semi-analytical model to investigate the impact of coiling method on MI[Reference Tao, Su, Ma, Wang and Zhou48]. According to their simulation result, it is shown that cylinder coiling shows much better MI properties than normal spiral coiling; also, appropriate bending radius of active fiber still has impact on MI mitigation, in general, smaller bending radius often reveals higher MI threshold. However, a too small bending radius may reduce effective mode area, which will result in other deteriorative nonlinear effects; thus it is necessary to make a compromise between MI and nonlinear effects.
5 Single-mode operation
Power scaling of fiber laser systems vigorously demands novel-innovative active fiber designs. To avoid detrimental nonlinear effects, few-mode fibers are adopted to substitute conventional single-mode fibers in high-power laser systems. And most of them have a large mode area (LMA) with a certain number of guided modes; for that, the possibility of mode coupling between FM (fundamental mode) and HOMs (high-order modes) creates the backdrop for transverse mode instability (TMI). LMA fibers with efforts to implement single-mode operation have made significant breakthroughs in recent years.
To achieve single-mode operation, the ultra-low-NA fiber is one of the most promising candidates in LMA fibers. In fact, researchers have acquired more than 1.36 kW laser output based on a low-NA (
![]() ${<}$
0.05) fiber as early as 2004[Reference Jeong, Sahu, Payne and Nilsson7]. Due to the fast development of rare-earth doped fibers, several low-NA preforms with large core diameter as well as uniform refractive index profile were fabricated by MCVD in conjunction of the solution doping technique[Reference Wang, Gray, Walton, Li, Chen, Liu and Zenteno49, Reference Peng, Zhan, Ni, Wang, Wang, Gao, Li, Wang, Jing and Lin50] or sol-gel process combined with high-temperature sintering[Reference Shi, Zhou, Ni, Xiao, Zhan, Zhang and Lin51]. Moreover, fibers with NA of
${<}$
0.05) fiber as early as 2004[Reference Jeong, Sahu, Payne and Nilsson7]. Due to the fast development of rare-earth doped fibers, several low-NA preforms with large core diameter as well as uniform refractive index profile were fabricated by MCVD in conjunction of the solution doping technique[Reference Wang, Gray, Walton, Li, Chen, Liu and Zenteno49, Reference Peng, Zhan, Ni, Wang, Wang, Gao, Li, Wang, Jing and Lin50] or sol-gel process combined with high-temperature sintering[Reference Shi, Zhou, Ni, Xiao, Zhan, Zhang and Lin51]. Moreover, fibers with NA of
![]() ${\sim}$
0.028 were successfully fabricated based on a large amount of post-processing[Reference Xu, Lin, Wang, Feng, Zhang, Zhou, Chen, Zhang, Wang, Yu and Hu52]. Several low-NA fibers fabricated by MCVD combined with solution doping technology were verified in a multikilowatt laser system. Vincent et al. reported a 1.6 kW nearly diffraction-limited output generated in an ultra-low-NA SIF with a
${\sim}$
0.028 were successfully fabricated based on a large amount of post-processing[Reference Xu, Lin, Wang, Feng, Zhang, Zhou, Chen, Zhang, Wang, Yu and Hu52]. Several low-NA fibers fabricated by MCVD combined with solution doping technology were verified in a multikilowatt laser system. Vincent et al. reported a 1.6 kW nearly diffraction-limited output generated in an ultra-low-NA SIF with a
![]() $52~\unicode[STIX]{x03BC}\text{m}$
core diameter and a core NA of 0.025[Reference Kong, Dunn, Parsons, Dong, Hawkins, Jones and Dong53]. Besides, a 3 kW laser output without PD and MI was achieved based on a low-NA fiber with a core diameter of
$52~\unicode[STIX]{x03BC}\text{m}$
core diameter and a core NA of 0.025[Reference Kong, Dunn, Parsons, Dong, Hawkins, Jones and Dong53]. Besides, a 3 kW laser output without PD and MI was achieved based on a low-NA fiber with a core diameter of
![]() $35~\unicode[STIX]{x03BC}\text{m}$
[Reference Petit, Tumminelli, Minelly and Khitrov54]. Very recently, Beier et al. presented a narrow linewidth single-mode fiber amplifier system up to 4.4 kW with single-mode beam quality achieved by lowering the NA of the fiber to
$35~\unicode[STIX]{x03BC}\text{m}$
[Reference Petit, Tumminelli, Minelly and Khitrov54]. Very recently, Beier et al. presented a narrow linewidth single-mode fiber amplifier system up to 4.4 kW with single-mode beam quality achieved by lowering the NA of the fiber to
![]() ${\sim}$
0.04[Reference Khitrov, Minelly, Tumminelli, Petit and Pooler55]. With low NA, the maximum effective mode area was reached up to
${\sim}$
0.04[Reference Khitrov, Minelly, Tumminelli, Petit and Pooler55]. With low NA, the maximum effective mode area was reached up to
![]() $1000~\unicode[STIX]{x03BC}\text{m}^{2}$
[Reference Beier, Moeller, Nold, Sattler, Kuhn, Hupel, Hein, Haarlammert, Schreiber, Eberhardt and Tünnermann56]. However, the reduction of NA will decrease the tolerance for fiber bending, which is not conducive to integration.
$1000~\unicode[STIX]{x03BC}\text{m}^{2}$
[Reference Beier, Moeller, Nold, Sattler, Kuhn, Hupel, Hein, Haarlammert, Schreiber, Eberhardt and Tünnermann56]. However, the reduction of NA will decrease the tolerance for fiber bending, which is not conducive to integration.
In general, the mode area of a fiber depends on its core size and index profile, while the extraction efficiency of FM is determined by the index profile together with the doping distribution. Thus, it is potential to achieve single-mode operation in LMA active fibers by the modification of conventional step-index fibers. For example, adding low-index trenches around the fiber core can greatly reduce the bending loss of FM, and improve the bending tolerance for low-NA fibers. With this approach, the so-called trench-assisted low-NA fibers, recently, have been regarded as a suitable design for mode area scaling in effective single-mode regime. Wang et al. proposed a novel trench-assisted fiber with two low-index trenches in the cladding and four layers of high-index trenches in the core, allowing single-mode operation with an effective mode area of
![]() $1100~\unicode[STIX]{x03BC}\text{m}^{2}$
at a bending radius of 15 cm[Reference Wang, Lou, Lu, Sheng, Zhao and Hua57]. A multitrench fiber (MTF) with a
$1100~\unicode[STIX]{x03BC}\text{m}^{2}$
at a bending radius of 15 cm[Reference Wang, Lou, Lu, Sheng, Zhao and Hua57]. A multitrench fiber (MTF) with a
![]() $30~\unicode[STIX]{x03BC}\text{m}$
diameter core, ensures single-mode operation in a wide range of bending diameter by inducing resonant coupling between core and ring modes. The mode area was further extended to
$30~\unicode[STIX]{x03BC}\text{m}$
diameter core, ensures single-mode operation in a wide range of bending diameter by inducing resonant coupling between core and ring modes. The mode area was further extended to
![]() $3100~\unicode[STIX]{x03BC}\text{m}^{2}$
with
$3100~\unicode[STIX]{x03BC}\text{m}^{2}$
with
![]() $90~\unicode[STIX]{x03BC}\text{m}$
diameter core[Reference Jain, Jung, Kim and Sahu58]. With the parabolic profile in the fiber core, a modified two-layer low-index trench fiber[Reference Sun, Kang, Wang, Liu and Jian59] was proposed to provide better HOMs suppression and bending resistance than initial MTFs[Reference Jain, Baskiotis and Sahu60]. Another advantage is that trench-assisted fiber can be fabricated by MCVD coupled with a rod in tube, and they have shown fair compatibility in all-fiber laser systems. To reduce the complexity of fabrication, a single-trench fiber (STF) was reported[Reference Jain, Jung, Nunez-Velazquez and Sahu61]. The Yb-doped core was surrounded by a high-index resonant ring with a refractive index close to that of the core. By adjusting the parameters such as distance between core and ring, ring thickness and
$90~\unicode[STIX]{x03BC}\text{m}$
diameter core[Reference Jain, Jung, Kim and Sahu58]. With the parabolic profile in the fiber core, a modified two-layer low-index trench fiber[Reference Sun, Kang, Wang, Liu and Jian59] was proposed to provide better HOMs suppression and bending resistance than initial MTFs[Reference Jain, Baskiotis and Sahu60]. Another advantage is that trench-assisted fiber can be fabricated by MCVD coupled with a rod in tube, and they have shown fair compatibility in all-fiber laser systems. To reduce the complexity of fabrication, a single-trench fiber (STF) was reported[Reference Jain, Jung, Nunez-Velazquez and Sahu61]. The Yb-doped core was surrounded by a high-index resonant ring with a refractive index close to that of the core. By adjusting the parameters such as distance between core and ring, ring thickness and
![]() $\unicode[STIX]{x0394}n$
, an STF with a
$\unicode[STIX]{x0394}n$
, an STF with a
![]() $40~\unicode[STIX]{x03BC}\text{m}$
core diameter exhibited high suppression of HOM by high bending loss and delocalization, while an effective mode area of
$40~\unicode[STIX]{x03BC}\text{m}$
core diameter exhibited high suppression of HOM by high bending loss and delocalization, while an effective mode area of
![]() ${\sim}1000~\unicode[STIX]{x03BC}\text{m}^{2}$
was achieved at the bend radius of 20 cm.
${\sim}1000~\unicode[STIX]{x03BC}\text{m}^{2}$
was achieved at the bend radius of 20 cm.
By an optimal rare-earth dopant distribution, preferential gain of FM while suppression of HOM can be realized, and this is the so-called gain management technique, corresponding to confined-doped fiber. Through selectively doping across the core, Yuan et al. proposed a hybrid profile fiber with an effective mode area of
![]() $2168~\unicode[STIX]{x03BC}\text{m}^{2}$
and an extraction efficiency of fundamental mode up to 60%[Reference Yuan and Gong62]. Experiments have shown that confined-doped ytterbium fibers greatly reduced threshold and enhanced laser efficiency. No beam quality deterioration was observed with output power increasing[Reference Marciante, Roides, Shkunov and Rockwell63]. Further, numerical simulations pointed out that tailoring the radial dopant profile helped boost the extraction efficiency of fundamental mode to 90%[Reference Gong, Yuan, Li, Yan, Zhang and Liao64, Reference Wang, Huang, Leng, Guo and Jiang65].
$2168~\unicode[STIX]{x03BC}\text{m}^{2}$
and an extraction efficiency of fundamental mode up to 60%[Reference Yuan and Gong62]. Experiments have shown that confined-doped ytterbium fibers greatly reduced threshold and enhanced laser efficiency. No beam quality deterioration was observed with output power increasing[Reference Marciante, Roides, Shkunov and Rockwell63]. Further, numerical simulations pointed out that tailoring the radial dopant profile helped boost the extraction efficiency of fundamental mode to 90%[Reference Gong, Yuan, Li, Yan, Zhang and Liao64, Reference Wang, Huang, Leng, Guo and Jiang65].
Further improvements in effective mode area can be accomplished via photonic crystal fibers (PCFs). PCF, which was earliest made in the University of Bath by stack and draw technique[Reference Knight, Birks, Russell and Atkin66], allows single-mode operation in a wide wavelength range[Reference Russell67]. And since then it has been recognized as one of the most promising solutions for very large mode area (VLMA) fibers operating in a single-mode regime. LMA PCFs for single-mode operation can be grouped into two categories: rod-type large-pitch PCF and leaky channel PCF, both possessing the hexagonal structure and cores surrounded by resonant elements for delocalization of HOMs. A rod-type PCF has achieved a mode field diameter as large as
![]() $105~\unicode[STIX]{x03BC}\text{m}$
[Reference Eidam, Rothhardt, Stutzki, Jansen, Hädrich, Carstens, Jauregui, Limpert and Tünnermann68]. Such rod-type fibers generally should be kept straight to avoid bend distortion, so it is not compact in practical applications. The leaky channel PCF offers a better bend tolerance with the potential of single-mode output and large mode area[Reference Dasgupta, Hayes and Richardson69]. Depending on the surrounding region, there are mainly three approaches to realize effective single-mode LMA operation[Reference Limpert, Stutzki, Jansen, Otto, Eidam, Jauregui and Tünnermann70]. A theoretically endless periodic structure with a single missing hole can be the first approach, while it cannot be practically achieved. The second is to exploit the ‘modal sieve’ effect[Reference Wong, Peng, McLaughlin and Dong71]. Large air holes with diameters dozens of times larger than the operating wavelength are arranged around the LMA-doped core. By adjusting the fiber parameters, a robust single-mode operation with several thousand
$105~\unicode[STIX]{x03BC}\text{m}$
[Reference Eidam, Rothhardt, Stutzki, Jansen, Hädrich, Carstens, Jauregui, Limpert and Tünnermann68]. Such rod-type fibers generally should be kept straight to avoid bend distortion, so it is not compact in practical applications. The leaky channel PCF offers a better bend tolerance with the potential of single-mode output and large mode area[Reference Dasgupta, Hayes and Richardson69]. Depending on the surrounding region, there are mainly three approaches to realize effective single-mode LMA operation[Reference Limpert, Stutzki, Jansen, Otto, Eidam, Jauregui and Tünnermann70]. A theoretically endless periodic structure with a single missing hole can be the first approach, while it cannot be practically achieved. The second is to exploit the ‘modal sieve’ effect[Reference Wong, Peng, McLaughlin and Dong71]. Large air holes with diameters dozens of times larger than the operating wavelength are arranged around the LMA-doped core. By adjusting the fiber parameters, a robust single-mode operation with several thousand
![]() $\unicode[STIX]{x03BC}\text{m}^{2}$
was achieved to the required HOM mode suppression[Reference Dong, Wu, McKay, Fu, Li and Winful72, Reference Dong, Li and Peng73]. The last approach is the index-guiding PCF with arrangement of tiny air holes, which exhibits a step-index-like guiding mechanism[Reference Mortensen, Folkenberg, Nielsen and Hansen74]. In recent years, index-guiding PCF has been further developed by incorporating photonic bandgap structures. This structure allows resonant coupling of HOMs from the core. With the so-called distributed-mode filter (DMF), a single-mode photonic bandgap rod-type fiber amplifier with a large mode field diameter of
$\unicode[STIX]{x03BC}\text{m}^{2}$
was achieved to the required HOM mode suppression[Reference Dong, Wu, McKay, Fu, Li and Winful72, Reference Dong, Li and Peng73]. The last approach is the index-guiding PCF with arrangement of tiny air holes, which exhibits a step-index-like guiding mechanism[Reference Mortensen, Folkenberg, Nielsen and Hansen74]. In recent years, index-guiding PCF has been further developed by incorporating photonic bandgap structures. This structure allows resonant coupling of HOMs from the core. With the so-called distributed-mode filter (DMF), a single-mode photonic bandgap rod-type fiber amplifier with a large mode field diameter of
![]() ${\sim}59~\unicode[STIX]{x03BC}\text{m}$
was reported[Reference Alkeskjold, Laurila, Scolari and Broeng75].
${\sim}59~\unicode[STIX]{x03BC}\text{m}$
was reported[Reference Alkeskjold, Laurila, Scolari and Broeng75].
Apart from the aforementioned designs, there are many other LMA fibers with brand-new operation mechanisms. Fermann[Reference Fermann76] has proposed that careful injection of the seed light allows only the fundamental mode of the fiber to be excited in multimode fiber. However, with the growing mode area, exciting only one mode becomes increasingly challenging. Index-guiding chirally coupled core (CCC) fiber provides resonant filtering of HOMs based on quasi-phase-match conditions. Effective single-mode operation was achieved in MOPA based on CCC air-clad fiber with
![]() $37~\unicode[STIX]{x03BC}\text{m}$
diameter[Reference Zhu, Hu, Ma and Galvanauskas77]. Then modified CCC fiber structure was proposed, where an octagon-shaped Yb-doped core larger than
$37~\unicode[STIX]{x03BC}\text{m}$
diameter[Reference Zhu, Hu, Ma and Galvanauskas77]. Then modified CCC fiber structure was proposed, where an octagon-shaped Yb-doped core larger than
![]() $50~\unicode[STIX]{x03BC}\text{m}$
was surrounded by eight side cores (shown in Figure 4)[Reference Ma, Zhu, Hu, Kaplan and Galvanauskas78]. Very recently, a triple-clad CCC fiber with
$50~\unicode[STIX]{x03BC}\text{m}$
was surrounded by eight side cores (shown in Figure 4)[Reference Ma, Zhu, Hu, Kaplan and Galvanauskas78]. Very recently, a triple-clad CCC fiber with
![]() $85~\unicode[STIX]{x03BC}\text{m}$
diameter was used to provide robust single-mode operation in an amplification system[Reference Pei, Ruppe, Chen, Sheikhsofla, Nees and Galvanauskas79]. However, CCC fibers require complex fabrication process and are very sensitive to fiber parameters. Moreover, resonance matching can be extremely challenging when further scaling the mode field area.
$85~\unicode[STIX]{x03BC}\text{m}$
diameter was used to provide robust single-mode operation in an amplification system[Reference Pei, Ruppe, Chen, Sheikhsofla, Nees and Galvanauskas79]. However, CCC fibers require complex fabrication process and are very sensitive to fiber parameters. Moreover, resonance matching can be extremely challenging when further scaling the mode field area.

Figure 4. Polygonal-CCC fiber structure[Reference Ma, Zhu, Hu, Kaplan and Galvanauskas78].
LMA fibers based on thermal guiding, index-antiguiding[Reference Jansen, Stutzki, Otto, Jauregui, Limpert and Tünnermann80] and gain-guided, index-antiguided[Reference Chen, McComb, Sudesh, Richardson and Bass81–Reference Wang, Chen, Hageman, Kim, Richardson, Xiong, Ballato and Bass84] mechanisms have come up as interesting approaches for LMA single-mode operation. However, they are still in the theoretical research stage with limited certifications for effective single-mode operation in high-power fiber lasers.
6 Conclusion
In conclusion, we have reviewed the current state of the art in the Yb-doped fiber in relation to fiber fabrication and performance consideration such as laser power stability and beam quality. Our review has highlighted that the PD and the MI are significant factors that limit the reliable commercial systems. And these also are likely to be highly challenging for the laser power levels climbing and the fiber laser application extension. We note that the fiber co-dopants composition, structure design and fiber fabrication are the fundamental methods to improve the performance of Yb-doped fiber. And it is interesting to see that those are also effective ways for the decrease of PD and the increase of MI thresholds. The optimization of Yb-doped silicate fibers seems to have come into
![]() $\text{Ce}/\text{Al}$
co-doping from
$\text{Ce}/\text{Al}$
co-doping from
![]() $\text{P}/\text{Al}$
co-doping and ultimately from high Al co-doping. With the deep research on photo-bleaching, it is now an available solution to mitigate PD, although this technique requires an injection scheme in fiber lasers. CCC fibers and ultra-low-NA LAM fibers have attracted intensive attention for the effective single-mode operation. However, these special fibers require a complex fabrication process and high control accuracy. An impressive technological improvement based on MCVD or completely new technologies is expected to be developed for a higher performance fiber.
$\text{P}/\text{Al}$
co-doping and ultimately from high Al co-doping. With the deep research on photo-bleaching, it is now an available solution to mitigate PD, although this technique requires an injection scheme in fiber lasers. CCC fibers and ultra-low-NA LAM fibers have attracted intensive attention for the effective single-mode operation. However, these special fibers require a complex fabrication process and high control accuracy. An impressive technological improvement based on MCVD or completely new technologies is expected to be developed for a higher performance fiber.