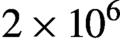1 Introduction
Laser-driven nuclear fusion and its byproduct, neutron generation, is achieved in spherical plasma compressions created by delivering multi-kilojoule pulses from the world’s largest lasers either directly to the target (direct drive)[Reference Craxton, Anderson, Boehly, Goncharov, Harding, Knauerl, McCrory, McKenty, Meyerhofer, Myatt, Schmitt, Sethian, Short, Skupsky, Theobald, Kruer, Tanaka, Betti, Collins, Delettrez, Hu, Marozas, Maximov, Michel, Radha, Reganl, Sangster, Seka, Solodov, Soures, Stoeckl and Zuegel1] or indirectly by converting these pulses into X-rays in a hohlraum[Reference Hurricane, Callahan, Casey, Celliers, Cerjan, Dewald, Dittrich, Döppner, Hinkel, Hopkins, Kline, Le Pape, Ma, MacPhee, Milovich, Pak, Park, Patel, Remington, Salmonson, Springer and Tommasini2, Reference Ping, Smalyuk, Amendt, Tommasini, Field, Khan, Bennett, Dewald, Graziani, Johnson and Landen3]. The latter approach produced a record yield of ![]() $1.9\times {10}^{16}$ neutrons employing 1.5 MJ of laser pulse energy[Reference Le Pape, Hopkins, Divol, Pak, Dewald, Bhandarkar, Bennedetti, Bunn, Biener, Crippen, Casey, Edgell, Fittinghoff, Gatu-Johnson, Goyon, Haan, Hatarik, Havre, Ho, Izumi, Jaquez, Khan, Kyrala, Ma, Mackinnon, MacPhee, MacGowan, Meezan, Milovich, Millot, Michel, Nagel, Nikroo, Patel, Ralph, Ross, Rice, Strozzi, Stadermann, Volegov, Yeamans, Weber, Wild, Callahan and Hurricane4]. However, these large lasers can fire at a repetition rate often limited to a few shots per day, and therefore offer limited accessibility to conduct comprehensive studies in a broad range of fundamental research and applications. The ability to drive fusion reactions and to produce neutron flashes at much higher repetition rates using compact lasers is therefore of significant interest. This would, for example, open the possibility to study the astrophysical-related processes of nucleosynthesis to form heavier elements over a broad range of parameters[Reference Chen, Negoita, Spohr, d’Humières, Pomerantz and Fuchs5], and to study the structure and dynamics of matter by neutron spectroscopy[Reference Mitchell6], scattering[Reference Taylor, Dunne, Bennington, Ansell, Gardner, Norreys, Broome, Findlay and Nelmes7], and imaging[Reference Lehmann, Kaestner, Josic, Hartmann and Mannes8–Reference Mizutani, Abe, Arikawa, Nishibata, Yogo, Mirfayzi, Nishimura, Mima, Fujioka, Nakai, Shiraga and Kodama10]. However, target engineering is required to efficiently generate the plasma conditions to drive nuclear reactions with compact joule-level lasers. Studies have utilized different types of targets that include thin foils of deuterated materials[Reference Higginson, McNaney, Swift, Petrov, Davis, Frenje, Jarrott, Kodama, Lancaster, Mackinnon, Nakamura, Patel, Tynan and Beg11, Reference Higginson, Gray, King, Dance, Williamson, Butler, Wilson, Capdessus, Armstrong, Green, Hawkes, Martin, Wei, Mirfayzi, Yuan, Kar, Borghesi, Clarke, Neely and McKenna12], deuterated clusters[Reference Zweiback, Smith, Cowan, Hays, Wharton, Yanovsky and Ditmire13–Reference Zweiback, Cowan, Hartley, Howell, Wharton, Crane, Yanovsky and Hays19], cryogenic D2[Reference Alejo, Krygier, Ahmed, Morrison, Clarke, Fuchs, Green, Green, Jung and Kleinschmidt20, Reference Norreys, Fews, Beg, Bell, Dangor, Lee, Nelson, Schmidt, Tatarakis and Cable21], and heavy water jets and spray[Reference Ter-Avetisyan, Schnürer, Hilscher, Jahnke, Busch, Nickles and Sandner22–Reference Soloveva, Andreyanova, Barionb, Ciullob, Engelsc, Fotyeva, Ivshina, Kochendaa, Kravchenkoa, Kravtsova, Larionova, Rozhdestvenskya, Shermana, Solovyeva, Trofimova, Vasilyeva and Vznuzdaeva24].
$1.9\times {10}^{16}$ neutrons employing 1.5 MJ of laser pulse energy[Reference Le Pape, Hopkins, Divol, Pak, Dewald, Bhandarkar, Bennedetti, Bunn, Biener, Crippen, Casey, Edgell, Fittinghoff, Gatu-Johnson, Goyon, Haan, Hatarik, Havre, Ho, Izumi, Jaquez, Khan, Kyrala, Ma, Mackinnon, MacPhee, MacGowan, Meezan, Milovich, Millot, Michel, Nagel, Nikroo, Patel, Ralph, Ross, Rice, Strozzi, Stadermann, Volegov, Yeamans, Weber, Wild, Callahan and Hurricane4]. However, these large lasers can fire at a repetition rate often limited to a few shots per day, and therefore offer limited accessibility to conduct comprehensive studies in a broad range of fundamental research and applications. The ability to drive fusion reactions and to produce neutron flashes at much higher repetition rates using compact lasers is therefore of significant interest. This would, for example, open the possibility to study the astrophysical-related processes of nucleosynthesis to form heavier elements over a broad range of parameters[Reference Chen, Negoita, Spohr, d’Humières, Pomerantz and Fuchs5], and to study the structure and dynamics of matter by neutron spectroscopy[Reference Mitchell6], scattering[Reference Taylor, Dunne, Bennington, Ansell, Gardner, Norreys, Broome, Findlay and Nelmes7], and imaging[Reference Lehmann, Kaestner, Josic, Hartmann and Mannes8–Reference Mizutani, Abe, Arikawa, Nishibata, Yogo, Mirfayzi, Nishimura, Mima, Fujioka, Nakai, Shiraga and Kodama10]. However, target engineering is required to efficiently generate the plasma conditions to drive nuclear reactions with compact joule-level lasers. Studies have utilized different types of targets that include thin foils of deuterated materials[Reference Higginson, McNaney, Swift, Petrov, Davis, Frenje, Jarrott, Kodama, Lancaster, Mackinnon, Nakamura, Patel, Tynan and Beg11, Reference Higginson, Gray, King, Dance, Williamson, Butler, Wilson, Capdessus, Armstrong, Green, Hawkes, Martin, Wei, Mirfayzi, Yuan, Kar, Borghesi, Clarke, Neely and McKenna12], deuterated clusters[Reference Zweiback, Smith, Cowan, Hays, Wharton, Yanovsky and Ditmire13–Reference Zweiback, Cowan, Hartley, Howell, Wharton, Crane, Yanovsky and Hays19], cryogenic D2[Reference Alejo, Krygier, Ahmed, Morrison, Clarke, Fuchs, Green, Green, Jung and Kleinschmidt20, Reference Norreys, Fews, Beg, Bell, Dangor, Lee, Nelson, Schmidt, Tatarakis and Cable21], and heavy water jets and spray[Reference Ter-Avetisyan, Schnürer, Hilscher, Jahnke, Busch, Nickles and Sandner22–Reference Soloveva, Andreyanova, Barionb, Ciullob, Engelsc, Fotyeva, Ivshina, Kochendaa, Kravchenkoa, Kravtsova, Larionova, Rozhdestvenskya, Shermana, Solovyeva, Trofimova, Vasilyeva and Vznuzdaeva24].
We have recently demonstrated that the interaction of ultrashort laser pulses of relativistic intensity with arrays of aligned deuterated nanowires (NWs) can accelerate deuterons to sufficient kinetic energies to efficiently produce nuclear fusion reactions and short neutron pulses. Experiments were conducted irradiating deuterated polyethylene (CD2) NWs with femtosecond laser pulses from a petawatt-class laser that can fire at repetition rates of up to 3.3 Hz[Reference Wang, Wang, Rockwood, Luther, Hollinger, Curtis, Calvi, Menoni and Rocca25]. Irradiation of arrays of 200–400 nm diameter NWs with an intensity of 8 × 1019 W cm–2 accelerated deuterons to energies up to 3 MeV[Reference Curtis, Calvi, Tinsley, Hollinger, Kaymak, Pukhov, Wang, Rockwood, Wang, Shlyaptsev and Rocca26]. Single-shot D–D neutron generation with ultra-high-contrast laser pulses of 1.6 J energy was measured to greatly surpass that in flat solid CD2 target irradiated with the same laser pulses owing to increased laser absorption and more efficient acceleration of ions. Our target design consists of an array of high-aspect-ratio vertically aligned CD2 NWs with an average density amounting to a significant fraction of CD2 solid density. In this scheme, ultra-high-contrast femtosecond laser pulses can be nearly completely absorbed by the NW arrays[Reference Purvis, Shlyaptsev, Hollinger, Bargsten, Pukhov, Prieto, Wang, Luther, Yin, Wang and Rocca27, Reference Bargsten, Hollinger, Capeluto, Kaymak, Pukhov, Wang, Rockwood, Wang, Keiss, Tommasini, London, Park, Busquet, Klapisch, Shlyaptsev and Rocca28]. Our previous work has shown that high-energy deuterons can be efficiently generated by irradiating arrays of vertically aligned high-aspect-ratio CD2 NWs with ultra-high-contrast pulses of relativistic intensities from a compact laser. The use of sufficiently short laser pulses allows for very efficient coupling of the pulse energy deep into the NW array, heating a volume of near-solid-density material several micrometers in depth to extreme temperatures. Optical field ionization initially generates a plasma concentrated at the tip of the NWs. The electrons ripped from the material are accelerated in the space between the NWs by a strong ponderomotive interaction[Reference Moreau, Hollinger, Calvi, Wang, Wang, Capeluto, Rockwood, Curtis, Kasdorf, Shlyaptsev, Kaymak, Pukhov and Rocca29]. The accelerated electrons are characterized by a three times higher electron temperature and an integrated flux ![]() $22$ times larger with respect to foil targets[Reference Moreau, Hollinger, Calvi, Wang, Wang, Capeluto, Rockwood, Curtis, Kasdorf, Shlyaptsev, Kaymak, Pukhov and Rocca29]. Electrons accelerated in the laser backward direction form a space charge sheath in front or the target, where ions are accelerated to multi-megaelectronvolt energy towards the laser by transverse normal sheath acceleration (TNSA)[Reference Curtis, Hollinger, Calvi, Wang, Huanyu, Wang, Pukhov, Kaymak, Baumann, Tinsley, Shlyaptsev and Rocca30]. Electron collisions heat the material until the NWs explode filling the gaps with a dense plasma. Before the gaps are filled with an overdense plasma, laser pulses can penetrate the NW array for a depth of several microns, allowing volumetric heating[Reference Bargsten, Hollinger, Capeluto, Kaymak, Pukhov, Wang, Rockwood, Wang, Keiss, Tommasini, London, Park, Busquet, Klapisch, Shlyaptsev and Rocca28].
$22$ times larger with respect to foil targets[Reference Moreau, Hollinger, Calvi, Wang, Wang, Capeluto, Rockwood, Curtis, Kasdorf, Shlyaptsev, Kaymak, Pukhov and Rocca29]. Electrons accelerated in the laser backward direction form a space charge sheath in front or the target, where ions are accelerated to multi-megaelectronvolt energy towards the laser by transverse normal sheath acceleration (TNSA)[Reference Curtis, Hollinger, Calvi, Wang, Huanyu, Wang, Pukhov, Kaymak, Baumann, Tinsley, Shlyaptsev and Rocca30]. Electron collisions heat the material until the NWs explode filling the gaps with a dense plasma. Before the gaps are filled with an overdense plasma, laser pulses can penetrate the NW array for a depth of several microns, allowing volumetric heating[Reference Bargsten, Hollinger, Capeluto, Kaymak, Pukhov, Wang, Rockwood, Wang, Keiss, Tommasini, London, Park, Busquet, Klapisch, Shlyaptsev and Rocca28].
The choice of the separation between NWs (![]() $d$) is therefore critical to ensure laser pulse penetration deep into the array. As a rule of thumb, the pulse duration should be small compared with the characteristic time that the plasma takes to fill the free space owing to hydrodynamic expansion (
$d$) is therefore critical to ensure laser pulse penetration deep into the array. As a rule of thumb, the pulse duration should be small compared with the characteristic time that the plasma takes to fill the free space owing to hydrodynamic expansion (![]() $d/2{c}_{\mathrm{s}}$, where
$d/2{c}_{\mathrm{s}}$, where ![]() ${c}_{\mathrm{s}}$ is the acoustic velocity). However, simulations show different mechanisms can affect the gap filling time and the laser penetration[Reference Purvis, Shlyaptsev, Hollinger, Bargsten, Pukhov, Prieto, Wang, Luther, Yin, Wang and Rocca27, Reference Bargsten, Hollinger, Capeluto, Kaymak, Pukhov, Wang, Rockwood, Wang, Keiss, Tommasini, London, Park, Busquet, Klapisch, Shlyaptsev and Rocca28, Reference Kaymak, Pukhov, Shlyaptsev and Rocca31]. As electrons are accelerated by the ponderomotive force to high speeds towards the substrate, a return current opposite to the direction of the laser beam appears to balance the charge. This return current gives rise to a nano-pinch effect that compresses the NWs, increasing the local energy density, and altering the NW expansion[Reference Kaymak, Pukhov, Shlyaptsev and Rocca31]. At sufficiently high irradiation intensity relativistically induced transparency[Reference Palaniyappan, Hegelich, Wu, Jung, Gautier, Yin, Albright, Johnson, Shimada, Letzring, Offermann, Ren, Huang, Hörlein, Dromey, Fernandez and Shah32, Reference Fernández, Gautier, Huang, Palaniyappan, Albright, Bang, Dyer, Favalli, Hunter, Mendez, Roth, Swinhoe, Bradley, Deppert, Espy, Falk, Guler, Hamilton, Hegelich, Henzlova, Ianakiev, Iliev, Johnson, Kleinschmidt, Losko, McCary, Mocko, Nelson, Roycroft, Cordoba, Schanz, Schaumann, Schmidt, Sefkow, Shimada, Taddeucci, Tebartz, Vogel, Vold, Wurden and Yin33] can also aid deep laser penetration even after the inter-wire gaps are filled with an overdense plasma[Reference Moreau, Hollinger, Calvi, Wang, Wang, Capeluto, Rockwood, Curtis, Kasdorf, Shlyaptsev, Kaymak, Pukhov and Rocca29, Reference Curtis, Hollinger, Calvi, Wang, Huanyu, Wang, Pukhov, Kaymak, Baumann, Tinsley, Shlyaptsev and Rocca30, Reference Hollinger, Wang, Wang, Moreau, Capeluto, Song, Rockwood, Bayarsaikhan, Kaymak, Pukhov, Shlyaptsev and Rocca34]. For example, at an intensity of 3 × 1021 W cm–2 the normalized vector potential at
${c}_{\mathrm{s}}$ is the acoustic velocity). However, simulations show different mechanisms can affect the gap filling time and the laser penetration[Reference Purvis, Shlyaptsev, Hollinger, Bargsten, Pukhov, Prieto, Wang, Luther, Yin, Wang and Rocca27, Reference Bargsten, Hollinger, Capeluto, Kaymak, Pukhov, Wang, Rockwood, Wang, Keiss, Tommasini, London, Park, Busquet, Klapisch, Shlyaptsev and Rocca28, Reference Kaymak, Pukhov, Shlyaptsev and Rocca31]. As electrons are accelerated by the ponderomotive force to high speeds towards the substrate, a return current opposite to the direction of the laser beam appears to balance the charge. This return current gives rise to a nano-pinch effect that compresses the NWs, increasing the local energy density, and altering the NW expansion[Reference Kaymak, Pukhov, Shlyaptsev and Rocca31]. At sufficiently high irradiation intensity relativistically induced transparency[Reference Palaniyappan, Hegelich, Wu, Jung, Gautier, Yin, Albright, Johnson, Shimada, Letzring, Offermann, Ren, Huang, Hörlein, Dromey, Fernandez and Shah32, Reference Fernández, Gautier, Huang, Palaniyappan, Albright, Bang, Dyer, Favalli, Hunter, Mendez, Roth, Swinhoe, Bradley, Deppert, Espy, Falk, Guler, Hamilton, Hegelich, Henzlova, Ianakiev, Iliev, Johnson, Kleinschmidt, Losko, McCary, Mocko, Nelson, Roycroft, Cordoba, Schanz, Schaumann, Schmidt, Sefkow, Shimada, Taddeucci, Tebartz, Vogel, Vold, Wurden and Yin33] can also aid deep laser penetration even after the inter-wire gaps are filled with an overdense plasma[Reference Moreau, Hollinger, Calvi, Wang, Wang, Capeluto, Rockwood, Curtis, Kasdorf, Shlyaptsev, Kaymak, Pukhov and Rocca29, Reference Curtis, Hollinger, Calvi, Wang, Huanyu, Wang, Pukhov, Kaymak, Baumann, Tinsley, Shlyaptsev and Rocca30, Reference Hollinger, Wang, Wang, Moreau, Capeluto, Song, Rockwood, Bayarsaikhan, Kaymak, Pukhov, Shlyaptsev and Rocca34]. For example, at an intensity of 3 × 1021 W cm–2 the normalized vector potential at ![]() $\lambda =400\ \mathrm{nm}$ is
$\lambda =400\ \mathrm{nm}$ is ![]() ${a}_{\rm o}\sim 18.7$ which implies a relativistic factor
${a}_{\rm o}\sim 18.7$ which implies a relativistic factor 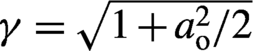 $\gamma =\sqrt{1+{a}_{\rm o}^2/2}$ of the order of 13. It follows that this effect increases the critical density to
$\gamma =\sqrt{1+{a}_{\rm o}^2/2}$ of the order of 13. It follows that this effect increases the critical density to 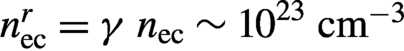 ${n}_{\rm ec}^r=\gamma\ {n}_{\rm ec}\sim {10}^{23}\ \mathrm{c}{\mathrm{m}}^{-3}$. Therefore, at high intensities the laser can propagate into the plasma even when the gaps are filled with a classically overdense plasma.
${n}_{\rm ec}^r=\gamma\ {n}_{\rm ec}\sim {10}^{23}\ \mathrm{c}{\mathrm{m}}^{-3}$. Therefore, at high intensities the laser can propagate into the plasma even when the gaps are filled with a classically overdense plasma.
In addition to the front TNSA field external to the NWs, simulations show that there also exists an internal quasi-static TNSA field within the NW array that accelerates the ions in the direction perpendicular to the NW surface. This radial field that surrounds each of the NWs is formed owing to the displacement of so-called Brunel electrons from the NW surfaces into the voids by the laser electric field. The radial acceleration due to the internal TNSA field accelerates ions in the close vicinity to the NW surface, after which they dissipate their energy colliding with the surrounding material or the CD2 substrate, opening a path to efficiently drive D–D fusion reactions and quasi-monoenergetic neutron generation with joule-level lasers. D–D neutron generation in CD2 NW targets irradiated at an intensity of 8 × 1019 W cm–2 was measured to reach ![]() $2\times {10}^6$ neutrons per joule[Reference Curtis, Calvi, Tinsley, Hollinger, Kaymak, Pukhov, Wang, Rockwood, Wang, Shlyaptsev and Rocca26], an increase of about 500 times with respect to flat solid targets irradiated with the same laser pulses. Following this first demonstration, irradiation with 8 J laser pulses was measured to generate up to 1.2 × 107 D–D fusion neutrons per shot[Reference Curtis, Hollinger, Calvi, Wang, Huanyu, Wang, Pukhov, Kaymak, Baumann, Tinsley, Shlyaptsev and Rocca30].
$2\times {10}^6$ neutrons per joule[Reference Curtis, Calvi, Tinsley, Hollinger, Kaymak, Pukhov, Wang, Rockwood, Wang, Shlyaptsev and Rocca26], an increase of about 500 times with respect to flat solid targets irradiated with the same laser pulses. Following this first demonstration, irradiation with 8 J laser pulses was measured to generate up to 1.2 × 107 D–D fusion neutrons per shot[Reference Curtis, Hollinger, Calvi, Wang, Huanyu, Wang, Pukhov, Kaymak, Baumann, Tinsley, Shlyaptsev and Rocca30].
Here we focus on the development of CD2 NW array targets to produce ultra-high-energy density plasmas where D–D fusion can be efficiently produced. We also summarize results of neutron production comparing NW arrays targets with flat targets made of the same material.
2 NW array fabrication
Arrays of vertically aligned CD2 NWs were fabricated by a multi-step process schematized in Figure 1. In general, the technique consists of extruding CD2 into the pores of an anodic aluminum oxide (AAO) template, followed by the template dissolution, and an appropriate sample drying process to preserve the NWs vertically aligned by avoiding their collapse owing to surface tension. The AAO templates are formed by electrochemical anodization of pure aluminum. They consist of parallel arrays of holes surrounded by hexagonal cells of aluminum oxide that grow perpendicular to the metallic surface as the anodization advances, forming a structure that resembles a honeycomb[Reference Liu, Tian and Zhang35, Reference Ruiz-Clavijo, Caballero-Calero and Martín-González36]. They are commercially available (e.g., SmartMembrane). The first step in the fabrication process is to extrude a CD2 thin film into the pores of the template. Figure 1(a) shows a schematic of the sample mounting for this step. The CD2 thin film is fabricated by applying a compressive force of 4 tons over an area of approximately 5 cm2 (~800 kg cm–2) on 100 mg of CD2 pellets (Aldrich CAS: 25549-98-8 or PolymerSource P40901-dPE) using a hydraulic press. The porous AAO template consists of an array of parallel aligned pores of 200 or 400 nm diameter in a hexagonal two-dimensional arrangement, with an interpore distance of approximately 480 or 810 nm and an average density of 16% or 19% solid density, respectively. One side of the membrane is covered by crystalline aluminum to avoid the extruded CD2 breaking through the template. The thickness of the membrane (5–15 μm) defines the pore depth and fixes the length of the NWs. The CD2 thin film is placed in between the side of the template with open pores facing the CD2 material and a polished Teflon disk. A polished Al slab is placed on top of the AAO to apply a constant pressure over the whole template using a screw and a spring. The whole assembly is placed in a furnace at a constant temperature for 25 min (230°C for Aldrich CD2 and 130°C for PolymerSource CD2). This temperature is high enough to ensure that the polymer is melted into the pores while preventing thermal degradation of the material.

Figure 1 Procedure for the fabrication of CD2 NW arrays. (a) A CD2 thin film is extruded through the pores of an AAO template at a pressure P and selected temperatures between 130°C and 230°C. (b) The sample is mounted on a carbon stub, subsequently the template is dissolved in NaOH at 50°C, and (c) the NWs are dried in an SPD. (d) SEM image of an array of vertically aligned CD2 NWs.
The next step after extruding the CD2 through the pores and cooling down the sample to room temperature consists of dissolving the template in sodium hydroxide (NaOH). The sample is mounted on a holder consisting of a carbon stub for electron microscopy; the choice of this material was based on its chemical compatibility with the NaOH. The remaining CD2 thin film is detached from the Teflon disk and mounted on the carbon holder using a double-sided copper tape, as shown in Figure 1(b). The AAO template is dissolved in a 10 mol/L NaOH bath at 50°C under constant stirring, using a temperature-controlled hot plate. From this step until the end of the procedure, special care is taken to keep the NWs into the liquid to avoid their drying in air, which otherwise would lead to their collapse owing to surface tension. When the template is completely dissolved the NWs are rinsed with milliQ water and the pH is tracked, exchanging NaOH and water until they are totally clean. A supercritical point dryer (SPD) is used to dry the samples to avoid bunching of the NWs by surface tension, preserving their vertical alignment. Figure 1(e) shows scanning electron microscopy (SEM) image of a typical processed target, where the arrangement of vertical distinct NWs can be observed.
In our previous work, the SPD technique was shown to be adequate for producing metal NWs[Reference Purvis, Shlyaptsev, Hollinger, Bargsten, Pukhov, Prieto, Wang, Luther, Yin, Wang and Rocca27, Reference Bargsten, Hollinger, Capeluto, Kaymak, Pukhov, Wang, Rockwood, Wang, Keiss, Tommasini, London, Park, Busquet, Klapisch, Shlyaptsev and Rocca28, Reference Hollinger, Wang, Wang, Moreau, Capeluto, Song, Rockwood, Bayarsaikhan, Kaymak, Pukhov, Shlyaptsev and Rocca34]. However, polyethylene is a very soft material (Young’s modulus of LDPE is 200–300 MPa and 600–1500 MPa for HDPE[Reference Mark37]); it is challenging to obtain a good NW alignment and adequate inter-wire separation over large areas, as the wires tend to bend and bunch, even when using SPD. A van der Graaf generator was used to separate bunched NWs. For this procedure, the target was mounted on the generator dome as shown in Figure 2(a). When charged by the van der Graaf generator, individual NWs are pushed away from each other, creating a vertical alignment. Figures 2(b) and 2(c) show SEM images of a sample before and after charging with the van der Graaf generator. Owing to the low Young’s modulus, arrays of high-aspect-ratio polyethylene NWs of small diameter are challenging to make. We have fabricated NWs of 200 and 400 nm diameter with lengths ranging from 5 to 15 μm. The typical CD2 substrate thickness is 200–300 μm. Arrays with thinner substrates, down to 50 μm, were also fabricated.

Figure 2 (a) Schematic representation of an NW target mounted on the van der Graaf generator dome. (b), (c) SEM images of a sample before and after charging, respectively.
3 Experimental results
CD2 NW arrays were irradiated by the ALEPH 400 PW class laser at Colorado State University[Reference Wang, Wang, Rockwood, Luther, Hollinger, Curtis, Calvi, Menoni and Rocca25]. Aleph 400 is a 400 nm frequency-doubled Ti:sapphire laser that was used in the experiments described in the following to deliver pulses with intensities of up to 3 × 1021 W cm–2. A KDP crystal was used to double the frequency of the laser and obtain ultra-high-contrast (>1012) pulses. Ultra-high-contrast pulses are essential in this type of experiment as pre-pulses can destroy the NWs before the arrival of the main pulse, hindering the energy coupling in a large volume near-solid density plasma. An initial set of experiments was conducted with pulses of 60 fs full width at half maximum (FWHM) with energy up to 1.65 J. In a second series of measurements pulses of approximately 45 fs duration and pulse energies up to 8 J were used. For a 0.5-inch diameter CD2 NW target the number of shots per target is limited to about 12, to ensure that one shot does not alter the nanostructure in the location of the next shot. Cutting the target and spacing the samples by 10 mm we have performed up to 20 shots from one such target. A larger number of shots can be made without breaking vacuum if samples from several targets are mounted in the same target mount. The experimental setup is schematically illustrated in Figure 3(a). In all cases we performed single-shot irradiation experiments in which the target was displaced between shots to renew the surface. An f/2 off-axis parabolic mirror was used to focus the beam into a focal spot of approximately 1.6 μm diameter on the target, impinging at an angle of 22.5° with respect to the target normal. A Thomson parabola ion spectrometer (TPIS), placed at 75 cm away from the target, was used to characterize the energy of ions that were accelerated along the target normal and backward direction, as schematized in Figure 3(a). In this instrument the electromagnetic fields that deflect the ions are generated by two electrically biased permanent Nd magnets that are separated by 6 mm to generate a B field of 0.18 T on-axis, measured using a Hall probe. The magnets were biased to create a potential difference of 3500 V. A 100 μm pinhole is placed at the entrance of the TPIS to collimate the beam before the ions go through the collinear fields where they are deflected to impinge on a pair of matched microchannel plates (MCPs) stacked in a chevron configuration. The spatial information encoded in the emitted electrons is transferred into a phosphor screen deposited onto an optical fiber bundle which is imaged onto a charge coupled device (CCD). We have developed a method to experimentally calibrate the energy of the ions arriving at the MCPs of the TPIS. It consists of a time-of-flight measurement in which the MCPs are gated by a fast-rising voltage pulse. Measurements of the arrival time of the gate pulse to the MCPs with respect to the arrival of the laser pulse to the target allow to determine the maximum velocity and energy of each of the ion species for each voltage setting. The measured ion traces were compared with those computed by Simion®[Reference Dahl38]. D–D neutrons were detected by an array of four EJ-228 plastic scintillator/photomultiplier sets (Hamamatsu H2431–50) of time-of-flight neutron detectors placed at different locations around the target. Their different distances from the target allowed for time-of-flight neutron energy measurements. The neutron detectors were shielded with 10-cm-thick Pb on the side facing the plasma, and by 5-cm-thick Pb on all other sides to reduce the impinging X-ray flux onto the detector.

Figure 3 (a) Experimental setup for ion energy spectra and neutron measurements. Femtosecond laser pulses of relativistic intensity are focused onto CD2 targets. A Thompson parabola is used to determine the energy spectra of the accelerated ions. The neutron flux is detected using an array of four scintillator/ photomultiplier neutron time of flight detectors (in the detectors: gray, lead; orange, scintillator). (b), (d) TPIS ion traces and (c), (e) deuteron energy spectra corresponding to an NW target and a flat target, respectively. The irradiation intensity is approximately 3 × 1021 W cm–2.
Both 200 and 400 nm diameter NW arrays were observed to produce a significant number of neutrons. The optimum NW diameter and spacing depend on the characteristics of the laser pulse used. The data presented here is limited to 200 nm diameter NWs. Figures 3(b) and 3(d) illustrate the typical single-shot ion-energy spectra for NW arrays of 200 nm diameter CD2 NWs and for flat CD2 solid targets irradiated with 45 fs duration laser pulses at an intensity of ~3 × 1021 W cm–2. Traces corresponding to H, D, and C ions are observed. Figures 3(c) and 3(e) show the corresponding deuteron energy spectra. The cutoff kinetic energy for the deuterons from the NW target is nearly twice that corresponding to CD2 flat targets irradiated with the same laser pulses. Although deuterons from the flat target are accelerated up to 6 MeV, deuterons ejected from the CD2 NW arrays reach an energy of approximately 11.5 MeV. The angular distribution of the accelerated ions was measured using CR39 track detectors covered with aluminum filters. In the case of ions with cutoff energies of the order of 0.4 MeV or less, for which the flux is high, the ion trackers were placed at 300 cm from the target to avoid saturation of the detectors. For ions with cutoff energies of approximately 1 MeV, they were placed at 195 cm from the target. The CR39 trackers were inserted at the end of vacuum tubes which were spaced at angular intervals of 22.5°, as shown in Figure 4(a). Angles less than 22.5° were blocked by the focusing parabola. Figure 4(b) shows the measured angular distribution for deuterons with energies greater than 1 and 1.3 MeV, whereas the data in Figure 4(c) corresponds to deuterons with energies greater than 0.3 and 0.4 MeV, respectively. The comparison between the two figures shows that the higher-energy ions are better collimated. This trend continues for higher ion energies. To measure the angular distribution of deuterons with energy greater than 13 MeV, CR39 trackers filtered by 250 ![]() $\mu$m thick copper foils mounted along the edge of a thin 10 cm radius of curvature circular stainless steel ‘sickle’ which was placed inside the vacuum chamber. Eleven CR39 detectors were positioned on it at different angles ranging from –65° to +65°. The mount was thin to avoid blocking a significant fraction of the incident laser beam. This circular trace array was positioned directly in the laser beam path at a distance of 10 cm from the target equal to the circle radius[Reference Curtis, Hollinger, Calvi, Wang, Huanyu, Wang, Pukhov, Kaymak, Baumann, Tinsley, Shlyaptsev and Rocca30]. The data shows that ions with this larger energy are highly directional, contained within a 7.5° FWHM cone[Reference Curtis, Hollinger, Calvi, Wang, Huanyu, Wang, Pukhov, Kaymak, Baumann, Tinsley, Shlyaptsev and Rocca30]. No ions were detected when the filter thickness was increased to 300 μm, which filters deuterons with energies less than 15 MeV.
$\mu$m thick copper foils mounted along the edge of a thin 10 cm radius of curvature circular stainless steel ‘sickle’ which was placed inside the vacuum chamber. Eleven CR39 detectors were positioned on it at different angles ranging from –65° to +65°. The mount was thin to avoid blocking a significant fraction of the incident laser beam. This circular trace array was positioned directly in the laser beam path at a distance of 10 cm from the target equal to the circle radius[Reference Curtis, Hollinger, Calvi, Wang, Huanyu, Wang, Pukhov, Kaymak, Baumann, Tinsley, Shlyaptsev and Rocca30]. The data shows that ions with this larger energy are highly directional, contained within a 7.5° FWHM cone[Reference Curtis, Hollinger, Calvi, Wang, Huanyu, Wang, Pukhov, Kaymak, Baumann, Tinsley, Shlyaptsev and Rocca30]. No ions were detected when the filter thickness was increased to 300 μm, which filters deuterons with energies less than 15 MeV.

Figure 4 (a) Experimental setup used to measure the angular distributions of deuterons with cutoff energies of less than 1.3 MeV energy. Filtered CR39 detectors are placed at the end of the vacuum tubes, at 195 cm from the target. (b) Measured angular distribution for deuterons with cutoff energies of 1 MeV and 1.3 MeV. (c) Similar data for deuterons with cutoff energies of 0.3 MeV and 0.4 MeV obtained at 300 cm from the target.
The deuteron spectra from an array of CD2 NWs exhibit good overlap with the D–D fusion cross-section, enabling efficient laser-driven fusion reactions and the generation of neutron pulses. The four-neutron time-of-fight detectors placed at different distances from the target show a peak at an energy of 2.45 MeV characteristic of D–D fusion reactions. As shown in Figure 5, NW targets exhibit an approximately 500 times increase in D–D neutron production as compared with flat targets of the same material irradiated at the same conditions. The highest yield shots at an irradiation intensity of 8 × 1019 W cm–2 produced 2.2 × 106 neutrons per joule of laser energy. Following these initial results higher production of neutrons was recently reported using CD2 NW arrays[Reference Curtis, Hollinger, Calvi, Wang, Huanyu, Wang, Pukhov, Kaymak, Baumann, Tinsley, Shlyaptsev and Rocca30, Reference Rubovič, Bonasera, Burian, Cao, Fu, Kong, Lan, Lou, Luo, Lv, Mah, Mae, Ma, Meduna, Mei, Mora, Pan, Shou, Sýkora, Veselský, Wang, Wang, Yan, Zhang, Zhao, Zhao and Žemlička39].

Figure 5 Time-of-flight neutron detector signals for a CD2 NW (blue trace) array and solid flat target (red trace). The amplitude of the red trace is multiplied by a factor of 10 for clarity. The histogram shows the average number of neutrons generated from 11 laser shots in each case. The neutron yield is approximately 500 times larger in the case of NWs. The data corresponds to an irradiation intensity of 8 × 1019 W cm–2 (after Curtis et al.[Reference Curtis, Calvi, Tinsley, Hollinger, Kaymak, Pukhov, Wang, Rockwood, Wang, Shlyaptsev and Rocca26]).
4 Conclusions
In this work, we have described a method for the fabrication of CD2 nanostructured targets to efficiently drive D–D fusion reactions with intense ultrashort pulse lasers. The targets fabricated consist of arrays of vertically aligned CD2 NWs of 200 or 400 nm diameter with an average density of 16% or 19% solid and lengths up to 15 μm. The fabrication consists of a multistep process that combines the heated extrusion of deuterated polyethylene into a porous template, dissolution of the template, supercritical drying, and charging with a van der Graaf generator. Targets with other NW diameters or average density can also be fabricated selecting templates with different porosities. These targets allow for efficient coupling of relativistic laser pulses into a near-solid plasmas in which deuterons are accelerated to megaelectronvolt energies resulting in D–D fusion reactions and flashes of 2.45 MeV neutrons. Irradiation of the CD2 NW arrays with high-contrast femtosecond laser pulses of 8 × 1019 W cm–2 intensity produced neutron flashes of 2.2 × 106 neutrons per joule, a two to three orders of magnitude increase with respect to flat targets of the same material.
Acknowledgments
This work was supported by the Air Force Office of Scientific Research under award number FA9550-17-1-0278. The experiments were conducted at Colorado State University’s ALEPH petawatt-class laser facility supported by LaserNet US with grant DE-SC0019076 from the US Department of Energy, Office of Science, Fusion Energy Sciences.