1. Introduction
By chirped pulse amplification, a higher laser intensity has been realized, and high-intensity short-pulse lasers are now available for applications. On the other hand, ion beams are useful for medical ion cancer therapy, basic particle physics, controlled nuclear fusion, high-energy sources, and so on[Reference Bulanov and Khoroshkov1–Reference Miyazaki, Kawata, Sonobe and Kikuchi10]. The energy of ions, which are accelerated in an interaction between an intense laser pulse and a gas target, is over a few tens of MeV[Reference Nakamura, Kawata, Sonobe, Miyazaki, Kong and Kikuchi11–Reference Margarone, Klimo, Kim, Prokůpek, Limpouch, Jeong, Mocek, Pšikal, Kim, Proška, Nam, Štolcová, Choi, Lee, Sung, Yu and Korn25]. The issues in laser ion acceleration include ion beam collimation[Reference Miyazaki, Kawata, Sonobe and Kikuchi10, Reference Nakamura, Kawata, Sonobe, Miyazaki, Kong and Kikuchi11, Reference Sonobe, Kawata, Miyazaki, Nakamura and Kikuchi15], ion energy spectrum control, ion production efficiency[Reference Nodera, Kawata, Onuma, Limpouch, Klimo and Kikuchi24, Reference Margarone, Klimo, Kim, Prokůpek, Limpouch, Jeong, Mocek, Pšikal, Kim, Proška, Nam, Štolcová, Choi, Lee, Sung, Yu and Korn25], ion energy control, and ion beam bunching. Depending on the ion beam applications, the ion particle energy and the ion energy spectrum should be controlled as well as the ion beam quality. For example, ion beam cancer therapy needs 200–250 MeV for proton energy[Reference Giap and Chuang26]. In recent research, ions have been accelerated in an interaction of an intense laser pulse with a solid target or a near-critical density plasma[Reference Nakamura, Kawata, Sonobe, Miyazaki, Kong and Kikuchi11–Reference Margarone, Klimo, Kim, Prokůpek, Limpouch, Jeong, Mocek, Pšikal, Kim, Proška, Nam, Štolcová, Choi, Lee, Sung, Yu and Korn25]. However, the ion particle energy tends to be relatively low, as shown above, and the ion beam controllability would remain unsolved.
The present paper shows a new concept for a future laser ion accelerator, which should have an ion source, ion collimator, ion beam buncher, and ion post acceleration devices. Based on the laser ion accelerator components, the ion particle energy and the ion energy spectrum are controlled, and a future compact laser ion accelerator could be designed and realized for ion cancer therapy or for ion material treatment. Such a compact laser ion accelerator would provide a future daily-use ion accelerator.
The present paper shows first a concept of a future laser ion accelerator for ion cancer therapy. Then each component is discussed including ion sources by a solid target or a lower density gas plasma target, an ion post acceleration, an ion beam collimator and an ion beam buncher. In the post acceleration, a higher ion particle energy and the energy spectrum control are realized in a laser–plasma interaction; a few hundreds of MeV of the proton beam energy is successfully achieved by several times of the ion post-accelerations in the laser–plasma interaction. In addition, a mono-energetic proton beam is also produced. Based on these research results on the laser ion accelerator components, the new concept for the laser ion accelerator become realistic for the future laser ion cancer therapy.
In this study, we performed 2.5-dimensional particle-in-cell simulations[Reference Langdon and Lasinski27]to investigate the laser ion acceleration. When an intense laser pulse interacts with a target plasma, it accelerates some of the target electrons. The electrons are accelerated by the intense laser and create an electric charge separation. The charge separation provides a strong electric field, for example, typically a few MV
![]() $\sim 10~ {\rm MV}~ \mu {\rm m}^{-1}$
, by which the target ions are accelerated. This ion acceleration mechanism is called TNSA (target normal sheath acceleration). In TNSA, the acceleration electric field is normal to the target surface. TNSA is widely used for the ion source. However, the target deformation and the edge effect of the acceleration electric field induce an ion beam divergence transversely. Therefore, a collimation device is required. In this paper we present a solid target, which has holes behind the target for the collimation. The holes behind the target suppress the source protons’ divergence by reducing the ion source edge field. The target high-energy electrons also form a high current and generate the azimuthal magnetic field that of kT order. In the laser–plasma interaction, the ion dynamics is affected directly by the electric field and the behavior of the electrons[Reference Nakamura, Bulanov, Esirkepov and Kando16–Reference Borghesi, Mackinnon, Campbell, Hicks, Kar, Patel, Price, Romagnani, Schiavi and Willi18]. Especially in an underdense gas target, the electron current forms a strong magnetic field inside the gas target, and during the increase phase of the azimuthal magnetic field the inductive strong electric field is generated by Faraday’s law. The ions are also accelerated by the inductive electric field in the gas plasma target. When the inductive field speed coincides with the ion beam speed, the ions are continuously accelerated.
$\sim 10~ {\rm MV}~ \mu {\rm m}^{-1}$
, by which the target ions are accelerated. This ion acceleration mechanism is called TNSA (target normal sheath acceleration). In TNSA, the acceleration electric field is normal to the target surface. TNSA is widely used for the ion source. However, the target deformation and the edge effect of the acceleration electric field induce an ion beam divergence transversely. Therefore, a collimation device is required. In this paper we present a solid target, which has holes behind the target for the collimation. The holes behind the target suppress the source protons’ divergence by reducing the ion source edge field. The target high-energy electrons also form a high current and generate the azimuthal magnetic field that of kT order. In the laser–plasma interaction, the ion dynamics is affected directly by the electric field and the behavior of the electrons[Reference Nakamura, Bulanov, Esirkepov and Kando16–Reference Borghesi, Mackinnon, Campbell, Hicks, Kar, Patel, Price, Romagnani, Schiavi and Willi18]. Especially in an underdense gas target, the electron current forms a strong magnetic field inside the gas target, and during the increase phase of the azimuthal magnetic field the inductive strong electric field is generated by Faraday’s law. The ions are also accelerated by the inductive electric field in the gas plasma target. When the inductive field speed coincides with the ion beam speed, the ions are continuously accelerated.
2. A concept for a future laser ion accelerator
Figure 1 shows a concept proposed for a future laser ion accelerator. In an intense laser interaction with a target, first ions are generated at an ion source device. In this paper we focus on proton beam generation. The protons are accelerated by the strong electric field produced at the target by the laser–target interaction, in which the target electrons are expelled quickly and the target becomes a plasma. The high-energy electrons move around the target and the target ions stay at rest during a short period of
![]() $\sim $
fs (
$\sim $
fs (
![]() $= 10^{-15}{\rm s}$
). Between the ions and the high-energy electrons, a strong electric field is generated, and it accelerates the protons gradually. In the ion source stage the ion beam tends to have a broad energy spectrum and a transverse divergence. For ion cancer therapy as an example application, the ion energy spectrum should be mono-energetic and the ion energy should be about 200–250 MeV to deposit the ion energy into cancer cells inside a human body.
$= 10^{-15}{\rm s}$
). Between the ions and the high-energy electrons, a strong electric field is generated, and it accelerates the protons gradually. In the ion source stage the ion beam tends to have a broad energy spectrum and a transverse divergence. For ion cancer therapy as an example application, the ion energy spectrum should be mono-energetic and the ion energy should be about 200–250 MeV to deposit the ion energy into cancer cells inside a human body.

Figure 1. (Color online) Concept of an example future laser ion accelerator. An intense laser illuminates a target, and a proton beam is generated at the ion source. The ion beam has a transverse divergence, and the proton energy is lower at the laser ion source. For ion cancer therapy as an example application, the proton energy must be 200–250 MeV to kill the cancer inside a human body. Therefore, further post-acceleration devices would be required to enhance the proton energy to achieve 200–250 MeV of proton energy and also to control the ion energy spectrum. In addition, ion collimators are also needed to suppress the ion beam divergence. In order to compress the ion beam longitudinally, a beam buncher may be required. All the components are realized by laser–target interactions in this example concept.
Therefore, the laser ion accelerator would need post-acceleration devices to enhance the ion energy and collimators to suppress the ion divergence, as well as beam bunchers to compress the ion beam longitudinally. Depending on the requirements for the proton energy and the beam radius, the laser ion accelerator would be designed appropriately, as shown in Figure 1.
3. Components of the laser ion accelerator
This section presents each component constituting the laser ion accelerator as shown in Figure 1. The ion sources are first discussed, and then the post-acceleration, the collimator, and the buncher are presented.
3.1. Proton beam source by a structured solid foil target
One of issues in laser ion acceleration is the energy conversion efficiency from the laser to ions; the energy conversion efficiency is low in actual experiments. When an intense short-pulse laser illuminates a thin foil, electrons in the foil obtain the laser energy and move around the thin foil. Some of the electrons placed at the surface irradiated by the laser are accelerated. The electrons form a strong electric field, and the ions are accelerated by the electric field. At the same time the electrons form a high current and generate a magnetic field[Reference Nakamura and Kawata14, Reference Sonobe, Kawata, Miyazaki, Nakamura and Kikuchi15]. The laser gives its energy mainly to the electrons near the thin-foil surface. The surface reflects a significant part of the laser energy. So the energy conversion efficiency from the laser to ions tends to be low. In our study, we employ an intense short-pulse laser and a double-layer hole target which consists of hydrogen and aluminum in 2.5-dimensional particle-in-cell simulations (see Figures 2(a) and 2(b)). The reason why we employ aluminum is to prevent the target deformation. Aluminum ions are heavier than hydrogen, and the aluminum supplies more electrons than hydrogen. The maximum energy of the protons is about a few MeV in the plain target. A significant increase in the energy conversion efficiency is demonstrated, and the maximum energy with the multihole target is shown in Figure 2(b). The holes, transpiercing the foil target, help drastically to increase the laser energy absorption[Reference Wang, Sheng and Zhang23, Reference Nodera, Kawata, Onuma, Limpouch, Klimo and Kikuchi24]. This idea for efficient laser ion acceleration by a fine structure was also proved by a recent experiment[Reference Margarone, Klimo, Kim, Prokůpek, Limpouch, Jeong, Mocek, Pšikal, Kim, Proška, Nam, Štolcová, Choi, Lee, Sung, Yu and Korn25].
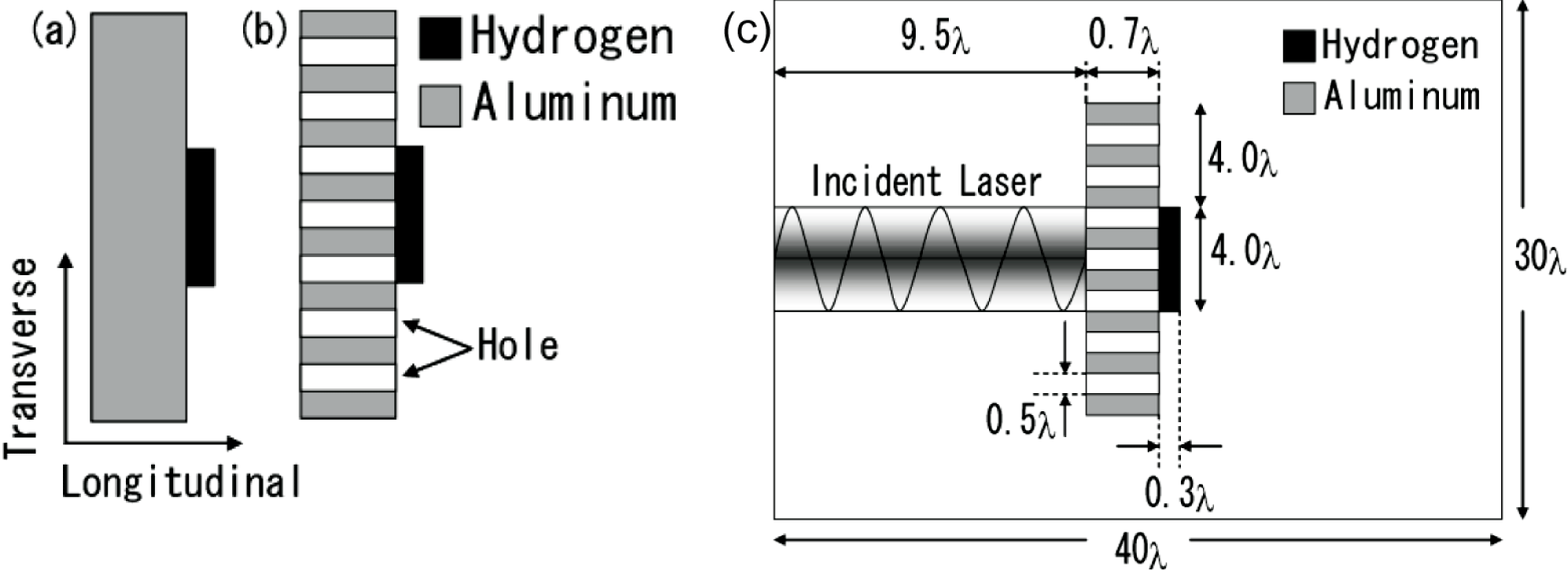
Figure 2. Thin-foil targets: (a) a plain target, (b) a multihole target, and (c) the target structure used in this study. An intense short-pulse laser gives electrons its energy, and the hot electrons are accelerated. The electrons form a strong electric field, and the protons are accelerated. The target surface reflects the laser. In the multihole target, the holes transpiercing the target help to enhance the laser–proton energy conversion efficiency. We employ a double-layer target which consists of Al and H. The Al layer has a linear density gradient in
![]() $0.5\lambda $
. The calculation area is
$0.5\lambda $
. The calculation area is
![]() $40\lambda $
in the longitudinal direction and
$40\lambda $
in the longitudinal direction and
![]() $30\lambda $
in the transverse direction. The hole diameter is
$30\lambda $
in the transverse direction. The hole diameter is
![]() $0.5\lambda $
, and the hole distance is also
$0.5\lambda $
, and the hole distance is also
![]() $0.5\lambda $
.
$0.5\lambda $
.
Figure 2(c) shows a conceptual diagram of the multihole target. We employ a linear density gradient in
![]() $0.5\lambda $
to the target at the laser illumination surface to include a pre-pulse effect of the laser. The laser intensity is
$0.5\lambda $
to the target at the laser illumination surface to include a pre-pulse effect of the laser. The laser intensity is
![]() $I = 1.0\times 10^{20 }~ {\rm W~ cm}^{-2}$
, the laser spot diameter is
$I = 1.0\times 10^{20 }~ {\rm W~ cm}^{-2}$
, the laser spot diameter is
![]() $4.0\lambda $
, and the pulse duration is 20 fs. The laser transverse profile has a Gaussian distribution. The laser wavelength is
$4.0\lambda $
, and the pulse duration is 20 fs. The laser transverse profile has a Gaussian distribution. The laser wavelength is
![]() $\lambda = 1.053~ \mu {\rm m}$
. The calculation area is
$\lambda = 1.053~ \mu {\rm m}$
. The calculation area is
![]() $40\lambda $
in the longitudinal direction and
$40\lambda $
in the longitudinal direction and
![]() $30\lambda $
in the transverse direction. The free boundary condition is employed so that the boundaries do not reflect particles and waves. The ionization degree of the Al layer is 11. The initial Al target peak density is the solid one (
$30\lambda $
in the transverse direction. The free boundary condition is employed so that the boundaries do not reflect particles and waves. The ionization degree of the Al layer is 11. The initial Al target peak density is the solid one (
![]() $n_{i}= 42n_{c}$
), and the density of the flat hydrogen layer is
$n_{i}= 42n_{c}$
), and the density of the flat hydrogen layer is
![]() $42n_{c}$
. The initial particle temperatures are 1 keV. Here,
$42n_{c}$
. The initial particle temperatures are 1 keV. Here,
![]() $n_{c}$
stands for the critical density, at which the plasma electron frequency is identical to the laser frequency. The hole diameter is
$n_{c}$
stands for the critical density, at which the plasma electron frequency is identical to the laser frequency. The hole diameter is
![]() $0.5\lambda $
.
$0.5\lambda $
.
First, we demonstrate the improvement of energy conversion efficiency from laser to protons by the multihole target (Figure 2(b)). Figure 3 show the distributions of the proton energy versus the longitudinal direction for both the cases of (a) the plain target and (b) the multihole target at 500 fs. Figures 3(a) and 3(b) show that the protons in the multihole target are accelerated in the longitudinal direction more than those in the plain target. The maximum energy of the protons is 3.14 MeV in the plain target and is 10.0 MeV in the multihole target. Figure 4 shows the total-energy histories of the protons and electrons in both cases. The peak of the laser intensity irradiates the target surface at about 55 fs, and the total energy of the electrons reaches the peak at about 60 fs. In Figure 4, the total energy of the protons reaches about
![]() $5.3\times 10^{2}~ {\rm J~ m}^{-1}$
in the plain target and
$5.3\times 10^{2}~ {\rm J~ m}^{-1}$
in the plain target and
![]() $3.1\times 10^{3}~ {\rm J~ m}^{-1}$
in the multihole target at 500 fs. The energy conversion efficiencies to the protons are 1.5% in the plain target and 9.3% in the multihole target. Figure 5 shows the hot-electron energy distributions
$3.1\times 10^{3}~ {\rm J~ m}^{-1}$
in the multihole target at 500 fs. The energy conversion efficiencies to the protons are 1.5% in the plain target and 9.3% in the multihole target. Figure 5 shows the hot-electron energy distributions
![]() $f$
in both cases at 80 fs. In Figure 5, the hot-electron temperature is 0.38 MeV in the multihole target and 0.30 MeV in the plain target. The electric field formed in the multihole target is stronger than that in the plain target, and the maximum value of the electric fields is
$f$
in both cases at 80 fs. In Figure 5, the hot-electron temperature is 0.38 MeV in the multihole target and 0.30 MeV in the plain target. The electric field formed in the multihole target is stronger than that in the plain target, and the maximum value of the electric fields is
![]() $13.1~ {\rm MV}~ \mu {\rm m}^{-1}$
for the plain target and
$13.1~ {\rm MV}~ \mu {\rm m}^{-1}$
for the plain target and
![]() $27.5~ {\rm MV}~ \mu {\rm m}^{-1}$
for the multihole target at 60 fs. Figure 6 shows the histories of the accelerated-proton number in both cases, and in Figure 6 the protons have energy over 0.1 MeV and are accelerated forward of the target. In Figure 6, the number of protons in the multihole target at 500 fs reaches about 2.7 times as many as that in the plain target. In the multihole target, the strong electric field, which is about twice as large as that of the plain target, accelerates the protons significantly and contributes the increase in the accelerated proton number. Therefore, the total-proton energy reaches about six times as much as that in the plain target.
$27.5~ {\rm MV}~ \mu {\rm m}^{-1}$
for the multihole target at 60 fs. Figure 6 shows the histories of the accelerated-proton number in both cases, and in Figure 6 the protons have energy over 0.1 MeV and are accelerated forward of the target. In Figure 6, the number of protons in the multihole target at 500 fs reaches about 2.7 times as many as that in the plain target. In the multihole target, the strong electric field, which is about twice as large as that of the plain target, accelerates the protons significantly and contributes the increase in the accelerated proton number. Therefore, the total-proton energy reaches about six times as much as that in the plain target.

Figure 3. Distributions of the proton kinetic energy at 500 fs: (a) the plain target and (b) the multihole target. The proton kinetic energies become significantly high in the multihole target.

Figure 4. Total-energy histories of the protons and electrons (a) in the plain target and (b) in the multihole target. The solid lines and the dotted lines are the histories of the electrons and the protons, respectively.
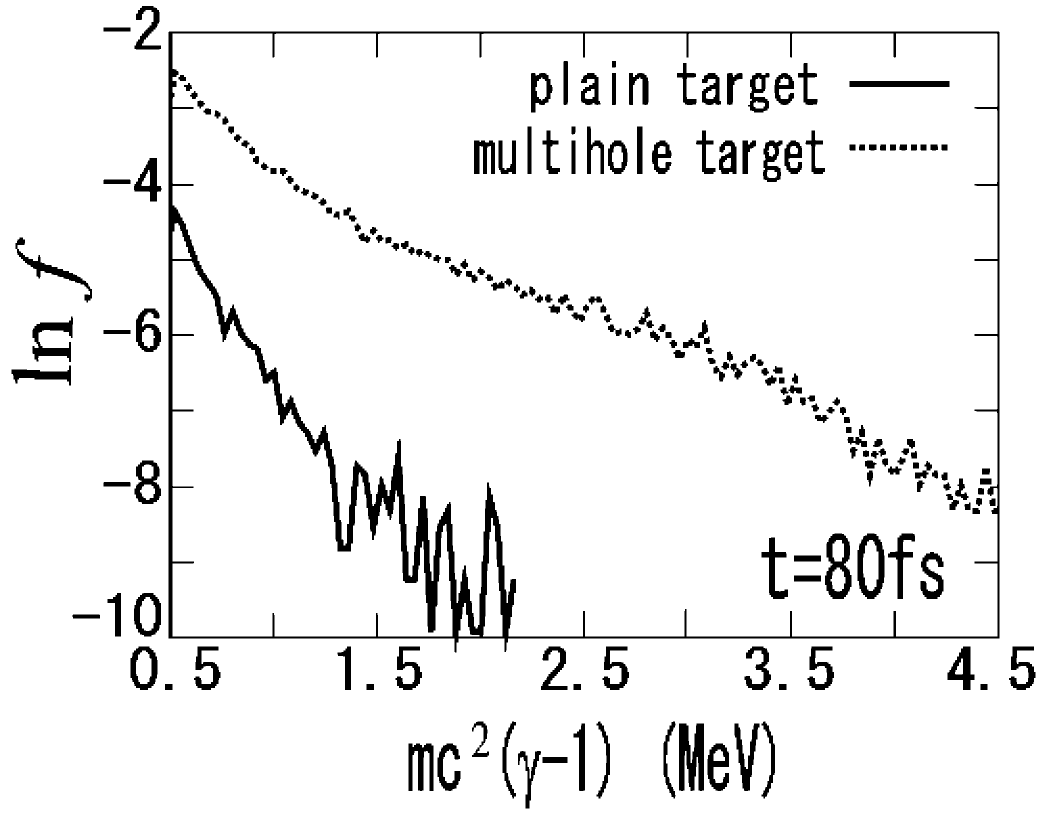
Figure 5. Energy spectra of the hot electrons at 80 fs. The solid line presents the distribution in the plain target and the dotted line shows the distribution in the multihole target.

Figure 6. Histories of the total number of the protons over 0.1 MeV in the plain target and the multihole target. The solid line shows the history in the plain target and the dotted line shows the history in the multihole target. The proton number in the multihole target becomes about 2.7 times larger than that in the plain target at 500 fs.
3.2. Proton beam source by an underdense gas plasma target
Another promising candidate for the ion source target is an underdense gas plasma, which can be created repetitively by a expanded thin plasma foil illuminated by a prepulse as an example or by a gas nozzle. In this simulation study, the hydrogen plasma target is located in
![]() $9.5\lambda < X < 29.5\lambda $
and
$9.5\lambda < X < 29.5\lambda $
and
![]() $11.0\lambda < Y < 39.0\lambda $
in the simulation box. The target density is
$11.0\lambda < Y < 39.0\lambda $
in the simulation box. The target density is
![]() $0.7n_{c}$
, and the edge region density has a linear gradient scale from
$0.7n_{c}$
, and the edge region density has a linear gradient scale from
![]() $0n_{c}$
to the maximum density of
$0n_{c}$
to the maximum density of
![]() $0.7n_{c}$
with a linear density gradient of
$0.7n_{c}$
with a linear density gradient of
![]() $2\lambda $
in the
$2\lambda $
in the
![]() $X$
and
$X$
and
![]() $Y$
directions at the target edges. The laser intensity is
$Y$
directions at the target edges. The laser intensity is
![]() $I=1.0 \times 10^{20}~ {\rm W~ cm}^{-2}$
. The laser spot diameter is
$I=1.0 \times 10^{20}~ {\rm W~ cm}^{-2}$
. The laser spot diameter is
![]() $10.0\lambda $
, the laser is focused on the left edge of each target, and the pulse duration is 40 fs. The transverse profile of the laser beam is Gaussian, and the laser temporal profile is also Gaussian. The laser wavelength is
$10.0\lambda $
, the laser is focused on the left edge of each target, and the pulse duration is 40 fs. The transverse profile of the laser beam is Gaussian, and the laser temporal profile is also Gaussian. The laser wavelength is
![]() $\lambda =1.053~ \mu {\rm m}$
. The simulation box is
$\lambda =1.053~ \mu {\rm m}$
. The simulation box is
![]() $80\lambda $
in the longitudinal direction and
$80\lambda $
in the longitudinal direction and
![]() $50\lambda $
in the transverse direction.
$50\lambda $
in the transverse direction.
The protons are accelerated by the TNSA mechanism and the dipole vortex mechanism[Reference Nakamura, Bulanov, Esirkepov and Kando16]at the linear density gradient behind the target surface. Figure 7 shows the longitudinal electric fields, which contribute the ion acceleration at (a)
![]() $t=130~ {\rm fs}$
and (b) 180 fs, and the magnetic fields at (c)
$t=130~ {\rm fs}$
and (b) 180 fs, and the magnetic fields at (c)
![]() $t=130~ {\rm fs}$
and (d) 190 fs. The maximum acceleration electric field reaches
$t=130~ {\rm fs}$
and (d) 190 fs. The maximum acceleration electric field reaches
![]() $16.7~ {\rm MV}~ \mu {\rm m}^{-1}$
at the end of the target area, and the maximum magnetic field reaches 37.0 kT in the first acceleration. The maximum proton energy is 38.9 MeV at 700 fs, and the energy conversion efficiency is 35.5% from the laser to the accelerated (
$16.7~ {\rm MV}~ \mu {\rm m}^{-1}$
at the end of the target area, and the maximum magnetic field reaches 37.0 kT in the first acceleration. The maximum proton energy is 38.9 MeV at 700 fs, and the energy conversion efficiency is 35.5% from the laser to the accelerated (
![]() $>$
20 MeV) protons.
$>$
20 MeV) protons.

Figure 7. The intense laser interacts with the hydrogen gas plasma, and protons are accelerated at the target rear surface by TNSA and magnetic vortex acceleration. The longitudinal electric fields, which contribute the ion acceleration at (a)
![]() $t=130$
fs and (b) 180 fs, and the magnetic fields at (c)
$t=130$
fs and (b) 180 fs, and the magnetic fields at (c)
![]() $t=130$
fs and (d) 180 fs. At the same time, the laser generates high-energy electrons inside the target. A transverse magnetic field is also formed along the channel in the laser–plasma interaction. During the increase phase of the magnetic field an inductive longitudinal electric field is created.
$t=130$
fs and (d) 180 fs. At the same time, the laser generates high-energy electrons inside the target. A transverse magnetic field is also formed along the channel in the laser–plasma interaction. During the increase phase of the magnetic field an inductive longitudinal electric field is created.
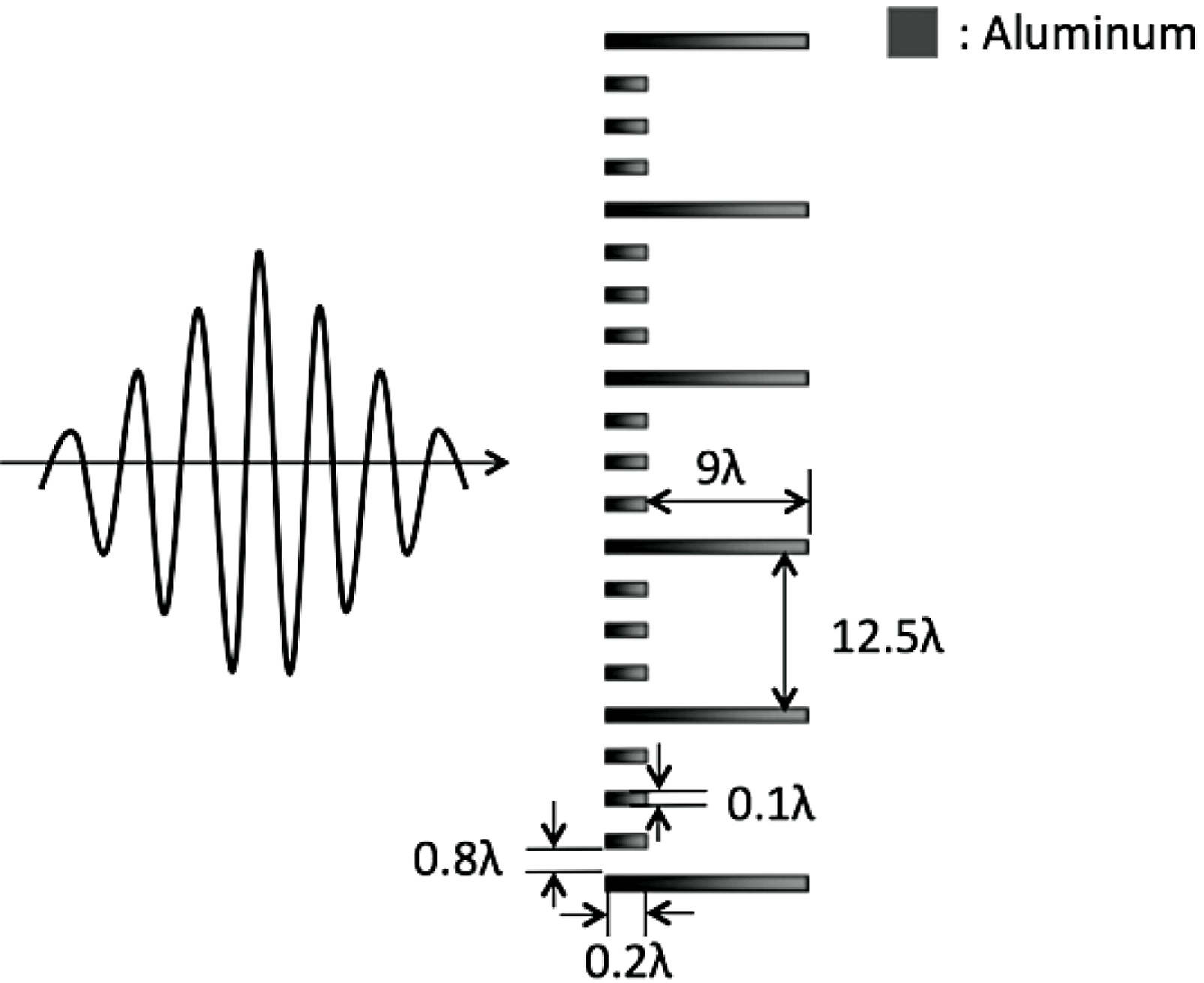
Figure 8. A collimation device for the ion beam. The Al structured target is illuminated by an intense laser. The fine structure absorbs the laser energy efficiently, and generates high-energy electrons. The electrons move around the target, and at the right-hand side the electric field is created normally to the target surface. The transverse field is generated by the electrons and collimates the proton beam.
3.3. Ion beam collimation by a structured solid target
The laser-based ion accelerator also needs a collimation device, which reduces the ion beam transverse divergence[Reference Miyazaki, Kawata, Sonobe and Kikuchi10, Reference Nakamura, Kawata, Sonobe, Miyazaki, Kong and Kikuchi11, Reference Sonobe, Kawata, Miyazaki, Nakamura and Kikuchi15]. The ion beam, generated by the laser ion source discussed above, has a small transverse velocity due the plasma target deformation and also the beam self-charge. The collimation device reduces the ion transverse velocity to collimate the ion beam. Therefore, the collimation devices would be installed in the laser ion accelerator as shown in Figure 1. In this study, the structured target shown in Figure 8 is employed. The proton beam obtained in Figure 3(b) is introduced to the collimation device. The fine structure of the target left layer in Figure 8 absorbs the laser energy efficiently, and generates high-energy electrons. The electrons move around the target, and create a strong electric field normally to the target surface. At the collimation target right-hand side there is a larger-scale structure, at which the TNSA field is created. The transverse electric field is also generated at the right area of the target, and it reduces the proton transverse divergence. In this case, the laser intensity is
![]() $5\times 10^{19}~ {\rm W~ cm}^{-2}$
, the pulse length is 100 fs, and the spot size is
$5\times 10^{19}~ {\rm W~ cm}^{-2}$
, the pulse length is 100 fs, and the spot size is
![]() $30\lambda $
. Figure 9 shows the electric field distribution; the transverse field reduces the proton transverse divergence. Figure 10 presents the proton beam divergence distributions for the original input proton beam and for the proton beam collimated by the transverse electric field. The proton beam is successfully collimated by the collimation device shown in Figure 8.
$30\lambda $
. Figure 9 shows the electric field distribution; the transverse field reduces the proton transverse divergence. Figure 10 presents the proton beam divergence distributions for the original input proton beam and for the proton beam collimated by the transverse electric field. The proton beam is successfully collimated by the collimation device shown in Figure 8.
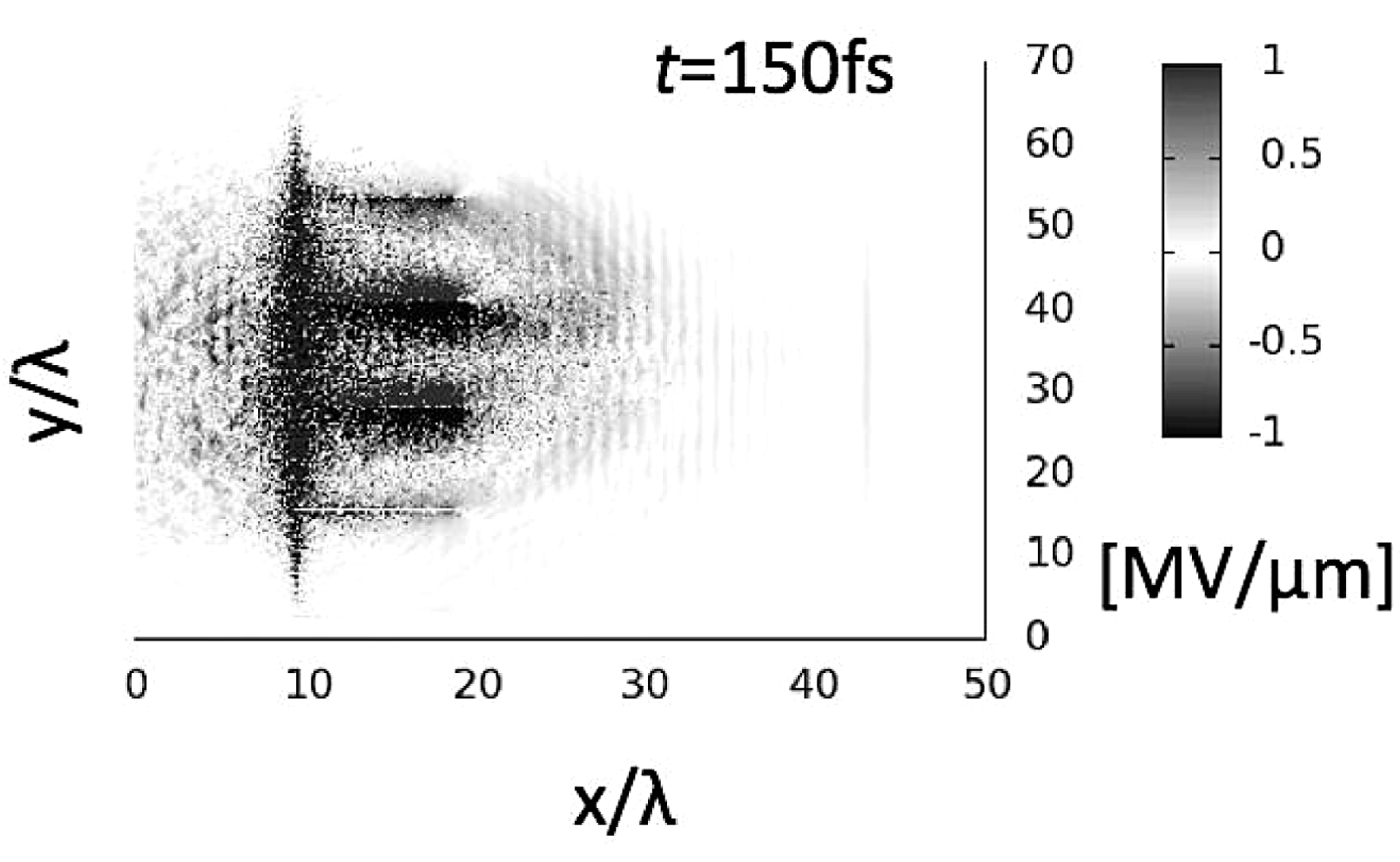
Figure 9. The transverse electric field is successfully generated, and reduces the proton divergence.
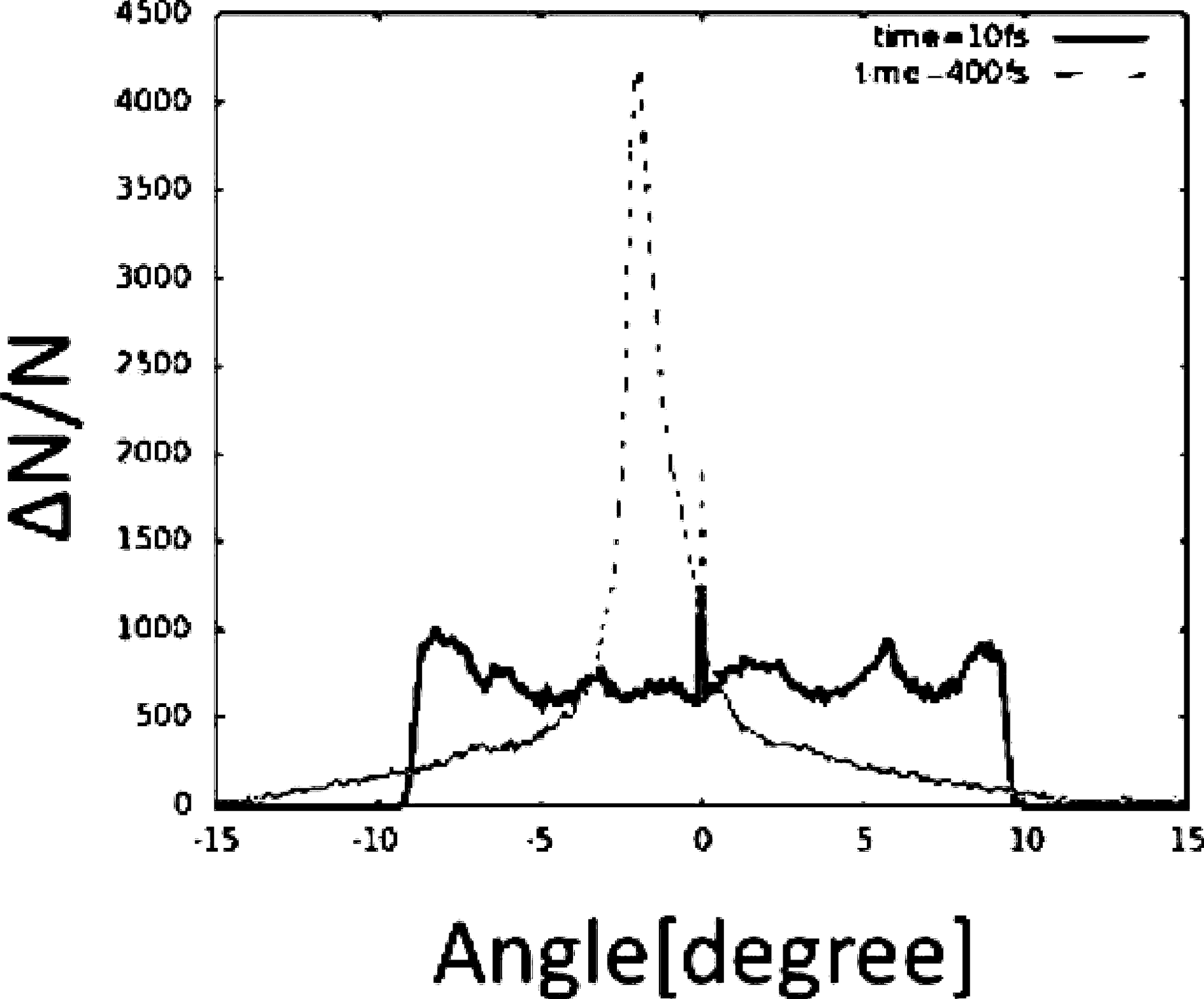
Figure 10. Divergence angle distributions for the original proton beam and for the collimated beam. The collimation device reduces the proton transverse divergence successfully.
The collimation device of the structured solid target needs care to be taken so that the transpiercing ion beam is collimated well: when the ion beam passes through the target striding over the multiple holes at the right side in Figure 8, it may case the ion beam split transversely depending on the laser intensity and also on the hole size. Therefore, preferably the hole size is slightly larger than the ion beam diameter and the ion beam passes through the hole center. In addition, when the laser intensity is strong compared with the optimal one, the transverse collimation electric field becomes stronger, and consequently the ion beam is focused behind the target. Depending on the application purpose, the collimation device should be designed appropriately.
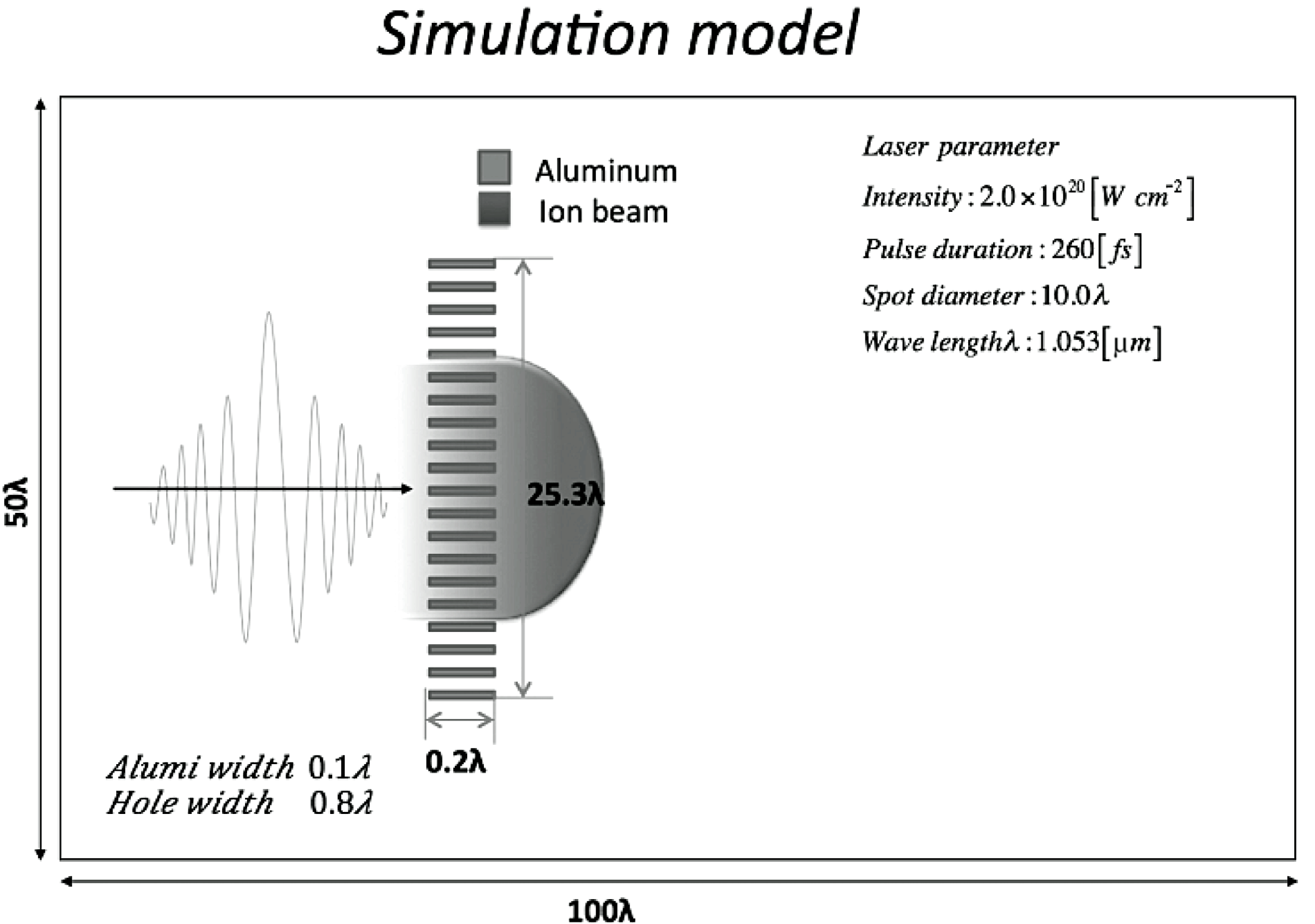
Figure 11. A bunching device illuminated by an intense laser. The structured Al target absorbs the laser efficiently, and a strong electric field is generated to accelerate the ion beam tail in this specific case.
In addition to the collimation device in Figure 8, Lund and his colleagues have proposed another collimation device using thin foils[Reference Lund, Cohen and Ni28]. The thin foils prevent the electron return current and also shield the ion beam self-charge by the mirror charge so that the ion beam self-magnetic field contributes the ion beam collimation. Nakamura et al. [Reference Nakamura, Bulanov, Esirkepov and Kando16]proposed another mechanism to collimate the ion beam by using the magnetic vortex acceleration field, which is formed at the rear surface of the under-dense plasma target.
3.4. Ion beam bunching device
In order to reduce the proton energy divergence and to reduce the ion beam longitudinal length, a bunching device would be required. As discussed above, when a structured solid target (see Figure 11) is illuminated by an intense laser, a strong electric field is generated at the target rear side. The electric field contributes the ion beam tail acceleration to reduce the ion beam energy divergence. In this study, the laser intensity is
![]() $2\times 10^{20}~ {\rm W~ cm}^{-2}$
, the laser spot size is
$2\times 10^{20}~ {\rm W~ cm}^{-2}$
, the laser spot size is
![]() $10\lambda $
, and the laser pulse length is 160 fs. A structured Al target is employed (see Figure 11). The target thickness is
$10\lambda $
, and the laser pulse length is 160 fs. A structured Al target is employed (see Figure 11). The target thickness is
![]() $0.2\lambda $
, the target piercing-hole size is
$0.2\lambda $
, the target piercing-hole size is
![]() $0.8\lambda $
, the Al wall thickness is
$0.8\lambda $
, the Al wall thickness is
![]() $0.1\lambda $
, and the target right edge is located at
$0.1\lambda $
, and the target right edge is located at
![]() $x=10\lambda $
. When the ion beam tail reaches the target left surface, the incoming laser pulse starts to illuminate the target in this specific case.
$x=10\lambda $
. When the ion beam tail reaches the target left surface, the incoming laser pulse starts to illuminate the target in this specific case.
Figures 11 and 12 show the results for the proton beam bunching. Initially the proton beam has the velocity divergence (
![]() $\Delta Vx$
) as shown in Figures 12(d), 12(g), and 13. If the buncher is not used, the proton beam is elongated, as shown in Figures 12(e), 12(f), and 13(a). However, when the buncher is employed, the proton beam velocity divergence is reduced successfully and the proton beam length is kept short, as shown in Figures 12(h), 12(i), and 13(b). When the laser interacts with the structured target, a TNSA field is created, as shown in Figures 12(a)–12(c). The pre-accelerated ion beam is introduced to the bunching device, and the tail of the ion beam is well accelerated to compensate the velocity difference (see Figures 12(h), 12(i), and Figure 13(b)).
$\Delta Vx$
) as shown in Figures 12(d), 12(g), and 13. If the buncher is not used, the proton beam is elongated, as shown in Figures 12(e), 12(f), and 13(a). However, when the buncher is employed, the proton beam velocity divergence is reduced successfully and the proton beam length is kept short, as shown in Figures 12(h), 12(i), and 13(b). When the laser interacts with the structured target, a TNSA field is created, as shown in Figures 12(a)–12(c). The pre-accelerated ion beam is introduced to the bunching device, and the tail of the ion beam is well accelerated to compensate the velocity difference (see Figures 12(h), 12(i), and Figure 13(b)).

Figure 12. (Color online) At the bunching device the TNSA acceleration field is generated (see (a)–(c)). The pre-accelerated proton beam is introduced to the bunching field (see (d) and (g)). With the longitudinal velocity divergence, the proton beam is elongated (see (e) and (f)). When the bunching device is used, the proton beam velocity divergence is reduced significantly, as shown in (h) and (i).

Figure 13. The pre-accelerated proton beam is introduced to the bunching device. At
![]() $t=0$
the proton beam has the velocity divergence. With the longitudinal velocity divergence, the proton beam is elongated (see (a)). When the bunching device is used, the proton beam velocity divergence is reduced well as shown in (b).
$t=0$
the proton beam has the velocity divergence. With the longitudinal velocity divergence, the proton beam is elongated (see (a)). When the bunching device is used, the proton beam velocity divergence is reduced well as shown in (b).
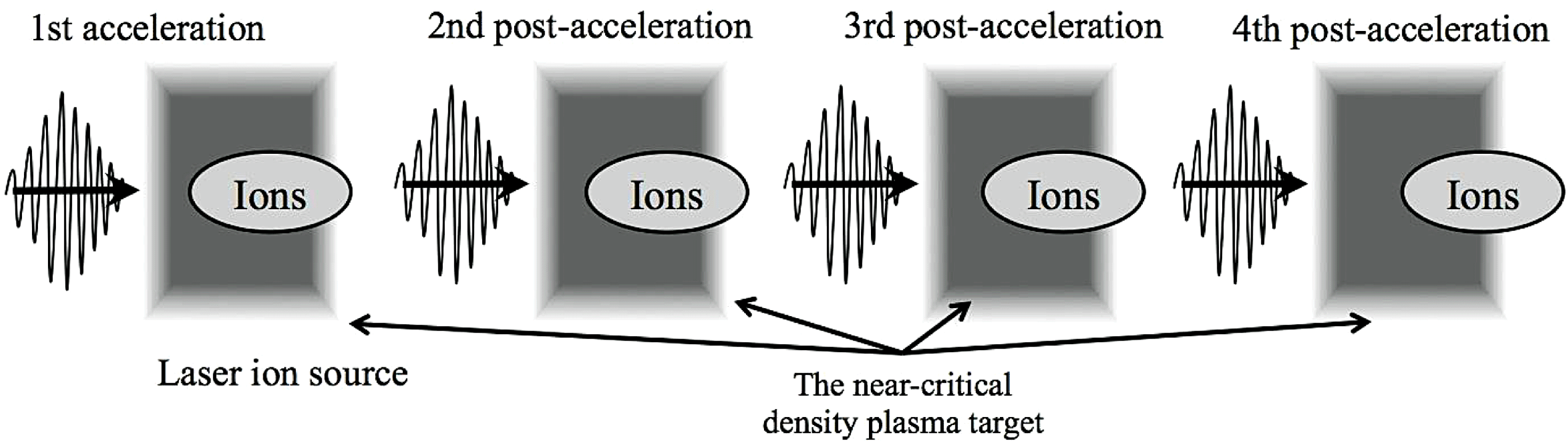
Figure 14. The conceptual diagram for post-acceleration in the laser–plasma interaction. The ions generated from the laser ion source are accelerated by several-stage post-acceleration. We employ a near-critical density plasma target, which consists of hydrogen. In this example, four-stage ion acceleration is performed.
3.5. Multi-stage ion acceleration
By the ion beam source based on the laser–target interaction, protons are accelerated to a few MeV (
![]() $\sim $
10 MeV) by the laser intensity of the order of
$\sim $
10 MeV) by the laser intensity of the order of
![]() $10^{20}~ {\rm W~ cm}^{-2}$
. For proton cancer therapy, the proton energy should reach about 200–250 MeV. In addition, the proton energy spectrum should also be controlled well. Therefore, an additional acceleration and a method for energy spectrum control are required for ion beam cancer therapy. The result in Figure 7 also shows that the gas plasma target would provide a promising post-acceleration device. In this subsection we investigate the multi-stage ion acceleration shown in Figure 14.
$10^{20}~ {\rm W~ cm}^{-2}$
. For proton cancer therapy, the proton energy should reach about 200–250 MeV. In addition, the proton energy spectrum should also be controlled well. Therefore, an additional acceleration and a method for energy spectrum control are required for ion beam cancer therapy. The result in Figure 7 also shows that the gas plasma target would provide a promising post-acceleration device. In this subsection we investigate the multi-stage ion acceleration shown in Figure 14.
When the intense laser pulse propagates through the plasma, it accelerates some of the electrons. The electrons form a high current and generate an azimuthal magnetic field in the underdense plasma. The electrons form a strong magnetic field, and during the increase in the azimuthal magnetic field an inductive strong electric field is generated by the Faraday law. The ions are accelerated by the inductive electric field inside the plasma, as well as the TNSA mechanism and the dipole vortex mechanism[Reference Nakamura, Bulanov, Esirkepov and Kando16]at the target rear side. Here, the laser and target employed are identical to those in Figure 7.
In the first acceleration stage, first the protons are accelerated by the TNSA mechanism and the dipole vortex mechanism behind the target surface. Then, the high-energy ions propagate to the next (second) post-acceleration. The third and fourth ion post-accelerations then take place. In the first and second acceleration stages, the beam ions are mainly accelerated by the TNSA acceleration and dipole vortex acceleration mechanisms. However, in the third and fourth post-accelerations the ions are accelerated by the inductive acceleration based on the Faraday law inside the plasma target as well as the TNSA and dipole vortex acceleration mechanisms behind the target surface. When an intense short-pulse laser illuminates the near-critical density plasma, the inductive acceleration field moves with a speed
![]() $v_{g}$
, which is less than
$v_{g}$
, which is less than
![]() $c$
depending on the plasma density:
$c$
depending on the plasma density:
![]() $v_{g} =c\sqrt{1-\omega _{pe}^{2} /\omega ^{2}} $
, where
$v_{g} =c\sqrt{1-\omega _{pe}^{2} /\omega ^{2}} $
, where
![]() $c$
is the speed of light,
$c$
is the speed of light,
![]() $\omega _{pe}$
the electron plasma frequency, and
$\omega _{pe}$
the electron plasma frequency, and
![]() $\omega $
the laser frequency. Additionally, the beam protons have a higher speed especially in the fourth stage, compared with that in the first and second stages. Therefore, the inductively accelerated ions are kept accelerating for a long time inside the near-critical density plasma target. The distance between the two adjacent targets is
$\omega $
the laser frequency. Additionally, the beam protons have a higher speed especially in the fourth stage, compared with that in the first and second stages. Therefore, the inductively accelerated ions are kept accelerating for a long time inside the near-critical density plasma target. The distance between the two adjacent targets is
![]() $60\lambda $
. The simulation in this study is divided into four successive simulations to reduce the computation time. One target is located in one stage, in which a laser accelerates ions. The ions accelerated are loaded to the next simulation stage. This simulation procedure is performed to simulate the multi-stage acceleration. The hydrogen plasma target is located in
$60\lambda $
. The simulation in this study is divided into four successive simulations to reduce the computation time. One target is located in one stage, in which a laser accelerates ions. The ions accelerated are loaded to the next simulation stage. This simulation procedure is performed to simulate the multi-stage acceleration. The hydrogen plasma target is located in
![]() $9.5\lambda < X < 29.5\lambda $
and
$9.5\lambda < X < 29.5\lambda $
and
![]() $11.0\lambda < Y < 39.0\lambda $
in each simulation box. The target density is
$11.0\lambda < Y < 39.0\lambda $
in each simulation box. The target density is
![]() $0.7n_{c}$
, and the edge region density has a linear gradient scale from
$0.7n_{c}$
, and the edge region density has a linear gradient scale from
![]() $0n_{c}$
to the maximum density of
$0n_{c}$
to the maximum density of
![]() $0.7n_{c}$
with a linear density gradient of
$0.7n_{c}$
with a linear density gradient of
![]() $2\lambda $
in the
$2\lambda $
in the
![]() $X$
and
$X$
and
![]() $Y$
directions at the target edges. Here,
$Y$
directions at the target edges. Here,
![]() $n_{c }= m\varepsilon _{0}\omega ^{2}/e^{2}$
is the critical density,
$n_{c }= m\varepsilon _{0}\omega ^{2}/e^{2}$
is the critical density,
![]() $ m$
is the electron mass,
$ m$
is the electron mass,
![]() $e$
is the charge of an electron, and
$e$
is the charge of an electron, and
![]() $\varepsilon _{0}$
is dielectric constant in vacuum, respectively. The target model and the lasers employed are identical for all four acceleration stages. For the staging from one stage to the next, the beam ions accelerated are extracted from the right boundary of the simulation box and then transferred to the left boundary of the next simulation box, so that the beam loading is smooth to the next stage. The ion beam transport is consistently computed between the two stages: for example, the ion beam divergence and the beam-ion self-charge interaction are naturally included during the beam transport between the stages, although the simulation is divided into the four stages. The distance between the two adjacent targets is
$\varepsilon _{0}$
is dielectric constant in vacuum, respectively. The target model and the lasers employed are identical for all four acceleration stages. For the staging from one stage to the next, the beam ions accelerated are extracted from the right boundary of the simulation box and then transferred to the left boundary of the next simulation box, so that the beam loading is smooth to the next stage. The ion beam transport is consistently computed between the two stages: for example, the ion beam divergence and the beam-ion self-charge interaction are naturally included during the beam transport between the stages, although the simulation is divided into the four stages. The distance between the two adjacent targets is
![]() $60\lambda $
, and is so short that additional ion beam bunching and focusing elements are not required. In another view, it may be also reasonable to think of the four-stage targets employed in this study as one longer target with gaps of
$60\lambda $
, and is so short that additional ion beam bunching and focusing elements are not required. In another view, it may be also reasonable to think of the four-stage targets employed in this study as one longer target with gaps of
![]() $60\lambda $
. In actual experiments multiple targets would be separated sufficiently far. In our simulations, for example, the first laser pulse interacts with the first target, and then the target debris is well expanded and blown off so that the next laser pulse impinging from the left area can reach the next target safely without a significant influence of the former target debris. In addition, after the laser pulse interacts with the target, the laser pulse is depleted well in the target so that the second–fourth targets survive successfully without the illumination of the former laser pulses. The target longitudinal length is selected to deplete the laser pulse energy sufficiently inside the target.
$60\lambda $
. In actual experiments multiple targets would be separated sufficiently far. In our simulations, for example, the first laser pulse interacts with the first target, and then the target debris is well expanded and blown off so that the next laser pulse impinging from the left area can reach the next target safely without a significant influence of the former target debris. In addition, after the laser pulse interacts with the target, the laser pulse is depleted well in the target so that the second–fourth targets survive successfully without the illumination of the former laser pulses. The target longitudinal length is selected to deplete the laser pulse energy sufficiently inside the target.
Figure 15 shows the histories of the maximum proton energy from the first acceleration to the fourth post-acceleration. The maximum proton energy is 38.9 MeV in the first acceleration at 700 fs, 89.9 MeV in the second post-acceleration at 600 fs, and 149 MeV in the third post-acceleration at 500 fs. Finally, the maximum proton energy reaches 254 MeV in the fourth ion post-acceleration at 450 fs.
In particular, in the fourth stage the proton energy is about 150–250 MeV during the inductive acceleration phase (Figure 15), and the proton speed is about
![]() $0.566_c \mbox{--} 0.653_c$
, which almost corresponds to
$0.566_c \mbox{--} 0.653_c$
, which almost corresponds to
![]() $v_{g}\sim 0.548c$
(the speed of a laser in a plasma density of
$v_{g}\sim 0.548c$
(the speed of a laser in a plasma density of
![]() $0.7n_{\mathrm{c}}$
). Therefore, in the fourth stage the ions are accelerated continuously by the inductive field in the target, and then accelerated further by the TNSA and the magnetic vortex mechanisms successfully. The continuous acceleration by the inductive field is realized and provides the ion energy jump in the fourth stage in Figure 15, because the ion speed coincides well with the moving inductive field.
$0.7n_{\mathrm{c}}$
). Therefore, in the fourth stage the ions are accelerated continuously by the inductive field in the target, and then accelerated further by the TNSA and the magnetic vortex mechanisms successfully. The continuous acceleration by the inductive field is realized and provides the ion energy jump in the fourth stage in Figure 15, because the ion speed coincides well with the moving inductive field.
Figure 16(a) shows the acceleration electric field
![]() $Ex$
along the center line of target in the longitudinal direction. The black solid line is
$Ex$
along the center line of target in the longitudinal direction. The black solid line is
![]() $Ex$
at
$Ex$
at
![]() $t=90~ {\rm fs}$
and the grey dotted line is
$t=90~ {\rm fs}$
and the grey dotted line is
![]() $Ex$
at
$Ex$
at
![]() $t=160~ {\rm fs}$
for the fourth post-acceleration in Figure 16(a). The inductive electric field for the ion acceleration is generated inside the near-critical density plasma target (Figure 16(a) solid line). The acceleration electric field for TNSA is generated behind the target (Figure 16(a) dotted line). Figure 16(b) shows the proton spatial distributions and Figure 16(c) shows the proton energy distributions in
$t=160~ {\rm fs}$
for the fourth post-acceleration in Figure 16(a). The inductive electric field for the ion acceleration is generated inside the near-critical density plasma target (Figure 16(a) solid line). The acceleration electric field for TNSA is generated behind the target (Figure 16(a) dotted line). Figure 16(b) shows the proton spatial distributions and Figure 16(c) shows the proton energy distributions in
![]() $20.0\lambda < Y < 30.0\lambda $
at
$20.0\lambda < Y < 30.0\lambda $
at
![]() $t=0~ {\rm fs}$
, 90 fs, 160 fs, 240 fs, and 450 fs. The proton energy reaches 254 MeV at
$t=0~ {\rm fs}$
, 90 fs, 160 fs, 240 fs, and 450 fs. The proton energy reaches 254 MeV at
![]() $t=450~ {\rm fs}$
. In this study the laser spot size is
$t=450~ {\rm fs}$
. In this study the laser spot size is
![]() $10\lambda $
, and as shown in Figures 16(b) and (c) the core protons accelerated are almost located in
$10\lambda $
, and as shown in Figures 16(b) and (c) the core protons accelerated are almost located in
![]() $20.0\lambda < Y < 30.0\lambda $
.
$20.0\lambda < Y < 30.0\lambda $
.

Figure 15. The histories of the maximum proton energy from the first acceleration to the fourth post-acceleration. The maximum proton energy is remarkably accelerated by the four-stages acceleration. The maximum proton energy is finally about 254.0 MeV in the fourth post-acceleration at 450 fs.

Figure 16. Acceleration electric fields averaged over the laser one cycle along the center line of the plasma target in the longitudinal direction. The black solid line is
![]() $Ex$
at
$Ex$
at
![]() $t=90$
fs and the grey dotted line is at
$t=90$
fs and the grey dotted line is at
![]() $t=160$
fs in the fourth post-acceleration. (b) The proton spatial distributions at
$t=160$
fs in the fourth post-acceleration. (b) The proton spatial distributions at
![]() $t=0$
fs, 90 fs, 160 fs, 240 fs, and 450 fs. The color shows the energy of the protons. (c) The energy distributions at
$t=0$
fs, 90 fs, 160 fs, 240 fs, and 450 fs. The color shows the energy of the protons. (c) The energy distributions at
![]() $t=0$
fs, 90 fs, 160 fs, 240 fs, and 450 fs for the protons existing in
$t=0$
fs, 90 fs, 160 fs, 240 fs, and 450 fs for the protons existing in
![]() $20.0\lambda < Y < 30.0\lambda $
at 450 fs. The maximum proton energy finally reaches 254 MeV in the fourth post-acceleration at 450 fs.
$20.0\lambda < Y < 30.0\lambda $
at 450 fs. The maximum proton energy finally reaches 254 MeV in the fourth post-acceleration at 450 fs.
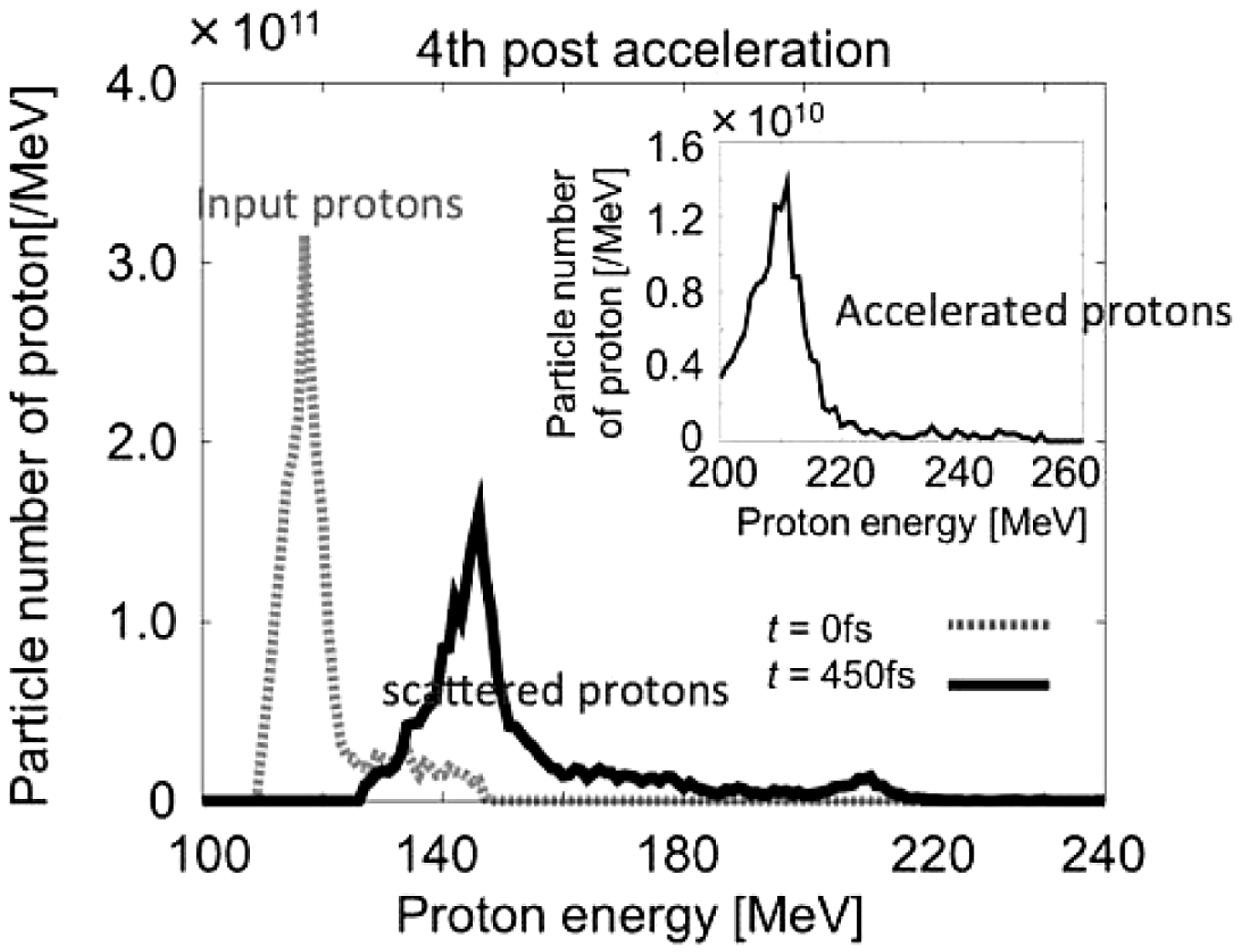
Figure 17. Energy spectra of protons in the fourth post-acceleration. The dotted lines are the input ion beam to the fourth stage, and the solid lines are the output ion beam. Figures present all the ions, including the scattered ions transversely, and the inset figure shows the high-energy core part of the beam ions located in
![]() $20.0\lambda < Y < 30.0\lambda $
. The core part of the beam ion is useful for practical purposes.
$20.0\lambda < Y < 30.0\lambda $
. The core part of the beam ion is useful for practical purposes.
Figure 17 shows the ion beam energy spectra for the fourth post-acceleration. The dotted line shows the input protons to the fourth stage, and the solid line shows the output protons from the fourth stage. Figure 17 present all the ions, including the scattered ions transversely (see Figure 16(b)). The inset figures in Figure 17 show the high-energy core part of the beam ions located in
![]() $20.0\lambda < Y < 30.0\lambda $
, and the core part of the beam ions could be useful for practical purposes. The inset figure in Figure 17 shows that a quasi mono-energetic energy spectrum is also realized in the multi-stage ion acceleration.
$20.0\lambda < Y < 30.0\lambda $
, and the core part of the beam ions could be useful for practical purposes. The inset figure in Figure 17 shows that a quasi mono-energetic energy spectrum is also realized in the multi-stage ion acceleration.
In the present case, our simulation parameter study shows that the synchronization timing requirement
![]() $\Delta t$
between the laser pulse and the ion beam is about 10 fs, so that the decrease in the ion maximal energy is limited by 10.2%. The TNSA field and the inductive acceleration field are generated by the laser pulse, whose pulse duration time is 40 fs in this study. The laser pulse risetime
$\Delta t$
between the laser pulse and the ion beam is about 10 fs, so that the decrease in the ion maximal energy is limited by 10.2%. The TNSA field and the inductive acceleration field are generated by the laser pulse, whose pulse duration time is 40 fs in this study. The laser pulse risetime
![]() $T_{\mathrm{Lr}}$
is
$T_{\mathrm{Lr}}$
is
![]() $\sim $
20 fs. The risetime
$\sim $
20 fs. The risetime
![]() $T_{\mathrm{Lr}}$
defines the duration time for the inductive acceleration field in the plasmas. Therefore, the synchronization requirement should be less than the laser risetime:
$T_{\mathrm{Lr}}$
defines the duration time for the inductive acceleration field in the plasmas. Therefore, the synchronization requirement should be less than the laser risetime:
![]() $\Delta t \ll T_{\mathrm{Lr}}$
.
$\Delta t \ll T_{\mathrm{Lr}}$
.
In addition to the timing issue, there are issues remaining including the laser alignment error, the effect of the target density profile modulation, the target position alignment error, the target production method, and the repetitive operation method. These issues should be studied further in the near future.
In addition to the present multi-staging ion acceleration study, we have also performed simulations on a staged ion acceleration in which a two-stage ion acceleration is studied[Reference Kawata29]. In this simulation the two targets are simulated in one simulation box, and so the effects of the target debris on the next target and of the laser ember are also studied; the studies on the two-stage ion acceleration also support the results presented in this subsection.
4. Discussions
In this paper we have proposed and discussed the concept for a future laser ion accelerator. The laser ion accelerator would consist of an ion source, ion beam collimators, ion beam bunchers, and post-accelerators, depending on the requirements for the ion particle energy, the ion energy spectrum, the beam radius, and the ion beam pulse length. Then for each a realistic component was also proposed and studied. In the laser ion acceleration, ions are accelerated by the strong electric field, generated by the interaction of the intense laser with the target. The electric field is created by the TNSA field and the inductive electric field. The acceleration field gradient is rather large (
![]() ${>} 10~ {\rm GV~ m}^{-1}$
) compared with that (
${>} 10~ {\rm GV~ m}^{-1}$
) compared with that (
![]() ${<} 100~ {\rm MV~ m}^{-1}$
) of a conventional accelerator. Based on the scientific results presented in this paper, a realistic laser ion accelerator could be designed as shown in Figure 1. Each component and combinations of the components provide a high controllability of the ion beam generated by the laser ion accelerator to meet variable requirements for a laser ion accelerator.
${<} 100~ {\rm MV~ m}^{-1}$
) of a conventional accelerator. Based on the scientific results presented in this paper, a realistic laser ion accelerator could be designed as shown in Figure 1. Each component and combinations of the components provide a high controllability of the ion beam generated by the laser ion accelerator to meet variable requirements for a laser ion accelerator.
The ion sources proposed in this paper realized a high energy conversion efficiency of more than a few tens of percent by using a fine structure solid target (Figure 2) or using a lower-density gas target (Figure 7). In order to enhance and to control the ion energy and the ion energy spectrum, the gas target provides an efficient inductive post-acceleration device. Proton energy of 200–250 MV was achieved and a mono-energetic energy spectrum was also realized. Laser-produced ion beams tend to have a transverse divergence. For the ion beam collimation a structured target (Figure 8) was also proposed to collimate the proton beam.
Conventional ion accelerators for the ion cancer therapy tend to be a large size and to be expensive. The laser ion accelerator proposed in this paper may open a new method to produce a controlled ion beam for cancer therapy because of its smaller size and its reasonable cost.
The novel laser ion accelerator was proposed toward a future ion cancer therapy, and the laser accelerator proposed provides a flexible capability to adjust the requirements. However, there are some issues remained to be studied further: for example, the laser ion accelerator would need multiple laser pulses with different focusing points with a high repetition rate, say 1–10 Hz or so, to kill the cancer cells. Repetitive operation of an intense laser system might be available even today at an intensity of the order of
![]() $10^{20}~ {\rm W~ cm}^{-2}$
or more. So the repetitive laser operation may need further studies. The present efficiency of the laser pulse oscillation itself is rather low, almost less than 1%. Another issue is how to prepare and install the targets in the repetitive operation environment. A prepulse-illuminated thin film or a gas jet nozzle would work well to produce the gas target repetitively employed in this study. In addition, the structured thin-foil target could be prepared in a tape form for repetitive usage. For the ion source and for the post acceleration device, the laser-based acceleration and post-acceleration provide a high acceleration gradient, and they contribute to shorten the accelerator devices. Conventional collimation and bunching devices could also substitute the laser-based collimators and bunchers, depending on the required quality for the ion beam. These issues should be studied in the near future to obtain a laser ion accelerator for cancer therapy.
$10^{20}~ {\rm W~ cm}^{-2}$
or more. So the repetitive laser operation may need further studies. The present efficiency of the laser pulse oscillation itself is rather low, almost less than 1%. Another issue is how to prepare and install the targets in the repetitive operation environment. A prepulse-illuminated thin film or a gas jet nozzle would work well to produce the gas target repetitively employed in this study. In addition, the structured thin-foil target could be prepared in a tape form for repetitive usage. For the ion source and for the post acceleration device, the laser-based acceleration and post-acceleration provide a high acceleration gradient, and they contribute to shorten the accelerator devices. Conventional collimation and bunching devices could also substitute the laser-based collimators and bunchers, depending on the required quality for the ion beam. These issues should be studied in the near future to obtain a laser ion accelerator for cancer therapy.
Acknowledgements
This work is partly supported by MEXT, JSPS, ASHULA project/ILE/Osaka University, CORE (Center for Optical Research and Education, Utsunomiya University, Japan), Fudan University, and Shanghai University. The authors would also like to express their appreciation to Prof. Daniel Margarone, Prof. Z. M. Sheng, Prof. J. Limpouch, Prof. O. Klimo, and Prof. A. Andreev, for their fruitful discussions on the subject.


















