Article contents
Uncountable existentially closed groups in locally finite group classes
Published online by Cambridge University Press: 18 May 2009
Extract
In this paper, 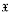 will always denote a local class of locally finite groups, which is closed with respect to subgroups, homomorphic images, extensions, and with respect to cartesian powers of finite
will always denote a local class of locally finite groups, which is closed with respect to subgroups, homomorphic images, extensions, and with respect to cartesian powers of finite 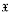 -groups. Examples for x are the classes L ℐπ of all locally finite π-groups and L(ℐπ ∩
-groups. Examples for x are the classes L ℐπ of all locally finite π-groups and L(ℐπ ∩ 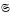 ) of all locally soluble π-groups (where π is a fixed set of primes). In [4], a wreath product construction was used in the study of existentially closed
) of all locally soluble π-groups (where π is a fixed set of primes). In [4], a wreath product construction was used in the study of existentially closed 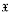 -groups (=e.c.
-groups (=e.c. 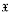 -groups); the restrictive type of construction available in [4] permitted results for only countable groups. This drawback was then removed partially in [5] with the help of permutational products. Nevertheless, the techniques essentially only permitted amalgamation of
-groups); the restrictive type of construction available in [4] permitted results for only countable groups. This drawback was then removed partially in [5] with the help of permutational products. Nevertheless, the techniques essentially only permitted amalgamation of 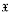 -groups with locally nilpotent π-groups. Thus, satisfactory results could be obtained for L
-groups with locally nilpotent π-groups. Thus, satisfactory results could be obtained for L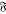 p-groups (resp. locally nilpotent π-groups) [6], while the theory remained incomplete in all other cases.
p-groups (resp. locally nilpotent π-groups) [6], while the theory remained incomplete in all other cases.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1990
References
REFERENCES
- 2
- Cited by

