No CrossRef data available.
Article contents
Semiabelian varieties and transcendence on Weierstrass sigma functions
Part of:
Abelian varieties and schemes
Algebraic number theory: local and $p$-adic fields
Diophantine approximation, transcendental number theory
Published online by Cambridge University Press: 25 November 2024
Abstract
We establish new results on complex and 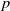 $p$-adic linear independence on a class of semiabelian varieties. As applications, we obtain transcendence results concerning complex and
$p$-adic linear independence on a class of semiabelian varieties. As applications, we obtain transcendence results concerning complex and 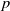 $p$-adic Weierstrass sigma functions associated with elliptic curves.
$p$-adic Weierstrass sigma functions associated with elliptic curves.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust
Footnotes
Dedicated to my Father-in-law, Dr. Ngoc Quang Le on the occasion of his 65th birthday.
References
Bertolin, C., Philippon, P., Saha, B. and Saha, E., Semi-abelian analogues of schanuel conjecture and applications, J. Algebra 596 (2022), 250–288.CrossRefGoogle Scholar
Bertrand, D., Sous-groupes à un paramètre p-adique de variétés de groupe, Invent. Math. 40(2) (1977), 171–193.CrossRefGoogle Scholar
Bourbaki, N., Elements of Mathematics. Lie groups and Lie algebras. Part I: Chapters 1–3. English translantion., Actualities scientifiques et industrielles, Herman, Adiwes International Series in Mathematics, (Hermann, Publishers in Arts and Science; Reading, Mass.: Addison-Wesley Publishing Company, Paris, 1975), XVII.Google Scholar
Conrad, B., A modern proof of chevalley’s theorem on algebraic groups, J. Ramanujan Math. Soc. 17 (2002), 1–18.Google Scholar
Fuchs, C. and Pham, D. H., The p-adic analytic subgroup theorem revisited, p-Adic Num. Ultrametr. Anal. Appl. 7 (2015), 143–156.CrossRefGoogle Scholar
Lang, S., Transcendental points on group varieties, Topology 1(4) (1962), 313–318.CrossRefGoogle Scholar
Lutz, E., Sur l’équation Y
2 = AX
3 − AX − B dans les corps p-adiques, J. Reine Angew. Math. 177 (1937), 238–247.CrossRefGoogle Scholar
Matev, T., The p-adic analytic subgroup theorem and applications. Available at http://arxiv.org/pdf/1010.3156v1.pdf
Google Scholar
Perucca, A., On the order of the reductions of points on abelian varieties and tori, PhD Thesis (Università di Roma La Sapienza, 2008).Google Scholar
Pham, D. H., Linear independence on simple abelian varieties, Period. Math. Hung. 89(1) (2024), 23–31.CrossRefGoogle Scholar
Waldschmidt, M., Nombres transcendants et fonctions sigma de weierstrass, C. R. Math. Rep. Acad. Sci. Can 1(2) (1978/1979), 111–114.Google Scholar
Waldschmidt, M., Nombres transcendants et groupes algébriques, Astérisques 69-70, (Société Mathématique de France, Paris, 1987).Google Scholar
Weil, A., Sur les fonctions elliptiques
 $\mathfrak{p}$
-adiques, Note aux C. R. Acad. Sc. Paris 203 (1936), 22–24.Google Scholar
$\mathfrak{p}$
-adiques, Note aux C. R. Acad. Sc. Paris 203 (1936), 22–24.Google Scholar
Wüstholz, G., Some remarks on a conjecture of Waldschmidt, Diophantine approximations and transcendental numbers (Luminy 1982), Progr. Math. 31, Birkhäuser Boston, Boston, MA, 1983, 329–336.Google Scholar
Wüstholz, G., Algebraische Punkte auf Analytischen Untergruppen algebraischer Gruppen, Ann. Math. 129 (1989), 501–517.CrossRefGoogle Scholar


