Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
CHEN, GANGYI
and
LI, HAIZHONG
2011.
SCALAR CURVATURE OF HYPERSURFACES WITH CONSTANT MEAN CURVATURE IN UNIT SPHERES.
International Journal of Mathematics,
Vol. 22,
Issue. 01,
p.
131.
DENG, QIN-TAO
GU, HUI-LING
and
SU, YAN-HUI
2012.
CONSTANT MEAN CURVATURE HYPERSURFACES IN SPHERES.
Glasgow Mathematical Journal,
Vol. 54,
Issue. 1,
p.
77.
ZHANG, QIN
2012.
SCALAR CURVATURE OF HYPERSURFACES WITH CONSTANT MEAN CURVATURE IN SPHERES.
Glasgow Mathematical Journal,
Vol. 54,
Issue. 1,
p.
67.
Xu, Hong-wei
and
Xu, Zhi-yuan
2013.
The second pinching theorem for hypersurfaces with constant mean curvature in a sphere.
Mathematische Annalen,
Vol. 356,
Issue. 3,
p.
869.
Xu, Hong-wei
and
Xu, Zhi-yuan
2014.
A new characterization of the Clifford torus via scalar curvature pinching.
Journal of Functional Analysis,
Vol. 267,
Issue. 10,
p.
3931.

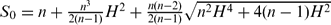 .
.