Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Harlander, Jens
1997.
Embeddings into efficient groups.
Proceedings of the Edinburgh Mathematical Society,
Vol. 40,
Issue. 2,
p.
317.
Steinberg, Benjamin
2025.
The homology of completely simple semigroups.
Semigroup Forum,
Vol. 110,
Issue. 3,
p.
745.


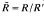 = R/R', the abelianized normal subgroup
= R/R', the abelianized normal subgroup 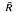 is called the relation module determined by the presentation (1). For a detailed discussion of this subject we refer to Gruenberg [
is called the relation module determined by the presentation (1). For a detailed discussion of this subject we refer to Gruenberg [