No CrossRef data available.
Article contents
RATIONAL GROUP ACTIONS ON AFFINE PI-ALGEBRAS
Published online by Cambridge University Press: 01 October 2013
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let R be an affine PI-algebra over an algebraically closed field 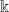 $\mathbb{k}$ and let G be an affine algebraic
$\mathbb{k}$ and let G be an affine algebraic 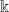 $\mathbb{k}$-group that acts rationally by algebra automorphisms on R. For R prime and G a torus, we show that R has only finitely many G-prime ideals if and only if the action of G on the centre of R is multiplicity free. This extends a standard result on affine algebraic G-varieties. Under suitable hypotheses on R and G, we also prove a PI-version of a well-known result on spherical varieties and a version of Schelter's catenarity theorem for G-primes.
$\mathbb{k}$-group that acts rationally by algebra automorphisms on R. For R prime and G a torus, we show that R has only finitely many G-prime ideals if and only if the action of G on the centre of R is multiplicity free. This extends a standard result on affine algebraic G-varieties. Under suitable hypotheses on R and G, we also prove a PI-version of a well-known result on spherical varieties and a version of Schelter's catenarity theorem for G-primes.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 2013
References
REFERENCES
1.Abrams, G., Bell, J. P. and Rangaswamy, K. M., The Dixmier–Moeglin equivalence for Leavitt path algebras Algebr. Represent. Theory 15 (3) (2012), 407–425.Google Scholar
3.Bergman, G. M., Lifting prime ideals to extensions by centralizing elements, unpublished, University of California, Berkeley.Google Scholar
4.Bergman, G. M., More on extensions by centralizing elements, unpublished, University of California, Berkeley.Google Scholar
5.Borel, A., Linear algebraic groups, 2nd ed., Graduate Texts in Mathematics, vol. 126 (Springer-Verlag, New York, 1991).Google Scholar
6.Bourbaki, N., Éléments de mathématique, Fasc. XXIII, Hermann, Paris, 1973, Livre II: Algèbre. Chapitre 8: Modules et anneaux semi-simples, Nouveau tirage de l'édition de 1958, Actualités Scientifiques et Industrielles, No. 1261.Google Scholar
7.Brown, K. A. and Goodearl, K. R., Lectures on algebraic quantum groups, Advanced Courses in Mathematics – CRM Barcelona (Birkhäuser Verlag, Basel, 2002).Google Scholar
8.Cauchon, G., Effacement des dérivations et spectres premiers des algèbres quantiques, J. Algebra 260 (2) (2003), 476–518.Google Scholar
9.Cauchon, G., Spectre premier de O q(M n(k)): image canonique et séparation normale, J. Algebra 260 (2) (2003), 519–569.Google Scholar
10.Goodearl, K. R. and Letzter, E. S., Prime ideals in skew and q-skew polynomial rings, Mem. Amer. Math. Soc. 109 (521) (1994), vi+106.Google Scholar
11.Goodearl, K. R. and Letzter, E. S., The Dixmier–Moeglin equivalence in quantum coordinate rings and quantized Weyl algebras, Trans. Amer. Math. Soc. 352 (3) (2000), 1381–1403.Google Scholar
12.Hodges, T. J., Levasseur, T. and Toro, M., Algebraic structure of multiparameter quantum groups, Adv. Math. 126 (1) (1997), 52–92.Google Scholar
13.Jantzen, J. C., Representations of algebraic groups, 2nd ed., Mathematical Surveys and Monographs, vol. 107 (American Mathematical Society, Providence, RI, 2003).Google Scholar
14.Joseph, A., Quantum groups and their primitive ideals, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], vol. 29, (Springer-Verlag, Berlin, 1995).Google Scholar
15.Kaplansky, I., Rings with a polynomial identity, Bull. Amer. Math. Soc. 54 (1948), 575–580.CrossRefGoogle Scholar
16.Knop, F., On the set of orbits for a Borel subgroup, Comment. Math. Helv. 70 (2) (1995), 285–309.Google Scholar
17.Kraft, H., Geometrische Methoden in der Invariantentheorie, Aspects of Mathematics, D1 (Friedr. Vieweg & Sohn, Braunschweig, 1984).Google Scholar
18.Krause, G. R. and Lenagan, T. H., Growth of algebras and Gelfand–Kirillov dimension, revised ed., Graduate Studies in Mathematics, vol. 22 (American Mathematical Society, Providence, RI, 2000).Google Scholar
19.Launois, S., Lenagan, T. H. and Rigal, L., Prime ideals in the quantum Grassmannian, Selecta Math. (N.S.) 13 (4) (2008), 697–725.Google Scholar
20.Lorenz, M., Finite normalizing extensions of rings, Math. Z. 176 (4) (1981), 447–484.CrossRefGoogle Scholar
21.Lorenz, M., Group actions and rational ideals, Algebra Number Theory 2 (4) (2008), 467–499.Google Scholar
22.Lorenz, M., Algebraic group actions on noncommutative spectra, Transform. Groups 14 (3) (2009), 649–675.Google Scholar
23.Malliavin, M.-P., Caténarité et théorème d'intersection en algèbre non commutative, Séminaire d'Algèbre Paul Dubreil 31ème année (Paris, 1977–1978), Lecture Notes in Mathematics, vol. 740 (Springer, Berlin, 1979), 408–431.Google Scholar
24.Martindale, W. S. III, Prime rings satisfying a generalized polynomial identity, J. Algebra 12 (1969), 576–584. MR MR0238897 (39 #257)CrossRefGoogle Scholar
25.McConnell, J. C. and Robson, J. C., Noncommutative Noetherian rings, revised ed., Graduate Studies in Mathematics, vol. 30 (American Mathematical Society, Providence, RI, 2001), With the cooperation of L. W. Small.Google Scholar
26.Montgomery, S., Hopf algebras and their actions on rings, CBMS Regional Conference Series in Mathematics, vol. 82 (CBMS, Washington, DC, 1993).Google Scholar
27.Procesi, C., Rings with polynomial identities Pure and Applied Mathematics, vol. 17 (Marcel Dekker Inc., New York, 1973).Google Scholar
28.Reiner, I., Maximal orders, London Mathematical Society Monographs, New Series, vol. 28 (The Clarendon Press, Oxford University Press, Oxford, 2003); corrected reprint of the 1975 original, with a foreword by M. J. Taylor.Google Scholar
29.Robson, J. C. and Small, L. W., Liberal extensions, Proc. London Math. Soc. (3) 42 (1) (1981), 87–103.Google Scholar
30.Rowen, L. H., Ring theory, Vol. II, Pure and Applied Mathematics, vol. 128 (Academic Press, Boston, MA, 1988).Google Scholar
31.Vonessen, N., Actions of linearly reductive groups on affine PI algebras, Mem. Amer. Math. Soc. 81 (414) (1989), iv+106.Google Scholar
32.Waterhouse, W. C., Introduction to affine group schemes, Graduate Texts in Mathematics, vol. 66 (Springer-Verlag, New York, 1979).Google Scholar

