No CrossRef data available.
Article contents
On twisted group ring isomorphism problem for p-groups
Part of:
Rings and algebras arising under various constructions
Structure and classification of infinite or finite groups
Representation theory of groups
Published online by Cambridge University Press: 16 February 2024
Abstract
In this article, we explore the problem of determining isomorphisms between the twisted complex group algebras of finite 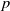 $p$-groups. This problem bears similarity to the classical group algebra isomorphism problem and has been recently examined by Margolis-Schnabel. Our focus lies on a specific invariant, referred to as the generalized corank, which relates to the twisted complex group algebra isomorphism problem. We provide a solution for non-abelian
$p$-groups. This problem bears similarity to the classical group algebra isomorphism problem and has been recently examined by Margolis-Schnabel. Our focus lies on a specific invariant, referred to as the generalized corank, which relates to the twisted complex group algebra isomorphism problem. We provide a solution for non-abelian 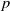 $p$-groups with generalized corank at most three.
$p$-groups with generalized corank at most three.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust
References
Berkovich, Y. G., On the order of the commutator subgroup and the Schur multiplier of a finite
 $p$
-group, J. Algebra 144(2) (1991), 269–272.CrossRefGoogle Scholar
$p$
-group, J. Algebra 144(2) (1991), 269–272.CrossRefGoogle Scholar
Coleman, D. B., Finite groups with isomorphic group algebras, Trans. Am. Math. Soc. 105 (1962), 1–8.CrossRefGoogle Scholar
Dade, E. C., Deux groupes finis distincts ayant la même algèbre de groupe sur tout corps, Math. Z. 119 (1971), 345–348.CrossRefGoogle Scholar
Ellis, G., On the Schur multiplier of
 $p$
-groups, Comm. Algebra 27(9) (1999), 4173–4177.CrossRefGoogle Scholar
$p$
-groups, Comm. Algebra 27(9) (1999), 4173–4177.CrossRefGoogle Scholar
Green, J. A., On the number of automorphisms of a finite group, Proc. Roy. Soc. London Ser. A 237 (1956), 574–581.Google Scholar
Hatui, S., Characterization of finite
 $p$
-groups by their Schur multiplier, Proc. Indian Acad. Sci. Math. Sci. 128(4) (2018), Paper No. 49, 9.CrossRefGoogle Scholar
$p$
-groups by their Schur multiplier, Proc. Indian Acad. Sci. Math. Sci. 128(4) (2018), Paper No. 49, 9.CrossRefGoogle Scholar
Hatui, S. and Singla, P., On Schur multiplier and projective representations of Heisenberg groups, J. Pure Appl. Algebra 225(11) (2021), Paper No. 106742, 16.CrossRefGoogle Scholar
Hertweck, M., A counterexample to the isomorphism problem for integral group rings, Ann. Math (2) 154(1) (2001), 115–138.CrossRefGoogle Scholar
Hochschild, G. and Serre, J.-P., Cohomology of group extensions, Trans. Am. Math. Soc. 74 (1953), 110–134.CrossRefGoogle Scholar
Isaacs, I. M., Character theory of finite groups (AMS Chelsea Publishing, Providence, RI, 2006), Corrected reprint of the 1976 original [Academic Press, New York; MR0460423].Google Scholar
James, R., The groups of order
 $p^{6}$
(
$p^{6}$
(
 $p$
an odd prime), Math. Comp. 34(150) (1980), 613–637.Google Scholar
$p$
an odd prime), Math. Comp. 34(150) (1980), 613–637.Google Scholar
Karpilovsky, G., Finite groups with isomorphic group algebras, Illinois J. Math. 25(1) (1981), 107–111.CrossRefGoogle Scholar
Karpilovsky, G., Projective representations of finite groups, Monographs and Textbooks in Pure and Applied Mathematics, vol. 94 (Marcel Dekker, Inc, New York, 1985).Google Scholar
Margolis, L., The modular isomorphism problem: a survey, Jahresber. Dtsch. Math.-Ver. 124(3) (2022),157–196.CrossRefGoogle Scholar
Margolis, L. and Del Rio, A., Finite subgroups of group rings: a survey (2018), arXiv preprint arXiv: 1809.00718.Google Scholar
Margolis, L. and Schnabel, O., Twisted group ring isomorphism problem, Q. J. Math. 69(4) (2018), 1195–1219.Google Scholar
Margolis, L. and Schnabel, O., The twisted group ring isomorphism problem over fields, Israel J. Math. 238(1) (2020), 209–242.CrossRefGoogle Scholar
Margolis, L. and Schnabel, O., Twisted group ring isomorphism problem and infinite cohomology groups, J. Pure Appl. Algebra 227(4) (2023), Paper No. 107258, 31.CrossRefGoogle Scholar
Niroomand, P., On the order of Schur multiplier of non-abelian
 $p$
-groups, J. Algebra 322(12) (2009), 4479–4482.CrossRefGoogle Scholar
$p$
-groups, J. Algebra 322(12) (2009), 4479–4482.CrossRefGoogle Scholar
Niroomand, P., Characterizing finite
 $p$
-groups by their Schur multipliers, C. R. Math. Acad. Sci. Paris 350(19-20) (2012), 867–870.CrossRefGoogle Scholar
$p$
-groups by their Schur multipliers, C. R. Math. Acad. Sci. Paris 350(19-20) (2012), 867–870.CrossRefGoogle Scholar
Niroomand, P., A note on the Schur multiplier of groups of prime power order, Ric. Mat. 61(2) (2012), 341–346.CrossRefGoogle Scholar
Niroomand, P., Characterizing finite
 $p$
-groups by their Schur multipliers,
$p$
-groups by their Schur multipliers,
 $t(G)=5$
, Math. Rep. (Bucur.) 17(67) (2) (2015), 249–254.Google Scholar
$t(G)=5$
, Math. Rep. (Bucur.) 17(67) (2) (2015), 249–254.Google Scholar
Niroomand, P., Classifying
 $p$
-groups by their Schur multipliers, Math. Rep. (Bucur.) 20(70) (3) (2018), 279–284.Google Scholar
$p$
-groups by their Schur multipliers, Math. Rep. (Bucur.) 20(70) (3) (2018), 279–284.Google Scholar
Perlis, S. and Walker, G. L., Abelian group algebras of finite order, Trans. Am. Math. Soc. 68 (1950), 420–426.CrossRefGoogle Scholar
Polcino Milies, C. and Sehgal, S. K., An introduction to group rings, Algebra and Applications, vol. 1 (Kluwer Academic Publishers, Dordrecht, 2002).CrossRefGoogle Scholar
Sandling, R., The isomorphism problem for group rings: a survey, in Orders and their Applications: Proceedings of a Conference held in Oberwolfach, West Germany June 3-9 (Oxford University Press, 1985), 256–288.CrossRefGoogle Scholar
Schur, J., Untersuchungen über die Darstellung der endlichen Gruppen durch gebrochene lineare Substitutionen, J. Reine Angew. Math. 132 (1907), 85–137.Google Scholar
Zhou, X. M., On the order of Schur multipliers of finite
 $p$
-groups, Comm. Algebra 22(1) (1994), 1–8.CrossRefGoogle Scholar
$p$
-groups, Comm. Algebra 22(1) (1994), 1–8.CrossRefGoogle Scholar


