Article contents
ON SEPARATION OF VARIABLES AND COMPLETENESS OF THE BETHE ANSATZ FOR QUANTUM 

Published online by Cambridge University Press: 01 February 2009
Abstract
In this paper, we discuss implications of the results obtained in [5]. It was shown there that eigenvectors of the Bethe algebra of the quantum 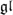 N Gaudin model are in a one-to-one correspondence with Fuchsian differential operators with polynomial kernel. Here, we interpret this fact as a separation of variables in the
N Gaudin model are in a one-to-one correspondence with Fuchsian differential operators with polynomial kernel. Here, we interpret this fact as a separation of variables in the 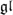 N Gaudin model. Having a Fuchsian differential operator with polynomial kernel, we construct the corresponding eigenvector of the Bethe algebra. It was shown in [5] that the Bethe algebra has simple spectrum if the evaluation parameters of the Gaudin model are generic. In that case, our Bethe ansatz construction produces an eigenbasis of the Bethe algebra.
N Gaudin model. Having a Fuchsian differential operator with polynomial kernel, we construct the corresponding eigenvector of the Bethe algebra. It was shown in [5] that the Bethe algebra has simple spectrum if the evaluation parameters of the Gaudin model are generic. In that case, our Bethe ansatz construction produces an eigenbasis of the Bethe algebra.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 2009
References
REFERENCES
- 9
- Cited by

