Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Pigno, Vincent
and
Pinner, Christopher
2017.
Binomial Character Sums Modulo Prime Powers.
Journal de théorie des nombres de Bordeaux,
Vol. 28,
Issue. 1,
p.
39.

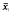 , where
, where 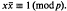 We consider the sum
We consider the sum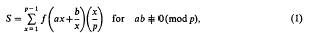
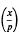 is the Legendre symbol. The sum is zero if
is the Legendre symbol. The sum is zero if 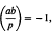 as is clear on replacing
as is clear on replacing