Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-01-26T21:37:41.717Z Has data issue: false hasContentIssue false
  • English
  • Français

On non-commutative regular local rings

Published online by Cambridge University Press:  18 May 2009

P. F. Smith
P. F. Smith
Affiliation:
University of Glasgow, Department of Mathematics, University Gardens, Glasgow, G12 8Qw
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let R be a ring (with identity). We shall call R a local ring if R is aright noetherian ring such that the Jacobson radical M is a maximal ideal (and so is the only maximal ideal), 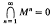and R/M is a simple artinian ring. A local ring R with maximal ideal M is called regular if there exists a chain

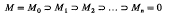
of ideals Mi of such that Mi–1/Mi is generated by a central regular element of R/Mi (1 ≦ i ≦ n). For such a ring R, Walker [6, Theorem 2. 7] proved that R is prime and n is the right global dimension of R, the Krull dimension of R, the homological dimension of theR-module R/M and the supremum of the lengths of chains of prime ideals of R. Such regular local rings will be called n-dimensional. The aim of this note is to give examples of regular local rings. These arise as localizations of universal enveloping algebras of nilpotent Lie algebras over fields and localizations of group algebras of certain finitely generated finite-by-nilpotent groups.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 17 , Issue 2 , July 1976 , pp. 98 - 102
Copyright
Copyright © Glasgow Mathematical Journal Trust 1976

References

REFERENCES

1.Hall, P., Finiteness conditions for soluble groups, Proc. London Math. Soc. (3) 4 (1954), 419–436.Google Scholar
2.Kaplansky, I., Commutative rings (Allyn and Bacon, 1970).Google Scholar
3.McConnell, J. C., The intersection theorem for a class of non-commutative rings, Proc. London Math. Soc. (3) 17 (1967), 487–498.CrossRefGoogle Scholar
4.Roseblade, J. E. and Smith, P. F., A note on hypercentral group rings, J. London Math. Soc.; to appear.Google Scholar
5.Smith, P. F., Localization and the AR property, Proc. London Math. Soc. (3) 22 (1971), 39–68.CrossRefGoogle Scholar
6.Walker, R., Local rings and normalizing sets of elements, Proc. London Math. Soc. (3) 24 (1972), 27–45.CrossRefGoogle Scholar