No CrossRef data available.
Article contents
NON-COCOMMUTATIVE C*-BIALGEBRA DEFINED AS THE DIRECT SUM OF FREE GROUP C*-ALGEBRAS
Part of:
Topological (rings and) algebras with an involution
Hopf algebras, quantum groups and related topics
Published online by Cambridge University Press: 21 July 2015
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Leti 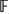 ${\Bbb F}$n be the free group of rank n and let
${\Bbb F}$n be the free group of rank n and let 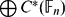 $\bigoplus C^{*}({\Bbb F}_{n})$ denote the direct sum of full group C*-algebras
$\bigoplus C^{*}({\Bbb F}_{n})$ denote the direct sum of full group C*-algebras 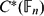 $C^{*}({\Bbb F}_{n})$ of
$C^{*}({\Bbb F}_{n})$ of 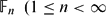 ${\Bbb F}_{n} (1\leq n<\infty$). We introduce a new comultiplication Δϕ on
${\Bbb F}_{n} (1\leq n<\infty$). We introduce a new comultiplication Δϕ on 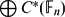 $\bigoplus C^{*}({\Bbb F}_{n})$ such that
$\bigoplus C^{*}({\Bbb F}_{n})$ such that 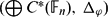 $(\bigoplus C^{*}({\Bbb F}_{n}),\,\Delta_{\varphi})$ is a non-cocommutative C*-bialgebra. With respect to Δϕ, the tensor product π⊗ϕπ′ of any two representations π and π′ of free groups is defined. The operation ×ϕ is associative and non-commutative. We compute its tensor product formulas of several representations.
$(\bigoplus C^{*}({\Bbb F}_{n}),\,\Delta_{\varphi})$ is a non-cocommutative C*-bialgebra. With respect to Δϕ, the tensor product π⊗ϕπ′ of any two representations π and π′ of free groups is defined. The operation ×ϕ is associative and non-commutative. We compute its tensor product formulas of several representations.
MSC classification
Secondary:
16T10: Bialgebras
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 2015
References
REFERENCES
2.Akemann, C., Wassermann, S. and Weaver, N., Pure states on free group C*-algebras. Glasgow Math. J. 52 (1) (2010), 151–154.CrossRefGoogle Scholar
3.Blackadar, B., Operator algebras, Theory of C*-algebras and von Neumann algebras (Springer-Verlag, Berlin Heidelberg, New York, 2006).Google Scholar
4.Brown, N. P. and Ozawa, N., C*-algebras and finite-dimensional approximations (American Mathematical Society, 2008).CrossRefGoogle Scholar
5.Burger, M. and de la Harpe, P., Constructing irreducible representations of discrete groups, Proc. Indian Acad. Sci. Math. Sci. 107 (3) (1997), 223–235.CrossRefGoogle Scholar
6.Davidson, K. R., C*-algebras by example (American Mathematical Society, 1996).CrossRefGoogle Scholar
7.Enock, M. and Schwartz, J. M., Kac algebras and duality of locally compact groups (Springer-Verlag, 1992).CrossRefGoogle Scholar
8.Hatem, H., Decomposition of quasi-regular representations induced from discrete subgroups of nilpotent Lie groups, Lett. Math. Phys. 81 (2) (2007), 135–150.Google Scholar
9.Herschend, M., On the representation ring of a quiver. Algebr. Represent. Theor. 12 (2009), 513–541.CrossRefGoogle Scholar
11.Kawamura, K., A tensor product of representations of Cuntz algebras, Lett. Math. Phys. 82 (1) (2007), 91–104.CrossRefGoogle Scholar
12.Kawamura, K., C*-bialgebra defined by the direct sum of Cuntz algebras, J.Algebra 319 (9) (2008), 3935–3959.CrossRefGoogle Scholar
13.Kawamura, K., C*-bialgebra defined as the direct sum of Cuntz-Krieger algebras, Commun. Algebra 37 (11) (2009), 4065–4078.CrossRefGoogle Scholar
14.Kawamura, K., Tensor products of type III factor representations of Cuntz-Krieger algebras, Algebr. Represent. Theor. 16 (5) (2013), 1397–1407.CrossRefGoogle Scholar
15.Kustermans, J. and Vaes, S., The operator algebra approach to quantum groups. Proc. Natl. Acad. Sci. USA 97 (2) (2000), 547–552.CrossRefGoogle ScholarPubMed
16.Mackey, G. W., The theory of unitary group representations (The University of Chicago Press Chicago and London, 1976).Google Scholar
17.Magnus, W., Karrass, A. and Solitar, D., Combinatorial group theory (Interscience Publishers, 1966).Google Scholar
18.Masuda, T., Nakagami, Y. and Woronowicz, S. L., A C*-algebraic framework for quantum groups, Int. J. Math. 14 (9) (2003), 903–1001.CrossRefGoogle Scholar
19.Obata, N., Induced representation of infinite discrete groups –-intertwining number theorem and its applications (Japanese). Research on coadjoint orbits in representation theory (Kyoto, 1989), Surikaisekikenkyusho Kokyuroku No. 715 (1990), 22–50.Google Scholar
21.Powers, R. T., Simplicity of the C*-algebra associated with the free group on two generators, Duke Math. J. 42 (1975), 151–156.CrossRefGoogle Scholar
22.Yoshizawa, H., Some remarks on unitary representations of the free group. Osaka Math. J. 3 (1) (1951), 55–63.Google Scholar

