Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Brown, R
Johnson, D.L
and
Robertson, E.F
1987.
Some computations of non-abelian tensor products of groups.
Journal of Algebra,
Vol. 111,
Issue. 1,
p.
177.
Brown, Ronald
and
Loday, Jean-Louis
1987.
Van Kampen theorems for diagrams of spaces.
Topology,
Vol. 26,
Issue. 3,
p.
311.
Ellis, Graham J.
1987.
Non-abelian exterior products of lie algebras and an exact sequence in the homology of lie algebras.
Journal of Pure and Applied Algebra,
Vol. 46,
Issue. 2-3,
p.
111.
Ellis, Graham J.
1988.
Higher dimensional crossed modules of algebras.
Journal of Pure and Applied Algebra,
Vol. 52,
Issue. 3,
p.
277.
Conduche´, Daniel
and
Ellis, Graham J.
1989.
Quelques proprie´te´s homologiques des modules pre´croise´s.
Journal of Algebra,
Vol. 123,
Issue. 2,
p.
327.
Ellis, Graham J
1989.
An algebraic derivation of a certain exact sequence.
Journal of Algebra,
Vol. 127,
Issue. 1,
p.
178.
Brown, Ronald
1990.
Homotopy Theory and Related Topics.
Vol. 1418,
Issue. ,
p.
105.
Ellis, Graham J.
1991.
A non-abelian tensor product of Lie algebras.
Glasgow Mathematical Journal,
Vol. 33,
Issue. 1,
p.
101.
Conduché, Daniel
and
Rodríguez-Fernández, Celso
1992.
Non-abelian tensor and exterior products modulo q and universal q-central relative extension.
Journal of Pure and Applied Algebra,
Vol. 78,
Issue. 2,
p.
139.
Ellis, Graham J.
1993.
On five well-known commutator identities.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 54,
Issue. 1,
p.
1.
Ellis, Graham
1993.
Crossed squares and combinatorial homotopy.
Mathematische Zeitschrift,
Vol. 214,
Issue. 1,
p.
93.
Ellis, Graham
and
Hardie, Keith
1995.
A projective homotopy theory of crossedG-modules.
Applied Categorical Structures,
Vol. 3,
Issue. 3,
p.
201.
Ellis, Graham
1998.
The Schur Multiplier of a Pair of Groups.
Applied Categorical Structures,
Vol. 6,
Issue. 3,
p.
355.
Ellis, Graham
1998.
On the Schur multiplier of a quotient of a direct product of groups.
Bulletin of the Australian Mathematical Society,
Vol. 58,
Issue. 3,
p.
495.
Ellis, Graham
1998.
On the capability of groups.
Proceedings of the Edinburgh Mathematical Society,
Vol. 41,
Issue. 3,
p.
487.
Ellis, Graham
and
Kholodna, Irina
1999.
Three-Dimensional Presentations for the Groups of Order at Most 30.
LMS Journal of Computation and Mathematics,
Vol. 2,
Issue. ,
p.
93.
Inassaridze, Nick
2001.
ON NONABELIAN TENSOR PRODUCT MODULOqOF GROUPS.
Communications in Algebra,
Vol. 29,
Issue. 6,
p.
2657.
Frøyshov, Kim A.
2013.
On the existence of representations of finitely presented groups in compact Lie groups.
Topology and its Applications,
Vol. 160,
Issue. 15,
p.
1987.
Inassaridze, N.
2016.
Some Aspects of Homotopic Algebra and Non-Abelian (CO)Homology Theories.
Journal of Mathematical Sciences,
Vol. 213,
Issue. 1,
p.
1.
Donadze, Guram
Inassaridze, Nick
and
Ladra, Manuel
2017.
Non-abelian tensor and exterior products of multiplicative Lie rings.
Forum Mathematicum,
Vol. 29,
Issue. 3,
p.
563.
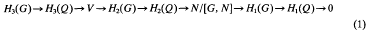
 ,
,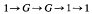

 .
. .
.
