Hostname: page-component-cb9f654ff-mwwwr Total loading time: 0 Render date: 2025-09-02T05:51:31.190Z Has data issue: false hasContentIssue false
  • English
  • Français

LOCALIZATIONS OF THE HEARTS OF COTORSION PAIRS

Part of: Abelian categories Representation theory of rings and algebras

Published online by Cambridge University Press:  03 July 2019

YU LIU
YU LIU*
Affiliation:
School of Mathematics, Southwest Jiaotong University, Chengdu 611756, China e-mail: liuyu86@swjtu.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this article, we study localizations of hearts of cotorsion pairs (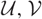$\mathcal{U}, \mathcal{V}$) where 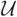$\mathcal{U}$ is rigid on an extriangulated category 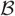$\mathcal{B}$. The hearts of such cotorsion pairs are equivalent to the functor categories over the stable category of 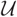$\mathcal{U}$ (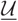$\bmod \underline{\mathcal{U}}$). Inspired by Marsh and Palu (Nagoya Math. J. 225(2017), 64–99), we consider the mutation (in the sense of Iyama and Yoshino, Invent. Math. 172(1) (2008), 117–168) of 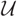$\mathcal{U}$ that induces a cotorsion pair (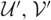$\mathcal{U}^{\prime}, \mathcal{V}^{\prime}$). Generally speaking, the hearts of (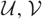$\mathcal{U}, \mathcal{V}$) and (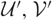$\mathcal{U}^{\prime}, \mathcal{V}^{\prime}$) are not equivalent to each other, but we will give a generalized pseudo-Morita equivalence between certain localizations of their hearts.

MSC classification

Primary: 16G99: None of the above, but in this section
Secondary: 18E99: None of the above, but in this section

Information

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 62 , Issue 3 , September 2020 , pp. 564 - 583
Copyright
© Glasgow Mathematical Journal Trust 2019

References

Abe, N. and Nakaoka, H., General heart construction on a triangulated category (II): Associated cohomological functor, Appl. Categ. Struct. 20(2) (2012), 162–174.CrossRefGoogle Scholar
Auslander, M., Coherent functors, in 1966 Proceedings of the Conference on Categorical Algebra, La Jolla, California (Springer, New York, 1965), 189–231.Google Scholar
Beilinson, A. A., Bernstein, J. and Deligne, P., pervers, Faisceaux, Analysis and topology on singular spaces, I (Luminy 1981), Astérisque, 100, (Soc. Math. France, Pairs, 1982), 5–171.Google Scholar
Buan, A. B. and Marsh, R. J., From triangulated categories to module categories via localisation, Trans. Amer. Math. Soc. 365(6) (2013), 2845–2861.CrossRefGoogle Scholar
Buan, A. B. and Marsh, R. J., From triangulated categories to module categories via localisation II: calculus of fractions, J. Lond. Math. Soc. 87(2) (2013), 643.Google Scholar
Demonet, L. and Liu, Y., Quotients of exact categories by cluster tilting subcategories as module categories, J. Pure Appl. Alg. 217 (2013), 2282–2297.CrossRefGoogle Scholar
Gabriel, P. and Zisman, M., Calculus of fractions and homotopy theory, in Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 35 (Springer-Verlag New York Inc., New York, 1967).Google Scholar
Happel, D., Triangulated categories in the representation theory of finite-dimensional algebras, in London Mathematical Society, Lecture Note Series, vol. 119, (Cambridge University Press, Cambridge, 1988), x+208.Google Scholar
Iyama, O. and Yoshino, Y., Mutation in triangulated categories and rigid Cohen–Macaulay modules, Invent. Math. 172(1) (2008), 117–168.CrossRefGoogle Scholar
Liu, Y., Hearts of twin cotorsion pairs on exact categories, J. Algebra. 394 (2013), 245–284.CrossRefGoogle Scholar
Liu, Y., Half exact functors associated with general hearts on exact categories. arXiv: 1305.1433.Google Scholar
Liu, Y. and Nakaoka, H., Hearts of twin Cotorsion pairs on extriangulated categories, J. Algebra 528 (2019), 96–149.CrossRefGoogle Scholar
Marsh, R. J. and Palu, Y., Nearly Morita equivalences and rigid objects, Nagoya Math. J. 225(2017), 64–99.CrossRefGoogle Scholar
Nakaoka, H., General heart construction on a triangulated category (I): unifying t-structures and cluster tilting subcategories, Appl. Categ. Struct. 19(6) (2011), 879–899.CrossRefGoogle Scholar
Nakaoka, H., General heart construction for twin torsion pairs on triangulated categories, J. Algebra 374 (2013), 195–215.CrossRefGoogle Scholar
Nakaoka, H., Equivalence of hearts of twin cotorsion pairs on triangulated categories, Comm. Algebra 44(10) (2016), 4302–4326.CrossRefGoogle Scholar
Nakaoka, H. and Palu, Y., Mutation via hovey twin cotorsion pairs and model structures in extriangulated categories. arXiv:1605.05607.Google Scholar
Zhou, Y. and Zhu, B., Mutation of torsion pairs in triangulated categories and its geometric realization, Algebr. Represent. Theory 21(4) (2018), 817–832.CrossRefGoogle Scholar