Article contents
Lattice subgroups of free congruence groups
Published online by Cambridge University Press: 18 May 2009
Extract
Let Г(1) denote the homogeneous modular group of 2 × 2 matrices with integral entries and determinant 1. Let 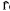 (1) be the inhomogeneous modular group of 2 × 2 integral matrices of determinant 1 in which a matrix is identified with its negative.
(1) be the inhomogeneous modular group of 2 × 2 integral matrices of determinant 1 in which a matrix is identified with its negative. 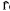 (N), the principal congruence subgroup of level N, is the subgroup of
(N), the principal congruence subgroup of level N, is the subgroup of 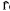 (1) consisting of all T ∈
(1) consisting of all T ∈ 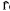 (1) for which T ≡ ± I (mod N), where N is a positive integer and I is the identity matrix. A subgroup
(1) for which T ≡ ± I (mod N), where N is a positive integer and I is the identity matrix. A subgroup 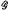 of
of 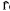 (1) is said to be a congruence group of level N if
(1) is said to be a congruence group of level N if 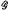 contains
contains 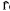 (N) and N is the least such integer. Similarly, we denote by Г(N) the principal congruence subgroup of level N of Г(1), consisting of those T∈(1) for which T ≡ I (mod N), and we say that a sub group
(N) and N is the least such integer. Similarly, we denote by Г(N) the principal congruence subgroup of level N of Г(1), consisting of those T∈(1) for which T ≡ I (mod N), and we say that a sub group 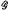 of Г(1) is a congruence group of level N if
of Г(1) is a congruence group of level N if 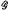 contains Г (N) and N is minimal with respect to this property. In a recent paper [9] Rankin considered lattice subgroups of a free congruence subgroup
contains Г (N) and N is minimal with respect to this property. In a recent paper [9] Rankin considered lattice subgroups of a free congruence subgroup 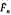 of rank n of
of rank n of 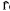 (1). By a lattice subgroup of
(1). By a lattice subgroup of 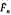 we mean a subgroup of
we mean a subgroup of 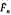 which contains the commutator group
which contains the commutator group 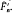 . In particular, he showed that, if
. In particular, he showed that, if 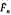 is a congruence group of level N and if
is a congruence group of level N and if 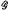 is a lattice congruence subgroup of
is a lattice congruence subgroup of 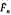 of level qr, where r is the largest divisor of qr prime to N, then N divides q and r divides 12. He then posed the problem of finding an upper bound for the factor q. It is the purpose of this paper to find such an upper bound for q. We also consider bounds for the factor r.
of level qr, where r is the largest divisor of qr prime to N, then N divides q and r divides 12. He then posed the problem of finding an upper bound for the factor q. It is the purpose of this paper to find such an upper bound for q. We also consider bounds for the factor r.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1969
References
REFERENCES
- 9
- Cited by

