No CrossRef data available.
Article contents
ISOMETRIES AND DISCRETE ISOMETRY SUBGROUPS OF HYPERBOLIC SPACES
Published online by Cambridge University Press: 01 January 2009
Abstract
Let 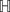 n be the n-dimensional hyperbolic space with n ≥ 2. Suppose that G is a discrete, sense-preserving subgroup of Isom
n be the n-dimensional hyperbolic space with n ≥ 2. Suppose that G is a discrete, sense-preserving subgroup of Isom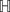 n, the isometry group of
n, the isometry group of 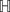 n. Let p be the projection map from
n. Let p be the projection map from 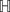 n to the quotient space M =
n to the quotient space M = 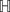 n/G. The first goal of this paper is to prove that for any a ∈ ∂
n/G. The first goal of this paper is to prove that for any a ∈ ∂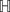 n (the sphere at infinity of
n (the sphere at infinity of 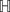 n), there exists an open neighbourhood U of a in
n), there exists an open neighbourhood U of a in 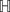 n ∪ ∂
n ∪ ∂ 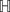 n such that p is an isometry on U ∩
n such that p is an isometry on U ∩ 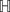 n if and only if a ∈ oΩ(G) (the domain of proper discontinuity of G). This is a generalization of the main result discussed in the work by Y. D. Kim (A theorem on discrete, torsion free subgroups of Isom
n if and only if a ∈ oΩ(G) (the domain of proper discontinuity of G). This is a generalization of the main result discussed in the work by Y. D. Kim (A theorem on discrete, torsion free subgroups of Isom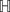 n, Geometriae Dedicata109 (2004), 51–57). The second goal is to obtain a new characterization for the elements of Isom
n, Geometriae Dedicata109 (2004), 51–57). The second goal is to obtain a new characterization for the elements of Isom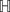 n by using a class of hyperbolic geometric objects: hyperbolic isosceles right triangles. The proof is based on a geometric approach.
n by using a class of hyperbolic geometric objects: hyperbolic isosceles right triangles. The proof is based on a geometric approach.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 2008

