Hostname: page-component-cb9f654ff-fg9bn Total loading time: 0 Render date: 2025-08-30T19:30:47.265Z Has data issue: false hasContentIssue false
  • English
  • Français

Higher-dimensional Auslander–Reiten theory on (d+2)-angulated categories

Part of: Representation theory of rings and algebras

Published online by Cambridge University Press:  27 October 2021

Panyue Zhou Open the ORCID record for Panyue Zhou [Opens in a new window]
Panyue Zhou*
Affiliation:
College of Mathematics, Hunan Institute of Science and Technology, 414006 Yueyang, Hunan, P. R. China e-mail: panyuezhou@163.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 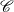$\mathscr{C}$ be a 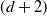$(d+2)$-angulated category with d-suspension functor 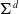$\Sigma^d$. Our main results show that every Serre functor on 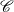$\mathscr{C}$ is a 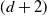$(d+2)$-angulated functor. We also show that 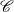$\mathscr{C}$ has a Serre functor 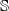$\mathbb{S}$ if and only if 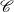$\mathscr{C}$ has Auslander–Reiten 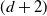$(d+2)$-angles. Moreover, 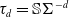$\tau_d=\mathbb{S}\Sigma^{-d}$ where 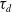$\tau_d$ is d-Auslander–Reiten translation. These results generalize work by Bondal–Kapranov and Reiten–Van den Bergh. As an application, we prove that for a strongly functorially finite subcategory 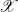$\mathscr{X}$ of 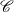$\mathscr{C}$, the quotient category 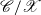$\mathscr{C}/\mathscr{X}$ is a 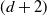$(d+2)$-angulated category if and only if 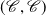$(\mathscr{C},\mathscr{C})$ is an 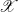$\mathscr{X}$-mutation pair, and if and only if 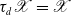$\tau_d\mathscr{X} =\mathscr{X}$.

Keywords

triangulated categories(d+2)-angulated categoriesAuslander-Reiten (d+2)-anglesSerre functor

MSC classification

Primary: 16G70: Auslander-Reiten sequences (almost split sequences) and Auslander-Reiten quivers

Information

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 64 , Issue 3 , September 2022 , pp. 527 - 547
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

This work was supported by the Scientific Research Fund of Hunan Provincial Education Department (Grant No. 19B239) and the National Natural Science Foundation of China (Grant No. 11901190).

References

E., Arentz-Hansen, P., Bergh and M., Thaule, The morphism axiom for N-angulated categories, Theory Appl. Categ. 31(18) (2016), 477–483.Google Scholar
M., Auslander and I., Reiten, Representation theory of Artin algebras. IV. Invariants given by almost split sequences, Comm. Algebra 5(5) (1977), 443–518.CrossRefGoogle Scholar
R., Bocklandt, Graded Calabi–Yau algebras of dimension 3, with an appendix “The signs of Serre duality” by M. Van den Bergh, J. Pure Appl. Algebra 212(1) (2008), 14–32.CrossRefGoogle Scholar
A., Bondal and M., Kapranov, Representable functors, Serre functors, and mutations, Math. USSR-Izvestiya 35(3) (1990), 519–541.CrossRefGoogle Scholar
P., Bergh and M., Thaule, The axioms for n-angulated categories, Algebr. Geom. Topol. 13(4) (2013), 2405–2428.CrossRefGoogle Scholar
P., Bergh and M., Thaule, The Grothendieck group of an n-angulated category, J. Pure Appl. Algebra 218(2) (2014), 354–366.CrossRefGoogle Scholar
F., Fedele, Auslander-Reiten $(d+2)$ -angles in subcategories and a $(d+2)$ -angulated generalisation of a theorem by Brüning, J. Pure Appl. Algebra 223(8) (2019), 3554–3580.CrossRefGoogle Scholar
C., Geiss, B., Keller and S., Oppermann, n-angulated categories, J. Reine Angew. Math. 675 (2013), 101–120.Google Scholar
O., Iyama and Y., Yoshino, Mutations in triangulated categories and rigid Cohen-Macaulay modules, Invent. Math. 172(1) (2008), 117–168.CrossRefGoogle Scholar
G., Jasso, n-abelian and n-exact categories, Math. Z. 283(3–4) (2016), 703–759.CrossRefGoogle Scholar
P., Jørgensen, Quotients of cluster categories, Proc. Roy. Soc. Edinburgh Sect. A 140(1) (2010), 65–81.CrossRefGoogle Scholar
Z., Lin, n-angulated quotient categories induced by mutation pairs, Czechoslovak Math. J. 65(4) (2015) 953–968.CrossRefGoogle Scholar
Z., Lin, Right n-angulated categories arising from covariantly finite subcategories, Comm. Algebra 45(2) (2017), 828–840.CrossRefGoogle Scholar
S., Oppermann and H., Thomas, Higher-dimensional cluster combinatorics and representation theory, J. Eur. Math. Soc. 14(6) (2012), 1679–1737.CrossRefGoogle Scholar
I., Reiten and M., Van den Bergh, Noetherian hereditary Abelian categories satisfying Serre duality, J. Amer. Math. Soc. 15(2) (2002), 295–366.CrossRefGoogle Scholar
P., Zhang, Triangulated categories and derived categories (Chinese, Science Press, 2015).Google Scholar