Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
BIRKENMEIER, G. F.
MUTLU, F. TAKIL
NEBİYEV, C.
SOKMEZ, N.
and
TERCAN, A.
2012.
GOLDIE*-SUPPLEMENTED MODULES – CORRIGENDUM.
Glasgow Mathematical Journal,
Vol. 54,
Issue. 2,
p.
479.
KURATOMI, YOSUKE
2014.
DIRECT SUMS OF H-SUPPLEMENTED MODULES.
Journal of Algebra and Its Applications,
Vol. 13,
Issue. 01,
p.
1350075.
Hosseinpour, M.
Ungor, B.
Talebi, Y.
and
Harmanci, A.
2017.
A generalization of the classof principally lifting modules.
Rocky Mountain Journal of Mathematics,
Vol. 47,
Issue. 5,
Güroğlu, A. T.
and
Meriç, E. T.
2018.
Principally Goldie*-Lifting Modules.
Ukrainian Mathematical Journal,
Vol. 70,
Issue. 7,
p.
1042.
NEBİYEV, Celil
and
ÖKTEN, Hasan Hüseyin
2022.
Finitely Essential Supplemented Modules.
Erzincan Üniversitesi Fen Bilimleri Enstitüsü Dergisi,
Vol. 15,
Issue. 1,
p.
304.
NEBİYEV, Celil
and
ÖKTEN, Hasan Hüseyin
2022.
Some Properties of r-Small Submodules.
Erzincan Üniversitesi Fen Bilimleri Enstitüsü Dergisi,
Vol. 15,
Issue. 3,
p.
996.
KOŞAR, Berna
2022.
Some Properties of Amply Weak Essential Supplemented Modules.
Erzincan Üniversitesi Fen Bilimleri Enstitüsü Dergisi,
Vol. 15,
Issue. 1,
p.
387.
Wadi, Adnan Saleh
and
Hasan, Wasan Khalid
2023.
⊕ μ*–essential – Supplemented modules.
Vol. 2591,
Issue. ,
p.
050028.
Güroğlu, Ayşe Tuğba
2023.
Totally Goldie*-Supplemented Modules.
Mathematics,
Vol. 11,
Issue. 21,
p.
4427.
Baanoon, Hiba R
and
Khalid, Wasan
2023.
On $\boldsymbol{e^{*}}$-supplemented Modules.
Missouri Journal of Mathematical Sciences,
Vol. 35,
Issue. 1,
Güroğlu, Ayşe Tuğba
2023.
Cofinitely Goldie*-Supplemented Modules.
Journal of New Theory,
p.
35.
Fandi, Firas Sh.
2023.
On essential T-Goldie* lifting modules.
Vol. 2834,
Issue. ,
p.
080126.
Nebiyev, Celil
and
Sökmez, Nurhan
2024.
Some properties of r-supplemented modules.
Miskolc Mathematical Notes,
Vol. 25,
Issue. 2,
p.
957.
Koşar, Berna
and
Ökten, Hasan Hüseyin
2024.
Amply socle supplemented modules.
Miskolc Mathematical Notes,
Vol. 25,
Issue. 1,
p.
367.
Moradiani, Sara
Moussavi, Ahmad
and
Zahiri, Masoome
2024.
A characterization of Goldie extending trivial Morita contexts.
Journal of Algebra and Its Applications,
Vol. 23,
Issue. 08,
Abbas, Muntaha Khudhair
Talebi, Yahya
and
Hadi, Inaam Mohammed Ali
2025.
T – supplement submodules and TZ - supplement submodules.
Vol. 3282,
Issue. ,
p.
040010.
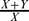 is small in
is small in 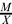 and
and 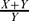 is small in
is small in 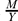 . We show that the β* relation is an equivalence relation and has good behaviour with respect to addition of submodules, homomorphisms and supplements. We apply these results to introduce the class of
. We show that the β* relation is an equivalence relation and has good behaviour with respect to addition of submodules, homomorphisms and supplements. We apply these results to introduce the class of 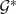 -supplemented modules and to investigate this class and the class of H-supplemented modules. These classes are located among various well-known classes of modules related to the class of lifting modules. Moreover these classes are used to explore an open question of S. H. Mohamed and B. J. Mueller. Examples are provided to illustrate and delimit the theory.
-supplemented modules and to investigate this class and the class of H-supplemented modules. These classes are located among various well-known classes of modules related to the class of lifting modules. Moreover these classes are used to explore an open question of S. H. Mohamed and B. J. Mueller. Examples are provided to illustrate and delimit the theory.
