Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Evans, Ronald J.
1979.
Discrete free products of two complex cyclic matrix groups.
Glasgow Mathematical Journal,
Vol. 20,
Issue. 1,
p.
69.

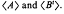 It is shown that
It is shown that 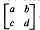 of determinant ±1 with integer entries satisfying |
of determinant ±1 with integer entries satisfying |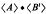 .
.