Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Duncan, J.
and
Taylor, P. J.
1976.
10.—Norm Inequalities for C*-algebras.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 75,
Issue. 2,
p.
119.
Huruya, Tadashi
1977.
The normed space numerical index of 𝐶*-algebras.
Proceedings of the American Mathematical Society,
Vol. 63,
Issue. 2,
p.
289.
Green, Michael D.
1977.
The lattice structure of C*-algebras and their duals.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 81,
Issue. 2,
p.
245.
1977.
C*-Algebras.
Vol. 15,
Issue. ,
p.
486.
Lin, C.-S.
1987.
On commutativity of C*-algebras.
Glasgow Mathematical Journal,
Vol. 29,
Issue. 1,
p.
93.
Iochum, B.
Loupias, G.
and
Rodriguez-Palacios, A.
1989.
Commutativity ofC*-algebras and associativity ofJB*-algebras.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 106,
Issue. 2,
p.
281.
Mena, J.F
Payá, R
Rodríguez, A
and
Yost, D.T
1991.
Absolutely proximinal subspaces of Banach spaces.
Journal of Approximation Theory,
Vol. 65,
Issue. 1,
p.
46.
Wu, Wei
2000.
An order characterization of commutativity for 𝐶*-algebras.
Proceedings of the American Mathematical Society,
Vol. 129,
Issue. 4,
p.
983.
Amin, Kaidi El
Campoy, Antonio Morales
and
Palacios, Angel Rodriguez
2001.
Geometrical Properties of the Product of a $C^*$-Algebra.
Rocky Mountain Journal of Mathematics,
Vol. 31,
Issue. 1,
Spain, P. G.
2001.
Recent Advances in Operator Theory and Related Topics.
p.
561.
El Amin, Kaidi
Campoy, Antonio Morales
and
Palacios, Angel Rodríguez
2001.
Recent Progress in Functional Analysis, Proceedings of the International Functional Analysis Meeting on the Occasion of the 70th Birthday of Professor Manuel Valdivia.
Vol. 189,
Issue. ,
p.
379.
Jeang, Jyh-Shyang
and
Ko, Chun-Chieh
2004.
On the commutativity of C* -algebras.
manuscripta mathematica,
Vol. 115,
Issue. 2,
p.
195.
Palacios, Ángel Rodríguez
2010.
Banach space characterizations of unitaries: A survey.
Journal of Mathematical Analysis and Applications,
Vol. 369,
Issue. 1,
p.
168.
Molnár, Lajos
2014.
A Few Conditions for aC*-Algebra to Be Commutative.
Abstract and Applied Analysis,
Vol. 2014,
Issue. ,
p.
1.
Abe, Toshikazu
and
Hatori, Osamu
2016.
On a characterization of commutativity for $$C^*$$ C ∗ -algebras via gyrogroup operations.
Periodica Mathematica Hungarica,
Vol. 72,
Issue. 2,
p.
248.
Hatori, Osamu
2017.
Commuting pairs of self-adjoint elements in C
*-algebras.
Mathematica Slovaca,
Vol. 67,
Issue. 1,
p.
209.
Ghahramani, H.
and
Sattari, S.
2019.
Characterization of reflexive closure of some operator algebras acting on Hilbert
$${C^{\star}}$$
C
⋆
-modules.
Acta Mathematica Hungarica,
Vol. 157,
Issue. 1,
p.
158.
Mabrouk, Mohamed
and
Zamani, Ali
2023.
An extension of the a-numerical radius on $$C^*$$-algebras.
Banach Journal of Mathematical Analysis,
Vol. 17,
Issue. 3,
Cabezas, David
and
Peralta, Antonio M.
2024.
Estimations of the Numerical Index of a JB$$^*$$-Triple.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 47,
Issue. 1,
Molnár, Lajos
2024.
Some new characterizations of central positive elements in C⁎-algebras.
Journal of Mathematical Analysis and Applications,
Vol. 534,
Issue. 2,
p.
128055.

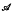 be a
be a 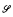 be the self-adjoint elements of
be the self-adjoint elements of 