Article contents
A THEORY OF COMPLEXITY, CONDITION, AND ROUNDOFF
Published online by Cambridge University Press: 27 February 2015
Abstract
We develop a theory of complexity for numerical computations that takes into account the condition of the input data and allows for roundoff in the computations. We follow the lines of the theory developed by Blum, Shub and Smale for computations over 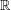 $\mathbb{R}$ (which in turn followed those of the classical, discrete, complexity theory as laid down by Cook, Karp, and Levin, among others). In particular, we focus on complexity classes of decision problems and, paramount among them, on appropriate versions of the classes
$\mathbb{R}$ (which in turn followed those of the classical, discrete, complexity theory as laid down by Cook, Karp, and Levin, among others). In particular, we focus on complexity classes of decision problems and, paramount among them, on appropriate versions of the classes 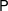 $\mathsf{P}$,
$\mathsf{P}$, 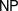 $\mathsf{NP}$, and
$\mathsf{NP}$, and 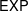 $\mathsf{EXP}$ of polynomial, nondeterministic polynomial, and exponential time, respectively. We prove some basic relationships between these complexity classes, and provide natural NP-complete problems.
$\mathsf{EXP}$ of polynomial, nondeterministic polynomial, and exponential time, respectively. We prove some basic relationships between these complexity classes, and provide natural NP-complete problems.
Information
- Type
- Research Article
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/3.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author 2015
References
- 3
- Cited by

