Article contents
SQUARE-INTEGRABILITY OF THE MIRZAKHANI FUNCTION AND STATISTICS OF SIMPLE CLOSED GEODESICS ON HYPERBOLIC SURFACES
Published online by Cambridge University Press: 04 February 2020
Abstract
Given integers 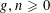 $g,n\geqslant 0$ satisfying
$g,n\geqslant 0$ satisfying 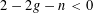 $2-2g-n<0$, let
$2-2g-n<0$, let 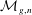 ${\mathcal{M}}_{g,n}$ be the moduli space of connected, oriented, complete, finite area hyperbolic surfaces of genus
${\mathcal{M}}_{g,n}$ be the moduli space of connected, oriented, complete, finite area hyperbolic surfaces of genus 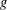 $g$ with
$g$ with  $n$ cusps. We study the global behavior of the Mirzakhani function
$n$ cusps. We study the global behavior of the Mirzakhani function 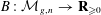 $B:{\mathcal{M}}_{g,n}\rightarrow \mathbf{R}_{{\geqslant}0}$ which assigns to
$B:{\mathcal{M}}_{g,n}\rightarrow \mathbf{R}_{{\geqslant}0}$ which assigns to 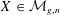 $X\in {\mathcal{M}}_{g,n}$ the Thurston measure of the set of measured geodesic laminations on
$X\in {\mathcal{M}}_{g,n}$ the Thurston measure of the set of measured geodesic laminations on 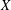 $X$ of hyperbolic length
$X$ of hyperbolic length 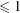 ${\leqslant}1$. We improve bounds of Mirzakhani describing the behavior of this function near the cusp of
${\leqslant}1$. We improve bounds of Mirzakhani describing the behavior of this function near the cusp of 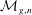 ${\mathcal{M}}_{g,n}$ and deduce that
${\mathcal{M}}_{g,n}$ and deduce that 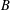 $B$ is square-integrable with respect to the Weil–Petersson volume form. We relate this knowledge of
$B$ is square-integrable with respect to the Weil–Petersson volume form. We relate this knowledge of 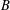 $B$ to statistics of counting problems for simple closed hyperbolic geodesics.
$B$ to statistics of counting problems for simple closed hyperbolic geodesics.
MSC classification
Information
- Type
- Differential Geometry and Geometric Analysis
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s) 2020
References
- 6
- Cited by

