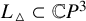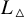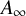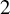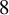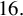1 Introduction
The main result of the present paper is a complete computation of the open Gromov-Witten disk invariants of the Chiang Lagrangian [Reference Chiang8] in
![]() $\mathbb {C}P^3.$
The Chiang Lagrangian is not fixed by any anti-symplectic involution [Reference Evans and Lekili10]. Multiple phenomena are observed that have not appeared in previous computations of open Gromov-Witten invariants for Lagrangian submanifolds fixed by anti-symplectic involutions. Our computation relies on direct geometric arguments combined with general structure theorems governing the invariants including the open WDVV equations of [Reference Solomon and Tukachinsky48] and results of the present paper.
$\mathbb {C}P^3.$
The Chiang Lagrangian is not fixed by any anti-symplectic involution [Reference Evans and Lekili10]. Multiple phenomena are observed that have not appeared in previous computations of open Gromov-Witten invariants for Lagrangian submanifolds fixed by anti-symplectic involutions. Our computation relies on direct geometric arguments combined with general structure theorems governing the invariants including the open WDVV equations of [Reference Solomon and Tukachinsky48] and results of the present paper.
1.1 Invariants
To formulate our results, we recall relevant background on open and closed Gromov-Witten invariants. Let
![]() $(X,\omega )$
be a symplectic manifold of real dimension
$(X,\omega )$
be a symplectic manifold of real dimension
![]() $2n$
, let
$2n$
, let
![]() $L \subset X$
be a Lagrangian submanifold and let J be an
$L \subset X$
be a Lagrangian submanifold and let J be an
![]() $\omega $
-tame almost complex structure. For simplicity, assume L is a connected, spin Lagrangian submanifold with
$\omega $
-tame almost complex structure. For simplicity, assume L is a connected, spin Lagrangian submanifold with
![]() $H^{*}(L;\mathbb {R}) \simeq H^{*}(S^n;\mathbb {R})$
and
$H^{*}(L;\mathbb {R}) \simeq H^{*}(S^n;\mathbb {R})$
and
![]() $[L] = 0 \in H_n(X;\mathbb {R}).$
We refer the reader to [Reference Solomon and Tukachinsky46] for a fuller account of settings where open Gromov-Witten invariants can be defined. Write
$[L] = 0 \in H_n(X;\mathbb {R}).$
We refer the reader to [Reference Solomon and Tukachinsky46] for a fuller account of settings where open Gromov-Witten invariants can be defined. Write
![]() $\widehat {H}^{*}(X,L;\mathbb {R}) = H^0(L;\mathbb {R})\oplus H^{>0}(X,L;\mathbb {R}).$
Let
$\widehat {H}^{*}(X,L;\mathbb {R}) = H^0(L;\mathbb {R})\oplus H^{>0}(X,L;\mathbb {R}).$
Let
![]() $y : H^n(L;\mathbb {R}) \to \widehat {H}^{n+1}(X,L;\mathbb {R})$
denote the boundary map from the short exact sequence of the pair
$y : H^n(L;\mathbb {R}) \to \widehat {H}^{n+1}(X,L;\mathbb {R})$
denote the boundary map from the short exact sequence of the pair
![]() $(X,L).$
Choose a map
$(X,L).$
Choose a map
![]() $P_{\mathbb {R}} : \widehat {H}^{n+1}(X,L;\mathbb {R})\to H^n(L;\mathbb {R})$
left-inverse to
$P_{\mathbb {R}} : \widehat {H}^{n+1}(X,L;\mathbb {R})\to H^n(L;\mathbb {R})$
left-inverse to
![]() $y.$
For
$y.$
For
![]() $\beta \in H_2(X,L;\mathbb {Z})$
and
$\beta \in H_2(X,L;\mathbb {Z})$
and
![]() $k,l \geq 0,$
let
$k,l \geq 0,$
let
denote the open Gromov-Witten invariants of [Reference Solomon and Tukachinsky48]. The multilinear maps
![]() $\overline {OGW}\!_{\beta ,k}$
are invariants of the symplectic manifold and the Lagrangian submanifold L up to Hamiltonian isotopy. When
$\overline {OGW}\!_{\beta ,k}$
are invariants of the symplectic manifold and the Lagrangian submanifold L up to Hamiltonian isotopy. When
![]() $\beta $
belongs to the image of the natural map
$\beta $
belongs to the image of the natural map
![]() $\varpi : H_2(X;\mathbb {Z}) \to H_2(X,L;\mathbb {Z}),$
the invariants
$\varpi : H_2(X;\mathbb {Z}) \to H_2(X,L;\mathbb {Z}),$
the invariants
![]() $\overline {OGW}\!_{\beta ,0}$
depend on the choice of
$\overline {OGW}\!_{\beta ,0}$
depend on the choice of
![]() $P_{\mathbb {R}}.$
Explicit formulas for this dependence are given in Propositions 1.1 and 8.1 below.
$P_{\mathbb {R}}.$
Explicit formulas for this dependence are given in Propositions 1.1 and 8.1 below.
The invariants
![]() $\overline {OGW}\!$
can be described as follows. Let
$\overline {OGW}\!$
can be described as follows. Let
![]() $A_1,\ldots ,A_l \in \widehat {H}^{*}(X,L;\mathbb {R}).$
Assume first that either
$A_1,\ldots ,A_l \in \widehat {H}^{*}(X,L;\mathbb {R}).$
Assume first that either
![]() $k> 0$
or
$k> 0$
or
![]() $\beta $
does not belong to the image of
$\beta $
does not belong to the image of
![]() $\varpi .$
The invariant
$\varpi .$
The invariant
![]() $\overline {OGW}\!_{\beta ,k}(A_1,\ldots ,A_l)$
counts J-holomorphic disks
$\overline {OGW}\!_{\beta ,k}(A_1,\ldots ,A_l)$
counts J-holomorphic disks
![]() $u: (D,\partial D) \to (X,L)$
representing
$u: (D,\partial D) \to (X,L)$
representing
![]() $\beta $
with boundary passing through k chosen points on L and interior passing through chosen cycles on X Poincaré dual to
$\beta $
with boundary passing through k chosen points on L and interior passing through chosen cycles on X Poincaré dual to
![]() $A_1,\ldots ,A_l,$
together with correction terms that compensate for disk bubbling. The correction terms come from bounding cochains in the Fukaya
$A_1,\ldots ,A_l,$
together with correction terms that compensate for disk bubbling. The correction terms come from bounding cochains in the Fukaya
![]() $A_\infty $
algebra associated to
$A_\infty $
algebra associated to
![]() $L.$
The assumption
$L.$
The assumption
![]() $H^{*}(L;\mathbb {R}) \simeq H^{*}(S^n;\mathbb {R})$
is used in [Reference Solomon and Tukachinsky46] to show vanishing of obstruction classes that arise in the construction of the bounding cochains following the method of Fukaya-Oh-Ohta-Ono [Reference Fukaya, Oh, Ohta and Ono14].
$H^{*}(L;\mathbb {R}) \simeq H^{*}(S^n;\mathbb {R})$
is used in [Reference Solomon and Tukachinsky46] to show vanishing of obstruction classes that arise in the construction of the bounding cochains following the method of Fukaya-Oh-Ohta-Ono [Reference Fukaya, Oh, Ohta and Ono14].
In the case
![]() $k = 0$
and
$k = 0$
and
![]() $\beta \in \operatorname {\mathrm {Im}} \varpi ,$
it is necessary to add an additional correction term to the above-mentioned counts of J-holomorphic disks to obtain an invariant. The additional correction term counts J-holomorphic spheres in X passing through an
$\beta \in \operatorname {\mathrm {Im}} \varpi ,$
it is necessary to add an additional correction term to the above-mentioned counts of J-holomorphic disks to obtain an invariant. The additional correction term counts J-holomorphic spheres in X passing through an
![]() $n+1$
chain C in X with
$n+1$
chain C in X with
![]() $\partial C = L.$
This term compensates for the fact that the boundary of a J-holomorphic disk can collapse to a point in L forming a J-holomorphic sphere. The topological type of the chain C is characterized by the map
$\partial C = L.$
This term compensates for the fact that the boundary of a J-holomorphic disk can collapse to a point in L forming a J-holomorphic sphere. The topological type of the chain C is characterized by the map
![]() $P_{\mathbb {R}} : \widehat {H}^{n+1}(X,L;\mathbb {R})\to H^n(L;\mathbb {R})$
mentioned above, which is given by the integration of differential forms over
$P_{\mathbb {R}} : \widehat {H}^{n+1}(X,L;\mathbb {R})\to H^n(L;\mathbb {R})$
mentioned above, which is given by the integration of differential forms over
![]() $C.$
See Remark 4.12 in [Reference Solomon and Tukachinsky48].
$C.$
See Remark 4.12 in [Reference Solomon and Tukachinsky48].
Suppose L is fixed by an anti-symplectic involution,
![]() $\dim L = 2$
or
$\dim L = 2$
or
![]() $3$
, and either
$3$
, and either
![]() $k> 0$
or
$k> 0$
or
![]() $\beta \notin \operatorname {\mathrm {Im}} \varpi .$
Then, it is shown in [Reference Solomon and Tukachinsky46] that the invariants
$\beta \notin \operatorname {\mathrm {Im}} \varpi .$
Then, it is shown in [Reference Solomon and Tukachinsky46] that the invariants
![]() $\overline {OGW}\!_{\beta ,k}(\cdots )$
coincide with invariants defined by straightforward counting of J-holomorphic disks [Reference Cho9, Reference Solomon45] or real J-holomorphic spheres [Reference Welschinger50, Reference Welschinger51]. When L is the Chiang Lagrangian, which is not fixed by any anti-symplectic involution, the invariants
$\overline {OGW}\!_{\beta ,k}(\cdots )$
coincide with invariants defined by straightforward counting of J-holomorphic disks [Reference Cho9, Reference Solomon45] or real J-holomorphic spheres [Reference Welschinger50, Reference Welschinger51]. When L is the Chiang Lagrangian, which is not fixed by any anti-symplectic involution, the invariants
![]() $\overline {OGW}\!$
do not coincide with straightforward disk counts in general. See Section 1.2.2 below. Closely related invariants were defined in [Reference Welschinger52], and a comparison can be found in [Reference Chen5].
$\overline {OGW}\!$
do not coincide with straightforward disk counts in general. See Section 1.2.2 below. Closely related invariants were defined in [Reference Welschinger52], and a comparison can be found in [Reference Chen5].
Although the definition of the invariants
![]() $\overline {OGW}\!$
is quite abstract, they have a rich structure that makes them explicitly computable in many situations. This structure includes the open WDVV equations recalled in Theorem 2.2, the open axioms recalled in Proposition 2.2, and the wall-crossing formula recalled in Theorem 2.3. Moreover, the relative quantum cohomology ring of the pair
$\overline {OGW}\!$
is quite abstract, they have a rich structure that makes them explicitly computable in many situations. This structure includes the open WDVV equations recalled in Theorem 2.2, the open axioms recalled in Proposition 2.2, and the wall-crossing formula recalled in Theorem 2.3. Moreover, the relative quantum cohomology ring of the pair
![]() $(X,L)$
recalled in Section 2.8 encodes the invariants
$(X,L)$
recalled in Section 2.8 encodes the invariants
![]() $\overline {OGW}\!$
along with the genus zero closed Gromov-Witten invariants of X.
$\overline {OGW}\!$
along with the genus zero closed Gromov-Witten invariants of X.
The genus zero closed Gromov-Witten invariants of X are given by multilinear maps
for
![]() $\beta \in H_2(X;\mathbb {Z})$
and
$\beta \in H_2(X;\mathbb {Z})$
and
![]() $l \geq 0.$
For
$l \geq 0.$
For
![]() $A_1,\ldots , A_l \in H^{*}(X;\mathbb {Q}),$
the invariant
$A_1,\ldots , A_l \in H^{*}(X;\mathbb {Q}),$
the invariant
![]() ${GW}_\beta (A_1,\ldots ,A_l)$
counts J-holomorphic maps
${GW}_\beta (A_1,\ldots ,A_l)$
counts J-holomorphic maps
![]() $S^2 \to X$
representing the class
$S^2 \to X$
representing the class
![]() $\beta $
and passing through chosen cycles Poincaré dual to
$\beta $
and passing through chosen cycles Poincaré dual to
![]() $A_1,\ldots ,A_l.$
We recall the basic properties of these invariants in Section 2.
$A_1,\ldots ,A_l.$
We recall the basic properties of these invariants in Section 2.
1.2 Statement of results
Let
![]() $L_\triangle $
denote the Chiang Lagrangian in
$L_\triangle $
denote the Chiang Lagrangian in
![]() $\mathbb {C}P^3$
. In particular,
$\mathbb {C}P^3$
. In particular,
![]() $L_\triangle $
is a rational homology sphere, so the open Gromov-Witten invariants
$L_\triangle $
is a rational homology sphere, so the open Gromov-Witten invariants
![]() $\overline {OGW}\!_{\beta ,k}$
are defined. The definition of
$\overline {OGW}\!_{\beta ,k}$
are defined. The definition of
![]() $L_\triangle $
is recalled in Section 3. Write
$L_\triangle $
is recalled in Section 3. Write
![]() $\Gamma _0 = [1] \in H^0(L_\triangle ;\mathbb {R}) = \widehat {H}^0(\mathbb {C}P^3,L_\triangle ;\mathbb {R}),$
and for
$\Gamma _0 = [1] \in H^0(L_\triangle ;\mathbb {R}) = \widehat {H}^0(\mathbb {C}P^3,L_\triangle ;\mathbb {R}),$
and for
![]() $j = 1,2,3,$
write
$j = 1,2,3,$
write
Write
![]() $\Delta _j=[\omega ^j] \in H^{*}(\mathbb {C}P^3;\mathbb {R})$
. Take
$\Delta _j=[\omega ^j] \in H^{*}(\mathbb {C}P^3;\mathbb {R})$
. Take
![]() $P_{\mathbb {R}}$
to be the unique left-inverse of y such that
$P_{\mathbb {R}}$
to be the unique left-inverse of y such that
![]() $\ker (P_{\mathbb {R}})=\mathrm {span}\{\Gamma _2\}$
. In light of Lemma 3.4 below, we identify
$\ker (P_{\mathbb {R}})=\mathrm {span}\{\Gamma _2\}$
. In light of Lemma 3.4 below, we identify
![]() $H_2(\mathbb {C}P^3,L_\triangle ;\mathbb {Z}) \simeq \mathbb {Z}.$
Our main results are the following.
$H_2(\mathbb {C}P^3,L_\triangle ;\mathbb {Z}) \simeq \mathbb {Z}.$
Our main results are the following.
Theorem 1.1. The open WDVV equations imply the following relations for the invariants
![]() $\overline {OGW}\!_{\beta , k}$
of
$\overline {OGW}\!_{\beta , k}$
of
![]() $(\mathbb {C}P^3, L_\triangle ).$
$(\mathbb {C}P^3, L_\triangle ).$
-
1. For
 $k \geq 1, l \geq 1 $
, and
$k \geq 1, l \geq 1 $
, and
 $I = \{ j_2,\ldots ,j_l\}$
,
$I = \{ j_2,\ldots ,j_l\}$
,  $$ \begin{align*} & \overline{OGW}\!_{\beta, k} (\Gamma_{j_1}, \Gamma_{j_2},\ldots,\Gamma_{j_l}) \\ &\quad = -\sum_{\substack{\varpi(\hat{\beta}) + \beta_1 = \beta \\ \beta_1 \not= \beta \\ I_1 \sqcup I_2 = I}} \sum_{i = 0}^{3} {GW}_{\hat{\beta}}(\Delta_{j_1 -1}, \Delta_1, \Delta_{I_1}, \Delta_i) \overline{OGW}\!_{\beta_1, k} (\Gamma_{3-i}, \Gamma_{I_2})\\ &\qquad +\sum_{\substack{\beta_1 +\beta_2 = \beta \\ k_1 + k_2 = k - 1 \\ I_1 \sqcup I_2 = I}}\binom{k-1}{k_1} \bigg( \overline{OGW}\!_{\beta_1, k_1} (\Gamma_{j_1 - 1}, \Gamma_1, \Gamma_{I_1}) \overline{OGW}\!_{\beta_2, k_2+2} (\Gamma_{I_2})\\ & \qquad -\overline{OGW}\!_{\beta_1, k_1 + 1}(\Gamma_{j_1 -1}, \Gamma_{I_1})\overline{OGW}\!_{\beta_2, k_2 + 1} (\Gamma_1, \Gamma_{I_2}) \bigg). \end{align*} $$
$$ \begin{align*} & \overline{OGW}\!_{\beta, k} (\Gamma_{j_1}, \Gamma_{j_2},\ldots,\Gamma_{j_l}) \\ &\quad = -\sum_{\substack{\varpi(\hat{\beta}) + \beta_1 = \beta \\ \beta_1 \not= \beta \\ I_1 \sqcup I_2 = I}} \sum_{i = 0}^{3} {GW}_{\hat{\beta}}(\Delta_{j_1 -1}, \Delta_1, \Delta_{I_1}, \Delta_i) \overline{OGW}\!_{\beta_1, k} (\Gamma_{3-i}, \Gamma_{I_2})\\ &\qquad +\sum_{\substack{\beta_1 +\beta_2 = \beta \\ k_1 + k_2 = k - 1 \\ I_1 \sqcup I_2 = I}}\binom{k-1}{k_1} \bigg( \overline{OGW}\!_{\beta_1, k_1} (\Gamma_{j_1 - 1}, \Gamma_1, \Gamma_{I_1}) \overline{OGW}\!_{\beta_2, k_2+2} (\Gamma_{I_2})\\ & \qquad -\overline{OGW}\!_{\beta_1, k_1 + 1}(\Gamma_{j_1 -1}, \Gamma_{I_1})\overline{OGW}\!_{\beta_2, k_2 + 1} (\Gamma_1, \Gamma_{I_2}) \bigg). \end{align*} $$
-
2. For
 $k \geq 2, l \geq 0$
, and
$k \geq 2, l \geq 0$
, and
 $I = \{j_1,\ldots ,j_l\}$
,
$I = \{j_1,\ldots ,j_l\}$
,  $$ \begin{align*} &\overline{OGW}\!_{\beta, k} (\Gamma_{j_1},\ldots,\Gamma_{j_l}) \overline{OGW}\!_{2, 0} (\Gamma_2, \Gamma_2) \\ & \quad = \sum_{\substack{ \varpi(\hat{\beta}) + \beta_1 = \beta+2 \\I_1 \sqcup I_2 = I}} \sum_{i = 0}^{3} {GW}_{\hat{\beta}}(\Delta_2, \Delta_2, \Delta_{I_1}, \Delta_i) \overline{OGW}\!_{\beta_1, k-1}(\Gamma_{3-i}, \Gamma_{I_2})\\ &\qquad + \sum_{\substack{\beta_1 + \beta_2 = \beta +2 \\ k_1 + k_2 = k-2 \\ I_1 \sqcup I_2 = I} } \binom{k-2}{k_1} \overline{OGW}\!_{\beta_1, k_1 + 1} (\Gamma_2, \Gamma_{I_1}) \overline{OGW}\!_{\beta_2, k_2 + 1} ( \Gamma_2, \Gamma_{I_2})\\ & \qquad -\sum_{\substack{\beta_1 + \beta_2 = \beta + 2 \\ k_1 + k_2 = k-2 \\ I_1 \sqcup I_2 = I \\ (\beta_1, k_1) \neq (\beta, k-2) }} \binom{k-2}{k_1} \overline{OGW}\!_{\beta_1, k_1 + 2}(\Gamma_{I_1}) \overline{OGW}\!_{\beta_2, k_2}(\Gamma_2, \Gamma_2, \Gamma_{I_2}). \end{align*} $$
$$ \begin{align*} &\overline{OGW}\!_{\beta, k} (\Gamma_{j_1},\ldots,\Gamma_{j_l}) \overline{OGW}\!_{2, 0} (\Gamma_2, \Gamma_2) \\ & \quad = \sum_{\substack{ \varpi(\hat{\beta}) + \beta_1 = \beta+2 \\I_1 \sqcup I_2 = I}} \sum_{i = 0}^{3} {GW}_{\hat{\beta}}(\Delta_2, \Delta_2, \Delta_{I_1}, \Delta_i) \overline{OGW}\!_{\beta_1, k-1}(\Gamma_{3-i}, \Gamma_{I_2})\\ &\qquad + \sum_{\substack{\beta_1 + \beta_2 = \beta +2 \\ k_1 + k_2 = k-2 \\ I_1 \sqcup I_2 = I} } \binom{k-2}{k_1} \overline{OGW}\!_{\beta_1, k_1 + 1} (\Gamma_2, \Gamma_{I_1}) \overline{OGW}\!_{\beta_2, k_2 + 1} ( \Gamma_2, \Gamma_{I_2})\\ & \qquad -\sum_{\substack{\beta_1 + \beta_2 = \beta + 2 \\ k_1 + k_2 = k-2 \\ I_1 \sqcup I_2 = I \\ (\beta_1, k_1) \neq (\beta, k-2) }} \binom{k-2}{k_1} \overline{OGW}\!_{\beta_1, k_1 + 2}(\Gamma_{I_1}) \overline{OGW}\!_{\beta_2, k_2}(\Gamma_2, \Gamma_2, \Gamma_{I_2}). \end{align*} $$
-
3. For
 $l \geq 2$
, and
$l \geq 2$
, and
 $I = \{j_3,\ldots ,j_l\}$
,
$I = \{j_3,\ldots ,j_l\}$
,  $$ \begin{align*} \overline{OGW}\!_{\beta, k} (\Gamma_{j_1},\ldots,\Gamma_{j_l})& =\overline{OGW}\!_{\beta, k} (\Gamma_{j_1-1},\Gamma_{j_2+1},\Gamma_{j_3},\ldots,\Gamma_{j_l})\\ &\quad + \sum_{\substack{ \varpi(\hat{\beta}) + \beta_1 = \beta \\\beta_1 \neq \beta \\I_1 \sqcup I_2 = I}} \sum_{i = 0}^{3} \bigg({GW}_{\hat{\beta}}(\Delta_1, \Delta_{j_2}, \Delta_{I_1}, \Delta_i) \overline{OGW}\!_{\beta_1, k}(\Gamma_{3-i}, \Gamma_{j_1-1}, \Gamma_{I_2})\\ &\quad -{GW}_{\hat{\beta}}(\Delta_1, \Delta_{j_1-1}, \Delta_{I_1}, \Delta_i) \overline{OGW}\!_{\beta_1, k}(\Gamma_{3-i}, \Gamma_{j_2}, \Gamma_{I_2})\bigg)\\ &\quad +\sum_{\substack{\beta_1 + \beta_2 = \beta \\ k_1 + k_2 = k \\ I_1 \sqcup I_2 = I }} \binom{k}{k_1} \bigg( \overline{OGW}\!_{\beta_1, k_1 }(\Gamma_1, \Gamma_{j_1-1}, \Gamma_{I_1}) \overline{OGW}\!_{\beta_2, k_2+1}(\Gamma_{j_2}, \Gamma_{I_2})\\ &\quad -\overline{OGW}\!_{\beta_1, k_1}(\Gamma_1, \Gamma_{j_2}, \Gamma_{I_1})\overline{OGW}\!_{\beta_2, k_2+1}(\Gamma_{j_1-1}, \Gamma_{I_2})\bigg). \end{align*} $$
$$ \begin{align*} \overline{OGW}\!_{\beta, k} (\Gamma_{j_1},\ldots,\Gamma_{j_l})& =\overline{OGW}\!_{\beta, k} (\Gamma_{j_1-1},\Gamma_{j_2+1},\Gamma_{j_3},\ldots,\Gamma_{j_l})\\ &\quad + \sum_{\substack{ \varpi(\hat{\beta}) + \beta_1 = \beta \\\beta_1 \neq \beta \\I_1 \sqcup I_2 = I}} \sum_{i = 0}^{3} \bigg({GW}_{\hat{\beta}}(\Delta_1, \Delta_{j_2}, \Delta_{I_1}, \Delta_i) \overline{OGW}\!_{\beta_1, k}(\Gamma_{3-i}, \Gamma_{j_1-1}, \Gamma_{I_2})\\ &\quad -{GW}_{\hat{\beta}}(\Delta_1, \Delta_{j_1-1}, \Delta_{I_1}, \Delta_i) \overline{OGW}\!_{\beta_1, k}(\Gamma_{3-i}, \Gamma_{j_2}, \Gamma_{I_2})\bigg)\\ &\quad +\sum_{\substack{\beta_1 + \beta_2 = \beta \\ k_1 + k_2 = k \\ I_1 \sqcup I_2 = I }} \binom{k}{k_1} \bigg( \overline{OGW}\!_{\beta_1, k_1 }(\Gamma_1, \Gamma_{j_1-1}, \Gamma_{I_1}) \overline{OGW}\!_{\beta_2, k_2+1}(\Gamma_{j_2}, \Gamma_{I_2})\\ &\quad -\overline{OGW}\!_{\beta_1, k_1}(\Gamma_1, \Gamma_{j_2}, \Gamma_{I_1})\overline{OGW}\!_{\beta_2, k_2+1}(\Gamma_{j_1-1}, \Gamma_{I_2})\bigg). \end{align*} $$
Theorem 1.2. Consider the choice of spin structure and orientation on
![]() $L_\triangle $
given in Section 3.2. Then
$L_\triangle $
given in Section 3.2. Then
It follows from the open WDVV equations that
![]() $\overline {OGW}\!_{2,0}(\Gamma _2, \Gamma _2)=\frac {35}{64}.$
$\overline {OGW}\!_{2,0}(\Gamma _2, \Gamma _2)=\frac {35}{64}.$
We call the invariants
![]() $\overline {OGW}\!_{1,1}, \overline {OGW}\!_{1,0}(\Gamma _2)$
and
$\overline {OGW}\!_{1,1}, \overline {OGW}\!_{1,0}(\Gamma _2)$
and
![]() $\overline {OGW}\!_{2,0}(\Gamma )$
basic invariants. Theorem 1.6 below shows that these invariants are given by straightforward counts of J-holomorphic disks without correction terms. Thus, we can compute the basic invariants using the theory of axial disks developed by Evans-Lekili [Reference Evans and Lekili10] and Smith [Reference Smith43, Reference Smith44] for computing the Floer cohomology of the Chiang Lagrangian and other homogeneous Lagrangian submanifolds. Since the Chiang Lagrangian is not fixed by an anti-symplectic involution, the techniques of real algebraic geometry used in other computations of open Gromov-Witten invariants [Reference Chen and Zinger7, Reference Horev and Solomon28, Reference Hugtenburg and Tukachinsky29, Reference Solomon and Tukachinsky48] are not available.
$\overline {OGW}\!_{2,0}(\Gamma )$
basic invariants. Theorem 1.6 below shows that these invariants are given by straightforward counts of J-holomorphic disks without correction terms. Thus, we can compute the basic invariants using the theory of axial disks developed by Evans-Lekili [Reference Evans and Lekili10] and Smith [Reference Smith43, Reference Smith44] for computing the Floer cohomology of the Chiang Lagrangian and other homogeneous Lagrangian submanifolds. Since the Chiang Lagrangian is not fixed by an anti-symplectic involution, the techniques of real algebraic geometry used in other computations of open Gromov-Witten invariants [Reference Chen and Zinger7, Reference Horev and Solomon28, Reference Hugtenburg and Tukachinsky29, Reference Solomon and Tukachinsky48] are not available.
Corollary 1.3. The genus zero open Gromov-Witten invariants of
![]() $(\mathbb {C}P^3, L_\triangle )$
are entirely determined by the open WDVV equations, the axioms of
$(\mathbb {C}P^3, L_\triangle )$
are entirely determined by the open WDVV equations, the axioms of
![]() $\overline {OGW}\!$
, the wall-crossing formula Theorem 2.3, the genus zero closed Gromov-Witten invariants of
$\overline {OGW}\!$
, the wall-crossing formula Theorem 2.3, the genus zero closed Gromov-Witten invariants of
![]() $\mathbb {C}P^3$
, and the values computed in Theorem 1.2.
$\mathbb {C}P^3$
, and the values computed in Theorem 1.2.
Samples values for the invariants
![]() $\overline {OGW}\!$
computed using Theorems 1.1 and 1.2 are given in Tables 1 and 2.
$\overline {OGW}\!$
computed using Theorems 1.1 and 1.2 are given in Tables 1 and 2.
Table 1 Values of invariants with boundary constraints only.

Table 2 Values of
![]() $\overline {OGW}\!_{\beta ,0}(\Gamma _2^{\otimes l_2},\Gamma _3^{\otimes l_3})$
. The value of
$\overline {OGW}\!_{\beta ,0}(\Gamma _2^{\otimes l_2},\Gamma _3^{\otimes l_3})$
. The value of
![]() $l_2$
is determined by
$l_2$
is determined by
![]() $\beta $
and
$\beta $
and
![]() $l_3$
by the open degree axiom.
$l_3$
by the open degree axiom.

1.2.1 Monotonicity versus periodicity
In other computations [Reference Itenberg, Kharlamov and Shustin30, Reference Itenberg, Kharlamov and Shustin31, Reference Itenberg, Kharlamov and Shustin32, Reference Pandharipande, Solomon and Walcher40, Reference Solomon and Tukachinsky48, Reference Horev and Solomon28, Reference Farajzadeh Tehrani11, Reference Chen and Zinger7], the absolute values of
![]() $\overline {OGW}\!_{\beta ,k}$
or invariants of a similar flavor are monotonically increasing in
$\overline {OGW}\!_{\beta ,k}$
or invariants of a similar flavor are monotonically increasing in
![]() $\beta .$
In the case of
$\beta .$
In the case of
![]() $(\mathbb {C}P^3,L_\triangle )$
, we see that these values are not monotonically increasing. Interestingly, it appears that the only persistent violation of monotonicity occurs periodically:
$(\mathbb {C}P^3,L_\triangle )$
, we see that these values are not monotonically increasing. Interestingly, it appears that the only persistent violation of monotonicity occurs periodically:
![]() $|\overline {OGW}\!_{\beta -1,\beta -1}|>|\overline {OGW}\!_{\beta ,\beta }|$
for
$|\overline {OGW}\!_{\beta -1,\beta -1}|>|\overline {OGW}\!_{\beta ,\beta }|$
for
![]() $\beta \in 8\mathbb {Z}$
at least up to
$\beta \in 8\mathbb {Z}$
at least up to
![]() $\beta = 32.$
$\beta = 32.$
Another unusual periodicity is visible in the signs of the invariants presented in Table 1, which repeat with period
![]() $16.$
Moreover, the sign is inverted when
$16.$
Moreover, the sign is inverted when
![]() $\beta $
is increased by
$\beta $
is increased by
![]() $8.$
$8.$
1.2.2 Bounding cochain corrections and denominators
In [Reference Evans and Lekili10], Evans-Lekili proved that there are exactly two J-holomorphic disks representing the class
![]() $\beta = 2 \in H_2(\mathbb {C}P^3,L_\triangle ;\mathbb {Z})$
passing through a specific choice of two points in
$\beta = 2 \in H_2(\mathbb {C}P^3,L_\triangle ;\mathbb {Z})$
passing through a specific choice of two points in
![]() $L_\triangle $
. This does not coincide with our computation
$L_\triangle $
. This does not coincide with our computation
![]() $\overline {OGW}\!_{2,2}=-\frac {5}{4}$
. The discrepancy reflects correction terms arising from a bounding cochain in the Fukaya
$\overline {OGW}\!_{2,2}=-\frac {5}{4}$
. The discrepancy reflects correction terms arising from a bounding cochain in the Fukaya
![]() $A_\infty $
algebra of
$A_\infty $
algebra of
![]() $L_\triangle .$
The correction terms need not be whole numbers. In fact, all invariants with only boundary constraints that are not whole numbers indicate the presence of nontrivial correction terms. Table 1 provides several examples. When interior constraints are present, open Gromov-Witten invariants may be non-integral even in the absence of correction terms [Reference Horev and Solomon28].
$L_\triangle .$
The correction terms need not be whole numbers. In fact, all invariants with only boundary constraints that are not whole numbers indicate the presence of nontrivial correction terms. Table 1 provides several examples. When interior constraints are present, open Gromov-Witten invariants may be non-integral even in the absence of correction terms [Reference Horev and Solomon28].
As far as we have calculated, for the Chiang Lagrangian
![]() $L_\triangle $
, the denominators appearing in the invariants
$L_\triangle $
, the denominators appearing in the invariants
![]() $\overline {OGW}\!_{\beta ,k}$
with only boundary constraints are always powers of
$\overline {OGW}\!_{\beta ,k}$
with only boundary constraints are always powers of
![]() $4.$
In the presence of interior constraints, powers of
$4.$
In the presence of interior constraints, powers of
![]() $2$
appear as well. Examining the proof of the existence of bounding cochains in [Reference Solomon and Tukachinsky46], we can see where denominators of
$2$
appear as well. Examining the proof of the existence of bounding cochains in [Reference Solomon and Tukachinsky46], we can see where denominators of
![]() $4$
arise. Namely, the proof uses a
$4$
arise. Namely, the proof uses a
![]() $1$
-cochain h with real coefficients with coboundary equal to a
$1$
-cochain h with real coefficients with coboundary equal to a
![]() $2$
-cocycle g representing the generator of
$2$
-cocycle g representing the generator of
![]() $H^2(L_\triangle ;\mathbb {Z}) \simeq \mathbb {Z}/4\mathbb {Z}.$
Since
$H^2(L_\triangle ;\mathbb {Z}) \simeq \mathbb {Z}/4\mathbb {Z}.$
Since
![]() $[4g] = 0 \in H^2(L_\triangle ;\mathbb {Z}),$
there exists an integral
$[4g] = 0 \in H^2(L_\triangle ;\mathbb {Z}),$
there exists an integral
![]() $1$
-cochain
$1$
-cochain
![]() $\tilde h$
with coboundary equal to
$\tilde h$
with coboundary equal to
![]() $4g$
. So, we can take
$4g$
. So, we can take
![]() $h = \frac {\tilde h}4.$
This is the source of the powers of
$h = \frac {\tilde h}4.$
This is the source of the powers of
![]() $4$
in the denominators of the invariants
$4$
in the denominators of the invariants
![]() $\overline {OGW}\!_{\beta ,k}.$
$\overline {OGW}\!_{\beta ,k}.$
In contrast, the invariants
![]() $\overline {OGW}\!_{\beta ,k}$
with only boundary constraints for the Lagrangian submanifold
$\overline {OGW}\!_{\beta ,k}$
with only boundary constraints for the Lagrangian submanifold
![]() $\mathbb {R} P^{n} \subset \mathbb {C} P^{n}$
with n odd are shown in [Reference Solomon and Tukachinsky48] to be whole numbers. For
$\mathbb {R} P^{n} \subset \mathbb {C} P^{n}$
with n odd are shown in [Reference Solomon and Tukachinsky48] to be whole numbers. For
![]() $n = 3,$
these invariants are shown in [Reference Solomon and Tukachinsky46] to be straightforward disk counts, but for
$n = 3,$
these invariants are shown in [Reference Solomon and Tukachinsky46] to be straightforward disk counts, but for
![]() $n \geq 5$
, they presumably include correction terms arising from bounding cochains. Since
$n \geq 5$
, they presumably include correction terms arising from bounding cochains. Since
![]() $H^{2i}(\mathbb {R} P^n;\mathbb {Z}) \simeq \mathbb {Z}/2$
for
$H^{2i}(\mathbb {R} P^n;\mathbb {Z}) \simeq \mathbb {Z}/2$
for
![]() $0 < i < n/2,$
by the reasoning of the preceding paragraph, one might expect to see powers of
$0 < i < n/2,$
by the reasoning of the preceding paragraph, one might expect to see powers of
![]() $2$
in the denominators of the invariants
$2$
in the denominators of the invariants
![]() $\overline {OGW}\!_{\beta ,k}.$
However, since
$\overline {OGW}\!_{\beta ,k}.$
However, since
![]() $\mathbb {R} P^n$
is fixed by an anti-symplectic involution, (i.e., complex conjugation), holomorphic disks come in pairs. So, in the proof of the existence of bounding cochains in [Reference Solomon and Tukachinsky46], one needs only a
$\mathbb {R} P^n$
is fixed by an anti-symplectic involution, (i.e., complex conjugation), holomorphic disks come in pairs. So, in the proof of the existence of bounding cochains in [Reference Solomon and Tukachinsky46], one needs only a
![]() $(2i-1)$
-cochain h with coboundary equal to twice a
$(2i-1)$
-cochain h with coboundary equal to twice a
![]() $2i$
-cocycle g representing the generator of
$2i$
-cocycle g representing the generator of
![]() $H^{2i}(\mathbb {R} P^n;\mathbb {Z})$
. But
$H^{2i}(\mathbb {R} P^n;\mathbb {Z})$
. But
![]() $[2g] = 0 \in H^{2i}(\mathbb {R} P^n;\mathbb {Z})$
, so h can be chosen to be integral. This explains the absence of denominators. A similar argument should apply for other Lagrangian submanifolds L fixed by an anti-symplectic involution. If all torsion in
$[2g] = 0 \in H^{2i}(\mathbb {R} P^n;\mathbb {Z})$
, so h can be chosen to be integral. This explains the absence of denominators. A similar argument should apply for other Lagrangian submanifolds L fixed by an anti-symplectic involution. If all torsion in
![]() $H^{2i}(L;\mathbb {Z})$
has order
$H^{2i}(L;\mathbb {Z})$
has order
![]() $2$
, then the invariants
$2$
, then the invariants
![]() $\overline {OGW}\!_{\beta ,k}$
should be integral. More generally, if
$\overline {OGW}\!_{\beta ,k}$
should be integral. More generally, if
![]() $H^{2i}(L;\mathbb {Z})$
contains torsion of even order, the rate of growth of the power of
$H^{2i}(L;\mathbb {Z})$
contains torsion of even order, the rate of growth of the power of
![]() $2$
in the denominator of
$2$
in the denominator of
![]() $\overline {OGW}\!_{\beta ,k}$
as a function of
$\overline {OGW}\!_{\beta ,k}$
as a function of
![]() $\omega (\beta )$
should be slower when L is fixed by an anti-symplectic involution than otherwise. In particular, the behavior of denominators in the invariants
$\omega (\beta )$
should be slower when L is fixed by an anti-symplectic involution than otherwise. In particular, the behavior of denominators in the invariants
![]() $\overline {OGW}\!_{\beta ,k}$
could potentially be used to prove that a Lagrangian submanifold is not fixed by an anti-symplectic involution.
$\overline {OGW}\!_{\beta ,k}$
could potentially be used to prove that a Lagrangian submanifold is not fixed by an anti-symplectic involution.
1.2.3 Mixed disk and sphere invariants
As mentioned above, the invariants
![]() $\overline {OGW}\!_{\beta ,k}$
for
$\overline {OGW}\!_{\beta ,k}$
for
![]() $\beta \in \operatorname {\mathrm {Im}}\varpi $
and
$\beta \in \operatorname {\mathrm {Im}}\varpi $
and
![]() $k = 0$
count J-holomorphic disks and J-holomorphic spheres together. In other computations [Reference Solomon and Tukachinsky48, Reference Hugtenburg and Tukachinsky29], these mixed disk and sphere invariants vanish for a natural choice of
$k = 0$
count J-holomorphic disks and J-holomorphic spheres together. In other computations [Reference Solomon and Tukachinsky48, Reference Hugtenburg and Tukachinsky29], these mixed disk and sphere invariants vanish for a natural choice of
![]() $P_{\mathbb {R}}.$
Another family of invariants combining counts of J-holomorphic maps of different topology has also been shown to vanish in certain examples [Reference Farajzadeh Tehrani11].
$P_{\mathbb {R}}.$
Another family of invariants combining counts of J-holomorphic maps of different topology has also been shown to vanish in certain examples [Reference Farajzadeh Tehrani11].
We show that the mixed disk and sphere invariants of
![]() $(\mathbb {C}P^3,L_\triangle )$
do not vanish. As shown in Lemma 3.4 below, the map
$(\mathbb {C}P^3,L_\triangle )$
do not vanish. As shown in Lemma 3.4 below, the map
![]() $\varpi : H_2(\mathbb {C}P^3;\mathbb {Z}) \to H_2(\mathbb {C}P^3,L_\triangle ;\mathbb {Z})\simeq \mathbb {Z}$
is given by multiplication by
$\varpi : H_2(\mathbb {C}P^3;\mathbb {Z}) \to H_2(\mathbb {C}P^3,L_\triangle ;\mathbb {Z})\simeq \mathbb {Z}$
is given by multiplication by
![]() $4.$
So, the nonvanishing of mixed disk and sphere invariants is visible in Table 2 for
$4.$
So, the nonvanishing of mixed disk and sphere invariants is visible in Table 2 for
![]() $\beta = 4,8.$
In fact, Corollary 1.4 below asserts that this nonvanishing persists for any choice of
$\beta = 4,8.$
In fact, Corollary 1.4 below asserts that this nonvanishing persists for any choice of
![]() $P_{\mathbb {R}}.$
$P_{\mathbb {R}}.$
Let
![]() $\rho : \widehat {H}^{4}(\mathbb {C}P^3,L_\triangle ;\mathbb {R})\rightarrow H^{4}(\mathbb {C}P^3;\mathbb {R})$
denote the natural map. Let
$\rho : \widehat {H}^{4}(\mathbb {C}P^3,L_\triangle ;\mathbb {R})\rightarrow H^{4}(\mathbb {C}P^3;\mathbb {R})$
denote the natural map. Let
![]() $P_{\mathbb {R}},P_{\mathbb {R}}^{\prime }$
be two choices of left inverse maps of y with associated invariants
$P_{\mathbb {R}},P_{\mathbb {R}}^{\prime }$
be two choices of left inverse maps of y with associated invariants
![]() $\overline {OGW}\!_{\beta ,k}$
and
$\overline {OGW}\!_{\beta ,k}$
and
![]() $\overline {OGW}\!\,'\!\!_{\beta ,k}$
, respectively. The long exact sequence of the pair
$\overline {OGW}\!\,'\!\!_{\beta ,k}$
, respectively. The long exact sequence of the pair
![]() $(\mathbb {C}P^3,L_\triangle )$
implies there exists a map
$(\mathbb {C}P^3,L_\triangle )$
implies there exists a map
such that
![]() $\mathfrak {p}_{\mathbb {R}}\circ \rho =P_{\mathbb {R}}-P_{\mathbb {R}}^{\prime }.$
We use Poincaré duality to identify
$\mathfrak {p}_{\mathbb {R}}\circ \rho =P_{\mathbb {R}}-P_{\mathbb {R}}^{\prime }.$
We use Poincaré duality to identify
![]() $H^3(L_\triangle ;\mathbb {R})\simeq \mathbb {R}.$
$H^3(L_\triangle ;\mathbb {R})\simeq \mathbb {R}.$
Theorem 1.1. For
![]() $\beta \in \operatorname {\mathrm {Im}} \varpi ,$
we have
$\beta \in \operatorname {\mathrm {Im}} \varpi ,$
we have
Corollary 1.4. There is no map
![]() $P_{\mathbb {R}}:\widehat {H}^{4}(\mathbb {C}P^3,L_\triangle ;\mathbb {R})\rightarrow H^3(L_\triangle ;\mathbb {R})$
such that
$P_{\mathbb {R}}:\widehat {H}^{4}(\mathbb {C}P^3,L_\triangle ;\mathbb {R})\rightarrow H^3(L_\triangle ;\mathbb {R})$
such that
![]() $\overline {OGW}\!_{\beta ,k}$
vanishes for every
$\overline {OGW}\!_{\beta ,k}$
vanishes for every
![]() $\beta \in \operatorname {\mathrm {Im}}\varpi $
and
$\beta \in \operatorname {\mathrm {Im}}\varpi $
and
![]() $k=0.$
$k=0.$
Proposition 1.1 is a special case of Proposition 8.1, which gives the analogous statement for X a general symplectic manifold and L a connected spin Lagrangian submanifold with
![]() $H^{*}(L;\mathbb {R}) \simeq H^{*}(S^n;\mathbb {R})$
and
$H^{*}(L;\mathbb {R}) \simeq H^{*}(S^n;\mathbb {R})$
and
![]() $[L] = 0 \in H_n(X;\mathbb {R}).$
In fact, Proposition 8.1 remains valid in all situations where the invariants
$[L] = 0 \in H_n(X;\mathbb {R}).$
In fact, Proposition 8.1 remains valid in all situations where the invariants
![]() $\overline {OGW}\!$
are defined in [Reference Solomon and Tukachinsky48].
$\overline {OGW}\!$
are defined in [Reference Solomon and Tukachinsky48].
1.2.4 Relative quantum cohomology
It follows from Corollary 1.3 that we can compute the big relative quantum cohomology of
![]() $(\mathbb {C}P^3,L_\triangle ).$
The resulting ring does not appear to have a tractable presentation by generators and relations. However, the small relative quantum cohomology of
$(\mathbb {C}P^3,L_\triangle ).$
The resulting ring does not appear to have a tractable presentation by generators and relations. However, the small relative quantum cohomology of
![]() $(\mathbb {C}P^3,L_\triangle )$
is more accessible.
$(\mathbb {C}P^3,L_\triangle )$
is more accessible.
Theorem 1.5. The small relative quantum cohomology of
![]() $(\mathbb {C}P^3,L_\triangle )$
is given by
$(\mathbb {C}P^3,L_\triangle )$
is given by
with
Computations of small relative quantum cohomology for a variety of pairs
![]() $(X,L)$
are given in [Reference Hugtenburg and Tukachinsky29]. However, all Lagrangian submanifolds considered there are fixed by an anti-symplectic involution. The definitions of big and small quantum cohomology are recalled in Section 2.8.
$(X,L)$
are given in [Reference Hugtenburg and Tukachinsky29]. However, all Lagrangian submanifolds considered there are fixed by an anti-symplectic involution. The definitions of big and small quantum cohomology are recalled in Section 2.8.
1.2.5 Invariants without corrections
The proof of Theorem 1.2 depends on the following general result, which says when the invariants
![]() $\overline {OGW}\!_{\beta ,k}$
can be computed without taking into account correction terms from bounding cochains. For simplicity, we continue as in Section 1.1 with L a connected spin Lagrangian with
$\overline {OGW}\!_{\beta ,k}$
can be computed without taking into account correction terms from bounding cochains. For simplicity, we continue as in Section 1.1 with L a connected spin Lagrangian with
![]() $H^{*}(L;\mathbb {R}) \simeq H^{*}(S^n;\mathbb {R}).$
A similar result holds in other settings where the invariants
$H^{*}(L;\mathbb {R}) \simeq H^{*}(S^n;\mathbb {R}).$
A similar result holds in other settings where the invariants
![]() $\overline {OGW}\!$
can be defined. For
$\overline {OGW}\!$
can be defined. For
![]() $\beta \in H_2(X,L;\mathbb {Z})$
, define
$\beta \in H_2(X,L;\mathbb {Z})$
, define
Let
![]() $\sigma _k = (k-1)!$
for
$\sigma _k = (k-1)!$
for
![]() $k \in \mathbb {Z}_{>0}$
and let
$k \in \mathbb {Z}_{>0}$
and let
![]() $\sigma _0 = 1.$
$\sigma _0 = 1.$
Theorem 1.6. Let
![]() $k \in \mathbb {Z}_{\geq 0}$
and
$k \in \mathbb {Z}_{\geq 0}$
and
![]() $\beta \in H_2(X,L;\mathbb {Z})$
satisfy either
$\beta \in H_2(X,L;\mathbb {Z})$
satisfy either
![]() $k> 0$
or
$k> 0$
or
![]() $\beta \not \in \operatorname {\mathrm {Im}} \varpi $
. Let
$\beta \not \in \operatorname {\mathrm {Im}} \varpi $
. Let
![]() $A_{j}\in \widehat {H}^{*}(X,L;\mathbb {R})$
. Let
$A_{j}\in \widehat {H}^{*}(X,L;\mathbb {R})$
. Let
![]() $\bar {b}\in A^n(L;\mathbb {R})$
such that
$\bar {b}\in A^n(L;\mathbb {R})$
such that
![]() $\text {PD}([\bar {b}])=pt$
, and let
$\text {PD}([\bar {b}])=pt$
, and let
![]() $a_{j}$
be a representative of
$a_{j}$
be a representative of
![]() $A_{j}$
. Suppose that for every
$A_{j}$
. Suppose that for every
one of the following two conditions is satisfied:
-
1.
 $1-\mu (\tilde {\beta }) +j(n-1) + \sum _{i\in I} (|A_{i}|-2)<0,$
or
$1-\mu (\tilde {\beta }) +j(n-1) + \sum _{i\in I} (|A_{i}|-2)<0,$
or -
2.
 $1-\mu (\tilde {\beta }) +j(n-1) + \sum _{i\in I} (|A_{i}|-2)\ge n-1.$
$1-\mu (\tilde {\beta }) +j(n-1) + \sum _{i\in I} (|A_{i}|-2)\ge n-1.$
Then,
 $$\begin{align*}\overline{OGW}\!_{\beta,k}(A_{1},\ldots,A_{l})= (-1)^n \sigma_k\int_{\mathcal{M}_{k,l}(\beta)} \bigwedge_{j=1}^{l} evi^{\beta*}_j a_{j} \bigwedge_{j=1}^{k}evb^{\beta*}_j\bar{b}. \end{align*}$$
$$\begin{align*}\overline{OGW}\!_{\beta,k}(A_{1},\ldots,A_{l})= (-1)^n \sigma_k\int_{\mathcal{M}_{k,l}(\beta)} \bigwedge_{j=1}^{l} evi^{\beta*}_j a_{j} \bigwedge_{j=1}^{k}evb^{\beta*}_j\bar{b}. \end{align*}$$
Theorem 1.6 is a special case of Theorem 4.19. The basic invariants
![]() $\overline {OGW}\!_{1,1}, \overline {OGW}\!_{1,0}(\Gamma _2)$
and
$\overline {OGW}\!_{1,1}, \overline {OGW}\!_{1,0}(\Gamma _2)$
and
![]() $\overline {OGW}\!_{2,0}(\Gamma _3)$
of Theorem 1.2 are exactly the invariants to which Theorem 1.6 applies for L the Chiang Lagrangian.
$\overline {OGW}\!_{2,0}(\Gamma _3)$
of Theorem 1.2 are exactly the invariants to which Theorem 1.6 applies for L the Chiang Lagrangian.
1.2.6 Orientation, spin structure and signs
We prove general formulas governing the dependence of the invariants
![]() $\overline {OGW}\!_{\beta ,k}$
on the spin structure and orientation of L, which appear as the spin axiom 7 and the orientation axiom 8 of Proposition 2.2. See also Lemmas 4.5 and 4.6. We use the spin and orientation axioms to deduce vanishing results for certain open Gromov-Witten invariants, which are formulated in Corollaries 4.7 and 4.8.
$\overline {OGW}\!_{\beta ,k}$
on the spin structure and orientation of L, which appear as the spin axiom 7 and the orientation axiom 8 of Proposition 2.2. See also Lemmas 4.5 and 4.6. We use the spin and orientation axioms to deduce vanishing results for certain open Gromov-Witten invariants, which are formulated in Corollaries 4.7 and 4.8.
A significant part of the present paper is devoted to computing the signs of the three basic invariants of Theorem 1.2. The spin and orientation axioms show that by changing the orientation and spin structure on
![]() $L_\triangle $
, one can adjust the signs of any two of the basic invariants arbitrarily. Moreover, changing the orientation and spin structure only affects the signs of invariants but not their absolute values.
$L_\triangle $
, one can adjust the signs of any two of the basic invariants arbitrarily. Moreover, changing the orientation and spin structure only affects the signs of invariants but not their absolute values.
However, it can be seen from the proof of Lemma 6.1 that if the sign of one of the three basic invariants is changed while the two others are held fixed, then the absolute values of non-basic invariants change. Qualitatively, the denominators of invariants cease to be powers of two.
1.2.7 Arithmetic structure of the open WDVV equations
From the perspective of Theorem 1.1, it is surprising that only powers of
![]() $2$
appear in the denominators of the invariants
$2$
appear in the denominators of the invariants
![]() $\overline {OGW}\!$
for the Chiang Lagrangian
$\overline {OGW}\!$
for the Chiang Lagrangian
![]() $L_\triangle .$
Indeed, to use relation 2 for recursive computations, it is necessary to divide by
$L_\triangle .$
Indeed, to use relation 2 for recursive computations, it is necessary to divide by
![]() $\overline {OGW}\!_{2,0}(\Gamma _2,\Gamma _2) = \frac {35}{64}.$
A priori, this should introduce factors of
$\overline {OGW}\!_{2,0}(\Gamma _2,\Gamma _2) = \frac {35}{64}.$
A priori, this should introduce factors of
![]() $5$
and
$5$
and
![]() $7$
in denominators, but unexpected cancellations occur so that only factors of
$7$
in denominators, but unexpected cancellations occur so that only factors of
![]() $2$
remain.
$2$
remain.
To test the rigidity of these cancellations, we searched for rational numbers
![]() $v \neq 1/4$
that upon substitution for the value of
$v \neq 1/4$
that upon substitution for the value of
![]() $\overline {OGW}\!_{1,0}(\Gamma _2)$
in the recursive scheme of Corollary 1.3 yield
$\overline {OGW}\!_{1,0}(\Gamma _2)$
in the recursive scheme of Corollary 1.3 yield
![]() $\overline {OGW}\!_{k,k}$
with denominator a power of
$\overline {OGW}\!_{k,k}$
with denominator a power of
![]() $2$
for
$2$
for
![]() $k = 1,\ldots ,M.$
As M increases, the magnitudes of the possible numerators and denominators of v increase. For
$k = 1,\ldots ,M.$
As M increases, the magnitudes of the possible numerators and denominators of v increase. For
![]() $M = 4,$
the v with smallest numerator and denominator that we found is
$M = 4,$
the v with smallest numerator and denominator that we found is
For this choice of
![]() $v,$
the value for
$v,$
the value for
![]() $\overline {OGW}\!_{5,5}$
given by the recursive scheme has denominator
$\overline {OGW}\!_{5,5}$
given by the recursive scheme has denominator
![]() $7.$
$7.$
Therefore, we reach the following conclusion. Suppose it were possible to formalize the heuristic argument of Section 1.2.2 to prove geometrically that the invariants
![]() $\overline {OGW}\!_{\beta ,k}$
can only have powers of
$\overline {OGW}\!_{\beta ,k}$
can only have powers of
![]() $2$
for denominators. Then, it seems reasonable to expect that the basic invariant
$2$
for denominators. Then, it seems reasonable to expect that the basic invariant
![]() $\overline {OGW}\!_{1,0}(\Gamma _2)$
could be deduced from the other two basic invariants, the open WDVV equations, the axioms of
$\overline {OGW}\!_{1,0}(\Gamma _2)$
could be deduced from the other two basic invariants, the open WDVV equations, the axioms of
![]() $\overline {OGW}\!$
, and the closed Gromov-Witten invariants of
$\overline {OGW}\!$
, and the closed Gromov-Witten invariants of
![]() $\mathbb {C}P^3.$
$\mathbb {C}P^3.$
If it were necessary to compute only two basic invariants geometrically, it would not be necessary to compute their signs. Indeed, these signs could be adjusted arbitrarily by changing the orientation and spin structure on
![]() $L_\triangle $
as noted in Section 1.2.6. Thus, the computations of this paper could be simplified significantly. In fact, this strategy can be generalized for an arbitrary pair
$L_\triangle $
as noted in Section 1.2.6. Thus, the computations of this paper could be simplified significantly. In fact, this strategy can be generalized for an arbitrary pair
![]() $(X,L)$
as outlined below.
$(X,L)$
as outlined below.
1.3 Directions for future research
Remarkably, Theorem 1.6 applies exactly for those invariants that are needed as initial values for the recursions given by Theorem 1.1. It is an interesting question to determine to what extent this phenomenon persists more generally.
We expect the techniques of the present paper to extend to the other Platonic Lagrangians studied by Smith [Reference Smith43] and more general homogeneous Lagrangians [Reference Bedulli and Gori3, Reference Gasparim, San Martin and Valencia23, Reference Konstantinov33]
Motivated by the discussion of Section 1.2.7, we formulate the following two hypotheses. These hypotheses should hold for a large class of Lagrangian submanifolds
![]() $L \subset X$
, but some restrictions are necessary.
$L \subset X$
, but some restrictions are necessary.
-
1. The invariants
 $\overline {OGW}\!_{\beta ,k}$
are rational of the form
$\overline {OGW}\!_{\beta ,k}$
are rational of the form
 $\frac {m}{p_1^{a_1}\cdots p_N^{a_N}}$
where
$\frac {m}{p_1^{a_1}\cdots p_N^{a_N}}$
where
 $p_1,\ldots ,p_N$
are the primes that occur as orders of torsion elements in
$p_1,\ldots ,p_N$
are the primes that occur as orders of torsion elements in
 $H^{*}(L;\mathbb {Z}).$
$H^{*}(L;\mathbb {Z}).$
-
2. Let
 $\mathcal {A}$
be a minimal set of the invariants
$\mathcal {A}$
be a minimal set of the invariants
 $\overline {OGW}\!_{\beta ,k}$
from which all other invariants can be deduced using the open WDVV equations, the axioms of
$\overline {OGW}\!_{\beta ,k}$
from which all other invariants can be deduced using the open WDVV equations, the axioms of
 $\overline {OGW}\!$
, the wall-crossing formula, and the closed GW invariants of X. Let
$\overline {OGW}\!$
, the wall-crossing formula, and the closed GW invariants of X. Let
 $\mathcal {B} \subset \mathcal {A}$
be defined in the same way as
$\mathcal {B} \subset \mathcal {A}$
be defined in the same way as
 $\mathcal {A}$
except that we are also allowed to use hypothesis 1 to deduce the other invariants. Then
$\mathcal {A}$
except that we are also allowed to use hypothesis 1 to deduce the other invariants. Then
 $\mathcal {B}$
is a proper subset of
$\mathcal {B}$
is a proper subset of
 $\mathcal {A}.$
$\mathcal {A}.$
Hypothesis 1 follows from the heuristic argument of Section 1.2.2 applied to L of general topology. It should admit a geometric proof. Hypothesis 2 is a statement about the arithmetic structure of the open WDVV equation. In the case of the Chiang Lagrangian, we can take
![]() $\mathcal {A}$
to be the basic invariants
$\mathcal {A}$
to be the basic invariants
![]() $\overline {OGW}\!_{1,1}, \overline {OGW}\!_{1,0}(\Gamma _2)$
and
$\overline {OGW}\!_{1,1}, \overline {OGW}\!_{1,0}(\Gamma _2)$
and
![]() $\overline {OGW}\!_{2,0}(\Gamma _3)$
. Then, the calculations presented in Section 1.2.7 indicate that the invariants
$\overline {OGW}\!_{2,0}(\Gamma _3)$
. Then, the calculations presented in Section 1.2.7 indicate that the invariants
![]() $\overline {OGW}\!_{1,1}$
and
$\overline {OGW}\!_{1,1}$
and
![]() $\overline {OGW}\!_{2,0}(\Gamma _3)$
suffice for
$\overline {OGW}\!_{2,0}(\Gamma _3)$
suffice for
![]() $\mathcal {B}.$
However, in the case
$\mathcal {B}.$
However, in the case
![]() $(X,L) = (\mathbb {C} P^n, \mathbb {R} P^n)$
, one can see that hypothesis 2 does not hold as follows. It is shown in [Reference Solomon and Tukachinsky48, Corollary 1.9] that one can take
$(X,L) = (\mathbb {C} P^n, \mathbb {R} P^n)$
, one can see that hypothesis 2 does not hold as follows. It is shown in [Reference Solomon and Tukachinsky48, Corollary 1.9] that one can take
![]() $\mathcal {A}$
to consist of a single invariant. It follows from either the spin axiom 7 or the orientation axiom 8 of Proposition 2.2 that by changing the spin structure or orientation on L, the sign of this single invariant can be changed without affecting the absolute value of the others – in particular, without violating hypothesis 1. Thus,
$\mathcal {A}$
to consist of a single invariant. It follows from either the spin axiom 7 or the orientation axiom 8 of Proposition 2.2 that by changing the spin structure or orientation on L, the sign of this single invariant can be changed without affecting the absolute value of the others – in particular, without violating hypothesis 1. Thus,
![]() $\mathcal {B}$
cannot be smaller than
$\mathcal {B}$
cannot be smaller than
![]() $\mathcal {A}.$
Another case where hypothesis 2 does not hold is when X is the quadric hypersurface in
$\mathcal {A}.$
Another case where hypothesis 2 does not hold is when X is the quadric hypersurface in
![]() $\mathbb {C} P^{n+1}$
given by
$\mathbb {C} P^{n+1}$
given by
![]() $\sum _{i = 0}^n z_i^2 - z_{n+1}^2 = 0$
and L is the real locus. This is explained in Remark 4.9 based on results of [Reference Hugtenburg and Tukachinsky29], which are related to the orientation axiom.
$\sum _{i = 0}^n z_i^2 - z_{n+1}^2 = 0$
and L is the real locus. This is explained in Remark 4.9 based on results of [Reference Hugtenburg and Tukachinsky29], which are related to the orientation axiom.
We observe the following common feature of the forgoing exceptions to hypothesis 2. In both cases, one can take
![]() $\mathcal {A}$
to contain a single invariant, while there are one or more geometric degree of freedom affecting the values of the invariants: in the case
$\mathcal {A}$
to contain a single invariant, while there are one or more geometric degree of freedom affecting the values of the invariants: in the case
![]() $(X,L) = (\mathbb {C} P^n,\mathbb {R} P^n)$
, there are choices of spin structure and orientation, and in the case of the quadric, there is the choice of orientation. The presence of more geometric degrees of freedom than the size of
$(X,L) = (\mathbb {C} P^n,\mathbb {R} P^n)$
, there are choices of spin structure and orientation, and in the case of the quadric, there is the choice of orientation. The presence of more geometric degrees of freedom than the size of
![]() $\mathcal {A}$
forces a measure of flexibility in the open WDVV equations. In contrast, for the Chiang Lagrangian,
$\mathcal {A}$
forces a measure of flexibility in the open WDVV equations. In contrast, for the Chiang Lagrangian,
![]() $\mathcal {A}$
contains three invariants, while there are only two geometric degrees of freedom, the choices of spin structure and orientation. So, the equations can be sufficiently rigid for hypothesis 2 to hold.
$\mathcal {A}$
contains three invariants, while there are only two geometric degrees of freedom, the choices of spin structure and orientation. So, the equations can be sufficiently rigid for hypothesis 2 to hold.
1.4 Outline
In Section 2, we recall general definitions and results on closed and open Gromov-Witten invariants that will be useful in the other sections. This includes the closed and open axioms, the closed and the open WDVV equations, the wall-crossing formula, and the definitions of small and big relative quantum cohomology.
In Section 3, we recall from [Reference Smith43] a family of Lagrangian homology spheres in Fano threefolds called Platonic Lagrangians. We focus mainly on the Chiang Lagrangian
![]() $L_\triangle $
, which is a special case of this construction, and recall some of its basic properties.
$L_\triangle $
, which is a special case of this construction, and recall some of its basic properties.
Section 4 contains results related to Fukaya
![]() $A_\infty $
algebras, bounding cochains and the superpotential. We recall definitions and results on obstruction theory for bounding cochains from [Reference Solomon and Tukachinsky46]. These are used to prove Theorem 4.19, which gives a criterion for open Gromov-Witten invariants to coincide with straightforward counts of J-holomorphic disks. Theorem 1.6, which is needed for Section 5, is obtained as a special case. We also prove Lemmas 4.5 and 4.6, from which we deduce the spin axiom 7 and the orientation axiom 8 of Proposition 2.2.
$A_\infty $
algebras, bounding cochains and the superpotential. We recall definitions and results on obstruction theory for bounding cochains from [Reference Solomon and Tukachinsky46]. These are used to prove Theorem 4.19, which gives a criterion for open Gromov-Witten invariants to coincide with straightforward counts of J-holomorphic disks. Theorem 1.6, which is needed for Section 5, is obtained as a special case. We also prove Lemmas 4.5 and 4.6, from which we deduce the spin axiom 7 and the orientation axiom 8 of Proposition 2.2.
The goal of Section 5 is to compute the basic invariants that serve as initial values for the recursive formulas. In Sections 5.1-5.3, we recall definitions and results about the anticanonical divisor, the Maslov class and axial disks. In Section 5.4, we give the definition of a spin Riemann-Hilbert pair, recall results on canonical orientations, and prove some new ones. Section 5.5 contains results concerning Riemann-Hilbert pairs arising from a certain type of axial disk. We use these results to compute the basic invariants geometrically in Sections 5.6-5.8.
Section 6 contains the proofs of Theorem 1.1 and Corollary 1.3, which give recursive formulas that determine all open Gromov-Witten invariants of
![]() $(\mathbb {C}P^3,L_\triangle )$
from the three basic invariants.
$(\mathbb {C}P^3,L_\triangle )$
from the three basic invariants.
In Section 7, we compute the small relative cohomology of
![]() $(\mathbb {C}P^3, L_\triangle )$
.
$(\mathbb {C}P^3, L_\triangle )$
.
In Section 8, we recall definitions and results concerning the map
![]() $P_{\mathbb {R}}$
from [Reference Solomon and Tukachinsky48]. These results are used to prove Proposition 8.1, which shows how the invariants
$P_{\mathbb {R}}$
from [Reference Solomon and Tukachinsky48]. These results are used to prove Proposition 8.1, which shows how the invariants
![]() $\overline {OGW}\!$
depend on the map
$\overline {OGW}\!$
depend on the map
![]() $P_{\mathbb {R}}.$
Proposition 1.1 is obtained as a special case. Finally, we prove Corollary 1.4.
$P_{\mathbb {R}}.$
Proposition 1.1 is obtained as a special case. Finally, we prove Corollary 1.4.
2 Background
In this section, we recall definitions and properties of open and closed Gromov-Witten invariants and relative quantum cohomology.
2.1 Invariants
Let
![]() $(X,\omega )$
be a closed symplectic manifold. For
$(X,\omega )$
be a closed symplectic manifold. For
![]() $\beta \in H_2(X;\mathbb {Z})$
and
$\beta \in H_2(X;\mathbb {Z})$
and
![]() $l \geq 0,$
let
$l \geq 0,$
let
denote the standard closed genus zero Gromov-Witten invariant. This invariant counts J-holomorphic maps
![]() $S^2 \to X$
representing the class
$S^2 \to X$
representing the class
![]() $\beta $
passing through cycles Poincaré dual to l cohomology classes on
$\beta $
passing through cycles Poincaré dual to l cohomology classes on
![]() $X.$
$X.$
Let
![]() $L \subset X$
be a closed Lagrangian submanifold. Genus zero open Gromov-Witten invariants are analogous invariants that count J-holomorphic maps
$L \subset X$
be a closed Lagrangian submanifold. Genus zero open Gromov-Witten invariants are analogous invariants that count J-holomorphic maps
![]() $(D,\partial D) \to (X,L)$
along with correction terms arising from bounding cochains. To simplify the exposition, we focus on the case that L is connected and spin, with
$(D,\partial D) \to (X,L)$
along with correction terms arising from bounding cochains. To simplify the exposition, we focus on the case that L is connected and spin, with
![]() $H^{*}(L;\mathbb {R})\simeq H^{*}(S^n; \mathbb {R})$
and
$H^{*}(L;\mathbb {R})\simeq H^{*}(S^n; \mathbb {R})$
and
![]() $[L] = 0 \in H_n(X;\mathbb {R})$
. These conditions hold for the Chiang Lagrangian. Similar results are known [Reference Solomon and Tukachinsky46] in the case that L is only relatively spin or
$[L] = 0 \in H_n(X;\mathbb {R})$
. These conditions hold for the Chiang Lagrangian. Similar results are known [Reference Solomon and Tukachinsky46] in the case that L is only relatively spin or
![]() $[L] \neq 0 \in H_n(X;\mathbb {R}).$
$[L] \neq 0 \in H_n(X;\mathbb {R}).$
Consider the subcomplex of differential forms on X consisting of those with trivial integral on
![]() $L,$
$L,$
 $$\begin{align*}\widehat{A}^{*}(X,L;\mathbb{R}):=\left\{\eta\in A^{*}(X;\mathbb{R})\Big| \int_L \eta|_L=0\right\}.\end{align*}$$
$$\begin{align*}\widehat{A}^{*}(X,L;\mathbb{R}):=\left\{\eta\in A^{*}(X;\mathbb{R})\Big| \int_L \eta|_L=0\right\}.\end{align*}$$
For an
![]() $\mathbb {R}$
-algebra
$\mathbb {R}$
-algebra
![]() $\Upsilon $
, write
$\Upsilon $
, write
Observe that
For
![]() $\beta \in H_2(X,L;\mathbb {Z})$
and
$\beta \in H_2(X,L;\mathbb {Z})$
and
![]() $k,l \geq 0,$
let
$k,l \geq 0,$
let
denote the open Gromov-Witten invariants of [Reference Solomon and Tukachinsky46]. The definition is recalled in Section 4.2. For
![]() $\beta \in H_2(X,L;\mathbb {Z})$
and
$\beta \in H_2(X,L;\mathbb {Z})$
and
![]() $k,l \geq 0,$
let
$k,l \geq 0,$
let
denote the enhanced invariants defined in [Reference Solomon and Tukachinsky48]. The definition is recalled in 8. These invariants combine counts of J-holomorphic disks and J-holomorphic spheres. With the exception of the case that
![]() $\beta $
belongs to the image of the natural map
$\beta $
belongs to the image of the natural map
and
![]() $k = 0,$
we have
$k = 0,$
we have
![]() $\overline {OGW}\! _{\beta ,k} = {OGW}_{\beta ,k}.$
In the exceptional case,
$\overline {OGW}\! _{\beta ,k} = {OGW}_{\beta ,k}.$
In the exceptional case,
![]() ${OGW}_{\beta ,k} = 0,$
but
${OGW}_{\beta ,k} = 0,$
but
![]() $\overline {OGW}\!_{\beta ,k}$
need not vanish. By the assumption
$\overline {OGW}\!_{\beta ,k}$
need not vanish. By the assumption
![]() $[L] = 0 \in H_n(X;\mathbb {R}),$
there is a short exact sequence
$[L] = 0 \in H_n(X;\mathbb {R}),$
there is a short exact sequence
For
![]() $k=0$
and
$k=0$
and
![]() $\beta \in \mathrm {Im \varpi }$
, the definition of the enhanced invariants
$\beta \in \mathrm {Im \varpi }$
, the definition of the enhanced invariants
![]() $\overline {OGW}\!_{\beta ,k}$
depends on the choice of a linear map
$\overline {OGW}\!_{\beta ,k}$
depends on the choice of a linear map
that is a left-inverse to the map y in the short exact sequence. A choice of
![]() $P_{\mathbb {R}}$
is equivalent to a splitting of (2.1). We extend
$P_{\mathbb {R}}$
is equivalent to a splitting of (2.1). We extend
![]() $P_{\mathbb {R}}$
to a map
$P_{\mathbb {R}}$
to a map
![]() $P_{\mathbb {R}}: \widehat {H}^{*}(X,L;\mathbb {R}) \to H^n(L;\mathbb {R})$
by setting it to zero outside
$P_{\mathbb {R}}: \widehat {H}^{*}(X,L;\mathbb {R}) \to H^n(L;\mathbb {R})$
by setting it to zero outside
![]() $\widehat {H}^{n+1}(X,L;\mathbb {R})$
.
$\widehat {H}^{n+1}(X,L;\mathbb {R})$
.
2.2 Axioms
The closed Gromov-Witten invariants satisfy the following properties [Reference Behrend4, Reference Fukaya and Ono22, Reference Kontsevich and Manin34, Reference Li and Tian36, Reference McDuff and Salamon38, Reference McDuff and Salamon37, Reference Ruan and Tian41, Reference Ruan and Tian42].
Theorem 2.1. Let
![]() $\beta \in H_2(X,\mathbb {Z})$
and let
$\beta \in H_2(X,\mathbb {Z})$
and let
![]() $A_1,\ldots ,A_k\in H^{*}(X;\mathbb {R})$
.
$A_1,\ldots ,A_k\in H^{*}(X;\mathbb {R})$
.
-
1. (Effective) If
 $\omega (\beta )<0$
, then
$\omega (\beta )<0$
, then
 ${GW}_{\beta }(A_1,\ldots ,A_k)=0.$
${GW}_{\beta }(A_1,\ldots ,A_k)=0.$
-
2. (Symmetry) For each permutation
 $\sigma \in S_k$
, where
$\sigma \in S_k$
, where $$\begin{align*}{GW}_{\beta}(A_{\sigma(1)},\ldots,A_{\sigma(k)})=(-1)^{s_\sigma(A)}{GW}_{\beta}(A_1,\ldots,A_k),\end{align*}$$
$$\begin{align*}{GW}_{\beta}(A_{\sigma(1)},\ldots,A_{\sigma(k)})=(-1)^{s_\sigma(A)}{GW}_{\beta}(A_1,\ldots,A_k),\end{align*}$$
 $s_\sigma (A):=\sum _{\substack {i<j\\ \sigma (i)<\sigma (j)}}|A_i|\cdot |A_j|.$
$s_\sigma (A):=\sum _{\substack {i<j\\ \sigma (i)<\sigma (j)}}|A_i|\cdot |A_j|.$
-
3. (Degree) If
 $GW_{\beta }(A_1,\ldots ,A_k)\ne 0,$
then
$GW_{\beta }(A_1,\ldots ,A_k)\ne 0,$
then  $$ \begin{align*}\sum_{i=1}^k|A_i|-2k+6= 2n+ 2c_1(\beta).\end{align*} $$
$$ \begin{align*}\sum_{i=1}^k|A_i|-2k+6= 2n+ 2c_1(\beta).\end{align*} $$
-
4. (Fundamental Class) If
 $(\beta ,k)\ne (0,3)$
and
$(\beta ,k)\ne (0,3)$
and
 $k\ge 1,$
then
$k\ge 1,$
then  $$ \begin{align*} GW_{\beta}(A_1,\ldots,A_{k-1},1)=0. \end{align*} $$
$$ \begin{align*} GW_{\beta}(A_1,\ldots,A_{k-1},1)=0. \end{align*} $$
-
5. (Divisor) If
 $(\beta ,k)\ne (0,3)$
,
$(\beta ,k)\ne (0,3)$
,
 $|A_k|=2$
and
$|A_k|=2$
and
 $k\ge 1,$
then
$k\ge 1,$
then  $$ \begin{align*} {GW}_{\beta}(A_1,\ldots,A_k)={GW}_{\beta}(A_1,\ldots,A_{k-1})\cdot \int_\beta A_k.\end{align*} $$
$$ \begin{align*} {GW}_{\beta}(A_1,\ldots,A_k)={GW}_{\beta}(A_1,\ldots,A_{k-1})\cdot \int_\beta A_k.\end{align*} $$
-
6. (Zero) If
 $k \ne 3$
, then
$k \ne 3$
, then
 $GW_{0}(A_1,\ldots ,A_k)=0$
. If
$GW_{0}(A_1,\ldots ,A_k)=0$
. If
 $k=3,$
then
$k=3,$
then  $$ \begin{align*}GW_{0}(A_1,A_2,A_3)= \int_XA_1\smile A_2\smile A_3.\end{align*} $$
$$ \begin{align*}GW_{0}(A_1,A_2,A_3)= \int_XA_1\smile A_2\smile A_3.\end{align*} $$
-
7. (Deformation invariance) The invariants
 ${GW}_\beta $
remain constant under deformations of the symplectic form
${GW}_\beta $
remain constant under deformations of the symplectic form
 $\omega $
.
$\omega $
.
The enhanced open invariants
![]() $\overline {OGW}\!$
satisfy the following properties.
$\overline {OGW}\!$
satisfy the following properties.
Theorem 2.2. Let
![]() $\beta \in H_2(X,L;\mathbb {Z})$
, let
$\beta \in H_2(X,L;\mathbb {Z})$
, let
![]() $k \in \mathbb {Z}_{\geq 0}$
and let
$k \in \mathbb {Z}_{\geq 0}$
and let
![]() $A_1,\ldots ,A_l\in \widehat {H}^{*}(X,L;\mathbb {R})$
.
$A_1,\ldots ,A_l\in \widehat {H}^{*}(X,L;\mathbb {R})$
.
-
1. (Effective) If
 $\omega (\beta )<0,$
then
$\omega (\beta )<0,$
then
 $\overline {OGW}\!_{\beta ,k}(A_1,\ldots ,A_k)=0.$
$\overline {OGW}\!_{\beta ,k}(A_1,\ldots ,A_k)=0.$
-
2. (Symmetry) For each permutation
 $\sigma \in S_l$
, where
$\sigma \in S_l$
, where $$\begin{align*}\overline{OGW}\!_{\beta,k}(A_{\sigma(1)},\ldots,A_{\sigma(l)})=(-1)^{s_\sigma(A)}\overline{OGW}\!_{\beta}(A_1,\ldots,A_l),\end{align*}$$
$$\begin{align*}\overline{OGW}\!_{\beta,k}(A_{\sigma(1)},\ldots,A_{\sigma(l)})=(-1)^{s_\sigma(A)}\overline{OGW}\!_{\beta}(A_1,\ldots,A_l),\end{align*}$$
 $s_\sigma (A):=\sum _{\substack {i<j\\ \sigma (i)<\sigma (j)}}|A_i|\cdot |A_j|.$
$s_\sigma (A):=\sum _{\substack {i<j\\ \sigma (i)<\sigma (j)}}|A_i|\cdot |A_j|.$
-
3. (Degree) If
 $\overline {OGW}\!_{\beta ,k}(A_1,\ldots ,A_l)\ne 0,$
then
$\overline {OGW}\!_{\beta ,k}(A_1,\ldots ,A_l)\ne 0,$
then  $$\begin{align*}n-3+\mu(\beta)+k+2l=kn+\sum_{j=1}^l | A_j|.\end{align*}$$
$$\begin{align*}n-3+\mu(\beta)+k+2l=kn+\sum_{j=1}^l | A_j|.\end{align*}$$
-
4. (Unit/ Fundamental class)
 $$\begin{align*}\overline{OGW}\!_{\beta,k}(1,A_1,\ldots,A_{l-1})= \left\{\begin{array}{ll} -1, & (\beta,k,l)=(\beta_0,1,1)\\ P_{\mathbb{R}}(A_1), & (\beta,k,l)=(\beta_0,0,2)\\ 0, & \mathrm{otherwise}. \end{array} \right. \end{align*}$$
$$\begin{align*}\overline{OGW}\!_{\beta,k}(1,A_1,\ldots,A_{l-1})= \left\{\begin{array}{ll} -1, & (\beta,k,l)=(\beta_0,1,1)\\ P_{\mathbb{R}}(A_1), & (\beta,k,l)=(\beta_0,0,2)\\ 0, & \mathrm{otherwise}. \end{array} \right. \end{align*}$$
-
5. (Zero)
 $$\begin{align*}\overline{OGW}\!_{\beta_0,k}(A_1,\ldots,A_l)= \left\{\begin{array}{ll} -1, & (k,l)=(1,1)\ and\ A_1=1\\ P_{\mathbb{R}}(A_1\smile A_2), & (k,l)=(0,2)\\ 0, &\mathrm{otherwise}. \end{array} \right. \end{align*}$$
$$\begin{align*}\overline{OGW}\!_{\beta_0,k}(A_1,\ldots,A_l)= \left\{\begin{array}{ll} -1, & (k,l)=(1,1)\ and\ A_1=1\\ P_{\mathbb{R}}(A_1\smile A_2), & (k,l)=(0,2)\\ 0, &\mathrm{otherwise}. \end{array} \right. \end{align*}$$
-
6. (Divisor) If
 $| A_l|=2$
, then
$| A_l|=2$
, then  $$\begin{align*}\overline{OGW}\!_{\beta,k}(A_1,\ldots,A_l)= \int_\beta A_l\cdot\overline{OGW}\!_{\beta,k}(A_1,\ldots,A_{l-1}).\end{align*}$$
$$\begin{align*}\overline{OGW}\!_{\beta,k}(A_1,\ldots,A_l)= \int_\beta A_l\cdot\overline{OGW}\!_{\beta,k}(A_1,\ldots,A_{l-1}).\end{align*}$$
-
7. (Spin) Changing the spin structure on L by the action of
 $\alpha \in H^1(L;\mathbb {Z}/2\mathbb {Z})$
changes the sign of
$\alpha \in H^1(L;\mathbb {Z}/2\mathbb {Z})$
changes the sign of
 $\overline {OGW}\!_{\beta ,k}(A_1,...,A_l)$
by the sign
$\overline {OGW}\!_{\beta ,k}(A_1,...,A_l)$
by the sign
 $(-1)^{\alpha (\partial \beta )}.$
$(-1)^{\alpha (\partial \beta )}.$
-
8. (Orientation) Changing the orientation of L changes the sign of
 $\overline {OGW}\!_{\beta ,k}(A_1,...,A_l)$
by the sign
$\overline {OGW}\!_{\beta ,k}(A_1,...,A_l)$
by the sign
 $(-1)^{k+1}.$
$(-1)^{k+1}.$
-
9. (Deformation invariance) The invariants
 $\overline {OGW}\!_{\beta ,k}$
remain constant under deformations of the symplectic form
$\overline {OGW}\!_{\beta ,k}$
remain constant under deformations of the symplectic form
 $\omega $
for which L remains Lagrangian.
$\omega $
for which L remains Lagrangian.
Proof. Axioms 3–6 are given in Proposition 4.19 from [Reference Solomon and Tukachinsky48]. The analogs of Axioms 2 and 9 for the invariants
![]() ${OGW}$
are given in Theorem 4 of [Reference Solomon and Tukachinsky46]. The analogs of Axioms 7 and 8 for the invariants
${OGW}$
are given in Theorem 4 of [Reference Solomon and Tukachinsky46]. The analogs of Axioms 7 and 8 for the invariants
![]() ${OGW}$
are given in Lemmas 4.5 and 4.6 below, respectively. The extension to the invariants
${OGW}$
are given in Lemmas 4.5 and 4.6 below, respectively. The extension to the invariants
![]() $\overline {OGW}\!$
is similar to the proof of Proposition 4.19 in [Reference Solomon and Tukachinsky48]. Axiom 1 follows from the fact that the Novikov ring
$\overline {OGW}\!$
is similar to the proof of Proposition 4.19 in [Reference Solomon and Tukachinsky48]. Axiom 1 follows from the fact that the Novikov ring
![]() $\Lambda $
consists of power series in
$\Lambda $
consists of power series in
![]() $T^\beta $
for
$T^\beta $
for
![]() $\omega (\beta ) \geq 0.$
Indeed, the enhanced superpotential
$\omega (\beta ) \geq 0.$
Indeed, the enhanced superpotential
![]() $\overline {\Omega }$
is defined in Section 1.3.3 in [Reference Solomon and Tukachinsky48] as an element of the ring
$\overline {\Omega }$
is defined in Section 1.3.3 in [Reference Solomon and Tukachinsky48] as an element of the ring
![]() $R_W.$
$R_W.$
2.3 Bases
Let
![]() $\Delta _i \in H^{*}(X;\mathbb {R})$
for
$\Delta _i \in H^{*}(X;\mathbb {R})$
for
![]() $i = 0,\ldots ,N,$
be a basis and let
$i = 0,\ldots ,N,$
be a basis and let
![]() $\Gamma _i \in \ker (P_{\mathbb {R}}) \subset \widehat {H}^{*}(X,L;\mathbb {R})$
be the unique classes such that
$\Gamma _i \in \ker (P_{\mathbb {R}}) \subset \widehat {H}^{*}(X,L;\mathbb {R})$
be the unique classes such that
![]() $\rho (\Gamma _i) = \Delta _i$
. Let
$\rho (\Gamma _i) = \Delta _i$
. Let
![]() $\Gamma _{N+1} = y(1).$
We also write
$\Gamma _{N+1} = y(1).$
We also write
![]() $\Gamma _\diamond = y(1).$
For convenience, set
$\Gamma _\diamond = y(1).$
For convenience, set
![]() $\Delta _{N+1} = 0.$
$\Delta _{N+1} = 0.$
2.4 Novikov rings
Let
![]() $\mu : H_2(X,L;\mathbb {Z}) \to \mathbb {Z}$
denote the Maslov index. Define Novikov coefficients rings
$\mu : H_2(X,L;\mathbb {Z}) \to \mathbb {Z}$
denote the Maslov index. Define Novikov coefficients rings
 $$ \begin{gather*} \Lambda:=\left\{\sum_{i=0}^\infty a_iT^{\beta_i}|a_i\in \mathbb{R}, \beta_i\in H_2(X,L;\mathbb{Z}), \omega(\beta_i)\ge0, \lim_{i\rightarrow \infty}{\omega(\beta_i)}=\infty \right\},\\ \Lambda_c:=\left\{\sum_{j=0}^\infty a_jT^{\varpi(\beta_j)}|a_j\in \mathbb{R}, \beta_j\in H_2(X;\mathbb{Z}), \omega(\beta_j)\ge0, \lim_{j\rightarrow \infty}{\omega(\beta_j)}=\infty \right\}\leqslant \Lambda. \end{gather*} $$
$$ \begin{gather*} \Lambda:=\left\{\sum_{i=0}^\infty a_iT^{\beta_i}|a_i\in \mathbb{R}, \beta_i\in H_2(X,L;\mathbb{Z}), \omega(\beta_i)\ge0, \lim_{i\rightarrow \infty}{\omega(\beta_i)}=\infty \right\},\\ \Lambda_c:=\left\{\sum_{j=0}^\infty a_jT^{\varpi(\beta_j)}|a_j\in \mathbb{R}, \beta_j\in H_2(X;\mathbb{Z}), \omega(\beta_j)\ge0, \lim_{j\rightarrow \infty}{\omega(\beta_j)}=\infty \right\}\leqslant \Lambda. \end{gather*} $$
Gradings on
![]() $\Lambda , \Lambda _c$
are defined by declaring
$\Lambda , \Lambda _c$
are defined by declaring
![]() $|T^\beta | = \mu (\beta ).$
Let
$|T^\beta | = \mu (\beta ).$
Let
 $$ \begin{gather*} R_W = \Lambda[[t_0,\ldots,t_{N+1},s]], \\ Q_W = \Lambda_c[[t_0,\ldots,t_{N+1}]], \qquad Q_U = \Lambda_c[[t_0,\ldots,t_N]]. \end{gather*} $$
$$ \begin{gather*} R_W = \Lambda[[t_0,\ldots,t_{N+1},s]], \\ Q_W = \Lambda_c[[t_0,\ldots,t_{N+1}]], \qquad Q_U = \Lambda_c[[t_0,\ldots,t_N]]. \end{gather*} $$
Gradings on
![]() $R_W,Q_W,Q_U,$
are defined by declaring
$R_W,Q_W,Q_U,$
are defined by declaring
![]() $|t_i| = 2-|\Gamma _i|,\, |s| = 1-n.$
$|t_i| = 2-|\Gamma _i|,\, |s| = 1-n.$
2.5 Potentials
The closed Gromov-Witten potential is given by
 $$\begin{align*}\Phi(t_0,\ldots,t_N) = \sum_{\substack{\beta \in H_2(X;\mathbb{Z}) \\ r_i \geq 0}} \frac{T^{\varpi(\beta)} t_N^{r_N} \cdots t_0^{r_0}}{r_N! \cdots r_0!}GW_\beta(\Delta_0^{\otimes r_0} \otimes \cdots \otimes \Delta_N^{\otimes r_N}) \in Q_U.\end{align*}$$
$$\begin{align*}\Phi(t_0,\ldots,t_N) = \sum_{\substack{\beta \in H_2(X;\mathbb{Z}) \\ r_i \geq 0}} \frac{T^{\varpi(\beta)} t_N^{r_N} \cdots t_0^{r_0}}{r_N! \cdots r_0!}GW_\beta(\Delta_0^{\otimes r_0} \otimes \cdots \otimes \Delta_N^{\otimes r_N}) \in Q_U.\end{align*}$$
The enhanced superpotential, which encodes the enhanced open Gromov-Witten invariants
![]() $\overline {OGW}\!_{\beta ,k},$
is given by
$\overline {OGW}\!_{\beta ,k},$
is given by
 $$ \begin{align} \overline{\Omega}(s,t_0,\ldots,t_{N+1}) = \sum_{\substack{\beta\in H_2(X,L;\mathbb{Z})\\k\ge 0\\r_i\ge 0}}\frac{T^\beta s^k t_{N+1}^{r_{N+1}} \cdots t_0^{r_0}}{k! r_{N+1}! \cdots r_0!} \overline{OGW}\!_{\beta,k}(\Gamma_0^{\otimes r_0}\otimes \cdots \otimes \Gamma_{N+1}^{\otimes r_{N+1}}) \in R_W. \end{align} $$
$$ \begin{align} \overline{\Omega}(s,t_0,\ldots,t_{N+1}) = \sum_{\substack{\beta\in H_2(X,L;\mathbb{Z})\\k\ge 0\\r_i\ge 0}}\frac{T^\beta s^k t_{N+1}^{r_{N+1}} \cdots t_0^{r_0}}{k! r_{N+1}! \cdots r_0!} \overline{OGW}\!_{\beta,k}(\Gamma_0^{\otimes r_0}\otimes \cdots \otimes \Gamma_{N+1}^{\otimes r_{N+1}}) \in R_W. \end{align} $$
2.6 WDVV equations
Let
and let
![]() $g^{ij}$
denote the inverse matrix. The following WDVV equations hold for the closed Gromov-Witten potential [Reference Behrend4, Reference Fukaya and Ono22, Reference Kontsevich and Manin34, Reference Li and Tian36, Reference McDuff and Salamon38, Reference McDuff and Salamon37, Reference Ruan and Tian41, Reference Ruan and Tian42, Reference Witten53].
$g^{ij}$
denote the inverse matrix. The following WDVV equations hold for the closed Gromov-Witten potential [Reference Behrend4, Reference Fukaya and Ono22, Reference Kontsevich and Manin34, Reference Li and Tian36, Reference McDuff and Salamon38, Reference McDuff and Salamon37, Reference Ruan and Tian41, Reference Ruan and Tian42, Reference Witten53].
Theorem 2.1 (Closed WDVV equations).
For all quadruples of integers
![]() $i,j,k,l\in \{0,\ldots , n\}$
, the function
$i,j,k,l\in \{0,\ldots , n\}$
, the function
![]() $\Phi =\Phi ^{\mathbb {C}P^n}$
satisfies
$\Phi =\Phi ^{\mathbb {C}P^n}$
satisfies
 $$\begin{align*}\sum_{\mu, \nu=0}^N \partial_{t_i} \partial_{t_j}\partial_{t_\nu}\Phi\cdot g^{\nu \mu}\cdot \partial_{t_\mu} \partial_{t_k} \partial_{t_l}\Phi= \sum_{\mu, \nu=0}^N \partial_{t_j} \partial_{t_k}\partial_{t_\nu}\Phi\cdot g^{\nu \mu}\cdot \partial_{t_\mu} \partial_{t_i} \partial_{t_l}\Phi. \end{align*}$$
$$\begin{align*}\sum_{\mu, \nu=0}^N \partial_{t_i} \partial_{t_j}\partial_{t_\nu}\Phi\cdot g^{\nu \mu}\cdot \partial_{t_\mu} \partial_{t_k} \partial_{t_l}\Phi= \sum_{\mu, \nu=0}^N \partial_{t_j} \partial_{t_k}\partial_{t_\nu}\Phi\cdot g^{\nu \mu}\cdot \partial_{t_\mu} \partial_{t_i} \partial_{t_l}\Phi. \end{align*}$$
The following is Corollary 1.6 from [Reference Solomon and Tukachinsky48].
Theorem 2.2 (Open WDVV equations).
For
![]() $u, v, w = 0,\ldots , N+1,$
we have the open WDVV equations
$u, v, w = 0,\ldots , N+1,$
we have the open WDVV equations
 $$ \begin{align} & \sum_{l,m = 0}^N \partial_{t_u} \partial_{t_l} \overline{\Omega} \cdot g^{lm} \cdot \partial_{t_m} \partial_{t_w} \partial_{t_v} \Phi - \partial_{t_u} \partial_s \overline{\Omega} \cdot \partial_{t_w} \partial_{t_v} \overline{\Omega} \notag\\ & \quad =\sum_{l,m = 0}^N \partial_{t_u} \partial_{t_w} \partial_{t_l} \Phi \cdot g^{lm} \cdot \partial_{t_m} \partial_{t_v} \overline{\Omega} - \partial_{t_u} \partial_{t_w} \overline{\Omega} \cdot \partial_{t_v} \partial_s \overline{\Omega}, \end{align} $$
$$ \begin{align} & \sum_{l,m = 0}^N \partial_{t_u} \partial_{t_l} \overline{\Omega} \cdot g^{lm} \cdot \partial_{t_m} \partial_{t_w} \partial_{t_v} \Phi - \partial_{t_u} \partial_s \overline{\Omega} \cdot \partial_{t_w} \partial_{t_v} \overline{\Omega} \notag\\ & \quad =\sum_{l,m = 0}^N \partial_{t_u} \partial_{t_w} \partial_{t_l} \Phi \cdot g^{lm} \cdot \partial_{t_m} \partial_{t_v} \overline{\Omega} - \partial_{t_u} \partial_{t_w} \overline{\Omega} \cdot \partial_{t_v} \partial_s \overline{\Omega}, \end{align} $$
 $$ \begin{align} \sum_{l,m = 0}^N \partial_s \partial_{t_l} \overline{\Omega} \cdot g^{lm} \cdot \partial_{t_m} \partial_{t_w} \partial_{t_v} \Phi - \partial_s^2 \overline{\Omega} \cdot \partial_{t_w} \partial_{t_v} \overline{\Omega} = -\partial_s \partial_{t_w} \overline{\Omega}\cdot \partial_{t_v} \partial_s \overline{\Omega}. \end{align} $$
$$ \begin{align} \sum_{l,m = 0}^N \partial_s \partial_{t_l} \overline{\Omega} \cdot g^{lm} \cdot \partial_{t_m} \partial_{t_w} \partial_{t_v} \Phi - \partial_s^2 \overline{\Omega} \cdot \partial_{t_w} \partial_{t_v} \overline{\Omega} = -\partial_s \partial_{t_w} \overline{\Omega}\cdot \partial_{t_v} \partial_s \overline{\Omega}. \end{align} $$
2.7 Wall-crossing
Define
The following is Theorem 6 from [Reference Solomon and Tukachinsky48].
Theorem 2.3 (Wall crossing).
Suppose
![]() $[L]=0$
. Then the invariants
$[L]=0$
. Then the invariants
![]() $\overline {OGW}\!_{\beta ,k}$
satisfy
$\overline {OGW}\!_{\beta ,k}$
satisfy
2.8 Relative quantum cohomology
Abbreviate
 $$\begin{align*}\Delta= \sum_{i=0}^N t_i\Delta_i,\quad \Gamma= \sum_{i=0}^{N+1} t_i\Gamma_i.\end{align*}$$
$$\begin{align*}\Delta= \sum_{i=0}^N t_i\Delta_i,\quad \Gamma= \sum_{i=0}^{N+1} t_i\Gamma_i.\end{align*}$$
The underlying module of the big relative quantum cohomology is
The big relative quantum product
is given by

In Theorem 7 of [Reference Solomon and Tukachinsky48], it is shown that the product ![]() is associative and graded commutative. Though in [Reference Solomon and Tukachinsky48] the definition of
is associative and graded commutative. Though in [Reference Solomon and Tukachinsky48] the definition of ![]() is based on a chain-level construction, the above explicit formula follows from Lemma 5.11 in [Reference Solomon and Tukachinsky48].
is based on a chain-level construction, the above explicit formula follows from Lemma 5.11 in [Reference Solomon and Tukachinsky48].
The underlying module of the small relative quantum cohomology is
The small relative quantum product
is given by specializing the big relative quantum product to
![]() $t_0 = \cdots =t_{N+1} = 0.$
So, it too is associated and graded commutative. Explicitly,
$t_0 = \cdots =t_{N+1} = 0.$
So, it too is associated and graded commutative. Explicitly, ![]() is given by
is given by

3 The Chiang Lagrangian
In this section, we describe the construction of the Chiang Lagrangian along with an orientation and spin structure. Then, we prove some lemmas concerning its topology.
3.1 Geometric construction
The following is largely based on [Reference Smith43]. Consider the fundamental representation V of
![]() $\text {SL}(2, \mathbb {C}).$
Projectifying, we obtain an action of
$\text {SL}(2, \mathbb {C}).$
Projectifying, we obtain an action of
![]() $\text {SL}(2, \mathbb {C})$
on
$\text {SL}(2, \mathbb {C})$
on
![]() $\mathbb {C}P^1 = \mathbb {P}(V).$
Taking the d-fold symmetric product, we obtain an action of
$\mathbb {C}P^1 = \mathbb {P}(V).$
Taking the d-fold symmetric product, we obtain an action of
![]() $\text {SL}(2, \mathbb {C})$
on
$\text {SL}(2, \mathbb {C})$
on
![]() $\text {Sym}^d \mathbb {C}P^1 = \mathbb {C}P^d.$
Equivalently, we can consider the d-fold symmetric power
$\text {Sym}^d \mathbb {C}P^1 = \mathbb {C}P^d.$
Equivalently, we can consider the d-fold symmetric power
![]() $S^d V$
and projectify to obtain an action of
$S^d V$
and projectify to obtain an action of
![]() $\text {SL}(2, \mathbb {C})$
on
$\text {SL}(2, \mathbb {C})$
on
![]() $\mathbb {P}(S^dV) = \mathbb {C}P^d.$
$\mathbb {P}(S^dV) = \mathbb {C}P^d.$
Fix
![]() $d\ge 3$
, and a configuration C of d distinct points in
$d\ge 3$
, and a configuration C of d distinct points in
![]() $\mathbb {C}P^1$
. Then, the
$\mathbb {C}P^1$
. Then, the
![]() $\text {SL}(2, \mathbb {C})$
-orbit of C in
$\text {SL}(2, \mathbb {C})$
-orbit of C in
![]() $\text {Sym}^d \mathbb {C}P^1 \cong \mathbb {P}S^dV$
is a three-dimensional complex submanifold, of which the
$\text {Sym}^d \mathbb {C}P^1 \cong \mathbb {P}S^dV$
is a three-dimensional complex submanifold, of which the
![]() $\text {SU}(2)$
-orbit is a three-dimensional totally real submanifold. The stabilizer of C in
$\text {SU}(2)$
-orbit is a three-dimensional totally real submanifold. The stabilizer of C in
![]() $\text {SL}(2, \mathbb {C})$
is a finite subgroup of
$\text {SL}(2, \mathbb {C})$
is a finite subgroup of
![]() $\text {SU}(2)$
which we denote by
$\text {SU}(2)$
which we denote by
![]() $\Gamma _C.$
In [Reference Aluffi and Faber1], Aluffi and Faber identify those configurations C for which the
$\Gamma _C.$
In [Reference Aluffi and Faber1], Aluffi and Faber identify those configurations C for which the
![]() $\text {SL}(2, \mathbb {C})$
-orbit has smooth closure
$\text {SL}(2, \mathbb {C})$
-orbit has smooth closure
![]() $X_C$
in
$X_C$
in
![]() $\mathbb {P}S^dV$
. There are four cases: the vertices of an equilateral triangle on a great circle in
$\mathbb {P}S^dV$
. There are four cases: the vertices of an equilateral triangle on a great circle in
![]() $\mathbb {C}P^1$
, which we denote by
$\mathbb {C}P^1$
, which we denote by
![]() $\triangle $
, and the vertices of a regular tetrahedron, octahedron and icosahedron in
$\triangle $
, and the vertices of a regular tetrahedron, octahedron and icosahedron in
![]() $\mathbb {C}P^1$
, which we denote by
$\mathbb {C}P^1$
, which we denote by
![]() $T, O$
and I, respectively.
$T, O$
and I, respectively.
In each case, the restriction of the
![]() $\text {SU}(2)$
-action to
$\text {SU}(2)$
-action to
![]() $X_C$
with the Fubini- Study Kähler form is Hamiltonian with the moment map
$X_C$
with the Fubini- Study Kähler form is Hamiltonian with the moment map
![]() $m: \mathbb {P}S^dV\rightarrow \mathfrak {su}(2)^{*}$
which is defined by
$m: \mathbb {P}S^dV\rightarrow \mathfrak {su}(2)^{*}$
which is defined by
 $$\begin{align*}\langle m([z]), \xi \rangle=\frac{i}{2}\frac{z^\dagger\varphi(\xi)z}{z^\dagger z}, \qquad \xi\in \mathfrak{su}(2), \end{align*}$$
$$\begin{align*}\langle m([z]), \xi \rangle=\frac{i}{2}\frac{z^\dagger\varphi(\xi)z}{z^\dagger z}, \qquad \xi\in \mathfrak{su}(2), \end{align*}$$
where
![]() $\varphi :\mathfrak {su}(2)\rightarrow \mathrm {Mat}_{(d+1)\times (d+1)}(\mathbb {C})$
is given by the representation
$\varphi :\mathfrak {su}(2)\rightarrow \mathrm {Mat}_{(d+1)\times (d+1)}(\mathbb {C})$
is given by the representation
![]() $S^dV.$
The
$S^dV.$
The
![]() $\text {SU}(2)$
-orbits of the configurations
$\text {SU}(2)$
-orbits of the configurations
![]() $\triangle , T, O$
and I all lie in the zero sets of the respective moment maps, so they are Lagrangian. We denote these orbits by
$\triangle , T, O$
and I all lie in the zero sets of the respective moment maps, so they are Lagrangian. We denote these orbits by
![]() $L_C$
.
$L_C$
.
The Chiang Lagrangian is
![]() $L_{\triangle } \subset X_{\triangle } = \mathbb {P}S^3V \cong \mathbb {C}P^3$
. It is the space of all the equilateral triangles on great circles in
$L_{\triangle } \subset X_{\triangle } = \mathbb {P}S^3V \cong \mathbb {C}P^3$
. It is the space of all the equilateral triangles on great circles in
![]() $\mathbb {C}P^1.$
Topologically,
$\mathbb {C}P^1.$
Topologically,
![]() $L_{\triangle }$
is the quotient of
$L_{\triangle }$
is the quotient of
![]() $\text {SU}(2)$
by the binary dihedral subgroup
$\text {SU}(2)$
by the binary dihedral subgroup
![]() $\Gamma _\triangle $
of order 12.
$\Gamma _\triangle $
of order 12.
To work with the Chiang Lagrangian, we will need the following additional notations. Let
![]() $W_\triangle $
denote the Zariski open
$W_\triangle $
denote the Zariski open
![]() $\text {SL}(2, \mathbb {C})$
-orbit in
$\text {SL}(2, \mathbb {C})$
-orbit in
![]() $\mathbb {C}P^3$
, and let
$\mathbb {C}P^3$
, and let
![]() $Y_\triangle $
denote its complement.
$Y_\triangle $
denote its complement.
![]() $Y_\triangle $
consists of those
$Y_\triangle $
consists of those
![]() $3$
-point configurations in
$3$
-point configurations in
![]() $\mathbb {C}P^3$
where at least
$\mathbb {C}P^3$
where at least
![]() $2$
of the points coincide. Let
$2$
of the points coincide. Let
![]() $N_\triangle \subset Y_\triangle $
be the subvariety consisting of those configurations where all
$N_\triangle \subset Y_\triangle $
be the subvariety consisting of those configurations where all
![]() $3$
points coincide. If
$3$
points coincide. If
![]() $[z_0:\ldots :z_3]$
are standard coordinates on
$[z_0:\ldots :z_3]$
are standard coordinates on
![]() $\mathbb {P}S^3 V$
, then the roots of the polynomial
$\mathbb {P}S^3 V$
, then the roots of the polynomial
correspond (with multiplicity) to the
![]() $3$
-tuple of points obtained by viewing
$3$
-tuple of points obtained by viewing
![]() $[z]$
as a point of
$[z]$
as a point of
![]() $\text {Sym}^3 \mathbb {C}P^1$
. We count
$\text {Sym}^3 \mathbb {C}P^1$
. We count
![]() $\infty $
as a root with multiplicity
$\infty $
as a root with multiplicity
![]() $3 - \deg f$
. Consequently,
$3 - \deg f$
. Consequently,
![]() $Y_\triangle $
is defined by the vanishing of the discriminant
$Y_\triangle $
is defined by the vanishing of the discriminant
![]() $\triangle (f)$
of f.
$\triangle (f)$
of f.
3.2 Orientation and spin structure
Let
![]() $\alpha ,\beta ,\gamma $
be a basis of
$\alpha ,\beta ,\gamma $
be a basis of
![]() $\mathfrak {su}(2)$
corresponding to infinitesimal right-handed rotations about a right-handed set of orthonormal axes. The infinitesimal group action gives rise to a frame for
$\mathfrak {su}(2)$
corresponding to infinitesimal right-handed rotations about a right-handed set of orthonormal axes. The infinitesimal group action gives rise to a frame for
![]() $TL_\triangle ,$
$TL_\triangle ,$
where
![]() $z\in L_\triangle .$
Let
$z\in L_\triangle .$
Let
![]() $\mathfrak {o}_\triangle $
be the orientation on
$\mathfrak {o}_\triangle $
be the orientation on
![]() $L_\triangle $
such that this frame is positively oriented. Let
$L_\triangle $
such that this frame is positively oriented. Let
![]() $\mathfrak {s}_\triangle $
be the spin structure on
$\mathfrak {s}_\triangle $
be the spin structure on
![]() $L_\triangle $
such that this frame can be lifted to the associated double cover of the frame bundle.
$L_\triangle $
such that this frame can be lifted to the associated double cover of the frame bundle.
3.3 Topological lemmas
Equip
![]() $\mathbb {P}S^3V \cong \mathbb {C}P^3$
with the Fubini-Study Kähler form
$\mathbb {P}S^3V \cong \mathbb {C}P^3$
with the Fubini-Study Kähler form
![]() $\omega $
such that
$\omega $
such that
![]() $\int _{\mathbb {C}P^1} \omega =1$
. The following lemma is given in Section 4.3 of [Reference Evans and Lekili10].
$\int _{\mathbb {C}P^1} \omega =1$
. The following lemma is given in Section 4.3 of [Reference Evans and Lekili10].
Lemma 3.1.
![]() $H_1(L_\triangle ;\mathbb {Z})=\mathbb {Z} /4\mathbb {Z}.$
$H_1(L_\triangle ;\mathbb {Z})=\mathbb {Z} /4\mathbb {Z}.$
Lemma 3.2.
![]() $H_2(L_\triangle ;\mathbb {Z})=0$
.
$H_2(L_\triangle ;\mathbb {Z})=0$
.
Proof. By Poincaré duality, it suffices to show
![]() $H^1(L;\mathbb {Z})=0$
. By the universal coefficients theorem, we get the following short exact sequence
$H^1(L;\mathbb {Z})=0$
. By the universal coefficients theorem, we get the following short exact sequence
By Lemma 3.1
![]() $H_1(L_\triangle ;\mathbb {Z})=\mathbb {Z}/4\mathbb {Z}$
. In addition,
$H_1(L_\triangle ;\mathbb {Z})=\mathbb {Z}/4\mathbb {Z}$
. In addition,
![]() $L_\triangle $
is connected, so
$L_\triangle $
is connected, so
![]() $H_0(L_\triangle ;\mathbb {Z})=\mathbb {Z}$
. Hence, we get an exact sequence
$H_0(L_\triangle ;\mathbb {Z})=\mathbb {Z}$
. Hence, we get an exact sequence
![]() $ 0\rightarrow H^1(L_\triangle ;\mathbb {Z})\rightarrow 0, $
which yields
$ 0\rightarrow H^1(L_\triangle ;\mathbb {Z})\rightarrow 0, $
which yields
![]() $H^1(L_\triangle ;\mathbb {Z})=0$
.
$H^1(L_\triangle ;\mathbb {Z})=0$
.
The following is Lemma 4.4.1 from [Reference Evans and Lekili10].
Lemma 3.3. The Chiang Lagrangian
![]() $L_\triangle $
has minimal Maslov number equal to
$L_\triangle $
has minimal Maslov number equal to
![]() $2.$
$2.$
For
![]() $\zeta \in H_2(\mathbb {C}P^3;\mathbb {Z})$
, we denote by
$\zeta \in H_2(\mathbb {C}P^3;\mathbb {Z})$
, we denote by
![]() $c_1(\zeta )$
the evaluation of the first Chern class of
$c_1(\zeta )$
the evaluation of the first Chern class of
![]() $\mathbb {C}P^3$
on
$\mathbb {C}P^3$
on
![]() $\zeta $
. Let
$\zeta $
. Let
![]() $\xi = [\mathbb {C}P^1]\in H_2(\mathbb {C}P^3;\mathbb {Z})$
, so
$\xi = [\mathbb {C}P^1]\in H_2(\mathbb {C}P^3;\mathbb {Z})$
, so
![]() $c_1(\xi )=4$
.
$c_1(\xi )=4$
.
Lemma 3.4. The long exact sequence of the pair
![]() $(\mathbb {C}P^3,L_\triangle )$
gives the short exact sequence
$(\mathbb {C}P^3,L_\triangle )$
gives the short exact sequence
with
![]() $H_2(\mathbb {C}P^3,L_\triangle ;\mathbb {Z}) \simeq \mathbb {Z} \simeq H_2(\mathbb {C}P^3;\mathbb {Z})$
, and the map
$H_2(\mathbb {C}P^3,L_\triangle ;\mathbb {Z}) \simeq \mathbb {Z} \simeq H_2(\mathbb {C}P^3;\mathbb {Z})$
, and the map
![]() $\varpi $
is given by multiplication by 4.
$\varpi $
is given by multiplication by 4.
Proof. Consider the long exact sequence
where
and Lemma 3.1 gives
![]() $H_1(L_\triangle ;\mathbb {Z})\simeq \mathbb {Z}/4\mathbb {Z}.$
By Lemma 3.2, we have
$H_1(L_\triangle ;\mathbb {Z})\simeq \mathbb {Z}/4\mathbb {Z}.$
By Lemma 3.2, we have
![]() $H_2(L_\triangle ;\mathbb {Z})=0$
, so we get the short exact sequence
$H_2(L_\triangle ;\mathbb {Z})=0$
, so we get the short exact sequence
We have two possibilities:
-
1. The short exact sequence (3.1) is split, so
 $H_2(\mathbb {C}P^3,L_\triangle ;\mathbb {Z}) \simeq \mathbb {Z}\oplus \mathbb {Z}/4\mathbb {Z}$
. Thus, (3.1) is isomorphic to where
$H_2(\mathbb {C}P^3,L_\triangle ;\mathbb {Z}) \simeq \mathbb {Z}\oplus \mathbb {Z}/4\mathbb {Z}$
. Thus, (3.1) is isomorphic to where $$\begin{align*}0\rightarrow \mathbb{Z} \overset{\varpi}{\rightarrow} \mathbb{Z}\oplus\mathbb{Z}/4\mathbb{Z} \rightarrow \mathbb{Z}/4\mathbb{Z}\rightarrow0, \end{align*}$$
$$\begin{align*}0\rightarrow \mathbb{Z} \overset{\varpi}{\rightarrow} \mathbb{Z}\oplus\mathbb{Z}/4\mathbb{Z} \rightarrow \mathbb{Z}/4\mathbb{Z}\rightarrow0, \end{align*}$$
 $$\begin{align*}\varpi(x)= (x,0). \end{align*}$$
$$\begin{align*}\varpi(x)= (x,0). \end{align*}$$
-
2. The short exact sequence (3.1) is not split, so
 $H_2(\mathbb {C}P^3,L_\triangle ;\mathbb {Z})=\mathbb {Z}$
. Thus, (3.1) is isomorphic to where
$H_2(\mathbb {C}P^3,L_\triangle ;\mathbb {Z})=\mathbb {Z}$
. Thus, (3.1) is isomorphic to where $$\begin{align*}0\rightarrow \mathbb{Z} \overset{\varpi}{\rightarrow} \mathbb{Z} \rightarrow \mathbb{Z}/4\mathbb{Z}\rightarrow0,\end{align*}$$
$$\begin{align*}0\rightarrow \mathbb{Z} \overset{\varpi}{\rightarrow} \mathbb{Z} \rightarrow \mathbb{Z}/4\mathbb{Z}\rightarrow0,\end{align*}$$
 $$\begin{align*}\varpi(x)= 4x.\end{align*}$$
$$\begin{align*}\varpi(x)= 4x.\end{align*}$$
In case 1, the Maslov index is given by
Since
![]() $\mu (\varpi (\xi ))=2c_1(\xi ) = 8$
, it follows that
$\mu (\varpi (\xi ))=2c_1(\xi ) = 8$
, it follows that
![]() $k=8$
is in contradiction to Lemma 3.3. Therefore, we must be in case 2.
$k=8$
is in contradiction to Lemma 3.3. Therefore, we must be in case 2.
In light of Lemma 3.4, let
![]() $\tilde {\xi }\in H_2(\mathbb {C}P^3,L_\triangle ;\mathbb {Z})$
be the generator such that
$\tilde {\xi }\in H_2(\mathbb {C}P^3,L_\triangle ;\mathbb {Z})$
be the generator such that
![]() $\varpi (\xi )=4\tilde {\xi }$
. Recall
$\varpi (\xi )=4\tilde {\xi }$
. Recall
![]() $\Gamma _1=[\omega ]\in H^2(\mathbb {C}P^3,L_\triangle ;\mathbb {Z})$
.
$\Gamma _1=[\omega ]\in H^2(\mathbb {C}P^3,L_\triangle ;\mathbb {Z})$
.
Lemma 3.5. We have
 $$\begin{align*}\int_{\tilde{\xi}} \Gamma_1 = \frac{1}{4}. \end{align*}$$
$$\begin{align*}\int_{\tilde{\xi}} \Gamma_1 = \frac{1}{4}. \end{align*}$$
Proof. We have
 $$\begin{align*}4\int_{\tilde{\xi}}\Gamma_1= \int_{\varpi(\xi)}\omega = \int_\xi\omega=1. \end{align*}$$
$$\begin{align*}4\int_{\tilde{\xi}}\Gamma_1= \int_{\varpi(\xi)}\omega = \int_\xi\omega=1. \end{align*}$$
4 Bounding cochains and open Gromov-Witten invariants
In this section, we recall the definition of the Fukaya
![]() $A_\infty $
algebra of a Lagrangian submanifold following [Reference Fukaya12, Reference Fukaya13, Reference Fukaya, Oh, Ohta and Ono17, Reference Fukaya, Oh, Ohta and Ono15, Reference Fukaya, Oh, Ohta and Ono16, Reference Fukaya, Oh, Ohta and Ono14, Reference Solomon and Tukachinsky47]. We recall the notion of bounding cochains from [Reference Fukaya, Oh, Ohta and Ono14] and the invariants
$A_\infty $
algebra of a Lagrangian submanifold following [Reference Fukaya12, Reference Fukaya13, Reference Fukaya, Oh, Ohta and Ono17, Reference Fukaya, Oh, Ohta and Ono15, Reference Fukaya, Oh, Ohta and Ono16, Reference Fukaya, Oh, Ohta and Ono14, Reference Solomon and Tukachinsky47]. We recall the notion of bounding cochains from [Reference Fukaya, Oh, Ohta and Ono14] and the invariants
![]() ${OGW}_{\beta ,k}$
of [Reference Solomon and Tukachinsky46] mentioned in Section 2.1. Additionally, we recall results concerning bounding cochains from [Reference Solomon and Tukachinsky46]. We use these results to prove Theorem 4.19, from which Theorem 1.6 follows as a special case. These theorems give a class of open Gromov-Witten invariants which coincide with straightforward counts of J-holomorphic disks without corrections from bounding chains. Theorem 1.6 plays an essential role in the computation of the basic invariants of Theorem 1.2. We also prove Lemmas 4.5 and 4.6 concerning the affect of change of spin structure and orientation on the invariants
${OGW}_{\beta ,k}$
of [Reference Solomon and Tukachinsky46] mentioned in Section 2.1. Additionally, we recall results concerning bounding cochains from [Reference Solomon and Tukachinsky46]. We use these results to prove Theorem 4.19, from which Theorem 1.6 follows as a special case. These theorems give a class of open Gromov-Witten invariants which coincide with straightforward counts of J-holomorphic disks without corrections from bounding chains. Theorem 1.6 plays an essential role in the computation of the basic invariants of Theorem 1.2. We also prove Lemmas 4.5 and 4.6 concerning the affect of change of spin structure and orientation on the invariants
![]() ${OGW}.$
These lemmas are used to prove parts 7 and 8 of Proposition 2.2.
${OGW}.$
These lemmas are used to prove parts 7 and 8 of Proposition 2.2.
Throughout this section,
![]() $(X, \omega )$
is a symplectic manifold of real dimension
$(X, \omega )$
is a symplectic manifold of real dimension
![]() $2n$
and
$2n$
and
![]() $L\subset X$
is a connected Lagrangian submanifold with relative spin structure
$L\subset X$
is a connected Lagrangian submanifold with relative spin structure
![]() $\mathfrak {s}$
. The notion of a relative spin structure appeared in [Reference Fukaya, Oh, Ohta and Ono14]. See also [Reference Wehrheim and Woodward49]. In particular, a relative spin structure determines an orientation on L. Let J be an
$\mathfrak {s}$
. The notion of a relative spin structure appeared in [Reference Fukaya, Oh, Ohta and Ono14]. See also [Reference Wehrheim and Woodward49]. In particular, a relative spin structure determines an orientation on L. Let J be an
![]() $\omega $
-tame almost complex structure on X.
$\omega $
-tame almost complex structure on X.
4.1 Moduli spaces
Denote by
![]() $\mathcal {M}_{k+1,l}(\beta )$
the moduli space of J-holomorphic genus zero open stable maps
$\mathcal {M}_{k+1,l}(\beta )$
the moduli space of J-holomorphic genus zero open stable maps
![]() $u:(D, \partial D) \rightarrow (X,L)$
of degree
$u:(D, \partial D) \rightarrow (X,L)$
of degree
![]() $\beta $
with one boundary component,
$\beta $
with one boundary component,
![]() $k+1$
boundary marked points and l interior marked points. The boundary points are labeled according to their cyclic order. We denote elements in
$k+1$
boundary marked points and l interior marked points. The boundary points are labeled according to their cyclic order. We denote elements in
![]() $\mathcal {M}_{k+1,l}(\beta )$
by
$\mathcal {M}_{k+1,l}(\beta )$
by
![]() $[u;z_0,\ldots ,z_k,w_1,\ldots ,w_l]$
, where
$[u;z_0,\ldots ,z_k,w_1,\ldots ,w_l]$
, where
![]() $z_i\in \partial D$
and
$z_i\in \partial D$
and
![]() $w_i\in \operatorname {\mathrm {int}} D$
. Denote by
$w_i\in \operatorname {\mathrm {int}} D$
. Denote by
the evaluation maps associated to boundary marked points and to the interior marked points respectively.
Denote by
![]() $\mathcal {M}^S_{k,l}(\beta )$
the moduli space of genus zero J-holomorphic open stable maps
$\mathcal {M}^S_{k,l}(\beta )$
the moduli space of genus zero J-holomorphic open stable maps
![]() $u:(D, \partial D) \rightarrow (X,L)$
of degree
$u:(D, \partial D) \rightarrow (X,L)$
of degree
![]() $\beta $
with one boundary component, k unordered boundary points, and l interior marked points. It comes with evaluation maps as in the case of
$\beta $
with one boundary component, k unordered boundary points, and l interior marked points. It comes with evaluation maps as in the case of
![]() $\mathcal {M}_{k,l}(\beta )$
.
$\mathcal {M}_{k,l}(\beta )$
.
We assume that all J-holomorphic genus zero open stable maps with one boundary component are regular and the moduli spaces
![]() $\mathcal {M}_{k+1,l}(\beta ),\mathcal {M}^S_{k,l}(\beta )$
are smooth orbifolds with corners. In addition, we assume that the evaluation maps
$\mathcal {M}_{k+1,l}(\beta ),\mathcal {M}^S_{k,l}(\beta )$
are smooth orbifolds with corners. In addition, we assume that the evaluation maps
![]() $evb^\beta _0$
are proper submersions. These assumptions should hold for
$evb^\beta _0$
are proper submersions. These assumptions should hold for
![]() $(X,L) = (\mathbb {C}P^3,L_\triangle )$
and J the standard complex structure on
$(X,L) = (\mathbb {C}P^3,L_\triangle )$
and J the standard complex structure on
![]() $\mathbb {C}P^3$
by Remark 1.6 of [Reference Solomon and Tukachinsky47] in light of the transitive action of
$\mathbb {C}P^3$
by Remark 1.6 of [Reference Solomon and Tukachinsky47] in light of the transitive action of
![]() $\text {SL}(4,\mathbb {C})$
on
$\text {SL}(4,\mathbb {C})$
on
![]() $\mathbb {C} P^3$
and the transitive action of the subgroup
$\mathbb {C} P^3$
and the transitive action of the subgroup
![]() $\text {SU}(2) \subset \text {SL}(4,\mathbb {C})$
on
$\text {SU}(2) \subset \text {SL}(4,\mathbb {C})$
on
![]() $L_\triangle $
. The arguments of the present section extend to arbitrary targets
$L_\triangle $
. The arguments of the present section extend to arbitrary targets
![]() $(X,\omega ,L)$
and arbitrary
$(X,\omega ,L)$
and arbitrary
![]() $\omega $
-tame almost complex structures J given the virtual fundamental class techniques of [Reference Fukaya12, Reference Fukaya13, Reference Fukaya, Oh, Ohta and Ono14, Reference Fukaya, Oh, Ohta and Ono15, Reference Fukaya, Oh, Ohta and Ono16, Reference Fukaya, Oh, Ohta and Ono17, Reference Fukaya, Oh, Ohta and Ono19, Reference Fukaya, Oh, Ohta and Ono18, Reference Fukaya, Oh, Ohta and Ono20, Reference Fukaya, Oh, Ohta and Ono21, Reference Fukaya and Ono22]. Alternatively, it should be possible to use the polyfold theory of [Reference Hofer, Wysocki and Zehnder24, Reference Hofer, Wysocki and Zehnder27, Reference Hofer, Wysocki and Zehnder26, Reference Hofer, Wysocki and Zehnder25, Reference Li and Wehrheim35]. The relative spin structure
$\omega $
-tame almost complex structures J given the virtual fundamental class techniques of [Reference Fukaya12, Reference Fukaya13, Reference Fukaya, Oh, Ohta and Ono14, Reference Fukaya, Oh, Ohta and Ono15, Reference Fukaya, Oh, Ohta and Ono16, Reference Fukaya, Oh, Ohta and Ono17, Reference Fukaya, Oh, Ohta and Ono19, Reference Fukaya, Oh, Ohta and Ono18, Reference Fukaya, Oh, Ohta and Ono20, Reference Fukaya, Oh, Ohta and Ono21, Reference Fukaya and Ono22]. Alternatively, it should be possible to use the polyfold theory of [Reference Hofer, Wysocki and Zehnder24, Reference Hofer, Wysocki and Zehnder27, Reference Hofer, Wysocki and Zehnder26, Reference Hofer, Wysocki and Zehnder25, Reference Li and Wehrheim35]. The relative spin structure
![]() $\mathfrak {s}$
determines an orientation on
$\mathfrak {s}$
determines an orientation on
![]() $\mathcal {M}_{k+1,l}(\beta ),\mathcal {M}^S_{k,l}(\beta )$
as in Chapter 8 of [Reference Fukaya, Oh, Ohta and Ono14].
$\mathcal {M}_{k+1,l}(\beta ),\mathcal {M}^S_{k,l}(\beta )$
as in Chapter 8 of [Reference Fukaya, Oh, Ohta and Ono14].
4.2 The Fukaya
 $A_\infty $
algebra
$A_\infty $
algebra
Denote by
![]() $A^{*}(X;\mathbb {R})$
the ring of differential forms on X with coefficients in
$A^{*}(X;\mathbb {R})$
the ring of differential forms on X with coefficients in
![]() $\mathbb {R}$
. For
$\mathbb {R}$
. For
![]() $m>0$
, denote by
$m>0$
, denote by
![]() $\widetilde {A}^m(X,L;\mathbb {R})$
differential m-forms on X that vanish on L, and denote by
$\widetilde {A}^m(X,L;\mathbb {R})$
differential m-forms on X that vanish on L, and denote by
![]() $\widetilde {A}^0(X,L;\mathbb {R})$
functions on X that are constant on L. Define
$\widetilde {A}^0(X,L;\mathbb {R})$
functions on X that are constant on L. Define
By Lemma 5.14 from[Reference Solomon and Tukachinsky46], if
![]() $H^{*}(L;\mathbb {R})\simeq H^{*}(S^n;\mathbb {R})$
, then
$H^{*}(L;\mathbb {R})\simeq H^{*}(S^n;\mathbb {R})$
, then
![]() $\widehat {H}^{*}(X,L;\mathbb {R})\simeq \widetilde {H}^{*}(X,L;\mathbb {R})$
. Denote by
$\widehat {H}^{*}(X,L;\mathbb {R})\simeq \widetilde {H}^{*}(X,L;\mathbb {R})$
. Denote by
![]() $\beta _0$
the zero element of
$\beta _0$
the zero element of
![]() $H_2(X,L;\mathbb {Z})$
.
$H_2(X,L;\mathbb {Z})$
.
Recall the definition of the Novikov ring
![]() $\Lambda $
from Section 2.4. Let
$\Lambda $
from Section 2.4. Let
![]() $s,t_0,\ldots ,t_M$
, be formal variables with degrees in
$s,t_0,\ldots ,t_M$
, be formal variables with degrees in
![]() $\mathbb {Z}$
. Set
$\mathbb {Z}$
. Set
thought of as differential graded algebras with trivial differential. Define a valuation
by
 $$\begin{align*}\nu\left(\sum_{j=0}^\infty a_jT^{\beta_j}s^{k_j}\prod_{a=0}^Mt_a^{l_{aj}}\right) = \inf_{\substack{j\\a_j\ne 0}} \left(\omega(\beta_j)+k_j+\sum_{a=0}^M l_{a_j}\right). \end{align*}$$
$$\begin{align*}\nu\left(\sum_{j=0}^\infty a_jT^{\beta_j}s^{k_j}\prod_{a=0}^Mt_a^{l_{aj}}\right) = \inf_{\substack{j\\a_j\ne 0}} \left(\omega(\beta_j)+k_j+\sum_{a=0}^M l_{a_j}\right). \end{align*}$$
Whenever a tensor product (resp. direct sum) of modules with valuation is written, we mean the completed tensor product (resp. direct sum). Set
In particular, the gradings on C and D take into account the degrees of
![]() $T^\beta , s,t_j$
, and the degrees of the differential forms. The valuation
$T^\beta , s,t_j$
, and the degrees of the differential forms. The valuation
![]() $\nu $
induces valuations on
$\nu $
induces valuations on
![]() $\Lambda ,Q,C,D$
and their tensor products, which we also denote by
$\Lambda ,Q,C,D$
and their tensor products, which we also denote by
![]() $\nu $
. Let
$\nu $
. Let
Let
Let
![]() $\gamma \in \mathcal {I}_QD$
be a closed form with
$\gamma \in \mathcal {I}_QD$
be a closed form with
![]() $|\gamma |=2$
. For example, given closed differential forms
$|\gamma |=2$
. For example, given closed differential forms
![]() $\gamma _j\in \widetilde {A}^{*}(X,L;\mathbb {R})$
for
$\gamma _j\in \widetilde {A}^{*}(X,L;\mathbb {R})$
for
![]() $j=0,\ldots ,M,$
take
$j=0,\ldots ,M,$
take
![]() $t_j$
of degree
$t_j$
of degree
![]() $2-|\gamma _j|$
and
$2-|\gamma _j|$
and
![]() $\gamma :=\sum _{j=0}^Mt_j\gamma _j$
. Define maps
$\gamma :=\sum _{j=0}^Mt_j\gamma _j$
. Define maps
by
and for
![]() $k\ge 0$
when
$k\ge 0$
when
![]() $(k,\beta )\ne (1,\beta _0)$
, by
$(k,\beta )\ne (1,\beta _0)$
, by
 $$ \begin{align} \mathfrak{m}^{\gamma,\beta}_k(\alpha_1,\ldots,\alpha_k):=(-1)^{\sum_{j=1}^kj(|\alpha_j|+1)+1} \sum_{\substack{l\ge0}}\frac{1}{l!}{evb_0^\beta}_* (\bigwedge_{j=1}^l(evi_j^\beta)^{*}\gamma\wedge \bigwedge_{j=1}^k (evb_j^\beta)^{*}\alpha_j ). \end{align} $$
$$ \begin{align} \mathfrak{m}^{\gamma,\beta}_k(\alpha_1,\ldots,\alpha_k):=(-1)^{\sum_{j=1}^kj(|\alpha_j|+1)+1} \sum_{\substack{l\ge0}}\frac{1}{l!}{evb_0^\beta}_* (\bigwedge_{j=1}^l(evi_j^\beta)^{*}\gamma\wedge \bigwedge_{j=1}^k (evb_j^\beta)^{*}\alpha_j ). \end{align} $$
The push-forward
![]() $evb^\beta _{0_*}$
is given by integration over the fiber, which is well-defined because
$evb^\beta _{0_*}$
is given by integration over the fiber, which is well-defined because
![]() $evb^\beta _0$
is a proper submersion. Define also
$evb^\beta _0$
is a proper submersion. Define also
by
 $$\begin{align*}\mathfrak{m}^{\gamma}_k:= \sum_{\substack{\beta\in H_2(X,L;\mathbb{Z})}}T^\beta\mathfrak{m}_k^{\gamma,\beta}. \end{align*}$$
$$\begin{align*}\mathfrak{m}^{\gamma}_k:= \sum_{\substack{\beta\in H_2(X,L;\mathbb{Z})}}T^\beta\mathfrak{m}_k^{\gamma,\beta}. \end{align*}$$
Furthermore, define
 $$ \begin{align*}\mathfrak{m}^\gamma_{-1} := \sum_{\substack{\beta\in H_2(X,L;\mathbb{Z}), \\ l\ge 0}} \frac{1}{l!} T^\beta \int_{\mathcal{M}_{0,l}(\beta)} \bigwedge_{j=1}^l (evi^\beta_j)^{*}\gamma.\end{align*} $$
$$ \begin{align*}\mathfrak{m}^\gamma_{-1} := \sum_{\substack{\beta\in H_2(X,L;\mathbb{Z}), \\ l\ge 0}} \frac{1}{l!} T^\beta \int_{\mathcal{M}_{0,l}(\beta)} \bigwedge_{j=1}^l (evi^\beta_j)^{*}\gamma.\end{align*} $$
The following is Proposition 2.6 from [Reference Solomon and Tukachinsky47].
Theorem 4.1. The operations
![]() $\{\mathfrak {m}_k^\gamma \}_{k\ge 0}$
define an
$\{\mathfrak {m}_k^\gamma \}_{k\ge 0}$
define an
![]() $A_\infty $
structure on C. That is, for any
$A_\infty $
structure on C. That is, for any
![]() $\alpha _1,\ldots ,\alpha _{k+1}\in C$
and
$\alpha _1,\ldots ,\alpha _{k+1}\in C$
and
![]() $k\in \mathbb {Z}_{\ge 0},$
$k\in \mathbb {Z}_{\ge 0},$
 $$\begin{align*}\sum_{\substack{k_1+k_2=k+1\\ 1\le i \le k_1}}(-1)^{\sum_{j=1}^{i-1}(|\alpha_j|+1)}\mathfrak{m}_{k_1}(\alpha_1,\ldots,\alpha_{i-1},\mathfrak{m}_{k_2}(\alpha_i,\ldots,\alpha_{i+k_2-1}),\alpha_{i+k_2},\ldots,\alpha_k)=0. \end{align*}$$
$$\begin{align*}\sum_{\substack{k_1+k_2=k+1\\ 1\le i \le k_1}}(-1)^{\sum_{j=1}^{i-1}(|\alpha_j|+1)}\mathfrak{m}_{k_1}(\alpha_1,\ldots,\alpha_{i-1},\mathfrak{m}_{k_2}(\alpha_i,\ldots,\alpha_{i+k_2-1}),\alpha_{i+k_2},\ldots,\alpha_k)=0. \end{align*}$$
The following is Proposition 3.1 from [Reference Solomon and Tukachinsky47].
Theorem 4.2. The operations
![]() $\mathfrak {m}_k$
are R-multilinear. Namely, for any
$\mathfrak {m}_k$
are R-multilinear. Namely, for any
![]() $\alpha _1,\ldots ,\alpha _{k+1}\in C$
and
$\alpha _1,\ldots ,\alpha _{k+1}\in C$
and
![]() $a\in R$
,
$a\in R$
,
Theorem 4.3. For
![]() $k\ge 0$
and
$k\ge 0$
and
![]() $\omega (\beta )=0$
,
$\omega (\beta )=0$
,
 $$\begin{align*}\mathfrak{m}^{\gamma,\beta}_k(\alpha_1,\ldots,\alpha_k)= \begin{cases} d\alpha_1, & (\beta,k)=(\beta_0,1),\\ (-1)^{|\alpha_1|}\alpha_1\wedge\alpha_2, & (\beta,k)=(\beta_0,2),\\ -\gamma_1|_L, & (\beta,k)=(\beta_0, 0),\\ 0, & \text{otherwise}. \end{cases} \end{align*}$$
$$\begin{align*}\mathfrak{m}^{\gamma,\beta}_k(\alpha_1,\ldots,\alpha_k)= \begin{cases} d\alpha_1, & (\beta,k)=(\beta_0,1),\\ (-1)^{|\alpha_1|}\alpha_1\wedge\alpha_2, & (\beta,k)=(\beta_0,2),\\ -\gamma_1|_L, & (\beta,k)=(\beta_0, 0),\\ 0, & \text{otherwise}. \end{cases} \end{align*}$$
Proof. If
![]() $\beta \ne \beta _0$
and
$\beta \ne \beta _0$
and
![]() $\omega (\beta )=0$
, then
$\omega (\beta )=0$
, then
![]() $\mathcal {M}_{k+1,l}=\emptyset $
. If
$\mathcal {M}_{k+1,l}=\emptyset $
. If
![]() $\beta =\beta _0$
, see Proposition 3.8 in [Reference Solomon and Tukachinsky47].
$\beta =\beta _0$
, see Proposition 3.8 in [Reference Solomon and Tukachinsky47].
Let
![]() $\langle \ , \ \rangle $
denote the Poincaré pairing
$\langle \ , \ \rangle $
denote the Poincaré pairing
The following is Proposition 3.1 from [Reference Solomon and Tukachinsky47].
Theorem 4.4. Let
![]() $a\in R$
and
$a\in R$
and
![]() $\alpha _1,\ldots ,\alpha _{k+1}\in C$
. The Poincaré pairing satisfies the following:
$\alpha _1,\ldots ,\alpha _{k+1}\in C$
. The Poincaré pairing satisfies the following:
The following is Proposition 3.3 from [Reference Solomon and Tukachinsky47].
Theorem 4.5. For
![]() $\alpha _1,\ldots ,\alpha _{k+1}\in C$
,
$\alpha _1,\ldots ,\alpha _{k+1}\in C$
,
4.3 Bounding pairs, the superpotential and invariants
Definition 4.1. A bounding pair with respect to J is a pair
![]() $(\gamma ,b)$
where
$(\gamma ,b)$
where
![]() $\gamma \in \mathcal {I}_Q D$
is closed with
$\gamma \in \mathcal {I}_Q D$
is closed with
![]() $|\gamma |=2$
and
$|\gamma |=2$
and
![]() $b\in \mathcal {I}_R C$
with
$b\in \mathcal {I}_R C$
with
![]() $ |b|=1, $
such that
$ |b|=1, $
such that
In this situation, b is called a bounding cochain for
![]() $\mathfrak {m}^\gamma $
.
$\mathfrak {m}^\gamma $
.
The definition of bounding pair appeared in [Reference Solomon and Tukachinsky46], and the definition of bounding cochain appeared in [Reference Fukaya, Oh, Ohta and Ono14].
Let
![]() $\gamma \in \mathcal {I}_Q D $
,
$\gamma \in \mathcal {I}_Q D $
,
![]() $b\in \mathcal {I}_R C$
. The standard superpotential [Reference Fukaya13] is given by
$b\in \mathcal {I}_R C$
. The standard superpotential [Reference Fukaya13] is given by
 $$\begin{align*}\widehat{\Omega}(\gamma, b):=\widehat{\Omega}_J(\gamma, b):= (-1)^n\left(\sum_{k\ge 0} \frac{1}{k+1} \langle \mathfrak{m}^\gamma_k(b^{\otimes k}), b\rangle + \mathfrak{m}^\gamma_{-1}\right). \end{align*}$$
$$\begin{align*}\widehat{\Omega}(\gamma, b):=\widehat{\Omega}_J(\gamma, b):= (-1)^n\left(\sum_{k\ge 0} \frac{1}{k+1} \langle \mathfrak{m}^\gamma_k(b^{\otimes k}), b\rangle + \mathfrak{m}^\gamma_{-1}\right). \end{align*}$$
Intuitively,
![]() $\widehat {\Omega }$
counts J-holomorphic disks with constraints
$\widehat {\Omega }$
counts J-holomorphic disks with constraints
![]() $\gamma $
in the interior and b on the boundary. Modification is necessary in order to avoid J-holomorphic disks the boundary of which can degenerate to a point, forming a J-holomorphic sphere. We say that a monomial element of R is of type
$\gamma $
in the interior and b on the boundary. Modification is necessary in order to avoid J-holomorphic disks the boundary of which can degenerate to a point, forming a J-holomorphic sphere. We say that a monomial element of R is of type
![]() $\mathcal {D}$
if it has the form
$\mathcal {D}$
if it has the form
![]() $a\, T^{\beta }s^0t_0^{j_0}\cdots t_N^{j_N}$
with
$a\, T^{\beta }s^0t_0^{j_0}\cdots t_N^{j_N}$
with
![]() $a\in \mathbb {R}$
and
$a\in \mathbb {R}$
and
![]() $\beta \in \operatorname {\mathrm {Im}}(\varpi )$
. Following [Reference Solomon and Tukachinsky46], in the present paper, the superpotential is defined by
$\beta \in \operatorname {\mathrm {Im}}(\varpi )$
. Following [Reference Solomon and Tukachinsky46], in the present paper, the superpotential is defined by
Definition 3.12 from [Reference Solomon and Tukachinsky46] gives a notion of gauge equivalence between a bounding pair
![]() $(\gamma ,b)$
with respect to J and a bounding pair
$(\gamma ,b)$
with respect to J and a bounding pair
![]() $(\gamma ',b')$
with respect to another almost complex structure
$(\gamma ',b')$
with respect to another almost complex structure
![]() $J'.$
Let
$J'.$
Let
![]() $\sim $
denote the resulting equivalence relation. For a graded module M, we denote by
$\sim $
denote the resulting equivalence relation. For a graded module M, we denote by
![]() $(M)_j$
the degree j part of the module.
$(M)_j$
the degree j part of the module.
Define a map
by
 $$\begin{align*}\varrho([\gamma,b]):=\left([\gamma],\int_Lb\right). \end{align*}$$
$$\begin{align*}\varrho([\gamma,b]):=\left([\gamma],\int_Lb\right). \end{align*}$$
By Lemma 3.16 in [Reference Solomon and Tukachinsky46],
![]() $\varrho $
is well defined. The following is Theorem 1 from [Reference Solomon and Tukachinsky46].
$\varrho $
is well defined. The following is Theorem 1 from [Reference Solomon and Tukachinsky46].
Theorem 4.2. If
![]() $(\gamma ,b)\sim (\gamma ',b')$
, then
$(\gamma ,b)\sim (\gamma ',b')$
, then
![]() $\Omega _J(\gamma ,b)=\Omega _{J'}(\gamma ',b')$
.
$\Omega _J(\gamma ,b)=\Omega _{J'}(\gamma ',b')$
.
The following is Theorem 2 from [Reference Solomon and Tukachinsky46].
Theorem 4.3. Assume
![]() $H^{*}(L;\mathbb {R})=H^{*}(S^n;\mathbb {R})$
. Then
$H^{*}(L;\mathbb {R})=H^{*}(S^n;\mathbb {R})$
. Then
![]() $\varrho $
is bijective.
$\varrho $
is bijective.
Fix
![]() $\Gamma _0,\ldots ,\Gamma _M$
a basis of
$\Gamma _0,\ldots ,\Gamma _M$
a basis of
![]() $\widetilde {H}^{*}(X,L;\mathbb {R})$
, set
$\widetilde {H}^{*}(X,L;\mathbb {R})$
, set
![]() $|t_j|=2-|\Gamma _j|$
, and take
$|t_j|=2-|\Gamma _j|$
, and take
 $$\begin{align*}\Gamma:=\sum_{j=0}^Mt_j\Gamma_j\in (\mathcal{I}_Q\widetilde{H}^{*}(X,L;\mathbb{R}))_2.\end{align*}$$
$$\begin{align*}\Gamma:=\sum_{j=0}^Mt_j\Gamma_j\in (\mathcal{I}_Q\widetilde{H}^{*}(X,L;\mathbb{R}))_2.\end{align*}$$
By Theorem 4.3, choose a bounding pair
![]() $(\gamma ,b)$
such that
$(\gamma ,b)$
such that
By Theorem 4.2, the superpotential
![]() $\Omega =\Omega (\gamma ,b)$
is independent of the choice of
$\Omega =\Omega (\gamma ,b)$
is independent of the choice of
![]() $(\gamma ,b)$
.
$(\gamma ,b)$
.
Definition 4.4. The open Gromov-Witten invariants of
![]() $(X,L)$
,
$(X,L)$
,
are defined by setting
and extending linearly to general input.
The following is Proposition 5.2 from [Reference Solomon and Tukachinsky46].
Theorem 4.6. The invariants
![]() $\mathrm {OGW}_{\beta ,k}$
are independent of the choice of a basis.
$\mathrm {OGW}_{\beta ,k}$
are independent of the choice of a basis.
4.4 Changes of spin structure and orientation
The following Lemmas describe the dependence of the invariants
![]() ${OGW}_{\beta ,k}$
on the spin structure and the orientation of
${OGW}_{\beta ,k}$
on the spin structure and the orientation of
![]() $L.$
$L.$
Lemma 4.5. Changing the spin structure on L by the action of
![]() $\alpha \in H^1(L;\mathbb {Z}/2\mathbb {Z})$
changes
$\alpha \in H^1(L;\mathbb {Z}/2\mathbb {Z})$
changes
![]() ${OGW}_{\beta ,k}(\cdots )$
by multiplication by
${OGW}_{\beta ,k}(\cdots )$
by multiplication by
![]() $(-1)^{\alpha (\partial \beta )}.$
$(-1)^{\alpha (\partial \beta )}.$
Proof. In the following proof, we add a superscript
![]() $\mathfrak {s}$
to the
$\mathfrak {s}$
to the
![]() $A_\infty $
operations, superpotential and open Gromov-Witten invariants to indicate the spin structure used to construct them. By Lemma 2.10 of [Reference Solomon45], the orientations of
$A_\infty $
operations, superpotential and open Gromov-Witten invariants to indicate the spin structure used to construct them. By Lemma 2.10 of [Reference Solomon45], the orientations of
![]() $\mathcal {M}_{k+1,l}(\beta )$
induced by
$\mathcal {M}_{k+1,l}(\beta )$
induced by
![]() $\mathfrak {s}$
and
$\mathfrak {s}$
and
![]() $\alpha \cdot \mathfrak {s}$
differ by a sign of
$\alpha \cdot \mathfrak {s}$
differ by a sign of
![]() $(-1)^{\alpha (\partial \beta )}$
. So,
$(-1)^{\alpha (\partial \beta )}$
. So,
Let
![]() $\mathfrak {f}_R : R \to R$
be the
$\mathfrak {f}_R : R \to R$
be the
![]() $\mathbb {R}$
algebra automorphism that sends
$\mathbb {R}$
algebra automorphism that sends
![]() $T^\beta $
to
$T^\beta $
to
![]() $(-1)^{\alpha (\partial \beta )}T^\beta $
and acts trivially on the other formal variables. Then, the R module automorphism
$(-1)^{\alpha (\partial \beta )}T^\beta $
and acts trivially on the other formal variables. Then, the R module automorphism
is a strict
![]() $A_\infty $
homomorphism between the
$A_\infty $
homomorphism between the
![]() $A_\infty $
structures
$A_\infty $
structures
![]() $\mathfrak {m}_k^{\mathfrak {s}}$
and
$\mathfrak {m}_k^{\mathfrak {s}}$
and
![]() $\mathfrak {m}_k^{\alpha \cdot \mathfrak {s}}$
and preserves the pairing
$\mathfrak {m}_k^{\alpha \cdot \mathfrak {s}}$
and preserves the pairing
![]() $\langle \cdot ,\cdot \rangle $
. So, if b is a bounding cochain for
$\langle \cdot ,\cdot \rangle $
. So, if b is a bounding cochain for
![]() $\mathfrak {m}_k^{\mathfrak {s}}$
with
$\mathfrak {m}_k^{\mathfrak {s}}$
with
![]() $\int _L b = s$
, then
$\int _L b = s$
, then
![]() $\mathfrak {f}(b)$
is a bounding cochain for
$\mathfrak {f}(b)$
is a bounding cochain for
![]() $\mathfrak {m}_k^{\alpha \cdot \mathfrak {s}}$
with
$\mathfrak {m}_k^{\alpha \cdot \mathfrak {s}}$
with
![]() $\int _L \mathfrak {f}(b) = s$
and
$\int _L \mathfrak {f}(b) = s$
and
![]() $\mathfrak {f}(\Omega ^{\mathfrak {s}}(\gamma ,b)) = \Omega ^{\alpha \cdot \mathfrak {s}}(\gamma ,\mathfrak {f}(b)).$
By Definition 4.4, we obtain
$\mathfrak {f}(\Omega ^{\mathfrak {s}}(\gamma ,b)) = \Omega ^{\alpha \cdot \mathfrak {s}}(\gamma ,\mathfrak {f}(b)).$
By Definition 4.4, we obtain
 $$ \begin{align*} {OGW}^{\alpha\cdot\mathfrak{s}}_{\beta,k}(\Gamma_{i_1},\ldots,\Gamma_{i_l}) & = [T^\beta]\partial_{t_{i_1}}\cdots\partial_{t_{i_l}}\partial_s^k \Omega^{\alpha\cdot\mathfrak{s}}(\gamma,\mathfrak{f}(b)))|_{s=0,t_j=0} \\ &=[T^{\beta}]\partial_{t_{i_1}}\cdots\partial_{t_{i_l}}\partial_s^k\mathfrak{f}(\Omega^{\mathfrak{s}}(\gamma,b))|_{s=0,t_j=0} \\ &=(-1)^{\alpha(\partial\beta)} [T^\beta]\partial_{t_{i_1}}\cdots\partial_{t_{i_l}}\partial_s^k(\Omega^{\mathfrak{s}}(\gamma,b))|_{s=0,t_j=0} \\ &=(-1)^{\alpha(\partial\beta)} {OGW}^{\mathfrak{s}}_{\beta,k}(\Gamma_{i_1},\ldots,\Gamma_{i_l}). \end{align*} $$
$$ \begin{align*} {OGW}^{\alpha\cdot\mathfrak{s}}_{\beta,k}(\Gamma_{i_1},\ldots,\Gamma_{i_l}) & = [T^\beta]\partial_{t_{i_1}}\cdots\partial_{t_{i_l}}\partial_s^k \Omega^{\alpha\cdot\mathfrak{s}}(\gamma,\mathfrak{f}(b)))|_{s=0,t_j=0} \\ &=[T^{\beta}]\partial_{t_{i_1}}\cdots\partial_{t_{i_l}}\partial_s^k\mathfrak{f}(\Omega^{\mathfrak{s}}(\gamma,b))|_{s=0,t_j=0} \\ &=(-1)^{\alpha(\partial\beta)} [T^\beta]\partial_{t_{i_1}}\cdots\partial_{t_{i_l}}\partial_s^k(\Omega^{\mathfrak{s}}(\gamma,b))|_{s=0,t_j=0} \\ &=(-1)^{\alpha(\partial\beta)} {OGW}^{\mathfrak{s}}_{\beta,k}(\Gamma_{i_1},\ldots,\Gamma_{i_l}). \end{align*} $$
Lemma 4.6. Changing the orientation of L changes
![]() ${OGW}_{\beta ,k}(\Gamma _{i_1},\ldots ,\Gamma _{i_l})$
by multiplication by
${OGW}_{\beta ,k}(\Gamma _{i_1},\ldots ,\Gamma _{i_l})$
by multiplication by
![]() $(-1)^{k+1}.$
$(-1)^{k+1}.$
Proof. In the following proof, we add a superscript
![]() $\mathfrak {o}$
to the
$\mathfrak {o}$
to the
![]() $A_\infty $
operations, superpotential, Poincaré pairing,
$A_\infty $
operations, superpotential, Poincaré pairing,
![]() $\int _L$
and open Gromov-Witten invariants to indicate the orientation used to construct them. By Lemma 2.9 from [Reference Solomon45], changing the orientation of L reverses the orientation of
$\int _L$
and open Gromov-Witten invariants to indicate the orientation used to construct them. By Lemma 2.9 from [Reference Solomon45], changing the orientation of L reverses the orientation of
![]() $\mathcal {M}_{k+1,l}(\beta )$
. Since the relative orientation is not changed, it follows that
$\mathcal {M}_{k+1,l}(\beta )$
. Since the relative orientation is not changed, it follows that
Let
![]() $\mathfrak {f}_R : R \to R$
be the
$\mathfrak {f}_R : R \to R$
be the
![]() $\mathbb {R}$
algebra automorphism that sends s to
$\mathbb {R}$
algebra automorphism that sends s to
![]() $-s$
and acts trivially on the other formal variables. Then, the R module automorphism
$-s$
and acts trivially on the other formal variables. Then, the R module automorphism
is a strict
![]() $A_\infty $
homomorphism between the
$A_\infty $
homomorphism between the
![]() $A_\infty $
structures
$A_\infty $
structures
![]() $\mathfrak {m}_k^{\mathfrak {o}}$
and
$\mathfrak {m}_k^{\mathfrak {o}}$
and
![]() $\mathfrak {m}_k^{-\mathfrak {o}}$
that satisfies
$\mathfrak {m}_k^{-\mathfrak {o}}$
that satisfies
Similarly,
![]() $\int _L^{\mathfrak {o}} = - \int _L^{-\mathfrak {o}}.$
So, if b is a bounding cochain for
$\int _L^{\mathfrak {o}} = - \int _L^{-\mathfrak {o}}.$
So, if b is a bounding cochain for
![]() $\mathfrak {m}_k^{\mathfrak {o}}$
with
$\mathfrak {m}_k^{\mathfrak {o}}$
with
![]() $\int _L^{\mathfrak {o}} b=s$
, then
$\int _L^{\mathfrak {o}} b=s$
, then
![]() $\mathfrak {f}(b)$
is a bounding cochain for
$\mathfrak {f}(b)$
is a bounding cochain for
![]() $\mathfrak {m}_k^{-\mathfrak {o}}$
with
$\mathfrak {m}_k^{-\mathfrak {o}}$
with
![]() $\int _L^{-\mathfrak {o}} \mathfrak {f}(b)=s$
and
$\int _L^{-\mathfrak {o}} \mathfrak {f}(b)=s$
and
![]() $\mathfrak {f}(\Omega ^{\mathfrak {o}}(\gamma ,b))=-\Omega ^{-\mathfrak {o}}(\gamma ,\mathfrak {f}(b))$
. By Definition 4.4, we obtain
$\mathfrak {f}(\Omega ^{\mathfrak {o}}(\gamma ,b))=-\Omega ^{-\mathfrak {o}}(\gamma ,\mathfrak {f}(b))$
. By Definition 4.4, we obtain
 $$ \begin{align*} {OGW}^{-\mathfrak{o}}_{\beta,k}(\Gamma_{i_1},\ldots,\Gamma_{i_l})&:= [T^\beta]\partial_{t_{i_1}}\cdots\partial_{t_{i_l}}\partial_s^k(\Omega^{-\mathfrak{o}}(\gamma,\mathfrak{f}(b)))|_{s=0,t_j=0}\\ &=- [T^{\beta}] \partial_{t_{i_1}}\cdots\partial_{t_{i_l}}\partial_s^k\mathfrak{f}(\Omega^{\mathfrak{o}}(\gamma,b))|_{s=0,t_j=0}\\ &=(-1)^{k+1}[T^\beta]\partial_{t_{i_1}}\cdots\partial_{t_{i_l}}\partial_s^k(\Omega^{\mathfrak{o}}(\gamma,b))|_{s=0,t_j=0}\\ &=(-1)^{k+1}{OGW}^{\mathfrak{o}}_{\beta,k}(\Gamma_{i_1},\ldots,\Gamma_{i_l}). \end{align*} $$
$$ \begin{align*} {OGW}^{-\mathfrak{o}}_{\beta,k}(\Gamma_{i_1},\ldots,\Gamma_{i_l})&:= [T^\beta]\partial_{t_{i_1}}\cdots\partial_{t_{i_l}}\partial_s^k(\Omega^{-\mathfrak{o}}(\gamma,\mathfrak{f}(b)))|_{s=0,t_j=0}\\ &=- [T^{\beta}] \partial_{t_{i_1}}\cdots\partial_{t_{i_l}}\partial_s^k\mathfrak{f}(\Omega^{\mathfrak{o}}(\gamma,b))|_{s=0,t_j=0}\\ &=(-1)^{k+1}[T^\beta]\partial_{t_{i_1}}\cdots\partial_{t_{i_l}}\partial_s^k(\Omega^{\mathfrak{o}}(\gamma,b))|_{s=0,t_j=0}\\ &=(-1)^{k+1}{OGW}^{\mathfrak{o}}_{\beta,k}(\Gamma_{i_1},\ldots,\Gamma_{i_l}). \end{align*} $$
We apply the preceding lemmas to prove vanishing results for the invariants
![]() $\overline {OGW}\!$
of certain Lagrangian submanifolds
$\overline {OGW}\!$
of certain Lagrangian submanifolds
![]() $L \subset X.$
The case
$L \subset X.$
The case
![]() $n = 3$
and k even of the following corollary has been proved previously in [Reference Chen and Zinger6, Proposition 1.3] by a different method, which goes back to an observation of Mikhalkin [Reference Welschinger51, Remark 2.4].
$n = 3$
and k even of the following corollary has been proved previously in [Reference Chen and Zinger6, Proposition 1.3] by a different method, which goes back to an observation of Mikhalkin [Reference Welschinger51, Remark 2.4].
Corollary 4.7. Consider
![]() $(X,L) = (\mathbb {C} P^n,\mathbb {R} P^n)$
with n odd. Let
$(X,L) = (\mathbb {C} P^n,\mathbb {R} P^n)$
with n odd. Let
![]() $\alpha \in H^1(\mathbb {R} P^n;\mathbb {Z})$
be the generator. The invariants
$\alpha \in H^1(\mathbb {R} P^n;\mathbb {Z})$
be the generator. The invariants
![]() $\overline {OGW}\!_{\beta ,k}(\cdots )$
vanish when
$\overline {OGW}\!_{\beta ,k}(\cdots )$
vanish when
![]() $k + \alpha (\partial \beta )$
is even.
$k + \alpha (\partial \beta )$
is even.
Proof. We identify
![]() $H_2(\mathbb {C} P^n,\mathbb {R} P^n;\mathbb {Z})$
with
$H_2(\mathbb {C} P^n,\mathbb {R} P^n;\mathbb {Z})$
with
![]() $\mathbb {Z}$
by the isomorphism taking the generator with positive symplectic area to
$\mathbb {Z}$
by the isomorphism taking the generator with positive symplectic area to
![]() $1 \in \mathbb {Z}.$
It is shown in [Reference Solomon and Tukachinsky48, Corollary 1.9] that all the invariants
$1 \in \mathbb {Z}.$
It is shown in [Reference Solomon and Tukachinsky48, Corollary 1.9] that all the invariants
![]() $\overline {OGW}\!_{\beta ,k}(\cdots )$
are determined by the open WDVV equations, the axioms of
$\overline {OGW}\!_{\beta ,k}(\cdots )$
are determined by the open WDVV equations, the axioms of
![]() $\overline {OGW}\!$
, the wall-crossing formula Theorem 2.3, the closed Gromov-Witten invariants of
$\overline {OGW}\!$
, the wall-crossing formula Theorem 2.3, the closed Gromov-Witten invariants of
![]() $\mathbb {C} P^n,$
and the value of
$\mathbb {C} P^n,$
and the value of
![]() $\overline {OGW}\!_{1,2}.$
If we simultaneously change the spin structure on
$\overline {OGW}\!_{1,2}.$
If we simultaneously change the spin structure on
![]() $\mathbb {R} P^n$
by
$\mathbb {R} P^n$
by
![]() $\alpha $
and reverse the orientation, then Lemma 4.5 and Lemma 4.6 imply that
$\alpha $
and reverse the orientation, then Lemma 4.5 and Lemma 4.6 imply that
![]() $\overline {OGW}\!_{\beta ,k}(\cdots )$
changes by multiplication by
$\overline {OGW}\!_{\beta ,k}(\cdots )$
changes by multiplication by
![]() $(-1)^{k + 1 + \alpha (\partial \beta )}.$
In particular
$(-1)^{k + 1 + \alpha (\partial \beta )}.$
In particular
![]() $\overline {OGW}\!_{1,2}$
remains unchanged. But since all the invariants
$\overline {OGW}\!_{1,2}$
remains unchanged. But since all the invariants
![]() $\overline {OGW}\!_{\beta ,k}(\cdots )$
are determined from
$\overline {OGW}\!_{\beta ,k}(\cdots )$
are determined from
![]() $\overline {OGW}\!_{1,2}$
in a way that does not depend on the spin structure or the orientation of
$\overline {OGW}\!_{1,2}$
in a way that does not depend on the spin structure or the orientation of
![]() $\mathbb {R} P^n,$
they must also remain unchanged. So, when
$\mathbb {R} P^n,$
they must also remain unchanged. So, when
![]() $k + 1+\alpha (\partial \beta )$
is odd,
$k + 1+\alpha (\partial \beta )$
is odd,
![]() $\overline {OGW}\!_{\beta ,k}(\cdots )$
must vanish.
$\overline {OGW}\!_{\beta ,k}(\cdots )$
must vanish.
The following was obtained by a different method in [Reference Hugtenburg and Tukachinsky29, Lemma 6.8].
Corollary 4.8. Take X to be the quadric hypersurface in
![]() $\mathbb {C} P^{n+1}$
given by
$\mathbb {C} P^{n+1}$
given by
![]() $\sum _{i = 0}^n z_i^2 - z_{n+1}^2 = 0$
and L to be the real locus. Then
$\sum _{i = 0}^n z_i^2 - z_{n+1}^2 = 0$
and L to be the real locus. Then
![]() $\overline {OGW}\!_{\beta ,k}(\cdots )$
vanishes when k is even.
$\overline {OGW}\!_{\beta ,k}(\cdots )$
vanishes when k is even.
Proof. We identify
![]() $H_2(X,L;\mathbb {Z})$
with
$H_2(X,L;\mathbb {Z})$
with
![]() $\mathbb {Z}$
by the isomorphism taking the generator with positive symplectic area to
$\mathbb {Z}$
by the isomorphism taking the generator with positive symplectic area to
![]() $1 \in \mathbb {Z}.$
It is shown in [Reference Hugtenburg and Tukachinsky29, Theorem 7] that all the invariants
$1 \in \mathbb {Z}.$
It is shown in [Reference Hugtenburg and Tukachinsky29, Theorem 7] that all the invariants
![]() $\overline {OGW}\!_{\beta ,k}(\cdots )$
are determined by the open WDVV equations, the axioms of
$\overline {OGW}\!_{\beta ,k}(\cdots )$
are determined by the open WDVV equations, the axioms of
![]() $\overline {OGW}\!$
, the wall-crossing formula Theorem 2.3, the closed Gromov-Witten invariants of
$\overline {OGW}\!$
, the wall-crossing formula Theorem 2.3, the closed Gromov-Witten invariants of
![]() $\mathbb {C} P^n,$
and the value of
$\mathbb {C} P^n,$
and the value of
![]() $\overline {OGW}\!_{1,3}.$
If we reverse the orientation of L, then Lemma 4.6 asserts that
$\overline {OGW}\!_{1,3}.$
If we reverse the orientation of L, then Lemma 4.6 asserts that
![]() $\overline {OGW}\!_{\beta ,k}(\cdots )$
changes by multiplication by
$\overline {OGW}\!_{\beta ,k}(\cdots )$
changes by multiplication by
![]() $(-1)^{k + 1}.$
In particular,
$(-1)^{k + 1}.$
In particular,
![]() $\overline {OGW}\!_{1,3}$
remains unchanged. But since all the invariants
$\overline {OGW}\!_{1,3}$
remains unchanged. But since all the invariants
![]() $\overline {OGW}\!_{\beta ,k}(\cdots )$
are determined from
$\overline {OGW}\!_{\beta ,k}(\cdots )$
are determined from
![]() $\overline {OGW}\!_{1,3}$
in a way that does not depend on the orientation of
$\overline {OGW}\!_{1,3}$
in a way that does not depend on the orientation of
![]() $L,$
they must also remain unchanged. So, when
$L,$
they must also remain unchanged. So, when
![]() $k + 1$
is odd,
$k + 1$
is odd,
![]() $\overline {OGW}\!_{\beta ,k}(\cdots )$
must vanish.
$\overline {OGW}\!_{\beta ,k}(\cdots )$
must vanish.
Remark 4.9. Let
![]() $(X,L)$
be as in Corollary 4.8. It is shown in [Reference Hugtenburg and Tukachinsky29, Prop. 6.9] that the vanishing result of Corollary 4.8 implies that changing the sign of the invariant
$(X,L)$
be as in Corollary 4.8. It is shown in [Reference Hugtenburg and Tukachinsky29, Prop. 6.9] that the vanishing result of Corollary 4.8 implies that changing the sign of the invariant
![]() $\overline {OGW}\!_{1,3},$
from which all the other invariants
$\overline {OGW}\!_{1,3},$
from which all the other invariants
![]() $\overline {OGW}\!$
are determined by a recursion, does not affect the absolute value of other invariants. Consequently, hypothesis 2 of Section 1.3 cannot hold for this choice of
$\overline {OGW}\!$
are determined by a recursion, does not affect the absolute value of other invariants. Consequently, hypothesis 2 of Section 1.3 cannot hold for this choice of
![]() $(X,L).$
The proof of Corollary 4.8 is based on the tension between the fact that all invariants are determined recursively from a single invariant, and the freedom in the choice of the orientation of L, which affects the values of invariants through Lemma 4.6. Thus, it seems natural to restrict hypothesis 2 to
$(X,L).$
The proof of Corollary 4.8 is based on the tension between the fact that all invariants are determined recursively from a single invariant, and the freedom in the choice of the orientation of L, which affects the values of invariants through Lemma 4.6. Thus, it seems natural to restrict hypothesis 2 to
![]() $(X,L)$
where such tension is not present. That is, the number of geometric degrees of freedom in the definition of invariants should not exceed the number of invariants from which all others are determined by recursions that do not depend on these degrees of freedom.
$(X,L)$
where such tension is not present. That is, the number of geometric degrees of freedom in the definition of invariants should not exceed the number of invariants from which all others are determined by recursions that do not depend on these degrees of freedom.
4.5 Obstruction theory
The goal of the present section is the proof of Lemma 4.18, which refines the existence result for bounding cochains given in Proposition 3.4 of [Reference Solomon and Tukachinsky46]. For this purpose, we recall relevant parts of the obstruction theoretic construction of bounding cochains given there. The basic idea goes back to [Reference Fukaya, Oh, Ohta and Ono14].
Let
denote the completed tensor algebra. For
![]() $x\in \mathcal {I}_RC$
, abbreviate
$x\in \mathcal {I}_RC$
, abbreviate
Moreover, define
by
Any element
![]() $\alpha \in C$
can be written as
$\alpha \in C$
can be written as
 $$ \begin{align} \alpha=\sum_{i=1}^\infty\lambda_i\alpha_i, \qquad \alpha_i\in A^{*}(L),\quad \lambda_i=T^{{\beta}_i}s^{k_i}\prod_{a=0}^M t_a^{l_{a_i}},\quad \lim_{i}\nu(\lambda_i)=\infty. \end{align} $$
$$ \begin{align} \alpha=\sum_{i=1}^\infty\lambda_i\alpha_i, \qquad \alpha_i\in A^{*}(L),\quad \lambda_i=T^{{\beta}_i}s^{k_i}\prod_{a=0}^M t_a^{l_{a_i}},\quad \lim_{i}\nu(\lambda_i)=\infty. \end{align} $$
Define a filtration
![]() $F^E$
on R, C by
$F^E$
on R, C by
Definition 4.10. A multiplicative submonoid
![]() $G\subset R$
is sababa if it can be written as a list
$G\subset R$
is sababa if it can be written as a list
such that
![]() $i<j\Rightarrow \nu (\lambda _i)\le \nu (\lambda _j).$
$i<j\Rightarrow \nu (\lambda _i)\le \nu (\lambda _j).$
For
![]() $j=1,\ldots ,m,$
and elements
$j=1,\ldots ,m,$
and elements
![]() $\alpha _j=\sum _i\lambda _{ij}\alpha _{ij}\in C$
decomposed as in (4.6), denote by
$\alpha _j=\sum _i\lambda _{ij}\alpha _{ij}\in C$
decomposed as in (4.6), denote by
![]() $G(\alpha _1,\ldots ,\alpha _m)$
the multiplicative monoid generated by
$G(\alpha _1,\ldots ,\alpha _m)$
the multiplicative monoid generated by
![]() $\{\pm T^\beta \,|\,\beta \in \Pi _\infty \}$
,
$\{\pm T^\beta \,|\,\beta \in \Pi _\infty \}$
,
![]() $\{t_j\}_{j=0}^N$
, and
$\{t_j\}_{j=0}^N$
, and
![]() $\{\lambda _{ij}\}_{i,j}$
. The following is Lemma 3.3 from [Reference Solomon and Tukachinsky46].
$\{\lambda _{ij}\}_{i,j}$
. The following is Lemma 3.3 from [Reference Solomon and Tukachinsky46].
Lemma 4.11. For
![]() $\alpha _1,\ldots ,\alpha _m\in \mathcal {I}_R$
, the monoid
$\alpha _1,\ldots ,\alpha _m\in \mathcal {I}_R$
, the monoid
![]() $G(\alpha _1,\ldots ,\alpha _m)$
is sababa.
$G(\alpha _1,\ldots ,\alpha _m)$
is sababa.
For
![]() $\alpha _1,\ldots ,\alpha _m\in \mathcal {I}_R$
, write the image of
$\alpha _1,\ldots ,\alpha _m\in \mathcal {I}_R$
, write the image of
![]() $G=G(\alpha _1,\ldots ,\alpha _m)$
under
$G=G(\alpha _1,\ldots ,\alpha _m)$
under
![]() $\nu $
as the sequence
$\nu $
as the sequence
![]() $\{E_0^G=0, E^G_1, E^G_2,\ldots \}$
with
$\{E_0^G=0, E^G_1, E^G_2,\ldots \}$
with
![]() $E_i^G<E^G_{i+1}$
. Let
$E_i^G<E^G_{i+1}$
. Let
![]() $\kappa ^G_i\in \mathbb {Z}_{\ge 0}$
be the largest index such that
$\kappa ^G_i\in \mathbb {Z}_{\ge 0}$
be the largest index such that
![]() $\nu (\lambda _{\kappa _i^G})=E^G_i$
. In the future, we omit G from the notation and simply write
$\nu (\lambda _{\kappa _i^G})=E^G_i$
. In the future, we omit G from the notation and simply write
![]() $E_i,\kappa _i$
since G will be fixed in each instance and no confusion should occur.
$E_i,\kappa _i$
since G will be fixed in each instance and no confusion should occur.
Given
![]() $\alpha \in C$
, a differential form with coefficients in R, we denote by
$\alpha \in C$
, a differential form with coefficients in R, we denote by
![]() $(\alpha )_j \in C$
the summand of differential form of degree j in
$(\alpha )_j \in C$
the summand of differential form of degree j in
![]() $\alpha $
. Let
$\alpha $
. Let
![]() $\Upsilon '$
be an
$\Upsilon '$
be an
![]() $\mathbb {R}-$
vector space, let
$\mathbb {R}-$
vector space, let
![]() $\Upsilon "=R, Q,$
or
$\Upsilon "=R, Q,$
or
![]() $\Lambda ,$
and let
$\Lambda ,$
and let
![]() $\Upsilon =\Upsilon '\otimes \Upsilon "$
. For
$\Upsilon =\Upsilon '\otimes \Upsilon "$
. For
![]() $x\in \Upsilon $
and a monomial
$x\in \Upsilon $
and a monomial
![]() $\lambda \in \Upsilon ",$
denote by
$\lambda \in \Upsilon ",$
denote by
![]() $[\lambda ](x)\in \Upsilon '$
the coefficient of
$[\lambda ](x)\in \Upsilon '$
the coefficient of
![]() $\lambda $
in x.
$\lambda $
in x.
Fix a sababa multiplicative monoid
![]() $G=\{\lambda _j\}_{j=0}^\infty \subset R$
ordered as in (4.7). Let
$G=\{\lambda _j\}_{j=0}^\infty \subset R$
ordered as in (4.7). Let
![]() $l\ge 0.$
Suppose we have
$l\ge 0.$
Suppose we have
![]() $b_{(l)}\in C$
with
$b_{(l)}\in C$
with
![]() $|b_{(l)}|=1$
, and
$|b_{(l)}|=1$
, and
Define the obstruction cochains
![]() $o_j\in A^{*}(L)$
for
$o_j\in A^{*}(L)$
for
![]() $j=\kappa _l+1,\ldots ,\kappa _{l+1}$
to be
$j=\kappa _l+1,\ldots ,\kappa _{l+1}$
to be
Lemmas 4.12–4.17 are Lemmas 3.5–3.10 from [Reference Solomon and Tukachinsky46].
Lemma 4.12.
![]() $|o_j|=2-|\lambda _j|$
.
$|o_j|=2-|\lambda _j|$
.
Lemma 4.13.
![]() $do_j=0$
.
$do_j=0$
.
Lemma 4.14. If
![]() $|\lambda _j|=2,$
then
$|\lambda _j|=2,$
then
![]() $o_j=c_j\cdot 1$
for some
$o_j=c_j\cdot 1$
for some
![]() $c_j\in \mathbb {R}.$
If
$c_j\in \mathbb {R}.$
If
![]() $|\lambda _j|\ne 2,$
then
$|\lambda _j|\ne 2,$
then
![]() $o_j\in A^{>0}(L;\mathbb {R})$
.
$o_j\in A^{>0}(L;\mathbb {R})$
.
Lemma 4.15. If
![]() $|\lambda _j| = 2-n$
and
$|\lambda _j| = 2-n$
and
![]() $(db_{(l)})_n = 0,$
then
$(db_{(l)})_n = 0,$
then
![]() $o_j = 0$
.
$o_j = 0$
.
Lemma 4.16. Suppose for all
![]() $j\in \{\kappa _l+1,\ldots ,\kappa _{l+1}\}$
such that
$j\in \{\kappa _l+1,\ldots ,\kappa _{l+1}\}$
such that
![]() $|\lambda _j|\ne 2$
, there exist
$|\lambda _j|\ne 2$
, there exist
![]() $b_j\in A^{1-|\lambda _j|}(L;\mathbb {R})$
such that
$b_j\in A^{1-|\lambda _j|}(L;\mathbb {R})$
such that
![]() $(-1)^{|\lambda _j|}db_j=-o_j.$
Then
$(-1)^{|\lambda _j|}db_j=-o_j.$
Then
 $$\begin{align*}b_{(l+1)}:=b_{(l)}+\sum_{\substack{\kappa_l+1\le j\le \kappa_{l+1}\\ |\lambda_j|\ne 2}}\lambda_jb_j \end{align*}$$
$$\begin{align*}b_{(l+1)}:=b_{(l)}+\sum_{\substack{\kappa_l+1\le j\le \kappa_{l+1}\\ |\lambda_j|\ne 2}}\lambda_jb_j \end{align*}$$
satisfies
Lemma 4.17. Let
![]() $\zeta \in \mathcal {I}_R C$
. Then
$\zeta \in \mathcal {I}_R C$
. Then
![]() $\mathfrak {m}^{\gamma }(e^\zeta )\equiv 0\pmod {F^{E_0}C}.$
$\mathfrak {m}^{\gamma }(e^\zeta )\equiv 0\pmod {F^{E_0}C}.$
Lemma 4.18. Let
![]() $b_0\in C$
such that
$b_0\in C$
such that
Then there exists a bounding cochain b, such that
-
1.
 $b\equiv b_0 \pmod {R^+}$
,
$b\equiv b_0 \pmod {R^+}$
, -
2.
 $\int _L b=\int _L b_0$
,
$\int _L b=\int _L b_0$
, -
3.
 $(b)_j=(b_0)_j$
where
$(b)_j=(b_0)_j$
where
 $j\in \{n-1,n\}$
.
$j\in \{n-1,n\}$
.
Proof. We follow the proof of Proposition 3.4 from [Reference Solomon and Tukachinsky46]. Define
![]() $b_{(0)}:=b_0$
. By Lemma 4.17, the cochain
$b_{(0)}:=b_0$
. By Lemma 4.17, the cochain
![]() $b_{(0)}$
satisfies
$b_{(0)}$
satisfies
Moreover,
![]() $|b_{(0)}|=1$
,
$|b_{(0)}|=1$
,
![]() $\int _L b_{(0)}=\int _L b_0$
,
$\int _L b_{(0)}=\int _L b_0$
,
![]() $(db_{(0)})_n=0$
, and
$(db_{(0)})_n=0$
, and
![]() $(b_{(0)})_j=(b_0)_j$
where
$(b_{(0)})_j=(b_0)_j$
where
![]() $j\in \{n-1,n\}$
. Observe also that
$j\in \{n-1,n\}$
. Observe also that
![]() $F^{E_0}C \subset R^+C$
. Proceed by induction. Suppose we have
$F^{E_0}C \subset R^+C$
. Proceed by induction. Suppose we have
![]() $b_{(l)}\in C$
such that
$b_{(l)}\in C$
such that
![]() $|b_{(l)}|=1$
,
$|b_{(l)}|=1$
,
![]() $b_{(l)}\equiv b_0 \pmod {R^+C}$
, and
$b_{(l)}\equiv b_0 \pmod {R^+C}$
, and
 $$ \begin{gather*} (db_{(l)})_n =0,\qquad\int_L b_{(l)}=\int_L b_0,\\ (b_{(l)})_j=(b_0)_j \quad j\in \{n-1,n\},\qquad \mathfrak{m}^\gamma(e^{b_{(l)}})\equiv c_{(l)}\cdot 1\pmod{F^{E_l}C},\quad c_{(l)}\in (\mathcal{I}_R)_2. \end{gather*} $$
$$ \begin{gather*} (db_{(l)})_n =0,\qquad\int_L b_{(l)}=\int_L b_0,\\ (b_{(l)})_j=(b_0)_j \quad j\in \{n-1,n\},\qquad \mathfrak{m}^\gamma(e^{b_{(l)}})\equiv c_{(l)}\cdot 1\pmod{F^{E_l}C},\quad c_{(l)}\in (\mathcal{I}_R)_2. \end{gather*} $$
By Lemma 4.13, we have
![]() $do_j=0$
, and by Lemma 4.12, we have
$do_j=0$
, and by Lemma 4.12, we have
![]() $o_j\in A^{2-|\lambda _j|}(L;\mathbb {R}).$
In order to apply Lemma 4.16, we need to find forms
$o_j\in A^{2-|\lambda _j|}(L;\mathbb {R}).$
In order to apply Lemma 4.16, we need to find forms
![]() $b_j\in A^{1-|\lambda _j|}(L;\mathbb {R})$
such that
$b_j\in A^{1-|\lambda _j|}(L;\mathbb {R})$
such that
![]() $(-1)^{|\lambda _j|}db_j=-o_j$
for all
$(-1)^{|\lambda _j|}db_j=-o_j$
for all
![]() $j\in \{\kappa _l+1,\ldots ,\kappa _{l+1}\}$
such that
$j\in \{\kappa _l+1,\ldots ,\kappa _{l+1}\}$
such that
![]() $|\lambda _j|\ne 2.$
Since
$|\lambda _j|\ne 2.$
Since
![]() $F^{E_l}C \subset R^+C,$
we have
$F^{E_l}C \subset R^+C,$
we have
It follows that
![]() $o_j=0$
when
$o_j=0$
when
![]() $\lambda _j\not \in R^+$
, so we choose
$\lambda _j\not \in R^+$
, so we choose
![]() $b_j=0$
. Hence, we may assume
$b_j=0$
. Hence, we may assume
![]() $\lambda _j\in R^+$
. If
$\lambda _j\in R^+$
. If
![]() $|\lambda _j|= 2-n,$
since
$|\lambda _j|= 2-n,$
since
![]() $(db_{(l)})_n =0$
, Lemma 4.15 gives
$(db_{(l)})_n =0$
, Lemma 4.15 gives
![]() $o_j = 0,$
so we choose
$o_j = 0,$
so we choose
![]() $b_j = 0.$
If
$b_j = 0.$
If
![]() $2-n < |\lambda _j|<~2,$
then
$2-n < |\lambda _j|<~2,$
then
![]() $0 < |o_j| < n.$
The assumption
$0 < |o_j| < n.$
The assumption
![]() $H^{*}(L;\mathbb {R})\simeq H^{*}(S^n;\mathbb {R})$
implies
$H^{*}(L;\mathbb {R})\simeq H^{*}(S^n;\mathbb {R})$
implies
![]() $[o_j] = 0 \in H^{*}(L;\mathbb {R}),$
so we choose
$[o_j] = 0 \in H^{*}(L;\mathbb {R}),$
so we choose
![]() $b_j$
such that
$b_j$
such that
![]() $(-1)^{|\lambda _j|}db_j = -o_j.$
For other possible values of
$(-1)^{|\lambda _j|}db_j = -o_j.$
For other possible values of
![]() $|\lambda _j|,$
degree considerations imply
$|\lambda _j|,$
degree considerations imply
![]() $o_j = 0,$
so we choose
$o_j = 0,$
so we choose
![]() $b_j =0.$
By Lemma 4.16,
$b_j =0.$
By Lemma 4.16,
![]() $b_{(l+1)}:=b_{(l)}+\sum _{\substack {\kappa _l+1\le j\le \kappa _{l+1}\\ |\lambda _j|\ne 2}}\lambda _jb_j$
satisfies
$b_{(l+1)}:=b_{(l)}+\sum _{\substack {\kappa _l+1\le j\le \kappa _{l+1}\\ |\lambda _j|\ne 2}}\lambda _jb_j$
satisfies
Since
![]() $b_j=0$
when
$b_j=0$
when
![]() $\lambda _j\not \in R^+$
, it follows that
$\lambda _j\not \in R^+$
, it follows that
![]() $b_{(l+1)}\equiv b_{(l)}\equiv b_0 \pmod {R^+C}$
. Since
$b_{(l+1)}\equiv b_{(l)}\equiv b_0 \pmod {R^+C}$
. Since
![]() $b_j = 0$
when
$b_j = 0$
when
![]() $|\lambda _j| = 2-n$
, it follows that
$|\lambda _j| = 2-n$
, it follows that
![]() $(b_{(l+1)})_{n-1}=(b_{(l)})_{n-1}=(b_{(0)})_{n-1}$
, and that
$(b_{(l+1)})_{n-1}=(b_{(l)})_{n-1}=(b_{(0)})_{n-1}$
, and that
![]() $(db_{(l+1)})_n = (db_{(l)})_n=0$
. In addition,
$(db_{(l+1)})_n = (db_{(l)})_n=0$
. In addition,
![]() $b_j = 0$
when
$b_j = 0$
when
![]() $|\lambda _j| = 1-n$
. Thus,
$|\lambda _j| = 1-n$
. Thus,
![]() $(b_{(l+1)})_{n}=(b_{(l)})_{n}=(b_{(0)})_{n},$
and
$(b_{(l+1)})_{n}=(b_{(l)})_{n}=(b_{(0)})_{n},$
and
![]() $\int _L b_{(l+1)}=\int _L b_{(l)}=\int _L b_0$
. The inductive process gives rise to a convergent sequence
$\int _L b_{(l+1)}=\int _L b_{(l)}=\int _L b_0$
. The inductive process gives rise to a convergent sequence
![]() $\{b_{(l)}\}_{l=0}^\infty $
where
$\{b_{(l)}\}_{l=0}^\infty $
where
![]() $b_{(l)}$
is bounding modulo
$b_{(l)}$
is bounding modulo
![]() $F^{E_l}C$
. Taking the limit as l goes to infinity, we obtain
$F^{E_l}C$
. Taking the limit as l goes to infinity, we obtain
4.6 Straightforward counts
In the following, we will be using the following notation conventions. For
![]() $k\ge 1$
, denote by
$k\ge 1$
, denote by
![]() $[k]$
the set
$[k]$
the set
![]() $[k]:= \{1,\ldots ,k \}.$
For
$[k]:= \{1,\ldots ,k \}.$
For
![]() $N>0$
, we denote
$N>0$
, we denote
![]() $t:= (t_1,\ldots ,t_N)$
. Similarly, we denote by
$t:= (t_1,\ldots ,t_N)$
. Similarly, we denote by
![]() $\alpha $
an N-tuple where all the components are taken from the set
$\alpha $
an N-tuple where all the components are taken from the set
![]() $\mathbb {Z}_{\ge 0}$
; that is,
$\mathbb {Z}_{\ge 0}$
; that is,
We denote
![]() $t^\alpha := t_1^{\alpha _1}\cdots t_N^{\alpha _N}$
. Recall the definition of
$t^\alpha := t_1^{\alpha _1}\cdots t_N^{\alpha _N}$
. Recall the definition of
![]() $P_\beta $
from (1.1).
$P_\beta $
from (1.1).
Theorem 4.19. Let
![]() $A_{j}\in \widetilde {H}^{*}(X,L;\mathbb {R})$
. Let
$A_{j}\in \widetilde {H}^{*}(X,L;\mathbb {R})$
. Let
![]() $\bar {b}\in A^n(L;\mathbb {R})$
such that
$\bar {b}\in A^n(L;\mathbb {R})$
such that
![]() $\text {PD}([\bar {b}])=pt$
, and let
$\text {PD}([\bar {b}])=pt$
, and let
![]() $a_{j}$
be a representative of
$a_{j}$
be a representative of
![]() $A_{j}$
. Let
$A_{j}$
. Let
![]() $\sigma _k = (k-1)!$
for
$\sigma _k = (k-1)!$
for
![]() $k \in \mathbb {Z}_{>0}$
and let
$k \in \mathbb {Z}_{>0}$
and let
![]() $\sigma _0 = 1.$
Then,
$\sigma _0 = 1.$
Then,
 $$ \begin{align*} {OGW}_{\beta,k}(A_{1},\ldots,A_{l}) &= (-1)^n \sigma_k\int_{\mathcal{M}_{k,l}(\beta)} \bigwedge_{j=1}^{l} evi^{\beta*}_j a_{j} \bigwedge_{j=1}^{k}evb^{\beta*}_j\bar{b} \\ &=(-1)^n\int_{\mathcal{M}^S_{k,l}(\beta)} \bigwedge_{j=1}^{l} evi^{\beta*}_j a_{j} \bigwedge_{j=1}^{k}evb^{\beta*}_j\bar{b} \end{align*} $$
$$ \begin{align*} {OGW}_{\beta,k}(A_{1},\ldots,A_{l}) &= (-1)^n \sigma_k\int_{\mathcal{M}_{k,l}(\beta)} \bigwedge_{j=1}^{l} evi^{\beta*}_j a_{j} \bigwedge_{j=1}^{k}evb^{\beta*}_j\bar{b} \\ &=(-1)^n\int_{\mathcal{M}^S_{k,l}(\beta)} \bigwedge_{j=1}^{l} evi^{\beta*}_j a_{j} \bigwedge_{j=1}^{k}evb^{\beta*}_j\bar{b} \end{align*} $$
if for every
one of the following two conditions is satisfied:
-
1.
 $1-\mu (\tilde {\beta }) +j(n-1) + \sum _{i\in I} (|A_{i}|-2)<0,$
or
$1-\mu (\tilde {\beta }) +j(n-1) + \sum _{i\in I} (|A_{i}|-2)<0,$
or -
2.
 $1-\mu (\tilde {\beta }) +j(n-1) + \sum _{i\in I} (|A_{i}|-2)\ge n-1.$
$1-\mu (\tilde {\beta }) +j(n-1) + \sum _{i\in I} (|A_{i}|-2)\ge n-1.$
Proof. Let
![]() $\Gamma _0,\ldots ,\Gamma _M$
be a basis of
$\Gamma _0,\ldots ,\Gamma _M$
be a basis of
![]() $\widetilde {H}^{*}(X,L;\mathbb {R})$
with
$\widetilde {H}^{*}(X,L;\mathbb {R})$
with
![]() $\Gamma _0 = 1$
. From multilinearity of
$\Gamma _0 = 1$
. From multilinearity of
![]() ${OGW}$
and Proposition 4.6, it suffices to prove the lemma for
${OGW}$
and Proposition 4.6, it suffices to prove the lemma for
![]() $\mathrm {OGW}_{\beta ,k}(\Gamma _0^{\otimes {r_0}}\otimes \cdots \otimes \Gamma _M^{\otimes {r_M}})$
. By the unit axiom 4, we can assume that
$\mathrm {OGW}_{\beta ,k}(\Gamma _0^{\otimes {r_0}}\otimes \cdots \otimes \Gamma _M^{\otimes {r_M}})$
. By the unit axiom 4, we can assume that
![]() $r_0=0$
, and by the zero axiom 5, we can assume that
$r_0=0$
, and by the zero axiom 5, we can assume that
![]() $\beta \ne \beta _0$
. We have
$\beta \ne \beta _0$
. We have
![]() $\gamma = \sum _{i=1}^M t_i \gamma _i$
, where
$\gamma = \sum _{i=1}^M t_i \gamma _i$
, where
![]() $\gamma _i$
is a representative of
$\gamma _i$
is a representative of
![]() $\Gamma _i\in \widetilde {H}^{*}(X,L;\mathbb {R})$
. Let
$\Gamma _i\in \widetilde {H}^{*}(X,L;\mathbb {R})$
. Let
![]() $b_{0,1,0}\in A^n(L;\mathbb {R})$
be a representative of the Poincaré dual of a point. Since by Proposition 4.3 we have
$b_{0,1,0}\in A^n(L;\mathbb {R})$
be a representative of the Poincaré dual of a point. Since by Proposition 4.3 we have
it follows by Lemma 4.18 that there exists a bounding cochain
![]() $b\in C$
such that
$b\in C$
such that
![]() $b\equiv s\cdot b_{0,1,0} \pmod {R^+C}$
, and
$b\equiv s\cdot b_{0,1,0} \pmod {R^+C}$
, and
Write
![]() $b=s\cdot b_{0,1,0}+\sum T^{\tilde {\beta }}s^j t^\alpha b_{\tilde {\beta },j,\alpha }$
, where
$b=s\cdot b_{0,1,0}+\sum T^{\tilde {\beta }}s^j t^\alpha b_{\tilde {\beta },j,\alpha }$
, where
Since
it follows that
 $$\begin{align*}|b_{\tilde {\beta},j, \alpha}|= 1-\mu(\tilde {\beta}) -j(1-n) - \sum_{i=1}^M \alpha_i(2-|\gamma_i|). \end{align*}$$
$$\begin{align*}|b_{\tilde {\beta},j, \alpha}|= 1-\mu(\tilde {\beta}) -j(1-n) - \sum_{i=1}^M \alpha_i(2-|\gamma_i|). \end{align*}$$
Hence, if conditions 1 and 2 are satisfied, then by (4.8) we must have
![]() $b_{\tilde {\beta },j,\alpha }=0$
when
$b_{\tilde {\beta },j,\alpha }=0$
when
Define
and denote
 $$\begin{align*}b' = s\cdot b_{0,1,0}+ \sum_{\substack{\omega(\tilde{\beta})=\omega(\beta)\\ 0\le j\le k\\ 0\le\alpha_i\le r_i}} T^{\tilde{\beta}}s^j t^\alpha b_{\tilde{\beta},j,\alpha}.\end{align*}$$
$$\begin{align*}b' = s\cdot b_{0,1,0}+ \sum_{\substack{\omega(\tilde{\beta})=\omega(\beta)\\ 0\le j\le k\\ 0\le\alpha_i\le r_i}} T^{\tilde{\beta}}s^j t^\alpha b_{\tilde{\beta},j,\alpha}.\end{align*}$$
Since
![]() $b'\equiv b \pmod {JC}$
, it follows that
$b'\equiv b \pmod {JC}$
, it follows that
Hence, it suffices to consider
![]() $\Omega (\gamma ,b')$
instead of
$\Omega (\gamma ,b')$
instead of
![]() $\Omega (\gamma ,b)$
in the computation of
$\Omega (\gamma ,b)$
in the computation of
![]() $\mathrm {OGW}_{\beta ,k}(\Gamma _1^{\otimes {r_1}}\otimes \cdots \otimes \Gamma _M^{\otimes {r_M}})$
. Since
$\mathrm {OGW}_{\beta ,k}(\Gamma _1^{\otimes {r_1}}\otimes \cdots \otimes \Gamma _M^{\otimes {r_M}})$
. Since
by Proposition 4.3, for every
![]() $m\ge 0$
,
$m\ge 0$
,
![]() $0\le j\le k$
and
$0\le j\le k$
and
![]() $\tilde {\beta }\in H_2(X,L;\mathbb {Z})$
such that
$\tilde {\beta }\in H_2(X,L;\mathbb {Z})$
such that
![]() $\omega (\tilde {\beta })=0$
, we get
$\omega (\tilde {\beta })=0$
, we get
So, by Proposition 4.5 for every
![]() $1\le i\le m$
, we get
$1\le i\le m$
, we get
Hence,
 $$ \begin{align} [T^\beta](\partial_{t_1}^{r_1}\ldots \partial_{t_M}^{r_M}\partial^k_s(\langle\sum_{m\ge0} \mathfrak{m}^{\gamma}_m &(b^{\prime\otimes{m}}), b'\rangle)) =\notag \\ &=(\partial_{t_1}^{r_1}\ldots \partial_{t_M}^{r_M}\partial^k_s( \langle \mathfrak{m}^{\gamma,\beta}_{k-1}(s\cdot b_{0,1,0},\ldots,s\cdot b_{0,1,0}),s\cdot b_{0,1,0}\rangle)). \end{align} $$
$$ \begin{align} [T^\beta](\partial_{t_1}^{r_1}\ldots \partial_{t_M}^{r_M}\partial^k_s(\langle\sum_{m\ge0} \mathfrak{m}^{\gamma}_m &(b^{\prime\otimes{m}}), b'\rangle)) =\notag \\ &=(\partial_{t_1}^{r_1}\ldots \partial_{t_M}^{r_M}\partial^k_s( \langle \mathfrak{m}^{\gamma,\beta}_{k-1}(s\cdot b_{0,1,0},\ldots,s\cdot b_{0,1,0}),s\cdot b_{0,1,0}\rangle)). \end{align} $$
Denote
![]() $l=\sum _{i=1}^Mr_i.$
For
$l=\sum _{i=1}^Mr_i.$
For
![]() $k=0$
, we get
$k=0$
, we get
 $$ \begin{align*} {OGW}_{\beta,0}(\Gamma_1^{\otimes{r_1}}\otimes\cdots\otimes\Gamma_M^{\otimes{r_M}})&= [T^\beta](\partial_{t_1}^{r_1}\ldots \partial_{t_M}^{r_M}\partial^k_s\Omega|_{s=0,t_j=0})\\ &=(-1)^n [T^\beta](\partial_{t_1}^{r_1}\ldots \partial_{t_M}^{r_M}\mathfrak{m}^\gamma_{-1})\\ &= (-1)^n\int_{\mathcal{M}_{0,l}(\beta)} \bigwedge_{j=1}^{r_1} evi^{\beta*}_j \gamma_1\cdots\bigwedge_{j=1}^{r_M} evi^{\beta*}_j \gamma_M, \end{align*} $$
$$ \begin{align*} {OGW}_{\beta,0}(\Gamma_1^{\otimes{r_1}}\otimes\cdots\otimes\Gamma_M^{\otimes{r_M}})&= [T^\beta](\partial_{t_1}^{r_1}\ldots \partial_{t_M}^{r_M}\partial^k_s\Omega|_{s=0,t_j=0})\\ &=(-1)^n [T^\beta](\partial_{t_1}^{r_1}\ldots \partial_{t_M}^{r_M}\mathfrak{m}^\gamma_{-1})\\ &= (-1)^n\int_{\mathcal{M}_{0,l}(\beta)} \bigwedge_{j=1}^{r_1} evi^{\beta*}_j \gamma_1\cdots\bigwedge_{j=1}^{r_M} evi^{\beta*}_j \gamma_M, \end{align*} $$
where
![]() $\mathcal {M}_{0,l}(\beta )=\mathcal {M}^S_{0,l}(\beta ).$
For
$\mathcal {M}_{0,l}(\beta )=\mathcal {M}^S_{0,l}(\beta ).$
For
![]() $k\ne 0$
, we get
$k\ne 0$
, we get
 $$ \begin{align*} {OGW}_{\beta,k}(\Gamma_1^{\otimes{r_1}}\otimes&\cdots\otimes\Gamma_M^{\otimes{r_M}}) = \\ & = [T^\beta](\partial_{t_1}^{r_1}\ldots \partial_{t_M}^{r_M}\partial^k_s\Omega|_{s=0,t_j=0})\\ &\!\overset{(4.9)}=(-1)^n \frac{1}{k}\cdot [T^\beta](\partial_{t_1}^{r_1}\ldots \partial_{t_M}^{r_M}\partial_s^k\langle \mathfrak{m}^\gamma_{k-1} ((s\cdot b_{0,1,0})^{\otimes {k-1}}), s\cdot b_{0,1,0} \rangle)\\ &\!\!\!\!\!\overset{(4.2) + (4.4)}=(-1)^{1+(1-n)\frac{k(k-1)}{2}}\cdot(k-1)!\cdot [T^\beta](\partial_{t_1}^{r_1}\ldots \partial_{t_M}^{r_M}\langle \mathfrak{m}^\gamma_{k-1} ( b_{0,1,0}^{\otimes {k-1}}), b_{0,1,0} \rangle)\\ &\overset{(4.1)}= (k-1)!\cdot \left\langle evb^{\beta}_{0*}\bigwedge_{j=1}^{l} evi^{\beta*}_j \gamma_{a_j} \bigwedge_{j=1}^{k-1}evb^{\beta*}_j(b_{0,1,0})), b_{0,1,0} \right\rangle\\ &\overset{(4.3)}= (-1)^n(k-1)!\int_{\mathcal{M}_{k,l}(\beta)} \bigwedge_{j=1}^{l} evi^{\beta*}_j \gamma_{a_j} \bigwedge_{j=1}^{k}evb^{\beta*}_j(b_{0,1,0}). \end{align*} $$
$$ \begin{align*} {OGW}_{\beta,k}(\Gamma_1^{\otimes{r_1}}\otimes&\cdots\otimes\Gamma_M^{\otimes{r_M}}) = \\ & = [T^\beta](\partial_{t_1}^{r_1}\ldots \partial_{t_M}^{r_M}\partial^k_s\Omega|_{s=0,t_j=0})\\ &\!\overset{(4.9)}=(-1)^n \frac{1}{k}\cdot [T^\beta](\partial_{t_1}^{r_1}\ldots \partial_{t_M}^{r_M}\partial_s^k\langle \mathfrak{m}^\gamma_{k-1} ((s\cdot b_{0,1,0})^{\otimes {k-1}}), s\cdot b_{0,1,0} \rangle)\\ &\!\!\!\!\!\overset{(4.2) + (4.4)}=(-1)^{1+(1-n)\frac{k(k-1)}{2}}\cdot(k-1)!\cdot [T^\beta](\partial_{t_1}^{r_1}\ldots \partial_{t_M}^{r_M}\langle \mathfrak{m}^\gamma_{k-1} ( b_{0,1,0}^{\otimes {k-1}}), b_{0,1,0} \rangle)\\ &\overset{(4.1)}= (k-1)!\cdot \left\langle evb^{\beta}_{0*}\bigwedge_{j=1}^{l} evi^{\beta*}_j \gamma_{a_j} \bigwedge_{j=1}^{k-1}evb^{\beta*}_j(b_{0,1,0})), b_{0,1,0} \right\rangle\\ &\overset{(4.3)}= (-1)^n(k-1)!\int_{\mathcal{M}_{k,l}(\beta)} \bigwedge_{j=1}^{l} evi^{\beta*}_j \gamma_{a_j} \bigwedge_{j=1}^{k}evb^{\beta*}_j(b_{0,1,0}). \end{align*} $$
The diffeomorphism of
![]() $\mathcal {M}^S_{k,l}(\beta )$
corresponding to relabeling boundary marked points by a permutation
$\mathcal {M}^S_{k,l}(\beta )$
corresponding to relabeling boundary marked points by a permutation
![]() $\sigma \in S_k$
preserves or reverses orientation depending on
$\sigma \in S_k$
preserves or reverses orientation depending on
![]() $sgn(\sigma )$
. Let
$sgn(\sigma )$
. Let
![]() $\sigma \in S_k$
be a permutation. Denote by
$\sigma \in S_k$
be a permutation. Denote by
![]() $\mathcal {M}_{\sigma (k),l}(\beta )$
the moduli space obtained from
$\mathcal {M}_{\sigma (k),l}(\beta )$
the moduli space obtained from
![]() $\mathcal {M}_{k,l}(\beta )$
by relabeling boundary marked points by
$\mathcal {M}_{k,l}(\beta )$
by relabeling boundary marked points by
![]() $\sigma $
. So,
$\sigma $
. So,
 $$ \begin{align*} \int_{\mathcal{M}_{k,l}(\beta)} \bigwedge_{j=1}^{l} evi^{\beta*}_j\gamma_{a_j} \bigwedge_{j=1}^{k}evb^{\beta*}_j(b_{0,1,0})&= sgn(\sigma)\int_{\mathcal{M}_{\sigma(k),l}(\beta)} \bigwedge_{j=1}^{l} evi^{\beta*}_j \gamma_{a_j} \bigwedge_{j=1}^{k}evb^{\beta*}_{\sigma(j)}(b_{0,1,0})\\ &=sgn(\sigma)^2\int_{\mathcal{M}_{\sigma(k),l}(\beta)} \bigwedge_{j=1}^{l} evi^{\beta*}_j \gamma_{a_j} \bigwedge_{j=1}^{k}evb^{\beta*}_j(b_{0,1,0})\\ &=\int_{\mathcal{M}_{\sigma(k),l}(\beta)}\bigwedge_{j=1}^{l} evi^{\beta*}_j \gamma_{a_j} \bigwedge_{j=1}^{k}evb^{\beta*}_j(b_{0,1,0}). \end{align*} $$
$$ \begin{align*} \int_{\mathcal{M}_{k,l}(\beta)} \bigwedge_{j=1}^{l} evi^{\beta*}_j\gamma_{a_j} \bigwedge_{j=1}^{k}evb^{\beta*}_j(b_{0,1,0})&= sgn(\sigma)\int_{\mathcal{M}_{\sigma(k),l}(\beta)} \bigwedge_{j=1}^{l} evi^{\beta*}_j \gamma_{a_j} \bigwedge_{j=1}^{k}evb^{\beta*}_{\sigma(j)}(b_{0,1,0})\\ &=sgn(\sigma)^2\int_{\mathcal{M}_{\sigma(k),l}(\beta)} \bigwedge_{j=1}^{l} evi^{\beta*}_j \gamma_{a_j} \bigwedge_{j=1}^{k}evb^{\beta*}_j(b_{0,1,0})\\ &=\int_{\mathcal{M}_{\sigma(k),l}(\beta)}\bigwedge_{j=1}^{l} evi^{\beta*}_j \gamma_{a_j} \bigwedge_{j=1}^{k}evb^{\beta*}_j(b_{0,1,0}). \end{align*} $$
Therefore, since
![]() $\mathcal {M}_{k,l}^S(\beta ) = \coprod _{\sigma \in S_k} \mathcal {M}_{\sigma (k),l}(\beta ),$
it follows that
$\mathcal {M}_{k,l}^S(\beta ) = \coprod _{\sigma \in S_k} \mathcal {M}_{\sigma (k),l}(\beta ),$
it follows that
 $$\begin{align*}{OGW}_{\beta,k}(\Gamma_1^{\otimes{r_1}}\otimes\cdots\otimes\Gamma_M^{\otimes{r_M}})= (-1)^n \int_{\mathcal{M}^S_{k,l}(\beta)} \bigwedge_{j=1}^{l} evi^{\beta*}_j \gamma_{a_j} \bigwedge_{j=1}^{k}evb^{\beta*}_j(b_{0,1,0}). \end{align*}$$
$$\begin{align*}{OGW}_{\beta,k}(\Gamma_1^{\otimes{r_1}}\otimes\cdots\otimes\Gamma_M^{\otimes{r_M}})= (-1)^n \int_{\mathcal{M}^S_{k,l}(\beta)} \bigwedge_{j=1}^{l} evi^{\beta*}_j \gamma_{a_j} \bigwedge_{j=1}^{k}evb^{\beta*}_j(b_{0,1,0}). \end{align*}$$
Proof of Theorem 1.6.
By Lemma 5.14 of [Reference Solomon and Tukachinsky46], if
![]() $H^{*}(L;\mathbb {R})\simeq H^{*}(S^n;\mathbb {R})$
, then
$H^{*}(L;\mathbb {R})\simeq H^{*}(S^n;\mathbb {R})$
, then
![]() $\widehat {H}^{*}(X,L;\mathbb {R})\simeq \widetilde {H}^{*}(X,L;\mathbb {R})$
. Recall that if
$\widehat {H}^{*}(X,L;\mathbb {R})\simeq \widetilde {H}^{*}(X,L;\mathbb {R})$
. Recall that if
![]() $k\ne 0$
or
$k\ne 0$
or
![]() $\beta \not \in \operatorname {\mathrm {Im}} \varpi $
, then
$\beta \not \in \operatorname {\mathrm {Im}} \varpi $
, then
![]() $\overline {OGW}\!_{\beta ,k}={OGW}_{\beta ,k}$
. Thus, when
$\overline {OGW}\!_{\beta ,k}={OGW}_{\beta ,k}$
. Thus, when
![]() $k\ne 0$
or
$k\ne 0$
or
![]() $\beta \not \in \operatorname {\mathrm {Im}} \varpi $
, Theorem 4.19 yields Theorem 1.6.
$\beta \not \in \operatorname {\mathrm {Im}} \varpi $
, Theorem 4.19 yields Theorem 1.6.
5 Computation of basic invariants
In order to use the recursive formula to compute the open Gromov Witten invariants of the Chiang Lagrangian
![]() $L_\triangle ,$
we need the initial values for the recursive formula, which are given by the following theorems. Fix the orientation
$L_\triangle ,$
we need the initial values for the recursive formula, which are given by the following theorems. Fix the orientation
![]() $\mathfrak {o}_\triangle $
and the spin structure
$\mathfrak {o}_\triangle $
and the spin structure
![]() $\mathfrak {s}_\triangle $
on
$\mathfrak {s}_\triangle $
on
![]() $L_\triangle $
as defined in Section 3.2.
$L_\triangle $
as defined in Section 3.2.
Theorem 5.1.
![]() $\overline {OGW}\!_{1, 1} = -3$
.
$\overline {OGW}\!_{1, 1} = -3$
.
Theorem 5.2.
![]() $\overline {OGW}\!_{1, 0}(\Gamma _2) =\frac {1}{4}$
.
$\overline {OGW}\!_{1, 0}(\Gamma _2) =\frac {1}{4}$
.
Theorem 5.3.
![]() $\overline {OGW}\!_{2, 0}(\Gamma _3) = 1$
.
$\overline {OGW}\!_{2, 0}(\Gamma _3) = 1$
.
The proofs appear below.
5.1 Intersections with the compactification divisor
Recall from Section 3.1 the definition of the Chiang Lagrangian
![]() $L_\triangle \subset X_\triangle \simeq \mathbb {C} P^3 \simeq \text {Sym}^3\mathbb {C}P^1.$
Recall also the definitions of the discriminant locus
$L_\triangle \subset X_\triangle \simeq \mathbb {C} P^3 \simeq \text {Sym}^3\mathbb {C}P^1.$
Recall also the definitions of the discriminant locus
![]() $Y_\triangle \subset X_\triangle $
and the subvariety
$Y_\triangle \subset X_\triangle $
and the subvariety
![]() $N_\triangle \subset Y_\triangle .$
$N_\triangle \subset Y_\triangle .$
Lemma 5.4.
![]() $\mathbb {C}P^3$
is Fano with anticanonical divisor
$\mathbb {C}P^3$
is Fano with anticanonical divisor
![]() $Y_{\triangle }$
.
$Y_{\triangle }$
.
Proof. The proof is part of Section 3.4 in [Reference Smith43].
The following is Lemma 3.1 from [Reference Auroux2].
Lemma 5.5. If L is special Lagrangian in the complement of an anticanonical divisor Y in a compact Kähler manifold X, then the Maslov index of a disk
![]() $u: (D, \partial D) \rightarrow (X, L)$
is given by twice the algebraic intersection number
$u: (D, \partial D) \rightarrow (X, L)$
is given by twice the algebraic intersection number
![]() $[u] \cdot [Y]$
.
$[u] \cdot [Y]$
.
The following is Lemma 3.7 from [Reference Smith43].
Lemma 5.6. A clean intersection of a holomorphic disk u with
![]() $N_{\triangle }$
contributes at least 2 to the intersection number
$N_{\triangle }$
contributes at least 2 to the intersection number
![]() $[u]\cdot [Y_{\triangle }]$
. A non-clean intersection contributes at least 3.
$[u]\cdot [Y_{\triangle }]$
. A non-clean intersection contributes at least 3.
5.2 Axial disks
The following is Definition 2.1 from [Reference Smith43].
Definition 5.7. If X is a complex manifold carrying an action of a compact Lie group K by holomorphic automorphisms, and L is a totally real submanifold which is an orbit of the K-action, then we say
![]() $(X,L)$
is K-homogeneous.
$(X,L)$
is K-homogeneous.
Example 5.8. The pair
![]() $(\mathbb {C}P^3,L_\triangle )$
is
$(\mathbb {C}P^3,L_\triangle )$
is
![]() $\text {SU}(2)$
-homogeneous as explained in Section 3.1.
$\text {SU}(2)$
-homogeneous as explained in Section 3.1.
The following is Definition 2.3 from [Reference Smith43].
Definition 5.9. Let
![]() $(X, L)$
be K-homogeneous. If
$(X, L)$
be K-homogeneous. If
![]() $u: (D, \partial D) \rightarrow (X, L)$
is a holomorphic disk, and there exists a smooth group homomorphism
$u: (D, \partial D) \rightarrow (X, L)$
is a holomorphic disk, and there exists a smooth group homomorphism
![]() $R: \mathbb {R} \rightarrow K$
such that (possibly after reparametrizing u) we have
$R: \mathbb {R} \rightarrow K$
such that (possibly after reparametrizing u) we have
![]() $u(e^{i\theta } z) = R(\theta )u(z)$
for all
$u(e^{i\theta } z) = R(\theta )u(z)$
for all
![]() $z \in D$
and all
$z \in D$
and all
![]() $\theta \in \mathbb {R}$
, then we say u is axial. Let
$\theta \in \mathbb {R}$
, then we say u is axial. Let
![]() $\xi \in \mathfrak {k} = \operatorname {Lie}(K).$
We say that u is axial of type
$\xi \in \mathfrak {k} = \operatorname {Lie}(K).$
We say that u is axial of type
![]() $\xi $
if
$\xi $
if
![]() $\dot R(0)$
belongs to the orbit of
$\dot R(0)$
belongs to the orbit of
![]() $\xi $
under the adjoint action of K.
$\xi $
under the adjoint action of K.
Thinking of
![]() $\mathbb {C}P^1$
as
$\mathbb {C}P^1$
as
![]() $\mathbb {C} \cup \{\infty \}$
, we identify
$\mathbb {C} \cup \{\infty \}$
, we identify
![]() $\mathbb {C}P^1 \simeq S^2$
by stereographic projection from the north pole. Thus, the complex structure on the
$\mathbb {C}P^1 \simeq S^2$
by stereographic projection from the north pole. Thus, the complex structure on the
![]() $2$
-sphere is given by left-handed rotation around the outward normal by an angle of
$2$
-sphere is given by left-handed rotation around the outward normal by an angle of
![]() $\pi /2.$
$\pi /2.$
For concreteness, we choose
![]() $\triangle $
to be the triangle with vertices
$\triangle $
to be the triangle with vertices
 $$\begin{align*}c_1=(0,0,1),\quad c_2=\left(\frac{\sqrt{3}}{2},0,-\frac{1}{2}\right),\quad c_3=\left(-\frac{\sqrt{3}}{2},0,-\frac{1}{2}\right).\end{align*}$$
$$\begin{align*}c_1=(0,0,1),\quad c_2=\left(\frac{\sqrt{3}}{2},0,-\frac{1}{2}\right),\quad c_3=\left(-\frac{\sqrt{3}}{2},0,-\frac{1}{2}\right).\end{align*}$$
By abuse of notation, we also denote by
![]() $\triangle $
the point
$\triangle $
the point
![]() $[c_1,c_2,c_3]\in \text {Sym}^3\mathbb {C}P^1.$
$[c_1,c_2,c_3]\in \text {Sym}^3\mathbb {C}P^1.$
Let
![]() $\xi _v\in \mathfrak {su}(2)$
be the infinitesimal right-handed rotation about the z axis and let
$\xi _v\in \mathfrak {su}(2)$
be the infinitesimal right-handed rotation about the z axis and let
![]() $\xi _f\in \mathfrak {su}(2)$
be the infinitesimal right-handed rotation about the y axis scaled so that for
$\xi _f\in \mathfrak {su}(2)$
be the infinitesimal right-handed rotation about the y axis scaled so that for
![]() $\xi = \xi _v,\xi _f,$
we have
$\xi = \xi _v,\xi _f,$
we have
![]() $\{t \in \mathbb {R}: e^{2\pi \xi t}\cdot \triangle = \triangle \} =\mathbb {Z}$
. Thus,
$\{t \in \mathbb {R}: e^{2\pi \xi t}\cdot \triangle = \triangle \} =\mathbb {Z}$
. Thus,
![]() $\xi _v,\xi _f,$
are generators of rotations about the vertex
$\xi _v,\xi _f,$
are generators of rotations about the vertex
![]() $c_1$
and the center of the face of the triangle, respectively, as shown in Figure 1.
$c_1$
and the center of the face of the triangle, respectively, as shown in Figure 1.

Figure 1 The choice of
![]() $\xi _v, \xi _f$
for the configuration
$\xi _v, \xi _f$
for the configuration
![]() $\triangle $
.
$\triangle $
.
Example 5.10 (Axial Maslov 2 disk).
Consider the homomorphism
given by
Let
![]() $u: (D,\partial D) \to (\mathbb {C}P^3,L_\triangle )$
be given by
$u: (D,\partial D) \to (\mathbb {C}P^3,L_\triangle )$
be given by
![]() $u(z)=e^{-i\xi _v\log z}\cdot \triangle $
. See below for more explicit formulas. Then u satisfies
$u(z)=e^{-i\xi _v\log z}\cdot \triangle $
. See below for more explicit formulas. Then u satisfies
![]() $u(e^{i\theta }z)=R(\theta )u(z),$
so it is an axial disk of type
$u(e^{i\theta }z)=R(\theta )u(z),$
so it is an axial disk of type
![]() $\xi _v$
.
$\xi _v$
.
Recall we denote by
![]() $c_1,c_2,c_3$
the vertices of the triangle
$c_1,c_2,c_3$
the vertices of the triangle
![]() $\triangle $
. The stereographic projection from the north pole
$\triangle $
. The stereographic projection from the north pole
is given by
 $$\begin{align*}p(x,y,z)= \left\{\begin{array}{ll} \frac{x+iy}{1-z}, & z\ne1\\ \infty, & z=1. \end{array} \right. \end{align*}$$
$$\begin{align*}p(x,y,z)= \left\{\begin{array}{ll} \frac{x+iy}{1-z}, & z\ne1\\ \infty, & z=1. \end{array} \right. \end{align*}$$
We have
Since
![]() $\xi _v$
is the generator of a rotation about the vertex
$\xi _v$
is the generator of a rotation about the vertex
![]() $c_1$
, the flow of
$c_1$
, the flow of
![]() $\xi _v$
is given by
$\xi _v$
is given by
for some
![]() $\chi \in \mathbb {R}.$
Since
$\chi \in \mathbb {R}.$
Since
![]() $\xi _v$
is normalized so that
$\xi _v$
is normalized so that
we have
![]() $\chi = \frac {1}{2}$
and
$\chi = \frac {1}{2}$
and
Hence, for
![]() $z\in D$
, we get
$z\in D$
, we get
 $$ \begin{align*} u(z)&= e^{-i\xi_v\log z}\cdot \triangle\\ &=\big[ \ [1:\varphi_{\xi_v}^{-i\log z}(\overline{c}_1)], \ [1:\varphi_{\xi_v}^{-i\log z}(\overline{c}_2)], \ [1: \varphi_{\xi_v}^{-i\log z}(\overline{c}_3)]\ \big]\\ &=\big[ \ [0:1], \ [1:\sqrt{\frac{z}{3}}] , \ [1:-\sqrt{\frac{z}{3}}] \ \big]\in \text{Sym}^3(\mathbb{C}P^1). \end{align*} $$
$$ \begin{align*} u(z)&= e^{-i\xi_v\log z}\cdot \triangle\\ &=\big[ \ [1:\varphi_{\xi_v}^{-i\log z}(\overline{c}_1)], \ [1:\varphi_{\xi_v}^{-i\log z}(\overline{c}_2)], \ [1: \varphi_{\xi_v}^{-i\log z}(\overline{c}_3)]\ \big]\\ &=\big[ \ [0:1], \ [1:\sqrt{\frac{z}{3}}] , \ [1:-\sqrt{\frac{z}{3}}] \ \big]\in \text{Sym}^3(\mathbb{C}P^1). \end{align*} $$
Hence, we can write
![]() $u(z)= [0:1:0: -\frac {z}{3}]\in \mathbb {C}P^3.$
$u(z)= [0:1:0: -\frac {z}{3}]\in \mathbb {C}P^3.$
We can describe u geometrically as follows. The boundary of u is obtained by the action of
![]() $R(\theta )$
on
$R(\theta )$
on
![]() $\triangle $
. Call an isosceles triangle narrow if the congruent sides are longer than the base. A point in the interior of u is described by a narrow isosceles triangle on a great circle where the north pole is the apex. For example, the triangle
$\triangle $
. Call an isosceles triangle narrow if the congruent sides are longer than the base. A point in the interior of u is described by a narrow isosceles triangle on a great circle where the north pole is the apex. For example, the triangle
![]() $c_1d_2d_3$
in Figure 2 represents a point in the interior of u. Note that as
$c_1d_2d_3$
in Figure 2 represents a point in the interior of u. Note that as
![]() $z\rightarrow 0$
, the vertices
$z\rightarrow 0$
, the vertices
![]() $c_2$
and
$c_2$
and
![]() $c_3$
move toward the south pole, so u intersects
$c_3$
move toward the south pole, so u intersects
![]() $Y_{\triangle }$
in a single point. So,
$Y_{\triangle }$
in a single point. So,
![]() $[u]\cdot [Y_{\triangle }]\ge 1$
. The proof of Lemma 3.8 in [Reference Smith43] shows that equality holds. Hence, by Lemma 5.5, u is a Maslov 2 disk.
$[u]\cdot [Y_{\triangle }]\ge 1$
. The proof of Lemma 3.8 in [Reference Smith43] shows that equality holds. Hence, by Lemma 5.5, u is a Maslov 2 disk.

Figure 2 A Maslov 2 disk passing through
![]() $\triangle $
.
$\triangle $
.
Example 5.11 (Axial Maslov 4 disk).
Consider the homomorphism
given by
The disk
![]() $u:(D,\partial D) \to (\mathbb {C}P^3,L_\triangle )$
given by
$u:(D,\partial D) \to (\mathbb {C}P^3,L_\triangle )$
given by
![]() $u(z)=e^{-i\xi _f\log z}\cdot \triangle $
satisfies
$u(z)=e^{-i\xi _f\log z}\cdot \triangle $
satisfies
![]() $u(e^{i\theta }z)=R(\theta )u(z),$
so it is axial of type
$u(e^{i\theta }z)=R(\theta )u(z),$
so it is axial of type
![]() $\xi _f$
.
$\xi _f$
.
We can describe u geometrically as follows. The boundary of u is obtained by the action of
![]() $R(\theta )$
on
$R(\theta )$
on
![]() $\triangle $
. The interior of u is given by all the equilateral triangles on northern lines of latitude if we take
$\triangle $
. The interior of u is given by all the equilateral triangles on northern lines of latitude if we take
![]() $r:=(0,-1,0)$
for the north pole. For example, the triangle
$r:=(0,-1,0)$
for the north pole. For example, the triangle
![]() $s_1s_2s_3$
in Figure 3 represents an interior point of
$s_1s_2s_3$
in Figure 3 represents an interior point of
![]() $u.$
Since u intersects
$u.$
Since u intersects
![]() $N_\triangle $
at the unique point
$N_\triangle $
at the unique point
![]() $[r,r,r]$
, it follows by Lemma 5.6 that
$[r,r,r]$
, it follows by Lemma 5.6 that
![]() $[u]\cdot [Y_{\triangle }] \geq 2.$
The proof of Lemma 3.8 in [Reference Smith43] shows that equality holds. Hence, by Lemma 5.5, u is a Maslov 4 disk.
$[u]\cdot [Y_{\triangle }] \geq 2.$
The proof of Lemma 3.8 in [Reference Smith43] shows that equality holds. Hence, by Lemma 5.5, u is a Maslov 4 disk.

Figure 3 A Maslov 4 disk passing through
![]() $\triangle $
.
$\triangle $
.
5.3 Classification of holomorphic disks
The following definition is given in Section 4 from [Reference Smith43].
Definition 5.12. The intersection points of a holomorphic disk
![]() $u:(D,\partial D)\rightarrow (\mathbb {C}P^3, L_\triangle )$
with the compactification divisor
$u:(D,\partial D)\rightarrow (\mathbb {C}P^3, L_\triangle )$
with the compactification divisor
![]() $Y_{\triangle }$
are called poles of u.
$Y_{\triangle }$
are called poles of u.
The following is Definition 4.6 from [Reference Smith43]. Recall from Section 3.1 the definition of
![]() $\Gamma _\triangle .$
$\Gamma _\triangle .$
Definition 5.13. A pole germ is the germ (at 0) of a holomorphic map
![]() $u,$
from an open neighborhood of
$u,$
from an open neighborhood of
![]() $0$
in
$0$
in
![]() $\mathbb {C}$
to
$\mathbb {C}$
to
![]() $\mathbb {C}P^3,$
such that
$\mathbb {C}P^3,$
such that
![]() $u^{-1}(Y_{\triangle })$
contains
$u^{-1}(Y_{\triangle })$
contains
![]() $0$
as an isolated point. More generally, for a Riemann surface
$0$
as an isolated point. More generally, for a Riemann surface
![]() $\Sigma $
and a point
$\Sigma $
and a point
![]() $a\in \Sigma ,$
one can speak of a pole germ at
$a\in \Sigma ,$
one can speak of a pole germ at
![]() $a.$
If we do not specify ‘at a’, then we are implicitly working at
$a.$
If we do not specify ‘at a’, then we are implicitly working at
![]() $0$
in
$0$
in
![]() $\mathbb {C}.$
We define an equivalence relation on pole germs at a by
$\mathbb {C}.$
We define an equivalence relation on pole germs at a by
![]() $u_1\sim u_2$
if and only if there exists a germ of holomorphic map
$u_1\sim u_2$
if and only if there exists a germ of holomorphic map
![]() $A,$
from a neighborhood of a in
$A,$
from a neighborhood of a in
![]() $\Sigma $
to
$\Sigma $
to
![]() $\mathrm {SL}(2,\mathbb {C}),$
such that
$\mathrm {SL}(2,\mathbb {C}),$
such that
![]() $u_2=A\cdot u_1.$
The principal part of a pole germ u is its equivalence class
$u_2=A\cdot u_1.$
The principal part of a pole germ u is its equivalence class
![]() $[u]_a$
under this relation.
$[u]_a$
under this relation.
We say a pole germ u is of type
![]() $\xi \in \mathfrak {su}(2)$
and order
$\xi \in \mathfrak {su}(2)$
and order
![]() $k\in \mathbb {Z}_{\ge 1}$
if its principal part is
$k\in \mathbb {Z}_{\ge 1}$
if its principal part is
and
![]() $\xi $
is scaled so that
$\xi $
is scaled so that
![]() $\{t\in \mathbb {R}: e^{2\pi \xi t}\in \Gamma _\triangle \}=\mathbb {Z}$
.
$\{t\in \mathbb {R}: e^{2\pi \xi t}\in \Gamma _\triangle \}=\mathbb {Z}$
.
Example 5.14. An axial disk of type
![]() $\xi $
has a pole germ of type
$\xi $
has a pole germ of type
![]() $\xi $
and order
$\xi $
and order
![]() $1$
.
$1$
.
The following is Lemma 4.10 from [Reference Smith43].
Lemma 5.15. A pole germ u is of type
![]() $\xi _v$
if and only if
$\xi _v$
if and only if
![]() $u(0) \in Y_\triangle \backslash N_\triangle $
.
$u(0) \in Y_\triangle \backslash N_\triangle $
.
The following is Corollary 4.13 from [Reference Smith43].
Lemma 5.16. All Maslov index
![]() $2$
holomorphic disks
$2$
holomorphic disks
![]() $u: (D,\partial D)\to (\mathbb {C}P^3,L_\triangle )$
are, up to reparametrization, of the form
$u: (D,\partial D)\to (\mathbb {C}P^3,L_\triangle )$
are, up to reparametrization, of the form
for
![]() $A\in \text {SU}(2)$
. In particular, they are all axial.
$A\in \text {SU}(2)$
. In particular, they are all axial.
The following is Corollary 4.14 from [Reference Smith43].
Lemma 5.17. Suppose
![]() $u : (D,\partial D) \to (\mathbb {C}P^3,L_\triangle )$
is a holomorphic disk of Maslov index 4. Then either u has two poles of type
$u : (D,\partial D) \to (\mathbb {C}P^3,L_\triangle )$
is a holomorphic disk of Maslov index 4. Then either u has two poles of type
![]() $\xi _v$
and order
$\xi _v$
and order
![]() $1$
, one pole of type
$1$
, one pole of type
![]() $\xi _v$
and order
$\xi _v$
and order
![]() $2$
, or one pole of type
$2$
, or one pole of type
![]() $\xi _f$
and order
$\xi _f$
and order
![]() $1$
. In the last case, the disk is axial of type
$1$
. In the last case, the disk is axial of type
![]() $\xi _f$
.
$\xi _f$
.
Recall the notation for moduli spaces of holomorphic disks from Section 4.1. The following is Corollary 4.21 from [Reference Smith43].
Lemma 5.18. Let
![]() $u : (D,\partial D) \to (\mathbb {C}P^3,L_\triangle )$
be an axial disk of type
$u : (D,\partial D) \to (\mathbb {C}P^3,L_\triangle )$
be an axial disk of type
![]() $\xi _f$
. Then for any
$\xi _f$
. Then for any
![]() $w \in \operatorname {\mathrm {int}} D$
, the evaluation map
$w \in \operatorname {\mathrm {int}} D$
, the evaluation map
is a submersion at
![]() $[u;w]$
.
$[u;w]$
.
Lemma 5.19. Let
![]() $a,b\in \mathbb {C}P^1$
be two sufficiently close points. There exists a unique point
$a,b\in \mathbb {C}P^1$
be two sufficiently close points. There exists a unique point
![]() $c\in \mathbb {C}P^1$
such that there exists a holomorphic disk
$c\in \mathbb {C}P^1$
such that there exists a holomorphic disk
![]() $u:(D, \partial D)\rightarrow (\mathbb {C}P^3,L_\triangle )$
of Maslov index 2 passing through
$u:(D, \partial D)\rightarrow (\mathbb {C}P^3,L_\triangle )$
of Maslov index 2 passing through
![]() $[a, b, c]\in \text {Sym}^3\mathbb {C}P^1 = \mathbb {C}P^3.$
This disk is unique up to reparameterization.
$[a, b, c]\in \text {Sym}^3\mathbb {C}P^1 = \mathbb {C}P^3.$
This disk is unique up to reparameterization.
Proof. Following Example 5.10, we call an isosceles triangle narrow if the congruent sides are longer than the base. Since
![]() $a,b,$
are sufficiently close, they cannot belong to an equilateral triangle on a great circle, so a point of the form
$a,b,$
are sufficiently close, they cannot belong to an equilateral triangle on a great circle, so a point of the form
![]() $[a,b,c]$
must be in
$[a,b,c]$
must be in
![]() $\mathbb {C}P^3\setminus L_\triangle .$
Thus, if a J-holomorphic disk
$\mathbb {C}P^3\setminus L_\triangle .$
Thus, if a J-holomorphic disk
![]() $u : (D,\partial D) \to (\mathbb {C}P^3,L_\triangle )$
passes through a point of the form
$u : (D,\partial D) \to (\mathbb {C}P^3,L_\triangle )$
passes through a point of the form
![]() $[a,b,c],$
then
$[a,b,c],$
then
![]() $[a,b,c] \in u(\operatorname {\mathrm {int}} D).$
By Lemma 5.16, all J-holomorphic disks
$[a,b,c] \in u(\operatorname {\mathrm {int}} D).$
By Lemma 5.16, all J-holomorphic disks
![]() $u: (D,\partial D) \to (\mathbb {C}P^3,L_\triangle )$
of Maslov index
$u: (D,\partial D) \to (\mathbb {C}P^3,L_\triangle )$
of Maslov index
![]() $2$
have the form
$2$
have the form
![]() $u(z)=A\cdot e^{-i\xi _v\log z}\cdot \triangle .$
For such
$u(z)=A\cdot e^{-i\xi _v\log z}\cdot \triangle .$
For such
![]() $u,$
it follows from the geometric explanation given in Example 5.10 that a point of
$u,$
it follows from the geometric explanation given in Example 5.10 that a point of
![]() $u(\operatorname {\mathrm {int}}{D} )$
is given by the vertices of a narrow isosceles triangle with apex
$u(\operatorname {\mathrm {int}}{D} )$
is given by the vertices of a narrow isosceles triangle with apex
![]() $A \cdot (0,0,1).$
So, since
$A \cdot (0,0,1).$
So, since
![]() $a,b,$
are sufficiently close, if u passes through
$a,b,$
are sufficiently close, if u passes through
![]() $[a,b,c]$
, then
$[a,b,c]$
, then
![]() $a,b,c,$
must be the vertices of a narrow isosceles triangle on a great circle with apex
$a,b,c,$
must be the vertices of a narrow isosceles triangle on a great circle with apex
![]() $c = A \cdot (0,1,1).$
We claim that such c is unique. Indeed, the points a and b are sufficiently close, so they determine a unique great circle. In addition, there exists a unique point c on the great circle such that the triangle with vertices
$c = A \cdot (0,1,1).$
We claim that such c is unique. Indeed, the points a and b are sufficiently close, so they determine a unique great circle. In addition, there exists a unique point c on the great circle such that the triangle with vertices
![]() $a,b,c,$
is narrow isosceles. The condition
$a,b,c,$
is narrow isosceles. The condition
![]() $c = A \cdot (0,0,1)$
determines A up to the action of
$c = A \cdot (0,0,1)$
determines A up to the action of
![]() $S^1 = \operatorname {\mathrm {Stab}}_{(0,0,1)} \subset \text {SU}(2).$
This
$S^1 = \operatorname {\mathrm {Stab}}_{(0,0,1)} \subset \text {SU}(2).$
This
![]() $S^1$
acts on u by reparameterization.
$S^1$
acts on u by reparameterization.
Lemma 5.20. Let
![]() $p\in N_\triangle .$
There exists an axial disk of type
$p\in N_\triangle .$
There exists an axial disk of type
![]() $\xi _f$
that passes through
$\xi _f$
that passes through
![]() $p.$
This disk is unique up to reparameterization.
$p.$
This disk is unique up to reparameterization.
Proof. Let
![]() $q\in \mathbb {C}P^1$
such that
$q\in \mathbb {C}P^1$
such that
![]() $p:=[q,q,q].$
Denote
$p:=[q,q,q].$
Denote
![]() $r:=(0,-1,0)$
. By definition, the general axial disk of type
$r:=(0,-1,0)$
. By definition, the general axial disk of type
![]() $\xi _f$
has the form
$\xi _f$
has the form
![]() $u(z)=A\cdot e^{-i\xi _f\log z}\cdot \triangle .$
It follows from Example 5.11 that such a disk intersects
$u(z)=A\cdot e^{-i\xi _f\log z}\cdot \triangle .$
It follows from Example 5.11 that such a disk intersects
![]() $N_\triangle $
at the unique point
$N_\triangle $
at the unique point
![]() $[A\cdot r,A\cdot r,A\cdot r].$
Let
$[A\cdot r,A\cdot r,A\cdot r].$
Let
![]() $A\in \text {SU}(2)$
be a rotation such that
$A\in \text {SU}(2)$
be a rotation such that
![]() $A\cdot r=q.$
Then
$A\cdot r=q.$
Then
![]() $u(0) = p.$
However, the condition
$u(0) = p.$
However, the condition
![]() $A\cdot r = q$
determines A up to the action of
$A\cdot r = q$
determines A up to the action of
![]() $S^1 = \operatorname {\mathrm {Stab}}_{q} \subset \text {SU}(2).$
This
$S^1 = \operatorname {\mathrm {Stab}}_{q} \subset \text {SU}(2).$
This
![]() $S^1$
acts on u by reparameterization.
$S^1$
acts on u by reparameterization.
5.4 Riemann-Hilbert pairs
Definition 5.21. A Riemann-Hilbert pair consists of holomorphic rank n vector bundle
![]() $E\rightarrow D$
over the closed unit disk with a smooth totally real n-dimensional subbundle
$E\rightarrow D$
over the closed unit disk with a smooth totally real n-dimensional subbundle
![]() $F\subset E|_{\partial D}$
. A spin Riemann-Hilbert pair is a Riemann-Hilbert pair
$F\subset E|_{\partial D}$
. A spin Riemann-Hilbert pair is a Riemann-Hilbert pair
![]() $(E,F)$
along with an orientation and spin structure on
$(E,F)$
along with an orientation and spin structure on
![]() $F.$
$F.$
Definition 5.22. Let
![]() $(E,F)$
,
$(E,F)$
,
![]() $(E',F')$
be spin Riemann-Hilbert pairs. An isomorphism of Riemann-Hilbert pairs
$(E',F')$
be spin Riemann-Hilbert pairs. An isomorphism of Riemann-Hilbert pairs
![]() $(E,F)\rightarrow (E',F')$
consists of
$(E,F)\rightarrow (E',F')$
consists of
-
1. a biholomorphism
 $f:D\rightarrow D$
, and
$f:D\rightarrow D$
, and -
2. a holomorphic isomorphism of bundles
 $\phi :E\rightarrow E'$
covering f such that
$\phi :E\rightarrow E'$
covering f such that
 $\phi |_{\partial D}$
takes F to
$\phi |_{\partial D}$
takes F to
 $F'$
.
$F'$
.
If
![]() $(E,F)$
and
$(E,F)$
and
![]() $(E',F')$
are spin Riemann-Hilbert pairs, we say that
$(E',F')$
are spin Riemann-Hilbert pairs, we say that
![]() $(f,\phi )$
is an isomorphism if additionally,
$(f,\phi )$
is an isomorphism if additionally,
![]() $\phi |_F : F \to F'$
preserves orientation and spin structure. We may refer to the pair
$\phi |_F : F \to F'$
preserves orientation and spin structure. We may refer to the pair
![]() $(f,\phi )$
by
$(f,\phi )$
by
![]() $\phi $
alone.
$\phi $
alone.
Let
![]() $(E,F)$
be a Riemann-Hilbert pair. Since D is contractible, we identify E with the trivial bundle
$(E,F)$
be a Riemann-Hilbert pair. Since D is contractible, we identify E with the trivial bundle
![]() $\underline {\mathbb {C}}^n$
, and thus, the pair is determined by the subbundle F. A totally real subspace of
$\underline {\mathbb {C}}^n$
, and thus, the pair is determined by the subbundle F. A totally real subspace of
![]() $\mathbb {C}^n$
is described by
$\mathbb {C}^n$
is described by
![]() $A\cdot \mathbb {R}^n$
where
$A\cdot \mathbb {R}^n$
where
![]() $A\in GL(n,\mathbb {C})$
. Moreover,
$A\in GL(n,\mathbb {C})$
. Moreover,
![]() $A' \in GL(n,\mathbb {C})$
gives the same totally real subspace if and only if
$A' \in GL(n,\mathbb {C})$
gives the same totally real subspace if and only if
![]() $A^{-1}A'\in GL(n,\mathbb {R})$
. The fibers of a totally real subbundle
$A^{-1}A'\in GL(n,\mathbb {R})$
. The fibers of a totally real subbundle
![]() $F \subset \underline {\mathbb {C}}^n$
can be written as
$F \subset \underline {\mathbb {C}}^n$
can be written as
![]() $F_z=A(z)\cdot \mathbb {R}^n$
where
$F_z=A(z)\cdot \mathbb {R}^n$
where
![]() $A(z)\in GL(n,\mathbb {C})$
, so such a family of matrices
$A(z)\in GL(n,\mathbb {C})$
, so such a family of matrices
![]() $\{A(z)\}_{z\in \partial D}$
determines a Riemann-Hilbert pair.
$\{A(z)\}_{z\in \partial D}$
determines a Riemann-Hilbert pair.
Let
![]() $F^\kappa \subset \underline {\mathbb {C}}$
denote the totally real subbundle given by
$F^\kappa \subset \underline {\mathbb {C}}$
denote the totally real subbundle given by
![]() $F^\kappa _z= z^{\kappa /2}\mathbb {R}$
and let
$F^\kappa _z= z^{\kappa /2}\mathbb {R}$
and let
![]() $F^{\kappa _1,\kappa _2}\subset \underline {\mathbb {C}}^2$
denote the totally real subbundle given by
$F^{\kappa _1,\kappa _2}\subset \underline {\mathbb {C}}^2$
denote the totally real subbundle given by
![]() $F^{\kappa _1,\kappa _2}_z= z^{\kappa _1/2}\mathbb {R}\oplus z^{\kappa _2/2}\mathbb {R}.$
The following is Theorem 1 from [Reference Oh39].
$F^{\kappa _1,\kappa _2}_z= z^{\kappa _1/2}\mathbb {R}\oplus z^{\kappa _2/2}\mathbb {R}.$
The following is Theorem 1 from [Reference Oh39].
Theorem 5.23. Any Riemann-Hilbert pair
![]() $(E,F)$
splits as a direct sum of Riemann-Hilbert pairs
$(E,F)$
splits as a direct sum of Riemann-Hilbert pairs
where
![]() $\kappa _i\in \mathbb {Z}$
.
$\kappa _i\in \mathbb {Z}$
.
If the boundary real subbundle F is orientable, which is equivalent to having even total index, by Theorem 5.23, we can write
where
![]() $\kappa _i$
and
$\kappa _i$
and
![]() ${\kappa _1}_i+{\kappa _2}_i$
are even numbers. Hence, each summand is orientable.
${\kappa _1}_i+{\kappa _2}_i$
are even numbers. Hence, each summand is orientable.
For a Riemann-Hilbert pair
![]() $(E,F),$
let
$(E,F),$
let
denote the Cauchy-Riemann operator determined by the holomorphic structure on E. Let
![]() $\det \bar {\partial }_{(E,F)}$
denote the Fredholm determinant. Abbreviate
$\det \bar {\partial }_{(E,F)}$
denote the Fredholm determinant. Abbreviate
The following is a special case of Proposition 2.8 from [Reference Solomon45].
Theorem 5.1. Let
![]() $(E,F)$
be a spin Riemann-Hilbert pair. Then
$(E,F)$
be a spin Riemann-Hilbert pair. Then
![]() $\det \bar {\partial }_{(E,F)}$
admits a canonical orientation. If
$\det \bar {\partial }_{(E,F)}$
admits a canonical orientation. If
![]() $\phi :(E,F)\rightarrow (E',F')$
is an isomorphism of spin Riemann-Hilbert pairs, then the induced isomorphism
$\phi :(E,F)\rightarrow (E',F')$
is an isomorphism of spin Riemann-Hilbert pairs, then the induced isomorphism
preserves the canonical orientation. Furthermore, the canonical orientation varies continuously in a family of Cauchy-Riemann operators.
The following is a consequence of the proof of a special case of Lemma 8.1 from [Reference Solomon45].
Lemma 5.24. Suppose
is a short exact sequence of real vector bundles over a base
![]() $B.$
Then an orientation on any two of
$B.$
Then an orientation on any two of
![]() $V, V' , V"$
naturally induces an orientation on the third. A spin structure on any two of
$V, V' , V"$
naturally induces an orientation on the third. A spin structure on any two of
![]() $V, V' , V"$
naturally induces a spin structure on the third.
$V, V' , V"$
naturally induces a spin structure on the third.
Suppose now that
![]() $V',V"$
are oriented and spin and equip
$V',V"$
are oriented and spin and equip
![]() $V = V' \oplus V"$
with the induced orientation and spin structure. If
$V = V' \oplus V"$
with the induced orientation and spin structure. If
![]() $\xi ^{\prime }_1,\ldots ,\xi ^{\prime }_{k'}$
(resp.
$\xi ^{\prime }_1,\ldots ,\xi ^{\prime }_{k'}$
(resp.
![]() $\xi ^{\prime \prime }_1,\ldots ,\xi ^{\prime \prime }_{k"})$
is an oriented frame of
$\xi ^{\prime \prime }_1,\ldots ,\xi ^{\prime \prime }_{k"})$
is an oriented frame of
![]() $V'$
(resp.
$V'$
(resp.
![]() $V"$
) that lifts to the associated spin bundle, then
$V"$
) that lifts to the associated spin bundle, then
![]() $\xi ^{\prime }_1 \oplus 0,\ldots ,\xi ^{\prime }_{k'} \oplus 0, 0 \oplus \xi ^{\prime \prime }_1,\ldots ,0\oplus \xi ^{\prime \prime }_{k"}$
is an oriented frame of
$\xi ^{\prime }_1 \oplus 0,\ldots ,\xi ^{\prime }_{k'} \oplus 0, 0 \oplus \xi ^{\prime \prime }_1,\ldots ,0\oplus \xi ^{\prime \prime }_{k"}$
is an oriented frame of
![]() $V' \oplus V"$
that lifts to the associated spin bundle.
$V' \oplus V"$
that lifts to the associated spin bundle.
In light of Lemma 5.24, the direct sum of spin Riemann-Hilbert pairs is naturally a spin Riemann-Hilbert pair. The following can be deduced from the proof of Proposition 8.4 from [Reference Solomon45].
Lemma 5.25. Let
![]() $(E,F)$
be a spin Riemann-Hilbert pair. If
$(E,F)$
be a spin Riemann-Hilbert pair. If
![]() $(E,F)$
splits as a direct sum of spin Riemann-Hilbert pairs
$(E,F)$
splits as a direct sum of spin Riemann-Hilbert pairs
![]() $(E',F')\oplus (E",F")$
, then the isomorphism
$(E',F')\oplus (E",F")$
, then the isomorphism
is orientation-preserving.
Remark 5.26. An oriented real line bundle has a canonical spin structure. So, a one-dimensional Riemann-Hilbert pair with an orientation on the real bundle determines a spin Riemann-Hilbert pair. We will use this implicitly below.
The proof of the following lemma is given as a part of the proof of Theorem C.4.1 in [Reference McDuff and Salamon38].
Lemma 5.27. If
![]() $\kappa \ge -1$
, then
$\kappa \ge -1$
, then
![]() $\ker \bar {\partial }_{\kappa }$
can be written explicitly as
$\ker \bar {\partial }_{\kappa }$
can be written explicitly as
 $$\begin{align*}\ker\bar{\partial}_{\kappa}=\{\sum_{j=0}^{\kappa}a_jz^j| \ a_j\in\mathbb{C} \text{ and } a_j=\bar{a}_{\kappa-j}\} \end{align*}$$
$$\begin{align*}\ker\bar{\partial}_{\kappa}=\{\sum_{j=0}^{\kappa}a_jz^j| \ a_j\in\mathbb{C} \text{ and } a_j=\bar{a}_{\kappa-j}\} \end{align*}$$
and
![]() $\operatorname {\mathrm {Coker}}(\bar {\partial }_{\kappa }) = 0.$
In particular,
$\operatorname {\mathrm {Coker}}(\bar {\partial }_{\kappa }) = 0.$
In particular,
![]() $\dim \ker \bar {\partial }_{\kappa } = \kappa +1.$
$\dim \ker \bar {\partial }_{\kappa } = \kappa +1.$
Below, we often use the fact that if
![]() $(E,F)$
is a Riemann-Hilbert pair with
$(E,F)$
is a Riemann-Hilbert pair with
![]() $\operatorname {\mathrm {Coker}} \bar {\partial }_{(E,F)} = 0,$
then an orientation of
$\operatorname {\mathrm {Coker}} \bar {\partial }_{(E,F)} = 0,$
then an orientation of
![]() $\det \bar {\partial }_{(E,F)}$
is the same as an orientation of
$\det \bar {\partial }_{(E,F)}$
is the same as an orientation of
![]() $\ker \bar {\partial }_{(E,F)}.$
$\ker \bar {\partial }_{(E,F)}.$
Lemma 5.28. Evaluation at 1 defines an orientation-preserving isomorphism
Proof. This follows from the definition of the orientation on
![]() $\det (\partial _0)$
given in Section 2 of [Reference Solomon45].
$\det (\partial _0)$
given in Section 2 of [Reference Solomon45].
The following is Lemma A.2.1 from [Reference Smith44].
Lemma 5.29. Let
![]() $(E,F)$
be a rank 1 Riemann-Hilbert pair of Maslov index
$(E,F)$
be a rank 1 Riemann-Hilbert pair of Maslov index
![]() $2$
. Evaluation at
$2$
. Evaluation at
![]() $0$
and
$0$
and
![]() $1$
defines an isomorphism
$1$
defines an isomorphism
Moreover, for any choice of orientation on
![]() $F,$
this isomorphism is orientation-preserving if the codomain is oriented by the complex structure on
$F,$
this isomorphism is orientation-preserving if the codomain is oriented by the complex structure on
![]() $E_0$
and the orientation on
$E_0$
and the orientation on
![]() $F_1$
.
$F_1$
.
We choose an orientation on
![]() $F^2$
such that the frame z is positively oriented. By Remark 5.26, this choice of orientation determines a spin structure on
$F^2$
such that the frame z is positively oriented. By Remark 5.26, this choice of orientation determines a spin structure on
![]() $F^2.$
$F^2.$
Lemma 5.30. The orientation on
![]() $\ker \bar {\partial }_2$
is determined by the ordered basis
$\ker \bar {\partial }_2$
is determined by the ordered basis
Proof. By Lemma 5.27, we have
Consider the map
from Lemma 5.29. Orient the fiber
![]() $\underline {\mathbb {C}}_0$
by its complex structure and the fiber
$\underline {\mathbb {C}}_0$
by its complex structure and the fiber
![]() $F^2_1 = \mathbb {R} \subset \underline {\mathbb {C}}_1$
by the basis
$F^2_1 = \mathbb {R} \subset \underline {\mathbb {C}}_1$
by the basis
![]() $1$
. By Lemma 5.29, the map
$1$
. By Lemma 5.29, the map
![]() $f_2$
is orientation-preserving. Since
$f_2$
is orientation-preserving. Since
is an oriented basis, it follows that the basis
determines the orientation on
![]() $\ker \bar {\partial }_2.$
$\ker \bar {\partial }_2.$
We choose the orientation on
![]() $F^{1,1}$
such that the frame
$F^{1,1}$
such that the frame
 $$\begin{align*}\zeta(z)=\begin{pmatrix} \frac{z+1}{4}\\ \frac{-i(1-z)}{4} \end{pmatrix}, \quad \eta(z)=\begin{pmatrix} \frac{i(1-z)}{4}\\ \frac{z+1}{4} \end{pmatrix}\end{align*}$$
$$\begin{align*}\zeta(z)=\begin{pmatrix} \frac{z+1}{4}\\ \frac{-i(1-z)}{4} \end{pmatrix}, \quad \eta(z)=\begin{pmatrix} \frac{i(1-z)}{4}\\ \frac{z+1}{4} \end{pmatrix}\end{align*}$$
is positively oriented. In addition, we choose the spin structure on
![]() $F^{1,1}$
such that this frame can be lifted to the associated double cover of the frame bundle.
$F^{1,1}$
such that this frame can be lifted to the associated double cover of the frame bundle.
Lemma 5.31. Evaluation at zero
defines an isomorphism. If the codomain is oriented by the complex structure on
![]() $\underline {\mathbb {C}}^2_0,$
this isomorphism is orientation-preserving.
$\underline {\mathbb {C}}^2_0,$
this isomorphism is orientation-preserving.
Proof. By Lemma 5.27, the map
![]() $f_{1,1}$
defines an isomorphism. We degenerate
$f_{1,1}$
defines an isomorphism. We degenerate
![]() $(\underline {\mathbb {C}}^2,F^{1,1})$
to
$(\underline {\mathbb {C}}^2,F^{1,1})$
to
![]() $(\underline {\mathbb {C}}^2,F^{0,2})$
in order to determine the orientation on
$(\underline {\mathbb {C}}^2,F^{0,2})$
in order to determine the orientation on
![]() $\ker \bar {\partial }_{1,1}$
. Consider the family of loops
$\ker \bar {\partial }_{1,1}$
. Consider the family of loops
given by
 $$\begin{align*}A_t(z)=\begin{pmatrix} {\frac{1+t^2z}{2}} & \frac{t(z-1)}{2i}\\ \frac{t(1-z)}{2i} & {\frac{t^2+z}{2}} \end{pmatrix}.\end{align*}$$
$$\begin{align*}A_t(z)=\begin{pmatrix} {\frac{1+t^2z}{2}} & \frac{t(z-1)}{2i}\\ \frac{t(1-z)}{2i} & {\frac{t^2+z}{2}} \end{pmatrix}.\end{align*}$$
We claim that the family of boundary conditions
![]() $F(t)$
given by
$F(t)$
given by
![]() $F(t)_z = A_t(z) \cdot \mathbb {R}^2$
is a degeneration from
$F(t)_z = A_t(z) \cdot \mathbb {R}^2$
is a degeneration from
![]() $F^{1,1}$
to
$F^{1,1}$
to
![]() $F^{0,2}.$
Indeed,
$F^{0,2}.$
Indeed,
 $$\begin{align*}A_0(z)=\begin{pmatrix} 1 & 0\\ 0 & z \end{pmatrix}\begin{pmatrix} \frac{1}{2} & 0\\ 0 & \frac{1}{2} \end{pmatrix}, \qquad A_1(z)=\begin{pmatrix} z^{\frac{1}{2}} & 0\\ 0 & z^{\frac{1}{2}} \end{pmatrix}\begin{pmatrix} {\frac{z^{-\frac{1}{2}}+z^{\frac{1}{2}}}{2}} & \frac{z^{\frac{1}{2}}-z^{-\frac{1}{2}}}{2i}\\ \frac{z^{-\frac{1}{2}}-z^{\frac{1}{2}}}{2i} & {\frac{z^{-\frac{1}{2}}+z^{\frac{1}{2}}}{2}} \end{pmatrix},\end{align*}$$
$$\begin{align*}A_0(z)=\begin{pmatrix} 1 & 0\\ 0 & z \end{pmatrix}\begin{pmatrix} \frac{1}{2} & 0\\ 0 & \frac{1}{2} \end{pmatrix}, \qquad A_1(z)=\begin{pmatrix} z^{\frac{1}{2}} & 0\\ 0 & z^{\frac{1}{2}} \end{pmatrix}\begin{pmatrix} {\frac{z^{-\frac{1}{2}}+z^{\frac{1}{2}}}{2}} & \frac{z^{\frac{1}{2}}-z^{-\frac{1}{2}}}{2i}\\ \frac{z^{-\frac{1}{2}}-z^{\frac{1}{2}}}{2i} & {\frac{z^{-\frac{1}{2}}+z^{\frac{1}{2}}}{2}} \end{pmatrix},\end{align*}$$
where the matrix
 $$\begin{align*}\begin{pmatrix} {\frac{z^{-\frac{1}{2}}+z^{\frac{1}{2}}}{2}} & \frac{z^{\frac{1}{2}}-z^{-\frac{1}{2}}}{2i}\\ \frac{z^{-\frac{1}{2}}-z^{\frac{1}{2}}}{2i} & {\frac{z^{-\frac{1}{2}}+z^{\frac{1}{2}}}{2}} \end{pmatrix}\end{align*}$$
$$\begin{align*}\begin{pmatrix} {\frac{z^{-\frac{1}{2}}+z^{\frac{1}{2}}}{2}} & \frac{z^{\frac{1}{2}}-z^{-\frac{1}{2}}}{2i}\\ \frac{z^{-\frac{1}{2}}-z^{\frac{1}{2}}}{2i} & {\frac{z^{-\frac{1}{2}}+z^{\frac{1}{2}}}{2}} \end{pmatrix}\end{align*}$$
is an invertible real matrix for every
![]() $z\in \partial D.$
The family of frames given by the columns of
$z\in \partial D.$
The family of frames given by the columns of
![]() $A_t$
gives rise to a continuous family of orientations and spin structures on
$A_t$
gives rise to a continuous family of orientations and spin structures on
![]() $F(t)$
. The orientation on
$F(t)$
. The orientation on
![]() $F(1)$
coincides with the orientation on
$F(1)$
coincides with the orientation on
![]() $F^{1,1}.$
The orientation on
$F^{1,1}.$
The orientation on
![]() $F(0)$
coincides with the direct sum orientation
$F(0)$
coincides with the direct sum orientation
![]() $F^{0,2} = F^0 \oplus F^2.$
The spin structure on
$F^{0,2} = F^0 \oplus F^2.$
The spin structure on
![]() $F(1)$
coincides with the spin structure on
$F(1)$
coincides with the spin structure on
![]() $F^{1,1}$
and the spin structure on
$F^{1,1}$
and the spin structure on
![]() $F(0)$
coincides with the direct sum spin structure on
$F(0)$
coincides with the direct sum spin structure on
![]() $F^{0,2}$
as in Lemma 5.24. Let
$F^{0,2}$
as in Lemma 5.24. Let
 $$\begin{align*}R(t):=\begin{pmatrix} 1 & 0\\ 0 & t \end{pmatrix}, \quad B(t,z):=\frac{1}{4}\begin{pmatrix} (3+t^2)+(t^2-1)z & i(1-t^2)+i(t^2-1)z\\ i(\frac{1}{t}-t)+i(t-\frac{1}{t})z & (3t+\frac{1}{t})+(\frac{1}{t}-t)z \end{pmatrix}.\end{align*}$$
$$\begin{align*}R(t):=\begin{pmatrix} 1 & 0\\ 0 & t \end{pmatrix}, \quad B(t,z):=\frac{1}{4}\begin{pmatrix} (3+t^2)+(t^2-1)z & i(1-t^2)+i(t^2-1)z\\ i(\frac{1}{t}-t)+i(t-\frac{1}{t})z & (3t+\frac{1}{t})+(\frac{1}{t}-t)z \end{pmatrix}.\end{align*}$$
Then
![]() $B(t,z)$
is an invertible holomorphic matrix on D for every
$B(t,z)$
is an invertible holomorphic matrix on D for every
![]() $t\in (0,1]$
, and the matrices satisfy
$t\in (0,1]$
, and the matrices satisfy
Hence,
![]() $B(t,z)$
is an isomorphism between
$B(t,z)$
is an isomorphism between
![]() $(\underline {\mathbb {C}}^2, F(1))$
and
$(\underline {\mathbb {C}}^2, F(1))$
and
![]() $(\underline {\mathbb {C}}^2, F(t))$
for every
$(\underline {\mathbb {C}}^2, F(t))$
for every
![]() $t\in (0,1]$
. Denote by
$t\in (0,1]$
. Denote by
![]() $\bar {\partial }(t)$
the family of the Cauchy-Riemann operators obtained from
$\bar {\partial }(t)$
the family of the Cauchy-Riemann operators obtained from
![]() $(\underline {\mathbb {C}}^2, F(t))$
for
$(\underline {\mathbb {C}}^2, F(t))$
for
![]() $t\in (0,1]$
. Note that
$t\in (0,1]$
. Note that
![]() $\ker \bar {\partial }(1)=\ker \bar {\partial }_{1,1}$
. By Lemma 5.27, the vectors
$\ker \bar {\partial }(1)=\ker \bar {\partial }_{1,1}$
. By Lemma 5.27, the vectors
 $$\begin{align*}\begin{pmatrix} 1+z\\ 0 \end{pmatrix},\quad \begin{pmatrix} i(1-z)\\ 0 \end{pmatrix},\quad \begin{pmatrix} 0\\ 1+z \end{pmatrix},\quad \begin{pmatrix} 0\\ i(1-z) \end{pmatrix} \end{align*}$$
$$\begin{align*}\begin{pmatrix} 1+z\\ 0 \end{pmatrix},\quad \begin{pmatrix} i(1-z)\\ 0 \end{pmatrix},\quad \begin{pmatrix} 0\\ 1+z \end{pmatrix},\quad \begin{pmatrix} 0\\ i(1-z) \end{pmatrix} \end{align*}$$
form a basis for
![]() $\ker \bar {\partial }_{1,1}.$
So, the following vectors form a basis for
$\ker \bar {\partial }_{1,1}.$
So, the following vectors form a basis for
![]() $\ker \bar {\partial }(t)$
:
$\ker \bar {\partial }(t)$
:
 $$\begin{align*}v_{1,t}(z):=B(t,z)\begin{pmatrix} 1+z\\ 0 \end{pmatrix}, \quad v_{2,t}(z):=B(t,z)\begin{pmatrix} i(1-z)\\ 0 \end{pmatrix}, \end{align*}$$
$$\begin{align*}v_{1,t}(z):=B(t,z)\begin{pmatrix} 1+z\\ 0 \end{pmatrix}, \quad v_{2,t}(z):=B(t,z)\begin{pmatrix} i(1-z)\\ 0 \end{pmatrix}, \end{align*}$$
 $$\begin{align*}v_{3,t}(z):=B(t,z)\begin{pmatrix} 0\\ 1+z \end{pmatrix}, \quad v_{4,t}(z):=B(t,z)\begin{pmatrix} 0\\ i(1-z) \end{pmatrix}.\end{align*}$$
$$\begin{align*}v_{3,t}(z):=B(t,z)\begin{pmatrix} 0\\ 1+z \end{pmatrix}, \quad v_{4,t}(z):=B(t,z)\begin{pmatrix} 0\\ i(1-z) \end{pmatrix}.\end{align*}$$
Let
 $$ \begin{align*} w_{1,t}(z)&:=v_{1,t}(z)-v_{4,t}(z)=\begin{pmatrix} zt^2+1\\ izt-it \end{pmatrix}, \\ w_{2,t}(z)&:=v_{1,t}(z)+v_{4,t}(z)=\frac{1}{2}\begin{pmatrix} z^2(t^2-1)+2z+t^2+1\\ iz^2(t-\frac{1}{t})+i(t+\frac{1}{t})-2izt \end{pmatrix},\\ w_{3,t}(z)&:=v_{2,t}(z)-v_{3,t}(z)=\frac{1}{2}\begin{pmatrix} iz^2(1-t^2)+(1+t^2)i-2iz\\ z^2(t-\frac{1}{t})-t-\frac{1}{t}-2zt \end{pmatrix}, \\ w_{4,t}(z)&:=v_{2,t}(z)+v_{3,t}(z)=\begin{pmatrix} -iz+i\\ t+\frac{z}{t} \end{pmatrix}. \end{align*} $$
$$ \begin{align*} w_{1,t}(z)&:=v_{1,t}(z)-v_{4,t}(z)=\begin{pmatrix} zt^2+1\\ izt-it \end{pmatrix}, \\ w_{2,t}(z)&:=v_{1,t}(z)+v_{4,t}(z)=\frac{1}{2}\begin{pmatrix} z^2(t^2-1)+2z+t^2+1\\ iz^2(t-\frac{1}{t})+i(t+\frac{1}{t})-2izt \end{pmatrix},\\ w_{3,t}(z)&:=v_{2,t}(z)-v_{3,t}(z)=\frac{1}{2}\begin{pmatrix} iz^2(1-t^2)+(1+t^2)i-2iz\\ z^2(t-\frac{1}{t})-t-\frac{1}{t}-2zt \end{pmatrix}, \\ w_{4,t}(z)&:=v_{2,t}(z)+v_{3,t}(z)=\begin{pmatrix} -iz+i\\ t+\frac{z}{t} \end{pmatrix}. \end{align*} $$
For
![]() $i=2,3,4,$
define
$i=2,3,4,$
define
![]() $u_{i,t}(z):=tw_{i,t}(z)$
when
$u_{i,t}(z):=tw_{i,t}(z)$
when
![]() $t>0,$
and
$t>0,$
and
![]() $u_{i,0}(z):=\lim _{t\rightarrow 0}tw_{i,t}(z).$
In addition, define
$u_{i,0}(z):=\lim _{t\rightarrow 0}tw_{i,t}(z).$
In addition, define
![]() $u_{1,t}(z):=w_{1,t}(z).$
Note that the bases
$u_{1,t}(z):=w_{1,t}(z).$
Note that the bases
determine the same orientation on
![]() $\ker \bar {\partial }(t)$
for
$\ker \bar {\partial }(t)$
for
![]() $t\in (0,1]$
. We have
$t\in (0,1]$
. We have
 $$ \begin{align*} u_{1,0}(z)&= \begin{pmatrix} 1\\ 0 \end{pmatrix},\\ u_{2,0}(z)&= \frac{1}{2}\begin{pmatrix} 0\\ i(1-z^2) \end{pmatrix},\\ u_{3,0}(z)&= -\frac{1}{2}\begin{pmatrix} 0\\ z^2+1 \end{pmatrix},\\ u_{4,0}(z)&= \begin{pmatrix} 0\\ z \end{pmatrix}. \end{align*} $$
$$ \begin{align*} u_{1,0}(z)&= \begin{pmatrix} 1\\ 0 \end{pmatrix},\\ u_{2,0}(z)&= \frac{1}{2}\begin{pmatrix} 0\\ i(1-z^2) \end{pmatrix},\\ u_{3,0}(z)&= -\frac{1}{2}\begin{pmatrix} 0\\ z^2+1 \end{pmatrix},\\ u_{4,0}(z)&= \begin{pmatrix} 0\\ z \end{pmatrix}. \end{align*} $$
By Lemma 5.30, the basis
![]() $\{-u_{3,0},u_{2,0},u_{4,0}\}$
determines the orientation on
$\{-u_{3,0},u_{2,0},u_{4,0}\}$
determines the orientation on
![]() $\ker \bar {\partial }_2$
, and by Lemma 5.28, the vector
$\ker \bar {\partial }_2$
, and by Lemma 5.28, the vector
![]() $u_{1,0}(z)$
determines the orientation on
$u_{1,0}(z)$
determines the orientation on
![]() $\ker \bar {\partial }_0.$
Hence, by Lemma 5.25, the basis
$\ker \bar {\partial }_0.$
Hence, by Lemma 5.25, the basis
determines the orientation on
![]() $\ker \bar {\partial }(0)$
. Continuity implies that
$\ker \bar {\partial }(0)$
. Continuity implies that
![]() $\{u_{1,t}, u_{2,t}, u_{3,t}, u_{4,t}\}$
is positively oriented for every
$\{u_{1,t}, u_{2,t}, u_{3,t}, u_{4,t}\}$
is positively oriented for every
![]() $t\in [0,1],$
and so is
$t\in [0,1],$
and so is
![]() $\{v_{1,t}, v_{2,t}, v_{3,t}, v_{4,t}\}$
for
$\{v_{1,t}, v_{2,t}, v_{3,t}, v_{4,t}\}$
for
![]() $t\in (0,1]$
. Hence, the basis
$t\in (0,1]$
. Hence, the basis
 $$\begin{align*}v_{1,1}= \begin{pmatrix} 1+z\\ 0 \end{pmatrix}, \quad v_{2,1}= \begin{pmatrix} i(1-z)\\ 0 \end{pmatrix}, \quad v_{3,1}= \begin{pmatrix} 0\\ 1+z \end{pmatrix}, \quad v_{4,1}= \begin{pmatrix} 0\\ i(1-z) \end{pmatrix}\end{align*}$$
$$\begin{align*}v_{1,1}= \begin{pmatrix} 1+z\\ 0 \end{pmatrix}, \quad v_{2,1}= \begin{pmatrix} i(1-z)\\ 0 \end{pmatrix}, \quad v_{3,1}= \begin{pmatrix} 0\\ 1+z \end{pmatrix}, \quad v_{4,1}= \begin{pmatrix} 0\\ i(1-z) \end{pmatrix}\end{align*}$$
is positively oriented. Therefore,
![]() $f_{1,1}$
is orientation-preserving.
$f_{1,1}$
is orientation-preserving.
The orientation convention for
![]() $\partial D$
is the counter-clockwise orientation. For a point
$\partial D$
is the counter-clockwise orientation. For a point
![]() $z\in \partial D$
, we identify
$z\in \partial D$
, we identify
![]() $T_z\partial D$
with
$T_z\partial D$
with
![]() $iz\mathbb {R},$
so
$iz\mathbb {R},$
so
![]() $iz$
is a positively oriented basis. The following definition is the orientation convention for
$iz$
is a positively oriented basis. The following definition is the orientation convention for
![]() $\mathrm {PSL}(2,\mathbb {R})$
in [Reference Fukaya, Oh, Ohta and Ono14].
$\mathrm {PSL}(2,\mathbb {R})$
in [Reference Fukaya, Oh, Ohta and Ono14].
Definition 5.32. Let
![]() $z_0, z_1, z_2\in \partial D$
be three distinct points in anticlockwise order. Consider the embedding
$z_0, z_1, z_2\in \partial D$
be three distinct points in anticlockwise order. Consider the embedding
The orientation on
![]() $\mathrm {PSL}(2,\mathbb {R})$
is determined such that F is orientation-reversing.
$\mathrm {PSL}(2,\mathbb {R})$
is determined such that F is orientation-reversing.
Consider the Lie algebra
![]() $\mathfrak {psl}(2,\mathbb {R}).$
Let
$\mathfrak {psl}(2,\mathbb {R}).$
Let
 $$\begin{align*}\eta_1=\begin{pmatrix} 1 & 0\\ 0 & -1 \end{pmatrix}, \quad \eta_2= \begin{pmatrix} 0 & 0\\ 1 & 0 \end{pmatrix},\quad \eta_3= \begin{pmatrix} 0 & 1\\ 0 & 0 \end{pmatrix}\end{align*}$$
$$\begin{align*}\eta_1=\begin{pmatrix} 1 & 0\\ 0 & -1 \end{pmatrix}, \quad \eta_2= \begin{pmatrix} 0 & 0\\ 1 & 0 \end{pmatrix},\quad \eta_3= \begin{pmatrix} 0 & 1\\ 0 & 0 \end{pmatrix}\end{align*}$$
be a basis for this algebra.
Lemma 5.33.
![]() $\{\eta _1,\eta _2,\eta _3\}$
is a positively oriented basis of
$\{\eta _1,\eta _2,\eta _3\}$
is a positively oriented basis of
![]() $\mathfrak {psl}(2,\mathbb {R}).$
$\mathfrak {psl}(2,\mathbb {R}).$
Proof. Let
![]() $\mathbb {H}$
denote the closed upper half plane and let
$\mathbb {H}$
denote the closed upper half plane and let
![]() $\overline {\mathbb {H}}$
denote the compactification by adding a point at infinity. Since there is a biholomorphism
$\overline {\mathbb {H}}$
denote the compactification by adding a point at infinity. Since there is a biholomorphism
![]() $D\rightarrow \overline {\mathbb {H}}$
, we can identify the range of the map F from Definition 5.32 with
$D\rightarrow \overline {\mathbb {H}}$
, we can identify the range of the map F from Definition 5.32 with
![]() $\partial \overline {\mathbb {H}}\times \partial \overline {\mathbb {H}} \times \partial \overline {\mathbb {H}}$
. Choose
$\partial \overline {\mathbb {H}}\times \partial \overline {\mathbb {H}} \times \partial \overline {\mathbb {H}}$
. Choose
The orientation of
is determined by the basis
We have
 $$ \begin{align*} \frac{d}{dt}|_{t=0}\exp(t\eta_1)\cdot z&=\frac{d}{dt}|_{t=0}\begin{pmatrix} e^t & 0\\ 0 & e^{-t} \end{pmatrix}\cdot z\\ &=\frac{d}{dt}|_{t=0}\frac{e^tz}{e^{-t}}\\ &=2z. \end{align*} $$
$$ \begin{align*} \frac{d}{dt}|_{t=0}\exp(t\eta_1)\cdot z&=\frac{d}{dt}|_{t=0}\begin{pmatrix} e^t & 0\\ 0 & e^{-t} \end{pmatrix}\cdot z\\ &=\frac{d}{dt}|_{t=0}\frac{e^tz}{e^{-t}}\\ &=2z. \end{align*} $$
Similarly,
Hence,
Since
 $$\begin{align*}\det\ \begin{pmatrix} -2 & 0 & 2 \\ -1 & 0 & -1 \\ 1 & 1 & 1 \end{pmatrix} < 0, \end{align*}$$
$$\begin{align*}\det\ \begin{pmatrix} -2 & 0 & 2 \\ -1 & 0 & -1 \\ 1 & 1 & 1 \end{pmatrix} < 0, \end{align*}$$
it follows that F is orientation-reversing. Thus, by Definition 5.32, the basis
![]() $\{\eta _1, \eta _2, \eta _3\}$
is positively oriented.
$\{\eta _1, \eta _2, \eta _3\}$
is positively oriented.
Lemma 5.34. The action of
![]() $\mathrm {PSL}(2,\mathbb {R})$
on D induces an isomorphism
$\mathrm {PSL}(2,\mathbb {R})$
on D induces an isomorphism
which is orientation-reversing.
Proof. Identify D with the one-point compactified upper half plane
![]() $\overline {\mathbb {H}}$
and identify the Riemann-Hilbert pair
$\overline {\mathbb {H}}$
and identify the Riemann-Hilbert pair
![]() $(\underline {\mathbb {C}},F^2)$
with the Riemann-Hilbert pair
$(\underline {\mathbb {C}},F^2)$
with the Riemann-Hilbert pair
![]() $(T\overline {\mathbb {H}},T\partial \overline {\mathbb {H}}).$
The latter identification preserves the canonical orientation on the determinant line by Proposition 5.1. The map
$(T\overline {\mathbb {H}},T\partial \overline {\mathbb {H}}).$
The latter identification preserves the canonical orientation on the determinant line by Proposition 5.1. The map
![]() $\mathcal {D}$
is given by
$\mathcal {D}$
is given by
Let
![]() $ev:=ev_i\oplus ev_0$
, where
$ev:=ev_i\oplus ev_0$
, where
![]() $ev_i$
and
$ev_i$
and
![]() $ev_0$
are the evaluation maps at i and
$ev_0$
are the evaluation maps at i and
![]() $0$
, respectively. By Lemma 5.29,
$0$
, respectively. By Lemma 5.29,
![]() $\mathcal {D}$
is orientation reversing if and only if
$\mathcal {D}$
is orientation reversing if and only if
![]() $ev\circ \mathcal {D}$
is orientation reversing. Consider the points
$ev\circ \mathcal {D}$
is orientation reversing. Consider the points
![]() $0,i\in \overline {\mathbb {H}}$
. The basis
$0,i\in \overline {\mathbb {H}}$
. The basis
is positively oriented basis of
![]() $T_i\overline {\mathbb {H}}\oplus T_0\partial \overline {\mathbb {H}}$
. By the calculation of the previous lemma, we have
$T_i\overline {\mathbb {H}}\oplus T_0\partial \overline {\mathbb {H}}$
. By the calculation of the previous lemma, we have
Since
 $$\begin{align*}\det\ \begin{pmatrix} 0 & 2 & 0 \\ 1 & 0 & 0 \\ 1 & 0 & 1 \end{pmatrix} < 0, \end{align*}$$
$$\begin{align*}\det\ \begin{pmatrix} 0 & 2 & 0 \\ 1 & 0 & 0 \\ 1 & 0 & 1 \end{pmatrix} < 0, \end{align*}$$
it follows that
![]() $\mathcal {D}$
is orientation-reversing.
$\mathcal {D}$
is orientation-reversing.
5.5 Riemann-Hilbert pairs and holomorphic disks
Let
![]() $(X,J)$
be an n-dimensional complex manifold, and let
$(X,J)$
be an n-dimensional complex manifold, and let
![]() $L\subset X$
be a smooth totally real n-dimensional submanifold. A holomorphic disk
$L\subset X$
be a smooth totally real n-dimensional submanifold. A holomorphic disk
![]() $u:(D,\partial D)\rightarrow (X,L)$
gives rise to a holomorphic vector bundle
$u:(D,\partial D)\rightarrow (X,L)$
gives rise to a holomorphic vector bundle
![]() $u^{*}TX\rightarrow D$
and a smooth totally real subbundle
$u^{*}TX\rightarrow D$
and a smooth totally real subbundle
![]() $u|_{\partial D}^{*}TL\subset u^{*}TX|_{\partial D}$
. Thus, we obtain a Riemann-Hilbert pair
$u|_{\partial D}^{*}TL\subset u^{*}TX|_{\partial D}$
. Thus, we obtain a Riemann-Hilbert pair
![]() $(E_u,F_u)$
associated to
$(E_u,F_u)$
associated to
![]() $u.$
$u.$
5.5.1 A useful example
Lemma 5.35. Let
![]() $u:(D,\partial D)\rightarrow (\mathbb {C}P^3,L_\triangle )$
be the holomorphic disk given by
$u:(D,\partial D)\rightarrow (\mathbb {C}P^3,L_\triangle )$
be the holomorphic disk given by
![]() $u(z)=e^{-i\xi _v\log z}\cdot \triangle .$
Let
$u(z)=e^{-i\xi _v\log z}\cdot \triangle .$
Let
![]() $\theta _1,\theta _2 \in \mathfrak {su}(2)$
be such that
$\theta _1,\theta _2 \in \mathfrak {su}(2)$
be such that
![]() $\xi _v,\theta _1,\theta _2$
form a basis of
$\xi _v,\theta _1,\theta _2$
form a basis of
![]() $\mathfrak {su}(2).$
Equip
$\mathfrak {su}(2).$
Equip
![]() $L_\triangle $
with the orientation and spin structure arising from the trivialization of
$L_\triangle $
with the orientation and spin structure arising from the trivialization of
![]() $TL_\triangle $
given by the infinitesimal action of
$TL_\triangle $
given by the infinitesimal action of
![]() $\mathfrak {su}(2)$
and the basis
$\mathfrak {su}(2)$
and the basis
![]() $\xi _v,\theta _1,\theta _2.$
Let
$\xi _v,\theta _1,\theta _2.$
Let
Then, the sections
form a holomorphic frame. Moreover, there is an isomorphism of spin Riemann-Hilbert pairs
given by
 $$ \begin{align} \frac{\xi_v}{z}\cdot u\mapsto \begin{pmatrix} 1\\ 0\\ 0 \end{pmatrix},\quad\theta_1\cdot u \mapsto \begin{pmatrix} 0\\ 1\\ 0 \end{pmatrix},\quad \theta_2\cdot u\mapsto \begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix}. \end{align} $$
$$ \begin{align} \frac{\xi_v}{z}\cdot u\mapsto \begin{pmatrix} 1\\ 0\\ 0 \end{pmatrix},\quad\theta_1\cdot u \mapsto \begin{pmatrix} 0\\ 1\\ 0 \end{pmatrix},\quad \theta_2\cdot u\mapsto \begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix}. \end{align} $$
Proof. Recalling Example 5.10, we see that the kernel of the infinitesimal action of
![]() $\mathfrak {sl}(2,\mathbb {C}) $
at
$\mathfrak {sl}(2,\mathbb {C}) $
at
![]() $u(0)$
is spanned by
$u(0)$
is spanned by
![]() $\xi _v$
. Given this, Smith (Reference Smith44, Appendix A.3) shows that the sections (5.1) form a holomorphic frame for
$\xi _v$
. Given this, Smith (Reference Smith44, Appendix A.3) shows that the sections (5.1) form a holomorphic frame for
![]() $E.$
We split
$E.$
We split
![]() $(E,F)$
by
$(E,F)$
by
 $$ \begin{align*} E=\left< \frac{\xi_v}{z}\cdot u\right>_{\mathbb{C}} \oplus \left< \theta_1\cdot u \right>_{\mathbb{C}}\oplus \left< \theta_1\cdot u \right>_{\mathbb{C}}, \end{align*} $$
$$ \begin{align*} E=\left< \frac{\xi_v}{z}\cdot u\right>_{\mathbb{C}} \oplus \left< \theta_1\cdot u \right>_{\mathbb{C}}\oplus \left< \theta_1\cdot u \right>_{\mathbb{C}}, \end{align*} $$
 $$ \begin{align*} F=z\left< \frac{\xi_v}{z}\cdot u\right>_{\mathbb{R}} \oplus \left< \theta_1\cdot u \right>_{\mathbb{R}}\oplus \left< \theta_1\cdot u \right>_{\mathbb{R}}. \end{align*} $$
$$ \begin{align*} F=z\left< \frac{\xi_v}{z}\cdot u\right>_{\mathbb{R}} \oplus \left< \theta_1\cdot u \right>_{\mathbb{R}}\oplus \left< \theta_1\cdot u \right>_{\mathbb{R}}. \end{align*} $$
It follows that the formula (5.2) gives the desired isomorphism
![]() $\Psi .$
Recall the choices of the spin structures and orientations of
$\Psi .$
Recall the choices of the spin structures and orientations of
![]() $F^2$
and
$F^2$
and
![]() $F^0$
given in Section 5.4. By Lemma 5.24, the frame
$F^0$
given in Section 5.4. By Lemma 5.24, the frame
 $$\begin{align*}\begin{pmatrix} z\\ 0\\ 0 \end{pmatrix},\quad \begin{pmatrix} 0\\ 1\\ 0 \end{pmatrix},\quad \begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix} \end{align*}$$
$$\begin{align*}\begin{pmatrix} z\\ 0\\ 0 \end{pmatrix},\quad \begin{pmatrix} 0\\ 1\\ 0 \end{pmatrix},\quad \begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix} \end{align*}$$
of
![]() $F^2\oplus F^0\oplus F^0$
is positively oriented and can be lifted to the associate double cover of the frame bundle. Therefore, the isomorphism
$F^2\oplus F^0\oplus F^0$
is positively oriented and can be lifted to the associate double cover of the frame bundle. Therefore, the isomorphism
![]() $\Psi $
preserves orientation and spin structure.
$\Psi $
preserves orientation and spin structure.
5.5.2 Orientation convention for disk moduli spaces
Let
![]() $(X,\omega )$
be a symplectic manifold with
$(X,\omega )$
be a symplectic manifold with
![]() $\omega $
-tame (integrable) complex structure
$\omega $
-tame (integrable) complex structure
![]() $J,$
and let
$J,$
and let
![]() $L \subset X$
be a Lagrangian submanifold. Let
$L \subset X$
be a Lagrangian submanifold. Let
![]() $\widetilde {\mathcal {M}}(\beta )$
denote the space of parameterized J-holomorphic maps
$\widetilde {\mathcal {M}}(\beta )$
denote the space of parameterized J-holomorphic maps
![]() $u: (D^2,\partial D^2) \to (X,L)$
such that
$u: (D^2,\partial D^2) \to (X,L)$
such that
![]() $u_*([D^2,\partial D^2]) = \beta $
. Each
$u_*([D^2,\partial D^2]) = \beta $
. Each
![]() $u \in \widetilde {\mathcal {M}}(\beta )$
determines a Riemann-Hilbert pair
$u \in \widetilde {\mathcal {M}}(\beta )$
determines a Riemann-Hilbert pair
![]() $(E_u,F_u) = (u^{*}TX,u^{*}TL)$
as explained above. For the following discussion, we assume that the linear Cauchy-Riemann operator
$(E_u,F_u) = (u^{*}TX,u^{*}TL)$
as explained above. For the following discussion, we assume that the linear Cauchy-Riemann operator
![]() $\bar \partial _{(E_u,F_u)} : \Gamma ((D^2,\partial D^2),(E_u,F_u)) \to \Gamma (D^2,\Omega ^{0,1}(E_u))$
is surjective for every u, so
$\bar \partial _{(E_u,F_u)} : \Gamma ((D^2,\partial D^2),(E_u,F_u)) \to \Gamma (D^2,\Omega ^{0,1}(E_u))$
is surjective for every u, so
![]() $\widetilde {\mathcal {M}}(\beta )$
is a smooth manifold and there is a canonical isomorphism
$\widetilde {\mathcal {M}}(\beta )$
is a smooth manifold and there is a canonical isomorphism
Thus, Proposition 5.1 gives a canonical orientation of
![]() $\widetilde {\mathcal {M}}(\beta ).$
$\widetilde {\mathcal {M}}(\beta ).$
We discuss now the relevant conventions concerning the orientations of the moduli spaces
![]() $\mathcal {M}_{k+1,l}(\beta )$
of unparameterized stable J-holomorphic maps with marked points. The following definition is Convention 8.2.1 from [Reference Fukaya, Oh, Ohta and Ono14].
$\mathcal {M}_{k+1,l}(\beta )$
of unparameterized stable J-holomorphic maps with marked points. The following definition is Convention 8.2.1 from [Reference Fukaya, Oh, Ohta and Ono14].
Definition 5.36. Let G be an oriented Lie group with a smooth, proper, free right action on an oriented manifold M. For
![]() $p \in M,$
let
$p \in M,$
let
![]() $\varphi _p : G \to M$
be given by
$\varphi _p : G \to M$
be given by
![]() $g \mapsto p\cdot g.$
Let
$g \mapsto p\cdot g.$
Let
![]() $\pi : M \to M/G$
be the quotient map. Split the short exact sequence
$\pi : M \to M/G$
be the quotient map. Split the short exact sequence
to obtain an isomorphism
The quotient orientation on
![]() $M/G$
is determined by the condition that the preceding isomorphism preserves orientation for all
$M/G$
is determined by the condition that the preceding isomorphism preserves orientation for all
![]() $p \in M$
.
$p \in M$
.
The following definition is based on [Reference Fukaya, Oh, Ohta and Ono14, p. 698].
Definition 5.37. Let
![]() $U \subset \widetilde {\mathcal {M}}(\beta ) \times (\partial D^2)^{k+1} \times (\operatorname {\mathrm {int}} D^2)^l$
denote the open subset where the marked points are pairwise disjoint and the cyclic ordering on the boundary marked points given by the orientation on
$U \subset \widetilde {\mathcal {M}}(\beta ) \times (\partial D^2)^{k+1} \times (\operatorname {\mathrm {int}} D^2)^l$
denote the open subset where the marked points are pairwise disjoint and the cyclic ordering on the boundary marked points given by the orientation on
![]() $\partial D^2$
induced from the complex orientation of
$\partial D^2$
induced from the complex orientation of
![]() $D^2$
agrees with the order of the labels. Thus, points of U are tuples
$D^2$
agrees with the order of the labels. Thus, points of U are tuples
![]() $(u,z,w)$
where
$(u,z,w)$
where
An automorphism of the disk
![]() $\psi \in \mathrm {PSL}_2(\mathbb {R})$
acts on U by
$\psi \in \mathrm {PSL}_2(\mathbb {R})$
acts on U by
The orientation of
![]() $\mathcal {M}_{k+1,l}(\beta )$
is determined by the quotient orientation on the open subset
$\mathcal {M}_{k+1,l}(\beta )$
is determined by the quotient orientation on the open subset
![]() $U/PSL_2(\mathbb {R}) \subset \mathcal {M}_{k+1,l}(\beta ).$
$U/PSL_2(\mathbb {R}) \subset \mathcal {M}_{k+1,l}(\beta ).$
5.6 Computation of
 $\overline {OGW}_{1, 1}$
$\overline {OGW}_{1, 1}$
Recall from Section 4 that we denote by
![]() $\mathcal {M}_{k+1,l}(\beta )$
the moduli space of holomorphic disks
$\mathcal {M}_{k+1,l}(\beta )$
the moduli space of holomorphic disks
![]() $u:(D, \partial D)\rightarrow (\mathbb {C}P^3,L_\triangle )$
representing a class
$u:(D, \partial D)\rightarrow (\mathbb {C}P^3,L_\triangle )$
representing a class
![]() $\beta \in H_2(\mathbb {C}P^3,L_\triangle ;\mathbb {Z})$
with
$\beta \in H_2(\mathbb {C}P^3,L_\triangle ;\mathbb {Z})$
with
![]() $k+1$
boundary points and l interior points. We denote elements in
$k+1$
boundary points and l interior points. We denote elements in
![]() $\mathcal {M}_{k+1,l}(\beta )$
by
$\mathcal {M}_{k+1,l}(\beta )$
by
![]() $[u;z_0,\ldots ,z_k,w_1,\ldots ,w_l]$
, where
$[u;z_0,\ldots ,z_k,w_1,\ldots ,w_l]$
, where
![]() $z_i\in \partial D$
and
$z_i\in \partial D$
and
![]() $w_i\in \mathrm {int}D$
. Consider the moduli space
$w_i\in \mathrm {int}D$
. Consider the moduli space
![]() $\mathcal {M}_{1,0}(1)$
, and the evaluation map
$\mathcal {M}_{1,0}(1)$
, and the evaluation map
The following lemma is part of Proposition 4.2 from [Reference Smith43].
Lemma 5.38. The evaluation map
![]() $evb_0:\mathcal {M}_{1,0}(1)\rightarrow L_\triangle $
is a covering map of degree
$evb_0:\mathcal {M}_{1,0}(1)\rightarrow L_\triangle $
is a covering map of degree
![]() $\pm 3$
.
$\pm 3$
.
Proof of Theorem 5.1.
By Theorem 1.6, we have
 $$\begin{align*}\overline{OGW}\!_{1,1}= - \int_{\mathcal{M}_{1,0}(1)}{evb_0}^{*}\bar{b},\end{align*}$$
$$\begin{align*}\overline{OGW}\!_{1,1}= - \int_{\mathcal{M}_{1,0}(1)}{evb_0}^{*}\bar{b},\end{align*}$$
where
![]() $\text {PD}([\bar {b}])=pt$
. Hence,
$\text {PD}([\bar {b}])=pt$
. Hence,
![]() $\overline {OGW}\!_{1,1}$
is determined by the degree of the map
$\overline {OGW}\!_{1,1}$
is determined by the degree of the map
![]() $evb_0$
, and Lemma 5.38 gives
$evb_0$
, and Lemma 5.38 gives
![]() $\overline {OGW}\!_{1,1}=\mp 3,$
where the sign depends on whether
$\overline {OGW}\!_{1,1}=\mp 3,$
where the sign depends on whether
![]() $evb_0$
preserves or reverses orientation.
$evb_0$
preserves or reverses orientation.
We show that
![]() $evb_0$
preserves orientation. Choose
$evb_0$
preserves orientation. Choose
![]() $\theta _1,\theta _2$
that together with
$\theta _1,\theta _2$
that together with
![]() $\xi _v$
form a basis of
$\xi _v$
form a basis of
![]() $\mathfrak {su}(2).$
Equip
$\mathfrak {su}(2).$
Equip
![]() $L_\triangle $
with the orientation and spin structure arising from the trivialization of
$L_\triangle $
with the orientation and spin structure arising from the trivialization of
![]() $TL_\triangle $
given by the infinitesimal action of
$TL_\triangle $
given by the infinitesimal action of
![]() $\mathfrak {su}(2)$
and the basis
$\mathfrak {su}(2)$
and the basis
![]() $\xi _v,\theta _1,\theta _2.$
The orientation of this basis does not affect the calculation below, in accordance with the orientation axiom Proposition 2.2 8.
$\xi _v,\theta _1,\theta _2.$
The orientation of this basis does not affect the calculation below, in accordance with the orientation axiom Proposition 2.2 8.
Let
![]() $u:(D,\partial D)\rightarrow (\mathbb {C}P^3,L_\triangle )$
be a holomorphic disk of Maslov index 2. Let
$u:(D,\partial D)\rightarrow (\mathbb {C}P^3,L_\triangle )$
be a holomorphic disk of Maslov index 2. Let
By Lemma 5.16, we can write
![]() $u(z)=A\cdot e^{-i\xi _v \log z}\cdot \triangle $
, where
$u(z)=A\cdot e^{-i\xi _v \log z}\cdot \triangle $
, where
![]() $A\in \text {SU}(2)$
. We may assume that A is the identity since acting by
$A\in \text {SU}(2)$
. We may assume that A is the identity since acting by
![]() $A^{-1}$
does not change the isomorphism class of
$A^{-1}$
does not change the isomorphism class of
![]() $(E,F)$
.
$(E,F)$
.
Let
![]() $z\in \partial D$
and let
$z\in \partial D$
and let
![]() $\zeta \in T_z\partial D$
denote the unit vector in the direction of the orientation. By Definition 5.37, the oriented tangent space of
$\zeta \in T_z\partial D$
denote the unit vector in the direction of the orientation. By Definition 5.37, the oriented tangent space of
![]() $\mathcal {M}_{1,0}(1)$
at
$\mathcal {M}_{1,0}(1)$
at
![]() $[u;z]$
is given by
$[u;z]$
is given by
By Proposition 5.1 and Lemma 5.35, we have an orientation-preserving isomorphism
By Lemma 5.27, we have an orientation-reversing isomorphism
The linearization of the action of
![]() $\mathrm {PSL}_2(\mathbb {R})$
in Definition 5.37 composed with the projection on
$\mathrm {PSL}_2(\mathbb {R})$
in Definition 5.37 composed with the projection on
![]() $\ker \bar \partial _2$
gives the map
$\ker \bar \partial _2$
gives the map
![]() $\mathcal {D}:\mathfrak {psl}(2,\mathbb {R})\rightarrow \ker \bar {\partial }_2$
of Lemma 5.34. So, by Definition 5.36 and Lemmas 5.34 and 5.27, we have an orientation-preserving isomorphism
$\mathcal {D}:\mathfrak {psl}(2,\mathbb {R})\rightarrow \ker \bar {\partial }_2$
of Lemma 5.34. So, by Definition 5.36 and Lemmas 5.34 and 5.27, we have an orientation-preserving isomorphism
given by
Abbreviate
Thus, by Lemmas 5.25 and 5.28, the orientation on
![]() $T_{[u:z]}\mathcal {M}_{1,0}(1)$
is given by the basis
$T_{[u:z]}\mathcal {M}_{1,0}(1)$
is given by the basis
![]() $\bar {\theta }_1, \bar {\theta }_2, \bar {\zeta }$
. In order to show that
$\bar {\theta }_1, \bar {\theta }_2, \bar {\zeta }$
. In order to show that
![]() $evb_0$
preserves orientation, it suffices to show that
$evb_0$
preserves orientation, it suffices to show that
preserves orientation when
![]() $z=1$
. The tangent vector
$z=1$
. The tangent vector
![]() $\zeta \in T_1 \partial D$
is represented by the path
$\zeta \in T_1 \partial D$
is represented by the path
![]() $t \mapsto e^{it}.$
So,
$t \mapsto e^{it}.$
So,
 $$\begin{align*}devb_{0_{[u;1]}}(\bar{\zeta}) = du_1(\zeta) = \left.\frac{d}{dt}u(e^{it})\right|{}_{t=0}= \left.\frac{d}{dt} e^{t\xi_v}\right|{}_{t = 0} = \xi_v\cdot u(1). \end{align*}$$
$$\begin{align*}devb_{0_{[u;1]}}(\bar{\zeta}) = du_1(\zeta) = \left.\frac{d}{dt}u(e^{it})\right|{}_{t=0}= \left.\frac{d}{dt} e^{t\xi_v}\right|{}_{t = 0} = \xi_v\cdot u(1). \end{align*}$$
Since
it follows that
![]() $evb_0$
preserves orientation. Therefore,
$evb_0$
preserves orientation. Therefore,
![]() $\overline {OGW}\!_{1,1}=-3$
.
$\overline {OGW}\!_{1,1}=-3$
.
5.7 Computation of
 $\overline {OGW}_{1, 0}(\Gamma _2)$
$\overline {OGW}_{1, 0}(\Gamma _2)$
By Theorem 1.6, we have
 $$ \begin{align*} \overline{OGW}\!_{1, 0}(\Gamma_2)= -\int_{\mathcal{M}_{0,1}(1)}evi_1^{*}\gamma_2, \end{align*} $$
$$ \begin{align*} \overline{OGW}\!_{1, 0}(\Gamma_2)= -\int_{\mathcal{M}_{0,1}(1)}evi_1^{*}\gamma_2, \end{align*} $$
where
![]() $\gamma _2$
is a a differential form representing
$\gamma _2$
is a a differential form representing
![]() $\Gamma _2 \in H^4(\mathbb {C}P^3, L_\triangle; \mathbb {R})$
. By Poincaré-Lefschetz duality, we have
$\Gamma _2 \in H^4(\mathbb {C}P^3, L_\triangle; \mathbb {R})$
. By Poincaré-Lefschetz duality, we have
![]() $H^4(\mathbb {C}P^3, L_\triangle; \mathbb {R}) \simeq H_2(\mathbb {C}P^3 \backslash L_\triangle ;\mathbb {R})$
. Hence, our strategy for computing
$H^4(\mathbb {C}P^3, L_\triangle; \mathbb {R}) \simeq H_2(\mathbb {C}P^3 \backslash L_\triangle ;\mathbb {R})$
. Hence, our strategy for computing
![]() $\overline {OGW}\!_{1,0}(\Gamma _2)$
is to find a complex curve in
$\overline {OGW}\!_{1,0}(\Gamma _2)$
is to find a complex curve in
![]() $\mathbb {C}P^3\setminus L_\triangle $
representing the Poincaré-Lefschetz dual to
$\mathbb {C}P^3\setminus L_\triangle $
representing the Poincaré-Lefschetz dual to
![]() $\Gamma _2,$
and determine how many holomorphic disks intersect it.
$\Gamma _2,$
and determine how many holomorphic disks intersect it.
Any complex subvariety
![]() $\Upsilon \subset \mathbb {C}P^3 \backslash L_\triangle $
of complex dimension 2 represents
$\Upsilon \subset \mathbb {C}P^3 \backslash L_\triangle $
of complex dimension 2 represents
![]() $k\text {PD}([\omega ])$
where
$k\text {PD}([\omega ])$
where
![]() $k \in \mathbb {Z}$
is the degree of
$k \in \mathbb {Z}$
is the degree of
![]() $\Upsilon $
(i.e., the number of intersection points with a generic line). Consider complex subvarieties
$\Upsilon $
(i.e., the number of intersection points with a generic line). Consider complex subvarieties
![]() $\Upsilon _1, \Upsilon _2$
of degree
$\Upsilon _1, \Upsilon _2$
of degree
![]() $k_1, k_2$
, respectively, in general position. Then
$k_1, k_2$
, respectively, in general position. Then
![]() $\Upsilon _1 \cap \Upsilon _2$
represents
$\Upsilon _1 \cap \Upsilon _2$
represents
![]() $k_1k_2\text {PD}([\omega ^2])$
, and thus,
$k_1k_2\text {PD}([\omega ^2])$
, and thus,
![]() $\text {PD}(\Gamma _2) = [\Upsilon _1 \cap \Upsilon _2] / (k_1k_2)$
.
$\text {PD}(\Gamma _2) = [\Upsilon _1 \cap \Upsilon _2] / (k_1k_2)$
.
We consider the case where
![]() $\Upsilon _1, \Upsilon _2$
are small perturbations of the anticanonical divisor
$\Upsilon _1, \Upsilon _2$
are small perturbations of the anticanonical divisor
![]() $Y_\triangle $
. For
$Y_\triangle $
. For
![]() $i = 1, 2$
, let
$i = 1, 2$
, let
![]() $g_i \in \text {SU}(2)$
be lifts of rotations by arbitrary small angles
$g_i \in \text {SU}(2)$
be lifts of rotations by arbitrary small angles
![]() $\epsilon _i$
about different axes. Write
$\epsilon _i$
about different axes. Write
Note that
![]() $\Upsilon _i\subset \mathbb {C}P^3\setminus L_\triangle $
since
$\Upsilon _i\subset \mathbb {C}P^3\setminus L_\triangle $
since
![]() $\epsilon _i$
are small.
$\epsilon _i$
are small.
Theorem 5.2.
![]() $\deg \Upsilon _i = 4$
$\deg \Upsilon _i = 4$
Proof. Write
![]() $a=[a_0:a_1]$
,
$a=[a_0:a_1]$
,
![]() $b=[b_0: b_1]\in \mathbb {C}P^1$
. Identifying
$b=[b_0: b_1]\in \mathbb {C}P^1$
. Identifying
![]() $\mathbb {C}P^3$
with the projectivization of the space of homogeneous polynomials of degree
$\mathbb {C}P^3$
with the projectivization of the space of homogeneous polynomials of degree
![]() $3$
in two variables, we can write
$3$
in two variables, we can write
where
![]() $(g_i)_{kl}$
are the components of the matrix
$(g_i)_{kl}$
are the components of the matrix
![]() $g_i.$
Hence, we have an embedding
$g_i.$
Hence, we have an embedding
where
![]() $f_i^j$
are homogeneous polynomials of bidegree
$f_i^j$
are homogeneous polynomials of bidegree
![]() $(2,1),$
such that
$(2,1),$
such that
![]() $\Upsilon _i=\operatorname {\mathrm {Im}} f_i$
.
$\Upsilon _i=\operatorname {\mathrm {Im}} f_i$
.
Let
![]() $H_1$
and
$H_1$
and
![]() $H_2$
be hyperplanes in
$H_2$
be hyperplanes in
![]() $\mathbb {C}P^3$
given by
$\mathbb {C}P^3$
given by
The intersection
![]() $H_1\cap H_2$
is a generic line, so we have
$H_1\cap H_2$
is a generic line, so we have
The preimages
![]() $f_i^{-1}(H_1)$
and
$f_i^{-1}(H_1)$
and
![]() $f_i^{-1}(H_2)$
are the vanishing sets of the polynomials
$f_i^{-1}(H_2)$
are the vanishing sets of the polynomials
 $$\begin{align*}p^h_i(a,b)=\sum_{j=0}^3 h_jf_i^j(a,b),\qquad p^k_i(a,b)=\sum_{j=0}^3 k_jf_i^j(a,b) \end{align*}$$
$$\begin{align*}p^h_i(a,b)=\sum_{j=0}^3 h_jf_i^j(a,b),\qquad p^k_i(a,b)=\sum_{j=0}^3 k_jf_i^j(a,b) \end{align*}$$
of bidegree
![]() $(2,1)$
. Denote by
$(2,1)$
. Denote by
![]() $\pi _1, \pi _2 : \mathbb {C}P^1 \times \mathbb {C}P^1 \rightarrow \mathbb {C}P^1$
the projection maps. Let
$\pi _1, \pi _2 : \mathbb {C}P^1 \times \mathbb {C}P^1 \rightarrow \mathbb {C}P^1$
the projection maps. Let
So,
The polynomials
![]() $p^h_i, p^k_i,$
define sections of the line bundle
$p^h_i, p^k_i,$
define sections of the line bundle
![]() $\mathcal {O}(2,1).$
So,
$\mathcal {O}(2,1).$
So,
 $$ \begin{align*} \# \Upsilon_i \cap H_1 \cap H_2 &= \# f_i^{-1}(H_1 \cap H_2) = \# f_i^{-1}(H_1) \cap f_i^{-1}(H_2) \\ &= \int_{\mathbb{C}P^1 \times \mathbb{C}P^1} c_1(\mathcal{O}(2,1)) \smile c_1(\mathcal{O}(2,1)) = 4. \end{align*} $$
$$ \begin{align*} \# \Upsilon_i \cap H_1 \cap H_2 &= \# f_i^{-1}(H_1 \cap H_2) = \# f_i^{-1}(H_1) \cap f_i^{-1}(H_2) \\ &= \int_{\mathbb{C}P^1 \times \mathbb{C}P^1} c_1(\mathcal{O}(2,1)) \smile c_1(\mathcal{O}(2,1)) = 4. \end{align*} $$
Proof of Theorem 5.2.
Let
![]() $\gamma _2$
be a a differential form representing
$\gamma _2$
be a a differential form representing
![]() $\Gamma _2 \in H^4(\mathbb {C}P^3, L_\triangle; \mathbb {R})$
. We show below that
$\Gamma _2 \in H^4(\mathbb {C}P^3, L_\triangle; \mathbb {R})$
. We show below that
![]() $evi_1$
is transverse to
$evi_1$
is transverse to
![]() $\Upsilon _1 \cap \Upsilon _2.$
Thus, by Theorem 1.6 and Poincaré duality, we have
$\Upsilon _1 \cap \Upsilon _2.$
Thus, by Theorem 1.6 and Poincaré duality, we have
 $$ \begin{align} \overline{OGW}\!_{1, 0}(\Gamma_2)= -\int_{\mathcal{M}_{0,1}(1)}evi_1^{*}\gamma_2 = -\frac{\# evi_1^{-1}(\Upsilon_1 \cap \Upsilon_2)}{\deg \Upsilon_1 \deg \Upsilon_2}. \end{align} $$
$$ \begin{align} \overline{OGW}\!_{1, 0}(\Gamma_2)= -\int_{\mathcal{M}_{0,1}(1)}evi_1^{*}\gamma_2 = -\frac{\# evi_1^{-1}(\Upsilon_1 \cap \Upsilon_2)}{\deg \Upsilon_1 \deg \Upsilon_2}. \end{align} $$
So, we need to count Maslov 2 disks passing through
![]() $\Upsilon _1 \cap \Upsilon _2$
with sign given by the orientation of the moduli space
$\Upsilon _1 \cap \Upsilon _2$
with sign given by the orientation of the moduli space
![]() $\mathcal {M}_{0,1}(1)$
and the complex orientation of the normal bundle to
$\mathcal {M}_{0,1}(1)$
and the complex orientation of the normal bundle to
![]() $\Upsilon _1 \cap \Upsilon _2.$
$\Upsilon _1 \cap \Upsilon _2.$
We represent a point of
![]() $\Upsilon _i$
by three dots with an arrow between two of them labeled by
$\Upsilon _i$
by three dots with an arrow between two of them labeled by
![]() $g_i$
as follows.
$g_i$
as follows.
Hence, a point of
![]() $\Upsilon _1 \cap \Upsilon _2$
is represented by three dots with two arrows between them labeled by
$\Upsilon _1 \cap \Upsilon _2$
is represented by three dots with two arrows between them labeled by
![]() $g_1$
and
$g_1$
and
![]() $g_2$
. There are 6 types up to continuous deformations:
$g_2$
. There are 6 types up to continuous deformations:


More explicitly,
 $$ \begin{align*} \Theta_1 &=\{ [a, g_1(a), g_2g_1(a)] \in \text{Sym}^3 \mathbb{C}P^1|\ a\in \mathbb{C}P^1\}, \\ \Theta_2 &=\{ [a, g_1(a), g_2^{-1}g_1(a)] \in \text{Sym}^3 \mathbb{C}P^1|\ a\in \mathbb{C}P^1 \}, \\ \Theta_3&=\{ [a, g_2(a), g_1g_2(a)] \in \text{Sym}^3 \mathbb{C}P^1|\ a\in \mathbb{C}P^1 \}, \\ \Theta_4&=\{ [a, g_1^{-1}(a), g_2g_1^{-1}(a)] \in \text{Sym}^3 \mathbb{C}P^1|\ a\in \mathbb{C}P^1\}, \\ \Theta_5&=\{[a, g_1(a), c]\in \text{Sym}^3 \mathbb{C}P^1 |\ a,c \in \mathbb{C}P^1, \ g_2g_1(a) = a\}, \\ \Theta_6 &= \{[a, g_1(a), c] \in \text{Sym}^3 \mathbb{C}P^1 | \ a,c \in \mathbb{C}P^1,\ g_2^{-1} g_1(a) = a \}. \end{align*} $$
$$ \begin{align*} \Theta_1 &=\{ [a, g_1(a), g_2g_1(a)] \in \text{Sym}^3 \mathbb{C}P^1|\ a\in \mathbb{C}P^1\}, \\ \Theta_2 &=\{ [a, g_1(a), g_2^{-1}g_1(a)] \in \text{Sym}^3 \mathbb{C}P^1|\ a\in \mathbb{C}P^1 \}, \\ \Theta_3&=\{ [a, g_2(a), g_1g_2(a)] \in \text{Sym}^3 \mathbb{C}P^1|\ a\in \mathbb{C}P^1 \}, \\ \Theta_4&=\{ [a, g_1^{-1}(a), g_2g_1^{-1}(a)] \in \text{Sym}^3 \mathbb{C}P^1|\ a\in \mathbb{C}P^1\}, \\ \Theta_5&=\{[a, g_1(a), c]\in \text{Sym}^3 \mathbb{C}P^1 |\ a,c \in \mathbb{C}P^1, \ g_2g_1(a) = a\}, \\ \Theta_6 &= \{[a, g_1(a), c] \in \text{Sym}^3 \mathbb{C}P^1 | \ a,c \in \mathbb{C}P^1,\ g_2^{-1} g_1(a) = a \}. \end{align*} $$
Since each of
![]() $\Theta _1,\ldots ,\Theta _4$
is the image of a map
$\Theta _1,\ldots ,\Theta _4$
is the image of a map
![]() $\mathbb {C}P^1 \to \mathbb {C}P^3$
of degree 3, it follows that
$\mathbb {C}P^1 \to \mathbb {C}P^3$
of degree 3, it follows that
![]() $\deg \Theta _1 = \ldots = \deg \Theta _4 =3.$
We claim that each of
$\deg \Theta _1 = \ldots = \deg \Theta _4 =3.$
We claim that each of
![]() $\Theta _5, \Theta _6$
is a union of two lines. Indeed, both
$\Theta _5, \Theta _6$
is a union of two lines. Indeed, both
![]() $g_2g_1$
and
$g_2g_1$
and
![]() $g_2^{-1}g_1$
have two eigenvectors, so there are two choices for
$g_2^{-1}g_1$
have two eigenvectors, so there are two choices for
![]() $a\in \mathbb {C}P^1$
. Each such choice a gives a line
$a\in \mathbb {C}P^1$
. Each such choice a gives a line
![]() $\{[a, g_1(a), c]|\ c\in \mathbb {C}P^1 \}.$
Hence,
$\{[a, g_1(a), c]|\ c\in \mathbb {C}P^1 \}.$
Hence,
![]() $\deg \Theta _5 = \deg \Theta _6 = 2$
. Therefore,
$\deg \Theta _5 = \deg \Theta _6 = 2$
. Therefore,
![]() $\sum _{i=1}^6 \deg \Theta _i=16$
. By Bezout’s theorem and Proposition 5.2, we have
$\sum _{i=1}^6 \deg \Theta _i=16$
. By Bezout’s theorem and Proposition 5.2, we have
Since the degrees coincide, it follows that each
![]() $\Theta _i$
occurs with multiplicity
$\Theta _i$
occurs with multiplicity
![]() $1$
in the intersection
$1$
in the intersection
![]() $\Upsilon _1 \cap \Upsilon _2.$
In particular, the intersection is generically transverse.
$\Upsilon _1 \cap \Upsilon _2.$
In particular, the intersection is generically transverse.
By Lemma 5.16, all Maslov 2 disks are axial of the form
![]() $u(z)=A\cdot e^{-i\xi _v\log z}\cdot \triangle $
. Let
$u(z)=A\cdot e^{-i\xi _v\log z}\cdot \triangle $
. Let
![]() $p_1, p_2, p_3 \in \mathbb {C}P^1$
such that
$p_1, p_2, p_3 \in \mathbb {C}P^1$
such that
![]() $[p_1, p_2, p_3]\in \text {Sym}^3 \mathbb {C}P^1$
is in the image of a Maslov index
$[p_1, p_2, p_3]\in \text {Sym}^3 \mathbb {C}P^1$
is in the image of a Maslov index
![]() $2$
disk. As in Example 5.10, there exist
$2$
disk. As in Example 5.10, there exist
![]() $i,j\in \{1,2,3\}$
such that
$i,j\in \{1,2,3\}$
such that
![]() $d(p_i,p_j)\ge e$
, where e is the distance between two vertices in an equilateral triangle on a great circle in
$d(p_i,p_j)\ge e$
, where e is the distance between two vertices in an equilateral triangle on a great circle in
![]() $\mathbb {C}P^1$
. By choosing
$\mathbb {C}P^1$
. By choosing
![]() $\epsilon _i$
sufficiently small,
$\epsilon _i$
sufficiently small,
![]() $\Theta _1,\ldots , \Theta _4$
can be brought arbitrarily close to the locus
$\Theta _1,\ldots , \Theta _4$
can be brought arbitrarily close to the locus
![]() $N_\triangle $
where all 3 points coincide. This rules out a Maslov index 2 disk passing through them. Hence, the number of Maslov 2 disks through
$N_\triangle $
where all 3 points coincide. This rules out a Maslov index 2 disk passing through them. Hence, the number of Maslov 2 disks through
![]() $\Upsilon _1 \cap \Upsilon _2$
is equal to the number of Maslov
$\Upsilon _1 \cap \Upsilon _2$
is equal to the number of Maslov
![]() $2$
disks through
$2$
disks through
![]() $\Theta _5$
and
$\Theta _5$
and
![]() $\Theta _6.$
Since a and
$\Theta _6.$
Since a and
![]() $g_1(a)$
are sufficiently close, it follows by Lemma 5.19 that one such disk passes through each of the lines making up
$g_1(a)$
are sufficiently close, it follows by Lemma 5.19 that one such disk passes through each of the lines making up
![]() $\Theta _5, \Theta _6,$
for a total of four disks.
$\Theta _5, \Theta _6,$
for a total of four disks.
Next, we determine the sign with which each disk passing through
![]() $\Theta _5$
and
$\Theta _5$
and
![]() $\Theta _6$
contributes to
$\Theta _6$
contributes to
![]() $\# evi_1^{-1}(\Upsilon _1 \cap \Upsilon _2).$
The treatment of
$\# evi_1^{-1}(\Upsilon _1 \cap \Upsilon _2).$
The treatment of
![]() $\Theta _5$
and
$\Theta _5$
and
![]() $\Theta _6$
is parallel, so we focus on
$\Theta _6$
is parallel, so we focus on
![]() $\Theta _6$
. Let
$\Theta _6$
. Let
![]() $a \in \mathbb {C}P^1$
be one of the two solutions of
$a \in \mathbb {C}P^1$
be one of the two solutions of
![]() $g_2^{-1}g_1(a) = a$
as in the above formula for
$g_2^{-1}g_1(a) = a$
as in the above formula for
![]() $\Theta _6.$
Denote by
$\Theta _6.$
Denote by
![]() $\Theta _6^a$
the corresponding component of
$\Theta _6^a$
the corresponding component of
![]() $\Theta _6.$
Let
$\Theta _6.$
Let
![]() $[u;w]\in \mathcal {M}_{0,1}(1)$
with
$[u;w]\in \mathcal {M}_{0,1}(1)$
with
![]() $u(w) \in \Theta _6^a$
. Let
$u(w) \in \Theta _6^a$
. Let
![]() $(\nu _{\Theta _6})_{u(w)}:= T_{u(w)}\mathbb {C}P^3/ T_{u(w)}\Theta _6$
be the normal space to
$(\nu _{\Theta _6})_{u(w)}:= T_{u(w)}\mathbb {C}P^3/ T_{u(w)}\Theta _6$
be the normal space to
![]() $\Theta _6$
at
$\Theta _6$
at
![]() $u(w)$
equipped with the complex orientation. The differential
$u(w)$
equipped with the complex orientation. The differential
![]() ${devi_1}_{[u;w]}$
induces a linear map
${devi_1}_{[u;w]}$
induces a linear map
We show
![]() $\overline {devi_1}_{[u;w]}$
is an orientation-reversing isomorphism.
$\overline {devi_1}_{[u;w]}$
is an orientation-reversing isomorphism.

Figure 4 The triangle
![]() $u(w)$
.
$u(w)$
.
By Lemma 5.16, we can write
![]() $u(z)=A\cdot e^{-i\xi _v\log z}\cdot \triangle $
. By applying an appropriate rotation to
$u(z)=A\cdot e^{-i\xi _v\log z}\cdot \triangle $
. By applying an appropriate rotation to
![]() $\mathbb {C}P^1 = S^2$
, which does not affect orientations, we may assume that a and
$\mathbb {C}P^1 = S^2$
, which does not affect orientations, we may assume that a and
![]() $g_1(a)$
are positioned in the
$g_1(a)$
are positioned in the
![]() $xz$
plane symmetrically about the south pole as in Figure 4. It follows from Example 5.10 that we may take A to be the identify matrix. We begin by finding an oriented basis for
$xz$
plane symmetrically about the south pole as in Figure 4. It follows from Example 5.10 that we may take A to be the identify matrix. We begin by finding an oriented basis for
![]() $T_{[u;w]}\mathcal {M}_{0,1}(1)$
. Let
$T_{[u;w]}\mathcal {M}_{0,1}(1)$
. Let
We choose
![]() $\theta _1,\theta _2 \in \mathfrak {su}(2)$
to be lifts of infinitesimal right-handed rotations around the x-axis and the y-axis, respectively. Thus, the trivialization of
$\theta _1,\theta _2 \in \mathfrak {su}(2)$
to be lifts of infinitesimal right-handed rotations around the x-axis and the y-axis, respectively. Thus, the trivialization of
![]() $TL_\triangle $
given by the infinitesimal action of
$TL_\triangle $
given by the infinitesimal action of
![]() $\mathfrak {su}(2)$
and the basis
$\mathfrak {su}(2)$
and the basis
![]() $\xi _v,\theta _1,\theta _2,$
determines the orientation and the spin structure of
$\xi _v,\theta _1,\theta _2,$
determines the orientation and the spin structure of
![]() $L_\triangle $
given in Section 3.2. Let
$L_\triangle $
given in Section 3.2. Let
![]() $w\in \operatorname {\mathrm {int}} D$
. The tangent space of
$w\in \operatorname {\mathrm {int}} D$
. The tangent space of
![]() $\mathcal {M}_{0,1}(1)$
at
$\mathcal {M}_{0,1}(1)$
at
![]() $[u;w]$
is given by
$[u;w]$
is given by
Consider the canonical identification
![]() $\mathbb {C}\simeq T_w D$
. We denote by
$\mathbb {C}\simeq T_w D$
. We denote by
![]() $\hat {x}$
and
$\hat {x}$
and
![]() $\hat {y}$
the vectors in
$\hat {y}$
the vectors in
![]() $T_w D$
that correspond to
$T_w D$
that correspond to
![]() $1$
and i in
$1$
and i in
![]() $\mathbb {C}$
, respectively. Hence, the basis
$\mathbb {C}$
, respectively. Hence, the basis
![]() $\{\hat {x}, \hat {y}\}$
determines the orientation on
$\{\hat {x}, \hat {y}\}$
determines the orientation on
![]() $T_w D$
that induced by its complex structure. By Proposition 5.1 and Lemmas 5.25, 5.28, 5.34 and 5.35, we have an orientation-reversing isomorphism
$T_w D$
that induced by its complex structure. By Proposition 5.1 and Lemmas 5.25, 5.28, 5.34 and 5.35, we have an orientation-reversing isomorphism
given by
Abbreviate
Thus,
![]() $\{-\bar \theta _1, \bar \theta _2,\bar {x}, \bar {y}\}$
is an oriented basis for
$\{-\bar \theta _1, \bar \theta _2,\bar {x}, \bar {y}\}$
is an oriented basis for
![]() $T_{[u;w]}\mathcal {M}_{0,1}(1)$
.
$T_{[u;w]}\mathcal {M}_{0,1}(1)$
.
Next, we compute
![]() $devi_1$
on
$devi_1$
on
![]() $\bar x, \bar y.$
Indeed,
$\bar x, \bar y.$
Indeed,
 $$ \begin{align*} du_w(\hat{x})=\left.\frac{d}{dt}\right|{}_{t=0}e^{-i\xi_v\log(w+t)}\cdot \triangle = \frac{-i\xi_v}{w}\cdot u(w), \end{align*} $$
$$ \begin{align*} du_w(\hat{x})=\left.\frac{d}{dt}\right|{}_{t=0}e^{-i\xi_v\log(w+t)}\cdot \triangle = \frac{-i\xi_v}{w}\cdot u(w), \end{align*} $$
and
 $$ \begin{align*} du_w(\hat{y})=\left.\frac{d}{dt}\right|{}_{t=0}e^{-i\xi_v\log(w+it)}\cdot \triangle = \frac{\xi_v}{w}\cdot u(w). \end{align*} $$
$$ \begin{align*} du_w(\hat{y})=\left.\frac{d}{dt}\right|{}_{t=0}e^{-i\xi_v\log(w+it)}\cdot \triangle = \frac{\xi_v}{w}\cdot u(w). \end{align*} $$
It follows that
To determine whether
![]() $\overline {devi_1}_{[u;w]}$
preserves orientation, it is helpful to work in a holomorphic coordinate chart on
$\overline {devi_1}_{[u;w]}$
preserves orientation, it is helpful to work in a holomorphic coordinate chart on
![]() $\text {Sym}^3(\mathbb {C}P^1)$
. Let
$\text {Sym}^3(\mathbb {C}P^1)$
. Let
be given by
Recall the stereographic projection p from Example 5.10. Observe that
Since
![]() $a \neq g_1(a)$
, we may choose an open
$a \neq g_1(a)$
, we may choose an open
![]() $U \subset \mathbb {C}^3$
containing
$U \subset \mathbb {C}^3$
containing
![]() $(p(a),p(g_1(a)),0)$
such that
$(p(a),p(g_1(a)),0)$
such that
![]() $\hat \psi = \psi |_U$
is a biholomorphism onto its image. Then
$\hat \psi = \psi |_U$
is a biholomorphism onto its image. Then
Observe that the normal bundle to
![]() $\hat \Theta _6^a$
is canonically identified with
$\hat \Theta _6^a$
is canonically identified with
![]() $\mathbb {C}^2 \times \{0\} \subset \mathbb {C}^3.$
Let
$\mathbb {C}^2 \times \{0\} \subset \mathbb {C}^3.$
Let
![]() $\pi : \mathbb {C}^3 \to \mathbb {C}^2$
be the projection onto the first two factors, and let
$\pi : \mathbb {C}^3 \to \mathbb {C}^2$
be the projection onto the first two factors, and let
Since
![]() $\hat \psi $
is biholomorphic and thus orientation preserving, it suffices to determine whether the map
$\hat \psi $
is biholomorphic and thus orientation preserving, it suffices to determine whether the map
preserves orientation.
We proceed to compute
![]() $d\widehat {evi_1}$
on the oriented basis
$d\widehat {evi_1}$
on the oriented basis
![]() $\{-\bar \theta _1,\bar \theta _2,\bar x,\bar y\}$
of
$\{-\bar \theta _1,\bar \theta _2,\bar x,\bar y\}$
of
![]() $T_{[u;w]}\mathcal {M}_{0,1}(1)$
. By Example 5.10, we have
$T_{[u;w]}\mathcal {M}_{0,1}(1)$
. By Example 5.10, we have
 $$ \begin{align} (p(a),p(g_1(a)))= \pi\circ \hat \psi^{-1}\circ u(w) = \left(\sqrt{\frac{w}{3}},-\sqrt{\frac{w}3}\right). \end{align} $$
$$ \begin{align} (p(a),p(g_1(a)))= \pi\circ \hat \psi^{-1}\circ u(w) = \left(\sqrt{\frac{w}{3}},-\sqrt{\frac{w}3}\right). \end{align} $$
Since a lies in the
![]() $xz$
plane, it follows that
$xz$
plane, it follows that
![]() $p(a)\in \mathbb {R}$
, and consequently,
$p(a)\in \mathbb {R}$
, and consequently,
![]() $w \in \mathbb {R}_{>0}.$
Recall the map
$w \in \mathbb {R}_{>0}.$
Recall the map
![]() $\varphi ^t_{\xi _v}$
from Example 5.10. For
$\varphi ^t_{\xi _v}$
from Example 5.10. For
![]() $z \in \mathbb {C},$
we have
$z \in \mathbb {C},$
we have
So, by equations (5.4) and (5.5), we obtain
 $$ \begin{gather*} d\widehat{evi_1}(\bar y) = \pi\circ d(\hat\psi)^{-1}\left(\frac{\xi_v}{w}\cdot u(w)\right) =\frac{1}{w}(\frac{i\sqrt{w}}{2\sqrt{3}}, -\frac{i\sqrt{w}}{2\sqrt{3}}), \\ d\widehat{evi_1}(\bar x) = \pi \circ d(\hat\psi)^{-1}\left(\frac{-i\xi_v}{w}\cdot u(w)\right) = \frac{1}{w}(\frac{\sqrt{w}}{2\sqrt{3}}, -\frac{\sqrt{w}}{2\sqrt{3}}). \end{gather*} $$
$$ \begin{gather*} d\widehat{evi_1}(\bar y) = \pi\circ d(\hat\psi)^{-1}\left(\frac{\xi_v}{w}\cdot u(w)\right) =\frac{1}{w}(\frac{i\sqrt{w}}{2\sqrt{3}}, -\frac{i\sqrt{w}}{2\sqrt{3}}), \\ d\widehat{evi_1}(\bar x) = \pi \circ d(\hat\psi)^{-1}\left(\frac{-i\xi_v}{w}\cdot u(w)\right) = \frac{1}{w}(\frac{\sqrt{w}}{2\sqrt{3}}, -\frac{\sqrt{w}}{2\sqrt{3}}). \end{gather*} $$
However, we can see by stereographically projecting Figure 4 or by direct calculation that
Since
 $$\begin{align*}\det\ \begin{pmatrix} 0 & -1 & 0 & -1\\ -1 & 0 & -1 & 0\\ \frac{1}{2\sqrt{3w}} & 0 & -\frac{1}{2\sqrt{3w}} &0\\ 0 & \frac{1}{2\sqrt{3w}} & 0 &-\frac{1}{2\sqrt{3w}} \end{pmatrix}=-\frac{1}{3w}<0, \end{align*}$$
$$\begin{align*}\det\ \begin{pmatrix} 0 & -1 & 0 & -1\\ -1 & 0 & -1 & 0\\ \frac{1}{2\sqrt{3w}} & 0 & -\frac{1}{2\sqrt{3w}} &0\\ 0 & \frac{1}{2\sqrt{3w}} & 0 &-\frac{1}{2\sqrt{3w}} \end{pmatrix}=-\frac{1}{3w}<0, \end{align*}$$
it follows that the basis
is not complex oriented. Thus,
![]() $d\widehat {evi_1}$
and consequently also
$d\widehat {evi_1}$
and consequently also
![]() $\overline {devi_1}$
reverse orientation.
$\overline {devi_1}$
reverse orientation.
Therefore, each of the 4 Maslov 2 disks passing through
![]() $\Upsilon _1\cap \Upsilon _2$
contributes to the signed count
$\Upsilon _1\cap \Upsilon _2$
contributes to the signed count
![]() $\# evi_1^{-1}(\Upsilon _1 \cap \Upsilon _2)$
with sign
$\# evi_1^{-1}(\Upsilon _1 \cap \Upsilon _2)$
with sign
![]() $-1$
. By Proposition 5.2 and equation (5.3), we obtain
$-1$
. By Proposition 5.2 and equation (5.3), we obtain
5.8 Computation of
 $\overline {OGW}_{2, 0}(\Gamma _3)$
$\overline {OGW}_{2, 0}(\Gamma _3)$
Proof of Theorem 5.3.
By Theorem 1.6, we have
 $$\begin{align*}\overline{OGW}\!_{2, 0}(\Gamma_3)= -\int_{\mathcal{M}_{0,1}(2)}evi_1^{*}\gamma_3,\end{align*}$$
$$\begin{align*}\overline{OGW}\!_{2, 0}(\Gamma_3)= -\int_{\mathcal{M}_{0,1}(2)}evi_1^{*}\gamma_3,\end{align*}$$
where
![]() $\gamma _3$
is a representative of
$\gamma _3$
is a representative of
![]() $\Gamma _3$
. Since
$\Gamma _3$
. Since
![]() $\Gamma _3$
is Poincaré dual to a point, it follows that
$\Gamma _3$
is Poincaré dual to a point, it follows that
where
![]() $p \in \mathbb {C} P^3$
is a regular value of
$p \in \mathbb {C} P^3$
is a regular value of
![]() $evi_1$
.
$evi_1$
.
Let
![]() $p \in N_\triangle $
. First, we show that p is a regular value of
$p \in N_\triangle $
. First, we show that p is a regular value of
![]() $evi_1$
and compute
$evi_1$
and compute
![]() $\#evi_1^{-1}(p)$
up to sign. We claim that any Maslov 4 disk u that passes through p is an axial disk of type
$\#evi_1^{-1}(p)$
up to sign. We claim that any Maslov 4 disk u that passes through p is an axial disk of type
![]() $\xi _f.$
Indeed, by Lemma 5.4,
$\xi _f.$
Indeed, by Lemma 5.4,
![]() $Y_{\triangle }$
is an anticanonical divisor, so by Lemma 5.5, the Maslov index of u is given by twice the algebraic intersection number
$Y_{\triangle }$
is an anticanonical divisor, so by Lemma 5.5, the Maslov index of u is given by twice the algebraic intersection number
![]() $[u] \cdot [Y_{\triangle }]$
. Hence,
$[u] \cdot [Y_{\triangle }]$
. Hence,
![]() $[u] \cdot [Y_{\triangle }] = 2$
. Thus, Lemma 5.6 implies that u intersects
$[u] \cdot [Y_{\triangle }] = 2$
. Thus, Lemma 5.6 implies that u intersects
![]() $Y_{\triangle }$
only at p. Hence, by Lemma 5.15, a pole germ of u is not of type
$Y_{\triangle }$
only at p. Hence, by Lemma 5.15, a pole germ of u is not of type
![]() $\xi _v$
. So, by Lemma 5.17, u is an axial disk of type
$\xi _v$
. So, by Lemma 5.17, u is an axial disk of type
![]() $\xi _f$
as claimed. Thus, Lemma 5.18 guarantees that p is a regular value of
$\xi _f$
as claimed. Thus, Lemma 5.18 guarantees that p is a regular value of
![]() $evi_1$
. Since by Lemma 5.20 there exists a unique axial disk of type
$evi_1$
. Since by Lemma 5.20 there exists a unique axial disk of type
![]() $\xi _f$
of Maslov index
$\xi _f$
of Maslov index
![]() $4$
that passes through
$4$
that passes through
![]() $p,$
it follows that
$p,$
it follows that
![]() $\# evi_1^{-1}(p)=\pm 1$
.
$\# evi_1^{-1}(p)=\pm 1$
.
It remains to show that in fact
![]() $\# evi_1^{-1}(p)= -1$
. Let
$\# evi_1^{-1}(p)= -1$
. Let
![]() $r:=(0,-1,0),$
and choose
$r:=(0,-1,0),$
and choose
Let
![]() $u:(D,\partial D)\rightarrow (\mathbb {C}P^3,L_\triangle )$
be the J-holomorphic disk of Maslov index 4 that intersects
$u:(D,\partial D)\rightarrow (\mathbb {C}P^3,L_\triangle )$
be the J-holomorphic disk of Maslov index 4 that intersects
![]() $N_\triangle $
at p. As shown above, u is an axial disk of type
$N_\triangle $
at p. As shown above, u is an axial disk of type
![]() $\xi _f$
, so by Example 5.11, we have
$\xi _f$
, so by Example 5.11, we have
![]() $u(z)= e^{-i\xi _f \log z}\cdot \triangle $
. Let
$u(z)= e^{-i\xi _f \log z}\cdot \triangle $
. Let
We construct frames for E and F as follows. Let
![]() $\alpha \in \mathfrak {su}(2)$
be an infinitesimal right-handed rotation about the
$\alpha \in \mathfrak {su}(2)$
be an infinitesimal right-handed rotation about the
![]() $-x$
axis, and let
$-x$
axis, and let
![]() $\beta \in \mathfrak {su}(2)$
be an infinitesimal right-handed rotation about the z axis. Recall that
$\beta \in \mathfrak {su}(2)$
be an infinitesimal right-handed rotation about the z axis. Recall that
![]() $\xi _f$
is an infinitesimal right-handed rotation about the y axis, so
$\xi _f$
is an infinitesimal right-handed rotation about the y axis, so
![]() $\xi _f, \alpha , \beta $
is a basis of
$\xi _f, \alpha , \beta $
is a basis of
![]() $\mathfrak {su}(2)$
corresponding to infinitesimal right-handed rotations about a right-handed set of orthogonal axes as in the definition of the orientation
$\mathfrak {su}(2)$
corresponding to infinitesimal right-handed rotations about a right-handed set of orthogonal axes as in the definition of the orientation
![]() $\mathfrak {o}_\triangle $
and spin structure
$\mathfrak {o}_\triangle $
and spin structure
![]() $\mathfrak {s}_\triangle $
on
$\mathfrak {s}_\triangle $
on
![]() $L_\triangle $
given in Section 3.2. Since
$L_\triangle $
given in Section 3.2. Since
![]() $u(0)=p,$
and we have taken the complex structure on
$u(0)=p,$
and we have taken the complex structure on
![]() $\mathbb {C}P^1$
given by left-handed rotation around the outward normal by an angle of
$\mathbb {C}P^1$
given by left-handed rotation around the outward normal by an angle of
![]() $\pi /2,$
it follows that
$\pi /2,$
it follows that
![]() $i\beta \cdot u(0)= -\alpha \cdot u(0).$
See Figure 5. Thus, the kernel of the infinitesimal action of
$i\beta \cdot u(0)= -\alpha \cdot u(0).$
See Figure 5. Thus, the kernel of the infinitesimal action of
![]() $\mathfrak {sl}(2,\mathbb {C})$
at
$\mathfrak {sl}(2,\mathbb {C})$
at
![]() $u(0)$
is spanned by
$u(0)$
is spanned by
![]() $\xi _f$
and by
$\xi _f$
and by
![]() $\alpha +i\beta $
. So, it follows from the argument of Smith [Reference Smith44, Appendix A.3] that the following sections give a holomorphic frame of
$\alpha +i\beta $
. So, it follows from the argument of Smith [Reference Smith44, Appendix A.3] that the following sections give a holomorphic frame of
![]() $E:$
$E:$
Taking
![]() $\mathbb {C}$
-linear combinations, we see that
$\mathbb {C}$
-linear combinations, we see that
is also a holomorphic frame of
![]() $E.$
Since
$E.$
Since
![]() $\xi _f, \alpha , \beta $
is a basis of
$\xi _f, \alpha , \beta $
is a basis of
![]() $\mathfrak {su}(2)$
, the sections
$\mathfrak {su}(2)$
, the sections
give a frame of for
![]() $F.$
This frame is
$F.$
This frame is
![]() $\mathfrak {o}_\triangle $
oriented and can be lifted to the double cover of the frame bundle of F associated to
$\mathfrak {o}_\triangle $
oriented and can be lifted to the double cover of the frame bundle of F associated to
![]() $\mathfrak {s}_\triangle $
because of how we have chosen
$\mathfrak {s}_\triangle $
because of how we have chosen
![]() $\alpha ,\beta $
.
$\alpha ,\beta $
.

Figure 5 The rotations
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
at p.
$\beta $
at p.
Let
![]() $\Psi : E \to \underline {\mathbb {C}}^3$
be the isomorphism given by
$\Psi : E \to \underline {\mathbb {C}}^3$
be the isomorphism given by
 $$\begin{align*}\frac{\xi_f}{z}\cdot u\mapsto \begin{pmatrix} 1\\ 0\\ 0 \end{pmatrix}, \quad \frac{(1+z)\alpha+i(1-z)\beta}{z}\cdot u\mapsto \begin{pmatrix} 0\\ 1\\ 0 \end{pmatrix}, \quad \frac{(1+z)\beta-i(1-z)\alpha}{z}\cdot u\mapsto \begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix}. \end{align*}$$
$$\begin{align*}\frac{\xi_f}{z}\cdot u\mapsto \begin{pmatrix} 1\\ 0\\ 0 \end{pmatrix}, \quad \frac{(1+z)\alpha+i(1-z)\beta}{z}\cdot u\mapsto \begin{pmatrix} 0\\ 1\\ 0 \end{pmatrix}, \quad \frac{(1+z)\beta-i(1-z)\alpha}{z}\cdot u\mapsto \begin{pmatrix} 0\\ 0\\ 1 \end{pmatrix}. \end{align*}$$
Since
 $$\begin{align*}\xi_f\cdot u\mapsto \begin{pmatrix} z\\ 0\\ 0 \end{pmatrix}, \quad\alpha\cdot u \mapsto \begin{pmatrix} 0\\ \frac{z+1}{4}\\ \frac{-i(1-z)}{4} \end{pmatrix},\quad \beta\cdot u\mapsto \begin{pmatrix} 0\\ \frac{i(1-z)}{4}\\ \frac{z+1}{4} \end{pmatrix}, \end{align*}$$
$$\begin{align*}\xi_f\cdot u\mapsto \begin{pmatrix} z\\ 0\\ 0 \end{pmatrix}, \quad\alpha\cdot u \mapsto \begin{pmatrix} 0\\ \frac{z+1}{4}\\ \frac{-i(1-z)}{4} \end{pmatrix},\quad \beta\cdot u\mapsto \begin{pmatrix} 0\\ \frac{i(1-z)}{4}\\ \frac{z+1}{4} \end{pmatrix}, \end{align*}$$
we see that
![]() $\Psi :(E,F) \to (\underline {\mathbb {C}}^3,F^{2} \oplus F^{1,1}).$
Recall the choices of spin structures and orientations on
$\Psi :(E,F) \to (\underline {\mathbb {C}}^3,F^{2} \oplus F^{1,1}).$
Recall the choices of spin structures and orientations on
![]() $F^2$
and
$F^2$
and
![]() $F^{1,1}$
given in Section 5.4. By Lemma 5.24, the frame
$F^{1,1}$
given in Section 5.4. By Lemma 5.24, the frame
 $$\begin{align*}\begin{pmatrix} z\\ 0\\ 0 \end{pmatrix},\quad \begin{pmatrix} 0\\ \frac{z+1}{4}\\ \frac{-i(1-z)}{4} \end{pmatrix},\quad \begin{pmatrix} 0\\ \frac{i(1-z)}{4}\\ \frac{z+1}{4} \end{pmatrix}\end{align*}$$
$$\begin{align*}\begin{pmatrix} z\\ 0\\ 0 \end{pmatrix},\quad \begin{pmatrix} 0\\ \frac{z+1}{4}\\ \frac{-i(1-z)}{4} \end{pmatrix},\quad \begin{pmatrix} 0\\ \frac{i(1-z)}{4}\\ \frac{z+1}{4} \end{pmatrix}\end{align*}$$
of
![]() $F^2\oplus F^{1,1}$
is positively oriented and can be lifted to the spin double cover of the frame bundle. Hence, the isomorphism
$F^2\oplus F^{1,1}$
is positively oriented and can be lifted to the spin double cover of the frame bundle. Hence, the isomorphism
![]() $\Psi $
preserves orientation and spin structure. Thus, by Lemma 5.25, we obtain an orientation preserving isomorphism
$\Psi $
preserves orientation and spin structure. Thus, by Lemma 5.25, we obtain an orientation preserving isomorphism
where
![]() $w\in \mathrm {int}D$
. By Lemma 5.34, this gives an orientation-reversing isomorphism
$w\in \mathrm {int}D$
. By Lemma 5.34, this gives an orientation-reversing isomorphism
It suffices to show that
reverses orientation when
![]() $w=0$
. Denote by
$w=0$
. Denote by
![]() $f_D:T_0D\rightarrow \mathbb {C}$
the canonical isomorphism, and recall that
$f_D:T_0D\rightarrow \mathbb {C}$
the canonical isomorphism, and recall that
![]() $f_{1,1}: \ker \bar {\partial }_{1,1}\rightarrow \underline {\mathbb {C}}^2_0$
is the evaluation map at zero. In the following commutative diagram of isomorphisms, the left vertical arrow reverses orientation, and the right vertical arrow preserves orientation.
$f_{1,1}: \ker \bar {\partial }_{1,1}\rightarrow \underline {\mathbb {C}}^2_0$
is the evaluation map at zero. In the following commutative diagram of isomorphisms, the left vertical arrow reverses orientation, and the right vertical arrow preserves orientation.

So, it suffices to show that
![]() $f_{1,1}\oplus f_D$
preserves orientation. Since
$f_{1,1}\oplus f_D$
preserves orientation. Since
![]() $f_D:T_0D\rightarrow \mathbb {C}$
preserves orientation, and by Lemma 5.31 the map
$f_D:T_0D\rightarrow \mathbb {C}$
preserves orientation, and by Lemma 5.31 the map
![]() $f_{1,1}$
preserves orientation, it follows that
$f_{1,1}$
preserves orientation, it follows that
![]() $f_{1,1}\oplus f_D$
preserves orientation as desired.
$f_{1,1}\oplus f_D$
preserves orientation as desired.
6 Recursions
Proof of Theorem 1.1.
Recall
![]() $\Delta _i=[\omega ^i]\in H^{*}(X;\mathbb {R}),$
for
$\Delta _i=[\omega ^i]\in H^{*}(X;\mathbb {R}),$
for
![]() $i=0,\ldots ,3.$
So, by the definition of
$i=0,\ldots ,3.$
So, by the definition of
![]() $g^{ij}$
given in Section 2.6, it follows that
$g^{ij}$
given in Section 2.6, it follows that
![]() $g^{ij}=\delta _{i,3-j}.$
In order to derive recursion 1, let
$g^{ij}=\delta _{i,3-j}.$
In order to derive recursion 1, let
![]() $I = \{j_2,\ldots ,j_l\}.$
Apply
$I = \{j_2,\ldots ,j_l\}.$
Apply
![]() $\partial _s^{k-1} \partial _{t_I}$
=
$\partial _s^{k-1} \partial _{t_I}$
=
![]() $\partial _s^{k-1} \partial _{t_{j_2}} \ldots \partial _{t_{j_l}}$
to equation (2.4) with
$\partial _s^{k-1} \partial _{t_{j_2}} \ldots \partial _{t_{j_l}}$
to equation (2.4) with
![]() $v={j_1-1}$
,
$v={j_1-1}$
,
![]() $w=1$
. We consider the coefficients of
$w=1$
. We consider the coefficients of
![]() $T^{\beta }$
and evaluate at
$T^{\beta }$
and evaluate at
![]() $s=t_j=0$
. Using the closed zero axiom Proposition 2.16, we single out instances of
$s=t_j=0$
. Using the closed zero axiom Proposition 2.16, we single out instances of
![]() $\overline {OGW}\!_{\beta , k}(\Gamma _{j_1},\Gamma _I)$
and obtain
$\overline {OGW}\!_{\beta , k}(\Gamma _{j_1},\Gamma _I)$
and obtain
 $$ \begin{align*} &[T^{\beta}]\sum_{i=0}^3(\partial_s^{k-1} \partial_{t_I}(\partial_s \partial_{t_{3-i}} \overline{\Omega} \cdot \partial_{t_i} \partial_{t_w} \partial_{t_v} \Phi )|_{s=t_j=0})=\\ &\qquad = \overline{OGW}\!_{\beta, k} (\Gamma_{j_1},\ldots, \Gamma_{j_l})+ \sum_{\substack{\varpi(\hat{\beta}) + \beta_1 = \beta \\ I_1 \sqcup I_2 = I \\ \beta_1 \neq \beta}} \sum_{i = 0}^{3} {GW}_{\hat{\beta}}(\Delta_1, \Delta_{j_1-1}, \Delta_{I_1}, \Delta_i) \overline{OGW}\!_{\beta_1, k} (\Gamma_{3-i}, \Gamma_{I_2}), \\ &[T^{\beta}](\partial_s^{k-1} \partial_{t_I}(\partial_s^2 \overline{\Omega} \cdot \partial_{t_{w}} \partial_{t_v} \overline{\Omega} )|_{s=t_j=0})= \\ &\qquad =\sum_{\substack{\beta_1 + \beta_2 = \beta \\ k_1 + k_2 = k-1 \\ I_1 \sqcup I_2 = I }} \binom{k-1}{k_1} \overline{OGW}\!_{\beta_1, k_1}(\Gamma_{j_1-1}, \Gamma_1, \Gamma_{I_1}) \overline{OGW}\!_{\beta_2, k_2+2} (\Gamma_{I_2}), \\ &[T^{\beta}](\partial_s^{k-1} \partial_{t_I}(\partial_{s} \partial_{t_w} \overline{\Omega} \cdot \partial_{t_v} \partial_s \overline{\Omega} )|_{s=t_j=0})= \\ & \qquad =\sum_{\substack{\beta_1 + \beta_2 = \beta \\ k_1 + k_2 = k-1 \\ I_1 \sqcup I_2 = I }} \binom{k-1}{k_1} \overline{OGW}\!_{\beta_1, k_1+1}(\Gamma_{j_1-1}, \Gamma_{I_1}) \overline{OGW}\!_{\beta_2, k_2+1} (\Gamma_1, \Gamma_{I_2}). \end{align*} $$
$$ \begin{align*} &[T^{\beta}]\sum_{i=0}^3(\partial_s^{k-1} \partial_{t_I}(\partial_s \partial_{t_{3-i}} \overline{\Omega} \cdot \partial_{t_i} \partial_{t_w} \partial_{t_v} \Phi )|_{s=t_j=0})=\\ &\qquad = \overline{OGW}\!_{\beta, k} (\Gamma_{j_1},\ldots, \Gamma_{j_l})+ \sum_{\substack{\varpi(\hat{\beta}) + \beta_1 = \beta \\ I_1 \sqcup I_2 = I \\ \beta_1 \neq \beta}} \sum_{i = 0}^{3} {GW}_{\hat{\beta}}(\Delta_1, \Delta_{j_1-1}, \Delta_{I_1}, \Delta_i) \overline{OGW}\!_{\beta_1, k} (\Gamma_{3-i}, \Gamma_{I_2}), \\ &[T^{\beta}](\partial_s^{k-1} \partial_{t_I}(\partial_s^2 \overline{\Omega} \cdot \partial_{t_{w}} \partial_{t_v} \overline{\Omega} )|_{s=t_j=0})= \\ &\qquad =\sum_{\substack{\beta_1 + \beta_2 = \beta \\ k_1 + k_2 = k-1 \\ I_1 \sqcup I_2 = I }} \binom{k-1}{k_1} \overline{OGW}\!_{\beta_1, k_1}(\Gamma_{j_1-1}, \Gamma_1, \Gamma_{I_1}) \overline{OGW}\!_{\beta_2, k_2+2} (\Gamma_{I_2}), \\ &[T^{\beta}](\partial_s^{k-1} \partial_{t_I}(\partial_{s} \partial_{t_w} \overline{\Omega} \cdot \partial_{t_v} \partial_s \overline{\Omega} )|_{s=t_j=0})= \\ & \qquad =\sum_{\substack{\beta_1 + \beta_2 = \beta \\ k_1 + k_2 = k-1 \\ I_1 \sqcup I_2 = I }} \binom{k-1}{k_1} \overline{OGW}\!_{\beta_1, k_1+1}(\Gamma_{j_1-1}, \Gamma_{I_1}) \overline{OGW}\!_{\beta_2, k_2+1} (\Gamma_1, \Gamma_{I_2}). \end{align*} $$
Substituting the expressions in (2.4) gives the required recursion.
In order to derive recursion 2, let
![]() $I = \{j_1,\ldots ,j_l\}.$
Apply
$I = \{j_1,\ldots ,j_l\}.$
Apply
![]() $\partial _s^{k-2} \partial _{t_I}$
=
$\partial _s^{k-2} \partial _{t_I}$
=
![]() $\partial _s^{k-2} \partial _{j_1} \ldots \partial _{j_l}$
to equation (2.4) with
$\partial _s^{k-2} \partial _{j_1} \ldots \partial _{j_l}$
to equation (2.4) with
![]() $v=2$
,
$v=2$
,
![]() $w=2$
. We consider the coefficients of
$w=2$
. We consider the coefficients of
![]() $T^{\beta +2}$
and evaluate at
$T^{\beta +2}$
and evaluate at
![]() $s=t_j=0$
. We obtain
$s=t_j=0$
. We obtain
 $$ \begin{align*} &[T^{\beta+2}]\sum_{i=0}^3(\partial_s^{k-2} \partial_{t_I}(\partial_s\partial_{t_{3-i}} \overline{\Omega}\cdot\partial_{t_i} \partial_{t_w} \partial_{t_v} \Phi)|_{s=t_j=0})= \\ &\qquad =\sum_{\substack{\varpi(\hat{\beta}) + \beta_1 = \beta+2 \\ I_1 \sqcup I_2 = I }} \sum_{i = 0}^{3} {GW}_{\hat{\beta}}(\Delta_2, \Delta_2, \Delta_{I_1}, \Delta_i) \overline{OGW}\!_{\beta_1, k-1} (\Gamma_{3-i}, \Gamma_{I_2}), \\ &[T^{\beta+2}](\partial_s^{k-2} \partial_{t_I}(\partial_s^2 \overline{\Omega} \cdot \partial_{t_w} \partial_{t_v} \overline{\Omega} )|_{s=t_j=0})= \\ &\qquad =\overline{OGW}\!_{2, 0}(\Gamma_2, \Gamma_2) \overline{OGW}\!_{\beta, k} (\Gamma_{j_1},\ldots,\Gamma_{j_l})\\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ +\sum_{\substack{\beta_1 + \beta_2 = \beta+2 \\ k_1 + k_2 = k-2 \\ (\beta_1,k_1)\ne(2,0)\\ I_1 \sqcup I_2 = I }} \binom{k-2}{k_1} \overline{OGW}\!_{\beta_1, k_1}(\Gamma_2, \Gamma_2, \Gamma_{I_1}) \overline{OGW}\!_{\beta_2, k_2+2} (\Gamma_{I_2}), \\ &[T^{\beta+2}](\partial_s^{k-2} \partial_{t_I}(\partial_{s} \partial_{t_w} \overline{\Omega} \cdot \partial_{t_v} \partial_s \overline{\Omega}) |_{s=t_j=0})= \\ &\qquad =\sum_{\substack{\beta_1 + \beta_2 = \beta+2 \\ k_1 + k_2 = k-2 \\ I_1 \sqcup I_2 = I }} \binom{k-2}{k_1} \overline{OGW}\!_{\beta_1, k_1+1}(\Gamma_2, \Gamma_{I_1}) \overline{OGW}\!_{\beta_2, k_2+1} (\Gamma_2, \Gamma_{I_1}). \end{align*} $$
$$ \begin{align*} &[T^{\beta+2}]\sum_{i=0}^3(\partial_s^{k-2} \partial_{t_I}(\partial_s\partial_{t_{3-i}} \overline{\Omega}\cdot\partial_{t_i} \partial_{t_w} \partial_{t_v} \Phi)|_{s=t_j=0})= \\ &\qquad =\sum_{\substack{\varpi(\hat{\beta}) + \beta_1 = \beta+2 \\ I_1 \sqcup I_2 = I }} \sum_{i = 0}^{3} {GW}_{\hat{\beta}}(\Delta_2, \Delta_2, \Delta_{I_1}, \Delta_i) \overline{OGW}\!_{\beta_1, k-1} (\Gamma_{3-i}, \Gamma_{I_2}), \\ &[T^{\beta+2}](\partial_s^{k-2} \partial_{t_I}(\partial_s^2 \overline{\Omega} \cdot \partial_{t_w} \partial_{t_v} \overline{\Omega} )|_{s=t_j=0})= \\ &\qquad =\overline{OGW}\!_{2, 0}(\Gamma_2, \Gamma_2) \overline{OGW}\!_{\beta, k} (\Gamma_{j_1},\ldots,\Gamma_{j_l})\\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ +\sum_{\substack{\beta_1 + \beta_2 = \beta+2 \\ k_1 + k_2 = k-2 \\ (\beta_1,k_1)\ne(2,0)\\ I_1 \sqcup I_2 = I }} \binom{k-2}{k_1} \overline{OGW}\!_{\beta_1, k_1}(\Gamma_2, \Gamma_2, \Gamma_{I_1}) \overline{OGW}\!_{\beta_2, k_2+2} (\Gamma_{I_2}), \\ &[T^{\beta+2}](\partial_s^{k-2} \partial_{t_I}(\partial_{s} \partial_{t_w} \overline{\Omega} \cdot \partial_{t_v} \partial_s \overline{\Omega}) |_{s=t_j=0})= \\ &\qquad =\sum_{\substack{\beta_1 + \beta_2 = \beta+2 \\ k_1 + k_2 = k-2 \\ I_1 \sqcup I_2 = I }} \binom{k-2}{k_1} \overline{OGW}\!_{\beta_1, k_1+1}(\Gamma_2, \Gamma_{I_1}) \overline{OGW}\!_{\beta_2, k_2+1} (\Gamma_2, \Gamma_{I_1}). \end{align*} $$
Substituting the expressions in (2.4) gives the required recursion.
Recursion 3 is derived in the same way as recursion (a) in Theorem 10 from [Reference Solomon and Tukachinsky48].
Lemma 6.1.
![]() $\overline {OGW}\!_{2,0}(\Gamma _2, \Gamma _2)=\frac {35}{64}.$
$\overline {OGW}\!_{2,0}(\Gamma _2, \Gamma _2)=\frac {35}{64}.$
Proof. In Theorems 5.1–5.3, we computed
By recursion 3 of Theorem 1.1, we get
By the open divisor axiom Proposition 2.26, we get
In order to prove Corollary 1.3 we will need the following lemma.
Lemma 6.2. Assume
![]() $|\Gamma _{i_j}|\ge 4.$
If
$|\Gamma _{i_j}|\ge 4.$
If
![]() $\overline {OGW}\!_{1,k}(\Gamma _{i_1},\ldots ,\Gamma _{i_l})\ne 0$
. Then
$\overline {OGW}\!_{1,k}(\Gamma _{i_1},\ldots ,\Gamma _{i_l})\ne 0$
. Then
![]() $(k,l)=(1,0)$
or
$(k,l)=(1,0)$
or
![]() $(k,l)=(0,1)$
and
$(k,l)=(0,1)$
and
![]() $|\Gamma _{i_1}|=4$
.
$|\Gamma _{i_1}|=4$
.
Proof. By the open degree axiom Proposition 2.23 and Lemma 3.3,
 $$ \begin{align*} & \beta=1 \implies 2+2l=2k+\sum_{j=1}^l |\Gamma_{i_j}| \\ &\implies 2(k-1)+\sum_{j=1}^l (|\Gamma_{i_j}|-2)=0. \end{align*} $$
$$ \begin{align*} & \beta=1 \implies 2+2l=2k+\sum_{j=1}^l |\Gamma_{i_j}| \\ &\implies 2(k-1)+\sum_{j=1}^l (|\Gamma_{i_j}|-2)=0. \end{align*} $$
Both summands are positive when
![]() $k>1.$
Hence, equality can hold only if
$k>1.$
Hence, equality can hold only if
![]() $(k,l)=(1,0),$
or
$(k,l)=(1,0),$
or
![]() $(k,l)=(0,1)$
and
$(k,l)=(0,1)$
and
![]() $|\Gamma _{i_1}|=4$
.
$|\Gamma _{i_1}|=4$
.
Proof of Corollary 1.3.
By Theorem 2.3, invariants with interior constraints in
![]() $\Gamma _{\diamond }$
are computable in terms of invariants with interior constraints of the form
$\Gamma _{\diamond }$
are computable in terms of invariants with interior constraints of the form
![]() $\Gamma _j=[\omega ^j]$
. Furthermore, by the open unit and divisor axioms Proposition 2.24,6, we may assume that
$\Gamma _j=[\omega ^j]$
. Furthermore, by the open unit and divisor axioms Proposition 2.24,6, we may assume that
![]() $|\Gamma _j| \geqslant 4$
. Finally, assume for convenience that interior constraints are written in ascending degree order. It follows from the open degree axiom Proposition 2.23 that for any
$|\Gamma _j| \geqslant 4$
. Finally, assume for convenience that interior constraints are written in ascending degree order. It follows from the open degree axiom Proposition 2.23 that for any
![]() $\beta ,$
there are only finitely many values of
$\beta ,$
there are only finitely many values of
![]() $k,l,$
for which there may be nonzero invariants with constraints of the above type. Hence, we give a process for computing
$k,l,$
for which there may be nonzero invariants with constraints of the above type. Hence, we give a process for computing
![]() $\overline {OGW}\!_{\beta , k}(\Gamma _{i_1}, \ldots , \Gamma _{i_l})$
which is inductive on
$\overline {OGW}\!_{\beta , k}(\Gamma _{i_1}, \ldots , \Gamma _{i_l})$
which is inductive on
![]() $(\beta , k, l, i_1)$
with respect to the lexicographical order on
$(\beta , k, l, i_1)$
with respect to the lexicographical order on
![]() $\mathbb {Z}^{\oplus 4}_{\geqslant 0}$
.
$\mathbb {Z}^{\oplus 4}_{\geqslant 0}$
.
Consider a triple
![]() $(\beta , k, l)$
with
$(\beta , k, l)$
with
![]() $ k + l < 2 $
. If
$ k + l < 2 $
. If
![]() $\beta =0$
, by the open zero axiom Proposition 2.25, all invariants vanish. For
$\beta =0$
, by the open zero axiom Proposition 2.25, all invariants vanish. For
![]() $\beta =1,2$
all possible values have been computed explicitly in Theorem 1.2. Indeed, if
$\beta =1,2$
all possible values have been computed explicitly in Theorem 1.2. Indeed, if
![]() $\beta =1$
, this follows from Lemma 6.2. If
$\beta =1$
, this follows from Lemma 6.2. If
![]() $\beta =2,$
we have
$\beta =2,$
we have
 $$ \begin{align*} & \beta=2 \implies 4+2l=2k+\sum_{j=1}^l |\Gamma_{i_j}| \\ &\implies 2(k-2)+\sum_{j=1}^l (|\Gamma_{i_j}|-2)=0. \end{align*} $$
$$ \begin{align*} & \beta=2 \implies 4+2l=2k+\sum_{j=1}^l |\Gamma_{i_j}| \\ &\implies 2(k-2)+\sum_{j=1}^l (|\Gamma_{i_j}|-2)=0. \end{align*} $$
Equality can only hold if
![]() $k=0$
,
$k=0$
,
![]() $l=1$
and
$l=1$
and
![]() $|\Gamma _{i_1}|=6$
. Similarly, the open degree axiom implies that for
$|\Gamma _{i_1}|=6$
. Similarly, the open degree axiom implies that for
![]() $\beta \geqslant 3$
, the only invariants that do not vanish have
$\beta \geqslant 3$
, the only invariants that do not vanish have
![]() $k+l \geqslant 2$
.
$k+l \geqslant 2$
.
Consider a triple
![]() $(\beta , k, l)$
with
$(\beta , k, l)$
with
![]() $ k + l \geqslant 2 $
. If
$ k + l \geqslant 2 $
. If
![]() $l \geqslant 2$
, by Theorem 1.1 3 and the open divisor and zero axiom, we can express the invariant
$l \geqslant 2$
, by Theorem 1.1 3 and the open divisor and zero axiom, we can express the invariant
![]() $\overline {OGW}\!_{\beta , k}(\Gamma _{i_1}, \ldots , \Gamma _{i_l})$
as a combination of invariants
$\overline {OGW}\!_{\beta , k}(\Gamma _{i_1}, \ldots , \Gamma _{i_l})$
as a combination of invariants
![]() $\overline {OGW}\!_{\beta ',k'}(\Gamma _{j_1},\ldots ,\Gamma _{j_{l'}})$
that either have
$\overline {OGW}\!_{\beta ',k'}(\Gamma _{j_1},\ldots ,\Gamma _{j_{l'}})$
that either have
![]() $\beta ' < \beta ,$
or
$\beta ' < \beta ,$
or
![]() $\beta ' = \beta , k' = k$
and
$\beta ' = \beta , k' = k$
and
![]() $l'< l,$
or
$l'< l,$
or
![]() $\beta ' = \beta , k' = k, l'=l$
and
$\beta ' = \beta , k' = k, l'=l$
and
![]() $ j_1 < i_1$
. Thus, the invariant is reduced to invariants with data of smaller lexicographical order, known by induction.
$ j_1 < i_1$
. Thus, the invariant is reduced to invariants with data of smaller lexicographical order, known by induction.
Note that by Lemma 6.1, we have
![]() $\overline {OGW}\!_{2,0}(\Gamma _2,\Gamma _2)\ne 0$
. So, if
$\overline {OGW}\!_{2,0}(\Gamma _2,\Gamma _2)\ne 0$
. So, if
![]() $k \geqslant 2$
, by Theorem 1.1 2, we can express the required invariant in terms of invariants that are either of smaller degree or have equal degree and fewer boundary marked points. Indeed, in formula 2, the closed zero axiom Proposition 2.13 and the open zero axiom imply that all the products involving invariants with degree
$k \geqslant 2$
, by Theorem 1.1 2, we can express the required invariant in terms of invariants that are either of smaller degree or have equal degree and fewer boundary marked points. Indeed, in formula 2, the closed zero axiom Proposition 2.13 and the open zero axiom imply that all the products involving invariants with degree
![]() $ \beta +2$
vanish. By Lemma 3.4, the map
$ \beta +2$
vanish. By Lemma 3.4, the map
![]() $\varpi $
is given by multiplication by
$\varpi $
is given by multiplication by
![]() $4.$
This and Lemma 6.2 imply that products involving invariants with degree
$4.$
This and Lemma 6.2 imply that products involving invariants with degree
![]() $\beta +1 $
do not occur.
$\beta +1 $
do not occur.
If
![]() $k \geqslant 1$
and
$k \geqslant 1$
and
![]() $ l\geqslant $
1, by Theorem 1.1 1, the open zero axiom and the closed zero axiom, we can express the required invariant in terms of invariants that are of smaller degree.
$ l\geqslant $
1, by Theorem 1.1 1, the open zero axiom and the closed zero axiom, we can express the required invariant in terms of invariants that are of smaller degree.
7 Small relative quantum cohomology
In this section, we compute the small relative quantum cohomology of
![]() $(\mathbb {C}P^3,L_\triangle ).$
$(\mathbb {C}P^3,L_\triangle ).$
Lemma 7.1.
![]() $\overline {OGW}\!_{2,2}=-\frac {5}{4}.$
$\overline {OGW}\!_{2,2}=-\frac {5}{4}.$
Proof. By recursion 1 of Theorem 1.1, we get
In Theorem 5.1, we computed
![]() $\overline {OGW}\!_{1,1}=-3.$
Thus, by the open divisor axiom Proposition 2.26, we get
$\overline {OGW}\!_{1,1}=-3.$
Thus, by the open divisor axiom Proposition 2.26, we get
![]() $\overline {OGW}\!_{2,1}(\Gamma _2)=-\frac {9}{16}.$
By recursion 2 of Theorem 1.1, we get
$\overline {OGW}\!_{2,1}(\Gamma _2)=-\frac {9}{16}.$
By recursion 2 of Theorem 1.1, we get
Lemma 6.1 gives
![]() $\overline {OGW}\!_{2,0}(\Gamma _2,\Gamma _2)=\frac {35}{64},$
and the number of lines through a point and two lines is
$\overline {OGW}\!_{2,0}(\Gamma _2,\Gamma _2)=\frac {35}{64},$
and the number of lines through a point and two lines is
![]() ${GW}_1(\Delta _2,\Delta _2, \Delta _3)=1.$
So, by the open unit axiom Proposition 2.24, we get
${GW}_1(\Delta _2,\Delta _2, \Delta _3)=1.$
So, by the open unit axiom Proposition 2.24, we get
 $$\begin{align*}\overline{OGW}\!_{2,2}= \frac{-1 +\frac{81}{256}}{\frac{35}{64}} = -\frac{5}{4}. \end{align*}$$
$$\begin{align*}\overline{OGW}\!_{2,2}= \frac{-1 +\frac{81}{256}}{\frac{35}{64}} = -\frac{5}{4}. \end{align*}$$
Recall the definition of
![]() $\Gamma _\diamond $
from Section 2.7. By Lemma 3.4, we have
$\Gamma _\diamond $
from Section 2.7. By Lemma 3.4, we have
![]() $H_2(\mathbb {C}P^3, L_\triangle ;\mathbb {Z})=\mathbb {Z},$
and the map
$H_2(\mathbb {C}P^3, L_\triangle ;\mathbb {Z})=\mathbb {Z},$
and the map
is given by
![]() $m\mapsto 4m.$
Hence, since
$m\mapsto 4m.$
Hence, since
![]() $g^{ij}=\delta _{i,3-j}$
, it follows that the relative small quantum product (2.6) for
$g^{ij}=\delta _{i,3-j}$
, it follows that the relative small quantum product (2.6) for
![]() $(X,L)=(\mathbb {C}P^3, L_\triangle )$
is given by
$(X,L)=(\mathbb {C}P^3, L_\triangle )$
is given by

Proof of Theorem 1.5.
We claim that
![]() $QH^{*}(\mathbb {C}P^3, L_\triangle )$
is generated as a ring by
$QH^{*}(\mathbb {C}P^3, L_\triangle )$
is generated as a ring by
![]() $1,T, \Gamma _1, \Gamma _\diamond .$
Indeed, by the open degree axiom Proposition 2.2 3 and the closed degree axiom Proposition 2.13, we obtain
$1,T, \Gamma _1, \Gamma _\diamond .$
Indeed, by the open degree axiom Proposition 2.2 3 and the closed degree axiom Proposition 2.13, we obtain
So, by the closed zero axiom Proposition 2.1 6, the open divisor axiom Proposition 2.2 6 and Theorem 5.2, we get
and
Consider the ring
![]() $\mathbb {R}[x,y][[q^{1/4}]]/I$
with
$\mathbb {R}[x,y][[q^{1/4}]]/I$
with
 $$\begin{align*}I=\left( x^4-q-\frac{1}{2}q^{1/2}y-\frac{3}{64}q^{1/4}y,\ y^2+\frac{5}{4}q^{1/2}y,\ xy-\frac{3}{4}q^{1/4}y \right).\end{align*}$$
$$\begin{align*}I=\left( x^4-q-\frac{1}{2}q^{1/2}y-\frac{3}{64}q^{1/4}y,\ y^2+\frac{5}{4}q^{1/2}y,\ xy-\frac{3}{4}q^{1/4}y \right).\end{align*}$$
Let
be the ring homomorphism defined by
Hence,
 $$ \begin{align} \phi(x)^2=\Gamma_2,\quad \phi(x)^3-\frac{\phi(q^{\frac{1}{4}})}{16}\phi(y)=\Gamma_3. \end{align} $$
$$ \begin{align} \phi(x)^2=\Gamma_2,\quad \phi(x)^3-\frac{\phi(q^{\frac{1}{4}})}{16}\phi(y)=\Gamma_3. \end{align} $$
In order to show the map
![]() $\phi $
is well defined, it suffices to show that the generators of the ideal I are sent to
$\phi $
is well defined, it suffices to show that the generators of the ideal I are sent to
![]() $0.$
Using the closed degree axiom, the wall crossing formula Theorem 2.3 and the open degree axiom, we obtain
$0.$
Using the closed degree axiom, the wall crossing formula Theorem 2.3 and the open degree axiom, we obtain

The number of lines through two points and a plane is
![]() ${GW}_1(\Delta _1,\Delta _3,\Delta _3)=1$
. Hence, by Theorem 5.3, Theorem 5.1 and the open divisor axiom, we get
${GW}_1(\Delta _1,\Delta _3,\Delta _3)=1$
. Hence, by Theorem 5.3, Theorem 5.1 and the open divisor axiom, we get
So,
By the wall crossing formula Theorem 2.3 and the open degree axiom, we get

Hence, by Lemma 7.1, we get
![]() $\phi (y^2+\frac {5}{4}q^{1/2}y)=0.$
Using the wall crossing formula Theorem 2.3, the open degree and divisor axioms, and Theorem 5.1, we get
$\phi (y^2+\frac {5}{4}q^{1/2}y)=0.$
Using the wall crossing formula Theorem 2.3, the open degree and divisor axioms, and Theorem 5.1, we get

So,
![]() $\phi (xy-\frac {3}{4}q^{1/4}y)=0.$
Thus, the map
$\phi (xy-\frac {3}{4}q^{1/4}y)=0.$
Thus, the map
![]() $\phi $
is well defined. It is surjective because its image generates
$\phi $
is well defined. It is surjective because its image generates
![]() $QH^{*}(\mathbb {C}P^3, L_\triangle )$
by equation (7.1).
$QH^{*}(\mathbb {C}P^3, L_\triangle )$
by equation (7.1).
Abbreviate
We think of M and N as modules over the local ring
![]() $\mathbb {R}[[q^{1/4}]].$
Consider the induced map
$\mathbb {R}[[q^{1/4}]].$
Consider the induced map
It follows from the definition of the ideal I that
![]() $M/mM$
is a real vector space with basis
$M/mM$
is a real vector space with basis
![]() $1,y,x,x^2,x^3$
. Since
$1,y,x,x^2,x^3$
. Since
![]() $\bar {\phi }$
is surjective and
$\bar {\phi }$
is surjective and
it follows that
![]() $\bar {\phi }$
is injective. Since
$\bar {\phi }$
is injective. Since
![]() $\ker \phi /m\ker \phi \subset \ker \bar {\phi }=0,$
it follows that
$\ker \phi /m\ker \phi \subset \ker \bar {\phi }=0,$
it follows that
![]() $m\ker \phi =\ker \phi .$
Since
$m\ker \phi =\ker \phi .$
Since
![]() $\mathbb {R}[[q^{1/4}]]$
is a local ring with maximal ideal m, Nakayama’s lemma gives
$\mathbb {R}[[q^{1/4}]]$
is a local ring with maximal ideal m, Nakayama’s lemma gives
![]() $\ker \phi =0.$
Therefore,
$\ker \phi =0.$
Therefore,
![]() $\phi $
is an isomorphism.
$\phi $
is an isomorphism.
8 Dependence of invariants on left inverse
In this section, we review in greater detail the dependence of the invariants
![]() $\overline {OGW}\!_{\beta ,k}$
on the map
$\overline {OGW}\!_{\beta ,k}$
on the map
![]() $P_{\mathbb {R}}.$
We quantify this dependence in Proposition 8.1, from which we obtain Proposition 1.1 as a special case. Finally, we prove Corollary 1.4.
$P_{\mathbb {R}}.$
We quantify this dependence in Proposition 8.1, from which we obtain Proposition 1.1 as a special case. Finally, we prove Corollary 1.4.
In the present section, we continue in the setting of Section 2.1. In particular,
![]() $L\subset X$
is a connected spin Lagrangian submanifold with
$L\subset X$
is a connected spin Lagrangian submanifold with
![]() $H^{*}(L;\mathbb {R}) \simeq H^{*}(S^n;\mathbb {R})$
and
$H^{*}(L;\mathbb {R}) \simeq H^{*}(S^n;\mathbb {R})$
and
![]() $[L] = 0 \in H_n(X;\mathbb {R}).$
Recall the definition of the map
$[L] = 0 \in H_n(X;\mathbb {R}).$
Recall the definition of the map
![]() $P_{\mathbb {R}}: \widehat {H}^{n+1}(X,L;\mathbb {R}) \to H^n(L;\mathbb {R})$
from Section 2.1. In this section, we extend
$P_{\mathbb {R}}: \widehat {H}^{n+1}(X,L;\mathbb {R}) \to H^n(L;\mathbb {R})$
from Section 2.1. In this section, we extend
![]() $P_{\mathbb {R}}$
to a map
$P_{\mathbb {R}}$
to a map
![]() $P_{\mathbb {R}}: \widehat {H}^{*}(X,L;\mathbb {R}) \to H^n(L;\mathbb {R})$
by setting it to zero outside
$P_{\mathbb {R}}: \widehat {H}^{*}(X,L;\mathbb {R}) \to H^n(L;\mathbb {R})$
by setting it to zero outside
![]() $\widehat {H}^{n+1}(X,L;\mathbb {R})$
. We use Poincaré duality to identify
$\widehat {H}^{n+1}(X,L;\mathbb {R})$
. We use Poincaré duality to identify
![]() $H^n(L;\mathbb {R})\simeq \mathbb {R}.$
Let
$H^n(L;\mathbb {R})\simeq \mathbb {R}.$
Let
![]() $\rho : \widehat {H}^{*}(X,L;\mathbb {R})\rightarrow H^{*}(X;\mathbb {R})$
denote the natural map. Consider
$\rho : \widehat {H}^{*}(X,L;\mathbb {R})\rightarrow H^{*}(X;\mathbb {R})$
denote the natural map. Consider
![]() $P_{\mathbb {R}},P_{\mathbb {R}}^{\prime }$
with associated invariants
$P_{\mathbb {R}},P_{\mathbb {R}}^{\prime }$
with associated invariants
![]() $\overline {OGW}\!_{\beta ,k}$
and
$\overline {OGW}\!_{\beta ,k}$
and
![]() $\overline {OGW}\!\,'\!\!_{\beta ,k}$
, respectively. The long exact sequence of the pair
$\overline {OGW}\!\,'\!\!_{\beta ,k}$
, respectively. The long exact sequence of the pair
![]() $(X,L)$
implies there exists a unique map
$(X,L)$
implies there exists a unique map
such that
![]() $\mathfrak {p}_{\mathbb {R}}\circ \rho =P_{\mathbb {R}}-P_{\mathbb {R}}^{\prime }.$
Let
$\mathfrak {p}_{\mathbb {R}}\circ \rho =P_{\mathbb {R}}-P_{\mathbb {R}}^{\prime }.$
Let
![]() $\Delta _0,\ldots ,\Delta _N\in H^{*}(X;\mathbb {R})$
be a basis. Recall that
$\Delta _0,\ldots ,\Delta _N\in H^{*}(X;\mathbb {R})$
be a basis. Recall that
and
![]() $g^{ij}$
denotes the inverse matrix.
$g^{ij}$
denotes the inverse matrix.
Theorem 8.1. Let
![]() $A_1,..,A_l\in \widehat {H}^{*}(X,L;\mathbb {R})$
.
$A_1,..,A_l\in \widehat {H}^{*}(X,L;\mathbb {R})$
.
 $$\begin{align*}\overline{OGW}\!_{\beta,0}(A_1,\ldots,A_l)-\overline{OGW}\!\,'\!\!_{\beta,0}(A_1,\ldots,A_l)=\sum_{\substack{\tilde {\beta}\in H_2(X;\mathbb{Z})\\ \varpi(\tilde {\beta})=\beta}} g^{ij}{GW}_{\tilde {\beta}}(\Delta_i,\rho(A_1),\ldots,\rho(A_l))\mathfrak{p}_{\mathbb{R}}(\Delta_j).\end{align*}$$
$$\begin{align*}\overline{OGW}\!_{\beta,0}(A_1,\ldots,A_l)-\overline{OGW}\!\,'\!\!_{\beta,0}(A_1,\ldots,A_l)=\sum_{\substack{\tilde {\beta}\in H_2(X;\mathbb{Z})\\ \varpi(\tilde {\beta})=\beta}} g^{ij}{GW}_{\tilde {\beta}}(\Delta_i,\rho(A_1),\ldots,\rho(A_l))\mathfrak{p}_{\mathbb{R}}(\Delta_j).\end{align*}$$
Remark 8.1. Proposition 8.1 continues to hold in the more general setting of [Reference Solomon and Tukachinsky48] without change. We have formulated it only for the case of L spin and
![]() $H^{*}(L;\mathbb {R}) \simeq H^{*}(S^n;\mathbb {R})$
to streamline the exposition since the Chiang Lagrangian satisfies these assumptions.
$H^{*}(L;\mathbb {R}) \simeq H^{*}(S^n;\mathbb {R})$
to streamline the exposition since the Chiang Lagrangian satisfies these assumptions.
In order to prove Proposition 8.1, we will need a number of results from [Reference Solomon and Tukachinsky48], which we now summarize. The proof appears toward the end of this section. Recall the definition of the rings
![]() $Q_W$
and
$Q_W$
and
![]() $R_W$
from Section 2.4. Define
$R_W$
from Section 2.4. Define
by
This is a map of complexes when
![]() $R_W$
is equipped with the trivial differential. The cone
$R_W$
is equipped with the trivial differential. The cone
![]() $C(\mathfrak {i})$
is the complex with underlying graded
$C(\mathfrak {i})$
is the complex with underlying graded
![]() $Q_W$
module
$Q_W$
module
![]() $A^{*}(X;Q_W)\oplus R_W[-n-1]$
and differential
$A^{*}(X;Q_W)\oplus R_W[-n-1]$
and differential
Note that if
![]() $[L]=0\in H_n(X;\mathbb {R}),$
then
$[L]=0\in H_n(X;\mathbb {R}),$
then
![]() $\operatorname {\mathrm {Coker}}\mathfrak {i}\simeq R_W[-n-1]$
. Thus, we consider the following commutative diagram with exact rows and columns, which is taken from Section 4.4 in [Reference Solomon and Tukachinsky48] except that
$\operatorname {\mathrm {Coker}}\mathfrak {i}\simeq R_W[-n-1]$
. Thus, we consider the following commutative diagram with exact rows and columns, which is taken from Section 4.4 in [Reference Solomon and Tukachinsky48] except that
![]() $\operatorname {\mathrm {Coker}}\mathfrak {i}$
is replaced with
$\operatorname {\mathrm {Coker}}\mathfrak {i}$
is replaced with
![]() $R_W[-n-1].$
$R_W[-n-1].$

Here,
![]() $\bar a : Q_W \to R_W$
is the inclusion and
$\bar a : Q_W \to R_W$
is the inclusion and
![]() $\bar q : R_W \to R_W/Q_W$
is the quotient map. Let
$\bar q : R_W \to R_W/Q_W$
is the quotient map. Let
be a left inverse to the map
![]() $\bar {x}$
from the diagram (8.1) satisfying the following two conditions. The first condition is that
$\bar {x}$
from the diagram (8.1) satisfying the following two conditions. The first condition is that
This condition and the exactness of the diagram (8.1) imply that there exists a unique
![]() $P_Q:\widehat {H}^{*}(X,L;Q_W)\rightarrow Q_W$
such that the following diagram commutes:
$P_Q:\widehat {H}^{*}(X,L;Q_W)\rightarrow Q_W$
such that the following diagram commutes:

The second condition is that there exists
![]() $P_{\mathbb {R}} : \widehat {H}^{*}(X,L;\mathbb {R}) \rightarrow \mathbb {R}$
, such that
$P_{\mathbb {R}} : \widehat {H}^{*}(X,L;\mathbb {R}) \rightarrow \mathbb {R}$
, such that
The following is Lemma 4.10 from [Reference Solomon and Tukachinsky48].
Lemma 8.2.
![]() $P_Q\circ \bar {y}_Q=\operatorname {\mathrm {Id}}$
.
$P_Q\circ \bar {y}_Q=\operatorname {\mathrm {Id}}$
.
The following is Lemma 4.11 from [Reference Solomon and Tukachinsky48].
Lemma 8.3. Let
![]() $l:\widehat {H}^{*}(X,L;\mathbb {R})\rightarrow \mathbb {R}$
satisfy
$l:\widehat {H}^{*}(X,L;\mathbb {R})\rightarrow \mathbb {R}$
satisfy
![]() $l\circ y=\operatorname {\mathrm {Id}}.$
There exists a unique choice of
$l\circ y=\operatorname {\mathrm {Id}}.$
There exists a unique choice of
![]() $P:H^{*}(C(\mathfrak {i}))\rightarrow R_W$
satisfying conditions (8.2) and (8.4) such that
$P:H^{*}(C(\mathfrak {i}))\rightarrow R_W$
satisfying conditions (8.2) and (8.4) such that
![]() $l=P_{\mathbb {R}}$
. Moreover,
$l=P_{\mathbb {R}}$
. Moreover,
![]() $\ker P= a(\ker P_Q)$
.
$\ker P= a(\ker P_Q)$
.
Let
![]() $\Psi \in C(\mathfrak {i})$
be the relative potential defined in Section 1.3.1 in [Reference Solomon and Tukachinsky48]. The definition of
$\Psi \in C(\mathfrak {i})$
be the relative potential defined in Section 1.3.1 in [Reference Solomon and Tukachinsky48]. The definition of
![]() $\overline {\Omega }$
given in Section 1.3.3 in [Reference Solomon and Tukachinsky48] is
$\overline {\Omega }$
given in Section 1.3.3 in [Reference Solomon and Tukachinsky48] is
This together with (2.2) and Lemma 8.3 makes precise the dependence of the invariants
![]() $\overline {OGW}\!_{\beta ,k}$
on
$\overline {OGW}\!_{\beta ,k}$
on
![]() $P_{\mathbb {R}}.$
To quantify this dependence, we recall another lemma.
$P_{\mathbb {R}}.$
To quantify this dependence, we recall another lemma.
Denote by
![]() $\rho ^{*}: Q_U\rightarrow Q_W$
the inclusion map. Recall the map
$\rho ^{*}: Q_U\rightarrow Q_W$
the inclusion map. Recall the map
![]() $\pi $
from diagram (8.1). The following is Lemma 5.9 from [Reference Solomon and Tukachinsky48]
$\pi $
from diagram (8.1). The following is Lemma 5.9 from [Reference Solomon and Tukachinsky48]
Lemma 8.4.
![]() $\pi (\Psi )=\rho ^{*}(\nabla \Phi ).$
$\pi (\Psi )=\rho ^{*}(\nabla \Phi ).$
Proof of Proposition 8.1.
Apply Lemma 8.3 to obtain maps
![]() $P,P,'$
corresponding to
$P,P,'$
corresponding to
![]() $P_{\mathbb {R}},P_{\mathbb {R}}^{\prime },$
that are left inverses to
$P_{\mathbb {R}},P_{\mathbb {R}}^{\prime },$
that are left inverses to
![]() $\bar {x}$
and satisfy conditions (8.2) and (8.4). Denote by
$\bar {x}$
and satisfy conditions (8.2) and (8.4). Denote by
![]() $P_Q, P_Q^{\prime }$
the corresponding maps from diagram (8.3). Since
$P_Q, P_Q^{\prime }$
the corresponding maps from diagram (8.3). Since
the maps
![]() $P-P'$
,
$P-P'$
,
![]() $P_Q-P_Q^{\prime },$
factor through
$P_Q-P_Q^{\prime },$
factor through
![]() $H^{*}(X;Q_W)$
. Consequently, there exist unique maps
$H^{*}(X;Q_W)$
. Consequently, there exist unique maps
![]() $\mathfrak {p},\mathfrak {p}_Q,$
such that the following diagram commutes.
$\mathfrak {p},\mathfrak {p}_Q,$
such that the following diagram commutes.

Indeed, since
then
![]() $(P_Q-P_Q^{\prime })(\ker \rho _Q)=0.$
By diagram (8.1),
$(P_Q-P_Q^{\prime })(\ker \rho _Q)=0.$
By diagram (8.1),
![]() $\rho _Q$
is surjective. Thus, for every
$\rho _Q$
is surjective. Thus, for every
![]() $\tilde {\eta }\in \rho _Q^{-1}(\eta )$
, we define
$\tilde {\eta }\in \rho _Q^{-1}(\eta )$
, we define
![]() $\mathfrak {p}_Q(\eta )= (P_Q-P_Q^{\prime })(\tilde {\eta })$
. Hence,
$\mathfrak {p}_Q(\eta )= (P_Q-P_Q^{\prime })(\tilde {\eta })$
. Hence,
![]() $\mathfrak {p}_Q$
is determined by
$\mathfrak {p}_Q$
is determined by
![]() $P_Q$
and
$P_Q$
and
![]() $P_Q^{\prime }.$
A similar argument applies for
$P_Q^{\prime }.$
A similar argument applies for
![]() $\mathfrak {p}.$
Since
$\mathfrak {p}.$
Since
 $$ \begin{align*} (\mathfrak{p}_{\mathbb{R}}\otimes\operatorname{\mathrm{Id}}_Q)\circ \rho_Q&=(\mathfrak{p}_{\mathbb{R}}\otimes\operatorname{\mathrm{Id}}_Q)\circ (\rho\otimes \operatorname{\mathrm{Id}}_Q)\\ &= (\mathfrak{p}_{\mathbb{R}}\circ\rho)\otimes\operatorname{\mathrm{Id}}_Q\\ &=(P_{\mathbb{R}}-P_{\mathbb{R}}^{\prime})\otimes \operatorname{\mathrm{Id}}_Q\\ &=P_Q-P_Q^{\prime}, \end{align*} $$
$$ \begin{align*} (\mathfrak{p}_{\mathbb{R}}\otimes\operatorname{\mathrm{Id}}_Q)\circ \rho_Q&=(\mathfrak{p}_{\mathbb{R}}\otimes\operatorname{\mathrm{Id}}_Q)\circ (\rho\otimes \operatorname{\mathrm{Id}}_Q)\\ &= (\mathfrak{p}_{\mathbb{R}}\circ\rho)\otimes\operatorname{\mathrm{Id}}_Q\\ &=(P_{\mathbb{R}}-P_{\mathbb{R}}^{\prime})\otimes \operatorname{\mathrm{Id}}_Q\\ &=P_Q-P_Q^{\prime}, \end{align*} $$
it follows by the uniqueness of
![]() $\mathfrak {p}_Q$
that
$\mathfrak {p}_Q$
that
Let
![]() $\overline {OGW}\!$
,
$\overline {OGW}\!$
,
![]() $ \overline {OGW}\!'$
be the Gromov-Witten invariants correspond to P and
$ \overline {OGW}\!'$
be the Gromov-Witten invariants correspond to P and
![]() $P'$
, respectively, and let
$P'$
, respectively, and let
![]() $\overline {\Omega }$
,
$\overline {\Omega }$
,
![]() $\overline {\Omega }'$
be the corresponding superpotentials.
$\overline {\Omega }'$
be the corresponding superpotentials.
From multilinearity of
![]() $\overline {OGW}\!_{\beta ,k}$
, it suffices to prove this proposition for
$\overline {OGW}\!_{\beta ,k}$
, it suffices to prove this proposition for
![]() $A_i=\Gamma _i.$
By (8.5), diagram (8.6), and Lemma 8.4, we get
$A_i=\Gamma _i.$
By (8.5), diagram (8.6), and Lemma 8.4, we get
 $$ \begin{align*} \overline{\Omega}-\overline{\Omega}'&=(P-P')\Psi\\ &=(\mathfrak{p}\circ \pi)\Psi\\ &=\mathfrak{p}(\rho^{*}(\nabla \Phi))\\ &=\bar{a}\circ \mathfrak{p}_Q(\rho^{*}(\nabla \Phi)). \end{align*} $$
$$ \begin{align*} \overline{\Omega}-\overline{\Omega}'&=(P-P')\Psi\\ &=(\mathfrak{p}\circ \pi)\Psi\\ &=\mathfrak{p}(\rho^{*}(\nabla \Phi))\\ &=\bar{a}\circ \mathfrak{p}_Q(\rho^{*}(\nabla \Phi)). \end{align*} $$
Recall that
![]() $[T^\beta ]$
denotes the coefficient of
$[T^\beta ]$
denotes the coefficient of
![]() $T^\beta .$
So,
$T^\beta .$
So,
By (2.2), we have
Since
![]() $\mathfrak {p}_Q=\mathfrak {p}_{\mathbb {R}}\otimes \operatorname {\mathrm {Id}}_Q$
and
$\mathfrak {p}_Q=\mathfrak {p}_{\mathbb {R}}\otimes \operatorname {\mathrm {Id}}_Q$
and
![]() $\nabla \Phi =g^{ij}\Delta _j\partial _i\Phi ,$
it follows that
$\nabla \Phi =g^{ij}\Delta _j\partial _i\Phi ,$
it follows that
 $$ \begin{align*} [T^\beta]\partial_{t_{i_1}}\cdots\partial_{t_{i_l}}(\bar{a}\circ \mathfrak{p}_Q(\rho^{*}(\nabla \Phi)))|_{s=t_i=0}&=[T^\beta]\partial_{t_{i_1}}\cdots\partial_{t_{i_l}}(\bar{a}\circ \mathfrak{p}_Q(\rho^{*}(g^{ij}\Delta_j\partial_i\Phi)))|_{s=t_i=0}\\ &=[T^\beta]\partial_{t_{i_1}}\cdots\partial_{t_{i_l}}( \mathfrak{p}_{\mathbb{R}}(\Delta_j)g^{ij}\partial_i\Phi)|_{s=t_i=0}\\ &=\sum_{\substack{\tilde {\beta}\in H_2(X;\mathbb{Z})\\ \varpi(\tilde {\beta})=\beta}} g^{ij}{GW}_{\tilde {\beta}}(\Delta_i,\Delta_{i_1},\ldots,\Delta_{i_l})\mathfrak{p}_{\mathbb{R}}(\Delta_j), \end{align*} $$
$$ \begin{align*} [T^\beta]\partial_{t_{i_1}}\cdots\partial_{t_{i_l}}(\bar{a}\circ \mathfrak{p}_Q(\rho^{*}(\nabla \Phi)))|_{s=t_i=0}&=[T^\beta]\partial_{t_{i_1}}\cdots\partial_{t_{i_l}}(\bar{a}\circ \mathfrak{p}_Q(\rho^{*}(g^{ij}\Delta_j\partial_i\Phi)))|_{s=t_i=0}\\ &=[T^\beta]\partial_{t_{i_1}}\cdots\partial_{t_{i_l}}( \mathfrak{p}_{\mathbb{R}}(\Delta_j)g^{ij}\partial_i\Phi)|_{s=t_i=0}\\ &=\sum_{\substack{\tilde {\beta}\in H_2(X;\mathbb{Z})\\ \varpi(\tilde {\beta})=\beta}} g^{ij}{GW}_{\tilde {\beta}}(\Delta_i,\Delta_{i_1},\ldots,\Delta_{i_l})\mathfrak{p}_{\mathbb{R}}(\Delta_j), \end{align*} $$
which completes the proof.
Proof of Proposition 1.1.
Lemma 3.4 asserts that
![]() $\varpi $
is given by multiplication by
$\varpi $
is given by multiplication by
![]() $4$
. Recall the choice of the basis
$4$
. Recall the choice of the basis
![]() $\Gamma _i \in \widehat H^{*}(\mathbb {C}P^3,L_\triangle ;\mathbb {R})$
from Section 1. Since
$\Gamma _i \in \widehat H^{*}(\mathbb {C}P^3,L_\triangle ;\mathbb {R})$
from Section 1. Since
![]() $P_{\mathbb {R}}(\Gamma _i)\ne 0$
only if
$P_{\mathbb {R}}(\Gamma _i)\ne 0$
only if
![]() $i=2,$
it follows that
$i=2,$
it follows that
![]() $\mathfrak {p}_{\mathbb {R}}(\Delta _i)\ne 0$
only if
$\mathfrak {p}_{\mathbb {R}}(\Delta _i)\ne 0$
only if
![]() $i=2.$
Hence, since
$i=2.$
Hence, since
![]() $g^{ij}=\delta _{i,3-j}$
, it follows by Proposition 8.1, Lemma 3.5 and the closed divisor axiom Proposition 2.15 that
$g^{ij}=\delta _{i,3-j}$
, it follows by Proposition 8.1, Lemma 3.5 and the closed divisor axiom Proposition 2.15 that
Proof of Corollary 1.4.
Assume there exists a map
![]() $P^{\prime }_{\mathbb {R}}$
such that
$P^{\prime }_{\mathbb {R}}$
such that
![]() $\overline {OGW}\!_{\beta ,k}'$
vanishes where
$\overline {OGW}\!_{\beta ,k}'$
vanishes where
![]() $k=0$
and
$k=0$
and
![]() $\beta \in \operatorname {\mathrm {Im}}\varpi .$
Hence, by Proposition 1.1, we get
$\beta \in \operatorname {\mathrm {Im}}\varpi .$
Hence, by Proposition 1.1, we get
where
![]() $\beta \in \operatorname {\mathrm {Im}}\varpi .$
By Table 2, we have
$\beta \in \operatorname {\mathrm {Im}}\varpi .$
By Table 2, we have
Since the number of lines through two points is
![]() ${GW}_{1}(\Delta _3,\Delta _3)=1,$
we get
${GW}_{1}(\Delta _3,\Delta _3)=1,$
we get
However, the number of lines through a point and two lines is
![]() ${GW}_{1}(\Delta _2,\Delta _2,\Delta _3)=1,$
so
${GW}_{1}(\Delta _2,\Delta _2,\Delta _3)=1,$
so
which is a contradiction.
Acknowledgements
The authors would like to thank J. Evans, O. Kedar, C.-C. M. Liu, J. Smith and S. Tukachinsky for helpful conversations. The authors were partially funded by ISF grants 569/18 and 1127/22.
Competing interests
The authors have no competing interest to declare.