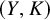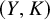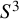1. Introduction
Every knot K in
![]() $S^3$
bounds a piecewise-linear (PL) disk in the 4-ball, namely, by taking the cone on the pair
$S^3$
bounds a piecewise-linear (PL) disk in the 4-ball, namely, by taking the cone on the pair
![]() $(S^3, K)$
(this disk in not locally flat, and throughout, we will not impose any local-flatness conditions on our PL surfaces). Resolving a conjecture of Zeeman [Reference Zeeman12], Akbulut [Reference Akbulut1] gave an example of a contractible 4-manifold X and a knot
$(S^3, K)$
(this disk in not locally flat, and throughout, we will not impose any local-flatness conditions on our PL surfaces). Resolving a conjecture of Zeeman [Reference Zeeman12], Akbulut [Reference Akbulut1] gave an example of a contractible 4-manifold X and a knot
![]() $K \subset \partial X$
, such that K does not bound a PL disk in X. However, Akbulut’s K does bound a PL disk in a different contractible 4-manifold
$K \subset \partial X$
, such that K does not bound a PL disk in X. However, Akbulut’s K does bound a PL disk in a different contractible 4-manifold
![]() $X'$
with
$X'$
with
![]() $\partial X' = \partial X$
. Levine [Reference Levine5] proved the stronger result that there exist manifold-knot pairs
$\partial X' = \partial X$
. Levine [Reference Levine5] proved the stronger result that there exist manifold-knot pairs
![]() $(Y, K)$
, such that Y bounds a smooth, contractible 4-manifold X and that K does not bound a PL disk in X nor in any other integer homology ball
$(Y, K)$
, such that Y bounds a smooth, contractible 4-manifold X and that K does not bound a PL disk in X nor in any other integer homology ball
![]() $X'$
with
$X'$
with
![]() $\partial X' = Y$
. In light of Levine’s [Reference Levine5] result, a natural question to ask is: Given a knot K in an integer homology 3-sphere Y, such that Y bounds an integer homology 4-ball, what’s the minimum genus of a PL surface
$\partial X' = Y$
. In light of Levine’s [Reference Levine5] result, a natural question to ask is: Given a knot K in an integer homology 3-sphere Y, such that Y bounds an integer homology 4-ball, what’s the minimum genus of a PL surface
![]() $\Sigma $
in an integer homology ball X, such that
$\Sigma $
in an integer homology ball X, such that
![]() $\partial (X,\Sigma ) = (Y,K)$
? We observe that such a surface
$\partial (X,\Sigma ) = (Y,K)$
? We observe that such a surface
![]() $\Sigma $
always exists, since K is null-homologous and thus bounds a surface in Y, which may be pushed slightly into any bounding
$\Sigma $
always exists, since K is null-homologous and thus bounds a surface in Y, which may be pushed slightly into any bounding
![]() $4$
-manifold.
$4$
-manifold.
Our main result is that this notion of PL genus can be arbitrarily large. Throughout, let
![]() $(Y_n, K_n) = \big (S^3_{-1}(T_{2n,2n+1}) \# -S^3_{-1}(T_{2n,2n+1}), \mu _{2n-1,-1} \# U \big )$
, where
$(Y_n, K_n) = \big (S^3_{-1}(T_{2n,2n+1}) \# -S^3_{-1}(T_{2n,2n+1}), \mu _{2n-1,-1} \# U \big )$
, where
![]() $\mu _{2n-1,-1}$
denotes the
$\mu _{2n-1,-1}$
denotes the
![]() $(2n-1, -1)$
-cable of the meridian in
$(2n-1, -1)$
-cable of the meridian in
![]() $S^3_{-1}(T_{2n,2n+1})$
and U denotes the unknot in
$S^3_{-1}(T_{2n,2n+1})$
and U denotes the unknot in
![]() $-S^3_{-1}(T_{2n,2n+1})$
.
$-S^3_{-1}(T_{2n,2n+1})$
.
Theorem 1.1. Any PL surface
![]() $\Sigma $
in any integer homology ball X, such that
$\Sigma $
in any integer homology ball X, such that
![]() $\partial (X, \Sigma ) = (Y_n, K_n)$
must have genus at least
$\partial (X, \Sigma ) = (Y_n, K_n)$
must have genus at least
![]() $n-1$
, for
$n-1$
, for
![]() $n \in \mathbb {Z}_{>0}$
.
$n \in \mathbb {Z}_{>0}$
.
We prove Theorem 1.1 by reinterpreting PL surfaces in terms of cobordisms inside of homology cobordisms. Recall that a homology cobordism from
![]() $Y_0$
to
$Y_0$
to
![]() $Y_1$
is a smooth, compact 4-manifold W, such that
$Y_1$
is a smooth, compact 4-manifold W, such that
![]() $\partial W = Y_0 \sqcup Y_1$
and that the map
$\partial W = Y_0 \sqcup Y_1$
and that the map
![]() $i_* \colon H_*(Y_j; \mathbb {Z}) \to H_*(W; \mathbb {Z})$
induced by inclusion is an isomorphism for
$i_* \colon H_*(Y_j; \mathbb {Z}) \to H_*(W; \mathbb {Z})$
induced by inclusion is an isomorphism for
![]() $j=0,1$
. Let
$j=0,1$
. Let
![]() $\Sigma $
be a genus g PL surface in an integer homology ball X, such that
$\Sigma $
be a genus g PL surface in an integer homology ball X, such that
![]() $\partial (X, \Sigma ) = (Y_n, K_n)$
. Up to isotopy, we may assume that
$\partial (X, \Sigma ) = (Y_n, K_n)$
. Up to isotopy, we may assume that
![]() $\Sigma $
is smooth, except at finitely many singular points, each of which is modeled on the cone of a smooth knot
$\Sigma $
is smooth, except at finitely many singular points, each of which is modeled on the cone of a smooth knot
![]() $J_i$
in
$J_i$
in
![]() $S^3$
(see, for example, [Reference Hom, Levine and Lidman4, Theorem A.1]). By deleting neighborhoods of arcs in
$S^3$
(see, for example, [Reference Hom, Levine and Lidman4, Theorem A.1]). By deleting neighborhoods of arcs in
![]() $\Sigma $
connecting the cone points, we obtain a genus g cobordism from the knot
$\Sigma $
connecting the cone points, we obtain a genus g cobordism from the knot
![]() $J = J_1 \# \dots \# J_m$
to K in a homology cobordism from
$J = J_1 \# \dots \# J_m$
to K in a homology cobordism from
![]() $S^3$
to Y.
$S^3$
to Y.
Let K be a knot in a homology null-bordant homology sphere Y. We consider cobordisms of pairs
such that W is a homology cobordism from
![]() $S^3$
to Y. The cobordism distance between
$S^3$
to Y. The cobordism distance between
![]() $(Y,K)$
and
$(Y,K)$
and
![]() $(S^3, J)$
is the minimal genus of S in any such pair
$(S^3, J)$
is the minimal genus of S in any such pair
![]() $(W, S)$
. By the preceding discussion, Theorem 1.1 is an immediate consequence of the following result.
$(W, S)$
. By the preceding discussion, Theorem 1.1 is an immediate consequence of the following result.
Theorem 1.2. The cobordism distance between
![]() $(Y_n,K_n)$
and any knot in
$(Y_n,K_n)$
and any knot in
![]() $S^3$
is at least
$S^3$
is at least
![]() $n-1$
.
$n-1$
.
We prove Theorem 1.2 using Heegaard Floer homology [Reference Ozsváth and Szabó8], specifically Zemke’s cobordism maps [Reference Zemke13]. Our obstruction relies on two key properties:
-
1. Consider a cobordism of pairs
where W is a homology cobordism and S has genus g. For any $$ \begin{align*}(W, S) \colon (S^3, J) \to (Y_n, K_n),\end{align*} $$
$$ \begin{align*}(W, S) \colon (S^3, J) \to (Y_n, K_n),\end{align*} $$
 $(c_1, c_2) \in (2\mathbb {Z})^2$
, such that
$(c_1, c_2) \in (2\mathbb {Z})^2$
, such that
 $c_1 +c_2 = -2g$
and
$c_1 +c_2 = -2g$
and
 $c_1, c_2 \leq 0$
, there exists a local map with bigrading
$c_1, c_2 \leq 0$
, there exists a local map with bigrading $$ \begin{align*} f_{W, S} \colon \operatorname{CFK}(S^3, J) \to \operatorname{CFK}(Y_n, K_n) \end{align*} $$
$$ \begin{align*} f_{W, S} \colon \operatorname{CFK}(S^3, J) \to \operatorname{CFK}(Y_n, K_n) \end{align*} $$
 $(c_1, c_2)$
. Similarly, we may consider a cobordism in the opposite direction, from
$(c_1, c_2)$
. Similarly, we may consider a cobordism in the opposite direction, from
 $(Y_n, K_n)$
to
$(Y_n, K_n)$
to
 $(S^3, J)$
(see [Reference Zemke13, Theorems 1.4 and 1.7]).
$(S^3, J)$
(see [Reference Zemke13, Theorems 1.4 and 1.7]).
-
2. The Heegaard Floer homology of
 $S^3$
is especially simple; namely,
$S^3$
is especially simple; namely,
 $\operatorname {HF}^-(S^3) = \mathbb {F}[U]$
. In particular, U acts nontrivally on any nontrivial element of
$\operatorname {HF}^-(S^3) = \mathbb {F}[U]$
. In particular, U acts nontrivally on any nontrivial element of
 $\operatorname {HF}^-(S^3)$
, or equivalently,
$\operatorname {HF}^-(S^3)$
, or equivalently,
 $\operatorname {HF}^-(S^3)$
contains no U-torsion.
$\operatorname {HF}^-(S^3)$
contains no U-torsion.
The proof of Theorem 1.2 relies on showing that
![]() $\operatorname {CFK}(Y_n, K_n)$
is sufficiently complicated so as to not admit local maps to and from
$\operatorname {CFK}(Y_n, K_n)$
is sufficiently complicated so as to not admit local maps to and from
![]() $\operatorname {CFK}(S^3, J)$
of certain bigradings (see Section 2 for more details).
$\operatorname {CFK}(S^3, J)$
of certain bigradings (see Section 2 for more details).
For constructing our examples
![]() $(Y_n, K_n)$
, we rely on recent work of the last author [Reference Zhou14], which combines work of Hedden-Levine [Reference Hedden and Levine3] and Truong [Reference Truong11] to give a description of the knot Floer complex for
$(Y_n, K_n)$
, we rely on recent work of the last author [Reference Zhou14], which combines work of Hedden-Levine [Reference Hedden and Levine3] and Truong [Reference Truong11] to give a description of the knot Floer complex for
![]() $(p, 1)$
-cables of the meridian in the image of surgery along a knot in
$(p, 1)$
-cables of the meridian in the image of surgery along a knot in
![]() $S^3$
. Preliminaries on this filtered mapping cone are given in Section 3 and the computation is carried out in Section 4.
$S^3$
. Preliminaries on this filtered mapping cone are given in Section 3 and the computation is carried out in Section 4.
2. Cobordism obstruction
In this section, we introduce a cobordism obstruction for manifold-knot pairs and prove Theorem 1.2 by applying the obstruction to the pairs
![]() $(Y_n, K_n)$
, calling upon the computational results in the later part of the paper. In addition, we compute the values of the concordance homomorphisms
$(Y_n, K_n)$
, calling upon the computational results in the later part of the paper. In addition, we compute the values of the concordance homomorphisms
![]() $\varphi _{i,j}$
of [Reference Dai, Hom, Stoffregen and Truong2] on the family
$\varphi _{i,j}$
of [Reference Dai, Hom, Stoffregen and Truong2] on the family
![]() $(Y_n, K_n)$
, which may be of independent interest.
$(Y_n, K_n)$
, which may be of independent interest.
We start with some preliminaries on knot Floer homology. Knot Floer homology was defined by Ozsváth-Szabó [Reference Ozsváth and Szabó7] and Rasmussen [Reference Rasmussen10]. We associate, following the conventions of Zemke [Reference Zemke13], to a manifold-knot pair
![]() $(Y,K)$
a chain complex
$(Y,K)$
a chain complex
![]() $ \operatorname {CFK}_{\mathbb {F}[\mathcal {U},{\mathcal {V}}]}(Y,K) = \operatorname {CFK}(Y,K) $
over the polynomial ring
$ \operatorname {CFK}_{\mathbb {F}[\mathcal {U},{\mathcal {V}}]}(Y,K) = \operatorname {CFK}(Y,K) $
over the polynomial ring
![]() $\mathbb {F}[\mathcal {U},{\mathcal {V}}],$
where
$\mathbb {F}[\mathcal {U},{\mathcal {V}}],$
where
![]() $\mathbb {F} = \mathbb {Z}/2\mathbb {Z}$
, called the knot Floer complex. This chain complex is a free module generated by intersecting points of two Lagrangians in a symmetric product of a Heegaard surface, equipped with differentials by counting holomorphic disks, weighted over the intersection numbers with the two basepoints. The topological invariance of
$\mathbb {F} = \mathbb {Z}/2\mathbb {Z}$
, called the knot Floer complex. This chain complex is a free module generated by intersecting points of two Lagrangians in a symmetric product of a Heegaard surface, equipped with differentials by counting holomorphic disks, weighted over the intersection numbers with the two basepoints. The topological invariance of
![]() $\operatorname {CFK}(Y,K)$
up to chain homotopy equivalence over
$\operatorname {CFK}(Y,K)$
up to chain homotopy equivalence over
![]() $\mathbb {F}[\mathcal {U},{\mathcal {V}}]$
is due to Ozsváth-Szabó and Rasmussen.
$\mathbb {F}[\mathcal {U},{\mathcal {V}}]$
is due to Ozsváth-Szabó and Rasmussen.
The knot Floer complex
![]() $\operatorname {CFK}(Y,K)$
comes with a bigrading, namely
$\operatorname {CFK}(Y,K)$
comes with a bigrading, namely
![]() $(\operatorname {\mathrm {gr}}_{\mathcal {U}}, \operatorname {\mathrm {gr}}_{{\mathcal {V}}})$
, where
$(\operatorname {\mathrm {gr}}_{\mathcal {U}}, \operatorname {\mathrm {gr}}_{{\mathcal {V}}})$
, where
![]() $\mathcal {U}, {\mathcal {V}}$
, and
$\mathcal {U}, {\mathcal {V}}$
, and
![]() $\partial $
each have bigrading
$\partial $
each have bigrading
![]() $(-2,0), (0,-2)$
and
$(-2,0), (0,-2)$
and
![]() $(-1,-1)$
, respectively. The Alexander grading of a homogeneous element
$(-1,-1)$
, respectively. The Alexander grading of a homogeneous element
![]() $x\in \operatorname {CFK}(Y,K) $
is defined by
$x\in \operatorname {CFK}(Y,K) $
is defined by
![]() $A(x)=\frac {1}{2}(\operatorname {\mathrm {gr}}_{\mathcal {U}}(x) - \operatorname {\mathrm {gr}}_{{\mathcal {V}}}(x))$
.
$A(x)=\frac {1}{2}(\operatorname {\mathrm {gr}}_{\mathcal {U}}(x) - \operatorname {\mathrm {gr}}_{{\mathcal {V}}}(x))$
.
A chain map between two complexes is called a local map if it induces an isomorphism on the
![]() $(\mathcal {U},{\mathcal {V}})$
-localized homology. Following from a special case of [Reference Zemke13, Theorem 1.4], the next theorem provides the main technical input for the obstruction.
$(\mathcal {U},{\mathcal {V}})$
-localized homology. Following from a special case of [Reference Zemke13, Theorem 1.4], the next theorem provides the main technical input for the obstruction.
Theorem 2.1 (Theorem 1.4 in [Reference Zemke13])
Suppose that
![]() $(W,S) \colon \thinspace (Y_1,K_1) \rightarrow (Y_2, K_2)$
is a cobordism between the manifold-knot pairs
$(W,S) \colon \thinspace (Y_1,K_1) \rightarrow (Y_2, K_2)$
is a cobordism between the manifold-knot pairs
![]() $(Y_1,K_1)$
and
$(Y_1,K_1)$
and
![]() $(Y_2, K_2)$
, such that W is a homology cobordism and S is of genus
$(Y_2, K_2)$
, such that W is a homology cobordism and S is of genus
![]() $g.$
Then, for any given
$g.$
Then, for any given
![]() $(c_1,c_2)\in (2\mathbb {Z})^2$
, such that
$(c_1,c_2)\in (2\mathbb {Z})^2$
, such that
![]() $c_1+c_2=-2g$
and
$c_1+c_2=-2g$
and
![]() $c_1, c_2 \leq 0$
, there exists a local map
$c_1, c_2 \leq 0$
, there exists a local map
with bigrading
![]() $(c_1,c_2)$
.
$(c_1,c_2)$
.
In particular, when
![]() $g(S)=0$
, namely, when
$g(S)=0$
, namely, when
![]() $(Y_1,K_1)$
and
$(Y_1,K_1)$
and
![]() $(Y_2, K_2)$
are homology concordant, then the cobordism map
$(Y_2, K_2)$
are homology concordant, then the cobordism map
![]() $f_{W, S}$
is a local map that preserves the bigrading.
$f_{W, S}$
is a local map that preserves the bigrading.
Definition 2.2. Two bigraded chain complexes
![]() $C_1$
and
$C_1$
and
![]() $C_2$
over
$C_2$
over
![]() $\mathbb {F}[\mathcal {U},{\mathcal {V}}]$
are locally equivalent if there exist bigrading-preserving local maps
$\mathbb {F}[\mathcal {U},{\mathcal {V}}]$
are locally equivalent if there exist bigrading-preserving local maps
It is straightforward to verify that local equivalence is an equivalence relation. By turning the cobordism around, we thus obtain that homology concordance induces local equivalence of the knot Floer complexes. Since the cobordism distance is invariant over the homology concordance class, we study the local equivalence class of the knot Floer complexes of the interested manifold-knot pairs.
Due to computational reasons, it is somewhat easier to first consider
that is, the orientation reversal of the manifold-knot pairs that appear in the Section 1. Observe that
![]() $-(S^3_{-1}(T_{2n,2n+1}), \mu _{2n-1,-1})$
is equivalent to
$-(S^3_{-1}(T_{2n,2n+1}), \mu _{2n-1,-1})$
is equivalent to
![]() $(S^3_{1}(-T_{2n,2n+1}), \mu _{2n-1,1})$
. According to Lemma 4.3, over the ring
$(S^3_{1}(-T_{2n,2n+1}), \mu _{2n-1,1})$
. According to Lemma 4.3, over the ring
![]() $\mathbb {F}[U,U^{-1}],$
the complex
$\mathbb {F}[U,U^{-1}],$
the complex
![]() $X^\infty _{2n-1} (-T_{2n,2n+1}) \langle 2n-1 \rangle $
represents the local equivalence class of
$X^\infty _{2n-1} (-T_{2n,2n+1}) \langle 2n-1 \rangle $
represents the local equivalence class of
![]() $\operatorname {CFK}^\infty (S^3_{1}(-T_{2n,2n+1}), \mu _{2n-1,1})$
for all
$\operatorname {CFK}^\infty (S^3_{1}(-T_{2n,2n+1}), \mu _{2n-1,1})$
for all
![]() $n\geq 3$
(see the beginning of Section 3 for more about the knot Floer complex
$n\geq 3$
(see the beginning of Section 3 for more about the knot Floer complex
![]() $\operatorname {CFK}^\infty (Y,K)$
defined over the ring
$\operatorname {CFK}^\infty (Y,K)$
defined over the ring
![]() $\mathbb {F}[U,U^{-1}]$
).
$\mathbb {F}[U,U^{-1}]$
).
Recall that the knot Floer complex enjoys a Künneth principle by [Reference Ozsváth and Szabó7, Theorem 7.1]. Since
![]() $-(Y_n,K_n) = \big (S^3_{1}(-T_{2n,2n+1}),\mu _{2n-1,1}\big ) \# \big (S^3_{-1}(T_{2n,2n+1}), U \big ) $
, the knot Floer complex of the pair
$-(Y_n,K_n) = \big (S^3_{1}(-T_{2n,2n+1}),\mu _{2n-1,1}\big ) \# \big (S^3_{-1}(T_{2n,2n+1}), U \big ) $
, the knot Floer complex of the pair
![]() $-(Y_n,K_n)$
is locally equivalent to
$-(Y_n,K_n)$
is locally equivalent to
![]() $\operatorname {CFK}^\infty (S^3_{1}(-T_{2n,2n+1}), \mu _{2n-1,1})$
tensored with a trivial complex, with the Maslov grading adjusted such that the tensored complex has d–invariant equal to
$\operatorname {CFK}^\infty (S^3_{1}(-T_{2n,2n+1}), \mu _{2n-1,1})$
tensored with a trivial complex, with the Maslov grading adjusted such that the tensored complex has d–invariant equal to
![]() $0.$
Translate this into the ring
$0.$
Translate this into the ring
![]() $\mathbb {F}[\mathcal {U},{\mathcal {V}}]$
; for
$\mathbb {F}[\mathcal {U},{\mathcal {V}}]$
; for
![]() $n\geq 1,$
let
$n\geq 1,$
let
![]() $C_n$
denote the complex corresponding to
$C_n$
denote the complex corresponding to
![]() $X^\infty _{2n-1} (-T_{2n,2n+1}) \langle 2n-1 \rangle $
, with a
$X^\infty _{2n-1} (-T_{2n,2n+1}) \langle 2n-1 \rangle $
, with a
![]() $(d(S^3_{-1}(T_{2n,2n+1})),d(S^3_{-1}(T_{2n,2n+1})))$
bigrading shift. Then
$(d(S^3_{-1}(T_{2n,2n+1})),d(S^3_{-1}(T_{2n,2n+1})))$
bigrading shift. Then
![]() $C_n$
represents the local equivalence class of the complex
$C_n$
represents the local equivalence class of the complex
![]() $\operatorname {CFK}_{\mathbb {F}[\mathcal {U},{\mathcal {V}}]}(-(Y_n,K_n)) $
(see Figure 3 for an example when
$\operatorname {CFK}_{\mathbb {F}[\mathcal {U},{\mathcal {V}}]}(-(Y_n,K_n)) $
(see Figure 3 for an example when
![]() $n=3).$
$n=3).$

Figure 1 The complex
![]() $C_3^*$
, defined to be the dual complex of
$C_3^*$
, defined to be the dual complex of
![]() $C_3$
. The axes indicate the
$C_3$
. The axes indicate the
![]() $\mathcal {U}$
and
$\mathcal {U}$
and
![]() ${\mathcal {V}}$
actions. The solid dots are generators, marked abstractly, missing actual
${\mathcal {V}}$
actions. The solid dots are generators, marked abstractly, missing actual
![]() $\mathcal {U},{\mathcal {V}}$
decorations, and the edges represent the differentials.
$\mathcal {U},{\mathcal {V}}$
decorations, and the edges represent the differentials.
Proposition 2.3. For
![]() $n\geq 3,$
the complex
$n\geq 3,$
the complex
![]() $C_n$
is characterized by
$C_n$
is characterized by
 $$ \begin{align} \partial \alpha_s &= \begin{cases} \mathcal{U}^{\frac{n(n-1)}{2}} {\mathcal{V}}^{\frac{n(n-1)}{2}}b^{(1)}_{n-1}, \qquad &s=1 \\ \mathcal{U}^{\frac{n(n+1)}{2} -s + 1 } {\mathcal{V}}^{\frac{n(n+1)}{2}} b_{n}^{(s-1)} + \mathcal{U}^{\frac{n(n-1)}{2}} {\mathcal{V}}^{\frac{n(n-1)}{2}}b^{(s)}_{n-1}, & 2\leq s \leq n-2\\ \mathcal{U}^{\frac{n(n-1)}{2} + n -s + 1 } {\mathcal{V}}^{\frac{n(n+1)}{2}} b_{n}^{(s-1)} + \mathcal{U}^{\frac{n(n+1)}{2}} {\mathcal{V}}^{\frac{n(n-1)}{2} - n + s + 1 } b_{n}^{(s)} & n-1\leq s \leq n+1\\ \mathcal{U}^{\frac{n(n-1)}{2}} {\mathcal{V}}^{\frac{n(n-1)}{2}}b^{(s-1)}_{n+1} + \mathcal{U}^{\frac{n(n+1)}{2}}{\mathcal{V}}^{\frac{n(n-1)}{2} -n + s + 1 } b_{n}^{(s)}, & n+2\leq s \leq 2n-2\\ \mathcal{U}^{\frac{n(n-1)}{2}} {\mathcal{V}}^{\frac{n(n-1)}{2}}b^{(2n-2)}_{n+1}, \qquad &s = 2n-1 \end{cases} \end{align} $$
$$ \begin{align} \partial \alpha_s &= \begin{cases} \mathcal{U}^{\frac{n(n-1)}{2}} {\mathcal{V}}^{\frac{n(n-1)}{2}}b^{(1)}_{n-1}, \qquad &s=1 \\ \mathcal{U}^{\frac{n(n+1)}{2} -s + 1 } {\mathcal{V}}^{\frac{n(n+1)}{2}} b_{n}^{(s-1)} + \mathcal{U}^{\frac{n(n-1)}{2}} {\mathcal{V}}^{\frac{n(n-1)}{2}}b^{(s)}_{n-1}, & 2\leq s \leq n-2\\ \mathcal{U}^{\frac{n(n-1)}{2} + n -s + 1 } {\mathcal{V}}^{\frac{n(n+1)}{2}} b_{n}^{(s-1)} + \mathcal{U}^{\frac{n(n+1)}{2}} {\mathcal{V}}^{\frac{n(n-1)}{2} - n + s + 1 } b_{n}^{(s)} & n-1\leq s \leq n+1\\ \mathcal{U}^{\frac{n(n-1)}{2}} {\mathcal{V}}^{\frac{n(n-1)}{2}}b^{(s-1)}_{n+1} + \mathcal{U}^{\frac{n(n+1)}{2}}{\mathcal{V}}^{\frac{n(n-1)}{2} -n + s + 1 } b_{n}^{(s)}, & n+2\leq s \leq 2n-2\\ \mathcal{U}^{\frac{n(n-1)}{2}} {\mathcal{V}}^{\frac{n(n-1)}{2}}b^{(2n-2)}_{n+1}, \qquad &s = 2n-1 \end{cases} \end{align} $$
 $$ \begin{align} \partial \widetilde{\alpha}_s &= \begin{cases} \mathcal{U}^n b_{n}^{(s)} + {\mathcal{V}}^{n-s-1} b_{n-1}^{(s)}, &\hspace{5em} 1\leq s \leq n-2\\ \mathcal{U}^{s-n} b_{n+1}^{(s)} + {\mathcal{V}}^{n} b_{n}^{(s)}, &\hspace{5em} n+1\leq s \leq 2n-2. \end{cases} \end{align} $$
$$ \begin{align} \partial \widetilde{\alpha}_s &= \begin{cases} \mathcal{U}^n b_{n}^{(s)} + {\mathcal{V}}^{n-s-1} b_{n-1}^{(s)}, &\hspace{5em} 1\leq s \leq n-2\\ \mathcal{U}^{s-n} b_{n+1}^{(s)} + {\mathcal{V}}^{n} b_{n}^{(s)}, &\hspace{5em} n+1\leq s \leq 2n-2. \end{cases} \end{align} $$
Proof. This is a direct translation from Lemma 4.4.
This allows us to compute the values of the family of concordance homomorphisms
![]() $\varphi _{i,j}$
defined in [Reference Dai, Hom, Stoffregen and Truong2, Definition 8.1], as follows.
$\varphi _{i,j}$
defined in [Reference Dai, Hom, Stoffregen and Truong2, Definition 8.1], as follows.
Proposition 2.4. For each
![]() $n\geq 3,$
we have
$n\geq 3,$
we have
 $$ \begin{align} \varphi_{i,0}(C_n) &= \begin{cases} -1, \hspace{3em} &1\leq i \leq n-2\\ -n+2, &i=n. \end{cases} \end{align} $$
$$ \begin{align} \varphi_{i,0}(C_n) &= \begin{cases} -1, \hspace{3em} &1\leq i \leq n-2\\ -n+2, &i=n. \end{cases} \end{align} $$
and
![]() $\varphi _{i,j}(C_n)=0$
for all other i and
$\varphi _{i,j}(C_n)=0$
for all other i and
![]() $j.$
$j.$
Proof. The complexes over
![]() $\mathbb {F}[\mathcal {U},{\mathcal {V}}]$
can be translated to complexes over the ring
$\mathbb {F}[\mathcal {U},{\mathcal {V}}]$
can be translated to complexes over the ring
![]() $\mathbb {X}$
defined in [Reference Dai, Hom, Stoffregen and Truong2] using the maps
$\mathbb {X}$
defined in [Reference Dai, Hom, Stoffregen and Truong2] using the maps

Due to its simple form, it is not hard to formulate a change of a basis under which
![]() $C_n$
becomes a standard complex (see [Reference Dai, Hom, Stoffregen and Truong2, Section 5.1]). In particular, the invariants
$C_n$
becomes a standard complex (see [Reference Dai, Hom, Stoffregen and Truong2, Section 5.1]). In particular, the invariants
![]() $a_i$
of
$a_i$
of
![]() $C_n$
with i odd (see [Reference Dai, Hom, Stoffregen and Truong2, Definition 6.1]) are given by the sequence
$C_n$
with i odd (see [Reference Dai, Hom, Stoffregen and Truong2, Definition 6.1]) are given by the sequence
 $$ \begin{align*} \Bigg( \underbrace{-\Big(\frac{n(n-1)}{2},\frac{n(n-1)}{2}\Big), -(n,0), } _{\text{repeats } n-2 \text{ times}} \cdots, -\Big(\frac{n(n+1)}{2}, \frac{n(n-1)}{2} \Big), -\Big(\frac{n(n+1)}{2}, \frac{n(n-1)}{2}+1 \Big),\\ \underbrace{-\Big(\frac{n(n+1)}{2}, \frac{n(n-1)}{2} +2 \Big), -(1,0), \cdots, -\Big(\frac{n(n+1)}{2}, \frac{n(n-1)}{2} +s+1 \Big), -(s,0)}_{\text{for } 1\leq s\leq n-2 }, \cdots \Bigg). \end{align*} $$
$$ \begin{align*} \Bigg( \underbrace{-\Big(\frac{n(n-1)}{2},\frac{n(n-1)}{2}\Big), -(n,0), } _{\text{repeats } n-2 \text{ times}} \cdots, -\Big(\frac{n(n+1)}{2}, \frac{n(n-1)}{2} \Big), -\Big(\frac{n(n+1)}{2}, \frac{n(n-1)}{2}+1 \Big),\\ \underbrace{-\Big(\frac{n(n+1)}{2}, \frac{n(n-1)}{2} +2 \Big), -(1,0), \cdots, -\Big(\frac{n(n+1)}{2}, \frac{n(n-1)}{2} +s+1 \Big), -(s,0)}_{\text{for } 1\leq s\leq n-2 }, \cdots \Bigg). \end{align*} $$
The computations for the values of
![]() $\varphi _{i,j}(C_n)$
immediately follow.
$\varphi _{i,j}(C_n)$
immediately follow.
Similarly, for the case
![]() $n=2$
, Lemma 4.5 yields the following.
$n=2$
, Lemma 4.5 yields the following.
Lemma 2.5. We have
and
![]() $\varphi _{i,j}(C_2)=0$
for all other i and
$\varphi _{i,j}(C_2)=0$
for all other i and
![]() $j.$
$j.$
As a consequence, we can compute the
![]() $\tau $
invariant of the manifold-knot pair
$\tau $
invariant of the manifold-knot pair
![]() $(Y_n, K_n)$
.
$(Y_n, K_n)$
.
Proposition 2.6. For all
![]() $n\geq 1,$
$n\geq 1,$
Proof. The
![]() $\tau $
invariant can be computed from
$\tau $
invariant can be computed from
![]() $\varphi _{i,j}$
by [Reference Dai, Hom, Stoffregen and Truong2, Proposition 1.4]. For
$\varphi _{i,j}$
by [Reference Dai, Hom, Stoffregen and Truong2, Proposition 1.4]. For
![]() $n\geq 3,$
$n\geq 3,$
 $$ \begin{align*} \tau(C_n) &= n(-n+2) - \sum^{n-2}_{i=1} i - \sum^{n}_{i=1} i \\ &=- 2n^2 + 3n -1. \end{align*} $$
$$ \begin{align*} \tau(C_n) &= n(-n+2) - \sum^{n-2}_{i=1} i - \sum^{n}_{i=1} i \\ &=- 2n^2 + 3n -1. \end{align*} $$
When
![]() $n=2,$
$n=2,$
The complex
![]() $C_1$
is locally trivial, so
$C_1$
is locally trivial, so
![]() $\tau (C_1)=0$
. The result now follows from the fact that
$\tau (C_1)=0$
. The result now follows from the fact that
![]() $\tau $
is additive in the concordance group.
$\tau $
is additive in the concordance group.
According to [Reference Ozsváth and Szabó7, Proposition 3.8], the knot Floer complex of the mirror knot is the dual complex to the original knot. Therefore, the local equivalence class of
![]() $\operatorname {CFK}(Y_n,K_n)$
is given by the dual complex of
$\operatorname {CFK}(Y_n,K_n)$
is given by the dual complex of
![]() $C_n$
; denote it by
$C_n$
; denote it by
![]() $C^*_n.$
Denote by
$C^*_n.$
Denote by
![]() $\alpha _s^*$
and
$\alpha _s^*$
and
![]() $\widetilde {\alpha }_s^*$
the dual of
$\widetilde {\alpha }_s^*$
the dual of
![]() $\alpha _s,\widetilde {\alpha }_s$
, respectively, and similarly denote by
$\alpha _s,\widetilde {\alpha }_s$
, respectively, and similarly denote by
![]() $b^{*,(s)}_i$
the dual of
$b^{*,(s)}_i$
the dual of
![]() $b^{(s)}_i$
.
$b^{(s)}_i$
.
Proposition 2.7. For
![]() $n\geq 3,$
the complex
$n\geq 3,$
the complex
![]() $C^*_n$
is characterized by the following
$C^*_n$
is characterized by the following
 $$ \begin{align} \partial b^{*,(s)}_{n} &= \begin{cases} \mathcal{U}^{\frac{n(n+1)}{2}-s} {\mathcal{V}}^{\frac{n(n+1)}{2}} \alpha^*_{s+1} + \mathcal{U}^n \widetilde{\alpha}^*_s, \qquad &1\leq s \leq n-2\\ \mathcal{U}^{\frac{n(n+1)}{2}}{\mathcal{V}}^{\frac{n(n-1)}{2}-n+s+1} \alpha_s^* + \mathcal{U}^{\frac{n(n+1)}{2}-s} {\mathcal{V}}^{\frac{n(n+1)}{2}} \alpha_{s+1}^*, &n-1 \leq s \leq n\\ \mathcal{U}^{\frac{n(n+1)}{2}}{\mathcal{V}}^{\frac{n(n-1)}{2}-n+s+1} \alpha_s^* + {\mathcal{V}}^n \widetilde{\alpha}_s^*, &n+1 \leq s \leq 2n-2 \end{cases} \end{align} $$
$$ \begin{align} \partial b^{*,(s)}_{n} &= \begin{cases} \mathcal{U}^{\frac{n(n+1)}{2}-s} {\mathcal{V}}^{\frac{n(n+1)}{2}} \alpha^*_{s+1} + \mathcal{U}^n \widetilde{\alpha}^*_s, \qquad &1\leq s \leq n-2\\ \mathcal{U}^{\frac{n(n+1)}{2}}{\mathcal{V}}^{\frac{n(n-1)}{2}-n+s+1} \alpha_s^* + \mathcal{U}^{\frac{n(n+1)}{2}-s} {\mathcal{V}}^{\frac{n(n+1)}{2}} \alpha_{s+1}^*, &n-1 \leq s \leq n\\ \mathcal{U}^{\frac{n(n+1)}{2}}{\mathcal{V}}^{\frac{n(n-1)}{2}-n+s+1} \alpha_s^* + {\mathcal{V}}^n \widetilde{\alpha}_s^*, &n+1 \leq s \leq 2n-2 \end{cases} \end{align} $$
Proof. This follows from Proposition 2.3 and the fact that
![]() $C^*_n$
is the dual complex of
$C^*_n$
is the dual complex of
![]() $C_n$
.
$C_n$
.
We record a few salient features of the complex
![]() $C^*_n$
for
$C^*_n$
for
![]() $n\geq 3$
from Proposition 2.7:
$n\geq 3$
from Proposition 2.7:
Lemma 2.8. We have the inequalities
Similarly,
Proof. We have
Note also the equalities:
In particular,
for
![]() $1\leq s\leq n-2.$
$1\leq s\leq n-2.$
From here, the claim of the lemma follows for
![]() $\alpha _s^*$
for all
$\alpha _s^*$
for all
![]() $1\leq s \leq n-1$
. The statement for
$1\leq s \leq n-1$
. The statement for
![]() $\widetilde {\alpha }_s^*$
follows from (9).
$\widetilde {\alpha }_s^*$
follows from (9).
The case of
![]() $\operatorname {\mathrm {gr}}_{\mathcal {U}}$
follows similarly, where we use
$\operatorname {\mathrm {gr}}_{\mathcal {U}}$
follows similarly, where we use
and also calculate:
In particular,
for
![]() $n+1\leq s\leq 2n-2.$
From here, the claim of the lemma follows for
$n+1\leq s\leq 2n-2.$
From here, the claim of the lemma follows for
![]() $\alpha _s^*$
for all
$\alpha _s^*$
for all
![]() $n+1\leq s \leq 2n-1$
. The statement for
$n+1\leq s \leq 2n-1$
. The statement for
![]() $\widetilde {\alpha }_s^*$
follows from (11).
$\widetilde {\alpha }_s^*$
follows from (11).
Lemma 2.9. For
![]() $n\geq 3$
, let
$n\geq 3$
, let
![]() $\phi \colon C^*_n\to C^*_n$
be a chain map of bigrading
$\phi \colon C^*_n\to C^*_n$
be a chain map of bigrading
![]() $(c_1,c_2)$
, where
$(c_1,c_2)$
, where
![]() $c_1>-2n$
and
$c_1>-2n$
and
![]() $c_2>-2n$
. Then,
$c_2>-2n$
. Then,
![]() $\phi (\alpha _n^*)$
is either an
$\phi (\alpha _n^*)$
is either an
![]() $\mathbb {F}[\mathcal {U}, {\mathcal {V}}]$
-multiple of
$\mathbb {F}[\mathcal {U}, {\mathcal {V}}]$
-multiple of
![]() $\alpha _n^*$
or
$\alpha _n^*$
or
![]() $0$
.
$0$
.
Proof. By Lemma 2.8, all of the other generators of
![]() $C^*_n$
, which are cycles, have either
$C^*_n$
, which are cycles, have either
![]() $\mathcal {U}$
-grading or
$\mathcal {U}$
-grading or
![]() ${\mathcal {V}}$
-grading less than that of
${\mathcal {V}}$
-grading less than that of
![]() $\phi (\alpha _n^*)$
. No linear combination of the
$\phi (\alpha _n^*)$
. No linear combination of the
![]() $b^{*}$
-type terms is a cycle, and so
$b^{*}$
-type terms is a cycle, and so
![]() $\phi (\alpha _n^*)$
is supported only by
$\phi (\alpha _n^*)$
is supported only by
![]() $\langle \alpha _n^*\rangle $
.
$\langle \alpha _n^*\rangle $
.
Lemma 2.10. For
![]() $n\geq 3$
, let
$n\geq 3$
, let
![]() $\phi \colon C^*_n\to C^*_n$
be a homogeneous chain map with degree as in Lemma 2.9 and so that
$\phi \colon C^*_n\to C^*_n$
be a homogeneous chain map with degree as in Lemma 2.9 and so that
![]() $\phi (\alpha _n^*)$
is a boundary in
$\phi (\alpha _n^*)$
is a boundary in
![]() $C^*_n\otimes \mathbb {F}[\mathcal {U},{\mathcal {V}}=1]/(\mathcal {U}^{n-1})$
. Then,
$C^*_n\otimes \mathbb {F}[\mathcal {U},{\mathcal {V}}=1]/(\mathcal {U}^{n-1})$
. Then,
![]() $\phi (\alpha _n^*)$
must be divisible by
$\phi (\alpha _n^*)$
must be divisible by
![]() $\mathcal {U}^{n-1}$
.
$\mathcal {U}^{n-1}$
.
Proof. From Lemma 2.9,
![]() $\phi (\alpha _n^*)=c\alpha _n^*$
for some
$\phi (\alpha _n^*)=c\alpha _n^*$
for some
![]() $c\in \mathbb {F}[\mathcal {U}, {\mathcal {V}}]$
. Considering the differential of
$c\in \mathbb {F}[\mathcal {U}, {\mathcal {V}}]$
. Considering the differential of
![]() $C_n^*$
mod
$C_n^*$
mod
![]() ${\mathcal {V}}=1,\mathcal {U}^{n-1}=0$
, we obtain that
${\mathcal {V}}=1,\mathcal {U}^{n-1}=0$
, we obtain that
![]() $c\alpha _n^*$
is a boundary over this quotient ring if and only if
$c\alpha _n^*$
is a boundary over this quotient ring if and only if
![]() $\mathcal {U}^{n-1}\mid c$
.
$\mathcal {U}^{n-1}\mid c$
.
We say that a chain complex D over
![]() $\mathbb {F}[\mathcal {U}, {\mathcal {V}}]$
is
$\mathbb {F}[\mathcal {U}, {\mathcal {V}}]$
is
![]() $S^3$
-knotlike if
$S^3$
-knotlike if
![]() $H_*(D\otimes \mathbb {F}[\mathcal {U}, {\mathcal {V}}=1]) = \mathbb {F}[\mathcal {U}]$
. Recall that for a knot
$H_*(D\otimes \mathbb {F}[\mathcal {U}, {\mathcal {V}}=1]) = \mathbb {F}[\mathcal {U}]$
. Recall that for a knot
![]() $K \subset Y,$
by setting
$K \subset Y,$
by setting
![]() ${\mathcal {V}} =1 $
in
${\mathcal {V}} =1 $
in
![]() $\operatorname {CFK}(Y,K)$
and taking the homology, one recovers the Heegaard Floer homology
$\operatorname {CFK}(Y,K)$
and taking the homology, one recovers the Heegaard Floer homology
![]() $\operatorname {HF}^-(Y)$
. In particular, if D is the knot Floer complex of a knot in
$\operatorname {HF}^-(Y)$
. In particular, if D is the knot Floer complex of a knot in
![]() $S^3$
, then D is
$S^3$
, then D is
![]() $S^3$
-knotlike.
$S^3$
-knotlike.
Lemma 2.11. For
![]() $n\geq 3$
, let f be a map from
$n\geq 3$
, let f be a map from
![]() $C_n^*$
to an
$C_n^*$
to an
![]() $S^3$
-knotlike complex D, and let g be a map from D to
$S^3$
-knotlike complex D, and let g be a map from D to
![]() $C_n^*$
. Then,
$C_n^*$
. Then,
![]() $gf(\alpha _n^*)$
is a boundary in
$gf(\alpha _n^*)$
is a boundary in
![]() $C^*_n\otimes \mathbb {F}[\mathcal {U},{\mathcal {V}}=1]/(\mathcal {U}^{n-1})$
.
$C^*_n\otimes \mathbb {F}[\mathcal {U},{\mathcal {V}}=1]/(\mathcal {U}^{n-1})$
.
Proof. We have, by considering
![]() $b^{*,(n-1)}_n$
, that
$b^{*,(n-1)}_n$
, that
is a boundary. Setting
![]() ${\mathcal {V}}=1$
,
${\mathcal {V}}=1$
,
Since any cycle in an
![]() $S^3$
-knotlike complex that is
$S^3$
-knotlike complex that is
![]() $\mathcal {U}$
-torsion in
$\mathcal {U}$
-torsion in
![]() $({\mathcal {V}}=1)$
homology is actually zero in homology, we have that
$({\mathcal {V}}=1)$
homology is actually zero in homology, we have that
is a boundary in
![]() $D/({\mathcal {V}}=1).$
So
$D/({\mathcal {V}}=1).$
So
![]() $f(\alpha _n^*)$
is a boundary in
$f(\alpha _n^*)$
is a boundary in
![]() $D/({\mathcal {V}}=1,\mathcal {U}^{n-1}=0)$
. Since g is a chain map, the same holds for
$D/({\mathcal {V}}=1,\mathcal {U}^{n-1}=0)$
. Since g is a chain map, the same holds for
![]() $gf(\alpha _n^*)$
.
$gf(\alpha _n^*)$
.
Lemma 2.12. For
![]() $n\geq 3$
, let f be a local map from
$n\geq 3$
, let f be a local map from
![]() $C_n^*$
to a knotlike complex D. There does not exist a local map
$C_n^*$
to a knotlike complex D. There does not exist a local map
![]() $g\colon D\to C_n^*$
, so that
$g\colon D\to C_n^*$
, so that
![]() $g\circ f$
is of bigrading
$g\circ f$
is of bigrading
![]() $(c_1,c_2)$
with
$(c_1,c_2)$
with
![]() $c_1>-2n+2$
and
$c_1>-2n+2$
and
![]() $c_2>-2n$
.
$c_2>-2n$
.
Proof. Suppose such a g exists. Since f and g are local and
![]() $\alpha ^*_n$
generates the
$\alpha ^*_n$
generates the
![]() $(\mathcal {U}, {\mathcal {V}})$
-localized homology, it follows that
$(\mathcal {U}, {\mathcal {V}})$
-localized homology, it follows that
![]() $gf(\alpha _n^*) \neq 0$
. Hence, by Lemma 2.9, we obtain that
$gf(\alpha _n^*) \neq 0$
. Hence, by Lemma 2.9, we obtain that
By Lemma 2.11,
![]() $gf(\alpha _n^*)$
is a boundary mod
$gf(\alpha _n^*)$
is a boundary mod
![]() $\mathcal {U}^{n-1}=0,{\mathcal {V}}=1$
, and so by Lemma 2.10, we have
$\mathcal {U}^{n-1}=0,{\mathcal {V}}=1$
, and so by Lemma 2.10, we have
![]() $n-1\leq -c_1/2$
. That is,
$n-1\leq -c_1/2$
. That is,
![]() $-2n + 2 \geq c_1>-2n+2$
, a contradiction.
$-2n + 2 \geq c_1>-2n+2$
, a contradiction.
Proof of Theorem 1.2
When
![]() $n=2,$
for any knot
$n=2,$
for any knot
![]() $J\subset S^3$
, by [Reference Dai, Hom, Stoffregen and Truong2, Theorem 10.1], we have
$J\subset S^3$
, by [Reference Dai, Hom, Stoffregen and Truong2, Theorem 10.1], we have
![]() $\varphi _{i,j}(S^3,J)=0$
for any
$\varphi _{i,j}(S^3,J)=0$
for any
![]() $ j\neq 0,$
so Lemma 2.5 obstructs the existence of a homology concordance between
$ j\neq 0,$
so Lemma 2.5 obstructs the existence of a homology concordance between
![]() $(Y_2,K_2)$
and
$(Y_2,K_2)$
and
![]() $(S^3,J)$
.
$(S^3,J)$
.
Now suppose
![]() $n \geq 3.$
Say that there is a pair
$n \geq 3.$
Say that there is a pair
![]() $(W,S)$
as in the discussion preceding Theorem 1.2, with S of genus
$(W,S)$
as in the discussion preceding Theorem 1.2, with S of genus
![]() $g\leq n-2$
. Then, for any choice of
$g\leq n-2$
. Then, for any choice of
![]() $(c_1,c_2),(d_1,d_2)\in (2\mathbb {Z})^2$
so that
$(c_1,c_2),(d_1,d_2)\in (2\mathbb {Z})^2$
so that
![]() $c_i,d_i\leq 0$
and
$c_i,d_i\leq 0$
and
![]() $c_1+c_2=-2g=d_1+d_2$
, there exist local maps
$c_1+c_2=-2g=d_1+d_2$
, there exist local maps
![]() $f\colon C_n\to \operatorname {CFK}(J)$
and
$f\colon C_n\to \operatorname {CFK}(J)$
and
![]() $g\colon \operatorname {CFK}(J)\to C_n$
of bigrading
$g\colon \operatorname {CFK}(J)\to C_n$
of bigrading
![]() $(c_1,c_2)$
,
$(c_1,c_2)$
,
![]() $(d_1,d_2)$
, respectively. Let f be of bigrading
$(d_1,d_2)$
, respectively. Let f be of bigrading
![]() $(0,-2g)$
and g be of bigrading
$(0,-2g)$
and g be of bigrading
![]() $(-2g,0)$
. By hypothesis,
$(-2g,0)$
. By hypothesis,
![]() $-2g\geq -2n+4$
, and so Lemma 2.12 applies to show that such
$-2g\geq -2n+4$
, and so Lemma 2.12 applies to show that such
![]() $f,g$
do not exist, a contradiction.
$f,g$
do not exist, a contradiction.
3. Preliminaries on the filtered mapping cone formula
We start by reviewing the original definition of the knot Floer complex over the ring
![]() $\mathbb {F}[U,U^{-1}]$
by Ozsváth and Szabó, as this is the setting where the filtered mapping cone formula can be most conveniently defined.
$\mathbb {F}[U,U^{-1}]$
by Ozsváth and Szabó, as this is the setting where the filtered mapping cone formula can be most conveniently defined.
In the original definition, the knot Floer complex is freely generated by the intersecting points of the two Lagrangians over the ring
![]() $\mathbb {F}[U,U^{-1}]$
, where the differentials similarly count the holomorphic disks but are weighted over the intersection number with only one of the basepoints. The datum of the other basepoint is encoded in the Alexander grading. This version of the knot Floer complex is denoted by
$\mathbb {F}[U,U^{-1}]$
, where the differentials similarly count the holomorphic disks but are weighted over the intersection number with only one of the basepoints. The datum of the other basepoint is encoded in the Alexander grading. This version of the knot Floer complex is denoted by
![]() $\operatorname {CFK}^\infty (Y,K)$
, and commonly depicted in an
$\operatorname {CFK}^\infty (Y,K)$
, and commonly depicted in an
![]() $(i,j)$
–plane, where the j–coordinate is given by the Alexander grading, and the i–coordinate is the normalized filtration level naturally induced by the U–action. We will often think of
$(i,j)$
–plane, where the j–coordinate is given by the Alexander grading, and the i–coordinate is the normalized filtration level naturally induced by the U–action. We will often think of
![]() $\operatorname {CFK}^\infty (Y,K)$
as a chain complex with an extra filtration given by the Alexander grading. By collapsing the Alexander filtration, one recovers a chain complex associated to the underlying three-manifold,
$\operatorname {CFK}^\infty (Y,K)$
as a chain complex with an extra filtration given by the Alexander grading. By collapsing the Alexander filtration, one recovers a chain complex associated to the underlying three-manifold,
![]() $\operatorname {CF}^\infty (Y)$
.
$\operatorname {CF}^\infty (Y)$
.
There is a Maslov grading on
![]() $\operatorname {CFK}^\infty (Y,K)$
, corresponding to
$\operatorname {CFK}^\infty (Y,K)$
, corresponding to
![]() $\operatorname {\mathrm {gr}}_{\mathcal {U}}$
; multiplication by U on
$\operatorname {\mathrm {gr}}_{\mathcal {U}}$
; multiplication by U on
![]() $\operatorname {CFK}^\infty (Y,K)$
is equivalent to multiplication by
$\operatorname {CFK}^\infty (Y,K)$
is equivalent to multiplication by
![]() $\mathcal {U}{\mathcal {V}}$
on
$\mathcal {U}{\mathcal {V}}$
on
![]() $\operatorname {CFK}_{\mathbb {F}[\mathcal {U},{\mathcal {V}}]}(Y,K)$
. Although the setting is slightly different,
$\operatorname {CFK}_{\mathbb {F}[\mathcal {U},{\mathcal {V}}]}(Y,K)$
. Although the setting is slightly different,
![]() $\operatorname {CFK}^\infty (Y,K)$
contains the same information as
$\operatorname {CFK}^\infty (Y,K)$
contains the same information as
![]() $\operatorname {CFK}_{\mathbb {F}[\mathcal {U},{\mathcal {V}}]}(Y,K)$
does. In the setting of
$\operatorname {CFK}_{\mathbb {F}[\mathcal {U},{\mathcal {V}}]}(Y,K)$
does. In the setting of
![]() $\operatorname {CFK}^\infty (Y,K)$
, the local equivalence reads as follows.
$\operatorname {CFK}^\infty (Y,K)$
, the local equivalence reads as follows.
Definition 3.1. Two filtered chain complex
![]() $C_1$
and
$C_1$
and
![]() $C_2$
over
$C_2$
over
![]() $\mathbb {F}[U,U^{-1}]$
are locally equivalent if there exist Maslov grading-preserving filtered local maps
$\mathbb {F}[U,U^{-1}]$
are locally equivalent if there exist Maslov grading-preserving filtered local maps
For the rest of the paper, we will always use the knot Floer complex
![]() $\operatorname {CFK}^\infty (Y,K)$
. Next, we recall the filtered mapping cone formula from [Reference Zhou14] for the reader; this is our main computational tool.
$\operatorname {CFK}^\infty (Y,K)$
. Next, we recall the filtered mapping cone formula from [Reference Zhou14] for the reader; this is our main computational tool.
Let
![]() $K\subset S^3$
be a knot with genus equal to
$K\subset S^3$
be a knot with genus equal to
![]() $g.$
For a given positive integer p, let
$g.$
For a given positive integer p, let
![]() $\mu _{p,1}$
denote the
$\mu _{p,1}$
denote the
![]() $(p,1)$
-cable of the meridian of K in the
$(p,1)$
-cable of the meridian of K in the
![]() $+1$
-surgery on
$+1$
-surgery on
![]() $K.$
According to [Reference Zhou14, Theorem 1.9], the knot Floer complex
$K.$
According to [Reference Zhou14, Theorem 1.9], the knot Floer complex
![]() $\operatorname {CFK}^\infty (S^3_{1}(K),\mu _{p,1})$
is a filtered chain homotopy equivalent to the doubly filtered chain complex
$\operatorname {CFK}^\infty (S^3_{1}(K),\mu _{p,1})$
is a filtered chain homotopy equivalent to the doubly filtered chain complex
![]() $X^\infty _p(K)$
, defined to be the mapping cone of
$X^\infty _p(K)$
, defined to be the mapping cone of
 $$ \begin{align} \bigoplus^{g+p-1}_{s=-g+1}A_s \xrightarrow{v_s+h_s} \bigoplus^{g+p-1}_{s=-g+2}B_s, \end{align} $$
$$ \begin{align} \bigoplus^{g+p-1}_{s=-g+1}A_s \xrightarrow{v_s+h_s} \bigoplus^{g+p-1}_{s=-g+2}B_s, \end{align} $$
where each
![]() $A_s$
and
$A_s$
and
![]() $B_s$
are isomorphic to
$B_s$
are isomorphic to
![]() $\operatorname {CFK}^\infty (S^3,K)$
, coming with the
$\operatorname {CFK}^\infty (S^3,K)$
, coming with the
![]() $(i,j)$
coordinate. The map
$(i,j)$
coordinate. The map
![]() $v_s\colon \thinspace A_s \to B_s $
is the identity, and the map
$v_s\colon \thinspace A_s \to B_s $
is the identity, and the map
![]() $h_s\colon \thinspace A_s \to B_{s+1} $
is the reflection along
$h_s\colon \thinspace A_s \to B_{s+1} $
is the reflection along
![]() $i=j$
precomposed with
$i=j$
precomposed with
![]() $U^s$
. Note that there are corresponding versions of the filtered mapping cone formula for the hat, minus, and infinity flavors of knot Floer homology. In the following computation, we will consistently use the infinity version of the
$U^s$
. Note that there are corresponding versions of the filtered mapping cone formula for the hat, minus, and infinity flavors of knot Floer homology. In the following computation, we will consistently use the infinity version of the
![]() $A_s$
and
$A_s$
and
![]() $B_s$
complexes and
$B_s$
complexes and
![]() $v_s$
and
$v_s$
and
![]() $h_s$
maps, so we repress the superindices.
$h_s$
maps, so we repress the superindices.
Let
![]() $\mathcal {I}$
and
$\mathcal {I}$
and
![]() $\mathcal {J}$
be the double filtrations, and let
$\mathcal {J}$
be the double filtrations, and let
![]() $\operatorname {\mathrm {gr}}_M$
be the absolute Maslov grading on the filtered mapping cone complex
$\operatorname {\mathrm {gr}}_M$
be the absolute Maslov grading on the filtered mapping cone complex
![]() $X^\infty _p(K)$
. We will reserve letters
$X^\infty _p(K)$
. We will reserve letters
![]() $\mathcal {I}$
and
$\mathcal {I}$
and
![]() $\mathcal {J}$
solely for this purpose throughout the paper. We have
$\mathcal {J}$
solely for this purpose throughout the paper. We have
for
![]() $[\mathbf {x},i,j] \in A_{s}$
,
$[\mathbf {x},i,j] \in A_{s}$
,
and for
![]() $[\mathbf {x},i,j] \in B_{s}$
,
$[\mathbf {x},i,j] \in B_{s}$
,
Here,
![]() $\widetilde {\operatorname {\mathrm {gr}}}$
denotes the absolute Maslov grading on the original chain complex
$\widetilde {\operatorname {\mathrm {gr}}}$
denotes the absolute Maslov grading on the original chain complex
![]() $\operatorname {CFK}^\infty (S^3,K)$
. It is straightforward to check that for
$\operatorname {CFK}^\infty (S^3,K)$
. It is straightforward to check that for
![]() $s<-g+1$
, the map
$s<-g+1$
, the map
![]() $h_s$
induces an isomorphism on the homology; for
$h_s$
induces an isomorphism on the homology; for
![]() $s>g+p-1,$
the map
$s>g+p-1,$
the map
![]() $v_s(K)$
induces an isomorphism on the homology, which justifies the truncation of the mapping cone.
$v_s(K)$
induces an isomorphism on the homology, which justifies the truncation of the mapping cone.
The general strategy for computation involves finding a reduced basis for
![]() $X^\infty _p(K),$
where every term in the differential strictly lowers at least one of the filtrations. This can be achieved through a cancellation process (see, for example [Reference Lipshitz6, Proposition 11.57]) as follows: suppose
$X^\infty _p(K),$
where every term in the differential strictly lowers at least one of the filtrations. This can be achieved through a cancellation process (see, for example [Reference Lipshitz6, Proposition 11.57]) as follows: suppose
![]() $\partial x_i = y_i\ + $
lower filtration terms, where the double filtration of
$\partial x_i = y_i\ + $
lower filtration terms, where the double filtration of
![]() $y_i$
is the same as
$y_i$
is the same as
![]() $x_i$
, then the subcomplex of
$x_i$
, then the subcomplex of
![]() $X^\infty _p(K)$
generated by all such
$X^\infty _p(K)$
generated by all such
![]() $\{x_i, \partial x_i\}$
is acyclic, and the
$\{x_i, \partial x_i\}$
is acyclic, and the
![]() $X^\infty _p(K)$
quotient by this complex is reduced. Alternatively, one can view the above process as a change of basis, that splits off acyclic summands which individually lie entirely in one double-filtration level.
$X^\infty _p(K)$
quotient by this complex is reduced. Alternatively, one can view the above process as a change of basis, that splits off acyclic summands which individually lie entirely in one double-filtration level.
There is an apparent symmetry on the mapping cone as follows. Let
![]() $[\mathbf {x},i,j] \mapsto [\psi (\mathbf {x}),j,i]$
be a homotopy equivalence that realizes the symmetry on the original chain complex
$[\mathbf {x},i,j] \mapsto [\psi (\mathbf {x}),j,i]$
be a homotopy equivalence that realizes the symmetry on the original chain complex
![]() $\operatorname {CFK}^\infty (S^3,K)$
. In the following lemma, we use a subindex to mark elements from
$\operatorname {CFK}^\infty (S^3,K)$
. In the following lemma, we use a subindex to mark elements from
![]() $A_s$
or
$A_s$
or
![]() $B_s$
.
$B_s$
.
Proposition 3.2. Let
![]() $\Psi \colon \thinspace X^\infty _p(K) \longrightarrow X^\infty _p(K)$
be the map, defined as
$\Psi \colon \thinspace X^\infty _p(K) \longrightarrow X^\infty _p(K)$
be the map, defined as
for
![]() $[\mathbf {x},i,j]_s \in A_{s}$
,
$[\mathbf {x},i,j]_s \in A_{s}$
,
for
![]() $[\mathbf {x},i,j]_s \in B_{s}$
,
$[\mathbf {x},i,j]_s \in B_{s}$
,
Then,
![]() $\Psi $
is a chain map that realizes a homotopy equivalence on the doubly filtered chain complex
$\Psi $
is a chain map that realizes a homotopy equivalence on the doubly filtered chain complex
![]() $\operatorname {CFK}^\infty (S^3_{1}(K),\mu _{p,1})$
that switches the
$\operatorname {CFK}^\infty (S^3_{1}(K),\mu _{p,1})$
that switches the
![]() $\mathcal {I}$
and
$\mathcal {I}$
and
![]() $\mathcal {J}$
filtrations.
$\mathcal {J}$
filtrations.
Proof. By definition,
![]() $\Psi $
is U–equivariant, so it suffices to show
$\Psi $
is U–equivariant, so it suffices to show
![]() $\Psi $
realizes the symmetry for any one
$\Psi $
realizes the symmetry for any one
![]() $\mathcal {I}$
and
$\mathcal {I}$
and
![]() $\mathcal {J}$
value.
$\mathcal {J}$
value.
Over each chain complex
![]() $A_s,$
by (14) and (15), we have
$A_s,$
by (14) and (15), we have
![]() $\{\mathcal {I}=0 \}=\max \{i,j-s\}$
and
$\{\mathcal {I}=0 \}=\max \{i,j-s\}$
and
![]() $\{\mathcal {J}=ps - \frac {p(p-1)}{2} \}=\max \{i-p,j-s\}$
. Compute
$\{\mathcal {J}=ps - \frac {p(p-1)}{2} \}=\max \{i-p,j-s\}$
. Compute
 $$ \begin{align*} \Psi(\{\mathcal{I}=0 \}_s) & = U^{\frac{(p-1)(p-2s)}{2}}\max\{i-s,j\}_{p-s}\\ & = U^{\frac{(p-1)(p-2s)}{2}+(p-s)}\max\{i-p,j-(p-s)\}_{p-s}\\ & = U^{\frac{p^2+p-2ps}{2}}\{\mathcal{J}=p(p-s) - \frac{p(p-1)}{2} \}_{p-s}\\ & = \{\mathcal{J}=0\}_{p-s} \\ \Psi(\{\mathcal{J}=ps - \frac{p(p-1)}{2} \}_s) &= U^{\frac{(p-1)(p-2s)}{2}}\max\{i-s,j-p\}_{p-s} \\ &= U^{\frac{(p-1)(p-2s)}{2}-s}\max\{i,j-(p-s)\}_{p-s}\\ &= \{\mathcal{I}=ps - \frac{p(p-1)}{2} \}_{p-s}, \end{align*} $$
$$ \begin{align*} \Psi(\{\mathcal{I}=0 \}_s) & = U^{\frac{(p-1)(p-2s)}{2}}\max\{i-s,j\}_{p-s}\\ & = U^{\frac{(p-1)(p-2s)}{2}+(p-s)}\max\{i-p,j-(p-s)\}_{p-s}\\ & = U^{\frac{p^2+p-2ps}{2}}\{\mathcal{J}=p(p-s) - \frac{p(p-1)}{2} \}_{p-s}\\ & = \{\mathcal{J}=0\}_{p-s} \\ \Psi(\{\mathcal{J}=ps - \frac{p(p-1)}{2} \}_s) &= U^{\frac{(p-1)(p-2s)}{2}}\max\{i-s,j-p\}_{p-s} \\ &= U^{\frac{(p-1)(p-2s)}{2}-s}\max\{i,j-(p-s)\}_{p-s}\\ &= \{\mathcal{I}=ps - \frac{p(p-1)}{2} \}_{p-s}, \end{align*} $$
while the computations for
![]() $B_s$
are similar and left for the reader. Moreover, by definition, we have
$B_s$
are similar and left for the reader. Moreover, by definition, we have
![]() $\Psi \circ v_s = h_s \circ \Psi ,$
and
$\Psi \circ v_s = h_s \circ \Psi ,$
and
![]() $\Psi \circ h_s = v_s \circ \Psi ,$
therefore,
$\Psi \circ h_s = v_s \circ \Psi ,$
therefore,
![]() $\Psi $
is a chain map.
$\Psi $
is a chain map.
4. Cables of the knot meridian of
 $-T_{2n,2n+1}$
$-T_{2n,2n+1}$
In this section, we perform the filtered mapping cone computation, which determines the knot Floer complex in Proposition 2.3 and Lemma 2.5.
Given
![]() $n\geq 1$
, let
$n\geq 1$
, let
![]() $T_{2n,2n+1}$
be the
$T_{2n,2n+1}$
be the
![]() $(2n,2n+1)$
-torus knot, with genus equal to
$(2n,2n+1)$
-torus knot, with genus equal to
![]() $n(2n-1).$
It is a fun exercise to compute its Alexander polynomial as follows
$n(2n-1).$
It is a fun exercise to compute its Alexander polynomial as follows
 $$ \begin{align*} \frac{(t^{2n(2n+1)}-1)(t-1)}{(t^{2n}-1)(t^{2n+1}-1)}=& \frac{t^{(2n-1)(2n+1)} + t^{(2n-2)(2n+1)} + \cdots + 1}{t^{2n-1} + t^{2n-2} + \cdots + 1}=\\ 1+\sum^{2n-2}_{i=0}\big( t^{(2n-i)(2n-1)-i} &- t^{(2n-i)(2n-1)-2i-1} \big). \end{align*} $$
$$ \begin{align*} \frac{(t^{2n(2n+1)}-1)(t-1)}{(t^{2n}-1)(t^{2n+1}-1)}=& \frac{t^{(2n-1)(2n+1)} + t^{(2n-2)(2n+1)} + \cdots + 1}{t^{2n-1} + t^{2n-2} + \cdots + 1}=\\ 1+\sum^{2n-2}_{i=0}\big( t^{(2n-i)(2n-1)-i} &- t^{(2n-i)(2n-1)-2i-1} \big). \end{align*} $$
For example, if we let
![]() $S_{2n}(i)= \big ( t^{(2n-i)(2n-1)-i} - t^{(2n-i)(2n-1)-2i-1} \big ) \big ( t^{2n-1} + t^{2n-2} + \cdots + 1 \big )$
for
$S_{2n}(i)= \big ( t^{(2n-i)(2n-1)-i} - t^{(2n-i)(2n-1)-2i-1} \big ) \big ( t^{2n-1} + t^{2n-2} + \cdots + 1 \big )$
for
![]() $i=0,1,\cdots , 2n-2$
, by induction, we obtain that for
$i=0,1,\cdots , 2n-2$
, by induction, we obtain that for
![]() $0 \leq \ell \leq 2n-2$
$0 \leq \ell \leq 2n-2$
 $$ \begin{align*} \sum^{\ell}_{i=0} S_{2n}(i) = t^{(2n-1)(2n+1)} + \cdots + t^{(2n-\ell -1)(2n+1)} -t^{(2n-\ell)(2n-1)-\ell -1 } - \cdots - t^{(2n-\ell)(2n-1)-2\ell -1}. \end{align*} $$
$$ \begin{align*} \sum^{\ell}_{i=0} S_{2n}(i) = t^{(2n-1)(2n+1)} + \cdots + t^{(2n-\ell -1)(2n+1)} -t^{(2n-\ell)(2n-1)-\ell -1 } - \cdots - t^{(2n-\ell)(2n-1)-2\ell -1}. \end{align*} $$
Taking
![]() $\ell $
to be
$\ell $
to be
![]() $2n-2$
leads to the answer.
$2n-2$
leads to the answer.
Torus knots are L–space knots. Therefore, according to [Reference Ozsváth and Szabó9, Theorem 1.2], the knot Floer complex
![]() $\operatorname {CFK}^\infty (S^3,T_{2n,2n+1})$
is generated by
$\operatorname {CFK}^\infty (S^3,T_{2n,2n+1})$
is generated by
![]() $a^*_i$
with coordinate
$a^*_i$
with coordinate
![]() $(0, \frac {(2n-i)(2n-i+1)}{2} - \frac {i(i-1)}{2} )$
for
$(0, \frac {(2n-i)(2n-i+1)}{2} - \frac {i(i-1)}{2} )$
for
![]() $i \in \{1, \cdots , 2n\}$
and
$i \in \{1, \cdots , 2n\}$
and
![]() $b^*_i$
with coordinate
$b^*_i$
with coordinate
![]() $(0, \frac {(2n-i)(2n-i+1)}{2}- \frac {i(i+1)}{2} )$
for
$(0, \frac {(2n-i)(2n-i+1)}{2}- \frac {i(i+1)}{2} )$
for
![]() $i \in \{1, \cdots , 2n-1\}$
(this is, in fact, a set of generators coming from a
$i \in \{1, \cdots , 2n-1\}$
(this is, in fact, a set of generators coming from a
![]() $\widehat {HFK}$
model), where the differentials are given by
$\widehat {HFK}$
model), where the differentials are given by
It follows from [Reference Ozsváth and Szabó7, Proposition 3.8], that the knot Floer complex of the mirror knot is the dual complex to the original knot. Therefore,
![]() $\operatorname {CFK}^\infty (S^3,-T_{2n,2n+1})$
is generated by
$\operatorname {CFK}^\infty (S^3,-T_{2n,2n+1})$
is generated by
![]() $a_i$
with coordinate
$a_i$
with coordinate
![]() $(0, -\frac {(2n-i)(2n-i+1)}{2} + \frac {i(i-1)}{2} )$
for
$(0, -\frac {(2n-i)(2n-i+1)}{2} + \frac {i(i-1)}{2} )$
for
![]() $i \in \{1, \cdots , 2n\}$
and
$i \in \{1, \cdots , 2n\}$
and
![]() $b_i$
with coordinate
$b_i$
with coordinate
![]() $(0, -\frac {(2n-i)(2n-i+1)}{2}+\frac {i(i+1)}{2} )$
for
$(0, -\frac {(2n-i)(2n-i+1)}{2}+\frac {i(i+1)}{2} )$
for
![]() $i \in \{1, \cdots , 2n-1\}$
(simply by taking
$i \in \{1, \cdots , 2n-1\}$
(simply by taking
![]() $a_i$
to be the dual of
$a_i$
to be the dual of
![]() $a^*_i$
and
$a^*_i$
and
![]() $b_i$
to be the dual of
$b_i$
to be the dual of
![]() $b^*_i$
). As a notational shorthand, we will let
$b^*_i$
). As a notational shorthand, we will let ![]() and
and ![]() Note that
Note that
![]() $g_a(n,i) +i = g_b(n,i)$
. The differentials are given by
$g_a(n,i) +i = g_b(n,i)$
. The differentials are given by
 $$ \begin{align*} \partial a_i = \begin{cases} Ub_{i}, &\qquad i=1\\ b_{i-1}, &\qquad i=2n\\ U^i b_{i} + b_{i-1}, &\qquad \text{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} \partial a_i = \begin{cases} Ub_{i}, &\qquad i=1\\ b_{i-1}, &\qquad i=2n\\ U^i b_{i} + b_{i-1}, &\qquad \text{otherwise.} \end{cases} \end{align*} $$
Note that the (horizontal) arrow from
![]() $a_i$
to
$a_i$
to
![]() $b_i$
is of length i, while the (vertical) arrow from
$b_i$
is of length i, while the (vertical) arrow from
![]() $a_i$
to
$a_i$
to
![]() $b_{i-1}$
is of length
$b_{i-1}$
is of length
![]() $2n-i+1$
(see Figure 2 for an example of
$2n-i+1$
(see Figure 2 for an example of
![]() $\operatorname {CFK}^\infty (S^3,-T_{2n,2n+1})$
when
$\operatorname {CFK}^\infty (S^3,-T_{2n,2n+1})$
when
![]() $n=3)$
.
$n=3)$
.

Figure 2 The knot Floer complex
![]() $\operatorname {CFK}^\infty (S^3,-T_{6,7})$
. The solid dots are generators. The differentials point to lower filtration levels, and the numbers indicate their lengths.
$\operatorname {CFK}^\infty (S^3,-T_{6,7})$
. The solid dots are generators. The differentials point to lower filtration levels, and the numbers indicate their lengths.
The interesting examples are given by the pair
![]() $(S^{3}_{1}(-T_{2n,2n+1}),\mu _{2n-1,1})$
, where
$(S^{3}_{1}(-T_{2n,2n+1}),\mu _{2n-1,1})$
, where
![]() $\mu _{2n-1,1}$
is the
$\mu _{2n-1,1}$
is the
![]() $(2n-1,1)$
-cable of the dual knot. To compute the knot Floer complex of said examples, we apply the filtered mapping cone formula for the cables of the dual knot on
$(2n-1,1)$
-cable of the dual knot. To compute the knot Floer complex of said examples, we apply the filtered mapping cone formula for the cables of the dual knot on
![]() $-T_{2n.2n+1}$
, with the surgery coefficient equal to
$-T_{2n.2n+1}$
, with the surgery coefficient equal to
![]() $+1.$
Following the recipe described in Section 3, the filtered chain complex
$+1.$
Following the recipe described in Section 3, the filtered chain complex
![]() $\operatorname {CFK}^\infty (S^{3}_{1}(-T_{2n,2n+1}),\mu _{2n-1,1})$
is filtered homotopy equivalent to the filtered complex
$\operatorname {CFK}^\infty (S^{3}_{1}(-T_{2n,2n+1}),\mu _{2n-1,1})$
is filtered homotopy equivalent to the filtered complex
![]() $X^\infty _{2n-1}(-T_{2n,2n+1})$
defined by the mapping cone of
$X^\infty _{2n-1}(-T_{2n,2n+1})$
defined by the mapping cone of
 $$ \begin{align*} \bigoplus^{(n+1)(2n-1)-1}_{s=-n(2n-1)+1}A_s \xrightarrow{v_s+h_s} \bigoplus^{(n+1)(2n-1)-1}_{s=-n(2n-1)+2}B_s.\end{align*} $$
$$ \begin{align*} \bigoplus^{(n+1)(2n-1)-1}_{s=-n(2n-1)+1}A_s \xrightarrow{v_s+h_s} \bigoplus^{(n+1)(2n-1)-1}_{s=-n(2n-1)+2}B_s.\end{align*} $$
Through the isomorphism with
![]() $\operatorname {CFK}^\infty (S^3,-T_{2n,2n+1})$
, denote the corresponding generators in
$\operatorname {CFK}^\infty (S^3,-T_{2n,2n+1})$
, denote the corresponding generators in
![]() $A_s$
by
$A_s$
by
![]() $a^{(s)}_i$
and
$a^{(s)}_i$
and
![]() $b^{(s)}_i$
, and the generators in
$b^{(s)}_i$
, and the generators in
![]() $B_s$
by
$B_s$
by
![]() $a^{\prime (s)}_i$
and
$a^{\prime (s)}_i$
and
![]() $b^{\prime (s)}_i$
, for suitable i and s. Recall that we use
$b^{\prime (s)}_i$
, for suitable i and s. Recall that we use
![]() $\mathcal {I}$
and
$\mathcal {I}$
and
![]() $\mathcal {J}$
specifically for the double filtrations on the entire mapping cone complex. Using the formulas given by (14), (15), (17), and (18), the computations for the
$\mathcal {J}$
specifically for the double filtrations on the entire mapping cone complex. Using the formulas given by (14), (15), (17), and (18), the computations for the
![]() $\mathcal {I}$
and
$\mathcal {I}$
and
![]() $\mathcal {J}$
filtrations of the generators described above are quite straightforward. We collect the result in a following lemma, with
$\mathcal {J}$
filtrations of the generators described above are quite straightforward. We collect the result in a following lemma, with
![]() $g_a(n,i)$
and
$g_a(n,i)$
and
![]() $g_b(n,i)$
the quantities defined in the previous paragraph. Also define a notational shorthand
$g_b(n,i)$
the quantities defined in the previous paragraph. Also define a notational shorthand
Note that
![]() $f(n,s-1) + n = f(n,s).$
$f(n,s-1) + n = f(n,s).$
Lemma 4.1. In the complex
![]() $X^\infty _{2n-1} (-T_{2n,2n+1})$
, we have
$X^\infty _{2n-1} (-T_{2n,2n+1})$
, we have
 $$ \begin{align} \mathcal{J}(a^{(s)}_i) &= \begin{cases}f(n,s)+g_a(n,i)-s, \qquad &s \leq g_a(n,i)+2n-1 \\ f(n,s-1), \qquad &s> g_a(n,i)+2n-1 \end{cases}\end{align} $$
$$ \begin{align} \mathcal{J}(a^{(s)}_i) &= \begin{cases}f(n,s)+g_a(n,i)-s, \qquad &s \leq g_a(n,i)+2n-1 \\ f(n,s-1), \qquad &s> g_a(n,i)+2n-1 \end{cases}\end{align} $$
 $$ \begin{align} \mathcal{J}(b^{(s)}_i) &= \begin{cases}f(n,s)+g_b(n,i)-s, \qquad &s \leq g_b(n,i)+2n-1 \\ f(n,s-1), \qquad &s> g_b(n,i)+2n-1; \end{cases} \end{align} $$
$$ \begin{align} \mathcal{J}(b^{(s)}_i) &= \begin{cases}f(n,s)+g_b(n,i)-s, \qquad &s \leq g_b(n,i)+2n-1 \\ f(n,s-1), \qquad &s> g_b(n,i)+2n-1; \end{cases} \end{align} $$
For the rest of the computation, we assume that
![]() $n \geq 3$
(the case when
$n \geq 3$
(the case when
![]() $n=1, 2$
does not fit into the following model. Instead, the results of those two cases are recorded in Lemma 4.5.).
$n=1, 2$
does not fit into the following model. Instead, the results of those two cases are recorded in Lemma 4.5.).
We first aim to obtain a reduced model of the generators of
![]() $X^\infty _{2n-1} (-T_{2n,2n+1})$
. Up to filtered homotopy equivalence (as a subcomplex of
$X^\infty _{2n-1} (-T_{2n,2n+1})$
. Up to filtered homotopy equivalence (as a subcomplex of
![]() $X^\infty _{2n-1} (-T_{2n,2n+1})$
), each
$X^\infty _{2n-1} (-T_{2n,2n+1})$
), each
![]() $B_s$
is one-dimensional. Indeed, quotienting out
$B_s$
is one-dimensional. Indeed, quotienting out
![]() $\{a^{\prime (s)}_i,\partial a^{\prime (s)}_i\}_{2\leq i\leq 2n}$
leaves us with a sole generator
$\{a^{\prime (s)}_i,\partial a^{\prime (s)}_i\}_{2\leq i\leq 2n}$
leaves us with a sole generator
![]() $ a^{\prime (s)}_1$
in each
$ a^{\prime (s)}_1$
in each
![]() $B_s$
.
$B_s$
.
Each
![]() $A_s$
is a subcomplex of the quotient complex
$A_s$
is a subcomplex of the quotient complex
![]() $\bigoplus _s A_s$
, which inherits the
$\bigoplus _s A_s$
, which inherits the
![]() $(\mathcal {I},\mathcal {J})$
filtration naturally. We would like to obtain a reduced model for each
$(\mathcal {I},\mathcal {J})$
filtration naturally. We would like to obtain a reduced model for each
![]() $A_s$
. For the next part, let
$A_s$
. For the next part, let
![]() $\partial $
temporarily denote the differential restricted to each subquotient-complex
$\partial $
temporarily denote the differential restricted to each subquotient-complex
![]() $A_s$
, as opposed to the differential on the entire chain complex
$A_s$
, as opposed to the differential on the entire chain complex
![]() $X^\infty _{2n-1} (-T_{2n,2n+1})$
. There are two types of complex
$X^\infty _{2n-1} (-T_{2n,2n+1})$
. There are two types of complex
![]() $A_s$
, depending on the dimension of the reduced model.
$A_s$
, depending on the dimension of the reduced model.
When
![]() $s\in [-n(2n-1),-n(2n-1)+2n] \cup \{-n(2n-1) + 2jn-1, -n(2n-1) + 2jn\}_{1\leq j \leq 2n-2} \cup [n(2n-1)-1,(n+1)(2n-1) -1] ,$
after quotienting out
$s\in [-n(2n-1),-n(2n-1)+2n] \cup \{-n(2n-1) + 2jn-1, -n(2n-1) + 2jn\}_{1\leq j \leq 2n-2} \cup [n(2n-1)-1,(n+1)(2n-1) -1] ,$
after quotienting out
![]() $\{a^{(s)}_i, \partial a^{(s)}_i\}_{2\leq i\leq 2n-1}$
, the reduced model of
$\{a^{(s)}_i, \partial a^{(s)}_i\}_{2\leq i\leq 2n-1}$
, the reduced model of
![]() $A_s$
is three-dimensional.
$A_s$
is three-dimensional.
-
○ When
 $s\in [-n(2n-1),-n(2n-1)+2n]$
, the reduced model is generated by
$s\in [-n(2n-1),-n(2n-1)+2n]$
, the reduced model is generated by
 $\{a^{(s)}_{2n},b^{(s)}_{1},a^{(s)}_{1}\}$
with modified differentials:
$\{a^{(s)}_{2n},b^{(s)}_{1},a^{(s)}_{1}\}$
with modified differentials:  $$ \begin{align*} \partial a^{(s)}_{1}= U b^{(s)}_{1}, \hspace{6em} \partial a^{(s)}_{2n}= U^{-n(2n-1)+1} b^{(s)}_{1}. \end{align*} $$
$$ \begin{align*} \partial a^{(s)}_{1}= U b^{(s)}_{1}, \hspace{6em} \partial a^{(s)}_{2n}= U^{-n(2n-1)+1} b^{(s)}_{1}. \end{align*} $$
-
○ When
 $s\in \{-n(2n-1) + 2jn-1, -n(2n-1) + 2jn\}_{1\leq j \leq 2n-2}$
,the reduced model is generated by
$s\in \{-n(2n-1) + 2jn-1, -n(2n-1) + 2jn\}_{1\leq j \leq 2n-2}$
,the reduced model is generated by
 $\{a^{(s)}_{2n},b^{(s)}_{j},a^{(s)}_{1}\}$
and modified differentials are
$\{a^{(s)}_{2n},b^{(s)}_{j},a^{(s)}_{1}\}$
and modified differentials are  $$ \begin{align*} \hspace{1.2em} \partial a^{(s)}_{1}= U^{\frac{j(j+1)}{2}} b^{(s)}_{j}, \hspace{4em} \partial a^{(s)}_{2n}= U^{-n(2n-1)+\frac{j(j+1)}{2}} b^{(s)}_{j}. \end{align*} $$
$$ \begin{align*} \hspace{1.2em} \partial a^{(s)}_{1}= U^{\frac{j(j+1)}{2}} b^{(s)}_{j}, \hspace{4em} \partial a^{(s)}_{2n}= U^{-n(2n-1)+\frac{j(j+1)}{2}} b^{(s)}_{j}. \end{align*} $$
-
○ When
 $s\in [n(2n-1)-1,(n+1)(2n-1) -1]$
, the reduced model is generated by
$s\in [n(2n-1)-1,(n+1)(2n-1) -1]$
, the reduced model is generated by
 $\{a^{(s)}_{2n},b^{(s)}_{2n-1},a^{(s)}_{1}\}$
with modified differentials
$\{a^{(s)}_{2n},b^{(s)}_{2n-1},a^{(s)}_{1}\}$
with modified differentials  $$ \begin{align*} \partial a^{(s)}_{1}= U^{n(2n-1)} b^{(s)}_{2n-1}, \hspace{5em} \partial a^{(s)}_{2n}= b^{(s)}_{2n-1}. \hspace{2em} \end{align*} $$
$$ \begin{align*} \partial a^{(s)}_{1}= U^{n(2n-1)} b^{(s)}_{2n-1}, \hspace{5em} \partial a^{(s)}_{2n}= b^{(s)}_{2n-1}. \hspace{2em} \end{align*} $$
When
![]() $s\in \bigcup _{1\leq j \leq 2n-2} [-n(2n-1) + 2jn+1, -n(2n-1) + 2(j+1)n-2]$
, the reduced model of
$s\in \bigcup _{1\leq j \leq 2n-2} [-n(2n-1) + 2jn+1, -n(2n-1) + 2(j+1)n-2]$
, the reduced model of
![]() $A_s$
is five-dimensional. Indeed, quotienting out
$A_s$
is five-dimensional. Indeed, quotienting out
![]() $\{a^{(s)}_i, \partial a^{(s)}_i\}_{j\in [2,j]\cup [j+2,2n-1]}$
leaves us with generators
$\{a^{(s)}_i, \partial a^{(s)}_i\}_{j\in [2,j]\cup [j+2,2n-1]}$
leaves us with generators
![]() $\{a^{(s)}_{2n}, b^{(s)}_{j+1}, a^{(s)}_{j+1}, b^{(s)}_{j},a^{(s)}_{1}\}$
. The difference here from the previous case is that both terms in
$\{a^{(s)}_{2n}, b^{(s)}_{j+1}, a^{(s)}_{j+1}, b^{(s)}_{j},a^{(s)}_{1}\}$
. The difference here from the previous case is that both terms in
![]() $\partial a^{(s)}_{j+1}$
strictly decrease
$\partial a^{(s)}_{j+1}$
strictly decrease
![]() $\mathcal {I}$
or
$\mathcal {I}$
or
![]() $\mathcal {J}$
grading, and therefore survive into the reduced complex. The modified differentials are given by
$\mathcal {J}$
grading, and therefore survive into the reduced complex. The modified differentials are given by
 $$ \begin{gather*} \begin{aligned} &\partial a^{(s)}_{1}= U^{\frac{j(j+1)}{2}} b^{(s)}_{j}, \hspace{3em} &\partial a^{(s)}_{j+1}= b^{(s)}_{j} + U^{j+1} b^{(s)}_{j+1},\\ & \partial a^{(s)}_{2n} = U^{-n(2n-1)+\frac{(j+1)(j+2)}{2}} b^{(s)}_{j+1}. & \end{aligned} \end{gather*} $$
$$ \begin{gather*} \begin{aligned} &\partial a^{(s)}_{1}= U^{\frac{j(j+1)}{2}} b^{(s)}_{j}, \hspace{3em} &\partial a^{(s)}_{j+1}= b^{(s)}_{j} + U^{j+1} b^{(s)}_{j+1},\\ & \partial a^{(s)}_{2n} = U^{-n(2n-1)+\frac{(j+1)(j+2)}{2}} b^{(s)}_{j+1}. & \end{aligned} \end{gather*} $$
Finally, consider the entire chain complex
![]() $X^\infty _{2n-1} (-T_{2n,2n+1})$
, using the reduced models for both
$X^\infty _{2n-1} (-T_{2n,2n+1})$
, using the reduced models for both
![]() $A_s$
and
$A_s$
and
![]() $B_s.$
Let
$B_s.$
Let
![]() $\partial $
denote the differential on the entire mapping cone complex (including
$\partial $
denote the differential on the entire mapping cone complex (including
![]() $v_s$
and
$v_s$
and
![]() $h_s$
maps). Observe that
$h_s$
maps). Observe that
![]() $h_s(U^{-s} a^{(s)}_{2n})=a^{\prime (s+1)}_{1}= v_{s+1}(a^{(s+1)}_{1})$
for
$h_s(U^{-s} a^{(s)}_{2n})=a^{\prime (s+1)}_{1}= v_{s+1}(a^{(s+1)}_{1})$
for
![]() $-n(2n-1)+1\leq s \leq n(2n-1)$
, while
$-n(2n-1)+1\leq s \leq n(2n-1)$
, while
![]() $\mathcal {I}(U^{-s} a^{(s)}_{2n})=\mathcal {I}(a^{\prime (s+1)}_{1}) = \mathcal {I}(a^{(s+1)}_{1})$
and
$\mathcal {I}(U^{-s} a^{(s)}_{2n})=\mathcal {I}(a^{\prime (s+1)}_{1}) = \mathcal {I}(a^{(s+1)}_{1})$
and
![]() $\mathcal {J}(U^{-s} a^{(s)}_{2n})=\mathcal {J}(a^{\prime (s+1)}_{1})\leq \mathcal {J}(a^{(s+1)}_{1})$
, where the last equality is reached when
$\mathcal {J}(U^{-s} a^{(s)}_{2n})=\mathcal {J}(a^{\prime (s+1)}_{1})\leq \mathcal {J}(a^{(s+1)}_{1})$
, where the last equality is reached when
![]() $s\geq -(n-1)(2n-1).$
Thus, we may quotient out
$s\geq -(n-1)(2n-1).$
Thus, we may quotient out
![]() $\{a^{(s)}_{2n}, \partial a^{(s)}_{2n}\}$
for
$\{a^{(s)}_{2n}, \partial a^{(s)}_{2n}\}$
for
![]() $-n(2n-1)+1\leq s \leq n(2n-1)$
. If we let
$-n(2n-1)+1\leq s \leq n(2n-1)$
. If we let
![]() $\alpha _s$
denote the image of
$\alpha _s$
denote the image of
![]() $a^{(s)}_{1}$
in the quotient for
$a^{(s)}_{1}$
in the quotient for
![]() $-n(2n-1)+1 \leq s \leq n(2n-1)+1$
, notice that for
$-n(2n-1)+1 \leq s \leq n(2n-1)+1$
, notice that for
![]() $-n(2n-1)+2 \leq s \leq n(2n-1)+1$
, this amounts to a change of basis
$-n(2n-1)+2 \leq s \leq n(2n-1)+1$
, this amounts to a change of basis
![]() $ a^{(s)}_{1} \mapsto U^{-s+1}a^{(s-1)}_{2n} + a^{(s)}_{1}$
followed by a homotopy equivalence. Similarly, we may quotient out
$ a^{(s)}_{1} \mapsto U^{-s+1}a^{(s-1)}_{2n} + a^{(s)}_{1}$
followed by a homotopy equivalence. Similarly, we may quotient out
![]() $\{a^{(s)}_{1}, \partial a^{(s)}_{1}\}$
for
$\{a^{(s)}_{1}, \partial a^{(s)}_{1}\}$
for
![]() $n(2n-1)+2\leq s \leq (n+1)(2n-1)-1$
.
$n(2n-1)+2\leq s \leq (n+1)(2n-1)-1$
.
We have obtained a reduced model for
![]() $X^\infty _{2n-1} (-T_{2n,2n+1})$
. Observe that no generator in
$X^\infty _{2n-1} (-T_{2n,2n+1})$
. Observe that no generator in
![]() $B_s$
survives into the reduced basis. Moreover, from the viewpoint of the quotient complex, the induced differential
$B_s$
survives into the reduced basis. Moreover, from the viewpoint of the quotient complex, the induced differential
![]() $\partial $
restricted to
$\partial $
restricted to
![]() $A_s$
is a map
$A_s$
is a map
![]() $\partial \colon \thinspace A_s \rightarrow A_s \oplus A_{s-1}$
for
$\partial \colon \thinspace A_s \rightarrow A_s \oplus A_{s-1}$
for
![]() $-n(2n-1)+2\leq s\leq n$
, viewing
$-n(2n-1)+2\leq s\leq n$
, viewing
![]() $\alpha _s$
as an element of
$\alpha _s$
as an element of
![]() $A_s$
. However, we will generally adopt the viewpoint of a change of basis, and view
$A_s$
. However, we will generally adopt the viewpoint of a change of basis, and view
![]() $\alpha _s$
as an element of
$\alpha _s$
as an element of
![]() $A_s \oplus A_{s-1}$
, mainly because this plays well with the symmetry on the mapping cone complex.
$A_s \oplus A_{s-1}$
, mainly because this plays well with the symmetry on the mapping cone complex.
Considering the symmetry on
![]() $X^\infty _{2n-1} (-T_{2n,2n+1})$
(see Proposition 3.2), our strategy would be to focus on the “first half” of the complex, namely, the mapping cone of
$X^\infty _{2n-1} (-T_{2n,2n+1})$
(see Proposition 3.2), our strategy would be to focus on the “first half” of the complex, namely, the mapping cone of
 $$ \begin{align*} \bigoplus_{s=-n(2n-1)+1}^{ n-1} A_s \xrightarrow{ v_s+h_s} \bigoplus_{s=-n(2n-1)+2}^{n} B_s, \end{align*} $$
$$ \begin{align*} \bigoplus_{s=-n(2n-1)+1}^{ n-1} A_s \xrightarrow{ v_s+h_s} \bigoplus_{s=-n(2n-1)+2}^{n} B_s, \end{align*} $$
which under the current basis is simply the chain complex
 $$ \begin{align*} \bigoplus_{s=-n(2n-1)+1}^{n-1} A_s. \end{align*} $$
$$ \begin{align*} \bigoplus_{s=-n(2n-1)+1}^{n-1} A_s. \end{align*} $$
So, let us summarize the generators and relations of this first half complex in the following lemma (we also include those
![]() $A_s$
where s is in the interval
$A_s$
where s is in the interval
![]() $[n, 2n-1]$
for the continuity). Let
$[n, 2n-1]$
for the continuity). Let
![]() $\widetilde {\alpha }_s$
denote
$\widetilde {\alpha }_s$
denote
![]() $a^{(s)}_{j+1}$
when
$a^{(s)}_{j+1}$
when
![]() $s\in [-n(2n-1) + 2jn+1, -n(2n-1) + 2(j+1)n-2]$
for each
$s\in [-n(2n-1) + 2jn+1, -n(2n-1) + 2(j+1)n-2]$
for each
![]() $1\leq j \leq n.$
$1\leq j \leq n.$
Lemma 4.2. Under the reduced basis chosen above, we have
-
○ For
 $s\in [-n(2n-1)+1, -n(2n-1)+2n],$
the complex
$s\in [-n(2n-1)+1, -n(2n-1)+2n],$
the complex
 $A_s$
is generated by
$A_s$
is generated by
 $\alpha _s$
and
$\alpha _s$
and
 $ b^{(s)}_{1}$
, where the differentials are given by (27)
$ b^{(s)}_{1}$
, where the differentials are given by (27) $$ \begin{align} \partial \alpha_s &= \begin{cases} Ub^{(s)}_{1}, &\qquad s=-n(2n-1)+1 \hspace{8em} \\ U^{-s+2}b^{(s-1)}_{1} + Ub^{(s)}_{1} , &\qquad s>-n(2n-1)+1. \end{cases} \end{align} $$
$$ \begin{align} \partial \alpha_s &= \begin{cases} Ub^{(s)}_{1}, &\qquad s=-n(2n-1)+1 \hspace{8em} \\ U^{-s+2}b^{(s-1)}_{1} + Ub^{(s)}_{1} , &\qquad s>-n(2n-1)+1. \end{cases} \end{align} $$
-
○ For
 $s\in [-n(2n-1) + 2jn+1, -n(2n-1) + 2(j+1)n-2]$
with some
$s\in [-n(2n-1) + 2jn+1, -n(2n-1) + 2(j+1)n-2]$
with some
 $1\leq j \leq n,$
the complex
$1\leq j \leq n,$
the complex
 $A_s$
is generated by
$A_s$
is generated by
 $\alpha _s, \widetilde {\alpha }_s, b^{(s)}_{j}$
and
$\alpha _s, \widetilde {\alpha }_s, b^{(s)}_{j}$
and
 $ b^{(s)}_{j+1}$
, where the differentials are given by (28)
$ b^{(s)}_{j+1}$
, where the differentials are given by (28) $$ \begin{align} \partial \alpha_s &= \begin{cases} U^{-s+1+\frac{j(j+1)}{2}} b^{(s-1)}_{j} + U^{\frac{j(j+1)}{2}} b^{(s)}_{j} , &\qquad s=-n(2n-1) + 2jn+1,\\ U^{-s+1+\frac{(j+1)(j+2)}{2}} b^{(s-1)}_{j+1} + U^{\frac{j(j+1)}{2}} b^{(s)}_{j} , &\qquad s>-n(2n-1) + 2jn+1, \end{cases} \end{align} $$
(29)
$$ \begin{align} \partial \alpha_s &= \begin{cases} U^{-s+1+\frac{j(j+1)}{2}} b^{(s-1)}_{j} + U^{\frac{j(j+1)}{2}} b^{(s)}_{j} , &\qquad s=-n(2n-1) + 2jn+1,\\ U^{-s+1+\frac{(j+1)(j+2)}{2}} b^{(s-1)}_{j+1} + U^{\frac{j(j+1)}{2}} b^{(s)}_{j} , &\qquad s>-n(2n-1) + 2jn+1, \end{cases} \end{align} $$
(29) $$ \begin{align} \partial \widetilde{\alpha}_s &= b^{(s)}_{j} + U^{j+1} b^{(s)}_{j+1}. \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\ \ \quad\qquad \end{align} $$
$$ \begin{align} \partial \widetilde{\alpha}_s &= b^{(s)}_{j} + U^{j+1} b^{(s)}_{j+1}. \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\ \ \quad\qquad \end{align} $$
-
○ For
 $s\in \{-n(2n-1) + 2jn-1, -n(2n-1) + 2jn\}$
with some
$s\in \{-n(2n-1) + 2jn-1, -n(2n-1) + 2jn\}$
with some
 $2\leq j \leq n,$
the complex
$2\leq j \leq n,$
the complex
 $A_s$
is generated by
$A_s$
is generated by
 $\alpha _s$
and
$\alpha _s$
and
 $ b^{(s)}_{j}$
, where the differentials are given by (30)
$ b^{(s)}_{j}$
, where the differentials are given by (30) $$ \begin{align} &\partial \alpha_s = U^{-s+1+\frac{j(j+1)}{2}} b^{(s-1)}_{j} + U^{\frac{j(j+1)}{2}} b^{(s)}_{j}. \hspace{16.5em} \end{align} $$
$$ \begin{align} &\partial \alpha_s = U^{-s+1+\frac{j(j+1)}{2}} b^{(s-1)}_{j} + U^{\frac{j(j+1)}{2}} b^{(s)}_{j}. \hspace{16.5em} \end{align} $$
Proof. This follows from the earlier discussion.
We prove in the next lemma that, up to local equivalence, we can further truncate the mapping cone. Define
![]() $X^\infty _{2n-1} (-T_{2n,2n+1}) \langle \ell \rangle $
for
$X^\infty _{2n-1} (-T_{2n,2n+1}) \langle \ell \rangle $
for
![]() $\ell \in \mathbb {Z}$
to be the filtered mapping cone
$\ell \in \mathbb {Z}$
to be the filtered mapping cone
 $$ \begin{align*} \bigoplus^{\ell}_{s=-\ell+2n-1}A_s \xrightarrow{v_s+h_s} \bigoplus^{\ell}_{s=-\ell+2n}B_s, \end{align*} $$
$$ \begin{align*} \bigoplus^{\ell}_{s=-\ell+2n-1}A_s \xrightarrow{v_s+h_s} \bigoplus^{\ell}_{s=-\ell+2n}B_s, \end{align*} $$
which under the reduced basis simplifies to the filtered chain complex
 $$ \begin{align*} \bigoplus^{\ell}_{s=-\ell+2n-1}A_s. \end{align*} $$
$$ \begin{align*} \bigoplus^{\ell}_{s=-\ell+2n-1}A_s. \end{align*} $$
Note that under this notation
![]() $X^\infty _{2n-1} (-T_{2n,2n+1}) = X^\infty _{2n-1} (-T_{2n,2n+1}) \langle (n+1)(2n-1) -1 \rangle $
.
$X^\infty _{2n-1} (-T_{2n,2n+1}) = X^\infty _{2n-1} (-T_{2n,2n+1}) \langle (n+1)(2n-1) -1 \rangle $
.
Lemma 4.3. Up to a change of basis, the filtered complex
![]() $X^\infty _{2n-1} (-T_{2n,2n+1})$
is isomorphic to
$X^\infty _{2n-1} (-T_{2n,2n+1})$
is isomorphic to
![]() $ X^\infty _{2n-1} (-T_{2n,2n+1}) \langle 2n-1 \rangle \oplus D $
, where
$ X^\infty _{2n-1} (-T_{2n,2n+1}) \langle 2n-1 \rangle \oplus D $
, where
![]() $H_*(D)=0$
.
$H_*(D)=0$
.
Proof. It suffices to show for any
![]() $2n \leq \ell \leq (n+1)(2n-1) -1,$
the complex
$2n \leq \ell \leq (n+1)(2n-1) -1,$
the complex
![]() $X^\infty _{2n-1} (-T_{2n,2n+1}) \langle \ell \rangle $
is isomorphic to
$X^\infty _{2n-1} (-T_{2n,2n+1}) \langle \ell \rangle $
is isomorphic to
![]() $X^\infty _{2n-1} (-T_{2n,2n+1}) \langle \ell -1 \rangle \oplus D'$
up to a change of basis, where
$X^\infty _{2n-1} (-T_{2n,2n+1}) \langle \ell -1 \rangle \oplus D'$
up to a change of basis, where
![]() $H_*(D')=0$
. For every such
$H_*(D')=0$
. For every such
![]() $\ell $
, we will demonstrate a filtered change of basis, such that the complex
$\ell $
, we will demonstrate a filtered change of basis, such that the complex
![]() $A_{-\ell +2n-1}$
becomes a summand. Following from the symmetry given by Proposition 3.2, there is also a filtered change of basis, such that
$A_{-\ell +2n-1}$
becomes a summand. Following from the symmetry given by Proposition 3.2, there is also a filtered change of basis, such that
![]() $A_{\ell }$
becomes a summand under the new basis as required. Let
$A_{\ell }$
becomes a summand under the new basis as required. Let
![]() $s=-\ell +2n-1.$
Recall that we view
$s=-\ell +2n-1.$
Recall that we view
![]() $\alpha _s$
as an element in
$\alpha _s$
as an element in
![]() $A_{s}\oplus A_{s-1}.$
$A_{s}\oplus A_{s-1}.$
-
○ For
 $s\in [-n(2n-1)+2, -n(2n-1)+2n+1],$
perform the change of basis According to (27) and (28), this splits off an acyclic summand as required. Since
$s\in [-n(2n-1)+2, -n(2n-1)+2n+1],$
perform the change of basis According to (27) and (28), this splits off an acyclic summand as required. Since
 $\mathcal {J}(\alpha _{s}) = \mathcal {J}(a_1^{s})>\mathcal {J}(a_1^{s-1}) = \mathcal {J}(\alpha _{s-1})$
, by (23), this change of basis is clearly filtered.
$\mathcal {J}(\alpha _{s}) = \mathcal {J}(a_1^{s})>\mathcal {J}(a_1^{s-1}) = \mathcal {J}(\alpha _{s-1})$
, by (23), this change of basis is clearly filtered.
-
○ For
 $s\in [-n(2n-1) + 2jn+2, -n(2n-1) + 2(j+1)n-1]$
for some
$s\in [-n(2n-1) + 2jn+2, -n(2n-1) + 2(j+1)n-1]$
for some
 $1\leq j \leq n-1,$
and when
$1\leq j \leq n-1,$
and when
 $s\leq 1$
, perform the change of basis According to (28), (29), and (30), this splits off an acyclic summand as required. This change of basis is clearly filtered when
$s\leq 1$
, perform the change of basis According to (28), (29), and (30), this splits off an acyclic summand as required. This change of basis is clearly filtered when
 $s\leq 1$
(the equality is reached in the interval associated to
$s\leq 1$
(the equality is reached in the interval associated to
 $j=n-1$
).
$j=n-1$
).
-
○ For
 $s\in \{-n(2n-1) + 2jn, -n(2n-1) + 2jn+1\}$
with some
$s\in \{-n(2n-1) + 2jn, -n(2n-1) + 2jn+1\}$
with some
 $2\leq j \leq n-1$
(noting that
$2\leq j \leq n-1$
(noting that
 $s<0$
always holds), perform the change of basis This change of basis is again clearly filtered.
$s<0$
always holds), perform the change of basis This change of basis is again clearly filtered.
Therefore, the local equivalence class of
![]() $X^\infty _{2n-1} (-T_{2n,2n+1})$
is given by
$X^\infty _{2n-1} (-T_{2n,2n+1})$
is given by
![]() $\bigoplus ^{2n-1}_{s=0}A_s$
under the reduced basis. The differentials in this complex are already given by Lemma 4.2, and the filtrations of the generators are given by Lemma 4.1. In the following lemma, we will work out the
$\bigoplus ^{2n-1}_{s=0}A_s$
under the reduced basis. The differentials in this complex are already given by Lemma 4.2, and the filtrations of the generators are given by Lemma 4.1. In the following lemma, we will work out the
![]() $\mathcal {J}$
–filtration shifts between the generators that are related by a differential.
$\mathcal {J}$
–filtration shifts between the generators that are related by a differential.
Suppose
![]() $U^c \beta $
is a nontrivial term in
$U^c \beta $
is a nontrivial term in
![]() $\partial \alpha $
, where
$\partial \alpha $
, where
![]() $\beta $
is used to represent some
$\beta $
is used to represent some
![]() $b_i^{(s)}$
and
$b_i^{(s)}$
and
![]() $\alpha $
is used to represent some
$\alpha $
is used to represent some
![]() $\alpha _s$
or
$\alpha _s$
or
![]() $\widetilde {\alpha }_s$
. Define
$\widetilde {\alpha }_s$
. Define
and, similarly define
![]() $\Delta _{\mathcal {I}}$
and
$\Delta _{\mathcal {I}}$
and
![]() $\Delta _{\mathcal {J}}$
.
$\Delta _{\mathcal {J}}$
.
Lemma 4.4. Generators in the reduced basis of
![]() $\bigoplus ^{2n-1}_{s=0}A_s$
satisfy the following.
$\bigoplus ^{2n-1}_{s=0}A_s$
satisfy the following.
Proof. We collect in Table 1 the filtrations of the generators in the reduced basis of
![]() $\bigoplus ^{2n-1}_{s=0}A_s$
from Lemma 4.1. Note that
$\bigoplus ^{2n-1}_{s=0}A_s$
from Lemma 4.1. Note that
![]() $g_b(n,n)=0$
and
$g_b(n,n)=0$
and
![]() $g_a(n,n)=-n$
. The
$g_a(n,n)=-n$
. The
![]() $\mathcal {I}$
filtrations of the generators are all
$\mathcal {I}$
filtrations of the generators are all
![]() $0$
(so this is, in fact, a reduced model of
$0$
(so this is, in fact, a reduced model of
![]() $\widehat {HFK}.$
)
$\widehat {HFK}.$
)
Table 1 The filtrations of the generators in the reduced basis of
![]() $\bigoplus^{2n-1}_{s=0}\ {A}_{s}$
.
$\bigoplus^{2n-1}_{s=0}\ {A}_{s}$
.

To show (32) and (33), first, by (28), we have
![]() $\Delta _{\mathcal {I}}(\alpha _s,b_{n-1}^{(s)}) = \frac {n(n-1)}{2}.$
Compute
$\Delta _{\mathcal {I}}(\alpha _s,b_{n-1}^{(s)}) = \frac {n(n-1)}{2}.$
Compute
 $$ \begin{align*} \Delta_{\mathcal{J}}(\alpha_s,b_{n-1}^{(s)}) &= \mathcal{J}(\alpha_s) - \mathcal{J}(b_{n-1}^{(s)}) + \frac{n(n-1)}{2}\\ &= \frac{n(n-1)}{2}, \end{align*} $$
$$ \begin{align*} \Delta_{\mathcal{J}}(\alpha_s,b_{n-1}^{(s)}) &= \mathcal{J}(\alpha_s) - \mathcal{J}(b_{n-1}^{(s)}) + \frac{n(n-1)}{2}\\ &= \frac{n(n-1)}{2}, \end{align*} $$
which proves (32), and (33) follows from the symmetry given by Proposition 3.2.
To show (34) and (35), first, by (28) and (30), we have
![]() $\Delta _{\mathcal {I}}(\alpha _s,b_{n}^{(s-1)}) = \frac {n(n+1)}{2} - s + 1.$
Compute
$\Delta _{\mathcal {I}}(\alpha _s,b_{n}^{(s-1)}) = \frac {n(n+1)}{2} - s + 1.$
Compute
 $$ \begin{align*} \Delta_{\mathcal{J}}(\alpha_s,b_{n}^{(s-1)}) &= \mathcal{J}(\alpha_s) - \mathcal{J}(b_{n}^{(s-1)}) + \frac{n(n+1)}{2} - s + 1\\ &= \frac{n(n+1)}{2}, \end{align*} $$
$$ \begin{align*} \Delta_{\mathcal{J}}(\alpha_s,b_{n}^{(s-1)}) &= \mathcal{J}(\alpha_s) - \mathcal{J}(b_{n}^{(s-1)}) + \frac{n(n+1)}{2} - s + 1\\ &= \frac{n(n+1)}{2}, \end{align*} $$
which proves (34), and (35) follows from the symmetry given by Proposition 3.2.
The rest of the results follow from similar computations and are left for the reader.
When
![]() $n=1$
and
$n=1$
and
![]() $2$
, the local equivalence class of the complex
$2$
, the local equivalence class of the complex
![]() $X^\infty _{n} (-T_{2n,2n+1})$
can be decided following a similar vein. We record the result in the next lemma, and the computations are left to the reader as an exercise.
$X^\infty _{n} (-T_{2n,2n+1})$
can be decided following a similar vein. We record the result in the next lemma, and the computations are left to the reader as an exercise.
Lemma 4.5. When
![]() $n=1$
, the complex
$n=1$
, the complex
![]() $X^\infty _{1} (-T_{2,3})$
is locally trivial.
$X^\infty _{1} (-T_{2,3})$
is locally trivial.
When
![]() $n=2$
, the complex
$n=2$
, the complex
![]() $X^\infty _{2} (-T_{4,5})$
has a local complex characterized by the following.
$X^\infty _{2} (-T_{4,5})$
has a local complex characterized by the following.
 $$ \begin{align*} \partial \alpha_1 &= U^3 b_2^{(1)},\\ \partial \alpha_2 &= U^2 b_2^{(1)} + U^3 b_2^{(2)},\\ \partial \alpha_3 &= U b_2^{(1)};\\ \Delta_{\mathcal{I},\mathcal{J}}&(\alpha_1, b_2^{(1)}) = (3,1),\\ \Delta_{\mathcal{I},\mathcal{J}}&(\alpha_2, b_2^{(1)}) = (2,3),\\ \Delta_{\mathcal{I},\mathcal{J}}&(\alpha_2, b_2^{(2)}) = (3,2),\\ \Delta_{\mathcal{I},\mathcal{J}}&(\alpha_3, b_2^{(2)}) = (1,3).\\ \end{align*} $$
$$ \begin{align*} \partial \alpha_1 &= U^3 b_2^{(1)},\\ \partial \alpha_2 &= U^2 b_2^{(1)} + U^3 b_2^{(2)},\\ \partial \alpha_3 &= U b_2^{(1)};\\ \Delta_{\mathcal{I},\mathcal{J}}&(\alpha_1, b_2^{(1)}) = (3,1),\\ \Delta_{\mathcal{I},\mathcal{J}}&(\alpha_2, b_2^{(1)}) = (2,3),\\ \Delta_{\mathcal{I},\mathcal{J}}&(\alpha_2, b_2^{(2)}) = (3,2),\\ \Delta_{\mathcal{I},\mathcal{J}}&(\alpha_3, b_2^{(2)}) = (1,3).\\ \end{align*} $$

Figure 3 A reduced basis for the complex
![]() $X^\infty _{5} (-T_{6,7}) \langle 5 \rangle $
, where the coordinates are given by
$X^\infty _{5} (-T_{6,7}) \langle 5 \rangle $
, where the coordinates are given by
![]() $\mathcal {I}$
and
$\mathcal {I}$
and
![]() $\mathcal {J}$
filtrations. The generators are marked abstractly, without U powers. The edges represent the differentials; the edge with
$\mathcal {J}$
filtrations. The generators are marked abstractly, without U powers. The edges represent the differentials; the edge with
![]() $*$
depicts an instance of the fact that
$*$
depicts an instance of the fact that
![]() $\Delta _{\mathcal {I}}(\alpha _n, b_{n}^{(n)}) = \Delta _{\mathcal {I}}(\alpha _{n+1},b_{n}^{(n)}) + n $
.
$\Delta _{\mathcal {I}}(\alpha _n, b_{n}^{(n)}) = \Delta _{\mathcal {I}}(\alpha _{n+1},b_{n}^{(n)}) + n $
.
Acknowledgements
The authors would like to thank Irving Dai, Tye Lidman, Chuck Livingston, Dan Margalit, and Linh Truong for helpful conversations, and the anonymous referee for helpful comments. JH and HZ were supported by NSF grant DMS-2104144 and a Simons Fellowship. MS was supported by NSF grant DMS-1952755. This work was done while JH and HZ were in residence at the Simons Laufer Mathematical Sciences Institute (formerly MSRI) during Fall 2023, supported by NSF Grant DMS-1928930.
Competing interests
The authors have no competing interest to declare.
Ethical standards
The research meets all ethical guidelines, including adherence to the legal requirements of the study country.