0 Introduction
The nilpotent and
![]() $\mathrm {SL}_2$
-orbit theorems of Schmid have been fundamental in understanding the degeneration of Hodge structure, particularly in the context of integral variation of Hodge structures. However, their complete generalization to complex variations of Hodge structure remains unproven. This paper aims to the study of Schmid’s nilpotent orbit theorem for complex variations of Hodge structure. The main result of this paper is the main component of the nilpotent orbit theorem.
$\mathrm {SL}_2$
-orbit theorems of Schmid have been fundamental in understanding the degeneration of Hodge structure, particularly in the context of integral variation of Hodge structures. However, their complete generalization to complex variations of Hodge structure remains unproven. This paper aims to the study of Schmid’s nilpotent orbit theorem for complex variations of Hodge structure. The main result of this paper is the main component of the nilpotent orbit theorem.
Theorem A. Let X be a complex manifold, and let
![]() $D=\sum _{i=1}^{\ell } D_i$
be a simple normal crossing divisor on X. Let
$D=\sum _{i=1}^{\ell } D_i$
be a simple normal crossing divisor on X. Let
![]() $(V, \nabla , F^{\bullet }, Q)$
be a complex polarized variation of Hodge structure on
$(V, \nabla , F^{\bullet }, Q)$
be a complex polarized variation of Hodge structure on
![]() $X\backslash D$
. Then for any multi-index
$X\backslash D$
. Then for any multi-index
![]() $\boldsymbol {\alpha }=(\alpha _1,\ldots ,\alpha _{\ell })\in \mathbb {R}^{\ell }$
,
$\boldsymbol {\alpha }=(\alpha _1,\ldots ,\alpha _{\ell })\in \mathbb {R}^{\ell }$
,
![]() $F^p_{\boldsymbol {\alpha }}:=j_{*}F^p\cap V_{\boldsymbol {\alpha }}^{\mathrm {Del}}$
and
$F^p_{\boldsymbol {\alpha }}:=j_{*}F^p\cap V_{\boldsymbol {\alpha }}^{\mathrm {Del}}$
and
![]() $F^{p}_{\boldsymbol {\alpha }}/F^{p+1}_{\boldsymbol {\alpha }}$
are both locally free sheaves. Here,
$F^{p}_{\boldsymbol {\alpha }}/F^{p+1}_{\boldsymbol {\alpha }}$
are both locally free sheaves. Here,
![]() $V_{\boldsymbol {\alpha }}^{\mathrm {Del}}$
is the Deligne extension of the flat bundle
$V_{\boldsymbol {\alpha }}^{\mathrm {Del}}$
is the Deligne extension of the flat bundle
![]() $(V,\nabla )$
with the eigenvalues of the residue of
$(V,\nabla )$
with the eigenvalues of the residue of
![]() $\nabla $
over
$\nabla $
over
![]() $D_i$
lying in
$D_i$
lying in
![]() $[-\alpha _i,-\alpha _i+1)$
.
$[-\alpha _i,-\alpha _i+1)$
.
We prove moreover that the grading
![]() $\oplus _{p+q=m}F^{p}_{\boldsymbol {\alpha }}/F^{p+1}_{\boldsymbol {\alpha }}$
is naturally identified with
$\oplus _{p+q=m}F^{p}_{\boldsymbol {\alpha }}/F^{p+1}_{\boldsymbol {\alpha }}$
is naturally identified with
![]() $\oplus _{p+q=m}\mathcal {P}_{\!\boldsymbol {\alpha }} E^{p,q}$
, where
$\oplus _{p+q=m}\mathcal {P}_{\!\boldsymbol {\alpha }} E^{p,q}$
, where
![]() $\mathcal {P}_{\!\boldsymbol {\alpha }} E^{p,q}$
is the prolongation of the Hodge bundles
$\mathcal {P}_{\!\boldsymbol {\alpha }} E^{p,q}$
is the prolongation of the Hodge bundles
![]() $ E^{p,q}:=F^{p}/F^{p+1}$
in terms of the norm growth of the Hodge metric (see §1.6 for the definition).
$ E^{p,q}:=F^{p}/F^{p+1}$
in terms of the norm growth of the Hodge metric (see §1.6 for the definition).
Based on Theorem A, we can generalize main parts of Schmid’s nilpotent orbit theorem to complex polarized variation of Hodge structure.
Theorem B. Let
![]() $(V,\nabla ,F^{\bullet },Q)$
be a complex polarized variation of Hodge structure on
$(V,\nabla ,F^{\bullet },Q)$
be a complex polarized variation of Hodge structure on
![]() $(\Delta ^{*})^p\times \Delta ^q$
. Denote by
$(\Delta ^{*})^p\times \Delta ^q$
. Denote by
![]() $\Phi :\mathbb {H}^{p}\times \Delta ^q\to \mathscr {D}$
its period mapping, where
$\Phi :\mathbb {H}^{p}\times \Delta ^q\to \mathscr {D}$
its period mapping, where
![]() $\mathscr {D}$
is the period domain and
$\mathscr {D}$
is the period domain and
![]() $\mathbb {H}=\{z\in \mathbb {C}\mid \Re z<0\}$
. Let us denote by
$\mathbb {H}=\{z\in \mathbb {C}\mid \Re z<0\}$
. Let us denote by
![]() $2\pi iR_i$
is the logarithm of the monodromy operator associated to the counterclockwise generator of the fundamental group of the i-th copy of
$2\pi iR_i$
is the logarithm of the monodromy operator associated to the counterclockwise generator of the fundamental group of the i-th copy of
![]() $\Delta ^{*}$
in
$\Delta ^{*}$
in
![]() $(\Delta ^{*})^p$
, whose eigenvalues lie in
$(\Delta ^{*})^p$
, whose eigenvalues lie in
![]() $(2\pi i (\alpha _i-1), 2\pi i \alpha _i]$
for some
$(2\pi i (\alpha _i-1), 2\pi i \alpha _i]$
for some
![]() $\boldsymbol {\alpha }\in \mathbb {R}^{p}$
. Then for the holomorphic mapping
$\boldsymbol {\alpha }\in \mathbb {R}^{p}$
. Then for the holomorphic mapping
![]() $\Psi :(\Delta ^{*})^p\times \Delta ^q\to \check {\mathscr {D}}$
induced by
$\Psi :(\Delta ^{*})^p\times \Delta ^q\to \check {\mathscr {D}}$
induced by
![]() $\tilde {\Psi }:= \exp (\sum _{i=1}^{p}z_iR_i)\circ \Phi (z,w)$
,
$\tilde {\Psi }:= \exp (\sum _{i=1}^{p}z_iR_i)\circ \Phi (z,w)$
,
-
(i)
 $\Psi $
extends holomorphically to
$\Psi $
extends holomorphically to
 $\Delta ^{p+q}$
;
$\Delta ^{p+q}$
; -
(ii) the holomorphic mapping
is horizontal, where $$ \begin{align*} \vartheta: \mathbb{H}^{p}\times \Delta^q&\to \check{\mathscr{D}}\\ (z,w)&\mapsto \exp\left(-\sum_{i=1}^{p}z_iR_i\right)\circ a(w) \end{align*} $$
$$ \begin{align*} \vartheta: \mathbb{H}^{p}\times \Delta^q&\to \check{\mathscr{D}}\\ (z,w)&\mapsto \exp\left(-\sum_{i=1}^{p}z_iR_i\right)\circ a(w) \end{align*} $$
 $a(w):=\Psi (0,w)$
, and
$a(w):=\Psi (0,w)$
, and
 $\check {\mathscr {D}}$
is the compact dual of the period domain
$\check {\mathscr {D}}$
is the compact dual of the period domain
 $\mathscr {D}$
.
$\mathscr {D}$
.
-
(iii) In the one variable case,
 $ \exp (-zR)\circ a$
lies in
$ \exp (-zR)\circ a$
lies in
 $\mathscr {D}$
when
$\mathscr {D}$
when
 $\Re z\leq -C$
for some
$\Re z\leq -C$
for some
 $C>0$
. Moreover, we have the distance estimate if
$C>0$
. Moreover, we have the distance estimate if $$ \begin{align*} d_{ {\mathscr{D}}}( \exp(-zR)\circ a, \Phi(z))\leq C' |\Re z|^{\beta}e^{\delta \Re z} \quad\mbox{for some}\quad C',\delta,\beta>0 \end{align*} $$
$$ \begin{align*} d_{ {\mathscr{D}}}( \exp(-zR)\circ a, \Phi(z))\leq C' |\Re z|^{\beta}e^{\delta \Re z} \quad\mbox{for some}\quad C',\delta,\beta>0 \end{align*} $$
 $\Re z\leq -C$
.
$\Re z\leq -C$
.
When
![]() $(V,\nabla ) $
has quasi-unipotent monodromies around D, Theorems A and B are contained in Schmid’s nilpotent orbit theorem [Reference Schmid10]. Under this monodromy assumption, he proved Theorem B.(iii) for the case of several variables.
$(V,\nabla ) $
has quasi-unipotent monodromies around D, Theorems A and B are contained in Schmid’s nilpotent orbit theorem [Reference Schmid10]. Under this monodromy assumption, he proved Theorem B.(iii) for the case of several variables.
Theorems A and B were also proved by Sabbah and Schnell [Reference Sabbah and Schnell9] for the case of one variable in a different way. Their methods can be extended to prove the general case.
Our proof of Theorem A is based on Mochizuki’s work on the prolongation of acceptable bundles [Reference Mochizuki8] and methods in
![]() $L^2$
-estimates. The proof of Theorems B.(ii) and B.(iii) essentially follows Schmid’s method in [Reference Schmid10].
$L^2$
-estimates. The proof of Theorems B.(ii) and B.(iii) essentially follows Schmid’s method in [Reference Schmid10].
We conclude the introduction by explaining applications of the main result in this paper. One application is related to the work [Reference Wu13] on the injectivity and vanishing theorem for
![]() $\mathbb {R}$
-Hodge modules. We remark that in [Reference Wu13
Reference Wu, Lemma 2.10], nilpotent orbit theorem for real variation of Hodge structures was claimed. It seems to the author that the proof needs some amplification, and as such, Theorem A complements the proof presented therein.
$\mathbb {R}$
-Hodge modules. We remark that in [Reference Wu13
Reference Wu, Lemma 2.10], nilpotent orbit theorem for real variation of Hodge structures was claimed. It seems to the author that the proof needs some amplification, and as such, Theorem A complements the proof presented therein.
Another potential further application is on the complex Hodge modules. It is well-established that Saito’s theory of mixed Hodge modules fundamentally relies on the nilpotent orbit theorem. Currently, Sabbah and Schnell are developing the theory of mixed Hodge modules for complex Hodge structures. We remark that the nilpotent orbit theorem established in this paper should serve as a foundational component in their work.
1 Preliminary
1.1 Complex polarized variations of Hodge structure
Let us briefly recall the definition of polarized Hodge structure. We refer the readers to [Reference Simpson12, Reference Sabbah and Schnell9] for more details. A Hodge structure of weight w on a complex vector space V is a decomposition
and a polarization is a Hermitian pairing
![]() $Q: V \otimes _{\mathbb {C}} \bar {V} \rightarrow \mathbb {C}$
such that the above decomposition is orthogonal with respect to Q and such that
$Q: V \otimes _{\mathbb {C}} \bar {V} \rightarrow \mathbb {C}$
such that the above decomposition is orthogonal with respect to Q and such that
![]() $(-1)^q Q$
is positive definite on the subspace
$(-1)^q Q$
is positive definite on the subspace
![]() $V^{p, q}$
. For any
$V^{p, q}$
. For any
![]() $v\in V$
, its Hodge norm is defined
$v\in V$
, its Hodge norm is defined
where
![]() $v^{p,q}$
is the
$v^{p,q}$
is the
![]() $(p,q)$
-component of v in the Hodge decomposition
$(p,q)$
-component of v in the Hodge decomposition
![]() $V=\bigoplus _{p+q=w} V^{p, q}$
. Such a polarized Hodge structure induces the Hodge filtration
$V=\bigoplus _{p+q=w} V^{p, q}$
. Such a polarized Hodge structure induces the Hodge filtration
![]() $F^{\bullet } V$
of V defined by
$F^{\bullet } V$
of V defined by
As introduced by [Reference Simpson12], a complex polarized variation of Hodge structure
![]() $(V=\bigoplus _{r+s=w} V^{r, s}, \nabla , Q)$
of weight w on a complex manifold U consists of the following data:
$(V=\bigoplus _{r+s=w} V^{r, s}, \nabla , Q)$
of weight w on a complex manifold U consists of the following data:
-
(a) a smooth vector bundle V with a Hodge decomposition
 $V=\bigoplus _{r+s=w} V^{r, s}$
;
$V=\bigoplus _{r+s=w} V^{r, s}$
; -
(b) a flat connection
 $\nabla $
satisfies the Griffiths’ transversality condition (1.1)
$\nabla $
satisfies the Griffiths’ transversality condition (1.1) $$ \begin{align} \nabla: {V}^{r, s} \rightarrow A^{0,1}(V^{r+1, s+1}) \oplus A^{1,0}\left(V^{r, s}\right) \oplus A^{0,1}(V^{r, s}) \oplus {A}^{1,0}(V^{r-1, s+1}); \end{align} $$
$$ \begin{align} \nabla: {V}^{r, s} \rightarrow A^{0,1}(V^{r+1, s+1}) \oplus A^{1,0}\left(V^{r, s}\right) \oplus A^{0,1}(V^{r, s}) \oplus {A}^{1,0}(V^{r-1, s+1}); \end{align} $$
-
(c) a parallel Hermitian form Q which makes the Hodge decomposition orthogonal and which on
 $\mathrm {V}^{r, s}$
is positive definite if r is even and negative definite if r is odd.
$\mathrm {V}^{r, s}$
is positive definite if r is even and negative definite if r is odd.
We decompose
![]() $\nabla =\bar {\theta }+\partial +\bar {\partial }+\theta $
according to the above transversality condition in Equation (1.1). The most important component of the connection turns out to be the Higgs field, which is the linear operator
$\nabla =\bar {\theta }+\partial +\bar {\partial }+\theta $
according to the above transversality condition in Equation (1.1). The most important component of the connection turns out to be the Higgs field, which is the linear operator
We decompose
![]() $\nabla =\nabla '+\nabla "$
into its (1,0)-component
$\nabla =\nabla '+\nabla "$
into its (1,0)-component
![]() $\nabla ': A^0(V) \rightarrow A^{1,0}(V)$
and its
$\nabla ': A^0(V) \rightarrow A^{1,0}(V)$
and its
![]() $(0,1)$
-component
$(0,1)$
-component
![]() $\nabla ": A^0(V) \rightarrow A^{0,1}(V)$
. Then
$\nabla ": A^0(V) \rightarrow A^{0,1}(V)$
. Then
![]() $\nabla "$
gives V the structure of a holomorphic vector bundle, which we denote by the symbol
$\nabla "$
gives V the structure of a holomorphic vector bundle, which we denote by the symbol
![]() $\mathcal V$
, and
$\mathcal V$
, and
![]() $\nabla '$
defines an integrable holomorphic connection
$\nabla '$
defines an integrable holomorphic connection
![]() $\nabla ': \mathcal V \rightarrow \Omega _U^1 \otimes _{\mathscr {O}_U} \mathcal V$
on this bundle. The condition on
$\nabla ': \mathcal V \rightarrow \Omega _U^1 \otimes _{\mathscr {O}_U} \mathcal V$
on this bundle. The condition on
![]() $\nabla $
in Equation (1.1) is saying that the Hodge filtration
$\nabla $
in Equation (1.1) is saying that the Hodge filtration
is a holomorphic subbundles of
![]() $\mathcal V$
, and that the connection
$\mathcal V$
, and that the connection
![]() $\nabla '$
satisfies Griffiths’ transversality relation
$\nabla '$
satisfies Griffiths’ transversality relation
Note that
![]() $(V^{p,q},\bar {{\partial }})$
defines a holomorphic vector bundle, denoted by
$(V^{p,q},\bar {{\partial }})$
defines a holomorphic vector bundle, denoted by
![]() $E^{p,q}$
. From the above point of view, the Higgs field is simply the holomorphic operator
$E^{p,q}$
. From the above point of view, the Higgs field is simply the holomorphic operator
Denote by
![]() $(E,\theta )=(\oplus _{p+q=w}E^{p,q}, \theta )$
, which is called the system of Hodge bundles relative to the
$(E,\theta )=(\oplus _{p+q=w}E^{p,q}, \theta )$
, which is called the system of Hodge bundles relative to the
![]() $\mathbb {C}$
-VHS
$\mathbb {C}$
-VHS
![]() $(V=\oplus _{p+q=w}V^{p,q},\nabla ,Q)$
. Let us define
$(V=\oplus _{p+q=w}V^{p,q},\nabla ,Q)$
. Let us define
![]() $h_{p,q}:=(-1)^pQ$
, which is a Hermitian metric for
$h_{p,q}:=(-1)^pQ$
, which is a Hermitian metric for
![]() $E^{p,q}$
by Item (c). For the Hermitian metric
$E^{p,q}$
by Item (c). For the Hermitian metric
![]() $h=\oplus _{p+q=w}h_{p,q}$
of E, the component
$h=\oplus _{p+q=w}h_{p,q}$
of E, the component
![]() $\bar {\theta }:V^{r,s}\to A^{0,1}(V^{r+1,s-1})$
is the adjoint of
$\bar {\theta }:V^{r,s}\to A^{0,1}(V^{r+1,s-1})$
is the adjoint of
![]() $\theta $
with respect to h. Since the primary objective of this paper is to establish the nilpotent orbit theorem for
$\theta $
with respect to h. Since the primary objective of this paper is to establish the nilpotent orbit theorem for
![]() $\mathbb {C}$
-VHS, we will adopt the notation
$\mathbb {C}$
-VHS, we will adopt the notation
![]() $(V, \nabla , F^{\bullet } V, Q)$
to represent the
$(V, \nabla , F^{\bullet } V, Q)$
to represent the
![]() $\mathbb {C}$
-VHS, as the Hodge filtration
$\mathbb {C}$
-VHS, as the Hodge filtration
![]() $F^{\bullet } V$
plays a central role in the nilpotent orbit theorem.
$F^{\bullet } V$
plays a central role in the nilpotent orbit theorem.
1.2 Deligne extension
Let X be a complex manifold, and let D be a simple normal crossing divisor on X. For the flat bundle
![]() $(V, \nabla )$
defined on
$(V, \nabla )$
defined on
![]() $U:=X\backslash D$
, Deligne introduced a way to extend it across D. We recall this construction briefly and refer the readers to [Reference Schmid10, Reference Mochizuki7, Reference Sabbah and Schnell9] for more details. For any point
$U:=X\backslash D$
, Deligne introduced a way to extend it across D. We recall this construction briefly and refer the readers to [Reference Schmid10, Reference Mochizuki7, Reference Sabbah and Schnell9] for more details. For any point
![]() $x\in D$
, we choose an admissible coordinate
$x\in D$
, we choose an admissible coordinate
![]() $(\Omega ;z_1,\ldots ,z_n)$
such that
$(\Omega ;z_1,\ldots ,z_n)$
such that
![]() $\Omega \simeq \Delta ^{n}$
and
$\Omega \simeq \Delta ^{n}$
and
![]() $D\cap \Omega =(z_1\ldots z_p=0)$
(see Definition 1.1 for the definition). Write
$D\cap \Omega =(z_1\ldots z_p=0)$
(see Definition 1.1 for the definition). Write
![]() $q=n-p$
. The fundamental group
$q=n-p$
. The fundamental group
![]() $\pi _1\big ((\Delta ^{*})^p\times \Delta ^q\big )$
is generated by elements
$\pi _1\big ((\Delta ^{*})^p\times \Delta ^q\big )$
is generated by elements
![]() $\gamma _1,\ldots ,\gamma _p$
, where
$\gamma _1,\ldots ,\gamma _p$
, where
![]() $\gamma _j$
may be identified with the counterclockwise generator of the fundamental group of the j-th copy of
$\gamma _j$
may be identified with the counterclockwise generator of the fundamental group of the j-th copy of
![]() $\Delta ^{*}$
in
$\Delta ^{*}$
in
![]() $(\Delta ^{*})^p$
. We denote by
$(\Delta ^{*})^p$
. We denote by
![]() $V^{\nabla }$
the space of multivalued flat sections of
$V^{\nabla }$
the space of multivalued flat sections of
![]() $(V,\nabla )$
, which is a finite-dimensional
$(V,\nabla )$
, which is a finite-dimensional
![]() $\mathbb {C}$
-vector space. Set
$\mathbb {C}$
-vector space. Set
![]() $T_j$
to be the monodromy transformation with respect to
$T_j$
to be the monodromy transformation with respect to
![]() $\gamma _j$
, which pairwise commute and are endomorphisms of
$\gamma _j$
, which pairwise commute and are endomorphisms of
![]() $V^{\nabla }$
; that is, for any multivalued section
$V^{\nabla }$
; that is, for any multivalued section
![]() $v(t_1,\ldots ,t_{p+q})\in V^{\nabla }$
, one has
$v(t_1,\ldots ,t_{p+q})\in V^{\nabla }$
, one has
and
![]() $[T_j,T_k]=0$
for any
$[T_j,T_k]=0$
for any
![]() $j,k=1,\ldots ,p$
. Let us write
$j,k=1,\ldots ,p$
. Let us write
![]() $Sp(T_j)$
the set of eigenvalues of
$Sp(T_j)$
the set of eigenvalues of
![]() $T_j$
, and for any
$T_j$
, and for any
![]() $\lambda _j\in Sp(T_j)$
, we denote by
$\lambda _j\in Sp(T_j)$
, we denote by
![]() $\mathbb {E}(T_j,\lambda _j)\subset V^{\nabla }$
the corresponding eigenspace. We know that all
$\mathbb {E}(T_j,\lambda _j)\subset V^{\nabla }$
the corresponding eigenspace. We know that all
![]() $\lambda _j\in Sp(T_j)$
has norm
$\lambda _j\in Sp(T_j)$
has norm
![]() $1$
(see, e.g., [Reference Sabbah and Schnell9]). Write
$1$
(see, e.g., [Reference Sabbah and Schnell9]). Write
![]() $Sp:=\prod _{i=1}^pSp(T_j)$
. For
$Sp:=\prod _{i=1}^pSp(T_j)$
. For
![]() $\boldsymbol {\lambda }=(\lambda _1,\ldots ,\lambda _p)$
, we define
$\boldsymbol {\lambda }=(\lambda _1,\ldots ,\lambda _p)$
, we define
Since
![]() $T_j$
pairwise commute, one has
$T_j$
pairwise commute, one has
and
![]() $\mathbb {E}_{\boldsymbol {\lambda }}$
is an invariant subspace of
$\mathbb {E}_{\boldsymbol {\lambda }}$
is an invariant subspace of
![]() $T_j$
for any
$T_j$
for any
![]() $\boldsymbol {\lambda }\in Sp$
and any j.
$\boldsymbol {\lambda }\in Sp$
and any j.
Let us fix a p-tuple
![]() $\boldsymbol {\alpha }:=(\alpha _1,\ldots ,\alpha _p)\in \mathbb {R}^p$
. Then for
$\boldsymbol {\alpha }:=(\alpha _1,\ldots ,\alpha _p)\in \mathbb {R}^p$
. Then for
![]() $\boldsymbol {\lambda }\in Sp$
, there exists a unique
$\boldsymbol {\lambda }\in Sp$
, there exists a unique
![]() $\beta _i\in (\alpha _i-1, \alpha _i]$
such that
$\beta _i\in (\alpha _i-1, \alpha _i]$
such that
![]() $\exp (2\pi i \beta _i)=\lambda _i$
. Since
$\exp (2\pi i \beta _i)=\lambda _i$
. Since
![]() $\lambda _i^{-1}T_i|_{ \mathbb {E}_{\boldsymbol {\lambda }}}$
is unipotent, its logarithm can be defined as
$\lambda _i^{-1}T_i|_{ \mathbb {E}_{\boldsymbol {\lambda }}}$
is unipotent, its logarithm can be defined as
 $$ \begin{align*}\log( \lambda_i^{-1}T_i|_{ \mathbb{E}_{\boldsymbol{\lambda}}}):=\sum_{k=1}^{\infty}(-1)^{k+1}\frac{(\lambda_i^{-1}T_i|_{ \mathbb{E}_{\boldsymbol{\lambda}}}-I)^k}{k}. \end{align*} $$
$$ \begin{align*}\log( \lambda_i^{-1}T_i|_{ \mathbb{E}_{\boldsymbol{\lambda}}}):=\sum_{k=1}^{\infty}(-1)^{k+1}\frac{(\lambda_i^{-1}T_i|_{ \mathbb{E}_{\boldsymbol{\lambda}}}-I)^k}{k}. \end{align*} $$
We denote
![]() $N_i:=\frac {\log ( \lambda _i^{-1}T_i|_{ \mathbb {E}_{\boldsymbol {\lambda }}})}{2\pi i}$
. Then for any
$N_i:=\frac {\log ( \lambda _i^{-1}T_i|_{ \mathbb {E}_{\boldsymbol {\lambda }}})}{2\pi i}$
. Then for any
![]() $v\in \mathbb {E}_{\boldsymbol {\lambda }}$
, we define
$v\in \mathbb {E}_{\boldsymbol {\lambda }}$
, we define
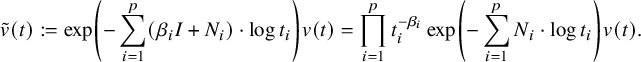 $$ \begin{align} \tilde{v}(t):=\exp\left(- \sum_{i=1}^{p}( \beta_iI+N_i)\cdot \log t_i \right)v(t) = \prod_{i=1}^{p}t_i^{-\beta_i}\exp\left(- \sum_{i=1}^{p}N_i\cdot \log t_i \right)v(t). \end{align} $$
$$ \begin{align} \tilde{v}(t):=\exp\left(- \sum_{i=1}^{p}( \beta_iI+N_i)\cdot \log t_i \right)v(t) = \prod_{i=1}^{p}t_i^{-\beta_i}\exp\left(- \sum_{i=1}^{p}N_i\cdot \log t_i \right)v(t). \end{align} $$
One can check that
![]() $\tilde {v}$
is single valued and that
$\tilde {v}$
is single valued and that
![]() $\nabla ^{0,1}\tilde {v}=0$
. We now fix a basis
$\nabla ^{0,1}\tilde {v}=0$
. We now fix a basis
![]() $v_1,\ldots ,v_r$
of
$v_1,\ldots ,v_r$
of
![]() $V^{\nabla }$
such that each
$V^{\nabla }$
such that each
![]() $v_i$
belongs to some
$v_i$
belongs to some
![]() $\mathbb {E}_{\boldsymbol {\lambda }}$
. Then the holomorphic sections
$\mathbb {E}_{\boldsymbol {\lambda }}$
. Then the holomorphic sections
![]() $\tilde {v}_1,\ldots ,\tilde {v}_r$
of
$\tilde {v}_1,\ldots ,\tilde {v}_r$
of
![]() $\mathcal V$
defines a prolongation of
$\mathcal V$
defines a prolongation of
![]() $\mathcal V$
over X which we denoted by
$\mathcal V$
over X which we denoted by
![]() $V^{\mathrm {Del}}_{\boldsymbol {\alpha }}$
. One can check that this construction does not depend on our choice of the basis. This is called the Deligne extension of the flat bundle
$V^{\mathrm {Del}}_{\boldsymbol {\alpha }}$
. One can check that this construction does not depend on our choice of the basis. This is called the Deligne extension of the flat bundle
![]() $(V,\nabla )$
with the eigenvalues of the residue of
$(V,\nabla )$
with the eigenvalues of the residue of
![]() $\nabla $
over
$\nabla $
over
![]() $D_i$
lying in
$D_i$
lying in
![]() $[-\alpha _i,-\alpha _i+1)$
. Note that it is defined for any flat bundle
$[-\alpha _i,-\alpha _i+1)$
. Note that it is defined for any flat bundle
![]() $(V,\nabla )$
(not necessarily complex variation of Hodge structure).
$(V,\nabla )$
(not necessarily complex variation of Hodge structure).
If
![]() $(V,\nabla )$
underlies a complex polarized variation of Hodge structure
$(V,\nabla )$
underlies a complex polarized variation of Hodge structure
![]() $(V, \nabla , F^{\bullet } V, Q)$
, we define
$(V, \nabla , F^{\bullet } V, Q)$
, we define
![]() $ F^p_{\boldsymbol {\alpha }}:=j_{*}F^p\cap V_{\boldsymbol {\alpha }}^{\mathrm {Del}}. $
It is called the extension of the Hodge filtration. It should be noted that, a priori, we do not know whether
$ F^p_{\boldsymbol {\alpha }}:=j_{*}F^p\cap V_{\boldsymbol {\alpha }}^{\mathrm {Del}}. $
It is called the extension of the Hodge filtration. It should be noted that, a priori, we do not know whether
![]() $F^p_{\boldsymbol {\alpha }}$
is locally free.
$F^p_{\boldsymbol {\alpha }}$
is locally free.
1.3 Acceptable bundles
Definition 1.1 (Admissible coordinate)
Let X be a complex manifold, and let D be a simple normal crossing divisor. Let x be a point of X, and assume that
![]() $\{D_{j}\}_{ j=1,\ldots ,\ell }$
are the components of D containing p. An admissible coordinate around x is the tuple
$\{D_{j}\}_{ j=1,\ldots ,\ell }$
are the components of D containing p. An admissible coordinate around x is the tuple
![]() $(\Omega ;z_1,\ldots ,z_n;\varphi )$
(or simply
$(\Omega ;z_1,\ldots ,z_n;\varphi )$
(or simply
![]() $(\Omega ;z_1,\ldots ,z_n)$
if no confusion arises) where
$(\Omega ;z_1,\ldots ,z_n)$
if no confusion arises) where
-
○
 $\Omega $
is an open subset of X containing x.
$\Omega $
is an open subset of X containing x. -
○ There is a holomorphic isomorphism
 $\varphi :\Omega \to \Delta ^n$
such that
$\varphi :\Omega \to \Delta ^n$
such that
 $\varphi (D_j)=(z_j=0)$
for any
$\varphi (D_j)=(z_j=0)$
for any
 $j=1,\ldots ,\ell $
.
$j=1,\ldots ,\ell $
.
We shall write
![]() $\Omega ^{*}:=\Omega -D$
,
$\Omega ^{*}:=\Omega -D$
,
![]() $\Omega (r):=\{z\in \Omega \mid |z_i|<r, \, \forall i=1,\ldots ,n\}$
and
$\Omega (r):=\{z\in \Omega \mid |z_i|<r, \, \forall i=1,\ldots ,n\}$
and
![]() $\Omega ^{*}(r):=\Omega (r)\cap \Omega ^{*}$
.
$\Omega ^{*}(r):=\Omega (r)\cap \Omega ^{*}$
.
We define a (incomplete) Poincaré-type metric
![]() $\omega _P$
on
$\omega _P$
on
![]() $(\Delta ^{*})^{\ell }\times \Delta ^{n-\ell }$
by
$(\Delta ^{*})^{\ell }\times \Delta ^{n-\ell }$
by
 $$ \begin{align} \omega_P=\sum_{j=1}^{\ell}\frac{\sqrt{-1}dz_j\wedge d\bar{z}_j}{|z_j|^2(\log |z_j|^2)^2}+\sum_{k=\ell+1}^{n} \sqrt{-1}dz_k\wedge d\bar{z}_k. \end{align} $$
$$ \begin{align} \omega_P=\sum_{j=1}^{\ell}\frac{\sqrt{-1}dz_j\wedge d\bar{z}_j}{|z_j|^2(\log |z_j|^2)^2}+\sum_{k=\ell+1}^{n} \sqrt{-1}dz_k\wedge d\bar{z}_k. \end{align} $$
Note that
 $$ \begin{align*} \omega_P=i\partial\bar{\partial} \log \left(\prod_{j=1}^{\ell}(-\log |z_j|^2)^{-1} \cdot \prod_{k=\ell+1}^{n}\exp(|z_k|^2)\right). \end{align*} $$
$$ \begin{align*} \omega_P=i\partial\bar{\partial} \log \left(\prod_{j=1}^{\ell}(-\log |z_j|^2)^{-1} \cdot \prod_{k=\ell+1}^{n}\exp(|z_k|^2)\right). \end{align*} $$
For any system of Hodge bundles
![]() $(E,\theta ,h)$
, we have the following crucial norm estimate for its Higgs field
$(E,\theta ,h)$
, we have the following crucial norm estimate for its Higgs field
![]() $\theta $
. The one-dimensional case is due to Simpson [Reference Simpson11, Theorem 1] and the general case was proved by Mochizuki in [Reference Mochizuki5, Proposition 4.1]. Its proof relies on a clever use of Ahlfors–Schwarz lemma.
$\theta $
. The one-dimensional case is due to Simpson [Reference Simpson11, Theorem 1] and the general case was proved by Mochizuki in [Reference Mochizuki5, Proposition 4.1]. Its proof relies on a clever use of Ahlfors–Schwarz lemma.
Theorem 1.2. Let
![]() $(E,\theta ,h)$
be a system of Hodge bundle on
$(E,\theta ,h)$
be a system of Hodge bundle on
![]() $X\backslash D$
. Then for any point
$X\backslash D$
. Then for any point
![]() $x\in D$
, it has an admissible coordinate
$x\in D$
, it has an admissible coordinate
![]() $(\Omega ;z_1,\ldots ,z_n)$
such that the norm
$(\Omega ;z_1,\ldots ,z_n)$
such that the norm
![]() $ | \theta |_{h,\omega _P}\leq C $
holds over
$ | \theta |_{h,\omega _P}\leq C $
holds over
![]() $\Omega ^{*}$
for some constant
$\Omega ^{*}$
for some constant
![]() $C>0$
. Here,
$C>0$
. Here,
![]() $| \theta |_{h,\omega _P}$
denotes the norm of
$| \theta |_{h,\omega _P}$
denotes the norm of
![]() $\theta $
with respect to h and
$\theta $
with respect to h and
![]() $\omega _P$
.
$\omega _P$
.
Here, we also recall the following definition in [Reference Mochizuki7, Definition 2.7].
Definition 1.3 (Acceptable bundle)
Let
![]() $(E, h)$
be a Hermitian vector bundle over
$(E, h)$
be a Hermitian vector bundle over
![]() $X\backslash D$
. We say that
$X\backslash D$
. We say that
![]() $(E, h)$
is an acceptable at
$(E, h)$
is an acceptable at
![]() $p\in D$
, if the following holds: There is an admissible coordinate
$p\in D$
, if the following holds: There is an admissible coordinate
![]() $(\Omega ;z_1,\ldots ,z_n)$
around p such that the norm
$(\Omega ;z_1,\ldots ,z_n)$
around p such that the norm
![]() $\lvert R(E,h) \rvert _{h,\omega _P}\leq C$
for some
$\lvert R(E,h) \rvert _{h,\omega _P}\leq C$
for some
![]() $C>0$
. Here,
$C>0$
. Here,
![]() $R(E,h)$
is the Chern curvature of
$R(E,h)$
is the Chern curvature of
![]() $(E,h)$
. When
$(E,h)$
. When
![]() $(E_,h)$
is acceptable at any point p of D, it is called acceptable.
$(E_,h)$
is acceptable at any point p of D, it is called acceptable.
Hodge filtrations and Hodge bundles endowed with the Hodge metric are all acceptable.
Lemma 1.4. Let
![]() $(V, \nabla , F^{\bullet }, Q)$
be a complex polarized variation of Hodge structure of weight m on
$(V, \nabla , F^{\bullet }, Q)$
be a complex polarized variation of Hodge structure of weight m on
![]() $X\backslash D$
. Let h (resp.
$X\backslash D$
. Let h (resp.
![]() $h_{p,q}$
) be the Hermitian metric on V (resp. on
$h_{p,q}$
) be the Hermitian metric on V (resp. on
![]() $E^{p,q}$
) introduced in §1.1. Consider the induced Hermitian metric
$E^{p,q}$
) introduced in §1.1. Consider the induced Hermitian metric
![]() $h_p:=h|_{F^p}$
on the Hodge filtration
$h_p:=h|_{F^p}$
on the Hodge filtration
![]() $F^p$
. Then both
$F^p$
. Then both
![]() $(F^p, h_p)$
and
$(F^p, h_p)$
and
![]() $(E^{p,q},h_{p,q})$
are acceptable bundles.
$(E^{p,q},h_{p,q})$
are acceptable bundles.
Proof. We write
![]() $\theta _{p,q}:=\theta |_{E^{p,q}}$
and let
$\theta _{p,q}:=\theta |_{E^{p,q}}$
and let
![]() $\theta _{p,q}^{\dagger }:E^{p-1,q+1}\to A^{0,1}(E^{p,q})$
be its adjoint with respect to
$\theta _{p,q}^{\dagger }:E^{p-1,q+1}\to A^{0,1}(E^{p,q})$
be its adjoint with respect to
![]() $h_{p,q}$
. For the Hermitian bundle
$h_{p,q}$
. For the Hermitian bundle
![]() $(F^p, h_p)$
, its curvature is
$(F^p, h_p)$
, its curvature is
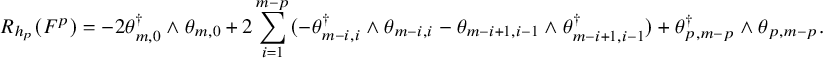 $$ \begin{align*} R_{h_p}(F^p)=- 2\theta_{m,0}^{\dagger}\wedge\theta_{m,0}+ 2\sum_{i=1}^{m-p}(-\theta_{m-i,i}^{\dagger}\wedge \theta_{m-i,i}-\theta_{m-i+1,i-1}\wedge\theta_{m-i+1,i-1}^{\dagger})+\theta_{p,m-p}^{\dagger}\wedge\theta_{p,m-p}. \end{align*} $$
$$ \begin{align*} R_{h_p}(F^p)=- 2\theta_{m,0}^{\dagger}\wedge\theta_{m,0}+ 2\sum_{i=1}^{m-p}(-\theta_{m-i,i}^{\dagger}\wedge \theta_{m-i,i}-\theta_{m-i+1,i-1}\wedge\theta_{m-i+1,i-1}^{\dagger})+\theta_{p,m-p}^{\dagger}\wedge\theta_{p,m-p}. \end{align*} $$
The curvature of the bundle
![]() $(E^{p,q},h_{p,q})$
is
$(E^{p,q},h_{p,q})$
is
By Theorem 1.2, for any point
![]() $x\in D$
there is an admissible coordinate
$x\in D$
there is an admissible coordinate
![]() $(\Omega ;z_1,\ldots ,z_n)$
around x such that the norm
$(\Omega ;z_1,\ldots ,z_n)$
around x such that the norm
holds over
![]() $\Omega ^{*}$
for some constant
$\Omega ^{*}$
for some constant
![]() $C>0$
. Since
$C>0$
. Since
![]() $\theta _{p,q}^{\dagger }$
is the adjoint of
$\theta _{p,q}^{\dagger }$
is the adjoint of
![]() $\theta _{p,q}$
with respect to
$\theta _{p,q}$
with respect to
![]() $h_{p,q}$
, one has
$h_{p,q}$
, one has
![]() $ | \theta ^{\dagger }_{p,q}|_{h,\omega _P}\leq C $
for any p. It follows that
$ | \theta ^{\dagger }_{p,q}|_{h,\omega _P}\leq C $
for any p. It follows that
![]() $|R_{h_p}(F^p)|_{h_{p,q},\omega _P}\leq C'$
and
$|R_{h_p}(F^p)|_{h_{p,q},\omega _P}\leq C'$
and
![]() $| R_{h_{p,q}}(E_{p,q})|_{h_{p,q},\omega _P}\leq C'$
for some
$| R_{h_{p,q}}(E_{p,q})|_{h_{p,q},\omega _P}\leq C'$
for some
![]() $C'>0$
. Hence,
$C'>0$
. Hence,
![]() $(F^p, h_p)$
and
$(F^p, h_p)$
and
![]() $(E^{p,q},h_{p,q})$
are both acceptable.
$(E^{p,q},h_{p,q})$
are both acceptable.
1.4 Adapted to log order
We recall some notions in [Reference Mochizuki7, §2.2.2]. Let X be a complex manifold, D be a simple normal crossing divisor on X and E be a holomorphic vector bundle on
![]() $X\backslash D$
such that
$X\backslash D$
such that
![]() $E|_{X\backslash D}$
is equipped with a Hermitian metric h. Let
$E|_{X\backslash D}$
is equipped with a Hermitian metric h. Let
![]() $\boldsymbol {v}=(v_1,\ldots ,v_r)$
be a smooth frame of
$\boldsymbol {v}=(v_1,\ldots ,v_r)$
be a smooth frame of
![]() $E|_{X\backslash D}$
. We obtain the
$E|_{X\backslash D}$
. We obtain the
![]() $H(r)$
-valued function
$H(r)$
-valued function
![]() $H(h,\boldsymbol {v})$
defined over
$H(h,\boldsymbol {v})$
defined over
![]() $X\backslash D$
, whose
$X\backslash D$
, whose
![]() $(i,j)$
-component is given by
$(i,j)$
-component is given by
![]() $h(v_i,v_j)$
.
$h(v_i,v_j)$
.
Let us consider the case
![]() $X=\mathbb {D}^n$
and
$X=\mathbb {D}^n$
and
![]() $D=\sum _{i=1}^{\ell }D_i$
with
$D=\sum _{i=1}^{\ell }D_i$
with
![]() $D_i=(z_i=0)$
. We have the coordinate
$D_i=(z_i=0)$
. We have the coordinate
![]() $(z_1,\ldots ,z_n)$
. Let h, E and
$(z_1,\ldots ,z_n)$
. Let h, E and
![]() $\boldsymbol {v}$
be as above.
$\boldsymbol {v}$
be as above.
Definition 1.5. A smooth frame
![]() $\boldsymbol {v}$
on
$\boldsymbol {v}$
on
![]() $X\backslash D$
is called adapted up to log order, if the following inequalities hold over
$X\backslash D$
is called adapted up to log order, if the following inequalities hold over
![]() $X\backslash D$
:
$X\backslash D$
:
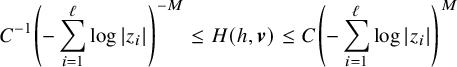 $$ \begin{align*} C^{-1}\left(-\sum_{i=1}^{\ell}\log |z_i|\right)^{-M}\leq H(h,\boldsymbol{v})\leq C\left(-\sum_{i=1}^{\ell}\log |z_i|\right)^{M} \end{align*} $$
$$ \begin{align*} C^{-1}\left(-\sum_{i=1}^{\ell}\log |z_i|\right)^{-M}\leq H(h,\boldsymbol{v})\leq C\left(-\sum_{i=1}^{\ell}\log |z_i|\right)^{M} \end{align*} $$
for some positive numbers M and C.
1.5 Parabolic vector bundles
In this subsection, we recall the notions of parabolic (vector) bundles. For more details, we refer to [Reference Mochizuki6]. Let X be a complex manifold,
![]() $D=\sum _{i=1}^{\ell }D_i$
be a reduced simple normal crossing divisor,
$D=\sum _{i=1}^{\ell }D_i$
be a reduced simple normal crossing divisor,
![]() $U=X\backslash D$
be the complement of D and
$U=X\backslash D$
be the complement of D and
![]() $j:U\to X$
be the inclusion.
$j:U\to X$
be the inclusion.
Definition 1.6. A parabolic bundle
![]() $ \mathcal {P}_{*} E$
on
$ \mathcal {P}_{*} E$
on
![]() $(X, D)$
is a holomorphic vector bundle E on U, together with an
$(X, D)$
is a holomorphic vector bundle E on U, together with an
![]() $\mathbb {R}^{\ell }$
-indexed filtration
$\mathbb {R}^{\ell }$
-indexed filtration
![]() $\mathcal {P}_{\!\boldsymbol {\alpha }}E$
(parabolic structure) by locally free subsheaves of
$\mathcal {P}_{\!\boldsymbol {\alpha }}E$
(parabolic structure) by locally free subsheaves of
![]() $j_{*}E$
such that
$j_{*}E$
such that
-
(i)
 $\boldsymbol {\alpha }\in \mathbb {R}^{\ell }$
and
$\boldsymbol {\alpha }\in \mathbb {R}^{\ell }$
and
 $\mathcal {P}_{\!\boldsymbol {\alpha }}E|_U=E$
.
$\mathcal {P}_{\!\boldsymbol {\alpha }}E|_U=E$
. -
(ii)
 $\mathcal {P}_{\!\boldsymbol {\alpha }} E\subset {\mathcal P}_{\!\boldsymbol {\beta }}E$
if
$\mathcal {P}_{\!\boldsymbol {\alpha }} E\subset {\mathcal P}_{\!\boldsymbol {\beta }}E$
if
 $\alpha _i\leq \beta _i$
for all i.
$\alpha _i\leq \beta _i$
for all i. -
(iii) For
 $1\leq i\leq \ell $
,
$1\leq i\leq \ell $
,
 $\mathcal {P}_{\boldsymbol {\alpha }+\boldsymbol {1}_i}E= \mathcal {P}_{\!\boldsymbol {\alpha }}E\otimes \mathcal O_X(D_i)$
, where
$\mathcal {P}_{\boldsymbol {\alpha }+\boldsymbol {1}_i}E= \mathcal {P}_{\!\boldsymbol {\alpha }}E\otimes \mathcal O_X(D_i)$
, where
 $\boldsymbol {1}_i=(0,\ldots , 1, \ldots , 0)$
with
$\boldsymbol {1}_i=(0,\ldots , 1, \ldots , 0)$
with
 $1$
in the i-th component.
$1$
in the i-th component. -
(iv)
 $\mathcal {P}_{\boldsymbol {\alpha }+\boldsymbol {\varepsilon }}E= \mathcal {P}_{\!\boldsymbol {\alpha }}E$
for any vector
$\mathcal {P}_{\boldsymbol {\alpha }+\boldsymbol {\varepsilon }}E= \mathcal {P}_{\!\boldsymbol {\alpha }}E$
for any vector
 $\boldsymbol {\epsilon }=(\epsilon , \ldots , \epsilon )$
with
$\boldsymbol {\epsilon }=(\epsilon , \ldots , \epsilon )$
with
 $0<\epsilon \ll 1$
.
$0<\epsilon \ll 1$
. -
(v) The set of weights
 $\{\boldsymbol {\alpha } \mid \mathcal {P}_{\!\boldsymbol {\alpha }}E/\mathcal {P}_{\! <\boldsymbol {\alpha }}E\} \not = 0$
is discrete in
$\{\boldsymbol {\alpha } \mid \mathcal {P}_{\!\boldsymbol {\alpha }}E/\mathcal {P}_{\! <\boldsymbol {\alpha }}E\} \not = 0$
is discrete in
 $\mathbb {R}^{\ell }$
.
$\mathbb {R}^{\ell }$
.
1.6 Prolongation via norm growth
Let X be a complex manifold,
![]() $D=\sum _{i=1}^{\ell }D_i$
be a simple normal crossing divisor,
$D=\sum _{i=1}^{\ell }D_i$
be a simple normal crossing divisor,
![]() $U=X\backslash D$
be the complement of D and
$U=X\backslash D$
be the complement of D and
![]() $j:U\to X$
be the inclusion. Let
$j:U\to X$
be the inclusion. Let
![]() $(E,h)$
be a Hermitian vector bundle on U. For any
$(E,h)$
be a Hermitian vector bundle on U. For any
![]() $\boldsymbol {\alpha }=(a_1,\ldots ,a_{\ell })\in \mathbb {R}^{\ell }$
, we can prolong E over X by a sheaf of
$\boldsymbol {\alpha }=(a_1,\ldots ,a_{\ell })\in \mathbb {R}^{\ell }$
, we can prolong E over X by a sheaf of
![]() $\mathcal O_X$
-module
$\mathcal O_X$
-module
![]() $\mathcal {P}_{\!\boldsymbol {\alpha }}E$
as follows:
$\mathcal {P}_{\!\boldsymbol {\alpha }}E$
as follows:
 $$ \begin{align*} \mathcal{P}_{\!\boldsymbol{\alpha}} E(U)=\left\{\sigma\in\Gamma(U\backslash D,E|_{U\backslash D})\mid |\sigma|_h\lesssim {\prod_{i=1}^{\ell}|z_i|^{-\alpha_i-\varepsilon}}\ \ \mbox{for all}\ \varepsilon>0\right\}. \end{align*} $$
$$ \begin{align*} \mathcal{P}_{\!\boldsymbol{\alpha}} E(U)=\left\{\sigma\in\Gamma(U\backslash D,E|_{U\backslash D})\mid |\sigma|_h\lesssim {\prod_{i=1}^{\ell}|z_i|^{-\alpha_i-\varepsilon}}\ \ \mbox{for all}\ \varepsilon>0\right\}. \end{align*} $$
In [Reference Mochizuki8, Theorem 21.3.1], Mochizuki proved that the prolongation of acceptable bundles defined above are parabolic bundles.
Theorem 1.7 (Mochizuki)
Let
![]() $(E,h)$
be an acceptable bundle over
$(E,h)$
be an acceptable bundle over
![]() $X\backslash D$
. Then
$X\backslash D$
. Then
![]() $ \mathcal {P}_{*} E$
defined above is a parabolic bundle.
$ \mathcal {P}_{*} E$
defined above is a parabolic bundle.
1.7 Period domain and period mapping
In this subsection, we quickly review the definitions of period domain and period mapping. We refer the readers to [Reference Carlson, Müller-Stach and Peters1, Reference Klingler, Koziarz and Maubon4, Reference Sabbah and Schnell9] for more details.
Let
![]() $(V=\oplus _{p+q=m}V^{p,q},Q)$
be a polarized complex Hodge structure of weight m defined in §1.1. Recall that the Hodge filtration is defined to be
$(V=\oplus _{p+q=m}V^{p,q},Q)$
be a polarized complex Hodge structure of weight m defined in §1.1. Recall that the Hodge filtration is defined to be
![]() $F^p:=\oplus _{i\geq p}V^{i,m-i}$
. After fixing m and
$F^p:=\oplus _{i\geq p}V^{i,m-i}$
. After fixing m and
![]() $\dim _{\mathbb {C}}F^p$
, the set of all such filtration
$\dim _{\mathbb {C}}F^p$
, the set of all such filtration
![]() $F^{\bullet }$
is a complex flag manifold, which is denoted by
$F^{\bullet }$
is a complex flag manifold, which is denoted by
![]() $\check {\mathscr {D}}$
. It is a closed submanifold of a product of Grassmannians and is thus a projective manifold. The subset
$\check {\mathscr {D}}$
. It is a closed submanifold of a product of Grassmannians and is thus a projective manifold. The subset
![]() $\mathscr {D}$
of all complex polarized Hodge structures are charcterized by
$\mathscr {D}$
of all complex polarized Hodge structures are charcterized by
-
(a)
 $ F^p=F^p\cap (F^{p+1})^{\perp }\oplus F^{p+1}$
.
$ F^p=F^p\cap (F^{p+1})^{\perp }\oplus F^{p+1}$
. -
(b)
 $(-1)^pQ$
is positive definite over
$(-1)^pQ$
is positive definite over
 $F^p\cap (F^{p+1})^{\perp }$
.
$F^p\cap (F^{p+1})^{\perp }$
.
It is an open submanifold of
![]() $\check {\mathscr {D}}$
. We usually write F instead of
$\check {\mathscr {D}}$
. We usually write F instead of
![]() $F^{\bullet }$
to lighten the notation. Since the groups
$F^{\bullet }$
to lighten the notation. Since the groups
![]() $\mathrm {GL}(V)$
and
$\mathrm {GL}(V)$
and
![]() $G:=U(V,Q)$
act transitively on
$G:=U(V,Q)$
act transitively on
![]() $\check {\mathscr {D}}$
and
$\check {\mathscr {D}}$
and
![]() $\mathscr {D}$
, respectively,
$\mathscr {D}$
, respectively,
![]() $\check {\mathscr {D}}$
and
$\check {\mathscr {D}}$
and
![]() $\mathscr {D}$
are thus homogeneous spaces.
$\mathscr {D}$
are thus homogeneous spaces.
For any Hodge structure
![]() $F\in \check {\mathscr {D}}$
, the holomorphic tangent space
$F\in \check {\mathscr {D}}$
, the holomorphic tangent space
![]() $T_{\check {\mathscr {D}},F}$
of
$T_{\check {\mathscr {D}},F}$
of
![]() $\check {\mathscr {D}}$
at F is identified with
$\check {\mathscr {D}}$
at F is identified with
For any
![]() $A\in \mathrm {\small End}(V)$
, we denote by
$A\in \mathrm {\small End}(V)$
, we denote by
![]() $[A]_F$
its image in
$[A]_F$
its image in
![]() $T_{\check {\mathscr {D}},F} $
.
$T_{\check {\mathscr {D}},F} $
.
A tangent vector
![]() $[A]_F$
in
$[A]_F$
in
![]() $T_{\check {\mathscr {D}},F}$
is called horizontal if
$T_{\check {\mathscr {D}},F}$
is called horizontal if
![]() $A(F^p)\subset F^{p-1}$
for all p. The subbundle of
$A(F^p)\subset F^{p-1}$
for all p. The subbundle of
![]() $T_{\check {\mathscr {D}}}$
consisting of horizontal vectors is denoted by
$T_{\check {\mathscr {D}}}$
consisting of horizontal vectors is denoted by
![]() $T_{\check {\mathscr {D}}}^{-1,1}$
, and one can show that it is a holomorphic subbundle of
$T_{\check {\mathscr {D}}}^{-1,1}$
, and one can show that it is a holomorphic subbundle of
![]() $T_{\check {\mathscr {D}}}$
. A holomorphic map
$T_{\check {\mathscr {D}}}$
. A holomorphic map
![]() $f:\Omega \to \check {\mathscr {D}}$
from a complex manifold
$f:\Omega \to \check {\mathscr {D}}$
from a complex manifold
![]() $\Omega $
is called horizontal if
$\Omega $
is called horizontal if
![]() $df: T_{\Omega }\to f^{*}T_{\check {\mathscr {D}}}$
factors through
$df: T_{\Omega }\to f^{*}T_{\check {\mathscr {D}}}$
factors through
![]() $f^{*}T_{\check {\mathscr {D}}}^{-1,1}$
.
$f^{*}T_{\check {\mathscr {D}}}^{-1,1}$
.
A complex (unpolarized) variation of Hodge structure
![]() $(V=\oplus _{p+q=m},\nabla )$
over a complex manifold
$(V=\oplus _{p+q=m},\nabla )$
over a complex manifold
![]() $\Omega $
induces a horizontal holomorphic map
$\Omega $
induces a horizontal holomorphic map
![]() $\Phi : \tilde {\Omega }\to \check {\mathscr {D}}$
by the Griffiths’ transversality, where
$\Phi : \tilde {\Omega }\to \check {\mathscr {D}}$
by the Griffiths’ transversality, where
![]() $\tilde {\Omega }$
is the universal cover of
$\tilde {\Omega }$
is the universal cover of
![]() $\Omega $
. Here, we choose the reference space of
$\Omega $
. Here, we choose the reference space of
![]() $\check {\mathscr {D}}$
to be the space of multivalued flat sections
$\check {\mathscr {D}}$
to be the space of multivalued flat sections
![]() $V^{\nabla }$
.
$V^{\nabla }$
.
![]() $\Phi $
is called the period mapping associated to
$\Phi $
is called the period mapping associated to
![]() $(V,\nabla ,F^{\bullet })$
. When this complex variation of Hodge structure is moreover polarized,
$(V,\nabla ,F^{\bullet })$
. When this complex variation of Hodge structure is moreover polarized,
![]() $\Phi $
factors through
$\Phi $
factors through
![]() $\mathscr {D}$
.
$\mathscr {D}$
.
2 Nilpotent orbit theorem
2.1 Two results of
 $L^2$
-estimate
$L^2$
-estimate
Set
![]() $X=\Delta ^n$
and
$X=\Delta ^n$
and
![]() $D=(z_1\cdots z_{\ell }=0)$
. We equip the complement
$D=(z_1\cdots z_{\ell }=0)$
. We equip the complement
![]() $U:=X\backslash D$
with the Poincaré metric
$U:=X\backslash D$
with the Poincaré metric
![]() $\omega _P$
defined in Equation (1.3). Write
$\omega _P$
defined in Equation (1.3). Write
Lemma 2.1. Let
![]() $(F, h_F)$
be a Hermitian vector bundle on U such that
$(F, h_F)$
be a Hermitian vector bundle on U such that
![]() $|R_{h_F}(F)|\leq C\omega _P$
for some constant
$|R_{h_F}(F)|\leq C\omega _P$
for some constant
![]() $C>0$
. Then for any section
$C>0$
. Then for any section
![]() $\eta \in \mathscr {C}^{\infty }(U, \Lambda ^{0,1}T_U^{*}\otimes F)$
such that
$\eta \in \mathscr {C}^{\infty }(U, \Lambda ^{0,1}T_U^{*}\otimes F)$
such that
![]() $|\eta |_{h_F,\omega _P}\lesssim \prod _{j=1}^{\ell }|z_j|^{\varepsilon }$
for some
$|\eta |_{h_F,\omega _P}\lesssim \prod _{j=1}^{\ell }|z_j|^{\varepsilon }$
for some
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $\bar {\partial }\eta =0$
, there exists
$\bar {\partial }\eta =0$
, there exists
![]() $\sigma \in \mathscr {C}^{\infty }(U, F)$
such that
$\sigma \in \mathscr {C}^{\infty }(U, F)$
such that
![]() $\bar {\partial } \sigma =\eta $
and
$\bar {\partial } \sigma =\eta $
and
 $$ \begin{align*} \int_{U} |\sigma|^2_{h_F} \prod_{j=1}^{\ell}(-\log |z_j|^2)^{N} d\mbox{vol}_{\omega_P}<\infty \end{align*} $$
$$ \begin{align*} \int_{U} |\sigma|^2_{h_F} \prod_{j=1}^{\ell}(-\log |z_j|^2)^{N} d\mbox{vol}_{\omega_P}<\infty \end{align*} $$
for some
![]() $N\gg 1$
.
$N\gg 1$
.
Proof. For the line bundle
![]() $K_U^{-1}$
endowed with the natural metric g induced by
$K_U^{-1}$
endowed with the natural metric g induced by
![]() $\omega _P$
, it is acceptable. Hence, for the Hermitian vector bundle
$\omega _P$
, it is acceptable. Hence, for the Hermitian vector bundle
![]() $(E, h):=(K_U^{-1}\otimes F, g\cdot h_F)$
, it is also acceptable. It follows from [Reference Deng and Hao3, Lemma 1.10] that one can choose
$(E, h):=(K_U^{-1}\otimes F, g\cdot h_F)$
, it is also acceptable. It follows from [Reference Deng and Hao3, Lemma 1.10] that one can choose
![]() $N\gg 1$
such that
$N\gg 1$
such that
where “
![]() $\geq _{Nak}$
” stands for Nakano semipositive (see [Reference Demailly2, Définition 2.2]). For the function
$\geq _{Nak}$
” stands for Nakano semipositive (see [Reference Demailly2, Définition 2.2]). For the function
 $$ \begin{align} \varphi:=\log \left(\prod_{j=1}^{\ell}(-\log |z_j|^2)^{-1} \cdot \prod_{k=\ell+1}^{n}\exp(|z_k|^2)\right), \end{align} $$
$$ \begin{align} \varphi:=\log \left(\prod_{j=1}^{\ell}(-\log |z_j|^2)^{-1} \cdot \prod_{k=\ell+1}^{n}\exp(|z_k|^2)\right), \end{align} $$
one has
![]() $ i\partial \bar {\partial } \log \varphi =\omega _P. $
For any
$ i\partial \bar {\partial } \log \varphi =\omega _P. $
For any
![]() $k\in \mathbb {Z}$
, we define a new metric
$k\in \mathbb {Z}$
, we define a new metric
![]() $h(k)=h\cdot e^{-k\varphi }$
for E. Therefore,
$h(k)=h\cdot e^{-k\varphi }$
for E. Therefore,
Note that
![]() $\mathscr {C}^{\infty }(U, \Lambda ^{n,1}T_U^{*}\otimes E)=\mathscr {C}^{\infty }(U, \Lambda ^{0,1}T_U^{*}\otimes F)$
with
$\mathscr {C}^{\infty }(U, \Lambda ^{n,1}T_U^{*}\otimes E)=\mathscr {C}^{\infty }(U, \Lambda ^{0,1}T_U^{*}\otimes F)$
with
![]() $|\eta |_{h,\omega _P}=|\eta |_{h_F,\omega _P}$
. Since
$|\eta |_{h,\omega _P}=|\eta |_{h_F,\omega _P}$
. Since
![]() $|\eta |_{h_F,\omega _P}\lesssim \prod _{j=1}^{\ell }|z_j|^{\varepsilon }$
,
$|\eta |_{h_F,\omega _P}\lesssim \prod _{j=1}^{\ell }|z_j|^{\varepsilon }$
,
![]() $|\eta |_{h(N),\omega _P}\leq C'$
for some
$|\eta |_{h(N),\omega _P}\leq C'$
for some
![]() $C'>0$
. Hence,
$C'>0$
. Hence,
![]() $\lVert \eta \rVert _{h(N), \omega _P}<\infty $
. Thanks to the Demailly–Hörmander
$\lVert \eta \rVert _{h(N), \omega _P}<\infty $
. Thanks to the Demailly–Hörmander
![]() $L^2$
-estimate [Reference Demailly2, Théorème 4.1 and Remarque 4.2], there exists
$L^2$
-estimate [Reference Demailly2, Théorème 4.1 and Remarque 4.2], there exists
![]() $ \sigma \in \mathscr {C}^{\infty }(U, K_U\otimes E)= \mathscr {C}^{\infty }(U, F)$
such that
$ \sigma \in \mathscr {C}^{\infty }(U, K_U\otimes E)= \mathscr {C}^{\infty }(U, F)$
such that
![]() $ \bar {\partial } \sigma =\eta $
and
$ \bar {\partial } \sigma =\eta $
and
![]() $\lVert \sigma \rVert _{h(N)}<\infty $
. Here, we note that the smoothness of
$\lVert \sigma \rVert _{h(N)}<\infty $
. Here, we note that the smoothness of
![]() $\sigma $
follows from the elliptic regularity of the Laplacian. The lemma is proved.
$\sigma $
follows from the elliptic regularity of the Laplacian. The lemma is proved.
Lemma 2.2. Let
![]() $(E, h)$
be a Hermitian vector bundle on U such that
$(E, h)$
be a Hermitian vector bundle on U such that
![]() $|R_{h}(E)|\leq C\omega _P$
for some constant
$|R_{h}(E)|\leq C\omega _P$
for some constant
![]() $C>0$
. Assume that
$C>0$
. Assume that
![]() $\sigma \in H^0(U,E)$
such that
$\sigma \in H^0(U,E)$
such that
![]() $\lVert \sigma \rVert _{h(N)}<\infty $
for some integer
$\lVert \sigma \rVert _{h(N)}<\infty $
for some integer
![]() $N\geq 1$
, where
$N\geq 1$
, where
![]() $h(N):=h\cdot e^{-N\varphi }$
with
$h(N):=h\cdot e^{-N\varphi }$
with
![]() $\varphi $
defined in Equation (2.2), then over
$\varphi $
defined in Equation (2.2), then over
![]() $U(\frac {1}{2})$
,
$U(\frac {1}{2})$
,
![]() $|\sigma |_{h}\lesssim \prod _{j=1}^{\ell }|z_j|^{-\varepsilon }$
for any
$|\sigma |_{h}\lesssim \prod _{j=1}^{\ell }|z_j|^{-\varepsilon }$
for any
![]() $\varepsilon>0$
.
$\varepsilon>0$
.
Proof. Since
![]() $|R_{h}(E)|\leq C\omega _P$
for some constant
$|R_{h}(E)|\leq C\omega _P$
for some constant
![]() $C>0$
, it follows from [Reference Deng and Hao3, Lemma 1.10] that
$C>0$
, it follows from [Reference Deng and Hao3, Lemma 1.10] that
![]() $(E,h(-N'))$
is Griffiths’ seminegative for some
$(E,h(-N'))$
is Griffiths’ seminegative for some
![]() $N'\gg 1$
, where
$N'\gg 1$
, where
![]() $h(-N'):=h\cdot e^{N'\varphi }$
with
$h(-N'):=h\cdot e^{N'\varphi }$
with
![]() $\varphi $
defined in Equation (2.2). One can show that
$\varphi $
defined in Equation (2.2). One can show that
![]() $\log |\sigma |^2_{h(-N')}$
is a plurisubharmonic function. For any
$\log |\sigma |^2_{h(-N')}$
is a plurisubharmonic function. For any
![]() $z\in U^{*}(\frac {1}{2})$
, one has
$z\in U^{*}(\frac {1}{2})$
, one has
 $$ \begin{align*} \log |\sigma(z)|^2_{h(-N')}&\leqslant \frac{4^n}{\pi^n \prod_{i=1}^{\ell}|z_i|^2}\int_{\Omega_z} \log |\sigma(w)|^2_{h(-N')}d\mbox{vol}_{g}\\ &\leqslant \log \left(\frac{4^n}{\pi^n \prod_{i=1}^{\ell}|z_i|^2}\cdot \int_{\Omega_z} |\sigma(w)|^2_{h(-N')}d\mbox{vol}_{g}\right)\\ &\leqslant \log \left(C \int_{\Omega_z} \frac{1}{ \prod_{i=1}^{\ell}|w_i|^2}|\sigma(w)|^2_{h(-N')}d\mbox{vol}_{g}\right)\\ &\leqslant C_1+ \log \int_{\Omega_z} |\sigma(w)|^2_{h(-N')}\cdot |\prod_{i=1}^{\ell}(\log |w_i|^2)^2| d\mbox{vol}_{\omega_P}\\ & \leqslant C_2+\log \int_{\Omega_z} |\sigma(w)|^2_{h(N)}d\mbox{vol}_{\omega_P}\\ &\leqslant C_2+\log \lVert \sigma\rVert_{h(N)}^2, \end{align*} $$
$$ \begin{align*} \log |\sigma(z)|^2_{h(-N')}&\leqslant \frac{4^n}{\pi^n \prod_{i=1}^{\ell}|z_i|^2}\int_{\Omega_z} \log |\sigma(w)|^2_{h(-N')}d\mbox{vol}_{g}\\ &\leqslant \log \left(\frac{4^n}{\pi^n \prod_{i=1}^{\ell}|z_i|^2}\cdot \int_{\Omega_z} |\sigma(w)|^2_{h(-N')}d\mbox{vol}_{g}\right)\\ &\leqslant \log \left(C \int_{\Omega_z} \frac{1}{ \prod_{i=1}^{\ell}|w_i|^2}|\sigma(w)|^2_{h(-N')}d\mbox{vol}_{g}\right)\\ &\leqslant C_1+ \log \int_{\Omega_z} |\sigma(w)|^2_{h(-N')}\cdot |\prod_{i=1}^{\ell}(\log |w_i|^2)^2| d\mbox{vol}_{\omega_P}\\ & \leqslant C_2+\log \int_{\Omega_z} |\sigma(w)|^2_{h(N)}d\mbox{vol}_{\omega_P}\\ &\leqslant C_2+\log \lVert \sigma\rVert_{h(N)}^2, \end{align*} $$
where
![]() $\Omega _z:=\{w\in U^{*}\mid |w_i-z_i|\leq \frac {|z_i|}{2} \mbox { for } i\leq \ell; |w_i-z_i|\leq \frac {1}{2} \mbox { for } i>\ell \}$
and g is the Euclidean metric.
$\Omega _z:=\{w\in U^{*}\mid |w_i-z_i|\leq \frac {|z_i|}{2} \mbox { for } i\leq \ell; |w_i-z_i|\leq \frac {1}{2} \mbox { for } i>\ell \}$
and g is the Euclidean metric.
![]() $C_1, C_2 $
are two positive constants which do not depend on
$C_1, C_2 $
are two positive constants which do not depend on
![]() $z\in U^{*}(\frac {1}{2})$
. The first inequality is due to the mean value inequality, and the second one follows from the Jensen inequality. It follows that
$z\in U^{*}(\frac {1}{2})$
. The first inequality is due to the mean value inequality, and the second one follows from the Jensen inequality. It follows that
 $$ \begin{align*} |\sigma(z)|_{h}&=|\sigma(z)|_{h(-N')}\cdot \left(\prod_{j=1}^{\ell}(-\log |z_j|^2)^{\frac{N'}{2}} \cdot \prod_{k=\ell+1}^{n}\exp(|z_k|^2)^{-\frac{N'}{2}}\right) \\ &\leq \exp\left(\frac{C_2}{2}\right)\cdot \lVert \sigma\rVert_{h(N)}\cdot \left(\prod_{j=1}^{\ell}(-\log |z_j|^2)^{\frac{N'}{2}} \cdot \prod_{k=\ell+1}^{n}\exp(|z_k|^2)^{-\frac{N'}{2}}\right)\lesssim \prod_{i=1}^{\ell}|z_i|^{-\varepsilon} \end{align*} $$
$$ \begin{align*} |\sigma(z)|_{h}&=|\sigma(z)|_{h(-N')}\cdot \left(\prod_{j=1}^{\ell}(-\log |z_j|^2)^{\frac{N'}{2}} \cdot \prod_{k=\ell+1}^{n}\exp(|z_k|^2)^{-\frac{N'}{2}}\right) \\ &\leq \exp\left(\frac{C_2}{2}\right)\cdot \lVert \sigma\rVert_{h(N)}\cdot \left(\prod_{j=1}^{\ell}(-\log |z_j|^2)^{\frac{N'}{2}} \cdot \prod_{k=\ell+1}^{n}\exp(|z_k|^2)^{-\frac{N'}{2}}\right)\lesssim \prod_{i=1}^{\ell}|z_i|^{-\varepsilon} \end{align*} $$
for any
![]() $\varepsilon>0$
.
$\varepsilon>0$
.
2.2 Proof of Theorem A
We first prove that the Deligne extension of the flat bundle underlying a complex variation of Hodge structure coincides with the prolongation defined in §1.6.
Proposition 2.3. Let X be a complex manifold,
![]() $D=\sum _{i=1}^{\ell }D_i$
be a simple normal crossing divisor. For a complex variation of Hodge structure
$D=\sum _{i=1}^{\ell }D_i$
be a simple normal crossing divisor. For a complex variation of Hodge structure
![]() $(V,\nabla ,F^{\bullet },h)$
defined on
$(V,\nabla ,F^{\bullet },h)$
defined on
![]() $U:=X\backslash D$
, one has
$U:=X\backslash D$
, one has
![]() $V_{\boldsymbol {\alpha }}^{\mathrm {Del}}=\mathcal {P}_{\! \boldsymbol {\alpha }}V$
for any multi-index
$V_{\boldsymbol {\alpha }}^{\mathrm {Del}}=\mathcal {P}_{\! \boldsymbol {\alpha }}V$
for any multi-index
![]() $\boldsymbol {\alpha }\in \mathbb {R}^{\ell }$
, where
$\boldsymbol {\alpha }\in \mathbb {R}^{\ell }$
, where
![]() $\mathcal {P}_{\! \boldsymbol {\alpha }}V$
is the prolongation of V defined in §1.6.
$\mathcal {P}_{\! \boldsymbol {\alpha }}V$
is the prolongation of V defined in §1.6.
Proof.
Step 1: We prove that
![]() $V_{\boldsymbol {\alpha }}^{\mathrm {Del}}\subset \mathcal {P}_{\! \boldsymbol {\alpha }}V$
. We will use the notation in §1.2. Since this is a local problem, we can assume that
$V_{\boldsymbol {\alpha }}^{\mathrm {Del}}\subset \mathcal {P}_{\! \boldsymbol {\alpha }}V$
. We will use the notation in §1.2. Since this is a local problem, we can assume that
![]() $X=\Delta ^n$
and
$X=\Delta ^n$
and
![]() $D=(t_1\cdots t_p=0)$
. By the construction of
$D=(t_1\cdots t_p=0)$
. By the construction of
![]() $V_{\boldsymbol {\alpha }}^{\mathrm {Del}}$
, one can take a basis
$V_{\boldsymbol {\alpha }}^{\mathrm {Del}}$
, one can take a basis
![]() $v_1,\ldots ,v_r$
of
$v_1,\ldots ,v_r$
of
![]() $V^{\nabla }$
with each
$V^{\nabla }$
with each
![]() $v_i\in \mathbb {E}_{\boldsymbol {\lambda }(v_i)}$
for some
$v_i\in \mathbb {E}_{\boldsymbol {\lambda }(v_i)}$
for some
![]() $\boldsymbol {\lambda }(v_i)\in Sp$
such that
$\boldsymbol {\lambda }(v_i)\in Sp$
such that
![]() $\{\tilde {v}_1,\ldots ,\tilde {v}_r\}$
defined in Equation (1.2) forms a basis of
$\{\tilde {v}_1,\ldots ,\tilde {v}_r\}$
defined in Equation (1.2) forms a basis of
![]() $V_{\boldsymbol {\alpha }}^{\mathrm {Del}}$
. It thus suffices to estimate the norm
$V_{\boldsymbol {\alpha }}^{\mathrm {Del}}$
. It thus suffices to estimate the norm
 $$ \begin{align*} \tilde{v}(t):=\exp\left(- \sum_{i=1}^{p}( \beta_iI+N_i)\cdot \log t_i \right)v(t) = \prod_{i=1}^{p}t_i^{-\beta_i}\exp\left(- \sum_{i=1}^{p}N_i\cdot \log t_i \right)v(t) \end{align*} $$
$$ \begin{align*} \tilde{v}(t):=\exp\left(- \sum_{i=1}^{p}( \beta_iI+N_i)\cdot \log t_i \right)v(t) = \prod_{i=1}^{p}t_i^{-\beta_i}\exp\left(- \sum_{i=1}^{p}N_i\cdot \log t_i \right)v(t) \end{align*} $$
for any
![]() $\boldsymbol {\lambda }$
and
$\boldsymbol {\lambda }$
and
![]() $v\in \mathbb {E}_{\boldsymbol {\lambda }}$
.
$v\in \mathbb {E}_{\boldsymbol {\lambda }}$
.
By the weaker norm estimate in [Reference Mochizuki7, Lemma 9.31] for general harmonic bundles, there exists a frame
![]() $v_1,\ldots ,v_r$
of
$v_1,\ldots ,v_r$
of
![]() $V^{\nabla }$
with each
$V^{\nabla }$
with each
![]() $v_i\in \mathbb {E}_{\boldsymbol {\lambda }(v_i)}$
and
$v_i\in \mathbb {E}_{\boldsymbol {\lambda }(v_i)}$
and
![]() $\{a_{ij}\}_{i=1,\ldots ,r; j=1,\ldots ,p}\subset \mathbb {R}$
such that if we put
$\{a_{ij}\}_{i=1,\ldots ,r; j=1,\ldots ,p}\subset \mathbb {R}$
such that if we put
![]() $ {v}^{\prime }_i:=v_i\cdot \prod _{j=1}^{p}|t_j|^{-a_{ij}}, $
then for the multivalued smooth sections
$ {v}^{\prime }_i:=v_i\cdot \prod _{j=1}^{p}|t_j|^{-a_{ij}}, $
then for the multivalued smooth sections
![]() ${\boldsymbol {v}}'=({v}^{\prime }_1,\ldots , {v}^{\prime }_r)$
, over a given sector of U one has the norm estimate
${\boldsymbol {v}}'=({v}^{\prime }_1,\ldots , {v}^{\prime }_r)$
, over a given sector of U one has the norm estimate
 $$ \begin{align} \left(\prod_{i=1}^p|\log |t_i||\right)^{-M}\lesssim H(h, {\boldsymbol{v}'}) \lesssim \left(\prod_{i=1}^p|\log |t_i||\right)^M \end{align} $$
$$ \begin{align} \left(\prod_{i=1}^p|\log |t_i||\right)^{-M}\lesssim H(h, {\boldsymbol{v}'}) \lesssim \left(\prod_{i=1}^p|\log |t_i||\right)^M \end{align} $$
for some
![]() $M>0$
. Here, h is the Hodge metric and
$M>0$
. Here, h is the Hodge metric and
![]() $H(h, {\boldsymbol {v}'}) $
is the
$H(h, {\boldsymbol {v}'}) $
is the
![]() $H(r)$
-valued function defined in §1.4.
$H(r)$
-valued function defined in §1.4.
Fix some
![]() $\{t_1,\ldots ,t_{p}\}\subset \Delta ^{*}$
. For each
$\{t_1,\ldots ,t_{p}\}\subset \Delta ^{*}$
. For each
![]() $\ell =1,\ldots ,p$
, over any sector of
$\ell =1,\ldots ,p$
, over any sector of
![]() $\Delta ^{*}$
, we have
$\Delta ^{*}$
, we have
by the Hodge norm estimate in one-dimensional case in [Reference Sabbah and Schnell9, Reference Simpson11]. Together with Equation (2.3), it implies that
![]() $a_{ij}=0$
for all
$a_{ij}=0$
for all
![]() ${i=1,\ldots ,r; j=1,\ldots ,\ell }$
. Therefore, we conclude that over a given sector of U one has the norm estimate
${i=1,\ldots ,r; j=1,\ldots ,\ell }$
. Therefore, we conclude that over a given sector of U one has the norm estimate
 $$ \begin{align} \left(\prod_{i=1}^p|\log |t_i||\right)^{-M}\lesssim H(h,{\boldsymbol{v}}) \lesssim \left(\prod_{i=1}^p|\log |t_i||\right)^M. \end{align} $$
$$ \begin{align} \left(\prod_{i=1}^p|\log |t_i||\right)^{-M}\lesssim H(h,{\boldsymbol{v}}) \lesssim \left(\prod_{i=1}^p|\log |t_i||\right)^M. \end{align} $$
Then for any multivalued flat section
![]() $v\in V^{\nabla }$
, over any given sector of U one has
$v\in V^{\nabla }$
, over any given sector of U one has
 $$ \begin{align*}\left(\prod_{i=1}^p|\log |t_i||\right)^{-M}\lesssim|v(t)|_h\lesssim \left(\prod_{i=1}^p|\log |t_i||\right)^M\end{align*} $$
$$ \begin{align*}\left(\prod_{i=1}^p|\log |t_i||\right)^{-M}\lesssim|v(t)|_h\lesssim \left(\prod_{i=1}^p|\log |t_i||\right)^M\end{align*} $$
for some
![]() $M>0$
. Since all
$M>0$
. Since all
![]() $N_i$
are nilpotent and pairwise commute,
$N_i$
are nilpotent and pairwise commute,
 $$ \begin{align*}\exp\left(- \sum_{i=1}^{p}N_i\cdot \log t_i \right)v(t)=\sum_{i=1}^{p}\sum_{k=0}^{N}\frac{1}{k!}(\log t_i)^k(N_i^k v)(t) \end{align*} $$
$$ \begin{align*}\exp\left(- \sum_{i=1}^{p}N_i\cdot \log t_i \right)v(t)=\sum_{i=1}^{p}\sum_{k=0}^{N}\frac{1}{k!}(\log t_i)^k(N_i^k v)(t) \end{align*} $$
for some integer
![]() $N>0$
. Note that if
$N>0$
. Note that if
![]() $v\in \mathbb {E}_{\boldsymbol {\lambda }}$
, we also have
$v\in \mathbb {E}_{\boldsymbol {\lambda }}$
, we also have
![]() $N_i^k v\in \mathbb {E}_{\boldsymbol {\lambda }} $
for any
$N_i^k v\in \mathbb {E}_{\boldsymbol {\lambda }} $
for any
![]() $k\geq 0$
. Since one can cover
$k\geq 0$
. Since one can cover
![]() $X\backslash D$
by finitely many sectors, this proves the norm estimate
$X\backslash D$
by finitely many sectors, this proves the norm estimate
 $$ \begin{align*}|\exp\left(- \sum_{i=1}^{p}N_i\cdot \log t_i \right)v(t)|_h\lesssim \left(\prod_{i=1}^p|\log |t_i||\right)^{M'} \end{align*} $$
$$ \begin{align*}|\exp\left(- \sum_{i=1}^{p}N_i\cdot \log t_i \right)v(t)|_h\lesssim \left(\prod_{i=1}^p|\log |t_i||\right)^{M'} \end{align*} $$
for some
![]() $M'>0$
. Hence,
$M'>0$
. Hence,
 $$ \begin{align*} |\tilde{v}(t)|_h \lesssim \prod_{i=1}^{p}|t_i|^{-\beta_i-\varepsilon}\lesssim\prod_{i=1}^{p}|t_i|^{-\alpha_i-\varepsilon} \end{align*} $$
$$ \begin{align*} |\tilde{v}(t)|_h \lesssim \prod_{i=1}^{p}|t_i|^{-\beta_i-\varepsilon}\lesssim\prod_{i=1}^{p}|t_i|^{-\alpha_i-\varepsilon} \end{align*} $$
for any
![]() $\varepsilon>0.$
This proves the inclusion
$\varepsilon>0.$
This proves the inclusion
![]() $V_{\boldsymbol {\alpha }}^{\mathrm {Del}}\subset \mathcal {P}_{\! \boldsymbol {\alpha }}V$
by the definition of
$V_{\boldsymbol {\alpha }}^{\mathrm {Del}}\subset \mathcal {P}_{\! \boldsymbol {\alpha }}V$
by the definition of
![]() $\mathcal {P}_{\!\boldsymbol {\alpha }} V$
in §1.6.
$\mathcal {P}_{\!\boldsymbol {\alpha }} V$
in §1.6.
Step 2: We prove that
![]() $\mathcal {P}_{\! \boldsymbol {\alpha }}V\subset V_{\boldsymbol {\alpha }}^{\mathrm {Del}}$
. First, we note that the decomposition
$\mathcal {P}_{\! \boldsymbol {\alpha }}V\subset V_{\boldsymbol {\alpha }}^{\mathrm {Del}}$
. First, we note that the decomposition
![]() $V^{\nabla }=\oplus _{\boldsymbol {\lambda }\in Sp}\mathbb {E}_{\boldsymbol {\lambda }}$
induces a decomposition of the flat bundle
$V^{\nabla }=\oplus _{\boldsymbol {\lambda }\in Sp}\mathbb {E}_{\boldsymbol {\lambda }}$
induces a decomposition of the flat bundle
![]() $(V,\nabla )$
into
$(V,\nabla )$
into
where
![]() $(V(\boldsymbol {\lambda }), \nabla |_{V(\boldsymbol {\lambda })})$
is the flat subbundle induced by
$(V(\boldsymbol {\lambda }), \nabla |_{V(\boldsymbol {\lambda })})$
is the flat subbundle induced by
![]() $\mathbb {E}_{\boldsymbol {\lambda }}$
. We fix a basis
$\mathbb {E}_{\boldsymbol {\lambda }}$
. We fix a basis
![]() $(v_1,\ldots ,v_r)\in V^{\nabla }$
such that
$(v_1,\ldots ,v_r)\in V^{\nabla }$
such that
![]() $v_i\in \mathbb {E}_{\boldsymbol {\lambda }(v_i)}$
for some
$v_i\in \mathbb {E}_{\boldsymbol {\lambda }(v_i)}$
for some
![]() $\boldsymbol {\lambda }(v_i) \in Sp$
. This means that such basis is compatible with the above decomposition (2.5); namely,
$\boldsymbol {\lambda }(v_i) \in Sp$
. This means that such basis is compatible with the above decomposition (2.5); namely,
![]() $v_j$
is a mutivalued flat section of
$v_j$
is a mutivalued flat section of
![]() $(V(\boldsymbol {\lambda }(v_j)), \nabla |_{V(\boldsymbol {\lambda }(v_j))})$
. Consider the dual bundle
$(V(\boldsymbol {\lambda }(v_j)), \nabla |_{V(\boldsymbol {\lambda }(v_j))})$
. Consider the dual bundle
![]() $V^{*}$
of V, and it can endowed with the natural connection
$V^{*}$
of V, and it can endowed with the natural connection
![]() $\nabla $
defined by
$\nabla $
defined by
for
![]() $\mu $
and v sections in
$\mu $
and v sections in
![]() $V^{*}$
and V, respectively.
$V^{*}$
and V, respectively.
![]() $(V^{*},\nabla )$
is thus also a flat bundle. Moreover,
$(V^{*},\nabla )$
is thus also a flat bundle. Moreover,
![]() $(V^{*})^{\nabla }$
is the dual space of
$(V^{*})^{\nabla }$
is the dual space of
![]() $(V^{\nabla })$
. Consider the dual basis
$(V^{\nabla })$
. Consider the dual basis
![]() $(v_1^{*},\ldots ,v^{*}_r)$
of
$(v_1^{*},\ldots ,v^{*}_r)$
of
![]() $(v_1,\ldots ,v_r)$
. Since
$(v_1,\ldots ,v_r)$
. Since
one has
![]() $v_i^{*}\in (V^{*})^{\nabla }$
. Recall that
$v_i^{*}\in (V^{*})^{\nabla }$
. Recall that
![]() $T_j$
is the monodromy transformation of
$T_j$
is the monodromy transformation of
![]() $(V,\nabla )$
with respect to
$(V,\nabla )$
with respect to
![]() $\gamma _j$
defined by
$\gamma _j$
defined by
for any
![]() $v\in V^{\nabla }$
. Let us denote by
$v\in V^{\nabla }$
. Let us denote by
![]() $\tilde {T}_j$
the monodromy transformation of
$\tilde {T}_j$
the monodromy transformation of
![]() $(V,\nabla )$
with respect to
$(V,\nabla )$
with respect to
![]() $\gamma _j$
defined by
$\gamma _j$
defined by
for any
![]() $\mu \in (V^{*})^{\nabla }$
. Then for any
$\mu \in (V^{*})^{\nabla }$
. Then for any
![]() $v\in V^{\nabla }$
and any
$v\in V^{\nabla }$
and any
![]() $\mu \in (V^{*})^{\nabla }$
one has
$\mu \in (V^{*})^{\nabla }$
one has
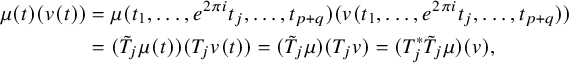 $$ \begin{align*} \mu(t)(v(t))&=\mu(t_1,\ldots,e^{2\pi i}t_j,\ldots,t_{p+q})(v(t_1,\ldots,e^{2\pi i}t_j,\ldots,t_{p+q}))\\ &=(\tilde{T}_j\mu(t))(T_jv(t))=(\tilde{T}_j\mu)(T_j v)=(T_j^{*}\tilde{T}_j \mu)(v), \end{align*} $$
$$ \begin{align*} \mu(t)(v(t))&=\mu(t_1,\ldots,e^{2\pi i}t_j,\ldots,t_{p+q})(v(t_1,\ldots,e^{2\pi i}t_j,\ldots,t_{p+q}))\\ &=(\tilde{T}_j\mu(t))(T_jv(t))=(\tilde{T}_j\mu)(T_j v)=(T_j^{*}\tilde{T}_j \mu)(v), \end{align*} $$
where
![]() $T_j^{*}:(V^{*})^{\nabla }\to (V^{*})^{\nabla }$
is the adjoint of
$T_j^{*}:(V^{*})^{\nabla }\to (V^{*})^{\nabla }$
is the adjoint of
![]() $T_j$
. Hence
$T_j$
. Hence
It follows that
![]() $Sp(\tilde {T}_j)=\{\lambda ^{-1} \}_{\lambda \in Sp(T_i)}$
. Set
$Sp(\tilde {T}_j)=\{\lambda ^{-1} \}_{\lambda \in Sp(T_i)}$
. Set
![]() $\mathbb {E}(\tilde {T}_j,\lambda _j)\subset (V^{*})^{\nabla }$
to be the corresponding eigenspace of
$\mathbb {E}(\tilde {T}_j,\lambda _j)\subset (V^{*})^{\nabla }$
to be the corresponding eigenspace of
![]() $\lambda _j\in Sp(\tilde {T}_j)$
. We know that all
$\lambda _j\in Sp(\tilde {T}_j)$
. We know that all
![]() $\lambda _j\in Sp(\tilde {T}_j)$
have norm
$\lambda _j\in Sp(\tilde {T}_j)$
have norm
![]() $1$
since
$1$
since
![]() $(V^{*},\nabla )$
admits a complex variation of Hodge structure. For
$(V^{*},\nabla )$
admits a complex variation of Hodge structure. For
![]() $\boldsymbol {\lambda }=(\lambda _1,\ldots ,\lambda _p)\in Sp$
, we define
$\boldsymbol {\lambda }=(\lambda _1,\ldots ,\lambda _p)\in Sp$
, we define
Since
![]() $T_j^{\prime }s$
are pairwise commute, one has
$T_j^{\prime }s$
are pairwise commute, one has
and
![]() $\tilde {E}_{\boldsymbol {\lambda }}$
is an invariant subspace of
$\tilde {E}_{\boldsymbol {\lambda }}$
is an invariant subspace of
![]() $\tilde {T}_j$
for any
$\tilde {T}_j$
for any
![]() $\boldsymbol {\lambda }\in Sp$
and any j.
$\boldsymbol {\lambda }\in Sp$
and any j.
By Lemma 2.4 below, one can show that for any
![]() $\mu \in \tilde {\mathbb {E}}_{\boldsymbol {\lambda '}}$
and
$\mu \in \tilde {\mathbb {E}}_{\boldsymbol {\lambda '}}$
and
![]() $v\in \mathbb {E}_{\boldsymbol {\lambda }}$
,
$v\in \mathbb {E}_{\boldsymbol {\lambda }}$
,
![]() $\mu (v)=0$
if
$\mu (v)=0$
if
![]() $\boldsymbol {\lambda }\neq \boldsymbol {\lambda }'$
, which implies that
$\boldsymbol {\lambda }\neq \boldsymbol {\lambda }'$
, which implies that
![]() $ v_j^{*}\in \tilde {\mathbb {E}}_{\boldsymbol {\lambda }(v_j)}. $
$ v_j^{*}\in \tilde {\mathbb {E}}_{\boldsymbol {\lambda }(v_j)}. $
For
![]() $\boldsymbol {\lambda }\in Sp$
, there exists a unique
$\boldsymbol {\lambda }\in Sp$
, there exists a unique
![]() $\beta _i\in (\alpha _i-1, \alpha _i]$
such that
$\beta _i\in (\alpha _i-1, \alpha _i]$
such that
![]() $\exp (2\pi i \beta _i)=\lambda _i$
. Denote
$\exp (2\pi i \beta _i)=\lambda _i$
. Denote
![]() $N_i:=\frac {\log ( \lambda _i^{-1}T_i|_{ \mathbb {E}_{\boldsymbol {\lambda }}})}{2\pi i}$
. Recall that for any
$N_i:=\frac {\log ( \lambda _i^{-1}T_i|_{ \mathbb {E}_{\boldsymbol {\lambda }}})}{2\pi i}$
. Recall that for any
![]() $v\in \mathbb {E}_{\boldsymbol {\lambda }}$
, we define
$v\in \mathbb {E}_{\boldsymbol {\lambda }}$
, we define
 $$ \begin{align*} \tilde{v}(t):=\exp\left(- \sum_{i=1}^{p}( \beta_iI+N_i)\cdot \log t_i \right)v(t) = \prod_{i=1}^{p}t_i^{-\beta_i}\exp\left(- \sum_{i=1}^{p}N_i\cdot \log t_i \right)v(t). \end{align*} $$
$$ \begin{align*} \tilde{v}(t):=\exp\left(- \sum_{i=1}^{p}( \beta_iI+N_i)\cdot \log t_i \right)v(t) = \prod_{i=1}^{p}t_i^{-\beta_i}\exp\left(- \sum_{i=1}^{p}N_i\cdot \log t_i \right)v(t). \end{align*} $$
Likewise, since
![]() $\lambda _i\tilde {T}_i|_{ \tilde {\mathbb {E}}_{\boldsymbol {\lambda }}}$
is unipotent, its logarithm can be defined as
$\lambda _i\tilde {T}_i|_{ \tilde {\mathbb {E}}_{\boldsymbol {\lambda }}}$
is unipotent, its logarithm can be defined as
 $$ \begin{align*}\log( \lambda_i \tilde{T}_i|_{ \tilde{\mathbb{E}}_{\boldsymbol{\lambda}}}):=\sum_{k=1}^{\infty}(-1)^{k+1}\frac{(\lambda_i\tilde{T}_i|_{ \tilde{\mathbb{E}}_{\boldsymbol{\lambda}}}-I)^k}{k}. \end{align*} $$
$$ \begin{align*}\log( \lambda_i \tilde{T}_i|_{ \tilde{\mathbb{E}}_{\boldsymbol{\lambda}}}):=\sum_{k=1}^{\infty}(-1)^{k+1}\frac{(\lambda_i\tilde{T}_i|_{ \tilde{\mathbb{E}}_{\boldsymbol{\lambda}}}-I)^k}{k}. \end{align*} $$
Write
![]() $\tilde {N}_i:=\frac {\log ( \lambda _i \tilde {T}_i|_{ \tilde {\mathbb {E}}_{\boldsymbol {\lambda }}})}{2\pi i}$
. Then for any
$\tilde {N}_i:=\frac {\log ( \lambda _i \tilde {T}_i|_{ \tilde {\mathbb {E}}_{\boldsymbol {\lambda }}})}{2\pi i}$
. Then for any
![]() $\mu \in \tilde { \mathbb {E}}_{\boldsymbol {\lambda }}$
, we define
$\mu \in \tilde { \mathbb {E}}_{\boldsymbol {\lambda }}$
, we define
 $$ \begin{align} \tilde{\mu}(t):=\exp\left(- \sum_{i=1}^{p}( -\beta_iI+\tilde{N}_i)\cdot \log t_i \right)\mu(t) = \prod_{i=1}^{p}t_i^{\beta_i}\exp\left(- \sum_{i=1}^{p}\tilde{N}_i\cdot \log t_i \right)\mu(t). \end{align} $$
$$ \begin{align} \tilde{\mu}(t):=\exp\left(- \sum_{i=1}^{p}( -\beta_iI+\tilde{N}_i)\cdot \log t_i \right)\mu(t) = \prod_{i=1}^{p}t_i^{\beta_i}\exp\left(- \sum_{i=1}^{p}\tilde{N}_i\cdot \log t_i \right)\mu(t). \end{align} $$
Since
![]() $\tilde {T}_i=(T_i^{*})^{-1}$
, one has
$\tilde {T}_i=(T_i^{*})^{-1}$
, one has
![]() $ \tilde {N}_j=-N_j^{*} $
. Therefore,
$ \tilde {N}_j=-N_j^{*} $
. Therefore,
 $$ \begin{align*} \tilde{\mu}(t)(\tilde{v}(t))&=\exp\left(- \sum_{i=1}^{p}\tilde{N}_i\cdot \log t_i \right)\mu(t)\left(\exp\left(- \sum_{i=1}^{p}N_i\cdot \log t_i \right)v(t)\right) \\ &=\exp\left(\sum_{i=1}^{p} {N}^{*}_i\cdot \log t_i \right)\mu(t)\left(\exp\left(- \sum_{i=1}^{p}N_i\cdot \log t_i \right)v(t)\right) \\ &= \mu(v)=\mbox{constant}. \end{align*} $$
$$ \begin{align*} \tilde{\mu}(t)(\tilde{v}(t))&=\exp\left(- \sum_{i=1}^{p}\tilde{N}_i\cdot \log t_i \right)\mu(t)\left(\exp\left(- \sum_{i=1}^{p}N_i\cdot \log t_i \right)v(t)\right) \\ &=\exp\left(\sum_{i=1}^{p} {N}^{*}_i\cdot \log t_i \right)\mu(t)\left(\exp\left(- \sum_{i=1}^{p}N_i\cdot \log t_i \right)v(t)\right) \\ &= \mu(v)=\mbox{constant}. \end{align*} $$
This implies that
![]() $\tilde {v}_i^{*}(t)(\tilde {v}_j(t))=v_i^{*}(v_j)\equiv \delta _{ij}$
if
$\tilde {v}_i^{*}(t)(\tilde {v}_j(t))=v_i^{*}(v_j)\equiv \delta _{ij}$
if
![]() $\boldsymbol {\lambda }=\boldsymbol {\lambda }'$
, where
$\boldsymbol {\lambda }=\boldsymbol {\lambda }'$
, where
![]() $\tilde {v}^{*}_i$
is defined in Equation (2.7) in terms of
$\tilde {v}^{*}_i$
is defined in Equation (2.7) in terms of
![]() $ v_i^{*}\in \tilde {\mathbb {E}}_{\boldsymbol {\lambda }(v_i)}. $
$ v_i^{*}\in \tilde {\mathbb {E}}_{\boldsymbol {\lambda }(v_i)}. $
If
![]() $\mu \in \tilde { \mathbb {E}}_{\boldsymbol {\lambda }}$
and
$\mu \in \tilde { \mathbb {E}}_{\boldsymbol {\lambda }}$
and
![]() $v\in \mathbb {E}_{\boldsymbol {\lambda }'}$
with
$v\in \mathbb {E}_{\boldsymbol {\lambda }'}$
with
![]() $\boldsymbol {\lambda }\neq \boldsymbol {\lambda }'$
, the above construction shows that
$\boldsymbol {\lambda }\neq \boldsymbol {\lambda }'$
, the above construction shows that
![]() $ \tilde {\mu } $
and
$ \tilde {\mu } $
and
![]() $\tilde {v}$
are holomorphic sections of
$\tilde {v}$
are holomorphic sections of
![]() $V^{*}(\boldsymbol {\lambda })$
and
$V^{*}(\boldsymbol {\lambda })$
and
![]() $V(\boldsymbol {\lambda }')$
. Here,
$V(\boldsymbol {\lambda }')$
. Here,
![]() $V(\boldsymbol {\lambda }')$
is the invariant flat subbundle of
$V(\boldsymbol {\lambda }')$
is the invariant flat subbundle of
![]() $(V,\nabla )$
defined in Equation (2.5), and
$(V,\nabla )$
defined in Equation (2.5), and
![]() $V^{*}(\boldsymbol {\lambda })$
is defined to be the invariant flat subbundle of
$V^{*}(\boldsymbol {\lambda })$
is defined to be the invariant flat subbundle of
![]() $(V^{*},\nabla )$
generated by
$(V^{*},\nabla )$
generated by
![]() $\tilde {E}_{\boldsymbol {\lambda }}$
. Hence,
$\tilde {E}_{\boldsymbol {\lambda }}$
. Hence,
![]() $\tilde {v}^{*}_i$
and
$\tilde {v}^{*}_i$
and
![]() $\tilde {v}_j$
are holomorphic sections of
$\tilde {v}_j$
are holomorphic sections of
![]() $V^{*}(\boldsymbol {\lambda }(v_i))$
and
$V^{*}(\boldsymbol {\lambda }(v_i))$
and
![]() $V(\boldsymbol {\lambda }(v_j))$
, respectively. This shows that
$V(\boldsymbol {\lambda }(v_j))$
, respectively. This shows that
![]() $\tilde {v}_i^{*}(t)(\tilde {v}_j(t))\equiv 0$
for
$\tilde {v}_i^{*}(t)(\tilde {v}_j(t))\equiv 0$
for
![]() $\boldsymbol {\lambda }\neq \boldsymbol {\lambda }'$
by Lemma 2.4.
$\boldsymbol {\lambda }\neq \boldsymbol {\lambda }'$
by Lemma 2.4.
In conclusion, we prove that
![]() $\tilde {v}^{*}_1,\ldots , \tilde {v}^{*}_r$
is the dual frame of
$\tilde {v}^{*}_1,\ldots , \tilde {v}^{*}_r$
is the dual frame of
![]() $\tilde {v}_1,\ldots ,\tilde {v}_r$
.
$\tilde {v}_1,\ldots ,\tilde {v}_r$
.
Recall that
![]() $v_j\in \mathbb {E}_{\boldsymbol {\lambda }(v_j)}$
for some
$v_j\in \mathbb {E}_{\boldsymbol {\lambda }(v_j)}$
for some
![]() $\boldsymbol {\lambda }(v_j)\in Sp$
. There exists a unique
$\boldsymbol {\lambda }(v_j)\in Sp$
. There exists a unique
![]() $\beta (v_j)_i\in (\alpha _i-1, \alpha _i]$
such that
$\beta (v_j)_i\in (\alpha _i-1, \alpha _i]$
such that
![]() $\exp (2\pi i \beta (v_j)_i)=\boldsymbol {\lambda }(v_j)_i$
. Define a smooth section
$\exp (2\pi i \beta (v_j)_i)=\boldsymbol {\lambda }(v_j)_i$
. Define a smooth section
![]() $\tilde {v}_j^{\prime }=\tilde {v}_j\cdot \prod _{i=1}^p |t_i|^{\beta (v_j)_i}$
. By the norm estimate in the first step, for all
$\tilde {v}_j^{\prime }=\tilde {v}_j\cdot \prod _{i=1}^p |t_i|^{\beta (v_j)_i}$
. By the norm estimate in the first step, for all
![]() $\tilde {v}_j^{\prime }$
one has the norm estimate
$\tilde {v}_j^{\prime }$
one has the norm estimate
 $$ \begin{align*}|\tilde{v}_j^{\prime}|_h\lesssim \left(\prod_{i=1}^p|\log |t_i||\right)^{M} \end{align*} $$
$$ \begin{align*}|\tilde{v}_j^{\prime}|_h\lesssim \left(\prod_{i=1}^p|\log |t_i||\right)^{M} \end{align*} $$
for some
![]() $M>0$
. It follows that
$M>0$
. It follows that
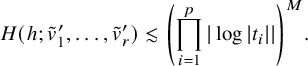 $$ \begin{align*}H(h; \tilde{v}^{\prime}_1,\ldots,\tilde{v}_r^{\prime})\lesssim \left(\prod_{i=1}^p|\log |t_i||\right)^{M}. \end{align*} $$
$$ \begin{align*}H(h; \tilde{v}^{\prime}_1,\ldots,\tilde{v}_r^{\prime})\lesssim \left(\prod_{i=1}^p|\log |t_i||\right)^{M}. \end{align*} $$
Here,
![]() $H(h; \tilde {v}_1^{\prime },\ldots , \tilde {v}_r^{\prime })$
is a
$H(h; \tilde {v}_1^{\prime },\ldots , \tilde {v}_r^{\prime })$
is a
![]() $r\times r$
-matrix function whose
$r\times r$
-matrix function whose
![]() $(i,j)$
-component is
$(i,j)$
-component is
![]() $h(\tilde {v}_i^{\prime },\tilde {v}_j^{\prime })$
. On the other hand, we put
$h(\tilde {v}_i^{\prime },\tilde {v}_j^{\prime })$
. On the other hand, we put
![]() $\mu ^{\prime }_i=\tilde {v}^{*}_i\cdot \prod _{j=1}^p |t_j|^{-\beta (v_i)_j}$
. Since complex polarized variation of Hodge structure is functorial by taking dual,
$\mu ^{\prime }_i=\tilde {v}^{*}_i\cdot \prod _{j=1}^p |t_j|^{-\beta (v_i)_j}$
. Since complex polarized variation of Hodge structure is functorial by taking dual,
![]() $(V^{*},\nabla )$
admits a complex polarized variation of Hodge structure whose Hodge metric is the dual metric
$(V^{*},\nabla )$
admits a complex polarized variation of Hodge structure whose Hodge metric is the dual metric
![]() $h^{*}$
of the Hodge metric h for
$h^{*}$
of the Hodge metric h for
![]() $(V,\nabla ,F^{\bullet },Q)$
. In the same manner, we obtain
$(V,\nabla ,F^{\bullet },Q)$
. In the same manner, we obtain
 $$ \begin{align*}|\mu_i^{\prime}|_{h^{*}}\lesssim \left(\prod_{i=1}^p|\log |t_i||\right)^{M'} \end{align*} $$
$$ \begin{align*}|\mu_i^{\prime}|_{h^{*}}\lesssim \left(\prod_{i=1}^p|\log |t_i||\right)^{M'} \end{align*} $$
for every
![]() $\mu _i^{\prime }$
and some
$\mu _i^{\prime }$
and some
![]() $M'>0$
. This implies that
$M'>0$
. This implies that
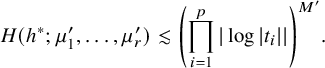 $$ \begin{align*}H(h^{*}; \mu^{\prime}_1,\ldots,\mu^{\prime}_r)\lesssim \left(\prod_{i=1}^p|\log |t_i||\right)^{M'}. \end{align*} $$
$$ \begin{align*}H(h^{*}; \mu^{\prime}_1,\ldots,\mu^{\prime}_r)\lesssim \left(\prod_{i=1}^p|\log |t_i||\right)^{M'}. \end{align*} $$
By our construction,
![]() $\mu ^{\prime }_1,\ldots ,\mu ^{\prime }_r$
is the dual of the smooth frame
$\mu ^{\prime }_1,\ldots ,\mu ^{\prime }_r$
is the dual of the smooth frame
![]() $\tilde {v}^{\prime }_1,\ldots ,\tilde {v}^{\prime }_r$
. It follows that
$\tilde {v}^{\prime }_1,\ldots ,\tilde {v}^{\prime }_r$
. It follows that
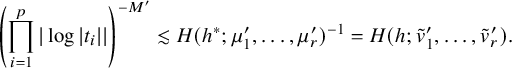 $$ \begin{align*}\left(\prod_{i=1}^p|\log |t_i||\right)^{-M'}\lesssim H(h^{*}; \mu^{\prime}_1,\ldots,\mu^{\prime}_r)^{-1}= H(h; \tilde{v}^{\prime}_1,\ldots,\tilde{v}_r^{\prime}). \end{align*} $$
$$ \begin{align*}\left(\prod_{i=1}^p|\log |t_i||\right)^{-M'}\lesssim H(h^{*}; \mu^{\prime}_1,\ldots,\mu^{\prime}_r)^{-1}= H(h; \tilde{v}^{\prime}_1,\ldots,\tilde{v}_r^{\prime}). \end{align*} $$
Hence,
 $$ \begin{align} \left(\prod_{i=1}^p|\log |t_i||\right)^{-M'}\lesssim H(h; \tilde{v}^{\prime}_1,\ldots,\tilde{v}_r^{\prime})\lesssim \left(\prod_{i=1}^p|\log |t_i||\right)^{M}. \end{align} $$
$$ \begin{align} \left(\prod_{i=1}^p|\log |t_i||\right)^{-M'}\lesssim H(h; \tilde{v}^{\prime}_1,\ldots,\tilde{v}_r^{\prime})\lesssim \left(\prod_{i=1}^p|\log |t_i||\right)^{M}. \end{align} $$
Now, we are ready to prove the inclusion
![]() $\mathcal {P}_{\! \boldsymbol {\alpha }}V\subset V_{\boldsymbol {\alpha }}^{\mathrm {Del}}$
. For any
$\mathcal {P}_{\! \boldsymbol {\alpha }}V\subset V_{\boldsymbol {\alpha }}^{\mathrm {Del}}$
. For any
![]() $s\in \mathcal {P}_{\!\boldsymbol {\alpha }} V(U)$
, it can be written as
$s\in \mathcal {P}_{\!\boldsymbol {\alpha }} V(U)$
, it can be written as
![]() $ s=\sum _{i=1}^rf_i \tilde {v}_i, $
where
$ s=\sum _{i=1}^rf_i \tilde {v}_i, $
where
![]() $f_i$
is a holomorphic function on U. By Equation (2.8) one has
$f_i$
is a holomorphic function on U. By Equation (2.8) one has
 $$ \begin{align*}\sum_{i=1}^r |f_i|^2\cdot \prod_{j=1}^{p}|t_j|^{-2\beta(v_i)_j} \cdot \left(\prod_{k=1}^p|\log |t_k||\right)^{-2M'}\lesssim |s|^2_h\lesssim\prod_{i=1}^p|t_j|^{-2\alpha_j-\varepsilon} \end{align*} $$
$$ \begin{align*}\sum_{i=1}^r |f_i|^2\cdot \prod_{j=1}^{p}|t_j|^{-2\beta(v_i)_j} \cdot \left(\prod_{k=1}^p|\log |t_k||\right)^{-2M'}\lesssim |s|^2_h\lesssim\prod_{i=1}^p|t_j|^{-2\alpha_j-\varepsilon} \end{align*} $$
for any
![]() $\varepsilon>0$
. Since
$\varepsilon>0$
. Since
![]() $\beta (v_i)_j\in (\alpha _j-1,\alpha _j]$
, one can choose
$\beta (v_i)_j\in (\alpha _j-1,\alpha _j]$
, one can choose
![]() $\delta>0$
such that
$\delta>0$
such that
![]() $\beta (v_i)_j-\alpha +1> \delta $
for all
$\beta (v_i)_j-\alpha +1> \delta $
for all
![]() $v_i$
and every
$v_i$
and every
![]() $j=1,\ldots ,p$
. The above inequality implies that for every
$j=1,\ldots ,p$
. The above inequality implies that for every
![]() $f_i$
,
$f_i$
,
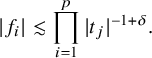 $$ \begin{align*}|f_i|\lesssim \prod_{i=1}^p|t_j|^{-1+\delta}. \end{align*} $$
$$ \begin{align*}|f_i|\lesssim \prod_{i=1}^p|t_j|^{-1+\delta}. \end{align*} $$
Hence, all
![]() $f_i$
extend to holomorphic functions over X. This proves that
$f_i$
extend to holomorphic functions over X. This proves that
![]() $s\in V_{\boldsymbol {\alpha }}^{\mathrm { Del}}(X)$
since
$s\in V_{\boldsymbol {\alpha }}^{\mathrm { Del}}(X)$
since
![]() $\tilde {v}_1,\ldots , \tilde {v}_r$
is a holomorphic basis of
$\tilde {v}_1,\ldots , \tilde {v}_r$
is a holomorphic basis of
![]() $V_{\boldsymbol {\alpha }}^{\mathrm {Del}}$
by the definition of Deligne extension in §1.2. The inclusion
$V_{\boldsymbol {\alpha }}^{\mathrm {Del}}$
by the definition of Deligne extension in §1.2. The inclusion
![]() $\mathcal {P}_{\! \boldsymbol {\alpha }}V\subset V_{\boldsymbol {\alpha }}^{\mathrm {Del}}$
is proved. We complete the proof of the proposition.
$\mathcal {P}_{\! \boldsymbol {\alpha }}V\subset V_{\boldsymbol {\alpha }}^{\mathrm {Del}}$
is proved. We complete the proof of the proposition.
We leave the proof of the following lemma of linear algebra to the reader.
Lemma 2.4. Let
![]() $T:V\to V$
be an isomorphism of a finite-dimensional
$T:V\to V$
be an isomorphism of a finite-dimensional
![]() $\mathbb {C}$
-vector space V. Decompose
$\mathbb {C}$
-vector space V. Decompose
![]() $V=V_{\lambda _1}\oplus \ldots \oplus V_{\lambda _k}$
into eigenspaces of T, where
$V=V_{\lambda _1}\oplus \ldots \oplus V_{\lambda _k}$
into eigenspaces of T, where
![]() $\lambda _i$
is a eigenvalue of T and
$\lambda _i$
is a eigenvalue of T and
![]() $V_{\lambda _i}$
is the corresponding eigenspace. Denote by
$V_{\lambda _i}$
is the corresponding eigenspace. Denote by
![]() $V^{*}$
the dual vector space. Then for the isomorphism
$V^{*}$
the dual vector space. Then for the isomorphism
![]() $(T^{*})^{-1}:V^{*}\to V^{*}$
, its eigenvalues are
$(T^{*})^{-1}:V^{*}\to V^{*}$
, its eigenvalues are
![]() $\lambda _1^{-1},\ldots , \lambda _k^{-1}$
and its eigenspace decomposition is
$\lambda _1^{-1},\ldots , \lambda _k^{-1}$
and its eigenspace decomposition is
![]() $V^{*}=V^{*}_{\lambda ^{-1}_1}\oplus \ldots \oplus V^{*}_{\lambda ^{-1}_k}$
, where
$V^{*}=V^{*}_{\lambda ^{-1}_1}\oplus \ldots \oplus V^{*}_{\lambda ^{-1}_k}$
, where
![]() $V^{*}_{\lambda ^{-1}_j}$
is the corresponding eigenspace of
$V^{*}_{\lambda ^{-1}_j}$
is the corresponding eigenspace of
![]() $\lambda _j^{-1}$
. Moreover, one has
$\lambda _j^{-1}$
. Moreover, one has
![]() $\mu (v)=0$
if
$\mu (v)=0$
if
![]() $\mu \in V^{*}_{\lambda ^{-1}_i}$
and
$\mu \in V^{*}_{\lambda ^{-1}_i}$
and
![]() $v\in V_{\lambda _j}$
with
$v\in V_{\lambda _j}$
with
![]() $i\neq j$
.
$i\neq j$
.
Theorem 2.5. Let X be a complex manifold, and let
![]() $D=\sum _{i=1}^{\ell } D_i$
be a simple normal crossing divisor on X. Let
$D=\sum _{i=1}^{\ell } D_i$
be a simple normal crossing divisor on X. Let
![]() $(V, \nabla , F^{\bullet }, Q)$
be a complex polarized variation of Hodge structure of weight m on
$(V, \nabla , F^{\bullet }, Q)$
be a complex polarized variation of Hodge structure of weight m on
![]() $X\backslash D$
. Let
$X\backslash D$
. Let
![]() ${\mathcal P}_{*}F^p$
and
${\mathcal P}_{*}F^p$
and
![]() ${\mathcal P}_{*} E_{p,m-p}$
be the induced filtered bundle of Hermitian bundles
${\mathcal P}_{*} E_{p,m-p}$
be the induced filtered bundle of Hermitian bundles
![]() $(F^p, h_p)$
and
$(F^p, h_p)$
and
![]() $(E_{p,m-p}, h_{p,m-p})$
defined in §1.6. Then for every p,
$(E_{p,m-p}, h_{p,m-p})$
defined in §1.6. Then for every p,
![]() ${\mathcal P}_{*}F^p$
and
${\mathcal P}_{*}F^p$
and
![]() ${\mathcal P}_{*} E_{p,m-p}$
are parabolic bundles and for each multi-index
${\mathcal P}_{*} E_{p,m-p}$
are parabolic bundles and for each multi-index
![]() $\alpha \in \mathbb {R}^{\ell }$
, there is a natural exact sequence
$\alpha \in \mathbb {R}^{\ell }$
, there is a natural exact sequence
Proof. By Lemma 1.4,
![]() $(F^p, h_p)$
and
$(F^p, h_p)$
and
![]() $(E_{p,m-p}, h_{p,m-p})$
are acceptable bundles for every p. It follows from Theorem 1.7 that
$(E_{p,m-p}, h_{p,m-p})$
are acceptable bundles for every p. It follows from Theorem 1.7 that
![]() ${\mathcal P}_{*}F^p$
and
${\mathcal P}_{*}F^p$
and
![]() ${\mathcal P}_{*} E_{p,m-p}$
defined in §1.6 are parabolic ones.
${\mathcal P}_{*} E_{p,m-p}$
defined in §1.6 are parabolic ones.
We first show that we can define
which is exact. Note that we have the following exact sequence
on
![]() $X\backslash D$
by the definition of
$X\backslash D$
by the definition of
![]() $\mathbb {C}$
-VHS. Pick any
$\mathbb {C}$
-VHS. Pick any
![]() $x\in D$
and any admissible coordinate
$x\in D$
and any admissible coordinate
![]() $(\Omega ;z_1,\ldots ,z_n)$
centering at x such that
$(\Omega ;z_1,\ldots ,z_n)$
centering at x such that
![]() $D\cap \Omega =(z_1\cdots z_k=0)$
. By the prolongation via norm growth defined in §1.6, any section
$D\cap \Omega =(z_1\cdots z_k=0)$
. By the prolongation via norm growth defined in §1.6, any section
![]() $s\in \mathcal {P}_{\!\boldsymbol {\alpha }} F^{p+1}(\Omega )$
satisfies that
$s\in \mathcal {P}_{\!\boldsymbol {\alpha }} F^{p+1}(\Omega )$
satisfies that
![]() $s\in F^{p+1}(\Omega \backslash D)$
and
$s\in F^{p+1}(\Omega \backslash D)$
and
![]() $|s|_{h^{p+1}}\lesssim \prod _{i=1}^{k}|z_i|^{-\alpha _i-\varepsilon }$
for any
$|s|_{h^{p+1}}\lesssim \prod _{i=1}^{k}|z_i|^{-\alpha _i-\varepsilon }$
for any
![]() $\varepsilon>0$
. Since
$\varepsilon>0$
. Since
![]() $h_{p+1}$
is the induced metric of
$h_{p+1}$
is the induced metric of
![]() $h_p$
on
$h_p$
on
![]() $F^{p+1}$
, it follows that
$F^{p+1}$
, it follows that
 $$ \begin{align} |s|_{h_{p+1}}=|s|_{h_p} \lesssim \prod_{i=1}^{k}|z_i|^{-\alpha_i-\varepsilon} \end{align} $$
$$ \begin{align} |s|_{h_{p+1}}=|s|_{h_p} \lesssim \prod_{i=1}^{k}|z_i|^{-\alpha_i-\varepsilon} \end{align} $$
for any
![]() $\varepsilon>0$
. Hence, the inclusion
$\varepsilon>0$
. Hence, the inclusion
![]() $F^{p+1}\subset F^p$
also results in the inclusion
$F^{p+1}\subset F^p$
also results in the inclusion
![]() $\mathcal {P}_{\!\boldsymbol {\alpha }} F^{p+1}\subset \mathcal {P}_{\!\boldsymbol {\alpha }} F^{p}$
. We proved that Equation (2.10) is exact in the left.
$\mathcal {P}_{\!\boldsymbol {\alpha }} F^{p+1}\subset \mathcal {P}_{\!\boldsymbol {\alpha }} F^{p}$
. We proved that Equation (2.10) is exact in the left.
Note that the metric
![]() $h_{p,m-p}$
on
$h_{p,m-p}$
on
![]() $E_{p,m-p}$
is the quotient metric of
$E_{p,m-p}$
is the quotient metric of
![]() $h_p$
. It follows that for any section
$h_p$
. It follows that for any section
![]() $s\in \mathcal {P}_{\!\boldsymbol {\alpha }} F^{p}(\Omega )$
, we have
$s\in \mathcal {P}_{\!\boldsymbol {\alpha }} F^{p}(\Omega )$
, we have
 $$ \begin{align*}|q(s)|_{h_{p,m-p}}\leq |s|_{h_p}\lesssim \prod_{i=1}^{k}|z_i|^{-\alpha_i-\varepsilon}\end{align*} $$
$$ \begin{align*}|q(s)|_{h_{p,m-p}}\leq |s|_{h_p}\lesssim \prod_{i=1}^{k}|z_i|^{-\alpha_i-\varepsilon}\end{align*} $$
for any
![]() $\varepsilon>0$
. Hence, the quotient
$\varepsilon>0$
. Hence, the quotient
![]() $q:F^p\to E_{p,m-p}$
induces the morphism
$q:F^p\to E_{p,m-p}$
induces the morphism
![]() $\mathcal {P}_{\! \boldsymbol {\alpha }}F^p\to \mathcal {P}_{\!\boldsymbol {\alpha }} E_{p,m-p}$
and thus Equation (2.10) can be defined. Next, we will show that Equation (2.10) is exact in the middle.
$\mathcal {P}_{\! \boldsymbol {\alpha }}F^p\to \mathcal {P}_{\!\boldsymbol {\alpha }} E_{p,m-p}$
and thus Equation (2.10) can be defined. Next, we will show that Equation (2.10) is exact in the middle.
Take any section
![]() $s\in \mathcal {P}_{\!\boldsymbol {\alpha }} F^{p}(\Omega )$
such that
$s\in \mathcal {P}_{\!\boldsymbol {\alpha }} F^{p}(\Omega )$
such that
![]() $q(s)=0$
. Thanks to the exactness in Equation (2.11), we have
$q(s)=0$
. Thanks to the exactness in Equation (2.11), we have
![]() $s\in F^{p+1}(\Omega \backslash D)$
. By Equation (2.12), we conclude that
$s\in F^{p+1}(\Omega \backslash D)$
. By Equation (2.12), we conclude that
![]() $s\in \mathcal {P}_{\!\boldsymbol {\alpha }} F^{p+1}(\Omega )$
. This implies the exactness of Equation (2.10).
$s\in \mathcal {P}_{\!\boldsymbol {\alpha }} F^{p+1}(\Omega )$
. This implies the exactness of Equation (2.10).
In what follows, we will prove that Equation (2.10) is exact on the right. It suffices to prove that for any point
![]() $x\in D$
and any section
$x\in D$
and any section
![]() $s\in \mathcal {P}_{\!\boldsymbol {\alpha }} E_{p,m-p}(\Omega )$
, where
$s\in \mathcal {P}_{\!\boldsymbol {\alpha }} E_{p,m-p}(\Omega )$
, where
![]() $\Omega $
is a neighborhood of x, there is a section
$\Omega $
is a neighborhood of x, there is a section
![]() $\tilde {s}\in \mathcal {P}_{\! \boldsymbol {\alpha }}F^p(\Omega ')$
for some smaller neighborhood
$\tilde {s}\in \mathcal {P}_{\! \boldsymbol {\alpha }}F^p(\Omega ')$
for some smaller neighborhood
![]() $\Omega '$
of x such that
$\Omega '$
of x such that
![]() $q(\tilde {s})=s|_{\Omega '}$
. We shall construct such
$q(\tilde {s})=s|_{\Omega '}$
. We shall construct such
![]() $\tilde {s}$
by utilizing the previous results on
$\tilde {s}$
by utilizing the previous results on
![]() $L^2$
-estimate in Lemmas 2.1 and 2.2.
$L^2$
-estimate in Lemmas 2.1 and 2.2.
Since this is a local problem, we can assume that
![]() $X=\Delta ^n$
,
$X=\Delta ^n$
,
![]() $D=(z_1\cdots z_{\ell }=0)$
and x is the origin. We equip the complement
$D=(z_1\cdots z_{\ell }=0)$
and x is the origin. We equip the complement
![]() $U:=X\backslash D$
with the Poincaré metric
$U:=X\backslash D$
with the Poincaré metric
![]() $\omega _P$
. Let
$\omega _P$
. Let
![]() $X(r)$
and
$X(r)$
and
![]() $U(r)$
be defined as in Equation (2.1). By the semicontinuity of the parabolic bundle in Definition 1.6.(iv), we can choose
$U(r)$
be defined as in Equation (2.1). By the semicontinuity of the parabolic bundle in Definition 1.6.(iv), we can choose
![]() $\boldsymbol {\beta }\in \mathbb {R}^{\ell }$
such that
$\boldsymbol {\beta }\in \mathbb {R}^{\ell }$
such that
![]() $\beta _i>\alpha _i$
and
$\beta _i>\alpha _i$
and
Pick any
![]() $s\in \mathcal {P}_{\!\boldsymbol {\alpha }} E_{p,m-p}(X)$
. Then
$s\in \mathcal {P}_{\!\boldsymbol {\alpha }} E_{p,m-p}(X)$
. Then
![]() $s\in H^0(U, E_{p,m-p})$
with
$s\in H^0(U, E_{p,m-p})$
with
![]() $|s|_{h_{p,m-p}}\lesssim \prod _{i=1}^{\ell }|z_i|^{-\alpha _i-\varepsilon }$
for any
$|s|_{h_{p,m-p}}\lesssim \prod _{i=1}^{\ell }|z_i|^{-\alpha _i-\varepsilon }$
for any
![]() $\varepsilon>0$
. We will construct a section
$\varepsilon>0$
. We will construct a section
![]() $\tilde {s}\in H^0(U(r), F^p)$
for some
$\tilde {s}\in H^0(U(r), F^p)$
for some
![]() $0<r<1$
such that
$0<r<1$
such that
![]() $q(\tilde {s})=s|_{U(r)}$
and
$q(\tilde {s})=s|_{U(r)}$
and
![]() $|\tilde {s}|_{h_p}\lesssim \prod _{i=1}^{\ell }|z_i|^{-\beta _i-\varepsilon }$
for any
$|\tilde {s}|_{h_p}\lesssim \prod _{i=1}^{\ell }|z_i|^{-\beta _i-\varepsilon }$
for any
![]() $\varepsilon>0$
. Note that there is a canonical smooth isomorphism (and isometry)
$\varepsilon>0$
. Note that there is a canonical smooth isomorphism (and isometry)
such that the holomorphic structure of
![]() $F^p$
via
$F^p$
via
![]() $\Phi $
is defined by
$\Phi $
is defined by
 $$ \begin{align*}\begin{bmatrix} \bar{\partial}_{F^{p+1}} & \theta_{p+1,m-p-1}^{\dagger} \\ 0 & \bar{\partial}_{E_{p,m-p}}, \end{bmatrix}, \end{align*} $$
$$ \begin{align*}\begin{bmatrix} \bar{\partial}_{F^{p+1}} & \theta_{p+1,m-p-1}^{\dagger} \\ 0 & \bar{\partial}_{E_{p,m-p}}, \end{bmatrix}, \end{align*} $$
where
![]() $ \theta _{p+1,m-p-1}^{\dagger }$
is the adjoint of
$ \theta _{p+1,m-p-1}^{\dagger }$
is the adjoint of
![]() $\theta _{p+1,m-p-1}$
with respect to
$\theta _{p+1,m-p-1}$
with respect to
![]() $h_{p+1,m-p-1}$
. If
$h_{p+1,m-p-1}$
. If
![]() $q(\tilde {s})=s$
, then
$q(\tilde {s})=s$
, then
![]() $\Phi (\tilde {s})=[\sigma , s]$
for some
$\Phi (\tilde {s})=[\sigma , s]$
for some
![]() $\sigma \in \mathscr {C}^{\infty }(U, F^{p+1})$
such that
$\sigma \in \mathscr {C}^{\infty }(U, F^{p+1})$
such that
 $$ \begin{align*}\begin{bmatrix} \bar{\partial}_{F^{p+1}} & \theta_{p+1,m-p-1}^{\dagger} \\ 0 & \bar{\partial}_{E_{p,m-p}} \end{bmatrix} \begin{bmatrix} \sigma \\ s \end{bmatrix}=0. \end{align*} $$
$$ \begin{align*}\begin{bmatrix} \bar{\partial}_{F^{p+1}} & \theta_{p+1,m-p-1}^{\dagger} \\ 0 & \bar{\partial}_{E_{p,m-p}} \end{bmatrix} \begin{bmatrix} \sigma \\ s \end{bmatrix}=0. \end{align*} $$
Hence,
![]() $\bar {\partial }_{F^{p+1}}\sigma =-\theta _{p+1,m-p-1}^{\dagger } s$
. We will solve this
$\bar {\partial }_{F^{p+1}}\sigma =-\theta _{p+1,m-p-1}^{\dagger } s$
. We will solve this
![]() $\bar {\partial }$
-equation with proper norm estimate.
$\bar {\partial }$
-equation with proper norm estimate.
By Theorem 1.2, after we replace U by
![]() $U(r)$
for some
$U(r)$
for some
![]() $0<r<1$
, we have
$0<r<1$
, we have
![]() $|\theta _{p+1,m-p-1}|_{h,\omega _P}\leq C$
over U. This implies that
$|\theta _{p+1,m-p-1}|_{h,\omega _P}\leq C$
over U. This implies that
![]() $|\theta _{p+1,m-p-1}^{\dagger }|_{h,\omega _P}\leq C$
over U. Hence,
$|\theta _{p+1,m-p-1}^{\dagger }|_{h,\omega _P}\leq C$
over U. Hence,
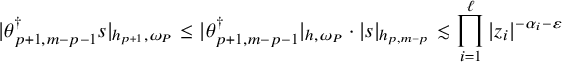 $$ \begin{align*} |\theta_{p+1,m-p-1}^{\dagger} s|_{h_{p+1},\omega_P} \leq |\theta_{p+1,m-p-1}^{\dagger}|_{h, \omega_P}\cdot |s|_{h_{p,m-p}} \lesssim \prod_{i=1}^{\ell}|z_i|^{-\alpha_i-\varepsilon} \end{align*} $$
$$ \begin{align*} |\theta_{p+1,m-p-1}^{\dagger} s|_{h_{p+1},\omega_P} \leq |\theta_{p+1,m-p-1}^{\dagger}|_{h, \omega_P}\cdot |s|_{h_{p,m-p}} \lesssim \prod_{i=1}^{\ell}|z_i|^{-\alpha_i-\varepsilon} \end{align*} $$
for any
![]() $\varepsilon>0$
. We now introduce a new metric for
$\varepsilon>0$
. We now introduce a new metric for
![]() $F^{p}$
defined by
$F^{p}$
defined by
 $$ \begin{align*}h_{p}(\boldsymbol{\beta}):=h_{p}\cdot \prod_{i=1}^{\ell}|z_i|^{\beta_i}.\end{align*} $$
$$ \begin{align*}h_{p}(\boldsymbol{\beta}):=h_{p}\cdot \prod_{i=1}^{\ell}|z_i|^{\beta_i}.\end{align*} $$
Since
![]() $\beta _i>\alpha _i$
for each i, we have
$\beta _i>\alpha _i$
for each i, we have
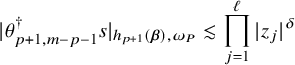 $$ \begin{align*}|\theta_{p+1,m-p-1}^{\dagger} s|_{h_{p+1}(\boldsymbol{\beta}),\omega_P} \lesssim \prod_{j=1}^{\ell}|z_j|^{\delta}\end{align*} $$
$$ \begin{align*}|\theta_{p+1,m-p-1}^{\dagger} s|_{h_{p+1}(\boldsymbol{\beta}),\omega_P} \lesssim \prod_{j=1}^{\ell}|z_j|^{\delta}\end{align*} $$
for some
![]() $\delta>0$
. Note that
$\delta>0$
. Note that
![]() $\theta _{p+1,m-p-1}^{\dagger } s\in A^{0,1}(E_{p+1,m-p-1})$
. We have
$\theta _{p+1,m-p-1}^{\dagger } s\in A^{0,1}(E_{p+1,m-p-1})$
. We have
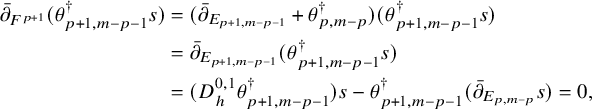 $$ \begin{align*} \bar{\partial}_{F^{p+1}}(\theta_{p+1,m-p-1}^{\dagger} s)&=(\bar{\partial}_{E_{p+1,m-p-1}}+\theta_{p,m-p}^{\dagger})(\theta_{p+1,m-p-1}^{\dagger} s)\\ & = \bar{\partial}_{E_{p+1,m-p-1}} (\theta_{p+1,m-p-1}^{\dagger} s)\\ &= (D_{h}^{0,1}\theta_{p+1,m-p-1}^{\dagger})s-\theta_{p+1,m-p-1}^{\dagger}(\bar{\partial}_{E_{p,m-p} }s)=0, \end{align*} $$
$$ \begin{align*} \bar{\partial}_{F^{p+1}}(\theta_{p+1,m-p-1}^{\dagger} s)&=(\bar{\partial}_{E_{p+1,m-p-1}}+\theta_{p,m-p}^{\dagger})(\theta_{p+1,m-p-1}^{\dagger} s)\\ & = \bar{\partial}_{E_{p+1,m-p-1}} (\theta_{p+1,m-p-1}^{\dagger} s)\\ &= (D_{h}^{0,1}\theta_{p+1,m-p-1}^{\dagger})s-\theta_{p+1,m-p-1}^{\dagger}(\bar{\partial}_{E_{p,m-p} }s)=0, \end{align*} $$
where the second equality follows from
![]() $\theta _{p+1,m-p-1}^{\dagger }\wedge \theta _{m-p}^{\dagger }=0$
, and the last one follows from
$\theta _{p+1,m-p-1}^{\dagger }\wedge \theta _{m-p}^{\dagger }=0$
, and the last one follows from
![]() $D_h^{0,1}(\theta ^{\dagger })=0$
. Here,
$D_h^{0,1}(\theta ^{\dagger })=0$
. Here,
![]() $D_h$
is the Chern connection for the Hodge bundle
$D_h$
is the Chern connection for the Hodge bundle
![]() $(E=\oplus _{p+q=m}E_{p,q},h)$
. Since
$(E=\oplus _{p+q=m}E_{p,q},h)$
. Since
![]() $(F^{p+1}, h_{p+1}(\boldsymbol {\beta }))$
is also acceptable by Lemma 1.4, we can invoke Lemma 2.1 to find some
$(F^{p+1}, h_{p+1}(\boldsymbol {\beta }))$
is also acceptable by Lemma 1.4, we can invoke Lemma 2.1 to find some
![]() $\sigma \in \mathscr {C}^{\infty }(U, F^{p+1})$
such that
$\sigma \in \mathscr {C}^{\infty }(U, F^{p+1})$
such that
and
for some
![]() $N\gg 1$
. Here,
$N\gg 1$
. Here,
![]() $h_{p+1}(\boldsymbol {\beta },N)$
is a new metric for
$h_{p+1}(\boldsymbol {\beta },N)$
is a new metric for
![]() $F^{p+1}$
define by
$F^{p+1}$
define by
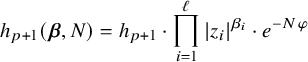 $$ \begin{align*}h_{p+1}(\boldsymbol{\beta},N)=h_{p+1}\cdot \prod_{i=1}^{\ell}|z_i|^{\beta_i}\cdot e^{-N\varphi} \end{align*} $$
$$ \begin{align*}h_{p+1}(\boldsymbol{\beta},N)=h_{p+1}\cdot \prod_{i=1}^{\ell}|z_i|^{\beta_i}\cdot e^{-N\varphi} \end{align*} $$
with
![]() $\varphi $
defined in Equation (2.2). Since
$\varphi $
defined in Equation (2.2). Since
![]() $|s|_{h_{p,m-p}}\lesssim \prod _{i=1}^{\ell }|z_i|^{-\alpha _i-\varepsilon }$
for any
$|s|_{h_{p,m-p}}\lesssim \prod _{i=1}^{\ell }|z_i|^{-\alpha _i-\varepsilon }$
for any
![]() $\varepsilon>0$
, it follows that
$\varepsilon>0$
, it follows that
![]() $ |s|_{h_{p,m-p}(\boldsymbol {\beta },N)}<C$
for some constant
$ |s|_{h_{p,m-p}(\boldsymbol {\beta },N)}<C$
for some constant
![]() $C>0$
, where we define
$C>0$
, where we define
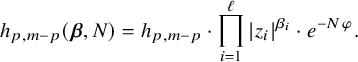 $$ \begin{align*}h_{p,m-p}(\boldsymbol{\beta},N)=h_{p,m-p}\cdot \prod_{i=1}^{\ell}|z_i|^{\beta_i}\cdot e^{-N\varphi}. \end{align*} $$
$$ \begin{align*}h_{p,m-p}(\boldsymbol{\beta},N)=h_{p,m-p}\cdot \prod_{i=1}^{\ell}|z_i|^{\beta_i}\cdot e^{-N\varphi}. \end{align*} $$
Thus, the section
![]() $\tilde {s}:=\Phi ^{-1}([\sigma ,s])$
is a holomorphic section of
$\tilde {s}:=\Phi ^{-1}([\sigma ,s])$
is a holomorphic section of
![]() $F^p$
such that
$F^p$
such that
Since
![]() $(F^p, h_p(\boldsymbol {\beta }))$
is also acceptable by Lemma 1.4, thanks to Lemma 2.2, over some
$(F^p, h_p(\boldsymbol {\beta }))$
is also acceptable by Lemma 1.4, thanks to Lemma 2.2, over some
![]() $U(r) $
for
$U(r) $
for
![]() $0<r<1$
we have
$0<r<1$
we have
![]() $|\tilde {s}|_{h_p(\boldsymbol {\beta })}\lesssim \prod _{j=1}^{\ell }|z_j|^{-\varepsilon }$
for any
$|\tilde {s}|_{h_p(\boldsymbol {\beta })}\lesssim \prod _{j=1}^{\ell }|z_j|^{-\varepsilon }$
for any
![]() $\varepsilon>0$
. Therefore,
$\varepsilon>0$
. Therefore,
![]() $|\tilde {s}|_{h_p}\lesssim \prod _{j=1}^{\ell }|z_j|^{-\beta _j-\varepsilon }$
for any
$|\tilde {s}|_{h_p}\lesssim \prod _{j=1}^{\ell }|z_j|^{-\beta _j-\varepsilon }$
for any
![]() $\varepsilon>0$
. It follows that
$\varepsilon>0$
. It follows that
![]() $ \tilde {s}\in {\mathcal P}_{\boldsymbol {\beta }} F^p(X(r)). $
By Equation (2.13), we conclude that
$ \tilde {s}\in {\mathcal P}_{\boldsymbol {\beta }} F^p(X(r)). $
By Equation (2.13), we conclude that
![]() $\tilde {s}\in {\mathcal P}_{\boldsymbol {\alpha }} F^p(X(r'))$
for some
$\tilde {s}\in {\mathcal P}_{\boldsymbol {\alpha }} F^p(X(r'))$
for some
![]() $0<r'<1$
. This implies the right exactness of Equation (2.9) as
$0<r'<1$
. This implies the right exactness of Equation (2.9) as
![]() $q(\tilde {s})=s$
. The theorem is proved.
$q(\tilde {s})=s$
. The theorem is proved.
Let us prove Theorem A.
Proof of Theorem A
Thanks to Proposition 2.3, we have
![]() $V^{\mathrm {Del}}_{\boldsymbol {\alpha }}=\mathcal {P}_{\!\boldsymbol {\alpha }} V$
. By Lemma 1.4,
$V^{\mathrm {Del}}_{\boldsymbol {\alpha }}=\mathcal {P}_{\!\boldsymbol {\alpha }} V$
. By Lemma 1.4,
![]() $(F^p, h_p)$
and
$(F^p, h_p)$
and
![]() $(E_{p,m-p}, h_{p,m-p})$
are acceptable bundles for any p. It follows from Theorem 1.7 that the induced filtered bundle
$(E_{p,m-p}, h_{p,m-p})$
are acceptable bundles for any p. It follows from Theorem 1.7 that the induced filtered bundle
![]() ${\mathcal P}_{*}F^p$
and
${\mathcal P}_{*}F^p$
and
![]() ${\mathcal P}_{*} E_{p,m-p} $
defined in §1.6 are parabolic ones. In particular,
${\mathcal P}_{*} E_{p,m-p} $
defined in §1.6 are parabolic ones. In particular,
![]() $\mathcal {P}_{\!\boldsymbol {\alpha }} F^p$
and
$\mathcal {P}_{\!\boldsymbol {\alpha }} F^p$
and
![]() $\mathcal {P}_{\!\boldsymbol {\alpha }} E_{p,m-p} $
are locally free sheaves. Denote by
$\mathcal {P}_{\!\boldsymbol {\alpha }} E_{p,m-p} $
are locally free sheaves. Denote by
![]() $j:X\backslash D\to X$
the inclusion map. Note that
$j:X\backslash D\to X$
the inclusion map. Note that
Hence, the exact sequence (2.9) in Theorem 2.5 implies the following one
In particular,
![]() $F^p_{\boldsymbol {\alpha }}/F^{p+1}_{\boldsymbol {\alpha }}$
is isomorphic to
$F^p_{\boldsymbol {\alpha }}/F^{p+1}_{\boldsymbol {\alpha }}$
is isomorphic to
![]() $\mathcal {P}_{\!\boldsymbol {\alpha }} E_{p,m-p}$
, which is thus locally free. The theorem is proved.
$\mathcal {P}_{\!\boldsymbol {\alpha }} E_{p,m-p}$
, which is thus locally free. The theorem is proved.
2.3 On the nilpotent orbit theorem
In this subsection, we apply Theorem A to prove Theorem B following closely Schmid’s original method [Reference Schmid10, p. 288-289]. We will use the notations and conventions in §1.7.
Let
![]() $(V,\nabla ,F^{\bullet },Q)$
be a complex polarized variation of Hodge structure on
$(V,\nabla ,F^{\bullet },Q)$
be a complex polarized variation of Hodge structure on
![]() $(\Delta ^{*})^p\times \Delta ^q$
. Denote by
$(\Delta ^{*})^p\times \Delta ^q$
. Denote by
![]() $\Phi :\mathbb {H}^{p}\times \Delta ^q\to \mathscr {D}$
its period mapping, where we set
$\Phi :\mathbb {H}^{p}\times \Delta ^q\to \mathscr {D}$
its period mapping, where we set
 $$ \begin{align*} \mathbb{H}^{p}\times \Delta^q&\to\Delta^n\\ (z,w)&\mapsto (e^{z_1},\ldots,e^{z_p},w) \end{align*} $$
$$ \begin{align*} \mathbb{H}^{p}\times \Delta^q&\to\Delta^n\\ (z,w)&\mapsto (e^{z_1},\ldots,e^{z_p},w) \end{align*} $$
to be the uniformizing map. Let
![]() $T_j$
be the monodromy transformation defined in §1.2. For some fixed
$T_j$
be the monodromy transformation defined in §1.2. For some fixed
![]() $\boldsymbol {\alpha }\in \mathbb {R}^p$
, there exist
$\boldsymbol {\alpha }\in \mathbb {R}^p$
, there exist
![]() $S_i, N_i\in \mathrm {\small End}(V^{\nabla })$
such that
$S_i, N_i\in \mathrm {\small End}(V^{\nabla })$
such that
-
○
 $T_i=\exp (2\pi i (S_i+N_i))$
;
$T_i=\exp (2\pi i (S_i+N_i))$
; -
○
 $[S_i,S_j]=0$
,
$[S_i,S_j]=0$
,
 $[S_i,N_j]=0$
, and
$[S_i,N_j]=0$
, and
 $[N_i, N_j]=0$
;
$[N_i, N_j]=0$
; -
○
 $S_i$
is semisimple whose eigenvalues lying in
$S_i$
is semisimple whose eigenvalues lying in
 $(\alpha _i-1,\alpha _i]$
and
$(\alpha _i-1,\alpha _i]$
and
 $N_i$
is nilpotent.
$N_i$
is nilpotent.
Let us define
 $$ \begin{align*} \tilde{\Psi}(z,w):=\exp\left(\sum_{i=1}^{p}(S_i+N_i)z_i\right)\Phi(z,w), \end{align*} $$
$$ \begin{align*} \tilde{\Psi}(z,w):=\exp\left(\sum_{i=1}^{p}(S_i+N_i)z_i\right)\Phi(z,w), \end{align*} $$
which satisfies
![]() $\tilde {\Psi }(z_1,\ldots ,z_i+2\pi i,\ldots , z_p,w)=\tilde {\Psi }(z,w)$
for
$\tilde {\Psi }(z_1,\ldots ,z_i+2\pi i,\ldots , z_p,w)=\tilde {\Psi }(z,w)$
for
![]() $i=1,\ldots ,p$
. It thus descends to a single-valued map
$i=1,\ldots ,p$
. It thus descends to a single-valued map
![]() $\Psi :(\Delta ^{*})^p\times \Delta ^q\to \check {\mathscr {D}}$
such that
$\Psi :(\Delta ^{*})^p\times \Delta ^q\to \check {\mathscr {D}}$
such that
![]() $\Psi (e^{z_1},\ldots ,e^{z_p},w)=\tilde {\Psi }(z,w)$
.
$\Psi (e^{z_1},\ldots ,e^{z_p},w)=\tilde {\Psi }(z,w)$
.
Lemma 2.6. The twisted holomorphic map
![]() $\Psi $
extends holomorphically to
$\Psi $
extends holomorphically to
![]() $\Delta ^{p+q}$
.
$\Delta ^{p+q}$
.
Proof. We use the notations in §1.2. We fix a basis
![]() $v_1,\ldots ,v_r$
of
$v_1,\ldots ,v_r$
of
![]() $V^{\nabla }$
such that each
$V^{\nabla }$
such that each
![]() $v_i$
belongs to some
$v_i$
belongs to some
![]() $\mathbb {E}_{\boldsymbol {\lambda }}$
. Then the sections
$\mathbb {E}_{\boldsymbol {\lambda }}$
. Then the sections
![]() $\tilde {v}_1,\ldots ,\tilde {v}_r$
defined in Equation (1.2) induces a trivialization
$\tilde {v}_1,\ldots ,\tilde {v}_r$
defined in Equation (1.2) induces a trivialization
where
![]() $V^{\mathrm {Del}}_{\boldsymbol {\alpha }}$
is the Deligne extension. Under such trivialization, the Hodge filtration
$V^{\mathrm {Del}}_{\boldsymbol {\alpha }}$
is the Deligne extension. Under such trivialization, the Hodge filtration
![]() $F^{\bullet }_{\boldsymbol {\alpha }}(t_1,\ldots ,t_{p+1})$
becomes
$F^{\bullet }_{\boldsymbol {\alpha }}(t_1,\ldots ,t_{p+1})$
becomes
![]() $\Psi (t_1,\ldots ,t_{p+1})$
. Thanks to Theorem A, the Hodge filtration
$\Psi (t_1,\ldots ,t_{p+1})$
. Thanks to Theorem A, the Hodge filtration
![]() $F^{\bullet }_{\boldsymbol {\alpha }}$
extends to locally free sheaves over
$F^{\bullet }_{\boldsymbol {\alpha }}$
extends to locally free sheaves over
![]() $\Delta ^{p+q}$
such that
$\Delta ^{p+q}$
such that
![]() $F^p_{\boldsymbol {\alpha }}/F^{p+1}_{\boldsymbol {\alpha }}$
is also locally free. Therefore,
$F^p_{\boldsymbol {\alpha }}/F^{p+1}_{\boldsymbol {\alpha }}$
is also locally free. Therefore,
![]() $\Psi $
extends holomorphic maps over
$\Psi $
extends holomorphic maps over
![]() $\Delta ^{p+q}$
.
$\Delta ^{p+q}$
.
This lemma thus proves Theorem B.(i). We write
![]() $a(w):=\Psi (0,w)$
. In general, it does not lie in
$a(w):=\Psi (0,w)$
. In general, it does not lie in
![]() $\mathscr {D}$
.
$\mathscr {D}$
.
The following well-known result follows from the fact that
![]() $\mathrm {GL}(V^{\nabla })$
acts transitively on
$\mathrm {GL}(V^{\nabla })$
acts transitively on
![]() $\check {\mathscr {D}}$
.
$\check {\mathscr {D}}$
.
Lemma 2.7. For any
![]() $g\in \mathrm {GL}(V^{\nabla })$
, consider the left translation
$g\in \mathrm {GL}(V^{\nabla })$
, consider the left translation
![]() $L_g:\check {\mathscr {D}}\to \check {\mathscr {D}}$
with
$L_g:\check {\mathscr {D}}\to \check {\mathscr {D}}$
with
![]() $L_g(F):=g F$
. Then
$L_g(F):=g F$
. Then
Recall that for any
![]() $A\in \mathrm {\small End}(V^{\nabla })$
and any
$A\in \mathrm {\small End}(V^{\nabla })$
and any
![]() $F\in \check {\mathscr {D}}$
, we denote by
$F\in \check {\mathscr {D}}$
, we denote by
![]() $[A]_F$
the image of A under the natural map
$[A]_F$
the image of A under the natural map
![]() $\mathrm {\small End}(V^{\nabla })\to T_{\check {\mathscr {D}},F}$
.
$\mathrm {\small End}(V^{\nabla })\to T_{\check {\mathscr {D}},F}$
.
Lemma 2.8. For each
![]() $i=1,\ldots ,p$
,
$i=1,\ldots ,p$
,
![]() $[S_i+N_i]_{a(w)}\subset T_{\check {\mathscr {D}},a(w)}^{-1,1}$
.
$[S_i+N_i]_{a(w)}\subset T_{\check {\mathscr {D}},a(w)}^{-1,1}$
.
Proof. Since
 $$ \begin{align*}\tilde{\Psi}_{*}\left(\frac{{\partial}}{{\partial} z_i}\right)(z,w)=[S_i+N_i]_{\tilde{\Psi}(z,w)}+ (L_{\exp(\sum_{i=1}^{p}(S_i+N_i)z_i)})_{*}\Phi_{*}\left(\frac{{\partial}}{{\partial} z_i}\right)(z,w), \end{align*} $$
$$ \begin{align*}\tilde{\Psi}_{*}\left(\frac{{\partial}}{{\partial} z_i}\right)(z,w)=[S_i+N_i]_{\tilde{\Psi}(z,w)}+ (L_{\exp(\sum_{i=1}^{p}(S_i+N_i)z_i)})_{*}\Phi_{*}\left(\frac{{\partial}}{{\partial} z_i}\right)(z,w), \end{align*} $$
![]() $\Phi _{*}(\frac {{\partial }}{{\partial } z_i})$
is horizontal since
$\Phi _{*}(\frac {{\partial }}{{\partial } z_i})$
is horizontal since
![]() $\Phi $
is a horizontal mapping by §1.7. By Lemma 2.7,
$\Phi $
is a horizontal mapping by §1.7. By Lemma 2.7,
![]() $(L_{\exp (\sum _{i=1}^{p}(S_i+N_i)z_i)})_{*}\Phi _{*}(\frac {{\partial }}{{\partial } z_i})(z,w)$
is horizontal. On the other hand,
$(L_{\exp (\sum _{i=1}^{p}(S_i+N_i)z_i)})_{*}\Phi _{*}(\frac {{\partial }}{{\partial } z_i})(z,w)$
is horizontal. On the other hand,
 $$ \begin{align*}\tilde{\Psi}_{*}\left(\frac{{\partial}}{{\partial} z_i}\right)(z,w)=\Psi_{*}\left(\frac{{\partial}}{{\partial} t_i}\right)(e^{z_1},\ldots,e^{z_p},w)\cdot e^{z_i} \end{align*} $$
$$ \begin{align*}\tilde{\Psi}_{*}\left(\frac{{\partial}}{{\partial} z_i}\right)(z,w)=\Psi_{*}\left(\frac{{\partial}}{{\partial} t_i}\right)(e^{z_1},\ldots,e^{z_p},w)\cdot e^{z_i} \end{align*} $$
which tends to zero if
![]() $\Re z_i\to -\infty $
and
$\Re z_i\to -\infty $
and
![]() $\Re z_j\leq C$
for other j. By the continuity, this implies that
$\Re z_j\leq C$
for other j. By the continuity, this implies that
We are ready to prove Theorem B.(ii).
Lemma 2.9. The holomorphic mapping
 $$ \begin{align*} \vartheta: \mathbb{H}^{p}\times \Delta^q&\to\check{\mathscr{D}}\\ (z,w)&\mapsto \exp\left(-\sum_{i=1}^{p}z_i(S_i+N_i)\right)\circ a(w) \end{align*} $$
$$ \begin{align*} \vartheta: \mathbb{H}^{p}\times \Delta^q&\to\check{\mathscr{D}}\\ (z,w)&\mapsto \exp\left(-\sum_{i=1}^{p}z_i(S_i+N_i)\right)\circ a(w) \end{align*} $$
is horizontal.
Proof. Note that
![]() $\vartheta _{*}(\frac {{\partial }}{{\partial } z_i})=[S_i+N_i]_{\vartheta (z,w)}$
. Since
$\vartheta _{*}(\frac {{\partial }}{{\partial } z_i})=[S_i+N_i]_{\vartheta (z,w)}$
. Since
![]() $[S_i,N_i]=0$
, one has
$[S_i,N_i]=0$
, one has
It then follows from Lemmas 2.7 and 2.8 that
![]() $ [S_i+N_i]_{\vartheta (z,w)}\in T_{\check {\mathscr {D}},\vartheta (z,w)}^{-1,1}$
. We conclude that
$ [S_i+N_i]_{\vartheta (z,w)}\in T_{\check {\mathscr {D}},\vartheta (z,w)}^{-1,1}$
. We conclude that
![]() $\vartheta _{*}(\frac {{\partial }}{{\partial } z_i})$
is horizontal.
$\vartheta _{*}(\frac {{\partial }}{{\partial } z_i})$
is horizontal.
On the other hand, one has
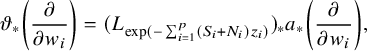 $$ \begin{align*}\vartheta_{*}\left(\frac{{\partial}}{{\partial} w_i}\right)=(L_{\exp(-\sum_{i=1}^{p}(S_i+N_i)z_i)})_{*}a_{*}\left(\frac{{\partial}}{{\partial} w_i}\right),\end{align*} $$
$$ \begin{align*}\vartheta_{*}\left(\frac{{\partial}}{{\partial} w_i}\right)=(L_{\exp(-\sum_{i=1}^{p}(S_i+N_i)z_i)})_{*}a_{*}\left(\frac{{\partial}}{{\partial} w_i}\right),\end{align*} $$
and
 $$ \begin{align*}{\Psi}_{*}\left(\frac{{\partial}}{{\partial} w_i}\right)(e^z,w)=\tilde{\Psi}_{*}\left(\frac{{\partial}}{{\partial} w_i}\right)(z,w):=(L_{\exp(\sum_{i=1}^{p}(S_i+N_i)z_i)})_{*}\Phi_{*}\left(\frac{{\partial}}{{\partial} w_i}\right)(z,w). \end{align*} $$
$$ \begin{align*}{\Psi}_{*}\left(\frac{{\partial}}{{\partial} w_i}\right)(e^z,w)=\tilde{\Psi}_{*}\left(\frac{{\partial}}{{\partial} w_i}\right)(z,w):=(L_{\exp(\sum_{i=1}^{p}(S_i+N_i)z_i)})_{*}\Phi_{*}\left(\frac{{\partial}}{{\partial} w_i}\right)(z,w). \end{align*} $$
Since
![]() $\Phi _{*}(\frac {{\partial }}{{\partial } w_i})$
is horizontal, by Lemma 2.7,
$\Phi _{*}(\frac {{\partial }}{{\partial } w_i})$
is horizontal, by Lemma 2.7,
 $$ \begin{align*}\tilde{\Psi}_{*}\left(\frac{{\partial}}{{\partial} w_i}\right)(z,w):=(L_{\exp(\sum_{i=1}^{p}(S_i+N_i)z_i)})_{*}\Phi_{*}\left(\frac{{\partial}}{{\partial} w_i}\right)(z,w)\end{align*} $$
$$ \begin{align*}\tilde{\Psi}_{*}\left(\frac{{\partial}}{{\partial} w_i}\right)(z,w):=(L_{\exp(\sum_{i=1}^{p}(S_i+N_i)z_i)})_{*}\Phi_{*}\left(\frac{{\partial}}{{\partial} w_i}\right)(z,w)\end{align*} $$
is horizontal, and thus
![]() ${\Psi }_{*}(\frac {{\partial }}{{\partial } w_i})(e^z,w)$
is horizontal. Letting
${\Psi }_{*}(\frac {{\partial }}{{\partial } w_i})(e^z,w)$
is horizontal. Letting
![]() $\Re z_i\to -\infty $
for
$\Re z_i\to -\infty $
for
![]() $i=1,\ldots , p$
, we conclude that
$i=1,\ldots , p$
, we conclude that
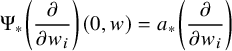 $$ \begin{align*}{\Psi}_{*}\left(\frac{{\partial}}{{\partial} w_i}\right)(0,w)=a_{*}\left(\frac{{\partial}}{{\partial} w_i}\right) \end{align*} $$
$$ \begin{align*}{\Psi}_{*}\left(\frac{{\partial}}{{\partial} w_i}\right)(0,w)=a_{*}\left(\frac{{\partial}}{{\partial} w_i}\right) \end{align*} $$
is also horizontal. We apply Lemma 2.7 again to conclude that
![]() $\vartheta _{*}(\frac {{\partial }}{{\partial } w_i})$
is horizontal. In conclusion,
$\vartheta _{*}(\frac {{\partial }}{{\partial } w_i})$
is horizontal. In conclusion,
![]() $\vartheta $
is a horizontal mapping. We proved Theorem B.(ii).
$\vartheta $
is a horizontal mapping. We proved Theorem B.(ii).
The rest of the paper is devoted to the proof of Theorem B.(iii). We will only deal with the case of one variable. We first start a lemma in linear algebra whose proof is direct (cf. [Reference Sabbah and Schnell9, §7.5] for a detailed proof).
Lemma 2.10. Let
![]() $S\in \mathrm {\small End}(V^{\nabla })$
be semisimple with real eigenvalues. Then there exists a constant
$S\in \mathrm {\small End}(V^{\nabla })$
be semisimple with real eigenvalues. Then there exists a constant
![]() $C>0$
such that
$C>0$
such that
where
![]() $\lambda _{\max }$
and
$\lambda _{\max }$
and
![]() $\lambda _{\min }$
are the largest and smallest eigenvalue of S. Let
$\lambda _{\min }$
are the largest and smallest eigenvalue of S. Let
![]() $N\in \mathrm {\small End}(V^{\nabla })$
be nilpotent. Then
$N\in \mathrm {\small End}(V^{\nabla })$
be nilpotent. Then
for some
![]() $C',m>0$
.
$C',m>0$
.
Here, we fix a reference polarized Hodge structure
![]() $o\in \mathscr {D}$
which induces metrics for
$o\in \mathscr {D}$
which induces metrics for
![]() $V^{\nabla }$
and
$V^{\nabla }$
and
![]() $\mathrm {\small End}(V^{\nabla })$
.
$\mathrm {\small End}(V^{\nabla })$
.
![]() $\lVert \mathrm {Ad}\, e^{xS}\rVert $
is the operator norm with respect to such metric of
$\lVert \mathrm {Ad}\, e^{xS}\rVert $
is the operator norm with respect to such metric of
![]() $\mathrm {\small End}(V^{\nabla })$
.
$\mathrm {\small End}(V^{\nabla })$
.
The following two lemmas are due to Schmid [Reference Schmid10, Lemmas 8.12 & 8.19]. They are stated for period domains of real Hodge structures. However, their proofs can be generalized to period domains of complex polarized Hodge structures verbatim, and we thus omit their proofs here.
Lemma 2.11. If
![]() $g\in \mathrm {GL}(V^{\nabla })$
, then for some natural distance
$g\in \mathrm {GL}(V^{\nabla })$
, then for some natural distance
![]() $d_{\check {\mathscr {D}}}$
of
$d_{\check {\mathscr {D}}}$
of
![]() $\check {\mathscr {D}}$
, we have
$\check {\mathscr {D}}$
, we have
for any points
![]() $a,b\in \check {\mathscr {D}}$
.
$a,b\in \check {\mathscr {D}}$
.
Lemma 2.12. Let
![]() $\Phi :\mathbb {H}\to \mathscr {D}$
be the period map associated to a complex polarized variation of Hodge structure on
$\Phi :\mathbb {H}\to \mathscr {D}$
be the period map associated to a complex polarized variation of Hodge structure on
![]() $\Delta ^{*}$
. Fix
$\Delta ^{*}$
. Fix
![]() $\alpha ,k>0$
and a reference point
$\alpha ,k>0$
and a reference point
![]() $o\in \mathscr {D}$
. Choose
$o\in \mathscr {D}$
. Choose
![]() $g(z)\in G=U(V^{\nabla },Q)$
such that
$g(z)\in G=U(V^{\nabla },Q)$
such that
![]() $g(z)\cdot o=\Phi (z)$
. Then there exist
$g(z)\cdot o=\Phi (z)$
. Then there exist
![]() $C,\beta>0$
such that if
$C,\beta>0$
such that if
![]() $|\Im z|\leq k$
, one has
$|\Im z|\leq k$
, one has
for
![]() $\Re z<-\alpha $
. Here,
$\Re z<-\alpha $
. Here,
![]() $\lVert \mathrm {Ad}\, g(z)^{-1}\rVert $
is the operator norm defined in Lemma 2.10.
$\lVert \mathrm {Ad}\, g(z)^{-1}\rVert $
is the operator norm defined in Lemma 2.10.
By [Reference Sabbah and Schnell9, §4.1], we know that
![]() $G:=U(V^{\nabla },Q)$
acts transitively on the period domain
$G:=U(V^{\nabla },Q)$
acts transitively on the period domain
![]() $\mathscr {D}$
, and
$\mathscr {D}$
, and
![]() $\mathscr {D}$
admits a natural G-invariant distance
$\mathscr {D}$
admits a natural G-invariant distance
![]() $d_{\mathscr {D}}$
.
$d_{\mathscr {D}}$
.
Proof of Theorem B.(iii)
Let
![]() $T\in \mathrm {GL}(V^{\nabla })$
be the monodromy operator associated to the counterclockwise generator of
$T\in \mathrm {GL}(V^{\nabla })$
be the monodromy operator associated to the counterclockwise generator of
![]() $\pi _1(\Delta ^{*})$
. Note that
$\pi _1(\Delta ^{*})$
. Note that
![]() $T\in G:=U(V^{\nabla },Q)$
. Recall that there exist commuting
$T\in G:=U(V^{\nabla },Q)$
. Recall that there exist commuting
![]() $S,N\in \mathrm { GL}(V^{\nabla })$
such that
$S,N\in \mathrm { GL}(V^{\nabla })$
such that
-
○
 $\exp (2\pi i(S+N))=T$
;
$\exp (2\pi i(S+N))=T$
; -
○ S is semisimple with eigenvalues lying in
 $(\alpha -1,\alpha ]$
;
$(\alpha -1,\alpha ]$
; -
○ N is nilpotent.
Denote by
![]() $a=\Psi (0)$
. Then for
$a=\Psi (0)$
. Then for
![]() $|t|$
small enough, one has
$|t|$
small enough, one has
which is equivalent to that
when
![]() $x\leq -M$
for some
$x\leq -M$
for some
![]() $M>0$
. Here, we write
$M>0$
. Here, we write
![]() $z=x+i y$
. Assume now
$z=x+i y$
. Assume now
![]() $|y|\leq 2\pi $
and
$|y|\leq 2\pi $
and
![]() $x\leq -M$
. Then
$x\leq -M$
. Then
 $$ \begin{align} d_{\check{\mathscr{D}}}(\exp(-(S+N)z)a, \Phi(z))&\leq \lVert\mathrm{Ad}\, \exp((S+N)z)\rVert \cdot d_{\check{\mathscr{D}}}(a, \Psi(e^z) ) \nonumber\\&\leq \lVert\mathrm{Ad}\, \exp(Nx)\rVert\cdot \lVert\mathrm{Ad}\, \exp(i(S+N) y)\rVert\cdot \lVert\mathrm{ Ad}\, \exp(S x)\rVert \cdot d_{\check{\mathscr{D}}}(a, \Psi(e^z) ) \nonumber\\&\leq C_1 \lVert\mathrm{Ad}\, \exp(Nx)\rVert \cdot \lVert\mathrm{Ad}\, \exp(S x)\rVert \cdot d_{\check{\mathscr{D}}}(a, \Psi(e^z) ) \nonumber\\&\leq C_2 |x|^{m}\cdot \exp( (\lambda_{\max}-\lambda_{\min})\cdot|x|)\cdot d_{\check{\mathscr{D}}}(a, \Psi(e^z) )\nonumber\\&\leq C_3 |x|^{m}\cdot \exp( (\lambda_{\max}-\lambda_{\min})\cdot|x|)\cdot e^x \leq C_3 |x|^me^{\delta x}. \end{align} $$
$$ \begin{align} d_{\check{\mathscr{D}}}(\exp(-(S+N)z)a, \Phi(z))&\leq \lVert\mathrm{Ad}\, \exp((S+N)z)\rVert \cdot d_{\check{\mathscr{D}}}(a, \Psi(e^z) ) \nonumber\\&\leq \lVert\mathrm{Ad}\, \exp(Nx)\rVert\cdot \lVert\mathrm{Ad}\, \exp(i(S+N) y)\rVert\cdot \lVert\mathrm{ Ad}\, \exp(S x)\rVert \cdot d_{\check{\mathscr{D}}}(a, \Psi(e^z) ) \nonumber\\&\leq C_1 \lVert\mathrm{Ad}\, \exp(Nx)\rVert \cdot \lVert\mathrm{Ad}\, \exp(S x)\rVert \cdot d_{\check{\mathscr{D}}}(a, \Psi(e^z) ) \nonumber\\&\leq C_2 |x|^{m}\cdot \exp( (\lambda_{\max}-\lambda_{\min})\cdot|x|)\cdot d_{\check{\mathscr{D}}}(a, \Psi(e^z) )\nonumber\\&\leq C_3 |x|^{m}\cdot \exp( (\lambda_{\max}-\lambda_{\min})\cdot|x|)\cdot e^x \leq C_3 |x|^me^{\delta x}. \end{align} $$
The first inequality is due to Lemma 2.11, the third one holds since
![]() $|y|\leq 2\pi $
, the fourth one follows from Lemma 2.10, and the fifth one follows from Equation (2.15). Here,
$|y|\leq 2\pi $
, the fourth one follows from Lemma 2.10, and the fifth one follows from Equation (2.15). Here,
![]() $\lambda _{\max }$
and
$\lambda _{\max }$
and
![]() $\lambda _{\min }$
are the largest and smallest eigenvalue of S. Therefore,
$\lambda _{\min }$
are the largest and smallest eigenvalue of S. Therefore,
![]() $\lambda _{\max }-\lambda _{\min }<1$
, and thus the last inequality can be achieved for some
$\lambda _{\max }-\lambda _{\min }<1$
, and thus the last inequality can be achieved for some
![]() $\delta>0$
. Here,
$\delta>0$
. Here,
![]() $C_1,\ldots ,C_3>0$
are some positive constants.
$C_1,\ldots ,C_3>0$
are some positive constants.
Fix a reference point
![]() $o\in \mathscr {D}$
, and let
$o\in \mathscr {D}$
, and let
![]() $g(z)\in G$
such that
$g(z)\in G$
such that
![]() $g(z)\cdot o=\Phi (z)$
. By Lemmas 2.11 and 2.12 together with Equation (2.16), one gets
$g(z)\cdot o=\Phi (z)$
. By Lemmas 2.11 and 2.12 together with Equation (2.16), one gets
if
![]() $|y|\leq 2\pi $
and
$|y|\leq 2\pi $
and
![]() $x<-M_2$
for some
$x<-M_2$
for some
![]() $M_2\geq M$
and
$M_2\geq M$
and
![]() $C_4,\beta>0$
. Pick a small neighborhood U of o in
$C_4,\beta>0$
. Pick a small neighborhood U of o in
![]() $\mathscr {D}$
such that the distance functions
$\mathscr {D}$
such that the distance functions
![]() $d_{\mathscr {D}}$
and
$d_{\mathscr {D}}$
and
![]() $d_{\check {\mathscr {D}}}$
are mutually bounded over U. By Equation (2.17) when
$d_{\check {\mathscr {D}}}$
are mutually bounded over U. By Equation (2.17) when
![]() $|y|\leq 2\pi $
,
$|y|\leq 2\pi $
,
![]() $x\leq -M_3$
for some
$x\leq -M_3$
for some
![]() $M_3\geq M_2$
,
$M_3\geq M_2$
,
![]() $g(z)^{-1}\exp (-(S+N)z)a$
will be entirely contained in U. Note that
$g(z)^{-1}\exp (-(S+N)z)a$
will be entirely contained in U. Note that
![]() $g(z)\in G$
, it follows that
$g(z)\in G$
, it follows that
![]() $ \exp (-(S+N)z)a\in \mathscr {D}$
if
$ \exp (-(S+N)z)a\in \mathscr {D}$
if
![]() $|y|\leq 2\pi $
and
$|y|\leq 2\pi $
and
![]() $x\leq -M_3$
. When
$x\leq -M_3$
. When
![]() $|y|>2\pi $
and
$|y|>2\pi $
and
![]() $x\leq -M_3$
, we find some integer
$x\leq -M_3$
, we find some integer
![]() $\ell $
such that
$\ell $
such that
![]() $|y-2\pi \ell |\leq 2\pi $
. Then
$|y-2\pi \ell |\leq 2\pi $
. Then
![]() $\exp (-(S+N)(z-2\pi i\ell ))a\in \mathscr {D}$
. Since
$\exp (-(S+N)(z-2\pi i\ell ))a\in \mathscr {D}$
. Since
![]() $ \exp (-(S+N)z)a=T^{-\ell }\exp (-(S+N)(z-2\pi i\ell ))a$
and
$ \exp (-(S+N)z)a=T^{-\ell }\exp (-(S+N)(z-2\pi i\ell ))a$
and
![]() $T\in G$
, it follows that
$T\in G$
, it follows that
![]() $ \exp (-(S+N)z)a\in \mathscr {D}$
. In conclusion,
$ \exp (-(S+N)z)a\in \mathscr {D}$
. In conclusion,
![]() $ \exp (-(S+N)z)a\in \mathscr {D}$
if
$ \exp (-(S+N)z)a\in \mathscr {D}$
if
![]() $x\leq -M_3$
. We prove the first claim in Theorem B.(iii).
$x\leq -M_3$
. We prove the first claim in Theorem B.(iii).
Recall that the distance functions
![]() $d_{\mathscr {D}}$
and
$d_{\mathscr {D}}$
and
![]() $d_{\check {\mathscr {D}}}$
are mutually bounded over U. By Equation (2.17) again for some
$d_{\check {\mathscr {D}}}$
are mutually bounded over U. By Equation (2.17) again for some
![]() $C_5>0$
we have
$C_5>0$
we have
for
![]() $|y|\leq 2\pi $
,
$|y|\leq 2\pi $
,
![]() $x\leq -M_3$
. Since the action of
$x\leq -M_3$
. Since the action of
![]() $g(z)$
is
$g(z)$
is
![]() $d_{\mathscr {D}}$
-distance invariant, we obtain the distance estimate
$d_{\mathscr {D}}$
-distance invariant, we obtain the distance estimate
for
![]() $|y|\leq 2\pi $
,
$|y|\leq 2\pi $
,
![]() $x\leq -M_3$
. When
$x\leq -M_3$
. When
![]() $|y|>2\pi $
and
$|y|>2\pi $
and
![]() $x\leq -M_3$
, one picks some integer
$x\leq -M_3$
, one picks some integer
![]() $\ell $
such that
$\ell $
such that
![]() $|y-2\pi \ell |\leq 2\pi $
. Then
$|y-2\pi \ell |\leq 2\pi $
. Then
In other words,
As T is also
![]() $d_{\mathscr {D}}$
-distance invariant, it follows that
$d_{\mathscr {D}}$
-distance invariant, it follows that
for
![]() $x\leq -M_3$
. The distance estimate is obtained.
$x\leq -M_3$
. The distance estimate is obtained.
Acknowledgements
This paper is motivated by a question asked by Junchao Shentu, to whom I express my gratitude. I especially thank Christian Schnell for his personal notes and discussions on the nilpotent orbit theorem in 2020 and 2022, and sending me the preprint [Reference Sabbah and Schnell9]. I also thank the referees for their valuable suggestions, which have greatly improved the paper.
Competing interest
The authors have no competing interest to declare.
Funding statement
The author acknowledges the support of the French Agence Nationale de la Recherche (ANR) under reference ANR-21-CE40-0010.



