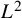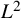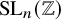1 Introduction
Eisenstein series are ubiquitous in the theory of automorphic forms, in particular, they are crucially used by Langlands, and later by Arthur, in their seminal works on the development of the spectral decomposition of the space of automorphic forms of a reductive group and the trace formula (see [Reference Arthur6, Reference Langlands36, Reference Langlands37, Reference Lapid38]. Many important questions in number theory and automorphic forms rely directly upon certain analytic properties of the Eisenstein series, for example, their complex analytic properties including the location and order of their poles and their various growth properties near the cusps.
The Eisenstein series, in contrast with cusp forms, do not decay near the cusps; in fact, they have polynomial growth. The rate of growth depends precisely on the constant terms of the Eisenstein series. In particular, the unitary Eisenstein series (barely!) fail to be square-integrable on the noncompact fundamental domain. However, it is quite natural to wonder how the
![]() $L^2$
-norms of unitary Eisenstein series grow locally (i.e., on a fixed compact subset of the fundamental domain), in terms of their Archimedean and non-Archimedean parameters.
$L^2$
-norms of unitary Eisenstein series grow locally (i.e., on a fixed compact subset of the fundamental domain), in terms of their Archimedean and non-Archimedean parameters.
In this paper, we study the general local
![]() $L^2$
-bound of a unitary Eisenstein series on a reductive group over a number field. We refer to [Reference Lapid38, Section 5.3], where such questions are considered and the relations with other important automorphic and analytic questions, for example, location and order of the poles of the Eisenstein series and classification of the residual spectrum, are discussed. Informally, we prove sharp upper bounds for the averages of the squared local
$L^2$
-bound of a unitary Eisenstein series on a reductive group over a number field. We refer to [Reference Lapid38, Section 5.3], where such questions are considered and the relations with other important automorphic and analytic questions, for example, location and order of the poles of the Eisenstein series and classification of the residual spectrum, are discussed. Informally, we prove sharp upper bounds for the averages of the squared local
![]() $L^2$
-norms of the Eisenstein series over certain short families, for a large class of reductive algebraic groups; see Theorems 2 and 3. We refer to Section 1.1 for precise and detailed discussions of the problems and our results.
$L^2$
-norms of the Eisenstein series over certain short families, for a large class of reductive algebraic groups; see Theorems 2 and 3. We refer to Section 1.1 for precise and detailed discussions of the problems and our results.
Our estimates of the local
![]() $L^2$
-norms of the Eisenstein series are potentially useful to answer many interesting number-theoretic questions, in particular, the problems that are approached via the spectral theory of various noncompact arithmetic symmetric spaces. Such approaches often face serious analytic difficulties due to the existence of the continuous spectrum and require estimates for various local
$L^2$
-norms of the Eisenstein series are potentially useful to answer many interesting number-theoretic questions, in particular, the problems that are approached via the spectral theory of various noncompact arithmetic symmetric spaces. Such approaches often face serious analytic difficulties due to the existence of the continuous spectrum and require estimates for various local
![]() $L^p$
-norms of the Eisenstein series. Our estimates and the methods to prove them seem to be utilizable to overcome the analytic hurdles that arise via the local
$L^p$
-norms of the Eisenstein series. Our estimates and the methods to prove them seem to be utilizable to overcome the analytic hurdles that arise via the local
![]() $L^2$
-norms of the Eisenstein series, at least in certain cases.
$L^2$
-norms of the Eisenstein series, at least in certain cases.
As a proof-of-concept, we prove the optimal lifting property for
![]() $\mathrm {SL}_n(\mathbb {Z}/q\mathbb {Z})$
in Theorem 5 for square-free q, as well as the Sarnak–Xue counting property in Theorem 4, for the principal congruence subgroups of
$\mathrm {SL}_n(\mathbb {Z}/q\mathbb {Z})$
in Theorem 5 for square-free q, as well as the Sarnak–Xue counting property in Theorem 4, for the principal congruence subgroups of
![]() $\mathrm {SL}_n(\mathbb {Z})$
of square-free level. Assing–Blomer recently proved those theorems conditional on the local
$\mathrm {SL}_n(\mathbb {Z})$
of square-free level. Assing–Blomer recently proved those theorems conditional on the local
![]() $L^2$
-bounds of the Eisenstein series (see [Reference Assing and Blomer8]). Thus, we make their results unconditional. We refer to Section 1.3 for a detailed discussion. In a sequel [Reference Jana and Kamber32], we prove optimal Diophantine exponent for
$L^2$
-bounds of the Eisenstein series (see [Reference Assing and Blomer8]). Thus, we make their results unconditional. We refer to Section 1.3 for a detailed discussion. In a sequel [Reference Jana and Kamber32], we prove optimal Diophantine exponent for
![]() $\mathrm {SL}_n(\mathbb {Z}[1/p])$
, as expected in a series of influential works by Ghosh–Gorodnik–Nevo (e.g. see [Reference Ghosh, Gorodnik and Nevo26]), assuming Sarnak’s density hypothesis. The proof of the main results in [Reference Jana and Kamber32] crucially depends on (a slightly weaker version of) Theorem 1 below; see [Reference Jana and Kamber32, Section 4.8]. We refer the reader to [Reference Jana and Kamber32] for a detailed discussion of this problem and our proof.
$\mathrm {SL}_n(\mathbb {Z}[1/p])$
, as expected in a series of influential works by Ghosh–Gorodnik–Nevo (e.g. see [Reference Ghosh, Gorodnik and Nevo26]), assuming Sarnak’s density hypothesis. The proof of the main results in [Reference Jana and Kamber32] crucially depends on (a slightly weaker version of) Theorem 1 below; see [Reference Jana and Kamber32, Section 4.8]. We refer the reader to [Reference Jana and Kamber32] for a detailed discussion of this problem and our proof.
Let us now discuss the motivating questions and our results.
1.1 Local
 $L^2$
-bound
$L^2$
-bound
Let G be a reductive algebraic group over a number field F. Let
![]() $\mathbb {A}$
be the adele ring of F. Also let
$\mathbb {A}$
be the adele ring of F. Also let
![]() $\mathbb {A}_f$
be the finite adeles and
$\mathbb {A}_f$
be the finite adeles and
![]() $F_\infty := F\otimes \mathbb {R}$
. Given a Levi subgroup M of G, let
$F_\infty := F\otimes \mathbb {R}$
. Given a Levi subgroup M of G, let
![]() $\mathfrak {a}_M^*$
be the
$\mathfrak {a}_M^*$
be the
![]() $\mathbb {R}$
-vector space spanned by F-rational characters of M, and
$\mathbb {R}$
-vector space spanned by F-rational characters of M, and
![]() $(\mathfrak {a}_M^G)^*$
the
$(\mathfrak {a}_M^G)^*$
the
![]() $\mathbb {R}$
-vector space spanned by characters that are trivial on G. Let
$\mathbb {R}$
-vector space spanned by characters that are trivial on G. Let
![]() $H_M\colon M(\mathbb {A}) \to \mathfrak {a}_M$
the natural map, and
$H_M\colon M(\mathbb {A}) \to \mathfrak {a}_M$
the natural map, and
![]() $M(\mathbb {A})^1$
the kernel of
$M(\mathbb {A})^1$
the kernel of
![]() $H_M$
. We denote by
$H_M$
. We denote by
![]() $M_0$
a minimal Levi subgroup.
$M_0$
a minimal Levi subgroup.
Let P be a parabolic subgroup of G with Levi subgroup M. We denote
![]() $\mathfrak {a}_P = \mathfrak {a}_M$
. Let
$\mathfrak {a}_P = \mathfrak {a}_M$
. Let
![]() $\varphi $
be in
$\varphi $
be in
![]() $\mathcal {A}^2(P)$
, which is the pre-Hilbert space of square-integrable automorphic forms on
$\mathcal {A}^2(P)$
, which is the pre-Hilbert space of square-integrable automorphic forms on
![]() $N(\mathbb {A})M(F)\backslash G(\mathbb {A})$
. Let
$N(\mathbb {A})M(F)\backslash G(\mathbb {A})$
. Let
![]() $\lambda $
be an element of
$\lambda $
be an element of
![]() $(\mathfrak {a}_{M,\mathbb {C}}^G)^* := (\mathfrak {a}_{M}^G)^*\otimes _{\mathbb {R}} \mathbb {C}$
. Following Langlands in [Reference Langlands37] (also see [Reference Arthur6, Chapter 7]), we construct an Eisenstein series
$(\mathfrak {a}_{M,\mathbb {C}}^G)^* := (\mathfrak {a}_{M}^G)^*\otimes _{\mathbb {R}} \mathbb {C}$
. Following Langlands in [Reference Langlands37] (also see [Reference Arthur6, Chapter 7]), we construct an Eisenstein series
![]() $\mathrm {Eis}(\varphi ,\lambda )$
attached to
$\mathrm {Eis}(\varphi ,\lambda )$
attached to
![]() $\varphi $
and
$\varphi $
and
![]() $\lambda $
(see the details of the construction in Section 3.3).
$\lambda $
(see the details of the construction in Section 3.3).
Let
![]() $\varphi $
be a unit vector (see Section 3.1 for the definition of the norm on
$\varphi $
be a unit vector (see Section 3.1 for the definition of the norm on
![]() $\mathcal {A}^2(P)$
) with
$\mathcal {A}^2(P)$
) with
![]() $\nu (\varphi )$
being a measurement of the complexity of
$\nu (\varphi )$
being a measurement of the complexity of
![]() $\varphi $
. We will later use a more nuanced notion of complexity (both Archimedean and non-Archimedean) (see Section 4.1 for precise definitions). Finally, let
$\varphi $
. We will later use a more nuanced notion of complexity (both Archimedean and non-Archimedean) (see Section 4.1 for precise definitions). Finally, let
![]() $\lambda \in i(\mathfrak {a}_M^G)^*$
be purely imaginary, so that
$\lambda \in i(\mathfrak {a}_M^G)^*$
be purely imaginary, so that
![]() $\mathrm {Eis}(\varphi ,\lambda )$
appears in the spectral decomposition of
$\mathrm {Eis}(\varphi ,\lambda )$
appears in the spectral decomposition of
![]() $L^2(G(F)\backslash G(\mathbb {A})^1)$
. Here and elsewhere in the paper,
$L^2(G(F)\backslash G(\mathbb {A})^1)$
. Here and elsewhere in the paper,
![]() $\,\mathrm {d}\lambda $
will denote the real-valued Lebesgue measure on
$\,\mathrm {d}\lambda $
will denote the real-valued Lebesgue measure on
![]() $i(\mathfrak {a}_M^G)^*$
as in, for example, [Reference Arthur6].
$i(\mathfrak {a}_M^G)^*$
as in, for example, [Reference Arthur6].
We ask the following two questions with (presumably, strictly) decreasing levels of difficulty. Let
![]() $\Omega $
be a fixed compact set in a fundamental domain of
$\Omega $
be a fixed compact set in a fundamental domain of
![]() $G(F)\backslash G(\mathbb {A})^1$
. How do
$G(F)\backslash G(\mathbb {A})^1$
. How do
 $$ \begin{align} \intop_\Omega|\mathrm{Eis}(\varphi,\lambda)(g)|^2\,\mathrm{d} g \end{align} $$
$$ \begin{align} \intop_\Omega|\mathrm{Eis}(\varphi,\lambda)(g)|^2\,\mathrm{d} g \end{align} $$
and
 $$ \begin{align} \intop_{\|\lambda'-\lambda\|\le 1}\intop_\Omega|\mathrm{Eis}(\varphi,\lambda')(g)|^2\,\mathrm{d} g\,\mathrm{d}\lambda' \end{align} $$
$$ \begin{align} \intop_{\|\lambda'-\lambda\|\le 1}\intop_\Omega|\mathrm{Eis}(\varphi,\lambda')(g)|^2\,\mathrm{d} g\,\mathrm{d}\lambda' \end{align} $$
grow as
![]() $\nu (\varphi )+\|\lambda \|\to \infty $
?
$\nu (\varphi )+\|\lambda \|\to \infty $
?
Here is our general expectation regarding the estimates of the above integrals.
as
![]() $\nu (\varphi )+\|\lambda \|\to \infty $
.
$\nu (\varphi )+\|\lambda \|\to \infty $
.
Let
![]() $\varphi $
be spherical at all places, and
$\varphi $
be spherical at all places, and
![]() $\nu (\varphi )$
denote the size of the Laplace eigenvalue of
$\nu (\varphi )$
denote the size of the Laplace eigenvalue of
![]() $\varphi $
. If
$\varphi $
. If
![]() $G=\mathrm {GL}_2$
and
$G=\mathrm {GL}_2$
and
![]() $\mathrm {Eis}(\varphi ,\lambda )$
is the nonholomorphic spherical Eisenstein series, then it is a classical result that (1.1) indeed satisfies (1.3) (see Section 1.4). For
$\mathrm {Eis}(\varphi ,\lambda )$
is the nonholomorphic spherical Eisenstein series, then it is a classical result that (1.1) indeed satisfies (1.3) (see Section 1.4). For
![]() $G=\mathrm {GL}_3$
, Miller in [Reference Miller43] proved that (1.2) satisfies (1.3) (see Section 1.4 for more discussions). For
$G=\mathrm {GL}_3$
, Miller in [Reference Miller43] proved that (1.2) satisfies (1.3) (see Section 1.4 for more discussions). For
![]() $G=\mathrm {GL}_n$
, Zhang in [Reference Zhang56] showed that if
$G=\mathrm {GL}_n$
, Zhang in [Reference Zhang56] showed that if
![]() $\mathrm {Eis}(\varphi ,\lambda )$
is the maximal parabolic degenerate Eisenstein series, that is induced from the trivial representation of the Levi subgroup
$\mathrm {Eis}(\varphi ,\lambda )$
is the maximal parabolic degenerate Eisenstein series, that is induced from the trivial representation of the Levi subgroup
![]() $\mathrm {GL}_{n-1}\times \mathrm {GL}_1$
, then (1.1) satisfies (1.3)Footnote
1
. As far as we know, these are the only examples where a poly-logarithmic strength bound is known for all the Eisenstein series for either (1.1) or (1.2), at least for higher rank groups.
$\mathrm {GL}_{n-1}\times \mathrm {GL}_1$
, then (1.1) satisfies (1.3)Footnote
1
. As far as we know, these are the only examples where a poly-logarithmic strength bound is known for all the Eisenstein series for either (1.1) or (1.2), at least for higher rank groups.
Remark 1.1. In this remark, we comment on a few topics in the existing literature that have similar flavour as the local
![]() $L^2$
-bound question in this paper. One may wonder about the size of the analogous local (and global, for cuspidal forms)
$L^2$
-bound question in this paper. One may wonder about the size of the analogous local (and global, for cuspidal forms)
![]() $L^p$
-bound of automorphic forms for any
$L^p$
-bound of automorphic forms for any
![]() $1\le p\le \infty $
. For compact manifolds, general polynomial bounds in
$1\le p\le \infty $
. For compact manifolds, general polynomial bounds in
![]() $\nu (\varphi )$
were obtained by Sogge [Reference Sogge54], and there have been many improvements in various aspects. On arithmetic locally symmetric spaces local
$\nu (\varphi )$
were obtained by Sogge [Reference Sogge54], and there have been many improvements in various aspects. On arithmetic locally symmetric spaces local
![]() $L^\infty $
-norms for cuspidal automorphic forms have been studied quite a lot, in particular, quite extensively for small rank groups. We refer to [Reference Blomer and Maga13] for the case of
$L^\infty $
-norms for cuspidal automorphic forms have been studied quite a lot, in particular, quite extensively for small rank groups. We refer to [Reference Blomer and Maga13] for the case of
![]() $\mathrm {GL}_n(\mathbb {R})$
, to [Reference Marshall42] for general semisimple groups and the references therein. The proofs there are via the pretrace formula, which can also be made to work to prove similar bounds for the local
$\mathrm {GL}_n(\mathbb {R})$
, to [Reference Marshall42] for general semisimple groups and the references therein. The proofs there are via the pretrace formula, which can also be made to work to prove similar bounds for the local
![]() $L^\infty $
-bounds of the short averages of the square of the Eisenstein series in case of noncompact spaces. We also remark that local
$L^\infty $
-bounds of the short averages of the square of the Eisenstein series in case of noncompact spaces. We also remark that local
![]() $L^\infty $
-bound of general Eisenstein series may not satisfy (1.3) (see, e.g. [Reference Blomer11, Theorem 2]). On the other hand, the local
$L^\infty $
-bound of general Eisenstein series may not satisfy (1.3) (see, e.g. [Reference Blomer11, Theorem 2]). On the other hand, the local
![]() $L^\infty $
bounds of the cusp forms (similarly, of an average of Eisenstein series) on
$L^\infty $
bounds of the cusp forms (similarly, of an average of Eisenstein series) on
![]() $\mathrm {GL}_n$
as in [Reference Blomer and Maga13] often do not hold globally (i.e. uniformly near the cusp) (see [Reference Brumley and Templier14]).
$\mathrm {GL}_n$
as in [Reference Blomer and Maga13] often do not hold globally (i.e. uniformly near the cusp) (see [Reference Brumley and Templier14]).
1.2 Main results
In this section, we state our main results. Informally, we prove that, for a large class of groups, (1.2) indeed can be estimated poly-logarithmically in
![]() $\nu (\varphi )+\|\lambda \|$
; as expected in (1.3). Before stating the most general result in our paper, we first give the state-of-the-art result for
$\nu (\varphi )+\|\lambda \|$
; as expected in (1.3). Before stating the most general result in our paper, we first give the state-of-the-art result for
![]() $\mathrm {GL}_n$
that is possible to state in classical language and without detailed notations.
$\mathrm {GL}_n$
that is possible to state in classical language and without detailed notations.
Theorem 1. Let
![]() $G= \mathrm {GL}_n$
and P be a parabolic subgroup of G. Let
$G= \mathrm {GL}_n$
and P be a parabolic subgroup of G. Let
![]() $\varphi _0\in \mathcal {A}^2(P)$
be a unit that is spherical at all places. Moreover, suppose that
$\varphi _0\in \mathcal {A}^2(P)$
be a unit that is spherical at all places. Moreover, suppose that
![]() $\varphi _0$
is an eigenfunction of the full Hecke algebra at the non-Archimedean places and the ring of invariant differential operators in the centre of the universal enveloping algebra at the Archimedean places. Then, for any
$\varphi _0$
is an eigenfunction of the full Hecke algebra at the non-Archimedean places and the ring of invariant differential operators in the centre of the universal enveloping algebra at the Archimedean places. Then, for any
![]() $\lambda _0\in i(\mathfrak {a}_P^G)^*$
, we have
$\lambda _0\in i(\mathfrak {a}_P^G)^*$
, we have
 $$\begin{align*}\intop_{\substack{{\lambda\in i(\mathfrak{a}_P^G)^*} \\ \|\lambda-\lambda_0\|\le 1}}\intop_\Omega|\mathrm{Eis}(\varphi_0,\lambda)(x)|^2\,\mathrm{d} x\,\mathrm{d} \lambda \ll_\Omega \left(\log(1+\nu(\varphi_0)+\|\lambda_0\|)\right)^{n-1}, \end{align*}$$
$$\begin{align*}\intop_{\substack{{\lambda\in i(\mathfrak{a}_P^G)^*} \\ \|\lambda-\lambda_0\|\le 1}}\intop_\Omega|\mathrm{Eis}(\varphi_0,\lambda)(x)|^2\,\mathrm{d} x\,\mathrm{d} \lambda \ll_\Omega \left(\log(1+\nu(\varphi_0)+\|\lambda_0\|)\right)^{n-1}, \end{align*}$$
where
![]() $\nu (\varphi _0)$
is the size of the Laplace eigenvalue of
$\nu (\varphi _0)$
is the size of the Laplace eigenvalue of
![]() $\varphi _0$
.
$\varphi _0$
.
Remark 1.2. Actually, Theorem 1 is true for any
![]() $\varphi $
that lies in the
$\varphi $
that lies in the
![]() $\pi $
-isotypic subspace
$\pi $
-isotypic subspace
![]() $\mathcal {A}_\pi ^2(P)$
for some representation
$\mathcal {A}_\pi ^2(P)$
for some representation
![]() $\pi $
of
$\pi $
of
![]() $M(\mathbb {A})$
and is only required to be spherical at the Archimedean places and invariant by any
$M(\mathbb {A})$
and is only required to be spherical at the Archimedean places and invariant by any
![]() $K\subset \mathrm {GL}_n(\mathbb {A}_f)$
, with
$K\subset \mathrm {GL}_n(\mathbb {A}_f)$
, with
![]() $\ll $
replaced by
$\ll $
replaced by
![]() $\ll _K$
. The dependency of the constant on K could, a priori, be large, for example, polynomial in
$\ll _K$
. The dependency of the constant on K could, a priori, be large, for example, polynomial in
![]() $\mathrm {level}(K)$
(see Section 4.1 for the definition of level). One may expect a polylogarithmic dependence on the level, but we can only prove it when
$\mathrm {level}(K)$
(see Section 4.1 for the definition of level). One may expect a polylogarithmic dependence on the level, but we can only prove it when
![]() $\varphi $
is associated with unramified cuspidal datum, as in Theorem 2.
$\varphi $
is associated with unramified cuspidal datum, as in Theorem 2.
Now, we describe our full results. First, we recall certain terminologies (that are fully explained in the body of the paper).
-
• Following Langlands, a cuspidal datum
 $\chi $
is a
$\chi $
is a
 $G(F)$
-conjugacy class of pairs
$G(F)$
-conjugacy class of pairs
 $(L,\sigma )$
, where L is a Levi subgroup of G defined over F and
$(L,\sigma )$
, where L is a Levi subgroup of G defined over F and
 $\sigma $
is a cuspidal representation of
$\sigma $
is a cuspidal representation of
 $L(\mathbb {A})$
(see Section 3.1). Moreover, we recall the notion of unramifiedness of a cuspidal datum, due to Arthur, which ensures that the datum has a trivial stabilizer (see [Reference Arthur6, Section 15]Footnote
2
).
$L(\mathbb {A})$
(see Section 3.1). Moreover, we recall the notion of unramifiedness of a cuspidal datum, due to Arthur, which ensures that the datum has a trivial stabilizer (see [Reference Arthur6, Section 15]Footnote
2
). -
• We discuss certain estimates of various intertwining operators. The following terminologies are due to Finis–Lapid–Müller.
-
– We say G satisfies property (tempered winding number, TWN+) if the first derivatives of the global normalization factors of the intertwining operators satisfy certain estimates (see Section 5.1).
-
– We say G satisfies property (bounded degree, BD) if the first derivatives of the local normalized intertwining operators satisfy certain estimates (see Section 5.2).
-
-
• For any Levi subgroup M, let
 $\Pi _2(M)$
denote the isomorphism class of representations of
$\Pi _2(M)$
denote the isomorphism class of representations of
 $M(\mathbb {A})$
appearing discretely in
$M(\mathbb {A})$
appearing discretely in
 $L^2(M(F) \backslash M(\mathbb {A}))$
(see Section 3.1).
$L^2(M(F) \backslash M(\mathbb {A}))$
(see Section 3.1). -
• For a parabolic subgroup P with Levi subgroup M,
 $\chi $
a cuspidal datum and
$\chi $
a cuspidal datum and
 $\pi \in \Pi _2(M)$
, let
$\pi \in \Pi _2(M)$
, let
 $\mathcal {A}^2(P)_{\chi ,\pi }$
denote the
$\mathcal {A}^2(P)_{\chi ,\pi }$
denote the
 $(\chi ,\pi )$
-isotypic part of
$(\chi ,\pi )$
-isotypic part of
 $\mathcal {A}^2(P)$
(see Section 3.1).
$\mathcal {A}^2(P)$
(see Section 3.1). -
• We fix (good) maximal compact subgroups
 $K_\infty $
of
$K_\infty $
of
 $G(F_\infty )$
and
$G(F_\infty )$
and
 $K_f$
of
$K_f$
of
 $G(\mathbb {A}_f)$
. For
$G(\mathbb {A}_f)$
. For
 $\tau \in \widehat {K_\infty }$
, which is the unitary dual of
$\tau \in \widehat {K_\infty }$
, which is the unitary dual of
 $K_\infty $
, we write
$K_\infty $
, we write
 $\mathcal {A}^2(P)^{\tau ,K}$
for the space of functions in
$\mathcal {A}^2(P)^{\tau ,K}$
for the space of functions in
 $\mathcal {A}^2(P)$
which are right K-invariant and belong to
$\mathcal {A}^2(P)$
which are right K-invariant and belong to
 $\tau $
-isotypic subspace. We define
$\tau $
-isotypic subspace. We define
 $\mathcal {A}^2_{\chi ,\pi }(P)^{\tau ,K}$
similarly (see Section 3.1).
$\mathcal {A}^2_{\chi ,\pi }(P)^{\tau ,K}$
similarly (see Section 3.1). -
• We bound the integrals over
 $\Omega $
in (1.1) and (1.2) via the inner product of truncated Eisenstein series. We work with a truncation operator
$\Omega $
in (1.1) and (1.2) via the inner product of truncated Eisenstein series. We work with a truncation operator
 $\Lambda ^T$
, as defined by Arthur, where T is a sufficiently dominant element in
$\Lambda ^T$
, as defined by Arthur, where T is a sufficiently dominant element in
 $\mathfrak {a}_{M_0}$
. We also define
$\mathfrak {a}_{M_0}$
. We also define
 $d(T)$
to be a measurement of how dominant T is (see Section 3.4 for details).
$d(T)$
to be a measurement of how dominant T is (see Section 3.4 for details). -
• Finally, we fix certain measurements of the Archimedean complexity of a representation
 $\pi $
of a real group by the size of its Casimir eigenvalue, denoted by
$\pi $
of a real group by the size of its Casimir eigenvalue, denoted by
 $\nu (\pi )$
and certain measurement of the non-Archimedean complexity of an open compact subgroup K of
$\nu (\pi )$
and certain measurement of the non-Archimedean complexity of an open compact subgroup K of
 $G(\mathbb {A}_f)$
by its depth and level, denoted by
$G(\mathbb {A}_f)$
by its depth and level, denoted by
 $\mathrm {level}(K)$
(see Section 4.1). To give a sense of their sizes for
$\mathrm {level}(K)$
(see Section 4.1). To give a sense of their sizes for
 $G=\mathrm {GL}_2$
, if
$G=\mathrm {GL}_2$
, if
 $\pi $
is principal series representations induced from
$\pi $
is principal series representations induced from
 $|.|^{it}\otimes |.|^{-it}$
, then
$|.|^{it}\otimes |.|^{-it}$
, then
 $\nu (\pi )\asymp 1+t^2$
, and if K is the principal congruence subgroup of level q, then
$\nu (\pi )\asymp 1+t^2$
, and if K is the principal congruence subgroup of level q, then
 $\mathrm {level}(K)=q$
.
$\mathrm {level}(K)=q$
.
Here is our first main theorem.
Theorem 2. Assume that G satisfies properties (TWN+) and (BD). Let P be a parabolic subgroup of G with Levi subgroup M and
![]() $\pi _0\in \Pi _2(M)$
. Moreover, assume that
$\pi _0\in \Pi _2(M)$
. Moreover, assume that
![]() $\chi :=(M,\pi _0)$
is an unramified cuspidal datum of G. Let
$\chi :=(M,\pi _0)$
is an unramified cuspidal datum of G. Let
![]() $\tau \in \widehat {K_\infty }$
and
$\tau \in \widehat {K_\infty }$
and
![]() $K\subset K_f$
be an open-compact. Then
$K\subset K_f$
be an open-compact. Then
 $$\begin{align*}\intop_{\substack{{\lambda\in i(\mathfrak{a}_M^G)^*} \\ \|\lambda-\lambda_0\|\le 1}} \|\Lambda^T \mathrm{Eis}(\varphi_0,\lambda)\|_{2}^2 \,\mathrm{d} \lambda \ll \Big((1+\|T\|)\,\log \left(1+\nu(\pi_{0,\infty})+\|\lambda_0\|+\nu(\tau)+\mathrm{level}(K)\right)\Big)^{\dim\mathfrak{a}_M^G}, \end{align*}$$
$$\begin{align*}\intop_{\substack{{\lambda\in i(\mathfrak{a}_M^G)^*} \\ \|\lambda-\lambda_0\|\le 1}} \|\Lambda^T \mathrm{Eis}(\varphi_0,\lambda)\|_{2}^2 \,\mathrm{d} \lambda \ll \Big((1+\|T\|)\,\log \left(1+\nu(\pi_{0,\infty})+\|\lambda_0\|+\nu(\tau)+\mathrm{level}(K)\right)\Big)^{\dim\mathfrak{a}_M^G}, \end{align*}$$
for any unit
![]() $\varphi _0\in \mathcal {A}^2_{\chi ,\pi _0}(P)^{\tau ,K}$
and
$\varphi _0\in \mathcal {A}^2_{\chi ,\pi _0}(P)^{\tau ,K}$
and
![]() $\lambda _0\in i(\mathfrak {a}_M^G)^*$
.
$\lambda _0\in i(\mathfrak {a}_M^G)^*$
.
Remark 1.3. The implicit constant in Theorem 2 depends only on G. For G and
![]() $\chi $
as in the statement, Theorem 2 proves that the integral (1.2) grows poly-logarithmically in all the parameters, verifying (1.3). For
$\chi $
as in the statement, Theorem 2 proves that the integral (1.2) grows poly-logarithmically in all the parameters, verifying (1.3). For
![]() $\mathrm {GL}_n$
, when Theorem 2 applies, it is more general than Theorem 1 in the level and weight aspect, since it gives poly-logarithmic dependence on the level and is not restricted to
$\mathrm {GL}_n$
, when Theorem 2 applies, it is more general than Theorem 1 in the level and weight aspect, since it gives poly-logarithmic dependence on the level and is not restricted to
![]() $K_\infty $
-invariant vectors.
$K_\infty $
-invariant vectors.
Of course, Theorem 2 excludes a ‘narrow’ class of cuspidal data that are not unramified. For example, for
![]() $G=\mathrm {GL}_n$
, a Levi subgroup is of the form
$G=\mathrm {GL}_n$
, a Levi subgroup is of the form
![]() $M\cong \mathrm {GL}_{n_1}\times \dots \times \mathrm {GL}_{n_k}$
, and a representation
$M\cong \mathrm {GL}_{n_1}\times \dots \times \mathrm {GL}_{n_k}$
, and a representation
![]() $\pi \in \Pi _2(M)$
satisfies
$\pi \in \Pi _2(M)$
satisfies
![]() $\pi \cong \pi _1\otimes \dots \otimes \pi _k$
, where
$\pi \cong \pi _1\otimes \dots \otimes \pi _k$
, where
![]() $\pi _i \in \Pi _2(\mathrm {GL}_{n_i})$
. Theorem 2 will apply to
$\pi _i \in \Pi _2(\mathrm {GL}_{n_i})$
. Theorem 2 will apply to
![]() $\pi $
if and only if each
$\pi $
if and only if each
![]() $\pi _i$
is cuspidal, and
$\pi _i$
is cuspidal, and
![]() $\pi _i \not \cong \pi _j$
for
$\pi _i \not \cong \pi _j$
for
![]() $i\ne j$
.
$i\ne j$
.
In Theorem 3, we give a result towards the expectation in (1.3) for G with the similar level of generalities considered in Theorem 2 and
![]() $\tau $
being trivial but for all cuspidal data
$\tau $
being trivial but for all cuspidal data
![]() $\chi $
. Before stating the theorem precisely, we introduce a new quantity below, which roughly measures the number of discrete series representations with specific
$\chi $
. Before stating the theorem precisely, we introduce a new quantity below, which roughly measures the number of discrete series representations with specific
![]() $K_\infty K_f$
-type that arises from a given cuspidal datum.
$K_\infty K_f$
-type that arises from a given cuspidal datum.
Definition 1.4. Let
![]() $\tau \in \widehat {K_\infty }$
and
$\tau \in \widehat {K_\infty }$
and
![]() $K\subset K_f$
be an open-compact. For any cuspidal datum
$K\subset K_f$
be an open-compact. For any cuspidal datum
![]() $\chi $
of G, we define
$\chi $
of G, we define
 $$\begin{align*}F(\chi;\tau,K):=\sum_{P\supset P_0}\dim\left(\mathcal{A}^2_{\chi}(P)^{\tau,K}\right)=\sum_{P\supset P_0}\sum_{\pi\in \Pi_2(M_P)}\dim\left(\mathcal{A}^2_{\chi,\pi}(P)^{\tau,K}\right). \end{align*}$$
$$\begin{align*}F(\chi;\tau,K):=\sum_{P\supset P_0}\dim\left(\mathcal{A}^2_{\chi}(P)^{\tau,K}\right)=\sum_{P\supset P_0}\sum_{\pi\in \Pi_2(M_P)}\dim\left(\mathcal{A}^2_{\chi,\pi}(P)^{\tau,K}\right). \end{align*}$$
Here,
![]() $P_0$
is some fixed minimal parabolic subgroup containing
$P_0$
is some fixed minimal parabolic subgroup containing
![]() $M_0$
and
$M_0$
and
![]() $P\supset P_0$
are called standard parabolic subgroups.
$P\supset P_0$
are called standard parabolic subgroups.
Theorem 3. Assume that G satisfies properties (TWN+) and (BD). Let
![]() $\chi :=(M,\pi _0)$
be any cuspidal datum of G. Then
$\chi :=(M,\pi _0)$
be any cuspidal datum of G. Then
 $$ \begin{align*} \sum_{P\supset P_0}&\sum_{\pi\in\Pi_2(M_P)}\sum_{\varphi\in\mathcal{B}_{\chi,\pi}(P)^{K_\infty K}}\intop_{\substack{{\lambda\in i(\mathfrak{a}_P^G)^*} \\ \|\lambda-\lambda_0\|\le 1}} \|\Lambda^T \mathrm{Eis}(\varphi,\lambda) \|^2_2 \,\mathrm{d} \lambda \\ \ll & \Big((1+\|T\|)\,\log(1+\nu(\pi_{0,\infty})+\|\lambda_0\|+\mathrm{level}(K))\Big)^{\dim\mathfrak{a}_M^G}F(\chi;\mathrm{triv},K), \end{align*} $$
$$ \begin{align*} \sum_{P\supset P_0}&\sum_{\pi\in\Pi_2(M_P)}\sum_{\varphi\in\mathcal{B}_{\chi,\pi}(P)^{K_\infty K}}\intop_{\substack{{\lambda\in i(\mathfrak{a}_P^G)^*} \\ \|\lambda-\lambda_0\|\le 1}} \|\Lambda^T \mathrm{Eis}(\varphi,\lambda) \|^2_2 \,\mathrm{d} \lambda \\ \ll & \Big((1+\|T\|)\,\log(1+\nu(\pi_{0,\infty})+\|\lambda_0\|+\mathrm{level}(K))\Big)^{\dim\mathfrak{a}_M^G}F(\chi;\mathrm{triv},K), \end{align*} $$
where
![]() $\mathcal {B}_{\chi ,\pi }(P)^{K_\infty K}$
denotes an orthonormal basis of
$\mathcal {B}_{\chi ,\pi }(P)^{K_\infty K}$
denotes an orthonormal basis of
![]() $\mathcal {A}^2_{\chi ,\pi }(P)^{K_\infty K}$
and
$\mathcal {A}^2_{\chi ,\pi }(P)^{K_\infty K}$
and
![]() $\lambda _0\in i(\mathfrak {a}_M^G)^*$
.
$\lambda _0\in i(\mathfrak {a}_M^G)^*$
.
Remark 1.5. Note that the
![]() $(P,\pi )$
-summand on the left-hand side above vanishes identically unless
$(P,\pi )$
-summand on the left-hand side above vanishes identically unless
![]() $\mathcal {A}^2_{\chi ,\pi }(P)^{K_\infty K}\neq \{0\}$
. In fact, the total number of nonzero
$\mathcal {A}^2_{\chi ,\pi }(P)^{K_\infty K}\neq \{0\}$
. In fact, the total number of nonzero
![]() $(P,\pi ,\varphi )$
-summands on the left-hand side is finite and equals to
$(P,\pi ,\varphi )$
-summands on the left-hand side is finite and equals to
![]() $F(\chi ;\mathrm {triv},K)$
(the
$F(\chi ;\mathrm {triv},K)$
(the
![]() $\lambda $
-integral, however, may be empty if
$\lambda $
-integral, however, may be empty if
![]() $\lambda _0 \in i(\mathfrak {a}_M^G)^* \subset i(\mathfrak {a}_{M_0}^G)^*$
is far from
$\lambda _0 \in i(\mathfrak {a}_M^G)^* \subset i(\mathfrak {a}_{M_0}^G)^*$
is far from
![]() $i(\mathfrak {a}_{P}^G)^* \subset i(\mathfrak {a}_{M_0}^G)^*$
). Thus, Theorem 3 on average is of the same strength as Theorem 2, that is, the integral in (1.2) on average satisfies the estimate in (1.3).
$i(\mathfrak {a}_{P}^G)^* \subset i(\mathfrak {a}_{M_0}^G)^*$
). Thus, Theorem 3 on average is of the same strength as Theorem 2, that is, the integral in (1.2) on average satisfies the estimate in (1.3).
In particular, by the positivity of the left-hand side in Theorem 3, we obtain the following corollary.
Corollary 1.6. Assume that G and
![]() $\chi $
are as in Theorem 3. Let P be a parabolic subgroup of G and
$\chi $
are as in Theorem 3. Let P be a parabolic subgroup of G and
![]() $\pi \in \Pi _2(M_P)$
, such that
$\pi \in \Pi _2(M_P)$
, such that
![]() $\mathcal {A}^2_{\chi ,\pi }(P)\neq \{0\}$
. Then
$\mathcal {A}^2_{\chi ,\pi }(P)\neq \{0\}$
. Then
 $$ \begin{align*} \intop_{\substack{{\lambda\in i(\mathfrak{a}_P^G)^*} \\ \|\lambda-\lambda_0\|\le 1}} &\|\Lambda^T \mathrm{Eis}(\varphi_0,\lambda) \|^2_2 \,\mathrm{d} \lambda \\ \ll & \Big((1+\|T\|)\,\log(1+\nu(\pi_{\infty})+\|\lambda_0\|+\mathrm{level}(K))\Big)^{\dim\mathfrak{a}_M^G}F(\chi;\mathrm{triv},K), \end{align*} $$
$$ \begin{align*} \intop_{\substack{{\lambda\in i(\mathfrak{a}_P^G)^*} \\ \|\lambda-\lambda_0\|\le 1}} &\|\Lambda^T \mathrm{Eis}(\varphi_0,\lambda) \|^2_2 \,\mathrm{d} \lambda \\ \ll & \Big((1+\|T\|)\,\log(1+\nu(\pi_{\infty})+\|\lambda_0\|+\mathrm{level}(K))\Big)^{\dim\mathfrak{a}_M^G}F(\chi;\mathrm{triv},K), \end{align*} $$
for any unit
![]() $\varphi _0\in \mathcal {A}^2_{\chi ,\pi }(P)^{K_\infty K}$
and
$\varphi _0\in \mathcal {A}^2_{\chi ,\pi }(P)^{K_\infty K}$
and
![]() $\lambda _0\in i(\mathfrak {a}_{P}^G)^*$
.
$\lambda _0\in i(\mathfrak {a}_{P}^G)^*$
.
Remark 1.7. Let us focus on
![]() $\mathrm {GL}_n$
. In this case, understanding
$\mathrm {GL}_n$
. In this case, understanding
![]() $F(\chi ;\mathrm {triv},K)$
boils down to a local question, as we know for which
$F(\chi ;\mathrm {triv},K)$
boils down to a local question, as we know for which
![]() $\pi $
it holds that
$\pi $
it holds that
![]() $\mathcal {A}^2_{\chi ,\pi }\ne \{0\}$
thanks to [Reference Mœglin and Waldspurger44]. Then one can show that when
$\mathcal {A}^2_{\chi ,\pi }\ne \{0\}$
thanks to [Reference Mœglin and Waldspurger44]. Then one can show that when
![]() $\pi _0$
is cuspidal it holds that
$\pi _0$
is cuspidal it holds that
However, when
![]() $\pi _0$
is not cuspidal,
$\pi _0$
is not cuspidal,
![]() $F(\chi ;\mathrm {triv},K)$
can be a lot larger than
$F(\chi ;\mathrm {triv},K)$
can be a lot larger than
![]() $\dim \mathcal {A}^2_{\chi ,\pi _0}(P)^{K_\infty K}$
, which eventually leads to a nonoptimal result, when averaging over a basis of
$\dim \mathcal {A}^2_{\chi ,\pi _0}(P)^{K_\infty K}$
, which eventually leads to a nonoptimal result, when averaging over a basis of
![]() $\mathcal {A}^2_{\chi ,\pi _0}(P)^{K_\infty K}$
.
$\mathcal {A}^2_{\chi ,\pi _0}(P)^{K_\infty K}$
.
For general groups, the size of
![]() $F(\chi ;\tau ,K)$
has two components: the local component, namely, the dimension of the
$F(\chi ;\tau ,K)$
has two components: the local component, namely, the dimension of the
![]() $K_\infty K_f$
-type subspace and the global component, namely, the number and multiplicity of square-integrable representations (with a given
$K_\infty K_f$
-type subspace and the global component, namely, the number and multiplicity of square-integrable representations (with a given
![]() $K_\infty K_f\cap M(\mathbb {A})$
-type) that are attached to
$K_\infty K_f\cap M(\mathbb {A})$
-type) that are attached to
![]() $\chi $
.
$\chi $
.
The local component could, potentially, be quite larger than
![]() $\log (\|\nu (\tau )\|+\mathrm {level}(K))$
but by uniform admissibility (see [Reference Bernšteĭn10]) is bounded depending only on
$\log (\|\nu (\tau )\|+\mathrm {level}(K))$
but by uniform admissibility (see [Reference Bernšteĭn10]) is bounded depending only on
![]() $\tau $
and K. This nonoptimal dependence on
$\tau $
and K. This nonoptimal dependence on
![]() $\mathrm {level}(K)$
even for
$\mathrm {level}(K)$
even for
![]() $\mathrm {GL}_n$
is the main weakness of Theorem 3 relative to Theorem 2. Also, Theorem 3 is restricted to
$\mathrm {GL}_n$
is the main weakness of Theorem 3 relative to Theorem 2. Also, Theorem 3 is restricted to
![]() $\tau =\mathrm {triv}$
, but this should not be a major issue.
$\tau =\mathrm {triv}$
, but this should not be a major issue.
The global component should, at least conjecturally, be small, and, in fact, bounded (perhaps depending on K). Its understanding depends eventually upon the classification of the residual spectrum. In other words, it depends on how the residual spectrum arises from the residues of the Eisenstein series induced from cuspidal representations, which in turn asks for highly nontrivial analytic properties of the Eisenstein series. All of the above problems are still wide open for general reductive groups, and understanding them for classical groups seems like a very interesting question that we plan to address in future work.
Remark 1.8. One may wonder whether one can obtain an estimate for the pointwise bound of the local
![]() $L^2$
-norms in (1.1) from corresponding bounds for their
$L^2$
-norms in (1.1) from corresponding bounds for their
![]() $\lambda $
-averages in Corollary 1.6. In principle, one may attempt this via a contour-shifting argument and employing the functional equation of the Eisenstein series. This kind of approach is prevalent in analytic number theory: for example, bounding central L-value
$\lambda $
-averages in Corollary 1.6. In principle, one may attempt this via a contour-shifting argument and employing the functional equation of the Eisenstein series. This kind of approach is prevalent in analytic number theory: for example, bounding central L-value
![]() $L(1/2+iT)$
for some automorphic representation for large T, by sharp estimation of
$L(1/2+iT)$
for some automorphic representation for large T, by sharp estimation of
![]() $\int _{T-H}^{T+H}|L(1/2+it)|^2\,\mathrm {d} t$
for some
$\int _{T-H}^{T+H}|L(1/2+it)|^2\,\mathrm {d} t$
for some
![]() $H\le T$
, shifting the
$H\le T$
, shifting the
![]() $it$
-contour and applying functional equation of the L-function (see, e.g. [Reference Good28]). Clearly, to apply the above contour-shifting method in our case, we need to crucially understand meromorphic properties of the Eisenstein series away from the unitary axis, in particular, the location of its poles and residues. On
$it$
-contour and applying functional equation of the L-function (see, e.g. [Reference Good28]). Clearly, to apply the above contour-shifting method in our case, we need to crucially understand meromorphic properties of the Eisenstein series away from the unitary axis, in particular, the location of its poles and residues. On
![]() $\mathrm {GL}_n$
, this is essentially equivalent to understanding strong zero-free regions of various Rankin–Selberg L-functions. Our current knowledge of such zero-free regions is rather limited and only yields a polynomial strength bound in the question (1.1).
$\mathrm {GL}_n$
, this is essentially equivalent to understanding strong zero-free regions of various Rankin–Selberg L-functions. Our current knowledge of such zero-free regions is rather limited and only yields a polynomial strength bound in the question (1.1).
1.3 Applications
While estimating the local
![]() $L^2$
-bound of the Eisenstein series is interesting in its own right, it is also very useful in applications to number theory and Diophantine approximation. As a matter of fact, we came to study
$L^2$
-bound of the Eisenstein series is interesting in its own right, it is also very useful in applications to number theory and Diophantine approximation. As a matter of fact, we came to study
![]() $L^2$
-bounds of the Eisenstein series while trying to understand certain number theoretic problems via the spectral theory of automorphic forms.
$L^2$
-bounds of the Eisenstein series while trying to understand certain number theoretic problems via the spectral theory of automorphic forms.
We already mentioned the sequel [Reference Jana and Kamber32], where we use the results of this work to prove optimal Diophantine exponent for
![]() $\mathrm {SL}_n$
assuming Sarnak’s density hypothesis.
$\mathrm {SL}_n$
assuming Sarnak’s density hypothesis.
Here, we give two other applications of the
![]() $L^2$
-bounds of the Eisenstein series, concerning the principal congruence subgroups of
$L^2$
-bounds of the Eisenstein series, concerning the principal congruence subgroups of
![]() $\mathrm {SL}_n(\mathbb {Z})$
. Let
$\mathrm {SL}_n(\mathbb {Z})$
. Let
![]() $\Gamma (1) := \mathrm {SL}_n(\mathbb {Z})$
, and let
$\Gamma (1) := \mathrm {SL}_n(\mathbb {Z})$
, and let
![]() $\Gamma (q) := \ker (\Gamma (1) \xrightarrow {\mod q} \mathrm {SL}_n(\mathbb {Z}/q\mathbb {Z}))$
be its principal congruence subgroup. By strong approximation,
$\Gamma (q) := \ker (\Gamma (1) \xrightarrow {\mod q} \mathrm {SL}_n(\mathbb {Z}/q\mathbb {Z}))$
be its principal congruence subgroup. By strong approximation,
![]() $\Gamma (1)/ \Gamma (q) \cong \mathrm {SL}_n(\mathbb {Z}/q\mathbb {Z})$
. Let
$\Gamma (1)/ \Gamma (q) \cong \mathrm {SL}_n(\mathbb {Z}/q\mathbb {Z})$
. Let
![]() $\|\cdot \|$
be the Frobenius norm on
$\|\cdot \|$
be the Frobenius norm on
![]() $\mathrm {SL}_n(\mathbb {R})$
, that is
$\mathrm {SL}_n(\mathbb {R})$
, that is
![]() $\|g\|^2 = \sum _{i,j} |g_{i,j}|^2$
(as a matter of fact, one can consider any other norm as well).
$\|g\|^2 = \sum _{i,j} |g_{i,j}|^2$
(as a matter of fact, one can consider any other norm as well).
The first problem is about counting the number of elements
There are two regimes in which this problem is well understood. In the regime
![]() $R< Cq$
, where
$R< Cq$
, where
![]() $C=C(n)$
is some small constant, it is simple to show that
$C=C(n)$
is some small constant, it is simple to show that
In the regime where q is fixed and
![]() $R\to \infty $
(or at least a large power of q), it holds that
$R\to \infty $
(or at least a large power of q), it holds that
 $$ \begin{align} \# \{\gamma \in \Gamma(q) \mid \|\gamma\| \le R\} = c_n\frac{R^{n(n-1)}}{\#\mathrm{SL}_n(\mathbb{Z}/q\mathbb{Z})}+ O(R^{n(n-1)-\delta_n}) \end{align} $$
$$ \begin{align} \# \{\gamma \in \Gamma(q) \mid \|\gamma\| \le R\} = c_n\frac{R^{n(n-1)}}{\#\mathrm{SL}_n(\mathbb{Z}/q\mathbb{Z})}+ O(R^{n(n-1)-\delta_n}) \end{align} $$
with
![]() $c_n$
an explicit constant, and
$c_n$
an explicit constant, and
![]() $\delta _n>0$
a small constant. This follows from the work of Duke, Rudnick and Sarnak [Reference Duke, Rudnick and Sarnak16, Theorem 1.10] and is based on spectral methodsFootnote
3
.
$\delta _n>0$
a small constant. This follows from the work of Duke, Rudnick and Sarnak [Reference Duke, Rudnick and Sarnak16, Theorem 1.10] and is based on spectral methodsFootnote
3
.
Sarnak and Xue ([Reference Sarnak and Xue52, Conjecture 2], see also [Reference Sarnak53]) made the following conjecture, which addresses the intermediate range when R is a small power of q:
 $$\begin{align*}\# \{\gamma \in \Gamma(q) \mid \|\gamma\| \le R\} \ll_\epsilon \frac{R^{n(n-1)+\epsilon}}{|\mathrm{SL}_n(\mathbb{Z}/q\mathbb{Z})|}+ R^{n(n-1)/2}. \end{align*}$$
$$\begin{align*}\# \{\gamma \in \Gamma(q) \mid \|\gamma\| \le R\} \ll_\epsilon \frac{R^{n(n-1)+\epsilon}}{|\mathrm{SL}_n(\mathbb{Z}/q\mathbb{Z})|}+ R^{n(n-1)/2}. \end{align*}$$
In a recent work, Assing and Blomer [Reference Assing and Blomer8, Theorem 1.4] essentially confirm the above Sarnak–Xue conjecture showing that
 $$ \begin{align} \# \{\gamma \in \Gamma(q) \mid \|\gamma\| \le R\} \ll_\epsilon (Rq)^\epsilon\left(\frac{R^{n(n-1)}}{q^{n^2-1}}+R^{n(n-1)/2}\right), \end{align} $$
$$ \begin{align} \# \{\gamma \in \Gamma(q) \mid \|\gamma\| \le R\} \ll_\epsilon (Rq)^\epsilon\left(\frac{R^{n(n-1)}}{q^{n^2-1}}+R^{n(n-1)/2}\right), \end{align} $$
conditional on a difficult conjecture, namely [Reference Assing and Blomer8, Hypothesis 1], on the local
![]() $L^2$
-bound of the Eisenstein series. This hypothesis is slightly weaker than the expected bound in (1.3) for the integral (1.1). In Theorem 4, we make Assing–Blomer’s result unconditional, by employing the method of proving Theorem 3, while also using their work as a crucial input.
$L^2$
-bound of the Eisenstein series. This hypothesis is slightly weaker than the expected bound in (1.3) for the integral (1.1). In Theorem 4, we make Assing–Blomer’s result unconditional, by employing the method of proving Theorem 3, while also using their work as a crucial input.
Theorem 4. Let q be a square-free integer. Then Equation (1.5) holds for every
![]() $\epsilon>0$
and every
$\epsilon>0$
and every
![]() $R\ge 1$
.
$R\ge 1$
.
The second application we have is the problem of optimal lifting. Recall that by strong approximation for
![]() $\mathrm {SL}_n$
, the map
$\mathrm {SL}_n$
, the map
![]() $\mathrm {SL}_n(\mathbb {Z}) \to \mathrm {SL}_n(\mathbb {Z}/q\mathbb {Z})$
is onto. We may therefore ask, given
$\mathrm {SL}_n(\mathbb {Z}) \to \mathrm {SL}_n(\mathbb {Z}/q\mathbb {Z})$
is onto. We may therefore ask, given
![]() $\overline {\gamma } \in \mathrm {SL}_n(\mathbb {Z} / q\mathbb {Z})$
, to find a lift of it to
$\overline {\gamma } \in \mathrm {SL}_n(\mathbb {Z} / q\mathbb {Z})$
, to find a lift of it to
![]() $\gamma \in \mathrm {SL}_n(\mathbb {Z})$
, with
$\gamma \in \mathrm {SL}_n(\mathbb {Z})$
, with
![]() $\|\gamma \|$
minimal. Gorodnik–Nevo studied this problem in a general context and proved that for every
$\|\gamma \|$
minimal. Gorodnik–Nevo studied this problem in a general context and proved that for every
![]() $\overline {\gamma }$
, it is possible to find a lift
$\overline {\gamma }$
, it is possible to find a lift
![]() $\gamma $
with
$\gamma $
with
![]() $\|\gamma \| \ll _\epsilon q^{C_n+\epsilon }$
where
$\|\gamma \| \ll _\epsilon q^{C_n+\epsilon }$
where
![]() $C_n$
is some explicit constant (see [Reference Gorodnik and Nevo29, Theorem 1.1]). One may then wonder what is the smallest
$C_n$
is some explicit constant (see [Reference Gorodnik and Nevo29, Theorem 1.1]). One may then wonder what is the smallest
![]() $C_n$
so that the statement holds for it. A simple lower bound is
$C_n$
so that the statement holds for it. A simple lower bound is
![]() $C_n \ge 1+1/n$
, which follows from Equation (1.4) (with
$C_n \ge 1+1/n$
, which follows from Equation (1.4) (with
![]() $q=1$
) and the fact that
$q=1$
) and the fact that
![]() $|\mathrm {SL}_n(\mathbb {Z}/q\mathbb {Z})| \gg _\epsilon q^{n^2-1-\epsilon }$
, but it is not the correct answer. In [Reference Kamber and Varjú34], by the second author and Pétér Varjú (which was completed after this work), it is shown that the correct answer is
$|\mathrm {SL}_n(\mathbb {Z}/q\mathbb {Z})| \gg _\epsilon q^{n^2-1-\epsilon }$
, but it is not the correct answer. In [Reference Kamber and Varjú34], by the second author and Pétér Varjú (which was completed after this work), it is shown that the correct answer is
![]() $C_n= 2$
(following weaker results of [Reference Sarnak51]). More precisely, the authors showed that for every q and
$C_n= 2$
(following weaker results of [Reference Sarnak51]). More precisely, the authors showed that for every q and
![]() $\overline {\gamma } \in \mathrm {SL}_n(\mathbb {Z} / q\mathbb {Z})$
, there is a lift
$\overline {\gamma } \in \mathrm {SL}_n(\mathbb {Z} / q\mathbb {Z})$
, there is a lift
![]() $\gamma \in \mathrm {SL}_n(\mathbb {Z})$
with
$\gamma \in \mathrm {SL}_n(\mathbb {Z})$
with
![]() $\|\gamma \| \ll _n q^2 \log q$
. In the other direction, they show that for every n,
$\|\gamma \| \ll _n q^2 \log q$
. In the other direction, they show that for every n,
![]() $\epsilon>0$
, and for every q, there is
$\epsilon>0$
, and for every q, there is
![]() $\overline {\gamma } \in \mathrm {SL}_n(\mathbb {Z} / q\mathbb {Z})$
, such that every lift
$\overline {\gamma } \in \mathrm {SL}_n(\mathbb {Z} / q\mathbb {Z})$
, such that every lift
![]() $\gamma \in \mathrm {SL}_n(\mathbb {Z})$
of
$\gamma \in \mathrm {SL}_n(\mathbb {Z})$
of
![]() $\overline {\gamma }$
satisfies
$\overline {\gamma }$
satisfies
![]() $\|\gamma \| \gg _{n,\epsilon } q^{2-\epsilon }$
.
$\|\gamma \| \gg _{n,\epsilon } q^{2-\epsilon }$
.
In contrast to the results of [Reference Kamber and Varjú34], Sarnak [Reference Sarnak51] observed that when one considers almost all the elements instead of all the elements, the simple lower bound
![]() $C_n=1+1/n$
should be the correct answer to the problem, and proved it for
$C_n=1+1/n$
should be the correct answer to the problem, and proved it for
![]() $n=2$
. This property is expected to hold in a general context, and we call it optimal lifting. We again refer to [Reference Golubev and Kamber27] for a detailed discussion of the general problem of optimal lifting, and to [Reference Kamber and Lavner33] for this specific problem.
$n=2$
. This property is expected to hold in a general context, and we call it optimal lifting. We again refer to [Reference Golubev and Kamber27] for a detailed discussion of the general problem of optimal lifting, and to [Reference Kamber and Lavner33] for this specific problem.
In the recent work of Assing and Blomer [Reference Assing and Blomer8, Theorem 1.4], they essentially solved the optimal lifting problem (see the statement of Theorem 5) but, again, conditional on [Reference Assing and Blomer8, Hypothesis 1]. Once again, in Theorem 5, employing the method of proving Theorem 3 and crucially inputting one of the main results of [Reference Assing and Blomer8], we make the above result of Assing–Blomer’s unconditional.
Theorem 5. For every
![]() $\epsilon>0$
, there is
$\epsilon>0$
, there is
![]() $\delta>0$
, such that for every square-free integer q, the number of elements in
$\delta>0$
, such that for every square-free integer q, the number of elements in
![]() $\overline {\gamma }\in \mathrm {SL}_n(\mathbb {Z}/q\mathbb {Z})$
without a lift
$\overline {\gamma }\in \mathrm {SL}_n(\mathbb {Z}/q\mathbb {Z})$
without a lift
![]() $\gamma \in \mathrm {SL}_n(\mathbb {Z})$
with
$\gamma \in \mathrm {SL}_n(\mathbb {Z})$
with
![]() $\|\gamma \| \le q^{1+1/n+\epsilon }$
is at most
$\|\gamma \| \le q^{1+1/n+\epsilon }$
is at most
![]() $O(q^{n^2-1-\delta })$
.
$O(q^{n^2-1-\delta })$
.
We now add a few remarks regarding Theorems 4 and 5.
Remark 1.9. While Theorems 4 and 5 are limited to q square-free (except for
![]() $n=2$
, where Sarnak’s proof holds for all q), our method can prove them for general q assuming Sarnak’s density conjecture, which is implied by the generalized Ramanujan conjecture (GRC) for cusp forms of
$n=2$
, where Sarnak’s proof holds for all q), our method can prove them for general q assuming Sarnak’s density conjecture, which is implied by the generalized Ramanujan conjecture (GRC) for cusp forms of
![]() $\mathrm {GL}_n$
over
$\mathrm {GL}_n$
over
![]() $\mathbb {Q}$
. More generally, unconditionally and independently of (most of) the work of Assing–Blomer, one can get slightly weaker results, with the exponents multiplied by
$\mathbb {Q}$
. More generally, unconditionally and independently of (most of) the work of Assing–Blomer, one can get slightly weaker results, with the exponents multiplied by
![]() $1+2\delta /(n-1)$
, where
$1+2\delta /(n-1)$
, where
![]() $0 \le \delta \le (n-1)/2$
is the best approximation for the (GRC) for
$0 \le \delta \le (n-1)/2$
is the best approximation for the (GRC) for
![]() $\mathrm {GL}_n$
over
$\mathrm {GL}_n$
over
![]() $\mathbb {Q}$
. Specifically, one has
$\mathbb {Q}$
. Specifically, one has
![]() $\delta \le \frac {1}{2}-\frac {1}{1+n^2}$
(see [Reference Sarnak50]).
$\delta \le \frac {1}{2}-\frac {1}{1+n^2}$
(see [Reference Sarnak50]).
Remark 1.10. Conjecturally, similar ‘Sarnak–Xue Counting’ and ‘Optimal Lifting’ theorems should hold more generally, in particular, for congruence subgroups of arithmetic lattices in semisimple Lie groups. We refer to [Reference Golubev and Kamber27], where those conjectures are discussed at length (for the specific problem of
![]() $\Gamma (q)$
see [Reference Golubev and Kamber27, Section 2.6]). In particular, for uniform (cocompact) lattices one can prove that Sarnak–Xue counting and optimal lifting follow from Sarnak’s density conjecture in automorphic forms, which is, presumably, a true approximation of the (false) naive Ramanujan conjecture (see [Reference Golubev and Kamber27]). For nonuniform lattices, this implication is unknown, because of the analytic difficulties coming from the Eisenstein series. The techniques of this paper allow us to essentially overcome those analytic difficulties, for nonuniform lattices in groups different than
$\Gamma (q)$
see [Reference Golubev and Kamber27, Section 2.6]). In particular, for uniform (cocompact) lattices one can prove that Sarnak–Xue counting and optimal lifting follow from Sarnak’s density conjecture in automorphic forms, which is, presumably, a true approximation of the (false) naive Ramanujan conjecture (see [Reference Golubev and Kamber27]). For nonuniform lattices, this implication is unknown, because of the analytic difficulties coming from the Eisenstein series. The techniques of this paper allow us to essentially overcome those analytic difficulties, for nonuniform lattices in groups different than
![]() $\mathrm {GL}_n$
, as long as properties (TWN+) and (BD) are known. For principal congruence subgroups of
$\mathrm {GL}_n$
, as long as properties (TWN+) and (BD) are known. For principal congruence subgroups of
![]() $\mathrm {SL}_n(\mathbb {Z})$
of square-free level, Assing–Blomer proved Sarnak’s density conjecture, which allows in combination with this work to deduce the two theorems.
$\mathrm {SL}_n(\mathbb {Z})$
of square-free level, Assing–Blomer proved Sarnak’s density conjecture, which allows in combination with this work to deduce the two theorems.
Remark 1.11. We note, that in this paper, we do not attempt to prove [Reference Assing and Blomer8, Hypothesis 1], and it remains an interesting and hard open question. We refer to Section 1.6 for a discussion.
1.4 Difficulties in higher rank
In this section, we try to describe the difficulties one faces while trying to estimate (1.1) and (1.2).
We start with a toy-example – estimating (1.1) for a low-rank group. We take
![]() $G=\mathrm {GL}_2$
over
$G=\mathrm {GL}_2$
over
![]() $\mathbb {Q}$
,
$\mathbb {Q}$
,
![]() $M=\mathrm {GL}_1\times \mathrm {GL}_1$
, P the Borel subgroup in G,
$M=\mathrm {GL}_1\times \mathrm {GL}_1$
, P the Borel subgroup in G,
![]() $\pi =\mathrm {triv}\times \mathrm {triv}$
and
$\pi =\mathrm {triv}\times \mathrm {triv}$
and
![]() $\lambda =(it,-it)$
with
$\lambda =(it,-it)$
with
![]() $t\in \mathbb {R}$
. We take
$t\in \mathbb {R}$
. We take
![]() $\varphi \in \mathcal {A}^2(P)_\pi $
to be the
$\varphi \in \mathcal {A}^2(P)_\pi $
to be the
![]() $\mathrm {O}_2(\mathbb {R})\mathrm {GL}_2(\hat {\mathbb {Z}})$
-invariant unit vector. In the classical language,
$\mathrm {O}_2(\mathbb {R})\mathrm {GL}_2(\hat {\mathbb {Z}})$
-invariant unit vector. In the classical language,
![]() $\mathrm {Eis}(\varphi ,\lambda )$
is the same as
$\mathrm {Eis}(\varphi ,\lambda )$
is the same as
![]() $E(\cdot ,1/2+it)$
. The classical Maass–Selberg relations (see [Reference Miller43, pp.153]) yield that
$E(\cdot ,1/2+it)$
. The classical Maass–Selberg relations (see [Reference Miller43, pp.153]) yield that
 $$ \begin{align*} &\|\Lambda^TE(\cdot,1/2+it)\|^2_2 \,=\lim_{t'\to t}\langle\Lambda^TE(\cdot,1/2+it'),\Lambda^TE(\cdot,1/2+it)\rangle\\ &=\lim_{t'\to t}\left(\frac{e^{iT(t'-t)}}{i(t'-t)}+\frac{\overline{c(it')}e^{iT(t'+t)}}{i(t'+t)}-\frac{c(it)e^{-iT(t'+t)}}{i(t'+t)}-\frac{{c(it')}\overline{c(it)}e^{-iT(t'-t)}}{i(t'-t)}\right)\\ &=2T-\frac{c'(it)}{c(it)} + \Re\left(\frac{c(it)e^{-2itT}}{t}\right)\ll T\log(1+|t|). \end{align*} $$
$$ \begin{align*} &\|\Lambda^TE(\cdot,1/2+it)\|^2_2 \,=\lim_{t'\to t}\langle\Lambda^TE(\cdot,1/2+it'),\Lambda^TE(\cdot,1/2+it)\rangle\\ &=\lim_{t'\to t}\left(\frac{e^{iT(t'-t)}}{i(t'-t)}+\frac{\overline{c(it')}e^{iT(t'+t)}}{i(t'+t)}-\frac{c(it)e^{-iT(t'+t)}}{i(t'+t)}-\frac{{c(it')}\overline{c(it)}e^{-iT(t'-t)}}{i(t'-t)}\right)\\ &=2T-\frac{c'(it)}{c(it)} + \Re\left(\frac{c(it)e^{-2itT}}{t}\right)\ll T\log(1+|t|). \end{align*} $$
Here,
![]() $c(s)$
is the scattering matrix appearing in the constant term of
$c(s)$
is the scattering matrix appearing in the constant term of
![]() $E(\cdot ,1/2+it)$
, given by
$E(\cdot ,1/2+it)$
, given by
![]() $\frac {\xi (s)}{\xi (1+s)}$
, where
$\frac {\xi (s)}{\xi (1+s)}$
, where
![]() $\xi (s)$
is the completed Riemann zeta function. The last estimate follows from the standard zero-free region of the Riemann zeta function. Now, we explain the difficulties we face if we try to prove the statement given in (1.3), by generalizing the method above.
$\xi (s)$
is the completed Riemann zeta function. The last estimate follows from the standard zero-free region of the Riemann zeta function. Now, we explain the difficulties we face if we try to prove the statement given in (1.3), by generalizing the method above.
-
1. The case when
 $\mathrm {Eis}(\varphi ,\lambda )$
is the minimal parabolic Eisenstein series for
$\mathrm {Eis}(\varphi ,\lambda )$
is the minimal parabolic Eisenstein series for
 $\mathrm {GL}_n$
is a natural higher-rank analogue of the above. Higher rank Maass–Selberg relations are in this case more complicated than the
$\mathrm {GL}_n$
is a natural higher-rank analogue of the above. Higher rank Maass–Selberg relations are in this case more complicated than the
 $\mathrm {GL}_2$
version. The number of summands in the formula is (
$\mathrm {GL}_2$
version. The number of summands in the formula is (
 $n!)^2$
. Moreover, each summand will likely have (a priori, higher-order) poles as
$n!)^2$
. Moreover, each summand will likely have (a priori, higher-order) poles as
 $\lambda '\to \lambda $
. The manoeuvre of ‘grouping terms’ which cancel each other’s poles, analogous to the
$\lambda '\to \lambda $
. The manoeuvre of ‘grouping terms’ which cancel each other’s poles, analogous to the
 $\mathrm {GL}_2$
case, is, in fact, combinatorially quite involved. Such complications arise already for
$\mathrm {GL}_2$
case, is, in fact, combinatorially quite involved. Such complications arise already for
 $\mathrm {GL}_3$
, as can be seen in [Reference Miller43].
$\mathrm {GL}_3$
, as can be seen in [Reference Miller43]. -
2. Apparently, the next difficult case is when
 $\mathrm {Eis}(\varphi ,\lambda )$
is induced from a cuspidal representation of a nonminimal parabolic, that is
$\mathrm {Eis}(\varphi ,\lambda )$
is induced from a cuspidal representation of a nonminimal parabolic, that is
 $\varphi $
is a cusp form. Apart from solving the combinatorial problem that arises in the limit procedure, one also needs to know certain strong estimates of the logarithmic (a priori, high) derivatives of the intertwining operators. When the Eisenstein series is spherical everywhere, such estimates can be described via the zero-free region of various Rankin–Selberg L-functions for
$\varphi $
is a cusp form. Apart from solving the combinatorial problem that arises in the limit procedure, one also needs to know certain strong estimates of the logarithmic (a priori, high) derivatives of the intertwining operators. When the Eisenstein series is spherical everywhere, such estimates can be described via the zero-free region of various Rankin–Selberg L-functions for
 $\mathrm {GL}_{m_1}\times \mathrm {GL}_{m_2}$
with
$\mathrm {GL}_{m_1}\times \mathrm {GL}_{m_2}$
with
 $m_1+m_2\le n$
at the edge of the critical strips. However, the quality and generality of the zero-free region that is required to prove (1.3) is still out of reach.
$m_1+m_2\le n$
at the edge of the critical strips. However, the quality and generality of the zero-free region that is required to prove (1.3) is still out of reach. -
3. We remark that Langlands (see [Reference Arthur6, Proposition 15.3]) proved the Maass–Selberg relations, but only when the underlying representation
 $\pi $
of
$\pi $
of
 $M(\mathbb {A})$
is cuspidal. Arthur, in [Reference Arthur5], proved an approximate Maass–Selberg relation for a general discrete series
$M(\mathbb {A})$
is cuspidal. Arthur, in [Reference Arthur5], proved an approximate Maass–Selberg relation for a general discrete series
 $\pi $
. However, the precision and generality of the approximation that we need to prove (1.3) is not available. In fact, the required precision in Arthur’s approximate Maass–Selberg formula can be obtained only via the classification of discrete series representations, in particular, how the residual spectrum arises from the Eisenstein series induced from cusp forms. This, in turn, requires understanding deep meromorphic properties of the Eisenstein series, in particular, the locations, orders and residues of their poles.
$\pi $
. However, the precision and generality of the approximation that we need to prove (1.3) is not available. In fact, the required precision in Arthur’s approximate Maass–Selberg formula can be obtained only via the classification of discrete series representations, in particular, how the residual spectrum arises from the Eisenstein series induced from cusp forms. This, in turn, requires understanding deep meromorphic properties of the Eisenstein series, in particular, the locations, orders and residues of their poles. -
4. When we move from
 $\mathrm {GL}_n$
to general reductive groups, all of the above difficulties persist prominently. First of all, our ignorance of the classification of the discrete series, equivalently the required meromorphic properties of a general Eisenstein series, hinders the very first step of estimating the
$\mathrm {GL}_n$
to general reductive groups, all of the above difficulties persist prominently. First of all, our ignorance of the classification of the discrete series, equivalently the required meromorphic properties of a general Eisenstein series, hinders the very first step of estimating the
 $L^2$
-norm via the Maass–Selberg relations. Even in the case of the Eisenstein series induced from cuspidal representations, the limit procedure requires a deep understanding of the meromorphic properties of the intertwining operators and the size of the (a priori, high) derivatives of the same — none of which is yet in the grasp of the current literature.
$L^2$
-norm via the Maass–Selberg relations. Even in the case of the Eisenstein series induced from cuspidal representations, the limit procedure requires a deep understanding of the meromorphic properties of the intertwining operators and the size of the (a priori, high) derivatives of the same — none of which is yet in the grasp of the current literature.
Primarily, this is why, in this paper, we try to estimate (1.2) for general Eisenstein series on general reductive groups not via the Maass–Selberg formula, rather via the spectral side of the Arthur–Selberg trace formula. We explain this in the next subsection.
In a future work, in order to estimate (1.1) for
![]() $\mathrm {GL}_n$
using the Maass–Selberg relations, we plan to address some of the issues pointed to above and, in particular, to give a robust method of understanding the combinatorics and corresponding limit problem mentioned above.
$\mathrm {GL}_n$
using the Maass–Selberg relations, we plan to address some of the issues pointed to above and, in particular, to give a robust method of understanding the combinatorics and corresponding limit problem mentioned above.
Remark 1.12. There is one case in which the Maass–Selberg relations do yield a nice formula, and it is exactly the unramified case of Theorem 2. The Maass–Selberg relations, in this case, are given in Lemma 3.1 and essentially reduce to understanding a certain operator we denote by
![]() $\mathcal {M}_M^T(\lambda ,P)$
, defined by a certain limit. Arthur’s method of
$\mathcal {M}_M^T(\lambda ,P)$
, defined by a certain limit. Arthur’s method of
![]() $(G,M)$
-family gives a way to calculate the limit in the formula. More precisely, Finis–Lapid–Müller [Reference Finis, Lapid and Müller21], generalizing previous results of Arthur in the spherical case, essentially gave a formula for
$(G,M)$
-family gives a way to calculate the limit in the formula. More precisely, Finis–Lapid–Müller [Reference Finis, Lapid and Müller21], generalizing previous results of Arthur in the spherical case, essentially gave a formula for
![]() $\mathcal {M}_M^T(\lambda ,P)$
, given in Proposition 5.7. The formula is a polynomial in T with coefficients given by certain intertwining operators and their first derivatives, given along linearly independent directions. Then, when we take
$\mathcal {M}_M^T(\lambda ,P)$
, given in Proposition 5.7. The formula is a polynomial in T with coefficients given by certain intertwining operators and their first derivatives, given along linearly independent directions. Then, when we take
![]() $\lambda $
-average over a short interval around
$\lambda $
-average over a short interval around
![]() $\lambda _0$
, we can use properties (TWN+) (and (BD) for general congruence subgroups) to deduce a bound on
$\lambda _0$
, we can use properties (TWN+) (and (BD) for general congruence subgroups) to deduce a bound on
![]() $\mathcal {M}_M^T(\lambda ,P)$
, given in Proposition 5.5, from which Theorem 2 follows. This technique can be traced back at least to [Reference Müller49] (for
$\mathcal {M}_M^T(\lambda ,P)$
, given in Proposition 5.5, from which Theorem 2 follows. This technique can be traced back at least to [Reference Müller49] (for
![]() $\mathrm {GL}_n$
and a fixed level) and was formalized in [Reference Finis, Lapid and Müller22].
$\mathrm {GL}_n$
and a fixed level) and was formalized in [Reference Finis, Lapid and Müller22].
1.5 High level sketch for the proof of Theorem 3
Our proof of Theorem 3 uses the Arthur–Selberg trace formula, or more precisely, Arthur’s development of the spectral side of the trace formula and Finis–Lapid–Müller’s refinement of it.
As we described in the previous subsection, it is quite difficult to estimate
![]() $\|\Lambda ^T \mathrm {Eis}(\varphi _0,\lambda _0)\|^2_2$
pointwise in
$\|\Lambda ^T \mathrm {Eis}(\varphi _0,\lambda _0)\|^2_2$
pointwise in
![]() $\lambda _0$
. Proving an estimate on a
$\lambda _0$
. Proving an estimate on a
![]() $\lambda $
-average over a short interval around
$\lambda $
-average over a short interval around
![]() $\lambda _0$
seems to be more tractable. Moreover, in our proof, we also need to average over
$\lambda _0$
seems to be more tractable. Moreover, in our proof, we also need to average over
![]() $\varphi $
in an orthonormal basis, equivalence classes of associated parabolic subgroups and discrete series representations of the Levi of these parabolic subgroups.
$\varphi $
in an orthonormal basis, equivalence classes of associated parabolic subgroups and discrete series representations of the Levi of these parabolic subgroups.
For a sufficiently dominant truncation parameter T and a bi-
![]() $K_\infty K$
-invariant test function f on
$K_\infty K$
-invariant test function f on
![]() $G(\mathbb {A})$
, Arthur defined a distribution
$G(\mathbb {A})$
, Arthur defined a distribution
![]() $J_\chi ^T(f)$
on the spectral side, that (for
$J_\chi ^T(f)$
on the spectral side, that (for
![]() $d(T)$
sufficiently large) essentially can be given by a weighted sum over
$d(T)$
sufficiently large) essentially can be given by a weighted sum over
![]() $P\supset P_0$
of
$P\supset P_0$
of
 $$\begin{align*}\sum_{\pi\in\Pi_2(M_P)}\sum_{\varphi\in\mathcal{B}_{\chi,\pi}(P)}\int_{i(\mathfrak{a}_M^G)^*}\tilde{f}(\mu_\pi+\lambda)\|\Lambda^T\mathrm{Eis}(\varphi,\lambda)\|^2\,\mathrm{d}\lambda,\end{align*}$$
$$\begin{align*}\sum_{\pi\in\Pi_2(M_P)}\sum_{\varphi\in\mathcal{B}_{\chi,\pi}(P)}\int_{i(\mathfrak{a}_M^G)^*}\tilde{f}(\mu_\pi+\lambda)\|\Lambda^T\mathrm{Eis}(\varphi,\lambda)\|^2\,\mathrm{d}\lambda,\end{align*}$$
where
![]() $\mu _\pi $
is the Langlands parameter of
$\mu _\pi $
is the Langlands parameter of
![]() $\pi $
(which is necessarily spherical as an
$\pi $
(which is necessarily spherical as an
![]() $M(\mathbb {A})$
-a representation) and
$M(\mathbb {A})$
-a representation) and
![]() $\tilde {f}$
is the spherical transform of f.
$\tilde {f}$
is the spherical transform of f.
We choose an f with bounded support via the Paley–Wiener theory and the theory of spherical inversion so that spherical transform
![]() $\tilde {f}$
localizes at
$\tilde {f}$
localizes at
![]() $\mu _\pi +\lambda \approx \mu _{\pi _0}+\lambda _0$
, and so that
$\mu _\pi +\lambda \approx \mu _{\pi _0}+\lambda _0$
, and so that
![]() $J_\chi ^T(f)$
majorizes the left-hand side of the estimate in Theorem 3. Our goal, now, is to estimate
$J_\chi ^T(f)$
majorizes the left-hand side of the estimate in Theorem 3. Our goal, now, is to estimate
![]() $J_\chi ^T(f)$
satisfactorily.
$J_\chi ^T(f)$
satisfactorily.
Arthur, in his deep work to develop the spectral side of the trace formula, showed that
![]() $J_\chi ^T(f)$
is a polynomial in T whose coefficients are given in terms of certain intertwining operators and their derivatives. More precisely,
$J_\chi ^T(f)$
is a polynomial in T whose coefficients are given in terms of certain intertwining operators and their derivatives. More precisely,
![]() $J_\chi ^T(f)$
essentially takes the form of a weighted sum over
$J_\chi ^T(f)$
essentially takes the form of a weighted sum over
![]() $P\supset P_0$
of
$P\supset P_0$
of
 $$\begin{align*}\sum_{\pi\in\Pi_2(M_P)}\sum_{L\supset M_P}\int_{i(\mathfrak{a}_L^G)^*}\tilde{f}(\lambda)\mathrm{tr}\left(\mathcal{M}_L^T(P,\lambda)\mid_{\mathcal{A}_{\chi,\pi}^2(P)^{K_\infty K}}\right)\,\mathrm{d}\lambda.\end{align*}$$
$$\begin{align*}\sum_{\pi\in\Pi_2(M_P)}\sum_{L\supset M_P}\int_{i(\mathfrak{a}_L^G)^*}\tilde{f}(\lambda)\mathrm{tr}\left(\mathcal{M}_L^T(P,\lambda)\mid_{\mathcal{A}_{\chi,\pi}^2(P)^{K_\infty K}}\right)\,\mathrm{d}\lambda.\end{align*}$$
The combinatorial formula of Finis–Lapid–Müller allows us to understand
![]() $\mathcal {M}_L^T(P,\lambda )$
in terms of a certain linear combination of various rank one intertwining operators and their first derivatives. We can then use the bound on
$\mathcal {M}_L^T(P,\lambda )$
in terms of a certain linear combination of various rank one intertwining operators and their first derivatives. We can then use the bound on
![]() $\mathcal {M}_L^T(P,\lambda )$
given in Proposition 5.5 that are yielded by properties (TWN+) and (BD), together with the Paley–Wiener theory to conclude the proof.
$\mathcal {M}_L^T(P,\lambda )$
given in Proposition 5.5 that are yielded by properties (TWN+) and (BD), together with the Paley–Wiener theory to conclude the proof.
The fact that we only see the first derivative of the intertwiners in the above formula circumvents the difficulty that arises because of, a priori, high derivatives of the same in the Maass–Selberg formula, as described in Section 1.4. Moreover, the formula above, which is yielded by the theory of
![]() $(G,L)$
-families due to Arthur and Finis–Lapid–Müller, bypasses the combinatorial complications that arise in the limit procedure in the Maass–Selberg formula, as described in Section 1.4.
$(G,L)$
-families due to Arthur and Finis–Lapid–Müller, bypasses the combinatorial complications that arise in the limit procedure in the Maass–Selberg formula, as described in Section 1.4.
It is worth noting that we do not use the geometric side of the trace formula, rather only use the two different expressions of the spectral side given in Proposition 6.1 (the spectral side of the pretrace formula) and Proposition 6.2 (the spectral side of the trace formula) (also see Proposition 6.3). We also remark that we crucially use the spectral decomposition for a specific cuspidal datum. This is presumably different than a usual proof of, for example, Weyl law (see, e.g. [Reference Finis and Lapid20], [Reference Lindenstrauss and Venkatesh41]), where one does another sum over all cuspidal data in addition to the averages in Theorem 3. This extra average will not give us the result of the strength as in, for example, Theorem 1. The primary reason is that the contribution from the cusp forms will dominate. This way, we may only achieve a polynomial strength dependence on
![]() $\mathrm {level}(K)$
in Theorem 1 (and Remark 1.2) as opposed to a poly-logarithmic strength.
$\mathrm {level}(K)$
in Theorem 1 (and Remark 1.2) as opposed to a poly-logarithmic strength.
1.6 On the proof of the applications
The proofs of the applications do not use Theorems 3 or 2 directly, but instead use very similar methods. The reason that we cannot use the theorems directly is explained in Remark 1.7.
Instead, one can prove the theorems by proving a weighted version of Theorem 3, where representations are weighted by how far they are from being tempered. Our method allows such a modification, by using a function
![]() $h_{R,q}$
on
$h_{R,q}$
on
![]() $\mathrm {GL}_n(\mathbb {A})$
that is essentially the characteristic function of the R-radius ball at the Archimedean places and of
$\mathrm {GL}_n(\mathbb {A})$
that is essentially the characteristic function of the R-radius ball at the Archimedean places and of
![]() $K(q)$
at the non-Archimedean places, where
$K(q)$
at the non-Archimedean places, where
![]() $K(q)$
is the principal congruence subgroup of level q of
$K(q)$
is the principal congruence subgroup of level q of
![]() $\mathrm {GL}_n$
over the finite adeles (see Section 4.1 below for the definition). This requires increasing
$\mathrm {GL}_n$
over the finite adeles (see Section 4.1 below for the definition). This requires increasing
![]() $d(T)$
sufficiently slowly so that Arthur’s formulæ will still hold.
$d(T)$
sufficiently slowly so that Arthur’s formulæ will still hold.
In practice, we use the full distribution
![]() $J^T$
of Arthur, over the entire spectrum. The idea is to compare two different formulæ of Arthur for
$J^T$
of Arthur, over the entire spectrum. The idea is to compare two different formulæ of Arthur for
![]() $J^T(h_{R,q})$
. On the one hand, the spectral side of the trace formula allows us to give a bound on
$J^T(h_{R,q})$
. On the one hand, the spectral side of the trace formula allows us to give a bound on
![]() $J^T(h_{R,q})$
, given in Proposition 8.1. This is done by using the bound on
$J^T(h_{R,q})$
, given in Proposition 8.1. This is done by using the bound on
![]() $\mathcal {M}_L^T(\lambda ,P)$
given in Proposition 5.5 to reduce the problem to a sum, which is bounded in the work of Assing–Blomer [Reference Assing and Blomer8, Theorem 7.1].
$\mathcal {M}_L^T(\lambda ,P)$
given in Proposition 5.5 to reduce the problem to a sum, which is bounded in the work of Assing–Blomer [Reference Assing and Blomer8, Theorem 7.1].
The other formula for
![]() $J^T(h_{R,q})$
, which requires that
$J^T(h_{R,q})$
, which requires that
![]() $d(T)$
will be sufficiently large (actually depending logarithmically on R), can be seen as a pretrace formula and leads to a bound on the usual kernel of
$d(T)$
will be sufficiently large (actually depending logarithmically on R), can be seen as a pretrace formula and leads to a bound on the usual kernel of
![]() $h_{R,q}$
, given in Proposition 8.3. The bound on the kernel of
$h_{R,q}$
, given in Proposition 8.3. The bound on the kernel of
![]() $h_{R,q}$
by standard methods (e.g, [Reference Sarnak51, Reference Golubev and Kamber27]) leads to the proofs of both Theorems 4 and 5.
$h_{R,q}$
by standard methods (e.g, [Reference Sarnak51, Reference Golubev and Kamber27]) leads to the proofs of both Theorems 4 and 5.
We finally remark that similar ideas, of using two formulæ for
![]() $J^T(h)$
, were recently used by Finis–Lapid to provide a remainder term for Weyl law for a large class of arithmetic noncompact locally symmetric spaces [Reference Finis and Lapid20]. However, [Reference Finis and Lapid20] compares the pretrace formula with the geometric side of the trace formula, not the spectral side.
$J^T(h)$
, were recently used by Finis–Lapid to provide a remainder term for Weyl law for a large class of arithmetic noncompact locally symmetric spaces [Reference Finis and Lapid20]. However, [Reference Finis and Lapid20] compares the pretrace formula with the geometric side of the trace formula, not the spectral side.
1.7 Added in proof
After the completion of this article, Assing, Blomer and Nelson [Reference Assing, Blomer and Nelson9] extended the results of [Reference Assing and Blomer8]. In particular, they show that in Theorems 4 and 5, the assumption that q is square-free can be removed.
1.8 Conventions
As usual in analytic number theory, we use
![]() $\epsilon $
to denote a small positive constant, whose actual value may change from line to line. We use Vinogradov’s notations
$\epsilon $
to denote a small positive constant, whose actual value may change from line to line. We use Vinogradov’s notations
![]() $\gg $
and
$\gg $
and
![]() $\ll $
, whose implied constants are understood to depend only on the group G and the number field F.
$\ll $
, whose implied constants are understood to depend only on the group G and the number field F.
2 General preliminaries
Let F denote a number field with integer ring
![]() $\mathfrak {o}$
. The letter v will usually (unless mentioned otherwise) denote an arbitrary place of F, and
$\mathfrak {o}$
. The letter v will usually (unless mentioned otherwise) denote an arbitrary place of F, and
![]() $F_v$
will denote the v-adic completion of F. Let G denote a reductive group defined over F. Let
$F_v$
will denote the v-adic completion of F. Let G denote a reductive group defined over F. Let
![]() $\mathbb {A}$
denote the adele ring of F. Also let
$\mathbb {A}$
denote the adele ring of F. Also let
![]() $\mathbb {A}_f$
denote the finite adeles and
$\mathbb {A}_f$
denote the finite adeles and
![]() $F_\infty := F\otimes \mathbb {R}$
.
$F_\infty := F\otimes \mathbb {R}$
.
Below, we briefly discuss the main ingredients and quantities in our proof. We primarily follow the notations of [Reference Finis, Lapid and Müller21, Section 2.1] and [Reference Finis, Lapid and Müller22, Section 4].
2.1 Brief structure theory of reductive groups
Let
![]() $T_0$
denote a fixed maximal F-split torus of G. Let
$T_0$
denote a fixed maximal F-split torus of G. Let
![]() $M_0$
denote the centralizer of
$M_0$
denote the centralizer of
![]() $T_0$
in G, which is a minimal Levi subgroup. Let
$T_0$
in G, which is a minimal Levi subgroup. Let
![]() $\mathcal {L}$
denote the finite set of Levi subgroups defined over F containing
$\mathcal {L}$
denote the finite set of Levi subgroups defined over F containing
![]() $M_0$
. Given
$M_0$
. Given
![]() $M\in \mathcal {L}$
, let
$M\in \mathcal {L}$
, let
![]() $\mathcal {L}(M) \subset \mathcal {L}$
denote the (finite) set of Levi subgroups containing M and
$\mathcal {L}(M) \subset \mathcal {L}$
denote the (finite) set of Levi subgroups containing M and
![]() $\mathcal {P}(M)$
denote the (finite) set of parabolic subgroups defined over F with Levi subgroup M. We also fix a minimal parabolic subgroup
$\mathcal {P}(M)$
denote the (finite) set of parabolic subgroups defined over F with Levi subgroup M. We also fix a minimal parabolic subgroup
![]() $P_0 \supset M_0$
.
$P_0 \supset M_0$
.
Let
![]() $T_M$
denote the split part of the identity component of the centre of M. We denote
$T_M$
denote the split part of the identity component of the centre of M. We denote
![]() ${W(M) := N_{G}(M)/M}$
, where
${W(M) := N_{G}(M)/M}$
, where
![]() $N_G(M)$
denotes the normalizer of M in G. We denote the Weyl group of
$N_G(M)$
denotes the normalizer of M in G. We denote the Weyl group of
![]() $(G,T_0)$
by
$(G,T_0)$
by
![]() $W_0 := W(M_0)$
. We can identify
$W_0 := W(M_0)$
. We can identify
![]() $W(M)$
as a subgroup of
$W(M)$
as a subgroup of
![]() $W_0$
.
$W_0$
.
Let
![]() $\mathfrak {a}_M^*$
denote the
$\mathfrak {a}_M^*$
denote the
![]() $\mathbb {R}$
-vector space spanned by the lattice
$\mathbb {R}$
-vector space spanned by the lattice
![]() $X^*(M)$
of F-rational characters of M, and let
$X^*(M)$
of F-rational characters of M, and let
![]() $\mathfrak {a}_{M,\mathbb {C}}^* := \mathfrak {a}_M^*\otimes _{\mathbb {R}} \mathbb {C}$
. For
$\mathfrak {a}_{M,\mathbb {C}}^* := \mathfrak {a}_M^*\otimes _{\mathbb {R}} \mathbb {C}$
. For
![]() $M_1 \subset M_2$
, it holds that
$M_1 \subset M_2$
, it holds that
![]() $\mathfrak {a}_{M_2}^* \subset \mathfrak {a}_{M_1}^*$
with a well-defined complement
$\mathfrak {a}_{M_2}^* \subset \mathfrak {a}_{M_1}^*$
with a well-defined complement
![]() $\mathfrak {a}_{M_1}^* = \mathfrak {a}_{M_2}^*\oplus (\mathfrak {a}_{M_1}^{M_2})^*$
. Let
$\mathfrak {a}_{M_1}^* = \mathfrak {a}_{M_2}^*\oplus (\mathfrak {a}_{M_1}^{M_2})^*$
. Let
![]() $\mathfrak {a}_M$
denote the dual space of
$\mathfrak {a}_M$
denote the dual space of
![]() $\mathfrak {a}_M^*$
, and we fix a pairing
$\mathfrak {a}_M^*$
, and we fix a pairing
![]() $\langle ,\rangle $
between
$\langle ,\rangle $
between
![]() $\mathfrak {a}_M$
and
$\mathfrak {a}_M$
and
![]() $\mathfrak {a}_M^*$
. For
$\mathfrak {a}_M^*$
. For
![]() $P\in \mathcal {P}(M)$
, we write
$P\in \mathcal {P}(M)$
, we write
![]() $\mathfrak {a}_P =\mathfrak {a}_M$
.
$\mathfrak {a}_P =\mathfrak {a}_M$
.
We choose a
![]() $W_0$
-invariant inner product on
$W_0$
-invariant inner product on
![]() $\mathfrak {a}_0:= \mathfrak {a}_{M_0}$
, which also defines measures on
$\mathfrak {a}_0:= \mathfrak {a}_{M_0}$
, which also defines measures on
![]() $\mathfrak {a}_M$
and
$\mathfrak {a}_M$
and
![]() $\mathfrak {a}_M^*$
for all
$\mathfrak {a}_M^*$
for all
![]() $M\in \mathcal {L}$
. We normalize all measures as in [Reference Arthur6, Section 7], similar to [Reference Finis, Lapid and Müller21].
$M\in \mathcal {L}$
. We normalize all measures as in [Reference Arthur6, Section 7], similar to [Reference Finis, Lapid and Müller21].
For
![]() $P\in \mathcal {P}(M)$
, we write
$P\in \mathcal {P}(M)$
, we write
![]() $M_P=M$
. Let
$M_P=M$
. Let
![]() $N_P$
denote the unipotent radical of P. Let
$N_P$
denote the unipotent radical of P. Let
![]() $\Sigma _P \subset (\mathfrak {a}_{P}^{G})^*$
denote the set of roots of
$\Sigma _P \subset (\mathfrak {a}_{P}^{G})^*$
denote the set of roots of
![]() $T_M$
on the Lie algebra of
$T_M$
on the Lie algebra of
![]() $N_P$
. Let
$N_P$
. Let
![]() $\Delta _P$
denote the subset of simple roots of
$\Delta _P$
denote the subset of simple roots of
![]() $\Sigma _P$
. Let
$\Sigma _P$
. Let
![]() $\Sigma _M := \cup _{P\in \mathcal {P}(M)}\Sigma _P$
. Given two parabolics
$\Sigma _M := \cup _{P\in \mathcal {P}(M)}\Sigma _P$
. Given two parabolics
![]() $P,Q\in \mathcal {P}(M)$
, we say that P and Q are adjacent along
$P,Q\in \mathcal {P}(M)$
, we say that P and Q are adjacent along
![]() $\alpha \in \Sigma _M$
and write
$\alpha \in \Sigma _M$
and write
![]() $P|^{\alpha } Q$
if
$P|^{\alpha } Q$
if
![]() $\Sigma _P = \Sigma _Q \setminus \{-\alpha \} \cup \{\alpha \}$
.
$\Sigma _P = \Sigma _Q \setminus \{-\alpha \} \cup \{\alpha \}$
.
Let
![]() $A_0$
denote the identity component of
$A_0$
denote the identity component of
![]() $T_0(\mathbb {R})$
. We let
$T_0(\mathbb {R})$
. We let
![]() $A_M := A_0 \cap T_M(\mathbb {R})$
. Let
$A_M := A_0 \cap T_M(\mathbb {R})$
. Let
![]() $H_M\colon M(\mathbb {A})\to \mathfrak {a}_M$
denote the natural homomorphism defined by
$H_M\colon M(\mathbb {A})\to \mathfrak {a}_M$
denote the natural homomorphism defined by
for any
![]() $\chi \in X^*(M)$
. Here,
$\chi \in X^*(M)$
. Here,
![]() $|\cdot |_{\mathbb {A}}$
denotes the homomorphism from
$|\cdot |_{\mathbb {A}}$
denotes the homomorphism from
![]() $\mathbb {A}^\times \to \mathbb {R}^+$
given by
$\mathbb {A}^\times \to \mathbb {R}^+$
given by
![]() $|\cdot |_{\mathbb {A}}:=\prod _v|\cdot |_v$
, where
$|\cdot |_{\mathbb {A}}:=\prod _v|\cdot |_v$
, where
![]() $|\cdot |_v$
denotes the usual absolute value on
$|\cdot |_v$
denotes the usual absolute value on
![]() $F_v$
. Let
$F_v$
. Let
![]() $M(\mathbb {A})^1 \subset M(\mathbb {A})$
denote the kernel of
$M(\mathbb {A})^1 \subset M(\mathbb {A})$
denote the kernel of
![]() $H_M$
. It holds that
$H_M$
. It holds that
![]() $M(\mathbb {A}) = A_M \times M(\mathbb {A})^1$
.
$M(\mathbb {A}) = A_M \times M(\mathbb {A})^1$
.
We fix a maximal compact subgroup
![]() $K_\infty $
of
$K_\infty $
of
![]() $G(F_\infty )$
and a maximal open-compact subgroup
$G(F_\infty )$
and a maximal open-compact subgroup
![]() $K_f$
of
$K_f$
of
![]() $G(\mathbb {A}_f)$
. Finally, we fix the maximal compact subgroup
$G(\mathbb {A}_f)$
. Finally, we fix the maximal compact subgroup
![]() $K_{\mathbb {A}} := K_\infty K_f$
of
$K_{\mathbb {A}} := K_\infty K_f$
of
![]() $G(\mathbb {A})$
and assume that it is admissible relative to
$G(\mathbb {A})$
and assume that it is admissible relative to
![]() $M_0$
, so that for every
$M_0$
, so that for every
![]() $P\in \mathcal {P}(M_0)$
, an Iwasawa decomposition
$P\in \mathcal {P}(M_0)$
, an Iwasawa decomposition
![]() $G(\mathbb {A}) = P(\mathbb {A})K_{\mathbb {A}}$
holds.
$G(\mathbb {A}) = P(\mathbb {A})K_{\mathbb {A}}$
holds.
Given
![]() $M\in \mathcal {M}$
and
$M\in \mathcal {M}$
and
![]() $P\in \mathcal {P}(M)$
, let
$P\in \mathcal {P}(M)$
, let
![]() $H_P\colon G(\mathbb {A}) \to \mathfrak {a}_P$
denote the extension of
$H_P\colon G(\mathbb {A}) \to \mathfrak {a}_P$
denote the extension of
![]() $H_M$
to a left
$H_M$
to a left
![]() $N_P(\mathbb {A})$
and right
$N_P(\mathbb {A})$
and right
![]() $K_{\mathbb {A}}$
-invariant map.
$K_{\mathbb {A}}$
-invariant map.
3 Global preliminaries
3.1 Automorphic forms
Given
![]() $M\in \mathcal {L}$
, let
$M\in \mathcal {L}$
, let
denote the discrete part of the spectrum of
![]() $L^2(M(F)A_M\backslash M(\mathbb {A}))$
, that is the Hilbert sum of all irreducible subrepresentations of
$L^2(M(F)A_M\backslash M(\mathbb {A}))$
, that is the Hilbert sum of all irreducible subrepresentations of
![]() $M(\mathbb {A})$
on the space.
$M(\mathbb {A})$
on the space.
Let
![]() $\Pi _2(M)$
denoteFootnote
4
the countable set of equivalence classes of irreducible unitary representation of
$\Pi _2(M)$
denoteFootnote
4
the countable set of equivalence classes of irreducible unitary representation of
![]() $M(\mathbb {A})$
appearing in
$M(\mathbb {A})$
appearing in
![]() $L^2_{\mathrm {disc}}(M(F) \backslash M(\mathbb {A})^1)$
. Each element
$L^2_{\mathrm {disc}}(M(F) \backslash M(\mathbb {A})^1)$
. Each element
![]() $\pi \in \Pi _2(M)$
is an abstract unitary representation of
$\pi \in \Pi _2(M)$
is an abstract unitary representation of
![]() $M(\mathbb {A})$
. By abuse of notations, we consider each
$M(\mathbb {A})$
. By abuse of notations, we consider each
![]() $\pi \in \Pi _2(M)$
also as a representation of
$\pi \in \Pi _2(M)$
also as a representation of
![]() $M(\mathbb {A})^1$
. By Flath’s tensor product theorem (see [Reference Flath23]), each
$M(\mathbb {A})^1$
. By Flath’s tensor product theorem (see [Reference Flath23]), each
![]() $\pi \in \Pi _2(M)$
can be considered as a tensor product of local representations
$\pi \in \Pi _2(M)$
can be considered as a tensor product of local representations
![]() $\pi = \otimes _v \pi _v$
, where
$\pi = \otimes _v \pi _v$
, where
![]() $\pi _v$
is a representation of
$\pi _v$
is a representation of
![]() $M(F_v)$
. We denote the finite part of the representation
$M(F_v)$
. We denote the finite part of the representation
![]() $\otimes _{v<\infty }\pi _v$
by
$\otimes _{v<\infty }\pi _v$
by
![]() $\pi _f$
, and the infinite part of the representation
$\pi _f$
, and the infinite part of the representation
![]() $\otimes _{v\mid \infty }\pi _v$
by
$\otimes _{v\mid \infty }\pi _v$
by
![]() $\pi _\infty $
.
$\pi _\infty $
.
Let
![]() $P\in \mathcal {P}(M)$
and
$P\in \mathcal {P}(M)$
and
![]() $\mathcal {A}^2(P)$
denote the set of automorphic forms
$\mathcal {A}^2(P)$
denote the set of automorphic forms
![]() $\varphi $
on
$\varphi $
on
![]() $N_P(\mathbb {A})M(F)\backslash G(\mathbb {A})$
that are square-integrable, that is
$N_P(\mathbb {A})M(F)\backslash G(\mathbb {A})$
that are square-integrable, that is
![]() $\varphi $
satisfies
$\varphi $
satisfies
where
![]() $\delta _P$
is the modular character attached to P (in particular,
$\delta _P$
is the modular character attached to P (in particular,
![]() $\varphi (amk)=\delta _P^{1/2}(a)\varphi (mk)$
for
$\varphi (amk)=\delta _P^{1/2}(a)\varphi (mk)$
for
![]() $a\in A_M$
,
$a\in A_M$
,
![]() $m\in M(\mathbb {A})^1$
and
$m\in M(\mathbb {A})^1$
and
![]() $k\in K_{\mathbb {A}}$
). Then
$k\in K_{\mathbb {A}}$
). Then
![]() $\mathcal {A}^2(P)$
is a pre-Hilbert space, with an inner product
$\mathcal {A}^2(P)$
is a pre-Hilbert space, with an inner product
 $$\begin{align*}\langle\varphi_1,\varphi_2\rangle_{\mathcal{A}^2(P)} := \intop_{A_M M(F) N_P(\mathbb{A}) \backslash G(\mathbb{A})} \varphi_1(g) \overline{\varphi_2(g)} \,\mathrm{d} g. \end{align*}$$
$$\begin{align*}\langle\varphi_1,\varphi_2\rangle_{\mathcal{A}^2(P)} := \intop_{A_M M(F) N_P(\mathbb{A}) \backslash G(\mathbb{A})} \varphi_1(g) \overline{\varphi_2(g)} \,\mathrm{d} g. \end{align*}$$
Sometimes, we shorthand
![]() $\|\cdot \|_{\mathcal {A}^2(G)}$
as
$\|\cdot \|_{\mathcal {A}^2(G)}$
as
![]() $\|\cdot \|_2$
. Let
$\|\cdot \|_2$
. Let
![]() $\overline {\mathcal {A}^2(P)}$
denote the Hilbert space completion of
$\overline {\mathcal {A}^2(P)}$
denote the Hilbert space completion of
![]() $\mathcal {A}^2(P)$
. For
$\mathcal {A}^2(P)$
. For
![]() $\pi \in \Pi _2(M)$
, we will also denote
$\pi \in \Pi _2(M)$
, we will also denote
![]() $\mathcal {A}^2_\pi (P)\subset \mathcal {A}^2(P)$
to be the subspace of
$\mathcal {A}^2_\pi (P)\subset \mathcal {A}^2(P)$
to be the subspace of
![]() $\varphi $
, such that
$\varphi $
, such that
![]() $\delta _P^{-1/2}\varphi (\cdot k)$
lies in the
$\delta _P^{-1/2}\varphi (\cdot k)$
lies in the
![]() $\pi $
-isotypic subspace of
$\pi $
-isotypic subspace of
![]() $L^2_{\mathrm {disc},\pi }(A_M M(F) \backslash M(\mathbb {A}))\subset L^2_{\mathrm {disc}}(A_M M(F) \backslash M(\mathbb {A}))$
for every
$L^2_{\mathrm {disc},\pi }(A_M M(F) \backslash M(\mathbb {A}))\subset L^2_{\mathrm {disc}}(A_M M(F) \backslash M(\mathbb {A}))$
for every
![]() $k\in K_{\mathbb {A}}$
.
$k\in K_{\mathbb {A}}$
.
Given
![]() $\lambda \in i(\mathfrak {a}_P^G)^*$
, let
$\lambda \in i(\mathfrak {a}_P^G)^*$
, let
![]() $\rho (P,\lambda ,\cdot )$
denote the unitary representation of
$\rho (P,\lambda ,\cdot )$
denote the unitary representation of
![]() $G(\mathbb {A})$
on
$G(\mathbb {A})$
on
![]() $\overline {\mathcal {A}^2(P)}$
, given by
$\overline {\mathcal {A}^2(P)}$
, given by
The representation
![]() $\rho (P,\lambda ,\cdot )$
is isomorphic to
$\rho (P,\lambda ,\cdot )$
is isomorphic to
(see [Reference Finis, Lapid and Müller22, Section 4.2]). We remark that the action of every compact subgroup of
![]() $G(\mathbb {A})$
on
$G(\mathbb {A})$
on
![]() $\mathcal {A}^2(P)$
does not depend on
$\mathcal {A}^2(P)$
does not depend on
![]() $\lambda $
.
$\lambda $
.
Recall that a cuspidal datum
![]() $\chi $
is a
$\chi $
is a
![]() $G(F)$
-conjugacy class of pairs
$G(F)$
-conjugacy class of pairs
![]() $(L,\sigma )$
, where L is a Levi subgroup of G defined over F and
$(L,\sigma )$
, where L is a Levi subgroup of G defined over F and
![]() $\sigma $
is a cuspidal representation of
$\sigma $
is a cuspidal representation of
![]() $L(\mathbb {A})$
(see [Reference Arthur6, Section 12] for a detailed discussion). We have a coarse spectral decomposition
$L(\mathbb {A})$
(see [Reference Arthur6, Section 12] for a detailed discussion). We have a coarse spectral decomposition
(see [Reference Arthur6, (12.5)]). Here and elsewhere,
![]() $\widehat {\oplus }$
denotes a Hilbert space direct sum. We have a similar coarse spectral decomposition of
$\widehat {\oplus }$
denotes a Hilbert space direct sum. We have a similar coarse spectral decomposition of
![]() $\mathcal {A}^2(P)$
(see [Reference Arthur6, p.66–67]). Let
$\mathcal {A}^2(P)$
(see [Reference Arthur6, p.66–67]). Let
![]() $\mathcal {A}^2_\chi (P)$
denote the
$\mathcal {A}^2_\chi (P)$
denote the
![]() $\chi $
-part of this spectral decomposition. Finally, we also write
$\chi $
-part of this spectral decomposition. Finally, we also write
and
![]() $\mathcal {A}^2_{\chi ,\pi }(P) := \mathcal {A}^2_{\chi }(P) \cap \mathcal {A}^2_{\pi }(P)$
.
$\mathcal {A}^2_{\chi ,\pi }(P) := \mathcal {A}^2_{\chi }(P) \cap \mathcal {A}^2_{\pi }(P)$
.
3.2 Some discussion of the coarse spectral expansion
Since this topic is less standard, for the convenience of the reader, we add here a discussion of the coarse spectral decomposition.
We start with the group
![]() $\mathrm {GL}_n$
, in which case, the coarse spectral decomposition is well understood. Thanks to the multiplicity one theorem, each cuspidal representation
$\mathrm {GL}_n$
, in which case, the coarse spectral decomposition is well understood. Thanks to the multiplicity one theorem, each cuspidal representation
![]() $\sigma $
of a Levi subgroup L appears with multiplicity one, that is
$\sigma $
of a Levi subgroup L appears with multiplicity one, that is
Next, let us describe some of the results of [Reference Mœglin and Waldspurger44]. First, we recall that given a cuspidal representation
![]() $\sigma $
of
$\sigma $
of
![]() $\mathrm {GL}_a(\mathbb {A})$
and
$\mathrm {GL}_a(\mathbb {A})$
and
![]() $b>0$
, one may construct a Speh representation
$b>0$
, one may construct a Speh representation
![]() $\operatorname {Speh}(\sigma ,b)$
of
$\operatorname {Speh}(\sigma ,b)$
of
![]() $\mathrm {GL}_{ab}(\mathbb {A})$
, which is the unique irreducible quotient of the induction of
$\mathrm {GL}_{ab}(\mathbb {A})$
, which is the unique irreducible quotient of the induction of
![]() $\sigma ^{\otimes b}$
from the Levi subgroup
$\sigma ^{\otimes b}$
from the Levi subgroup
![]() $\mathrm {GL}_a(\mathbb {A})^b$
and twisted by the character
$\mathrm {GL}_a(\mathbb {A})^b$
and twisted by the character
![]() $\mathrm {GL}_a(\mathbb {A})^b\ni (g_1,g_2,\dots ,g_b)\mapsto |\det (g_1)|^{(b-1)/2}|\det (g_2)|^{(b-3)/2}\dots |\det (g_b)|^{(1-b)/2}$
. It holds that
$\mathrm {GL}_a(\mathbb {A})^b\ni (g_1,g_2,\dots ,g_b)\mapsto |\det (g_1)|^{(b-1)/2}|\det (g_2)|^{(b-3)/2}\dots |\det (g_b)|^{(1-b)/2}$
. It holds that
![]() $\operatorname {Speh}(\sigma ,b) \in \Pi _2(\mathrm {GL}_{ab})$
, and each representation
$\operatorname {Speh}(\sigma ,b) \in \Pi _2(\mathrm {GL}_{ab})$
, and each representation
![]() $\pi \in \Pi _2(\mathrm {GL}_n)$
is isomorphic to a unique Speh representation
$\pi \in \Pi _2(\mathrm {GL}_n)$
is isomorphic to a unique Speh representation
![]() $\operatorname {Speh}(\sigma ,b)$
for some
$\operatorname {Speh}(\sigma ,b)$
for some
![]() $b\mid n$
and cuspidal representation
$b\mid n$
and cuspidal representation
![]() $\sigma $
of
$\sigma $
of
![]() $\mathrm {GL}_{n/b}(\mathbb {A})$
. Note that the
$\mathrm {GL}_{n/b}(\mathbb {A})$
. Note that the
![]() $b=1$
case corresponds to the cuspidal representations in
$b=1$
case corresponds to the cuspidal representations in
![]() $\Pi _2(\mathrm {GL}_n)$
.
$\Pi _2(\mathrm {GL}_n)$
.
Now, if M is a Levi subgroup of
![]() $\mathrm {GL}_n$
of a parabolic P, for each
$\mathrm {GL}_n$
of a parabolic P, for each
![]() $\pi \in \Pi _2(M)$
, there is a unique cuspidal datum
$\pi \in \Pi _2(M)$
, there is a unique cuspidal datum
![]() $\chi $
, such that
$\chi $
, such that
![]() $\mathcal {A}^2_{\chi ,\pi }(P)\ne \{0\}$
, and the multiplicity of
$\mathcal {A}^2_{\chi ,\pi }(P)\ne \{0\}$
, and the multiplicity of
![]() $\pi $
in the space
$\pi $
in the space
![]() $L^2_{\mathrm {disc}}(A_MM(F) \backslash M(\mathbb {A}))$
is equal to
$L^2_{\mathrm {disc}}(A_MM(F) \backslash M(\mathbb {A}))$
is equal to
![]() $1$
. More precisely, if
$1$
. More precisely, if
![]() $M \cong \mathrm {GL}_{n_1}\times \dots \times \mathrm {GL}_{n_k}$
is the standard Levi subgroup, and
$M \cong \mathrm {GL}_{n_1}\times \dots \times \mathrm {GL}_{n_k}$
is the standard Levi subgroup, and
![]() $\pi = \pi _1 \otimes \dots \otimes \pi _k$
, then one can write (uniquely)
$\pi = \pi _1 \otimes \dots \otimes \pi _k$
, then one can write (uniquely)
![]() $n_i = a_i b_i$
, find a cuspidal representation
$n_i = a_i b_i$
, find a cuspidal representation
![]() $\sigma _i \in \Pi _2(\mathrm {GL}_{a_i})$
and write
$\sigma _i \in \Pi _2(\mathrm {GL}_{a_i})$
and write
![]() $\pi _i = \operatorname {Speh}(\sigma _i,b_i)$
. In this case, let
$\pi _i = \operatorname {Speh}(\sigma _i,b_i)$
. In this case, let
![]() $L:=\mathrm {GL}_{a_1}^{b_1}\times \dots \times \mathrm {GL}_{a_k}^{b_k}$
and
$L:=\mathrm {GL}_{a_1}^{b_1}\times \dots \times \mathrm {GL}_{a_k}^{b_k}$
and
![]() $\sigma := \sigma _1^{\otimes b_1}\otimes \dots \otimes \sigma _k^{\otimes b_k} \in \Pi _2(L)$
be cuspidal. If
$\sigma := \sigma _1^{\otimes b_1}\otimes \dots \otimes \sigma _k^{\otimes b_k} \in \Pi _2(L)$
be cuspidal. If
![]() $\chi $
is the cuspidal datum corresponding to
$\chi $
is the cuspidal datum corresponding to
![]() $(L,\sigma )$
, then
$(L,\sigma )$
, then
![]() $\mathcal {A}^2_{\chi ,\pi }(P)\ne \{0\}$
.
$\mathcal {A}^2_{\chi ,\pi }(P)\ne \{0\}$
.
The procedure can be reversed, but one should be a bit careful about the fact that cuspidal datum is only defined up to equivalence. In general, given a Levi L and
![]() $\sigma \in \Pi _2(L)$
cuspidal, let
$\sigma \in \Pi _2(L)$
cuspidal, let
![]() $\chi :=(L,\sigma )$
be the cuspidal datum and P be a standard parabolic containing L as a Levi subgroup. Then there are at most
$\chi :=(L,\sigma )$
be the cuspidal datum and P be a standard parabolic containing L as a Levi subgroup. Then there are at most
![]() $n_P:= |\sum _{P'\sim P} W(\mathfrak {a}_{P},\mathfrak {a}_{P'})|\le |W_0|=n!$
other pairs
$n_P:= |\sum _{P'\sim P} W(\mathfrak {a}_{P},\mathfrak {a}_{P'})|\le |W_0|=n!$
other pairs
![]() $(L',\sigma ')$
of Levi subgroups
$(L',\sigma ')$
of Levi subgroups
![]() $L'\supset M_0$
and cuspidal representations
$L'\supset M_0$
and cuspidal representations
![]() $\sigma '\in \Pi _2(L')$
in
$\sigma '\in \Pi _2(L')$
in
![]() $\chi $
(see [Reference Arthur6, Section 12]). Given such a pair
$\chi $
(see [Reference Arthur6, Section 12]). Given such a pair
![]() $(L,\sigma )$
and a Levi subgroup
$(L,\sigma )$
and a Levi subgroup
![]() $L\subset M$
, we get at most one residual representation in
$L\subset M$
, we get at most one residual representation in
![]() $L^2_{\mathrm {disc},\chi }(A_M M(F) \backslash M(\mathbb {A}))$
. All in all, there are at most
$L^2_{\mathrm {disc},\chi }(A_M M(F) \backslash M(\mathbb {A}))$
. All in all, there are at most
![]() $n!$
pairs of standard parabolics P and
$n!$
pairs of standard parabolics P and
![]() $\pi \in \Pi _2(M_P)$
, such that
$\pi \in \Pi _2(M_P)$
, such that
![]() $\mathcal {A}^2_{\chi ,\pi }(P)\ne \{0\}$
.
$\mathcal {A}^2_{\chi ,\pi }(P)\ne \{0\}$
.
For groups that are different than
![]() $\mathrm {GL}_n$
, the situation becomes much more involved. An interesting case is the group
$\mathrm {GL}_n$
, the situation becomes much more involved. An interesting case is the group
![]() $G=G_2$
. By [Reference Mœglin and Waldspurger45, Appendix III], for
$G=G_2$
. By [Reference Mœglin and Waldspurger45, Appendix III], for
![]() $\chi = (M_0,\mathrm {triv})$
(the torus and the trivial representation of it), there are infinitely many different
$\chi = (M_0,\mathrm {triv})$
(the torus and the trivial representation of it), there are infinitely many different
![]() $\pi \in \Pi _2(G)$
, such that
$\pi \in \Pi _2(G)$
, such that
(see also [Reference Kim35, Reference Žampera55] for complete results about the residual spectrum in this case). Moreover, by [Reference Gan, Gurevich and Jiang24], for some
![]() $\pi \in \Pi _2(G)$
, there are two different cuspidal data
$\pi \in \Pi _2(G)$
, there are two different cuspidal data
![]() $\chi _1,\chi _2$
, such that
$\chi _1,\chi _2$
, such that
with
![]() $\chi _1$
associated with the subgroup G and
$\chi _1$
associated with the subgroup G and
![]() $\chi _2$
associated with a proper parabolic subgroup. Finally, the multiplicity of
$\chi _2$
associated with a proper parabolic subgroup. Finally, the multiplicity of
![]() $\pi $
in
$\pi $
in
![]() $L^2_{\mathrm {disc},\chi _1,\pi }(A_G G(F) \backslash G(\mathbb {A}))$
can be arbitrarily large.
$L^2_{\mathrm {disc},\chi _1,\pi }(A_G G(F) \backslash G(\mathbb {A}))$
can be arbitrarily large.
3.3 Eisenstein series
Given
![]() $\varphi \in \mathcal {A}^2(P)$
and
$\varphi \in \mathcal {A}^2(P)$
and
![]() $\lambda \in (\mathfrak {a}_{P,\mathbb {C}}^G)^*$
, we define a corresponding Eisenstein series, as
$\lambda \in (\mathfrak {a}_{P,\mathbb {C}}^G)^*$
, we define a corresponding Eisenstein series, as
 $$\begin{align*}\mathrm{Eis}(\varphi,\lambda)(g) := \sum_{\gamma \in P(F) \backslash G(F)} \varphi(\gamma g) e^{\langle \lambda, H_P(\gamma g)\rangle }. \end{align*}$$
$$\begin{align*}\mathrm{Eis}(\varphi,\lambda)(g) := \sum_{\gamma \in P(F) \backslash G(F)} \varphi(\gamma g) e^{\langle \lambda, H_P(\gamma g)\rangle }. \end{align*}$$
The above converges absolutely if
![]() $\lambda $
is sufficiently dominantFootnote
5
. One can then, via Langlands’ deep work (see, e.g. [Reference Langlands36]), meromorphically continue
$\lambda $
is sufficiently dominantFootnote
5
. One can then, via Langlands’ deep work (see, e.g. [Reference Langlands36]), meromorphically continue
![]() $\mathrm {Eis}(\varphi ,\lambda )$
to all
$\mathrm {Eis}(\varphi ,\lambda )$
to all
![]() $\lambda \in (\mathfrak {a}_{P,\mathbb {C}}^G)^*$
.
$\lambda \in (\mathfrak {a}_{P,\mathbb {C}}^G)^*$
.
It holds that the Eisenstein series intertwines the representation
![]() $\rho (P,\lambda ,\cdot )$
. Namely, it holds that
$\rho (P,\lambda ,\cdot )$
. Namely, it holds that
for
![]() $y\in G(\mathbb {A})$
.
$y\in G(\mathbb {A})$
.
3.4 Truncation
Recall the minimal parabolic subgroup
![]() $P_0 \in \mathcal {P}(M_0)$
. Given
$P_0 \in \mathcal {P}(M_0)$
. Given
![]() $T\in \mathfrak {a}_{M_0}^G$
, let
$T\in \mathfrak {a}_{M_0}^G$
, let
Given T with
![]() $d(T)$
sufficiently large, Arthur (following Langlands; see [Reference Arthur6, Section 13]) defined certain truncation operator
$d(T)$
sufficiently large, Arthur (following Langlands; see [Reference Arthur6, Section 13]) defined certain truncation operator
![]() $\Lambda ^T$
, which acts on locally integrable functions on
$\Lambda ^T$
, which acts on locally integrable functions on
![]() $G(F) \backslash G(\mathbb {A})^1$
. We do not need the exact definition of
$G(F) \backslash G(\mathbb {A})^1$
. We do not need the exact definition of
![]() $\Lambda ^T$
but just the following properties of it.
$\Lambda ^T$
but just the following properties of it.
Let f be a locally integrable function on
![]() $G(F)\backslash G(\mathbb {A})^1$
.
$G(F)\backslash G(\mathbb {A})^1$
.
-
1.
 $\Lambda ^Tf$
is rapidly decaying. In particular, if
$\Lambda ^Tf$
is rapidly decaying. In particular, if
 $\lambda \in (\mathfrak {a}_{P,\mathbb {C}}^G)^*$
is away from any pole of
$\lambda \in (\mathfrak {a}_{P,\mathbb {C}}^G)^*$
is away from any pole of
 $\mathrm {Eis}(\varphi ,\lambda )$
, then
$\mathrm {Eis}(\varphi ,\lambda )$
, then
 $\Lambda ^T\mathrm {Eis}(\varphi ,\lambda )$
is square-integrable.
$\Lambda ^T\mathrm {Eis}(\varphi ,\lambda )$
is square-integrable. -
2. Given any compact
 $\Omega \subset G(F)\backslash G(\mathbb {A})^1$
, there is a
$\Omega \subset G(F)\backslash G(\mathbb {A})^1$
, there is a
 $C(\Omega )>0$
, such that for every
$C(\Omega )>0$
, such that for every
 $T\in \mathfrak {a}_{M_0}^G$
with
$T\in \mathfrak {a}_{M_0}^G$
with
 $d(T)>C(\Omega )$
, it holds that
$d(T)>C(\Omega )$
, it holds that
 $\Lambda ^Tf\mid _\Omega =f\mid _\Omega $
(see [Reference Lapid40, Lemma 6.2]).
$\Lambda ^Tf\mid _\Omega =f\mid _\Omega $
(see [Reference Lapid40, Lemma 6.2]). -
3. When
 $\alpha (T)\le \alpha (T')$
for every
$\alpha (T)\le \alpha (T')$
for every
 $\alpha \in \Delta _{P_0}$
, it holds that
$\alpha \in \Delta _{P_0}$
, it holds that
 $\Lambda ^{T'}\Lambda ^{T}=\Lambda ^T$
and
$\Lambda ^{T'}\Lambda ^{T}=\Lambda ^T$
and
 $\|\Lambda ^{T'}f\|_2\ge \|\Lambda ^T f\|_2$
(see [Reference Finis and Lapid20, Section 3.3]).
$\|\Lambda ^{T'}f\|_2\ge \|\Lambda ^T f\|_2$
(see [Reference Finis and Lapid20, Section 3.3]).
3.5 Intertwining operators
We follow [Reference Finis, Lapid and Müller22, Section 4.2] to define intertwining operators and to record their relevant properties.
For
![]() $P,Q \in \mathcal {P}(M)$
and
$P,Q \in \mathcal {P}(M)$
and
![]() $\lambda \in \mathfrak {a}^*_{M,\mathbb {C}}$
, we define the standard intertwining operator
$\lambda \in \mathfrak {a}^*_{M,\mathbb {C}}$
, we define the standard intertwining operator
by
 $$ \begin{align} (M_{Q|P}(\lambda)\varphi)(x) := \intop_{N_Q(\mathbb{A})\cap N_P(\mathbb{A}) \backslash N_Q(\mathbb{A})}\varphi(nx) e^{\langle \lambda, H_P(nx) - H_Q(x)\rangle} \,\mathrm{d} n. \end{align} $$
$$ \begin{align} (M_{Q|P}(\lambda)\varphi)(x) := \intop_{N_Q(\mathbb{A})\cap N_P(\mathbb{A}) \backslash N_Q(\mathbb{A})}\varphi(nx) e^{\langle \lambda, H_P(nx) - H_Q(x)\rangle} \,\mathrm{d} n. \end{align} $$
The above integral converges absolutely for sufficiently dominant
![]() $\lambda $
. It can then be meromorphically continued for all
$\lambda $
. It can then be meromorphically continued for all
![]() $\lambda \in \mathfrak {a}^*_{M,\mathbb {C}}$
. It can be checked that
$\lambda \in \mathfrak {a}^*_{M,\mathbb {C}}$
. It can be checked that
![]() $M_{Q\mid P}(\lambda )^{-1}=M_{P\mid Q}(\lambda )$
and for
$M_{Q\mid P}(\lambda )^{-1}=M_{P\mid Q}(\lambda )$
and for
![]() $\lambda \in i(\mathfrak {a}_M^G)^*$
the operator
$\lambda \in i(\mathfrak {a}_M^G)^*$
the operator
![]() $M_{Q\mid P}(\lambda )$
is unitary.
$M_{Q\mid P}(\lambda )$
is unitary.
For each
![]() $\pi \in \Pi _2(M)$
, we denote the restriction of
$\pi \in \Pi _2(M)$
, we denote the restriction of
![]() $M_{Q\mid P}(\lambda )$
on
$M_{Q\mid P}(\lambda )$
on
![]() $\mathcal {A}^2_\pi (P)$
by
$\mathcal {A}^2_\pi (P)$
by
![]() $M_{Q\mid P}(\pi ,\lambda ):\mathcal {A}^2_\pi (P)\to \mathcal {A}^2_\pi (Q)$
. On the other hand, we can define an intertwiner from
$M_{Q\mid P}(\pi ,\lambda ):\mathcal {A}^2_\pi (P)\to \mathcal {A}^2_\pi (Q)$
. On the other hand, we can define an intertwiner from
that can be densely defined on K-finite and
![]() $Z\left (\mathrm {Lie}(G(F_\infty ))\otimes _{\mathbb {R}}\mathbb {C}\right )$
-finite subspace of
$Z\left (\mathrm {Lie}(G(F_\infty ))\otimes _{\mathbb {R}}\mathbb {C}\right )$
-finite subspace of
![]() $\mathrm {Ind}_{P(\mathbb {A})}^{G(\mathbb {A})}\pi $
as in (3.1) (first, for sufficiently dominant
$\mathrm {Ind}_{P(\mathbb {A})}^{G(\mathbb {A})}\pi $
as in (3.1) (first, for sufficiently dominant
![]() $\lambda $
, then by meromorphic continuation). Then we have a unique canonical isomorphism of
$\lambda $
, then by meromorphic continuation). Then we have a unique canonical isomorphism of
![]() $G(\mathbb {A}_f)\times \left (\mathrm {Lie}(G(F_\infty ))\otimes _{\mathbb {R}}\mathbb {C},K_\infty \right )$
-modules (see [Reference Finis, Lapid and Müller22, Section 4.2])
$G(\mathbb {A}_f)\times \left (\mathrm {Lie}(G(F_\infty ))\otimes _{\mathbb {R}}\mathbb {C},K_\infty \right )$
-modules (see [Reference Finis, Lapid and Müller22, Section 4.2])
(similarly,
![]() $j_Q$
) that can be characterized by
$j_Q$
) that can be characterized by
(see [Reference Müller48, (2.3)] and discussion around it).
Endowing
![]() $\mathrm {Hom}_{M(\mathbb {A})}\left (\pi ,L^2(A_MM(F) \backslash M(\mathbb {A}))\right )$
with the inner product
$\mathrm {Hom}_{M(\mathbb {A})}\left (\pi ,L^2(A_MM(F) \backslash M(\mathbb {A}))\right )$
with the inner product
![]() $\langle f_1,f_2\rangle = f_2^*f_1$
, where
$\langle f_1,f_2\rangle = f_2^*f_1$
, where
![]() $*$
denotes adjoint (notice that by Schur’s lemma,
$*$
denotes adjoint (notice that by Schur’s lemma,
![]() $f_2^* f_1$
is a scalar), we note that
$f_2^* f_1$
is a scalar), we note that
![]() $j_P$
is an isometry.
$j_P$
is an isometry.
Now, in the rest of this subsection, let
![]() $P|^\alpha Q$
for some
$P|^\alpha Q$
for some
![]() $\alpha \in \Sigma _M$
. In this case,
$\alpha \in \Sigma _M$
. In this case,
![]() $M_{Q\mid P}(\lambda )$
depends only upon
$M_{Q\mid P}(\lambda )$
depends only upon
![]() $\langle \lambda ,\alpha ^\vee \rangle $
. Let
$\langle \lambda ,\alpha ^\vee \rangle $
. Let
![]() $\varpi \in \mathfrak {a}_M^*$
be such that
$\varpi \in \mathfrak {a}_M^*$
be such that
![]() $\langle \varpi ,\alpha ^\vee \rangle =1$
. We have
$\langle \varpi ,\alpha ^\vee \rangle =1$
. We have
for any
![]() $s\in \mathbb {C}$
avoiding poles of the operators on both sides of above. Here,
$s\in \mathbb {C}$
avoiding poles of the operators on both sides of above. Here,
![]() $n_\alpha (\pi ,s)$
, a global normalizing factor, is a meromorphic function in s. Moreover, if
$n_\alpha (\pi ,s)$
, a global normalizing factor, is a meromorphic function in s. Moreover, if
![]() $s\in i\mathbb {R}$
, then
$s\in i\mathbb {R}$
, then
![]() $|n_\alpha (\pi ,s)|=1$
. The operator
$|n_\alpha (\pi ,s)|=1$
. The operator
is a factorizable normalized intertwining operator, so that
Here, ![]() for almost all v. Moreover, if
for almost all v. Moreover, if
![]() $s\in i\mathbb {R}$
, then
$s\in i\mathbb {R}$
, then
![]() $R_{Q\mid P}(\pi ,s)$
is unitary (see [Reference Arthur6, Theorem 21.4] for details).
$R_{Q\mid P}(\pi ,s)$
is unitary (see [Reference Arthur6, Theorem 21.4] for details).
3.6 Langlands inner product formula
For
![]() $Q\in \mathcal {P}(M)$
, we let
$Q\in \mathcal {P}(M)$
, we let
 $$\begin{align*}\theta_Q(\Lambda) := v_{\Delta_Q}^{-1}\prod_{\beta \in \Delta_Q}\langle \Lambda,\beta^\vee \rangle,\quad \Lambda\in \mathfrak{a}_{M_0,\mathbb{C},}^* \end{align*}$$
$$\begin{align*}\theta_Q(\Lambda) := v_{\Delta_Q}^{-1}\prod_{\beta \in \Delta_Q}\langle \Lambda,\beta^\vee \rangle,\quad \Lambda\in \mathfrak{a}_{M_0,\mathbb{C},}^* \end{align*}$$
where
![]() $v_{\Delta _Q}$
is the covolume of the lattice in
$v_{\Delta _Q}$
is the covolume of the lattice in
![]() $\mathfrak {a}_Q^G$
spanned by
$\mathfrak {a}_Q^G$
spanned by
![]() $\{\beta ^\vee \mid \beta \in \Delta _Q\}$
.
$\{\beta ^\vee \mid \beta \in \Delta _Q\}$
.
For
![]() $T\in \mathfrak {a}_{M_0}^G$
, we also define
$T\in \mathfrak {a}_{M_0}^G$
, we also define
![]() $Y_Q(T)$
as the projection to
$Y_Q(T)$
as the projection to
![]() $\mathfrak {a}_M^G$
of
$\mathfrak {a}_M^G$
of
![]() $t^{-1}(T-T_0)+T_0$
, where
$t^{-1}(T-T_0)+T_0$
, where
![]() $t \in W_0$
is an element, such that
$t \in W_0$
is an element, such that
![]() $P_0 \subset tQ $
, and
$P_0 \subset tQ $
, and
![]() $T_0 \in a_M^G$
is the element defined by Arthur in [Reference Arthur2, Lemma 1.1] (also see the discussion around [Reference Arthur6, (9.4)]).
$T_0 \in a_M^G$
is the element defined by Arthur in [Reference Arthur2, Lemma 1.1] (also see the discussion around [Reference Arthur6, (9.4)]).
Let
![]() $\chi = (M,\pi )$
be a cuspidal datum and
$\chi = (M,\pi )$
be a cuspidal datum and
![]() $\varphi ,\varphi ' \in \mathcal {A}^2_{\chi ,\pi }(P)$
, namely,
$\varphi ,\varphi ' \in \mathcal {A}^2_{\chi ,\pi }(P)$
, namely,
![]() $\varphi $
and
$\varphi $
and
![]() $\varphi '$
are cusp forms. In this case, Langlands, generalizing the classical Maass–Selberg relations, obtained a formula for the inner product of two truncated Eisenstein series attached to
$\varphi '$
are cusp forms. In this case, Langlands, generalizing the classical Maass–Selberg relations, obtained a formula for the inner product of two truncated Eisenstein series attached to
![]() $\varphi $
and
$\varphi $
and
![]() $\varphi '$
(see [Reference Arthur6, Proposition 15.3]). The formula involves sums over various Weyl elements and parabolic subgroups of quantities involving (twisted) intertwining operators,
$\varphi '$
(see [Reference Arthur6, Proposition 15.3]). The formula involves sums over various Weyl elements and parabolic subgroups of quantities involving (twisted) intertwining operators,
![]() $\theta _Q$
, and
$\theta _Q$
, and
![]() $Y_Q$
. There is also an approximate version of the formula, due to Arthur in [Reference Arthur5], when
$Y_Q$
. There is also an approximate version of the formula, due to Arthur in [Reference Arthur5], when
![]() $\varphi $
or
$\varphi $
or
![]() $\varphi '$
are not cuspidal. However, we do not need any of these formulæ here, but only a special case that we describe below.
$\varphi '$
are not cuspidal. However, we do not need any of these formulæ here, but only a special case that we describe below.
For any two parabolic subgroups
![]() $P,Q\supset P_0$
, let
$P,Q\supset P_0$
, let
![]() $W(\mathfrak {a}_P,\mathfrak {a}_Q)$
be the set of distinct linear isomorphisms from
$W(\mathfrak {a}_P,\mathfrak {a}_Q)$
be the set of distinct linear isomorphisms from
![]() $\mathfrak {a}_P\subset \mathfrak {a}_{P_0}$
to
$\mathfrak {a}_P\subset \mathfrak {a}_{P_0}$
to
![]() $\mathfrak {a}_Q\subset \mathfrak {a}_{P_0}$
, induced by elements of
$\mathfrak {a}_Q\subset \mathfrak {a}_{P_0}$
, induced by elements of
![]() $W_0$
. For any
$W_0$
. For any
![]() $Q\in \mathcal {P}(M)$
and
$Q\in \mathcal {P}(M)$
and
![]() $P_0\subset P$
, there is a natural action of
$P_0\subset P$
, there is a natural action of
![]() $W(\mathfrak {a}_P,\mathfrak {a}_Q)$
on
$W(\mathfrak {a}_P,\mathfrak {a}_Q)$
on
![]() $\Pi _2(M)$
. Following [Reference Arthur6, Section 15], we call
$\Pi _2(M)$
. Following [Reference Arthur6, Section 15], we call
![]() $\chi $
unramified if, for every
$\chi $
unramified if, for every
![]() $(M,\pi )\in \chi $
, the stabilizer of
$(M,\pi )\in \chi $
, the stabilizer of
![]() $\pi $
in
$\pi $
in
![]() $W(\mathfrak {a}_P,\mathfrak {a}_P)$
is trivial. We warn again that this notion should not be confused with the unramifiedness of representations of reductive groups over local fields.
$W(\mathfrak {a}_P,\mathfrak {a}_P)$
is trivial. We warn again that this notion should not be confused with the unramifiedness of representations of reductive groups over local fields.
In the unramified case, we record the Langlands inner product formula.
Lemma 3.1. Let
![]() $\chi :=(M,\pi )$
be any unramified cuspidal datum and
$\chi :=(M,\pi )$
be any unramified cuspidal datum and
![]() $\varphi ,\varphi '\in \mathcal {A}_{\chi ,\pi }^2(P)$
. Then we have
$\varphi ,\varphi '\in \mathcal {A}_{\chi ,\pi }^2(P)$
. Then we have
 $$ \begin{align*} \langle \Lambda^T \mathrm{Eis}(\varphi,\lambda), \Lambda^T \mathrm{Eis}(\varphi',\lambda) \rangle_{\mathcal{A}^2(G)} = \lim_{\Lambda \to 0} \sum_{Q\in \mathcal{P}(M)} e^{\langle \Lambda, Y_Q(T) \rangle}\frac{\langle M_{Q|P}(\lambda+\Lambda)\varphi,M_{Q|P}(\lambda)\varphi'\rangle_{\mathcal{A}^2(Q)}}{\theta_Q(\Lambda)}. \end{align*} $$
$$ \begin{align*} \langle \Lambda^T \mathrm{Eis}(\varphi,\lambda), \Lambda^T \mathrm{Eis}(\varphi',\lambda) \rangle_{\mathcal{A}^2(G)} = \lim_{\Lambda \to 0} \sum_{Q\in \mathcal{P}(M)} e^{\langle \Lambda, Y_Q(T) \rangle}\frac{\langle M_{Q|P}(\lambda+\Lambda)\varphi,M_{Q|P}(\lambda)\varphi'\rangle_{\mathcal{A}^2(Q)}}{\theta_Q(\Lambda)}. \end{align*} $$
Proof. We refer to [Reference Finis, Lapid and Müller21, pp.185] and note that
![]() $M_{Q\mid P}(1,\lambda )$
in this reference is the same as
$M_{Q\mid P}(1,\lambda )$
in this reference is the same as
![]() $M_{Q\mid P}(\lambda )$
.
$M_{Q\mid P}(\lambda )$
.
4 Local preliminaries
4.1 Parameters associated with a representation
Let
![]() $M\in \mathcal {L}$
. The goal of this subsection is to associate various parameters measuring the complexity of a certain representation
$M\in \mathcal {L}$
. The goal of this subsection is to associate various parameters measuring the complexity of a certain representation
![]() $\pi \in \Pi _2(M)$
.
$\pi \in \Pi _2(M)$
.
4.1.1 Non-Archimedean complexity
First, following [Reference Finis, Lapid and Müller22, Section 5.1], for any open-compact subgroup
![]() $K\subset K_f$
, we recall the notion
$K\subset K_f$
, we recall the notion
![]() $\mathrm {level}(K)$
. Fix
$\mathrm {level}(K)$
. Fix
![]() $\iota :G\to \mathrm {GL}(V)$
a faithful F-rational representation and an
$\iota :G\to \mathrm {GL}(V)$
a faithful F-rational representation and an
![]() $\mathfrak {o}$
-lattice
$\mathfrak {o}$
-lattice
![]() $\Lambda \subset V$
so that the stabilizer of
$\Lambda \subset V$
so that the stabilizer of
![]() $\hat {\mathfrak {o}}\otimes \Lambda \subset \mathbb {A}_f\otimes V$
in
$\hat {\mathfrak {o}}\otimes \Lambda \subset \mathbb {A}_f\otimes V$
in
![]() $G(\mathbb {A}_f)$
is
$G(\mathbb {A}_f)$
is
![]() $K_f$
. Then, for any ideal
$K_f$
. Then, for any ideal
![]() $\mathfrak {q}\subset \mathfrak {o}$
, we define the principal congruence subgroup of level
$\mathfrak {q}\subset \mathfrak {o}$
, we define the principal congruence subgroup of level
![]() $\mathfrak {q}$
by
$\mathfrak {q}$
by
Now, we define
![]() $\mathrm {level}(K)$
to be the index
$\mathrm {level}(K)$
to be the index
![]() $[\mathfrak {o}:\mathfrak {q}_K]$
, where
$[\mathfrak {o}:\mathfrak {q}_K]$
, where
![]() $\mathfrak {q}_K\subset \mathfrak {o}$
is the largest ideal
$\mathfrak {q}_K\subset \mathfrak {o}$
is the largest ideal
![]() $\mathfrak {q}$
, such that
$\mathfrak {q}$
, such that
![]() $K\supset K({\mathfrak {q}})$
. On the other hand, given a representation
$K\supset K({\mathfrak {q}})$
. On the other hand, given a representation
![]() $\pi _f$
of
$\pi _f$
of
![]() $G(\mathbb {A}_f)$
, we define
$G(\mathbb {A}_f)$
, we define
![]() $\mathrm {level}(\pi _f)$
as the minimum over
$\mathrm {level}(\pi _f)$
as the minimum over
![]() $\mathrm {level}(K)$
, such that
$\mathrm {level}(K)$
, such that
![]() $\pi _f$
has a nontrivial K-invariant vector.Footnote
6
$\pi _f$
has a nontrivial K-invariant vector.Footnote
6
Given a representation
![]() $\pi _f$
of
$\pi _f$
of
![]() $M(\mathbb {A}_f)$
and
$M(\mathbb {A}_f)$
and
![]() $\alpha \in \Sigma _M$
, we recall the quantity
$\alpha \in \Sigma _M$
, we recall the quantity
![]() $\mathrm {level}_M(\pi _f,\hat {M}_\alpha ^+)$
, as defined in [Reference Finis, Lapid and Müller22, Sections 5.1–5.2], which measures the complexity of
$\mathrm {level}_M(\pi _f,\hat {M}_\alpha ^+)$
, as defined in [Reference Finis, Lapid and Müller22, Sections 5.1–5.2], which measures the complexity of
![]() $\pi _f$
. In this paper, we do not need to know
$\pi _f$
. In this paper, we do not need to know
![]() $\mathrm {level}_M(\pi _f,\hat {M}_\alpha ^+)$
explicitly, but only an upper bound that we describe below.
$\mathrm {level}_M(\pi _f,\hat {M}_\alpha ^+)$
explicitly, but only an upper bound that we describe below.
Lemma 4.1. Let
![]() $K\subset K_f$
be an open-compact subgroup. Assume that
$K\subset K_f$
be an open-compact subgroup. Assume that
![]() $\pi \in \Pi _2(M)$
is such that
$\pi \in \Pi _2(M)$
is such that
![]() $\mathcal {A}^2_\pi (P)^{K} \neq \{0\}$
for some
$\mathcal {A}^2_\pi (P)^{K} \neq \{0\}$
for some
![]() $P\in \mathcal {P}(M)$
, that is the parabolic induction of
$P\in \mathcal {P}(M)$
, that is the parabolic induction of
![]() $\pi _f$
to
$\pi _f$
to
![]() $G(\mathbb {A}_f)$
has a K-invariant vector. Then we have
$G(\mathbb {A}_f)$
has a K-invariant vector. Then we have
Proof. It follows from [Reference Finis, Lapid and Müller22, Lemma 5.12] that
where
![]() $G_M^+\subset G$
is a certain subgroup and
$G_M^+\subset G$
is a certain subgroup and
![]() $\mathrm {level}(K;G_M^+)$
denotes the relative level of K in respect to
$\mathrm {level}(K;G_M^+)$
denotes the relative level of K in respect to
![]() $G_M^+$
as defined in [Reference Finis, Lapid and Müller22, Section 5.1]. The lemma follows from the fact that
$G_M^+$
as defined in [Reference Finis, Lapid and Müller22, Section 5.1]. The lemma follows from the fact that
![]() $\mathrm {level}(K;G_M^+)\le \mathrm {level}(K)$
(see [Reference Finis, Lapid and Müller22, Section 5.1]).
$\mathrm {level}(K;G_M^+)\le \mathrm {level}(K)$
(see [Reference Finis, Lapid and Müller22, Section 5.1]).
4.1.2 Archimedean complexity
Let
![]() $\pi _\infty $
be a smooth representation of
$\pi _\infty $
be a smooth representation of
![]() $M(F_\infty )$
. Let
$M(F_\infty )$
. Let
![]() $\alpha \in \Sigma _M$
. We recall the quantity
$\alpha \in \Sigma _M$
. We recall the quantity
![]() $\Lambda _M(\pi _\infty ;\hat {M}_\alpha )$
, as defined in [Reference Finis, Lapid and Müller22, Sections 5.1–5.2], which measures the complexity of
$\Lambda _M(\pi _\infty ;\hat {M}_\alpha )$
, as defined in [Reference Finis, Lapid and Müller22, Sections 5.1–5.2], which measures the complexity of
![]() $\pi _\infty $
as a representation of
$\pi _\infty $
as a representation of
![]() $M(F_\infty )$
. In this paper, we do not need to know
$M(F_\infty )$
. In this paper, we do not need to know
![]() $\Lambda _M(\pi _\infty ;\hat {M}_\alpha )$
explicitly, but only an upper bound that we describe below.
$\Lambda _M(\pi _\infty ;\hat {M}_\alpha )$
explicitly, but only an upper bound that we describe below.
Let
![]() $\nu (\pi _\infty )$
be the eigenvalue for
$\nu (\pi _\infty )$
be the eigenvalue for
![]() $\pi _\infty $
of the Casimir operator of
$\pi _\infty $
of the Casimir operator of
![]() $M(F_\infty )$
. Similarly, given
$M(F_\infty )$
. Similarly, given
![]() $\tau \in \widehat {K_\infty }$
, let
$\tau \in \widehat {K_\infty }$
, let
![]() $\nu (\tau )$
be the Casimir eigenvalue of
$\nu (\tau )$
be the Casimir eigenvalue of
![]() $\tau $
.
$\tau $
.
Lemma 4.2. Let
![]() $\tau \in \widehat {K_\infty }$
. Assume that
$\tau \in \widehat {K_\infty }$
. Assume that
![]() $\pi \in \Pi _2(M)$
is such that
$\pi \in \Pi _2(M)$
is such that
![]() $\mathcal {A}_\pi ^2(P)^{\tau }\neq \{0\}$
for some
$\mathcal {A}_\pi ^2(P)^{\tau }\neq \{0\}$
for some
![]() $P\in \mathcal {P}(M)$
, that is, the parabolic induction of
$P\in \mathcal {P}(M)$
, that is, the parabolic induction of
![]() $\pi _\infty $
to
$\pi _\infty $
to
![]() $G(F_\infty )$
has a nonzero vector whose
$G(F_\infty )$
has a nonzero vector whose
![]() $K_\infty $
-type is
$K_\infty $
-type is
![]() $\tau $
. Then we have
$\tau $
. Then we have
Proof. It follows from [Reference Finis, Lapid and Müller22, (10)–(11)] that
where
![]() $\tau '\in \widehat {K_\infty }$
runs over the lowest
$\tau '\in \widehat {K_\infty }$
runs over the lowest
![]() $K_\infty $
-types of
$K_\infty $
-types of
![]() $\mathrm {Ind}_{P(F_\infty )}^{G(F_\infty )}\pi _\infty $
. We conclude by noting that the lowest
$\mathrm {Ind}_{P(F_\infty )}^{G(F_\infty )}\pi _\infty $
. We conclude by noting that the lowest
![]() $K_\infty $
-types have the smallest Casimir eigenvalues (equivalently, the smallest infinitesimal characters).
$K_\infty $
-types have the smallest Casimir eigenvalues (equivalently, the smallest infinitesimal characters).
4.2 The spherical function
In the rest of this section, we only work over the Archimedean places, that is
![]() $F_\infty $
(see [Reference Duistermaat, Kolk and Varadarajan15, Section 3] for references to the material below).
$F_\infty $
(see [Reference Duistermaat, Kolk and Varadarajan15, Section 3] for references to the material below).
Let
![]() $G_\infty := A_G \backslash G(F_\infty )$
and
$G_\infty := A_G \backslash G(F_\infty )$
and
![]() $K_\infty $
be a maximal compact subgroup in
$K_\infty $
be a maximal compact subgroup in
![]() $G_\infty $
. Choose a maximal
$G_\infty $
. Choose a maximal
![]() $\mathbb {R}$
-split torus
$\mathbb {R}$
-split torus
![]() $T_\infty \subset G_\infty $
, which we may assume to contain
$T_\infty \subset G_\infty $
, which we may assume to contain
![]() $T_0(F_\infty )$
and contained in
$T_0(F_\infty )$
and contained in
![]() $M_0(F_\infty )$
. Let
$M_0(F_\infty )$
. Let
![]() ${W_\infty := N_{G_\infty }(T_\infty )/T_\infty }$
be the Weyl group of
${W_\infty := N_{G_\infty }(T_\infty )/T_\infty }$
be the Weyl group of
![]() $G_\infty $
relative to
$G_\infty $
relative to
![]() $T_\infty $
. Let
$T_\infty $
. Let
![]() $T_\infty ^0$
be the connected component of the identity of
$T_\infty ^0$
be the connected component of the identity of
![]() $T_\infty $
and
$T_\infty $
and
![]() $\mathfrak {a}_\infty $
be the Lie algebra of
$\mathfrak {a}_\infty $
be the Lie algebra of
![]() $T_\infty ^0$
.
$T_\infty ^0$
.
We remark that for any Levi
![]() $M\supset M_0$
, the embedding
$M\supset M_0$
, the embedding
![]() $T_\infty \to M(F_\infty )$
defines a projection
$T_\infty \to M(F_\infty )$
defines a projection
![]() $\mathfrak {a}_\infty \twoheadrightarrow \mathfrak {a}_{M}^G$
and an embedding
$\mathfrak {a}_\infty \twoheadrightarrow \mathfrak {a}_{M}^G$
and an embedding
![]() $(\mathfrak {a}_{M}^G)^* \hookrightarrow \mathfrak {a}_\infty ^*$
(see [Reference Arthur6, pp.118]).
$(\mathfrak {a}_{M}^G)^* \hookrightarrow \mathfrak {a}_\infty ^*$
(see [Reference Arthur6, pp.118]).
We let
![]() $M_{0,\infty }$
be the Levi subgroup, which is the normalizer of
$M_{0,\infty }$
be the Levi subgroup, which is the normalizer of
![]() $T_\infty $
in
$T_\infty $
in
![]() $G_\infty $
. Let
$G_\infty $
. Let
![]() $B_\infty $
be a Borel subgroup containing
$B_\infty $
be a Borel subgroup containing
![]() $M_{0,\infty }$
as a Levi subgroup and also containing
$M_{0,\infty }$
as a Levi subgroup and also containing
![]() $P_0(F_\infty )$
. Let
$P_0(F_\infty )$
. Let
![]() $N_\infty $
be the unipotent radical of
$N_\infty $
be the unipotent radical of
![]() $B_\infty $
. We have the Iwasawa decomposition
$B_\infty $
. We have the Iwasawa decomposition
![]() $G_\infty = B_\infty K_\infty = N_\infty T_\infty ^0 K_\infty $
.
$G_\infty = B_\infty K_\infty = N_\infty T_\infty ^0 K_\infty $
.
Using the exponential map from
![]() $\mathfrak {a}_\infty $
to
$\mathfrak {a}_\infty $
to
![]() $T_\infty ^0$
, each element
$T_\infty ^0$
, each element
![]() $\mu \in \mathfrak {a}_{\infty ,\mathbb {C}}^*:=(\mathfrak {a}_\infty \otimes _{\mathbb {R}}\mathbb {C})^*$
defines a character
$\mu \in \mathfrak {a}_{\infty ,\mathbb {C}}^*:=(\mathfrak {a}_\infty \otimes _{\mathbb {R}}\mathbb {C})^*$
defines a character
![]() $\chi _\mu $
of
$\chi _\mu $
of
![]() $T_\infty $
, which is trivial on
$T_\infty $
, which is trivial on
![]() $T_\infty /T_\infty ^0$
. It extends, via
$T_\infty /T_\infty ^0$
. It extends, via
![]() $N_\infty $
-invariance, to a character of
$N_\infty $
-invariance, to a character of
![]() $B_\infty $
. Let
$B_\infty $
. Let
![]() $\delta _\infty \colon B_\infty \to \mathbb {R}_{>0}$
be the modular character of
$\delta _\infty \colon B_\infty \to \mathbb {R}_{>0}$
be the modular character of
![]() $B_\infty $
, which is attached to the character
$B_\infty $
, which is attached to the character
![]() $\chi _{2\rho _\infty }$
, where
$\chi _{2\rho _\infty }$
, where
![]() $2\rho _\infty $
is the sum of all the roots of the action of
$2\rho _\infty $
is the sum of all the roots of the action of
![]() $T_\infty $
on the Lie algebra of
$T_\infty $
on the Lie algebra of
![]() $N_\infty $
, weighted by the dimensions of the corresponding root spaces.
$N_\infty $
, weighted by the dimensions of the corresponding root spaces.
Given
![]() $g \in G_\infty $
, we let
$g \in G_\infty $
, we let
![]() $a(g)$
be its
$a(g)$
be its
![]() $T_\infty ^0$
part according to the Iwasawa decomposition
$T_\infty ^0$
part according to the Iwasawa decomposition
![]() $G_\infty = N_\infty T_\infty ^0 K_\infty $
. We define the spherical function
$G_\infty = N_\infty T_\infty ^0 K_\infty $
. We define the spherical function
![]() $\eta _\mu \colon G_\infty \to \mathbb {C}$
corresponding to
$\eta _\mu \colon G_\infty \to \mathbb {C}$
corresponding to
![]() $\mu \in \mathfrak {a}_{\infty ,\mathbb {C}}^*$
by
$\mu \in \mathfrak {a}_{\infty ,\mathbb {C}}^*$
by
 $$\begin{align*}\eta_\mu(g) := \intop_{K_\infty}\chi_{\mu+\rho_\infty}(a(kg))\,\mathrm{d} k. \end{align*}$$
$$\begin{align*}\eta_\mu(g) := \intop_{K_\infty}\chi_{\mu+\rho_\infty}(a(kg))\,\mathrm{d} k. \end{align*}$$
Thus,
![]() $\eta _\mu $
is bi
$\eta _\mu $
is bi
![]() $K_\infty $
-invariant. Here,
$K_\infty $
-invariant. Here,
![]() $\,\mathrm {d} k$
denotes the probability Haar measure on
$\,\mathrm {d} k$
denotes the probability Haar measure on
![]() $K_\infty $
.
$K_\infty $
.
4.3 Spherical representation
We call an irreducible admissible representation
![]() $(\pi ,V)$
of
$(\pi ,V)$
of
![]() $G_\infty $
spherical if
$G_\infty $
spherical if
![]() $\pi $
has a nonzero
$\pi $
has a nonzero
![]() $K_\infty $
-invariant vector. We can construct all irreducible admissible spherical representations of
$K_\infty $
-invariant vector. We can construct all irreducible admissible spherical representations of
![]() $G_\infty $
from the unitarily induced principal series representations. Let
$G_\infty $
from the unitarily induced principal series representations. Let
![]() $\mu \in \mathfrak {a}_{\infty ,\mathbb {C}}^*$
and
$\mu \in \mathfrak {a}_{\infty ,\mathbb {C}}^*$
and
![]() $\mathrm {Ind}_{B_\infty }^{G_\infty }\chi _\mu $
denotes the normalized parabolic induction of
$\mathrm {Ind}_{B_\infty }^{G_\infty }\chi _\mu $
denotes the normalized parabolic induction of
![]() $\chi _\mu $
from
$\chi _\mu $
from
![]() $B_\infty $
to
$B_\infty $
to
![]() $G_\infty $
. It is an admissible representation and has a unique irreducible spherical subquotient. Conversely, for any irreducible spherical representation
$G_\infty $
. It is an admissible representation and has a unique irreducible spherical subquotient. Conversely, for any irreducible spherical representation
![]() $(\pi ,V)$
, we can find a (unique up to
$(\pi ,V)$
, we can find a (unique up to
![]() $W_\infty $
-action)
$W_\infty $
-action)
![]() $\mu _\pi \in \mathfrak {a}_{\infty ,\mathbb {C}}^*$
, such that
$\mu _\pi \in \mathfrak {a}_{\infty ,\mathbb {C}}^*$
, such that
![]() $\pi $
appears as the unique spherical subquotient of
$\pi $
appears as the unique spherical subquotient of
![]() $\mathrm {Ind}_{B_\infty }^{G_\infty }\chi _{\mu _\pi }$
. In this case, we call
$\mathrm {Ind}_{B_\infty }^{G_\infty }\chi _{\mu _\pi }$
. In this case, we call
![]() $\mu _\pi $
the Langlands parameter of
$\mu _\pi $
the Langlands parameter of
![]() $\pi $
. When
$\pi $
. When
![]() $\pi $
is also unitary, it holds that
$\pi $
is also unitary, it holds that
![]() $\|\Re (\mu _\pi )\| \le \|\rho _\infty \|$
and
$\|\Re (\mu _\pi )\| \le \|\rho _\infty \|$
and
![]() $1+\|\mu _\pi \|^2\asymp 1+ \nu (\pi )$
(more precisely,
$1+\|\mu _\pi \|^2\asymp 1+ \nu (\pi )$
(more precisely,
![]() $\nu (\pi ) = \|\rho _\infty \|^2- \|\Re (\mu _\pi )\|^2 + \|\Im (\mu _\pi )\|^2$
) (see [Reference Duistermaat, Kolk and Varadarajan15, (3.17)]).
$\nu (\pi ) = \|\rho _\infty \|^2- \|\Re (\mu _\pi )\|^2 + \|\Im (\mu _\pi )\|^2$
) (see [Reference Duistermaat, Kolk and Varadarajan15, (3.17)]).
If
![]() $\pi $
is spherical, then the
$\pi $
is spherical, then the
![]() $K_\infty $
-invariant vector of
$K_\infty $
-invariant vector of
![]() $\pi $
is unique up to multiplication by a scalar. Let
$\pi $
is unique up to multiplication by a scalar. Let ![]() be the characteristic function on
be the characteristic function on
![]() $K_\infty $
. Then
$K_\infty $
. Then ![]() is well-defined and acts as a projection onto the
is well-defined and acts as a projection onto the
![]() $K_\infty $
-invariant subspace of V. Let
$K_\infty $
-invariant subspace of V. Let
![]() $0\neq v\in \pi $
be a
$0\neq v\in \pi $
be a
![]() $K_\infty $
-invariant vector. It follows from the definition of the spherical function that
$K_\infty $
-invariant vector. It follows from the definition of the spherical function that ![]() .
.
Let
![]() $M_\infty $
be any Levi subgroup of
$M_\infty $
be any Levi subgroup of
![]() $G_\infty $
, having
$G_\infty $
, having
![]() $T_\infty $
as a maximal split torus. We can associate to each irreducible admissible spherical (containing a nonzero
$T_\infty $
as a maximal split torus. We can associate to each irreducible admissible spherical (containing a nonzero
![]() $K_\infty \cap M_\infty $
-invariant vector) representation
$K_\infty \cap M_\infty $
-invariant vector) representation
![]() $\pi $
of
$\pi $
of
![]() $M_\infty $
a Langlands parameter
$M_\infty $
a Langlands parameter
![]() $\mu _\pi \in \mathfrak {a}_{\infty ,\mathbb {C}}^*$
, defined up to
$\mu _\pi \in \mathfrak {a}_{\infty ,\mathbb {C}}^*$
, defined up to
![]() $W_{M,\infty }=N_{M_\infty }(T_\infty )/T_\infty \subset W_\infty $
. Moreover, if
$W_{M,\infty }=N_{M_\infty }(T_\infty )/T_\infty \subset W_\infty $
. Moreover, if
![]() $Q_\infty $
is a parabolic subgroup of
$Q_\infty $
is a parabolic subgroup of
![]() $G_\infty $
with
$G_\infty $
with
![]() $M_\infty $
as its Levi subgroup,
$M_\infty $
as its Levi subgroup,
![]() $\mathrm {Ind}_{Q_\infty }^{G_\infty }\pi $
has a unique spherical subrepresentation. On the other hand, if
$\mathrm {Ind}_{Q_\infty }^{G_\infty }\pi $
has a unique spherical subrepresentation. On the other hand, if
![]() $\mathrm {Ind}_{Q_\infty }^{G_\infty }\pi $
has a
$\mathrm {Ind}_{Q_\infty }^{G_\infty }\pi $
has a
![]() $K_\infty $
-invariant vector, then
$K_\infty $
-invariant vector, then
![]() $\pi $
necessarily has a
$\pi $
necessarily has a
![]() $K_\infty \cap M_\infty $
-invariant vector. In any case, by the transitivity of induction,
$K_\infty \cap M_\infty $
-invariant vector. In any case, by the transitivity of induction,
![]() $\mu _\pi $
is also the Langlands parameter of the spherical subquotient of
$\mu _\pi $
is also the Langlands parameter of the spherical subquotient of
![]() $\mathrm {Ind}_{Q_\infty }^{G_\infty }\pi $
(however, the new parameter is defined up to
$\mathrm {Ind}_{Q_\infty }^{G_\infty }\pi $
(however, the new parameter is defined up to
![]() $W_\infty $
).
$W_\infty $
).
4.4 The spherical transform
We call the convolution algebra on
![]() $C_c^\infty (K_\infty \backslash G_\infty / K_\infty )$
the spherical Hecke algebra of
$C_c^\infty (K_\infty \backslash G_\infty / K_\infty )$
the spherical Hecke algebra of
![]() $G_\infty $
. For
$G_\infty $
. For
![]() ${h \in C_c^\infty (K_\infty \backslash G_\infty / K_\infty )}$
, we let
${h \in C_c^\infty (K_\infty \backslash G_\infty / K_\infty )}$
, we let
![]() $\tilde {h}\colon \mathfrak {a}_{\infty ,\mathbb {C}}^* \to \mathbb {C}$
be the spherical transform of h, defined by
$\tilde {h}\colon \mathfrak {a}_{\infty ,\mathbb {C}}^* \to \mathbb {C}$
be the spherical transform of h, defined by
 $$\begin{align*}\tilde{h}(\mu) := \intop_{G_\infty } h(g) \eta_\mu(g) \,\mathrm{d} g. \end{align*}$$
$$\begin{align*}\tilde{h}(\mu) := \intop_{G_\infty } h(g) \eta_\mu(g) \,\mathrm{d} g. \end{align*}$$
If
![]() $\pi $
is spherical and
$\pi $
is spherical and
![]() $0\neq v\in \pi $
is a
$0\neq v\in \pi $
is a
![]() $K_\infty $
-invariant vector, then it holds that
$K_\infty $
-invariant vector, then it holds that
 $$\begin{align*}\pi(h)v = \intop_{G_\infty} h(g) \pi(g) v \,\mathrm{d} g = \tilde{h}(\mu_\pi)v. \end{align*}$$
$$\begin{align*}\pi(h)v = \intop_{G_\infty} h(g) \pi(g) v \,\mathrm{d} g = \tilde{h}(\mu_\pi)v. \end{align*}$$
We define the Abel–Satake transform (also known as Harish-Chandra transform) to be the map
![]() $\mathcal {S}:C_c(K_\infty \backslash G_\infty / K_\infty )\to C_c(T_\infty )$
defined by
$\mathcal {S}:C_c(K_\infty \backslash G_\infty / K_\infty )\to C_c(T_\infty )$
defined by
 $$\begin{align*}h\mapsto \mathcal{S} h : a\mapsto \delta_\infty(a)^{1/2} \intop_{N_\infty}h(an)\,\mathrm{d} n, \end{align*}$$
$$\begin{align*}h\mapsto \mathcal{S} h : a\mapsto \delta_\infty(a)^{1/2} \intop_{N_\infty}h(an)\,\mathrm{d} n, \end{align*}$$
where
![]() $\,\mathrm {d} n$
is a Haar measure on
$\,\mathrm {d} n$
is a Haar measure on
![]() $N_\infty $
. Since
$N_\infty $
. Since
![]() $\mathcal {S} h$
is left-
$\mathcal {S} h$
is left-
![]() $K_\infty \cap T_\infty $
-invariant, it is actually a map on
$K_\infty \cap T_\infty $
-invariant, it is actually a map on
![]() $T_\infty ^0$
. We have the exponential map
$T_\infty ^0$
. We have the exponential map
![]() $\exp \colon \mathfrak {a}_\infty \to T_\infty ^0$
, which gives an identification of
$\exp \colon \mathfrak {a}_\infty \to T_\infty ^0$
, which gives an identification of
![]() $\mathfrak {a}_\infty $
with
$\mathfrak {a}_\infty $
with
![]() $T_\infty ^0$
. So we may as well realize
$T_\infty ^0$
. So we may as well realize
![]() $\mathcal {S} h \in C_c(\mathfrak {a}_\infty )$
after precomposing with the
$\mathcal {S} h \in C_c(\mathfrak {a}_\infty )$
after precomposing with the
![]() $\exp $
map. It holds that
$\exp $
map. It holds that
![]() $\mathcal {S} f$
is
$\mathcal {S} f$
is
![]() $W_\infty $
-invariant. In fact, Gangolli showed that
$W_\infty $
-invariant. In fact, Gangolli showed that
is an isomorphism of topological algebras (see [Reference Duistermaat, Kolk and Varadarajan15, eq.(3.21)] (also see [Reference Gangolli25]). Let us denote the Fourier–Laplace transform
![]() $C_c(\mathfrak {a}_\infty )\to C(\mathfrak {a}_{\infty ,\mathbb {C}}^*)$
by the map
$C_c(\mathfrak {a}_\infty )\to C(\mathfrak {a}_{\infty ,\mathbb {C}}^*)$
by the map
 $$\begin{align*}h\mapsto \hat{h}:\mu\mapsto \intop_{\mathfrak{a}_\infty} h(\alpha) e^{\langle\mu, \alpha\rangle}\,\mathrm{d}\alpha,\end{align*}$$
$$\begin{align*}h\mapsto \hat{h}:\mu\mapsto \intop_{\mathfrak{a}_\infty} h(\alpha) e^{\langle\mu, \alpha\rangle}\,\mathrm{d}\alpha,\end{align*}$$
Harish-Chandra showed that the spherical transform
![]() $\tilde {h} = \widehat {\mathcal {S}(h)}$
. Here,
$\tilde {h} = \widehat {\mathcal {S}(h)}$
. Here,
![]() $\,\mathrm {d}\alpha $
denotes the Lebesgue measure inherited from the
$\,\mathrm {d}\alpha $
denotes the Lebesgue measure inherited from the
![]() $\mathbb {R}$
-vector space structure of
$\mathbb {R}$
-vector space structure of
![]() $\mathfrak {a}_\infty $
.
$\mathfrak {a}_\infty $
.
4.5 The Paley–Wiener theorem
Recall the Abel–Satake transform
![]() $\mathcal {S}$
above. Gangolli (see [Reference Duistermaat, Kolk and Varadarajan15, eq.(3.22)]) proved that if
$\mathcal {S}$
above. Gangolli (see [Reference Duistermaat, Kolk and Varadarajan15, eq.(3.22)]) proved that if
![]() $h\in C_c^\infty (\mathfrak {a}_\infty )^{W_\infty }$
is such that
$h\in C_c^\infty (\mathfrak {a}_\infty )^{W_\infty }$
is such that
![]() $\mathrm {supp} (h) \subset \{\alpha \in \mathfrak {a}_\infty \mid \|\alpha \|\le b\}$
, then
$\mathrm {supp} (h) \subset \{\alpha \in \mathfrak {a}_\infty \mid \|\alpha \|\le b\}$
, then
We also record the classical Paley–Wiener theorem, which implies that for
![]() $h\in C_c^\infty (\mathfrak {a}_\infty )^{W_\infty }$
with support in
$h\in C_c^\infty (\mathfrak {a}_\infty )^{W_\infty }$
with support in
![]() $\{\alpha \in \mathfrak {a}_\infty \mid \|\alpha \|\le b\}$
, we have
$\{\alpha \in \mathfrak {a}_\infty \mid \|\alpha \|\le b\}$
, we have
for every
![]() $N\ge 0$
.
$N\ge 0$
.
5 A bound on an intertwining operator
In this section, we prove Theorem 2 and provide one of the main ingredients of the proof of Theorem 3.
First, we record the required estimates of the logarithmic derivatives of the normalizing factors and the normalized intertwining operators, denoted by properties (TWN+) and (BD), respectively.
5.1 Property (TWN+)
In [Reference Finis and Lapid18, Definition 3.3]Footnote
7
, the authors defined the (TWN+) property, strong version, of a reductive group. Property (TWN+) is a global property that concerns the size of the logarithmic derivative of
![]() $n_\alpha (\pi ,s)$
. Below, we record an implication of property (TWN+) which we will use in this article.
$n_\alpha (\pi ,s)$
. Below, we record an implication of property (TWN+) which we will use in this article.
Lemma 5.1. Let G satisfy property (TWN+). Let
![]() $M\in \mathcal {L}$
be proper,
$M\in \mathcal {L}$
be proper,
![]() $\pi \in \Pi _2(M)$
and
$\pi \in \Pi _2(M)$
and
![]() $\alpha \in \Sigma _M$
. Let
$\alpha \in \Sigma _M$
. Let
![]() $K\subset K_f$
be open-compact and
$K\subset K_f$
be open-compact and
![]() $\tau \in \widehat {K_\infty }$
so that
$\tau \in \widehat {K_\infty }$
so that
![]() $\mathcal {A}^2_\pi (P)^{\tau ,K}\neq \{0\}$
for some
$\mathcal {A}^2_\pi (P)^{\tau ,K}\neq \{0\}$
for some
![]() $P\in \mathcal {P}(M)$
. Then it holds that
$P\in \mathcal {P}(M)$
. Then it holds that
 $$\begin{align*}\intop_{t_0}^{t_0+1} \left|\frac{n^{\prime}_\alpha(\pi,it)}{n_\alpha(\pi,it)}\right| \,\mathrm{d} t \ll \log \left(1+|t_0|+\nu(\pi_\infty)+\nu(\tau)+\mathrm{level}(K)\right), \end{align*}$$
$$\begin{align*}\intop_{t_0}^{t_0+1} \left|\frac{n^{\prime}_\alpha(\pi,it)}{n_\alpha(\pi,it)}\right| \,\mathrm{d} t \ll \log \left(1+|t_0|+\nu(\pi_\infty)+\nu(\tau)+\mathrm{level}(K)\right), \end{align*}$$
for any
![]() $t_0\in \mathbb {R}$
.
$t_0\in \mathbb {R}$
.
Proof. Note that
![]() $|n_\alpha (\pi ,it)|=1$
. Now the proof follows immediately by applying Lemmas 4.1 and 4.2 to the inequality in [Reference Finis and Lapid18, Definition 3.3].
$|n_\alpha (\pi ,it)|=1$
. Now the proof follows immediately by applying Lemmas 4.1 and 4.2 to the inequality in [Reference Finis and Lapid18, Definition 3.3].
Finally, we keep a record that property (TWN+) is not vacuous.
Proposition 5.2. [Reference Finis and Lapid18, Theorem 3.11]. Property (TWN+) holds for G being
![]() $\mathrm {GL}_n$
and its inner form, a quasi-split classical groupFootnote
8
, and
$\mathrm {GL}_n$
and its inner form, a quasi-split classical groupFootnote
8
, and
![]() $G_2$
. Moreover, it holds for any group whose derived group coincides with the derived group of any group mentioned above.
$G_2$
. Moreover, it holds for any group whose derived group coincides with the derived group of any group mentioned above.
5.2 Property (BD)
In [Reference Finis and Lapid19, Definitions 1–2], the authors defined the (BD) property of a reductive group. Property (BD) is a local property that concerns the size of the logarithmic derivative of
![]() $R_{Q\mid P}(\pi _v,s)$
. Below, we record an implication of property (BD) which we will use in this article.
$R_{Q\mid P}(\pi _v,s)$
. Below, we record an implication of property (BD) which we will use in this article.
Lemma 5.3. Let G satisfy property (BD) at every place. Let
![]() $M\in \mathcal {L}$
be proper,
$M\in \mathcal {L}$
be proper,
![]() $\pi \in \Pi _2(M)$
and
$\pi \in \Pi _2(M)$
and
![]() $P,Q\in \mathcal {P}(M)$
be adjacent. Let
$P,Q\in \mathcal {P}(M)$
be adjacent. Let
![]() $K\subset K_f$
be open-compact and
$K\subset K_f$
be open-compact and
![]() $\tau \in \widehat {K_\infty }$
so that
$\tau \in \widehat {K_\infty }$
so that
![]() $\mathcal {A}^2_\pi (P)^{\tau ,K}\neq \{0\}$
. Then it holds that
$\mathcal {A}^2_\pi (P)^{\tau ,K}\neq \{0\}$
. Then it holds that
 $$\begin{align*}\intop_{t_0}^{t_0+1} \,\left\|R_{Q|P}(\pi,it)^{-1} R_{Q|P}^\prime(\pi,it)\vert_{\left(\mathrm{Ind}_{P(\mathbb{A})}^{G(\mathbb{A})}\pi\right)^{\tau,K}}\right\|_{\mathrm{op}} \,\mathrm{d} t \ll \log \left(1+\nu(\tau)+\mathrm{level}(K)\right), \end{align*}$$
$$\begin{align*}\intop_{t_0}^{t_0+1} \,\left\|R_{Q|P}(\pi,it)^{-1} R_{Q|P}^\prime(\pi,it)\vert_{\left(\mathrm{Ind}_{P(\mathbb{A})}^{G(\mathbb{A})}\pi\right)^{\tau,K}}\right\|_{\mathrm{op}} \,\mathrm{d} t \ll \log \left(1+\nu(\tau)+\mathrm{level}(K)\right), \end{align*}$$
for any
![]() $t_0\in \mathbb {R}$
.
$t_0\in \mathbb {R}$
.
To prove Lemma 5.3, we use a different formulation of property (BD), namely, [Reference Finis, Lapid and Müller22, Definition 5.9]. This formulation is implied by the formulation in [Reference Finis and Lapid19, Definitions 1–2] (see [Reference Finis and Lapid19, Remark 3]).
Proof. We closely follow the proof of [Reference Finis, Lapid and Müller22, Proposition 5.16]. As
![]() $R_{Q\mid P}(\pi ,s)=\prod _v R_{Q\mid P}(\pi _v,s)$
and as
$R_{Q\mid P}(\pi ,s)=\prod _v R_{Q\mid P}(\pi _v,s)$
and as
![]() $R_{Q\mid P}(\pi _v,s)\vert _{\left (\mathrm {Ind}_{P(F_v)}^{G(F_v)}\pi _v\right )^{K_v}}$
is independent of s for almost all v (see [Reference Finis, Lapid and Müller22, Remark 5.13]), it is enough to show that
$R_{Q\mid P}(\pi _v,s)\vert _{\left (\mathrm {Ind}_{P(F_v)}^{G(F_v)}\pi _v\right )^{K_v}}$
is independent of s for almost all v (see [Reference Finis, Lapid and Müller22, Remark 5.13]), it is enough to show that
 $$\begin{align*}\intop_{t_0}^{t_0+1} \,\left\|R_{Q|P}(\pi_\infty,it)^{-1} R_{Q|P}^\prime(\pi_\infty,it)\vert_{\left(\mathrm{Ind}_{P(F_\infty)}^{G(F_\infty)}\pi_\infty\right)^{\tau}}\right\|_{\mathrm{op}} \,\mathrm{d} t \ll \log \left(1+\nu(\tau)\right),\end{align*}$$
$$\begin{align*}\intop_{t_0}^{t_0+1} \,\left\|R_{Q|P}(\pi_\infty,it)^{-1} R_{Q|P}^\prime(\pi_\infty,it)\vert_{\left(\mathrm{Ind}_{P(F_\infty)}^{G(F_\infty)}\pi_\infty\right)^{\tau}}\right\|_{\mathrm{op}} \,\mathrm{d} t \ll \log \left(1+\nu(\tau)\right),\end{align*}$$
and for each non-Archimedean v
 $$\begin{align*}\intop_{t_0}^{t_0+1} \,\kern1pt\left\|R_{Q|P}(\pi_v,it)^{-1} R_{Q|P}^\prime(\pi_v,it)\vert_{\left(\mathrm{Ind}_{P(F_v)}^{G(F_v)}\pi_v\right)^{K_v}}\right\|_{\mathrm{op}} \,\mathrm{d} t \ll \log \left(1+\mathrm{level}(K_v)\right),\end{align*}$$
$$\begin{align*}\intop_{t_0}^{t_0+1} \,\kern1pt\left\|R_{Q|P}(\pi_v,it)^{-1} R_{Q|P}^\prime(\pi_v,it)\vert_{\left(\mathrm{Ind}_{P(F_v)}^{G(F_v)}\pi_v\right)^{K_v}}\right\|_{\mathrm{op}} \,\mathrm{d} t \ll \log \left(1+\mathrm{level}(K_v)\right),\end{align*}$$
where
![]() $K=\prod _{v<\infty }K_v$
and
$K=\prod _{v<\infty }K_v$
and
![]() $\mathrm {level}(K_v)$
is the v-adic factor of
$\mathrm {level}(K_v)$
is the v-adic factor of
![]() $\mathrm {level}(K)$
and the implied constant is uniform in v (i.e. uniform in the order
$\mathrm {level}(K)$
and the implied constant is uniform in v (i.e. uniform in the order
![]() $q_v$
of the corresponding residue fields).
$q_v$
of the corresponding residue fields).
To prove the non-Archimedean part, we only modify [Reference Finis, Lapid and Müller22, (14)]. Keeping the same notations (in particular, denoting
![]() $R_{Q\mid P}(\pi _v,s)\vert _{\left (\mathrm {Ind}_{P(F_v)}^{G(F_v)}\pi _v\right )^{K_v}} = A_v(q_v^{-s})$
) and assumptions as in [Reference Finis, Lapid and Müller22], we bound
$R_{Q\mid P}(\pi _v,s)\vert _{\left (\mathrm {Ind}_{P(F_v)}^{G(F_v)}\pi _v\right )^{K_v}} = A_v(q_v^{-s})$
) and assumptions as in [Reference Finis, Lapid and Müller22], we bound
 $$ \begin{align*} \intop_{t_0}^{t_0+1} \,\kern1pt&\left\|R_{Q|P}(\pi_v,it)^{-1} R_{Q|P}^\prime(\pi_v,it)\vert_{\left(\mathrm{Ind}_{P(F_v)}^{G(F_v)}\pi_v\right)^{K_v}}\right\|_{\mathrm{op}} \,\mathrm{d} t\\ &=\log q_v\intop_{t_0}^{t_0+1} \|A^{\prime}_v(q_v^{-it})\|_{\mathrm{op}} \,\mathrm{d} t \ll \log q_v\intop_{S^1}\|A^{\prime}_v(z)\|_{\mathrm{op}}|\,\mathrm{d} z|, \end{align*} $$
$$ \begin{align*} \intop_{t_0}^{t_0+1} \,\kern1pt&\left\|R_{Q|P}(\pi_v,it)^{-1} R_{Q|P}^\prime(\pi_v,it)\vert_{\left(\mathrm{Ind}_{P(F_v)}^{G(F_v)}\pi_v\right)^{K_v}}\right\|_{\mathrm{op}} \,\mathrm{d} t\\ &=\log q_v\intop_{t_0}^{t_0+1} \|A^{\prime}_v(q_v^{-it})\|_{\mathrm{op}} \,\mathrm{d} t \ll \log q_v\intop_{S^1}\|A^{\prime}_v(z)\|_{\mathrm{op}}|\,\mathrm{d} z|, \end{align*} $$
where the last estimate follows by changing variable
![]() $q_v^{-it}\mapsto z$
. In the first equality above, the factor
$q_v^{-it}\mapsto z$
. In the first equality above, the factor
![]() $\log q_v$
comes from
$\log q_v$
comes from
In the second estimate above, we have changed variable
On the other hand, as t moves along
![]() $[t_0,t_0+1]\subset \mathbb {R}$
, the variable z winds
$[t_0,t_0+1]\subset \mathbb {R}$
, the variable z winds
![]() $S^1$
asymptotically
$S^1$
asymptotically
![]() $\log q_v$
times, uniformly in
$\log q_v$
times, uniformly in
![]() $t_0$
. From here, we follow the discussion after [Reference Finis, Lapid and Müller22, (14)] and conclude.
$t_0$
. From here, we follow the discussion after [Reference Finis, Lapid and Müller22, (14)] and conclude.
To prove the Archimedean part, we first modify [Reference Finis, Lapid and Müller22, Lemma 5.19] and its proof. Keeping the same notations and assumptions as in [Reference Finis, Lapid and Müller22], we claim that
 $$\begin{align*}\intop_{t_0}^{t_0+1}\|A'(it)\|_{\mathrm{op}}\,\mathrm{d} t \ll \sum_{1\le j\le m:\,u_j\neq 0} \min \left(1,\frac{1}{|u_j|}\right).\end{align*}$$
$$\begin{align*}\intop_{t_0}^{t_0+1}\|A'(it)\|_{\mathrm{op}}\,\mathrm{d} t \ll \sum_{1\le j\le m:\,u_j\neq 0} \min \left(1,\frac{1}{|u_j|}\right).\end{align*}$$
Here,
![]() $A(s)=A_\infty (s)=R_{Q\mid P}(\pi _\infty ,s)\vert _{\left (\mathrm {Ind}_{P(F_\infty )}^{G(F_\infty )}\pi _\infty \right )^{\tau }}$
. Following the proof of [Reference Finis, Lapid and Müller22, Lemma 5.19], we see that the above claim follows from the following claim
$A(s)=A_\infty (s)=R_{Q\mid P}(\pi _\infty ,s)\vert _{\left (\mathrm {Ind}_{P(F_\infty )}^{G(F_\infty )}\pi _\infty \right )^{\tau }}$
. Following the proof of [Reference Finis, Lapid and Müller22, Lemma 5.19], we see that the above claim follows from the following claim
 $$\begin{align*}\intop_{t_0}^{t_0+1} |\phi_w'(it)| \,\mathrm{d} t \ll \min \left( 1, 1/|u|\right), \end{align*}$$
$$\begin{align*}\intop_{t_0}^{t_0+1} |\phi_w'(it)| \,\mathrm{d} t \ll \min \left( 1, 1/|u|\right), \end{align*}$$
where
![]() $w=u+iv$
with
$w=u+iv$
with
![]() $u,v\in \mathbb {R}$
,
$u,v\in \mathbb {R}$
,
If
![]() $u\neq 0$
, we clearly have
$u\neq 0$
, we clearly have
 $$\begin{align*}\intop_{t_0}^{t_0+1}|\phi^{\prime}_w(it)|\,\mathrm{d} t \ll \intop_{t_0}^{t_0+1}\frac{1}{|u|}\,\mathrm{d} t \ll \frac{1}{|u|}.\end{align*}$$
$$\begin{align*}\intop_{t_0}^{t_0+1}|\phi^{\prime}_w(it)|\,\mathrm{d} t \ll \intop_{t_0}^{t_0+1}\frac{1}{|u|}\,\mathrm{d} t \ll \frac{1}{|u|}.\end{align*}$$
We also have
 $$\begin{align*}\intop_{t_0}^{t_0+1}|\phi^{\prime}_w(it)|\,\mathrm{d} t \le \intop_{\mathbb{R}}\frac{2|u|}{u^2+(t-v)^2}\,\mathrm{d} t =\left.2\arctan\left(\frac{t-v}{|u|}\right)\right\vert{}^{\infty}_{-\infty} = 2\pi.\end{align*}$$
$$\begin{align*}\intop_{t_0}^{t_0+1}|\phi^{\prime}_w(it)|\,\mathrm{d} t \le \intop_{\mathbb{R}}\frac{2|u|}{u^2+(t-v)^2}\,\mathrm{d} t =\left.2\arctan\left(\frac{t-v}{|u|}\right)\right\vert{}^{\infty}_{-\infty} = 2\pi.\end{align*}$$
Thus, the claim follows.
Now, it follows from the discussion and the proof in [Reference Finis, Lapid and Müller22, pp.620–621] that
 $$\begin{align*}\intop_{t_0}^{t_0+1} \,\left\|R_{Q|P}(\pi_\infty,it)^{-1} R_{Q|P}^\prime(\pi_\infty,it)\vert_{\left(\mathrm{Ind}_{P(F_\infty)}^{G(F_\infty)}\pi_\infty\right)^{\tau}}\right\|_{\mathrm{op}} \,\mathrm{d} t \ll \sum_{j=1}^r\sum_{k=1}^m\min\left(1,\frac{1}{|u_j-ck|}\right),\end{align*}$$
$$\begin{align*}\intop_{t_0}^{t_0+1} \,\left\|R_{Q|P}(\pi_\infty,it)^{-1} R_{Q|P}^\prime(\pi_\infty,it)\vert_{\left(\mathrm{Ind}_{P(F_\infty)}^{G(F_\infty)}\pi_\infty\right)^{\tau}}\right\|_{\mathrm{op}} \,\mathrm{d} t \ll \sum_{j=1}^r\sum_{k=1}^m\min\left(1,\frac{1}{|u_j-ck|}\right),\end{align*}$$
where
![]() $|u_j|,r\ll _G 1$
,
$|u_j|,r\ll _G 1$
,
and
![]() $c>0$
depends only on M. We conclude the proof in the Archimedean case by noting that the double sum above is bounded by
$c>0$
depends only on M. We conclude the proof in the Archimedean case by noting that the double sum above is bounded by
![]() $\ll _{G,M}\log m$
.
$\ll _{G,M}\log m$
.
Finally, we keep a record that the property (BD) is not vacuous.
Proposition 5.4. [Reference Finis and Lapid19, Corollary 1]. Property (BD) holds at every place if G is
![]() $\mathrm {GL}_n$
or its inner form, or a split group of rank
$\mathrm {GL}_n$
or its inner form, or a split group of rank
![]() $2$
. It also holds at every non
$2$
. It also holds at every non
![]() $2$
-adic place if G is special orthogonal, or symplectic.
$2$
-adic place if G is special orthogonal, or symplectic.
Fix
![]() $T\in \mathfrak {a}_{M_0}^G$
. Let
$T\in \mathfrak {a}_{M_0}^G$
. Let
![]() $M\in \mathcal {L}$
, and fix
$M\in \mathcal {L}$
, and fix
![]() $P\in \mathcal {P}(M)$
. For
$P\in \mathcal {P}(M)$
. For
![]() $Q\in \mathcal {P}(M)$
and
$Q\in \mathcal {P}(M)$
and
![]() $\lambda ,\Lambda \in i(\mathfrak {a}_M^G)^*$
, we define an operator
$\lambda ,\Lambda \in i(\mathfrak {a}_M^G)^*$
, we define an operator
![]() $\mathcal {M}_Q^T(\lambda ,\Lambda ,P)$
acting on
$\mathcal {M}_Q^T(\lambda ,\Lambda ,P)$
acting on
![]() $\mathcal {A}^2(P)$
by
$\mathcal {A}^2(P)$
by
Similarly, for
![]() $L\in \mathcal {L}(M)$
,
$L\in \mathcal {L}(M)$
,
![]() $Q\in \mathcal {P}(L)$
and
$Q\in \mathcal {P}(L)$
and
![]() $\lambda ,\Lambda \in i(\mathfrak {a}_L^G)^* \subset i(\mathfrak {a}_M^G)^*$
, we define
$\lambda ,\Lambda \in i(\mathfrak {a}_L^G)^* \subset i(\mathfrak {a}_M^G)^*$
, we define
for arbitrary
![]() $Q_1\subset Q$
,
$Q_1\subset Q$
,
![]() $Q_1 \in \mathcal {P}(M)$
. The choice of
$Q_1 \in \mathcal {P}(M)$
. The choice of
![]() $Q_1$
does not matter here. Here, in the left-hand side,
$Q_1$
does not matter here. Here, in the left-hand side,
![]() $\lambda ,\Lambda $
are realized as restrictions on
$\lambda ,\Lambda $
are realized as restrictions on
![]() $\mathfrak {a}_L$
(see [Reference Arthur6, pp.133]).
$\mathfrak {a}_L$
(see [Reference Arthur6, pp.133]).
Following definitions in [Reference Arthur6, Section 21], the set
![]() $\{ \mathcal {M}_Q^T(\lambda ,\Lambda ,P) \}_{Q\in \mathcal {P}(L)}$
is an example of a ‘
$\{ \mathcal {M}_Q^T(\lambda ,\Lambda ,P) \}_{Q\in \mathcal {P}(L)}$
is an example of a ‘
![]() $(G,L)$
-family’ (see [Reference Arthur6, Section 17] for a general discussion on
$(G,L)$
-family’ (see [Reference Arthur6, Section 17] for a general discussion on
![]() $(G,M)$
-family). For
$(G,M)$
-family). For
![]() $L\in \mathcal {L}(M)$
and
$L\in \mathcal {L}(M)$
and
![]() $\lambda \in i(\mathfrak {a}_L^G)^*$
, we define the operator
$\lambda \in i(\mathfrak {a}_L^G)^*$
, we define the operator
![]() $\mathcal {M}^T_L(\lambda ,P)$
as the value at
$\mathcal {M}^T_L(\lambda ,P)$
as the value at
![]() $\Lambda =0$
of
$\Lambda =0$
of
 $$\begin{align*}\sum_{Q \in \mathcal{P}(L)}\frac{\mathcal{M}_Q^T(\lambda,\Lambda,P)}{\theta_Q(\Lambda)}. \end{align*}$$
$$\begin{align*}\sum_{Q \in \mathcal{P}(L)}\frac{\mathcal{M}_Q^T(\lambda,\Lambda,P)}{\theta_Q(\Lambda)}. \end{align*}$$
Below, we prove the main estimate on the operator norm of
![]() $\mathcal {M}^T_L(\lambda ,P)$
.
$\mathcal {M}^T_L(\lambda ,P)$
.
Proposition 5.5. Assume that G satisfies properties (TWN+) and (BD). Fix
![]() $M\in \mathcal {L}$
,
$M\in \mathcal {L}$
,
![]() $P\in \mathcal {P}(M)$
and
$P\in \mathcal {P}(M)$
and
![]() $L\in \mathcal {L}(M)$
. Let
$L\in \mathcal {L}(M)$
. Let
![]() $\tau \in \widehat {K_\infty }$
,
$\tau \in \widehat {K_\infty }$
,
![]() $K\subset K_f$
be an open-compact and
$K\subset K_f$
be an open-compact and
![]() $\pi \in \Pi _2(M)$
. Then, for every
$\pi \in \Pi _2(M)$
. Then, for every
![]() $\lambda _0 \in i(\mathfrak {a}_L^G)^*$
,
$\lambda _0 \in i(\mathfrak {a}_L^G)^*$
,
 $$\begin{align*}\intop_{\substack{\lambda\in i(\mathfrak{a}_L^G)^* \\ \|\lambda-\lambda_0\|\le 1}}\left\|\mathcal{M}^T_L(\lambda,P)|_{\mathcal{A}^2_\pi(P)^{\tau,K}} \right\|_{\mathrm{op}} \,\mathrm{d} \lambda \ll \left(\|T\|\,\log \left(1+\nu(\tau)+\nu(\pi_\infty)+\|\lambda_0\|+\mathrm{level}(K)\right)\right)^{\dim \mathfrak{a}_L^G}, \end{align*}$$
$$\begin{align*}\intop_{\substack{\lambda\in i(\mathfrak{a}_L^G)^* \\ \|\lambda-\lambda_0\|\le 1}}\left\|\mathcal{M}^T_L(\lambda,P)|_{\mathcal{A}^2_\pi(P)^{\tau,K}} \right\|_{\mathrm{op}} \,\mathrm{d} \lambda \ll \left(\|T\|\,\log \left(1+\nu(\tau)+\nu(\pi_\infty)+\|\lambda_0\|+\mathrm{level}(K)\right)\right)^{\dim \mathfrak{a}_L^G}, \end{align*}$$
where
![]() $T\in \mathfrak {a}_{M_0}^G$
with sufficiently large
$T\in \mathfrak {a}_{M_0}^G$
with sufficiently large
![]() $d(T)$
.
$d(T)$
.
Before proving Proposition 5.5, we give a proof of Theorem 2.
Proof of Theorem 2.
Using Lemma 3.1 and the fact that
![]() $M_{Q\mid P}(\lambda )$
unitary for
$M_{Q\mid P}(\lambda )$
unitary for
![]() $\lambda \in i(\mathfrak {a}_M^G)^*$
, and recalling Equation (5.1), we can write
$\lambda \in i(\mathfrak {a}_M^G)^*$
, and recalling Equation (5.1), we can write
We conclude using Proposition 5.5 and that
![]() $\varphi $
is a unit.
$\varphi $
is a unit.
The rest of this section is devoted to the proof of Proposition 5.5.
Let
![]() $P|^\alpha Q$
for some
$P|^\alpha Q$
for some
![]() $\alpha \in \Sigma _M$
. Let
$\alpha \in \Sigma _M$
. Let
![]() $\varpi \in \mathfrak {a}_M^*$
be such that
$\varpi \in \mathfrak {a}_M^*$
be such that
![]() $\langle \varpi ,\alpha ^\vee \rangle =1$
. We define
$\langle \varpi ,\alpha ^\vee \rangle =1$
. We define
as in [Reference Finis, Lapid and Müller22, Section 4.3] as an operator from
![]() $\mathcal {A}^2(P)$
to
$\mathcal {A}^2(P)$
to
![]() $\mathcal {A}^2(P)$
. Here
$\mathcal {A}^2(P)$
. Here
![]() $D_{\varpi }M_{Q|P}(\lambda )$
is the derivative of
$D_{\varpi }M_{Q|P}(\lambda )$
is the derivative of
![]() $M_{Q|P}(\lambda )$
in the direction
$M_{Q|P}(\lambda )$
in the direction
![]() $\varpi $
. The definition is independent of the choice of
$\varpi $
. The definition is independent of the choice of
![]() $\varpi $
; see [Reference Finis, Lapid and Müller22, pp.608].
$\varpi $
; see [Reference Finis, Lapid and Müller22, pp.608].
Lemma 5.6. Keep the notations as above and assumptions as in Proposition 5.5. We have
 $$\begin{align*}\intop_{t_0}^{t_0+1} \,\left\| \delta_{Q|P}(it\varpi)|_{\mathcal{A}^2_{\pi}(P)^{\tau,K}} \right\|_{\mathrm{op}} \,\mathrm{d} t \ll \log\left(1+\nu(\tau)+\nu(\pi_\infty)+|t_0|+\mathrm{level}(K)\right), \end{align*}$$
$$\begin{align*}\intop_{t_0}^{t_0+1} \,\left\| \delta_{Q|P}(it\varpi)|_{\mathcal{A}^2_{\pi}(P)^{\tau,K}} \right\|_{\mathrm{op}} \,\mathrm{d} t \ll \log\left(1+\nu(\tau)+\nu(\pi_\infty)+|t_0|+\mathrm{level}(K)\right), \end{align*}$$
for any
![]() $t_0\in \mathbb {R}$
.
$t_0\in \mathbb {R}$
.
Proof. We take the inverse on both sides of (3.2) and compose it with the derivative of (3.2) and obtain
Recall that
![]() $j_P$
can be chosen to be isometric, that is
$j_P$
can be chosen to be isometric, that is
![]() $\|j_P\|=1$
. We conclude the proof by applying Lemmas 5.1 and 5.3.
$\|j_P\|=1$
. We conclude the proof by applying Lemmas 5.1 and 5.3.
Given
![]() $L \in \mathcal {L}(M)$
, we let
$L \in \mathcal {L}(M)$
, we let
![]() $\mathfrak {B}_{P,L}$
be the set of tuples
$\mathfrak {B}_{P,L}$
be the set of tuples
![]() $\underline {\beta } = (\beta _1^\vee ,...,\beta _m^\vee )$
of
$\underline {\beta } = (\beta _1^\vee ,...,\beta _m^\vee )$
of
![]() $\Sigma _P^\vee $
with
$\Sigma _P^\vee $
with
![]() $m:=\dim \mathfrak {a}^G_L$
, such that their projection to
$m:=\dim \mathfrak {a}^G_L$
, such that their projection to
![]() $\mathfrak {a}_L^G$
form a basis of
$\mathfrak {a}_L^G$
form a basis of
![]() $\mathfrak {a}_L^G$
. We denote
$\mathfrak {a}_L^G$
. We denote
![]() $\mathrm {vol}(\underline {\beta })$
to be the covolume of the lattice generated by the projection of
$\mathrm {vol}(\underline {\beta })$
to be the covolume of the lattice generated by the projection of
![]() $\beta _1^\vee ,...,\beta _m^\vee $
in
$\beta _1^\vee ,...,\beta _m^\vee $
in
![]() $\mathfrak {a}_L^G$
. Let
$\mathfrak {a}_L^G$
. Let
In [Reference Finis, Lapid and Müller21, pp.179–180], (also see [Reference Finis, Lapid and Müller22, pp.608–609]) the authors define a mapFootnote 9
For
![]() $P|^\beta P'$
, we find
$P|^\beta P'$
, we find
![]() $\alpha _{P,P^\prime }\in \mathfrak {a}_M^*$
, such that
$\alpha _{P,P^\prime }\in \mathfrak {a}_M^*$
, such that
Such an
![]() $\alpha _{P,P'}$
exists (see [Reference Finis, Lapid and Müller21, pp.186]). Finally, for
$\alpha _{P,P'}$
exists (see [Reference Finis, Lapid and Müller21, pp.186]). Finally, for
![]() $\xi \in \Xi _L(\underline {\beta })$
, we define the operator
$\xi \in \Xi _L(\underline {\beta })$
, we define the operator
 $$ \begin{align} \Delta_{\xi}^T(P,\lambda) := \frac{\mathrm{vol}(\underline{\beta})}{m!}M_{P\mid P_1^{\prime}}(\lambda) \bigg(\delta_{P_1|P_1^{\prime}}(\lambda)&+\langle\alpha_{P_1,P_1^{\prime}},T-T_0\rangle\mathrm{Id}\bigg) M_{P_1^{\prime}|P_2^{\prime}}(\lambda)\nonumber\\ &\quad\dots \bigg(\delta_{P_m|P_m^{\prime}}(\lambda)+\langle{\alpha}_{P_m,P_m^{\prime}},T-T_0\rangle\mathrm{Id}\bigg)M_{P_m^{\prime}|P}(\lambda). \end{align} $$
$$ \begin{align} \Delta_{\xi}^T(P,\lambda) := \frac{\mathrm{vol}(\underline{\beta})}{m!}M_{P\mid P_1^{\prime}}(\lambda) \bigg(\delta_{P_1|P_1^{\prime}}(\lambda)&+\langle\alpha_{P_1,P_1^{\prime}},T-T_0\rangle\mathrm{Id}\bigg) M_{P_1^{\prime}|P_2^{\prime}}(\lambda)\nonumber\\ &\quad\dots \bigg(\delta_{P_m|P_m^{\prime}}(\lambda)+\langle{\alpha}_{P_m,P_m^{\prime}},T-T_0\rangle\mathrm{Id}\bigg)M_{P_m^{\prime}|P}(\lambda). \end{align} $$
Note that the definition of
![]() $\Delta _\xi ^T(P,\lambda )$
, here, looks a little different from [Reference Finis, Lapid and Müller21, pp.186], although they are the same. This is because the definition of
$\Delta _\xi ^T(P,\lambda )$
, here, looks a little different from [Reference Finis, Lapid and Müller21, pp.186], although they are the same. This is because the definition of
![]() $\delta _{P_i\mid P_i'}$
in [Reference Finis, Lapid and Müller21, pp.179] is different than ours (also compare with the definition of
$\delta _{P_i\mid P_i'}$
in [Reference Finis, Lapid and Müller21, pp.179] is different than ours (also compare with the definition of
![]() $\Delta ^T_\xi (P,\lambda )$
in [Reference Finis, Lapid and Müller22, pp.609]).
$\Delta ^T_\xi (P,\lambda )$
in [Reference Finis, Lapid and Müller22, pp.609]).
Following, Proposition 5.7 expresses the operator
![]() $\mathcal {M}^T_L$
in terms of
$\mathcal {M}^T_L$
in terms of
![]() $\Delta ^T_\xi $
. A proof of this is essentially contained in [Reference Finis, Lapid and Müller21, Theorem 4].
$\Delta ^T_\xi $
. A proof of this is essentially contained in [Reference Finis, Lapid and Müller21, Theorem 4].
Proposition 5.7. Keep the same notations as in Proposition 5.5. We have
 $$\begin{align*}\mathcal{M}_L^T(P,\lambda) = \sum_{\underline{\beta}\in \mathfrak{B}_{P,L}} \Delta_{\xi(\underline{\beta})}^T(P,\lambda) \end{align*}$$
$$\begin{align*}\mathcal{M}_L^T(P,\lambda) = \sum_{\underline{\beta}\in \mathfrak{B}_{P,L}} \Delta_{\xi(\underline{\beta})}^T(P,\lambda) \end{align*}$$
as operators on
![]() $\mathcal {A}^2_{\pi }(P)^{\tau ,K}$
.
$\mathcal {A}^2_{\pi }(P)^{\tau ,K}$
.
Proof. We closely follow the proof of [Reference Finis, Lapid and Müller21, Theorem 4]. The Taylor expansion
![]() $\mathcal {A}_Q$
of
$\mathcal {A}_Q$
of
form a compatible family (in the sense of [Reference Finis, Lapid and Müller21]), when restricted to the finite-dimensional subspace
![]() $\mathcal {A}_\pi ^2(P)^{\tau ,K}$
. This follows from the argument in [Reference Finis, Lapid and Müller21, pp.185] for
$\mathcal {A}_\pi ^2(P)^{\tau ,K}$
. This follows from the argument in [Reference Finis, Lapid and Müller21, pp.185] for
![]() $s=1$
. On the other hand, the Taylor series
$s=1$
. On the other hand, the Taylor series
![]() $c_Q$
of
$c_Q$
of
![]() $e^{\langle \Lambda ,Y_Q(T)\rangle }$
at
$e^{\langle \Lambda ,Y_Q(T)\rangle }$
at
![]() $\Lambda =0$
form a scalar-valued compatible family. Thus, following the argument in [Reference Finis, Lapid and Müller21, pp.186], we conclude that
$\Lambda =0$
form a scalar-valued compatible family. Thus, following the argument in [Reference Finis, Lapid and Müller21, pp.186], we conclude that
![]() $c_Q\mathcal {A}_Q$
form a compatible family when restricted to the finite-dimensional subspace
$c_Q\mathcal {A}_Q$
form a compatible family when restricted to the finite-dimensional subspace
![]() $\mathcal {A}_\pi ^2(P)^{\tau ,K}$
. Hence, as in [Reference Finis, Lapid and Müller21], we compute the limit of (5.1) at
$\mathcal {A}_\pi ^2(P)^{\tau ,K}$
. Hence, as in [Reference Finis, Lapid and Müller21], we compute the limit of (5.1) at
![]() $\Lambda =0$
using [Reference Finis and Lapid17, Theorem 8.1], which concludes the proof.
$\Lambda =0$
using [Reference Finis and Lapid17, Theorem 8.1], which concludes the proof.
Finally, we can prove Proposition 5.5.
Proof of Proposition 5.5.
Using Proposition 5.7, we see that it is enough to bound for each
![]() $\beta \in \mathfrak {B}_{P,L}$
,
$\beta \in \mathfrak {B}_{P,L}$
,
 $$\begin{align*}\intop_{\substack{{\lambda\in i(\mathfrak{a}_L^G)^*} \\ \|\lambda-\lambda_0\|\le 1}}\left\| \Delta_{\xi(\underline{\beta})}^T(P,\lambda)|_{\mathcal{A}^2_\pi(P)^{\tau,K}} \right\|_{\mathrm{op}} \,\mathrm{d} \lambda \ll \left(\|T\|\,\log \left(1+\nu(\tau)+\nu(\pi_\infty)+\|\lambda_0\|+\mathrm{level}(K)\right)\right)^{m}. \end{align*}$$
$$\begin{align*}\intop_{\substack{{\lambda\in i(\mathfrak{a}_L^G)^*} \\ \|\lambda-\lambda_0\|\le 1}}\left\| \Delta_{\xi(\underline{\beta})}^T(P,\lambda)|_{\mathcal{A}^2_\pi(P)^{\tau,K}} \right\|_{\mathrm{op}} \,\mathrm{d} \lambda \ll \left(\|T\|\,\log \left(1+\nu(\tau)+\nu(\pi_\infty)+\|\lambda_0\|+\mathrm{level}(K)\right)\right)^{m}. \end{align*}$$
Let
![]() $\vartheta _i\in (\mathfrak {a}_L^G)^*$
be the dual basis to
$\vartheta _i\in (\mathfrak {a}_L^G)^*$
be the dual basis to
![]() $\beta _j^\vee $
. Using this basis, the above integral can be majorized by
$\beta _j^\vee $
. Using this basis, the above integral can be majorized by
 $$\begin{align*}\ll \intop_{\substack{{\lambda=i\sum_{j=1}^mt_j\vartheta_j}\\{t_j\in\mathbb{R},\,|t_j-t_{0,j}| \le C}}}\left\|\Delta_{\xi(\underline{\beta})}^T(P,\lambda)|_{\mathcal{A}^2_\pi(P)^{\tau,K}} \right\|_{\mathrm{op}} \,\mathrm{d} \lambda,\end{align*}$$
$$\begin{align*}\ll \intop_{\substack{{\lambda=i\sum_{j=1}^mt_j\vartheta_j}\\{t_j\in\mathbb{R},\,|t_j-t_{0,j}| \le C}}}\left\|\Delta_{\xi(\underline{\beta})}^T(P,\lambda)|_{\mathcal{A}^2_\pi(P)^{\tau,K}} \right\|_{\mathrm{op}} \,\mathrm{d} \lambda,\end{align*}$$
where
![]() $it_{0,j}:=\langle \lambda _0,\beta _j^\vee \rangle $
and C is a constant, depending only on the root system. Now we recall (5.3) and use the fact that
$it_{0,j}:=\langle \lambda _0,\beta _j^\vee \rangle $
and C is a constant, depending only on the root system. Now we recall (5.3) and use the fact that
![]() $M_{Q|P}(\lambda )$
is unitary for purely imaginary
$M_{Q|P}(\lambda )$
is unitary for purely imaginary
![]() $\lambda $
to see that the above integral can be bounded by
$\lambda $
to see that the above integral can be bounded by
 $$\begin{align*}\prod_{j=1}^m\intop_{|t_j - t_{0,j}| \le C} \left(\left\|\delta_{P_j|P_j^\prime}(i\vartheta_jt_j)|_{\mathcal{A}^2_\pi(P^{\prime}_j)^{\tau,K}}\right\|_{\mathrm{op}}+\|T\|\right) \,\mathrm{d} t_j. \end{align*}$$
$$\begin{align*}\prod_{j=1}^m\intop_{|t_j - t_{0,j}| \le C} \left(\left\|\delta_{P_j|P_j^\prime}(i\vartheta_jt_j)|_{\mathcal{A}^2_\pi(P^{\prime}_j)^{\tau,K}}\right\|_{\mathrm{op}}+\|T\|\right) \,\mathrm{d} t_j. \end{align*}$$
We conclude the proof by dividing the above interval in the j’th integral in
![]() $O(1)$
number of length one subinterval centring the points of size
$O(1)$
number of length one subinterval centring the points of size
![]() $O(t_{0,j})$
and applying Lemma 5.6 for the integral over each subinterval.
$O(t_{0,j})$
and applying Lemma 5.6 for the integral over each subinterval.
6 The spectral side of the trace formula
For any
![]() $M\in \mathcal {L}$
and
$M\in \mathcal {L}$
and
![]() $\pi \in \Pi _2(M)$
, we denote
$\pi \in \Pi _2(M)$
, we denote
![]() $\mathcal {B}_{\chi ,\pi }(P)$
to be an orthonormal basis of
$\mathcal {B}_{\chi ,\pi }(P)$
to be an orthonormal basis of
![]() $\mathcal {A}^2_{\chi ,\pi }(P)$
. Let
$\mathcal {A}^2_{\chi ,\pi }(P)$
. Let
![]() $h\in C_c^\infty (G(\mathbb {A})^1)$
be a
$h\in C_c^\infty (G(\mathbb {A})^1)$
be a
![]() $K_\infty K_f$
-finite function and
$K_\infty K_f$
-finite function and
![]() $T\in \mathfrak {a}_{M_0}^G$
with sufficiently large
$T\in \mathfrak {a}_{M_0}^G$
with sufficiently large
![]() $d(T)$
.
$d(T)$
.
Let
![]() $\chi $
be cuspidal data. In [Reference Arthur1, Section 3], Arthur defined a distribution
$\chi $
be cuspidal data. In [Reference Arthur1, Section 3], Arthur defined a distribution
![]() $J_\chi ^T(h)$
via a geometric expansion (for
$J_\chi ^T(h)$
via a geometric expansion (for
![]() $d(T)$
sufficiently large) and showed that
$d(T)$
sufficiently large) and showed that
![]() $J_\chi ^T(h)$
is a polynomial in T. We do not need to know the exact definition of the distribution
$J_\chi ^T(h)$
is a polynomial in T. We do not need to know the exact definition of the distribution
![]() $J_\chi ^T(h)$
but will record spectral formulæ for it that will be useful for us.
$J_\chi ^T(h)$
but will record spectral formulæ for it that will be useful for us.
We recall certain norm
![]() $\|g\|$
on
$\|g\|$
on
![]() $G(\mathbb {A})\ni g$
as defined in [Reference Arthur3, pp.1252–1253]. For
$G(\mathbb {A})\ni g$
as defined in [Reference Arthur3, pp.1252–1253]. For
![]() $P \supset P_0$
, we let
$P \supset P_0$
, we let
where
![]() $\sim $
denotes association.
$\sim $
denotes association.
Proposition 6.1. [Reference Arthur3, Proposition 2.2] There is a constant
![]() $C_0>0$
, such that if
$C_0>0$
, such that if
then
 $$\begin{align*}J_\chi^T(h)= \sum_{P\supset P_0} \frac{1}{n_P}\sum_{\pi \in \Pi_2(M_P)} \sum_{\varphi \in \mathcal{B}_{\chi,\pi}(P)}\intop_{i (\mathfrak{a}_P^G)^*} \langle \Lambda^T \mathrm{Eis}(\rho(P,\lambda,h)\varphi,\lambda),\Lambda^T \mathrm{Eis}(\varphi,\lambda) \rangle_{\mathcal{A}^2(G)} \,\mathrm{d} \lambda, \end{align*}$$
$$\begin{align*}J_\chi^T(h)= \sum_{P\supset P_0} \frac{1}{n_P}\sum_{\pi \in \Pi_2(M_P)} \sum_{\varphi \in \mathcal{B}_{\chi,\pi}(P)}\intop_{i (\mathfrak{a}_P^G)^*} \langle \Lambda^T \mathrm{Eis}(\rho(P,\lambda,h)\varphi,\lambda),\Lambda^T \mathrm{Eis}(\varphi,\lambda) \rangle_{\mathcal{A}^2(G)} \,\mathrm{d} \lambda, \end{align*}$$
and moreover, is a polynomial in T.
The
![]() $\pi $
-sum in Proposition 6.1 is actually finite (see [Reference Arthur3, pp.1245]), although we will not use this fact in this paper.
$\pi $
-sum in Proposition 6.1 is actually finite (see [Reference Arthur3, pp.1245]), although we will not use this fact in this paper.
The polynomial expression of
![]() $J_\chi ^T(h)$
can be explicitly calculated. We record the expression in the following Proposition 6.2.
$J_\chi ^T(h)$
can be explicitly calculated. We record the expression in the following Proposition 6.2.
For
![]() $L\in \mathcal {L}(M)$
, let
$L\in \mathcal {L}(M)$
, let
![]() $W^L(M_P)$
be the set of
$W^L(M_P)$
be the set of
![]() $w\in W(M)$
, such that
$w\in W(M)$
, such that
We record the following important proposition. For each
![]() $w\in W^L(M_P)$
, we consider the intertwining operator
$w\in W^L(M_P)$
, we consider the intertwining operator
![]() $M(P,w)$
defined in [Reference Arthur4, pp.1309]. We do not need an explicit definition (which is a bit convoluted) of this operator but only need some of its properties, which are described below.
$M(P,w)$
defined in [Reference Arthur4, pp.1309]. We do not need an explicit definition (which is a bit convoluted) of this operator but only need some of its properties, which are described below.
Proposition 6.2. The quantity
![]() $J_\chi ^T(h)$
is equal to
$J_\chi ^T(h)$
is equal to
 $$\begin{align*}\sum_{P\supset P_0} \frac{1}{n_P}\sum_{\pi \in \Pi_2(M_P)}\sum_{L\in\mathcal{L}(M_P)}\sum_{w\in W^L(M_P)}\iota_w \intop_{i(\mathfrak{a}_{L}^G)^*} \mathrm{tr} \left(\mathcal{M}^T_{L}(P,\lambda)M(P,w)\rho(P,\lambda,h)|_{\mathcal{A}^2_{\chi,\pi}(P)}\right) \,\mathrm{d} \lambda,\end{align*}$$
$$\begin{align*}\sum_{P\supset P_0} \frac{1}{n_P}\sum_{\pi \in \Pi_2(M_P)}\sum_{L\in\mathcal{L}(M_P)}\sum_{w\in W^L(M_P)}\iota_w \intop_{i(\mathfrak{a}_{L}^G)^*} \mathrm{tr} \left(\mathcal{M}^T_{L}(P,\lambda)M(P,w)\rho(P,\lambda,h)|_{\mathcal{A}^2_{\chi,\pi}(P)}\right) \,\mathrm{d} \lambda,\end{align*}$$
where
![]() $\iota _w:=\left |\det \left ((w-1)\mid _{\mathfrak {a}^L_M}\right )\right |$
.
$\iota _w:=\left |\det \left ((w-1)\mid _{\mathfrak {a}^L_M}\right )\right |$
.
Arthur in [Reference Arthur3, Reference Arthur4] proved Proposition 6.2 only for
![]() $T=T_0$
, but below, we show that the same arguments can also be made to work for general T.
$T=T_0$
, but below, we show that the same arguments can also be made to work for general T.
Proof. We fix a Weyl group invariant test function
![]() $B\in C_c^\infty (i(\mathfrak {a}_{M_0}^G)^*)^{W_0}$
with
$B\in C_c^\infty (i(\mathfrak {a}_{M_0}^G)^*)^{W_0}$
with
![]() $B(0)=1$
. As in [Reference Arthur3, pp.1273], for
$B(0)=1$
. As in [Reference Arthur3, pp.1273], for
![]() $\epsilon>0$
and
$\epsilon>0$
and
![]() $\pi \in \Pi _2(M)$
, we define
$\pi \in \Pi _2(M)$
, we define
where
![]() $\mu _\pi \in \mathfrak {a}_{M_0,\mathbb {C}}^*$
is the infinitesimal character of
$\mu _\pi \in \mathfrak {a}_{M_0,\mathbb {C}}^*$
is the infinitesimal character of
![]() $\pi $
. Combining [Reference Arthur3, Theorem 6.3(ii)] and [Reference Arthur4, Theorem 4.1], we obtain that
$\pi $
. Combining [Reference Arthur3, Theorem 6.3(ii)] and [Reference Arthur4, Theorem 4.1], we obtain that
![]() $J_\chi ^T(h)$
is equal to the limit of
$J_\chi ^T(h)$
is equal to the limit of
 $$\begin{align*}\sum_{P\supset P_0} \frac{1}{n_P}\sum_{L\in\mathcal{L}(M_P)}\sum_{w\in W^L(M_P)}\iota_w \sum_{\pi \in \Pi_2(M_P)}\intop_{i(\mathfrak{a}_{L}^G)^*} \mathrm{tr} \left(\mathcal{M}^T_{L}(P,\lambda)M(P,w)\rho(P,\lambda,h)|_{\mathcal{A}^2_{\chi,\pi}(P)}\right) B_\pi^\epsilon(\lambda) \,\mathrm{d} \lambda\end{align*}$$
$$\begin{align*}\sum_{P\supset P_0} \frac{1}{n_P}\sum_{L\in\mathcal{L}(M_P)}\sum_{w\in W^L(M_P)}\iota_w \sum_{\pi \in \Pi_2(M_P)}\intop_{i(\mathfrak{a}_{L}^G)^*} \mathrm{tr} \left(\mathcal{M}^T_{L}(P,\lambda)M(P,w)\rho(P,\lambda,h)|_{\mathcal{A}^2_{\chi,\pi}(P)}\right) B_\pi^\epsilon(\lambda) \,\mathrm{d} \lambda\end{align*}$$
as
![]() $\epsilon \to 0$
. Now, if we show that for each
$\epsilon \to 0$
. Now, if we show that for each
![]() $P\in \mathcal {P}$
,
$P\in \mathcal {P}$
,
![]() $L\in \mathcal {L}(M_P)$
, and
$L\in \mathcal {L}(M_P)$
, and
![]() $w\in W^L(M_P)$
$w\in W^L(M_P)$
 $$\begin{align*}\sum_{\pi \in \Pi_2(M_P)}\intop_{i(\mathfrak{a}_{L}^G)^*} \left|\mathrm{tr} \left(\mathcal{M}^T_{L}(P,\lambda)M(P,w)\rho(P,\lambda,h)|_{\mathcal{A}^2_{\chi,\pi}(P)}\right)\right|\,\mathrm{d} \lambda<\infty,\end{align*}$$
$$\begin{align*}\sum_{\pi \in \Pi_2(M_P)}\intop_{i(\mathfrak{a}_{L}^G)^*} \left|\mathrm{tr} \left(\mathcal{M}^T_{L}(P,\lambda)M(P,w)\rho(P,\lambda,h)|_{\mathcal{A}^2_{\chi,\pi}(P)}\right)\right|\,\mathrm{d} \lambda<\infty,\end{align*}$$
then by dominated convergence, we can pass the
![]() $\epsilon \to 0$
limit inside and conclude.
$\epsilon \to 0$
limit inside and conclude.
Now we work as in [Reference Finis, Lapid and Müller21, Section 5.1] to show the above absolute convergence. As the intertwiner
![]() $M(P,w)$
commutes with the group action
$M(P,w)$
commutes with the group action
![]() $\rho $
and is unitary (see [Reference Finis, Lapid and Müller21, pp.184]), we have
$\rho $
and is unitary (see [Reference Finis, Lapid and Müller21, pp.184]), we have
Here, on the right-hand side above and elsewhere,
![]() $\|\cdot \|_1$
denotes the trace norm of the corresponding operator. Moreover, using Proposition 5.7, it suffices to show that
$\|\cdot \|_1$
denotes the trace norm of the corresponding operator. Moreover, using Proposition 5.7, it suffices to show that
 $$\begin{align*}\sum_{\pi \in \Pi_2(M_P)}\intop_{i(\mathfrak{a}_{L}^G)^*}\left\|\Delta_\xi^T(P,\lambda)\rho(P,\lambda,h)|_{\mathcal{A}^2_{\chi,\pi}(P)}\right\|_1 \,\mathrm{d} \lambda <\infty,\end{align*}$$
$$\begin{align*}\sum_{\pi \in \Pi_2(M_P)}\intop_{i(\mathfrak{a}_{L}^G)^*}\left\|\Delta_\xi^T(P,\lambda)\rho(P,\lambda,h)|_{\mathcal{A}^2_{\chi,\pi}(P)}\right\|_1 \,\mathrm{d} \lambda <\infty,\end{align*}$$
for any
![]() $\underline {\beta }\in \mathcal {B}_{P,L}$
and
$\underline {\beta }\in \mathcal {B}_{P,L}$
and
![]() $\xi \in \Xi _L(\underline {\beta })$
. As h is
$\xi \in \Xi _L(\underline {\beta })$
. As h is
![]() $K_f$
-finite, there exists an open-compact
$K_f$
-finite, there exists an open-compact
![]() $K_h\subset K_f$
, such that h is right
$K_h\subset K_f$
, such that h is right
![]() $K_h$
-invariant. Now decomposing into
$K_h$
-invariant. Now decomposing into
![]() $K_\infty $
-types, it suffices to show that
$K_\infty $
-types, it suffices to show that
 $$\begin{align*}\sum_{\tau\in\widehat{K_\infty}}\sum_{\pi \in \Pi_2(M_P)}\intop_{i(\mathfrak{a}_{L}^G)^*}\left\|\Delta_\xi^T(P,\lambda)\rho(P,\lambda,h)|_{\mathcal{A}^2_{\chi,\pi}(P)^{\tau,K_h}}\right\|_1 \,\mathrm{d} \lambda <\infty.\end{align*}$$
$$\begin{align*}\sum_{\tau\in\widehat{K_\infty}}\sum_{\pi \in \Pi_2(M_P)}\intop_{i(\mathfrak{a}_{L}^G)^*}\left\|\Delta_\xi^T(P,\lambda)\rho(P,\lambda,h)|_{\mathcal{A}^2_{\chi,\pi}(P)^{\tau,K_h}}\right\|_1 \,\mathrm{d} \lambda <\infty.\end{align*}$$
Working, as in [Reference Finis, Lapid and Müller21, Section 5.1], with the Laplacian on
![]() $G(F_\infty )$
, noting that h is compactly supported and using
$G(F_\infty )$
, noting that h is compactly supported and using
![]() $\|A\mid _V\|_1\le \dim (V)\|A\|_{\mathrm {op}}$
, we obtain the above integral is bounded by
$\|A\mid _V\|_1\le \dim (V)\|A\|_{\mathrm {op}}$
, we obtain the above integral is bounded by
 $$\begin{align*}\ll_{h,N} \dim\left(\mathcal{A}_{\chi,\pi}^2(P)^{\tau,K_h}\right)\intop_{i(\mathfrak{a}_{L}^G)^*}(1+\|\lambda\|+\nu(\pi_\infty)+\nu(\tau))^{-N}\left\|\Delta^T_{\xi}(P,\lambda)\mid_{\mathcal{A}^2_{\chi,\pi}(P)^{\tau,K_h}}\right\|_{\mathrm{op}}\,\mathrm{d}\lambda,\end{align*}$$
$$\begin{align*}\ll_{h,N} \dim\left(\mathcal{A}_{\chi,\pi}^2(P)^{\tau,K_h}\right)\intop_{i(\mathfrak{a}_{L}^G)^*}(1+\|\lambda\|+\nu(\pi_\infty)+\nu(\tau))^{-N}\left\|\Delta^T_{\xi}(P,\lambda)\mid_{\mathcal{A}^2_{\chi,\pi}(P)^{\tau,K_h}}\right\|_{\mathrm{op}}\,\mathrm{d}\lambda,\end{align*}$$
for any
![]() $N>0$
. Now we use (5.3) and work as in the proof of Proposition 5.5 to bound
$N>0$
. Now we use (5.3) and work as in the proof of Proposition 5.5 to bound
 $$\begin{align*}\left\|\Delta^T_{\xi}(P,\lambda)\mid_{\mathcal{A}^2_{\chi,\pi}(P)^{\tau,K_h}}\right\|_{\mathrm{op}}\ll_T \prod_{j} \left(1+\left\|\delta_{P_j|P_j^\prime}(i\vartheta_jt_j)|_{\mathcal{A}^2_\pi(P^{\prime}_j)^{\tau,K_h}}\right\|_{\mathrm{op}}\right), \end{align*}$$
$$\begin{align*}\left\|\Delta^T_{\xi}(P,\lambda)\mid_{\mathcal{A}^2_{\chi,\pi}(P)^{\tau,K_h}}\right\|_{\mathrm{op}}\ll_T \prod_{j} \left(1+\left\|\delta_{P_j|P_j^\prime}(i\vartheta_jt_j)|_{\mathcal{A}^2_\pi(P^{\prime}_j)^{\tau,K_h}}\right\|_{\mathrm{op}}\right), \end{align*}$$
where, following the notation in the proof of Proposition 5.5, above, we have written
![]() $\lambda =i\sum _jt_j\vartheta _j$
with
$\lambda =i\sum _jt_j\vartheta _j$
with
![]() $\vartheta _j\in (\mathfrak {a}_L^G)^*$
. Finally, from here on, proceeding as in [Reference Finis, Lapid and Müller21, Section 5.1], we conclude the proof.
$\vartheta _j\in (\mathfrak {a}_L^G)^*$
. Finally, from here on, proceeding as in [Reference Finis, Lapid and Müller21, Section 5.1], we conclude the proof.
We denote
![]() $\mathcal {A}^2_{\pi }(P):=\bigoplus _{\chi }\mathcal {A}^2_{\chi ,\pi }(P)$
and
$\mathcal {A}^2_{\pi }(P):=\bigoplus _{\chi }\mathcal {A}^2_{\chi ,\pi }(P)$
and
![]() $\mathcal {B}_\pi (P):=\bigcup _\chi \mathcal {B}_{\chi ,\pi }(P)$
, which is an orthonormal basis of
$\mathcal {B}_\pi (P):=\bigcup _\chi \mathcal {B}_{\chi ,\pi }(P)$
, which is an orthonormal basis of
![]() $\mathcal {A}^2_\pi (P)$
. On the other hand, the sum
$\mathcal {A}^2_\pi (P)$
. On the other hand, the sum
where
![]() $\chi $
runs over all equivalence classes of cuspidal data, is absolutely convergent (see [Reference Arthur6, pp.80]).
$\chi $
runs over all equivalence classes of cuspidal data, is absolutely convergent (see [Reference Arthur6, pp.80]).
Proposition 6.3. Let T be as in Proposition 6.1. Then
 $$ \begin{align*} &J^T(h)= \sum_{P\supset P_0} \frac{1}{n_P}\sum_{\pi \in \Pi_2(M_P)} \sum_{\varphi \in \mathcal{B}_{\pi}(P)}\intop_{i (\mathfrak{a}_P^G)^*} \langle \Lambda^T \mathrm{Eis}(\rho(P,\lambda,h)\varphi,\lambda),\Lambda^T \mathrm{Eis}(\varphi,\lambda) \rangle_{\mathcal{A}^2(G)} \,\mathrm{d} \lambda\\ &=\sum_{P\supset P_0} \frac{1}{n_P}\sum_{\pi \in \Pi_2(M_P)}\sum_{L\in\mathcal{L}(M_P)}\sum_{w\in W^L(M_P)}\iota_w \intop_{i(\mathfrak{a}_{L}^G)^*} \mathrm{tr} \left(\mathcal{M}^T_{L}(P,\lambda)M(P,w)\rho(P,\lambda,h)|_{\mathcal{A}^2_{\pi}(P)}\right) \,\mathrm{d} \lambda, \end{align*} $$
$$ \begin{align*} &J^T(h)= \sum_{P\supset P_0} \frac{1}{n_P}\sum_{\pi \in \Pi_2(M_P)} \sum_{\varphi \in \mathcal{B}_{\pi}(P)}\intop_{i (\mathfrak{a}_P^G)^*} \langle \Lambda^T \mathrm{Eis}(\rho(P,\lambda,h)\varphi,\lambda),\Lambda^T \mathrm{Eis}(\varphi,\lambda) \rangle_{\mathcal{A}^2(G)} \,\mathrm{d} \lambda\\ &=\sum_{P\supset P_0} \frac{1}{n_P}\sum_{\pi \in \Pi_2(M_P)}\sum_{L\in\mathcal{L}(M_P)}\sum_{w\in W^L(M_P)}\iota_w \intop_{i(\mathfrak{a}_{L}^G)^*} \mathrm{tr} \left(\mathcal{M}^T_{L}(P,\lambda)M(P,w)\rho(P,\lambda,h)|_{\mathcal{A}^2_{\pi}(P)}\right) \,\mathrm{d} \lambda, \end{align*} $$
where
![]() $\iota _w$
and
$\iota _w$
and
![]() $M(P,w)$
are as in Proposition 6.2.
$M(P,w)$
are as in Proposition 6.2.
7 Bounds for a specific maximal compact
In this section, we prove Theorem 3. First, we develop some necessary local ingredients that go in the proof.
7.1 Choice of test function
We freely use the notations of Section 4.2. Recall that
![]() $\mathfrak {a}_\infty $
is the Lie algebra of a maximal
$\mathfrak {a}_\infty $
is the Lie algebra of a maximal
![]() $\mathbb {R}$
-split torus of
$\mathbb {R}$
-split torus of
![]() $G(F_\infty )$
. Let
$G(F_\infty )$
. Let
![]() $\delta>0$
be a sufficiently small constant. We choose a fixed
$\delta>0$
be a sufficiently small constant. We choose a fixed
![]() $L^1$
-normalized nonnegative test function
$L^1$
-normalized nonnegative test function
![]() $f_{0,\delta }$
on
$f_{0,\delta }$
on
![]() $\mathfrak {a}_\infty $
supported on the ball of radius
$\mathfrak {a}_\infty $
supported on the ball of radius
![]() $\delta /2$
around
$\delta /2$
around
![]() $0$
. Let
$0$
. Let
![]() $f_{\delta }:=f_{0,\delta }*f_{0,\delta }^*$
, where for any
$f_{\delta }:=f_{0,\delta }*f_{0,\delta }^*$
, where for any
![]() $f\in C_c(\mathfrak {a}_\infty )$
, we define
$f\in C_c(\mathfrak {a}_\infty )$
, we define
![]() $f^*(\alpha ) := \overline {f(-\alpha )}$
. It holds that
$f^*(\alpha ) := \overline {f(-\alpha )}$
. It holds that
![]() $\widehat {f^*}(\mu ) = \overline {\hat {f}(-\overline {\mu })}$
. Thus,
$\widehat {f^*}(\mu ) = \overline {\hat {f}(-\overline {\mu })}$
. Thus,
![]() $\widehat {f_{\delta }}$
is nonnegative on
$\widehat {f_{\delta }}$
is nonnegative on
![]() $i\mathfrak {a}_\infty ^*$
. Note that
$i\mathfrak {a}_\infty ^*$
. Note that
![]() $f_{\delta }$
is also nonnegative,
$f_{\delta }$
is also nonnegative,
![]() $L^1$
-normalized and supported on the ball of radius
$L^1$
-normalized and supported on the ball of radius
![]() $\delta $
around
$\delta $
around
![]() $0$
.
$0$
.
We fix
Now, we make
![]() $\delta>0$
small enough so that
$\delta>0$
small enough so that
This follows from continuity and the fact that
![]() $\widehat {f_\delta }(0)=1$
.
$\widehat {f_\delta }(0)=1$
.
Given
![]() $\mu _0 \in i\mathfrak {a}_\infty ^*$
, we define
$\mu _0 \in i\mathfrak {a}_\infty ^*$
, we define
![]() $f_{\mu _0} \in C_c^\infty (\mathfrak {a}_\infty )^{W_\infty }$
by
$f_{\mu _0} \in C_c^\infty (\mathfrak {a}_\infty )^{W_\infty }$
by
so that
Finally, we define
Thus, the spherical transform of
![]() $h_{\mu _0}$
is
$h_{\mu _0}$
is
(see Section 4.4). Then
![]() $h_{\mu _0}$
satisfies the following properties:
$h_{\mu _0}$
satisfies the following properties:
-
1. The support of
 $h_{\mu _0}$
is bounded independently of
$h_{\mu _0}$
is bounded independently of
 $\mu _0$
, which follows from (4.1).
$\mu _0$
, which follows from (4.1). -
2.
 $\tilde {h}_{\mu _0}(\mu ) \ge 0$
, if
$\tilde {h}_{\mu _0}(\mu ) \ge 0$
, if
 $\mu = -w\overline {\mu }$
for some
$\mu = -w\overline {\mu }$
for some
 $w\in W_\infty $
; in particular, if
$w\in W_\infty $
; in particular, if
 $\mu \in i\mathfrak {a}_\infty ^*$
, or more generally, if
$\mu \in i\mathfrak {a}_\infty ^*$
, or more generally, if
 $\mu $
is the Langlands parameter of a unitary representation. This is immediate from
$\mu $
is the Langlands parameter of a unitary representation. This is immediate from
 $W_\infty $
-invariance of
$W_\infty $
-invariance of
 $\widehat {f_{\mu _0}}$
.
$\widehat {f_{\mu _0}}$
. -
3. There is a constant b depending only on the support of
 $f_\delta $
, such that for every
$f_\delta $
, such that for every
 $N>0$
, it holds that which follows from (4.2).
$N>0$
, it holds that which follows from (4.2). $$\begin{align*}|\tilde{h}_{\mu_0}(\mu)| \ll_{N} \sum_{w \in W_\infty}\exp(b\|\Re(\mu)\|)(1+\|w\mu-\mu_0\|)^{-N}, \end{align*}$$
$$\begin{align*}|\tilde{h}_{\mu_0}(\mu)| \ll_{N} \sum_{w \in W_\infty}\exp(b\|\Re(\mu)\|)(1+\|w\mu-\mu_0\|)^{-N}, \end{align*}$$
-
4. For
 $C_0$
as in (7.1), we have that if
$C_0$
as in (7.1), we have that if
 $\|\mu -\mu _0\| \le C_0$
, then
$\|\mu -\mu _0\| \le C_0$
, then
 $|\tilde {h}_{\mu _0}(\mu )| \ge 1/10$
, perhaps after making
$|\tilde {h}_{\mu _0}(\mu )| \ge 1/10$
, perhaps after making
 $\delta>0$
smaller.
$\delta>0$
smaller.
To see the last claim, it suffices to show that
Working similarly to the proof of [Reference Finis, Lapid and Müller21, Lemma 3.2], below, we prove the above sufficient formulation. We see that
 $$ \begin{align*} \widehat{f_\delta}(\mu) &=\intop_{\mathfrak{a}_\infty}f_\delta(\alpha)\left(e^{i\langle\Im(\mu),\alpha\rangle}-e^{i\langle\Im(\mu),\alpha\rangle}+e^{\langle\mu,\alpha\rangle}\right)\,\mathrm{d}\alpha\\ &=\widehat{f_\delta}\left(i\Im(\mu)\right) + \intop_{\mathfrak{a}_\infty}f_\delta(\alpha)e^{i\langle\Im(\mu),\alpha\rangle}\left(e^{\langle\Re(\mu),\alpha\rangle}-1\right)\,\mathrm{d}\alpha. \end{align*} $$
$$ \begin{align*} \widehat{f_\delta}(\mu) &=\intop_{\mathfrak{a}_\infty}f_\delta(\alpha)\left(e^{i\langle\Im(\mu),\alpha\rangle}-e^{i\langle\Im(\mu),\alpha\rangle}+e^{\langle\mu,\alpha\rangle}\right)\,\mathrm{d}\alpha\\ &=\widehat{f_\delta}\left(i\Im(\mu)\right) + \intop_{\mathfrak{a}_\infty}f_\delta(\alpha)e^{i\langle\Im(\mu),\alpha\rangle}\left(e^{\langle\Re(\mu),\alpha\rangle}-1\right)\,\mathrm{d}\alpha. \end{align*} $$
As
![]() $\|\Re (\mu )\|\le C_0$
, we have
$\|\Re (\mu )\|\le C_0$
, we have
![]() $|e^{\langle \Re (\mu ),\alpha \rangle }-1|<C_1\delta $
for
$|e^{\langle \Re (\mu ),\alpha \rangle }-1|<C_1\delta $
for
![]() $\alpha $
lying in a
$\alpha $
lying in a
![]() $\delta $
-radius ball around the origin and for certain
$\delta $
-radius ball around the origin and for certain
![]() $C_1$
depending on
$C_1$
depending on
![]() $C_0$
. Consequently, we have
$C_0$
. Consequently, we have
as
![]() $\widehat {f_\delta }\left (i\Im (\mu )\right )\ge 0$
. Thus, upon applying (7.2), and the fact that
$\widehat {f_\delta }\left (i\Im (\mu )\right )\ge 0$
. Thus, upon applying (7.2), and the fact that
we obtain
for some
![]() $C_2$
depending on
$C_2$
depending on
![]() $C_0$
and the group. We conclude by making
$C_0$
and the group. We conclude by making
![]() $\delta $
sufficiently small.
$\delta $
sufficiently small.
7.2 Langlands parameters
Let
![]() $\chi :=(M_1,\pi _1)$
be a cuspidal datum, determined by a Levi subgroup
$\chi :=(M_1,\pi _1)$
be a cuspidal datum, determined by a Levi subgroup
![]() $M_1$
and a representation
$M_1$
and a representation
![]() $\pi _1 \in \Pi _2(M_1)$
. Let
$\pi _1 \in \Pi _2(M_1)$
. Let
![]() $P_1 \supset P_0$
be such that
$P_1 \supset P_0$
be such that
![]() $M_1 = M_{P_1}$
. We assume that
$M_1 = M_{P_1}$
. We assume that
![]() $\pi _{1,\infty }$
is spherical, that is, has a nonzero
$\pi _{1,\infty }$
is spherical, that is, has a nonzero
![]() $K_\infty \cap M_1(F_\infty )$
-invariant vector, so we may associate to it a Langlands parameter
$K_\infty \cap M_1(F_\infty )$
-invariant vector, so we may associate to it a Langlands parameter
![]() $\mu _{\pi _1}$
.
$\mu _{\pi _1}$
.
We first notice that
![]() $\chi $
is actually an equivalence class, whose size by [Reference Arthur6, Section 12], is at most
$\chi $
is actually an equivalence class, whose size by [Reference Arthur6, Section 12], is at most
We let
![]() $(M_1,\pi _1),...,(M_k,\pi _k)$
be the elements in this equivalence class, with
$(M_1,\pi _1),...,(M_k,\pi _k)$
be the elements in this equivalence class, with
![]() $k\le n_{P_1} \le n_{P_0}$
, and
$k\le n_{P_1} \le n_{P_0}$
, and
![]() $M_i = M_{P_i}$
for
$M_i = M_{P_i}$
for
![]() $P_i \supset P_0$
, all associated with
$P_i \supset P_0$
, all associated with
![]() $P_1$
. Notice that the Langlands parameter
$P_1$
. Notice that the Langlands parameter
![]() $\mu _{\pi _i}$
is in the
$\mu _{\pi _i}$
is in the
![]() $W_\infty $
-orbit of
$W_\infty $
-orbit of
![]() $\mu _{\pi _1}$
, so
$\mu _{\pi _1}$
, so
![]() $\|\mu _{\pi _i}\|=\|\mu _{\pi _1}\|$
.
$\|\mu _{\pi _i}\|=\|\mu _{\pi _1}\|$
.
Now, let
![]() $P\supset P_0$
and
$P\supset P_0$
and
![]() $\pi \in \Pi _2(M_P)$
so that
$\pi \in \Pi _2(M_P)$
so that
![]() $\mathcal {A}_{\chi ,\pi }^2(P)^{K_\infty K}\neq \{0\}$
. It follows from the Langlands construction of the residual spectrum that
$\mathcal {A}_{\chi ,\pi }^2(P)^{K_\infty K}\neq \{0\}$
. It follows from the Langlands construction of the residual spectrum that
![]() $\pi $
is defined using iterated residues from an Eisenstein series of one of the
$\pi $
is defined using iterated residues from an Eisenstein series of one of the
![]() $\pi _i$
,
$\pi _i$
,
![]() $1\le i\le k$
, for some
$1\le i\le k$
, for some
![]() $P_i \sim P$
. Let
$P_i \sim P$
. Let
![]() $\rho _\pi \in (\mathfrak {a}_{M_i}^M)^* \subset (\mathfrak {a}_{M_0}^G)^* \subset (\mathfrak {a}_\infty )^*$
be the point where the residual representation is defined by iterated residues (see, e.g. [Reference Arthur5, Section 2]). Then
$\rho _\pi \in (\mathfrak {a}_{M_i}^M)^* \subset (\mathfrak {a}_{M_0}^G)^* \subset (\mathfrak {a}_\infty )^*$
be the point where the residual representation is defined by iterated residues (see, e.g. [Reference Arthur5, Section 2]). Then
![]() $\mu _\pi = \mu _{\pi _i}+\rho _\pi $
. The crucial point here is that
$\mu _\pi = \mu _{\pi _i}+\rho _\pi $
. The crucial point here is that
![]() $\rho _\pi $
is real and universally bounded (in fact,
$\rho _\pi $
is real and universally bounded (in fact,
![]() $\|\rho _\pi \|\le \|\rho _\infty \|$
, where
$\|\rho _\pi \|\le \|\rho _\infty \|$
, where
![]() $\rho _\infty $
is as in Section 4.2). Therefore,
$\rho _\infty $
is as in Section 4.2). Therefore,
![]() $\|\mu _{\pi }-\mu _{\pi _i}\|\le \|\rho _\infty \|$
and
$\|\mu _{\pi }-\mu _{\pi _i}\|\le \|\rho _\infty \|$
and
The above properties of
![]() $\rho _\pi $
follow from Langlands’ construction of the residual spectrum (see e.g. [Reference Müller47, pp.1152, Proof of Lemma 4.3]).
$\rho _\pi $
follow from Langlands’ construction of the residual spectrum (see e.g. [Reference Müller47, pp.1152, Proof of Lemma 4.3]).
Next, the Langlands parameter of
![]() $\mathrm {Ind}_{P(F_\infty )}^{G(F_\infty )}\left (\pi _\infty \otimes e^{\langle \lambda , H_{M_P}(\cdot ) \rangle }\right )$
for
$\mathrm {Ind}_{P(F_\infty )}^{G(F_\infty )}\left (\pi _\infty \otimes e^{\langle \lambda , H_{M_P}(\cdot ) \rangle }\right )$
for
![]() $\lambda \in (\mathfrak {a}_{P,\mathbb {C}}^G)^*$
is
$\lambda \in (\mathfrak {a}_{P,\mathbb {C}}^G)^*$
is
![]() $\mu _{\pi ,\lambda }:=\mu _\pi +\lambda $
.Footnote
10
If
$\mu _{\pi ,\lambda }:=\mu _\pi +\lambda $
.Footnote
10
If
![]() $\lambda \in i(\mathfrak {a}_P^G)^*$
, then this induction is unitary. Correspondingly, it holds that
$\lambda \in i(\mathfrak {a}_P^G)^*$
, then this induction is unitary. Correspondingly, it holds that
-
•
 $\|\Re (\mu _{\pi ,\lambda })\|\le \|\rho _{\infty }\|$
, and
$\|\Re (\mu _{\pi ,\lambda })\|\le \|\rho _{\infty }\|$
, and -
• there is a
 $w\in W_\infty $
so that
$w\in W_\infty $
so that
 $-\overline {\mu _{\pi ,\lambda }}=w\mu _{\pi ,\lambda }$
(as a matter of fact, we may choose
$-\overline {\mu _{\pi ,\lambda }}=w\mu _{\pi ,\lambda }$
(as a matter of fact, we may choose
 $w \in N_{M_P(F_\infty )}(T_\infty )/T_\infty \subset W_\infty $
)
$w \in N_{M_P(F_\infty )}(T_\infty )/T_\infty \subset W_\infty $
)
(see, e.g. [Reference Duistermaat, Kolk and Varadarajan15, Proposition 3.4].
We now prove Theorem 3.
Proof of Theorem 3.
We use property (3) in Section 3.4 to assume that T in Theorem 3 is such that
![]() $d(T)$
is sufficiently large (in terms of G and F) but fixed.
$d(T)$
is sufficiently large (in terms of G and F) but fixed.
We assume that the cuspidal datum
![]() $\chi :=(M,\pi _0)$
with the equivalence class
$\chi :=(M,\pi _0)$
with the equivalence class
![]() $(M_1,\pi _1),\dots ,(M_k,\pi _k)$
as above. Recall that
$(M_1,\pi _1),\dots ,(M_k,\pi _k)$
as above. Recall that
![]() $\|\mu _{\pi _0}\|\asymp \|\mu _{\pi _i}\|$
.
$\|\mu _{\pi _0}\|\asymp \|\mu _{\pi _i}\|$
.
Let
![]() $i\mathfrak {a}_\infty \ni \mu _j := i \Im (\mu _{\pi _j})+\lambda _0$
for
$i\mathfrak {a}_\infty \ni \mu _j := i \Im (\mu _{\pi _j})+\lambda _0$
for
![]() $j=1,\dots ,k$
. We construct
$j=1,\dots ,k$
. We construct
![]() $h_{\mu _j}$
as in Section 7.1, with the choice of
$h_{\mu _j}$
as in Section 7.1, with the choice of
![]() $C_0$
given in (7.1). Now let
$C_0$
given in (7.1). Now let
![]() $h_j \in C_c^\infty (G(\mathbb {A})^1)$
be of the form
$h_j \in C_c^\infty (G(\mathbb {A})^1)$
be of the form
Note that Item 1 implies that support of
![]() $h_j$
has bounded measure.
$h_j$
has bounded measure.
Clearly, for any
![]() $P\supset P_0$
and
$P\supset P_0$
and
![]() $\lambda \in i(\mathfrak {a}_{P}^G)^*$
, the operator
$\lambda \in i(\mathfrak {a}_{P}^G)^*$
, the operator
![]() $\rho (P,\lambda ,h_j)$
projects on
$\rho (P,\lambda ,h_j)$
projects on
![]() $\mathcal {A}^2(P)^{K_\infty K}$
. Moreover, for any
$\mathcal {A}^2(P)^{K_\infty K}$
. Moreover, for any
![]() $\pi \in \Pi _2(M_P)$
and
$\pi \in \Pi _2(M_P)$
and
![]() $\varphi \in \mathcal {A}^2_{\chi ,\pi }(P)^{K_\infty K}$
, we have
$\varphi \in \mathcal {A}^2_{\chi ,\pi }(P)^{K_\infty K}$
, we have
Recall from the discussion about the Langlands parameters above that there exists
![]() $w\in W_\infty $
so that
$w\in W_\infty $
so that
![]() $w\mu _{\pi ,\lambda }=-\overline {\mu _{\pi ,\lambda }}$
. Thus, using Item 2, we obtain that
$w\mu _{\pi ,\lambda }=-\overline {\mu _{\pi ,\lambda }}$
. Thus, using Item 2, we obtain that
On the other hand, if
![]() $\|\lambda -\lambda _0\|\le 1$
, and
$\|\lambda -\lambda _0\|\le 1$
, and
![]() $P\supset P_0$
and
$P\supset P_0$
and
![]() $\pi \in \Pi _2(M_P)$
are such that
$\pi \in \Pi _2(M_P)$
are such that
![]() $\mathcal {A}_{\chi ,\pi }^2(P)\neq \{0\}$
, then by the discussion above, there is
$\mathcal {A}_{\chi ,\pi }^2(P)\neq \{0\}$
, then by the discussion above, there is
![]() $1\le j\le k$
, such that
$1\le j\le k$
, such that
Hence, applying Item 4 it holds that
Now, we fix
![]() $T\in \mathfrak {a}_{M_0}^G$
with sufficiently large
$T\in \mathfrak {a}_{M_0}^G$
with sufficiently large
![]() $d(T)$
and apply Proposition 6.1 to write
$d(T)$
and apply Proposition 6.1 to write
 $$\begin{align*}J_\chi^T(h_j) = \sum_{P\supset P_0}\frac{1}{n_P}\sum_{\pi\in\Pi_2(M_P)}\sum_{\varphi\in\mathcal{B}_{\chi,\pi}(P)^{K_\infty K}}\intop_{i(\mathfrak{a}_P^G)^*}\tilde{h}_{\mu_j}(\mu_{\pi,\lambda})\|\Lambda^T\mathrm{Eis}(\varphi,\lambda)\|^2_2\,\mathrm{d}\lambda.\end{align*}$$
$$\begin{align*}J_\chi^T(h_j) = \sum_{P\supset P_0}\frac{1}{n_P}\sum_{\pi\in\Pi_2(M_P)}\sum_{\varphi\in\mathcal{B}_{\chi,\pi}(P)^{K_\infty K}}\intop_{i(\mathfrak{a}_P^G)^*}\tilde{h}_{\mu_j}(\mu_{\pi,\lambda})\|\Lambda^T\mathrm{Eis}(\varphi,\lambda)\|^2_2\,\mathrm{d}\lambda.\end{align*}$$
Here,
![]() $\mathcal {B}_{\chi ,\pi }(P)^{K_\infty K}$
is an orthonormal basis of
$\mathcal {B}_{\chi ,\pi }(P)^{K_\infty K}$
is an orthonormal basis of
![]() $\mathcal {A}_{\chi ,\pi }^2(P)^{K_\infty K}$
. Using the above properties of
$\mathcal {A}_{\chi ,\pi }^2(P)^{K_\infty K}$
. Using the above properties of
![]() $\tilde {h}_{\mu _j}$
, we obtain that
$\tilde {h}_{\mu _j}$
, we obtain that
 $$\begin{align*}\sum_j J_\chi^T(h_j)\gg \sum_{P\supset P_0}\sum_{\pi\in\Pi_2(M_P)}\sum_{\varphi\in\mathcal{B}_{\chi,\pi}(P)^{K_\infty K}}\intop_{\substack{{\lambda\in i(\mathfrak{a}_P^G)^*} \\ \|\lambda-\lambda_0\|\le 1}}\|\Lambda^T\mathrm{Eis}(\varphi,\lambda)\|^2_2\,\mathrm{d}\lambda.\end{align*}$$
$$\begin{align*}\sum_j J_\chi^T(h_j)\gg \sum_{P\supset P_0}\sum_{\pi\in\Pi_2(M_P)}\sum_{\varphi\in\mathcal{B}_{\chi,\pi}(P)^{K_\infty K}}\intop_{\substack{{\lambda\in i(\mathfrak{a}_P^G)^*} \\ \|\lambda-\lambda_0\|\le 1}}\|\Lambda^T\mathrm{Eis}(\varphi,\lambda)\|^2_2\,\mathrm{d}\lambda.\end{align*}$$
Note that the right-hand side above equals to the left-hand side of the estimate in Theorem 3.
Hence, it remains to bound
![]() $J_\chi ^T(h_j)$
for
$J_\chi ^T(h_j)$
for
![]() $j=1,\dots ,k$
. As the proof is the same for all j without loss of generality, we will bound for
$j=1,\dots ,k$
. As the proof is the same for all j without loss of generality, we will bound for
![]() $j=1$
and write
$j=1$
and write
![]() $h=h_1$
.
$h=h_1$
.
Using Proposition 6.2, we see that
 $$\begin{align*}J_\chi^T(h)\ll \sum_{P\supset P_0}\max_{L\in\mathcal{L}(M_P)}\max_{w\in W^L(M_P)}\sum_{\pi\in\Pi_2(M_P)}\intop_{i(\mathfrak{a}_{L}^G)^*} \mathrm{tr}\left(\mathcal{M}_{L}^T(P,\lambda)M(P,w) \rho(P,\lambda,h)|_{\mathcal{A}_{\chi,\pi}^2(P)}\right)\,\mathrm{d}\lambda. \end{align*}$$
$$\begin{align*}J_\chi^T(h)\ll \sum_{P\supset P_0}\max_{L\in\mathcal{L}(M_P)}\max_{w\in W^L(M_P)}\sum_{\pi\in\Pi_2(M_P)}\intop_{i(\mathfrak{a}_{L}^G)^*} \mathrm{tr}\left(\mathcal{M}_{L}^T(P,\lambda)M(P,w) \rho(P,\lambda,h)|_{\mathcal{A}_{\chi,\pi}^2(P)}\right)\,\mathrm{d}\lambda. \end{align*}$$
Recall that
![]() $\rho (P,\lambda ,h)\mid _{\mathcal {A}_{\chi ,\pi }^2(P)}$
projects on
$\rho (P,\lambda ,h)\mid _{\mathcal {A}_{\chi ,\pi }^2(P)}$
projects on
![]() $\mathcal {A}_{\chi ,\pi }^2(P)^{K_\infty K}$
and acts there by the scalar
$\mathcal {A}_{\chi ,\pi }^2(P)^{K_\infty K}$
and acts there by the scalar
![]() $\tilde {h}_{\mu _1}(\mu _\pi +\lambda )$
. Noting that
$\tilde {h}_{\mu _1}(\mu _\pi +\lambda )$
. Noting that
![]() $M(P,w)$
is unitary and commutes with
$M(P,w)$
is unitary and commutes with
![]() $\rho (P,\lambda ,h)$
, we get that the integral on the right-hand side above is bounded by
$\rho (P,\lambda ,h)$
, we get that the integral on the right-hand side above is bounded by
 $$\begin{align*}\dim\,\left(\mathcal{A}_{\chi,\pi}^2(P)^{K_\infty K}\right)\intop_{i(\mathfrak{a}_{L}^G)^*}\tilde{h}_{\mu_1}(\mu_\pi+\lambda) \left\|\mathcal{M}_{L}^T(P,\lambda)|_{\mathcal{A}_{\chi,\pi}^2(P)^{K_\infty K}}\right\|_{\mathrm{op}}\,\mathrm{d} \lambda. \end{align*}$$
$$\begin{align*}\dim\,\left(\mathcal{A}_{\chi,\pi}^2(P)^{K_\infty K}\right)\intop_{i(\mathfrak{a}_{L}^G)^*}\tilde{h}_{\mu_1}(\mu_\pi+\lambda) \left\|\mathcal{M}_{L}^T(P,\lambda)|_{\mathcal{A}_{\chi,\pi}^2(P)^{K_\infty K}}\right\|_{\mathrm{op}}\,\mathrm{d} \lambda. \end{align*}$$
Applying Item 3, we can bound the inner integral in the above display by
 $$ \begin{align} \ll_N\max_{w\in W_\infty}\intop_{i(\mathfrak{a}_L^G)^*}\left(1+\|w\lambda+wi\Im(\mu_\pi)-\lambda_0-i\Im(\mu_{\pi_1})\|\right)^{-N}\left\|\mathcal{M}_{L}^T(P,\lambda)|_{\mathcal{A}_{\chi,\pi}^2(P)^{K_\infty K}}\right\|_{\mathrm{op}} \,\mathrm{d} \lambda. \end{align} $$
$$ \begin{align} \ll_N\max_{w\in W_\infty}\intop_{i(\mathfrak{a}_L^G)^*}\left(1+\|w\lambda+wi\Im(\mu_\pi)-\lambda_0-i\Im(\mu_{\pi_1})\|\right)^{-N}\left\|\mathcal{M}_{L}^T(P,\lambda)|_{\mathcal{A}_{\chi,\pi}^2(P)^{K_\infty K}}\right\|_{\mathrm{op}} \,\mathrm{d} \lambda. \end{align} $$
For each
![]() $w\in W_\infty $
, we define
$w\in W_\infty $
, we define
Using (7.3), we obtain
Thus, for each w, we bound the integral on the right-hand side of (7.4) by
 $$ \begin{align} \intop_{i(\mathfrak{a}_L^G)^*}\left(1+\|\lambda-\lambda_1\|\right)^{-N}&\left\|\mathcal{M}_{L}^T(P,\lambda)|_{\mathcal{A}_{\chi,\pi}^2(P)^{K_\infty K}}\right\|_{\mathrm{op}} \,\mathrm{d} \lambda\nonumber\\ &\qquad\le\sum_{m=1}^\infty\frac{1}{m^N}\intop_{{\substack{{\lambda\in i(\mathfrak{a}_L^G)^*} \\ m-1\le\|\lambda-\lambda_1\|\le m}}}\left\|\mathcal{M}_{L}^T(P,\lambda)|_{\mathcal{A}_{\chi,\pi}^2(P)^{K_\infty K}}\right\|_{\mathrm{op}} \,\mathrm{d} \lambda. \end{align} $$
$$ \begin{align} \intop_{i(\mathfrak{a}_L^G)^*}\left(1+\|\lambda-\lambda_1\|\right)^{-N}&\left\|\mathcal{M}_{L}^T(P,\lambda)|_{\mathcal{A}_{\chi,\pi}^2(P)^{K_\infty K}}\right\|_{\mathrm{op}} \,\mathrm{d} \lambda\nonumber\\ &\qquad\le\sum_{m=1}^\infty\frac{1}{m^N}\intop_{{\substack{{\lambda\in i(\mathfrak{a}_L^G)^*} \\ m-1\le\|\lambda-\lambda_1\|\le m}}}\left\|\mathcal{M}_{L}^T(P,\lambda)|_{\mathcal{A}_{\chi,\pi}^2(P)^{K_\infty K}}\right\|_{\mathrm{op}} \,\mathrm{d} \lambda. \end{align} $$
We can find
![]() $\{\eta _l\}_{l=1}^{n}\subset i(\mathfrak {a}_L^G)^*$
with
$\{\eta _l\}_{l=1}^{n}\subset i(\mathfrak {a}_L^G)^*$
with
![]() $\|\eta _l\|\le m$
and
$\|\eta _l\|\le m$
and
![]() $n\ll m^{\dim \mathfrak {a}_L^G}$
, such that
$n\ll m^{\dim \mathfrak {a}_L^G}$
, such that
Thus, the integral on the right-hand side of (7.5) is bounded by
 $$\begin{align*}\sum_{l=1}^n\intop_{{\substack{{\lambda\in i(\mathfrak{a}_L^G)^*} \\ \|\lambda-\lambda_1-\eta_l\|\le 1}}}\left\|\mathcal{M}_{L}^T(P,\lambda)|_{\mathcal{A}_{\chi,\pi}^2(P)^{K_\infty K}}\right\|_{\mathrm{op}} \,\mathrm{d} \lambda.\end{align*}$$
$$\begin{align*}\sum_{l=1}^n\intop_{{\substack{{\lambda\in i(\mathfrak{a}_L^G)^*} \\ \|\lambda-\lambda_1-\eta_l\|\le 1}}}\left\|\mathcal{M}_{L}^T(P,\lambda)|_{\mathcal{A}_{\chi,\pi}^2(P)^{K_\infty K}}\right\|_{\mathrm{op}} \,\mathrm{d} \lambda.\end{align*}$$
We apply Proposition 5.5 to estimate the above integral and obtain that
 $$ \begin{align*} \intop_{i(\mathfrak{a}_{L}^G)^*}\tilde{h}_{\mu_1}(\mu_\pi+\lambda) &\left\|\mathcal{M}_{L}^T(P,\lambda)|_{\mathcal{A}_{\chi,\pi}^2(P)^{K_\infty K}}\right\|_{\mathrm{op}} \,\mathrm{d} \lambda\\ &\qquad\ll_{N}\max_{w\in W_\infty}\sum_{m=1}^\infty\frac{1}{m^N}\sum_{l=1}^n\left(\|T\|\,\log\left(1+\|\lambda_1+\eta_l\|+\nu(\pi_\infty)+\mathrm{level}(K)\right)\right)^{\dim\mathfrak{a}_L^G.} \end{align*} $$
$$ \begin{align*} \intop_{i(\mathfrak{a}_{L}^G)^*}\tilde{h}_{\mu_1}(\mu_\pi+\lambda) &\left\|\mathcal{M}_{L}^T(P,\lambda)|_{\mathcal{A}_{\chi,\pi}^2(P)^{K_\infty K}}\right\|_{\mathrm{op}} \,\mathrm{d} \lambda\\ &\qquad\ll_{N}\max_{w\in W_\infty}\sum_{m=1}^\infty\frac{1}{m^N}\sum_{l=1}^n\left(\|T\|\,\log\left(1+\|\lambda_1+\eta_l\|+\nu(\pi_\infty)+\mathrm{level}(K)\right)\right)^{\dim\mathfrak{a}_L^G.} \end{align*} $$
Using the bounds of
![]() $\lambda _1$
,
$\lambda _1$
,
![]() $\eta _l$
, and n, the right-hand side above is bounded by
$\eta _l$
, and n, the right-hand side above is bounded by
 $$ \begin{align*} \ll_{N}\sum_{m=1}^\infty\frac{1}{m^{N-\dim\mathfrak{a}_L^G}}&\left(\|T\|\,\log\left(1+m+\|\lambda_0\|+\nu(\pi_{1,\infty})+\mathrm{level}(K)\right)\right)^{\dim\mathfrak{a}_L^G}\\ &\ll\left(\|T\|\,\log\left(1+\|\lambda_0\|+\nu(\pi_{1,\infty})+\mathrm{level}(K)\right)\right)^{\dim\mathfrak{a}_L^G}, \end{align*} $$
$$ \begin{align*} \ll_{N}\sum_{m=1}^\infty\frac{1}{m^{N-\dim\mathfrak{a}_L^G}}&\left(\|T\|\,\log\left(1+m+\|\lambda_0\|+\nu(\pi_{1,\infty})+\mathrm{level}(K)\right)\right)^{\dim\mathfrak{a}_L^G}\\ &\ll\left(\|T\|\,\log\left(1+\|\lambda_0\|+\nu(\pi_{1,\infty})+\mathrm{level}(K)\right)\right)^{\dim\mathfrak{a}_L^G}, \end{align*} $$
by making N large enough. Thus, we obtain
 $$ \begin{align*} J_\chi^T(h) \ll \sum_{P\supset P_0}\max_{L\in\mathcal{L}(M_P)}\sum_{\pi\in\Pi_2(M_P)}\dim\ &\left(\mathcal{A}_{\chi,\pi}^2(P)^{K_\infty K}\right)\\ &\qquad\times\left(\|T\|\,\log\left(1+\|\lambda_0\|+\nu(\pi_{1,\infty})+\mathrm{level}(K)\right)\right)^{\dim\mathfrak{a}_L^G}. \end{align*} $$
$$ \begin{align*} J_\chi^T(h) \ll \sum_{P\supset P_0}\max_{L\in\mathcal{L}(M_P)}\sum_{\pi\in\Pi_2(M_P)}\dim\ &\left(\mathcal{A}_{\chi,\pi}^2(P)^{K_\infty K}\right)\\ &\qquad\times\left(\|T\|\,\log\left(1+\|\lambda_0\|+\nu(\pi_{1,\infty})+\mathrm{level}(K)\right)\right)^{\dim\mathfrak{a}_L^G}. \end{align*} $$
We conclude noting that
![]() $\max _{L\in \mathcal {L}(M_P)}\dim \mathfrak {a}_L^G=\dim \mathfrak {a}_M^G$
.
$\max _{L\in \mathcal {L}(M_P)}\dim \mathfrak {a}_L^G=\dim \mathfrak {a}_M^G$
.
We now prove Corollary 1.6 and Theorem 1.
Proof of Corollary 1.6.
By symmetries of the Eisenstein series, we may assume that
![]() $P\supset P_0$
. Let
$P\supset P_0$
. Let
![]() $\chi = (M,\pi _0)$
be as in the statement of the corollary. Then, by (7.3), it holds that
$\chi = (M,\pi _0)$
be as in the statement of the corollary. Then, by (7.3), it holds that
![]() $1+\nu (\pi _{\infty }) \asymp 1+ \nu (\pi _{0,\infty })$
and the claim follows from Theorem 3.
$1+\nu (\pi _{\infty }) \asymp 1+ \nu (\pi _{0,\infty })$
and the claim follows from Theorem 3.
Proof of Theorem 1.
We will prove the slightly stronger statement given in Remark 1.2.
The classification of the residual spectrum for
![]() $\mathrm {GL}_n$
due to Mœglin and Waldspurger [Reference Mœglin and Waldspurger45] (see Section 3.2) implies that for every
$\mathrm {GL}_n$
due to Mœglin and Waldspurger [Reference Mœglin and Waldspurger45] (see Section 3.2) implies that for every
![]() $\chi $
and
$\chi $
and
![]() $P\supset P_0$
it holds that
$P\supset P_0$
it holds that
The classification also implies that the multiplicity of
![]() $\pi $
in
$\pi $
in
![]() $L^2_{\mathrm {disc},\chi }(A_{M_P}M_P(F) \backslash M(\mathbb {A}))$
is at most
$L^2_{\mathrm {disc},\chi }(A_{M_P}M_P(F) \backslash M(\mathbb {A}))$
is at most
![]() $1$
. So the representation
$1$
. So the representation
![]() $\rho (P,0,\cdot )$
on
$\rho (P,0,\cdot )$
on
![]() $\mathcal {A}^2_{\chi ,\pi }(P)$
is isomorphic to
$\mathcal {A}^2_{\chi ,\pi }(P)$
is isomorphic to
![]() $\mathrm {Ind}_{P(\mathbb {A})}^{G(\mathbb {A})} \pi $
, and, in particular
$\mathrm {Ind}_{P(\mathbb {A})}^{G(\mathbb {A})} \pi $
, and, in particular
On the other hand, we may write
![]() $\pi = \otimes _v^\prime \pi _v$
and obtain
$\pi = \otimes _v^\prime \pi _v$
and obtain
where
![]() $K_\infty K = \prod _v K_v$
.
$K_\infty K = \prod _v K_v$
.
Now using uniform admissibility due to Bernstein [Reference Bernšteĭn10], which says that
we deduce that
 $$\begin{align*}F(\chi;\mathrm{triv},K) = \sum_{P\supset P_0}\sum_{\pi\in\Pi_2(M_P)}\dim \left(\mathcal{A}^2_{\chi,\pi}(P)^{K_\infty K}\right) \ll_{n,K} 1. \end{align*}$$
$$\begin{align*}F(\chi;\mathrm{triv},K) = \sum_{P\supset P_0}\sum_{\pi\in\Pi_2(M_P)}\dim \left(\mathcal{A}^2_{\chi,\pi}(P)^{K_\infty K}\right) \ll_{n,K} 1. \end{align*}$$
Let
![]() $\chi _0$
be a cuspidal datum and
$\chi _0$
be a cuspidal datum and
![]() $\pi _0\in \Pi _2(M_P)$
, such that
$\pi _0\in \Pi _2(M_P)$
, such that
![]() $\varphi _0\in \mathcal {A}^2_{\chi _0,\pi _0}(P)^{K_\infty K}$
. Then we have
$\varphi _0\in \mathcal {A}^2_{\chi _0,\pi _0}(P)^{K_\infty K}$
. Then we have
![]() $\nu (\varphi _0)\asymp \nu (\pi _{0,\infty })$
. Now the result follows from Corollary 1.6 along with Propositions 5.2 and 5.4.
$\nu (\varphi _0)\asymp \nu (\pi _{0,\infty })$
. Now the result follows from Corollary 1.6 along with Propositions 5.2 and 5.4.
8 Optimal lifting after Assing–Blomer
In this section, we prove Theorems 4 and 5. Aligning with our usual convention of suppressing the dependence on G in Vinogradov’s notations, we also suppress the dependence on n in this section.
We start with a discussion of the link between the adelic setting of the group
![]() $\mathrm {GL}_n$
and the classical setting of
$\mathrm {GL}_n$
and the classical setting of
![]() $\mathrm {SL}_n(\mathbb {R})$
. A good place to follow is [Reference Lapid and Müller39, Section 3].
$\mathrm {SL}_n(\mathbb {R})$
. A good place to follow is [Reference Lapid and Müller39, Section 3].
From now on, let
![]() $G:=\mathrm {GL}_n$
over
$G:=\mathrm {GL}_n$
over
![]() $\mathbb {Q}$
. We identify
$\mathbb {Q}$
. We identify
![]() $A_G$
as the positive scalar matrices in
$A_G$
as the positive scalar matrices in
![]() $G(\mathbb {R})$
. Note that
$G(\mathbb {R})$
. Note that
![]() $G(\mathbb {R})/A_G \cong \mathrm {SL}_n(\mathbb {R})\times \{\pm 1\}$
. We can therefore identify
$G(\mathbb {R})/A_G \cong \mathrm {SL}_n(\mathbb {R})\times \{\pm 1\}$
. We can therefore identify
 $$\begin{align*}G(\mathbb{A})^1 = (G(\mathbb{R})/A_G)\times \sideset{}{'}\prod_p G(\mathbb{Q}_p), \end{align*}$$
$$\begin{align*}G(\mathbb{A})^1 = (G(\mathbb{R})/A_G)\times \sideset{}{'}\prod_p G(\mathbb{Q}_p), \end{align*}$$
where
![]() $\prime $
denotes the restricted product relative to
$\prime $
denotes the restricted product relative to
![]() $G(\mathbb {Z}_p)$
.
$G(\mathbb {Z}_p)$
.
Given an integer
![]() $q>0$
with prime factorization
$q>0$
with prime factorization
![]() $q= \prod _{p<\infty } p^{r_p}$
with
$q= \prod _{p<\infty } p^{r_p}$
with
![]() $r_p\in \mathbb {Z}_{\ge 0}$
, let
$r_p\in \mathbb {Z}_{\ge 0}$
, let
![]() $K(q) \subset G(\mathbb {A}_f)$
be the principal congruence subgroup of level q. We have
$K(q) \subset G(\mathbb {A}_f)$
be the principal congruence subgroup of level q. We have
![]() $K(q) = \prod _{p<\infty } K_p(q)$
, where
$K(q) = \prod _{p<\infty } K_p(q)$
, where
The group
![]() $\mathrm {SL}_n(\mathbb {R})$
acts from the right on the space
$\mathrm {SL}_n(\mathbb {R})$
acts from the right on the space
![]() $G(\mathbb {Q})A_G\backslash G(\mathbb {A})/ K(q)$
. The space decomposes into
$G(\mathbb {Q})A_G\backslash G(\mathbb {A})/ K(q)$
. The space decomposes into
![]() $\varphi (q)$
(
$\varphi (q)$
(
![]() $\varphi $
being Euler’s totient function) connected components, determined by the determinant map into
$\varphi $
being Euler’s totient function) connected components, determined by the determinant map into
Each orbit is isomorphic to
![]() $\Gamma (q) \backslash \mathrm {SL}_n(\mathbb {R})$
, where
$\Gamma (q) \backslash \mathrm {SL}_n(\mathbb {R})$
, where
![]() $\Gamma (q)$
is the principal congruence subgroup of level q of
$\Gamma (q)$
is the principal congruence subgroup of level q of
![]() $\Gamma (1):= \mathrm {SL}_n(\mathbb {Z})$
.
$\Gamma (1):= \mathrm {SL}_n(\mathbb {Z})$
.
Let
![]() $K_\infty ^0 = \mathrm {SO}(n)$
, which is a maximal compact subgroup of
$K_\infty ^0 = \mathrm {SO}(n)$
, which is a maximal compact subgroup of
![]() $\mathrm {SL}_n(\mathbb {R})$
, and an index
$\mathrm {SL}_n(\mathbb {R})$
, and an index
![]() $2$
subgroup of the maximal compact subgroup
$2$
subgroup of the maximal compact subgroup
![]() $K_\infty := \mathrm {O}(n)$
of
$K_\infty := \mathrm {O}(n)$
of
![]() $G(\mathbb {R})$
. Let
$G(\mathbb {R})$
. Let
![]() $\|\cdot \|$
denote the Frobenius norm on
$\|\cdot \|$
denote the Frobenius norm on
![]() $\mathrm {SL}_n(\mathbb {R})$
, given by
$\mathrm {SL}_n(\mathbb {R})$
, given by
![]() $g\mapsto \sqrt {\mathrm {tr} (g^\top g)}$
. We note that the norm is both left and right
$g\mapsto \sqrt {\mathrm {tr} (g^\top g)}$
. We note that the norm is both left and right
![]() $K_\infty ^0$
-invariant. It holds that
$K_\infty ^0$
-invariant. It holds that
For
![]() $R>n$
, we define
$R>n$
, we define
Note that
see [Reference Duke, Rudnick and Sarnak16, Appendix 1], which also calculates the precise coefficient
![]() $c_n$
.
$c_n$
.
We now construct a test function in the Archimedean Hecke algebra following [Reference Assing and Blomer8, Section 2.7]. Let
![]() $h_0\colon \mathbb {R}_{\ge 0}\to [0,1]$
be a smooth nonnegative function with
$h_0\colon \mathbb {R}_{\ge 0}\to [0,1]$
be a smooth nonnegative function with
![]() $h_0(x)=1$
for
$h_0(x)=1$
for
![]() $x\in [0,n]$
and
$x\in [0,n]$
and
![]() $h_0(x)=0$
for
$h_0(x)=0$
for
![]() $x>2n$
. For
$x>2n$
. For
![]() $R>0$
, we define
$R>0$
, we define
 $$\begin{align*}h_R\in C_c^\infty(K_\infty^0 \backslash \mathrm{SL}_n(\mathbb{R}) /K_\infty^0),\quad g\mapsto \frac{1}{\|h_0(\frac{\| \cdot\|}{R})\|_{L^1}}h_0\left(\frac{\| g\|}{R}\right).\end{align*}$$
$$\begin{align*}h_R\in C_c^\infty(K_\infty^0 \backslash \mathrm{SL}_n(\mathbb{R}) /K_\infty^0),\quad g\mapsto \frac{1}{\|h_0(\frac{\| \cdot\|}{R})\|_{L^1}}h_0\left(\frac{\| g\|}{R}\right).\end{align*}$$
A direct consequence of [Reference Assing and Blomer8, (2.34)–(2.35)] is that the spherical transform of
![]() $h_R$
satisfies
$h_R$
satisfies
for
![]() $\mu \in \mathfrak {a}^*_{0,\mathbb {C}}$
, such that
$\mu \in \mathfrak {a}^*_{0,\mathbb {C}}$
, such that
![]() $w\mu =-\overline {\mu }$
for some
$w\mu =-\overline {\mu }$
for some
![]() $w\in W_\infty $
(and, in particular, for any
$w\in W_\infty $
(and, in particular, for any
![]() $\mu \in \mathfrak {a}^*_{0,\mathbb {C}}$
corresponding to the Langlands parameters of a unitary representation). Here,
$\mu \in \mathfrak {a}^*_{0,\mathbb {C}}$
corresponding to the Langlands parameters of a unitary representation). Here,
![]() $\|\mu \|_\infty $
denotes the
$\|\mu \|_\infty $
denotes the
![]() $\ell ^\infty $
-norm of
$\ell ^\infty $
-norm of
![]() $\mu $
when
$\mu $
when
![]() $\mathfrak {a}^*_{0,\mathbb {C}}$
is realized as a complex n-tuple.
$\mathfrak {a}^*_{0,\mathbb {C}}$
is realized as a complex n-tuple.
For the non-Archimedean part, we let
![]() $h_q\in C_c^\infty (G(\mathbb {A}_f))$
be the normalized characteristic function of
$h_q\in C_c^\infty (G(\mathbb {A}_f))$
be the normalized characteristic function of
![]() $K(q)$
, that is
$K(q)$
, that is
Let
![]() $h_{R,q,1} \in C_c^\infty (G(\mathbb {A})^1)$
be given by
$h_{R,q,1} \in C_c^\infty (G(\mathbb {A})^1)$
be given by
Finally, let
![]() $h_{R,q} = h_{R,q,1}*h_{R,q,1}^{*}$
, where
$h_{R,q} = h_{R,q,1}*h_{R,q,1}^{*}$
, where
![]() $h^*(g):=\overline {h(g^{-1})}$
. In other words, we have
$h^*(g):=\overline {h(g^{-1})}$
. In other words, we have
Clearly,
![]() $h_{R,q}\in C_c^\infty (G(\mathbb {A})^1)$
and is bi-
$h_{R,q}\in C_c^\infty (G(\mathbb {A})^1)$
and is bi-
![]() $K_\infty ^0K_f$
-finite.
$K_\infty ^0K_f$
-finite.
The following is the main technical result of this section and will be used to prove Theorems 4 and 5. First, we recall the definition of
![]() $J^T(h)$
from (6.1).
$J^T(h)$
from (6.1).
Proposition 8.1. For any q square-free and any
![]() $R>1$
, it holds that for every
$R>1$
, it holds that for every
![]() $\epsilon>0$
$\epsilon>0$
for any
![]() $T\in \mathfrak {a}_{M_0}$
.
$T\in \mathfrak {a}_{M_0}$
.
Remark 8.2. As will be evident from the proof, the summand q comes from the
![]() $\varphi (q)$
possible Dirichlet characters modulo q. The factor
$\varphi (q)$
possible Dirichlet characters modulo q. The factor
![]() $R^{-n(n-1)}q^{n^2}$
comes from the contribution of cusp forms. The number of such forms with bounded Laplacian eigenvalues is
$R^{-n(n-1)}q^{n^2}$
comes from the contribution of cusp forms. The number of such forms with bounded Laplacian eigenvalues is
![]() $\asymp [K(1):K(q)] \ll q^{n^2}$
, and the contribution of each such form to
$\asymp [K(1):K(q)] \ll q^{n^2}$
, and the contribution of each such form to
![]() $J^T(h_{R,q})$
assuming the (GRC) is
$J^T(h_{R,q})$
assuming the (GRC) is
![]() $R^{-n(n-1)}$
. The results of Assing and Blomer [Reference Assing and Blomer8, Theorem 1.1] on the density hypothesis allow us to prove the proposition unconditionally of the GRC. However, a significant difficulty arises to control the continuous spectrum, as also experienced in [Reference Assing and Blomer8], managing that is the main contribution of Proposition 8.1.
$R^{-n(n-1)}$
. The results of Assing and Blomer [Reference Assing and Blomer8, Theorem 1.1] on the density hypothesis allow us to prove the proposition unconditionally of the GRC. However, a significant difficulty arises to control the continuous spectrum, as also experienced in [Reference Assing and Blomer8], managing that is the main contribution of Proposition 8.1.
We will assume Proposition 8.1 for now and prove Theorems 4 and 5. In the next subsection, we prove Proposition 8.6 using Proposition 8.1 and then deduce these two theorems from it in the following two subsections. At the end of this section, we prove Proposition 8.1.
8.1 Initial reductions
Let us fix
![]() $R_0>n$
and a compact domain
$R_0>n$
and a compact domain
![]() $\Omega \subset G(\mathbb {Q})\backslash G(\mathbb {A})^1$
of the form
$\Omega \subset G(\mathbb {Q})\backslash G(\mathbb {A})^1$
of the form
![]() $\Omega := G(\mathbb {Q}) \backslash B_{R_0}\times K(1)$
. The implied constants in various estimates below are allowed to depend on
$\Omega := G(\mathbb {Q}) \backslash B_{R_0}\times K(1)$
. The implied constants in various estimates below are allowed to depend on
![]() $R_0$
, however, we will not mention it in the notations. We define the adelic kernel
$R_0$
, however, we will not mention it in the notations. We define the adelic kernel
![]() $K_{h_{R,q}}(x,y)$
by
$K_{h_{R,q}}(x,y)$
by
 $$\begin{align*}K_{h_{R,q}}(x,y) := \sum_{\gamma \in G(\mathbb{Q})} h_{R,q}(x^{-1}\gamma y), \end{align*}$$
$$\begin{align*}K_{h_{R,q}}(x,y) := \sum_{\gamma \in G(\mathbb{Q})} h_{R,q}(x^{-1}\gamma y), \end{align*}$$
for
![]() $x,y \in G(\mathbb {A})^1$
.
$x,y \in G(\mathbb {A})^1$
.
Proposition 8.3. There is a constant C (possibly depending on
![]() $R_0$
), such that if
$R_0$
), such that if
![]() $d(T) \ge C (1+\log (R))$
, then it holds that
$d(T) \ge C (1+\log (R))$
, then it holds that
 $$\begin{align*}\intop_\Omega K_{h_{R,q}}(x,x) \,\mathrm{d} x \le J^T(h_{R,q}), \end{align*}$$
$$\begin{align*}\intop_\Omega K_{h_{R,q}}(x,x) \,\mathrm{d} x \le J^T(h_{R,q}), \end{align*}$$
for any R and q.
Proof. We start with the spectral decomposition of
![]() $K_{h_{R,q}}(x,x)$
(see, e.g. [Reference Arthur6, (7.6)]) which implies that
$K_{h_{R,q}}(x,x)$
(see, e.g. [Reference Arthur6, (7.6)]) which implies that
 $$ \begin{align*} &\intop_{\Omega} K_{h_{R,q}}(x,x) \,\mathrm{d} x \\ =& \sum_{P\supset P_0}\frac{1}{n_P} \sum_{\pi \in \Pi_2(M_P)} \sum_{\varphi \in \mathcal{B}_\pi(P)} \intop_{i (\mathfrak{a}_P^G)^*}\intop_\Omega \mathrm{Eis}(\rho(P,\lambda,h_{R,q})\varphi,\lambda)(x)\overline{\mathrm{Eis}(\varphi,\lambda)(x)} \,\mathrm{d} x \,\mathrm{d} \lambda. \end{align*} $$
$$ \begin{align*} &\intop_{\Omega} K_{h_{R,q}}(x,x) \,\mathrm{d} x \\ =& \sum_{P\supset P_0}\frac{1}{n_P} \sum_{\pi \in \Pi_2(M_P)} \sum_{\varphi \in \mathcal{B}_\pi(P)} \intop_{i (\mathfrak{a}_P^G)^*}\intop_\Omega \mathrm{Eis}(\rho(P,\lambda,h_{R,q})\varphi,\lambda)(x)\overline{\mathrm{Eis}(\varphi,\lambda)(x)} \,\mathrm{d} x \,\mathrm{d} \lambda. \end{align*} $$
Note that absolute convergence of the spectral side [Reference Finis, Lapid and Müller21] allows us to pull the
![]() $\Omega $
-integral inside. Here, we choose a basis
$\Omega $
-integral inside. Here, we choose a basis
![]() $\mathcal {B}_\pi (P)$
, such that each of its elements is either
$\mathcal {B}_\pi (P)$
, such that each of its elements is either
![]() $K_\infty ^0K(q)$
-invariant or orthogonal to the
$K_\infty ^0K(q)$
-invariant or orthogonal to the
![]() $K_\infty ^0K(q)$
-invariant subspace.
$K_\infty ^0K(q)$
-invariant subspace.
From the definition of
![]() $h_{R,q}$
, we note that the operator
$h_{R,q}$
, we note that the operator
![]() $\rho (P,\lambda ,h_{R,q})$
projects
$\rho (P,\lambda ,h_{R,q})$
projects
![]() $\mathcal {A}^2_\pi (P)$
onto
$\mathcal {A}^2_\pi (P)$
onto
![]() $\mathcal {A}^2_\pi (P)^{K_\infty ^0K(q)}$
, and acts on it by the scalar
$\mathcal {A}^2_\pi (P)^{K_\infty ^0K(q)}$
, and acts on it by the scalar
![]() $(\tilde {h}_R\cdot \tilde {h}^*_R)(\mu _\pi +\lambda )=|\tilde {h}_R(\mu _\pi +\lambda )|^2$
. Focusing on the innermost integral above and assuming that
$(\tilde {h}_R\cdot \tilde {h}^*_R)(\mu _\pi +\lambda )=|\tilde {h}_R(\mu _\pi +\lambda )|^2$
. Focusing on the innermost integral above and assuming that
![]() $\varphi $
is
$\varphi $
is
![]() $K_\infty ^0K(q)$
-invariant, we have
$K_\infty ^0K(q)$
-invariant, we have
 $$ \begin{align*} \intop_\Omega \mathrm{Eis}(\rho(P,\lambda,h_{R,q})\varphi,\lambda)(x)\overline{\mathrm{Eis}(\varphi,\lambda))(x)} \,\mathrm{d} x = |\tilde{h}_R(\mu_\pi+\lambda)|^2\intop_\Omega|\mathrm{Eis}(\varphi,\lambda)(x)|^2 \,\mathrm{d} x. \end{align*} $$
$$ \begin{align*} \intop_\Omega \mathrm{Eis}(\rho(P,\lambda,h_{R,q})\varphi,\lambda)(x)\overline{\mathrm{Eis}(\varphi,\lambda))(x)} \,\mathrm{d} x = |\tilde{h}_R(\mu_\pi+\lambda)|^2\intop_\Omega|\mathrm{Eis}(\varphi,\lambda)(x)|^2 \,\mathrm{d} x. \end{align*} $$
On the other hand, by property (2) of Section 3.4, we have
 $$ \begin{align*} \intop_\Omega |\mathrm{Eis}(\varphi,\lambda)(x)|^2 \,\mathrm{d} x \le \intop_{G(\mathbb{Q}) \backslash G(\mathbb{A})} |\Lambda^T\mathrm{Eis}(\varphi,\lambda)(x)|^2 \,\mathrm{d} x \end{align*} $$
$$ \begin{align*} \intop_\Omega |\mathrm{Eis}(\varphi,\lambda)(x)|^2 \,\mathrm{d} x \le \intop_{G(\mathbb{Q}) \backslash G(\mathbb{A})} |\Lambda^T\mathrm{Eis}(\varphi,\lambda)(x)|^2 \,\mathrm{d} x \end{align*} $$
for
![]() $d(T)$
sufficiently large. Plugging this into the above integral and reverse engineering the above manipulation with
$d(T)$
sufficiently large. Plugging this into the above integral and reverse engineering the above manipulation with
![]() $h_{R,q}$
, we deduce that
$h_{R,q}$
, we deduce that
 $$ \begin{align*} &\intop_{\Omega} K_{f}(x,x) \,\mathrm{d} x \\ \le& \sum_{P\supset P_0} \frac{1}{n_P} \sum_{\pi \in \Pi_2(M_P)} \sum_{\varphi \in \mathcal{B}_\pi(P)} \intop_{i (\mathfrak{a}_P^G)^*} \langle \Lambda^T\mathrm{Eis}(\rho(P,\lambda,h_{R,q})\varphi,\lambda), \Lambda^T\mathrm{Eis}(\varphi,\lambda) \rangle_{\mathcal{A}^2(G)} \,\mathrm{d} \lambda. \end{align*} $$
$$ \begin{align*} &\intop_{\Omega} K_{f}(x,x) \,\mathrm{d} x \\ \le& \sum_{P\supset P_0} \frac{1}{n_P} \sum_{\pi \in \Pi_2(M_P)} \sum_{\varphi \in \mathcal{B}_\pi(P)} \intop_{i (\mathfrak{a}_P^G)^*} \langle \Lambda^T\mathrm{Eis}(\rho(P,\lambda,h_{R,q})\varphi,\lambda), \Lambda^T\mathrm{Eis}(\varphi,\lambda) \rangle_{\mathcal{A}^2(G)} \,\mathrm{d} \lambda. \end{align*} $$
Now, the statement of the proposition follows from Proposition 6.3.
Corollary 8.4. Let q be square-free. There is an
![]() $x\in \Omega $
, such that
$x\in \Omega $
, such that
for every
![]() $\epsilon>0$
.
$\epsilon>0$
.
We move the discussion to the classical language. We let
![]() $K_{h_{R}*h_{R}^*}^q(x,y)$
be the classical automorphic kernel of
$K_{h_{R}*h_{R}^*}^q(x,y)$
be the classical automorphic kernel of
![]() $h_R*h_R^*$
, that is
$h_R*h_R^*$
, that is
 $$\begin{align*}K_{h_R*h_R^*}^q(x,y) = \sum_{\gamma \in \Gamma(q)} (h_R*h_R^*)(x^{-1}\gamma y), \end{align*}$$
$$\begin{align*}K_{h_R*h_R^*}^q(x,y) = \sum_{\gamma \in \Gamma(q)} (h_R*h_R^*)(x^{-1}\gamma y), \end{align*}$$
where
![]() $x,y \in \Gamma (q) \backslash \mathrm {SL}_n(\mathbb {R})$
.
$x,y \in \Gamma (q) \backslash \mathrm {SL}_n(\mathbb {R})$
.
Lemma 8.5. Let q be square-free, there is an
![]() $x\in \Gamma (q) \backslash B_{R_0} \subset \Gamma (q) \backslash \mathrm {SL}_n(\mathbb {R})$
, such that
$x\in \Gamma (q) \backslash B_{R_0} \subset \Gamma (q) \backslash \mathrm {SL}_n(\mathbb {R})$
, such that
for every
![]() $\epsilon>0$
.
$\epsilon>0$
.
Proof. This follows from the classical-adelic dictionary. Let
![]() $x_0 \in B_{R_0} \times K(1) \subset G(\mathbb {A})^1$
be a representative point from Corollary 8.4, and let
$x_0 \in B_{R_0} \times K(1) \subset G(\mathbb {A})^1$
be a representative point from Corollary 8.4, and let
![]() $x := x_{0,\infty } \in B_{R_0} \subset \mathrm {SL}_n(\mathbb {R})$
be its
$x := x_{0,\infty } \in B_{R_0} \subset \mathrm {SL}_n(\mathbb {R})$
be its
![]() $\infty $
-coordinate.
$\infty $
-coordinate.
We claim that
which implies the claim together with Corollary 8.4 and the fact that
![]() $\mathrm {vol}(K(q)) \ll _\epsilon q^{-n^2+\epsilon }$
.
$\mathrm {vol}(K(q)) \ll _\epsilon q^{-n^2+\epsilon }$
.
Indeed,
 $$ \begin{align*} K_{h_{R,q}}(x_0,x_0) = \sum_{\gamma \in G(\mathbb{Q})} h_{R,q}(x_0^{-1}\gamma x_0) = \sum_{\gamma \in G(\mathbb{Q})}(h_R*h_R)^*(x_{0,\infty}^{-1}\gamma x_{0,\infty})h_q(x_{0,f}^{-1}\gamma x_{0,f}). \end{align*} $$
$$ \begin{align*} K_{h_{R,q}}(x_0,x_0) = \sum_{\gamma \in G(\mathbb{Q})} h_{R,q}(x_0^{-1}\gamma x_0) = \sum_{\gamma \in G(\mathbb{Q})}(h_R*h_R)^*(x_{0,\infty}^{-1}\gamma x_{0,\infty})h_q(x_{0,f}^{-1}\gamma x_{0,f}). \end{align*} $$
An element
![]() $\gamma \in G(\mathbb {Q})$
that has nonzero contribution to the above sum must satisfy
$\gamma \in G(\mathbb {Q})$
that has nonzero contribution to the above sum must satisfy
![]() $x_{0,\infty }^{-1}\gamma x_{0,\infty } \in \mathrm {SL}_n(\mathbb {R})$
, so
$x_{0,\infty }^{-1}\gamma x_{0,\infty } \in \mathrm {SL}_n(\mathbb {R})$
, so
![]() $\gamma \in \mathrm {SL}_n(\mathbb {R})$
. Also, it must hold that
$\gamma \in \mathrm {SL}_n(\mathbb {R})$
. Also, it must hold that
![]() $x_{0,f}^{-1}\gamma x_{0,f} \in K(q)$
. In addition, since
$x_{0,f}^{-1}\gamma x_{0,f} \in K(q)$
. In addition, since
![]() $x_{0,f}\in K(1)$
and
$x_{0,f}\in K(1)$
and
![]() $K(q)$
is normal in
$K(q)$
is normal in
![]() $K(1)$
, it holds that
$K(1)$
, it holds that
![]() $\gamma \in K(q)$
. Therefore,
$\gamma \in K(q)$
. Therefore,
![]() $\gamma \in \Gamma (q) \subset \mathrm {SL}_n(\mathbb {Z})$
, and
$\gamma \in \Gamma (q) \subset \mathrm {SL}_n(\mathbb {Z})$
, and
![]() $h_q(x_{0,f}^{-1}\gamma x_{0,f})=\frac {1}{\mathrm {vol}(K(q))}$
. Therefore,
$h_q(x_{0,f}^{-1}\gamma x_{0,f})=\frac {1}{\mathrm {vol}(K(q))}$
. Therefore,
 $$\begin{align*}K_{h_{R,q}}(x_0,x_0) = \mathrm{vol}(K(q))^{-1}\sum_{\gamma \in \Gamma(q)}(h_R*h_R)^*(x^{-1}\gamma x) = \mathrm{vol}(K(q))^{-1} K_{h_R*h_R^*}^q(x,x), \end{align*}$$
$$\begin{align*}K_{h_{R,q}}(x_0,x_0) = \mathrm{vol}(K(q))^{-1}\sum_{\gamma \in \Gamma(q)}(h_R*h_R)^*(x^{-1}\gamma x) = \mathrm{vol}(K(q))^{-1} K_{h_R*h_R^*}^q(x,x), \end{align*}$$
and the proof is complete.
We now claim that we may replace
![]() $x \in B_{R_0}$
with
$x \in B_{R_0}$
with
![]() $x=e$
in Lemma 8.5.
$x=e$
in Lemma 8.5.
Proposition 8.6. Let q be square-free. It holds that
for every
![]() $\epsilon>0$
.
$\epsilon>0$
.
Proof. Let x be the point from Lemma 8.5. We choose for x a representative in
![]() $B_{R_0}$
. This implies that for
$B_{R_0}$
. This implies that for
![]() $C>0$
sufficiently large and for every
$C>0$
sufficiently large and for every
![]() $g\in \mathrm {SL}_n(\mathbb {R})$
, we have
$g\in \mathrm {SL}_n(\mathbb {R})$
, we have
From the definition of
![]() $h_{R}$
, the above implies that for
$h_{R}$
, the above implies that for
![]() $c>0$
sufficiently small (e.g.
$c>0$
sufficiently small (e.g.
![]() $c=C^{-1}/2$
) and every
$c=C^{-1}/2$
) and every
![]() $g\in \mathrm {SL}_n(\mathbb {R})$
$g\in \mathrm {SL}_n(\mathbb {R})$
and therefore, for every
![]() $\gamma \in \Gamma (q)$
,
$\gamma \in \Gamma (q)$
,
We deduce using Lemma 8.5 that
After changing R to
![]() $cR$
, the proposition follows.
$cR$
, the proposition follows.
8.2 Proof of Theorem 4
We adopt the notations developed for the classical spectral decomposition of
![]() $L^2(\Gamma (q) \backslash \mathrm {SL}_n(\mathbb {R}) / K_\infty ^0)$
in [Reference Assing and Blomer8, Section 2.5]. We write the spectral decomposition of the kernel of
$L^2(\Gamma (q) \backslash \mathrm {SL}_n(\mathbb {R}) / K_\infty ^0)$
in [Reference Assing and Blomer8, Section 2.5]. We write the spectral decomposition of the kernel of
![]() $h \in C_c^\infty (K_\infty ^0 \backslash \mathrm {SL}_n(\mathbb {R}) / K_\infty ^0)$
as
$h \in C_c^\infty (K_\infty ^0 \backslash \mathrm {SL}_n(\mathbb {R}) / K_\infty ^0)$
as
 $$ \begin{align} K_h^q(x,y) = \intop_{\Gamma(q)} \tilde{h}(\mu_\varpi) \varpi(x)\overline{\varpi(y)}\,\mathrm{d} \varpi, \end{align} $$
$$ \begin{align} K_h^q(x,y) = \intop_{\Gamma(q)} \tilde{h}(\mu_\varpi) \varpi(x)\overline{\varpi(y)}\,\mathrm{d} \varpi, \end{align} $$
where
![]() $\intop _{\Gamma (q)} V_\varpi \,\mathrm {d} \varpi $
is a spectral decomposition of
$\intop _{\Gamma (q)} V_\varpi \,\mathrm {d} \varpi $
is a spectral decomposition of
![]() $L^2(\Gamma (q) \backslash \mathrm {SL}_n(\mathbb {R}) / K_\infty ^0)$
, respecting the unramified Hecke algebra (see [Reference Assing and Blomer8, Section 2.5] for more details). This classical spectral decomposition may be deduced from the more precise adelic spectral decomposition (e.g. [Reference Arthur6, (7.6)]). The value
$L^2(\Gamma (q) \backslash \mathrm {SL}_n(\mathbb {R}) / K_\infty ^0)$
, respecting the unramified Hecke algebra (see [Reference Assing and Blomer8, Section 2.5] for more details). This classical spectral decomposition may be deduced from the more precise adelic spectral decomposition (e.g. [Reference Arthur6, (7.6)]). The value
![]() $\mu _\varpi $
is the Langlands parameter of the
$\mu _\varpi $
is the Langlands parameter of the
![]() $K_\infty ^0$
-invariant representation
$K_\infty ^0$
-invariant representation
![]() $V_\varpi $
.
$V_\varpi $
.
Lemma 8.7. We have
for any
![]() $h\in C_c^\infty (K_\infty ^0 \backslash \mathrm {SL}_n(\mathbb {R}) / K_\infty ^0)$
.
$h\in C_c^\infty (K_\infty ^0 \backslash \mathrm {SL}_n(\mathbb {R}) / K_\infty ^0)$
.
Proof. We have
 $$ \begin{align*} K_{h*h}^q(e,e) = \intop_{\Gamma(q)}\tilde{h}(\mu_\varpi)^2|\varpi(e)|^2\,\mathrm{d}\varpi \le \intop_{\Gamma(q)}|\tilde{h}(\mu_\varpi)|^2|\varpi(e)|^2\,\mathrm{d}\varpi = K_{h*h^*}^q(e,e), \end{align*} $$
$$ \begin{align*} K_{h*h}^q(e,e) = \intop_{\Gamma(q)}\tilde{h}(\mu_\varpi)^2|\varpi(e)|^2\,\mathrm{d}\varpi \le \intop_{\Gamma(q)}|\tilde{h}(\mu_\varpi)|^2|\varpi(e)|^2\,\mathrm{d}\varpi = K_{h*h^*}^q(e,e), \end{align*} $$
where the first and last equalities follow from the spectral decompositions of the corresponding kernels as in (8.3).
Proof of Theorem 4.
Let ![]() be the normalized characteristic function of the ball
be the normalized characteristic function of the ball
![]() $B_R$
. It holds for every
$B_R$
. It holds for every
![]() $g\in \mathrm {SL}_n(\mathbb {R})$
that
$g\in \mathrm {SL}_n(\mathbb {R})$
that
![]() $h_{R}^{(1)}(g)\ll h_{R}(g)$
, which, upon applying Lemma 8.7 and Proposition 8.6, implies that
$h_{R}^{(1)}(g)\ll h_{R}(g)$
, which, upon applying Lemma 8.7 and Proposition 8.6, implies that
Notice that the kernel
![]() $K_{h_{R}^{(1)}*h_{R}^{(1)}}^q(e,e)$
is well-defined even though
$K_{h_{R}^{(1)}*h_{R}^{(1)}}^q(e,e)$
is well-defined even though
![]() $h_{R}^{(1)}$
is not smooth. The same will be true for other functions below.
$h_{R}^{(1)}$
is not smooth. The same will be true for other functions below.
Next, we claim that for
![]() $c>0$
sufficiently small and R sufficiently large, it holds that for every
$c>0$
sufficiently small and R sufficiently large, it holds that for every
![]() $g\in \mathrm {SL}_n(\mathbb {R})$
$g\in \mathrm {SL}_n(\mathbb {R})$
To prove this claim, notice that
For
![]() $c>0$
small enough and R large enough, the above is
$c>0$
small enough and R large enough, the above is
![]() $\gg 1$
as long as
$\gg 1$
as long as
![]() $\|g\| \le c R^2$
. Indeed, we may assume that g is diagonal with positive values on the diagonal. Then
$\|g\| \le c R^2$
. Indeed, we may assume that g is diagonal with positive values on the diagonal. Then
![]() $B_R \cap gB_R^{-1}$
contains all the element of the form
$B_R \cap gB_R^{-1}$
contains all the element of the form
![]() $g^{1/2} x$
, for
$g^{1/2} x$
, for
![]() $\|x\| \le C$
(for
$\|x\| \le C$
(for
![]() $c>0$
sufficiently small relative to C). Therefore, for every
$c>0$
sufficiently small relative to C). Therefore, for every
![]() $g\in \mathrm {SL}_n(\mathbb {R})$
,
$g\in \mathrm {SL}_n(\mathbb {R})$
,
Using (8.1), we deduce that (8.5) holds. Thus, using (8.4), we obtain

Using (8.1) once again and changing R to
![]() $\sqrt {R}$
, we complete the proof.
$\sqrt {R}$
, we complete the proof.
8.3 Proof Theorem 5
To prove the theorem, we first prove a couple of lemmata. Fix
![]() $\eta>0$
. We consider the function
$\eta>0$
. We consider the function
![]() $m_R:=h_R*h_{R^\eta }$
.
$m_R:=h_R*h_{R^\eta }$
.
Lemma 8.8. There is a
![]() $\delta>0$
depending only on
$\delta>0$
depending only on
![]() $\eta $
, such that for every q square-free and
$\eta $
, such that for every q square-free and
![]() $R\ge q^{1+1/n}$
$R\ge q^{1+1/n}$
Proof. We apply the spectral decomposition as in (8.3) to obtain
 $$\begin{align*}K_{m_R*m_R^*}^q(e,e)= \intop_{\Gamma(q)} |\tilde{m}_R(\mu_\varpi)|^2 |\varpi(e)|^2 \,\mathrm{d} \varpi. \end{align*}$$
$$\begin{align*}K_{m_R*m_R^*}^q(e,e)= \intop_{\Gamma(q)} |\tilde{m}_R(\mu_\varpi)|^2 |\varpi(e)|^2 \,\mathrm{d} \varpi. \end{align*}$$
Among the automorphic forms
![]() $\varpi $
appearing in the spectral decomposition, we have the
$\varpi $
appearing in the spectral decomposition, we have the
![]() $L^2$
-normalized constant function
$L^2$
-normalized constant function
![]() $\varpi _{\mathrm {triv}}$
, for which it holds that
$\varpi _{\mathrm {triv}}$
, for which it holds that
Also, using the facts that
![]() $\tilde {m}_R(\lambda ) = \tilde {h}_R(\lambda ) \tilde {h}_{R^\eta }(\lambda )$
and
$\tilde {m}_R(\lambda ) = \tilde {h}_R(\lambda ) \tilde {h}_{R^\eta }(\lambda )$
and
![]() $\tilde {h}_R(\mu _{\varpi _{\mathrm {triv}}})=\|h_R\|_1=1$
, it follows that
$\tilde {h}_R(\mu _{\varpi _{\mathrm {triv}}})=\|h_R\|_1=1$
, it follows that
![]() $\tilde {m}_R(\mu _{\varpi _{\mathrm {triv}}}) =1=\|m_R\|_1$
.
$\tilde {m}_R(\mu _{\varpi _{\mathrm {triv}}}) =1=\|m_R\|_1$
.
On the other hand, there is a
![]() $\delta _1>0$
, such that for every
$\delta _1>0$
, such that for every
![]() $\varpi \ne \varpi _{\mathrm {triv}}$
, it holds that
$\varpi \ne \varpi _{\mathrm {triv}}$
, it holds that
![]() $\|\Re (\mu _\varpi )\|_\infty \le (n-1)/2-\delta _1$
. This follows from the explicit property (T) for
$\|\Re (\mu _\varpi )\|_\infty \le (n-1)/2-\delta _1$
. This follows from the explicit property (T) for
![]() $n\ge 3$
(where we may actually take
$n\ge 3$
(where we may actually take
![]() $\delta _1 =1/2$
), and from Selberg’s spectral gap theorem for
$\delta _1 =1/2$
), and from Selberg’s spectral gap theorem for
![]() $n=2$
(see [Reference Sarnak50]).
$n=2$
(see [Reference Sarnak50]).
Using (8.2), we deduce that there is a
![]() $\delta _2>0$
depending only on
$\delta _2>0$
depending only on
![]() $\eta $
(and n), such that for
$\eta $
(and n), such that for
![]() $\varpi \ne \varpi _{\mathrm {triv}}$
$\varpi \ne \varpi _{\mathrm {triv}}$
Combining all the information above, we obtain
 $$ \begin{align*} &K_{m_R*m_R^*}^q(e,e) - \frac{1}{\mathrm{vol}(\Gamma(q) \backslash \mathrm{SL}_n(\mathbb{R}))} = \intop_{\varpi \ne \varpi_{\mathrm{triv}}} |\tilde{m}_R(\mu_\varpi)|^2 |\varpi(e)|^2 \,\mathrm{d} \varpi \\ & \le R^{-2\delta_2} \intop_{\varpi \ne \varpi_{\mathrm{triv}}} |\tilde{ h}_R(\mu_\varpi)|^2 |\varpi(e)|^2 \,\mathrm{d} \varpi \le R^{-2\delta_2} K_{h_R*h_R^*}^q(e,e). \end{align*} $$
$$ \begin{align*} &K_{m_R*m_R^*}^q(e,e) - \frac{1}{\mathrm{vol}(\Gamma(q) \backslash \mathrm{SL}_n(\mathbb{R}))} = \intop_{\varpi \ne \varpi_{\mathrm{triv}}} |\tilde{m}_R(\mu_\varpi)|^2 |\varpi(e)|^2 \,\mathrm{d} \varpi \\ & \le R^{-2\delta_2} \intop_{\varpi \ne \varpi_{\mathrm{triv}}} |\tilde{ h}_R(\mu_\varpi)|^2 |\varpi(e)|^2 \,\mathrm{d} \varpi \le R^{-2\delta_2} K_{h_R*h_R^*}^q(e,e). \end{align*} $$
The claim now follows from Proposition 8.6.
Lemma 8.9. Let
![]() $M_R^q\colon \Gamma (q) \backslash \mathrm {SL}_n(\mathbb {R}) \to \mathbb {R}$
be the function
$M_R^q\colon \Gamma (q) \backslash \mathrm {SL}_n(\mathbb {R}) \to \mathbb {R}$
be the function
![]() $M_R^q(x):= \sum _{\gamma \in \Gamma (q)} m_R(\gamma x)$
. Then
$M_R^q(x):= \sum _{\gamma \in \Gamma (q)} m_R(\gamma x)$
. Then
Proof. We see that
 $$ \begin{align*} K_{m_R*m_R^*}^q(e,e) = \sum_{\gamma \in \Gamma(q)} (m_R*m_R^*)(\gamma) =\sum_{\gamma\in \Gamma(q)} \intop_{x\in \mathrm{SL}_n(\mathbb{R})}m_R(x)m_R(\gamma^{-1} x) \,\mathrm{d} x. \end{align*} $$
$$ \begin{align*} K_{m_R*m_R^*}^q(e,e) = \sum_{\gamma \in \Gamma(q)} (m_R*m_R^*)(\gamma) =\sum_{\gamma\in \Gamma(q)} \intop_{x\in \mathrm{SL}_n(\mathbb{R})}m_R(x)m_R(\gamma^{-1} x) \,\mathrm{d} x. \end{align*} $$
Folding the integral over
![]() $\Gamma (q)$
, we obtain the above equals
$\Gamma (q)$
, we obtain the above equals
 $$\begin{align*}\intop_{x\in \Gamma(q) \backslash \mathrm{SL}_n(\mathbb{R})}\sum_{\gamma_1\in \Gamma(q)} m_R(\gamma_1 x)\sum_{\gamma\in \Gamma(q)}m_R(\gamma^{-1} \gamma _1 x) \,\mathrm{d} x = \intop_{x\in \Gamma(q) \backslash \mathrm{SL}_n(\mathbb{R})} M_R^q( x)M_R^q( x) \,\mathrm{d} x. \end{align*}$$
$$\begin{align*}\intop_{x\in \Gamma(q) \backslash \mathrm{SL}_n(\mathbb{R})}\sum_{\gamma_1\in \Gamma(q)} m_R(\gamma_1 x)\sum_{\gamma\in \Gamma(q)}m_R(\gamma^{-1} \gamma _1 x) \,\mathrm{d} x = \intop_{x\in \Gamma(q) \backslash \mathrm{SL}_n(\mathbb{R})} M_R^q( x)M_R^q( x) \,\mathrm{d} x. \end{align*}$$
We conclude that the above is
![]() $\|M_R^q\|^2_2$
as
$\|M_R^q\|^2_2$
as
![]() $m_R$
is real-valued.
$m_R$
is real-valued.
Proof of Theorem 5.
Let
![]() $U_q \in L^2 (\Gamma (q) \backslash \mathrm {SL}_n(\mathbb {R}))$
be the
$U_q \in L^2 (\Gamma (q) \backslash \mathrm {SL}_n(\mathbb {R}))$
be the
![]() $L^1$
-normalized constant function on
$L^1$
-normalized constant function on
![]() $\Gamma (q) \backslash \mathrm {SL}_n(\mathbb {R})$
. Then by Lemma 8.9, the fact that
$\Gamma (q) \backslash \mathrm {SL}_n(\mathbb {R})$
. Then by Lemma 8.9, the fact that
 $$\begin{align*}\intop_{\Gamma(q) \backslash \mathrm{SL}_n(\mathbb{R})} M_R^q(x) \,\mathrm{d} x = \intop_{\mathrm{SL}_n(\mathbb{R})} m_R(x) \,\mathrm{d} x=1, \end{align*}$$
$$\begin{align*}\intop_{\Gamma(q) \backslash \mathrm{SL}_n(\mathbb{R})} M_R^q(x) \,\mathrm{d} x = \intop_{\mathrm{SL}_n(\mathbb{R})} m_R(x) \,\mathrm{d} x=1, \end{align*}$$
and Lemma 8.8, we have that there is a
![]() $\delta>0$
depending only on
$\delta>0$
depending only on
![]() $\eta>0$
, such that for
$\eta>0$
, such that for
![]() $R\ge q^{1+1/n}$
$R\ge q^{1+1/n}$
We identify
![]() $\overline {g}\in \Gamma (q)\backslash \Gamma (1) \cong \mathrm {SL}_n(\mathbb {Z}/q\mathbb {Z})$
with some representative of it in
$\overline {g}\in \Gamma (q)\backslash \Gamma (1) \cong \mathrm {SL}_n(\mathbb {Z}/q\mathbb {Z})$
with some representative of it in
![]() $\Gamma (1):=\mathrm {SL}_n(\mathbb {Z})\subset \mathrm {SL}_n(\mathbb {R})$
. We notice that if
$\Gamma (1):=\mathrm {SL}_n(\mathbb {Z})\subset \mathrm {SL}_n(\mathbb {R})$
. We notice that if
![]() $\overline {g}$
has no lift to
$\overline {g}$
has no lift to
![]() $\Gamma (1)$
of size bounded by
$\Gamma (1)$
of size bounded by
![]() $C_1R^{1+\eta }$
for certain sufficiently large but fixed
$C_1R^{1+\eta }$
for certain sufficiently large but fixed
![]() $C_1>0$
, then for all
$C_1>0$
, then for all
![]() $\gamma \in \Gamma (q)$
, we have
$\gamma \in \Gamma (q)$
, we have
for certain
![]() $C_3>0$
sufficiently large, where
$C_3>0$
sufficiently large, where
![]() $w\in \Gamma (1)\backslash \mathrm {SL}_n(\mathbb {R})$
with
$w\in \Gamma (1)\backslash \mathrm {SL}_n(\mathbb {R})$
with
![]() $\|w\|\le C_2$
for certain
$\|w\|\le C_2$
for certain
![]() $C_2\ge n$
. Consequently, noting that the support of
$C_2\ge n$
. Consequently, noting that the support of
![]() $m_R$
is on
$m_R$
is on
![]() $g\in \mathrm {SL}_n(\mathbb {R})$
, such that
$g\in \mathrm {SL}_n(\mathbb {R})$
, such that
![]() $\|g\| \le C_4R^{1+\eta }$
for certain fixed
$\|g\| \le C_4R^{1+\eta }$
for certain fixed
![]() $C_4>0$
, we conclude that
$C_4>0$
, we conclude that
Thus, for such
![]() $\overline {g}$
, we have
$\overline {g}$
, we have
 $$\begin{align*}\intop_{\substack{w\in\mathcal{F}\\ \|w\|\le C_2}} \left|M_R^q(\overline{g}w)-\frac{1}{\mathrm{vol}(\Gamma(q)\backslash \mathrm{SL}_n(\mathbb{R}))}\right|^2 \,\mathrm{d} w \gg \frac{1}{\mathrm{vol}(\Gamma(q)\backslash \mathrm{SL}_n(\mathbb{R}))^2} \gg \frac{1}{q^{2(n^2-1)}}, \end{align*}$$
$$\begin{align*}\intop_{\substack{w\in\mathcal{F}\\ \|w\|\le C_2}} \left|M_R^q(\overline{g}w)-\frac{1}{\mathrm{vol}(\Gamma(q)\backslash \mathrm{SL}_n(\mathbb{R}))}\right|^2 \,\mathrm{d} w \gg \frac{1}{\mathrm{vol}(\Gamma(q)\backslash \mathrm{SL}_n(\mathbb{R}))^2} \gg \frac{1}{q^{2(n^2-1)}}, \end{align*}$$
where
![]() $\mathcal {F}\subseteq \mathrm {SL}_n(\mathbb {R})$
is the standard (i.e. containing identity) fundamental domain of
$\mathcal {F}\subseteq \mathrm {SL}_n(\mathbb {R})$
is the standard (i.e. containing identity) fundamental domain of
![]() $\Gamma (1)\backslash \mathrm {SL}_n(\mathbb {R})$
. Summing the above over such
$\Gamma (1)\backslash \mathrm {SL}_n(\mathbb {R})$
. Summing the above over such
![]() $\overline {g}$
, we obtain
$\overline {g}$
, we obtain
 $$\begin{align*}\frac{N(q,C_1R^{1+\eta})}{q^{2(n^2-1)}} \ll \sum_{\overline{g} \in \Gamma(q) \backslash \Gamma(1)} \intop_{\mathcal{F}} \left|M_R^q(\overline{g}w)-\frac{1}{\mathrm{vol}(\Gamma(q)\backslash \mathrm{SL}_n(\mathbb{R}))}\right|^2 \,\mathrm{d} w, \end{align*}$$
$$\begin{align*}\frac{N(q,C_1R^{1+\eta})}{q^{2(n^2-1)}} \ll \sum_{\overline{g} \in \Gamma(q) \backslash \Gamma(1)} \intop_{\mathcal{F}} \left|M_R^q(\overline{g}w)-\frac{1}{\mathrm{vol}(\Gamma(q)\backslash \mathrm{SL}_n(\mathbb{R}))}\right|^2 \,\mathrm{d} w, \end{align*}$$
where
![]() $N(q,R)$
is the number of
$N(q,R)$
is the number of
![]() $\overline {g} \in \mathrm {SL}_n(\mathbb {Z}/q\mathbb {Z})$
without a lift to
$\overline {g} \in \mathrm {SL}_n(\mathbb {Z}/q\mathbb {Z})$
without a lift to
![]() $\Gamma (1)$
of norm bounded by R. Note that
$\Gamma (1)$
of norm bounded by R. Note that
 $$\begin{align*}\sum_{\overline{g} \in \Gamma(q) \backslash \Gamma(1)}\left|M_R^q(\overline{g}w)-\frac{1}{\mathrm{vol}(\Gamma(q)\backslash \mathrm{SL}_n(\mathbb{R}))}\right|^2\end{align*}$$
$$\begin{align*}\sum_{\overline{g} \in \Gamma(q) \backslash \Gamma(1)}\left|M_R^q(\overline{g}w)-\frac{1}{\mathrm{vol}(\Gamma(q)\backslash \mathrm{SL}_n(\mathbb{R}))}\right|^2\end{align*}$$
as a function of w is left-invariant by
![]() $\Gamma (1)$
. Thus, we can write the w-integral of the above over
$\Gamma (1)$
. Thus, we can write the w-integral of the above over
![]() $\mathcal {F}$
as
$\mathcal {F}$
as
 $$ \begin{align*} \sum_{\overline{g} \in \Gamma(q) \backslash \Gamma(1)} \intop_{\Gamma(1)\backslash \mathrm{SL}_n(\mathbb{R})} \left|M_R^q(\overline{g}w)-\frac{1}{\mathrm{vol}(\Gamma(q)\backslash \mathrm{SL}_n(\mathbb{R}))}\right|^2 \,\mathrm{d} w =\|M_R^q - U_q \|_2^2. \end{align*} $$
$$ \begin{align*} \sum_{\overline{g} \in \Gamma(q) \backslash \Gamma(1)} \intop_{\Gamma(1)\backslash \mathrm{SL}_n(\mathbb{R})} \left|M_R^q(\overline{g}w)-\frac{1}{\mathrm{vol}(\Gamma(q)\backslash \mathrm{SL}_n(\mathbb{R}))}\right|^2 \,\mathrm{d} w =\|M_R^q - U_q \|_2^2. \end{align*} $$
On the other hand, for
![]() $R \ge q^{1+1/n}$
, we have
$R \ge q^{1+1/n}$
, we have
which follows from (8.6). Finally, plugging in
![]() $R= q^{1+1/n}$
, we get that for
$R= q^{1+1/n}$
, we get that for
![]() $C>0$
sufficiently large
$C>0$
sufficiently large
Modifying
![]() $\eta $
, we conclude the proof.
$\eta $
, we conclude the proof.
8.4 Proof of Proposition 8.1
We start by applying the second formulation of
![]() $J^T(h)$
as in Proposition 6.3. Note that
$J^T(h)$
as in Proposition 6.3. Note that
![]() $\rho (P,\lambda , h_{R,q})\mid _{\mathcal {A}^2_\pi (P)}$
projects onto
$\rho (P,\lambda , h_{R,q})\mid _{\mathcal {A}^2_\pi (P)}$
projects onto
![]() $\mathcal {A}^2_\pi (P)^{K_\infty ^0 K(q)}$
. Thus, working as in the proof of Theorem 3, it suffices to show that
$\mathcal {A}^2_\pi (P)^{K_\infty ^0 K(q)}$
. Thus, working as in the proof of Theorem 3, it suffices to show that
 $$ \begin{align} &\sum_{P\supset P_0}\max_{L\in\mathcal{L}(M_P)}\sum_{\pi\in\Pi_2(M_P)}\dim\left(\mathcal{A}_{\pi}^2(P)^{K_\infty^0 K(q)}\right)\nonumber\\ &\quad\times\intop_{i(\mathfrak{a}_{L}^G)^*}|\tilde{h}_{R}(\mu_\pi+\lambda)|^2\left\|\mathcal{M}_{L}^T(P,\lambda)|_{\mathcal{A}_{\pi}^2(P)^{K_\infty^0 K(q)}}\right\|_{\mathrm{op}}\,\mathrm{d} \lambda \ll_\epsilon \|T\|^{n-1}(Rq)^\epsilon(q+R^{-n(n-1)}q^{n^2}). \end{align} $$
$$ \begin{align} &\sum_{P\supset P_0}\max_{L\in\mathcal{L}(M_P)}\sum_{\pi\in\Pi_2(M_P)}\dim\left(\mathcal{A}_{\pi}^2(P)^{K_\infty^0 K(q)}\right)\nonumber\\ &\quad\times\intop_{i(\mathfrak{a}_{L}^G)^*}|\tilde{h}_{R}(\mu_\pi+\lambda)|^2\left\|\mathcal{M}_{L}^T(P,\lambda)|_{\mathcal{A}_{\pi}^2(P)^{K_\infty^0 K(q)}}\right\|_{\mathrm{op}}\,\mathrm{d} \lambda \ll_\epsilon \|T\|^{n-1}(Rq)^\epsilon(q+R^{-n(n-1)}q^{n^2}). \end{align} $$
We apply (8.2) to bound the inner integral on the left-hand side of the above by
 $$\begin{align*}\ll_{N,\epsilon} R^{-n(n-1)+2n\|\Re(\mu_\pi)\|_\infty+\epsilon}\intop_{i(\mathfrak{a}_{L}^G)^*}(1+\|\mu_\pi+\lambda\|)^{-N}\left\|\mathcal{M}_{L}^T(P,\lambda)|_{\mathcal{A}_{\pi}^2(P)^{K_\infty^0 K(q)}}\right\|_{\mathrm{op}}\,\mathrm{d} \lambda.\end{align*}$$
$$\begin{align*}\ll_{N,\epsilon} R^{-n(n-1)+2n\|\Re(\mu_\pi)\|_\infty+\epsilon}\intop_{i(\mathfrak{a}_{L}^G)^*}(1+\|\mu_\pi+\lambda\|)^{-N}\left\|\mathcal{M}_{L}^T(P,\lambda)|_{\mathcal{A}_{\pi}^2(P)^{K_\infty^0 K(q)}}\right\|_{\mathrm{op}}\,\mathrm{d} \lambda.\end{align*}$$
As
![]() $\pi $
is a representation of
$\pi $
is a representation of
![]() $M(\mathbb {A})^1$
and
$M(\mathbb {A})^1$
and
![]() $\lambda \in i(\mathfrak {a}_M^G)^*$
, we have
$\lambda \in i(\mathfrak {a}_M^G)^*$
, we have
![]() $\langle \mu _\pi ,\lambda \rangle =0$
, consequently, we have
$\langle \mu _\pi ,\lambda \rangle =0$
, consequently, we have
![]() $\|\mu _\pi +\lambda \|^2\asymp \|\mu _\pi \|^2+\|\lambda \|^2$
. Thus, the above integral can be bounded by
$\|\mu _\pi +\lambda \|^2\asymp \|\mu _\pi \|^2+\|\lambda \|^2$
. Thus, the above integral can be bounded by
 $$\begin{align*}(1+\|\mu_\pi\|)^{-N/2}\intop_{i(\mathfrak{a}_{L}^G)^*}(1+\|\lambda\|)^{-N/2}\left\|\mathcal{M}_{L}^T(P,\lambda)|_{\mathcal{A}_{\pi}^2(P)^{K_\infty^0 K(q)}}\right\|_{\mathrm{op}}\,\mathrm{d} \lambda.\end{align*}$$
$$\begin{align*}(1+\|\mu_\pi\|)^{-N/2}\intop_{i(\mathfrak{a}_{L}^G)^*}(1+\|\lambda\|)^{-N/2}\left\|\mathcal{M}_{L}^T(P,\lambda)|_{\mathcal{A}_{\pi}^2(P)^{K_\infty^0 K(q)}}\right\|_{\mathrm{op}}\,\mathrm{d} \lambda.\end{align*}$$
To estimate the above integral, we proceed exactly as in the proof Theorem 3. We first write it as the sum of the subintegrals over
![]() $m-1\le \|\lambda \|\le m$
where m varies over
$m-1\le \|\lambda \|\le m$
where m varies over
![]() $\mathbb {N}$
. We further majorize each subintegral by a sum of integrals over
$\mathbb {N}$
. We further majorize each subintegral by a sum of integrals over
![]() $\|\lambda -\eta \|\le 1$
with
$\|\lambda -\eta \|\le 1$
with
![]() $\eta \in i(\mathfrak {a}^G_L)^*$
and
$\eta \in i(\mathfrak {a}^G_L)^*$
and
![]() $\|\eta \|\ll m$
. Finally, we apply Proposition 5.5 to bound each integral after making N large enough. This gives us
$\|\eta \|\ll m$
. Finally, we apply Proposition 5.5 to bound each integral after making N large enough. This gives us
 $$\begin{align*}\intop_{i(\mathfrak{a}_{L}^G)^*}(1+\|\lambda\|)^{-N/2}\left\|\mathcal{M}_{L}^T(P,\lambda)|_{\mathcal{A}_{\pi}^2(P)^{K_\infty^0 K(q)}}\right\|_{\mathrm{op}}\,\mathrm{d} \lambda\ll \left(\|T\|\log(1+\|\mu_\pi\|+\mathrm{level}(K(q))\right)^{\dim\mathfrak{a}^G_L}.\end{align*}$$
$$\begin{align*}\intop_{i(\mathfrak{a}_{L}^G)^*}(1+\|\lambda\|)^{-N/2}\left\|\mathcal{M}_{L}^T(P,\lambda)|_{\mathcal{A}_{\pi}^2(P)^{K_\infty^0 K(q)}}\right\|_{\mathrm{op}}\,\mathrm{d} \lambda\ll \left(\|T\|\log(1+\|\mu_\pi\|+\mathrm{level}(K(q))\right)^{\dim\mathfrak{a}^G_L}.\end{align*}$$
Hence, we obtain
 $$ \begin{align} \max_{L\in\mathcal{L}(M_P)}\intop_{i(\mathfrak{a}_{L}^G)^*}|\tilde{h}_{R}(\mu_\pi+\lambda)|^2&\left\|\mathcal{M}_{L}^T(P,\lambda)|_{\mathcal{A}_{\pi}^2(P)^{K_\infty^0 K(q)}}\right\|_{\mathrm{op}}\,\mathrm{d} \lambda\nonumber\\ &\qquad\ll_{\epsilon,N} \|T\|^{n-1}(Rq)^\epsilon R^{-n(n-1)+2n\|\Re(\mu_\pi)\|_\infty}(1+\|\mu_\pi\|)^{-N}, \end{align} $$
$$ \begin{align} \max_{L\in\mathcal{L}(M_P)}\intop_{i(\mathfrak{a}_{L}^G)^*}|\tilde{h}_{R}(\mu_\pi+\lambda)|^2&\left\|\mathcal{M}_{L}^T(P,\lambda)|_{\mathcal{A}_{\pi}^2(P)^{K_\infty^0 K(q)}}\right\|_{\mathrm{op}}\,\mathrm{d} \lambda\nonumber\\ &\qquad\ll_{\epsilon,N} \|T\|^{n-1}(Rq)^\epsilon R^{-n(n-1)+2n\|\Re(\mu_\pi)\|_\infty}(1+\|\mu_\pi\|)^{-N}, \end{align} $$
for all sufficiently large
![]() $N>0$
.
$N>0$
.
Now, we move on to estimate the
![]() $\pi $
-sum in (8.7). First, let us estimate the contribution for
$\pi $
-sum in (8.7). First, let us estimate the contribution for
![]() $\|\mu _\pi \|\ge (Rq)^\epsilon $
. Dividing into dyadic intervals, and using (8.8) and the fact that
$\|\mu _\pi \|\ge (Rq)^\epsilon $
. Dividing into dyadic intervals, and using (8.8) and the fact that
![]() $\|\Re (\mu _\pi )\|_\infty \ll 1$
, we estimate this contribution by
$\|\Re (\mu _\pi )\|_\infty \ll 1$
, we estimate this contribution by
 $$\begin{align*}\ll(Rq)^{O(1)}\sum_{m\ge (Rq)^\epsilon}\sum_{\substack{\pi\in\Pi_2(M_P)\\ \|\mu_\pi\|\asymp m}}\dim\left(\mathcal{A}_{\pi}^2(P)^{K_\infty^0 K(q)}\right)\|\mu_\pi\|^{-N}.\end{align*}$$
$$\begin{align*}\ll(Rq)^{O(1)}\sum_{m\ge (Rq)^\epsilon}\sum_{\substack{\pi\in\Pi_2(M_P)\\ \|\mu_\pi\|\asymp m}}\dim\left(\mathcal{A}_{\pi}^2(P)^{K_\infty^0 K(q)}\right)\|\mu_\pi\|^{-N}.\end{align*}$$
There is an absolute K, such that the inner sum is bounded by
![]() $\ll m^{-N}(mq)^K$
, which follows from [Reference Assing and Blomer8, (7.2)], classification of discrete series [Reference Mœglin and Waldspurger44] and local Weyl law [Reference Müller49] (also see the discussion in [Reference Assing and Blomer8, pp.35]). Making N large enough, we can bound the above double sum by
$\ll m^{-N}(mq)^K$
, which follows from [Reference Assing and Blomer8, (7.2)], classification of discrete series [Reference Mœglin and Waldspurger44] and local Weyl law [Reference Müller49] (also see the discussion in [Reference Assing and Blomer8, pp.35]). Making N large enough, we can bound the above double sum by
![]() $\ll _N(Rq)^{-N}$
. Thus, we may restrict the
$\ll _N(Rq)^{-N}$
. Thus, we may restrict the
![]() $\pi $
-sum in (8.7) with
$\pi $
-sum in (8.7) with
![]() $\|\mu _\pi \|\le (Rq)^\epsilon $
. We conclude the proof by applying Lemma 8.10 below.
$\|\mu _\pi \|\le (Rq)^\epsilon $
. We conclude the proof by applying Lemma 8.10 below.
Lemma 8.10. We have
 $$\begin{align*}\sum_{P\supset P_0}\sum_{\substack{\pi\in\Pi_2(M_P)\\ \|\mu_\pi\|\le (Rq)^\epsilon}}\dim\left(\mathcal{A}_{\pi}^2(P)^{K_\infty^0 K(q)}\right)R^{2n\|\Re(\mu_\pi)\|_\infty}\ll_\epsilon (Rq)^\epsilon q(R^{n(n-1)}+q^{n^2-1}),\end{align*}$$
$$\begin{align*}\sum_{P\supset P_0}\sum_{\substack{\pi\in\Pi_2(M_P)\\ \|\mu_\pi\|\le (Rq)^\epsilon}}\dim\left(\mathcal{A}_{\pi}^2(P)^{K_\infty^0 K(q)}\right)R^{2n\|\Re(\mu_\pi)\|_\infty}\ll_\epsilon (Rq)^\epsilon q(R^{n(n-1)}+q^{n^2-1}),\end{align*}$$
with
![]() $R,q$
as in Proposition 8.1.
$R,q$
as in Proposition 8.1.
The statement and the proof below are quite similar to those of [Reference Assing and Blomer8, Theorem 7.1]. To make the similarities comprehensible, we make the dictionary that T and M in [Reference Assing and Blomer8] are
![]() $R^n$
and
$R^n$
and
![]() $(Rq)^\epsilon $
, respectively, in our case.
$(Rq)^\epsilon $
, respectively, in our case.
Proof. First, trivially, we have
 $$ \begin{align*} \sum_{P\supset P_0}\sum_{\substack{\pi\in\Pi_2(M_P)\\ \|\mu_\pi\|\le (Rq)^\epsilon}}\dim&\left(\mathcal{A}_{\pi}^2(P)^{K_\infty^0 K(q)}\right)R^{2n\|\Re(\mu_\pi)\|_\infty}\\ &\qquad\le \sum_{P\supset P_0}\sum_{\substack{\pi\in\Pi_2(M_P)\\ \|\mu_\pi\|\le (Rq)^\epsilon}}\dim\left(\mathcal{A}_{\pi}^2(P)^{K_\infty^0 K(q)}\right)R^{2n\|\Re(\mu_\pi)\|_\infty}\intop_{\substack{\lambda\in i(\mathfrak{a}_P^G)^*\\ \|\lambda\|\le (Rq)^\epsilon}}\,\mathrm{d}\lambda. \end{align*} $$
$$ \begin{align*} \sum_{P\supset P_0}\sum_{\substack{\pi\in\Pi_2(M_P)\\ \|\mu_\pi\|\le (Rq)^\epsilon}}\dim&\left(\mathcal{A}_{\pi}^2(P)^{K_\infty^0 K(q)}\right)R^{2n\|\Re(\mu_\pi)\|_\infty}\\ &\qquad\le \sum_{P\supset P_0}\sum_{\substack{\pi\in\Pi_2(M_P)\\ \|\mu_\pi\|\le (Rq)^\epsilon}}\dim\left(\mathcal{A}_{\pi}^2(P)^{K_\infty^0 K(q)}\right)R^{2n\|\Re(\mu_\pi)\|_\infty}\intop_{\substack{\lambda\in i(\mathfrak{a}_P^G)^*\\ \|\lambda\|\le (Rq)^\epsilon}}\,\mathrm{d}\lambda. \end{align*} $$
In the classical language as in [Reference Assing and Blomer8, Theorem 7.1], the right-hand side above is bounded by
 $$ \begin{align} q\int_{\substack{\Gamma(q)\\ \|\mu_\varpi\|\le 2(Rq)^\epsilon}} R^{2n\|\Re(\mu_\varpi)\|_\infty}\,\mathrm{d}\varpi. \end{align} $$
$$ \begin{align} q\int_{\substack{\Gamma(q)\\ \|\mu_\varpi\|\le 2(Rq)^\epsilon}} R^{2n\|\Re(\mu_\varpi)\|_\infty}\,\mathrm{d}\varpi. \end{align} $$
For the relevant notations, we refer to [Reference Assing and Blomer8, Section 2]. The factor q comes from the
![]() $\varphi (q) \le q$
possible twists by Dirichlet characters when moving from the adelic to the classical language (see [Reference Assing and Blomer8, Section 2.6.2] and also [Reference Lapid and Müller39, Section 3.4]).
$\varphi (q) \le q$
possible twists by Dirichlet characters when moving from the adelic to the classical language (see [Reference Assing and Blomer8, Section 2.6.2] and also [Reference Lapid and Müller39, Section 3.4]).
If
![]() $R\le R_0:=q^{1+1/n}(Rq)^{-\epsilon }$
for sufficiently small
$R\le R_0:=q^{1+1/n}(Rq)^{-\epsilon }$
for sufficiently small
![]() $\epsilon>0$
, we directly apply [Reference Assing and Blomer8, Theorem 7.1] to bound the integral in (8.9) by
$\epsilon>0$
, we directly apply [Reference Assing and Blomer8, Theorem 7.1] to bound the integral in (8.9) by
![]() $\ll _\epsilon (Rq)^\epsilon q^{n^2-1}$
.
$\ll _\epsilon (Rq)^\epsilon q^{n^2-1}$
.
If
![]() $R> R_0$
, then we work as in [Reference Assing and Blomer8, Section 8.2]. Note that
$R> R_0$
, then we work as in [Reference Assing and Blomer8, Section 8.2]. Note that
![]() $\|\Re (\mu _\varpi )\|_\infty \le \frac {n-1}{2}$
(which is attained when
$\|\Re (\mu _\varpi )\|_\infty \le \frac {n-1}{2}$
(which is attained when
![]() $\varpi $
is one-dimensional). In this case, we write the integral in (8.9) as
$\varpi $
is one-dimensional). In this case, we write the integral in (8.9) as
 $$\begin{align*}(R/R_0)^{n(n-1)}\int_{\substack{\Gamma(q)\\ \|\mu_\varpi\|\le 2(Rq)^\epsilon}} R_0^{2n\|\Re(\mu_\varpi)\|_\infty}\,\mathrm{d}\varpi\ll_\epsilon (Rq)^\epsilon R^{n(n-1)}.\end{align*}$$
$$\begin{align*}(R/R_0)^{n(n-1)}\int_{\substack{\Gamma(q)\\ \|\mu_\varpi\|\le 2(Rq)^\epsilon}} R_0^{2n\|\Re(\mu_\varpi)\|_\infty}\,\mathrm{d}\varpi\ll_\epsilon (Rq)^\epsilon R^{n(n-1)}.\end{align*}$$
This completes the proof.
Acknowledgements
The authors thank Erez Lapid for several fruitful discussions, his interest in this work and his encouragement. The authors also thank Valentin Blomer for discussions relating to this work and [Reference Assing and Blomer8] and Paul Nelson for several useful comments on an earlier draft of this paper. The first author thanks Shreyasi Datta for various enlightening conversations and her immense support during this project. The first author also thanks Max Planck Institute for Mathematics, Bonn where most of the work was completed during his stay there. The second author is supported by the European Research Council under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 803711). Finally, the authors generously thank the anonymous referees for carefully reading the paper and suggesting numerous improvements.
Competing interest
The authors have no competing interest to declare.