Article contents
NONCOMMUTATIVE DE LEEUW THEOREMS
Published online by Cambridge University Press: 12 October 2015
Abstract
Let 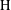 $\text{H}$ be a subgroup of some locally compact group
$\text{H}$ be a subgroup of some locally compact group 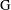 $\text{G}$. Assume that
$\text{G}$. Assume that 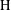 $\text{H}$ is approximable by discrete subgroups and that
$\text{H}$ is approximable by discrete subgroups and that 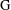 $\text{G}$ admits neighborhood bases which are almost invariant under conjugation by finite subsets of
$\text{G}$ admits neighborhood bases which are almost invariant under conjugation by finite subsets of 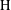 $\text{H}$. Let
$\text{H}$. Let 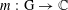 $m:\text{G}\rightarrow \mathbb{C}$ be a bounded continuous symbol giving rise to an
$m:\text{G}\rightarrow \mathbb{C}$ be a bounded continuous symbol giving rise to an 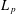 $L_{p}$-bounded Fourier multiplier (not necessarily completely bounded) on the group von Neumann algebra of
$L_{p}$-bounded Fourier multiplier (not necessarily completely bounded) on the group von Neumann algebra of 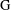 $\text{G}$ for some
$\text{G}$ for some 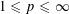 $1\leqslant p\leqslant \infty$. Then,
$1\leqslant p\leqslant \infty$. Then, 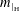 $m_{\mid _{\text{H}}}$ yields an
$m_{\mid _{\text{H}}}$ yields an 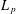 $L_{p}$-bounded Fourier multiplier on the group von Neumann algebra of
$L_{p}$-bounded Fourier multiplier on the group von Neumann algebra of 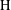 $\text{H}$ provided that the modular function
$\text{H}$ provided that the modular function 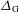 ${\rm\Delta}_{\text{G}}$ is equal to 1 over
${\rm\Delta}_{\text{G}}$ is equal to 1 over 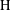 $\text{H}$. This is a noncommutative form of de Leeuw’s restriction theorem for a large class of pairs
$\text{H}$. This is a noncommutative form of de Leeuw’s restriction theorem for a large class of pairs 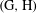 $(\text{G},\text{H})$. Our assumptions on
$(\text{G},\text{H})$. Our assumptions on 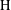 $\text{H}$ are quite natural, and they recover the classical result. The main difference with de Leeuw’s original proof is that we replace dilations of Gaussians by other approximations of the identity for which certain new estimates on almost-multiplicative maps are crucial. Compactification via lattice approximation and periodization theorems are also investigated.
$\text{H}$ are quite natural, and they recover the classical result. The main difference with de Leeuw’s original proof is that we replace dilations of Gaussians by other approximations of the identity for which certain new estimates on almost-multiplicative maps are crucial. Compactification via lattice approximation and periodization theorems are also investigated.
MSC classification
Information
- Type
- Research Article
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s) 2015
References
- 13
- Cited by


