1 Introduction
Motives were introduced by Alexander Grothendieck in the 1960s and since then they became a fundamental tool for investigating the structure of algebraic varieties. In particular, the study of Chow motives of twisted flag varieties has led to the solution of several classical problems in the theory of algebraic groups. More precisely, it was the J-invariant that played an important role in the progress on the Kaplansky problem about possible values of the u-invariant of fields by Vishik [Reference Vishik44], in the solution of a problem of Serre about groups of type
![]() $\mathsf E_8$
[Reference Semenov40, Reference Garibaldi and Semenov8], and a conjecture of Rost about groups of type
$\mathsf E_8$
[Reference Semenov40, Reference Garibaldi and Semenov8], and a conjecture of Rost about groups of type
![]() $\mathsf {E}_7$
[Reference Garibaldi, Petrov and Semenov7].
$\mathsf {E}_7$
[Reference Garibaldi, Petrov and Semenov7].
The J-invariant is a discrete invariant which describes the motivic behavior of the variety of Borel subgroups of a semisimple linear algebraic group. It was first introduced by Vishik in [Reference Vishik43] in the case of orthogonal groups, and then generalized in [Reference Petrov, Semenov and Zainoulline30] to other algebraic groups.
Recently, the first and the third authors generalized in [Reference Petrov and Semenov29] the J-invariant to other oriented cohomology theories in the sense of Levine–Morel [Reference Levine and Morel19]. Their approach gives a ‘categorified’ version of the invariant: for an oriented cohomology theory
![]() $A^*$
and for a split semisimple algebraic group G, the corresponding J-invariant is a certain quotient bi-algebra of
$A^*$
and for a split semisimple algebraic group G, the corresponding J-invariant is a certain quotient bi-algebra of
![]() $A^*(G)$
. Using the Milnor–Moore Theorem on the classification of Hopf algebras, one can show that the new definition coincides with the old one in the case
$A^*(G)$
. Using the Milnor–Moore Theorem on the classification of Hopf algebras, one can show that the new definition coincides with the old one in the case
![]() $A^*=\mathrm {CH}^*(-;\,\mathbb F_p)$
.
$A^*=\mathrm {CH}^*(-;\,\mathbb F_p)$
.
Thus, to understand the J-invariant for general oriented cohomology theories, one has to analyze the structure of the cohomology
![]() $A^*(G)$
of a split group. In the present article, we focus on the algebraic Morava K-theory of orthogonal groups. Note that the algebraic Morava K-theory and Morava motives have a deep connection with Galois cohomology as was already recognized by Voevodsky in his program of the proof of the Bloch–Kato conjecture [Reference Voevodsky47] and further investigated in [Reference Semenov and Sechin41]. The algebraic Morava K-theory has also applications to the structure of torsion in Chow rings of twisted flag varieties (see [Reference Semenov and Sechin41]). Besides, the algebraic Morava K-theory plays an important role in the study of isotropic motives [Reference Vishik45, Reference Vishik46] and in particular the description of the Balmer spectrum of the Morel-Voevodsky
$A^*(G)$
of a split group. In the present article, we focus on the algebraic Morava K-theory of orthogonal groups. Note that the algebraic Morava K-theory and Morava motives have a deep connection with Galois cohomology as was already recognized by Voevodsky in his program of the proof of the Bloch–Kato conjecture [Reference Voevodsky47] and further investigated in [Reference Semenov and Sechin41]. The algebraic Morava K-theory has also applications to the structure of torsion in Chow rings of twisted flag varieties (see [Reference Semenov and Sechin41]). Besides, the algebraic Morava K-theory plays an important role in the study of isotropic motives [Reference Vishik45, Reference Vishik46] and in particular the description of the Balmer spectrum of the Morel-Voevodsky
![]() $\mathbb A^1$
-stable homotopy category [Reference Du and Vishik5].
$\mathbb A^1$
-stable homotopy category [Reference Du and Vishik5].
The computation of the cohomology of Lie groups was a classical problem in algebraic topology dating back to Cartan, which gave rise to the theory of Hopf algebras. A uniform description of the cohomology rings of simple compact Lie groups and of the Chow rings of corresponding algebraic groups can be found in [Reference Kac16]. The computation of the co-multiplication was finished in [Reference Ishitoya, Kono and Toda14].
The topological K-theory of simple Lie groups was computed by Atiyah and Hirzebruch, Hodgkin [Reference Hodgkin11] and Araki [Reference Araki2], and the (higher) algebraic K-theory of algebraic groups was computed by Levine [Reference Levine18], Merkurjev [Reference Merkurjev22] and others (also for twisted forms).
In turn, the topological Morava K-theory of simple compact Lie groups is not known in many cases. Some cases were computed by Yagita [Reference Yagita50, Reference Yagita51], Rao [Reference Rao33, Reference Rao35, Reference Rao37], Nishimoto [Reference Nishimoto27], Mimura [Reference Mimura and Nishimoto24] and many others (see, for example, [Reference Hunton, Mimura, Nishimoto and Schuster13]). In particular, the topological Morava K-theory of orthogonal (and spinor) groups is known only additively by [Reference Rao33, Reference Nishimoto27], but the multiplication and co-multiplication is not known (see [Reference Rao35, Reference Rao36, Reference Rao37] for partial results).
However, the algebraic Morava K-theory seems to behave much better. In our previous article [Reference Geldhauser, Lavrenov, Petrov and Sechin9], we described
![]() $\mathrm K(n)^*(\mathrm {SO}_m)$
as an algebra. Combining our technique with computations of Rao [Reference Rao35] we prove the following:
$\mathrm K(n)^*(\mathrm {SO}_m)$
as an algebra. Combining our technique with computations of Rao [Reference Rao35] we prove the following:
Theorem (Theorem 4.1).
The algebra structure of
![]() $\mathrm K(n)^*(\mathrm {SO}_m)$
is given by
$\mathrm K(n)^*(\mathrm {SO}_m)$
is given by
where
![]() $s=\mathrm {min}\left (\lfloor \frac {m-1}{2}\rfloor ,\,2^{n}-1\right )$
and
$s=\mathrm {min}\left (\lfloor \frac {m-1}{2}\rfloor ,\,2^{n}-1\right )$
and
![]() $e_{2i}$
stands for
$e_{2i}$
stands for
![]() $0$
if
$0$
if
![]() $2i>s$
, cf. [Reference Geldhauser, Lavrenov, Petrov and Sechin9, Theorem 6.13]. The reduced co-multiplication
$2i>s$
, cf. [Reference Geldhauser, Lavrenov, Petrov and Sechin9, Theorem 6.13]. The reduced co-multiplication
![]() $\widetilde \Delta (x)=\Delta (x)-x\otimes 1-1\otimes x$
is given by
$\widetilde \Delta (x)=\Delta (x)-x\otimes 1-1\otimes x$
is given by
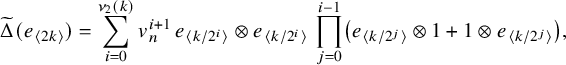 $$ \begin{align*}\widetilde\Delta(e_{\langle2k\rangle})=\sum_{i=0}^{\nu_2(k)}v_n^{i+1}\,e_{\langle k/2^{i}\rangle}\otimes e_{\langle k/2^{i}\rangle}\,\prod_{j=0}^{i-1}\left(e_{\langle k/2^{j}\rangle}\otimes1+1\otimes e_{\langle k/2^{j}\rangle}\right), \end{align*} $$
$$ \begin{align*}\widetilde\Delta(e_{\langle2k\rangle})=\sum_{i=0}^{\nu_2(k)}v_n^{i+1}\,e_{\langle k/2^{i}\rangle}\otimes e_{\langle k/2^{i}\rangle}\,\prod_{j=0}^{i-1}\left(e_{\langle k/2^{j}\rangle}\otimes1+1\otimes e_{\langle k/2^{j}\rangle}\right), \end{align*} $$
where
![]() $\langle t\rangle $
stands for
$\langle t\rangle $
stands for
![]() $2^n-1-t$
,
$2^n-1-t$
,
![]() $k>0$
, and
$k>0$
, and
![]() $\nu _2(k)$
is the
$\nu _2(k)$
is the
![]() $2$
-adic valuation of k, that is,
$2$
-adic valuation of k, that is,
![]() $k/2^{\,\nu _2(k)}$
is an odd integer, and
$k/2^{\,\nu _2(k)}$
is an odd integer, and
In other words, for a fixed n, the algebra and the co-algebra structures of the n-th Morava K-theory of orthogonal groups
![]() $\mathrm {SO}_m$
stabilize for
$\mathrm {SO}_m$
stabilize for
![]() $m\geq 2^{n+1}-1$
. In the range
$m\geq 2^{n+1}-1$
. In the range
![]() $m\leq 2^{n+1}$
, the algebra structure of the Morava K-theory coincides with the algebra structure of the Chow theory, but the co-algebra structure of the Morava K-theory coincides with the co-algebra structure of the Chow theory only for
$m\leq 2^{n+1}$
, the algebra structure of the Morava K-theory coincides with the algebra structure of the Chow theory, but the co-algebra structure of the Morava K-theory coincides with the co-algebra structure of the Chow theory only for
![]() $m\leq 2^{n}$
. In the intermediate range
$m\leq 2^{n}$
. In the intermediate range
![]() $2^n< m\leq 2^{n+1}$
, the co-algebra structure is given by the theorem above.
$2^n< m\leq 2^{n+1}$
, the co-algebra structure is given by the theorem above.
An important step in our arguments is a comparison of the algebraic and topological Morava K-theories. Recall that for a compact connected Lie group K, and the corresponding reductive group
![]() $G=K_{\mathbb C}$
, there is a natural map
$G=K_{\mathbb C}$
, there is a natural map
from the algebraic cobordism of Levine–Morel of G to the complex cobordism of K. Yagita conjectured in [Reference Yagita52] that this map is injective and obtained partial results in this direction; however, his conjecture remains open. However, it is natural to consider an analogue of this conjecture for the Morava K-theory. Using our computations of
![]() $\mathrm K(n)^*(\mathrm {SO}_m)$
, we show in Section 3 that the natural map
$\mathrm K(n)^*(\mathrm {SO}_m)$
, we show in Section 3 that the natural map
is indeed injective. Next, in Section 4, we use the computations of [Reference Rao35] to deduce the co-algebra structure of
![]() $\mathrm K(n)^*(\mathrm {SO}_m)$
for all n and m.
$\mathrm K(n)^*(\mathrm {SO}_m)$
for all n and m.
In the last part of the article, we apply our computations of the algebraic Morava K-theory of orthogonal groups and provide a complete motivic decomposition of connected components of all generic maximal orthogonal Grassmannians:
Theorem (Corollary 6.3).
Let
![]() $n\in \mathbb N\setminus 0$
, and let q be a quadratic form of dimension m with trivial discriminant and denote by
$n\in \mathbb N\setminus 0$
, and let q be a quadratic form of dimension m with trivial discriminant and denote by
![]() $J(q)$
its (classical Chow) J-invariant [Reference Vishik43, Definition 5.11]. Assume that
$J(q)$
its (classical Chow) J-invariant [Reference Vishik43, Definition 5.11]. Assume that
(e.g., this holds for a generic quadratic form q). Let X denote a connected component of its maximal orthogonal Grassmannian (see Section 6). Then the following holds.
-
1. The
 $\mathrm K(n)$
-motive
$\mathrm K(n)$
-motive
 $\mathcal M_{\mathrm K(n)}(X)$
of X is indecomposable for
$\mathcal M_{\mathrm K(n)}(X)$
of X is indecomposable for
 $m\leq 2^{n+1}-2$
.
$m\leq 2^{n+1}-2$
. -
2. The
 $\mathrm K(n)$
-motive
$\mathrm K(n)$
-motive
 $\mathcal M_{\mathrm K(n)}(X)$
of X has
$\mathcal M_{\mathrm K(n)}(X)$
of X has
 $2^{\lfloor \frac {m-1}{2}\rfloor -2^n+2}$
indecomposable summands of rank
$2^{\lfloor \frac {m-1}{2}\rfloor -2^n+2}$
indecomposable summands of rank
 $2^{2^n-2}$
for
$2^{2^n-2}$
for
 $m\geq 2^{n+1}-1$
.
$m\geq 2^{n+1}-1$
.
Note that our previous results describing the structure of Morava motives of maximal orthogonal Grassmannians [Reference Geldhauser, Lavrenov, Petrov and Sechin9] did not use the co-algebra structure of
![]() $\mathrm K(n)^*({\mathrm {SO}_m})$
and gave only a partial decomposition of the Morava motive.
$\mathrm K(n)^*({\mathrm {SO}_m})$
and gave only a partial decomposition of the Morava motive.
2 Morava K-theory and related (co)homology theories
2.1 Algebraic cohomology theories
We work over a field k with
![]() $\mathrm {char}(k)=0$
, and denote by
$\mathrm {char}(k)=0$
, and denote by
![]() $\mathcal S\mathsf m_k$
the category of smooth quasi-projective varieties over k. We often denote
$\mathcal S\mathsf m_k$
the category of smooth quasi-projective varieties over k. We often denote
![]() $\mathrm {pt}=\mathrm {Spec}(k)$
.
$\mathrm {pt}=\mathrm {Spec}(k)$
.
We consider oriented cohomology theories on
![]() $\mathcal S\mathsf m_k$
as defined by Levine–Morel [Reference Levine and Morel19, Definition 1.1.2]. In order to distinguish these from generalized cohomology theories of topological spaces (discussed below), we sometimes call them algebraic cohomology theories. Let
$\mathcal S\mathsf m_k$
as defined by Levine–Morel [Reference Levine and Morel19, Definition 1.1.2]. In order to distinguish these from generalized cohomology theories of topological spaces (discussed below), we sometimes call them algebraic cohomology theories. Let
![]() $\Omega ^*$
denote the algebraic cobordism of Levine–Morel [Reference Levine and Morel19] – that is, the universal oriented cohomology theory [Reference Levine and Morel19, Theorem 1.2.6].
$\Omega ^*$
denote the algebraic cobordism of Levine–Morel [Reference Levine and Morel19] – that is, the universal oriented cohomology theory [Reference Levine and Morel19, Theorem 1.2.6].
Let
![]() $\mathbb L$
be the Lazard ring classifying formal group laws (see [Reference Ravenel38, Definition A2.1.1]). In other words, for any commutative ring R, the formal group laws over R are in one-to-one correspondence with the ring homomorphisms
$\mathbb L$
be the Lazard ring classifying formal group laws (see [Reference Ravenel38, Definition A2.1.1]). In other words, for any commutative ring R, the formal group laws over R are in one-to-one correspondence with the ring homomorphisms
![]() $\mathbb L\rightarrow R$
[Reference Ravenel38, Theorem A2.1.8]. The Lazard ring
$\mathbb L\rightarrow R$
[Reference Ravenel38, Theorem A2.1.8]. The Lazard ring
![]() $\mathbb L$
is isomorphic to a polynomial ring
$\mathbb L$
is isomorphic to a polynomial ring
![]() $\mathbb Z[x_1,x_2,\ldots ]$
of infinitely many variables [Reference Ravenel38, Theorem A2.1.10]. By [Reference Levine and Morel19, Theorem 1.2.7],
$\mathbb Z[x_1,x_2,\ldots ]$
of infinitely many variables [Reference Ravenel38, Theorem A2.1.10]. By [Reference Levine and Morel19, Theorem 1.2.7],
![]() $\Omega ^*(\mathrm {pt})\cong \mathbb L$
.
$\Omega ^*(\mathrm {pt})\cong \mathbb L$
.
We would like to warn the reader that
![]() $\mathbb L$
is graded in [Reference Ravenel38] in such a way that
$\mathbb L$
is graded in [Reference Ravenel38] in such a way that
![]() $|x_i|=2i$
; however, using the grading induced from
$|x_i|=2i$
; however, using the grading induced from
![]() $\Omega ^*(\mathrm {pt})$
, we have
$\Omega ^*(\mathrm {pt})$
, we have
![]() $|x_i|=-i$
. In the present paper, we stick to the latter convention. If R is a commutative graded ring, then the graded homomorphisms
$|x_i|=-i$
. In the present paper, we stick to the latter convention. If R is a commutative graded ring, then the graded homomorphisms
![]() $\mathbb L\rightarrow R$
classify the formal group laws F which are homogeneous of degree
$\mathbb L\rightarrow R$
classify the formal group laws F which are homogeneous of degree
![]() $1$
as elements of
$1$
as elements of
![]() $R[\![x,y]\!]$
.
$R[\![x,y]\!]$
.
Given a commutative, graded
![]() $\mathbb L$
-algebra R, it is easy to see that
$\mathbb L$
-algebra R, it is easy to see that
![]() $A^*=\Omega ^*(-)\otimes _{\mathbb L}R$
also has a natural structure of an oriented cohomology theory. If F is a formal group law classified by
$A^*=\Omega ^*(-)\otimes _{\mathbb L}R$
also has a natural structure of an oriented cohomology theory. If F is a formal group law classified by
![]() $\mathbb L\rightarrow R$
, we will say that
$\mathbb L\rightarrow R$
, we will say that
![]() $A^*$
is a free theory corresponding to F and sometimes denote
$A^*$
is a free theory corresponding to F and sometimes denote
![]() $F_A=F$
.
$F_A=F$
.
Example 2.1.
-
1. For the localization
 $\mathbb L_{(2)}=\mathbb L\otimes _{\mathbb Z}\mathbb Z_{(2)}$
at the prime ideal
$\mathbb L_{(2)}=\mathbb L\otimes _{\mathbb Z}\mathbb Z_{(2)}$
at the prime ideal
 $(2)=2\mathbb Z\trianglelefteq \mathbb Z$
and for the natural map
$(2)=2\mathbb Z\trianglelefteq \mathbb Z$
and for the natural map
 $\mathbb L\rightarrow \mathbb L_{(2)}$
, we denote the corresponding free theory by
$\mathbb L\rightarrow \mathbb L_{(2)}$
, we denote the corresponding free theory by  $$ \begin{align*}\Omega_{(2)}^*=\Omega^*(-)\otimes_{\mathbb L}\mathbb L_{(2)}=\Omega^*(-)\otimes_{\mathbb Z}\mathbb Z_{(2)}. \end{align*} $$
$$ \begin{align*}\Omega_{(2)}^*=\Omega^*(-)\otimes_{\mathbb L}\mathbb L_{(2)}=\Omega^*(-)\otimes_{\mathbb Z}\mathbb Z_{(2)}. \end{align*} $$
-
2. Let
 $V=\mathbb Z_{(2)}[v_1,v_2,\ldots ]$
with
$V=\mathbb Z_{(2)}[v_1,v_2,\ldots ]$
with
 $|v_i|=1-2^i$
and let F denote the universal
$|v_i|=1-2^i$
and let F denote the universal
 $2$
-typical formal group law over V of [Reference Ravenel38, Theorem A2.1.25] (we remark again that
$2$
-typical formal group law over V of [Reference Ravenel38, Theorem A2.1.25] (we remark again that
 $v_i$
are graded in a different way in [Reference Ravenel38]). We remark that the map classifying F induces a surjective map
$v_i$
are graded in a different way in [Reference Ravenel38]). We remark that the map classifying F induces a surjective map
 $\mathbb L_{(2)}\twoheadrightarrow V$
by [Reference Ravenel38, Theorem A2.1.25]. The corresponding free theory is the algebraic Brown–Peterson cohomology theory. One can similarly define Brown–Peterson theories for odd primes p; however, in this article, we will only consider the case
$\mathbb L_{(2)}\twoheadrightarrow V$
by [Reference Ravenel38, Theorem A2.1.25]. The corresponding free theory is the algebraic Brown–Peterson cohomology theory. One can similarly define Brown–Peterson theories for odd primes p; however, in this article, we will only consider the case $$ \begin{align*}\mathrm{BP}^*=\Omega^*(-)\otimes_{\mathbb L}\mathbb Z_{(2)}[v_1,v_2,\ldots]=\Omega_{(2)}^*(-)\otimes_{\mathbb L_{(2)}}V \end{align*} $$
$$ \begin{align*}\mathrm{BP}^*=\Omega^*(-)\otimes_{\mathbb L}\mathbb Z_{(2)}[v_1,v_2,\ldots]=\Omega_{(2)}^*(-)\otimes_{\mathbb L_{(2)}}V \end{align*} $$
 $p=2$
.
$p=2$
.
-
3. For a fixed natural number
 $n>0$
, let
$n>0$
, let
 $I(2,\,n)=(2, v_1,\ldots , v_{n-1})$
be an ideal in V, and consider the composite map
$I(2,\,n)=(2, v_1,\ldots , v_{n-1})$
be an ideal in V, and consider the composite map
 $\mathbb L\rightarrow V\rightarrow V/I(2,\,n)=\mathbb F_2[v_n,v_{n+1},\ldots ]$
. Then the algebraic
$\mathbb L\rightarrow V\rightarrow V/I(2,\,n)=\mathbb F_2[v_n,v_{n+1},\ldots ]$
. Then the algebraic
 $\mathrm {P}(n)^*$
theory is by definition
$\mathrm {P}(n)^*$
theory is by definition  $$ \begin{align*}\mathrm P(n)^*=\Omega^*(-)\otimes_{\mathbb L}\mathbb F_2[v_n,v_{n+1},\ldots]=\mathrm{BP}^*(-)\otimes_{V}V/I(2,\,n). \end{align*} $$
$$ \begin{align*}\mathrm P(n)^*=\Omega^*(-)\otimes_{\mathbb L}\mathbb F_2[v_n,v_{n+1},\ldots]=\mathrm{BP}^*(-)\otimes_{V}V/I(2,\,n). \end{align*} $$
-
4. Consider the composition of
 $\mathbb L\rightarrow \mathbb F_2[v_n,v_{n+1},\ldots ]$
with the natural quotient map
$\mathbb L\rightarrow \mathbb F_2[v_n,v_{n+1},\ldots ]$
with the natural quotient map
 $\mathbb F_2[v_n,v_{n+1},\ldots ]\rightarrow \mathbb F_2[v_n]$
. Then the corresponding free theory is the algebraic connective Morava K-theory.
$\mathbb F_2[v_n,v_{n+1},\ldots ]\rightarrow \mathbb F_2[v_n]$
. Then the corresponding free theory is the algebraic connective Morava K-theory. $$ \begin{align*}\mathrm{CK}(n)^*=\Omega^*(-)\otimes_{\mathbb L}\mathbb F_2[v_n]=\mathrm P(n)^*(-)\otimes_{V/I(2,\,n)}\mathbb F_2[v_n] \end{align*} $$
$$ \begin{align*}\mathrm{CK}(n)^*=\Omega^*(-)\otimes_{\mathbb L}\mathbb F_2[v_n]=\mathrm P(n)^*(-)\otimes_{V/I(2,\,n)}\mathbb F_2[v_n] \end{align*} $$
-
5. Consider the composition of
 $\mathbb L\rightarrow \mathbb F_2[v_n]$
with the natural localization map
$\mathbb L\rightarrow \mathbb F_2[v_n]$
with the natural localization map
 $\mathbb F_2[v_n]\rightarrow \mathbb F_2[v_n^{\pm 1}]$
. Then the corresponding free theory is the algebraic periodic Morava K-theory which we will usually call simply the Morava K-theory.
$\mathbb F_2[v_n]\rightarrow \mathbb F_2[v_n^{\pm 1}]$
. Then the corresponding free theory is the algebraic periodic Morava K-theory which we will usually call simply the Morava K-theory. $$ \begin{align*}\mathrm{K}(n)^*=\Omega^*(-)\otimes_{\mathbb L}\mathbb F_2[v_n^{\pm1}]=\mathrm{CK}(n)^*(-)\otimes_{\mathbb F_2[v_n]}\mathbb F_2[v_n^{\pm1}] \end{align*} $$
$$ \begin{align*}\mathrm{K}(n)^*=\Omega^*(-)\otimes_{\mathbb L}\mathbb F_2[v_n^{\pm1}]=\mathrm{CK}(n)^*(-)\otimes_{\mathbb F_2[v_n]}\mathbb F_2[v_n^{\pm1}] \end{align*} $$
-
6. Consider the composition of
 $\mathbb L\rightarrow \mathbb F_2[v_n]$
with the natural quotient map
$\mathbb L\rightarrow \mathbb F_2[v_n]$
with the natural quotient map
 $\mathbb F_2[v_n]\rightarrow \mathbb F_2$
. Then the corresponding free theory is the usual Chow theory with
$\mathbb F_2[v_n]\rightarrow \mathbb F_2$
. Then the corresponding free theory is the usual Chow theory with $$ \begin{align*}\mathrm{Ch}^*=\mathrm{CH}^*(-;\,\mathbb F_2)=\Omega^*(-)\otimes_{\mathbb L}\mathbb F_2=\mathrm{CK}(n)^*(-)\otimes_{\mathbb F_2[v_n]}\mathbb F_2 \end{align*} $$
$$ \begin{align*}\mathrm{Ch}^*=\mathrm{CH}^*(-;\,\mathbb F_2)=\Omega^*(-)\otimes_{\mathbb L}\mathbb F_2=\mathrm{CK}(n)^*(-)\otimes_{\mathbb F_2[v_n]}\mathbb F_2 \end{align*} $$
 $\mathbb F_2$
-coefficients by [Reference Levine and Morel19, Theorem 1.2.19].
$\mathbb F_2$
-coefficients by [Reference Levine and Morel19, Theorem 1.2.19].
In the next subsection, we consider topological versions of these theories. We also remark that in the present paper, we do not work with bi-graded algebraic cohomology theories of [Reference Yagita53, Reference Levine and Tripathi20, Reference Yagita54] related to Morava K-theories.
2.2 Topological (co)homology theories
We refer the reader to [Reference Adams1] for a general introduction to generalized (co)homology theories, and to [Reference Ravenel38, Chapter 4] for a survey of different theories related to the Morava K-theory. A more detailed exposition of these topics can be found in [Reference Rudyak39].
For a spectrum E (CW-spectrum in terminology of [Reference Adams1, Part III, Chapter 2]) and a CW-complex X, we consider (unreduced) generalized homology and cohomology theories
represented by E (see [Reference Adams1, Part III, Chapter 6]), where
![]() $X_+=X\sqcup *$
,
$X_+=X\sqcup *$
,
![]() $\Sigma ^\infty $
denotes the suspension spectrum functor and
$\Sigma ^\infty $
denotes the suspension spectrum functor and
![]() $\mathbb S$
is the sphere spectrum.
$\mathbb S$
is the sphere spectrum.
Example 2.2.
-
1. Let
 $\mathrm {MU}$
denote the complex cobordism spectrum (see, for example, [Reference Ravenel38, Chapter IV, Section 1] or [Reference Rudyak39, Chapter VII]). By Quillen’s Theorem [Reference Ravenel38, Theorem 4.1.6], the complex cobordism of a point
$\mathrm {MU}$
denote the complex cobordism spectrum (see, for example, [Reference Ravenel38, Chapter IV, Section 1] or [Reference Rudyak39, Chapter VII]). By Quillen’s Theorem [Reference Ravenel38, Theorem 4.1.6], the complex cobordism of a point
 $*$
is canonically isomorphic to the Lazard ring
$*$
is canonically isomorphic to the Lazard ring
 $\mathbb L$
, and the isomorphism doubles the grading (i.e.,
$\mathbb L$
, and the isomorphism doubles the grading (i.e.,
 $\mathrm {MU}^{2k+1}(*)=0$
and
$\mathrm {MU}^{2k+1}(*)=0$
and
 $\mathrm {MU}^{2k}(*)=\mathbb L^k$
).
$\mathrm {MU}^{2k}(*)=\mathbb L^k$
). -
2. We can consider the
 $2$
-local complex cobordism – that is, the spectrum where
$2$
-local complex cobordism – that is, the spectrum where $$ \begin{align*}\mathrm{MU}_{(2)}=\mathrm{MU}\wedge\mathbb S_{(2)}, \end{align*} $$
$$ \begin{align*}\mathrm{MU}_{(2)}=\mathrm{MU}\wedge\mathbb S_{(2)}, \end{align*} $$
 $\mathbb S_{(2)}$
is the Moore spectrum of type
$\mathbb S_{(2)}$
is the Moore spectrum of type
 $\mathbb Z_{(2)}$
(see [Reference Adams1, Part III, Example 6.6]). The spectrum
$\mathbb Z_{(2)}$
(see [Reference Adams1, Part III, Example 6.6]). The spectrum
 $\mathrm {MU}_{(2)}$
inherits the canonical ring structure from
$\mathrm {MU}_{(2)}$
inherits the canonical ring structure from
 $\mathrm {MU}$
(see, for example, [Reference Rudyak39, Chapter II, Theorem 5.15]). We also remark that for a finite CW-complex X, we have (see [Reference Adams1, Part III, Proposition 6.9]), in particular,
$\mathrm {MU}$
(see, for example, [Reference Rudyak39, Chapter II, Theorem 5.15]). We also remark that for a finite CW-complex X, we have (see [Reference Adams1, Part III, Proposition 6.9]), in particular, $$ \begin{align*}\mathrm{MU}_{(2)}^*(X)=\mathrm{MU}^*(X)\otimes_{\mathbb Z}\mathbb Z_{(2)} \end{align*} $$
$$ \begin{align*}\mathrm{MU}_{(2)}^*(X)=\mathrm{MU}^*(X)\otimes_{\mathbb Z}\mathbb Z_{(2)} \end{align*} $$
 $\mathrm {MU}_{(2)}^*(*)\cong \mathbb L_{(2)}$
.
$\mathrm {MU}_{(2)}^*(*)\cong \mathbb L_{(2)}$
.
-
3. We will denote
 $\mathrm {BP}_{\mathrm {top}}$
(or also
$\mathrm {BP}_{\mathrm {top}}$
(or also
 $\mathrm {BP}^{\mathrm {top}}$
) the Brown–Peterson spectrum; see [Reference Ravenel38, Theorem 4.1.12] or [Reference Rudyak39, Chapter VII, Definition 3.20]. It is an associative commutative ring spectrum, and a natural map (2.1)of ring spectra is a retraction. There is a natural isomorphism
$\mathrm {BP}^{\mathrm {top}}$
) the Brown–Peterson spectrum; see [Reference Ravenel38, Theorem 4.1.12] or [Reference Rudyak39, Chapter VII, Definition 3.20]. It is an associative commutative ring spectrum, and a natural map (2.1)of ring spectra is a retraction. There is a natural isomorphism $$ \begin{align} \mathrm{MU}_{(2)}\rightarrow\mathrm{BP}_{\mathrm{top}} \end{align} $$
$$ \begin{align} \mathrm{MU}_{(2)}\rightarrow\mathrm{BP}_{\mathrm{top}} \end{align} $$
 $V\cong \mathrm {BP}_{\mathrm {top}}^*(*)$
(which doubles the grading), and the map (2.1) evaluated on
$V\cong \mathrm {BP}_{\mathrm {top}}^*(*)$
(which doubles the grading), and the map (2.1) evaluated on
 $*$
induces a natural map
$*$
induces a natural map
 $\mathbb L_{(2)}\twoheadrightarrow V$
; see Example 2.1 (2). We will refer to
$\mathbb L_{(2)}\twoheadrightarrow V$
; see Example 2.1 (2). We will refer to
 $\mathrm {BP}^{\mathrm {top}}_*$
and
$\mathrm {BP}^{\mathrm {top}}_*$
and
 $\mathrm {BP}_{\mathrm {top}}^*$
as the topological Brown–Peterson (co)homology theories.
$\mathrm {BP}_{\mathrm {top}}^*$
as the topological Brown–Peterson (co)homology theories.
-
4. Let us also denote by
 $\mathrm P(n)_{\mathrm {top}}$
(or
$\mathrm P(n)_{\mathrm {top}}$
(or
 $\mathrm P(n)^{\mathrm {top}}$
) the spectrum defined by killing
$\mathrm P(n)^{\mathrm {top}}$
) the spectrum defined by killing
 $I(2,n)$
in the spectrum
$I(2,n)$
in the spectrum
 $\mathrm {BP}_{\mathrm {top}}$
(see Example 2.1 (3)). In other words, we put
$\mathrm {BP}_{\mathrm {top}}$
(see Example 2.1 (3)). In other words, we put
 $\mathrm P(0)_{\mathrm {top}}=\mathrm {BP}_{\mathrm {top}}$
, and
$\mathrm P(0)_{\mathrm {top}}=\mathrm {BP}_{\mathrm {top}}$
, and
 $\mathrm P(n+1)_{\mathrm {top}}$
is the cofiber of the map (see [Reference Ravenel38, Chapter 4, Section 2] and also [Reference Nassau25]). The ring
$\mathrm P(n+1)_{\mathrm {top}}$
is the cofiber of the map (see [Reference Ravenel38, Chapter 4, Section 2] and also [Reference Nassau25]). The ring $$ \begin{align*}\Sigma^{2(2^n-1)}\mathrm P(n)_{\mathrm{top}}\stackrel{v_n}{\longrightarrow}\mathrm P(n)_{\mathrm{top}} \end{align*} $$
$$ \begin{align*}\Sigma^{2(2^n-1)}\mathrm P(n)_{\mathrm{top}}\stackrel{v_n}{\longrightarrow}\mathrm P(n)_{\mathrm{top}} \end{align*} $$
 $\mathrm P(n)_{\mathrm {top}}^*(*)$
is naturally isomorphic to
$\mathrm P(n)_{\mathrm {top}}^*(*)$
is naturally isomorphic to
 $\mathbb F_2[v_n,v_{n+1},\ldots ]$
.
$\mathbb F_2[v_n,v_{n+1},\ldots ]$
.
-
5. Killing the ideal
 $(v_{n+1},v_{n+2},\ldots )$
in the spectrum
$(v_{n+1},v_{n+2},\ldots )$
in the spectrum
 $\mathrm P(n)_{\mathrm {top}}$
, we obtain the connected Morava K-theory spectrum
$\mathrm P(n)_{\mathrm {top}}$
, we obtain the connected Morava K-theory spectrum
 $\mathrm {k}(n)$
, which we will prefer to denote
$\mathrm {k}(n)$
, which we will prefer to denote
 $\mathrm {CK}(n)_{\mathrm {top}}$
or
$\mathrm {CK}(n)_{\mathrm {top}}$
or
 $\mathrm {CK}(n)^{\mathrm {top}}$
in this paper; see [Reference Ravenel38, Chapter 4, Section 2]. The ring
$\mathrm {CK}(n)^{\mathrm {top}}$
in this paper; see [Reference Ravenel38, Chapter 4, Section 2]. The ring
 $\mathrm {CK}(n)_{\mathrm {top}}^*(*)$
is isomorphic to
$\mathrm {CK}(n)_{\mathrm {top}}^*(*)$
is isomorphic to
 $\mathbb F_2[v_n]$
. We refer to
$\mathbb F_2[v_n]$
. We refer to
 $\mathrm {CK}(n)^{\mathrm {top}}_*$
and
$\mathrm {CK}(n)^{\mathrm {top}}_*$
and
 $\mathrm {CK}(n)_{\mathrm {top}}^*$
as the topological connective Morava K-theory (co)homology.
$\mathrm {CK}(n)_{\mathrm {top}}^*$
as the topological connective Morava K-theory (co)homology. -
6. One defines the Morava K-theory spectrum
 $\mathrm K(n)_{\mathrm {top}}$
or
$\mathrm K(n)_{\mathrm {top}}$
or
 $\mathrm K(n)^{\mathrm {top}}$
as the directed colimit of the sequence (see [Reference Ravenel38, Chapter 4, Section 2]). We refer to
$\mathrm K(n)^{\mathrm {top}}$
as the directed colimit of the sequence (see [Reference Ravenel38, Chapter 4, Section 2]). We refer to $$ \begin{align*}\mathrm{k}(n)\stackrel{v_n}{\longrightarrow}\Sigma^{2(1-2^n)}\mathrm{k}(n)\stackrel{v_n}{\longrightarrow}\Sigma^{4(1-2^n)}\mathrm{k}(n)\stackrel{v_n}{\longrightarrow}\ldots \end{align*} $$
$$ \begin{align*}\mathrm{k}(n)\stackrel{v_n}{\longrightarrow}\Sigma^{2(1-2^n)}\mathrm{k}(n)\stackrel{v_n}{\longrightarrow}\Sigma^{4(1-2^n)}\mathrm{k}(n)\stackrel{v_n}{\longrightarrow}\ldots \end{align*} $$
 $\mathrm {K}(n)^{\mathrm {top}}_*$
and
$\mathrm {K}(n)^{\mathrm {top}}_*$
and
 $\mathrm {K}(n)_{\mathrm {top}}^*$
as the topological (periodic) Morava K-theory (co)homology. We remark that
$\mathrm {K}(n)_{\mathrm {top}}^*$
as the topological (periodic) Morava K-theory (co)homology. We remark that
 $\mathrm K(n)^*_{\mathrm {top}}(X)$
coincides with the ring theoretic localization of
$\mathrm K(n)^*_{\mathrm {top}}(X)$
coincides with the ring theoretic localization of
 $\mathrm {CK}(n)^*_{\mathrm {top}}$
by the powers of
$\mathrm {CK}(n)^*_{\mathrm {top}}$
by the powers of
 $v_n$
(cf. [Reference Johnson and Wilson15, Section 2]) for a finite CW-complex X – in particular,
$v_n$
(cf. [Reference Johnson and Wilson15, Section 2]) for a finite CW-complex X – in particular,
 $\mathrm K(n)^*_{\mathrm {top}}(*)\cong \mathbb F_2[v_n^{\pm 1}]$
.
$\mathrm K(n)^*_{\mathrm {top}}(*)\cong \mathbb F_2[v_n^{\pm 1}]$
.
-
7. The Eilenberg–MacLane spectrum
 $\mathrm H\mathbb Z/2$
of type
$\mathrm H\mathbb Z/2$
of type
 $\mathbb Z/2$
can in fact be obtained from
$\mathbb Z/2$
can in fact be obtained from
 $\mathrm {BP}_{\mathrm {top}}$
by killing
$\mathrm {BP}_{\mathrm {top}}$
by killing
 $(2,v_1,v_2,\ldots )$
(see [Reference Ravenel38, Chapter 4]). The corresponding (co)homology theories are the usual (co)homology
$(2,v_1,v_2,\ldots )$
(see [Reference Ravenel38, Chapter 4]). The corresponding (co)homology theories are the usual (co)homology
 $\mathrm H_*(-;\,\mathbb F_2)$
and
$\mathrm H_*(-;\,\mathbb F_2)$
and
 $\mathrm H^*(-;\,\mathbb F_2)$
with
$\mathrm H^*(-;\,\mathbb F_2)$
with
 $\mathrm {mod}\ 2$
coefficients.
$\mathrm {mod}\ 2$
coefficients.
Observe that
![]() $\mathrm P(n)_{\mathrm {top}}$
does not admit a commutative multiplicative structure (for
$\mathrm P(n)_{\mathrm {top}}$
does not admit a commutative multiplicative structure (for
![]() $p=2$
); however, it has exactly two multiplicative structures
$p=2$
); however, it has exactly two multiplicative structures
for which
![]() $\mathrm {P}(n)_{\mathrm {top}}$
is a
$\mathrm {P}(n)_{\mathrm {top}}$
is a
![]() $\mathrm {BP}_{\mathrm {top}}$
-algebra spectrum, and, moreover,
$\mathrm {BP}_{\mathrm {top}}$
-algebra spectrum, and, moreover,
![]() $\mu _1=\mu _2\circ \tau $
where
$\mu _1=\mu _2\circ \tau $
where
![]() $\tau $
denotes the switch
$\tau $
denotes the switch
![]() $\tau \colon X\wedge Y\rightarrow Y\wedge X$
(see [Reference Würgler49, Proposition 2.4] and [Reference Nassau25, Reference Nassau26]). Therefore, the algebra structure of
$\tau \colon X\wedge Y\rightarrow Y\wedge X$
(see [Reference Würgler49, Proposition 2.4] and [Reference Nassau25, Reference Nassau26]). Therefore, the algebra structure of
![]() $\mathrm P(n)^*_{\mathrm {top}}(X)$
with respect to any of
$\mathrm P(n)^*_{\mathrm {top}}(X)$
with respect to any of
![]() $\mu _i$
determines the other one. The same is true for the multiplicative structures on
$\mu _i$
determines the other one. The same is true for the multiplicative structures on
![]() $\mathrm {CK}(n)_{\mathrm {top}}$
and
$\mathrm {CK}(n)_{\mathrm {top}}$
and
![]() $\mathrm {K}(n)_{\mathrm {top}}$
; cf. [Reference Würgler49, Remark 2.6], and see also [Reference Strickland42].
$\mathrm {K}(n)_{\mathrm {top}}$
; cf. [Reference Würgler49, Remark 2.6], and see also [Reference Strickland42].
2.3 Comparison of algebraic and topological cohomology theories
Consider a field extension
![]() $k\subseteq \mathbb C$
. Then there is a natural map from the discussed (algebraic) oriented cohomology theories to their topological versions.
$k\subseteq \mathbb C$
. Then there is a natural map from the discussed (algebraic) oriented cohomology theories to their topological versions.
Observe that for
![]() $X\in \mathcal S\mathsf m_k$
, we obtain an oriented cohomology theory
$X\in \mathcal S\mathsf m_k$
, we obtain an oriented cohomology theory
(see [Reference Levine and Morel19, Example 1.2.10]). Then by the universality of
![]() $\Omega ^*$
, we obtain a canonical map
$\Omega ^*$
, we obtain a canonical map
Since
![]() $\mathrm {MU}^{*}_{(2)}(X(\mathbb C))$
has the structure of an
$\mathrm {MU}^{*}_{(2)}(X(\mathbb C))$
has the structure of an
![]() $\mathbb L_{(2)}$
-module, localizing at
$\mathbb L_{(2)}$
-module, localizing at
![]() $(2)$
, we also obtain a morphism of oriented cohomology theories
$(2)$
, we also obtain a morphism of oriented cohomology theories
![]() $\Omega ^*_{(2)}\rightarrow \mathrm {MU}^*_{(2)}$
.
$\Omega ^*_{(2)}\rightarrow \mathrm {MU}^*_{(2)}$
.
For
![]() $A=\mathrm {BP},\,\mathrm {P}(n),\,\mathrm {CK}(n)$
, consider the diagram
$A=\mathrm {BP},\,\mathrm {P}(n),\,\mathrm {CK}(n)$
, consider the diagram
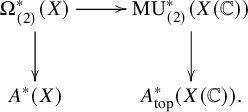
Since the generators of
![]() $\mathrm {Ker}(\mathbb L_{(2)}\twoheadrightarrow A^*(\mathrm {pt}))$
act as zero on
$\mathrm {Ker}(\mathbb L_{(2)}\twoheadrightarrow A^*(\mathrm {pt}))$
act as zero on
![]() $A^*_{\mathrm {top}}(X(\mathbb C))$
, we conclude that the top horizontal map induces a natural map from
$A^*_{\mathrm {top}}(X(\mathbb C))$
, we conclude that the top horizontal map induces a natural map from
![]() $A^*(X)$
to
$A^*(X)$
to
![]() $A^*_{\mathrm {top}}(X(\mathbb C))$
. Passing to the localization, we also obtain a natural map from
$A^*_{\mathrm {top}}(X(\mathbb C))$
. Passing to the localization, we also obtain a natural map from
![]() $\mathrm {K}(n)^*(X)$
to
$\mathrm {K}(n)^*(X)$
to
![]() $\mathrm {K}(n)^*_{\mathrm {top}}(X(\mathbb C))$
.
$\mathrm {K}(n)^*_{\mathrm {top}}(X(\mathbb C))$
.
Moreover, since the natural map
![]() $\mathrm {BP}^*(X)\rightarrow \mathrm {BP}_{\mathrm {top}}^*(X(\mathbb C))$
respects the multiplication, and
$\mathrm {BP}^*(X)\rightarrow \mathrm {BP}_{\mathrm {top}}^*(X(\mathbb C))$
respects the multiplication, and
![]() $\mu _i$
from (2.2) are compatible with the multiplicative structure on
$\mu _i$
from (2.2) are compatible with the multiplicative structure on
![]() $\mathrm {BP}_{\mathrm {top}}$
, we conclude that the natural map
$\mathrm {BP}_{\mathrm {top}}$
, we conclude that the natural map
![]() $\mathrm P(n)^*(X)\rightarrow \mathrm P(n)^*_{\mathrm {top}}(X(\mathbb C))$
is a ring homomorphism for any choice of
$\mathrm P(n)^*(X)\rightarrow \mathrm P(n)^*_{\mathrm {top}}(X(\mathbb C))$
is a ring homomorphism for any choice of
![]() $\mu _i$
(cf. [Reference Würgler49, (2.3)(i)] and [Reference Nassau25, Reference Nassau26]). The same statement remains true for the multiplicative structures on
$\mu _i$
(cf. [Reference Würgler49, (2.3)(i)] and [Reference Nassau25, Reference Nassau26]). The same statement remains true for the multiplicative structures on
![]() $\mathrm {CK}(n)_{\mathrm {top}}$
and
$\mathrm {CK}(n)_{\mathrm {top}}$
and
![]() $\mathrm {K}(n)_{\mathrm {top}}$
; cf. [Reference Würgler49, Remark 2.6].
$\mathrm {K}(n)_{\mathrm {top}}$
; cf. [Reference Würgler49, Remark 2.6].
2.4 Atiyah–Hirzebruch spectral sequences
For a finite CW-complex X, its filtration by r-skeletons
![]() $X^r$
$X^r$
induces the Atiyah–Hirzebruch spectral sequences
for any spectrum E; see [Reference Adams1, Part III, Chapter 7].
We remark that the morphism of spectra
![]() $ \mathrm {CK}(n)_{\mathrm {top}}\rightarrow \mathrm K(n)_{\mathrm {top}} $
induces a morphism of the Atiyah–Hirzebruch spectral sequences for
$ \mathrm {CK}(n)_{\mathrm {top}}\rightarrow \mathrm K(n)_{\mathrm {top}} $
induces a morphism of the Atiyah–Hirzebruch spectral sequences for
![]() $\mathrm {CK}(n)_{\mathrm {top}}^*(X)$
and
$\mathrm {CK}(n)_{\mathrm {top}}^*(X)$
and
![]() $\mathrm K(n)_{\mathrm {top}}^*(X)$
. On the second page, this map coincides with the localization; in particular, it is injective. As a result, if the Atiyah–Hirzebruch spectral sequence for
$\mathrm K(n)_{\mathrm {top}}^*(X)$
. On the second page, this map coincides with the localization; in particular, it is injective. As a result, if the Atiyah–Hirzebruch spectral sequence for
![]() $\mathrm {K}(n)_{\mathrm {top}}^*(X)$
collapses at the second page, we see that the Atiyah–Hirzebruch spectral sequence for
$\mathrm {K}(n)_{\mathrm {top}}^*(X)$
collapses at the second page, we see that the Atiyah–Hirzebruch spectral sequence for
![]() $\mathrm {CK}(n)_{\mathrm {top}}^*(X)$
also collapses. In particular, the following holds.
$\mathrm {CK}(n)_{\mathrm {top}}^*(X)$
also collapses. In particular, the following holds.
Proposition 2.3. Let X be a finite CW-complex,
![]() $n\in \mathbb N$
, and assume that the Atiyah–Hirzebruch spectral sequence
$n\in \mathbb N$
, and assume that the Atiyah–Hirzebruch spectral sequence
![]() $\mathrm H^p\big (X;\,\mathrm K(n)^{\mathrm {top}}_q(*)\big )\Rightarrow \mathrm K(n)_{\mathrm {top}}^{p+q}(X)$
collapses at the second page.
$\mathrm H^p\big (X;\,\mathrm K(n)^{\mathrm {top}}_q(*)\big )\Rightarrow \mathrm K(n)_{\mathrm {top}}^{p+q}(X)$
collapses at the second page.
Then
![]() $\mathrm {CK}(n)_{\mathrm {top}}^*(X)$
is a free graded
$\mathrm {CK}(n)_{\mathrm {top}}^*(X)$
is a free graded
![]() $\mathbb F_2[v_n]$
-module of rank
$\mathbb F_2[v_n]$
-module of rank
![]() $\mathrm {dim}_{\mathbb F_2\,}\mathrm {H}^*(X;\,\mathbb F_2)$
, and the natural map
$\mathrm {dim}_{\mathbb F_2\,}\mathrm {H}^*(X;\,\mathbb F_2)$
, and the natural map
![]() $\mathrm {CK}(n)_{\mathrm {top}}\rightarrow \mathrm H\mathbb Z/2$
induces an isomorphism
$\mathrm {CK}(n)_{\mathrm {top}}\rightarrow \mathrm H\mathbb Z/2$
induces an isomorphism
We will also need the following result proven in [Reference Johnson and Wilson15, Section 4].
Proposition 2.4. Let X be a finite CW-complex,
![]() $n\in \mathbb N\setminus 0$
. Then the following are equivalent.
$n\in \mathbb N\setminus 0$
. Then the following are equivalent.
-
1. The Atiyah–Hirzebruch spectral sequence
collapses (at the second page). $$ \begin{align*}\mathrm H_p(X;\,\mathrm P(n)^{\mathrm{top}}_q(*))\Longrightarrow \mathrm P(n)^{\mathrm{top}}_{p+q}(X) \end{align*} $$
$$ \begin{align*}\mathrm H_p(X;\,\mathrm P(n)^{\mathrm{top}}_q(*))\Longrightarrow \mathrm P(n)^{\mathrm{top}}_{p+q}(X) \end{align*} $$
-
2.
 $\mathrm {P}(n)^{\mathrm {top}}_{*}(X)$
is a free
$\mathrm {P}(n)^{\mathrm {top}}_{*}(X)$
is a free
 $\mathbb F_2[v_n,v_{n+1},\ldots ]$
-module of rank
$\mathbb F_2[v_n,v_{n+1},\ldots ]$
-module of rank
 $\mathrm {dim}_{\mathbb F_2\,}\mathrm H_*(X;\,\mathbb F_2)$
, and the canonical map
$\mathrm {dim}_{\mathbb F_2\,}\mathrm H_*(X;\,\mathbb F_2)$
, and the canonical map
 $\mathrm P(n)^{\mathrm {top}}\rightarrow \mathrm H\mathbb Z/2$
induces an isomorphism
$\mathrm P(n)^{\mathrm {top}}\rightarrow \mathrm H\mathbb Z/2$
induces an isomorphism  $$ \begin{align*}\mathrm P(n)^{\mathrm{top}}_{*}(X)\otimes_{\mathbb F_2[v_n,v_{n+1},\ldots]}\mathbb F_2\cong\mathrm H_*(X;\mathbb F_2). \end{align*} $$
$$ \begin{align*}\mathrm P(n)^{\mathrm{top}}_{*}(X)\otimes_{\mathbb F_2[v_n,v_{n+1},\ldots]}\mathbb F_2\cong\mathrm H_*(X;\mathbb F_2). \end{align*} $$
-
3. The canonical map
 $\mathrm P(n)^{\mathrm {top}}_{*}(X)\rightarrow \mathrm H_*(X;\mathbb F_2)$
is surjective.
$\mathrm P(n)^{\mathrm {top}}_{*}(X)\rightarrow \mathrm H_*(X;\mathbb F_2)$
is surjective. -
4. The Atiyah–Hirzebruch spectral sequence
collapses. $$ \begin{align*}\mathrm H_p(X;\,\mathrm{CK}(n)^{\mathrm{top}}_q(*))\Longrightarrow \mathrm{CK}(n)^{\mathrm{top}}_{p+q}(X) \end{align*} $$
$$ \begin{align*}\mathrm H_p(X;\,\mathrm{CK}(n)^{\mathrm{top}}_q(*))\Longrightarrow \mathrm{CK}(n)^{\mathrm{top}}_{p+q}(X) \end{align*} $$
-
5.
 $\mathrm {CK}(n)^{\mathrm {top}}_{*}(X)$
is a free
$\mathrm {CK}(n)^{\mathrm {top}}_{*}(X)$
is a free
 $\mathbb F_2[v_n]$
-module of rank
$\mathbb F_2[v_n]$
-module of rank
 $\mathrm {dim}_{\mathbb F_2\,}\mathrm H_*(X;\,\mathbb F_2)$
, and the natural map
$\mathrm {dim}_{\mathbb F_2\,}\mathrm H_*(X;\,\mathbb F_2)$
, and the natural map
 $\mathrm {CK}(n)^{\mathrm {top}}\rightarrow \mathrm H\mathbb Z/2$
induces an isomorphism
$\mathrm {CK}(n)^{\mathrm {top}}\rightarrow \mathrm H\mathbb Z/2$
induces an isomorphism  $$ \begin{align*}\mathrm{CK}(n)^{\mathrm{top}}_{*}(X)\otimes_{\mathbb F_2[v_n]}\mathbb F_2\cong\mathrm H_*(X;\mathbb F_2). \end{align*} $$
$$ \begin{align*}\mathrm{CK}(n)^{\mathrm{top}}_{*}(X)\otimes_{\mathbb F_2[v_n]}\mathbb F_2\cong\mathrm H_*(X;\mathbb F_2). \end{align*} $$
-
6. The canonical map
 $\mathrm {CK}(n)^{\mathrm {top}}_{*}(X)\rightarrow \mathrm H_*(X;\mathbb F_2)$
is surjective.
$\mathrm {CK}(n)^{\mathrm {top}}_{*}(X)\rightarrow \mathrm H_*(X;\mathbb F_2)$
is surjective.
If the equivalent conditions (1)–(6) hold, then one also has the following.
-
7. The canonical map
 $\mathrm P(n)^{\mathrm {top}}\rightarrow \mathrm {CK}(n)^{\mathrm {top}}$
induces an isomorphism
$\mathrm P(n)^{\mathrm {top}}\rightarrow \mathrm {CK}(n)^{\mathrm {top}}$
induces an isomorphism  $$ \begin{align*}\mathrm P(n)^{\mathrm{top}}_{*}(X)\otimes_{\mathbb F_2[v_n,v_{n+1},\ldots]}\mathbb F_2[v_n]\cong\mathrm{CK}(n)^{\mathrm{top}}_*(X). \end{align*} $$
$$ \begin{align*}\mathrm P(n)^{\mathrm{top}}_{*}(X)\otimes_{\mathbb F_2[v_n,v_{n+1},\ldots]}\mathbb F_2[v_n]\cong\mathrm{CK}(n)^{\mathrm{top}}_*(X). \end{align*} $$
-
8. There is a canonical isomorphism
 $$ \begin{align*}\mathrm{CK}(n)^*_{\mathrm{top}}(X)\cong\mathrm{Hom}_{\mathbb F_2[v_n]}(\mathrm{CK}(n)^{\mathrm{top}}_*(X),\,\mathbb F_2[v_n]). \end{align*} $$
$$ \begin{align*}\mathrm{CK}(n)^*_{\mathrm{top}}(X)\cong\mathrm{Hom}_{\mathbb F_2[v_n]}(\mathrm{CK}(n)^{\mathrm{top}}_*(X),\,\mathbb F_2[v_n]). \end{align*} $$
Proof. The implications
are straightforward. For
![]() $(3)\Rightarrow (1)$
, see [Reference Rao34, Proposition 1.1] (cf. [Reference Johnson and Wilson15, Proof of Theorem 4.16]).
$(3)\Rightarrow (1)$
, see [Reference Rao34, Proposition 1.1] (cf. [Reference Johnson and Wilson15, Proof of Theorem 4.16]).
Assume that
![]() $(6)$
holds. Then by [Reference Johnson and Wilson15, Theorem 4.8 and Remark 4.9], one has that the natural map
$(6)$
holds. Then by [Reference Johnson and Wilson15, Theorem 4.8 and Remark 4.9], one has that the natural map
![]() $\mathrm P(n)^{\mathrm {top}}_*(X)\rightarrow \mathrm {CK}(n)^{\mathrm {top}}_*(X)$
is surjective. In particular,
$\mathrm P(n)^{\mathrm {top}}_*(X)\rightarrow \mathrm {CK}(n)^{\mathrm {top}}_*(X)$
is surjective. In particular,
![]() $(6)\Rightarrow (3)$
. This finishes the proof of equivalence (1)–(6). Moreover, we see that the induced surjection
$(6)\Rightarrow (3)$
. This finishes the proof of equivalence (1)–(6). Moreover, we see that the induced surjection
is in fact an isomorphism by (2) and (5) comparing the dimensions. Therefore,
![]() $(6)\Rightarrow (7)$
. Finally, for
$(6)\Rightarrow (7)$
. Finally, for
![]() $(4)\Rightarrow (8)$
, see [Reference Adams1, Lemma 13.9].
$(4)\Rightarrow (8)$
, see [Reference Adams1, Lemma 13.9].
We remark that for the periodic topological Morava K-theory, there is a canonical isomorphism
for any finite CW-complex X; see, for example, [Reference Würgler48, Section 8].
3 An analogue of Yagita’s conjecture for Morava K-theory
3.1 Yagita’s conjecture
Let K be a compact connected Lie group, T its maximal torus, and
![]() $\pi \colon K\rightarrow K/T$
the natural projection. Denote by
$\pi \colon K\rightarrow K/T$
the natural projection. Denote by
![]() $G=K_{\mathbb C}$
the corresponding (split) reductive group over
$G=K_{\mathbb C}$
the corresponding (split) reductive group over
![]() $\mathbb C$
. Kac observes in [Reference Kac16] that the results of Grothendieck [Reference Grothendieck10] imply that
$\mathbb C$
. Kac observes in [Reference Kac16] that the results of Grothendieck [Reference Grothendieck10] imply that
where the latter is a subring in
![]() $\mathrm H^*(K;\,\mathbb F_p)$
(and the isomorphism doubles the grading).
$\mathrm H^*(K;\,\mathbb F_p)$
(and the isomorphism doubles the grading).
In the article [Reference Yagita52], Yagita conjectured that the same is true for the cobordism theories. Recall that
![]() $\mathrm {MU}^*$
denotes the complex cobordism theory, and
$\mathrm {MU}^*$
denotes the complex cobordism theory, and
![]() $\Omega ^*$
denotes the algebraic cobordism theory of Levine–Morel. Yagita shows in [Reference Yagita52, Theorem 1.1] that for the ideal
$\Omega ^*$
denotes the algebraic cobordism theory of Levine–Morel. Yagita shows in [Reference Yagita52, Theorem 1.1] that for the ideal
![]() $I=(p,x_{p-1},x_{p^2-1},\ldots )$
in
$I=(p,x_{p-1},x_{p^2-1},\ldots )$
in
![]() $\mathbb L\cong \mathbb Z[x_1,x_2,\ldots ]$
and for a simply-connected compact Lie group K, one has an isomorphism
$\mathbb L\cong \mathbb Z[x_1,x_2,\ldots ]$
and for a simply-connected compact Lie group K, one has an isomorphism
Then he remarks that the same seems to be true without ‘
![]() $/I^2$
’.
$/I^2$
’.
In the present article, we consider the following analogue of the above statements for the Morava K-theory.
Conjecture 1. Let K be a compact connected Lie group, T its maximal torus, and
![]() $\pi \colon K\rightarrow K/T$
the natural projection. Denote by
$\pi \colon K\rightarrow K/T$
the natural projection. Denote by
![]() $G=K_{\mathbb C}$
the corresponding (split) reductive group over
$G=K_{\mathbb C}$
the corresponding (split) reductive group over
![]() $\mathbb C$
. Then for
$\mathbb C$
. Then for
![]() $A=\mathrm K(n)$
or
$A=\mathrm K(n)$
or
![]() $A=\mathrm {CK}(n)$
, one has
$A=\mathrm {CK}(n)$
, one has
We will prove the above conjecture for groups
![]() $K=\mathrm {SO}(m)$
and
$K=\mathrm {SO}(m)$
and
![]() $K=\mathrm {Spin}(m)$
.
$K=\mathrm {Spin}(m)$
.
3.2 Iwasawa decomposition
As above, let K be a compact connected Lie group, T its maximal torus,
![]() $G=K_{\mathbb C}$
the corresponding reductive group with split maximal torus
$G=K_{\mathbb C}$
the corresponding reductive group with split maximal torus
![]() $T_{\mathbb C}$
, and B a Borel subgroup of G containing
$T_{\mathbb C}$
, and B a Borel subgroup of G containing
![]() $T_{\mathbb C}$
.
$T_{\mathbb C}$
.
Using the Iwasawa decomposition
![]() $G=KAN$
, see [Reference Bump3, Theorem 26.3], where
$G=KAN$
, see [Reference Bump3, Theorem 26.3], where
![]() $A\cong (\mathbb R_{>0})^{l}$
, and N is a unipotent radical of B (in particular, A and N are contractible), we conclude that
$A\cong (\mathbb R_{>0})^{l}$
, and N is a unipotent radical of B (in particular, A and N are contractible), we conclude that
![]() $E^*(G)=E^*(K)$
for any (topological) cohomology theory
$E^*(G)=E^*(K)$
for any (topological) cohomology theory
![]() $E^*$
. Since
$E^*$
. Since
![]() $B\cap K=T$
, we also conclude that
$B\cap K=T$
, we also conclude that
Lemma 3.1. Under the above identification, the natural map
is an isomorphism for
![]() $A=\mathrm {CK}(n)$
,
$A=\mathrm {CK}(n)$
,
![]() $\mathrm K(n)$
.
$\mathrm K(n)$
.
Proof. The integral cohomology of
![]() $K/T$
is a free module with a basis given by classes of Schubert varieties; in particular, it is concentrated in even degrees. Since
$K/T$
is a free module with a basis given by classes of Schubert varieties; in particular, it is concentrated in even degrees. Since
![]() $\mathrm {MU}^*(*)$
and
$\mathrm {MU}^*(*)$
and
![]() $\mathrm {CK}(n)_{\mathrm {top}}^*(*)$
are also even graded, the Atiyah–Hirzebruch spectral sequences
$\mathrm {CK}(n)_{\mathrm {top}}^*(*)$
are also even graded, the Atiyah–Hirzebruch spectral sequences
collapse at the second page for
![]() $A=\mathrm {MU}$
,
$A=\mathrm {MU}$
,
![]() $\mathrm {CK}(n)_{\mathrm {top}}$
. In particular, the natural map
$\mathrm {CK}(n)_{\mathrm {top}}$
. In particular, the natural map
is surjective.
The Bruhat decomposition gives a cellular decomposition for
![]() $K/T$
; therefore, the natural map
$K/T$
; therefore, the natural map
![]() $\Omega ^*(G/B)\rightarrow \mathrm {MU}^*(K/T)$
is an isomorphism by [Reference Hornbostel and Kiritchenko12, Theorem 6.1]. Then the induced map
$\Omega ^*(G/B)\rightarrow \mathrm {MU}^*(K/T)$
is an isomorphism by [Reference Hornbostel and Kiritchenko12, Theorem 6.1]. Then the induced map
![]() $\mathrm {CK}(n)^*(G/B)\rightarrow \mathrm {CK}(n)_{\mathrm {top}}^*(K/T)$
is a surjective map between free
$\mathrm {CK}(n)^*(G/B)\rightarrow \mathrm {CK}(n)_{\mathrm {top}}^*(K/T)$
is a surjective map between free
![]() $\mathbb {F}_2[v_n]$
-modules of the same rank (cf. [Reference Calmès, Petrov and Zainoulline4, Lemma 13.7], Proposition 2.4); therefore, it is also an isomorphism.
$\mathbb {F}_2[v_n]$
-modules of the same rank (cf. [Reference Calmès, Petrov and Zainoulline4, Lemma 13.7], Proposition 2.4); therefore, it is also an isomorphism.
Taking the localization by the powers of
![]() $v_n$
, we conclude that
$v_n$
, we conclude that
is an isomorphism as well.
We can summarize the discussion above with the following result.
Proposition 3.2. In the above notation, let
![]() $A=\mathrm K(n)$
or
$A=\mathrm K(n)$
or
![]() $A=\mathrm {CK}(n)$
. Let
$A=\mathrm {CK}(n)$
. Let
![]() $\pi \colon K\rightarrow K/T$
denote the natural projection, and consider the diagram
$\pi \colon K\rightarrow K/T$
denote the natural projection, and consider the diagram
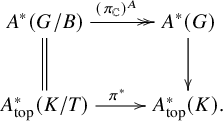
Then
![]() $\pi ^*\big (A^*_{\mathrm {top}}(K/T)\big )$
is isomorphic to the image of
$\pi ^*\big (A^*_{\mathrm {top}}(K/T)\big )$
is isomorphic to the image of
![]() $A^*(G)$
in
$A^*(G)$
in
![]() $A^*_{\mathrm {top}}(K)$
.
$A^*_{\mathrm {top}}(K)$
.
Corollary 3.3. Conjecture 1 is equivalent to the injectivity of the natural map
![]() $A^*(G)\rightarrow A^*_{\mathrm {top}}(K)$
.
$A^*(G)\rightarrow A^*_{\mathrm {top}}(K)$
.
3.3 Connective Morava K-theory of orthogonal groups
In [Reference Geldhauser, Lavrenov, Petrov and Sechin9, Theorem 6.13], we computed the algebraic periodic Morava K-theory of special orthogonal groups
![]() $\mathrm K(n)^*(\mathrm {SO}_m)$
. We can also compute the connective Morava K-theory of
$\mathrm K(n)^*(\mathrm {SO}_m)$
. We can also compute the connective Morava K-theory of
![]() $\mathrm {SO}_m$
as a simple corollary of the techniques of [Reference Geldhauser, Lavrenov, Petrov and Sechin9].
$\mathrm {SO}_m$
as a simple corollary of the techniques of [Reference Geldhauser, Lavrenov, Petrov and Sechin9].
Recall that
for
![]() $s=\lfloor \frac {m-1}{2}\rfloor $
, and
$s=\lfloor \frac {m-1}{2}\rfloor $
, and
![]() $e_k=0$
for
$e_k=0$
for
![]() $k>s$
. We will also need the following results.
$k>s$
. We will also need the following results.
Lemma 3.4. Let
![]() $m\in \mathbb N\setminus 0$
and let Q denote a split projective quadric of dimension
$m\in \mathbb N\setminus 0$
and let Q denote a split projective quadric of dimension
![]() $m-2$
. Denote by
$m-2$
. Denote by
![]() $l\in \mathrm {Ch}(Q)$
the class of the maximal isotropic subspace in Q. Then the following results hold.
$l\in \mathrm {Ch}(Q)$
the class of the maximal isotropic subspace in Q. Then the following results hold.
-
1. The pullback
along the canonical map $$ \begin{align*}\mathrm{Ch}^*(Q)\rightarrow\mathrm{Ch}^*(\mathrm{SO}_m) \end{align*} $$
$$ \begin{align*}\mathrm{Ch}^*(Q)\rightarrow\mathrm{Ch}^*(\mathrm{SO}_m) \end{align*} $$
 $\mathrm {SO}_m\rightarrow Q$
sends l to
$\mathrm {SO}_m\rightarrow Q$
sends l to
 $e_s$
.
$e_s$
.
-
2. Let
 $n\in \mathbb N\setminus 0$
be such that
$n\in \mathbb N\setminus 0$
be such that
 $m\geq 2^{n+1}+1$
. Then the canonical map sends
$m\geq 2^{n+1}+1$
. Then the canonical map sends $$ \begin{align*}\mathrm{CK}(n)^*(Q)\rightarrow\mathrm{CK}(n)^*(\mathrm{SO}_m) \end{align*} $$
$$ \begin{align*}\mathrm{CK}(n)^*(Q)\rightarrow\mathrm{CK}(n)^*(\mathrm{SO}_m) \end{align*} $$
 $v_nl$
and
$v_nl$
and
 $l^2$
to
$l^2$
to
 $0$
.
$0$
.
-
3. For any
 $n\in \mathbb N\setminus 0$
, let x denote the image of l under the canonical map Then
$n\in \mathbb N\setminus 0$
, let x denote the image of l under the canonical map Then $$ \begin{align*}\mathrm{CK}(n)^*(Q)\rightarrow\mathrm{CK}(n)^*(\mathrm{SO}_m). \end{align*} $$
$$ \begin{align*}\mathrm{CK}(n)^*(Q)\rightarrow\mathrm{CK}(n)^*(\mathrm{SO}_m). \end{align*} $$
 $\mathrm {CK}(n)^*(\mathrm {SO}_m)/x\cong \mathrm {CK}(n)^*(\mathrm {SO}_{m-2}).$
$\mathrm {CK}(n)^*(\mathrm {SO}_m)/x\cong \mathrm {CK}(n)^*(\mathrm {SO}_{m-2}).$
Proof. For (1), see [Reference Petrov and Semenov29, Lemma 7.2]. The proof of [Reference Geldhauser, Lavrenov, Petrov and Sechin9, Theorem 5.1] can be repeated verbatim to obtain (2). For (3), see [Reference Geldhauser, Lavrenov, Petrov and Sechin9, Proposition 5.2].
Next, we prove the following theorem.
Theorem 3.5. For all n,
![]() $m\in \mathbb N\setminus 0$
the ring
$m\in \mathbb N\setminus 0$
the ring
![]() $\mathrm {CK}(n)^*(\mathrm {SO}_m)$
is (non-canonically) isomorphic to
$\mathrm {CK}(n)^*(\mathrm {SO}_m)$
is (non-canonically) isomorphic to
where
![]() $s=\lfloor \frac {m-1}{2}\rfloor $
, and
$s=\lfloor \frac {m-1}{2}\rfloor $
, and
![]() $e_k=0$
for
$e_k=0$
for
![]() $k>s$
.
$k>s$
.
Proof. For
![]() $m\leq 2^{n+1}$
, see [Reference Geldhauser, Lavrenov, Petrov and Sechin9, Theorem 6.10]. For
$m\leq 2^{n+1}$
, see [Reference Geldhauser, Lavrenov, Petrov and Sechin9, Theorem 6.10]. For
![]() $m\geq 2^{n+1}+1$
, we will argue by induction.
$m\geq 2^{n+1}+1$
, we will argue by induction.
In the notation of Lemma 3.4, consider arbitrary lifts
![]() $\widetilde e_i$
of the elements
$\widetilde e_i$
of the elements
![]() ${e_i\in \mathrm {CK}(n)^*(\mathrm {SO}_{m-2})}$
to
${e_i\in \mathrm {CK}(n)^*(\mathrm {SO}_{m-2})}$
to
![]() $\mathrm {CK}(n)^*(\mathrm {SO}_m)$
. These lifts together with x generate
$\mathrm {CK}(n)^*(\mathrm {SO}_m)$
. These lifts together with x generate
![]() $\mathrm {CK}(n)^*(\mathrm {SO}_m)$
as an algebra.
$\mathrm {CK}(n)^*(\mathrm {SO}_m)$
as an algebra.
First, we will construct a map from R to
![]() $\mathrm {CK}(n)^*(\mathrm {SO}_m)$
sending
$\mathrm {CK}(n)^*(\mathrm {SO}_m)$
sending
![]() $e_i$
to
$e_i$
to
![]() $\widetilde e_i$
for
$\widetilde e_i$
for
![]() $i<s$
, and sending
$i<s$
, and sending
![]() $e_s$
to x.
$e_s$
to x.
Using Lemma 3.4 (2) we have
![]() $v_nx=0$
and
$v_nx=0$
and
![]() $x^2=0$
.
$x^2=0$
.
We claim that
![]() $v_n\widetilde e_i=0$
for
$v_n\widetilde e_i=0$
for
![]() $2^n\leq i<s$
. Using the inductive assumption, we obtain
$2^n\leq i<s$
. Using the inductive assumption, we obtain
![]() $v_n\widetilde e_i=xz$
for some
$v_n\widetilde e_i=xz$
for some
![]() $z\in \mathrm {CK}(n)^*(\mathrm {SO}_m)$
. Decompose z as a linear combination of monomials in
$z\in \mathrm {CK}(n)^*(\mathrm {SO}_m)$
. Decompose z as a linear combination of monomials in
![]() $\widetilde e_i$
and x. Since
$\widetilde e_i$
and x. Since
![]() $v_nx=0$
, we can assume that this linear combination has
$v_nx=0$
, we can assume that this linear combination has
![]() $\mathbb F_2$
-coefficients, rather than just
$\mathbb F_2$
-coefficients, rather than just
![]() $\mathbb F_2[v_n]$
-. Moreover, since
$\mathbb F_2[v_n]$
-. Moreover, since
![]() $x^2=0$
, we can assume that this linear combination consists only of monomials in
$x^2=0$
, we can assume that this linear combination consists only of monomials in
![]() $\widetilde e_i$
(and not in x). However, the image of
$\widetilde e_i$
(and not in x). However, the image of
![]() $xz$
in
$xz$
in
![]() $\mathrm {Ch}^*(\mathrm {SO}_m)$
is
$\mathrm {Ch}^*(\mathrm {SO}_m)$
is
![]() $0$
. In other words, the image of z in
$0$
. In other words, the image of z in
![]() $\mathrm {Ch}^*(\mathrm {SO}_m)$
is a linear combination in
$\mathrm {Ch}^*(\mathrm {SO}_m)$
is a linear combination in
![]() $e_1,\ldots ,e_{s-1}$
which is annihilated by
$e_1,\ldots ,e_{s-1}$
which is annihilated by
![]() $e_s$
. This can only happen if the image of z in
$e_s$
. This can only happen if the image of z in
![]() $\mathrm {Ch}^*(\mathrm {SO}_m)$
is zero. In other words, z is divisible by
$\mathrm {Ch}^*(\mathrm {SO}_m)$
is zero. In other words, z is divisible by
![]() $v_n$
, but this implies that
$v_n$
, but this implies that
![]() $xz=0$
.
$xz=0$
.
Similarly, one shows that
![]() $\widetilde e_i^2-\widetilde e_{2i}=0$
for
$\widetilde e_i^2-\widetilde e_{2i}=0$
for
![]() $2i<s$
. Finally, we have to show that
$2i<s$
. Finally, we have to show that
![]() $\widetilde e_{s/2}^{\,2}=x$
for s even. By induction, we know that
$\widetilde e_{s/2}^{\,2}=x$
for s even. By induction, we know that
![]() $\widetilde e_{s/2}^{\,2}=xz$
for some z. Then
$\widetilde e_{s/2}^{\,2}=xz$
for some z. Then
![]() $\widetilde e_{s/2}^{\,2}-x=x(z-1)$
, and we can argue for
$\widetilde e_{s/2}^{\,2}-x=x(z-1)$
, and we can argue for
![]() $z-1$
as above to obtain the claim.
$z-1$
as above to obtain the claim.
In other words, the map from R to
![]() $\mathrm {CK}(n)^*(\mathrm {SO}_m)$
is well defined (and surjective). Then
$\mathrm {CK}(n)^*(\mathrm {SO}_m)$
is well defined (and surjective). Then
![]() $\mathrm {CK}(n)^*(\mathrm {SO}_m)=R/(f_i)$
for some
$\mathrm {CK}(n)^*(\mathrm {SO}_m)=R/(f_i)$
for some
![]() $f_1,\ldots ,f_k\in R$
. However, the images of
$f_1,\ldots ,f_k\in R$
. However, the images of
![]() $f_i$
in
$f_i$
in
![]() $\mathrm {CK}(n)^*(\mathrm {SO}_{m-2})$
should also be
$\mathrm {CK}(n)^*(\mathrm {SO}_{m-2})$
should also be
![]() $0$
; therefore,
$0$
; therefore,
![]() $f_i=e_sg_i$
for some
$f_i=e_sg_i$
for some
![]() $g_i$
by induction. We can again assume that
$g_i$
by induction. We can again assume that
![]() $g_i$
are polynomials in
$g_i$
are polynomials in
![]() $e_i$
for
$e_i$
for
![]() $i<s$
with
$i<s$
with
![]() $\mathbb F_2$
-coefficients. However,
$\mathbb F_2$
-coefficients. However,
![]() $f_i$
should equal
$f_i$
should equal
![]() $0$
modulo
$0$
modulo
![]() $v_n$
, since we can specialize
$v_n$
, since we can specialize
![]() $\mathrm {CK}(n)^*(\mathrm {SO}_m)$
to
$\mathrm {CK}(n)^*(\mathrm {SO}_m)$
to
![]() $\mathrm {Ch}^*(\mathrm {SO}_m)$
. This again implies that
$\mathrm {Ch}^*(\mathrm {SO}_m)$
. This again implies that
![]() $g_i$
are divisible by
$g_i$
are divisible by
![]() $v_n$
, and therefore,
$v_n$
, and therefore,
![]() $f_i=0$
.
$f_i=0$
.
3.4 Injectivity Theorem
In this subsection we will prove Conjecture 1 for special othogonal and spinor groups.
Lemma 3.6. Assume that for a compact connected Lie group K the Atiyah–Hirzebruch spectral sequence
![]() $\mathrm H^p\big (K;\,\mathrm K(n)_q^{\mathrm {top}}(*)\big )\Rightarrow \mathrm K(n)_{\mathrm {top}}^{p+q}(K)$
collapses at the second page. Then the natural maps
$\mathrm H^p\big (K;\,\mathrm K(n)_q^{\mathrm {top}}(*)\big )\Rightarrow \mathrm K(n)_{\mathrm {top}}^{p+q}(K)$
collapses at the second page. Then the natural maps
are injective.
Proof. Let
![]() $G=K_{\mathbb C}$
denote the corresponding reductive group. We conclude by Proposition 2.3 that
$G=K_{\mathbb C}$
denote the corresponding reductive group. We conclude by Proposition 2.3 that
![]() $\mathrm {CK}(n)_{\mathrm {top}}^*(K)$
is a free
$\mathrm {CK}(n)_{\mathrm {top}}^*(K)$
is a free
![]() $\mathbb F_2[v_n]$
-module. Consider the diagram
$\mathbb F_2[v_n]$
-module. Consider the diagram
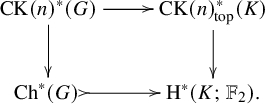
Take an element
![]() $x\in \mathrm {CK}(n)^*(G)$
which is not divisible by
$x\in \mathrm {CK}(n)^*(G)$
which is not divisible by
![]() $v_n$
. Then the injectivity of the bottom horizontal arrow implies that the image of x in
$v_n$
. Then the injectivity of the bottom horizontal arrow implies that the image of x in
![]() $\mathrm {CK}(n)_{\mathrm {top}}^*(K)$
cannot be zero. Since
$\mathrm {CK}(n)_{\mathrm {top}}^*(K)$
cannot be zero. Since
![]() $\mathrm {CK}(n)_{\mathrm {top}}^*(K)$
cannot have a
$\mathrm {CK}(n)_{\mathrm {top}}^*(K)$
cannot have a
![]() $v_n$
-torsion, we conclude that the top horizontal arrow is injective.
$v_n$
-torsion, we conclude that the top horizontal arrow is injective.
Finally, since
![]() $\mathrm {CK}(n)_{\mathrm {top}}^*(K)$
cannot have a
$\mathrm {CK}(n)_{\mathrm {top}}^*(K)$
cannot have a
![]() $v_n$
-torsion, and the natural map
$v_n$
-torsion, and the natural map
coincides with the localization, we conclude that this map is injective. This implies that
is also injective.
Remark 3.7. In this paper, we are only interested in orthogonal groups, and therefore only work with Morava K-theories for
![]() $p=2$
. However, we remark that the above argument clearly remains valid for odd p.
$p=2$
. However, we remark that the above argument clearly remains valid for odd p.
Theorem 3.8. Let
![]() $K=\mathrm {SO}(m)$
or
$K=\mathrm {SO}(m)$
or
![]() $K=\mathrm {Spin}(m)$
(for any
$K=\mathrm {Spin}(m)$
(for any
![]() $m\in \mathbb N$
), and
$m\in \mathbb N$
), and
![]() $G=K_{\mathbb C}$
. Then the natural maps
$G=K_{\mathbb C}$
. Then the natural maps
are injective.
Proof. First, assume that
![]() $m\leq 2^{n+1}$
. Under this condition, the Atiyah–Hirzebruch spectral sequence
$m\leq 2^{n+1}$
. Under this condition, the Atiyah–Hirzebruch spectral sequence
![]() $\mathrm H^p\big (K;\,\mathrm K(n)_q^{\mathrm {top}}(*)\big )\Rightarrow \mathrm K(n)_{\mathrm {top}}^{p+q}(K)$
collapses by [Reference Nishimoto27, Theorems 2.4 and 3.2]. Therefore, the claim follows from Lemma 3.6.
$\mathrm H^p\big (K;\,\mathrm K(n)_q^{\mathrm {top}}(*)\big )\Rightarrow \mathrm K(n)_{\mathrm {top}}^{p+q}(K)$
collapses by [Reference Nishimoto27, Theorems 2.4 and 3.2]. Therefore, the claim follows from Lemma 3.6.
Next, consider the case
![]() $m>2^{n+1}$
, and assume that the natural map from the algebraic Morava K-theory
$m>2^{n+1}$
, and assume that the natural map from the algebraic Morava K-theory
![]() $\mathrm K(n)^*(G)$
to the topological one
$\mathrm K(n)^*(G)$
to the topological one
![]() $\mathrm K(n)^*_{\mathrm {top}}(K)$
is not injective. Consider the natural inclusion of
$\mathrm K(n)^*_{\mathrm {top}}(K)$
is not injective. Consider the natural inclusion of
![]() $K_0=\mathrm {SO}(2^{n+1})$
for m even or
$K_0=\mathrm {SO}(2^{n+1})$
for m even or
![]() $K_0=\mathrm {SO}(2^{n+1}-1)$
for m odd into K, and denote
$K_0=\mathrm {SO}(2^{n+1}-1)$
for m odd into K, and denote
![]() $G_0=(K_0)_{\mathbb C}$
. Consider the following diagram
$G_0=(K_0)_{\mathbb C}$
. Consider the following diagram
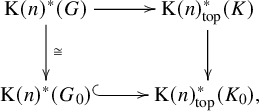
where the left vertical arrow is an isomorphism by [Reference Geldhauser, Lavrenov, Petrov and Sechin9, Theorem 5.1]. Then a simple diagram chase provides a contradiction.
Finally, assume that the natural map from
![]() $\mathrm {CK}(n)^*(G)$
to
$\mathrm {CK}(n)^*(G)$
to
![]() $\mathrm {CK}(n)^*_{\mathrm {top}}(K)$
is not injective, and take an element x in the kernel. Since x maps to
$\mathrm {CK}(n)^*_{\mathrm {top}}(K)$
is not injective, and take an element x in the kernel. Since x maps to
![]() $0$
in
$0$
in
![]() $\mathrm {Ch}^*(G)$
, we conclude that
$\mathrm {Ch}^*(G)$
, we conclude that
![]() $x=v_ny$
for some y. However, since the image of x in
$x=v_ny$
for some y. However, since the image of x in
![]() $\mathrm {K}(n)^*(G)$
is also
$\mathrm {K}(n)^*(G)$
is also
![]() $0$
, we conclude that x (and therefore y) is a
$0$
, we conclude that x (and therefore y) is a
![]() $v_n^{\mathbb Z}$
-torsion. However, using Theorem 3.5, we conclude that if y is a
$v_n^{\mathbb Z}$
-torsion. However, using Theorem 3.5, we conclude that if y is a
![]() $v_n^{\mathbb Z}$
-torsion, then in fact,
$v_n^{\mathbb Z}$
-torsion, then in fact,
![]() $v_ny=0$
. This finishes the proof.
$v_ny=0$
. This finishes the proof.
Conjecture 1 for special othogonal and spinor groups now follows from Corollary 3.3.
Remark 3.9. Observe that in the case
![]() $m>2^{n+1}$
, the proof of Theorem 3.8 relies on the results of [Reference Geldhauser, Lavrenov, Petrov and Sechin9]. We do not know how to prove Conjecture 1 without actually computing
$m>2^{n+1}$
, the proof of Theorem 3.8 relies on the results of [Reference Geldhauser, Lavrenov, Petrov and Sechin9]. We do not know how to prove Conjecture 1 without actually computing
![]() $\mathrm K(n)^*(G)$
(as a module).
$\mathrm K(n)^*(G)$
(as a module).
4 Computation of the co-multiplication
4.1 Statement of results
In [Reference Geldhauser, Lavrenov, Petrov and Sechin9, Theorem 6.13], the algebra structure of
![]() $\mathrm K(n)^*(\mathrm {SO}_m)$
is described. As an application of the Yagita conjecture, we can also deduce the co-algebra structure using results in topology.
$\mathrm K(n)^*(\mathrm {SO}_m)$
is described. As an application of the Yagita conjecture, we can also deduce the co-algebra structure using results in topology.
Theorem 4.1. The algebra structure of
![]() $\mathrm K(n)^*(\mathrm {SO}_m)$
is given by
$\mathrm K(n)^*(\mathrm {SO}_m)$
is given by
where
![]() $s=\mathrm {min}\left (\lfloor \frac {m-1}{2}\rfloor ,\,2^{n}-1\right )$
and
$s=\mathrm {min}\left (\lfloor \frac {m-1}{2}\rfloor ,\,2^{n}-1\right )$
and
![]() $e_{2i}$
stands for
$e_{2i}$
stands for
![]() $0$
if
$0$
if
![]() $2i>s$
. The reduced co-multiplication
$2i>s$
. The reduced co-multiplication
![]() $\widetilde \Delta (x)=\Delta (x)-x\otimes 1-1\otimes x$
is given by
$\widetilde \Delta (x)=\Delta (x)-x\otimes 1-1\otimes x$
is given by
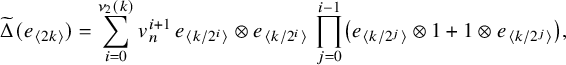 $$ \begin{align*}\widetilde\Delta(e_{\langle 2k\rangle})=\sum_{i=0}^{\nu_2(k)}v_n^{i+1}\,e_{\langle k/2^{i}\rangle}\otimes e_{\langle k/2^{i}\rangle}\,\prod_{j=0}^{i-1}\left(e_{\langle k/2^{j}\rangle}\otimes1+1\otimes e_{\langle k/2^{j}\rangle}\right), \end{align*} $$
$$ \begin{align*}\widetilde\Delta(e_{\langle 2k\rangle})=\sum_{i=0}^{\nu_2(k)}v_n^{i+1}\,e_{\langle k/2^{i}\rangle}\otimes e_{\langle k/2^{i}\rangle}\,\prod_{j=0}^{i-1}\left(e_{\langle k/2^{j}\rangle}\otimes1+1\otimes e_{\langle k/2^{j}\rangle}\right), \end{align*} $$
where
![]() $\langle t\rangle $
stands for
$\langle t\rangle $
stands for
![]() $2^n-1-t$
,
$2^n-1-t$
,
![]() $k>0$
and
$k>0$
and
![]() $\nu _2(k)$
is a
$\nu _2(k)$
is a
![]() $2$
-adic valuation of k, that is,
$2$
-adic valuation of k, that is,
![]() $k/2^{\,\nu _2(k)}$
is an odd integer, and
$k/2^{\,\nu _2(k)}$
is an odd integer, and
Moreover,
![]() $e_1$
coincides with the first Chern class
$e_1$
coincides with the first Chern class
![]() $c_1^{\mathrm {K}(n)}(e_1^{\mathrm {CH}})$
of the generator
$c_1^{\mathrm {K}(n)}(e_1^{\mathrm {CH}})$
of the generator
![]() $e_1^{\mathrm {CH}}$
of
$e_1^{\mathrm {CH}}$
of
![]() $\mathrm {CH}^1(\mathrm {SO}_m;\mathbb Z)=\mathrm {Pic}(\mathrm {SO}_m)$
.
$\mathrm {CH}^1(\mathrm {SO}_m;\mathbb Z)=\mathrm {Pic}(\mathrm {SO}_m)$
.
For the computation of
![]() $\mathrm {CH}^1(\mathrm {SO}_m;\mathbb Z)$
, see [Reference Marlin21, Théorème 7], and
$\mathrm {CH}^1(\mathrm {SO}_m;\mathbb Z)$
, see [Reference Marlin21, Théorème 7], and
![]() $c_1^{\mathrm {K}(n)}$
is defined in [Reference Levine and Morel19, Chapter I, Subsection 1.1]).
$c_1^{\mathrm {K}(n)}$
is defined in [Reference Levine and Morel19, Chapter I, Subsection 1.1]).
We remark that as a corollary, we also obtain the Hopf algebra structure of
(cf. [Reference Geldhauser, Lavrenov, Petrov and Sechin9, Corollary 6.15]). In the following, we provide a few examples.
Example 4.2. It is easy to see that all
![]() $e_{2j-1}^2=e_{4j-2}\in \mathrm {K}(n)^*(\mathrm {SO}_m)$
are primitive. Indeed, let
$e_{2j-1}^2=e_{4j-2}\in \mathrm {K}(n)^*(\mathrm {SO}_m)$
are primitive. Indeed, let
![]() $2j-1=\langle 2k\rangle =2^n-1-2k$
for some
$2j-1=\langle 2k\rangle =2^n-1-2k$
for some
![]() $0\leq k\leq 2^{n-1}-1$
. Then
$0\leq k\leq 2^{n-1}-1$
. Then
![]() $2\langle k/2^i\rangle \geq 2^{n}$
for all
$2\langle k/2^i\rangle \geq 2^{n}$
for all
![]() $i\geq 0$
, and therefore,
$i\geq 0$
, and therefore,
Similarly, for
![]() $m\leq 2^n$
, all
$m\leq 2^n$
, all
![]() $e_{2i-1}$
are primitive.
$e_{2i-1}$
are primitive.
Example 4.3. Since
![]() $e_1^{2^n}=0$
in
$e_1^{2^n}=0$
in
![]() $\mathrm K(n)^*(\mathrm {SO}_m)$
, we conclude that
$\mathrm K(n)^*(\mathrm {SO}_m)$
, we conclude that
by, for example, [Reference Petrov and Semenov28, Subsection 2.3] (cf. also [Reference Geldhauser, Lavrenov, Petrov and Sechin9, Lemma 6.12]). Similarly, for odd j, we have
4.2 Homology of special orthogonal groups
We remark that the topological Morava K-theory of the special orthogonal group is computed as an
![]() $\mathbb F_2[v_n^{\pm 1}]$
-module in [Reference Rao33, Theorem 1] and [Reference Nishimoto27, Theorem 2.10]. The algebra and co-algebra structure of
$\mathbb F_2[v_n^{\pm 1}]$
-module in [Reference Rao33, Theorem 1] and [Reference Nishimoto27, Theorem 2.10]. The algebra and co-algebra structure of
![]() $\mathrm K(n)^*_{\mathrm {top}}\big (\mathrm {SO}(m)\big )$
are not known for an arbitrary m; see [Reference Rao36, Reference Rao37] for partial results.
$\mathrm K(n)^*_{\mathrm {top}}\big (\mathrm {SO}(m)\big )$
are not known for an arbitrary m; see [Reference Rao36, Reference Rao37] for partial results.
However, for
![]() $m=2^{n+1}-1$
, both algebra and co-algebra structure of the topological Morava K-theory
$m=2^{n+1}-1$
, both algebra and co-algebra structure of the topological Morava K-theory
![]() $\mathrm K(n)^*_{\mathrm {top}}\big (\mathrm {SO}(2^{n+1}-1)\big )$
are known by [Reference Rao35]. Due to the stabilization of the algebraic Morava K-theory [Reference Geldhauser, Lavrenov, Petrov and Sechin9, Theorem 5.1], this is already sufficient for the computation of the co-multiplication of
$\mathrm K(n)^*_{\mathrm {top}}\big (\mathrm {SO}(2^{n+1}-1)\big )$
are known by [Reference Rao35]. Due to the stabilization of the algebraic Morava K-theory [Reference Geldhauser, Lavrenov, Petrov and Sechin9, Theorem 5.1], this is already sufficient for the computation of the co-multiplication of
![]() $\mathrm K(n)^*\big (\mathrm {SO}_m\big )$
for all m.
$\mathrm K(n)^*\big (\mathrm {SO}_m\big )$
for all m.
First, we recall the Hopf algebra structure of
![]() $\mathrm H_*\big (\mathrm {SO}(2^{n+1}-1);\,\mathbb F_2\big )$
.
$\mathrm H_*\big (\mathrm {SO}(2^{n+1}-1);\,\mathbb F_2\big )$
.
For a Hopf algebra
![]() $H=\mathbb F_2[x]/x^{2^k}$
with x primitive, we denote the dual basis of the dual Hopf algebra
$H=\mathbb F_2[x]/x^{2^k}$
with x primitive, we denote the dual basis of the dual Hopf algebra
![]() $H^\vee $
by
$H^\vee $
by
![]() $\gamma _j$
(i.e.,
$\gamma _j$
(i.e.,
![]() $\langle x^i,\,\gamma _j\rangle =\delta _{ij}$
). One easily checks that the multiplication and the co-multiplication in
$\langle x^i,\,\gamma _j\rangle =\delta _{ij}$
). One easily checks that the multiplication and the co-multiplication in
![]() $H^\vee $
are given by
$H^\vee $
are given by
 $$ \begin{align*}\gamma_i\cdot\gamma_j=\frac{(i+j)!}{i!j!}\gamma_{i+j}\ \text{ and }\ \Delta(\gamma_k)=\sum_{t=0}^k\gamma_t\otimes\gamma_{k-t}. \end{align*} $$
$$ \begin{align*}\gamma_i\cdot\gamma_j=\frac{(i+j)!}{i!j!}\gamma_{i+j}\ \text{ and }\ \Delta(\gamma_k)=\sum_{t=0}^k\gamma_t\otimes\gamma_{k-t}. \end{align*} $$
Such an algebra
![]() $H^\vee $
is called the algebra of divided powers, and we denote it by
$H^\vee $
is called the algebra of divided powers, and we denote it by
![]() $\Gamma _k$
. By [Reference Kac16, Theorem 6 (d)], we know that
$\Gamma _k$
. By [Reference Kac16, Theorem 6 (d)], we know that
where
 $$ \begin{align} k_i=\left\lfloor\mathrm{log}_2\left(\frac{2^{n+1}-2}{2i-1}\right)\right\rfloor \end{align} $$
$$ \begin{align} k_i=\left\lfloor\mathrm{log}_2\left(\frac{2^{n+1}-2}{2i-1}\right)\right\rfloor \end{align} $$
for
![]() $i\leq 2^{n-1}$
. Set additionally
$i\leq 2^{n-1}$
. Set additionally
![]() $k_i=0$
for
$k_i=0$
for
![]() $i>2^{n-1}$
(in fact, formula (4.1) also gives
$i>2^{n-1}$
(in fact, formula (4.1) also gives
![]() $k_i=0$
for
$k_i=0$
for
![]() $i>2^{n-1}$
). Then
$i>2^{n-1}$
). Then
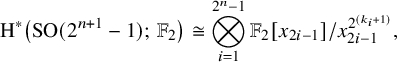 $$ \begin{align*}\mathrm H^*\big(\mathrm{SO}(2^{n+1}-1);\,\mathbb F_2\big)\cong\bigotimes_{i=1}^{2^n-1}\mathbb F_2[x_{2i-1}]/x_{2i-1}^{2^{(k_i+1)}}, \end{align*} $$
$$ \begin{align*}\mathrm H^*\big(\mathrm{SO}(2^{n+1}-1);\,\mathbb F_2\big)\cong\bigotimes_{i=1}^{2^n-1}\mathbb F_2[x_{2i-1}]/x_{2i-1}^{2^{(k_i+1)}}, \end{align*} $$
and dualizing the above formula, we obtain
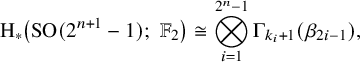 $$ \begin{align} \mathrm H_*\big(\mathrm{SO}(2^{n+1}-1);\,\,\mathbb F_2\big)\cong\bigotimes_{i=1}^{2^n-1}\Gamma_{k_i+1}(\beta_{2i-1}), \end{align} $$
$$ \begin{align} \mathrm H_*\big(\mathrm{SO}(2^{n+1}-1);\,\,\mathbb F_2\big)\cong\bigotimes_{i=1}^{2^n-1}\Gamma_{k_i+1}(\beta_{2i-1}), \end{align} $$
where
![]() $\Gamma _{k_i+1}(\beta _{2i-1})$
denotes the dual Hopf algebra to
$\Gamma _{k_i+1}(\beta _{2i-1})$
denotes the dual Hopf algebra to
![]() $\mathbb F_2[x_{2i-1}]/x_{2i-1}^{2^{(k_i+1)}}$
, and the basis elements of
$\mathbb F_2[x_{2i-1}]/x_{2i-1}^{2^{(k_i+1)}}$
, and the basis elements of
![]() $\Gamma _{k_i+1}(\beta _{2i-1})$
are denoted by
$\Gamma _{k_i+1}(\beta _{2i-1})$
are denoted by
![]() $\gamma _t(\beta _{2i-1})$
. We write
$\gamma _t(\beta _{2i-1})$
. We write
![]() $\beta _{2i-1}$
for
$\beta _{2i-1}$
for
![]() $\gamma _1(\beta _{2i-1})$
.
$\gamma _1(\beta _{2i-1})$
.
4.3 Rao’s Theorem
In fact, the multiplication and the co-multiplication of
are computed in [Reference Rao35]. We will reproduce this result in this subsection.
Observe also that
![]() $\mathrm P(n)^*_{\mathrm {top}}\big (\mathrm {SO}(2^{n+1}-1)\big )$
admits a canonical co-algebra structure induced by the multiplication in
$\mathrm P(n)^*_{\mathrm {top}}\big (\mathrm {SO}(2^{n+1}-1)\big )$
admits a canonical co-algebra structure induced by the multiplication in
![]() $\mathrm {SO}(2^{n+1}-1)$
; however, it is not a Hopf algebra. More precisely, the co-multiplication map
$\mathrm {SO}(2^{n+1}-1)$
; however, it is not a Hopf algebra. More precisely, the co-multiplication map
![]() $\Delta $
does not preserve the multiplication,
$\Delta $
does not preserve the multiplication,
![]() $\Delta (xy)\neq \Delta (x)\Delta (y)$
. The reason for this is that the multiplicative structure on
$\Delta (xy)\neq \Delta (x)\Delta (y)$
. The reason for this is that the multiplicative structure on
![]() $\mathrm P(n)^{\mathrm {top}}$
does not commute with a twist
$\mathrm P(n)^{\mathrm {top}}$
does not commute with a twist
![]() $\tau \colon X\wedge Y\rightarrow Y\wedge X$
(see [Reference Rao34, Corollary 1.6]).
$\tau \colon X\wedge Y\rightarrow Y\wedge X$
(see [Reference Rao34, Corollary 1.6]).
It is proven in [Reference Rao32, Theorem 1.1] that there exists a filtration on the topological homology theory
![]() $\mathrm P(n)_*^{\mathrm {top}}\big (\mathrm {SO}(2^{n+1}-1)\big )$
(which respects the multiplication and the co-multiplication) such that the graded (co-)algebra associated with this filtration is isomorphic to
$\mathrm P(n)_*^{\mathrm {top}}\big (\mathrm {SO}(2^{n+1}-1)\big )$
(which respects the multiplication and the co-multiplication) such that the graded (co-)algebra associated with this filtration is isomorphic to
![]() $\mathrm H_*\big (\mathrm {SO}(2^{n+1}-1);\,\,\mathbb F_2[v_n,v_{n+1},\ldots ]\big )$
.
$\mathrm H_*\big (\mathrm {SO}(2^{n+1}-1);\,\,\mathbb F_2[v_n,v_{n+1},\ldots ]\big )$
.
Moreover, in [Reference Rao35], the lifts of
![]() $\gamma _t(\beta _{2i-1})$
from (4.2) to
$\gamma _t(\beta _{2i-1})$
from (4.2) to
![]() $\mathrm P(n)_*^{\mathrm {top}}\big (\mathrm {SO}(2^{n+1}-1)\big )$
(which we will denote by the same symbols) are chosen in such a way, that the following theorem holds.
$\mathrm P(n)_*^{\mathrm {top}}\big (\mathrm {SO}(2^{n+1}-1)\big )$
(which we will denote by the same symbols) are chosen in such a way, that the following theorem holds.
Theorem 4.4 (Rao).
For
![]() $1\leq i\leq 2^n-1$
and
$1\leq i\leq 2^n-1$
and
![]() $1\leq t\leq 2^{k_i}$
, where
$1\leq t\leq 2^{k_i}$
, where
![]() $k_i$
are given by (4.1), there exist elements
$k_i$
are given by (4.1), there exist elements
![]() $\gamma _t(\beta _{2i-1})\in \mathrm P(n)_*^{\mathrm {top}}\big (\mathrm {SO}(2^{n+1}-1)\big )$
which lift the corresponding elements of
$\gamma _t(\beta _{2i-1})\in \mathrm P(n)_*^{\mathrm {top}}\big (\mathrm {SO}(2^{n+1}-1)\big )$
which lift the corresponding elements of
![]() $\mathrm H_*(\mathrm {SO}(2^{n+1}-1);\,\mathbb F_2)$
described in Subsection 4.2. Moreover, the following statements hold.
$\mathrm H_*(\mathrm {SO}(2^{n+1}-1);\,\mathbb F_2)$
described in Subsection 4.2. Moreover, the following statements hold.
-
1. The ordered set
(with an arbitrary choice of order) simply generates $$ \begin{align*}M=\{\gamma_{2^s}(\beta_{2i-1})\mid1\leq i\leq2^n-1,\ 0\leq s\leq k_i\} \end{align*} $$
$$ \begin{align*}M=\{\gamma_{2^s}(\beta_{2i-1})\mid1\leq i\leq2^n-1,\ 0\leq s\leq k_i\} \end{align*} $$
 $\mathrm P(n)_*^{\mathrm {top}}\big (\mathrm {SO}(2^{n+1}-1)\big )$
. By this, we mean that the monomials
$\mathrm P(n)_*^{\mathrm {top}}\big (\mathrm {SO}(2^{n+1}-1)\big )$
. By this, we mean that the monomials
 $g_1g_2\ldots g_k$
, for
$g_1g_2\ldots g_k$
, for
 $g_i<g_{i+1}\in M$
,
$g_i<g_{i+1}\in M$
,
 $k\geq 0$
, form a basis of
$k\geq 0$
, form a basis of
 $\mathrm P(n)_*^{\mathrm {top}}\big (\mathrm {SO}(2^{n+1}-1)\big )$
over
$\mathrm P(n)_*^{\mathrm {top}}\big (\mathrm {SO}(2^{n+1}-1)\big )$
over
 ${\mathbb {F}}_2[v_n,v_{n+1},\ldots ]$
.
${\mathbb {F}}_2[v_n,v_{n+1},\ldots ]$
.
-
2. For
 $1\leq i\leq 2^{n}-1$
,
$1\leq i\leq 2^{n}-1$
,
 $1\leq t\leq 2^{k_i}$
, we have
$1\leq t\leq 2^{k_i}$
, we have  $$ \begin{align*}\Delta(\gamma_t(\beta_{2i-1}))=\sum_{s=0}^t\gamma_s(\beta_{2i-1})\otimes\gamma_{t-s}(\beta_{2i-1}). \end{align*} $$
$$ \begin{align*}\Delta(\gamma_t(\beta_{2i-1}))=\sum_{s=0}^t\gamma_s(\beta_{2i-1})\otimes\gamma_{t-s}(\beta_{2i-1}). \end{align*} $$
-
3. For
 $1\leq i\leq 2^{n-1}$
,
$1\leq i\leq 2^{n-1}$
,
 $1\leq s,t< 2^{k_i}$
, we have
$1\leq s,t< 2^{k_i}$
, we have  $$ \begin{align*}\gamma_s(\beta_{2i-1})\cdot\gamma_t(\beta_{2i-1})=\frac{(s+t)!}{s!\,t!}\gamma_{s+t}(\beta_{2i-1}). \end{align*} $$
$$ \begin{align*}\gamma_s(\beta_{2i-1})\cdot\gamma_t(\beta_{2i-1})=\frac{(s+t)!}{s!\,t!}\gamma_{s+t}(\beta_{2i-1}). \end{align*} $$
-
4. For
 $1\leq i\leq 2^{n-1}$
and
$1\leq i\leq 2^{n-1}$
and
 $j=(2i-1)2^{k_i-1}-2^{n-1}$
, we have
$j=(2i-1)2^{k_i-1}-2^{n-1}$
, we have  $$ \begin{align*}\gamma_{2^{k_i}}(\beta_{2i-1})^2=[\gamma_{2^{k_i}}(\beta_{2i-1}),\,\beta_{2i-1}]\cdot\gamma_{2^{k_i}-1}(\beta_{2i-1})+v_n\gamma_2(\beta_{2j-1}). \end{align*} $$
$$ \begin{align*}\gamma_{2^{k_i}}(\beta_{2i-1})^2=[\gamma_{2^{k_i}}(\beta_{2i-1}),\,\beta_{2i-1}]\cdot\gamma_{2^{k_i}-1}(\beta_{2i-1})+v_n\gamma_2(\beta_{2j-1}). \end{align*} $$
-
5. The quotient algebra of
 $\mathrm P(n)_*^{\mathrm {top}}\big (\mathrm {SO}(2^{n+1}-1)\big )$
modulo the ideal generated by
$\mathrm P(n)_*^{\mathrm {top}}\big (\mathrm {SO}(2^{n+1}-1)\big )$
modulo the ideal generated by
 $\beta _{2i-1}$
,
$\beta _{2i-1}$
,
 $1\leq i\leq 2^n-1$
, is commutative.
$1\leq i\leq 2^n-1$
, is commutative.
Proof. For (1), see [Reference Rao35, Proposition 3.1], for (2), see [Reference Rao35, Proposition 2.4 and Lemma 3.4], for (3), see [Reference Rao35, Lemma 3.4], for (4), see [Reference Rao35, Proposition 5.8]. To obtain (5), it suffices to show that the commutators of all generators are
![]() $0$
modulo
$0$
modulo
![]() $\beta _{2i-1}$
. This is shown in [Reference Rao35, Lemmas 3.2–3.4, Corollary 5.3, Propositions 5.4–5.5, Lemma 5.7].
$\beta _{2i-1}$
. This is shown in [Reference Rao35, Lemmas 3.2–3.4, Corollary 5.3, Propositions 5.4–5.5, Lemma 5.7].
Remark 4.5. In fact, in [Reference Rao35], the rest of the algebra and co-algebra structures of
![]() $\mathrm P(n)_*^{\mathrm {top}}\big (\mathrm {SO}(2^{n+1}-1)\big )$
is also computed, but we will not need it in this paper.
$\mathrm P(n)_*^{\mathrm {top}}\big (\mathrm {SO}(2^{n+1}-1)\big )$
is also computed, but we will not need it in this paper.
It will be more convenient for us to work with
![]() $\mathrm {CK}(n)_{\mathrm {top}}$
rather than
$\mathrm {CK}(n)_{\mathrm {top}}$
rather than
![]() $\mathrm P(n)_{\mathrm {top}}$
. Recall that
$\mathrm P(n)_{\mathrm {top}}$
. Recall that
and
by Proposition 2.4.
4.4 Algebraic part of
 $\mathrm {CK}(n)_*^{\mathrm {top}}\big (\mathrm {SO}(2^{n+1}-1)\big )$
$\mathrm {CK}(n)_*^{\mathrm {top}}\big (\mathrm {SO}(2^{n+1}-1)\big )$
We recall that for a field extension
![]() $k\subseteq L$
, the restriction map
$k\subseteq L$
, the restriction map
![]() $\mathrm {res}^L_k$
induces an isomorphism on
$\mathrm {res}^L_k$
induces an isomorphism on
![]() $A^*(\mathrm {SO}_m)$
for any free theory
$A^*(\mathrm {SO}_m)$
for any free theory
![]() $A^*$
. Therefore, instead of an arbitrary field of characteristic zero, we can take
$A^*$
. Therefore, instead of an arbitrary field of characteristic zero, we can take
![]() $k=\mathbb Q$
or
$k=\mathbb Q$
or
![]() $k=\mathbb C$
. The latter choice allows us to apply Yagita’s conjecture.
$k=\mathbb C$
. The latter choice allows us to apply Yagita’s conjecture.
Recall that the natural map from
![]() $\mathrm {Ch}^*(\mathrm {SO}_{m})$
to
$\mathrm {Ch}^*(\mathrm {SO}_{m})$
to
![]() $\mathrm {H}^*(\mathrm {SO}(m);\,\mathbb F_2)$
is injective (see Subsection 3.1), and its image coincides with the set of squares in
$\mathrm {H}^*(\mathrm {SO}(m);\,\mathbb F_2)$
is injective (see Subsection 3.1), and its image coincides with the set of squares in
![]() $\mathrm {H}^*(\mathrm {SO}(m);\,\mathbb F_2)$
(cf. [Reference Kac16, Remark after Theorem 6]). In Proposition 4.6 below, we will dualize the above statement to determine the ‘algebraic part’ of
$\mathrm {H}^*(\mathrm {SO}(m);\,\mathbb F_2)$
(cf. [Reference Kac16, Remark after Theorem 6]). In Proposition 4.6 below, we will dualize the above statement to determine the ‘algebraic part’ of
![]() $\mathrm H_*(\mathrm {SO}_m;\,\mathbb F_2)$
.
$\mathrm H_*(\mathrm {SO}_m;\,\mathbb F_2)$
.
Proposition 4.6. In the notation of Subsection 4.2,
![]() $\mathrm {Ch}^*(\mathrm {SO}_{2^{n+1}-1})^\vee $
is isomorphic as a Hopf algebra to the quotient of
$\mathrm {Ch}^*(\mathrm {SO}_{2^{n+1}-1})^\vee $
is isomorphic as a Hopf algebra to the quotient of
![]() $\mathrm {H}_*(\mathrm {SO}(2^{n+1}-1);\,\mathbb F_2)$
modulo the ideal generated by
$\mathrm {H}_*(\mathrm {SO}(2^{n+1}-1);\,\mathbb F_2)$
modulo the ideal generated by
![]() $\beta _{2i-1}$
for all
$\beta _{2i-1}$
for all
![]() $1\leq i\leq 2^n-1$
.
$1\leq i\leq 2^n-1$
.
We recall the proof in the Appendix A1 for the convenience of the reader.
Corollary 4.7. In the notation of Proposition 4.6, denote by
![]() $\gamma _{t}(\alpha _{2i-1})$
the images of
$\gamma _{t}(\alpha _{2i-1})$
the images of
![]() $\gamma _{2t}(\beta _{2i-1})$
in
$\gamma _{2t}(\beta _{2i-1})$
in
![]() $\mathrm {Ch}^*(\mathrm {SO}_{2^{n+1}-1})^\vee $
for
$\mathrm {Ch}^*(\mathrm {SO}_{2^{n+1}-1})^\vee $
for
![]() $1\leq i\leq 2^{n-1}$
,
$1\leq i\leq 2^{n-1}$
,
![]() $1\leq t<2^{k_i}$
. Then
$1\leq t<2^{k_i}$
. Then
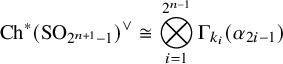 $$ \begin{align*}\mathrm{Ch}^*(\mathrm{SO}_{2^{n+1}-1})^\vee\cong\bigotimes_{i=1}^{2^{n-1}}\Gamma_{k_i}(\alpha_{2i-1}) \end{align*} $$
$$ \begin{align*}\mathrm{Ch}^*(\mathrm{SO}_{2^{n+1}-1})^\vee\cong\bigotimes_{i=1}^{2^{n-1}}\Gamma_{k_i}(\alpha_{2i-1}) \end{align*} $$
as a Hopf algebra.
Now we will prove analogues of these results for the connective Morava K-theory. As above, let
![]() $\mathrm {CK}(n)^*(\mathrm {SO}_m)^\vee $
denote the Hopf algebra over
$\mathrm {CK}(n)^*(\mathrm {SO}_m)^\vee $
denote the Hopf algebra over
![]() $\mathbb F_2[v_n]$
dual to
$\mathbb F_2[v_n]$
dual to
![]() $\mathrm {CK}(n)^*(\mathrm {SO}_m)$
. Recall that we denote
$\mathrm {CK}(n)^*(\mathrm {SO}_m)$
. Recall that we denote
![]() $\gamma _t(\beta _{2i-1})$
in homology and their lifts to
$\gamma _t(\beta _{2i-1})$
in homology and their lifts to
![]() $\mathrm {CK}(n)^{\mathrm {top}}_*(\mathrm {SO}_m)$
by the same symbols by some abuse of notation.
$\mathrm {CK}(n)^{\mathrm {top}}_*(\mathrm {SO}_m)$
by the same symbols by some abuse of notation.
Proposition 4.8. In the notation of Theorem 4.4,
![]() $\mathrm {CK}(n)^*(\mathrm {SO}_{2^{n+1}-1})^\vee $
is isomorphic to the quotient of
$\mathrm {CK}(n)^*(\mathrm {SO}_{2^{n+1}-1})^\vee $
is isomorphic to the quotient of
![]() $\mathrm {CK}(n)_*^{\mathrm {top}}(\mathrm {SO}(2^{n+1}-1))$
modulo the ideal generated by
$\mathrm {CK}(n)_*^{\mathrm {top}}(\mathrm {SO}(2^{n+1}-1))$
modulo the ideal generated by
![]() $\beta _{2i-1}$
for all
$\beta _{2i-1}$
for all
![]() $1\leq i\leq 2^n-1$
as an algebra and a co-algebra.
$1\leq i\leq 2^n-1$
as an algebra and a co-algebra.
Proof. Consider the map
dual to the natural inclusion
![]() $\mathrm {CK}(n)^*(\mathrm {SO}_{2^{n+1}-1})\hookrightarrow \mathrm {CK}(n)_{\mathrm {top}}^*(\mathrm {SO}({2^{n+1}-1}))$
, and denote
$\mathrm {CK}(n)^*(\mathrm {SO}_{2^{n+1}-1})\hookrightarrow \mathrm {CK}(n)_{\mathrm {top}}^*(\mathrm {SO}({2^{n+1}-1}))$
, and denote
Using Propositions 2.4 and 4.6, we conclude that
![]() $\mathrm {CK}(n)^*(\mathrm {SO}_{2^{n+1}-1})^\vee $
is generated over
$\mathrm {CK}(n)^*(\mathrm {SO}_{2^{n+1}-1})^\vee $
is generated over
![]() $\mathbb F_2[v_n]$
by the monomials
$\mathbb F_2[v_n]$
by the monomials
![]() $g_1\ldots g_k$
, where
$g_1\ldots g_k$
, where
![]() $g_i$
lie in
$g_i$
lie in
In fact, comparing the ranks, we conclude that these monomials form a basis. Moreover, by Proposition 4.6, we conclude that
![]() $\overline \beta _{2i-1}$
are divisible by
$\overline \beta _{2i-1}$
are divisible by
![]() $v_n$
. Let
$v_n$
. Let
in
![]() $\mathrm {CK}(n)^*(\mathrm {SO}_{2^{n+1}-1})^\vee $
, where P is not divisible by
$\mathrm {CK}(n)^*(\mathrm {SO}_{2^{n+1}-1})^\vee $
, where P is not divisible by
![]() $v_n$
(i.e., the image of P in
$v_n$
(i.e., the image of P in
![]() $\mathrm {Ch}^*(\mathrm {SO}_{2^{n+1}-1})^\vee $
is nonzero). Since (4.3) is a morphism of algebras and co-algebras, and
$\mathrm {Ch}^*(\mathrm {SO}_{2^{n+1}-1})^\vee $
is nonzero). Since (4.3) is a morphism of algebras and co-algebras, and
![]() $\beta _{2i-1}$
is primitive by Theorem 4.4, we conclude that P is primitive modulo
$\beta _{2i-1}$
is primitive by Theorem 4.4, we conclude that P is primitive modulo
![]() $v_n$
. This implies that P coincides with a sum of
$v_n$
. This implies that P coincides with a sum of
![]() $\overline \gamma _2(\beta _{2j-1})$
for some
$\overline \gamma _2(\beta _{2j-1})$
for some
![]() $1\leq j\leq 2^{n-1}$
modulo
$1\leq j\leq 2^{n-1}$
modulo
![]() $v_n$
by Corollary 4.7. Comparing the gradings
$v_n$
by Corollary 4.7. Comparing the gradings
we conclude that
![]() $a=1$
and P is congruent just to
$a=1$
and P is congruent just to
![]() $\overline \gamma _2(\beta _{2j-1})$
modulo
$\overline \gamma _2(\beta _{2j-1})$
modulo
![]() $v_n$
(rather than to a sum of several
$v_n$
(rather than to a sum of several
![]() $\overline \gamma _2(\beta _{2j-1})$
). Moreover,
$\overline \gamma _2(\beta _{2j-1})$
). Moreover,
![]() $2j-1\geq 2^{n-1}-1$
(under this condition,
$2j-1\geq 2^{n-1}-1$
(under this condition,
![]() $k_j=1$
),
$k_j=1$
),
![]() $i\leq j$
(in particular,
$i\leq j$
(in particular,
![]() $i\leq 2^{n-1}$
), and
$i\leq 2^{n-1}$
), and
![]() $i=j$
implies that
$i=j$
implies that
![]() $i=2^{n-1}$
.
$i=2^{n-1}$
.
Take the largest i such that
![]() $\overline \beta _{2i-1}\neq 0$
and let
$\overline \beta _{2i-1}\neq 0$
and let
Since
![]() $k_j=1$
, we conclude that
$k_j=1$
, we conclude that
by Theorem 4.4 (4). However,
by Theorem 4.4 (3). We do not know yet that
![]() $\mathrm {CK}(n)^*(\mathrm {SO}_{2^{n+1}-1})^\vee $
is commutative; however, all commutators are divisible by
$\mathrm {CK}(n)^*(\mathrm {SO}_{2^{n+1}-1})^\vee $
is commutative; however, all commutators are divisible by
![]() $v_n$
in
$v_n$
in
![]() $\mathrm {CK}(n)^*(\mathrm {SO}_{2^{n+1}-1})^\vee $
, and we obtain
$\mathrm {CK}(n)^*(\mathrm {SO}_{2^{n+1}-1})^\vee $
, and we obtain
For
![]() $i<2^{n-1}$
, we have
$i<2^{n-1}$
, we have
![]() $\overline \beta _{2j-1}=0$
(by the choice of i), and therefore,
$\overline \beta _{2j-1}=0$
(by the choice of i), and therefore,
but the image of
![]() $\gamma _2(\beta _{2i-1})$
in
$\gamma _2(\beta _{2i-1})$
in
![]() $\mathrm {Ch}^*(\mathrm {SO}_{2^{n+1}-1})^\vee $
is nonzero. This provides a contradiction.
$\mathrm {Ch}^*(\mathrm {SO}_{2^{n+1}-1})^\vee $
is nonzero. This provides a contradiction.
Finally, let
![]() $i=2^{n-1}$
. Then
$i=2^{n-1}$
. Then
and using again the fact that all commutators are divisible by
![]() $v_n$
and
$v_n$
and
![]() $\overline \beta _{2^n-1}=v_n\overline \gamma _2(\beta _{2^n-1})+v_n^2R$
, we obtain
$\overline \beta _{2^n-1}=v_n\overline \gamma _2(\beta _{2^n-1})+v_n^2R$
, we obtain
which again provides a contradiction.
Therefore, all
![]() $\overline \beta _{2i-1}$
are equal to zero, and
$\overline \beta _{2i-1}$
are equal to zero, and
![]() $\varphi $
factors through the quotient modulo the ideal generated by
$\varphi $
factors through the quotient modulo the ideal generated by
![]() $\beta _{2i-1}$
. Comparing the ranks, we obtain the claim.
$\beta _{2i-1}$
. Comparing the ranks, we obtain the claim.
Corollary 4.9. The Hopf algebra
![]() $\mathrm {CK}(n)^*(\mathrm {SO}_{2^{n+1}-1})^\vee $
is commutative.
$\mathrm {CK}(n)^*(\mathrm {SO}_{2^{n+1}-1})^\vee $
is commutative.
Proof. This follows from Theorem 4.4 (5).
We are going to reuse the notation for
![]() $\gamma _t(\alpha _{2i-1})$
in
$\gamma _t(\alpha _{2i-1})$
in
![]() $\mathrm {Ch}^*(\mathrm {SO}_{2^{n+1}-1})^\vee $
also for their lifts to
$\mathrm {Ch}^*(\mathrm {SO}_{2^{n+1}-1})^\vee $
also for their lifts to
![]() $\mathrm {CK}(n)^*(\mathrm {SO}_{2^{n+1}-1})^\vee $
. In the notation of the proof of Proposition 4.8, denote
$\mathrm {CK}(n)^*(\mathrm {SO}_{2^{n+1}-1})^\vee $
. In the notation of the proof of Proposition 4.8, denote
in
![]() $\mathrm {CK}(n)^*(\mathrm {SO}_m)^\vee $
for
$\mathrm {CK}(n)^*(\mathrm {SO}_m)^\vee $
for
![]() $1\leq i\leq 2^{n-1}$
,
$1\leq i\leq 2^{n-1}$
,
![]() $1\leq t\leq 2^{k_i-1}$
, and denote additionally
$1\leq t\leq 2^{k_i-1}$
, and denote additionally
for
![]() $t<2^{k_i-1}$
. We also reuse below the notation
$t<2^{k_i-1}$
. We also reuse below the notation
![]() $\Gamma _{k_i}(\alpha _{2i-1})$
for the algebra of divided differences over
$\Gamma _{k_i}(\alpha _{2i-1})$
for the algebra of divided differences over
![]() $\mathbb F_2[v_n]$
(rather than
$\mathbb F_2[v_n]$
(rather than
![]() $\mathbb F_2$
).
$\mathbb F_2$
).
Proposition 4.10. In the notation above,
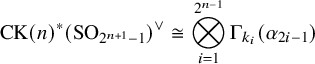 $$ \begin{align*}\mathrm{CK}(n)^*(\mathrm{SO}_{2^{n+1}-1})^\vee\cong\bigotimes_{i=1}^{2^{n-1}}\Gamma_{k_i}(\alpha_{2i-1}) \end{align*} $$
$$ \begin{align*}\mathrm{CK}(n)^*(\mathrm{SO}_{2^{n+1}-1})^\vee\cong\bigotimes_{i=1}^{2^{n-1}}\Gamma_{k_i}(\alpha_{2i-1}) \end{align*} $$
is an isomorphism of co-algebras, and the multiplication table of
![]() $\mathrm {CK}(n)^*(\mathrm {SO}_{2^{n+1}-1})^\vee $
can be deduced from the identities
$\mathrm {CK}(n)^*(\mathrm {SO}_{2^{n+1}-1})^\vee $
can be deduced from the identities
for
![]() $1\leq i\leq 2^{n-1}$
,
$1\leq i\leq 2^{n-1}$
,
![]() $1\leq s,t< 2^{k_i-1}$
, and
$1\leq s,t< 2^{k_i-1}$
, and
for
![]() $1\leq i\leq 2^{n-1}$
,
$1\leq i\leq 2^{n-1}$
,
![]() $2j-1=(2i-1)2^{k_i}-2^{n}+1$
.
$2j-1=(2i-1)2^{k_i}-2^{n}+1$
.
Proof. The identity (4.4) and the formula
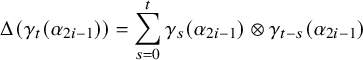 $$ \begin{align} \Delta(\gamma_t(\alpha_{2i-1}))=\sum_{s=0}^t\gamma_s(\alpha_{2i-1})\otimes\gamma_{t-s}(\alpha_{2i-1}) \end{align} $$
$$ \begin{align} \Delta(\gamma_t(\alpha_{2i-1}))=\sum_{s=0}^t\gamma_s(\alpha_{2i-1})\otimes\gamma_{t-s}(\alpha_{2i-1}) \end{align} $$
for
![]() $1\leq t\leq 2^{k_i-1}$
follow from Theorem 4.4. Using this and the fact that
$1\leq t\leq 2^{k_i-1}$
follow from Theorem 4.4. Using this and the fact that
![]() $\mathrm {CK}(n)^*(\mathrm {SO}_{2^{n+1}-1})^\vee $
is a Hopf algebra, we can prove (4.6) for all
$\mathrm {CK}(n)^*(\mathrm {SO}_{2^{n+1}-1})^\vee $
is a Hopf algebra, we can prove (4.6) for all
![]() $1\leq t<2^{k_i}$
, and obtain the first claim. Finally, (4.5) follows from Theorem 4.4 (4) and Corollary 4.9.
$1\leq t<2^{k_i}$
, and obtain the first claim. Finally, (4.5) follows from Theorem 4.4 (4) and Corollary 4.9.
4.5 The co-algebra structure of
 $\mathrm {CK}(n)^*(\mathrm {SO}_m)$
$\mathrm {CK}(n)^*(\mathrm {SO}_m)$
Dualizing the above result, we obtain the following
Proposition 4.11. The algebraic Morava K-theory
![]() $\mathrm {CK}(n)^*(\mathrm {SO}_{2^{n+1}-1})$
can be identified as an algebra with
$\mathrm {CK}(n)^*(\mathrm {SO}_{2^{n+1}-1})$
can be identified as an algebra with
where
![]() $k_i$
are given by (4.1). Denote additionally
$k_i$
are given by (4.1). Denote additionally
![]() $e_{2k}=e_k^2$
. The reduced co-multiplication
$e_{2k}=e_k^2$
. The reduced co-multiplication
![]() $\widetilde \Delta (x)=\Delta (x)-x\otimes 1-1\otimes x$
of
$\widetilde \Delta (x)=\Delta (x)-x\otimes 1-1\otimes x$
of
![]() $\mathrm {CK}(n)^*(\mathrm {SO}_{2^{n+1}-1})$
under the above identification is given by
$\mathrm {CK}(n)^*(\mathrm {SO}_{2^{n+1}-1})$
under the above identification is given by
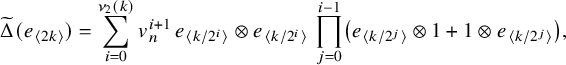 $$ \begin{align} \widetilde\Delta(e_{\langle 2k\rangle})=\sum_{i=0}^{\nu_2(k)}v_n^{i+1}\,e_{\langle k/2^{i}\rangle}\otimes e_{\langle k/2^{i}\rangle}\,\prod_{j=0}^{i-1}\left(e_{\langle k/2^{j}\rangle}\otimes1+1\otimes e_{\langle k/2^{j}\rangle}\right), \end{align} $$
$$ \begin{align} \widetilde\Delta(e_{\langle 2k\rangle})=\sum_{i=0}^{\nu_2(k)}v_n^{i+1}\,e_{\langle k/2^{i}\rangle}\otimes e_{\langle k/2^{i}\rangle}\,\prod_{j=0}^{i-1}\left(e_{\langle k/2^{j}\rangle}\otimes1+1\otimes e_{\langle k/2^{j}\rangle}\right), \end{align} $$
where
![]() $\langle t\rangle $
stands for
$\langle t\rangle $
stands for
![]() $2^n-1-t$
,
$2^n-1-t$
,
![]() $k>0$
, and
$k>0$
, and
![]() $\nu _2(k)$
is the
$\nu _2(k)$
is the
![]() $2$
-adic valuation of k, i.e.,
$2$
-adic valuation of k, i.e.,
![]() $k/2^{\,\nu _2(k)}$
is an odd integer, and
$k/2^{\,\nu _2(k)}$
is an odd integer, and
Proof. We will denote by
![]() $\Big \langle \ ,\ \Big \rangle $
the natural pairing of
$\Big \langle \ ,\ \Big \rangle $
the natural pairing of
![]() $\mathrm {CK}(n)^*(\mathrm {SO}_{2^{n+1}-1})$
with
$\mathrm {CK}(n)^*(\mathrm {SO}_{2^{n+1}-1})$
with
![]() $\mathrm {CK}(n)^*(\mathrm {SO}_{2^{n+1}-1})^\vee $
.
$\mathrm {CK}(n)^*(\mathrm {SO}_{2^{n+1}-1})^\vee $
.
Let
![]() $e_{2i-1}$
denote the dual elements to
$e_{2i-1}$
denote the dual elements to
![]() $\alpha _{2i-1}$
. Then the first claim follows from Proposition 4.10. To compute
$\alpha _{2i-1}$
. Then the first claim follows from Proposition 4.10. To compute
![]() $\Delta (e_{2^n-1})$
, observe that
$\Delta (e_{2^n-1})$
, observe that
can only be nonzero for the basis elements
![]() $1\otimes \alpha _{2^n-1}$
,
$1\otimes \alpha _{2^n-1}$
,
![]() $\alpha _{2^n-1}\otimes 1$
and
$\alpha _{2^n-1}\otimes 1$
and
![]() $\alpha _{2^n-1}\otimes \alpha _{2^n-1}$
in the right-hand side of the pairing
$\alpha _{2^n-1}\otimes \alpha _{2^n-1}$
in the right-hand side of the pairing
![]() $\Big \langle \ ,\,\Big \rangle $
by Proposition 4.10. Similarly, for odd j, we see that
$\Big \langle \ ,\,\Big \rangle $
by Proposition 4.10. Similarly, for odd j, we see that
![]() $2^{n-1}-1+j$
is even; that is, if
$2^{n-1}-1+j$
is even; that is, if
![]() $2j-1=(2i-1)2^{k_i}-2^{n}+1$
, then
$2j-1=(2i-1)2^{k_i}-2^{n}+1$
, then
![]() $k_i>1$
. This also implies that
$k_i>1$
. This also implies that
can only be nonzero for the basis elements
![]() $1\otimes \alpha _{2j-1}$
,
$1\otimes \alpha _{2j-1}$
,
![]() $\alpha _{2j-1}\otimes 1$
and
$\alpha _{2j-1}\otimes 1$
and
![]() $\gamma _{2^{k_i-1}}(\alpha _{2i-1})\otimes \gamma _{2^{k_i-1}}(\alpha _{2i-1})$
, where
$\gamma _{2^{k_i-1}}(\alpha _{2i-1})\otimes \gamma _{2^{k_i-1}}(\alpha _{2i-1})$
, where
![]() $2j-1=(2i-1)2^{k_i}-2^{n}+1$
by Proposition 4.10.
$2j-1=(2i-1)2^{k_i}-2^{n}+1$
by Proposition 4.10.
However, if j is even, then
![]() $k_i=1$
, that is,
$k_i=1$
, that is,
![]() $\alpha _{2i-1}^2=v_n\alpha _{2j-1}$
, and
$\alpha _{2i-1}^2=v_n\alpha _{2j-1}$
, and
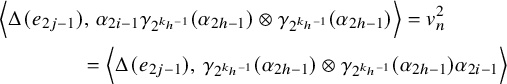 $$ \begin{align*} &\Big\langle\Delta(e_{2j-1}),\,\alpha_{2i-1}\gamma_{2^{k_h-1}}(\alpha_{2h-1})\otimes\gamma_{2^{k_h-1}}(\alpha_{2h-1})\Big\rangle=v_n^2\qquad\qquad\qquad\\ &\qquad\qquad=\Big\langle\Delta(e_{2j-1}),\,\gamma_{2^{k_h-1}}(\alpha_{2h-1})\otimes\gamma_{2^{k_h-1}}(\alpha_{2h-1})\alpha_{2i-1}\Big\rangle \end{align*} $$
$$ \begin{align*} &\Big\langle\Delta(e_{2j-1}),\,\alpha_{2i-1}\gamma_{2^{k_h-1}}(\alpha_{2h-1})\otimes\gamma_{2^{k_h-1}}(\alpha_{2h-1})\Big\rangle=v_n^2\qquad\qquad\qquad\\ &\qquad\qquad=\Big\langle\Delta(e_{2j-1}),\,\gamma_{2^{k_h-1}}(\alpha_{2h-1})\otimes\gamma_{2^{k_h-1}}(\alpha_{2h-1})\alpha_{2i-1}\Big\rangle \end{align*} $$
for
![]() $2i-1=(2h-1)2^{k_h}-2^{n}+1$
. Let us denote
$2i-1=(2h-1)2^{k_h}-2^{n}+1$
. Let us denote
![]() $2j-1=2^n-1-2k$
. Then we have
$2j-1=2^n-1-2k$
. Then we have
![]() $2i-1=2^{n}-1-k$
, and
$2i-1=2^{n}-1-k$
, and
![]() $2h-1=2^{n}-1-\frac k2$
. Moreover, if k is divisible by
$2h-1=2^{n}-1-\frac k2$
. Moreover, if k is divisible by
![]() $4$
, we see that h is even and we can continue this process by induction.
$4$
, we see that h is even and we can continue this process by induction.
Denoting
![]() $\langle t\rangle =2^n-1-t$
, we obtain formula (4.7).
$\langle t\rangle =2^n-1-t$
, we obtain formula (4.7).
We can now compute
![]() $\mathrm {CK}(n)^*(\mathrm {SO}_m)$
for
$\mathrm {CK}(n)^*(\mathrm {SO}_m)$
for
![]() $m\leq 2^{n+1}$
as a corollary of the above proposition.
$m\leq 2^{n+1}$
as a corollary of the above proposition.
Proposition 4.12. For
![]() $m\leq 2^{n+1}$
, the algebra structure of
$m\leq 2^{n+1}$
, the algebra structure of
![]() $\mathrm {CK}(n)^*(\mathrm {SO}_m)$
is given by
$\mathrm {CK}(n)^*(\mathrm {SO}_m)$
is given by
where
![]() $s=\lfloor \frac {m-1}{2}\rfloor $
and
$s=\lfloor \frac {m-1}{2}\rfloor $
and
![]() $e_{k}$
stands for
$e_{k}$
stands for
![]() $0$
if
$0$
if
![]() $k>s$
. The reduced co-multiplication
$k>s$
. The reduced co-multiplication
![]() $\widetilde \Delta (x)=\Delta (x)-x\otimes 1-1\otimes x$
is given by
$\widetilde \Delta (x)=\Delta (x)-x\otimes 1-1\otimes x$
is given by
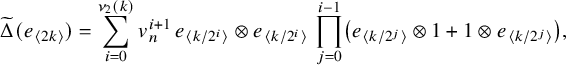 $$ \begin{align*}\widetilde\Delta(e_{\langle 2k\rangle})=\sum_{i=0}^{\nu_2(k)}v_n^{i+1}\,e_{\langle k/2^{i}\rangle}\otimes e_{\langle k/2^{i}\rangle}\,\prod_{j=0}^{i-1}\left(e_{\langle k/2^{j}\rangle}\otimes1+1\otimes e_{\langle k/2^{j}\rangle}\right), \end{align*} $$
$$ \begin{align*}\widetilde\Delta(e_{\langle 2k\rangle})=\sum_{i=0}^{\nu_2(k)}v_n^{i+1}\,e_{\langle k/2^{i}\rangle}\otimes e_{\langle k/2^{i}\rangle}\,\prod_{j=0}^{i-1}\left(e_{\langle k/2^{j}\rangle}\otimes1+1\otimes e_{\langle k/2^{j}\rangle}\right), \end{align*} $$
where
![]() $\langle t\rangle $
stands for
$\langle t\rangle $
stands for
![]() $2^n-1-t$
,
$2^n-1-t$
,
![]() $k>0$
, and
$k>0$
, and
![]() $\nu _2(k)$
is the
$\nu _2(k)$
is the
![]() $2$
-adic valuation of k, that is,
$2$
-adic valuation of k, that is,
![]() $k/2^{\,\nu _2(k)}$
is an odd integer, and
$k/2^{\,\nu _2(k)}$
is an odd integer, and
Moreover,
![]() $e_1$
coincides with the first Chern class
$e_1$
coincides with the first Chern class
![]() $c_1^{\mathrm {CK}(n)}(e_1^{\mathrm {CH}})$
of the generator
$c_1^{\mathrm {CK}(n)}(e_1^{\mathrm {CH}})$
of the generator
![]() $e_1^{\mathrm {CH}}$
of
$e_1^{\mathrm {CH}}$
of
![]() $\mathrm {CH}^1(\mathrm {SO}_m;\mathbb Z)$
.
$\mathrm {CH}^1(\mathrm {SO}_m;\mathbb Z)$
.
Proof. First, assume that m is odd. We know that the natural map
coincides with taking a quotient modulo
![]() $e_k$
for
$e_k$
for
![]() $k>\lfloor \frac {m-1}{2}\rfloor $
. Therefore, the corresponding map on the connective Morava K-theories
$k>\lfloor \frac {m-1}{2}\rfloor $
. Therefore, the corresponding map on the connective Morava K-theories
is surjective by Nakayama’s Lemma (see [Reference Geldhauser, Lavrenov, Petrov and Sechin9, Lemma 5.5]), and the images of
![]() $e_k$
become divisible by
$e_k$
become divisible by
![]() $v_n$
for
$v_n$
for
![]() $k>\lfloor \frac {m-1}{2}\rfloor $
.
$k>\lfloor \frac {m-1}{2}\rfloor $
.
Denote the image of
![]() $e_i$
in
$e_i$
in
![]() $\mathrm {CK}(n)^*(\mathrm {SO}_{m})$
by
$\mathrm {CK}(n)^*(\mathrm {SO}_{m})$
by
![]() $\overline e_i$
and let
$\overline e_i$
and let
for some P not divisible by
![]() $v_n$
. We will show that such an equation is impossible by formal reasons; therefore, in fact
$v_n$
. We will show that such an equation is impossible by formal reasons; therefore, in fact
![]() $\overline e_k=0$
for
$\overline e_k=0$
for
![]() $k>\lfloor \frac {m-1}{2}\rfloor $
.
$k>\lfloor \frac {m-1}{2}\rfloor $
.
Let
![]() $k=2^t(2^n-1-2j)$
and let
$k=2^t(2^n-1-2j)$
and let
![]() $\langle t\rangle $
denote
$\langle t\rangle $
denote
![]() $2^n-1-t$
. Then
$2^n-1-t$
. Then
and therefore,
For
![]() $k=2^n-1$
, we obtain
$k=2^n-1$
, we obtain
which implies that the image of P in
![]() $\mathrm {Ch}^*(\mathrm {SO}_{m})$
is primitive and therefore coincides with
$\mathrm {Ch}^*(\mathrm {SO}_{m})$
is primitive and therefore coincides with
![]() $\sum e_{2h-1}^{2^{d_h}}$
for some
$\sum e_{2h-1}^{2^{d_h}}$
for some
![]() $0\leq d_h<\lfloor \log _2\left (\frac {m-1}{2h-1}\right )\rfloor $
(cf. [Reference Geldhauser, Lavrenov, Petrov and Sechin9, Lemma 6.1 a)]). Then
$0\leq d_h<\lfloor \log _2\left (\frac {m-1}{2h-1}\right )\rfloor $
(cf. [Reference Geldhauser, Lavrenov, Petrov and Sechin9, Lemma 6.1 a)]). Then
and comparing the gradings, we have
for each h. However,
![]() $a\geq 1$
and
$a\geq 1$
and
![]() $2^{d_h}(2h-1)\leq \frac {m-1}{2}$
; therefore, the above identity is impossible. This shows that
$2^{d_h}(2h-1)\leq \frac {m-1}{2}$
; therefore, the above identity is impossible. This shows that
![]() $\overline e_{2^n-1}=0$
.
$\overline e_{2^n-1}=0$
.
Take the largest k such that
Then by (4.8), we conclude that
and the image of P in
![]() $\mathrm {Ch}^*(\mathrm {SO}_{m})$
is primitive. Then
$\mathrm {Ch}^*(\mathrm {SO}_{m})$
is primitive. Then
as above, and
for each h. But again,
![]() $a\geq 1$
,
$a\geq 1$
,
![]() $k>\lfloor \frac {m-1}{2}\rfloor $
and
$k>\lfloor \frac {m-1}{2}\rfloor $
and
![]() $2^{d_h}(2h-1)\leq \frac {m-1}{2}$
; therefore, the above identity is impossible.
$2^{d_h}(2h-1)\leq \frac {m-1}{2}$
; therefore, the above identity is impossible.
This shows that all
![]() $\overline e_k=0$
for
$\overline e_k=0$
for
![]() $k>\lfloor \frac {m-1}{2}\rfloor $
. Comparing the ranks, we obtain the claim for odd m (cf. [Reference Geldhauser, Lavrenov, Petrov and Sechin9, Theorem 6.10]).
$k>\lfloor \frac {m-1}{2}\rfloor $
. Comparing the ranks, we obtain the claim for odd m (cf. [Reference Geldhauser, Lavrenov, Petrov and Sechin9, Theorem 6.10]).
Now assume that m is even. As we already remarked, we can assume that
![]() $k=\mathbb C$
; in particular, we can consider the natural map
$k=\mathbb C$
; in particular, we can consider the natural map
![]() $\mathrm {SO}_{m-1}\rightarrow \mathrm {SO}_m$
induces a surjection on Chow rings
$\mathrm {SO}_{m-1}\rightarrow \mathrm {SO}_m$
induces a surjection on Chow rings
(in fact, an isomorphism) (cf., for example, [Reference Pittie31, Section 2]), and therefore, a surjection on
![]() $\mathrm {CK}(n)^*$
by Nakayama’s Lemma [Reference Geldhauser, Lavrenov, Petrov and Sechin9, Lemma 5.5]. Comparing the ranks, we conclude that
$\mathrm {CK}(n)^*$
by Nakayama’s Lemma [Reference Geldhauser, Lavrenov, Petrov and Sechin9, Lemma 5.5]. Comparing the ranks, we conclude that
is an isomorphism of Hopf algebras (cf. [Reference Geldhauser, Lavrenov, Petrov and Sechin9, Theorem 6.10]).
Finally, we will show that
![]() $e_1$
coincides with the first Chern class of a certain bundle. Let
$e_1$
coincides with the first Chern class of a certain bundle. Let
![]() $e_1^{\mathrm {CH}}$
denote a generator of
$e_1^{\mathrm {CH}}$
denote a generator of
![]() $\mathrm {CH}^1(\mathrm {SO}_m;\,\mathbb Z)$
, and
$\mathrm {CH}^1(\mathrm {SO}_m;\,\mathbb Z)$
, and
![]() $e_1'=c_1^{\mathrm {CK}(n)}(e_1^{\mathrm {CH}})$
. The images of
$e_1'=c_1^{\mathrm {CK}(n)}(e_1^{\mathrm {CH}})$
. The images of
![]() $e_1$
and
$e_1$
and
![]() $e_1'$
coincide in
$e_1'$
coincide in
![]() $\mathrm {Ch}^*(\mathrm {SO}_m)$
, and
$\mathrm {Ch}^*(\mathrm {SO}_m)$
, and
see the proof of [Reference Geldhauser, Lavrenov, Petrov and Sechin9, Lemma 6.12]. Since
![]() $e_{2i-1}^{2^n}=0$
in
$e_{2i-1}^{2^n}=0$
in
![]() $\mathrm {CK}(n)^*(\mathrm {SO}_m)$
for all i, we conclude that
$\mathrm {CK}(n)^*(\mathrm {SO}_m)$
for all i, we conclude that
![]() $(e_1')^{2^n}=0$
, and therefore,
$(e_1')^{2^n}=0$
, and therefore,
by, for example, [Reference Petrov and Semenov28, Subsection 2.3]. Let
for some P not divisible by
![]() $v_n$
. Again, we will show that the above equation is impossible by formal reasons.
$v_n$
. Again, we will show that the above equation is impossible by formal reasons.
Indeed, one has
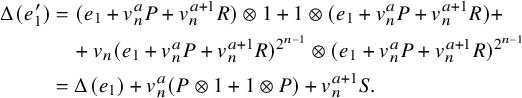 $$ \begin{align*} \Delta(e_1')&=(e_1+v_n^aP+v_n^{a+1}R)\otimes1+1\otimes(e_1+v_n^aP+v_n^{a+1}R)+\\ &\quad+v_n(e_1+v_n^aP+v_n^{a+1}R)^{2^{n-1}}\otimes(e_1+v_n^aP+v_n^{a+1}R)^{2^{n-1}}\\ &=\Delta(e_1)+v_n^a(P\otimes1+1\otimes P)+v_n^{a+1}S. \end{align*} $$
$$ \begin{align*} \Delta(e_1')&=(e_1+v_n^aP+v_n^{a+1}R)\otimes1+1\otimes(e_1+v_n^aP+v_n^{a+1}R)+\\ &\quad+v_n(e_1+v_n^aP+v_n^{a+1}R)^{2^{n-1}}\otimes(e_1+v_n^aP+v_n^{a+1}R)^{2^{n-1}}\\ &=\Delta(e_1)+v_n^a(P\otimes1+1\otimes P)+v_n^{a+1}S. \end{align*} $$
However,
This implies that P becomes primitive modulo
![]() $v_n$
; that is,
$v_n$
; that is,
and
where
![]() $a\geq 1$
and
$a\geq 1$
and
![]() $2^{d_h}(2h-1)\leq \frac {m-1}{2}\leq 2^n-1$
. Therefore, the above identity is impossible and
$2^{d_h}(2h-1)\leq \frac {m-1}{2}\leq 2^n-1$
. Therefore, the above identity is impossible and
![]() $e_1'=e_1$
.
$e_1'=e_1$
.
Finally, we will compute the co-multiplication in
![]() $\mathrm {CK}(n)^*(\mathrm {SO}_m)$
for
$\mathrm {CK}(n)^*(\mathrm {SO}_m)$
for
![]() $m>2^{n+1}$
.
$m>2^{n+1}$
.
Theorem 4.13. For all m,
![]() $n\in \mathbb N\setminus 0$
the algebra structure of
$n\in \mathbb N\setminus 0$
the algebra structure of
![]() $\mathrm {CK}(n)^*(\mathrm {SO}_m)$
is given by
$\mathrm {CK}(n)^*(\mathrm {SO}_m)$
is given by
where
![]() $s=\lfloor \frac {m-1}{2}\rfloor $
and
$s=\lfloor \frac {m-1}{2}\rfloor $
and
![]() $e_{k}$
stands for
$e_{k}$
stands for
![]() $0$
if
$0$
if
![]() $k>s$
. The reduced co-multiplication
$k>s$
. The reduced co-multiplication
![]() $\widetilde \Delta (x)=\Delta (x)-x\otimes 1-1\otimes x$
is given by
$\widetilde \Delta (x)=\Delta (x)-x\otimes 1-1\otimes x$
is given by
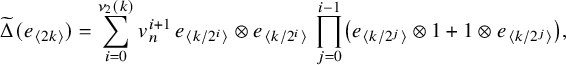 $$ \begin{align*}\widetilde\Delta(e_{\langle 2k\rangle})=\sum_{i=0}^{\nu_2(k)}v_n^{i+1}\,e_{\langle k/2^{i}\rangle}\otimes e_{\langle k/2^{i}\rangle}\,\prod_{j=0}^{i-1}\left(e_{\langle k/2^{j}\rangle}\otimes1+1\otimes e_{\langle k/2^{j}\rangle}\right), \end{align*} $$
$$ \begin{align*}\widetilde\Delta(e_{\langle 2k\rangle})=\sum_{i=0}^{\nu_2(k)}v_n^{i+1}\,e_{\langle k/2^{i}\rangle}\otimes e_{\langle k/2^{i}\rangle}\,\prod_{j=0}^{i-1}\left(e_{\langle k/2^{j}\rangle}\otimes1+1\otimes e_{\langle k/2^{j}\rangle}\right), \end{align*} $$
where
![]() $\langle t\rangle $
stands for
$\langle t\rangle $
stands for
![]() $2^n-1-t$
,
$2^n-1-t$
,
![]() $0<k<2^{n-1}$
, and
$0<k<2^{n-1}$
, and
![]() $\nu _2(k)$
is the
$\nu _2(k)$
is the
![]() $2$
-adic valuation of k, i.e.,
$2$
-adic valuation of k, i.e.,
![]() $k/2^{\,\nu _2(k)}$
is an odd integer,
$k/2^{\,\nu _2(k)}$
is an odd integer,
and
for
![]() $k>2^{n-1}$
. Moreover,
$k>2^{n-1}$
. Moreover,
![]() $e_1$
coincides with the first Chern class
$e_1$
coincides with the first Chern class
![]() $c_1^{\mathrm {CK}(n)}(e_1^{\mathrm {CH}})$
of the generator
$c_1^{\mathrm {CK}(n)}(e_1^{\mathrm {CH}})$
of the generator
![]() $e_1^{\mathrm {CH}}$
of
$e_1^{\mathrm {CH}}$
of
![]() $\mathrm {CH}^1(\mathrm {SO}_m;\mathbb Z)$
.
$\mathrm {CH}^1(\mathrm {SO}_m;\mathbb Z)$
.
Proof. For
![]() $m\leq 2^{n+1}$
, the claim follows from Proposition 4.12. Assume that
$m\leq 2^{n+1}$
, the claim follows from Proposition 4.12. Assume that
![]() $m>2^{n+1}$
and denote
$m>2^{n+1}$
and denote
![]() $m_0=2^{n+1}-1$
for m odd, and
$m_0=2^{n+1}-1$
for m odd, and
![]() $m_0=2^{n+1}$
for m even.
$m_0=2^{n+1}$
for m even.
The claim about the algebra structure is proven in Theorem 3.5. Moreover, from the proof of Theorem 3.5, it follows that one can take any lift of
![]() $e_1\in \mathrm {CK}(n)^*(\mathrm {SO}_{m_0})$
as a generator
$e_1\in \mathrm {CK}(n)^*(\mathrm {SO}_{m_0})$
as a generator
![]() $e_1\in \mathrm {CK}(n)^*(\mathrm {SO}_{m})$
. Therefore, we can assume that
$e_1\in \mathrm {CK}(n)^*(\mathrm {SO}_{m})$
. Therefore, we can assume that
![]() $e_1=c_1^{\mathrm {CK}(n)}(e_1^{\mathrm {CH}})$
is the first Chern class of the generator
$e_1=c_1^{\mathrm {CK}(n)}(e_1^{\mathrm {CH}})$
is the first Chern class of the generator
![]() $e_1^{\mathrm {CH}}$
of
$e_1^{\mathrm {CH}}$
of
![]() $\mathrm {CH}^1(\mathrm {SO}_m;\mathbb Z)$
.
$\mathrm {CH}^1(\mathrm {SO}_m;\mathbb Z)$
.
Denote
![]() $H=\mathrm {CK}(n)^*(\mathrm {SO}_{m})$
,
$H=\mathrm {CK}(n)^*(\mathrm {SO}_{m})$
,
![]() $I=(e_{2^n},e_{2^n+1},\ldots ,e_s)\trianglelefteq H$
, and
$I=(e_{2^n},e_{2^n+1},\ldots ,e_s)\trianglelefteq H$
, and
Then one also has
Observe that all generators of I have degree at least
![]() $2^n$
and are annihilated by
$2^n$
and are annihilated by
![]() $v_n$
. This implies that
$v_n$
. This implies that
![]() $H\otimes _{\mathbb F_2[v_n]}I+I\otimes _{\mathbb F_2[v_n]}H$
does not have nonzero elements of degree less than
$H\otimes _{\mathbb F_2[v_n]}I+I\otimes _{\mathbb F_2[v_n]}H$
does not have nonzero elements of degree less than
![]() $2^n$
.
$2^n$
.
For
![]() $0<k<2^{n-1}$
, we conclude by Proposition 4.11 that
$0<k<2^{n-1}$
, we conclude by Proposition 4.11 that
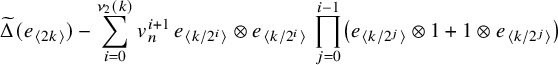 $$ \begin{align*}\widetilde\Delta(e_{\langle 2k\rangle})-\sum_{i=0}^{\nu_2(k)}v_n^{i+1}\,e_{\langle k/2^{i}\rangle}\otimes e_{\langle k/2^{i}\rangle}\,\prod_{j=0}^{i-1}\left(e_{\langle k/2^{j}\rangle}\otimes1+1\otimes e_{\langle k/2^{j}\rangle}\right) \end{align*} $$
$$ \begin{align*}\widetilde\Delta(e_{\langle 2k\rangle})-\sum_{i=0}^{\nu_2(k)}v_n^{i+1}\,e_{\langle k/2^{i}\rangle}\otimes e_{\langle k/2^{i}\rangle}\,\prod_{j=0}^{i-1}\left(e_{\langle k/2^{j}\rangle}\otimes1+1\otimes e_{\langle k/2^{j}\rangle}\right) \end{align*} $$
is a (homogeneous) element of
![]() $H\otimes _{\mathbb F_2[v_n]}I+I\otimes _{\mathbb F_2[v_n]}H$
of degree
$H\otimes _{\mathbb F_2[v_n]}I+I\otimes _{\mathbb F_2[v_n]}H$
of degree
![]() $\langle 2k\rangle <2^n$
. Therefore, this element is
$\langle 2k\rangle <2^n$
. Therefore, this element is
![]() $0$
. Similarly,
$0$
. Similarly,
![]() $\widetilde \Delta (e_{2^n-1})-v_n\,e_{2^{n}-1}\otimes e_{2^{n}-1}=0$
.
$\widetilde \Delta (e_{2^n-1})-v_n\,e_{2^{n}-1}\otimes e_{2^{n}-1}=0$
.
It remains to compute
![]() $\Delta (e_{2k-1})$
for
$\Delta (e_{2k-1})$
for
![]() $k>2^{n-1}$
. Let
$k>2^{n-1}$
. Let
![]() $I'=(e_{2k-1},e_{2k},\ldots ,e_s)$
and
$I'=(e_{2k-1},e_{2k},\ldots ,e_s)$
and
![]() $H':=H/I'=\mathrm {CK}(n)^*(\mathrm {SO}_{m'})$
for
$H':=H/I'=\mathrm {CK}(n)^*(\mathrm {SO}_{m'})$
for
![]() $m'=4k-3$
for m odd or
$m'=4k-3$
for m odd or
![]() $m'=4k-2$
for m even. Observe that
$m'=4k-2$
for m even. Observe that
![]() $\Delta (e_{2k-1})$
lies in the kernel of the map
$\Delta (e_{2k-1})$
lies in the kernel of the map
and the latter kernel coincides with
![]() $H\otimes _{\mathbb F_2[v_n]}I'+I'\otimes _{\mathbb F_2[v_n]}H$
. However,
$H\otimes _{\mathbb F_2[v_n]}I'+I'\otimes _{\mathbb F_2[v_n]}H$
. However,
![]() $\Delta (e_{2k-1})$
is homogeneous of degree
$\Delta (e_{2k-1})$
is homogeneous of degree
![]() $2k-1$
, and the only nonzero element of
$2k-1$
, and the only nonzero element of
![]() $I'$
of degree less than or equal to
$I'$
of degree less than or equal to
![]() $2k-1$
is
$2k-1$
is
![]() $e_{2k-1}$
itself. This implies that
$e_{2k-1}$
itself. This implies that
![]() $\Delta (e_{2k-1})$
is a linear combination of
$\Delta (e_{2k-1})$
is a linear combination of
![]() $1\otimes e_{2k-1}$
and
$1\otimes e_{2k-1}$
and
![]() $e_{2k-1}\otimes 1$
, which finishes the proof.
$e_{2k-1}\otimes 1$
, which finishes the proof.
Now Theorem 4.1 also follows.
5 Morava J-invariant for orthogonal groups
5.1 A generalized J-invariant
Let
![]() $G=\mathrm {SO}_{m}$
denote a (split) special orthogonal group and let
$G=\mathrm {SO}_{m}$
denote a (split) special orthogonal group and let
![]() $E\in \mathrm H^1(k,\,G)$
be a torsor corresponding to a quadratic form
$E\in \mathrm H^1(k,\,G)$
be a torsor corresponding to a quadratic form
![]() $q\colon V\rightarrow k$
(with trivial discriminant), see [Reference Knus, Merkurjev, Rost and Tignol17, (29.29)]. For a free theory
$q\colon V\rightarrow k$
(with trivial discriminant), see [Reference Knus, Merkurjev, Rost and Tignol17, (29.29)]. For a free theory
![]() $A^*$
, the extension of scalars
$A^*$
, the extension of scalars
![]() $\overline k/k$
induces a natural map
$\overline k/k$
induces a natural map
![]() $A^*(E)\rightarrow A^*(G)$
. Following [Reference Petrov and Semenov29, Definition 4.6], we give the following definition.
$A^*(E)\rightarrow A^*(G)$
. Following [Reference Petrov and Semenov29, Definition 4.6], we give the following definition.
Definition 1. In the notation above, we call
the (generalized) J-invariant of E (or q) corresponding to the theory
![]() $A^*$
.
$A^*$
.
By [Reference Petrov and Semenov29, Lemma 4.5],
![]() $H^*_A(E)$
is a quotient bi-algebra of
$H^*_A(E)$
is a quotient bi-algebra of
![]() $A^*(G)$
. Therefore, after classification of bi-ideals in
$A^*(G)$
. Therefore, after classification of bi-ideals in
![]() $\mathrm {CK}(n)^*(G)$
obtained in Subsection 5.2, we will be able to prove the following result.
$\mathrm {CK}(n)^*(G)$
obtained in Subsection 5.2, we will be able to prove the following result.
Theorem 5.1. For all n,
![]() $m\in \mathbb N\setminus 0$
and
$m\in \mathbb N\setminus 0$
and
![]() $E\in \mathrm H^1(k,\,\mathrm {SO}_m)$
, one has
$E\in \mathrm H^1(k,\,\mathrm {SO}_m)$
, one has
where
![]() $\overline e_i$
denotes the image of
$\overline e_i$
denotes the image of
![]() $e_i\in \mathrm {CK}(n)^*(\mathrm {SO}_m)$
in
$e_i\in \mathrm {CK}(n)^*(\mathrm {SO}_m)$
in
![]() $H^*_{\mathrm {CK}(n)}(E)$
(see Theorem 4.13).
$H^*_{\mathrm {CK}(n)}(E)$
(see Theorem 4.13).
In other words, the J-invariants for the Chow theory
![]() $\mathrm {Ch}^*$
and for the connective Morava K-theory
$\mathrm {Ch}^*$
and for the connective Morava K-theory
![]() $\mathrm {CK}(n)^*$
carry the same information. As a consequence, we clearly obtain the following corollary.
$\mathrm {CK}(n)^*$
carry the same information. As a consequence, we clearly obtain the following corollary.
Corollary 5.2. For n,
![]() $m\in \mathbb N\setminus 0$
and
$m\in \mathbb N\setminus 0$
and
![]() $E\in \mathrm H^1(k,\,\mathrm {SO}_m)$
, one has
$E\in \mathrm H^1(k,\,\mathrm {SO}_m)$
, one has
where
![]() $\overline e_i$
denotes the image of
$\overline e_i$
denotes the image of
![]() $e_i\in \mathrm {K}(n)^*(\mathrm {SO}_m)$
in
$e_i\in \mathrm {K}(n)^*(\mathrm {SO}_m)$
in
![]() $H^*_{\mathrm {K}(n)}(E)$
(see Theorem 4.1).
$H^*_{\mathrm {K}(n)}(E)$
(see Theorem 4.1).
In other words, the J-invariant for the periodic Morava K-theory can be obtained from the usual J-invariant for
![]() $\mathrm {Ch}^*$
by an appropriate truncation.
$\mathrm {Ch}^*$
by an appropriate truncation.
5.2 Saturated bi-ideals in
 $\mathrm {CK}(n)^*(\mathrm {SO}_m)$
$\mathrm {CK}(n)^*(\mathrm {SO}_m)$
We call a submodule N in a
![]() $\mathbb F_2[v_n]$
-module M saturated, if
$\mathbb F_2[v_n]$
-module M saturated, if
![]() $v_nx\in N\Rightarrow x\in N$
for any
$v_nx\in N\Rightarrow x\in N$
for any
![]() $x\in M$
. We will need the following technical result.
$x\in M$
. We will need the following technical result.
Lemma 5.3.
![]() $1)$
Let M be a graded, finitely generated
$1)$
Let M be a graded, finitely generated
![]() $\mathbb F_2[v_n]$
-module, and
$\mathbb F_2[v_n]$
-module, and
![]() $N\leq M$
be its (graded) submodule. Then N is saturated if and only if
$N\leq M$
be its (graded) submodule. Then N is saturated if and only if
![]() $M/N$
is free.
$M/N$
is free.
![]() $2)$
Let H be a graded, finitely generated
$2)$
Let H be a graded, finitely generated
![]() $\mathbb F_2[v_n]$
-algebra, and I its (homogeneous) saturated ideal. Then
$\mathbb F_2[v_n]$
-algebra, and I its (homogeneous) saturated ideal. Then
![]() $I\otimes H+H\otimes I$
is a saturated ideal of
$I\otimes H+H\otimes I$
is a saturated ideal of
![]() $H\otimes H$
.
$H\otimes H$
.
Proof. The first claim is obvious. To get 2), one only has to observe that
is free, and use 1).
We will also need the following well-known corollary of the Milnor–Moore Theorem [Reference Milnor and Moore23, Theorem 7.16]. We provide a proof in Section A2 for the convenience of the reader.
Lemma 5.4. Let
![]() $H=\mathbb F_{2}[e_1,\,e_3,\ldots ,e_{2r-1}]/(e_{1}^{2^{k_1}},\,e_{3}^{2^{k_2}},\ldots ,\,e_{2r-1}^{2^{k_r}})$
be a commutative, graded Hopf algebra with
$H=\mathbb F_{2}[e_1,\,e_3,\ldots ,e_{2r-1}]/(e_{1}^{2^{k_1}},\,e_{3}^{2^{k_2}},\ldots ,\,e_{2r-1}^{2^{k_r}})$
be a commutative, graded Hopf algebra with
![]() $e_{2i-1}$
primitive of degree
$e_{2i-1}$
primitive of degree
![]() $2i-1$
. Then any (homogeneous) bi-ideal I of H coincides with the ideal
$2i-1$
. Then any (homogeneous) bi-ideal I of H coincides with the ideal
for some
![]() $0\leq a_{i}\leq k_i$
.
$0\leq a_{i}\leq k_i$
.
For
![]() $m\leq 2^{n+1}$
, we will give a description of saturated bi-ideals in
$m\leq 2^{n+1}$
, we will give a description of saturated bi-ideals in
![]() $\mathrm {CK}(n)^*(\mathrm {SO}_m)$
analogues to Lemma 5.4. First, we will need the following technical result (cf. [Reference Geldhauser, Lavrenov, Petrov and Sechin9, Lemma 6.11]).
$\mathrm {CK}(n)^*(\mathrm {SO}_m)$
analogues to Lemma 5.4. First, we will need the following technical result (cf. [Reference Geldhauser, Lavrenov, Petrov and Sechin9, Lemma 6.11]).
Lemma 5.5. Let n, m, j, k be positive integers such that
![]() $m\leq 2^{n+1}$
, and
$m\leq 2^{n+1}$
, and
![]() $j,\,k\leq \left \lfloor \frac {m+1}{4}\right \rfloor $
. Then the equation
$j,\,k\leq \left \lfloor \frac {m+1}{4}\right \rfloor $
. Then the equation
has no integral solutions
![]() $x>0$
,
$x>0$
,
![]() $0\leq y<\left \lfloor \mathrm {log}_2\left (\frac {m-1}{2j-1}\right )\right \rfloor $
,
$0\leq y<\left \lfloor \mathrm {log}_2\left (\frac {m-1}{2j-1}\right )\right \rfloor $
,
![]() $z\geq 0$
.
$z\geq 0$
.
Proof. Since
![]() $ (2j-1)2^y=(2k-1)2^z+(2^n-1)x\geq 2^n, $
we have
$ (2j-1)2^y=(2k-1)2^z+(2^n-1)x\geq 2^n, $
we have
 $$ \begin{align*}2^{y+1}\geq\frac{2^{n+1}}{2j-1}\geq\frac{m}{2j-1}>\frac{m-1}{2j-1}. \end{align*} $$
$$ \begin{align*}2^{y+1}\geq\frac{2^{n+1}}{2j-1}\geq\frac{m}{2j-1}>\frac{m-1}{2j-1}. \end{align*} $$
In other words,
![]() $y+1>\left \lfloor \mathrm {log}_2\left (\frac {m-1}{2j-1}\right )\right \rfloor $
contradicting the assumptions.
$y+1>\left \lfloor \mathrm {log}_2\left (\frac {m-1}{2j-1}\right )\right \rfloor $
contradicting the assumptions.
Proposition 5.6. Let
for
![]() $m\leq 2^{n+1}$
,
$m\leq 2^{n+1}$
,
![]() $r=\lfloor \frac {m+1}{4}\rfloor $
,
$r=\lfloor \frac {m+1}{4}\rfloor $
,
![]() $k_i=\left \lfloor \mathrm {log}_2\left (\frac {m-1}{2i-1}\right )\right \rfloor $
(see Proposition 4.12). Then any homogeneous saturated bi-ideal I of H coincides with the ideal
$k_i=\left \lfloor \mathrm {log}_2\left (\frac {m-1}{2i-1}\right )\right \rfloor $
(see Proposition 4.12). Then any homogeneous saturated bi-ideal I of H coincides with the ideal
for some
![]() $0\leq a_i\leq k_i$
.
$0\leq a_i\leq k_i$
.
Proof. Let
![]() $\overline {(\ )}$
denote the image modulo
$\overline {(\ )}$
denote the image modulo
![]() $v_n$
. Since
$v_n$
. Since
![]() $\overline I$
is also a bi-ideal, we conclude by Lemma 5.4 that
$\overline I$
is also a bi-ideal, we conclude by Lemma 5.4 that
for some
![]() $0\leq a_i\leq k_i$
. We claim that
$0\leq a_i\leq k_i$
. We claim that
with the same indices
![]() $a_k$
. In fact, it is enough to show that
$a_k$
. In fact, it is enough to show that
![]() $e_k^{2^{a_k}}\in I$
for all k, and comparing dimensions, we will get the claim.
$e_k^{2^{a_k}}\in I$
for all k, and comparing dimensions, we will get the claim.
Assume that
![]() $e_k^{2^{a_k}}\not \in I$
for some k, fix an arbitrary lift
$e_k^{2^{a_k}}\not \in I$
for some k, fix an arbitrary lift
![]() $E_{2k-1}$
of
$E_{2k-1}$
of
![]() $\overline e_{2k-1}^{2^{a_{k}}}$
to an element of I, and write
$\overline e_{2k-1}^{2^{a_{k}}}$
to an element of I, and write
for
![]() $\overline P\neq 0\in \overline H$
. We will show that it is possible to find another lift
$\overline P\neq 0\in \overline H$
. We will show that it is possible to find another lift
![]() $E_{2k-1}'\in I$
of
$E_{2k-1}'\in I$
of
![]() $\overline e_{2k-1}^{2^{a_k}}$
with greater a in the decomposition (5.1). Continuing this process, we will eventually show that
$\overline e_{2k-1}^{2^{a_k}}$
with greater a in the decomposition (5.1). Continuing this process, we will eventually show that
![]() $P=0$
by the degree reasons.
$P=0$
by the degree reasons.
Case 1. First, we will show that if
![]() $\overline e_{2k-1}^{\,2^e}\in \overline I$
for some
$\overline e_{2k-1}^{\,2^e}\in \overline I$
for some
![]() $e>0$
, then in fact,
$e>0$
, then in fact,
![]() $e_{2k-1}^{\,2^e}\in I$
.
$e_{2k-1}^{\,2^e}\in I$
.
Let
![]() $E_{2k-1}$
denote a pre-image of
$E_{2k-1}$
denote a pre-image of
![]() $\overline e_{2k-1}^{2^{e}}$
in I, and write
$\overline e_{2k-1}^{2^{e}}$
in I, and write
for
![]() $\overline P\neq 0\in \overline H$
. Observe that
$\overline P\neq 0\in \overline H$
. Observe that
![]() $e_{2k-1}^{2^{e}}$
is primitive in H (see Example 4.2). Then, applying
$e_{2k-1}^{2^{e}}$
is primitive in H (see Example 4.2). Then, applying
![]() $\widetilde \Delta $
to (5.2), we get
$\widetilde \Delta $
to (5.2), we get
since I is a bi-ideal. By Lemma 5.3, we conclude that
that is, the class of
![]() $\overline P$
is primitive in
$\overline P$
is primitive in
![]() $\overline H/\,\overline I$
, and therefore,
$\overline H/\,\overline I$
, and therefore,
![]() $\overline P$
is congruent modulo
$\overline P$
is congruent modulo
![]() $\overline I$
to
$\overline I$
to
![]() $\sum _{i\in \mathcal {I}} \overline e_{2i-1}^{2^{s_i}}$
for some
$\sum _{i\in \mathcal {I}} \overline e_{2i-1}^{2^{s_i}}$
for some
![]() $0\leq s_i<a_i$
and some index set
$0\leq s_i<a_i$
and some index set
![]() $\mathcal {I}\subseteq \{1,\ldots ,r\}$
(see [Reference Geldhauser, Lavrenov, Petrov and Sechin9, Lemma 6.1 a)]). Comparing the codimensions, we obtain an equation
$\mathcal {I}\subseteq \{1,\ldots ,r\}$
(see [Reference Geldhauser, Lavrenov, Petrov and Sechin9, Lemma 6.1 a)]). Comparing the codimensions, we obtain an equation
However, this equation has no solutions by Lemma 5.5. Therefore,
![]() $\mathcal {I}=\emptyset $
and, thus,
$\mathcal {I}=\emptyset $
and, thus,
![]() $\overline P\in \overline I$
.
$\overline P\in \overline I$
.
Take a pre-image
![]() $Q\in I$
of
$Q\in I$
of
![]() $\overline P$
. Then
$\overline P$
. Then
![]() $P-Q$
is divisible by
$P-Q$
is divisible by
![]() $v_n$
, (i.e., there exist
$v_n$
, (i.e., there exist
![]() $P'\in H$
such that
$P'\in H$
such that
![]() $P-Q=v_nP'$
). Therefore,
$P-Q=v_nP'$
). Therefore,
(i.e., we obtain a pre-image of
![]() $\overline e_{2k-1}^{\,2^{e}}$
in I with a greater a than in (5.2)). Continuing this process, we will eventually show that
$\overline e_{2k-1}^{\,2^{e}}$
in I with a greater a than in (5.2)). Continuing this process, we will eventually show that
![]() $e_{2k-1}^{2^{e}}\in I$
.
$e_{2k-1}^{2^{e}}\in I$
.
Case 2. By Case 1, we can assume that
![]() $a_k=0$
. We use the notation
$a_k=0$
. We use the notation
![]() $\langle t\rangle =2^n-1-t$
from Proposition 4.12, and denote
$\langle t\rangle =2^n-1-t$
from Proposition 4.12, and denote
![]() $\langle 2j\rangle =2k-1$
. We can assume, moreover, that k is the largest possible (i.e., j is the least possible) such that
$\langle 2j\rangle =2k-1$
. We can assume, moreover, that k is the largest possible (i.e., j is the least possible) such that
![]() $a_k=0$
and
$a_k=0$
and
![]() $e_{2k-1}\not \in I$
.
$e_{2k-1}\not \in I$
.
Our aim is to prove that
![]() $\overline P\in \overline I\otimes \overline H+\overline H\otimes \overline I$
and use the same argument as in Case 1 to find a presentation as (5.1) with a greater a.
$\overline P\in \overline I\otimes \overline H+\overline H\otimes \overline I$
and use the same argument as in Case 1 to find a presentation as (5.1) with a greater a.
Applying
![]() $\widetilde \Delta $
to (5.1), we obtain
$\widetilde \Delta $
to (5.1), we obtain
where
![]() $v_n^2R=\widetilde \Delta (e_{\langle 2j\rangle })-v_ne_{\langle j\rangle }\otimes e_{\langle j\rangle }$
is determined by Theorem 4.13.
$v_n^2R=\widetilde \Delta (e_{\langle 2j\rangle })-v_ne_{\langle j\rangle }\otimes e_{\langle j\rangle }$
is determined by Theorem 4.13.
Subcase 2.1. For
![]() $j=0$
(i.e.,
$j=0$
(i.e.,
![]() $2k-1=2^n-1$
), observe that
$2k-1=2^n-1$
), observe that
![]() $R=0$
. Using that
$R=0$
. Using that
![]() $E_{2^n-1}\otimes E_{2^n-1}\in I\otimes I$
, we obtain by (5.1) that
$E_{2^n-1}\otimes E_{2^n-1}\in I\otimes I$
, we obtain by (5.1) that
for
![]() $R'=e_{2^n-1}\otimes P+P\otimes e_{2^n-1}+v_n^{a}P\otimes P$
. As above, this implies that
$R'=e_{2^n-1}\otimes P+P\otimes e_{2^n-1}+v_n^{a}P\otimes P$
. As above, this implies that
![]() $\overline P$
becomes primitive modulo
$\overline P$
becomes primitive modulo
![]() $\overline I$
; however,
$\overline I$
; however,
![]() $\overline H/\,\overline I$
does not have primitive elements of the required degree by Lemma 5.5. This implies that
$\overline H/\,\overline I$
does not have primitive elements of the required degree by Lemma 5.5. This implies that
![]() $\overline P\in \overline I$
, and therefore, we can find a new lift
$\overline P\in \overline I$
, and therefore, we can find a new lift
![]() $E_{2^n-1}'$
for
$E_{2^n-1}'$
for
![]() $\overline e_{2^n-1}$
with greater a in the decomposition (5.1). Continuing this process, we will eventually prove that
$\overline e_{2^n-1}$
with greater a in the decomposition (5.1). Continuing this process, we will eventually prove that
![]() $e_{2^n-1}\in I$
.
$e_{2^n-1}\in I$
.
Subcase 2.2. Now consider the case
![]() $j>0$
. The proof in this case is divided in three steps.
$j>0$
. The proof in this case is divided in three steps.
Step 1. First, we show that that
![]() $\overline e_{\langle j\rangle }\in \overline I$
. Indeed, if
$\overline e_{\langle j\rangle }\in \overline I$
. Indeed, if
![]() $a>1$
, we obtain that
$a>1$
, we obtain that
![]() $\overline e_{\langle j\rangle }\otimes \overline e_{\langle j\rangle }\in \overline I\otimes \overline H+\overline H\otimes \overline I$
by Lemma 5.3, and therefore,
$\overline e_{\langle j\rangle }\otimes \overline e_{\langle j\rangle }\in \overline I\otimes \overline H+\overline H\otimes \overline I$
by Lemma 5.3, and therefore,
![]() $\overline e_{\langle j\rangle }\in \overline I$
. If
$\overline e_{\langle j\rangle }\in \overline I$
. If
![]() $a=1$
, we similarly obtain that
$a=1$
, we similarly obtain that
![]() $\overline e_{\langle j\rangle }\otimes \overline e_{\langle j\rangle }+\widetilde \Delta (\overline P)\in \overline I\otimes \overline H+\overline H\otimes \overline I$
.
$\overline e_{\langle j\rangle }\otimes \overline e_{\langle j\rangle }+\widetilde \Delta (\overline P)\in \overline I\otimes \overline H+\overline H\otimes \overline I$
.
Consider the natural basis of
![]() $\overline H$
consisting of the monomials in
$\overline H$
consisting of the monomials in
![]() $\overline e_{2i-1}$
. Then the part of this basis divisible by
$\overline e_{2i-1}$
. Then the part of this basis divisible by
![]() $\overline e_{2i-1}^{\,2^{a_i}}$
for some i is a basis of
$\overline e_{2i-1}^{\,2^{a_i}}$
for some i is a basis of
![]() $\overline I$
, and the tensor product
$\overline I$
, and the tensor product
![]() $\overline H\otimes \overline H$
has a natural basis consisting of decomposable tensors of basis elements.
$\overline H\otimes \overline H$
has a natural basis consisting of decomposable tensors of basis elements.
Observe that
![]() $\widetilde \Delta (\overline P)$
cannot have a monomial
$\widetilde \Delta (\overline P)$
cannot have a monomial
![]() $\overline e_{\langle j\rangle }\otimes \overline e_{\langle j\rangle }$
in its decomposition as a sum of basis elements (this follows from the facts that
$\overline e_{\langle j\rangle }\otimes \overline e_{\langle j\rangle }$
in its decomposition as a sum of basis elements (this follows from the facts that
![]() $\overline e_{2i-1}$
are primitive, and
$\overline e_{2i-1}$
are primitive, and
![]() ${2n\choose n}\equiv 0\ \mod 2$
). Therefore, we obtain that
${2n\choose n}\equiv 0\ \mod 2$
). Therefore, we obtain that
![]() $\overline e_{\langle j\rangle }\otimes \overline e_{\langle j\rangle }\in \overline I\otimes \overline H+\overline H\otimes \overline I$
, and
$\overline e_{\langle j\rangle }\otimes \overline e_{\langle j\rangle }\in \overline I\otimes \overline H+\overline H\otimes \overline I$
, and
![]() $\overline e_{\langle j\rangle }\in \overline I$
.
$\overline e_{\langle j\rangle }\in \overline I$
.
Step 2. Now we will show that in fact
![]() $e_{\langle j\rangle }\in I$
. Recall that we chose k in such a way that
$e_{\langle j\rangle }\in I$
. Recall that we chose k in such a way that
![]() $2k-1=\langle 2j\rangle $
is the largest possible number such that
$2k-1=\langle 2j\rangle $
is the largest possible number such that
![]() $a_k=0$
and
$a_k=0$
and
![]() $e_{2k-1}\not \in I$
. Since
$e_{2k-1}\not \in I$
. Since
![]() $\overline e_{\langle j\rangle }\in \overline I$
, we conclude that
$\overline e_{\langle j\rangle }\in \overline I$
, we conclude that
![]() $\overline e_{\langle j\rangle }$
is equal to
$\overline e_{\langle j\rangle }$
is equal to
![]() $\overline e_{2i-1}^{\,2^{a_i+e}}$
for some i and
$\overline e_{2i-1}^{\,2^{a_i+e}}$
for some i and
![]() $e\geq 0$
. However, if
$e\geq 0$
. However, if
![]() $a_i+e>0$
, we already proved that
$a_i+e>0$
, we already proved that
![]() $e_{2i-1}^{\,2^{a_i+e}}\in I$
(see Case 1). But if
$e_{2i-1}^{\,2^{a_i+e}}\in I$
(see Case 1). But if
![]() $a_i=0=e$
, we know that
$a_i=0=e$
, we know that
![]() $e_{2i-1}\in I$
by the choice of k. In both cases, we obtain that
$e_{2i-1}\in I$
by the choice of k. In both cases, we obtain that
![]() $e_{\langle j\rangle }\in I$
.
$e_{\langle j\rangle }\in I$
.
Step 3. Finally, we show that
![]() $e_{\langle 2j\rangle }\in I$
. Since
$e_{\langle 2j\rangle }\in I$
. Since
![]() $e_{\langle j\rangle }\in I$
by Step 2, we conclude that
$e_{\langle j\rangle }\in I$
by Step 2, we conclude that
by Theorem 4.13. Consequently, applying
![]() $\widetilde \Delta $
to (5.1), we have
$\widetilde \Delta $
to (5.1), we have
and therefore,
![]() $\widetilde \Delta (P)\in I\otimes H+H\otimes I$
by Lemma 5.3. As above, this implies that
$\widetilde \Delta (P)\in I\otimes H+H\otimes I$
by Lemma 5.3. As above, this implies that
![]() $\overline P$
becomes primitive modulo
$\overline P$
becomes primitive modulo
![]() $\overline I$
; however,
$\overline I$
; however,
![]() $\overline H/\,\overline I$
does not have primitive elements of the required degree by Lemma 5.5. This implies that
$\overline H/\,\overline I$
does not have primitive elements of the required degree by Lemma 5.5. This implies that
![]() $\overline P\in \overline I$
, and therefore, we can find a new lift
$\overline P\in \overline I$
, and therefore, we can find a new lift
![]() $E_{2k-1}'$
for
$E_{2k-1}'$
for
![]() $\overline e_{2k-1}$
with greater a in the decomposition (5.1). Continuing this process, we will eventually prove that
$\overline e_{2k-1}$
with greater a in the decomposition (5.1). Continuing this process, we will eventually prove that
![]() $e_{2k-1}=e_{\langle 2j\rangle }\in I$
. This finishes the proof of Subcase 2.2.
$e_{2k-1}=e_{\langle 2j\rangle }\in I$
. This finishes the proof of Subcase 2.2.
We proved that
![]() $e_{2i-1}^{2^{a_i}}\in I$
, and it remains to observe that they clearly generate I since it is true modulo
$e_{2i-1}^{2^{a_i}}\in I$
, and it remains to observe that they clearly generate I since it is true modulo
![]() $v_n$
and I is saturated.
$v_n$
and I is saturated.
5.3 The J-invariant for the connective Morava K-theory
Let n,
![]() $m\in \mathbb N\setminus 0$
. For
$m\in \mathbb N\setminus 0$
. For
![]() $m\leq 2^{n+1}$
, we put
$m\leq 2^{n+1}$
, we put
![]() $m_0=m$
, and for
$m_0=m$
, and for
![]() $m>2^{n+1}$
, let
$m>2^{n+1}$
, let
![]() $m_0=2^{n+1}-1$
for an odd m and
$m_0=2^{n+1}-1$
for an odd m and
![]() $m_0=2^{n+1}$
for an even m. Denote
$m_0=2^{n+1}$
for an even m. Denote
For a smooth irreducible variety X and a free theory
![]() $A^*$
, the
$A^*$
, the
![]() $A^*(\mathrm {pt})$
-algebra
$A^*(\mathrm {pt})$
-algebra
![]() $A^*(X)$
is naturally augmented via
$A^*(X)$
is naturally augmented via
where
![]() $\eta $
denotes the generic point of X (see [Reference Levine and Morel19, Remark 1.2.12]). We denote by
$\eta $
denotes the generic point of X (see [Reference Levine and Morel19, Remark 1.2.12]). We denote by
![]() $A^*(X)^+$
the augmentation ideal.
$A^*(X)^+$
the augmentation ideal.
For
![]() $E\in \mathrm H^1(k,\,\mathrm {SO}_m)$
, consider the natural map
$E\in \mathrm H^1(k,\,\mathrm {SO}_m)$
, consider the natural map
![]() $\mathrm {CK}(n)^*(E)\rightarrow \mathrm {CK}(n)^*(\mathrm {SO}_m)$
induced by the restriction of scalars. Denote by I the ideal of H generated by the image of the map
$\mathrm {CK}(n)^*(E)\rightarrow \mathrm {CK}(n)^*(\mathrm {SO}_m)$
induced by the restriction of scalars. Denote by I the ideal of H generated by the image of the map
and denote by
![]() $I_0$
the ideal of
$I_0$
the ideal of
![]() $H_0$
generated by the image of
$H_0$
generated by the image of
where the map
![]() $H\rightarrow H_0$
is the pullback along the natural closed embedding
$H\rightarrow H_0$
is the pullback along the natural closed embedding
![]() $\mathrm {SO}_{m_0}\hookrightarrow \mathrm {SO}_{m}$
. In other words,
$\mathrm {SO}_{m_0}\hookrightarrow \mathrm {SO}_{m}$
. In other words,
![]() $H/I$
is the generalized J-invariant of E in the sense of Definition 1, and I is a bi-ideal of H by [Reference Petrov and Semenov29, Lemma 4.5].
$H/I$
is the generalized J-invariant of E in the sense of Definition 1, and I is a bi-ideal of H by [Reference Petrov and Semenov29, Lemma 4.5].
Lemma 5.7. In the notation above,
![]() $I_0$
is a saturated bi-ideal of
$I_0$
is a saturated bi-ideal of
![]() $H_0$
.
$H_0$
.
Proof. It is easy to see that
![]() $I_0$
is also a bi-ideal of
$I_0$
is also a bi-ideal of
![]() $H_0$
as an image of I.
$H_0$
as an image of I.
Let
![]() $J_0$
denote the saturation of
$J_0$
denote the saturation of
![]() $I_0$
, that is,
$I_0$
, that is,
For
![]() $x\in J_0$
, one has
$x\in J_0$
, one has
and therefore,
![]() $J_0$
is a bi-ideal by Lemma 5.3. Then, by Proposition 5.6,
$J_0$
is a bi-ideal by Lemma 5.3. Then, by Proposition 5.6,
We will show that in fact
![]() $e_{2i-1}^{2^{a_i}}\in I_0$
.
$e_{2i-1}^{2^{a_i}}\in I_0$
.
Since
![]() $v_n^te_{2i-1}^{2^{a_i}}\in I_0$
, there exist homogeneous elements
$v_n^te_{2i-1}^{2^{a_i}}\in I_0$
, there exist homogeneous elements
![]() $h_k\in H_0$
and
$h_k\in H_0$
and
such that
![]() $v_n^te_{2i-1}^{2^{a_i}}=\sum x_kh_k$
. However, since the codimension of
$v_n^te_{2i-1}^{2^{a_i}}=\sum x_kh_k$
. However, since the codimension of
![]() $e_{2i-1}^{2^{a_i}}$
is less than or equal to
$e_{2i-1}^{2^{a_i}}$
is less than or equal to
![]() $2^n-1$
, we can assume that for each k, either
$2^n-1$
, we can assume that for each k, either
![]() $x_k$
or
$x_k$
or
![]() $h_k$
has degree less than
$h_k$
has degree less than
![]() $0$
(if the degree of
$0$
(if the degree of
![]() $x_kh_k$
is
$x_kh_k$
is
![]() $0$
, use additionally that
$0$
, use additionally that
![]() $e_{2i-1}\in H^+_0$
). By a theorem of Levine–Morel, the algebraic cobordism is generated by the elements of non-negative degrees [Reference Levine and Morel19, Theorem 1.2.14]. This implies that either
$e_{2i-1}\in H^+_0$
). By a theorem of Levine–Morel, the algebraic cobordism is generated by the elements of non-negative degrees [Reference Levine and Morel19, Theorem 1.2.14]. This implies that either
![]() $x_k$
or
$x_k$
or
![]() $h_k$
is divisible by
$h_k$
is divisible by
![]() $v_n$
. In other words, there exist
$v_n$
. In other words, there exist
![]() $h_k'\in H_0$
and
$h_k'\in H_0$
and
![]() $x_k'\in \mathrm {Im}\big (\mathrm {CK}(n)^*(E)^+\rightarrow H\rightarrow H_0\big )$
such that
$x_k'\in \mathrm {Im}\big (\mathrm {CK}(n)^*(E)^+\rightarrow H\rightarrow H_0\big )$
such that
Since
![]() $H_0$
does not have
$H_0$
does not have
![]() $v_n$
-torsion, we conclude that
$v_n$
-torsion, we conclude that
![]() $ v_n^{t-1}e_{2i-1}^{2^{a_i}}\in I_0. $
Continuing this process, we obtain the claim.
$ v_n^{t-1}e_{2i-1}^{2^{a_i}}\in I_0. $
Continuing this process, we obtain the claim.
Next, we prove the following theorem.
Theorem 5.8. For H and
![]() $H_0$
as above, let I be a (homogeneous) bi-ideal of H such that its image
$H_0$
as above, let I be a (homogeneous) bi-ideal of H such that its image
![]() $I_0$
in
$I_0$
in
![]() $H_0$
is saturated. Then
$H_0$
is saturated. Then
for some
![]() $0\leq a_i\leq k_i$
. In particular, I is determined by its image modulo
$0\leq a_i\leq k_i$
. In particular, I is determined by its image modulo
![]() $v_n$
.
$v_n$
.
Proof. For
![]() $m\leq 2^{n+1}$
, the claim is proven in Proposition 5.6. We assume that
$m\leq 2^{n+1}$
, the claim is proven in Proposition 5.6. We assume that
![]() $m>2^{n+1}$
and argue by induction.
$m>2^{n+1}$
and argue by induction.
We denote the reduction modulo
![]() $v_n$
by
$v_n$
by
![]() $\,\overline {\phantom {x}}$
. Let
$\,\overline {\phantom {x}}$
. Let
![]() $ \overline I=(\overline e_1^{\,2^{a_1}},\ldots ,\overline e_{2r-1}^{\,2^{a_{r}}}) $
according to Lemma 5.4. Let
$ \overline I=(\overline e_1^{\,2^{a_1}},\ldots ,\overline e_{2r-1}^{\,2^{a_{r}}}) $
according to Lemma 5.4. Let
![]() $s=\lfloor \frac {m-1}{2}\rfloor $
.
$s=\lfloor \frac {m-1}{2}\rfloor $
.
Case 1. Assume that
![]() $e_s\neq e_{2i-1}^{2^{a_{i}}}$
for all i. Since
$e_s\neq e_{2i-1}^{2^{a_{i}}}$
for all i. Since
![]() $I/e_s$
is a bi-ideal in
$I/e_s$
is a bi-ideal in
![]() $H/e_s$
such that
$H/e_s$
such that
![]() $(I/e_s)_0$
is saturated, using the induction, we have
$(I/e_s)_0$
is saturated, using the induction, we have
Then there exist
![]() $E_1,\ldots ,E_r\in I$
such that
$E_1,\ldots ,E_r\in I$
such that
![]() $E_i-e_{2i-1}^{2^{a_i}}=e_s\cdot x_i$
. Since
$E_i-e_{2i-1}^{2^{a_i}}=e_s\cdot x_i$
. Since
![]() $e_s^2=0$
and
$e_s^2=0$
and
![]() $v_ne_s=0$
, we can assume that
$v_ne_s=0$
, we can assume that
![]() $x_i$
are polynomials with
$x_i$
are polynomials with
![]() $\mathbb F_2$
-coefficients in
$\mathbb F_2$
-coefficients in
![]() $e_1,\ldots ,e_{s-1}$
. However,
$e_1,\ldots ,e_{s-1}$
. However,
and this can only happen if
![]() $\overline x_i\in \overline I$
. Then
$\overline x_i\in \overline I$
. Then
![]() $ x_i-\sum e_{2j-1}^{2^{a_j}}\cdot y_{ij} = v_nz_i $
for some
$ x_i-\sum e_{2j-1}^{2^{a_j}}\cdot y_{ij} = v_nz_i $
for some
![]() $y_{ij}$
,
$y_{ij}$
,
![]() $z_i\in H$
. Then one has
$z_i\in H$
. Then one has
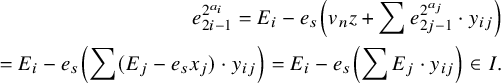 $$ \begin{align*} e_{2i-1}^{2^{a_i}}=E_i-e_s\left(v_nz+\sum e_{2j-1}^{2^{a_j}}\cdot y_{ij}\right)\\=E_i-e_s\left(\sum (E_j-e_sx_j)\cdot y_{ij}\right)=E_i-e_s\left(\sum E_j\cdot y_{ij}\right)\in I. \end{align*} $$
$$ \begin{align*} e_{2i-1}^{2^{a_i}}=E_i-e_s\left(v_nz+\sum e_{2j-1}^{2^{a_j}}\cdot y_{ij}\right)\\=E_i-e_s\left(\sum (E_j-e_sx_j)\cdot y_{ij}\right)=E_i-e_s\left(\sum E_j\cdot y_{ij}\right)\in I. \end{align*} $$
It remains to prove that
![]() $I\subseteq (e_1^{2^{a_1}},\ldots ,e_{2r-1}^{2^{a_r}})$
. Take
$I\subseteq (e_1^{2^{a_1}},\ldots ,e_{2r-1}^{2^{a_r}})$
. Take
![]() $x\in I$
. Then
$x\in I$
. Then
![]() $x-\sum e_{2i-1}^{2^{a_i}}\, x_{i}=e_sz$
for some
$x-\sum e_{2i-1}^{2^{a_i}}\, x_{i}=e_sz$
for some
![]() $x_i$
,
$x_i$
,
![]() $z\in H$
. Again, we can assume that z is a polynomial with
$z\in H$
. Again, we can assume that z is a polynomial with
![]() $\mathbb F_2$
-coefficients in
$\mathbb F_2$
-coefficients in
![]() $e_1,\ldots ,e_{s-1}$
. But
$e_1,\ldots ,e_{s-1}$
. But
![]() $\overline e_s\,\overline z\in \overline I$
, and therefore,
$\overline e_s\,\overline z\in \overline I$
, and therefore,
![]() $\overline z\in \overline I$
(i.e.,
$\overline z\in \overline I$
(i.e.,
![]() $z-\sum e_{2j-1}^{2^{a_j}}\, y_{j}=v_nw$
for some
$z-\sum e_{2j-1}^{2^{a_j}}\, y_{j}=v_nw$
for some
![]() $y_j$
,
$y_j$
,
![]() $w\in H$
). Therefore,
$w\in H$
). Therefore,
which proves the claim.
Case 2. Assume that
![]() $e_s= e_{2i_0-1}^{2^{a_{i_0}}}$
for some
$e_s= e_{2i_0-1}^{2^{a_{i_0}}}$
for some
![]() $i_0$
. Again,
$i_0$
. Again,
![]() $I/e_s$
is a bi-ideal in
$I/e_s$
is a bi-ideal in
![]() $H/e_s$
such that
$H/e_s$
such that
![]() $(I/e_s)_0$
is saturated. Then using the induction, we have
$(I/e_s)_0$
is saturated. Then using the induction, we have
where
![]() $\widehat e_s$
means that we excluded
$\widehat e_s$
means that we excluded
![]() $e_s=e_{2i_0-1}^{2^{a_{i_0}}}$
from
$e_s=e_{2i_0-1}^{2^{a_{i_0}}}$
from
![]() $e_1^{2^{a_1}},\ldots ,e_{2r-1}^{2^{a_r}}$
. As above, we can find
$e_1^{2^{a_1}},\ldots ,e_{2r-1}^{2^{a_r}}$
. As above, we can find
![]() $E_i\in I$
such that
$E_i\in I$
such that
![]() $E_i-e_{2i-1}^{2^{a_i}}=e_sx_i$
for
$E_i-e_{2i-1}^{2^{a_i}}=e_sx_i$
for
![]() $i\neq i_0$
and some
$i\neq i_0$
and some
![]() $x_i\in H$
, and
$x_i\in H$
, and
![]() $e_s+v_ny\in I$
for some
$e_s+v_ny\in I$
for some
![]() $y\in H$
. Since the image of
$y\in H$
. Since the image of
![]() $e_s+v_ny$
coincides with the image of
$e_s+v_ny$
coincides with the image of
![]() $v_ny$
in
$v_ny$
in
![]() $I_0$
, and the latter ideal is saturated, we conclude that the image of y lies in
$I_0$
, and the latter ideal is saturated, we conclude that the image of y lies in
![]() $I_0$
. Then there exist
$I_0$
. Then there exist
![]() $y_i\in H$
such that the image of
$y_i\in H$
such that the image of
![]() $Y=\sum e_{2i-1}^{2^{a_i}}\,y_i$
in
$Y=\sum e_{2i-1}^{2^{a_i}}\,y_i$
in
![]() $H_0$
coincides with the image of y. Obviously, the image of
$H_0$
coincides with the image of y. Obviously, the image of
![]() $Y'=\sum E_i\,y_i$
also coincides with the image of Y. But the kernel of
$Y'=\sum E_i\,y_i$
also coincides with the image of Y. But the kernel of
![]() $H\rightarrow H_0$
is annihilated by
$H\rightarrow H_0$
is annihilated by
![]() $v_n$
; in other words,
$v_n$
; in other words,
But then
![]() $e_s=(e_s+v_ny)-v_nY'\in I$
. Therefore,
$e_s=(e_s+v_ny)-v_nY'\in I$
. Therefore,
![]() $e_{2i-1}^{2^{a_i}}=E_i-e_s\,x_i\in I$
.
$e_{2i-1}^{2^{a_i}}=E_i-e_s\,x_i\in I$
.
Finally, it remains to show that
![]() $I\subseteq (e_1^{2^{a_1}},\ldots ,e_{2r-1}^{2^{a_r}})$
. Let
$I\subseteq (e_1^{2^{a_1}},\ldots ,e_{2r-1}^{2^{a_r}})$
. Let
![]() $x\in I$
. Then
$x\in I$
. Then
for some
![]() $z_i$
,
$z_i$
,
![]() $w\in H$
by induction. The claim follows.
$w\in H$
by induction. The claim follows.
6 Motivic decomposition of maximal orthogonal Grassmannians
6.1 Statement of results
For a non-degenerate quadratic form
![]() $q\colon V\rightarrow k$
with trivial discriminant, let
$q\colon V\rightarrow k$
with trivial discriminant, let
![]() $\mathrm {OGr}(q)$
denote the variety of maximal totally isotropic subspaces of V. If q is odd dimensional, denote
$\mathrm {OGr}(q)$
denote the variety of maximal totally isotropic subspaces of V. If q is odd dimensional, denote
![]() $X=\mathrm {OGr}(q)$
, and if q is even-dimensional, denote by X one of the (isomorphic) connected components of
$X=\mathrm {OGr}(q)$
, and if q is even-dimensional, denote by X one of the (isomorphic) connected components of
![]() $\mathrm {OGr}(q)$
(see [Reference Elman, Karpenko and Merkurjev6, Section 86]). Since X is generically split, the decomposition of its Morava motive can be described in terms of the Hopf algebra structure of
$\mathrm {OGr}(q)$
(see [Reference Elman, Karpenko and Merkurjev6, Section 86]). Since X is generically split, the decomposition of its Morava motive can be described in terms of the Hopf algebra structure of
![]() $\mathrm K(n)^*(\mathrm {SO}_m)$
by [Reference Petrov and Semenov29, Theorem 5.7]; cf. [Reference Geldhauser, Lavrenov, Petrov and Sechin9, Corollary 6.14]. In particular, for a generic quadratic form q, we will determine the
$\mathrm K(n)^*(\mathrm {SO}_m)$
by [Reference Petrov and Semenov29, Theorem 5.7]; cf. [Reference Geldhauser, Lavrenov, Petrov and Sechin9, Corollary 6.14]. In particular, for a generic quadratic form q, we will determine the
![]() $\mathrm K(n)$
-motivic decomposition of X.
$\mathrm K(n)$
-motivic decomposition of X.
More generally, if
![]() $\mathrm {dim}\,q=2l+1$
or
$\mathrm {dim}\,q=2l+1$
or
![]() $\mathrm {dim}\,q=2l$
, following [Reference Vishik43, Definition 5.11], we define
$\mathrm {dim}\,q=2l$
, following [Reference Vishik43, Definition 5.11], we define
![]() $J(q)$
as a subset of
$J(q)$
as a subset of
![]() $\{1,\ldots ,l\}$
such that
$\{1,\ldots ,l\}$
such that
![]() $i\in J(q)$
iff the image of
$i\in J(q)$
iff the image of
![]() $e_i$
in
$e_i$
in
![]() $H^*_{\mathrm {Ch}}(q)$
is
$H^*_{\mathrm {Ch}}(q)$
is
![]() $0$
(see Definition 1). By [Reference Vishik43, Main Theorem 5.8], one can recover
$0$
(see Definition 1). By [Reference Vishik43, Main Theorem 5.8], one can recover
We will need the theorem of the first and the third authors [Reference Petrov and Semenov29, Theorem 5.7] in the case
![]() $A^*=\mathrm K(n)^*$
,
$A^*=\mathrm K(n)^*$
,
![]() $G=\mathrm {SO}_m$
(cf. also [Reference Geldhauser, Lavrenov, Petrov and Sechin9, Corollary 6.14]).
$G=\mathrm {SO}_m$
(cf. also [Reference Geldhauser, Lavrenov, Petrov and Sechin9, Corollary 6.14]).
Theorem 6.1 (Theorem 5.7 [Reference Petrov and Semenov29]).
For
![]() $n\in \mathbb N\setminus 0$
, let q be a quadratic form of dimension m with trivial discriminant. Let X denote the connected component of its maximal orthogonal Grassmannian. Then there exists a
$n\in \mathbb N\setminus 0$
, let q be a quadratic form of dimension m with trivial discriminant. Let X denote the connected component of its maximal orthogonal Grassmannian. Then there exists a
![]() $\mathrm K(n)$
-motive
$\mathrm K(n)$
-motive
![]() $\mathcal R$
such that the
$\mathcal R$
such that the
![]() $\mathrm K(n)$
-motive of X decomposes as
$\mathrm K(n)$
-motive of X decomposes as
for some multiset of non-negative integers
![]() $\mathcal {I}$
. Moreover, the rank of
$\mathcal {I}$
. Moreover, the rank of
![]() $\mathcal R$
equals the rank of
$\mathcal R$
equals the rank of
![]() $H^*_{\mathrm K(n)}(q)$
.
$H^*_{\mathrm K(n)}(q)$
.
Observe that the the rank of
![]() $\mathcal R$
is determined by
$\mathcal R$
is determined by
![]() $J(q)$
by Corollary 5.2. Using the developed techniques, we can now prove a more precise version of the above result.
$J(q)$
by Corollary 5.2. Using the developed techniques, we can now prove a more precise version of the above result.
Theorem 6.2. In the notation of Theorem 6.1, if
![]() $m\leq 2^{n+1}-2$
or
$m\leq 2^{n+1}-2$
or
![]() $2^n-1\in J(q)$
, then
$2^n-1\in J(q)$
, then
![]() $\mathcal R$
is indecomposable. If
$\mathcal R$
is indecomposable. If
![]() $m\geq 2^{n+1}-1$
and
$m\geq 2^{n+1}-1$
and
![]() $2^n-1\not \in J(q)$
, then
$2^n-1\not \in J(q)$
, then
![]() $\mathcal R$
decomposes as a sum of two non-isomorphic indecomposable motives of the same rank.
$\mathcal R$
decomposes as a sum of two non-isomorphic indecomposable motives of the same rank.
As an immediate corollary, we obtain the following result.
Corollary 6.3. In the notation of Theorem 6.1, assume additionally that
(e.g., a generic quadratic form). Then the following holds.
-
1. The
 $\mathrm K(n)$
-motive
$\mathrm K(n)$
-motive
 $\mathcal M_{\mathrm K(n)}(X)$
of X is indecomposable for
$\mathcal M_{\mathrm K(n)}(X)$
of X is indecomposable for
 $m\leq 2^{n+1}-2$
.
$m\leq 2^{n+1}-2$
. -
2. The
 $\mathrm K(n)$
-motive
$\mathrm K(n)$
-motive
 $\mathcal M_{\mathrm K(n)}(X)$
of X has
$\mathcal M_{\mathrm K(n)}(X)$
of X has
 $2^{\lfloor \frac {m-1}{2}\rfloor -2^n+2}$
indecomposable summands of rank
$2^{\lfloor \frac {m-1}{2}\rfloor -2^n+2}$
indecomposable summands of rank
 $2^{2^n-2}$
for
$2^{2^n-2}$
for
 $m\geq 2^{n+1}-1$
.
$m\geq 2^{n+1}-1$
.
Remark 6.4. Compare the above corollary with [Reference Geldhauser, Lavrenov, Petrov and Sechin9, Corollary 6.14]. We proved there that the motive of X is decomposable for
![]() $m\geq 2^{n+1}+1$
. We could not prove at that time, however, that for
$m\geq 2^{n+1}+1$
. We could not prove at that time, however, that for
![]() $m=2^{n+1}-1,2^{n+1}$
, the motive of X is also decomposable.
$m=2^{n+1}-1,2^{n+1}$
, the motive of X is also decomposable.
In the case of generic q, we also did not claim that the summands found in [Reference Geldhauser, Lavrenov, Petrov and Sechin9, Corollary 6.14] are indecomposable. In fact, they decompose as a sum of two motives of the same rank.
Proof of Corollary 6.3.
According to Theorem 6.1, there exists a
![]() $\mathrm K(n)$
-motive
$\mathrm K(n)$
-motive
![]() $\mathcal R$
such that the
$\mathcal R$
such that the
![]() $\mathrm K(n)$
-motive of X decomposes as
$\mathrm K(n)$
-motive of X decomposes as
for some multiset of integers
![]() $\mathcal {I}$
; moreover, the rank of
$\mathcal {I}$
; moreover, the rank of
![]() $\mathcal R$
equals the rank of
$\mathcal R$
equals the rank of
![]() $H^*_{\mathrm K(n)}(q)$
.
$H^*_{\mathrm K(n)}(q)$
.
By Corollary 5.2, we conclude that
where the last equality follows from the assumption on the J-invariant of q.
We can now compare the ranks of
![]() $\mathrm K(n)^*(\mathrm {SO}_m)$
and
$\mathrm K(n)^*(\mathrm {SO}_m)$
and
![]() $\mathrm K(n)^*(\overline X)$
to determine the cardinality of
$\mathrm K(n)^*(\overline X)$
to determine the cardinality of
![]() $\mathcal I$
. By [Reference Geldhauser, Lavrenov, Petrov and Sechin9, Theorem 6.13], the rank of
$\mathcal I$
. By [Reference Geldhauser, Lavrenov, Petrov and Sechin9, Theorem 6.13], the rank of
![]() $\mathrm K(n)^*(\mathrm {SO}_m)$
equals
$\mathrm K(n)^*(\mathrm {SO}_m)$
equals
![]() $2^{\lfloor \frac {m-1}{2}\rfloor }$
for
$2^{\lfloor \frac {m-1}{2}\rfloor }$
for
![]() $m\leq 2^{n+1}$
, and
$m\leq 2^{n+1}$
, and
![]() $2^{2^n-1}$
for
$2^{2^n-1}$
for
![]() $m>2^{n+1}$
. However, the rank of
$m>2^{n+1}$
. However, the rank of
![]() $\mathrm K(n)^*(\overline X)$
always equals
$\mathrm K(n)^*(\overline X)$
always equals
![]() $2^{\lfloor \frac {m-1}{2}\rfloor }$
. This implies that
$2^{\lfloor \frac {m-1}{2}\rfloor }$
. This implies that
![]() $|\mathcal I|=1$
for
$|\mathcal I|=1$
for
![]() $m\leq 2^{n+1}$
, and
$m\leq 2^{n+1}$
, and
![]() $|\mathcal I|=2^{\lfloor \frac {m-1}{2}\rfloor -2^n+1}$
for
$|\mathcal I|=2^{\lfloor \frac {m-1}{2}\rfloor -2^n+1}$
for
![]() $m>2^{n+1}$
.
$m>2^{n+1}$
.
It remains to use that
![]() $\mathcal R$
is indecomposable for
$\mathcal R$
is indecomposable for
![]() $m\leq 2^{n+1}-2$
, and that
$m\leq 2^{n+1}-2$
, and that
![]() $\mathcal R$
has two indecomposable summands of the same rank for
$\mathcal R$
has two indecomposable summands of the same rank for
![]() $m>2^{n+1}-2$
by Theorem 6.2.
$m>2^{n+1}-2$
by Theorem 6.2.
The next section will be devoted to the proof Theorem 6.2.
6.2 Idempotents in
 $\mathrm K(n)^*(\mathrm {SO}_m)^{\vee }$
$\mathrm K(n)^*(\mathrm {SO}_m)^{\vee }$
Dualizing Proposition 4.12, we obtain the following description of the Hopf algebra
![]() $\mathrm {CK}(n)^*(\mathrm {SO}_m)^{\vee }$
for
$\mathrm {CK}(n)^*(\mathrm {SO}_m)^{\vee }$
for
![]() $m\leq 2^{n+1}$
.
$m\leq 2^{n+1}$
.
Proposition 6.5. In the notation of Proposition 4.10, for an odd
![]() $m\leq 2^{n+1}-1$
, the natural map
$m\leq 2^{n+1}-1$
, the natural map
coincides with the inclusion of a sub-algebra generated by
![]() $\gamma _t(\alpha _{2i-1})$
for
$\gamma _t(\alpha _{2i-1})$
for
![]() $1\leq i\leq r$
and
$1\leq i\leq r$
and
![]() $1\leq t<2^{d_i}$
, where
$1\leq t<2^{d_i}$
, where
![]() $r=\lfloor \frac {m+1}{4}\rfloor $
and
$r=\lfloor \frac {m+1}{4}\rfloor $
and
![]() $d_i=\left \lfloor \log _2\left (\frac {m-1}{2i-1}\right )\right \rfloor $
. In particular,
$d_i=\left \lfloor \log _2\left (\frac {m-1}{2i-1}\right )\right \rfloor $
. In particular,
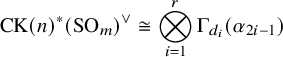 $$ \begin{align*}\mathrm{CK}(n)^*(\mathrm{SO}_{m})^\vee\cong\bigotimes_{i=1}^{r}\Gamma_{d_i}(\alpha_{2i-1}) \end{align*} $$
$$ \begin{align*}\mathrm{CK}(n)^*(\mathrm{SO}_{m})^\vee\cong\bigotimes_{i=1}^{r}\Gamma_{d_i}(\alpha_{2i-1}) \end{align*} $$
is an isomorphism of co-algebras, and the multiplication table of
![]() $\mathrm {CK}(n)^*(\mathrm {SO}_{m})^\vee $
can be deduced from the identities (4.4) and (4.5) of Proposition 4.10. For m even, there is an isomorphism of Hopf algebras
$\mathrm {CK}(n)^*(\mathrm {SO}_{m})^\vee $
can be deduced from the identities (4.4) and (4.5) of Proposition 4.10. For m even, there is an isomorphism of Hopf algebras
As a corollary, we obtain an analogous result for the periodic algebraic Morava K-theories
![]() $\mathrm {K}(n)^*(\mathrm {SO}_m)^{\vee }$
for
$\mathrm {K}(n)^*(\mathrm {SO}_m)^{\vee }$
for
![]() $m\leq 2^{n+1}$
. Therefore, to determine the idempotents of
$m\leq 2^{n+1}$
. Therefore, to determine the idempotents of
![]() $\mathrm {K}(n)^*(\mathrm {SO}_m)^{\vee }$
for all m, it is enough to consider only the case
$\mathrm {K}(n)^*(\mathrm {SO}_m)^{\vee }$
for all m, it is enough to consider only the case
![]() $m=2^{n+1}-1$
.
$m=2^{n+1}-1$
.
Proposition 6.6. In the notation of Proposition 4.10, the only non-trivial idempotents in
![]() $\mathrm {K}(n)^*(\mathrm {SO}_{2^{n+1}-1})^{\vee }$
are
$\mathrm {K}(n)^*(\mathrm {SO}_{2^{n+1}-1})^{\vee }$
are
Proof. Let e be an idempotent in
![]() $\mathrm {K}(n)^*(\mathrm {SO}_{2^{n+1}-1})^{\vee }$
. Decompose it in the basis of monomials
$\mathrm {K}(n)^*(\mathrm {SO}_{2^{n+1}-1})^{\vee }$
. Decompose it in the basis of monomials
where
![]() $0\leq t_i<2^{k_i}$
, and observe that
$0\leq t_i<2^{k_i}$
, and observe that
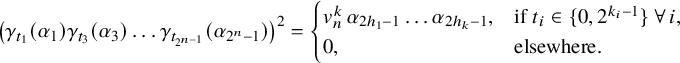 $$ \begin{align*}\big(\gamma_{t_1}(\alpha_{1})\gamma_{t_3}(\alpha_{3})\ldots\gamma_{t_{2^{n-1}}}(\alpha_{2^n-1})\big)^2= \begin{cases} v_n^k\,\alpha_{2h_1-1}\ldots\alpha_{2h_k-1},&\text{if}\ t_i\in\{0,2^{k_i-1}\}\ \forall\,i,\\ 0,&\text{elsewhere}. \end{cases} \end{align*} $$
$$ \begin{align*}\big(\gamma_{t_1}(\alpha_{1})\gamma_{t_3}(\alpha_{3})\ldots\gamma_{t_{2^{n-1}}}(\alpha_{2^n-1})\big)^2= \begin{cases} v_n^k\,\alpha_{2h_1-1}\ldots\alpha_{2h_k-1},&\text{if}\ t_i\in\{0,2^{k_i-1}\}\ \forall\,i,\\ 0,&\text{elsewhere}. \end{cases} \end{align*} $$
Since
![]() $e^2=e$
, we conclude that e can contain only monomials of the form
$e^2=e$
, we conclude that e can contain only monomials of the form
(with some coefficients from
![]() $\mathbb F_2[v_n^{\pm 1}]$
) in its decomposition. However,
$\mathbb F_2[v_n^{\pm 1}]$
) in its decomposition. However,
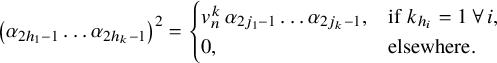 $$ \begin{align*}\big(\alpha_{2h_1-1}\ldots\alpha_{2h_k-1}\big)^2= \begin{cases} v_n^k\,\alpha_{2j_1-1}\ldots\alpha_{2j_k-1},&\text{if}\ k_{h_i}=1\ \forall\,i,\\ 0,&\text{elsewhere}. \end{cases} \end{align*} $$
$$ \begin{align*}\big(\alpha_{2h_1-1}\ldots\alpha_{2h_k-1}\big)^2= \begin{cases} v_n^k\,\alpha_{2j_1-1}\ldots\alpha_{2j_k-1},&\text{if}\ k_{h_i}=1\ \forall\,i,\\ 0,&\text{elsewhere}. \end{cases} \end{align*} $$
The condition
![]() $k_{h_i}=1$
is equivalent to
$k_{h_i}=1$
is equivalent to
![]() $2^{n-2}<h_i\leq 2^{n-1}$
, and the fact
$2^{n-2}<h_i\leq 2^{n-1}$
, and the fact
![]() $e^2=e$
implies that e contains only monomials
$e^2=e$
implies that e contains only monomials
![]() $\alpha _{2h_1-1}\ldots \alpha _{2h_k-1}$
with
$\alpha _{2h_1-1}\ldots \alpha _{2h_k-1}$
with
![]() $2^{n-2}<h_i\leq 2^{n-1}$
in its decomposition. Recall that
$2^{n-2}<h_i\leq 2^{n-1}$
in its decomposition. Recall that
for
![]() $2j_i-1=2(2h_i-1)-2^n+1$
, and
$2j_i-1=2(2h_i-1)-2^n+1$
, and
![]() $2j_i-1$
cannot be greater than
$2j_i-1$
cannot be greater than
![]() $2h_i-1$
for
$2h_i-1$
for
![]() $2^{n-2}<h_i\leq 2^{n-1}$
. Moreover,
$2^{n-2}<h_i\leq 2^{n-1}$
. Moreover,
![]() $2j_i-1=2h_i-1$
can only happen for
$2j_i-1=2h_i-1$
can only happen for
![]() $2h_i-1=2^n-1$
. Then assume that e contains a monomial
$2h_i-1=2^n-1$
. Then assume that e contains a monomial
![]() $\alpha _{2h_1-1}\ldots \alpha _{2h_k-1}$
in its decomposition distinct from
$\alpha _{2h_1-1}\ldots \alpha _{2h_k-1}$
in its decomposition distinct from
![]() $1$
and
$1$
and
![]() $\alpha _{2^n-1}$
, and take the greatest such monomial in the lexicographical order. Then
$\alpha _{2^n-1}$
, and take the greatest such monomial in the lexicographical order. Then
![]() $e^2$
cannot contain this monomial, which provides a contradiction.
$e^2$
cannot contain this monomial, which provides a contradiction.
Then e is a linear combination of
![]() $1$
and
$1$
and
![]() $\alpha _{2^n-1}$
, and it remains to observe that
$\alpha _{2^n-1}$
, and it remains to observe that
![]() $e^2=e$
implies that
$e^2=e$
implies that
![]() $1$
can only have the coefficient
$1$
can only have the coefficient
![]() $0$
or
$0$
or
![]() $1$
, and
$1$
, and
![]() $\alpha _{2^n-1}$
can only have the coefficient
$\alpha _{2^n-1}$
can only have the coefficient
![]() $0$
or
$0$
or
![]() $v_n^{-1}$
in the decomposition of e.
$v_n^{-1}$
in the decomposition of e.
As a corollary of Propositions 6.5 and 6.6, we obtain the following result.
Corollary 6.7. The ring
![]() $\mathrm {K}(n)^*(\mathrm {SO}_{m})^{\vee }$
does not contain nontrivial idempotents for
$\mathrm {K}(n)^*(\mathrm {SO}_{m})^{\vee }$
does not contain nontrivial idempotents for
![]() $m\leq 2^{n+1}-2$
.
$m\leq 2^{n+1}-2$
.
For a quadratic form q of dimension m with trivial discriminant, it follows from Corollary 5.2, that
for
![]() $0\leq a_i\leq k_i$
determined by
$0\leq a_i\leq k_i$
determined by
![]() $J(q)$
, and
$J(q)$
, and
![]() $r=\mathrm {min}\left (\left \lfloor \frac {m+1}{4}\right \rfloor ,\,2^{n-1}\right )$
. Dually,
$r=\mathrm {min}\left (\left \lfloor \frac {m+1}{4}\right \rfloor ,\,2^{n-1}\right )$
. Dually,
![]() $H^*_{\mathrm K(n)}(q)^\vee $
can be identified with a subalgebra
$H^*_{\mathrm K(n)}(q)^\vee $
can be identified with a subalgebra
![]() $\bigotimes _{i=1}^{r}\Gamma _{a_i}(\alpha _{2i-1})$
in
$\bigotimes _{i=1}^{r}\Gamma _{a_i}(\alpha _{2i-1})$
in
![]() $\mathrm K(n)(\mathrm {SO}_m)^\vee $
. In particular, we get the following corollary.
$\mathrm K(n)(\mathrm {SO}_m)^\vee $
. In particular, we get the following corollary.
Corollary 6.8. In the notation above, if
![]() $m\leq 2^{n+1}-2$
or
$m\leq 2^{n+1}-2$
or
![]() $2^n-1\in J(q)$
, then
$2^n-1\in J(q)$
, then
![]() $H^*_{\mathrm K(n)}(q)^\vee $
does not contain non-trivial idempotents. If
$H^*_{\mathrm K(n)}(q)^\vee $
does not contain non-trivial idempotents. If
![]() $m\geq 2^{n+1}-1$
and
$m\geq 2^{n+1}-1$
and
![]() $2^n-1\not \in J(q)$
, then the only nontrivial idempotents in
$2^n-1\not \in J(q)$
, then the only nontrivial idempotents in
![]() $\mathrm {K}(n)^*(\mathrm {SO}_{2^{n+1}-1})^{\vee }$
are
$\mathrm {K}(n)^*(\mathrm {SO}_{2^{n+1}-1})^{\vee }$
are
![]() $v_n^{-1}\alpha _{2^n-1}$
and
$v_n^{-1}\alpha _{2^n-1}$
and
![]() $1-v_n^{-1}\alpha _{2^n-1}$
.
$1-v_n^{-1}\alpha _{2^n-1}$
.
Proof. By Proposition 6.6,
![]() $H^*_{\mathrm K(n)}(q)^\vee $
contains non-trivial idempotents if and only if
$H^*_{\mathrm K(n)}(q)^\vee $
contains non-trivial idempotents if and only if
![]() $\alpha _{2^n-1}\in H^*_{\mathrm K(n)}(q)^\vee $
(i.e.,
$\alpha _{2^n-1}\in H^*_{\mathrm K(n)}(q)^\vee $
(i.e.,
![]() $e_{2^n-1}$
does not map to zero in
$e_{2^n-1}$
does not map to zero in
![]() $H^*_{\mathrm K(n)}$
). The latter exactly means that
$H^*_{\mathrm K(n)}$
). The latter exactly means that
![]() $2^n-1\not \in J(q)$
.
$2^n-1\not \in J(q)$
.
Now we are ready to finish the proof of Theorem 6.2.
Proof of Theorem 6.2.
According to [Reference Petrov and Semenov29, Theorem 5.7], there is a one-to-one correspondence between motivic decompositions of
![]() $\mathcal R$
in the category of
$\mathcal R$
in the category of
![]() $\mathrm K(n)$
-motives and direct sum decompositions of
$\mathrm K(n)$
-motives and direct sum decompositions of
![]() $H^*_{\mathrm K(n)}(q)^{\vee }$
as a module over itself.
$H^*_{\mathrm K(n)}(q)^{\vee }$
as a module over itself.
However,
![]() $H^*_{\mathrm K(n)}(q)^{\vee }$
is indecomposable as a module over itself for
$H^*_{\mathrm K(n)}(q)^{\vee }$
is indecomposable as a module over itself for
![]() $m\leq 2^{n+1}-2$
or
$m\leq 2^{n+1}-2$
or
![]() $2^n-1\in J(q)$
by Corollary 6.8; therefore,
$2^n-1\in J(q)$
by Corollary 6.8; therefore,
![]() $\mathcal R$
is also indecomposable in these cases.
$\mathcal R$
is also indecomposable in these cases.
If
![]() $m\geq 2^{n+1}-1$
and
$m\geq 2^{n+1}-1$
and
![]() $2^n-1\not \in J(q)$
, then the only nontrivial idempotents in
$2^n-1\not \in J(q)$
, then the only nontrivial idempotents in
![]() $H^*_{\mathrm K(n)}(q)^{\vee }$
are
$H^*_{\mathrm K(n)}(q)^{\vee }$
are
![]() $v_n^{-1}\alpha _{2^n-1}$
and
$v_n^{-1}\alpha _{2^n-1}$
and
![]() $1-v_n^{-1}\alpha _{2^n-1}$
. The corresponding modules
$1-v_n^{-1}\alpha _{2^n-1}$
. The corresponding modules
![]() $H_1=v_n^{-1}\alpha _{2^n-1}H^*_{\mathrm K(n)}(q)^{\vee }$
and
$H_1=v_n^{-1}\alpha _{2^n-1}H^*_{\mathrm K(n)}(q)^{\vee }$
and
![]() $H_2=(1-v_n^{-1}\alpha _{2^n-1})H^*_{\mathrm K(n)}(q)^{\vee }$
have equal ranks, but they are not isomorphic as
$H_2=(1-v_n^{-1}\alpha _{2^n-1})H^*_{\mathrm K(n)}(q)^{\vee }$
have equal ranks, but they are not isomorphic as
![]() $H^*_{\mathrm K(n)}(q)^{\vee }$
-modules (
$H^*_{\mathrm K(n)}(q)^{\vee }$
-modules (
![]() $\alpha _{2^n-1}$
acts as the identity on the first one, and as zero on the second one).
$\alpha _{2^n-1}$
acts as the identity on the first one, and as zero on the second one).
Therefore, the motive
![]() $\mathcal R$
also decomposes as a sum
$\mathcal R$
also decomposes as a sum
![]() $\mathcal R\cong \mathcal R_1\oplus \mathcal R_2$
for indecomposable
$\mathcal R\cong \mathcal R_1\oplus \mathcal R_2$
for indecomposable
![]() $\mathcal R_i$
,
$\mathcal R_i$
,
![]() $i=1,2$
. It remains to observe that these summands cannot be isomorphic. Indeed, the realisation
$i=1,2$
. It remains to observe that these summands cannot be isomorphic. Indeed, the realisation
![]() $\alpha _\star $
of the isomorphism
$\alpha _\star $
of the isomorphism
![]() $\alpha \in \mathrm K(n)^*(X\times X)$
between
$\alpha \in \mathrm K(n)^*(X\times X)$
between
![]() $\mathcal R_i$
defines an isomorphism of
$\mathcal R_i$
defines an isomorphism of
![]() $H_{\mathrm K(n)}(q)^{\vee }$
-modules between
$H_{\mathrm K(n)}(q)^{\vee }$
-modules between
![]() $H_i$
by [Reference Petrov and Semenov29, Theorem 4.14], which is impossible.
$H_i$
by [Reference Petrov and Semenov29, Theorem 4.14], which is impossible.
Remark 6.9. We remark that for
![]() $m\geq 2^{n+1}-1$
, the
$m\geq 2^{n+1}-1$
, the
![]() $\mathrm K(n)$
-motive of X detects whether
$\mathrm K(n)$
-motive of X detects whether
![]() $2^n-1\in J(q)$
in the following way. If all indecomposable summands of
$2^n-1\in J(q)$
in the following way. If all indecomposable summands of
![]() $\mathcal M_{\mathrm K(n)}(X)$
are isomorphic to each other up to a shift, then
$\mathcal M_{\mathrm K(n)}(X)$
are isomorphic to each other up to a shift, then
![]() $2^n-1\in J(q)$
. However, if there are two indecomposable summands of
$2^n-1\in J(q)$
. However, if there are two indecomposable summands of
![]() $\mathcal M_{\mathrm K(n)}(X)$
which are not isomorphic to each other up to a shift, then
$\mathcal M_{\mathrm K(n)}(X)$
which are not isomorphic to each other up to a shift, then
![]() $2^n-1\not \in J(q)$
.
$2^n-1\not \in J(q)$
.
A Appendices
A1 Algebraic part of
 $\mathrm {H}_*\big (\mathrm {SO}(2^{n+1}-1);\,\mathbb F_2\big )$
$\mathrm {H}_*\big (\mathrm {SO}(2^{n+1}-1);\,\mathbb F_2\big )$
In this appendix, we will give a proof of Proposition 4.6. By [Reference Kac16, Remark after Theorem 6], the natural map
is injective and its image coincides with the set of squares in
![]() $\mathrm {H}^*(\mathrm {SO}(m);\,\mathbb F_2)$
. In Proposition 4.6, we dualized this statement. To give a detailed proof, we will use the following result.
$\mathrm {H}^*(\mathrm {SO}(m);\,\mathbb F_2)$
. In Proposition 4.6, we dualized this statement. To give a detailed proof, we will use the following result.
Lemma A1.1. For an
![]() $\mathbb F_2$
-algebra H, consider the switch map
$\mathbb F_2$
-algebra H, consider the switch map
![]() $\tau \colon H\otimes H\rightarrow H\otimes H$
sending
$\tau \colon H\otimes H\rightarrow H\otimes H$
sending
![]() $a\otimes b$
to
$a\otimes b$
to
![]() $b\otimes a$
. Let
$b\otimes a$
. Let
![]() $H\otimes H^\tau $
denote the submodule of
$H\otimes H^\tau $
denote the submodule of
![]() $\tau $
-invariant elements, and
$\tau $
-invariant elements, and
![]() $H\otimes H_\tau $
the module of
$H\otimes H_\tau $
the module of
![]() $\tau $
-coinvariants (i.e., the kernel and the cokernel of the map
$\tau $
-coinvariants (i.e., the kernel and the cokernel of the map
![]() $\mathrm {id}+\tau $
. Consider the map
$\mathrm {id}+\tau $
. Consider the map
given as a composition of the natural inclusion
![]() $H\otimes H^\tau \hookrightarrow H\otimes H$
followed by the multiplication
$H\otimes H^\tau \hookrightarrow H\otimes H$
followed by the multiplication
![]() $\mathrm m\colon H\otimes H\rightarrow H$
. The image of
$\mathrm m\colon H\otimes H\rightarrow H$
. The image of
![]() $\mathrm {sq}$
coincides with the submodule of H generated by squares.
$\mathrm {sq}$
coincides with the submodule of H generated by squares.
Then the dual map to a switch
![]() $\tau ^\vee $
coincides with the switch on
$\tau ^\vee $
coincides with the switch on
![]() $H^\vee \otimes H^\vee $
, and the dual map to
$H^\vee \otimes H^\vee $
, and the dual map to
![]() $\mathrm {sq}$
,
$\mathrm {sq}$
,
is given by the class of the co-multiplication
![]() $\Delta =\mathrm m^\vee $
.
$\Delta =\mathrm m^\vee $
.
Proof. Take an additive basis
![]() $\{e_i\}$
of H, and let
$\{e_i\}$
of H, and let
![]() $\{f_i\}$
denote the dual basis of
$\{f_i\}$
denote the dual basis of
![]() $H^\vee $
. Then
$H^\vee $
. Then
and therefore,
![]() $\tau ^\vee (f_i\otimes f_j)=f_j\otimes f_i$
; in particular,
$\tau ^\vee (f_i\otimes f_j)=f_j\otimes f_i$
; in particular,
The last claim is clear.
Let
![]() $\mathrm {Ch}^*(\mathrm {SO}_m)^\vee $
denote the Hopf algebra dual to
$\mathrm {Ch}^*(\mathrm {SO}_m)^\vee $
denote the Hopf algebra dual to
![]() $\mathrm {Ch}^*(\mathrm {SO}_m)$
.
$\mathrm {Ch}^*(\mathrm {SO}_m)$
.
Proposition A1.2 (Proposition 4.6).
In the notation of Subsection 4.2, the Hopf algebra
![]() $\mathrm {Ch}^*(\mathrm {SO}_{2^{n+1}-1})^\vee $
is isomorphic to the quotient of
$\mathrm {Ch}^*(\mathrm {SO}_{2^{n+1}-1})^\vee $
is isomorphic to the quotient of
![]() $\mathrm {H}_*(\mathrm {SO}(2^{n+1}-1);\,\mathbb F_2)$
modulo the ideal generated by
$\mathrm {H}_*(\mathrm {SO}(2^{n+1}-1);\,\mathbb F_2)$
modulo the ideal generated by
![]() $\beta _{2i-1}$
for all
$\beta _{2i-1}$
for all
![]() $1\leq i\leq 2^n-1$
.
$1\leq i\leq 2^n-1$
.
Proof. Denote
![]() $H=\mathrm {H}^*(\mathrm {SO}(2^{n+1}-1);\,\mathbb F_2)$
and
$H=\mathrm {H}^*(\mathrm {SO}(2^{n+1}-1);\,\mathbb F_2)$
and
![]() $H^\vee =\mathrm {H}_*(\mathrm {SO}(2^{n+1}-1);\,\mathbb F_2)$
its dual.
$H^\vee =\mathrm {H}_*(\mathrm {SO}(2^{n+1}-1);\,\mathbb F_2)$
its dual.
Consider the right exact sequence
where
![]() $\mathrm {sq}$
is the map defined in Lemma A1.1. Then
$\mathrm {sq}$
is the map defined in Lemma A1.1. Then
![]() $C^\vee $
is the kernel of the map
$C^\vee $
is the kernel of the map
![]() $\mathrm {sq}^\vee $
.
$\mathrm {sq}^\vee $
.
By Lemma A1.1, we easily see that
![]() $\beta _{2i-1}$
lies in the kernel of
$\beta _{2i-1}$
lies in the kernel of
![]() $\mathrm {sq}^\vee $
for all i,
$\mathrm {sq}^\vee $
for all i,
![]() $1\leq i\leq 2^n-1$
: in fact,
$1\leq i\leq 2^n-1$
: in fact,
![]() $\beta _{2i-1}$
are primitive, and
$\beta _{2i-1}$
are primitive, and
vanishes in
![]() $H^\vee \otimes H^\vee _\tau $
.
$H^\vee \otimes H^\vee _\tau $
.
Since
![]() $\mathrm {Ch}^*(\mathrm {SO}_{2^{n+1}-1})$
coincides with
$\mathrm {Ch}^*(\mathrm {SO}_{2^{n+1}-1})$
coincides with
![]() $\mathrm {Im}(\mathrm {sq})$
, we conclude that
$\mathrm {Im}(\mathrm {sq})$
, we conclude that
is exact; in particular, the kernel of the map
![]() $H^\vee \twoheadrightarrow \mathrm {Ch}^*(\mathrm {SO}_{2^{n+1}-1})^\vee $
contains
$H^\vee \twoheadrightarrow \mathrm {Ch}^*(\mathrm {SO}_{2^{n+1}-1})^\vee $
contains
![]() $\beta _{2i-1}$
,
$\beta _{2i-1}$
,
![]() $1\leq i\leq 2^n-1$
.
$1\leq i\leq 2^n-1$
.
However, the natural map
![]() $\mathrm {Ch}^*(\mathrm {SO}_{2^{n+1}-1})\hookrightarrow H$
is a morphism of algebras and co-algebras; therefore, the dual map is also a morphism of algebras and co-algebras. Therefore, all multiples of
$\mathrm {Ch}^*(\mathrm {SO}_{2^{n+1}-1})\hookrightarrow H$
is a morphism of algebras and co-algebras; therefore, the dual map is also a morphism of algebras and co-algebras. Therefore, all multiples of
![]() $\beta _{2i-1}$
are also mapped to zero in
$\beta _{2i-1}$
are also mapped to zero in
![]() $\mathrm {Ch}^*(\mathrm {SO}_{2^{n+1}-1})^\vee $
.
$\mathrm {Ch}^*(\mathrm {SO}_{2^{n+1}-1})^\vee $
.
Comparing the dimensions, we obtain the claim. More precisely, the set of monomials
(where
![]() $k_i$
are given by (4.1) and
$k_i$
are given by (4.1) and
![]() $\gamma _0(\beta _{2i-1})$
stands for
$\gamma _0(\beta _{2i-1})$
stands for
![]() $1$
) has the same cardinality as the dimension of
$1$
) has the same cardinality as the dimension of
![]() $\mathrm {Ch}^*(\mathrm {SO}_{2^{n+1}-1})$
, and the images of these monomials generate
$\mathrm {Ch}^*(\mathrm {SO}_{2^{n+1}-1})$
, and the images of these monomials generate
![]() $\mathrm {Ch}^*(\mathrm {SO}_{2^{n+1}-1})^\vee $
.
$\mathrm {Ch}^*(\mathrm {SO}_{2^{n+1}-1})^\vee $
.
A2 Bi-ideals in
 $\mathrm {Ch}^*(\mathrm {SO}_m)$
$\mathrm {Ch}^*(\mathrm {SO}_m)$
In this appendix, we give a proof of Lemma 5.4. This result is well known and included only for the convenience of the reader. We recall the following classical theorem.
Theorem A2.1 (Milnor–Moore).
If H is a non-negatively graded, primitively generated, commutative, finite dimensional bi-algebra over
![]() $\mathbb F_p$
, with
$\mathbb F_p$
, with
![]() $H_0 = \mathbb F_p$
, then there is an isomorphism of bi-algebras
$H_0 = \mathbb F_p$
, then there is an isomorphism of bi-algebras
for some
![]() $l_i$
, where
$l_i$
, where
![]() $y_i$
are primitive.
$y_i$
are primitive.
In fact, a much more general theorem is proven in [Reference Milnor and Moore23, Theorem 7.16]. Now we can give a proof of Lemma 5.4.
Lemma A2.2 (Lemma 5.4).
Let
![]() $H=\mathbb F_{2}[e_1,\,e_3,\ldots ,e_{2r-1}]/(e_{1}^{2^{k_1}},e_{3}^{2^{k_2}},\ldots ,e_{2r-1}^{2^{k_r}})$
be a commutative, graded Hopf algebra with
$H=\mathbb F_{2}[e_1,\,e_3,\ldots ,e_{2r-1}]/(e_{1}^{2^{k_1}},e_{3}^{2^{k_2}},\ldots ,e_{2r-1}^{2^{k_r}})$
be a commutative, graded Hopf algebra with
![]() $e_{2i-1}$
primitive of degree
$e_{2i-1}$
primitive of degree
![]() $2i-1$
. Then any (homogeneous) bi-ideal I of H coincides with the ideal
$2i-1$
. Then any (homogeneous) bi-ideal I of H coincides with the ideal
for some
![]() $0\leq a_{i}\leq k_i$
.
$0\leq a_{i}\leq k_i$
.
Proof. Since
![]() $H/I$
is still a non-negatively graded commutative co-commutative Hopf algebra with
$H/I$
is still a non-negatively graded commutative co-commutative Hopf algebra with
![]() $(H/I)_0=\mathbb F_2$
, it is isomorphic to
$(H/I)_0=\mathbb F_2$
, it is isomorphic to
for some primitive
![]() $\overline y_i$
and some
$\overline y_i$
and some
![]() $l_i$
by Theorem A2.1. Take arbitrary pre-images
$l_i$
by Theorem A2.1. Take arbitrary pre-images
![]() $y_i\in H$
of
$y_i\in H$
of
![]() $\overline y_i$
. Since the images
$\overline y_i$
. Since the images
![]() $\overline e_{2k-1}$
of
$\overline e_{2k-1}$
of
![]() $e_{2k-1}$
are primitive in
$e_{2k-1}$
are primitive in
![]() $H/I$
, they have the form
$H/I$
, they have the form
for some
![]() $i_j$
and
$i_j$
and
![]() $b_j<l_{i_j}$
(see [Reference Geldhauser, Lavrenov, Petrov and Sechin9, Lemma 6.1 a)]). Comparing the dimensions, we conclude that
$b_j<l_{i_j}$
(see [Reference Geldhauser, Lavrenov, Petrov and Sechin9, Lemma 6.1 a)]). Comparing the dimensions, we conclude that
![]() $b_i=0$
and
$b_i=0$
and
![]() $\mathrm {deg}(y_{i_j})=2k-1$
. Let
$\mathrm {deg}(y_{i_j})=2k-1$
. Let
for the above set of
![]() $i_j$
. Then
$i_j$
. Then
![]() $e_{2k-1}-\sum y_{i_j}\in I$
, and
$e_{2k-1}-\sum y_{i_j}\in I$
, and
![]() $y_{i_j}^{2^{a_{k}}}\in I$
, and therefore,
$y_{i_j}^{2^{a_{k}}}\in I$
, and therefore,
Now let
and consider the map of Hopf algebras
We will show that
![]() $\varphi $
is injective on the set of primitive elements. Indeed, primitive elements of
$\varphi $
is injective on the set of primitive elements. Indeed, primitive elements of
![]() $H/J$
have the form
$H/J$
have the form
for some set of
![]() $k_h$
and
$k_h$
and
![]() $c_h<a_{k_h}$
. The image of
$c_h<a_{k_h}$
. The image of
![]() $e_{2k_h-1}$
under
$e_{2k_h-1}$
under
![]() $\varphi $
coincides with the sum
$\varphi $
coincides with the sum
![]() $\sum \overline y_{i_j}$
where
$\sum \overline y_{i_j}$
where
![]() $\mathrm {deg}(y_{i_j})=2k_h-1$
. Comparing degrees, we conclude that the sets of
$\mathrm {deg}(y_{i_j})=2k_h-1$
. Comparing degrees, we conclude that the sets of
![]() $y_{i_j}$
for different
$y_{i_j}$
for different
![]() $k_h$
have empty intersection. Therefore,
$k_h$
have empty intersection. Therefore,
implies that
![]() $y_{i_j}^{2^{c_h}}=0$
for all
$y_{i_j}^{2^{c_h}}=0$
for all
![]() $i_j=i_j(k_h)$
and all
$i_j=i_j(k_h)$
and all
![]() $k_h$
. However, this implies that
$k_h$
. However, this implies that
![]() $c_h\geq \mathrm {max}(l_{i_j})=a_{k_h}$
, which leads to a contradiction.
$c_h\geq \mathrm {max}(l_{i_j})=a_{k_h}$
, which leads to a contradiction.
Finally, we conclude that
![]() $\varphi $
is injective by [Reference Geldhauser, Lavrenov, Petrov and Sechin9, Lemma 6.8].
$\varphi $
is injective by [Reference Geldhauser, Lavrenov, Petrov and Sechin9, Lemma 6.8].
A3 Restrictions on J-invariant
The following statement combined with Theorem 5.1 provides certain restrictions on the Chow J-invariant of Vishik. However, these restrictions are not new.
Proposition A3.1. In the notation of Proposition 4.12, let
![]() $m\leq 2^{n+1}$
, and let I be a homogeneous saturated bi-ideal of
$m\leq 2^{n+1}$
, and let I be a homogeneous saturated bi-ideal of
![]() $\mathrm {CK}(n)^*(\mathrm {SO}_m)$
. Assume that
$\mathrm {CK}(n)^*(\mathrm {SO}_m)$
. Assume that
![]() $e_{2^n-1-2k}\in I$
. Then
$e_{2^n-1-2k}\in I$
. Then
![]() $e_{2^n-1-k}\in I$
.
$e_{2^n-1-k}\in I$
.
Proof. Since
by Proposition 5.6, our assumption is equivalent to
![]() $j_{2^{n-1}-k}=0$
. Since I is a bi-ideal, one has
$j_{2^{n-1}-k}=0$
. Since I is a bi-ideal, one has
This implies that
by Lemma 5.3, and therefore,
![]() $\overline e_{2^n-1-k}\in \overline I$
. However, since
$\overline e_{2^n-1-k}\in \overline I$
. However, since
we conclude that
![]() $j_t\leq d$
for
$j_t\leq d$
for
![]() $2^n-1-k=2^d(2t-1)$
. Using Theorem 5.1, we conclude that
$2^n-1-k=2^d(2t-1)$
. Using Theorem 5.1, we conclude that
![]() $e_{2^n-1-k}\in J$
.
$e_{2^n-1-k}\in J$
.
We will show now how to deduce the above restrictions from old results.
Let
![]() $J(q)$
denote Vishik’s original J-invariant [Reference Vishik43, Definition 5.11] of quadratic form q of dimension m. By Theorem 5.1, we conclude
$J(q)$
denote Vishik’s original J-invariant [Reference Vishik43, Definition 5.11] of quadratic form q of dimension m. By Theorem 5.1, we conclude
![]() $J(q)$
is a subset of
$J(q)$
is a subset of
![]() $\{1,2,\ldots ,\left \lfloor \frac {m-1}{2}\right \rfloor \}$
such that
$\{1,2,\ldots ,\left \lfloor \frac {m-1}{2}\right \rfloor \}$
such that
![]() $i\in J(q)$
if and only if
$i\in J(q)$
if and only if
![]() $e_{i}$
is rational in
$e_{i}$
is rational in
![]() $\mathrm {CK}(n)(\mathrm {SO}_m)$
.
$\mathrm {CK}(n)(\mathrm {SO}_m)$
.
Vishik proved in [Reference Vishik43, Proposition 5.12] that if
![]() $i\in J(q)$
and
$i\in J(q)$
and
![]() $t\in \mathbb N\setminus 0$
such that
$t\in \mathbb N\setminus 0$
such that
![]() $i+t\leq \left \lfloor \frac {m-1}{2}\right \rfloor $
and
$i+t\leq \left \lfloor \frac {m-1}{2}\right \rfloor $
and
![]() ${i\choose t}\equiv 1\ \mod 2$
, then
${i\choose t}\equiv 1\ \mod 2$
, then
![]() $i+t\in J(q)$
. In fact, he proved that
$i+t\in J(q)$
. In fact, he proved that
![]() $S^t(e_i)=e_{i+t}$
in this case, where
$S^t(e_i)=e_{i+t}$
in this case, where
![]() $S^i$
denotes the i-th Steenrod operation; see [Reference Elman, Karpenko and Merkurjev6, Chapter XI and Chapter XVI, Section 89].
$S^i$
denotes the i-th Steenrod operation; see [Reference Elman, Karpenko and Merkurjev6, Chapter XI and Chapter XVI, Section 89].
Proposition A3.2. In the notation above, let
![]() $k=2^{a_1}+2^{a_2}+\ldots +2^{a_t}$
where
$k=2^{a_1}+2^{a_2}+\ldots +2^{a_t}$
where
![]() $a_1=\nu _2(k)$
and
$a_1=\nu _2(k)$
and
![]() $a_{i+1}=\nu _2(k-2^{a_1}-\ldots -2^{a_i})$
,
$a_{i+1}=\nu _2(k-2^{a_1}-\ldots -2^{a_i})$
,
![]() $0\leq a_1<a_2<\ldots <a_t$
. Then
$0\leq a_1<a_2<\ldots <a_t$
. Then
Proof. Let
![]() $\pi \colon \mathbb N\cup 0\rightarrow 2^{\mathbb N\cup 0}$
be the injection given by the base
$\pi \colon \mathbb N\cup 0\rightarrow 2^{\mathbb N\cup 0}$
be the injection given by the base
![]() $2$
expansions. For any
$2$
expansions. For any
![]() $n\in \mathbb N\cup 0$
, the set
$n\in \mathbb N\cup 0$
, the set
![]() $\pi (n)$
consists of all those
$\pi (n)$
consists of all those
![]() $m\in \mathbb N\cup 0$
such that the base
$m\in \mathbb N\cup 0$
such that the base
![]() $2$
expansion of n has
$2$
expansion of n has
![]() $1$
in the m-th position. For any
$1$
in the m-th position. For any
![]() $i,\, n\in \mathbb N\cup 0$
, the binomial coefficient
$i,\, n\in \mathbb N\cup 0$
, the binomial coefficient
![]() ${n\choose i}$
is odd if and only if
${n\choose i}$
is odd if and only if
![]() $\pi (i)\subseteq \pi (n)$
(see [Reference Elman, Karpenko and Merkurjev6, Lemma 78.6]).
$\pi (i)\subseteq \pi (n)$
(see [Reference Elman, Karpenko and Merkurjev6, Lemma 78.6]).
It is enough to show that
![]() ${2^n-1-2k+2^{a_1}+\ldots +2^{a_i}\choose 2^{a_{i+1}}}\equiv 1\quad \mod 2$
. Obviously,
${2^n-1-2k+2^{a_1}+\ldots +2^{a_i}\choose 2^{a_{i+1}}}\equiv 1\quad \mod 2$
. Obviously,
in particular,
![]() $\pi (k)=\{a_1,\ldots ,a_t\}$
,
$\pi (k)=\{a_1,\ldots ,a_t\}$
,
![]() $\pi (2k)=\{a_1+1,\ldots ,a_t+1\}$
, and, obviously,
$\pi (2k)=\{a_1+1,\ldots ,a_t+1\}$
, and, obviously,
![]() $\pi (2^n-1)=\{0,1,\ldots , n-1\}$
. In other words, identifying
$\pi (2^n-1)=\{0,1,\ldots , n-1\}$
. In other words, identifying
![]() $\pi $
with the base
$\pi $
with the base
![]() $2$
expansion, we conclude that
$2$
expansion, we conclude that
![]() $\pi (2^n-1-2k)$
has
$\pi (2^n-1-2k)$
has
![]() $0$
-s in positions
$0$
-s in positions
![]() $a_i+1$
and
$a_i+1$
and
![]() $1$
-s in all other positions from
$1$
-s in all other positions from
![]() $0$
to
$0$
to
![]() $n-1$
. Then it is easy to see that
$n-1$
. Then it is easy to see that
![]() $\pi (2^n-1-2k+2^{a_1}+\ldots +2^{a_i})$
has
$\pi (2^n-1-2k+2^{a_1}+\ldots +2^{a_i})$
has
![]() $1$
in position
$1$
in position
![]() $a_{i+1}$
, that is,
$a_{i+1}$
, that is,
![]() $\pi (2^{a_{i+1}})\subseteq \pi (2^n-1-2k+2^{a_1}+\ldots +2^{a_i})$
.
$\pi (2^{a_{i+1}})\subseteq \pi (2^n-1-2k+2^{a_1}+\ldots +2^{a_i})$
.
Acknowledgements
We would like to thank sincerely Markus Land for his valuable comments on the subject of the article.
Competing interest
The authors have no competing interests to declare.
Financial support
The first author was supported by the DFG grant AN 1545/4-1. The research of the second author was mostly carried out at the Ludwig-Maximilians-Universität München, and partly at the St. Petersburg Leonhard Euler International Mathematical Institute supported by the Ministry of Science and Higher Education of the Russian Federation (agreement no. 075–15–2022–287) and BASIS foundation grant ‘Young Russia Mathematics’, and partly at the Bar-Ilan University supported by ISF grant 1994/20. The third author was supported by the Foundation for the Advancement of Theoretical Physics and Mathematics ‘BASIS’.



