Article contents
Modularity lifting results in parallel weight one and applications to the Artin conjecture: the tamely ramified case
Published online by Cambridge University Press: 10 July 2014
Abstract
We extend the modularity lifting result of P. Kassaei (‘Modularity lifting in parallel weight one’,J. Amer. Math. Soc.26 (1) (2013), 199–225) to allow Galois representations with some ramification at 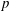 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$ . We also prove modularity mod 5 of certain Galois representations. We use these results to prove new cases of the strong Artin conjecture over totally real fields in which 5 is unramified. As an ingredient of the proof, we provide a general result on the automatic analytic continuation of overconvergent
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$ . We also prove modularity mod 5 of certain Galois representations. We use these results to prove new cases of the strong Artin conjecture over totally real fields in which 5 is unramified. As an ingredient of the proof, we provide a general result on the automatic analytic continuation of overconvergent 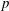 $p$ -adic Hilbert modular forms of finite slope which substantially generalizes a similar result in P. Kassaei (‘Modularity lifting in parallel weight one’, J. Amer. Math. Soc.26 (1) (2013), 199–225).
$p$ -adic Hilbert modular forms of finite slope which substantially generalizes a similar result in P. Kassaei (‘Modularity lifting in parallel weight one’, J. Amer. Math. Soc.26 (1) (2013), 199–225).
MSC classification
Information
- Type
- Research Article
- Information
- Creative Commons
- The online version of this article is published within an Open Access environment subject to the conditions of the Creative Commons Attribution licence .
- Copyright
- © The Author(s) 2014
References
- 4
- Cited by

