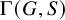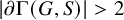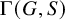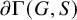1. Introduction
Hyperfiniteness is a property of countable Borel equivalence relations that measures their complexity. It is a classical topic in descriptive set theory that has been attracting people’s interest for decades, and its research is still active to this day. Because any countable Borel equivalence relation is the orbit equivalence relation of a Borel action of a countable group by the Feldman–Moore theorem (see Definition 2.6 and [Reference Feldman and Moore7]), people have investigated orbit equivalence relations of group actions. Historically, study on amenable groups preceded toward a long-standing open problem asking whether all orbit equivalence relations of Borel actions of countable amenable groups are hyperfinite. Remarkable progress on this problem includes partial yet crucial results for
![]() $\mathbb {Z}^n$
in [Reference Weiss21], finitely generated groups with polynomial growth in [Reference Jackson, Kechris and Louveau13], countable abelian groups in [Reference Gao and Jackson9] and polycyclic groups in [Reference Conley, Jackson, Marks, Seward and Tucker-Drob4].
$\mathbb {Z}^n$
in [Reference Weiss21], finitely generated groups with polynomial growth in [Reference Jackson, Kechris and Louveau13], countable abelian groups in [Reference Gao and Jackson9] and polycyclic groups in [Reference Conley, Jackson, Marks, Seward and Tucker-Drob4].
On the other hand, there was not much progress made for non-amenable groups until very recently and this is the focus of this paper. To the best of my knowledge, the only result of hyperfiniteness in absence of measures in non-amenable case before 2010s was obtained by Dougherty, Jackson and Kechris in [Reference Dougherty, Jackson and Kechris6], where they proved that the action of the free group
![]() $F_2$
on the Gromov boundary is hyperfinite. A breakthrough in this direction was achieved by Huang, Sabok and Shinko in [Reference Huang, Sabok and Shinko11], where they generalized this result to cubulated hyperbolic groups. In [Reference Marquis and Sabok16], Marquis and Sabok succeeded in proving hyperfiniteness of boundary actions of hyperbolic groups in full generality. This was further generalized to finitely generated relatively hyperbolic groups by Karpinski in [Reference Karpinski14]. Other important results in non-amenable case are [Reference Przytycki and Sabok20] by Przytycki and Sabok, where they proved that actions of mapping class groups on the Gromov boundaries of the arc complex and the curve complex are hyperfinite, and [Reference Naryshkin and Vaccaro18] by Naryshkin and Vaccaro, where they proved that boundary actions of hyperbolic groups have finite Borel asymptotic dimension, which strengthen [Reference Marquis and Sabok16].
$F_2$
on the Gromov boundary is hyperfinite. A breakthrough in this direction was achieved by Huang, Sabok and Shinko in [Reference Huang, Sabok and Shinko11], where they generalized this result to cubulated hyperbolic groups. In [Reference Marquis and Sabok16], Marquis and Sabok succeeded in proving hyperfiniteness of boundary actions of hyperbolic groups in full generality. This was further generalized to finitely generated relatively hyperbolic groups by Karpinski in [Reference Karpinski14]. Other important results in non-amenable case are [Reference Przytycki and Sabok20] by Przytycki and Sabok, where they proved that actions of mapping class groups on the Gromov boundaries of the arc complex and the curve complex are hyperfinite, and [Reference Naryshkin and Vaccaro18] by Naryshkin and Vaccaro, where they proved that boundary actions of hyperbolic groups have finite Borel asymptotic dimension, which strengthen [Reference Marquis and Sabok16].
Most of the above results in non-amenable case can be summarized by saying that the involved groups admit a non-elementary acylindrical action on a hyperbolic space with a hyperfinite action on the Gromov boundary. In this paper, we show that this is true for a much wider class of groups by proving the following theorem.
Theorem 1.1. For any countable acylindrically hyperbolic group G, there exists a generating set S of G such that the corresponding Cayley graph
![]() $\Gamma (G,S)$
is hyperbolic,
$\Gamma (G,S)$
is hyperbolic,
![]() $|\partial \Gamma (G,S)|>2$
, the natural action of G on
$|\partial \Gamma (G,S)|>2$
, the natural action of G on
![]() $\Gamma (G,S)$
is acylindrical and the natural action of G on the Gromov boundary
$\Gamma (G,S)$
is acylindrical and the natural action of G on the Gromov boundary
![]() $\partial \Gamma (G,S)$
is hyperfinite.
$\partial \Gamma (G,S)$
is hyperfinite.
Note that acylindrically hyperbolic groups do not need to be finitely generated. The new portion of Theorem 1.1 is the hyperfiniteness of the action on the Gromov boundary, while the other conditions were proved by Osin in [Reference Osin19]. Also, the generating set S in Theorem 1.1 is the same as the one constructed in [Reference Osin19, Theorem 5.4]. The class of acylindrically hyperbolic groups is broad and includes many examples of interest: non-elementary hyperbolic and relatively hyperbolic groups, all but finitely many mapping class groups of punctured closed surfaces,
![]() $Out(F_n)$
for any
$Out(F_n)$
for any
![]() $n\ge 2$
, directly indecomposable right angled Artin groups, non-virtually cyclic graphical small cancellation groups including some Gromov monsters (see [Reference Gruber and Sisto10]), one relator groups with at least three generators, Higman group, most orientable 3-manifold groups (see [Reference Minasyan and Osin17]) and many others. Proving hyperfiniteness in this broad class faces some difficulties that didn’t appear in previous results. For exmaple, for acylindrically hyperbolic groups, there is no canonical generating set in general, local compactness of geodesic ray bundles is lacking (see [Reference Marquis and Sabok16, Section 1]), and elements of the Gromov boundary may not be represented by geodesic rays. We circumvent these difficulties by bringing a new insight on the Gromov boundaries of acylindrically hyperbolic groups, which we explain in Section 3 and Section 6 and by building on the work of Naryshkin and Vaccaro in [Reference Naryshkin and Vaccaro18]. In [Reference Naryshkin and Vaccaro18], given a hyperbolic group G with a finite symmetric generating set S, they constructed an injective Borel measurable map from
$n\ge 2$
, directly indecomposable right angled Artin groups, non-virtually cyclic graphical small cancellation groups including some Gromov monsters (see [Reference Gruber and Sisto10]), one relator groups with at least three generators, Higman group, most orientable 3-manifold groups (see [Reference Minasyan and Osin17]) and many others. Proving hyperfiniteness in this broad class faces some difficulties that didn’t appear in previous results. For exmaple, for acylindrically hyperbolic groups, there is no canonical generating set in general, local compactness of geodesic ray bundles is lacking (see [Reference Marquis and Sabok16, Section 1]), and elements of the Gromov boundary may not be represented by geodesic rays. We circumvent these difficulties by bringing a new insight on the Gromov boundaries of acylindrically hyperbolic groups, which we explain in Section 3 and Section 6 and by building on the work of Naryshkin and Vaccaro in [Reference Naryshkin and Vaccaro18]. In [Reference Naryshkin and Vaccaro18], given a hyperbolic group G with a finite symmetric generating set S, they constructed an injective Borel measurable map from
![]() $\partial G$
to
$\partial G$
to
![]() $S^{\mathbb {N}}$
that Borel reduces a finite index subequivalence relation of the orbit equivalence relation
$S^{\mathbb {N}}$
that Borel reduces a finite index subequivalence relation of the orbit equivalence relation
![]() $E_G^{\partial G}$
to the tail equivalence relation
$E_G^{\partial G}$
to the tail equivalence relation
![]() $E_t(S)$
, thereby hyperfiniteness of
$E_t(S)$
, thereby hyperfiniteness of
![]() $E_t(S)$
implied hyperfiniteness of
$E_t(S)$
implied hyperfiniteness of
![]() $E_G^{\partial G}$
.
$E_G^{\partial G}$
.
Moreover, Theorem 1.1 has the following application to topological amenability of group actions. Corollary 1.2 is interesting because it contrasts with the fact that some Gromov monsters are acylindrically hyperbolic, and these groups don’t admit a topologically amenable action on any compact Hausdorff space as they’re non-exact.
Corollary 1.2. For any countable acylindrically hyperbolic group G, there exists a generating set S of G such that the corresponding Cayley graph
![]() $\Gamma (G,S)$
is hyperbolic,
$\Gamma (G,S)$
is hyperbolic,
![]() $|\partial \Gamma (G,S)|>2$
, the natural action of G on
$|\partial \Gamma (G,S)|>2$
, the natural action of G on
![]() $\Gamma (G,S)$
is acylindrical and the natural action of G on the Gromov boundary
$\Gamma (G,S)$
is acylindrical and the natural action of G on the Gromov boundary
![]() $\partial \Gamma (G,S)$
is topologically amenable.
$\partial \Gamma (G,S)$
is topologically amenable.
The paper is organized as follows. In Section 2, we discuss the necessary definitions and known results about hyperfinite Borel equivalence relations and acylindrically hyperbolic groups. In Section 3, we introduce a new way to represent elements of the Gromov boundary of an acylindrically hyperbolic group for a nice generating set by building on the work of Osin in [Reference Osin19]. In Section 4, we give a proof of Theorem 1.1 by using techniques developed in Section 3. In Section 5, we introduce topological amenability of group actions and prove Corollary 1.2. In Section 6, we summarize more results on the Gromov boundaries of acylindrically hyperbolic groups that are not necessary in the proof of Theorem 1.1 but are of independent interest for possible future use. Section 6 is independent of Section 4 and Section 5 and can be read as another continuation of Section 3.
2. Preliminary
2.1. Descriptive set theory
In this section, we review concepts in descriptive set theory.
Definition 2.1. A Polish space is a separable completely metrizable topological space.
Definition 2.2. A measurable space
![]() $(X,\mathcal {B})$
is called a standard Borel space if there exists a topology
$(X,\mathcal {B})$
is called a standard Borel space if there exists a topology
![]() $\mathcal {O}$
on X such that
$\mathcal {O}$
on X such that
![]() $(X,\mathcal {O})$
is a Polish space and
$(X,\mathcal {O})$
is a Polish space and
![]() $\mathcal {B}(\mathcal {O})=\mathcal {B}$
holds, where
$\mathcal {B}(\mathcal {O})=\mathcal {B}$
holds, where
![]() $\mathcal {B}(\mathcal {O})$
is the
$\mathcal {B}(\mathcal {O})$
is the
![]() $\sigma $
-algebra on X generated by
$\sigma $
-algebra on X generated by
![]() $\mathcal {O}$
.
$\mathcal {O}$
.
Definition 2.3. Let X be a standard Borel space and E be an equivalence relation on X. E is called Borel if E is a Borel subset of
![]() $X\times X$
. E is called countable (resp. finite) if for any
$X\times X$
. E is called countable (resp. finite) if for any
![]() $x\in X$
, the set
$x\in X$
, the set
![]() $\{ y\in X \mid (x,y)\in E \}$
is countable (resp. finite).
$\{ y\in X \mid (x,y)\in E \}$
is countable (resp. finite).
Remark 2.4. The word ‘countable Borel equivalence relation’ is often abbreviated to ‘CBER’.
Definition 2.5. Let X be a standard Borel space. A countable Borel equivalence relation E on X is called hyperfinite if there exist finite Borel equivalence relations
![]() $(E_n)_{n=1}^\infty $
on X such that
$(E_n)_{n=1}^\infty $
on X such that
![]() $E_n\subset E_{n+1}$
for any
$E_n\subset E_{n+1}$
for any
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $E=\bigcup _{n=1}^\infty E_n$
.
$E=\bigcup _{n=1}^\infty E_n$
.
Definition 2.6 and Definition 2.8 are two important examples of CBERs in this paper.
Definition 2.6. Suppose that a group G acts on a set S. The equivalence relation
![]() $E_G^S$
on S is defined as follows: For
$E_G^S$
on S is defined as follows: For
![]() $x,y\in S$
,
$x,y\in S$
,
![]() $E_G^S$
is called the orbit equivalence relation on S.
$E_G^S$
is called the orbit equivalence relation on S.
Lemma 2.7 is straightforward, but we record the proof for convenience of readers.
Lemma 2.7. Suppose that a countable group G acts on a standard Borel space S as Borel isomorphism, then
![]() $E_G^S$
is a CBER.
$E_G^S$
is a CBER.
Proof. For any
![]() $g\in G$
, the set
$g\in G$
, the set
![]() $\mathrm {Graph}(g)$
defined by
$\mathrm {Graph}(g)$
defined by
![]() $\mathrm {Graph}(g)=\{(x,gx)\in S\times S \mid x\in S\}$
is Borel since
$\mathrm {Graph}(g)=\{(x,gx)\in S\times S \mid x\in S\}$
is Borel since
![]() $g\colon S \to S$
is Borel measurable. Since G is countable and we have
$g\colon S \to S$
is Borel measurable. Since G is countable and we have
![]() $E_G^S=\bigcup _{g\in G} \mathrm {Graph}(g)$
, the set
$E_G^S=\bigcup _{g\in G} \mathrm {Graph}(g)$
, the set
![]() $E_G^S$
is also Borel, being the countable union of Borel sets. Finally, for any
$E_G^S$
is also Borel, being the countable union of Borel sets. Finally, for any
![]() $x\in S$
, the orbit equivalence class of x is exactly
$x\in S$
, the orbit equivalence class of x is exactly
![]() $G x$
, which is countable since G is countable. Thus,
$G x$
, which is countable since G is countable. Thus,
![]() $E_G^S$
is a CBER.
$E_G^S$
is a CBER.
Recall that any countable set
![]() $\Omega $
with the discrete topology is a Polish space. Hence,
$\Omega $
with the discrete topology is a Polish space. Hence,
![]() $\Omega ^{\mathbb {N}}$
endowed with the product topology is a Polish space.
$\Omega ^{\mathbb {N}}$
endowed with the product topology is a Polish space.
Definition 2.8. Let
![]() $\Omega $
be a countable set. The equivalence relation
$\Omega $
be a countable set. The equivalence relation
![]() $E_t(\Omega )$
on
$E_t(\Omega )$
on
![]() $\Omega ^{\mathbb {N}}$
is defined as follows: For
$\Omega ^{\mathbb {N}}$
is defined as follows: For
![]() $w_0=(s_1,s_2,\cdots ), w_1=(t_1,t_2,\cdots ) \in \Omega ^{\mathbb {N}}$
,
$w_0=(s_1,s_2,\cdots ), w_1=(t_1,t_2,\cdots ) \in \Omega ^{\mathbb {N}}$
,
![]() $E_t(\Omega )$
is called the tail equivalence relation on
$E_t(\Omega )$
is called the tail equivalence relation on
![]() $\Omega ^{\mathbb {N}}$
.
$\Omega ^{\mathbb {N}}$
.
We list some facts needed for the proof of Theorem 1.1. Proposition 2.9 is a particular case of [Reference Dougherty, Jackson and Kechris6, Corollary 8.2].
Proposition 2.9 (cf. [Reference Dougherty, Jackson and Kechris6, Corollary 8.2])
For any countable set
![]() $\Omega $
, the tail equivalence relation
$\Omega $
, the tail equivalence relation
![]() $E_t(\Omega )$
on
$E_t(\Omega )$
on
![]() $\Omega ^{\mathbb {N}}$
is a hyperfinite CBER.
$\Omega ^{\mathbb {N}}$
is a hyperfinite CBER.
Proposition 2.10 [Reference Jackson, Kechris and Louveau13, Proposition 1.3.(vii)]
Let X be a standard Borel space and
![]() $E,F$
be countable Borel equivalence relations on X. If
$E,F$
be countable Borel equivalence relations on X. If
![]() $E\subset F$
, E is hyperfinite and every F-equivalence class contains only finitely many E-classes, then F is hyperfinite.
$E\subset F$
, E is hyperfinite and every F-equivalence class contains only finitely many E-classes, then F is hyperfinite.
2.2. The Gromov boundary of a hyperbolic space
In this section, we review the Gromov boundary of a hyperbolic space. For more on the Gromov boundary, readers are referred to [Reference Bridson and Haefliger2].
Definition 2.11. Let
![]() $(S,d_S)$
be a metric space. For
$(S,d_S)$
be a metric space. For
![]() $x,y,z\in S$
, we define
$x,y,z\in S$
, we define
![]() $(x,y)_z^S$
by
$(x,y)_z^S$
by
Proposition 2.12. For any geodesic metric space
![]() $(S,d_S)$
, the following conditions are equivalent.
$(S,d_S)$
, the following conditions are equivalent.
(1) There exists
![]() $\delta \in \mathbb {N}$
satisfying the following property. Let
$\delta \in \mathbb {N}$
satisfying the following property. Let
![]() $x,y,z\in S$
, and let p be a geodesic path from z to x and q be a geodesic path from z to y. If two points
$x,y,z\in S$
, and let p be a geodesic path from z to x and q be a geodesic path from z to y. If two points
![]() $a\in p$
and
$a\in p$
and
![]() $b\in q$
satisfy
$b\in q$
satisfy
![]() $d_S(z,a)=d_S(z,b)\le (x,y)_z^S$
, then we have
$d_S(z,a)=d_S(z,b)\le (x,y)_z^S$
, then we have
![]() $d_S(a,b) \le \delta $
.
$d_S(a,b) \le \delta $
.
(2) There exists
![]() $\delta \in \mathbb {N}$
such that for any
$\delta \in \mathbb {N}$
such that for any
![]() $w,x,y,z \in S$
, we have
$w,x,y,z \in S$
, we have
Definition 2.13. A geodesic metric space S is called hyperbolic if S satisfies the equivalent conditions (1) and (2) in Proposition 2.12. We call a hyperbolic space
![]() $\delta $
-hyperbolic with
$\delta $
-hyperbolic with
![]() $\delta \in \mathbb {N}$
if
$\delta \in \mathbb {N}$
if
![]() $\delta $
satisfies both of (1) and (2) in Proposition 2.12. A connected graph
$\delta $
satisfies both of (1) and (2) in Proposition 2.12. A connected graph
![]() $\Gamma $
is called hyperbolic, if the geodesic metric space
$\Gamma $
is called hyperbolic, if the geodesic metric space
![]() $(\Gamma ,d_\Gamma )$
is hyperbolic, where
$(\Gamma ,d_\Gamma )$
is hyperbolic, where
![]() $d_\Gamma $
is the graph metric of
$d_\Gamma $
is the graph metric of
![]() $\Gamma $
.
$\Gamma $
.
In the remainder of this section, suppose that
![]() $(S,d_S)$
is a hyperbolic geodesic metric space.
$(S,d_S)$
is a hyperbolic geodesic metric space.
Definition 2.14. A sequence
![]() $(x_n)_{n=1}^\infty $
of elements of S is said to converge to infinity if we have
$(x_n)_{n=1}^\infty $
of elements of S is said to converge to infinity if we have
![]() $\lim _{i,j\to \infty } (x_i,x_j)_o^S =\infty $
for some (equivalently any)
$\lim _{i,j\to \infty } (x_i,x_j)_o^S =\infty $
for some (equivalently any)
![]() $o\in S$
. For two sequences
$o\in S$
. For two sequences
![]() $(x_n)_{n=1}^\infty ,(y_n)_{n=1}^\infty $
in S converging to infinity, we define the relation
$(x_n)_{n=1}^\infty ,(y_n)_{n=1}^\infty $
in S converging to infinity, we define the relation
![]() $\sim $
by
$\sim $
by
![]() $(x_n)_{n=1}^\infty \sim (y_n)_{n=1}^\infty $
if we have
$(x_n)_{n=1}^\infty \sim (y_n)_{n=1}^\infty $
if we have
![]() $\lim _{i,j\to \infty } (x_i,y_j)_o^S =\infty $
for some (equivalently any)
$\lim _{i,j\to \infty } (x_i,y_j)_o^S =\infty $
for some (equivalently any)
![]() $o\in S$
.
$o\in S$
.
Remark 2.15. It’s not difficult to see that the relation
![]() $\sim $
in Definition 2.14 is an equivalence relation by using the condition (2) of Proposition 2.12.
$\sim $
in Definition 2.14 is an equivalence relation by using the condition (2) of Proposition 2.12.
Definition 2.16. The quotient set
![]() $\partial S$
is defined by
$\partial S$
is defined by
and called Gromov boundary of S.
Remark 2.17. The set
![]() $\partial S$
is sometimes called the sequential boundary of S. Note that
$\partial S$
is sometimes called the sequential boundary of S. Note that
![]() $\partial S$
sometimes coincides with the geodesic boundary of S (e.g., when S is a proper metric space), but this is not the case in general.
$\partial S$
sometimes coincides with the geodesic boundary of S (e.g., when S is a proper metric space), but this is not the case in general.
Definition 2.18. For
![]() $o\in S$
and
$o\in S$
and
![]() $\xi ,\eta \in S\cup \partial S$
, we define
$\xi ,\eta \in S\cup \partial S$
, we define
![]() $(\xi ,\eta )_o^S$
by
$(\xi ,\eta )_o^S$
by
where we define
![]() $\xi =[(x_n)_{n=1}^\infty ]$
as follows. If
$\xi =[(x_n)_{n=1}^\infty ]$
as follows. If
![]() $\xi \in \partial S$
, then
$\xi \in \partial S$
, then
![]() $(x_n)_{n=1}^\infty $
is a sequence in S converging to infinity such that
$(x_n)_{n=1}^\infty $
is a sequence in S converging to infinity such that
![]() $\xi $
represents the equivalence class of
$\xi $
represents the equivalence class of
![]() $(x_n)_{n=1}^\infty $
. If
$(x_n)_{n=1}^\infty $
. If
![]() $\xi \in S$
, then
$\xi \in S$
, then
![]() $(x_n)_{n=1}^\infty $
is constant with
$(x_n)_{n=1}^\infty $
is constant with
![]() $x_n \equiv \xi $
. We define
$x_n \equiv \xi $
. We define
![]() $\eta =[(y_n)_{n=1}^\infty ]$
in the same way.
$\eta =[(y_n)_{n=1}^\infty ]$
in the same way.
Proposition 2.19. For any hyperbolic geodesic metric space
![]() $(S,d_S)$
, there exists a unique topology
$(S,d_S)$
, there exists a unique topology
![]() $\mathcal {O}_S$
on
$\mathcal {O}_S$
on
![]() $S\cup \partial S$
such that the relative topology of
$S\cup \partial S$
such that the relative topology of
![]() $\mathcal {O}_S$
on S coincides with the metric topology of
$\mathcal {O}_S$
on S coincides with the metric topology of
![]() $d_S$
and for any
$d_S$
and for any
![]() $\xi \in \partial S$
and
$\xi \in \partial S$
and
![]() $o\in S$
, the sets
$o\in S$
, the sets
![]() $(U(o,\xi ,n))_{n=1}^\infty $
defined by
$(U(o,\xi ,n))_{n=1}^\infty $
defined by
form a neighborhood basis of
![]() $\mathcal {O}_S$
at
$\mathcal {O}_S$
at
![]() $\xi $
.
$\xi $
.
Remark 2.20. When a group G acts on S isometrically, this action naturally extends to the homeomorphic action on
![]() $S\cup \partial S$
.
$S\cup \partial S$
.
The following proposition is a variation of [Reference Bridson and Haefliger2, Proposition 3.21] and can be proved in the same way. Indeed, in the statement of [Reference Bridson and Haefliger2, Proposition 3.21], the domain of D below is
![]() $(\partial S)^2$
.
$(\partial S)^2$
.
Proposition 2.21. For any
![]() $o\in S$
, there exist a map
$o\in S$
, there exist a map
![]() $D \colon (S\cup \partial S)^2 \to [0,\infty )$
and constants
$D \colon (S\cup \partial S)^2 \to [0,\infty )$
and constants
![]() $\varepsilon ,\varepsilon '>0$
with
$\varepsilon ,\varepsilon '>0$
with
![]() $\varepsilon '\le \sqrt {2}-1$
satisfying the following three conditions.
$\varepsilon '\le \sqrt {2}-1$
satisfying the following three conditions.
-
(i)
 $D(x,y)=D(y,x)$
for any
$D(x,y)=D(y,x)$
for any
 $x,y \in S\cup \partial S$
.
$x,y \in S\cup \partial S$
. -
(ii)
 $D(x,z) \le D(x,y)+D(y,z)$
for any
$D(x,z) \le D(x,y)+D(y,z)$
for any
 $x,y,z \in S\cup \partial S$
.
$x,y,z \in S\cup \partial S$
. -
(iii)
 $(1-2\varepsilon ')e^{-\varepsilon (x,y)_o^S} \le D(x,y) \le e^{-\varepsilon (x,y)_o^S}$
for any
$(1-2\varepsilon ')e^{-\varepsilon (x,y)_o^S} \le D(x,y) \le e^{-\varepsilon (x,y)_o^S}$
for any
 $x,y \in S\cup \partial S$
.
$x,y \in S\cup \partial S$
.
For convenience, if
![]() $(x,y)_o^S=\infty $
, then we define
$(x,y)_o^S=\infty $
, then we define
![]() $e^{-\varepsilon (x,y)_o^S}=0$
.
$e^{-\varepsilon (x,y)_o^S}=0$
.
Remark 2.22. For any
![]() $x\in S$
, we have
$x\in S$
, we have
![]() $(1-2\varepsilon ')e^{-\varepsilon d_S(o,x)} \le \inf _{y\in S\cup \partial S}D(x,y)$
by
$(1-2\varepsilon ')e^{-\varepsilon d_S(o,x)} \le \inf _{y\in S\cup \partial S}D(x,y)$
by
![]() $\sup _{y \in S\cup \partial S} (x,y)_o^S \le d_S(o,x)$
. Hence, the map D in Proposition 2.21 is not a metric on
$\sup _{y \in S\cup \partial S} (x,y)_o^S \le d_S(o,x)$
. Hence, the map D in Proposition 2.21 is not a metric on
![]() $(S\cup \partial S)^2$
. However, D is a metric on
$(S\cup \partial S)^2$
. However, D is a metric on
![]() $(\partial S)^2$
. This metric
$(\partial S)^2$
. This metric
![]() $D|_{(\partial S)^2}$
is called a visual metric and the metric topology of
$D|_{(\partial S)^2}$
is called a visual metric and the metric topology of
![]() $D|_{(\partial S)^2}$
on
$D|_{(\partial S)^2}$
on
![]() $(\partial S)^2$
coincides with the relative topology of
$(\partial S)^2$
coincides with the relative topology of
![]() $\mathcal {O}_S$
in Proposition 2.19.
$\mathcal {O}_S$
in Proposition 2.19.
2.3. Hull–Osin’s separating cosets of hyperbolically embedded subgroups
In this section, we review hyperbolically embedded subgroups and Hull–Osin’s separating cosets. The notion of separating cosets of hyperbolically embedded subgroups was first introduced by Hull and Osin in [Reference Hull and Osin12] and further developed by Osin in [Reference Osin19]. There are two differences in the definition of separating cosets in [Reference Hull and Osin12] and in [Reference Osin19], though other terminologies and related propositions are mostly the same between them. This difference is explained in Remark 2.33. With regards to this difference, we follow definitions and notations of [Reference Osin19] in our discussion. We begin with defining auxiliary concepts.
Definition 2.23. Let
![]() $m,n\in \mathbb {Z}$
and let
$m,n\in \mathbb {Z}$
and let
![]() $\Gamma $
be a connected graph with the graph metric
$\Gamma $
be a connected graph with the graph metric
![]() $d_\Gamma $
. A path p in
$d_\Gamma $
. A path p in
![]() $\Gamma $
is a graph homomorphism from one of
$\Gamma $
is a graph homomorphism from one of
![]() $[m,n]$
,
$[m,n]$
,
![]() $[m,\infty )$
or
$[m,\infty )$
or
![]() $\mathbb {R}$
to
$\mathbb {R}$
to
![]() $\Gamma $
, where each domain is considered as a graph with a vertex set
$\Gamma $
, where each domain is considered as a graph with a vertex set
![]() $\mathbb {Z}\cap [m,n]$
,
$\mathbb {Z}\cap [m,n]$
,
![]() $\mathbb {Z}\cap [m,\infty )$
and
$\mathbb {Z}\cap [m,\infty )$
and
![]() $\mathbb {Z}$
, respectively. When we want to emphasize that the domain is
$\mathbb {Z}$
, respectively. When we want to emphasize that the domain is
![]() $[m,\infty )$
(resp.
$[m,\infty )$
(resp.
![]() $\mathbb {R}$
), we call p an infinite path (resp. bi-infinite path). A subpath q of a path p is a path obtained by restricting p to a subset of the domain of p. For vertices x and y of
$\mathbb {R}$
), we call p an infinite path (resp. bi-infinite path). A subpath q of a path p is a path obtained by restricting p to a subset of the domain of p. For vertices x and y of
![]() $\Gamma $
, a path p from x to y is a path p with the domain
$\Gamma $
, a path p from x to y is a path p with the domain
![]() $[m,n]$
satisfying
$[m,n]$
satisfying
![]() $p(m)=x$
and
$p(m)=x$
and
![]() $p(n)=y$
. We also denote the initial point x of p by
$p(n)=y$
. We also denote the initial point x of p by
![]() $p_-$
and the terminal point y by
$p_-$
and the terminal point y by
![]() $p_+$
. A path p is called closed if
$p_+$
. A path p is called closed if
![]() $p_-=p_+$
. Similarly, an infinite path p from x is a path satisfying
$p_-=p_+$
. Similarly, an infinite path p from x is a path satisfying
![]() $p(m)=x$
and we denote the initial point x of p by
$p(m)=x$
and we denote the initial point x of p by
![]() $p_-$
. A path p is called geodesic if p is a distance-preserving map from its domain to
$p_-$
. A path p is called geodesic if p is a distance-preserving map from its domain to
![]() $(\Gamma ,d_\Gamma )$
. An infinite geodesic path is also called a geodesic ray. Since geodesic paths are injective, we often identify their images with maps. For example, we will denote a geodesic ray p by
$(\Gamma ,d_\Gamma )$
. An infinite geodesic path is also called a geodesic ray. Since geodesic paths are injective, we often identify their images with maps. For example, we will denote a geodesic ray p by
![]() $p=(x_0,x_1,x_2,\cdots )$
, where each
$p=(x_0,x_1,x_2,\cdots )$
, where each
![]() $x_i$
is a vertex of
$x_i$
is a vertex of
![]() $\Gamma $
and each pair
$\Gamma $
and each pair
![]() $(x_i,x_{i+1})$
is adjacent. Also, for a geodesic path p, if q is its subpath from x to y (resp. its infinite subpath from x), we denote q by
$(x_i,x_{i+1})$
is adjacent. Also, for a geodesic path p, if q is its subpath from x to y (resp. its infinite subpath from x), we denote q by
![]() $p_{[x,y]}$
(resp.
$p_{[x,y]}$
(resp.
![]() $p_{[x,\infty )}$
).
$p_{[x,\infty )}$
).
Remark 2.24. For two paths p and q satisfying
![]() $p_+=q_-$
, we can define the path
$p_+=q_-$
, we can define the path
![]() $pq$
by concatenating p and q. Also, for a path p from x to y, we can define the path
$pq$
by concatenating p and q. Also, for a path p from x to y, we can define the path
![]() $p^{-1}$
to be the path from y to x obtained by reversing the direction of p.
$p^{-1}$
to be the path from y to x obtained by reversing the direction of p.
Remark 2.25. For vertices x and y of
![]() $\Gamma $
, we sometimes denote a geodesic path from x to y by
$\Gamma $
, we sometimes denote a geodesic path from x to y by
![]() $[x,y]$
, though it’s not necessarily unique.
$[x,y]$
, though it’s not necessarily unique.
Definition 2.26. Suppose that G is a group, X is a subset of G and
![]() $\{H_\lambda \}_{\lambda \in \Lambda }$
is a collection of subgroups of G such that the set
$\{H_\lambda \}_{\lambda \in \Lambda }$
is a collection of subgroups of G such that the set
![]() $X\cup \bigcup _{\lambda \in \Lambda }H_\lambda $
generates G. We denote
$X\cup \bigcup _{\lambda \in \Lambda }H_\lambda $
generates G. We denote
![]() $\mathcal {H} = \bigsqcup _{\lambda \in \Lambda }(H_\lambda \setminus \{1\})$
and
$\mathcal {H} = \bigsqcup _{\lambda \in \Lambda }(H_\lambda \setminus \{1\})$
and
![]() $X\sqcup \mathcal {H}$
to mean sets of labels. Note that these unions are disjoint as sets of labels, not as subsets of G. Let
$X\sqcup \mathcal {H}$
to mean sets of labels. Note that these unions are disjoint as sets of labels, not as subsets of G. Let
![]() $\Gamma (G, X\sqcup \mathcal {H})$
be the Cayley graph of G with respect to
$\Gamma (G, X\sqcup \mathcal {H})$
be the Cayley graph of G with respect to
![]() $X\sqcup \mathcal {H}$
, which allows loops and multiple edges, that is, its vertex set is G and its positive edge set is
$X\sqcup \mathcal {H}$
, which allows loops and multiple edges, that is, its vertex set is G and its positive edge set is
![]() $G\times (X\sqcup \mathcal {H})$
. The graph
$G\times (X\sqcup \mathcal {H})$
. The graph
![]() $\Gamma (G,X\sqcup \mathcal {H})$
is called a relative Cayley graph. For each
$\Gamma (G,X\sqcup \mathcal {H})$
is called a relative Cayley graph. For each
![]() $\lambda \in \Lambda $
, we consider the Cayley graph
$\lambda \in \Lambda $
, we consider the Cayley graph
![]() $\Gamma (H_\lambda ,H_\lambda \setminus \{1\})$
, which is a subgraph of
$\Gamma (H_\lambda ,H_\lambda \setminus \{1\})$
, which is a subgraph of
![]() $\Gamma (G,X\sqcup \mathcal {H})$
, and define a metric
$\Gamma (G,X\sqcup \mathcal {H})$
, and define a metric
![]() $\widehat {d}_{\lambda }\colon H_\lambda \times H_\lambda \to [0,\infty ]$
as follows. We say that a path p in
$\widehat {d}_{\lambda }\colon H_\lambda \times H_\lambda \to [0,\infty ]$
as follows. We say that a path p in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
is
$\Gamma (G,X\sqcup \mathcal {H})$
is
![]() $\lambda $
-admissible if p doesn’t contain any edge of
$\lambda $
-admissible if p doesn’t contain any edge of
![]() $\Gamma (H_\lambda ,H_\lambda \setminus \{1\})$
. Note that p can contain an edge whose label is an element of
$\Gamma (H_\lambda ,H_\lambda \setminus \{1\})$
. Note that p can contain an edge whose label is an element of
![]() $H_\lambda $
(e.g., the case when the initial vertex of the edge is not in
$H_\lambda $
(e.g., the case when the initial vertex of the edge is not in
![]() $H_\lambda $
) and also p can pass vertices of
$H_\lambda $
) and also p can pass vertices of
![]() $\Gamma (H_\lambda ,H_\lambda \setminus \{1\})$
. For
$\Gamma (H_\lambda ,H_\lambda \setminus \{1\})$
. For
![]() $f,g\in H_\lambda $
, we define
$f,g\in H_\lambda $
, we define
![]() $\widehat {d}_{\lambda }(f,g)$
to be the minimum of lengths of all
$\widehat {d}_{\lambda }(f,g)$
to be the minimum of lengths of all
![]() $\lambda $
-admissible paths from f to g. If there is no
$\lambda $
-admissible paths from f to g. If there is no
![]() $\lambda $
-admissible path from f to g, then we define
$\lambda $
-admissible path from f to g, then we define
![]() $\widehat {d}_{\lambda }(f,g)$
by
$\widehat {d}_{\lambda }(f,g)$
by
![]() $\widehat {d}_{\lambda }(f,g)=\infty $
. For convenience, we extend
$\widehat {d}_{\lambda }(f,g)=\infty $
. For convenience, we extend
![]() $\widehat {d}_{\lambda }$
to
$\widehat {d}_{\lambda }$
to
![]() $\widehat {d}_{\lambda }\colon G\times G \to [0,\infty ]$
by defining
$\widehat {d}_{\lambda }\colon G\times G \to [0,\infty ]$
by defining
![]() $\widehat {d}_{\lambda }(f,g)=\widehat {d}_{\lambda }(1,f^{-1}g)$
if
$\widehat {d}_{\lambda }(f,g)=\widehat {d}_{\lambda }(1,f^{-1}g)$
if
![]() $f^{-1}g\in H_\lambda $
and
$f^{-1}g\in H_\lambda $
and
![]() $\widehat {d}_{\lambda }(f,g)=\infty $
otherwise. The metric
$\widehat {d}_{\lambda }(f,g)=\infty $
otherwise. The metric
![]() $\widehat {d}_{\lambda }$
is called the relative metric.
$\widehat {d}_{\lambda }$
is called the relative metric.
Definition 2.27. Suppose that G is a group and
![]() $\{H_\lambda \}_{\lambda \in \Lambda }$
is a collection of subgroups of G. For a subset X of G,
$\{H_\lambda \}_{\lambda \in \Lambda }$
is a collection of subgroups of G. For a subset X of G,
![]() $\{H_\lambda \}_{\lambda \in \Lambda }$
is said to be hyperbolically embedded in
$\{H_\lambda \}_{\lambda \in \Lambda }$
is said to be hyperbolically embedded in
![]() $(G,X)$
(and denoted by
$(G,X)$
(and denoted by
![]() $\{H_\lambda \}_{\lambda \in \Lambda } \hookrightarrow _h (G,X)$
), if it satisfies the two conditions below.
$\{H_\lambda \}_{\lambda \in \Lambda } \hookrightarrow _h (G,X)$
), if it satisfies the two conditions below.
-
(1) The set
 $X\cup (\bigcup _{\lambda \in \Lambda }H_\lambda )$
generates G and the graph
$X\cup (\bigcup _{\lambda \in \Lambda }H_\lambda )$
generates G and the graph
 $\Gamma (G,X\sqcup \mathcal {H})$
is hyperbolic.
$\Gamma (G,X\sqcup \mathcal {H})$
is hyperbolic. -
(2) For any
 $\lambda \in \Lambda $
,
$\lambda \in \Lambda $
,
 $(H_\lambda ,\widehat {d}_{\lambda })$
is locally finite, that is, for any
$(H_\lambda ,\widehat {d}_{\lambda })$
is locally finite, that is, for any
 $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
 $\{g\in H_\lambda \mid \widehat {d}_{\lambda }(1,g)\le n\}$
is finite.
$\{g\in H_\lambda \mid \widehat {d}_{\lambda }(1,g)\le n\}$
is finite.
A collection of subgroups
![]() $\{H_\lambda \}_{\lambda \in \Lambda }$
is also said to be hyperbolically embedded in G (and denoted by
$\{H_\lambda \}_{\lambda \in \Lambda }$
is also said to be hyperbolically embedded in G (and denoted by
![]() $\{H_\lambda \}_{\lambda \in \Lambda } \hookrightarrow _h G$
), if there exists a subset X of G such that
$\{H_\lambda \}_{\lambda \in \Lambda } \hookrightarrow _h G$
), if there exists a subset X of G such that
![]() $\{H_\lambda \}_{\lambda \in \Lambda } \hookrightarrow _h (G,X)$
.
$\{H_\lambda \}_{\lambda \in \Lambda } \hookrightarrow _h (G,X)$
.
In the remainder of this section, suppose that
![]() $\{H_\lambda \}_{\lambda \in \Lambda }$
is hyperbolically embedded in
$\{H_\lambda \}_{\lambda \in \Lambda }$
is hyperbolically embedded in
![]() $(G,X)$
as in Definition 2.27. We next prepare concepts to define separating cosets.
$(G,X)$
as in Definition 2.27. We next prepare concepts to define separating cosets.
Definition 2.28 [Reference Osin19, Definition 4.1]
Suppose that p is a path in the relative Cayley graph
![]() $\Gamma (G,X\sqcup \mathcal {H})$
. A subpath q of p is called an
$\Gamma (G,X\sqcup \mathcal {H})$
. A subpath q of p is called an
![]() $H_\lambda $
-subpath if the labels of all edges of q are in
$H_\lambda $
-subpath if the labels of all edges of q are in
![]() $H_\lambda $
. In the case that p is a closed path, q can be a subpath of any cyclic shift of p. An
$H_\lambda $
. In the case that p is a closed path, q can be a subpath of any cyclic shift of p. An
![]() $H_\lambda $
-subpath q of a path p is called
$H_\lambda $
-subpath q of a path p is called
![]() $H_\lambda $
-component if q is not contained in any longer
$H_\lambda $
-component if q is not contained in any longer
![]() $H_\lambda $
-subpath of p. In the case that p is a closed path, we require that q is not contained in any longer
$H_\lambda $
-subpath of p. In the case that p is a closed path, we require that q is not contained in any longer
![]() $H_\lambda $
-subpath of any cyclic shift of p. Furthermore, by a component, we mean an
$H_\lambda $
-subpath of any cyclic shift of p. Furthermore, by a component, we mean an
![]() $H_\lambda $
-component for some
$H_\lambda $
-component for some
![]() $H_\lambda $
. Two
$H_\lambda $
. Two
![]() $H_\lambda $
-components
$H_\lambda $
-components
![]() $q_1$
and
$q_1$
and
![]() $q_2$
of a path p are called connected if all vertices of
$q_2$
of a path p are called connected if all vertices of
![]() $q_1$
and
$q_1$
and
![]() $q_2$
are in the same
$q_2$
are in the same
![]() $H_\lambda $
-coset. An
$H_\lambda $
-coset. An
![]() $H_\lambda $
-component q of a path p is called isolated if q is not connected to any other
$H_\lambda $
-component q of a path p is called isolated if q is not connected to any other
![]() $H_\lambda $
-component of p.
$H_\lambda $
-component of p.
Remark 2.29. Note that all vertices of an
![]() $H_\lambda $
-component lie in the same
$H_\lambda $
-component lie in the same
![]() $H_\lambda $
-coset.
$H_\lambda $
-coset.
Proposition 2.30 is a particular case of [Reference Dahmani, Guirardel and Osin5, Proposition 4.13] and plays a crucial role in this paper.
Proposition 2.30 [Reference Hull and Osin12, Lemma 2.4]
There exists a constant
![]() $C>0$
such that for any geodesic n-gon p in
$C>0$
such that for any geodesic n-gon p in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
and any isolated
$\Gamma (G,X\sqcup \mathcal {H})$
and any isolated
![]() $H_\lambda $
-component a of p, we have
$H_\lambda $
-component a of p, we have
In the remainder of section, we fix any constant
![]() $D>0$
with
$D>0$
with
We can now define separating cosets.
Definition 2.31 [Reference Osin19, Definition 4.3]
A path p in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
is said to penetrate a coset
$\Gamma (G,X\sqcup \mathcal {H})$
is said to penetrate a coset
![]() $xH_\lambda $
for some
$xH_\lambda $
for some
![]() $\lambda \in \Lambda $
if p decomposes into
$\lambda \in \Lambda $
if p decomposes into
![]() $p_1ap_2$
, where
$p_1ap_2$
, where
![]() $p_1,p_2$
are possibly trivial, a is an
$p_1,p_2$
are possibly trivial, a is an
![]() $H_\lambda $
-component and
$H_\lambda $
-component and
![]() $a_-\in xH_\lambda $
. Note that if p is geodesic, p penetrates any coset of
$a_-\in xH_\lambda $
. Note that if p is geodesic, p penetrates any coset of
![]() $H_\lambda $
at most once. In this case, a is called the component of p corresponding to
$H_\lambda $
at most once. In this case, a is called the component of p corresponding to
![]() $xH_\lambda $
and also the vertices
$xH_\lambda $
and also the vertices
![]() $a_-$
and
$a_-$
and
![]() $a_+$
are called the entrance and exit points of p and are denoted by
$a_+$
are called the entrance and exit points of p and are denoted by
![]() $p_{in}(xH_\lambda )$
and
$p_{in}(xH_\lambda )$
and
![]() $p_{out}(xH_\lambda )$
, respectively. If in addition we have
$p_{out}(xH_\lambda )$
, respectively. If in addition we have
![]() $\widehat {d}_{\lambda }(a_-,a_+)>D$
, then p is said to essentially penetrates
$\widehat {d}_{\lambda }(a_-,a_+)>D$
, then p is said to essentially penetrates
![]() $xH_\lambda $
. For
$xH_\lambda $
. For
![]() $f,g\in G$
and
$f,g\in G$
and
![]() $\lambda \in \Lambda $
if there exists a geodesic path from f to g in
$\lambda \in \Lambda $
if there exists a geodesic path from f to g in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
which essentially penetrates an
$\Gamma (G,X\sqcup \mathcal {H})$
which essentially penetrates an
![]() $H_\lambda $
-coset
$H_\lambda $
-coset
![]() $xH_\lambda $
, then
$xH_\lambda $
, then
![]() $xH_\lambda $
is called an
$xH_\lambda $
is called an
![]() $(f,g;D)$
-separating coset. The set of all
$(f,g;D)$
-separating coset. The set of all
![]() $(f,g;D)$
-separating cosets of subgroups from the collection
$(f,g;D)$
-separating cosets of subgroups from the collection
![]() $\{H_\lambda \}_{\lambda \in \Lambda }$
is denoted by
$\{H_\lambda \}_{\lambda \in \Lambda }$
is denoted by
![]() $S(f,g;D)$
.
$S(f,g;D)$
.
Remark 2.32. If a geodesic path p penetrates an
![]() $H_\lambda $
-coset
$H_\lambda $
-coset
![]() $xH_\lambda $
, then the component a of p corresponding to
$xH_\lambda $
, then the component a of p corresponding to
![]() $xH_\lambda $
consists of a single edge and is isolated in p by minimality of the length of p.
$xH_\lambda $
consists of a single edge and is isolated in p by minimality of the length of p.
Remark 2.33. First, in [Reference Hull and Osin12, Definition 3.1], whenever
![]() $f,g\in G$
are in the same
$f,g\in G$
are in the same
![]() $H_\lambda $
-coset
$H_\lambda $
-coset
![]() $xH_\lambda $
for some
$xH_\lambda $
for some
![]() $\lambda \in \Lambda $
,
$\lambda \in \Lambda $
,
![]() $xH_\lambda $
is included in
$xH_\lambda $
is included in
![]() $S(f,g;D)$
, but in our Definition 2.31,
$S(f,g;D)$
, but in our Definition 2.31,
![]() $S(f,g;D)$
can be empty even in this case. Secondly, in [Reference Hull and Osin12, Definition 3.1], separating cosets are considered for each subgroup
$S(f,g;D)$
can be empty even in this case. Secondly, in [Reference Hull and Osin12, Definition 3.1], separating cosets are considered for each subgroup
![]() $H_\lambda $
separately, being denoted by
$H_\lambda $
separately, being denoted by
![]() $S_\lambda (f,g;D)$
, but in our Definition 2.31, we consider separating cosets of all subgroups from the collection
$S_\lambda (f,g;D)$
, but in our Definition 2.31, we consider separating cosets of all subgroups from the collection
![]() $\{H_\lambda \}_{\lambda \in \Lambda }$
all together.
$\{H_\lambda \}_{\lambda \in \Lambda }$
all together.
The following lemma is immediate from the above definition.
Lemma 2.34. For any
![]() $f,g,h\in G$
and any
$f,g,h\in G$
and any
![]() $\lambda \in \Lambda $
, the following hold.
$\lambda \in \Lambda $
, the following hold.
-
(a)
 $S(f,g;D)=S(g,f;D)$
.
$S(f,g;D)=S(g,f;D)$
. -
(b)
 $S(hf,hg;D)=\{hxH_\lambda \mid xH_\lambda \in S(f,g;D)\}$
.
$S(hf,hg;D)=\{hxH_\lambda \mid xH_\lambda \in S(f,g;D)\}$
.
We list some results on separating cosets so that readers have a better understanding.
Lemma 2.35 (cf. [Reference Osin19, Lemma 4.5])
For any
![]() $f,g\in G$
and any
$f,g\in G$
and any
![]() $xH_\lambda \in S(f,g;D)$
, every path in
$xH_\lambda \in S(f,g;D)$
, every path in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
connecting f to g and composed of at most two geodesic segments penetrates
$\Gamma (G,X\sqcup \mathcal {H})$
connecting f to g and composed of at most two geodesic segments penetrates
![]() $xH_\lambda $
.
$xH_\lambda $
.
The following lemma makes
![]() $S(f,g;D)$
into a totally ordered set.
$S(f,g;D)$
into a totally ordered set.
Lemma 2.36 [Reference Osin19, Lemma 4.6]
Let
![]() $f,g\in G$
, and suppose that a geodesic path p from f to g penetrates a coset
$f,g\in G$
, and suppose that a geodesic path p from f to g penetrates a coset
![]() $xH_\lambda $
for some
$xH_\lambda $
for some
![]() $\lambda \in \Lambda $
and decomposes into
$\lambda \in \Lambda $
and decomposes into
![]() $p=p_1ap_2$
, where
$p=p_1ap_2$
, where
![]() $p_1,p_2$
are possibly trivial and a is a component corresponding to
$p_1,p_2$
are possibly trivial and a is a component corresponding to
![]() $xH_\lambda $
. Then, we have
$xH_\lambda $
. Then, we have
![]() $d_{X\cup \mathcal {H}}(f,a_-)=d_{X\cup \mathcal {H}}(f,xH_\lambda )$
.
$d_{X\cup \mathcal {H}}(f,a_-)=d_{X\cup \mathcal {H}}(f,xH_\lambda )$
.
Definition 2.37 [Reference Osin19, Definition 4.7]
Given any
![]() $f,g\in G$
, a relation
$f,g\in G$
, a relation
![]() $\preceq $
on the set
$\preceq $
on the set
![]() $S(f,g;D)$
is defined as follows: For any
$S(f,g;D)$
is defined as follows: For any
![]() $C_1,C_2 \in S(f,g;D)$
,
$C_1,C_2 \in S(f,g;D)$
,
Lemma 2.38 [Reference Osin19, Lemma 4.8]
For any
![]() $f,g\in G$
, the relation
$f,g\in G$
, the relation
![]() $\preceq $
is a linear order on
$\preceq $
is a linear order on
![]() $S(f,g;D)$
and any geodesic path p in
$S(f,g;D)$
and any geodesic path p in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from f to g penetrates all
$\Gamma (G,X\sqcup \mathcal {H})$
from f to g penetrates all
![]() $(f,g;D)$
-separating cosets according to the order
$(f,g;D)$
-separating cosets according to the order
![]() $\preceq $
. In particular,
$\preceq $
. In particular,
![]() $S(f,g;D)$
is finite. That is,
$S(f,g;D)$
is finite. That is,
for some
![]() $n\in \mathbb {N}$
and p decomposes into
$n\in \mathbb {N}$
and p decomposes into
![]() $p=p_1a_1\cdots p_na_np_{n+1}$
, where
$p=p_1a_1\cdots p_na_np_{n+1}$
, where
![]() $a_i$
is the component of p corresponding to
$a_i$
is the component of p corresponding to
![]() $C_i$
for each
$C_i$
for each
![]() $i\in \{1,\cdots , n\}$
.
$i\in \{1,\cdots , n\}$
.
2.4. Acylindrically hyperbolic group
Theorem 2.39 is a simplified version of [Reference Osin19, Theorem 1.2]. For more details on acylindrically hyperbolic groups, readers are referred to [Reference Osin19].
Theorem 2.39. For any group G, the following conditions are equivalent.
-
(AH 1) There exists a generating set X of G such that the corresponding Cayley graph
 $\Gamma (G,X)$
is hyperbolic,
$\Gamma (G,X)$
is hyperbolic,
 $|\partial \Gamma (G,X)|>2$
, and the natural action of G on
$|\partial \Gamma (G,X)|>2$
, and the natural action of G on
 $\Gamma (G,X)$
is acylindrical.
$\Gamma (G,X)$
is acylindrical. -
(AH 4) G contains a proper infinite hyperbolically embedded subgroup.
Definition 2.40. A group G is called acylindrically hyperbolic if G satisfies the equivalent conditions
![]() $(AH_1)$
and
$(AH_1)$
and
![]() $(AH_4)$
from Theorem 2.39.
$(AH_4)$
from Theorem 2.39.
The following results were obtained in [Reference Osin19, Section 5] in proving the implication
![]() $(AH_4)\Rightarrow (AH_1)$
in Theorem 2.39. In Theorem 2.41 below, we consider separating cosets for
$(AH_4)\Rightarrow (AH_1)$
in Theorem 2.39. In Theorem 2.41 below, we consider separating cosets for
![]() $\{H_\lambda \}_{\lambda \in \Lambda } \hookrightarrow _h (G,X)$
and the metric
$\{H_\lambda \}_{\lambda \in \Lambda } \hookrightarrow _h (G,X)$
and the metric
![]() $d_{\Gamma (G,Y\sqcup \mathcal {H})}(\cdot ,\cdot )$
is denoted by
$d_{\Gamma (G,Y\sqcup \mathcal {H})}(\cdot ,\cdot )$
is denoted by
![]() $d_{Y\cup \mathcal {H}}(\cdot ,\cdot )$
for brevity.
$d_{Y\cup \mathcal {H}}(\cdot ,\cdot )$
for brevity.
Theorem 2.41 (cf. [Reference Osin19, Theorem 5.4, Lemma 5.10])
Suppose that G is a group, X is a subset of G and
![]() $\{H_\lambda \}_{\lambda \in \Lambda }$
is a collection of subgroups of G hyperbolically embedded in
$\{H_\lambda \}_{\lambda \in \Lambda }$
is a collection of subgroups of G hyperbolically embedded in
![]() $(G,X)$
. Let
$(G,X)$
. Let
![]() $C>0$
as in Proposition 2.30, and let
$C>0$
as in Proposition 2.30, and let
![]() $D>0$
satisfy
$D>0$
satisfy
![]() $D \ge 3C$
as in equation (3). We also define the subset Y of G by
$D \ge 3C$
as in equation (3). We also define the subset Y of G by
Then, we have for any
![]() $f,g \in G$
,
$f,g \in G$
,
If in addition
![]() $\Lambda $
is finite, then the following hold.
$\Lambda $
is finite, then the following hold.
-
(a)
 $\{H_\lambda \}_{\lambda \in \Lambda } \hookrightarrow _h (G,Y)$
.
$\{H_\lambda \}_{\lambda \in \Lambda } \hookrightarrow _h (G,Y)$
. -
(b) The action of G on
 $\Gamma (G,Y\sqcup \mathcal {H})$
is acylindrical.
$\Gamma (G,Y\sqcup \mathcal {H})$
is acylindrical.
Remark 2.42. In [Reference Osin19, Section 5], the condition
![]() $|\Lambda |<\infty $
is assumed in all lemmas for proving
$|\Lambda |<\infty $
is assumed in all lemmas for proving
![]() $(AH_4)\Rightarrow (AH_1)$
including [Reference Osin19, Lemma 5.10], which corresponds to the inequality (5) in Theorem 2.41. However, the condition
$(AH_4)\Rightarrow (AH_1)$
including [Reference Osin19, Lemma 5.10], which corresponds to the inequality (5) in Theorem 2.41. However, the condition
![]() $|\Lambda |<\infty $
is not used in the proof of [Reference Osin19, Lemma 5.10], so we omit it in equation (5) for our discussion in Section 3 and Section 6. Actually, the condition
$|\Lambda |<\infty $
is not used in the proof of [Reference Osin19, Lemma 5.10], so we omit it in equation (5) for our discussion in Section 3 and Section 6. Actually, the condition
![]() $|\Lambda |<\infty $
is not used in the proof of [Reference Osin19, Theorem 5.4 (a)] either.
$|\Lambda |<\infty $
is not used in the proof of [Reference Osin19, Theorem 5.4 (a)] either.
Lemma 2.43 [Reference Osin19, Lemma 5.12]
Let G be a group, H a subgroup of G, X a subset of G. If H is non-degenerate (i.e., H is a proper infinite subgroup of G) and
![]() $H\hookrightarrow _h (G,X)$
, then the action of G on
$H\hookrightarrow _h (G,X)$
, then the action of G on
![]() $\Gamma (G,X\sqcup H)$
is non-elementary (i.e.,
$\Gamma (G,X\sqcup H)$
is non-elementary (i.e.,
![]() $|\partial \Gamma (G,X\sqcup H)|>2$
).
$|\partial \Gamma (G,X\sqcup H)|>2$
).
3. Path representatives of the Gromov boundary
Throughout this section, suppose that G is a group, X is a subset of G and
![]() $\{H_\lambda \}_{\lambda \in \Lambda }$
is a collection of subgroups of G hyperbolically embedded in
$\{H_\lambda \}_{\lambda \in \Lambda }$
is a collection of subgroups of G hyperbolically embedded in
![]() $(G,X)$
. Let
$(G,X)$
. Let
![]() $C>0$
as in Proposition 2.30 and fix
$C>0$
as in Proposition 2.30 and fix
![]() $D>0$
satisfying
$D>0$
satisfying
![]() $D\ge 3C$
as in equation (3). We also define the subset Y of G by
$D\ge 3C$
as in equation (3). We also define the subset Y of G by
![]() $Y=\{y \in G \mid S(1,y;D)= \emptyset \}$
as in Theorem 2.41.
$Y=\{y \in G \mid S(1,y;D)= \emptyset \}$
as in Theorem 2.41.
In this section, we will show that elements of the Gromov boundary of the Cayley graph
![]() $\Gamma (G,Y\sqcup \mathcal {H})$
are represented by nice geodesic rays in
$\Gamma (G,Y\sqcup \mathcal {H})$
are represented by nice geodesic rays in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
(see Proposition 3.22). The nice geodesic rays are characterized by penetrating infinitely many cosets deeply enough (see Lemma 3.20). By using these path representatives of boundary points, we will extend the notion of Hull–Osin’s separating cosets to allow a point in the Gromov boundary (see Definition 3.25). We will also investigate the relation between the path representatives and the topology of
$\Gamma (G,X\sqcup \mathcal {H})$
(see Proposition 3.22). The nice geodesic rays are characterized by penetrating infinitely many cosets deeply enough (see Lemma 3.20). By using these path representatives of boundary points, we will extend the notion of Hull–Osin’s separating cosets to allow a point in the Gromov boundary (see Definition 3.25). We will also investigate the relation between the path representatives and the topology of
![]() $\partial \Gamma (G,Y\sqcup \mathcal {H})$
(see Proposition 3.23 and Proposition 3.29).
$\partial \Gamma (G,Y\sqcup \mathcal {H})$
(see Proposition 3.23 and Proposition 3.29).
For brevity, we will denote
![]() $d_{\Gamma (G,X\sqcup \mathcal {H})}(\cdot ,\cdot )$
and
$d_{\Gamma (G,X\sqcup \mathcal {H})}(\cdot ,\cdot )$
and
![]() $(\cdot ,\cdot )_\cdot ^{\Gamma (G,X\sqcup \mathcal {H})}$
by
$(\cdot ,\cdot )_\cdot ^{\Gamma (G,X\sqcup \mathcal {H})}$
by
![]() $d_{X\cup \mathcal {H}}(\cdot ,\cdot )$
and
$d_{X\cup \mathcal {H}}(\cdot ,\cdot )$
and
![]() $(\cdot ,\cdot )_\cdot ^{X\cup \mathcal {H}}$
, respectively (see equation (1)). This will be the same for
$(\cdot ,\cdot )_\cdot ^{X\cup \mathcal {H}}$
, respectively (see equation (1)). This will be the same for
![]() $\Gamma (G,Y\sqcup \mathcal {H})$
as well. We also emphasize that we will consider separating cosets and relative metrics for
$\Gamma (G,Y\sqcup \mathcal {H})$
as well. We also emphasize that we will consider separating cosets and relative metrics for
![]() $\{H_\lambda \}_{\lambda \in \Lambda } \hookrightarrow _h (G,X)$
, hence we use the notations
$\{H_\lambda \}_{\lambda \in \Lambda } \hookrightarrow _h (G,X)$
, hence we use the notations
![]() $S(\cdot ,\cdot ;D)$
and
$S(\cdot ,\cdot ;D)$
and
![]() $\widehat {d}_{\lambda }(\cdot ,\cdot )$
without including X in them.
$\widehat {d}_{\lambda }(\cdot ,\cdot )$
without including X in them.
As preparation of our discussion, we list auxiliary results that immediately follow from Section 2.3 but have not been recorded explicitly. They’re from Lemma 3.1 up to Lemma 3.5.
Lemma 3.1. Let p be a geodesic path in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
between two vertices and q be a subpath of p, then we have
$\Gamma (G,X\sqcup \mathcal {H})$
between two vertices and q be a subpath of p, then we have
![]() $S(q_-,q_+;D) \subset S(p_-,p_+;D)$
.
$S(q_-,q_+;D) \subset S(p_-,p_+;D)$
.
Proof. Let
![]() $p=p_1qp_2$
be decomposition of p into subpaths
$p=p_1qp_2$
be decomposition of p into subpaths
![]() $p_1$
, q and
$p_1$
, q and
![]() $p_2$
. For any
$p_2$
. For any
![]() $H_\lambda $
-coset
$H_\lambda $
-coset
![]() $xH_\lambda \in S(q_-,q_+;D)$
, there exists a geodesic path
$xH_\lambda \in S(q_-,q_+;D)$
, there exists a geodesic path
![]() $\alpha $
in
$\alpha $
in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from
$\Gamma (G,X\sqcup \mathcal {H})$
from
![]() $q_-$
to
$q_-$
to
![]() $q_+$
that essentially penetrates
$q_+$
that essentially penetrates
![]() $xH_\lambda $
. Since
$xH_\lambda $
. Since
![]() $p_1\alpha p_2$
is a geodesic path in
$p_1\alpha p_2$
is a geodesic path in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from
$\Gamma (G,X\sqcup \mathcal {H})$
from
![]() $p_-$
to
$p_-$
to
![]() $p_+$
that essentially penetrates
$p_+$
that essentially penetrates
![]() $xH_\lambda $
, we have
$xH_\lambda $
, we have
![]() $xH_\lambda \in S(p_-,p_+;D)$
.
$xH_\lambda \in S(p_-,p_+;D)$
.
Lemma 3.2 means that if two geodesic paths from the same point penetrate the same coset, then their entrance points are close.
Lemma 3.2. Let
![]() $o\in G$
and suppose that B is an
$o\in G$
and suppose that B is an
![]() $H_\lambda $
-coset for some
$H_\lambda $
-coset for some
![]() $\lambda \in \Lambda $
and that
$\lambda \in \Lambda $
and that
![]() $p,q$
are (possibly infinite) geodesic paths from o in
$p,q$
are (possibly infinite) geodesic paths from o in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
that penetrate B. Then, we have
$\Gamma (G,X\sqcup \mathcal {H})$
that penetrate B. Then, we have
![]() $\widehat {d}_{\lambda }(p_{in}(B),q_{in}(B)) \le 3C$
.
$\widehat {d}_{\lambda }(p_{in}(B),q_{in}(B)) \le 3C$
.
Proof. Let
![]() $x=p_{in}(B)$
and
$x=p_{in}(B)$
and
![]() $y=q_{in}(B)$
for brevity, and let e be the edge in
$y=q_{in}(B)$
for brevity, and let e be the edge in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from x to y whose label is in
$\Gamma (G,X\sqcup \mathcal {H})$
from x to y whose label is in
![]() $H_\lambda $
. Since
$H_\lambda $
. Since
![]() $p,q$
are geodesic in
$p,q$
are geodesic in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
and penetrates B, e is an isolated component in the geodesic triangle
$\Gamma (G,X\sqcup \mathcal {H})$
and penetrates B, e is an isolated component in the geodesic triangle
![]() $p_{[o,x]}e(q_{[o,y]})^{-1}$
by Remark 2.32. This implies
$p_{[o,x]}e(q_{[o,y]})^{-1}$
by Remark 2.32. This implies
![]() $\widehat {d}_\lambda (x,y)\le 3C$
by Proposition 2.30.
$\widehat {d}_\lambda (x,y)\le 3C$
by Proposition 2.30.
Lemma 3.3 means that the distance between two cosets can be measured by a geodesic path penetrating both of them.
Lemma 3.3. Suppose that p is a (possibly infinite) geodesic path in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from
$\Gamma (G,X\sqcup \mathcal {H})$
from
![]() $p_-\in G$
. If p penetrates two distinct cosets
$p_-\in G$
. If p penetrates two distinct cosets
![]() $C_0,C_1$
satisfying
$C_0,C_1$
satisfying
![]() $d_{X\cup \mathcal {H}}(p_-,C_0)< d_{X\cup \mathcal {H}}(p_-,C_1)$
, then we have
$d_{X\cup \mathcal {H}}(p_-,C_0)< d_{X\cup \mathcal {H}}(p_-,C_1)$
, then we have
Proof. Let
![]() $p=p_1ap_2bp_3$
be decomposition of p into subpaths such that
$p=p_1ap_2bp_3$
be decomposition of p into subpaths such that
![]() $a,b$
are components of p corresponding to
$a,b$
are components of p corresponding to
![]() $C_0,C_1$
, respectively. By
$C_0,C_1$
, respectively. By
![]() $a_+\in C_0$
and
$a_+\in C_0$
and
![]() $b_-\in C_1$
, we have
$b_-\in C_1$
, we have
![]() $d_{X\cup \mathcal {H}}(C_0,C_1) \le d_{X\cup \mathcal {H}}(a_+,b_-)$
. Suppose for contradiction that there exist
$d_{X\cup \mathcal {H}}(C_0,C_1) \le d_{X\cup \mathcal {H}}(a_+,b_-)$
. Suppose for contradiction that there exist
![]() $x\in C_0, y\in C_1$
such that
$x\in C_0, y\in C_1$
such that
![]() $d_{X\cup \mathcal {H}}(x,y) < d_{X\cup \mathcal {H}}(a_+,b_-)$
. By
$d_{X\cup \mathcal {H}}(x,y) < d_{X\cup \mathcal {H}}(a_+,b_-)$
. By
![]() $x,a_-\in C_0$
and
$x,a_-\in C_0$
and
![]() $y,b_+\in C_1$
, we have
$y,b_+\in C_1$
, we have
![]() $d_{X\cup \mathcal {H}}(a_-,x)\le 1$
and
$d_{X\cup \mathcal {H}}(a_-,x)\le 1$
and
![]() $d_{X\cup \mathcal {H}}(y,b_+) \le 1$
. This implies
$d_{X\cup \mathcal {H}}(y,b_+) \le 1$
. This implies
 $$ \begin{align*} d_{X\cup\mathcal{H}}(a_-,b_+) &\le d_{X\cup\mathcal{H}}(a_-,x)+d_{X\cup\mathcal{H}}(x,y)+d_{X\cup\mathcal{H}}(y,b_+)\\ &< 1+d_{X\cup\mathcal{H}}(a_+,b_-)+1 =d_{X\cup\mathcal{H}}(a_-,b_+), \end{align*} $$
$$ \begin{align*} d_{X\cup\mathcal{H}}(a_-,b_+) &\le d_{X\cup\mathcal{H}}(a_-,x)+d_{X\cup\mathcal{H}}(x,y)+d_{X\cup\mathcal{H}}(y,b_+)\\ &< 1+d_{X\cup\mathcal{H}}(a_+,b_-)+1 =d_{X\cup\mathcal{H}}(a_-,b_+), \end{align*} $$
which is a contradiction. Hence, we also have
![]() $d_{X\cup \mathcal {H}}(a_+,b_-) \le d_{X\cup \mathcal {H}}(C_0,C_1)$
.
$d_{X\cup \mathcal {H}}(a_+,b_-) \le d_{X\cup \mathcal {H}}(C_0,C_1)$
.

Figure 1 Proof of Lemma 3.4.

Figure 2 Proof of Lemma 3.5.
Lemma 3.4 is analogous to Lemma 3.2.
Lemma 3.4. Suppose that
![]() $C_0,C_1$
are cosets of
$C_0,C_1$
are cosets of
![]() $H_{\lambda _0}, H_{\lambda _1}$
, respectively, with
$H_{\lambda _0}, H_{\lambda _1}$
, respectively, with
![]() $C_0\neq C_1$
and that
$C_0\neq C_1$
and that
![]() $p,q$
are (possibly infinite) geodesic paths in
$p,q$
are (possibly infinite) geodesic paths in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from
$\Gamma (G,X\sqcup \mathcal {H})$
from
![]() $p_-,q_- \in G$
, respectively, that penetrate
$p_-,q_- \in G$
, respectively, that penetrate
![]() $C_0$
and
$C_0$
and
![]() $C_1$
satisfying
$C_1$
satisfying
![]() $d_{X\cup \mathcal {H}}(p_-,C_0) < d_{X\cup \mathcal {H}}(p_-,C_1)$
and
$d_{X\cup \mathcal {H}}(p_-,C_0) < d_{X\cup \mathcal {H}}(p_-,C_1)$
and
![]() $d_{X\cup \mathcal {H}}(q_-,C_0) < d_{X\cup \mathcal {H}}(q_-,C_1)$
. Then, we have
$d_{X\cup \mathcal {H}}(q_-,C_0) < d_{X\cup \mathcal {H}}(q_-,C_1)$
. Then, we have
![]() $\widehat {d}_{\lambda _0}(p_{out}(C_0),q_{out}(C_0)) \le 4C$
and
$\widehat {d}_{\lambda _0}(p_{out}(C_0),q_{out}(C_0)) \le 4C$
and
![]() $\widehat {d}_{\lambda _1}(p_{in}(C_1),q_{in}(C_1)) \le 4C$
.
$\widehat {d}_{\lambda _1}(p_{in}(C_1),q_{in}(C_1)) \le 4C$
.
Proof. Let
![]() $x_0=p_{out}(C_0), x_1=p_{in}(C_1), y_0=q_{out}(C_0), y_1=q_{in}(C_1)$
for brevity, and let
$x_0=p_{out}(C_0), x_1=p_{in}(C_1), y_0=q_{out}(C_0), y_1=q_{in}(C_1)$
for brevity, and let
![]() $e_0,e_1$
be edges in
$e_0,e_1$
be edges in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
such that
$\Gamma (G,X\sqcup \mathcal {H})$
such that
![]() $e_0$
is from
$e_0$
is from
![]() $x_0$
to
$x_0$
to
![]() $y_0$
with its label in
$y_0$
with its label in
![]() $H_{\lambda _0}$
and
$H_{\lambda _0}$
and
![]() $e_1$
is from
$e_1$
is from
![]() $x_1$
to
$x_1$
to
![]() $y_1$
with its label in
$y_1$
with its label in
![]() $H_{\lambda _1}$
. Since the subpaths
$H_{\lambda _1}$
. Since the subpaths
![]() $p_{[x_0,x_1]},q_{[y_0,y_1]}$
don’t penetrate
$p_{[x_0,x_1]},q_{[y_0,y_1]}$
don’t penetrate
![]() $C_0$
nor
$C_0$
nor
![]() $C_1$
by Remark 2.32 and we have
$C_1$
by Remark 2.32 and we have
![]() $C_0\neq C_1$
,
$C_0\neq C_1$
,
![]() $e_0$
and
$e_0$
and
![]() $e_1$
are isolated components of the geodesic quadrilateral
$e_1$
are isolated components of the geodesic quadrilateral
![]() $e_0 q_{[y_0,y_1]} e_1^{-1} (p_{[x_0,x_1]})^{-1}$
. This implies
$e_0 q_{[y_0,y_1]} e_1^{-1} (p_{[x_0,x_1]})^{-1}$
. This implies
![]() $\widehat {d}_{\lambda _0}(x_0,y_0)\le 4C$
and
$\widehat {d}_{\lambda _0}(x_0,y_0)\le 4C$
and
![]() $\widehat {d}_{\lambda _1}(x_1,y_1)\le 4C$
by Proposition 2.30.
$\widehat {d}_{\lambda _1}(x_1,y_1)\le 4C$
by Proposition 2.30.
Lemma 3.5 is useful to find separating cosets of a pair of elements in G.
Lemma 3.5. Let
![]() $o,x,y\in G$
and
$o,x,y\in G$
and
![]() $S(o,x;D)=\{C_1\preceq C_2\preceq \cdots \preceq C_n\}$
. If a geodesic path q in
$S(o,x;D)=\{C_1\preceq C_2\preceq \cdots \preceq C_n\}$
. If a geodesic path q in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from o to y penetrates
$\Gamma (G,X\sqcup \mathcal {H})$
from o to y penetrates
![]() $C_i$
for some
$C_i$
for some
![]() $i\in \{1,\cdots ,n\}$
, then we have
$i\in \{1,\cdots ,n\}$
, then we have
![]() $C_j\in S(o,y;D)$
for any j with
$C_j\in S(o,y;D)$
for any j with
![]() $j<i$
.
$j<i$
.
Proof. Let q penetrate
![]() $C_i$
and
$C_i$
and
![]() $j\in \mathbb {N}$
satisfy
$j\in \mathbb {N}$
satisfy
![]() $j<i$
. By
$j<i$
. By
![]() $C_j\in S(o,x;D)$
, their exists a geodesic path p in
$C_j\in S(o,x;D)$
, their exists a geodesic path p in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from o to x that essentially penetrates
$\Gamma (G,X\sqcup \mathcal {H})$
from o to x that essentially penetrates
![]() $C_j$
. Note that p penetrates
$C_j$
. Note that p penetrates
![]() $C_i$
by Lemma 2.38. Let
$C_i$
by Lemma 2.38. Let
![]() $p=p_1 a p_2$
,
$p=p_1 a p_2$
,
![]() $q=q_1 b q_2$
be decomposition of
$q=q_1 b q_2$
be decomposition of
![]() $p,q$
into subpaths such that
$p,q$
into subpaths such that
![]() $a,b$
are
$a,b$
are
![]() $H_\lambda $
-component of
$H_\lambda $
-component of
![]() $p,q$
corresponding to
$p,q$
corresponding to
![]() $C_i$
, respectively. Let e be the edge from
$C_i$
, respectively. Let e be the edge from
![]() $a_-$
to
$a_-$
to
![]() $b_+$
in
$b_+$
in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
whose label is in
$\Gamma (G,X\sqcup \mathcal {H})$
whose label is in
![]() $H_\lambda $
. Since we have
$H_\lambda $
. Since we have
![]() $d_{X\cup \mathcal {H}}(o,a_-)=d_{X\cup \mathcal {H}}(o,b_-)=d_{X\cup \mathcal {H}}(o,C_i)$
by Lemma 2.36, the path
$d_{X\cup \mathcal {H}}(o,a_-)=d_{X\cup \mathcal {H}}(o,b_-)=d_{X\cup \mathcal {H}}(o,C_i)$
by Lemma 2.36, the path
![]() $p_1eq_2$
from o to y is geodesic in
$p_1eq_2$
from o to y is geodesic in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
and essentially penetrates
$\Gamma (G,X\sqcup \mathcal {H})$
and essentially penetrates
![]() $C_j$
. This implies
$C_j$
. This implies
![]() $C_j \in S(o,y;D)$
.
$C_j \in S(o,y;D)$
.
First of all, we verify hyperbolicity of
![]() $\Gamma (G,Y\sqcup \mathcal {H})$
. Lemma 3.7 is straightforward from [Reference Bowditch1, Proposition 3.1], which is stated below in a simplified way, but we write down the proof for completeness. Also, Lemma 3.7 (a) is actually known by [Reference Osin19, Lemma 5.6] since its proof doesn’t use the condition
$\Gamma (G,Y\sqcup \mathcal {H})$
. Lemma 3.7 is straightforward from [Reference Bowditch1, Proposition 3.1], which is stated below in a simplified way, but we write down the proof for completeness. Also, Lemma 3.7 (a) is actually known by [Reference Osin19, Lemma 5.6] since its proof doesn’t use the condition
![]() $|\Lambda |<\infty $
(see Remark 2.42). Lemma 3.7 (b) is new and plays an important role in this paper together with the inequality (5) in Theorem 2.41.
$|\Lambda |<\infty $
(see Remark 2.42). Lemma 3.7 (b) is new and plays an important role in this paper together with the inequality (5) in Theorem 2.41.
Proposition 3.6 (cf. [Reference Bowditch1, Proposition 3.1])
Given
![]() $h\ge 0$
, there exists
$h\ge 0$
, there exists
![]() $k(h)\ge 0$
with the following property. Suppose that
$k(h)\ge 0$
with the following property. Suppose that
![]() $\Gamma $
is a connected graph and that for each pair of vertices
$\Gamma $
is a connected graph and that for each pair of vertices
![]() $x,y\in \Gamma $
, we have associated a connected subgraph
$x,y\in \Gamma $
, we have associated a connected subgraph
![]() $\mathcal {L}(x,y)$
of
$\mathcal {L}(x,y)$
of
![]() $\Gamma $
with
$\Gamma $
with
![]() $x,y \in \mathcal {L}(x,y)$
satisfying (1) and (2) below. (Here, we define
$x,y \in \mathcal {L}(x,y)$
satisfying (1) and (2) below. (Here, we define
![]() $\mathcal {N}(A,h)=\{v\in \Gamma \mid \exists w\in A ~\mathrm {s.t.}~ d_{\Gamma }(v,w)\le h \}$
.)
$\mathcal {N}(A,h)=\{v\in \Gamma \mid \exists w\in A ~\mathrm {s.t.}~ d_{\Gamma }(v,w)\le h \}$
.)
-
(1) For any vertices
 $x,y,z\in \Gamma $
,
$x,y,z\in \Gamma $
,
 $\mathcal {L}(x,y) \subset \mathcal {N}(\mathcal {L}(x,z)\cup \mathcal {L}(z,y),h)$
.
$\mathcal {L}(x,y) \subset \mathcal {N}(\mathcal {L}(x,z)\cup \mathcal {L}(z,y),h)$
. -
(2) For any vertices
 $x,y \in \Gamma $
with
$x,y \in \Gamma $
with
 $d_{\Gamma }(x,y) \le 1$
, the diameter of
$d_{\Gamma }(x,y) \le 1$
, the diameter of
 $\mathcal {L}(x,y)$
in
$\mathcal {L}(x,y)$
in
 $\Gamma $
is at most h.
$\Gamma $
is at most h.
Then,
![]() $\Gamma $
is
$\Gamma $
is
![]() $k(h)$
-hyperbolic and for any two vertices
$k(h)$
-hyperbolic and for any two vertices
![]() $x,y\in \Gamma $
, the Hausdorff distance between
$x,y\in \Gamma $
, the Hausdorff distance between
![]() $\mathcal {L}(x,y)$
and any geodesic path in
$\mathcal {L}(x,y)$
and any geodesic path in
![]() $\Gamma $
from x to y is bounded above by
$\Gamma $
from x to y is bounded above by
![]() $k(h)$
.
$k(h)$
.
Lemma 3.7. The following hold.
-
(a) We have
 $X\subset Y$
and
$X\subset Y$
and
 $\Gamma (G,Y\sqcup \mathcal {H})$
is hyperbolic.
$\Gamma (G,Y\sqcup \mathcal {H})$
is hyperbolic. -
(b) There exists
 $M_X \in \mathbb {N}$
such that for any
$M_X \in \mathbb {N}$
such that for any
 $x,y \in G$
, any geodesic path
$x,y \in G$
, any geodesic path
 $\alpha $
in
$\alpha $
in
 $\Gamma (G,X\sqcup \mathcal {H})$
from x to y and any geodesic path
$\Gamma (G,X\sqcup \mathcal {H})$
from x to y and any geodesic path
 $\beta $
in
$\beta $
in
 $\Gamma (G, Y\sqcup \mathcal {H})$
from x to y, the Hausforff distance between
$\Gamma (G, Y\sqcup \mathcal {H})$
from x to y, the Hausforff distance between
 $\alpha $
and
$\alpha $
and
 $\beta $
in
$\beta $
in
 $\Gamma (G,Y\sqcup \mathcal {H})$
is bounded above by
$\Gamma (G,Y\sqcup \mathcal {H})$
is bounded above by
 $M_X$
.
$M_X$
.
Proof. If
![]() $x\in X$
and
$x\in X$
and
![]() $x\neq 1$
, then the edge in
$x\neq 1$
, then the edge in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from
$\Gamma (G,X\sqcup \mathcal {H})$
from
![]() $1$
to x with the label
$1$
to x with the label
![]() $x\in X$
is geodesic in
$x\in X$
is geodesic in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
. Since this path consisting of one edge has no
$\Gamma (G,X\sqcup \mathcal {H})$
. Since this path consisting of one edge has no
![]() $H_\lambda $
-component for any
$H_\lambda $
-component for any
![]() $\lambda \in \Lambda $
, we have
$\lambda \in \Lambda $
, we have
![]() $S(1,x;D)=\emptyset $
by Lemma 2.38. This implies
$S(1,x;D)=\emptyset $
by Lemma 2.38. This implies
![]() $x\in Y$
, hence
$x\in Y$
, hence
![]() $X\subset Y$
. We will check the two conditions in Proposition 3.6 considering
$X\subset Y$
. We will check the two conditions in Proposition 3.6 considering
![]() $\Gamma =\Gamma (G,Y\sqcup \mathcal {H})$
. Note that
$\Gamma =\Gamma (G,Y\sqcup \mathcal {H})$
. Note that
![]() $\Gamma (G,X\sqcup \mathcal {H})$
is a subgraph of
$\Gamma (G,X\sqcup \mathcal {H})$
is a subgraph of
![]() $\Gamma (G,Y\sqcup \mathcal {H})$
by
$\Gamma (G,Y\sqcup \mathcal {H})$
by
![]() $X\subset Y$
. For each pair
$X\subset Y$
. For each pair
![]() $(x,y)$
of elements of G, fix a geodesic path
$(x,y)$
of elements of G, fix a geodesic path
![]() $\gamma _{x,y}$
in
$\gamma _{x,y}$
in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from x to y and define
$\Gamma (G,X\sqcup \mathcal {H})$
from x to y and define
![]() $\mathcal {L}(x,y)=\gamma _{x,y}$
. Since
$\mathcal {L}(x,y)=\gamma _{x,y}$
. Since
![]() $\Gamma (G,X\sqcup \mathcal {H})$
is
$\Gamma (G,X\sqcup \mathcal {H})$
is
![]() $\delta _X$
-hyperbolic with
$\delta _X$
-hyperbolic with
![]() $\delta _X\in \mathbb {N}$
(see Definition 2.27 (1)), Proposition 3.6 (1) is satisfied with
$\delta _X\in \mathbb {N}$
(see Definition 2.27 (1)), Proposition 3.6 (1) is satisfied with
![]() $h=\delta _X$
. Next, let
$h=\delta _X$
. Next, let
![]() $x,y\in G$
satisfy
$x,y\in G$
satisfy
![]() $d_{Y\cup \mathcal {H}}(x,y)\le 1$
, then
$d_{Y\cup \mathcal {H}}(x,y)\le 1$
, then
![]() $S(x,y;D)=\emptyset $
. Hence, for any vertex
$S(x,y;D)=\emptyset $
. Hence, for any vertex
![]() $z\in \gamma _{x,y}$
, we have
$z\in \gamma _{x,y}$
, we have
![]() $S(x,z;D)=\emptyset $
by Lemma 3.1. This implies
$S(x,z;D)=\emptyset $
by Lemma 3.1. This implies
![]() $d_{Y\cup \mathcal {H}}(x,z)\le 1$
. Hence, the diameter of
$d_{Y\cup \mathcal {H}}(x,z)\le 1$
. Hence, the diameter of
![]() $p_{x,y}$
in
$p_{x,y}$
in
![]() $\Gamma (G,Y\sqcup \mathcal {H})$
is at most 2, which verifies Proposition 3.6 (2). Since both conditions in Proposition 3.6 are satisfied with
$\Gamma (G,Y\sqcup \mathcal {H})$
is at most 2, which verifies Proposition 3.6 (2). Since both conditions in Proposition 3.6 are satisfied with
![]() $h=\max \{\delta _X,2\}$
, the graph
$h=\max \{\delta _X,2\}$
, the graph
![]() $\Gamma (G,Y\sqcup \mathcal {H})$
is
$\Gamma (G,Y\sqcup \mathcal {H})$
is
![]() $k(h)$
-hyperbolic. Also, let
$k(h)$
-hyperbolic. Also, let
![]() $x,y \in G$
and let
$x,y \in G$
and let
![]() $\alpha $
be a geodesic path in
$\alpha $
be a geodesic path in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from x to y, and
$\Gamma (G,X\sqcup \mathcal {H})$
from x to y, and
![]() $\beta $
be a geodesic path in
$\beta $
be a geodesic path in
![]() $\Gamma (G, Y\sqcup \mathcal {H})$
from x to y. By Proposition 3.6, the Hausdorff distance between
$\Gamma (G, Y\sqcup \mathcal {H})$
from x to y. By Proposition 3.6, the Hausdorff distance between
![]() $\beta $
and
$\beta $
and
![]() $\gamma _{x,y}$
in
$\gamma _{x,y}$
in
![]() $\Gamma (G,Y\sqcup \mathcal {H})$
is at most
$\Gamma (G,Y\sqcup \mathcal {H})$
is at most
![]() $k(h)$
and by
$k(h)$
and by
![]() $\delta _X$
-hyperbolicity of
$\delta _X$
-hyperbolicity of
![]() $\Gamma (G,X\sqcup \mathcal {H})$
, the Hausdorff distance between
$\Gamma (G,X\sqcup \mathcal {H})$
, the Hausdorff distance between
![]() $\alpha $
and
$\alpha $
and
![]() $\gamma _{x,y}$
in
$\gamma _{x,y}$
in
![]() $\Gamma (G,Y\sqcup \mathcal {H})$
is at most
$\Gamma (G,Y\sqcup \mathcal {H})$
is at most
![]() $\delta _X$
. Thus, the statement (b) holds with
$\delta _X$
. Thus, the statement (b) holds with
![]() $M_X=k(h)+\delta _X$
.
$M_X=k(h)+\delta _X$
.
In the remainder of this section, let
![]() $\Gamma (G,Y\sqcup \mathcal {H})$
(resp.
$\Gamma (G,Y\sqcup \mathcal {H})$
(resp.
![]() $\Gamma (G,X\sqcup \mathcal {H})$
) be
$\Gamma (G,X\sqcup \mathcal {H})$
) be
![]() $\delta _Y$
-hyperbolic (resp.
$\delta _Y$
-hyperbolic (resp.
![]() $\delta _X$
-hyperbolic) with
$\delta _X$
-hyperbolic) with
![]() $\delta _X,\delta _Y \in \mathbb {N}$
.
$\delta _X,\delta _Y \in \mathbb {N}$
.
Remark 3.8. Note that
![]() $\delta _Y$
and
$\delta _Y$
and
![]() $M_X$
depend only on X by the proof of Lemma 3.7.
$M_X$
depend only on X by the proof of Lemma 3.7.
The point of Theorem 2.41 equation (5) and Lemma 3.7 (b) is that we can deal with geodesic paths in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
as if they are quasi-geodesic in
$\Gamma (G,X\sqcup \mathcal {H})$
as if they are quasi-geodesic in
![]() $\Gamma (G,Y\sqcup \mathcal {H})$
, though they’re actually not. This will become clear by results from Lemma 3.9 up to Lemma 3.11 below. Lemma 3.9 is mostly applied to two elements
$\Gamma (G,Y\sqcup \mathcal {H})$
, though they’re actually not. This will become clear by results from Lemma 3.9 up to Lemma 3.11 below. Lemma 3.9 is mostly applied to two elements
![]() $g_1,g_2$
except in the proof of Proposition 3.22.
$g_1,g_2$
except in the proof of Proposition 3.22.
Lemma 3.9. Let
![]() $R\in \mathbb {N}$
,
$R\in \mathbb {N}$
,
![]() $(g_i)_{i\in \mathbb {N}},o \in G$
, and suppose that
$(g_i)_{i\in \mathbb {N}},o \in G$
, and suppose that
![]() $p_i$
is a geodesic path in
$p_i$
is a geodesic path in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from o to
$\Gamma (G,X\sqcup \mathcal {H})$
from o to
![]() $g_i$
for each
$g_i$
for each
![]() $i\in \mathbb {N}$
. If
$i\in \mathbb {N}$
. If
![]() $(g_i,g_j)_o^{Y\cup \mathcal {H}}\ge R$
for any
$(g_i,g_j)_o^{Y\cup \mathcal {H}}\ge R$
for any
![]() $i,j\in \mathbb {N}$
, then there exist vertices
$i,j\in \mathbb {N}$
, then there exist vertices
![]() $v_i \in p_i$
for each
$v_i \in p_i$
for each
![]() $i\in \mathbb {N}$
such that for any
$i\in \mathbb {N}$
such that for any
![]() $i,j\in \mathbb {N}$
, we have
$i,j\in \mathbb {N}$
, we have
Proof. For each
![]() $i \in \mathbb {N}$
, let
$i \in \mathbb {N}$
, let
![]() $[o,g_i]$
be a geodesic path in
$[o,g_i]$
be a geodesic path in
![]() $\Gamma (G,Y\sqcup \mathcal {H})$
from o to
$\Gamma (G,Y\sqcup \mathcal {H})$
from o to
![]() $g_i$
and
$g_i$
and
![]() $w_i \in [o,g_i]$
be a vertex satisfying
$w_i \in [o,g_i]$
be a vertex satisfying
![]() $d_{Y\cup \mathcal {H}} (o,w_i)=R$
. By
$d_{Y\cup \mathcal {H}} (o,w_i)=R$
. By
![]() $(g_i,g_j)_o^{Y\cup \mathcal {H}}\ge R$
, we have
$(g_i,g_j)_o^{Y\cup \mathcal {H}}\ge R$
, we have
![]() $d_{Y\cup \mathcal {H}}(w_i,w_j) \le \delta _Y$
for any
$d_{Y\cup \mathcal {H}}(w_i,w_j) \le \delta _Y$
for any
![]() $i,j \in \mathbb {N}$
. By Lemma 3.7 (b), for each
$i,j \in \mathbb {N}$
. By Lemma 3.7 (b), for each
![]() $i\in \mathbb {N}$
, there exists a vertex
$i\in \mathbb {N}$
, there exists a vertex
![]() $v_i \in p_i$
such that
$v_i \in p_i$
such that
![]() $d_{Y\cup \mathcal {H}}(v_i,w_i) \le M_X$
. We have for any
$d_{Y\cup \mathcal {H}}(v_i,w_i) \le M_X$
. We have for any
![]() $i,j\in \mathbb {N}$
,
$i,j\in \mathbb {N}$
,
 $$ \begin{align*} &d_{Y\cup\mathcal{H}}(v_i,v_j) \le d_{Y\cup\mathcal{H}}(v_i,w_i) + d_{Y\cup\mathcal{H}}(w_i,w_j) + d_{Y\cup\mathcal{H}}(w_j,v_j) \le \delta_Y + 2M_X \\ \mathrm{and}~~~~~ &d_{Y\cup\mathcal{H}}(o, v_i) \ge d_{Y\cup\mathcal{H}}(o, w_i) - d_{Y\cup\mathcal{H}}(w_i,v_i) \ge R-M_X.\\[-34pt] \end{align*} $$
$$ \begin{align*} &d_{Y\cup\mathcal{H}}(v_i,v_j) \le d_{Y\cup\mathcal{H}}(v_i,w_i) + d_{Y\cup\mathcal{H}}(w_i,w_j) + d_{Y\cup\mathcal{H}}(w_j,v_j) \le \delta_Y + 2M_X \\ \mathrm{and}~~~~~ &d_{Y\cup\mathcal{H}}(o, v_i) \ge d_{Y\cup\mathcal{H}}(o, w_i) - d_{Y\cup\mathcal{H}}(w_i,v_i) \ge R-M_X.\\[-34pt] \end{align*} $$
Lemma 3.10 below can be considered as the converse of Lemma 3.9.
Lemma 3.10. Let
![]() $o,x,y \in G$
, and suppose that
$o,x,y \in G$
, and suppose that
![]() $p,q$
are geodesic paths in
$p,q$
are geodesic paths in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
such that p is from o to x and q is from o to y. If there exist vertices
$\Gamma (G,X\sqcup \mathcal {H})$
such that p is from o to x and q is from o to y. If there exist vertices
![]() $v\in p$
and
$v\in p$
and
![]() $w\in q$
such that
$w\in q$
such that
![]() $d_{Y\cup \mathcal {H}}(o,v) \ge R$
and
$d_{Y\cup \mathcal {H}}(o,v) \ge R$
and
![]() $d_{Y\cup \mathcal {H}}(v,w) \le K$
with some
$d_{Y\cup \mathcal {H}}(v,w) \le K$
with some
![]() $R,K\in \mathbb {N}$
, then we have
$R,K\in \mathbb {N}$
, then we have
![]() $(x,y)_o^{Y\cup \mathcal {H}}\ge R-(K+3M_X) - 2\delta _Y$
.
$(x,y)_o^{Y\cup \mathcal {H}}\ge R-(K+3M_X) - 2\delta _Y$
.
Proof. Take geodesic paths
![]() $[o,x],[o,y]$
in
$[o,x],[o,y]$
in
![]() $\Gamma (G,Y\sqcup \mathcal {H})$
. By Lemma 3.7 (b), there exist vertices
$\Gamma (G,Y\sqcup \mathcal {H})$
. By Lemma 3.7 (b), there exist vertices
![]() $a\in [o,x], b \in [o,y]$
such that
$a\in [o,x], b \in [o,y]$
such that
![]() $d_{Y\cup \mathcal {H}}(a,v) \le M_X$
and
$d_{Y\cup \mathcal {H}}(a,v) \le M_X$
and
![]() $d_{Y\cup \mathcal {H}}(b,w) \le M_X$
. We have
$d_{Y\cup \mathcal {H}}(b,w) \le M_X$
. We have
 $$ \begin{align*} d_{Y\cup\mathcal{H}}(a,b) &\le d_{Y\cup\mathcal{H}}(a,v) + d_{Y\cup\mathcal{H}}(v,w) + d_{Y\cup\mathcal{H}}(w,b) \le K + 2M_X, \\ d_{Y\cup\mathcal{H}}(o,a) &\ge d_{Y\cup\mathcal{H}}(o,v)- d_{Y\cup\mathcal{H}}(a,v) \ge R-M_X, \\ \mathrm{and}~~~~~ d_{Y\cup\mathcal{H}}(o,b) &\ge d_{Y\cup\mathcal{H}}(o,v)- (d_{Y\cup\mathcal{H}}(v,w) + d_{Y\cup\mathcal{H}}(w,b)) \ge R-(K+M_X). \end{align*} $$
$$ \begin{align*} d_{Y\cup\mathcal{H}}(a,b) &\le d_{Y\cup\mathcal{H}}(a,v) + d_{Y\cup\mathcal{H}}(v,w) + d_{Y\cup\mathcal{H}}(w,b) \le K + 2M_X, \\ d_{Y\cup\mathcal{H}}(o,a) &\ge d_{Y\cup\mathcal{H}}(o,v)- d_{Y\cup\mathcal{H}}(a,v) \ge R-M_X, \\ \mathrm{and}~~~~~ d_{Y\cup\mathcal{H}}(o,b) &\ge d_{Y\cup\mathcal{H}}(o,v)- (d_{Y\cup\mathcal{H}}(v,w) + d_{Y\cup\mathcal{H}}(w,b)) \ge R-(K+M_X). \end{align*} $$
This implies
![]() $(a,b)_o^{Y\cup \mathcal {H}} \ge d_{Y\cup \mathcal {H}}(o,a)-d_{Y\cup \mathcal {H}}(a,b) \ge R-(K+3M_X)$
. Note
$(a,b)_o^{Y\cup \mathcal {H}} \ge d_{Y\cup \mathcal {H}}(o,a)-d_{Y\cup \mathcal {H}}(a,b) \ge R-(K+3M_X)$
. Note
![]() $(x,a)_o^{Y\cup \mathcal {H}}=d_{Y\cup \mathcal {H}}(o,a)$
and
$(x,a)_o^{Y\cup \mathcal {H}}=d_{Y\cup \mathcal {H}}(o,a)$
and
![]() $(y,b)_o^{Y\cup \mathcal {H}}=d_{Y\cup \mathcal {H}}(o,b)$
since
$(y,b)_o^{Y\cup \mathcal {H}}=d_{Y\cup \mathcal {H}}(o,b)$
since
![]() $[o,a], [o,b]$
are geodesic in
$[o,a], [o,b]$
are geodesic in
![]() $\Gamma (Y\cup \mathcal {H})$
. Hence,
$\Gamma (Y\cup \mathcal {H})$
. Hence,
 $$ \begin{align*} (x,y)_o^{Y\cup\mathcal{H}} &\ge \min\{(x,a)_o^{Y\cup\mathcal{H}}, (a,b)_o^{Y\cup\mathcal{H}}, (b,y)_o^{Y\cup\mathcal{H}} \}-2\delta_Y \\ &\ge R-(K+3M_X) - 2\delta_Y.\\[-34pt] \end{align*} $$
$$ \begin{align*} (x,y)_o^{Y\cup\mathcal{H}} &\ge \min\{(x,a)_o^{Y\cup\mathcal{H}}, (a,b)_o^{Y\cup\mathcal{H}}, (b,y)_o^{Y\cup\mathcal{H}} \}-2\delta_Y \\ &\ge R-(K+3M_X) - 2\delta_Y.\\[-34pt] \end{align*} $$
Lemma 3.11 describes slim triangle property of
![]() $\Gamma (G,Y\sqcup \mathcal {H})$
using separating cosets.
$\Gamma (G,Y\sqcup \mathcal {H})$
using separating cosets.
Lemma 3.11. Let
![]() $o,x,y \in G$
and
$o,x,y \in G$
and
![]() $S(o,x;D)=\{C_1\preceq C_2\preceq \cdots \preceq C_n\}$
. If q is a geodesic path in
$S(o,x;D)=\{C_1\preceq C_2\preceq \cdots \preceq C_n\}$
. If q is a geodesic path in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from o to y and
$\Gamma (G,X\sqcup \mathcal {H})$
from o to y and
![]() $i\in \{1,\cdots ,n\}$
satisfies
$i\in \{1,\cdots ,n\}$
satisfies
![]() $3d_{Y\cup \mathcal {H}}(x,y)+1 \le n-i$
, then q penetrates
$3d_{Y\cup \mathcal {H}}(x,y)+1 \le n-i$
, then q penetrates
![]() $C_i$
.
$C_i$
.
Proof. Let
![]() $i \in \{1,\cdots ,n\}$
satisfy
$i \in \{1,\cdots ,n\}$
satisfy
![]() $3d_{Y\cup \mathcal {H}}(x,y)+1 \le n-i$
, and take a geodesic path r in
$3d_{Y\cup \mathcal {H}}(x,y)+1 \le n-i$
, and take a geodesic path r in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from y to x. Since the path
$\Gamma (G,X\sqcup \mathcal {H})$
from y to x. Since the path
![]() $qr$
is from o to x and composed of two geodesic segments, one of q or r penetrates
$qr$
is from o to x and composed of two geodesic segments, one of q or r penetrates
![]() $C_i$
by Lemma 2.35. Suppose for contradiction that r penetrates
$C_i$
by Lemma 2.35. Suppose for contradiction that r penetrates
![]() $C_i$
. This implies
$C_i$
. This implies
![]() $C_j\in S(x,y;D)$
for any
$C_j\in S(x,y;D)$
for any
![]() $j\in \{i+1,\cdots ,n\}$
by applying Lemma 3.5 to
$j\in \{i+1,\cdots ,n\}$
by applying Lemma 3.5 to
![]() $r^{-1}$
and
$r^{-1}$
and
![]() $S(x,o;D)=\{C_n \preceq \cdots \preceq C_1\}$
. This and equation (5) imply
$S(x,o;D)=\{C_n \preceq \cdots \preceq C_1\}$
. This and equation (5) imply
This is a contradiction. Hence, q penetrates
![]() $C_i$
.
$C_i$
.
Hull–Osin’s separating cosets have been defined only for a pair of group elements. Now, we define separating cosets for geodesic rays. This notion is useful to clarify nice geodesic rays in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
mentioned at the beginning of this section.
$\Gamma (G,X\sqcup \mathcal {H})$
mentioned at the beginning of this section.
Definition 3.12. Let
![]() $\gamma =(x_0,x_1,\cdots )$
be a geodesic ray in
$\gamma =(x_0,x_1,\cdots )$
be a geodesic ray in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
. We define
$\Gamma (G,X\sqcup \mathcal {H})$
. We define
 $$\begin{align*}S(\gamma;D)=\bigcup_{n=0}^\infty S(x_0,x_n;D), \end{align*}$$
$$\begin{align*}S(\gamma;D)=\bigcup_{n=0}^\infty S(x_0,x_n;D), \end{align*}$$
and call an element in
![]() $S(\gamma ;D)$
a
$S(\gamma ;D)$
a
![]() $(\gamma ;D)$
-separating coset.
$(\gamma ;D)$
-separating coset.
Remark 3.13. By Lemma 3.1, we have
![]() $S(x_0,x_{n-1};D) \subset S(x_0,x_n;D)$
for any
$S(x_0,x_{n-1};D) \subset S(x_0,x_n;D)$
for any
![]() $n\in \mathbb {N}$
. This implies
$n\in \mathbb {N}$
. This implies
We collect basic properties of separating cosets for geodesic rays from Lemma 3.14 up to Lemma 3.18.
Lemma 3.14. Suppose that
![]() $\gamma $
is a geodesic ray in
$\gamma $
is a geodesic ray in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
, then
$\Gamma (G,X\sqcup \mathcal {H})$
, then
![]() $\gamma $
penetrates all
$\gamma $
penetrates all
![]() $(\gamma ;D)$
-separating cosets exactly once.
$(\gamma ;D)$
-separating cosets exactly once.
Proof. Let
![]() $\gamma =(x_0,x_1,\cdots )$
and
$\gamma =(x_0,x_1,\cdots )$
and
![]() $B\in S(\gamma ;D)$
. There exists
$B\in S(\gamma ;D)$
. There exists
![]() $n\in \mathbb {N}$
such that
$n\in \mathbb {N}$
such that
![]() $B\in S(x_0,x_n;D)$
. By Lemma 2.38,
$B\in S(x_0,x_n;D)$
. By Lemma 2.38,
![]() $\gamma _{[x_0,x_n]}$
penetrates B, hence so does
$\gamma _{[x_0,x_n]}$
penetrates B, hence so does
![]() $\gamma $
. If
$\gamma $
. If
![]() $\gamma $
penetrates an
$\gamma $
penetrates an
![]() $H_\lambda $
-coset more than once, then
$H_\lambda $
-coset more than once, then
![]() $\gamma $
can be shortened by an edge whose label is in
$\gamma $
can be shortened by an edge whose label is in
![]() $H_\lambda $
, which contradicts that
$H_\lambda $
, which contradicts that
![]() $\gamma $
is geodesic in
$\gamma $
is geodesic in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
.
$\Gamma (G,X\sqcup \mathcal {H})$
.
Note that in Lemma 3.14, the fact that
![]() $\gamma $
penetrates all
$\gamma $
penetrates all
![]() $(\gamma ;D)$
-separating cosets doesn’t trivially follow from the definition of
$(\gamma ;D)$
-separating cosets doesn’t trivially follow from the definition of
![]() $S(\gamma ;D)$
because by Definition 3.12, an
$S(\gamma ;D)$
because by Definition 3.12, an
![]() $H_\lambda $
-coset C is in
$H_\lambda $
-coset C is in
![]() $S(\gamma ;D)$
if and only if there exist
$S(\gamma ;D)$
if and only if there exist
![]() $n\in \mathbb {N}$
and a geodesic path p in
$n\in \mathbb {N}$
and a geodesic path p in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from
$\Gamma (G,X\sqcup \mathcal {H})$
from
![]() $x_0$
to
$x_0$
to
![]() $x_n$
such that p essentially penetrates C, and p may not be a subpath of
$x_n$
such that p essentially penetrates C, and p may not be a subpath of
![]() $\gamma $
.
$\gamma $
.
Lemma 3.15 is analogous to Lemma 2.36.
Lemma 3.15. Suppose that a geodesic ray
![]() $\gamma $
in
$\gamma $
in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
penetrates an
$\Gamma (G,X\sqcup \mathcal {H})$
penetrates an
![]() $H_\lambda $
-coset B, then we have
$H_\lambda $
-coset B, then we have
![]() $d_{X\cup \mathcal {H}}(\gamma _-,\gamma _{in}(B))=d_{X\cup \mathcal {H}}(\gamma _-,B)$
.
$d_{X\cup \mathcal {H}}(\gamma _-,\gamma _{in}(B))=d_{X\cup \mathcal {H}}(\gamma _-,B)$
.
Proof. Let
![]() $\gamma =(x_0,x_1,\cdots )$
. Take
$\gamma =(x_0,x_1,\cdots )$
. Take
![]() $n\in \mathbb {N}$
satisfying
$n\in \mathbb {N}$
satisfying
![]() $d_{X\cup \mathcal {H}}(\gamma _-,\gamma _{out}(B))<d_{X\cup \mathcal {H}}(\gamma _-,x_n)$
, then we have
$d_{X\cup \mathcal {H}}(\gamma _-,\gamma _{out}(B))<d_{X\cup \mathcal {H}}(\gamma _-,x_n)$
, then we have
![]() $d_{X\cup \mathcal {H}}(\gamma _-,B)=d_{X\cup \mathcal {H}}(\gamma _-,(\gamma _{[x_0,x_n]})_{in}(B))=d_{X\cup \mathcal {H}}(\gamma _-,\gamma _{in}(B))$
by Lemma 2.36.
$d_{X\cup \mathcal {H}}(\gamma _-,B)=d_{X\cup \mathcal {H}}(\gamma _-,(\gamma _{[x_0,x_n]})_{in}(B))=d_{X\cup \mathcal {H}}(\gamma _-,\gamma _{in}(B))$
by Lemma 2.36.
As in Definition 2.37, we can align separating cosets for a geodesic ray based on the order of their penetration.
Definition 3.16. Given a geodesic ray
![]() $\gamma $
in
$\gamma $
in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
, a relation
$\Gamma (G,X\sqcup \mathcal {H})$
, a relation
![]() $\preceq $
on the set
$\preceq $
on the set
![]() $S(\gamma ;D)$
is defined as follows: For any
$S(\gamma ;D)$
is defined as follows: For any
![]() $C_1,C_2 \in S(\gamma ;D)$
,
$C_1,C_2 \in S(\gamma ;D)$
,
Remark 3.17. By Lemma 3.14 and Lemma 3.15, the relation
![]() $\preceq $
in Definition 3.16 is a well-order on
$\preceq $
in Definition 3.16 is a well-order on
![]() $S(\gamma ;D)$
. We will denote
$S(\gamma ;D)$
. We will denote
![]() $S(\gamma ;D)=\{C_1\preceq C_2\preceq \cdots \}$
considering this order.
$S(\gamma ;D)=\{C_1\preceq C_2\preceq \cdots \}$
considering this order.
In Lemma 3.18, given a finite collection of separating cosets of a geodesic ray, we find how long subpath of the geodesic ray we have to take to contain them.
Lemma 3.18. Let
![]() $\gamma =(x_0,x_1,\cdots )$
be a geodesic ray in
$\gamma =(x_0,x_1,\cdots )$
be a geodesic ray in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
and
$\Gamma (G,X\sqcup \mathcal {H})$
and
![]() $S(\gamma ;D)=\{C_1\preceq C_2\preceq \cdots \}$
. For any
$S(\gamma ;D)=\{C_1\preceq C_2\preceq \cdots \}$
. For any
![]() $N,\ell \in \mathbb {N}$
satisfying
$N,\ell \in \mathbb {N}$
satisfying
![]() $d_{X\cup \mathcal {H}}(x_0,\gamma _{out}(C_{N+1})) \le d_{X\cup \mathcal {H}}(x_0,x_\ell )$
, we have
$d_{X\cup \mathcal {H}}(x_0,\gamma _{out}(C_{N+1})) \le d_{X\cup \mathcal {H}}(x_0,x_\ell )$
, we have
![]() $\{C_1,\cdots ,C_N\} \subset S(x_0,x_\ell ;D)$
. Moreover, letting
$\{C_1,\cdots ,C_N\} \subset S(x_0,x_\ell ;D)$
. Moreover, letting
![]() $S(x_0,x_\ell ;D)=\{B_1\preceq \cdots \preceq B_N\preceq \cdots \}$
, we have
$S(x_0,x_\ell ;D)=\{B_1\preceq \cdots \preceq B_N\preceq \cdots \}$
, we have
![]() $B_n=C_n$
for any
$B_n=C_n$
for any
![]() $n\in \{1,\cdots ,N\}$
.
$n\in \{1,\cdots ,N\}$
.
Proof. By
![]() $d_{X\cup \mathcal {H}}(x_0,\gamma _{out}(C_{N+1})) \le d_{X\cup \mathcal {H}}(x_0,x_\ell )$
, the subpath
$d_{X\cup \mathcal {H}}(x_0,\gamma _{out}(C_{N+1})) \le d_{X\cup \mathcal {H}}(x_0,x_\ell )$
, the subpath
![]() $\gamma _{[x_0,x_\ell ]}$
penetrates
$\gamma _{[x_0,x_\ell ]}$
penetrates
![]() $C_{N+1}$
. Take
$C_{N+1}$
. Take
![]() $k\in \mathbb {N}$
such that
$k\in \mathbb {N}$
such that
![]() $\{C_1,\cdots ,C_{N+1}\}\subset S(x_0,x_k;D)$
. By applying Lemma 3.5 to
$\{C_1,\cdots ,C_{N+1}\}\subset S(x_0,x_k;D)$
. By applying Lemma 3.5 to
![]() $x_0,x_k,\gamma _{[x_0,x_\ell ]}$
, we have
$x_0,x_k,\gamma _{[x_0,x_\ell ]}$
, we have
![]() $\{C_1,\cdots ,C_N\}\subset S(x_0,x_\ell ;D)$
. Let
$\{C_1,\cdots ,C_N\}\subset S(x_0,x_\ell ;D)$
. Let
![]() $S(x_0,x_\ell ;D)=\{B_1\preceq \cdots \preceq B_N\preceq \cdots \}$
. We have
$S(x_0,x_\ell ;D)=\{B_1\preceq \cdots \preceq B_N\preceq \cdots \}$
. We have
![]() $B_1\preceq C_1$
by
$B_1\preceq C_1$
by
![]() $C_1\in S(x_0,x_\ell ;D)$
and by minimality of
$C_1\in S(x_0,x_\ell ;D)$
and by minimality of
![]() $B_1$
in
$B_1$
in
![]() $(S(x_0,x_\ell ;D),\preceq )$
. On the other hand, by minimality of
$(S(x_0,x_\ell ;D),\preceq )$
. On the other hand, by minimality of
![]() $C_1$
in
$C_1$
in
![]() $(S(\gamma ;D),\preceq )$
, we also have
$(S(\gamma ;D),\preceq )$
, we also have
![]() $C_1\preceq B_1$
, hence
$C_1\preceq B_1$
, hence
![]() $B_1=C_1$
. Repeating the same argument inductively, we can see
$B_1=C_1$
. Repeating the same argument inductively, we can see
![]() $B_n=C_n$
for any
$B_n=C_n$
for any
![]() $n\in \{1,\cdots ,N\}$
.
$n\in \{1,\cdots ,N\}$
.
We can now characterize nice geodesic rays in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
and study their properties. Lemma 3.20 lists several equivalent conditions of Definition 3.19.
$\Gamma (G,X\sqcup \mathcal {H})$
and study their properties. Lemma 3.20 lists several equivalent conditions of Definition 3.19.
Definition 3.19. We say that a geodesic ray
![]() $\gamma =(x_0,x_1,\cdots )$
in
$\gamma =(x_0,x_1,\cdots )$
in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
converges to infinity in
$\Gamma (G,X\sqcup \mathcal {H})$
converges to infinity in
![]() $\Gamma (G,Y\sqcup \mathcal {H})$
if the sequence
$\Gamma (G,Y\sqcup \mathcal {H})$
if the sequence
![]() $(x_n)_{n=1}^\infty $
in G converges to infinity in
$(x_n)_{n=1}^\infty $
in G converges to infinity in
![]() $\Gamma (G,Y\sqcup \mathcal {H})$
.
$\Gamma (G,Y\sqcup \mathcal {H})$
.
Lemma 3.20. Suppose that
![]() $\gamma =(x_0,x_1,\cdots )$
is a geodesic ray in
$\gamma =(x_0,x_1,\cdots )$
is a geodesic ray in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
, then (i)–(vi) below are all equivalent.
$\Gamma (G,X\sqcup \mathcal {H})$
, then (i)–(vi) below are all equivalent.
-
(i) The geodesic ray
 $\gamma $
converges to infinity in
$\gamma $
converges to infinity in
 $\Gamma (G,Y\sqcup \mathcal {H})$
.
$\Gamma (G,Y\sqcup \mathcal {H})$
. -
(ii) There exists a subsequence
 $(x_{n_k})_{k=1}^\infty $
that converges to infinity in
$(x_{n_k})_{k=1}^\infty $
that converges to infinity in
 $\Gamma (G,Y\sqcup \mathcal {H})$
.
$\Gamma (G,Y\sqcup \mathcal {H})$
. -
(iii)
 $|S(\gamma ;D)|=\infty $
.
$|S(\gamma ;D)|=\infty $
. -
(iv) There exists a subsequence
 $(x_{n_k})_{k=1}^\infty $
such that
$(x_{n_k})_{k=1}^\infty $
such that
 $\lim _{k\to \infty } |S(x_0,x_{n_k};D)| = \infty $
.
$\lim _{k\to \infty } |S(x_0,x_{n_k};D)| = \infty $
. -
(v)
 $\lim _{n\to \infty } d_{Y\cup \mathcal {H}}(x_0,x_n) =\infty $
.
$\lim _{n\to \infty } d_{Y\cup \mathcal {H}}(x_0,x_n) =\infty $
. -
(vi) There exists a subsequence
 $(x_{n_k})_{k=1}^\infty $
such that
$(x_{n_k})_{k=1}^\infty $
such that
 $\lim _{k\to \infty } d_{Y\cup \mathcal {H}}(x_0,x_{n_k}) =\infty $
.
$\lim _{k\to \infty } d_{Y\cup \mathcal {H}}(x_0,x_{n_k}) =\infty $
.
Proof. (i)
![]() $\Rightarrow $
(ii) and (v)
$\Rightarrow $
(ii) and (v)
![]() $\Rightarrow $
(vi) are trivial. (iii)
$\Rightarrow $
(vi) are trivial. (iii)
![]() $\Rightarrow $
(iv) follows from Remark 3.13. (i)
$\Rightarrow $
(iv) follows from Remark 3.13. (i)
![]() $\Rightarrow $
(v) and (ii)
$\Rightarrow $
(v) and (ii)
![]() $\Rightarrow $
(vi) follow from the definition of the Gromov product (see equation (1)). (iii)
$\Rightarrow $
(vi) follow from the definition of the Gromov product (see equation (1)). (iii)
![]() $\Leftrightarrow $
(v) and (iv)
$\Leftrightarrow $
(v) and (iv)
![]() $\Leftrightarrow $
(vi) follow from equation (5). We are left to show (iv)
$\Leftrightarrow $
(vi) follow from equation (5). We are left to show (iv)
![]() $\Rightarrow $
(iii) and (v)
$\Rightarrow $
(iii) and (v)
![]() $\Rightarrow $
(i).
$\Rightarrow $
(i).
![]() $\underline {\mathrm {(iv)}\Rightarrow \mathrm {(iii)}}$
By Remark 3.13, we have
$\underline {\mathrm {(iv)}\Rightarrow \mathrm {(iii)}}$
By Remark 3.13, we have
Thus,
![]() $\lim _{k\to \infty } |S(x_0,x_{n_k};D)| = \infty $
implies
$\lim _{k\to \infty } |S(x_0,x_{n_k};D)| = \infty $
implies
![]() $|S(\gamma ;D)|=\lim _{n\to \infty } |S(x_0,x_n;D)| = \infty $
.
$|S(\gamma ;D)|=\lim _{n\to \infty } |S(x_0,x_n;D)| = \infty $
.
![]() $\underline {\mathrm {(v)}\Rightarrow \mathrm {(i)}}$
For any
$\underline {\mathrm {(v)}\Rightarrow \mathrm {(i)}}$
For any
![]() $R\in \mathbb {N}$
, define
$R\in \mathbb {N}$
, define
![]() $R_1=R+3M_X+2\delta _Y$
. By (v), there exists
$R_1=R+3M_X+2\delta _Y$
. By (v), there exists
![]() $N\in \mathbb {N}$
such that
$N\in \mathbb {N}$
such that
![]() $d_{Y\cup \mathcal {H}}(x_0,x_N) \ge R_1$
. Hence, for any
$d_{Y\cup \mathcal {H}}(x_0,x_N) \ge R_1$
. Hence, for any
![]() $n,m\ge N$
, we have
$n,m\ge N$
, we have
![]() $(x_n,x_m)_{x_0}^{Y\cup \mathcal {H}}\ge R_1-3M_X-2\delta _Y=R$
by Lemma 3.10 applied to
$(x_n,x_m)_{x_0}^{Y\cup \mathcal {H}}\ge R_1-3M_X-2\delta _Y=R$
by Lemma 3.10 applied to
![]() $o=x_0, x=x_n, y=x_m, v=x_N, w=x_N$
. This implies
$o=x_0, x=x_n, y=x_m, v=x_N, w=x_N$
. This implies
![]() $\liminf _{n,m\to \infty }(x_n,x_m)_{x_0}^{Y\cup \mathcal {H}} \ge \inf _{n,m\ge N} (x_n,x_m)_{x_0}^{Y\cup \mathcal {H}} \ge R$
for any
$\liminf _{n,m\to \infty }(x_n,x_m)_{x_0}^{Y\cup \mathcal {H}} \ge \inf _{n,m\ge N} (x_n,x_m)_{x_0}^{Y\cup \mathcal {H}} \ge R$
for any
![]() $R\in \mathbb {N}$
. Thus,
$R\in \mathbb {N}$
. Thus,
![]() $\lim _{n,m\to \infty }(x_n,x_m)_{x_0}^{Y\cup \mathcal {H}}=\infty $
.
$\lim _{n,m\to \infty }(x_n,x_m)_{x_0}^{Y\cup \mathcal {H}}=\infty $
.
In Definition 3.21 below, we summarize notations related to limits of the nice geodesic rays, which we will use in what follows.
Definition 3.21. For a sequence
![]() $(x_n)_{n=1}^\infty $
of elements of G that is convergent in
$(x_n)_{n=1}^\infty $
of elements of G that is convergent in
![]() $\Gamma (G,Y\sqcup \mathcal {H})\cup \partial \Gamma (G,Y\sqcup \mathcal {H})$
, we denote its limit point by
$\Gamma (G,Y\sqcup \mathcal {H})\cup \partial \Gamma (G,Y\sqcup \mathcal {H})$
, we denote its limit point by
![]() $Y\text{-}{\lim} _{n\to \infty }x_n$
. For a geodesic ray
$Y\text{-}{\lim} _{n\to \infty }x_n$
. For a geodesic ray
![]() $\gamma =(x_0,x_1,\cdots )$
in
$\gamma =(x_0,x_1,\cdots )$
in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
such that the sequence
$\Gamma (G,X\sqcup \mathcal {H})$
such that the sequence
![]() $(x_n)_{n=1}^\infty $
is convergent in
$(x_n)_{n=1}^\infty $
is convergent in
![]() $\Gamma (G,Y\sqcup \mathcal {H})\cup \partial \Gamma (G,Y\sqcup \mathcal {H})$
, we also denote its limit point by
$\Gamma (G,Y\sqcup \mathcal {H})\cup \partial \Gamma (G,Y\sqcup \mathcal {H})$
, we also denote its limit point by
![]() $Y\text{-}{\lim}\ \gamma $
. Note that when we write
$Y\text{-}{\lim}\ \gamma $
. Note that when we write
![]() $Y\text{-}{\lim} _{n\to \infty }x_n \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
for a sequence
$Y\text{-}{\lim} _{n\to \infty }x_n \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
for a sequence
![]() $(x_n)_{n=1}^\infty $
in G, it implicitly means that
$(x_n)_{n=1}^\infty $
in G, it implicitly means that
![]() $(x_n)_{n=1}^\infty $
converges to infinity in
$(x_n)_{n=1}^\infty $
converges to infinity in
![]() $\Gamma (G,Y\sqcup \mathcal {H})$
and its limit point in
$\Gamma (G,Y\sqcup \mathcal {H})$
and its limit point in
![]() $\partial \Gamma (G,Y\sqcup \mathcal {H})$
is
$\partial \Gamma (G,Y\sqcup \mathcal {H})$
is
![]() $Y\text{-}{\lim} _{n\to \infty }x_n$
. This is the same for
$Y\text{-}{\lim} _{n\to \infty }x_n$
. This is the same for
![]() $Y\text{-}{\lim}\ \gamma \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
as well. We use the notations
$Y\text{-}{\lim}\ \gamma \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
as well. We use the notations
![]() $X\text{-}{\lim} _{n\to \infty }x_n$
and
$X\text{-}{\lim} _{n\to \infty }x_n$
and
![]() $X\text{-}{\lim}\ \gamma $
similarly.
$X\text{-}{\lim}\ \gamma $
similarly.

Figure 3 Proof of Proposition 3.22.
We will now show that any element of G and any point in
![]() $\partial \Gamma (G,Y\sqcup \mathcal {H})$
can be connected by a geodesic ray in
$\partial \Gamma (G,Y\sqcup \mathcal {H})$
can be connected by a geodesic ray in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
, and by using this we will extend the notion of Hull–Osin’s separating cosets to allow a point in the Gromov boundary. We emphasize that, in Proposition 3.22, the path
$\Gamma (G,X\sqcup \mathcal {H})$
, and by using this we will extend the notion of Hull–Osin’s separating cosets to allow a point in the Gromov boundary. We emphasize that, in Proposition 3.22, the path
![]() $\gamma $
below is not necessarily geodesic nor quasi-geodesic in
$\gamma $
below is not necessarily geodesic nor quasi-geodesic in
![]() $\Gamma (G,Y\sqcup \mathcal {H})$
.
$\Gamma (G,Y\sqcup \mathcal {H})$
.
Proposition 3.22. For any
![]() $o\in G$
and any
$o\in G$
and any
![]() $\xi \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
, there exists a geodesic ray
$\xi \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
, there exists a geodesic ray
![]() $\gamma $
in
$\gamma $
in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from o such that
$\Gamma (G,X\sqcup \mathcal {H})$
from o such that
![]() $Y\text{-}{\lim}\ \gamma =\xi \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
.
$Y\text{-}{\lim}\ \gamma =\xi \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
.
Proof. Let
![]() $(g_n)_{n=1}^\infty $
be a sequence of elements of G that converges to
$(g_n)_{n=1}^\infty $
be a sequence of elements of G that converges to
![]() $\xi $
. For each
$\xi $
. For each
![]() $n\in \mathbb {N}$
, take a geodesic path
$n\in \mathbb {N}$
, take a geodesic path
![]() $\gamma _n$
in
$\gamma _n$
in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from o to
$\Gamma (G,X\sqcup \mathcal {H})$
from o to
![]() $g_n$
. Since
$g_n$
. Since
![]() $\lim _{i,j\to \infty } (g_i,g_j)_o^{Y\cup \mathcal {H}} = \infty $
, there exists a subsequence
$\lim _{i,j\to \infty } (g_i,g_j)_o^{Y\cup \mathcal {H}} = \infty $
, there exists a subsequence
![]() $(g_{0k})_{k=1}^\infty $
of
$(g_{0k})_{k=1}^\infty $
of
![]() $(g_n)_{n=1}^\infty $
such that
$(g_n)_{n=1}^\infty $
such that
By Lemma 3.9 and equation (6), there exist vertices
![]() $v_{0k} \in \gamma _{0k}$
for each
$v_{0k} \in \gamma _{0k}$
for each
![]() $k \in \mathbb {N}$
satisfying
$k \in \mathbb {N}$
satisfying
![]() $d_{Y\cup \mathcal {H}}(v_{0k},v_{0\ell }) \le \delta _Y + 2M_X$
and
$d_{Y\cup \mathcal {H}}(v_{0k},v_{0\ell }) \le \delta _Y + 2M_X$
and
![]() $d_{Y\cup \mathcal {H}}(o, v_{0\ell }) \ge 2(3(\delta _Y + 2M_X)+4) + 1$
for any
$d_{Y\cup \mathcal {H}}(o, v_{0\ell }) \ge 2(3(\delta _Y + 2M_X)+4) + 1$
for any
![]() $k,\ell \in \mathbb {N}$
. This and equation (5) imply for any
$k,\ell \in \mathbb {N}$
. This and equation (5) imply for any
![]() $k,\ell \in \mathbb {N}$
,
$k,\ell \in \mathbb {N}$
,
Let
![]() $m=|S(o,v_{01};D)|$
and
$m=|S(o,v_{01};D)|$
and
![]() $S(o,v_{01};D)=\{C_1\preceq C_2\preceq \cdots \preceq C_m\}$
. Since equation (7) implies
$S(o,v_{01};D)=\{C_1\preceq C_2\preceq \cdots \preceq C_m\}$
. Since equation (7) implies
![]() $3d_{Y\cup \mathcal {H}}(v_{0k},v_{01})+1 \le m-3$
, the path
$3d_{Y\cup \mathcal {H}}(v_{0k},v_{01})+1 \le m-3$
, the path
![]() $\gamma _{0k}$
penetrates
$\gamma _{0k}$
penetrates
![]() $C_1$
,
$C_1$
,
![]() $C_2$
, and
$C_2$
, and
![]() $C_3$
for any
$C_3$
for any
![]() $k\in \mathbb {N}$
by Lemma 3.11. Let
$k\in \mathbb {N}$
by Lemma 3.11. Let
![]() $C_3$
be an
$C_3$
be an
![]() $H_\lambda $
-coset. For each
$H_\lambda $
-coset. For each
![]() $k \in \mathbb {N}$
, let
$k \in \mathbb {N}$
, let
![]() $a_{0k-}$
and
$a_{0k-}$
and
![]() $a_{0k+}$
be the entrance and exit points of
$a_{0k+}$
be the entrance and exit points of
![]() $\gamma _{0k}$
in
$\gamma _{0k}$
in
![]() $C_3$
. Since
$C_3$
. Since
![]() $\gamma _{0k}$
is geodesic in
$\gamma _{0k}$
is geodesic in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
for each
$\Gamma (G,X\sqcup \mathcal {H})$
for each
![]() $k\in \mathbb {N}$
, we have
$k\in \mathbb {N}$
, we have
by Lemma 3.2. Since the relative metric
![]() $\widehat {d}_{\lambda }$
is locally finite (see Definition 2.27), the set
$\widehat {d}_{\lambda }$
is locally finite (see Definition 2.27), the set
![]() $\{a_{0k-} \mid k\in \mathbb {N}\}$
is finite. Hence, there exist
$\{a_{0k-} \mid k\in \mathbb {N}\}$
is finite. Hence, there exist
![]() $a_1 \in \{a_{0k-} \mid k\in \mathbb {N}\}$
and a subsequence
$a_1 \in \{a_{0k-} \mid k\in \mathbb {N}\}$
and a subsequence
![]() $(g_{1'k})_{k=1}^\infty $
of
$(g_{1'k})_{k=1}^\infty $
of
![]() $(g_{0k})_{k=1}^\infty $
such that
$(g_{0k})_{k=1}^\infty $
such that
![]() $a_1 \in \gamma _{1'k}$
for any
$a_1 \in \gamma _{1'k}$
for any
![]() $k\in \mathbb {N}$
. Note
$k\in \mathbb {N}$
. Note
![]() $S(o,a_1;D) \ge 1$
since we have
$S(o,a_1;D) \ge 1$
since we have
![]() $C_1 \in S(o,a_1;D)$
by Lemma 3.5. By
$C_1 \in S(o,a_1;D)$
by Lemma 3.5. By
![]() $\lim _{k,\ell \to \infty } (g_{1'k},g_{1'\ell })_o^{Y\cup \mathcal {H}} = \infty $
, there exists a subsequence
$\lim _{k,\ell \to \infty } (g_{1'k},g_{1'\ell })_o^{Y\cup \mathcal {H}} = \infty $
, there exists a subsequence
![]() $(g_{1k})_{k=1}^\infty $
of
$(g_{1k})_{k=1}^\infty $
of
![]() $(g_{1'k})_{k=1}^\infty $
such that
$(g_{1'k})_{k=1}^\infty $
such that
Note
![]() $a_1 \in \gamma _{1k}$
for any
$a_1 \in \gamma _{1k}$
for any
![]() $k\in \mathbb {N}$
. By the same argument as
$k\in \mathbb {N}$
. By the same argument as
![]() $(g_{0k})_{k=1}^\infty $
, we can see that there exist
$(g_{0k})_{k=1}^\infty $
, we can see that there exist
![]() $a_2 \in G$
and a subsequence
$a_2 \in G$
and a subsequence
![]() $(g_{2'k})_{k=1}^\infty $
of
$(g_{2'k})_{k=1}^\infty $
of
![]() $(g_{1k})_{k=1}^\infty $
such that
$(g_{1k})_{k=1}^\infty $
such that
![]() $a_2 \in \gamma _{2'k}$
for any
$a_2 \in \gamma _{2'k}$
for any
![]() $k\in \mathbb {N}$
and
$k\in \mathbb {N}$
and
![]() $|S(o,a_2;D)| \ge |S(o,a_1;D)| +1$
. The latter inequality comes from the term
$|S(o,a_2;D)| \ge |S(o,a_1;D)| +1$
. The latter inequality comes from the term
![]() $|S(o,a_1;D)|+4$
in equation (8), which corresponds to
$|S(o,a_1;D)|+4$
in equation (8), which corresponds to
![]() $4$
in equation (6). By repeating this argument, we can see that there exist
$4$
in equation (6). By repeating this argument, we can see that there exist
![]() $a_1,a_2,\cdots \in G$
and a sequence of subsequences
$a_1,a_2,\cdots \in G$
and a sequence of subsequences
![]() $(g_{1k})_{k=1}^\infty \supset (g_{2k})_{k=1}^\infty \supset \cdots $
satisfying (i) and (ii) below for any
$(g_{1k})_{k=1}^\infty \supset (g_{2k})_{k=1}^\infty \supset \cdots $
satisfying (i) and (ii) below for any
![]() $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
.
-
(i)
 $\{a_1,\cdots ,a_n\}\subset \gamma _{nk}$
for any
$\{a_1,\cdots ,a_n\}\subset \gamma _{nk}$
for any
 $k\in \mathbb {N}$
.
$k\in \mathbb {N}$
. -
(ii)
 $|S(o,a_{n+1};D)| \ge |S(o,a_n;D)|+1$
.
$|S(o,a_{n+1};D)| \ge |S(o,a_n;D)|+1$
.
Take the diagonal sequence
![]() $(g_{kk})_{k=1}^\infty $
, then for any
$(g_{kk})_{k=1}^\infty $
, then for any
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $(g_{kk})_{k=n}^\infty $
is a subsequence of
$(g_{kk})_{k=n}^\infty $
is a subsequence of
![]() $(g_{nk})_{k=1}^\infty $
. Hence,
$(g_{nk})_{k=1}^\infty $
. Hence,
![]() $\{a_1,\cdots ,a_n\}\subset \gamma _{nn}$
for any
$\{a_1,\cdots ,a_n\}\subset \gamma _{nn}$
for any
![]() $n\in \mathbb {N}$
. Note that (ii) and Lemma 3.1 imply
$n\in \mathbb {N}$
. Note that (ii) and Lemma 3.1 imply
![]() $d_{X\cup \mathcal {H}}(o,a_n) < d_{X\cup \mathcal {H}}(o,a_{n+1})$
for any
$d_{X\cup \mathcal {H}}(o,a_n) < d_{X\cup \mathcal {H}}(o,a_{n+1})$
for any
![]() $n\in \mathbb {N}$
. Define the path
$n\in \mathbb {N}$
. Define the path
![]() $\gamma \colon [0,\infty ) \to \Gamma (G,X\sqcup \mathcal {H})$
by
$\gamma \colon [0,\infty ) \to \Gamma (G,X\sqcup \mathcal {H})$
by
 $$\begin{align*}\gamma=\bigcup_{n=1}^\infty \gamma_{nn[a_{n-1},a_n]}, \end{align*}$$
$$\begin{align*}\gamma=\bigcup_{n=1}^\infty \gamma_{nn[a_{n-1},a_n]}, \end{align*}$$
where we define
![]() $a_0$
by
$a_0$
by
![]() $a_0=o$
for convenience. the path
$a_0=o$
for convenience. the path
![]() $\gamma $
is a geodesic ray since for any
$\gamma $
is a geodesic ray since for any
![]() $n \in \mathbb {N}$
, we have
$n \in \mathbb {N}$
, we have
 $$\begin{align*}\sum_{i=1}^n |\gamma_{ii[a_{i-1},a_i]}| = \sum_{i=1}^n d_{X\cup\mathcal{H}}(a_{i-1},a_i) = \sum_{i=1}^n |\gamma_{nn[a_{i-1},a_i]}| = |\gamma_{nn[o,a_n]}| =d_{X\cup\mathcal{H}}(o,a_n). \end{align*}$$
$$\begin{align*}\sum_{i=1}^n |\gamma_{ii[a_{i-1},a_i]}| = \sum_{i=1}^n d_{X\cup\mathcal{H}}(a_{i-1},a_i) = \sum_{i=1}^n |\gamma_{nn[a_{i-1},a_i]}| = |\gamma_{nn[o,a_n]}| =d_{X\cup\mathcal{H}}(o,a_n). \end{align*}$$
Since we have
![]() $\lim _{n\to \infty } |S(o,a_n;D)| = \infty $
by (ii) and
$\lim _{n\to \infty } |S(o,a_n;D)| = \infty $
by (ii) and
![]() $(a_n)_{n=1}^\infty $
is a subsequence of
$(a_n)_{n=1}^\infty $
is a subsequence of
![]() $\gamma $
, the path
$\gamma $
, the path
![]() $\gamma $
converges to infinity in
$\gamma $
converges to infinity in
![]() $\Gamma (G,Y\sqcup \mathcal {H})$
by Lemma 3.20 and we have
$\Gamma (G,Y\sqcup \mathcal {H})$
by Lemma 3.20 and we have
![]() $Y\text{-}{\lim}\ \gamma = Y\text{-}{\lim} _{n\to \infty } a_n$
.
$Y\text{-}{\lim}\ \gamma = Y\text{-}{\lim} _{n\to \infty } a_n$
.
Finally, we will show
![]() $Y\text{-}{\lim}\ \gamma = \xi \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
. Since we have
$Y\text{-}{\lim}\ \gamma = \xi \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
. Since we have
![]() $\xi = Y\text{-}{\lim} _{n\to \infty } g_n =Y\text{-}{\lim} _{n\to \infty } g_{nn}$
, it’s enough to show
$\xi = Y\text{-}{\lim} _{n\to \infty } g_n =Y\text{-}{\lim} _{n\to \infty } g_{nn}$
, it’s enough to show
![]() $Y\text{-}{\lim} _{n\to \infty } a_n=Y\text{-}{\lim} _{n\to \infty } g_{nn} \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
. For any
$Y\text{-}{\lim} _{n\to \infty } a_n=Y\text{-}{\lim} _{n\to \infty } g_{nn} \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
. For any
![]() $R\in \mathbb {N}$
, there exists
$R\in \mathbb {N}$
, there exists
![]() $N\in \mathbb {N}$
such that
$N\in \mathbb {N}$
such that
![]() $d_{Y\cup \mathcal {H}}(o,a_N)\ge R+3M_X+2\delta _Y$
since we have
$d_{Y\cup \mathcal {H}}(o,a_N)\ge R+3M_X+2\delta _Y$
since we have
![]() $\lim _{n\to \infty } d_{Y\cup \mathcal {H}}(o,a_n)=\infty $
by Lemma 3.20. Hence, for any
$\lim _{n\to \infty } d_{Y\cup \mathcal {H}}(o,a_n)=\infty $
by Lemma 3.20. Hence, for any
![]() $m,n\ge N$
, we have
$m,n\ge N$
, we have
![]() $(a_m,g_{nn})_o^{Y\cup \mathcal {H}} \ge R$
by Lemma 3.10 applied to
$(a_m,g_{nn})_o^{Y\cup \mathcal {H}} \ge R$
by Lemma 3.10 applied to
![]() $x=a_m, y=g_{nn}, v=a_N, w=a_N$
. This implies
$x=a_m, y=g_{nn}, v=a_N, w=a_N$
. This implies
![]() $\lim _{m,n\to \infty } (a_m,g_{nn})_o^{Y\cup \mathcal {H}} = \infty $
, hence
$\lim _{m,n\to \infty } (a_m,g_{nn})_o^{Y\cup \mathcal {H}} = \infty $
, hence
![]() $Y\text{-}{\lim} _{n\to \infty } a_n=Y\text{-}{\lim} _{n\to \infty } g_{nn}$
in
$Y\text{-}{\lim} _{n\to \infty } a_n=Y\text{-}{\lim} _{n\to \infty } g_{nn}$
in
![]() $\partial \Gamma (G,Y\sqcup \mathcal {H})$
.
$\partial \Gamma (G,Y\sqcup \mathcal {H})$
.
We next show that as the limit points of geodesic rays in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
get closer to one another in
$\Gamma (G,X\sqcup \mathcal {H})$
get closer to one another in
![]() $\partial \Gamma (G,Y\sqcup \mathcal {H})$
, the geodesic rays have more common separating cosets. Proposition 3.23 has two important corollaries, Corollary 3.24 and Corollary 3.28.
$\partial \Gamma (G,Y\sqcup \mathcal {H})$
, the geodesic rays have more common separating cosets. Proposition 3.23 has two important corollaries, Corollary 3.24 and Corollary 3.28.
Proposition 3.23. Let
![]() $o\in G$
,
$o\in G$
,
![]() $\xi \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
, and suppose that
$\xi \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
, and suppose that
![]() $\alpha $
is a geodesic ray in
$\alpha $
is a geodesic ray in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from o such that
$\Gamma (G,X\sqcup \mathcal {H})$
from o such that
![]() $Y\text{-}{\lim}\ \alpha = \xi \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
. Let
$Y\text{-}{\lim}\ \alpha = \xi \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
. Let
![]() $S(\alpha ,D)=\{C_1\preceq C_2 \preceq \cdots \}$
. Then, for any
$S(\alpha ,D)=\{C_1\preceq C_2 \preceq \cdots \}$
. Then, for any
![]() $N\in \mathbb {N}$
, there exists an open neighborhood U of
$N\in \mathbb {N}$
, there exists an open neighborhood U of
![]() $\xi $
in
$\xi $
in
![]() $\partial \Gamma (G,Y\sqcup \mathcal {H})$
such that any geodesic ray
$\partial \Gamma (G,Y\sqcup \mathcal {H})$
such that any geodesic ray
![]() $\beta $
in
$\beta $
in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from o satisfying
$\Gamma (G,X\sqcup \mathcal {H})$
from o satisfying
![]() $Y\text{-}{\lim}\ \beta \in U$
penetrates
$Y\text{-}{\lim}\ \beta \in U$
penetrates
![]() $C_n$
for any
$C_n$
for any
![]() $n\in \{1,\cdots ,N\}$
.
$n\in \{1,\cdots ,N\}$
.
Proof. Given
![]() $N\in \mathbb {N}$
, define
$N\in \mathbb {N}$
, define
![]() $R\in \mathbb {N}$
by
$R\in \mathbb {N}$
by
Let
![]() $\eta \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
satisfy
$\eta \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
satisfy
![]() $(\xi ,\eta )_o^{Y\cup \mathcal {H}}> R$
(see equation (2)) and
$(\xi ,\eta )_o^{Y\cup \mathcal {H}}> R$
(see equation (2)) and
![]() $\beta $
be a geodesic ray in
$\beta $
be a geodesic ray in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from o such that
$\Gamma (G,X\sqcup \mathcal {H})$
from o such that
![]() $Y\text{-}{\lim}\ \beta =\eta $
. Let
$Y\text{-}{\lim}\ \beta =\eta $
. Let
![]() $\alpha =(x_0,x_1,\cdots )$
and
$\alpha =(x_0,x_1,\cdots )$
and
![]() $\beta =(y_0,y_1,\cdots )$
. It’s not difficult to see from equation (2) that
$\beta =(y_0,y_1,\cdots )$
. It’s not difficult to see from equation (2) that
![]() $(\xi ,\eta )_o^{Y\cup \mathcal {H}}> R$
implies
$(\xi ,\eta )_o^{Y\cup \mathcal {H}}> R$
implies
Hence, there exists
![]() $k\in \mathbb {N}$
such that
$k\in \mathbb {N}$
such that
![]() $(x_k,y_k)_o^{Y\cup \mathcal {H}}> R-2\delta _Y$
. By Lemma 3.9 applied to
$(x_k,y_k)_o^{Y\cup \mathcal {H}}> R-2\delta _Y$
. By Lemma 3.9 applied to
![]() $o,x_k,y_k,\alpha _{[o,x_k]},\beta _{[o,y_k]}$
, there exist
$o,x_k,y_k,\alpha _{[o,x_k]},\beta _{[o,y_k]}$
, there exist
![]() $\ell ,m$
with
$\ell ,m$
with
![]() $\ell ,m \le k$
such that
$\ell ,m \le k$
such that
![]() $d_{Y\cup \mathcal {H}} (x_\ell ,y_m) \le \delta _Y+2M_X$
and
$d_{Y\cup \mathcal {H}} (x_\ell ,y_m) \le \delta _Y+2M_X$
and
![]() $d_{Y\cup \mathcal {H}} (o,x_\ell ) \ge R-2\delta _Y-M_X$
. This implies, together with equation (5) in Theorem 2.41 and equation (9),
$d_{Y\cup \mathcal {H}} (o,x_\ell ) \ge R-2\delta _Y-M_X$
. This implies, together with equation (5) in Theorem 2.41 and equation (9),
Let
![]() $L=|S(o,x_\ell ;D)|$
and
$L=|S(o,x_\ell ;D)|$
and
![]() $S(o,x_\ell ;D)=\{B_1\preceq \cdots \preceq B_L\}$
. By Lemma 3.11,
$S(o,x_\ell ;D)=\{B_1\preceq \cdots \preceq B_L\}$
. By Lemma 3.11,
![]() $\beta _{[y_0,y_m]}$
penetrates
$\beta _{[y_0,y_m]}$
penetrates
![]() $B_n$
for any
$B_n$
for any
![]() $n\in \{1,\cdots ,N\}$
since equation (10) implies
$n\in \{1,\cdots ,N\}$
since equation (10) implies
![]() $3d_{Y\cup \mathcal {H}} (x_\ell ,y_m)+1\le L-N$
. Meanwhile, suppose
$3d_{Y\cup \mathcal {H}} (x_\ell ,y_m)+1\le L-N$
. Meanwhile, suppose
![]() $d_{X\cup \mathcal {H}}(o,x_\ell ) \le d_{X\cup \mathcal {H}}(o,\alpha _{out}(C_{N+1}))$
for contradiction, then we have
$d_{X\cup \mathcal {H}}(o,x_\ell ) \le d_{X\cup \mathcal {H}}(o,\alpha _{out}(C_{N+1}))$
for contradiction, then we have
![]() $\alpha _{[o,x_\ell ]} \subset \alpha _{[o,\alpha _{out}(C_{N+1})]}$
. This implies
$\alpha _{[o,x_\ell ]} \subset \alpha _{[o,\alpha _{out}(C_{N+1})]}$
. This implies
![]() $|S(o,x_\ell ;D)| \le |S(o,\alpha _{out}(C_{N+1});D)| \le N+1$
by Lemma 3.1. This contradicts that we get
$|S(o,x_\ell ;D)| \le |S(o,\alpha _{out}(C_{N+1});D)| \le N+1$
by Lemma 3.1. This contradicts that we get
![]() $N+2\le |S(o,x_\ell ;D)|$
by equation (10). Thus, we have
$N+2\le |S(o,x_\ell ;D)|$
by equation (10). Thus, we have
![]() $d_{X\cup \mathcal {H}}(o,\alpha _{out}(C_{N+1})) < d_{X\cup \mathcal {H}}(o,x_\ell )$
. Hence, we have
$d_{X\cup \mathcal {H}}(o,\alpha _{out}(C_{N+1})) < d_{X\cup \mathcal {H}}(o,x_\ell )$
. Hence, we have
![]() $B_n=C_n$
for any
$B_n=C_n$
for any
![]() $n\in \{1,\cdots ,N\}$
by Lemma 3.18. Thus,
$n\in \{1,\cdots ,N\}$
by Lemma 3.18. Thus,
![]() $\beta $
penetrates
$\beta $
penetrates
![]() $C_n$
for any
$C_n$
for any
![]() $n\in \{1,\cdots ,N\}$
. Finally, since the set
$n\in \{1,\cdots ,N\}$
. Finally, since the set
![]() $V=\{\eta \in \partial \Gamma (G,Y\sqcup \mathcal {H}) \mid (\xi ,\eta )_o^{Y\cup \mathcal {H}}> R \}$
is a neighborhood of
$V=\{\eta \in \partial \Gamma (G,Y\sqcup \mathcal {H}) \mid (\xi ,\eta )_o^{Y\cup \mathcal {H}}> R \}$
is a neighborhood of
![]() $\xi $
, there exists an open set U of
$\xi $
, there exists an open set U of
![]() $\partial \Gamma (G,Y\sqcup \mathcal {H})$
such that
$\partial \Gamma (G,Y\sqcup \mathcal {H})$
such that
![]() $\xi \in U$
and
$\xi \in U$
and
![]() $U\subset V$
. This U satisfies the statement for N.
$U\subset V$
. This U satisfies the statement for N.
Corollary 3.24 is the final step to extend the notion of Hull–Osin’s separating cosets, which is done in Definition 3.25.
Corollary 3.24. Let
![]() $o\in G$
and suppose that
$o\in G$
and suppose that
![]() $\alpha ,\beta $
are geodesic rays in
$\alpha ,\beta $
are geodesic rays in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from o such that
$\Gamma (G,X\sqcup \mathcal {H})$
from o such that
![]() $Y\text{-}{\lim}\ \alpha = Y\text{-}{\lim}\ \beta \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
. Then, we have
$Y\text{-}{\lim}\ \alpha = Y\text{-}{\lim}\ \beta \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
. Then, we have
![]() $S(\alpha ;D)=S(\beta ;D)$
.
$S(\alpha ;D)=S(\beta ;D)$
.
Proof. Let
![]() $\alpha =(x_0,x_1,\cdots )$
,
$\alpha =(x_0,x_1,\cdots )$
,
![]() $\beta =(y_0,y_1,\cdots )$
, and
$\beta =(y_0,y_1,\cdots )$
, and
![]() $S(\alpha ;D)=\{C_1 \preceq C_2\preceq \cdots \}$
. By Proposition 3.23,
$S(\alpha ;D)=\{C_1 \preceq C_2\preceq \cdots \}$
. By Proposition 3.23,
![]() $\beta $
penetrates
$\beta $
penetrates
![]() $C_n$
for any
$C_n$
for any
![]() $n\in \mathbb {N}$
since
$n\in \mathbb {N}$
since
![]() $Y\text{-}{\lim}\ \beta $
is obviously contained in any open neighborhood of
$Y\text{-}{\lim}\ \beta $
is obviously contained in any open neighborhood of
![]() $Y\text{-}{\lim}\ \alpha $
. For any
$Y\text{-}{\lim}\ \alpha $
. For any
![]() $n\in \mathbb {N}$
, there exists
$n\in \mathbb {N}$
, there exists
![]() $k\in \mathbb {N}$
such that
$k\in \mathbb {N}$
such that
![]() $\{C_1, \cdots ,C_{n+1}\} \subset S(o,x_k;D)$
. Let
$\{C_1, \cdots ,C_{n+1}\} \subset S(o,x_k;D)$
. Let
![]() $\ell \in \mathbb {N}$
satisfy
$\ell \in \mathbb {N}$
satisfy
![]() $d_{X\cup \mathcal {H}}(o,\beta _{out}(C_{n+1}))\le d_{X\cup \mathcal {H}}(o,y_\ell )$
. By Lemma 3.5, we have
$d_{X\cup \mathcal {H}}(o,\beta _{out}(C_{n+1}))\le d_{X\cup \mathcal {H}}(o,y_\ell )$
. By Lemma 3.5, we have
![]() $\{C_1, \cdots ,C_n\} \subset S(o,y_\ell ;D)\subset S(\beta ;D)$
. This implies
$\{C_1, \cdots ,C_n\} \subset S(o,y_\ell ;D)\subset S(\beta ;D)$
. This implies
![]() $S(\alpha ;D) \subset S(\beta ;D)$
. Similarly, we can also see
$S(\alpha ;D) \subset S(\beta ;D)$
. Similarly, we can also see
![]() $S(\beta ;D) \subset S(\alpha ;D)$
.
$S(\beta ;D) \subset S(\alpha ;D)$
.
Definition 3.25. Given
![]() $x\in G$
and
$x\in G$
and
![]() $\xi \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
, we take a geodesic ray
$\xi \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
, we take a geodesic ray
![]() $\gamma $
in
$\gamma $
in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
satisfying
$\Gamma (G,X\sqcup \mathcal {H})$
satisfying
![]() $\gamma _-=x$
and
$\gamma _-=x$
and
![]() $Y\text{-}{\lim}\ \gamma =\xi $
and define the set of cosets
$Y\text{-}{\lim}\ \gamma =\xi $
and define the set of cosets
![]() $S(x,\xi ;D)$
by
$S(x,\xi ;D)$
by
We call an element of
![]() $S(x,\xi ;D)$
a
$S(x,\xi ;D)$
a
![]() $(x,\xi ;D)$
-separating coset.
$(x,\xi ;D)$
-separating coset.
Remark 3.26. By Proposition 3.22 and Corollary 3.24, Definition 3.25 is well-defined, that is,
![]() $\gamma $
above exists and
$\gamma $
above exists and
![]() $S(x,\xi ;D)$
doesn’t depend on
$S(x,\xi ;D)$
doesn’t depend on
![]() $\gamma $
. Also,
$\gamma $
. Also,
![]() $S(x,\xi ;D)$
is exactly the set of all cosets that are essentially penetrated by some geodesic ray
$S(x,\xi ;D)$
is exactly the set of all cosets that are essentially penetrated by some geodesic ray
![]() $\gamma $
in
$\gamma $
in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from x with
$\Gamma (G,X\sqcup \mathcal {H})$
from x with
![]() $Y\text{-}{\lim}\ \gamma =\xi $
.
$Y\text{-}{\lim}\ \gamma =\xi $
.
We will next show in Corollary 3.28 that two geodesic rays in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
having the same limit in
$\Gamma (G,X\sqcup \mathcal {H})$
having the same limit in
![]() $\partial \Gamma (G,Y\sqcup \mathcal {H})$
penetrate the same separating cosets after going far enough. This will play an important role to show hyperfiniteness in the proof of Theorem 1.1. We begin with an auxiliary lemma. Lemma 3.27 is a well-known fact, but we write down a sketch of the proof for completeness.
$\partial \Gamma (G,Y\sqcup \mathcal {H})$
penetrate the same separating cosets after going far enough. This will play an important role to show hyperfiniteness in the proof of Theorem 1.1. We begin with an auxiliary lemma. Lemma 3.27 is a well-known fact, but we write down a sketch of the proof for completeness.
Lemma 3.27. Suppose that
![]() $\Gamma $
is a connected graph, x is a vertex and
$\Gamma $
is a connected graph, x is a vertex and
![]() $\beta =(y_0,y_1,\cdots )$
is a geodesic ray. Then, there exists
$\beta =(y_0,y_1,\cdots )$
is a geodesic ray. Then, there exists
![]() $k\in \mathbb {N}$
such that for any geodesic path p from x to
$k\in \mathbb {N}$
such that for any geodesic path p from x to
![]() $y_k$
, the path
$y_k$
, the path
![]() $p\beta _{[y_k,\infty )}$
is a geodesic ray.
$p\beta _{[y_k,\infty )}$
is a geodesic ray.
Proof. Define the map
![]() $f \colon \mathbb {N}\to \mathbb {Z}$
by
$f \colon \mathbb {N}\to \mathbb {Z}$
by
![]() $f(n)=d_\Gamma (y_n,y_0)-d_\Gamma (y_n,x)$
. Since
$f(n)=d_\Gamma (y_n,y_0)-d_\Gamma (y_n,x)$
. Since
![]() $\beta $
is geodesic, we have
$\beta $
is geodesic, we have
![]() $f(n)=n-d_\Gamma (y_n,x), \forall n\in \mathbb {N}$
. This and
$f(n)=n-d_\Gamma (y_n,x), \forall n\in \mathbb {N}$
. This and
![]() $|d_\Gamma (y_{n+1},x)-d_\Gamma (y_n,x)|\le 1, \forall n\in \mathbb {N}$
imply that f is non-decreasing. The map f is also bounded above by
$|d_\Gamma (y_{n+1},x)-d_\Gamma (y_n,x)|\le 1, \forall n\in \mathbb {N}$
imply that f is non-decreasing. The map f is also bounded above by
![]() $d_\Gamma (y_0,x)$
. Hence, there exists
$d_\Gamma (y_0,x)$
. Hence, there exists
![]() $k\in \mathbb {N}$
such that
$k\in \mathbb {N}$
such that
![]() $f(n)=f(k)$
for any n with
$f(n)=f(k)$
for any n with
![]() $n\ge k$
. Since this implies
$n\ge k$
. Since this implies
![]() $d_\Gamma (y_n,x)=d_\Gamma (y_n,y_k)+d_\Gamma (y_k,x)$
for any n with
$d_\Gamma (y_n,x)=d_\Gamma (y_n,y_k)+d_\Gamma (y_k,x)$
for any n with
![]() $n\ge k$
, this k satisfies the statement.
$n\ge k$
, this k satisfies the statement.

Figure 4 Proof of Corollary 3.28.
Corollary 3.28. Suppose that
![]() $\alpha ,\beta $
are geodesic rays in
$\alpha ,\beta $
are geodesic rays in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
that converge to infinity in
$\Gamma (G,X\sqcup \mathcal {H})$
that converge to infinity in
![]() $\Gamma (G,Y\sqcup \mathcal {H})$
, and let
$\Gamma (G,Y\sqcup \mathcal {H})$
, and let
![]() $S(\alpha ;D)=\{C_1\preceq C_2\preceq \cdots \}$
. If
$S(\alpha ;D)=\{C_1\preceq C_2\preceq \cdots \}$
. If
![]() $Y\text{-}{\lim}\ \alpha =Y\text{-}{\lim}\ \beta $
in
$Y\text{-}{\lim}\ \alpha =Y\text{-}{\lim}\ \beta $
in
![]() $\partial \Gamma (G,Y\sqcup \mathcal {H})$
, then there exists
$\partial \Gamma (G,Y\sqcup \mathcal {H})$
, then there exists
![]() $N\in \mathbb {N}$
such that for any
$N\in \mathbb {N}$
such that for any
![]() $n\ge N$
,
$n\ge N$
,
![]() $\beta $
penetrates
$\beta $
penetrates
![]() $C_n$
satisfying
$C_n$
satisfying
![]() $d_{X\cup \mathcal {H}}(\beta _-,C_n)<d_{X\cup \mathcal {H}}(\beta _-,C_{n+1})$
and we have, when
$d_{X\cup \mathcal {H}}(\beta _-,C_n)<d_{X\cup \mathcal {H}}(\beta _-,C_{n+1})$
and we have, when
![]() $C_n$
is an
$C_n$
is an
![]() $H_\lambda $
-coset,
$H_\lambda $
-coset,
Proof. Let
![]() $\beta =(y_0,y_1,\cdots )$
. By applying Lemma 3.27 to
$\beta =(y_0,y_1,\cdots )$
. By applying Lemma 3.27 to
![]() $\Gamma (G,X\sqcup \mathcal {H})$
, there exist
$\Gamma (G,X\sqcup \mathcal {H})$
, there exist
![]() $k\in \mathbb {N}$
and a geodesic path p in
$k\in \mathbb {N}$
and a geodesic path p in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from
$\Gamma (G,X\sqcup \mathcal {H})$
from
![]() $\alpha _-$
to
$\alpha _-$
to
![]() $y_k$
such that the path
$y_k$
such that the path
![]() $\gamma $
defined by
$\gamma $
defined by
![]() $\gamma =p\beta _{[y_k,\infty )}$
is a geodesic ray in
$\gamma =p\beta _{[y_k,\infty )}$
is a geodesic ray in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
. By
$\Gamma (G,X\sqcup \mathcal {H})$
. By
![]() $\gamma _{[y_k,\infty )}=\beta _{[y_k,\infty )}$
, we have
$\gamma _{[y_k,\infty )}=\beta _{[y_k,\infty )}$
, we have
![]() $Y\text{-}{\lim}\ \gamma =Y\text{-}{\lim}\ \beta =Y\text{-}{\lim}\ \alpha $
. This implies
$Y\text{-}{\lim}\ \gamma =Y\text{-}{\lim}\ \beta =Y\text{-}{\lim}\ \alpha $
. This implies
![]() $S(\gamma ;D)=S(\alpha ;D)$
by Corollary 3.24. Hence,
$S(\gamma ;D)=S(\alpha ;D)$
by Corollary 3.24. Hence,
![]() $\gamma $
penetrates
$\gamma $
penetrates
![]() $C_n$
for any
$C_n$
for any
![]() $n\in \mathbb {N}$
by Lemma 3.14. Note that
$n\in \mathbb {N}$
by Lemma 3.14. Note that
![]() $|S(\gamma ;D)|=\infty $
implies
$|S(\gamma ;D)|=\infty $
implies
![]() $\lim _{n\to \infty } d_{X\cup \mathcal {H}}(\gamma _-, \gamma _{in}(C_n))=\infty $
. Hence, there exists
$\lim _{n\to \infty } d_{X\cup \mathcal {H}}(\gamma _-, \gamma _{in}(C_n))=\infty $
. Hence, there exists
![]() $N\ge 2$
such that
$N\ge 2$
such that
![]() $d_{X\cup \mathcal {H}}(\gamma _-, \gamma _{in}(C_{N-1}))>d_{X\cup \mathcal {H}}(\gamma _-, y_k)$
. By
$d_{X\cup \mathcal {H}}(\gamma _-, \gamma _{in}(C_{N-1}))>d_{X\cup \mathcal {H}}(\gamma _-, y_k)$
. By
![]() $\gamma _{[y_k,\infty )}=\beta _{[y_k,\infty )}$
, the path
$\gamma _{[y_k,\infty )}=\beta _{[y_k,\infty )}$
, the path
![]() $\beta $
penetrates
$\beta $
penetrates
![]() $C_n$
for any
$C_n$
for any
![]() $n\ge N-1$
. Let
$n\ge N-1$
. Let
![]() $n\ge N$
and
$n\ge N$
and
![]() $C_n$
be an
$C_n$
be an
![]() $H_\lambda $
-coset. By
$H_\lambda $
-coset. By
![]() $C_{n-1}\preceq C_n$
and
$C_{n-1}\preceq C_n$
and
![]() $\gamma _-=\alpha _-$
, we have
$\gamma _-=\alpha _-$
, we have
![]() $d_{X\cup \mathcal {H}}(\gamma _-, C_{n-1})<d_{X\cup \mathcal {H}}(\gamma _-, C_n)$
. This implies
$d_{X\cup \mathcal {H}}(\gamma _-, C_{n-1})<d_{X\cup \mathcal {H}}(\gamma _-, C_n)$
. This implies
 $$ \begin{align*} d_{X\cup\mathcal{H}}(\beta_-, C_n)-d_{X\cup\mathcal{H}}(\beta_-, C_{n-1}) &=d_{X\cup\mathcal{H}}(y_k, \beta_{in}(C_n))-d_{X\cup\mathcal{H}}(y_k, \beta_{in}(C_{n-1})) \\ &=d_{X\cup\mathcal{H}}(y_k, \gamma_{in}(C_n))-d_{X\cup\mathcal{H}}(y_k, \gamma_{in}(C_{n-1})) \\ &=d_{X\cup\mathcal{H}}(\gamma_-, C_n)-d_{X\cup\mathcal{H}}(\gamma_-, C_{n-1})>0. \end{align*} $$
$$ \begin{align*} d_{X\cup\mathcal{H}}(\beta_-, C_n)-d_{X\cup\mathcal{H}}(\beta_-, C_{n-1}) &=d_{X\cup\mathcal{H}}(y_k, \beta_{in}(C_n))-d_{X\cup\mathcal{H}}(y_k, \beta_{in}(C_{n-1})) \\ &=d_{X\cup\mathcal{H}}(y_k, \gamma_{in}(C_n))-d_{X\cup\mathcal{H}}(y_k, \gamma_{in}(C_{n-1})) \\ &=d_{X\cup\mathcal{H}}(\gamma_-, C_n)-d_{X\cup\mathcal{H}}(\gamma_-, C_{n-1})>0. \end{align*} $$
Hence, we have
![]() $\widehat {d}_{\lambda }(\alpha _{in}(C_n), \beta _{in}(C_n)) \le 4C$
by applying Lemma 3.4 to
$\widehat {d}_{\lambda }(\alpha _{in}(C_n), \beta _{in}(C_n)) \le 4C$
by applying Lemma 3.4 to
![]() $C_{n-1},C_n,\alpha ,\beta $
. Similarly, we have
$C_{n-1},C_n,\alpha ,\beta $
. Similarly, we have
![]() $\widehat {d}_{\lambda }(\alpha _{out}(C_n), \beta _{out}(C_n)) \le 4C$
by applying Lemma 3.4 to
$\widehat {d}_{\lambda }(\alpha _{out}(C_n), \beta _{out}(C_n)) \le 4C$
by applying Lemma 3.4 to
![]() $C_n,C_{n+1},\alpha ,\beta $
.
$C_n,C_{n+1},\alpha ,\beta $
.
Finally, we show that if the limit points in
![]() $\partial \Gamma (G,X\sqcup \mathcal {H})$
of geodesic rays in
$\partial \Gamma (G,X\sqcup \mathcal {H})$
of geodesic rays in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
are convergent, then their limit points in
$\Gamma (G,X\sqcup \mathcal {H})$
are convergent, then their limit points in
![]() $\partial \Gamma (G,Y\sqcup \mathcal {H})$
are also convergent. Proposition 3.29 can be considered as opposite to Proposition 3.23. This will become clear in Proposition 6.2.
$\partial \Gamma (G,Y\sqcup \mathcal {H})$
are also convergent. Proposition 3.29 can be considered as opposite to Proposition 3.23. This will become clear in Proposition 6.2.
Proposition 3.29. Let
![]() $o\in G$
and suppose that
$o\in G$
and suppose that
![]() $\alpha $
is a geodesic ray in
$\alpha $
is a geodesic ray in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from o converging to infinity in
$\Gamma (G,X\sqcup \mathcal {H})$
from o converging to infinity in
![]() $\Gamma (G,Y\sqcup \mathcal {H})$
. For any open neighborhood U of
$\Gamma (G,Y\sqcup \mathcal {H})$
. For any open neighborhood U of
![]() $Y\text{-}{\lim}\ \alpha $
in
$Y\text{-}{\lim}\ \alpha $
in
![]() $\partial \Gamma (G,Y\sqcup \mathcal {H})$
, there exists an open neighborhood V of
$\partial \Gamma (G,Y\sqcup \mathcal {H})$
, there exists an open neighborhood V of
![]() $X\text{-}{\lim}\ \alpha $
in
$X\text{-}{\lim}\ \alpha $
in
![]() $\partial \Gamma (G,X\sqcup \mathcal {H})$
such that if a geodesic ray
$\partial \Gamma (G,X\sqcup \mathcal {H})$
such that if a geodesic ray
![]() $\beta $
in
$\beta $
in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from o converging to infinity in
$\Gamma (G,X\sqcup \mathcal {H})$
from o converging to infinity in
![]() $\Gamma (G,Y\sqcup \mathcal {H})$
satisfies
$\Gamma (G,Y\sqcup \mathcal {H})$
satisfies
![]() $X\text{-}{\lim}\ \beta \in V$
, then we have
$X\text{-}{\lim}\ \beta \in V$
, then we have
![]() $Y\text{-}{\lim}\ \beta \in U$
.
$Y\text{-}{\lim}\ \beta \in U$
.
Proof. Let
![]() $\alpha =(x_0,x_1,\cdots )$
. For any open neighborhood U of
$\alpha =(x_0,x_1,\cdots )$
. For any open neighborhood U of
![]() $Y\text{-}{\lim}\ \alpha $
in
$Y\text{-}{\lim}\ \alpha $
in
![]() $\partial \Gamma (G,Y\sqcup \mathcal {H})$
, there exists
$\partial \Gamma (G,Y\sqcup \mathcal {H})$
, there exists
![]() $R\in \mathbb {N}$
such that
$R\in \mathbb {N}$
such that
by Proposition 2.19. We define
![]() $R_1=R+\delta _X+3M_X+2\delta _Y$
. Since we have
$R_1=R+\delta _X+3M_X+2\delta _Y$
. Since we have
![]() $\lim _{n\to \infty }d_{Y\cup \mathcal {H}}(o,x_n)=\infty $
by Lemma 3.20, there exists
$\lim _{n\to \infty }d_{Y\cup \mathcal {H}}(o,x_n)=\infty $
by Lemma 3.20, there exists
![]() $N\in \mathbb {N}$
such that
$N\in \mathbb {N}$
such that
By Proposition 2.19, there exists an open neighborhood V of
![]() $X\text{-}{\lim}\ \alpha $
in
$X\text{-}{\lim}\ \alpha $
in
![]() $\partial \Gamma (G,X\sqcup \mathcal {H})$
such that
$\partial \Gamma (G,X\sqcup \mathcal {H})$
such that
We show that V satisfies the statement. Let
![]() $\beta =(y_0,y_1,\cdots )$
be a geodesic ray in
$\beta =(y_0,y_1,\cdots )$
be a geodesic ray in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from o converging to infinity in
$\Gamma (G,X\sqcup \mathcal {H})$
from o converging to infinity in
![]() $\Gamma (G,Y\sqcup \mathcal {H})$
such that
$\Gamma (G,Y\sqcup \mathcal {H})$
such that
![]() $X\text{-}{\lim}\ \beta \in V$
. By equation (13), it’s not difficult to see
$X\text{-}{\lim}\ \beta \in V$
. By equation (13), it’s not difficult to see
![]() $\liminf _{i,j\to \infty }(x_i,y_j)_o^{X\cup \mathcal {H}}>N$
. Since
$\liminf _{i,j\to \infty }(x_i,y_j)_o^{X\cup \mathcal {H}}>N$
. Since
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are geodesic rays in
$\beta $
are geodesic rays in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from o, this implies
$\Gamma (G,X\sqcup \mathcal {H})$
from o, this implies
Hence, for any
![]() $n,m\ge N$
, we have
$n,m\ge N$
, we have
![]() $(x_{n},y_{m})_o^{Y\cup \mathcal {H}} \ge R_1-(\delta _X+3M_X)-2\delta _Y=R$
by applying Lemma 3.10 to
$(x_{n},y_{m})_o^{Y\cup \mathcal {H}} \ge R_1-(\delta _X+3M_X)-2\delta _Y=R$
by applying Lemma 3.10 to
![]() $\alpha _{[o,x_n]}, \beta _{[o,y_m]},x=x_n,y=y_m,v=x_N,w=y_N$
. This implies
$\alpha _{[o,x_n]}, \beta _{[o,y_m]},x=x_n,y=y_m,v=x_N,w=y_N$
. This implies
Hence, we have
![]() $Y\text{-}{\lim}\ \beta \in U$
by equation (12).
$Y\text{-}{\lim}\ \beta \in U$
by equation (12).
4. Proof of main theorem
In this section, we prove Theorem 1.1. We follow the approach of [Reference Naryshkin and Vaccaro18], where they gave another proof of the fact that the action of any hyperbolic group on its Gromov boundary is hyperfinite. Their approach goes as follows. Given a hyperbolic group G with a finite symmetric generating set S, we fix a well-order on S. This order induces the lexicographic order
![]() $\le _{\mathrm {lex}}$
on
$\le _{\mathrm {lex}}$
on
![]() $S^{\mathbb {N}}$
, which enables us to pick for
$S^{\mathbb {N}}$
, which enables us to pick for
![]() $\xi \in \partial G$
, a geodesic ray from
$\xi \in \partial G$
, a geodesic ray from
![]() $1$
to
$1$
to
![]() $\xi $
in the Cayley graph
$\xi $
in the Cayley graph
![]() $\Gamma (G,S)$
whose label is the minimum in
$\Gamma (G,S)$
whose label is the minimum in
![]() $(S^{\mathbb {N}},\le _{\mathrm {lex}})$
among all such geodesic rays. This defines an injective Borel measurable map from
$(S^{\mathbb {N}},\le _{\mathrm {lex}})$
among all such geodesic rays. This defines an injective Borel measurable map from
![]() $\partial G$
to
$\partial G$
to
![]() $S^{\mathbb {N}}$
that Borel reduces a finite index subequivalence relation of the orbit equivalence relation
$S^{\mathbb {N}}$
that Borel reduces a finite index subequivalence relation of the orbit equivalence relation
![]() $E_G^{\partial G}$
to the tail equivalence relation
$E_G^{\partial G}$
to the tail equivalence relation
![]() $E_t(S)$
, thereby hyperfiniteness of
$E_t(S)$
, thereby hyperfiniteness of
![]() $E_t(S)$
implies hyperfiniteness of
$E_t(S)$
implies hyperfiniteness of
![]() $E_G^{\partial G}$
.
$E_G^{\partial G}$
.
We first verify in Lemma 4.1 that the Gromov boundary is a Polish space (see Definition 2.1). Actually, we can show slightly more. It’s interesting to know whether the statement of Lemma 4.1 holds for any completely metrizable hyperbolic space, that is, whether
![]() $S\cup \partial S$
is completely metrizable for any completely metrizable hyperbolic space S. For a graph
$S\cup \partial S$
is completely metrizable for any completely metrizable hyperbolic space S. For a graph
![]() $\Gamma $
, we denote its vertex set by
$\Gamma $
, we denote its vertex set by
![]() $V(\Gamma )$
. The proof below uses that
$V(\Gamma )$
. The proof below uses that
![]() $V(\Gamma )$
is discrete.
$V(\Gamma )$
is discrete.
Lemma 4.1. For any hyperbolic graph
![]() $\Gamma $
, the topological space
$\Gamma $
, the topological space
![]() $V(\Gamma )\cup \partial \Gamma $
is completely metrizable. If in addition
$V(\Gamma )\cup \partial \Gamma $
is completely metrizable. If in addition
![]() $V(\Gamma )$
is countable, then
$V(\Gamma )$
is countable, then
![]() $V(\Gamma )\cup \partial \Gamma $
is Polish.
$V(\Gamma )\cup \partial \Gamma $
is Polish.
Proof. Fix a vertex
![]() $o\in \Gamma $
, and take the map
$o\in \Gamma $
, and take the map
![]() $D \colon (\Gamma \cup \partial \Gamma )^2 \to [0,\infty )$
and constants
$D \colon (\Gamma \cup \partial \Gamma )^2 \to [0,\infty )$
and constants
![]() $\varepsilon ,\varepsilon '>0$
as in Proposition 2.21. We define the map
$\varepsilon ,\varepsilon '>0$
as in Proposition 2.21. We define the map
![]() $\widetilde {D} \colon (V(\Gamma )\cup \partial \Gamma )^2 \to [0,\infty )$
by
$\widetilde {D} \colon (V(\Gamma )\cup \partial \Gamma )^2 \to [0,\infty )$
by
![]() $\widetilde {D}(x,y)=D(x,y)$
if
$\widetilde {D}(x,y)=D(x,y)$
if
![]() $x\neq y$
and
$x\neq y$
and
![]() $\widetilde {D}(x,y)=0$
if
$\widetilde {D}(x,y)=0$
if
![]() $x=y$
. By Proposition 2.21, it’s not difficult to see that
$x=y$
. By Proposition 2.21, it’s not difficult to see that
![]() $\widetilde {D}$
is a metric and the metric topology of
$\widetilde {D}$
is a metric and the metric topology of
![]() $\widetilde {D}$
coincides with the relative topology of
$\widetilde {D}$
coincides with the relative topology of
![]() $\mathcal {O}_\Gamma $
on
$\mathcal {O}_\Gamma $
on
![]() $V(\Gamma )\cup \partial \Gamma $
(see Proposition 2.19). Here, we used discreteness of
$V(\Gamma )\cup \partial \Gamma $
(see Proposition 2.19). Here, we used discreteness of
![]() $(V(\Gamma ), \mathcal {O}_\Gamma |_{V(\Gamma )})$
since the metric topology of
$(V(\Gamma ), \mathcal {O}_\Gamma |_{V(\Gamma )})$
since the metric topology of
![]() $\widetilde {D}$
on
$\widetilde {D}$
on
![]() $V(\Gamma )$
is discrete by Remark 2.22. We will show that
$V(\Gamma )$
is discrete by Remark 2.22. We will show that
![]() $\widetilde {D}$
is complete. Let
$\widetilde {D}$
is complete. Let
![]() $(x_n)_{n=1}^\infty $
be a Cauchy sequence of
$(x_n)_{n=1}^\infty $
be a Cauchy sequence of
![]() $(V(\Gamma )\cup \partial \Gamma ,\widetilde {D})$
. Since
$(V(\Gamma )\cup \partial \Gamma ,\widetilde {D})$
. Since
![]() $V(\Gamma )$
is dense in
$V(\Gamma )$
is dense in
![]() $V(\Gamma )\cup \partial \Gamma $
, we can take for each
$V(\Gamma )\cup \partial \Gamma $
, we can take for each
![]() $n\in \mathbb {N}$
, a vertex
$n\in \mathbb {N}$
, a vertex
![]() $y_n\in V(\Gamma )$
such that
$y_n\in V(\Gamma )$
such that
![]() $\widetilde {D}(x_n,y_n)\le \frac {1}{n}$
. The sequence
$\widetilde {D}(x_n,y_n)\le \frac {1}{n}$
. The sequence
![]() $(y_n)_{n=1}^\infty $
in
$(y_n)_{n=1}^\infty $
in
![]() $V(\Gamma )$
is also a Cauchy sequence in the metric
$V(\Gamma )$
is also a Cauchy sequence in the metric
![]() $\widetilde {D}$
and it’s enough to show that
$\widetilde {D}$
and it’s enough to show that
![]() $(y_n)_{n=1}^\infty $
is convergent. If there exists a constant subsequence
$(y_n)_{n=1}^\infty $
is convergent. If there exists a constant subsequence
![]() $(y_{n_k})_{k=1}^\infty $
(i.e.,
$(y_{n_k})_{k=1}^\infty $
(i.e.,
![]() $y_{n_k}\equiv y$
for some
$y_{n_k}\equiv y$
for some
![]() $y\in V(\Gamma )$
), then
$y\in V(\Gamma )$
), then
![]() $(y_n)_{n=1}^\infty $
converges to y in
$(y_n)_{n=1}^\infty $
converges to y in
![]() $\widetilde {D}$
. If there is no constant subsequence of
$\widetilde {D}$
. If there is no constant subsequence of
![]() $(y_n)_{n=1}^\infty $
, then there exists a subsequence
$(y_n)_{n=1}^\infty $
, then there exists a subsequence
![]() $(y_{n_k})_{k=1}^\infty $
whose elements are all distinct. This implies
$(y_{n_k})_{k=1}^\infty $
whose elements are all distinct. This implies
![]() $\widetilde {D}(y_{n_k},y_{n_\ell })=D(y_{n_k},y_{n_\ell })$
for any
$\widetilde {D}(y_{n_k},y_{n_\ell })=D(y_{n_k},y_{n_\ell })$
for any
![]() $k\neq \ell $
. Since this implies
$k\neq \ell $
. Since this implies
![]() $\lim _{k,\ell \to \infty } (y_{n_k},y_{n_\ell })_o^\Gamma =\infty $
, the sequence
$\lim _{k,\ell \to \infty } (y_{n_k},y_{n_\ell })_o^\Gamma =\infty $
, the sequence
![]() $(y_{n_k})_{k=1}^\infty $
converges to some
$(y_{n_k})_{k=1}^\infty $
converges to some
![]() $y \in \partial \Gamma $
in
$y \in \partial \Gamma $
in
![]() $\mathcal {O}_\Gamma $
. Hence,
$\mathcal {O}_\Gamma $
. Hence,
![]() $(y_n)_{n=1}^\infty $
converges to y as well. Thus,
$(y_n)_{n=1}^\infty $
converges to y as well. Thus,
![]() $V(\Gamma )\cup \partial \Gamma $
is completely metrizable with
$V(\Gamma )\cup \partial \Gamma $
is completely metrizable with
![]() $\widetilde {D}$
. If
$\widetilde {D}$
. If
![]() $V(\Gamma )$
is countable,
$V(\Gamma )$
is countable,
![]() $V(\Gamma )$
is a countable dense subset of
$V(\Gamma )$
is a countable dense subset of
![]() $V(\Gamma )\cup \partial \Gamma $
. Hence,
$V(\Gamma )\cup \partial \Gamma $
. Hence,
![]() $V(\Gamma )\cup \partial \Gamma $
is Polish.
$V(\Gamma )\cup \partial \Gamma $
is Polish.
From here up to Lemma 4.9, suppose that G is a countable group, X is a subset of G and
![]() $\{H_\lambda \}_{\lambda \in \Lambda }$
is a countable collection of subgroups of G hyperbolically embedded in
$\{H_\lambda \}_{\lambda \in \Lambda }$
is a countable collection of subgroups of G hyperbolically embedded in
![]() $(G,X)$
. Let
$(G,X)$
. Let
![]() $C>0$
as in Proposition 2.30, and fix
$C>0$
as in Proposition 2.30, and fix
![]() $D>0$
satisfying
$D>0$
satisfying
![]() $D\ge 3C$
as in equation (3). We also define the subset Y of G by
$D\ge 3C$
as in equation (3). We also define the subset Y of G by
![]() $Y=\{y \in G \mid S(1,y;D)= \emptyset \}$
as in Theorem 2.41. The difference from Section 3 is that we assume G and
$Y=\{y \in G \mid S(1,y;D)= \emptyset \}$
as in Theorem 2.41. The difference from Section 3 is that we assume G and
![]() $\Lambda $
are countable.
$\Lambda $
are countable.
Since
![]() $X\sqcup \mathcal {H}$
is countable, we fix a well-order
$X\sqcup \mathcal {H}$
is countable, we fix a well-order
![]() $\le $
on
$\le $
on
![]() $X\sqcup \mathcal {H}$
by some injection
$X\sqcup \mathcal {H}$
by some injection
![]() $X\sqcup \mathcal {H} \hookrightarrow \mathbb {N}$
. The lexicographic order
$X\sqcup \mathcal {H} \hookrightarrow \mathbb {N}$
. The lexicographic order
![]() $\le _{\mathrm {lex}}$
on
$\le _{\mathrm {lex}}$
on
![]() $(X\sqcup \mathcal {H})^{\mathbb {N}}$
is naturally defined from the order
$(X\sqcup \mathcal {H})^{\mathbb {N}}$
is naturally defined from the order
![]() $\le $
on
$\le $
on
![]() $X\sqcup \mathcal {H}$
, that is, for
$X\sqcup \mathcal {H}$
, that is, for
![]() $w_0=(s_1,s_2,\cdots ), w_1=(t_1,t_2,\cdots ) \in (X\sqcup \mathcal {H})^{\mathbb {N}}$
, we have
$w_0=(s_1,s_2,\cdots ), w_1=(t_1,t_2,\cdots ) \in (X\sqcup \mathcal {H})^{\mathbb {N}}$
, we have
 $$\begin{align*}w_0 <_{\mathrm{lex}} w_1 \iff \exists n\in\mathbb{N} ~\mathrm{s.t.}~ \left(\bigwedge_{i<n} s_i=t_i \right) \wedge s_n<t_n. \end{align*}$$
$$\begin{align*}w_0 <_{\mathrm{lex}} w_1 \iff \exists n\in\mathbb{N} ~\mathrm{s.t.}~ \left(\bigwedge_{i<n} s_i=t_i \right) \wedge s_n<t_n. \end{align*}$$
Similarly, we define the lexicographic order
![]() $\le _{\mathrm {lex}}$
on
$\le _{\mathrm {lex}}$
on
![]() $(X\sqcup \mathcal {H})^n$
for each
$(X\sqcup \mathcal {H})^n$
for each
![]() $n\in \mathbb {N}$
. Note that
$n\in \mathbb {N}$
. Note that
![]() $(X\sqcup \mathcal {H})^{\mathbb {N}}$
becomes a Polish space with the product topology as mentioned in Section 2.1.
$(X\sqcup \mathcal {H})^{\mathbb {N}}$
becomes a Polish space with the product topology as mentioned in Section 2.1.
As suggested at the beginning of this section, the important step of the proof of Theorem 1.1 is for a boundary point
![]() $\xi \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
, picking one geodesic ray in
$\xi \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
, picking one geodesic ray in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from
$\Gamma (G,X\sqcup \mathcal {H})$
from
![]() $1$
to
$1$
to
![]() $\xi $
in a Borel way. This is done by reading the labels of all geodesic rays from
$\xi $
in a Borel way. This is done by reading the labels of all geodesic rays from
![]() $1$
to
$1$
to
![]() $\xi $
and comparing these labels by the lexicographic order defined above. Definition 4.2 and Definition 4.3 are for setting up notations for the labeling.
$\xi $
and comparing these labels by the lexicographic order defined above. Definition 4.2 and Definition 4.3 are for setting up notations for the labeling.
Definition 4.2. For
![]() $w=(s_1,s_2,\cdots )\in (X\sqcup \mathcal {H})^{\mathbb {N}}$
, we define the infinite path
$w=(s_1,s_2,\cdots )\in (X\sqcup \mathcal {H})^{\mathbb {N}}$
, we define the infinite path
![]() $\gamma ^w$
from
$\gamma ^w$
from
![]() $1\in G$
in
$1\in G$
in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
by
$\Gamma (G,X\sqcup \mathcal {H})$
by
![]() $\gamma ^w=(1,x_{w,1},x_{w,2},\cdots )$
, where the n-th vertex
$\gamma ^w=(1,x_{w,1},x_{w,2},\cdots )$
, where the n-th vertex
![]() $x_{w,n}$
is defined by
$x_{w,n}$
is defined by
for each
![]() $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
.
Definition 4.3. For
![]() $\xi \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
, we define the subset
$\xi \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
, we define the subset
![]() $\mathcal {G}(\xi )$
of
$\mathcal {G}(\xi )$
of
![]() $(X\sqcup \mathcal {H})^{\mathbb {N}}$
by
$(X\sqcup \mathcal {H})^{\mathbb {N}}$
by
Remark 4.4. Note that the condition
![]() $Y\text{-}{\lim}\ \gamma ^w=\xi $
in Definition 4.3 implicitly requires that
$Y\text{-}{\lim}\ \gamma ^w=\xi $
in Definition 4.3 implicitly requires that
![]() $\gamma ^w$
converges to infinity in
$\gamma ^w$
converges to infinity in
![]() $\Gamma (G,Y\sqcup \mathcal {H})$
(see Definition 3.21). Also, for any
$\Gamma (G,Y\sqcup \mathcal {H})$
(see Definition 3.21). Also, for any
![]() $\xi \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
, the set
$\xi \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
, the set
![]() $\mathcal {G}(\xi )$
is nonempty by Proposition 3.22.
$\mathcal {G}(\xi )$
is nonempty by Proposition 3.22.
We will show that picking one geodesic ray from
![]() $\mathcal {G}(\xi )$
is possible in Corollary 4.6. Lemma 4.5 is the auxiliary lemma for this.
$\mathcal {G}(\xi )$
is possible in Corollary 4.6. Lemma 4.5 is the auxiliary lemma for this.
Lemma 4.5. For any
![]() $\xi \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
, the set
$\xi \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
, the set
![]() $\mathcal {G}(\xi )$
is closed in
$\mathcal {G}(\xi )$
is closed in
![]() $(X\sqcup \mathcal {H})^{\mathbb {N}}$
.
$(X\sqcup \mathcal {H})^{\mathbb {N}}$
.
Proof. Note that
![]() $(X\sqcup \mathcal {H})^{\mathbb {N}}$
is metrizable. Suppose that a sequence
$(X\sqcup \mathcal {H})^{\mathbb {N}}$
is metrizable. Suppose that a sequence
![]() $(w_i)_{i=1}^\infty $
in
$(w_i)_{i=1}^\infty $
in
![]() $\mathcal {G}(\xi )$
converges to
$\mathcal {G}(\xi )$
converges to
![]() $w\in (X\sqcup \mathcal {H})^{\mathbb {N}}$
. It’s straightforward to see that
$w\in (X\sqcup \mathcal {H})^{\mathbb {N}}$
. It’s straightforward to see that
![]() $\gamma ^w$
is geodesic in
$\gamma ^w$
is geodesic in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
. We will first show
$\Gamma (G,X\sqcup \mathcal {H})$
. We will first show
![]() $|S(\gamma ^w;D)|=\infty $
. Let
$|S(\gamma ^w;D)|=\infty $
. Let
![]() $S(1,\xi ;D)=\{C_1\preceq C_2 \preceq \cdots \}$
(see Definition 3.25). Since
$S(1,\xi ;D)=\{C_1\preceq C_2 \preceq \cdots \}$
(see Definition 3.25). Since
![]() $w_i\in \mathcal {G}(\xi )$
implies
$w_i\in \mathcal {G}(\xi )$
implies
![]() $S(\gamma ^{w_i};D)=S(1,\xi ;D)$
for any
$S(\gamma ^{w_i};D)=S(1,\xi ;D)$
for any
![]() $i\in \mathbb {N}$
, we have for any
$i\in \mathbb {N}$
, we have for any
![]() $i,n\in \mathbb {N}$
,
$i,n\in \mathbb {N}$
,
by Lemma 3.15. For any
![]() $N\in \mathbb {N}$
, we define k by
$N\in \mathbb {N}$
, we define k by
![]() $k=d_{X\cup \mathcal {H}}(1,C_{N+1})+1$
. Since
$k=d_{X\cup \mathcal {H}}(1,C_{N+1})+1$
. Since
![]() $(w_i)_{i=1}^\infty $
converges to w, there exists
$(w_i)_{i=1}^\infty $
converges to w, there exists
![]() $I\in \mathbb {N}$
such that
$I\in \mathbb {N}$
such that
![]() $x_{w_I,m}=x_{w,m}$
for any
$x_{w_I,m}=x_{w,m}$
for any
![]() $m\in \{1,\cdots ,k\}$
(see Definition 4.2). This implies
$m\in \{1,\cdots ,k\}$
(see Definition 4.2). This implies
![]() $ \{C_1,\cdots ,C_N\} \subset S(1,x_{w_I,k};D)=S(1,x_{w,k};D) \subset S(\gamma ^w;D) $
by equation (14) and Lemma 3.18. Hence, we have
$ \{C_1,\cdots ,C_N\} \subset S(1,x_{w_I,k};D)=S(1,x_{w,k};D) \subset S(\gamma ^w;D) $
by equation (14) and Lemma 3.18. Hence, we have
![]() $|S(\gamma ^w;D)|=\infty $
since
$|S(\gamma ^w;D)|=\infty $
since
![]() $N\in \mathbb {N}$
is arbitrary. Since
$N\in \mathbb {N}$
is arbitrary. Since
![]() $(w_i)_{i=1}\infty $
converges to w,
$(w_i)_{i=1}\infty $
converges to w,
![]() $(X\text{-}{\lim}\ \gamma ^{w_i})_{i=1}\infty $
converges to
$(X\text{-}{\lim}\ \gamma ^{w_i})_{i=1}\infty $
converges to
![]() $X\text{-}{\lim}\ \gamma ^w$
in
$X\text{-}{\lim}\ \gamma ^w$
in
![]() $\partial \Gamma (G,X\sqcup \mathcal {H})$
. Hence,
$\partial \Gamma (G,X\sqcup \mathcal {H})$
. Hence,
![]() $(Y\text{-}{\lim}\ \gamma ^{w_i})_{i=1}\infty $
converges to
$(Y\text{-}{\lim}\ \gamma ^{w_i})_{i=1}\infty $
converges to
![]() $Y\text{-}{\lim}\ \gamma ^w$
in
$Y\text{-}{\lim}\ \gamma ^w$
in
![]() $\partial \Gamma (G,Y\sqcup \mathcal {H})$
by Proposition 3.29. This implies
$\partial \Gamma (G,Y\sqcup \mathcal {H})$
by Proposition 3.29. This implies
![]() $Y\text{-}{\lim}\ \gamma ^w=\xi $
by
$Y\text{-}{\lim}\ \gamma ^w=\xi $
by
![]() $Y\text{-}{\lim}\ \gamma ^{w_i}=\xi , \forall i\in \mathbb {N}$
. Thus, we have
$Y\text{-}{\lim}\ \gamma ^{w_i}=\xi , \forall i\in \mathbb {N}$
. Thus, we have
![]() $w\in \mathcal {G}(\xi )$
.
$w\in \mathcal {G}(\xi )$
.
Corollary 4.6. For any
![]() $\xi \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
, the element
$\xi \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
, the element
![]() $\min _{\le _{\mathrm {lex}}} \mathcal {G}(\xi )$
exists.
$\min _{\le _{\mathrm {lex}}} \mathcal {G}(\xi )$
exists.
Proof. For each
![]() $n\in \mathbb {N}$
, we define the element
$n\in \mathbb {N}$
, we define the element
![]() $s_{\xi ,n}\in X\sqcup \mathcal {H}$
and the subset
$s_{\xi ,n}\in X\sqcup \mathcal {H}$
and the subset
![]() $\mathcal {G}(\xi )_n$
of
$\mathcal {G}(\xi )_n$
of
![]() $\mathcal {G}(\xi )$
inductively as follows:
$\mathcal {G}(\xi )$
inductively as follows:
 $$ \begin{align*} s_{\xi,1}&=\min \{ s_1 \in (X\sqcup\mathcal{H},\le) \mid \exists w\in \mathcal{G}(\xi) ~\mathrm{s.t.}~ w=(s_1,s_2,\cdots) \}, \\ \mathcal{G}(\xi)_1&=\{ w\in \mathcal{G}(\xi) \mid w=(s_{\xi,1},s_2,\cdots) \}, \\ s_{\xi,n+1}&=\min \{ s_{n+1} \in (X\sqcup\mathcal{H},\le) \mid \exists w\in \mathcal{G}(\xi)_n ~\mathrm{s.t.}~ w=(s_{\xi,1},\cdots,s_{\xi,n},s_{n+1},\cdots) \}, \\ \mathcal{G}(\xi)_{n+1}&=\{ w\in \mathcal{G}(\xi)_n \mid w=(s_{\xi,1},\cdots,s_{\xi,n},s_{\xi,n+1},\cdots) \}. \end{align*} $$
$$ \begin{align*} s_{\xi,1}&=\min \{ s_1 \in (X\sqcup\mathcal{H},\le) \mid \exists w\in \mathcal{G}(\xi) ~\mathrm{s.t.}~ w=(s_1,s_2,\cdots) \}, \\ \mathcal{G}(\xi)_1&=\{ w\in \mathcal{G}(\xi) \mid w=(s_{\xi,1},s_2,\cdots) \}, \\ s_{\xi,n+1}&=\min \{ s_{n+1} \in (X\sqcup\mathcal{H},\le) \mid \exists w\in \mathcal{G}(\xi)_n ~\mathrm{s.t.}~ w=(s_{\xi,1},\cdots,s_{\xi,n},s_{n+1},\cdots) \}, \\ \mathcal{G}(\xi)_{n+1}&=\{ w\in \mathcal{G}(\xi)_n \mid w=(s_{\xi,1},\cdots,s_{\xi,n},s_{\xi,n+1},\cdots) \}. \end{align*} $$
Note that each
![]() $\mathcal {G}(\xi )_n$
is nonempty since
$\mathcal {G}(\xi )_n$
is nonempty since
![]() $\mathcal {G}(\xi )$
is nonempty. We define the element
$\mathcal {G}(\xi )$
is nonempty. We define the element
![]() $w_\xi \in (X\sqcup \mathcal {H})^{\mathbb {N}}$
by
$w_\xi \in (X\sqcup \mathcal {H})^{\mathbb {N}}$
by
![]() $w_\xi =(s_{\xi ,1},s_{\xi ,2},s_{\xi ,3},\cdots )$
and take an element
$w_\xi =(s_{\xi ,1},s_{\xi ,2},s_{\xi ,3},\cdots )$
and take an element
![]() $w_n \in \mathcal {G}(\xi )_n$
for each
$w_n \in \mathcal {G}(\xi )_n$
for each
![]() $n\in \mathbb {N}$
. Since
$n\in \mathbb {N}$
. Since
![]() $(w_n)_{n=1}\infty $
converges to
$(w_n)_{n=1}\infty $
converges to
![]() $w_\xi $
in
$w_\xi $
in
![]() $(X\sqcup \mathcal {H})^{\mathbb {N}}$
, we have
$(X\sqcup \mathcal {H})^{\mathbb {N}}$
, we have
![]() $w_\xi \in \mathcal {G}(\xi )$
by Lemma 4.5. Since
$w_\xi \in \mathcal {G}(\xi )$
by Lemma 4.5. Since
![]() $w_\xi \in \bigcap _{n=1}^\infty \mathcal {G}(\xi )_n$
, we have
$w_\xi \in \bigcap _{n=1}^\infty \mathcal {G}(\xi )_n$
, we have
![]() $w_\xi \le _{\mathrm {lex}} w$
for any
$w_\xi \le _{\mathrm {lex}} w$
for any
![]() $w\in \mathcal {G}(\xi )$
.
$w\in \mathcal {G}(\xi )$
.
Definition 4.7 below is well-defined by Corollary 4.6.
Definition 4.7. We define the map
![]() $\Phi \colon \partial \Gamma (G,Y\sqcup \mathcal {H}) \to (X\sqcup \mathcal {H})^{\mathbb {N}}$
by
$\Phi \colon \partial \Gamma (G,Y\sqcup \mathcal {H}) \to (X\sqcup \mathcal {H})^{\mathbb {N}}$
by
For each
![]() $\xi \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
, we denote
$\xi \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
, we denote
![]() $\Phi (\xi )=(s_{\xi ,1},s_{\xi ,2},s_{\xi ,3},\cdots )$
.
$\Phi (\xi )=(s_{\xi ,1},s_{\xi ,2},s_{\xi ,3},\cdots )$
.
We will show that the map
![]() $\Phi (\xi )$
is injective and continuous in Lemma 4.8 and Lemma 4.9. This will finish the step of picking a geodesic ray for a boundary point.
$\Phi (\xi )$
is injective and continuous in Lemma 4.8 and Lemma 4.9. This will finish the step of picking a geodesic ray for a boundary point.
Lemma 4.8. The map
![]() $\Phi \colon \partial \Gamma (G,Y\sqcup \mathcal {H}) \to (X\sqcup \mathcal {H})^{\mathbb {N}} $
is injective.
$\Phi \colon \partial \Gamma (G,Y\sqcup \mathcal {H}) \to (X\sqcup \mathcal {H})^{\mathbb {N}} $
is injective.
Proof. This follows since we have
![]() $\xi =Y\text{-}{\lim}\ \gamma ^{\Phi (\xi )}$
for any
$\xi =Y\text{-}{\lim}\ \gamma ^{\Phi (\xi )}$
for any
![]() $\xi \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
.
$\xi \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
.
Recall that we put the discrete topology on the countable set
![]() $X\sqcup \mathcal {H}$
and the product topology on
$X\sqcup \mathcal {H}$
and the product topology on
![]() $(X\sqcup \mathcal {H})^{\mathbb {N}}$
.
$(X\sqcup \mathcal {H})^{\mathbb {N}}$
.
Lemma 4.9. The map
![]() $\Phi \colon \partial \Gamma (G,Y\sqcup \mathcal {H}) \to (X\sqcup \mathcal {H})^{\mathbb {N}}$
is continuous.
$\Phi \colon \partial \Gamma (G,Y\sqcup \mathcal {H}) \to (X\sqcup \mathcal {H})^{\mathbb {N}}$
is continuous.
Proof. It’s enough to show that for any
![]() $\xi \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
and any
$\xi \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
and any
![]() $k\in \mathbb {N}$
, there exists an open neighborhood U of
$k\in \mathbb {N}$
, there exists an open neighborhood U of
![]() $\xi $
in
$\xi $
in
![]() $\partial \Gamma (G,Y\sqcup \mathcal {H})$
such that
$\partial \Gamma (G,Y\sqcup \mathcal {H})$
such that
![]() $s_{\eta ,n}=s_{\xi ,n}$
for any
$s_{\eta ,n}=s_{\xi ,n}$
for any
![]() $\eta \in U$
and any
$\eta \in U$
and any
![]() $n\in \{1,\cdots ,k\}$
. Indeed, given
$n\in \{1,\cdots ,k\}$
. Indeed, given
![]() $\xi \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
, the open sets
$\xi \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
, the open sets
![]() $\{V_k\}_{k=1}^\infty $
defined by
$\{V_k\}_{k=1}^\infty $
defined by
![]() $V_k=\{(s_n)_{n=1}^\infty \in (X\sqcup \mathcal {H})^{\mathbb {N}} \mid s_n=s_{\xi ,n}, \forall n\in \{1,\cdots ,k\} \}$
form a neighborhood basis of
$V_k=\{(s_n)_{n=1}^\infty \in (X\sqcup \mathcal {H})^{\mathbb {N}} \mid s_n=s_{\xi ,n}, \forall n\in \{1,\cdots ,k\} \}$
form a neighborhood basis of
![]() $\Phi (\xi )$
. Hence, for any open neighborhood V of
$\Phi (\xi )$
. Hence, for any open neighborhood V of
![]() $\Phi (\xi )$
, there exists
$\Phi (\xi )$
, there exists
![]() $k\in \mathbb {N}$
such that
$k\in \mathbb {N}$
such that
![]() $V_k \subset V$
. For this k, we will be able to take an open neighborhood U of
$V_k \subset V$
. For this k, we will be able to take an open neighborhood U of
![]() $\xi $
such that
$\xi $
such that
![]() $\Phi (U)\subset V_k$
. This will imply continuity of
$\Phi (U)\subset V_k$
. This will imply continuity of
![]() $\Phi $
at
$\Phi $
at
![]() $\xi $
. Hence, we will get continuity of
$\xi $
. Hence, we will get continuity of
![]() $\Phi $
since
$\Phi $
since
![]() $\xi \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
is arbitrary.
$\xi \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
is arbitrary.
Let
![]() $S(1,\xi ;D)=\{C_1\preceq C_2 \preceq \cdots \}$
(see Definition 3.25). By
$S(1,\xi ;D)=\{C_1\preceq C_2 \preceq \cdots \}$
(see Definition 3.25). By
![]() $\lim _{i\to \infty }d_{X\cup \mathcal {H}}(1,C_i)=\infty $
, there exists
$\lim _{i\to \infty }d_{X\cup \mathcal {H}}(1,C_i)=\infty $
, there exists
![]() $N\in \mathbb {N}$
such that
$N\in \mathbb {N}$
such that
![]() $d_{X\cup \mathcal {H}}(1,C_N)> k$
. By Proposition 3.23, there exists an open neighborhood U of
$d_{X\cup \mathcal {H}}(1,C_N)> k$
. By Proposition 3.23, there exists an open neighborhood U of
![]() $\xi $
in
$\xi $
in
![]() $\partial \Gamma (G,Y\sqcup \mathcal {H})$
such that for any
$\partial \Gamma (G,Y\sqcup \mathcal {H})$
such that for any
![]() $\eta \in U$
and any
$\eta \in U$
and any
![]() $w \in \mathcal {G}(\eta )$
, the path
$w \in \mathcal {G}(\eta )$
, the path
![]() $\gamma ^w$
penetrates
$\gamma ^w$
penetrates
![]() $C_i$
for any
$C_i$
for any
![]() $i\in \{1,\cdots ,N\}$
. Let
$i\in \{1,\cdots ,N\}$
. Let
![]() $\eta \in U$
. We define m by
$\eta \in U$
. We define m by
![]() $m=d_{X\cup \mathcal {H}}(1,C_N)$
for brevity and let
$m=d_{X\cup \mathcal {H}}(1,C_N)$
for brevity and let
![]() $C_N$
be an
$C_N$
be an
![]() $H_\lambda $
-coset. We claim
$H_\lambda $
-coset. We claim
 $$ \begin{align} \begin{aligned} &\{(s_1,\cdots,s_m) \in (X\sqcup\mathcal{H})^m \mid \exists w\in\mathcal{G}(\eta) ~\mathrm{s.t.}~ w=(s_1,\cdots,s_m,\cdots) \} \\ =& \{(s_1,\cdots,s_m) \in (X\sqcup\mathcal{H})^m \mid \exists w\in\mathcal{G}(\xi) ~\mathrm{s.t.}~ w=(s_1,\cdots,s_m,\cdots) \}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\{(s_1,\cdots,s_m) \in (X\sqcup\mathcal{H})^m \mid \exists w\in\mathcal{G}(\eta) ~\mathrm{s.t.}~ w=(s_1,\cdots,s_m,\cdots) \} \\ =& \{(s_1,\cdots,s_m) \in (X\sqcup\mathcal{H})^m \mid \exists w\in\mathcal{G}(\xi) ~\mathrm{s.t.}~ w=(s_1,\cdots,s_m,\cdots) \}. \end{aligned} \end{align} $$
Indeed, for any
![]() $w_1\in \mathcal {G}(\eta )$
and
$w_1\in \mathcal {G}(\eta )$
and
![]() $w_2\in \mathcal {G}(\xi )$
, let
$w_2\in \mathcal {G}(\xi )$
, let
![]() $e_1,e_2$
be the edges in
$e_1,e_2$
be the edges in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
whose labels are in
$\Gamma (G,X\sqcup \mathcal {H})$
whose labels are in
![]() $H_\lambda $
such that
$H_\lambda $
such that
![]() $e_1$
is from
$e_1$
is from
![]() $\gamma ^{w_1}_{in}(C_N)$
to
$\gamma ^{w_1}_{in}(C_N)$
to
![]() $\gamma ^{w_2}_{out}(C_N)$
and
$\gamma ^{w_2}_{out}(C_N)$
and
![]() $e_2$
is from
$e_2$
is from
![]() $\gamma ^{w_2}_{in}(C_N)$
to
$\gamma ^{w_2}_{in}(C_N)$
to
![]() $\gamma ^{w_1}_{out}(C_N)$
. We have
$\gamma ^{w_1}_{out}(C_N)$
. We have
![]() $x_{w_1,m}=\gamma ^{w_1}_{in}(C_N)$
,
$x_{w_1,m}=\gamma ^{w_1}_{in}(C_N)$
,
![]() $x_{w_1,m+1}=\gamma ^{w_1}_{out}(C_N)$
,
$x_{w_1,m+1}=\gamma ^{w_1}_{out}(C_N)$
,
![]() $x_{w_2,m}=\gamma ^{w_2}_{in}(C_N)$
, and
$x_{w_2,m}=\gamma ^{w_2}_{in}(C_N)$
, and
![]() $x_{w_2,m+1}=\gamma ^{w_2}_{out}(C_N)$
by Lemma 2.36. Hence, the paths
$x_{w_2,m+1}=\gamma ^{w_2}_{out}(C_N)$
by Lemma 2.36. Hence, the paths
![]() $\alpha _1,\alpha _2$
defined by
$\alpha _1,\alpha _2$
defined by
are geodesic in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
. By
$\Gamma (G,X\sqcup \mathcal {H})$
. By
![]() $Y\text{-}{\lim}\ \alpha _1=Y\text{-}{\lim}\ \gamma ^{w_2}=\xi $
and
$Y\text{-}{\lim}\ \alpha _1=Y\text{-}{\lim}\ \gamma ^{w_2}=\xi $
and
![]() $Y\text{-}{\lim}\ \alpha _2=Y\text{-}{\lim}\ \gamma ^{w_1}=\eta $
, we have
$Y\text{-}{\lim}\ \alpha _2=Y\text{-}{\lim}\ \gamma ^{w_1}=\eta $
, we have
![]() $\alpha _1\in \mathcal {G}(\xi )$
and
$\alpha _1\in \mathcal {G}(\xi )$
and
![]() $\alpha _2 \in \mathcal {G}(\eta )$
. This implies equation (15). By equation (15), we have
$\alpha _2 \in \mathcal {G}(\eta )$
. This implies equation (15). By equation (15), we have
![]() $s_{\eta ,n}=s_{\xi ,n}$
for any
$s_{\eta ,n}=s_{\xi ,n}$
for any
![]() $n\in \{1,\cdots ,m\}$
.
$n\in \{1,\cdots ,m\}$
.

Figure 5 Proof of Proposition 4.10.
We are now ready to show hyperfiniteness of the boundary action in Proposition 4.10, which is essentially the proof of Theorem 1.1. The difference of the conditions in Proposition 4.10 from those at the beginning of this section is that we further assume that
![]() $\Lambda $
is finite.
$\Lambda $
is finite.
Proposition 4.10. Suppose that G is a countable group, X is a subset of G and
![]() $\{H_\lambda \}_{\lambda \in \Lambda }$
is a finite collection of subgroups of G hyperbolically embedded in
$\{H_\lambda \}_{\lambda \in \Lambda }$
is a finite collection of subgroups of G hyperbolically embedded in
![]() $(G,X)$
. Let
$(G,X)$
. Let
![]() $C>0$
as in Proposition 2.30, and fix
$C>0$
as in Proposition 2.30, and fix
![]() $D>0$
satisfying
$D>0$
satisfying
![]() $D\ge 3C$
. We also define the subset Y of G by
$D\ge 3C$
. We also define the subset Y of G by
![]() $Y=\{y \in G \mid S(1,y;D)= \emptyset \}$
as in equation (4). Then, the orbit equivalence relation
$Y=\{y \in G \mid S(1,y;D)= \emptyset \}$
as in equation (4). Then, the orbit equivalence relation
![]() $E_G$
on
$E_G$
on
![]() $\partial \Gamma (G,Y\sqcup \mathcal {H})$
induced by the action
$\partial \Gamma (G,Y\sqcup \mathcal {H})$
induced by the action
![]() $G\curvearrowright \partial \Gamma (G,Y\sqcup \mathcal {H})$
is a hyperfinite CBER.
$G\curvearrowright \partial \Gamma (G,Y\sqcup \mathcal {H})$
is a hyperfinite CBER.
Proof. Since G is countable,
![]() $\partial \Gamma (G,Y\sqcup \mathcal {H})$
is Polish being a closed subset of the Polish space
$\partial \Gamma (G,Y\sqcup \mathcal {H})$
is Polish being a closed subset of the Polish space
![]() $G\cup \Gamma (G,Y\sqcup \mathcal {H})$
by Lemma 4.1. Since
$G\cup \Gamma (G,Y\sqcup \mathcal {H})$
by Lemma 4.1. Since
![]() $\partial \Gamma (G,Y\sqcup \mathcal {H})$
is a Polish space and G is a countable group acting on
$\partial \Gamma (G,Y\sqcup \mathcal {H})$
is a Polish space and G is a countable group acting on
![]() $\partial \Gamma (G,Y\sqcup \mathcal {H})$
homeomorphically,
$\partial \Gamma (G,Y\sqcup \mathcal {H})$
homeomorphically,
![]() $E_G$
is a CBER by Lemma 2.7. We will show that
$E_G$
is a CBER by Lemma 2.7. We will show that
![]() $E_G$
is hyperfinite. Define the subsets
$E_G$
is hyperfinite. Define the subsets
![]() $R,R_1$
of
$R,R_1$
of
![]() $(\partial \Gamma (G,Y\sqcup \mathcal {H}))^2$
by
$(\partial \Gamma (G,Y\sqcup \mathcal {H}))^2$
by
![]() $R=(\Phi \times \Phi )^{-1}(E_t(X\sqcup \mathcal {H}))$
and
$R=(\Phi \times \Phi )^{-1}(E_t(X\sqcup \mathcal {H}))$
and
![]() $R_1=R\cap E_G$
(see Definition 2.8 for
$R_1=R\cap E_G$
(see Definition 2.8 for
![]() $E_t(X\sqcup \mathcal {H})$
). Since
$E_t(X\sqcup \mathcal {H})$
). Since
![]() $E_t(X\sqcup \mathcal {H})$
is hyperfinite by Proposition 2.9 and the map
$E_t(X\sqcup \mathcal {H})$
is hyperfinite by Proposition 2.9 and the map
![]() $\Phi $
is an injective Borel measurable map by Lemma 4.8 and Lemma 4.9, R is a hyperfinite CBER on
$\Phi $
is an injective Borel measurable map by Lemma 4.8 and Lemma 4.9, R is a hyperfinite CBER on
![]() $\partial \Gamma (G,Y\sqcup \mathcal {H})$
. Hence,
$\partial \Gamma (G,Y\sqcup \mathcal {H})$
. Hence,
![]() $R_1$
is also hyperfinite. We define the constant K by
$R_1$
is also hyperfinite. We define the constant K by
 $$ \begin{align} K=\left( \max_{\lambda\in\Lambda} |\{h\in H_\lambda \mid \widehat{d}_{\lambda}(1,h)\le 4C \}| \right)^2. \end{align} $$
$$ \begin{align} K=\left( \max_{\lambda\in\Lambda} |\{h\in H_\lambda \mid \widehat{d}_{\lambda}(1,h)\le 4C \}| \right)^2. \end{align} $$
Note
![]() $K<\infty $
, since
$K<\infty $
, since
![]() $\Lambda $
is finite by our assumption and each
$\Lambda $
is finite by our assumption and each
![]() $\widehat {d}_{\lambda }$
is locally finite. We will show that each
$\widehat {d}_{\lambda }$
is locally finite. We will show that each
![]() $E_G$
-class is composed of at most K equivalence classes of
$E_G$
-class is composed of at most K equivalence classes of
![]() $R_1$
. This implies that
$R_1$
. This implies that
![]() $E_G$
is hyperfinite by Proposition 2.10. Suppose for contradiction that there exist
$E_G$
is hyperfinite by Proposition 2.10. Suppose for contradiction that there exist
![]() $\xi _0,\xi _1,\cdots ,\xi _K \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
such that
$\xi _0,\xi _1,\cdots ,\xi _K \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
such that
![]() $(\xi _i,\xi _j)\in E_G \setminus R_1$
for any distinct
$(\xi _i,\xi _j)\in E_G \setminus R_1$
for any distinct
![]() $i,j\in \{0,1,\cdots ,K\}$
(i.e.,
$i,j\in \{0,1,\cdots ,K\}$
(i.e.,
![]() $i\neq j$
). For each
$i\neq j$
). For each
![]() $i\in \{0,1,\cdots ,K\}$
, there exists
$i\in \{0,1,\cdots ,K\}$
, there exists
![]() $g_i \in G$
such that
$g_i \in G$
such that
![]() $g_i\xi _i = \xi _0$
by
$g_i\xi _i = \xi _0$
by
![]() $(\xi _i,\xi _0)\in E_G$
. We take
$(\xi _i,\xi _0)\in E_G$
. We take
![]() $g_0=1$
. Let
$g_0=1$
. Let
![]() $ S(\gamma ^{\Phi (\xi _0)};D)=\{C_1\preceq C_2\preceq \cdots \}. $
By Corollary 3.28, there exists
$ S(\gamma ^{\Phi (\xi _0)};D)=\{C_1\preceq C_2\preceq \cdots \}. $
By Corollary 3.28, there exists
![]() $N_0\in \mathbb {N}$
such that for any
$N_0\in \mathbb {N}$
such that for any
![]() $i\in \{0,1,\cdots ,K\}$
and any
$i\in \{0,1,\cdots ,K\}$
and any
![]() $n\ge N_0$
, the path
$n\ge N_0$
, the path
![]() $g_i\gamma ^{\Phi (\xi _i)}$
penetrates
$g_i\gamma ^{\Phi (\xi _i)}$
penetrates
![]() $C_n$
and satisfies equation (11). Define
$C_n$
and satisfies equation (11). Define
![]() $m_i$
by
$m_i$
by
for each
![]() $i\in \{0,1,\cdots ,K\}$
. Note
$i\in \{0,1,\cdots ,K\}$
. Note
![]() $m_0=d_{X\cup \mathcal {H}}(1,C_{N_0})$
. For any distinct
$m_0=d_{X\cup \mathcal {H}}(1,C_{N_0})$
. For any distinct
![]() $i,j\in \{0,1,\cdots ,K\}$
,
$i,j\in \{0,1,\cdots ,K\}$
,
![]() $(\xi _i,\xi _j)\notin R_1$
implies
$(\xi _i,\xi _j)\notin R_1$
implies
![]() $(\Phi (\xi _i),\Phi (\xi _j))\notin E_t(X\sqcup \mathcal {H})$
. Hence, there exists
$(\Phi (\xi _i),\Phi (\xi _j))\notin E_t(X\sqcup \mathcal {H})$
. Hence, there exists
![]() $k\in \mathbb {N}$
such that
$k\in \mathbb {N}$
such that
for any distinct
![]() $i,j\in \{0,1,\cdots ,K\}$
. On the other hand, there exists
$i,j\in \{0,1,\cdots ,K\}$
. On the other hand, there exists
![]() $N_1\in \mathbb {N}$
such that
$N_1\in \mathbb {N}$
such that
![]() $d_{X\cup \mathcal {H}}(1,\gamma _{in}^{\Phi (\xi _0)}(C_{N_1}))> m_0+k$
by
$d_{X\cup \mathcal {H}}(1,\gamma _{in}^{\Phi (\xi _0)}(C_{N_1}))> m_0+k$
by
![]() $\lim _{n\to \infty }d_{X\cup \mathcal {H}}(1,\gamma _{in}^{\Phi (\xi _0)}(C_n)) = \infty $
. Define
$\lim _{n\to \infty }d_{X\cup \mathcal {H}}(1,\gamma _{in}^{\Phi (\xi _0)}(C_n)) = \infty $
. Define
![]() $\ell \in \mathbb {N}$
by
$\ell \in \mathbb {N}$
by
![]() $\ell =d_{X\cup \mathcal {H}}(C_{N_0},C_{N_1})+1$
. By Lemma 3.3, we have
$\ell =d_{X\cup \mathcal {H}}(C_{N_0},C_{N_1})+1$
. By Lemma 3.3, we have
for any
![]() $i\in \{0,1,\cdots ,K\}$
. In particular,
$i\in \{0,1,\cdots ,K\}$
. In particular,
![]() $m_0+\ell =d_{X\cup \mathcal {H}}(1,\gamma _{in}^{\Phi (\xi _0)}(C_{N_1}))> m_0+k$
implies
$m_0+\ell =d_{X\cup \mathcal {H}}(1,\gamma _{in}^{\Phi (\xi _0)}(C_{N_1}))> m_0+k$
implies
![]() $\ell> k$
. By equation (11), the set
$\ell> k$
. By equation (11), the set
has at most K elements (see equation (16)). Hence, by the pigeonhole principle, there exist distinct
![]() $i,j\in \{0,1,\cdots ,K\}$
such that
$i,j\in \{0,1,\cdots ,K\}$
such that
By equation (18), minimality of
![]() $\Phi (\xi _i)$
in
$\Phi (\xi _i)$
in
![]() $(\mathcal {G}(\xi _i), \le _{\mathrm {lex}})$
, and minimality of
$(\mathcal {G}(\xi _i), \le _{\mathrm {lex}})$
, and minimality of
![]() $\Phi (\xi _j)$
in
$\Phi (\xi _j)$
in
![]() $(\mathcal {G}(\xi _j), \le _{\mathrm {lex}})$
, we have
$(\mathcal {G}(\xi _j), \le _{\mathrm {lex}})$
, we have
Indeed, suppose for contradiction that equation (19) doesn’t hold. We assume without loss of generality,
![]() $(s_{\xi _i,m_i+1},\cdots ,s_{\xi _i,m_i+\ell }) <_{{\mathrm {lex}}} (s_{\xi _j,m_j+1},\cdots ,s_{\xi _j,m_j+\ell })$
and define
$(s_{\xi _i,m_i+1},\cdots ,s_{\xi _i,m_i+\ell }) <_{{\mathrm {lex}}} (s_{\xi _j,m_j+1},\cdots ,s_{\xi _j,m_j+\ell })$
and define
![]() $a,b$
by
$a,b$
by
![]() $a=(g_i\gamma ^{\Phi (\xi _i)})_{in}(C_{N_0})$
and
$a=(g_i\gamma ^{\Phi (\xi _i)})_{in}(C_{N_0})$
and
![]() $b=(g_i\gamma ^{\Phi (\xi _i)})_{in}(C_{N_1})$
for brevity. By equation (18), the path
$b=(g_i\gamma ^{\Phi (\xi _i)})_{in}(C_{N_1})$
for brevity. By equation (18), the path
is well-defined. Since
![]() $\alpha $
is a geodesic ray in
$\alpha $
is a geodesic ray in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from
$\Gamma (G,X\sqcup \mathcal {H})$
from
![]() $g_j$
satisfying
$g_j$
satisfying
![]() $Y\text{-}{\lim}\ \alpha = Y\text{-}{\lim}\ g_j\gamma ^{\Phi (\xi _j)}=g_j \xi _j$
, the path
$Y\text{-}{\lim}\ \alpha = Y\text{-}{\lim}\ g_j\gamma ^{\Phi (\xi _j)}=g_j \xi _j$
, the path
![]() $g_j^{-1}\alpha $
is a geodesic ray from 1 with
$g_j^{-1}\alpha $
is a geodesic ray from 1 with
![]() $Y\text{-}{\lim}\ g_j^{-1}\alpha = \xi _j$
. Hence, we have
$Y\text{-}{\lim}\ g_j^{-1}\alpha = \xi _j$
. Hence, we have
![]() $\mathbf {Lab}(\alpha )=\mathbf {Lab}(g_j^{-1}\alpha )\in \mathcal {G}(\xi _j)$
, where
$\mathbf {Lab}(\alpha )=\mathbf {Lab}(g_j^{-1}\alpha )\in \mathcal {G}(\xi _j)$
, where
![]() $\mathbf {Lab}$
denotes labels of paths in
$\mathbf {Lab}$
denotes labels of paths in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
. On the other hand, we have
$\Gamma (G,X\sqcup \mathcal {H})$
. On the other hand, we have
![]() $\mathbf {Lab}(\alpha )<_{{\mathrm {lex}}} \mathbf {Lab}(g_j\gamma ^{\Phi (\xi _j)})=\Phi (\xi _j)$
by
$\mathbf {Lab}(\alpha )<_{{\mathrm {lex}}} \mathbf {Lab}(g_j\gamma ^{\Phi (\xi _j)})=\Phi (\xi _j)$
by
![]() $(s_{\xi _i,m_i+1},\cdots ,s_{\xi _i,m_i+\ell }) <_{{\mathrm {lex}}} (s_{\xi _j,m_j+1},\cdots ,s_{\xi _j,m_j+\ell })$
. This contradicts that
$(s_{\xi _i,m_i+1},\cdots ,s_{\xi _i,m_i+\ell }) <_{{\mathrm {lex}}} (s_{\xi _j,m_j+1},\cdots ,s_{\xi _j,m_j+\ell })$
. This contradicts that
![]() $\Phi (\xi _j)$
is minimal in
$\Phi (\xi _j)$
is minimal in
![]() $(\mathcal {G}(\xi _j), \le _{\mathrm {lex}})$
. Hence, we have
$(\mathcal {G}(\xi _j), \le _{\mathrm {lex}})$
. Hence, we have
![]() $(s_{\xi _i,m_i+1},\cdots ,s_{\xi _i,m_i+\ell }) \ge _{{\mathrm {lex}}} (s_{\xi _j,m_j+1},\cdots ,s_{\xi _j,m_j+\ell })$
. We can also show the converse inequality from minimality of
$(s_{\xi _i,m_i+1},\cdots ,s_{\xi _i,m_i+\ell }) \ge _{{\mathrm {lex}}} (s_{\xi _j,m_j+1},\cdots ,s_{\xi _j,m_j+\ell })$
. We can also show the converse inequality from minimality of
![]() $\Phi (\xi _i)$
in
$\Phi (\xi _i)$
in
![]() $(\mathcal {G}(\xi _i), \le _{\mathrm {lex}})$
. Thus, we get equation (19), which contradicts equation (17) by
$(\mathcal {G}(\xi _i), \le _{\mathrm {lex}})$
. Thus, we get equation (19), which contradicts equation (17) by
![]() $\ell>k$
.
$\ell>k$
.
Proof of Theorem 1.1
By Theorem 2.39
![]() $(AH_4)$
, there exist a proper infinite subgroup H and a subset X of G such that
$(AH_4)$
, there exist a proper infinite subgroup H and a subset X of G such that
![]() $H\hookrightarrow _h (G,X)$
. Let
$H\hookrightarrow _h (G,X)$
. Let
![]() $C>0$
as in Proposition 2.30, and fix
$C>0$
as in Proposition 2.30, and fix
![]() $D>0$
satisfying
$D>0$
satisfying
![]() $D\ge 3C$
. We also define the subset Y of G by
$D\ge 3C$
. We also define the subset Y of G by
![]() $Y=\{y \in G \mid S(1,y;D)= \emptyset \}$
as in equation (4). By Theorem 2.41 and Lemma 2.43, the Caylay graph
$Y=\{y \in G \mid S(1,y;D)= \emptyset \}$
as in equation (4). By Theorem 2.41 and Lemma 2.43, the Caylay graph
![]() $\Gamma (G,Y\sqcup H)$
is hyperbolic,
$\Gamma (G,Y\sqcup H)$
is hyperbolic,
![]() $|\partial \Gamma (G,Y\sqcup H)|>2$
, and the action of G on
$|\partial \Gamma (G,Y\sqcup H)|>2$
, and the action of G on
![]() $\Gamma (G,Y\sqcup H)$
is acylindrical. By Proposition 4.10, the orbit equivalence relation
$\Gamma (G,Y\sqcup H)$
is acylindrical. By Proposition 4.10, the orbit equivalence relation
![]() $E_G$
induced by the action of G on
$E_G$
induced by the action of G on
![]() $\partial \Gamma (G,Y\sqcup H)$
is hyperfinite. Thus,
$\partial \Gamma (G,Y\sqcup H)$
is hyperfinite. Thus,
![]() $S=Y\cup H$
is a generator of G satisfying the statement of Theorem 1.1.
$S=Y\cup H$
is a generator of G satisfying the statement of Theorem 1.1.
5. Application to topologically amenable actions
In this short section, by applying Theorem 1.1 we will prove that any countable acylindrically hyperbolic group admits a topologically amenable action on a Polish space (see Theorem 5.5). We begin with introducing some facts about topologically amenable actions and stabilizers of boundary points for a group acting on a hyperbolic space. For more on topologically amenable actions, readers are referred to [Reference Brown and Ozawa3].
Definition 5.1. Suppose that G is a countable group and X is a Polish space. A homeomorphic action
![]() $G\curvearrowright X$
is called topologically amenable if for any finite subset S of G, any compact set K of X and any
$G\curvearrowright X$
is called topologically amenable if for any finite subset S of G, any compact set K of X and any
![]() $\varepsilon>0$
, there exists a continuous map
$\varepsilon>0$
, there exists a continuous map
![]() $p\colon X\to \mathrm {Prob}(G)$
such that
$p\colon X\to \mathrm {Prob}(G)$
such that
Theorem 5.2 immediately follows from Theorem A.1.1 and Theorem A.3.1 of [Reference Frisch, Kechris, Shinko and Vidnyánszky8] and connects hyperfiniteness and topological amenability of group actions. Note that in Theorem A.3.1 of [Reference Frisch, Kechris, Shinko and Vidnyánszky8], the condition that the Polish space is
![]() $\sigma $
-compact is used only to show that topological amenability implies Borel amenability.
$\sigma $
-compact is used only to show that topological amenability implies Borel amenability.
Theorem 5.2. Let
![]() $G \curvearrowright X$
be a homeomorphic action of a countable group G on a Polish space X. If
$G \curvearrowright X$
be a homeomorphic action of a countable group G on a Polish space X. If
![]() $E_G^X$
is hyperfinite and for any
$E_G^X$
is hyperfinite and for any
![]() $x\in X$
, its stabilizer
$x\in X$
, its stabilizer
![]() $\mathrm {Stab}_G(x)=\{g\in G \mid gx=x\}$
is amenable, then
$\mathrm {Stab}_G(x)=\{g\in G \mid gx=x\}$
is amenable, then
![]() $G\curvearrowright X$
is topologically amenable.
$G\curvearrowright X$
is topologically amenable.
Proof. Hyperfiniteness of
![]() $E_G^X$
and amenability of stabilizers imply Borel amenability of the action
$E_G^X$
and amenability of stabilizers imply Borel amenability of the action
![]() $G\curvearrowright X$
by [Reference Frisch, Kechris, Shinko and Vidnyánszky8, Theorem A.1.1]. Borel amenability trivially implies measure-amenability by their definitions. Measure-amenability implies topological amenability by [Reference Frisch, Kechris, Shinko and Vidnyánszky8, Theorem A.3.1].
$G\curvearrowright X$
by [Reference Frisch, Kechris, Shinko and Vidnyánszky8, Theorem A.1.1]. Borel amenability trivially implies measure-amenability by their definitions. Measure-amenability implies topological amenability by [Reference Frisch, Kechris, Shinko and Vidnyánszky8, Theorem A.3.1].
We will next show that boundary stabilizers of a group acting acylindrically on a hyperbolic space are amenable in Lemma 5.4. Lemma 5.3 is auxiliary for Lemma 5.4. Both of these lemmas should be well-known to experts, but I will record the sketch of proofs for convenience of readers. Note that the
![]() $(1,\delta )$
-quasi-geodesic ray p in Lemma 5.3 may not be continuous.
$(1,\delta )$
-quasi-geodesic ray p in Lemma 5.3 may not be continuous.
Lemma 5.3. Suppose that
![]() $(S,d_S)$
is a
$(S,d_S)$
is a
![]() $\delta $
-hyperbolic geodesic metric space with
$\delta $
-hyperbolic geodesic metric space with
![]() $\delta \in \mathbb {N}$
, then for any
$\delta \in \mathbb {N}$
, then for any
![]() $o\in S$
and
$o\in S$
and
![]() $\xi \in \partial S$
, there exists a
$\xi \in \partial S$
, there exists a
![]() $(1,\delta )$
-quasi-geodesic ray p from o to
$(1,\delta )$
-quasi-geodesic ray p from o to
![]() $\xi $
, that is,
$\xi $
, that is,
![]() $p\colon [0,\infty )\to S$
satisfies
$p\colon [0,\infty )\to S$
satisfies
![]() $p(0)=o$
,
$p(0)=o$
,
![]() $\sup _{s,t\in [0,\infty )}|d_S(p(s),p(t))-|s-t||\le \delta $
and
$\sup _{s,t\in [0,\infty )}|d_S(p(s),p(t))-|s-t||\le \delta $
and
![]() $\lim _{s\to \infty }p(s)=\xi $
.
$\lim _{s\to \infty }p(s)=\xi $
.
Proof. Let
![]() $(x_n)_{n=1}^\infty $
be a sequence of points in S that converges to
$(x_n)_{n=1}^\infty $
be a sequence of points in S that converges to
![]() $\xi $
. By taking a subsequence of
$\xi $
. By taking a subsequence of
![]() $(x_n)_{n=1}^\infty $
if necessary, we may assume that for any
$(x_n)_{n=1}^\infty $
if necessary, we may assume that for any
![]() $n,m\in \mathbb {N}$
with
$n,m\in \mathbb {N}$
with
![]() $n\le m$
,
$n\le m$
,
![]() $(x_n,x_m)_o^S\ge n$
holds since we have
$(x_n,x_m)_o^S\ge n$
holds since we have
![]() $\lim _{n,m\to \infty }(x_n,x_m)_o^S=\infty $
. For each
$\lim _{n,m\to \infty }(x_n,x_m)_o^S=\infty $
. For each
![]() $n\in \mathbb {N}$
, take a geodesic path
$n\in \mathbb {N}$
, take a geodesic path
![]() $p_n$
from o to
$p_n$
from o to
![]() $x_n$
. Note that
$x_n$
. Note that
![]() $(x_n,x_m)_o^S\ge n$
implies
$(x_n,x_m)_o^S\ge n$
implies
![]() $d_S(o,x_n)\ge n$
for any
$d_S(o,x_n)\ge n$
for any
![]() $n\in \mathbb {N}$
. Define the map
$n\in \mathbb {N}$
. Define the map
![]() $p\colon [0,\infty ) \to S$
as follows. For each
$p\colon [0,\infty ) \to S$
as follows. For each
![]() $n\in \mathbb {N}$
, p isometrically maps
$n\in \mathbb {N}$
, p isometrically maps
![]() $[n-1,n)$
to the subpath
$[n-1,n)$
to the subpath
![]() $q_n$
of
$q_n$
of
![]() $p_n$
satisfying
$p_n$
satisfying
![]() $d_S(o,q_{n-})=n-1$
. By
$d_S(o,q_{n-})=n-1$
. By
![]() $d_S(o,q_{1-})=0$
, we have
$d_S(o,q_{1-})=0$
, we have
![]() $p(0)=o$
. Let
$p(0)=o$
. Let
![]() $s,t\ge 0$
with
$s,t\ge 0$
with
![]() $s\le t$
, then there exist
$s\le t$
, then there exist
![]() $n,m\in \mathbb {N}$
such that
$n,m\in \mathbb {N}$
such that
![]() $s\in [n-1,n)$
and
$s\in [n-1,n)$
and
![]() $t\in [m-1,m)$
. We have
$t\in [m-1,m)$
. We have
![]() $n\le m$
. Let
$n\le m$
. Let
![]() $a\in S$
be the unique point on
$a\in S$
be the unique point on
![]() $p_m$
satisfying
$p_m$
satisfying
![]() $d_S(o,a)=s$
. Since a and
$d_S(o,a)=s$
. Since a and
![]() $p(t)$
are both on the geodesic path
$p(t)$
are both on the geodesic path
![]() $p_m$
, we have
$p_m$
, we have
![]() $d_S(a,p(t))=d_S(o,p(t))-d_S(o,a)=t-s$
. By
$d_S(a,p(t))=d_S(o,p(t))-d_S(o,a)=t-s$
. By
![]() $(x_n,x_m)_o^S\ge n>s$
, we have
$(x_n,x_m)_o^S\ge n>s$
, we have
![]() $d_S(p(s),a)\le \delta $
. Hence, we have
$d_S(p(s),a)\le \delta $
. Hence, we have
for any
![]() $s,t\ge 0$
with
$s,t\ge 0$
with
![]() $s\le t$
. It’s not difficult to show that for any
$s\le t$
. It’s not difficult to show that for any
![]() $N\in \mathbb {N}$
, if
$N\in \mathbb {N}$
, if
![]() $n,m\ge N$
, then
$n,m\ge N$
, then
![]() $(x_n,p(m))_o^S\ge N-\delta $
. This implies
$(x_n,p(m))_o^S\ge N-\delta $
. This implies
![]() $\lim _{s\to \infty }p(s)=\xi $
.
$\lim _{s\to \infty }p(s)=\xi $
.
Lemma 5.4. Suppose that
![]() $(S,d_S)$
is a
$(S,d_S)$
is a
![]() $\delta $
-hyperbolic geodesic metric space with
$\delta $
-hyperbolic geodesic metric space with
![]() $\delta \in \mathbb {N}$
and a group G acts on S isometrically and acylindrically. Then, for any
$\delta \in \mathbb {N}$
and a group G acts on S isometrically and acylindrically. Then, for any
![]() $\xi \in \partial S$
, the stabilizer
$\xi \in \partial S$
, the stabilizer
![]() $\mathrm {Stab}_G(\xi )$
of
$\mathrm {Stab}_G(\xi )$
of
![]() $\xi $
is virtually cyclic.
$\xi $
is virtually cyclic.
Proof. Let
![]() $\xi \in \partial S$
and
$\xi \in \partial S$
and
![]() $H=\mathrm {Stab}_G(\xi )$
. Since the action
$H=\mathrm {Stab}_G(\xi )$
. Since the action
![]() $G \curvearrowright S$
is acylindrical so is
$G \curvearrowright S$
is acylindrical so is
![]() $H\curvearrowright S$
. Hence, by [Reference Osin19, Theorem 1.1] H satisfies exactly one of the following three conditions: (a) H has bounded orbits; (b) H is virtually cyclic and contains a loxodromic element; (c) H contains infinitely many independent loxodromic elements. Since H fixes
$H\curvearrowright S$
. Hence, by [Reference Osin19, Theorem 1.1] H satisfies exactly one of the following three conditions: (a) H has bounded orbits; (b) H is virtually cyclic and contains a loxodromic element; (c) H contains infinitely many independent loxodromic elements. Since H fixes
![]() $\xi $
, (c) cannot occur. We will show that in case (a), H is finite (hence virtually cyclic). Fix
$\xi $
, (c) cannot occur. We will show that in case (a), H is finite (hence virtually cyclic). Fix
![]() $o\in S$
, and define
$o\in S$
, and define
![]() $\varepsilon $
by
$\varepsilon $
by
![]() $\varepsilon =\sup _{g\in H}d(o,go)<\infty $
. By Morse lemma (see [Reference Bridson and Haefliger2, Chapter III. H, Theorem 1.7]), there exists a constant
$\varepsilon =\sup _{g\in H}d(o,go)<\infty $
. By Morse lemma (see [Reference Bridson and Haefliger2, Chapter III. H, Theorem 1.7]), there exists a constant
![]() $K(\delta )>0$
such that for any
$K(\delta )>0$
such that for any
![]() $(1,\delta )$
-quasi-geodesic path q and any geodesic path
$(1,\delta )$
-quasi-geodesic path q and any geodesic path
![]() $q'$
from
$q'$
from
![]() $q_-$
to
$q_-$
to
![]() $q_+$
, the Hausdorff distance between q and
$q_+$
, the Hausdorff distance between q and
![]() $q'$
is at most
$q'$
is at most
![]() $K(\delta )$
. Define
$K(\delta )$
. Define
![]() $\varepsilon '$
by
$\varepsilon '$
by
![]() $\varepsilon '=\varepsilon +4K(\delta )+7\delta $
. Since
$\varepsilon '=\varepsilon +4K(\delta )+7\delta $
. Since
![]() $H\curvearrowright S$
is acylindrical, there exist
$H\curvearrowright S$
is acylindrical, there exist
![]() $R,M\in \mathbb {N}$
such that for any
$R,M\in \mathbb {N}$
such that for any
![]() $x,y\in S$
with
$x,y\in S$
with
![]() $d_S(x,y)\ge R$
,
$d_S(x,y)\ge R$
,
By Lemma 5.3, there exists a
![]() $(1,\delta )$
-quasi-geodesic ray p from o to
$(1,\delta )$
-quasi-geodesic ray p from o to
![]() $\xi $
. Let
$\xi $
. Let
![]() $g\in H$
, then by
$g\in H$
, then by
![]() $g\xi =\xi $
the path
$g\xi =\xi $
the path
![]() $gp$
is a
$gp$
is a
![]() $(1,\delta )$
-quasi-geodesic ray from
$(1,\delta )$
-quasi-geodesic ray from
![]() $go$
to
$go$
to
![]() $\xi $
. Take a real number
$\xi $
. Take a real number
![]() $s>0$
satisfying
$s>0$
satisfying
![]() $d_S(o,p(s))>\max \{\varepsilon +K(\delta ),R\}$
, then by Morse lemma and
$d_S(o,p(s))>\max \{\varepsilon +K(\delta ),R\}$
, then by Morse lemma and
![]() $d_S(o,p(s))> d_S(o,go)+K(\delta )$
, there exists
$d_S(o,p(s))> d_S(o,go)+K(\delta )$
, there exists
![]() $t>0$
such that
$t>0$
such that
![]() $d_S(p(s),gp(t))\le 2K(\delta )+2\delta $
. This implies
$d_S(p(s),gp(t))\le 2K(\delta )+2\delta $
. This implies
 $$ \begin{align*} d_S(gp(s),gp(t)) &=d_S(p(s),p(t)) \le |s-t|+\delta \le |d_S(o,p(s))-d_S(go,gp(t))| + 3\delta \\ &\le d_S(o,go)+d_S(p(s),gp(t)) + 3\delta \le \varepsilon+ 2K(\delta)+2\delta+ 3\delta. \end{align*} $$
$$ \begin{align*} d_S(gp(s),gp(t)) &=d_S(p(s),p(t)) \le |s-t|+\delta \le |d_S(o,p(s))-d_S(go,gp(t))| + 3\delta \\ &\le d_S(o,go)+d_S(p(s),gp(t)) + 3\delta \le \varepsilon+ 2K(\delta)+2\delta+ 3\delta. \end{align*} $$
Hence, we have
![]() $d_S(o,go)\le \varepsilon '$
and
$d_S(o,go)\le \varepsilon '$
and
![]() $d_S(p(s),gp(s))\le d_S(p(s),gp(t))+d_S(gp(t),gp(s))\le \varepsilon '$
for any
$d_S(p(s),gp(s))\le d_S(p(s),gp(t))+d_S(gp(t),gp(s))\le \varepsilon '$
for any
![]() $g\in H$
. By
$g\in H$
. By
![]() $d_S(o,p(s))>R$
and equation (20), this implies
$d_S(o,p(s))>R$
and equation (20), this implies
![]() $|H|\le M$
.
$|H|\le M$
.
Now, we show topological amenability of the boundary action. We restate Corollary 1.2 as Theorem 5.5 here. This is an immediate corollary of the above facts and Theorem 1.1.
Theorem 5.5. For any countable acylindrically hyperbolic group G, there exists a generating set S of G such that the corresponding Cayley graph
![]() $\Gamma (G,S)$
is hyperbolic,
$\Gamma (G,S)$
is hyperbolic,
![]() $|\partial \Gamma (G,S)|>2$
, the natural action of G on
$|\partial \Gamma (G,S)|>2$
, the natural action of G on
![]() $\Gamma (G,S)$
is acylindrical, and the natural action of G on the Gromov boundary
$\Gamma (G,S)$
is acylindrical, and the natural action of G on the Gromov boundary
![]() $\partial \Gamma (G,S)$
is topologically amenable.
$\partial \Gamma (G,S)$
is topologically amenable.
Proof. Take the generating set S of G in Theorem 1.1. Since the action
![]() $G \curvearrowright \Gamma (G,S)$
is acylindrical, the stabilizer
$G \curvearrowright \Gamma (G,S)$
is acylindrical, the stabilizer
![]() $\mathrm {Stab}_G(\xi )$
is amenable for any
$\mathrm {Stab}_G(\xi )$
is amenable for any
![]() $\xi \in \partial \Gamma (G,S)$
by Lemma 5.4. This and hyperfiniteness of the action
$\xi \in \partial \Gamma (G,S)$
by Lemma 5.4. This and hyperfiniteness of the action
![]() $G\curvearrowright \partial \Gamma (G,S)$
imply that
$G\curvearrowright \partial \Gamma (G,S)$
imply that
![]() $G\curvearrowright \partial \Gamma (G,S)$
is topologically amenable by Theorem 5.2.
$G\curvearrowright \partial \Gamma (G,S)$
is topologically amenable by Theorem 5.2.
6. Appendix (more on path representatives)
This section is continuation of Section 3.
![]() $G,X,\{H_\lambda \}_{\lambda \in \Lambda },C,D,Y$
are the same as were defined at the beginning of Section 3. We will list more results on path representatives of the Gromov boundary
$G,X,\{H_\lambda \}_{\lambda \in \Lambda },C,D,Y$
are the same as were defined at the beginning of Section 3. We will list more results on path representatives of the Gromov boundary
![]() $\partial \Gamma (G,Y\sqcup \mathcal {H})$
for possible future use.
$\partial \Gamma (G,Y\sqcup \mathcal {H})$
for possible future use.
After recording the result that
![]() $\partial \Gamma (G,Y\sqcup \mathcal {H})$
is homeomorphic to a certain subset of
$\partial \Gamma (G,Y\sqcup \mathcal {H})$
is homeomorphic to a certain subset of
![]() $\partial \Gamma (G,X\sqcup \mathcal {H})$
(see Proposition 6.2), which was essentially proved in Section 3, we will first show that any two distinct points of
$\partial \Gamma (G,X\sqcup \mathcal {H})$
(see Proposition 6.2), which was essentially proved in Section 3, we will first show that any two distinct points of
![]() $\partial \Gamma (G,Y\sqcup \mathcal {H})$
can be connected by a bi-infinite geodesic path in
$\partial \Gamma (G,Y\sqcup \mathcal {H})$
can be connected by a bi-infinite geodesic path in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
(see Proposition 6.5). By using this path representative, we will extend the notion of Hull–Osin’s separating cosets to pairs of points in
$\Gamma (G,X\sqcup \mathcal {H})$
(see Proposition 6.5). By using this path representative, we will extend the notion of Hull–Osin’s separating cosets to pairs of points in
![]() $\partial \Gamma (G,Y\sqcup \mathcal {H})$
(see Definition 6.9). Finally, we will verify that this generalization of separating cosets to boundary points satisfies similar properties to those of Hull–Osin’s separating cosets (see Lemma 6.11 and Proposition 6.14).
$\partial \Gamma (G,Y\sqcup \mathcal {H})$
(see Definition 6.9). Finally, we will verify that this generalization of separating cosets to boundary points satisfies similar properties to those of Hull–Osin’s separating cosets (see Lemma 6.11 and Proposition 6.14).
In Definition 6.1, we define the set of limit points in
![]() $\partial \Gamma (G,X\sqcup \mathcal {H})$
of all nice geodesic rays in
$\partial \Gamma (G,X\sqcup \mathcal {H})$
of all nice geodesic rays in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
. This set turns out to be homeomorphic to
$\Gamma (G,X\sqcup \mathcal {H})$
. This set turns out to be homeomorphic to
![]() $\partial \Gamma (G,Y\sqcup \mathcal {H})$
.
$\partial \Gamma (G,Y\sqcup \mathcal {H})$
.
Definition 6.1. We define the subset A of
![]() $\partial \Gamma (G,X\sqcup \mathcal {H})$
by
$\partial \Gamma (G,X\sqcup \mathcal {H})$
by
For
![]() $\xi '\in A$
, take a geodesic ray
$\xi '\in A$
, take a geodesic ray
![]() $\gamma $
in
$\gamma $
in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
such that
$\Gamma (G,X\sqcup \mathcal {H})$
such that
![]() $|S(\gamma ;D)|=\infty $
and
$|S(\gamma ;D)|=\infty $
and
![]() $ X\text{-}{\lim}\ \gamma =\xi '$
. The geodesic ray
$ X\text{-}{\lim}\ \gamma =\xi '$
. The geodesic ray
![]() $\gamma $
converges to infinity in
$\gamma $
converges to infinity in
![]() $\Gamma (G,Y\sqcup \mathcal {H})$
by Lemma 3.20 and the limit point
$\Gamma (G,Y\sqcup \mathcal {H})$
by Lemma 3.20 and the limit point
![]() $Y\text{-}{\lim}\ \gamma $
is independent of
$Y\text{-}{\lim}\ \gamma $
is independent of
![]() $\gamma $
taken for
$\gamma $
taken for
![]() $\xi '$
by Proposition 3.29 and Lemma 3.27. Hence, this defines the well-defined map
$\xi '$
by Proposition 3.29 and Lemma 3.27. Hence, this defines the well-defined map
![]() $\Psi \colon A \to \partial \Gamma (G,Y\sqcup \mathcal {H})$
by
$\Psi \colon A \to \partial \Gamma (G,Y\sqcup \mathcal {H})$
by
Proposition 6.2. The map
![]() $\Psi $
is a homeomorphism from A to
$\Psi $
is a homeomorphism from A to
![]() $\partial \Gamma (G,Y\sqcup \mathcal {H})$
.
$\partial \Gamma (G,Y\sqcup \mathcal {H})$
.
Proof. Injectivity and surjectivity of
![]() $\Psi $
follow from Corollary 3.28 and Proposition 3.22, respectively. Continuity of
$\Psi $
follow from Corollary 3.28 and Proposition 3.22, respectively. Continuity of
![]() $\Psi $
and
$\Psi $
and
![]() $\Psi ^{-1}$
follow from Proposition 3.29 and Proposition 3.23, respectively.
$\Psi ^{-1}$
follow from Proposition 3.29 and Proposition 3.23, respectively.
Remark 6.3. By Proposition 6.2 and the Luzin–Souslin Theorem (see [Reference Kechris15, Corollary 15.2]) for
![]() $\Psi ^{-1}$
, the set A is Borel in
$\Psi ^{-1}$
, the set A is Borel in
![]() $\partial \Gamma (G,X\sqcup \mathcal {H})$
. It’s interesting to know whether the geodesic boundary is Borel or not in
$\partial \Gamma (G,X\sqcup \mathcal {H})$
. It’s interesting to know whether the geodesic boundary is Borel or not in
![]() $\partial \Gamma (G,X\sqcup \mathcal {H})$
. Recall that the geodesic boundary of a geodesic hyperbolic metric space S is the set of all points in the Gromov boundary
$\partial \Gamma (G,X\sqcup \mathcal {H})$
. Recall that the geodesic boundary of a geodesic hyperbolic metric space S is the set of all points in the Gromov boundary
![]() $\partial S$
that can be realized as the limit point of a geodesic ray in S.
$\partial S$
that can be realized as the limit point of a geodesic ray in S.
We will now begin our discussion to extend the notion of Hull–Osin’s separating cosets to pairs of boundary points, which completes in Definition 6.9. Definition 6.4 sets up notations for the endpoints of a bi-infinite geodesic path.
Definition 6.4. Suppose that
![]() $\gamma =(\cdots ,x_{-1},x_0,x_1,\cdots )$
is a bi-infinite geodesic path in
$\gamma =(\cdots ,x_{-1},x_0,x_1,\cdots )$
is a bi-infinite geodesic path in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
such that the sequences
$\Gamma (G,X\sqcup \mathcal {H})$
such that the sequences
![]() $(x_n)_{n=1}^\infty $
and
$(x_n)_{n=1}^\infty $
and
![]() $(x_n)_{n=-1}^{-\infty }$
converge to infinity in
$(x_n)_{n=-1}^{-\infty }$
converge to infinity in
![]() $\Gamma (G,Y\sqcup \mathcal {H})$
. We denote the limit point
$\Gamma (G,Y\sqcup \mathcal {H})$
. We denote the limit point
![]() $Y\text{-}{\lim} _{n\to \infty }x_n$
in
$Y\text{-}{\lim} _{n\to \infty }x_n$
in
![]() $\partial \Gamma (G,Y\sqcup \mathcal {H})$
by
$\partial \Gamma (G,Y\sqcup \mathcal {H})$
by
![]() $Y\text{-}{\lim}\ \gamma _+$
and the limit point
$Y\text{-}{\lim}\ \gamma _+$
and the limit point
![]() $Y\text{-}{\lim} _{n\to -\infty }x_n$
in
$Y\text{-}{\lim} _{n\to -\infty }x_n$
in
![]() $\partial \Gamma (G,Y\sqcup \mathcal {H})$
by
$\partial \Gamma (G,Y\sqcup \mathcal {H})$
by
![]() $Y\text{-}{\lim}\ \gamma _-$
.
$Y\text{-}{\lim}\ \gamma _-$
.
As we did in Proposition 3.22, we first show that two distinct boundary points can be connected by a bi-infinite geodesic path of the smaller Cayley graph.
Proposition 6.5. For any two distinct points
![]() $\xi ,\eta \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
, there exists a bi-infinite geodesic path
$\xi ,\eta \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
, there exists a bi-infinite geodesic path
![]() $\gamma $
in
$\gamma $
in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
such that
$\Gamma (G,X\sqcup \mathcal {H})$
such that
![]() $Y\text{-}{\lim}\ \gamma _- =\xi $
and
$Y\text{-}{\lim}\ \gamma _- =\xi $
and
![]() $Y\text{-}{\lim}\ \gamma _+ =\eta $
.
$Y\text{-}{\lim}\ \gamma _+ =\eta $
.
Proof. By Proposition 3.22, fix geodesic rays
![]() $\alpha =(1,x_1,x_2,\cdots ), \beta =(1,y_1,y_2,\cdots )$
in
$\alpha =(1,x_1,x_2,\cdots ), \beta =(1,y_1,y_2,\cdots )$
in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from
$\Gamma (G,X\sqcup \mathcal {H})$
from
![]() $1$
such that
$1$
such that
![]() $Y\text{-}{\lim}\ \alpha = \xi $
and
$Y\text{-}{\lim}\ \alpha = \xi $
and
![]() $Y\text{-}{\lim}\ \beta = \eta $
. Since
$Y\text{-}{\lim}\ \beta = \eta $
. Since
![]() $\xi \neq \eta $
, it’s straightforward to see that there exist
$\xi \neq \eta $
, it’s straightforward to see that there exist
![]() $R,m_0\in \mathbb {N}$
such that for any
$R,m_0\in \mathbb {N}$
such that for any
![]() $i,j \ge m_0$
,
$i,j \ge m_0$
,
For each
![]() $n \ge m_0$
, fix a geodesic path
$n \ge m_0$
, fix a geodesic path
![]() $\gamma _n$
in
$\gamma _n$
in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from
$\Gamma (G,X\sqcup \mathcal {H})$
from
![]() $x_n$
to
$x_n$
to
![]() $y_n$
. Also, take a geodesic path
$y_n$
. Also, take a geodesic path
![]() $[x_n,y_n]$
in
$[x_n,y_n]$
in
![]() $\Gamma (G,Y\sqcup \mathcal {H})$
for each
$\Gamma (G,Y\sqcup \mathcal {H})$
for each
![]() $n \ge m_0$
, then there exists a vertex
$n \ge m_0$
, then there exists a vertex
![]() $z^{\prime }_n \in [x_n,y_n]$
such that
$z^{\prime }_n \in [x_n,y_n]$
such that
![]() $d_{Y\cup \mathcal {H}}(1,z^{\prime }_n) \le R+\delta _Y$
by equation (21) and we can take a vertex
$d_{Y\cup \mathcal {H}}(1,z^{\prime }_n) \le R+\delta _Y$
by equation (21) and we can take a vertex
![]() $z_n\in \gamma _n$
satisfying
$z_n\in \gamma _n$
satisfying
![]() $d_{Y\cup \mathcal {H}}(z^{\prime }_n,z_n) \le M_X$
by Lemma 3.7 (b). This
$d_{Y\cup \mathcal {H}}(z^{\prime }_n,z_n) \le M_X$
by Lemma 3.7 (b). This
![]() $z_n$
satisfies
$z_n$
satisfies
for each
![]() $n\ge m_0$
. Let
$n\ge m_0$
. Let
![]() $S(\alpha ;D)=\{C_1^\alpha \preceq C_2^\alpha \preceq \cdots \}$
and
$S(\alpha ;D)=\{C_1^\alpha \preceq C_2^\alpha \preceq \cdots \}$
and
![]() $S(\beta ;D)=\{C_1^\beta \preceq C_2^\beta \preceq \cdots \}$
, and let each
$S(\beta ;D)=\{C_1^\beta \preceq C_2^\beta \preceq \cdots \}$
, and let each
![]() $C_i^\alpha $
(resp.
$C_i^\alpha $
(resp.
![]() $C_i^\beta $
) be a coset of
$C_i^\beta $
) be a coset of
![]() $H_{\lambda _i^\alpha }$
(resp.
$H_{\lambda _i^\alpha }$
(resp.
![]() $H_{\lambda _i^\beta }$
). Define I by
$H_{\lambda _i^\beta }$
). Define I by
![]() $I=3(R+\delta _Y+M_X)+2$
. We claim that for any
$I=3(R+\delta _Y+M_X)+2$
. We claim that for any
![]() $i,n\in \mathbb {N}$
satisfying
$i,n\in \mathbb {N}$
satisfying
![]() $I\le i$
and
$I\le i$
and
![]() $d_{X\cup \mathcal {H}}(1,\alpha _{out}(C_{i+1}^\alpha )) \le n$
,
$d_{X\cup \mathcal {H}}(1,\alpha _{out}(C_{i+1}^\alpha )) \le n$
,
![]() $\gamma _n$
penetrates
$\gamma _n$
penetrates
![]() $C_i^\alpha $
. Indeed, let
$C_i^\alpha $
. Indeed, let
![]() $S(x_n,1;D)=\{B_1\preceq \cdots \preceq B_m\}$
. By applying Lemma 3.18 to
$S(x_n,1;D)=\{B_1\preceq \cdots \preceq B_m\}$
. By applying Lemma 3.18 to
![]() $\alpha $
and
$\alpha $
and
![]() $S(1,x_n;D)$
, we have
$S(1,x_n;D)$
, we have
![]() $B_{m-(j-1)}=C_j^\alpha $
for any
$B_{m-(j-1)}=C_j^\alpha $
for any
![]() $j\in \{1,\cdots ,i\}$
. Since we have
$j\in \{1,\cdots ,i\}$
. Since we have
![]() $3d_{Y\cup \mathcal {H}}(1,z_n)+1 \le i-1$
, the path
$3d_{Y\cup \mathcal {H}}(1,z_n)+1 \le i-1$
, the path
![]() $\gamma _n$
penetrates
$\gamma _n$
penetrates
![]() $C_i^\alpha (=B_{m-(i-1)})$
by applying Lemma 3.11 to
$C_i^\alpha (=B_{m-(i-1)})$
by applying Lemma 3.11 to
![]() $x_n,1,\gamma _{[x_n,z_n]}$
. By applying Lemma 3.2 to
$x_n,1,\gamma _{[x_n,z_n]}$
. By applying Lemma 3.2 to
![]() $(\alpha _{[1,x_n]})^{-1}$
and
$(\alpha _{[1,x_n]})^{-1}$
and
![]() $\gamma _n$
, we have
$\gamma _n$
, we have
In the same way, we can also see that for any
![]() $i,n\in \mathbb {N}$
satisfying
$i,n\in \mathbb {N}$
satisfying
![]() $I\le i$
and
$I\le i$
and
![]() $d_{X\cup \mathcal {H}}(1,\beta _{out}(C_{i+1}^\beta )) \le n$
, the path
$d_{X\cup \mathcal {H}}(1,\beta _{out}(C_{i+1}^\beta )) \le n$
, the path
![]() $\gamma _n$
penetrates
$\gamma _n$
penetrates
![]() $C_i^\beta $
and we have
$C_i^\beta $
and we have
![]() $\widehat {d}_{\lambda _i^\beta }(\beta _{out}(C_i^\beta ), \gamma _{n~out}(C_i^\beta )) \le 3C$
. Since
$\widehat {d}_{\lambda _i^\beta }(\beta _{out}(C_i^\beta ), \gamma _{n~out}(C_i^\beta )) \le 3C$
. Since
![]() $\widehat {d}_{\lambda _i^\alpha }$
and
$\widehat {d}_{\lambda _i^\alpha }$
and
![]() $\widehat {d}_{\lambda _i^\beta }$
are locally finite for any
$\widehat {d}_{\lambda _i^\beta }$
are locally finite for any
![]() $i\in \mathbb {N}$
, the sets
$i\in \mathbb {N}$
, the sets
![]() $A_i,B_i$
defined by
$A_i,B_i$
defined by
are finite for any
![]() $i\in \mathbb {N}$
. Hence, by the above claim for
$i\in \mathbb {N}$
. Hence, by the above claim for
![]() $i=I$
, there exist a subsequence
$i=I$
, there exist a subsequence
![]() $(\gamma _{1k})_{k=1}^\infty $
of
$(\gamma _{1k})_{k=1}^\infty $
of
![]() $(\gamma _n)_{n=m_1}^\infty $
and vertices
$(\gamma _n)_{n=m_1}^\infty $
and vertices
![]() $a_1\in A_I$
,
$a_1\in A_I$
,
![]() $b_1\in B_I$
such that
$b_1\in B_I$
such that
![]() $\{a_1,b_1\}\subset \gamma _{1k}$
for any
$\{a_1,b_1\}\subset \gamma _{1k}$
for any
![]() $k\in \mathbb {N}$
. By repeating this argument for
$k\in \mathbb {N}$
. By repeating this argument for
![]() $i=I+1,I+2,\cdots $
and taking subsequences, we can see that there exist a sequence of subsequences
$i=I+1,I+2,\cdots $
and taking subsequences, we can see that there exist a sequence of subsequences
![]() $(\gamma _{1k})_{k=1}^\infty \supset (\gamma _{2k})_{k=1}^\infty \supset \cdots $
and vertices
$(\gamma _{1k})_{k=1}^\infty \supset (\gamma _{2k})_{k=1}^\infty \supset \cdots $
and vertices
![]() $a_n \in A_{I+n-1}$
,
$a_n \in A_{I+n-1}$
,
![]() $b_n \in B_{I+n-1}$
for each
$b_n \in B_{I+n-1}$
for each
![]() $n\in \mathbb {N}$
such that
$n\in \mathbb {N}$
such that
![]() $\{a_n,\cdots ,a_1,b_1,\cdots ,b_n\} \subset \gamma _{nk}$
for any
$\{a_n,\cdots ,a_1,b_1,\cdots ,b_n\} \subset \gamma _{nk}$
for any
![]() $n,k\in \mathbb {N}$
. Take the diagonal sequence
$n,k\in \mathbb {N}$
. Take the diagonal sequence
![]() $(\gamma _{kk})_{k=1}^\infty $
, then for any
$(\gamma _{kk})_{k=1}^\infty $
, then for any
![]() $n,k\in \mathbb {N}$
satisfying
$n,k\in \mathbb {N}$
satisfying
![]() $k\ge n$
, we have
$k\ge n$
, we have
Define the bi-infinite path
![]() $\gamma $
in
$\gamma $
in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
by
$\Gamma (G,X\sqcup \mathcal {H})$
by
 $$\begin{align*}\gamma =\bigcup_{i=2}^\infty \gamma_{nn[a_n,a_{n-1}]} \cup \gamma_{11[a_1,b_1]} \cup \bigcup_{n=2}^\infty \gamma_{nn[b_{n-1},b_n]}. \end{align*}$$
$$\begin{align*}\gamma =\bigcup_{i=2}^\infty \gamma_{nn[a_n,a_{n-1}]} \cup \gamma_{11[a_1,b_1]} \cup \bigcup_{n=2}^\infty \gamma_{nn[b_{n-1},b_n]}. \end{align*}$$
By equation (23),
![]() $\gamma $
is geodesic in
$\gamma $
is geodesic in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
. By
$\Gamma (G,X\sqcup \mathcal {H})$
. By
![]() $d_{Y\cup \mathcal {H}}(a_n, \alpha _{out}(C_{I+n-1}^\alpha ))\le 1, \forall n\in \mathbb {N}$
and
$d_{Y\cup \mathcal {H}}(a_n, \alpha _{out}(C_{I+n-1}^\alpha ))\le 1, \forall n\in \mathbb {N}$
and
![]() $Y\text{-}{\lim} _{n\to \infty } \alpha _{out}(C_{I+n-1}^\alpha )=\xi $
, we have
$Y\text{-}{\lim} _{n\to \infty } \alpha _{out}(C_{I+n-1}^\alpha )=\xi $
, we have
![]() $Y\text{-}{\lim} _{n\to \infty } a_n=\xi $
. This implies
$Y\text{-}{\lim} _{n\to \infty } a_n=\xi $
. This implies
![]() $Y\text{-}{\lim}\ \gamma _-=Y\text{-}{\lim} _{n\to \infty } a_n=\xi $
by Lemma 3.20. Similarly,
$Y\text{-}{\lim}\ \gamma _-=Y\text{-}{\lim} _{n\to \infty } a_n=\xi $
by Lemma 3.20. Similarly,
![]() $Y\text{-}{\lim} _{n\to \infty } b_n=\eta $
implies
$Y\text{-}{\lim} _{n\to \infty } b_n=\eta $
implies
![]() $Y\text{-}{\lim}\ \gamma _+=\eta $
.
$Y\text{-}{\lim}\ \gamma _+=\eta $
.

Figure 6 The bi-infinite path
![]() $\gamma $
in the proof of Proposition 6.5.
$\gamma $
in the proof of Proposition 6.5.
As in Definition 3.12 and Definition 3.16, we next define separating cosets for a bi-infinite geodesic path and align these separating cosets based on the order of their penetration.
Definition 6.6. For a bi-infinite geodesic path
![]() $\gamma =(\cdots ,x_{-1},x_0,x_1,\cdots )$
in
$\gamma =(\cdots ,x_{-1},x_0,x_1,\cdots )$
in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
, we define the set
$\Gamma (G,X\sqcup \mathcal {H})$
, we define the set
![]() $S(\gamma ;D)$
of cosets by
$S(\gamma ;D)$
of cosets by
We call an element of
![]() $S(\gamma ;D)$
a
$S(\gamma ;D)$
a
![]() $(\gamma ;D)$
-separating coset.
$(\gamma ;D)$
-separating coset.
Remark 6.7. In Definition 6.6, we have
![]() $S(\gamma ;D)=\bigcup _{n\in \mathbb {N}}S(x_{-n},x_n;D)$
by Lemma 3.1. Also, since
$S(\gamma ;D)=\bigcup _{n\in \mathbb {N}}S(x_{-n},x_n;D)$
by Lemma 3.1. Also, since
![]() $\gamma $
penetrates all cosets in
$\gamma $
penetrates all cosets in
![]() $S(\gamma ;D)$
by Lemma 2.35, we can define the relation
$S(\gamma ;D)$
by Lemma 2.35, we can define the relation
![]() $\preceq $
on
$\preceq $
on
![]() $S(\gamma ;D)$
as follows: for any
$S(\gamma ;D)$
as follows: for any
![]() $C_1,C_2 \in S(\gamma ;D)$
,
$C_1,C_2 \in S(\gamma ;D)$
,
We can see that the relation
![]() $\preceq $
is a linear order. We write
$\preceq $
is a linear order. We write
![]() $S(\gamma ;D)=\{\cdots \preceq C_{-1} \preceq C_0 \preceq C_1 \preceq \cdots \}$
considering this order.
$S(\gamma ;D)=\{\cdots \preceq C_{-1} \preceq C_0 \preceq C_1 \preceq \cdots \}$
considering this order.
As in Corollary 3.24, we finally show that two bi-infinite geodesic paths with the same endpoints have the same separating cosets. This enables us to define separating cosets for a pair of boundary points using a bi-infinite geodesic path connecting them.
Lemma 6.8. Suppose that
![]() $\xi ,\eta \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
are distinct and
$\xi ,\eta \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
are distinct and
![]() $\alpha ,\beta $
are bi-infinite geodesic paths in
$\alpha ,\beta $
are bi-infinite geodesic paths in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
such that
$\Gamma (G,X\sqcup \mathcal {H})$
such that
![]() $Y\text{-}{\lim}\ \alpha _-=Y\text{-}{\lim}\ \beta _-=\xi $
and
$Y\text{-}{\lim}\ \alpha _-=Y\text{-}{\lim}\ \beta _-=\xi $
and
![]() $Y\text{-}{\lim}\ \alpha _+=Y\text{-}{\lim}\ \beta _+=\eta $
. Then, we have
$Y\text{-}{\lim}\ \alpha _+=Y\text{-}{\lim}\ \beta _+=\eta $
. Then, we have
![]() $S(\alpha ;D)=S(\beta ;D)$
.
$S(\alpha ;D)=S(\beta ;D)$
.
Proof. Let
![]() $\alpha =(\cdots ,x_{-1},x_0,x_1,\cdots )$
and
$\alpha =(\cdots ,x_{-1},x_0,x_1,\cdots )$
and
![]() $S(\alpha ;D)=\{ \cdots \preceq C_{-1} \preceq C_0 \preceq C_1 \preceq \cdots \}$
. By
$S(\alpha ;D)=\{ \cdots \preceq C_{-1} \preceq C_0 \preceq C_1 \preceq \cdots \}$
. By
![]() $Y\text{-}{\lim}\ \alpha _-=Y\text{-}{\lim}\ \beta _-$
,
$Y\text{-}{\lim}\ \alpha _-=Y\text{-}{\lim}\ \beta _-$
,
![]() $Y\text{-}{\lim}\ \alpha _+=Y\text{-}{\lim}\ \beta _+$
, and Corollary 3.28, there exists
$Y\text{-}{\lim}\ \alpha _+=Y\text{-}{\lim}\ \beta _+$
, and Corollary 3.28, there exists
![]() $N\in \mathbb {N}$
such that
$N\in \mathbb {N}$
such that
![]() $\beta $
penetrates
$\beta $
penetrates
![]() $C_{-n}$
and
$C_{-n}$
and
![]() $C_n$
for any
$C_n$
for any
![]() $n\ge N$
. For any
$n\ge N$
. For any
![]() $i\in \mathbb {Z}$
, there exists
$i\in \mathbb {Z}$
, there exists
![]() $m \in \mathbb {N}$
such that
$m \in \mathbb {N}$
such that
![]() $C_i \in S(x_{-m},x_m;D)$
by Remark 6.7. For N and m, there exists
$C_i \in S(x_{-m},x_m;D)$
by Remark 6.7. For N and m, there exists
![]() $n\ge N$
such that
$n\ge N$
such that
![]() $\alpha _{[x_{-m},x_m]}\subset \alpha _{[\alpha _{out}(C_{-n}),\alpha _{in}(C_n)]}$
. Since this implies
$\alpha _{[x_{-m},x_m]}\subset \alpha _{[\alpha _{out}(C_{-n}),\alpha _{in}(C_n)]}$
. Since this implies
![]() $C_i \in S(\alpha _{out}(C_{-n}),\alpha _{in}(C_n);D)$
by Lemma 3.1, there exists a geodesic path p in
$C_i \in S(\alpha _{out}(C_{-n}),\alpha _{in}(C_n);D)$
by Lemma 3.1, there exists a geodesic path p in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from
$\Gamma (G,X\sqcup \mathcal {H})$
from
![]() $\alpha _{out}(C_{-n})$
to
$\alpha _{out}(C_{-n})$
to
![]() $\alpha _{in}(C_n)$
that essentially penetrates
$\alpha _{in}(C_n)$
that essentially penetrates
![]() $C_i$
. Let
$C_i$
. Let
![]() $C_{-n},C_n$
be cosets of
$C_{-n},C_n$
be cosets of
![]() $H_{\lambda _{-n}}, H_{\lambda _n}$
, respectively, and let
$H_{\lambda _{-n}}, H_{\lambda _n}$
, respectively, and let
![]() $e_1,e_2$
be the edges of
$e_1,e_2$
be the edges of
![]() $\Gamma (G,X\sqcup \mathcal {H})$
with their labels in
$\Gamma (G,X\sqcup \mathcal {H})$
with their labels in
![]() $H_{\lambda _{-n}}, H_{\lambda _n}$
, respectively, such that
$H_{\lambda _{-n}}, H_{\lambda _n}$
, respectively, such that
![]() $e_1$
is from
$e_1$
is from
![]() $\beta _{in}(C_{-n})$
to
$\beta _{in}(C_{-n})$
to
![]() $\alpha _{out}(C_{-n})$
and
$\alpha _{out}(C_{-n})$
and
![]() $e_2$
is from
$e_2$
is from
![]() $\alpha _{in}(C_{n})$
to
$\alpha _{in}(C_{n})$
to
![]() $\beta _{out}(C_{n})$
. Since we have
$\beta _{out}(C_{n})$
. Since we have
![]() $d_{X\cup \mathcal {H}}(\alpha _{out}(C_{-n}),\alpha _{in}(C_{n}))=d_{X\cup \mathcal {H}}(\beta _{out}(C_{-n}),\beta _{in}(C_{n}))=d_{X\cup \mathcal {H}}(C_{-n},C_n)$
by Lemma 3.3, the path
$d_{X\cup \mathcal {H}}(\alpha _{out}(C_{-n}),\alpha _{in}(C_{n}))=d_{X\cup \mathcal {H}}(\beta _{out}(C_{-n}),\beta _{in}(C_{n}))=d_{X\cup \mathcal {H}}(C_{-n},C_n)$
by Lemma 3.3, the path
![]() $e_1pe_2$
from
$e_1pe_2$
from
![]() $\beta _{in}(C_{-n})$
to
$\beta _{in}(C_{-n})$
to
![]() $\beta _{out}(C_{n})$
is geodesic in
$\beta _{out}(C_{n})$
is geodesic in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
and essentially penetrates
$\Gamma (G,X\sqcup \mathcal {H})$
and essentially penetrates
![]() $C_i$
. This implies
$C_i$
. This implies
![]() $C_i \in S(\beta _{in}(C_{-n}),\beta _{out}(C_{n});D) \subset S(\beta ;D)$
. Hence, we have
$C_i \in S(\beta _{in}(C_{-n}),\beta _{out}(C_{n});D) \subset S(\beta ;D)$
. Hence, we have
![]() $S(\alpha ;D) \subset S(\beta ;D)$
. Similarly, we can also see
$S(\alpha ;D) \subset S(\beta ;D)$
. Similarly, we can also see
![]() $S(\beta ;D) \subset S(\alpha ;D)$
.
$S(\beta ;D) \subset S(\alpha ;D)$
.
We can now extend the notion of Hull–Osin’s separating cosets to a pair of boundary points in the same way as Definition 3.25.
Definition 6.9. For
![]() $\xi ,\eta \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
with
$\xi ,\eta \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
with
![]() $\xi \neq \eta $
, we take a bi-infinite geodesic path
$\xi \neq \eta $
, we take a bi-infinite geodesic path
![]() $\gamma $
in
$\gamma $
in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
satisfying
$\Gamma (G,X\sqcup \mathcal {H})$
satisfying
![]() $Y\text{-}{\lim}\ \gamma _-=\xi $
and
$Y\text{-}{\lim}\ \gamma _-=\xi $
and
![]() $Y\text{-}{\lim}\ \gamma _+=\eta $
, and define the set
$Y\text{-}{\lim}\ \gamma _+=\eta $
, and define the set
![]() $S(\xi ,\eta ;D)$
of cosets by
$S(\xi ,\eta ;D)$
of cosets by
We call an element of
![]() $S(\xi ,\eta ;D)$
a
$S(\xi ,\eta ;D)$
a
![]() $(\xi ,\eta ;D)$
-separating coset. For convenience, we also define
$(\xi ,\eta ;D)$
-separating coset. For convenience, we also define
![]() $S(\xi ,\xi ;D)$
by
$S(\xi ,\xi ;D)$
by
![]() $S(\xi ,\xi ;D)=\emptyset $
for any
$S(\xi ,\xi ;D)=\emptyset $
for any
![]() $\xi \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
.
$\xi \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
.
Remark 6.10. Definition 6.9 is well-defined by Proposition 6.5 and Lemma 6.8. Also,
![]() $S(\xi ,\eta ;D)$
is exactly the set of all cosets that are essentially penetrated by some bi-infinite geodesic path
$S(\xi ,\eta ;D)$
is exactly the set of all cosets that are essentially penetrated by some bi-infinite geodesic path
![]() $\gamma $
in
$\gamma $
in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
satisfying
$\Gamma (G,X\sqcup \mathcal {H})$
satisfying
![]() $Y\text{-}{\lim}\ \gamma _-=\xi $
and
$Y\text{-}{\lim}\ \gamma _-=\xi $
and
![]() $Y\text{-}{\lim}\ \gamma _+=\eta $
.
$Y\text{-}{\lim}\ \gamma _+=\eta $
.

Figure 7 Proof of Lemma 6.11.
Our next goal is to show Proposition 6.14, which is an analogue of [Reference Hull and Osin12, Lemma 3.9]. We first prepare auxiliary results. For distinct elements
![]() $\xi ,\eta \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
, if a bi-infinite geodesic path in
$\xi ,\eta \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
, if a bi-infinite geodesic path in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
satisfies
$\Gamma (G,X\sqcup \mathcal {H})$
satisfies
![]() $Y\text{-}{\lim}\ \gamma _-=\xi $
and
$Y\text{-}{\lim}\ \gamma _-=\xi $
and
![]() $Y\text{-}{\lim}\ \gamma _+=\eta $
, then we say that
$Y\text{-}{\lim}\ \gamma _+=\eta $
, then we say that
![]() $\gamma $
is from
$\gamma $
is from
![]() $\xi $
to
$\xi $
to
![]() $\eta $
.
$\eta $
.
Lemma 6.11 below is analogous to Lemma 2.35.
Lemma 6.11. Let
![]() $D\ge 6C$
. For any distinct elements
$D\ge 6C$
. For any distinct elements
![]() $\xi ,\eta ,\zeta \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
and any
$\xi ,\eta ,\zeta \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
and any
![]() $B\in S(\xi ,\eta ;D)$
, B is either penetrated by all bi-infinite geodesic paths in
$B\in S(\xi ,\eta ;D)$
, B is either penetrated by all bi-infinite geodesic paths in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from
$\Gamma (G,X\sqcup \mathcal {H})$
from
![]() $\xi $
to
$\xi $
to
![]() $\zeta $
or penetrated by all bi-infinite geodesic paths in
$\zeta $
or penetrated by all bi-infinite geodesic paths in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from
$\Gamma (G,X\sqcup \mathcal {H})$
from
![]() $\zeta $
to
$\zeta $
to
![]() $\eta $
.
$\eta $
.
Proof. Let
![]() $S(\xi ,\eta ;D)=\{ \cdots \preceq C_{-1} \preceq C_0 \preceq C_1 \preceq \cdots \}$
, and suppose that there exist
$S(\xi ,\eta ;D)=\{ \cdots \preceq C_{-1} \preceq C_0 \preceq C_1 \preceq \cdots \}$
, and suppose that there exist
![]() $j\in \mathbb {Z}$
and a bi-infinite geodesic path q in
$j\in \mathbb {Z}$
and a bi-infinite geodesic path q in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from
$\Gamma (G,X\sqcup \mathcal {H})$
from
![]() $\xi $
to
$\xi $
to
![]() $\zeta $
that doesn’t penetrate
$\zeta $
that doesn’t penetrate
![]() $C_j$
. Take a bi-infinite geodesic path p in
$C_j$
. Take a bi-infinite geodesic path p in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from
$\Gamma (G,X\sqcup \mathcal {H})$
from
![]() $\xi $
to
$\xi $
to
![]() $\eta $
that essentially penetrates
$\eta $
that essentially penetrates
![]() $C_j$
. For any bi-infinite geodesic path
$C_j$
. For any bi-infinite geodesic path
![]() $\alpha $
in
$\alpha $
in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from
$\Gamma (G,X\sqcup \mathcal {H})$
from
![]() $\zeta $
to
$\zeta $
to
![]() $\eta $
, there exists an
$\eta $
, there exists an
![]() $H_\lambda $
-coset
$H_\lambda $
-coset
![]() $B'$
and
$B'$
and
![]() $i,k\in \mathbb {Z}$
with
$i,k\in \mathbb {Z}$
with
![]() $i<j<k$
such that
$i<j<k$
such that
![]() $B'$
(resp.
$B'$
(resp.
![]() $C_i$
,
$C_i$
,
![]() $C_k$
) is penetrated by both q and
$C_k$
) is penetrated by both q and
![]() $\alpha $
(resp. p and q, p and
$\alpha $
(resp. p and q, p and
![]() $\alpha $
) by Corollary 3.28. Note
$\alpha $
) by Corollary 3.28. Note
![]() $B'\neq C_j$
since q doesn’t penetrate
$B'\neq C_j$
since q doesn’t penetrate
![]() $C_j$
. Let
$C_j$
. Let
![]() $C_i,C_j,C_k$
be cosets of
$C_i,C_j,C_k$
be cosets of
![]() $H_{\lambda _i},H_{\lambda _j},H_{\lambda _k}$
, respectively, and let
$H_{\lambda _i},H_{\lambda _j},H_{\lambda _k}$
, respectively, and let
![]() $e_1,e_2,e_3$
be the edges in
$e_1,e_2,e_3$
be the edges in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
with their labels in
$\Gamma (G,X\sqcup \mathcal {H})$
with their labels in
![]() $H_{\lambda _i},H_{\lambda },H_{\lambda _k}$
, respectively, such that
$H_{\lambda _i},H_{\lambda },H_{\lambda _k}$
, respectively, such that
![]() $e_1$
is from
$e_1$
is from
![]() $p_{out}(C_i)$
to
$p_{out}(C_i)$
to
![]() $q_{out}(C_i)$
,
$q_{out}(C_i)$
,
![]() $e_2$
is from
$e_2$
is from
![]() $q_{in}(B')$
to
$q_{in}(B')$
to
![]() $\alpha _{out}(B')$
, and
$\alpha _{out}(B')$
, and
![]() $e_3$
is from
$e_3$
is from
![]() $\alpha _{in}(C_k)$
to
$\alpha _{in}(C_k)$
to
![]() $p_{in}(C_k)$
. If
$p_{in}(C_k)$
. If
![]() $\alpha $
doesn’t penetrate
$\alpha $
doesn’t penetrate
![]() $C_j$
, then the component of
$C_j$
, then the component of
![]() $p_{[p_{out}(C_i), p_{in}(C_k)]}$
corresponding to
$p_{[p_{out}(C_i), p_{in}(C_k)]}$
corresponding to
![]() $C_j$
is isolated in the geodesic hexagon
$C_j$
is isolated in the geodesic hexagon
![]() $e_1q_{[q_{out}(C_i),q_{in}(B')]} e_2 \alpha _{[\alpha _{out}(B'), \alpha _{in}(C_k)]} e_3 (p_{[p_{out}(C_i),p_{in}(C_k)]})^{-1}$
by
$e_1q_{[q_{out}(C_i),q_{in}(B')]} e_2 \alpha _{[\alpha _{out}(B'), \alpha _{in}(C_k)]} e_3 (p_{[p_{out}(C_i),p_{in}(C_k)]})^{-1}$
by
![]() $C_j\notin \{C_i,C_k,B'\}$
. This implies
$C_j\notin \{C_i,C_k,B'\}$
. This implies
![]() $\widehat {d}_{\lambda _j}(p_{in}(C_j),p_{out}(C_j))\le 6C$
by Proposition 2.30. This contradicts that p essentially penetrates
$\widehat {d}_{\lambda _j}(p_{in}(C_j),p_{out}(C_j))\le 6C$
by Proposition 2.30. This contradicts that p essentially penetrates
![]() $C_j$
since we assume
$C_j$
since we assume
![]() $D\ge 6C$
. Thus,
$D\ge 6C$
. Thus,
![]() $\alpha $
penetrates
$\alpha $
penetrates
![]() $C_j$
.
$C_j$
.
Lemma 6.12 below means that if a geodesic ray converges to one endpoint of a bi-infinite geodesic path, then the geodesic ray penetrates separating cosets of the bi-infinite path in the same order as the order of the separating cosets.

Figure 8 Proof of Lemma 6.12.
Lemma 6.12. Let
![]() $D\ge 4C$
. Suppose that
$D\ge 4C$
. Suppose that
![]() $\xi ,\eta \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
are distinct and
$\xi ,\eta \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
are distinct and
![]() $\alpha $
is a geodesic ray in
$\alpha $
is a geodesic ray in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from
$\Gamma (G,X\sqcup \mathcal {H})$
from
![]() $\alpha _- \in G$
to
$\alpha _- \in G$
to
![]() $\eta $
. Let
$\eta $
. Let
![]() $S(\xi ,\eta ;D)=\{ \cdots \preceq C_{-1} \preceq C_0 \preceq C_1 \preceq \cdots \}$
. If
$S(\xi ,\eta ;D)=\{ \cdots \preceq C_{-1} \preceq C_0 \preceq C_1 \preceq \cdots \}$
. If
![]() $\alpha $
penetrates
$\alpha $
penetrates
![]() $C_i$
for some
$C_i$
for some
![]() $i\in \mathbb {Z}$
, then the subpath
$i\in \mathbb {Z}$
, then the subpath
![]() $\alpha _{[\alpha _{out}(C_i),\infty )}$
penetrates
$\alpha _{[\alpha _{out}(C_i),\infty )}$
penetrates
![]() $C_{i+1}$
.
$C_{i+1}$
.
Proof. By
![]() $C_{i+1}\in S(\xi ,\eta ;D)$
, there exists a bi-infinite geodesic path
$C_{i+1}\in S(\xi ,\eta ;D)$
, there exists a bi-infinite geodesic path
![]() $\beta $
in
$\beta $
in
![]() $\Gamma (X\sqcup \mathcal {H})$
from
$\Gamma (X\sqcup \mathcal {H})$
from
![]() $\xi $
to
$\xi $
to
![]() $\eta $
that essentially penetrates
$\eta $
that essentially penetrates
![]() $C_{i+1}$
. By
$C_{i+1}$
. By
![]() $Y\text{-}{\lim}\ \alpha =Y\text{-}{\lim}\ \beta _+=\eta $
and Corollary 3.28, there exists j with
$Y\text{-}{\lim}\ \alpha =Y\text{-}{\lim}\ \beta _+=\eta $
and Corollary 3.28, there exists j with
![]() $j>i+1$
such that
$j>i+1$
such that
![]() $C_j$
is penetrated by both
$C_j$
is penetrated by both
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
and satisfies
$\beta $
and satisfies
![]() $d_{X\cup \mathcal {H}}(\alpha _-,\alpha _{in}(C_i))<d_{X\cup \mathcal {H}}(\alpha _-,\alpha _{in}(C_j))$
. Note that
$d_{X\cup \mathcal {H}}(\alpha _-,\alpha _{in}(C_i))<d_{X\cup \mathcal {H}}(\alpha _-,\alpha _{in}(C_j))$
. Note that
![]() $\beta $
penetrates
$\beta $
penetrates
![]() $C_i$
. Let
$C_i$
. Let
![]() $C_i,C_{i+1},C_j$
be cosets of
$C_i,C_{i+1},C_j$
be cosets of
![]() $H_{\lambda _i},H_{\lambda _{i+1}}, H_{\lambda _j}$
, respectively, and let
$H_{\lambda _i},H_{\lambda _{i+1}}, H_{\lambda _j}$
, respectively, and let
![]() $e_1,e_2$
be the edges in
$e_1,e_2$
be the edges in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
with their labels in
$\Gamma (G,X\sqcup \mathcal {H})$
with their labels in
![]() $H_{\lambda _i},H_{\lambda _j}$
, respectively, such that
$H_{\lambda _i},H_{\lambda _j}$
, respectively, such that
![]() $e_1$
is from
$e_1$
is from
![]() $\alpha _{out}(C_i)$
to
$\alpha _{out}(C_i)$
to
![]() $\beta _{out}(C_i)$
and
$\beta _{out}(C_i)$
and
![]() $e_2$
is from
$e_2$
is from
![]() $\alpha _{in}(C_j)$
to
$\alpha _{in}(C_j)$
to
![]() $\beta _{in}(C_j)$
. If the subpath
$\beta _{in}(C_j)$
. If the subpath
![]() $\alpha _{[\alpha _{out}(C_i),\infty )}$
doesn’t penetrate
$\alpha _{[\alpha _{out}(C_i),\infty )}$
doesn’t penetrate
![]() $C_{i+1}$
, then the component of
$C_{i+1}$
, then the component of
![]() $\beta _{[\beta _{out}(C_i),\beta _{in}(C_j)]}$
corresponding to
$\beta _{[\beta _{out}(C_i),\beta _{in}(C_j)]}$
corresponding to
![]() $C_{i+1}$
is isolated in the geodesic quadrilateral
$C_{i+1}$
is isolated in the geodesic quadrilateral
![]() $e_1 \beta _{[\beta _{out}(C_i),\beta _{in}(C_j)]} e_2^{-1} (\alpha _{[\alpha _{out}(C_i),\alpha _{in}(C_j)]})^{-1}$
by
$e_1 \beta _{[\beta _{out}(C_i),\beta _{in}(C_j)]} e_2^{-1} (\alpha _{[\alpha _{out}(C_i),\alpha _{in}(C_j)]})^{-1}$
by
![]() $C_{i+1}\notin \{C_i,C_j\}$
. This implies
$C_{i+1}\notin \{C_i,C_j\}$
. This implies
![]() $\widehat {d}_{\lambda _{i+1}}(\beta _{in}(C_{i+1}),\beta _{out}(C_{i+1}))\le 4C$
by Proposition 2.30. This contradicts that
$\widehat {d}_{\lambda _{i+1}}(\beta _{in}(C_{i+1}),\beta _{out}(C_{i+1}))\le 4C$
by Proposition 2.30. This contradicts that
![]() $\beta $
essentially penetrates
$\beta $
essentially penetrates
![]() $C_{i+1}$
since we assume
$C_{i+1}$
since we assume
![]() $D\ge 4C$
. Thus,
$D\ge 4C$
. Thus,
![]() $\alpha _{[\alpha _{out}(C_i),\infty )}$
penetrates
$\alpha _{[\alpha _{out}(C_i),\infty )}$
penetrates
![]() $C_{i+1}$
.
$C_{i+1}$
.
Lemma 6.13 below enables us to create a new bi-infinite geodesic ray by concatenating two geodesic paths.

Figure 9 Proof of Lemma 6.13.
Lemma 6.13. Suppose that
![]() $\xi ,\eta \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
are distinct,
$\xi ,\eta \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
are distinct,
![]() $\alpha $
is a geodesic ray in
$\alpha $
is a geodesic ray in
![]() $\Gamma (X\sqcup \mathcal {H})$
from
$\Gamma (X\sqcup \mathcal {H})$
from
![]() $\alpha _-\in G$
to
$\alpha _-\in G$
to
![]() $\eta $
, and
$\eta $
, and
![]() $\beta $
is a bi-infinite geodesic path in
$\beta $
is a bi-infinite geodesic path in
![]() $\Gamma (X\sqcup \mathcal {H})$
from
$\Gamma (X\sqcup \mathcal {H})$
from
![]() $\xi $
to
$\xi $
to
![]() $\eta $
. If
$\eta $
. If
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
penetrate an
$\beta $
penetrate an
![]() $H_\lambda $
-coset B satisfying
$H_\lambda $
-coset B satisfying
![]() $\widehat {d}_{H_\lambda }(\beta _{in}(B),\beta _{out}(B))> 3C$
and e is the edge in
$\widehat {d}_{H_\lambda }(\beta _{in}(B),\beta _{out}(B))> 3C$
and e is the edge in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from
$\Gamma (G,X\sqcup \mathcal {H})$
from
![]() $\beta _{in}(B)$
to
$\beta _{in}(B)$
to
![]() $\alpha _{out}(B)$
whose label is in
$\alpha _{out}(B)$
whose label is in
![]() $H_{\lambda }$
, then the bi-infinite path
$H_{\lambda }$
, then the bi-infinite path
![]() $\beta _{(-\infty ,\beta _{in}(B)]} e \alpha _{[\alpha _{out}(B),\infty )}$
is geodesic in
$\beta _{(-\infty ,\beta _{in}(B)]} e \alpha _{[\alpha _{out}(B),\infty )}$
is geodesic in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
.
$\Gamma (G,X\sqcup \mathcal {H})$
.
Proof. Let
![]() $\alpha =(x_0,x_1,\cdots )$
and
$\alpha =(x_0,x_1,\cdots )$
and
![]() $\beta =(\cdots ,y_{-1},y_0,y_1,\cdots )$
, and let
$\beta =(\cdots ,y_{-1},y_0,y_1,\cdots )$
, and let
![]() $N\in \mathbb {Z}$
satisfy
$N\in \mathbb {Z}$
satisfy
![]() $y_N=\beta _{in}(B)$
. Fix
$y_N=\beta _{in}(B)$
. Fix
![]() $i\in \mathbb {Z}$
with
$i\in \mathbb {Z}$
with
![]() $i<N$
. There exist
$i<N$
. There exist
![]() $k\in \mathbb {N}$
and a geodesic path p in
$k\in \mathbb {N}$
and a geodesic path p in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from
$\Gamma (G,X\sqcup \mathcal {H})$
from
![]() $y_i$
to
$y_i$
to
![]() $x_k$
such that the path
$x_k$
such that the path
![]() $p\alpha _{[x_k,\infty )}$
is geodesic in
$p\alpha _{[x_k,\infty )}$
is geodesic in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
by Lemma 3.27. By
$\Gamma (G,X\sqcup \mathcal {H})$
by Lemma 3.27. By
![]() $Y\text{-}{\lim}\ \alpha =Y\text{-}{\lim}\ \beta _+=\eta $
and Corollary 3.28, there exists a
$Y\text{-}{\lim}\ \alpha =Y\text{-}{\lim}\ \beta _+=\eta $
and Corollary 3.28, there exists a
![]() $H_{\lambda _1}$
-coset
$H_{\lambda _1}$
-coset
![]() $B_1 \in S(\alpha ,D)$
such that
$B_1 \in S(\alpha ,D)$
such that
![]() $\beta $
penetrates
$\beta $
penetrates
![]() $B_1$
and we have
$B_1$
and we have
![]() $d_{X\cup \mathcal {H}}(x_0, x_k)<d_{X\cup \mathcal {H}}(x_0,\alpha _{in}(B_1))$
and
$d_{X\cup \mathcal {H}}(x_0, x_k)<d_{X\cup \mathcal {H}}(x_0,\alpha _{in}(B_1))$
and
![]() $d_{X\cup \mathcal {H}}(y_i, \beta _{in}(B))<d_{X\cup \mathcal {H}}(y_i,\beta _{in}(B_1))$
. Let
$d_{X\cup \mathcal {H}}(y_i, \beta _{in}(B))<d_{X\cup \mathcal {H}}(y_i,\beta _{in}(B_1))$
. Let
![]() $e_1$
be the edge in
$e_1$
be the edge in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from
$\Gamma (G,X\sqcup \mathcal {H})$
from
![]() $\alpha _{in}(B_1)$
to
$\alpha _{in}(B_1)$
to
![]() $\beta _{in}(B_1)$
whose label is in
$\beta _{in}(B_1)$
whose label is in
![]() $H_{\lambda _1}$
. Define the path q by
$H_{\lambda _1}$
. Define the path q by
![]() $q=p\alpha _{[x_k,\alpha _{in}(B_1)]}$
, and consider the geodesic triangle
$q=p\alpha _{[x_k,\alpha _{in}(B_1)]}$
, and consider the geodesic triangle
![]() $\Delta =qe_1 (\beta _{[y_i,\beta _{in}(B_1)]})^{-1}$
. The component of
$\Delta =qe_1 (\beta _{[y_i,\beta _{in}(B_1)]})^{-1}$
. The component of
![]() $\beta _{[y_i,\beta _{in}(B_1)]}$
corresponding to B cannot be isolated in
$\beta _{[y_i,\beta _{in}(B_1)]}$
corresponding to B cannot be isolated in
![]() $\Delta $
by Proposition 2.30 and
$\Delta $
by Proposition 2.30 and
![]() $\widehat {d}_{H_\lambda }(\beta _{in}(B),\beta _{out}(B))> 3C$
. By this and
$\widehat {d}_{H_\lambda }(\beta _{in}(B),\beta _{out}(B))> 3C$
. By this and
![]() $B\neq B_1$
, the path q penetrates B. Hence, we have
$B\neq B_1$
, the path q penetrates B. Hence, we have
 $$ \begin{align*} d_{X\cup\mathcal{H}}(y_i,\beta_{in}(B))&=d_{X\cup\mathcal{H}}(y_i,q_{in}(B))~ (=d_{X\cup\mathcal{H}}(y_i,B)) \\ \mathrm{and}~~~~~ d_{X\cup\mathcal{H}}(\alpha_{out}(B), \alpha_{in}(B_1))&=d_{X\cup\mathcal{H}}(q_{out}(B), \alpha_{in}(B_1)) ~(=d_{X\cup\mathcal{H}}(\alpha_{in}(B_1),B)) \end{align*} $$
$$ \begin{align*} d_{X\cup\mathcal{H}}(y_i,\beta_{in}(B))&=d_{X\cup\mathcal{H}}(y_i,q_{in}(B))~ (=d_{X\cup\mathcal{H}}(y_i,B)) \\ \mathrm{and}~~~~~ d_{X\cup\mathcal{H}}(\alpha_{out}(B), \alpha_{in}(B_1))&=d_{X\cup\mathcal{H}}(q_{out}(B), \alpha_{in}(B_1)) ~(=d_{X\cup\mathcal{H}}(\alpha_{in}(B_1),B)) \end{align*} $$
by Lemma 2.36. This implies
 $$ \begin{align*} |\beta_{[y_i,\beta_{in}(B)]} e \alpha_{[\alpha_{out}(B),\alpha_{in}(B_1)]}| &\le d_{X\cup\mathcal{H}}(y_i,\beta_{in}(B)) + 1 + d_{X\cup\mathcal{H}}(\alpha_{out}(B), \alpha_{in}(B_1)) \\ &=d_{X\cup\mathcal{H}}(y_i,q_{in}(B))+1+d_{X\cup\mathcal{H}}(q_{out}(B), \alpha_{in}(B_1))\\ &=|q|=d_{X\cup\mathcal{H}}(y_i,\alpha_{in}(B_1)). \end{align*} $$
$$ \begin{align*} |\beta_{[y_i,\beta_{in}(B)]} e \alpha_{[\alpha_{out}(B),\alpha_{in}(B_1)]}| &\le d_{X\cup\mathcal{H}}(y_i,\beta_{in}(B)) + 1 + d_{X\cup\mathcal{H}}(\alpha_{out}(B), \alpha_{in}(B_1)) \\ &=d_{X\cup\mathcal{H}}(y_i,q_{in}(B))+1+d_{X\cup\mathcal{H}}(q_{out}(B), \alpha_{in}(B_1))\\ &=|q|=d_{X\cup\mathcal{H}}(y_i,\alpha_{in}(B_1)). \end{align*} $$
Hence, the path r defined by
![]() $r=\beta _{[y_i,\beta _{in}(B)]} e \alpha _{[\alpha _{out}(B),\alpha _{in}(B_1)]}$
is geodesic in
$r=\beta _{[y_i,\beta _{in}(B)]} e \alpha _{[\alpha _{out}(B),\alpha _{in}(B_1)]}$
is geodesic in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
and has the same endpoints as q. This implies that
$\Gamma (G,X\sqcup \mathcal {H})$
and has the same endpoints as q. This implies that
![]() $\beta _{[y_i,\beta _{in}(B)]} e \alpha _{[\alpha _{out}(B),\infty )}(=r\alpha _{[\alpha _{in}(B_1),\infty )})$
is geodesic in
$\beta _{[y_i,\beta _{in}(B)]} e \alpha _{[\alpha _{out}(B),\infty )}(=r\alpha _{[\alpha _{in}(B_1),\infty )})$
is geodesic in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
since
$\Gamma (G,X\sqcup \mathcal {H})$
since
![]() $q\alpha _{[\alpha _{in}(B_1),\infty )}(= p \alpha _{[x_k,\infty )]})$
is geodesic in
$q\alpha _{[\alpha _{in}(B_1),\infty )}(= p \alpha _{[x_k,\infty )]})$
is geodesic in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
. Since i with
$\Gamma (G,X\sqcup \mathcal {H})$
. Since i with
![]() $i<N$
is arbitrary, this implies that
$i<N$
is arbitrary, this implies that
![]() $\beta _{(-\infty ,\beta _{in}(B)]} e \alpha _{[\alpha _{out}(B),\infty )}$
is geodesic in
$\beta _{(-\infty ,\beta _{in}(B)]} e \alpha _{[\alpha _{out}(B),\infty )}$
is geodesic in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
.
$\Gamma (G,X\sqcup \mathcal {H})$
.

Figure 10 Proof of Proposition 6.14.
We are now ready to show Proposition 6.14. The proof is similar to [Reference Hull and Osin12, Lemma 3.9] modulo the above auxiliary lemmas.
Proposition 6.14. Let
![]() $D\ge 11C$
. For any
$D\ge 11C$
. For any
![]() $\xi ,\eta ,\zeta \in G \cup \partial \Gamma (G,Y\sqcup \mathcal {H})$
,
$\xi ,\eta ,\zeta \in G \cup \partial \Gamma (G,Y\sqcup \mathcal {H})$
,
![]() $S(\xi ,\eta ;D)$
can be decomposed into
$S(\xi ,\eta ;D)$
can be decomposed into
![]() $S(\xi ,\eta ;D)=S'\sqcup S" \sqcup F$
such that
$S(\xi ,\eta ;D)=S'\sqcup S" \sqcup F$
such that
![]() $S'\subset S(\xi ,\zeta ;D)$
,
$S'\subset S(\xi ,\zeta ;D)$
,
![]() $S"\subset S(\zeta ,\eta ;D)$
, and
$S"\subset S(\zeta ,\eta ;D)$
, and
![]() $|F|\le 4$
.
$|F|\le 4$
.
Proof. We will only show the case where
![]() $\xi ,\eta ,\zeta \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
and
$\xi ,\eta ,\zeta \in \partial \Gamma (G,Y\sqcup \mathcal {H})$
and
![]() $\xi ,\eta ,\zeta $
are all distinct because the proof of other cases is similar. Let
$\xi ,\eta ,\zeta $
are all distinct because the proof of other cases is similar. Let
![]() $S(\xi ,\eta ;D)=\{ \cdots \preceq C_{-1} \preceq C_0 \preceq C_1 \preceq \cdots \}$
, and define
$S(\xi ,\eta ;D)=\{ \cdots \preceq C_{-1} \preceq C_0 \preceq C_1 \preceq \cdots \}$
, and define
![]() $\mathcal {P}_\xi =\{i\in \mathbb {Z} \mid \forall \gamma \colon {\mathrm {bi}}\text{-} \textrm {infinite geodesic path in }\Gamma (G,X\sqcup \mathcal {H}) \textrm { from }\xi \textrm { to }\zeta \textrm { penetrates } C_i \}$
and
$\mathcal {P}_\xi =\{i\in \mathbb {Z} \mid \forall \gamma \colon {\mathrm {bi}}\text{-} \textrm {infinite geodesic path in }\Gamma (G,X\sqcup \mathcal {H}) \textrm { from }\xi \textrm { to }\zeta \textrm { penetrates } C_i \}$
and
![]() $\mathcal {P}_\eta =\{i\in \mathbb {Z} \mid \forall \gamma \colon \textrm { bi}\text{-} \textrm {infinite geodesic path in } \Gamma (G,X\sqcup \mathcal {H}) \textrm { from }\zeta \textrm { to }\eta \textrm { penetrates } C_i \}$
. By Lemma 6.11, we have
$\mathcal {P}_\eta =\{i\in \mathbb {Z} \mid \forall \gamma \colon \textrm { bi}\text{-} \textrm {infinite geodesic path in } \Gamma (G,X\sqcup \mathcal {H}) \textrm { from }\zeta \textrm { to }\eta \textrm { penetrates } C_i \}$
. By Lemma 6.11, we have
![]() $\mathbb {Z}=\mathcal {P}_\xi \cup \mathcal {P}_\eta $
. Suppose for contradiction that there exists a sequence
$\mathbb {Z}=\mathcal {P}_\xi \cup \mathcal {P}_\eta $
. Suppose for contradiction that there exists a sequence
![]() $(i_k)_{k=1}^\infty $
in
$(i_k)_{k=1}^\infty $
in
![]() $\mathcal {P}_\xi $
such that
$\mathcal {P}_\xi $
such that
![]() $\lim _{k\to \infty }i_k=\infty $
. Take bi-infinite geodesic paths
$\lim _{k\to \infty }i_k=\infty $
. Take bi-infinite geodesic paths
![]() $p,q$
in
$p,q$
in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
such that p is from
$\Gamma (G,X\sqcup \mathcal {H})$
such that p is from
![]() $\xi $
to
$\xi $
to
![]() $\zeta $
and q is from
$\zeta $
and q is from
![]() $\xi $
to
$\xi $
to
![]() $\eta $
. Since
$\eta $
. Since
![]() $i_k\in \mathcal {P}_\xi $
implies
$i_k\in \mathcal {P}_\xi $
implies
![]() $d_{Y\cup \mathcal {H}}(p_{in}(C_{i_k}), q_{in}(C_{i_k}))\le 1$
for any
$d_{Y\cup \mathcal {H}}(p_{in}(C_{i_k}), q_{in}(C_{i_k}))\le 1$
for any
![]() $k\in \mathbb {N}$
, we have
$k\in \mathbb {N}$
, we have
![]() $\zeta =\lim _{k\to \infty } p_{in}(C_{i_k})=\lim _{k\to \infty } q_{in}(C_{i_k})=\xi $
. This contradicts our assumption that
$\zeta =\lim _{k\to \infty } p_{in}(C_{i_k})=\lim _{k\to \infty } q_{in}(C_{i_k})=\xi $
. This contradicts our assumption that
![]() $\xi ,\eta ,\zeta $
are distinct. Hence, there exists
$\xi ,\eta ,\zeta $
are distinct. Hence, there exists
![]() $i_1\in \mathbb {Z}$
such that
$i_1\in \mathbb {Z}$
such that
![]() $\mathcal {P}_\xi \cap [i_1,\infty )=\emptyset $
. Similarly, we can see
$\mathcal {P}_\xi \cap [i_1,\infty )=\emptyset $
. Similarly, we can see
![]() $\mathcal {P}_\eta \cap (-\infty ,i_2]=\emptyset $
for some
$\mathcal {P}_\eta \cap (-\infty ,i_2]=\emptyset $
for some
![]() $i_2\in \mathbb {Z}$
. In particular,
$i_2\in \mathbb {Z}$
. In particular,
![]() $\mathcal {P}_\eta $
is nonempty and
$\mathcal {P}_\eta $
is nonempty and
![]() $\min \mathcal {P}_\eta $
exists. Define N by
$\min \mathcal {P}_\eta $
exists. Define N by
![]() $N=\min \mathcal {P}_\eta $
.
$N=\min \mathcal {P}_\eta $
.
We claim
![]() $\{C_i \mid i\ge N+2\}\subset S(\zeta ,\eta ;D)$
. Fix a bi-infinite geodesic path
$\{C_i \mid i\ge N+2\}\subset S(\zeta ,\eta ;D)$
. Fix a bi-infinite geodesic path
![]() $\beta $
in
$\beta $
in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from
$\Gamma (G,X\sqcup \mathcal {H})$
from
![]() $\zeta $
to
$\zeta $
to
![]() $\eta $
. By
$\eta $
. By
![]() $N\in \mathcal {P}_\eta $
, the path
$N\in \mathcal {P}_\eta $
, the path
![]() $\beta $
penetrates
$\beta $
penetrates
![]() $C_N$
. Hence, the subpath
$C_N$
. Hence, the subpath
![]() $\beta _{[\beta _{out}(C_N),\infty )}$
penetrates
$\beta _{[\beta _{out}(C_N),\infty )}$
penetrates
![]() $C_{N+1}$
by Lemma 6.12. Let
$C_{N+1}$
by Lemma 6.12. Let
![]() $C_{N+1}$
be an
$C_{N+1}$
be an
![]() $H_\lambda $
-coset, then we have
$H_\lambda $
-coset, then we have
![]() $\widehat {d}_{\lambda }(\beta _{in}(C_{N+1}), \beta _{out}(C_{N+1}))> 3C$
. Indeed, take a bi-infinite geodesic path
$\widehat {d}_{\lambda }(\beta _{in}(C_{N+1}), \beta _{out}(C_{N+1}))> 3C$
. Indeed, take a bi-infinite geodesic path
![]() $p'$
in
$p'$
in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from
$\Gamma (G,X\sqcup \mathcal {H})$
from
![]() $\xi $
to
$\xi $
to
![]() $\eta $
that essentially penetrates
$\eta $
that essentially penetrates
![]() $C_N$
. By applying Lemma 3.4 to
$C_N$
. By applying Lemma 3.4 to
![]() $C_N$
and
$C_N$
and
![]() $C_{N+1}$
, we have
$C_{N+1}$
, we have
![]() $\widehat {d}_{\lambda }(p^{\prime }_{in}(C_{N+1}),\beta _{in}(C_{N+1})) \le 4C$
. By the same argument for
$\widehat {d}_{\lambda }(p^{\prime }_{in}(C_{N+1}),\beta _{in}(C_{N+1})) \le 4C$
. By the same argument for
![]() $C_{N+1}$
and
$C_{N+1}$
and
![]() $C_{N+2}$
, we can also see
$C_{N+2}$
, we can also see
![]() $\widehat {d}_{\lambda }(p^{\prime }_{out}(C_{N+1}),\beta _{out}(C_{N+1}))\le 4C$
. Since
$\widehat {d}_{\lambda }(p^{\prime }_{out}(C_{N+1}),\beta _{out}(C_{N+1}))\le 4C$
. Since
![]() $p'$
essentially penetrates
$p'$
essentially penetrates
![]() $C_{N+1}$
, this implies
$C_{N+1}$
, this implies
 $$ \begin{align} \begin{aligned} &\widehat{d}_{\lambda}(\beta_{in}(C_{N+1}), \beta_{out}(C_{N+1})) \\ &\ge \widehat{d}_{\lambda}(p^{\prime}_{in}(C_{N+1}),p^{\prime}_{out}(C_{N+1})) - \widehat{d}_{\lambda}(\beta_{in}(C_{N+1}),p^{\prime}_{in}(C_{N+1}))-\widehat{d}_{\lambda}(\beta_{out}(C_{N+1}),p^{\prime}_{out}(C_{N+1}))\\ &> D-4C-4C \ge 3C. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\widehat{d}_{\lambda}(\beta_{in}(C_{N+1}), \beta_{out}(C_{N+1})) \\ &\ge \widehat{d}_{\lambda}(p^{\prime}_{in}(C_{N+1}),p^{\prime}_{out}(C_{N+1})) - \widehat{d}_{\lambda}(\beta_{in}(C_{N+1}),p^{\prime}_{in}(C_{N+1}))-\widehat{d}_{\lambda}(\beta_{out}(C_{N+1}),p^{\prime}_{out}(C_{N+1}))\\ &> D-4C-4C \ge 3C. \end{aligned} \end{align} $$
For any
![]() $i\ge N+2$
, there exists a bi-infinite geodesic path
$i\ge N+2$
, there exists a bi-infinite geodesic path
![]() $\alpha $
in
$\alpha $
in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from
$\Gamma (G,X\sqcup \mathcal {H})$
from
![]() $\xi $
to
$\xi $
to
![]() $\eta $
that essentially penetrates
$\eta $
that essentially penetrates
![]() $C_i$
. Note that
$C_i$
. Note that
![]() $\alpha $
penetrates
$\alpha $
penetrates
![]() $C_{N+1}$
. Let e be the edge in
$C_{N+1}$
. Let e be the edge in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
from
$\Gamma (G,X\sqcup \mathcal {H})$
from
![]() $\beta _{in}(C_{N+1})$
to
$\beta _{in}(C_{N+1})$
to
![]() $\alpha _{out}(C_{N+1})$
whose label is in
$\alpha _{out}(C_{N+1})$
whose label is in
![]() $H_{\lambda }$
. By Lemma 6.13, the bi-infinite path
$H_{\lambda }$
. By Lemma 6.13, the bi-infinite path
![]() $\gamma $
defined by
$\gamma $
defined by
![]() $\gamma =\beta _{(-\infty ,\beta _{in}(C_{N+1})]} e \alpha _{[\alpha _{out}(C_{N+1}),\infty )}$
is geodesic in
$\gamma =\beta _{(-\infty ,\beta _{in}(C_{N+1})]} e \alpha _{[\alpha _{out}(C_{N+1}),\infty )}$
is geodesic in
![]() $\Gamma (G,X\sqcup \mathcal {H})$
and essentially penetrates
$\Gamma (G,X\sqcup \mathcal {H})$
and essentially penetrates
![]() $C_i$
. This implies
$C_i$
. This implies
![]() $C_i\in S(\gamma ;D)$
. On the other hand, we have
$C_i\in S(\gamma ;D)$
. On the other hand, we have
![]() $S(\gamma ;D)=S(\zeta ,\eta ;D)$
by
$S(\gamma ;D)=S(\zeta ,\eta ;D)$
by
![]() $Y\text{-}{\lim}\ \gamma _-=Y\text{-}{\lim}\ \beta _-=\zeta $
and
$Y\text{-}{\lim}\ \gamma _-=Y\text{-}{\lim}\ \beta _-=\zeta $
and
![]() $Y\text{-}{\lim}\ \gamma _+=Y\text{-}{\lim}\ \alpha _+=\eta $
. Thus, we have
$Y\text{-}{\lim}\ \gamma _+=Y\text{-}{\lim}\ \alpha _+=\eta $
. Thus, we have
![]() $\{C_i \mid i\ge N+2\}\subset S(\zeta ,\eta ;D)$
. Similarly, we can also see
$\{C_i \mid i\ge N+2\}\subset S(\zeta ,\eta ;D)$
. Similarly, we can also see
![]() $\{C_i \mid i\le N-3\}\subset S(\xi ,\zeta ;D)$
since we have
$\{C_i \mid i\le N-3\}\subset S(\xi ,\zeta ;D)$
since we have
![]() $N-1\in \mathcal {P}_\xi $
by
$N-1\in \mathcal {P}_\xi $
by
![]() $\mathbb {Z}=\mathcal {P}_\xi \cup \mathcal {P}_\eta $
and
$\mathbb {Z}=\mathcal {P}_\xi \cup \mathcal {P}_\eta $
and
![]() $N=\min \mathcal {P}_\eta $
. Thus, we get the desired decomposition by defining
$N=\min \mathcal {P}_\eta $
. Thus, we get the desired decomposition by defining
![]() $S',S",F$
by
$S',S",F$
by
![]() $S'=\{C_i \mid i\le N-3\}$
,
$S'=\{C_i \mid i\le N-3\}$
,
![]() $S"=\{C_i \mid i\ge N+2\}$
and
$S"=\{C_i \mid i\ge N+2\}$
and
![]() $F=\{C_{N-2},C_{N-1},C_{N},C_{N+1}\}$
.
$F=\{C_{N-2},C_{N-1},C_{N},C_{N+1}\}$
.
Acknowledgement
I would like to thank the anonymous referee for many helpful comments, which greatly improved exposition of this paper.
Competing interest
The authors have no competing interest to declare.
Funding statement
None.