Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Elduque, Eva
and
Mustată, Mircea
2021.
О гипотезе Тесье: случай логканонических порогов.
Математический сборник,
Vol. 212,
Issue. 3,
p.
175.
Kim, Dano
2021.
On a question of Teissier.
Annali di Matematica Pura ed Applicata (1923 -),
Vol. 200,
Issue. 5,
p.
2305.
Elduque, E.
and
Mustaţă, M.
2021.
On a conjecture of Teissier: the case of log canonical thresholds.
Sbornik: Mathematics,
Vol. 212,
Issue. 3,
p.
433.
Glazer, Itay
and
Hendel, Yotam I.
2021.
On singularity properties of convolutions of algebraic morphisms ‐ the general case.
Journal of the London Mathematical Society,
Vol. 103,
Issue. 4,
p.
1453.
Nguyen, Kien Huu
2021.
Arithmetic and Geometry over Local Fields.
Vol. 2275,
Issue. ,
p.
61.
Jung, Seung-Jo
Kim, In-Kyun
Saito, Morihiko
and
Yoon, Youngho
2022.
Hodge ideals and spectrum of isolated hypersurface singularities.
Annales de l'Institut Fourier,
Vol. 72,
Issue. 2,
p.
465.
Blanco, Guillem
2022.
An algorithm for Hodge ideals.
Mathematics of Computation,
Wu, Lei
2022.
Characteristic cycles associated to holonomic $${\mathscr {D}}$$-modules.
Mathematische Zeitschrift,
Vol. 301,
Issue. 2,
p.
2059.
Castaño Domínguez, Alberto
Narváez Macarro, Luis
and
Sevenheck, Christian
2022.
Hodge ideals of free divisors.
Selecta Mathematica,
Vol. 28,
Issue. 3,
Àlvarez Montaner, Josep
Hernández, Daniel J.
Jeffries, Jack
Núñez-Betancourt, Luis
Teixeira, Pedro
and
Witt, Emily E.
2022.
Bernstein–Sato functional equations, V-filtrations, and multiplier ideals of direct summands.
Communications in Contemporary Mathematics,
Vol. 24,
Issue. 10,
Jung, Seung-Jo
Kim, In-Kyun
Saito, Morihiko
and
Yoon, Youngho
2022.
Briançon-Skoda exponents and the maximal root of reduced Bernstein-Sato polynomials.
Selecta Mathematica,
Vol. 28,
Issue. 4,
Friedman, Robert
and
Laza, Radu
2023.
The higher Du Bois and higher rational properties for isolated singularities.
Journal of Algebraic Geometry,
Vol. 33,
Issue. 3,
p.
493.
Chen, Bingyi
2023.
Vanishing for Hodge Ideals of ℚ-Divisors.
International Mathematics Research Notices,
Vol. 2023,
Issue. 1,
p.
185.
Olano, Sebastián
2023.
Weighted Hodge ideals of reduced divisors.
Forum of Mathematics, Sigma,
Vol. 11,
Issue. ,
Mustaţă, Mircea
Olano, Sebastián
Popa, Mihnea
and
Witaszek, Jakub
2023.
The Du Bois complex of a hypersurface and the minimal exponent.
Duke Mathematical Journal,
Vol. 172,
Issue. 7,
Vo, Anh Duc
2024.
Vanishing theorem for Hodge ideals on smooth hypersurfaces.
Mathematische Zeitschrift,
Vol. 308,
Issue. 2,
Chen, Qianyu
Dirks, Bradley
Mustaţă, Mircea
and
Olano, Sebastián
2024.
𝑉-filtrations and minimal exponents for local complete intersections.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 0,
Issue. 0,
Chen, Qianyu
Dirks, Bradley
and
Mustaţă, Mircea
2024.
The minimal exponent and k-rationality for local complete intersections.
Journal de l’École polytechnique — Mathématiques,
Vol. 11,
Issue. ,
p.
849.
Lee, Jonghyun
2025.
Multiplicative Thom-Sebastiani for Bernstein-Sato polynomials.
Journal of Algebra,
Vol. 664,
Issue. ,
p.
247.
CHEN, QIANYU
Dirks , Bradley
and
Mustata , Mircea
2025.
THE MINIMAL EXPONENT OF CONES OVER SMOOTH
COMPLETE INTERSECTION PROJECTIVE VARIETIES.
Revue Roumaine Mathematiques Pures Appliquees,
Vol. LXIX,
Issue. 3-4,
p.
33.
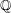 $\mathbb{Q}$-DIVISORS,
$\mathbb{Q}$-DIVISORS, 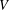 $V$-FILTRATION, AND MINIMAL EXPONENT
$V$-FILTRATION, AND MINIMAL EXPONENT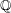 $\mathbb{Q}$-divisors in terms of the
$\mathbb{Q}$-divisors in terms of the 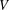 $V$-filtration induced by a local defining equation, inspired by a result of Saito in the reduced case. We deduce basic properties of Hodge ideals in this generality, and relate them to Bernstein–Sato polynomials. As a consequence of our study we establish general properties of the minimal exponent, a refined version of the log canonical threshold, and bound it in terms of discrepancies on log resolutions, addressing a question of Lichtin and Kollár.
$V$-filtration induced by a local defining equation, inspired by a result of Saito in the reduced case. We deduce basic properties of Hodge ideals in this generality, and relate them to Bernstein–Sato polynomials. As a consequence of our study we establish general properties of the minimal exponent, a refined version of the log canonical threshold, and bound it in terms of discrepancies on log resolutions, addressing a question of Lichtin and Kollár.