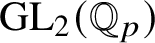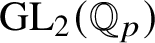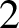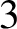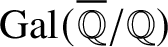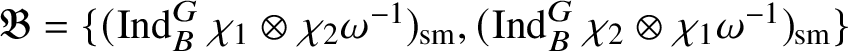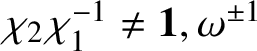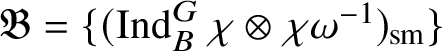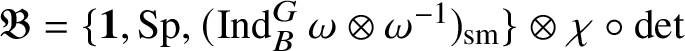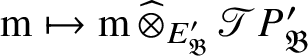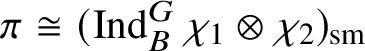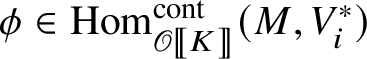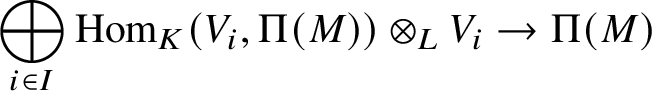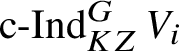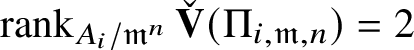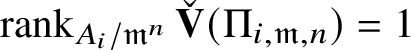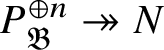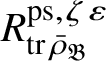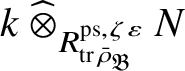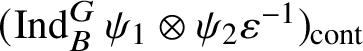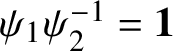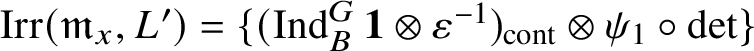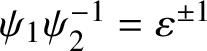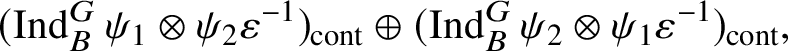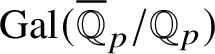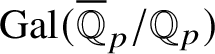1 Introduction
Recently, Lue Pan gave a new proof of the Fontaine–Mazur conjecture for Hodge–Tate representations of
![]() $\operatorname {\mathrm {Gal}}(\overline {\mathbb Q}/\mathbb {Q})$
with equal Hodge–Tate weights [Reference Pan38]. One of the ingredients in his proof are the Bernstein-centre type of results for the category of mod p representations of
$\operatorname {\mathrm {Gal}}(\overline {\mathbb Q}/\mathbb {Q})$
with equal Hodge–Tate weights [Reference Pan38]. One of the ingredients in his proof are the Bernstein-centre type of results for the category of mod p representations of
![]() $\operatorname {\mathrm {GL}}_2(\mathbb {Q}_p)$
proved in [Reference Paškūnas39, Reference Paškūnas41]. This caused him to impose some restrictions on the Galois representations at p, when
$\operatorname {\mathrm {GL}}_2(\mathbb {Q}_p)$
proved in [Reference Paškūnas39, Reference Paškūnas41]. This caused him to impose some restrictions on the Galois representations at p, when
![]() $p=2$
and
$p=2$
and
![]() $p=3$
. In this paper we remove these restrictions by proving the required finiteness results in these remaining cases (Theorem 7.3).
$p=3$
. In this paper we remove these restrictions by proving the required finiteness results in these remaining cases (Theorem 7.3).
Let L be a finite extension of
![]() $\mathbb {Q}_p$
with ring of integers
$\mathbb {Q}_p$
with ring of integers
![]() $\mathscr O$
and residue field k. Let
$\mathscr O$
and residue field k. Let
![]() $G=\operatorname {\mathrm {GL}}_2 (\mathbb {Q}_p)$
and let
$G=\operatorname {\mathrm {GL}}_2 (\mathbb {Q}_p)$
and let
![]() $\operatorname {\mathrm {Mod}}^{\mathrm {sm}}_{G}(\mathscr O)$
be the category of smooth G-representations on
$\operatorname {\mathrm {Mod}}^{\mathrm {sm}}_{G}(\mathscr O)$
be the category of smooth G-representations on
![]() $\mathscr O$
-torsion modules. Let
$\mathscr O$
-torsion modules. Let
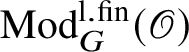 $\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G}(\mathscr O)$
be the full subcategory of
$\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G}(\mathscr O)$
be the full subcategory of
![]() $\operatorname {\mathrm {Mod}}^{\mathrm {sm}}_{G}(\mathscr O)$
consisting of representations which are equal to the union of their subrepresentations of finite length. This is equivalent to the requirement that every finitely generated subrepresentation be of finite length, and we call such representations locally finite. We fix a character
$\operatorname {\mathrm {Mod}}^{\mathrm {sm}}_{G}(\mathscr O)$
consisting of representations which are equal to the union of their subrepresentations of finite length. This is equivalent to the requirement that every finitely generated subrepresentation be of finite length, and we call such representations locally finite. We fix a character
![]() $\zeta :Z\rightarrow \mathscr O^{\times }$
of the centre of G, and let
$\zeta :Z\rightarrow \mathscr O^{\times }$
of the centre of G, and let
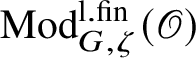 $\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O)$
be the full subcategory of
$\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O)$
be the full subcategory of
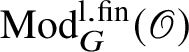 $\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G}(\mathscr O)$
consisting of representations with central character
$\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G}(\mathscr O)$
consisting of representations with central character
![]() $\zeta $
. The category
$\zeta $
. The category
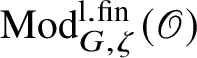 $\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O)$
is locally finite and by general results of Gabriel [Reference Gabriel31] decomposes as a product
$\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O)$
is locally finite and by general results of Gabriel [Reference Gabriel31] decomposes as a product
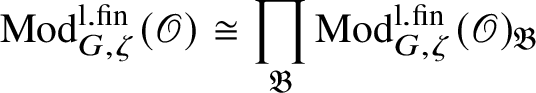 $$ \begin{align*} \operatorname{\mathrm{Mod}}^{\mathrm{l.fin}}_{G, \zeta}(\mathscr O)\cong \prod_{\mathfrak B} \operatorname{\mathrm{Mod}}^{\mathrm{l.fin}}_{G, \zeta}(\mathscr O)_{\mathfrak B} \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Mod}}^{\mathrm{l.fin}}_{G, \zeta}(\mathscr O)\cong \prod_{\mathfrak B} \operatorname{\mathrm{Mod}}^{\mathrm{l.fin}}_{G, \zeta}(\mathscr O)_{\mathfrak B} \end{align*} $$
of indecomposable subcategories, called blocks. Moreover, each block is antiequivalent to the category of pseudocompact modules over a pseudocompact ring
![]() $E_{\mathfrak B}$
. The centre of the ring
$E_{\mathfrak B}$
. The centre of the ring
![]() $E_{\mathfrak B}$
, which we denote by
$E_{\mathfrak B}$
, which we denote by
![]() $Z_{\mathfrak B}$
, is naturally isomorphic to the centre of the category
$Z_{\mathfrak B}$
, is naturally isomorphic to the centre of the category
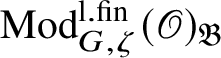 $\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G,\zeta }(\mathscr O)_{\mathfrak B}$
, which by definition is the ring of natural transformations of the identity functor. This means that
$\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G,\zeta }(\mathscr O)_{\mathfrak B}$
, which by definition is the ring of natural transformations of the identity functor. This means that
![]() $Z_{\mathfrak B}$
acts functorially on every object in
$Z_{\mathfrak B}$
acts functorially on every object in
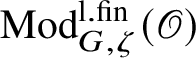 $\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O)$
. The finiteness result in the title is an analogue of a result of Bernstein in the theory of smooth representations of p-adic groups on
$\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O)$
. The finiteness result in the title is an analogue of a result of Bernstein in the theory of smooth representations of p-adic groups on
![]() $\mathbb {C}$
-vector spaces [Reference Bernstein5, Proposition 3.3]:
$\mathbb {C}$
-vector spaces [Reference Bernstein5, Proposition 3.3]:
Theorem 1.1. The ring
![]() $Z_{\mathfrak B}$
is Noetherian, and
$Z_{\mathfrak B}$
is Noetherian, and
![]() $E_{\mathfrak B}$
is a finitely generated
$E_{\mathfrak B}$
is a finitely generated
![]() $Z_{\mathfrak B}$
-module.
$Z_{\mathfrak B}$
-module.
To prove the theorem we use in an essential way the direct connection between the
![]() $\operatorname {\mathrm {GL}}_2 (\mathbb {Q}_p)$
representations and the representations of the absolute Galois group of
$\operatorname {\mathrm {GL}}_2 (\mathbb {Q}_p)$
representations and the representations of the absolute Galois group of
![]() $\mathbb {Q}_p$
, which we denote by
$\mathbb {Q}_p$
, which we denote by
![]() $\mathscr G_{\mathbb {Q}_p}$
, discovered by Colmez in [Reference Colmez19], via his celebrated Montreal functor
$\mathscr G_{\mathbb {Q}_p}$
, discovered by Colmez in [Reference Colmez19], via his celebrated Montreal functor
![]() $\check {\mathbf {V}}$
, which we review in Section 4.4.
$\check {\mathbf {V}}$
, which we review in Section 4.4.
For each fixed block
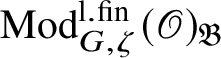 $\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O)_{\mathfrak B}$
there is a finite extension
$\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O)_{\mathfrak B}$
there is a finite extension
![]() $L'$
of L with ring of integers
$L'$
of L with ring of integers
![]() $\mathscr O'$
, such that
$\mathscr O'$
, such that
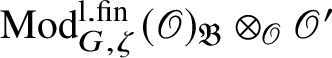 $\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O)_{\mathfrak B}\otimes _{\mathscr O} {\mathscr O}'$
decomposes into a finite product of indecomposable subcategories, each of which remains indecomposable after a further extension of scalars. Such absolutely indecomposable blocks have been classified in [Reference Paškūnas40], and they correspond to semisimple representations
$\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O)_{\mathfrak B}\otimes _{\mathscr O} {\mathscr O}'$
decomposes into a finite product of indecomposable subcategories, each of which remains indecomposable after a further extension of scalars. Such absolutely indecomposable blocks have been classified in [Reference Paškūnas40], and they correspond to semisimple representations
![]() $\bar {\rho }: \mathscr G_{\mathbb {Q}_p}\rightarrow \operatorname {\mathrm {GL}}_2(k)$
, which are either absolutely irreducible or a direct sum of two characters. This bijection realises the semisimple mod p local Langlands correspondence established in a visionary paper of Breuil [Reference Breuil9].
$\bar {\rho }: \mathscr G_{\mathbb {Q}_p}\rightarrow \operatorname {\mathrm {GL}}_2(k)$
, which are either absolutely irreducible or a direct sum of two characters. This bijection realises the semisimple mod p local Langlands correspondence established in a visionary paper of Breuil [Reference Breuil9].
If
![]() $\bar {\rho }$
is absolutely irreducible, then
$\bar {\rho }$
is absolutely irreducible, then
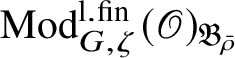 $\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O)_{\mathfrak B_{\bar {\rho }}}$
contains only one irreducible object
$\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O)_{\mathfrak B_{\bar {\rho }}}$
contains only one irreducible object
![]() $\pi $
, satisfying
$\pi $
, satisfying
![]() $\check {\mathbf {V}}(\pi ^{\vee })\cong \bar {\rho }$
, where
$\check {\mathbf {V}}(\pi ^{\vee })\cong \bar {\rho }$
, where
![]() $\vee $
denotes the Pontryagin dual. Moreover,
$\vee $
denotes the Pontryagin dual. Moreover,
![]() $\pi $
is not a subquotient of any parabolically induced representation; such representations are called supersingular.
$\pi $
is not a subquotient of any parabolically induced representation; such representations are called supersingular.
If
![]() $\bar {\rho }=\chi _1 \oplus \chi _2$
, where
$\bar {\rho }=\chi _1 \oplus \chi _2$
, where
![]() $\chi _1, \chi _2: \mathscr G_{\mathbb {Q}_p}\rightarrow k^{\times }$
are characters, then the irreducible objects in
$\chi _1, \chi _2: \mathscr G_{\mathbb {Q}_p}\rightarrow k^{\times }$
are characters, then the irreducible objects in
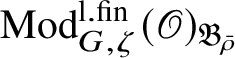 $\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O)_{\mathfrak B_{\bar {\rho }}}$
are the irreducible subquotients of the representation
$\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O)_{\mathfrak B_{\bar {\rho }}}$
are the irreducible subquotients of the representation
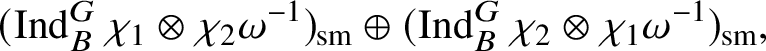 $$ \begin{align*} (\operatorname{\mathrm{Ind}}^G_B \chi_1\otimes \chi_2 \omega^{-1})_{\mathrm{sm}}\oplus (\operatorname{\mathrm{Ind}}^G_B \chi_2\otimes \chi_1 \omega^{-1})_{\mathrm{sm}}, \end{align*} $$
$$ \begin{align*} (\operatorname{\mathrm{Ind}}^G_B \chi_1\otimes \chi_2 \omega^{-1})_{\mathrm{sm}}\oplus (\operatorname{\mathrm{Ind}}^G_B \chi_2\otimes \chi_1 \omega^{-1})_{\mathrm{sm}}, \end{align*} $$
where we consider
![]() $\chi _1, \chi _2$
as characters of
$\chi _1, \chi _2$
as characters of
![]() $\mathbb {Q}_p^{\times }$
via the Artin map
$\mathbb {Q}_p^{\times }$
via the Artin map
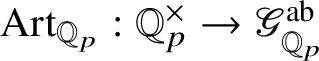 $\operatorname {\mathrm {Art}}_{\mathbb {Q}_p}: \mathbb {Q}_p^{\times } \rightarrow \mathscr G_{\mathbb {Q}_p}^{\mathrm {ab}}$
, and
$\operatorname {\mathrm {Art}}_{\mathbb {Q}_p}: \mathbb {Q}_p^{\times } \rightarrow \mathscr G_{\mathbb {Q}_p}^{\mathrm {ab}}$
, and
![]() $\omega (x)= x \lvert x\rvert \pmod {p}$
for all
$\omega (x)= x \lvert x\rvert \pmod {p}$
for all
![]() $x\in \mathbb {Q}_p^{\times }$
corresponds to the cyclotomic character modulo p. (See Section 4.1 for an explicit list.)
$x\in \mathbb {Q}_p^{\times }$
corresponds to the cyclotomic character modulo p. (See Section 4.1 for an explicit list.)
All the blocks, except when p is either
![]() $2$
or
$2$
or
![]() $3$
and
$3$
and
![]() $\bar {\rho }=\chi \oplus \chi \omega $
, have been well understood in [Reference Paškūnas39, Reference Paškūnas41]. These exceptional blocks are the main focus of this paper, but our arguments work for all p and all blocks.
$\bar {\rho }=\chi \oplus \chi \omega $
, have been well understood in [Reference Paškūnas39, Reference Paškūnas41]. These exceptional blocks are the main focus of this paper, but our arguments work for all p and all blocks.
The action of
![]() $Z_{\mathfrak B_{\bar {\rho }}}$
induces a functorial ring homomorphism
$Z_{\mathfrak B_{\bar {\rho }}}$
induces a functorial ring homomorphism
for every object
![]() $\tau $
in
$\tau $
in
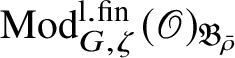 $\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O)_{\mathfrak B_{\bar {\rho }}}$
. Since
$\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O)_{\mathfrak B_{\bar {\rho }}}$
. Since
![]() $\check {\mathbf {V}}$
is a functor, it induces a ring homomorphism
$\check {\mathbf {V}}$
is a functor, it induces a ring homomorphism
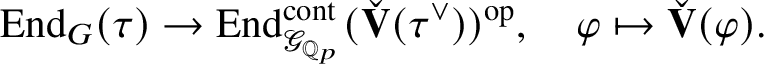 $$ \begin{align*} \operatorname{\mathrm{End}}_{G}(\tau)\rightarrow \operatorname{\mathrm{End}}^{\mathrm{cont}}_{\mathscr G_{\mathbb{Q}_p}}(\check{\mathbf{V}}(\tau^{\vee}))^{\mathrm{op}},\quad \varphi\mapsto \check{\mathbf{V}}(\varphi). \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{End}}_{G}(\tau)\rightarrow \operatorname{\mathrm{End}}^{\mathrm{cont}}_{\mathscr G_{\mathbb{Q}_p}}(\check{\mathbf{V}}(\tau^{\vee}))^{\mathrm{op}},\quad \varphi\mapsto \check{\mathbf{V}}(\varphi). \end{align*} $$
We denote the action of
![]() $\mathscr G_{\mathbb {Q}_p}$
on
$\mathscr G_{\mathbb {Q}_p}$
on
![]() $\check {\mathbf {V}} (\tau ^{\vee })$
by
$\check {\mathbf {V}} (\tau ^{\vee })$
by
![]() $\rho _{\check {\mathbf {V}} (\tau ^{\vee })}$
.
$\rho _{\check {\mathbf {V}} (\tau ^{\vee })}$
.
Let
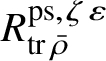 $R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr} \bar {\rho }}$
be the universal deformation ring parameterising pseudorepresentations lifting
$R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr} \bar {\rho }}$
be the universal deformation ring parameterising pseudorepresentations lifting
![]() $\operatorname {tr} \bar {\rho }$
with determinant
$\operatorname {tr} \bar {\rho }$
with determinant
![]() $\zeta \varepsilon $
, where
$\zeta \varepsilon $
, where
![]() $\varepsilon $
is the p-adic cyclotomic character. We may evaluate the universal pseudorepresentation
$\varepsilon $
is the p-adic cyclotomic character. We may evaluate the universal pseudorepresentation
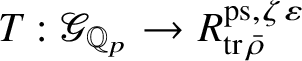 $T: \mathscr G_{\mathbb {Q}_p} \rightarrow R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }}$
at
$T: \mathscr G_{\mathbb {Q}_p} \rightarrow R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }}$
at
![]() $g\in \mathscr G_{\mathbb {Q}_p}$
to obtain an element
$g\in \mathscr G_{\mathbb {Q}_p}$
to obtain an element
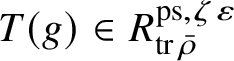 $T(g)\in R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }}$
.
$T(g)\in R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }}$
.
Theorem 1.2. There is an
![]() $\mathscr O$
-algebra homomorphism
$\mathscr O$
-algebra homomorphism
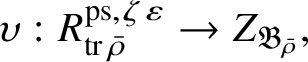 $$ \begin{align} \upsilon: R^{\mathrm{ps}, \zeta\varepsilon}_{\operatorname{tr} \bar{\rho}}\rightarrow Z_{\mathfrak B_{\bar{\rho}}}, \end{align} $$
$$ \begin{align} \upsilon: R^{\mathrm{ps}, \zeta\varepsilon}_{\operatorname{tr} \bar{\rho}}\rightarrow Z_{\mathfrak B_{\bar{\rho}}}, \end{align} $$
satisfying the following compatibility property with the Colmez’s functor: For all
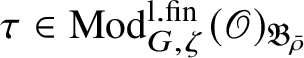 $\tau \in \operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O)_{\mathfrak B_{\bar {\rho }}}$
and all
$\tau \in \operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O)_{\mathfrak B_{\bar {\rho }}}$
and all
![]() $g\in \mathscr G_{\mathbb {Q}_p}$
, we have
$g\in \mathscr G_{\mathbb {Q}_p}$
, we have
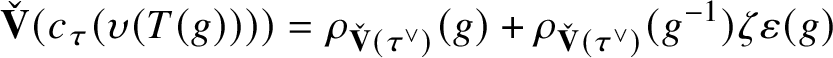 $$ \begin{align*} \check{\mathbf{V}}(c_{\tau}(\upsilon(T(g))))= \rho_{\check{\mathbf{V}}(\tau^{\vee})}(g) + \rho_{\check{\mathbf{V}}(\tau^{\vee})}(g^{-1}) \zeta\varepsilon(g) \end{align*} $$
$$ \begin{align*} \check{\mathbf{V}}(c_{\tau}(\upsilon(T(g))))= \rho_{\check{\mathbf{V}}(\tau^{\vee})}(g) + \rho_{\check{\mathbf{V}}(\tau^{\vee})}(g^{-1}) \zeta\varepsilon(g) \end{align*} $$
in
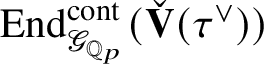 $\operatorname {\mathrm {End}}_{\mathscr G_{\mathbb {Q}_p}}^{\mathrm {cont}} (\check {\mathbf {V}} (\tau ^{\vee }))$
.
$\operatorname {\mathrm {End}}_{\mathscr G_{\mathbb {Q}_p}}^{\mathrm {cont}} (\check {\mathbf {V}} (\tau ^{\vee }))$
.
The construction of the map (1) is the main point of this paper. Outside the exceptional cases, it has been established in [Reference Paškūnas39, Reference Paškūnas41] using a different argument from ours. Our main result is the following:
Theorem 1.3. The map (1) makes
![]() $Z_{\mathfrak B_{\bar {\rho }}}$
and
$Z_{\mathfrak B_{\bar {\rho }}}$
and
![]() $E_{\mathfrak B_{\bar {\rho }}}$
into finitely generated
$E_{\mathfrak B_{\bar {\rho }}}$
into finitely generated
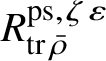 $R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }}$
-modules.
$R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }}$
-modules.
Since
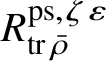 $R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }}$
is known to be Noetherian by the work of Chenevier [Reference Chenevier18], Theorem 1.3 implies Theorem 1.1. Moreover, Theorems 1.2 and 1.3 are sufficient to remove the restrictions in Lue Pan’s paper. Further, we can re-prove most of the results concerning Banach-space representations in [Reference Paškūnas39] (see Section 6.2 and Corollary 6.16).
$R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }}$
is known to be Noetherian by the work of Chenevier [Reference Chenevier18], Theorem 1.3 implies Theorem 1.1. Moreover, Theorems 1.2 and 1.3 are sufficient to remove the restrictions in Lue Pan’s paper. Further, we can re-prove most of the results concerning Banach-space representations in [Reference Paškūnas39] (see Section 6.2 and Corollary 6.16).
To give a flavour of the results on Banach-space representations, we will explain a special case. Let
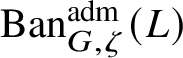 $\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)$
be the category of admissible unitary L-Banach-space representations of G with central character
$\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)$
be the category of admissible unitary L-Banach-space representations of G with central character
![]() $\zeta $
. This category is abelian [Reference Schneider and Teitelbaum44]. By [Reference Colmez, Dospinescu and Paškūnas21], Colmez’s functor induces a bijection between the equivalence classes of absolutely irreducible nonordinary
$\zeta $
. This category is abelian [Reference Schneider and Teitelbaum44]. By [Reference Colmez, Dospinescu and Paškūnas21], Colmez’s functor induces a bijection between the equivalence classes of absolutely irreducible nonordinary
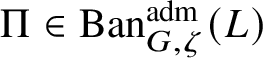 $\Pi \in \operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)$
and absolutely irreducible Galois representations
$\Pi \in \operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)$
and absolutely irreducible Galois representations
![]() $\rho : \mathscr G_{\mathbb {Q}_p}\rightarrow \operatorname {\mathrm {GL}}_2(L)$
. We show that there are no extensions between
$\rho : \mathscr G_{\mathbb {Q}_p}\rightarrow \operatorname {\mathrm {GL}}_2(L)$
. We show that there are no extensions between
![]() $\Pi $
and other irreducible representations in
$\Pi $
and other irreducible representations in
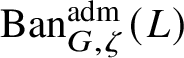 $\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)$
; hence
$\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)$
; hence
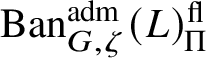 $\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)^{\mathrm {fl}}_{\Pi }$
is a direct summand of
$\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)^{\mathrm {fl}}_{\Pi }$
is a direct summand of
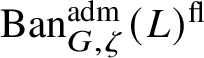 $\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)^{\mathrm {fl}}$
, where the superscript ‘
$\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)^{\mathrm {fl}}$
, where the superscript ‘
![]() $\mathrm {fl}$
’ indicates finite length and the subscript
$\mathrm {fl}$
’ indicates finite length and the subscript
![]() $\Pi $
indicates that all the irreducible subquotients are isomorphic to
$\Pi $
indicates that all the irreducible subquotients are isomorphic to
![]() $\Pi $
. We show in Corollary 6.16 that
$\Pi $
. We show in Corollary 6.16 that
![]() $\check {\mathbf {V}}$
induces an antiequivalence of categories between
$\check {\mathbf {V}}$
induces an antiequivalence of categories between
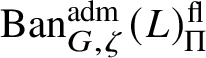 $\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)^{\mathrm {fl}}_{\Pi }$
and the category of modules of finite length over
$\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)^{\mathrm {fl}}_{\Pi }$
and the category of modules of finite length over
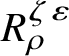 $R^{\zeta \varepsilon }_{\rho }$
, the universal deformation ring of
$R^{\zeta \varepsilon }_{\rho }$
, the universal deformation ring of
![]() $\rho $
parameterising deformations of
$\rho $
parameterising deformations of
![]() $\rho $
with determinant equal to
$\rho $
with determinant equal to
![]() $\zeta \varepsilon $
to local Artinian L-algebras. Such results were known before for
$\zeta \varepsilon $
to local Artinian L-algebras. Such results were known before for
![]() $p\ge 5$
[Reference Paškūnas39], and under assumptions on the reduction modulo p of a G-invariant lattice in
$p\ge 5$
[Reference Paškūnas39], and under assumptions on the reduction modulo p of a G-invariant lattice in
![]() $\Pi $
if
$\Pi $
if
![]() $p=2$
or
$p=2$
or
![]() $p=3$
[Reference Paškūnas41].
$p=3$
[Reference Paškūnas41].
Let
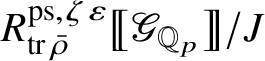 be the largest quotient of
be the largest quotient of
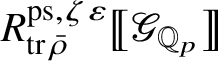 such that the Cayley–Hamilton theorem holds for the universal pseudorepresentation with determinant
such that the Cayley–Hamilton theorem holds for the universal pseudorepresentation with determinant
![]() $\zeta \varepsilon $
lifting
$\zeta \varepsilon $
lifting
![]() $\operatorname {tr} \bar {\rho }$
. Such algebras have been studied by Bellaïche and Chenevier [Reference Bellaïche and Chenevier3, Reference Chenevier18]; they play a key role in this paper. The subscript ‘
$\operatorname {tr} \bar {\rho }$
. Such algebras have been studied by Bellaïche and Chenevier [Reference Bellaïche and Chenevier3, Reference Chenevier18]; they play a key role in this paper. The subscript ‘
![]() $\mathrm {tf}$
’ will indicate the maximal
$\mathrm {tf}$
’ will indicate the maximal
![]() $\mathscr O$
-torsion-free quotient. Our second main result asserts the following:
$\mathscr O$
-torsion-free quotient. Our second main result asserts the following:
Theorem 1.4. The essential image of
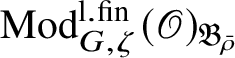 $\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O)_{\mathfrak B_{\bar {\rho }}}$
under
$\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O)_{\mathfrak B_{\bar {\rho }}}$
under
![]() $\check {\mathbf {V}}$
is antiequivalent to the category of pseudocompact
$\check {\mathbf {V}}$
is antiequivalent to the category of pseudocompact
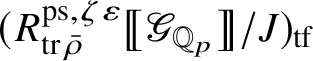 -modules. The map (1) induces an isomorphism
-modules. The map (1) induces an isomorphism
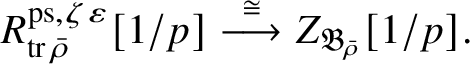 $$ \begin{align} R^{\mathrm{ps}, \zeta\varepsilon}_{\operatorname{tr} \bar{\rho}}[1/p]\overset{\cong}{\longrightarrow}Z_{\mathfrak B_{\bar{\rho}}}[1/p]. \end{align} $$
$$ \begin{align} R^{\mathrm{ps}, \zeta\varepsilon}_{\operatorname{tr} \bar{\rho}}[1/p]\overset{\cong}{\longrightarrow}Z_{\mathfrak B_{\bar{\rho}}}[1/p]. \end{align} $$
Moreover, if
![]() $p\neq 2$
, then
$p\neq 2$
, then
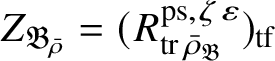 $Z_{\mathfrak B_{\bar {\rho }}}= (R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}})_{\mathrm {tf}}$
, and if
$Z_{\mathfrak B_{\bar {\rho }}}= (R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}})_{\mathrm {tf}}$
, and if
![]() $p=2$
, then the cokernel of map (1) is killed by
$p=2$
, then the cokernel of map (1) is killed by
![]() $2$
.
$2$
.
Corollary 1.5.
![]() $Z_{\mathfrak B_{\bar {\rho }}}$
is a complete local Noetherian
$Z_{\mathfrak B_{\bar {\rho }}}$
is a complete local Noetherian
![]() $\mathscr O$
-algebra with residue field k. It is
$\mathscr O$
-algebra with residue field k. It is
![]() $\mathscr O$
-torsion-free, and
$\mathscr O$
-torsion-free, and
![]() $Z_{\mathfrak B_{\bar {\rho }}} [1/p]$
is normal.
$Z_{\mathfrak B_{\bar {\rho }}} [1/p]$
is normal.
If we are not in the exceptional cases, then Theorem 1.3 is proved in [Reference Paškūnas39, Reference Paškūnas41] essentially by computing first
![]() $E_{\mathfrak B}$
and then its centre
$E_{\mathfrak B}$
and then its centre
![]() $Z_{\mathfrak B}$
. Moreover, it is proved there that map (1) is an isomorphism and
$Z_{\mathfrak B}$
. Moreover, it is proved there that map (1) is an isomorphism and
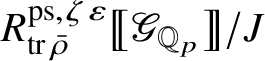 is
is
![]() $\mathscr O$
-torsion-free. The argument in this paper, sketched in Section 1.1, is different: We do not compute
$\mathscr O$
-torsion-free. The argument in this paper, sketched in Section 1.1, is different: We do not compute
![]() $E_{\mathfrak B}$
.
$E_{\mathfrak B}$
.
Our original strategy for proving formula (2) in this paper was to use an argument of Gabber in [Reference Kisin34, Appendix]. We showed that
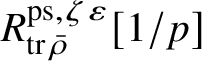 $R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr} \bar {\rho}}[1/p]$
is normal,
$R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr} \bar {\rho}}[1/p]$
is normal,
![]() $Z_{\mathfrak B}[1/p]$
is reduced, and map (1) induces a bijection on maximal spectra
$Z_{\mathfrak B}[1/p]$
is reduced, and map (1) induces a bijection on maximal spectra
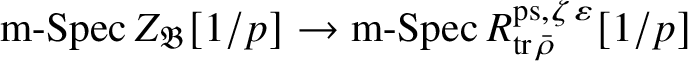 $\operatorname {\mathrm {m-Spec}} Z_{\mathfrak B}[1/p]\rightarrow \operatorname {\mathrm {m-Spec}} R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr} \bar {\rho }} [1/p]$
and an isomorphism of the residue fields. However, this is replaced by a different argument in the final version, which also proves the first part of Theorem 1.4. One important ingredient in the proof is results of Colmez, Dospinescu and the first author [Reference Colmez, Dospinescu and Paškūnas21, Reference Colmez, Dospinescu and Paškūnas22] which imply that the universal framed deformation of
$\operatorname {\mathrm {m-Spec}} Z_{\mathfrak B}[1/p]\rightarrow \operatorname {\mathrm {m-Spec}} R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr} \bar {\rho }} [1/p]$
and an isomorphism of the residue fields. However, this is replaced by a different argument in the final version, which also proves the first part of Theorem 1.4. One important ingredient in the proof is results of Colmez, Dospinescu and the first author [Reference Colmez, Dospinescu and Paškūnas21, Reference Colmez, Dospinescu and Paškūnas22] which imply that the universal framed deformation of
![]() $\bar {\rho }$
with determinant
$\bar {\rho }$
with determinant
![]() $\zeta \varepsilon $
lies in the image of
$\zeta \varepsilon $
lies in the image of
![]() $\check {\mathbf {V}}$
. We show in Appendix A that
$\check {\mathbf {V}}$
. We show in Appendix A that
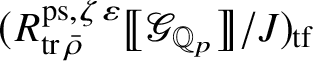 acts faithfully on this representation using the theory of Cayley–Hamilton algebras [Reference Procesi43].
acts faithfully on this representation using the theory of Cayley–Hamilton algebras [Reference Procesi43].
The normality of the ring
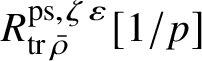 $R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr} \bar {\rho }}[1/p]$
is proved in Appendix A, where we show that if the generic fibre of the framed deformation ring
$R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr} \bar {\rho }}[1/p]$
is proved in Appendix A, where we show that if the generic fibre of the framed deformation ring
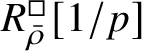 $R^{\square }_{\bar {\rho }} [1/p]$
is normal, then
$R^{\square }_{\bar {\rho }} [1/p]$
is normal, then
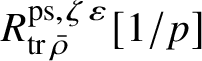 $R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr} \bar {\rho }}[1/p]$
and the corresponding rigid analytic space
$R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr} \bar {\rho }}[1/p]$
and the corresponding rigid analytic space
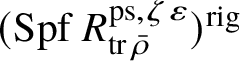 $(\operatorname {\mathrm {Spf}} R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr} \bar {\rho }})^{\mathrm {rig}}$
are normal. The same applies to the deformation rings without the fixed-determinant condition. In fact, we prove this statement not only for
$(\operatorname {\mathrm {Spf}} R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr} \bar {\rho }})^{\mathrm {rig}}$
are normal. The same applies to the deformation rings without the fixed-determinant condition. In fact, we prove this statement not only for
![]() $\mathscr G_{\mathbb {Q}_p}$
but for any profinite group satisfying Mazur’s finiteness condition at p. We then show that
$\mathscr G_{\mathbb {Q}_p}$
but for any profinite group satisfying Mazur’s finiteness condition at p. We then show that
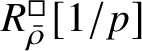 $R^{\square }_{\bar {\rho }}[1/p]$
is normal for all
$R^{\square }_{\bar {\rho }}[1/p]$
is normal for all
![]() $2$
-dimensional semisimple representations of
$2$
-dimensional semisimple representations of
![]() $\mathscr G_{\mathbb {Q}_p}$
; the hard cases are precisely those corresponding to the exceptional blocks. If
$\mathscr G_{\mathbb {Q}_p}$
; the hard cases are precisely those corresponding to the exceptional blocks. If
![]() $p=2$
, then the assertion has been shown in [Reference Colmez, Dospinescu and Paškūnas22], and if
$p=2$
, then the assertion has been shown in [Reference Colmez, Dospinescu and Paškūnas22], and if
![]() $p=3$
, then we give a proof in Appendix A based on Böckle’s explicit description of the framed deformation ring in [Reference Böckle7]. We note that the argument of [Reference Colmez, Dospinescu and Paškūnas22] has been generalised by Iyengar [Reference Iyengar33], showing that when
$p=3$
, then we give a proof in Appendix A based on Böckle’s explicit description of the framed deformation ring in [Reference Böckle7]. We note that the argument of [Reference Colmez, Dospinescu and Paškūnas22] has been generalised by Iyengar [Reference Iyengar33], showing that when
![]() $\bar {\rho }$
is the trivial d-dimensional representation of the absolute Galois group of a p-adic field, containing a
$\bar {\rho }$
is the trivial d-dimensional representation of the absolute Galois group of a p-adic field, containing a
![]() $4$
th root of unity if
$4$
th root of unity if
![]() $p=2$
, then
$p=2$
, then
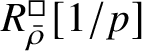 $R^{\square }_{\bar {\rho }}[1/p]$
is normal, so our results also apply in this setting. We expectFootnote
1
the rings
$R^{\square }_{\bar {\rho }}[1/p]$
is normal, so our results also apply in this setting. We expectFootnote
1
the rings
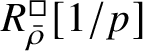 $R^{\square }_{\bar {\rho }}[1/p]$
to be normal for any d-dimensional representation
$R^{\square }_{\bar {\rho }}[1/p]$
to be normal for any d-dimensional representation
![]() $\bar {\rho }$
of
$\bar {\rho }$
of
![]() $\mathscr G_F$
, where F is a finite extension of
$\mathscr G_F$
, where F is a finite extension of
![]() $\mathbb {Q}_p$
.
$\mathbb {Q}_p$
.
1.1 A sketch of the proof
We will now explain the construction of the map (1). To fix ideas we will discuss a special case:
![]() $p=2$
,
$p=2$
,
![]() $\bar {\rho }=\mathbf 1 \oplus \omega $
and
$\bar {\rho }=\mathbf 1 \oplus \omega $
and
![]() $\zeta =\mathbf 1$
. Since the cyclotomic character is trivial modulo
$\zeta =\mathbf 1$
. Since the cyclotomic character is trivial modulo
![]() $2$
,
$2$
,
![]() $\bar {\rho }=\mathbf 1 \oplus \mathbf 1$
. The corresponding block has two irreducible representations: the trivial
$\bar {\rho }=\mathbf 1 \oplus \mathbf 1$
. The corresponding block has two irreducible representations: the trivial
![]() $\mathbf 1$
and the smooth Steinberg representation
$\mathbf 1$
and the smooth Steinberg representation
![]() $\operatorname {\mathrm {Sp}}$
. Instead of working with representations on
$\operatorname {\mathrm {Sp}}$
. Instead of working with representations on
![]() $\mathscr O$
-torsion modules, it is more convenient to use Pontryagin duality and work with representations of G on compact
$\mathscr O$
-torsion modules, it is more convenient to use Pontryagin duality and work with representations of G on compact
![]() $\mathscr O$
-modules. We denote by
$\mathscr O$
-modules. We denote by
![]() ${\mathfrak C}(\mathscr O)_{\mathfrak B}$
the category antiequivalent to
${\mathfrak C}(\mathscr O)_{\mathfrak B}$
the category antiequivalent to
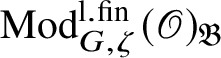 $\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O)_{\mathfrak B}$
under Pontryagin duality.
$\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O)_{\mathfrak B}$
under Pontryagin duality.
Let
![]() $P_{\mathbf 1^{\vee }}$
and
$P_{\mathbf 1^{\vee }}$
and
![]() $P_{\operatorname {\mathrm {Sp}}^{\vee }}$
be projective envelopes of
$P_{\operatorname {\mathrm {Sp}}^{\vee }}$
be projective envelopes of
![]() $\mathbf 1^{\vee }$
and
$\mathbf 1^{\vee }$
and
![]() $\operatorname {\mathrm {Sp}}^{\vee }$
in
$\operatorname {\mathrm {Sp}}^{\vee }$
in
![]() ${\mathfrak C}(\mathscr O)_{\mathfrak B}$
, respectively. Then
${\mathfrak C}(\mathscr O)_{\mathfrak B}$
, respectively. Then
![]() $P_{\mathfrak B}:= P_{\mathbf 1^{\vee }}\oplus P_{\operatorname {\mathrm {Sp}}^{\vee }}$
is a projective generator of
$P_{\mathfrak B}:= P_{\mathbf 1^{\vee }}\oplus P_{\operatorname {\mathrm {Sp}}^{\vee }}$
is a projective generator of
![]() ${\mathfrak C}(\mathscr O)_{\mathfrak B}$
, and by results of Gabriel [Reference Gabriel31] the category
${\mathfrak C}(\mathscr O)_{\mathfrak B}$
, and by results of Gabriel [Reference Gabriel31] the category
![]() ${\mathfrak C}(\mathscr O)_{\mathfrak B}$
is equivalent to the category of pseudocompact modules of
${\mathfrak C}(\mathscr O)_{\mathfrak B}$
is equivalent to the category of pseudocompact modules of
![]() $E_{\mathfrak B}:=\operatorname {\mathrm {End}}_{{\mathfrak C}(\mathscr O)}(P_{\mathfrak B})$
. The equivalence is induced by the functors
$E_{\mathfrak B}:=\operatorname {\mathrm {End}}_{{\mathfrak C}(\mathscr O)}(P_{\mathfrak B})$
. The equivalence is induced by the functors
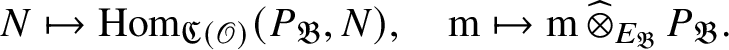 $$ \begin{align*} N\mapsto \operatorname{\mathrm{Hom}}_{{\mathfrak C}(\mathscr O)}(P_{\mathfrak B}, N),\quad \mathrm m\mapsto \mathrm m \operatorname{\mathrm{\mathbin{\widehat{\otimes}}}}_{E_{\mathfrak B}} P_{\mathfrak B}. \end{align*} $$
$$ \begin{align*} N\mapsto \operatorname{\mathrm{Hom}}_{{\mathfrak C}(\mathscr O)}(P_{\mathfrak B}, N),\quad \mathrm m\mapsto \mathrm m \operatorname{\mathrm{\mathbin{\widehat{\otimes}}}}_{E_{\mathfrak B}} P_{\mathfrak B}. \end{align*} $$
The centre
![]() $Z_{\mathfrak B}$
of the category
$Z_{\mathfrak B}$
of the category
![]() ${\mathfrak C}(\mathscr O)_{\mathfrak B}$
is naturally isomorphic to the centre of the ring
${\mathfrak C}(\mathscr O)_{\mathfrak B}$
is naturally isomorphic to the centre of the ring
![]() $E_{\mathfrak B}$
.
$E_{\mathfrak B}$
.
Colmez’s functor kills all objects on which
![]() $\operatorname {\mathrm {SL}}_2(\mathbb {Q}_p)$
acts trivially, and these form a thick subcategory. Thus
$\operatorname {\mathrm {SL}}_2(\mathbb {Q}_p)$
acts trivially, and these form a thick subcategory. Thus
![]() $\check {\mathbf {V}}$
factors through the quotient category, which we denote by
$\check {\mathbf {V}}$
factors through the quotient category, which we denote by
![]() $\mathfrak Q(\mathscr O)_{\mathfrak B}$
; let
$\mathfrak Q(\mathscr O)_{\mathfrak B}$
; let
![]() $\mathscr T: {\mathfrak C}(\mathscr O)_{\mathfrak B}\rightarrow \mathfrak Q(\mathscr O)_{\mathfrak B}$
be the quotient functor. Moreover,
$\mathscr T: {\mathfrak C}(\mathscr O)_{\mathfrak B}\rightarrow \mathfrak Q(\mathscr O)_{\mathfrak B}$
be the quotient functor. Moreover,
![]() $\check {\mathbf {V}}$
induces an equivalence of categories between
$\check {\mathbf {V}}$
induces an equivalence of categories between
![]() $\mathfrak Q(\mathscr O)_{\mathfrak B}$
and its essential image under
$\mathfrak Q(\mathscr O)_{\mathfrak B}$
and its essential image under
![]() $\check {\mathbf {V}}$
. To prove this, one needs to show that
$\check {\mathbf {V}}$
. To prove this, one needs to show that
![]() $\check {\mathbf {V}}$
sends nonsplit extensions to nonsplit extensions; such arguments are originally due to Colmez, and in the case
$\check {\mathbf {V}}$
sends nonsplit extensions to nonsplit extensions; such arguments are originally due to Colmez, and in the case
![]() $p=2$
this has been shown by the second author [Reference Tung47].
$p=2$
this has been shown by the second author [Reference Tung47].
Since
![]() $\mathscr T (\mathbf 1^{\vee })=0$
, then
$\mathscr T (\mathbf 1^{\vee })=0$
, then
![]() $\mathscr T (\operatorname {\mathrm {Sp}}^{\vee })$
is the only irreducible object in
$\mathscr T (\operatorname {\mathrm {Sp}}^{\vee })$
is the only irreducible object in
![]() $\mathfrak Q(\mathscr O)_{\mathfrak B}$
up to isomorphism. Moreover, it is shown in [Reference Paškūnas39] that
$\mathfrak Q(\mathscr O)_{\mathfrak B}$
up to isomorphism. Moreover, it is shown in [Reference Paškūnas39] that
![]() $\mathscr T (P_{\operatorname {\mathrm {Sp}}^{\vee }})$
is a projective envelope of
$\mathscr T (P_{\operatorname {\mathrm {Sp}}^{\vee }})$
is a projective envelope of
![]() $\mathscr T (\operatorname {\mathrm {Sp}}^{\vee })$
, and
$\mathscr T (\operatorname {\mathrm {Sp}}^{\vee })$
, and
![]() $\mathscr T$
induces an isomorphism
$\mathscr T$
induces an isomorphism
Since
![]() $\mathscr T (\operatorname {\mathrm {Sp}}^{\vee })$
is the only irreducible object in
$\mathscr T (\operatorname {\mathrm {Sp}}^{\vee })$
is the only irreducible object in
![]() $\mathfrak Q(\mathscr O)_{\mathfrak B}$
, then
$\mathfrak Q(\mathscr O)_{\mathfrak B}$
, then
![]() $\mathscr T (P_{\operatorname {\mathrm {Sp}}^{\vee }})$
is a projective generator of
$\mathscr T (P_{\operatorname {\mathrm {Sp}}^{\vee }})$
is a projective generator of
![]() $\mathfrak Q(\mathscr O)_{\mathfrak B}$
, and thus
$\mathfrak Q(\mathscr O)_{\mathfrak B}$
, and thus
![]() $\mathfrak Q(\mathscr O)_{\mathfrak B}$
is equivalent to the category of pseudocompact
$\mathfrak Q(\mathscr O)_{\mathfrak B}$
is equivalent to the category of pseudocompact
![]() $E_{\mathfrak B}'$
-modules. This implies that
$E_{\mathfrak B}'$
-modules. This implies that
![]() $\mathscr T (P_{\operatorname {\mathrm {Sp}}^{\vee }})$
– and hence, by equivalence of categories,
$\mathscr T (P_{\operatorname {\mathrm {Sp}}^{\vee }})$
– and hence, by equivalence of categories,
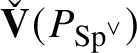 $\check {\mathbf {V}} (P_{\operatorname {\mathrm {Sp}}^{\vee }})$
– is flat over
$\check {\mathbf {V}} (P_{\operatorname {\mathrm {Sp}}^{\vee }})$
– is flat over
![]() $E_{\mathfrak B}'$
. Since
$E_{\mathfrak B}'$
. Since
![]() $\check {\mathbf {V}} (\operatorname {\mathrm {Sp}}^{\vee })$
is a
$\check {\mathbf {V}} (\operatorname {\mathrm {Sp}}^{\vee })$
is a
![]() $1$
-dimensional representation of
$1$
-dimensional representation of
![]() $\mathscr G_{\mathbb {Q}_p}$
, in fact the trivial representation with our normalisations, an application of Nakayama’s lemma shows that
$\mathscr G_{\mathbb {Q}_p}$
, in fact the trivial representation with our normalisations, an application of Nakayama’s lemma shows that
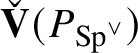 $\check {\mathbf {V}} (P_{\operatorname {\mathrm {Sp}}^{\vee }})$
is a free
$\check {\mathbf {V}} (P_{\operatorname {\mathrm {Sp}}^{\vee }})$
is a free
![]() $E_{\mathfrak B}'$
-module of rank
$E_{\mathfrak B}'$
-module of rank
![]() $1$
. The action of
$1$
. The action of
![]() $\mathscr G_{\mathbb {Q}_p}$
on
$\mathscr G_{\mathbb {Q}_p}$
on
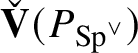 $\check {\mathbf {V}} (P_{\operatorname {\mathrm {Sp}}^{\vee }})$
commutes with the action of
$\check {\mathbf {V}} (P_{\operatorname {\mathrm {Sp}}^{\vee }})$
commutes with the action of
![]() $E_{\mathfrak B}'$
and so induces a homomorphism
$E_{\mathfrak B}'$
and so induces a homomorphism
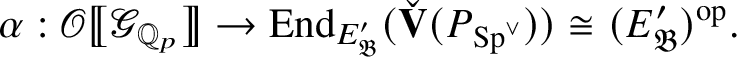
We show that this map is surjective. In general, the argument is carried out in Section 2 in an abstract setting, and then in Proposition 4.18 we verify that the conditions of the abstract setting are satisfied. However, in the special case under consideration, the argument is easier: Since
![]() $\check {\mathbf {V}}$
induces an equivalence of categories between
$\check {\mathbf {V}}$
induces an equivalence of categories between
![]() $\mathfrak Q(\mathscr O)_{\mathfrak B}$
and its essential image, the
$\mathfrak Q(\mathscr O)_{\mathfrak B}$
and its essential image, the
![]() $E_{\mathfrak B}'$
-cosocle and
$E_{\mathfrak B}'$
-cosocle and
-cosocle of
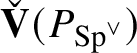 $\check {\mathbf {V}} (P_{\operatorname {\mathrm {Sp}}^{\vee }})$
coincide. This implies that there is
$\check {\mathbf {V}} (P_{\operatorname {\mathrm {Sp}}^{\vee }})$
coincide. This implies that there is
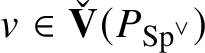 $v\in \check {\mathbf {V}} (P_{\operatorname {\mathrm {Sp}}^{\vee }} )$
, which is a generator of
$v\in \check {\mathbf {V}} (P_{\operatorname {\mathrm {Sp}}^{\vee }} )$
, which is a generator of
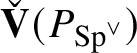 $\check {\mathbf {V}} (P_{\operatorname {\mathrm {Sp}}^{\vee }} )$
as both an
$\check {\mathbf {V}} (P_{\operatorname {\mathrm {Sp}}^{\vee }} )$
as both an
![]() $E_{\mathfrak B}'$
- and an
$E_{\mathfrak B}'$
- and an
-module. This implies that
![]() $\alpha $
is surjective.
$\alpha $
is surjective.
We also show in Section 3 that the natural map
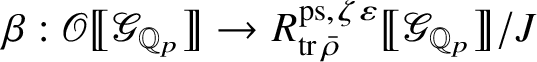
is surjective, where
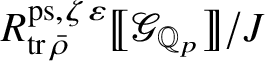
is the largest quotient of
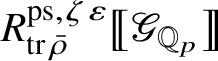
such that the Cayley–Hamilton theorem holds for the universal pseudorepresentation with determinant
![]() $\zeta \varepsilon $
lifting
$\zeta \varepsilon $
lifting
![]() $\operatorname {tr} \bar {\rho }$
.
$\operatorname {tr} \bar {\rho }$
.
The idea is to show that
![]() $\operatorname {\mathrm {Ker}} \alpha $
contains
$\operatorname {\mathrm {Ker}} \alpha $
contains
![]() $\operatorname {\mathrm {Ker}} \beta $
, since this implies that the action of
$\operatorname {\mathrm {Ker}} \beta $
, since this implies that the action of
![]() $\mathscr G_{\mathbb {Q}_p}$
on
$\mathscr G_{\mathbb {Q}_p}$
on
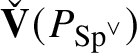 $\check {\mathbf {V}} (P_{\operatorname {\mathrm {Sp}}^{\vee }} )$
induces surjections:
$\check {\mathbf {V}} (P_{\operatorname {\mathrm {Sp}}^{\vee }} )$
induces surjections:
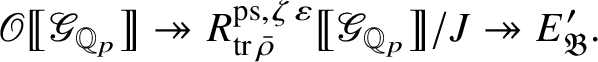
This is proved using the results of Berger and Breuil [Reference Berger and Breuil4] on universal unitary completions of locally algebraic principal series and density arguments already used in [Reference Colmez, Dospinescu and Paškūnas21] and also in [Reference Tung46]. Morally, the argument should be that
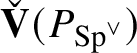 $\check {\mathbf {V}} (P_{\operatorname {\mathrm {Sp}}^{\vee }} )$
injects into the product of all
$\check {\mathbf {V}} (P_{\operatorname {\mathrm {Sp}}^{\vee }} )$
injects into the product of all
![]() $2$
-dimensional crystabelline representations of
$2$
-dimensional crystabelline representations of
![]() $\mathscr G_{\mathbb {Q}_p}$
with mod p reduction isomorphic to
$\mathscr G_{\mathbb {Q}_p}$
with mod p reduction isomorphic to
![]() $\bar {\rho }$
and determinant
$\bar {\rho }$
and determinant
![]() $\zeta \varepsilon $
; then an element in
$\zeta \varepsilon $
; then an element in
![]() $\operatorname {\mathrm {Ker}} \beta $
would kill this product, and hence
$\operatorname {\mathrm {Ker}} \beta $
would kill this product, and hence
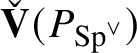 $\check {\mathbf {V}} (P_{\operatorname {\mathrm {Sp}}^{\vee }} )$
. In reality the argument is technically a bit more complicated: We also have to consider deformations of such representations to local Artinian L-algebras (see Section 5).
$\check {\mathbf {V}} (P_{\operatorname {\mathrm {Sp}}^{\vee }} )$
. In reality the argument is technically a bit more complicated: We also have to consider deformations of such representations to local Artinian L-algebras (see Section 5).
Wang-Erickson proved in [Reference Wang-Erickson48] that
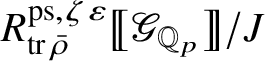
is a finitely generated
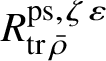 $R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr} \bar {\rho }}$
-module. The surjection (3) implies that the image of
$R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr} \bar {\rho }}$
-module. The surjection (3) implies that the image of
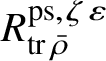 $R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr} \bar {\rho }}$
is contained in the centre of
$R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr} \bar {\rho }}$
is contained in the centre of
![]() $E_{\mathfrak B}'$
, which we denote by
$E_{\mathfrak B}'$
, which we denote by
![]() $Z_{\mathfrak B}'$
. Moreover, both
$Z_{\mathfrak B}'$
. Moreover, both
![]() $E_{\mathfrak B}'$
and
$E_{\mathfrak B}'$
and
![]() $Z_{\mathfrak B}'$
are finite
$Z_{\mathfrak B}'$
are finite
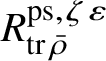 $R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr} \bar {\rho }}$
-modules. We show that formula (3) induces an isomorphism
$R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr} \bar {\rho }}$
-modules. We show that formula (3) induces an isomorphism
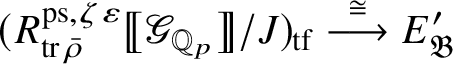
by showing that the universal framed deformation of
![]() $\bar {\rho }$
with determinant
$\bar {\rho }$
with determinant
![]() $\zeta \varepsilon $
lies in the image of
$\zeta \varepsilon $
lies in the image of
![]() $\check {\mathbf {V}}$
using [Reference Colmez, Dospinescu and Paškūnas21, Reference Colmez, Dospinescu and Paškūnas22], and
$\check {\mathbf {V}}$
using [Reference Colmez, Dospinescu and Paškūnas21, Reference Colmez, Dospinescu and Paškūnas22], and
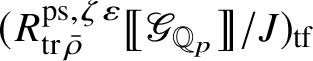 acts faithfully on it (see Proposition A.11). The assertions about the centre in Theorem 1.4, with
acts faithfully on it (see Proposition A.11). The assertions about the centre in Theorem 1.4, with
![]() $Z_{\mathfrak B}'$
instead of
$Z_{\mathfrak B}'$
instead of
![]() $Z_{\mathfrak B}$
, are proved by studying the centre of
$Z_{\mathfrak B}$
, are proved by studying the centre of
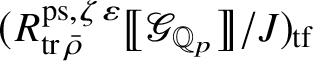 . This argument is carried out in Appendix A for d-dimensional representations of any profinite group, satisfying Mazur’s finiteness condition at p.
. This argument is carried out in Appendix A for d-dimensional representations of any profinite group, satisfying Mazur’s finiteness condition at p.
We then transfer this result from
![]() $E_{\mathfrak B}'$
and
$E_{\mathfrak B}'$
and
![]() $Z_{\mathfrak B}'$
to
$Z_{\mathfrak B}'$
to
![]() $E_{\mathfrak B}$
and
$E_{\mathfrak B}$
and
![]() $Z_{\mathfrak B}$
. Let
$Z_{\mathfrak B}$
. Let
![]() $M_{\mathfrak B}$
be the kernel of
$M_{\mathfrak B}$
be the kernel of
![]() $P_{\mathfrak B}\rightarrow (P_{\mathfrak B})_{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )}$
. We show that
$P_{\mathfrak B}\rightarrow (P_{\mathfrak B})_{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )}$
. We show that
by examining various exact sequences and showing that certain
![]() $\operatorname {\mathrm {Ext}}$
-groups vanish. We also show that the cosocle of
$\operatorname {\mathrm {Ext}}$
-groups vanish. We also show that the cosocle of
![]() $M_{\mathfrak B}$
is a direct sum of finitely many copies of
$M_{\mathfrak B}$
is a direct sum of finitely many copies of
![]() $\operatorname {\mathrm {Sp}}^{\vee }$
. Thus
$\operatorname {\mathrm {Sp}}^{\vee }$
. Thus
![]() $M_{\mathfrak B}$
is a quotient of
$M_{\mathfrak B}$
is a quotient of
![]() $ (P_{\mathfrak B}' )^{\oplus n}$
for some
$ (P_{\mathfrak B}' )^{\oplus n}$
for some
![]() $n\ge 1$
. This allows us to conclude that
$n\ge 1$
. This allows us to conclude that
![]() $\operatorname {\mathrm {End}}_{{\mathfrak C}(\mathscr O)}(M_{\mathfrak B})$
and its centre are finitely generated
$\operatorname {\mathrm {End}}_{{\mathfrak C}(\mathscr O)}(M_{\mathfrak B})$
and its centre are finitely generated
![]() $Z_{\mathfrak B}'$
-modules, which finishes the proof of Theorem 1.3. The arguments showing the finiteness of
$Z_{\mathfrak B}'$
-modules, which finishes the proof of Theorem 1.3. The arguments showing the finiteness of
![]() $E_{\mathfrak B}$
and
$E_{\mathfrak B}$
and
![]() $Z_{\mathfrak B}$
over
$Z_{\mathfrak B}$
over
![]() $Z_{\mathfrak B}'$
are carried out in Section 4.3. Then with some more effort we are able to show that
$Z_{\mathfrak B}'$
are carried out in Section 4.3. Then with some more effort we are able to show that
![]() $Z_{\mathfrak B}'=Z_{\mathfrak B}$
(Corollary 6.15).
$Z_{\mathfrak B}'=Z_{\mathfrak B}$
(Corollary 6.15).
1.2 What is left to do?
Although we believe that our results will suffice for most number-theoretic applications – for example, [Reference Pan38] – to complete the programme started in [Reference Paškūnas39], one would have to compute the ring
![]() $E_{\mathfrak B}$
in the exceptional cases. This will be harder than [Reference Paškūnas39, Section 10.5], which is already quite involved. We expect that the map (3) induces isomorphisms
$E_{\mathfrak B}$
in the exceptional cases. This will be harder than [Reference Paškūnas39, Section 10.5], which is already quite involved. We expect that the map (3) induces isomorphisms
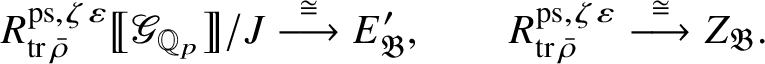
This is known to hold for all blocks except for the exceptional ones. Theorem 1.4 implies that to prove this result, it would be enough to show that
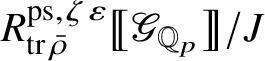
is
![]() $\mathscr O$
-torsion-free, and for the second isomorphism in the case
$\mathscr O$
-torsion-free, and for the second isomorphism in the case
![]() $p=3$
it would be enough to showFootnote
2
that
$p=3$
it would be enough to showFootnote
2
that
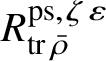 $R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr} \bar {\rho }}$
is
$R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr} \bar {\rho }}$
is
![]() $\mathscr O$
-torsion-free.
$\mathscr O$
-torsion-free.
It seems likely that using the results of this paper, one can remove the restriction on the prime p in Lue Pan’s work [Reference Pan37] on the Fontaine–Mazur conjecture in the residually reducible case, which generalises the work of Skinner and Wiles. We hope to return to these questions in future work.
2 Endomorphism rings
Let E be a pseudocompact
![]() $\mathscr O$
-algebra and let
$\mathscr O$
-algebra and let
![]() $\mathrm {PC}(E)$
be the category of left pseudocompact E-modules (see [Reference Brumer12], [Reference Gabriel31, Section IV.3]. Let
$\mathrm {PC}(E)$
be the category of left pseudocompact E-modules (see [Reference Brumer12], [Reference Gabriel31, Section IV.3]. Let
![]() $\operatorname {\mathrm {Irr}}(E)$
be the set of equivalence classes of irreducible objects in
$\operatorname {\mathrm {Irr}}(E)$
be the set of equivalence classes of irreducible objects in
![]() $\mathrm {PC}(E)$
.
$\mathrm {PC}(E)$
.
Let M be in
![]() $\mathrm {PC}(E)$
. We assume that we are given a continuous E-linear action of a profinite group
$\mathrm {PC}(E)$
. We assume that we are given a continuous E-linear action of a profinite group
![]() $\mathscr G$
on M, which makes M into a pseudocompact module over the completed group algebra
$\mathscr G$
on M, which makes M into a pseudocompact module over the completed group algebra
![]() . The action induces a homomorphism of
. The action induces a homomorphism of
![]() $\mathscr O$
-algebras
$\mathscr O$
-algebras
![]() . In this section we will study when this map is surjective, as well as its kernel.
. In this section we will study when this map is surjective, as well as its kernel.
If N is a pseudocompact E-module, which is finitely generated as an E-module, then we may present it as
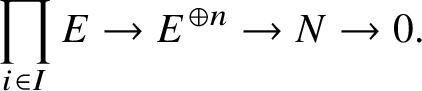 $$ \begin{align*} \prod_{i\in I} E \rightarrow E^{\oplus n} \rightarrow N \rightarrow 0. \end{align*} $$
$$ \begin{align*} \prod_{i\in I} E \rightarrow E^{\oplus n} \rightarrow N \rightarrow 0. \end{align*} $$
By applying
![]() $\operatorname {\mathrm {Hom}}^{\mathrm {cont}}_E(\ast , M)$
we obtain an exact sequence
$\operatorname {\mathrm {Hom}}^{\mathrm {cont}}_E(\ast , M)$
we obtain an exact sequence
We thus may identify
![]() $\operatorname {\mathrm {Hom}}^{\mathrm {cont}}_E(N, M)$
with a closed submodule of
$\operatorname {\mathrm {Hom}}^{\mathrm {cont}}_E(N, M)$
with a closed submodule of
![]() $M^{\oplus n}$
, which makes
$M^{\oplus n}$
, which makes
![]() $\operatorname {\mathrm {Hom}}^{\mathrm {cont}}_E(N, M)$
into a pseudocompact left
$\operatorname {\mathrm {Hom}}^{\mathrm {cont}}_E(N, M)$
into a pseudocompact left
![]() -module.
-module.
Lemma 2.1. Let N be a finitely generated projective E-module and let
![]() $\mathrm m$
be a right pseudocompact
$\mathrm m$
be a right pseudocompact
![]() -module. Then the natural map
-module. Then the natural map
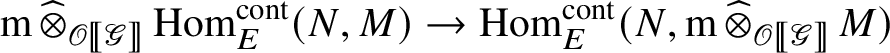
is an isomorphism.
Proof. Since N is finitely generated and projective, we may present it as
where
![]() $F\cong E^{\oplus n}$
and e is an idempotent. In particular, N is a pseudocompact E-module. The map (4) is induced by a continuous bilinear map
$F\cong E^{\oplus n}$
and e is an idempotent. In particular, N is a pseudocompact E-module. The map (4) is induced by a continuous bilinear map
It is an isomorphism if
![]() $N=F$
. The general case follows by applying the idempotent e to the isomorphism obtained for
$N=F$
. The general case follows by applying the idempotent e to the isomorphism obtained for
![]() $N=F$
.
$N=F$
.
Lemma 2.2. Let
![]() $\{\rho _i\}_{i\in I}$
be a family of pairwise distinct absolutely irreducible right pseudocompact
$\{\rho _i\}_{i\in I}$
be a family of pairwise distinct absolutely irreducible right pseudocompact
![]() -modules. Then the map
-modules. Then the map
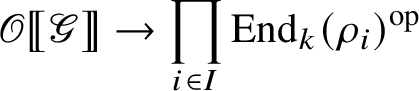
is surjective.
Proof. Since
![]() $\mathscr G$
is profinite, each
$\mathscr G$
is profinite, each
![]() $\rho _i$
is a finite-dimensional k-vector space. Thus
$\rho _i$
is a finite-dimensional k-vector space. Thus
![]() , given by the action, is continuous for the discrete topology on the target. Since
, given by the action, is continuous for the discrete topology on the target. Since
![]() $\rho _i$
is absolutely irreducible,
$\rho _i$
is absolutely irreducible,
![]() $\varphi _i$
is surjective. Moreover,
$\varphi _i$
is surjective. Moreover,
![]() $\operatorname {\mathrm {Ker}} \varphi _i$
is an open maximal two-sided ideal of
$\operatorname {\mathrm {Ker}} \varphi _i$
is an open maximal two-sided ideal of
![]() . If
. If
![]() $i\neq j$
, then
$i\neq j$
, then
![]() $\rho _i\not \cong \rho _j$
, and thus
$\rho _i\not \cong \rho _j$
, and thus
![]() . This implies that for every finite subset F of I, the map
. This implies that for every finite subset F of I, the map
![]() is surjective. Thus the image of map (5) is dense for the product topology on the target. On the other hand, map (5) is a continuous map between pseudocompact
is surjective. Thus the image of map (5) is dense for the product topology on the target. On the other hand, map (5) is a continuous map between pseudocompact
![]() $\mathscr O$
-modules, and thus its image is closed, which implies surjectivity.
$\mathscr O$
-modules, and thus its image is closed, which implies surjectivity.
If M is in
![]() $\mathrm {PC}(E)$
, then we let
$\mathrm {PC}(E)$
, then we let
![]() $\mathfrak r(M)$
be the intersection of open maximal submodules of M. Then
$\mathfrak r(M)$
be the intersection of open maximal submodules of M. Then
![]() $\mathfrak r(E)$
is a closed two-sided ideal of E and
$\mathfrak r(E)$
is a closed two-sided ideal of E and
![]() $\mathfrak r(M)$
is the closure of
$\mathfrak r(M)$
is the closure of
![]() $\mathfrak r(E) M$
inside M.
$\mathfrak r(E) M$
inside M.
Proposition 2.3. Let us assume that the following hold:
-
1. M is a finitely generated projective E-module.
-
2.
 $M/\mathfrak r(M) = \operatorname {\mathrm {cosoc}}_{\mathscr G} M$
.
$M/\mathfrak r(M) = \operatorname {\mathrm {cosoc}}_{\mathscr G} M$
. -
3. For all
 $S\in \operatorname {\mathrm {Irr}}(E)$
such that
$S\in \operatorname {\mathrm {Irr}}(E)$
such that  $$ \begin{align*} \rho_S:=\operatorname{\mathrm{Hom}}_{E}^{\mathrm{cont}}(M, S)\neq 0, \end{align*} $$
$$ \begin{align*} \rho_S:=\operatorname{\mathrm{Hom}}_{E}^{\mathrm{cont}}(M, S)\neq 0, \end{align*} $$
 $\dim _k \rho _S$
is finite and
$\dim _k \rho _S$
is finite and
 $\rho _S$
is an absolutely irreducible representation of
$\rho _S$
is an absolutely irreducible representation of
 $\mathscr G$
.
$\mathscr G$
.
-
4. If
 $S, S'\in \operatorname {\mathrm {Irr}}(E)$
and
$S, S'\in \operatorname {\mathrm {Irr}}(E)$
and
 $S\not \cong S'$
, then
$S\not \cong S'$
, then
 $\operatorname {\mathrm {Hom}}_{\mathscr G} (\rho _S, \rho _{S'} )=0$
.
$\operatorname {\mathrm {Hom}}_{\mathscr G} (\rho _S, \rho _{S'} )=0$
.
Then the map
![]() is surjective.
is surjective.
Proof. For
![]() $S\in \operatorname {\mathrm {Irr}}(E)$
, we let
$S\in \operatorname {\mathrm {Irr}}(E)$
, we let
![]() $\overline {M}_S$
be the smallest quotient of M such that
$\overline {M}_S$
be the smallest quotient of M such that
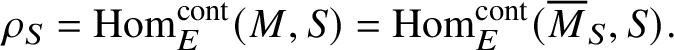 $$ \begin{align*} \rho_S=\operatorname{\mathrm{Hom}}_E^{\mathrm{cont}}(M, S)=\operatorname{\mathrm{Hom}}_E^{\mathrm{cont}}(\overline{M}_S, S). \end{align*} $$
$$ \begin{align*} \rho_S=\operatorname{\mathrm{Hom}}_E^{\mathrm{cont}}(M, S)=\operatorname{\mathrm{Hom}}_E^{\mathrm{cont}}(\overline{M}_S, S). \end{align*} $$
It follows from assumption (3) that these subspaces are finite-dimensional. Thus
![]() $\overline {M}_S\cong S^{\oplus d}$
such that
$\overline {M}_S\cong S^{\oplus d}$
such that
![]() $d \cdot \dim _k \operatorname {\mathrm {End}}_E^{\mathrm {cont}}(S)= \dim _k \rho _S$
. Since S is irreducible,
$d \cdot \dim _k \operatorname {\mathrm {End}}_E^{\mathrm {cont}}(S)= \dim _k \rho _S$
. Since S is irreducible,
![]() $\operatorname {\mathrm {End}}_E^{\mathrm {cont}}(S)$
is a skew field. It acts on
$\operatorname {\mathrm {End}}_E^{\mathrm {cont}}(S)$
is a skew field. It acts on
![]() $\rho _S$
, and this action commutes with the action of
$\rho _S$
, and this action commutes with the action of
![]() $\mathscr G$
. Since
$\mathscr G$
. Since
![]() $\rho _S$
is absolutely irreducible, we conclude that
$\rho _S$
is absolutely irreducible, we conclude that
![]() $\operatorname {\mathrm {End}}_E^{\mathrm {cont}}(S)=k$
and
$\operatorname {\mathrm {End}}_E^{\mathrm {cont}}(S)=k$
and
![]() $\dim _k \rho _S=d$
. Thus
$\dim _k \rho _S=d$
. Thus
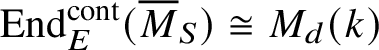 $\operatorname {\mathrm {End}}^{\mathrm {cont}}_E ( \overline {M}_S )\cong M_d(k)$
and thus does not have nontrivial two-sided ideals. Hence, the natural right action of
$\operatorname {\mathrm {End}}^{\mathrm {cont}}_E ( \overline {M}_S )\cong M_d(k)$
and thus does not have nontrivial two-sided ideals. Hence, the natural right action of
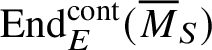 $\operatorname {\mathrm {End}}^{\mathrm {cont}}_E ( \overline {M}_S )$
on
$\operatorname {\mathrm {End}}^{\mathrm {cont}}_E ( \overline {M}_S )$
on
![]() $\rho _S$
induces an injective ring homomorphism
$\rho _S$
induces an injective ring homomorphism
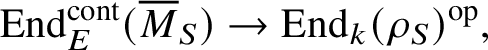 $$ \begin{align} \operatorname{\mathrm{End}}_E^{\mathrm{cont}}( \overline{M}_S) \rightarrow \operatorname{\mathrm{End}}_k(\rho_S)^{\mathrm{op}}, \end{align} $$
$$ \begin{align} \operatorname{\mathrm{End}}_E^{\mathrm{cont}}( \overline{M}_S) \rightarrow \operatorname{\mathrm{End}}_k(\rho_S)^{\mathrm{op}}, \end{align} $$
which has to be surjective, as both k-vector spaces have dimension equal to
![]() $d^2$
.
$d^2$
.
The isomorphism
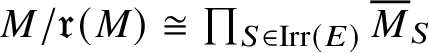 $M/\mathfrak r(M) \cong \prod _{S\in \operatorname {\mathrm {Irr}}(E)} \overline {M}_S$
induces an isomorphism
$M/\mathfrak r(M) \cong \prod _{S\in \operatorname {\mathrm {Irr}}(E)} \overline {M}_S$
induces an isomorphism
 $$ \begin{align*} \operatorname{\mathrm{End}}_E^{\mathrm{cont}}( M /\mathfrak r(M)) \cong \prod_{S\in \operatorname{\mathrm{Irr}}(E)} \operatorname{\mathrm{End}}_E^{\mathrm{cont}}(\overline{M}_S). \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{End}}_E^{\mathrm{cont}}( M /\mathfrak r(M)) \cong \prod_{S\in \operatorname{\mathrm{Irr}}(E)} \operatorname{\mathrm{End}}_E^{\mathrm{cont}}(\overline{M}_S). \end{align*} $$
Since
![]() $\rho _S \not \cong \rho _{S'}$
if
$\rho _S \not \cong \rho _{S'}$
if
![]() $S\not \cong S'$
, it follows from Lemma 2.2 together with isomorphism (6) that the action of
$S\not \cong S'$
, it follows from Lemma 2.2 together with isomorphism (6) that the action of
on
![]() $M /\mathfrak r(M)$
induces a surjection
$M /\mathfrak r(M)$
induces a surjection
Since M is projective and
![]() $M/\mathfrak r(M)$
is prosemisimple, we have
$M/\mathfrak r(M)$
is prosemisimple, we have
If
![]() $\mathrm m$
is an irreducible right pseudocompact
$\mathrm m$
is an irreducible right pseudocompact
-module and
![]() $\mathfrak a$
is its annihilator, then
$\mathfrak a$
is its annihilator, then
is a finite-dimensional simple k-algebra, and thus
is semisimple as a left
-module, and thus
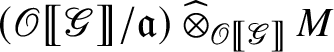
is semisimple as a left
-module. Hence, the surjection
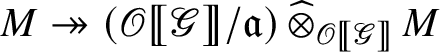
factors through as
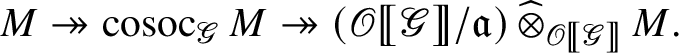
Moreover, the maps become isomorphisms after application of
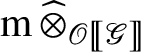
. Thus
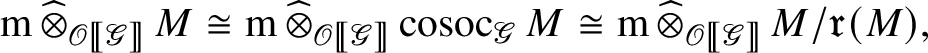
as
![]() $M/\mathfrak r(M)= \operatorname {\mathrm {cosoc}}_{\mathscr G} M$
by assumption. Lemma 2.1 together with formula (9) implies that by applying
$M/\mathfrak r(M)= \operatorname {\mathrm {cosoc}}_{\mathscr G} M$
by assumption. Lemma 2.1 together with formula (9) implies that by applying
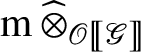
to formula (8), we obtain isomorphisms
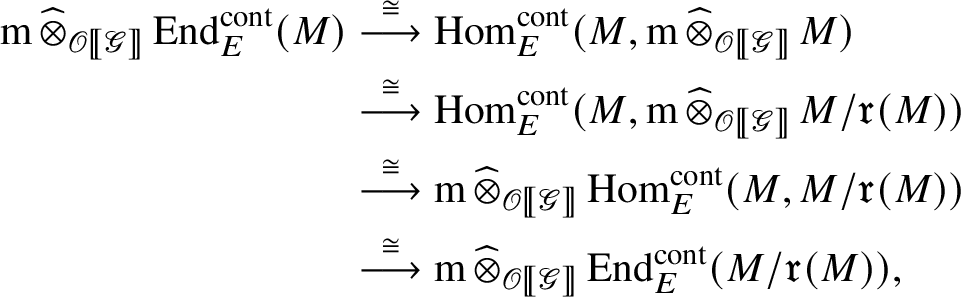
where the
![]() $\mathscr G$
-action on
$\mathscr G$
-action on
![]() $\operatorname {\mathrm {End}}^{\mathrm {cont}}_E(M)$
and
$\operatorname {\mathrm {End}}^{\mathrm {cont}}_E(M)$
and
![]() $\operatorname {\mathrm {End}}^{\mathrm {cont}}_E(M/\mathfrak r(M))$
is given by
$\operatorname {\mathrm {End}}^{\mathrm {cont}}_E(M/\mathfrak r(M))$
is given by
![]() $(g.\varphi )(v):= g (\varphi (v))$
.
$(g.\varphi )(v):= g (\varphi (v))$
.
If the map
is not surjective, then its cokernel is a nonzero left pseudocompact
-module and thus will have an irreducible quotient
![]() $\mathrm m'$
. If we let
$\mathrm m'$
. If we let
![]() $\mathrm m= \operatorname {\mathrm {Hom}}_k(\mathrm m', k)$
with the right
$\mathrm m= \operatorname {\mathrm {Hom}}_k(\mathrm m', k)$
with the right
-action, then
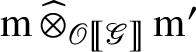
is nonzero, as the evaluation map
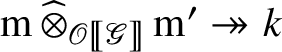
is nonzero. By construction, the composition
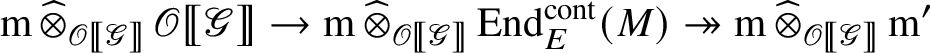
is the zero map. Thus
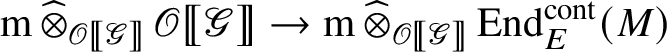
cannot be surjective. However, the commutative diagram
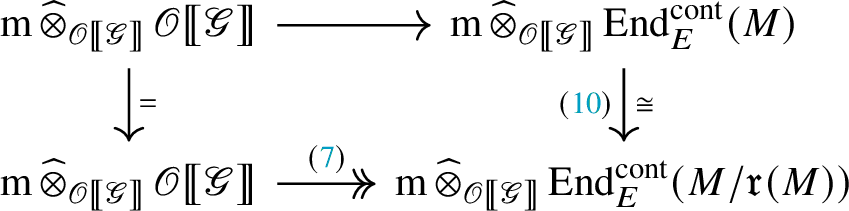
implies that the top horizontal arrow is surjective, yielding a contradiction.
We remind the reader that as a consequence of the topological Nakayama’s lemma [Reference Gille, Polo, Artin, Bertin, Gabriel, Raynaud and Serre32, Exposé VIIB, Lemma 0.3.3], the following holds:
Lemma 2.4. Let N be a pseudocompact left E-module. Then N is projective in
![]() $\mathrm {PC}(E)$
if and only if the functor
$\mathrm {PC}(E)$
if and only if the functor
![]() $\mathrm m \mapsto \mathrm m\operatorname {\mathrm {\mathbin {\widehat {\otimes }}}}_E N$
from the category of right pseudocompact E-modules to the category of abelian groups is exact. In this case,
$\mathrm m \mapsto \mathrm m\operatorname {\mathrm {\mathbin {\widehat {\otimes }}}}_E N$
from the category of right pseudocompact E-modules to the category of abelian groups is exact. In this case,
![]() $N\twoheadrightarrow N/\mathfrak r(N)$
is a projective envelope of
$N\twoheadrightarrow N/\mathfrak r(N)$
is a projective envelope of
![]() $N/\mathfrak r(N)$
.
$N/\mathfrak r(N)$
.
Corollary 2.5. If in addition to the assumptions of Proposition 2.3 we assume that
![]() $M/\mathfrak r(M) \cong E/\mathfrak r(E)$
as E-modules, then M is a free E-module of rank
$M/\mathfrak r(M) \cong E/\mathfrak r(E)$
as E-modules, then M is a free E-module of rank
![]() $1$
and the action of
$1$
and the action of
on M induces a surjection
which is uniquely determined up to a conjugation by
![]() $E^{\times }$
.
$E^{\times }$
.
We will now give a characterisation of the kernel of
![]() in favourable settings.
in favourable settings.
Let
![]() $\mathrm m$
be a finite-dimensional L-vector space with continuous
$\mathrm m$
be a finite-dimensional L-vector space with continuous
![]() $\mathscr O$
-linear action of E on the right. The image of E in
$\mathscr O$
-linear action of E on the right. The image of E in
![]() $\operatorname {\mathrm {End}}_L(\mathrm m)$
is a compact
$\operatorname {\mathrm {End}}_L(\mathrm m)$
is a compact
![]() $\mathscr O$
-module, and thus E stabilises an
$\mathscr O$
-module, and thus E stabilises an
![]() $\mathscr O$
-lattice
$\mathscr O$
-lattice
![]() $\mathrm m^0$
in
$\mathrm m^0$
in
![]() $\mathrm m$
. The action of
$\mathrm m$
. The action of
![]() on M induces a continuous left action of
on M induces a continuous left action of
![]() on
on
![]() $\mathrm m^0\operatorname {\mathrm {\mathbin {\widehat {\otimes }}}}_E M$
and hence on
$\mathrm m^0\operatorname {\mathrm {\mathbin {\widehat {\otimes }}}}_E M$
and hence on
Lemma 2.6. Let
![]() $\{\mathrm m_i\}_{i\in I}$
be a family of finite-dimensional L-vector spaces with continuous right
$\{\mathrm m_i\}_{i\in I}$
be a family of finite-dimensional L-vector spaces with continuous right
![]() $\mathscr O$
-linear action of E. For each
$\mathscr O$
-linear action of E. For each
![]() $i\in I$
, let
$i\in I$
, let
![]() $\mathfrak a_i$
be the E-annihilator of
$\mathfrak a_i$
be the E-annihilator of
![]() $\mathrm m_i$
and let
$\mathrm m_i$
and let
![]() $\mathfrak b_i$
be the
$\mathfrak b_i$
be the
-annihilator of
![]() $\mathrm m_i \otimes _E M$
. If M is a free E-module of finite rank and
$\mathrm m_i \otimes _E M$
. If M is a free E-module of finite rank and
![]() $\bigcap _{i\in I} \mathfrak a_i=0$
, then
$\bigcap _{i\in I} \mathfrak a_i=0$
, then
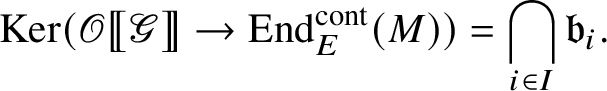
Proof. For each
![]() $i\in I$
, let
$i\in I$
, let
![]() $\mathfrak c_i$
be the
$\mathfrak c_i$
be the
![]() $\operatorname {\mathrm {End}}_E^{\mathrm {cont}}(M)$
-annihilator of
$\operatorname {\mathrm {End}}_E^{\mathrm {cont}}(M)$
-annihilator of
![]() $\mathrm m_i \otimes _E M$
. Since
$\mathrm m_i \otimes _E M$
. Since
![]() $\mathfrak b_i$
is the preimage of
$\mathfrak b_i$
is the preimage of
![]() $\mathfrak c_i$
in
$\mathfrak c_i$
in
![]() , it is enough to show that
, it is enough to show that
![]() $\bigcap _{i\in I} \mathfrak c_i=0$
.
$\bigcap _{i\in I} \mathfrak c_i=0$
.
Let
![]() $w_1, \dotsc , w_n$
be an E-basis of M. Then we may identify
$w_1, \dotsc , w_n$
be an E-basis of M. Then we may identify
![]() $\operatorname {\mathrm {End}}_E^{\mathrm {cont}}(M)$
with
$\operatorname {\mathrm {End}}_E^{\mathrm {cont}}(M)$
with
![]() $M_n(E)$
by mapping
$M_n(E)$
by mapping
![]() $\varphi $
to the matrix
$\varphi $
to the matrix
![]() $ (a_{kj} )$
, given by
$ (a_{kj} )$
, given by
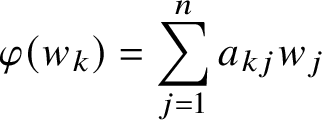 $$ \begin{align*} \varphi(w_k)= \sum_{j=1}^n a_{kj} w_j \end{align*} $$
$$ \begin{align*} \varphi(w_k)= \sum_{j=1}^n a_{kj} w_j \end{align*} $$
for all
![]() $1\le k\le n$
. If
$1\le k\le n$
. If
![]() $v\in \mathrm m_i$
, then
$v\in \mathrm m_i$
, then
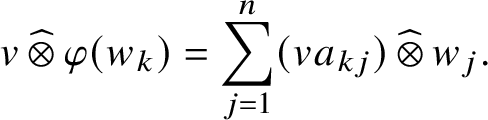 $$ \begin{align*} v \operatorname{\mathrm{\mathbin{\widehat{\otimes}}}} \varphi(w_k)= \sum_{j=1}^n ( v a_{kj})\operatorname{\mathrm{\mathbin{\widehat{\otimes}}}} w_j. \end{align*} $$
$$ \begin{align*} v \operatorname{\mathrm{\mathbin{\widehat{\otimes}}}} \varphi(w_k)= \sum_{j=1}^n ( v a_{kj})\operatorname{\mathrm{\mathbin{\widehat{\otimes}}}} w_j. \end{align*} $$
Thus
![]() $\varphi $
annihilates
$\varphi $
annihilates
![]() $\mathrm m_i\otimes _E M$
if and only if
$\mathrm m_i\otimes _E M$
if and only if
![]() $v a_{kj}=0$
for all
$v a_{kj}=0$
for all
![]() $v\in \mathrm m_i$
and all
$v\in \mathrm m_i$
and all
![]() $1\le k, j\le n$
, which is equivalent to
$1\le k, j\le n$
, which is equivalent to
![]() $\varphi \in M_n(\mathfrak a_i)$
. Since
$\varphi \in M_n(\mathfrak a_i)$
. Since
![]() $\bigcap _{i\in I} \mathfrak a_i=0$
, we have
$\bigcap _{i\in I} \mathfrak a_i=0$
, we have
![]() $\bigcap _{i\in I} M_n(\mathfrak a_i)=0$
and thus
$\bigcap _{i\in I} M_n(\mathfrak a_i)=0$
and thus
![]() $\bigcap _{i\in I} \mathfrak c_i=0$
.
$\bigcap _{i\in I} \mathfrak c_i=0$
.
3 Pseudorepresentations
Let
![]() $\mathscr G$
be a profinite group and let
$\mathscr G$
be a profinite group and let
![]() $\bar {\rho }$
be a continuous semisimple representation of
$\bar {\rho }$
be a continuous semisimple representation of
![]() $\mathscr G$
on a
$\mathscr G$
on a
![]() $2$
-dimensional k-vector space. We fix a continuous group homomorphism
$2$
-dimensional k-vector space. We fix a continuous group homomorphism
![]() $\psi : \mathscr G\rightarrow \mathscr O^{\times }$
lifting
$\psi : \mathscr G\rightarrow \mathscr O^{\times }$
lifting
![]() $\det \bar {\rho }$
. Let
$\det \bar {\rho }$
. Let
![]() $D^{\mathrm {ps}, \psi }$
be the functor from the category of augmented Artinian
$D^{\mathrm {ps}, \psi }$
be the functor from the category of augmented Artinian
![]() $\mathscr O$
-algebras with residue field k to the category of sets, which maps
$\mathscr O$
-algebras with residue field k to the category of sets, which maps
![]() $(A, \mathfrak m_A)$
to the set of continuous functions
$(A, \mathfrak m_A)$
to the set of continuous functions
![]() $t: \mathscr G \rightarrow A$
satisfying the following conditions:
$t: \mathscr G \rightarrow A$
satisfying the following conditions:
-
•
 $t(1)=2$
.
$t(1)=2$
. -
•
 $t(g) \equiv \operatorname {tr} \bar {\rho }(g)\pmod {\mathfrak m_A}, \quad \forall g\in \mathscr G$
.
$t(g) \equiv \operatorname {tr} \bar {\rho }(g)\pmod {\mathfrak m_A}, \quad \forall g\in \mathscr G$
. -
•
 $t(gh)=t(hg), \quad \forall g, h\in \mathscr G$
.
$t(gh)=t(hg), \quad \forall g, h\in \mathscr G$
. -
•
 $\psi (g) t (g^{-1} h )-t(g)t(h) +t(gh)=0, \quad \forall g, h\in \mathscr G$
.
$\psi (g) t (g^{-1} h )-t(g)t(h) +t(gh)=0, \quad \forall g, h\in \mathscr G$
.
The data
![]() $(t, \psi )$
determines a continuous polynomial law of homogeneous degree
$(t, \psi )$
determines a continuous polynomial law of homogeneous degree
![]() $2$
on
$2$
on
![]() $\mathscr G$
(see [Reference Chenevier18, Lemma 1.9]). This deformation problem is prorepresentable by a local
$\mathscr G$
(see [Reference Chenevier18, Lemma 1.9]). This deformation problem is prorepresentable by a local
![]() $\mathscr O$
-algebra
$\mathscr O$
-algebra
![]() $R^{\mathrm {ps}, \psi }$
with residue field k, complete with respect to profinite topology. We denote by
$R^{\mathrm {ps}, \psi }$
with residue field k, complete with respect to profinite topology. We denote by
![]() $T: \mathscr G\rightarrow R^{\mathrm {ps}, \psi }$
the universal deformation. We extend it
$T: \mathscr G\rightarrow R^{\mathrm {ps}, \psi }$
the universal deformation. We extend it
![]() $R^{\mathrm {ps}, \psi }$
-linearly to a continuous function
$R^{\mathrm {ps}, \psi }$
-linearly to a continuous function
![]() . The homomorphism
. The homomorphism
![]() $\psi : \mathscr G \rightarrow \mathscr O^{\times }$
induces a continuous
$\psi : \mathscr G \rightarrow \mathscr O^{\times }$
induces a continuous
![]() $\mathscr O$
-algebra homomorphism
$\mathscr O$
-algebra homomorphism
![]() , which we extend
, which we extend
![]() $R^{\mathrm {ps}, \psi }$
-linearly to a continuous
$R^{\mathrm {ps}, \psi }$
-linearly to a continuous
![]() $R^{\mathrm {ps}, \psi }$
-algebra homomorphism
$R^{\mathrm {ps}, \psi }$
-algebra homomorphism
![]() . Let J be the closed two-sided ideal of
. Let J be the closed two-sided ideal of
![]() generated by
generated by
![]() $a^2- T(a) a + \psi (a)$
for all
$a^2- T(a) a + \psi (a)$
for all
![]() .
.
Proposition 3.1. The ring homomorphism
![]() is surjective.
is surjective.
Proof. Let
![]() $\overline {R}$
and C be the images of
$\overline {R}$
and C be the images of
![]() $R^{\mathrm {ps}, \psi }$
and
$R^{\mathrm {ps}, \psi }$
and
![]() in
in
![]() , respectively. Since
, respectively. Since
![]() $R^{\mathrm {ps}, \psi }$
,
$R^{\mathrm {ps}, \psi }$
,
![]() and
and
![]() are pseudocompact
are pseudocompact
![]() $\mathscr O$
-modules,
$\mathscr O$
-modules,
![]() $\overline {R}$
and C are closed subrings of
$\overline {R}$
and C are closed subrings of
![]() . It is enough to show that C contains
. It is enough to show that C contains
![]() $\overline {R}$
, since in this case we deduce that C contains the image of
$\overline {R}$
, since in this case we deduce that C contains the image of
![]() , which is equal to
, which is equal to
![]() .
.
Let
![]() $B= \overline {R}\cap C$
and let
$B= \overline {R}\cap C$
and let
![]() $\mathfrak m_B$
be the intersection of B with the maximal ideal of
$\mathfrak m_B$
be the intersection of B with the maximal ideal of
![]() $\overline {R}$
. Then B is a closed subring of
$\overline {R}$
. Then B is a closed subring of
![]() $\overline {R}$
. This implies that B is complete for the profinite topology. If
$\overline {R}$
. This implies that B is complete for the profinite topology. If
![]() $x\in \mathfrak m_B$
, then
$x\in \mathfrak m_B$
, then
![]() $1+x$
has an inverse in B given by the geometric series. Since B is an
$1+x$
has an inverse in B given by the geometric series. Since B is an
![]() $\mathscr O$
-algebra and the residue field of
$\mathscr O$
-algebra and the residue field of
![]() $\overline {R}$
is k, we conclude that
$\overline {R}$
is k, we conclude that
![]() $(B, \mathfrak m_B)$
is a local ring with residue field k.
$(B, \mathfrak m_B)$
is a local ring with residue field k.
Let
![]() $\overline {T}$
be the specialisation of T along
$\overline {T}$
be the specialisation of T along
![]() $R^{\mathrm {ps}, \psi }\twoheadrightarrow \overline {R}$
. The relation
$R^{\mathrm {ps}, \psi }\twoheadrightarrow \overline {R}$
. The relation
![]() $g^2 - \overline {T}(g) g +\psi (g)=0$
in
$g^2 - \overline {T}(g) g +\psi (g)=0$
in
![]() implies that
implies that
![]() $\overline {T}(g)= g + g^{-1} \psi (g)$
. Thus
$\overline {T}(g)= g + g^{-1} \psi (g)$
. Thus
![]() $\overline {T}$
takes values in B. The universal property of
$\overline {T}$
takes values in B. The universal property of
![]() $R^{\mathrm {ps}, \psi }$
implies that there is a continuous homomorphism of
$R^{\mathrm {ps}, \psi }$
implies that there is a continuous homomorphism of
![]() $\mathscr O$
-algebras
$\mathscr O$
-algebras
![]() $\varphi : R^{\mathrm {ps}, \psi } \rightarrow B$
, such that
$\varphi : R^{\mathrm {ps}, \psi } \rightarrow B$
, such that
![]() $\varphi (T(g))= \overline {T}(g)$
for all
$\varphi (T(g))= \overline {T}(g)$
for all
![]() $g\in \mathscr G$
. Using the universal property of
$g\in \mathscr G$
. Using the universal property of
![]() $R^{\mathrm {ps}, \psi }$
again, we conclude that if we compose
$R^{\mathrm {ps}, \psi }$
again, we conclude that if we compose
![]() $\varphi $
with the inclusion
$\varphi $
with the inclusion
![]() $B \subset \overline {R}$
, we get back the surjection
$B \subset \overline {R}$
, we get back the surjection
![]() $R^{\mathrm {ps}, \psi }\twoheadrightarrow \overline {R}$
that we started with. Thus
$R^{\mathrm {ps}, \psi }\twoheadrightarrow \overline {R}$
that we started with. Thus
![]() $B=\overline {R}$
.
$B=\overline {R}$
.
Remark 3.2. The proposition does not hold if we do not fix the determinant or consider representations
![]() $\bar {\rho }$
of dimension greater than
$\bar {\rho }$
of dimension greater than
![]() $2$
. Counterexamples may be obtained with
$2$
. Counterexamples may be obtained with
![]() $\mathscr G=\mathbb {Z}_p$
and
$\mathscr G=\mathbb {Z}_p$
and
![]() $\bar {\rho }$
trivial representation of
$\bar {\rho }$
trivial representation of
![]() $\mathscr G$
on an n-dimensional k-vector space, using [Reference Chenevier18, Examples 1.7(i) and 1.11(i)].
$\mathscr G$
on an n-dimensional k-vector space, using [Reference Chenevier18, Examples 1.7(i) and 1.11(i)].
4 Representations of
 $\operatorname {\mathrm {GL}}_2 (\mathbb {Q}_p )$
$\operatorname {\mathrm {GL}}_2 (\mathbb {Q}_p )$
Let G be a p-adic analytic group and let Z be its centre. We let
![]() $\operatorname {\mathrm {Mod}}^{\mathrm {sm}}_G(\mathscr O)$
be the category of smooth representations of G on
$\operatorname {\mathrm {Mod}}^{\mathrm {sm}}_G(\mathscr O)$
be the category of smooth representations of G on
![]() $\mathscr O$
-torsion modules. Using Pontryagin duality,
$\mathscr O$
-torsion modules. Using Pontryagin duality,
![]() $\pi \mapsto \pi ^{\vee }:=\operatorname {\mathrm {Hom}}_{\mathscr O}(\pi , L/\mathscr O)$
equipped with the compact open topology induces an antiequivalence of categories between
$\pi \mapsto \pi ^{\vee }:=\operatorname {\mathrm {Hom}}_{\mathscr O}(\pi , L/\mathscr O)$
equipped with the compact open topology induces an antiequivalence of categories between
![]() $\operatorname {\mathrm {Mod}}^{\mathrm {sm}}_G(\mathscr O)$
and the category
$\operatorname {\mathrm {Mod}}^{\mathrm {sm}}_G(\mathscr O)$
and the category
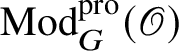 $\operatorname {\mathrm {Mod}}^{\mathrm {pro}}_G(\mathscr O)$
of linearly compact
$\operatorname {\mathrm {Mod}}^{\mathrm {pro}}_G(\mathscr O)$
of linearly compact
![]() $\mathscr O$
-modules with a continuous G-action [Reference Emerton28, Lemma 2.2.7]. The inverse is given by
$\mathscr O$
-modules with a continuous G-action [Reference Emerton28, Lemma 2.2.7]. The inverse is given by
![]() $M \mapsto M^{\vee }:=\operatorname {\mathrm {Hom}}^{\mathrm {cont}}_{\mathscr O}(M, L/\mathscr O)$
. In particular, if G is compact, then
$M \mapsto M^{\vee }:=\operatorname {\mathrm {Hom}}^{\mathrm {cont}}_{\mathscr O}(M, L/\mathscr O)$
. In particular, if G is compact, then
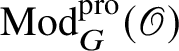 $\operatorname {\mathrm {Mod}}^{\mathrm {pro}}_G(\mathscr O)$
is the category of linearly compact
$\operatorname {\mathrm {Mod}}^{\mathrm {pro}}_G(\mathscr O)$
is the category of linearly compact
![]() -modules, where
-modules, where
![]() is the completed group algebra. We define
is the completed group algebra. We define
![]() $\operatorname {\mathrm {Mod}}^{\mathrm {sm}}_G(k)$
and
$\operatorname {\mathrm {Mod}}^{\mathrm {sm}}_G(k)$
and
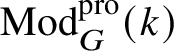 $\operatorname {\mathrm {Mod}}^{\mathrm {pro}}_G(k)$
the same way, with
$\operatorname {\mathrm {Mod}}^{\mathrm {pro}}_G(k)$
the same way, with
![]() $\mathscr O$
replaced by k. Moreover, for a continuous character
$\mathscr O$
replaced by k. Moreover, for a continuous character
![]() $\zeta : Z \rightarrow \mathscr O^\times $
, adding the subscript
$\zeta : Z \rightarrow \mathscr O^\times $
, adding the subscript
![]() $\zeta $
in any of these categories indicates the corresponding full subcategory of G-representations on which Z acts by
$\zeta $
in any of these categories indicates the corresponding full subcategory of G-representations on which Z acts by
![]() $\zeta $
. Denote by
$\zeta $
. Denote by
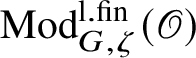 $\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O)$
the full subcategory of
$\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O)$
the full subcategory of
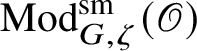 $\operatorname {\mathrm {Mod}}^{\mathrm {sm}}_{G, \zeta }(\mathscr O)$
consisting of representations in
$\operatorname {\mathrm {Mod}}^{\mathrm {sm}}_{G, \zeta }(\mathscr O)$
consisting of representations in
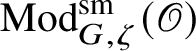 $\operatorname {\mathrm {Mod}}^{\mathrm {sm}}_{G, \zeta }(\mathscr O)$
which are equal to the union of their subrepresentations of finite length. We let
$\operatorname {\mathrm {Mod}}^{\mathrm {sm}}_{G, \zeta }(\mathscr O)$
which are equal to the union of their subrepresentations of finite length. We let
![]() $\mathfrak C(\mathscr O)$
be the full subcategory of
$\mathfrak C(\mathscr O)$
be the full subcategory of
 $\operatorname {\mathrm {Mod}}^{\mathrm {pro}}_G(\mathscr O)$
antiequivalent to
$\operatorname {\mathrm {Mod}}^{\mathrm {pro}}_G(\mathscr O)$
antiequivalent to
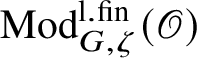 $\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O)$
under the Pontryagin duality.
$\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O)$
under the Pontryagin duality.
4.1 Blocks
From now on, we will assume
![]() $G = \operatorname {\mathrm {GL}}_2 (\mathbb {Q}_p )$
. Every irreducible object
$G = \operatorname {\mathrm {GL}}_2 (\mathbb {Q}_p )$
. Every irreducible object
![]() $\pi $
of
$\pi $
of
![]() $\operatorname {\mathrm {Mod}}^{\mathrm {sm}}_G(\mathscr O)$
is killed by
$\operatorname {\mathrm {Mod}}^{\mathrm {sm}}_G(\mathscr O)$
is killed by
![]() $\varpi $
and hence is an object of
$\varpi $
and hence is an object of
![]() $\operatorname {\mathrm {Mod}}^{\mathrm {sm}}_G(k)$
.
$\operatorname {\mathrm {Mod}}^{\mathrm {sm}}_G(k)$
.
Let
![]() $\operatorname {\mathrm {Irr}}_{G, \zeta }$
be the set of irreducible representations in
$\operatorname {\mathrm {Irr}}_{G, \zeta }$
be the set of irreducible representations in
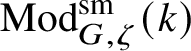 $\operatorname {\mathrm {Mod}}^{\mathrm {sm}}_{G, \zeta }(k)$
. We write
$\operatorname {\mathrm {Mod}}^{\mathrm {sm}}_{G, \zeta }(k)$
. We write
![]() $\pi \leftrightarrow \pi '$
if
$\pi \leftrightarrow \pi '$
if
![]() $\pi \cong \pi '$
or
$\pi \cong \pi '$
or
 $\operatorname {\mathrm {Ext}}^1_{G, \zeta }(\pi , \pi ') \neq 0$
or
$\operatorname {\mathrm {Ext}}^1_{G, \zeta }(\pi , \pi ') \neq 0$
or
 $\operatorname {\mathrm {Ext}}^1_{G, \zeta }(\pi ', \pi ) \neq 0$
, where
$\operatorname {\mathrm {Ext}}^1_{G, \zeta }(\pi ', \pi ) \neq 0$
, where
 $\operatorname {\mathrm {Ext}}^1_{G, \zeta }(\pi , \pi ')$
is the Yoneda extension group of
$\operatorname {\mathrm {Ext}}^1_{G, \zeta }(\pi , \pi ')$
is the Yoneda extension group of
![]() $\pi '$
by
$\pi '$
by
![]() $\pi $
in
$\pi $
in
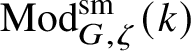 $\operatorname {\mathrm {Mod}}^{\mathrm {sm}}_{G, \zeta }(k)$
. We write
$\operatorname {\mathrm {Mod}}^{\mathrm {sm}}_{G, \zeta }(k)$
. We write
![]() $\pi \sim \pi '$
if there exist
$\pi \sim \pi '$
if there exist
![]() $\pi _1, \dotsc , \pi _n \in \operatorname {\mathrm {Irr}}_{G, \zeta }$
such that
$\pi _1, \dotsc , \pi _n \in \operatorname {\mathrm {Irr}}_{G, \zeta }$
such that
![]() $\pi \cong \pi _1$
,
$\pi \cong \pi _1$
,
![]() $\pi ' \cong \pi _n$
and
$\pi ' \cong \pi _n$
and
![]() $\pi _i \leftrightarrow \pi _{i+1}$
for
$\pi _i \leftrightarrow \pi _{i+1}$
for
![]() $1 \leq i \leq n-1$
. The relation
$1 \leq i \leq n-1$
. The relation
![]() $\sim $
is an equivalence relation on
$\sim $
is an equivalence relation on
![]() $\operatorname {\mathrm {Irr}}_{G, \zeta }$
. A block is an equivalence class of
$\operatorname {\mathrm {Irr}}_{G, \zeta }$
. A block is an equivalence class of
![]() $\sim $
.
$\sim $
.
Barthel and Livné [Reference Barthel and Livné2] and Breuil [Reference Breuil9] have classified the absolutely irreducible smooth representations
![]() $\pi $
admitting a central character. The blocks containing an absolutely irreducible representation have been determined in [Reference Paškūnas40, Corollary 6.2]. We have the following cases:
$\pi $
admitting a central character. The blocks containing an absolutely irreducible representation have been determined in [Reference Paškūnas40, Corollary 6.2]. We have the following cases:
-
(i)
 $\mathfrak B = \{ \pi \}$
with
$\mathfrak B = \{ \pi \}$
with
 $\pi $
supersingular.
$\pi $
supersingular. -
(ii)
 $\mathfrak B = \{ (\operatorname {\mathrm {Ind}}_B^G\chi _1 \otimes \chi _2 \omega ^{-1} )_{\mathrm {sm}}, (\operatorname {\mathrm {Ind}}_B^G\chi _2 \otimes \chi _1 \omega ^{-1} )_{\mathrm {sm}} \}$
with
$\mathfrak B = \{ (\operatorname {\mathrm {Ind}}_B^G\chi _1 \otimes \chi _2 \omega ^{-1} )_{\mathrm {sm}}, (\operatorname {\mathrm {Ind}}_B^G\chi _2 \otimes \chi _1 \omega ^{-1} )_{\mathrm {sm}} \}$
with
 $\chi _2 \chi _1^{-1} \neq \mathbf 1, \omega ^{\pm 1}$
.
$\chi _2 \chi _1^{-1} \neq \mathbf 1, \omega ^{\pm 1}$
. -
(iii)
 $p>2$
and
$p>2$
and
 $\mathfrak B = \{ (\operatorname {\mathrm {Ind}}_B^G \chi \otimes \chi \omega ^{-1} )_{\mathrm {sm}} \}$
.
$\mathfrak B = \{ (\operatorname {\mathrm {Ind}}_B^G \chi \otimes \chi \omega ^{-1} )_{\mathrm {sm}} \}$
. -
(iv)
 $p \geq 5$
and
$p \geq 5$
and
 $\mathfrak B = \{ \mathbf 1, \operatorname {\mathrm {Sp}}, (\operatorname {\mathrm {Ind}}^G_B \omega \otimes \omega ^{-1} )_{\mathrm {sm}} \} \otimes \chi \circ \det $
.
$\mathfrak B = \{ \mathbf 1, \operatorname {\mathrm {Sp}}, (\operatorname {\mathrm {Ind}}^G_B \omega \otimes \omega ^{-1} )_{\mathrm {sm}} \} \otimes \chi \circ \det $
. -
(v)
 $p=3$
and
$p=3$
and
 $\mathfrak B = \{ \mathbf 1, \operatorname {\mathrm {Sp}}, \omega \circ \det , \operatorname {\mathrm {Sp}} \otimes \omega \circ \det \} \otimes \chi \circ \det $
.
$\mathfrak B = \{ \mathbf 1, \operatorname {\mathrm {Sp}}, \omega \circ \det , \operatorname {\mathrm {Sp}} \otimes \omega \circ \det \} \otimes \chi \circ \det $
. -
(vi)
 $p=2$
and
$p=2$
and
 $\mathfrak B = \{ \mathbf 1, \operatorname {\mathrm {Sp}} \} \otimes \chi \circ \det $
.
$\mathfrak B = \{ \mathbf 1, \operatorname {\mathrm {Sp}} \} \otimes \chi \circ \det $
.
In these cases,
![]() $\chi , \chi _1, \chi _2: \mathbb {Q}_p^{\times } \rightarrow k^{\times }$
are smooth characters and
$\chi , \chi _1, \chi _2: \mathbb {Q}_p^{\times } \rightarrow k^{\times }$
are smooth characters and
![]() $\omega : \mathbb {Q}_p^{\times } \rightarrow k^{\times }$
is the character
$\omega : \mathbb {Q}_p^{\times } \rightarrow k^{\times }$
is the character
![]() $\omega (x) = x \lvert x\rvert \pmod {\varpi }$
, and
$\omega (x) = x \lvert x\rvert \pmod {\varpi }$
, and
![]() $\operatorname {\mathrm {Sp}}$
is the Steinberg representation defined by the exact sequence
$\operatorname {\mathrm {Sp}}$
is the Steinberg representation defined by the exact sequence
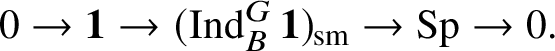 $$ \begin{align*} 0 \rightarrow \mathbf 1 \rightarrow (\operatorname{\mathrm{Ind}}_B^G \mathbf 1)_{\mathrm{sm}} \rightarrow \operatorname{\mathrm{Sp}} \rightarrow 0. \end{align*} $$
$$ \begin{align*} 0 \rightarrow \mathbf 1 \rightarrow (\operatorname{\mathrm{Ind}}_B^G \mathbf 1)_{\mathrm{sm}} \rightarrow \operatorname{\mathrm{Sp}} \rightarrow 0. \end{align*} $$
If
![]() $\pi \in \operatorname {\mathrm {Irr}}_{G, \zeta }$
is not absolutely irreducible then there is a finite extension
$\pi \in \operatorname {\mathrm {Irr}}_{G, \zeta }$
is not absolutely irreducible then there is a finite extension
![]() $k'$
of k, such that
$k'$
of k, such that
![]() $\pi \otimes _k k'$
is a finite direct sum of absolutely irreducible representations, see [Reference Paškūnas39, Proposition 5.11], so no information is lost by working with absolutely irreducible representations.
$\pi \otimes _k k'$
is a finite direct sum of absolutely irreducible representations, see [Reference Paškūnas39, Proposition 5.11], so no information is lost by working with absolutely irreducible representations.
Given a block
![]() $\mathfrak B$
, we denote by
$\mathfrak B$
, we denote by
![]() $\pi _{\mathfrak B}$
the direct sum of all representations in
$\pi _{\mathfrak B}$
the direct sum of all representations in
![]() $\mathfrak B$
and let
$\mathfrak B$
and let
![]() $P_{\mathfrak B}$
be a projective envelope of
$P_{\mathfrak B}$
be a projective envelope of
![]() $\pi _{\mathfrak B}^{\vee }$
in
$\pi _{\mathfrak B}^{\vee }$
in
![]() $\mathfrak C(\mathscr O)$
. Then
$\mathfrak C(\mathscr O)$
. Then
![]() $E_{\mathfrak B} = \operatorname {\mathrm {End}}_{\mathfrak C(\mathscr O)}(P_{\mathfrak B})$
is a pseudocompact
$E_{\mathfrak B} = \operatorname {\mathrm {End}}_{\mathfrak C(\mathscr O)}(P_{\mathfrak B})$
is a pseudocompact
![]() $\mathscr O$
-algebra. We denote the centre of
$\mathscr O$
-algebra. We denote the centre of
![]() $E_{\mathfrak B}$
by
$E_{\mathfrak B}$
by
![]() $Z_{\mathfrak B}$
.
$Z_{\mathfrak B}$
.
By [Reference Paškūnas39, Corollary 5.35], the category
![]() $\mathfrak C(\mathscr O)$
decomposes into a direct product of subcategories
$\mathfrak C(\mathscr O)$
decomposes into a direct product of subcategories
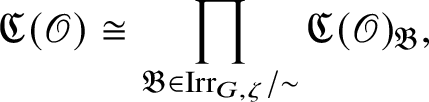 $$ \begin{align} \mathfrak C(\mathscr O) \cong \prod_{\mathfrak B \in \operatorname{\mathrm{Irr}}_{G, \zeta} / \sim} \mathfrak C(\mathscr O)_{\mathfrak B}, \end{align} $$
$$ \begin{align} \mathfrak C(\mathscr O) \cong \prod_{\mathfrak B \in \operatorname{\mathrm{Irr}}_{G, \zeta} / \sim} \mathfrak C(\mathscr O)_{\mathfrak B}, \end{align} $$
where the objects of
![]() $\mathfrak C(\mathscr O)_{\mathfrak B}$
are those M in
$\mathfrak C(\mathscr O)_{\mathfrak B}$
are those M in
![]() $\mathfrak C(\mathscr O)$
such that for every irreducible subquotient S of M,
$\mathfrak C(\mathscr O)$
such that for every irreducible subquotient S of M,
![]() $S^{\vee }$
lies in
$S^{\vee }$
lies in
![]() $\mathfrak B$
. Moreover, the category
$\mathfrak B$
. Moreover, the category
![]() $\mathfrak C(\mathscr O)_{\mathfrak B}$
is equivalent to the category of compact right
$\mathfrak C(\mathscr O)_{\mathfrak B}$
is equivalent to the category of compact right
![]() $E_{\mathfrak B}$
-modules and the centre of
$E_{\mathfrak B}$
-modules and the centre of
![]() $\mathfrak C(\mathscr O)_{\mathfrak B}$
is isomorphic to
$\mathfrak C(\mathscr O)_{\mathfrak B}$
is isomorphic to
![]() $Z_{\mathfrak B}$
[Reference Paškūnas39, Proposition 5.45].
$Z_{\mathfrak B}$
[Reference Paškūnas39, Proposition 5.45].
Lemma 4.1. If
![]() $\mathfrak B$
contains an absolutely irreducible representation, then
$\mathfrak B$
contains an absolutely irreducible representation, then
![]() $Z_{\mathfrak B}$
is a local pseudocompact
$Z_{\mathfrak B}$
is a local pseudocompact
![]() $\mathscr O$
-algebra with residue field k.
$\mathscr O$
-algebra with residue field k.
Proof. If
![]() $\pi $
is absolutely irreducible, then
$\pi $
is absolutely irreducible, then
![]() $\operatorname {\mathrm {End}}_G(\pi )=k$
, and thus the action of
$\operatorname {\mathrm {End}}_G(\pi )=k$
, and thus the action of
![]() $Z_{\mathfrak B}$
on
$Z_{\mathfrak B}$
on
![]() $\pi $
defines a homomorphism of
$\pi $
defines a homomorphism of
![]() $\mathscr O$
-algebras
$\mathscr O$
-algebras
![]() $c_{\pi }: Z_{\mathfrak B}\rightarrow k$
. If
$c_{\pi }: Z_{\mathfrak B}\rightarrow k$
. If
![]() $\pi , \pi '\in \mathfrak B$
are distinct and there is a nonsplit extension
$\pi , \pi '\in \mathfrak B$
are distinct and there is a nonsplit extension
![]() $0\rightarrow \pi \rightarrow \tau \rightarrow \pi '\rightarrow 0$
, then
$0\rightarrow \pi \rightarrow \tau \rightarrow \pi '\rightarrow 0$
, then
![]() $\operatorname {\mathrm {End}}_G(\tau )=k$
, and we conclude that
$\operatorname {\mathrm {End}}_G(\tau )=k$
, and we conclude that
![]() $c_{\pi }=c_{\tau }=c_{\pi '}$
. Using the transitivity property of the relation
$c_{\pi }=c_{\tau }=c_{\pi '}$
. Using the transitivity property of the relation
![]() $\sim $
on
$\sim $
on
![]() $\operatorname {\mathrm {Irr}}_{G, \zeta }$
, we conclude that
$\operatorname {\mathrm {Irr}}_{G, \zeta }$
, we conclude that
![]() $c_{\pi }=c_{\pi '}$
for all
$c_{\pi }=c_{\pi '}$
for all
![]() $\pi , \pi '\in \mathfrak B$
. It follows from the proof of [Reference Gabriel31, Proposition IV.4.12] that the Jacobson radical of
$\pi , \pi '\in \mathfrak B$
. It follows from the proof of [Reference Gabriel31, Proposition IV.4.12] that the Jacobson radical of
![]() $Z_{\mathfrak B}$
consists of elements that kill all the irreducible representations. Thus
$Z_{\mathfrak B}$
consists of elements that kill all the irreducible representations. Thus
![]() $\operatorname {\mathrm {Ker}} c_{\pi }$
is the maximal ideal of
$\operatorname {\mathrm {Ker}} c_{\pi }$
is the maximal ideal of
![]() $Z_{\mathfrak B}$
with residue field k. The last assertion follows from the fact that
$Z_{\mathfrak B}$
with residue field k. The last assertion follows from the fact that
![]() $Z_{\mathfrak B}$
is closed in
$Z_{\mathfrak B}$
is closed in
![]() $E_{\mathfrak B}$
and [Reference Gabriel31, Proposition IV.4.13].
$E_{\mathfrak B}$
and [Reference Gabriel31, Proposition IV.4.13].
Lemma 4.2. Let P be projective in
![]() $\mathfrak C(\mathscr O)$
. Then
$\mathfrak C(\mathscr O)$
. Then
![]() $P^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )} = 0$
.
$P^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )} = 0$
.
Proof. Let J be the Pontryagin dual of P. Then J is injective in
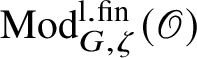 $\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O)$
and the assertion is equivalent to
$\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O)$
and the assertion is equivalent to
![]() $J_{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )} = 0$
. Let N be the unipotent subgroup
$J_{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )} = 0$
. Let N be the unipotent subgroup
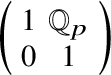 $ \left(\begin{smallmatrix} 1 & \mathbb {Q}_p \\ 0 & 1 \end{smallmatrix} \right)$
. Then by [Reference Emerton29, Proposition 3.6.2] and [Reference Emerton and Paškūnas30, Corollary 3.12], we have
$ \left(\begin{smallmatrix} 1 & \mathbb {Q}_p \\ 0 & 1 \end{smallmatrix} \right)$
. Then by [Reference Emerton29, Proposition 3.6.2] and [Reference Emerton and Paškūnas30, Corollary 3.12], we have
![]() $J_{N} = 0$
. Thus
$J_{N} = 0$
. Thus
![]() $J_{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )} = 0$
and the lemma follows. Alternatively, one can deduce the statement from Proposition 4.3.
$J_{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )} = 0$
and the lemma follows. Alternatively, one can deduce the statement from Proposition 4.3.
Proposition 4.3. Let P and M be in
![]() ${\mathfrak C}(\mathscr O)$
, such that P is projective and
${\mathfrak C}(\mathscr O)$
, such that P is projective and
![]() $M/\varpi M$
is of finite length. Then
$M/\varpi M$
is of finite length. Then
![]() $\operatorname {\mathrm {Hom}}_{{\mathfrak C}(\mathscr O)}(M, P)=0$
.
$\operatorname {\mathrm {Hom}}_{{\mathfrak C}(\mathscr O)}(M, P)=0$
.
Proof. Let
![]() $K'$
be a compact open pro-p subgroup of
$K'$
be a compact open pro-p subgroup of
![]() $\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )$
such that
$\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )$
such that
![]() $K' \cap Z = \{1\}$
. Then P is projective in
$K' \cap Z = \{1\}$
. Then P is projective in
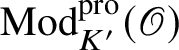 $\operatorname {\mathrm {Mod}}^{\mathrm {pro}}_{K'}(\mathscr O)$
by [Reference Emerton and Paškūnas30, Corollary 3.10], and thus
$\operatorname {\mathrm {Mod}}^{\mathrm {pro}}_{K'}(\mathscr O)$
by [Reference Emerton and Paškūnas30, Corollary 3.10], and thus
![]() for some index set I. Thus it is enough to show that
for some index set I. Thus it is enough to show that
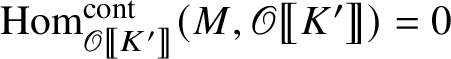 . The topological Nakayama’s lemma for compact
. The topological Nakayama’s lemma for compact
![]() $\mathscr O$
-modules implies that it is enough to show that
$\mathscr O$
-modules implies that it is enough to show that
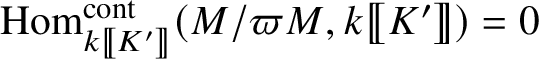 . Since
. Since
![]() $M/\varpi M$
is of finite length, it is enough to show that
$M/\varpi M$
is of finite length, it is enough to show that
![]() for every
for every
![]() $\pi \in \mathfrak B$
. This follows from [Reference Paškūnas42, Lemma 5.16]. Note that if
$\pi \in \mathfrak B$
. This follows from [Reference Paškūnas42, Lemma 5.16]. Note that if
![]() $K_n= 1+ M_2 (2 p^n \mathbb {Z}_p )$
and
$K_n= 1+ M_2 (2 p^n \mathbb {Z}_p )$
and
![]() $K_n'= K_n\cap \operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )$
, then
$K_n'= K_n\cap \operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )$
, then
![]() $K_n= K_n' ( Z\cap K_n)$
and so
$K_n= K_n' ( Z\cap K_n)$
and so
![]() $\pi ^{K_n}= \pi ^{K^{\prime }_n}$
as
$\pi ^{K_n}= \pi ^{K^{\prime }_n}$
as
![]() $Z\cap K_n$
acts trivially on
$Z\cap K_n$
acts trivially on
![]() $\pi $
; so the argument in [Reference Paškūnas42, Lemma 5.16] carries over to the restriction of
$\pi $
; so the argument in [Reference Paškūnas42, Lemma 5.16] carries over to the restriction of
![]() $\pi $
to
$\pi $
to
![]() $\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )$
.
$\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )$
.
We will denote by
![]() $\operatorname {\mathrm {Ord}}_B$
Emerton’s functor of ordinary parts [Reference Emerton28].
$\operatorname {\mathrm {Ord}}_B$
Emerton’s functor of ordinary parts [Reference Emerton28].
Lemma 4.4. Let
![]() $\pi \hookrightarrow J$
be an injective envelope of
$\pi \hookrightarrow J$
be an injective envelope of
![]() $\pi \in \mathfrak B$
in
$\pi \in \mathfrak B$
in
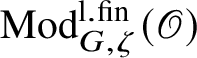 $\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O)$
. If
$\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O)$
. If
![]() $\pi $
is supersingular, then
$\pi $
is supersingular, then
![]() $\operatorname {\mathrm {Ord}}_B J=0$
. If
$\operatorname {\mathrm {Ord}}_B J=0$
. If
![]() $\pi $
is an irreducible subquotient of
$\pi $
is an irreducible subquotient of
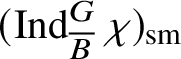 $ (\operatorname {\mathrm {Ind}}_{\overline {B}}^G \chi )_{\mathrm {sm}}$
for some character
$ (\operatorname {\mathrm {Ind}}_{\overline {B}}^G \chi )_{\mathrm {sm}}$
for some character
![]() $\chi : T\rightarrow k^{\times }$
, where
$\chi : T\rightarrow k^{\times }$
, where
![]() $\overline {B}$
is the subgroup of lower triangular matrices, then
$\overline {B}$
is the subgroup of lower triangular matrices, then
![]() $\operatorname {\mathrm {Ord}}_B J$
is isomorphic to an injective envelope of
$\operatorname {\mathrm {Ord}}_B J$
is isomorphic to an injective envelope of
![]() $\chi $
in
$\chi $
in
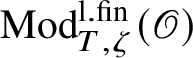 $\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{T, \zeta }(\mathscr O)$
, and also in
$\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{T, \zeta }(\mathscr O)$
, and also in
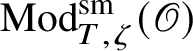 $\operatorname {\mathrm {Mod}}^{\mathrm {sm}}_{T, \zeta }(\mathscr O)$
.
$\operatorname {\mathrm {Mod}}^{\mathrm {sm}}_{T, \zeta }(\mathscr O)$
.
Proof. Since J is injective and
![]() $\operatorname {\mathrm {Ord}}_B$
is adjoint to parabolic induction, which is an exact functor,
$\operatorname {\mathrm {Ord}}_B$
is adjoint to parabolic induction, which is an exact functor,
![]() $\operatorname {\mathrm {Ord}}_B J$
is injective in
$\operatorname {\mathrm {Ord}}_B J$
is injective in
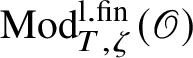 $\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{T, \zeta }(\mathscr O)$
. Thus it is a direct sum of injective envelopes of characters of T. Moreover,
$\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{T, \zeta }(\mathscr O)$
. Thus it is a direct sum of injective envelopes of characters of T. Moreover,
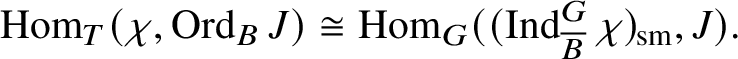 $$ \begin{align} \operatorname{\mathrm{Hom}}_T(\chi, \operatorname{\mathrm{Ord}}_B J)\cong\operatorname{\mathrm{Hom}}_G( (\operatorname{\mathrm{Ind}}_{\overline{B}}^G \chi)_{\mathrm{sm}}, J). \end{align} $$
$$ \begin{align} \operatorname{\mathrm{Hom}}_T(\chi, \operatorname{\mathrm{Ord}}_B J)\cong\operatorname{\mathrm{Hom}}_G( (\operatorname{\mathrm{Ind}}_{\overline{B}}^G \chi)_{\mathrm{sm}}, J). \end{align} $$
Since J is an injective envelope of
![]() $\pi $
, this group is nonzero if and only if
$\pi $
, this group is nonzero if and only if
![]() $\pi $
is a subquotient of
$\pi $
is a subquotient of
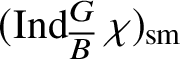 $ (\operatorname {\mathrm {Ind}}_{\overline {B}}^G \chi )_{\mathrm {sm}}$
, in which case the dimension of the spaces in formula (12) is equal to the multiplicity with which
$ (\operatorname {\mathrm {Ind}}_{\overline {B}}^G \chi )_{\mathrm {sm}}$
, in which case the dimension of the spaces in formula (12) is equal to the multiplicity with which
![]() $\pi $
occurs as a subquotient of
$\pi $
occurs as a subquotient of
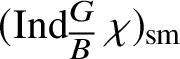 $ (\operatorname {\mathrm {Ind}}_{\overline {B}}^G \chi )_{\mathrm {sm}}$
. If
$ (\operatorname {\mathrm {Ind}}_{\overline {B}}^G \chi )_{\mathrm {sm}}$
. If
![]() $\pi $
is supersingular, then it does not occur as a subquotient of principal series, and thus
$\pi $
is supersingular, then it does not occur as a subquotient of principal series, and thus
![]() $\operatorname {\mathrm {Ord}}_B J=0$
. Otherwise, it follows from [Reference Barthel and Livné2] that there is a unique character
$\operatorname {\mathrm {Ord}}_B J=0$
. Otherwise, it follows from [Reference Barthel and Livné2] that there is a unique character
![]() $\chi $
such that the multiplicity is nonzero, in which case it is equal to
$\chi $
such that the multiplicity is nonzero, in which case it is equal to
![]() $1$
. This proves the first assertion. The same (albeit easier) proof as in [Reference Paškūnas39, Proposition 5.16] implies that every injective object in
$1$
. This proves the first assertion. The same (albeit easier) proof as in [Reference Paškūnas39, Proposition 5.16] implies that every injective object in
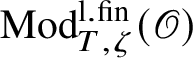 $\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{T, \zeta }(\mathscr O)$
is also injective in
$\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{T, \zeta }(\mathscr O)$
is also injective in
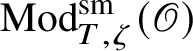 $\operatorname {\mathrm {Mod}}^{\mathrm {sm}}_{T, \zeta }(\mathscr O)$
.
$\operatorname {\mathrm {Mod}}^{\mathrm {sm}}_{T, \zeta }(\mathscr O)$
.
Lemma 4.5. Let
![]() $\pi \hookrightarrow J$
be an injective envelope of
$\pi \hookrightarrow J$
be an injective envelope of
![]() $\pi \in \mathfrak B$
in
$\pi \in \mathfrak B$
in
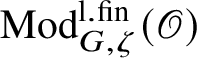 $\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O)$
. If
$\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O)$
. If
![]() $\pi $
is not a character, then
$\pi $
is not a character, then
![]() $J^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )}=0$
; otherwise
$J^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )}=0$
; otherwise
![]() $ (J^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )} )^{\vee }$
is nonzero and finitely generated over
$ (J^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )} )^{\vee }$
is nonzero and finitely generated over
![]() $\mathscr O$
.
$\mathscr O$
.
Proof. If
![]() $J^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )}$
is nonzero, then
$J^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )}$
is nonzero, then
![]() $\pi \cap J^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )}$
is nonzero, as
$\pi \cap J^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )}$
is nonzero, as
![]() $\pi \hookrightarrow J$
is essential. Since
$\pi \hookrightarrow J$
is essential. Since
![]() $\pi $
is absolutely irreducible, we deduce that it is a character and is the G-socle of
$\pi $
is absolutely irreducible, we deduce that it is a character and is the G-socle of
![]() $J^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )}$
. Note that the action of G on
$J^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )}$
. Note that the action of G on
![]() $J^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )}$
factors through
$J^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )}$
factors through
 $$ \begin{align*} G / Z \operatorname{\mathrm{SL}}_2(\mathbb{Q}_p) \cong \mathbb{Q}_p^{\times} / (\mathbb{Q}_p^{\times})^2 \cong \begin{cases} \mathbb Z / 2 \mathbb Z \times \mathbb Z / 2 \mathbb Z &\text{if } p>2, \\ \mathbb Z / 2 \mathbb Z \times \mathbb Z / 2 \mathbb Z \times \mathbb Z / 2 \mathbb Z &\text{if } p=2. \end{cases} \end{align*} $$
$$ \begin{align*} G / Z \operatorname{\mathrm{SL}}_2(\mathbb{Q}_p) \cong \mathbb{Q}_p^{\times} / (\mathbb{Q}_p^{\times})^2 \cong \begin{cases} \mathbb Z / 2 \mathbb Z \times \mathbb Z / 2 \mathbb Z &\text{if } p>2, \\ \mathbb Z / 2 \mathbb Z \times \mathbb Z / 2 \mathbb Z \times \mathbb Z / 2 \mathbb Z &\text{if } p=2. \end{cases} \end{align*} $$
It follows that
![]() $J^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )}[\varpi ]$
is a finite-dimensional k-vector space. Dually, this implies that
$J^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )}[\varpi ]$
is a finite-dimensional k-vector space. Dually, this implies that
![]() $ (J^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )} )^{\vee } / \varpi (J^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )} )^{\vee }$
is finite-dimensional over k, and the lemma follows from Nakayama’s lemma.
$ (J^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )} )^{\vee } / \varpi (J^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )} )^{\vee }$
is finite-dimensional over k, and the lemma follows from Nakayama’s lemma.
Lemma 4.6. Let J be injective in
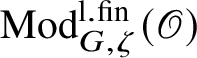 $\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O)$
and
$\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O)$
and
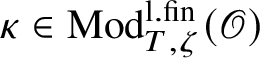 $\kappa \in \operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{T, \zeta }(\mathscr O)$
be such that
$\kappa \in \operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{T, \zeta }(\mathscr O)$
be such that
![]() $\kappa ^{\vee }$
is a finitely generated
$\kappa ^{\vee }$
is a finitely generated
![]() $\mathscr O$
-module. Then
$\mathscr O$
-module. Then
![]() $\operatorname {\mathrm {Hom}}_T(\operatorname {\mathrm {Ord}}_B J, \kappa ) = 0$
.
$\operatorname {\mathrm {Hom}}_T(\operatorname {\mathrm {Ord}}_B J, \kappa ) = 0$
.
Proof. The following is an analogue of Proposition 4.3 in an easier setting. Let
![]() $T_0$
to be an open torsion-free pro-p subgroup of
$T_0$
to be an open torsion-free pro-p subgroup of
![]() $T\cap \operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )$
. Since
$T\cap \operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )$
. Since
![]() $\operatorname {\mathrm {Ord}}_B J$
is injective in
$\operatorname {\mathrm {Ord}}_B J$
is injective in
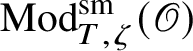 $\operatorname {\mathrm {Mod}}^{\mathrm {sm}}_{T,\zeta }(\mathscr O)$
by Lemma 4.4, it is injective in
$\operatorname {\mathrm {Mod}}^{\mathrm {sm}}_{T,\zeta }(\mathscr O)$
by Lemma 4.4, it is injective in
![]() $\operatorname {\mathrm {Mod}}^{\mathrm {sm}}_{T_0}(\mathscr O)$
, as restriction to
$\operatorname {\mathrm {Mod}}^{\mathrm {sm}}_{T_0}(\mathscr O)$
, as restriction to
![]() $T_0$
is adjoint to
$T_0$
is adjoint to
 $\operatorname {\mathrm {c-Ind}}_{ZT_0}^{T}$
, which is exact. Thus the Pontryagin dual of
$\operatorname {\mathrm {c-Ind}}_{ZT_0}^{T}$
, which is exact. Thus the Pontryagin dual of
![]() $\operatorname {\mathrm {Ord}}_B J$
is isomorphic to
$\operatorname {\mathrm {Ord}}_B J$
is isomorphic to
for some index set I. Hence, it suffices to show that
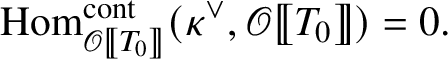
This is clear, as
is isomorphic to the ring of formal power series in one variable and
![]() $\kappa ^{\vee }$
is a finitely generated
$\kappa ^{\vee }$
is a finitely generated
![]() $\mathscr O$
-module.
$\mathscr O$
-module.
Lemma 4.7. Let
![]() $\tau $
be a smooth representation of G whose irreducible subquotients consist of characters in
$\tau $
be a smooth representation of G whose irreducible subquotients consist of characters in
![]() $\mathfrak B$
. Then
$\mathfrak B$
. Then
![]() $\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )$
acts trivially on
$\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )$
acts trivially on
![]() $\tau $
and there is an exact sequence
$\tau $
and there is an exact sequence
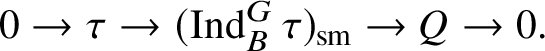 $$ \begin{align} 0 \rightarrow \tau \rightarrow (\operatorname{\mathrm{Ind}}^G_B \tau)_{\mathrm{sm}} \rightarrow Q \rightarrow 0. \end{align} $$
$$ \begin{align} 0 \rightarrow \tau \rightarrow (\operatorname{\mathrm{Ind}}^G_B \tau)_{\mathrm{sm}} \rightarrow Q \rightarrow 0. \end{align} $$
Moreover, the irreducible subquotients of Q are twists of
![]() $\operatorname {\mathrm {Sp}}$
by a character. In particular,
$\operatorname {\mathrm {Sp}}$
by a character. In particular,
![]() $\operatorname {\mathrm {Hom}}_G(\tau , Q)=0$
.
$\operatorname {\mathrm {Hom}}_G(\tau , Q)=0$
.
Proof. Since
![]() $\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )$
acts trivially on
$\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )$
acts trivially on
![]() $\tau $
by [Reference Tung47, Lemma 1.2.1], the unipotent radical of B acts trivially on
$\tau $
by [Reference Tung47, Lemma 1.2.1], the unipotent radical of B acts trivially on
![]() $\tau $
. Thus
$\tau $
. Thus
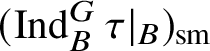 $ (\operatorname {\mathrm {Ind}}^G_B \tau \rvert _{B} )_{\mathrm {sm}}$
coincides with the parabolic induction. Since the map
$ (\operatorname {\mathrm {Ind}}^G_B \tau \rvert _{B} )_{\mathrm {sm}}$
coincides with the parabolic induction. Since the map
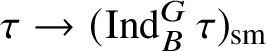 $\tau \rightarrow (\operatorname {\mathrm {Ind}}^G_B \tau )_{\mathrm {sm}}$
defined by
$\tau \rightarrow (\operatorname {\mathrm {Ind}}^G_B \tau )_{\mathrm {sm}}$
defined by
![]() $v \mapsto (g \mapsto gv)$
is G-equivariant and injective, we obtain the first assertion.
$v \mapsto (g \mapsto gv)$
is G-equivariant and injective, we obtain the first assertion.
To show the second assertion, we choose an increasing and exhaustive filtration
![]() $ \{R^j \}_{j \geq 0}$
of
$ \{R^j \}_{j \geq 0}$
of
![]() $\tau $
such that
$\tau $
such that
![]() $R^j / R^{j-1}$
is a character for each j. Then we have
$R^j / R^{j-1}$
is a character for each j. Then we have
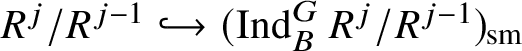 $R^j / R^{j-1} \hookrightarrow (\operatorname {\mathrm {Ind}}^G_B R^j / R^{j-1} )_{\mathrm {sm}}$
with quotient isomorphic to a twist of
$R^j / R^{j-1} \hookrightarrow (\operatorname {\mathrm {Ind}}^G_B R^j / R^{j-1} )_{\mathrm {sm}}$
with quotient isomorphic to a twist of
![]() $\operatorname {\mathrm {Sp}}$
by a character. Thus the second assertion follows from the exactness of
$\operatorname {\mathrm {Sp}}$
by a character. Thus the second assertion follows from the exactness of
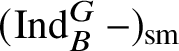 $ (\operatorname {\mathrm {Ind}}^G_B - )_{\mathrm {sm}}$
.
$ (\operatorname {\mathrm {Ind}}^G_B - )_{\mathrm {sm}}$
.
Lemma 4.8. Let J be injective in
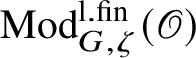 $\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O)$
and let
$\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O)$
and let
![]() $\tau $
and Q be as in Lemma 4.7. If
$\tau $
and Q be as in Lemma 4.7. If
![]() $\tau ^{\vee }$
is finitely generated over
$\tau ^{\vee }$
is finitely generated over
![]() $\mathscr O$
, then
$\mathscr O$
, then
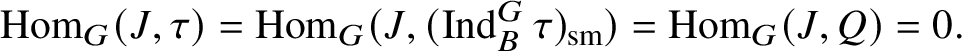 $$ \begin{align*} \operatorname{\mathrm{Hom}}_G(J, \tau) = \operatorname{\mathrm{Hom}}_G(J, (\operatorname{\mathrm{Ind}}^G_B \tau)_{\mathrm{sm}})= \operatorname{\mathrm{Hom}}_G(J, Q) = 0. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Hom}}_G(J, \tau) = \operatorname{\mathrm{Hom}}_G(J, (\operatorname{\mathrm{Ind}}^G_B \tau)_{\mathrm{sm}})= \operatorname{\mathrm{Hom}}_G(J, Q) = 0. \end{align*} $$
Proof. Since
![]() $\tau ^{\vee }$
is finitely generated over
$\tau ^{\vee }$
is finitely generated over
![]() $\mathscr O$
, then
$\mathscr O$
, then
![]() $\tau [\varpi ]$
is a finite k-vector space, and thus
$\tau [\varpi ]$
is a finite k-vector space, and thus
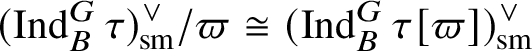 $$ \begin{align*} (\operatorname{\mathrm{Ind}}^G_B \tau )_{\mathrm{sm}}^{\vee}/ \varpi \cong (\operatorname{\mathrm{Ind}}^G_B \tau[\varpi])_{\mathrm{sm}}^{\vee} \end{align*} $$
$$ \begin{align*} (\operatorname{\mathrm{Ind}}^G_B \tau )_{\mathrm{sm}}^{\vee}/ \varpi \cong (\operatorname{\mathrm{Ind}}^G_B \tau[\varpi])_{\mathrm{sm}}^{\vee} \end{align*} $$
is of finite length in
![]() ${\mathfrak C}(\mathscr O)$
and the assertion follows from Proposition 4.3.
${\mathfrak C}(\mathscr O)$
and the assertion follows from Proposition 4.3.
Proposition 4.9. Let J and
![]() $\tau $
be as in Lemma 4.8. Then
$\tau $
be as in Lemma 4.8. Then
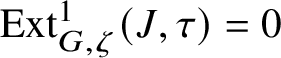 $\operatorname {\mathrm {Ext}}^1_{G, \zeta }(J, \tau ) = 0$
.
$\operatorname {\mathrm {Ext}}^1_{G, \zeta }(J, \tau ) = 0$
.
Proof. Consider an exact sequence
![]() $0 \rightarrow \tau \rightarrow I \rightarrow J \rightarrow 0$
. Applying
$0 \rightarrow \tau \rightarrow I \rightarrow J \rightarrow 0$
. Applying
![]() $\operatorname {\mathrm {Ord}}_B$
to it, we get an exact sequence
$\operatorname {\mathrm {Ord}}_B$
to it, we get an exact sequence
of smooth T-representations. It is proved in [Reference Emerton and Paškūnas30] that the functors
![]() $H^i\operatorname {\mathrm {Ord}}_B$
in [Reference Emerton29] coincide with the derived functors
$H^i\operatorname {\mathrm {Ord}}_B$
in [Reference Emerton29] coincide with the derived functors
![]() $\mathbb R^i\operatorname {\mathrm {Ord}}_B$
. Moreover,
$\mathbb R^i\operatorname {\mathrm {Ord}}_B$
. Moreover,
![]() $H^1\operatorname {\mathrm {Ord}}_B$
coincides with the N-coinvariants twisted by the character
$H^1\operatorname {\mathrm {Ord}}_B$
coincides with the N-coinvariants twisted by the character
![]() $\alpha ^{-1}$
, where
$\alpha ^{-1}$
, where
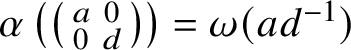 $\alpha \left( \left( \begin {smallmatrix} a & 0 \\ 0 & d\end {smallmatrix} \right) \right)=\omega (a d^{-1} )$
, by [Reference Emerton29, Proposition 3.6.2].
$\alpha \left( \left( \begin {smallmatrix} a & 0 \\ 0 & d\end {smallmatrix} \right) \right)=\omega (a d^{-1} )$
, by [Reference Emerton29, Proposition 3.6.2].
Since
![]() $\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )$
acts trivially on
$\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )$
acts trivially on
![]() $\tau $
, we have
$\tau $
, we have
![]() $\operatorname {\mathrm {Ord}}_B \tau =0$
and
$\operatorname {\mathrm {Ord}}_B \tau =0$
and
![]() $\mathbb R^1 \operatorname {\mathrm {Ord}}_B \tau \cong \tau \otimes \alpha ^{-1}$
. Thus the exact sequence reduces to
$\mathbb R^1 \operatorname {\mathrm {Ord}}_B \tau \cong \tau \otimes \alpha ^{-1}$
. Thus the exact sequence reduces to
Since the middle map is zero by Lemma 4.6, the map
![]() $\tau \hookrightarrow I$
induces an isomorphism
$\tau \hookrightarrow I$
induces an isomorphism
![]() $\tau \cong I_N$
of T-representations and hence
$\tau \cong I_N$
of T-representations and hence
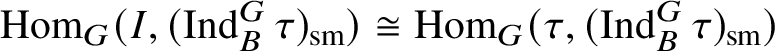 $$ \begin{align} \operatorname{\mathrm{Hom}}_G(I, (\operatorname{\mathrm{Ind}}^G_B \tau)_{\mathrm{sm}}) \cong \operatorname{\mathrm{Hom}}_G(\tau, (\operatorname{\mathrm{Ind}}^G_B \tau)_{\mathrm{sm}}) \end{align} $$
$$ \begin{align} \operatorname{\mathrm{Hom}}_G(I, (\operatorname{\mathrm{Ind}}^G_B \tau)_{\mathrm{sm}}) \cong \operatorname{\mathrm{Hom}}_G(\tau, (\operatorname{\mathrm{Ind}}^G_B \tau)_{\mathrm{sm}}) \end{align} $$
by the adjunction formula.
It follows from Lemma 4.8 that the first three terms in the long exact sequence obtained by applying
![]() $\operatorname {\mathrm {Hom}}_G(J, -)$
to formula (13) are zero. Thus by applying
$\operatorname {\mathrm {Hom}}_G(J, -)$
to formula (13) are zero. Thus by applying
![]() $\operatorname {\mathrm {Hom}}_G(I, -)\rightarrow \operatorname {\mathrm {Hom}}_G(\tau ,-)$
to formula (13), we obtain the following commutative diagram with exact columns:
$\operatorname {\mathrm {Hom}}_G(I, -)\rightarrow \operatorname {\mathrm {Hom}}_G(\tau ,-)$
to formula (13), we obtain the following commutative diagram with exact columns:
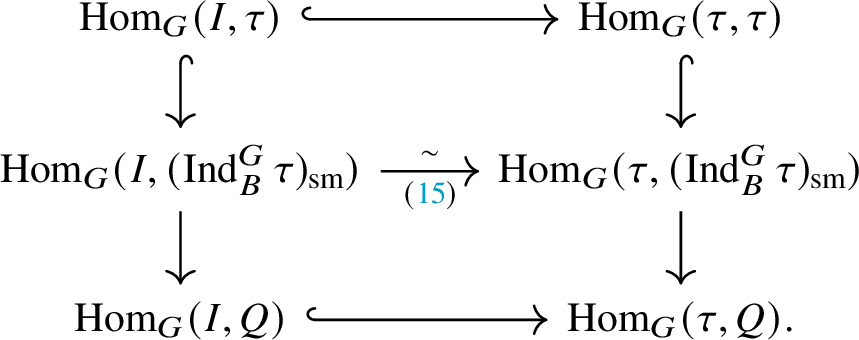
The last part of Lemma 4.7 says that
![]() $\operatorname {\mathrm {Hom}}_G(\tau , Q)=0$
and hence
$\operatorname {\mathrm {Hom}}_G(\tau , Q)=0$
and hence
![]() $\operatorname {\mathrm {Hom}}_G(I, Q)=0$
. Thus all the maps in the top square of the diagram are isomorphisms. The preimage of
$\operatorname {\mathrm {Hom}}_G(I, Q)=0$
. Thus all the maps in the top square of the diagram are isomorphisms. The preimage of
![]() $\operatorname {\mathrm {id}}_{\tau }\in \operatorname {\mathrm {Hom}}_G(\tau , \tau )$
in
$\operatorname {\mathrm {id}}_{\tau }\in \operatorname {\mathrm {Hom}}_G(\tau , \tau )$
in
![]() $\operatorname {\mathrm {Hom}}_G(I, \tau )$
splits the exact sequence
$\operatorname {\mathrm {Hom}}_G(I, \tau )$
splits the exact sequence
![]() $0 \rightarrow \tau \rightarrow I \rightarrow J \rightarrow 0$
. This proves the proposition.
$0 \rightarrow \tau \rightarrow I \rightarrow J \rightarrow 0$
. This proves the proposition.
4.2 Quotient category
Let
![]() $\mathfrak T(\mathscr O)$
be the full subcategory of
$\mathfrak T(\mathscr O)$
be the full subcategory of
![]() $\mathfrak C(\mathscr O)$
whose objects have trivial
$\mathfrak C(\mathscr O)$
whose objects have trivial
![]() $\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )$
-action. By [Reference Paškūnas39, Lemma 10.25] (for
$\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )$
-action. By [Reference Paškūnas39, Lemma 10.25] (for
![]() $p>2$
) and [Reference Tung47, Lemma 1.2.1] (for
$p>2$
) and [Reference Tung47, Lemma 1.2.1] (for
![]() $p=2$
),
$p=2$
),
![]() $\mathfrak T(\mathscr O)$
is a thick subcategory of
$\mathfrak T(\mathscr O)$
is a thick subcategory of
![]() $\mathfrak C(\mathscr O)$
and hence we may consider the quotient category
$\mathfrak C(\mathscr O)$
and hence we may consider the quotient category
![]() $\mathfrak Q(\mathscr O) := \mathfrak C(\mathscr O) / \mathfrak T(\mathscr O)$
. Let
$\mathfrak Q(\mathscr O) := \mathfrak C(\mathscr O) / \mathfrak T(\mathscr O)$
. Let
![]() $\mathscr T: \mathfrak C(\mathscr O) \rightarrow \mathfrak Q(\mathscr O)$
be the quotient functor; we note that
$\mathscr T: \mathfrak C(\mathscr O) \rightarrow \mathfrak Q(\mathscr O)$
be the quotient functor; we note that
![]() $\mathscr T$
is the identity on objects. It is shown in [Reference Paškūnas39, Section 10.3] that
$\mathscr T$
is the identity on objects. It is shown in [Reference Paškūnas39, Section 10.3] that
![]() $\mathfrak Q(\mathscr O)$
is an abelian category with enough projectives and
$\mathfrak Q(\mathscr O)$
is an abelian category with enough projectives and
![]() $\mathscr T$
is an exact functor.
$\mathscr T$
is an exact functor.
For a block
![]() $\mathfrak B$
, we denote
$\mathfrak B$
, we denote
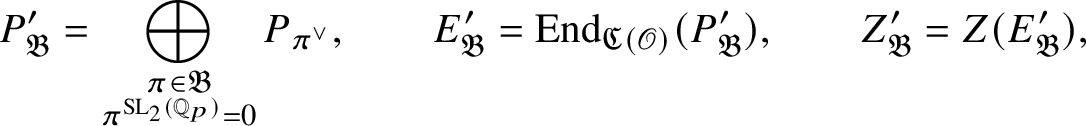 $$ \begin{align*} P_{\mathfrak B}' = \bigoplus_{\substack{\pi \in \mathfrak B \\ \pi^{\operatorname{\mathrm{SL}}_2(\mathbb{Q}_p)} = 0}} P_{\pi^{\vee}}, \qquad E_{\mathfrak B}' = \operatorname{\mathrm{End}}_{\mathfrak C(\mathscr O)}(P_{\mathfrak B}'), \qquad Z_{\mathfrak B}' = Z(E_{\mathfrak B}'), \end{align*} $$
$$ \begin{align*} P_{\mathfrak B}' = \bigoplus_{\substack{\pi \in \mathfrak B \\ \pi^{\operatorname{\mathrm{SL}}_2(\mathbb{Q}_p)} = 0}} P_{\pi^{\vee}}, \qquad E_{\mathfrak B}' = \operatorname{\mathrm{End}}_{\mathfrak C(\mathscr O)}(P_{\mathfrak B}'), \qquad Z_{\mathfrak B}' = Z(E_{\mathfrak B}'), \end{align*} $$
where
![]() $P_{\pi ^{\vee }}$
is a projective envelope of
$P_{\pi ^{\vee }}$
is a projective envelope of
![]() $\pi ^{\vee }$
in
$\pi ^{\vee }$
in
![]() $\mathfrak C(\mathscr O)$
.
$\mathfrak C(\mathscr O)$
.
Proposition 4.10. Let
![]() $\mathfrak B$
be a block.
$\mathfrak B$
be a block.
-
1.
 $\mathscr T P_{\mathfrak B}'$
is a projective object of
$\mathscr T P_{\mathfrak B}'$
is a projective object of
 $\mathfrak Q(\mathscr O)$
and
$\mathfrak Q(\mathscr O)$
and
 $E_{\mathfrak B}' \cong \operatorname {\mathrm {End}}_{\mathfrak Q(\mathscr O)} (\mathscr T P_{\mathfrak B}' )$
.
$E_{\mathfrak B}' \cong \operatorname {\mathrm {End}}_{\mathfrak Q(\mathscr O)} (\mathscr T P_{\mathfrak B}' )$
. -
2. The functor
 $M \mapsto \operatorname {\mathrm {Hom}}_{\mathfrak Q(\mathscr O)} (\mathscr T P_{\mathfrak B}', M )$
defines an equivalence of categories between
$M \mapsto \operatorname {\mathrm {Hom}}_{\mathfrak Q(\mathscr O)} (\mathscr T P_{\mathfrak B}', M )$
defines an equivalence of categories between
 $\mathfrak Q(\mathscr O)_{\mathfrak B}$
and the category of pseudocompact right
$\mathfrak Q(\mathscr O)_{\mathfrak B}$
and the category of pseudocompact right
 $E_{\mathfrak B}'$
-modules, with the inverse given by
$E_{\mathfrak B}'$
-modules, with the inverse given by
 $\mathrm m \mapsto \mathrm m \operatorname {\mathrm {\mathbin {\widehat {\otimes }}}}_{E_{\mathfrak B}'} \mathscr T P_{\mathfrak B}'$
.
$\mathrm m \mapsto \mathrm m \operatorname {\mathrm {\mathbin {\widehat {\otimes }}}}_{E_{\mathfrak B}'} \mathscr T P_{\mathfrak B}'$
.
Proof. See [Reference Paškūnas39, Lemma 10.27] for the first assertion and [Reference Gabriel31, Section IV.4, Theorem 4, Corollaries 1 and 5] for the second assertion.
4.3 The centre
In this section we will prove key results toward showing that
![]() $E_{\mathfrak B}$
and
$E_{\mathfrak B}$
and
![]() $Z_{\mathfrak B}$
are finite over
$Z_{\mathfrak B}$
are finite over
![]() $Z_{\mathfrak B}'$
. If
$Z_{\mathfrak B}'$
. If
![]() $\mathfrak B$
is of type (i), (ii) or (iii), then we have
$\mathfrak B$
is of type (i), (ii) or (iii), then we have
![]() $P_{\mathfrak B}=P_{\mathfrak B}'$
and thus
$P_{\mathfrak B}=P_{\mathfrak B}'$
and thus
![]() $Z_{\mathfrak B}=Z_{\mathfrak B}'$
.
$Z_{\mathfrak B}=Z_{\mathfrak B}'$
.
Lemma 4.11. Let E be a ring with centre Z and let
![]() $\mathrm m$
be a finitely generated (right) E-module. Assume that Z is Noetherian and E is (module) finite over Z. Then
$\mathrm m$
be a finitely generated (right) E-module. Assume that Z is Noetherian and E is (module) finite over Z. Then
![]() $\operatorname {\mathrm {End}}_E(\mathrm m)$
and its centre
$\operatorname {\mathrm {End}}_E(\mathrm m)$
and its centre
![]() $Z(\operatorname {\mathrm {End}}_E(\mathrm m))$
are Noetherian and finite over Z.
$Z(\operatorname {\mathrm {End}}_E(\mathrm m))$
are Noetherian and finite over Z.
Proof. Since
![]() $\mathrm m$
is finitely generated over E, there is a surjection
$\mathrm m$
is finitely generated over E, there is a surjection
![]() $E^{\oplus n} \twoheadrightarrow \mathrm m$
for some n. This induces an injection
$E^{\oplus n} \twoheadrightarrow \mathrm m$
for some n. This induces an injection
![]() $\operatorname {\mathrm {End}}_E(\mathrm m) \hookrightarrow \operatorname {\mathrm {Hom}}_E (E^{\oplus n}, \mathrm m )$
and a surjection
$\operatorname {\mathrm {End}}_E(\mathrm m) \hookrightarrow \operatorname {\mathrm {Hom}}_E (E^{\oplus n}, \mathrm m )$
and a surjection
![]() $M_n(E^{\mathrm {op}}) \cong \operatorname {\mathrm {End}}_E (E^{\oplus n} ) \twoheadrightarrow \operatorname {\mathrm {Hom}}_E (E^{\oplus n}, \mathrm m )$
of Z-modules. Since
$M_n(E^{\mathrm {op}}) \cong \operatorname {\mathrm {End}}_E (E^{\oplus n} ) \twoheadrightarrow \operatorname {\mathrm {Hom}}_E (E^{\oplus n}, \mathrm m )$
of Z-modules. Since
![]() $M_n(E^{\mathrm {op}})$
is finite over
$M_n(E^{\mathrm {op}})$
is finite over
![]() $E^{\mathrm {op}}$
, it is finite and Noetherian over Z. It follows that
$E^{\mathrm {op}}$
, it is finite and Noetherian over Z. It follows that
![]() $\operatorname {\mathrm {Hom}}_E (E^{\oplus n}, \mathrm m )$
and thus
$\operatorname {\mathrm {Hom}}_E (E^{\oplus n}, \mathrm m )$
and thus
![]() $\operatorname {\mathrm {End}}_E(\mathrm m)$
, which can be identified with a Z-submodule of
$\operatorname {\mathrm {End}}_E(\mathrm m)$
, which can be identified with a Z-submodule of
![]() $\operatorname {\mathrm {Hom}}_E (E^{\oplus n}, \mathrm m )$
, are finite and Noetherian over Z. This proves the lemma.
$\operatorname {\mathrm {Hom}}_E (E^{\oplus n}, \mathrm m )$
, are finite and Noetherian over Z. This proves the lemma.
Lemma 4.12. Let
![]() $M_{\mathfrak B} = \ker (P_{\mathfrak B} \rightarrow (P_{\mathfrak B})_{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )} )$
. Then the following hold:
$M_{\mathfrak B} = \ker (P_{\mathfrak B} \rightarrow (P_{\mathfrak B})_{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )} )$
. Then the following hold:
-
1.
 $(M_{\mathfrak B})_{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )} = 0$
.
$(M_{\mathfrak B})_{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )} = 0$
. -
2. For all
 $\pi \in \mathfrak B$
,
$\pi \in \mathfrak B$
,
 $\operatorname {\mathrm {Hom}}_{\mathfrak C(\mathscr O)} (M_{\mathfrak B}, \pi ^{\vee } )$
is finite-dimensional over k.
$\operatorname {\mathrm {Hom}}_{\mathfrak C(\mathscr O)} (M_{\mathfrak B}, \pi ^{\vee } )$
is finite-dimensional over k.
Proof. It suffices to consider the block
![]() $\mathfrak B$
of type (iv), (v) or (vi); otherwise
$\mathfrak B$
of type (iv), (v) or (vi); otherwise
![]() $M_{\mathfrak B} = P_{\mathfrak B}$
and the assertion is trivial. Let
$M_{\mathfrak B} = P_{\mathfrak B}$
and the assertion is trivial. Let
![]() $J_{\mathfrak B}$
be the Pontryagin dual of
$J_{\mathfrak B}$
be the Pontryagin dual of
![]() $P_{\mathfrak B}$
. Then we have an exact sequence
$P_{\mathfrak B}$
. Then we have an exact sequence
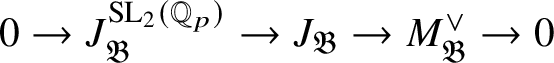 $0 \rightarrow J_{\mathfrak B}^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )} \rightarrow J_{\mathfrak B} \rightarrow M_{\mathfrak B}^{\vee } \rightarrow 0$
. By applying
$0 \rightarrow J_{\mathfrak B}^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )} \rightarrow J_{\mathfrak B} \rightarrow M_{\mathfrak B}^{\vee } \rightarrow 0$
. By applying
![]() $\operatorname {\mathrm {Hom}}_{\operatorname {\mathrm {GL}}_2 (\mathbb {Q}_p )}(\pi , -)$
, we get a long exact sequence
$\operatorname {\mathrm {Hom}}_{\operatorname {\mathrm {GL}}_2 (\mathbb {Q}_p )}(\pi , -)$
, we get a long exact sequence
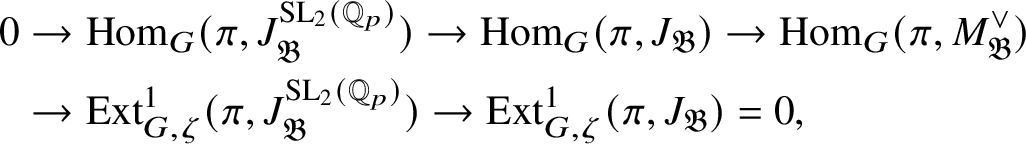 $$ \begin{align*} 0 &\rightarrow \operatorname{\mathrm{Hom}}_{G}(\pi, J_{\mathfrak B}^{\operatorname{\mathrm{SL}}_2(\mathbb{Q}_p)}) \rightarrow \operatorname{\mathrm{Hom}}_{G}(\pi, J_{\mathfrak B}) \rightarrow \operatorname{\mathrm{Hom}}_{G}(\pi, M_{\mathfrak B}^{\vee}) \\ &\rightarrow \operatorname{\mathrm{Ext}}^1_{G, \zeta}(\pi, J_{\mathfrak B}^{\operatorname{\mathrm{SL}}_2(\mathbb{Q}_p)}) \rightarrow \operatorname{\mathrm{Ext}}^1_{G, \zeta}(\pi, J_{\mathfrak B}) = 0, \end{align*} $$
$$ \begin{align*} 0 &\rightarrow \operatorname{\mathrm{Hom}}_{G}(\pi, J_{\mathfrak B}^{\operatorname{\mathrm{SL}}_2(\mathbb{Q}_p)}) \rightarrow \operatorname{\mathrm{Hom}}_{G}(\pi, J_{\mathfrak B}) \rightarrow \operatorname{\mathrm{Hom}}_{G}(\pi, M_{\mathfrak B}^{\vee}) \\ &\rightarrow \operatorname{\mathrm{Ext}}^1_{G, \zeta}(\pi, J_{\mathfrak B}^{\operatorname{\mathrm{SL}}_2(\mathbb{Q}_p)}) \rightarrow \operatorname{\mathrm{Ext}}^1_{G, \zeta}(\pi, J_{\mathfrak B}) = 0, \end{align*} $$
where
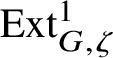 $\operatorname {\mathrm {Ext}}^1_{G, \zeta }$
is the extension group in
$\operatorname {\mathrm {Ext}}^1_{G, \zeta }$
is the extension group in
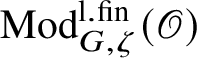 $\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O)$
.
$\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O)$
.
If
![]() $\pi \in \mathfrak B$
is a character, then both
$\pi \in \mathfrak B$
is a character, then both
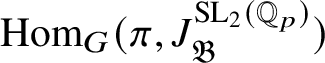 $\operatorname {\mathrm {Hom}}_{G} (\pi , J_{\mathfrak B}^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )} )$
and
$\operatorname {\mathrm {Hom}}_{G} (\pi , J_{\mathfrak B}^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )} )$
and
![]() $\operatorname {\mathrm {Hom}}_{G}(\pi , J_{\mathfrak B})$
are
$\operatorname {\mathrm {Hom}}_{G}(\pi , J_{\mathfrak B})$
are
![]() $1$
-dimensional over k, and
$1$
-dimensional over k, and
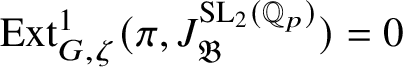 $\operatorname {\mathrm {Ext}}^1_{G, \zeta } (\pi , J_{\mathfrak B}^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )} ) = 0$
by [Reference Tung47, Lemma 1.2.1]. Thus
$\operatorname {\mathrm {Ext}}^1_{G, \zeta } (\pi , J_{\mathfrak B}^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )} ) = 0$
by [Reference Tung47, Lemma 1.2.1]. Thus
![]() $\operatorname {\mathrm {Hom}}_G (\pi , M_{\mathfrak B}^{\vee } ) = 0$
and the first assertion follows (see [Reference Colmez and Dospinescu20, Lemma III.40] for another proof).
$\operatorname {\mathrm {Hom}}_G (\pi , M_{\mathfrak B}^{\vee } ) = 0$
and the first assertion follows (see [Reference Colmez and Dospinescu20, Lemma III.40] for another proof).
If
![]() $\pi \in \mathfrak B$
is not a character, then
$\pi \in \mathfrak B$
is not a character, then
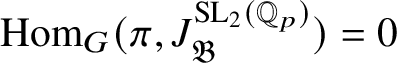 $\operatorname {\mathrm {Hom}}_{G} (\pi , J_{\mathfrak B}^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )} ) = 0$
and
$\operatorname {\mathrm {Hom}}_{G} (\pi , J_{\mathfrak B}^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )} ) = 0$
and
![]() $\operatorname {\mathrm {Hom}}_{G}(\pi , J_{\mathfrak B})$
is
$\operatorname {\mathrm {Hom}}_{G}(\pi , J_{\mathfrak B})$
is
![]() $1$
-dimensional over k. Since
$1$
-dimensional over k. Since
![]() $\pi $
is killed by
$\pi $
is killed by
![]() $\varpi $
, for the second assertion it is enough to show that
$\varpi $
, for the second assertion it is enough to show that
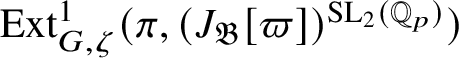 $\operatorname {\mathrm {Ext}}^1_{G, \zeta } (\pi , (J_{\mathfrak B}[\varpi ])^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )} )$
is finite-dimensional over k. This holds, because
$\operatorname {\mathrm {Ext}}^1_{G, \zeta } (\pi , (J_{\mathfrak B}[\varpi ])^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )} )$
is finite-dimensional over k. This holds, because
![]() $(J_{\mathfrak B}[\varpi ])^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )}$
is of finite length by Lemma 4.5, and if
$(J_{\mathfrak B}[\varpi ])^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )}$
is of finite length by Lemma 4.5, and if
![]() $\chi $
is a character, then
$\chi $
is a character, then
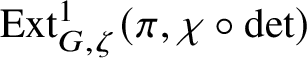 $\operatorname {\mathrm {Ext}}^1_{G, \zeta }(\pi , \chi \circ \det )$
is finite-dimensional.
$\operatorname {\mathrm {Ext}}^1_{G, \zeta }(\pi , \chi \circ \det )$
is finite-dimensional.
Corollary 4.13. There is a surjection
![]() $ (P_{\mathfrak B}' )^{\oplus n} \twoheadrightarrow M_{\mathfrak B}$
for some
$ (P_{\mathfrak B}' )^{\oplus n} \twoheadrightarrow M_{\mathfrak B}$
for some
![]() $n \in \mathbb {N}$
.
$n \in \mathbb {N}$
.
Proof. This follows from Lemma 4.12, which shows that the cosocle of
![]() $M_{\mathfrak B}$
contains no characters and each irreducible representation in
$M_{\mathfrak B}$
contains no characters and each irreducible representation in
![]() $\mathfrak B$
appears with finite multiplicity.
$\mathfrak B$
appears with finite multiplicity.
Lemma 4.14. Both
![]() $\operatorname {\mathrm {Hom}}_{\mathfrak C(\mathscr O)}(P_{\mathfrak B} / M_{\mathfrak B}, P_{\mathfrak B})$
and
$\operatorname {\mathrm {Hom}}_{\mathfrak C(\mathscr O)}(P_{\mathfrak B} / M_{\mathfrak B}, P_{\mathfrak B})$
and
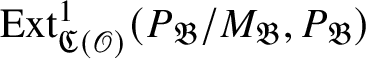 $\operatorname {\mathrm {Ext}}^1_{\mathfrak C(\mathscr O)}(P_{\mathfrak B} / M_{\mathfrak B}, P_{\mathfrak B})$
are equal to zero.
$\operatorname {\mathrm {Ext}}^1_{\mathfrak C(\mathscr O)}(P_{\mathfrak B} / M_{\mathfrak B}, P_{\mathfrak B})$
are equal to zero.
Proof. The first assertion follows because
![]() $\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )$
acts trivially on
$\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )$
acts trivially on
![]() $P_{\mathfrak B} / M_{\mathfrak B}$
and
$P_{\mathfrak B} / M_{\mathfrak B}$
and
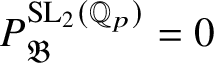 $P_{\mathfrak B}^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )} = 0$
(see Lemma 4.2), and the second assertion follows from Proposition 4.9 applied to
$P_{\mathfrak B}^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )} = 0$
(see Lemma 4.2), and the second assertion follows from Proposition 4.9 applied to
![]() $J=P_{\mathfrak B}^{\vee }$
and
$J=P_{\mathfrak B}^{\vee }$
and
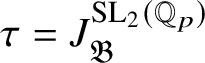 $\tau = J_{\mathfrak B}^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )}$
. It follows from Lemma 4.5 that
$\tau = J_{\mathfrak B}^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )}$
. It follows from Lemma 4.5 that
![]() $\tau ^{\vee }$
is a finitely generated
$\tau ^{\vee }$
is a finitely generated
![]() $\mathscr O$
-module.
$\mathscr O$
-module.
Proposition 4.15. There is a natural isomorphism
![]() $E_{\mathfrak B} \cong \operatorname {\mathrm {End}}_{\mathfrak C(\mathscr O)}(M_{\mathfrak B})$
. In particular,
$E_{\mathfrak B} \cong \operatorname {\mathrm {End}}_{\mathfrak C(\mathscr O)}(M_{\mathfrak B})$
. In particular,
![]() $Z_{\mathfrak B} \cong Z(\operatorname {\mathrm {End}}_{\mathfrak C(\mathscr O)}(M_{\mathfrak B}))$
.
$Z_{\mathfrak B} \cong Z(\operatorname {\mathrm {End}}_{\mathfrak C(\mathscr O)}(M_{\mathfrak B}))$
.
Proof. Set
![]() $\phi \in E_{\mathfrak B} = \operatorname {\mathrm {End}}_{\mathfrak C(\mathscr O)}(P_{\mathfrak B})$
. Then the composition
$\phi \in E_{\mathfrak B} = \operatorname {\mathrm {End}}_{\mathfrak C(\mathscr O)}(P_{\mathfrak B})$
. Then the composition
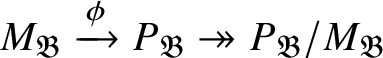 $M_{\mathfrak B} \xrightarrow {\phi } P_{\mathfrak B} \twoheadrightarrow P_{\mathfrak B} / M_{\mathfrak B}$
is the zero map, since
$M_{\mathfrak B} \xrightarrow {\phi } P_{\mathfrak B} \twoheadrightarrow P_{\mathfrak B} / M_{\mathfrak B}$
is the zero map, since
![]() $\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )$
acts trivially on
$\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )$
acts trivially on
![]() $P_{\mathfrak B} / M_{\mathfrak B} \cong (P_{\mathfrak B})_{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )}$
and
$P_{\mathfrak B} / M_{\mathfrak B} \cong (P_{\mathfrak B})_{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )}$
and
![]() $(M_{\mathfrak B})_{\operatorname {\mathrm {SL}} (\mathbb {Q}_p )}= 0$
by Lemma 4.12. Thus
$(M_{\mathfrak B})_{\operatorname {\mathrm {SL}} (\mathbb {Q}_p )}= 0$
by Lemma 4.12. Thus
![]() $\phi $
maps
$\phi $
maps
![]() $M_{\mathfrak B}$
to
$M_{\mathfrak B}$
to
![]() $M_{\mathfrak B}$
, and restriction to
$M_{\mathfrak B}$
, and restriction to
![]() $M_{\mathfrak B}$
induces a ring homomorphism
$M_{\mathfrak B}$
induces a ring homomorphism
![]() $E_{\mathfrak B} \rightarrow \operatorname {\mathrm {End}}_{\mathfrak C(\mathscr O)}(M_{\mathfrak B})$
.
$E_{\mathfrak B} \rightarrow \operatorname {\mathrm {End}}_{\mathfrak C(\mathscr O)}(M_{\mathfrak B})$
.
Applying the functor
![]() $\operatorname {\mathrm {Hom}}_{\mathfrak C(\mathscr O)}(M_{\mathfrak B}, -)$
to the exact sequence
$\operatorname {\mathrm {Hom}}_{\mathfrak C(\mathscr O)}(M_{\mathfrak B}, -)$
to the exact sequence
![]() $0 \rightarrow M_{\mathfrak B} \rightarrow P_{\mathfrak B} \rightarrow P_{\mathfrak B}/M_{\mathfrak B} \rightarrow 0$
, we get the exact sequence
$0 \rightarrow M_{\mathfrak B} \rightarrow P_{\mathfrak B} \rightarrow P_{\mathfrak B}/M_{\mathfrak B} \rightarrow 0$
, we get the exact sequence
Since the last term is equal to zero by Lemma 4.12, we obtain
![]() $\operatorname {\mathrm {End}}_{\mathfrak C(\mathscr O)}(M_{\mathfrak B}) \cong \operatorname {\mathrm {Hom}}_{\mathfrak C(\mathscr O)}(M_{\mathfrak B}, P_{\mathfrak B})$
. On the other hand, by applying the functor
$\operatorname {\mathrm {End}}_{\mathfrak C(\mathscr O)}(M_{\mathfrak B}) \cong \operatorname {\mathrm {Hom}}_{\mathfrak C(\mathscr O)}(M_{\mathfrak B}, P_{\mathfrak B})$
. On the other hand, by applying the functor
![]() $\operatorname {\mathrm {Hom}}_{\mathfrak C(\mathscr O)}(-, P_{\mathfrak B})$
to the same short exact sequence, we get the exact sequence
$\operatorname {\mathrm {Hom}}_{\mathfrak C(\mathscr O)}(-, P_{\mathfrak B})$
to the same short exact sequence, we get the exact sequence
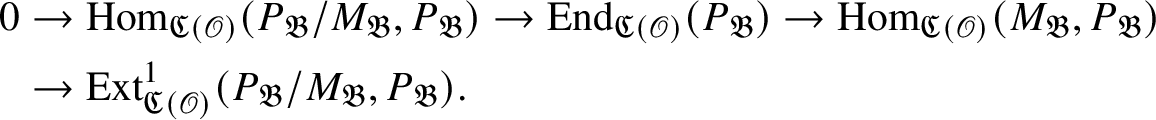 $$ \begin{align*} 0 &\rightarrow \operatorname{\mathrm{Hom}}_{\mathfrak C(\mathscr O)}(P_{\mathfrak B} / M_{\mathfrak B}, P_{\mathfrak B}) \rightarrow \operatorname{\mathrm{End}}_{\mathfrak C(\mathscr O)}(P_{\mathfrak B}) \rightarrow \operatorname{\mathrm{Hom}}_{\mathfrak C(\mathscr O)}(M_{\mathfrak B}, P_{\mathfrak B}) \\ &\rightarrow \operatorname{\mathrm{Ext}}^1_{\mathfrak C(\mathscr O)}(P_{\mathfrak B} / M_{\mathfrak B}, P_{\mathfrak B}). \end{align*} $$
$$ \begin{align*} 0 &\rightarrow \operatorname{\mathrm{Hom}}_{\mathfrak C(\mathscr O)}(P_{\mathfrak B} / M_{\mathfrak B}, P_{\mathfrak B}) \rightarrow \operatorname{\mathrm{End}}_{\mathfrak C(\mathscr O)}(P_{\mathfrak B}) \rightarrow \operatorname{\mathrm{Hom}}_{\mathfrak C(\mathscr O)}(M_{\mathfrak B}, P_{\mathfrak B}) \\ &\rightarrow \operatorname{\mathrm{Ext}}^1_{\mathfrak C(\mathscr O)}(P_{\mathfrak B} / M_{\mathfrak B}, P_{\mathfrak B}). \end{align*} $$
Since
![]() $\operatorname {\mathrm {Hom}}_{\mathfrak C(\mathscr O)}(P_{\mathfrak B} / M_{\mathfrak B}, P_{\mathfrak B}) = 0$
and
$\operatorname {\mathrm {Hom}}_{\mathfrak C(\mathscr O)}(P_{\mathfrak B} / M_{\mathfrak B}, P_{\mathfrak B}) = 0$
and
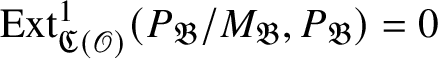 $\operatorname {\mathrm {Ext}}^1_{\mathfrak C(\mathscr O)}(P_{\mathfrak B} / M_{\mathfrak B}, P_{\mathfrak B}) = 0$
by Lemma 4.14, we deduce
$\operatorname {\mathrm {Ext}}^1_{\mathfrak C(\mathscr O)}(P_{\mathfrak B} / M_{\mathfrak B}, P_{\mathfrak B}) = 0$
by Lemma 4.14, we deduce
![]() $\operatorname {\mathrm {End}}_{\mathfrak C(\mathscr O)}(P_{\mathfrak B}) \cong \operatorname {\mathrm {Hom}}_{\mathfrak C(\mathscr O)}(M_{\mathfrak B}, P_{\mathfrak B})$
and the proposition follows.
$\operatorname {\mathrm {End}}_{\mathfrak C(\mathscr O)}(P_{\mathfrak B}) \cong \operatorname {\mathrm {Hom}}_{\mathfrak C(\mathscr O)}(M_{\mathfrak B}, P_{\mathfrak B})$
and the proposition follows.
Corollary 4.16. There is a natural surjective homomorphism
Proof. Note that we have
![]() $(M_{\mathfrak B})^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )} = 0$
by Lemma 4.2 and
$(M_{\mathfrak B})^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )} = 0$
by Lemma 4.2 and
![]() $(M_{\mathfrak B})_{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )} = 0$
by Lemma 4.12. It follows from [Reference Paškūnas39, Lemma 10.26] that the functor
$(M_{\mathfrak B})_{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )} = 0$
by Lemma 4.12. It follows from [Reference Paškūnas39, Lemma 10.26] that the functor
![]() $\mathscr T$
induces an isomorphism
$\mathscr T$
induces an isomorphism
Since
![]() $Z_{\mathfrak B}'$
is the centre of
$Z_{\mathfrak B}'$
is the centre of
![]() $\mathfrak Q(\mathscr O)_{\mathfrak B}$
, it acts on
$\mathfrak Q(\mathscr O)_{\mathfrak B}$
, it acts on
![]() $\mathscr T M_{\mathfrak B}$
, and this action induces a homomorphism
$\mathscr T M_{\mathfrak B}$
, and this action induces a homomorphism
![]() $Z_{\mathfrak B}'\rightarrow Z (\operatorname {\mathrm {End}}_{\mathfrak Q(\mathscr O)}(\mathscr T M_{\mathfrak B}) )$
, which we may compose with the previous isomorphism to obtain a homomorphism
$Z_{\mathfrak B}'\rightarrow Z (\operatorname {\mathrm {End}}_{\mathfrak Q(\mathscr O)}(\mathscr T M_{\mathfrak B}) )$
, which we may compose with the previous isomorphism to obtain a homomorphism
![]() $Z_{\mathfrak B}'\rightarrow Z (\operatorname {\mathrm {End}}_{\mathfrak C(\mathscr O)}(M_{\mathfrak B}) )$
. Since
$Z_{\mathfrak B}'\rightarrow Z (\operatorname {\mathrm {End}}_{\mathfrak C(\mathscr O)}(M_{\mathfrak B}) )$
. Since
![]() $Z_{\mathfrak B}$
is the centre of
$Z_{\mathfrak B}$
is the centre of
![]() ${\mathfrak C}(\mathscr O)_{\mathfrak B}$
, a similar argument shows that
${\mathfrak C}(\mathscr O)_{\mathfrak B}$
, a similar argument shows that
![]() $Z_{\mathfrak B}'$
is a
$Z_{\mathfrak B}'$
is a
![]() $Z_{\mathfrak B}$
-algebra and the surjection
$Z_{\mathfrak B}$
-algebra and the surjection
![]() $ (P_{\mathfrak B}' )^{\oplus n} \twoheadrightarrow M_{\mathfrak B}$
in Corollary 4.13 is
$ (P_{\mathfrak B}' )^{\oplus n} \twoheadrightarrow M_{\mathfrak B}$
in Corollary 4.13 is
![]() $Z_{\mathfrak B}$
-equivariant. It induces a
$Z_{\mathfrak B}$
-equivariant. It induces a
![]() $Z_{\mathfrak B}$
-equivariant surjection
$Z_{\mathfrak B}$
-equivariant surjection
![]() $ (\mathscr T P_{\mathfrak B}' )^{\oplus n} \twoheadrightarrow \mathscr T M_{\mathfrak B}$
. We deduce that the map
$ (\mathscr T P_{\mathfrak B}' )^{\oplus n} \twoheadrightarrow \mathscr T M_{\mathfrak B}$
. We deduce that the map
is a homomorphism of
![]() $Z_{\mathfrak B}$
-algebras. Proposition 4.15 implies that the composition
$Z_{\mathfrak B}$
-algebras. Proposition 4.15 implies that the composition
is the identity map, which implies that the homomorphism is surjective.
4.4 Colmez’s Montreal functor
Let
![]() $\mathscr G_{\mathbb {Q}_p}$
be the absolute Galois group of
$\mathscr G_{\mathbb {Q}_p}$
be the absolute Galois group of
![]() $\mathbb {Q}_p$
. We will consider
$\mathbb {Q}_p$
. We will consider
![]() $\zeta $
as a character of
$\zeta $
as a character of
![]() $\mathscr G_{\mathbb {Q}_p}$
via local class field theory, normalised so that the uniformisers correspond to geometric Frobenius. Let
$\mathscr G_{\mathbb {Q}_p}$
via local class field theory, normalised so that the uniformisers correspond to geometric Frobenius. Let
![]() $\varepsilon : \mathscr G_{\mathbb {Q}_p} \rightarrow \mathbb {Z}_p^{\times }$
be the p-adic cyclotomic character.
$\varepsilon : \mathscr G_{\mathbb {Q}_p} \rightarrow \mathbb {Z}_p^{\times }$
be the p-adic cyclotomic character.
Colmez [Reference Colmez19] has defined an exact and covariant functor
![]() $\mathbf V$
from the category of smooth, finite-length representations of G on
$\mathbf V$
from the category of smooth, finite-length representations of G on
![]() $\mathscr O$
-torsion modules with a central character to the category of continuous finite-length representations of
$\mathscr O$
-torsion modules with a central character to the category of continuous finite-length representations of
![]() $\mathscr G_{\mathbb {Q}_p}$
on
$\mathscr G_{\mathbb {Q}_p}$
on
![]() $\mathscr O$
-torsion modules. This functor is modified in [Reference Paškūnas39, Section 5.7] to an exact covariant functor
$\mathscr O$
-torsion modules. This functor is modified in [Reference Paškūnas39, Section 5.7] to an exact covariant functor
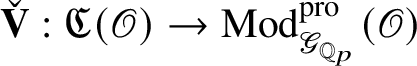 $$ \begin{align*} \check{\mathbf{V}}: \mathfrak C(\mathscr O) \rightarrow \operatorname{\mathrm{Mod}}^{\mathrm{pro}}_{\mathscr G_{\mathbb{Q}_p}}(\mathscr O) \end{align*} $$
$$ \begin{align*} \check{\mathbf{V}}: \mathfrak C(\mathscr O) \rightarrow \operatorname{\mathrm{Mod}}^{\mathrm{pro}}_{\mathscr G_{\mathbb{Q}_p}}(\mathscr O) \end{align*} $$
as follows. Let M be in
![]() $\mathfrak C(\mathscr O)$
; if it is of finite length, we define
$\mathfrak C(\mathscr O)$
; if it is of finite length, we define
![]() $\check {\mathbf {V}}(M) := \mathbf V (M^\vee )^\vee (\zeta \varepsilon )$
, where
$\check {\mathbf {V}}(M) := \mathbf V (M^\vee )^\vee (\zeta \varepsilon )$
, where
![]() $\vee $
denotes the Pontryagin dual. For general
$\vee $
denotes the Pontryagin dual. For general
![]() $M \in \mathfrak C(\mathscr O)$
, we may write
$M \in \mathfrak C(\mathscr O)$
, we may write
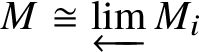 $M \cong \varprojlim M_i$
, with
$M \cong \varprojlim M_i$
, with
![]() $M_i$
of finite length in
$M_i$
of finite length in
![]() $\mathfrak C(\mathscr O)$
, and define
$\mathfrak C(\mathscr O)$
, and define
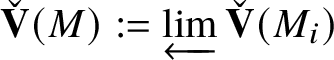 $\check {\mathbf {V}}(M) := \varprojlim \check {\mathbf {V}}(M_i)$
. With this normalisation, we have the following:
$\check {\mathbf {V}}(M) := \varprojlim \check {\mathbf {V}}(M_i)$
. With this normalisation, we have the following:
-
•
 $\check {\mathbf {V}} (\pi ^{\vee } ) = 0$
if
$\check {\mathbf {V}} (\pi ^{\vee } ) = 0$
if
 $\pi \cong \chi \circ \det $
.
$\pi \cong \chi \circ \det $
. -
•
 $\check {\mathbf {V}} (\pi ^{\vee } )= \chi _1$
if
$\check {\mathbf {V}} (\pi ^{\vee } )= \chi _1$
if
 $\pi \cong (\operatorname {\mathrm {Ind}}^G_B \chi _1 \otimes \chi _2 )_{\mathrm {sm}}$
.
$\pi \cong (\operatorname {\mathrm {Ind}}^G_B \chi _1 \otimes \chi _2 )_{\mathrm {sm}}$
. -
•
 $\check {\mathbf {V}} (\pi ^{\vee } ) = \chi $
if
$\check {\mathbf {V}} (\pi ^{\vee } ) = \chi $
if
 $\pi \cong \operatorname {\mathrm {Sp}} \otimes \chi \circ \det $
.
$\pi \cong \operatorname {\mathrm {Sp}} \otimes \chi \circ \det $
. -
•
 $\check {\mathbf {V}} (\pi ^{\vee } ) = \mathbf V(\pi )$
is a
$\check {\mathbf {V}} (\pi ^{\vee } ) = \mathbf V(\pi )$
is a
 $2$
-dimensional absolutely irreducible Galois representation if
$2$
-dimensional absolutely irreducible Galois representation if
 $\pi $
is supersingular.
$\pi $
is supersingular.
The functor
![]() $\check {\mathbf {V}}$
induces a bijection
$\check {\mathbf {V}}$
induces a bijection
![]() $\mathfrak B\mapsto \bar {\rho }_{\mathfrak B}$
between blocks containing an absolutely irreducible representation and equivalence classes of semisimple representations
$\mathfrak B\mapsto \bar {\rho }_{\mathfrak B}$
between blocks containing an absolutely irreducible representation and equivalence classes of semisimple representations
![]() $\bar {\rho }: \mathscr G_{\mathbb {Q}_p}\rightarrow \operatorname {\mathrm {GL}}_2(k)$
such that all irreducible summands of
$\bar {\rho }: \mathscr G_{\mathbb {Q}_p}\rightarrow \operatorname {\mathrm {GL}}_2(k)$
such that all irreducible summands of
![]() $\bar {\rho }$
are absolutely irreducible. The representation
$\bar {\rho }$
are absolutely irreducible. The representation
![]() $\bar {\rho }_{\mathfrak B}$
can be described explicitly according to the classification of blocks given in Section 4.1: in case (i),
$\bar {\rho }_{\mathfrak B}$
can be described explicitly according to the classification of blocks given in Section 4.1: in case (i),
![]() $\bar {\rho }_{\mathfrak B}=\check {\mathbf {V}} (\pi ^{\vee } )$
is absolutely irreducible; in case (ii),
$\bar {\rho }_{\mathfrak B}=\check {\mathbf {V}} (\pi ^{\vee } )$
is absolutely irreducible; in case (ii),
![]() $\bar {\rho }_{\mathfrak B}=\chi _1\oplus \chi _2$
; in cases (iii) and (vi),
$\bar {\rho }_{\mathfrak B}=\chi _1\oplus \chi _2$
; in cases (iii) and (vi),
![]() $\bar {\rho }_{\mathfrak B}=\chi \oplus \chi $
; and in cases (iv) and (v),
$\bar {\rho }_{\mathfrak B}=\chi \oplus \chi $
; and in cases (iv) and (v),
![]() $\bar {\rho }_{\mathfrak B}= \chi \oplus \chi \omega $
.
$\bar {\rho }_{\mathfrak B}= \chi \oplus \chi \omega $
.
Since the functor
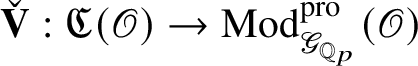 $\check {\mathbf {V}}: \mathfrak C(\mathscr O) \rightarrow \operatorname {\mathrm {Mod}}^{\mathrm {pro}}_{\mathscr G_{\mathbb {Q}_p}}(\mathscr O)$
kills characters and hence every object in
$\check {\mathbf {V}}: \mathfrak C(\mathscr O) \rightarrow \operatorname {\mathrm {Mod}}^{\mathrm {pro}}_{\mathscr G_{\mathbb {Q}_p}}(\mathscr O)$
kills characters and hence every object in
![]() $\mathfrak T(\mathscr O)$
, it factors through
$\mathfrak T(\mathscr O)$
, it factors through
![]() $\mathscr T: \mathfrak C(\mathscr O) \rightarrow \mathfrak Q(\mathscr O)$
. We denote
$\mathscr T: \mathfrak C(\mathscr O) \rightarrow \mathfrak Q(\mathscr O)$
. We denote
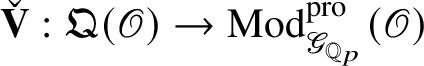 $\check {\mathbf {V}}: \mathfrak Q(\mathscr O) \rightarrow \operatorname {\mathrm {Mod}}^{\mathrm {pro}}_{\mathscr G_{\mathbb {Q}_p}}(\mathscr O)$
by the same letter.
$\check {\mathbf {V}}: \mathfrak Q(\mathscr O) \rightarrow \operatorname {\mathrm {Mod}}^{\mathrm {pro}}_{\mathscr G_{\mathbb {Q}_p}}(\mathscr O)$
by the same letter.
Proposition 4.17. For each block
![]() $\mathfrak B$
, the functor
$\mathfrak B$
, the functor
![]() $\check {\mathbf {V}}$
induces an equivalence of categories between
$\check {\mathbf {V}}$
induces an equivalence of categories between
![]() $\mathfrak Q(\mathscr O)_{\mathfrak B}$
and its essential image in
$\mathfrak Q(\mathscr O)_{\mathfrak B}$
and its essential image in
 $\operatorname {\mathrm {Mod}}^{\mathrm {pro}}_{\mathscr G_{\mathbb {Q}_p}}(\mathscr O)$
.
$\operatorname {\mathrm {Mod}}^{\mathrm {pro}}_{\mathscr G_{\mathbb {Q}_p}}(\mathscr O)$
.
Proof. This is due to [Reference Paškūnas39] for cases (i)–(iv), [Reference Tung46, Proposition 2.8] for case (v) and [Reference Tung47, Proposition 1.3.2] for case (iv).
Proposition 4.18. The map
 is surjective. Moreover, if
is surjective. Moreover, if
![]() $\mathfrak B$
is supersingular, then
$\mathfrak B$
is supersingular, then
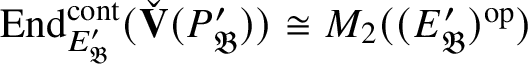 $\operatorname {\mathrm {End}}_{E_{\mathfrak B}'}^{\mathrm {cont}} (\check {\mathbf {V}} (P_{\mathfrak B}' ) )\cong M_2 ( (E_{\mathfrak B}' )^{\mathrm {op}} )$
; otherwise,
$\operatorname {\mathrm {End}}_{E_{\mathfrak B}'}^{\mathrm {cont}} (\check {\mathbf {V}} (P_{\mathfrak B}' ) )\cong M_2 ( (E_{\mathfrak B}' )^{\mathrm {op}} )$
; otherwise,
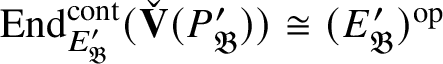 $\operatorname {\mathrm {End}}_{E_{\mathfrak B}'}^{\mathrm {cont}} (\check {\mathbf {V}} (P_{\mathfrak B}' ) )\cong (E_{\mathfrak B}' )^{\mathrm {op}}$
.
$\operatorname {\mathrm {End}}_{E_{\mathfrak B}'}^{\mathrm {cont}} (\check {\mathbf {V}} (P_{\mathfrak B}' ) )\cong (E_{\mathfrak B}' )^{\mathrm {op}}$
.
Proof. It suffices to show that
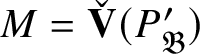 $M=\check {\mathbf {V}} (P_{\mathfrak B}' )$
satisfies all four conditions in Proposition 2.3. We note that the functor
$M=\check {\mathbf {V}} (P_{\mathfrak B}' )$
satisfies all four conditions in Proposition 2.3. We note that the functor
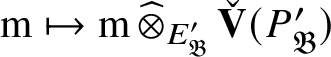 $\mathrm m \mapsto \mathrm m \operatorname {\mathrm {\mathbin {\widehat {\otimes }}}}_{E_{\mathfrak B}'} \check {\mathbf {V}} (P_{\mathfrak B}' )$
is exact by the equivalence of categories in Proposition 4.10(2), the exactness of
$\mathrm m \mapsto \mathrm m \operatorname {\mathrm {\mathbin {\widehat {\otimes }}}}_{E_{\mathfrak B}'} \check {\mathbf {V}} (P_{\mathfrak B}' )$
is exact by the equivalence of categories in Proposition 4.10(2), the exactness of
![]() $\check {\mathbf {V}}$
and the isomorphism
$\check {\mathbf {V}}$
and the isomorphism
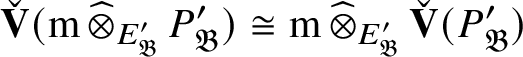 $$ \begin{align*} \check{\mathbf{V}}(\mathrm m \operatorname{\mathrm{\mathbin{\widehat{\otimes}}}}_{E_{\mathfrak B}'} P_{\mathfrak B}') \cong \mathrm m \operatorname{\mathrm{\mathbin{\widehat{\otimes}}}}_{E_{\mathfrak B}'} \check{\mathbf{V}}(P_{\mathfrak B}') \end{align*} $$
$$ \begin{align*} \check{\mathbf{V}}(\mathrm m \operatorname{\mathrm{\mathbin{\widehat{\otimes}}}}_{E_{\mathfrak B}'} P_{\mathfrak B}') \cong \mathrm m \operatorname{\mathrm{\mathbin{\widehat{\otimes}}}}_{E_{\mathfrak B}'} \check{\mathbf{V}}(P_{\mathfrak B}') \end{align*} $$
(see the proof of [Reference Paškūnas39, Lemma 5.53]). Thus by Lemma 2.4,
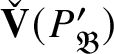 $\check {\mathbf {V}} (P_{\mathfrak B}' )$
is a projective
$\check {\mathbf {V}} (P_{\mathfrak B}' )$
is a projective
![]() $E_{\mathfrak B}'$
-module. Let
$E_{\mathfrak B}'$
-module. Let
![]() $\mathfrak r$
be the Jacobson radical of
$\mathfrak r$
be the Jacobson radical of
![]() $E_{\mathfrak B}'$
. Since
$E_{\mathfrak B}'$
. Since
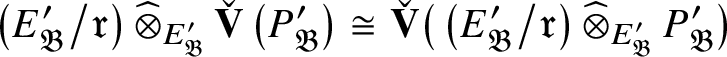 $$ \begin{align*} \left(E_{\mathfrak B}'\middle/{\mathfrak r}\right)\operatorname{\mathrm{\mathbin{\widehat{\otimes}}}}_{E_{\mathfrak B}'}\check{\mathbf{V}}\left(P_{\mathfrak B}'\right)\cong \check{\mathbf{V}}\big(\left(E_{\mathfrak B}'\middle/\mathfrak r\right) \operatorname{\mathrm{\mathbin{\widehat{\otimes}}}}_{E_{\mathfrak B}'} P_{\mathfrak B}'\big) \end{align*} $$
$$ \begin{align*} \left(E_{\mathfrak B}'\middle/{\mathfrak r}\right)\operatorname{\mathrm{\mathbin{\widehat{\otimes}}}}_{E_{\mathfrak B}'}\check{\mathbf{V}}\left(P_{\mathfrak B}'\right)\cong \check{\mathbf{V}}\big(\left(E_{\mathfrak B}'\middle/\mathfrak r\right) \operatorname{\mathrm{\mathbin{\widehat{\otimes}}}}_{E_{\mathfrak B}'} P_{\mathfrak B}'\big) \end{align*} $$
is either a
![]() $1$
- or a
$1$
- or a
![]() $2$
-dimensional k-vector space, the topological Nakayama’s lemma implies that
$2$
-dimensional k-vector space, the topological Nakayama’s lemma implies that
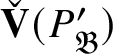 $\check {\mathbf {V}} (P_{\mathfrak B}' )$
is a finitely generated
$\check {\mathbf {V}} (P_{\mathfrak B}' )$
is a finitely generated
![]() $E_{\mathfrak B}'$
-module, and thus Proposition 2.3(1) holds. Proposition 4.17 implies that Proposition 2.3(2) holds.
$E_{\mathfrak B}'$
-module, and thus Proposition 2.3(1) holds. Proposition 4.17 implies that Proposition 2.3(2) holds.
If
![]() $\mathrm m$
is a right pseudocompact
$\mathrm m$
is a right pseudocompact
![]() $E_{\mathfrak B}'$
-module then [Reference Brumer12, Lemma 2.4] implies that
$E_{\mathfrak B}'$
-module then [Reference Brumer12, Lemma 2.4] implies that
 $$ \begin{align} \operatorname{\mathrm{Hom}}_{\mathscr O}^{\mathrm{cont}}( \mathrm m \operatorname{\mathrm{\mathbin{\widehat{\otimes}}}}_{E_{\mathfrak B}'} \check{\mathbf{V}}(P_{\mathfrak B}') , k) \cong \operatorname{\mathrm{Hom}}_{E_{\mathfrak B}'}^{\mathrm{cont}}( \check{\mathbf{V}}(P_{\mathfrak B}'), \operatorname{\mathrm{Hom}}_{\mathscr O}^{\mathrm{cont}}(\mathrm m, k)). \end{align} $$
$$ \begin{align} \operatorname{\mathrm{Hom}}_{\mathscr O}^{\mathrm{cont}}( \mathrm m \operatorname{\mathrm{\mathbin{\widehat{\otimes}}}}_{E_{\mathfrak B}'} \check{\mathbf{V}}(P_{\mathfrak B}') , k) \cong \operatorname{\mathrm{Hom}}_{E_{\mathfrak B}'}^{\mathrm{cont}}( \check{\mathbf{V}}(P_{\mathfrak B}'), \operatorname{\mathrm{Hom}}_{\mathscr O}^{\mathrm{cont}}(\mathrm m, k)). \end{align} $$
Since in our situation
![]() $E_{\mathfrak B}'$
is a compact
$E_{\mathfrak B}'$
is a compact
![]() $\mathscr O$
-algebra, the irreducible (left or right)
$\mathscr O$
-algebra, the irreducible (left or right)
![]() $E_{\mathfrak B}'$
-modules are finite-dimensional vector spaces with discrete topology, and thus the map
$E_{\mathfrak B}'$
-modules are finite-dimensional vector spaces with discrete topology, and thus the map
![]() $\mathrm m\mapsto \mathrm m^*:=\operatorname {\mathrm {Hom}}_k(\mathrm m, k)$
induces a bijection between irreducible left and irreducible right
$\mathrm m\mapsto \mathrm m^*:=\operatorname {\mathrm {Hom}}_k(\mathrm m, k)$
induces a bijection between irreducible left and irreducible right
![]() $E_{\mathfrak B}'$
-modules. Moreover, if
$E_{\mathfrak B}'$
-modules. Moreover, if
![]() $\mathrm m$
is an irreducible right
$\mathrm m$
is an irreducible right
![]() $E_{\mathfrak B}'$
-module, then it follows from formula (16) that
$E_{\mathfrak B}'$
-module, then it follows from formula (16) that
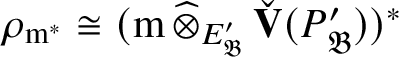 $\rho _{\mathrm m^*}\cong (\mathrm m \operatorname {\mathrm {\mathbin {\widehat {\otimes }}}}_{E_{\mathfrak B}'} \check {\mathbf {V}} (P_{\mathfrak B}' ) )^*$
; thus Proposition 2.3(3) and (4) follow from Proposition 4.17.
$\rho _{\mathrm m^*}\cong (\mathrm m \operatorname {\mathrm {\mathbin {\widehat {\otimes }}}}_{E_{\mathfrak B}'} \check {\mathbf {V}} (P_{\mathfrak B}' ) )^*$
; thus Proposition 2.3(3) and (4) follow from Proposition 4.17.
If
![]() $\mathfrak B$
is supersingular, then it contains only one irreducible
$\mathfrak B$
is supersingular, then it contains only one irreducible
![]() $\pi $
, which is not a character. Thus
$\pi $
, which is not a character. Thus
![]() $P_{\mathfrak B}=P_{\mathfrak B}'$
,
$P_{\mathfrak B}=P_{\mathfrak B}'$
,
![]() $E_{\mathfrak B}=E_{\mathfrak B}'$
is a local ring and
$E_{\mathfrak B}=E_{\mathfrak B}'$
is a local ring and
![]() $k\operatorname {\mathrm {\mathbin {\widehat {\otimes }}}}_{E_{\mathfrak B}} P_{\mathfrak B}= \pi ^{\vee }$
. Thus
$k\operatorname {\mathrm {\mathbin {\widehat {\otimes }}}}_{E_{\mathfrak B}} P_{\mathfrak B}= \pi ^{\vee }$
. Thus
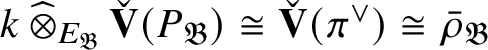 $ k\operatorname {\mathrm {\mathbin {\widehat {\otimes }}}}_{E_{\mathfrak B}} \check {\mathbf {V}}(P_{\mathfrak B})\cong \check {\mathbf {V}} (\pi ^{\vee } )\cong \bar {\rho }_{\mathfrak B}$
is an absolutely irreducible
$ k\operatorname {\mathrm {\mathbin {\widehat {\otimes }}}}_{E_{\mathfrak B}} \check {\mathbf {V}}(P_{\mathfrak B})\cong \check {\mathbf {V}} (\pi ^{\vee } )\cong \bar {\rho }_{\mathfrak B}$
is an absolutely irreducible
![]() $2$
-dimensional representation. Since
$2$
-dimensional representation. Since
![]() $E_{\mathfrak B}$
is a local ring, we deduce that
$E_{\mathfrak B}$
is a local ring, we deduce that
![]() $\check {\mathbf {V}}(P_{\mathfrak B})$
is a free
$\check {\mathbf {V}}(P_{\mathfrak B})$
is a free
![]() $E_{\mathfrak B}$
-module of rank
$E_{\mathfrak B}$
-module of rank
![]() $2$
. Thus
$2$
. Thus
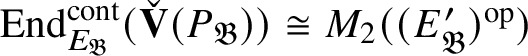 $\operatorname {\mathrm {End}}^{\mathrm {cont}}_{E_{\mathfrak B}} (\check {\mathbf {V}}(P_{\mathfrak B}) )\cong M_2 ( (E_{\mathfrak B}' )^{\mathrm {op}} )$
.
$\operatorname {\mathrm {End}}^{\mathrm {cont}}_{E_{\mathfrak B}} (\check {\mathbf {V}}(P_{\mathfrak B}) )\cong M_2 ( (E_{\mathfrak B}' )^{\mathrm {op}} )$
.
If
![]() $\mathfrak B$
is of type (iii) or (vi), then the block in the quotient category contains only one irreducible object, and Colmez’s functor maps it to a
$\mathfrak B$
is of type (iii) or (vi), then the block in the quotient category contains only one irreducible object, and Colmez’s functor maps it to a
![]() $1$
-dimensional
$1$
-dimensional
![]() $\mathscr G_{\mathbb {Q}_p}$
-representation. The same argument as in the supersingular case shows that
$\mathscr G_{\mathbb {Q}_p}$
-representation. The same argument as in the supersingular case shows that
![]() $E_{\mathfrak B}'$
is a local ring and
$E_{\mathfrak B}'$
is a local ring and
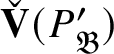 $\check {\mathbf {V}} (P_{\mathfrak B}' )$
is a free
$\check {\mathbf {V}} (P_{\mathfrak B}' )$
is a free
![]() $E_{\mathfrak B}'$
-module of rank
$E_{\mathfrak B}'$
-module of rank
![]() $1$
, and thus
$1$
, and thus
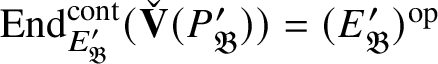 $\operatorname {\mathrm {End}}_{E_{\mathfrak B}'}^{\mathrm {cont}} (\check {\mathbf {V}} (P_{\mathfrak B}' ) )= (E_{\mathfrak B}' )^{\mathrm {op}}$
.
$\operatorname {\mathrm {End}}_{E_{\mathfrak B}'}^{\mathrm {cont}} (\check {\mathbf {V}} (P_{\mathfrak B}' ) )= (E_{\mathfrak B}' )^{\mathrm {op}}$
.
If
![]() $\mathfrak B$
is of type (ii), (iv) or (v), then
$\mathfrak B$
is of type (ii), (iv) or (v), then
![]() $\mathfrak Q(\mathscr O)_{\mathfrak B}$
contains exactly two irreducible objects, and Colmez’s functor sends them to distinct
$\mathfrak Q(\mathscr O)_{\mathfrak B}$
contains exactly two irreducible objects, and Colmez’s functor sends them to distinct
![]() $1$
-dimensional
$1$
-dimensional
![]() $\mathscr G_{\mathbb {Q}_p}$
-representations
$\mathscr G_{\mathbb {Q}_p}$
-representations
![]() $\chi _1, \chi _2$
. It follows from Corollary 2.5 that
$\chi _1, \chi _2$
. It follows from Corollary 2.5 that
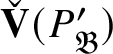 $\check {\mathbf {V}}(P_{\mathfrak B}')$
is a free
$\check {\mathbf {V}}(P_{\mathfrak B}')$
is a free
![]() $E_{\mathfrak B}'$
-module of rank
$E_{\mathfrak B}'$
-module of rank
![]() $1$
, and thus
$1$
, and thus
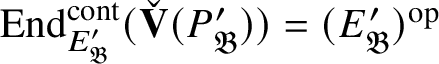 $\operatorname {\mathrm {End}}_{E_{\mathfrak B}'}^{\mathrm {cont}} (\check {\mathbf {V}} (P_{\mathfrak B}' ) )= (E_{\mathfrak B}' )^{\mathrm {op}}$
.
$\operatorname {\mathrm {End}}_{E_{\mathfrak B}'}^{\mathrm {cont}} (\check {\mathbf {V}} (P_{\mathfrak B}' ) )= (E_{\mathfrak B}' )^{\mathrm {op}}$
.
4.5 Banach-space representations
Let
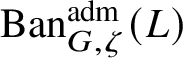 $\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)$
be the category of admissible unitary L-Banach-space representations [Reference Schneider and Teitelbaum44, Section 3] on which Z acts by the character
$\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)$
be the category of admissible unitary L-Banach-space representations [Reference Schneider and Teitelbaum44, Section 3] on which Z acts by the character
![]() $\zeta $
. We note that
$\zeta $
. We note that
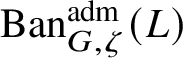 $\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)$
is an abelian category [Reference Schneider and Teitelbaum44, Theorem 3.5]. Any
$\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)$
is an abelian category [Reference Schneider and Teitelbaum44, Theorem 3.5]. Any
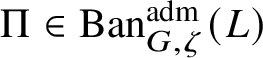 $\Pi \in \operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)$
has an open, bounded and G-invariant lattice
$\Pi \in \operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)$
has an open, bounded and G-invariant lattice
![]() $\Theta $
, and
$\Theta $
, and
![]() $\Theta \otimes _{\mathscr O} k$
is an admissible smooth k-representation of G. Let
$\Theta \otimes _{\mathscr O} k$
is an admissible smooth k-representation of G. Let
![]() $\Theta ^d = \operatorname {\mathrm {Hom}}_{\mathscr O}(\Theta , {\mathscr O})$
be the Schikhof dual of
$\Theta ^d = \operatorname {\mathrm {Hom}}_{\mathscr O}(\Theta , {\mathscr O})$
be the Schikhof dual of
![]() $\Theta $
endowed with the topology of pointwise convergence. Then
$\Theta $
endowed with the topology of pointwise convergence. Then
![]() $\Theta ^d$
is an object of
$\Theta ^d$
is an object of
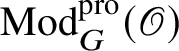 $\operatorname {\mathrm {Mod}}^{\mathrm {pro}}_G(\mathscr O)$
[Reference Paškūnas39, Lemma 4.4]. If
$\operatorname {\mathrm {Mod}}^{\mathrm {pro}}_G(\mathscr O)$
[Reference Paškūnas39, Lemma 4.4]. If
![]() $\Theta ^d$
is in
$\Theta ^d$
is in
![]() $\mathfrak C(\mathscr O)$
, then
$\mathfrak C(\mathscr O)$
, then
![]() $\Xi ^d$
is in
$\Xi ^d$
is in
![]() $\mathfrak C(\mathscr O)$
for every open bounded G-invariant lattice
$\mathfrak C(\mathscr O)$
for every open bounded G-invariant lattice
![]() $\Xi $
in
$\Xi $
in
![]() $\Pi $
, since
$\Pi $
, since
![]() $\Theta $
and
$\Theta $
and
![]() $\Xi $
are commensurable and
$\Xi $
are commensurable and
![]() $\mathfrak C(\mathscr O)$
is closed under subquotients [Reference Paškūnas39, Lemma 4.6].
$\mathfrak C(\mathscr O)$
is closed under subquotients [Reference Paškūnas39, Lemma 4.6].
If
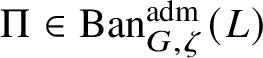 $\Pi \in \operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)$
, then we let
$\Pi \in \operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)$
, then we let
where
![]() $\Theta $
is any open bounded G-invariant lattice in
$\Theta $
is any open bounded G-invariant lattice in
![]() $\Pi $
. Then
$\Pi $
. Then
![]() $\check {\mathbf {V}}$
is exact and contravariant on
$\check {\mathbf {V}}$
is exact and contravariant on
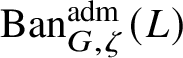 $\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)$
.
$\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)$
.
5 Density
5.1 Capture
Let
![]() $G = \operatorname {\mathrm {GL}}_2 (\mathbb {Q}_p )$
and
$G = \operatorname {\mathrm {GL}}_2 (\mathbb {Q}_p )$
and
![]() $K = \operatorname {\mathrm {GL}}_2 (\mathbb {Z}_p )$
. Write Z for the centre of G and
$K = \operatorname {\mathrm {GL}}_2 (\mathbb {Z}_p )$
. Write Z for the centre of G and
![]() $Z(K)$
for the centre of K. Let
$Z(K)$
for the centre of K. Let
![]() $\psi : Z(K) \rightarrow \mathscr O^{\times }$
be a continuous character. We identify Z with
$\psi : Z(K) \rightarrow \mathscr O^{\times }$
be a continuous character. We identify Z with
![]() $\mathbb {Q}_p^{\times }$
and
$\mathbb {Q}_p^{\times }$
and
![]() $Z(K)$
with
$Z(K)$
with
![]() $\mathbb {Z}_p^{\times }$
via the map
$\mathbb {Z}_p^{\times }$
via the map
![]() $ \left(\begin{smallmatrix} x & 0 \\ 0 & x \end{smallmatrix} \right) \mapsto x$
.
$ \left(\begin{smallmatrix} x & 0 \\ 0 & x \end{smallmatrix} \right) \mapsto x$
.
Lemma 5.1. Let
![]() $\{V_i\}_{i \in I}$
be a family of continuous representations of K on finite-dimensional L-vector spaces with central character
$\{V_i\}_{i \in I}$
be a family of continuous representations of K on finite-dimensional L-vector spaces with central character
![]() $\psi $
, and let
$\psi $
, and let
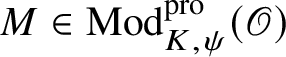 $M \in \operatorname {\mathrm {Mod}}^{\mathrm {pro}}_{K, \psi }(\mathscr O)$
be
$M \in \operatorname {\mathrm {Mod}}^{\mathrm {pro}}_{K, \psi }(\mathscr O)$
be
![]() $\mathscr O$
-torsion-free. The following conditions are equivalent:
$\mathscr O$
-torsion-free. The following conditions are equivalent:
-
1. For all
 $i \in I$
, the smallest quotient
$i \in I$
, the smallest quotient
 $M \twoheadrightarrow Q$
such that
$M \twoheadrightarrow Q$
such that
 is equal to M.
is equal to M. -
2. The intersection of the kernels of all
 for each
for each
 $i \in I$
is equal to zero.
$i \in I$
is equal to zero. -
3. The image of the evaluation map
is a dense subspace, where $$ \begin{align*} \bigoplus_{i \in I} \operatorname{\mathrm{Hom}}_K(V_i, \Pi(M)) \otimes_L V_i \rightarrow \Pi(M) \end{align*} $$
$$ \begin{align*} \bigoplus_{i \in I} \operatorname{\mathrm{Hom}}_K(V_i, \Pi(M)) \otimes_L V_i \rightarrow \Pi(M) \end{align*} $$
 $\Pi (M) := \operatorname {\mathrm {Hom}}^{\mathrm {cont}}_{\mathscr O}(M, L)$
is an L-Banach space equipped with the supremum norm.
$\Pi (M) := \operatorname {\mathrm {Hom}}^{\mathrm {cont}}_{\mathscr O}(M, L)$
is an L-Banach space equipped with the supremum norm.
Proof. See [Reference Colmez, Dospinescu and Paškūnas21, Lemmas 2.7 and 2.10].
Definition 5.2. We say that
![]() $\{V_i\}_{i \in I}$
captures M if it satisfies one of the equivalent conditions in Lemma 5.1.
$\{V_i\}_{i \in I}$
captures M if it satisfies one of the equivalent conditions in Lemma 5.1.
Since
![]() $1+p\mathbb {Z}_p$
(resp.,
$1+p\mathbb {Z}_p$
(resp.,
![]() $1+4\mathbb Z_2$
) is a free pro-p group of rank 1 if
$1+4\mathbb Z_2$
) is a free pro-p group of rank 1 if
![]() $p>2$
(resp.,
$p>2$
(resp.,
![]() $p=2$
), there are a smooth nontrivial character
$p=2$
), there are a smooth nontrivial character
![]() $\chi : \mathbb {Z}_p^\times \rightarrow L^\times $
and a continuous character
$\chi : \mathbb {Z}_p^\times \rightarrow L^\times $
and a continuous character
![]() $\eta _0 : \mathbb {Z}_p^{\times } \rightarrow L^\times $
such that
$\eta _0 : \mathbb {Z}_p^{\times } \rightarrow L^\times $
such that
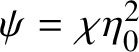 $\psi = \chi \eta _0^2$
. Let e be the smallest integer such that
$\psi = \chi \eta _0^2$
. Let e be the smallest integer such that
![]() $\chi $
is trivial on
$\chi $
is trivial on
![]() $1+p^e\mathbb {Z}_p$
. Let
$1+p^e\mathbb {Z}_p$
. Let
 $$ \begin{align*} J = \left(\begin{smallmatrix} \mathbb{Z}_p^\times & \mathbb{Z}_p \\ p^e \mathbb{Z}_p & \mathbb{Z}_p^\times \end{smallmatrix}\right) \end{align*} $$
$$ \begin{align*} J = \left(\begin{smallmatrix} \mathbb{Z}_p^\times & \mathbb{Z}_p \\ p^e \mathbb{Z}_p & \mathbb{Z}_p^\times \end{smallmatrix}\right) \end{align*} $$
and let
![]() $\chi \otimes \mathbf 1: J \rightarrow L^\times $
be the character which sends
$\chi \otimes \mathbf 1: J \rightarrow L^\times $
be the character which sends
![]() $ \left(\begin{smallmatrix} a & b \\ c & d \end{smallmatrix} \right)$
to
$ \left(\begin{smallmatrix} a & b \\ c & d \end{smallmatrix} \right)$
to
![]() $\chi (a)$
. Then the representation
$\chi (a)$
. Then the representation
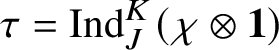 $\tau =\operatorname {\mathrm {Ind}}^{K}_{J} (\chi \otimes \mathbf 1)$
is a principal series type. That is, for an irreducible smooth
$\tau =\operatorname {\mathrm {Ind}}^{K}_{J} (\chi \otimes \mathbf 1)$
is a principal series type. That is, for an irreducible smooth
![]() $\overline {L}$
-representation
$\overline {L}$
-representation
![]() $\pi $
of G, we have
$\pi $
of G, we have
![]() $\operatorname {\mathrm {Hom}}_{L[K]}(\tau , \pi ) \neq 0$
if and only if
$\operatorname {\mathrm {Hom}}_{L[K]}(\tau , \pi ) \neq 0$
if and only if
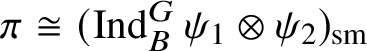 $\pi \cong (\operatorname {\mathrm {Ind}}^G_B \psi _1 \otimes \psi _2 )_{\mathrm {sm}}$
, where B is a Borel subgroup and
$\pi \cong (\operatorname {\mathrm {Ind}}^G_B \psi _1 \otimes \psi _2 )_{\mathrm {sm}}$
, where B is a Borel subgroup and
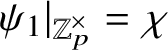 $\psi _1\rvert _{\mathbb {Z}_p^\times } = \chi $
and
$\psi _1\rvert _{\mathbb {Z}_p^\times } = \chi $
and
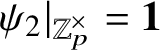 $\psi _2\rvert _{\mathbb {Z}_p^\times } = \mathbf 1$
[Reference Breuil and Mézard11, Section A2.2].
$\psi _2\rvert _{\mathbb {Z}_p^\times } = \mathbf 1$
[Reference Breuil and Mézard11, Section A2.2].
Proposition 5.3. The family
 $$ \begin{align*} \{\operatorname{\mathrm{Ind}}^{K}_{J} (\chi \otimes \mathbf 1) \otimes \operatorname{\mathrm{Sym}}^{2a} L^2 \otimes (\det)^{-a} \otimes \eta \eta_0 \circ \det \}_{a \in \mathbb{N} , \eta}, \end{align*} $$
$$ \begin{align*} \{\operatorname{\mathrm{Ind}}^{K}_{J} (\chi \otimes \mathbf 1) \otimes \operatorname{\mathrm{Sym}}^{2a} L^2 \otimes (\det)^{-a} \otimes \eta \eta_0 \circ \det \}_{a \in \mathbb{N} , \eta}, \end{align*} $$
where
![]() $\eta $
runs over all the characters with
$\eta $
runs over all the characters with
![]() $\eta ^2 = \mathbf 1$
, captures every projective object in
$\eta ^2 = \mathbf 1$
, captures every projective object in
 $\operatorname {\mathrm {Mod}}^{\mathrm {pro}}_{K, \psi ^{-1}}(\mathscr O)$
.
$\operatorname {\mathrm {Mod}}^{\mathrm {pro}}_{K, \psi ^{-1}}(\mathscr O)$
.
Proof. See [Reference Paškūnas41, Proposition 2.7].
We will denote the family of representations in this proposition by
![]() $\{V_i\}_{i\in I}$
. We note that each
$\{V_i\}_{i\in I}$
. We note that each
![]() $V_i$
is a twist of a locally algebraic representation by a unitary character
$V_i$
is a twist of a locally algebraic representation by a unitary character
![]() $\eta _0$
, which might not be locally algebraic. However, twisting by its inverse will get us to a locally algebraic situation, which is sufficient for all arguments that follow.
$\eta _0$
, which might not be locally algebraic. However, twisting by its inverse will get us to a locally algebraic situation, which is sufficient for all arguments that follow.
5.2 Locally algebraic vectors in
 $\Pi (P)$
$\Pi (P)$
Let
![]() $\zeta : Z \rightarrow \mathscr O^{\times }$
be a continuous character and
$\zeta : Z \rightarrow \mathscr O^{\times }$
be a continuous character and
![]() $\psi = \zeta \rvert _{K}$
. Let P be a projective object in
$\psi = \zeta \rvert _{K}$
. Let P be a projective object in
![]() $\mathfrak C(\mathscr O)$
and
$\mathfrak C(\mathscr O)$
and
![]() $E = \operatorname {\mathrm {End}}_{\mathfrak C(\mathscr O)}(P)$
. In particular, P is a torsion-free compact linear-topological
$E = \operatorname {\mathrm {End}}_{\mathfrak C(\mathscr O)}(P)$
. In particular, P is a torsion-free compact linear-topological
![]() $\mathscr O$
-module. Define
$\mathscr O$
-module. Define
with the topology induced by the supremum norm. Then we have
![]() $E [1/p ] \cong \operatorname {\mathrm {End}}^{\mathrm {cont}}_{G}(\Pi (P))$
.
$E [1/p ] \cong \operatorname {\mathrm {End}}^{\mathrm {cont}}_{G}(\Pi (P))$
.
If V is a continuous representation of K on a finite-dimensional L-vector space, then
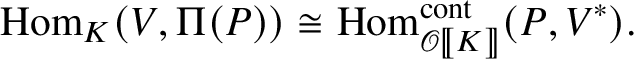
Since P is projective in
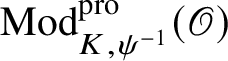 $\operatorname {\mathrm {Mod}}^{\mathrm {pro}}_{K, \psi ^{-1}}(\mathscr O)$
by [Reference Emerton and Paškūnas30, Corollary 3.10], the family of finite-dimensional K-representations associated to
$\operatorname {\mathrm {Mod}}^{\mathrm {pro}}_{K, \psi ^{-1}}(\mathscr O)$
by [Reference Emerton and Paškūnas30, Corollary 3.10], the family of finite-dimensional K-representations associated to
![]() $\psi $
in Proposition 5.3, which we denote by
$\psi $
in Proposition 5.3, which we denote by
![]() $\{V_i\}_{i \in I}$
, captures P. We view
$\{V_i\}_{i \in I}$
, captures P. We view
![]() $V_i$
as a representation of
$V_i$
as a representation of
![]() $KZ$
by letting
$KZ$
by letting
![]() $ \left(\begin{smallmatrix} \varpi & 0 \\ 0 & \varpi \end{smallmatrix} \right)$
act by
$ \left(\begin{smallmatrix} \varpi & 0 \\ 0 & \varpi \end{smallmatrix} \right)$
act by
![]() $\zeta (\varpi )$
.
$\zeta (\varpi )$
.
Proposition 5.4. For each
![]() $i \in I$
, we define
$i \in I$
, we define
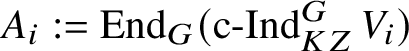 $A_i := \operatorname {\mathrm {End}}_G (\operatorname {\mathrm {c-Ind}}^G_{KZ} V_i )$
. Then
$A_i := \operatorname {\mathrm {End}}_G (\operatorname {\mathrm {c-Ind}}^G_{KZ} V_i )$
. Then
-
1.
 $A_i$
is isomorphic to
$A_i$
is isomorphic to
 $L[T]$
and
$L[T]$
and -
2.
 $\operatorname {\mathrm {c-Ind}}^G_{KZ} V_i$
is flat over
$\operatorname {\mathrm {c-Ind}}^G_{KZ} V_i$
is flat over
 $A_i$
.
$A_i$
.
Proof. We may write
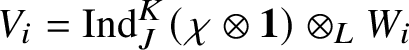 $V_i= \operatorname {\mathrm {Ind}}^{K}_{J} (\chi \otimes \mathbf 1)\otimes _L W_i$
, where the action of
$V_i= \operatorname {\mathrm {Ind}}^{K}_{J} (\chi \otimes \mathbf 1)\otimes _L W_i$
, where the action of
![]() $KZ$
on
$KZ$
on
![]() $W_i$
extends to an action of G (see Proposition 5.3). Then
$W_i$
extends to an action of G (see Proposition 5.3). Then
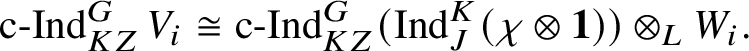 $$ \begin{align*} \operatorname{\mathrm{c-Ind}}^G_{KZ} V_i \cong \operatorname{\mathrm{c-Ind}}^G_{KZ}(\operatorname{\mathrm{Ind}}^{K}_{J} (\chi \otimes \mathbf 1))\otimes_L W_i. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{c-Ind}}^G_{KZ} V_i \cong \operatorname{\mathrm{c-Ind}}^G_{KZ}(\operatorname{\mathrm{Ind}}^{K}_{J} (\chi \otimes \mathbf 1))\otimes_L W_i. \end{align*} $$
Here we view
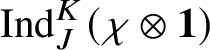 $\operatorname {\mathrm {Ind}}^{K}_{J} (\chi \otimes \mathbf 1)$
as a representation of
$\operatorname {\mathrm {Ind}}^{K}_{J} (\chi \otimes \mathbf 1)$
as a representation of
![]() $KZ$
by letting
$KZ$
by letting
![]() $ \left(\begin{smallmatrix} \varpi & 0 \\ 0 & \varpi \end{smallmatrix} \right)$
act on
$ \left(\begin{smallmatrix} \varpi & 0 \\ 0 & \varpi \end{smallmatrix} \right)$
act on
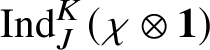 $\operatorname {\mathrm {Ind}}^{K}_{J} (\chi \otimes \mathbf 1)$
by
$\operatorname {\mathrm {Ind}}^{K}_{J} (\chi \otimes \mathbf 1)$
by
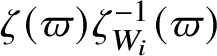 $\zeta (\varpi ) \zeta ^{-1}_{W_i}( \varpi )$
, where
$\zeta (\varpi ) \zeta ^{-1}_{W_i}( \varpi )$
, where
![]() $\zeta _{W_i}$
is the central character of
$\zeta _{W_i}$
is the central character of
![]() $W_i$
. Since the restriction of
$W_i$
. Since the restriction of
![]() $W_i$
to any compact open subgroup of G remains absolutely irreducible, the isomorphism induces an isomorphism of L-algebras
$W_i$
to any compact open subgroup of G remains absolutely irreducible, the isomorphism induces an isomorphism of L-algebras
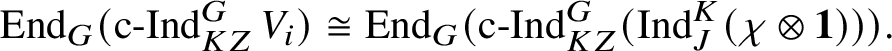 $$ \begin{align*} \operatorname{\mathrm{End}}_G(\operatorname{\mathrm{c-Ind}}^G_{KZ} V_i) \cong \operatorname{\mathrm{End}}_G(\operatorname{\mathrm{c-Ind}}^G_{KZ}(\operatorname{\mathrm{Ind}}^{K}_{J} (\chi \otimes \mathbf 1))). \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{End}}_G(\operatorname{\mathrm{c-Ind}}^G_{KZ} V_i) \cong \operatorname{\mathrm{End}}_G(\operatorname{\mathrm{c-Ind}}^G_{KZ}(\operatorname{\mathrm{Ind}}^{K}_{J} (\chi \otimes \mathbf 1))). \end{align*} $$
Thus we may assume that
![]() $W_i$
is the trivial representation.
$W_i$
is the trivial representation.
By [Reference Bushnell and Kutzko14], the K-type
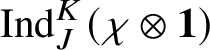 $\operatorname {\mathrm {Ind}}^{K}_{J} (\chi \otimes \mathbf 1)$
is a G-cover of the
$\operatorname {\mathrm {Ind}}^{K}_{J} (\chi \otimes \mathbf 1)$
is a G-cover of the
![]() $K_M$
-type
$K_M$
-type
![]() $\chi \otimes \mathbf 1$
, where
$\chi \otimes \mathbf 1$
, where
![]() $M = \mathbb {Q}_p^{\times } \times \mathbb {Q}_p^{\times }$
and
$M = \mathbb {Q}_p^{\times } \times \mathbb {Q}_p^{\times }$
and
![]() $K_M = \mathbb {Z}_p^{\times } \times \mathbb {Z}_p^{\times }$
. Thus there is an algebra isomorphism
$K_M = \mathbb {Z}_p^{\times } \times \mathbb {Z}_p^{\times }$
. Thus there is an algebra isomorphism
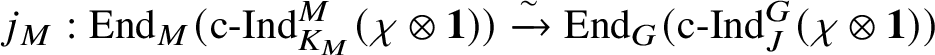 $$ \begin{align*} j_M: \operatorname{\mathrm{End}}_{M}(\operatorname{\mathrm{c-Ind}}^M_{K_M} (\chi \otimes \mathbf 1)) \xrightarrow{\sim} \operatorname{\mathrm{End}}_G(\operatorname{\mathrm{c-Ind}}^G_J(\chi \otimes \mathbf 1)) \end{align*} $$
$$ \begin{align*} j_M: \operatorname{\mathrm{End}}_{M}(\operatorname{\mathrm{c-Ind}}^M_{K_M} (\chi \otimes \mathbf 1)) \xrightarrow{\sim} \operatorname{\mathrm{End}}_G(\operatorname{\mathrm{c-Ind}}^G_J(\chi \otimes \mathbf 1)) \end{align*} $$
such that for each
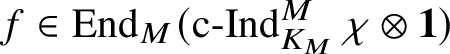 $f \in \operatorname {\mathrm {End}}_{M} (\operatorname {\mathrm {c-Ind}}^M_{K_M} \chi \otimes \mathbf 1 )$
, we have
$f \in \operatorname {\mathrm {End}}_{M} (\operatorname {\mathrm {c-Ind}}^M_{K_M} \chi \otimes \mathbf 1 )$
, we have
![]() $\operatorname {\mathrm {Supp}}(j_M f) = J \operatorname {\mathrm {Supp}}(f) J$
. It follows that
$\operatorname {\mathrm {Supp}}(j_M f) = J \operatorname {\mathrm {Supp}}(f) J$
. It follows that
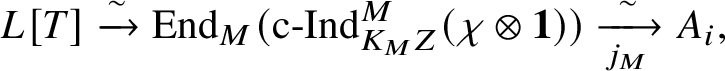 $$ \begin{align*} L[T] \xrightarrow{\sim} \operatorname{\mathrm{End}}_{M}(\operatorname{\mathrm{c-Ind}}^{M}_{K_MZ} (\chi \otimes \mathbf 1)) \xrightarrow[j_M]{\sim} A_i, \end{align*} $$
$$ \begin{align*} L[T] \xrightarrow{\sim} \operatorname{\mathrm{End}}_{M}(\operatorname{\mathrm{c-Ind}}^{M}_{K_MZ} (\chi \otimes \mathbf 1)) \xrightarrow[j_M]{\sim} A_i, \end{align*} $$
where T maps to an element in
![]() $A_i$
supported at
$A_i$
supported at
 $JZ \left(\begin{smallmatrix} p & 0 \\ 0 & 1 \end{smallmatrix} \right) JZ$
. Here we view
$JZ \left(\begin{smallmatrix} p & 0 \\ 0 & 1 \end{smallmatrix} \right) JZ$
. Here we view
![]() $\chi \otimes \mathbf 1$
as a representation of
$\chi \otimes \mathbf 1$
as a representation of
![]() $K_M Z$
by letting
$K_M Z$
by letting
![]() $ \left(\begin{smallmatrix} \varpi & 0 \\ 0 & \varpi \end{smallmatrix} \right)$
act by
$ \left(\begin{smallmatrix} \varpi & 0 \\ 0 & \varpi \end{smallmatrix} \right)$
act by
![]() $\zeta (\varpi )$
. This shows the first assertion.
$\zeta (\varpi )$
. This shows the first assertion.
To prove the second assertion, it suffices to show that
 $\operatorname {\mathrm {c-Ind}}^G_{KZ} V_i$
is torsion-free, since
$\operatorname {\mathrm {c-Ind}}^G_{KZ} V_i$
is torsion-free, since
![]() $A_i$
is a principal ideal domain. After tensoring with
$A_i$
is a principal ideal domain. After tensoring with
![]() $\overline {L}$
, this is equivalent to
$\overline {L}$
, this is equivalent to
 $\operatorname {\mathrm {c-Ind}}^G_{KZ} V_i$
having no
$\operatorname {\mathrm {c-Ind}}^G_{KZ} V_i$
having no
![]() $T - \lambda $
torsion, which is easily seen using the fact that the functions in
$T - \lambda $
torsion, which is easily seen using the fact that the functions in
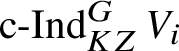 $\operatorname {\mathrm {c-Ind}}^G_{KZ} V_i$
are compactly supported.
$\operatorname {\mathrm {c-Ind}}^G_{KZ} V_i$
are compactly supported.
In particular, Frobenius reciprocity gives
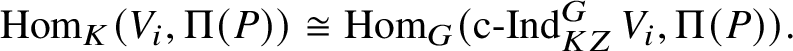 $$ \begin{align} \operatorname{\mathrm{Hom}}_K(V_i, \Pi(P)) \cong \operatorname{\mathrm{Hom}}_G(\operatorname{\mathrm{c-Ind}}^G_{KZ} V_i, \Pi(P)). \end{align} $$
$$ \begin{align} \operatorname{\mathrm{Hom}}_K(V_i, \Pi(P)) \cong \operatorname{\mathrm{Hom}}_G(\operatorname{\mathrm{c-Ind}}^G_{KZ} V_i, \Pi(P)). \end{align} $$
Hence
![]() $\operatorname {\mathrm {Hom}}_K(V_i, \Pi (P))$
is naturally an
$\operatorname {\mathrm {Hom}}_K(V_i, \Pi (P))$
is naturally an
![]() $A_i$
-module and we may transport the action of
$A_i$
-module and we may transport the action of
![]() $A_i$
onto
$A_i$
onto
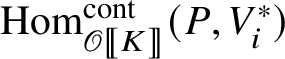 via formula (17).
via formula (17).
If V is a continuous representation of K on a finite-dimensional L-vector space and if
![]() $\Theta $
is an open, bounded K-invariant lattice in V, let
$\Theta $
is an open, bounded K-invariant lattice in V, let
![]() $\lvert \cdot \rvert $
be the norm on
$\lvert \cdot \rvert $
be the norm on
![]() $V^*$
given by
$V^*$
given by
![]() $\lvert \ell \rvert := \mathop {\mathrm {sup}}_{v \in \Theta } \lvert \ell (v)\rvert $
, so that
$\lvert \ell \rvert := \mathop {\mathrm {sup}}_{v \in \Theta } \lvert \ell (v)\rvert $
, so that
![]() $\Theta ^d = \operatorname {\mathrm {Hom}}_{\mathscr O}(\Theta , \mathscr O)$
is the unit ball in
$\Theta ^d = \operatorname {\mathrm {Hom}}_{\mathscr O}(\Theta , \mathscr O)$
is the unit ball in
![]() $V^*$
with respect to
$V^*$
with respect to
![]() $\lvert \cdot \rvert $
. The topology on
$\lvert \cdot \rvert $
. The topology on
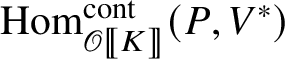 is given by the norm
is given by the norm
![]() $\lVert \phi \rVert := \mathop {\mathrm {sup}}_{v \in P} \lvert \phi (v)\rvert $
, and
$\lVert \phi \rVert := \mathop {\mathrm {sup}}_{v \in P} \lvert \phi (v)\rvert $
, and
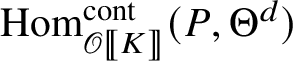 is the unit ball in this Banach space.
is the unit ball in this Banach space.
Proposition 5.5. For all
![]() $i \in I$
, the submodule
$i \in I$
, the submodule
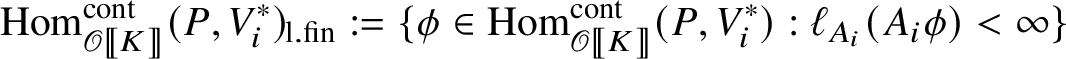
is dense in
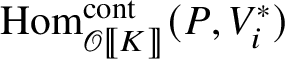
, where
![]() $\ell _{A_i}(A_i \phi )$
is the length of
$\ell _{A_i}(A_i \phi )$
is the length of
![]() $A_i \phi $
as an
$A_i \phi $
as an
![]() $A_i$
-module.
$A_i$
-module.
Proof. See [Reference Colmez, Dospinescu and Paškūnas21, Proposition 2.19].
Proposition 5.6. Let
![]() $\mathfrak m$
be a maximal ideal of
$\mathfrak m$
be a maximal ideal of
![]() $A_i$
and let
$A_i$
and let
![]() $\Pi $
be a completion of
$\Pi $
be a completion of
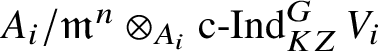 $A_i / \mathfrak m^n \otimes _{A_i} \operatorname {\mathrm {c-Ind}}^G_{KZ} V_i$
with respect to a G-invariant norm. Then
$A_i / \mathfrak m^n \otimes _{A_i} \operatorname {\mathrm {c-Ind}}^G_{KZ} V_i$
with respect to a G-invariant norm. Then
![]() $\Pi $
is the universal unitary completion of
$\Pi $
is the universal unitary completion of
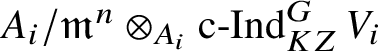 $A_i / \mathfrak m^n \otimes _{A_i} \operatorname {\mathrm {c-Ind}}^G_{KZ} V_i$
. Moreover, the action of
$A_i / \mathfrak m^n \otimes _{A_i} \operatorname {\mathrm {c-Ind}}^G_{KZ} V_i$
. Moreover, the action of
![]() $A_i$
on
$A_i$
on
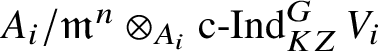 $A_i / \mathfrak m^n \otimes _{A_i} \operatorname {\mathrm {c-Ind}}^G_{KZ} V_i$
extends to a continuous action of
$A_i / \mathfrak m^n \otimes _{A_i} \operatorname {\mathrm {c-Ind}}^G_{KZ} V_i$
extends to a continuous action of
![]() $A_i$
on
$A_i$
on
![]() $\Pi $
.
$\Pi $
.
Proof. Let
![]() $\Pi ^{\circ }$
be a G-invariant
$\Pi ^{\circ }$
be a G-invariant
![]() $\mathscr O$
-lattice of
$\mathscr O$
-lattice of
![]() $\Pi $
. Then
$\Pi $
. Then
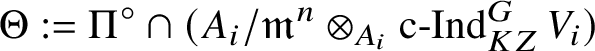 $$ \begin{align*} \Theta := \Pi^{\circ} \cap (A_i / \mathfrak m^n \otimes_{A_i} \operatorname{\mathrm{c-Ind}}^G_{KZ} V_i) \end{align*} $$
$$ \begin{align*} \Theta := \Pi^{\circ} \cap (A_i / \mathfrak m^n \otimes_{A_i} \operatorname{\mathrm{c-Ind}}^G_{KZ} V_i) \end{align*} $$
is a G-invariant
![]() $\mathscr O$
-lattice of
$\mathscr O$
-lattice of
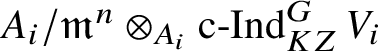 $A_i / \mathfrak m^n \otimes _{A_i} \operatorname {\mathrm {c-Ind}}^G_{KZ} V_i$
. By [Reference Emerton27, Proposition 1.17], it suffices to show that
$A_i / \mathfrak m^n \otimes _{A_i} \operatorname {\mathrm {c-Ind}}^G_{KZ} V_i$
. By [Reference Emerton27, Proposition 1.17], it suffices to show that
![]() $\Theta $
is of finite type over
$\Theta $
is of finite type over
![]() $\mathscr O[G]$
.
$\mathscr O[G]$
.
By Proposition 5.4(i), we have that
![]() $\kappa (\mathfrak m) := A_i / \mathfrak m \cong L[T] / f(T)$
– where
$\kappa (\mathfrak m) := A_i / \mathfrak m \cong L[T] / f(T)$
– where
![]() $f(T) \in L[T]$
is an irreducible polynomial – is a finite extension of L. Define a finite, increasing, exhaustive filtration
$f(T) \in L[T]$
is an irreducible polynomial – is a finite extension of L. Define a finite, increasing, exhaustive filtration
![]() $ \{ R^j \}_{n \geq j \geq 0}$
of
$ \{ R^j \}_{n \geq j \geq 0}$
of
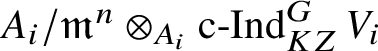 $A_i / \mathfrak m^n \otimes _{A_i} \operatorname {\mathrm {c-Ind}}^G_{KZ} V_i$
by G-invariant
$A_i / \mathfrak m^n \otimes _{A_i} \operatorname {\mathrm {c-Ind}}^G_{KZ} V_i$
by G-invariant
![]() $A_i$
-submodules
$A_i$
-submodules
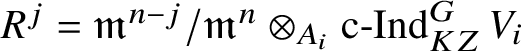 $R^j = \mathfrak m^{n-j} / \mathfrak m^n \otimes _{A_i} \operatorname {\mathrm {c-Ind}}^G_{KZ} V_i$
. Then we have
$R^j = \mathfrak m^{n-j} / \mathfrak m^n \otimes _{A_i} \operatorname {\mathrm {c-Ind}}^G_{KZ} V_i$
. Then we have
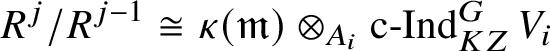 $$ \begin{align*} R^j / R^{j-1} \cong \kappa(\mathfrak m) \otimes_{A_i} \operatorname{\mathrm{c-Ind}}^G_{KZ} V_i \end{align*} $$
$$ \begin{align*} R^j / R^{j-1} \cong \kappa(\mathfrak m) \otimes_{A_i} \operatorname{\mathrm{c-Ind}}^G_{KZ} V_i \end{align*} $$
for each j and
![]() $ \{ \Theta ^j := \Theta \cap R^j \}_{n \geq j \geq 0}$
is a finite, increasing, exhaustive filtration of
$ \{ \Theta ^j := \Theta \cap R^j \}_{n \geq j \geq 0}$
is a finite, increasing, exhaustive filtration of
![]() $\Theta $
such that
$\Theta $
such that
![]() $\Theta ^j$
is a G-invariant
$\Theta ^j$
is a G-invariant
![]() $\mathscr O$
-lattice of
$\mathscr O$
-lattice of
![]() $R^j$
for each j. Moreover,
$R^j$
for each j. Moreover,
![]() $\Theta ^j / \Theta ^{j-1}$
gives rise to a G-invariant
$\Theta ^j / \Theta ^{j-1}$
gives rise to a G-invariant
![]() $\mathscr O$
-lattice of
$\mathscr O$
-lattice of
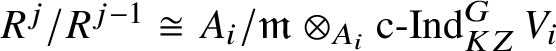 $R^j / R^{j-1} \cong A_i / \mathfrak m \otimes _{A_i} \operatorname {\mathrm {c-Ind}}^G_{KZ} V_i$
, and thus is finitely generated over
$R^j / R^{j-1} \cong A_i / \mathfrak m \otimes _{A_i} \operatorname {\mathrm {c-Ind}}^G_{KZ} V_i$
, and thus is finitely generated over
![]() $\mathscr O[G]$
by the proof of [Reference Berger and Breuil4, Theorem 4.3.1]. This implies that
$\mathscr O[G]$
by the proof of [Reference Berger and Breuil4, Theorem 4.3.1]. This implies that
![]() $\Theta $
is finitely generated over
$\Theta $
is finitely generated over
![]() $\mathscr O[G]$
, and the first assertion follows.
$\mathscr O[G]$
, and the first assertion follows.
If
![]() $\phi \in A_i$
, then
$\phi \in A_i$
, then
![]() $\phi (\Theta ) \subset \varpi ^n \Theta $
for some
$\phi (\Theta ) \subset \varpi ^n \Theta $
for some
![]() $n\in \mathbb Z$
, as
$n\in \mathbb Z$
, as
![]() $\Theta $
is finitely generated over
$\Theta $
is finitely generated over
![]() $\mathscr O[G]$
. This implies the second assertion.
$\mathscr O[G]$
. This implies the second assertion.
We denote the universal unitary completion of
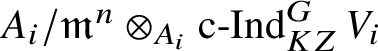 $A_i / \mathfrak m^n \otimes _{A_i} \operatorname {\mathrm {c-Ind}}^G_{KZ} V_i$
by
$A_i / \mathfrak m^n \otimes _{A_i} \operatorname {\mathrm {c-Ind}}^G_{KZ} V_i$
by
![]() $\Pi _{i,\mathfrak m, n}$
. If
$\Pi _{i,\mathfrak m, n}$
. If
![]() $n=1$
, then
$n=1$
, then
![]() $\Pi _{i,\mathfrak m, 1}$
is the universal unitary completion of
$\Pi _{i,\mathfrak m, 1}$
is the universal unitary completion of
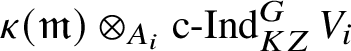 $\kappa (\mathfrak m) \otimes _{A_i} \operatorname {\mathrm {c-Ind}}^G_{KZ} V_i$
studied in [Reference Berger and Breuil4, Theorem 4.3.1] and [Reference Breuil and Emerton10, Proposition 2.2.1].
$\kappa (\mathfrak m) \otimes _{A_i} \operatorname {\mathrm {c-Ind}}^G_{KZ} V_i$
studied in [Reference Berger and Breuil4, Theorem 4.3.1] and [Reference Breuil and Emerton10, Proposition 2.2.1].
Corollary 5.7. If
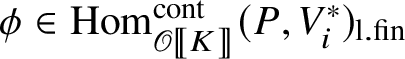 is such that
is such that
![]() $A_i \phi \cong A_i / \mathfrak m^n$
for a maximal ideal
$A_i \phi \cong A_i / \mathfrak m^n$
for a maximal ideal
![]() $\mathfrak m$
of
$\mathfrak m$
of
![]() $A_i$
, then
$A_i$
, then
![]() $\phi $
induces an injection
$\phi $
induces an injection
![]() $\Pi _{i,\mathfrak m, n} \hookrightarrow \Pi (P)$
. Moreover,
$\Pi _{i,\mathfrak m, n} \hookrightarrow \Pi (P)$
. Moreover,
![]() $\Pi _{i,\mathfrak m, n}$
admits a filtration of length n such that each graded piece is isomorphic to the universal unitary completion
$\Pi _{i,\mathfrak m, n}$
admits a filtration of length n such that each graded piece is isomorphic to the universal unitary completion
![]() $\Pi _{i,\mathfrak m, 1}$
of
$\Pi _{i,\mathfrak m, 1}$
of
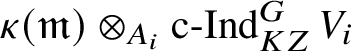 $\kappa (\mathfrak m) \otimes _{A_i} \operatorname {\mathrm {c-Ind}}^G_{KZ} V_i$
.
$\kappa (\mathfrak m) \otimes _{A_i} \operatorname {\mathrm {c-Ind}}^G_{KZ} V_i$
.
Proof. The assumption
![]() $A_i \phi \cong A_i / \mathfrak m^n$
implies that
$A_i \phi \cong A_i / \mathfrak m^n$
implies that
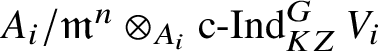 $A_i / \mathfrak m^n \otimes _{A_i} \operatorname {\mathrm {c-Ind}}^G_{KZ} V_i$
injects into
$A_i / \mathfrak m^n \otimes _{A_i} \operatorname {\mathrm {c-Ind}}^G_{KZ} V_i$
injects into
![]() $\Pi (P)$
. The first assertion follows immediately from Proposition 5.6. To show the second assertion, we let
$\Pi (P)$
. The first assertion follows immediately from Proposition 5.6. To show the second assertion, we let
![]() $ \{R^j \}_{n \geq j \geq 0}$
be the filtration of
$ \{R^j \}_{n \geq j \geq 0}$
be the filtration of
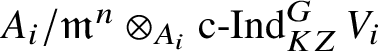 $A_i / \mathfrak m^n \otimes _{A_i} \operatorname {\mathrm {c-Ind}}^G_{KZ} V_i$
defined in Proposition 5.6. Let
$A_i / \mathfrak m^n \otimes _{A_i} \operatorname {\mathrm {c-Ind}}^G_{KZ} V_i$
defined in Proposition 5.6. Let
![]() $\Pi ^j$
be the closure of
$\Pi ^j$
be the closure of
![]() $R^j$
in
$R^j$
in
![]() $\Pi _{i,\mathfrak m, n}$
; then
$\Pi _{i,\mathfrak m, n}$
; then
![]() $\Pi ^n= \Pi _{i,\mathfrak m,n}$
. Since
$\Pi ^n= \Pi _{i,\mathfrak m,n}$
. Since
![]() $\mathfrak m R^j = R^{j-1}$
, we have
$\mathfrak m R^j = R^{j-1}$
, we have
![]() $\mathfrak m \Pi ^j = \Pi ^{j-1}$
and hence
$\mathfrak m \Pi ^j = \Pi ^{j-1}$
and hence
![]() $\Pi ^j= \mathfrak m^{n-j} \Pi _{i,\mathfrak m,n}$
. If
$\Pi ^j= \mathfrak m^{n-j} \Pi _{i,\mathfrak m,n}$
. If
![]() $\Pi ^j= \Pi ^{j-1}$
, then
$\Pi ^j= \Pi ^{j-1}$
, then
![]() $\Pi ^j=\mathfrak m \Pi ^j$
and hence
$\Pi ^j=\mathfrak m \Pi ^j$
and hence
![]() $\Pi ^j= \mathfrak m^j \Pi ^j= \mathfrak m^n \Pi _{i,\mathfrak m,n}=0$
. Since
$\Pi ^j= \mathfrak m^j \Pi ^j= \mathfrak m^n \Pi _{i,\mathfrak m,n}=0$
. Since
![]() $\Pi ^j\neq 0$
for
$\Pi ^j\neq 0$
for
![]() $1\le j\le n$
, we conclude that
$1\le j\le n$
, we conclude that
![]() $\Pi ^j\neq \Pi ^{j-1}$
for
$\Pi ^j\neq \Pi ^{j-1}$
for
![]() $1\le j\le n$
. Moreover,
$1\le j\le n$
. Moreover,
![]() $\Pi ^j / \Pi ^{j-1}$
contains
$\Pi ^j / \Pi ^{j-1}$
contains
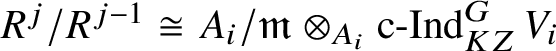 $R^j / R^{j-1} \cong A_i / \mathfrak m \otimes _{A_i} \operatorname {\mathrm {c-Ind}}^G_{KZ} V_i$
as a dense subspace, and thus is isomorphic to
$R^j / R^{j-1} \cong A_i / \mathfrak m \otimes _{A_i} \operatorname {\mathrm {c-Ind}}^G_{KZ} V_i$
as a dense subspace, and thus is isomorphic to
![]() $\Pi _{i,\mathfrak m, 1}$
. This proves the corollary.
$\Pi _{i,\mathfrak m, 1}$
. This proves the corollary.
Note that the image of any
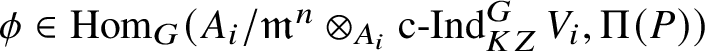 $\phi \in \operatorname {\mathrm {Hom}}_G (A_i / \mathfrak m^n \otimes _{A_i} \operatorname {\mathrm {c-Ind}}^G_{KZ} V_i, \Pi (P) )$
is isomorphic to
$\phi \in \operatorname {\mathrm {Hom}}_G (A_i / \mathfrak m^n \otimes _{A_i} \operatorname {\mathrm {c-Ind}}^G_{KZ} V_i, \Pi (P) )$
is isomorphic to
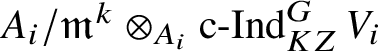 $A_i / \mathfrak m^k \otimes _{A_i} \operatorname {\mathrm {c-Ind}}^G_{KZ} V_i$
for some
$A_i / \mathfrak m^k \otimes _{A_i} \operatorname {\mathrm {c-Ind}}^G_{KZ} V_i$
for some
![]() $0 \leq k \leq n$
. Hence it induces an injection
$0 \leq k \leq n$
. Hence it induces an injection
![]() $\Pi _{i, \mathfrak m, k} \hookrightarrow \Pi (P)$
by Corollary 5.7.
$\Pi _{i, \mathfrak m, k} \hookrightarrow \Pi (P)$
by Corollary 5.7.
Proposition 5.8. Let P be a projective object in
![]() $\mathfrak C(\mathscr O)$
. Then the image of the evaluation map
$\mathfrak C(\mathscr O)$
. Then the image of the evaluation map
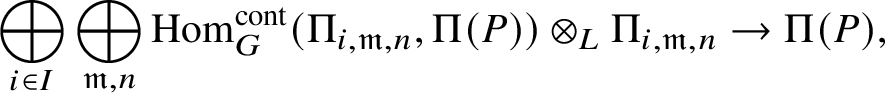 $$ \begin{align*} \bigoplus_{i \in I} \bigoplus_{\mathfrak m, n} \operatorname{\mathrm{Hom}}^{\mathrm{cont}}_{G}(\Pi_{i,\mathfrak m, n}, \Pi(P)) \otimes_L \Pi_{i,\mathfrak m, n} \rightarrow \Pi(P), \end{align*} $$
$$ \begin{align*} \bigoplus_{i \in I} \bigoplus_{\mathfrak m, n} \operatorname{\mathrm{Hom}}^{\mathrm{cont}}_{G}(\Pi_{i,\mathfrak m, n}, \Pi(P)) \otimes_L \Pi_{i,\mathfrak m, n} \rightarrow \Pi(P), \end{align*} $$
where
![]() $\mathfrak m$
runs through maximal ideals of
$\mathfrak m$
runs through maximal ideals of
![]() $A_i$
and
$A_i$
and
![]() $n \in \mathbb {N}$
is a dense subspace.
$n \in \mathbb {N}$
is a dense subspace.
Proof. Let
![]() $\Pi $
be the closure of the image of the evaluation map and M the image of P under
$\Pi $
be the closure of the image of the evaluation map and M the image of P under
![]() $\operatorname {\mathrm {Hom}}^{\mathrm {cont}}_{L}(\Pi (P), L) \twoheadrightarrow \operatorname {\mathrm {Hom}}^{\mathrm {cont}}_{L}(\Pi , L)$
. Then we have
$\operatorname {\mathrm {Hom}}^{\mathrm {cont}}_{L}(\Pi (P), L) \twoheadrightarrow \operatorname {\mathrm {Hom}}^{\mathrm {cont}}_{L}(\Pi , L)$
. Then we have
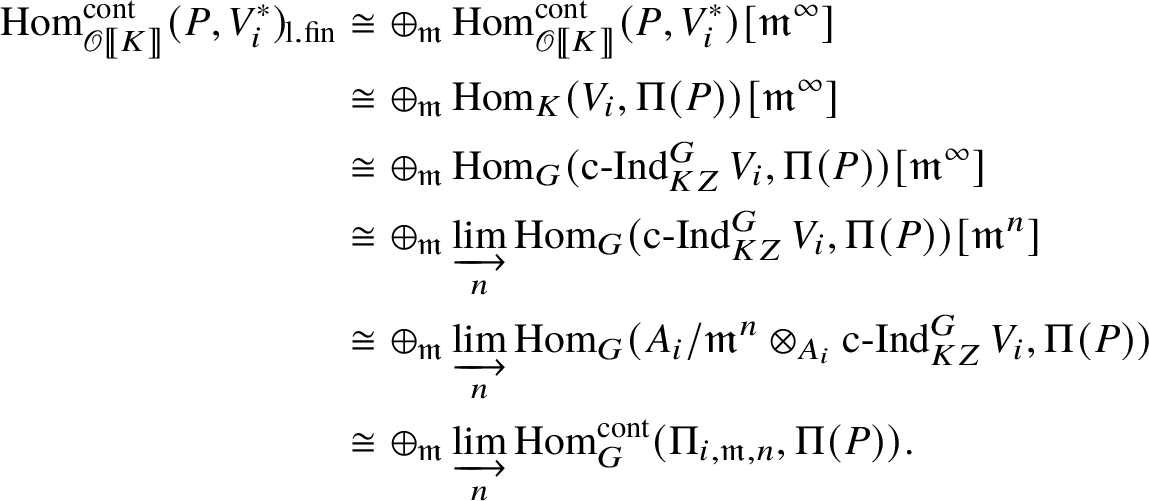
Here the first isomorphism is due to the fact that any module M over a commutative ring A such that every finitely generated submodule is of finite length admits a decomposition
![]() $M \cong \oplus _{\mathfrak m} M[\mathfrak m^{\infty }]$
with
$M \cong \oplus _{\mathfrak m} M[\mathfrak m^{\infty }]$
with
![]() $\mathfrak m$
running through maximal ideals of A. The second isomorphism is given by formula (17), and the last isomorphism is due to Corollary 5.7. Similarly, we have
$\mathfrak m$
running through maximal ideals of A. The second isomorphism is given by formula (17), and the last isomorphism is due to Corollary 5.7. Similarly, we have
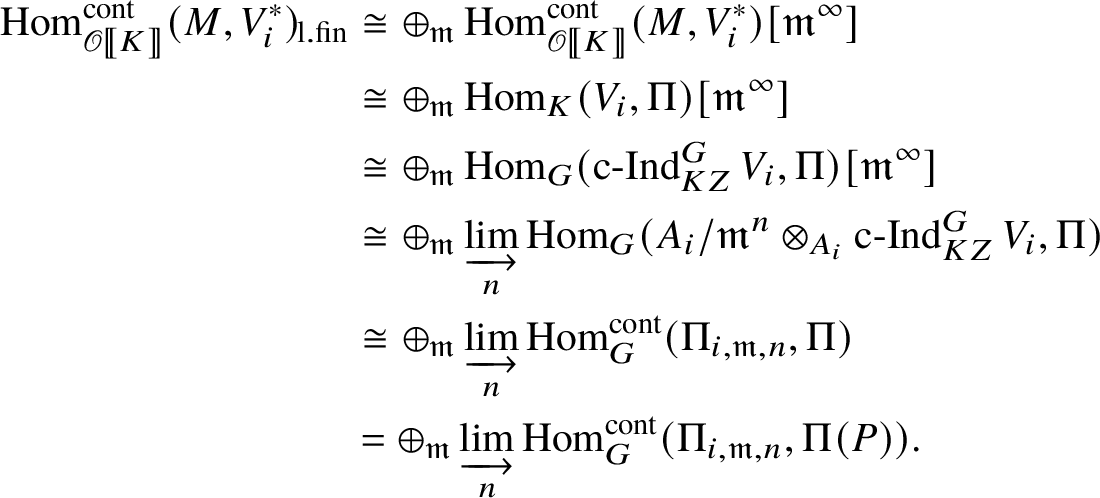
Thus by Proposition 5.5, we have
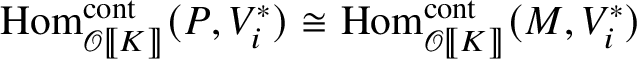
for each
![]() $i \in I$
. Combining this with Lemma 5.1, we deduce the proposition.
$i \in I$
. Combining this with Lemma 5.1, we deduce the proposition.
Corollary 5.9. Define
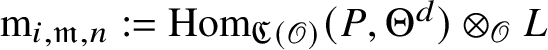 $\mathrm m_{i,\mathfrak m, n} := \operatorname {\mathrm {Hom}}_{\mathfrak C(\mathscr O)} (P, \Theta ^d ) \otimes _{\mathscr O} L$
, where
$\mathrm m_{i,\mathfrak m, n} := \operatorname {\mathrm {Hom}}_{\mathfrak C(\mathscr O)} (P, \Theta ^d ) \otimes _{\mathscr O} L$
, where
![]() $\Theta $
is an open bounded G-invariant lattice in
$\Theta $
is an open bounded G-invariant lattice in
![]() $\Pi _{i,\mathfrak m, n}$
. Then
$\Pi _{i,\mathfrak m, n}$
. Then
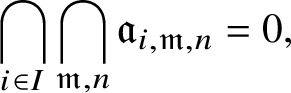 $$ \begin{align*} \bigcap_{i \in I} \bigcap_{\mathfrak m, n} \mathfrak{a}_{i,\mathfrak m, n} = 0, \end{align*} $$
$$ \begin{align*} \bigcap_{i \in I} \bigcap_{\mathfrak m, n} \mathfrak{a}_{i,\mathfrak m, n} = 0, \end{align*} $$
where
![]() $\mathfrak {a}_{i,\mathfrak m, n} := \operatorname {\mathrm {ann}}_E (\mathrm m_{i,\mathfrak m, n} )$
.
$\mathfrak {a}_{i,\mathfrak m, n} := \operatorname {\mathrm {ann}}_E (\mathrm m_{i,\mathfrak m, n} )$
.
Proof. For
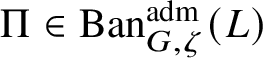 $\Pi \in \operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)$
with a G-invariant
$\Pi \in \operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)$
with a G-invariant
![]() $\mathscr O$
-lattice
$\mathscr O$
-lattice
![]() $\Theta $
, we have
$\Theta $
, we have
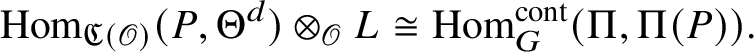 $$ \begin{align*} \operatorname{\mathrm{Hom}}_{\mathfrak C(\mathscr O)}(P, \Theta^d) \otimes_{\mathscr O} L \cong \operatorname{\mathrm{Hom}}^{\mathrm{cont}}_{G}(\Pi, \Pi(P)). \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Hom}}_{\mathfrak C(\mathscr O)}(P, \Theta^d) \otimes_{\mathscr O} L \cong \operatorname{\mathrm{Hom}}^{\mathrm{cont}}_{G}(\Pi, \Pi(P)). \end{align*} $$
Thus the evaluation map in Proposition 5.8 induces an
![]() $E [1/p ]$
-homomorphism
$E [1/p ]$
-homomorphism
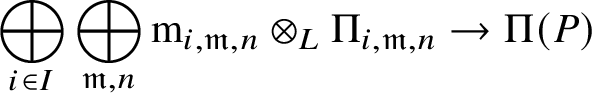 $$ \begin{align*} \bigoplus_{i \in I} \bigoplus_{\mathfrak m, n} \mathrm m_{i,\mathfrak m, n} \otimes_L \Pi_{i,\mathfrak m, n} \rightarrow \Pi(P) \end{align*} $$
$$ \begin{align*} \bigoplus_{i \in I} \bigoplus_{\mathfrak m, n} \mathrm m_{i,\mathfrak m, n} \otimes_L \Pi_{i,\mathfrak m, n} \rightarrow \Pi(P) \end{align*} $$
with a dense image. Since
![]() $E [1/p ]$
acts faithfully on the right-hand side of the map, it acts faithfully on the left-hand side as well. This proves the corollary, since the E-action on the left-hand side factors through the quotient
$E [1/p ]$
acts faithfully on the right-hand side of the map, it acts faithfully on the left-hand side as well. This proves the corollary, since the E-action on the left-hand side factors through the quotient
![]() $E / \bigcap _{i \in I} \bigcap _{\mathfrak m, n} \mathfrak {a}_{i,\mathfrak m, n}$
.
$E / \bigcap _{i \in I} \bigcap _{\mathfrak m, n} \mathfrak {a}_{i,\mathfrak m, n}$
.
6 Main results
Given a block
![]() $\mathfrak B$
, we have defined
$\mathfrak B$
, we have defined
![]() $\pi _{\mathfrak B}$
,
$\pi _{\mathfrak B}$
,
![]() $P_{\mathfrak B}$
and
$P_{\mathfrak B}$
and
![]() $E_{\mathfrak B}$
in Section 4.1 and
$E_{\mathfrak B}$
in Section 4.1 and
![]() $P_{\mathfrak B}'$
and
$P_{\mathfrak B}'$
and
![]() $E_{\mathfrak B}'$
in Section 4.2. We assume that all irreducibles in
$E_{\mathfrak B}'$
in Section 4.2. We assume that all irreducibles in
![]() $\mathfrak B$
are absolutely irreducible. This can be achieved by replacing k with a finite extension. Let
$\mathfrak B$
are absolutely irreducible. This can be achieved by replacing k with a finite extension. Let
![]() $\bar {\rho }_{\mathfrak B}$
be the
$\bar {\rho }_{\mathfrak B}$
be the
![]() $2$
-dimensional semisimple Galois representation of
$2$
-dimensional semisimple Galois representation of
![]() $\mathscr G_{\mathbb {Q}_p}$
over k defined by
$\mathscr G_{\mathbb {Q}_p}$
over k defined by
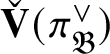 $\check {\mathbf {V}} (\pi _{\mathfrak B}^{\vee } )$
in cases (i), (ii), (iv) and (v), and by a direct sum of two copies of
$\check {\mathbf {V}} (\pi _{\mathfrak B}^{\vee } )$
in cases (i), (ii), (iv) and (v), and by a direct sum of two copies of
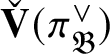 $\check {\mathbf {V}} (\pi _{\mathfrak B}^{\vee } )$
in cases (iii) and (vi); see Section 4.4 for an explicit description. We write
$\check {\mathbf {V}} (\pi _{\mathfrak B}^{\vee } )$
in cases (iii) and (vi); see Section 4.4 for an explicit description. We write
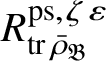 $R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
for the universal pseudodeformation ring of
$R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
for the universal pseudodeformation ring of
![]() $\operatorname {tr} \bar {\rho }_{\mathfrak B}$
with a fixed determinant
$\operatorname {tr} \bar {\rho }_{\mathfrak B}$
with a fixed determinant
![]() $\zeta \varepsilon $
. This ring is Noetherian by [Reference Chenevier18, Proposition F]. We let
$\zeta \varepsilon $
. This ring is Noetherian by [Reference Chenevier18, Proposition F]. We let
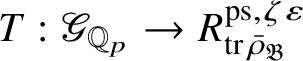 $T: \mathscr G_{\mathbb {Q}_p}\rightarrow R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
be the universal object (see Section 3).
$T: \mathscr G_{\mathbb {Q}_p}\rightarrow R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
be the universal object (see Section 3).
6.1 Finiteness
Let
![]() $\{V_i \}_{i \in I}$
be a family of K-representations defined in Proposition 5.3 and let
$\{V_i \}_{i \in I}$
be a family of K-representations defined in Proposition 5.3 and let
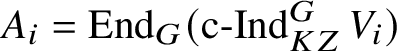 $A_i = \operatorname {\mathrm {End}}_G (\operatorname {\mathrm {c-Ind}}^G_{KZ} V_i )$
. For each
$A_i = \operatorname {\mathrm {End}}_G (\operatorname {\mathrm {c-Ind}}^G_{KZ} V_i )$
. For each
![]() $i \in I$
, a maximal ideal
$i \in I$
, a maximal ideal
![]() $\mathfrak m$
of
$\mathfrak m$
of
![]() $A_i$
and
$A_i$
and
![]() $n \in \mathbb {N}$
, we write
$n \in \mathbb {N}$
, we write
![]() $\Pi _{i,\mathfrak m, n}$
for the universal unitary completion of
$\Pi _{i,\mathfrak m, n}$
for the universal unitary completion of
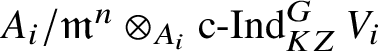 $A_i / \mathfrak m^n \otimes _{A_i} \operatorname {\mathrm {c-Ind}}^G_{KZ} V_i$
.
$A_i / \mathfrak m^n \otimes _{A_i} \operatorname {\mathrm {c-Ind}}^G_{KZ} V_i$
.
Lemma 6.1. Assume
![]() $\Pi _{i,\mathfrak m, n}$
is a subrepresentation of
$\Pi _{i,\mathfrak m, n}$
is a subrepresentation of
![]() $\Pi (P_{\mathfrak B}' )$
. Then
$\Pi (P_{\mathfrak B}' )$
. Then
![]() $\check {\mathbf {V}} (\Pi _{i,\mathfrak m, n} )$
is a finite free
$\check {\mathbf {V}} (\Pi _{i,\mathfrak m, n} )$
is a finite free
![]() $A_{i} / \mathfrak m^n$
-module of rank equal to
$A_{i} / \mathfrak m^n$
-module of rank equal to
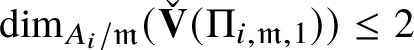 $\dim _{A_i / \mathfrak m} (\check {\mathbf {V}} (\Pi _{i,\mathfrak m, 1} ) ) \leq 2$
. Moreover,
$\dim _{A_i / \mathfrak m} (\check {\mathbf {V}} (\Pi _{i,\mathfrak m, 1} ) ) \leq 2$
. Moreover,
-
(i) if
 $\mathop {\mathrm {rank}}\nolimits _{A_i / \mathfrak m^n} \check {\mathbf {V}} (\Pi _{i,\mathfrak m, n} ) = 2$
, then
$\mathop {\mathrm {rank}}\nolimits _{A_i / \mathfrak m^n} \check {\mathbf {V}} (\Pi _{i,\mathfrak m, n} ) = 2$
, then
 $\check {\mathbf {V}} (\Pi _{i,\mathfrak m, n} )$
is a deformation to
$\check {\mathbf {V}} (\Pi _{i,\mathfrak m, n} )$
is a deformation to
 $A_{i} / \mathfrak m^n$
of the absolutely irreducible
$A_{i} / \mathfrak m^n$
of the absolutely irreducible
 $2$
-dimensional L-representation
$2$
-dimensional L-representation
 $\check {\mathbf {V}} (\Pi _{i,\mathfrak m, 1} )$
of
$\check {\mathbf {V}} (\Pi _{i,\mathfrak m, 1} )$
of
 $\mathscr G_{\mathbb {Q}_p}$
; and
$\mathscr G_{\mathbb {Q}_p}$
; and -
(ii) if
 $\mathop {\mathrm {rank}}\nolimits _{A_{i} / \mathfrak m^n} \check {\mathbf {V}} (\Pi _{i,\mathfrak m, n} ) = 1$
, then the action of
$\mathop {\mathrm {rank}}\nolimits _{A_{i} / \mathfrak m^n} \check {\mathbf {V}} (\Pi _{i,\mathfrak m, n} ) = 1$
, then the action of
 $\mathscr G_{\mathbb {Q}_p}$
on
$\mathscr G_{\mathbb {Q}_p}$
on
 $\check {\mathbf {V}} (\Pi _{i,\mathfrak m, n} )$
is given by an
$\check {\mathbf {V}} (\Pi _{i,\mathfrak m, n} )$
is given by an
 $(A_{i} / \mathfrak m^n)^{\times }$
-valued character lifting
$(A_{i} / \mathfrak m^n)^{\times }$
-valued character lifting
 $\check {\mathbf {V}} (\Pi _{i,\mathfrak m, 1} )$
.
$\check {\mathbf {V}} (\Pi _{i,\mathfrak m, 1} )$
.
Proof. Since
![]() $V_i$
is a principal series type, the
$V_i$
is a principal series type, the
![]() $\mathscr G_{\mathbb {Q}_p}$
-module
$\mathscr G_{\mathbb {Q}_p}$
-module
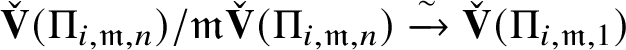 $$ \begin{align*} \check{\mathbf{V}}(\Pi_{i,\mathfrak m, n}) / \mathfrak m \check{\mathbf{V}}(\Pi_{i,\mathfrak m, n}) \xrightarrow{\sim} \check{\mathbf{V}}(\Pi_{i,\mathfrak m, 1}) \end{align*} $$
$$ \begin{align*} \check{\mathbf{V}}(\Pi_{i,\mathfrak m, n}) / \mathfrak m \check{\mathbf{V}}(\Pi_{i,\mathfrak m, n}) \xrightarrow{\sim} \check{\mathbf{V}}(\Pi_{i,\mathfrak m, 1}) \end{align*} $$
has dimension
![]() $r \leq 2$
over
$r \leq 2$
over
![]() $\kappa (\mathfrak m) := A_i / \mathfrak m$
by [Reference Berger and Breuil4, Theorem 4.3.1] and [Reference Breuil and Emerton10, Proposition 2.2.1]. Nakayama’s lemma implies that we have a surjection
$\kappa (\mathfrak m) := A_i / \mathfrak m$
by [Reference Berger and Breuil4, Theorem 4.3.1] and [Reference Breuil and Emerton10, Proposition 2.2.1]. Nakayama’s lemma implies that we have a surjection
Proposition 5.7 and the exactness of
![]() $\check {\mathbf {V}}$
imply that
$\check {\mathbf {V}}$
imply that
![]() $\check {\mathbf {V}} (\Pi _{i,\mathfrak m, n} )$
has length
$\check {\mathbf {V}} (\Pi _{i,\mathfrak m, n} )$
has length
![]() $nr$
as an
$nr$
as an
![]() $A_i / \mathfrak m^n$
-module. Hence the surjection is an isomorphism and the lemma follows.
$A_i / \mathfrak m^n$
-module. Hence the surjection is an isomorphism and the lemma follows.
Lemma 6.2. Under the same assumptions as in Lemma 6.1, there is a natural map
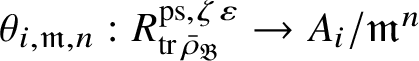 $\theta _{i,\mathfrak m, n}: R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}} \rightarrow A_i / \mathfrak m^n$
, which induces a map
$\theta _{i,\mathfrak m, n}: R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}} \rightarrow A_i / \mathfrak m^n$
, which induces a map
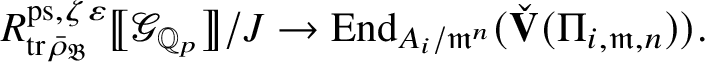
Proof. If
![]() $\check {\mathbf {V}} (\Pi _{i,\mathfrak m, n} )$
is of rank
$\check {\mathbf {V}} (\Pi _{i,\mathfrak m, n} )$
is of rank
![]() $2$
over
$2$
over
![]() $A_i/\mathfrak m^n$
, it follows from Lemma 6.1(i) that
$A_i/\mathfrak m^n$
, it follows from Lemma 6.1(i) that
![]() $\check {\mathbf {V}} (\Pi _{i,\mathfrak m, n} )$
is a deformation of the
$\check {\mathbf {V}} (\Pi _{i,\mathfrak m, n} )$
is a deformation of the
![]() $2$
-dimensional Galois representation
$2$
-dimensional Galois representation
![]() $\check {\mathbf {V}} (\Pi _{i,\mathfrak m, 1} )$
to
$\check {\mathbf {V}} (\Pi _{i,\mathfrak m, 1} )$
to
![]() $A_i/{\mathfrak m}^n$
with determinant
$A_i/{\mathfrak m}^n$
with determinant
![]() $\zeta \varepsilon $
. It follows from [Reference Chenevier18, Section 4.1, Theorem 3.17] that there is an
$\zeta \varepsilon $
. It follows from [Reference Chenevier18, Section 4.1, Theorem 3.17] that there is an
![]() $\mathscr O$
-algebra map
$\mathscr O$
-algebra map
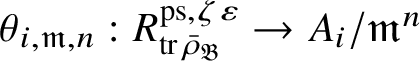 $\theta _{i,\mathfrak m, n}: R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}} \rightarrow A_i / \mathfrak m^n$
such that the specialisation of T along
$\theta _{i,\mathfrak m, n}: R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}} \rightarrow A_i / \mathfrak m^n$
such that the specialisation of T along
![]() $\theta _{i,\mathfrak m, n}$
is equal to
$\theta _{i,\mathfrak m, n}$
is equal to
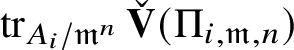 $\operatorname {tr}_{A_i/{\mathfrak m}^n} \check {\mathbf {V}} (\Pi _{i,\mathfrak m, n} )$
. This map induces a homomorphism of
$\operatorname {tr}_{A_i/{\mathfrak m}^n} \check {\mathbf {V}} (\Pi _{i,\mathfrak m, n} )$
. This map induces a homomorphism of
![]() $\mathscr O$
-algebras
$\mathscr O$
-algebras
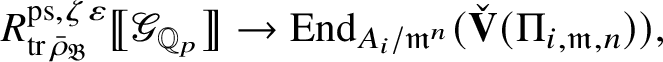
and Cayley–Hamilton for
![]() $M_2(A_i / \mathfrak m^n)$
implies that J lies in the kernel of this map.
$M_2(A_i / \mathfrak m^n)$
implies that J lies in the kernel of this map.
If
![]() $\check {\mathbf {V}} (\Pi _{i,\mathfrak m, n} )$
is given by a character
$\check {\mathbf {V}} (\Pi _{i,\mathfrak m, n} )$
is given by a character
![]() $\chi _{i,\mathfrak m, n}: \mathscr G_{\mathbb {Q}_p} \rightarrow (A_i / \mathfrak m^n)^{\times }$
, then the same argument applies to the representation
$\chi _{i,\mathfrak m, n}: \mathscr G_{\mathbb {Q}_p} \rightarrow (A_i / \mathfrak m^n)^{\times }$
, then the same argument applies to the representation
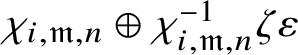 $\chi _{i,\mathfrak m, n} \oplus \chi _{i,\mathfrak m,n}^{-1} \zeta \varepsilon $
, so that we get a map
$\chi _{i,\mathfrak m, n} \oplus \chi _{i,\mathfrak m,n}^{-1} \zeta \varepsilon $
, so that we get a map
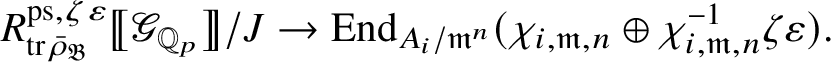
Its image commutes with the idempotent which projects onto the direct summand
![]() $\chi _{i,\mathfrak m, n}$
. Hence, the image is contained in
$\chi _{i,\mathfrak m, n}$
. Hence, the image is contained in
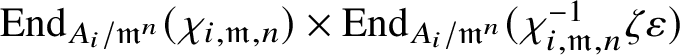 $\operatorname {\mathrm {End}}_{A_i / \mathfrak m^n} (\chi _{i,\mathfrak m, n} )\times \operatorname {\mathrm {End}}_{A_i / \mathfrak m^n} (\chi _{i,\mathfrak m,n}^{-1}\zeta \varepsilon )$
, and we may project to
$\operatorname {\mathrm {End}}_{A_i / \mathfrak m^n} (\chi _{i,\mathfrak m, n} )\times \operatorname {\mathrm {End}}_{A_i / \mathfrak m^n} (\chi _{i,\mathfrak m,n}^{-1}\zeta \varepsilon )$
, and we may project to
![]() $\operatorname {\mathrm {End}}_{A_i / \mathfrak m^n} (\chi _{i,\mathfrak m, n} )$
to obtain the required homomorphism.
$\operatorname {\mathrm {End}}_{A_i / \mathfrak m^n} (\chi _{i,\mathfrak m, n} )$
to obtain the required homomorphism.
In Propositions 3.1 and 4.18, we established surjections

Theorem 6.3. The maps just given induce a surjection
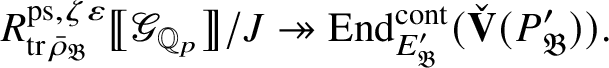
In particular,
![]() $E_{\mathfrak B}'$
and
$E_{\mathfrak B}'$
and
![]() $Z_{\mathfrak B}'$
are finite over
$Z_{\mathfrak B}'$
are finite over
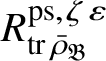 $R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
and hence Noetherian.
$R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
and hence Noetherian.
Proof. For the first part we have to show that
![]() $\operatorname {\mathrm {Ker}} \beta \subset \operatorname {\mathrm {Ker}} \alpha $
. Let
$\operatorname {\mathrm {Ker}} \beta \subset \operatorname {\mathrm {Ker}} \alpha $
. Let
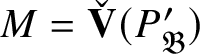 $M = \check {\mathbf {V}} (P_{\mathfrak B}' )$
and define
$M = \check {\mathbf {V}} (P_{\mathfrak B}' )$
and define
![]() $\mathrm m_{i,\mathfrak m, n} := \mathrm m (\Pi _{i,\mathfrak m, n} )$
, with
$\mathrm m_{i,\mathfrak m, n} := \mathrm m (\Pi _{i,\mathfrak m, n} )$
, with
![]() $i,\mathfrak m, n$
as in Corollary 5.9. Then the assumptions in Lemma 2.6 are satisfied by Corollary 5.9. It follows that the kernel of
$i,\mathfrak m, n$
as in Corollary 5.9. Then the assumptions in Lemma 2.6 are satisfied by Corollary 5.9. It follows that the kernel of
![]() $\alpha $
is given by
$\alpha $
is given by
![]() $\cap _{i \in I} \cap _{\mathfrak m, n} \mathfrak b_{i,\mathfrak m, n}$
, where
$\cap _{i \in I} \cap _{\mathfrak m, n} \mathfrak b_{i,\mathfrak m, n}$
, where
![]() $\mathfrak b_{i,\mathfrak m, n}$
is the
$\mathfrak b_{i,\mathfrak m, n}$
is the
![]() -annihilator of
-annihilator of
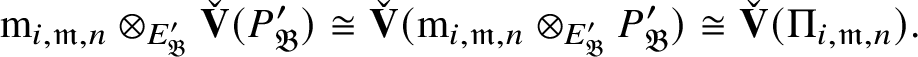 $$ \begin{align*} \mathrm m_{i,\mathfrak m, n} \otimes_{E_{\mathfrak B}'} \check{\mathbf{V}}(P_{\mathfrak B}') \cong \check{\mathbf{V}}(\mathrm m_{i,\mathfrak m, n} \otimes_{E_{\mathfrak B}'} P_{\mathfrak B}') \cong \check{\mathbf{V}}(\Pi_{i,\mathfrak m, n}). \end{align*} $$
$$ \begin{align*} \mathrm m_{i,\mathfrak m, n} \otimes_{E_{\mathfrak B}'} \check{\mathbf{V}}(P_{\mathfrak B}') \cong \check{\mathbf{V}}(\mathrm m_{i,\mathfrak m, n} \otimes_{E_{\mathfrak B}'} P_{\mathfrak B}') \cong \check{\mathbf{V}}(\Pi_{i,\mathfrak m, n}). \end{align*} $$
Since the action of
![]() on
on
![]() $\check {\mathbf {V}} (\Pi _{i,\mathfrak m, n} )$
factors through
$\check {\mathbf {V}} (\Pi _{i,\mathfrak m, n} )$
factors through
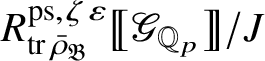 by Lemma 6.2,
by Lemma 6.2,
![]() $\mathfrak b_{i,\mathfrak m, n}$
contains the kernel of
$\mathfrak b_{i,\mathfrak m, n}$
contains the kernel of
![]() $\beta $
and hence
$\beta $
and hence
![]() $\operatorname {\mathrm {Ker}} \beta \subset \operatorname {\mathrm {Ker}} \alpha $
.
$\operatorname {\mathrm {Ker}} \beta \subset \operatorname {\mathrm {Ker}} \alpha $
.
The second assertion is a consequence of the first assertion and the finiteness of
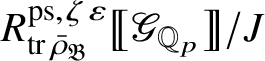 over
over
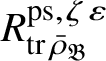 $R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
[Reference Wang-Erickson48, Proposition 3.6].
$R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
[Reference Wang-Erickson48, Proposition 3.6].
Corollary 6.4.
![]() $E_{\mathfrak B}$
and
$E_{\mathfrak B}$
and
![]() $Z_{\mathfrak B}$
are finite over
$Z_{\mathfrak B}$
are finite over
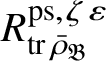 $R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
and hence Noetherian.
$R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
and hence Noetherian.
Proof. By [Reference Paškūnas39, Lemma 10.26], we have
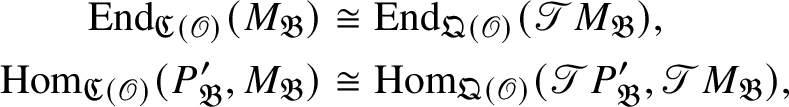 $$ \begin{align*} \operatorname{\mathrm{End}}_{\mathfrak C(\mathscr O)}(M_{\mathfrak B}) &\cong \operatorname{\mathrm{End}}_{\mathfrak Q(\mathscr O)}(\mathscr T M_{\mathfrak B}), \\ \operatorname{\mathrm{Hom}}_{\mathfrak C(\mathscr O)}(P_{\mathfrak B}', M_{\mathfrak B}) &\cong \operatorname{\mathrm{Hom}}_{\mathfrak Q(\mathscr O)}(\mathscr T P_{\mathfrak B}', \mathscr T M_{\mathfrak B}), \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{End}}_{\mathfrak C(\mathscr O)}(M_{\mathfrak B}) &\cong \operatorname{\mathrm{End}}_{\mathfrak Q(\mathscr O)}(\mathscr T M_{\mathfrak B}), \\ \operatorname{\mathrm{Hom}}_{\mathfrak C(\mathscr O)}(P_{\mathfrak B}', M_{\mathfrak B}) &\cong \operatorname{\mathrm{Hom}}_{\mathfrak Q(\mathscr O)}(\mathscr T P_{\mathfrak B}', \mathscr T M_{\mathfrak B}), \end{align*} $$
since
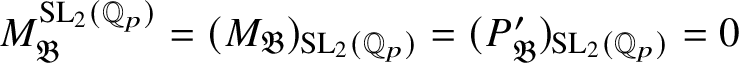 $M_{\mathfrak B}^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )} = (M_{\mathfrak B})_{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )} = (P_{\mathfrak B}' )_{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )} = 0$
. Define
$M_{\mathfrak B}^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )} = (M_{\mathfrak B})_{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )} = (P_{\mathfrak B}' )_{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )} = 0$
. Define
![]() $\mathrm m := \operatorname {\mathrm {Hom}}_{\mathfrak C(\mathscr O)} (P_{\mathfrak B}', M_{\mathfrak B} )$
, which is a finitely generated right
$\mathrm m := \operatorname {\mathrm {Hom}}_{\mathfrak C(\mathscr O)} (P_{\mathfrak B}', M_{\mathfrak B} )$
, which is a finitely generated right
![]() $E_{\mathfrak B}'$
-module by Corollary 4.13. Moreover, we have
$E_{\mathfrak B}'$
-module by Corollary 4.13. Moreover, we have
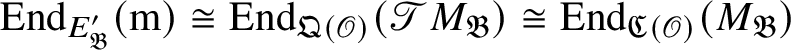 $$ \begin{align*} \operatorname{\mathrm{End}}_{E_{\mathfrak B}'}(\mathrm m) \cong \operatorname{\mathrm{End}}_{\mathfrak Q(\mathscr O)}(\mathscr T M_{\mathfrak B})\cong \operatorname{\mathrm{End}}_{\mathfrak C(\mathscr O)}(M_{\mathfrak B}) \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{End}}_{E_{\mathfrak B}'}(\mathrm m) \cong \operatorname{\mathrm{End}}_{\mathfrak Q(\mathscr O)}(\mathscr T M_{\mathfrak B})\cong \operatorname{\mathrm{End}}_{\mathfrak C(\mathscr O)}(M_{\mathfrak B}) \end{align*} $$
by Proposition 4.10(2) and the isomorphism above. Theorem 6.3 implies that the conditions of Lemma 4.11 are satisfied with
![]() $E=E_{\mathfrak B}'$
and
$E=E_{\mathfrak B}'$
and
![]() $Z=Z_{\mathfrak B}'$
. Thus
$Z=Z_{\mathfrak B}'$
. Thus
![]() $\operatorname {\mathrm {End}}_{\mathfrak C(\mathscr O)}(M_{\mathfrak B})$
and its centre are finite over
$\operatorname {\mathrm {End}}_{\mathfrak C(\mathscr O)}(M_{\mathfrak B})$
and its centre are finite over
![]() $Z_{\mathfrak B}'$
, and thus finite over
$Z_{\mathfrak B}'$
, and thus finite over
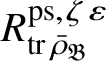 $R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
by Theorem 6.3, and hence Noetherian. This implies the corollary, since
$R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
by Theorem 6.3, and hence Noetherian. This implies the corollary, since
![]() $\operatorname {\mathrm {End}}_{\mathfrak C(\mathscr O)}(M_{\mathfrak B}) \cong E_{\mathfrak B}$
and
$\operatorname {\mathrm {End}}_{\mathfrak C(\mathscr O)}(M_{\mathfrak B}) \cong E_{\mathfrak B}$
and
![]() $Z (\operatorname {\mathrm {End}}_{\mathfrak C(\mathscr O)}(M_{\mathfrak B}) ) \cong Z_{\mathfrak B}$
by Proposition 4.15.
$Z (\operatorname {\mathrm {End}}_{\mathfrak C(\mathscr O)}(M_{\mathfrak B}) ) \cong Z_{\mathfrak B}$
by Proposition 4.15.
Remark 6.5. Since
![]() $Z_{\mathfrak B}$
is Noetherian, the
$Z_{\mathfrak B}$
is Noetherian, the
![]() $\mathfrak m$
-adic topology coincides with the linearly compact topology in Lemma 4.1.
$\mathfrak m$
-adic topology coincides with the linearly compact topology in Lemma 4.1.
Let us spell out the properties of the map
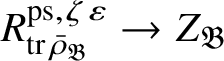 $R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}\rightarrow Z_{\mathfrak B}$
constructed in Corollary 6.4. Since
$R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}\rightarrow Z_{\mathfrak B}$
constructed in Corollary 6.4. Since
![]() $Z_{\mathfrak B}$
acts functorially on every object in
$Z_{\mathfrak B}$
acts functorially on every object in
![]() ${\mathfrak C}(\mathscr O)_{\mathfrak B}$
, the homomorphism
${\mathfrak C}(\mathscr O)_{\mathfrak B}$
, the homomorphism
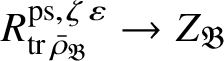 $R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}\rightarrow Z_{\mathfrak B}$
induces a functorial ring homomorphism
$R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}\rightarrow Z_{\mathfrak B}$
induces a functorial ring homomorphism
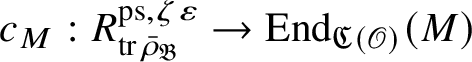 $$ \begin{align*} c_M: R^{\mathrm{ps}, \zeta\varepsilon}_{\operatorname{tr}\bar{\rho}_{\mathfrak B}} \rightarrow \operatorname{\mathrm{End}}_{{\mathfrak C}(\mathscr O)}(M) \end{align*} $$
$$ \begin{align*} c_M: R^{\mathrm{ps}, \zeta\varepsilon}_{\operatorname{tr}\bar{\rho}_{\mathfrak B}} \rightarrow \operatorname{\mathrm{End}}_{{\mathfrak C}(\mathscr O)}(M) \end{align*} $$
for every object M in
![]() ${\mathfrak C}(\mathscr O)$
. Since
${\mathfrak C}(\mathscr O)$
. Since
![]() $\check {\mathbf {V}}$
is a functor, it induces a ring homomorphism
$\check {\mathbf {V}}$
is a functor, it induces a ring homomorphism
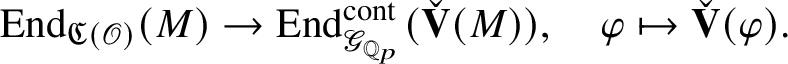 $$ \begin{align*} \operatorname{\mathrm{End}}_{{\mathfrak C}(\mathscr O)}(M)\rightarrow \operatorname{\mathrm{End}}^{\mathrm{cont}}_{\mathscr G_{\mathbb{Q}_p}}(\check{\mathbf{V}}(M)),\quad \varphi\mapsto \check{\mathbf{V}}(\varphi). \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{End}}_{{\mathfrak C}(\mathscr O)}(M)\rightarrow \operatorname{\mathrm{End}}^{\mathrm{cont}}_{\mathscr G_{\mathbb{Q}_p}}(\check{\mathbf{V}}(M)),\quad \varphi\mapsto \check{\mathbf{V}}(\varphi). \end{align*} $$
We denote the action of
![]() $\mathscr G_{\mathbb {Q}_p}$
on
$\mathscr G_{\mathbb {Q}_p}$
on
![]() $\check {\mathbf {V}}(M)$
by
$\check {\mathbf {V}}(M)$
by
![]() $\rho _{\check {\mathbf {V}}(M)}$
. Finally, for all
$\rho _{\check {\mathbf {V}}(M)}$
. Finally, for all
![]() $g\in \mathscr G_{\mathbb {Q}_p}$
we may evaluate the universal pseudorepresentation
$g\in \mathscr G_{\mathbb {Q}_p}$
we may evaluate the universal pseudorepresentation
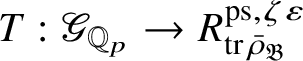 $T: \mathscr G_{\mathbb {Q}_p} \rightarrow R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
at
$T: \mathscr G_{\mathbb {Q}_p} \rightarrow R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
at
![]() $g\in \mathscr G_{\mathbb {Q}_p}$
to obtain an element
$g\in \mathscr G_{\mathbb {Q}_p}$
to obtain an element
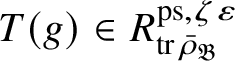 $T(g)\in R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
.
$T(g)\in R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
.
Proposition 6.6. For each
![]() $M\in {\mathfrak C}(\mathscr O)_{\mathfrak B}$
and each
$M\in {\mathfrak C}(\mathscr O)_{\mathfrak B}$
and each
![]() $g\in \mathscr G_{\mathbb {Q}_p}$
,
$g\in \mathscr G_{\mathbb {Q}_p}$
,
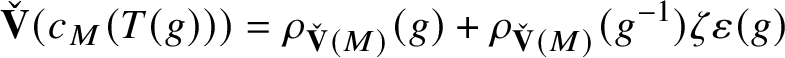 $$ \begin{align*} \check{\mathbf{V}}(c_M(T(g)))= \rho_{\check{\mathbf{V}}(M)}(g) + \rho_{\check{\mathbf{V}}(M)}(g^{-1}) \zeta\varepsilon(g) \end{align*} $$
$$ \begin{align*} \check{\mathbf{V}}(c_M(T(g)))= \rho_{\check{\mathbf{V}}(M)}(g) + \rho_{\check{\mathbf{V}}(M)}(g^{-1}) \zeta\varepsilon(g) \end{align*} $$
in
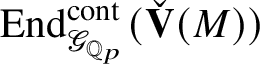 $\operatorname {\mathrm {End}}_{\mathscr G_{\mathbb {Q}_p}}^{\mathrm {cont}} (\check {\mathbf {V}}(M) )$
.
$\operatorname {\mathrm {End}}_{\mathscr G_{\mathbb {Q}_p}}^{\mathrm {cont}} (\check {\mathbf {V}}(M) )$
.
Proof. Since
![]() $g^2 -T(g)g + \zeta \varepsilon (g)=0$
in
$g^2 -T(g)g + \zeta \varepsilon (g)=0$
in
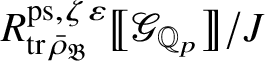 , the equality
, the equality
![]() $T(g)\operatorname {\mathrm {id}} = g + \zeta \varepsilon (g) g^{-1}$
holds in that ring. The rest is just unravelling the definitions.
$T(g)\operatorname {\mathrm {id}} = g + \zeta \varepsilon (g) g^{-1}$
holds in that ring. The rest is just unravelling the definitions.
Since
![]() $P_{\mathfrak B}$
is a projective generator for
$P_{\mathfrak B}$
is a projective generator for
![]() ${\mathfrak C}(\mathscr O)_{\mathfrak B}$
, the functor
${\mathfrak C}(\mathscr O)_{\mathfrak B}$
, the functor
induces an equivalence of categories between
![]() ${\mathfrak C}(\mathscr O)_{\mathfrak B}$
and the category of right pseudocompact
${\mathfrak C}(\mathscr O)_{\mathfrak B}$
and the category of right pseudocompact
![]() $E_{\mathfrak B}$
-modules. The inverse functor is given by
$E_{\mathfrak B}$
-modules. The inverse functor is given by
![]() $\mathrm m \mapsto \mathrm m \operatorname {\mathrm {\mathbin {\widehat {\otimes }}}}_{E_{\mathfrak B}} P_{\mathfrak B}$
.
$\mathrm m \mapsto \mathrm m \operatorname {\mathrm {\mathbin {\widehat {\otimes }}}}_{E_{\mathfrak B}} P_{\mathfrak B}$
.
Corollary 6.7. For N in
![]() ${\mathfrak C}(\mathscr O)_{\mathfrak B}$
the following assertions are equivalent:
${\mathfrak C}(\mathscr O)_{\mathfrak B}$
the following assertions are equivalent:
-
1. There is a surjection
 $P_{\mathfrak B}^{\oplus n} \twoheadrightarrow N$
for some
$P_{\mathfrak B}^{\oplus n} \twoheadrightarrow N$
for some
 $n\ge 1$
.
$n\ge 1$
. -
2.
 $\mathrm m(N)$
is a finitely generated
$\mathrm m(N)$
is a finitely generated
 $E_{\mathfrak B}$
-module.
$E_{\mathfrak B}$
-module. -
3.
 $\mathrm m(N)$
is a finitely generated
$\mathrm m(N)$
is a finitely generated
 $R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
-module.
$R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
-module. -
4.
 $k\operatorname {\mathrm {\mathbin {\widehat {\otimes }}}}_{R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}} N$
is of finite length in
$k\operatorname {\mathrm {\mathbin {\widehat {\otimes }}}}_{R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}} N$
is of finite length in
 ${\mathfrak C}(\mathscr O)$
.
${\mathfrak C}(\mathscr O)$
. -
5. The cosocle of N in
 ${\mathfrak C}(\mathscr O)$
is of finite length.
${\mathfrak C}(\mathscr O)$
is of finite length.
The equivalent conditions hold if N is finitely generated over
![]() for a compact open subgroup H of G.
for a compact open subgroup H of G.
Proof. (1) implies (2), since
![]() $\mathrm m$
is exact. (2) implies (3) by Corollary 6.4. Since
$\mathrm m$
is exact. (2) implies (3) by Corollary 6.4. Since
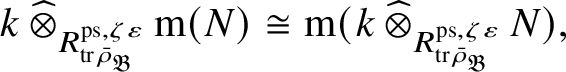 $$ \begin{align*} k\operatorname{\mathrm{\mathbin{\widehat{\otimes}}}}_{R^{\mathrm{ps}, \zeta\varepsilon}_{\operatorname{tr}\bar{\rho}_{\mathfrak B}}}\mathrm m(N)\cong \mathrm m( k\operatorname{\mathrm{\mathbin{\widehat{\otimes}}}}_{R^{\mathrm{ps}, \zeta\varepsilon}_{\operatorname{tr}\bar{\rho}_{\mathfrak B}}}N), \end{align*} $$
$$ \begin{align*} k\operatorname{\mathrm{\mathbin{\widehat{\otimes}}}}_{R^{\mathrm{ps}, \zeta\varepsilon}_{\operatorname{tr}\bar{\rho}_{\mathfrak B}}}\mathrm m(N)\cong \mathrm m( k\operatorname{\mathrm{\mathbin{\widehat{\otimes}}}}_{R^{\mathrm{ps}, \zeta\varepsilon}_{\operatorname{tr}\bar{\rho}_{\mathfrak B}}}N), \end{align*} $$
and the functor
![]() $\mathrm m$
is an antiequivalence, (3) implies (4). Let
$\mathrm m$
is an antiequivalence, (3) implies (4). Let
![]() $N \twoheadrightarrow \operatorname {\mathrm {cosoc}}(N)$
be the cosocle of N. Since the maximal ideal of
$N \twoheadrightarrow \operatorname {\mathrm {cosoc}}(N)$
be the cosocle of N. Since the maximal ideal of
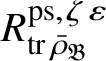 $R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
acts trivially on every semisimple object, the surjection factors through
$R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
acts trivially on every semisimple object, the surjection factors through
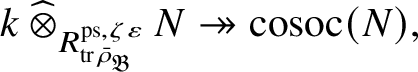 $$ \begin{align*} k\operatorname{\mathrm{\mathbin{\widehat{\otimes}}}}_{R^{\mathrm{ps}, \zeta\varepsilon}_{\operatorname{tr}\bar{\rho}_{\mathfrak B}}} N \twoheadrightarrow \operatorname{\mathrm{cosoc}}(N), \end{align*} $$
$$ \begin{align*} k\operatorname{\mathrm{\mathbin{\widehat{\otimes}}}}_{R^{\mathrm{ps}, \zeta\varepsilon}_{\operatorname{tr}\bar{\rho}_{\mathfrak B}}} N \twoheadrightarrow \operatorname{\mathrm{cosoc}}(N), \end{align*} $$
and so (4) implies (5). If
![]() $\operatorname {\mathrm {cosoc}}(N)$
is of finite length, then there is a surjection
$\operatorname {\mathrm {cosoc}}(N)$
is of finite length, then there is a surjection
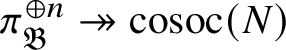 $\pi _{\mathfrak B}^{\oplus n} \twoheadrightarrow \operatorname {\mathrm {cosoc}}(N)$
for some
$\pi _{\mathfrak B}^{\oplus n} \twoheadrightarrow \operatorname {\mathrm {cosoc}}(N)$
for some
![]() $n\ge 1$
. Since
$n\ge 1$
. Since
![]() $P_{\mathfrak B}$
is projective, there is a map
$P_{\mathfrak B}$
is projective, there is a map
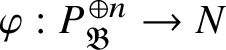 $\varphi : P_{\mathfrak B}^{\oplus n} \rightarrow N$
lifting
$\varphi : P_{\mathfrak B}^{\oplus n} \rightarrow N$
lifting
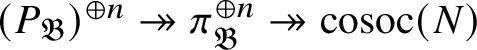 $(P_{\mathfrak B})^{\oplus n} \twoheadrightarrow \pi _{\mathfrak B}^{\oplus n} \twoheadrightarrow \operatorname {\mathrm {cosoc}}(N)$
. The cokernel of
$(P_{\mathfrak B})^{\oplus n} \twoheadrightarrow \pi _{\mathfrak B}^{\oplus n} \twoheadrightarrow \operatorname {\mathrm {cosoc}}(N)$
. The cokernel of
![]() $\varphi $
will have zero cosocle and hence
$\varphi $
will have zero cosocle and hence
![]() $\varphi $
is surjective, so that (5) implies (1).
$\varphi $
is surjective, so that (5) implies (1).
If N is finitely generated over
![]() , which we may assume to be pro-p, then
, which we may assume to be pro-p, then
![]() $ ((N/\varpi N)^{\vee } )^H$
is a finite-dimensional k-vector space, and hence the G-socle of
$ ((N/\varpi N)^{\vee } )^H$
is a finite-dimensional k-vector space, and hence the G-socle of
![]() $N^{\vee }$
is of finite length, which dually implies that (5) holds.
$N^{\vee }$
is of finite length, which dually implies that (5) holds.
Since every irreducible in
![]() $\mathfrak B$
is admissible, its Pontryagin dual is finitely generated over
$\mathfrak B$
is admissible, its Pontryagin dual is finitely generated over
![]() for any compact open subgroup H of G. It follows from Corollary 6.7(4) that
for any compact open subgroup H of G. It follows from Corollary 6.7(4) that
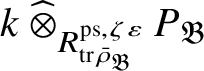 $k\operatorname {\mathrm {\mathbin {\widehat {\otimes }}}}_{R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}}P_{\mathfrak B}$
is also a finitely generated
$k\operatorname {\mathrm {\mathbin {\widehat {\otimes }}}}_{R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}}P_{\mathfrak B}$
is also a finitely generated
![]() -module. This implies that the assumptions made in [Reference Paškūnas39, Section 4] are satisfied with the category
-module. This implies that the assumptions made in [Reference Paškūnas39, Section 4] are satisfied with the category
![]() ${\mathfrak C}(\mathscr O)$
there equal to
${\mathfrak C}(\mathscr O)$
there equal to
![]() ${\mathfrak C}(\mathscr O)_{\mathfrak B}$
, and we will record some consequences.
${\mathfrak C}(\mathscr O)_{\mathfrak B}$
, and we will record some consequences.
6.2 Banach-space representations
The category
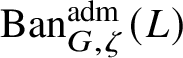 $\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)$
decomposes into a direct sum of categories [Reference Paškūnas39, Proposition 5.36]:
$\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)$
decomposes into a direct sum of categories [Reference Paškūnas39, Proposition 5.36]:
 $$ \begin{align} \operatorname{\mathrm{Ban}}^{\mathrm{adm}}_{G, \zeta}(L) \cong \bigoplus_{\mathfrak B \in \operatorname{\mathrm{Irr}}_{G, \zeta} / \sim} \operatorname{\mathrm{Ban}}^{\mathrm{adm}}_{G, \zeta}(L)_{\mathfrak B}, \end{align} $$
$$ \begin{align} \operatorname{\mathrm{Ban}}^{\mathrm{adm}}_{G, \zeta}(L) \cong \bigoplus_{\mathfrak B \in \operatorname{\mathrm{Irr}}_{G, \zeta} / \sim} \operatorname{\mathrm{Ban}}^{\mathrm{adm}}_{G, \zeta}(L)_{\mathfrak B}, \end{align} $$
where the objects of
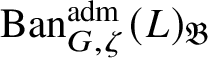 $\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)_{\mathfrak B}$
are those
$\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)_{\mathfrak B}$
are those
![]() $\Pi $
in
$\Pi $
in
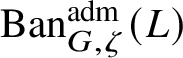 $\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)$
such that for every open bounded G-invariant lattice
$\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)$
such that for every open bounded G-invariant lattice
![]() $\Theta $
in
$\Theta $
in
![]() $\Pi $
, the irreducible subquotients of
$\Pi $
, the irreducible subquotients of
![]() $\Theta \otimes _{\mathscr O} k$
lie in
$\Theta \otimes _{\mathscr O} k$
lie in
![]() $\mathfrak B$
. This condition is equivalent to requiring that
$\mathfrak B$
. This condition is equivalent to requiring that
![]() $\Theta ^d$
be an object of
$\Theta ^d$
be an object of
![]() ${\mathfrak C}(\mathscr O)_{\mathfrak B}$
.
${\mathfrak C}(\mathscr O)_{\mathfrak B}$
.
As in the previous subsection, we fix a block
![]() $\mathfrak B$
consisting of absolutely irreducible representations. Let
$\mathfrak B$
consisting of absolutely irreducible representations. Let
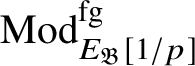 $\operatorname {\mathrm {Mod}}^{\mathrm {fg}}_{E_{\mathfrak B} [1/p ]}$
be the category of finitely generated right
$\operatorname {\mathrm {Mod}}^{\mathrm {fg}}_{E_{\mathfrak B} [1/p ]}$
be the category of finitely generated right
![]() $E_{\mathfrak B} [1/p ]$
-modules. The functor
$E_{\mathfrak B} [1/p ]$
-modules. The functor
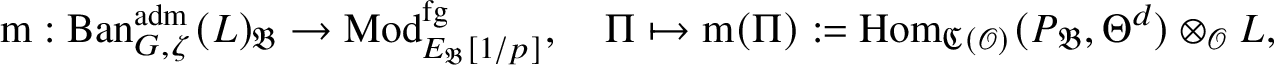 $$ \begin{align*} \mathrm m: \operatorname{\mathrm{Ban}}^{\mathrm{adm}}_{G, \zeta}(L)_{\mathfrak B} \rightarrow \operatorname{\mathrm{Mod}}^{\mathrm{fg}}_{E_{\mathfrak B}[1/p]}, \quad \Pi \mapsto \mathrm m(\Pi):= \operatorname{\mathrm{Hom}}_{{\mathfrak C}(\mathscr O)}(P_{\mathfrak B},\Theta^d)\otimes_{\mathscr O} L, \end{align*} $$
$$ \begin{align*} \mathrm m: \operatorname{\mathrm{Ban}}^{\mathrm{adm}}_{G, \zeta}(L)_{\mathfrak B} \rightarrow \operatorname{\mathrm{Mod}}^{\mathrm{fg}}_{E_{\mathfrak B}[1/p]}, \quad \Pi \mapsto \mathrm m(\Pi):= \operatorname{\mathrm{Hom}}_{{\mathfrak C}(\mathscr O)}(P_{\mathfrak B},\Theta^d)\otimes_{\mathscr O} L, \end{align*} $$
where
![]() $\Theta $
is any open bounded G-invariant lattice in
$\Theta $
is any open bounded G-invariant lattice in
![]() $\Pi $
and is exact, contravariant and fully faithful by [Reference Paškūnas39, Lemma 4.45]. Moreover, it induces an antiequivalence of categories
$\Pi $
and is exact, contravariant and fully faithful by [Reference Paškūnas39, Lemma 4.45]. Moreover, it induces an antiequivalence of categories
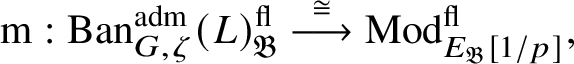 $$ \begin{align} \mathrm m: \operatorname{\mathrm{Ban}}^{\mathrm{adm}}_{G, \zeta}(L)_{\mathfrak B}^{\mathrm{fl}} \overset{\cong}{\longrightarrow} \operatorname{\mathrm{Mod}}^{\mathrm{fl}}_{E_{\mathfrak B}[1/p]}, \end{align} $$
$$ \begin{align} \mathrm m: \operatorname{\mathrm{Ban}}^{\mathrm{adm}}_{G, \zeta}(L)_{\mathfrak B}^{\mathrm{fl}} \overset{\cong}{\longrightarrow} \operatorname{\mathrm{Mod}}^{\mathrm{fl}}_{E_{\mathfrak B}[1/p]}, \end{align} $$
where the superscript ‘
![]() $\mathrm {fl}$
’ indicates the subcategories of objects of finite length in the respective categories [Reference Paškūnas39, Theorem 4.34]. We write antiequivalence instead of equivalence to indicate that
$\mathrm {fl}$
’ indicates the subcategories of objects of finite length in the respective categories [Reference Paškūnas39, Theorem 4.34]. We write antiequivalence instead of equivalence to indicate that
![]() $\mathrm m$
is contravariant.
$\mathrm m$
is contravariant.
If
![]() $\mathfrak m$
is a maximal ideal of
$\mathfrak m$
is a maximal ideal of
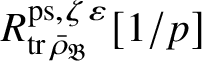 $R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}} [1/p ]$
, then we let
$R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}} [1/p ]$
, then we let
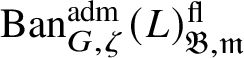 $\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)_{\mathfrak B, \mathfrak m}^{\mathrm {fl}}$
be the full subcategory of
$\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)_{\mathfrak B, \mathfrak m}^{\mathrm {fl}}$
be the full subcategory of
 $\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)$
consisting of finite-length Banach-space representations, which are killed by some power of
$\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)$
consisting of finite-length Banach-space representations, which are killed by some power of
![]() $\mathfrak m$
. The functor
$\mathfrak m$
. The functor
![]() $\mathrm m$
induces an antiequivalence between this category and the category of
$\mathrm m$
induces an antiequivalence between this category and the category of
![]() $E_{\mathfrak B} [1/p ]$
-modules of finite length, which are killed by a power of
$E_{\mathfrak B} [1/p ]$
-modules of finite length, which are killed by a power of
![]() $\mathfrak m$
. The Chinese remainder theorem [Reference Paškūnas39, Theorem 4.36] implies that we have an equivalence of categories
$\mathfrak m$
. The Chinese remainder theorem [Reference Paškūnas39, Theorem 4.36] implies that we have an equivalence of categories
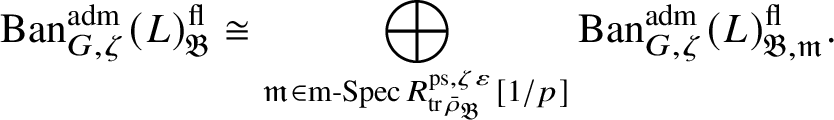 $$ \begin{align} \operatorname{\mathrm{Ban}}^{\mathrm{adm}}_{G, \zeta}(L)_{\mathfrak B}^{\mathrm{fl}}\cong \bigoplus_{\mathfrak m \in \operatorname{\mathrm{m-Spec}} R^{\mathrm{ps}, \zeta\varepsilon}_{\operatorname{tr}\bar{\rho}_{\mathfrak B}}[1/p]} \operatorname{\mathrm{Ban}}^{\mathrm{adm}}_{G, \zeta}(L)_{\mathfrak B, \mathfrak m}^{\mathrm{fl}}. \end{align} $$
$$ \begin{align} \operatorname{\mathrm{Ban}}^{\mathrm{adm}}_{G, \zeta}(L)_{\mathfrak B}^{\mathrm{fl}}\cong \bigoplus_{\mathfrak m \in \operatorname{\mathrm{m-Spec}} R^{\mathrm{ps}, \zeta\varepsilon}_{\operatorname{tr}\bar{\rho}_{\mathfrak B}}[1/p]} \operatorname{\mathrm{Ban}}^{\mathrm{adm}}_{G, \zeta}(L)_{\mathfrak B, \mathfrak m}^{\mathrm{fl}}. \end{align} $$
Corollary 6.8. If
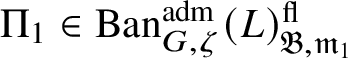 $\Pi _1\in \operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)_{\mathfrak B, \mathfrak m_1}^{\mathrm {fl}}$
and
$\Pi _1\in \operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)_{\mathfrak B, \mathfrak m_1}^{\mathrm {fl}}$
and
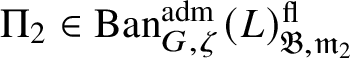 $\Pi _2\in \operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)_{\mathfrak B, \mathfrak m_2}^{\mathrm {fl}}$
for distinct maximal ideals
$\Pi _2\in \operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)_{\mathfrak B, \mathfrak m_2}^{\mathrm {fl}}$
for distinct maximal ideals
![]() $\mathfrak m_1$
and
$\mathfrak m_1$
and
![]() $\mathfrak m_2$
of
$\mathfrak m_2$
of
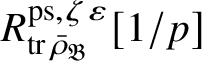 $R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}} [1/p ]$
, then the Yoneda
$R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}} [1/p ]$
, then the Yoneda
![]() $\operatorname {\mathrm {Ext}}^i(\Pi _1, \Pi _2)$
computed in
$\operatorname {\mathrm {Ext}}^i(\Pi _1, \Pi _2)$
computed in
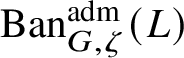 $\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)$
vanish for all
$\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)$
vanish for all
![]() $i\ge 0$
.
$i\ge 0$
.
Proof. It follows from formula (21) that the assertion holds for the Yoneda
![]() $\operatorname {\mathrm {Ext}}$
groups computed in
$\operatorname {\mathrm {Ext}}$
groups computed in
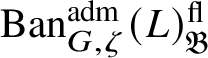 $\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)_{\mathfrak B}^{\mathrm {fl}}$
. It follows from [Reference Paškūnas39, Proposition 4.46, Corollary 4.48] that these coincide with Yoneda
$\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)_{\mathfrak B}^{\mathrm {fl}}$
. It follows from [Reference Paškūnas39, Proposition 4.46, Corollary 4.48] that these coincide with Yoneda
![]() $\operatorname {\mathrm {Ext}}$
groups computed in
$\operatorname {\mathrm {Ext}}$
groups computed in
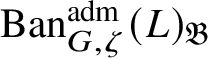 $\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)_{\mathfrak B}$
, which is a direct summand of
$\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)_{\mathfrak B}$
, which is a direct summand of
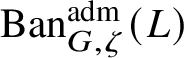 $\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)$
(see formaul (19)).
$\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)$
(see formaul (19)).
We will determine the set of isomorphism classes
![]() $\operatorname {\mathrm {Irr}}(\mathfrak m, L')$
of irreducible objects in
$\operatorname {\mathrm {Irr}}(\mathfrak m, L')$
of irreducible objects in
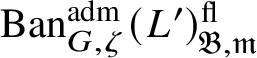 $\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L')_{\mathfrak B, \mathfrak m}^{\mathrm {fl}}$
for a sufficiently large finite extension
$\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L')_{\mathfrak B, \mathfrak m}^{\mathrm {fl}}$
for a sufficiently large finite extension
![]() $L'$
of L. Recall that
$L'$
of L. Recall that
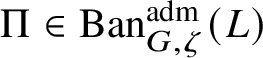 $\Pi \in \operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)$
is absolutely irreducible if
$\Pi \in \operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)$
is absolutely irreducible if
![]() $\Pi \otimes _L L'$
is irreducible in
$\Pi \otimes _L L'$
is irreducible in
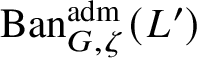 $\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L')$
for all finite extensions
$\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L')$
for all finite extensions
![]() $L'$
of L. It follows from formula (20) that for such
$L'$
of L. It follows from formula (20) that for such
![]() $\Pi $
, Schur’s lemma holds, so that
$\Pi $
, Schur’s lemma holds, so that
![]() $\operatorname {\mathrm {End}}^{\mathrm {cont}}_G(\Pi )=L$
. This result is also proved in [Reference Dospinescu and Schraen26] in a much more general setting. It follows from formula (20) that irreducibles in
$\operatorname {\mathrm {End}}^{\mathrm {cont}}_G(\Pi )=L$
. This result is also proved in [Reference Dospinescu and Schraen26] in a much more general setting. It follows from formula (20) that irreducibles in
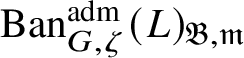 $\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)_{\mathfrak B, \mathfrak m}$
correspond to irreducible modules of the algebra
$\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)_{\mathfrak B, \mathfrak m}$
correspond to irreducible modules of the algebra
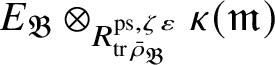 $E_{\mathfrak B} \otimes _{R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}} \kappa (\mathfrak m)$
. Corollary 6.4 implies that this algebra is finite-dimensional over
$E_{\mathfrak B} \otimes _{R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}} \kappa (\mathfrak m)$
. Corollary 6.4 implies that this algebra is finite-dimensional over
![]() $\kappa (\mathfrak m)$
, and thus
$\kappa (\mathfrak m)$
, and thus
![]() $\operatorname {\mathrm {Irr}}(\mathfrak m, L')$
is finite for every finite extension
$\operatorname {\mathrm {Irr}}(\mathfrak m, L')$
is finite for every finite extension
![]() $L'$
of L, and there is a finite extension
$L'$
of L, and there is a finite extension
![]() $L'$
of L such that all
$L'$
of L such that all
![]() $\Pi $
in
$\Pi $
in
![]() $\operatorname {\mathrm {Irr}}(\mathfrak m, L')$
are absolutely irreducible.
$\operatorname {\mathrm {Irr}}(\mathfrak m, L')$
are absolutely irreducible.
Proposition 6.9. Let
![]() $L'$
be a finite extension of L and let
$L'$
be a finite extension of L and let
![]() $\Pi $
be absolutely irreducible in
$\Pi $
be absolutely irreducible in
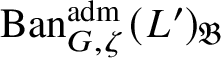 $\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L')_{\mathfrak B}$
. Let
$\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L')_{\mathfrak B}$
. Let
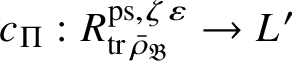 $c_{\Pi }: R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}\rightarrow L'$
be the composition
$c_{\Pi }: R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}\rightarrow L'$
be the composition
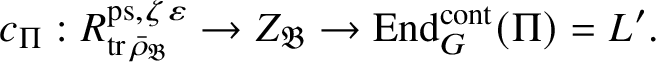 $$ \begin{align*} c_{\Pi}: R^{\mathrm{ps}, \zeta\varepsilon}_{\operatorname{tr}\bar{\rho}_{\mathfrak B}}\rightarrow Z_{\mathfrak B}\rightarrow \operatorname{\mathrm{End}}^{\mathrm{cont}}_G(\Pi)=L'. \end{align*} $$
$$ \begin{align*} c_{\Pi}: R^{\mathrm{ps}, \zeta\varepsilon}_{\operatorname{tr}\bar{\rho}_{\mathfrak B}}\rightarrow Z_{\mathfrak B}\rightarrow \operatorname{\mathrm{End}}^{\mathrm{cont}}_G(\Pi)=L'. \end{align*} $$
Then one of the following holds:
-
1. If
 $\Pi $
is a subquotient of
$\Pi $
is a subquotient of
 $ (\operatorname {\mathrm {Ind}}_B^G \psi _1\otimes \psi _2 \varepsilon ^{-1} )_{\mathrm {cont}}$
for some unitary characters
$ (\operatorname {\mathrm {Ind}}_B^G \psi _1\otimes \psi _2 \varepsilon ^{-1} )_{\mathrm {cont}}$
for some unitary characters
 $\psi _1, \psi _2: \mathbb {Q}_p^{\times } \rightarrow (L')^{\times }$
, then
$\psi _1, \psi _2: \mathbb {Q}_p^{\times } \rightarrow (L')^{\times }$
, then
 $T_{c_{\Pi }}= \psi _1+\psi _2$
;
$T_{c_{\Pi }}= \psi _1+\psi _2$
; -
2. otherwise,
 $\check {\mathbf {V}}(\Pi )$
is a
$\check {\mathbf {V}}(\Pi )$
is a
 $2$
-dimensional absolutely irreducible
$2$
-dimensional absolutely irreducible
 $L'$
-representation of
$L'$
-representation of
 $\mathscr G_{\mathbb {Q}_p}$
,
$\mathscr G_{\mathbb {Q}_p}$
,
 $\det \check {\mathbf {V}}(\Pi )= \zeta \varepsilon $
and
$\det \check {\mathbf {V}}(\Pi )= \zeta \varepsilon $
and
 $T_{c_{\Pi }}= \operatorname {tr} \check {\mathbf {V}}(\Pi )$
,
$T_{c_{\Pi }}= \operatorname {tr} \check {\mathbf {V}}(\Pi )$
,
where
![]() $T_{c_{\Pi }}$
is the specialisation of the universal pseudorepresentation
$T_{c_{\Pi }}$
is the specialisation of the universal pseudorepresentation
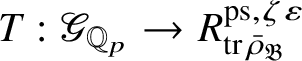 $T: \mathscr G_{\mathbb {Q}_p}\rightarrow R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
along
$T: \mathscr G_{\mathbb {Q}_p}\rightarrow R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
along
![]() $c_{\Pi }$
.
$c_{\Pi }$
.
Proof. Let
![]() $\Psi $
be the unitary principal series representation in (1). If
$\Psi $
be the unitary principal series representation in (1). If
![]() $\psi _1\neq \psi _2\varepsilon ^{-1}$
, then
$\psi _1\neq \psi _2\varepsilon ^{-1}$
, then
![]() $\Psi ^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )}=0$
, and by looking at its reduction modulo p one may conclude that
$\Psi ^{\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )}=0$
, and by looking at its reduction modulo p one may conclude that
![]() $\Psi $
is absolutely irreducible. If
$\Psi $
is absolutely irreducible. If
![]() $\psi _1= \psi _2\varepsilon $
, then
$\psi _1= \psi _2\varepsilon $
, then
![]() $\Psi $
is a nonsplit extension
$\Psi $
is a nonsplit extension
where
![]() $\widehat {\operatorname {\mathrm {Sp}}}$
is the universal unitary completion of the smooth Steinberg representation. This representation is absolutely irreducible, since its mod p reduction is. In both cases,
$\widehat {\operatorname {\mathrm {Sp}}}$
is the universal unitary completion of the smooth Steinberg representation. This representation is absolutely irreducible, since its mod p reduction is. In both cases,
![]() $\operatorname {\mathrm {End}}^{\mathrm {cont}}_G(\Psi )=L'$
, and thus
$\operatorname {\mathrm {End}}^{\mathrm {cont}}_G(\Psi )=L'$
, and thus
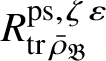 $R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
acts on all irreducible subquotients of
$R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
acts on all irreducible subquotients of
![]() $\Psi $
via the same homomorphism
$\Psi $
via the same homomorphism
![]() $c_{\Psi }$
. Since
$c_{\Psi }$
. Since
![]() $\check {\mathbf {V}}(\Psi )= \psi _2$
, regarded as a representation of
$\check {\mathbf {V}}(\Psi )= \psi _2$
, regarded as a representation of
![]() $\mathscr G_{\mathbb {Q}_p}$
via the class field theory,
$\mathscr G_{\mathbb {Q}_p}$
via the class field theory,
![]() $g + \varepsilon \zeta (g) g^{-1}$
acts on it via the scalar
$g + \varepsilon \zeta (g) g^{-1}$
acts on it via the scalar
![]() $\psi _2(g)+ \psi _2 (g^{-1} )\varepsilon \zeta (g) = \psi _2(g) + \psi _1(g)$
for all
$\psi _2(g)+ \psi _2 (g^{-1} )\varepsilon \zeta (g) = \psi _2(g) + \psi _1(g)$
for all
![]() $g\in \mathscr G_{\mathbb {Q}_p}$
. Proposition 6.6 implies that the specialisation of T at
$g\in \mathscr G_{\mathbb {Q}_p}$
. Proposition 6.6 implies that the specialisation of T at
![]() $c_{\Psi }$
is the character
$c_{\Psi }$
is the character
![]() $\psi _1+\psi _2$
.
$\psi _1+\psi _2$
.
If we are not in part (1), then [Reference Colmez, Dospinescu and Paškūnas21, Corollary 1.2, Theorem 1.9] imply that
![]() $\check {\mathbf {V}}(\Pi )$
is absolutely irreducible
$\check {\mathbf {V}}(\Pi )$
is absolutely irreducible
![]() $2$
-dimensional and
$2$
-dimensional and
![]() $\det \check {\mathbf {V}}(\Pi )= \zeta \varepsilon $
. A calculation with
$\det \check {\mathbf {V}}(\Pi )= \zeta \varepsilon $
. A calculation with
![]() $2\times 2$
matrices implies that
$2\times 2$
matrices implies that
![]() $g+ \zeta \varepsilon (g) g^{-1}$
acts on
$g+ \zeta \varepsilon (g) g^{-1}$
acts on
![]() $\check {\mathbf {V}}(\Pi )$
by a scalar
$\check {\mathbf {V}}(\Pi )$
by a scalar
![]() $ (\operatorname {tr} \check {\mathbf {V}}(\Pi ) )(g)$
. Proposition 6.6 implies that the specialisation of T at
$ (\operatorname {tr} \check {\mathbf {V}}(\Pi ) )(g)$
. Proposition 6.6 implies that the specialisation of T at
![]() $c_{\Psi }$
is the character
$c_{\Psi }$
is the character
![]() $\operatorname {tr} \check {\mathbf {V}}(\Pi )$
.
$\operatorname {tr} \check {\mathbf {V}}(\Pi )$
.
Corollary 6.10. Let
![]() $L'$
be a finite extension of L and let
$L'$
be a finite extension of L and let
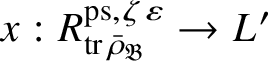 $x: R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}\rightarrow L'$
be an
$x: R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}\rightarrow L'$
be an
![]() $\mathscr O$
-algebra homomorphism. If
$\mathscr O$
-algebra homomorphism. If
![]() $T_x= \psi _1+ \psi _2$
for characters
$T_x= \psi _1+ \psi _2$
for characters
![]() $\psi _1, \psi _2:\mathscr G_{\mathbb {Q}_p} \rightarrow (L')^{\times }$
, then one of the following holds:
$\psi _1, \psi _2:\mathscr G_{\mathbb {Q}_p} \rightarrow (L')^{\times }$
, then one of the following holds:
-
1. If
 $\psi _1\psi _2^{-1}=\mathbf 1$
, then
$\psi _1\psi _2^{-1}=\mathbf 1$
, then
 $\operatorname {\mathrm {Irr}}(\mathfrak m_x, L')= \{ (\operatorname {\mathrm {Ind}}_B^G \mathbf 1\otimes \varepsilon ^{-1} )_{\mathrm {cont}}\otimes \psi _1\circ \det \}$
.
$\operatorname {\mathrm {Irr}}(\mathfrak m_x, L')= \{ (\operatorname {\mathrm {Ind}}_B^G \mathbf 1\otimes \varepsilon ^{-1} )_{\mathrm {cont}}\otimes \psi _1\circ \det \}$
. -
2. If
 $\psi _1 \psi _2^{-1}= \varepsilon ^{\pm 1}$
, then
$\psi _1 \psi _2^{-1}= \varepsilon ^{\pm 1}$
, then
 $\operatorname {\mathrm {Irr}}(\mathfrak m_x, L')= \{ \mathbf 1, \widehat {\operatorname {\mathrm {Sp}}}, (\operatorname {\mathrm {Ind}}_B^G \varepsilon \otimes \varepsilon ^{-1} )_{\mathrm {cont}} \} \otimes \psi \circ \det $
.
$\operatorname {\mathrm {Irr}}(\mathfrak m_x, L')= \{ \mathbf 1, \widehat {\operatorname {\mathrm {Sp}}}, (\operatorname {\mathrm {Ind}}_B^G \varepsilon \otimes \varepsilon ^{-1} )_{\mathrm {cont}} \} \otimes \psi \circ \det $
. -
3. If
 $\psi _1 \psi _2^{-1}\neq \varepsilon ^{\pm 1}, \mathbf 1$
, then
$\psi _1 \psi _2^{-1}\neq \varepsilon ^{\pm 1}, \mathbf 1$
, then  $$ \begin{align*} \operatorname{\mathrm{Irr}}(\mathfrak m_x, L')= \{ (\operatorname{\mathrm{Ind}}_B^G \psi_1\otimes \psi_2 \varepsilon^{-1})_{\mathrm{cont}}, (\operatorname{\mathrm{Ind}}_B^G \psi_2\otimes \psi_1 \varepsilon^{-1})_{\mathrm{cont}}\}, \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Irr}}(\mathfrak m_x, L')= \{ (\operatorname{\mathrm{Ind}}_B^G \psi_1\otimes \psi_2 \varepsilon^{-1})_{\mathrm{cont}}, (\operatorname{\mathrm{Ind}}_B^G \psi_2\otimes \psi_1 \varepsilon^{-1})_{\mathrm{cont}}\}, \end{align*} $$
where we consider
![]() $\psi _1$
and
$\psi _1$
and
![]() $\psi _2$
as unitary characters of
$\psi _2$
as unitary characters of
![]() $\mathbb {Q}_p^{\times }$
via the class field theory and
$\mathbb {Q}_p^{\times }$
via the class field theory and
![]() $\psi $
in (2) is either
$\psi $
in (2) is either
![]() $\psi _1$
or
$\psi _1$
or
![]() $\psi _2$
.
$\psi _2$
.
Proof. We have explained in the course of the proof of Proposition 6.9 that the representations listed in this corollary are absolutely irreducible and are contained in
![]() $\operatorname {\mathrm {Irr}}(\mathfrak m_x, L')$
. Moreover, using the functor of ordinary parts one may show that they are pairwise nonisomorphic.
$\operatorname {\mathrm {Irr}}(\mathfrak m_x, L')$
. Moreover, using the functor of ordinary parts one may show that they are pairwise nonisomorphic.
We will show that the list is exhaustive. We may enlarge
![]() $L'$
so that all
$L'$
so that all
![]() $\Pi \in \operatorname {\mathrm {Irr}}(\mathfrak m_x, L')$
are absolutely irreducible. Since
$\Pi \in \operatorname {\mathrm {Irr}}(\mathfrak m_x, L')$
are absolutely irreducible. Since
![]() $c_{\Pi }=x$
, we cannot be in part (2) of Proposition 6.9, and thus we must be in part (1), and hence
$c_{\Pi }=x$
, we cannot be in part (2) of Proposition 6.9, and thus we must be in part (1), and hence
![]() $\Pi $
is already in our list.
$\Pi $
is already in our list.
Proposition 6.11. Let
![]() $L'$
be a finite extension of L and let
$L'$
be a finite extension of L and let
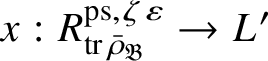 $x: R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}\rightarrow L'$
be an
$x: R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}\rightarrow L'$
be an
![]() $\mathscr O$
-algebra homomorphism. If
$\mathscr O$
-algebra homomorphism. If
![]() $T_x =\operatorname {tr} \rho $
, where
$T_x =\operatorname {tr} \rho $
, where
![]() $\rho : \mathscr G_{\mathbb {Q}_p}\rightarrow \operatorname {\mathrm {GL}}_2(L')$
is absolutely irreducible, then
$\rho : \mathscr G_{\mathbb {Q}_p}\rightarrow \operatorname {\mathrm {GL}}_2(L')$
is absolutely irreducible, then
![]() $\operatorname {\mathrm {Irr}}(\mathfrak m_x, L')=\{\Pi \}$
, with
$\operatorname {\mathrm {Irr}}(\mathfrak m_x, L')=\{\Pi \}$
, with
![]() $\Pi $
absolutely irreducible nonordinary and
$\Pi $
absolutely irreducible nonordinary and
![]() $\check {\mathbf {V}}(\Pi )\cong \rho $
.
$\check {\mathbf {V}}(\Pi )\cong \rho $
.
Proof. It follows from [Reference Colmez, Dospinescu and Paškūnas21, Theorem 1.1] that such
![]() $\Pi $
exists. We may enlarge
$\Pi $
exists. We may enlarge
![]() $L'$
so that all
$L'$
so that all
![]() $\Pi ' \in \operatorname {\mathrm {Irr}}(\mathfrak m_x, L')$
are absolutely irreducible. Since
$\Pi ' \in \operatorname {\mathrm {Irr}}(\mathfrak m_x, L')$
are absolutely irreducible. Since
![]() $c_{\Pi '}=x$
, we cannot be in part (1) of Proposition 6.9; thus we must be in part (2), and
$c_{\Pi '}=x$
, we cannot be in part (1) of Proposition 6.9; thus we must be in part (2), and
![]() $\operatorname {tr} \check {\mathbf {V}}(\Pi )=\operatorname {tr} \check {\mathbf {V}}(\Pi ')$
. Since both
$\operatorname {tr} \check {\mathbf {V}}(\Pi )=\operatorname {tr} \check {\mathbf {V}}(\Pi ')$
. Since both
![]() $\check {\mathbf {V}}(\Pi ')$
and
$\check {\mathbf {V}}(\Pi ')$
and
![]() $\check {\mathbf {V}}(\Pi )$
are absolutely irreducible, we deduce that
$\check {\mathbf {V}}(\Pi )$
are absolutely irreducible, we deduce that
![]() $\check {\mathbf {V}}(\Pi )\cong \check {\mathbf {V}}(\Pi ')$
, and [Reference Colmez, Dospinescu and Paškūnas21, Theorem 1.8] implies that
$\check {\mathbf {V}}(\Pi )\cong \check {\mathbf {V}}(\Pi ')$
, and [Reference Colmez, Dospinescu and Paškūnas21, Theorem 1.8] implies that
![]() $\Pi \cong \Pi '$
.
$\Pi \cong \Pi '$
.
6.3 The centre
We fix a block
![]() $\mathfrak B$
as in the previous section and explore the relation between
$\mathfrak B$
as in the previous section and explore the relation between
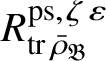 $R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
and
$R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
and
![]() $Z_{\mathfrak B}$
. So far we have constructed a finite map
$Z_{\mathfrak B}$
. So far we have constructed a finite map
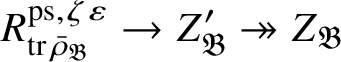 $$ \begin{align} R^{\mathrm{ps}, \zeta\varepsilon}_{\operatorname{tr}\bar{\rho}_{\mathfrak B}}\rightarrow Z_{\mathfrak B}'\twoheadrightarrow Z_{\mathfrak B} \end{align} $$
$$ \begin{align} R^{\mathrm{ps}, \zeta\varepsilon}_{\operatorname{tr}\bar{\rho}_{\mathfrak B}}\rightarrow Z_{\mathfrak B}'\twoheadrightarrow Z_{\mathfrak B} \end{align} $$
(Theorem 6.3 and Corollary 4.16). We show in Corollary A.14 that
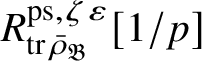 $R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}} [1/p ]$
is normal, and we know by [Reference Chenevier17, Theorem 2.1] that it is equidimensional, and the locus corresponding to absolutely irreducible pseudorepresentations is Zariski dense in
$R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}} [1/p ]$
is normal, and we know by [Reference Chenevier17, Theorem 2.1] that it is equidimensional, and the locus corresponding to absolutely irreducible pseudorepresentations is Zariski dense in
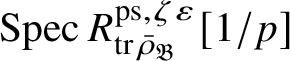 $\operatorname {\mathrm {Spec}} R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}} [1/p ]$
.
$\operatorname {\mathrm {Spec}} R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}} [1/p ]$
.
Proposition 6.12. Let
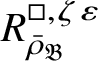 $R^{\square , \zeta \varepsilon }_{\bar {\rho }_{\mathfrak B}}$
be the universal framed deformation ring of
$R^{\square , \zeta \varepsilon }_{\bar {\rho }_{\mathfrak B}}$
be the universal framed deformation ring of
![]() $\bar {\rho }_{\mathfrak B}$
with fixed determinant
$\bar {\rho }_{\mathfrak B}$
with fixed determinant
![]() $\zeta \varepsilon $
, let S be its maximal
$\zeta \varepsilon $
, let S be its maximal
![]() $\mathscr O$
-torsion-free quotient and let
$\mathscr O$
-torsion-free quotient and let
![]() $V_S$
be a free S-module of rank
$V_S$
be a free S-module of rank
![]() $2$
with
$2$
with
![]() $\mathscr G_{\mathbb {Q}_p}$
-action induced by the universal deformation
$\mathscr G_{\mathbb {Q}_p}$
-action induced by the universal deformation
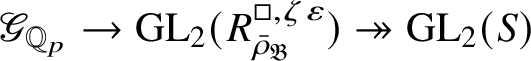 $\mathscr G_{\mathbb {Q}_p}\rightarrow \operatorname {\mathrm {GL}}_2 ( R^{\square , \zeta \varepsilon }_{\bar {\rho }_{\mathfrak B}} )\twoheadrightarrow \operatorname {\mathrm {GL}}_2(S)$
. There is N in
$\mathscr G_{\mathbb {Q}_p}\rightarrow \operatorname {\mathrm {GL}}_2 ( R^{\square , \zeta \varepsilon }_{\bar {\rho }_{\mathfrak B}} )\twoheadrightarrow \operatorname {\mathrm {GL}}_2(S)$
. There is N in
![]() ${\mathfrak C}(\mathscr O)$
with a continuous action of S, which commutes with the action of G, such that we have an isomorphism of
${\mathfrak C}(\mathscr O)$
with a continuous action of S, which commutes with the action of G, such that we have an isomorphism of
![]() $S [\mathscr G_{\mathbb {Q}_p} ]$
-modules
$S [\mathscr G_{\mathbb {Q}_p} ]$
-modules
![]() $\check {\mathbf {V}}(N)\cong V_{S}$
.
$\check {\mathbf {V}}(N)\cong V_{S}$
.
Proof. If
![]() $x\in \operatorname {\mathrm {m-Spec}} S [1/p ]$
, then the specialisation of
$x\in \operatorname {\mathrm {m-Spec}} S [1/p ]$
, then the specialisation of
![]() $V_S$
at x lies in the image of
$V_S$
at x lies in the image of
![]() $\check {\mathbf {V}}$
by [Reference Colmez, Dospinescu and Paškūnas22, Theorem 10.1]. Since
$\check {\mathbf {V}}$
by [Reference Colmez, Dospinescu and Paškūnas22, Theorem 10.1]. Since
![]() $S [1/p ]$
is reduced (Propositions A.9 and A.13) and Jacobson, such points will be dense, and the existence of such N follows from [Reference Colmez19, Theorem II.3.3].
$S [1/p ]$
is reduced (Propositions A.9 and A.13) and Jacobson, such points will be dense, and the existence of such N follows from [Reference Colmez19, Theorem II.3.3].
The subscript ‘
![]() $\mathrm {tf}$
’ will indicate the maximal
$\mathrm {tf}$
’ will indicate the maximal
![]() $\mathscr O$
-torsion-free quotient.
$\mathscr O$
-torsion-free quotient.
Theorem 6.13. The surjection
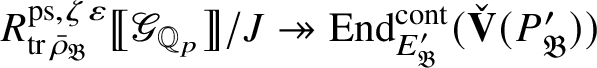 in Theorem 6.3 identifies
in Theorem 6.3 identifies
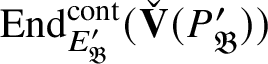 $\operatorname {\mathrm {End}}_{E_{\mathfrak B}'}^{\mathrm {cont}} (\check {\mathbf {V}} (P_{\mathfrak B}' ) )$
with
$\operatorname {\mathrm {End}}_{E_{\mathfrak B}'}^{\mathrm {cont}} (\check {\mathbf {V}} (P_{\mathfrak B}' ) )$
with
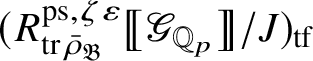 . In particular, map (22) induces an isomorphism
. In particular, map (22) induces an isomorphism
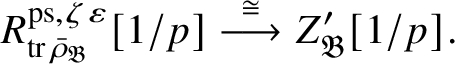 $$ \begin{align} R^{\mathrm{ps}, \zeta\varepsilon}_{\operatorname{tr}\bar{\rho}_{\mathfrak B}}[1/p]\overset{\cong}{\longrightarrow} Z_{\mathfrak B}'[1/p]. \end{align} $$
$$ \begin{align} R^{\mathrm{ps}, \zeta\varepsilon}_{\operatorname{tr}\bar{\rho}_{\mathfrak B}}[1/p]\overset{\cong}{\longrightarrow} Z_{\mathfrak B}'[1/p]. \end{align} $$
Moreover, if
![]() $p\neq 2$
, then
$p\neq 2$
, then
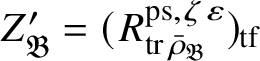 $Z_{\mathfrak B}'= (R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}} )_{\mathrm {tf}}$
, and if
$Z_{\mathfrak B}'= (R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}} )_{\mathrm {tf}}$
, and if
![]() $p=2$
, then the cokernel of map (22) is killed by
$p=2$
, then the cokernel of map (22) is killed by
![]() $2$
.
$2$
.
Proof. As already explained in the proof of Proposition 4.3, projective objects in
![]() ${\mathfrak C}(\mathscr O)$
are also projective in the category of compact
${\mathfrak C}(\mathscr O)$
are also projective in the category of compact
![]() -modules, where
-modules, where
![]() $K'$
is an open pro-p subgroup of
$K'$
is an open pro-p subgroup of
![]() $\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )$
intersecting Z trivially, and thus are
$\operatorname {\mathrm {SL}}_2 (\mathbb {Q}_p )$
intersecting Z trivially, and thus are
![]() $\mathscr O$
-torsion-free. Hence,
$\mathscr O$
-torsion-free. Hence,
![]() $P_{\mathfrak B}'$
is
$P_{\mathfrak B}'$
is
![]() $\mathscr O$
-torsion-free. Since
$\mathscr O$
-torsion-free. Since
![]() $E_{\mathfrak B}'$
and
$E_{\mathfrak B}'$
and
![]() $Z_{\mathfrak B}'$
act faithfully on
$Z_{\mathfrak B}'$
act faithfully on
![]() $P_{\mathfrak B}'$
, we deduce that both rings are
$P_{\mathfrak B}'$
, we deduce that both rings are
![]() $\mathscr O$
-torsion-free. Since
$\mathscr O$
-torsion-free. Since
 $\operatorname {\mathrm {End}}_{E_{\mathfrak B}'}^{\mathrm {cont}} (\check {\mathbf {V}} (P_{\mathfrak B}' ) )$
is either
$\operatorname {\mathrm {End}}_{E_{\mathfrak B}'}^{\mathrm {cont}} (\check {\mathbf {V}} (P_{\mathfrak B}' ) )$
is either
![]() $ (E_{\mathfrak B}' )^{\mathrm {op}}$
or
$ (E_{\mathfrak B}' )^{\mathrm {op}}$
or
![]() $M_2 (E_{\mathfrak B}' )$
by Proposition 4.18, we deduce that the map in Theorem 6.3 factors through
$M_2 (E_{\mathfrak B}' )$
by Proposition 4.18, we deduce that the map in Theorem 6.3 factors through
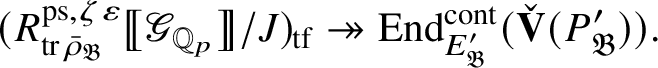
If a lies in the kernel of this map, then it will kill
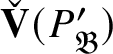 $\check {\mathbf {V}} (P_{\mathfrak B}' )$
and hence
$\check {\mathbf {V}} (P_{\mathfrak B}' )$
and hence
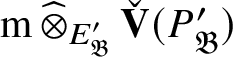 $\mathrm m\operatorname {\mathrm {\mathbin {\widehat {\otimes }}}}_{E_{\mathfrak B}'} \check {\mathbf {V}} (P_{\mathfrak B}' )$
for all compact right
$\mathrm m\operatorname {\mathrm {\mathbin {\widehat {\otimes }}}}_{E_{\mathfrak B}'} \check {\mathbf {V}} (P_{\mathfrak B}' )$
for all compact right
![]() $E_{\mathfrak B}'$
-modules. Thus a will kill all objects in the essential image of
$E_{\mathfrak B}'$
-modules. Thus a will kill all objects in the essential image of
![]() $\check {\mathbf {V}}$
, and it will therefore also kill the representation
$\check {\mathbf {V}}$
, and it will therefore also kill the representation
![]() $V_S$
defined in Proposition 6.12.
$V_S$
defined in Proposition 6.12.
It follows from Propositions A.9 and A.13 that the ring
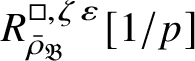 $R^{\square , \zeta \varepsilon }_{\bar {\rho }_{\mathfrak B}} [1/p ]$
is normal and the absolutely irreducible locus is dense in
$R^{\square , \zeta \varepsilon }_{\bar {\rho }_{\mathfrak B}} [1/p ]$
is normal and the absolutely irreducible locus is dense in
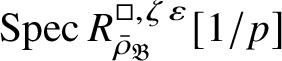 $\operatorname {\mathrm {Spec}} R^{\square , \zeta \varepsilon }_{\bar {\rho }_{\mathfrak B}} [1/p ]$
. Corollary A.7 implies that
$\operatorname {\mathrm {Spec}} R^{\square , \zeta \varepsilon }_{\bar {\rho }_{\mathfrak B}} [1/p ]$
. Corollary A.7 implies that
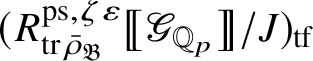 acts faithfully on
acts faithfully on
![]() $V_S$
, hence
$V_S$
, hence
![]() $a=0$
and formula (24) is injective.
$a=0$
and formula (24) is injective.
The assertions about the centre follow from Proposition A.11.
We immediately obtain the following:
Corollary 6.14.
![]() $Z_{\mathfrak B}'$
is a complete local Noetherian
$Z_{\mathfrak B}'$
is a complete local Noetherian
![]() $\mathscr O$
-algebra with residue field k. It is
$\mathscr O$
-algebra with residue field k. It is
![]() $\mathscr O$
-torsion-free and
$\mathscr O$
-torsion-free and
![]() $Z_{\mathfrak B}' [1/p ]$
is normal.
$Z_{\mathfrak B}' [1/p ]$
is normal.
Corollary 6.15.
![]() $Z_{\mathfrak B}= Z_{\mathfrak B}'$
.
$Z_{\mathfrak B}= Z_{\mathfrak B}'$
.
Proof. Since
![]() $Z_{\mathfrak B}$
acts faithfully on
$Z_{\mathfrak B}$
acts faithfully on
![]() $P_{\mathfrak B}$
it is
$P_{\mathfrak B}$
it is
![]() $\mathscr O$
-torsion-free. Thus it is enough to show that the surjection
$\mathscr O$
-torsion-free. Thus it is enough to show that the surjection
![]() $Z_{\mathfrak B}'\twoheadrightarrow Z_{\mathfrak B}$
(see Corollary 4.16) induces an isomorphism after inversion of p. Since
$Z_{\mathfrak B}'\twoheadrightarrow Z_{\mathfrak B}$
(see Corollary 4.16) induces an isomorphism after inversion of p. Since
![]() $Z_{\mathfrak B}' [1/p ]$
is reduced by Corollary 6.14, it is enough to show that
$Z_{\mathfrak B}' [1/p ]$
is reduced by Corollary 6.14, it is enough to show that
![]() $\operatorname {\mathrm {m-Spec}} Z_{\mathfrak B} [1/p ]$
contains a subset
$\operatorname {\mathrm {m-Spec}} Z_{\mathfrak B} [1/p ]$
contains a subset
![]() $\Sigma $
of
$\Sigma $
of
![]() $\operatorname {\mathrm {m-Spec}} Z_{\mathfrak B}' [1/p ]$
, which is dense in
$\operatorname {\mathrm {m-Spec}} Z_{\mathfrak B}' [1/p ]$
, which is dense in
![]() $\operatorname {\mathrm {Spec}} Z_{\mathfrak B}' [1/p ]$
. We may take
$\operatorname {\mathrm {Spec}} Z_{\mathfrak B}' [1/p ]$
. We may take
![]() $\Sigma $
to be the absolutely irreducible locus in
$\Sigma $
to be the absolutely irreducible locus in
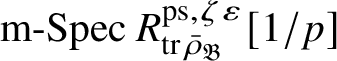 $\operatorname {\mathrm {m-Spec}} R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr} \bar {\rho }_{\mathfrak B}} [1/p ]$
, as it is dense in
$\operatorname {\mathrm {m-Spec}} R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr} \bar {\rho }_{\mathfrak B}} [1/p ]$
, as it is dense in
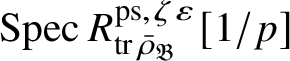 $\operatorname {\mathrm {Spec}} R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr} \bar {\rho }_{\mathfrak B}} [1/p ]$
by [Reference Chenevier17, Theorem 2.1] and lies in
$\operatorname {\mathrm {Spec}} R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr} \bar {\rho }_{\mathfrak B}} [1/p ]$
by [Reference Chenevier17, Theorem 2.1] and lies in
![]() $\operatorname {\mathrm {m-Spec}} Z_{\mathfrak B} [1/p ]$
by the main result of [Reference Colmez, Dospinescu and Paškūnas21].
$\operatorname {\mathrm {m-Spec}} Z_{\mathfrak B} [1/p ]$
by the main result of [Reference Colmez, Dospinescu and Paškūnas21].
Corollary 6.16. Let
![]() $L'$
be a finite extension of L and let
$L'$
be a finite extension of L and let
 $x: R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}} \rightarrow L'$
be an
$x: R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}} \rightarrow L'$
be an
![]() $\mathscr O$
-algebra homomorphism. If the specialisation of the universal pseudodeformation
$\mathscr O$
-algebra homomorphism. If the specialisation of the universal pseudodeformation
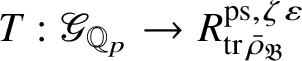 $T:\mathscr G_{\mathbb {Q}_p}\rightarrow R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
at x is not of the form
$T:\mathscr G_{\mathbb {Q}_p}\rightarrow R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
at x is not of the form
![]() $\psi + \psi \varepsilon $
, then
$\psi + \psi \varepsilon $
, then
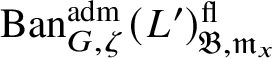 $\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L')^{\mathrm {fl}}_{\mathfrak B, \mathfrak m_x}$
is equivalent to the category of modules of finite length over the completion of
$\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L')^{\mathrm {fl}}_{\mathfrak B, \mathfrak m_x}$
is equivalent to the category of modules of finite length over the completion of
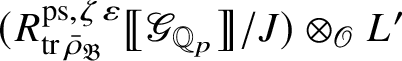 at
at
![]() $\mathfrak m_x$
.
$\mathfrak m_x$
.
Moreover, if
![]() $T_x =\operatorname {tr} \rho $
, where
$T_x =\operatorname {tr} \rho $
, where
![]() $\rho : \mathscr G_{\mathbb {Q}_p}\rightarrow \operatorname {\mathrm {GL}}_2(L')$
is absolutely irreducible, then
$\rho : \mathscr G_{\mathbb {Q}_p}\rightarrow \operatorname {\mathrm {GL}}_2(L')$
is absolutely irreducible, then
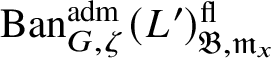 $\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L')^{\mathrm {fl}}_{\mathfrak B, \mathfrak m_x}$
is equivalent to the category of modules of finite length over the deformation ring
$\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L')^{\mathrm {fl}}_{\mathfrak B, \mathfrak m_x}$
is equivalent to the category of modules of finite length over the deformation ring
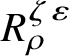 $R^{\zeta \varepsilon }_{\rho }$
, which parameterises the deformations of
$R^{\zeta \varepsilon }_{\rho }$
, which parameterises the deformations of
![]() $\rho $
with determinant
$\rho $
with determinant
![]() $\zeta \varepsilon $
to local Artinian
$\zeta \varepsilon $
to local Artinian
![]() $L'$
-algebras.
$L'$
-algebras.
In particular, if
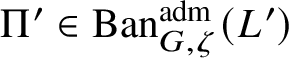 $\Pi '\in \operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L')$
is killed by
$\Pi '\in \operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L')$
is killed by
![]() $\mathfrak m_x$
then
$\mathfrak m_x$
then
![]() $\Pi '$
is isomorphic to a direct sum of finitely many copies of
$\Pi '$
is isomorphic to a direct sum of finitely many copies of
![]() $\Pi $
in Proposition 6.11.
$\Pi $
in Proposition 6.11.
Proof. After extending scalars, we may assume that
![]() $L=L'$
. If
$L=L'$
. If
![]() $T_x\neq \psi +\psi \varepsilon $
for any character
$T_x\neq \psi +\psi \varepsilon $
for any character
![]() $\psi $
, then it follows from Corollaries 6.10 and 6.11 that
$\psi $
, then it follows from Corollaries 6.10 and 6.11 that
![]() $\operatorname {\mathrm {Irr}}(\mathfrak m_x, L')$
does not contain characters. We may apply [Reference Paškūnas39, Theorem 4.36] to deduce that
$\operatorname {\mathrm {Irr}}(\mathfrak m_x, L')$
does not contain characters. We may apply [Reference Paškūnas39, Theorem 4.36] to deduce that
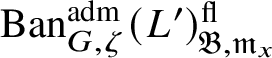 $\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L')^{\mathrm {fl}}_{\mathfrak B, \mathfrak m_x}$
is antiequivalent to the category of
$\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L')^{\mathrm {fl}}_{\mathfrak B, \mathfrak m_x}$
is antiequivalent to the category of
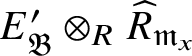 $E_{\mathfrak B}'\otimes _R \widehat {R}_{\mathfrak m_x}$
-modules of finite length, where
$E_{\mathfrak B}'\otimes _R \widehat {R}_{\mathfrak m_x}$
-modules of finite length, where
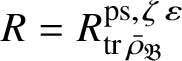 $R=R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
. Theorem 6.13 implies that this ring coincides with the completion of
$R=R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
. Theorem 6.13 implies that this ring coincides with the completion of
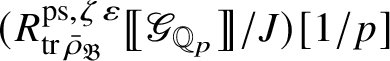 at
at
![]() $\mathfrak m_x$
.
$\mathfrak m_x$
.
Let us assume that
![]() $T_x= \operatorname {tr} \rho $
with
$T_x= \operatorname {tr} \rho $
with
![]() $\rho $
absolutely irreducible. Then
$\rho $
absolutely irreducible. Then
![]() $\operatorname {\mathrm {Irr}}(\mathfrak m_x, L')=\{\Pi \}$
, with
$\operatorname {\mathrm {Irr}}(\mathfrak m_x, L')=\{\Pi \}$
, with
![]() $\Pi $
absolutely irreducible by Proposition 6.11 and
$\Pi $
absolutely irreducible by Proposition 6.11 and
![]() $\check {\mathbf {V}}(\Pi )\cong \rho $
. It follows from [Reference Chenevier18, Sections 4.1 and 4.2] that
$\check {\mathbf {V}}(\Pi )\cong \rho $
. It follows from [Reference Chenevier18, Sections 4.1 and 4.2] that
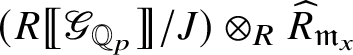 is an Azumaya algebra over
is an Azumaya algebra over
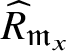 $\widehat {R}_{\mathfrak m_x}$
. Since
$\widehat {R}_{\mathfrak m_x}$
. Since
![]() $\rho $
is an absolutely irreducible
$\rho $
is an absolutely irreducible
![]() $2$
-dimensional module of
$2$
-dimensional module of
![]() , we conclude that
, we conclude that
![]() , and thus
, and thus
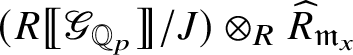 is isomorphic to the ring of
is isomorphic to the ring of
![]() $2\times 2$
matrices over
$2\times 2$
matrices over
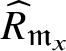 $\widehat {R}_{\mathfrak m_x}$
. Since
$\widehat {R}_{\mathfrak m_x}$
. Since
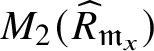 $M_2 (\widehat {R}_{\mathfrak m_x} )$
is Morita equivalent to
$M_2 (\widehat {R}_{\mathfrak m_x} )$
is Morita equivalent to
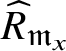 $\widehat {R}_{\mathfrak m_x}$
, which is isomorphic to
$\widehat {R}_{\mathfrak m_x}$
, which is isomorphic to
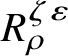 $R^{\zeta \varepsilon }_{\rho }$
by [Reference Kisin35, Lemma 2.3.3, Proposition 2.3.5], we obtain the first assertion.
$R^{\zeta \varepsilon }_{\rho }$
by [Reference Kisin35, Lemma 2.3.3, Proposition 2.3.5], we obtain the first assertion.
In particular, the full subcategory of
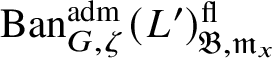 $\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L')^{\mathrm {fl}}_{\mathfrak B, \mathfrak m_x}$
consisting of representations killed by
$\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L')^{\mathrm {fl}}_{\mathfrak B, \mathfrak m_x}$
consisting of representations killed by
![]() $\mathfrak m_x$
is equivalent to the category of finite-dimensional vector spaces over
$\mathfrak m_x$
is equivalent to the category of finite-dimensional vector spaces over
![]() $L'$
, and hence the last assertion follows.
$L'$
, and hence the last assertion follows.
6.4 Complements
We will prove Theorem 1.1. Let
![]() $\mathfrak B$
be an arbitrary block, so that we do not assume that it contains an absolutely irreducible representation.
$\mathfrak B$
be an arbitrary block, so that we do not assume that it contains an absolutely irreducible representation.
If
![]() $\pi _1, \pi _2\in \operatorname {\mathrm {Irr}}_{G, \zeta }(k)$
, then it follows from [Reference Paškūnas39, Proposition 5.11] that there is a finite extension
$\pi _1, \pi _2\in \operatorname {\mathrm {Irr}}_{G, \zeta }(k)$
, then it follows from [Reference Paškūnas39, Proposition 5.11] that there is a finite extension
![]() $k'$
of k such that
$k'$
of k such that
![]() $\pi _1\otimes _k k'$
is a finite direct sum of absolutely irreducible representations; then
$\pi _1\otimes _k k'$
is a finite direct sum of absolutely irreducible representations; then
![]() $\pi _2\otimes _k k'$
is a finite direct sum of irreducible representations, each of them occurring with multiplicity
$\pi _2\otimes _k k'$
is a finite direct sum of irreducible representations, each of them occurring with multiplicity
![]() $1$
. It is implied by [Reference Paškūnas39, Proposition 5.33] that
$1$
. It is implied by [Reference Paškūnas39, Proposition 5.33] that
 $$ \begin{align} \operatorname{\mathrm{Ext}}^1_{k[G], \zeta}(\pi_1, \pi_2)\otimes_k k'\cong \operatorname{\mathrm{Ext}}^1_{k'[G],\zeta}(\pi_1\otimes_k k', \pi_2\otimes_k k'). \end{align} $$
$$ \begin{align} \operatorname{\mathrm{Ext}}^1_{k[G], \zeta}(\pi_1, \pi_2)\otimes_k k'\cong \operatorname{\mathrm{Ext}}^1_{k'[G],\zeta}(\pi_1\otimes_k k', \pi_2\otimes_k k'). \end{align} $$
If
 $\operatorname {\mathrm {Ext}}^1_{k[G], \zeta }(\pi _1, \pi _2)\neq 0$
, then it follows from this formula that there are irreducible summands
$\operatorname {\mathrm {Ext}}^1_{k[G], \zeta }(\pi _1, \pi _2)\neq 0$
, then it follows from this formula that there are irreducible summands
![]() $\pi _1'$
of
$\pi _1'$
of
![]() $\pi _1\otimes _k k'$
and
$\pi _1\otimes _k k'$
and
![]() $\pi _2'$
of
$\pi _2'$
of
![]() $\pi _2 \otimes _k k'$
such that
$\pi _2 \otimes _k k'$
such that
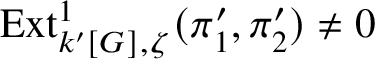 $\operatorname {\mathrm {Ext}}^1_{k'[G], \zeta } (\pi _1', \pi _2' )\neq 0$
. Since
$\operatorname {\mathrm {Ext}}^1_{k'[G], \zeta } (\pi _1', \pi _2' )\neq 0$
. Since
![]() $\pi _1'$
is absolutely irreducible, we conclude by inspecting the list of blocks in Section 4.1 that
$\pi _1'$
is absolutely irreducible, we conclude by inspecting the list of blocks in Section 4.1 that
![]() $\pi _2'$
is absolutely irreducible, and thus if
$\pi _2'$
is absolutely irreducible, and thus if
![]() $\mathfrak B$
is the block containing
$\mathfrak B$
is the block containing
![]() $\pi _1$
, then
$\pi _1$
, then
![]() $\pi \otimes _k k'$
is a finite direct sum of absolutely irreducible representations for all
$\pi \otimes _k k'$
is a finite direct sum of absolutely irreducible representations for all
![]() $\pi \in \mathfrak B$
.
$\pi \in \mathfrak B$
.
Let
![]() $L'$
be a finite extension of L with ring of integers
$L'$
be a finite extension of L with ring of integers
![]() $\mathscr O'$
and residue field
$\mathscr O'$
and residue field
![]() $k'$
. If
$k'$
. If
![]() $\pi ^{\prime }_1, \pi _2'\in \operatorname {\mathrm {Irr}}_{G,\zeta }(k')$
are absolutely irreducible, then it follows from [Reference Paškūnas39, Proposition 5.11] that there exist unique
$\pi ^{\prime }_1, \pi _2'\in \operatorname {\mathrm {Irr}}_{G,\zeta }(k')$
are absolutely irreducible, then it follows from [Reference Paškūnas39, Proposition 5.11] that there exist unique
![]() $\pi _1, \pi _2\in \operatorname {\mathrm {Irr}}_{G, \zeta }(k)$
such that
$\pi _1, \pi _2\in \operatorname {\mathrm {Irr}}_{G, \zeta }(k)$
such that
![]() $\pi _1'$
is a direct summand of
$\pi _1'$
is a direct summand of
![]() $\pi _1\otimes _k k'$
and
$\pi _1\otimes _k k'$
and
![]() $\pi _2'$
is a direct summand of
$\pi _2'$
is a direct summand of
![]() $\pi _2\otimes _k k'$
. It follows from formula (25) that if
$\pi _2\otimes _k k'$
. It follows from formula (25) that if
![]() $\pi _1'$
and
$\pi _1'$
and
![]() $\pi _2'$
lie in the same block in
$\pi _2'$
lie in the same block in
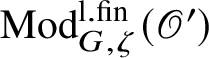 $\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O')$
, then
$\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O')$
, then
![]() $\pi _1$
and
$\pi _1$
and
![]() $\pi _2$
lie in the same block in
$\pi _2$
lie in the same block in
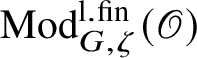 $\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O)$
.
$\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O)$
.
Thus if
![]() $\pi _1\in \mathfrak B$
and we let
$\pi _1\in \mathfrak B$
and we let
![]() $\mathfrak B_1, \dotsc , \mathfrak B_r$
be the blocks of irreducible subquotients of
$\mathfrak B_1, \dotsc , \mathfrak B_r$
be the blocks of irreducible subquotients of
![]() $\pi _1\otimes _k k'$
in
$\pi _1\otimes _k k'$
in
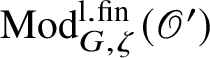 $\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O')$
and
$\operatorname {\mathrm {Mod}}^{\mathrm {l.fin}}_{G, \zeta }(\mathscr O')$
and
![]() $\mathfrak B\otimes _k k'$
be the set of isomorphism classes of irreducible subquotients of
$\mathfrak B\otimes _k k'$
be the set of isomorphism classes of irreducible subquotients of
![]() $\pi \otimes _k k'$
for all
$\pi \otimes _k k'$
for all
![]() $\pi \in \mathfrak B$
, then
$\pi \in \mathfrak B$
, then
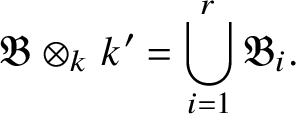 $$ \begin{align*} \mathfrak B\otimes_k k'= \bigcup_{i=1}^r \mathfrak B_i. \end{align*} $$
$$ \begin{align*} \mathfrak B\otimes_k k'= \bigcup_{i=1}^r \mathfrak B_i. \end{align*} $$
It follows from [Reference Paškūnas39, Corollary 5.40] that
![]() $P_{\mathfrak B}\otimes _{\mathscr O} \mathscr O'\cong \prod _{i=1}^r P_{\mathfrak B_i}$
and
$P_{\mathfrak B}\otimes _{\mathscr O} \mathscr O'\cong \prod _{i=1}^r P_{\mathfrak B_i}$
and
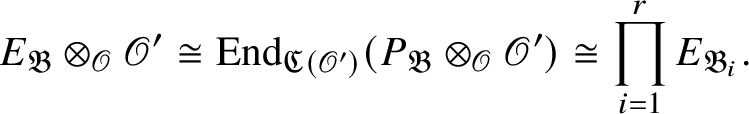 $$ \begin{align*} E_{\mathfrak B}\otimes_{\mathscr O} \mathscr O'\cong \operatorname{\mathrm{End}}_{{\mathfrak C}(\mathscr O')}(P_{\mathfrak B}\otimes_{\mathscr O} \mathscr O')\cong \prod_{i=1}^r E_{\mathfrak B_i}. \end{align*} $$
$$ \begin{align*} E_{\mathfrak B}\otimes_{\mathscr O} \mathscr O'\cong \operatorname{\mathrm{End}}_{{\mathfrak C}(\mathscr O')}(P_{\mathfrak B}\otimes_{\mathscr O} \mathscr O')\cong \prod_{i=1}^r E_{\mathfrak B_i}. \end{align*} $$
Since the blocks
![]() $\mathfrak B_i$
contain only absolutely irreducible representations, it follows from Corollary 6.4 that
$\mathfrak B_i$
contain only absolutely irreducible representations, it follows from Corollary 6.4 that
![]() $E_{\mathfrak B}\otimes _{\mathscr O} \mathscr O'$
is a finite module over its centre
$E_{\mathfrak B}\otimes _{\mathscr O} \mathscr O'$
is a finite module over its centre
![]() $Z(E_{\mathfrak B}\otimes _{\mathscr O} \mathscr O')$
and
$Z(E_{\mathfrak B}\otimes _{\mathscr O} \mathscr O')$
and
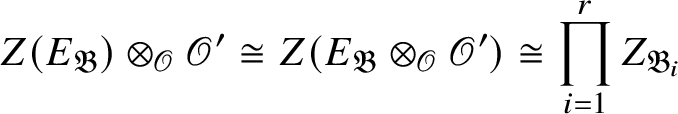 $$ \begin{align*} Z(E_{\mathfrak B})\otimes_{\mathscr O} \mathscr O'\cong Z(E_{\mathfrak B}\otimes_{\mathscr O} \mathscr O')\cong \prod_{i=1}^r Z_{\mathfrak B_i} \end{align*} $$
$$ \begin{align*} Z(E_{\mathfrak B})\otimes_{\mathscr O} \mathscr O'\cong Z(E_{\mathfrak B}\otimes_{\mathscr O} \mathscr O')\cong \prod_{i=1}^r Z_{\mathfrak B_i} \end{align*} $$
is Noetherian (see the argument in the proof of [Reference Dospinescu, Paškūnas and Schraen25, Lemma 4.14] for the first isomorphism). Since
![]() $\mathscr O'$
is a finite free
$\mathscr O'$
is a finite free
![]() $\mathscr O$
-module, this implies that
$\mathscr O$
-module, this implies that
![]() $Z(E_{\mathfrak B})$
is Noetherian, and
$Z(E_{\mathfrak B})$
is Noetherian, and
![]() $E_{\mathfrak B}$
is a finitely generated
$E_{\mathfrak B}$
is a finitely generated
![]() $Z_{\mathfrak B}$
-module, which finishes the proof of Theorem 1.1.
$Z_{\mathfrak B}$
-module, which finishes the proof of Theorem 1.1.
7 Application to Hecke eigenspaces
Let R be a linearly compact local
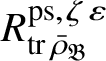 $R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
-algebra with residue field k; we do not assume that R is Noetherian. If
$R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
-algebra with residue field k; we do not assume that R is Noetherian. If
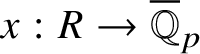 $x:R\rightarrow \overline {\mathbb {Q}}_p$
is an
$x:R\rightarrow \overline {\mathbb {Q}}_p$
is an
![]() $\mathscr O$
-algebra homomorphism, then we denote by
$\mathscr O$
-algebra homomorphism, then we denote by
![]() $T_x$
the specialisation of the universal pseudorepresentation
$T_x$
the specialisation of the universal pseudorepresentation
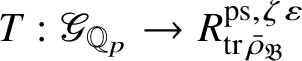 $T: \mathscr G_{\mathbb {Q}_p} \rightarrow R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
along
$T: \mathscr G_{\mathbb {Q}_p} \rightarrow R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
along
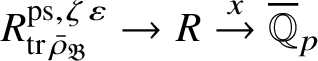 $R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}\rightarrow R \overset {x}{\rightarrow } \overline {\mathbb {Q}}_p$
.
$R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}\rightarrow R \overset {x}{\rightarrow } \overline {\mathbb {Q}}_p$
.
Let M be an object of
![]() ${\mathfrak C}(\mathscr O)_{\mathfrak B}$
, which we assume to be
${\mathfrak C}(\mathscr O)_{\mathfrak B}$
, which we assume to be
![]() $\mathscr O$
-torsion-free. Then
$\mathscr O$
-torsion-free. Then
![]() $\Pi (M):=\operatorname {\mathrm {Hom}}_{\mathscr O}^{\mathrm {cont}}(M, L)$
is a unitary L-Banach-space representation of G.
$\Pi (M):=\operatorname {\mathrm {Hom}}_{\mathscr O}^{\mathrm {cont}}(M, L)$
is a unitary L-Banach-space representation of G.
We assume that we are given a continuous action of R on M, which commutes with the action of G, such that the following hold:
-
• the action of R on M is faithful;
-
• the two actions of
 $R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
on M induced by the maps coincide; and
$R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
on M induced by the maps coincide; and $$ \begin{align*} R^{\mathrm{ps}, \zeta\varepsilon}_{\operatorname{tr}\bar{\rho}_{\mathfrak B}}\rightarrow R, \qquad R^{\mathrm{ps}, \zeta\varepsilon}_{\operatorname{tr}\bar{\rho}_{\mathfrak B}}\rightarrow Z_{\mathfrak B} \end{align*} $$
$$ \begin{align*} R^{\mathrm{ps}, \zeta\varepsilon}_{\operatorname{tr}\bar{\rho}_{\mathfrak B}}\rightarrow R, \qquad R^{\mathrm{ps}, \zeta\varepsilon}_{\operatorname{tr}\bar{\rho}_{\mathfrak B}}\rightarrow Z_{\mathfrak B} \end{align*} $$
-
• M is a finitely generated
 -module.
-module.
Theorem 7.1. Let
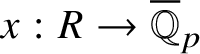 $x: R\rightarrow \overline {\mathbb {Q}}_p$
be an
$x: R\rightarrow \overline {\mathbb {Q}}_p$
be an
![]() $\mathscr O$
-algebra homomorphism and let
$\mathscr O$
-algebra homomorphism and let
![]() $\Pi (M)[\mathfrak m_x]$
be the subspace of
$\Pi (M)[\mathfrak m_x]$
be the subspace of
![]() $\Pi (M)$
annihilated by the kernel of x. Then under the foregoing assumptions,
$\Pi (M)$
annihilated by the kernel of x. Then under the foregoing assumptions,
![]() $\Pi (M)[\mathfrak m_x]$
is nonzero and is of finite length in
$\Pi (M)[\mathfrak m_x]$
is nonzero and is of finite length in
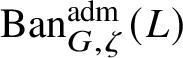 $\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)$
. Moreover,
$\operatorname {\mathrm {Ban}}^{\mathrm {adm}}_{G, \zeta }(L)$
. Moreover,
-
• if
 $T_x$
is the trace of an absolutely irreducible Galois representation defined over
$T_x$
is the trace of an absolutely irreducible Galois representation defined over
 $\kappa (x)$
, then for some multiplicity
$\kappa (x)$
, then for some multiplicity $$ \begin{align*} \Pi(M)[\mathfrak m_x]\cong \Pi^{\oplus m} \end{align*} $$
$$ \begin{align*} \Pi(M)[\mathfrak m_x]\cong \Pi^{\oplus m} \end{align*} $$
 $m>0$
, where
$m>0$
, where
 $\Pi $
is an absolutely irreducible nonordinary
$\Pi $
is an absolutely irreducible nonordinary
 $\kappa (x)$
-Banach-space representation of G satisfying
$\kappa (x)$
-Banach-space representation of G satisfying
 $\operatorname {tr} \check {\mathbf {V}}(\Pi )= T_x$
; and
$\operatorname {tr} \check {\mathbf {V}}(\Pi )= T_x$
; and
-
• if
 $T_x$
is the trace of a reducible Galois representation, then (after a possible extension of scalars) all the irreducible subquotients of
$T_x$
is the trace of a reducible Galois representation, then (after a possible extension of scalars) all the irreducible subquotients of
 $\Pi (M)[\mathfrak m_x]$
occur as subquotients of a direct sum of unitary parabolic induction where
$\Pi (M)[\mathfrak m_x]$
occur as subquotients of a direct sum of unitary parabolic induction where $$ \begin{align*} (\operatorname{\mathrm{Ind}}_B^G \psi_1 \otimes \psi_2 \varepsilon^{-1})_{\mathrm{cont}} \oplus (\operatorname{\mathrm{Ind}}_B^G \psi_2 \otimes \psi_1 \varepsilon^{-1})_{\mathrm{cont}}, \end{align*} $$
$$ \begin{align*} (\operatorname{\mathrm{Ind}}_B^G \psi_1 \otimes \psi_2 \varepsilon^{-1})_{\mathrm{cont}} \oplus (\operatorname{\mathrm{Ind}}_B^G \psi_2 \otimes \psi_1 \varepsilon^{-1})_{\mathrm{cont}}, \end{align*} $$
 $\psi _1, \psi _2:\mathscr G_{\mathbb {Q}_p} \rightarrow \kappa (x)^{\times }$
are characters such that
$\psi _1, \psi _2:\mathscr G_{\mathbb {Q}_p} \rightarrow \kappa (x)^{\times }$
are characters such that
 $T_x= \psi _1 + \psi _2$
.
$T_x= \psi _1 + \psi _2$
.
Proof. Since
![]() $P_{\mathfrak B}$
is a projective generator for
$P_{\mathfrak B}$
is a projective generator for
![]() ${\mathfrak C}(\mathscr O)_{\mathfrak B}$
, the functor
${\mathfrak C}(\mathscr O)_{\mathfrak B}$
, the functor
![]() $N \mapsto \mathrm m(N):= \operatorname {\mathrm {Hom}}_{{\mathfrak C}(\mathscr O)}(P_{\mathfrak B}, N)$
induces an equivalence of categories between
$N \mapsto \mathrm m(N):= \operatorname {\mathrm {Hom}}_{{\mathfrak C}(\mathscr O)}(P_{\mathfrak B}, N)$
induces an equivalence of categories between
![]() ${\mathfrak C}(\mathscr O)_{\mathfrak B}$
and the category of right pseudocompact
${\mathfrak C}(\mathscr O)_{\mathfrak B}$
and the category of right pseudocompact
![]() $E_{\mathfrak B}$
-modules. The inverse functor is given by
$E_{\mathfrak B}$
-modules. The inverse functor is given by
![]() $\mathrm m \mapsto \mathrm m \operatorname {\mathrm {\mathbin {\widehat {\otimes }}}}_{E_{\mathfrak B}} P_{\mathfrak B}$
. In particular, the assumption that R acts faithfully on M implies that R acts faithfully on
$\mathrm m \mapsto \mathrm m \operatorname {\mathrm {\mathbin {\widehat {\otimes }}}}_{E_{\mathfrak B}} P_{\mathfrak B}$
. In particular, the assumption that R acts faithfully on M implies that R acts faithfully on
![]() $\mathrm m(M)$
.
$\mathrm m(M)$
.
We claim that
![]() $\mathrm m(M)$
is a finitely generated R-module. The topological Nakayama’s lemma implies that it is enough to show that
$\mathrm m(M)$
is a finitely generated R-module. The topological Nakayama’s lemma implies that it is enough to show that
![]() $k \operatorname {\mathrm {\mathbin {\widehat {\otimes }}}}_R \mathrm m(M)$
is a finite-dimensional k-vector space. Since
$k \operatorname {\mathrm {\mathbin {\widehat {\otimes }}}}_R \mathrm m(M)$
is a finite-dimensional k-vector space. Since
![]() $k\operatorname {\mathrm {\mathbin {\widehat {\otimes }}}}_R \mathrm m(M)\cong \mathrm m (k \operatorname {\mathrm {\mathbin {\widehat {\otimes }}}}_R M )$
, it is enough to show that
$k\operatorname {\mathrm {\mathbin {\widehat {\otimes }}}}_R \mathrm m(M)\cong \mathrm m (k \operatorname {\mathrm {\mathbin {\widehat {\otimes }}}}_R M )$
, it is enough to show that
![]() $k\operatorname {\mathrm {\mathbin {\widehat {\otimes }}}}_R M$
is of finite length in
$k\operatorname {\mathrm {\mathbin {\widehat {\otimes }}}}_R M$
is of finite length in
![]() ${\mathfrak C}(\mathscr O)$
. Since by assumption M is a finitely generated
${\mathfrak C}(\mathscr O)$
. Since by assumption M is a finitely generated
![]() -module,
-module,
![]() $k\operatorname {\mathrm {\mathbin {\widehat {\otimes }}}}_R M$
is a finitely generated
$k\operatorname {\mathrm {\mathbin {\widehat {\otimes }}}}_R M$
is a finitely generated
![]() -module. Since by assumption the actions of
-module. Since by assumption the actions of
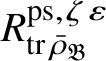 $R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
on M induced by
$R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
on M induced by
![]() $Z_{\mathfrak B}$
and by R, coincide we deduce that the maximal ideal of
$Z_{\mathfrak B}$
and by R, coincide we deduce that the maximal ideal of
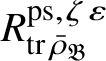 $R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
annihilates
$R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
annihilates
![]() $k\operatorname {\mathrm {\mathbin {\widehat {\otimes }}}}_R M$
. Corollary 6.7(4) applied to
$k\operatorname {\mathrm {\mathbin {\widehat {\otimes }}}}_R M$
. Corollary 6.7(4) applied to
![]() $N=k\operatorname {\mathrm {\mathbin {\widehat {\otimes }}}}_R M$
implies the claim.
$N=k\operatorname {\mathrm {\mathbin {\widehat {\otimes }}}}_R M$
implies the claim.
Since
![]() $\mathrm m(M)$
is a finitely generated and faithful R-module, its localisation
$\mathrm m(M)$
is a finitely generated and faithful R-module, its localisation
![]() $\mathrm m(M)_{\mathfrak m_x}$
is a finitely generated faithful
$\mathrm m(M)_{\mathfrak m_x}$
is a finitely generated faithful
![]() $R_{\mathfrak m_x}$
-module. If
$R_{\mathfrak m_x}$
-module. If
![]() $\mathrm m(M)\otimes _R \kappa (x)=0$
, then
$\mathrm m(M)\otimes _R \kappa (x)=0$
, then
![]() $\mathrm m(M)_{\mathfrak m_x}=0$
by Nakayama’s lemma, and since
$\mathrm m(M)_{\mathfrak m_x}=0$
by Nakayama’s lemma, and since
![]() $R_{\mathfrak m_x}$
acts faithfully,
$R_{\mathfrak m_x}$
acts faithfully,
![]() $R_{\mathfrak m_x}=0$
and hence
$R_{\mathfrak m_x}=0$
and hence
![]() $\kappa (x)=0$
, giving a contradiction. In particular,
$\kappa (x)=0$
, giving a contradiction. In particular,
![]() $\mathrm m(M)\otimes _{R}\kappa (x)$
is a nonzero, finite-dimensional
$\mathrm m(M)\otimes _{R}\kappa (x)$
is a nonzero, finite-dimensional
![]() $\kappa (x)$
-vector space. Since R is a compact
$\kappa (x)$
-vector space. Since R is a compact
![]() $\mathscr O$
-module and
$\mathscr O$
-module and
![]() $\kappa (x)$
is a subfield of
$\kappa (x)$
is a subfield of
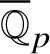 $\overline {\mathbb {Q}}_p$
, we have that
$\overline {\mathbb {Q}}_p$
, we have that
![]() $\kappa (x)$
is a finite extension of L and the image of R is contained in the ring of integers of
$\kappa (x)$
is a finite extension of L and the image of R is contained in the ring of integers of
![]() $\kappa (x)$
.
$\kappa (x)$
.
Let Q be the maximal
![]() $\mathscr O$
-torsion-free Hausdorff quotient of
$\mathscr O$
-torsion-free Hausdorff quotient of
![]() $M/\mathfrak m_x M$
. It follows from [Reference Schneider and Teitelbaum44, Proposition 1.3] that
$M/\mathfrak m_x M$
. It follows from [Reference Schneider and Teitelbaum44, Proposition 1.3] that
![]() $\Pi (Q)$
is a closed subspace of
$\Pi (Q)$
is a closed subspace of
![]() $\Pi (M)$
, which then implies that
$\Pi (M)$
, which then implies that
![]() $\Pi (Q)=\Pi (M)[\mathfrak m_x]$
. It follows from the equivalence of categories already explained that
$\Pi (Q)=\Pi (M)[\mathfrak m_x]$
. It follows from the equivalence of categories already explained that
![]() $\mathrm m(Q)$
is isomorphic to the image of
$\mathrm m(Q)$
is isomorphic to the image of
![]() $\mathrm m(M)$
in
$\mathrm m(M)$
in
![]() $\mathrm m(M)\otimes _{R}\kappa (x)$
. In particular, Q and thus
$\mathrm m(M)\otimes _{R}\kappa (x)$
. In particular, Q and thus
![]() $\Pi (Q)$
are nonzero.
$\Pi (Q)$
are nonzero.
The last two assertions follow from the antiequivalence (20) and Corollaries 6.10 and 6.16.
Remark 7.2. If M is finitely generated as a
![]() -module, then the argument in the proof of Theorem 7.1 shows that
-module, then the argument in the proof of Theorem 7.1 shows that
![]() $\mathrm m(M)$
is a finitely generated
$\mathrm m(M)$
is a finitely generated
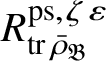 $R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
-module, and since R acts faithfully on
$R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
-module, and since R acts faithfully on
![]() $\mathrm m(M)$
, then R is a finitely generated
$\mathrm m(M)$
, then R is a finitely generated
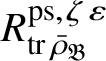 $R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
-module and hence is Noetherian.
$R^{\mathrm {ps}, \zeta \varepsilon }_{\operatorname {tr}\bar {\rho }_{\mathfrak B}}$
-module and hence is Noetherian.
The result allows us to remove the restrictions imposed on the Galois representation
![]() $\bar {\rho }_{\mathfrak m, p}$
in [Reference Pan38, Corollary 6.3.6], by taking M to be the Pontryagin dual of the representation denoted by
$\bar {\rho }_{\mathfrak m, p}$
in [Reference Pan38, Corollary 6.3.6], by taking M to be the Pontryagin dual of the representation denoted by
![]() $\tilde {H}^1(K^p, E/\mathscr O)_{\mathfrak m, \zeta '}$
in [Reference Pan38, Theorem 6.3.5] and taking R to be the closure of the subring generated by the Hecke operators in
$\tilde {H}^1(K^p, E/\mathscr O)_{\mathfrak m, \zeta '}$
in [Reference Pan38, Theorem 6.3.5] and taking R to be the closure of the subring generated by the Hecke operators in
![]() $\operatorname {\mathrm {End}}^{\mathrm {cont}}_{\mathscr O}(M)$
. Since [Reference Pan38, Corollary 6.3.6] is the only place where the restriction on p is used, the proof of [Reference Pan38, Theorem 6.4.7] goes through without a change to give the following result:
$\operatorname {\mathrm {End}}^{\mathrm {cont}}_{\mathscr O}(M)$
. Since [Reference Pan38, Corollary 6.3.6] is the only place where the restriction on p is used, the proof of [Reference Pan38, Theorem 6.4.7] goes through without a change to give the following result:
Theorem 7.3 Lue Pan +
 $\varepsilon $
$\varepsilon $
Let
![]() $\rho : \operatorname {\mathrm {Gal}} (\overline {\mathbb {Q}}/\mathbb {Q} )\rightarrow \operatorname {\mathrm {GL}}_2(L)$
be promodular and absolutely irreducible. If
$\rho : \operatorname {\mathrm {Gal}} (\overline {\mathbb {Q}}/\mathbb {Q} )\rightarrow \operatorname {\mathrm {GL}}_2(L)$
be promodular and absolutely irreducible. If
![]() $\rho $
is unramified outside finitely many places and
$\rho $
is unramified outside finitely many places and
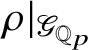 $\rho \rvert _{\mathscr G_{\mathbb {Q}_p}}$
is Hodge–Tate with weights
$\rho \rvert _{\mathscr G_{\mathbb {Q}_p}}$
is Hodge–Tate with weights
![]() $0,0$
, then
$0,0$
, then
![]() $\rho $
is associated to a weight
$\rho $
is associated to a weight
![]() $1$
modular form.
$1$
modular form.
The promodular condition means that the Hecke eigenvalues associated to
![]() $\rho $
appear in completed cohomology; see [Reference Pan38, Definition 6.1.2] for the precise definition. The original theorem in Lue Pan’s paper had to additionally assume that if p is
$\rho $
appear in completed cohomology; see [Reference Pan38, Definition 6.1.2] for the precise definition. The original theorem in Lue Pan’s paper had to additionally assume that if p is
![]() $2$
or
$2$
or
![]() $3$
, then
$3$
, then
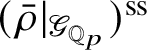 $ (\bar {\rho }\rvert _{\mathscr G_{\mathbb {Q}_p}} )^{\mathrm {ss}}$
is not isomorphic to
$ (\bar {\rho }\rvert _{\mathscr G_{\mathbb {Q}_p}} )^{\mathrm {ss}}$
is not isomorphic to
![]() $\chi \oplus \chi \omega $
for any character
$\chi \oplus \chi \omega $
for any character
![]() $\chi : \mathscr G_{\mathbb {Q}_p}\rightarrow k^{\times }$
.
$\chi : \mathscr G_{\mathbb {Q}_p}\rightarrow k^{\times }$
.
A Normality of
 $R^{\mathrm {ps}} [1/p ]$
$R^{\mathrm {ps}} [1/p ]$
Let
![]() $\mathscr G$
be a profinite group satisfying Mazur’s finiteness condition at p: The group of continuous group homomorphisms
$\mathscr G$
be a profinite group satisfying Mazur’s finiteness condition at p: The group of continuous group homomorphisms
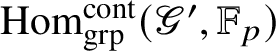 $\operatorname {\mathrm {Hom}}^{\mathrm {cont}}_{\mathrm {grp}} (\mathscr G', \mathbb F_p )$
is finite for every open subgroup
$\operatorname {\mathrm {Hom}}^{\mathrm {cont}}_{\mathrm {grp}} (\mathscr G', \mathbb F_p )$
is finite for every open subgroup
![]() $\mathscr G'$
of
$\mathscr G'$
of
![]() $\mathscr G$
. Let
$\mathscr G$
. Let
![]() $\bar {\rho }: \mathscr G \rightarrow \operatorname {\mathrm {GL}}_d(k)$
be a continuous semisimple representation such that all the irreducible summands of
$\bar {\rho }: \mathscr G \rightarrow \operatorname {\mathrm {GL}}_d(k)$
be a continuous semisimple representation such that all the irreducible summands of
![]() $\bar {\rho }$
are absolutely irreducible. Let
$\bar {\rho }$
are absolutely irreducible. Let
![]() $\psi : \mathscr G\rightarrow \mathscr O^{\times }$
be a character lifting
$\psi : \mathscr G\rightarrow \mathscr O^{\times }$
be a character lifting
![]() $\det \bar {\rho }$
. Let
$\det \bar {\rho }$
. Let
![]() $\bar {D}: k[\mathscr G]\rightarrow k$
be the pseudorepresentation associated to
$\bar {D}: k[\mathscr G]\rightarrow k$
be the pseudorepresentation associated to
![]() $\bar {\rho }$
in [Reference Chenevier18], so that
$\bar {\rho }$
in [Reference Chenevier18], so that
![]() $\bar {D}(1+t g)= \det (1 + t \bar {\rho }(g))$
for all
$\bar {D}(1+t g)= \det (1 + t \bar {\rho }(g))$
for all
![]() $g\in \mathscr G$
. We may consider the framed deformation ring
$g\in \mathscr G$
. We may consider the framed deformation ring
![]() $R^{\square }_{\bar {\rho }}$
, its quotient
$R^{\square }_{\bar {\rho }}$
, its quotient
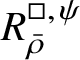 $R^{\square , \psi }_{\bar {\rho }}$
parameterising framed deformations of
$R^{\square , \psi }_{\bar {\rho }}$
parameterising framed deformations of
![]() $\bar {\rho }$
with determinant equal to
$\bar {\rho }$
with determinant equal to
![]() $\psi $
, the universal deformation ring
$\psi $
, the universal deformation ring
![]() $R^{\mathrm {ps}}$
of
$R^{\mathrm {ps}}$
of
![]() $\bar {D}$
, and its quotient
$\bar {D}$
, and its quotient
![]() $R^{\mathrm {ps}, \psi }$
parameterising deformations of
$R^{\mathrm {ps}, \psi }$
parameterising deformations of
![]() $\bar {D}$
with determinant
$\bar {D}$
with determinant
![]() $\psi $
. This last ring is constructed as follows: If
$\psi $
. This last ring is constructed as follows: If
![]() $D^u:\mathscr G\rightarrow R^{\mathrm {ps}}$
is the universal deformation of
$D^u:\mathscr G\rightarrow R^{\mathrm {ps}}$
is the universal deformation of
![]() $\bar {D}$
, then for each
$\bar {D}$
, then for each
![]() $g\in \mathscr G$
, we have that
$g\in \mathscr G$
, we have that
![]() $D^u(1 +t g)= a_0(g)+\dotsb +a_d(g)t^d$
, with
$D^u(1 +t g)= a_0(g)+\dotsb +a_d(g)t^d$
, with
![]() $a_i(g)\in R^{\mathrm {ps}}$
, and
$a_i(g)\in R^{\mathrm {ps}}$
, and
![]() $R^{\mathrm {ps}, \psi }$
is the quotient of
$R^{\mathrm {ps}, \psi }$
is the quotient of
![]() $R^{\mathrm {ps}}$
by the ideal generated
$R^{\mathrm {ps}}$
by the ideal generated
![]() $\psi (g) a_d(g)-1$
for all
$\psi (g) a_d(g)-1$
for all
![]() $g\in \mathscr G$
. The finiteness condition on
$g\in \mathscr G$
. The finiteness condition on
![]() $\mathscr G$
ensures that all these rings are Noetherian. The characteristic polynomial of the universal framed deformations of
$\mathscr G$
ensures that all these rings are Noetherian. The characteristic polynomial of the universal framed deformations of
![]() $\bar {\rho }$
induces maps
$\bar {\rho }$
induces maps
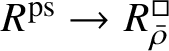 $R^{\mathrm {ps}}\rightarrow R^{\square }_{\bar {\rho }}$
and
$R^{\mathrm {ps}}\rightarrow R^{\square }_{\bar {\rho }}$
and
 $R^{\mathrm {ps}, \psi }\rightarrow R^{\square , \psi }_{\bar {\rho }}$
.
$R^{\mathrm {ps}, \psi }\rightarrow R^{\square , \psi }_{\bar {\rho }}$
.
Theorem A.1. If
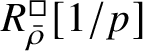 $R^{\square }_{\bar {\rho }} [1/p ]$
is normal, then both
$R^{\square }_{\bar {\rho }} [1/p ]$
is normal, then both
![]() $R^{\mathrm {ps}} [1/p ]$
and the associated rigid space
$R^{\mathrm {ps}} [1/p ]$
and the associated rigid space
![]() $(\operatorname {\mathrm {Spf}} R^{\mathrm {ps}})^{\mathrm {rig}}$
are normal.
$(\operatorname {\mathrm {Spf}} R^{\mathrm {ps}})^{\mathrm {rig}}$
are normal.
We also prove a version of the theorem with a fixed determinant. We apply this theorem to
![]() $\mathscr G=\mathscr G_{\mathbb {Q}_p}$
to prove that the rings
$\mathscr G=\mathscr G_{\mathbb {Q}_p}$
to prove that the rings
![]() $R^{\mathrm {ps}, \psi }, R^{\mathrm {ps}}$
and associated rigid analytic spaces are normal for all
$R^{\mathrm {ps}, \psi }, R^{\mathrm {ps}}$
and associated rigid analytic spaces are normal for all
![]() $2$
-dimensional
$2$
-dimensional
![]() $\bar {\rho }$
. There is essentially one case that we need to handle, namely
$\bar {\rho }$
. There is essentially one case that we need to handle, namely
![]() $\bar {\rho }= \mathbf 1 \oplus \omega $
, where
$\bar {\rho }= \mathbf 1 \oplus \omega $
, where
![]() $\omega $
is the cyclotomic character modulo p; in the other cases, all the rings are regular. The trickiest cases are when
$\omega $
is the cyclotomic character modulo p; in the other cases, all the rings are regular. The trickiest cases are when
![]() $p=2$
and
$p=2$
and
![]() $p=3$
. The case
$p=3$
. The case
![]() $p=2$
is treated in [Reference Colmez, Dospinescu and Paškūnas22]. We deal with the case
$p=2$
is treated in [Reference Colmez, Dospinescu and Paškūnas22]. We deal with the case
![]() $p=3$
using the work of Böckle [Reference Böckle7].
$p=3$
using the work of Böckle [Reference Böckle7].
The argument of [Reference Colmez, Dospinescu and Paškūnas22] has been extended by Iyengar in [Reference Iyengar33], to the case when
![]() $\bar {\rho }$
is the trivial d-dimensional representation of a Galois group of a p-adic field F, under the assumption that F contains a primitive
$\bar {\rho }$
is the trivial d-dimensional representation of a Galois group of a p-adic field F, under the assumption that F contains a primitive
![]() $4$
th root of unity if
$4$
th root of unity if
![]() $p=2$
. Thus our theorem applies in that setting.Footnote
3
$p=2$
. Thus our theorem applies in that setting.Footnote
3
We will split the proof into several steps. We start with commutative algebra lemmas and recall that all excellent rings are G-rings [45, Tag 07QS].
Lemma A.2. Let A be a G-ring and set
![]() $\mathfrak p\in \operatorname {\mathrm {Spec}} A$
. Then
$\mathfrak p\in \operatorname {\mathrm {Spec}} A$
. Then
![]() $A_{\mathfrak p}$
satisfies Serre’s condition
$A_{\mathfrak p}$
satisfies Serre’s condition
![]() $(R_i)$
(resp.,
$(R_i)$
(resp.,
![]() $(S_i)$
) if and only if the completion
$(S_i)$
) if and only if the completion
![]() $A_{\mathfrak p}$
at
$A_{\mathfrak p}$
at
![]() $\mathfrak p$
does.
$\mathfrak p$
does.
Proof. Let
![]() $B=A_{\mathfrak p}$
and let
$B=A_{\mathfrak p}$
and let
![]() $\hat {B}$
be the completion of
$\hat {B}$
be the completion of
![]() $A_{\mathfrak p}$
at
$A_{\mathfrak p}$
at
![]() $\mathfrak p$
. Since A is a G-ring, the fibre rings
$\mathfrak p$
. Since A is a G-ring, the fibre rings
![]() $\kappa (\mathfrak q)\otimes _B \hat {B}$
are regular for all
$\kappa (\mathfrak q)\otimes _B \hat {B}$
are regular for all
![]() $\mathfrak q\in \operatorname {\mathrm {Spec}} B$
. The assertion follows from [Reference Matsumura and Reid36, Theorem 23.9].
$\mathfrak q\in \operatorname {\mathrm {Spec}} B$
. The assertion follows from [Reference Matsumura and Reid36, Theorem 23.9].
Lemma A.3. Let A be a complete local Noetherian
![]() $\mathscr O$
-algebra with residue field k and
$\mathscr O$
-algebra with residue field k and
![]() , set
, set
![]() $\mathfrak q \in \operatorname {\mathrm {Spec}} B [1/p ]$
, and let
$\mathfrak q \in \operatorname {\mathrm {Spec}} B [1/p ]$
, and let
![]() $\mathfrak p$
be the image of
$\mathfrak p$
be the image of
![]() $\mathfrak q$
in
$\mathfrak q$
in
![]() $\operatorname {\mathrm {Spec}} A [1/p ]$
. Then
$\operatorname {\mathrm {Spec}} A [1/p ]$
. Then
![]() $A_{\mathfrak p}$
satisfies Serre’s condition
$A_{\mathfrak p}$
satisfies Serre’s condition
![]() $(R_i)$
(resp.,
$(R_i)$
(resp.,
![]() $(S_i)$
) if and only if
$(S_i)$
) if and only if
![]() $B_{\mathfrak q}$
does. In particular,
$B_{\mathfrak q}$
does. In particular,
![]() $A [1/p ]$
is normal if and only if
$A [1/p ]$
is normal if and only if
![]() $B [1/p ]$
is normal.
$B [1/p ]$
is normal.
Proof. The proof is a variation on [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and Shin15, Appendix A]. We may assume that A and hence B are
![]() $\mathscr O$
-torsion-free. Set
$\mathscr O$
-torsion-free. Set
![]() $\mathfrak p'\in \operatorname {\mathrm {Spec}} A_{\mathfrak p} \subset \operatorname {\mathrm {Spec}} A$
. We claim that the ring
$\mathfrak p'\in \operatorname {\mathrm {Spec}} A_{\mathfrak p} \subset \operatorname {\mathrm {Spec}} A$
. We claim that the ring
![]() $\kappa (\mathfrak p')\otimes _A B$
is regular. By Cohen’s structure theorem, there is a subring
$\kappa (\mathfrak p')\otimes _A B$
is regular. By Cohen’s structure theorem, there is a subring
![]() $C\subset A/\mathfrak p'$
such that C is formally smooth over
$C\subset A/\mathfrak p'$
such that C is formally smooth over
![]() $\mathscr O$
and
$\mathscr O$
and
![]() $A/\mathfrak p'$
is finite over C. Then
$A/\mathfrak p'$
is finite over C. Then
Since
![]() $A/\mathfrak p'$
is finite over C, we have
$A/\mathfrak p'$
is finite over C, we have
Thus
where
![]() $Q(C)$
is the quotient field of C. Since C is formally smooth over
$Q(C)$
is the quotient field of C. Since C is formally smooth over
![]() $\mathscr O$
, the ring
$\mathscr O$
, the ring
is isomorphic to a ring of formal power series over
![]() $\mathscr O$
, and thus is regular. Tensoring with
$\mathscr O$
, and thus is regular. Tensoring with
![]() $Q(C)$
over C is just localisation with respect to the multiplicative set
$Q(C)$
over C is just localisation with respect to the multiplicative set
![]() $C\setminus \{0\}$
, and thus
$C\setminus \{0\}$
, and thus
is regular. Since
![]() $Q(C)$
is of characteristic
$Q(C)$
is of characteristic
![]() $0$
, the extension
$0$
, the extension
![]() $\kappa (\mathfrak p)/ Q(C)$
is separable, and it follows from [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and Shin15, Lemma A.3] that
$\kappa (\mathfrak p)/ Q(C)$
is separable, and it follows from [Reference Caraiani, Emerton, Gee, Geraghty, Paškūnas and Shin15, Lemma A.3] that
is regular. We deduce that
![]() $\kappa (\mathfrak p')\otimes _{A_{\mathfrak p}} B_{\mathfrak q}$
is regular, since it is a localisation of
$\kappa (\mathfrak p')\otimes _{A_{\mathfrak p}} B_{\mathfrak q}$
is regular, since it is a localisation of
![]() $\kappa (\mathfrak p')\otimes _A B$
at
$\kappa (\mathfrak p')\otimes _A B$
at
![]() $\mathfrak q$
.
$\mathfrak q$
.
It follows from [Reference Matsumura and Reid36, Theorem 23.9] that
![]() $A_{\mathfrak p}$
satisfies
$A_{\mathfrak p}$
satisfies
![]() $(R_i)$
(resp.,
$(R_i)$
(resp.,
![]() $(S_i)$
) if and only if
$(S_i)$
) if and only if
![]() $B_{\mathfrak q}$
does. To conclude that
$B_{\mathfrak q}$
does. To conclude that
![]() $A [1/p ]$
is normal if and only if
$A [1/p ]$
is normal if and only if
![]() $B [1/p ]$
is, we only have to show that the map
$B [1/p ]$
is, we only have to show that the map
![]() $\operatorname {\mathrm {Spec}} B [1/p ]\rightarrow \operatorname {\mathrm {Spec}} A [1/p ]$
is surjective, and this is clear because
$\operatorname {\mathrm {Spec}} B [1/p ]\rightarrow \operatorname {\mathrm {Spec}} A [1/p ]$
is surjective, and this is clear because
![]() $(\mathfrak p, x_1, \dotsc , x_r)$
maps to
$(\mathfrak p, x_1, \dotsc , x_r)$
maps to
![]() $\mathfrak p$
.
$\mathfrak p$
.
Lemma A.4. Let
![]() $A\rightarrow B$
be a finite étale map of local rings. Then A satisfies Serre’s condition
$A\rightarrow B$
be a finite étale map of local rings. Then A satisfies Serre’s condition
![]() $(R_i)$
(resp.,
$(R_i)$
(resp.,
![]() $(S_i)$
) if and only if B does.
$(S_i)$
) if and only if B does.
Proof. If
![]() $\mathfrak p\in \operatorname {\mathrm {Spec}} A$
, then the fibre ring
$\mathfrak p\in \operatorname {\mathrm {Spec}} A$
, then the fibre ring
![]() $\kappa (\mathfrak p)\otimes _A B$
is a finite étale
$\kappa (\mathfrak p)\otimes _A B$
is a finite étale
![]() $\kappa (\mathfrak p)$
-algebra and hence a product of fields, and thus is regular. The assertion follows from [Reference Matsumura and Reid36, Theorem 23.9].
$\kappa (\mathfrak p)$
-algebra and hence a product of fields, and thus is regular. The assertion follows from [Reference Matsumura and Reid36, Theorem 23.9].
Proposition A.5. Let
![]() $L'$
be a finite extension of L and let
$L'$
be a finite extension of L and let
![]() $\rho : \mathscr G \rightarrow \operatorname {\mathrm {GL}}_n(L')$
be a continuous representation with mod p semisimplification isomorphic to
$\rho : \mathscr G \rightarrow \operatorname {\mathrm {GL}}_n(L')$
be a continuous representation with mod p semisimplification isomorphic to
![]() $\bar {\rho }$
. If
$\bar {\rho }$
. If
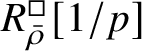 $R^{\square }_{\bar {\rho }} [1/p ]$
is normal, then the ring
$R^{\square }_{\bar {\rho }} [1/p ]$
is normal, then the ring
![]() $R^{\square }_{\rho }$
, representing the framed deformations of
$R^{\square }_{\rho }$
, representing the framed deformations of
![]() $\rho $
to Artinian
$\rho $
to Artinian
![]() $L'$
-algebras, is also normal.
$L'$
-algebras, is also normal.
Proof. We may choose a finite extension
![]() $L''$
of
$L''$
of
![]() $L'$
with the ring of integers
$L'$
with the ring of integers
![]() $\mathscr O''$
and residue field
$\mathscr O''$
and residue field
![]() $k''$
such that
$k''$
such that
![]() $\rho \otimes _{L'} L''$
has a
$\rho \otimes _{L'} L''$
has a
![]() $\mathscr G$
-invariant
$\mathscr G$
-invariant
![]() $\mathscr O''$
-lattice
$\mathscr O''$
-lattice
![]() $\Theta $
with
$\Theta $
with
![]() $\Theta \otimes _{\mathscr O''} k''\cong \bar {\rho }\otimes _k k''$
(see the proof of [Reference Colmez, Dospinescu and Paškūnas22, Lemma 9.5]). Thus
$\Theta \otimes _{\mathscr O''} k''\cong \bar {\rho }\otimes _k k''$
(see the proof of [Reference Colmez, Dospinescu and Paškūnas22, Lemma 9.5]). Thus
![]() $\Theta $
is a deformation of
$\Theta $
is a deformation of
![]() $\bar {\rho }\otimes _k k''$
to
$\bar {\rho }\otimes _k k''$
to
![]() $\mathscr O''$
.
$\mathscr O''$
.
It follows from Lemma A.4 that
![]() $R^{\square }_{\rho }$
is normal if and only if
$R^{\square }_{\rho }$
is normal if and only if
![]() $L''\otimes _{L'} R^{\square }_{\rho }$
is normal. The same argument shows that
$L''\otimes _{L'} R^{\square }_{\rho }$
is normal. The same argument shows that
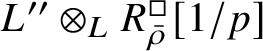 $L''\otimes _{L} R^{\square }_{\bar {\rho }} [1/p ]$
is normal. Moreover, we may identify
$L''\otimes _{L} R^{\square }_{\bar {\rho }} [1/p ]$
is normal. Moreover, we may identify
![]() $L''\otimes _{L'} R^{\square }_{\rho }$
with the framed deformation ring of
$L''\otimes _{L'} R^{\square }_{\rho }$
with the framed deformation ring of
![]() $\rho \otimes _{L'} L''$
to local Artinian
$\rho \otimes _{L'} L''$
to local Artinian
![]() $L''$
-algebras, and
$L''$
-algebras, and
 $\mathscr O''\otimes _{\mathscr O} R^{\square }_{\bar {\rho }}$
with the framed deformation ring of
$\mathscr O''\otimes _{\mathscr O} R^{\square }_{\bar {\rho }}$
with the framed deformation ring of
![]() $\bar {\rho }\otimes _k k''$
to local Artinian
$\bar {\rho }\otimes _k k''$
to local Artinian
![]() $\mathscr O''$
-algebras. After these identifications, we may assume that
$\mathscr O''$
-algebras. After these identifications, we may assume that
![]() $L=L'=L''$
, and so
$L=L'=L''$
, and so
![]() $\Theta $
is a deformation of
$\Theta $
is a deformation of
![]() $\bar {\rho }$
to
$\bar {\rho }$
to
![]() $\mathscr O$
and hence induces an
$\mathscr O$
and hence induces an
![]() $\mathscr O$
-algebra homomorphism
$\mathscr O$
-algebra homomorphism
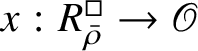 $x: R^{\square }_{\bar {\rho }} \rightarrow \mathscr O$
.
$x: R^{\square }_{\bar {\rho }} \rightarrow \mathscr O$
.
It follows from [Reference Kisin35, Lemma 2.3.3, Proposition 2.3.5] that
![]() $R^{\square }_{\rho }$
is isomorphic to the completion of
$R^{\square }_{\rho }$
is isomorphic to the completion of
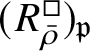 $ (R^{\square }_{\bar {\rho }} )_{\mathfrak p}$
at
$ (R^{\square }_{\bar {\rho }} )_{\mathfrak p}$
at
![]() $\mathfrak p=\operatorname {\mathrm {Ker}} x$
. Since
$\mathfrak p=\operatorname {\mathrm {Ker}} x$
. Since
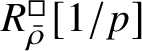 $R^{\square }_{\bar {\rho }} [1/p ]$
is normal,
$R^{\square }_{\bar {\rho }} [1/p ]$
is normal,
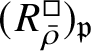 $ (R^{\square }_{\bar {\rho }} )_{\mathfrak p}$
will satisfy
$ (R^{\square }_{\bar {\rho }} )_{\mathfrak p}$
will satisfy
![]() $(R_1)$
and
$(R_1)$
and
![]() $(S_2)$
. Lemma A.2 implies that the same holds for the completion. Thus
$(S_2)$
. Lemma A.2 implies that the same holds for the completion. Thus
![]() $R^{\square }_{\rho }$
is normal by Serre’s criterion for normality [Reference Matsumura and Reid36, Theorem 23.8].
$R^{\square }_{\rho }$
is normal by Serre’s criterion for normality [Reference Matsumura and Reid36, Theorem 23.8].
Lemma A.6. Let A be a normal Noetherian ring and let G be a group acting on A by ring automorphisms. Then the subring of G-invariants
![]() $A^G$
is normal.
$A^G$
is normal.
Proof. If A is a domain, then the assertion is proved in [Reference Bruns and Herzog13, Proposition 6.4.1]. The same proof works in our setting, as we will explain for the lack of a reference. Since A is Noetherian and normal, it is a finite product of normal domains. Let
![]() $\operatorname {\mathrm {Frac}}(A)$
denote its total ring of fractions. Then
$\operatorname {\mathrm {Frac}}(A)$
denote its total ring of fractions. Then
![]() $\operatorname {\mathrm {Frac}}(A)$
is a finite product of fields. The group G acts on
$\operatorname {\mathrm {Frac}}(A)$
is a finite product of fields. The group G acts on
![]() $\operatorname {\mathrm {Frac}}(A)$
and we have
$\operatorname {\mathrm {Frac}}(A)$
and we have
We claim that
![]() $\operatorname {\mathrm {Frac}}(A)^G$
is a finite product of fields. The claim implies that
$\operatorname {\mathrm {Frac}}(A)^G$
is a finite product of fields. The claim implies that
![]() $\operatorname {\mathrm {Frac}}(A)^G$
is its own ring of fractions. Since A is normal, equation (26) implies that
$\operatorname {\mathrm {Frac}}(A)^G$
is its own ring of fractions. Since A is normal, equation (26) implies that
![]() $A^G$
is reduced and integrally closed in its ring of fractions and has only finitely many minimal prime ideals – and hence is normal by [45, Tag 037B, Lemma 10.37.16].
$A^G$
is reduced and integrally closed in its ring of fractions and has only finitely many minimal prime ideals – and hence is normal by [45, Tag 037B, Lemma 10.37.16].
To prove the claim, we note that
![]() $\operatorname {\mathrm {Spec}} \operatorname {\mathrm {Frac}}(A)$
consists of finitely many primes and is in bijection with the set
$\operatorname {\mathrm {Spec}} \operatorname {\mathrm {Frac}}(A)$
consists of finitely many primes and is in bijection with the set
![]() $\mathscr E$
of idempotents
$\mathscr E$
of idempotents
![]() $e\in \operatorname {\mathrm {Frac}}(A)$
, such that
$e\in \operatorname {\mathrm {Frac}}(A)$
, such that
![]() $e \operatorname {\mathrm {Frac}}(A) e$
is a field. We have
$e \operatorname {\mathrm {Frac}}(A) e$
is a field. We have
![]() $1=\sum _{e\in \mathscr E} e$
and
$1=\sum _{e\in \mathscr E} e$
and
![]() $e e'=0$
if
$e e'=0$
if
![]() $e\neq e'$
. If
$e\neq e'$
. If
![]() $e\in \operatorname {\mathrm {Frac}}(A)$
is a G-invariant idempotent, then
$e\in \operatorname {\mathrm {Frac}}(A)$
is a G-invariant idempotent, then
and thus we may assume that the action of G on
![]() $\mathscr E$
is transitive. If
$\mathscr E$
is transitive. If
![]() $x\in \operatorname {\mathrm {Frac}}(A)^G$
and
$x\in \operatorname {\mathrm {Frac}}(A)^G$
and
![]() $e x=0$
for some
$e x=0$
for some
![]() $e\in \mathscr E$
, then using the transitivity of the action we obtain that
$e\in \mathscr E$
, then using the transitivity of the action we obtain that
![]() $ex=0$
for all
$ex=0$
for all
![]() $e\in \mathscr E$
, and so
$e\in \mathscr E$
, and so
![]() $x=\sum _{e\in \mathscr E} ex=0$
. Hence, if
$x=\sum _{e\in \mathscr E} ex=0$
. Hence, if
![]() $x\in \operatorname {\mathrm {Frac}}(A)^G$
is nonzero, then
$x\in \operatorname {\mathrm {Frac}}(A)^G$
is nonzero, then
![]() $ex$
is nonzero, and we denote its inverse in the field
$ex$
is nonzero, and we denote its inverse in the field
![]() $e \operatorname {\mathrm {Frac}}(A) e$
by
$e \operatorname {\mathrm {Frac}}(A) e$
by
![]() $(xe)^{-1}$
. If we let
$(xe)^{-1}$
. If we let
![]() $y= \sum _{e\in \mathscr E} (xe)^{-1} e \in \operatorname {\mathrm {Frac}}(A)$
, then
$y= \sum _{e\in \mathscr E} (xe)^{-1} e \in \operatorname {\mathrm {Frac}}(A)$
, then
![]() $xy=1$
. Thus x is a unit in
$xy=1$
. Thus x is a unit in
![]() $\operatorname {\mathrm {Frac}}(A)$
and its inverse y is unique. Uniqueness implies that y is G-invariant. Thus if G acts transitively on
$\operatorname {\mathrm {Frac}}(A)$
and its inverse y is unique. Uniqueness implies that y is G-invariant. Thus if G acts transitively on
![]() $\mathscr E$
, then
$\mathscr E$
, then
![]() $\operatorname {\mathrm {Frac}}(A)^G$
is a field.
$\operatorname {\mathrm {Frac}}(A)^G$
is a field.
Proof of Theorem A.1. Let
![]() $D^u: \mathscr G\rightarrow R^{\mathrm {ps}}$
be the universal pseudorepresentation lifting
$D^u: \mathscr G\rightarrow R^{\mathrm {ps}}$
be the universal pseudorepresentation lifting
![]() $\overline {D}$
. Let
$\overline {D}$
. Let
![]() $\mathrm {CH}(D^u)$
be the closed two-sided ideal of
$\mathrm {CH}(D^u)$
be the closed two-sided ideal of
![]() defined in [Reference Chenevier18, Section 1.17], so that
defined in [Reference Chenevier18, Section 1.17], so that
![]() is the largest quotient of
is the largest quotient of
![]() where the Cayley–Hamilton theorem for
where the Cayley–Hamilton theorem for
![]() $D^u$
holds. Following [Reference Chenevier18, Section 1.17], we will call such an algebra a Cayley–Hamilton
$D^u$
holds. Following [Reference Chenevier18, Section 1.17], we will call such an algebra a Cayley–Hamilton
![]() $R^{\mathrm {ps}}$
-algebra of degree d. Then E is a finitely generated
$R^{\mathrm {ps}}$
-algebra of degree d. Then E is a finitely generated
![]() $R^{\mathrm {ps}}$
-module [Reference Wang-Erickson48, Proposition 3.6]. If
$R^{\mathrm {ps}}$
-module [Reference Wang-Erickson48, Proposition 3.6]. If
![]() $f: E\rightarrow M_d(B)$
is a homomorphism of
$f: E\rightarrow M_d(B)$
is a homomorphism of
![]() $R^{\mathrm {ps}}$
-algebras for a commutative
$R^{\mathrm {ps}}$
-algebras for a commutative
![]() $R^{\mathrm {ps}}$
-algebra B, then we say f is a homomorphism of Cayley–Hamilton algebras if
$R^{\mathrm {ps}}$
-algebra B, then we say f is a homomorphism of Cayley–Hamilton algebras if
![]() $\det \circ f: E\rightarrow B$
is equal to the specialisation of
$\det \circ f: E\rightarrow B$
is equal to the specialisation of
![]() $D^u$
along
$D^u$
along
![]() $R^{\mathrm {ps}}\rightarrow B$
.
$R^{\mathrm {ps}}\rightarrow B$
.
There is a commutative
![]() $R^{\mathrm {ps}}$
-algebra
$R^{\mathrm {ps}}$
-algebra
![]() $A^{\mathrm {gen}}$
together with a homomorphism of
$A^{\mathrm {gen}}$
together with a homomorphism of
![]() $R^{\mathrm {ps}}$
-algebras
$R^{\mathrm {ps}}$
-algebras
![]() $j: E\rightarrow M_d(A^{\mathrm {gen}})$
satisfying the following universal property: If
$j: E\rightarrow M_d(A^{\mathrm {gen}})$
satisfying the following universal property: If
![]() $f: E\rightarrow M_d(B)$
is a map of Cayley–Hamilton
$f: E\rightarrow M_d(B)$
is a map of Cayley–Hamilton
![]() $R^{\mathrm {ps}}$
-algebras for a commutative
$R^{\mathrm {ps}}$
-algebras for a commutative
![]() $R^{\mathrm {ps}}$
-algebra B, then there is a unique map
$R^{\mathrm {ps}}$
-algebra B, then there is a unique map
![]() $\tilde {f}: A^{\mathrm {gen}}\rightarrow B$
of
$\tilde {f}: A^{\mathrm {gen}}\rightarrow B$
of
![]() $R^{\mathrm {ps}}$
-algebras such that
$R^{\mathrm {ps}}$
-algebras such that
![]() $f= M_d (\tilde {f} )\circ j$
(see, for example, [Reference Wang-Erickson48, Theorem 3.8] or [Reference Böckle, Iyengar and Paškūnas8, Lemma 3.1]). Since E is finitely generated as an
$f= M_d (\tilde {f} )\circ j$
(see, for example, [Reference Wang-Erickson48, Theorem 3.8] or [Reference Böckle, Iyengar and Paškūnas8, Lemma 3.1]). Since E is finitely generated as an
![]() $R^{\mathrm {ps}}$
-module,
$R^{\mathrm {ps}}$
-module,
![]() $A^{\mathrm {gen}}$
is of finite type over
$A^{\mathrm {gen}}$
is of finite type over
![]() $R^{\mathrm {ps}}$
.
$R^{\mathrm {ps}}$
.
Let
![]() $\Lambda _i: E\rightarrow R^{\mathrm {ps}}$
,
$\Lambda _i: E\rightarrow R^{\mathrm {ps}}$
,
![]() $0\le i\le d$
, be the coefficients of the characteristic polynomial of
$0\le i\le d$
, be the coefficients of the characteristic polynomial of
![]() $D^u$
; these are homogeneous polynomial laws satisfying
$D^u$
; these are homogeneous polynomial laws satisfying
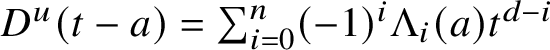 $D^{u}(t-a)= \sum _{i=0}^n (-1)^i \Lambda _i(a) t^{d-i}$
in
$D^{u}(t-a)= \sum _{i=0}^n (-1)^i \Lambda _i(a) t^{d-i}$
in
![]() $R^{\mathrm {ps}}[t]$
for all
$R^{\mathrm {ps}}[t]$
for all
![]() $a\in E$
[Reference Chenevier18, Section 1.10]. Now
$a\in E$
[Reference Chenevier18, Section 1.10]. Now
![]() $E [1/p ]$
is a
$E [1/p ]$
is a
![]() $\mathbb Q$
-algebra and the pair
$\mathbb Q$
-algebra and the pair
![]() $ (E [1/p ], \Lambda _1 )$
is a trace algebra satisfying the d-dimensional Cayley–Hamilton identity in the sense of [Reference Procesi43, Definition 2.6] (see [Reference Chenevier16, Footnote 10]). Moreover, for
$ (E [1/p ], \Lambda _1 )$
is a trace algebra satisfying the d-dimensional Cayley–Hamilton identity in the sense of [Reference Procesi43, Definition 2.6] (see [Reference Chenevier16, Footnote 10]). Moreover, for
![]() $\mathbb Q$
-algebras, the homomorphisms of Cayley–Hamilton algebras coincide with the notion of maps of algebras with traces in [Reference Procesi43, Section 2.5]. Thus
$\mathbb Q$
-algebras, the homomorphisms of Cayley–Hamilton algebras coincide with the notion of maps of algebras with traces in [Reference Procesi43, Section 2.5]. Thus
![]() $j: E [1/p ] \rightarrow M_d (A^{\mathrm {gen}} [1/p ] )$
is injective and its image is equal to the
$j: E [1/p ] \rightarrow M_d (A^{\mathrm {gen}} [1/p ] )$
is injective and its image is equal to the
![]() $\operatorname {\mathrm {GL}}_d$
-invariants [Reference Procesi43, Theorem 2.6]. Moreover,
$\operatorname {\mathrm {GL}}_d$
-invariants [Reference Procesi43, Theorem 2.6]. Moreover,
![]() $R^{\mathrm {ps}} [1/p ]= (A^{\mathrm {gen}} [1/p ] )^{\operatorname {\mathrm {GL}}_d}$
(see [Reference Chenevier16, Proposition 2.3] and [Reference Wang-Erickson48, Theorem 2.20]). By Lemma A.6 it is enough to show that
$R^{\mathrm {ps}} [1/p ]= (A^{\mathrm {gen}} [1/p ] )^{\operatorname {\mathrm {GL}}_d}$
(see [Reference Chenevier16, Proposition 2.3] and [Reference Wang-Erickson48, Theorem 2.20]). By Lemma A.6 it is enough to show that
![]() $A^{\mathrm {gen}} [1/p ]$
is normal. Further, it is enough to show that the localisation of
$A^{\mathrm {gen}} [1/p ]$
is normal. Further, it is enough to show that the localisation of
![]() $A^{\mathrm {gen}} [1/p ]$
at every maximal ideal is normal (see [45, Tag 037B, Lemma 10.37.10]). (The superscript ‘gen’ in
$A^{\mathrm {gen}} [1/p ]$
at every maximal ideal is normal (see [45, Tag 037B, Lemma 10.37.10]). (The superscript ‘gen’ in
![]() $A^{\mathrm {gen}}$
stands for generic matrices in [Reference Procesi43, Section 1.1].)
$A^{\mathrm {gen}}$
stands for generic matrices in [Reference Procesi43, Section 1.1].)
Let
![]() $\mathfrak m$
be a maximal ideal of
$\mathfrak m$
be a maximal ideal of
![]() $A^{\mathrm {gen}} [1/p ]$
. Its residue field
$A^{\mathrm {gen}} [1/p ]$
. Its residue field
![]() $\kappa (\mathfrak m)$
is a finite extension of L, as
$\kappa (\mathfrak m)$
is a finite extension of L, as
![]() $A^{\mathrm {gen}} [1/p ]$
is finitely generated over
$A^{\mathrm {gen}} [1/p ]$
is finitely generated over
![]() $R^{\mathrm {ps}} [1/p ]$
. By specialising j at
$R^{\mathrm {ps}} [1/p ]$
. By specialising j at
![]() $\mathfrak m$
we obtain a continuous representation
$\mathfrak m$
we obtain a continuous representation
![]() $\rho :\mathscr G\rightarrow \operatorname {\mathrm {GL}}_d(\kappa (\mathfrak m))$
such that
$\rho :\mathscr G\rightarrow \operatorname {\mathrm {GL}}_d(\kappa (\mathfrak m))$
such that
This implies that if we choose a
![]() $\mathscr G$
-invariant
$\mathscr G$
-invariant
![]() $\mathscr O_{\kappa (\mathfrak m)}$
-lattice
$\mathscr O_{\kappa (\mathfrak m)}$
-lattice
![]() $\Theta $
in
$\Theta $
in
![]() $\rho $
, then the semisimplification of
$\rho $
, then the semisimplification of
![]() $\Theta /\varpi _{\kappa (\mathfrak m)}\Theta $
is isomorphic to
$\Theta /\varpi _{\kappa (\mathfrak m)}\Theta $
is isomorphic to
![]() $\bar {\rho }$
, so that we are in the setup of Proposition A.5. The universal property of
$\bar {\rho }$
, so that we are in the setup of Proposition A.5. The universal property of
![]() $A^{\mathrm {gen}}$
implies that the completion of
$A^{\mathrm {gen}}$
implies that the completion of
![]() $A^{\mathrm {gen}} [1/p ]$
at
$A^{\mathrm {gen}} [1/p ]$
at
![]() $\mathfrak m$
is the universal framed deformation ring
$\mathfrak m$
is the universal framed deformation ring
![]() $R^{\square }_{\rho }$
, which is normal by Proposition A.5. Since
$R^{\square }_{\rho }$
, which is normal by Proposition A.5. Since
![]() $A^{\mathrm {gen}}$
is finitely generated over
$A^{\mathrm {gen}}$
is finitely generated over
![]() $R^{\mathrm {ps}}$
, which is a complete local Noetherian ring,
$R^{\mathrm {ps}}$
, which is a complete local Noetherian ring,
![]() $A^{\mathrm {gen}}$
and hence its localisation
$A^{\mathrm {gen}}$
and hence its localisation
![]() $ (A^{\mathrm {gen}} [1/p ] )_{\mathfrak m}$
are excellent, and thus a G-ring. Lemma A.2 implies that
$ (A^{\mathrm {gen}} [1/p ] )_{\mathfrak m}$
are excellent, and thus a G-ring. Lemma A.2 implies that
![]() $ (A^{\mathrm {gen}} [1/p ] )_{\mathfrak m}$
satisfies
$ (A^{\mathrm {gen}} [1/p ] )_{\mathfrak m}$
satisfies
![]() $(R_1)$
and
$(R_1)$
and
![]() $(S_2)$
and hence is normal.
$(S_2)$
and hence is normal.
Let
![]() $\tilde {R}$
be the normalisation of
$\tilde {R}$
be the normalisation of
![]() $R^{\mathrm {ps}}$
in
$R^{\mathrm {ps}}$
in
![]() $R^{\mathrm {ps}} [1/p ]$
. Then
$R^{\mathrm {ps}} [1/p ]$
. Then
![]() $(\operatorname {\mathrm {Spf}} R^{\mathrm {ps}})^{\mathrm {rig}}= (\operatorname {\mathrm {Spf}} \tilde {R} )^{\mathrm {rig}}$
[Reference de Jong24, Lemma 7.2.2]. Since
$(\operatorname {\mathrm {Spf}} R^{\mathrm {ps}})^{\mathrm {rig}}= (\operatorname {\mathrm {Spf}} \tilde {R} )^{\mathrm {rig}}$
[Reference de Jong24, Lemma 7.2.2]. Since
![]() $R^{\mathrm {ps}} [1/p ]$
is normal, so is
$R^{\mathrm {ps}} [1/p ]$
is normal, so is
![]() $\tilde {R}$
, and thus
$\tilde {R}$
, and thus
![]() $ (\operatorname {\mathrm {Spf}} \tilde {R} )^{\mathrm {rig}}$
is normal [Reference de Jong24, Proposition 7.2.4(c)]. Alternatively, one could use the fact that the local rings of
$ (\operatorname {\mathrm {Spf}} \tilde {R} )^{\mathrm {rig}}$
is normal [Reference de Jong24, Proposition 7.2.4(c)]. Alternatively, one could use the fact that the local rings of
![]() $(\operatorname {\mathrm {Spf}} R^{\mathrm {ps}})^{\mathrm {rig}}$
are excellent [Reference Conrad23, Theorem 1.1.3] and [Reference de Jong24, Lemma 7.1.9] together with Lemma A.2.
$(\operatorname {\mathrm {Spf}} R^{\mathrm {ps}})^{\mathrm {rig}}$
are excellent [Reference Conrad23, Theorem 1.1.3] and [Reference de Jong24, Lemma 7.1.9] together with Lemma A.2.
The following is a corollary to the proof; it does not require the assumption that
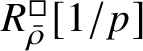 $R^{\square }_{\bar {\rho }} [1/p ]$
is normal:
$R^{\square }_{\bar {\rho }} [1/p ]$
is normal:
Corollary A.7. Let V be a free
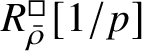 $R^{\square }_{\bar {\rho }} [1/p ]$
-module of rank d with
$R^{\square }_{\bar {\rho }} [1/p ]$
-module of rank d with
![]() $\mathscr G$
-action given by
$\mathscr G$
-action given by
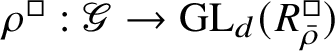 $\rho ^{\square }: \mathscr G \rightarrow \operatorname {\mathrm {GL}}_d (R^{\square }_{\bar {\rho }} )$
. Then
$\rho ^{\square }: \mathscr G \rightarrow \operatorname {\mathrm {GL}}_d (R^{\square }_{\bar {\rho }} )$
. Then
![]() acts faithfully on V. The same holds with the fixed determinant.
acts faithfully on V. The same holds with the fixed determinant.
Proof. We use the notation of the proof of Theorem A.1, so that
![]() and there is a map
and there is a map
![]() $j: E\rightarrow M_d(A^{\mathrm {gen}})$
satisfying a universal property. This map is an injection after inverting p. Let
$j: E\rightarrow M_d(A^{\mathrm {gen}})$
satisfying a universal property. This map is an injection after inverting p. Let
![]() $V^{\mathrm {gen}}$
be a free
$V^{\mathrm {gen}}$
be a free
![]() $A^{\mathrm {gen}}$
-module of rank d, with E-action given by j. Thus
$A^{\mathrm {gen}}$
-module of rank d, with E-action given by j. Thus
![]() $E [1/p ]$
acts faithfully on
$E [1/p ]$
acts faithfully on
![]() $V^{\mathrm {gen}} [1/p ]$
.
$V^{\mathrm {gen}} [1/p ]$
.
Suppose that
![]() $a\in E [1/p ]$
kills off V. Since
$a\in E [1/p ]$
kills off V. Since
![]() $E [1/p ]$
acts faithfully on
$E [1/p ]$
acts faithfully on
![]() $V^{\mathrm {gen}} [1/p ]$
, there is a maximal ideal
$V^{\mathrm {gen}} [1/p ]$
, there is a maximal ideal
![]() $\mathfrak m$
of
$\mathfrak m$
of
![]() $A^{\mathrm {gen}} [1/p ]$
such that a acts nontrivially on
$A^{\mathrm {gen}} [1/p ]$
such that a acts nontrivially on
![]() $V^{\mathrm {gen}}\otimes _{A^{\mathrm {gen}}} A^{\mathrm {gen}}_{\mathfrak m}$
. Let
$V^{\mathrm {gen}}\otimes _{A^{\mathrm {gen}}} A^{\mathrm {gen}}_{\mathfrak m}$
. Let
![]() $\hat {A}^{\mathrm {gen}}_{\mathfrak m}$
be the completion of
$\hat {A}^{\mathrm {gen}}_{\mathfrak m}$
be the completion of
![]() $A^{\mathrm {gen}}_{\mathfrak m}$
with respect to the maximal ideal. Since
$A^{\mathrm {gen}}_{\mathfrak m}$
with respect to the maximal ideal. Since
![]() $\hat {A}^{\mathrm {gen}}_{\mathfrak m}$
is faithfully flat over
$\hat {A}^{\mathrm {gen}}_{\mathfrak m}$
is faithfully flat over
![]() $A^{\mathrm {gen}}_{\mathfrak m}$
, a acts nontrivially on the completion of
$A^{\mathrm {gen}}_{\mathfrak m}$
, a acts nontrivially on the completion of
![]() $V^{\mathrm {gen}} [1/p ]$
at
$V^{\mathrm {gen}} [1/p ]$
at
![]() $\mathfrak m$
, which we denote by
$\mathfrak m$
, which we denote by
![]() $\hat {V}^{\mathrm {gen}}_{\mathfrak m}$
. However, as explained in the proof of Theorem A.1,
$\hat {V}^{\mathrm {gen}}_{\mathfrak m}$
. However, as explained in the proof of Theorem A.1,
![]() $\hat {V}^{\mathrm {gen}}_{\mathfrak m}$
is isomorphic as an E-module to the completion of V at a maximal ideal of
$\hat {V}^{\mathrm {gen}}_{\mathfrak m}$
is isomorphic as an E-module to the completion of V at a maximal ideal of
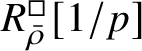 $R^{\square }_{\bar {\rho }} [1/p ]$
. Since a annihilates V, it will also annihilate the completion, giving a contradiction.
$R^{\square }_{\bar {\rho }} [1/p ]$
. Since a annihilates V, it will also annihilate the completion, giving a contradiction.
Define
![]() $E^{\psi }:= E\otimes _{R^{\mathrm {ps}}}R^{\mathrm {ps}, \psi }$
and
$E^{\psi }:= E\otimes _{R^{\mathrm {ps}}}R^{\mathrm {ps}, \psi }$
and
![]() $A^{\mathrm {gen}, \psi }:=A^{\mathrm {gen}}\otimes _{R^{\mathrm {ps}}}R^{\mathrm {ps}, \psi }$
. Then
$A^{\mathrm {gen}, \psi }:=A^{\mathrm {gen}}\otimes _{R^{\mathrm {ps}}}R^{\mathrm {ps}, \psi }$
. Then
![]() $j: E\rightarrow M_d(A^{\mathrm {gen}})$
induces a map
$j: E\rightarrow M_d(A^{\mathrm {gen}})$
induces a map
![]() $j: E^{\psi }\rightarrow M_d (A^{\mathrm {gen}, \psi } )$
which satisfies the same universal property as j. Then the same proof works with
$j: E^{\psi }\rightarrow M_d (A^{\mathrm {gen}, \psi } )$
which satisfies the same universal property as j. Then the same proof works with
![]() $A^{\mathrm {gen}, \psi }$
instead of
$A^{\mathrm {gen}, \psi }$
instead of
![]() $A^{\mathrm {gen}}$
.
$A^{\mathrm {gen}}$
.
Lemma A.8. Let R be a complete local Noetherian
![]() $\mathscr O$
-algebra with residue field k, and let
$\mathscr O$
-algebra with residue field k, and let
![]() $\rho : \mathscr G\rightarrow \operatorname {\mathrm {GL}}_d(R)$
be a continuous representation. Assume that R is
$\rho : \mathscr G\rightarrow \operatorname {\mathrm {GL}}_d(R)$
be a continuous representation. Assume that R is
![]() $\mathscr O$
-torsion-free and reduced, and the set of
$\mathscr O$
-torsion-free and reduced, and the set of
![]() $x\in \operatorname {\mathrm {m-Spec}} R [1/p ]$
such that
$x\in \operatorname {\mathrm {m-Spec}} R [1/p ]$
such that
![]() $\rho _x$
is absolutely irreducible is dense in
$\rho _x$
is absolutely irreducible is dense in
![]() $\operatorname {\mathrm {Spec}} R [1/p ]$
. Then
$\operatorname {\mathrm {Spec}} R [1/p ]$
. Then
consists of scalar matrices.
Proof. Set
![]() $X\in \mathscr C$
with matrix entries
$X\in \mathscr C$
with matrix entries
![]() $x_{ij}$
. Let
$x_{ij}$
. Let
![]() $\mathfrak p_1, \dotsc , \mathfrak p_n$
be the minimal primes of R. Since R is reduced, it embeds into
$\mathfrak p_1, \dotsc , \mathfrak p_n$
be the minimal primes of R. Since R is reduced, it embeds into
![]() $\prod _{s=1}^n \kappa (\mathfrak p_s)$
. It is enough to show that the image of X in
$\prod _{s=1}^n \kappa (\mathfrak p_s)$
. It is enough to show that the image of X in
![]() $M_d(\kappa (\mathfrak p_s))$
for
$M_d(\kappa (\mathfrak p_s))$
for
![]() $1\le s \le n$
is scalar, since if the images of
$1\le s \le n$
is scalar, since if the images of
![]() $x_{ij}$
and
$x_{ij}$
and
![]() $x_{ii}-x_{jj}$
for
$x_{ii}-x_{jj}$
for
![]() $i\neq j$
are zero in
$i\neq j$
are zero in
![]() $\kappa (\mathfrak p_s)$
for
$\kappa (\mathfrak p_s)$
for
![]() $1\le s\le n$
, then they are zero in A and so X is scalar. If
$1\le s\le n$
, then they are zero in A and so X is scalar. If
![]() $x\in \operatorname {\mathrm {m-Spec}} R [1/p ]$
is such that
$x\in \operatorname {\mathrm {m-Spec}} R [1/p ]$
is such that
![]() $\rho _x: \mathscr G\rightarrow \operatorname {\mathrm {GL}}_d(\kappa (x))$
is absolutely irreducible, then
$\rho _x: \mathscr G\rightarrow \operatorname {\mathrm {GL}}_d(\kappa (x))$
is absolutely irreducible, then
![]() $\mathscr C\otimes _R \kappa (x)$
is
$\mathscr C\otimes _R \kappa (x)$
is
![]() $1$
-dimensional. Since
$1$
-dimensional. Since
![]() $\mathfrak q\mapsto \dim _{\kappa (\mathfrak q )} \mathscr C\otimes _R \kappa (\mathfrak q)$
is upper semicontinuous and such x are dense, we deduce that
$\mathfrak q\mapsto \dim _{\kappa (\mathfrak q )} \mathscr C\otimes _R \kappa (\mathfrak q)$
is upper semicontinuous and such x are dense, we deduce that
![]() $\dim _{\kappa (\mathfrak p_s )} \mathscr C\otimes _R \kappa (\mathfrak p_s)=1$
for all minimal primes
$\dim _{\kappa (\mathfrak p_s )} \mathscr C\otimes _R \kappa (\mathfrak p_s)=1$
for all minimal primes
![]() $\mathfrak p_s$
. This implies that
$\mathfrak p_s$
. This implies that
![]() $\mathscr C\otimes _R \kappa (\mathfrak p_s)$
consists of scalar matrices.
$\mathscr C\otimes _R \kappa (\mathfrak p_s)$
consists of scalar matrices.
Proposition A.9. Assume that
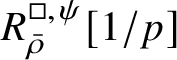 $R^{\square , \psi }_{\bar {\rho }} [1/p ]$
is nonzero. Then
$R^{\square , \psi }_{\bar {\rho }} [1/p ]$
is nonzero. Then
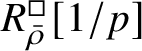 $R^{\square }_{\bar {\rho }} [1/p ]$
is normal (resp., reduced) if and only if
$R^{\square }_{\bar {\rho }} [1/p ]$
is normal (resp., reduced) if and only if
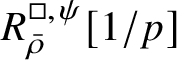 $R^{\square , \psi }_{\bar {\rho }} [1/p ]$
is normal (resp., reduced).
$R^{\square , \psi }_{\bar {\rho }} [1/p ]$
is normal (resp., reduced).
Proof. Let
![]() $\Gamma $
be the pro-p completion of the abelianisation of
$\Gamma $
be the pro-p completion of the abelianisation of
![]() $\mathscr G$
. Because
$\mathscr G$
. Because
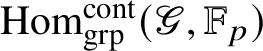 $\operatorname {\mathrm {Hom}}^{\mathrm {cont}}_{\mathrm {grp}} (\mathscr G, \mathbb F_p )$
is finite,
$\operatorname {\mathrm {Hom}}^{\mathrm {cont}}_{\mathrm {grp}} (\mathscr G, \mathbb F_p )$
is finite,
![]() $\Gamma \cong \Delta \times \mathbb {Z}_p^r$
, where
$\Gamma \cong \Delta \times \mathbb {Z}_p^r$
, where
![]() $\Delta $
is a finite p-group. The map
$\Delta $
is a finite p-group. The map
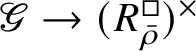 $\mathscr G\rightarrow (R^{\square }_{\bar {\rho }} )^{\times }$
,
$\mathscr G\rightarrow (R^{\square }_{\bar {\rho }} )^{\times }$
,
![]() $g\mapsto \psi (g)^{-1} \det \rho ^{\square }(g)$
, factors through
$g\mapsto \psi (g)^{-1} \det \rho ^{\square }(g)$
, factors through
![]() $\Gamma $
and thus induces an
$\Gamma $
and thus induces an
![]() $\mathscr O$
-algebra homomorphism
$\mathscr O$
-algebra homomorphism
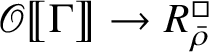 ; and
; and
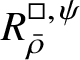 $R^{\square , \psi }_{\bar {\rho }}$
is equal to the quotient of
$R^{\square , \psi }_{\bar {\rho }}$
is equal to the quotient of
![]() $R^{\square }_{\bar {\rho }}$
by the augmentation ideal in
$R^{\square }_{\bar {\rho }}$
by the augmentation ideal in
![]() .
.
Let
![]() $\mathscr X(\Gamma )$
be the functor which sends a local Artinian
$\mathscr X(\Gamma )$
be the functor which sends a local Artinian
![]() $\mathscr O$
-algebra
$\mathscr O$
-algebra
![]() $(A, \mathfrak m_A)$
to the group of continuous characters
$(A, \mathfrak m_A)$
to the group of continuous characters
![]() $\chi : \Gamma \rightarrow 1+\mathfrak m_A$
. This functor is represented by
$\chi : \Gamma \rightarrow 1+\mathfrak m_A$
. This functor is represented by
![]() . For such
. For such
![]() $(A, \mathfrak m_A)$
, the group
$(A, \mathfrak m_A)$
, the group
![]() $\mathscr X(\Gamma )(A)$
acts on
$\mathscr X(\Gamma )(A)$
acts on
![]() $D^{\square }(A)$
by twisting. The action induces a homomorphism of local
$D^{\square }(A)$
by twisting. The action induces a homomorphism of local
![]() $\mathscr O$
-algebras
$\mathscr O$
-algebras
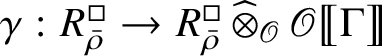 . Let
. Let
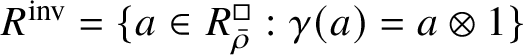 $R^{\mathrm {inv}}= \{ a\in R^{\square }_{\bar {\rho }}: \gamma (a)= a\otimes 1 \}$
be the subring of
$R^{\mathrm {inv}}= \{ a\in R^{\square }_{\bar {\rho }}: \gamma (a)= a\otimes 1 \}$
be the subring of
![]() $\mathscr X(\Gamma )$
-invariants in
$\mathscr X(\Gamma )$
-invariants in
![]() $R^{\square }_{\bar {\rho }}$
. Analogously,
$R^{\square }_{\bar {\rho }}$
. Analogously,
![]() $\mathscr X(\Delta )$
acts on
$\mathscr X(\Delta )$
acts on
![]() $D^{\square }$
, the action induces the map
$D^{\square }$
, the action induces the map
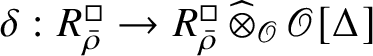 $\delta : R^{\square }_{\bar {\rho }}\rightarrow R^{\square }_{\bar {\rho }}\operatorname {\mathrm {\mathbin {\widehat {\otimes }}}}_{\mathscr O} \mathscr O[\Delta ]$
and we let
$\delta : R^{\square }_{\bar {\rho }}\rightarrow R^{\square }_{\bar {\rho }}\operatorname {\mathrm {\mathbin {\widehat {\otimes }}}}_{\mathscr O} \mathscr O[\Delta ]$
and we let
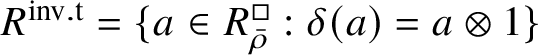 $R^{\mathrm {inv.t}}= \{ a\in R^{\square }_{\bar {\rho }}: \delta (a)= a\otimes 1 \}$
be the subring of
$R^{\mathrm {inv.t}}= \{ a\in R^{\square }_{\bar {\rho }}: \delta (a)= a\otimes 1 \}$
be the subring of
![]() $\mathscr X(\Delta )$
-invariants in
$\mathscr X(\Delta )$
-invariants in
![]() $R^{\square }_{\bar {\rho }}$
.
$R^{\square }_{\bar {\rho }}$
.
The action of
![]() $\mathscr X(\Gamma )$
and
$\mathscr X(\Gamma )$
and
![]() $\mathscr X(\Delta )$
on
$\mathscr X(\Delta )$
on
![]() $D^{\square }$
is free, since if
$D^{\square }$
is free, since if
![]() $\rho _A: \mathscr G_{\mathbb {Q}_p}\rightarrow \operatorname {\mathrm {GL}}_d(A)$
is a framed deformation of
$\rho _A: \mathscr G_{\mathbb {Q}_p}\rightarrow \operatorname {\mathrm {GL}}_d(A)$
is a framed deformation of
![]() $\bar {\rho }$
, then for each
$\bar {\rho }$
, then for each
![]() $g\in \mathscr G_{\mathbb {Q}_p}$
at least one matrix entry of
$g\in \mathscr G_{\mathbb {Q}_p}$
at least one matrix entry of
![]() $\rho _A(g)$
will not lie in
$\rho _A(g)$
will not lie in
![]() $\mathfrak m_A$
and thus is a unit. Hence,
$\mathfrak m_A$
and thus is a unit. Hence,
![]() $\rho _A(g)=\rho _A(g) \chi _A(g)$
for all
$\rho _A(g)=\rho _A(g) \chi _A(g)$
for all
![]() $g\in G$
implies that
$g\in G$
implies that
![]() $\chi _A$
is the trivial character.
$\chi _A$
is the trivial character.
The map
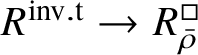 $R^{\mathrm {inv.t}} \rightarrow R^{\square }_{\bar {\rho }}$
is finite and becomes étale after inversion of p by [Reference Allen1, Proposition 1.1.11(2)]. Thus
$R^{\mathrm {inv.t}} \rightarrow R^{\square }_{\bar {\rho }}$
is finite and becomes étale after inversion of p by [Reference Allen1, Proposition 1.1.11(2)]. Thus
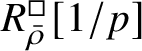 $R^{\square }_{\bar {\rho }} [1/p ]$
is normal if and only if
$R^{\square }_{\bar {\rho }} [1/p ]$
is normal if and only if
![]() $R^{\mathrm {inv.t}} [1/p ]$
is normal, by Lemma A.4. Since
$R^{\mathrm {inv.t}} [1/p ]$
is normal, by Lemma A.4. Since
![]() $R^{\mathrm {inv}}$
is the subring of
$R^{\mathrm {inv}}$
is the subring of
![]() $\mathscr X(\Gamma /\Delta )$
-invariants in
$\mathscr X(\Gamma /\Delta )$
-invariants in
![]() $R^{\mathrm {inv.t}}$
and
$R^{\mathrm {inv.t}}$
and
![]() $\Gamma /\Delta \cong \mathbb {Z}_p^r$
, we have
$\Gamma /\Delta \cong \mathbb {Z}_p^r$
, we have
![]() by [Reference Allen1, Proposition 1.1.11(2)]. Thus
by [Reference Allen1, Proposition 1.1.11(2)]. Thus
![]() $R^{\mathrm {inv.t}} [1/p ]$
is normal if and only if
$R^{\mathrm {inv.t}} [1/p ]$
is normal if and only if
![]() $R^{\mathrm {inv}} [1/p ]$
is normal, by Lemma A.3. The map
$R^{\mathrm {inv}} [1/p ]$
is normal, by Lemma A.3. The map
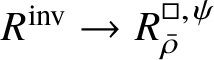 $R^{\mathrm {inv}}\rightarrow R^{\square , \psi }_{\bar {\rho }}$
is finite and becomes étale after inversion of p by [Reference Allen1, Proposition 1.1.11(3)]. Lemma A.4 implies that
$R^{\mathrm {inv}}\rightarrow R^{\square , \psi }_{\bar {\rho }}$
is finite and becomes étale after inversion of p by [Reference Allen1, Proposition 1.1.11(3)]. Lemma A.4 implies that
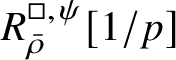 $R^{\square , \psi }_{\bar {\rho }} [1/p ]$
is normal if and only if
$R^{\square , \psi }_{\bar {\rho }} [1/p ]$
is normal if and only if
![]() $R^{\mathrm {inv}} [1/p ]$
is normal. Putting all the equivalences together proves the assertion.
$R^{\mathrm {inv}} [1/p ]$
is normal. Putting all the equivalences together proves the assertion.
Since reducedness is equivalent to (
![]() $R_0$
) and (
$R_0$
) and (
![]() $S_1$
), the same proof works.
$S_1$
), the same proof works.
Corollary A.10. If
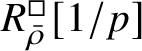 $R^{\square }_{\bar {\rho }} [1/p ]$
is normal, then
$R^{\square }_{\bar {\rho }} [1/p ]$
is normal, then
![]() $R^{\mathrm {ps}, \psi } [1/p ]$
and the associated rigid analytic space
$R^{\mathrm {ps}, \psi } [1/p ]$
and the associated rigid analytic space
![]() $ (\operatorname {\mathrm {Spf}} R^{\mathrm {ps}, \psi } )^{\mathrm {rig}}$
are normal.
$ (\operatorname {\mathrm {Spf}} R^{\mathrm {ps}, \psi } )^{\mathrm {rig}}$
are normal.
Proof. Proposition A.9 implies that
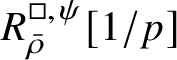 $R^{\square , \psi }_{\bar {\rho }} [1/p ]$
is normal. The proof of Theorem A.1, with
$R^{\square , \psi }_{\bar {\rho }} [1/p ]$
is normal. The proof of Theorem A.1, with
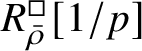 $R^{\square }_{\bar {\rho }} [1/p ]$
replaced by
$R^{\square }_{\bar {\rho }} [1/p ]$
replaced by
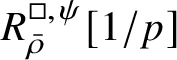 $R^{\square , \psi }_{\bar {\rho }} [1/p ]$
, implies the assertion.
$R^{\square , \psi }_{\bar {\rho }} [1/p ]$
, implies the assertion.
Proposition A.11. Let
![]() ,
,
![]() $E_{\mathrm {tf}}$
the maximal
$E_{\mathrm {tf}}$
the maximal
![]() $\mathscr O$
-torsion-free quotient of E,
$\mathscr O$
-torsion-free quotient of E,
![]() $Z(E_{\mathrm {tf}})$
the centre of
$Z(E_{\mathrm {tf}})$
the centre of
![]() $E_{\mathrm {tf}}$
and
$E_{\mathrm {tf}}$
and
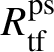 $R^{\mathrm {ps}}_{\mathrm {tf}}$
the maximal
$R^{\mathrm {ps}}_{\mathrm {tf}}$
the maximal
![]() $\mathscr O$
-torsion-free quotient of
$\mathscr O$
-torsion-free quotient of
![]() $R^{\mathrm {ps}}$
. Then
$R^{\mathrm {ps}}$
. Then
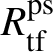 $R^{\mathrm {ps}}_{\mathrm {tf}}$
is a subring of
$R^{\mathrm {ps}}_{\mathrm {tf}}$
is a subring of
![]() $Z(E_{\mathrm {tf}})$
.
$Z(E_{\mathrm {tf}})$
.
If
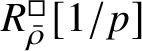 $R^{\square }_{\bar {\rho }} [1/p ]$
is reduced and the set
$R^{\square }_{\bar {\rho }} [1/p ]$
is reduced and the set
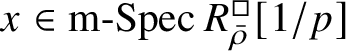 $x\in \operatorname {\mathrm {m-Spec}} R^{\square }_{\bar {\rho }} [1/p ]$
, such that
$x\in \operatorname {\mathrm {m-Spec}} R^{\square }_{\bar {\rho }} [1/p ]$
, such that
![]() $\rho ^{\square }_x$
is absolutely irreducible, is dense in
$\rho ^{\square }_x$
is absolutely irreducible, is dense in
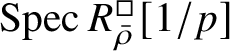 $\operatorname {\mathrm {Spec}} R^{\square }_{\bar {\rho }} [1/p ]$
, then
$\operatorname {\mathrm {Spec}} R^{\square }_{\bar {\rho }} [1/p ]$
, then
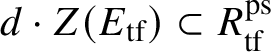 $d \cdot Z(E_{\mathrm {tf}}) \subset R^{\mathrm {ps}}_{\mathrm {tf}}$
. In particular, if
$d \cdot Z(E_{\mathrm {tf}}) \subset R^{\mathrm {ps}}_{\mathrm {tf}}$
. In particular, if
![]() $p\nmid d$
, then
$p\nmid d$
, then
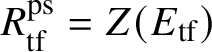 $R^{\mathrm {ps}}_{\mathrm {tf}}=Z(E_{\mathrm {tf}})$
. Moreover, the same holds for rings with fixed determinant.
$R^{\mathrm {ps}}_{\mathrm {tf}}=Z(E_{\mathrm {tf}})$
. Moreover, the same holds for rings with fixed determinant.
Proof. As in the proof of Theorem A.1, there is an injection
Moreover,
![]() $\operatorname {tr} \circ j$
induces a surjection
$\operatorname {tr} \circ j$
induces a surjection
![]() $E [1/p ]\twoheadrightarrow R^{\mathrm {ps}} [1/p ]$
. Thus
$E [1/p ]\twoheadrightarrow R^{\mathrm {ps}} [1/p ]$
. Thus
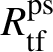 $R^{\mathrm {ps}}_{\mathrm {tf}}$
is a subring of
$R^{\mathrm {ps}}_{\mathrm {tf}}$
is a subring of
![]() $Z(E_{\mathrm {tf}})$
. Corollary A.7 gives us an injection
$Z(E_{\mathrm {tf}})$
. Corollary A.7 gives us an injection
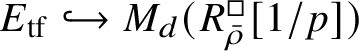 $E_{\mathrm {tf}} \hookrightarrow M_d (R^{\square }_{\bar {\rho }} [1/p ] )$
. If
$E_{\mathrm {tf}} \hookrightarrow M_d (R^{\square }_{\bar {\rho }} [1/p ] )$
. If
![]() $a\in E_{\mathrm {tf}}$
, then the characteristic polynomial of
$a\in E_{\mathrm {tf}}$
, then the characteristic polynomial of
![]() $j(a)$
has coefficients in
$j(a)$
has coefficients in
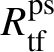 $R^{\mathrm {ps}}_{\mathrm {tf}}$
. Moreover,
$R^{\mathrm {ps}}_{\mathrm {tf}}$
. Moreover,
![]() $Z(E_{\mathrm {tf}})$
is contained in the centraliser of
$Z(E_{\mathrm {tf}})$
is contained in the centraliser of
![]() $\rho ^{\square }(\mathscr G)$
in
$\rho ^{\square }(\mathscr G)$
in
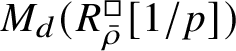 $M_d (R^{\square }_{\bar {\rho }} [1/p ] )$
. According to Lemma A.8, the centraliser is equal to scalar matrices. Since
$M_d (R^{\square }_{\bar {\rho }} [1/p ] )$
. According to Lemma A.8, the centraliser is equal to scalar matrices. Since
![]() $j(z)$
is a scalar matrix, we deduce that
$j(z)$
is a scalar matrix, we deduce that
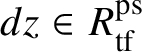 $d z \in R^{\mathrm {ps}}_{\mathrm {tf}}$
.
$d z \in R^{\mathrm {ps}}_{\mathrm {tf}}$
.
It follows from Proposition A.9 that
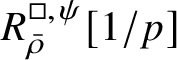 $R^{\square , \psi }_{\bar {\rho }} [1/p ]$
is reduced. Since twisting by characters does not change the property of being absolutely irreducible, the proof of Proposition A.9 shows that the absolutely irreducible locus is dense in
$R^{\square , \psi }_{\bar {\rho }} [1/p ]$
is reduced. Since twisting by characters does not change the property of being absolutely irreducible, the proof of Proposition A.9 shows that the absolutely irreducible locus is dense in
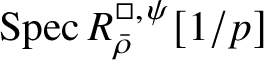 $\operatorname {\mathrm {Spec}} R^{\square , \psi }_{\bar {\rho }} [1/p ]$
. Then the same proof goes through.
$\operatorname {\mathrm {Spec}} R^{\square , \psi }_{\bar {\rho }} [1/p ]$
. Then the same proof goes through.
Proposition A.12. If
![]() $p=3$
,
$p=3$
,
![]() $\mathscr G=\mathscr G_{\mathbb Q_3}$
and
$\mathscr G=\mathscr G_{\mathbb Q_3}$
and
![]() $\bar {\rho }= \mathbf 1\oplus \omega $
, then
$\bar {\rho }= \mathbf 1\oplus \omega $
, then
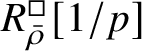 $R^{\square }_{\bar {\rho }} [1/p ]$
is normal.Footnote
4
$R^{\square }_{\bar {\rho }} [1/p ]$
is normal.Footnote
4
Proof. We will first relate the framed deformation ring
![]() $R^{\square }_{\bar {\rho }}$
to the ring studied in [Reference Böckle7]. Let
$R^{\square }_{\bar {\rho }}$
to the ring studied in [Reference Böckle7]. Let
![]() $\mu _3$
be the group of
$\mu _3$
be the group of
![]() $3$
rd roots of unity in
$3$
rd roots of unity in
![]() $\overline {\mathbb {Q}}_3$
, let
$\overline {\mathbb {Q}}_3$
, let
![]() $E=\mathbb Q_3(\mu _3)$
and let
$E=\mathbb Q_3(\mu _3)$
and let
![]() $E(3)$
be the compositum of all extensions
$E(3)$
be the compositum of all extensions
![]() $E \subset E' \subset \overline {\mathbb {Q}}_3$
such that
$E \subset E' \subset \overline {\mathbb {Q}}_3$
such that
![]() $[E':E]$
is a power of
$[E':E]$
is a power of
![]() $3$
. Then the Galois group
$3$
. Then the Galois group
![]() $\operatorname {\mathrm {Gal}}(E(3)/E)$
is the maximal pro-
$\operatorname {\mathrm {Gal}}(E(3)/E)$
is the maximal pro-
![]() $3$
quotient of
$3$
quotient of
![]() $\operatorname {\mathrm {Gal}} (\overline {\mathbb {Q}}_3/E )$
, and thus the map
$\operatorname {\mathrm {Gal}} (\overline {\mathbb {Q}}_3/E )$
, and thus the map
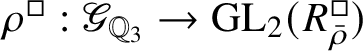 $\rho ^{\square }: \mathscr G_{\mathbb Q_3} \rightarrow \operatorname {\mathrm {GL}}_2 (R^{\square }_{\bar {\rho }} )$
factors through the surjection
$\rho ^{\square }: \mathscr G_{\mathbb Q_3} \rightarrow \operatorname {\mathrm {GL}}_2 (R^{\square }_{\bar {\rho }} )$
factors through the surjection
![]() $\mathscr G_{\mathbb Q_3}\twoheadrightarrow \operatorname {\mathrm {Gal}}(E(3)/\mathbb Q_3)$
. Since
$\mathscr G_{\mathbb Q_3}\twoheadrightarrow \operatorname {\mathrm {Gal}}(E(3)/\mathbb Q_3)$
. Since
![]() $\operatorname {\mathrm {Gal}}(E/ \mathbb Q_3)$
has order
$\operatorname {\mathrm {Gal}}(E/ \mathbb Q_3)$
has order
![]() $2$
, Schur–Zassenhaus implies that the surjection
$2$
, Schur–Zassenhaus implies that the surjection
![]() $\operatorname {\mathrm {Gal}}(E(3)/\mathbb Q_3)\twoheadrightarrow \operatorname {\mathrm {Gal}}(E/ \mathbb Q_3)$
has a splitting, which gives us an isomorphism
$\operatorname {\mathrm {Gal}}(E(3)/\mathbb Q_3)\twoheadrightarrow \operatorname {\mathrm {Gal}}(E/ \mathbb Q_3)$
has a splitting, which gives us an isomorphism
where
![]() $G=\{1, \sigma \}$
is a subgroup of
$G=\{1, \sigma \}$
is a subgroup of
![]() $\operatorname {\mathrm {Gal}}(E(3)/\mathbb Q_3)$
. One may define a closed subfunctor, denoted by
$\operatorname {\mathrm {Gal}}(E(3)/\mathbb Q_3)$
. One may define a closed subfunctor, denoted by
![]() $\mathrm {EH}_1$
in [Reference Böckle7], of the framed deformation functor
$\mathrm {EH}_1$
in [Reference Böckle7], of the framed deformation functor
![]() $D^{\square }$
such that
$D^{\square }$
such that
![]() $\mathrm {EH}_1(A)$
consists of pairs
$\mathrm {EH}_1(A)$
consists of pairs
![]() $(V_A, \beta _A)$
, where
$(V_A, \beta _A)$
, where
![]() $V_A$
is a deformation of
$V_A$
is a deformation of
![]() $\omega \oplus 1$
to A and
$\omega \oplus 1$
to A and
![]() $\beta _A=(v_1, v_2)$
is an A-basis of
$\beta _A=(v_1, v_2)$
is an A-basis of
![]() $V_A$
lifting a fixed basis
$V_A$
lifting a fixed basis
![]() $\beta _k$
of
$\beta _k$
of
![]() $\omega \oplus 1$
, such that
$\omega \oplus 1$
, such that
![]() $\sigma $
acts by
$\sigma $
acts by
![]() $-1$
on
$-1$
on
![]() $v_1$
and by
$v_1$
and by
![]() $1$
on
$1$
on
![]() $v_2$
. It follows from the Iwahori decomposition for the group
$v_2$
. It follows from the Iwahori decomposition for the group
![]() $1+M_2(\mathfrak m_A)$
that a framed deformation
$1+M_2(\mathfrak m_A)$
that a framed deformation
![]() $(V_A, \beta _A)\in D^{\square }(A)$
can be conjugated to a framed deformation in
$(V_A, \beta _A)\in D^{\square }(A)$
can be conjugated to a framed deformation in
![]() $\mathrm {EH}_1(A)$
by a unique element of the form
$\mathrm {EH}_1(A)$
by a unique element of the form
![]() $ \left( \begin {smallmatrix} 1 & b \\ 0 & 1 \end {smallmatrix} \right) \left( \begin {smallmatrix} 1 & 0\\ c & 1 \end {smallmatrix} \right)$
, with
$ \left( \begin {smallmatrix} 1 & b \\ 0 & 1 \end {smallmatrix} \right) \left( \begin {smallmatrix} 1 & 0\\ c & 1 \end {smallmatrix} \right)$
, with
![]() $b, c \in \mathfrak m_A$
. Hence if
$b, c \in \mathfrak m_A$
. Hence if
![]() $\mathrm {EH}_1$
is represented by R, then
$\mathrm {EH}_1$
is represented by R, then
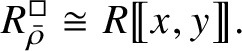
Now R is a complete intersection by [Reference Böckle7, Theorem 1.1], thus so is
![]() $R^{\square }_{\bar {\rho }}$
; and to show the normality of
$R^{\square }_{\bar {\rho }}$
; and to show the normality of
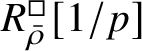 $R^{\square }_{\bar {\rho }} [1/p ]$
, it is enough to show that the singular locus in
$R^{\square }_{\bar {\rho }} [1/p ]$
, it is enough to show that the singular locus in
![]() $R [1/p ]$
has codimension at least
$R [1/p ]$
has codimension at least
![]() $2$
.
$2$
.
Let
![]() $\rho : \operatorname {\mathrm {Gal}}(E(3)/\mathbb Q_3)\rightarrow \operatorname {\mathrm {GL}}_2(R)$
be the representation obtained for the action of the Galois group on
$\rho : \operatorname {\mathrm {Gal}}(E(3)/\mathbb Q_3)\rightarrow \operatorname {\mathrm {GL}}_2(R)$
be the representation obtained for the action of the Galois group on
![]() $V_R$
with respect to the basis
$V_R$
with respect to the basis
![]() $\beta _{R}$
such that
$\beta _{R}$
such that
![]() $\rho (\sigma )= \left( \begin {smallmatrix} -1 & 0 \\ 0 & 1\end {smallmatrix} \right)$
. It follows from the argument of [Reference Colmez, Dospinescu and Paškūnas22, Lemma 4.1] that
$\rho (\sigma )= \left( \begin {smallmatrix} -1 & 0 \\ 0 & 1\end {smallmatrix} \right)$
. It follows from the argument of [Reference Colmez, Dospinescu and Paškūnas22, Lemma 4.1] that
![]() $x\in \operatorname {\mathrm {m-Spec}} R [1/p ]$
is singular if and only if there is an exact sequence
$x\in \operatorname {\mathrm {m-Spec}} R [1/p ]$
is singular if and only if there is an exact sequence
![]() $0\rightarrow \delta \rightarrow \rho _x \rightarrow \delta \varepsilon \rightarrow 0$
for some character
$0\rightarrow \delta \rightarrow \rho _x \rightarrow \delta \varepsilon \rightarrow 0$
for some character
![]() $\delta : \operatorname {\mathrm {Gal}}(E(3)/\mathbb Q_3)\rightarrow \kappa (x)^{\times }$
. Thus the singular locus is contained in the reducible locus, and it is enough to show that it has positive codimension inside the reducible locus: We know that R is a domain by [Reference Böckle7, Theorem 1.1], and there are absolutely irreducible lifts of
$\delta : \operatorname {\mathrm {Gal}}(E(3)/\mathbb Q_3)\rightarrow \kappa (x)^{\times }$
. Thus the singular locus is contained in the reducible locus, and it is enough to show that it has positive codimension inside the reducible locus: We know that R is a domain by [Reference Böckle7, Theorem 1.1], and there are absolutely irreducible lifts of
![]() $\bar {\rho }$
, so that the reducible locus has codimension
$\bar {\rho }$
, so that the reducible locus has codimension
![]() $1$
inside
$1$
inside
![]() $\operatorname {\mathrm {Spec}} R$
.
$\operatorname {\mathrm {Spec}} R$
.
We will now describe the ring R as computed in [Reference Böckle7] and compute the reducible locus. We know from [Reference Böckle7, Lemma 3.2] that the representation
![]() $\rho : \operatorname {\mathrm {Gal}}(E(3)/\mathbb Q_3)\rightarrow \operatorname {\mathrm {GL}}_2(R)$
factors through a quotient
$\rho : \operatorname {\mathrm {Gal}}(E(3)/\mathbb Q_3)\rightarrow \operatorname {\mathrm {GL}}_2(R)$
factors through a quotient
![]() $\operatorname {\mathrm {Gal}}(E(3)/\mathbb Q_3)\twoheadrightarrow P \rtimes G$
, where P is a pro-p group with generators
$\operatorname {\mathrm {Gal}}(E(3)/\mathbb Q_3)\twoheadrightarrow P \rtimes G$
, where P is a pro-p group with generators
![]() $x_1, x_2, x_3, x_4$
and one relation
$x_1, x_2, x_3, x_4$
and one relation
 $$ \begin{align*} r= x_1^3 [x_1, x_2][x_3, x_4][x_4, x_3^{-1}] [x_2, x_1^{-1}] x_1^3, \end{align*} $$
$$ \begin{align*} r= x_1^3 [x_1, x_2][x_3, x_4][x_4, x_3^{-1}] [x_2, x_1^{-1}] x_1^3, \end{align*} $$
where
![]() $[g, h]=g hg^{-1} h^{-1}$
. The action of
$[g, h]=g hg^{-1} h^{-1}$
. The action of
![]() $\sigma \in G$
on the generators is given by
$\sigma \in G$
on the generators is given by
 $$ \begin{align*} \sigma(x_1)= x_1^{-1}, \qquad \sigma(x_2)= x_2, \qquad \sigma(x_3)=x_3^{-1}, \qquad \sigma(x_4)=x_4. \end{align*} $$
$$ \begin{align*} \sigma(x_1)= x_1^{-1}, \qquad \sigma(x_2)= x_2, \qquad \sigma(x_3)=x_3^{-1}, \qquad \sigma(x_4)=x_4. \end{align*} $$
Let
![]() and let
and let
![]() $A_i\in \operatorname {\mathrm {GL}}_2(S)$
be the matrices
$A_i\in \operatorname {\mathrm {GL}}_2(S)$
be the matrices
 $$ \begin{align*} A_1&=\left(\begin{smallmatrix} \sqrt{1+bc} & b \\ c & \sqrt{1+bc}\end{smallmatrix}\right), & A_2&= \sqrt{1+a}\left(\begin{smallmatrix} \sqrt{1+d} & 0 \\ 0 & \sqrt{1+d}^{-1}\end{smallmatrix}\right), \\ A_3&=\left(\begin{smallmatrix} \sqrt{1+b'c'} & b' \\ c' & \sqrt{1+b'c'}\end{smallmatrix}\right), & A_4&= \sqrt{1+a'}\left(\begin{smallmatrix} \sqrt{1+d'} & 0 \\ 0 & \sqrt{1+d'}^{-1}\end{smallmatrix}\right), \end{align*} $$
$$ \begin{align*} A_1&=\left(\begin{smallmatrix} \sqrt{1+bc} & b \\ c & \sqrt{1+bc}\end{smallmatrix}\right), & A_2&= \sqrt{1+a}\left(\begin{smallmatrix} \sqrt{1+d} & 0 \\ 0 & \sqrt{1+d}^{-1}\end{smallmatrix}\right), \\ A_3&=\left(\begin{smallmatrix} \sqrt{1+b'c'} & b' \\ c' & \sqrt{1+b'c'}\end{smallmatrix}\right), & A_4&= \sqrt{1+a'}\left(\begin{smallmatrix} \sqrt{1+d'} & 0 \\ 0 & \sqrt{1+d'}^{-1}\end{smallmatrix}\right), \end{align*} $$
and let
 $$ \begin{align*} B= A_1^3 [A_1, A_2][A_3, A_4][A_4, A_3^{-1}] [A_2, A_1^{-1}] A_1^3. \end{align*} $$
$$ \begin{align*} B= A_1^3 [A_1, A_2][A_3, A_4][A_4, A_3^{-1}] [A_2, A_1^{-1}] A_1^3. \end{align*} $$
Then [Reference Böckle7, Theorem 4.1(c)] asserts that
![]() $R= S/I$
, where I is the ideal of S generated by the matrix entries of
$R= S/I$
, where I is the ideal of S generated by the matrix entries of
![]() $B - \left( \begin {smallmatrix}1 & 0 \\ 0 & 1\end {smallmatrix} \right)$
and
$B - \left( \begin {smallmatrix}1 & 0 \\ 0 & 1\end {smallmatrix} \right)$
and
![]() $\rho : P\rtimes G\rightarrow \operatorname {\mathrm {GL}}_2(R)$
is obtained by mapping
$\rho : P\rtimes G\rightarrow \operatorname {\mathrm {GL}}_2(R)$
is obtained by mapping
![]() $\sigma \mapsto \left( \begin {smallmatrix} -1 & 0 \\ 0 & 1\end {smallmatrix} \right)$
and
$\sigma \mapsto \left( \begin {smallmatrix} -1 & 0 \\ 0 & 1\end {smallmatrix} \right)$
and
![]() $x_i\mapsto A_i$
for
$x_i\mapsto A_i$
for
![]() $1\le i\le 4$
.
$1\le i\le 4$
.
It follows from this description that the locus in
![]() $\operatorname {\mathrm {Spec}} R$
parameterising reducible representations, where
$\operatorname {\mathrm {Spec}} R$
parameterising reducible representations, where
![]() $\sigma $
acts on the rank
$\sigma $
acts on the rank
![]() $1$
subrepresentation by
$1$
subrepresentation by
![]() $-1$
(resp.,
$-1$
(resp.,
![]() $1$
), is equal to
$1$
), is equal to
![]() $V( c, c')$
(resp.,
$V( c, c')$
(resp.,
![]() $V(b, b'))$
.
$V(b, b'))$
.
The images of
![]() $A_1$
and
$A_1$
and
![]() $A_3$
in
$A_3$
in
![]() $\operatorname {\mathrm {GL}}_2(R/( c, c'))$
are unipotent upper-triangular matrices. It is easy to compute the commutator of a unipotent upper-triangular matrix with a diagonal matrix. One obtains that the image of B in
$\operatorname {\mathrm {GL}}_2(R/( c, c'))$
are unipotent upper-triangular matrices. It is easy to compute the commutator of a unipotent upper-triangular matrix with a diagonal matrix. One obtains that the image of B in
![]() $\operatorname {\mathrm {GL}}_2(S/( c, c'))$
is the matrix
$\operatorname {\mathrm {GL}}_2(S/( c, c'))$
is the matrix
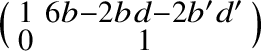 $ \left( \begin {smallmatrix} 1 & 6b- 2bd -2 b'd' \\ 0 & 1\end {smallmatrix} \right)$
. Thus
$ \left( \begin {smallmatrix} 1 & 6b- 2bd -2 b'd' \\ 0 & 1\end {smallmatrix} \right)$
. Thus
is an integral domain, as
![]() is factorial and
is factorial and
![]() $3b -bd -b'd'$
is an irreducible element in
$3b -bd -b'd'$
is an irreducible element in
![]() $S/(c, c')$
.
$S/(c, c')$
.
Let
![]() $X^{\mathrm {sing}}$
be the singular locus in
$X^{\mathrm {sing}}$
be the singular locus in
![]() $\operatorname {\mathrm {Spec}} R [1/p ]$
. The point
$\operatorname {\mathrm {Spec}} R [1/p ]$
. The point
![]() $x\in \operatorname {\mathrm {Spec}} R/(c,c')$
corresponding to the representation
$x\in \operatorname {\mathrm {Spec}} R/(c,c')$
corresponding to the representation
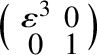 $ \big( \begin {smallmatrix} \varepsilon ^3 & 0 \\ 0 & 1 \end {smallmatrix} \big)$
will not lie in
$ \big( \begin {smallmatrix} \varepsilon ^3 & 0 \\ 0 & 1 \end {smallmatrix} \big)$
will not lie in
![]() $X^{\mathrm {sing}}$
, since this representation is not an extension of
$X^{\mathrm {sing}}$
, since this representation is not an extension of
![]() $\delta \varepsilon $
by
$\delta \varepsilon $
by
![]() $\delta $
. Thus
$\delta $
. Thus
![]() $X^{\mathrm {sing}} \cap \operatorname {\mathrm {Spec}} R/(c,c') [1/p ]$
is of codimension at least
$X^{\mathrm {sing}} \cap \operatorname {\mathrm {Spec}} R/(c,c') [1/p ]$
is of codimension at least
![]() $1$
. In the same way, we obtain that
$1$
. In the same way, we obtain that
![]() $X^{\mathrm {sing}} \cap \operatorname {\mathrm {Spec}} R/(b,b') [1/p ]$
is of codimension at least
$X^{\mathrm {sing}} \cap \operatorname {\mathrm {Spec}} R/(b,b') [1/p ]$
is of codimension at least
![]() $1$
in
$1$
in
![]() $\operatorname {\mathrm {Spec}} R/(b,b') [1/p ]$
. Thus
$\operatorname {\mathrm {Spec}} R/(b,b') [1/p ]$
. Thus
![]() $X^{\mathrm {sing}}$
is of codimension at least
$X^{\mathrm {sing}}$
is of codimension at least
![]() $1$
in the reducible locus in
$1$
in the reducible locus in
![]() $\operatorname {\mathrm {Spec}} R [1/p ]$
and of codimension at least
$\operatorname {\mathrm {Spec}} R [1/p ]$
and of codimension at least
![]() $2$
in
$2$
in
![]() $\operatorname {\mathrm {Spec}} R [1/p ]$
.
$\operatorname {\mathrm {Spec}} R [1/p ]$
.
Proposition A.13. If
![]() $\mathscr G=\mathscr G_{\mathbb {Q}_p}$
, then
$\mathscr G=\mathscr G_{\mathbb {Q}_p}$
, then
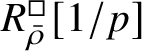 $R^{\square }_{\bar {\rho }} [1/p ]$
is normal and the absolutely irreducible locus is dense in
$R^{\square }_{\bar {\rho }} [1/p ]$
is normal and the absolutely irreducible locus is dense in
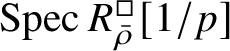 $\operatorname {\mathrm {Spec}} R^{\square }_{\bar {\rho }} [1/p ]$
for all semisimple
$\operatorname {\mathrm {Spec}} R^{\square }_{\bar {\rho }} [1/p ]$
for all semisimple
![]() $2$
-dimensional
$2$
-dimensional
![]() $\bar {\rho }$
.
$\bar {\rho }$
.
Proof. Since
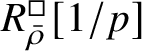 $R^{\square }_{\bar {\rho }} [1/p ]$
is excellent, the singular locus is closed in
$R^{\square }_{\bar {\rho }} [1/p ]$
is excellent, the singular locus is closed in
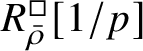 $R^{\square }_{\bar {\rho }} [1/p ]$
. If it is nonempty, then it will contain a maximal ideal x such that
$R^{\square }_{\bar {\rho }} [1/p ]$
. If it is nonempty, then it will contain a maximal ideal x such that
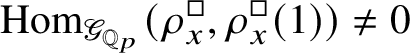 $$ \begin{align*} \operatorname{\mathrm{Hom}}_{\mathscr G_{\mathbb{Q}_p}}(\rho^{\square}_x, \rho^{\square}_x(1))\neq 0 \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Hom}}_{\mathscr G_{\mathbb{Q}_p}}(\rho^{\square}_x, \rho^{\square}_x(1))\neq 0 \end{align*} $$
(see [Reference Colmez, Dospinescu and Paškūnas22, Lemma 4.1]). Thus
![]() $\bar {\rho }$
is of the form
$\bar {\rho }$
is of the form
![]() $\bar {\chi } \oplus \bar {\chi } \omega $
. After twisting by a character, we may assume that
$\bar {\chi } \oplus \bar {\chi } \omega $
. After twisting by a character, we may assume that
![]() $\bar {\rho }= \mathbf 1 \oplus \omega $
. If
$\bar {\rho }= \mathbf 1 \oplus \omega $
. If
![]() $p=2$
or
$p=2$
or
![]() $p=3$
, then
$p=3$
, then
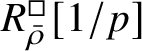 $R^{\square }_{\bar {\rho }} [1/p ]$
is normal by [Reference Colmez, Dospinescu and Paškūnas22, Proposition 4.3] or Proposition A.12, respectively. If
$R^{\square }_{\bar {\rho }} [1/p ]$
is normal by [Reference Colmez, Dospinescu and Paškūnas22, Proposition 4.3] or Proposition A.12, respectively. If
![]() $p\ge 5$
, it follows from the proof of [Reference Paškūnas39, Proposition B2, Theorem B.3], based on the work of Böckle [Reference Böckle6], that
$p\ge 5$
, it follows from the proof of [Reference Paškūnas39, Proposition B2, Theorem B.3], based on the work of Böckle [Reference Böckle6], that
![]() $R^{\square }_{\bar {\rho }}$
is formally smooth over
$R^{\square }_{\bar {\rho }}$
is formally smooth over
![]() . (The only change is that because in our setting
. (The only change is that because in our setting
![]() $\bar {\rho }$
is split, the generator
$\bar {\rho }$
is split, the generator
![]() $x_{p-2}$
maps to the matrix
$x_{p-2}$
maps to the matrix
![]() $ \left( \begin {smallmatrix} 1 & x \\ 0 & 1\end {smallmatrix} \right)$
instead of
$ \left( \begin {smallmatrix} 1 & x \\ 0 & 1\end {smallmatrix} \right)$
instead of
![]() $ \left( \begin {smallmatrix} 1 & 1 \\ 0 & 1\end {smallmatrix} \right)$
. This adds an extra variable but does not change the relation coming from [Reference Paškūnas39, equation (261)].) Thus
$ \left( \begin {smallmatrix} 1 & 1 \\ 0 & 1\end {smallmatrix} \right)$
. This adds an extra variable but does not change the relation coming from [Reference Paškūnas39, equation (261)].) Thus
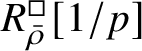 $R^{\square }_{\bar {\rho }} [1/p ]$
is normal.
$R^{\square }_{\bar {\rho }} [1/p ]$
is normal.
Hence,
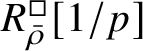 $R^{\square }_{\bar {\rho }} [1/p ]$
is a product of normal domains, and if the absolutely irreducible locus were not dense, there would be a component without absolutely irreducible points. (Let I be the ideal of
$R^{\square }_{\bar {\rho }} [1/p ]$
is a product of normal domains, and if the absolutely irreducible locus were not dense, there would be a component without absolutely irreducible points. (Let I be the ideal of
![]() $R^{\square }_{\bar {\rho }}$
generated by the matrix entries of
$R^{\square }_{\bar {\rho }}$
generated by the matrix entries of
![]() $ (\rho ^{\square }(gh)-\rho ^{\square }(hg) )^2$
for all
$ (\rho ^{\square }(gh)-\rho ^{\square }(hg) )^2$
for all
![]() $g, h\in \mathscr G_{\mathbb {Q}_p}$
. Then a specialisation of
$g, h\in \mathscr G_{\mathbb {Q}_p}$
. Then a specialisation of
![]() $\rho ^{\square }$
at
$\rho ^{\square }$
at
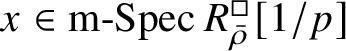 $x\in \operatorname {\mathrm {m-Spec}} R^{\square }_{\bar {\rho }} [1/p ]$
is absolutely irreducible over
$x\in \operatorname {\mathrm {m-Spec}} R^{\square }_{\bar {\rho }} [1/p ]$
is absolutely irreducible over
![]() $\kappa (x)$
if and only if
$\kappa (x)$
if and only if
![]() $x\not \in V(I)$
. Thus if an irreducible component of
$x\not \in V(I)$
. Thus if an irreducible component of
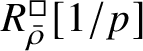 $R^{\square }_{\bar {\rho }} [1/p ]$
contains an absolutely irreducible point, then such points are dense in the component.) In the course of the proof of Proposition A.11, we have shown that
$R^{\square }_{\bar {\rho }} [1/p ]$
contains an absolutely irreducible point, then such points are dense in the component.) In the course of the proof of Proposition A.11, we have shown that
![]() $R^{\mathrm {ps}} [1/p ]$
is a subring of
$R^{\mathrm {ps}} [1/p ]$
is a subring of
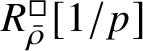 $R^{\square }_{\bar {\rho }} [1/p ]$
. Thus there would exist an irreducible component of
$R^{\square }_{\bar {\rho }} [1/p ]$
. Thus there would exist an irreducible component of
![]() $R^{\mathrm {ps}} [1/p ]$
without absolutely irreducible points. This would contradict [Reference Chenevier17, Theorem 2.1].
$R^{\mathrm {ps}} [1/p ]$
without absolutely irreducible points. This would contradict [Reference Chenevier17, Theorem 2.1].
Corollary A.14. If
![]() $\mathscr G=\mathscr G_{\mathbb {Q}_p}$
, then
$\mathscr G=\mathscr G_{\mathbb {Q}_p}$
, then
![]() $R^{\mathrm {ps}, \psi } [1/p ]$
,
$R^{\mathrm {ps}, \psi } [1/p ]$
,
![]() $R^{\mathrm {ps}} [1/p ]$
and the corresponding rigid analytic spaces are normal for all semisimple
$R^{\mathrm {ps}} [1/p ]$
and the corresponding rigid analytic spaces are normal for all semisimple
![]() $2$
-dimensional
$2$
-dimensional
![]() $\bar {\rho }$
.
$\bar {\rho }$
.
Acknowledgements
The first author would like to thank Toby Gee for organising a seminar on Lue Pan’s paper [Reference Pan38] and for the invitation to participate. Lue Pan’s paper was a major source of motivation to deal with the exceptional cases. The first author would also like to thank Patrick Allen and Gebhard Böckle for stimulating correspondence. Parts of the paper were written when the second author was visiting Academia Sinica. The second author would like to thank Carl Wang-Erickson for stimulating correspondence. The authors would like to thank Gabriel Dospinescu and Toby Gee for their detailed comments on an earlier draft. The authors would also like to thank the anonymous referee for a quick and thorough reading of the paper. We acknowledge support by the Open Access Publication Fund of the University of Duisburg-Essen.
Conflict of Interest
None.