1 Introduction
1.1 Motivation
Our results are motivated by the problem of classifying tracial von Neumann algebras up to elementary equivalence. Elementary equivalence is a central notion in model theory, which means that two objects have the same first-order theory. An equivalent characterization that is more familiar to operator algebraists follows from the Keisler-Shelah theorem: Two tracial von Neumann algebras M and N are elementarily equivalent (written
![]() $M \equiv N$
) if and only if there is some ultrafilter
$M \equiv N$
) if and only if there is some ultrafilter
![]() $\mathcal {U}$
on some index set such that the ultrapowers
$\mathcal {U}$
on some index set such that the ultrapowers
![]() $M^{\mathcal {U}}$
and
$M^{\mathcal {U}}$
and
![]() $N^{\mathcal {U}}$
are isomorphic.
$N^{\mathcal {U}}$
are isomorphic.
Von Neumann [Reference von Neumannvon49] showed that a von Neumann algebra with separable predual can be decomposed as a direct integral
![]() $M = \int _\Omega ^{\oplus } M_\omega \,d\omega $
over some measure space
$M = \int _\Omega ^{\oplus } M_\omega \,d\omega $
over some measure space
![]() $\Omega $
such that the center
$\Omega $
such that the center
![]() $Z(M) \subseteq M$
agrees with
$Z(M) \subseteq M$
agrees with
![]() $L^\infty (\Omega ) \subseteq \int _\Omega ^{\oplus } M_\omega \,d\omega $
, and hence reduced the classification of separable von Neumann algebras to that of factors. In the case where the von Neumann algebra admits a faithful normal tracial state, the factors are either matrix algebras or
$L^\infty (\Omega ) \subseteq \int _\Omega ^{\oplus } M_\omega \,d\omega $
, and hence reduced the classification of separable von Neumann algebras to that of factors. In the case where the von Neumann algebra admits a faithful normal tracial state, the factors are either matrix algebras or
![]() $\mathrm {II}_1$
factors. The classification of factors, even in the
$\mathrm {II}_1$
factors. The classification of factors, even in the
![]() $\mathrm {II}_1$
case, is an extremely challenging task. While Murray and von Neumann distinguished group von Neumann algebras
$\mathrm {II}_1$
case, is an extremely challenging task. While Murray and von Neumann distinguished group von Neumann algebras
![]() $L(G)$
for free groups versus amenable groups, it was not until the work of McDuff that infinitely many non-isomorphic
$L(G)$
for free groups versus amenable groups, it was not until the work of McDuff that infinitely many non-isomorphic
![]() $\mathrm {II}_1$
factors were shown to exist [Reference McDuffMcD69a, Reference McDuffMcD69b]. Recent breakthroughs have classified von Neumann algebras associated to large classes of groups using deformation/rigidity techniques (see, for example, [Reference Ioana, Popa and VaesIPV13, Reference Chifan, Ioana, Osin and SunCIOS23]), but are still very far from general
$\mathrm {II}_1$
factors were shown to exist [Reference McDuffMcD69a, Reference McDuffMcD69b]. Recent breakthroughs have classified von Neumann algebras associated to large classes of groups using deformation/rigidity techniques (see, for example, [Reference Ioana, Popa and VaesIPV13, Reference Chifan, Ioana, Osin and SunCIOS23]), but are still very far from general
![]() $\mathrm {II}_1$
factors.
$\mathrm {II}_1$
factors.
Through the study of ultrapowers and later the introduction (officially) of continuous model theory for von Neumann algebras in [Reference Farah, Hart and ShermanFHS14a], there was growing interest in classification of von Neumann algebras up to elementary equivalence, and many of the developments paralleled the early history of classification up to isomorphism. Farah, Hart and Sherman showed that property Gamma is axiomatizable, and hence, amenable von Neumann algebras and free group von Neumann algebras are not elementarily equivalent [Reference Farah, Hart and ShermanFHS14b, §3.2.2]; preservation of Gamma under elementary equivalence also follows from the earlier work of Fang, Ge and Li [Reference Fang, Ge and LiFGL06, Corollary 5.2]. Boutonnet, Chifan and Ioana showed that McDuff’s family of
![]() $\mathrm {II}_1$
factors are not elementarily equivalent [Reference Boutonnet, Chifan and IoanaBCI17]; see also [Reference Goldbring and HartGH17]. In the non-Gamma setting, the first examples proved to be non-elementarily equivalent were given in [Reference Chifan, Ioana and ElayavalliCIKE23], and further examples were obtained in [Reference Kunnawalkam Elayavalli and PatchellKP23].
$\mathrm {II}_1$
factors are not elementarily equivalent [Reference Boutonnet, Chifan and IoanaBCI17]; see also [Reference Goldbring and HartGH17]. In the non-Gamma setting, the first examples proved to be non-elementarily equivalent were given in [Reference Chifan, Ioana and ElayavalliCIKE23], and further examples were obtained in [Reference Kunnawalkam Elayavalli and PatchellKP23].
However, the more fundamental question about the analog of von Neumann’s disintegration theorem for elementary equivalence was not fully addressed (and similarly, there is not much written about classification of tracial von Neumann algebras with nontrivial center in practice, except for [Reference Chifan, Fernández Quero and TanCQT24]). Farah and Ghasemi showed, in general, that the theory of a direct integral is uniquely determined by the theories of the integrands [Reference Farah and GhasemiFG24, Corollary 3.8] (see also [Reference Ben Yaacov, Ibarlucía and TsankovBIT24, Theorem 18.3]). In the case where the integral is over an atomless probability space, this also follows from the work of Ben Yaacov on randomizations of metric structures [Reference Ben YaacovBen13].
Our goal in this paper is to establish a converse recovering the theory of the integrands from the theory of the integral for tracial von Neumann algebras, which was conjectured by Farah and Ghasemi in an earlier version of [Reference Farah and GhasemiFG24]. In other words, we will show that the integrands in the direct integral can be recovered up to elementary equivalence if the integral is known up to elementary equivalence. After the first draft of this paper appeared, Ben Yaacov, Ibarlucía and Tsankov added a general version of this result to their systematic treatment of direct integrals, affine logic and continuous logic; see [Reference Ben Yaacov, Ibarlucía and TsankovBIT24, Theorem 20.13].
1.2 Results
We require a slight technical hypothesis to rule out different multiplicities of the same factor occurring in the diffuse part of the measure space in the direct integral decomposition. For example, suppose that
![]() $(\Omega ,\mu )$
is diffuse (i.e., has no atoms) and
$(\Omega ,\mu )$
is diffuse (i.e., has no atoms) and
![]() $(M_\omega )_{\omega \in \Omega }$
are a measurable field of pairwise non-elementarily equivalent tracial factors. Let
$(M_\omega )_{\omega \in \Omega }$
are a measurable field of pairwise non-elementarily equivalent tracial factors. Let
![]() $(\tilde {\Omega },\tilde {\mu }) = (\Omega \sqcup \Omega ,\frac {1}{2} \mu \oplus \frac {1}{2} \mu )$
, and consider the measurable field
$(\tilde {\Omega },\tilde {\mu }) = (\Omega \sqcup \Omega ,\frac {1}{2} \mu \oplus \frac {1}{2} \mu )$
, and consider the measurable field
![]() $(N_\omega )_{\omega \in \tilde {\Omega }}$
on
$(N_\omega )_{\omega \in \tilde {\Omega }}$
on
![]() $\tilde {\Omega }$
consisting of two copies of
$\tilde {\Omega }$
consisting of two copies of
![]() $(M_\omega )_{\omega \in \Omega }$
. Then it follows from [Reference Farah and GhasemiFG24, Corollary 3.8] that
$(M_\omega )_{\omega \in \Omega }$
. Then it follows from [Reference Farah and GhasemiFG24, Corollary 3.8] that
![]() $\int _\Omega (M_\omega ,\tau _\omega ) \,d\mu (\omega )$
is elementarily equivalent to
$\int _\Omega (M_\omega ,\tau _\omega ) \,d\mu (\omega )$
is elementarily equivalent to
![]() $\int _{\tilde {\Omega }} N_\omega \,d\tilde {\mu }(\omega ) \cong \int _\Omega (M_\omega \oplus M_\omega ,\frac {1}{2} \tau _\omega \oplus \frac {1}{2} \tau _\omega )\,d\mu (\omega )$
, but there is no measurable isomorphism
$\int _{\tilde {\Omega }} N_\omega \,d\tilde {\mu }(\omega ) \cong \int _\Omega (M_\omega \oplus M_\omega ,\frac {1}{2} \tau _\omega \oplus \frac {1}{2} \tau _\omega )\,d\mu (\omega )$
, but there is no measurable isomorphism
![]() $(\Omega ,\mu ) \to (\Omega \sqcup \Omega ,\frac {1}{2} \mu \oplus \frac {1}{2} \mu )$
exhibiting elementary equivalence fiberwise because in
$(\Omega ,\mu ) \to (\Omega \sqcup \Omega ,\frac {1}{2} \mu \oplus \frac {1}{2} \mu )$
exhibiting elementary equivalence fiberwise because in
![]() $\Omega $
, all the elementary equivalence classes are distinct, but in
$\Omega $
, all the elementary equivalence classes are distinct, but in
![]() $\tilde {\Omega }$
, there are two copies of each elementary equivalence class. Hence, there is an unavoidable ambiguity due to the different possibly multiplicities of each elementary equivalence class over the underlying measure space. To rule out such examples, we add an assumption of ‘infinite multiplicity’ of each fiber in the direct integral decomposition.
$\tilde {\Omega }$
, there are two copies of each elementary equivalence class. Hence, there is an unavoidable ambiguity due to the different possibly multiplicities of each elementary equivalence class over the underlying measure space. To rule out such examples, we add an assumption of ‘infinite multiplicity’ of each fiber in the direct integral decomposition.
Given a probability space
![]() $(\Omega ,\mu )$
and a mapping F from
$(\Omega ,\mu )$
and a mapping F from
![]() $\Omega $
into some space
$\Omega $
into some space
![]() $\Omega '$
, we say that
$\Omega '$
, we say that
![]() $(\Omega ,\mu ,F)$
is stable under tensorization with
$(\Omega ,\mu ,F)$
is stable under tensorization with
![]() $L^\infty [0,1]$
, if there is a measurable isomorphism
$L^\infty [0,1]$
, if there is a measurable isomorphism
![]() $\Phi : (\Omega ,\mu ) \to (\Omega \otimes [0,1], \mu \otimes \operatorname {Leb})$
such that
$\Phi : (\Omega ,\mu ) \to (\Omega \otimes [0,1], \mu \otimes \operatorname {Leb})$
such that
![]() $F \circ \pi _1 \circ \Phi = F$
, where
$F \circ \pi _1 \circ \Phi = F$
, where
![]() $\pi _1$
is the first coordinate projection (see Lemma 4.6 for equivalent characterizations of this property). Note that the example in preceding paragraph created
$\pi _1$
is the first coordinate projection (see Lemma 4.6 for equivalent characterizations of this property). Note that the example in preceding paragraph created
![]() $\tilde {\Omega }$
by tensorizing
$\tilde {\Omega }$
by tensorizing
![]() $\Omega $
with a two-point space. Of course, the measure space
$\Omega $
with a two-point space. Of course, the measure space
![]() $\Omega $
in a direct integral decomposition can be expressed as a direct sum of an atomic one and an atomless (diffuse) one, and we only want to assume stability under tensorization for the diffuse part. Hence, our main result can be stated as follows; note that the converse to Theorem A follows from [Reference Farah and GhasemiFG24, Corollary 3.8]. See also Remark 4.7 for what happens without the stability assumption.
$\Omega $
in a direct integral decomposition can be expressed as a direct sum of an atomic one and an atomless (diffuse) one, and we only want to assume stability under tensorization for the diffuse part. Hence, our main result can be stated as follows; note that the converse to Theorem A follows from [Reference Farah and GhasemiFG24, Corollary 3.8]. See also Remark 4.7 for what happens without the stability assumption.
Theorem A. Let
![]() $(\Omega _1,\mu _1)$
and
$(\Omega _1,\mu _1)$
and
![]() $(\Omega _2,\mu _2)$
be standard Borel probability spaces, and let
$(\Omega _2,\mu _2)$
be standard Borel probability spaces, and let
![]() $(M,\tau ) = \int _{\Omega _1}^{\oplus } (M_\omega ,\tau _\omega ) \,d\mu _1(\omega )$
and
$(M,\tau ) = \int _{\Omega _1}^{\oplus } (M_\omega ,\tau _\omega ) \,d\mu _1(\omega )$
and
![]() $(N,\sigma ) = \int _{\Omega _2}^{\oplus } (N_\omega ,\sigma _\omega ) \,d\mu _2(\omega )$
be direct integrals of separable tracial factors. Suppose that the diffuse part of each decomposition is stable under tensorization with
$(N,\sigma ) = \int _{\Omega _2}^{\oplus } (N_\omega ,\sigma _\omega ) \,d\mu _2(\omega )$
be direct integrals of separable tracial factors. Suppose that the diffuse part of each decomposition is stable under tensorization with
![]() $L^\infty [0,1]$
. If
$L^\infty [0,1]$
. If
![]() $(M,\tau ) \equiv (N,\sigma )$
, then there exists an isomorphism of probability spaces (i.e., a measure-preserving map with measurable inverse up to null sets)
$(M,\tau ) \equiv (N,\sigma )$
, then there exists an isomorphism of probability spaces (i.e., a measure-preserving map with measurable inverse up to null sets)
![]() $f: \Omega _1 \to \Omega _2$
such that
$f: \Omega _1 \to \Omega _2$
such that
![]() $(M_\omega , \tau _\omega ) \equiv (N_{f(\omega )},\tau _{f(\omega )})$
for almost every
$(M_\omega , \tau _\omega ) \equiv (N_{f(\omega )},\tau _{f(\omega )})$
for almost every
![]() $\omega \in \Omega _1$
.
$\omega \in \Omega _1$
.
To give a simple example, we can obtain continuum many non-elementarily equivalent tracial von Neumann algebras with diffuse center as follows. Let P and Q be two non-elementarily equivalent
![]() $\mathrm {II}_1$
factors. Let
$\mathrm {II}_1$
factors. Let
![]() $M_c$
be the direct integral over
$M_c$
be the direct integral over
![]() $[0,1]$
where the fibers on
$[0,1]$
where the fibers on
![]() $[0,c]$
are P and the fibers on
$[0,c]$
are P and the fibers on
![]() $(c,1]$
are Q. Theorem A shows that
$(c,1]$
are Q. Theorem A shows that
![]() $M_c$
and
$M_c$
and
![]() $M_{c'}$
are not elementarily equivalent for
$M_{c'}$
are not elementarily equivalent for
![]() $c \neq c'$
.
$c \neq c'$
.
Our approach is based on constructing the ‘ultrafibers’ out of a direct integral
![]() $(M,\tau ) = \int _{\Omega }^{\oplus } (M_\omega ,\tau _\omega ) \,d\mu (\omega )$
associated to characters on
$(M,\tau ) = \int _{\Omega }^{\oplus } (M_\omega ,\tau _\omega ) \,d\mu (\omega )$
associated to characters on
![]() $L^\infty (\Omega )$
. While it is not possible to obtain the fiber
$L^\infty (\Omega )$
. While it is not possible to obtain the fiber
![]() $(M_\omega ,\tau _\omega )$
canonically as a
$(M_\omega ,\tau _\omega )$
canonically as a
![]() $\mathrm {C}^*$
-quotient of M since a point evaluation is not necessarily well defined on
$\mathrm {C}^*$
-quotient of M since a point evaluation is not necessarily well defined on
![]() $L^\infty (\Omega )$
, we can obtain a
$L^\infty (\Omega )$
, we can obtain a
![]() $\mathrm {C}^*$
-quotient corresponding to each character on
$\mathrm {C}^*$
-quotient corresponding to each character on
![]() $L^\infty (\Omega )$
. If
$L^\infty (\Omega )$
. If
![]() $\Omega $
was a discrete measurable space I, so that
$\Omega $
was a discrete measurable space I, so that
![]() $L^\infty (\Omega ) = \ell ^\infty (I)$
for the index set I, then a character would always be given by an ultrafilter on I, and then our ultrafiber would reduce to the ultraproduct of
$L^\infty (\Omega ) = \ell ^\infty (I)$
for the index set I, then a character would always be given by an ultrafilter on I, and then our ultrafiber would reduce to the ultraproduct of
![]() $(M_i,\tau _i)_{i \in I}$
with respect to this ultrafilter. As we will see, there is no need to assume that M is a direct integral in the classical sense; we can replace
$(M_i,\tau _i)_{i \in I}$
with respect to this ultrafilter. As we will see, there is no need to assume that M is a direct integral in the classical sense; we can replace
![]() $L^\infty (\Omega )$
by any central von Neumann subalgebra N of a tracial von Neumann algebra M, and so obtain an ultrafiber of M over N for any character on N (see §2.1). The possibility of this construction was already implicit in Wright’s 1954 work on the quotients of
$L^\infty (\Omega )$
by any central von Neumann subalgebra N of a tracial von Neumann algebra M, and so obtain an ultrafiber of M over N for any character on N (see §2.1). The possibility of this construction was already implicit in Wright’s 1954 work on the quotients of
![]() $\mathrm {AW}^*$
-algebras by maximal ideals [Reference WrightWri54]. See also [Reference Sinclair and SmithSS08, §A.3]. The ultrafibers studied here also closely relate with Keisler and Ben Yaacov’s work on randomizations of structures [Reference KeislerKei99, Reference Ben YaacovBen13]. Indeed, on careful inspection, the ultrafibers are exactly the fibers in the canonical realization of [Reference Ben YaacovBen13, Theorem 3.11]. Hence, our work gives a more operator-algebraic approach to randomizations for tracial von Neumann algebras.
$\mathrm {AW}^*$
-algebras by maximal ideals [Reference WrightWri54]. See also [Reference Sinclair and SmithSS08, §A.3]. The ultrafibers studied here also closely relate with Keisler and Ben Yaacov’s work on randomizations of structures [Reference KeislerKei99, Reference Ben YaacovBen13]. Indeed, on careful inspection, the ultrafibers are exactly the fibers in the canonical realization of [Reference Ben YaacovBen13, Theorem 3.11]. Hence, our work gives a more operator-algebraic approach to randomizations for tracial von Neumann algebras.
Note in addition that [Reference Ben Yaacov, Ibarlucía and TsankovBIT24] developed direct integrals in the non-separable setting more generally by relating affine logic with continuous logic and in particular showed the existence of direct integral decompositions for arbitrary (including non-separable) tracial von Neumann algebras [Reference Ben Yaacov, Ibarlucía and TsankovBIT24, Corollary 29.10]. See [Reference Ben Yaacov, Ibarlucía and TsankovBIT24, §9] for a discussion of combining direct integrals and ultraproducts. See also [Reference Ben Yaacov, Ibarlucía and TsankovBIT24, §20] for a general version of the result on unique distribution of theories, which works for affine theories that are simplicial. As our goal is to present these results for an operator algebraic audience, we focus here on the separable case.
Although here we argue using ultrafibers in order to minimize the model theory background needed to understand the proof, we also point out another, more model-theoretic way to prove Theorem A in the diffuse case using Ben Yaacov’s disintegration theorem [Reference Ben YaacovBen13, Theorem 3.32]. Ben Yaacov’s theorem deals with a two-sorted structure with an auxiliary sort representing the probability space used in the randomization (for instance, the space
![]() $(\Omega ,\mu )$
in a direct integral decomposition). Thus, to apply this result, one seeks to upgrade the plain structure of a tracial von Neumann algebra into a structure with an auxiliary sort for the center, which is a commutative tracial von Neumann algebra and hence corresponds to a probability space. The key point for this approach (which distinguishes tracial von Neumann algebras from certain other metric structures) is that the center is a definable set and the center-valued trace is a definable function, which follows from Dixmier averaging as in [Reference Farah, Hart and ShermanFHS13, Lemma 4.2]. Hence, the new upgraded structure is definable in terms of the plain tracial von Neumann algebra structure. From this, one can deduce that the center-valued interpretations of formulas are definable functions by similar reasoning as [Reference Ben YaacovBen13, Lemma 3.13]. We also remark that the disintegration result in [Reference Ben Yaacov, Ibarlucía and TsankovBIT24, Theorem 20.13] holds in greater generality, including situations where the fiberwise interpretations of formulas cannot be expressed as definable functions with respect to the original language in any sense; such definability is thus a stronger conclusion that requires stronger hypotheses.
$(\Omega ,\mu )$
in a direct integral decomposition). Thus, to apply this result, one seeks to upgrade the plain structure of a tracial von Neumann algebra into a structure with an auxiliary sort for the center, which is a commutative tracial von Neumann algebra and hence corresponds to a probability space. The key point for this approach (which distinguishes tracial von Neumann algebras from certain other metric structures) is that the center is a definable set and the center-valued trace is a definable function, which follows from Dixmier averaging as in [Reference Farah, Hart and ShermanFHS13, Lemma 4.2]. Hence, the new upgraded structure is definable in terms of the plain tracial von Neumann algebra structure. From this, one can deduce that the center-valued interpretations of formulas are definable functions by similar reasoning as [Reference Ben YaacovBen13, Lemma 3.13]. We also remark that the disintegration result in [Reference Ben Yaacov, Ibarlucía and TsankovBIT24, Theorem 20.13] holds in greater generality, including situations where the fiberwise interpretations of formulas cannot be expressed as definable functions with respect to the original language in any sense; such definability is thus a stronger conclusion that requires stronger hypotheses.
The special case of Theorem A when all the fibers are the same, so that the direct integral over
![]() $\Omega $
reduces to
$\Omega $
reduces to
![]() $L^\infty (\Omega ,\mu ) \overline {\otimes } M$
, is of particular note.
$L^\infty (\Omega ,\mu ) \overline {\otimes } M$
, is of particular note.
Corollary B. Let
![]() $(M,\tau _M)$
and
$(M,\tau _M)$
and
![]() $(N,\tau _N)$
be
$(N,\tau _N)$
be
![]() $\mathrm {II}_1$
factors, and let
$\mathrm {II}_1$
factors, and let
![]() $(\Omega ,\mu )$
be a standard Borel probability space. If
$(\Omega ,\mu )$
be a standard Borel probability space. If
![]() $L^\infty (\Omega ,\mu ) \overline {\otimes } (M,\tau _M) \equiv L^\infty (\Omega ,\mu ) \overline {\otimes } (N,\tau _N)$
, then
$L^\infty (\Omega ,\mu ) \overline {\otimes } (M,\tau _M) \equiv L^\infty (\Omega ,\mu ) \overline {\otimes } (N,\tau _N)$
, then
![]() $(M,\tau _M) \equiv (N,\tau _N)$
.
$(M,\tau _M) \equiv (N,\tau _N)$
.
This is related to the problem, which has become known as Ozawa’s question due a discussion on MathOverflow, of whether
![]() $L^\infty (\Omega ,\mu ) \overline {\otimes } M \cong L^\infty (\Omega ,\mu ) \overline {\otimes } N$
implies
$L^\infty (\Omega ,\mu ) \overline {\otimes } M \cong L^\infty (\Omega ,\mu ) \overline {\otimes } N$
implies
![]() $M \cong N$
in general (this is an exercise if we assume that M and N are separable); our result solves the analogous question for elementary equivalence. In fact, we are able to give a simpler and more ‘algebraic’ proof of Corollary B than the general case. In other words, we will be able to prove it from
$M \cong N$
in general (this is an exercise if we assume that M and N are separable); our result solves the analogous question for elementary equivalence. In fact, we are able to give a simpler and more ‘algebraic’ proof of Corollary B than the general case. In other words, we will be able to prove it from
![]() $\mathrm {C}^*$
-algebraic manipulations of our generalized ultraproducts once we know that the Keisler–Shelah characterization of elementary equivalence works for generalized ultrapowers (see Proposition C below).
$\mathrm {C}^*$
-algebraic manipulations of our generalized ultraproducts once we know that the Keisler–Shelah characterization of elementary equivalence works for generalized ultrapowers (see Proposition C below).
Now let us briefly describe the generalized ultraproduct construction in the case of ultrapowers. It is well known that ultrafilters on a (discrete) index set I are equivalent to pure states on
![]() $\ell ^\infty (I)$
. From this point of view, there is no need to restrict I to be a discrete measurable space. Thus, for a measure space
$\ell ^\infty (I)$
. From this point of view, there is no need to restrict I to be a discrete measurable space. Thus, for a measure space
![]() $(\Omega ,\mu )$
, we can consider a pure state
$(\Omega ,\mu )$
, we can consider a pure state
![]() $\mathcal {U}$
on
$\mathcal {U}$
on
![]() $L^\infty (\Omega ,\mu )$
as an ‘ultrafilter on a measure space’. Given a tracial von Neumann algebra
$L^\infty (\Omega ,\mu )$
as an ‘ultrafilter on a measure space’. Given a tracial von Neumann algebra
![]() $(M,\tau )$
, the ultrapower
$(M,\tau )$
, the ultrapower
![]() $M^{\mathcal {U}}$
can then be defined in an analogous way. Take the tracial state
$M^{\mathcal {U}}$
can then be defined in an analogous way. Take the tracial state
![]() $\mathcal {U} \circ (\operatorname {\mathrm {id}} \otimes \tau )$
on the
$\mathcal {U} \circ (\operatorname {\mathrm {id}} \otimes \tau )$
on the
![]() $L^\infty (\Omega ,\mu ) \overline {\otimes } M$
, and let
$L^\infty (\Omega ,\mu ) \overline {\otimes } M$
, and let
![]() $M^{\mathcal {U}}$
be the algebra generated by the GNS construction of this trace, which is a
$M^{\mathcal {U}}$
be the algebra generated by the GNS construction of this trace, which is a
![]() $\mathrm {C}^*$
-quotient of
$\mathrm {C}^*$
-quotient of
![]() $L^\infty (\Omega ,\mu ) \overline {\otimes } M$
. This
$L^\infty (\Omega ,\mu ) \overline {\otimes } M$
. This
![]() $M^{\mathcal {U}}$
is a special case of the ultrafiber construction described above; namely, it is the ultrafiber of
$M^{\mathcal {U}}$
is a special case of the ultrafiber construction described above; namely, it is the ultrafiber of
![]() $L^\infty (\Omega ,\mu ) \overline {\otimes } M$
associated to the character
$L^\infty (\Omega ,\mu ) \overline {\otimes } M$
associated to the character
![]() $\mathcal {U}$
on
$\mathcal {U}$
on
![]() $N = L^\infty (\Omega ,\mu )$
. To give a short proof of Corollary B, we only need the following fact, which allows us to extend the Keisler-Shelah characterization of elementary equivalence to the setting of ultrapowers over measure spaces.
$N = L^\infty (\Omega ,\mu )$
. To give a short proof of Corollary B, we only need the following fact, which allows us to extend the Keisler-Shelah characterization of elementary equivalence to the setting of ultrapowers over measure spaces.
Proposition C. Let
![]() $\mathcal {U}$
be a pure state on
$\mathcal {U}$
be a pure state on
![]() $L^\infty (\Omega ,\mu )$
for some measure space, and let
$L^\infty (\Omega ,\mu )$
for some measure space, and let
![]() $(M,\tau )$
be a tracial von Neumann algebra. Then
$(M,\tau )$
be a tracial von Neumann algebra. Then
![]() $M^{\mathcal {U}} \equiv M$
.
$M^{\mathcal {U}} \equiv M$
.
For Theorem A, we generalize this ultrapower construction by replacing
![]() $L^\infty (\Omega ,\mu )$
inside
$L^\infty (\Omega ,\mu )$
inside
![]() $L^\infty (\Omega ,\mu ) \otimes M$
with a general
$L^\infty (\Omega ,\mu ) \otimes M$
with a general
![]() $N \subseteq M$
such that N is contained in the center of M (for instance, N could be
$N \subseteq M$
such that N is contained in the center of M (for instance, N could be
![]() $L^\infty (\Omega ,\mu )$
inside a direct integral M). One of the key ingredients for all our results is the following analog of Łoś’s theorem in this setting, which is closely related to [Reference Ben YaacovBen13, Theorem 3.19]. We hope that our proof will make the result accessible to operator algebraists.
$L^\infty (\Omega ,\mu )$
inside a direct integral M). One of the key ingredients for all our results is the following analog of Łoś’s theorem in this setting, which is closely related to [Reference Ben YaacovBen13, Theorem 3.19]. We hope that our proof will make the result accessible to operator algebraists.
Theorem D (Łoś theorem for ultrafibers).
Let
![]() $(M,\tau )$
be a tracial von Neumann algebra, and let
$(M,\tau )$
be a tracial von Neumann algebra, and let
![]() $N \subseteq Z(M)$
. Let
$N \subseteq Z(M)$
. Let
![]() $E: M \to N$
be the trace-preserving conditional expectation. For each n-variate formula
$E: M \to N$
be the trace-preserving conditional expectation. For each n-variate formula
![]() $\phi $
, let
$\phi $
, let
![]() $\phi _E^M$
be the N-valued interpretation of
$\phi _E^M$
be the N-valued interpretation of
![]() $\phi $
on elements of M using E in place of the trace (see §3.2).
$\phi $
on elements of M using E in place of the trace (see §3.2).
Let
![]() $\mathcal {U}$
be a pure state on N and let
$\mathcal {U}$
be a pure state on N and let
![]() $M^{/E,\mathcal {U}} = M / I_{\mathcal {U}}$
be the ultrafiber (see §2.1). Let
$M^{/E,\mathcal {U}} = M / I_{\mathcal {U}}$
be the ultrafiber (see §2.1). Let
![]() $\overline {x} \in M^n$
and let
$\overline {x} \in M^n$
and let
![]() $\pi _{E,\mathcal {U}}: M \to M^{/E,\mathcal {U}}$
be the quotient map. Then for each formula
$\pi _{E,\mathcal {U}}: M \to M^{/E,\mathcal {U}}$
be the quotient map. Then for each formula
![]() $\phi $
, we have
$\phi $
, we have
In §5, we point out that, while these generalized ultraproducts are a useful tool, they do not necessarily produce new objects. Indeed, if we assume the continuum hypothesis, then we can show by standard techniques that each ultrafiber of a measurable field
![]() $(M_\omega ,\tau _\omega )$
can be realized as a discrete ultraproduct of some sequence of elements
$(M_\omega ,\tau _\omega )$
can be realized as a discrete ultraproduct of some sequence of elements
![]() $(M_{\omega _n},\tau _{\omega _n})$
.
$(M_{\omega _n},\tau _{\omega _n})$
.
It is natural to ask to what extent these results generalize beyond the tracial setting – that is, to von Neumann algebras with faithful normal states. Theorem D certainly applies for general metric structures, and hence for von Neumann algebras with states as axiomatized in [Reference DabrowskiDab19], [Reference Aruseelan, Goldbring, Hart and SinclairAGHS25, §5]. Theorem A relies on the fact that the center of ultraproducts is the ultraproduct of the center (see Proposition 2.8 and the proof of Proposition 4.3); this will fail for type
![]() $\mathrm {III}_0$
von Neumann algebras (see [Reference Aruseelan, Goldbring, Hart and SinclairAGHS25, Fact 8.5]). There may also be difficulty in the type
$\mathrm {III}_0$
von Neumann algebras (see [Reference Aruseelan, Goldbring, Hart and SinclairAGHS25, Fact 8.5]). There may also be difficulty in the type
![]() $\mathrm {II}_\infty $
setting due to the lack of axiomatizability of this class [Reference Aruseelan, Goldbring, Hart and SinclairAGHS25, Proposition 8.3]. However, we expect that the result will hold if the algebras and states in the direct integral decomposition are tracial or
$\mathrm {II}_\infty $
setting due to the lack of axiomatizability of this class [Reference Aruseelan, Goldbring, Hart and SinclairAGHS25, Proposition 8.3]. However, we expect that the result will hold if the algebras and states in the direct integral decomposition are tracial or
![]() $\mathrm {III}_\lambda $
for
$\mathrm {III}_\lambda $
for
![]() $\lambda> 0$
.
$\lambda> 0$
.
We close with a word of motivation on why the notions from continuous model theory, such as formulas, types and theories, are important for the study of operator algebras (other than for proving Theorem A). Indeed, since complete theories correspond to elementary equivalence classes, which in turn can be characterized in terms of ultraproducts, one might ask what we gain from formalizing the notion of theories through sentences. One reason is to provide a topology; since complete theories can be expressed as characters on a certain real
![]() $\mathrm {C}^*$
-algebra of sentences, the space of complete theories comes with a natural weak-
$\mathrm {C}^*$
-algebra of sentences, the space of complete theories comes with a natural weak-
![]() $*$
topology. This topology can be characterized by the fact that the theory of an ultraproduct
$*$
topology. This topology can be characterized by the fact that the theory of an ultraproduct
![]() $\prod _{\mathcal {U}} M_i$
is the ultralimit of the theories of
$\prod _{\mathcal {U}} M_i$
is the ultralimit of the theories of
![]() $M_i$
. If we look at things purely in terms of elementary equivalence classes (defined in terms of isomorphic ultrapowers), the topology could only be described in terms of sequences or nets by using the condition
$M_i$
. If we look at things purely in terms of elementary equivalence classes (defined in terms of isomorphic ultrapowers), the topology could only be described in terms of sequences or nets by using the condition
![]() $\operatorname {Th}(\prod _{\mathcal {U}} M_i) = \lim _{\mathcal {U}} \operatorname {Th}(M_I)$
, and it is not transparent what the open sets are, why this condition defines a topology, why the space is Hausdorff, etc. However, after defining theories properly using sentences, we obtain a compact metrizable space of complete theories, which is actually crucial for proving Theorem A in the diffuse case. The key point is that
$\operatorname {Th}(\prod _{\mathcal {U}} M_i) = \lim _{\mathcal {U}} \operatorname {Th}(M_I)$
, and it is not transparent what the open sets are, why this condition defines a topology, why the space is Hausdorff, etc. However, after defining theories properly using sentences, we obtain a compact metrizable space of complete theories, which is actually crucial for proving Theorem A in the diffuse case. The key point is that
![]() $\omega \mapsto \operatorname {Th}(M_\omega )$
is a measurable map from the underlying probability space into the space of theories with its Borel
$\omega \mapsto \operatorname {Th}(M_\omega )$
is a measurable map from the underlying probability space into the space of theories with its Borel
![]() $\sigma $
-algebra, that is,
$\sigma $
-algebra, that is,
![]() $\operatorname {Th}(M_\omega )$
is a random variable in the space of complete theories, and we show that the distribution of
$\operatorname {Th}(M_\omega )$
is a random variable in the space of complete theories, and we show that the distribution of
![]() $\operatorname {Th}(M_\omega )$
is uniquely determined if
$\operatorname {Th}(M_\omega )$
is uniquely determined if
![]() $\int _\Omega M_\omega $
is given up to elementary equivalence.
$\int _\Omega M_\omega $
is given up to elementary equivalence.
1.3 Notation
We assume familiarity with
![]() $\mathrm {C}^*$
-algebras and von Neumann algebras. For background, refer to [Reference Anantharaman and PopaAP16, Reference TakesakiTak79, Reference BlackadarBla06, Reference Brown and OzawaBO08]. We recall the following terminology and notation:
$\mathrm {C}^*$
-algebras and von Neumann algebras. For background, refer to [Reference Anantharaman and PopaAP16, Reference TakesakiTak79, Reference BlackadarBla06, Reference Brown and OzawaBO08]. We recall the following terminology and notation:
-
• A tracial von Neumann algebra is a pair
 $(M,\tau )$
where M is a (necessarily finite) von Neumann algebra and
$(M,\tau )$
where M is a (necessarily finite) von Neumann algebra and
 $\tau $
is a faithful normal tracial state.
$\tau $
is a faithful normal tracial state. -
• An embedding of tracial von Neumann algebras is a trace-preserving
 $*$
-homomorphism. Often M and N have a preferred trace in context, and an embedding
$*$
-homomorphism. Often M and N have a preferred trace in context, and an embedding
 $M \to N$
will still be assumed to be trace-preserving even if
$M \to N$
will still be assumed to be trace-preserving even if
 $\tau $
is not written explicitly.
$\tau $
is not written explicitly. -
•
 ${\lVert {\cdot }\rVert }$
signifies the operator norms on a von Neumann algebra or more generally a
${\lVert {\cdot }\rVert }$
signifies the operator norms on a von Neumann algebra or more generally a
 $C^\ast $
-algebra.
$C^\ast $
-algebra. -
•
 ${\lVert {\cdot }\rVert }_{2,\phi }$
denotes the
${\lVert {\cdot }\rVert }_{2,\phi }$
denotes the
 $2$
-norm with respect to a given state
$2$
-norm with respect to a given state
 $\phi $
– namely,
$\phi $
– namely,
 ${\lVert {x}\rVert }_{2,\phi } = \phi (x^*x)^{1/2}$
. In particular, when a tracial state is given by context, then
${\lVert {x}\rVert }_{2,\phi } = \phi (x^*x)^{1/2}$
. In particular, when a tracial state is given by context, then
 ${\lVert {\cdot }\rVert }_2$
will denote its associated
${\lVert {\cdot }\rVert }_2$
will denote its associated
 $2$
-norm.
$2$
-norm. -
•
 $Z(M)$
denotes the center of a von Neumann algebra M.
$Z(M)$
denotes the center of a von Neumann algebra M. -
•
 $M_{\operatorname {sa}}$
denotes the set of self-adjoint elements.
$M_{\operatorname {sa}}$
denotes the set of self-adjoint elements. -
•
 $M_+$
denotes the set of positive elements.
$M_+$
denotes the set of positive elements. -
•
 $U(M)$
denotes the set of unitary elements.
$U(M)$
denotes the set of unitary elements. -
•
 $(M)_1$
denotes the unit ball of M with respect to operator norm.
$(M)_1$
denotes the unit ball of M with respect to operator norm.
We also briefly recall a definition of direct integrals for tracial von Neumann algebras. Although von Neumann’s work defines direct integrals of von Neumann algebras based on direct integrals of the underlying Hilbert spaces, the direct integral can also be described directly in terms of algebra elements, thanks to the axiomatic characterizations of tracial von Neumann algebras as tracial
![]() $\mathrm {C}^*$
-algebras whose unit ball is complete in
$\mathrm {C}^*$
-algebras whose unit ball is complete in
![]() ${\lVert {\cdot }\rVert }_2$
[Reference Anantharaman and PopaAP16, Proposition 2.6.4]. This development is more suited to our purposes and consistent with the general definition for metric structures used in [Reference Farah and GhasemiFG24, Reference Ben Yaacov, Ibarlucía and TsankovBIT24].
${\lVert {\cdot }\rVert }_2$
[Reference Anantharaman and PopaAP16, Proposition 2.6.4]. This development is more suited to our purposes and consistent with the general definition for metric structures used in [Reference Farah and GhasemiFG24, Reference Ben Yaacov, Ibarlucía and TsankovBIT24].
Definition 1.1 (Measurable fields of tracial von Neumann algebras).
Let
![]() $(\Omega ,\mu )$
be a probability space (i.e., a measure space with
$(\Omega ,\mu )$
be a probability space (i.e., a measure space with
![]() $\mu (\Omega ) = 1$
). Let
$\mu (\Omega ) = 1$
). Let
![]() $(M_\omega ,\tau _\omega )$
be a collection of separable tracial von Neumann algebras indexed by
$(M_\omega ,\tau _\omega )$
be a collection of separable tracial von Neumann algebras indexed by
![]() $\omega \in \Omega $
. A section is a function
$\omega \in \Omega $
. A section is a function
![]() $f: \Omega \to \bigsqcup _{\omega \in \Omega } M_\omega $
with
$f: \Omega \to \bigsqcup _{\omega \in \Omega } M_\omega $
with
![]() $f(\omega ) \in M_\omega $
. Let
$f(\omega ) \in M_\omega $
. Let
![]() $(e_n)_{n \in \mathbb {N}}$
be a sequence of sections such that
$(e_n)_{n \in \mathbb {N}}$
be a sequence of sections such that
-
1.
 $e_1(\omega ) = 1$
.
$e_1(\omega ) = 1$
. -
2. For each
 $\omega $
,
$\omega $
,
 $(e_n(\omega ))_{n \in \mathbb {N}}$
is dense in
$(e_n(\omega ))_{n \in \mathbb {N}}$
is dense in
 $(M_\omega )_1$
with respect to
$(M_\omega )_1$
with respect to
 ${\lVert {\cdot }\rVert }_{2,\tau _\omega }$
.
${\lVert {\cdot }\rVert }_{2,\tau _\omega }$
. -
3. For each n-variable
 $*$
-polynomial p, the function
$*$
-polynomial p, the function
 $\omega \mapsto \tau _\omega [p(e_1(\omega ),\dots ,e_n(\omega ))]$
is measurable.
$\omega \mapsto \tau _\omega [p(e_1(\omega ),\dots ,e_n(\omega ))]$
is measurable.
Then we say that
![]() $(M_\omega , (e_n(\omega ))_{n \in \mathbb {N}})_{\omega \in \Omega }$
is a measurable field of (separable) tracial von Neumann algebras.
$(M_\omega , (e_n(\omega ))_{n \in \mathbb {N}})_{\omega \in \Omega }$
is a measurable field of (separable) tracial von Neumann algebras.
Definition 1.2. Continue the same setup as Definition 1.1.
-
1. A section
 $f: \omega \to \bigsqcup _{\omega \in \Omega } M_\omega $
is measurable if
$f: \omega \to \bigsqcup _{\omega \in \Omega } M_\omega $
is measurable if
 $\omega \mapsto \tau _\omega (e_n(\omega ) f(\omega ))$
is measurable for each
$\omega \mapsto \tau _\omega (e_n(\omega ) f(\omega ))$
is measurable for each
 $n \in \mathbb {N}$
.
$n \in \mathbb {N}$
. -
2. A section
 $f: \omega \to \bigsqcup _{\omega \in \Omega } M_\omega $
is bounded if
$f: \omega \to \bigsqcup _{\omega \in \Omega } M_\omega $
is bounded if
 $\omega \mapsto {\lVert {f(\omega )} \rVert }$
is bounded.
$\omega \mapsto {\lVert {f(\omega )} \rVert }$
is bounded. -
3. A simple section is a section of the form
 where
where
 $\lambda _j \in \mathbb {C}$
and
$\lambda _j \in \mathbb {C}$
and
 $(S_j)_{j=1}^n$
is a measurable partition of
$(S_j)_{j=1}^n$
is a measurable partition of
 $\Omega $
.
$\Omega $
.
Fact 1.3. Continue the same setup as Definition 1.1.
-
1. If
 $(S_j)_{j=1}^m$
is a measurable partition of
$(S_j)_{j=1}^m$
is a measurable partition of
 $\Omega $
and
$\Omega $
and
 $p_j$
is a non-commutative
$p_j$
is a non-commutative
 $*$
-polynomial in n variables, then
$*$
-polynomial in n variables, then  is a measurable section, so in particular, simple sections are measurable.
is a measurable section, so in particular, simple sections are measurable. -
2. If f is a measurable section, then
 $\omega \mapsto {\lVert {f(\omega )} \rVert }_{\tau _\omega ,2}$
is measurable since Hence, by polarization,
$\omega \mapsto {\lVert {f(\omega )} \rVert }_{\tau _\omega ,2}$
is measurable since Hence, by polarization,
 $\omega \mapsto \tau _\omega (f(\omega )^* g(\omega ))$
is measurable whenever f and g are measurable sections.
$\omega \mapsto \tau _\omega (f(\omega )^* g(\omega ))$
is measurable whenever f and g are measurable sections.
-
3. If f is a measurable section, then
 $\omega \mapsto {\lVert {f(\omega )} \rVert }$
is measurable since and
$\omega \mapsto {\lVert {f(\omega )} \rVert }$
is measurable since and
 $\tau _\omega (e_n(\omega )^* f(\omega ) e_m(\omega )) = \tau _\omega (f(\omega ) [e_m(\omega ) e_n(\omega )^*])$
is measurable by (1) and (2).
$\tau _\omega (e_n(\omega )^* f(\omega ) e_m(\omega )) = \tau _\omega (f(\omega ) [e_m(\omega ) e_n(\omega )^*])$
is measurable by (1) and (2).
-
4. If
 $f_n$
are measurable sections, f is a section, and
$f_n$
are measurable sections, f is a section, and
 $\lim _{n \to \infty } {\lVert {f_n(\omega ) - f(\omega )} \rVert }_{\tau _\omega ,2} = 0$
for a.e.
$\lim _{n \to \infty } {\lVert {f_n(\omega ) - f(\omega )} \rVert }_{\tau _\omega ,2} = 0$
for a.e.
 $\omega $
, then f is a measurable section.
$\omega $
, then f is a measurable section. -
5. Every bounded measurable section is a pointwise-
 ${\lVert {\cdot }\rVert }_2$
limit of simple sections
${\lVert {\cdot }\rVert }_2$
limit of simple sections
 $f_n$
such that
$f_n$
such that
 $\sup _\omega {\lVert {f_n(\omega )}\rVert } \leq \sup _\omega {\lVert {f(\omega )} \rVert }$
. Indeed, by rescaling, assume without loss of generality that
$\sup _\omega {\lVert {f_n(\omega )}\rVert } \leq \sup _\omega {\lVert {f(\omega )} \rVert }$
. Indeed, by rescaling, assume without loss of generality that
 ${\lVert {f(\omega )} \rVert } \leq 1$
. Then define
${\lVert {f(\omega )} \rVert } \leq 1$
. Then define
 $m(\omega ,n)$
recursively with
$m(\omega ,n)$
recursively with
 $m(\omega ,1) = 1$
and Then
$m(\omega ,1) = 1$
and Then $$\begin{align*}m(\omega,n+1) = \begin{cases} n+1, & \text{ if } {\lVert {e_{n+1}(\omega) - f(\omega)}\rVert}_{2,\tau_\omega} < {\lVert {e_{m(\omega,n)}(\omega) - f(\omega)} \rVert}_{2,\tau_\omega} \\ m(\omega,n), & \text{ else.} \end{cases} \end{align*}$$
$$\begin{align*}m(\omega,n+1) = \begin{cases} n+1, & \text{ if } {\lVert {e_{n+1}(\omega) - f(\omega)}\rVert}_{2,\tau_\omega} < {\lVert {e_{m(\omega,n)}(\omega) - f(\omega)} \rVert}_{2,\tau_\omega} \\ m(\omega,n), & \text{ else.} \end{cases} \end{align*}$$
 $f_n(\omega ) := e_{m(\omega ,n)}(\omega )$
is a simple section and
$f_n(\omega ) := e_{m(\omega ,n)}(\omega )$
is a simple section and
 ${\lVert {f_n(\omega ) - f(\omega )}\rVert }_{2,\tau _\omega } \to 0$
.
${\lVert {f_n(\omega ) - f(\omega )}\rVert }_{2,\tau _\omega } \to 0$
.
-
6. Bounded measurable sections form a
 $*$
-algebra under pointwise multiplication. To show closure under products, let f and g by bounded measurable sections and let
$*$
-algebra under pointwise multiplication. To show closure under products, let f and g by bounded measurable sections and let
 $f_n$
and
$f_n$
and
 $g_n$
be approximating sequences of simple sections as in (6). Then
$g_n$
be approximating sequences of simple sections as in (6). Then
 $f_n g_n$
is a measurable section by (1). We also have
$f_n g_n$
is a measurable section by (1). We also have
 ${\lVert {f_n(\omega ) g_n(\omega ) - f(\omega ) g(\omega )}\rVert }_{\tau _\omega ,2} \to 0$
for each
${\lVert {f_n(\omega ) g_n(\omega ) - f(\omega ) g(\omega )}\rVert }_{\tau _\omega ,2} \to 0$
for each
 $\omega $
, so
$\omega $
, so
 $fg$
is measurable by (5). Closure under addition and adjoint are left to the reader.
$fg$
is measurable by (5). Closure under addition and adjoint are left to the reader.
Definition 1.4 (Direct integrals of tracial von Neumann algebras).
Let
![]() $(\Omega ,\mu )$
and
$(\Omega ,\mu )$
and
![]() $(M_\omega , (e_n(\omega ))_{n \in \mathbb {N}})_{\omega \in \Omega }$
be as in Definition 1.1. The direct integral is the pair
$(M_\omega , (e_n(\omega ))_{n \in \mathbb {N}})_{\omega \in \Omega }$
be as in Definition 1.1. The direct integral is the pair
![]() $(M,\tau )$
given as follows:
$(M,\tau )$
given as follows:
-
1. M is the set of bounded measurable sections modulo equality almost everywhere.
-
2. The
 $*$
-algebra operations on M are defined pointwise on
$*$
-algebra operations on M are defined pointwise on
 $\Omega $
.
$\Omega $
. -
3. The norm on M is given by
 ${\lVert {f} \rVert } = \operatorname {esssup}_{\omega \in \Omega } {\lVert {f(\omega )} \rVert }$
.
${\lVert {f} \rVert } = \operatorname {esssup}_{\omega \in \Omega } {\lVert {f(\omega )} \rVert }$
. -
4. The trace
 $\tau $
is given by
$\tau $
is given by
 $\tau (f) = \int _{\Omega } \tau _\omega (f(\omega ))\,d\mu (\omega )$
.
$\tau (f) = \int _{\Omega } \tau _\omega (f(\omega ))\,d\mu (\omega )$
.
To see that
![]() $(M,\tau )$
is a tracial von Neumann algebra via [Reference Anantharaman and PopaAP16, Proposition 2.6.4], one first checks it is a
$(M,\tau )$
is a tracial von Neumann algebra via [Reference Anantharaman and PopaAP16, Proposition 2.6.4], one first checks it is a
![]() $\mathrm {C}^*$
-algebra with the norm given by the essential supremum as above, which is immediate once we know that
$\mathrm {C}^*$
-algebra with the norm given by the essential supremum as above, which is immediate once we know that
![]() $\omega \mapsto {\lVert {f(\omega )} \rVert }$
is measurable for each
$\omega \mapsto {\lVert {f(\omega )} \rVert }$
is measurable for each
![]() $f \in M$
. Then
$f \in M$
. Then
![]() $\tau $
is faithful since
$\tau $
is faithful since
![]() $\tau (f^*f) = 0$
implies that
$\tau (f^*f) = 0$
implies that
![]() $\tau _\omega (f(\omega )^*f(\omega )) = 0$
, and hence,
$\tau _\omega (f(\omega )^*f(\omega )) = 0$
, and hence,
![]() $f(\omega ) = 0$
almost everywhere. Finally, for completeness of the unit ball in
$f(\omega ) = 0$
almost everywhere. Finally, for completeness of the unit ball in
![]() ${\lVert {\cdot }\rVert }_{2,\tau }$
, suppose that
${\lVert {\cdot }\rVert }_{2,\tau }$
, suppose that
![]() $f_n$
is Cauchy in
$f_n$
is Cauchy in
![]() ${\lVert {\cdot }\rVert }_{2,\tau }$
. Take a subsequence
${\lVert {\cdot }\rVert }_{2,\tau }$
. Take a subsequence
![]() $f_{n(k)}$
such that
$f_{n(k)}$
such that
![]() $\sum _k {\lVert {f_{n(k)} - f_{n(k+1)}} \rVert }_{2,\tau }^2 < \infty $
, and observe that
$\sum _k {\lVert {f_{n(k)} - f_{n(k+1)}} \rVert }_{2,\tau }^2 < \infty $
, and observe that
![]() $f_{n(k)}(\omega )$
converges in
$f_{n(k)}(\omega )$
converges in
![]() ${\lVert {\cdot }\rVert }_{2,\tau _\omega }$
almost everywhere to some
${\lVert {\cdot }\rVert }_{2,\tau _\omega }$
almost everywhere to some
![]() $f(\omega )$
. By Fact 1.3 (5), f is measurable. It also follows from standard measure-theory arguments that
$f(\omega )$
. By Fact 1.3 (5), f is measurable. It also follows from standard measure-theory arguments that
![]() $f_n \to f$
in
$f_n \to f$
in
![]() ${\lVert {\cdot }\rVert }_{2,\tau }$
.
${\lVert {\cdot }\rVert }_{2,\tau }$
.
We remark that the set of measurable sections, and hence the direct integral, can depend on the choice of
![]() $e_n(\omega )$
. However, as in [Reference Ben Yaacov, Ibarlucía and TsankovBIT24, Remark 8.13], if two sequences
$e_n(\omega )$
. However, as in [Reference Ben Yaacov, Ibarlucía and TsankovBIT24, Remark 8.13], if two sequences
![]() $(e_n(\omega ))_{n \in \mathbb {N}}$
and
$(e_n(\omega ))_{n \in \mathbb {N}}$
and
![]() $(e_n'(\omega ))_{n \in \mathbb {N}}$
are measurable with respect to each other, then a bounded section f is measurable with respect to
$(e_n'(\omega ))_{n \in \mathbb {N}}$
are measurable with respect to each other, then a bounded section f is measurable with respect to
![]() $(e_n)_{n \in \mathbb {N}}$
if and only if it is measurable with respect to
$(e_n)_{n \in \mathbb {N}}$
if and only if it is measurable with respect to
![]() $(e_n')_{n \in \mathbb {N}}$
in light of Fact 1.3 (5) and (4), and hence, the direct integrals are the same.
$(e_n')_{n \in \mathbb {N}}$
in light of Fact 1.3 (5) and (4), and hence, the direct integrals are the same.
1.4 Organization
The rest of the paper is organized as follows:
-
• §2 explains the construction of ultrafibers and ultraproducts associated to pure states on a commutative von Neumann algebra, and how to deduce Corollary B from Proposition C.
-
• §3 describes the N-valued interpretation of formulas for some
 $N \subseteq Z(M)$
and proves Theorem D.
$N \subseteq Z(M)$
and proves Theorem D. -
• §4 defines the distribution of theories and shows that it can be recovered when a tracial von Neumann algebra is given up to elementary equivalence, thus proving Theorem A.
-
• §5 shows that under continuum hypothesis, an ultrafiber associated to a separable direct integral will in fact be isomorphic to an ultraproduct over the natural numbers of some of the fibers.
-
• §6 applies the ultrafiber construction to ultraproducts of random matrix algebras. This gives a new way of making a ‘deterministic selection’ of elements in an ultraproduct representing the large-n limit of random matrix models, which sidesteps measurability problems inherent in the study of ultralimits.
2 Ultrafibers and generalized ultrapowers
2.1 Construction of ultrafibers
As motivation, we recall the relationship between ultrafilters on discrete sets and characters. A character on a commutative (unital)
![]() $\mathrm {C}^*$
-algebra is a multiplicative linear functional into the complex numbers. It is a standard fact that characters are equivalent to pure states, or extreme points in the spaces of states (positive linear functionals of norm
$\mathrm {C}^*$
-algebra is a multiplicative linear functional into the complex numbers. It is a standard fact that characters are equivalent to pure states, or extreme points in the spaces of states (positive linear functionals of norm
![]() $1$
).
$1$
).
For an ultrafilter
![]() $\mathcal {U}$
on an index set I, the ultralimit
$\mathcal {U}$
on an index set I, the ultralimit
![]() $\lim _{\mathcal {U}}$
defines a character on
$\lim _{\mathcal {U}}$
defines a character on
![]() $l^\infty (I)$
. If
$l^\infty (I)$
. If
![]() $\mathcal {U} \neq \mathcal {V}$
, then there is a set
$\mathcal {U} \neq \mathcal {V}$
, then there is a set
![]() $A \subseteq I$
with
$A \subseteq I$
with
![]() $A \in \mathcal {U}$
but
$A \in \mathcal {U}$
but
![]() $A \notin \mathcal {V}$
, so
$A \notin \mathcal {V}$
, so ![]() but
but ![]() , whence the map
, whence the map
![]() $\mathcal {U} \mapsto \lim _{\mathcal {U}}$
is injective. In fact, it is also surjective, for if
$\mathcal {U} \mapsto \lim _{\mathcal {U}}$
is injective. In fact, it is also surjective, for if
![]() $\sigma $
is a character on
$\sigma $
is a character on
![]() $l^\infty (I)$
, then
$l^\infty (I)$
, then
![]() $\sigma $
must send any projection to either
$\sigma $
must send any projection to either
![]() $0$
or
$0$
or
![]() $1$
. As such, it is easy to verify that
$1$
. As such, it is easy to verify that
is an ultrafilter. For this ultrafilter, clearly ![]() for any projection
for any projection ![]() in
in
![]() $\ell ^\infty (I)$
. As projections densely span a von Neumann algebra, we see that
$\ell ^\infty (I)$
. As projections densely span a von Neumann algebra, we see that
![]() $\lim _{\mathcal {U}} = \sigma $
. Therefore, we shall use ultrafilters on I and characters on
$\lim _{\mathcal {U}} = \sigma $
. Therefore, we shall use ultrafilters on I and characters on
![]() $l^\infty (I)$
interchangeably and use the same symbol to denote both. We shall further generalize to use
$l^\infty (I)$
interchangeably and use the same symbol to denote both. We shall further generalize to use
![]() $\mathcal {U}$
and
$\mathcal {U}$
and
![]() $\mathcal {V}$
to denote characters on arbitrary commutative von Neumann algebras.
$\mathcal {V}$
to denote characters on arbitrary commutative von Neumann algebras.
Definition 2.1. Let M be a finite von Neumann algebra,
![]() $N \subseteq Z(M)$
be a subalgebra of its center,
$N \subseteq Z(M)$
be a subalgebra of its center,
![]() $E: M \to N$
be a normal, tracial, faithful conditional expectation, and
$E: M \to N$
be a normal, tracial, faithful conditional expectation, and
![]() $\mathcal {U}$
be a character on N. The ultrafiber of M w.r.t. E and
$\mathcal {U}$
be a character on N. The ultrafiber of M w.r.t. E and
![]() $\mathcal {U}$
, denoted by
$\mathcal {U}$
, denoted by
![]() $M^{/E, \mathcal {U}}$
, is given by
$M^{/E, \mathcal {U}}$
, is given by
where
![]() $I_{E, \mathcal {U}}$
is the closed ideal given by
$I_{E, \mathcal {U}}$
is the closed ideal given by
![]() $M^{/E, \mathcal {U}}$
shall always be regarded as equipped with the faithful tracial state
$M^{/E, \mathcal {U}}$
shall always be regarded as equipped with the faithful tracial state
![]() $\tau _{E, \mathcal {U}}$
given by
$\tau _{E, \mathcal {U}}$
given by
Consider the case where M is a direct sum
![]() $\oplus _{i \in I} M_i$
of tracial von Neumann algebra
$\oplus _{i \in I} M_i$
of tracial von Neumann algebra
![]() $(M_i,\tau _i)$
over some index set I; suppose
$(M_i,\tau _i)$
over some index set I; suppose
![]() $N = \ell ^\infty (I)$
and
$N = \ell ^\infty (I)$
and
![]() $E: M \to N$
is given by application of the trace on each direct summand. Suppose
$E: M \to N$
is given by application of the trace on each direct summand. Suppose
![]() $\mathcal {U}$
is the character given by the ultralimit associated to an ultrafilter on I, which we shall also denoted by
$\mathcal {U}$
is the character given by the ultralimit associated to an ultrafilter on I, which we shall also denoted by
![]() $\mathcal {U}$
. Then it is easy to verify that
$\mathcal {U}$
. Then it is easy to verify that
![]() $M^{/E, \mathcal {U}} = \prod _{\mathcal {U}} M_i$
. Hence, the ultrafiber construction generalizes the classical ultraproducts. We remark here that although our primary interest is in tracial von Neumann algebras, it is important in Definition 2.1 not to assume that M admits a faithful tracial state; indeed, if M had a faithful tracial state, then so would N, but if I is an uncoutable discrete set, then
$M^{/E, \mathcal {U}} = \prod _{\mathcal {U}} M_i$
. Hence, the ultrafiber construction generalizes the classical ultraproducts. We remark here that although our primary interest is in tracial von Neumann algebras, it is important in Definition 2.1 not to assume that M admits a faithful tracial state; indeed, if M had a faithful tracial state, then so would N, but if I is an uncoutable discrete set, then
![]() $\ell ^\infty (I)$
does not have a faithful state.
$\ell ^\infty (I)$
does not have a faithful state.
Proposition 2.2.
![]() $(M^{/E, \mathcal {U}}, \tau _{E, \mathcal {U}})$
is a tracial von Neumann algebra. Furthermore, any element of norm 1 in
$(M^{/E, \mathcal {U}}, \tau _{E, \mathcal {U}})$
is a tracial von Neumann algebra. Furthermore, any element of norm 1 in
![]() $M^{/E, \mathcal {U}}$
can be lifted to an element of norm 1 in M.
$M^{/E, \mathcal {U}}$
can be lifted to an element of norm 1 in M.
The proof follows similar lines as the proof that classical ultraproducts are tracial von Neumann algebras in [Reference Anantharaman and PopaAP16, Proposition 5.4.1]. We recall two ingredients from classical von Neumann algebra theory.
Lemma 2.3. Let N be a commutative von Neumann algebra,
![]() $\mathcal {U}$
be a character on N,
$\mathcal {U}$
be a character on N,
![]() $f \in N$
. For any
$f \in N$
. For any
![]() $\epsilon> 0$
, there exists a projection
$\epsilon> 0$
, there exists a projection
![]() $p \in N$
s.t.
$p \in N$
s.t.
![]() $\mathcal {U}(p) = 1$
and
$\mathcal {U}(p) = 1$
and
![]() $\|fp - \mathcal {U}(f)p\|_\infty \leq \epsilon $
.
$\|fp - \mathcal {U}(f)p\|_\infty \leq \epsilon $
.
Proof. Let
![]() $\Omega $
be the spectrum of N, and we shall regard f as a continuous function on
$\Omega $
be the spectrum of N, and we shall regard f as a continuous function on
![]() $\Omega $
. Then there exists an open neighborhood
$\Omega $
. Then there exists an open neighborhood
![]() $O \subseteq \Omega $
of
$O \subseteq \Omega $
of
![]() $\mathcal {U}$
s.t.
$\mathcal {U}$
s.t.
![]() $|f(t) - \mathcal {U}(f)| \leq \epsilon $
whenever
$|f(t) - \mathcal {U}(f)| \leq \epsilon $
whenever
![]() $t \in O$
. As clopen sets form a basis of topology for
$t \in O$
. As clopen sets form a basis of topology for
![]() $\Omega $
, O can be chosen to be clopen. Letting
$\Omega $
, O can be chosen to be clopen. Letting
![]() $p = 1_O$
concludes the proof.
$p = 1_O$
concludes the proof.
Lemma 2.4. Let M be a finite von Neumann algebra,
![]() $N \subseteq Z(M)$
be a subalgebra of its center,
$N \subseteq Z(M)$
be a subalgebra of its center,
![]() $E: M \to N$
be a normal, tracial, faithful conditional expectation. Then
$E: M \to N$
be a normal, tracial, faithful conditional expectation. Then
![]() $\|x\|_{E, 2, \infty } = \|E(x^\ast x)\|_\infty ^{1/2}$
defines a norm on M and
$\|x\|_{E, 2, \infty } = \|E(x^\ast x)\|_\infty ^{1/2}$
defines a norm on M and
![]() $(M)_1$
is complete under
$(M)_1$
is complete under
![]() $\|\cdot \|_{E, 2, \infty }$
.
$\|\cdot \|_{E, 2, \infty }$
.
Proof. That
![]() $\|\cdot \|_{E, 2, \infty }$
defines a norm is an easy exercise. To prove completeness, we let
$\|\cdot \|_{E, 2, \infty }$
defines a norm is an easy exercise. To prove completeness, we let
![]() $\{\varphi _i\}_{i \in I}$
be a maximal collection of normal states on N with disjoint supports. Then
$\{\varphi _i\}_{i \in I}$
be a maximal collection of normal states on N with disjoint supports. Then
![]() $\sum _{i \in I} \mathrm {supp}(\varphi _i) = 1$
, so the direct sum of the GNS representations of M, associated with
$\sum _{i \in I} \mathrm {supp}(\varphi _i) = 1$
, so the direct sum of the GNS representations of M, associated with
![]() $\varphi _i \circ E$
,
$\varphi _i \circ E$
,
is a faithful normal representation. Thus, a uniformly dense subset of positive linear functionals on M is of the form
where
![]() $I_0 \subseteq I$
is a finite subset and
$I_0 \subseteq I$
is a finite subset and
![]() $y_i \in M_+$
is supported on
$y_i \in M_+$
is supported on
![]() $\mathrm {supp}(\varphi _i)$
.
$\mathrm {supp}(\varphi _i)$
.
Now, let
![]() $(x_n) \subseteq (M)_1$
be a Cauchy sequence under
$(x_n) \subseteq (M)_1$
be a Cauchy sequence under
![]() $\|\cdot \|_{E, 2, \infty }$
. For any finite subset
$\|\cdot \|_{E, 2, \infty }$
. For any finite subset
![]() $I_0 \subseteq I$
and
$I_0 \subseteq I$
and
![]() $y_i \in M_+$
supported on
$y_i \in M_+$
supported on
![]() $\mathrm {supp}(\varphi _i)$
, we have
$\mathrm {supp}(\varphi _i)$
, we have
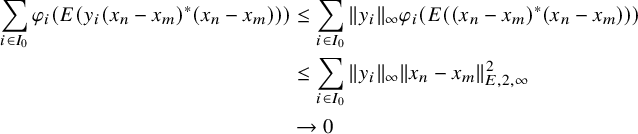 $$ \begin{align*} \begin{split} \sum_{i \in I_0} \varphi_i(E(y_i(x_n - x_m)^\ast (x_n - x_m))) &\leq \sum_{i \in I_0} \|y_i\|_\infty \varphi_i(E((x_n - x_m)^\ast (x_n - x_m)))\\ &\leq \sum_{i \in I_0} \|y_i\|_\infty \|x_n - x_m\|_{E, 2, \infty}^2\\ &\to 0 \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} \sum_{i \in I_0} \varphi_i(E(y_i(x_n - x_m)^\ast (x_n - x_m))) &\leq \sum_{i \in I_0} \|y_i\|_\infty \varphi_i(E((x_n - x_m)^\ast (x_n - x_m)))\\ &\leq \sum_{i \in I_0} \|y_i\|_\infty \|x_n - x_m\|_{E, 2, \infty}^2\\ &\to 0 \end{split} \end{align*} $$
as
![]() $n, m \to \infty $
. Hence, as
$n, m \to \infty $
. Hence, as
![]() $\|x_n\|_\infty \leq 1$
for all n, we see that
$\|x_n\|_\infty \leq 1$
for all n, we see that
![]() $x_n \to x$
in the strong
$x_n \to x$
in the strong
![]() $^\ast $
topology for some
$^\ast $
topology for some
![]() $x \in (M)_1$
.
$x \in (M)_1$
.
We claim that
![]() $\|x_n - x\|_{E, 2, \infty }^2 \to 0$
to conclude the proof. For any
$\|x_n - x\|_{E, 2, \infty }^2 \to 0$
to conclude the proof. For any
![]() $\epsilon> 0$
, there exists
$\epsilon> 0$
, there exists
![]() $N> 0$
s.t.
$N> 0$
s.t.
![]() $\|x_n - x_m\|_{E, 2, \infty }^2 \leq \epsilon $
whenever
$\|x_n - x_m\|_{E, 2, \infty }^2 \leq \epsilon $
whenever
![]() $n, m \geq N$
; that is,
$n, m \geq N$
; that is,
![]() $\|E((x_n - x_m)^\ast (x_n - x_m))\|_\infty \leq \epsilon $
. As
$\|E((x_n - x_m)^\ast (x_n - x_m))\|_\infty \leq \epsilon $
. As
![]() $x_m \to x$
in the strong
$x_m \to x$
in the strong
![]() $^\ast $
topology,
$^\ast $
topology,
![]() $(x_n - x_m)^\ast (x_n - x_m) \to (x_n - x)^\ast (x_n - x)$
in the strong
$(x_n - x_m)^\ast (x_n - x_m) \to (x_n - x)^\ast (x_n - x)$
in the strong
![]() $^\ast $
topology. As E is normal, we have
$^\ast $
topology. As E is normal, we have
![]() $E((x_n - x_m)^\ast (x_n - x_m)) \to E((x_n - x)^\ast (x_n - x))$
in the strong
$E((x_n - x_m)^\ast (x_n - x_m)) \to E((x_n - x)^\ast (x_n - x))$
in the strong
![]() $^\ast $
topology, whence
$^\ast $
topology, whence
![]() $\|E((x_n - x)^\ast (x_n - x))\|_\infty \leq \epsilon $
; that is,
$\|E((x_n - x)^\ast (x_n - x))\|_\infty \leq \epsilon $
; that is,
![]() $\|x_n - x\|_{E, 2, \infty }^2 \leq \epsilon $
whenever
$\|x_n - x\|_{E, 2, \infty }^2 \leq \epsilon $
whenever
![]() $n \geq N$
. The concludes the proof.
$n \geq N$
. The concludes the proof.
Proof of Proposition 2.2.
Let
![]() $q: M \to M^{/E, \mathcal {U}} = M/I_{E, \mathcal {U}}$
be the natural quotient map. We claim that
$q: M \to M^{/E, \mathcal {U}} = M/I_{E, \mathcal {U}}$
be the natural quotient map. We claim that
![]() $q((M)_1)$
is complete under
$q((M)_1)$
is complete under
![]() $\|\cdot \|_{\tau _{E, \mathcal {U}}, 2}$
. Granted the claim, then as
$\|\cdot \|_{\tau _{E, \mathcal {U}}, 2}$
. Granted the claim, then as
![]() $q((M)_1)$
is contained in
$q((M)_1)$
is contained in
![]() $(M^{/E, \mathcal {U}})_1$
and contains all elements of the latter space of operator norm strictly smaller than 1, consequently dense in the latter space under
$(M^{/E, \mathcal {U}})_1$
and contains all elements of the latter space of operator norm strictly smaller than 1, consequently dense in the latter space under
![]() $\|\cdot \|_{\tau _{E, \mathcal {U}}, 2}$
, we must have
$\|\cdot \|_{\tau _{E, \mathcal {U}}, 2}$
, we must have
![]() $q((M)_1) = (M^{/E, \mathcal {U}})_1$
and it is complete. Whence, it is a tracial von Neumann algebra with
$q((M)_1) = (M^{/E, \mathcal {U}})_1$
and it is complete. Whence, it is a tracial von Neumann algebra with
![]() $\tau _{E, \mathcal {U}}$
a faithful, normal, tracial state, by [Reference Anantharaman and PopaAP16, Proposition 2.6.4].
$\tau _{E, \mathcal {U}}$
a faithful, normal, tracial state, by [Reference Anantharaman and PopaAP16, Proposition 2.6.4].
To prove the claim, we let
![]() $(x_n) \subseteq q((M)_1)$
be a Cauchy sequence under
$(x_n) \subseteq q((M)_1)$
be a Cauchy sequence under
![]() $\|\cdot \|_{\tau _{E, \mathcal {U}}, 2}$
. By taking a subsequence if necessary, we may assume
$\|\cdot \|_{\tau _{E, \mathcal {U}}, 2}$
. By taking a subsequence if necessary, we may assume
![]() $\|x_n - x_{n+1}\|_{\tau _{E, \mathcal {U}}, 2} \leq 2^{-(n+1)}$
. We shall construct by induction a sequence
$\|x_n - x_{n+1}\|_{\tau _{E, \mathcal {U}}, 2} \leq 2^{-(n+1)}$
. We shall construct by induction a sequence ![]() , with
, with ![]() and
and ![]() . We start with an arbitrary
. We start with an arbitrary ![]() with
with ![]() . Now, assume
. Now, assume ![]() up to some n have been constructed, let
up to some n have been constructed, let ![]() be arbitrarily chosen with
be arbitrarily chosen with ![]() . Since,
. Since,
by Lemma 2.3, there exists a projection
![]() $p \in N$
s.t.
$p \in N$
s.t.
![]() $\mathcal {U}(p) = 1$
and
$\mathcal {U}(p) = 1$
and
Let ![]() . Since both
. Since both ![]() and
and ![]() have operator norms bounded by
have operator norms bounded by
![]() $1$
,
$1$
, ![]() as well. We have
as well. We have
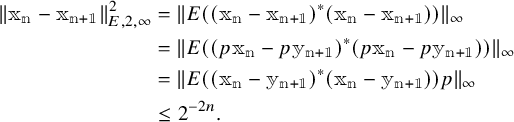
We also have
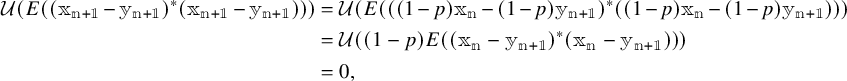
where in the final equality, we used that
![]() $\mathcal {U}(p) = 1$
and therefore
$\mathcal {U}(p) = 1$
and therefore
![]() $\mathcal {U}(1-p) = 0$
. Thus,
$\mathcal {U}(1-p) = 0$
. Thus, ![]() and
and ![]() . This concludes the inductive construction.
. This concludes the inductive construction.
By Lemma 2.4, ![]() for some
for some ![]() in
in
![]() $\|\cdot \|_{E, 2, \infty }$
. Let
$\|\cdot \|_{E, 2, \infty }$
. Let ![]() . We shall show that
. We shall show that
![]() $x_n \to x$
in
$x_n \to x$
in
![]() $\|\cdot \|_{\tau _{E, \mathcal {U}}, 2}$
to conclude the proof of the claim. Indeed,
$\|\cdot \|_{\tau _{E, \mathcal {U}}, 2}$
to conclude the proof of the claim. Indeed,

This proves the claim.
Definition 2.5 (Generalized ultrapowers).
Let
![]() $(M, \tau )$
be a tracial von Neumann algebra, A be an abelian von Neumann algebra, and
$(M, \tau )$
be a tracial von Neumann algebra, A be an abelian von Neumann algebra, and
![]() $\mathcal {U}$
be a character on A. The generalized ultrapower of M with respect to
$\mathcal {U}$
be a character on A. The generalized ultrapower of M with respect to
![]() $\mathcal {U}$
, denoted by
$\mathcal {U}$
, denoted by
![]() $M^{\mathcal {U}}$
, is given by
$M^{\mathcal {U}}$
, is given by
where
![]() $E: A \mathbin {\overline {\otimes }} M \to A$
is given by
$E: A \mathbin {\overline {\otimes }} M \to A$
is given by
![]() $E = \mathrm {Id} \otimes \tau $
. We shall denote the canonical trace on
$E = \mathrm {Id} \otimes \tau $
. We shall denote the canonical trace on
![]() $M^{\mathcal {U}}$
by
$M^{\mathcal {U}}$
by
![]() $\tau _{\mathcal {U}}$
. The map that sends
$\tau _{\mathcal {U}}$
. The map that sends
![]() $x \in M$
to the element represented by
$x \in M$
to the element represented by
![]() $1_A \otimes x$
in
$1_A \otimes x$
in
![]() $M^{\mathcal {U}}$
is a trace-preserving embedding and shall be called the diagonal embedding.
$M^{\mathcal {U}}$
is a trace-preserving embedding and shall be called the diagonal embedding.
Remark 2.6. Consider the case where
![]() $A = \ell ^\infty (I)$
, where I is an index set and
$A = \ell ^\infty (I)$
, where I is an index set and
![]() $\mathcal {U}$
is the character given by the ultralimit associated to an ultrafilter on I, which we shall also denote by
$\mathcal {U}$
is the character given by the ultralimit associated to an ultrafilter on I, which we shall also denote by
![]() $\mathcal {U}$
. Then
$\mathcal {U}$
. Then
![]() $M^{\mathcal {U}}$
, as defined here, is easily seen to be the same as the ordinary ultrapower of M with respect to
$M^{\mathcal {U}}$
, as defined here, is easily seen to be the same as the ordinary ultrapower of M with respect to
![]() $\mathcal {U}$
. The diagonal embedding is also the same map as in the ordinary case. Hence, this construction generalizes the ordinary ultrapowers.
$\mathcal {U}$
. The diagonal embedding is also the same map as in the ordinary case. Hence, this construction generalizes the ordinary ultrapowers.
2.2 Factoriality and centers
The center of
![]() $M^{/E,\mathcal {U}}$
behaves as one would expect based on the case of ultraproducts over discrete index sets [Reference Farah, Hart and ShermanFHS13, Corollary 4.3]. To set up the proof, we first recall the center-valued trace and the Dixmier averaging theorem.
$M^{/E,\mathcal {U}}$
behaves as one would expect based on the case of ultraproducts over discrete index sets [Reference Farah, Hart and ShermanFHS13, Corollary 4.3]. To set up the proof, we first recall the center-valued trace and the Dixmier averaging theorem.
Theorem 2.7. (Generalized Dixmier averaging theorem [Reference DixmierDix81, III.5, Cor. of Thm. 1]) Let M be a finite von Neumann algebra with center
![]() $Z(M)$
. Then there is a unique normal, faithful, tracial conditional expectation
$Z(M)$
. Then there is a unique normal, faithful, tracial conditional expectation
![]() $E: M \to Z(M)$
, called the center-valued trace. Furthermore, for each
$E: M \to Z(M)$
, called the center-valued trace. Furthermore, for each
![]() $x \in M$
, there exists a sequence
$x \in M$
, there exists a sequence
![]() $x_i$
, where each
$x_i$
, where each
![]() $x_i$
is a finite convex combination of unitary conjugates of x, such that
$x_i$
is a finite convex combination of unitary conjugates of x, such that
![]() $x_i \to E[x]$
in
$x_i \to E[x]$
in
![]() ${\lVert {\cdot }\rVert }_\infty $
.
${\lVert {\cdot }\rVert }_\infty $
.
Now the center of the ultrafiber can be evaluated as follows.
Proposition 2.8. Let M be a finite von Neumann algebra,
![]() $N \subseteq Z(M)$
be a subalgebra of its center,
$N \subseteq Z(M)$
be a subalgebra of its center,
![]() $E: M \to N$
be a normal, tracial, faithful conditional expectation, and
$E: M \to N$
be a normal, tracial, faithful conditional expectation, and
![]() $\mathcal {U}$
be a character on N. Let
$\mathcal {U}$
be a character on N. Let
![]() $\pi _{E,\mathcal {U}}: M \to M^{/E,\mathcal {U}}$
be the canonical projection map. Then
$\pi _{E,\mathcal {U}}: M \to M^{/E,\mathcal {U}}$
be the canonical projection map. Then
In particular, if
![]() $N = Z(M)$
and E is the center-valued trace, then
$N = Z(M)$
and E is the center-valued trace, then
![]() $M^{/E, \mathcal {U}}$
is a factor.
$M^{/E, \mathcal {U}}$
is a factor.
Proof. First, we show that
![]() $Z(M^{/E,\mathcal {U}}) = \pi _{E,\mathcal {U}}(Z(M))$
. It is immediate that
$Z(M^{/E,\mathcal {U}}) = \pi _{E,\mathcal {U}}(Z(M))$
. It is immediate that
![]() $\pi _{E,\mathcal {U}}(Z(M)) \subseteq Z(M^{/E,\mathcal {U}})$
since
$\pi _{E,\mathcal {U}}(Z(M)) \subseteq Z(M^{/E,\mathcal {U}})$
since
![]() $\pi _{E,\mathcal {U}}$
is a
$\pi _{E,\mathcal {U}}$
is a
![]() $*$
-homomorphism. Conversely, suppose that
$*$
-homomorphism. Conversely, suppose that
![]() $x \in Z(M^{/E,\mathcal {U}})$
, and fix
$x \in Z(M^{/E,\mathcal {U}})$
, and fix ![]() with
with ![]() . Let
. Let
![]() $E_0: M \to Z(M)$
be the center-valued trace. By the generalized Dixmier averaging theorem, there is a sequence
$E_0: M \to Z(M)$
be the center-valued trace. By the generalized Dixmier averaging theorem, there is a sequence
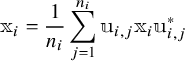
of convex combinations of unitary conjugates of ![]() such that
such that ![]() in norm. Since
in norm. Since ![]() and
and ![]() , we see that
, we see that ![]() . Hence,
. Hence, ![]() , and so
, and so ![]() , which implies that
, which implies that
![]() $x \in \pi _{E,\mathcal {U}}(Z(M))$
as desired.
$x \in \pi _{E,\mathcal {U}}(Z(M))$
as desired.
Next, we give an isomorphism
![]() $\pi _{E,\mathcal {U}}(Z(M)) \cong Z(M)^{/E|_{Z(M)},\mathcal {U}}$
. First, note that
$\pi _{E,\mathcal {U}}(Z(M)) \cong Z(M)^{/E|_{Z(M)},\mathcal {U}}$
. First, note that
![]() $E|_{Z(M)}$
is a faithful normal conditional expectation from
$E|_{Z(M)}$
is a faithful normal conditional expectation from
![]() $Z(M)$
onto N, and so
$Z(M)$
onto N, and so
![]() $Z(M)^{/E|_{Z(M)},\mathcal {U}}$
is well defined. Two elements
$Z(M)^{/E|_{Z(M)},\mathcal {U}}$
is well defined. Two elements ![]() and
and ![]() in
in
![]() $Z(M)$
represent the same element of
$Z(M)$
represent the same element of
![]() $Z(M)^{/E|_{Z(M)},\mathcal {U}}$
if and only if
$Z(M)^{/E|_{Z(M)},\mathcal {U}}$
if and only if ![]() if and only if
if and only if ![]() and
and ![]() represent the same element in
represent the same element in
![]() $M^{/E,\mathcal {U}}$
. Hence, there is a well-defined injective
$M^{/E,\mathcal {U}}$
. Hence, there is a well-defined injective
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $Z(M)^{/E|_{Z(M)},\mathcal {U}} \to M^{/E,\mathcal {U}}$
, and its image is clearly equal to
$Z(M)^{/E|_{Z(M)},\mathcal {U}} \to M^{/E,\mathcal {U}}$
, and its image is clearly equal to
![]() $\pi _{E,\mathcal {U}}(Z(M))$
.
$\pi _{E,\mathcal {U}}(Z(M))$
.
In the case that
![]() $N = Z(M)$
, then
$N = Z(M)$
, then
![]() $Z(M)^{/E|_{Z(M)},\mathcal {U}} \cong \mathbb {C}$
since
$Z(M)^{/E|_{Z(M)},\mathcal {U}} \cong \mathbb {C}$
since
![]() $\mathcal {U}$
is a pure state on
$\mathcal {U}$
is a pure state on
![]() $Z(M)$
, and hence
$Z(M)$
, and hence
![]() $Z(M^{/E,\mathcal {U}}) \cong \mathbb {C}$
, so
$Z(M^{/E,\mathcal {U}}) \cong \mathbb {C}$
, so
![]() $M^{/E,\mathcal {U}}$
is a factor.
$M^{/E,\mathcal {U}}$
is a factor.
2.3 Proof of Corollary B from Proposition C
Now we are ready to give a short proof of Corollary B showing that if M and N are
![]() $\mathrm {II}_1$
factors and
$\mathrm {II}_1$
factors and
![]() $M \otimes L^\infty [0,1] \equiv N \otimes L^\infty [0,1]$
, then
$M \otimes L^\infty [0,1] \equiv N \otimes L^\infty [0,1]$
, then
![]() $M \equiv N$
. We state it here in a slightly more general form. The only ingredients needed are the Keisler–Shelah theorm for ordinary ultraproducts, the generalized ultraproduct construction and Proposition C which shows that M is elementarily equivalent to each of its generalized ultrapowers, which we will be proven later in Proposition 3.20.
$M \equiv N$
. We state it here in a slightly more general form. The only ingredients needed are the Keisler–Shelah theorm for ordinary ultraproducts, the generalized ultraproduct construction and Proposition C which shows that M is elementarily equivalent to each of its generalized ultrapowers, which we will be proven later in Proposition 3.20.
Proposition 2.9. Let M and N be
![]() $\mathrm {II}_1$
factors. Let A and B be diffuse commutative tracial von Neumann algebras. If
$\mathrm {II}_1$
factors. Let A and B be diffuse commutative tracial von Neumann algebras. If
![]() $M \overline {\otimes } A \equiv N \overline {\otimes } B$
, then
$M \overline {\otimes } A \equiv N \overline {\otimes } B$
, then
![]() $M \equiv N$
.
$M \equiv N$
.
Proof of Proposition 2.9 / Corollary B.
Since
![]() $A \mathbin {\overline {\otimes }} M \equiv B \mathbin {\overline {\otimes }} N$
, the Keisler–Shelah theorem implies that
$A \mathbin {\overline {\otimes }} M \equiv B \mathbin {\overline {\otimes }} N$
, the Keisler–Shelah theorem implies that
![]() $A \mathbin {\overline {\otimes }} M \equiv B \mathbin {\overline {\otimes }} N$
admit isomorphic ultrapowers. In particular, there exists a character
$A \mathbin {\overline {\otimes }} M \equiv B \mathbin {\overline {\otimes }} N$
admit isomorphic ultrapowers. In particular, there exists a character
![]() $\mathcal {U}$
on some abelian von Neumann algebra C s.t. there exists a trace-preserving isomorphism
$\mathcal {U}$
on some abelian von Neumann algebra C s.t. there exists a trace-preserving isomorphism
![]() $\pi : (A \mathbin {\overline {\otimes }} M)^{\mathcal {U}} \to (B \mathbin {\overline {\otimes }} N)^{\mathcal {U}}$
. Since M is a factor,
$\pi : (A \mathbin {\overline {\otimes }} M)^{\mathcal {U}} \to (B \mathbin {\overline {\otimes }} N)^{\mathcal {U}}$
. Since M is a factor,
![]() $Z(A \mathbin {\overline {\otimes }} M) = A$
, so by Proposition 2.8, the center of
$Z(A \mathbin {\overline {\otimes }} M) = A$
, so by Proposition 2.8, the center of
![]() $(A \mathbin {\overline {\otimes }} M)^{\mathcal {U}}$
is
$(A \mathbin {\overline {\otimes }} M)^{\mathcal {U}}$
is
![]() $A^{\mathcal {U}}$
. Similarly,
$A^{\mathcal {U}}$
. Similarly,
![]() $Z((B \mathbin {\overline {\otimes }} N)^{\mathcal {U}}) = B^{\mathcal {U}}$
. Hence,
$Z((B \mathbin {\overline {\otimes }} N)^{\mathcal {U}}) = B^{\mathcal {U}}$
. Hence,
![]() $\pi $
must restrict to a trace-preserving isomorphism between
$\pi $
must restrict to a trace-preserving isomorphism between
![]() $A^{\mathcal {U}}$
and
$A^{\mathcal {U}}$
and
![]() $B^{\mathcal {U}}$
. We may thus identify these algebras via
$B^{\mathcal {U}}$
. We may thus identify these algebras via
![]() $\pi $
.
$\pi $
.
Let
![]() $\mathcal {V}$
be any character on
$\mathcal {V}$
be any character on
![]() $A^{\mathcal {U}} = B^{\mathcal {U}}$
. Let E denote the center-valued trace of
$A^{\mathcal {U}} = B^{\mathcal {U}}$
. Let E denote the center-valued trace of
![]() $(A \mathbin {\overline {\otimes }} M)^{\mathcal {U}}$
as well as the center-valued trace of
$(A \mathbin {\overline {\otimes }} M)^{\mathcal {U}}$
as well as the center-valued trace of
![]() $(B \mathbin {\overline {\otimes }} N)^{\mathcal {U}}$
. We again identify the two algebras via
$(B \mathbin {\overline {\otimes }} N)^{\mathcal {U}}$
. We again identify the two algebras via
![]() $\pi $
and note that the
$\pi $
and note that the
![]() $\pi $
must also preserve the center-valued trace. Hence, we must have
$\pi $
must also preserve the center-valued trace. Hence, we must have
Note that
![]() $(A \mathbin {\overline {\otimes }} M)^{\mathcal {U}}$
is, by definition, a quotient of
$(A \mathbin {\overline {\otimes }} M)^{\mathcal {U}}$
is, by definition, a quotient of
![]() $C \mathbin {\overline {\otimes }} A \mathbin {\overline {\otimes }} M$
. Let the natural quotient map be
$C \mathbin {\overline {\otimes }} A \mathbin {\overline {\otimes }} M$
. Let the natural quotient map be
![]() $q: C \mathbin {\overline {\otimes }} A \mathbin {\overline {\otimes }} M \to (A \mathbin {\overline {\otimes }} M)^{\mathcal {U}}$
. Then,
$q: C \mathbin {\overline {\otimes }} A \mathbin {\overline {\otimes }} M \to (A \mathbin {\overline {\otimes }} M)^{\mathcal {U}}$
. Then,
We also have
It follows from Dixmier averaging as in the proof of Proposition 2.8 that
![]() $E \circ q = q \circ (\mathrm {Id} \otimes \mathrm {Id} \otimes \tau )$
. Since q restricts to a *-homomorphism
$E \circ q = q \circ (\mathrm {Id} \otimes \mathrm {Id} \otimes \tau )$
. Since q restricts to a *-homomorphism
![]() $C \mathbin {\overline {\otimes }} A \to A^{\mathcal {U}}$
, we see that
$C \mathbin {\overline {\otimes }} A \to A^{\mathcal {U}}$
, we see that
![]() $\mathcal {V} \circ q|_{C \mathbin {\overline {\otimes }} A}$
is a character on
$\mathcal {V} \circ q|_{C \mathbin {\overline {\otimes }} A}$
is a character on
![]() $C \mathbin {\overline {\otimes }} A$
. Hence,
$C \mathbin {\overline {\otimes }} A$
. Hence,
But this means
![]() $[(A \mathbin {\overline {\otimes }} M)^{\mathcal {U}}]^{/E, \mathcal {V}} = M^{\mathcal {V} \circ q}$
. Similarly,
$[(A \mathbin {\overline {\otimes }} M)^{\mathcal {U}}]^{/E, \mathcal {V}} = M^{\mathcal {V} \circ q}$
. Similarly,
![]() $[(B \mathbin {\overline {\otimes }} N)^{\mathcal {U}}]^{/E, \mathcal {V}}$
is a generalized ultrapower of N as well. Hence, M and N admit generalized ultrapowers that are isomorphic, and so
$[(B \mathbin {\overline {\otimes }} N)^{\mathcal {U}}]^{/E, \mathcal {V}}$
is a generalized ultrapower of N as well. Hence, M and N admit generalized ultrapowers that are isomorphic, and so
![]() $M \equiv N$
by Proposition C and the transitivity of elementary equivalence.
$M \equiv N$
by Proposition C and the transitivity of elementary equivalence.
3 Łoś’s theorem and elementary equivalence
3.1 Model theory background
To state and prove Łoś’s theorem in this section, we must first review some background from continuous model theory, including formulas, sentences and theories. As this section is largely for readers who are less familiar with model theory, we aim to give minimal working definitions of the concepts for tracial von Neumann algebras, rather than completely general and proper definitions. Unlike [Reference Ben Yaacov, Berenstein, Henson, Usvyatsov, Chatzidakis, Macpherson, Pillay and WilkieBBHU08], we do not aim to describe metric structures in general. Unlike [Reference Farah, Hart and ShermanFHS14a], we do not need to prove that tracial von Neumann algebras fit into the general framework of metric structures (i.e., that they can be axiomatized in some metric language) since this has already been done. Hence, we can avoid the technicalities of setting up the sorts or domains, and defining the addition, multiplication, and adjoint functions on these domains, that were used in [Reference Farah, Hart and ShermanFHS14a], by simply working on the unit ball. We remark that another axiomatization was given in [Reference Ben Yaacov, Ibarlucía and TsankovBIT24, Proposition 29.4] which works entirely on the unit ball and uses a universal
![]() $\mathrm {C}^*$
-algebra to define the function symbols. For further background on continuous model theory, especially for tracial von Neumann algebras, refer to [Reference Ben Yaacov, Berenstein, Henson, Usvyatsov, Chatzidakis, Macpherson, Pillay and WilkieBBHU08, Reference Farah, Hart and ShermanFHS14a, Reference Goldbring and IovinoGol23, Reference JekelJek23, Reference Hart and GoldbringHar23, Reference Goldbring, Hart and GoldbringGH23].
$\mathrm {C}^*$
-algebra to define the function symbols. For further background on continuous model theory, especially for tracial von Neumann algebras, refer to [Reference Ben Yaacov, Berenstein, Henson, Usvyatsov, Chatzidakis, Macpherson, Pillay and WilkieBBHU08, Reference Farah, Hart and ShermanFHS14a, Reference Goldbring and IovinoGol23, Reference JekelJek23, Reference Hart and GoldbringHar23, Reference Goldbring, Hart and GoldbringGH23].
Formulas in continuous logic are analogous to formulas in classical first-order logic – that is, expressions composed of basic statements by applying quantifiers (for all, there exists) and connectives (and, or, not, if/then, etc.). The basic statements depend on the category of objects that we are working with. The signature gives the operations and relations for the category, which are used to generate the corresponding language, the set of formulas. For instance, for fields, there are binary operations
![]() $+$
and
$+$
and
![]() $\times $
,
$\times $
,
![]() $0$
-ary operations (constant symbols)
$0$
-ary operations (constant symbols)
![]() $0$
and
$0$
and
![]() $1$
, and the relation
$1$
, and the relation
![]() $=$
, so a basic statement in variables x and y might be
$=$
, so a basic statement in variables x and y might be
![]() $x \cdot (y + z) = x + y$
. Then first-order statements for fields are obtained using quantifiers and connectives. In continuous model theory, we make the following changes:
$x \cdot (y + z) = x + y$
. Then first-order statements for fields are obtained using quantifiers and connectives. In continuous model theory, we make the following changes:
-
• Instead of true/false-valued predicates, we consider real-valued predicates.
-
• Instead of logical operations that input and output true/false values, the connectives are continuous functions
 $\mathbb {R}^k \to \mathbb {R}$
.
$\mathbb {R}^k \to \mathbb {R}$
. -
• Instead of
 $\forall $
and
$\forall $
and
 $\exists $
, the quantifiers are
$\exists $
, the quantifiers are
 $\sup $
and
$\sup $
and
 $\inf $
.
$\inf $
.
Definition 3.1. Let X be an infinite set. Formulae in the language of tracial von Neumann algebras with variables from the set X are all formal expressions constructed recursively as follows:
-
1. A basic formula is an expression of the form
 $\varphi = \operatorname {\mathrm {Re}}\operatorname {\mathrm {tr}}(p(x_1,\dots ,x_n))$
and
$\varphi = \operatorname {\mathrm {Re}}\operatorname {\mathrm {tr}}(p(x_1,\dots ,x_n))$
and
 $\varphi = \operatorname {\mathrm {Im}}\operatorname {\mathrm {tr}}(p(x_1,\dots ,x_n))$
are formulae, for any
$\varphi = \operatorname {\mathrm {Im}}\operatorname {\mathrm {tr}}(p(x_1,\dots ,x_n))$
are formulae, for any
 $*$
-polynomial p in variables
$*$
-polynomial p in variables
 $x_1,\dots ,x_n$
from X.
$x_1,\dots ,x_n$
from X. -
2. If
 $\varphi _i$
is a formula for all
$\varphi _i$
is a formula for all
 $1 \leq i \leq n$
and if
$1 \leq i \leq n$
and if
 $f: \mathbb {R}^k \to \mathbb {R}$
is continuous, then
$f: \mathbb {R}^k \to \mathbb {R}$
is continuous, then
 $\varphi = f(\varphi _1, \cdots , \varphi _k)$
is a formula.
$\varphi = f(\varphi _1, \cdots , \varphi _k)$
is a formula. -
3. If
 $\varphi $
is a formula and
$\varphi $
is a formula and
 $y \in X$
, then
$y \in X$
, then
 $\sup _y \varphi $
and
$\sup _y \varphi $
and
 $\inf _y \varphi $
are formulas.
$\inf _y \varphi $
are formulas.
Example 3.2. An example of a formula would be
When we evaluate this formula in a particular tracial von Neumann algebra M, the suprema and infima will be taken over the unit ball.
In a formula, each occurrence of a variable is either free or bound to a quantifier
![]() $\sup $
or
$\sup $
or
![]() $\inf $
. In basic formulas, all occurrences of variables are free, and when applying connectives, the freeness or boundness of each occurrence of a variable is preserved. When applying
$\inf $
. In basic formulas, all occurrences of variables are free, and when applying connectives, the freeness or boundness of each occurrence of a variable is preserved. When applying
![]() $\sup _y$
or
$\sup _y$
or
![]() $\inf _y$
, all free occurrences of the variable y inside the formula become bound to the new quantifier, and the freeness or boundness of the others remains unchanged. It is possible that some variable occurs multiple times in a formula and one occurrence is bound to a quantifier while another occurrence is not – for instance, if we wrote
$\inf _y$
, all free occurrences of the variable y inside the formula become bound to the new quantifier, and the freeness or boundness of the others remains unchanged. It is possible that some variable occurs multiple times in a formula and one occurrence is bound to a quantifier while another occurrence is not – for instance, if we wrote
![]() $\tau (x) - \sup _x \tau (xy)$
. However, in this case, we could rename the bound occurrence of x as z and use the equivalent expression
$\tau (x) - \sup _x \tau (xy)$
. However, in this case, we could rename the bound occurrence of x as z and use the equivalent expression
![]() $\tau (x) - \sup _z \tau (zy)$
. Thus, we will always assume that our formulas have a distinct variable name associated to each quantifier. Moreover, we will usually list the free variables as arguments for each formula, so that
$\tau (x) - \sup _z \tau (zy)$
. Thus, we will always assume that our formulas have a distinct variable name associated to each quantifier. Moreover, we will usually list the free variables as arguments for each formula, so that
will usually denote a formula whose free variables are
![]() $\{x_1,\dots ,x_n\}$
, and more generally a formula whose free variables are a subset of
$\{x_1,\dots ,x_n\}$
, and more generally a formula whose free variables are a subset of
![]() $\{x_1,\dots ,x_n\}$
.
$\{x_1,\dots ,x_n\}$
.
Just like non-commutative polynomials, formulas for tracial von Neumann algebra are formal expressions, but they can be evaluated on particular elements in a particular von Neumann algebra M by plugging in operators into the non-commutative polynomials and evaluating the suprema and infima over the unit ball of M. (In fact, one can define formulas with quantifiers
![]() $\sup _{x \in (M)_r}$
and
$\sup _{x \in (M)_r}$
and
![]() $\inf _{x \in (M)_r}$
for each
$\inf _{x \in (M)_r}$
for each
![]() $r> 0$
; but by a change of variables
$r> 0$
; but by a change of variables
![]() $x \mapsto x/r$
, this can be transformed into a supremum or infimum over the unit ball, hence here we only consider the unit ball.)
$x \mapsto x/r$
, this can be transformed into a supremum or infimum over the unit ball, hence here we only consider the unit ball.)
Definition 3.3 (Interpretation of formulas).
Let
![]() $\varphi (x_1,\dots ,x_n)$
be a formula for tracial von Neumann algebras. Let
$\varphi (x_1,\dots ,x_n)$
be a formula for tracial von Neumann algebras. Let
![]() $\mathcal {M} = (M,\tau )$
be a tracial von Neumann algebra. Then the interpretation of
$\mathcal {M} = (M,\tau )$
be a tracial von Neumann algebra. Then the interpretation of
![]() $\varphi $
in
$\varphi $
in
![]() $\mathcal {M}$
is the mapping
$\mathcal {M}$
is the mapping
![]() $\phi ^{\mathcal {M}}: M^n \to \mathbb {R}$
described as follows:
$\phi ^{\mathcal {M}}: M^n \to \mathbb {R}$
described as follows:
-
• If
 $\varphi (x_1,\dots ,x_n) = \operatorname {\mathrm {Re}} \operatorname {\mathrm {tr}}(p(x_1,\dots ,x_n))$
is a basic formula, then
$\varphi (x_1,\dots ,x_n) = \operatorname {\mathrm {Re}} \operatorname {\mathrm {tr}}(p(x_1,\dots ,x_n))$
is a basic formula, then
 $\varphi ^{\mathcal {M}}(x_1,\dots ,x_n) = \tau (p(x_1,\dots ,x_n))$
; that is, we evaluate the polynomial on the given
$\varphi ^{\mathcal {M}}(x_1,\dots ,x_n) = \tau (p(x_1,\dots ,x_n))$
; that is, we evaluate the polynomial on the given
 $x_1$
, …,
$x_1$
, …,
 $x_n \in M$
.
$x_n \in M$
. -
• If
 $\varphi = f(\varphi _1,\dots ,\varphi _k)$
for a connective
$\varphi = f(\varphi _1,\dots ,\varphi _k)$
for a connective
 $f: \mathbb {R}^k \to \mathbb {R}$
, where
$f: \mathbb {R}^k \to \mathbb {R}$
, where
 $\varphi _i = \varphi _i(x_1,\dots ,x_n)$
, then
$\varphi _i = \varphi _i(x_1,\dots ,x_n)$
, then  $$\begin{align*}\varphi^{\mathcal{M}}(x_1,\dots,x_n) = f(\varphi^{\mathcal{M}}(x_1,\dots,x_n),\dots,\varphi_k^{\mathcal{M}}(x_1,\dots,x_n)). \end{align*}$$
$$\begin{align*}\varphi^{\mathcal{M}}(x_1,\dots,x_n) = f(\varphi^{\mathcal{M}}(x_1,\dots,x_n),\dots,\varphi_k^{\mathcal{M}}(x_1,\dots,x_n)). \end{align*}$$
-
• If
 $\varphi (x_1,\dots ,x_n) = \sup _y \psi (x_1,\dots ,x_n,y)$
, then
$\varphi (x_1,\dots ,x_n) = \sup _y \psi (x_1,\dots ,x_n,y)$
, then  $$\begin{align*}\varphi^{\mathcal{M}}(x_1,\dots,x_n) = \sup_{y \in M_1} \psi^{\mathcal{M}}(x_1,\dots,x_n,y). \end{align*}$$
$$\begin{align*}\varphi^{\mathcal{M}}(x_1,\dots,x_n) = \sup_{y \in M_1} \psi^{\mathcal{M}}(x_1,\dots,x_n,y). \end{align*}$$
Example 3.4. Consider the formula
![]() $\varphi (x) = \sup _y \operatorname {\mathrm {tr}}((xy - yx)^*(xy - yx))^{1/2}$
. Then
$\varphi (x) = \sup _y \operatorname {\mathrm {tr}}((xy - yx)^*(xy - yx))^{1/2}$
. Then
Then
![]() $\varphi ^{\mathcal {M}}(x) = 0$
if and only if
$\varphi ^{\mathcal {M}}(x) = 0$
if and only if
![]() $x \in Z(M)$
.
$x \in Z(M)$
.
A formula in
![]() $(x_1,\dots ,x_n)$
expresses certain information about
$(x_1,\dots ,x_n)$
expresses certain information about
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $x_1$
, …,
$x_1$
, …,
![]() $x_n$
. If there are no free variables, the formula is called a sentence, and its interpretation in
$x_n$
. If there are no free variables, the formula is called a sentence, and its interpretation in
![]() $\mathcal {M}$
expresses certain first-order information about
$\mathcal {M}$
expresses certain first-order information about
![]() $\mathcal {M}$
itself. This information is what we refer to as the theory of
$\mathcal {M}$
itself. This information is what we refer to as the theory of
![]() $\mathcal {M}$
. Note that in discrete logic, the theory of some object M is the set of all sentences in the language that are true for M. Since our sentences take real values, we describe the theory of M as the functional that assigns a real value to each sentence. More precisely, we use the following definition.
$\mathcal {M}$
. Note that in discrete logic, the theory of some object M is the set of all sentences in the language that are true for M. Since our sentences take real values, we describe the theory of M as the functional that assigns a real value to each sentence. More precisely, we use the following definition.
Definition 3.5.
-
• A sentence is a formula with no free variables.
-
• Denoting the set of sentences by
 $\mathcal {S}$
, the theory of
$\mathcal {S}$
, the theory of
 $\mathcal {M}$
is the map
$\mathcal {M}$
is the map
 $\operatorname {Th}(\mathcal {M}): \mathcal {S} \to \mathbb {R}, \varphi \mapsto \varphi ^{\mathcal {M}}$
.
$\operatorname {Th}(\mathcal {M}): \mathcal {S} \to \mathbb {R}, \varphi \mapsto \varphi ^{\mathcal {M}}$
. -
• Two tracial von Neumann algebras
 $\mathcal {M}$
and
$\mathcal {M}$
and
 $\mathcal {N}$
are elementarily equivalent, written
$\mathcal {N}$
are elementarily equivalent, written
 $\mathcal {M} \equiv \mathcal {N}$
, if
$\mathcal {M} \equiv \mathcal {N}$
, if
 $\operatorname {Th}(\mathcal {M}) = \operatorname {Th}(\mathcal {N})$
, or in other words,
$\operatorname {Th}(\mathcal {M}) = \operatorname {Th}(\mathcal {N})$
, or in other words,
 $\varphi ^{\mathcal {M}} = \varphi ^{\mathcal {N}}$
for all sentences
$\varphi ^{\mathcal {M}} = \varphi ^{\mathcal {N}}$
for all sentences
 $\varphi $
.
$\varphi $
. -
• An embedding
 $\iota : M \to N$
of tracial von Neumann algebras is said to be elementary if
$\iota : M \to N$
of tracial von Neumann algebras is said to be elementary if
 $\varphi ^N(\iota (x_1),\dots ,\iota (x_n)) = \varphi ^M(x_1,\dots ,x_n)$
for all formulas
$\varphi ^N(\iota (x_1),\dots ,\iota (x_n)) = \varphi ^M(x_1,\dots ,x_n)$
for all formulas
 $\varphi $
.
$\varphi $
.
In order to better describe the topology for the space of complete theories and to make the above definitions amenable to functional analysis, we will first describe how the set of formulas and the set of sentences in particular can be completed to a real
![]() $\mathrm {C}^*$
-algebra, and the theory of
$\mathrm {C}^*$
-algebra, and the theory of
![]() $\mathcal {M}$
corresponds to a character on this
$\mathcal {M}$
corresponds to a character on this
![]() $\mathrm {C}^*$
-algebra.
$\mathrm {C}^*$
-algebra.
Let
![]() $\mathcal {F}_X$
denote the set of formulas with free variables contained in the set X. We observe that since addition and multiplication are continuous functions
$\mathcal {F}_X$
denote the set of formulas with free variables contained in the set X. We observe that since addition and multiplication are continuous functions
![]() $\mathbb {R}^2 \to \mathbb {R}$
, they can be applied as connectives to formulas. This implies that
$\mathbb {R}^2 \to \mathbb {R}$
, they can be applied as connectives to formulas. This implies that
![]() $\mathcal {F}_X$
is an algebra over
$\mathcal {F}_X$
is an algebra over
![]() $\mathbb {R}$
. In order to obtain a
$\mathbb {R}$
. In order to obtain a
![]() $\mathrm {C}^*$
-algebra, we need a (semi)norm.
$\mathrm {C}^*$
-algebra, we need a (semi)norm.
Definition 3.6. For a formula
![]() $\varphi (x_1,\dots ,x_n)$
for tracial von Neumann algebras, the uniform seminorm is given by
$\varphi (x_1,\dots ,x_n)$
for tracial von Neumann algebras, the uniform seminorm is given by
where we take the supremum over all tracial von Neumann algebras
![]() $(M,\tau )$
as well as
$(M,\tau )$
as well as
![]() $x_1$
, …,
$x_1$
, …,
![]() $x_n$
.
$x_n$
.
It is easy to show by induction that
![]() ${\lVert {\varphi }\rVert }_u < \infty $
for every formula
${\lVert {\varphi }\rVert }_u < \infty $
for every formula
![]() $\varphi $
(this is a special case of Lemma 3.12 below). One starts with the basic formulas
$\varphi $
(this is a special case of Lemma 3.12 below). One starts with the basic formulas
![]() $\operatorname {\mathrm {tr}}(p(x_1,\dots ,x_n))$
and then shows that boundedness is preserved when applying connectives and quantifiers. Similarly, it is an exercise to check that for formulas
$\operatorname {\mathrm {tr}}(p(x_1,\dots ,x_n))$
and then shows that boundedness is preserved when applying connectives and quantifiers. Similarly, it is an exercise to check that for formulas
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
and
$\psi $
and
![]() $c \in \mathbb {R}$
,
$c \in \mathbb {R}$
,
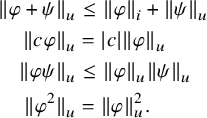 $$ \begin{align*} {\lVert{\varphi + \psi} \rVert}_u &\leq {\lVert {\varphi} \rVert}_i + {\lVert {\psi} \rVert}_u \\ {\lVert {c \varphi}\rVert}_u &= |c| {\lVert {\varphi} \rVert}_u \\ {\lVert {\varphi \psi} \rVert}_u & \leq {\lVert {\varphi} \rVert}_u {\lVert {\psi}\rVert}_u \\ {\lVert {\varphi^2} \rVert}_u &= {\lVert {\varphi}\rVert}_u^2. \end{align*} $$
$$ \begin{align*} {\lVert{\varphi + \psi} \rVert}_u &\leq {\lVert {\varphi} \rVert}_i + {\lVert {\psi} \rVert}_u \\ {\lVert {c \varphi}\rVert}_u &= |c| {\lVert {\varphi} \rVert}_u \\ {\lVert {\varphi \psi} \rVert}_u & \leq {\lVert {\varphi} \rVert}_u {\lVert {\psi}\rVert}_u \\ {\lVert {\varphi^2} \rVert}_u &= {\lVert {\varphi}\rVert}_u^2. \end{align*} $$
Definition 3.7. Fix a countable index set I (for instance,
![]() $I = \mathbb {N}$
). Let
$I = \mathbb {N}$
). Let
![]() $\mathcal {F}_X$
be the set of formulas
$\mathcal {F}_X$
be the set of formulas
![]() $\varphi $
with variables in
$\varphi $
with variables in
![]() $X \sqcup I$
such that the free variables of
$X \sqcup I$
such that the free variables of
![]() $\varphi $
are contained in X and the bound variables of
$\varphi $
are contained in X and the bound variables of
![]() $\varphi $
are contained in I. Thus, for instance,
$\varphi $
are contained in I. Thus, for instance,
![]() $\mathcal {F}_{\varnothing }$
is the set of sentences with variables in I. Then let
$\mathcal {F}_{\varnothing }$
is the set of sentences with variables in I. Then let
![]() $\mathcal {P}_X$
be the separation-completion of
$\mathcal {P}_X$
be the separation-completion of
![]() $\mathcal {F}_X$
with respect to the uniform norm. The elements of
$\mathcal {F}_X$
with respect to the uniform norm. The elements of
![]() $\mathcal {P}_X$
are called definable predicates with free variables in X.
$\mathcal {P}_X$
are called definable predicates with free variables in X.
Lemma 3.8.
![]() $\mathcal {P}_X$
is a commutative real
$\mathcal {P}_X$
is a commutative real
![]() $\mathrm {C}^*$
-algebra. Moreover, for each tracial von Neumann algebra
$\mathrm {C}^*$
-algebra. Moreover, for each tracial von Neumann algebra
![]() $\mathcal {M}$
, there is a unique
$\mathcal {M}$
, there is a unique
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\operatorname {\mathrm {Th}}(\mathcal {M}): \mathcal {P}_{\varnothing } \to \mathbb {R}$
such that
$\operatorname {\mathrm {Th}}(\mathcal {M}): \mathcal {P}_{\varnothing } \to \mathbb {R}$
such that
![]() $\operatorname {\mathrm {Th}}(\mathcal {M})(\varphi ) = \varphi ^{\mathcal {M}}$
for sentences
$\operatorname {\mathrm {Th}}(\mathcal {M})(\varphi ) = \varphi ^{\mathcal {M}}$
for sentences
![]() $\varphi $
.
$\varphi $
.
The fact that
![]() $\mathcal {P}_X$
is a commutative real
$\mathcal {P}_X$
is a commutative real
![]() $\mathrm {C}^*$
-algebra follows from the inqualities mentioned above. The fact that evaluation
$\mathrm {C}^*$
-algebra follows from the inqualities mentioned above. The fact that evaluation
![]() $\varphi \mapsto \varphi ^{\mathcal {M}}$
gives a
$\varphi \mapsto \varphi ^{\mathcal {M}}$
gives a
![]() $*$
-homomorphism on the algebra of sentences is immediate from the definition of the interpretation, specifically how it behaves on connectives. Since clearly
$*$
-homomorphism on the algebra of sentences is immediate from the definition of the interpretation, specifically how it behaves on connectives. Since clearly
![]() $|\varphi ^{\mathcal {M}}| \leq {\lVert {\varphi } \rVert }_u$
, this mapping extends to a
$|\varphi ^{\mathcal {M}}| \leq {\lVert {\varphi } \rVert }_u$
, this mapping extends to a
![]() $*$
-homomorphism on
$*$
-homomorphism on
![]() $\mathcal {P}_{\varnothing }$
. While above we defined
$\mathcal {P}_{\varnothing }$
. While above we defined
![]() $\operatorname {Th}(\mathcal {M})$
as a linear functional on
$\operatorname {Th}(\mathcal {M})$
as a linear functional on
![]() $\mathcal {S}$
, it also defines a linear functional on
$\mathcal {S}$
, it also defines a linear functional on
![]() $\mathcal {P}_{\varnothing }$
, and we will denote this functional also by
$\mathcal {P}_{\varnothing }$
, and we will denote this functional also by
![]() $\operatorname {Th}(\mathcal {M})$
since there is little risk of confusion.
$\operatorname {Th}(\mathcal {M})$
since there is little risk of confusion.
Proposition 3.9.
-
1. If
 $\mathcal {M}$
is a tracial von Neumann algebra, then
$\mathcal {M}$
is a tracial von Neumann algebra, then
 $\operatorname {Th}(\mathcal {M})$
is a character on
$\operatorname {Th}(\mathcal {M})$
is a character on
 $\mathcal {P}_{\varnothing }$
.
$\mathcal {P}_{\varnothing }$
. -
2. Conversely, every character on
 $\mathcal {P}_{\varnothing }$
is equal to
$\mathcal {P}_{\varnothing }$
is equal to
 $\operatorname {Th}(\mathcal {M})$
for some
$\operatorname {Th}(\mathcal {M})$
for some
 $\mathcal {M}$
.
$\mathcal {M}$
. -
3. If
 $\mathcal {M} = \prod _{\mathcal {U}} \mathcal {M}_i$
for some ultrafilter
$\mathcal {M} = \prod _{\mathcal {U}} \mathcal {M}_i$
for some ultrafilter
 $\mathcal {U}$
on an index set I, then
$\mathcal {U}$
on an index set I, then
 $\operatorname {Th}(\mathcal {M}) = \lim _{\mathcal {U}} \operatorname {Th}(\mathcal {M}_i)$
with respect to the weak-
$\operatorname {Th}(\mathcal {M}) = \lim _{\mathcal {U}} \operatorname {Th}(\mathcal {M}_i)$
with respect to the weak-
 $*$
topology.
$*$
topology.
This proposition is well-known in continuous model theory, so we merely sketch the proof in an expository way. We already explained why (1) is true. For point (3), we use Łoś’s theorem, which shows that for all sentences
![]() $\varphi $
,
$\varphi $
,
Because sentences give a
![]() ${\lVert {\cdot }\rVert }_u$
-dense subset of
${\lVert {\cdot }\rVert }_u$
-dense subset of
![]() $\mathcal {P}_{\varnothing }$
by construction, it follows that
$\mathcal {P}_{\varnothing }$
by construction, it follows that
![]() $\varphi ^{\mathcal {M}} = \lim _{\mathcal {U}} \varphi ^{\mathcal {M}_i}$
for all
$\varphi ^{\mathcal {M}} = \lim _{\mathcal {U}} \varphi ^{\mathcal {M}_i}$
for all
![]() $\varphi \in \mathcal {P}_{\varnothing }$
, and thus,
$\varphi \in \mathcal {P}_{\varnothing }$
, and thus,
![]() $\operatorname {Th}(\mathcal {M}) = \lim _{\mathcal {U}} \operatorname {Th}(\mathcal {M}_i)$
in the weak-
$\operatorname {Th}(\mathcal {M}) = \lim _{\mathcal {U}} \operatorname {Th}(\mathcal {M}_i)$
in the weak-
![]() $*$
topology.
$*$
topology.
Finally, for (2), recall by Gelfand duality that
![]() $\mathcal {P}_{\varnothing } \cong C(\mathcal {X};\mathbb {R})$
, where
$\mathcal {P}_{\varnothing } \cong C(\mathcal {X};\mathbb {R})$
, where
![]() $\mathcal {X}$
is the space of characters on
$\mathcal {X}$
is the space of characters on
![]() $\mathcal {P}_{\varnothing }$
with the weak-
$\mathcal {P}_{\varnothing }$
with the weak-
![]() $*$
topology, which is a compact Hausdorff space. We also have by definition of the uniform norm that
$*$
topology, which is a compact Hausdorff space. We also have by definition of the uniform norm that
Generally, if
![]() $\mathcal {Y}$
is a subset of a compact Hausdorff space
$\mathcal {Y}$
is a subset of a compact Hausdorff space
![]() $\mathcal {X}$
and if
$\mathcal {X}$
and if
then
![]() $\mathcal {Y}$
must be dense in
$\mathcal {Y}$
must be dense in
![]() $\mathcal {X}$
. Therefore, in our case, the points in
$\mathcal {X}$
. Therefore, in our case, the points in
![]() $\mathcal {X}$
of the form
$\mathcal {X}$
of the form
![]() $\operatorname {Th}(\mathcal {M})$
must be dense in
$\operatorname {Th}(\mathcal {M})$
must be dense in
![]() $\mathcal {X}$
. However, by point (2), they also form a closed set, and hence, they are all of
$\mathcal {X}$
. However, by point (2), they also form a closed set, and hence, they are all of
![]() $\mathcal {X}$
, meaning that every character on
$\mathcal {X}$
, meaning that every character on
![]() $\mathcal {P}_{\varnothing }$
is of the form
$\mathcal {P}_{\varnothing }$
is of the form
![]() $\operatorname {Th}(\mathcal {M})$
.
$\operatorname {Th}(\mathcal {M})$
.
The statement above that points of the form
![]() $\operatorname {Th}(\mathcal {M})$
give a closed set is essentially a functional-analytic viewpoint on the compactness theorem in continuous logic [Reference Ben Yaacov, Berenstein, Henson, Usvyatsov, Chatzidakis, Macpherson, Pillay and WilkieBBHU08, Theorem 5.8]. We close by recalling a basic fact about separability.
$\operatorname {Th}(\mathcal {M})$
give a closed set is essentially a functional-analytic viewpoint on the compactness theorem in continuous logic [Reference Ben Yaacov, Berenstein, Henson, Usvyatsov, Chatzidakis, Macpherson, Pillay and WilkieBBHU08, Theorem 5.8]. We close by recalling a basic fact about separability.
Lemma 3.10. Let X be a countable set of variables. The real
![]() $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
![]() $\mathcal {P}_X$
of formulas in the language of tracial von Neumann algebras with free variables from X is separable. Hence, the unit ball in the dual with the weak-
$\mathcal {P}_X$
of formulas in the language of tracial von Neumann algebras with free variables from X is separable. Hence, the unit ball in the dual with the weak-
![]() $*$
topology is metrizable, and the space of characters with the weak-
$*$
topology is metrizable, and the space of characters with the weak-
![]() $*$
topology is metrizable. In particular, the space of theories of tracial von Neumann algebras is compact and metrizable.
$*$
topology is metrizable. In particular, the space of theories of tracial von Neumann algebras is compact and metrizable.
Proof. Consider rational polynomial formulas defined in a similar way to formulas, except that
-
• The basic formulas are
 $\operatorname {\mathrm {Re}} \operatorname {\mathrm {tr}}(p(x_1,\dots ,x_n))$
and
$\operatorname {\mathrm {Re}} \operatorname {\mathrm {tr}}(p(x_1,\dots ,x_n))$
and
 $\operatorname {\mathrm {Im}} \operatorname {\mathrm {tr}}(p(x_1,\dots ,x_n))$
where p is a non-commutative
$\operatorname {\mathrm {Im}} \operatorname {\mathrm {tr}}(p(x_1,\dots ,x_n))$
where p is a non-commutative
 $*$
-polynomial with coefficients in
$*$
-polynomial with coefficients in
 $\mathbb {Q}[i]$
.
$\mathbb {Q}[i]$
. -
• The connectives are polynomial functions
 $\mathbb {R}^k \to \mathbb {R}$
with rational coefficients.
$\mathbb {R}^k \to \mathbb {R}$
with rational coefficients.
The set of rational polynomial formulas is countable if the underlying set of variables is countable. The rational polynomials in variables
![]() $X \sqcup I$
are dense in the space of all formulas with respect to
$X \sqcup I$
are dense in the space of all formulas with respect to
![]() ${\lVert {\cdot }\rVert }_u$
. To show this, one proceeds by induction on the complexity of the formula. For the base case, it suffices to approximate the coefficients of each non-commutative
${\lVert {\cdot }\rVert }_u$
. To show this, one proceeds by induction on the complexity of the formula. For the base case, it suffices to approximate the coefficients of each non-commutative
![]() $*$
-polynomial by elements of
$*$
-polynomial by elements of
![]() $\mathbb {Q}[i]$
and estimate the uniform norm of the difference. For applying a connective f to formulas
$\mathbb {Q}[i]$
and estimate the uniform norm of the difference. For applying a connective f to formulas
![]() $\phi _1$
, …,
$\phi _1$
, …,
![]() $\phi _k$
, recall by the Stone-Weierstrass theorem that f can be uniformly approximated by a polynomial on
$\phi _k$
, recall by the Stone-Weierstrass theorem that f can be uniformly approximated by a polynomial on
![]() $[-{\lVert {\varphi _1}\rVert }_u,{\lVert {\varphi _1}\rVert }_u] \times \dots \times [-{\lVert {\varphi _k}\rVert }_u, {\lVert {\varphi _k}\rVert }_u]$
. The case of applying a quantifier is immediate since
$[-{\lVert {\varphi _1}\rVert }_u,{\lVert {\varphi _1}\rVert }_u] \times \dots \times [-{\lVert {\varphi _k}\rVert }_u, {\lVert {\varphi _k}\rVert }_u]$
. The case of applying a quantifier is immediate since
Hence, rational polynomial formulas are dense in the space of formulas. The same holds when we restrict to formulas where the free variables are in X and the bound variables are in I. This shows separability of
![]() $\mathcal {P}_X$
since this is the separation-completion of the space of such formulas. Since
$\mathcal {P}_X$
since this is the separation-completion of the space of such formulas. Since
![]() $\mathcal {P}_X$
is separable, the weak-
$\mathcal {P}_X$
is separable, the weak-
![]() $*$
topology on the unit ball in the dual space is metrizable, and hence also the space of states and the space of characters are metrizable.
$*$
topology on the unit ball in the dual space is metrizable, and hence also the space of states and the space of characters are metrizable.
3.2 Operator-valued interpretations of formulas
In order to understand the theory of a direct integral
![]() $M = \int _\Omega M_\omega \,d\mu (\omega )$
, we must study the fiberwise evaluation
$M = \int _\Omega M_\omega \,d\mu (\omega )$
, we must study the fiberwise evaluation
for a formula
![]() $\varphi $
on
$\varphi $
on
![]() $x_1$
, …,
$x_1$
, …,
![]() $x_n \in M$
, which (we will see) is a measurable function on
$x_n \in M$
, which (we will see) is a measurable function on
![]() $\Omega $
. More generally, since we are interested in non-separable von Neumann algebras such as ultraproducts, we want to replace
$\Omega $
. More generally, since we are interested in non-separable von Neumann algebras such as ultraproducts, we want to replace
![]() $L^\infty (\Omega )$
by a von Neumann subalgebra
$L^\infty (\Omega )$
by a von Neumann subalgebra
![]() $N \subseteq Z(M)$
, and still make sense of ‘fiberwise evaluation’ of a formula with respect to N. This leads to the definition of N-valued interpretations of formulas; we show below in Lemma 3.17 that this agrees with the fiberwise evaluation in the case that M is a direct integral.
$N \subseteq Z(M)$
, and still make sense of ‘fiberwise evaluation’ of a formula with respect to N. This leads to the definition of N-valued interpretations of formulas; we show below in Lemma 3.17 that this agrees with the fiberwise evaluation in the case that M is a direct integral.
For (2) below, we recall that multivariable continuous function calculus is well defined on any commutative
![]() $\mathrm {C}^*$
-algebra. For (3), we recall that every bounded family of self-adjoint elements in a commutative von Neumann algebra has a supremum.
$\mathrm {C}^*$
-algebra. For (3), we recall that every bounded family of self-adjoint elements in a commutative von Neumann algebra has a supremum.
Definition 3.11 (N-valued interpretation of formulas).
Let M be a finite von Neumann algebra,
![]() $N \subseteq Z(M)$
be a subalgebra of its center, and
$N \subseteq Z(M)$
be a subalgebra of its center, and
![]() $E: M \to N$
be a normal, faithful, tracial conditional expectation. For formulas
$E: M \to N$
be a normal, faithful, tracial conditional expectation. For formulas
![]() $\varphi $
in the language of tracial von Neumann algebras in variables from a set X, we define the N-valued interpretation
$\varphi $
in the language of tracial von Neumann algebras in variables from a set X, we define the N-valued interpretation
![]() $\varphi _E^M(x_1,\dots ,x_n)$
as follows, by induction on the complexity of
$\varphi _E^M(x_1,\dots ,x_n)$
as follows, by induction on the complexity of
![]() $\varphi $
. Here, we write
$\varphi $
. Here, we write
![]() $\overline {x} = (x_1,\dots ,x_n)$
.
$\overline {x} = (x_1,\dots ,x_n)$
.
-
1. If
 $\varphi = \operatorname {\mathrm {Re}}\tau (p(\overline {x}))$
for some *-polynomial p, then
$\varphi = \operatorname {\mathrm {Re}}\tau (p(\overline {x}))$
for some *-polynomial p, then
 $\varphi ^M_E(\overline {x}) = \operatorname {\mathrm {Re}}(E(p(\overline {x})))$
. Similarly, if
$\varphi ^M_E(\overline {x}) = \operatorname {\mathrm {Re}}(E(p(\overline {x})))$
. Similarly, if
 $\varphi = \operatorname {\mathrm {Im}}\tau (p(\overline {x}))$
for some *-polynomial p, then
$\varphi = \operatorname {\mathrm {Im}}\tau (p(\overline {x}))$
for some *-polynomial p, then
 $\varphi ^M_E(\overline {x}) = \operatorname {\mathrm {Im}}(E(p(\overline {x})))$
.
$\varphi ^M_E(\overline {x}) = \operatorname {\mathrm {Im}}(E(p(\overline {x})))$
. -
2. If
 $\varphi = f(\varphi _1, \cdots , \varphi _k)$
where
$\varphi = f(\varphi _1, \cdots , \varphi _k)$
where
 $f: \mathbb {R}^l \to \mathbb {R}$
is a connective (i.e., a continuous function), then
$f: \mathbb {R}^l \to \mathbb {R}$
is a connective (i.e., a continuous function), then
 $\varphi ^M_E(\overline {x}) = f((\varphi _1)^M_E(\overline {x}), \cdots , (\varphi _n)^M_E(\overline {x}))$
, where f is applied in the sense of continuous functional calculus.
$\varphi ^M_E(\overline {x}) = f((\varphi _1)^M_E(\overline {x}), \cdots , (\varphi _n)^M_E(\overline {x}))$
, where f is applied in the sense of continuous functional calculus. -
3. If
 $\varphi = \sup _y \phi (\overline {x}, y)$
, then
$\varphi = \sup _y \phi (\overline {x}, y)$
, then
 $\varphi ^M_E(\overline {x}) = \sup _{y \in (M)_1} \psi ^M_E(\overline {x}, y)$
. Similarly, if
$\varphi ^M_E(\overline {x}) = \sup _{y \in (M)_1} \psi ^M_E(\overline {x}, y)$
. Similarly, if
 $\varphi = \inf _y \phi (\overline {x}, y)$
, then
$\varphi = \inf _y \phi (\overline {x}, y)$
, then
 $\varphi ^M_E(\overline {x}) = \inf _{y \in (M)_1} \psi ^M_E(\overline {x}, y)$
.
$\varphi ^M_E(\overline {x}) = \inf _{y \in (M)_1} \psi ^M_E(\overline {x}, y)$
.
We remark that in the case that
![]() $N = \mathbb {C}$
and
$N = \mathbb {C}$
and
![]() $E = \tau $
is a faithful, normal, tracial state, then
$E = \tau $
is a faithful, normal, tracial state, then
![]() $\varphi ^M_E$
reduces to the usual interpretation
$\varphi ^M_E$
reduces to the usual interpretation
![]() $\varphi ^M$
(Definition 3.3). As in that case, one can show by induction that the N-valued interpretation of every formula is bounded on the unit ball
$\varphi ^M$
(Definition 3.3). As in that case, one can show by induction that the N-valued interpretation of every formula is bounded on the unit ball
![]() $(M)_1^n$
, which is used in (3) above to show that the supremum exists in N.
$(M)_1^n$
, which is used in (3) above to show that the supremum exists in N.
Lemma 3.12. Let M be a finite von Neumann algebra,
![]() $N \subseteq Z(M)$
be a subalgebra of its center,
$N \subseteq Z(M)$
be a subalgebra of its center,
![]() $E: M \to N$
be a normal, faithful, tracial conditional expectation, and
$E: M \to N$
be a normal, faithful, tracial conditional expectation, and
![]() $\varphi $
be a formula with n free variables. Then there exists
$\varphi $
be a formula with n free variables. Then there exists
![]() $C> 0$
s.t.
$C> 0$
s.t.
![]() ${\lVert {\varphi ^M_E(\overline {x})}\rVert }_\infty \leq C$
for all
${\lVert {\varphi ^M_E(\overline {x})}\rVert }_\infty \leq C$
for all
![]() $\overline {x} \in (M)_1^n$
. Furthermore, C can be chosen independent of M, N and E.
$\overline {x} \in (M)_1^n$
. Furthermore, C can be chosen independent of M, N and E.
Proof. The case where
![]() $\varphi (\overline {x}) = \operatorname {\mathrm {Re}} \operatorname {\mathrm {tr}}(p(\overline {x}))$
or
$\varphi (\overline {x}) = \operatorname {\mathrm {Re}} \operatorname {\mathrm {tr}}(p(\overline {x}))$
or
![]() $\operatorname {\mathrm {Im}} \operatorname {\mathrm {tr}}(p(\overline {x}))$
follows by expanding the polynomial p termwise and using the triangle inequality and submultiplicativity of the operator norm. Next, suppose that
$\operatorname {\mathrm {Im}} \operatorname {\mathrm {tr}}(p(\overline {x}))$
follows by expanding the polynomial p termwise and using the triangle inequality and submultiplicativity of the operator norm. Next, suppose that
![]() $\varphi = f(\varphi _1,\dots ,\varphi _k)$
for some continuous
$\varphi = f(\varphi _1,\dots ,\varphi _k)$
for some continuous
![]() $f: \mathbb {R}^k \to \mathbb {R}$
. Since each of the
$f: \mathbb {R}^k \to \mathbb {R}$
. Since each of the
![]() $\varphi _j$
’s is bounded by some constant, the output
$\varphi _j$
’s is bounded by some constant, the output
![]() $f(\varphi _1,\dots ,\varphi _k)$
will also be bounded, by the spectral mapping property for continuous functional calculus. Finally, suppose that
$f(\varphi _1,\dots ,\varphi _k)$
will also be bounded, by the spectral mapping property for continuous functional calculus. Finally, suppose that
![]() $\varphi (\overline {x}) = \sup _y \psi (\overline {x},y)$
. Clearly, if
$\varphi (\overline {x}) = \sup _y \psi (\overline {x},y)$
. Clearly, if
![]() ${\lVert {\psi _E^M(\overline {x},y)}\rVert } \leq C$
for all y, then
${\lVert {\psi _E^M(\overline {x},y)}\rVert } \leq C$
for all y, then
![]() ${\lVert {\varphi _E^M(x)}\rVert }\leq C$
as well.
${\lVert {\varphi _E^M(x)}\rVert }\leq C$
as well.
A key ingredient for our version of Łoś’s theorem, as well as for handling other examples and applications, is the fact that when
![]() $\varphi = \sup _y \phi (\overline {x}, y)$
, there is a single y that realizes the supremum
$\varphi = \sup _y \phi (\overline {x}, y)$
, there is a single y that realizes the supremum
![]() $\sup _{y \in (M)_1} \psi ^M_E(\overline {x}, y)$
within error
$\sup _{y \in (M)_1} \psi ^M_E(\overline {x}, y)$
within error
![]() $\epsilon $
uniformly (i.e., in operator norm). In the case of a direct integral, this means that
$\epsilon $
uniformly (i.e., in operator norm). In the case of a direct integral, this means that
![]() $y(\omega )$
gets within
$y(\omega )$
gets within
![]() $\epsilon $
of the supremum on almost every fiber simultaneously. A similar statement is given in [Reference Ben YaacovBen13, Lemma 3.13] for randomizations.
$\epsilon $
of the supremum on almost every fiber simultaneously. A similar statement is given in [Reference Ben YaacovBen13, Lemma 3.13] for randomizations.
Proposition 3.13. Let M be a finite von Neumann algebra,
![]() $N \subseteq Z(M)$
be a subalgebra of its center,
$N \subseteq Z(M)$
be a subalgebra of its center,
![]() $E: M \to N$
be a normal, faithful, tracial conditional expectation, and
$E: M \to N$
be a normal, faithful, tracial conditional expectation, and
![]() $\varphi = \sup _y \psi (\overline {x}, y)$
where
$\varphi = \sup _y \psi (\overline {x}, y)$
where
![]() $\phi $
is a formula with
$\phi $
is a formula with
![]() $n + 1$
free variables. Then for any
$n + 1$
free variables. Then for any
![]() $\overline {x} = (x_1, \cdots , x_n)$
, tuple of elements of M, and
$\overline {x} = (x_1, \cdots , x_n)$
, tuple of elements of M, and
![]() $\epsilon> 0$
, there exists
$\epsilon> 0$
, there exists
![]() $y \in (M)_1$
such that
$y \in (M)_1$
such that
This property emerges from the ability to paste elements of the von Neumann algebra using partitions of unity on the commutative algebra. Recall that a projection-valued measure (PVM) over von Neumann algebra N is a collection
![]() $\{e_i\}_{i \in I}$
of pairwise orthogonal projections in N which sum up to 1. The relationship between projection-valued measures and operator-valued interpretations of formulas is as follows. This is parallel to the locality property for randomizations [Reference Ben YaacovBen13, Definition 3.12].
$\{e_i\}_{i \in I}$
of pairwise orthogonal projections in N which sum up to 1. The relationship between projection-valued measures and operator-valued interpretations of formulas is as follows. This is parallel to the locality property for randomizations [Reference Ben YaacovBen13, Definition 3.12].
Lemma 3.14. Let M be a finite von Neumann algebra,
![]() $N \subseteq Z(M)$
be a subalgebra of its center,
$N \subseteq Z(M)$
be a subalgebra of its center,
![]() $E: M \to N$
be a normal, faithful, tracial conditional expectation,
$E: M \to N$
be a normal, faithful, tracial conditional expectation,
![]() $\varphi $
be a formula with n free variables
$\varphi $
be a formula with n free variables
![]() $\overline {x} = (x_1, \cdots , x_n)$
. Let
$\overline {x} = (x_1, \cdots , x_n)$
. Let
![]() $\{e_j\}_{j \in J}$
be a PVM over N and
$\{e_j\}_{j \in J}$
be a PVM over N and
![]() $x_{i,j} \in (M)_1$
for
$x_{i,j} \in (M)_1$
for
![]() $i = 1, \dots , n$
and
$i = 1, \dots , n$
and
![]() $j \in J$
. Then
$j \in J$
. Then
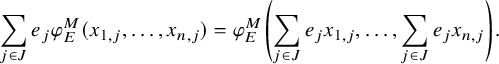 $$\begin{align*}\sum_{j \in J} e_j\varphi^M_E(x_{1,j},\dots,x_{n,j}) = \varphi^M_E\left( \sum_{j \in J} e_j x_{1,j},\dots, \sum_{j \in J} e_j x_{n,j} \right). \end{align*}$$
$$\begin{align*}\sum_{j \in J} e_j\varphi^M_E(x_{1,j},\dots,x_{n,j}) = \varphi^M_E\left( \sum_{j \in J} e_j x_{1,j},\dots, \sum_{j \in J} e_j x_{n,j} \right). \end{align*}$$
Proof. We proceed by induction on complexity of the formula. First, suppose
![]() $\varphi (\overline {x}) = \operatorname {\mathrm {Re}} \operatorname {\mathrm {tr}}(p(\overline {x}))$
, and hence,
$\varphi (\overline {x}) = \operatorname {\mathrm {Re}} \operatorname {\mathrm {tr}}(p(\overline {x}))$
, and hence,
![]() $\varphi _E^M(x_{1,j},\dots ,x_{n,j}) = \operatorname {\mathrm {Re}} E[p(x_{1,j},\dots ,x_{n,j})]$
. Write
$\varphi _E^M(x_{1,j},\dots ,x_{n,j}) = \operatorname {\mathrm {Re}} E[p(x_{1,j},\dots ,x_{n,j})]$
. Write
![]() $x_i = \sum _{j \in J} e_j x_{i,j}$
. Since
$x_i = \sum _{j \in J} e_j x_{i,j}$
. Since
![]() $e_j$
is central,
$e_j$
is central,
 $$ \begin{align*} e_j \operatorname{\mathrm{Re}} E[p(x_{1,j},\dots,x_{n,j})] &= e_j \operatorname{\mathrm{Re}} E[p(e_j x_{1,j},\dots,e_j x_{n,j})] \\ &= e_j \operatorname{\mathrm{Re}} E[p(e_j x_1,\dots,e_j x_n)] \\ &= e_j \operatorname{\mathrm{Re}} E[p(x_1,\dots,x_n)]. \end{align*} $$
$$ \begin{align*} e_j \operatorname{\mathrm{Re}} E[p(x_{1,j},\dots,x_{n,j})] &= e_j \operatorname{\mathrm{Re}} E[p(e_j x_{1,j},\dots,e_j x_{n,j})] \\ &= e_j \operatorname{\mathrm{Re}} E[p(e_j x_1,\dots,e_j x_n)] \\ &= e_j \operatorname{\mathrm{Re}} E[p(x_1,\dots,x_n)]. \end{align*} $$
Summing over j completes the proof for this case, and the imaginary part is similar.
Next, suppose that
![]() $\varphi = f(\varphi _1,\dots ,\varphi _k)$
for some continuous
$\varphi = f(\varphi _1,\dots ,\varphi _k)$
for some continuous
![]() $f: \mathbb {R}^k \to \mathbb {R}$
, such that
$f: \mathbb {R}^k \to \mathbb {R}$
, such that
![]() $\varphi _j$
satisfies the induction hypothesis. Let
$\varphi _j$
satisfies the induction hypothesis. Let
![]() $\overline {x}_j = (x_{1,j},\dots ,x_{n,j})$
. Then we have
$\overline {x}_j = (x_{1,j},\dots ,x_{n,j})$
. Then we have
because the mapping
![]() $N \to e_jN$
,
$N \to e_jN$
,
![]() $y \mapsto e_j y$
is a
$y \mapsto e_j y$
is a
![]() $*$
-homomorphism of commutative
$*$
-homomorphism of commutative
![]() $\mathrm {C}^*$
-algebras and therefore respects functional calculus. From here, we apply the induction hypothesis to
$\mathrm {C}^*$
-algebras and therefore respects functional calculus. From here, we apply the induction hypothesis to
![]() $\varphi _i$
and then argue similarly as in the first case.
$\varphi _i$
and then argue similarly as in the first case.
Now suppose that
![]() $\varphi (\overline {x}) = \sup _y \psi (\overline {x},y)$
where
$\varphi (\overline {x}) = \sup _y \psi (\overline {x},y)$
where
![]() $\psi $
satisfies the induction hypothesis. First, note that if
$\psi $
satisfies the induction hypothesis. First, note that if
![]() $(z_i)_{i \in I}$
is a family of self-adjoint operators in N and e is a projection in N, then
$(z_i)_{i \in I}$
is a family of self-adjoint operators in N and e is a projection in N, then
Indeed, clearly
![]() $e \sup _i z_i$
is an upper bound for
$e \sup _i z_i$
is an upper bound for
![]() $ez_i$
for each i, and hence,
$ez_i$
for each i, and hence,
![]() $e \sup _i z_i \geq \sup _i e z_i$
. However, let
$e \sup _i z_i \geq \sup _i e z_i$
. However, let
![]() $C = \sup _i {\lVert {z_i}\rVert }$
. Then clearly,
$C = \sup _i {\lVert {z_i}\rVert }$
. Then clearly,
![]() $(1 - e)C + \sup _i ez_i$
is an upper bound for each
$(1 - e)C + \sup _i ez_i$
is an upper bound for each
![]() $z_i$
, so that
$z_i$
, so that
![]() $\sup _i z_i \leq (1 - e)C + \sup _i ez_i$
, which implies
$\sup _i z_i \leq (1 - e)C + \sup _i ez_i$
, which implies
which proves the claim. Again, let
![]() $x_i = \sum _j e_j x_{i,j}$
. Note that
$x_i = \sum _j e_j x_{i,j}$
. Note that
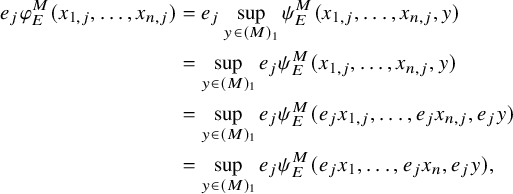 $$ \begin{align*} e_j \varphi_E^M(x_{1,j},\dots,x_{n,j}) &= e_j \sup_{y \in (M)_1} \psi_E^M(x_{1,j},\dots,x_{n,j},y) \\&= \sup_{y \in (M)_1} e_j \psi_E^M(x_{1,j},\dots,x_{n,j},y) \\&= \sup_{y \in (M)_1} e_j \psi_E^M(e_j x_{1,j},\dots,e_jx_{n,j}, e_jy) \\&= \sup_{y \in (M)_1} e_j \psi_E^M(e_j x_1,\dots,e_j x_n, e_j y), \end{align*} $$
$$ \begin{align*} e_j \varphi_E^M(x_{1,j},\dots,x_{n,j}) &= e_j \sup_{y \in (M)_1} \psi_E^M(x_{1,j},\dots,x_{n,j},y) \\&= \sup_{y \in (M)_1} e_j \psi_E^M(x_{1,j},\dots,x_{n,j},y) \\&= \sup_{y \in (M)_1} e_j \psi_E^M(e_j x_{1,j},\dots,e_jx_{n,j}, e_jy) \\&= \sup_{y \in (M)_1} e_j \psi_E^M(e_j x_1,\dots,e_j x_n, e_j y), \end{align*} $$
and by the reverse manipulations as before, this equals
![]() $e_j \varphi _E^M(x_1,\dots ,x_n)$
. Hence,
$e_j \varphi _E^M(x_1,\dots ,x_n)$
. Hence,
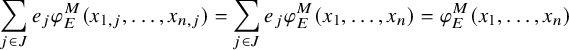 $$\begin{align*}\sum_{j \in J} e_j \varphi_E^M(x_{1,j},\dots,x_{n,j}) = \sum_{j \in J} e_j \varphi_E^M(x_1,\dots,x_n) = \varphi_E^M(x_1,\dots,x_n) \end{align*}$$
$$\begin{align*}\sum_{j \in J} e_j \varphi_E^M(x_{1,j},\dots,x_{n,j}) = \sum_{j \in J} e_j \varphi_E^M(x_1,\dots,x_n) = \varphi_E^M(x_1,\dots,x_n) \end{align*}$$
as desired. The case of an infimum is symmetrical; in fact, one can use the identity
to reduce it to the case of suprema and connectives.
The other ingredient that we need for Proposition 3.13 is a classical fact about suprema in commutative von Neumann algebras or, equivalently, about Stone spaces (which have already made their appearance in model theory of probability spaces [Reference Ben YaacovBen13, §2]). Lemma 3.15 serves a similar purpose for us as the measure-theoretic fact [Reference Ben YaacovBen13, Fact 3.30] used in [Reference Ben YaacovBen13, Lemma 3.31].
Lemma 3.15. Let N be a commutative von Neumann algebra, and let
![]() $\{z_i\}_{i \in I} \subset N_{sa}$
be a collection of elements which are uniformly bounded in norm. Then for any
$\{z_i\}_{i \in I} \subset N_{sa}$
be a collection of elements which are uniformly bounded in norm. Then for any
![]() $\epsilon> 0$
, there exists a PVM
$\epsilon> 0$
, there exists a PVM
![]() $\{e_j\}_{j \in J}$
over N, and for each j there exists
$\{e_j\}_{j \in J}$
over N, and for each j there exists
![]() $i_j \in I$
, s.t.
$i_j \in I$
, s.t.
![]() ${\lVert {\sup _{i \in I} z_i - \sum _j e_jz_{i_j}}\rVert } \leq \epsilon $
.
${\lVert {\sup _{i \in I} z_i - \sum _j e_jz_{i_j}}\rVert } \leq \epsilon $
.
Proof. Let
![]() $\Omega $
be the Gelfand spectrum of N, so that
$\Omega $
be the Gelfand spectrum of N, so that
![]() $N \cong C(\Omega )$
. We shall regard all
$N \cong C(\Omega )$
. We shall regard all
![]() $z_i$
as well as
$z_i$
as well as
![]() $z = \sup _{i \in I} z_i$
as continuous functions on
$z = \sup _{i \in I} z_i$
as continuous functions on
![]() $\Omega $
. Then by [Reference TakesakiTak79, Corollary III.1.16], there exists an open dense set
$\Omega $
. Then by [Reference TakesakiTak79, Corollary III.1.16], there exists an open dense set
![]() $O \subseteq \Omega $
s.t. for any
$O \subseteq \Omega $
s.t. for any
![]() $t \in O$
,
$t \in O$
,
![]() $z(t) = \sup _{i \in I} z_i(t)$
. We now consider a maximal collection
$z(t) = \sup _{i \in I} z_i(t)$
. We now consider a maximal collection
![]() $\{K_j\}_{j \in J}$
of nonempty pairwise disjoint clopen subsets s.t. for each j there exists
$\{K_j\}_{j \in J}$
of nonempty pairwise disjoint clopen subsets s.t. for each j there exists
![]() $i_j \in I$
with
$i_j \in I$
with
![]() $|z(t) - z_{i_j}(t)| < \epsilon $
for all
$|z(t) - z_{i_j}(t)| < \epsilon $
for all
![]() $t \in K_j$
. We claim that
$t \in K_j$
. We claim that
![]() $\cup K_j$
is dense. Indeed, assume otherwise, then
$\cup K_j$
is dense. Indeed, assume otherwise, then
![]() $U = \Omega \setminus \overline {\cup K_j}$
is a nonempty open set, whence so is
$U = \Omega \setminus \overline {\cup K_j}$
is a nonempty open set, whence so is
![]() $O \cap U$
. Fix any
$O \cap U$
. Fix any
![]() $t_0 \in O \cap U$
, as
$t_0 \in O \cap U$
, as
![]() $z(t_0) = \sup _{i \in I} z_i(t_0)$
, there exists some
$z(t_0) = \sup _{i \in I} z_i(t_0)$
, there exists some
![]() $z_i$
s.t.
$z_i$
s.t.
![]() $|z(t_0) - z_i(t_0)| < \epsilon $
. Continuity then implies
$|z(t_0) - z_i(t_0)| < \epsilon $
. Continuity then implies
![]() $|z(t) - z_i(t)| < \epsilon $
in some neighborhood K of
$|z(t) - z_i(t)| < \epsilon $
in some neighborhood K of
![]() $t_0$
. As clopen sets form a basis of topology for
$t_0$
. As clopen sets form a basis of topology for
![]() $\Omega $
(see [Reference TakesakiTak79, Definition III.1.6]), such a neighborhood can be chosen to be clopen and a subset of U. But then adding K to
$\Omega $
(see [Reference TakesakiTak79, Definition III.1.6]), such a neighborhood can be chosen to be clopen and a subset of U. But then adding K to
![]() $\{K_j\}$
shows the latter collection is not maximal, a contradiction. This shows that
$\{K_j\}$
shows the latter collection is not maximal, a contradiction. This shows that
![]() $\cup K_j$
is indeed dense. Let
$\cup K_j$
is indeed dense. Let
![]() $e_j = 1_{K_j}$
. Then
$e_j = 1_{K_j}$
. Then
![]() $|\sum _j e_j z_{i_j}(t) - z(t)| \leq \epsilon $
on a dense subset of
$|\sum _j e_j z_{i_j}(t) - z(t)| \leq \epsilon $
on a dense subset of
![]() $\Omega $
, and hence by continuity,
$\Omega $
, and hence by continuity,
![]() ${\lVert {\sum _j e_j z_{i_j}(t) - z(t)} \rVert } \leq \epsilon $
.
${\lVert {\sum _j e_j z_{i_j}(t) - z(t)} \rVert } \leq \epsilon $
.
Proof of Proposition 3.13.
As
![]() $\varphi ^M_E(\overline {x}) = \sup _{y \in (M)_1} \psi ^M_E(\overline {x}, y)$
, by Lemma 3.15, there exists a PVM
$\varphi ^M_E(\overline {x}) = \sup _{y \in (M)_1} \psi ^M_E(\overline {x}, y)$
, by Lemma 3.15, there exists a PVM
![]() $\{e_j\}_{j \in J}$
over N and elements
$\{e_j\}_{j \in J}$
over N and elements
![]() $y_j \in (M)_1$
such that
$y_j \in (M)_1$
such that
Let
![]() $y = \sum _j e_j y_j$
. By Lemma 3.14, to the decompositions
$y = \sum _j e_j y_j$
. By Lemma 3.14, to the decompositions
![]() $x_i = \sum _j e_j x_i$
and
$x_i = \sum _j e_j x_i$
and
![]() $y = \sum _j e_j y_j$
, we have
$y = \sum _j e_j y_j$
, we have
which concludes the proof.
We next note that for a tracial von Neumann algebra M, the N-valued interpretation of a formula
![]() $\varphi (x_1,\dots ,x_n)$
always defines a uniformly continuous function on
$\varphi (x_1,\dots ,x_n)$
always defines a uniformly continuous function on
![]() $(M)_1^n$
with respect to
$(M)_1^n$
with respect to
![]() $2$
-norm, which will be useful for various limiting arguments. This is a generalization of the well-known uniform continuity property for scalar-valued interpretations of formulas [Reference Ben Yaacov, Berenstein, Henson, Usvyatsov, Chatzidakis, Macpherson, Pillay and WilkieBBHU08, Theorem 3.5], and its proof proceeds in the same way by induction on the complexity of the formula, while also relying on Proposition 3.13.
$2$
-norm, which will be useful for various limiting arguments. This is a generalization of the well-known uniform continuity property for scalar-valued interpretations of formulas [Reference Ben Yaacov, Berenstein, Henson, Usvyatsov, Chatzidakis, Macpherson, Pillay and WilkieBBHU08, Theorem 3.5], and its proof proceeds in the same way by induction on the complexity of the formula, while also relying on Proposition 3.13.
Lemma 3.16. Let M be a finite von Neumann algebra,
![]() $N \subseteq Z(M)$
be a subalgebra of its center,
$N \subseteq Z(M)$
be a subalgebra of its center,
![]() $E: M \to N$
be a normal, faithful, tracial conditional expectation. Let
$E: M \to N$
be a normal, faithful, tracial conditional expectation. Let
![]() $\tau $
be a state on N, so that
$\tau $
be a state on N, so that
![]() $\tilde {\tau } = \tau \circ E$
is a tracial state on M. For each formula
$\tilde {\tau } = \tau \circ E$
is a tracial state on M. For each formula
![]() $\varphi (x_1,\dots ,x_n)$
, there exists a continuous increasing function
$\varphi (x_1,\dots ,x_n)$
, there exists a continuous increasing function
![]() $\delta : [0,\infty ) \to [0,\infty )$
such that for
$\delta : [0,\infty ) \to [0,\infty )$
such that for
![]() $\overline {x}$
,
$\overline {x}$
,
![]() $\overline {y} \in (M)_1^n$
, we have
$\overline {y} \in (M)_1^n$
, we have
where
![]() ${\lVert {\cdot }\rVert }_2$
denotes the
${\lVert {\cdot }\rVert }_2$
denotes the
![]() $2$
-norm associated to
$2$
-norm associated to
![]() $\tilde {\tau }$
. Furthermore,
$\tilde {\tau }$
. Furthermore,
![]() $\delta $
can be chosen independent of M, N, E, and
$\delta $
can be chosen independent of M, N, E, and
![]() $\tau $
.
$\tau $
.
Proof. We proceed by induction on the complexity of formulas. First, consider a basic formula
![]() $\operatorname {\mathrm {Re}} \operatorname {\mathrm {tr}}(p(x_1,\dots ,x_n))$
. By decomposing p into monomials, it suffices to show that
$\operatorname {\mathrm {Re}} \operatorname {\mathrm {tr}}(p(x_1,\dots ,x_n))$
. By decomposing p into monomials, it suffices to show that
![]() $E[x_{i_1} \dots x_{i_k}]$
is uniformly continuous on
$E[x_{i_1} \dots x_{i_k}]$
is uniformly continuous on
![]() $(M)_1^n$
. This follows easily from the inequalities
$(M)_1^n$
. This follows easily from the inequalities
![]() ${\lVert {xy}\rVert }_2 \leq \min ({\lVert {x}\rVert } {\lVert {y} \rVert }_2, {\lVert {x}\rVert }_2 {\lVert {y}\rVert })$
and
${\lVert {xy}\rVert }_2 \leq \min ({\lVert {x}\rVert } {\lVert {y} \rVert }_2, {\lVert {x}\rVert }_2 {\lVert {y}\rVert })$
and
![]() ${\lVert {E(x)}\rVert }_2 \leq {\lVert {x}\rVert }_2$
.
${\lVert {E(x)}\rVert }_2 \leq {\lVert {x}\rVert }_2$
.
Next, suppose that
![]() $\varphi = f(\varphi _1,\dots ,\varphi _k)$
for some
$\varphi = f(\varphi _1,\dots ,\varphi _k)$
for some
![]() $f: \mathbb {R}^k \to \mathbb {R}$
continuous, and formulas
$f: \mathbb {R}^k \to \mathbb {R}$
continuous, and formulas
![]() $\varphi _1$
, …,
$\varphi _1$
, …,
![]() $\varphi _k$
satisfying the conclusion of the lemma. By Lemma 3.12, each formula
$\varphi _k$
satisfying the conclusion of the lemma. By Lemma 3.12, each formula
![]() $\varphi _j$
is bounded by some constant
$\varphi _j$
is bounded by some constant
![]() $C_j$
. To obtain the conclusion for
$C_j$
. To obtain the conclusion for
![]() $\varphi $
, it suffices to show that the application of f by functional calculus defines a
$\varphi $
, it suffices to show that the application of f by functional calculus defines a
![]() ${\lVert {\cdot }\rVert }_2$
-uniformly continuous function
${\lVert {\cdot }\rVert }_2$
-uniformly continuous function
Note that in the case where f is a polynomial, this follows from the same reasoning as in the first step. Now fix a sequence of polynomials
![]() $f_j$
such that
$f_j$
such that
![]() $f_j \to f$
uniformly on
$f_j \to f$
uniformly on
![]() $[-C_1,C_1] \times \dots \times [-C_k,C_k]$
. The spectral mapping theorem implies uniform convergence of
$[-C_1,C_1] \times \dots \times [-C_k,C_k]$
. The spectral mapping theorem implies uniform convergence of
![]() $f_j \to f$
on N (and with bounds independent of the particular choice of N). Moreover, since uniform continuity is preserved under uniform limits, we see that f is
$f_j \to f$
on N (and with bounds independent of the particular choice of N). Moreover, since uniform continuity is preserved under uniform limits, we see that f is
![]() ${\lVert {\cdot }\rVert }_2$
-uniformly continuous.
${\lVert {\cdot }\rVert }_2$
-uniformly continuous.
Next, consider the case where
![]() $\varphi (\overline {x}) = \sup _y \psi (\overline {x},y)$
. Let
$\varphi (\overline {x}) = \sup _y \psi (\overline {x},y)$
. Let
![]() $\delta : [0,\infty ) \to [0,\infty )$
be the modulus of continuity associated to
$\delta : [0,\infty ) \to [0,\infty )$
be the modulus of continuity associated to
![]() $\psi $
, and suppose that
$\psi $
, and suppose that
![]() $\max _j {\lVert {x_j - x_j'}\rVert }_2 \leq \delta (\epsilon / 4)$
. By Proposition 3.13, there exists y such that
$\max _j {\lVert {x_j - x_j'}\rVert }_2 \leq \delta (\epsilon / 4)$
. By Proposition 3.13, there exists y such that
Furthermore, note that
Letting
![]() $[\cdot ]_+$
denote the positive part of a self-adjoint operator, we have
$[\cdot ]_+$
denote the positive part of a self-adjoint operator, we have
On the right-hand side, the first term is bounded by
![]() $\epsilon /4$
by our choice of y, and the last term is zero by definition of
$\epsilon /4$
by our choice of y, and the last term is zero by definition of
![]() $\varphi $
. Hence,
$\varphi $
. Hence,
where we have applied the uniform continuity condition on
![]() $\psi $
. A symmetrical argument shows that
$\psi $
. A symmetrical argument shows that
Overall,
provided that
![]() $\max _j {\lVert {x_j - x_j'}\rVert }_2 \leq \delta (\epsilon /4)$
. As before, the case of an infimum is symmetrical to the case of a supremum.
$\max _j {\lVert {x_j - x_j'}\rVert }_2 \leq \delta (\epsilon /4)$
. As before, the case of an infimum is symmetrical to the case of a supremum.
Now we show that if M has a direct integral decomposition, then the operator-valued interpretations of formulas coincide with their fiberwise interpretations.
Lemma 3.17. Suppose that
![]() $(M,\tau )$
is a tracial von Neumann algebra given as a direct integral
$(M,\tau )$
is a tracial von Neumann algebra given as a direct integral
![]() $(M,\tau ) = \int _\Omega ^{\oplus } (M_\omega ,\tau _\omega ) \,d\mu (\omega )$
. Let
$(M,\tau ) = \int _\Omega ^{\oplus } (M_\omega ,\tau _\omega ) \,d\mu (\omega )$
. Let
![]() $N = L^\infty (\Omega )$
and let
$N = L^\infty (\Omega )$
and let
![]() $E: M \to L^\infty (\Omega )$
be the faithful, normal, tracial conditional expectation given by
$E: M \to L^\infty (\Omega )$
be the faithful, normal, tracial conditional expectation given by
![]() $E[x](\omega ) = \tau _\omega (x(\omega ))$
. Let
$E[x](\omega ) = \tau _\omega (x(\omega ))$
. Let
![]() $\varphi $
be a formula in the language of tracial von Neumann algebras, and let
$\varphi $
be a formula in the language of tracial von Neumann algebras, and let
![]() $\overline {x} \in (M)_1^n$
. Then
$\overline {x} \in (M)_1^n$
. Then
![]() $\varphi ^M_E(\overline {x}) \in L^\infty (\Omega )$
is (up to a.e. equivalence) the function given by
$\varphi ^M_E(\overline {x}) \in L^\infty (\Omega )$
is (up to a.e. equivalence) the function given by
![]() $\Omega \ni \omega \mapsto \varphi ^{M_\omega }(\overline {x}(\omega ))$
. In particular,
$\Omega \ni \omega \mapsto \varphi ^{M_\omega }(\overline {x}(\omega ))$
. In particular,
![]() $\omega \mapsto \varphi ^{M_\omega }(\overline {x}(\omega ))$
is measurable.
$\omega \mapsto \varphi ^{M_\omega }(\overline {x}(\omega ))$
is measurable.
Proof. We proceed by induction on the complexity of formulas. The cases for basic formulas and adding connectives are straightforward and left to the reader. Now consider
![]() $\varphi = \sup _y \psi (\overline {x}, y)$
where the claim is already proved for
$\varphi = \sup _y \psi (\overline {x}, y)$
where the claim is already proved for
![]() $\psi $
.
$\psi $
.
Let
![]() $z(\omega ) = \varphi ^{M_\omega }(\overline {x}(\omega ))$
. First, let us verify that z is measurable (as in [Reference Farah and GhasemiFG24, Lemma 1.2]). Let
$z(\omega ) = \varphi ^{M_\omega }(\overline {x}(\omega ))$
. First, let us verify that z is measurable (as in [Reference Farah and GhasemiFG24, Lemma 1.2]). Let
![]() $(e_n)_{n> 0}$
be as in Definition 1.1, so that
$(e_n)_{n> 0}$
be as in Definition 1.1, so that
![]() $(e_n(\omega ))_{n> 0}$
is
$(e_n(\omega ))_{n> 0}$
is
![]() ${\lVert {\cdot }\rVert }_2$
-dense in
${\lVert {\cdot }\rVert }_2$
-dense in
![]() $(M_\omega )_1$
for every
$(M_\omega )_1$
for every
![]() $\omega $
. Note that
$\omega $
. Note that
![]() $\varphi ^{M_\omega }$
is uniformly continuous on
$\varphi ^{M_\omega }$
is uniformly continuous on
![]() $(M_\omega )_1$
with respect to
$(M_\omega )_1$
with respect to
![]() ${\lVert {\cdot }\rVert }_2$
by Lemma 3.16 in the case
${\lVert {\cdot }\rVert }_2$
by Lemma 3.16 in the case
![]() $N = \mathbb {C}$
. Therefore, for almost every
$N = \mathbb {C}$
. Therefore, for almost every
![]() $\omega $
,
$\omega $
,
Thus,
![]() $z(\omega ) = \varphi ^{M_\omega }(\overline {x}(\omega ))$
is the pointwise supremum of a countable collection of measurable functions, and hence, it is measurable.
$z(\omega ) = \varphi ^{M_\omega }(\overline {x}(\omega ))$
is the pointwise supremum of a countable collection of measurable functions, and hence, it is measurable.
We show that this agrees with the operator-valued supremum by proving two directions. Given
![]() $y \in (M)_1$
, writing y as a function
$y \in (M)_1$
, writing y as a function
![]() $\omega \mapsto y(\omega ) \in (M_\omega )_1$
defined almost everywhere, we have by induction hypothesis
$\omega \mapsto y(\omega ) \in (M_\omega )_1$
defined almost everywhere, we have by induction hypothesis
 $$ \begin{align*} \begin{split} \psi^M_E(\overline{x}, y)(\omega) &= \psi^{M_\omega}(\overline{x}(\omega), y(\omega))\\ &\leq \sup_{y_0 \in (M_\omega)_1} \psi^{M_\omega}(\overline{x}(\omega), y_0)\\ &= \varphi^{M_\omega}(\overline{x}(\omega)). \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} \psi^M_E(\overline{x}, y)(\omega) &= \psi^{M_\omega}(\overline{x}(\omega), y(\omega))\\ &\leq \sup_{y_0 \in (M_\omega)_1} \psi^{M_\omega}(\overline{x}(\omega), y_0)\\ &= \varphi^{M_\omega}(\overline{x}(\omega)). \end{split} \end{align*} $$
Hence, z is an upper bound for
![]() $\psi _E^M(\overline {x},y)$
in
$\psi _E^M(\overline {x},y)$
in
![]() $N_{\operatorname {\mathrm {sa}}}$
, and
$N_{\operatorname {\mathrm {sa}}}$
, and
However, since the operator supremum in
![]() $L^\infty (\Omega )$
agrees with the pointwise supremum almost everywhere,
$L^\infty (\Omega )$
agrees with the pointwise supremum almost everywhere,
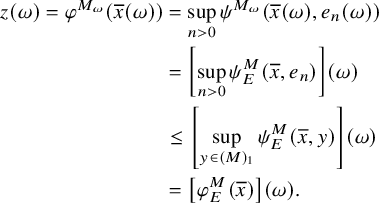 $$ \begin{align*} \begin{split} z(\omega) = \varphi^{M_\omega}(\overline{x}(\omega)) &= \sup_{n> 0} \psi^{M_\omega}(\overline{x}(\omega), e_n(\omega))\\ &= \left[ \sup_{n > 0} \psi^M_E(\overline{x}, e_n) \right](\omega)\\ &\leq \left[\sup_{y \in (M)_1} \psi^M_E(\overline{x}, y) \right](\omega)\\ &= \left[\varphi^M_E(\overline{x})\right](\omega). \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} z(\omega) = \varphi^{M_\omega}(\overline{x}(\omega)) &= \sup_{n> 0} \psi^{M_\omega}(\overline{x}(\omega), e_n(\omega))\\ &= \left[ \sup_{n > 0} \psi^M_E(\overline{x}, e_n) \right](\omega)\\ &\leq \left[\sup_{y \in (M)_1} \psi^M_E(\overline{x}, y) \right](\omega)\\ &= \left[\varphi^M_E(\overline{x})\right](\omega). \end{split} \end{align*} $$
Thus,
![]() $z \leq \varphi _E^M(\overline {x})$
. Thus, we have shown
$z \leq \varphi _E^M(\overline {x})$
. Thus, we have shown
![]() $z = \varphi _E^M(\overline {x})$
, as desired.
$z = \varphi _E^M(\overline {x})$
, as desired.
3.3 Łoś’s theorem for ultrafibers and generalized ultraproducts
The following theorem is an analog of Łoś’s theorem for ultrafibers.
Theorem 3.18 (Łoś’s theorem for ultrafibers; cf. [Reference Ben YaacovBen13, Theorem 3.19]).
Let M be a finite von Neumann algebra,
![]() $N \subseteq Z(M)$
be a subalgebra of its center,
$N \subseteq Z(M)$
be a subalgebra of its center,
![]() $E: M \to N$
be a normal, faithful, tracial conditional expectation. Let
$E: M \to N$
be a normal, faithful, tracial conditional expectation. Let
![]() $\mathcal {U}$
be a character on N and let
$\mathcal {U}$
be a character on N and let
![]() $\pi _{E,\mathcal {U}}: M \to M^{/E,\mathcal {U}}$
be the quotient map onto the ultrafiber. Then for every formula
$\pi _{E,\mathcal {U}}: M \to M^{/E,\mathcal {U}}$
be the quotient map onto the ultrafiber. Then for every formula
![]() $\varphi $
and every tuple
$\varphi $
and every tuple
![]() $\overline {x} \in (M)_1^n$
, we have
$\overline {x} \in (M)_1^n$
, we have
Proof. We proceed by induction on the complexity of
![]() $\varphi $
. For atomic formulas, this holds because for a non-commutative
$\varphi $
. For atomic formulas, this holds because for a non-commutative
![]() $*$
-polynomial p,
$*$
-polynomial p,
The case of adding connectives can also be proved easily from the fact that
![]() $\mathcal {U}$
is a
$\mathcal {U}$
is a
![]() $*$
-homomorphism from N to
$*$
-homomorphism from N to
![]() $\mathbb {C}$
and therefore commutes with continuous functional calculus.
$\mathbb {C}$
and therefore commutes with continuous functional calculus.
Next, suppose that
![]() $\varphi (\overline {x}) = \sup _y \psi (\overline {x},y)$
; the case of an infimum, of course, is symmetrical. We first show that
$\varphi (\overline {x}) = \sup _y \psi (\overline {x},y)$
; the case of an infimum, of course, is symmetrical. We first show that
![]() $\varphi ^{M^{/E, \mathcal {U}}}(\pi _{E,\mathcal {U}}(\overline {x})) \leq \mathcal {U}({\varphi ^M_E}(\overline {x}))$
. As noted in Proposition 2.2, any element
$\varphi ^{M^{/E, \mathcal {U}}}(\pi _{E,\mathcal {U}}(\overline {x})) \leq \mathcal {U}({\varphi ^M_E}(\overline {x}))$
. As noted in Proposition 2.2, any element
![]() $\hat {y}$
of norm at most
$\hat {y}$
of norm at most
![]() $1$
in
$1$
in
![]() $M^{/E, \mathcal {U}}$
can be lifted to an element y of norm at most
$M^{/E, \mathcal {U}}$
can be lifted to an element y of norm at most
![]() $1$
in M. From the induction hypothesis
$1$
in M. From the induction hypothesis
and since
![]() $\hat {y}$
was arbitrary,
$\hat {y}$
was arbitrary,
![]() $\varphi ^{M^{/E,\mathcal {U}}}(\pi _{E,\mathcal {U}}(\overline {x})) \leq \mathcal {U}(\varphi _E^M(\overline {x}))$
. For the other direction, fix
$\varphi ^{M^{/E,\mathcal {U}}}(\pi _{E,\mathcal {U}}(\overline {x})) \leq \mathcal {U}(\varphi _E^M(\overline {x}))$
. For the other direction, fix
![]() $\epsilon> 0$
. Then by Proposition 3.13, there exists
$\epsilon> 0$
. Then by Proposition 3.13, there exists
![]() $y \in (M)_1$
s.t.
$y \in (M)_1$
s.t.
![]() $\psi ^M_E(\overline {x}, y) \geq \varphi ^M_E(\overline {x}) - \epsilon $
. Then by induction hypothesis,
$\psi ^M_E(\overline {x}, y) \geq \varphi ^M_E(\overline {x}) - \epsilon $
. Then by induction hypothesis,
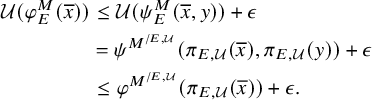 $$ \begin{align*} \begin{split} \mathcal{U}({\varphi^M_E}(\overline{x})) &\leq \mathcal{U}({\psi^M_E}(\overline{x}, y)) + \epsilon\\ &= \psi^{M^{/E, \mathcal{U}}}(\pi_{E,\mathcal{U}}(\overline{x}), \pi_{E,\mathcal{U}}(y)) + \epsilon\\ &\leq \varphi^{M^{/E, \mathcal{U}}}(\pi_{E,\mathcal{U}}(\overline{x})) + \epsilon. \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} \mathcal{U}({\varphi^M_E}(\overline{x})) &\leq \mathcal{U}({\psi^M_E}(\overline{x}, y)) + \epsilon\\ &= \psi^{M^{/E, \mathcal{U}}}(\pi_{E,\mathcal{U}}(\overline{x}), \pi_{E,\mathcal{U}}(y)) + \epsilon\\ &\leq \varphi^{M^{/E, \mathcal{U}}}(\pi_{E,\mathcal{U}}(\overline{x})) + \epsilon. \end{split} \end{align*} $$
Since
![]() $\epsilon $
was arbitrary,
$\epsilon $
was arbitrary,
![]() $\mathcal {U}({\varphi ^M_E}(\overline {x})) \leq \varphi ^{M^{/E, \mathcal {U}}}(\pi _{E,\mathcal {U}}(\overline {x}))$
, so the proof is complete.
$\mathcal {U}({\varphi ^M_E}(\overline {x})) \leq \varphi ^{M^{/E, \mathcal {U}}}(\pi _{E,\mathcal {U}}(\overline {x}))$
, so the proof is complete.
Remark 3.19. We showed earlier that for each formula
![]() $\varphi $
, there is a universal upper bound for
$\varphi $
, there is a universal upper bound for
![]() $\varphi _E^M$
. Now in light of Theorem 3.18, we know that for every pure state
$\varphi _E^M$
. Now in light of Theorem 3.18, we know that for every pure state
![]() $\mathcal {U}$
on N, we have
$\mathcal {U}$
on N, we have
Therefore,
and it follows that the evaluation map
![]() $\varphi \mapsto \varphi _E^M$
extends to the
$\varphi \mapsto \varphi _E^M$
extends to the
![]() $\mathrm {C}^*$
-algebra
$\mathrm {C}^*$
-algebra
![]() $\mathcal {P}_X$
of definable predicates from Definition 3.7.
$\mathcal {P}_X$
of definable predicates from Definition 3.7.
Furthermore, in the special case of ultrapowers over measure spaces, we have the following, which in particular proves Proposition C.
Proposition 3.20. Let A be a commutative von Neumann algebra and let
![]() $(M,\tau )$
be a tracial von Neumann algebra. Let
$(M,\tau )$
be a tracial von Neumann algebra. Let
![]() $\tilde {M} = A \overline {\otimes } M$
and let
$\tilde {M} = A \overline {\otimes } M$
and let
![]() $\tilde {E} = \operatorname {\mathrm {id}} \otimes \tau : \tilde {M} \to A$
. Let
$\tilde {E} = \operatorname {\mathrm {id}} \otimes \tau : \tilde {M} \to A$
. Let
![]() $\mathcal {U}$
be a pure state on A, so that
$\mathcal {U}$
be a pure state on A, so that
![]() $\tilde {M}^{/E,\mathcal {U}} = M^{\mathcal {U}}$
. Then for
$\tilde {M}^{/E,\mathcal {U}} = M^{\mathcal {U}}$
. Then for
![]() $\overline {x} \in (M)_1^n$
and formulas
$\overline {x} \in (M)_1^n$
and formulas
![]() $\varphi $
, we have
$\varphi $
, we have
In particular, for every sentence
![]() $\varphi $
, we have
$\varphi $
, we have
![]() $\varphi ^{M^{\mathcal {U}}} = \varphi ^M$
, so that
$\varphi ^{M^{\mathcal {U}}} = \varphi ^M$
, so that
![]() $M^{\mathcal {U}} \equiv M$
.
$M^{\mathcal {U}} \equiv M$
.
The first claim says that the mapping
![]() $M \to M^{\mathcal {U}}$
given by
$M \to M^{\mathcal {U}}$
given by
![]() $x \mapsto \pi _{E,\mathcal {U}}(1 \otimes x)$
is an elementary embedding (see 3.5). The second claim about sentences is the special case where
$x \mapsto \pi _{E,\mathcal {U}}(1 \otimes x)$
is an elementary embedding (see 3.5). The second claim about sentences is the special case where
![]() $\varphi $
has no free variables (or
$\varphi $
has no free variables (or
![]() $n = 0$
). Note that by Theorem 3.18, the first claim can be rewritten as
$n = 0$
). Note that by Theorem 3.18, the first claim can be rewritten as
Hence, since we want to prove the proposition for all pure states, the claim is equivalent to
We will prove this in greater generality, allowing
![]() $\tau : M \to \mathbb {C}$
to be replaced by a conditional expectation onto a central subalgebra.
$\tau : M \to \mathbb {C}$
to be replaced by a conditional expectation onto a central subalgebra.
Proposition 3.21. Let M be a finite von Neumann algebra,
![]() $N \subseteq Z(M)$
be a subalgebra of its center,
$N \subseteq Z(M)$
be a subalgebra of its center,
![]() $E: M \to N$
be a normal, faithful, tracial conditional expectation, and A be an abelian von Neumann algebra. Let
$E: M \to N$
be a normal, faithful, tracial conditional expectation, and A be an abelian von Neumann algebra. Let
![]() $\tilde {M} = A \mathbin {\overline {\otimes }} M$
and
$\tilde {M} = A \mathbin {\overline {\otimes }} M$
and
![]() $\tilde {E}: \tilde {M} \to A \mathbin {\overline {\otimes }} N$
be given by
$\tilde {E}: \tilde {M} \to A \mathbin {\overline {\otimes }} N$
be given by
![]() $\tilde {E} = \mathrm {Id} \otimes E$
. Then for any sentence
$\tilde {E} = \mathrm {Id} \otimes E$
. Then for any sentence
![]() $\varphi $
,
$\varphi $
,
![]() $\varphi ^{\tilde {M}}_{\tilde {E}} = 1_A \otimes \varphi ^M_E$
.
$\varphi ^{\tilde {M}}_{\tilde {E}} = 1_A \otimes \varphi ^M_E$
.
For the sake of induction, we will actually prove an even more general statement. Proposition 3.21 corresponds to the case of Proposition 3.22 where the index set J is a singleton and the projection-valued measure is simply
![]() $1_A$
.
$1_A$
.
Proposition 3.22. Let M be a finite von Neumann algebra,
![]() $N \subseteq Z(M)$
be a subalgebra of its center,
$N \subseteq Z(M)$
be a subalgebra of its center,
![]() $E: M \to N$
be a normal, faithful, tracial conditional expectation, and A be an abelian von Neumann algebra. Let
$E: M \to N$
be a normal, faithful, tracial conditional expectation, and A be an abelian von Neumann algebra. Let
![]() $\tilde {M} = A \mathbin {\overline {\otimes }} M$
and
$\tilde {M} = A \mathbin {\overline {\otimes }} M$
and
![]() $\tilde {E}: \tilde {M} \to A \overline {\otimes } N$
be given by
$\tilde {E}: \tilde {M} \to A \overline {\otimes } N$
be given by
![]() $\tilde {E} = \operatorname {\mathrm {id}} \otimes E$
. Let
$\tilde {E} = \operatorname {\mathrm {id}} \otimes E$
. Let
![]() $\varphi $
be a formula with n free variables. Let
$\varphi $
be a formula with n free variables. Let
![]() $x_i = \sum _{j \in J} e_j \otimes m_{i,j}$
for each
$x_i = \sum _{j \in J} e_j \otimes m_{i,j}$
for each
![]() $i \leq n$
, where
$i \leq n$
, where
![]() $\{e_j\}_{j \in J}$
is a PVM over A and
$\{e_j\}_{j \in J}$
is a PVM over A and
![]() $m_{i,j} \in (M)_1$
for all
$m_{i,j} \in (M)_1$
for all
![]() $j \in J$
. Also, write
$j \in J$
. Also, write
![]() $\overline {m}_j = (m_{1,j},\dots ,m_{n,j})$
. Then
$\overline {m}_j = (m_{1,j},\dots ,m_{n,j})$
. Then
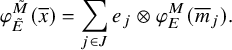 $$\begin{align*}\varphi^{\tilde{M}}_{\tilde{E}}(\overline{x}) = \sum_{j \in J} e_j \otimes \varphi^M_E(\overline{m}_j). \end{align*}$$
$$\begin{align*}\varphi^{\tilde{M}}_{\tilde{E}}(\overline{x}) = \sum_{j \in J} e_j \otimes \varphi^M_E(\overline{m}_j). \end{align*}$$
Proof. We proceed by induction on the complexity of the formula. As in the proof of Lemma 3.14, the cases for atomic formulae and adding connectives follows from the fact that
![]() $\tilde {M} \ni x \mapsto (e_j \otimes 1)x \in (e_j \otimes 1)\tilde {M}$
is a *-homomorphism. As before, the
$\tilde {M} \ni x \mapsto (e_j \otimes 1)x \in (e_j \otimes 1)\tilde {M}$
is a *-homomorphism. As before, the
![]() $\sup $
and
$\sup $
and
![]() $\inf $
cases are symmetrical, and so suppose that
$\inf $
cases are symmetrical, and so suppose that
![]() $\varphi (\overline {x}) = \sup _y \psi (\overline {x},y)$
where
$\varphi (\overline {x}) = \sup _y \psi (\overline {x},y)$
where
![]() $\psi $
satisfies the induction hypothesis.
$\psi $
satisfies the induction hypothesis.
Let
![]() $e_j$
,
$e_j$
,
![]() $m_{i,j}$
and
$m_{i,j}$
and
![]() $x_i$
be as in the theorem statement. Let
$x_i$
be as in the theorem statement. Let
![]() $\epsilon> 0$
. For each j, by Proposition 3.13, there exists
$\epsilon> 0$
. For each j, by Proposition 3.13, there exists
![]() $n_j$
such that
$n_j$
such that
Let
![]() $y = \sum _{j \in J} e_j \otimes n_j$
. Applying the induction hypothesis to
$y = \sum _{j \in J} e_j \otimes n_j$
. Applying the induction hypothesis to
![]() $\psi $
, we obtain
$\psi $
, we obtain
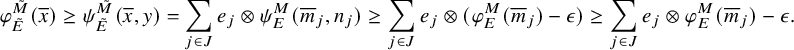 $$\begin{align*}\varphi_{\tilde{E}}^{\tilde{M}}(\overline{x}) \geq \psi_{\tilde{E}}^{\tilde{M}}(\overline{x},y) = \sum_{j \in J} e_j \otimes \psi_E^M(\overline{m}_j, n_j) \geq \sum_{j \in J} e_j \otimes (\varphi_E^M(\overline{m}_j) - \epsilon) \geq \sum_{j \in J} e_j \otimes \varphi_E^M(\overline{m}_j) - \epsilon. \end{align*}$$
$$\begin{align*}\varphi_{\tilde{E}}^{\tilde{M}}(\overline{x}) \geq \psi_{\tilde{E}}^{\tilde{M}}(\overline{x},y) = \sum_{j \in J} e_j \otimes \psi_E^M(\overline{m}_j, n_j) \geq \sum_{j \in J} e_j \otimes (\varphi_E^M(\overline{m}_j) - \epsilon) \geq \sum_{j \in J} e_j \otimes \varphi_E^M(\overline{m}_j) - \epsilon. \end{align*}$$
Therefore,
![]() $\varphi _{\tilde {E}}^{\tilde {M}}(\overline {x}) \geq \sum _{j \in J} e_j \otimes \varphi _E^M(\overline {m}_j)$
.
$\varphi _{\tilde {E}}^{\tilde {M}}(\overline {x}) \geq \sum _{j \in J} e_j \otimes \varphi _E^M(\overline {m}_j)$
.
In order to prove the reverse inequality, we start by considering y in certain a dense subset of
![]() $(\tilde {M})_1$
with respect to the strong-
$(\tilde {M})_1$
with respect to the strong-
![]() $*$
operator topology (SOT-
$*$
operator topology (SOT-
![]() $*$
). Let
$*$
). Let
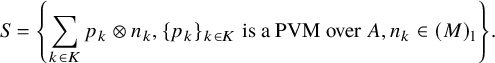 $$\begin{align*}S = \left\{\sum_{k \in K} p_k \otimes n_k, \{p_k\}_{k \in K}\textrm{ is a PVM over }A, n_k \in (M)_1 \right\}. \end{align*}$$
$$\begin{align*}S = \left\{\sum_{k \in K} p_k \otimes n_k, \{p_k\}_{k \in K}\textrm{ is a PVM over }A, n_k \in (M)_1 \right\}. \end{align*}$$
By the construction of tensor products and by the Kaplansky density theorem, S is dense in
![]() $(\tilde {M})_1$
. Suppose that
$(\tilde {M})_1$
. Suppose that
![]() $y = \sum _{k \in K} p_k \otimes n_k$
is in S. Then by the induction hypothesis applied to the partition
$y = \sum _{k \in K} p_k \otimes n_k$
is in S. Then by the induction hypothesis applied to the partition
![]() $(e_j p_k)_{j \in J, k \in K}$
, we have
$(e_j p_k)_{j \in J, k \in K}$
, we have
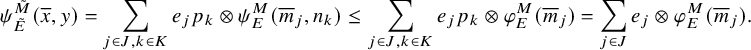 $$\begin{align*}\psi_{\tilde{E}}^{\tilde{M}}(\overline{x},y) = \sum_{j \in J, k \in K} e_j p_k \otimes \psi_E^M(\overline{m}_j,n_k) \leq \sum_{j \in J, k \in K} e_j p_k \otimes \varphi_E^M(\overline{m}_j) = \sum_{j \in J} e_j \otimes \varphi_E^M(\overline{m}_j). \end{align*}$$
$$\begin{align*}\psi_{\tilde{E}}^{\tilde{M}}(\overline{x},y) = \sum_{j \in J, k \in K} e_j p_k \otimes \psi_E^M(\overline{m}_j,n_k) \leq \sum_{j \in J, k \in K} e_j p_k \otimes \varphi_E^M(\overline{m}_j) = \sum_{j \in J} e_j \otimes \varphi_E^M(\overline{m}_j). \end{align*}$$
Next, suppose that y is a general element in
![]() $(\tilde {M})_1$
and write y as the limit of a net
$(\tilde {M})_1$
and write y as the limit of a net
![]() $y_i \in S$
. Since
$y_i \in S$
. Since
![]() $y_i \to y$
in SOT-
$y_i \to y$
in SOT-
![]() $*$
, we have that for every normal state
$*$
, we have that for every normal state
![]() $\tau $
on
$\tau $
on
![]() $A \overline {\otimes } N$
, we have
$A \overline {\otimes } N$
, we have
![]() ${\lVert {y_\ell - y}\rVert }_{2,\tau \circ \tilde {E}} \to 0$
. By Lemma 3.16, this implies that
${\lVert {y_\ell - y}\rVert }_{2,\tau \circ \tilde {E}} \to 0$
. By Lemma 3.16, this implies that
Therefore, since this holds for every normal state, we have
![]() $\psi _{\tilde {E}}^{\tilde {M}}(\overline {x},y_\ell ) \to \psi _{\tilde {E}}^{\tilde {M}}(\overline {x},y)$
. The preceding argument showed that
$\psi _{\tilde {E}}^{\tilde {M}}(\overline {x},y_\ell ) \to \psi _{\tilde {E}}^{\tilde {M}}(\overline {x},y)$
. The preceding argument showed that
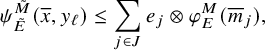 $$\begin{align*}\psi_{\tilde{E}}^{\tilde{M}}(\overline{x},y_\ell) \leq \sum_{j \in J} e_j \otimes \varphi_E^M(\overline{m}_j), \end{align*}$$
$$\begin{align*}\psi_{\tilde{E}}^{\tilde{M}}(\overline{x},y_\ell) \leq \sum_{j \in J} e_j \otimes \varphi_E^M(\overline{m}_j), \end{align*}$$
and therefore,
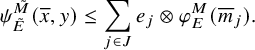 $$\begin{align*}\psi_{\tilde{E}}^{\tilde{M}}(\overline{x},y) \leq \sum_{j \in J} e_j \otimes \varphi_E^M(\overline{m}_j). \end{align*}$$
$$\begin{align*}\psi_{\tilde{E}}^{\tilde{M}}(\overline{x},y) \leq \sum_{j \in J} e_j \otimes \varphi_E^M(\overline{m}_j). \end{align*}$$
Since
![]() $y \in (\tilde {M})_1$
was arbitrary,
$y \in (\tilde {M})_1$
was arbitrary,
![]() $\varphi _{\tilde {E}}^{\tilde {M}}(\overline {x}) \leq \sum _{j \in J} e_j \otimes \varphi _E^M(\overline {m}_j)$
. We have now shown both inequalities so the proof is complete.
$\varphi _{\tilde {E}}^{\tilde {M}}(\overline {x}) \leq \sum _{j \in J} e_j \otimes \varphi _E^M(\overline {m}_j)$
. We have now shown both inequalities so the proof is complete.
This concludes the proof of Proposition 3.20 and so of Proposition C. This proposition allows the Keisler–Shelah characterization of elementary equivalence to be extended to ultrafilters on measure spaces. We recall the Keisler–Shelah theorem for ultraproducts on discrete index sets here.
Theorem 3.23 (Keisler–Shelah, see [Reference Ben Yaacov, Berenstein, Henson, Usvyatsov, Chatzidakis, Macpherson, Pillay and WilkieBBHU08, Theorem 5.7], [Reference Farah, Hart and ShermanFHS14b, Theorem 2.1(2)]).
![]() $(M, \tau _M) \equiv (N, \tau _N)$
iff there exists an index set I and an ultrafilter
$(M, \tau _M) \equiv (N, \tau _N)$
iff there exists an index set I and an ultrafilter
![]() $\mathcal {U}$
on I s.t.
$\mathcal {U}$
on I s.t.
![]() $(M,\tau _M)^{\mathcal {U}} \simeq (N,\tau _N)^{\mathcal {U}}$
.
$(M,\tau _M)^{\mathcal {U}} \simeq (N,\tau _N)^{\mathcal {U}}$
.
We now have the following corollary.
Corollary 3.24. Let
![]() $(M, \tau _M)$
and
$(M, \tau _M)$
and
![]() $(N, \tau _N)$
be two tracial von Neumann algebras. Then TFAE,
$(N, \tau _N)$
be two tracial von Neumann algebras. Then TFAE,
-
1.
 $(M, \tau _M) \equiv (N, \tau _N)$
;
$(M, \tau _M) \equiv (N, \tau _N)$
; -
2. There exists a character
 $\mathcal {U}$
on a commutative von Neumann algebra A s.t.
$\mathcal {U}$
on a commutative von Neumann algebra A s.t.
 $(M,\tau _M)^{\mathcal {U}} \simeq (N,\tau _N)^{\mathcal {U}}$
.
$(M,\tau _M)^{\mathcal {U}} \simeq (N,\tau _N)^{\mathcal {U}}$
.
Proof. (1)
![]() $\implies $
(2). If
$\implies $
(2). If
![]() $(M,\tau _M) \equiv (N,\tau _N)$
, then the Keisler-Shelah theorem implies that
$(M,\tau _M) \equiv (N,\tau _N)$
, then the Keisler-Shelah theorem implies that
![]() $M^{\mathcal {U}} \cong N^{\mathcal {U}}$
for some ultrafilter
$M^{\mathcal {U}} \cong N^{\mathcal {U}}$
for some ultrafilter
![]() $\mathcal {U}$
on a discrete index set (i.e., a pure state on
$\mathcal {U}$
on a discrete index set (i.e., a pure state on
![]() $\ell ^\infty (I)$
for some index set).
$\ell ^\infty (I)$
for some index set).
(2)
![]() $\implies $
(1). This follows from Proposition 3.20 and the transitivity of elementary equivalence.
$\implies $
(1). This follows from Proposition 3.20 and the transitivity of elementary equivalence.
4 Disintegration for elementary equivalence
The goal of this section is to prove Theorem A. It will become clear in the proof that the main case of interest is when the measure spaces are diffuse. In this case, we will see that the right perspective on this result is to look at the distribution of the theory
![]() $\mathrm {Th}(M_\omega )$
as a random variable with values in the space of theories of tracial factors (see [Reference Farah and GhasemiFG24, Definition 5.2]). The crux of the proof is to show that if
$\mathrm {Th}(M_\omega )$
as a random variable with values in the space of theories of tracial factors (see [Reference Farah and GhasemiFG24, Definition 5.2]). The crux of the proof is to show that if
![]() $M \equiv N$
, then the distribution of theories for M and N coincide.
$M \equiv N$
, then the distribution of theories for M and N coincide.
4.1 The distribution of theories
Suppose that M is a tracial von Neumann algebra,
![]() $N \subseteq Z(M)$
is a von Neumann subalgebra, and
$N \subseteq Z(M)$
is a von Neumann subalgebra, and
![]() $E: M \to N$
is the unique trace-preserving expectation. If
$E: M \to N$
is the unique trace-preserving expectation. If
![]() $\varphi $
is a sentence in the language of tracial von Neumann algebras, then
$\varphi $
is a sentence in the language of tracial von Neumann algebras, then
![]() $\varphi _E^M$
is an element of N. Since
$\varphi _E^M$
is an element of N. Since
![]() $(N,\tau |_N)$
is a commutative tracial von Neumann algebra, it is isomorphic to
$(N,\tau |_N)$
is a commutative tracial von Neumann algebra, it is isomorphic to
![]() $L^\infty (\Omega ,\mu )$
for some complete probability measure space. Thus,
$L^\infty (\Omega ,\mu )$
for some complete probability measure space. Thus,
![]() $\varphi _E^M$
can be regarded as a real random variable on
$\varphi _E^M$
can be regarded as a real random variable on
![]() $\Omega $
. Hence, it makes sense to speak of its probability distribution, which is its spectral measure on
$\Omega $
. Hence, it makes sense to speak of its probability distribution, which is its spectral measure on
![]() $\mathbb {R}$
with respect to the tracial state. More generally, we can consider the joint probability distribution of
$\mathbb {R}$
with respect to the tracial state. More generally, we can consider the joint probability distribution of
![]() $((\varphi _1)_E^M,\dots , (\varphi _k)_E^M)$
for several sentences
$((\varphi _1)_E^M,\dots , (\varphi _k)_E^M)$
for several sentences
![]() $\varphi _1$
, …,
$\varphi _1$
, …,
![]() $\varphi _k$
, which gives a probability measure on
$\varphi _k$
, which gives a probability measure on
![]() $\mathbb {R}^k$
. As a concrete example, recall that in the case that M is a direct integral over
$\mathbb {R}^k$
. As a concrete example, recall that in the case that M is a direct integral over
![]() $N = L^\infty (\Omega ,\mu )$
, then
$N = L^\infty (\Omega ,\mu )$
, then
![]() $\varphi _E^M$
coincides with the measurable function
$\varphi _E^M$
coincides with the measurable function
![]() $\omega \mapsto \varphi ^{M_\omega }$
. Thus, the elements
$\omega \mapsto \varphi ^{M_\omega }$
. Thus, the elements
![]() $((\varphi _1)_E^M,\dots , (\varphi _k)_E^M)$
are simply random variables on the underlying probability space for the direct integral.
$((\varphi _1)_E^M,\dots , (\varphi _k)_E^M)$
are simply random variables on the underlying probability space for the direct integral.
We actually want to consider the joint distribution of all sentences together, or equivalently, instead of looking at random variables in
![]() $\mathbb {R}^k$
, we want to look at random variables taking values in the space of theories of tracial von Neumann algebras. Recall from Definition 3.7 that
$\mathbb {R}^k$
, we want to look at random variables taking values in the space of theories of tracial von Neumann algebras. Recall from Definition 3.7 that
![]() $\mathcal {P}_\varnothing $
is the real
$\mathcal {P}_\varnothing $
is the real
![]() $\mathrm {C}^*$
-algebra obtained as the separation-completion of the algebra of sentences with respect to
$\mathrm {C}^*$
-algebra obtained as the separation-completion of the algebra of sentences with respect to
![]() ${\lVert {\cdot }\rVert }_u$
. We showed in Proposition 3.9 that theories of tracial von Neumann algebras are in bijection with characters on
${\lVert {\cdot }\rVert }_u$
. We showed in Proposition 3.9 that theories of tracial von Neumann algebras are in bijection with characters on
![]() $\mathcal {P}_{\varnothing }$
. Let
$\mathcal {P}_{\varnothing }$
. Let
![]() $\operatorname {\mathrm {Spec}}(\mathcal {P}_{\varnothing })$
be the space of characters, that is, the Gelfand spectrum, of
$\operatorname {\mathrm {Spec}}(\mathcal {P}_{\varnothing })$
be the space of characters, that is, the Gelfand spectrum, of
![]() $\mathcal {P}_{\varnothing }$
, equipped with the weak-
$\mathcal {P}_{\varnothing }$
, equipped with the weak-
![]() $*$
topology, so that
$*$
topology, so that
![]() $\mathcal {P}_{\varnothing } \cong C(\operatorname {\mathrm {Spec}}(\mathcal {P}_{\varnothing });\mathbb {R})$
. Given
$\mathcal {P}_{\varnothing } \cong C(\operatorname {\mathrm {Spec}}(\mathcal {P}_{\varnothing });\mathbb {R})$
. Given
![]() $N \subseteq M$
as above, there is a
$N \subseteq M$
as above, there is a
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\operatorname {\mathrm {ev}}_E^M: \mathcal {P}_{\varnothing } \to N$
given by
$\operatorname {\mathrm {ev}}_E^M: \mathcal {P}_{\varnothing } \to N$
given by
![]() $\varphi \mapsto \varphi _E^M$
for sentences (see Remark 3.19). Hence,
$\varphi \mapsto \varphi _E^M$
for sentences (see Remark 3.19). Hence,
![]() $\tau _N \circ \operatorname {\mathrm {ev}}_E^M$
is a state on
$\tau _N \circ \operatorname {\mathrm {ev}}_E^M$
is a state on
![]() $\mathcal {P}_{\varnothing }$
or, equivalently, a probability measure on
$\mathcal {P}_{\varnothing }$
or, equivalently, a probability measure on
![]() $\operatorname {\mathrm {Spec}}(\mathcal {P}_{\varnothing })$
, which is the distribution that we seek.
$\operatorname {\mathrm {Spec}}(\mathcal {P}_{\varnothing })$
, which is the distribution that we seek.
Definition 4.1 (Distribution of theories).
We denote by
![]() $\mathbb {T}_{\operatorname {\mathrm {tr}}} = \operatorname {\mathrm {Spec}}(\mathcal {P}_{\varnothing })$
the space of theories of tracial von Neumann algebras with the weak-
$\mathbb {T}_{\operatorname {\mathrm {tr}}} = \operatorname {\mathrm {Spec}}(\mathcal {P}_{\varnothing })$
the space of theories of tracial von Neumann algebras with the weak-
![]() $*$
topology. Given a tracial von Neumann algebra
$*$
topology. Given a tracial von Neumann algebra
![]() $(M,\tau )$
and
$(M,\tau )$
and
![]() $N \subseteq Z(M)$
, let
$N \subseteq Z(M)$
, let
![]() $E: M \to N$
be the unique trace-preserving conditional expectation. Let
$E: M \to N$
be the unique trace-preserving conditional expectation. Let
![]() $\operatorname {\mathrm {ev}}_E^M: \mathcal {P}_{\varnothing } \to N$
be the unique
$\operatorname {\mathrm {ev}}_E^M: \mathcal {P}_{\varnothing } \to N$
be the unique
![]() $*$
-homomorphism given by
$*$
-homomorphism given by
![]() $\varphi \mapsto \varphi _E^M$
on sentences (see Remark 3.19). The distribution of theories for M over N is the probability measure on
$\varphi \mapsto \varphi _E^M$
on sentences (see Remark 3.19). The distribution of theories for M over N is the probability measure on
![]() $\mathbb {T}_{\operatorname {\mathrm {tr}}}$
corresponding to the state
$\mathbb {T}_{\operatorname {\mathrm {tr}}}$
corresponding to the state
![]() $\tau |_N \circ \operatorname {\mathrm {ev}}_E^M$
on
$\tau |_N \circ \operatorname {\mathrm {ev}}_E^M$
on
![]() $\mathcal {P}_{\varnothing }$
.
$\mathcal {P}_{\varnothing }$
.
In the case that
![]() $N = Z(M)$
and E is the center-valued trace, then we call this probability measure simply the distribution of theories for M.
$N = Z(M)$
and E is the center-valued trace, then we call this probability measure simply the distribution of theories for M.
A more measure-theoretic description of the distribution of theories can be found in Farah and Ghasemi’s paper [Reference Farah and GhasemiFG24, Definition 5.2]. As one would expect, in the case of direct integrals, this can be formulated more concretely.
Lemma 4.2. Suppose
![]() $(M,\tau ) = \int _{\Omega }^{\oplus } (M_\omega ,\tau _\omega )$
is a direct integral of separable tracial von Neumann algebras. Then
$(M,\tau ) = \int _{\Omega }^{\oplus } (M_\omega ,\tau _\omega )$
is a direct integral of separable tracial von Neumann algebras. Then
![]() $\omega \mapsto \operatorname {\mathrm {Th}}(M_\omega ,\tau _\omega )$
is a random variable taking values in
$\omega \mapsto \operatorname {\mathrm {Th}}(M_\omega ,\tau _\omega )$
is a random variable taking values in
![]() $\mathbb {T}_{\operatorname {\mathrm {tr}}}$
, and the distribution of theories for M over N is the distribution of this random variable.
$\mathbb {T}_{\operatorname {\mathrm {tr}}}$
, and the distribution of theories for M over N is the distribution of this random variable.
Proof. First, to see why
![]() $\operatorname {\mathrm {Th}}(M_\omega ,\tau _\omega )$
is a measurable function, it suffices to show that each open set is measurable. Recall that
$\operatorname {\mathrm {Th}}(M_\omega ,\tau _\omega )$
is a measurable function, it suffices to show that each open set is measurable. Recall that
![]() $\mathbb {T}_{\operatorname {\mathrm {tr}}}$
is separable and metrizable, and the topology is generated by the continuous functions given by elements of
$\mathbb {T}_{\operatorname {\mathrm {tr}}}$
is separable and metrizable, and the topology is generated by the continuous functions given by elements of
![]() $\mathcal {P}_{\varnothing }$
, so it suffices to check that
$\mathcal {P}_{\varnothing }$
, so it suffices to check that
![]() $\omega \mapsto \operatorname {\mathrm {Th}}(M_\omega ,\tau _\omega )[\varphi ]$
is measurable for each
$\omega \mapsto \operatorname {\mathrm {Th}}(M_\omega ,\tau _\omega )[\varphi ]$
is measurable for each
![]() $\varphi \in \mathcal {P}_{\varnothing }$
. Since formulas give a dense subset of
$\varphi \in \mathcal {P}_{\varnothing }$
. Since formulas give a dense subset of
![]() $\mathcal {P}_{\varnothing }$
, it suffices to check measurability for formulas, which follows Lemma 3.17.
$\mathcal {P}_{\varnothing }$
, it suffices to check measurability for formulas, which follows Lemma 3.17.
Next, to show that the distribution of
![]() $\omega \mapsto \operatorname {\mathrm {Th}}(M_\omega ,\tau _\omega )$
agrees with the abstract distribution of theories, it suffices to check that both measures agree when integrated against any continuous function on
$\omega \mapsto \operatorname {\mathrm {Th}}(M_\omega ,\tau _\omega )$
agrees with the abstract distribution of theories, it suffices to check that both measures agree when integrated against any continuous function on
![]() $\mathbb {T}_{\operatorname {\mathrm {tr}}}$
. By Lemma 3.17, for a sentence
$\mathbb {T}_{\operatorname {\mathrm {tr}}}$
. By Lemma 3.17, for a sentence
![]() $\varphi $
, we have
$\varphi $
, we have
By density, this extends to all functions in
![]() $\mathcal {P}_{\varnothing } = C(\mathbb {T}_{\operatorname {\mathrm {tr}}};\mathbb {R})$
, so the claim is proved.
$\mathcal {P}_{\varnothing } = C(\mathbb {T}_{\operatorname {\mathrm {tr}}};\mathbb {R})$
, so the claim is proved.
In order to prove that the distribution of theories is preserved by elementary equivalence, we first show the following. The proof can be thought of as a generalization of the method for Corollary B.
Proposition 4.3. Let
![]() $(M, \tau )$
be a tracial von Neumann algebra, and let N be a von Neumann subalgebra of its center. Let
$(M, \tau )$
be a tracial von Neumann algebra, and let N be a von Neumann subalgebra of its center. Let
![]() $\mathcal {U}$
be a character on a commutative von Neumann algebra A, and consider the generalized ultrapowers
$\mathcal {U}$
be a character on a commutative von Neumann algebra A, and consider the generalized ultrapowers
![]() $N^{\mathcal {U}} \subseteq M^{\mathcal {U}}$
. Then the distribution of theories for M over N is the same as the distribution of theories for
$N^{\mathcal {U}} \subseteq M^{\mathcal {U}}$
. Then the distribution of theories for M over N is the same as the distribution of theories for
![]() $M^{\mathcal {U}}$
over
$M^{\mathcal {U}}$
over
![]() $N^{\mathcal {U}}$
. In particular, the distribution of theories for M over
$N^{\mathcal {U}}$
. In particular, the distribution of theories for M over
![]() $Z(M)$
is the same as that for
$Z(M)$
is the same as that for
![]() $M^{\mathcal {U}}$
over
$M^{\mathcal {U}}$
over
![]() $Z(M^{\mathcal {U}})$
.
$Z(M^{\mathcal {U}})$
.
Proof. Let q denote the natural quotient map
![]() $q: A \overline {\otimes } M \to M^{\mathcal {U}}$
. Note that the trace
$q: A \overline {\otimes } M \to M^{\mathcal {U}}$
. Note that the trace
![]() $\mathcal {U} \circ (\operatorname {\mathrm {id}}_A \otimes \tau )$
on
$\mathcal {U} \circ (\operatorname {\mathrm {id}}_A \otimes \tau )$
on
![]() $A \overline {\otimes } M$
restricts on
$A \overline {\otimes } M$
restricts on
![]() $A \overline {\otimes } N$
to the trace
$A \overline {\otimes } N$
to the trace
![]() $\mathcal {U} \circ (\operatorname {\mathrm {id}}_A \otimes \tau |_N)$
, and hence, we have a natural trace-preserving embedding
$\mathcal {U} \circ (\operatorname {\mathrm {id}}_A \otimes \tau |_N)$
, and hence, we have a natural trace-preserving embedding
![]() $N^{\mathcal {U}} \to M^{\mathcal {U}}$
. Furthermore, letting
$N^{\mathcal {U}} \to M^{\mathcal {U}}$
. Furthermore, letting
![]() $\tilde {E}: M^{\mathcal {U}} \to N^{\mathcal {U}}$
be the unique trace-preserving conditional expectation, we have
$\tilde {E}: M^{\mathcal {U}} \to N^{\mathcal {U}}$
be the unique trace-preserving conditional expectation, we have
Indeed, for each
![]() $x \in A \overline {\otimes } M$
,
$x \in A \overline {\otimes } M$
,
![]() $(\operatorname {\mathrm {id}}_A \otimes E)(x)$
is an element in
$(\operatorname {\mathrm {id}}_A \otimes E)(x)$
is an element in
![]() $A \overline {\otimes } N$
satisfying
$A \overline {\otimes } N$
satisfying
By applying
![]() $\mathcal {U}$
to both sides, we see that
$\mathcal {U}$
to both sides, we see that
![]() $q((\operatorname {\mathrm {id}}_A \otimes E)(x))$
is an element in
$q((\operatorname {\mathrm {id}}_A \otimes E)(x))$
is an element in
![]() $N^{\mathcal {U}}$
with the same inner product as
$N^{\mathcal {U}}$
with the same inner product as
![]() $q(x)$
with every element of
$q(x)$
with every element of
![]() $N^{\mathcal {U}}$
.
$N^{\mathcal {U}}$
.
Let
![]() $\mathcal {V}$
be a character on
$\mathcal {V}$
be a character on
![]() $N^{\mathcal {U}}$
. We claim that
$N^{\mathcal {U}}$
. We claim that
![]() $(M^{\mathcal {U}})^{/\tilde {E}, \mathcal {V}} \cong (A \mathbin {\overline {\otimes }} M)^{/\operatorname {\mathrm {id}}_A \otimes E, \mathcal {V} \circ q}$
. Indeed,
$(M^{\mathcal {U}})^{/\tilde {E}, \mathcal {V}} \cong (A \mathbin {\overline {\otimes }} M)^{/\operatorname {\mathrm {id}}_A \otimes E, \mathcal {V} \circ q}$
. Indeed,
![]() $(A \overline {\otimes } M)^{/\operatorname {\mathrm {id}}_A \otimes E,\mathcal {V} \circ q}$
is obtained by quotienting
$(A \overline {\otimes } M)^{/\operatorname {\mathrm {id}}_A \otimes E,\mathcal {V} \circ q}$
is obtained by quotienting
![]() $A \overline {\otimes } M$
by the ideal
$A \overline {\otimes } M$
by the ideal
![]() $\{x: \mathcal {V} \circ q \circ (\operatorname {\mathrm {id}}_A \otimes E)(x^*x) = 0\}$
. Meanwhile,
$\{x: \mathcal {V} \circ q \circ (\operatorname {\mathrm {id}}_A \otimes E)(x^*x) = 0\}$
. Meanwhile,
![]() $(M^{\mathcal {U}})^{/\tilde {E}, \mathcal {V}}$
is obtained by quotienting out the ideal
$(M^{\mathcal {U}})^{/\tilde {E}, \mathcal {V}}$
is obtained by quotienting out the ideal
![]() $\{x: \mathcal {U} \circ (\operatorname {\mathrm {id}}_A \otimes \tau )(x^*x) = 0\}$
, and then further quotienting by
$\{x: \mathcal {U} \circ (\operatorname {\mathrm {id}}_A \otimes \tau )(x^*x) = 0\}$
, and then further quotienting by
![]() $\{y \in M^{\mathcal {U}}: \mathcal {V} \circ \tilde {E}(y^*y) = 0\}$
. But by the first paragraph,
$\{y \in M^{\mathcal {U}}: \mathcal {V} \circ \tilde {E}(y^*y) = 0\}$
. But by the first paragraph,
![]() $\mathcal {V} \circ \tilde {E} \circ q = \mathcal {V} \circ q \circ (\operatorname {\mathrm {id}}_A \otimes E)$
, and hence, these two quotients are the same.
$\mathcal {V} \circ \tilde {E} \circ q = \mathcal {V} \circ q \circ (\operatorname {\mathrm {id}}_A \otimes E)$
, and hence, these two quotients are the same.
By Theorem 3.18, for every sentence
![]() $\varphi $
,
$\varphi $
,
Since
![]() $\mathcal {V}$
was an arbitrary pure state,
$\mathcal {V}$
was an arbitrary pure state,
By Proposition 3.21,
Therefore,
or in other words,
![]() $\varphi _{\tilde {E}}^{M^{\mathcal {U}}}$
equals the image of
$\varphi _{\tilde {E}}^{M^{\mathcal {U}}}$
equals the image of
![]() $\varphi _E^M$
under the diagonal embedding
$\varphi _E^M$
under the diagonal embedding
![]() $N \to N^{\mathcal {U}}$
. Since the diagonal embedding is trace-preserving, we have
$N \to N^{\mathcal {U}}$
. Since the diagonal embedding is trace-preserving, we have
Since this holds for all sentences
![]() $\varphi $
, we have proved that the distributions of theories agree.
$\varphi $
, we have proved that the distributions of theories agree.
Next, consider the second claim regarding the case where
![]() $N = Z(M)$
. By Proposition 2.8,
$N = Z(M)$
. By Proposition 2.8,
![]() $Z(M^{\mathcal {U}}) = Z(M)^{\mathcal {U}}$
, so this follows from the first claim.
$Z(M^{\mathcal {U}}) = Z(M)^{\mathcal {U}}$
, so this follows from the first claim.
Corollary 4.4. Let
![]() $(M, \tau _M)$
and
$(M, \tau _M)$
and
![]() $(N, \tau _N)$
be elementarily equivalent tracial von Neumann algebras. Then their distributions of theories coincide.
$(N, \tau _N)$
be elementarily equivalent tracial von Neumann algebras. Then their distributions of theories coincide.
Proof. By the Keisler-Shelah theorem (Theorem 3.23), there exists some ultrafilter such that
![]() $M^{\mathcal {U}} \cong N^{\mathcal {U}}$
, which of course implies that
$M^{\mathcal {U}} \cong N^{\mathcal {U}}$
, which of course implies that
![]() $M^{\mathcal {U}}$
and
$M^{\mathcal {U}}$
and
![]() $N^{\mathcal {U}}$
have the same distribution of theories. By Proposition 4.3, M and
$N^{\mathcal {U}}$
have the same distribution of theories. By Proposition 4.3, M and
![]() $M^{\mathcal {U}}$
have the same distribution of theories, and N and
$M^{\mathcal {U}}$
have the same distribution of theories, and N and
![]() $N^{\mathcal {U}}$
have the same distribution of theories. Hence, M and N have the same distribution of theories.
$N^{\mathcal {U}}$
have the same distribution of theories. Hence, M and N have the same distribution of theories.
4.2 Proof of Theorem A
First, we recall some measure theory background needed to create a measurable isomorphism that will exhibit fiberwise elementary equivalence. Recall that a standard Borel space is a measurable space isomorphic to a complete separable metric space equipped with its Borel
![]() $\sigma $
-algebra. Any two such spaces, if they have no atoms, are Borel-isomorphic, so that we can always assume without loss of generality that we are working on
$\sigma $
-algebra. Any two such spaces, if they have no atoms, are Borel-isomorphic, so that we can always assume without loss of generality that we are working on
![]() $[0,1]$
with its Borel
$[0,1]$
with its Borel
![]() $\sigma $
-algebra.
$\sigma $
-algebra.
Theorem 4.5 (Rokhlin disintegration theorem).
Let
![]() $\mu $
be a Borel measure on
$\mu $
be a Borel measure on
![]() $[0,1] \times [0,1]$
. Let
$[0,1] \times [0,1]$
. Let
![]() $\mu _1$
be the pushforward of
$\mu _1$
be the pushforward of
![]() $\mu $
under the first coordinate projection. Then there exists a family of probability measures
$\mu $
under the first coordinate projection. Then there exists a family of probability measures
![]() $(\nu _x)_{x \in [0,1]}$
such that
$(\nu _x)_{x \in [0,1]}$
such that
-
• For each Borel
 $A \subseteq [0,1]$
,
$A \subseteq [0,1]$
,
 $x \mapsto \nu _x(A)$
is Borel-measurable.
$x \mapsto \nu _x(A)$
is Borel-measurable. -
• For each Borel set A, let
 $A_x = \{y \in [0,1]: (x,y) \in A\}$
. Then
$A_x = \{y \in [0,1]: (x,y) \in A\}$
. Then
 $A_x$
is Borel measurable and
$A_x$
is Borel measurable and  $$\begin{align*}\mu(A) = \int_{[0,1]} \nu_x(A_x)\,d\mu_1(x). \end{align*}$$
$$\begin{align*}\mu(A) = \int_{[0,1]} \nu_x(A_x)\,d\mu_1(x). \end{align*}$$
One can easily obtain the following equivalent notions of a probability space having ‘diffuse fibers’ relative to a given random variable X. This result could also be deduced from certain versions of the spectral theorem or from direct integral decompositions of von Neumann algebras, but we prefer to give a more self-contained proof. Note that condition (3) is exactly the stability under tensorization assumed in Theorem A.
Lemma 4.6. Consider
![]() $[0,1]$
with Lebesgue measure. Let X be any Borel random variable
$[0,1]$
with Lebesgue measure. Let X be any Borel random variable
![]() $[0,1] \to [0,1]$
and let Y be the identity function
$[0,1] \to [0,1]$
and let Y be the identity function
![]() $[0,1] \to [0,1]$
. Let
$[0,1] \to [0,1]$
. Let
![]() $\mu _X \in \mathcal {P}([0,1])$
be the distribution of X – that is, the pushforward of Lebesgue measure by the function X. Similarly, let
$\mu _X \in \mathcal {P}([0,1])$
be the distribution of X – that is, the pushforward of Lebesgue measure by the function X. Similarly, let
![]() $\mu _{X,Y} \in \mathcal {P}([0,1] \times [0,1])$
be the distribution of
$\mu _{X,Y} \in \mathcal {P}([0,1] \times [0,1])$
be the distribution of
![]() $(X,Y)$
, or the pushforward Lebesgue measure under
$(X,Y)$
, or the pushforward Lebesgue measure under
![]() $(X,Y)$
. Let
$(X,Y)$
. Let
![]() $\pi _1, \pi _2: [0,1] \times [0,1] \to [0,1]$
denote the coordinate projections. The following are equivalent:
$\pi _1, \pi _2: [0,1] \times [0,1] \to [0,1]$
denote the coordinate projections. The following are equivalent:
-
1. For
 $\mu _X$
-almost every x, the measure
$\mu _X$
-almost every x, the measure
 $\nu _x$
in the disintegration for
$\nu _x$
in the disintegration for
 $\mu _{X,Y}$
from Theorem 4.5 has no atoms.
$\mu _{X,Y}$
from Theorem 4.5 has no atoms. -
2. There exists an isomorphism of measure spaces
 $\Phi : ([0,1],\operatorname {\mathrm {Leb}}) \to ([0,1],\mu _X) \times ([0,1],\operatorname {\mathrm {Leb}})$
such that
$\Phi : ([0,1],\operatorname {\mathrm {Leb}}) \to ([0,1],\mu _X) \times ([0,1],\operatorname {\mathrm {Leb}})$
such that
 $X = \pi _1 \circ \Phi $
.
$X = \pi _1 \circ \Phi $
. -
3. There exists an isomorphism of measure spaces
 $\Psi : ([0,1],\operatorname {\mathrm {Leb}}) \to ([0,1],\operatorname {\mathrm {Leb}}) \times ([0,1],\operatorname {\mathrm {Leb}})$
such that
$\Psi : ([0,1],\operatorname {\mathrm {Leb}}) \to ([0,1],\operatorname {\mathrm {Leb}}) \times ([0,1],\operatorname {\mathrm {Leb}})$
such that
 $X = X \circ \pi _1 \circ \Psi $
.
$X = X \circ \pi _1 \circ \Psi $
. -
4. There exists an isomorphism of measure spaces
 $\Psi : ([0,1],\operatorname {\mathrm {Leb}}) \to ([0,1],\operatorname {\mathrm {Leb}}) \times ([0,1],\operatorname {\mathrm {Leb}})$
and a random variable Z such that
$\Psi : ([0,1],\operatorname {\mathrm {Leb}}) \to ([0,1],\operatorname {\mathrm {Leb}}) \times ([0,1],\operatorname {\mathrm {Leb}})$
and a random variable Z such that
 $X = Z \circ \pi _1 \circ \Psi $
.
$X = Z \circ \pi _1 \circ \Psi $
. -
5. There exists a sequence of random variables
 $Z_n: [0,1] \to \{-1,1\}$
such that for all random variables
$Z_n: [0,1] \to \{-1,1\}$
such that for all random variables
 $W: [0,1] \to [0,1]$
, we have
$W: [0,1] \to [0,1]$
, we have
 ${\lVert {E[Z_n W \mid X]}\rVert }_{L^2} \to 0$
.
${\lVert {E[Z_n W \mid X]}\rVert }_{L^2} \to 0$
.
Proof. (1)
![]() $\implies $
(2). Note that
$\implies $
(2). Note that
![]() $([0,1],\operatorname {\mathrm {Leb}})$
is isomorphic to
$([0,1],\operatorname {\mathrm {Leb}})$
is isomorphic to
![]() $([0,1] \times [0,1], \mu _{X,Y})$
as a measure space since
$([0,1] \times [0,1], \mu _{X,Y})$
as a measure space since
![]() $(X,Y)$
generate the entire Borel
$(X,Y)$
generate the entire Borel
![]() $\sigma $
-algebra on
$\sigma $
-algebra on
![]() $[0,1]$
. Hence, it suffices to produce an isomorphism
$[0,1]$
. Hence, it suffices to produce an isomorphism
![]() $([0,1] \times [0,1], \mu _{X,Y}) \to ([0,1],\mu _X) \times ([0,1],\operatorname {\mathrm {Leb}})$
that preserves the first coordinate.
$([0,1] \times [0,1], \mu _{X,Y}) \to ([0,1],\mu _X) \times ([0,1],\operatorname {\mathrm {Leb}})$
that preserves the first coordinate.
Let
![]() $F_{\nu _x}: [0,1] \to [0,1]$
be the cumulative distribution function of
$F_{\nu _x}: [0,1] \to [0,1]$
be the cumulative distribution function of
![]() $\nu _x$
– that is,
$\nu _x$
– that is,
![]() $F_{\nu _x}(y) = \nu _x([0,y])$
. Since
$F_{\nu _x}(y) = \nu _x([0,y])$
. Since
![]() $\nu _x$
has no atoms,
$\nu _x$
has no atoms,
![]() $F_{\nu _x}$
is continuous. Since
$F_{\nu _x}$
is continuous. Since
![]() $F_{\nu _x}$
is an increasing surjective continuous function
$F_{\nu _x}$
is an increasing surjective continuous function
![]() $[0,1] \to [0,1]$
, there is a unique strictly increasing, right-continuous function
$[0,1] \to [0,1]$
, there is a unique strictly increasing, right-continuous function
![]() $G_x: [0,1] \to [0,1]$
such that
$G_x: [0,1] \to [0,1]$
such that
![]() $F_{\nu _x} \circ G_x = \operatorname {\mathrm {id}}$
. Let
$F_{\nu _x} \circ G_x = \operatorname {\mathrm {id}}$
. Let
![]() $F(x,y) = F_{\nu _x}(y)$
and let
$F(x,y) = F_{\nu _x}(y)$
and let
![]() $G(x,y) = G_x(y)$
. We claim that F and G are Borel-measurable. Indeed, note that
$G(x,y) = G_x(y)$
. We claim that F and G are Borel-measurable. Indeed, note that
which is Borel-measurable by the properties of the disintegration. However,
which is Borel-measurable since F is Borel-measurable. Note that
![]() $(F_{\nu _x})_* \nu _x = \operatorname {\mathrm {Leb}}$
since
$(F_{\nu _x})_* \nu _x = \operatorname {\mathrm {Leb}}$
since
![]() $(F_{\nu _x})_* \nu _x([0,t]) = \nu _x(F_{\nu _x}^{-1}([0,t])) = \nu _x([0,G_x(t)]) = F_{\nu _x}(G_x(t)) = t$
.
$(F_{\nu _x})_* \nu _x([0,t]) = \nu _x(F_{\nu _x}^{-1}([0,t])) = \nu _x([0,G_x(t)]) = F_{\nu _x}(G_x(t)) = t$
.
Now let
![]() $\tilde {F}(x,y) = (x, F(x,y))$
and
$\tilde {F}(x,y) = (x, F(x,y))$
and
![]() $\tilde {G}(x,y) = (x,G(x,y))$
. Note that
$\tilde {G}(x,y) = (x,G(x,y))$
. Note that
![]() $F(x,G(x,y)) = y$
by construction, and
$F(x,G(x,y)) = y$
by construction, and
![]() $\mu _{X,Y}$
-almost everywhere we have
$\mu _{X,Y}$
-almost everywhere we have
![]() $G(x,F(x,y)) = y$
since the set of jump discontinuities of
$G(x,F(x,y)) = y$
since the set of jump discontinuities of
![]() $G_x$
has measure zero, and hence,
$G_x$
has measure zero, and hence,
![]() $\tilde {F}$
and
$\tilde {F}$
and
![]() $\tilde {G}$
are inverses of each other almost everywhere. Moreover,
$\tilde {G}$
are inverses of each other almost everywhere. Moreover,
![]() $\tilde {F}_* \mu _{X,Y} = \mu _X \times \operatorname {\mathrm {Leb}}$
because using the disintegration theorem, for
$\tilde {F}_* \mu _{X,Y} = \mu _X \times \operatorname {\mathrm {Leb}}$
because using the disintegration theorem, for
![]() $h \in C([0,1] \times [0,1])$
,
$h \in C([0,1] \times [0,1])$
,
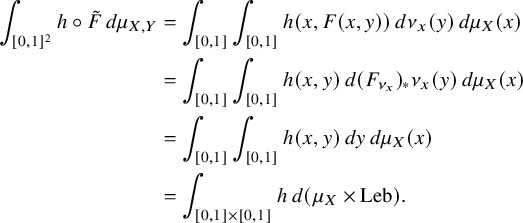 $$ \begin{align*} \int_{[0,1]^2} h \circ \tilde{F}\,d\mu_{X,Y} &= \int_{[0,1]} \int_{[0,1]} h(x,F(x,y))\,d\nu_x(y)\,d\mu_X(x) \\ &= \int_{[0,1]} \int_{[0,1]} h(x,y) \,d(F_{\nu_x})_*\nu_x(y)\,d\mu_X(x) \\ &= \int_{[0,1]} \int_{[0,1]} h(x,y)\,dy\,d\mu_X(x) \\ &= \int_{[0,1] \times [0,1]} h\,d(\mu_X \times \operatorname{\mathrm{Leb}}). \end{align*} $$
$$ \begin{align*} \int_{[0,1]^2} h \circ \tilde{F}\,d\mu_{X,Y} &= \int_{[0,1]} \int_{[0,1]} h(x,F(x,y))\,d\nu_x(y)\,d\mu_X(x) \\ &= \int_{[0,1]} \int_{[0,1]} h(x,y) \,d(F_{\nu_x})_*\nu_x(y)\,d\mu_X(x) \\ &= \int_{[0,1]} \int_{[0,1]} h(x,y)\,dy\,d\mu_X(x) \\ &= \int_{[0,1] \times [0,1]} h\,d(\mu_X \times \operatorname{\mathrm{Leb}}). \end{align*} $$
(2)
![]() $\implies $
(3). Let
$\implies $
(3). Let
![]() $\Phi $
be as in (2). Let
$\Phi $
be as in (2). Let
![]() $\Gamma : [0,1] \to [0,1] \times [0,1]$
be any isomorphism of measure spaces (for instance, one can take
$\Gamma : [0,1] \to [0,1] \times [0,1]$
be any isomorphism of measure spaces (for instance, one can take
![]() $\Gamma = \Phi $
). Then let
$\Gamma = \Phi $
). Then let
![]() $\Psi = (\Phi ^{-1} \times \operatorname {\mathrm {id}}_{[0,1]}) \circ (\operatorname {\mathrm {id}}_{[0,1]} \times \Gamma ) \circ \Phi $
. We leave the verification to the reader.
$\Psi = (\Phi ^{-1} \times \operatorname {\mathrm {id}}_{[0,1]}) \circ (\operatorname {\mathrm {id}}_{[0,1]} \times \Gamma ) \circ \Phi $
. We leave the verification to the reader.
(3)
![]() $\implies $
(4). This is immediate.
$\implies $
(4). This is immediate.
(4)
![]() $\implies $
(5). Let
$\implies $
(5). Let
![]() $\Psi $
be as in (4), and let
$\Psi $
be as in (4), and let
![]() $\tilde {X} = X \circ \pi _1 \circ \Psi $
. We can use the maps
$\tilde {X} = X \circ \pi _1 \circ \Psi $
. We can use the maps
![]() $\Psi $
and
$\Psi $
and
![]() $\Psi ^{-1}$
to transform between random variables on
$\Psi ^{-1}$
to transform between random variables on
![]() $[0,1] \times [0,1]$
and
$[0,1] \times [0,1]$
and
![]() $[0,1]$
; hence, it suffices to show that there are random variables
$[0,1]$
; hence, it suffices to show that there are random variables
![]() $Z_n: [0,1] \times [0,1] \to \{-1,1\}$
, such that for all random variables
$Z_n: [0,1] \times [0,1] \to \{-1,1\}$
, such that for all random variables
![]() $W: [0,1] \times [0,1] \to [0,1]$
, we have
$W: [0,1] \times [0,1] \to [0,1]$
, we have
![]() ${\lVert {E[Z_n W \mid \tilde {X}]} \rVert }_{L^2} \to 0$
. Let
${\lVert {E[Z_n W \mid \tilde {X}]} \rVert }_{L^2} \to 0$
. Let
![]() $f_n: [0,1] \to \{-1,1\}$
be a function that alternates between
$f_n: [0,1] \to \{-1,1\}$
be a function that alternates between
![]() $\pm 1$
on intervals of length
$\pm 1$
on intervals of length
![]() $2^{-n}$
. Let
$2^{-n}$
. Let
![]() $Z_n = f_n \circ \pi _2$
. Given Borel
$Z_n = f_n \circ \pi _2$
. Given Borel
![]() $W_1$
,
$W_1$
,
![]() $W_2: [0,1] \to \mathbb {R}$
, consider the tensor product
$W_2: [0,1] \to \mathbb {R}$
, consider the tensor product
![]() $W_1 \otimes W_2$
on
$W_1 \otimes W_2$
on
![]() $[0,1] \times [0,1]$
. Then
$[0,1] \times [0,1]$
. Then
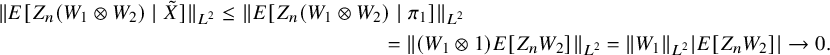 $$ \begin{align*} {\lVert{E[Z_n (W_1 \otimes W_2) \mid \tilde{X}]} \rVert}_{L^2} &\leq {\lVert{E[Z_n(W_1 \otimes W_2) \mid \pi_1]} \rVert}_{L^2} \\ &\qquad\qquad\qquad\qquad = {\lVert {(W_1 \otimes 1) E[Z_n W_2]}\rVert}_{L^2} = {\lVert{W_1} \rVert}_{L^2} | E[Z_n W_2]| \to 0. \end{align*} $$
$$ \begin{align*} {\lVert{E[Z_n (W_1 \otimes W_2) \mid \tilde{X}]} \rVert}_{L^2} &\leq {\lVert{E[Z_n(W_1 \otimes W_2) \mid \pi_1]} \rVert}_{L^2} \\ &\qquad\qquad\qquad\qquad = {\lVert {(W_1 \otimes 1) E[Z_n W_2]}\rVert}_{L^2} = {\lVert{W_1} \rVert}_{L^2} | E[Z_n W_2]| \to 0. \end{align*} $$
Since simple tensors span a dense subset of the probability space, the claim follows.
(5)
![]() $\implies $
(1). Use the same notation from the first step. Let
$\implies $
(1). Use the same notation from the first step. Let
![]() $S_\epsilon $
be the set of
$S_\epsilon $
be the set of
![]() $(x,y)$
such that
$(x,y)$
such that
![]() $\nu _x$
has an atom of size
$\nu _x$
has an atom of size
![]() $\geq \epsilon $
at y. We can write
$\geq \epsilon $
at y. We can write
and hence,
![]() $S_\epsilon $
is a Borel set since
$S_\epsilon $
is a Borel set since
![]() $(x,y) \mapsto F_{\nu _x}(y)$
is Borel-measurable. Let
$(x,y) \mapsto F_{\nu _x}(y)$
is Borel-measurable. Let
![]() $(S_\epsilon )_x$
be the slice
$(S_\epsilon )_x$
be the slice
![]() $\{y: (x,y) \in S_\epsilon \}$
. From this, it is not hard to see that
$\{y: (x,y) \in S_\epsilon \}$
. From this, it is not hard to see that
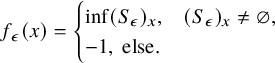 $$\begin{align*}f_\epsilon(x) = \begin{cases} \inf (S_\epsilon)_x, & (S_\epsilon)_x \neq \varnothing, \\ -1, \text{ else.} \end{cases} \end{align*}$$
$$\begin{align*}f_\epsilon(x) = \begin{cases} \inf (S_\epsilon)_x, & (S_\epsilon)_x \neq \varnothing, \\ -1, \text{ else.} \end{cases} \end{align*}$$
is a Borel function. Let
![]() $(Z_n)_{n \in \mathbb {N}}$
be a sequence of random variables as in (5). Let
$(Z_n)_{n \in \mathbb {N}}$
be a sequence of random variables as in (5). Let
![]() $W_\epsilon = \mathbf {1}_{Y = f_\epsilon (X)}$
. By passing to a subsequence, assume that
$W_\epsilon = \mathbf {1}_{Y = f_\epsilon (X)}$
. By passing to a subsequence, assume that
![]() $E[W_\epsilon Z_n \mid X] \to 0$
almost surely (that is,
$E[W_\epsilon Z_n \mid X] \to 0$
almost surely (that is,
![]() $\mu _X$
-almost everywhere). But note that when
$\mu _X$
-almost everywhere). But note that when
![]() $(S_\epsilon )_x \neq \varnothing $
, we have
$(S_\epsilon )_x \neq \varnothing $
, we have
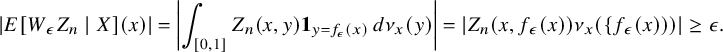 $$\begin{align*}|E[W_\epsilon Z_n \mid X](x)| = \left| \int_{[0,1]} Z_n(x,y) \mathbf{1}_{y = f_\epsilon(x)}\,d\nu_x(y) \right| = |Z_n(x,f_\epsilon(x)) \nu_x(\{f_\epsilon(x)))| \geq \epsilon. \end{align*}$$
$$\begin{align*}|E[W_\epsilon Z_n \mid X](x)| = \left| \int_{[0,1]} Z_n(x,y) \mathbf{1}_{y = f_\epsilon(x)}\,d\nu_x(y) \right| = |Z_n(x,f_\epsilon(x)) \nu_x(\{f_\epsilon(x)))| \geq \epsilon. \end{align*}$$
Therefore, whenever
![]() $E[W_\epsilon Z_n \mid X](x) \to 0$
, we have
$E[W_\epsilon Z_n \mid X](x) \to 0$
, we have
![]() $(S_\epsilon )_x = \varnothing $
. Hence, for
$(S_\epsilon )_x = \varnothing $
. Hence, for
![]() $\mu _X$
-almost every x, we have
$\mu _X$
-almost every x, we have
![]() $(S_\epsilon )_x = \varnothing $
. Since this holds for every
$(S_\epsilon )_x = \varnothing $
. Since this holds for every
![]() $\epsilon $
, we conclude that for
$\epsilon $
, we conclude that for
![]() $\mu _X$
-almost every x, the measure
$\mu _X$
-almost every x, the measure
![]() $\nu _x$
has no atoms.
$\nu _x$
has no atoms.
Proof of Theorem A.
The measure space
![]() $(\Omega _1,\mu _1)$
can be decomposed into countably many atoms and an atomless space, which we in turn can assume is
$(\Omega _1,\mu _1)$
can be decomposed into countably many atoms and an atomless space, which we in turn can assume is
![]() $([0,1],\operatorname {\mathrm {Leb}})$
. Thus, suppose that
$([0,1],\operatorname {\mathrm {Leb}})$
. Thus, suppose that
![]() $\Omega _1 = I \sqcup [0,1]$
and
$\Omega _1 = I \sqcup [0,1]$
and
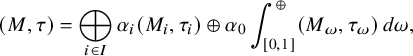 $$\begin{align*}(M,\tau) = \bigoplus_{i \in I} \alpha_i (M_i,\tau_i) \oplus \alpha_0 \int_{[0,1]}^{\oplus} (M_\omega,\tau_\omega)\,d\omega, \end{align*}$$
$$\begin{align*}(M,\tau) = \bigoplus_{i \in I} \alpha_i (M_i,\tau_i) \oplus \alpha_0 \int_{[0,1]}^{\oplus} (M_\omega,\tau_\omega)\,d\omega, \end{align*}$$
where
![]() $(\alpha _i)_{i \in I}$
are the weights of the atoms and
$(\alpha _i)_{i \in I}$
are the weights of the atoms and
![]() $\alpha _0 = 1 - \sum _{i \in I} \alpha _i$
. Let
$\alpha _0 = 1 - \sum _{i \in I} \alpha _i$
. Let
![]() $(M_0,\tau _0) = \int _{[0,1]}^{\oplus } (M_\omega ,\tau _\omega )\,d\omega $
. Similarly, suppose that
$(M_0,\tau _0) = \int _{[0,1]}^{\oplus } (M_\omega ,\tau _\omega )\,d\omega $
. Similarly, suppose that
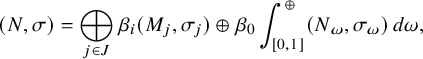 $$\begin{align*}(N,\sigma) = \bigoplus_{j \in J} \beta_i (M_j,\sigma_j) \oplus \beta_0 \int_{[0,1]}^{\oplus} (N_\omega,\sigma_\omega)\,d\omega, \end{align*}$$
$$\begin{align*}(N,\sigma) = \bigoplus_{j \in J} \beta_i (M_j,\sigma_j) \oplus \beta_0 \int_{[0,1]}^{\oplus} (N_\omega,\sigma_\omega)\,d\omega, \end{align*}$$
and let
![]() $(N_0,\sigma _0) = \int _{[0,1]}^{\oplus } (N_\omega ,\sigma _\omega )\,d\omega $
.
$(N_0,\sigma _0) = \int _{[0,1]}^{\oplus } (N_\omega ,\sigma _\omega )\,d\omega $
.
Since we assumed
![]() $(M,\tau ) \equiv (N,\sigma )$
, the Keisler-Shelah theorem yields some ultrafilter
$(M,\tau ) \equiv (N,\sigma )$
, the Keisler-Shelah theorem yields some ultrafilter
![]() $\mathcal {U}$
on some index set S such that
$\mathcal {U}$
on some index set S such that
![]() $(M,\tau )^{\mathcal {U}} \cong (N,\sigma )^{\mathcal {U}}$
. Note that there is an isomorphism
$(M,\tau )^{\mathcal {U}} \cong (N,\sigma )^{\mathcal {U}}$
. Note that there is an isomorphism
in the obvious way. Indeed, any element in the ultrapower
![]() $(M,\tau )^{\mathcal {U}}$
can be lifted to some tuple
$(M,\tau )^{\mathcal {U}}$
can be lifted to some tuple
![]() $(x_s)_{s \in S}$
over the index set S, which in turn can be decomposed as a direct sum of elements
$(x_s)_{s \in S}$
over the index set S, which in turn can be decomposed as a direct sum of elements
![]() $x_{s,i} \in M_i$
,
$x_{s,i} \in M_i$
,
![]() $i \in I \cup \{0\}$
. Moreover,
$i \in I \cup \{0\}$
. Moreover,
![]() ${\lVert {x_s}\rVert }_2 \to 0$
along the ultrafilter if and only if
${\lVert {x_s}\rVert }_2 \to 0$
along the ultrafilter if and only if
![]() ${\lVert {x_{s,i}}\rVert }_2 \to 0$
along the ultrafilter for each i. The elements
${\lVert {x_{s,i}}\rVert }_2 \to 0$
along the ultrafilter for each i. The elements
![]() $(M_i,\tau _i)^{\mathcal {U}}$
are factors for each
$(M_i,\tau _i)^{\mathcal {U}}$
are factors for each
![]() $i \in I$
(by Proposition 2.8 for instance), while
$i \in I$
(by Proposition 2.8 for instance), while
![]() $(M_0,\tau _0)^{\mathcal {U}}$
has diffuse center. Thus, the elements
$(M_0,\tau _0)^{\mathcal {U}}$
has diffuse center. Thus, the elements
![]() $1_{M_i}$
are exactly the minimal central projections in
$1_{M_i}$
are exactly the minimal central projections in
![]() $(M,\tau )^{\mathcal {U}}$
for
$(M,\tau )^{\mathcal {U}}$
for
![]() $i \in I$
.
$i \in I$
.
The analogous claims hold for
![]() $(N,\sigma )$
as well. Hence,
$(N,\sigma )$
as well. Hence,
![]() $(M,\tau )^{\mathcal {U}} \cong (N,\sigma )^{\mathcal {U}}$
becomes
$(M,\tau )^{\mathcal {U}} \cong (N,\sigma )^{\mathcal {U}}$
becomes
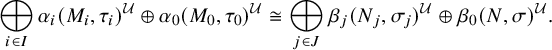 $$\begin{align*}\bigoplus_{i \in I} \alpha_i (M_i,\tau_i)^{\mathcal{U}} \oplus \alpha_0 (M_0,\tau_0)^{\mathcal{U}} \cong \bigoplus_{j \in J} \beta_j (N_j,\sigma_j)^{\mathcal{U}} \oplus \beta_0 (N,\sigma)^{\mathcal{U}}. \end{align*}$$
$$\begin{align*}\bigoplus_{i \in I} \alpha_i (M_i,\tau_i)^{\mathcal{U}} \oplus \alpha_0 (M_0,\tau_0)^{\mathcal{U}} \cong \bigoplus_{j \in J} \beta_j (N_j,\sigma_j)^{\mathcal{U}} \oplus \beta_0 (N,\sigma)^{\mathcal{U}}. \end{align*}$$
The isomorphism must map minimal central projections on the left-hand side to minimal central projections on the right-hand side. Therefore, there is a bijection
![]() $f_1: I \to J$
such that the identity in
$f_1: I \to J$
such that the identity in
![]() $(M_i,\tau _i)^{\mathcal {U}}$
is mapped to the identity in
$(M_i,\tau _i)^{\mathcal {U}}$
is mapped to the identity in
![]() $(N_{f_1(i)},\sigma _{f_1(i)})^{\mathcal {U}}$
under the isomorphism. It easily follows that
$(N_{f_1(i)},\sigma _{f_1(i)})^{\mathcal {U}}$
under the isomorphism. It easily follows that
![]() $\alpha _i = \beta _{f_1(i)}$
and
$\alpha _i = \beta _{f_1(i)}$
and
![]() $(M_i,\tau _i)^{\mathcal {U}} \cong (N_{f_1(i)},\sigma _{f_1(i)})^{\mathcal {U}}$
, which means that
$(M_i,\tau _i)^{\mathcal {U}} \cong (N_{f_1(i)},\sigma _{f_1(i)})^{\mathcal {U}}$
, which means that
![]() $(M_i,\tau _i) \equiv (N_{f(i)},\sigma _{f(i)})$
. Moreover, the remaining summands with diffuse center in the direct sum decomposition must also correspond under the isomorphism, so that
$(M_i,\tau _i) \equiv (N_{f(i)},\sigma _{f(i)})$
. Moreover, the remaining summands with diffuse center in the direct sum decomposition must also correspond under the isomorphism, so that
![]() $(M_0,\tau _0)^{\mathcal {U}} \cong (N_0,\sigma _0)^{\mathcal {U}}$
, which means that
$(M_0,\tau _0)^{\mathcal {U}} \cong (N_0,\sigma _0)^{\mathcal {U}}$
, which means that
![]() $(M_0,\tau _0) \equiv (N_0,\sigma _0)$
.
$(M_0,\tau _0) \equiv (N_0,\sigma _0)$
.
By Corollary 4.4,
![]() $(M_0,\tau _0)$
and
$(M_0,\tau _0)$
and
![]() $(N_0,\sigma _0)$
have the same distribution of theories. By Lemma 4.2, this means that the random variables
$(N_0,\sigma _0)$
have the same distribution of theories. By Lemma 4.2, this means that the random variables
![]() $X: \omega \mapsto \operatorname {\mathrm {Th}}(M_\omega ,\tau _\omega )$
and
$X: \omega \mapsto \operatorname {\mathrm {Th}}(M_\omega ,\tau _\omega )$
and
![]() $Y: \omega \mapsto \operatorname {\mathrm {Th}}(N_\omega ,\sigma _\omega )$
have the same distribution, or
$Y: \omega \mapsto \operatorname {\mathrm {Th}}(N_\omega ,\sigma _\omega )$
have the same distribution, or
![]() $\mu _X = \mu _Y$
as probability measures on
$\mu _X = \mu _Y$
as probability measures on
![]() $\mathbb {T}_{\operatorname {\mathrm {tr}}}$
. Let
$\mathbb {T}_{\operatorname {\mathrm {tr}}}$
. Let
![]() $g: \mathbb {T}_{\operatorname {\mathrm {tr}}} \to [0,1]$
be an isomorphism of standard Borel spaces, and let
$g: \mathbb {T}_{\operatorname {\mathrm {tr}}} \to [0,1]$
be an isomorphism of standard Borel spaces, and let
![]() $\tilde {X} = g \circ X$
. Since we assumed that the diffuse part of the direct integral decomposition satisfies stability under tensorization, it is easy to see that the random variable
$\tilde {X} = g \circ X$
. Since we assumed that the diffuse part of the direct integral decomposition satisfies stability under tensorization, it is easy to see that the random variable
![]() $\tilde {X}$
satisfies condition (3) of Lemma 4.6. Hence, by condition (2), there exists a measurable isomorphism
$\tilde {X}$
satisfies condition (3) of Lemma 4.6. Hence, by condition (2), there exists a measurable isomorphism
![]() $\tilde {\Phi }: ([0,1],\operatorname {\mathrm {Leb}}) \to ([0,1],\mu _{\tilde {X}}) \times ([0,1],\operatorname {\mathrm {Leb}})$
such that
$\tilde {\Phi }: ([0,1],\operatorname {\mathrm {Leb}}) \to ([0,1],\mu _{\tilde {X}}) \times ([0,1],\operatorname {\mathrm {Leb}})$
such that
![]() $\tilde {X} = \pi _1 \circ \tilde {\Phi }$
. Let
$\tilde {X} = \pi _1 \circ \tilde {\Phi }$
. Let
![]() $\Phi = (g^{-1} \times \operatorname {\mathrm {id}}) \circ \tilde {\Phi }: ([0,1],\operatorname {\mathrm {Leb}}) \to (\mathbb {T}_{\operatorname {\mathrm {tr}}},\mu _{X}) \times ([0,1],\operatorname {\mathrm {Leb}})$
; then we have
$\Phi = (g^{-1} \times \operatorname {\mathrm {id}}) \circ \tilde {\Phi }: ([0,1],\operatorname {\mathrm {Leb}}) \to (\mathbb {T}_{\operatorname {\mathrm {tr}}},\mu _{X}) \times ([0,1],\operatorname {\mathrm {Leb}})$
; then we have
![]() $X = \pi _1 \circ \Phi $
. Similarly, obtain an isomorphism
$X = \pi _1 \circ \Phi $
. Similarly, obtain an isomorphism
![]() $\Psi : ([0,1],\operatorname {\mathrm {Leb}}) \to (\mathbb {T}_{\operatorname {\mathrm {tr}}},\mu _{Y}) \times ([0,1],\operatorname {\mathrm {Leb}})$
such that
$\Psi : ([0,1],\operatorname {\mathrm {Leb}}) \to (\mathbb {T}_{\operatorname {\mathrm {tr}}},\mu _{Y}) \times ([0,1],\operatorname {\mathrm {Leb}})$
such that
![]() $Y = \pi _1 \circ \Psi $
.
$Y = \pi _1 \circ \Psi $
.
Then
![]() $f_0 = \Psi ^{-1} \circ \Phi $
gives an isomorphism
$f_0 = \Psi ^{-1} \circ \Phi $
gives an isomorphism
![]() $([0,1],\operatorname {\mathrm {Leb}}) \to ([0,1],\operatorname {\mathrm {Leb}})$
such that
$([0,1],\operatorname {\mathrm {Leb}}) \to ([0,1],\operatorname {\mathrm {Leb}})$
such that
![]() $Y \circ f_0 = X$
, meaning that
$Y \circ f_0 = X$
, meaning that
![]() $\operatorname {\mathrm {Th}}(N_{f_0(\omega )},\sigma _{f_0(\omega )}) = \operatorname {\mathrm {Th}}(M_\omega ,\tau _\omega )$
. Let
$\operatorname {\mathrm {Th}}(N_{f_0(\omega )},\sigma _{f_0(\omega )}) = \operatorname {\mathrm {Th}}(M_\omega ,\tau _\omega )$
. Let
![]() $f: I \sqcup [0,1] \to J \sqcup [0,1]$
be the function given by
$f: I \sqcup [0,1] \to J \sqcup [0,1]$
be the function given by
![]() $f|_I = f_1$
and
$f|_I = f_1$
and
![]() $f|_{[0,1]} = f_0$
. Then f is a bijection such that
$f|_{[0,1]} = f_0$
. Then f is a bijection such that
![]() $(N_{f(\omega )},\sigma _{f(\omega )}) \equiv (M_\omega , \tau _\omega )$
.
$(N_{f(\omega )},\sigma _{f(\omega )}) \equiv (M_\omega , \tau _\omega )$
.
Remark 4.7. In the setup of Theorem A, if we remove the hypothesis of stability under tensorization for the diffuse part of the direct integral decomposition, can we still find a measurable isomorphism
![]() $f: \Omega _1 \to \Omega _2$
such that
$f: \Omega _1 \to \Omega _2$
such that
![]() $M_\omega \equiv N_{f(\omega )}$
almost surely? We claim that the answer comes down to the behavior of the fiber measures in the distintegration of the diffuse parts of
$M_\omega \equiv N_{f(\omega )}$
almost surely? We claim that the answer comes down to the behavior of the fiber measures in the distintegration of the diffuse parts of
![]() $\Omega _1$
and
$\Omega _1$
and
![]() $\Omega _2$
over the random variables X and Y, respectively.
$\Omega _2$
over the random variables X and Y, respectively.
The proof given above still allows us to match up the direct summands over each atom in the probability spaces
![]() $(\Omega _1,\mu _1)$
and
$(\Omega _1,\mu _1)$
and
![]() $(\Omega _2,\mu _2)$
, and so it remains to consider what happens for the diffuse parts. So for simplicity, assume that there are no atoms in
$(\Omega _2,\mu _2)$
, and so it remains to consider what happens for the diffuse parts. So for simplicity, assume that there are no atoms in
![]() $\Omega _1$
and
$\Omega _1$
and
![]() $\Omega _2$
. Assume
$\Omega _2$
. Assume
![]() $\Omega _1$
and
$\Omega _1$
and
![]() $\Omega _2$
are standard Borel spaces. Disintegrate
$\Omega _2$
are standard Borel spaces. Disintegrate
![]() $\mu _1$
with respect to the random variable
$\mu _1$
with respect to the random variable
![]() $X(\omega ) = \operatorname {\mathrm {Th}}(M_\omega ,\tau _\omega )$
as
$X(\omega ) = \operatorname {\mathrm {Th}}(M_\omega ,\tau _\omega )$
as
![]() $\mu _1 = \int _{\mathbb {T}_{\operatorname {\mathrm {tr}}}} \nu _x \,d\mu _X(x)$
, where
$\mu _1 = \int _{\mathbb {T}_{\operatorname {\mathrm {tr}}}} \nu _x \,d\mu _X(x)$
, where
![]() $\nu _x \in \mathcal {P}(\Omega _1)$
is supported on
$\nu _x \in \mathcal {P}(\Omega _1)$
is supported on
![]() $S_x = \{\omega \in \Omega _1: X(\omega ) = x\}$
. This is possible since
$S_x = \{\omega \in \Omega _1: X(\omega ) = x\}$
. This is possible since
![]() $\Omega _1$
and
$\Omega _1$
and
![]() $\mathbb {T}_1$
are standard Borel spaces, hence isomorphic to
$\mathbb {T}_1$
are standard Borel spaces, hence isomorphic to
![]() $[0,1]$
as measure spaces, and for the same reason, Lemma 4.6 also applies to this disintegration. In particular, the hypothesis of stability under tensorization means precisely that for
$[0,1]$
as measure spaces, and for the same reason, Lemma 4.6 also applies to this disintegration. In particular, the hypothesis of stability under tensorization means precisely that for
![]() $\mu _X$
-a.e. x, the fiber measure
$\mu _X$
-a.e. x, the fiber measure
![]() $\nu _x$
is diffuse. Similarly, let
$\nu _x$
is diffuse. Similarly, let
![]() $\mu _2 = \int _{\mathbb {T}_{\operatorname {\mathrm {tr}}}} \tilde {\nu }_y\,d\mu _Y(y)$
where
$\mu _2 = \int _{\mathbb {T}_{\operatorname {\mathrm {tr}}}} \tilde {\nu }_y\,d\mu _Y(y)$
where
![]() $\tilde {\nu }_y$
is supported on
$\tilde {\nu }_y$
is supported on
![]() $\tilde {S}_y = \{\omega \in \Omega _2: Y(\omega ) = y\}$
. As in the proof above, we still have
$\tilde {S}_y = \{\omega \in \Omega _2: Y(\omega ) = y\}$
. As in the proof above, we still have
![]() $\mu _X = \mu _Y$
. By construction, for each
$\mu _X = \mu _Y$
. By construction, for each
![]() $x \in \mathbb {T}_{\operatorname {\mathrm {tr}}}$
, the tracial von Neumann algebras
$x \in \mathbb {T}_{\operatorname {\mathrm {tr}}}$
, the tracial von Neumann algebras
![]() $M_\omega $
for
$M_\omega $
for
![]() $\omega S_x$
and
$\omega S_x$
and
![]() $N_\omega $
for
$N_\omega $
for
![]() $\omega \in S_y$
have theory equal to x, and so they are all elementarily equivalent to each other.
$\omega \in S_y$
have theory equal to x, and so they are all elementarily equivalent to each other.
Thus, if the sizes of the atoms of the measures
![]() $\nu _x$
and
$\nu _x$
and
![]() $\tilde {\nu }_x$
agree for almost every x, then there is an isomorphism of
$\tilde {\nu }_x$
agree for almost every x, then there is an isomorphism of
![]() $(S_x,\nu _x)$
to
$(S_x,\nu _x)$
to
![]() $(\tilde {S}_x,\tilde {\nu }_x)$
. In this case, one can show that these maps can be chosen to depend measurably on x, or there is a measurable isomorphism
$(\tilde {S}_x,\tilde {\nu }_x)$
. In this case, one can show that these maps can be chosen to depend measurably on x, or there is a measurable isomorphism
![]() $f: (\Omega _1,\mu _1) \to (\Omega _2,\mu _2)$
sending
$f: (\Omega _1,\mu _1) \to (\Omega _2,\mu _2)$
sending
![]() $S_x$
to
$S_x$
to
![]() $\tilde {S}_x$
(we leave the details to the reader, but the idea is to measurably pick out atoms of a certain size in each fiber as in the proof of Lemma 4.6 (5)
$\tilde {S}_x$
(we leave the details to the reader, but the idea is to measurably pick out atoms of a certain size in each fiber as in the proof of Lemma 4.6 (5)
![]() $\implies $
(1)). Then
$\implies $
(1)). Then
![]() $X(\omega ) = \operatorname {\mathrm {Th}}(M_{\omega }) =Y(f(\omega )) = \operatorname {\mathrm {Th}}(N_{f(\omega )})$
, so that
$X(\omega ) = \operatorname {\mathrm {Th}}(M_{\omega }) =Y(f(\omega )) = \operatorname {\mathrm {Th}}(N_{f(\omega )})$
, so that
![]() $M_{\omega } \equiv N_{f(\omega )}$
almost everywhere. Conversely, if such a measurable isomorphism exists, then it is necessary that for
$M_{\omega } \equiv N_{f(\omega )}$
almost everywhere. Conversely, if such a measurable isomorphism exists, then it is necessary that for
![]() $\mu _X$
-a.e.
$\mu _X$
-a.e.
![]() $x \in \mathbb {T}_{\operatorname {\mathrm {tr}}}$
, the fiber measures
$x \in \mathbb {T}_{\operatorname {\mathrm {tr}}}$
, the fiber measures
![]() $\nu _x$
and
$\nu _x$
and
![]() $\tilde {\nu }_x$
have the same number of atoms of each size.
$\tilde {\nu }_x$
have the same number of atoms of each size.
5 Isomorphism classes of ultrafibers
In this section, we show that under the continuum hypothesis (CH), the ultrafibers obtained from separable algebras are all isomorphic to some ultraproduct over the natural numbers. More precisely, we show the following.
Proposition 5.1. Assume CH. Let
![]() $(\Omega ,\mu )$
be a standard Borel probability space and let
$(\Omega ,\mu )$
be a standard Borel probability space and let
![]() $\mathcal {U}$
be a pure state on
$\mathcal {U}$
be a pure state on
![]() $L^\infty (\Omega ,\mu )$
. Let
$L^\infty (\Omega ,\mu )$
. Let
![]() $(M_\omega )_{\omega \in \Omega }$
be a measurable field of separable tracial von Neumann algebras and write
$(M_\omega )_{\omega \in \Omega }$
be a measurable field of separable tracial von Neumann algebras and write
![]() $(M,\tau ) = \int _\Omega ^{\oplus } (M_\omega ,\tau _\omega )\,d\mu (\omega )$
, and let
$(M,\tau ) = \int _\Omega ^{\oplus } (M_\omega ,\tau _\omega )\,d\mu (\omega )$
, and let
![]() $E: M \to L^\infty (\Omega ,\mu )$
be the canonical expectation. Then there exists a sequence
$E: M \to L^\infty (\Omega ,\mu )$
be the canonical expectation. Then there exists a sequence
![]() $(\omega _n)_{n \in \mathbb {N}}$
in
$(\omega _n)_{n \in \mathbb {N}}$
in
![]() $\Omega $
and a non-principal ultrafilter
$\Omega $
and a non-principal ultrafilter
![]() $\mathcal {V}$
on
$\mathcal {V}$
on
![]() $\mathbb {N}$
such that
$\mathbb {N}$
such that
![]() $M^{/E,\mathcal {U}} \cong \prod _{n \to \mathcal {V}} M_{\omega _n}$
.
$M^{/E,\mathcal {U}} \cong \prod _{n \to \mathcal {V}} M_{\omega _n}$
.
We remark that Proposition 5.1 in particular applies to generalized ultrapowers over separable commutative tracial von Neumann algebras as follows. Suppose that
![]() $(M,\tau _M)$
is a tracial von Neumann algebra. Let A be a separable diffuse commutative tracial von Neumann algebra, and let
$(M,\tau _M)$
is a tracial von Neumann algebra. Let A be a separable diffuse commutative tracial von Neumann algebra, and let
![]() $\mathcal {U}$
is a character on A. We can assume without loss of generality that
$\mathcal {U}$
is a character on A. We can assume without loss of generality that
![]() $A = L^\infty (\Omega )$
, and then
$A = L^\infty (\Omega )$
, and then
![]() $A \overline {\otimes } M$
is identified with
$A \overline {\otimes } M$
is identified with
![]() $\int _\Omega ^\omega (M,\tau _M) \,d\omega $
, and the ultrafiber
$\int _\Omega ^\omega (M,\tau _M) \,d\omega $
, and the ultrafiber
![]() $M^{/E,\mathcal {U}}$
is exactly the generalized ultrapower
$M^{/E,\mathcal {U}}$
is exactly the generalized ultrapower
![]() $M^{\mathcal {U}}$
of Definition 2.5. Hence, the proposition implies that
$M^{\mathcal {U}}$
of Definition 2.5. Hence, the proposition implies that
![]() $M^{\mathcal {U}}$
is isomorphic to an ultrapower
$M^{\mathcal {U}}$
is isomorphic to an ultrapower
![]() $M^{\mathcal {V}}$
with respect to a non-principal ultrafilter
$M^{\mathcal {V}}$
with respect to a non-principal ultrafilter
![]() $\mathcal {V}$
on
$\mathcal {V}$
on
![]() $\mathbb {N}$
.
$\mathbb {N}$
.
The isomorphism in Theorem 5.1 arises from the following classic fact from model theory. The notions of density character and saturation are explained below.
Proposition 5.2 [Reference Farah, Hart and ShermanFHS14a, Proposition 4.13].
If
![]() $(M, \tau _M)$
and
$(M, \tau _M)$
and
![]() $(N, \tau _N)$
are saturated tracial von Neumann algebras of the same uncountable density character, then
$(N, \tau _N)$
are saturated tracial von Neumann algebras of the same uncountable density character, then
![]() $M \equiv N$
if and only if
$M \equiv N$
if and only if
![]() $M \cong N$
.
$M \cong N$
.
Recall that the density character of a metric space is the minimum cardinality of a dense subset or, equivalently, the maximum cardinality of a collection of disjoint balls. The density character of a tracial von Neumann algebra is understood with respect to the
![]() $L^2$
-metric, or equivalently, it refers to the density character of the predual. Thus, the first prerequisite for applying Proposition 5.2 is to determine the density character of the ultrafibers in question. We will show the density character is
$L^2$
-metric, or equivalently, it refers to the density character of the predual. Thus, the first prerequisite for applying Proposition 5.2 is to determine the density character of the ultrafibers in question. We will show the density character is
![]() $2^{\aleph _0}$
if the algebra has a diffuse part, and in fact, this is true even without assuming CH.
$2^{\aleph _0}$
if the algebra has a diffuse part, and in fact, this is true even without assuming CH.
Proposition 5.3. Let
![]() $(\Omega ,\mu )$
be a standard Borel probability space and let
$(\Omega ,\mu )$
be a standard Borel probability space and let
![]() $\mathcal {U}$
be a character on
$\mathcal {U}$
be a character on
![]() $L^\infty (\Omega ,\mu )$
. Assume that
$L^\infty (\Omega ,\mu )$
. Assume that
![]() $\mathcal {U}$
is not given by a point mass located at some atom of
$\mathcal {U}$
is not given by a point mass located at some atom of
![]() $\Omega $
. Let
$\Omega $
. Let
![]() $(M_\omega )_{\omega \in \Omega }$
be a measurable field of separable tracial von Neumann algebras and write
$(M_\omega )_{\omega \in \Omega }$
be a measurable field of separable tracial von Neumann algebras and write
![]() $(M,\tau ) = \int _\Omega ^{\oplus } (M_\omega ,\tau _\omega )\,d\mu (\omega )$
, and let
$(M,\tau ) = \int _\Omega ^{\oplus } (M_\omega ,\tau _\omega )\,d\mu (\omega )$
, and let
![]() $E: M \to L^\infty (\Omega ,\mu )$
be the canonical expectation.
$E: M \to L^\infty (\Omega ,\mu )$
be the canonical expectation.
-
1. If
 $M^{/E,\mathcal {U}}$
has a diffuse summand, then its density character is
$M^{/E,\mathcal {U}}$
has a diffuse summand, then its density character is
 $2^{\aleph _0}$
.
$2^{\aleph _0}$
. -
2. Otherwise,
 $M^{/E,\mathcal {U}}$
is a direct sum of matrix algebras, and hence is separable.
$M^{/E,\mathcal {U}}$
is a direct sum of matrix algebras, and hence is separable.
For the proof, we need one more property of the ultrafilters or characters on
![]() $L^\infty (\Omega )$
– namely, countable incompleteness. Recall that an ultrafilter
$L^\infty (\Omega )$
– namely, countable incompleteness. Recall that an ultrafilter
![]() $\mathcal {U}$
on an index set I is called countably incomplete if there exists a decreasing sequence of sets
$\mathcal {U}$
on an index set I is called countably incomplete if there exists a decreasing sequence of sets
![]() $\{A_n\}_{n = 1}^\infty \subseteq \mathcal {U}$
such that
$\{A_n\}_{n = 1}^\infty \subseteq \mathcal {U}$
such that
![]() $\bigcap _n A_n = \varnothing $
. For instance, all non-principal ultrafilters on
$\bigcap _n A_n = \varnothing $
. For instance, all non-principal ultrafilters on
![]() $\mathbb {N}$
are countably incomplete since we can take
$\mathbb {N}$
are countably incomplete since we can take
![]() $A_n = \{n,n+1,\dots \}$
. If we view the ultrafilter as a pure state on
$A_n = \{n,n+1,\dots \}$
. If we view the ultrafilter as a pure state on
![]() $\ell ^\infty (I)$
, then countable incompleteness means that there is a decreasing sequence of projections
$\ell ^\infty (I)$
, then countable incompleteness means that there is a decreasing sequence of projections
![]() $p_n$
such that
$p_n$
such that
![]() $\mathcal {U}(p_n) = 1$
and
$\mathcal {U}(p_n) = 1$
and
![]() $\bigwedge _{n \in \mathbb {N}} p_n = 0$
. Thus, we adapt the definition to characters on commutative von Neumann algebras as follows.
$\bigwedge _{n \in \mathbb {N}} p_n = 0$
. Thus, we adapt the definition to characters on commutative von Neumann algebras as follows.
Definition 5.4. Let
![]() $\mathcal {U}$
be a character on a commutative von Neumann algebra N. We say
$\mathcal {U}$
be a character on a commutative von Neumann algebra N. We say
![]() $\mathcal {U}$
is countably incomplete if there exists a decreasing sequence of projections.
$\mathcal {U}$
is countably incomplete if there exists a decreasing sequence of projections.
![]() $\{p_n\}_{n = 1}^\infty \subseteq N$
s.t.
$\{p_n\}_{n = 1}^\infty \subseteq N$
s.t.
![]() $p_n \searrow 0$
in SOT and
$p_n \searrow 0$
in SOT and
![]() $\mathcal {U}(p_n) = 1$
for all n.
$\mathcal {U}(p_n) = 1$
for all n.
Proposition 5.5. Let N be a commutative tracial von Neumann algebra and
![]() $\mathcal {U}$
a character on N. Then
$\mathcal {U}$
a character on N. Then
![]() $\mathcal {U}$
is countably incomplete unless there is a minimal projection p such that
$\mathcal {U}$
is countably incomplete unless there is a minimal projection p such that
![]() $px = \mathcal {U}(x) p$
for all
$px = \mathcal {U}(x) p$
for all
![]() $x \in N$
.
$x \in N$
.
Proof. First, consider the case where N is diffuse. By Maharam’s theorem [Reference MaharamMah42, Theorem 1], we may assume
![]() $(N, \tau _N) = L^\infty ([0, 1]^\kappa , \lambda ^{\otimes \kappa })$
for some infinite cardinal
$(N, \tau _N) = L^\infty ([0, 1]^\kappa , \lambda ^{\otimes \kappa })$
for some infinite cardinal
![]() $\kappa $
, where
$\kappa $
, where
![]() $\lambda $
is the Lebesgue measure. Thus,
$\lambda $
is the Lebesgue measure. Thus,
![]() $A = C([0, 1]^\kappa ) \subseteq N$
, so
$A = C([0, 1]^\kappa ) \subseteq N$
, so
![]() $\mathcal {U}$
necessarily restricts to a character on A, which must be of the form of the evaluation functional at some
$\mathcal {U}$
necessarily restricts to a character on A, which must be of the form of the evaluation functional at some
![]() $t \in [0, 1]^\kappa $
. For each positive integer n, let
$t \in [0, 1]^\kappa $
. For each positive integer n, let
![]() $f_n: [0, 1] \to [0, 1]$
be a continuous function s.t.
$f_n: [0, 1] \to [0, 1]$
be a continuous function s.t.
![]() $f_n = 1$
on
$f_n = 1$
on
![]() $[t(0) - 1/(2n), t(0) + 1/(2n)] \cap [0, 1]$
and
$[t(0) - 1/(2n), t(0) + 1/(2n)] \cap [0, 1]$
and
![]() $f_n = 0$
outside
$f_n = 0$
outside
![]() $[t(0) - 1/n, t(0) + 1/n] \cap [0, 1]$
. Let
$[t(0) - 1/n, t(0) + 1/n] \cap [0, 1]$
. Let
![]() $p: [0, 1]^\kappa \to [0, 1]$
be the projection map onto the zeroth coordinate. Then
$p: [0, 1]^\kappa \to [0, 1]$
be the projection map onto the zeroth coordinate. Then
![]() $g_n = f_n \circ p \in A$
. Furthermore, by definition
$g_n = f_n \circ p \in A$
. Furthermore, by definition
![]() $\mathcal {U}(g_n) = g_n(t) = 1$
. Let
$\mathcal {U}(g_n) = g_n(t) = 1$
. Let
![]() $p_n \in N$
be the projection corresponding to the set
$p_n \in N$
be the projection corresponding to the set
![]() $([t(0) - 1/n, t(0) + 1/n] \cap [0, 1]) \times [0, 1]^{\kappa \setminus \{0\}}$
. Then
$([t(0) - 1/n, t(0) + 1/n] \cap [0, 1]) \times [0, 1]^{\kappa \setminus \{0\}}$
. Then
![]() $p_n \geq g_n$
, so
$p_n \geq g_n$
, so
![]() $\mathcal {U}(p_n) = 1$
. We also have
$\mathcal {U}(p_n) = 1$
. We also have
![]() $\tau _N(p_n) \leq 2/n \to 0$
, so
$\tau _N(p_n) \leq 2/n \to 0$
, so
![]() $p_n \searrow 0$
.
$p_n \searrow 0$
.
Now consider the general case. Choose a family
![]() $(p_i)_{i \in I}$
of mutually orthogonal minimal projections in N that is maximal with respect to inclusion. Since N has a faithful state, I must be countable. Let
$(p_i)_{i \in I}$
of mutually orthogonal minimal projections in N that is maximal with respect to inclusion. Since N has a faithful state, I must be countable. Let
![]() $p = \sum _{i \in I} p_i$
. Then N is the direct sum of
$p = \sum _{i \in I} p_i$
. Then N is the direct sum of
![]() $pN$
and
$pN$
and
![]() $(1-p)N$
, and so the character
$(1-p)N$
, and so the character
![]() $\mathcal {U}$
must be supported on one of these two summands. If it is supported on
$\mathcal {U}$
must be supported on one of these two summands. If it is supported on
![]() $(1-p)N$
, then we can apply the diffuse case. If it is supported on
$(1-p)N$
, then we can apply the diffuse case. If it is supported on
![]() $pN$
, then the argument is the same as for
$pN$
, then the argument is the same as for
![]() $\ell ^\infty (\mathbb {N})$
.
$\ell ^\infty (\mathbb {N})$
.
Proof of Proposition 5.3.
(1) Suppose that p is a central projection such that
![]() $p M^{/E,\mathcal {U}}$
is diffuse, and hence it contains a copy of
$p M^{/E,\mathcal {U}}$
is diffuse, and hence it contains a copy of
![]() $L^\infty (\{-1,1\}^{\mathbb {N}})$
where
$L^\infty (\{-1,1\}^{\mathbb {N}})$
where
![]() $\{-1,1\}^{\mathbb {N}}$
is the probability space equipped with the infinite tensor product of the uniform measure
$\{-1,1\}^{\mathbb {N}}$
is the probability space equipped with the infinite tensor product of the uniform measure
![]() $\frac {1}{2} (\delta _{-1} + \delta _1)$
. Let
$\frac {1}{2} (\delta _{-1} + \delta _1)$
. Let
![]() $v_k: \{-1,1\}^{\mathbb {N}} \to \{-1,1\}$
be the kth coordinate projection, viewed as an element of
$v_k: \{-1,1\}^{\mathbb {N}} \to \{-1,1\}$
be the kth coordinate projection, viewed as an element of
![]() $pM^{/E,\mathcal {U}}$
. Note that
$pM^{/E,\mathcal {U}}$
. Note that
![]() $v_k$
is self-adjoint with
$v_k$
is self-adjoint with
![]() $v_k^2 = p$
, and the
$v_k^2 = p$
, and the
![]() $v_k$
’s commute. Since
$v_k$
’s commute. Since
![]() $M^{/E,\mathcal {U}}$
is a quotient of M, write
$M^{/E,\mathcal {U}}$
is a quotient of M, write
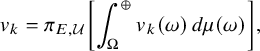 $$\begin{align*}v_k = \pi_{E,\mathcal{U}} \left[ \int_{\Omega}^{\oplus} v_k(\omega)\,d\mu(\omega) \right], \end{align*}$$
$$\begin{align*}v_k = \pi_{E,\mathcal{U}} \left[ \int_{\Omega}^{\oplus} v_k(\omega)\,d\mu(\omega) \right], \end{align*}$$
where
![]() $v_k(\omega ) \in (M_\omega )_1$
is self-adjoint. For
$v_k(\omega ) \in (M_\omega )_1$
is self-adjoint. For
![]() $n \in \mathbb {N}$
, let
$n \in \mathbb {N}$
, let
![]() $A_n \subseteq \Omega $
be the set of
$A_n \subseteq \Omega $
be the set of
![]() $\omega $
such that
$\omega $
such that
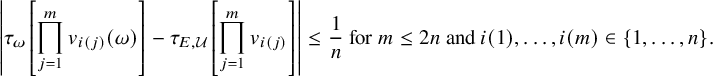 $$\begin{align*}\left| \tau_\omega\left[ \prod_{j=1}^m v_{i(j)}(\omega) \right] - \tau_{E,\mathcal{U}}\left[ \prod_{j=1}^m v_{i(j)} \right] \right| \leq \frac{1}{n} \text{ for } m \leq 2n \text{ and } i(1), \dots, i(m) \in \{1,\dots,n\}. \end{align*}$$
$$\begin{align*}\left| \tau_\omega\left[ \prod_{j=1}^m v_{i(j)}(\omega) \right] - \tau_{E,\mathcal{U}}\left[ \prod_{j=1}^m v_{i(j)} \right] \right| \leq \frac{1}{n} \text{ for } m \leq 2n \text{ and } i(1), \dots, i(m) \in \{1,\dots,n\}. \end{align*}$$
Note that because
![]() $\mathcal {U}$
evaluated on
$\mathcal {U}$
evaluated on
![]() $\omega \mapsto \tau _\omega \left [ \prod _{j=1}^m v_{i(j)}(\omega ) \right ]$
is equal to
$\omega \mapsto \tau _\omega \left [ \prod _{j=1}^m v_{i(j)}(\omega ) \right ]$
is equal to
![]() $\tau _{E,\mathcal {U}}\left [ \prod _{j=1}^m v_{i(j)} \right ]$
, we must have that
$\tau _{E,\mathcal {U}}\left [ \prod _{j=1}^m v_{i(j)} \right ]$
, we must have that
Also,
![]() $A_n$
is a decreasing sequence. Moreover, since
$A_n$
is a decreasing sequence. Moreover, since
![]() $\mathcal {U}$
is countably incomplete, choose a decreasing collection of subsets
$\mathcal {U}$
is countably incomplete, choose a decreasing collection of subsets
![]() $B_n$
such that
$B_n$
such that ![]() and
and
![]() $\mu (B_n) \to 0$
. Let
$\mu (B_n) \to 0$
. Let
![]() $C_n = A_n \cap B_n$
, so that
$C_n = A_n \cap B_n$
, so that ![]() and
and
![]() $\mu (C_n) \to 0$
. For each
$\mu (C_n) \to 0$
. For each
![]() $S \subseteq \mathbb {N}$
, define
$S \subseteq \mathbb {N}$
, define
where the product runs from left to right when the indices are written in increasing order. Suppose the sets S and
![]() $S'$
are not equal, and say they differ at some integer m. Fix some
$S'$
are not equal, and say they differ at some integer m. Fix some
![]() $n_0 \geq m$
. Then for
$n_0 \geq m$
. Then for
![]() $n \geq n_0$
, we have
$n \geq n_0$
, we have
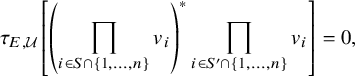 $$\begin{align*}\tau_{E,\mathcal{U}}\left[ \left( \prod_{i \in S \cap \{1,\dots,n\}} v_i \right)^* \prod_{i \in S' \cap \{1,\dots,n\}} v_i \right] = 0, \end{align*}$$
$$\begin{align*}\tau_{E,\mathcal{U}}\left[ \left( \prod_{i \in S \cap \{1,\dots,n\}} v_i \right)^* \prod_{i \in S' \cap \{1,\dots,n\}} v_i \right] = 0, \end{align*}$$
and hence by definition of
![]() $A_n$
, we have for
$A_n$
, we have for
![]() $\omega \in C_n \setminus C_{n+1}$
that
$\omega \in C_n \setminus C_{n+1}$
that
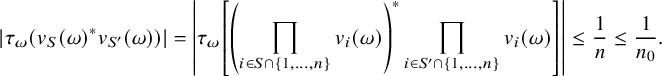 $$\begin{align*}|\tau_\omega(v_{S}(\omega)^* v_{S'}(\omega))| = \left|\tau_\omega\left[ \left( \prod_{i \in S \cap \{1,\dots,n\}} v_i(\omega)\right)^* \prod_{i \in S' \cap \{1,\dots,n\}} v_i(\omega) \right] \right| \leq \frac{1}{n} \leq \frac{1}{n_0}. \end{align*}$$
$$\begin{align*}|\tau_\omega(v_{S}(\omega)^* v_{S'}(\omega))| = \left|\tau_\omega\left[ \left( \prod_{i \in S \cap \{1,\dots,n\}} v_i(\omega)\right)^* \prod_{i \in S' \cap \{1,\dots,n\}} v_i(\omega) \right] \right| \leq \frac{1}{n} \leq \frac{1}{n_0}. \end{align*}$$
This holds on
![]() $\bigcup _{n \geq n_0} (C_n \setminus C_{n+1})$
, which equals
$\bigcup _{n \geq n_0} (C_n \setminus C_{n+1})$
, which equals
![]() $C_{n_0}$
up to null sets. Since
$C_{n_0}$
up to null sets. Since ![]() , we have that
, we have that
Since
![]() $n_0$
was arbitrary,
$n_0$
was arbitrary,
![]() $\tau _{E,\mathcal {U}}(v_S^* v_{S'}) = 0$
. Similar reasoning shows that
$\tau _{E,\mathcal {U}}(v_S^* v_{S'}) = 0$
. Similar reasoning shows that
![]() $\tau _{E,\mathcal {U}}(v_S^*v_S) = \tau _{E,\mathcal {U}}(p)$
. Therefore,
$\tau _{E,\mathcal {U}}(v_S^*v_S) = \tau _{E,\mathcal {U}}(p)$
. Therefore,
![]() $(v_S)_{S \subseteq \mathbb {N}}$
gives an orthogonal set of nonzero elements in
$(v_S)_{S \subseteq \mathbb {N}}$
gives an orthogonal set of nonzero elements in
![]() $pM$
of cardinality equal to
$pM$
of cardinality equal to
![]() $2^{\aleph _0}$
, so the density character is at least
$2^{\aleph _0}$
, so the density character is at least
![]() $2^{\aleph _0}$
.
$2^{\aleph _0}$
.
However, since M is separable, its cardinality is at most
![]() $2^{\aleph _0}$
. And
$2^{\aleph _0}$
. And
![]() $M^{/E,\mathcal {U}}$
is the image of M under the quotient map, and so its cardinality is at most
$M^{/E,\mathcal {U}}$
is the image of M under the quotient map, and so its cardinality is at most
![]() $2^{\aleph _0}$
. Hence, the density character is also at most
$2^{\aleph _0}$
. Hence, the density character is also at most
![]() $2^{\aleph _0}$
.
$2^{\aleph _0}$
.
(2) Suppose
![]() $M^{/E,\mathcal {U}}$
has no diffuse summand. Choose a family
$M^{/E,\mathcal {U}}$
has no diffuse summand. Choose a family
![]() $(p_i)_{i \in I}$
of mutually orthogonal minimal projections in
$(p_i)_{i \in I}$
of mutually orthogonal minimal projections in
![]() $Z(M^{/E,\mathcal {U}})$
that is maximal with respect to inclusion. This collection must be countable since
$Z(M^{/E,\mathcal {U}})$
that is maximal with respect to inclusion. This collection must be countable since
![]() $M^{/E,\mathcal {U}}$
has a faithful trace. We must have
$M^{/E,\mathcal {U}}$
has a faithful trace. We must have
![]() $\sum _{i \in I} p_i = 1$
, or else we could construct a minimal projection under the complement and contradict maximality. Note that
$\sum _{i \in I} p_i = 1$
, or else we could construct a minimal projection under the complement and contradict maximality. Note that
![]() $p_i M^{/E,\mathcal {U}}$
must be a factor, or else it would contain a nontrivial central projection and contradict minimality of
$p_i M^{/E,\mathcal {U}}$
must be a factor, or else it would contain a nontrivial central projection and contradict minimality of
![]() $p_i$
. Thus,
$p_i$
. Thus,
![]() $p_i M^{E,\mathcal {U}}$
must be a tracial factor that admits a minimal projection, and so is isomorphic to a matrix algebra.
$p_i M^{E,\mathcal {U}}$
must be a tracial factor that admits a minimal projection, and so is isomorphic to a matrix algebra.
Now that we have computed the density character of the generalized ultraproducts, we move on to saturation. Roughly speaking, saturation means that if some conditions have approximate solutions, then they have a solution; saturation is thus somewhat similar to compactness (see [Reference JekelJek24, Proposition 2.28]). The number of constants that can appear in the conditions is a specified cardinality
![]() $\kappa $
. The definition is as follows; see [Reference Ben Yaacov, Berenstein, Henson, Usvyatsov, Chatzidakis, Macpherson, Pillay and WilkieBBHU08, Definition 7.5], [Reference Farah, Hart and ShermanFHS14a, §4.4].
$\kappa $
. The definition is as follows; see [Reference Ben Yaacov, Berenstein, Henson, Usvyatsov, Chatzidakis, Macpherson, Pillay and WilkieBBHU08, Definition 7.5], [Reference Farah, Hart and ShermanFHS14a, §4.4].
Definition 5.6. Let M be a tracial von Neumann algebra. Let
![]() $A \subseteq (M)_1$
and let
$A \subseteq (M)_1$
and let
![]() $\Gamma $
be a collection of formulas whose free variables lie within
$\Gamma $
be a collection of formulas whose free variables lie within
![]() $\{x_1, \cdots , x_n\} \cup \{y_a\}_{a \in A}$
. with free variables
$\{x_1, \cdots , x_n\} \cup \{y_a\}_{a \in A}$
. with free variables
![]() $x_1,\dots ,x_n$
and
$x_1,\dots ,x_n$
and
![]() $(y_i)_{i \in I}$
.
$(y_i)_{i \in I}$
.
-
1. The collection
 $\Gamma $
is satisfiable in M if there exist
$\Gamma $
is satisfiable in M if there exist
 $x_1$
, …,
$x_1$
, …,
 $x_n \in (M)_1$
, such that
$x_n \in (M)_1$
, such that  $$\begin{align*}\varphi^M(x_1, \cdots, x_n, \{a\}_{a \in A}) = 0 \text{ for } \varphi \in \Gamma. \end{align*}$$
$$\begin{align*}\varphi^M(x_1, \cdots, x_n, \{a\}_{a \in A}) = 0 \text{ for } \varphi \in \Gamma. \end{align*}$$
-
2. The collection
 $\Gamma $
is finitely approximately satisfiable if, for every finite subset
$\Gamma $
is finitely approximately satisfiable if, for every finite subset
 $\Gamma _0 \subseteq \Gamma $
and every
$\Gamma _0 \subseteq \Gamma $
and every
 $\epsilon> 0$
, there exists
$\epsilon> 0$
, there exists
 $\{x_1, \cdots , x_n\} \subseteq (M)_1$
, such that
$\{x_1, \cdots , x_n\} \subseteq (M)_1$
, such that  $$\begin{align*}|\varphi^M(x_1, \cdots, x_n, \{a\}_{a \in A})| < \epsilon \text{ for } \varphi \in \Gamma_0. \end{align*}$$
$$\begin{align*}|\varphi^M(x_1, \cdots, x_n, \{a\}_{a \in A})| < \epsilon \text{ for } \varphi \in \Gamma_0. \end{align*}$$
-
3. Let
 $\kappa $
be an infinite cardinal. We say that M is
$\kappa $
be an infinite cardinal. We say that M is
 $\kappa $
-saturated if for every
$\kappa $
-saturated if for every
 $A \subseteq (M)_1$
with
$A \subseteq (M)_1$
with
 $|A| < \kappa $
and every collection
$|A| < \kappa $
and every collection
 $\Gamma $
as above, if
$\Gamma $
as above, if
 $\Gamma $
is finitely approximately satisfiable, then
$\Gamma $
is finitely approximately satisfiable, then
 $\Gamma $
is satisfiable.
$\Gamma $
is satisfiable. -
4. We call M countably saturated if it is
 $\aleph _1$
-saturated, meaning that the above condition holds whenever
$\aleph _1$
-saturated, meaning that the above condition holds whenever
 $|A| < \aleph _1$
(i.e., when A is countable).
$|A| < \aleph _1$
(i.e., when A is countable). -
5. We call M saturated if it is
 $\kappa $
-saturated where
$\kappa $
-saturated where
 $\kappa $
is the density character of M.
$\kappa $
is the density character of M.
Hence, in Proposition 5.2, the requirement is for M and N to be saturated with the cardinal specified by their density character. We showed in Proposition 5.3 that the density character of ultrafibers arising from a direct integral is
![]() $2^{\aleph _0}$
in the non-atomic case. Under CH, this equals
$2^{\aleph _0}$
in the non-atomic case. Under CH, this equals
![]() $\aleph _1$
, so in this case, countable saturation is enough to obtain saturation. It is well known that ultraproducts with respect to countably incomplete ultrafilters are countably saturated [Reference Ben Yaacov, Berenstein, Henson, Usvyatsov, Chatzidakis, Macpherson, Pillay and WilkieBBHU08, Proposition 7.6], [Reference Farah, Hart and ShermanFHS14a, Proposition 4.11]. Our next goal is to show the same conclusion for ultrafibers over continuous index sets by adapting the classic diagonalization argument.
$\aleph _1$
, so in this case, countable saturation is enough to obtain saturation. It is well known that ultraproducts with respect to countably incomplete ultrafilters are countably saturated [Reference Ben Yaacov, Berenstein, Henson, Usvyatsov, Chatzidakis, Macpherson, Pillay and WilkieBBHU08, Proposition 7.6], [Reference Farah, Hart and ShermanFHS14a, Proposition 4.11]. Our next goal is to show the same conclusion for ultrafibers over continuous index sets by adapting the classic diagonalization argument.
Proposition 5.7. Let M be a finite von Neumann algebra,
![]() $N \subseteq Z(M)$
be a subalgebra of its center,
$N \subseteq Z(M)$
be a subalgebra of its center,
![]() $E: M \to N$
be a normal, tracial, faithful conditional expectation, and
$E: M \to N$
be a normal, tracial, faithful conditional expectation, and
![]() $\mathcal {U}$
be a countably incomplete character on N. Then
$\mathcal {U}$
be a countably incomplete character on N. Then
![]() $M^{/E, \mathcal {U}}$
is countably saturated.
$M^{/E, \mathcal {U}}$
is countably saturated.
Proof. Let
![]() $A \subset (M^{/E, \mathcal {U}})_1$
be a countable set. For each
$A \subset (M^{/E, \mathcal {U}})_1$
be a countable set. For each
![]() $a \in A$
, fix a lift
$a \in A$
, fix a lift ![]() of a. Let
of a. Let
![]() $\Gamma $
be a collection of formulae whose free variables lie within
$\Gamma $
be a collection of formulae whose free variables lie within
![]() $\{x_1, \cdots , x_n\} \cup \{y_a\}_{a \in A}$
, and suppose that
$\{x_1, \cdots , x_n\} \cup \{y_a\}_{a \in A}$
, and suppose that
![]() $\Gamma $
is finitely approximately satisfiable in
$\Gamma $
is finitely approximately satisfiable in
![]() $M^{/E,\mathcal {U}}$
. First, we consider the case where
$M^{/E,\mathcal {U}}$
. First, we consider the case where
![]() $\Gamma $
is countable, so write
$\Gamma $
is countable, so write
![]() $\Gamma = \{\varphi _k: k \in \mathbb {N}\}$
.
$\Gamma = \{\varphi _k: k \in \mathbb {N}\}$
.
For each
![]() $m \in \mathbb {N}$
, since
$m \in \mathbb {N}$
, since
![]() $\Gamma $
is finitely satisfiable, fix
$\Gamma $
is finitely satisfiable, fix
![]() $x_1^{(m)},\dots ,x_n^{(m)} \in (M^{/E, \mathcal {U}})_1$
such that
$x_1^{(m)},\dots ,x_n^{(m)} \in (M^{/E, \mathcal {U}})_1$
such that
Let ![]() such that
such that ![]() . By Theorem 3.18, we have
. By Theorem 3.18, we have
By Lemma 2.3, there exists a projection
![]() $p_m \in N$
s.t.
$p_m \in N$
s.t.
![]() $\mathcal {U}(p_m) = 1$
and
$\mathcal {U}(p_m) = 1$
and
As
![]() $\mathcal {U}$
is countably incomplete, fix a sequence of projections
$\mathcal {U}$
is countably incomplete, fix a sequence of projections
![]() $q_n \searrow 0$
with
$q_n \searrow 0$
with
![]() $\mathcal {U}(q_n) = 1$
. Then let
$\mathcal {U}(q_n) = 1$
. Then let
![]() $e_m = (\bigwedge _{k = 1}^m p_k) \wedge q_m$
, so that
$e_m = (\bigwedge _{k = 1}^m p_k) \wedge q_m$
, so that
![]() $e_m \searrow 0$
and
$e_m \searrow 0$
and
![]() $e_m$
satisfies the same condition as
$e_m$
satisfies the same condition as
![]() $p_m$
above.
$p_m$
above.
Let
![]() $e_0' = 1 - e_1$
and
$e_0' = 1 - e_1$
and
![]() $e_m' = e_m - e_{m+1}$
for
$e_m' = e_m - e_{m+1}$
for
![]() $m \geq 1$
. Then
$m \geq 1$
. Then
![]() $(e_m')_{m=0}^\infty $
is a PVM over N. For
$(e_m')_{m=0}^\infty $
is a PVM over N. For
![]() $i = 1, \dots , n$
, define
$i = 1, \dots , n$
, define
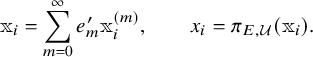
Given
![]() $m_0 \in \mathbb {N}$
, we have that
$m_0 \in \mathbb {N}$
, we have that
![]() $m \geq m_0$
,
$m \geq m_0$
,
and hence,
Therefore,
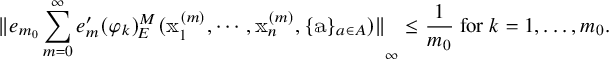
By Lemma 3.14, this means that
Since
![]() $\mathcal {U}(e_{m_0}) = 1$
, we therefore have by Theorem 3.18 that
$\mathcal {U}(e_{m_0}) = 1$
, we therefore have by Theorem 3.18 that
Since
![]() $m_0$
was arbitrary,
$m_0$
was arbitrary,
![]() $\varphi _k^{M^{/E,\mathcal {U}}}(x_1,\dots ,x_m,(a)_{a \in A}) = 0$
for all
$\varphi _k^{M^{/E,\mathcal {U}}}(x_1,\dots ,x_m,(a)_{a \in A}) = 0$
for all
![]() $k \in \mathbb {N}$
, and therefore,
$k \in \mathbb {N}$
, and therefore,
![]() $\Gamma $
is satisfiable.
$\Gamma $
is satisfiable.
It remains to remove the assumption that
![]() $\Gamma $
is countable. Consider a general
$\Gamma $
is countable. Consider a general
![]() $\Gamma = (\varphi _i)_{i \in I}$
associated to the same countable set A. By Lemma 3.10, choose a countable set of formulas
$\Gamma = (\varphi _i)_{i \in I}$
associated to the same countable set A. By Lemma 3.10, choose a countable set of formulas
![]() $\Lambda $
that is dense with respect to
$\Lambda $
that is dense with respect to
![]() ${\lVert {\cdot }\rVert }_u$
. For each
${\lVert {\cdot }\rVert }_u$
. For each
![]() $i \in I$
and
$i \in I$
and
![]() $m \in \mathbb {N}$
, choose
$m \in \mathbb {N}$
, choose
![]() $\lambda _{i,m} \in \Lambda $
such that
$\lambda _{i,m} \in \Lambda $
such that
![]() ${\lVert {\lambda _{i,m} - \varphi _i}\rVert }_u \leq 1/m$
. Let
${\lVert {\lambda _{i,m} - \varphi _i}\rVert }_u \leq 1/m$
. Let
Since
![]() $\lambda _{i,m}$
comes from the countable set
$\lambda _{i,m}$
comes from the countable set
![]() $\Lambda $
, the set
$\Lambda $
, the set
![]() $\Gamma ' = \{\psi _{i,m}: i \in I, m \in \mathbb {N}\}$
is countable. Furthermore, note that for each
$\Gamma ' = \{\psi _{i,m}: i \in I, m \in \mathbb {N}\}$
is countable. Furthermore, note that for each
![]() $i \in I$
,
$i \in I$
,
Thus, since
![]() $\Gamma $
is finitely approximately satisfiable, so is
$\Gamma $
is finitely approximately satisfiable, so is
![]() $\Gamma '$
. By the preceding argument,
$\Gamma '$
. By the preceding argument,
![]() $\Gamma '$
is satisfiable in M. If
$\Gamma '$
is satisfiable in M. If
![]() $(x_1,\dots ,x_n)$
satisfies
$(x_1,\dots ,x_n)$
satisfies
![]() $\Gamma '$
, then it satisfies
$\Gamma '$
, then it satisfies
![]() $|\varphi _i(x_1,\dots ,x_m,(a)_{a \in A})| \leq 2/m$
for all
$|\varphi _i(x_1,\dots ,x_m,(a)_{a \in A})| \leq 2/m$
for all
![]() $i \in I$
and
$i \in I$
and
![]() $m \in \mathbb {N}$
, and therefore, it satisfies
$m \in \mathbb {N}$
, and therefore, it satisfies
![]() $\Gamma $
, as desired.
$\Gamma $
, as desired.
Finally, we put the pieces together to complete the proof.
Proof of Proposition 5.1.
Consider a direct integral
![]() $(M,\tau ) = \int _\Omega ^{\oplus } (M_\omega ,\tau _\omega )\,d\mu (\omega )$
. Let
$(M,\tau ) = \int _\Omega ^{\oplus } (M_\omega ,\tau _\omega )\,d\mu (\omega )$
. Let
![]() $E: M \to L^\infty (\Omega ,\mu )$
be the canonical conditional expectation. First, we claim that
$E: M \to L^\infty (\Omega ,\mu )$
be the canonical conditional expectation. First, we claim that
Let
![]() $\operatorname {\mathrm {ev}}_E^M: \mathcal {P}_{\varnothing } \to L^\infty (\Omega ,\mu )$
be the evaluation map. By Theorem 3.18,
$\operatorname {\mathrm {ev}}_E^M: \mathcal {P}_{\varnothing } \to L^\infty (\Omega ,\mu )$
be the evaluation map. By Theorem 3.18,
![]() $\operatorname {\mathrm {Th}}(M^{/E,\mathcal {U}})$
is the mapping
$\operatorname {\mathrm {Th}}(M^{/E,\mathcal {U}})$
is the mapping
![]() $\mathcal {P}_{\varnothing } \to \mathbb {R}$
given by
$\mathcal {P}_{\varnothing } \to \mathbb {R}$
given by
![]() $\mathcal {U} \circ \operatorname {\mathrm {ev}}_E^M$
. For each
$\mathcal {U} \circ \operatorname {\mathrm {ev}}_E^M$
. For each
![]() $\varphi \in \mathcal {P}_{\varnothing }$
, we have
$\varphi \in \mathcal {P}_{\varnothing }$
, we have
Recall that
![]() $\varphi $
is equivalent to a continuous function on the compact Hausdorff space
$\varphi $
is equivalent to a continuous function on the compact Hausdorff space
![]() $\mathcal {X} = \operatorname {\mathrm {Spec}}(\mathcal {P}_{\varnothing })$
. If
$\mathcal {X} = \operatorname {\mathrm {Spec}}(\mathcal {P}_{\varnothing })$
. If
![]() $\mathcal {Y} \subseteq \mathcal {X}$
and we have
$\mathcal {Y} \subseteq \mathcal {X}$
and we have
![]() $|f(x)| \leq \sup _{y \in \mathcal {Y}} |f(y)|$
for all
$|f(x)| \leq \sup _{y \in \mathcal {Y}} |f(y)|$
for all
![]() $f \in C(\mathcal {X};\mathbb {R})$
, then
$f \in C(\mathcal {X};\mathbb {R})$
, then
![]() $x \in \overline {\mathcal {Y}}$
. Since the theories are characters corresponding to point evaluations, this shows in our case that
$x \in \overline {\mathcal {Y}}$
. Since the theories are characters corresponding to point evaluations, this shows in our case that
![]() $\operatorname {\mathrm {Th}}(M^{/E,\mathcal {U}})$
is in the closure of
$\operatorname {\mathrm {Th}}(M^{/E,\mathcal {U}})$
is in the closure of
![]() $\{\operatorname {\mathrm {Th}}(M_\omega ): \omega \in \Omega \}$
, as desired.
$\{\operatorname {\mathrm {Th}}(M_\omega ): \omega \in \Omega \}$
, as desired.
Now since the space of theories is separable and metrizable, there exists a sequence
![]() $\omega _n$
such that
$\omega _n$
such that
![]() $\operatorname {\mathrm {Th}}(M_{\omega _n}) \to \operatorname {\mathrm {Th}}(M^{/E,\mathcal {U}})$
. Fix a non-principal ultrafilter
$\operatorname {\mathrm {Th}}(M_{\omega _n}) \to \operatorname {\mathrm {Th}}(M^{/E,\mathcal {U}})$
. Fix a non-principal ultrafilter
![]() $\mathcal {V}$
on
$\mathcal {V}$
on
![]() $\mathbb {N}$
, and let
$\mathbb {N}$
, and let
![]() $N = \prod _{\mathcal {V}} (M_{\omega _n},\tau _{\omega _n})$
. By Łoś’s theorem,
$N = \prod _{\mathcal {V}} (M_{\omega _n},\tau _{\omega _n})$
. By Łoś’s theorem,
![]() $\operatorname {\mathrm {Th}}(N) = \lim _{n \to \mathcal {V}} \operatorname {\mathrm {Th}}(M_{\omega _n}) = \operatorname {\mathrm {Th}}(M^{/E,\mathcal {U}})$
.
$\operatorname {\mathrm {Th}}(N) = \lim _{n \to \mathcal {V}} \operatorname {\mathrm {Th}}(M_{\omega _n}) = \operatorname {\mathrm {Th}}(M^{/E,\mathcal {U}})$
.
By [Reference Farah and GhasemiFG24, Lemma 4.4, proof of Proposition 4.3], we have that N is atomic if and only if
![]() $M^{/E,\mathcal {U}}$
is atomic; moreover, the sizes of the atoms in the decomposition and the dimensions of the matrix algebras are uniquely determined by the theory. Thus, in the atomic case, we have
$M^{/E,\mathcal {U}}$
is atomic; moreover, the sizes of the atoms in the decomposition and the dimensions of the matrix algebras are uniquely determined by the theory. Thus, in the atomic case, we have
![]() $M^{/E,\mathcal {U}} \cong N$
.
$M^{/E,\mathcal {U}} \cong N$
.
Otherwise,
![]() $M^{/E,\mathcal {U}}$
and N both have a diffuse summand. By Proposition 5.3, the density character of
$M^{/E,\mathcal {U}}$
and N both have a diffuse summand. By Proposition 5.3, the density character of
![]() $M^{/E,\mathcal {U}}$
and of N is the continuum
$M^{/E,\mathcal {U}}$
and of N is the continuum
![]() $2^{\aleph _0}$
. Note that Proposition 5.7 implies that
$2^{\aleph _0}$
. Note that Proposition 5.7 implies that
![]() $M^{/E,\mathcal {U}}$
and N are countably saturated (i.e.,
$M^{/E,\mathcal {U}}$
and N are countably saturated (i.e.,
![]() $\aleph _1$
-saturated). By CH,
$\aleph _1$
-saturated). By CH,
![]() $\aleph _1 = 2^{\aleph _0}$
, and therefore,
$\aleph _1 = 2^{\aleph _0}$
, and therefore,
![]() $M^{/E,\mathcal {U}}$
and N are saturated, so by Proposition 5.2,
$M^{/E,\mathcal {U}}$
and N are saturated, so by Proposition 5.2,
![]() $M^{/E,\mathcal {U}} \cong N$
.
$M^{/E,\mathcal {U}} \cong N$
.
6 Random matrices and ultraproducts
Our goal in this section is to describe how ultrafibers shed light on the relationship between random matrices and ultraproducts. We denote by
![]() $\mathbb {M}_n$
the algebra of
$\mathbb {M}_n$
the algebra of
![]() $n \times n$
complex matrices equipped with the normalized trace
$n \times n$
complex matrices equipped with the normalized trace
![]() $\operatorname {\mathrm {tr}}_n$
. Suppose that
$\operatorname {\mathrm {tr}}_n$
. Suppose that
![]() $X^{(n)} = (X_i^{(n)})_{i \in I}$
is a tuple of random
$X^{(n)} = (X_i^{(n)})_{i \in I}$
is a tuple of random
![]() $n \times n$
matrices on the probability space
$n \times n$
matrices on the probability space
![]() $([0,1],\operatorname {\mathrm {Leb}})$
and suppose that
$([0,1],\operatorname {\mathrm {Leb}})$
and suppose that
![]() $\limsup _{n \to \infty } {\lVert {X_i^{(n)}}\rVert } < \infty $
almost surely. Fix also a free ultrafilter
$\limsup _{n \to \infty } {\lVert {X_i^{(n)}}\rVert } < \infty $
almost surely. Fix also a free ultrafilter
![]() $\mathcal {U}$
on
$\mathcal {U}$
on
![]() $\mathbb {N}$
. Then in what sense does the sequence
$\mathbb {N}$
. Then in what sense does the sequence
![]() $X_i^{(n)}$
define a random element in the ultraproduct
$X_i^{(n)}$
define a random element in the ultraproduct
![]() $\prod _{n \to \mathcal {U}} \mathbb {M}_n$
?
$\prod _{n \to \mathcal {U}} \mathbb {M}_n$
?
For concreteness, assume that
![]() $X_i^{(n)}$
is an independent family of matrices from the Gaussian unitary ensemble (GUE) (for background, see, for example, [Reference Anderson, Guionnet and ZeitouniAGZ09, Reference Mingo and SpeicherMS17]). For almost every
$X_i^{(n)}$
is an independent family of matrices from the Gaussian unitary ensemble (GUE) (for background, see, for example, [Reference Anderson, Guionnet and ZeitouniAGZ09, Reference Mingo and SpeicherMS17]). For almost every
![]() $\omega \in [0,1]$
, the sequence
$\omega \in [0,1]$
, the sequence
![]() $(X_i^{(n)}(\omega ))_{n \in \mathbb {N}}$
defines an element
$(X_i^{(n)}(\omega ))_{n \in \mathbb {N}}$
defines an element
![]() $X_i(\omega )$
in
$X_i(\omega )$
in
![]() $\mathcal {Q} = \prod _{n \to \mathcal {U}} \mathbb {M}_n$
. However,
$\mathcal {Q} = \prod _{n \to \mathcal {U}} \mathbb {M}_n$
. However,
![]() $\omega \mapsto X_i(\omega )$
is not measurable in the usual sense. Indeed, for
$\omega \mapsto X_i(\omega )$
is not measurable in the usual sense. Indeed, for
![]() $X_i(\omega )$
to be Bochner-measurable, it would have to almost surely take values in a separable subspace of
$X_i(\omega )$
to be Bochner-measurable, it would have to almost surely take values in a separable subspace of
![]() $\mathcal {Q}$
, which would imply there is some
$\mathcal {Q}$
, which would imply there is some
![]() $L^2$
ball
$L^2$
ball
![]() $B_r(Y)$
in
$B_r(Y)$
in
![]() $\mathcal {Q}$
such that
$\mathcal {Q}$
such that
![]() $\{\omega : X_i(\omega ) \in B_r(Y)\}$
has strictly positive measure with
$\{\omega : X_i(\omega ) \in B_r(Y)\}$
has strictly positive measure with
![]() $r < 1$
. Write
$r < 1$
. Write
![]() $Y = [Y^{(n)}]_{n \in \mathbb {N}}$
. Then this set can also be written as
$Y = [Y^{(n)}]_{n \in \mathbb {N}}$
. Then this set can also be written as
 $$ \begin{align*} \{\omega: \lim_{n \to \mathcal{U}} {\lVert {X_i^{(n)} - Y^{(n)}} \rVert}_2 < r\} &\subseteq \{\omega: \limsup_{n \to \mathcal{U}} {\lVert {X_i^{(n)}(\omega) - Y^{(n)}} \rVert}_2 < r\} \\ &\subseteq \limsup_{n \to \infty} \{\omega: {\lVert {X_i^{(n)}(\omega) - Y^{(n)}} \rVert}_2 < r\}. \end{align*} $$
$$ \begin{align*} \{\omega: \lim_{n \to \mathcal{U}} {\lVert {X_i^{(n)} - Y^{(n)}} \rVert}_2 < r\} &\subseteq \{\omega: \limsup_{n \to \mathcal{U}} {\lVert {X_i^{(n)}(\omega) - Y^{(n)}} \rVert}_2 < r\} \\ &\subseteq \limsup_{n \to \infty} \{\omega: {\lVert {X_i^{(n)}(\omega) - Y^{(n)}} \rVert}_2 < r\}. \end{align*} $$
Thus,
which is zero because the Gaussian measure of the r-ball vanishes as
![]() $n \to \infty $
if
$n \to \infty $
if
![]() $r < 1$
. It is difficult even to obtain weak-
$r < 1$
. It is difficult even to obtain weak-
![]() $*$
measurability for
$*$
measurability for
![]() $\omega \mapsto X_i(\omega )$
because the inner products with elements of
$\omega \mapsto X_i(\omega )$
because the inner products with elements of
![]() $\mathcal {Q}$
are not ordinary limits of inner products with elements of
$\mathcal {Q}$
are not ordinary limits of inner products with elements of
![]() $\mathbb {M}_n$
, but rather ultralimits. Even if we could achieve weak-
$\mathbb {M}_n$
, but rather ultralimits. Even if we could achieve weak-
![]() $*$
measurability, it would not be that helpful since the predual of the matrix ultraproduct is not separable; thus, many natural conditions we would want for the random matrix would end up producing uncountable unions and intersections. Hence, great care has to be taken in arguments that combine probability and ultraproducts as in [Reference Farah, Jekel and PiFJP23, Reference Jekel and PiJP24].
$*$
measurability, it would not be that helpful since the predual of the matrix ultraproduct is not separable; thus, many natural conditions we would want for the random matrix would end up producing uncountable unions and intersections. Hence, great care has to be taken in arguments that combine probability and ultraproducts as in [Reference Farah, Jekel and PiFJP23, Reference Jekel and PiJP24].
Therefore, rather than attempting to study
![]() $X_i$
as a map
$X_i$
as a map
![]() $[0,1] \to \prod _{n \to \mathcal {U}} \mathbb {M}_n$
, it seems much more natural to consider
$[0,1] \to \prod _{n \to \mathcal {U}} \mathbb {M}_n$
, it seems much more natural to consider
![]() $X_i$
as an element of
$X_i$
as an element of
![]() $\prod _{n \to \mathcal {U}} (L^\infty [0,1] \otimes \mathbb {M}_n)$
, which heuristically is more like a random variable on the non-separable probability space
$\prod _{n \to \mathcal {U}} (L^\infty [0,1] \otimes \mathbb {M}_n)$
, which heuristically is more like a random variable on the non-separable probability space
![]() $([0,1],\operatorname {\mathrm {Leb}})^{\mathcal {U}}$
corresponding to
$([0,1],\operatorname {\mathrm {Leb}})^{\mathcal {U}}$
corresponding to
![]() $L^\infty [0,1]^{\mathcal {U}}$
than on the probability space
$L^\infty [0,1]^{\mathcal {U}}$
than on the probability space
![]() $[0,1]$
itself. However, it is not even a random variable over
$[0,1]$
itself. However, it is not even a random variable over
![]() $([0,1],\operatorname {\mathrm {Leb}})^{\mathcal {U}}$
in the ordinary sense. And so, rather than trying to extract a deterministic element of
$([0,1],\operatorname {\mathrm {Leb}})^{\mathcal {U}}$
in the ordinary sense. And so, rather than trying to extract a deterministic element of
![]() $\prod _{n \to \mathcal {U}} \mathbb {M}_n$
from
$\prod _{n \to \mathcal {U}} \mathbb {M}_n$
from
![]() $X_i$
by choosing a point in some probability space, we can form an ultrafiber of
$X_i$
by choosing a point in some probability space, we can form an ultrafiber of
![]() $\prod _{n \to \mathcal {U}} (L^\infty [0,1] \otimes \mathbb {M}_n)$
using a pure state
$\prod _{n \to \mathcal {U}} (L^\infty [0,1] \otimes \mathbb {M}_n)$
using a pure state
![]() $\mathcal {V}$
on its center
$\mathcal {V}$
on its center
![]() $L^\infty [0,1]^{\mathcal {U}}$
. As we will see below, the ultrafiber M obtained from this process is larger than the subalgebra
$L^\infty [0,1]^{\mathcal {U}}$
. As we will see below, the ultrafiber M obtained from this process is larger than the subalgebra
![]() $Q = \prod _{n \to \mathcal {U}} \mathbb {M}_n \subseteq \prod _{n \to \mathcal {U}} (L^\infty [0,1] \otimes \mathbb {M}_n)$
corresponding to the deterministic matrices. In fact, the image of
$Q = \prod _{n \to \mathcal {U}} \mathbb {M}_n \subseteq \prod _{n \to \mathcal {U}} (L^\infty [0,1] \otimes \mathbb {M}_n)$
corresponding to the deterministic matrices. In fact, the image of
![]() $X_i$
in M will be freely independent of Q (for background on free independence, see [Reference Voiculescu, Dykema and NicaVDN92, Reference Anderson, Guionnet and ZeitouniAGZ09, Reference Mingo and SpeicherMS17]).
$X_i$
in M will be freely independent of Q (for background on free independence, see [Reference Voiculescu, Dykema and NicaVDN92, Reference Anderson, Guionnet and ZeitouniAGZ09, Reference Mingo and SpeicherMS17]).
Proposition 6.1. Let
![]() $\mathcal {U}$
be a free ultrafilter on
$\mathcal {U}$
be a free ultrafilter on
![]() $\mathbb {N}$
. Let
$\mathbb {N}$
. Let
![]() $N = \prod _{n \to \mathcal {U}} (L^\infty [0,1] \otimes \mathbb {M}_n)$
and let
$N = \prod _{n \to \mathcal {U}} (L^\infty [0,1] \otimes \mathbb {M}_n)$
and let
![]() $Q = \prod _{n \to \mathcal {U}} \mathbb {M}_n \subseteq N$
. Let
$Q = \prod _{n \to \mathcal {U}} \mathbb {M}_n \subseteq N$
. Let
![]() $\mathcal {V}$
be a pure state on
$\mathcal {V}$
be a pure state on
![]() $Z(N) \cong L^\infty [0,1]^{\mathcal {U}}$
, let
$Z(N) \cong L^\infty [0,1]^{\mathcal {U}}$
, let
![]() $E: N \to Z(N)$
be the trace-preserving conditional expectation, let
$E: N \to Z(N)$
be the trace-preserving conditional expectation, let
![]() $M = N^{/E,\mathcal {V}}$
be the corresponding ultrafiber, and let
$M = N^{/E,\mathcal {V}}$
be the corresponding ultrafiber, and let
![]() $\pi _{E,\mathcal {V}}: N \to M$
be the natural quotient map.
$\pi _{E,\mathcal {V}}: N \to M$
be the natural quotient map.
Let I be a countable index set and let
![]() $(X_i^{(n)})_{i \in I}$
be a family of independent GUE matrices on the probability space
$(X_i^{(n)})_{i \in I}$
be a family of independent GUE matrices on the probability space
![]() $([0,1],\operatorname {\mathrm {Leb}})$
. Let
$([0,1],\operatorname {\mathrm {Leb}})$
. Let
![]() $f: \mathbb {R} \to \mathbb {R}$
be a bounded continuous function with
$f: \mathbb {R} \to \mathbb {R}$
be a bounded continuous function with
![]() $f|_{[-2,2]} = \operatorname {\mathrm {id}}$
, and let
$f|_{[-2,2]} = \operatorname {\mathrm {id}}$
, and let
![]() $X_i = [f(X_i^{(n)})]_{n \in \mathbb {N}} \in N$
. Then
$X_i = [f(X_i^{(n)})]_{n \in \mathbb {N}} \in N$
. Then
-
1.
 $\pi _{E,\mathcal {V}}$
is injective on Q, and
$\pi _{E,\mathcal {V}}$
is injective on Q, and
 $\pi _{E,\mathcal {V}}(Q)$
is an elementary submodel of M.
$\pi _{E,\mathcal {V}}(Q)$
is an elementary submodel of M. -
2.
 $X_i$
does not depend on the particular choice of f.
$X_i$
does not depend on the particular choice of f. -
3. The elements
 $\pi _{E,\mathcal {V}}(X_i)$
are freely independent of each other and of
$\pi _{E,\mathcal {V}}(X_i)$
are freely independent of each other and of
 $\pi _{E,\mathcal {V}}(Q)$
.
$\pi _{E,\mathcal {V}}(Q)$
. -
4. For each
 $k+\ell $
-variable formula
$k+\ell $
-variable formula
 $\varphi $
, indices
$\varphi $
, indices
 $i_1$
, …,
$i_1$
, …,
 $i_k \in I$
, and elements
$i_k \in I$
, and elements
 $A_1$
, …,
$A_1$
, …,
 $A_\ell \in (Q)_1$
, the value of does not depend on
$A_\ell \in (Q)_1$
, the value of does not depend on $$\begin{align*}\varphi^{M}(\pi_{E,\mathcal{V}}(X_{i_1}/2),\dots,\pi_{E,\mathcal{V}}(X_{i_k}/2),\pi_{E,\mathcal{V}}(A_1),\dots,\pi_{E,\mathcal{V}}(A_\ell)) \end{align*}$$
$$\begin{align*}\varphi^{M}(\pi_{E,\mathcal{V}}(X_{i_1}/2),\dots,\pi_{E,\mathcal{V}}(X_{i_k}/2),\pi_{E,\mathcal{V}}(A_1),\dots,\pi_{E,\mathcal{V}}(A_\ell)) \end{align*}$$
 $\mathcal {V}$
(it only depends on
$\mathcal {V}$
(it only depends on
 $\mathcal {U}$
).
$\mathcal {U}$
).
Proof. (1) Note that
![]() $N = \prod _{n \to \mathcal {U}} (L^\infty [0,1] \otimes \mathbb {M}_n)$
is a quotient of
$N = \prod _{n \to \mathcal {U}} (L^\infty [0,1] \otimes \mathbb {M}_n)$
is a quotient of
let q denote the quotient map, and let
![]() $\tilde {E}: \tilde {N} \to Z(\tilde {N)} \cong L^\infty [0,1] \overline {\otimes } \ell ^\infty (\mathbb {N})$
be the center-valued trace. As in the proof of Proposition 4.3, we have
$\tilde {E}: \tilde {N} \to Z(\tilde {N)} \cong L^\infty [0,1] \overline {\otimes } \ell ^\infty (\mathbb {N})$
be the center-valued trace. As in the proof of Proposition 4.3, we have
Note also that
![]() $\tilde {N}$
can be viewed as a direct integral of
$\tilde {N}$
can be viewed as a direct integral of
![]() $M_n(\mathbb {C})$
over the probability space
$M_n(\mathbb {C})$
over the probability space
![]() $\bigsqcup _{n \in \mathbb {N}} [0,1]$
corresponding to the algebra
$\bigsqcup _{n \in \mathbb {N}} [0,1]$
corresponding to the algebra
![]() $L^\infty [0,1] \overline {\otimes } \ell ^\infty (\mathbb {N})$
(after fixing a probability measure on
$L^\infty [0,1] \overline {\otimes } \ell ^\infty (\mathbb {N})$
(after fixing a probability measure on
![]() $\mathbb {N}$
with full support, which, however, will play no role in the argument). For
$\mathbb {N}$
with full support, which, however, will play no role in the argument). For
![]() $j = 1$
, …, k, let
$j = 1$
, …, k, let
![]() $(A_j^{(n)})_{n \in \mathbb {N}} \in \bigoplus _{n \in \mathbb {N}} \mathbb {M}_n$
be a sequence of matrices bounded in operator norm, and let
$(A_j^{(n)})_{n \in \mathbb {N}} \in \bigoplus _{n \in \mathbb {N}} \mathbb {M}_n$
be a sequence of matrices bounded in operator norm, and let
Let
![]() $\varphi $
be a formula with k free variables. By considering these with respect to the direct integral decomposition over
$\varphi $
be a formula with k free variables. By considering these with respect to the direct integral decomposition over
![]() $L^\infty [0,1] \overline {\otimes } \ell ^\infty (\mathbb {N})$
and applying Lemma 3.17, we see that
$L^\infty [0,1] \overline {\otimes } \ell ^\infty (\mathbb {N})$
and applying Lemma 3.17, we see that
Then by Theorem 3.18, we have
 $$ \begin{align*} \varphi^{M}(\pi_{\tilde{E},\mathcal{V} \circ q}(\tilde{A}_1),\dots, \pi_{\tilde{E},\mathcal{V} \circ q}(\tilde{A}_k)) &= \mathcal{V} \circ q[\varphi_{\tilde{E}}^{\tilde{N}}(\tilde{A}_1,\dots,\tilde{A}_k)] \\ &= \mathcal{V} \circ q \left( 1_{L^\infty[0,1]} \otimes \bigoplus_{n \in \mathbb{N}} \varphi^{\mathbb{M}_n}(A_1^{(n)},\dots,A_k^{(n)}) \right) \\ &= \mathcal{V} \circ q \left( \bigoplus_{n \in \mathbb{N}} 1_{L^\infty[0,1]} \otimes \varphi^{\mathbb{M}_n}(A_1^{(n)},\dots,A_k^{(n)}) \right) \\ &= \mathcal{V} \left( 1_{N} \lim_{n \to \mathcal{U}} \varphi^{\mathbb{M}_n}(A_1^{(n)},\dots,A_k^{(n)}) \right) \\ &= \lim_{n \to \mathcal{U}} \varphi^{\mathbb{M}_n}(A_1^{(n)},\dots,A_k^{(n)}) \\ &= \varphi^{Q}(A_1,\dots,A_k), \end{align*} $$
$$ \begin{align*} \varphi^{M}(\pi_{\tilde{E},\mathcal{V} \circ q}(\tilde{A}_1),\dots, \pi_{\tilde{E},\mathcal{V} \circ q}(\tilde{A}_k)) &= \mathcal{V} \circ q[\varphi_{\tilde{E}}^{\tilde{N}}(\tilde{A}_1,\dots,\tilde{A}_k)] \\ &= \mathcal{V} \circ q \left( 1_{L^\infty[0,1]} \otimes \bigoplus_{n \in \mathbb{N}} \varphi^{\mathbb{M}_n}(A_1^{(n)},\dots,A_k^{(n)}) \right) \\ &= \mathcal{V} \circ q \left( \bigoplus_{n \in \mathbb{N}} 1_{L^\infty[0,1]} \otimes \varphi^{\mathbb{M}_n}(A_1^{(n)},\dots,A_k^{(n)}) \right) \\ &= \mathcal{V} \left( 1_{N} \lim_{n \to \mathcal{U}} \varphi^{\mathbb{M}_n}(A_1^{(n)},\dots,A_k^{(n)}) \right) \\ &= \lim_{n \to \mathcal{U}} \varphi^{\mathbb{M}_n}(A_1^{(n)},\dots,A_k^{(n)}) \\ &= \varphi^{Q}(A_1,\dots,A_k), \end{align*} $$
where
![]() $A_j$
is the image of
$A_j$
is the image of
![]() $[A_j^{(n)}]_{n \in \mathbb {N}}$
in Q. Note that
$[A_j^{(n)}]_{n \in \mathbb {N}}$
in Q. Note that
![]() $\pi _{\tilde {E},\mathcal {V} \circ q}(\tilde {A}_j) = \pi _{E,\mathcal {V}}(A_j)$
; we have shown that
$\pi _{\tilde {E},\mathcal {V} \circ q}(\tilde {A}_j) = \pi _{E,\mathcal {V}}(A_j)$
; we have shown that
for all formulas
![]() $\varphi $
and
$\varphi $
and
![]() $A_j \in Q$
. Taking
$A_j \in Q$
. Taking
![]() $\varphi $
to be the distance, we see that
$\varphi $
to be the distance, we see that
![]() $\pi _{E,\mathcal {V}}|_Q$
is isometric, and hence injective. And since this relation in fact holds for all formulas
$\pi _{E,\mathcal {V}}|_Q$
is isometric, and hence injective. And since this relation in fact holds for all formulas
![]() $\varphi $
, the mapping
$\varphi $
, the mapping
![]() $Q \to M$
is an elementary embedding.
$Q \to M$
is an elementary embedding.
(2) It is well known that for GUE matrices, we have
![]() $\lim _{n \to \infty } {\lVert {X_i^{(n)}} \rVert } = 2$
almost surely. Suppose f and g are two bounded continuous functions that both equal identity on
$\lim _{n \to \infty } {\lVert {X_i^{(n)}} \rVert } = 2$
almost surely. Suppose f and g are two bounded continuous functions that both equal identity on
![]() $[-2,2]$
. Given
$[-2,2]$
. Given
![]() $\epsilon> 0$
, there exists
$\epsilon> 0$
, there exists
![]() $\delta> 0$
such that
$\delta> 0$
such that
![]() $|f - g| < \epsilon $
on
$|f - g| < \epsilon $
on
![]() $[-2-\delta ,2+\delta ]$
. Thus, when
$[-2-\delta ,2+\delta ]$
. Thus, when
![]() ${\lVert {X_i^{(n)}}\rVert } \leq 2 + \delta $
, which happens for sufficiently large n almost surely, we have
${\lVert {X_i^{(n)}}\rVert } \leq 2 + \delta $
, which happens for sufficiently large n almost surely, we have
![]() ${\lVert {f(X_i^{(n)}) - g(X_i^{(n)})}\rVert } \leq \epsilon $
. Therefore,
${\lVert {f(X_i^{(n)}) - g(X_i^{(n)})}\rVert } \leq \epsilon $
. Therefore,
![]() $\limsup _{n \to \infty } {\lVert {f(X_i^{(n)}) - g(X_i^{(n)})} \rVert }_{L^2([0,1],\mathbb {M}_n)} \leq \epsilon $
, and since
$\limsup _{n \to \infty } {\lVert {f(X_i^{(n)}) - g(X_i^{(n)})} \rVert }_{L^2([0,1],\mathbb {M}_n)} \leq \epsilon $
, and since
![]() $\epsilon $
was arbitary, the limit is zero. This implies that
$\epsilon $
was arbitary, the limit is zero. This implies that
![]() $(f(X_i^{(n)}))_{n \in \mathbb {N}}$
and
$(f(X_i^{(n)}))_{n \in \mathbb {N}}$
and
![]() $(g(X_i^{(n)}))_{n \in \mathbb {N}}$
produce the same element of
$(g(X_i^{(n)}))_{n \in \mathbb {N}}$
produce the same element of
![]() $N = \prod _{n \to \mathcal {U}} (L^\infty [0,1] \otimes \mathbb {M}_n)$
.
$N = \prod _{n \to \mathcal {U}} (L^\infty [0,1] \otimes \mathbb {M}_n)$
.
(3) Recall that to show free independence of
![]() $(\pi _{E,\mathcal {V}}(X_i))_{i \in I}$
and
$(\pi _{E,\mathcal {V}}(X_i))_{i \in I}$
and
![]() $(\pi _{E,\mathcal {V}}(Q))$
, we need to show that for non-commutative polynomials
$(\pi _{E,\mathcal {V}}(Q))$
, we need to show that for non-commutative polynomials
![]() $p_1$
, …,
$p_1$
, …,
![]() $p_k$
and for
$p_k$
and for
![]() $A_1$
, …,
$A_1$
, …,
![]() $A_k \in Q$
, we have
$A_k \in Q$
, we have
 $$\begin{align*}\tau_{M} \left[ \prod_{j=1}^k (p_j((\pi_{E,\mathcal{V}}(X_i))_{i\in I}) - \tau_{M}[p_j((\pi_{E,\mathcal{V}}(X_i))_{i\in I})]) (\pi_{E,\mathcal{V}}(A_j) - \tau_{M}[\pi_{E,\mathcal{V}}(A_j)]) \right] = 0, \end{align*}$$
$$\begin{align*}\tau_{M} \left[ \prod_{j=1}^k (p_j((\pi_{E,\mathcal{V}}(X_i))_{i\in I}) - \tau_{M}[p_j((\pi_{E,\mathcal{V}}(X_i))_{i\in I})]) (\pi_{E,\mathcal{V}}(A_j) - \tau_{M}[\pi_{E,\mathcal{V}}(A_j)]) \right] = 0, \end{align*}$$
where the product is understood to run from left to right. We also have to prove similar claims for alternating strings that start with
![]() $A_1 - \tau (A_1)$
or end with
$A_1 - \tau (A_1)$
or end with
![]() $p_k((X_i)_{i \in I}) - \tau (p_k((X_i)_{i \in I}))$
, but the proof in these cases, of course, is symmetrical, so we focus on the first case written above. Since
$p_k((X_i)_{i \in I}) - \tau (p_k((X_i)_{i \in I}))$
, but the proof in these cases, of course, is symmetrical, so we focus on the first case written above. Since
![]() $\pi _{E,\mathcal {V}}: N \to M$
is a
$\pi _{E,\mathcal {V}}: N \to M$
is a
![]() $*$
-homomorphism and
$*$
-homomorphism and
![]() $\tau _{M} = \mathcal {V} \circ E$
, it suffices to show that
$\tau _{M} = \mathcal {V} \circ E$
, it suffices to show that
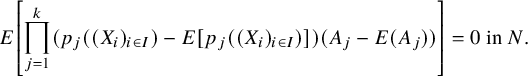 $$\begin{align*}E \left[ \prod_{j=1}^k (p_j((X_i)_{i\in I}) - E[p_j((X_i)_{i\in I})]) (A_j - E(A_j)) \right] = 0 \text{ in } N. \end{align*}$$
$$\begin{align*}E \left[ \prod_{j=1}^k (p_j((X_i)_{i\in I}) - E[p_j((X_i)_{i\in I})]) (A_j - E(A_j)) \right] = 0 \text{ in } N. \end{align*}$$
The latter is the element of the ultraproduct
![]() $\prod _{n \to \mathcal {U}} (L^\infty [0,1] \otimes \mathbb {M}_n)$
given by the sequence
$\prod _{n \to \mathcal {U}} (L^\infty [0,1] \otimes \mathbb {M}_n)$
given by the sequence
 $$\begin{align*}\operatorname{\mathrm{tr}}_n \left[ \prod_{j=1}^k (p_j((f(X_i^{(n)}))_{i\in I}) - \operatorname{\mathrm{tr}}_n[p_j((f(X_i^{(n)}))_{i\in I})]) (A_j^{(n)} - \operatorname{\mathrm{tr}}_n(A_j^{(n)})) \right], \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{tr}}_n \left[ \prod_{j=1}^k (p_j((f(X_i^{(n)}))_{i\in I}) - \operatorname{\mathrm{tr}}_n[p_j((f(X_i^{(n)}))_{i\in I})]) (A_j^{(n)} - \operatorname{\mathrm{tr}}_n(A_j^{(n)})) \right], \end{align*}$$
where
![]() $(A_j^{(n)})_{n \in \mathbb {N}}$
is a sequence representing
$(A_j^{(n)})_{n \in \mathbb {N}}$
is a sequence representing
![]() $A_j$
in Q. By Voiculescu’s asymptotic freeness theorem (see, for example, [Reference Anderson, Guionnet and ZeitouniAGZ09, Theorem 5.4.5]), this sequence of random variables converges to zero almost surely. Since they are bounded, they also converge to zero in
$A_j$
in Q. By Voiculescu’s asymptotic freeness theorem (see, for example, [Reference Anderson, Guionnet and ZeitouniAGZ09, Theorem 5.4.5]), this sequence of random variables converges to zero almost surely. Since they are bounded, they also converge to zero in
![]() $L^2$
as
$L^2$
as
![]() $n \to \infty $
. Therefore, this sequence of bounded random variables agrees with the zero element in N, as desired.
$n \to \infty $
. Therefore, this sequence of bounded random variables agrees with the zero element in N, as desired.
(4) This follows by a concentration of measure argument similar to [Reference Farah, Jekel and PiFJP23, Lemma 4.2], so we will proceed briefly here. By (2), assume without loss of generality that
![]() $|f| \leq 2$
everywhere. For
$|f| \leq 2$
everywhere. For
![]() $A_1$
, …,
$A_1$
, …,
![]() $A_\ell \in (Q)_1$
and for each j, lift
$A_\ell \in (Q)_1$
and for each j, lift
![]() $A_j$
to a sequence
$A_j$
to a sequence
![]() $(A_j^{(n)})_{n \in \mathbb {N}}$
where
$(A_j^{(n)})_{n \in \mathbb {N}}$
where
![]() $A_j^{(n)} \in (\mathbb {M}_n)_1$
. It suffices to check the claim on a dense set of formulas, such as the rational polynomial formulas in Lemma 3.10. These formulas are easily seen to be Lipschitz on the unit ball. Hence,
$A_j^{(n)} \in (\mathbb {M}_n)_1$
. It suffices to check the claim on a dense set of formulas, such as the rational polynomial formulas in Lemma 3.10. These formulas are easily seen to be Lipschitz on the unit ball. Hence,
is a Lipschitz function of
![]() $(X_{i_1}^{(n)}, \dots , X_{i_k}^{(n)})$
. Let
$(X_{i_1}^{(n)}, \dots , X_{i_k}^{(n)})$
. Let
![]() $a_n$
be its expectation. Then by Gaussian concentration of measure (see, for example, [Reference Anderson, Guionnet and ZeitouniAGZ09, Lemma 2.3.3]), we have that
$a_n$
be its expectation. Then by Gaussian concentration of measure (see, for example, [Reference Anderson, Guionnet and ZeitouniAGZ09, Lemma 2.3.3]), we have that
Therefore, the sequence
![]() $\varphi ^{\mathbb {M}_n}(f(X_{i_1}^{(n)})/2,\dots ,f(X_{i_k}^{(n)})/2,A_1^{(n)},\dots ,A_\ell ^{(n)})$
agrees in
$\varphi ^{\mathbb {M}_n}(f(X_{i_1}^{(n)})/2,\dots ,f(X_{i_k}^{(n)})/2,A_1^{(n)},\dots ,A_\ell ^{(n)})$
agrees in
![]() $L^\infty [0,1]^{\mathcal {U}}$
with the constant
$L^\infty [0,1]^{\mathcal {U}}$
with the constant
![]() $\lim _{n \to \mathcal {U}} a_n$
. It follows by similar reasoning to (1) that
$\lim _{n \to \mathcal {U}} a_n$
. It follows by similar reasoning to (1) that
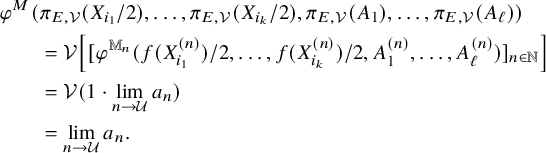 $$ \begin{align*} \varphi^{M}(&\pi_{E,\mathcal{V}}(X_{i_1}/2), \dots,\pi_{E,\mathcal{V}}(X_{i_k}/2),\pi_{E,\mathcal{V}}(A_1),\dots,\pi_{E,\mathcal{V}}(A_\ell)) \\ &= \mathcal{V} \left[ [\varphi^{\mathbb{M}_n}(f(X_{i_1}^{(n)})/2,\dots,f(X_{i_k}^{(n)})/2,A_1^{(n)},\dots,A_\ell^{(n)})]_{n \in \mathbb{N}} \right] \\ &= \mathcal{V} (1 \cdot \lim_{n \to \mathcal{U}} a_n) \\ &= \lim_{n \to \mathcal{U}} a_n. \end{align*} $$
$$ \begin{align*} \varphi^{M}(&\pi_{E,\mathcal{V}}(X_{i_1}/2), \dots,\pi_{E,\mathcal{V}}(X_{i_k}/2),\pi_{E,\mathcal{V}}(A_1),\dots,\pi_{E,\mathcal{V}}(A_\ell)) \\ &= \mathcal{V} \left[ [\varphi^{\mathbb{M}_n}(f(X_{i_1}^{(n)})/2,\dots,f(X_{i_k}^{(n)})/2,A_1^{(n)},\dots,A_\ell^{(n)})]_{n \in \mathbb{N}} \right] \\ &= \mathcal{V} (1 \cdot \lim_{n \to \mathcal{U}} a_n) \\ &= \lim_{n \to \mathcal{U}} a_n. \end{align*} $$
This is clearly independent of
![]() $\mathcal {V}$
, and only depends on
$\mathcal {V}$
, and only depends on
![]() $\mathcal {U}$
and
$\mathcal {U}$
and
![]() $A_1$
, …,
$A_1$
, …,
![]() $A_\ell $
.
$A_\ell $
.
Acknowledgements
We thank Ilijas Farah for bringing the problem of direct integrals and model theory to our attention. We thank Srivatsav Kunnawalkam Elayavalli, Jennifer Pi, Ionut Chifan and David Sherman for comments on a draft of the paper. We thank the referee for careful reading of the manuscript and helpful suggestions.
Competing interest
The authors have no competing interests to declare.
Funding statement
DG was partially supported by the National Science Foundation (US), grant DMS-2153805. DJ was partially supported by the National Sciences and Engineering Research Council (Canada), grant RGPIN-2017-05650, and the Danish Independent Research Fund, grant 1026-00371B and a Horizon Europe Marie Skłodowska-Curie Action FREEINFOGEOM, grant id: 101209517.






