Article contents
A CONTACT INVARIANT IN SUTURED MONOPOLE HOMOLOGY
Published online by Cambridge University Press: 10 June 2016
Abstract
We define an invariant of contact 3-manifolds with convex boundary using Kronheimer and Mrowka’s sutured monopole Floer homology theory ( 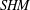 $SHM$ ). Our invariant can be viewed as a generalization of Kronheimer and Mrowka’s contact invariant for closed contact 3-manifolds and as the monopole Floer analogue of Honda, Kazez, and Matić’s contact invariant in sutured Heegaard Floer homology (
$SHM$ ). Our invariant can be viewed as a generalization of Kronheimer and Mrowka’s contact invariant for closed contact 3-manifolds and as the monopole Floer analogue of Honda, Kazez, and Matić’s contact invariant in sutured Heegaard Floer homology ( 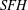 $SFH$ ). In the process of defining our invariant, we construct maps on
$SFH$ ). In the process of defining our invariant, we construct maps on 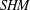 $SHM$ associated to contact handle attachments, analogous to those defined by Honda, Kazez, and Matić in
$SHM$ associated to contact handle attachments, analogous to those defined by Honda, Kazez, and Matić in 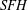 $SFH$ . We use these maps to establish a bypass exact triangle in
$SFH$ . We use these maps to establish a bypass exact triangle in 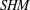 $SHM$ analogous to Honda’s in
$SHM$ analogous to Honda’s in 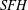 $SFH$ . This paper also provides the topological basis for the construction of similar gluing maps in sutured instanton Floer homology, which are used in Baldwin and Sivek [Selecta Math. (N.S.), 22(2) (2016), 939–978] to define a contact invariant in the instanton Floer setting.
$SFH$ . This paper also provides the topological basis for the construction of similar gluing maps in sutured instanton Floer homology, which are used in Baldwin and Sivek [Selecta Math. (N.S.), 22(2) (2016), 939–978] to define a contact invariant in the instanton Floer setting.
MSC classification
Information
- Type
- Research Article
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s) 2016
References
- 14
- Cited by


