1 Introduction
1.1 Overview
1.1.1 Traces and characters
In linear algebra, an important numerical invariant one can assign to an endomorphism
![]() $f\colon V \to V$
of a finite-dimensional k-vector space V is its trace
$f\colon V \to V$
of a finite-dimensional k-vector space V is its trace
![]() $ {\mathrm {tr}}(f \,\vert \, V) \in k$
. For example, the trace of the identity map on V is the dimension of V, regarded as a scalar in k. By combining various traces together, one obtains the notion of a character in representation theory: if V is a finite-dimensional linear representation of a finite group G, its character
$ {\mathrm {tr}}(f \,\vert \, V) \in k$
. For example, the trace of the identity map on V is the dimension of V, regarded as a scalar in k. By combining various traces together, one obtains the notion of a character in representation theory: if V is a finite-dimensional linear representation of a finite group G, its character
![]() $\chi _V\colon G\to k$
is the conjugation-invariant k-valued function on G defined by
$\chi _V\colon G\to k$
is the conjugation-invariant k-valued function on G defined by
![]() $\chi _V(g) = {\mathrm {tr}}(g \,\vert \, V)$
. This character encodes useful information about V, especially when
$\chi _V(g) = {\mathrm {tr}}(g \,\vert \, V)$
. This character encodes useful information about V, especially when
![]() $|G|$
is invertible in k. For instance, there is a simple formula for the dimension of the space of co-invariants
$|G|$
is invertible in k. For instance, there is a simple formula for the dimension of the space of co-invariants
![]() $V_G$
of the representation in terms of its character:
$V_G$
of the representation in terms of its character:
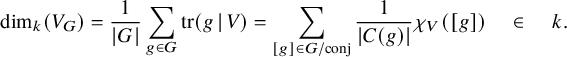 $$\begin{align*}\dim_k(V_G) = \frac{1}{|G|}\sum_{g\in G} {\mathrm{tr}}(g \,\vert \, V) = \sum_{[g]\in G/\mathrm{conj}} \frac{1}{|C(g)|} \chi_V([g]) \quad\in\quad k. \end{align*}$$
$$\begin{align*}\dim_k(V_G) = \frac{1}{|G|}\sum_{g\in G} {\mathrm{tr}}(g \,\vert \, V) = \sum_{[g]\in G/\mathrm{conj}} \frac{1}{|C(g)|} \chi_V([g]) \quad\in\quad k. \end{align*}$$
This formula is a special case of a more general induced character formula: given a (not-necessarily injective) group morphism
![]() $f\colon G \to H$
, the induced character formula expresses the character
$f\colon G \to H$
, the induced character formula expresses the character
![]() $\chi _{ {\mathrm {Ind}}_G^HV}$
of the induced representation
$\chi _{ {\mathrm {Ind}}_G^HV}$
of the induced representation
![]() $ {\mathrm {Ind}}_G^HV$
in terms of the character
$ {\mathrm {Ind}}_G^HV$
in terms of the character
![]() $\chi _V$
. The special case
$\chi _V$
. The special case
![]() $H=\{1\}$
recovers the dimension formula above.
$H=\{1\}$
recovers the dimension formula above.
The goal of this article is to generalize this story in several directions. To begin with, note that a finite-dimensional vector space is a dualizable object in the symmetric monoidal category
![]() $\mathrm {Vect}_k$
of vector spaces over k. We will study more generally dimensions, traces and characters of dualizable objects in an arbitrary presentably symmetric monoidal
$\mathrm {Vect}_k$
of vector spaces over k. We will study more generally dimensions, traces and characters of dualizable objects in an arbitrary presentably symmetric monoidal
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}$
, encompassing for example the notions of Euler characteristics and Lefschetz numbers in homotopy theory. Next, observe that a representation V of the group G can be encoded via a functor
$\mathscr {C}$
, encompassing for example the notions of Euler characteristics and Lefschetz numbers in homotopy theory. Next, observe that a representation V of the group G can be encoded via a functor
![]() $BG\to \mathrm {Vect}_k$
from the classifying space of G to the category of vector spaces over k. We will consider more generally functors
$BG\to \mathrm {Vect}_k$
from the classifying space of G to the category of vector spaces over k. We will consider more generally functors
![]() $A\to \mathscr {C}$
from an arbitrary space A, also known as
$A\to \mathscr {C}$
from an arbitrary space A, also known as
![]() $\mathscr {C}$
-valued local systems over A; in the case
$\mathscr {C}$
-valued local systems over A; in the case
![]() $\mathscr {C} = \mathrm {Sp}$
these are known as parametrized spectra over A. If A is connected, a local system over A can also be thought of as a
$\mathscr {C} = \mathrm {Sp}$
these are known as parametrized spectra over A. If A is connected, a local system over A can also be thought of as a
![]() $\mathscr {C}$
-valued representation of the (not necessarily discrete) loop group
$\mathscr {C}$
-valued representation of the (not necessarily discrete) loop group
![]() $\Omega _a A$
with respect to some basepoint a.
$\Omega _a A$
with respect to some basepoint a.
Note that conjugacy classes of elements of G can be identified with connected components of the free loop space
![]() $LBG$
of its classifying space
$LBG$
of its classifying space
![]() $BG$
. Accordingly, the conjugation-invariant character
$BG$
. Accordingly, the conjugation-invariant character
![]() $\chi _V\colon G \to k$
of some G-representation V may be identified with a locally constant function
$\chi _V\colon G \to k$
of some G-representation V may be identified with a locally constant function
![]() $LBG\to k$
. Generalizing this, we will assign to every local system of dualizable objects
$LBG\to k$
. Generalizing this, we will assign to every local system of dualizable objects
![]() $V\in \mathscr {C}^A$
a character
$V\in \mathscr {C}^A$
a character
which is a map from the free loop space
![]() $LA = {\mathrm {Map}}(S^1,A)$
of A to the endomorphism space of the unit object of
$LA = {\mathrm {Map}}(S^1,A)$
of A to the endomorphism space of the unit object of
![]() $\mathscr {C}$
. This character encodes the traces of the “monodromy actions” of free loops in A on the fibers of the local system V. Here, the endomorphism space
$\mathscr {C}$
. This character encodes the traces of the “monodromy actions” of free loops in A on the fibers of the local system V. Here, the endomorphism space ![]() plays the role of the set of scalars k.
plays the role of the set of scalars k.
The induced character formula, and in particular the formula above for the dimension of the coinvariants
![]() $V_G$
, involves division by
$V_G$
, involves division by
![]() $|G|$
, and hence is applicable only if
$|G|$
, and hence is applicable only if
![]() $|G|$
is invertible in k. This problem becomes more severe in the derived setting: if V is a dualizable object in the derived
$|G|$
is invertible in k. This problem becomes more severe in the derived setting: if V is a dualizable object in the derived
![]() $\infty $
-category
$\infty $
-category
![]() $D(k)$
of k equipped with a G-action, its object of coinvariants
$D(k)$
of k equipped with a G-action, its object of coinvariants
![]() $V_{hG}$
might not even be dualizable anymore if
$V_{hG}$
might not even be dualizable anymore if
![]() $|G|$
is not invertible in k. To deal with this problem for general
$|G|$
is not invertible in k. To deal with this problem for general
![]() $\mathscr {C}$
, we introduce the notion of a
$\mathscr {C}$
, we introduce the notion of a
![]() $\mathscr {C}$
-adjointable maps of spaces
$\mathscr {C}$
-adjointable maps of spaces
![]() $f \colon A \to B$
, see Definition 4.20. This property in particular ensures that for a pointwise dualizable local system
$f \colon A \to B$
, see Definition 4.20. This property in particular ensures that for a pointwise dualizable local system
![]() $V\colon A \to \mathscr {C}$
, its left Kan extension
$V\colon A \to \mathscr {C}$
, its left Kan extension
![]() $f_!V \colon B \to \mathscr {C}$
along f (playing the role of the induced representation) is pointwise dualizable as well, so that we may form its character. In such a situation, in the spirit of [Reference Ponto and Shulman58], we will provide an induced character formula which expresses the character of the left Kan extension
$f_!V \colon B \to \mathscr {C}$
along f (playing the role of the induced representation) is pointwise dualizable as well, so that we may form its character. In such a situation, in the spirit of [Reference Ponto and Shulman58], we will provide an induced character formula which expresses the character of the left Kan extension
![]() $f_!V\colon B \to \mathscr {C}$
in terms of the character of the original local system
$f_!V\colon B \to \mathscr {C}$
in terms of the character of the original local system
![]() $V\colon A \to \mathscr {C}$
.
$V\colon A \to \mathscr {C}$
.
Finally, the theory of characters can be generalized in a third direction, which is needed in some of the applications. The definition of the trace can naturally be extended to generalized endomorphisms of the form
![]() $f\colon X\to X\otimes Y$
, which results in a generalized trace map
$f\colon X\to X\otimes Y$
, which results in a generalized trace map ![]() . Given a space A and an A-indexed family of generalized endomorphisms
. Given a space A and an A-indexed family of generalized endomorphisms
![]() $f_a\colon X_a \to X_a\otimes Y$
, we may assign to it a map
$f_a\colon X_a \to X_a\otimes Y$
, we may assign to it a map ![]() , called the generalized character map of this family. We will develop our induced character formula in this generality.
, called the generalized character map of this family. We will develop our induced character formula in this generality.
1.1.2 Transfers
One of the applications of our generalized character theory is to the study of transfer maps in topology. Recall that a spectrum E represents a homology theory
![]() $E_*(-)$
as well as a cohomology theory
$E_*(-)$
as well as a cohomology theory
![]() $E^*(-)$
. In particular, we have for any map of spaces
$E^*(-)$
. In particular, we have for any map of spaces
![]() $f\colon A \to B$
induced maps on E-homology and E-cohomology
$f\colon A \to B$
induced maps on E-homology and E-cohomology
If f has suitably small fibers, we also have a wrong-way or transfer maps
going in the opposite direction. The map
![]() $f_!\colon E^*(A) \to E^*(B)$
on E-cohomology can be understood as a form of “integration along the fibers”. These transfer maps can be canonically refined to maps of spectra
$f_!\colon E^*(A) \to E^*(B)$
on E-cohomology can be understood as a form of “integration along the fibers”. These transfer maps can be canonically refined to maps of spectra
![]() $f^! \colon E\otimes B\to E\otimes A$
resp.
$f^! \colon E\otimes B\to E\otimes A$
resp.
![]() $f_!\colon E^A \to E^B$
. Transfer maps have a long history in algebraic topology, as described for example in [Reference Becker and Gottlieb11]. A trace-theoretic perspective on these transfer maps is developed by several authors, including [Reference Dold and Puppe21, Reference Ponto and Shulman59, Reference Ponto and Shulman57, Reference Ben-Zvi and Nadler14].
$f_!\colon E^A \to E^B$
. Transfer maps have a long history in algebraic topology, as described for example in [Reference Becker and Gottlieb11]. A trace-theoretic perspective on these transfer maps is developed by several authors, including [Reference Dold and Puppe21, Reference Ponto and Shulman59, Reference Ponto and Shulman57, Reference Ben-Zvi and Nadler14].
In this article, we study transfer maps in an arbitrary presentably symmetric monoidal
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}$
. Recall that
$\mathscr {C}$
. Recall that
![]() $\mathscr {C}$
admits a unique symmetric monoidal colimit-preserving functor
$\mathscr {C}$
admits a unique symmetric monoidal colimit-preserving functor ![]() , denoted
, denoted ![]() , which sends a space A to the colimit over A of the constant A-indexed diagram on
, which sends a space A to the colimit over A of the constant A-indexed diagram on ![]() . For example, for the
. For example, for the
![]() $\infty $
-category of spectra this is the unreduced suspension spectrum functor
$\infty $
-category of spectra this is the unreduced suspension spectrum functor
![]() $\Sigma ^{\infty }_+\colon \mathcal {S} \to \mathrm {Sp}$
, while for the derived
$\Sigma ^{\infty }_+\colon \mathcal {S} \to \mathrm {Sp}$
, while for the derived
![]() $\infty $
-category of a ring R this is the singular chain functor
$\infty $
-category of a ring R this is the singular chain functor
![]() $C_{\bullet }(-;R)\colon \mathcal {S} \to D(R)$
. Given a
$C_{\bullet }(-;R)\colon \mathcal {S} \to D(R)$
. Given a
![]() $\mathscr {C}$
-adjointable map of spaces
$\mathscr {C}$
-adjointable map of spaces
![]() $f\colon A\to B$
, we will define a transfer map of the form
$f\colon A\to B$
, we will define a transfer map of the form ![]() . This transfer
. This transfer
![]() $f^!$
will by construction be a B-shaped colimit of traces of generalized endomorphisms, and hence can be studied using the induced character formula. This recovers a description of the
$f^!$
will by construction be a B-shaped colimit of traces of generalized endomorphisms, and hence can be studied using the induced character formula. This recovers a description of the
![]() $\mathscr {C}$
-linear Becker-Gottlieb transfer
$\mathscr {C}$
-linear Becker-Gottlieb transfer
![]() $f^!$
in terms of the
$f^!$
in terms of the
![]() $\mathscr {C}$
-linear free loop space transfer of f, given for
$\mathscr {C}$
-linear free loop space transfer of f, given for
![]() $\mathscr {C} = \mathrm {Sp}$
by [Reference Lind and Malkiewich48].
$\mathscr {C} = \mathrm {Sp}$
by [Reference Lind and Malkiewich48].
Using the interpretation of the transfer maps in terms of characters, we address the problem of composability of transfer maps. We show by an example that, for two composable
![]() $\mathscr {C}$
-adjointable maps f and g, the relation
$\mathscr {C}$
-adjointable maps f and g, the relation
![]() $f^!g^! \simeq (gf)^!$
does not hold in full generality. We identify various conditions under which this relation does hold, recovering and refining some of the results of [Reference Lewis, May and Steinberger47] and [Reference Klein and Malkiewich43], and some of the related results of [Reference Lind and Malkiewich48]. Despite various attempts to answer it, the question of composability of the transfers for maps of spaces with compact (sometimes called ‘finitely dominated’) fibers in the case of
$f^!g^! \simeq (gf)^!$
does not hold in full generality. We identify various conditions under which this relation does hold, recovering and refining some of the results of [Reference Lewis, May and Steinberger47] and [Reference Klein and Malkiewich43], and some of the related results of [Reference Lind and Malkiewich48]. Despite various attempts to answer it, the question of composability of the transfers for maps of spaces with compact (sometimes called ‘finitely dominated’) fibers in the case of
![]() $\mathscr {C}=\mathrm {Sp}$
is still open. We hope that our methods and results could shed some new light on this problem. For example, Klein, Malkiewich and the third author [Reference Klein, Malkiewich and Ramzi44] use it to prove functoriality of the Becker-Gottlieb transfers at the level of
$\mathscr {C}=\mathrm {Sp}$
is still open. We hope that our methods and results could shed some new light on this problem. For example, Klein, Malkiewich and the third author [Reference Klein, Malkiewich and Ramzi44] use it to prove functoriality of the Becker-Gottlieb transfers at the level of
![]() $\pi _0$
.
$\pi _0$
.
1.1.3 Categorified traces
For an
![]() $\mathbb {E}_\infty $
-ring spectrum E, the E-cohomology
$\mathbb {E}_\infty $
-ring spectrum E, the E-cohomology
![]() $E^A$
of a space A admits a natural categorification, namely the
$E^A$
of a space A admits a natural categorification, namely the
![]() $\infty $
-category
$\infty $
-category
![]() $( {\mathrm {Mod}}_E)^A$
of local systems of E-modules on A. This categorification of cohomology also admits natural right and wrong-way maps: for a map of spaces
$( {\mathrm {Mod}}_E)^A$
of local systems of E-modules on A. This categorification of cohomology also admits natural right and wrong-way maps: for a map of spaces
![]() $g\colon A \to B$
, we have the restriction functor
$g\colon A \to B$
, we have the restriction functor
along with its right adjoint
given by right Kan extension along g. Objects
![]() $M \in ( {\mathrm {Mod}}_E)^A$
are local systems of E-modules on A, and we think of the right Kan extension
$M \in ( {\mathrm {Mod}}_E)^A$
are local systems of E-modules on A, and we think of the right Kan extension
![]() $g_*M \in ( {\mathrm {Mod}}_E)^B$
as fiberwise cohomology with local coefficients, i.e. as some sort of “categorified integration along the fibers”. When
$g_*M \in ( {\mathrm {Mod}}_E)^B$
as fiberwise cohomology with local coefficients, i.e. as some sort of “categorified integration along the fibers”. When
![]() $B = \mathrm {pt}$
, the object
$B = \mathrm {pt}$
, the object
![]() $g_*g^*E = E^A$
is precisely the E-cohomology of A. To summarize, cohomology both admits wrong-way maps and can be seen as a wrong-way map.
$g_*g^*E = E^A$
is precisely the E-cohomology of A. To summarize, cohomology both admits wrong-way maps and can be seen as a wrong-way map.
In a similar way, the key tool in studying our generalized characters and associated induced character formulas is the interaction between traces and categorification. The generality of the formalism of symmetric monoidal traces allows us to also apply it to symmetric monoidal
![]() $(\infty ,2)$
-categories, such as the
$(\infty ,2)$
-categories, such as the
![]() $(\infty ,2)$
-category of E-linear presentable
$(\infty ,2)$
-category of E-linear presentable
![]() $\infty $
-categories. While in symmetric monoidal
$\infty $
-categories. While in symmetric monoidal
![]() $(\infty ,1)$
-categories, traces can only be functorial in equivalences, in
$(\infty ,1)$
-categories, traces can only be functorial in equivalences, in
![]() $(\infty ,2)$
-categories they are functorial more generally in left adjoints. We will exploit this extra functoriality of categorified traces to understand the interaction of traces at a lower categorical level with colimits.
$(\infty ,2)$
-categories they are functorial more generally in left adjoints. We will exploit this extra functoriality of categorified traces to understand the interaction of traces at a lower categorical level with colimits.
In the case of the symmetric monoidal
![]() $(\infty ,2)$
-category
$(\infty ,2)$
-category
![]() $\mathrm {Pr}^{\text {L}}_{\mathrm {st}}$
of presentable stable
$\mathrm {Pr}^{\text {L}}_{\mathrm {st}}$
of presentable stable
![]() $\infty $
-categories the dimension of dualizable objects recovers a well-known invariant: topological Hochschild homology, classically defined in terms of the cyclic bar construction. The interpretation of topological Hochschild homology as a trace, when combined with the categorification of the induced character formula, allows us to compute the topological Hochschild homology of Thom spectra, recovering and generalizing the main result of [Reference Blumberg, Cohen and Schlichtkrull15].
$\infty $
-categories the dimension of dualizable objects recovers a well-known invariant: topological Hochschild homology, classically defined in terms of the cyclic bar construction. The interpretation of topological Hochschild homology as a trace, when combined with the categorification of the induced character formula, allows us to compute the topological Hochschild homology of Thom spectra, recovering and generalizing the main result of [Reference Blumberg, Cohen and Schlichtkrull15].
1.2 Main results
We shall now explain our approach to generalized character theory and its applications in more detail. For the remainder of this subsection, we fix a presentably symmetric monoidal
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}$
. We use the following notational convention to distinguish traces in
$\mathscr {C}$
. We use the following notational convention to distinguish traces in
![]() $\mathscr {C}$
from their categorifications:
$\mathscr {C}$
from their categorifications:
-
• Given an endomorphism f of a dualizable object X in
 $\mathscr {C}$
, we denote its trace in
$\mathscr {C}$
, we denote its trace in
 $\mathscr {C}$
by
$\mathscr {C}$
by  , and we write
, and we write
 $\dim (X) := {\mathrm {tr}}(\mathrm {id}_X)$
for its dimension;
$\dim (X) := {\mathrm {tr}}(\mathrm {id}_X)$
for its dimension; -
• Given a
 $\mathscr {C}$
-linear endomorphism
$\mathscr {C}$
-linear endomorphism
 $F\colon \mathscr {D} \to \mathscr {D}$
of a dualizable object
$F\colon \mathscr {D} \to \mathscr {D}$
of a dualizable object
 $\mathscr {D}$
in the symmetric monoidal
$\mathscr {D}$
in the symmetric monoidal
 $(\infty ,2)$
-category
$(\infty ,2)$
-category
 $ {\mathrm {Mod}}_{\mathscr {C}}$
of
$ {\mathrm {Mod}}_{\mathscr {C}}$
of
 $\mathscr {C}$
-linear presentable
$\mathscr {C}$
-linear presentable
 $\infty $
-categories, we denote its trace in
$\infty $
-categories, we denote its trace in
 $ {\mathrm {Mod}}_{\mathscr {C}}$
, called the
$ {\mathrm {Mod}}_{\mathscr {C}}$
, called the
 $\mathscr {C}$
-linear trace, by
$\mathscr {C}$
-linear trace, by
 $ {\mathrm {Tr}}_{\mathscr {C}}(F) \in {\mathrm {Fun}}_{\mathscr {C}}(\mathscr {C},\mathscr {C}) \simeq \mathscr {C}$
. When
$ {\mathrm {Tr}}_{\mathscr {C}}(F) \in {\mathrm {Fun}}_{\mathscr {C}}(\mathscr {C},\mathscr {C}) \simeq \mathscr {C}$
. When
 $F = \mathrm {id}_{\mathscr {D}}$
we will alternatively write
$F = \mathrm {id}_{\mathscr {D}}$
we will alternatively write
 $ {\mathrm {Tr}}_{\mathscr {C}}(\mathscr {D})$
for
$ {\mathrm {Tr}}_{\mathscr {C}}(\mathscr {D})$
for
 $ {\mathrm {Tr}}_{\mathscr {C}}(\mathrm {id}_{\mathscr {D}})$
.
$ {\mathrm {Tr}}_{\mathscr {C}}(\mathrm {id}_{\mathscr {D}})$
.
Consider a space A and let
![]() $V\colon A \to \mathscr {C}$
be a pointwise dualizable local system, in the sense that
$V\colon A \to \mathscr {C}$
be a pointwise dualizable local system, in the sense that
![]() $V_a \in \mathscr {C}$
is dualizable for all
$V_a \in \mathscr {C}$
is dualizable for all
![]() $a \in A$
. Every free loop
$a \in A$
. Every free loop
![]() $\gamma \in LA := {\mathrm {Map}}(S^1,A)$
induces an automorphism
$\gamma \in LA := {\mathrm {Map}}(S^1,A)$
induces an automorphism
![]() $\gamma \colon V_{\gamma (0)} \to V_{\gamma (0)}$
in
$\gamma \colon V_{\gamma (0)} \to V_{\gamma (0)}$
in
![]() $\mathscr {C}$
, and the traces of all these automorphisms assemble into the character of V:
$\mathscr {C}$
, and the traces of all these automorphisms assemble into the character of V:
Our first main result provides a description of this map via categorified traces. The
![]() $\infty $
-category of local systems
$\infty $
-category of local systems
![]() $\mathscr {C}^A$
is a dualizable object in
$\mathscr {C}^A$
is a dualizable object in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
, and its
$ {\mathrm {Mod}}_{\mathscr {C}}$
, and its
![]() $\mathscr {C}$
-linear trace is given by
$\mathscr {C}$
-linear trace is given by
where ![]() . The local system
. The local system
![]() $V\colon A \to \mathscr {C}$
determines a
$V\colon A \to \mathscr {C}$
determines a
![]() $\mathscr {C}$
-linear map
$\mathscr {C}$
-linear map
![]() $\mathscr {C}^A \to \mathscr {C}$
by
$\mathscr {C}^A \to \mathscr {C}$
by
![]() $\mathscr {C}$
-linear Yoneda extension, which by pointwise dualizability of V is a left adjoint in the
$\mathscr {C}$
-linear Yoneda extension, which by pointwise dualizability of V is a left adjoint in the
![]() $(\infty ,2)$
-category
$(\infty ,2)$
-category
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
. Since the
$ {\mathrm {Mod}}_{\mathscr {C}}$
. Since the
![]() $\mathscr {C}$
-linear trace is functorial in such left adjoints, this produces a map
$\mathscr {C}$
-linear trace is functorial in such left adjoints, this produces a map ![]() , or equivalently a map of spaces
, or equivalently a map of spaces ![]() . We show that this map is precisely the character of V.
. We show that this map is precisely the character of V.
In fact, we prove a somewhat more general claim, which is required for some of the applications. A pointwise dualizable local system V equipped with a generalized endomorphism
determines a morphism
![]() $(\mathscr {C}^A,\mathrm {id}_{\mathscr {C}^A}) \to (\mathscr {C},Y)$
in the
$(\mathscr {C}^A,\mathrm {id}_{\mathscr {C}^A}) \to (\mathscr {C},Y)$
in the
![]() $\infty $
-category of traceable endomorphisms in
$\infty $
-category of traceable endomorphisms in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
, see Definition 2.18. Upon applying the
$ {\mathrm {Mod}}_{\mathscr {C}}$
, see Definition 2.18. Upon applying the
![]() $\mathscr {C}$
-linear trace functor, this induces a map
$\mathscr {C}$
-linear trace functor, this induces a map ![]() , or equivalently a map of spaces
, or equivalently a map of spaces ![]() .
.
Theorem A (Proposition 5.14).
Let
![]() $V\colon A\to \mathscr {C}$
be a local system of dualizable objects, and
$V\colon A\to \mathscr {C}$
be a local system of dualizable objects, and
![]() $f\colon V\to V\otimes A^*Y$
a generalized endomorphism, where
$f\colon V\to V\otimes A^*Y$
a generalized endomorphism, where
![]() $Y\in \mathscr {C}$
. The map
$Y\in \mathscr {C}$
. The map
is the character of f, in the sense that
![]() $\chi _f(\gamma ) \simeq {\mathrm {tr}}(f\circ \overline {\gamma }\mid V)$
, naturally in the loop
$\chi _f(\gamma ) \simeq {\mathrm {tr}}(f\circ \overline {\gamma }\mid V)$
, naturally in the loop
![]() $\gamma $
.Footnote
1
$\gamma $
.Footnote
1
While the character
![]() $\chi _f$
encodes
$\chi _f$
encodes
![]() $(\infty ,1)$
-categorical traces, the above description in terms of categorified traces allows us to study it using the calculus of
$(\infty ,1)$
-categorical traces, the above description in terms of categorified traces allows us to study it using the calculus of
![]() $(\infty ,2)$
-categorical traces. In particular, it allows us to study the interaction of traces with colimits via a generalized induced character formula, as we will now explain.
$(\infty ,2)$
-categorical traces. In particular, it allows us to study the interaction of traces with colimits via a generalized induced character formula, as we will now explain.
Let
![]() $g\colon A \to B$
be a
$g\colon A \to B$
be a
![]() $\mathscr {C}$
-adjointable map of spaces, in the sense that the restriction functor
$\mathscr {C}$
-adjointable map of spaces, in the sense that the restriction functor
![]() $g^*\colon \mathscr {C}^B \to \mathscr {C}^A$
is a left adjoint in the
$g^*\colon \mathscr {C}^B \to \mathscr {C}^A$
is a left adjoint in the
![]() $(\infty ,2)$
-category
$(\infty ,2)$
-category
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
. Given a pointwise dualizable local system
$ {\mathrm {Mod}}_{\mathscr {C}}$
. Given a pointwise dualizable local system
![]() $V\colon A \to \mathscr {C}$
with character
$V\colon A \to \mathscr {C}$
with character ![]() , the left Kan extension
, the left Kan extension
![]() $g_!V\colon B \to \mathscr {C}$
of V is again pointwise dualizable (Proposition 4.33), and hence also admits a character
$g_!V\colon B \to \mathscr {C}$
of V is again pointwise dualizable (Proposition 4.33), and hence also admits a character ![]() . Our induced character formula then says that the character
. Our induced character formula then says that the character
![]() $\chi _{g_!V}$
can be expressed in terms of the character
$\chi _{g_!V}$
can be expressed in terms of the character
![]() $\chi _V$
as the following composite:
$\chi _V$
as the following composite:
Here the map ![]() is called the free loop transfer of g, and is obtained by applying the functoriality of
is called the free loop transfer of g, and is obtained by applying the functoriality of
![]() $\mathscr {C}$
-linear traces to the left adjoint
$\mathscr {C}$
-linear traces to the left adjoint
![]() $g^*$
in
$g^*$
in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
; see for example [Reference Lind and Malkiewich48] for an alternative description of this transfer map in the case
$ {\mathrm {Mod}}_{\mathscr {C}}$
; see for example [Reference Lind and Malkiewich48] for an alternative description of this transfer map in the case
![]() $\mathscr {C} = \mathrm {Sp}$
.
$\mathscr {C} = \mathrm {Sp}$
.
More generally, if the local system
![]() $V \in \mathscr {C}^A$
comes equipped with a generalized endomorphism
$V \in \mathscr {C}^A$
comes equipped with a generalized endomorphism
![]() $f\colon V\to V\otimes A^*Y$
, we can induce it along g to get a generalized endomorphism
$f\colon V\to V\otimes A^*Y$
, we can induce it along g to get a generalized endomorphism
We obtain a similar expression of the induced character
![]() $\chi _{ {\mathrm {Ind}}_g(f)}$
in terms of
$\chi _{ {\mathrm {Ind}}_g(f)}$
in terms of
![]() $\chi _f$
:
$\chi _f$
:
Theorem B (Induced character formula, Theorem 5.20).
Let
![]() $V\colon A\to \mathscr {C}$
be a local system of dualizable objects, and let
$V\colon A\to \mathscr {C}$
be a local system of dualizable objects, and let
![]() $f\colon V\to V\otimes A^*Y$
be a generalized endomorphism, where
$f\colon V\to V\otimes A^*Y$
be a generalized endomorphism, where
![]() $Y\in \mathscr {C}$
. For a
$Y\in \mathscr {C}$
. For a
![]() $\mathscr {C}$
-adjointable map of spaces
$\mathscr {C}$
-adjointable map of spaces
![]() $g\colon A\to B$
, the induced character
$g\colon A\to B$
, the induced character
![]() $\chi _{ {\mathrm {Ind}}_g(f)}$
is given by the composition
$\chi _{ {\mathrm {Ind}}_g(f)}$
is given by the composition
An important special case of this theorem is the case where B is a point and Y is the monoidal unit: we may compute the trace of the induced map
![]() $A_!f \colon A_!V \to A_!V$
on colimits as the composite
$A_!f \colon A_!V \to A_!V$
on colimits as the composite
In particular, this gives a formula of the dimension of a colimit of dualizable objects over a
![]() $\mathscr {C}$
-adjointable space.
$\mathscr {C}$
-adjointable space.
The induced character formula can itself be categorified. This categorification allows us to recover a result of Blumberg-Cohen-Schlichtkrull on the topological Hochschild homology of Thom spectra [Reference Blumberg, Cohen and Schlichtkrull15], and extend it from
![]() $\mathrm {Sp}$
to an arbitrary presentably symmetric monoidal
$\mathrm {Sp}$
to an arbitrary presentably symmetric monoidal
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}$
:
$\mathscr {C}$
:
Theorem C (Theorem 7.2, cf. [Reference Blumberg, Cohen and Schlichtkrull15, Theorem 1]).
Let G be an
![]() $\mathbb {E}_1$
-group in
$\mathbb {E}_1$
-group in
![]() $\mathcal {S}$
, and let
$\mathcal {S}$
, and let
![]() $\xi \colon G\to {\mathrm {Pic}}(\mathscr {C})$
be an
$\xi \colon G\to {\mathrm {Pic}}(\mathscr {C})$
be an
![]() $\mathbb {E}_1$
-group map. Then the Hochschild homology of the Thom object
$\mathbb {E}_1$
-group map. Then the Hochschild homology of the Thom object
![]() $\mathrm {Th}_{\mathscr {C}}(\xi )$
in
$\mathrm {Th}_{\mathscr {C}}(\xi )$
in
![]() $ {\mathrm {Alg}}(\mathscr {C})$
is the Thom object of the following composite:
$ {\mathrm {Alg}}(\mathscr {C})$
is the Thom object of the following composite:
where
![]() $\eta \colon B {\mathrm {Pic}}(\mathscr {C}) \to {\mathrm {Pic}}(\mathscr {C})$
is the Hopf map.
$\eta \colon B {\mathrm {Pic}}(\mathscr {C}) \to {\mathrm {Pic}}(\mathscr {C})$
is the Hopf map.
The proof of this theorem uses the following result, which is of independent interest and has previously been sketched by Douglas [Reference Douglas23] in the case of
![]() $\mathscr {C}= \mathrm {Sp}$
:
$\mathscr {C}= \mathrm {Sp}$
:
Theorem D (Theorem 7.13, cf. [Reference Douglas23, Proposition 3.13]).
Let A be a pointed connected space and let
![]() $\zeta \colon A \to {\mathrm {Mod}}_{\mathscr {C}}$
be a pointed map. Then there is an equivalence
$\zeta \colon A \to {\mathrm {Mod}}_{\mathscr {C}}$
be a pointed map. Then there is an equivalence
where
![]() $\Omega \zeta \colon \Omega A\to {\mathrm {Pic}}(\mathscr {C})$
is the
$\Omega \zeta \colon \Omega A\to {\mathrm {Pic}}(\mathscr {C})$
is the
![]() $\mathbb {E}_1$
-group map induced by
$\mathbb {E}_1$
-group map induced by
![]() $\zeta $
.
$\zeta $
.
Another application of our methods is to study Becker-Gottlieb transfers. First, using our induced character formula we reprove a result of Lind and Malkiewich [Reference Lind and Malkiewich48], expressing the Becker-Gottlieb transfer in terms of the free loop transfer, and again extend it from
![]() $\mathrm {Sp}$
to arbitrary
$\mathrm {Sp}$
to arbitrary
![]() $\mathscr {C}$
:
$\mathscr {C}$
:
Theorem E (Theorem 6.12, cf. [Reference Lind and Malkiewich48, Theorem 1.2]).
For a
![]() $\mathscr {C}$
-adjointable map of spaces
$\mathscr {C}$
-adjointable map of spaces
![]() $f\colon A \to B$
, the Becker-Gottlieb transfer
$f\colon A \to B$
, the Becker-Gottlieb transfer ![]() is given by the following composite:
is given by the following composite:
Here
![]() $c\colon B \to LB$
is the inclusion of B into
$c\colon B \to LB$
is the inclusion of B into
![]() $LB$
as the constant loops and
$LB$
as the constant loops and
![]() $e\colon LA \to A$
is the evaluation at the basepoint of
$e\colon LA \to A$
is the evaluation at the basepoint of
![]() $S^1$
.
$S^1$
.
Second, we address the problem of composability of the Becker-Gottlieb transfer, namely the question of whether there is a homotopy
![]() $(gf)^!\simeq f^!g^!$
for two composable
$(gf)^!\simeq f^!g^!$
for two composable
![]() $\mathscr {C}$
-adjointable maps f and g. While we observe that for a general symmetric monoidal
$\mathscr {C}$
-adjointable maps f and g. While we observe that for a general symmetric monoidal
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}$
the answer is negative, we discuss a number of cases where the answer is positive, see Theorem 6.18.
$\mathscr {C}$
the answer is negative, we discuss a number of cases where the answer is positive, see Theorem 6.18.
As a final application of the calculus of categorified traces, we reprove the additivity of traces in symmetric monoidal stable
![]() $\infty $
-categories.
$\infty $
-categories.
Theorem F (Theorem 5.27, cf. [Reference May54, Reference Ponto and Shulman59, Reference Ramzi61]).
Let
![]() $\mathscr {C}$
be a stable presentably symmetric monoidal
$\mathscr {C}$
be a stable presentably symmetric monoidal
![]() $\infty $
-category, and let
$\infty $
-category, and let ![]() be a bifiber sequence of dualizable objects in
be a bifiber sequence of dualizable objects in
![]() $\mathscr {C}$
. Let
$\mathscr {C}$
. Let
![]() $f_i\colon Z \otimes X_i \to X_i \otimes Y$
be morphisms fitting in a bifiber sequence in
$f_i\colon Z \otimes X_i \to X_i \otimes Y$
be morphisms fitting in a bifiber sequence in
![]() $\mathscr {C}^{[1]}$
of the formFootnote
2
$\mathscr {C}^{[1]}$
of the formFootnote
2
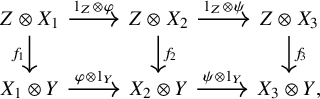
where the top and bottom sequences are obtained from the original bifiber sequence by tensoring with Z resp. Y. Then, there is a homotopy
1.3 Relation to other work
Our treatment of higher categorical traces follows [Reference Hoyois, Scherotzke and Sibilla37], which builds on foundations from [Reference Johnson-Freyd and Scheimbauer39].
Our induced character formula is largely inspired by the work of Ponto and Shulman [Reference Ponto and Shulman59]. Beyond the difference in implementation (derivators versus
![]() $\infty $
-categories), the main conceptual difference between their work and ours is that we consider indexing diagrams which are
$\infty $
-categories), the main conceptual difference between their work and ours is that we consider indexing diagrams which are
![]() $\infty $
-groupoids, rather than
$\infty $
-groupoids, rather than
![]() $1$
-categories. In particular, while [Reference Ponto and Shulman59, Lemma 10.4] can be used to obtain an analogue of the above identification
$1$
-categories. In particular, while [Reference Ponto and Shulman59, Lemma 10.4] can be used to obtain an analogue of the above identification
![]() $\chi _f(\gamma ) \simeq {\mathrm {tr}}(f \circ \gamma \,\vert \, V)$
for every individual free loop
$\chi _f(\gamma ) \simeq {\mathrm {tr}}(f \circ \gamma \,\vert \, V)$
for every individual free loop
![]() $\gamma \in LA$
, we obtain this identification naturally in
$\gamma \in LA$
, we obtain this identification naturally in
![]() $\gamma $
. This naturality is necessary to study families of generalized endomorphisms indexed over spaces, which is where our main applications lie. Compared to [Reference Ponto and Shulman59], a limitation of the current work is that our indexing diagrams are
$\gamma $
. This naturality is necessary to study families of generalized endomorphisms indexed over spaces, which is where our main applications lie. Compared to [Reference Ponto and Shulman59], a limitation of the current work is that our indexing diagrams are
![]() $\infty $
-groupoids as opposed to categories, or even weights. An extension of this work to the common generalization of
$\infty $
-groupoids as opposed to categories, or even weights. An extension of this work to the common generalization of
![]() $\infty $
-categorical weights is the subject of future work.
$\infty $
-categorical weights is the subject of future work.
Our work is also related to the work of Hoyois, Safronov, Scherotzke and Sibilla [Reference Hoyois, Safronov, Scherotzke and Sibilla38]. Their result [Reference Hoyois, Safronov, Scherotzke and Sibilla38, Corollary 5.3] looks formally analogous to our induced character formula, though it does not seem to apply to our situation, as the relevant symmetric monoidal functors are typically not rigid (cf. [Reference Hoyois, Safronov, Scherotzke and Sibilla38, Definition 2.15]), nor the relevant adjunctions ambidextrous (cf. [Reference Hoyois, Safronov, Scherotzke and Sibilla38, Definition 2.1]). It would be interesting to find a common framework which unifies both results.
1.4 Organization
This article is structured as follows. Sections 2, 3 and 4 are mostly expository. In Section 2 we recall the definition of generalized traces and of higher categorical traces following [Reference Hoyois, Scherotzke and Sibilla37]. In Section 3, we specialize the discussion to the symmetric monoidal
![]() $(\infty ,2)$
-category
$(\infty ,2)$
-category
![]() $ {\mathrm {Span}}(\mathscr {D})$
of spans and provide a detailed proof of the fact that dimensions in span categories can be naturally identified with free loop spaces. In Section 4, we specialize to the symmetric monoidal
$ {\mathrm {Span}}(\mathscr {D})$
of spans and provide a detailed proof of the fact that dimensions in span categories can be naturally identified with free loop spaces. In Section 4, we specialize to the symmetric monoidal
![]() $(\infty ,2)$
-category
$(\infty ,2)$
-category
![]() $ {\mathrm {Mod}}_{\mathscr {C}}(\mathrm {Pr}^{\text {L}})$
of
$ {\mathrm {Mod}}_{\mathscr {C}}(\mathrm {Pr}^{\text {L}})$
of
![]() $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
![]() $\infty $
-categories for a presentably symmetric monoidal
$\infty $
-categories for a presentably symmetric monoidal
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}$
. There, we study
$\mathscr {C}$
. There, we study
![]() $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
![]() $\infty $
-categories freely and cofreely generated by spaces, as well as their traces, and we introduce the key notion of
$\infty $
-categories freely and cofreely generated by spaces, as well as their traces, and we introduce the key notion of
![]() $\mathscr {C}$
-adjointable spaces (resp. maps). We also recall the trace interpretation of Hochschild homology.
$\mathscr {C}$
-adjointable spaces (resp. maps). We also recall the trace interpretation of Hochschild homology.
Section 5 forms the heart of this article. It is there that we introduce generalized characters, prove their description in terms of categorified traces, and deduce the induced character formula. It is also in this section that we prove the additivity of generalized traces.
Sections 6 and 7 contain two applications of the theory. In Section 6, we discuss the Becker-Gottlieb transfer. We start by recalling its definition and basic properties, and we then express it in terms of the free loop transfer. We also address the question of its composability: although the equivalence
![]() $(gf)^!\simeq f^!g^!$
fails in full generality, we prove that it holds in a number of cases. Finally, in Section 7, we study Thom objects and their module categories, and we recover and generalize the main result of [Reference Blumberg, Cohen and Schlichtkrull15], computing the topological Hochschild homology of Thom spectra.
$(gf)^!\simeq f^!g^!$
fails in full generality, we prove that it holds in a number of cases. Finally, in Section 7, we study Thom objects and their module categories, and we recover and generalize the main result of [Reference Blumberg, Cohen and Schlichtkrull15], computing the topological Hochschild homology of Thom spectra.
1.5 Conventions
We work in the context of
![]() $\infty $
-categories, defined as quasicategories, and will generally follow Lurie’s conventions from [Reference Lurie49] and [Reference Lurie51]. In particular, all categorical notions appearing here, such as (co)limits and adjoints, are meant to be interpreted in the
$\infty $
-categories, defined as quasicategories, and will generally follow Lurie’s conventions from [Reference Lurie49] and [Reference Lurie51]. In particular, all categorical notions appearing here, such as (co)limits and adjoints, are meant to be interpreted in the
![]() $\infty $
-categorical sense. For
$\infty $
-categorical sense. For
![]() $(\infty ,n)$
-categories, we follow [Reference Hoyois, Scherotzke and Sibilla37] and work in the setting of Barwick’s n-fold complete Segal spaces [Reference Barwick and Schommer-Pries6].Footnote
3
$(\infty ,n)$
-categories, we follow [Reference Hoyois, Scherotzke and Sibilla37] and work in the setting of Barwick’s n-fold complete Segal spaces [Reference Barwick and Schommer-Pries6].Footnote
3
-
(1) We denote mapping spaces in an
 $\infty $
-category
$\infty $
-category
 $\mathscr {C}$
by
$\mathscr {C}$
by
 $ {\mathrm {Map}}_{\mathscr {C}}(-,-)$
or just by
$ {\mathrm {Map}}_{\mathscr {C}}(-,-)$
or just by
 $ {\mathrm {Map}}(-,-)$
if
$ {\mathrm {Map}}(-,-)$
if
 $\mathscr {C}$
is clear from context. The notation
$\mathscr {C}$
is clear from context. The notation
 $ {\mathrm {Fun}}(-,-)$
is used for functor
$ {\mathrm {Fun}}(-,-)$
is used for functor
 $\infty $
-categories and
$\infty $
-categories and
 $ {\mathrm {Fun}}^{\mathrm {L}}$
for the full subcategory of
$ {\mathrm {Fun}}^{\mathrm {L}}$
for the full subcategory of
 $ {\mathrm {Fun}}$
spanned by colimit-preserving functors;
$ {\mathrm {Fun}}$
spanned by colimit-preserving functors; -
(2) We write
 $ {\mathrm {Hom}}_{\mathscr {E}}(-,-)$
for the mapping
$ {\mathrm {Hom}}_{\mathscr {E}}(-,-)$
for the mapping
 $\infty $
-category in an
$\infty $
-category in an
 $(\infty ,2)$
-category
$(\infty ,2)$
-category
 $\mathscr {E}$
;
$\mathscr {E}$
; -
(3) We let
 $\mathcal {S}$
,
$\mathcal {S}$
,
 $\mathrm {Sp}$
,
$\mathrm {Sp}$
,
 $\mathrm {Cat}_\infty $
,
$\mathrm {Cat}_\infty $
,
 $\widehat {\mathrm {Cat}}_\infty $
and
$\widehat {\mathrm {Cat}}_\infty $
and
 $\mathrm {Pr}^{\text {L}}$
denote, respectively, the
$\mathrm {Pr}^{\text {L}}$
denote, respectively, the
 $\infty $
-category of spaces, of spectra, of small
$\infty $
-category of spaces, of spectra, of small
 $\infty $
-categories, of possibly large
$\infty $
-categories, of possibly large
 $\infty $
-categories and of presentable
$\infty $
-categories and of presentable
 $\infty $
-categories;
$\infty $
-categories; -
(4) We denote by
 $(-)^\simeq \colon \mathrm {Cat}_\infty \to \mathcal {S}$
the maximal subgroupoid functor. For an
$(-)^\simeq \colon \mathrm {Cat}_\infty \to \mathcal {S}$
the maximal subgroupoid functor. For an
 $(\infty ,n)$
-category
$(\infty ,n)$
-category
 $\mathscr {E}$
, we let
$\mathscr {E}$
, we let
 $\iota _k\mathscr {E}$
denote its maximal sub-
$\iota _k\mathscr {E}$
denote its maximal sub-
 $(\infty ,k)$
-category; in particular,
$(\infty ,k)$
-category; in particular,
 $\iota _0$
and
$\iota _0$
and
 $(-)^\simeq $
agree when restricted to
$(-)^\simeq $
agree when restricted to
 $(\infty ,1)$
-categories;
$(\infty ,1)$
-categories; -
(5) Restriction along a functor f is denoted by
 $f^*$
, and left and right Kan extensions along f are denoted by
$f^*$
, and left and right Kan extensions along f are denoted by
 $f_!$
and
$f_!$
and
 $f_*$
respectively;
$f_*$
respectively; -
(6) For a space A, we abuse notation and denote by A also the unique map
 $A\to \mathrm {pt}$
, so that for example the functor
$A\to \mathrm {pt}$
, so that for example the functor
 $A_!\colon \mathscr {C}^A \to \mathscr {C}$
denotes
$A_!\colon \mathscr {C}^A \to \mathscr {C}$
denotes
 $ {\mathrm {colim}}_A$
;
$ {\mathrm {colim}}_A$
; -
(7) For an object
 $X\in \mathscr {C}$
, we will denote by
$X\in \mathscr {C}$
, we will denote by
 $X[A]$
the object
$X[A]$
the object
 $A_!A^*X$
, i.e. the A-indexed colimit of the constant diagram X;
$A_!A^*X$
, i.e. the A-indexed colimit of the constant diagram X; -
(8) Equivalences are denoted by the symbol
 $\simeq $
;
$\simeq $
; -
(9) For an
 $\infty $
-category
$\infty $
-category
 $\mathscr {C}$
with finite products, a commutative monoid in
$\mathscr {C}$
with finite products, a commutative monoid in
 $\mathscr {C}$
is a functor
$\mathscr {C}$
is a functor
 $M\colon {\mathrm {Fin}}_* \to \mathscr {C}$
satisfying the Segal condition
$M\colon {\mathrm {Fin}}_* \to \mathscr {C}$
satisfying the Segal condition  .
. -
(10) We define a symmetric monoidal
 $\infty $
-category as a commutative monoid in
$\infty $
-category as a commutative monoid in
 $\mathrm {Cat}_{\infty }$
; by [Reference Lurie51, Remark 2.4.2.6] this agrees with Lurie’s definition. More generally, we define a symmetric monoidal
$\mathrm {Cat}_{\infty }$
; by [Reference Lurie51, Remark 2.4.2.6] this agrees with Lurie’s definition. More generally, we define a symmetric monoidal
 $(\infty ,n)$
-category as a commutative monoid in
$(\infty ,n)$
-category as a commutative monoid in
 $\mathrm {Cat}_{(\infty ,n)}$
.
$\mathrm {Cat}_{(\infty ,n)}$
. -
(11) Given a symmetric monoidal
 $\infty $
-category
$\infty $
-category
 $\mathscr {C}$
, we denote its monoidal unit by
$\mathscr {C}$
, we denote its monoidal unit by  , or by
, or by  if there is no ambiguity. We occasionally use
if there is no ambiguity. We occasionally use  to denote the pointing of an
to denote the pointing of an
 $\mathbb {E}_0$
-monoidal category. We write
$\mathbb {E}_0$
-monoidal category. We write
 $\mathrm {pt}$
for terminal objects when they exist;
$\mathrm {pt}$
for terminal objects when they exist; -
(12) We typically denote tensor products in (symmetric) monoidal
 $\infty $
-categories by
$\infty $
-categories by
 $\otimes $
if there is no ambiguity;
$\otimes $
if there is no ambiguity; -
(13) We write
 $ {\mathrm {Alg}}(\mathscr {C})$
,
$ {\mathrm {Alg}}(\mathscr {C})$
,
 $ {\mathrm {CAlg}}(\mathscr {C})$
and
$ {\mathrm {CAlg}}(\mathscr {C})$
and
 $ {\mathrm {Alg}}_n(\mathscr {C})$
for the
$ {\mathrm {Alg}}_n(\mathscr {C})$
for the
 $\infty $
-categories of algebras, resp. commutative algebras, resp.
$\infty $
-categories of algebras, resp. commutative algebras, resp.
 $\mathbb {E}_n$
-algebras in a symmetric monoidal
$\mathbb {E}_n$
-algebras in a symmetric monoidal
 $\infty $
-category
$\infty $
-category
 $\mathscr {C}$
. Note that a commutative monoid in an
$\mathscr {C}$
. Note that a commutative monoid in an
 $\infty $
-category
$\infty $
-category
 $\mathscr {C}$
with finite products is the same as a commutative algebra in the cartesian monoidal structure on
$\mathscr {C}$
with finite products is the same as a commutative algebra in the cartesian monoidal structure on
 $\mathscr {C}$
, see [Reference Lurie51, Proposition 2.4.2.5].
$\mathscr {C}$
, see [Reference Lurie51, Proposition 2.4.2.5]. -
(14) We write
 $ {\mathrm {RMod}}_R(\mathscr {C})$
and
$ {\mathrm {RMod}}_R(\mathscr {C})$
and
 $ {\mathrm {LMod}}_R(\mathscr {C})$
for the
$ {\mathrm {LMod}}_R(\mathscr {C})$
for the
 $\infty $
-categories of right resp. left modules over an algebra object R in
$\infty $
-categories of right resp. left modules over an algebra object R in
 $\mathscr {C}$
. When R is a commutative algebra, we write
$\mathscr {C}$
. When R is a commutative algebra, we write
 $ {\mathrm {Mod}}_R(\mathscr {C})$
.
$ {\mathrm {Mod}}_R(\mathscr {C})$
.
2 Higher categorical traces
Let ![]() be a symmetric monoidal
be a symmetric monoidal
![]() $\infty $
-category. Recall that an object X of
$\infty $
-category. Recall that an object X of
![]() $\mathscr {C}$
is called dualizable if there is another object
$\mathscr {C}$
is called dualizable if there is another object
![]() $X^\vee $
and maps
$X^\vee $
and maps ![]() and
and ![]() that satisfy the triangle identities: the composites
that satisfy the triangle identities: the composites
are homotopic to the respective identities. Given an endomorphism
![]() $f\colon X\to X$
of a dualizable object X, we define its trace
$f\colon X\to X$
of a dualizable object X, we define its trace ![]() to be the following composition:
to be the following composition:
The trace construction admits a certain functoriality, which we will outline first and make precise below. Let us call an endomorphism
![]() $f\colon X \to X$
traceable if the object X is dualizable in
$f\colon X \to X$
traceable if the object X is dualizable in
![]() $\mathscr {C}$
, and let
$\mathscr {C}$
, and let
![]() $\mathscr {C}^{\mathrm {trl}} \subseteq {\mathrm {Map}}(B\mathbb {N}, \mathscr {C})$
denote the subspace of traceable endomorphisms. Then the assignment
$\mathscr {C}^{\mathrm {trl}} \subseteq {\mathrm {Map}}(B\mathbb {N}, \mathscr {C})$
denote the subspace of traceable endomorphisms. Then the assignment
![]() $f \mapsto {\mathrm {tr}}(f)$
can be enhanced to a map of spaces
$f \mapsto {\mathrm {tr}}(f)$
can be enhanced to a map of spaces
the details for this will be recalled in Section 2.2. In the case where
![]() $\mathscr {C}$
is a symmetric monoidal
$\mathscr {C}$
is a symmetric monoidal
![]() $(\infty ,2)$
-category, the trace construction admits additional functoriality. In this case, the mapping space
$(\infty ,2)$
-category, the trace construction admits additional functoriality. In this case, the mapping space ![]() upgrades to an
upgrades to an
![]() $\infty $
-category, which will be denoted by
$\infty $
-category, which will be denoted by
![]() $\Omega \mathscr {C}$
. Also the space
$\Omega \mathscr {C}$
. Also the space
![]() $\mathscr {C}^{\mathrm {trl}}$
can be upgraded to an
$\mathscr {C}^{\mathrm {trl}}$
can be upgraded to an
![]() $\infty $
-category, again denoted by
$\infty $
-category, again denoted by
![]() $\mathscr {C}^{\mathrm {trl}}$
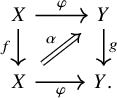
, whose morphisms are suitable morphisms between traceable endomorphisms. To describe these, recall that a morphism
$\mathscr {C}^{\mathrm {trl}}$
, whose morphisms are suitable morphisms between traceable endomorphisms. To describe these, recall that a morphism
![]() $\varphi \colon X \to Y$
in
$\varphi \colon X \to Y$
in
![]() $\mathscr {C}$
is called a left adjoint in
$\mathscr {C}$
is called a left adjoint in
![]() $\mathscr {C}$
if there exists a morphism
$\mathscr {C}$
if there exists a morphism
![]() $\varphi ^r\colon Y \to X$
together with 2-morphisms
$\varphi ^r\colon Y \to X$
together with 2-morphisms
![]() $\epsilon \colon \varphi \circ \varphi ^r \Rightarrow \mathrm {id}_Y$
and
$\epsilon \colon \varphi \circ \varphi ^r \Rightarrow \mathrm {id}_Y$
and
![]() $\eta \colon \mathrm {id}_X \Rightarrow \varphi ^r \circ \varphi $
satisfying the triangle identities: the composites
$\eta \colon \mathrm {id}_X \Rightarrow \varphi ^r \circ \varphi $
satisfying the triangle identities: the composites
are equivalent to the respective identity 2-morphisms. The morphisms in the
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}^{\mathrm {trl}}$
between two traceable endomorphisms
$\mathscr {C}^{\mathrm {trl}}$
between two traceable endomorphisms
![]() $f\colon X \to X$
and
$f\colon X \to X$
and
![]() $g\colon Y \to Y$
are pairs
$g\colon Y \to Y$
are pairs
![]() $(\varphi ,\alpha )$
consisting of a left adjoint morphism
$(\varphi ,\alpha )$
consisting of a left adjoint morphism
![]() $\varphi \colon X \to Y$
in
$\varphi \colon X \to Y$
in
![]() $\mathscr {C}$
together with a 2-morphism
$\mathscr {C}$
together with a 2-morphism
![]() $\alpha \colon \varphi f \Rightarrow g \varphi $
:
$\alpha \colon \varphi f \Rightarrow g \varphi $
:
Having these two
![]() $\infty $
-categories
$\infty $
-categories
![]() $\mathscr {C}^{\mathrm {trl}}$
and
$\mathscr {C}^{\mathrm {trl}}$
and
![]() $\Omega \mathscr {C}$
, the trace map can be upgraded to a functor of
$\Omega \mathscr {C}$
, the trace map can be upgraded to a functor of
![]() $\infty $
-categories
$\infty $
-categories
On objects, it still sends a traceable endomorphism f to its trace
![]() $ {\mathrm {tr}}(f)$
. On morphisms, it sends a morphism
$ {\mathrm {tr}}(f)$
. On morphisms, it sends a morphism
![]() $(\varphi ,\alpha )\colon (X,f) \to (Y,g)$
in
$(\varphi ,\alpha )\colon (X,f) \to (Y,g)$
in
![]() $\mathscr {C}^{\mathrm {trl}}$
to the morphism
$\mathscr {C}^{\mathrm {trl}}$
to the morphism
![]() $ {\mathrm {tr}}(\alpha )\colon {\mathrm {tr}}(f) \to {\mathrm {tr}}(g)$
in
$ {\mathrm {tr}}(\alpha )\colon {\mathrm {tr}}(f) \to {\mathrm {tr}}(g)$
in
![]() $\Omega \mathscr {C}$
obtained by considering the total composite in the following diagram:
$\Omega \mathscr {C}$
obtained by considering the total composite in the following diagram:
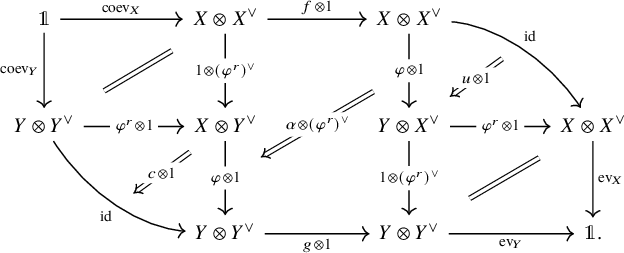
Here the morphism
![]() $(\varphi ^r)^{\vee }\colon X^{\vee } \to Y^{\vee }$
is the dual of the morphism
$(\varphi ^r)^{\vee }\colon X^{\vee } \to Y^{\vee }$
is the dual of the morphism
![]() $\varphi ^r\colon Y \to X$
, making the top-left and bottom-right squares commute.
$\varphi ^r\colon Y \to X$
, making the top-left and bottom-right squares commute.
The precise construction of this functoriality was worked out in [Reference Hoyois, Scherotzke and Sibilla37, Section 2]. In fact, they construct more generally for any
![]() $n \geq 1$
and any symmetric monoidal
$n \geq 1$
and any symmetric monoidal
![]() $(\infty ,n)$
-category
$(\infty ,n)$
-category
![]() $\mathscr {C}$
an
$\mathscr {C}$
an
![]() $(n-1)$
-functor
$(n-1)$
-functor
![]() $ {\mathrm {tr}}_{\mathscr {C}}\colon \mathscr {C}^{\mathrm {trl}} \to \Omega \mathscr {C}$
.Footnote
4
$ {\mathrm {tr}}_{\mathscr {C}}\colon \mathscr {C}^{\mathrm {trl}} \to \Omega \mathscr {C}$
.Footnote
4
The goal of this section is to give a detailed exposition of this
![]() $(n-1)$
-functor, following [Reference Hoyois, Scherotzke and Sibilla37, Section 2]. We will start in Section 2.1 with a brief recollection of generalized traces. In Section 2.2, we will discuss the functoriality of traces in the
$(n-1)$
-functor, following [Reference Hoyois, Scherotzke and Sibilla37, Section 2]. We will start in Section 2.1 with a brief recollection of generalized traces. In Section 2.2, we will discuss the functoriality of traces in the
![]() $(\infty ,1)$
-categorical setting, which will be bootstrapped up to the
$(\infty ,1)$
-categorical setting, which will be bootstrapped up to the
![]() $(\infty ,n)$
-categorical setting in Section 2.4. In the bootstrapping process, we make use of the notion of an (op)lax natural transformation between n-functors, which will be recalled in Section 2.3.
$(\infty ,n)$
-categorical setting in Section 2.4. In the bootstrapping process, we make use of the notion of an (op)lax natural transformation between n-functors, which will be recalled in Section 2.3.
2.1 Generalized traces
Let
![]() $\mathscr {C}$
be a symmetric monoidal
$\mathscr {C}$
be a symmetric monoidal
![]() $\infty $
-category, and let
$\infty $
-category, and let
![]() $X \in \mathscr {C}$
is a dualizable object, as defined in the introduction of this section. We will be interested in the generalized endomorphisms of X, that is, morphisms in
$X \in \mathscr {C}$
is a dualizable object, as defined in the introduction of this section. We will be interested in the generalized endomorphisms of X, that is, morphisms in
![]() $\mathscr {C}$
of the form
$\mathscr {C}$
of the form
where Y and Z are objects of
![]() $\mathscr {C}$
.
$\mathscr {C}$
.
Definition 2.1 (Generalized trace).
Given a generalized endomorphism
![]() $f\colon Z \otimes X \to X \otimes Y$
in
$f\colon Z \otimes X \to X \otimes Y$
in
![]() $\mathscr {C}$
, its generalized trace map
$\mathscr {C}$
, its generalized trace map
is defined as the following composition:
If Y and Z are the monoidal unit ![]() , the map
, the map ![]() is called the trace of the endomorphism
is called the trace of the endomorphism
![]() $f\colon X \to X$
. If f is the identity on X, we will call its trace the dimension
Footnote
5
of X:
$f\colon X \to X$
. If f is the identity on X, we will call its trace the dimension
Footnote
5
of X:
Remark 2.2. For simplicity, we will sometimes suppress the twist equivalence from the notation when writing down a (generalized) trace.
We now give several examples of dimensions and traces. For an extensive discussion of symmetric monoidal traces, including more examples, we refer the reader to [Reference Ponto and Shulman58].
Example 2.3. When ![]() , the trace of
, the trace of
![]() $f\colon Z \to Y$
is simply f itself:
$f\colon Z \to Y$
is simply f itself:
Example 2.4. When
![]() $\mathscr {C} = \mathscr {D}(R)$
is the derived
$\mathscr {C} = \mathscr {D}(R)$
is the derived
![]() $\infty $
-category of a commutative ring R, the notions of dimension and trace reduce to the notions of Euler characteristic and Lefschetz number of endomorphisms of perfect complexes. Similarly, when
$\infty $
-category of a commutative ring R, the notions of dimension and trace reduce to the notions of Euler characteristic and Lefschetz number of endomorphisms of perfect complexes. Similarly, when
![]() $\mathscr {C} = \mathrm {Sp}$
is the
$\mathscr {C} = \mathrm {Sp}$
is the
![]() $\infty $
-category of spectra and
$\infty $
-category of spectra and
![]() $X = \mathbb {S}[A]$
is the suspension spectrum of a finite CW-complex A, one recovers the Euler characteristic of A and the Lefschetz numbers of endomorphisms of A.
$X = \mathbb {S}[A]$
is the suspension spectrum of a finite CW-complex A, one recovers the Euler characteristic of A and the Lefschetz numbers of endomorphisms of A.
Example 2.5 (Field trace).
Consider a finite field extension
![]() $K \to L$
. The generalized trace of the multiplication map
$K \to L$
. The generalized trace of the multiplication map
![]() $L \otimes _K L \to L$
is a K-linear map
$L \otimes _K L \to L$
is a K-linear map
known as the field trace of L over K. It sends an element
![]() $\alpha \in L$
to the trace of the endomorphism
$\alpha \in L$
to the trace of the endomorphism
![]() $m_{\alpha }\colon L \to L$
given by multiplication by
$m_{\alpha }\colon L \to L$
given by multiplication by
![]() $\alpha $
.
$\alpha $
.
More generally, if k is a commutative ring and R is a dualizable k-algebra, applying the generalized trace construction to the multiplication map
![]() $R \otimes _k R \to R$
gives a k-linear trace map
$R \otimes _k R \to R$
gives a k-linear trace map
![]() $ {\mathrm {tr}}_{R/k}\colon R \to k$
.
$ {\mathrm {tr}}_{R/k}\colon R \to k$
.
Example 2.6 (Becker-Gottlieb transfer).
Let A be a compact space, so that its suspension spectrum
![]() $\mathbb {S}[A] \in \mathrm {Sp}$
is dualizable. The generalized trace of the diagonal
$\mathbb {S}[A] \in \mathrm {Sp}$
is dualizable. The generalized trace of the diagonal
![]() $\Delta \colon \mathbb {S}[A] \to \mathbb {S}[A \times A] \simeq \mathbb {S}[A] \otimes \mathbb {S}[A]$
is called the Becker-Gottlieb transfer of A. We will study this map in more detail in Section 6.
$\Delta \colon \mathbb {S}[A] \to \mathbb {S}[A \times A] \simeq \mathbb {S}[A] \otimes \mathbb {S}[A]$
is called the Becker-Gottlieb transfer of A. We will study this map in more detail in Section 6.
Remark 2.7. The formation of generalized traces is functorial in
![]() $\mathscr {C}$
: if
$\mathscr {C}$
: if
![]() $F\colon \mathscr {C} \to \mathscr {D}$
is a symmetric monoidal functor, then F preserves dualizable objects and it is easy to see that
$F\colon \mathscr {C} \to \mathscr {D}$
is a symmetric monoidal functor, then F preserves dualizable objects and it is easy to see that
![]() $ {\mathrm {tr}}(F(f) \,\vert \, F(X)) \simeq F( {\mathrm {tr}}(f \,\vert \, X))$
for every map
$ {\mathrm {tr}}(F(f) \,\vert \, F(X)) \simeq F( {\mathrm {tr}}(f \,\vert \, X))$
for every map
![]() $f\colon Z \otimes X \to X \otimes Y$
in
$f\colon Z \otimes X \to X \otimes Y$
in
![]() $\mathscr {C}$
.
$\mathscr {C}$
.
Remark 2.8. The generalized trace is functorial in Y and Z in the following sense: if
![]() $a\colon Z' \to Z$
and
$a\colon Z' \to Z$
and
![]() $b\colon Y \to Y'$
are morphisms in
$b\colon Y \to Y'$
are morphisms in
![]() $\mathscr {C}$
, then the generalized trace of the composite
$\mathscr {C}$
, then the generalized trace of the composite
is naturally equivalent to the composite
Observation 2.9 (Trace is symmetric monoidal).
Let
![]() $f\colon X \to X$
and
$f\colon X \to X$
and
![]() $g\colon Y \to Y$
be two traceable endomorphisms in
$g\colon Y \to Y$
be two traceable endomorphisms in
![]() $\mathscr {C}$
, i.e. X and Y are dualizable objects of
$\mathscr {C}$
, i.e. X and Y are dualizable objects of
![]() $\mathscr {C}$
. The tensor product
$\mathscr {C}$
. The tensor product
![]() $X \otimes Y$
is again dualizable, with evaluation and coevaluation given by the tensor product of those for X and Y. A simple computation shows that the trace of the endomorphism
$X \otimes Y$
is again dualizable, with evaluation and coevaluation given by the tensor product of those for X and Y. A simple computation shows that the trace of the endomorphism
![]() $f \otimes g\colon X \otimes Y \to X \otimes Y$
is equivalent to the tensor product of the traces of f and g:
$f \otimes g\colon X \otimes Y \to X \otimes Y$
is equivalent to the tensor product of the traces of f and g:
In Corollary 2.27, we will see that these equivalences can be made fully coherent.
2.2 Functoriality of traces
Let
![]() $\mathscr {C}$
be a symmetric monoidal
$\mathscr {C}$
be a symmetric monoidal
![]() $\infty $
-category. If X and
$\infty $
-category. If X and
![]() $X'$
are dualizable objects in
$X'$
are dualizable objects in
![]() $\mathscr {C}$
, then any equivalence
$\mathscr {C}$
, then any equivalence
![]() $X \simeq X'$
in
$X \simeq X'$
in
![]() $\mathscr {C}$
can be used to transfer the duality data from X to duality data on
$\mathscr {C}$
can be used to transfer the duality data from X to duality data on
![]() $X'$
, giving rise to a homotopy
$X'$
, giving rise to a homotopy
![]() $\dim (X) \simeq \dim (X')$
in
$\dim (X) \simeq \dim (X')$
in ![]() between the dimensions of X and
between the dimensions of X and
![]() $X'$
. It is possible to choose these homotopies in a fully coherent fashion. For a precise formulation of this claim, we need the following definitions:
$X'$
. It is possible to choose these homotopies in a fully coherent fashion. For a precise formulation of this claim, we need the following definitions:
Definition 2.10. Let
![]() $\mathscr {C} \in {\mathrm {CMon}}(\mathrm {Cat}_{\infty })$
be a symmetric monoidal
$\mathscr {C} \in {\mathrm {CMon}}(\mathrm {Cat}_{\infty })$
be a symmetric monoidal
![]() $\infty $
-category.
$\infty $
-category.
-
(1) We denote by
 $\mathscr {C}^{\mathrm {rig}} \subseteq \mathscr {C}$
the full subcategory spanned by the dualizable (a.k.a. ‘rigid’) objects;
$\mathscr {C}^{\mathrm {rig}} \subseteq \mathscr {C}$
the full subcategory spanned by the dualizable (a.k.a. ‘rigid’) objects; -
(2) We write
 $\mathscr {C}^{\mathrm {dbl}} \subseteq \mathscr {C}^{\simeq }$
for the full subgroupoid of dualizable objects and equivalences in
$\mathscr {C}^{\mathrm {dbl}} \subseteq \mathscr {C}^{\simeq }$
for the full subgroupoid of dualizable objects and equivalences in
 $\mathscr {C}$
, so that we have
$\mathscr {C}$
, so that we have
 $\mathscr {C}^{\mathrm {dbl}} = (\mathscr {C}^{\mathrm {rig}})^{\simeq }$
;
$\mathscr {C}^{\mathrm {dbl}} = (\mathscr {C}^{\mathrm {rig}})^{\simeq }$
; -
(3) We denote by
 $\mathscr {C}^{\mathrm {trl}} \subseteq {\mathrm {Fun}}(B\mathbb {N},\mathscr {C})^{\simeq }$
the full subgroupoid spanned by those endomorphisms
$\mathscr {C}^{\mathrm {trl}} \subseteq {\mathrm {Fun}}(B\mathbb {N},\mathscr {C})^{\simeq }$
the full subgroupoid spanned by those endomorphisms
 $f\colon X \to X$
where X is dualizable in
$f\colon X \to X$
where X is dualizable in
 $\mathscr {C}$
. We refer to such endomorphisms as the traceable endomorphisms.
$\mathscr {C}$
. We refer to such endomorphisms as the traceable endomorphisms. -
(4) We write
 for the space of endomorphisms of the monoidal unit
for the space of endomorphisms of the monoidal unit  of
of
 $\mathscr {C}$
.
$\mathscr {C}$
.
As we are about to make precise, the assignment
![]() $X \mapsto \dim (X)$
can be promoted to a map of spaces
$X \mapsto \dim (X)$
can be promoted to a map of spaces
naturally in
![]() $\mathscr {C}$
. Similarly, one can promote the assignment
$\mathscr {C}$
. Similarly, one can promote the assignment
![]() $(X,f) \mapsto {\mathrm {tr}}(f \,\vert \, X)$
to a map of spaces
$(X,f) \mapsto {\mathrm {tr}}(f \,\vert \, X)$
to a map of spaces
naturally in
![]() $\mathscr {C}$
. A convenient way of obtaining these two maps, as observed by [Reference Toën and Vezzosi64], is to use the fact that the functors
$\mathscr {C}$
. A convenient way of obtaining these two maps, as observed by [Reference Toën and Vezzosi64], is to use the fact that the functors
![]() $\mathscr {C} \mapsto \mathscr {C}^{\mathrm {dbl}}$
and
$\mathscr {C} \mapsto \mathscr {C}^{\mathrm {dbl}}$
and
![]() $\mathscr {C} \mapsto \mathscr {C}^{\mathrm {trl}}$
from symmetric monoidal
$\mathscr {C} \mapsto \mathscr {C}^{\mathrm {trl}}$
from symmetric monoidal
![]() $\infty $
-categories to spaces are corepresented by certain symmetric monoidal
$\infty $
-categories to spaces are corepresented by certain symmetric monoidal
![]() $\infty $
-categories
$\infty $
-categories
![]() $\mathrm {Fr}^{\mathrm {rig}}(\mathrm {pt})$
and
$\mathrm {Fr}^{\mathrm {rig}}(\mathrm {pt})$
and
![]() $\mathrm {Fr}^{\mathrm {rig}}(B\mathbb {N})$
. The main input for this is the following observation.
$\mathrm {Fr}^{\mathrm {rig}}(B\mathbb {N})$
. The main input for this is the following observation.
Lemma 2.11. The functor
![]() $(-)^{\mathrm {rig}}\colon {\mathrm {CAlg}}(\mathrm {Cat}_\infty ) \longrightarrow \mathrm {Cat}_{\infty }$
admits a left adjoint
$(-)^{\mathrm {rig}}\colon {\mathrm {CAlg}}(\mathrm {Cat}_\infty ) \longrightarrow \mathrm {Cat}_{\infty }$
admits a left adjoint
Proof. We will show that the assignment
![]() $\mathscr {C} \mapsto \mathscr {C}^{\mathrm {rig}}$
preserves limits and filtered colimits, so that it admits a left adjoint by the adjoint functor theorem. Recall that both the forgetful functor
$\mathscr {C} \mapsto \mathscr {C}^{\mathrm {rig}}$
preserves limits and filtered colimits, so that it admits a left adjoint by the adjoint functor theorem. Recall that both the forgetful functor
![]() $ {\mathrm {CAlg}}(\mathrm {Cat}_{\infty }) \to \mathrm {Cat}_{\infty }$
and the groupoid core functor
$ {\mathrm {CAlg}}(\mathrm {Cat}_{\infty }) \to \mathrm {Cat}_{\infty }$
and the groupoid core functor
![]() $(-)^{\simeq } \colon \mathrm {Cat}_{\infty } \to \mathcal {S}$
preserve limits and filtered colimits, and that fully faithful inclusions are closed under both limits and filtered colimits in
$(-)^{\simeq } \colon \mathrm {Cat}_{\infty } \to \mathcal {S}$
preserve limits and filtered colimits, and that fully faithful inclusions are closed under both limits and filtered colimits in
![]() $\mathrm {Cat}^{[1]}$
. Since the inclusion
$\mathrm {Cat}^{[1]}$
. Since the inclusion
![]() $\mathscr {C}^{\mathrm {rig}} \subseteq \mathscr {C}$
is a full subcategory for every
$\mathscr {C}^{\mathrm {rig}} \subseteq \mathscr {C}$
is a full subcategory for every
![]() $\mathscr {C}$
, we conclude that for every functor
$\mathscr {C}$
, we conclude that for every functor
![]() $I \to \mathrm {Cat}_{\infty }$
the canonical comparison maps
$I \to \mathrm {Cat}_{\infty }$
the canonical comparison maps
![]() $\lim _i \mathscr {C}^{\mathrm {rig}}_i \hookrightarrow \lim _i \mathscr {C}_i$
and, in case I is filtered,
$\lim _i \mathscr {C}^{\mathrm {rig}}_i \hookrightarrow \lim _i \mathscr {C}_i$
and, in case I is filtered,
![]() $ {\mathrm {colim}}_i \mathscr {C}_i^{\mathrm {rig}} \hookrightarrow {\mathrm {colim}}_i \mathscr {C}_i$
are fully faithful. All in all, we see that it remains to show that the functor
$ {\mathrm {colim}}_i \mathscr {C}_i^{\mathrm {rig}} \hookrightarrow {\mathrm {colim}}_i \mathscr {C}_i$
are fully faithful. All in all, we see that it remains to show that the functor
![]() $ {\mathrm {CAlg}}(\mathrm {Cat}_\infty ) \to \mathcal {S}$
sending
$ {\mathrm {CAlg}}(\mathrm {Cat}_\infty ) \to \mathcal {S}$
sending
![]() $\mathscr {C}$
to
$\mathscr {C}$
to
![]() $\mathscr {C}^{\mathrm {dbl}}$
preserves limits and filtered colimits.
$\mathscr {C}^{\mathrm {dbl}}$
preserves limits and filtered colimits.
By [Reference Lurie51, Lemma 4.6.1.10], the
![]() $\infty $
-groupoid
$\infty $
-groupoid
![]() $\mathscr {C}^{\mathrm {dbl}}$
is equivalent to the
$\mathscr {C}^{\mathrm {dbl}}$
is equivalent to the
![]() $\infty $
-category
$\infty $
-category
![]() $ {\mathrm {DDat}}(\mathscr {C})$
of duality data in
$ {\mathrm {DDat}}(\mathscr {C})$
of duality data in
![]() $\mathscr {C}$
, cf. [Reference Lurie51, Notation 4.6.1.8]. But the assignment
$\mathscr {C}$
, cf. [Reference Lurie51, Notation 4.6.1.8]. But the assignment
![]() $\mathscr {C} \mapsto {\mathrm {DDat}}(\mathscr {C})$
is easily seen to commute with limits and filtered colimits, finishing the proof.
$\mathscr {C} \mapsto {\mathrm {DDat}}(\mathscr {C})$
is easily seen to commute with limits and filtered colimits, finishing the proof.
For an
![]() $\infty $
-category I, the symmetric monoidal
$\infty $
-category I, the symmetric monoidal
![]() $\infty $
-category
$\infty $
-category
![]() $\mathrm {Fr}^{\mathrm {rig}}(I)$
comes equipped with a unit map
$\mathrm {Fr}^{\mathrm {rig}}(I)$
comes equipped with a unit map
![]() $I \to \mathrm {Fr}^{\mathrm {rig}}(I)$
which lands in dualizable objects. Restriction along this map induces for every symmetric monoidal
$I \to \mathrm {Fr}^{\mathrm {rig}}(I)$
which lands in dualizable objects. Restriction along this map induces for every symmetric monoidal
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}$
an equivalence of spaces
$\mathscr {C}$
an equivalence of spaces
In particular, specializing to
![]() $I = \mathrm {pt}$
and
$I = \mathrm {pt}$
and
![]() $I = B\mathbb {N}$
gives equivalences of spaces
$I = B\mathbb {N}$
gives equivalences of spaces
showing that the functors
![]() $(-)^{\mathrm {dbl}}, (-)^{\mathrm {trl}}\colon {\mathrm {CAlg}}(\mathrm {Cat}_{\infty }) \to \mathcal {S}$
are corepresentable.
$(-)^{\mathrm {dbl}}, (-)^{\mathrm {trl}}\colon {\mathrm {CAlg}}(\mathrm {Cat}_{\infty }) \to \mathcal {S}$
are corepresentable.
In the case of
![]() $B\mathbb {N}$
, we will denote the unit map by
$B\mathbb {N}$
, we will denote the unit map by
![]() $\gamma _{ {\mathrm {univ}}}\colon B\mathbb {N} \to \mathrm {Fr}^{\mathrm {rig}}(B\mathbb {N})$
, and refer to it as the ‘universal traceable endomorphism’. Forming its trace produces an element
$\gamma _{ {\mathrm {univ}}}\colon B\mathbb {N} \to \mathrm {Fr}^{\mathrm {rig}}(B\mathbb {N})$
, and refer to it as the ‘universal traceable endomorphism’. Forming its trace produces an element
![]() $ {\mathrm {tr}}(\gamma _{ {\mathrm {univ}}}) \in \Omega \mathrm {Fr}^{\mathrm {rig}}(B\mathbb {N})$
, thought of as the ‘universal trace’. By the Yoneda lemma, it determines for every
$ {\mathrm {tr}}(\gamma _{ {\mathrm {univ}}}) \in \Omega \mathrm {Fr}^{\mathrm {rig}}(B\mathbb {N})$
, thought of as the ‘universal trace’. By the Yoneda lemma, it determines for every
![]() $\mathscr {C} \in {\mathrm {CAlg}}(\mathrm {Cat}_{\infty })$
a natural map of spaces
$\mathscr {C} \in {\mathrm {CAlg}}(\mathrm {Cat}_{\infty })$
a natural map of spaces
![]() $ {\mathrm {tr}}\colon \mathscr {C}^{\mathrm {trl}} \to \Omega \mathscr {C}$
. More explicitly:
$ {\mathrm {tr}}\colon \mathscr {C}^{\mathrm {trl}} \to \Omega \mathscr {C}$
. More explicitly:
Definition 2.12. Given a symmetric monoidal
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}$
, we define the trace map
$\mathscr {C}$
, we define the trace map
![]() $ {\mathrm {tr}}\colon \mathscr {C}^{\mathrm {trl}} \to \Omega \mathscr {C}$
as the composite
$ {\mathrm {tr}}\colon \mathscr {C}^{\mathrm {trl}} \to \Omega \mathscr {C}$
as the composite
By Remark 2.7, this functor agrees on objects with the formula for the trace given in the beginning of this section.
The map
![]() $\dim \colon \mathscr {C}^{\mathrm {dbl}} \to \Omega \mathscr {C}$
may be produced in a similar way from the Yoneda lemma by using instead the ‘universal dimension’
$\dim \colon \mathscr {C}^{\mathrm {dbl}} \to \Omega \mathscr {C}$
may be produced in a similar way from the Yoneda lemma by using instead the ‘universal dimension’
![]() $\dim (\mathrm {pt}_{ {\mathrm {univ}}}) \in \Omega \mathrm {Fr}^{\mathrm {rig}}(\mathrm {pt})$
, where
$\dim (\mathrm {pt}_{ {\mathrm {univ}}}) \in \Omega \mathrm {Fr}^{\mathrm {rig}}(\mathrm {pt})$
, where
![]() $\mathrm {pt}_{ {\mathrm {univ}}} \in \mathrm {Fr}^{\mathrm {rig}}(\mathrm {pt})$
is the ‘universal dualizable object’. Alternatively, one can obtain the map
$\mathrm {pt}_{ {\mathrm {univ}}} \in \mathrm {Fr}^{\mathrm {rig}}(\mathrm {pt})$
is the ‘universal dualizable object’. Alternatively, one can obtain the map
![]() $\dim \colon \mathscr {C}^{\mathrm {dbl}} \to \Omega \mathscr {C}$
from the map
$\dim \colon \mathscr {C}^{\mathrm {dbl}} \to \Omega \mathscr {C}$
from the map
![]() $ {\mathrm {tr}}\colon \mathscr {C}^{\mathrm {trl}} \to \Omega \mathscr {C}$
by precomposing with the map
$ {\mathrm {tr}}\colon \mathscr {C}^{\mathrm {trl}} \to \Omega \mathscr {C}$
by precomposing with the map
![]() $\mathscr {C}^{\mathrm {dbl}} \to \mathscr {C}^{\mathrm {trl}}\colon X \mapsto (X,\mathrm {id})$
.
$\mathscr {C}^{\mathrm {dbl}} \to \mathscr {C}^{\mathrm {trl}}\colon X \mapsto (X,\mathrm {id})$
.
2.3 Lax and oplax transformations
When
![]() $\mathscr {C} \in {\mathrm {CMon}}(\mathrm {Cat}_{(\infty ,n)})$
is a symmetric monoidal
$\mathscr {C} \in {\mathrm {CMon}}(\mathrm {Cat}_{(\infty ,n)})$
is a symmetric monoidal
![]() $(\infty ,n)$
-category, then the traceable endomorphisms
$(\infty ,n)$
-category, then the traceable endomorphisms
![]() $f\colon X \to X$
in
$f\colon X \to X$
in
![]() $\mathscr {C}$
naturally form an
$\mathscr {C}$
naturally form an
![]() $(\infty ,n-1)$
-category
$(\infty ,n-1)$
-category
![]() $\mathscr {C}^{\mathrm {trl}}$
rather than just a space. The construction of this
$\mathscr {C}^{\mathrm {trl}}$
rather than just a space. The construction of this
![]() $(\infty ,n-1)$
-category proceeds by realizing it as a subcategory of the
$(\infty ,n-1)$
-category proceeds by realizing it as a subcategory of the
![]() $(\infty ,n)$
-category of functors
$(\infty ,n)$
-category of functors
![]() $B\mathbb {N} \to \mathscr {C}$
and symmetric monoidal oplax natural transformations between them, satisfying certain dualizability and adjointability constraints. In this subsection, we will recall the necessary background on lax and oplax transformations.
$B\mathbb {N} \to \mathscr {C}$
and symmetric monoidal oplax natural transformations between them, satisfying certain dualizability and adjointability constraints. In this subsection, we will recall the necessary background on lax and oplax transformations.
Following [Reference Hoyois, Scherotzke and Sibilla37], we will model
![]() $(\infty , n)$
-categories by Barwick’s n-fold complete Segal spaces
$(\infty , n)$
-categories by Barwick’s n-fold complete Segal spaces
![]() $\mathscr {C}\colon (\Delta ^{\mathrm {op}})^{\times n} \to \mathcal {S}$
[Reference Barwick and Schommer-Pries6, §Reference Ben-Zvi and Nadler14]. For an
$\mathscr {C}\colon (\Delta ^{\mathrm {op}})^{\times n} \to \mathcal {S}$
[Reference Barwick and Schommer-Pries6, §Reference Ben-Zvi and Nadler14]. For an
![]() $(\infty ,n)$
-category
$(\infty ,n)$
-category
![]() $\mathscr {C}$
and a vector
$\mathscr {C}$
and a vector
![]() $\vec {k} = (k_1,\dots ,k_n)\in \mathbb {N}^n$
, we denote by
$\vec {k} = (k_1,\dots ,k_n)\in \mathbb {N}^n$
, we denote by
![]() $\mathscr {C}_{\vec {k}}$
the value of
$\mathscr {C}_{\vec {k}}$
the value of
![]() $\mathscr {C}$
, considered as an n-fold complete Segal space, at
$\mathscr {C}$
, considered as an n-fold complete Segal space, at
![]() $([k_1],\dots ,[k_n])\in \Delta ^n$
. The collection of
$([k_1],\dots ,[k_n])\in \Delta ^n$
. The collection of
![]() $(\infty ,n)$
-categories assembles into an
$(\infty ,n)$
-categories assembles into an
![]() $\infty $
-category that we denote by
$\infty $
-category that we denote by
![]() $\mathrm {Cat}_{(\infty ,n)}$
. By a symmetric monoidal
$\mathrm {Cat}_{(\infty ,n)}$
. By a symmetric monoidal
![]() $(\infty ,n)$
-category we mean a commutative monoid in the
$(\infty ,n)$
-category we mean a commutative monoid in the
![]() $\infty $
-category
$\infty $
-category
![]() $\mathrm {Cat}_{(\infty ,n)}$
.
$\mathrm {Cat}_{(\infty ,n)}$
.
For each vector
![]() $\vec {k}\in \mathbb {N}^n$
, the functor
$\vec {k}\in \mathbb {N}^n$
, the functor
![]() $\mathrm {Cat}_{(\infty ,n)} \to \mathcal {S}$
given by
$\mathrm {Cat}_{(\infty ,n)} \to \mathcal {S}$
given by
![]() $\mathscr {C}\mapsto \mathscr {C}_{\vec {k}}$
is corepresentable by the so called ‘walking
$\mathscr {C}\mapsto \mathscr {C}_{\vec {k}}$
is corepresentable by the so called ‘walking
![]() $\vec {k}$
-tuple’
$\vec {k}$
-tuple’
![]() $\theta ^{\vec {k}}\in \mathrm {Cat}_{(\infty ,n)}$
(see [Reference Johnson-Freyd and Scheimbauer39, Definition 5.1, Remark 5.4]). Namely, we have a natural equivalence of spaces
$\theta ^{\vec {k}}\in \mathrm {Cat}_{(\infty ,n)}$
(see [Reference Johnson-Freyd and Scheimbauer39, Definition 5.1, Remark 5.4]). Namely, we have a natural equivalence of spaces
The
![]() $(\infty ,n)$
-categories
$(\infty ,n)$
-categories
![]() $\theta ^{\vec {k}}$
generate
$\theta ^{\vec {k}}$
generate
![]() $\mathrm {Cat}_{(\infty ,n)}$
under colimits. For
$\mathrm {Cat}_{(\infty ,n)}$
under colimits. For
![]() $n = 1$
, the
$n = 1$
, the
![]() $\infty $
-category
$\infty $
-category
![]() $\theta ^{(k)}$
is just the k-simplex
$\theta ^{(k)}$
is just the k-simplex
![]() $[k] \in \mathrm {Cat}_{(\infty ,1)}$
. The following are some examples for
$[k] \in \mathrm {Cat}_{(\infty ,1)}$
. The following are some examples for
![]() $n = 2$
:
$n = 2$
:

Given two
![]() $(\infty ,n)$
-categories
$(\infty ,n)$
-categories
![]() $\mathscr {C}$
and
$\mathscr {C}$
and
![]() $\mathscr {D}$
, one can form two new
$\mathscr {D}$
, one can form two new
![]() $(\infty ,n)$
-categories
$(\infty ,n)$
-categories
whose objects are the n-functors
![]() $\mathscr {C} \to \mathscr {D}$
and whose higher morphisms are given by certain (op)lax transformations (see [Reference Hoyois, Scherotzke and Sibilla37, §2.2]). We emphasize that there is no laxness in the objects of
$\mathscr {C} \to \mathscr {D}$
and whose higher morphisms are given by certain (op)lax transformations (see [Reference Hoyois, Scherotzke and Sibilla37, §2.2]). We emphasize that there is no laxness in the objects of
![]() $ {\mathrm {Fun}}_{\mathrm {lax}}(\mathscr {C},\mathscr {D})$
and
$ {\mathrm {Fun}}_{\mathrm {lax}}(\mathscr {C},\mathscr {D})$
and
![]() $ {\mathrm {Fun}}_{\mathrm {oplax}}(\mathscr {C},\mathscr {D})$
, only in the higher morphisms. These two
$ {\mathrm {Fun}}_{\mathrm {oplax}}(\mathscr {C},\mathscr {D})$
, only in the higher morphisms. These two
![]() $(\infty ,n)$
-categories are most easily described in terms of a certain conjectural monoidal structure
$(\infty ,n)$
-categories are most easily described in terms of a certain conjectural monoidal structure
![]() $\times ^{\mathrm {lax}}$
on
$\times ^{\mathrm {lax}}$
on
![]() $\mathrm {Cat}_{(\infty ,n)}$
, called the Gray product: for
$\mathrm {Cat}_{(\infty ,n)}$
, called the Gray product: for
![]() $(\infty ,n)$
-categories
$(\infty ,n)$
-categories
![]() $\mathscr {C}$
and
$\mathscr {C}$
and
![]() $\mathscr {D}$
, we would like to define the
$\mathscr {D}$
, we would like to define the
![]() $(\infty ,n)$
-categories
$(\infty ,n)$
-categories
![]() $ {\mathrm {Fun}}_{\mathrm {lax}}(\mathscr {C},\mathscr {D})$
and
$ {\mathrm {Fun}}_{\mathrm {lax}}(\mathscr {C},\mathscr {D})$
and
![]() $ {\mathrm {Fun}}_{\mathrm {oplax}}(\mathscr {C},\mathscr {D})$
via the natural isomorphisms
$ {\mathrm {Fun}}_{\mathrm {oplax}}(\mathscr {C},\mathscr {D})$
via the natural isomorphisms
 $$ \begin{align*} \begin{split} {\mathrm{Map}}(\mathscr{E}, {\mathrm{Fun}}_{\mathrm{lax}}(\mathscr{C},\mathscr{D})) &\simeq {\mathrm{Map}}(\mathscr{E} \times^{\mathrm{lax}} \mathscr{C}, \mathscr{D}) \\ {\mathrm{Map}}(\mathscr{E}, {\mathrm{Fun}}_{\mathrm{oplax}}(\mathscr{C},\mathscr{D})) &\simeq {\mathrm{Map}}(\mathscr{C} \times^{\mathrm{lax}} \mathscr{E}, \mathscr{D}) \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} {\mathrm{Map}}(\mathscr{E}, {\mathrm{Fun}}_{\mathrm{lax}}(\mathscr{C},\mathscr{D})) &\simeq {\mathrm{Map}}(\mathscr{E} \times^{\mathrm{lax}} \mathscr{C}, \mathscr{D}) \\ {\mathrm{Map}}(\mathscr{E}, {\mathrm{Fun}}_{\mathrm{oplax}}(\mathscr{C},\mathscr{D})) &\simeq {\mathrm{Map}}(\mathscr{C} \times^{\mathrm{lax}} \mathscr{E}, \mathscr{D}) \end{split} \end{align*} $$
for
![]() $\mathscr {E} \in \mathrm {Cat}_{(\infty ,n)}$
. Unfortunately, as far as we know the construction of the Gray product of
$\mathscr {E} \in \mathrm {Cat}_{(\infty ,n)}$
. Unfortunately, as far as we know the construction of the Gray product of
![]() $(\infty ,n)$
-categories with all of its expected properties is not yet fully furnished in the literature.
$(\infty ,n)$
-categories with all of its expected properties is not yet fully furnished in the literature.
To circumvent this technical difficulty, [Reference Johnson-Freyd and Scheimbauer39] observed that in order to define
![]() $ {\mathrm {Fun}}_{\mathrm {lax}}(-,-)$
and
$ {\mathrm {Fun}}_{\mathrm {lax}}(-,-)$
and
![]() $ {\mathrm {Fun}}_{\mathrm {oplax}}(-,-)$
one only needs the Gray products of the walking
$ {\mathrm {Fun}}_{\mathrm {oplax}}(-,-)$
one only needs the Gray products of the walking
![]() $\vec {k}$
-tuples
$\vec {k}$
-tuples
![]() $\theta ^{\vec {k}}$
. In [Reference Johnson-Freyd and Scheimbauer39, Definition 5.7], a combinatorial model is given for a Gray product
$\theta ^{\vec {k}}$
. In [Reference Johnson-Freyd and Scheimbauer39, Definition 5.7], a combinatorial model is given for a Gray product
![]() $\theta ^{\vec {k}}\times ^{\mathrm {lax}} \theta ^{\vec {\ell }}$
, which we denote by
$\theta ^{\vec {k}}\times ^{\mathrm {lax}} \theta ^{\vec {\ell }}$
, which we denote by
![]() $\theta ^{\vec {k},\vec {\ell }}$
. We have the following low-dimensional examples, cf. [Reference Johnson-Freyd and Scheimbauer39, Example 4.2,4.3]:
$\theta ^{\vec {k},\vec {\ell }}$
. We have the following low-dimensional examples, cf. [Reference Johnson-Freyd and Scheimbauer39, Example 4.2,4.3]:

The construction of
![]() $\theta ^{\vec {k},\vec {l}}$
is functorial in
$\theta ^{\vec {k},\vec {l}}$
is functorial in
![]() $\vec {k}, \vec {l} \in \Delta ^{n}$
, and satisfies
$\vec {k}, \vec {l} \in \Delta ^{n}$
, and satisfies
![]() $\theta ^{\vec {k},\vec {0}} \simeq \theta ^{\vec {k}} \simeq \theta ^{\vec {0},\vec {k}}$
. In particular, it comes equipped with a natural map
$\theta ^{\vec {k},\vec {0}} \simeq \theta ^{\vec {k}} \simeq \theta ^{\vec {0},\vec {k}}$
. In particular, it comes equipped with a natural map
![]() $\theta ^{\vec {k},\vec {l}} \to \theta ^{\vec {k}} \times \theta ^{\vec {l}}$
to the cartesian product. Using the
$\theta ^{\vec {k},\vec {l}} \to \theta ^{\vec {k}} \times \theta ^{\vec {l}}$
to the cartesian product. Using the
![]() $(\infty ,n)$
-categories
$(\infty ,n)$
-categories
![]() $\theta ^{\vec {k},\vec {l}}$
, one now defines
$\theta ^{\vec {k},\vec {l}}$
, one now defines
![]() $ {\mathrm {Fun}}_{\mathrm {lax}}(-,-)$
and
$ {\mathrm {Fun}}_{\mathrm {lax}}(-,-)$
and
![]() $ {\mathrm {Fun}}_{\mathrm {oplax}}(-,-)$
by the following two-step procedure:
$ {\mathrm {Fun}}_{\mathrm {oplax}}(-,-)$
by the following two-step procedure:
Definition 2.13. For
![]() $\mathscr {C} \in \mathrm {Cat}_{(\infty ,n)}$
and
$\mathscr {C} \in \mathrm {Cat}_{(\infty ,n)}$
and
![]() $\vec {k}\in \mathbb {N}^n$
, we define the following n-fold simplicial spaces:
$\vec {k}\in \mathbb {N}^n$
, we define the following n-fold simplicial spaces:
We then define n-fold simplicial spaces
![]() $ {\mathrm {Fun}}_{\mathrm {lax}}(\mathscr {E},\mathscr {C})$
and
$ {\mathrm {Fun}}_{\mathrm {lax}}(\mathscr {E},\mathscr {C})$
and
![]() $ {\mathrm {Fun}}_{\mathrm {oplax}}(\mathscr {E},\mathscr {D})$
by:
$ {\mathrm {Fun}}_{\mathrm {oplax}}(\mathscr {E},\mathscr {D})$
by:
 $$ \begin{align*} {\mathrm{Fun}}_{\mathrm{lax}}(\mathscr{E},\mathscr{C})_{\vec{k}}&:= {\mathrm{Map}}(\mathscr{E},{\mathrm{Fun}}_{\mathrm{oplax}}(\theta^{\vec{k}},\mathscr{C})),\\ {\mathrm{Fun}}_{\mathrm{oplax}}(\mathscr{E},\mathscr{C})_{\vec{k}}&:= {\mathrm{Map}}(\mathscr{E},{\mathrm{Fun}}_{\mathrm{lax}}(\theta^{\vec{k}},\mathscr{C})). \end{align*} $$
$$ \begin{align*} {\mathrm{Fun}}_{\mathrm{lax}}(\mathscr{E},\mathscr{C})_{\vec{k}}&:= {\mathrm{Map}}(\mathscr{E},{\mathrm{Fun}}_{\mathrm{oplax}}(\theta^{\vec{k}},\mathscr{C})),\\ {\mathrm{Fun}}_{\mathrm{oplax}}(\mathscr{E},\mathscr{C})_{\vec{k}}&:= {\mathrm{Map}}(\mathscr{E},{\mathrm{Fun}}_{\mathrm{lax}}(\theta^{\vec{k}},\mathscr{C})). \end{align*} $$
These are n-fold complete Segal spaces by [Reference Johnson-Freyd and Scheimbauer39, Corollary 5.19] and these constructions assemble into functors
It is immediate from the construction that these functors preserve limits in both variables. Furthermore, they come equipped with a natural map from the ordinary functor category: by precomposition with the maps
![]() $\theta ^{\vec {k},\vec {l}} \to \theta ^{\vec {k}} \times \theta ^{\vec {l}}$
one obtains maps
$\theta ^{\vec {k},\vec {l}} \to \theta ^{\vec {k}} \times \theta ^{\vec {l}}$
one obtains maps
Example 2.14. The low-dimensional simplices in the
![]() $(\infty ,n)$
-category
$(\infty ,n)$
-category
![]() $ {\mathrm {Fun}}_{\mathrm {lax}}([1], \mathscr {C})$
may be described as follows:
$ {\mathrm {Fun}}_{\mathrm {lax}}([1], \mathscr {C})$
may be described as follows:
-
(0) Objects are morphisms
 $X_0 \to X_1$
in
$X_0 \to X_1$
in
 $\mathscr {C}$
;
$\mathscr {C}$
; -
(1) m Morphisms are lax commuting squares

-
(2) 2-Morphisms are
 $3$
-dimensional diagrams of the following shape:
$3$
-dimensional diagrams of the following shape: 
Remark 2.15. In the case
![]() $n = 2$
, a full definition of the Gray product is given by [Reference Gagna, Harpaz and Lanari28] in terms of scaled simplicial sets: by [Reference Gagna, Harpaz and Lanari28, Corollary 2.15], their construction determines a presentably (non-symmetric) monoidal structure
$n = 2$
, a full definition of the Gray product is given by [Reference Gagna, Harpaz and Lanari28] in terms of scaled simplicial sets: by [Reference Gagna, Harpaz and Lanari28, Corollary 2.15], their construction determines a presentably (non-symmetric) monoidal structure
on the
![]() $\infty $
-category
$\infty $
-category
![]() $\mathrm {Cat}_{(\infty ,2)}$
. In [Reference Haugseng, Hebestreit, Linskens and Nuiten34, Proposition 5.1.9], it was computed that this lax product takes the expected values on pairs of simplices
$\mathrm {Cat}_{(\infty ,2)}$
. In [Reference Haugseng, Hebestreit, Linskens and Nuiten34, Proposition 5.1.9], it was computed that this lax product takes the expected values on pairs of simplices
![]() $[k] \in \mathrm {Cat}_{(\infty ,1)}$
(as in the example
$[k] \in \mathrm {Cat}_{(\infty ,1)}$
(as in the example
![]() $\theta ^{(1),(1)}$
above). Consequently, for
$\theta ^{(1),(1)}$
above). Consequently, for
![]() $\mathscr {C},\mathscr {D} \in \mathrm {Cat}_{(\infty ,1)}$
and
$\mathscr {C},\mathscr {D} \in \mathrm {Cat}_{(\infty ,1)}$
and
![]() $\mathscr {E} \in \mathrm {Cat}_{(\infty ,2)}$
, we have
$\mathscr {E} \in \mathrm {Cat}_{(\infty ,2)}$
, we have
In particular, the underlying
![]() $(\infty ,1)$
-category of
$(\infty ,1)$
-category of
![]() $ {\mathrm {Fun}}_{\mathrm {lax}}(\mathscr {D},\mathscr {E})$
can be described in terms of
$ {\mathrm {Fun}}_{\mathrm {lax}}(\mathscr {D},\mathscr {E})$
can be described in terms of
![]() $\times ^{\mathrm {lax}}$
.
$\times ^{\mathrm {lax}}$
.
Finally, we discuss the interaction of the constructions
![]() $ {\mathrm {Fun}}_{\mathrm {lax}}(-,-)$
and
$ {\mathrm {Fun}}_{\mathrm {lax}}(-,-)$
and
![]() $ {\mathrm {Fun}}_{\mathrm {oplax}}(-,-)$
with symmetric monoidal structures.
$ {\mathrm {Fun}}_{\mathrm {oplax}}(-,-)$
with symmetric monoidal structures.
Observation 2.16. If
![]() $\mathscr {D}$
is a symmetric monoidal
$\mathscr {D}$
is a symmetric monoidal
![]() $(\infty ,n)$
-category, i.e. a commutative monoid in
$(\infty ,n)$
-category, i.e. a commutative monoid in
![]() $\mathrm {Cat}_{(\infty ,n)}$
, then
$\mathrm {Cat}_{(\infty ,n)}$
, then
![]() $ {\mathrm {Fun}}_{\mathrm {lax}}(\mathscr {C},\mathscr {D})$
and
$ {\mathrm {Fun}}_{\mathrm {lax}}(\mathscr {C},\mathscr {D})$
and
![]() $ {\mathrm {Fun}}_{\mathrm {oplax}}(\mathscr {C},\mathscr {D})$
inherit canonical structures of symmetric monoidal
$ {\mathrm {Fun}}_{\mathrm {oplax}}(\mathscr {C},\mathscr {D})$
inherit canonical structures of symmetric monoidal
![]() $(\infty ,n)$
-categories as well. Indeed, since the functors
$(\infty ,n)$
-categories as well. Indeed, since the functors
![]() $ {\mathrm {Fun}}_{\mathrm {lax}}(\mathscr {C},-)$
and
$ {\mathrm {Fun}}_{\mathrm {lax}}(\mathscr {C},-)$
and
![]() $ {\mathrm {Fun}}_{\mathrm {oplax}}(\mathscr {C},-)$
preserve limits, and therefore in particular finite products, they preserve commutative monoids in
$ {\mathrm {Fun}}_{\mathrm {oplax}}(\mathscr {C},-)$
preserve limits, and therefore in particular finite products, they preserve commutative monoids in
![]() $\mathrm {Cat}_{(\infty ,n)}$
.
$\mathrm {Cat}_{(\infty ,n)}$
.
If both
![]() $\mathscr {C}$
and
$\mathscr {C}$
and
![]() $\mathscr {D}$
have symmetric monoidal structures, one can define the following variants of
$\mathscr {D}$
have symmetric monoidal structures, one can define the following variants of
![]() $ {\mathrm {Fun}}_{\mathrm {lax}}(\mathscr {C},\mathscr {D})$
and
$ {\mathrm {Fun}}_{\mathrm {lax}}(\mathscr {C},\mathscr {D})$
and
![]() $ {\mathrm {Fun}}_{\mathrm {oplax}}(\mathscr {C},\mathscr {D})$
in which the functors and (op)lax natural transformations are symmetric monoidal:
$ {\mathrm {Fun}}_{\mathrm {oplax}}(\mathscr {C},\mathscr {D})$
in which the functors and (op)lax natural transformations are symmetric monoidal:
Definition 2.17. Assume
![]() $\mathscr {C}$
and
$\mathscr {C}$
and
![]() $\mathscr {D}$
are symmetric monoidal
$\mathscr {D}$
are symmetric monoidal
![]() $(\infty ,n)$
-categories. We define
$(\infty ,n)$
-categories. We define
![]() $(\infty ,n)$
-categories
$(\infty ,n)$
-categories
![]() $ {\mathrm {Fun}}_{\mathrm {lax}}^{\otimes }(\mathscr {C},\mathscr {D})$
and
$ {\mathrm {Fun}}_{\mathrm {lax}}^{\otimes }(\mathscr {C},\mathscr {D})$
and
![]() $ {\mathrm {Fun}}_{\mathrm {oplax}}^{\otimes }(\mathscr {C},\mathscr {D})$
by the following representability conditions: for
$ {\mathrm {Fun}}_{\mathrm {oplax}}^{\otimes }(\mathscr {C},\mathscr {D})$
by the following representability conditions: for
![]() $\mathscr {E} \in \mathrm {Cat}_{(\infty ,n)}$
we have natural equivalences
$\mathscr {E} \in \mathrm {Cat}_{(\infty ,n)}$
we have natural equivalences
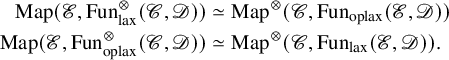 $$ \begin{align*} {\mathrm{Map}}(\mathscr{E}, {\mathrm{Fun}}_{\mathrm{lax}}^{\otimes}(\mathscr{C},\mathscr{D})) &\simeq {\mathrm{Map}}^{\otimes}(\mathscr{C}, {\mathrm{Fun}}_{\mathrm{oplax}}(\mathscr{E},\mathscr{D})) \\ {\mathrm{Map}}(\mathscr{E}, {\mathrm{Fun}}_{\mathrm{oplax}}^{\otimes}(\mathscr{C},\mathscr{D})) &\simeq {\mathrm{Map}}^{\otimes}(\mathscr{C}, {\mathrm{Fun}}_{\mathrm{lax}}(\mathscr{E},\mathscr{D})). \end{align*} $$
$$ \begin{align*} {\mathrm{Map}}(\mathscr{E}, {\mathrm{Fun}}_{\mathrm{lax}}^{\otimes}(\mathscr{C},\mathscr{D})) &\simeq {\mathrm{Map}}^{\otimes}(\mathscr{C}, {\mathrm{Fun}}_{\mathrm{oplax}}(\mathscr{E},\mathscr{D})) \\ {\mathrm{Map}}(\mathscr{E}, {\mathrm{Fun}}_{\mathrm{oplax}}^{\otimes}(\mathscr{C},\mathscr{D})) &\simeq {\mathrm{Map}}^{\otimes}(\mathscr{C}, {\mathrm{Fun}}_{\mathrm{lax}}(\mathscr{E},\mathscr{D})). \end{align*} $$
2.4 Higher categorical traces
In this section, we will recall from [Reference Hoyois, Scherotzke and Sibilla37] the definition of the symmetric monoidal
![]() $(n-1)$
-functor
$(n-1)$
-functor
![]() $ {\mathrm {tr}}\colon \mathscr {C}^{\mathrm {trl}} \to \Omega \mathscr {C}$
for a symmetric monoidal
$ {\mathrm {tr}}\colon \mathscr {C}^{\mathrm {trl}} \to \Omega \mathscr {C}$
for a symmetric monoidal
![]() $(\infty ,n)$
-category
$(\infty ,n)$
-category
![]() $\mathscr {C}$
. We will start by formally defining its source and target.
$\mathscr {C}$
. We will start by formally defining its source and target.
Definition 2.18. Let
![]() $\mathscr {C} \in {\mathrm {CAlg}}(\mathrm {Cat}_{(\infty ,n)})$
be a symmetric monoidal
$\mathscr {C} \in {\mathrm {CAlg}}(\mathrm {Cat}_{(\infty ,n)})$
be a symmetric monoidal
![]() $(\infty ,n)$
-category. We define the
$(\infty ,n)$
-category. We define the
![]() $(\infty ,n-1)$
-category
$(\infty ,n-1)$
-category
![]() $\mathscr {C}^{\mathrm {dbl}}$
of dualizable objects in
$\mathscr {C}^{\mathrm {dbl}}$
of dualizable objects in
![]() $\mathscr {C}$
as
$\mathscr {C}$
as
Similarly, we define the
![]() $(\infty ,n-1)$
-category
$(\infty ,n-1)$
-category
![]() $\mathscr {C}^{\mathrm {trl}}$
of traceable endomorphisms in
$\mathscr {C}^{\mathrm {trl}}$
of traceable endomorphisms in
![]() $\mathscr {C}$
as
$\mathscr {C}$
as
Precomposition with the symmetric monoidal functor
![]() $\mathrm {Fr}^{\mathrm {rig}}(B\mathbb {N}) \to \mathrm {Fr}^{\mathrm {rig}}(\mathrm {pt})$
induced by the map
$\mathrm {Fr}^{\mathrm {rig}}(B\mathbb {N}) \to \mathrm {Fr}^{\mathrm {rig}}(\mathrm {pt})$
induced by the map
![]() $B\mathbb {N} \to \mathrm {pt}$
gives an
$B\mathbb {N} \to \mathrm {pt}$
gives an
![]() $(n-1)$
-functor
$(n-1)$
-functor
![]() $\mathscr {C}^{\mathrm {dbl}} \to \mathscr {C}^{\mathrm {trl}}$
.
$\mathscr {C}^{\mathrm {dbl}} \to \mathscr {C}^{\mathrm {trl}}$
.
Remark 2.19. The application of the underlying
![]() $(\infty ,n-1)$
-category functor
$(\infty ,n-1)$
-category functor
![]() $\iota _{n-1}$
in the definition of
$\iota _{n-1}$
in the definition of
![]() $\mathscr {C}^{\mathrm {dbl}}$
and
$\mathscr {C}^{\mathrm {dbl}}$
and
![]() $\mathscr {C}^{\mathrm {trl}}$
is actually redundant as the
$\mathscr {C}^{\mathrm {trl}}$
is actually redundant as the
![]() $(\infty ,n)$
-categories to which it is applied are already
$(\infty ,n)$
-categories to which it is applied are already
![]() $(\infty ,n-1)$
-categories, cf. [Reference Hoyois, Scherotzke and Sibilla37, Remark 2.3].
$(\infty ,n-1)$
-categories, cf. [Reference Hoyois, Scherotzke and Sibilla37, Remark 2.3].
For
![]() $n = 1$
, there is an equivalence of
$n = 1$
, there is an equivalence of
![]() $\infty $
-groupoids
$\infty $
-groupoids
![]() $\iota _0 {\mathrm {Fun}}^{\otimes }_{\mathrm {oplax}}(-,-) \simeq {\mathrm {Map}}^{\otimes }(-,-)$
, and thus by corepresentability the definitions of the
$\iota _0 {\mathrm {Fun}}^{\otimes }_{\mathrm {oplax}}(-,-) \simeq {\mathrm {Map}}^{\otimes }(-,-)$
, and thus by corepresentability the definitions of the
![]() $\infty $
-groupoids
$\infty $
-groupoids
![]() $\mathscr {C}^{\mathrm {dbl}}$
and
$\mathscr {C}^{\mathrm {dbl}}$
and
![]() $\mathscr {C}^{\mathrm {trl}}$
agree with the ones from the previous subsection. For larger n, the constructions of
$\mathscr {C}^{\mathrm {trl}}$
agree with the ones from the previous subsection. For larger n, the constructions of
![]() $\mathscr {C}^{\mathrm {dbl}}$
and
$\mathscr {C}^{\mathrm {dbl}}$
and
![]() $\mathscr {C}^{\mathrm {trl}}$
are compatible with the inclusions
$\mathscr {C}^{\mathrm {trl}}$
are compatible with the inclusions
![]() $\mathrm {Cat}_{(\infty ,n)} \hookrightarrow \mathrm {Cat}_{(\infty ,n+1)}$
, in the sense that the following squares commute:
$\mathrm {Cat}_{(\infty ,n)} \hookrightarrow \mathrm {Cat}_{(\infty ,n+1)}$
, in the sense that the following squares commute:
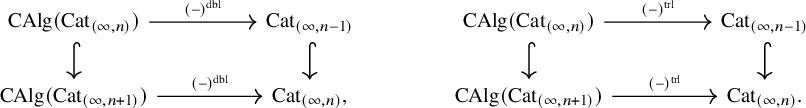
Moreover, these squares are vertically right adjointable: for
![]() $1 \leq k \leq n$
there are equivalences
$1 \leq k \leq n$
there are equivalences
It follows that the space of objects of the
![]() $(\infty ,n-1)$
-category
$(\infty ,n-1)$
-category
![]() $\mathscr {C}^{\mathrm {dbl}}$
is the space of dualizable objects in
$\mathscr {C}^{\mathrm {dbl}}$
is the space of dualizable objects in
![]() $\mathscr {C}$
, while the space of objects of
$\mathscr {C}$
, while the space of objects of
![]() $\mathscr {C}^{\mathrm {trl}}$
is the space of traceable endomorphisms in
$\mathscr {C}^{\mathrm {trl}}$
is the space of traceable endomorphisms in
![]() $\mathscr {C}$
.
$\mathscr {C}$
.
We will next show that also the morphisms in
![]() $\mathscr {C}^{\mathrm {dbl}}$
and
$\mathscr {C}^{\mathrm {dbl}}$
and
![]() $\mathscr {C}^{\mathrm {trl}}$
are as claimed in the introduction of this section.
$\mathscr {C}^{\mathrm {trl}}$
are as claimed in the introduction of this section.
Lemma 2.20. Let
![]() $\mathscr {C}$
be a symmetric monoidal
$\mathscr {C}$
be a symmetric monoidal
![]() $(\infty ,n)$
-category. For any
$(\infty ,n)$
-category. For any
![]() $(\infty ,n-1)$
-category
$(\infty ,n-1)$
-category
![]() $\mathscr {E}$
there are equivalences of spaces
$\mathscr {E}$
there are equivalences of spaces
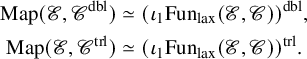 $$ \begin{align*} {\mathrm{Map}}(\mathscr{E},\mathscr{C}^{\mathrm{dbl}}) &\simeq (\iota_1{\mathrm{Fun}}_{\mathrm{lax}}(\mathscr{E},\mathscr{C}))^{\mathrm{dbl}},\\ {\mathrm{Map}}(\mathscr{E},\mathscr{C}^{\mathrm{trl}}) &\simeq (\iota_1{\mathrm{Fun}}_{\mathrm{lax}}(\mathscr{E},\mathscr{C}))^{\mathrm{trl}}. \end{align*} $$
$$ \begin{align*} {\mathrm{Map}}(\mathscr{E},\mathscr{C}^{\mathrm{dbl}}) &\simeq (\iota_1{\mathrm{Fun}}_{\mathrm{lax}}(\mathscr{E},\mathscr{C}))^{\mathrm{dbl}},\\ {\mathrm{Map}}(\mathscr{E},\mathscr{C}^{\mathrm{trl}}) &\simeq (\iota_1{\mathrm{Fun}}_{\mathrm{lax}}(\mathscr{E},\mathscr{C}))^{\mathrm{trl}}. \end{align*} $$
Proof. For the second equation, there are equivalences
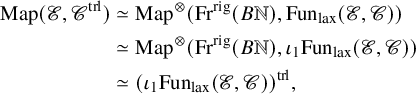 $$ \begin{align*} {\mathrm{Map}}(\mathscr{E},\mathscr{C}^{\mathrm{trl}}) &\simeq {\mathrm{Map}}^{\otimes}(\mathrm{Fr}^{\mathrm{rig}}(B\mathbb{N}),{\mathrm{Fun}}_{\mathrm{lax}}(\mathscr{E},\mathscr{C})) \\ &\simeq {\mathrm{Map}}^{\otimes}(\mathrm{Fr}^{\mathrm{rig}}(B\mathbb{N}),\iota_1{\mathrm{Fun}}_{\mathrm{lax}}(\mathscr{E},\mathscr{C}))\\ &\simeq (\iota_1{\mathrm{Fun}}_{\mathrm{lax}}(\mathscr{E},\mathscr{C}))^{\mathrm{trl}}, \end{align*} $$
$$ \begin{align*} {\mathrm{Map}}(\mathscr{E},\mathscr{C}^{\mathrm{trl}}) &\simeq {\mathrm{Map}}^{\otimes}(\mathrm{Fr}^{\mathrm{rig}}(B\mathbb{N}),{\mathrm{Fun}}_{\mathrm{lax}}(\mathscr{E},\mathscr{C})) \\ &\simeq {\mathrm{Map}}^{\otimes}(\mathrm{Fr}^{\mathrm{rig}}(B\mathbb{N}),\iota_1{\mathrm{Fun}}_{\mathrm{lax}}(\mathscr{E},\mathscr{C}))\\ &\simeq (\iota_1{\mathrm{Fun}}_{\mathrm{lax}}(\mathscr{E},\mathscr{C}))^{\mathrm{trl}}, \end{align*} $$
where the first equivalence is immediate from the definitions, the second equivalence holds as
![]() $\mathrm {Fr}^{\mathrm {rig}}(B\mathbb {N})$
is an
$\mathrm {Fr}^{\mathrm {rig}}(B\mathbb {N})$
is an
![]() $(\infty ,1)$
-category, and the third is the defining property of
$(\infty ,1)$
-category, and the third is the defining property of
![]() $\mathrm {Fr}^{\mathrm {rig}}(B\mathbb {N})$
. The computation for the first equation is analogous, using
$\mathrm {Fr}^{\mathrm {rig}}(B\mathbb {N})$
. The computation for the first equation is analogous, using
![]() $\mathrm {Fr}^{\mathrm {rig}}(\mathrm {pt})$
instead.
$\mathrm {Fr}^{\mathrm {rig}}(\mathrm {pt})$
instead.
Corollary 2.21 (cf. [Reference Hoyois, Scherotzke and Sibilla37, Lemma 2.4]).
Let
![]() $\mathscr {C}$
be an
$\mathscr {C}$
be an
![]() $(\infty ,n)$
-category. There are natural monomorphisms of
$(\infty ,n)$
-category. There are natural monomorphisms of
![]() $(\infty ,n)$
-categories
$(\infty ,n)$
-categories
An object
![]() $X \in \mathscr {C}$
is in
$X \in \mathscr {C}$
is in
![]() $\mathscr {C}^{\mathrm {dbl}}$
if and only if it is dualizable, and a morphism
$\mathscr {C}^{\mathrm {dbl}}$
if and only if it is dualizable, and a morphism
![]() $f\colon X \to Y$
between dualizable objects is in
$f\colon X \to Y$
between dualizable objects is in
![]() $\mathscr {C}^{\mathrm {dbl}}$
if and only if it is a left adjoint morphism. Similarly, an endomorphism
$\mathscr {C}^{\mathrm {dbl}}$
if and only if it is a left adjoint morphism. Similarly, an endomorphism
![]() $f\colon X \to X$
is an object in
$f\colon X \to X$
is an object in
![]() $\mathscr {C}^{\mathrm {trl}}$
if and only if X is dualizable, and a lax square
$\mathscr {C}^{\mathrm {trl}}$
if and only if X is dualizable, and a lax square
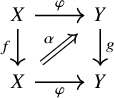
is a morphism in
![]() $\mathscr {C}^{\mathrm {trl}}$
if and only if X and Y are dualizable and
$\mathscr {C}^{\mathrm {trl}}$
if and only if X and Y are dualizable and
![]() $\varphi \colon X \to Y$
is a left adjoint in
$\varphi \colon X \to Y$
is a left adjoint in
![]() $\mathscr {C}$
.
$\mathscr {C}$
.
Proof. We start by producing the two monomorphisms. We will do this for
![]() $\mathscr {C}^{\mathrm {trl}}$
, and leave the case for
$\mathscr {C}^{\mathrm {trl}}$
, and leave the case for
![]() $\mathscr {C}^{\mathrm {dbl}}$
to the reader. For every
$\mathscr {C}^{\mathrm {dbl}}$
to the reader. For every
![]() $(\infty ,n-1)$
-category
$(\infty ,n-1)$
-category
![]() $\mathscr {E}$
, we consider the following natural composite map of spaces:
$\mathscr {E}$
, we consider the following natural composite map of spaces:
Note that the middle map is an inclusion of path components by definition of
![]() $(-)^{\mathrm {trl}}$
. By the Yoneda lemma, we obtain the desired monomorphism
$(-)^{\mathrm {trl}}$
. By the Yoneda lemma, we obtain the desired monomorphism
![]() $\mathscr {C}^{\mathrm {trl}} \hookrightarrow {\mathrm {Fun}}_{\mathrm {oplax}}(B\mathbb {N},\mathscr {C})$
.
$\mathscr {C}^{\mathrm {trl}} \hookrightarrow {\mathrm {Fun}}_{\mathrm {oplax}}(B\mathbb {N},\mathscr {C})$
.
We now prove the descriptions of the objects and morphisms of
![]() $\mathscr {C}^{\mathrm {dbl}}$
and
$\mathscr {C}^{\mathrm {dbl}}$
and
![]() $\mathscr {C}^{\mathrm {trl}}$
. As mentioned earlier, the statement on objects is clear from the equivalences
$\mathscr {C}^{\mathrm {trl}}$
. As mentioned earlier, the statement on objects is clear from the equivalences
![]() $\iota _0\mathscr {C}^{\mathrm {dbl}} \simeq (\iota _1\mathscr {C})^{\mathrm {dbl}}$
and
$\iota _0\mathscr {C}^{\mathrm {dbl}} \simeq (\iota _1\mathscr {C})^{\mathrm {dbl}}$
and
![]() $\iota _0\mathscr {C}^{\mathrm {trl}} \simeq (\iota _1\mathscr {C})^{\mathrm {trl}}$
. For the statement on morphisms, we apply Lemma 2.20 to
$\iota _0\mathscr {C}^{\mathrm {trl}} \simeq (\iota _1\mathscr {C})^{\mathrm {trl}}$
. For the statement on morphisms, we apply Lemma 2.20 to
![]() $\mathscr {E} = [1]$
to reduce to a statement about the dualizable objects of
$\mathscr {E} = [1]$
to reduce to a statement about the dualizable objects of
![]() $ {\mathrm {Fun}}_{\mathrm {lax}}([1],\mathscr {C})$
. This then becomes an instance of Lemma 2.4 in [Reference Hoyois, Scherotzke and Sibilla37], which says that an object
$ {\mathrm {Fun}}_{\mathrm {lax}}([1],\mathscr {C})$
. This then becomes an instance of Lemma 2.4 in [Reference Hoyois, Scherotzke and Sibilla37], which says that an object
![]() $(\varphi \colon X \to Y)$
of
$(\varphi \colon X \to Y)$
of
![]() $ {\mathrm {Fun}}_{\mathrm {lax}}([1],\mathscr {C})$
is dualizable if and only if X and Y are dualizable and
$ {\mathrm {Fun}}_{\mathrm {lax}}([1],\mathscr {C})$
is dualizable if and only if X and Y are dualizable and
![]() $\varphi \colon X \to Y$
is a left adjoint in
$\varphi \colon X \to Y$
is a left adjoint in
![]() $\mathscr {C}$
.
$\mathscr {C}$
.
The target
![]() $\Omega \mathscr {C}$
of the higher trace functor is the
$\Omega \mathscr {C}$
of the higher trace functor is the
![]() $(\infty ,n-1)$
-category of endomorphisms of the monoidal unit, defined formally as follows:
$(\infty ,n-1)$
-category of endomorphisms of the monoidal unit, defined formally as follows:
Definition 2.22. The
![]() $(\infty ,n-1)$
-category
$(\infty ,n-1)$
-category
![]() $\Omega \mathscr {C}$
is defined as the following pullbackFootnote
6
in
$\Omega \mathscr {C}$
is defined as the following pullbackFootnote
6
in
![]() $\mathrm {Cat}_{(\infty ,n-1)}$
:
$\mathrm {Cat}_{(\infty ,n-1)}$
:
That is, the objects of
![]() $\Omega \mathscr {C}$
are given by 1-morphisms
$\Omega \mathscr {C}$
are given by 1-morphisms ![]() in
in
![]() $\mathscr {C}$
, the morphisms are given by 2-morphisms
$\mathscr {C}$
, the morphisms are given by 2-morphisms
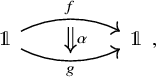
and so forth. If
![]() $\mathscr {C}$
is symmetric monoidal, then so is
$\mathscr {C}$
is symmetric monoidal, then so is
![]() $\Omega \mathscr {C}$
, as all the functors in the diagram of which
$\Omega \mathscr {C}$
, as all the functors in the diagram of which
![]() $\Omega \mathscr {C}$
is defined to be the limit are manifestly symmetric monoidal.
$\Omega \mathscr {C}$
is defined to be the limit are manifestly symmetric monoidal.
Proposition 2.23. For every
![]() $(\infty ,n-1)$
-category
$(\infty ,n-1)$
-category
![]() $\mathscr {E}$
the canonical map
$\mathscr {E}$
the canonical map
is an equivalence. In particular, there is an equivalence
Proof. In the special case
![]() $\mathscr {E} = \theta ^{\vec {k}}$
, the first statement is [Reference Hoyois, Scherotzke and Sibilla37, Proposition 2.6]. The general case follows from the fact that the
$\mathscr {E} = \theta ^{\vec {k}}$
, the first statement is [Reference Hoyois, Scherotzke and Sibilla37, Proposition 2.6]. The general case follows from the fact that the
![]() $(\infty ,n-1)$
-categories
$(\infty ,n-1)$
-categories
![]() $\theta ^{\vec {k}}$
generate
$\theta ^{\vec {k}}$
generate
![]() $\mathrm {Cat}_{(\infty ,n-1)}$
under colimits and both sides take colimits in the variable
$\mathrm {Cat}_{(\infty ,n-1)}$
under colimits and both sides take colimits in the variable
![]() $\mathscr {E}$
to limits.
$\mathscr {E}$
to limits.
For the second statement, we observe that
![]() $\Omega \iota _{k} \mathscr {C} \simeq \iota _{k-1} \Omega \mathscr {C}$
for
$\Omega \iota _{k} \mathscr {C} \simeq \iota _{k-1} \Omega \mathscr {C}$
for
![]() $1 \leq k \leq n-1$
, so that
$1 \leq k \leq n-1$
, so that
proving the claim.
We can now bootstrap the
![]() $(\infty ,1)$
-categorical trace map from Definition 2.12 to the
$(\infty ,1)$
-categorical trace map from Definition 2.12 to the
![]() $(\infty ,n)$
-categorical setting.
$(\infty ,n)$
-categorical setting.
Definition 2.24. Let
![]() $\mathscr {C}$
be a symmetric monoidal
$\mathscr {C}$
be a symmetric monoidal
![]() $(\infty ,n)$
-category. We define the trace functor
$(\infty ,n)$
-category. We define the trace functor
as the
![]() $(n-1)$
-functor inducing the following natural map of spaces for every
$(n-1)$
-functor inducing the following natural map of spaces for every
![]() $\mathscr {E} \in \mathrm {Cat}_{(\infty ,n-1)}$
:
$\mathscr {E} \in \mathrm {Cat}_{(\infty ,n-1)}$
:
Here the first and last equivalences are Lemma 2.20 and Proposition 2.23 respectively and the middle map is the trace map of spaces for the symmetric monoidal
![]() $(\infty ,1)$
-category
$(\infty ,1)$
-category
![]() $\iota _1 {\mathrm {Fun}}_{\mathrm {lax}}(\mathscr {E},\mathscr {C})$
, as defined in Definition 2.12.
$\iota _1 {\mathrm {Fun}}_{\mathrm {lax}}(\mathscr {E},\mathscr {C})$
, as defined in Definition 2.12.
We define the dimension functor
![]() $\dim \colon \mathscr {C}^{\mathrm {dbl}} \to \Omega \mathscr {C}$
as the
$\dim \colon \mathscr {C}^{\mathrm {dbl}} \to \Omega \mathscr {C}$
as the
![]() $(n-1)$
-functor obtained by precomposing
$(n-1)$
-functor obtained by precomposing
![]() $ {\mathrm {tr}}\colon \mathscr {C}^{\mathrm {trl}} \to \Omega \mathscr {C}$
with the map
$ {\mathrm {tr}}\colon \mathscr {C}^{\mathrm {trl}} \to \Omega \mathscr {C}$
with the map
![]() $\mathscr {C}^{\mathrm {dbl}} \to \mathscr {C}^{\mathrm {trl}}$
from Definition 2.18.
$\mathscr {C}^{\mathrm {dbl}} \to \mathscr {C}^{\mathrm {trl}}$
from Definition 2.18.
By definition, the
![]() $(n-1)$
-functor
$(n-1)$
-functor
![]() $ {\mathrm {tr}}\colon \mathscr {C}^{\mathrm {trl}} \to \Omega \mathscr {C}$
is on groupoid cores simply given by the trace map of the
$ {\mathrm {tr}}\colon \mathscr {C}^{\mathrm {trl}} \to \Omega \mathscr {C}$
is on groupoid cores simply given by the trace map of the
![]() $(\infty ,1)$
-category
$(\infty ,1)$
-category
![]() $\iota _1 \mathscr {C}$
, and thus it has the correct behavior on objects. The following lemma shows that also its behavior on morphisms is as described in the introduction of this section:
$\iota _1 \mathscr {C}$
, and thus it has the correct behavior on objects. The following lemma shows that also its behavior on morphisms is as described in the introduction of this section:
Lemma 2.25 (cf. [Reference Hoyois, Scherotzke and Sibilla37, Lemma 2.4]).
Let
![]() $f\colon X \to X$
and
$f\colon X \to X$
and
![]() $g\colon Y \to Y$
be traceable endomorphisms in
$g\colon Y \to Y$
be traceable endomorphisms in
![]() $\mathscr {C}$
, and let
$\mathscr {C}$
, and let
![]() $(\varphi ,\alpha )\colon (X,f) \to (Y,g)$
be a morphism in
$(\varphi ,\alpha )\colon (X,f) \to (Y,g)$
be a morphism in
![]() $\mathscr {C}^{\mathrm {trl}}$
as in (1), cf. Corollary 2.21. Then applying
$\mathscr {C}^{\mathrm {trl}}$
as in (1), cf. Corollary 2.21. Then applying
![]() $ {\mathrm {tr}}\colon \mathscr {C}^{\mathrm {trl}} \to \Omega \mathscr {C}$
gives the morphism
$ {\mathrm {tr}}\colon \mathscr {C}^{\mathrm {trl}} \to \Omega \mathscr {C}$
gives the morphism
![]() $ {\mathrm {tr}}(\alpha )\colon {\mathrm {tr}}(f) \to {\mathrm {tr}}(g)$
in
$ {\mathrm {tr}}(\alpha )\colon {\mathrm {tr}}(f) \to {\mathrm {tr}}(g)$
in
![]() $\Omega \mathscr {C}$
given by (2).
$\Omega \mathscr {C}$
given by (2).
Proof. Under the identification
![]() $ {\mathrm {Map}}([1],\mathscr {C}^{\mathrm {trl}}) \simeq (\iota _1 {\mathrm {Fun}}_{\mathrm {lax}}([1],\mathscr {C}))^{\mathrm {trl}}$
, the morphism
$ {\mathrm {Map}}([1],\mathscr {C}^{\mathrm {trl}}) \simeq (\iota _1 {\mathrm {Fun}}_{\mathrm {lax}}([1],\mathscr {C}))^{\mathrm {trl}}$
, the morphism
![]() $(\varphi ,\alpha )\colon (X,f) \to (Y,g)$
in
$(\varphi ,\alpha )\colon (X,f) \to (Y,g)$
in
![]() $\mathscr {C}^{\mathrm {trl}}$
corresponds to an endomorphism
$\mathscr {C}^{\mathrm {trl}}$
corresponds to an endomorphism
![]() $(f,g,\alpha )$
of the dualizable object
$(f,g,\alpha )$
of the dualizable object
![]() $(\varphi \colon X \to Y)$
in the symmetric monoidal
$(\varphi \colon X \to Y)$
in the symmetric monoidal
![]() $\infty $
-category
$\infty $
-category
![]() $ {\mathrm {Fun}}_{\mathrm {lax}}([1],\mathscr {C})$
, and the map
$ {\mathrm {Fun}}_{\mathrm {lax}}([1],\mathscr {C})$
, and the map
![]() $ {\mathrm {tr}}(\alpha )$
is by definition the trace of this endomorphism:
$ {\mathrm {tr}}(\alpha )$
is by definition the trace of this endomorphism:
In the proof of [Reference Hoyois, Scherotzke and Sibilla37, Lemma 2.4], the authors write down explicit duality data of
![]() $\varphi $
as an object of
$\varphi $
as an object of
![]() $ {\mathrm {Fun}}_{\mathrm {lax}}([1],\mathscr {C})$
, and plugging this in gives the explicit description of the map
$ {\mathrm {Fun}}_{\mathrm {lax}}([1],\mathscr {C})$
, and plugging this in gives the explicit description of the map
![]() $ {\mathrm {tr}}(\alpha )\colon {\mathrm {tr}}(f) \to {\mathrm {tr}}(g)$
as given in (2).
$ {\mathrm {tr}}(\alpha )\colon {\mathrm {tr}}(f) \to {\mathrm {tr}}(g)$
as given in (2).
We finish the section by showing that the trace functor
![]() $ {\mathrm {tr}}\colon \mathscr {C}^{\mathrm {trl}} \to \Omega \mathscr {C}$
admits a canonical enhancement to a symmetric monoidal
$ {\mathrm {tr}}\colon \mathscr {C}^{\mathrm {trl}} \to \Omega \mathscr {C}$
admits a canonical enhancement to a symmetric monoidal
![]() $(n-1)$
-functor.
$(n-1)$
-functor.
Lemma 2.26. The functors
 $$ \begin{align*} (-)^{\mathrm{trl}}\colon {\mathrm{CAlg}}(\mathrm{Cat}_{(\infty,n)}) &\to \mathrm{Cat}_{(\infty,n-1)} \\ \Omega\colon {\mathrm{CAlg}}(\mathrm{Cat}_{(\infty,n)}) &\to \mathrm{Cat}_{(\infty,n-1)} \end{align*} $$
$$ \begin{align*} (-)^{\mathrm{trl}}\colon {\mathrm{CAlg}}(\mathrm{Cat}_{(\infty,n)}) &\to \mathrm{Cat}_{(\infty,n-1)} \\ \Omega\colon {\mathrm{CAlg}}(\mathrm{Cat}_{(\infty,n)}) &\to \mathrm{Cat}_{(\infty,n-1)} \end{align*} $$
preserve limits.
Proof. The functor
![]() $\Omega (-)$
is the pullback of the limit-preserving functors sending
$\Omega (-)$
is the pullback of the limit-preserving functors sending
![]() $\mathscr {C}$
to
$\mathscr {C}$
to ![]() ,
,
![]() $\mathscr {C}_0 \times \mathscr {C}_0$
and
$\mathscr {C}_0 \times \mathscr {C}_0$
and
![]() $\mathscr {C}_1$
, and thus also
$\mathscr {C}_1$
, and thus also
![]() $\Omega $
preserves limits. For
$\Omega $
preserves limits. For
![]() $(-)^{\mathrm {trl}}$
, this follows from the fact that for every
$(-)^{\mathrm {trl}}$
, this follows from the fact that for every
![]() $\mathscr {E} \in \mathrm {Cat}_{(\infty ,n-1)}$
and
$\mathscr {E} \in \mathrm {Cat}_{(\infty ,n-1)}$
and
![]() $\mathscr {C} \in {\mathrm {CAlg}}(\mathrm {Cat}_{(\infty ,n)})$
there is an equivalence
$\mathscr {C} \in {\mathrm {CAlg}}(\mathrm {Cat}_{(\infty ,n)})$
there is an equivalence
where the right-hand side preserves limits in the variable
![]() $\mathscr {C} \in {\mathrm {CAlg}}(\mathrm {Cat}_{(\infty ,n)})$
.
$\mathscr {C} \in {\mathrm {CAlg}}(\mathrm {Cat}_{(\infty ,n)})$
.
Since the functors
![]() $(-)^{\mathrm {trl}}$
and
$(-)^{\mathrm {trl}}$
and
![]() $\Omega (-)$
in particular preserve finite products, they induce functors on commutative algebra objects. Employing the equivalence
$\Omega (-)$
in particular preserve finite products, they induce functors on commutative algebra objects. Employing the equivalence
![]() $ {\mathrm {CAlg}}(\mathrm {Cat}_{(\infty ,n)}) \simeq {\mathrm {CAlg}}( {\mathrm {CAlg}}(\mathrm {Cat}_{(\infty ,n)}))$
, we may regard every symmetric monoidal
$ {\mathrm {CAlg}}(\mathrm {Cat}_{(\infty ,n)}) \simeq {\mathrm {CAlg}}( {\mathrm {CAlg}}(\mathrm {Cat}_{(\infty ,n)}))$
, we may regard every symmetric monoidal
![]() $(\infty ,n)$
-category as a commutative algebra in the
$(\infty ,n)$
-category as a commutative algebra in the
![]() $\infty $
-category
$\infty $
-category
![]() $ {\mathrm {CAlg}}(\mathrm {Cat}_{(\infty ,n)})$
. This leads to a symmetric monoidal enhancement of the trace functor.
$ {\mathrm {CAlg}}(\mathrm {Cat}_{(\infty ,n)})$
. This leads to a symmetric monoidal enhancement of the trace functor.
Corollary 2.27 (cf. [Reference Hoyois, Scherotzke and Sibilla37, Definition 2.11]).
For every symmetric monoidal
![]() $(\infty ,n)$
-category
$(\infty ,n)$
-category
![]() $\mathscr {C}$
, the
$\mathscr {C}$
, the
![]() $(\infty ,n-1)$
-categories
$(\infty ,n-1)$
-categories
![]() $\mathscr {C}^{\mathrm {trl}}$
and
$\mathscr {C}^{\mathrm {trl}}$
and
![]() $\Omega \mathscr {C}$
admit canonical enhancements to symmetric monoidal
$\Omega \mathscr {C}$
admit canonical enhancements to symmetric monoidal
![]() $(n-1)$
-categories, and the trace functor
$(n-1)$
-categories, and the trace functor
![]() $ {\mathrm {tr}}\colon \mathscr {C}^{\mathrm {trl}} \to \Omega \mathscr {C}$
admits a canonical enhancement to a symmetric monoidal
$ {\mathrm {tr}}\colon \mathscr {C}^{\mathrm {trl}} \to \Omega \mathscr {C}$
admits a canonical enhancement to a symmetric monoidal
![]() $(n-1)$
-functor.
$(n-1)$
-functor.
3 Traces in the
 $(\infty ,2)$
-category of spans
$(\infty ,2)$
-category of spans
Consider an
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {D}$
which admits finite limits. In this section, we will compute dimensions and traces in a certain
$\mathscr {D}$
which admits finite limits. In this section, we will compute dimensions and traces in a certain
![]() $(\infty ,2)$
-categoryFootnote
7
$(\infty ,2)$
-categoryFootnote
7
![]() $ {\mathrm {Span}}(\mathscr {D})$
of spans (or correspondences) in
$ {\mathrm {Span}}(\mathscr {D})$
of spans (or correspondences) in
![]() $\mathscr {D}$
, to be recalled below. The objects of
$\mathscr {D}$
, to be recalled below. The objects of
![]() $ {\mathrm {Span}}(\mathscr {D})$
are given by the objects the objects of
$ {\mathrm {Span}}(\mathscr {D})$
are given by the objects the objects of
![]() $\mathscr {D}$
, and the
$\mathscr {D}$
, and the
![]() $\infty $
-category of morphisms from X to Y is equivalent to the
$\infty $
-category of morphisms from X to Y is equivalent to the
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {D}_{/(X \times Y)}$
of spans
$\mathscr {D}_{/(X \times Y)}$
of spans
![]() $X \leftarrow W \rightarrow Y$
. Composition is informally given by forming the pullback:
$X \leftarrow W \rightarrow Y$
. Composition is informally given by forming the pullback:
The
![]() $(\infty ,2)$
-category
$(\infty ,2)$
-category
![]() $ {\mathrm {Span}}(\mathscr {D})$
inherits a symmetric monoidal structure from the cartesian product on
$ {\mathrm {Span}}(\mathscr {D})$
inherits a symmetric monoidal structure from the cartesian product on
![]() $\mathscr {D}$
, and applying the constructions of Section 2.4 thus gives a trace functor
$\mathscr {D}$
, and applying the constructions of Section 2.4 thus gives a trace functor
The primary reason we are interested in traces in
![]() $ {\mathrm {Span}}(\mathscr {D})$
is the fact that, as a symmetric monoidal
$ {\mathrm {Span}}(\mathscr {D})$
is the fact that, as a symmetric monoidal
![]() $(\infty ,2)$
-category,
$(\infty ,2)$
-category,
![]() $ {\mathrm {Span}}(\mathscr {D})$
admits a universal property: it is the target of the universal symmetric monoidal bivariant theory
$ {\mathrm {Span}}(\mathscr {D})$
admits a universal property: it is the target of the universal symmetric monoidal bivariant theory
![]() $\mathscr {D}\to {\mathrm {Span}}(\mathscr {D})$
, in the sense of Definition 3.5. In particular, any other symmetric monoidal bivariant theory
$\mathscr {D}\to {\mathrm {Span}}(\mathscr {D})$
, in the sense of Definition 3.5. In particular, any other symmetric monoidal bivariant theory
![]() $F\colon \mathscr {D} \to \mathscr {E}$
factors uniquely through a symmetric monoidal 2-functor
$F\colon \mathscr {D} \to \mathscr {E}$
factors uniquely through a symmetric monoidal 2-functor
![]() $ {\mathrm {Span}}(\mathscr {D}) \to \mathscr {E}$
, which allows us to reduce computations of traces in
$ {\mathrm {Span}}(\mathscr {D}) \to \mathscr {E}$
, which allows us to reduce computations of traces in
![]() $\mathscr {E}$
to computations of traces in
$\mathscr {E}$
to computations of traces in
![]() $ {\mathrm {Span}}(\mathscr {D})$
.
$ {\mathrm {Span}}(\mathscr {D})$
.
A direct computation of traces in
![]() $ {\mathrm {Span}}(\mathscr {D})$
can be obtained from the description of composition in
$ {\mathrm {Span}}(\mathscr {D})$
can be obtained from the description of composition in
![]() $ {\mathrm {Span}}(\mathscr {D})$
given above. Observe first that every object in
$ {\mathrm {Span}}(\mathscr {D})$
given above. Observe first that every object in
![]() $ {\mathrm {Span}}(\mathscr {D})$
is dualizable: the evaluation and coevaluation maps for an object
$ {\mathrm {Span}}(\mathscr {D})$
is dualizable: the evaluation and coevaluation maps for an object
![]() $X \in \mathscr {D}$
are given by the spans
$X \in \mathscr {D}$
are given by the spans
where
![]() $\Delta $
denotes the diagonal of X. It follows that the dimension of X in
$\Delta $
denotes the diagonal of X. It follows that the dimension of X in
![]() $ {\mathrm {Span}}(\mathscr {D})$
is equivalent to the free loop space
$ {\mathrm {Span}}(\mathscr {D})$
is equivalent to the free loop space
![]() $LX$
, defined as the cotensoring
$LX$
, defined as the cotensoring
![]() $X^{S^1}$
of X by the circle
$X^{S^1}$
of X by the circle
![]() $S^1$
. Furthermore, if we consider an endomorphism of X in
$S^1$
. Furthermore, if we consider an endomorphism of X in
![]() $ {\mathrm {Span}}(\mathscr {D})$
given by a span
$ {\mathrm {Span}}(\mathscr {D})$
given by a span ![]() , then the trace of this endomorphism in
, then the trace of this endomorphism in
![]() $ {\mathrm {Span}}(\mathscr {D})$
is the equalizer
$ {\mathrm {Span}}(\mathscr {D})$
is the equalizer
![]() $ {\mathrm {Eq}}(f,g)$
of f and g in
$ {\mathrm {Eq}}(f,g)$
of f and g in
![]() $\mathscr {D}$
, see Definition 3.10 and Lemma 3.11.
$\mathscr {D}$
, see Definition 3.10 and Lemma 3.11.
The goal of this section is to give a careful account of (the functoriality of) these computations. In Section 3.1, we will recall the definition of the
![]() $(\infty ,2)$
-category
$(\infty ,2)$
-category
![]() $ {\mathrm {Span}}(\mathscr {D})$
, its universal property, and some of its features. In Section 3.2, we will show that the trace of the span
$ {\mathrm {Span}}(\mathscr {D})$
, its universal property, and some of its features. In Section 3.2, we will show that the trace of the span ![]() , viewed as an endomorphism in
, viewed as an endomorphism in
![]() $ {\mathrm {Span}}(\mathscr {D})$
, is the equalizer
$ {\mathrm {Span}}(\mathscr {D})$
, is the equalizer
![]() $ {\mathrm {Eq}}(f,g)$
of f and g, and in particular that there is an equivalence
$ {\mathrm {Eq}}(f,g)$
of f and g, and in particular that there is an equivalence
![]() $\dim _{ {\mathrm {Span}}(\mathscr {D})}(X) \simeq LX$
. Moreover, we will make the latter identification natural in
$\dim _{ {\mathrm {Span}}(\mathscr {D})}(X) \simeq LX$
. Moreover, we will make the latter identification natural in
![]() $X \in \mathscr {D}$
.
$X \in \mathscr {D}$
.
3.1 The
 $(\infty ,2)$
-category of spans
$(\infty ,2)$
-category of spans
We will start by introducing the
![]() $(\infty ,2)$
-category
$(\infty ,2)$
-category
![]() $ {\mathrm {Span}}(\mathscr {D})$
of spans associated with an
$ {\mathrm {Span}}(\mathscr {D})$
of spans associated with an
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {D}$
which admits finite limits. There are various ways to define
$\mathscr {D}$
which admits finite limits. There are various ways to define
![]() $ {\mathrm {Span}}(\mathscr {D})$
: explicitly as a 2-fold complete Segal space [Reference Haugseng32, Reference Gaitsgory and Rozenblyum29] generalizing Barwick’s
$ {\mathrm {Span}}(\mathscr {D})$
: explicitly as a 2-fold complete Segal space [Reference Haugseng32, Reference Gaitsgory and Rozenblyum29] generalizing Barwick’s
![]() $(\infty ,1)$
-categorical construction [Reference Barwick and Rognes5, Reference Barwick4], via bivariant fibrations [Reference Stefanich63], or via bivariant theories [Reference Macpherson53]. All these
$(\infty ,1)$
-categorical construction [Reference Barwick and Rognes5, Reference Barwick4], via bivariant fibrations [Reference Stefanich63], or via bivariant theories [Reference Macpherson53]. All these
![]() $(\infty ,2)$
-categories are equivalent because they satisfy a universal property: they come equipped with a functor
$(\infty ,2)$
-categories are equivalent because they satisfy a universal property: they come equipped with a functor
![]() $\mathscr {D} \to {\mathrm {Span}}(\mathscr {D})$
which is universal among bivariant theories from
$\mathscr {D} \to {\mathrm {Span}}(\mathscr {D})$
which is universal among bivariant theories from
![]() $\mathscr {D}$
into some
$\mathscr {D}$
into some
![]() $(\infty ,2)$
-category
$(\infty ,2)$
-category
![]() $\mathscr {E}$
, cf. Definition 3.2. For the purposes of this article, it is convenient to simply define
$\mathscr {E}$
, cf. Definition 3.2. For the purposes of this article, it is convenient to simply define
![]() $ {\mathrm {Span}}(\mathscr {D})$
via its universal property.
$ {\mathrm {Span}}(\mathscr {D})$
via its universal property.
Definition 3.1. An
![]() $\infty $
-category is called left exact if it has finite limits, and a functor is called left exact if it preserves finite limits. We let
$\infty $
-category is called left exact if it has finite limits, and a functor is called left exact if it preserves finite limits. We let
![]() $\mathrm {Cat}^{\mathrm {lex}}_{\infty }$
denote the
$\mathrm {Cat}^{\mathrm {lex}}_{\infty }$
denote the
![]() $\infty $
-category of (small) left exact
$\infty $
-category of (small) left exact
![]() $\infty $
-categories and left exact functors.
$\infty $
-categories and left exact functors.
Recall that a commutative square
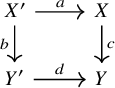
in an
![]() $(\infty ,2)$
-category
$(\infty ,2)$
-category
![]() $\mathscr {E}$
is called vertically right adjointable if the morphisms b and c admit right adjoints
$\mathscr {E}$
is called vertically right adjointable if the morphisms b and c admit right adjoints
![]() $b^r$
and
$b^r$
and
![]() $c^r$
in
$c^r$
in
![]() $\mathscr {E}$
, and the Beck-Chevalley map
$\mathscr {E}$
, and the Beck-Chevalley map
is an equivalence in
![]() $\mathscr {E}$
.
$\mathscr {E}$
.
Definition 3.2 [Reference Macpherson53, Section 3.2].
Let
![]() $\mathscr {D}$
be a left exact
$\mathscr {D}$
be a left exact
![]() $\infty $
-category and let
$\infty $
-category and let
![]() $\mathscr {E}$
be an
$\mathscr {E}$
be an
![]() $(\infty ,2)$
-category. A functor
$(\infty ,2)$
-category. A functor
![]() $F\colon \mathscr {D} \to \mathscr {E}$
is called a bivariant theory if the following two conditions are satisfied:
$F\colon \mathscr {D} \to \mathscr {E}$
is called a bivariant theory if the following two conditions are satisfied:
-
(1) For every morphism
 $f\colon A \to B$
in
$f\colon A \to B$
in
 $\mathscr {D}$
, the morphism
$\mathscr {D}$
, the morphism
 $F(f)\colon F(A) \to F(B)$
admits a right adjoint
$F(f)\colon F(A) \to F(B)$
admits a right adjoint
 $F(f)^r$
in
$F(f)^r$
in
 $\mathscr {E}$
;
$\mathscr {E}$
; -
(2) For every pullback square
in
 $\mathscr {D}$
, the induced square in
$\mathscr {D}$
, the induced square in
 $\mathscr {E}$
is vertically right adjointable.
$\mathscr {E}$
is vertically right adjointable.
Given another bivariant theory
![]() $F'\colon \mathscr {C} \to \mathscr {E}$
, a transformation
$F'\colon \mathscr {C} \to \mathscr {E}$
, a transformation
![]() $\alpha \colon F \Rightarrow F'$
is called bivariant if it commutes with the right adjoints of
$\alpha \colon F \Rightarrow F'$
is called bivariant if it commutes with the right adjoints of
![]() $F(f)$
: for every morphism
$F(f)$
: for every morphism
![]() $f\colon A \to B$
in
$f\colon A \to B$
in
![]() $\mathscr {D}$
, the resulting naturality square
$\mathscr {D}$
, the resulting naturality square
is vertically right adjointable.
We let
![]() $ {\mathrm {Biv}}(\mathscr {D}, \mathscr {E}) \subseteq {\mathrm {Fun}}(\mathscr {D},\mathscr {E})$
denote the
$ {\mathrm {Biv}}(\mathscr {D}, \mathscr {E}) \subseteq {\mathrm {Fun}}(\mathscr {D},\mathscr {E})$
denote the
![]() $(\infty ,2)$
-category of bivariant theories
$(\infty ,2)$
-category of bivariant theories
![]() $F\colon \mathscr {D} \to \mathscr {E}$
, bivariant transformations and arbitrary 3-transformations.
$F\colon \mathscr {D} \to \mathscr {E}$
, bivariant transformations and arbitrary 3-transformations.
We may now introduce
![]() $ {\mathrm {Span}}(\mathscr {D})$
as the
$ {\mathrm {Span}}(\mathscr {D})$
as the
![]() $(\infty ,2)$
-category equipped with the universal bivariant theory
$(\infty ,2)$
-category equipped with the universal bivariant theory
![]() $h_{\mathscr {D}}\colon \mathscr {D} \to {\mathrm {Span}}(\mathscr {D})$
.
$h_{\mathscr {D}}\colon \mathscr {D} \to {\mathrm {Span}}(\mathscr {D})$
.
Proposition 3.3 [Reference Macpherson53, Theorem 4.2.6].
Let
![]() $\mathscr {D}$
be a left exact
$\mathscr {D}$
be a left exact
![]() $\infty $
-category. There exists an
$\infty $
-category. There exists an
![]() $(\infty ,2)$
-category
$(\infty ,2)$
-category
![]() $ {\mathrm {Span}}(\mathscr {D})$
equipped with a bivariant theory
$ {\mathrm {Span}}(\mathscr {D})$
equipped with a bivariant theory
![]() $h_{\mathscr {D}}\colon \mathscr {D} \to {\mathrm {Span}}(\mathscr {D})$
satisfying the following property: for any other
$h_{\mathscr {D}}\colon \mathscr {D} \to {\mathrm {Span}}(\mathscr {D})$
satisfying the following property: for any other
![]() $(\infty ,2)$
-category
$(\infty ,2)$
-category
![]() $\mathscr {E}$
, composition with
$\mathscr {E}$
, composition with
![]() $h_{\mathscr {D}}$
induces an equivalence of
$h_{\mathscr {D}}$
induces an equivalence of
![]() $(\infty ,2)$
-categories
$(\infty ,2)$
-categories
The construction
![]() $\mathscr {D} \mapsto {\mathrm {Span}}(\mathscr {D})$
and the maps
$\mathscr {D} \mapsto {\mathrm {Span}}(\mathscr {D})$
and the maps
![]() $h_{\mathscr {D}}\colon \mathscr {D} \to {\mathrm {Span}}(\mathscr {D})$
uniquely assemble into a functor
$h_{\mathscr {D}}\colon \mathscr {D} \to {\mathrm {Span}}(\mathscr {D})$
uniquely assemble into a functor
![]() $ {\mathrm {Span}}\colon \mathrm {Cat}^{\mathrm {lex}}_{\infty } \to \mathrm {Cat}_{(\infty ,2)}$
equipped with a natural transformation h from the forgetful functor
$ {\mathrm {Span}}\colon \mathrm {Cat}^{\mathrm {lex}}_{\infty } \to \mathrm {Cat}_{(\infty ,2)}$
equipped with a natural transformation h from the forgetful functor
![]() $\mathrm {Cat}^{\mathrm {lex}}_{\infty } \to \mathrm {Cat}_{\infty } \hookrightarrow \mathrm {Cat}_{(\infty ,2)}$
.
$\mathrm {Cat}^{\mathrm {lex}}_{\infty } \to \mathrm {Cat}_{\infty } \hookrightarrow \mathrm {Cat}_{(\infty ,2)}$
.
Remark 3.4. MacPherson used the notation
![]() $ {\mathrm {Corr}}(\mathscr {D})$
instead of
$ {\mathrm {Corr}}(\mathscr {D})$
instead of
![]() $ {\mathrm {Span}}(\mathscr {D})$
and referred to it as the
$ {\mathrm {Span}}(\mathscr {D})$
and referred to it as the
![]() $(\infty ,2)$
-category of correspondences in
$(\infty ,2)$
-category of correspondences in
![]() $\mathscr {D}$
.
$\mathscr {D}$
.
The above universal property of
![]() $ {\mathrm {Span}}(\mathscr {D})$
admits a symmetric monoidal variant:
$ {\mathrm {Span}}(\mathscr {D})$
admits a symmetric monoidal variant:
Definition 3.5. Let
![]() $\mathscr {D}$
be a left exact
$\mathscr {D}$
be a left exact
![]() $\infty $
-category, equipped with the cartesian monoidal structure, and let
$\infty $
-category, equipped with the cartesian monoidal structure, and let
![]() $\mathscr {E}^{\otimes }$
be a symmetric monoidal
$\mathscr {E}^{\otimes }$
be a symmetric monoidal
![]() $(\infty ,2)$
-category. A symmetric monoidal functor
$(\infty ,2)$
-category. A symmetric monoidal functor
![]() $F\colon \mathscr {D}^{\times } \to \mathscr {E}^{\otimes }$
is called a symmetric monoidal bivariant theory if its underlying functor
$F\colon \mathscr {D}^{\times } \to \mathscr {E}^{\otimes }$
is called a symmetric monoidal bivariant theory if its underlying functor
![]() $\mathscr {D} \to \mathscr {E}$
is a bivariant theory.
$\mathscr {D} \to \mathscr {E}$
is a bivariant theory.
We let
![]() $ {\mathrm {Biv}}^{\otimes }(\mathscr {D}, \mathscr {E}) \subseteq {\mathrm {Fun}}^{\otimes }(\mathscr {D},\mathscr {E})$
denote the
$ {\mathrm {Biv}}^{\otimes }(\mathscr {D}, \mathscr {E}) \subseteq {\mathrm {Fun}}^{\otimes }(\mathscr {D},\mathscr {E})$
denote the
![]() $(\infty ,2)$
-category of symmetric monoidal bivariant theories
$(\infty ,2)$
-category of symmetric monoidal bivariant theories
![]() $F\colon \mathscr {D} \to \mathscr {E}$
, symmetric monoidal bivariant transformations and arbitrary 3-transformations.
$F\colon \mathscr {D} \to \mathscr {E}$
, symmetric monoidal bivariant transformations and arbitrary 3-transformations.
Proposition 3.6 [Reference Macpherson53, 4.4.6 Theorem].
Let
![]() $\mathscr {D}$
be a left exact
$\mathscr {D}$
be a left exact
![]() $\infty $
-category. There is a unique enhancement of
$\infty $
-category. There is a unique enhancement of
![]() $ {\mathrm {Span}}(\mathscr {D})$
to a symmetric monoidal
$ {\mathrm {Span}}(\mathscr {D})$
to a symmetric monoidal
![]() $(\infty ,2)$
-category together with an enhancement of the bivariant theory
$(\infty ,2)$
-category together with an enhancement of the bivariant theory
![]() $h_{\mathscr {D}}\colon \mathscr {D} \to {\mathrm {Span}}(\mathscr {D})$
to a symmetric monoidal bivariant theory. It satisfies the following property: for any other symmetric monoidal
$h_{\mathscr {D}}\colon \mathscr {D} \to {\mathrm {Span}}(\mathscr {D})$
to a symmetric monoidal bivariant theory. It satisfies the following property: for any other symmetric monoidal
![]() $(\infty ,2)$
-category
$(\infty ,2)$
-category
![]() $\mathscr {E}$
, composition with
$\mathscr {E}$
, composition with
![]() $h_{\mathscr {D}}$
induces an equivalence of
$h_{\mathscr {D}}$
induces an equivalence of
![]() $(\infty ,2)$
-categories
$(\infty ,2)$
-categories
The construction
![]() $\mathscr {D} \mapsto {\mathrm {Span}}(\mathscr {D})$
and the maps
$\mathscr {D} \mapsto {\mathrm {Span}}(\mathscr {D})$
and the maps
![]() $h_{\mathscr {D}}\colon \mathscr {D} \to {\mathrm {Span}}(\mathscr {D})$
uniquely assemble into a functor
$h_{\mathscr {D}}\colon \mathscr {D} \to {\mathrm {Span}}(\mathscr {D})$
uniquely assemble into a functor
![]() $ {\mathrm {Span}}\colon \mathrm {Cat}^{\mathrm {lex}}_{\infty } \to {\mathrm {CAlg}}(\mathrm {Cat}_{(\infty ,2)})$
equipped with a natural transformation h from the forgetful functor
$ {\mathrm {Span}}\colon \mathrm {Cat}^{\mathrm {lex}}_{\infty } \to {\mathrm {CAlg}}(\mathrm {Cat}_{(\infty ,2)})$
equipped with a natural transformation h from the forgetful functor
![]() $\mathrm {Cat}^{\mathrm {lex}}_{\infty } \to {\mathrm {CAlg}}(\mathrm {Cat}_{\infty }) \hookrightarrow {\mathrm {CAlg}}(\mathrm {Cat}_{(\infty ,2)})$
.
$\mathrm {Cat}^{\mathrm {lex}}_{\infty } \to {\mathrm {CAlg}}(\mathrm {Cat}_{\infty }) \hookrightarrow {\mathrm {CAlg}}(\mathrm {Cat}_{(\infty ,2)})$
.
In [Reference Stefanich63, Section 3.1], Stefanich introduces for every left exact
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {D}$
an explicit 2-fold complete Segal space
$\mathscr {D}$
an explicit 2-fold complete Segal space
![]() $2 {\mathrm {Corr}}(\mathscr {D})$
equipped with a functor
$2 {\mathrm {Corr}}(\mathscr {D})$
equipped with a functor
![]() $\mathscr {D} \to 2 {\mathrm {Corr}}(\mathscr {D})$
satisfying the universal property of
$\mathscr {D} \to 2 {\mathrm {Corr}}(\mathscr {D})$
satisfying the universal property of
![]() $h_{\mathscr {D}}\colon \mathscr {D} \to {\mathrm {Span}}(\mathscr {D})$
, cf. [Reference Stefanich63, Theorem 3.4.18]. In [Reference Stefanich63, Remark 3.1.10], the mapping spaces in
$h_{\mathscr {D}}\colon \mathscr {D} \to {\mathrm {Span}}(\mathscr {D})$
, cf. [Reference Stefanich63, Theorem 3.4.18]. In [Reference Stefanich63, Remark 3.1.10], the mapping spaces in
![]() $2 {\mathrm {Corr}}(\mathscr {D})$
are computed to be
$2 {\mathrm {Corr}}(\mathscr {D})$
are computed to be
for
![]() $d,d'\in \mathscr {D}$
. One observes from his computation (cf. [Reference Stefanich63, Notation 3.1.4, Notation 3.1.9, Remark 3.1.8]) that this identification is natural in the triple
$d,d'\in \mathscr {D}$
. One observes from his computation (cf. [Reference Stefanich63, Notation 3.1.4, Notation 3.1.9, Remark 3.1.8]) that this identification is natural in the triple
![]() $(\mathscr {D},d,d')$
. In particular, letting both d and
$(\mathscr {D},d,d')$
. In particular, letting both d and
![]() $d'$
be the final object of
$d'$
be the final object of
![]() $\mathscr {D}$
, we obtain the following result:
$\mathscr {D}$
, we obtain the following result:
Proposition 3.7 [Reference Stefanich63].
Let
![]() $\mathscr {D}$
be a left exact
$\mathscr {D}$
be a left exact
![]() $\infty $
-category. Then there is a functorial equivalence
$\infty $
-category. Then there is a functorial equivalence
We finish this subsection by recalling from [Reference Haugseng32, Reference Stefanich63] that all objects in
![]() $ {\mathrm {Span}}(\mathscr {D})$
are dualizable and that every morphism f in
$ {\mathrm {Span}}(\mathscr {D})$
are dualizable and that every morphism f in
![]() $\mathscr {D}$
gives rise to an adjunction in
$\mathscr {D}$
gives rise to an adjunction in
![]() $ {\mathrm {Span}}(\mathscr {D})$
between the associated left- and right-pointing morphisms.
$ {\mathrm {Span}}(\mathscr {D})$
between the associated left- and right-pointing morphisms.
Lemma 3.8 [Reference Haugseng32, Theorem 1.4], [Reference Stefanich63, Proposition 3.3.3].
For a left exact
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {D}$
and an object
$\mathscr {D}$
and an object
![]() $X \in \mathscr {D}$
, the span
$X \in \mathscr {D}$
, the span
is part of a duality datum exhibiting X as self-dual in
![]() $ {\mathrm {Span}}(\mathscr {D})$
. The coevaluation is given by the span
$ {\mathrm {Span}}(\mathscr {D})$
. The coevaluation is given by the span ![]() . In particular, every object in
. In particular, every object in
![]() $ {\mathrm {Span}}(\mathscr {D})$
is dualizable.
$ {\mathrm {Span}}(\mathscr {D})$
is dualizable.
Lemma 3.9 [Reference Stefanich63, Proposition 3.3.1], see also [Reference Haugseng32, Lemma 12.3].
For a morphism
![]() $f\colon X \to Y$
in
$f\colon X \to Y$
in
![]() $\mathscr {D}$
, the morphisms of spans
$\mathscr {D}$
, the morphisms of spans
are the counit resp. unit of an adjunction in
![]() $ {\mathrm {Span}}(\mathscr {D})$
between the span
$ {\mathrm {Span}}(\mathscr {D})$
between the span ![]() and the span
and the span ![]() .
.
3.2 Traces and dimensions in the
 $(\infty ,2)$
-category of spans
$(\infty ,2)$
-category of spans
In this subsection, we recall the folklore fact that the trace of an endomorphism ![]() in
in
![]() $ {\mathrm {Span}}(\mathscr {D})$
is given by the equalizer
$ {\mathrm {Span}}(\mathscr {D})$
is given by the equalizer
![]() $ {\mathrm {Eq}}(f,g)$
of f and g. An instance of this appears for example in [Reference Ben-Zvi and Nadler14, Section 4]. For completeness, we provide a proof of this fact. Furthermore, we will show that there is a natural identification
$ {\mathrm {Eq}}(f,g)$
of f and g. An instance of this appears for example in [Reference Ben-Zvi and Nadler14, Section 4]. For completeness, we provide a proof of this fact. Furthermore, we will show that there is a natural identification
![]() $\dim _{ {\mathrm {Span}}(\mathscr {D})}(X) \simeq LX$
for
$\dim _{ {\mathrm {Span}}(\mathscr {D})}(X) \simeq LX$
for
![]() $X \in \mathscr {D}$
.
$X \in \mathscr {D}$
.
Definition 3.10. Let
![]() $f,g\colon Z \to X$
be two maps in
$f,g\colon Z \to X$
be two maps in
![]() $\mathscr {D}$
. The equalizer
$\mathscr {D}$
. The equalizer
![]() $ {\mathrm {Eq}}(f,g)$
of f and g is defined via the pullback square
$ {\mathrm {Eq}}(f,g)$
of f and g is defined via the pullback square
When
![]() $Z = X$
and
$Z = X$
and
![]() $f = g = \mathrm {id}_X$
is the identity on X, we write the equalizer as
$f = g = \mathrm {id}_X$
is the identity on X, we write the equalizer as
and call it the free loop space, or the free loop object of X. Observe that it is equivalent to the cotensor
![]() $X^{S^1}$
of X by
$X^{S^1}$
of X by
![]() $S^1$
.
$S^1$
.
The proof that traces in
![]() $ {\mathrm {Span}}(\mathscr {D})$
are given by equalizers is a straightforward computation.
$ {\mathrm {Span}}(\mathscr {D})$
are given by equalizers is a straightforward computation.
Lemma 3.11. Consider an endomorphism in
![]() $ {\mathrm {Span}}(\mathscr {D})$
given by a span
$ {\mathrm {Span}}(\mathscr {D})$
given by a span ![]() . Under the equivalence
. Under the equivalence
![]() $\mathscr {D} \simeq \Omega {\mathrm {Span}}(\mathscr {D})$
of Proposition 3.7, the trace of this endomorphism is equivalent to the equalizer
$\mathscr {D} \simeq \Omega {\mathrm {Span}}(\mathscr {D})$
of Proposition 3.7, the trace of this endomorphism is equivalent to the equalizer
![]() $ {\mathrm {Eq}}(f,g) \in \mathscr {D}$
. In particular, the dimension of X in
$ {\mathrm {Eq}}(f,g) \in \mathscr {D}$
. In particular, the dimension of X in
![]() $ {\mathrm {Span}}(\mathscr {D})$
is equivalent to its free loop space
$ {\mathrm {Span}}(\mathscr {D})$
is equivalent to its free loop space
![]() $LX \in \mathscr {D}$
.
$LX \in \mathscr {D}$
.
Proof. Spelling out the definition of trace and plugging in the explicit duality data from Lemma 3.8, the trace is given by the following composite of spans:
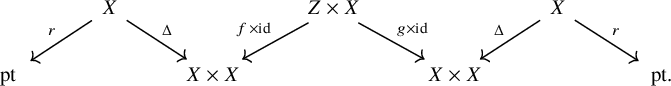
Observe that we have the following pullback diagram:
It follows that the above composite span is equivalent to the span ![]() , as desired.
, as desired.
The above computation of dimensions in
![]() $ {\mathrm {Span}}(\mathscr {D})$
gives rise to explicit descriptions of dimensions in
$ {\mathrm {Span}}(\mathscr {D})$
gives rise to explicit descriptions of dimensions in
![]() $(\infty ,2)$
-categories
$(\infty ,2)$
-categories
![]() $\mathscr {E}$
which receive a bivariant theory from
$\mathscr {E}$
which receive a bivariant theory from
![]() $\mathscr {D}$
:
$\mathscr {D}$
:
Corollary 3.12. Let
![]() $F\colon \mathscr {D} \to \mathscr {E}$
be a symmetric monoidal bivariant theory, with
$F\colon \mathscr {D} \to \mathscr {E}$
be a symmetric monoidal bivariant theory, with
![]() $\mathscr {D}$
and
$\mathscr {D}$
and
![]() $\mathscr {E}$
as in Definition 3.2.
$\mathscr {E}$
as in Definition 3.2.
-
(a) For every object
 $X \in \mathscr {D}$
, the composite exhibits the object
$X \in \mathscr {D}$
, the composite exhibits the object
 $F(X) \in \mathscr {E}$
as self-dual in
$F(X) \in \mathscr {E}$
as self-dual in
 $\mathscr {E}$
. In particular, objects in the image of F are dualizable.
$\mathscr {E}$
. In particular, objects in the image of F are dualizable.
-
(b) For every object
 $X \in \mathscr {D}$
, the dimension of
$X \in \mathscr {D}$
, the dimension of
 $F(X) \in \mathscr {E}$
is given by the composite
$F(X) \in \mathscr {E}$
is given by the composite 
Proof. By the universal property of the
![]() $(\infty ,2)$
-category
$(\infty ,2)$
-category
![]() $ {\mathrm {Span}}(\mathscr {D})$
, the functor F uniquely extends to a symmetric monoidal 2-functor
$ {\mathrm {Span}}(\mathscr {D})$
, the functor F uniquely extends to a symmetric monoidal 2-functor
![]() $F'\colon {\mathrm {Span}}(\mathscr {D}) \to \mathscr {E}$
. As
$F'\colon {\mathrm {Span}}(\mathscr {D}) \to \mathscr {E}$
. As
![]() $F'$
preserves duality data and adjunction data, statement a) thus follows from Lemma 3.8, while statement b) follows from Lemma 3.11.
$F'$
preserves duality data and adjunction data, statement a) thus follows from Lemma 3.8, while statement b) follows from Lemma 3.11.
3.2.1 Coherence
We have seen above that for an object X of a left exact
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {D}$
, the dimension of X in
$\mathscr {D}$
, the dimension of X in
![]() $ {\mathrm {Span}}(\mathscr {D})$
is given by its free loop space:
$ {\mathrm {Span}}(\mathscr {D})$
is given by its free loop space:
![]() $\dim _{ {\mathrm {Span}}(\mathscr {D})}(X) \simeq LX$
. The goal of the remainder of subsection is to make this calculation functorial in X, see Theorem 3.19 below. This is more subtle than it looks: to get at the functoriality of the trace functor, we need to produce all the higher duality data for the objects in
$\dim _{ {\mathrm {Span}}(\mathscr {D})}(X) \simeq LX$
. The goal of the remainder of subsection is to make this calculation functorial in X, see Theorem 3.19 below. This is more subtle than it looks: to get at the functoriality of the trace functor, we need to produce all the higher duality data for the objects in
![]() $ {\mathrm {Span}}(\mathscr {D})$
in a coherent fashion.
$ {\mathrm {Span}}(\mathscr {D})$
in a coherent fashion.
We will work around this problem by observing that the computation of dimensions in
![]() $ {\mathrm {Span}}(\mathscr {D})$
can be done uniformly in
$ {\mathrm {Span}}(\mathscr {D})$
can be done uniformly in
![]() $\mathscr {D} \in \mathrm {Cat}_{\infty }^{\mathrm {lex}}$
, allowing us to reduce to the ‘universal’ left exact
$\mathscr {D} \in \mathrm {Cat}_{\infty }^{\mathrm {lex}}$
, allowing us to reduce to the ‘universal’ left exact
![]() $\infty $
-category. More precisely, we will consider the left exact
$\infty $
-category. More precisely, we will consider the left exact
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {D} = (\mathcal {S}^{\mathrm {fin}})^{\mathrm {op}}$
, the opposite of the
$\mathscr {D} = (\mathcal {S}^{\mathrm {fin}})^{\mathrm {op}}$
, the opposite of the
![]() $\infty $
-category of finite spaces. By using the fact that
$\infty $
-category of finite spaces. By using the fact that
![]() $(\mathcal {S}^{\mathrm {fin}})^{\mathrm {op}}$
is freely generated under finite limits by the point
$(\mathcal {S}^{\mathrm {fin}})^{\mathrm {op}}$
is freely generated under finite limits by the point
![]() $\mathrm {pt} \in (\mathcal {S}^{\mathrm {fin}})^{\mathrm {op}}$
, it is possible to reduce the coherence problem to a non-coherent statement, which was solved in Lemma 3.11. In the remainder of this subsection, we will fill in the details of this proof strategy.
$\mathrm {pt} \in (\mathcal {S}^{\mathrm {fin}})^{\mathrm {op}}$
, it is possible to reduce the coherence problem to a non-coherent statement, which was solved in Lemma 3.11. In the remainder of this subsection, we will fill in the details of this proof strategy.
Lemma 3.13. The functor
![]() $h_{\mathscr {D}}\colon \mathscr {D} \to {\mathrm {Span}}(\mathscr {D})$
factors through the subcategory
$h_{\mathscr {D}}\colon \mathscr {D} \to {\mathrm {Span}}(\mathscr {D})$
factors through the subcategory
![]() $ {\mathrm {Span}}(\mathscr {D})^{\mathrm {dbl}}$
.
$ {\mathrm {Span}}(\mathscr {D})^{\mathrm {dbl}}$
.
Proof. Since
![]() $ {\mathrm {Span}}(\mathscr {D})^{\mathrm {dbl}} \hookrightarrow {\mathrm {Span}}(\mathscr {D})$
is a non-full subcategory by Corollary 2.21, it suffices to check this on the level of objects and morphisms. By Lemma 3.8,
$ {\mathrm {Span}}(\mathscr {D})^{\mathrm {dbl}} \hookrightarrow {\mathrm {Span}}(\mathscr {D})$
is a non-full subcategory by Corollary 2.21, it suffices to check this on the level of objects and morphisms. By Lemma 3.8,
![]() $h_{\mathscr {D}}$
carries every object in
$h_{\mathscr {D}}$
carries every object in
![]() $\mathscr {D}$
to a dualizable object of
$\mathscr {D}$
to a dualizable object of
![]() $ {\mathrm {Span}}(\mathscr {D})$
, and since
$ {\mathrm {Span}}(\mathscr {D})$
, and since
![]() $h_{\mathscr {D}}$
is a bivariant theory, it carries morphisms in
$h_{\mathscr {D}}$
is a bivariant theory, it carries morphisms in
![]() $\mathscr {D}$
to left adjoint morphisms in
$\mathscr {D}$
to left adjoint morphisms in
![]() $ {\mathrm {Span}}(\mathscr {D})$
. The statement thus follows from the description of objects and morphisms of
$ {\mathrm {Span}}(\mathscr {D})$
. The statement thus follows from the description of objects and morphisms of
![]() $ {\mathrm {Span}}(\mathscr {D})^{\mathrm {dbl}}$
given in Corollary 2.21.
$ {\mathrm {Span}}(\mathscr {D})^{\mathrm {dbl}}$
given in Corollary 2.21.
Remark 3.14. The functor
![]() $h_{\mathscr {D}}\colon \mathscr {D} \to {\mathrm {Span}}(\mathscr {D})^{\mathrm {dbl}}$
is in fact an equivalence of
$h_{\mathscr {D}}\colon \mathscr {D} \to {\mathrm {Span}}(\mathscr {D})^{\mathrm {dbl}}$
is in fact an equivalence of
![]() $\infty $
-categories. As we will not need this statement, we leave the proof to the reader.
$\infty $
-categories. As we will not need this statement, we leave the proof to the reader.
It is relatively straightforward to show that the equivalence
![]() $\dim _{ {\mathrm {Span}}(\mathscr {D})}(X) \simeq LX$
is natural with respect to equivalences in the
$\dim _{ {\mathrm {Span}}(\mathscr {D})}(X) \simeq LX$
is natural with respect to equivalences in the
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {D}$
.
$\mathscr {D}$
.
Lemma 3.15. For every left exact
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {D}$
, the following diagram naturally commutes:
$\mathscr {D}$
, the following diagram naturally commutes:
Proof. The four corners of the square are natural in
![]() $\mathscr {D} \in \mathrm {Cat}^{\mathrm {lex}}_{\infty }$
and the four edges form natural transformations. The assignment
$\mathscr {D} \in \mathrm {Cat}^{\mathrm {lex}}_{\infty }$
and the four edges form natural transformations. The assignment
![]() $\mathscr {D} \mapsto \mathscr {D}^{\simeq }$
is corepresented by the left exact
$\mathscr {D} \mapsto \mathscr {D}^{\simeq }$
is corepresented by the left exact
![]() $\infty $
-category
$\infty $
-category
![]() $(\mathcal {S}^{\mathrm {fin}})^{\mathrm {op}}$
. Indeed, the
$(\mathcal {S}^{\mathrm {fin}})^{\mathrm {op}}$
. Indeed, the
![]() $\infty $
-category
$\infty $
-category
![]() $\mathcal {S}^{\mathrm {fin}}$
is freely generated under finite colimits by the point, see (the proof of) [Reference Lurie49, Proposition 5.3.6.2]. It thus suffices, by the Yoneda lemma, to show that the two composites agree for
$\mathcal {S}^{\mathrm {fin}}$
is freely generated under finite colimits by the point, see (the proof of) [Reference Lurie49, Proposition 5.3.6.2]. It thus suffices, by the Yoneda lemma, to show that the two composites agree for
![]() $\mathscr {D} = (\mathcal {S}^{\mathrm {fin}})^{\mathrm {op}}$
when evaluated at the point
$\mathscr {D} = (\mathcal {S}^{\mathrm {fin}})^{\mathrm {op}}$
when evaluated at the point
![]() $\mathrm {pt} \in (\mathcal {S}^{\mathrm {fin}})^{\mathrm {op}}$
. This is an instance of Lemma 3.11.
$\mathrm {pt} \in (\mathcal {S}^{\mathrm {fin}})^{\mathrm {op}}$
. This is an instance of Lemma 3.11.
In order to enhance the above commutative diagram to a diagram defined on all of
![]() $\mathscr {D}$
rather than just its groupoid core
$\mathscr {D}$
rather than just its groupoid core
![]() $\mathscr {D}^{\simeq }$
, we will need some understanding of the interaction between span-categories and functor categories.
$\mathscr {D}^{\simeq }$
, we will need some understanding of the interaction between span-categories and functor categories.
Lemma 3.16. Let
![]() $\mathscr {E}$
and
$\mathscr {E}$
and
![]() $\mathscr {D}$
be
$\mathscr {D}$
be
![]() $\infty $
-categories such that
$\infty $
-categories such that
![]() $\mathscr {D}$
is left exact. The inclusion
$\mathscr {D}$
is left exact. The inclusion
![]() $ {\mathrm {Fun}}(\mathscr {E},\mathscr {D}) \hookrightarrow {\mathrm {Fun}}(\mathscr {E}, {\mathrm {Span}}(\mathscr {D})) \hookrightarrow {\mathrm {Fun}}_{\mathrm {lax}}(\mathscr {E}, {\mathrm {Span}}(\mathscr {D}))$
is a symmetric monoidal bivariant theory, i.e. it is symmetric monoidal, sends all morphisms to left adjoint morphisms and sends pullback squares to right adjointable squares.
$ {\mathrm {Fun}}(\mathscr {E},\mathscr {D}) \hookrightarrow {\mathrm {Fun}}(\mathscr {E}, {\mathrm {Span}}(\mathscr {D})) \hookrightarrow {\mathrm {Fun}}_{\mathrm {lax}}(\mathscr {E}, {\mathrm {Span}}(\mathscr {D}))$
is a symmetric monoidal bivariant theory, i.e. it is symmetric monoidal, sends all morphisms to left adjoint morphisms and sends pullback squares to right adjointable squares.
Proof. The inclusion
![]() $ {\mathrm {Fun}}(\mathscr {E},\mathscr {D}) \hookrightarrow {\mathrm {Fun}}_{\mathrm {lax}}(\mathscr {E}, {\mathrm {Span}}(\mathscr {D}))$
inherits a symmetric monoidal structure from applying the finite-product-preserving functor
$ {\mathrm {Fun}}(\mathscr {E},\mathscr {D}) \hookrightarrow {\mathrm {Fun}}_{\mathrm {lax}}(\mathscr {E}, {\mathrm {Span}}(\mathscr {D}))$
inherits a symmetric monoidal structure from applying the finite-product-preserving functor
![]() $ {\mathrm {Fun}}(\mathscr {E},-)$
to the symmetric monoidal functor
$ {\mathrm {Fun}}(\mathscr {E},-)$
to the symmetric monoidal functor
![]() $\mathscr {D} \to {\mathrm {Span}}(\mathscr {D})$
.
$\mathscr {D} \to {\mathrm {Span}}(\mathscr {D})$
.
Next, given a morphism
![]() $\alpha \colon F \to G$
in
$\alpha \colon F \to G$
in
![]() $ {\mathrm {Fun}}(\mathscr {E},\mathscr {D})$
, we have to show its image in
$ {\mathrm {Fun}}(\mathscr {E},\mathscr {D})$
, we have to show its image in
![]() $ {\mathrm {Fun}}_{\mathrm {lax}}(\mathscr {E}, {\mathrm {Span}}(\mathscr {D}))$
is a left adjoint. By [Reference Haugseng33, Theorem 4.6], it suffices to show that this image in
$ {\mathrm {Fun}}_{\mathrm {lax}}(\mathscr {E}, {\mathrm {Span}}(\mathscr {D}))$
is a left adjoint. By [Reference Haugseng33, Theorem 4.6], it suffices to show that this image in
![]() $ {\mathrm {Fun}}_{\mathrm {lax}}(\mathscr {E}, {\mathrm {Span}}(\mathscr {D}))$
comes from a morphism in the functor category
$ {\mathrm {Fun}}_{\mathrm {lax}}(\mathscr {E}, {\mathrm {Span}}(\mathscr {D}))$
comes from a morphism in the functor category
![]() $ {\mathrm {Fun}}(\mathscr {E}, {\mathrm {Span}}(\mathscr {D}))$
, and that for every
$ {\mathrm {Fun}}(\mathscr {E}, {\mathrm {Span}}(\mathscr {D}))$
, and that for every
![]() $e \in \mathscr {E}$
the map
$e \in \mathscr {E}$
the map
![]() $\alpha (e)\colon F(e) \to G(e)$
is a left adjoint morphism in
$\alpha (e)\colon F(e) \to G(e)$
is a left adjoint morphism in
![]() $ {\mathrm {Span}}(\mathscr {D})$
. But the former is automatic, and the latter follows from the fact that
$ {\mathrm {Span}}(\mathscr {D})$
. But the former is automatic, and the latter follows from the fact that
![]() $h_{\mathscr {D}}\colon \mathscr {D} \to {\mathrm {Span}}(\mathscr {D})$
sends morphisms to left adjoints.
$h_{\mathscr {D}}\colon \mathscr {D} \to {\mathrm {Span}}(\mathscr {D})$
sends morphisms to left adjoints.
Finally, given a pullback square
in
![]() $ {\mathrm {Fun}}(\mathscr {E},\mathscr {D})$
, we have to show that the resulting Beck-Chevalley map (see e.g. [Reference Carmeli, Schlank and Yanovski18, Section 2.2])
$ {\mathrm {Fun}}(\mathscr {E},\mathscr {D})$
, we have to show that the resulting Beck-Chevalley map (see e.g. [Reference Carmeli, Schlank and Yanovski18, Section 2.2])
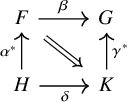
in
![]() $ {\mathrm {Fun}}_{\mathrm {lax}}(\mathscr {E}, {\mathrm {Span}}(\mathscr {D}))$
is an equivalence. For every
$ {\mathrm {Fun}}_{\mathrm {lax}}(\mathscr {E}, {\mathrm {Span}}(\mathscr {D}))$
is an equivalence. For every
![]() $e \in \mathscr {E}$
, evaluation of the pullback square at
$e \in \mathscr {E}$
, evaluation of the pullback square at
![]() $e \in \mathscr {E}$
gives a pullback square in
$e \in \mathscr {E}$
gives a pullback square in
![]() $\mathscr {D}$
. Hence, since
$\mathscr {D}$
. Hence, since
![]() $h_{\mathscr {D}}\colon \mathscr {D} \to {\mathrm {Span}}(\mathscr {D})$
is a bivariant theory, the above Beck-Chevalley map is an equivalence in
$h_{\mathscr {D}}\colon \mathscr {D} \to {\mathrm {Span}}(\mathscr {D})$
is a bivariant theory, the above Beck-Chevalley map is an equivalence in
![]() $ {\mathrm {Span}}(\mathscr {D})$
after evaluating at e:
$ {\mathrm {Span}}(\mathscr {D})$
after evaluating at e:
Since the 2-functors
![]() $\mathrm {ev}_e\colon {\mathrm {Fun}}_{\mathrm {lax}}(\mathscr {E}, {\mathrm {Span}}(\mathscr {D})) \to {\mathrm {Span}}(\mathscr {D})$
for
$\mathrm {ev}_e\colon {\mathrm {Fun}}_{\mathrm {lax}}(\mathscr {E}, {\mathrm {Span}}(\mathscr {D})) \to {\mathrm {Span}}(\mathscr {D})$
for
![]() $e \in \mathscr {E}$
are jointly conservative on morphism
$e \in \mathscr {E}$
are jointly conservative on morphism
![]() $\infty $
-categories, this gives the claim.
$\infty $
-categories, this gives the claim.
By the previous lemma, the symmetric monoidal inclusion
![]() $ {\mathrm {Fun}}(\mathscr {E},\mathscr {D}) \hookrightarrow {\mathrm {Fun}}_{\mathrm {lax}}(\mathscr {E}, {\mathrm {Span}}(\mathscr {D}))$
universally extends to a symmetric monoidal functor
$ {\mathrm {Fun}}(\mathscr {E},\mathscr {D}) \hookrightarrow {\mathrm {Fun}}_{\mathrm {lax}}(\mathscr {E}, {\mathrm {Span}}(\mathscr {D}))$
universally extends to a symmetric monoidal functor
The following lemma shows that this functor interacts well with the equivalence ![]() :
:
Lemma 3.17. For every
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {E}$
, there is a natural homotopy making the following diagram of
$\mathscr {E}$
, there is a natural homotopy making the following diagram of
![]() $\infty $
-groupoids commute:
$\infty $
-groupoids commute:

Proof. Under the identification
![]() $ {\mathrm {Fun}}(\mathscr {E},\mathscr {E}')^{\simeq } \simeq {\mathrm {Map}}_{\mathrm {Cat}_{\infty }}(\mathscr {E},\mathscr {E}')$
, the composite along the left and bottom of the diagram (3) constitutes a map from
$ {\mathrm {Fun}}(\mathscr {E},\mathscr {E}')^{\simeq } \simeq {\mathrm {Map}}_{\mathrm {Cat}_{\infty }}(\mathscr {E},\mathscr {E}')$
, the composite along the left and bottom of the diagram (3) constitutes a map from
![]() $ {\mathrm {Map}}_{\mathrm {Cat}_{\infty }}(\mathscr {E},\mathscr {D})$
to
$ {\mathrm {Map}}_{\mathrm {Cat}_{\infty }}(\mathscr {E},\mathscr {D})$
to
![]() $ {\mathrm {Map}}_{\mathrm {Cat}_{\infty }}(\mathscr {E},\Omega {\mathrm {Span}}(\mathscr {D}))$
which is natural in
$ {\mathrm {Map}}_{\mathrm {Cat}_{\infty }}(\mathscr {E},\Omega {\mathrm {Span}}(\mathscr {D}))$
which is natural in
![]() $\mathscr {E} \in \mathrm {Cat}_{\infty }$
. By the Yoneda lemma, it is thus induced by a functor
$\mathscr {E} \in \mathrm {Cat}_{\infty }$
. By the Yoneda lemma, it is thus induced by a functor
![]() $j_{\mathscr {D}}\colon \mathscr {D} \to \Omega {\mathrm {Span}}(\mathscr {D})$
. From the definition it is immediate that the functors
$j_{\mathscr {D}}\colon \mathscr {D} \to \Omega {\mathrm {Span}}(\mathscr {D})$
. From the definition it is immediate that the functors
![]() $i_{\mathscr {D}}$
and
$i_{\mathscr {D}}$
and
![]() $j_{\mathscr {D}}$
agree on groupoid cores and that the diagram (3) commutes if we replace
$j_{\mathscr {D}}$
agree on groupoid cores and that the diagram (3) commutes if we replace
![]() $i_{\mathscr {D}}$
by
$i_{\mathscr {D}}$
by
![]() $j_{\mathscr {D}}$
. It thus remains to show that the maps
$j_{\mathscr {D}}$
. It thus remains to show that the maps
![]() $i_{\mathscr {D}}$
and
$i_{\mathscr {D}}$
and
![]() $j_{\mathscr {D}}$
are equivalent as functors
$j_{\mathscr {D}}$
are equivalent as functors
![]() $\mathscr {D} \to \Omega {\mathrm {Span}}(\mathscr {D})$
.
$\mathscr {D} \to \Omega {\mathrm {Span}}(\mathscr {D})$
.
Note that the construction of
![]() $j_{\mathscr {D}}$
is natural in
$j_{\mathscr {D}}$
is natural in
![]() $\mathscr {D} \in \mathrm {Cat}^{\mathrm {lex}}_{\infty }$
. We may thus consider the composite
$\mathscr {D} \in \mathrm {Cat}^{\mathrm {lex}}_{\infty }$
. We may thus consider the composite
![]() $k_{\mathscr {D}}:= i^{-1}_{\mathscr {D}}j_{\mathscr {D}}\colon \mathscr {D} \to \mathscr {D}$
and regard it as an endomorphism
$k_{\mathscr {D}}:= i^{-1}_{\mathscr {D}}j_{\mathscr {D}}\colon \mathscr {D} \to \mathscr {D}$
and regard it as an endomorphism
![]() $k\colon U \to U$
of the forgetful functor
$k\colon U \to U$
of the forgetful functor
![]() $U\colon \mathrm {Cat}^{\mathrm {lex}}_{\infty } \to \mathrm {Cat}_{\infty }$
. We need to show that k is the identity of U. Since
$U\colon \mathrm {Cat}^{\mathrm {lex}}_{\infty } \to \mathrm {Cat}_{\infty }$
. We need to show that k is the identity of U. Since
![]() $i_{\mathscr {D}}$
and
$i_{\mathscr {D}}$
and
![]() $j_{\mathscr {D}}$
agree on groupoid cores, the induced map
$j_{\mathscr {D}}$
agree on groupoid cores, the induced map
![]() $k_{\mathscr {D}}\colon \mathscr {D}^{\simeq } \to \mathscr {D}^{\simeq }$
on groupoid cores is naturally equivalent to the identity. It thus remains to prove the following result, Lemma 3.18, which we record separately because of its independent interest.
$k_{\mathscr {D}}\colon \mathscr {D}^{\simeq } \to \mathscr {D}^{\simeq }$
on groupoid cores is naturally equivalent to the identity. It thus remains to prove the following result, Lemma 3.18, which we record separately because of its independent interest.
Lemma 3.18. Let
![]() $k\colon U \to U$
be an endomorphism of the forgetful functor
$k\colon U \to U$
be an endomorphism of the forgetful functor
![]() $U\colon \mathrm {Cat}^{\mathrm {lex}}_{\infty } \to \mathrm {Cat}_{\infty }$
. Assume that the induced endomorphism
$U\colon \mathrm {Cat}^{\mathrm {lex}}_{\infty } \to \mathrm {Cat}_{\infty }$
. Assume that the induced endomorphism
![]() $k^{\simeq }\colon U^{\simeq } \to U^{\simeq }$
of the functor
$k^{\simeq }\colon U^{\simeq } \to U^{\simeq }$
of the functor
![]() $U^{\simeq }\colon \mathrm {Cat}^{\mathrm {lex}}_{\infty } \to \mathcal {S}$
is equivalent to the identity of
$U^{\simeq }\colon \mathrm {Cat}^{\mathrm {lex}}_{\infty } \to \mathcal {S}$
is equivalent to the identity of
![]() $U^{\simeq }$
. Then k is equivalent to the identity of U.
$U^{\simeq }$
. Then k is equivalent to the identity of U.
Proof. The forgetful functor U admits a left adjoint
![]() $F\colon \mathrm {Cat}_{\infty } \to \mathrm {Cat}_{\infty }^{\mathrm {lex}}$
, sending an
$F\colon \mathrm {Cat}_{\infty } \to \mathrm {Cat}_{\infty }^{\mathrm {lex}}$
, sending an
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {E}$
to the subcategory of the presheaf category
$\mathscr {E}$
to the subcategory of the presheaf category
![]() $\mathrm {PSh}(\mathscr {E}^{\mathrm {op}})^{\mathrm {op}}$
generated under finite limits by the representable objects. In particular, the transformation
$\mathrm {PSh}(\mathscr {E}^{\mathrm {op}})^{\mathrm {op}}$
generated under finite limits by the representable objects. In particular, the transformation
![]() $k\colon U \to U$
corresponds to a transformation
$k\colon U \to U$
corresponds to a transformation
![]() $k'\colon \mathrm {id} \to U \circ F$
, and the problem translates to showing that
$k'\colon \mathrm {id} \to U \circ F$
, and the problem translates to showing that
![]() $k'$
is equivalent to the unit transformation
$k'$
is equivalent to the unit transformation
![]() $u\colon \mathrm {id} \to U \circ F$
.
$u\colon \mathrm {id} \to U \circ F$
.
First we will show that
![]() $k'$
factors through u via some transformation
$k'$
factors through u via some transformation
![]() $k"\colon \mathrm {id} \to \mathrm {id}$
. To see this, observe that for an
$k"\colon \mathrm {id} \to \mathrm {id}$
. To see this, observe that for an
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {E}$
the unit map
$\mathscr {E}$
the unit map
![]() $u_{\mathscr {E}}\colon \mathscr {E} \to U(F(\mathscr {E}))$
is fully faithful, both sides being full subcategories of
$u_{\mathscr {E}}\colon \mathscr {E} \to U(F(\mathscr {E}))$
is fully faithful, both sides being full subcategories of
![]() $\mathrm {PSh}(\mathscr {E}^{\mathrm {op}})^{\mathrm {op}}$
. It follows in particular that
$\mathrm {PSh}(\mathscr {E}^{\mathrm {op}})^{\mathrm {op}}$
. It follows in particular that
![]() $u\colon \mathrm {id} \to U \circ F$
is a monomorphism in
$u\colon \mathrm {id} \to U \circ F$
is a monomorphism in
![]() $ {\mathrm {Fun}}(\mathrm {Cat}_{\infty },\mathrm {Cat}_{\infty })$
, and thus it is a property for
$ {\mathrm {Fun}}(\mathrm {Cat}_{\infty },\mathrm {Cat}_{\infty })$
, and thus it is a property for
![]() $k'$
to factor through u. Moreover, as the property of factoring through a monomorphism in a functor category can be checked pointwise, it suffices to show that for each
$k'$
to factor through u. Moreover, as the property of factoring through a monomorphism in a functor category can be checked pointwise, it suffices to show that for each
![]() $\mathscr {E} \in \mathrm {Cat}_{\infty }$
the functor
$\mathscr {E} \in \mathrm {Cat}_{\infty }$
the functor
![]() $k^{\prime }_{\mathscr {E}}\colon \mathscr {E} \to U(F(\mathscr {E}))$
factors through
$k^{\prime }_{\mathscr {E}}\colon \mathscr {E} \to U(F(\mathscr {E}))$
factors through
![]() $u_{\mathscr {E}}\colon \mathscr {E} \to U(F(\mathscr {E}))$
via some map
$u_{\mathscr {E}}\colon \mathscr {E} \to U(F(\mathscr {E}))$
via some map
![]() $k^{\prime \prime }_{\mathscr {E}}\colon \mathscr {E} \to \mathscr {E}$
. By construction,
$k^{\prime \prime }_{\mathscr {E}}\colon \mathscr {E} \to \mathscr {E}$
. By construction,
![]() $k^{\prime }_{\mathscr {E}}\colon \mathscr {E} \to U(F(\mathscr {E}))$
is given by the composite
$k^{\prime }_{\mathscr {E}}\colon \mathscr {E} \to U(F(\mathscr {E}))$
is given by the composite
By assumption on k, the second map induces the identity on groupoid cores, proving that
![]() $k^{\prime }_{\mathscr {E}}$
factors through
$k^{\prime }_{\mathscr {E}}$
factors through
![]() $u_{\mathscr {E}}$
on objects. By fully faithfulness of
$u_{\mathscr {E}}$
on objects. By fully faithfulness of
![]() $u_{\mathscr {E}}\colon \mathscr {E} \to U(F(\mathscr {E}))$
this means
$u_{\mathscr {E}}\colon \mathscr {E} \to U(F(\mathscr {E}))$
this means
![]() $k^{\prime }_{\mathscr {E}}$
factors through
$k^{\prime }_{\mathscr {E}}$
factors through
![]() $u_{\mathscr {E}}$
as desired.
$u_{\mathscr {E}}$
as desired.
We are thus left with showing that the resulting endomorphism
![]() $k"\colon \mathrm {id}_{\mathrm {Cat}_{\infty }} \to \mathrm {id}_{\mathrm {Cat}_{\infty }}$
of the identity on
$k"\colon \mathrm {id}_{\mathrm {Cat}_{\infty }} \to \mathrm {id}_{\mathrm {Cat}_{\infty }}$
of the identity on
![]() $\mathrm {Cat}_{\infty }$
is equivalent to the identity. This is immediate: the space
$\mathrm {Cat}_{\infty }$
is equivalent to the identity. This is immediate: the space
![]() $ {\mathrm {End}}(\mathrm {id}_{\mathrm {Cat}_\infty })$
of endomorphisms of
$ {\mathrm {End}}(\mathrm {id}_{\mathrm {Cat}_\infty })$
of endomorphisms of
![]() $\mathrm {id}_{\mathrm {Cat}_{\infty }}$
is contractible. This follows from a theorem by Toën, which says that the full subcategory of
$\mathrm {id}_{\mathrm {Cat}_{\infty }}$
is contractible. This follows from a theorem by Toën, which says that the full subcategory of
![]() $ {\mathrm {Fun}}(\mathrm {Cat}_{\infty },\mathrm {Cat}_{\infty })$
spanned by the equivalences is equivalent to the discrete category
$ {\mathrm {Fun}}(\mathrm {Cat}_{\infty },\mathrm {Cat}_{\infty })$
spanned by the equivalences is equivalent to the discrete category
![]() $\{\mathrm {id}, (-)^{\mathrm {op}}\}$
, see [Reference Lurie50, Theorem 4.4.1].
$\{\mathrm {id}, (-)^{\mathrm {op}}\}$
, see [Reference Lurie50, Theorem 4.4.1].
We are now ready for the main theorem of this section.
Theorem 3.19. For every left exact
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {D}$
, the following diagram naturally commutes:
$\mathscr {D}$
, the following diagram naturally commutes:
Proof. By the Yoneda lemma, it suffices to prove that the diagram commutes after applying the functor
![]() $ {\mathrm {Map}}_{\mathrm {Cat}_{\infty }}(\mathscr {E},-) = {\mathrm {Fun}}(\mathscr {E},-)^{\simeq }$
for every
$ {\mathrm {Map}}_{\mathrm {Cat}_{\infty }}(\mathscr {E},-) = {\mathrm {Fun}}(\mathscr {E},-)^{\simeq }$
for every
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {E}$
, naturally in
$\mathscr {E}$
, naturally in
![]() $\mathscr {E}$
. Here we may use the following naturally commutative diagram:
$\mathscr {E}$
. Here we may use the following naturally commutative diagram:

The left square commutes by Lemma 3.15 applied to
![]() $ {\mathrm {Fun}}(\mathscr {E},\mathscr {D})$
. The top square commutes by definition of
$ {\mathrm {Fun}}(\mathscr {E},\mathscr {D})$
. The top square commutes by definition of
![]() $\Phi _{\mathscr {E},\mathscr {D}}$
. The right square commutes by definition of the higher categorical dimension functor (Definition 2.24). The bottom square commutes by Lemma 3.17. Finally, the middle square commutes by naturality of the dimension functor applied to the symmetric monoidal 2-functor
$\Phi _{\mathscr {E},\mathscr {D}}$
. The right square commutes by definition of the higher categorical dimension functor (Definition 2.24). The bottom square commutes by Lemma 3.17. Finally, the middle square commutes by naturality of the dimension functor applied to the symmetric monoidal 2-functor
![]() $\Phi _{\mathscr {E},\mathscr {D}}$
.
$\Phi _{\mathscr {E},\mathscr {D}}$
.
4 Traces of
 $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
 $\infty $
-categories
$\infty $
-categories
Let
![]() $\mathscr {C} \in {\mathrm {CAlg}}(\mathrm {Pr}^{\text {L}})$
be a presentably symmetric monoidal
$\mathscr {C} \in {\mathrm {CAlg}}(\mathrm {Pr}^{\text {L}})$
be a presentably symmetric monoidal
![]() $\infty $
-category, taken to be fixed. In this case, we can form the symmetric monoidal
$\infty $
-category, taken to be fixed. In this case, we can form the symmetric monoidal
![]() $(\infty ,2)$
-category
$(\infty ,2)$
-category
![]() $ {\mathrm {Mod}}_{\mathscr {C}} := {\mathrm {Mod}}_{\mathscr {C}}(\mathrm {Pr}^{\text {L}})$
of
$ {\mathrm {Mod}}_{\mathscr {C}} := {\mathrm {Mod}}_{\mathscr {C}}(\mathrm {Pr}^{\text {L}})$
of
![]() $\mathscr {C}$
-modules in
$\mathscr {C}$
-modules in
![]() $\mathrm {Pr}^{\text {L}}$
, with tensor product denoted by
$\mathrm {Pr}^{\text {L}}$
, with tensor product denoted by
![]() $\otimes _{\mathscr {C}}$
. We will refer to the objects of
$\otimes _{\mathscr {C}}$
. We will refer to the objects of
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
as
$ {\mathrm {Mod}}_{\mathscr {C}}$
as
![]() $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
![]() $\infty $
-categories, to its morphisms as
$\infty $
-categories, to its morphisms as
![]() $\mathscr {C}$
-linear functors and to its 2-morphisms as
$\mathscr {C}$
-linear functors and to its 2-morphisms as
![]() $\mathscr {C}$
-linear transformations. The mapping
$\mathscr {C}$
-linear transformations. The mapping
![]() $\infty $
-categories in
$\infty $
-categories in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
are
$ {\mathrm {Mod}}_{\mathscr {C}}$
are
![]() $ {\mathrm {Fun}}_{\mathscr {C}}(\mathscr {D},\mathscr {E})$
, the
$ {\mathrm {Fun}}_{\mathscr {C}}(\mathscr {D},\mathscr {E})$
, the
![]() $\infty $
-categories of
$\infty $
-categories of
![]() $\mathscr {C}$
-linear colimit preserving functors from
$\mathscr {C}$
-linear colimit preserving functors from
![]() $\mathscr {D}$
to
$\mathscr {D}$
to
![]() $\mathscr {E}$
; they come equipped with natural enhancements to
$\mathscr {E}$
; they come equipped with natural enhancements to
![]() $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
![]() $\infty $
-categories, making them into internal mapping objects in
$\infty $
-categories, making them into internal mapping objects in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
. We refer to [Reference Hoyois, Scherotzke and Sibilla37, Section 4.4] for a more precise discussion.
$ {\mathrm {Mod}}_{\mathscr {C}}$
. We refer to [Reference Hoyois, Scherotzke and Sibilla37, Section 4.4] for a more precise discussion.
The goal of this section is to study traces in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
, which provide a natural categorification of traces in
$ {\mathrm {Mod}}_{\mathscr {C}}$
, which provide a natural categorification of traces in
![]() $\mathscr {C}$
. As
$\mathscr {C}$
. As
![]() $\mathscr {C}$
is the monoidal unit of
$\mathscr {C}$
is the monoidal unit of
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
, the
$ {\mathrm {Mod}}_{\mathscr {C}}$
, the
![]() $\infty $
-category
$\infty $
-category
![]() $\Omega {\mathrm {Mod}}_{\mathscr {C}}$
of Definition 2.22 is given by the
$\Omega {\mathrm {Mod}}_{\mathscr {C}}$
of Definition 2.22 is given by the
![]() $\infty $
-category
$\infty $
-category
![]() $ {\mathrm {Fun}}_{\mathscr {C}}(\mathscr {C},\mathscr {C})$
of
$ {\mathrm {Fun}}_{\mathscr {C}}(\mathscr {C},\mathscr {C})$
of
![]() $\mathscr {C}$
-linear endofunctors of
$\mathscr {C}$
-linear endofunctors of
![]() $\mathscr {C}$
. Observe that evaluation at the monoidal unit
$\mathscr {C}$
. Observe that evaluation at the monoidal unit ![]() induces an equivalence
induces an equivalence ![]() , and thus postcomposing the trace functor of
, and thus postcomposing the trace functor of
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
with this identification yields a
$ {\mathrm {Mod}}_{\mathscr {C}}$
with this identification yields a
![]() $\mathscr {C}$
-valued trace functor. Since this functor will play an important role in the remainder of this paper, we give it its own notation and terminology.
$\mathscr {C}$
-valued trace functor. Since this functor will play an important role in the remainder of this paper, we give it its own notation and terminology.
Definition 4.1. The
![]() $\mathscr {C}$
-linear trace functor
$\mathscr {C}$
-linear trace functor
![]() $ {\mathrm {Tr}}_{\mathscr {C}}\colon {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}} \to \mathscr {C}$
is defined as the following composite:
$ {\mathrm {Tr}}_{\mathscr {C}}\colon {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}} \to \mathscr {C}$
is defined as the following composite:
For a dualizable
![]() $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {D}$
equipped with a
$\mathscr {D}$
equipped with a
![]() $\mathscr {C}$
-linear endofunctor
$\mathscr {C}$
-linear endofunctor
![]() $F\colon \mathscr {D} \to \mathscr {D}$
, we call the object
$F\colon \mathscr {D} \to \mathscr {D}$
, we call the object
![]() $ {\mathrm {Tr}}_{\mathscr {C}}(\mathscr {D},F) \in \mathscr {C}$
the
$ {\mathrm {Tr}}_{\mathscr {C}}(\mathscr {D},F) \in \mathscr {C}$
the
![]() $\mathscr {C}$
-linear trace of the pair
$\mathscr {C}$
-linear trace of the pair
![]() $(\mathscr {D},F)$
. When F is the identity endofunctor of
$(\mathscr {D},F)$
. When F is the identity endofunctor of
![]() $\mathscr {D}$
, we will denote this object by
$\mathscr {D}$
, we will denote this object by
![]() $ {\mathrm {Tr}}_{\mathscr {C}}(\mathscr {D})$
and call it the
$ {\mathrm {Tr}}_{\mathscr {C}}(\mathscr {D})$
and call it the
![]() $\mathscr {C}$
-linear trace of
$\mathscr {C}$
-linear trace of
![]() $\mathscr {D}$
.Footnote
8
$\mathscr {D}$
.Footnote
8
Example 4.2. Assume that
![]() $\mathscr {D} = \mathscr {C}$
, so that
$\mathscr {D} = \mathscr {C}$
, so that
![]() $F\colon \mathscr {C} \to \mathscr {C}$
is given by tensoring with an object
$F\colon \mathscr {C} \to \mathscr {C}$
is given by tensoring with an object
![]() $X \in \mathscr {C}$
. Then by Example 2.3 the
$X \in \mathscr {C}$
. Then by Example 2.3 the
![]() $\mathscr {C}$
-linear trace is simply given by X itself:
$\mathscr {C}$
-linear trace is simply given by X itself:
Example 4.3. For a space A, recall that the functor category
![]() $\mathscr {C}^A = {\mathrm {Fun}}(A,\mathscr {C})$
is dualizable in
$\mathscr {C}^A = {\mathrm {Fun}}(A,\mathscr {C})$
is dualizable in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
with dual given by
$ {\mathrm {Mod}}_{\mathscr {C}}$
with dual given by
![]() $\mathscr {C}^A$
itself; see Corollary 4.13 for details. An explicit computation shows that the
$\mathscr {C}^A$
itself; see Corollary 4.13 for details. An explicit computation shows that the
![]() $\mathscr {C}$
-linear trace of
$\mathscr {C}$
-linear trace of
![]() $\mathscr {C}^A$
is given as
$\mathscr {C}^A$
is given as
where
![]() $LA$
is the free loop space of A. This example will be treated in detail in Section 4.3 below.
$LA$
is the free loop space of A. This example will be treated in detail in Section 4.3 below.
Example 4.4. For an algebra object
![]() $R \in {\mathrm {Alg}}(\mathscr {C})$
, Lurie showed in [Reference Lurie51, Proposition 4.6.3.12] that the
$R \in {\mathrm {Alg}}(\mathscr {C})$
, Lurie showed in [Reference Lurie51, Proposition 4.6.3.12] that the
![]() $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
![]() $\infty $
-category
$\infty $
-category
![]() $ {\mathrm {RMod}}_R(\mathscr {C})$
of right-modules over R is dualizable in
$ {\mathrm {RMod}}_R(\mathscr {C})$
of right-modules over R is dualizable in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
, with dual given by the
$ {\mathrm {Mod}}_{\mathscr {C}}$
, with dual given by the
![]() $\infty $
-category
$\infty $
-category
![]() $ {\mathrm {LMod}}_R(\mathscr {C})$
of left-modules. It is a folklore fact, reviewed for completeness in Section 4.4, that the
$ {\mathrm {LMod}}_R(\mathscr {C})$
of left-modules. It is a folklore fact, reviewed for completeness in Section 4.4, that the
![]() $\mathscr {C}$
-linear trace of
$\mathscr {C}$
-linear trace of
![]() $ {\mathrm {RMod}}_R(\mathscr {C})$
is given by the
$ {\mathrm {RMod}}_R(\mathscr {C})$
is given by the
![]() $\mathscr {C}$
-linear (topological) Hochshild homology of R:
$\mathscr {C}$
-linear (topological) Hochshild homology of R:
More generally, for an R-bimodule M the
![]() $\mathscr {C}$
-linear trace of the functor
$\mathscr {C}$
-linear trace of the functor
![]() $- \otimes _R M\colon {\mathrm {RMod}}_R(\mathscr {C}) \to {\mathrm {RMod}}_R(\mathscr {C})$
is
$- \otimes _R M\colon {\mathrm {RMod}}_R(\mathscr {C}) \to {\mathrm {RMod}}_R(\mathscr {C})$
is
![]() $ {\mathrm {HH}}_{\mathscr {C}}(R;M) := R \otimes _{R\otimes R^{\mathrm {op}}} M$
.
$ {\mathrm {HH}}_{\mathscr {C}}(R;M) := R \otimes _{R\otimes R^{\mathrm {op}}} M$
.
Example 4.5. Let X be a locally compact Hausdorff space. Using proper base change, one can show that if
![]() $\mathscr {C}$
is stable, then the
$\mathscr {C}$
is stable, then the
![]() $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
![]() $\infty $
-category
$\infty $
-category
![]() $\mathrm {Shv}(X;\mathscr {C})$
of
$\mathrm {Shv}(X;\mathscr {C})$
of
![]() $\mathscr {C}$
-valued sheaves on X is dualizable in
$\mathscr {C}$
-valued sheaves on X is dualizable in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
with dual given by
$ {\mathrm {Mod}}_{\mathscr {C}}$
with dual given by
![]() $\mathrm {Shv}(X;\mathscr {C})$
itself. The evaluation and coevaluation maps can be written down explicitly in terms of proper pushforwards, and the resulting
$\mathrm {Shv}(X;\mathscr {C})$
itself. The evaluation and coevaluation maps can be written down explicitly in terms of proper pushforwards, and the resulting
![]() $\mathscr {C}$
-linear trace recovers the compactly supported cohomology of X with coefficients in
$\mathscr {C}$
-linear trace recovers the compactly supported cohomology of X with coefficients in
![]() $\mathscr {C}$
(see for example [Reference Kuo, Shende and Zhang45, Theorem 1.1]):
$\mathscr {C}$
(see for example [Reference Kuo, Shende and Zhang45, Theorem 1.1]):
Remark 4.6. By Corollary 2.27, the functor
![]() $ {\mathrm {Tr}}_{\mathscr {C}}$
admits a canonical refinement to a symmetric monoidal functor of
$ {\mathrm {Tr}}_{\mathscr {C}}$
admits a canonical refinement to a symmetric monoidal functor of
![]() $\infty $
-categories. In particular, given two
$\infty $
-categories. In particular, given two
![]() $\mathscr {C}$
-linear endofunctors
$\mathscr {C}$
-linear endofunctors
![]() $(\mathscr {D},F), (\mathscr {D}',F') \in {\mathrm {Mod}}^{\mathrm {trl}}_{\mathscr {C}}$
, there is a natural equivalence
$(\mathscr {D},F), (\mathscr {D}',F') \in {\mathrm {Mod}}^{\mathrm {trl}}_{\mathscr {C}}$
, there is a natural equivalence
Let us spell out the behavior of the
![]() $\mathscr {C}$
-linear trace functor on objects and morphisms. The
$\mathscr {C}$
-linear trace functor on objects and morphisms. The
![]() $\infty $
-category
$\infty $
-category
![]() $ {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}}$
is a (non-full)
$ {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}}$
is a (non-full)
![]() $(\infty ,1)$
-subcategory of the oplax functor category
$(\infty ,1)$
-subcategory of the oplax functor category
![]() $ {\mathrm {Fun}}_{\mathrm {oplax}}(B\mathbb {N}, {\mathrm {Mod}}_{\mathscr {C}})$
, see Corollary 2.21. Its objects are given by pairs
$ {\mathrm {Fun}}_{\mathrm {oplax}}(B\mathbb {N}, {\mathrm {Mod}}_{\mathscr {C}})$
, see Corollary 2.21. Its objects are given by pairs
![]() $(\mathscr {D},F)$
, where
$(\mathscr {D},F)$
, where
![]() $\mathscr {D} \in {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {dbl}}$
is a dualizable
$\mathscr {D} \in {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {dbl}}$
is a dualizable
![]() $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
![]() $\infty $
-category and
$\infty $
-category and
![]() $F\colon \mathscr {D} \to \mathscr {D}$
is a
$F\colon \mathscr {D} \to \mathscr {D}$
is a
![]() $\mathscr {C}$
-linear endofunctor. Its morphisms
$\mathscr {C}$
-linear endofunctor. Its morphisms
![]() $(\mathscr {D},F) \to (\mathscr {E},G)$
are pairs
$(\mathscr {D},F) \to (\mathscr {E},G)$
are pairs
![]() $(H,\alpha )$
, where
$(H,\alpha )$
, where
![]() $H\colon \mathscr {D} \to \mathscr {E}$
is a left adjoint morphism in
$H\colon \mathscr {D} \to \mathscr {E}$
is a left adjoint morphism in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
and where
$ {\mathrm {Mod}}_{\mathscr {C}}$
and where
![]() $\alpha \colon H \circ F \Rightarrow G \circ H$
is a
$\alpha \colon H \circ F \Rightarrow G \circ H$
is a
![]() $\mathscr {C}$
-linear transformation:
$\mathscr {C}$
-linear transformation:

For an object
![]() $(\mathscr {D},F)$
of
$(\mathscr {D},F)$
of
![]() $ {\mathrm {Mod}}^{\mathrm {trl}}_{\mathscr {C}}$
, its
$ {\mathrm {Mod}}^{\mathrm {trl}}_{\mathscr {C}}$
, its
![]() $\mathscr {C}$
-linear trace
$\mathscr {C}$
-linear trace
![]() $ {\mathrm {Tr}}_{\mathscr {C}}(\mathscr {D},F) \in \mathscr {C}$
is the image of the monoidal unit
$ {\mathrm {Tr}}_{\mathscr {C}}(\mathscr {D},F) \in \mathscr {C}$
is the image of the monoidal unit ![]() under the following composite:
under the following composite:
For a morphism
![]() $(H,\alpha )\colon (\mathscr {D},F) \to (\mathscr {E},G)$
in
$(H,\alpha )\colon (\mathscr {D},F) \to (\mathscr {E},G)$
in
![]() $ {\mathrm {Mod}}^{\mathrm {trl}}_{\mathscr {C}}$
, the map
$ {\mathrm {Mod}}^{\mathrm {trl}}_{\mathscr {C}}$
, the map
![]() $ {\mathrm {Tr}}_{\mathscr {C}}(H,\alpha )\colon {\mathrm {Tr}}_{\mathscr {C}}(\mathscr {D},F) \to {\mathrm {Tr}}_{\mathscr {C}}(\mathscr {E},G)$
is given by evaluating the following composite transformation at the monoidal unit
$ {\mathrm {Tr}}_{\mathscr {C}}(H,\alpha )\colon {\mathrm {Tr}}_{\mathscr {C}}(\mathscr {D},F) \to {\mathrm {Tr}}_{\mathscr {C}}(\mathscr {E},G)$
is given by evaluating the following composite transformation at the monoidal unit ![]() :
:
This section is organized as follows: in Section 4.1, we define and review basic properties of
![]() $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
![]() $\infty $
-categories freely and cofreely generated from spaces; in Section 4.2 we discuss maps of spaces f for which the pullback functor
$\infty $
-categories freely and cofreely generated from spaces; in Section 4.2 we discuss maps of spaces f for which the pullback functor
![]() $f^*$
admits a
$f^*$
admits a
![]() $\mathscr {C}$
-linear right adjoint, called
$\mathscr {C}$
-linear right adjoint, called
![]() $\mathscr {C}$
-adjointable maps; in Section 4.3 we compute the
$\mathscr {C}$
-adjointable maps; in Section 4.3 we compute the
![]() $\mathscr {C}$
-linear trace of
$\mathscr {C}$
-linear trace of
![]() $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
![]() $\infty $
-categories freely generated by spaces and the morphisms between them induced by maps of spaces, and in the case of
$\infty $
-categories freely generated by spaces and the morphisms between them induced by maps of spaces, and in the case of
![]() $\mathscr {C}$
-adjointable maps, we introduce a “wrong-way” morphism called the free loop transfer; in Section 4.4, we prove the folklore identification of Hochschild homology as a trace in the case of module categories; and finally in Section 4.5, we discuss the identification of
$\mathscr {C}$
-adjointable maps, we introduce a “wrong-way” morphism called the free loop transfer; in Section 4.4, we prove the folklore identification of Hochschild homology as a trace in the case of module categories; and finally in Section 4.5, we discuss the identification of
![]() $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
![]() $\infty $
-categories of local systems with module
$\infty $
-categories of local systems with module
![]() $\infty $
-categories over the correspnding loop spaces.
$\infty $
-categories over the correspnding loop spaces.
4.1 Free and cofree
 $ \mathscr {C}$
-linear
$ \mathscr {C}$
-linear
 $\infty $
-categories
$\infty $
-categories
There are two classes of
![]() $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
![]() $\infty $
-categories which will play an important role throughout this article: for every space A we have the free
$\infty $
-categories which will play an important role throughout this article: for every space A we have the free
![]() $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}[A]$
and the cofree
$\mathscr {C}[A]$
and the cofree
![]() $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}^A$
. The goal of this subsection is to recall the basic properties these
$\mathscr {C}^A$
. The goal of this subsection is to recall the basic properties these
![]() $\infty $
-categories have.
$\infty $
-categories have.
Definition 4.7. Let A be a space and let
![]() $\mathscr {D}$
be a
$\mathscr {D}$
be a
![]() $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
![]() $\infty $
-category. We define the
$\infty $
-category. We define the
![]() $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
![]() $\infty $
-categories
$\infty $
-categories
![]() $\mathscr {D}[A]$
and
$\mathscr {D}[A]$
and
![]() $\mathscr {D}^A$
by
$\mathscr {D}^A$
by
For a map
![]() $f\colon A \to B$
of spaces, we denote by
$f\colon A \to B$
of spaces, we denote by
the induced
![]() $\mathscr {C}$
-linear functors. Their right adjoints in
$\mathscr {C}$
-linear functors. Their right adjoints in
![]() $\widehat {\mathrm {Cat}}_{\infty }$
are denoted by
$\widehat {\mathrm {Cat}}_{\infty }$
are denoted by
We will show in Corollary 4.15 that there is an equivalence
![]() $\mathscr {D}[A] \simeq \mathscr {D}^A$
. Nevertheless, we choose to distinguish them in the notation to emphasize the different roles they play. Under this identification, the two functors called
$\mathscr {D}[A] \simeq \mathscr {D}^A$
. Nevertheless, we choose to distinguish them in the notation to emphasize the different roles they play. Under this identification, the two functors called
![]() $f^*$
get identified, justifying the notation.
$f^*$
get identified, justifying the notation.
Remark 4.8. Since the forgetful functors
![]() $ {\mathrm {Mod}}_{\mathscr {C}} \to \mathrm {Pr}^{\text {L}}$
and
$ {\mathrm {Mod}}_{\mathscr {C}} \to \mathrm {Pr}^{\text {L}}$
and
![]() $\mathrm {Pr}^{\text {L}} \to \mathrm {Cat}_{\infty }$
preserve limits, the underlying
$\mathrm {Pr}^{\text {L}} \to \mathrm {Cat}_{\infty }$
preserve limits, the underlying
![]() $\infty $
-category of
$\infty $
-category of
![]() $\mathscr {D}^A$
, and therefore also of
$\mathscr {D}^A$
, and therefore also of
![]() $\mathscr {D}[A]$
, is the functor category
$\mathscr {D}[A]$
, is the functor category
![]() $ {\mathrm {Fun}}(A,\mathscr {D})$
.
$ {\mathrm {Fun}}(A,\mathscr {D})$
.
The
![]() $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}[A]$
is called the free
$\mathscr {C}[A]$
is called the free
![]() $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
![]() $\infty $
-category on A, as the
$\infty $
-category on A, as the
![]() $\mathscr {C}$
-linear functors out of it into some
$\mathscr {C}$
-linear functors out of it into some
![]() $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {D}$
correspond to functors
$\mathscr {D}$
correspond to functors
![]() $A \to \mathscr {D}$
. In fact, we have the following stronger statement:
$A \to \mathscr {D}$
. In fact, we have the following stronger statement:
Lemma 4.9. Let
![]() $\mathscr {D}$
be a
$\mathscr {D}$
be a
![]() $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
![]() $\infty $
-category and let A be a space. There are natural equivalences of
$\infty $
-category and let A be a space. There are natural equivalences of
![]() $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
![]() $\infty $
-categories
$\infty $
-categories
Proof. As the functor
![]() $\mathscr {D}\otimes _{\mathscr {C}} -\colon {\mathrm {Mod}}_{\mathscr {C}} \to {\mathrm {Mod}}_{\mathscr {C}}$
preserves colimits, the first equivalence follows from the equivalence
$\mathscr {D}\otimes _{\mathscr {C}} -\colon {\mathrm {Mod}}_{\mathscr {C}} \to {\mathrm {Mod}}_{\mathscr {C}}$
preserves colimits, the first equivalence follows from the equivalence
![]() $\mathscr {D} \simeq \mathscr {D} \otimes _{\mathscr {C}} \mathscr {C}$
. Similarly, as the functor
$\mathscr {D} \simeq \mathscr {D} \otimes _{\mathscr {C}} \mathscr {C}$
. Similarly, as the functor
![]() $ {\mathrm {Fun}}_{\mathscr {C}}(-,\mathscr {D})\colon {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {op}} \to {\mathrm {Mod}}_{\mathscr {C}}$
turns colimits in
$ {\mathrm {Fun}}_{\mathscr {C}}(-,\mathscr {D})\colon {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {op}} \to {\mathrm {Mod}}_{\mathscr {C}}$
turns colimits in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
into limits, the second equivalence similarly follows from the fact that evaluation at
$ {\mathrm {Mod}}_{\mathscr {C}}$
into limits, the second equivalence similarly follows from the fact that evaluation at ![]() induces an equivalence
induces an equivalence ![]() .
.
Notation 4.10. We will frequently abuse notation and denote the
![]() $\mathscr {C}$
-linear functor associated with an object
$\mathscr {C}$
-linear functor associated with an object
![]() $X \in \mathscr {D}^A$
simply by
$X \in \mathscr {D}^A$
simply by
![]() $X\colon \mathscr {C}[A] \to \mathscr {D}$
, or sometimes by
$X\colon \mathscr {C}[A] \to \mathscr {D}$
, or sometimes by
![]() $X_{\mathscr {C}}\colon \mathscr {C}[A] \to \mathscr {D}$
when we need to distinguish it from X itself. For an object
$X_{\mathscr {C}}\colon \mathscr {C}[A] \to \mathscr {D}$
when we need to distinguish it from X itself. For an object
![]() $Y \in \mathscr {C}$
we will write
$Y \in \mathscr {C}$
we will write
![]() $Y\colon \mathscr {C} \to \mathscr {C}$
for the functor
$Y\colon \mathscr {C} \to \mathscr {C}$
for the functor
![]() $- \otimes Y\colon \mathscr {C} \to \mathscr {C}$
.
$- \otimes Y\colon \mathscr {C} \to \mathscr {C}$
.
The assignments
![]() $A \mapsto \mathscr {C}[A]$
and
$A \mapsto \mathscr {C}[A]$
and
![]() $A \mapsto \mathscr {D}^A$
satisfy various adjointability properties, making them bivariant theories in the sense of Definition 3.2.
$A \mapsto \mathscr {D}^A$
satisfy various adjointability properties, making them bivariant theories in the sense of Definition 3.2.
Proposition 4.11.
-
(1) The functor
 $\mathscr {C}[-]\colon \mathcal {S} \to {\mathrm {Mod}}_{\mathscr {C}}$
is a symmetric monoidal bivariant theory.
$\mathscr {C}[-]\colon \mathcal {S} \to {\mathrm {Mod}}_{\mathscr {C}}$
is a symmetric monoidal bivariant theory. -
(2) For every
 $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
 $\infty $
-category
$\infty $
-category
 $\mathscr {D}$
, the functors
$\mathscr {D}$
, the functors
 $\mathscr {D}[-]\colon \mathcal {S} \to {\mathrm {Mod}}_{\mathscr {C}}$
and
$\mathscr {D}[-]\colon \mathcal {S} \to {\mathrm {Mod}}_{\mathscr {C}}$
and
 $\mathscr {D}^{(-)}\colon \mathcal {S} \to {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {op}}$
are bivariant theories.
$\mathscr {D}^{(-)}\colon \mathcal {S} \to {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {op}}$
are bivariant theories. -
(3) For every
 $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
 $\infty $
-category
$\infty $
-category
 $\mathscr {D}$
, there are equivalences of bivariant theories
$\mathscr {D}$
, there are equivalences of bivariant theories  $$\begin{align*}\mathscr{D}\otimes_{\mathscr{C}}\mathscr{C}[-] \simeq \mathscr{D}[-] \qquad\qquad \text{ and } \qquad\qquad {\mathrm{Fun}}_{\mathscr{C}}(\mathscr{C}[-],\mathscr{D}) \simeq \mathscr{D}^{(-)}. \end{align*}$$
$$\begin{align*}\mathscr{D}\otimes_{\mathscr{C}}\mathscr{C}[-] \simeq \mathscr{D}[-] \qquad\qquad \text{ and } \qquad\qquad {\mathrm{Fun}}_{\mathscr{C}}(\mathscr{C}[-],\mathscr{D}) \simeq \mathscr{D}^{(-)}. \end{align*}$$
Proof. For part (1), notice that the functor
![]() $A \mapsto \mathscr {C}[A]$
factors through the symmetric monoidal 2-functor
$A \mapsto \mathscr {C}[A]$
factors through the symmetric monoidal 2-functor
![]() $\mathscr {C} \otimes _{\mathcal {S}} -\colon \mathrm {Pr}^{\text {L}} \to {\mathrm {Mod}}_{\mathscr {C}}$
. It thus suffices to show the claim when
$\mathscr {C} \otimes _{\mathcal {S}} -\colon \mathrm {Pr}^{\text {L}} \to {\mathrm {Mod}}_{\mathscr {C}}$
. It thus suffices to show the claim when
![]() $\mathscr {C} = \mathcal {S}$
. More concretely, this means we have to show that the functor
$\mathscr {C} = \mathcal {S}$
. More concretely, this means we have to show that the functor
![]() $\mathcal {S}[-]\colon \mathcal {S} \to \mathrm {Pr}^{\text {L}}$
is symmetric monoidal, sends maps of spaces to internal left adjoints in
$\mathcal {S}[-]\colon \mathcal {S} \to \mathrm {Pr}^{\text {L}}$
is symmetric monoidal, sends maps of spaces to internal left adjoints in
![]() $\mathrm {Pr}^{\text {L}}$
and sends pullback squares of spaces to right adjointable squares in
$\mathrm {Pr}^{\text {L}}$
and sends pullback squares of spaces to right adjointable squares in
![]() $\mathrm {Pr}^{\text {L}}$
. Symmetric monoidality of
$\mathrm {Pr}^{\text {L}}$
. Symmetric monoidality of
![]() $\mathcal {S}[-]\colon \mathcal {S} \to \mathrm {Pr}^{\text {L}}$
is automatic from the observation that it is the unique colimit-preserving symmetric monoidal functor
$\mathcal {S}[-]\colon \mathcal {S} \to \mathrm {Pr}^{\text {L}}$
is automatic from the observation that it is the unique colimit-preserving symmetric monoidal functor
![]() $\mathcal {S} \to \mathrm {Pr}^{\text {L}}$
. For the other two conditions, we use that for every space A there is an equivalence between
$\mathcal {S} \to \mathrm {Pr}^{\text {L}}$
. For the other two conditions, we use that for every space A there is an equivalence between
![]() $\mathcal {S}[A]$
and the
$\mathcal {S}[A]$
and the
![]() $\infty $
-category
$\infty $
-category
![]() $\mathrm {PSh}(A) := {\mathrm {Fun}}(A^{\mathrm {op}},\mathcal {S})$
of presheaves on A, see [Reference Lurie49, Theorem 5.1.5.6]. For a morphism of spaces
$\mathrm {PSh}(A) := {\mathrm {Fun}}(A^{\mathrm {op}},\mathcal {S})$
of presheaves on A, see [Reference Lurie49, Theorem 5.1.5.6]. For a morphism of spaces
![]() $f\colon A \to B$
, the induced functor
$f\colon A \to B$
, the induced functor
![]() $f_!\colon \mathrm {PSh}(A) \to \mathrm {PSh}(B)$
is given by left Kan extension. Consequently, the right adjoint
$f_!\colon \mathrm {PSh}(A) \to \mathrm {PSh}(B)$
is given by left Kan extension. Consequently, the right adjoint
![]() $f^*\colon \mathrm {PSh}(B) \to \mathrm {PSh}(A)$
is given by precomposing with f, and hence preserves colimits. We deduce that
$f^*\colon \mathrm {PSh}(B) \to \mathrm {PSh}(A)$
is given by precomposing with f, and hence preserves colimits. We deduce that
![]() $f^*$
is an internal right adjoint of
$f^*$
is an internal right adjoint of
![]() $f_!$
in
$f_!$
in
![]() $\mathrm {Pr}^{\text {L}}$
. It remains to show that
$\mathrm {Pr}^{\text {L}}$
. It remains to show that
![]() $\mathcal {S}[-]$
sends pullback squares of spaces to adjointable squares in
$\mathcal {S}[-]$
sends pullback squares of spaces to adjointable squares in
![]() $\mathrm {Pr}^{\text {L}}$
, which is an instance of [Reference Hopkins and Lurie36, Proposition 4.3.3]. This finishes the proof of part (1).
$\mathrm {Pr}^{\text {L}}$
, which is an instance of [Reference Hopkins and Lurie36, Proposition 4.3.3]. This finishes the proof of part (1).
Parts (2) and (3) follow immediately from part (1). Indeed, observe that the post-composition of a bivariant theory
![]() $\mathscr {D} \to \mathscr {E}$
with a 2-functor
$\mathscr {D} \to \mathscr {E}$
with a 2-functor
![]() $\mathscr {E} \to \mathscr {E}'$
is again a bivariant theory. Since
$\mathscr {E} \to \mathscr {E}'$
is again a bivariant theory. Since
![]() $\mathscr {D}\otimes _{\mathscr {C}} -$
and
$\mathscr {D}\otimes _{\mathscr {C}} -$
and
![]() $ {\mathrm {Fun}}_{\mathscr {C}}(-,\mathscr {D})\colon {\mathrm {Mod}}_{\mathscr {C}} \to {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {op}}$
are 2-functors, it thus follows from part (1) that the functors
$ {\mathrm {Fun}}_{\mathscr {C}}(-,\mathscr {D})\colon {\mathrm {Mod}}_{\mathscr {C}} \to {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {op}}$
are 2-functors, it thus follows from part (1) that the functors
![]() $\mathscr {D}\otimes _{\mathscr {C}} \mathscr {C}[-]$
and
$\mathscr {D}\otimes _{\mathscr {C}} \mathscr {C}[-]$
and
![]() $ {\mathrm {Fun}}_{\mathscr {C}}(\mathscr {C}[-],\mathscr {D})$
are bivariant theories. By the natural equivalences
$ {\mathrm {Fun}}_{\mathscr {C}}(\mathscr {C}[-],\mathscr {D})$
are bivariant theories. By the natural equivalences
![]() $\mathscr {D}\otimes _{\mathscr {C}} \mathscr {C}[-]\simeq \mathscr {D}[-]$
and
$\mathscr {D}\otimes _{\mathscr {C}} \mathscr {C}[-]\simeq \mathscr {D}[-]$
and
![]() $ {\mathrm {Fun}}_{\mathscr {C}}(\mathscr {C}[-],\mathscr {D}) \simeq \mathscr {D}^{(-)}$
of Lemma 4.9, parts (2) and (3) follow.
$ {\mathrm {Fun}}_{\mathscr {C}}(\mathscr {C}[-],\mathscr {D}) \simeq \mathscr {D}^{(-)}$
of Lemma 4.9, parts (2) and (3) follow.
Let us spell out some consequences of Proposition 4.11 in a more concrete form. There is for every pair of spaces A and B an equivalence
For every map
![]() $f\colon A \to B$
of spaces, the
$f\colon A \to B$
of spaces, the
![]() $\mathscr {C}$
-linear functor
$\mathscr {C}$
-linear functor
![]() $f_!\colon \mathscr {C}[A] \to \mathscr {C}[B]$
admits a
$f_!\colon \mathscr {C}[A] \to \mathscr {C}[B]$
admits a
![]() $\mathscr {C}$
-linear right adjoint
$\mathscr {C}$
-linear right adjoint
![]() $f^*\colon \mathscr {C}[B] \to \mathscr {C}[A]$
, and similarly the
$f^*\colon \mathscr {C}[B] \to \mathscr {C}[A]$
, and similarly the
![]() $\mathscr {C}$
-linear functor
$\mathscr {C}$
-linear functor
![]() $f^*\colon \mathscr {D}^B \to \mathscr {D}^A$
admits a
$f^*\colon \mathscr {D}^B \to \mathscr {D}^A$
admits a
![]() $\mathscr {C}$
-linear left adjoint
$\mathscr {C}$
-linear left adjoint
![]() $f_!\colon \mathscr {D}^A \to \mathscr {D}^B$
. Furthermore, for every pullback square of spaces
$f_!\colon \mathscr {D}^A \to \mathscr {D}^B$
. Furthermore, for every pullback square of spaces
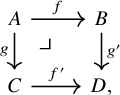
if we consider the two associated commutative squares in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
$ {\mathrm {Mod}}_{\mathscr {C}}$

then the left square is right adjointable in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
, while the right square is left adjointable.
$ {\mathrm {Mod}}_{\mathscr {C}}$
, while the right square is left adjointable.
Corollary 4.12. Let
![]() $\mathscr {D}$
be a
$\mathscr {D}$
be a
![]() $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
![]() $\infty $
-category. For every map
$\infty $
-category. For every map
![]() $f\colon A \to B$
of spaces, there are naturally commutative squares of
$f\colon A \to B$
of spaces, there are naturally commutative squares of
![]() $\mathscr {C}$
-linear functors
$\mathscr {C}$
-linear functors
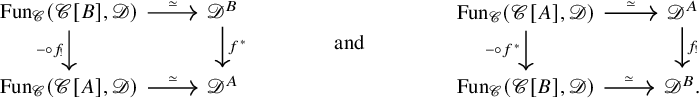
Proof. The left square is an instance of Lemma 4.9. The right square is obtained from the left square by passing to left adjoints.
As a corollary of Proposition 4.11, we obtain that the free
![]() $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
![]() $\infty $
-categories
$\infty $
-categories
![]() $\mathscr {C}[A]$
are dualizable in
$\mathscr {C}[A]$
are dualizable in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
.
$ {\mathrm {Mod}}_{\mathscr {C}}$
.
Corollary 4.13. For every space A, the
![]() $\mathscr {C}$
-linear pairing
$\mathscr {C}$
-linear pairing
is non-degenerate. In particular the
![]() $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}[A]$
is self-dual in
$\mathscr {C}[A]$
is self-dual in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
.
$ {\mathrm {Mod}}_{\mathscr {C}}$
.
Proof. By part (1) of Proposition 4.11, this is an instance of Corollary 3.12. The coevaluation is given by ![]() .
.
Under the self-duality of the free
![]() $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
![]() $\infty $
-categories
$\infty $
-categories
![]() $\mathscr {C}[A]$
, the functors
$\mathscr {C}[A]$
, the functors
![]() $f_!$
and
$f_!$
and
![]() $f^*$
are dual to each other, in the sense of the following lemma:
$f^*$
are dual to each other, in the sense of the following lemma:
Lemma 4.14. Let
![]() $f\colon A \to B$
be a map of spaces. Then the following diagrams commute:
$f\colon A \to B$
be a map of spaces. Then the following diagrams commute:
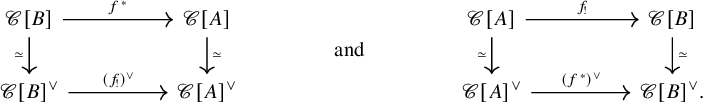
Proof. We will prove the commutativity of the left diagram. The proof for the right diagram is analogous and is left to the reader. Expanding the definition of
![]() $(f_!)^{\vee }$
by plugging in the explicit evaluation and coevaluation maps from Corollary 4.13, we see it is given by the composite
$(f_!)^{\vee }$
by plugging in the explicit evaluation and coevaluation maps from Corollary 4.13, we see it is given by the composite
Observe that the maps
![]() $\mathrm {id} \times (f,\mathrm {id})$
and
$\mathrm {id} \times (f,\mathrm {id})$
and
![]() $\Delta \times \mathrm {id}$
fit into a pullback square
$\Delta \times \mathrm {id}$
fit into a pullback square
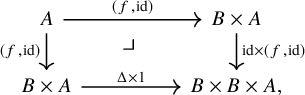
and thus it follows from part (1) of Proposition 4.11 that the above composite is homotopic to
But this composite is the functor
![]() $f^*\colon \mathscr {C}[B] \to \mathscr {C}[A]$
, as desired.
$f^*\colon \mathscr {C}[B] \to \mathscr {C}[A]$
, as desired.
We deduce from the previous lemma that the free and cofree
![]() $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
![]() $\infty $
-categories
$\infty $
-categories
![]() $\mathscr {C}[A]$
and
$\mathscr {C}[A]$
and
![]() $\mathscr {C}^A$
are equivalent, and that under this equivalence the functor
$\mathscr {C}^A$
are equivalent, and that under this equivalence the functor
![]() $f^*\colon \mathscr {C}[B] \to \mathscr {C}[A]$
agrees with
$f^*\colon \mathscr {C}[B] \to \mathscr {C}[A]$
agrees with
![]() $f^*\colon \mathscr {C}^B \to \mathscr {C}^A$
and
$f^*\colon \mathscr {C}^B \to \mathscr {C}^A$
and
![]() $f_!\colon \mathscr {C}[A] \to \mathscr {C}[B]$
agrees with
$f_!\colon \mathscr {C}[A] \to \mathscr {C}[B]$
agrees with
![]() $f_!\colon \mathscr {C}^A \to \mathscr {C}^B$
.
$f_!\colon \mathscr {C}^A \to \mathscr {C}^B$
.
Corollary 4.15. For every space A and every
![]() $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {D}$
, there is an equivalence
$\mathscr {D}$
, there is an equivalence
of
![]() $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
![]() $\infty $
-categories, natural in
$\infty $
-categories, natural in
![]() $A \in \mathcal {S}^{\simeq }$
. Furthermore, for every map
$A \in \mathcal {S}^{\simeq }$
. Furthermore, for every map
![]() $f\colon A \to B$
of spaces, the following diagrams commute:
$f\colon A \to B$
of spaces, the following diagrams commute:
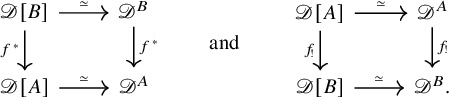
Proof. We will start by proving the equivalence
![]() $\mathscr {D}[A] \simeq \mathscr {D}^A$
. By self-duality of
$\mathscr {D}[A] \simeq \mathscr {D}^A$
. By self-duality of
![]() $\mathscr {C}[A]$
, the evaluation map
$\mathscr {C}[A]$
, the evaluation map
![]() $\mathscr {C}[A] \otimes _{\mathscr {C}} \mathscr {C}[A] \otimes _{\mathscr {C}} \mathscr {D} \to \mathscr {D}$
adjoints over to an equivalence
$\mathscr {C}[A] \otimes _{\mathscr {C}} \mathscr {C}[A] \otimes _{\mathscr {C}} \mathscr {D} \to \mathscr {D}$
adjoints over to an equivalence ![]() , which is natural in
, which is natural in
![]() $A \in \mathcal {S}^{\simeq }$
. By Lemma 4.9, the left-hand side of this equivalence is equivalent to
$A \in \mathcal {S}^{\simeq }$
. By Lemma 4.9, the left-hand side of this equivalence is equivalent to
![]() $\mathscr {D}[A]$
and the right-hand side is equivalent to
$\mathscr {D}[A]$
and the right-hand side is equivalent to
![]() $\mathscr {D}^A$
. Together, this gives the desired equivalence
$\mathscr {D}^A$
. Together, this gives the desired equivalence
![]() $\mathscr {D}[A] \simeq \mathscr {D}^A$
, naturally in
$\mathscr {D}[A] \simeq \mathscr {D}^A$
, naturally in
![]() $A \in \mathcal {S}^{\simeq }$
.
$A \in \mathcal {S}^{\simeq }$
.
Now we show that the two diagrams commute. The right diagram is obtained from the left one by passing to left adjoints, so it suffices to prove that the left diagram commutes. This follows from the following commutative diagram:

The left and right squares commutes by functoriality in A of the equivalences
![]() $\mathscr {D}[A] \simeq \mathscr {D} \otimes _{\mathscr {C}} \mathscr {C}[A]$
and
$\mathscr {D}[A] \simeq \mathscr {D} \otimes _{\mathscr {C}} \mathscr {C}[A]$
and
![]() $ {\mathrm {Fun}}_{\mathscr {C}}(\mathscr {C}[A],\mathscr {D}) \simeq \mathscr {D}^A$
from Lemma 4.9. The middle square commutes by Lemma 4.14.
$ {\mathrm {Fun}}_{\mathscr {C}}(\mathscr {C}[A],\mathscr {D}) \simeq \mathscr {D}^A$
from Lemma 4.9. The middle square commutes by Lemma 4.14.
Remark 4.16. The assignment
![]() $A \mapsto \mathscr {D}[A]$
can be turned into a contravariant functor via the right adjoints
$A \mapsto \mathscr {D}[A]$
can be turned into a contravariant functor via the right adjoints
![]() $f^*\colon \mathscr {D}[B] \to \mathscr {D}[A]$
. With this functoriality, the assignments
$f^*\colon \mathscr {D}[B] \to \mathscr {D}[A]$
. With this functoriality, the assignments
![]() $A \mapsto \mathscr {D}[A]$
and
$A \mapsto \mathscr {D}[A]$
and
![]() $A \mapsto \mathscr {D}^A$
are equivalent as functors
$A \mapsto \mathscr {D}^A$
are equivalent as functors
![]() $\mathcal {S}^{\mathrm {op}} \to {\mathrm {Mod}}_{\mathscr {C}}$
. Indeed, this follows from the observation that both send colimits of spaces to limits in
$\mathcal {S}^{\mathrm {op}} \to {\mathrm {Mod}}_{\mathscr {C}}$
. Indeed, this follows from the observation that both send colimits of spaces to limits in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
and agree on the point.
$ {\mathrm {Mod}}_{\mathscr {C}}$
and agree on the point.
Corollary 4.17. Let A be a space. Then the functors
![]() $a^*\colon \mathscr {C}[A] \to \mathscr {C}$
for
$a^*\colon \mathscr {C}[A] \to \mathscr {C}$
for
![]() $a \in A$
are jointly conservative.
$a \in A$
are jointly conservative.
Proof. Since this is true for the functors
![]() $a^*\colon \mathscr {C}^A \to \mathscr {C}$
, this follows directly from Corollary 4.15.
$a^*\colon \mathscr {C}^A \to \mathscr {C}$
, this follows directly from Corollary 4.15.
4.2 Adjointability in
 $ {\mathrm {Mod}}_{\mathscr {C}}$
$ {\mathrm {Mod}}_{\mathscr {C}}$
Since
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
is an
$ {\mathrm {Mod}}_{\mathscr {C}}$
is an
![]() $(\infty ,2)$
-category, there is a notion of a left adjoint morphism in
$(\infty ,2)$
-category, there is a notion of a left adjoint morphism in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
: a
$ {\mathrm {Mod}}_{\mathscr {C}}$
: a
![]() $\mathscr {C}$
-linear functor
$\mathscr {C}$
-linear functor
![]() $H\colon \mathscr {D} \to \mathscr {E}$
which admits a
$H\colon \mathscr {D} \to \mathscr {E}$
which admits a
![]() $\mathscr {C}$
-linear right adjoint
$\mathscr {C}$
-linear right adjoint
![]() $H^r\colon \mathscr {E} \to \mathscr {D}$
with
$H^r\colon \mathscr {E} \to \mathscr {D}$
with
![]() $\mathscr {C}$
-linear unit and counit. For emphasis, we will refer to the left adjoint morphisms in
$\mathscr {C}$
-linear unit and counit. For emphasis, we will refer to the left adjoint morphisms in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
as the internal left adjoints. By [Reference Lurie51, Remark 7.3.2.9], a
$ {\mathrm {Mod}}_{\mathscr {C}}$
as the internal left adjoints. By [Reference Lurie51, Remark 7.3.2.9], a
![]() $\mathscr {C}$
-linear functor
$\mathscr {C}$
-linear functor
![]() $H\colon \mathscr {D} \to \mathscr {E}$
is an internal left adjoint precisely when its right adjoint
$H\colon \mathscr {D} \to \mathscr {E}$
is an internal left adjoint precisely when its right adjoint
![]() $G\colon \mathscr {E} \to \mathscr {D}$
in
$G\colon \mathscr {E} \to \mathscr {D}$
in
![]() $\widehat {\mathrm {Cat}}_{\infty }$
preserves colimits and satisfies the right projection formula: the canonical map
$\widehat {\mathrm {Cat}}_{\infty }$
preserves colimits and satisfies the right projection formula: the canonical map
is an equivalence in
![]() $\mathscr {D}$
for all
$\mathscr {D}$
for all
![]() $X \in \mathscr {C}$
and
$X \in \mathscr {C}$
and
![]() $Y \in \mathscr {E}$
.
$Y \in \mathscr {E}$
.
In fact, it frequently happens that the projection formula comes for free:
Lemma 4.18. Let
![]() $H\colon \mathscr {D} \to \mathscr {E}$
be a
$H\colon \mathscr {D} \to \mathscr {E}$
be a
![]() $\mathscr {C}$
-linear functor whose right adjoint
$\mathscr {C}$
-linear functor whose right adjoint
![]() $G\colon \mathscr {E} \to \mathscr {D}$
in
$G\colon \mathscr {E} \to \mathscr {D}$
in
![]() $\widehat {\mathrm {Cat}}_{\infty }$
preserves colimits. Assume that one of the following two conditions hold:
$\widehat {\mathrm {Cat}}_{\infty }$
preserves colimits. Assume that one of the following two conditions hold:
-
(1) The presentable
 $\infty $
-category
$\infty $
-category
 $\mathscr {C}$
is an idempotent algebra in
$\mathscr {C}$
is an idempotent algebra in
 $\mathrm {Pr}^{\text {L}}$
;
$\mathrm {Pr}^{\text {L}}$
; -
(2) The dualizable objects in
 $\mathscr {C}$
generate
$\mathscr {C}$
generate
 $\mathscr {C}$
under colimits.
$\mathscr {C}$
under colimits.
Then H is an internal left adjoint in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
.
$ {\mathrm {Mod}}_{\mathscr {C}}$
.
Proof. In case (1),
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
is a full subcategory of
$ {\mathrm {Mod}}_{\mathscr {C}}$
is a full subcategory of
![]() $\mathrm {Pr}^{\text {L}}$
, so any right adjoint of H in
$\mathrm {Pr}^{\text {L}}$
, so any right adjoint of H in
![]() $\mathrm {Pr}^{\text {L}}$
is automatically a right adjoint of H in
$\mathrm {Pr}^{\text {L}}$
is automatically a right adjoint of H in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
. In case (2), we have to show that the map
$ {\mathrm {Mod}}_{\mathscr {C}}$
. In case (2), we have to show that the map
![]() $X \otimes G(Y) \to G(X \otimes Y)$
is an equivalence in
$X \otimes G(Y) \to G(X \otimes Y)$
is an equivalence in
![]() $\mathscr {D}$
for all
$\mathscr {D}$
for all
![]() $X \in \mathscr {C}$
and
$X \in \mathscr {C}$
and
![]() $Y \in \mathscr {E}$
. The assumption on G implies that both sides preserve colimits in X, and thus by the assumption on
$Y \in \mathscr {E}$
. The assumption on G implies that both sides preserve colimits in X, and thus by the assumption on
![]() $\mathscr {C}$
it will suffice to prove this whenever X is dualizable in
$\mathscr {C}$
it will suffice to prove this whenever X is dualizable in
![]() $\mathscr {C}$
. But in this case, if we let
$\mathscr {C}$
. But in this case, if we let
![]() $X^{\vee } \in \mathscr {C}$
denote a dual of X, we observe that the transformation
$X^{\vee } \in \mathscr {C}$
denote a dual of X, we observe that the transformation
![]() $X \otimes G(-) \to G(X \otimes -)$
is the total mate of the specified equivalence
$X \otimes G(-) \to G(X \otimes -)$
is the total mate of the specified equivalence ![]() , and thus is itself an equivalence.
, and thus is itself an equivalence.
Testing whether a
![]() $\mathscr {C}$
-linear functor out of a free
$\mathscr {C}$
-linear functor out of a free
![]() $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}[A]$
is an internal left adjoint can be done pointwise.
$\mathscr {C}[A]$
is an internal left adjoint can be done pointwise.
Lemma 4.19. A
![]() $\mathscr {C}$
-linear functor
$\mathscr {C}$
-linear functor
![]() $F\colon \mathscr {C}[A] \to \mathscr {D}$
is an internal left adjoint if and only if the composition
$F\colon \mathscr {C}[A] \to \mathscr {D}$
is an internal left adjoint if and only if the composition
![]() $F \circ a_!\colon \mathscr {C} \to \mathscr {D}$
is an internal left adjoint for every
$F \circ a_!\colon \mathscr {C} \to \mathscr {D}$
is an internal left adjoint for every
![]() $a\colon \mathrm {pt} \to A$
.
$a\colon \mathrm {pt} \to A$
.
Proof. Since internal left adjoints are closed under composition, one direction follows from the fact that the functors
![]() $a_!\colon \mathscr {C} \to \mathscr {C}[A]$
are internal left adjoints for every
$a_!\colon \mathscr {C} \to \mathscr {C}[A]$
are internal left adjoints for every
![]() $a \in A$
. For the other direction, assume that
$a \in A$
. For the other direction, assume that
![]() $F \circ a_!$
is an internal left adjoint for every
$F \circ a_!$
is an internal left adjoint for every
![]() $a \in A$
. We need to show that the right adjoint
$a \in A$
. We need to show that the right adjoint
![]() $G\colon \mathscr {D} \to \mathscr {C}[A]$
of F preserves colimits and satisfies the projection formula. For the projection formula, consider objects
$G\colon \mathscr {D} \to \mathscr {C}[A]$
of F preserves colimits and satisfies the projection formula. For the projection formula, consider objects
![]() $X \in \mathscr {C}$
and
$X \in \mathscr {C}$
and
![]() $Y \in \mathscr {D}$
. We need to show that the canonical map
$Y \in \mathscr {D}$
. We need to show that the canonical map
![]() $X \otimes G(Y) \to G(X \otimes Y)$
is an equivalence. As the functors
$X \otimes G(Y) \to G(X \otimes Y)$
is an equivalence. As the functors
![]() $a^*\colon \mathscr {C}[A] \to \mathscr {C}$
are jointly conservative by Corollary 4.17, this may be tested after applying
$a^*\colon \mathscr {C}[A] \to \mathscr {C}$
are jointly conservative by Corollary 4.17, this may be tested after applying
![]() $a^*$
for every a. But since
$a^*$
for every a. But since
![]() $a^*$
is
$a^*$
is
![]() $\mathscr {C}$
-linear, this map becomes the exchange map
$\mathscr {C}$
-linear, this map becomes the exchange map
![]() $X \otimes (a^* \circ G)(Y) \to (a^* \circ G)(X \otimes Y)$
for the composite
$X \otimes (a^* \circ G)(Y) \to (a^* \circ G)(X \otimes Y)$
for the composite
![]() $a^* \circ G$
, which is an equivalence by the assumption that
$a^* \circ G$
, which is an equivalence by the assumption that
![]() $F \circ a_!$
is an internal left adjoint. We conclude that G satisfies the projection formula. A similar argument shows that G preserves colimits.
$F \circ a_!$
is an internal left adjoint. We conclude that G satisfies the projection formula. A similar argument shows that G preserves colimits.
4.2.1 Adjointability for maps of spaces
We will be particularly interested in the internal left adjoints which are induced by a map of spaces
![]() $g\colon A \to B$
. In the covariant direction, we have the
$g\colon A \to B$
. In the covariant direction, we have the
![]() $\mathscr {C}$
-linear functor
$\mathscr {C}$
-linear functor
![]() $g_!\colon \mathscr {C}[A] \to \mathscr {C}[B]$
, which by Proposition 4.11(1) is always an internal left adjoint. In the contravariant direction, we have the
$g_!\colon \mathscr {C}[A] \to \mathscr {C}[B]$
, which by Proposition 4.11(1) is always an internal left adjoint. In the contravariant direction, we have the
![]() $\mathscr {C}$
-linear functor
$\mathscr {C}$
-linear functor
![]() $g^*\colon \mathscr {C}[B] \to \mathscr {C}[A]$
, which need not be an internal left adjoint in general. The class of morphisms for which this happens to be the case will play a mayor role throughout this article.
$g^*\colon \mathscr {C}[B] \to \mathscr {C}[A]$
, which need not be an internal left adjoint in general. The class of morphisms for which this happens to be the case will play a mayor role throughout this article.
Definition 4.20. We say that a map of spaces
![]() $g\colon A \to B$
is
$g\colon A \to B$
is
![]() $\mathscr {C}$
-adjointable if the
$\mathscr {C}$
-adjointable if the
![]() $\mathscr {C}$
-linear functor
$\mathscr {C}$
-linear functor
![]() $g^*\colon \mathscr {C}[B] \to \mathscr {C}[A]$
is an internal left adjoint in
$g^*\colon \mathscr {C}[B] \to \mathscr {C}[A]$
is an internal left adjoint in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
, i.e. its right adjoint
$ {\mathrm {Mod}}_{\mathscr {C}}$
, i.e. its right adjoint
![]() $g_*\colon \mathscr {C}[A] \to \mathscr {C}[B]$
preserves colimits and satisfies the projection formula. We say that a space A is
$g_*\colon \mathscr {C}[A] \to \mathscr {C}[B]$
preserves colimits and satisfies the projection formula. We say that a space A is
![]() $\mathscr {C}$
-adjointable if the map
$\mathscr {C}$
-adjointable if the map
![]() $A \to \mathrm {pt}$
is
$A \to \mathrm {pt}$
is
![]() $\mathscr {C}$
-adjointable.
$\mathscr {C}$
-adjointable.
It is immediate that the collection of
![]() $\mathscr {C}$
-adjointable maps is closed under composition and cartesian products.
$\mathscr {C}$
-adjointable maps is closed under composition and cartesian products.
Lemma 4.21. Let
![]() $g\colon A \to B$
be a map of spaces. If all of the fibers of g are
$g\colon A \to B$
be a map of spaces. If all of the fibers of g are
![]() $\mathscr {C}$
-adjointable, then g is
$\mathscr {C}$
-adjointable, then g is
![]() $\mathscr {C}$
-adjointable.
$\mathscr {C}$
-adjointable.
Proof. By Lemma 4.19, the
![]() $\mathscr {C}$
-linear functor
$\mathscr {C}$
-linear functor
![]() $g^*\colon \mathscr {C}[B] \to \mathscr {C}[A]$
is an internal left adjoint as soon as for every point
$g^*\colon \mathscr {C}[B] \to \mathscr {C}[A]$
is an internal left adjoint as soon as for every point
![]() $b\colon \mathrm {pt} \to B$
, the composite
$b\colon \mathrm {pt} \to B$
, the composite
![]() $g^* \circ b_!\colon \mathscr {C} \to \mathscr {C}[A]$
is an internal left adjoint. Letting
$g^* \circ b_!\colon \mathscr {C} \to \mathscr {C}[A]$
is an internal left adjoint. Letting
![]() $\iota _b\colon A_b \to A$
denote the inclusion of the fiber of g at b, this composite is equivalent to the
$\iota _b\colon A_b \to A$
denote the inclusion of the fiber of g at b, this composite is equivalent to the
![]() $\mathscr {C}$
-linear functor
$\mathscr {C}$
-linear functor
![]() $(\iota _b)_! \circ (A_b)^*\colon \mathscr {C} \to \mathscr {C}[A]$
. As
$(\iota _b)_! \circ (A_b)^*\colon \mathscr {C} \to \mathscr {C}[A]$
. As
![]() $(\iota _b)_!$
is always an internal left adjoint and
$(\iota _b)_!$
is always an internal left adjoint and
![]() $(A_b)^*$
is an internal left adjoint by assumption, this finishes the proof.
$(A_b)^*$
is an internal left adjoint by assumption, this finishes the proof.
Warning 4.22. The converse of the previous lemma is not true.Footnote
9
For a counterexample, consider the category
![]() $\mathscr {C}= \mathrm {Vect}_{k}$
of vector spaces over some field k of characteristic p and let G be the cyclic group of order p. Then the map
$\mathscr {C}= \mathrm {Vect}_{k}$
of vector spaces over some field k of characteristic p and let G be the cyclic group of order p. Then the map
![]() $f\colon \mathrm {pt}\to B^2G$
is
$f\colon \mathrm {pt}\to B^2G$
is
![]() $\mathscr {C}$
-adjointable, since the functor
$\mathscr {C}$
-adjointable, since the functor
![]() $f^*\colon {\mathrm {Fun}}(B^2G,\mathscr {C}) \to \mathscr {C}$
is an equivalence and thus in particular an internal left adjoint. However, the fiber
$f^*\colon {\mathrm {Fun}}(B^2G,\mathscr {C}) \to \mathscr {C}$
is an equivalence and thus in particular an internal left adjoint. However, the fiber
![]() $BG$
of f is not
$BG$
of f is not
![]() $\mathscr {C}$
-adjointable: applying the G-fixed point functor to the exact sequence
$\mathscr {C}$
-adjointable: applying the G-fixed point functor to the exact sequence
![]() $k[G] \to k \to 0$
gives the non-exact sequence
$k[G] \to k \to 0$
gives the non-exact sequence ![]() , showing that
, showing that
![]() $(BG)^*\colon \mathscr {C} \to {\mathrm {Fun}}(BG,\mathscr {C})$
does not preserve colimits.
$(BG)^*\colon \mathscr {C} \to {\mathrm {Fun}}(BG,\mathscr {C})$
does not preserve colimits.
Remark 4.23. The concept of
![]() $\mathscr {C}$
-adjointability is closely related to other notions appearing in the literature:
$\mathscr {C}$
-adjointability is closely related to other notions appearing in the literature:
-
1. In [Reference Barthel, Carmeli, Schlank and Yanovski3, Definition 2.15], a map of spaces
 $g\colon A \to B$
is called
$g\colon A \to B$
is called
 $\mathscr {C}$
-semiaffine if the restriction functor
$\mathscr {C}$
-semiaffine if the restriction functor
 $g^*\colon \mathscr {C}^B \to \mathscr {C}^A$
is an internal left adjoint in
$g^*\colon \mathscr {C}^B \to \mathscr {C}^A$
is an internal left adjoint in
 $ {\mathrm {Mod}}_{\mathscr {C}^B}$
. It is clear that any
$ {\mathrm {Mod}}_{\mathscr {C}^B}$
. It is clear that any
 $\mathscr {C}$
-semiaffine map is
$\mathscr {C}$
-semiaffine map is
 $\mathscr {C}$
-adjointable. Conversely, a variant of the proof of Lemma 4.21 shows that if all the fibers of g are
$\mathscr {C}$
-adjointable. Conversely, a variant of the proof of Lemma 4.21 shows that if all the fibers of g are
 $\mathscr {C}$
-adjointable, then g is
$\mathscr {C}$
-adjointable, then g is
 $\mathscr {C}$
-semiaffine. Indeed, the main observation is that for a point
$\mathscr {C}$
-semiaffine. Indeed, the main observation is that for a point
 $b \in B$
, the
$b \in B$
, the
 $\mathscr {C}^B$
-actions on
$\mathscr {C}^B$
-actions on
 $\mathscr {C}$
and
$\mathscr {C}$
and
 $\mathscr {C}^{A_b}$
are obtained from the
$\mathscr {C}^{A_b}$
are obtained from the
 $\mathscr {C}$
-action via the evaluation functor
$\mathscr {C}$
-action via the evaluation functor
 $b^*\colon \mathscr {C}^B \to \mathscr {C}$
, so that the functor
$b^*\colon \mathscr {C}^B \to \mathscr {C}$
, so that the functor
 $A_b^*\colon \mathscr {C} \to \mathscr {C}^{A_b}$
is a
$A_b^*\colon \mathscr {C} \to \mathscr {C}^{A_b}$
is a
 $\mathscr {C}^B$
-linear internal left adjoint if and only if it is a
$\mathscr {C}^B$
-linear internal left adjoint if and only if it is a
 $\mathscr {C}$
-linear internal left adjoint.
$\mathscr {C}$
-linear internal left adjoint. -
2. For a space A, there exists a ‘dualizing object’
 $D_A \in \mathscr {C}[A]$
and a ‘twisted norm map’
$D_A \in \mathscr {C}[A]$
and a ‘twisted norm map’
 $\mathrm {Nm}_A \colon A_!(- \otimes D_A)\to A_*$
which exhibits
$\mathrm {Nm}_A \colon A_!(- \otimes D_A)\to A_*$
which exhibits
 $A_!(- \otimes D_A)$
as the terminal
$A_!(- \otimes D_A)$
as the terminal
 $\mathscr {C}$
-linear approximation to the lax
$\mathscr {C}$
-linear approximation to the lax
 $\mathscr {C}$
-linear functor
$\mathscr {C}$
-linear functor
 $A_*$
. It follows that A is
$A_*$
. It follows that A is
 $\mathscr {C}$
-adjointable if and only if it is twisted
$\mathscr {C}$
-adjointable if and only if it is twisted
 $\mathscr {C}$
-ambidextrous, i.e. if the twisted norm map
$\mathscr {C}$
-ambidextrous, i.e. if the twisted norm map
 $\mathrm {Nm}_A$
is an equivalence.
$\mathrm {Nm}_A$
is an equivalence.When
 $\mathscr {C}$
is the
$\mathscr {C}$
is the
 $\infty $
-category of spectra, the parameterized spectrum
$\infty $
-category of spectra, the parameterized spectrum
 $D_A \in \mathrm {Sp}^A$
was introduced and studied by John Klein [Reference Klein41] and is called the dualizing spectrum of A.Footnote
10
The universal property of the twisted norm map in this setting was proved by [Reference Nikolaus and Scholze55, Theorem I.4.1(v)]. For general
$D_A \in \mathrm {Sp}^A$
was introduced and studied by John Klein [Reference Klein41] and is called the dualizing spectrum of A.Footnote
10
The universal property of the twisted norm map in this setting was proved by [Reference Nikolaus and Scholze55, Theorem I.4.1(v)]. For general
 $\mathscr {C}$
, the construction of the twisted norm map and a proof of its universal property appears in the article [Reference Cnossen20] by the second author, where in fact a more general version in the setting of parameterized homotopy theory is introduced.
$\mathscr {C}$
, the construction of the twisted norm map and a proof of its universal property appears in the article [Reference Cnossen20] by the second author, where in fact a more general version in the setting of parameterized homotopy theory is introduced.
Lemma 4.24 (cf. [Reference Lurie52, Lemma 21.1.2.14]).
The collection of
![]() $\mathscr {C}$
-adjointable maps is closed under retracts.
$\mathscr {C}$
-adjointable maps is closed under retracts.
Proof. Consider a retract diagram
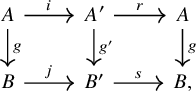
and assume that
![]() $g'$
is
$g'$
is
![]() $\mathscr {C}$
-adjointable. We have to show that
$\mathscr {C}$
-adjointable. We have to show that
![]() $g^*\colon \mathscr {C}[B]\to \mathscr {C}[A]$
is an internal left adjoint. This follows by writing
$g^*\colon \mathscr {C}[B]\to \mathscr {C}[A]$
is an internal left adjoint. This follows by writing
![]() $g^*$
as a retract of the composite
$g^*$
as a retract of the composite
![]() $r_!(g')^*j_!\colon \mathscr {C}[B]\to \mathscr {C}[A]$
: indeed, the right adjoint
$r_!(g')^*j_!\colon \mathscr {C}[B]\to \mathscr {C}[A]$
: indeed, the right adjoint
![]() $g_*$
is then also a retract of the composite
$g_*$
is then also a retract of the composite
![]() $j^*(g')_*r^*$
, compatibly with the projection formula maps. The fact that
$j^*(g')_*r^*$
, compatibly with the projection formula maps. The fact that
![]() $j^*(g')_*r^*$
satisfies the projection formula therefore implies that so does
$j^*(g')_*r^*$
satisfies the projection formula therefore implies that so does
![]() $g_*$
. Similarly, the fact that
$g_*$
. Similarly, the fact that
![]() $j^*(g')_*r^*$
preserves colimits implies that so does
$j^*(g')_*r^*$
preserves colimits implies that so does
![]() $g_*$
.
$g_*$
.
We next discuss some examples of
![]() $\mathscr {C}$
-adjointable spaces under various assumptions on
$\mathscr {C}$
-adjointable spaces under various assumptions on
![]() $\mathscr {C}$
. One source of such examples is the theory of ambidexterity developed by Hopkins and Lurie [Reference Hopkins and Lurie36]:
$\mathscr {C}$
. One source of such examples is the theory of ambidexterity developed by Hopkins and Lurie [Reference Hopkins and Lurie36]:
Example 4.25. If a space A is
![]() $\mathscr {C}$
-ambidextrous in the sense of [Reference Hopkins and Lurie36, Construction 4.1.8], then it is in particular
$\mathscr {C}$
-ambidextrous in the sense of [Reference Hopkins and Lurie36, Construction 4.1.8], then it is in particular
![]() $\mathscr {C}$
-adjointable: colimit-preservation of
$\mathscr {C}$
-adjointable: colimit-preservation of
![]() $A_*$
follows from the fact that it is a left adjoint of
$A_*$
follows from the fact that it is a left adjoint of
![]() $A^*$
[Reference Hopkins and Lurie36, Proposition 4.3.9], while the projection formula follows from [Reference Carmeli, Schlank and Yanovski18, Proposition 3.3.1]. In particular, if
$A^*$
[Reference Hopkins and Lurie36, Proposition 4.3.9], while the projection formula follows from [Reference Carmeli, Schlank and Yanovski18, Proposition 3.3.1]. In particular, if
![]() $\mathscr {C}$
is m-semiadditive, then by definition every m-finite space is
$\mathscr {C}$
is m-semiadditive, then by definition every m-finite space is
![]() $\mathscr {C}$
-ambidextrous and hence
$\mathscr {C}$
-ambidextrous and hence
![]() $\mathscr {C}$
-adjointable. This yields the following special cases:
$\mathscr {C}$
-adjointable. This yields the following special cases:
-
(-2) For every
 $\mathscr {C}$
the point
$\mathscr {C}$
the point
 $A = \mathrm {pt}$
is
$A = \mathrm {pt}$
is
 $\mathscr {C}$
-adjointable.
$\mathscr {C}$
-adjointable. -
(-1) For every pointed
 $\mathscr {C}$
, the empty space
$\mathscr {C}$
, the empty space
 $A=\varnothing $
is
$A=\varnothing $
is
 $\mathscr {C}$
-adjointable.
$\mathscr {C}$
-adjointable. -
(0) For every semiadditive
 $\mathscr {C}$
, every finite discrete set A is
$\mathscr {C}$
, every finite discrete set A is
 $\mathscr {C}$
-adjointable.
$\mathscr {C}$
-adjointable. -
(1) For every
 $1$
-semiadditive
$1$
-semiadditive
 $\mathscr {C}$
, and for every finite group G, the classifying space
$\mathscr {C}$
, and for every finite group G, the classifying space
 $A=BG$
is
$A=BG$
is
 $\mathscr {C}$
-adjointable.
$\mathscr {C}$
-adjointable. -
(∞) For every
 $\infty $
-semiadditive
$\infty $
-semiadditive
 $\mathscr {C}$
, every
$\mathscr {C}$
, every
 $\pi $
-finite space A is
$\pi $
-finite space A is
 $\mathscr {C}$
-adjointable.
$\mathscr {C}$
-adjointable.
For such spaces A, it follows that also all iterated loop spaces
![]() $\Omega ^k(A,a)$
for all
$\Omega ^k(A,a)$
for all
![]() $k \in \mathbb {N}$
and all basepoints
$k \in \mathbb {N}$
and all basepoints
![]() $a \in A$
are
$a \in A$
are
![]() $\mathscr {C}$
-adjointable, as they are also
$\mathscr {C}$
-adjointable, as they are also
![]() $\mathscr {C}$
-ambidextrous. Conversely, it follows directly from [Reference Hopkins and Lurie36, Proposition 4.3.9] that if A is an n-truncated space such that both A and all its iterated loop spaces
$\mathscr {C}$
-ambidextrous. Conversely, it follows directly from [Reference Hopkins and Lurie36, Proposition 4.3.9] that if A is an n-truncated space such that both A and all its iterated loop spaces
![]() $\Omega (A,a), \dots , \Omega ^n(A,a)$
are
$\Omega (A,a), \dots , \Omega ^n(A,a)$
are
![]() $\mathscr {C}$
-adjointable, then A is
$\mathscr {C}$
-adjointable, then A is
![]() $\mathscr {C}$
-ambidextrous.
$\mathscr {C}$
-ambidextrous.
A space can be
![]() $\mathscr {C}$
-adjointable without being
$\mathscr {C}$
-adjointable without being
![]() $\mathscr {C}$
-ambidextrous. For example, a space can be
$\mathscr {C}$
-ambidextrous. For example, a space can be
![]() $\mathscr {C}$
-adjointable for trivial reasons:
$\mathscr {C}$
-adjointable for trivial reasons:
Example 4.26. If
![]() $\mathscr {C}$
is an n-category (i.e., its mapping spaces are homotopically
$\mathscr {C}$
is an n-category (i.e., its mapping spaces are homotopically
![]() $(n-1)$
-truncated), then every n-connected space A is
$(n-1)$
-truncated), then every n-connected space A is
![]() $\mathscr {C}$
-adjointable, because the functor
$\mathscr {C}$
-adjointable, because the functor
![]() $A^*\colon \mathscr {C} \to \mathscr {C}^A$
is an equivalence, and hence in particular an internal left adjoint. In particular, if
$A^*\colon \mathscr {C} \to \mathscr {C}^A$
is an equivalence, and hence in particular an internal left adjoint. In particular, if
![]() $\mathscr {C}$
happens to be an ordinary category, then every simply-connected space is
$\mathscr {C}$
happens to be an ordinary category, then every simply-connected space is
![]() $\mathscr {C}$
-adjointable. Similarly, if
$\mathscr {C}$
-adjointable. Similarly, if
![]() $\mathscr {C}$
happens to be a poset, then any connected space is
$\mathscr {C}$
happens to be a poset, then any connected space is
![]() $\mathscr {C}$
-adjointable.
$\mathscr {C}$
-adjointable.
There are however also non-trivial examples of
![]() $\mathscr {C}$
-adjointable spaces which are not
$\mathscr {C}$
-adjointable spaces which are not
![]() $\mathscr {C}$
-ambidextrous.
$\mathscr {C}$
-ambidextrous.
Example 4.27. If
![]() $\mathscr {C}$
is stable, then every compact space is
$\mathscr {C}$
is stable, then every compact space is
![]() $\mathscr {C}$
-adjointable. To see this, we may reduce to the case
$\mathscr {C}$
-adjointable. To see this, we may reduce to the case
![]() $\mathscr {C} = \mathrm {Sp}$
by base changing along the unique map
$\mathscr {C} = \mathrm {Sp}$
by base changing along the unique map
![]() $\mathrm {Sp} \to \mathscr {C}$
in
$\mathrm {Sp} \to \mathscr {C}$
in
![]() $ {\mathrm {CAlg}}(\mathrm {Pr}^{\text {L}})$
, and to the case of a finite space A by Lemma 4.24. In this case, the functor
$ {\mathrm {CAlg}}(\mathrm {Pr}^{\text {L}})$
, and to the case of a finite space A by Lemma 4.24. In this case, the functor
![]() $A_*\colon \mathrm {Sp}[A] \to \mathrm {Sp}$
is a finite limit and thus commutes with colimits by stability. It follows from Lemma 4.18 that A is
$A_*\colon \mathrm {Sp}[A] \to \mathrm {Sp}$
is a finite limit and thus commutes with colimits by stability. It follows from Lemma 4.18 that A is
![]() $\mathscr {C}$
-adjointable.
$\mathscr {C}$
-adjointable.
More generally, the
![]() $\mathscr {C}$
-adjointable spaces are closed under pushouts when
$\mathscr {C}$
-adjointable spaces are closed under pushouts when
![]() $\mathscr {C}$
is stable.
$\mathscr {C}$
is stable.
Lemma 4.28. Assume
![]() $\mathscr {C}$
is stable. Then for every space B, the collection of
$\mathscr {C}$
is stable. Then for every space B, the collection of
![]() $\mathscr {C}$
-adjointable maps
$\mathscr {C}$
-adjointable maps
![]() $A \to B$
is closed under finite colimits in
$A \to B$
is closed under finite colimits in
![]() $\mathcal {S}_{/B}$
.
$\mathcal {S}_{/B}$
.
Proof. As
![]() $\mathscr {C}$
is pointed, the map
$\mathscr {C}$
is pointed, the map
![]() $\emptyset \to B$
is
$\emptyset \to B$
is
![]() $\mathscr {C}$
-adjointable. It will thus suffice to show that the
$\mathscr {C}$
-adjointable. It will thus suffice to show that the
![]() $\mathscr {C}$
-adjointable morphisms are closed under pushouts in
$\mathscr {C}$
-adjointable morphisms are closed under pushouts in
![]() $\mathcal {S}_{/B}$
. To this end, consider a pushout square of spaces
$\mathcal {S}_{/B}$
. To this end, consider a pushout square of spaces

Let
![]() $f\colon A \to B$
be a map of spaces, and define
$f\colon A \to B$
be a map of spaces, and define
![]() $f_i = f \circ j_i\colon A_i \to B$
for
$f_i = f \circ j_i\colon A_i \to B$
for
![]() $j=0,1,2$
, where
$j=0,1,2$
, where
![]() $j_0 = j_2 \circ \beta \simeq j_1 \circ \alpha $
. Assume that
$j_0 = j_2 \circ \beta \simeq j_1 \circ \alpha $
. Assume that
![]() $f_1$
,
$f_1$
,
![]() $f_2$
and
$f_2$
and
![]() $f_0$
are
$f_0$
are
![]() $\mathscr {C}$
-adjointable. We want to prove that the functor
$\mathscr {C}$
-adjointable. We want to prove that the functor
![]() $f^*\colon \mathscr {C}[B]\to \mathscr {C}[A]$
is an internal left adjoint, or equivalently, by Corollary 4.15, that the functor
$f^*\colon \mathscr {C}[B]\to \mathscr {C}[A]$
is an internal left adjoint, or equivalently, by Corollary 4.15, that the functor
![]() $f^*\colon {\mathrm {Fun}}(B,\mathscr {C}) \to {\mathrm {Fun}}(A,\mathscr {C})$
is an internal left adjoint.
$f^*\colon {\mathrm {Fun}}(B,\mathscr {C}) \to {\mathrm {Fun}}(A,\mathscr {C})$
is an internal left adjoint.
Let
![]() $I= \Lambda ^2_0$
denote the walking cospan. The cospan
$I= \Lambda ^2_0$
denote the walking cospan. The cospan ![]() defines a functor
defines a functor
![]() $I \to \mathcal {S}_{/B} \simeq {\mathrm {Fun}}(B,\mathcal {S})$
. We let
$I \to \mathcal {S}_{/B} \simeq {\mathrm {Fun}}(B,\mathcal {S})$
. We let
![]() $p\colon E \to I^{\mathrm {op}} \times B$
denote the unstraightening of the associated functor
$p\colon E \to I^{\mathrm {op}} \times B$
denote the unstraightening of the associated functor
![]() $I \times B \to \mathcal {S} \subseteq \mathrm {Cat}_{\infty }$
; note that the pullback of p along the inclusion
$I \times B \to \mathcal {S} \subseteq \mathrm {Cat}_{\infty }$
; note that the pullback of p along the inclusion
![]() $\{i\} \times B\to I^{\mathrm {op}}\times B$
is equivalent to the map
$\{i\} \times B\to I^{\mathrm {op}}\times B$
is equivalent to the map
![]() $f\colon A_i \to \{i\}\times B$
for
$f\colon A_i \to \{i\}\times B$
for
![]() $i=0,1,2$
. The above pushout diagram determines a functor
$i=0,1,2$
. The above pushout diagram determines a functor
![]() $g \colon E\to A$
which exhibits A as the groupoidification of E (see [Reference Lurie49, Corollary 3.3.4.6]). As
$g \colon E\to A$
which exhibits A as the groupoidification of E (see [Reference Lurie49, Corollary 3.3.4.6]). As
![]() $g\colon E\to A$
is a localization, the restriction functor
$g\colon E\to A$
is a localization, the restriction functor
![]() $g^*\colon {\mathrm {Fun}}(A,\mathscr {C})\to {\mathrm {Fun}}(E,\mathscr {C})$
is fully faithful, so that the counit
$g^*\colon {\mathrm {Fun}}(A,\mathscr {C})\to {\mathrm {Fun}}(E,\mathscr {C})$
is fully faithful, so that the counit
![]() $g_!g^*\to \mathrm {id}_{\mathscr {C}^A}$
is an equivalence. Letting
$g_!g^*\to \mathrm {id}_{\mathscr {C}^A}$
is an equivalence. Letting
![]() $f' := f \circ g\colon E \to B$
, it follows that the functor
$f' := f \circ g\colon E \to B$
, it follows that the functor
![]() $f^*\colon {\mathrm {Fun}}(B,\mathscr {C})\to {\mathrm {Fun}}(A,\mathscr {C})$
is
$f^*\colon {\mathrm {Fun}}(B,\mathscr {C})\to {\mathrm {Fun}}(A,\mathscr {C})$
is
![]() $\mathscr {C}$
-linearly equivalent to the following composite:
$\mathscr {C}$
-linearly equivalent to the following composite:
As the functor
![]() $g_!$
is an internal left adjoint, it will suffice to prove the same for
$g_!$
is an internal left adjoint, it will suffice to prove the same for
![]() ${f'}^*$
. This functor can in turn be
${f'}^*$
. This functor can in turn be
![]() $\mathscr {C}$
-linearly decomposed as the following composite:
$\mathscr {C}$
-linearly decomposed as the following composite:
where the first functor is given by precomposition with the projection
![]() $\mathrm {pr}_B\colon I^{\mathrm {op}} \times B \to B$
.
$\mathrm {pr}_B\colon I^{\mathrm {op}} \times B \to B$
.
The functor
![]() $\mathrm {pr}_B^*$
is obtained by tensoring the functor
$\mathrm {pr}_B^*$
is obtained by tensoring the functor
![]() $(I^{\mathrm {op}})^*\colon \mathrm {Sp} \to {\mathrm {Fun}}(I^{\mathrm {op}},\mathrm {Sp})$
with
$(I^{\mathrm {op}})^*\colon \mathrm {Sp} \to {\mathrm {Fun}}(I^{\mathrm {op}},\mathrm {Sp})$
with
![]() $ {\mathrm {Fun}}(B,\mathscr {C})$
in
$ {\mathrm {Fun}}(B,\mathscr {C})$
in
![]() $\mathrm {Pr}^{\text {L}}$
. Since finite limits in
$\mathrm {Pr}^{\text {L}}$
. Since finite limits in
![]() $\mathrm {Sp}$
commute with colimits, the functor
$\mathrm {Sp}$
commute with colimits, the functor
![]() $(I^{\mathrm {op}})^*\colon \mathrm {Sp} \to {\mathrm {Fun}}(I^{\mathrm {op}},\mathrm {Sp})$
is an internal left adjoint in
$(I^{\mathrm {op}})^*\colon \mathrm {Sp} \to {\mathrm {Fun}}(I^{\mathrm {op}},\mathrm {Sp})$
is an internal left adjoint in
![]() $\mathrm {Pr}^{\text {L}}_{\mathrm {st}}$
, and thus
$\mathrm {Pr}^{\text {L}}_{\mathrm {st}}$
, and thus
![]() $\mathrm {pr}_B^*\colon {\mathrm {Fun}}(B,\mathscr {C}) \to {\mathrm {Fun}}(I^{\mathrm {op}} \times B, \mathscr {C})$
is an internal left adjoint in
$\mathrm {pr}_B^*\colon {\mathrm {Fun}}(B,\mathscr {C}) \to {\mathrm {Fun}}(I^{\mathrm {op}} \times B, \mathscr {C})$
is an internal left adjoint in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
.
$ {\mathrm {Mod}}_{\mathscr {C}}$
.
It thus remains to show that
![]() $p^*$
is an internal left adjoint, i.e. that its right adjoint
$p^*$
is an internal left adjoint, i.e. that its right adjoint
![]() $p_*\colon {\mathrm {Fun}}(E,\mathscr {C}) \to {\mathrm {Fun}}(I^{\mathrm {op}},\mathscr {C})$
in
$p_*\colon {\mathrm {Fun}}(E,\mathscr {C}) \to {\mathrm {Fun}}(I^{\mathrm {op}},\mathscr {C})$
in
![]() $\widehat {\mathrm {Cat}}_{\infty }$
preserves colimits and satisfies the projection formula. The proof is similar to that of Lemma 4.21. The three evaluation functors
$\widehat {\mathrm {Cat}}_{\infty }$
preserves colimits and satisfies the projection formula. The proof is similar to that of Lemma 4.21. The three evaluation functors
![]() $\mathrm {ev}_i\colon {\mathrm {Fun}}(I^{\mathrm {op}} \times B,\mathscr {C})\to {\mathrm {Fun}}(B,\mathscr {C})$
for
$\mathrm {ev}_i\colon {\mathrm {Fun}}(I^{\mathrm {op}} \times B,\mathscr {C})\to {\mathrm {Fun}}(B,\mathscr {C})$
for
![]() $i \in I^{\mathrm {op}}$
are jointly conservative, and since projection formulas are compatible with
$i \in I^{\mathrm {op}}$
are jointly conservative, and since projection formulas are compatible with
![]() $\mathscr {C}$
-linear functors (cf. [Reference Carmeli, Schlank and Yanovski18, Lemma 2.2.4]) it suffices to check that each of the three composites
$\mathscr {C}$
-linear functors (cf. [Reference Carmeli, Schlank and Yanovski18, Lemma 2.2.4]) it suffices to check that each of the three composites
preserves colimits and satisfies the projection formula. In other words, letting
![]() $i \colon B \hookrightarrow I^{\mathrm {op}} \times B$
denote the inclusion of
$i \colon B \hookrightarrow I^{\mathrm {op}} \times B$
denote the inclusion of
![]() $B\simeq B \times \{i\}$
into
$B\simeq B \times \{i\}$
into
![]() $B \times I^{\mathrm {op}}$
, it suffices to check that for each
$B \times I^{\mathrm {op}}$
, it suffices to check that for each
![]() $i\in I^{\mathrm {op}}$
the composite
$i\in I^{\mathrm {op}}$
the composite
![]() $p^*\circ i_!\colon {\mathrm {Fun}}(B,\mathscr {C})\to {\mathrm {Fun}}(E,\mathscr {C})$
is an internal left adjoint. To this end, observe that for each
$p^*\circ i_!\colon {\mathrm {Fun}}(B,\mathscr {C})\to {\mathrm {Fun}}(E,\mathscr {C})$
is an internal left adjoint. To this end, observe that for each
![]() $i \in I^{\mathrm {op}}$
there is a pullback diagram
$i \in I^{\mathrm {op}}$
there is a pullback diagram
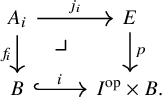
As p is a cartesian fibration, it follows from [Reference Lurie49, Proposition 4.1.2.11, Proposition 4.1.2.15]Footnote
11
that the Beck-Chevalley map
![]() ${j_i}_! \circ f_i^* \to p^*\circ i_!$
in
${j_i}_! \circ f_i^* \to p^*\circ i_!$
in
![]() $ {\mathrm {Fun}}^{\mathrm {L}}(\mathcal {S},\mathcal {S}^{E})$
is an equivalence. By tensoring with
$ {\mathrm {Fun}}^{\mathrm {L}}(\mathcal {S},\mathcal {S}^{E})$
is an equivalence. By tensoring with
![]() $\mathscr {C}$
, we obtain a similar equivalence of functors
$\mathscr {C}$
, we obtain a similar equivalence of functors
![]() $\mathscr {C} \to \mathscr {C}^E$
. By assumption on
$\mathscr {C} \to \mathscr {C}^E$
. By assumption on
![]() $f_i$
, the functor
$f_i$
, the functor
![]() $f_i^*\colon \mathscr {C}^B \to \mathscr {C}^{A_i}$
is an internal left adjoint, and the same is always true for
$f_i^*\colon \mathscr {C}^B \to \mathscr {C}^{A_i}$
is an internal left adjoint, and the same is always true for
![]() $(j_i)_!\colon \mathscr {C}^{A_i} \to \mathscr {C}^A$
. It thus follows that their composite
$(j_i)_!\colon \mathscr {C}^{A_i} \to \mathscr {C}^A$
. It thus follows that their composite
![]() $p^* \circ i_!\colon \mathscr {C}^B \to \mathscr {C}^E$
is an internal left adjoint as well, finishing the proof.
$p^* \circ i_!\colon \mathscr {C}^B \to \mathscr {C}^E$
is an internal left adjoint as well, finishing the proof.
As it turns out,
![]() $\mathscr {C}$
-adjointability becomes ubiquitous when we move one categorical level up.
$\mathscr {C}$
-adjointability becomes ubiquitous when we move one categorical level up.
Example 4.29.
Every space is
![]() $\mathrm {Pr}^{\text {L}}$
-adjointable. For n-truncated spaces, this is an instance of Example 4.25, using [Reference Hopkins and Lurie36, Example 4.3.11]. For a general space A, the colimit of any diagram
$\mathrm {Pr}^{\text {L}}$
-adjointable. For n-truncated spaces, this is an instance of Example 4.25, using [Reference Hopkins and Lurie36, Example 4.3.11]. For a general space A, the colimit of any diagram
![]() $F\colon A \to \mathrm {Pr}^{\text {L}}$
is computed as the limit of the associated diagram of right adjoints
$F\colon A \to \mathrm {Pr}^{\text {L}}$
is computed as the limit of the associated diagram of right adjoints
![]() $F^r \colon A^{\mathrm {op}} \to \mathrm {Pr}^{\text {R}}$
(see [Reference Lurie49]). Since A is a space, we have a natural isomorphism
$F^r \colon A^{\mathrm {op}} \to \mathrm {Pr}^{\text {R}}$
(see [Reference Lurie49]). Since A is a space, we have a natural isomorphism
![]() $F \simeq F^r$
and hence a natural isomorphism of functors
$F \simeq F^r$
and hence a natural isomorphism of functors
![]() $A_! \simeq A_*$
. Since
$A_! \simeq A_*$
. Since
![]() $A_!$
preserves colimits, so does
$A_!$
preserves colimits, so does
![]() $A_*$
. Since dualizable presentable
$A_*$
. Since dualizable presentable
![]() $\infty $
-categories generate
$\infty $
-categories generate
![]() $\mathrm {Pr}^{\text {L}}$
under colimits, cf. [Reference Ragimov and Schlank60, Lemma 7.14], the claim follows from lemma 4.18.
$\mathrm {Pr}^{\text {L}}$
under colimits, cf. [Reference Ragimov and Schlank60, Lemma 7.14], the claim follows from lemma 4.18.
It follows that, similarly, every space is
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
-adjointable for every
$ {\mathrm {Mod}}_{\mathscr {C}}$
-adjointable for every
![]() $\mathscr {C} \in {\mathrm {CAlg}}(\mathrm {Pr}^{\text {L}})$
.
$\mathscr {C} \in {\mathrm {CAlg}}(\mathrm {Pr}^{\text {L}})$
.
Remark 4.30. For a fixed space A and for large enough cardinals
![]() $\kappa $
(depending on A), the inclusion
$\kappa $
(depending on A), the inclusion
![]() $\mathrm {Pr}^{\text {L}}_\kappa \hookrightarrow \mathrm {Pr}^{\text {L}}$
preserves A-shaped limits. Therefore, for such
$\mathrm {Pr}^{\text {L}}_\kappa \hookrightarrow \mathrm {Pr}^{\text {L}}$
preserves A-shaped limits. Therefore, for such
![]() $\kappa $
, the above example also works in
$\kappa $
, the above example also works in
![]() $\mathrm {Pr}^{\text {L}}_\kappa $
.
$\mathrm {Pr}^{\text {L}}_\kappa $
.
4.2.2 Adjointability and dualizability
In the remainder of this subsection, we will discuss the close relationship between internal left adjoints in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
and dualizable objects in
$ {\mathrm {Mod}}_{\mathscr {C}}$
and dualizable objects in
![]() $\mathscr {C}$
. Recall from Notation 4.10 that every object
$\mathscr {C}$
. Recall from Notation 4.10 that every object
![]() $X \in \mathscr {C}^A$
gives rise to a
$X \in \mathscr {C}^A$
gives rise to a
![]() $\mathscr {C}$
-linear functor that we abusively also denote by
$\mathscr {C}$
-linear functor that we abusively also denote by
![]() $X\colon \mathscr {C}[A] \to \mathscr {C}$
.
$X\colon \mathscr {C}[A] \to \mathscr {C}$
.
Observation 4.31. For an object
![]() $Y\in \mathscr {C}$
, the morphism
$Y\in \mathscr {C}$
, the morphism
![]() $Y\colon \mathscr {C} \to \mathscr {C}$
in
$Y\colon \mathscr {C} \to \mathscr {C}$
in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
is an internal left adjoint if and only if Y is dualizable in
$ {\mathrm {Mod}}_{\mathscr {C}}$
is an internal left adjoint if and only if Y is dualizable in
![]() $\mathscr {C}$
. Indeed, the internal right adjoint of
$\mathscr {C}$
. Indeed, the internal right adjoint of
![]() $Y\colon \mathscr {C} \to \mathscr {C}$
is of the form
$Y\colon \mathscr {C} \to \mathscr {C}$
is of the form
![]() $Y^{\vee }\colon \mathscr {C} \to \mathscr {C}$
for some object
$Y^{\vee }\colon \mathscr {C} \to \mathscr {C}$
for some object
![]() $Y^{\vee } \in \mathscr {C}$
, and the unit and counit of the adjunction correspond to the evaluation and coevaluation maps forming the duality data. The triangle identities for the adjunction translate into the triangle identities for the duality.
$Y^{\vee } \in \mathscr {C}$
, and the unit and counit of the adjunction correspond to the evaluation and coevaluation maps forming the duality data. The triangle identities for the adjunction translate into the triangle identities for the duality.
Corollary 4.32. For
![]() $X \in \mathscr {C}^A$
, the functor
$X \in \mathscr {C}^A$
, the functor ![]() is an internal left adjoint if and only if X is pointwise dualizable.
is an internal left adjoint if and only if X is pointwise dualizable.
Proof. The composite of the functor
![]() $X\colon \mathscr {C}[A] \to \mathscr {C}$
with
$X\colon \mathscr {C}[A] \to \mathscr {C}$
with
![]() $a_!\colon \mathscr {C} \to \mathscr {C}[A]$
corresponds to
$a_!\colon \mathscr {C} \to \mathscr {C}[A]$
corresponds to
![]() $a^*X \in \mathscr {C}$
by Corollary 4.12. The claim thus follows from Observation 4.31 and Lemma 4.19.
$a^*X \in \mathscr {C}$
by Corollary 4.12. The claim thus follows from Observation 4.31 and Lemma 4.19.
In what follows, we equip the
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}^A$
with the pointwise symmetric monoidal structure. In particular, an object of
$\mathscr {C}^A$
with the pointwise symmetric monoidal structure. In particular, an object of
![]() $\mathscr {C}^A$
is dualizable if and only if it is pointwise dualizable.
$\mathscr {C}^A$
is dualizable if and only if it is pointwise dualizable.
Proposition 4.33 (cf. [Reference Carmeli, Schlank and Yanovski19, Proposition 2.5]).
Let
![]() $g\colon A \to B$
be a map of spaces and assume that g is
$g\colon A \to B$
be a map of spaces and assume that g is
![]() $\mathscr {C}$
-adjointable. Then the left Kan extension functor
$\mathscr {C}$
-adjointable. Then the left Kan extension functor
![]() $g_!\colon \mathscr {C}^A \to \mathscr {C}^B$
preserves dualizable objects. For a dualizable object
$g_!\colon \mathscr {C}^A \to \mathscr {C}^B$
preserves dualizable objects. For a dualizable object
![]() $X \in \mathscr {C}^A$
, the dual of
$X \in \mathscr {C}^A$
, the dual of
![]() $g_!(X) \in \mathscr {C}^B$
is given by
$g_!(X) \in \mathscr {C}^B$
is given by
![]() $g_*(X^\vee )$
. In particular, if A is a
$g_*(X^\vee )$
. In particular, if A is a
![]() $\mathscr {C}$
-adjointable space and
$\mathscr {C}$
-adjointable space and
![]() $X \in \mathscr {C}^A$
is dualizable, then
$X \in \mathscr {C}^A$
is dualizable, then
![]() $A_!X$
is dualizable with dual
$A_!X$
is dualizable with dual
![]() $A_*X^{\vee }$
.
$A_*X^{\vee }$
.
Proof. Assume that
![]() $X \in \mathscr {C}^A$
is dualizable. By Corollary 4.32, the associated
$X \in \mathscr {C}^A$
is dualizable. By Corollary 4.32, the associated
![]() $\mathscr {C}$
-linear functor
$\mathscr {C}$
-linear functor
![]() $X\colon \mathscr {C}[A] \to \mathscr {C}$
is an internal left adjoint. Since g is
$X\colon \mathscr {C}[A] \to \mathscr {C}$
is an internal left adjoint. Since g is
![]() $\mathscr {C}$
-adjointable, the
$\mathscr {C}$
-adjointable, the
![]() $\mathscr {C}$
-linear functor
$\mathscr {C}$
-linear functor
![]() $g^*\colon \mathscr {C}[B] \to \mathscr {C}[A]$
is also an internal left adjoint, and thus so is the composite
$g^*\colon \mathscr {C}[B] \to \mathscr {C}[A]$
is also an internal left adjoint, and thus so is the composite
By Corollary 4.12, this composite classifies the object
![]() $g_!X \in \mathscr {C}^B$
, and thus it follows from another application of Corollary 4.32 that
$g_!X \in \mathscr {C}^B$
, and thus it follows from another application of Corollary 4.32 that
![]() $g_!X$
is dualizable. The dual of
$g_!X$
is dualizable. The dual of
![]() $g_!X$
may now be computed by
$g_!X$
may now be computed by ![]() , where
, where
![]() $\hom _{\mathscr {D}}$
denotes the internal hom in a symmetric monoidal
$\hom _{\mathscr {D}}$
denotes the internal hom in a symmetric monoidal
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {D}$
.
$\mathscr {D}$
.
4.3 Traces of free
 $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
 $\infty $
-categories and free loop transfers
$\infty $
-categories and free loop transfers
Let A be a space and consider the free
![]() $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}[A]$
. By combining Corollary 3.12 and Proposition 4.11(1) we get that
$\mathscr {C}[A]$
. By combining Corollary 3.12 and Proposition 4.11(1) we get that
![]() $\mathscr {C}[A]$
is a dualizable object in
$\mathscr {C}[A]$
is a dualizable object in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
, and that its dimension in
$ {\mathrm {Mod}}_{\mathscr {C}}$
, and that its dimension in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
is given by the composite
$ {\mathrm {Mod}}_{\mathscr {C}}$
is given by the composite
where
![]() $LA = {\mathrm {Map}}(S^1,A) \in \mathcal {S}$
is the free loop space of A. By evaluating at the monoidal unit
$LA = {\mathrm {Map}}(S^1,A) \in \mathcal {S}$
is the free loop space of A. By evaluating at the monoidal unit ![]() , we thus obtain an equivalence
, we thus obtain an equivalence
When
![]() $f\colon A \to B$
is a map of spaces, applying the
$f\colon A \to B$
is a map of spaces, applying the
![]() $\mathscr {C}$
-linear trace functor
$\mathscr {C}$
-linear trace functor
![]() $ {\mathrm {Tr}}_{\mathscr {C}}$
to the internal left adjoint
$ {\mathrm {Tr}}_{\mathscr {C}}$
to the internal left adjoint
![]() $f_!\colon \mathscr {C}[A] \to \mathscr {C}[B]$
gives the map
$f_!\colon \mathscr {C}[A] \to \mathscr {C}[B]$
gives the map ![]() , see Corollary 4.41 below. In case the map f is
, see Corollary 4.41 below. In case the map f is
![]() $\mathscr {C}$
-adjointable, we also get a map in the opposite direction.
$\mathscr {C}$
-adjointable, we also get a map in the opposite direction.
Definition 4.34. Let
![]() $f\colon A \to B$
be a
$f\colon A \to B$
be a
![]() $\mathscr {C}$
-adjointable map of spaces, and consider the
$\mathscr {C}$
-adjointable map of spaces, and consider the
![]() $\mathscr {C}$
-linear functor
$\mathscr {C}$
-linear functor
![]() $f^*\colon \mathscr {C}[B] \to \mathscr {C}[A]$
, which by assumption is an internal left adjoint. The (
$f^*\colon \mathscr {C}[B] \to \mathscr {C}[A]$
, which by assumption is an internal left adjoint. The (
![]() $\mathscr {C}$
-linear) free loop transfer of f is the map
$\mathscr {C}$
-linear) free loop transfer of f is the map
obtained by applying the
![]() $\mathscr {C}$
-linear trace functor to
$\mathscr {C}$
-linear trace functor to
![]() $f^*$
.
$f^*$
.
The goal of the remainder of this section is to show that the equivalence ![]() is functorial in A, see Theorem 4.40 below. Since we have already solved a similar coherence problem for the computation of dimensions in the
is functorial in A, see Theorem 4.40 below. Since we have already solved a similar coherence problem for the computation of dimensions in the
![]() $(\infty ,2)$
-category
$(\infty ,2)$
-category
![]() $ {\mathrm {Span}}(\mathcal {S})$
in Section 3.2, the main ingredient will be a good understanding of the functor
$ {\mathrm {Span}}(\mathcal {S})$
in Section 3.2, the main ingredient will be a good understanding of the functor
![]() $\mathscr {C}[-]\colon {\mathrm {Span}}(\mathcal {S}) \to {\mathrm {Mod}}_{\mathscr {C}}$
obtained from the bivariant theory
$\mathscr {C}[-]\colon {\mathrm {Span}}(\mathcal {S}) \to {\mathrm {Mod}}_{\mathscr {C}}$
obtained from the bivariant theory
![]() $\mathscr {C}[-]\colon \mathcal {S} \to {\mathrm {Mod}}_{\mathscr {C}}$
of Proposition 4.11. More precisely, we will show that after applying
$\mathscr {C}[-]\colon \mathcal {S} \to {\mathrm {Mod}}_{\mathscr {C}}$
of Proposition 4.11. More precisely, we will show that after applying
![]() $\Omega $
this functor induces the functor
$\Omega $
this functor induces the functor ![]() .
.
We start with some preliminary results.
Lemma 4.35. Let
![]() $\mathscr {E}$
be a small
$\mathscr {E}$
be a small
![]() $(\infty ,2)$
-category. The
$(\infty ,2)$
-category. The
![]() $\infty $
-category
$\infty $
-category
![]() $\iota _1 {\mathrm {Fun}}(\mathscr {E},\mathrm {Pr}^{\text {L}})$
is cocomplete, and colimits therein are preserved under restriction along any
$\iota _1 {\mathrm {Fun}}(\mathscr {E},\mathrm {Pr}^{\text {L}})$
is cocomplete, and colimits therein are preserved under restriction along any
![]() $2$
-functor
$2$
-functor
![]() $\mathscr {E}'\to \mathscr {E}$
. In particular, colimits are computed pointwise.
$\mathscr {E}'\to \mathscr {E}$
. In particular, colimits are computed pointwise.
Proof. For every
![]() $\infty $
-category I, the colimit adjunction
$\infty $
-category I, the colimit adjunction
![]() $(\mathrm {Pr}^{\text {L}})^I \rightleftarrows \mathrm {Pr}^{\text {L}}$
is a
$(\mathrm {Pr}^{\text {L}})^I \rightleftarrows \mathrm {Pr}^{\text {L}}$
is a
![]() $2$
-adjunction: both the unit and co-unit transformations are transformations of
$2$
-adjunction: both the unit and co-unit transformations are transformations of
![]() $2$
-functors, and they induce the appropriate equivalences on mapping
$2$
-functors, and they induce the appropriate equivalences on mapping
![]() $\infty $
-categories rather than just spaces. In particular, it induces an adjunction
$\infty $
-categories rather than just spaces. In particular, it induces an adjunction
![]() $ {\mathrm {Fun}}(\mathscr {E},\mathrm {Pr}^{\text {L}})^I \simeq {\mathrm {Fun}}(\mathscr {E},(\mathrm {Pr}^{\text {L}})^I)\rightleftarrows {\mathrm {Fun}}(\mathscr {E},\mathrm {Pr}^{\text {L}})$
where the right adjoint is equivalent to the diagonal functor. The claim follows.
$ {\mathrm {Fun}}(\mathscr {E},\mathrm {Pr}^{\text {L}})^I \simeq {\mathrm {Fun}}(\mathscr {E},(\mathrm {Pr}^{\text {L}})^I)\rightleftarrows {\mathrm {Fun}}(\mathscr {E},\mathrm {Pr}^{\text {L}})$
where the right adjoint is equivalent to the diagonal functor. The claim follows.
Lemma 4.36. Evaluation at a point induces an equivalence of
![]() $(\infty ,2)$
-categories
$(\infty ,2)$
-categories
Proof. By the Yoneda lemma, it suffices to check that for every small
![]() $(\infty ,2)$
-category
$(\infty ,2)$
-category
![]() $\mathscr {E}$
the induced map of spaces
$\mathscr {E}$
the induced map of spaces
is an equivalence. By Lemma 4.35, the underlying
![]() $\infty $
-category of
$\infty $
-category of
![]() $ {\mathrm {Fun}}(\mathscr {E},\mathrm {Pr}^{\text {L}})$
is again cocomplete, and there is an equivalence
$ {\mathrm {Fun}}(\mathscr {E},\mathrm {Pr}^{\text {L}})$
is again cocomplete, and there is an equivalence
The composite map
is given by evaluation at a point, which is an equivalence by the universal property of the
![]() $\infty $
-category of spaces (see e.g. [Reference Lurie49, Theorem 5.1.5.6]).
$\infty $
-category of spaces (see e.g. [Reference Lurie49, Theorem 5.1.5.6]).
Definition 4.37. Define
![]() $ {\mathrm {Biv}}^{\mathrm {L}}(\mathcal {S},\mathrm {Pr}^{\text {L}}) \subseteq {\mathrm {Biv}}(\mathcal {S},\mathrm {Cat}_{\infty })$
as the sub-2-category consisting of the colimit-preserving bivariant functors
$ {\mathrm {Biv}}^{\mathrm {L}}(\mathcal {S},\mathrm {Pr}^{\text {L}}) \subseteq {\mathrm {Biv}}(\mathcal {S},\mathrm {Cat}_{\infty })$
as the sub-2-category consisting of the colimit-preserving bivariant functors
![]() $\mathcal {S} \to \mathrm {Pr}^{\text {L}} \subseteq \mathrm {Cat}_{\infty }$
.
$\mathcal {S} \to \mathrm {Pr}^{\text {L}} \subseteq \mathrm {Cat}_{\infty }$
.
Lemma 4.38. The inclusion
is an equivalence of
![]() $(\infty ,2)$
-categories.
$(\infty ,2)$
-categories.
Proof. Note that
![]() $ {\mathrm {Biv}}^{\mathrm {L}}(\mathcal {S},\mathrm {Pr}^{\text {L}})$
is a locally full sub-2-category of
$ {\mathrm {Biv}}^{\mathrm {L}}(\mathcal {S},\mathrm {Pr}^{\text {L}})$
is a locally full sub-2-category of
![]() $ {\mathrm {Fun}}^{\mathrm {L}}(\mathcal {S},\mathrm {Pr}^{\text {L}})$
, meaning that the induced maps on mapping categories are fully faithful. It will thus suffice to show the following two claims:
$ {\mathrm {Fun}}^{\mathrm {L}}(\mathcal {S},\mathrm {Pr}^{\text {L}})$
, meaning that the induced maps on mapping categories are fully faithful. It will thus suffice to show the following two claims:
-
(a) Any object in
 $ {\mathrm {Fun}}^{\mathrm {L}}(\mathcal {S},\mathrm {Pr}^{\text {L}})$
is a bivariant theory;
$ {\mathrm {Fun}}^{\mathrm {L}}(\mathcal {S},\mathrm {Pr}^{\text {L}})$
is a bivariant theory; -
(b) Any morphism in
 $ {\mathrm {Fun}}^{\mathrm {L}}(\mathcal {S},\mathrm {Pr}^{\text {L}})$
is a morphism of bivariant theories.
$ {\mathrm {Fun}}^{\mathrm {L}}(\mathcal {S},\mathrm {Pr}^{\text {L}})$
is a morphism of bivariant theories.
For claim (a), note that a colimit preserving functor
![]() $F\colon \mathcal {S} \to \mathrm {Pr}^{\text {L}}$
is necessarily of the form
$F\colon \mathcal {S} \to \mathrm {Pr}^{\text {L}}$
is necessarily of the form
![]() $A \mapsto \mathscr {D}[A]$
for
$A \mapsto \mathscr {D}[A]$
for
![]() $\mathscr {D} = F(\mathrm {pt}) \in \mathrm {Pr}^{\text {L}}$
, and thus claim (a) follows from Proposition 4.11(2). For claim (b), let
$\mathscr {D} = F(\mathrm {pt}) \in \mathrm {Pr}^{\text {L}}$
, and thus claim (a) follows from Proposition 4.11(2). For claim (b), let
![]() $\mathscr {D}_0$
and
$\mathscr {D}_0$
and
![]() $\mathscr {D}_1$
be presentable
$\mathscr {D}_1$
be presentable
![]() $\infty $
-categories, and let
$\infty $
-categories, and let
![]() $G\colon \mathscr {D}_0 \to \mathscr {D}_1$
be a colimit-preserving functor. We have to show that the associated morphism
$G\colon \mathscr {D}_0 \to \mathscr {D}_1$
be a colimit-preserving functor. We have to show that the associated morphism
![]() $\mathscr {D}_0[-] \to \mathscr {D}_1[-]$
in
$\mathscr {D}_0[-] \to \mathscr {D}_1[-]$
in
![]() $ {\mathrm {Fun}}^{\mathrm {L}}(\mathcal {S},\mathrm {Pr}^{\text {L}})$
is a morphism of bivariant theories, i.e. that for any map
$ {\mathrm {Fun}}^{\mathrm {L}}(\mathcal {S},\mathrm {Pr}^{\text {L}})$
is a morphism of bivariant theories, i.e. that for any map
![]() $f\colon A\to B$
of spaces the following commuting square is vertically right adjointable:
$f\colon A\to B$
of spaces the following commuting square is vertically right adjointable:
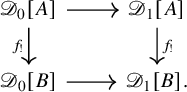
Under the identification
![]() $\mathscr {D}[A]\simeq \mathscr {D}^A$
, the Beck-Chevalley transformation of this square is the natural isomorphism rendering the following square commutative:
$\mathscr {D}[A]\simeq \mathscr {D}^A$
, the Beck-Chevalley transformation of this square is the natural isomorphism rendering the following square commutative:
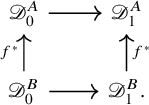
This proves that claim (b) holds, which finishes the proof that
![]() $ {\mathrm {Biv}}^{\mathrm {L}}(\mathcal {S},\mathrm {Pr}^{\text {L}})= {\mathrm {Fun}}^{\mathrm {L}}(\mathcal {S},\mathrm {Pr}^{\text {L}})$
.
$ {\mathrm {Biv}}^{\mathrm {L}}(\mathcal {S},\mathrm {Pr}^{\text {L}})= {\mathrm {Fun}}^{\mathrm {L}}(\mathcal {S},\mathrm {Pr}^{\text {L}})$
.
The functor
![]() $\mathcal {S}[-]\colon \mathcal {S} \to \mathrm {Pr}^{\text {L}}$
is a symmetric monoidal bivariant theory by Proposition 4.11(1), and hence by the universal property of the
$\mathcal {S}[-]\colon \mathcal {S} \to \mathrm {Pr}^{\text {L}}$
is a symmetric monoidal bivariant theory by Proposition 4.11(1), and hence by the universal property of the
![]() $(\infty ,2)$
-category
$(\infty ,2)$
-category
![]() $ {\mathrm {Span}}(\mathcal {S})$
uniquely extends to a symmetric monoidal 2-functor
$ {\mathrm {Span}}(\mathcal {S})$
uniquely extends to a symmetric monoidal 2-functor
![]() $\mathcal {S}[-]\colon {\mathrm {Span}}(\mathcal {S}) \to \mathrm {Pr}^{\text {L}}$
.
$\mathcal {S}[-]\colon {\mathrm {Span}}(\mathcal {S}) \to \mathrm {Pr}^{\text {L}}$
.
Proposition 4.39. The 2-functor
![]() $\mathcal {S}[-]\colon {\mathrm {Span}}(\mathcal {S}) \to \mathrm {Pr}^{\text {L}}$
is 2-fully-faithful, in the sense that it induces equivalences of mapping
$\mathcal {S}[-]\colon {\mathrm {Span}}(\mathcal {S}) \to \mathrm {Pr}^{\text {L}}$
is 2-fully-faithful, in the sense that it induces equivalences of mapping
![]() $\infty $
-categories
$\infty $
-categories
for all spaces
![]() $A,B \in \mathcal {S}$
. In particular, it induces an equivalence
$A,B \in \mathcal {S}$
. In particular, it induces an equivalence ![]() .
.
Proof. Consider the functor
called the ‘bivariant op-Yoneda functor’ in [Reference Macpherson53]. Here the functoriality in B is via post-composition, while the functoriality in A is via pullback. By [Reference Macpherson53, Corollary 3.7.5, Theorem 4.2.6], this is a bivariant theory and the induced 2-functor
![]() $ {\mathrm {Span}}(\mathcal {S}) \to {\mathrm {Biv}}(\mathcal {S},\mathrm {Cat}_{\infty })^{\mathrm {op}}$
is 2-fully faithful. Note that the bivariant op-Yoneda functor factors through the locally full sub-2-category
$ {\mathrm {Span}}(\mathcal {S}) \to {\mathrm {Biv}}(\mathcal {S},\mathrm {Cat}_{\infty })^{\mathrm {op}}$
is 2-fully faithful. Note that the bivariant op-Yoneda functor factors through the locally full sub-2-category
![]() $ {\mathrm {Biv}}^{\mathrm {L}}(\mathcal {S},\mathrm {Pr}^{\text {L}})^{\mathrm {op}}$
of
$ {\mathrm {Biv}}^{\mathrm {L}}(\mathcal {S},\mathrm {Pr}^{\text {L}})^{\mathrm {op}}$
of
![]() $ {\mathrm {Biv}}(\mathcal {S},\mathrm {Cat}_{\infty })^{\mathrm {op}}$
, and in particular, the map
$ {\mathrm {Biv}}(\mathcal {S},\mathrm {Cat}_{\infty })^{\mathrm {op}}$
, and in particular, the map
![]() $ {\mathrm {Span}}(\mathcal {S}) \to {\mathrm {Biv}}^{\mathrm { L}}(\mathcal {S},\mathrm {Pr}^{\text {L}})^{\mathrm {op}}$
is also 2-fully-faithful. By Lemma 4.38 and Lemma 4.36, the latter
$ {\mathrm {Span}}(\mathcal {S}) \to {\mathrm {Biv}}^{\mathrm { L}}(\mathcal {S},\mathrm {Pr}^{\text {L}})^{\mathrm {op}}$
is also 2-fully-faithful. By Lemma 4.38 and Lemma 4.36, the latter
![]() $(\infty ,2)$
-category is equivalent to
$(\infty ,2)$
-category is equivalent to
![]() $(\mathrm {Pr}^{\text {L}})^{\mathrm {op}}$
by evaluation at a point, and it follows that also the composite
$(\mathrm {Pr}^{\text {L}})^{\mathrm {op}}$
by evaluation at a point, and it follows that also the composite
is 2-fully faithful. Passing to opposites, we obtain a fully faithful embedding -
Spelling out what this composite is and using the natural equivalences
![]() $\mathcal {S}[A] \simeq \mathcal {S}^{A} \simeq \mathcal {S}_{/A}$
, one observes that it is the functor
$\mathcal {S}[A] \simeq \mathcal {S}^{A} \simeq \mathcal {S}_{/A}$
, one observes that it is the functor
![]() $\mathcal {S}[-]\colon {\mathrm {Span}}(\mathcal {S}) \to \mathrm {Pr}^{\text {L}}$
, which finishes the proof.
$\mathcal {S}[-]\colon {\mathrm {Span}}(\mathcal {S}) \to \mathrm {Pr}^{\text {L}}$
, which finishes the proof.
We now have the ingredients at hand to prove a coherent version of the equivalence ![]() .
.
Theorem 4.40. There is an equivalence
natural in the space
![]() $A\in \mathcal {S}$
, between the
$A\in \mathcal {S}$
, between the
![]() $\mathscr {C}$
-linear trace
$\mathscr {C}$
-linear trace
![]() $ {\mathrm {Tr}}_{\mathscr {C}}(\mathscr {C}[A])$
of
$ {\mathrm {Tr}}_{\mathscr {C}}(\mathscr {C}[A])$
of
![]() $\mathscr {C}[A]$
and the tensoring
$\mathscr {C}[A]$
and the tensoring ![]() of the monoidal unit
of the monoidal unit ![]() by the free loop space
by the free loop space
![]() $LA \in \mathcal {S}$
.
$LA \in \mathcal {S}$
.
Proof. Since the
![]() $\mathscr {C}$
-linear trace functor
$\mathscr {C}$
-linear trace functor
![]() $ {\mathrm {Tr}}_{\mathscr {C}}$
is natural in the variable
$ {\mathrm {Tr}}_{\mathscr {C}}$
is natural in the variable
![]() $\mathscr {C} \in {\mathrm {CAlg}}(\mathrm {Pr}^{\text {L}})$
, the symmetric monoidal colimit-preserving functor
$\mathscr {C} \in {\mathrm {CAlg}}(\mathrm {Pr}^{\text {L}})$
, the symmetric monoidal colimit-preserving functor ![]() gives rise to a commutative diagram
gives rise to a commutative diagram
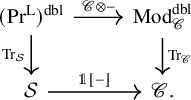
As
![]() $\mathscr {C}[A] \simeq \mathscr {C} \otimes \mathcal {S}[A]$
, it thus suffices to produce a natural equivalence of spaces
$\mathscr {C}[A] \simeq \mathscr {C} \otimes \mathcal {S}[A]$
, it thus suffices to produce a natural equivalence of spaces
Consider the functor
![]() $\mathcal {S}[-]\colon \mathcal {S} \to \mathrm {Pr}^{\text {L}}$
. By part (1) of Proposition 4.11, this functor is a symmetric monoidal bivariant theory and in particular it extends uniquely to a symmetric monoidal 2-functor
$\mathcal {S}[-]\colon \mathcal {S} \to \mathrm {Pr}^{\text {L}}$
. By part (1) of Proposition 4.11, this functor is a symmetric monoidal bivariant theory and in particular it extends uniquely to a symmetric monoidal 2-functor
![]() $\mathcal {S}[-]\colon {\mathrm {Span}}(\mathcal {S}) \to \mathrm {Pr}^{\text {L}}$
. We may now consider the following commutative diagram:
$\mathcal {S}[-]\colon {\mathrm {Span}}(\mathcal {S}) \to \mathrm {Pr}^{\text {L}}$
. We may now consider the following commutative diagram:

The left square commutes by Theorem 3.19. The middle square commutes by functoriality of the dimension functor, applied to the symmetric monoidal 2-functor
![]() $\mathcal {S}[-]\colon {\mathrm {Span}}(\mathcal {S}) \to \mathrm {Pr}^{\text {L}}$
. The right triangle commutes by definition. The functor
$\mathcal {S}[-]\colon {\mathrm {Span}}(\mathcal {S}) \to \mathrm {Pr}^{\text {L}}$
. The right triangle commutes by definition. The functor
![]() $i_{\mathcal {S}}\colon \mathcal {S} \to \Omega {\mathrm {Span}}(\mathcal {S})$
from Proposition 3.7 is an equivalence, and by Proposition 4.39 below also the functor
$i_{\mathcal {S}}\colon \mathcal {S} \to \Omega {\mathrm {Span}}(\mathcal {S})$
from Proposition 3.7 is an equivalence, and by Proposition 4.39 below also the functor
![]() $\Omega \mathcal {S}[-]\colon \Omega {\mathrm {Span}}(\mathcal {S}) \to \Omega \mathrm {Pr}^{\text {L}}$
is an equivalence. It follows that the bottom composite
$\Omega \mathcal {S}[-]\colon \Omega {\mathrm {Span}}(\mathcal {S}) \to \Omega \mathrm {Pr}^{\text {L}}$
is an equivalence. It follows that the bottom composite
![]() $\mathcal {S} \to \mathcal {S}$
is an equivalence. In particular, it is colimit preserving and hence given by
$\mathcal {S} \to \mathcal {S}$
is an equivalence. In particular, it is colimit preserving and hence given by
![]() $X\times (-)$
for some space X. Since the only space for which this functor is invertible is
$X\times (-)$
for some space X. Since the only space for which this functor is invertible is
![]() $X=\mathrm {pt}$
, we deduce that the bottom composite is homotopic to the identity on
$X=\mathrm {pt}$
, we deduce that the bottom composite is homotopic to the identity on
![]() $\mathcal {S}$
. Comparing the two outer paths in the diagram then gives the desired result.
$\mathcal {S}$
. Comparing the two outer paths in the diagram then gives the desired result.
Theorem 4.40 has the following immediate consequences:
Corollary 4.41. Let
![]() $f\colon A \to B$
be a map of spaces. Then applying the
$f\colon A \to B$
be a map of spaces. Then applying the
![]() $\mathscr {C}$
-linear trace functor
$\mathscr {C}$
-linear trace functor
![]() $ {\mathrm {Tr}}_{\mathscr {C}}$
to the internal left adjoint
$ {\mathrm {Tr}}_{\mathscr {C}}$
to the internal left adjoint
![]() $f_!\colon \mathscr {C}[A] \to \mathscr {C}[B]$
gives the map
$f_!\colon \mathscr {C}[A] \to \mathscr {C}[B]$
gives the map ![]() :
:
Corollary 4.42. For
![]() $(\mathscr {D},F) \in {\mathrm {Mod}}^{\mathrm {trl}}_{\mathscr {C}}$
and
$(\mathscr {D},F) \in {\mathrm {Mod}}^{\mathrm {trl}}_{\mathscr {C}}$
and
![]() $A \in \mathcal {S}$
, there is a natural equivalence
$A \in \mathcal {S}$
, there is a natural equivalence
Proof. By symmetric monoidality of
![]() $ {\mathrm {Tr}}_{\mathscr {C}}$
and the equivalence
$ {\mathrm {Tr}}_{\mathscr {C}}$
and the equivalence
![]() $(\mathscr {D},F)[A] \simeq (\mathscr {D},F) \otimes _{\mathscr {C}} \mathscr {C}[A]$
in
$(\mathscr {D},F)[A] \simeq (\mathscr {D},F) \otimes _{\mathscr {C}} \mathscr {C}[A]$
in
![]() $ {\mathrm {Mod}}^{\mathrm {trl}}_{\mathscr {C}}$
, this follows immediately from the natural equivalence
$ {\mathrm {Mod}}^{\mathrm {trl}}_{\mathscr {C}}$
, this follows immediately from the natural equivalence ![]() of Theorem 4.40.
of Theorem 4.40.
Corollary 4.43. For any space
![]() $A \in \mathcal {S}$
, the composite
$A \in \mathcal {S}$
, the composite
is the mate of the map ![]() induced by the inclusion of constant loops A into
induced by the inclusion of constant loops A into
![]() $LA$
.
$LA$
.
Proof. By Theorem 4.40 this composite is equivalent to the composite
The composite of the first two maps is the composition of the map
![]() $c\colon A \to LA$
and the equivalence
$c\colon A \to LA$
and the equivalence
![]() $LA \simeq {\mathrm {Map}}_{\mathcal {S}}(\mathrm {pt},LA)$
. From this, the description given in the statement of the corollary follows directly.
$LA \simeq {\mathrm {Map}}_{\mathcal {S}}(\mathrm {pt},LA)$
. From this, the description given in the statement of the corollary follows directly.
4.3.1 Traces of space-indexed families of maps
The functoriality of the
![]() $\mathscr {C}$
-linear trace functor
$\mathscr {C}$
-linear trace functor
![]() $ {\mathrm {Tr}}_{\mathscr {C}}$
is somewhat mysterious: although we gave an explicit description of what it does on objects and on morphisms, the higher coherences are not explicit due to the fact that
$ {\mathrm {Tr}}_{\mathscr {C}}$
is somewhat mysterious: although we gave an explicit description of what it does on objects and on morphisms, the higher coherences are not explicit due to the fact that
![]() $ {\mathrm {Tr}}_{\mathscr {C}}$
is defined by reduction to a universal example. In particular, given a family
$ {\mathrm {Tr}}_{\mathscr {C}}$
is defined by reduction to a universal example. In particular, given a family
![]() $\mathscr {D}_{\bullet }\colon A \to {\mathrm {Mod}}^{\mathrm {trl}}_{\mathscr {C}}$
indexed by some space A, the description we gave for
$\mathscr {D}_{\bullet }\colon A \to {\mathrm {Mod}}^{\mathrm {trl}}_{\mathscr {C}}$
indexed by some space A, the description we gave for
![]() $ {\mathrm {Tr}}_{\mathscr {C}}$
does not immediately provide a full description of the composite functor
$ {\mathrm {Tr}}_{\mathscr {C}}$
does not immediately provide a full description of the composite functor
![]() $ {\mathrm {Tr}}_{\mathscr {C}} \circ \mathscr {D}_{\bullet }\colon A \to \mathscr {C}$
. The goal of this subsection is to show that the situation improves when we try to compute the
$ {\mathrm {Tr}}_{\mathscr {C}} \circ \mathscr {D}_{\bullet }\colon A \to \mathscr {C}$
. The goal of this subsection is to show that the situation improves when we try to compute the
![]() $\mathscr {C}$
-linear traces of an A-indexed family of maps in
$\mathscr {C}$
-linear traces of an A-indexed family of maps in
![]() $ {\mathrm {Mod}}^{\mathrm {trl}}_{\mathscr {C}}$
with fixed source
$ {\mathrm {Mod}}^{\mathrm {trl}}_{\mathscr {C}}$
with fixed source
![]() $(\mathscr {D},F)$
and target
$(\mathscr {D},F)$
and target
![]() $(\mathscr {E},G)$
. More concretely, we have the following lemma:
$(\mathscr {E},G)$
. More concretely, we have the following lemma:
Lemma 4.44. For
![]() $(\mathscr {D},F), (\mathscr {E},G) \in {\mathrm {Mod}}^{\mathrm {trl}}_{\mathscr {C}}$
and
$(\mathscr {D},F), (\mathscr {E},G) \in {\mathrm {Mod}}^{\mathrm {trl}}_{\mathscr {C}}$
and
![]() $A \in \mathcal {S}$
, the following diagram commutes:
$A \in \mathcal {S}$
, the following diagram commutes:
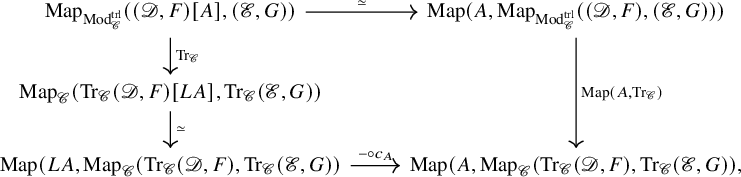
where
![]() $c\colon A \to LA$
is the inclusion of constant loops.
$c\colon A \to LA$
is the inclusion of constant loops.
Proof. By the Yoneda lemma, it suffices to prove this in the universal case, i.e. when
![]() $(\mathscr {E},G) = (\mathscr {D},F)[A]$
and only at the identity on
$(\mathscr {E},G) = (\mathscr {D},F)[A]$
and only at the identity on
![]() $(\mathscr {D},F)[A]$
. Expanding definitions, we thus need to show that the composite
$(\mathscr {D},F)[A]$
. Expanding definitions, we thus need to show that the composite
is the mate of the map
This follows directly from Corollary 4.43, using the equivalence
![]() $(\mathscr {D},F)[A] \simeq (\mathscr {D},F) \otimes _{\mathscr {C}} \mathscr {C}[A]$
in
$(\mathscr {D},F)[A] \simeq (\mathscr {D},F) \otimes _{\mathscr {C}} \mathscr {C}[A]$
in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}}$
and the symmetric monoidality of the functor
$ {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}}$
and the symmetric monoidality of the functor
![]() $ {\mathrm {Tr}}_{\mathscr {C}}$
.
$ {\mathrm {Tr}}_{\mathscr {C}}$
.
The content of Lemma 4.44 may more informally be described as follows. Let
![]() $(H,\alpha )\colon (\mathscr {D},F)[A] \to (\mathscr {E},G)$
be a morphism in
$(H,\alpha )\colon (\mathscr {D},F)[A] \to (\mathscr {E},G)$
be a morphism in
![]() $ {\mathrm {Mod}}^{\mathrm {trl}}_{\mathscr {C}}$
, and define for every
$ {\mathrm {Mod}}^{\mathrm {trl}}_{\mathscr {C}}$
, and define for every
![]() $a \in A$
the map
$a \in A$
the map
![]() $(H_a,\alpha _a)\colon (\mathscr {D},F) \to (\mathscr {E},G)$
in
$(H_a,\alpha _a)\colon (\mathscr {D},F) \to (\mathscr {E},G)$
in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}}$
by precomposition with
$ {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}}$
by precomposition with
![]() $a_!\colon (\mathscr {D},F) \to (\mathscr {D},F)[A]$
:
$a_!\colon (\mathscr {D},F) \to (\mathscr {D},F)[A]$
:
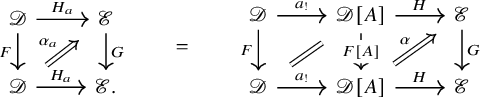
By applying
![]() $ {\mathrm {Tr}}_{\mathscr {C}}$
to the maps
$ {\mathrm {Tr}}_{\mathscr {C}}$
to the maps
![]() $(H_a,\alpha _a)$
, we get an A-indexed family of maps
$(H_a,\alpha _a)$
, we get an A-indexed family of maps
![]() $ {\mathrm {Tr}}_{\mathscr {C}}(\mathscr {D},F) \to {\mathrm {Tr}}_{\mathscr {C}}(\mathscr {E},G)$
in
$ {\mathrm {Tr}}_{\mathscr {C}}(\mathscr {D},F) \to {\mathrm {Tr}}_{\mathscr {C}}(\mathscr {E},G)$
in
![]() $\mathscr {C}$
, or equivalently a map
$\mathscr {C}$
, or equivalently a map
![]() $ {\mathrm {Tr}}_{\mathscr {C}}(\mathscr {D},F)[A] \to {\mathrm {Tr}}_{\mathscr {C}}(\mathscr {E},G)$
. Lemma 4.44 shows that this map is equivalent to the composite
$ {\mathrm {Tr}}_{\mathscr {C}}(\mathscr {D},F)[A] \to {\mathrm {Tr}}_{\mathscr {C}}(\mathscr {E},G)$
. Lemma 4.44 shows that this map is equivalent to the composite
where the first map is induced by the inclusion
![]() $c_A\colon A \to LA$
of the constant loops. In particular, we may compute the effect of
$c_A\colon A \to LA$
of the constant loops. In particular, we may compute the effect of
![]() $ {\mathrm {Tr}}_{\mathscr {C}}$
on the family of maps
$ {\mathrm {Tr}}_{\mathscr {C}}$
on the family of maps
![]() $(H_{a},\alpha _a)$
by computing the effect of
$(H_{a},\alpha _a)$
by computing the effect of
![]() $ {\mathrm {Tr}}_{\mathscr {C}}$
on the single map
$ {\mathrm {Tr}}_{\mathscr {C}}$
on the single map
![]() $(H,\alpha )\colon (\mathscr {D},F)[A] \to (\mathscr {E},G)$
.
$(H,\alpha )\colon (\mathscr {D},F)[A] \to (\mathscr {E},G)$
.
4.4 Hochschild homology as a
 $\mathscr {C}$
-linear trace
$\mathscr {C}$
-linear trace
One natural example of a dualizable object in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
is the
$ {\mathrm {Mod}}_{\mathscr {C}}$
is the
![]() $\infty $
-category
$\infty $
-category
![]() $ {\mathrm {RMod}}_R(\mathscr {C})$
of right modules in
$ {\mathrm {RMod}}_R(\mathscr {C})$
of right modules in
![]() $\mathscr {C}$
over an algebra
$\mathscr {C}$
over an algebra
![]() $R \in {\mathrm {Alg}}(\mathscr {C})$
. Its
$R \in {\mathrm {Alg}}(\mathscr {C})$
. Its
![]() $\mathscr {C}$
-linear trace
$\mathscr {C}$
-linear trace
![]() $ {\mathrm {Tr}}_{\mathscr {C}}( {\mathrm {RMod}}_R(\mathscr {C})) \in \mathscr {C}$
identifies with the more classically defined invariant known as the (topological) Hochschild homology of R. While this folklore identification will not be used in the rest of this article, we shall review it in detail for completeness.Footnote
12
$ {\mathrm {Tr}}_{\mathscr {C}}( {\mathrm {RMod}}_R(\mathscr {C})) \in \mathscr {C}$
identifies with the more classically defined invariant known as the (topological) Hochschild homology of R. While this folklore identification will not be used in the rest of this article, we shall review it in detail for completeness.Footnote
12
Definition 4.45. Let
![]() $R \in {\mathrm {Alg}}(\mathscr {C})$
be an associative algebra in
$R \in {\mathrm {Alg}}(\mathscr {C})$
be an associative algebra in
![]() $\mathscr {C}$
, and let M be an
$\mathscr {C}$
, and let M be an
![]() $(R,R)$
-bimodule. We define the Hochschild homology of the pair
$(R,R)$
-bimodule. We define the Hochschild homology of the pair
![]() $(R,M)$
as
$(R,M)$
as
where we regard R as a bimodule over itself via the left and right multiplication. The Hochschild homology of R is defined as
![]() $ {\mathrm {HH}}_{\mathscr {C}}(R) := {\mathrm {HH}}_{\mathscr {C}}(R,R)$
.
$ {\mathrm {HH}}_{\mathscr {C}}(R) := {\mathrm {HH}}_{\mathscr {C}}(R,R)$
.
Recall from [Reference Lurie51, Remark 4.8.4.8] that the
![]() $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
![]() $\infty $
-category
$\infty $
-category
![]() $ {\mathrm {RMod}}_R(\mathscr {C})$
of right R-modules is dualizable in
$ {\mathrm {RMod}}_R(\mathscr {C})$
of right R-modules is dualizable in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
, with dual given by
$ {\mathrm {Mod}}_{\mathscr {C}}$
, with dual given by
![]() $ {\mathrm {LMod}}_R(\mathscr {C})$
. For the identification of its
$ {\mathrm {LMod}}_R(\mathscr {C})$
. For the identification of its
![]() $\mathscr {C}$
-linear trace, we will need an explicit description of the evaluation and coevaluation maps for the duality data for
$\mathscr {C}$
-linear trace, we will need an explicit description of the evaluation and coevaluation maps for the duality data for
![]() $ {\mathrm {RMod}}_{R}(\mathscr {C})$
and
$ {\mathrm {RMod}}_{R}(\mathscr {C})$
and
![]() $ {\mathrm {LMod}}_R(\mathscr {C})$
. Alternatively, because of the equivalence
$ {\mathrm {LMod}}_R(\mathscr {C})$
. Alternatively, because of the equivalence
![]() $ {\mathrm {LMod}}_R(\mathscr {C}) \simeq {\mathrm {RMod}}_{R^{\mathrm {op}}}(\mathscr {C})$
, we may exhibit explicit duality data between
$ {\mathrm {LMod}}_R(\mathscr {C}) \simeq {\mathrm {RMod}}_{R^{\mathrm {op}}}(\mathscr {C})$
, we may exhibit explicit duality data between
![]() $ {\mathrm {RMod}}_R(\mathscr {C})$
and
$ {\mathrm {RMod}}_R(\mathscr {C})$
and
![]() $ {\mathrm {RMod}}_{R^{\mathrm {op}}}(\mathscr {C})$
. To this end, recall from [Reference Lurie51, Construction 4.6.3.7] that the
$ {\mathrm {RMod}}_{R^{\mathrm {op}}}(\mathscr {C})$
. To this end, recall from [Reference Lurie51, Construction 4.6.3.7] that the
![]() $(R,R)$
-bimodule R gives rise to an evaluation module
$(R,R)$
-bimodule R gives rise to an evaluation module
![]() $R^e \in {\mathrm {LMod}}_{R \otimes R^{\mathrm {op}}}(\mathscr {C})$
and a coevaluation module
$R^e \in {\mathrm {LMod}}_{R \otimes R^{\mathrm {op}}}(\mathscr {C})$
and a coevaluation module
![]() $R^c \in {\mathrm {RMod}}_{R \otimes R^{\mathrm {op}}}(\mathscr {C})$
.
$R^c \in {\mathrm {RMod}}_{R \otimes R^{\mathrm {op}}}(\mathscr {C})$
.
Lemma 4.46 [Reference Lurie51].
The composite
is the coevaluation of a duality datum in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
between
$ {\mathrm {Mod}}_{\mathscr {C}}$
between
![]() $ {\mathrm {RMod}}_{R}(\mathscr {C})$
and
$ {\mathrm {RMod}}_{R}(\mathscr {C})$
and
![]() $ {\mathrm {RMod}}_{R^{\mathrm {op}}}(\mathscr {C})$
. The evaluation is given by the composite
$ {\mathrm {RMod}}_{R^{\mathrm {op}}}(\mathscr {C})$
. The evaluation is given by the composite
Here, the first equivalence is an instance of [Reference Lurie51, Theorem 4.8.5.16(4)].
Proof. The two triangle identities are an immediate consequence of [Reference Lurie51, Proposition 4.6.3.12].
Using the above explicit identification of the duality data of the
![]() $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
![]() $\infty $
-category
$\infty $
-category
![]() $ {\mathrm {RMod}}_R(\mathscr {C})$
, we can now calculate that its
$ {\mathrm {RMod}}_R(\mathscr {C})$
, we can now calculate that its
![]() $\mathscr {C}$
-linear trace is the Hochschild homology of R.
$\mathscr {C}$
-linear trace is the Hochschild homology of R.
Proposition 4.47. Let
![]() $R \in {\mathrm {Alg}}(\mathscr {C})$
be an associative algebra in
$R \in {\mathrm {Alg}}(\mathscr {C})$
be an associative algebra in
![]() $\mathscr {C}$
, and let M be an
$\mathscr {C}$
, and let M be an
![]() $(R,R)$
-bimodule. Then there is an equivalence between the Hochschild homology of the pair
$(R,R)$
-bimodule. Then there is an equivalence between the Hochschild homology of the pair
![]() $(R,M)$
and the
$(R,M)$
and the
![]() $\mathscr {C}$
-linear trace of the
$\mathscr {C}$
-linear trace of the
![]() $\mathscr {C}$
-linear endofunctor
$\mathscr {C}$
-linear endofunctor
![]() $- \otimes _R M\colon {\mathrm {RMod}}_R(\mathscr {C}) \to {\mathrm {RMod}}_R(\mathscr {C})$
:
$- \otimes _R M\colon {\mathrm {RMod}}_R(\mathscr {C}) \to {\mathrm {RMod}}_R(\mathscr {C})$
:
In particular, there is an equivalence
Proof. Observe that the second statement is a special case of the first statement by taking
![]() $M = R$
, so we focus on the first statement. By definition of the trace, we have to compute the composite
$M = R$
, so we focus on the first statement. By definition of the trace, we have to compute the composite
Plugging in the evaluation and coevaluation maps described above, we see that this is given by the following composite:
where we abusively write M for the functor given by tensoring with M, and where
![]() $\boxtimes $
denotes the external tensor product defined in [Reference Lurie51, Notation 4.6.3.3]. The composite of the first two maps is classified by the right
$\boxtimes $
denotes the external tensor product defined in [Reference Lurie51, Notation 4.6.3.3]. The composite of the first two maps is classified by the right
![]() $(R \otimes R^{\mathrm {op}})$
-module
$(R \otimes R^{\mathrm {op}})$
-module
![]() $R^c \otimes _{R \otimes R^{\mathrm {op}}} (M \boxtimes R^{\mathrm {op}})$
, which is by definition precisely the image of M under the equivalence
$R^c \otimes _{R \otimes R^{\mathrm {op}}} (M \boxtimes R^{\mathrm {op}})$
, which is by definition precisely the image of M under the equivalence
![]() ${}_R\! {\mathrm {BMod}}_R(\mathscr {C}) \simeq {\mathrm {RMod}}_{R \otimes R^{\mathrm {op}}}(\mathscr {C})$
of [Reference Lurie51, Construction 4.6.3.9]. If we abusively denote this right
${}_R\! {\mathrm {BMod}}_R(\mathscr {C}) \simeq {\mathrm {RMod}}_{R \otimes R^{\mathrm {op}}}(\mathscr {C})$
of [Reference Lurie51, Construction 4.6.3.9]. If we abusively denote this right
![]() $(R \otimes R^{\mathrm {op}})$
-module again by M and similarly denote the left
$(R \otimes R^{\mathrm {op}})$
-module again by M and similarly denote the left
![]() $(R \otimes R^{\mathrm {op}})$
-module
$(R \otimes R^{\mathrm {op}})$
-module
![]() $R^e$
by R, we see that the above composite is given by the object
$R^e$
by R, we see that the above composite is given by the object
![]() $M \otimes _{R \otimes R^{\mathrm {op}}} R= {\mathrm {HH}}_{\mathscr {C}}(R,M)$
, as desired.
$M \otimes _{R \otimes R^{\mathrm {op}}} R= {\mathrm {HH}}_{\mathscr {C}}(R,M)$
, as desired.
Remark 4.48. The equivalence of Proposition 4.47 above, expressing Hochschild homology as a
![]() $\mathscr {C}$
-linear trace, is highly expected to be natural in the triple
$\mathscr {C}$
-linear trace, is highly expected to be natural in the triple
![]() $(\mathscr {C},R,M)$
. We emphasize that the above proof does not prove this stronger statement: as in the case of traces in
$(\mathscr {C},R,M)$
. We emphasize that the above proof does not prove this stronger statement: as in the case of traces in
![]() $(\infty ,2)$
-categories of spans, discussed in Section 3.2.1, the subtlety lies in making the above explicit duality data for
$(\infty ,2)$
-categories of spans, discussed in Section 3.2.1, the subtlety lies in making the above explicit duality data for
![]() $ {\mathrm {RMod}}_R(\mathscr {C})$
suitably natural in
$ {\mathrm {RMod}}_R(\mathscr {C})$
suitably natural in
![]() $\mathscr {C}$
and R. We will, however, not need this natural enhancement.
$\mathscr {C}$
and R. We will, however, not need this natural enhancement.
4.5 Free
 $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
 $\infty $
-categories as module categories
$\infty $
-categories as module categories
For a space A, we have seen that the free
![]() $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}[A]$
can be identified with the cofree
$\mathscr {C}[A]$
can be identified with the cofree
![]() $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}^A$
. In the case where A is a pointed connected space,
$\mathscr {C}^A$
. In the case where A is a pointed connected space,
![]() $\mathscr {C}[A]$
can also be identified with
$\mathscr {C}[A]$
can also be identified with ![]() , the
, the
![]() $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
![]() $\infty $
-category of modules in
$\infty $
-category of modules in
![]() $\mathscr {C}$
over the group algebra
$\mathscr {C}$
over the group algebra ![]() . We shall explain this in some detail to flesh out the rather strong naturality properties of this identification that will be required later on.
. We shall explain this in some detail to flesh out the rather strong naturality properties of this identification that will be required later on.
Recall from [Reference Lurie51, §4.8.5] the functor
which assigns to an algebra R in
![]() $\mathscr {C}$
the
$\mathscr {C}$
the
![]() $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
![]() $\infty $
-category
$\infty $
-category
![]() $ {\mathrm {RMod}}_R(\mathscr {C})$
of right R-modules in
$ {\mathrm {RMod}}_R(\mathscr {C})$
of right R-modules in
![]() $\mathscr {C}$
, pointed by R. This functor is fully faithful and admits a right adjoint ([Reference Lurie51, Theorem 4.8.5.11, Remark 4.8.5.12])
$\mathscr {C}$
, pointed by R. This functor is fully faithful and admits a right adjoint ([Reference Lurie51, Theorem 4.8.5.11, Remark 4.8.5.12])
which takes a
![]() $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {D}$
pointed by some
$\mathscr {D}$
pointed by some ![]() to the
to the
![]() $\mathscr {C}$
-object of endomorphisms of
$\mathscr {C}$
-object of endomorphisms of ![]() , viewed as an
, viewed as an
![]() $\mathbb {E}_1$
-algebra in
$\mathbb {E}_1$
-algebra in
![]() $\mathscr {C}$
.Footnote
13
$\mathscr {C}$
.Footnote
13
Lemma 4.49 (cf. [Reference Ben-Moshe, Carmeli, Schlank and Yanovski13, Proposition A.4]).
For a pointed connected space A, we have an equivalence
natural in both A and
![]() $\mathscr {C}$
.
$\mathscr {C}$
.
Proof. In light of the equivalence
![]() $\mathcal {S}_*^{\geq 1} \simeq \mathrm {Grp}(\mathcal {S})$
between pointed connected spaces and group objects in
$\mathcal {S}_*^{\geq 1} \simeq \mathrm {Grp}(\mathcal {S})$
between pointed connected spaces and group objects in
![]() $\mathcal {S}$
, we may equivalently produce a natural equivalence
$\mathcal {S}$
, we may equivalently produce a natural equivalence
for
![]() $G \in \mathrm {Grp}(\mathcal {S})$
. The canonical functors
$G \in \mathrm {Grp}(\mathcal {S})$
. The canonical functors ![]() and
and ![]() in
in
![]() $\mathrm {Pr}^{\text {L}}_{\mathcal {S}/}$
induce natural equivalences
$\mathrm {Pr}^{\text {L}}_{\mathcal {S}/}$
induce natural equivalences
in
![]() $( {\mathrm {Mod}}_{\mathscr {C}})_{\mathscr {C}/}$
; the first one since
$( {\mathrm {Mod}}_{\mathscr {C}})_{\mathscr {C}/}$
; the first one since
![]() $\mathscr {C} \otimes -$
preserves colimits and the second one by [Reference Lurie51, Theorem 4.8.4.6]. It thus remains to show that
$\mathscr {C} \otimes -$
preserves colimits and the second one by [Reference Lurie51, Theorem 4.8.4.6]. It thus remains to show that
![]() $\mathcal {S}[BG] \simeq {\mathrm {RMod}}_{G}(\mathcal {S})$
, or equivalently that
$\mathcal {S}[BG] \simeq {\mathrm {RMod}}_{G}(\mathcal {S})$
, or equivalently that
![]() $\mathcal {S}^{BG} \simeq {\mathrm {LMod}}_{G}(\mathcal {S})$
by passing to duals. Recalling from [Reference Lurie51, Notation 4.2.2.5] the
$\mathcal {S}^{BG} \simeq {\mathrm {LMod}}_{G}(\mathcal {S})$
by passing to duals. Recalling from [Reference Lurie51, Notation 4.2.2.5] the
![]() $\infty $
-category
$\infty $
-category
![]() $ {\mathrm {LMon}}_{G}(\mathcal {S})$
of spaces with a left action of G, we then have the following sequence of natural equivalences:
$ {\mathrm {LMon}}_{G}(\mathcal {S})$
of spaces with a left action of G, we then have the following sequence of natural equivalences:
here the equivalence on the left is straightening-unstraightening, the middle equivalence is [Reference Sati and Schreiber’62, Proposition 3.2.76] (see also [Reference Nikolaus, Schreiber and Stevenson56, 4.1]) and the equivalence on the right is [Reference Lurie51, Proposition 4.2.2.9].
Corollary 4.50. The following square naturally commutes:
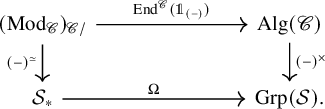
Here the right vertical functor sends an algebra
![]() $R \in {\mathrm {Alg}}(\mathscr {C})$
to the subgroup
$R \in {\mathrm {Alg}}(\mathscr {C})$
to the subgroup
![]() $R^{\times }$
of invertibles in the
$R^{\times }$
of invertibles in the
![]() $\mathbb {E}_1$
-monoid
$\mathbb {E}_1$
-monoid ![]() .
.
Proof. Passing to left adjoints, we may equivalently produce a commutative square of the form
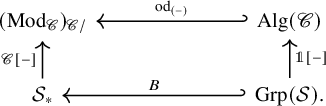
This is the content of Lemma 4.49.
Given an algebra
![]() $R\in {\mathrm {Alg}}(\mathscr {C})$
, a pointed map
$R\in {\mathrm {Alg}}(\mathscr {C})$
, a pointed map
![]() $\zeta \colon A \to {\mathrm {RMod}}_R(\mathscr {C})$
corresponds by adjunction to a pointed
$\zeta \colon A \to {\mathrm {RMod}}_R(\mathscr {C})$
corresponds by adjunction to a pointed
![]() $\mathscr {C}$
-linear functor
$\mathscr {C}$
-linear functor
![]() $\zeta _{\mathscr {C}} \colon \mathscr {C}[A] \to {\mathrm {RMod}}_R(\mathscr {C})$
, hence by the lemma to a pointed
$\zeta _{\mathscr {C}} \colon \mathscr {C}[A] \to {\mathrm {RMod}}_R(\mathscr {C})$
, hence by the lemma to a pointed
![]() $\mathscr {C}$
-linear functor
$\mathscr {C}$
-linear functor ![]() . This can be described in terms of the group map
. This can be described in terms of the group map
![]() $\Omega \zeta \colon \Omega A \to \Omega {\mathrm {RMod}}_R(\mathscr {C})$
, which under the equivalence
$\Omega \zeta \colon \Omega A \to \Omega {\mathrm {RMod}}_R(\mathscr {C})$
, which under the equivalence
corresponds to an algebra map ![]() .
.
Lemma 4.51. The composite
is given by extension of scalars along ![]() .
.
Proof. Since the functoriality of
![]() $ {\mathrm {RMod}}_{(-)}(\mathscr {C})$
is given by extension of scalars, this follows from a straightforward diagram chase in the above commutative square of adjunctions.
$ {\mathrm {RMod}}_{(-)}(\mathscr {C})$
is given by extension of scalars, this follows from a straightforward diagram chase in the above commutative square of adjunctions.
Remark 4.52. Let A be a pointed connected space. Combining Proposition 4.47, Lemma 4.49 and Theorem 4.40, we get a chain of equivalences
The resulting identification of the Hochschild homology of ![]() with the free loop spac
with the free loop spac ![]() is well-known among experts, and is usually stated and proved in terms of the cyclic bar construction. For example, when
is well-known among experts, and is usually stated and proved in terms of the cyclic bar construction. For example, when
![]() $\mathscr {C}$
is the
$\mathscr {C}$
is the
![]() $\infty $
-category of spectra, this is [Reference Nikolaus and Scholze55, Corollary IV.3.3]. For earlier references, one can consult [Reference Bökstedt, Hsiang and Madsen17, Proposition 3.7], or [Reference Goodwillie30, Lemma V.1.3] in the integral case.
$\infty $
-category of spectra, this is [Reference Nikolaus and Scholze55, Corollary IV.3.3]. For earlier references, one can consult [Reference Bökstedt, Hsiang and Madsen17, Proposition 3.7], or [Reference Goodwillie30, Lemma V.1.3] in the integral case.
5 Traces and characters via categorified traces
Let
![]() $\mathscr {C}$
be a presentably symmetric monoidal
$\mathscr {C}$
be a presentably symmetric monoidal
![]() $\infty $
-category, taken to be fixed. In this section, we will study the interaction between (generalized) traces in
$\infty $
-category, taken to be fixed. In this section, we will study the interaction between (generalized) traces in
![]() $\mathscr {C}$
and categorified traces in the
$\mathscr {C}$
and categorified traces in the
![]() $(\infty ,2)$
-category
$(\infty ,2)$
-category
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
of
$ {\mathrm {Mod}}_{\mathscr {C}}$
of
![]() $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
![]() $\infty $
-categories, studied in the previous section.
$\infty $
-categories, studied in the previous section.
The main ingredient for this interaction is the fact that one can express generalized traces in
![]() $\mathscr {C}$
in terms of
$\mathscr {C}$
in terms of
![]() $\mathscr {C}$
-linear traces, so let us start by explaining how this goes. Consider objects X, Y and Z of
$\mathscr {C}$
-linear traces, so let us start by explaining how this goes. Consider objects X, Y and Z of
![]() $\mathscr {C}$
, where X is dualizable, and let
$\mathscr {C}$
, where X is dualizable, and let
![]() $f\colon Z \otimes X \to X \otimes Y$
be a generalized endomorphism. Forming the tensor product with X gives a functor
$f\colon Z \otimes X \to X \otimes Y$
be a generalized endomorphism. Forming the tensor product with X gives a functor
![]() $X\colon \mathscr {C} \to \mathscr {C}$
, which by dualizability of X is an internal left adjoint, see Observation 4.31. Similarly we obtain
$X\colon \mathscr {C} \to \mathscr {C}$
, which by dualizability of X is an internal left adjoint, see Observation 4.31. Similarly we obtain
![]() $Y\colon \mathscr {C} \to \mathscr {C}$
and
$Y\colon \mathscr {C} \to \mathscr {C}$
and
![]() $Z\colon \mathscr {C} \to \mathscr {C}$
, and the morphism f corresponds to a
$Z\colon \mathscr {C} \to \mathscr {C}$
, and the morphism f corresponds to a
![]() $\mathscr {C}$
-linear natural transformation fitting in the following diagram:
$\mathscr {C}$
-linear natural transformation fitting in the following diagram:
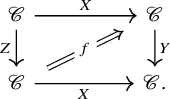
We denote by
![]() $(X,f)\colon (\mathscr {C},Z) \to (\mathscr {C},Y)$
the resulting morphism in
$(X,f)\colon (\mathscr {C},Z) \to (\mathscr {C},Y)$
the resulting morphism in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}}$
. Applying the
$ {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}}$
. Applying the
![]() $\mathscr {C}$
-linear trace functor to this map provides a morphism of the form
$\mathscr {C}$
-linear trace functor to this map provides a morphism of the form
here we use the identifications
![]() $ {\mathrm {Tr}}_{\mathscr {C}}(\mathscr {C},Z) = Z$
and
$ {\mathrm {Tr}}_{\mathscr {C}}(\mathscr {C},Z) = Z$
and
![]() $ {\mathrm {Tr}}_{\mathscr {C}}(\mathscr {C},Y) = Y$
of Example 4.2, which we will leave implicit from now on. The next lemma shows that this morphism is given by the generalized trace
$ {\mathrm {Tr}}_{\mathscr {C}}(\mathscr {C},Y) = Y$
of Example 4.2, which we will leave implicit from now on. The next lemma shows that this morphism is given by the generalized trace
![]() $ {\mathrm {tr}}(f \,\vert \, X)\colon Z \to Y$
of f.
$ {\mathrm {tr}}(f \,\vert \, X)\colon Z \to Y$
of f.
Lemma 5.1 (Trace comparison lemma, pointwise version).
Let X, Y and Z be objects of
![]() $\mathscr {C}$
, where X is dualizable, and let
$\mathscr {C}$
, where X is dualizable, and let
![]() $f\colon Z \otimes X \to X \otimes Y$
be a generalized endomorphism of X in
$f\colon Z \otimes X \to X \otimes Y$
be a generalized endomorphism of X in
![]() $\mathscr {C}$
. Then there is an equivalence
$\mathscr {C}$
. Then there is an equivalence
Proof. We compute
![]() $ {\mathrm {Tr}}_{\mathscr {C}}(X,f)$
using the description of the functoriality of
$ {\mathrm {Tr}}_{\mathscr {C}}(X,f)$
using the description of the functoriality of
![]() $ {\mathrm {Tr}}_{\mathscr {C}}$
from the diagram (4) on page 31. Since
$ {\mathrm {Tr}}_{\mathscr {C}}$
from the diagram (4) on page 31. Since
![]() $\mathscr {C}$
is the monoidal unit of
$\mathscr {C}$
is the monoidal unit of
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
, it is in particular self-dual, and we get
$ {\mathrm {Mod}}_{\mathscr {C}}$
, it is in particular self-dual, and we get
![]() $\mathscr {C} \otimes _{\mathscr {C}} \mathscr {C}^\vee \simeq \mathscr {C}$
. The right adjoint of
$\mathscr {C} \otimes _{\mathscr {C}} \mathscr {C}^\vee \simeq \mathscr {C}$
. The right adjoint of
![]() $X\colon \mathscr {C} \to \mathscr {C}$
is
$X\colon \mathscr {C} \to \mathscr {C}$
is
![]() $X^{\vee }\colon \mathscr {C} \to \mathscr {C}$
, whose
$X^{\vee }\colon \mathscr {C} \to \mathscr {C}$
, whose
![]() $\mathscr {C}$
-linear dual is again
$\mathscr {C}$
-linear dual is again
![]() $X^{\vee }\colon \mathscr {C} \to \mathscr {C}$
. It follows that the map
$X^{\vee }\colon \mathscr {C} \to \mathscr {C}$
. It follows that the map
![]() $ {\mathrm {Tr}}_{\mathscr {C}}(X,f)\colon Z \to Y$
is given by evaluating the following composite transformation at
$ {\mathrm {Tr}}_{\mathscr {C}}(X,f)\colon Z \to Y$
is given by evaluating the following composite transformation at ![]() :
:
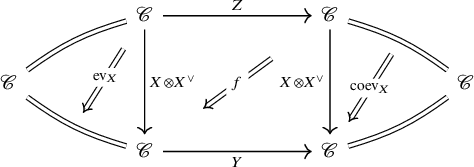
This is precisely the definition of the generalized trace
![]() $ {\mathrm {tr}}(f \,\vert \, X)\colon Z \to Y$
of f.
$ {\mathrm {tr}}(f \,\vert \, X)\colon Z \to Y$
of f.
The goal of this section is to exploit the above interaction to set up a generalized character theory to study these generalized traces in families indexed by spaces. Specifically, given an A-indexed family of generalized endomorphisms
we will associate a generalized character ![]() , encoding the generalized traces of twists of f by free loops in A. These generalized characters are the main object of study of this section, and of the entire article.
, encoding the generalized traces of twists of f by free loops in A. These generalized characters are the main object of study of this section, and of the entire article.
This section is organized as follows. We start in Section 5.1 with the definition of the generalized character ![]() , and prove an explicit description of it in terms of generalized traces of twists of f. Showing that the various pointwise descriptions we give are in fact natural equivalences is a bit subtle, and will be discussed in Section 5.2. In Section 5.3, we conclude the study of these characters with explicit formulas for induced and restricted characters.
, and prove an explicit description of it in terms of generalized traces of twists of f. Showing that the various pointwise descriptions we give are in fact natural equivalences is a bit subtle, and will be discussed in Section 5.2. In Section 5.3, we conclude the study of these characters with explicit formulas for induced and restricted characters.
In Section 5.4, we demonstrate another use of categorification to deduce the additivity of generalized traces from exactness properties of the
![]() $\mathscr {C}$
-linear trace functor
$\mathscr {C}$
-linear trace functor
![]() $ {\mathrm {Tr}}_{\mathscr {C}}$
. This final subsection is independent of first three subsections, in that it does not use our generalized character theory.
$ {\mathrm {Tr}}_{\mathscr {C}}$
. This final subsection is independent of first three subsections, in that it does not use our generalized character theory.
5.1 Generalized characters
Let G be a finite group, and let V be a finite-dimensional complex G-representation. The character
![]() $\chi _V\colon G \to \mathbb {C}$
of V is the function which assigns to every group element
$\chi _V\colon G \to \mathbb {C}$
of V is the function which assigns to every group element
![]() $g \in G$
the trace of the action map
$g \in G$
the trace of the action map
![]() $g\colon V \to V$
. The character of V is a class function: for two conjugate group elements g and
$g\colon V \to V$
. The character of V is a class function: for two conjugate group elements g and
![]() $g'$
, we have
$g'$
, we have
![]() $\chi _V(g) = \chi _V(g')$
. If we let
$\chi _V(g) = \chi _V(g')$
. If we let
![]() $G/\mathrm {conj}$
denote the set of conjugacy classes, it is thus natural to regard the character of V as a function
$G/\mathrm {conj}$
denote the set of conjugacy classes, it is thus natural to regard the character of V as a function
In this subsection, we will generalize the definition of characters in the following three ways:
-
(1) The category
 $\mathrm {Vect}_{\mathbb {C}}$
of complex vector spaces gets replaced by an arbitrary presentably symmetric monoidal
$\mathrm {Vect}_{\mathbb {C}}$
of complex vector spaces gets replaced by an arbitrary presentably symmetric monoidal
 $\infty $
-category
$\infty $
-category
 $\mathscr {C}$
, from now on taken to be fixed;
$\mathscr {C}$
, from now on taken to be fixed; -
(2) Instead of G-equivariant objects, regarded as local systems on the classifying space
 $BG$
, we will work with local systems on an arbitrary space A.
$BG$
, we will work with local systems on an arbitrary space A. -
(3) Rather than studying the character of an object, we will study the character associated to a generalized endomorphism of an object.
Taking inspiration from Lemma 5.1, our notion of generalized character map will be defined as the
![]() $\mathscr {C}$
-linear trace of a suitable map in
$\mathscr {C}$
-linear trace of a suitable map in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}}$
.
$ {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}}$
.
Construction 5.2. Assume given a space A, a dualizable object
![]() $X \in \mathscr {C}^A$
, and a generalized endomorphism of X in
$X \in \mathscr {C}^A$
, and a generalized endomorphism of X in
![]() $\mathscr {C}^A$
of the form
$\mathscr {C}^A$
of the form
![]() $f\colon X \to X \otimes A^*Y$
for some object
$f\colon X \to X \otimes A^*Y$
for some object
![]() $Y \in \mathscr {C}$
. We denote by
$Y \in \mathscr {C}$
. We denote by
![]() $(X,f)\colon \mathscr {C}[A] \to (\mathscr {C},Y)$
the map in
$(X,f)\colon \mathscr {C}[A] \to (\mathscr {C},Y)$
the map in
![]() $ {\mathrm {Mod}}^{\mathrm {trl}}_{\mathscr {C}}$
presented by the following diagram:
$ {\mathrm {Mod}}^{\mathrm {trl}}_{\mathscr {C}}$
presented by the following diagram:
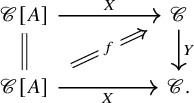
Here we regard X as a
![]() $\mathscr {C}$
-linear functor
$\mathscr {C}$
-linear functor
![]() $X\colon \mathscr {C}[A] \to \mathscr {C}$
using the equivalence
$X\colon \mathscr {C}[A] \to \mathscr {C}$
using the equivalence
![]() $ {\mathrm {Fun}}_{\mathscr {C}}(\mathscr {C}[A],\mathscr {C}) \simeq \mathscr {C}^A$
of Lemma 4.9, and we similarly regard f as a
$ {\mathrm {Fun}}_{\mathscr {C}}(\mathscr {C}[A],\mathscr {C}) \simeq \mathscr {C}^A$
of Lemma 4.9, and we similarly regard f as a
![]() $\mathscr {C}$
-linear transformation. Since X is pointwise dualizable, the functor
$\mathscr {C}$
-linear transformation. Since X is pointwise dualizable, the functor
![]() $X\colon \mathscr {C}[A] \to \mathscr {C}$
is an internal left adjoint by Corollary 4.32, and thus this diagram is indeed a morphism in
$X\colon \mathscr {C}[A] \to \mathscr {C}$
is an internal left adjoint by Corollary 4.32, and thus this diagram is indeed a morphism in
![]() $ {\mathrm {Mod}}^{\mathrm {trl}}_{\mathscr {C}}$
by Corollary 2.21.
$ {\mathrm {Mod}}^{\mathrm {trl}}_{\mathscr {C}}$
by Corollary 2.21.
The generalized character of f is obtained by applying the
![]() $\mathscr {C}$
-linear trace functor to the map
$\mathscr {C}$
-linear trace functor to the map
![]() $(X,f)\colon \mathscr {C}[A] \to (\mathscr {C},Y)$
.
$(X,f)\colon \mathscr {C}[A] \to (\mathscr {C},Y)$
.
Definition 5.3. Let A be a space,
![]() $X \in \mathscr {C}^A$
a local system of dualizable objects,
$X \in \mathscr {C}^A$
a local system of dualizable objects,
![]() $Y \in \mathscr {C}$
an object and
$Y \in \mathscr {C}$
an object and
![]() $f\colon X \to X \otimes A^*Y$
a morphism in
$f\colon X \to X \otimes A^*Y$
a morphism in
![]() $\mathscr {C}^A$
. We define the generalized character
$\mathscr {C}^A$
. We define the generalized character ![]() of f to be the map
of f to be the map
We will sometimes abuse notation by identifying it with its mate
When ![]() and
and
![]() $f=\mathrm {id}_X$
, we will write
$f=\mathrm {id}_X$
, we will write
![]() $\chi _X$
for
$\chi _X$
for
![]() $\chi _f$
.
$\chi _f$
.
Example 5.4. When
![]() $A = \mathrm {pt}$
, the data of f is a generalized endomorphism
$A = \mathrm {pt}$
, the data of f is a generalized endomorphism
![]() $f\colon X \to X \otimes Y$
in
$f\colon X \to X \otimes Y$
in
![]() $\mathscr {C}$
, and the character
$\mathscr {C}$
, and the character
![]() $\chi _f$
is just the generalized trace
$\chi _f$
is just the generalized trace ![]() by Lemma 5.1.
by Lemma 5.1.
Example 5.5 (Characters in representation theory).
When A is the classifying space
![]() $BG$
of a finite group G and
$BG$
of a finite group G and
![]() $\mathscr {C}$
is the (ordinary) category
$\mathscr {C}$
is the (ordinary) category
![]() $\mathrm {Vect}_{\mathbb {C}}$
of complex vector spaces, the data of X is that of a finite-dimensional complex G-representation V. Since there is an isomorphism of complex vector spaces
$\mathrm {Vect}_{\mathbb {C}}$
of complex vector spaces, the data of X is that of a finite-dimensional complex G-representation V. Since there is an isomorphism of complex vector spaces
the generalized character map
![]() $\chi _V\colon \mathbb {C}[LBG] \to \mathbb {C}$
may be identified with a function
$\chi _V\colon \mathbb {C}[LBG] \to \mathbb {C}$
may be identified with a function
We shall see in Corollary 5.8 that this is precisely the ordinary character of the G-representation V.
The goal of the remainder of this subsection is to give an explicit formula for the generalized character
![]() $\chi _f$
in terms of generalized traces. Concretely, we shall show that its value
$\chi _f$
in terms of generalized traces. Concretely, we shall show that its value ![]() on a free loop
on a free loop
![]() $\gamma \in LA$
is given by the following generalized trace:
$\gamma \in LA$
is given by the following generalized trace:
Here we let
![]() $a := \gamma (\ast )$
denote the basepoint of
$a := \gamma (\ast )$
denote the basepoint of
![]() $\gamma $
, and
$\gamma $
, and
![]() $\gamma \colon X_a \to X_a$
denotes the automorphism of
$\gamma \colon X_a \to X_a$
denotes the automorphism of
![]() $X_a$
induced by applying the functor
$X_a$
induced by applying the functor
![]() $X\colon A \to \mathscr {C}$
to the automorphism
$X\colon A \to \mathscr {C}$
to the automorphism ![]() in A.
in A.
The main ingredient in the proof of this character formula is the following lemma:
Lemma 5.6 (Loop indicator lemma, pointwise version).
Consider a free loop
![]() $\gamma \in LA$
with basepoint
$\gamma \in LA$
with basepoint
![]() $a := \gamma (\ast )$
, and consider the morphism
$a := \gamma (\ast )$
, and consider the morphism
![]() $(a_!,\gamma _!)\colon \mathscr {C} \to \mathscr {C}[A]$
in
$(a_!,\gamma _!)\colon \mathscr {C} \to \mathscr {C}[A]$
in
![]() $ {\mathrm {Mod}}^{\mathrm {trl}}_{\mathscr {C}}$
given by
$ {\mathrm {Mod}}^{\mathrm {trl}}_{\mathscr {C}}$
given by
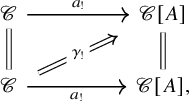
where
![]() $\gamma $
is regarded as a self-homotopy of the map
$\gamma $
is regarded as a self-homotopy of the map
![]() $a\colon \mathrm {pt} \to A$
. Then the
$a\colon \mathrm {pt} \to A$
. Then the
![]() $\mathscr {C}$
-linear trace
$\mathscr {C}$
-linear trace ![]() is homotopic to the map
is homotopic to the map ![]() induced from the map
induced from the map ![]() :
:
In other words, the map ![]() can be thought of as the “Dirac measure” supported at the loop
can be thought of as the “Dirac measure” supported at the loop
![]() $\gamma \in LA$
.
$\gamma \in LA$
.
Proof. By Proposition 4.11, the functor
![]() $\mathscr {C}[-]\colon \mathcal {S} \to {\mathrm {Mod}}_{\mathscr {C}}$
is a symmetric monoidal bivariant theory, and hence uniquely extends to a symmetric monoidal functor
$\mathscr {C}[-]\colon \mathcal {S} \to {\mathrm {Mod}}_{\mathscr {C}}$
is a symmetric monoidal bivariant theory, and hence uniquely extends to a symmetric monoidal functor
![]() $ {\mathrm {Span}}(\mathcal {S}) \to {\mathrm {Mod}}_{\mathscr {C}}$
. Since the formation of the categorified trace functor is manifestly natural in symmetric monoidal functors, the claim for
$ {\mathrm {Span}}(\mathcal {S}) \to {\mathrm {Mod}}_{\mathscr {C}}$
. Since the formation of the categorified trace functor is manifestly natural in symmetric monoidal functors, the claim for
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
follows from the analogous statement in the
$ {\mathrm {Mod}}_{\mathscr {C}}$
follows from the analogous statement in the
![]() $(\infty ,2)$
-category
$(\infty ,2)$
-category
![]() $ {\mathrm {Span}}(\mathcal {S})$
. It thus suffices to show that applying the trace functor to the morphism
$ {\mathrm {Span}}(\mathcal {S})$
. It thus suffices to show that applying the trace functor to the morphism
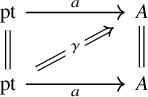
in
![]() $ {\mathrm {Span}}(\mathcal {S})^{\mathrm {trl}}$
yields the map
$ {\mathrm {Span}}(\mathcal {S})^{\mathrm {trl}}$
yields the map
![]() $\gamma \colon \mathrm {pt} \to LA$
in
$\gamma \colon \mathrm {pt} \to LA$
in
![]() $\Omega {\mathrm {Span}}(\mathcal {S}) \simeq \mathcal {S}$
.
$\Omega {\mathrm {Span}}(\mathcal {S}) \simeq \mathcal {S}$
.
To this end, recall from Lemma 3.8 that A is self-dual in
![]() $ {\mathrm {Span}}(\mathcal {S})$
with evaluation and coevaluation maps given by
$ {\mathrm {Span}}(\mathcal {S})$
with evaluation and coevaluation maps given by
We can now compute
![]() $ {\mathrm {Tr}}_{ {\mathrm {Span}}(\mathcal {S})}(a;\gamma )$
by substituting these evaluation and coevaluation maps into the diagram (2), which in our case assumes the form
$ {\mathrm {Tr}}_{ {\mathrm {Span}}(\mathcal {S})}(a;\gamma )$
by substituting these evaluation and coevaluation maps into the diagram (2), which in our case assumes the form
Here we identify objects and morphisms in
![]() $\mathcal {S}$
with their images under the inclusion
$\mathcal {S}$
with their images under the inclusion
![]() $h_{\mathcal {S}}\colon \mathcal {S} \hookrightarrow {\mathrm {Span}}(\mathcal {S})$
, and given a morphism
$h_{\mathcal {S}}\colon \mathcal {S} \hookrightarrow {\mathrm {Span}}(\mathcal {S})$
, and given a morphism
![]() $f\colon A \to B$
of spaces, we denote its right adjoint in
$f\colon A \to B$
of spaces, we denote its right adjoint in
![]() $ {\mathrm {Span}}(\mathcal {S})$
by
$ {\mathrm {Span}}(\mathcal {S})$
by
![]() $f^r\colon B \to A$
, as in Lemma 3.9. We can now explicitly identify each of the natural transformations in this diagram as a morphism in a suitable over-category of a space:
$f^r\colon B \to A$
, as in Lemma 3.9. We can now explicitly identify each of the natural transformations in this diagram as a morphism in a suitable over-category of a space:
-
(1) By the construction of the unit
 $2$
-morphism
$2$
-morphism
 $u\colon \mathrm {id}_{\mathrm {pt}} \to a^r \circ a$
, it corresponds via the equivalence to the map of spaces
$u\colon \mathrm {id}_{\mathrm {pt}} \to a^r \circ a$
, it corresponds via the equivalence to the map of spaces $$\begin{align*}{\mathrm{Hom}}_{{\mathrm{Span}}(\mathcal{S})}(\mathrm{pt},\mathrm{pt}) \simeq \mathcal{S} \end{align*}$$
$$\begin{align*}{\mathrm{Hom}}_{{\mathrm{Span}}(\mathcal{S})}(\mathrm{pt},\mathrm{pt}) \simeq \mathcal{S} \end{align*}$$
 $\mathrm {pt} \to \mathrm {pt} \times _A \mathrm {pt}$
classified by the square By definition,
$\mathrm {pt} \to \mathrm {pt} \times _A \mathrm {pt}$
classified by the square By definition,
 $\Omega _a A = \mathrm {pt} \times _A \mathrm {pt}$
, and the above square classifies the constant loop map
$\Omega _a A = \mathrm {pt} \times _A \mathrm {pt}$
, and the above square classifies the constant loop map
 $c_a \colon \mathrm {pt} \to \Omega _a A$
.
$c_a \colon \mathrm {pt} \to \Omega _a A$
.
-
(2) The
 $2$
-morphism
$2$
-morphism
 $\gamma \times a\colon (a,\mathrm {id})\circ a \to (\mathrm {id},a)\circ a$
corresponds via the equivalence to the automorphism of the map
$\gamma \times a\colon (a,\mathrm {id})\circ a \to (\mathrm {id},a)\circ a$
corresponds via the equivalence to the automorphism of the map $$\begin{align*}{\mathrm{Hom}}_{{\mathrm{Span}}(\mathcal{S})}(\mathrm{pt},A\times A) \simeq \mathcal{S}_{/A\times A} \end{align*}$$
$$\begin{align*}{\mathrm{Hom}}_{{\mathrm{Span}}(\mathcal{S})}(\mathrm{pt},A\times A) \simeq \mathcal{S}_{/A\times A} \end{align*}$$
 $a\times a \colon \mathrm {pt} \to A\times A$
given by applying
$a\times a \colon \mathrm {pt} \to A\times A$
given by applying
 $\gamma $
to the first coordinate. Composing it from the right with the evaluation map
$\gamma $
to the first coordinate. Composing it from the right with the evaluation map
 $A\times A \to \mathrm {pt}$
in
$A\times A \to \mathrm {pt}$
in
 $ {\mathrm {Span}}(\mathcal {S})$
amounts to pulling it back along the diagonal map
$ {\mathrm {Span}}(\mathcal {S})$
amounts to pulling it back along the diagonal map
 $\Delta \colon A\to A\times A$
and then applying the forgetful functor
$\Delta \colon A\to A\times A$
and then applying the forgetful functor
 $\mathcal {S}_{/A} \to \mathcal {S}$
. The space
$\mathcal {S}_{/A} \to \mathcal {S}$
. The space
 $\mathrm {pt} \times _{A\times A} A$
identifies with
$\mathrm {pt} \times _{A\times A} A$
identifies with
 $\Omega _a A$
, and the pullback of
$\Omega _a A$
, and the pullback of
 $(\gamma ,a)$
along
$(\gamma ,a)$
along
 $\Delta \colon A\to A\times A$
corresponds via this identification to the map
$\Delta \colon A\to A\times A$
corresponds via this identification to the map
 $\gamma \star (-)\colon \Omega _a A \to \Omega _a A$
of concatenation with
$\gamma \star (-)\colon \Omega _a A \to \Omega _a A$
of concatenation with
 $\gamma $
.
$\gamma $
.
-
(3) The
 $2$
-morphism
$2$
-morphism
 $c\times \mathrm {id} \colon (a,\mathrm {id})\circ (a,\mathrm {id})^r \to \mathrm {id}_{A\times A}$
corresponds via the equivalence to the commutative triangle
$c\times \mathrm {id} \colon (a,\mathrm {id})\circ (a,\mathrm {id})^r \to \mathrm {id}_{A\times A}$
corresponds via the equivalence to the commutative triangle $$\begin{align*}{\mathrm{Hom}}_{{\mathrm{Span}}(\mathcal{S})}(A\times A, A\times A) \simeq \mathcal{S}_{/A\times A \times A\times A} \end{align*}$$
regarded as a morphism in the over-category of
$$\begin{align*}{\mathrm{Hom}}_{{\mathrm{Span}}(\mathcal{S})}(A\times A, A\times A) \simeq \mathcal{S}_{/A\times A \times A\times A} \end{align*}$$
regarded as a morphism in the over-category of
 $A\times A \times A\times A$
. Precomposing it with the evaluation of A and post-composing with the coevaluation of A amounts to pulling it back along the map
$A\times A \times A\times A$
. Precomposing it with the evaluation of A and post-composing with the coevaluation of A amounts to pulling it back along the map
 $\Delta _A\times \Delta _A \colon A\times A \to A\times A \times A\times A$
and then applying the forgetful functor
$\Delta _A\times \Delta _A \colon A\times A \to A\times A \times A\times A$
and then applying the forgetful functor
 $\mathcal {S}_{/A\times A} \to \mathcal {S}$
. Now, pulling back the morphism
$\mathcal {S}_{/A\times A} \to \mathcal {S}$
. Now, pulling back the morphism
 $(a,\mathrm {id}_A, a, \mathrm {id}_A)$
along
$(a,\mathrm {id}_A, a, \mathrm {id}_A)$
along
 $\Delta _A \times \Delta _A$
gives the space
$\Delta _A \times \Delta _A$
gives the space
 $\Omega _a A$
, with a certain map to
$\Omega _a A$
, with a certain map to
 $A\times A$
that we then forget. Pulling back the map
$A\times A$
that we then forget. Pulling back the map
 $\Delta _{A\times A}$
along
$\Delta _{A\times A}$
along
 $\Delta _A \times \Delta _A$
gives the space
$\Delta _A \times \Delta _A$
gives the space
 $LA$
, again with a map to
$LA$
, again with a map to
 $A\times A$
that we forget. Finally, via these identifications, the map
$A\times A$
that we forget. Finally, via these identifications, the map
 $(a,\mathrm {id}_A)$
pulls back to the map
$(a,\mathrm {id}_A)$
pulls back to the map
 $\Omega _a A \to LA$
embedding the based loops at A inside the space of all free loops.
$\Omega _a A \to LA$
embedding the based loops at A inside the space of all free loops.
We thus deduce that the trace
![]() $ {\mathrm {Tr}}_{ {\mathrm {Span}}(\mathcal {S})}(a;\gamma ) $
is given by the composition
$ {\mathrm {Tr}}_{ {\mathrm {Span}}(\mathcal {S})}(a;\gamma ) $
is given by the composition
But this composition is clearly given by
![]() $\gamma \colon \mathrm {pt} \to LA$
, finishing the proof.
$\gamma \colon \mathrm {pt} \to LA$
, finishing the proof.
We may use Lemma 5.6 to prove the description of the character in terms of generalized traces.
Proposition 5.7 (Character formula, pointwise version).
Let A be a space, let
![]() $X\in \mathscr {C}^A$
be a dualizable object, let
$X\in \mathscr {C}^A$
be a dualizable object, let
![]() $Y\in \mathscr {C}$
be an object and let
$Y\in \mathscr {C}$
be an object and let
![]() $f\colon X \to X \otimes A^*Y$
be a generalized endomorphism. For every free loop
$f\colon X \to X \otimes A^*Y$
be a generalized endomorphism. For every free loop
![]() $\gamma \in LA$
with basepoint
$\gamma \in LA$
with basepoint
![]() $a := \gamma (\ast )$
, there is an equivalence
$a := \gamma (\ast )$
, there is an equivalence
Proof. Consider the following composition of morphisms in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}}$
:
$ {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}}$
:
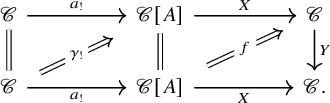
It follows from Corollary 4.12 that this composition is given by the morphism
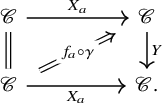
In particular, we deduce from the functoriality of
![]() $\mathscr {C}$
-linear trace functor that there is an identification
$\mathscr {C}$
-linear trace functor that there is an identification
The
![]() $\mathscr {C}$
-linear trace
$\mathscr {C}$
-linear trace
![]() $ {\mathrm {Tr}}_{\mathscr {C}}(X,f)$
is by definition the character
$ {\mathrm {Tr}}_{\mathscr {C}}(X,f)$
is by definition the character ![]() , and by Lemma 5.6 the
, and by Lemma 5.6 the
![]() $\mathscr {C}$
-linear trace
$\mathscr {C}$
-linear trace
![]() $ {\mathrm {Tr}}_{\mathscr {C}}(a_!,\gamma _!)$
is given by
$ {\mathrm {Tr}}_{\mathscr {C}}(a_!,\gamma _!)$
is given by ![]() . It follows that the left hand side of the above identification is given by the composite
. It follows that the left hand side of the above identification is given by the composite
which is exactly
![]() $\chi _f(\gamma )$
. On the other hand, we have by Lemma 5.1 that the right hand side,
$\chi _f(\gamma )$
. On the other hand, we have by Lemma 5.1 that the right hand side,
![]() $ {\mathrm {Tr}}_{\mathscr {C}}(X_a,f_a \circ \gamma )$
, is the generalized trace of the generalized endomorphism
$ {\mathrm {Tr}}_{\mathscr {C}}(X_a,f_a \circ \gamma )$
, is the generalized trace of the generalized endomorphism
![]() $f_a \circ \gamma \colon X_a \to X_a \otimes Y$
. The result follows.
$f_a \circ \gamma \colon X_a \to X_a \otimes Y$
. The result follows.
Corollary 5.8. Let A be a space and let
![]() $\gamma \in LA$
with
$\gamma \in LA$
with
![]() $a := \gamma (\mathrm {pt})$
. For
$a := \gamma (\mathrm {pt})$
. For
![]() $X\in \mathscr {C}[A]$
, we have
$X\in \mathscr {C}[A]$
, we have
Proof. This follows from Proposition 5.7 by taking ![]() and
and
![]() $f = \mathrm {id}_X$
.
$f = \mathrm {id}_X$
.
5.2 Coherence of trace formulas
In the previous subsection, we have shown various explicit formulas of
![]() $\mathscr {C}$
-linear traces. The goal of this subsection is to show that these formulas are natural in the input variables. This question is somewhat more subtle than one might first expect, due to the fact that the explicit description of the functoriality of the
$\mathscr {C}$
-linear traces. The goal of this subsection is to show that these formulas are natural in the input variables. This question is somewhat more subtle than one might first expect, due to the fact that the explicit description of the functoriality of the
![]() $\mathscr {C}$
-linear trace functor given at the beginning of Section 4 is a pointwise description which involves choices of duality data for the objects involved.
$\mathscr {C}$
-linear trace functor given at the beginning of Section 4 is a pointwise description which involves choices of duality data for the objects involved.
5.2.1 Coherent version of the trace comparison lemma
We will start by proving a natural version of the trace comparison lemma, Lemma 5.1, in space-indexed families of generalized endomorphisms. The main input will be the following observation about the interaction between
![]() $\mathscr {C}$
-linear traces and
$\mathscr {C}$
-linear traces and
![]() $\mathscr {C}^A$
-linear traces for a given space A. Since
$\mathscr {C}^A$
-linear traces for a given space A. Since
![]() $ {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}}$
is functorial in
$ {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}}$
is functorial in
![]() $\mathscr {C}$
, there is a coassembly map
$\mathscr {C}$
, there is a coassembly map
associated to the functor
![]() $ {\mathrm {Mod}}_{(-)}^{\mathrm {trl}}\colon {\mathrm {CAlg}}(\mathrm {Pr}^{\text {L}}) \to \mathrm {Pr}^{\text {L}}$
. Informally speaking, it sends a pair
$ {\mathrm {Mod}}_{(-)}^{\mathrm {trl}}\colon {\mathrm {CAlg}}(\mathrm {Pr}^{\text {L}}) \to \mathrm {Pr}^{\text {L}}$
. Informally speaking, it sends a pair
![]() $(\mathscr {D},F)$
to the functor
$(\mathscr {D},F)$
to the functor
where
![]() $\mathscr {D}_a = \mathscr {D} \otimes _{\mathscr {C}^A} \mathscr {C}$
is the base change of
$\mathscr {D}_a = \mathscr {D} \otimes _{\mathscr {C}^A} \mathscr {C}$
is the base change of
![]() $\mathscr {D}$
along the map
$\mathscr {D}$
along the map
![]() $a^*\colon \mathscr {C}^A \to \mathscr {C}$
in
$a^*\colon \mathscr {C}^A \to \mathscr {C}$
in
![]() $ {\mathrm {CAlg}}(\mathrm {Pr}^{\text {L}})$
and similarly for
$ {\mathrm {CAlg}}(\mathrm {Pr}^{\text {L}})$
and similarly for
![]() $F_a$
.
$F_a$
.
Lemma 5.9. For a space A, the following diagram commutes:
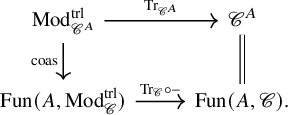
Proof. Viewing the right vertical map as the coassembly map for forgetful functor
![]() $ {\mathrm {CAlg}}(\mathrm {Pr}^{\text {L}})\to \mathrm {Pr}^{\text {L}}$
, the commutativity of the square follows from the naturality of the coassembly map.
$ {\mathrm {CAlg}}(\mathrm {Pr}^{\text {L}})\to \mathrm {Pr}^{\text {L}}$
, the commutativity of the square follows from the naturality of the coassembly map.
In other words, given a
![]() $\mathscr {C}^A$
-linear
$\mathscr {C}^A$
-linear
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {D}$
equipped with an endofunctor
$\mathscr {D}$
equipped with an endofunctor
![]() $F\colon \mathscr {D} \to \mathscr {D}$
, its
$F\colon \mathscr {D} \to \mathscr {D}$
, its
![]() $\mathscr {C}^A$
-linear trace
$\mathscr {C}^A$
-linear trace
![]() $ {\mathrm {Tr}}_{\mathscr {C}^A}(\mathscr {D},F) \in \mathscr {C}^A$
is the A-indexed family of objects of
$ {\mathrm {Tr}}_{\mathscr {C}^A}(\mathscr {D},F) \in \mathscr {C}^A$
is the A-indexed family of objects of
![]() $\mathscr {C}$
obtained by pointwise taking the
$\mathscr {C}$
obtained by pointwise taking the
![]() $\mathscr {C}$
-linear trace of the family
$\mathscr {C}$
-linear trace of the family
![]() $(\mathscr {D}_a,F_a)_{a \in A}$
:
$(\mathscr {D}_a,F_a)_{a \in A}$
:
We now obtain the following generalization of Lemma 5.1 for space-indexed family of generalized endomorphisms:
Lemma 5.10 (Trace comparison lemma, coherent version).
Let A be a space, let
![]() $X,Y,Z\colon A \to \mathscr {C}$
be A-indexed families of objects of
$X,Y,Z\colon A \to \mathscr {C}$
be A-indexed families of objects of
![]() $\mathscr {C}$
, and let
$\mathscr {C}$
, and let
![]() $f_a\colon Z_a \otimes X_a \to X_a \otimes Y_a$
be a family of generalized endomorphisms in
$f_a\colon Z_a \otimes X_a \to X_a \otimes Y_a$
be a family of generalized endomorphisms in
![]() $\mathscr {C}$
. Assume that
$\mathscr {C}$
. Assume that
![]() $X_a$
is dualizable in
$X_a$
is dualizable in
![]() $\mathscr {C}$
for every
$\mathscr {C}$
for every
![]() $a \in A$
. Then the choice of homotopy
$a \in A$
. Then the choice of homotopy
of Lemma 5.1 can be chosen to depend naturally on
![]() $a \in A$
.
$a \in A$
.
Proof. We may consider f as a generalized endomorphism
![]() $Z \otimes X \to X \otimes Y$
of X in
$Z \otimes X \to X \otimes Y$
of X in
![]() $\mathscr {C}^A$
. By Lemma 5.1, its generalized trace
$\mathscr {C}^A$
. By Lemma 5.1, its generalized trace
![]() $ {\mathrm {tr}}_{\mathscr {C}^A}(f \,\vert \, X)\colon Z \to Y$
in
$ {\mathrm {tr}}_{\mathscr {C}^A}(f \,\vert \, X)\colon Z \to Y$
in
![]() $\mathscr {C}^A$
is homotopic to the map
$\mathscr {C}^A$
is homotopic to the map
![]() $ {\mathrm {Tr}}_{\mathscr {C}^A}(X,f)$
obtained by forming the
$ {\mathrm {Tr}}_{\mathscr {C}^A}(X,f)$
obtained by forming the
![]() $\mathscr {C}^A$
-linear trace of the map
$\mathscr {C}^A$
-linear trace of the map
![]() $(X,f)\colon (\mathscr {C}^A,Z) \to (\mathscr {C}^A,Y)$
in
$(X,f)\colon (\mathscr {C}^A,Z) \to (\mathscr {C}^A,Y)$
in
![]() $ {\mathrm {Mod}}^{\mathrm {trl}}_{\mathscr {C}^A}$
:
$ {\mathrm {Mod}}^{\mathrm {trl}}_{\mathscr {C}^A}$
:
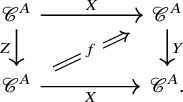
Since generalized traces are functorial under symmetric monoidal functors (Remark 2.7) the map
![]() $ {\mathrm {tr}}_{\mathscr {C}^A}(f \,\vert \, X)\colon Z \to Y$
in
$ {\mathrm {tr}}_{\mathscr {C}^A}(f \,\vert \, X)\colon Z \to Y$
in
![]() $\mathscr {C}^A$
corresponds to the A-indexed family of maps
$\mathscr {C}^A$
corresponds to the A-indexed family of maps
![]() $ {\mathrm {tr}}_{\mathscr {C}}(f_a \,\vert \, X_a)\colon Z_a \to Y_a$
:
$ {\mathrm {tr}}_{\mathscr {C}}(f_a \,\vert \, X_a)\colon Z_a \to Y_a$
:
For the same reason, we deduce from Lemma 5.9 that the map
![]() $ {\mathrm {Tr}}_{\mathscr {C}^A}(X,f)\colon Z \to Y$
in
$ {\mathrm {Tr}}_{\mathscr {C}^A}(X,f)\colon Z \to Y$
in
![]() $\mathscr {C}^A$
is given by the A-indexed family of maps
$\mathscr {C}^A$
is given by the A-indexed family of maps
![]() $ {\mathrm {Tr}}_{\mathscr {C}}(X_a,f_a)\colon Z_a \to Y_a$
:
$ {\mathrm {Tr}}_{\mathscr {C}}(X_a,f_a)\colon Z_a \to Y_a$
:
As
![]() $ {\mathrm {Tr}}_{\mathscr {C}^A}(X,f) \simeq {\mathrm {tr}}_{\mathscr {C}^A}(f \,\vert \, X) \in {\mathrm {Map}}_{\mathscr {C}^A}(Z,Y)$
, this finishes the proof.
$ {\mathrm {Tr}}_{\mathscr {C}^A}(X,f) \simeq {\mathrm {tr}}_{\mathscr {C}^A}(f \,\vert \, X) \in {\mathrm {Map}}_{\mathscr {C}^A}(Z,Y)$
, this finishes the proof.
5.2.2 Coherent version of the loop indicator lemma
We will next prove a coherent version of the loop indicator lemma, Lemma 5.6. Recall that the loop indicator lemma describes the effect of
![]() $ {\mathrm {Tr}}_{\mathscr {C}}$
on the map
$ {\mathrm {Tr}}_{\mathscr {C}}$
on the map
![]() $(a_!,\gamma _!)$
in
$(a_!,\gamma _!)$
in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}}$
, which is obtained from a free loop
$ {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}}$
, which is obtained from a free loop
![]() $\gamma \in LA$
by interpreting it as a self-homotopy of the basepoint inclusion
$\gamma \in LA$
by interpreting it as a self-homotopy of the basepoint inclusion
![]() $\gamma (\ast )\colon \mathrm {pt} \to A$
. We will start by generalizing this description to the case of an arbitrary self-homotopy of a map of spaces.
$\gamma (\ast )\colon \mathrm {pt} \to A$
. We will start by generalizing this description to the case of an arbitrary self-homotopy of a map of spaces.
Proposition 5.11. Let
![]() $f\colon A\to B$
be a map of spaces, and let
$f\colon A\to B$
be a map of spaces, and let
![]() $H\colon A \times S^1 \to B$
be a self-homotopy of f. Applying the functor
$H\colon A \times S^1 \to B$
be a self-homotopy of f. Applying the functor
![]() $\mathscr {C}[-]\colon \mathcal {S} \to {\mathrm {Mod}}_{\mathscr {C}}$
gives an automorphism
$\mathscr {C}[-]\colon \mathcal {S} \to {\mathrm {Mod}}_{\mathscr {C}}$
gives an automorphism
![]() $H_!$
of
$H_!$
of
![]() $f_!$
in
$f_!$
in
![]() $ {\mathrm {Fun}}_{\mathscr {C}}(\mathscr {C}[A],\mathscr {C}[B])$
, which gives rise to a morphism
$ {\mathrm {Fun}}_{\mathscr {C}}(\mathscr {C}[A],\mathscr {C}[B])$
, which gives rise to a morphism
![]() $(f_!,H_!)\colon \mathscr {C}[A] \to \mathscr {C}[B]$
in
$(f_!,H_!)\colon \mathscr {C}[A] \to \mathscr {C}[B]$
in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}}$
:
$ {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}}$
:
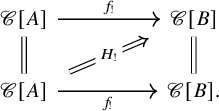
Applying
![]() $ {\mathrm {Tr}}_{\mathscr {C}}$
to this map gives the map
$ {\mathrm {Tr}}_{\mathscr {C}}$
to this map gives the map ![]() induced by the composite
induced by the composite
which informally sends a loop
![]() $\gamma \in LA$
in A to the loop
$\gamma \in LA$
in A to the loop
![]() $s\mapsto H(\gamma (s),s)$
in B.
$s\mapsto H(\gamma (s),s)$
in B.
Proof. Let
![]() $H_A\colon S^1 \to {\mathrm {Map}}(A,A \times S^1)$
denote the mate of the identity of
$H_A\colon S^1 \to {\mathrm {Map}}(A,A \times S^1)$
denote the mate of the identity of
![]() $A \times S^1$
. It is a self-homotopy of the map
$A \times S^1$
. It is a self-homotopy of the map
![]() $A \times b\colon A \to A \times S^1$
, where
$A \times b\colon A \to A \times S^1$
, where
![]() $b\colon \mathrm {pt} \to S^1$
is the inclusion of the basepoint. Observe that the self-homotopy
$b\colon \mathrm {pt} \to S^1$
is the inclusion of the basepoint. Observe that the self-homotopy
![]() $S^1 \to {\mathrm {Map}}(A,B)$
classified by H can be obtained from
$S^1 \to {\mathrm {Map}}(A,B)$
classified by H can be obtained from
![]() $H_A$
by postcomposing with
$H_A$
by postcomposing with
![]() $H\colon A \times S^1 \to B$
, and in particular the square in the statement of the proposition can be written as the composite of the squares
$H\colon A \times S^1 \to B$
, and in particular the square in the statement of the proposition can be written as the composite of the squares
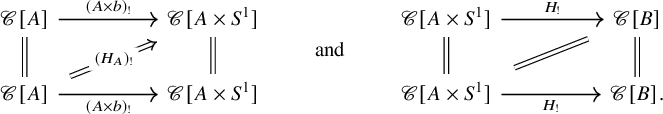
By Theorem 4.40, applying
![]() $ {\mathrm {Tr}}_{\mathscr {C}}$
to the right square gives the map
$ {\mathrm {Tr}}_{\mathscr {C}}$
to the right square gives the map ![]() . For the left square we observe that the homotopy
. For the left square we observe that the homotopy
![]() $H_A$
is equivalent to the product
$H_A$
is equivalent to the product
![]() $A \times H_b$
, where
$A \times H_b$
, where
![]() $H_b\colon S^1 \to {\mathrm {Map}}(\mathrm {pt}, S^1)$
is the canonical self-homotopy of
$H_b\colon S^1 \to {\mathrm {Map}}(\mathrm {pt}, S^1)$
is the canonical self-homotopy of
![]() $b\colon \mathrm {pt} \to S^1$
. By symmetric monoidality of
$b\colon \mathrm {pt} \to S^1$
. By symmetric monoidality of
![]() $ {\mathrm {Tr}}_{\mathscr {C}}$
, we thus find that
$ {\mathrm {Tr}}_{\mathscr {C}}$
, we thus find that
![]() $ {\mathrm {Tr}}_{\mathscr {C}}$
of the left square is given by
$ {\mathrm {Tr}}_{\mathscr {C}}$
of the left square is given by
By Lemma 5.6, applied to the identity
![]() $\gamma = \mathrm {id}_{S^1} \in LS^1$
, the map
$\gamma = \mathrm {id}_{S^1} \in LS^1$
, the map
![]() $ {\mathrm {Tr}}_{\mathscr {C}}(b_!,(H_b)_!))\colon \mathrm {pt} \to LS^1$
is exactly the map
$ {\mathrm {Tr}}_{\mathscr {C}}(b_!,(H_b)_!))\colon \mathrm {pt} \to LS^1$
is exactly the map ![]() . This finishes the proof.
. This finishes the proof.
In the following, let
![]() $d\colon L^2A \to LA$
denote the map induced by the diagonal
$d\colon L^2A \to LA$
denote the map induced by the diagonal
![]() $S^1 \to S^1 \times S^1$
, and let
$S^1 \to S^1 \times S^1$
, and let
![]() $\mathrm {can}_A\colon S^1 \to {\mathrm {Map}}(LA,A)$
denote the mate of the evaluation map
$\mathrm {can}_A\colon S^1 \to {\mathrm {Map}}(LA,A)$
denote the mate of the evaluation map
![]() $\mathrm {ev}_A\colon LA \times S^1 \to A$
. It is a canonical self-homotopy of the map
$\mathrm {ev}_A\colon LA \times S^1 \to A$
. It is a canonical self-homotopy of the map
![]() $e\colon LA \to A$
given by evaluation at
$e\colon LA \to A$
given by evaluation at
![]() $* \in S^1$
.
$* \in S^1$
.
Corollary 5.12. Applying
![]() $ {\mathrm {Tr}}_{\mathscr {C}}$
to the diagram
$ {\mathrm {Tr}}_{\mathscr {C}}$
to the diagram

gives the map ![]() .
.
Proof. By Proposition 5.11, the map ![]() is induced from the composite
is induced from the composite
where the first map sends a double loop
![]() $\gamma \colon S^1 \times S^1 \to A$
in A to the loop
$\gamma \colon S^1 \times S^1 \to A$
in A to the loop
![]() $(s\mapsto (\gamma (s,-),s))$
in
$(s\mapsto (\gamma (s,-),s))$
in
![]() $LA \times S^1$
. In particular, the composite is given by
$LA \times S^1$
. In particular, the composite is given by
![]() $\gamma \mapsto (s\mapsto \gamma (s,s))$
, which is precisely the map
$\gamma \mapsto (s\mapsto \gamma (s,s))$
, which is precisely the map
![]() $d\colon L^2A \to LA$
as claimed.
$d\colon L^2A \to LA$
as claimed.
All in all, we obtain a coherent version of the loop indicator lemma, Lemma 5.6.
Corollary 5.13 (Loop indicator lemma, coherent version).
For a space A, the equivalence
from Lemma 5.6 may be chosen naturally in
![]() $\gamma \in LA$
.
$\gamma \in LA$
.
Proof. Consider the map
![]() $(e_!,\mathrm {can}_{A,!})\colon \mathscr {C}[LA] \to \mathscr {C}[A]$
in
$(e_!,\mathrm {can}_{A,!})\colon \mathscr {C}[LA] \to \mathscr {C}[A]$
in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}}$
considered in Corollary 5.12. It corresponds to an
$ {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}}$
considered in Corollary 5.12. It corresponds to an
![]() $LA$
-indexed family of maps
$LA$
-indexed family of maps
![]() $\mathscr {C} \to \mathscr {C}[A]$
given at
$\mathscr {C} \to \mathscr {C}[A]$
given at
![]() $\gamma \in LA$
by precomposing with
$\gamma \in LA$
by precomposing with
![]() $\gamma _!\colon \mathscr {C} \to \mathscr {C}[LA]$
. We claim that this is the
$\gamma _!\colon \mathscr {C} \to \mathscr {C}[LA]$
. We claim that this is the
![]() $LA$
-indexed diagram of maps
$LA$
-indexed diagram of maps
![]() $(a_!,\gamma _!)\colon \mathscr {C} \to \mathscr {C}[A]$
whose
$(a_!,\gamma _!)\colon \mathscr {C} \to \mathscr {C}[A]$
whose
![]() $\mathscr {C}$
-linear trace we want to compute:
$\mathscr {C}$
-linear trace we want to compute:
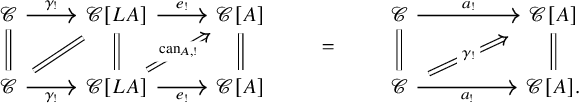
Indeed, one observes that evaluating the canonical homotopy
![]() $\mathrm {can}_A\colon S^1 \to {\mathrm {Map}}(LA,A)$
at
$\mathrm {can}_A\colon S^1 \to {\mathrm {Map}}(LA,A)$
at
![]() $\gamma \in LA$
gives the loop
$\gamma \in LA$
gives the loop
![]() $\gamma \colon S^1 \to A$
, functorially in
$\gamma \colon S^1 \to A$
, functorially in
![]() $\gamma $
. By Lemma 4.44, applying the
$\gamma $
. By Lemma 4.44, applying the
![]() $\mathscr {C}$
-linear trace functor
$\mathscr {C}$
-linear trace functor
![]() $ {\mathrm {Tr}}_{\mathscr {C}}$
to this family of maps in
$ {\mathrm {Tr}}_{\mathscr {C}}$
to this family of maps in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}}$
gives the map
$ {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}}$
gives the map ![]() which is the mate of the composite
which is the mate of the composite
By Corollary 5.12 the second map is the map ![]() , and thus the composite is the identity
, and thus the composite is the identity ![]() . The mate of this is the map
. The mate of this is the map ![]() which sends
which sends
![]() $\gamma $
to
$\gamma $
to ![]() , as desired.
, as desired.
5.2.3 Coherent version of the character formula
We are now in a position to prove that the formula for generalized characters given in Proposition 5.7 is natural in the loop
![]() $\gamma \in LA$
.
$\gamma \in LA$
.
Proposition 5.14 (Character formula, coherent version).
Let
![]() $X \in \mathscr {C}^A$
and
$X \in \mathscr {C}^A$
and
![]() $f\colon X \to X \otimes A^*Y$
be as in Proposition 5.7. Then the equivalence
$f\colon X \to X \otimes A^*Y$
be as in Proposition 5.7. Then the equivalence
of Proposition 5.7 is natural in
![]() $\gamma \in LA$
.
$\gamma \in LA$
.
Proof. We will go through the proof of Proposition 5.7 and check that everything is natural in
![]() $\gamma $
. For every
$\gamma $
. For every
![]() $\gamma \in LA$
, we consider the following composition of morphisms in
$\gamma \in LA$
, we consider the following composition of morphisms in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}}$
:
$ {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}}$
:

Observe that this identification is natural in
![]() $\gamma \in LA$
. By Lemma 5.10, the
$\gamma \in LA$
. By Lemma 5.10, the
![]() $\mathscr {C}$
-linear trace of the right-hand side can naturally be identified with the generalized trace of the map
$\mathscr {C}$
-linear trace of the right-hand side can naturally be identified with the generalized trace of the map
![]() $f_a \circ \gamma \colon X_a \to X_a \otimes Y$
. Furthermore, by Corollary 5.13 the
$f_a \circ \gamma \colon X_a \to X_a \otimes Y$
. Furthermore, by Corollary 5.13 the
![]() $\mathscr {C}$
-linear trace of
$\mathscr {C}$
-linear trace of
![]() $(a_!,\gamma _!)\colon \mathscr {C} \to \mathscr {C}[A]$
can naturally be identified with the morphism
$(a_!,\gamma _!)\colon \mathscr {C} \to \mathscr {C}[A]$
can naturally be identified with the morphism ![]() . Since we have
. Since we have
![]() $\chi _f = {\mathrm {Tr}}_{\mathscr {C}}(X,f)$
by definition, the above diagram thus gives a natural equivalence
$\chi _f = {\mathrm {Tr}}_{\mathscr {C}}(X,f)$
by definition, the above diagram thus gives a natural equivalence
finishing the proof.
Given a generalized endomorphism
![]() $f \colon X \to X \otimes A^*Y$
in
$f \colon X \to X \otimes A^*Y$
in
![]() $\mathscr {C}^A$
, its generalized trace in
$\mathscr {C}^A$
, its generalized trace in
![]() $\mathscr {C}^A$
is a map
$\mathscr {C}^A$
is a map ![]() , which by adjunction corresponds to a map
, which by adjunction corresponds to a map
It follows from the coherent character formula of Proposition 5.14 that the generalized trace
![]() $ {\mathrm {tr}}(f \,\vert \, X)$
of f can be obtained from the the character
$ {\mathrm {tr}}(f \,\vert \, X)$
of f can be obtained from the the character ![]() by precomposition with the inclusion of constant loops
by precomposition with the inclusion of constant loops ![]() .
.
Corollary 5.15. Let A be a space,
![]() $X \in \mathscr {C}^A$
a dualizable object and
$X \in \mathscr {C}^A$
a dualizable object and
![]() $f\colon X \to X \otimes A^*Y$
in
$f\colon X \to X \otimes A^*Y$
in
![]() $\mathscr {C}^A$
a generalized morphism. Then the following diagram commutes:
$\mathscr {C}^A$
a generalized morphism. Then the following diagram commutes:
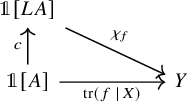
5.3 Restriction and induction of characters
In this subsection, we consider the behavior of the character maps under restriction and induction along maps of spaces
![]() $g\colon A \to B$
.
$g\colon A \to B$
.
Definition 5.16. Let
![]() $X \in \mathscr {C}^B$
be dualizable and let
$X \in \mathscr {C}^B$
be dualizable and let
![]() $f\colon X \to X \otimes B^*Y$
be a morphism in
$f\colon X \to X \otimes B^*Y$
be a morphism in
![]() $\mathscr {C}^B$
. We define the restriction of f along g as the the composite
$\mathscr {C}^B$
. We define the restriction of f along g as the the composite
Note that
![]() $g^*X \in \mathscr {C}^A$
is still pointwise dualizable, so
$g^*X \in \mathscr {C}^A$
is still pointwise dualizable, so
![]() $\mathrm {Res}_g(f)$
corresponds to an A-family of generalized endomorphisms
$\mathrm {Res}_g(f)$
corresponds to an A-family of generalized endomorphisms
Lemma 5.17 (Restricted character formula).
In the setting of Definition 5.16, the character ![]() of the restriction
of the restriction
![]() $\mathrm {Res}_g(f)\colon g^*X \to g^*X \otimes A^*Y$
is given by the composite
$\mathrm {Res}_g(f)\colon g^*X \to g^*X \otimes A^*Y$
is given by the composite
Proof. Regarding f as a transformation of
![]() $\mathscr {C}$
-linear functors
$\mathscr {C}$
-linear functors
![]() $\mathscr {C}[B] \to \mathscr {C}$
and
$\mathscr {C}[B] \to \mathscr {C}$
and
![]() $\mathrm {Res}_g(f)$
as a transformation of
$\mathrm {Res}_g(f)$
as a transformation of
![]() $\mathscr {C}$
-linear functors
$\mathscr {C}$
-linear functors
![]() $\mathscr {C}[A] \to \mathscr {C}$
, Corollary 4.12 tells us that
$\mathscr {C}[A] \to \mathscr {C}$
, Corollary 4.12 tells us that
![]() $\mathrm {Res}_g(f)$
is obtained from f by whiskering with the functor
$\mathrm {Res}_g(f)$
is obtained from f by whiskering with the functor
![]() $g_!\colon \mathscr {C}[A] \to \mathscr {C}[B]$
. In particular, we get the following equivalence of maps
$g_!\colon \mathscr {C}[A] \to \mathscr {C}[B]$
. In particular, we get the following equivalence of maps
![]() $\mathscr {C}[A] \to (\mathscr {C},Y)$
in
$\mathscr {C}[A] \to (\mathscr {C},Y)$
in
![]() $ {\mathrm {Mod}}^{\mathrm {trl}}_{\mathscr {C}}$
:
$ {\mathrm {Mod}}^{\mathrm {trl}}_{\mathscr {C}}$
:

We thus obtain the claim by applying the functor
![]() $ {\mathrm {Tr}}_{\mathscr {C}}\colon {\mathrm {Mod}}^{\mathrm {trl}}_{\mathscr {C}} \to \mathscr {C}$
.
$ {\mathrm {Tr}}_{\mathscr {C}}\colon {\mathrm {Mod}}^{\mathrm {trl}}_{\mathscr {C}} \to \mathscr {C}$
.
Definition 5.18. Let
![]() $X \in \mathscr {C}^A$
be dualizable and let
$X \in \mathscr {C}^A$
be dualizable and let
![]() $f\colon X \to X \otimes A^*Y$
be a morphism in
$f\colon X \to X \otimes A^*Y$
be a morphism in
![]() $\mathscr {C}^A$
. Assume that the map
$\mathscr {C}^A$
. Assume that the map
![]() $g\colon A \to B$
is
$g\colon A \to B$
is
![]() $\mathscr {C}$
-adjointable. We define the induction of f along g as the the composite
$\mathscr {C}$
-adjointable. We define the induction of f along g as the the composite
Note that the object
![]() $g_!X \in \mathscr {C}^B$
is again dualizable by Proposition 4.33, and thus
$g_!X \in \mathscr {C}^B$
is again dualizable by Proposition 4.33, and thus
![]() $ {\mathrm {Ind}}_g(f)$
corresponds to a B-family of generalized endomorphisms
$ {\mathrm {Ind}}_g(f)$
corresponds to a B-family of generalized endomorphisms
where
![]() $A_b$
is the fiber of
$A_b$
is the fiber of ![]() over
over
![]() $b\in B$
.
$b\in B$
.
Warning 5.19. Without the assumption that
![]() $g\colon A \to B$
is
$g\colon A \to B$
is
![]() $\mathscr {C}$
-adjointable, the object
$\mathscr {C}$
-adjointable, the object
![]() $g_!X\in \mathscr {C}^B$
will not in general be dualizable and the character of
$g_!X\in \mathscr {C}^B$
will not in general be dualizable and the character of
![]() $ {\mathrm {Ind}}_g(f)$
is not defined.
$ {\mathrm {Ind}}_g(f)$
is not defined.
Theorem 5.20 (Induced character formula).
In the setting of Definition 5.18, the character ![]() of the induction
of the induction
![]() $ {\mathrm {Ind}}_g(f)\colon g_!(X) \to g_!(X) \otimes B^*Y$
is given by the composition
$ {\mathrm {Ind}}_g(f)\colon g_!(X) \to g_!(X) \otimes B^*Y$
is given by the composition
Proof. The proof is essentially the same as that of Lemma 5.17. Regarding f as a transformation of
![]() $\mathscr {C}$
-linear functors
$\mathscr {C}$
-linear functors
![]() $\mathscr {C}[A] \to \mathscr {C}$
and
$\mathscr {C}[A] \to \mathscr {C}$
and
![]() $ {\mathrm {Ind}}_g(f)$
as a transformation of
$ {\mathrm {Ind}}_g(f)$
as a transformation of
![]() $\mathscr {C}$
-linear functors
$\mathscr {C}$
-linear functors
![]() $\mathscr {C}[B] \to \mathscr {C}$
, Corollary 4.12 tells us that
$\mathscr {C}[B] \to \mathscr {C}$
, Corollary 4.12 tells us that
![]() $ {\mathrm {Ind}}_g(f)$
is obtained from f by whiskering with the functor
$ {\mathrm {Ind}}_g(f)$
is obtained from f by whiskering with the functor
![]() $g^*\colon \mathscr {C}[B] \to \mathscr {C}[A]$
. In particular, we get the following equivalence of maps
$g^*\colon \mathscr {C}[B] \to \mathscr {C}[A]$
. In particular, we get the following equivalence of maps
![]() $\mathscr {C}[B] \to (\mathscr {C},Y)$
in
$\mathscr {C}[B] \to (\mathscr {C},Y)$
in
![]() $ {\mathrm {Mod}}^{\mathrm {trl}}_{\mathscr {C}}$
:
$ {\mathrm {Mod}}^{\mathrm {trl}}_{\mathscr {C}}$
:
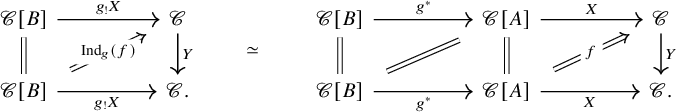
We thus obtain the claim by applying the functor
![]() $ {\mathrm {Tr}}_{\mathscr {C}}\colon {\mathrm {Mod}}^{\mathrm {trl}}_{\mathscr {C}} \to \mathscr {C}$
.
$ {\mathrm {Tr}}_{\mathscr {C}}\colon {\mathrm {Mod}}^{\mathrm {trl}}_{\mathscr {C}} \to \mathscr {C}$
.
As a special case of Theorem 5.20, we obtain main result of this section: a formula for the trace of a colimit of endomorphisms.
Corollary 5.21 (Traces and dimensions of colimits).
Let A be a
![]() $\mathscr {C}$
-adjointable space, and let
$\mathscr {C}$
-adjointable space, and let
![]() $X \in \mathscr {C}^A$
be a dualizable object. For an endomorphism
$X \in \mathscr {C}^A$
be a dualizable object. For an endomorphism
![]() $f\colon X \to X$
in
$f\colon X \to X$
in
![]() $\mathscr {C}^A$
, the trace of the induced endomorphism
$\mathscr {C}^A$
, the trace of the induced endomorphism
![]() $A_!(f)\colon A_!(X) \to A_!(X)$
on colimits over A is given by the composite
$A_!(f)\colon A_!(X) \to A_!(X)$
on colimits over A is given by the composite
In particular, the dimension
![]() $\dim (A_!(X))$
of the colimit of X is given by the composite
$\dim (A_!(X))$
of the colimit of X is given by the composite
5.4 Additivity of generalized traces
Let
![]() $V_1$
,
$V_1$
,
![]() $V_2$
and
$V_2$
and
![]() $V_3$
be finite-dimensional vector spaces over a field k, fitting in a short exact sequence
$V_3$
be finite-dimensional vector spaces over a field k, fitting in a short exact sequence ![]() . Assume that
. Assume that
![]() $V_i$
comes equipped with an endomorphism
$V_i$
comes equipped with an endomorphism
![]() $f_i\colon V_i \to V_i$
for
$f_i\colon V_i \to V_i$
for
![]() $i=1,2,3$
and that these fit into a commutative diagram
$i=1,2,3$
and that these fit into a commutative diagram
In this case, the trace of
![]() $f_2$
may be expressed in terms of the traces of
$f_2$
may be expressed in terms of the traces of
![]() $f_1$
and
$f_1$
and
![]() $f_3$
as follows:
$f_3$
as follows:
To see this, one may choose an identification
![]() $V_2 \simeq V_1 \oplus V_3$
and write the map
$V_2 \simeq V_1 \oplus V_3$
and write the map
![]() $f_2\colon V_2 \to V_2$
as a block matrix
$f_2\colon V_2 \to V_2$
as a block matrix
 $\begin {pmatrix} f_1 & g \\ 0 & f_3\end {pmatrix}\colon V_1 \oplus V_3 \to V_1 \oplus V_3$
for some map
$\begin {pmatrix} f_1 & g \\ 0 & f_3\end {pmatrix}\colon V_1 \oplus V_3 \to V_1 \oplus V_3$
for some map
![]() $g\colon V_3 \to V_1$
.
$g\colon V_3 \to V_1$
.
An additivity result for traces in more general general contexts, such as tensor-triangulated categories, has proved subtle. In [Reference Ferrand27], Daniel Ferrand provided an example of an endomorphism in the derived category of an exact triangle of perfect complexes for which the trace of the middle map is not equal to the sum of the traces of the two other ones. The issue can be phrased as a coherence problem: when regarding the short exact sequence as a cofiber sequence in the derived
![]() $\infty $
-category, the chain homotopies exhibiting the diagram as commutative should be suitably compatible with the null-homotopies witnessing the sequences as cofiber sequences. In particular, the bare triangulated category contains too little information to allow for an additivity result for traces.
$\infty $
-category, the chain homotopies exhibiting the diagram as commutative should be suitably compatible with the null-homotopies witnessing the sequences as cofiber sequences. In particular, the bare triangulated category contains too little information to allow for an additivity result for traces.
Since then, additivity of traces has been proved in more structured settings. In [Reference May54], May proved additivity of traces for tensor-triangulated categories coming from a stable closed symmetric monoidal model category. In [Reference Groth, Ponto and Shulman31], Groth, Ponto and Shulman translated the statement and proof of May’s result into the language of stable derivators. In fact, as Grothendieck explained in a letter to ThomasonFootnote 14 , the failure of additivity of traces in the bare triangulated setting was his main motivation for the development of the formalism of derivators, where mapping cones would be functorial. Finally, in [Reference Ponto and Shulman59], Ponto and Shulman gave a proof of the additivity of traces which is much closer to our approach.
The goal of this section is to give a new proof of additivity of generalized traces in a stable presentably symmetric monoidal
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}$
. Our method is fundamentally different from those of [Reference May54] and [Reference Groth, Ponto and Shulman31], in which the required homotopy between trace maps was produced directly via a large diagram chase. Instead, we will deduce the result from a categorification of the problem, similarly to [Reference Ponto and Shulman59]: the
$\mathscr {C}$
. Our method is fundamentally different from those of [Reference May54] and [Reference Groth, Ponto and Shulman31], in which the required homotopy between trace maps was produced directly via a large diagram chase. Instead, we will deduce the result from a categorification of the problem, similarly to [Reference Ponto and Shulman59]: the
![]() $\mathscr {C}$
-linear trace functor
$\mathscr {C}$
-linear trace functor
![]() $ {\mathrm {Tr}}_{\mathscr {C}}\colon {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}} \to \mathscr {C}$
is “additive” in a sense analogous to the “additive invariants” of [Reference Blumberg, Gepner and Tabuada16]. The advantage of this approach is that the additivity of the functor
$ {\mathrm {Tr}}_{\mathscr {C}}\colon {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}} \to \mathscr {C}$
is “additive” in a sense analogous to the “additive invariants” of [Reference Blumberg, Gepner and Tabuada16]. The advantage of this approach is that the additivity of the functor
![]() $ {\mathrm {Tr}}_{\mathscr {C}}$
is a property (sending localization sequences to cofiber sequences, cf. Theorem 5.23) rather than structure (a homotopy between the various trace maps). The approach in [Reference Ponto and Shulman59] is to use a variant of Corollary 5.21 with A being a
$ {\mathrm {Tr}}_{\mathscr {C}}$
is a property (sending localization sequences to cofiber sequences, cf. Theorem 5.23) rather than structure (a homotopy between the various trace maps). The approach in [Reference Ponto and Shulman59] is to use a variant of Corollary 5.21 with A being a
![]() $1$
-category in place of a space.
$1$
-category in place of a space.
For the convenience of the reader, we will recall from [Reference Hoyois, Scherotzke and Sibilla37] the relevant definitions and statements about the additivity of the categorical trace. Throughout this section,
![]() $\mathscr {C}$
is a fixed stable presentably symmetric monoidal
$\mathscr {C}$
is a fixed stable presentably symmetric monoidal
![]() $\infty $
-category.
$\infty $
-category.
Definition 5.22 [Reference Hoyois, Scherotzke and Sibilla37, Definition 3.2].
A sequence ![]() in
in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
is called a localization sequence if the following conditions hold:
$ {\mathrm {Mod}}_{\mathscr {C}}$
is called a localization sequence if the following conditions hold:
-
•
 $\iota $
and
$\iota $
and
 $\pi $
have
$\pi $
have
 $\mathscr {C}$
-linear right adjoints
$\mathscr {C}$
-linear right adjoints
 $\iota ^r$
and
$\iota ^r$
and
 $\pi ^r$
;
$\pi ^r$
; -
• the composite
 $\pi \iota \colon \mathscr {D} \to \mathscr {F}$
is the zero functor;
$\pi \iota \colon \mathscr {D} \to \mathscr {F}$
is the zero functor; -
• the unit
 $\eta \colon \mathrm {id}_{\mathscr {D}} \to \iota ^r \iota $
and the counit
$\eta \colon \mathrm {id}_{\mathscr {D}} \to \iota ^r \iota $
and the counit
 $\epsilon \colon \pi \pi ^r\to \mathrm {id}_{\mathscr {F}}$
are equivalences;
$\epsilon \colon \pi \pi ^r\to \mathrm {id}_{\mathscr {F}}$
are equivalences; -
• the sequence
 $\iota \iota ^r \to \mathrm {id}_{\mathscr {E}} \to \pi ^r\pi $
, with its unique nullhomotopy, is a cofiber sequence in
$\iota \iota ^r \to \mathrm {id}_{\mathscr {E}} \to \pi ^r\pi $
, with its unique nullhomotopy, is a cofiber sequence in
 $ {\mathrm {Fun}}_{\mathscr {C}}(\mathscr {E},\mathscr {E})$
.
$ {\mathrm {Fun}}_{\mathscr {C}}(\mathscr {E},\mathscr {E})$
.
A sequence ![]() in
in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}}$
is called a localization sequence if
$ {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}}$
is called a localization sequence if
![]() $\mathscr {D}\stackrel \iota \to \mathscr {E}\stackrel \pi \to \mathscr {F}$
is a localization sequence and moreover the morphisms
$\mathscr {D}\stackrel \iota \to \mathscr {E}\stackrel \pi \to \mathscr {F}$
is a localization sequence and moreover the morphisms
![]() $(\iota ,\alpha )$
and
$(\iota ,\alpha )$
and
![]() $(\pi ,\beta )$
are right adjointable in
$(\pi ,\beta )$
are right adjointable in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
.
$ {\mathrm {Mod}}_{\mathscr {C}}$
.
The assumption that the composite
![]() $\pi \iota $
in a localization sequence is the zero functor implies that the sequence
$\pi \iota $
in a localization sequence is the zero functor implies that the sequence
![]() $ {\mathrm {Tr}}_{\mathscr {C}}(\mathscr {D},F) \to {\mathrm {Tr}}_{\mathscr {C}}(\mathscr {E},G) \to {\mathrm {Tr}}_{\mathscr {C}}(\mathscr {F},H)$
in
$ {\mathrm {Tr}}_{\mathscr {C}}(\mathscr {D},F) \to {\mathrm {Tr}}_{\mathscr {C}}(\mathscr {E},G) \to {\mathrm {Tr}}_{\mathscr {C}}(\mathscr {F},H)$
in
![]() $\mathscr {C}$
obtained by applying
$\mathscr {C}$
obtained by applying
![]() $ {\mathrm {Tr}}_{\mathscr {C}}$
admits a canonical null-homotopy.
$ {\mathrm {Tr}}_{\mathscr {C}}$
admits a canonical null-homotopy.
Theorem 5.23 [Reference Hoyois, Scherotzke and Sibilla37, Theorem 3.4].
Let
be a localization sequence in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}}$
. Then the canonical null-homotopy exhibits the sequence
$ {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}}$
. Then the canonical null-homotopy exhibits the sequence
as a cofiber sequence in
![]() $\mathscr {C}$
.
$\mathscr {C}$
.
One might refer to this result as saying that the functor
![]() $ {\mathrm {Tr}}_{\mathscr {C}}$
is ‘localizing’, cf. [Reference Blumberg, Gepner and Tabuada16, Definition 8.1]. We will show next how this implies that
$ {\mathrm {Tr}}_{\mathscr {C}}$
is ‘localizing’, cf. [Reference Blumberg, Gepner and Tabuada16, Definition 8.1]. We will show next how this implies that
![]() $ {\mathrm {Tr}}_{\mathscr {C}}$
sends bifiber sequences between morphisms in
$ {\mathrm {Tr}}_{\mathscr {C}}$
sends bifiber sequences between morphisms in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}}$
to sums in mapping spaces in
$ {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}}$
to sums in mapping spaces in
![]() $\mathscr {C}$
.
$\mathscr {C}$
.
Definition 5.24. Let
![]() $(\mathscr {D},F)$
and
$(\mathscr {D},F)$
and
![]() $(\mathscr {E},G)$
be in
$(\mathscr {E},G)$
be in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}}$
and consider morphisms
$ {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}}$
and consider morphisms
![]() $(\iota _i,\alpha _i)\colon (\mathscr {D},F) \to (\mathscr {E},G)$
for
$(\iota _i,\alpha _i)\colon (\mathscr {D},F) \to (\mathscr {E},G)$
for
![]() $i = 1,2,3$
, that is,
$i = 1,2,3$
, that is,
![]() $\iota _i\colon \mathscr {D} \to \mathscr {E}$
is an internal left adjoint in
$\iota _i\colon \mathscr {D} \to \mathscr {E}$
is an internal left adjoint in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
and
$ {\mathrm {Mod}}_{\mathscr {C}}$
and
![]() $\alpha _i\colon \iota _i\circ F\to G\circ \iota _i$
is a morphism in
$\alpha _i\colon \iota _i\circ F\to G\circ \iota _i$
is a morphism in
![]() $ {\mathrm {Fun}}_{\mathscr {C}}(\mathscr {D},\mathscr {E})$
. We define a bifiber sequence
$ {\mathrm {Fun}}_{\mathscr {C}}(\mathscr {D},\mathscr {E})$
. We define a bifiber sequence
to be a bifiber sequence ![]() in
in
![]() $ {\mathrm {Fun}}_{\mathscr {C}}(\mathscr {D},\mathscr {E})$
which fits into a bifiber sequence in
$ {\mathrm {Fun}}_{\mathscr {C}}(\mathscr {D},\mathscr {E})$
which fits into a bifiber sequence in
![]() $ {\mathrm {Fun}}_{\mathscr {C}}(\mathscr {D},\mathscr {E})^{[1]}$
of the form
$ {\mathrm {Fun}}_{\mathscr {C}}(\mathscr {D},\mathscr {E})^{[1]}$
of the form
where the top (resp. bottom) bifiber sequence is obtained by precomposing with F (resp. postcomposing with G)
Remark 5.25. We emphasize at this point that the data of a bifiber sequence ![]() in a stable
in a stable
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {E}$
is that of a bicartesian square in
$\mathscr {E}$
is that of a bicartesian square in
![]() $\mathscr {E}$
of the form
$\mathscr {E}$
of the form
In particular, a bifiber sequence in
![]() $\mathscr {E}^{[1]}$
contains the data of a commutative cube in
$\mathscr {E}^{[1]}$
contains the data of a commutative cube in
![]() $\mathscr {E}$
. We will often leave the null-homotopy implicit in the notation to enhance readability.
$\mathscr {E}$
. We will often leave the null-homotopy implicit in the notation to enhance readability.
Corollary 5.26. Let
be a bifiber sequence of morphisms
![]() $(\mathscr {D},F) \to (\mathscr {E},G)$
in
$(\mathscr {D},F) \to (\mathscr {E},G)$
in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}}$
. There is an equivalence
$ {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}}$
. There is an equivalence
in the mapping space
![]() $ {\mathrm {Map}}_{\mathscr {C}}( {\mathrm {Tr}}_{\mathscr {C}}(\mathscr {D}, F), {\mathrm {Tr}}_{\mathscr {C}}(\mathscr {E}, G)))$
.
$ {\mathrm {Map}}_{\mathscr {C}}( {\mathrm {Tr}}_{\mathscr {C}}(\mathscr {D}, F), {\mathrm {Tr}}_{\mathscr {C}}(\mathscr {E}, G)))$
.
Proof. This is a standard trick due to Waldhausen, adapted to the current context. Consider the full subcategory
![]() $S_2(\mathscr {E}) \subseteq {\mathrm {Fun}}([1] \times [1], \mathscr {E})$
spanned by the bifiber sequences in
$S_2(\mathscr {E}) \subseteq {\mathrm {Fun}}([1] \times [1], \mathscr {E})$
spanned by the bifiber sequences in
![]() $\mathscr {E}$
. Equip
$\mathscr {E}$
. Equip
![]() $S_2(\mathscr {E})$
with the endomorphism
$S_2(\mathscr {E})$
with the endomorphism
![]() $S_2(G)\colon S_2(\mathscr {E})\to S_2(\mathscr {E})$
defined by pointwise application of G, which is well-defined as G preserves cofiber sequences. The
$S_2(G)\colon S_2(\mathscr {E})\to S_2(\mathscr {E})$
defined by pointwise application of G, which is well-defined as G preserves cofiber sequences. The
![]() $\infty $
-category
$\infty $
-category
![]() $S_2(\mathscr {E})$
is canonically
$S_2(\mathscr {E})$
is canonically
![]() $\mathscr {C}$
-linear, and as such it is equivalent to
$\mathscr {C}$
-linear, and as such it is equivalent to
![]() $\mathscr {E}^{[1]} \simeq \mathrm {PSh}([1]) \otimes \mathscr {E}$
. In particular,
$\mathscr {E}^{[1]} \simeq \mathrm {PSh}([1]) \otimes \mathscr {E}$
. In particular,
![]() $S_2(\mathscr {E})$
is dualizable in
$S_2(\mathscr {E})$
is dualizable in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
, and thus the pair
$ {\mathrm {Mod}}_{\mathscr {C}}$
, and thus the pair
![]() $(S_2(\mathscr {C}),S_2(G))$
forms an object of
$(S_2(\mathscr {C}),S_2(G))$
forms an object of
![]() $ {\mathrm {Mod}}^{\mathrm {trl}}_{\mathscr {C}}$
. It fits into a localization sequence
$ {\mathrm {Mod}}^{\mathrm {trl}}_{\mathscr {C}}$
. It fits into a localization sequence
see for example [Reference Blumberg, Gepner and Tabuada16, Proof of proposition 7.17]. By Theorem 5.23, the induced sequence
is a cofiber sequence in
![]() $\mathscr {C}$
, and thus the maps
$\mathscr {C}$
, and thus the maps
![]() $r\colon S_2(\mathscr {E}) \to \mathscr {E}$
and
$r\colon S_2(\mathscr {E}) \to \mathscr {E}$
and
![]() $p\colon S_2(\mathscr {E}) \to \mathscr {E}$
induce an equivalence
$p\colon S_2(\mathscr {E}) \to \mathscr {E}$
induce an equivalence
whose inverse is
![]() $( {\mathrm {Tr}}_{\mathscr {C}}(i), {\mathrm {Tr}}_{\mathscr {C}}(s))$
. In particular, the identity on
$( {\mathrm {Tr}}_{\mathscr {C}}(i), {\mathrm {Tr}}_{\mathscr {C}}(s))$
. In particular, the identity on
![]() $ {\mathrm {Tr}}_{\mathscr {C}}(S_2(\mathscr {E}),S_2(G))$
is equivalent to the sum of the maps
$ {\mathrm {Tr}}_{\mathscr {C}}(S_2(\mathscr {E}),S_2(G))$
is equivalent to the sum of the maps
![]() $ {\mathrm {Tr}}_{\mathscr {C}}(ir)$
and
$ {\mathrm {Tr}}_{\mathscr {C}}(ir)$
and
![]() $ {\mathrm {Tr}}_{\mathscr {C}}(sp)$
.
$ {\mathrm {Tr}}_{\mathscr {C}}(sp)$
.
Observe that a bifiber sequence ![]() as in Definition 5.24 is the same data as a map
as in Definition 5.24 is the same data as a map
![]() $(\iota ,\alpha )\colon (\mathscr {D},F) \to (S_2(\mathscr {E}),S_2(G))$
in
$(\iota ,\alpha )\colon (\mathscr {D},F) \to (S_2(\mathscr {E}),S_2(G))$
in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}}$
whose three components are given by
$ {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}}$
whose three components are given by
![]() $(\iota _i,\alpha _i)$
for
$(\iota _i,\alpha _i)$
for
![]() $i=1,2,3$
. After applying
$i=1,2,3$
. After applying
![]() $ {\mathrm {Tr}}_{\mathscr {C}}(-)$
, we then get that the map in
$ {\mathrm {Tr}}_{\mathscr {C}}(-)$
, we then get that the map in
![]() $\mathscr {C}$
$\mathscr {C}$
is equivalent to the sum of
where
![]() $\alpha _1$
and
$\alpha _1$
and
![]() $\alpha _3$
are dropped from the notation to enhance readability. In particular, if we postcompose it with the map induced by
$\alpha _3$
are dropped from the notation to enhance readability. In particular, if we postcompose it with the map induced by
![]() $S_2(\mathscr {E}) \to \mathscr {E}\colon (X,Y,Z) \mapsto Y$
, we get a homotopy
$S_2(\mathscr {E}) \to \mathscr {E}\colon (X,Y,Z) \mapsto Y$
, we get a homotopy
as desired.
As a consequence of the above additivity property of the
![]() $\mathscr {C}$
-linear trace functor, we immediately obtain the main result of this subsection: the additivity of generalized traces in
$\mathscr {C}$
-linear trace functor, we immediately obtain the main result of this subsection: the additivity of generalized traces in
![]() $\mathscr {C}$
.
$\mathscr {C}$
.
Theorem 5.27 (Additivity of generalized traces, cf. [Reference May54, Reference Ponto and Shulman59, Reference Ramzi61]).
Let
![]() $\mathscr {C}$
be a stable presentably symmetric monoidal
$\mathscr {C}$
be a stable presentably symmetric monoidal
![]() $\infty $
-category, and let
$\infty $
-category, and let ![]() be a bifiber sequence of dualizable objects in
be a bifiber sequence of dualizable objects in
![]() $\mathscr {C}$
. Let
$\mathscr {C}$
. Let
![]() $f_i\colon Z \otimes X_i \to X_i \otimes Y$
be morphisms fitting in bifiber sequence in
$f_i\colon Z \otimes X_i \to X_i \otimes Y$
be morphisms fitting in bifiber sequence in
![]() $\mathscr {C}^{[1]}$
of the form
$\mathscr {C}^{[1]}$
of the form
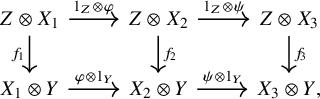
where the top and bottom sequences are obtained from the original bifiber sequence by tensoring with Z resp. Y. Then there is an equivalence
Proof. Recall from Lemma 5.1 that the generalized trace
![]() $ {\mathrm {tr}}(f_i \,\vert \, X_i)\colon Z \to Y$
of the generalized endomorphism
$ {\mathrm {tr}}(f_i \,\vert \, X_i)\colon Z \to Y$
of the generalized endomorphism
![]() $f_i\colon Z \otimes X_i \to X_i \otimes Y$
is the result of applying the
$f_i\colon Z \otimes X_i \to X_i \otimes Y$
is the result of applying the
![]() $\mathscr {C}$
-linear trace functor
$\mathscr {C}$
-linear trace functor
![]() $ {\mathrm {Tr}}_{\mathscr {C}}$
to the morphism
$ {\mathrm {Tr}}_{\mathscr {C}}$
to the morphism
![]() $(X_i,f_i)\colon (\mathscr {C},Z) \to (\mathscr {C},Y)$
in
$(X_i,f_i)\colon (\mathscr {C},Z) \to (\mathscr {C},Y)$
in
![]() $ {\mathrm {Mod}}^{\mathrm {trl}}_{\mathscr {C}}$
. One observes that the maps
$ {\mathrm {Mod}}^{\mathrm {trl}}_{\mathscr {C}}$
. One observes that the maps
![]() $\varphi \colon X_1 \to X_2$
and
$\varphi \colon X_1 \to X_2$
and
![]() $\psi \colon X_2 \to X_3$
induce a bifiber sequence
$\psi \colon X_2 \to X_3$
induce a bifiber sequence
of morphisms in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}}$
. It then follows from Corollary 5.26 that
$ {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {trl}}$
. It then follows from Corollary 5.26 that
![]() $ {\mathrm {tr}}(f_2 \,\vert \, X_2) \simeq {\mathrm {tr}}(f_1 \,\vert \, X_1) + {\mathrm {tr}}(f_3 \,\vert \, X_3)$
as desired.
$ {\mathrm {tr}}(f_2 \,\vert \, X_2) \simeq {\mathrm {tr}}(f_1 \,\vert \, X_1) + {\mathrm {tr}}(f_3 \,\vert \, X_3)$
as desired.
Remark 5.28. Replacing
![]() $\mathscr {C}$
with
$\mathscr {C}$
with
![]() $ {\mathrm {Ind}}(\mathscr {C}^{\mathrm {dbl}})$
, we see that we can drop the presentability assumption on
$ {\mathrm {Ind}}(\mathscr {C}^{\mathrm {dbl}})$
, we see that we can drop the presentability assumption on
![]() $\mathscr {C}$
.
$\mathscr {C}$
.
A special case of additivity of traces is the situation where
![]() $X_2 \simeq X_1 \oplus X_3$
is given by a direct sum. While this follows for stable
$X_2 \simeq X_1 \oplus X_3$
is given by a direct sum. While this follows for stable
![]() $\mathscr {C}$
from Theorem 5.27, the proof in this case is much more elementary and only requires
$\mathscr {C}$
from Theorem 5.27, the proof in this case is much more elementary and only requires
![]() $\mathscr {C}$
to be semiadditive, in the sense that finite products in
$\mathscr {C}$
to be semiadditive, in the sense that finite products in
![]() $\mathscr {C}$
are also finite coproducts. For completeness, we give a proof.
$\mathscr {C}$
are also finite coproducts. For completeness, we give a proof.
Lemma 5.29. Let
![]() $\mathscr {C}$
be a semiadditive presentably symmetric monoidal
$\mathscr {C}$
be a semiadditive presentably symmetric monoidal
![]() $\infty $
-category. Let
$\infty $
-category. Let
![]() $X_1$
and
$X_1$
and
![]() $X_2$
be dualizable objects, and set
$X_2$
be dualizable objects, and set
![]() $X := X_1 \oplus X_2$
. Consider morphisms
$X := X_1 \oplus X_2$
. Consider morphisms
![]() $f_i\colon Z \otimes X_i \to X_i \otimes Y$
for
$f_i\colon Z \otimes X_i \to X_i \otimes Y$
for
![]() $i = 1,2$
, and let
$i = 1,2$
, and let
![]() $f\colon Z \otimes X \to X \otimes Y$
be their direct sum. Then there is an equivalence
$f\colon Z \otimes X \to X \otimes Y$
be their direct sum. Then there is an equivalence
Proof. The object
![]() $X = X_1 \oplus X_2$
is dualizable, with duality data given by
$X = X_1 \oplus X_2$
is dualizable, with duality data given by
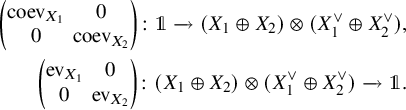
The result now follows from spelling out the definition of the generalized trace and the definition of addition of morphisms in
![]() $\mathscr {C}$
.
$\mathscr {C}$
.
6 The Becker-Gottlieb transfer
Let
![]() $f\colon A \to B$
be a map of spaces. By functoriality of the suspension spectrum functor, there is an induced map of spectra
$f\colon A \to B$
be a map of spaces. By functoriality of the suspension spectrum functor, there is an induced map of spectra
![]() $\mathbb {S}[f]\colon \mathbb {S}[A] \to \mathbb {S}[B]$
. When the fibers of f are compact, there is also a ‘wrong-way’ map
$\mathbb {S}[f]\colon \mathbb {S}[A] \to \mathbb {S}[B]$
. When the fibers of f are compact, there is also a ‘wrong-way’ map
![]() $f^!\colon \mathbb {S}[B] \to \mathbb {S}[A]$
, discovered by Becker and Gottlieb [Reference Becker and Gottlieb9, Reference Becker and Gottlieb10] and now known as the Becker-Gottlieb transfer. While the first construction in [Reference Becker and Gottlieb9] was geometric in nature and only for fiber bundles of smooth manifolds, Becker and Gottlieb realized in [Reference Becker and Gottlieb10] that their transfer map has a description purely in terms of duality data. In modern language: it is a special case of a generalized trace.
$f^!\colon \mathbb {S}[B] \to \mathbb {S}[A]$
, discovered by Becker and Gottlieb [Reference Becker and Gottlieb9, Reference Becker and Gottlieb10] and now known as the Becker-Gottlieb transfer. While the first construction in [Reference Becker and Gottlieb9] was geometric in nature and only for fiber bundles of smooth manifolds, Becker and Gottlieb realized in [Reference Becker and Gottlieb10] that their transfer map has a description purely in terms of duality data. In modern language: it is a special case of a generalized trace.
Because of the formal nature of generalized traces, the definition of the Becker-Gottlieb transfer makes sense in more general settings than spectra and maps of spaces with compact fibers. In [Reference Dwyer25], Dwyer introduces for every ring spectrum R the notion of an R-small fibration
![]() $f\colon A \to B$
, and constructs for every such fibration a transfer map of spectra of the form
$f\colon A \to B$
, and constructs for every such fibration a transfer map of spectra of the form
![]() $R[B] \to R[A]$
. More generally, if
$R[B] \to R[A]$
. More generally, if
![]() $\mathscr {C}$
is an arbitrary presentably symmetric monoidal
$\mathscr {C}$
is an arbitrary presentably symmetric monoidal
![]() $\infty $
-category, then there is for every
$\infty $
-category, then there is for every
![]() $\mathscr {C}$
-adjointable map
$\mathscr {C}$
-adjointable map
![]() $f\colon A \to B$
a Becker-Gottlieb transfer
$f\colon A \to B$
a Becker-Gottlieb transfer
When
![]() $\mathscr {C} = {\mathrm {RMod}}_R$
for a commutative ring spectrum R, this recovers Dwyer’s construction in the commutative case.
$\mathscr {C} = {\mathrm {RMod}}_R$
for a commutative ring spectrum R, this recovers Dwyer’s construction in the commutative case.
In this section, we will study these Becker-Gottlieb transfers utilizing the perspective on generalized traces developed earlier. We start by recalling the definition and the basic properties of Becker-Gottlieb transfers in Section 6.1. In Section 6.2, we will apply the methods from the previous sections to give a short proof of a theorem by John Lind and Cary Malkiewich [Reference Lind and Malkiewich48] which expresses the Becker-Gottlieb transfer ![]() as the composite of the inclusion of constant loops
as the composite of the inclusion of constant loops ![]() , the free loop transfer
, the free loop transfer ![]() and the evaluation map
and the evaluation map ![]() , see Theorem 6.12. In Section 6.3, we discuss the question of composability of Becker-Gottlieb transfers, and prove several instances where it holds. A simple counterexample when
, see Theorem 6.12. In Section 6.3, we discuss the question of composability of Becker-Gottlieb transfers, and prove several instances where it holds. A simple counterexample when
![]() $\mathscr {C}$
is the
$\mathscr {C}$
is the
![]() $\infty $
-category of rational vector spaces shows that this cannot be expected to hold in full generality. We end the section in Section 6.4 by explaining how keeping track of the naturality in the map f formally leads to a refinement of Theorem 6.12.
$\infty $
-category of rational vector spaces shows that this cannot be expected to hold in full generality. We end the section in Section 6.4 by explaining how keeping track of the naturality in the map f formally leads to a refinement of Theorem 6.12.
Throughout this section, we fix a presentably symmetric monoidal
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}$
.
$\mathscr {C}$
.
6.1 Definition and basic properties
For a space A, the diagonal map
![]() $\Delta _A\colon A \to A \times A$
induces a map in
$\Delta _A\colon A \to A \times A$
induces a map in
![]() $\mathscr {C}$
of the form
$\mathscr {C}$
of the form
If A is
![]() $\mathscr {C}$
-adjointable, then the object
$\mathscr {C}$
-adjointable, then the object ![]() is a dualizable object by Proposition 4.33, and thus we may form the generalized trace of this diagonal map. The resulting map, denoted
is a dualizable object by Proposition 4.33, and thus we may form the generalized trace of this diagonal map. The resulting map, denoted
is called the Becker-Gottlieb transfer of A.
For a relative version of this construction, consider a
![]() $\mathscr {C}$
-adjointable map of spaces
$\mathscr {C}$
-adjointable map of spaces
![]() $f\colon A \to B$
. For every fiber
$f\colon A \to B$
. For every fiber
![]() $A_b$
of f, the object
$A_b$
of f, the object ![]() is dualizable by Proposition 4.33, so that the above construction gives a B-indexed family of Becker-Gottlieb transfers
is dualizable by Proposition 4.33, so that the above construction gives a B-indexed family of Becker-Gottlieb transfers ![]() in
in
![]() $\mathscr {C}$
. Passing to colimits over B then gives a map
$\mathscr {C}$
. Passing to colimits over B then gives a map
called the Becker-Gottlieb transfer of f.
Throughout this section, we will frequently use arguments involving space-indexed families of objects or morphisms, and thus it will be convenient to set up some special notation for this. For a space B, consider the composite functor
where the first equivalence is the straightening equivalence and the second is given by post-composition with ![]() . It preserves colimits and is naturally symmetric monoidal. We think of the functor
. It preserves colimits and is naturally symmetric monoidal. We think of the functor ![]() as the B-parameterized analogue of the functor
as the B-parameterized analogue of the functor ![]() . Observe that it is compatible with restriction and pushforward: if
. Observe that it is compatible with restriction and pushforward: if
![]() $\beta \colon B' \to B$
is a map of spaces, then the following diagrams naturally commute:
$\beta \colon B' \to B$
is a map of spaces, then the following diagrams naturally commute:
Applying this to
![]() $\beta = f$
, we see in particular that
$\beta = f$
, we see in particular that ![]() for every space A over B. Applying it to the map
for every space A over B. Applying it to the map
![]() $B \to \mathrm {pt}$
, we see that
$B \to \mathrm {pt}$
, we see that ![]() .
.
Warning 6.1. The notation ![]() is abusive, as this object depends on a map of spaces
is abusive, as this object depends on a map of spaces
![]() $f\colon A \to B$
: at a point
$f\colon A \to B$
: at a point
![]() $b \in B$
it is given by
$b \in B$
it is given by ![]() . We emphasize that this is different from the object
. We emphasize that this is different from the object ![]() , which does not depend on f: it is given by
, which does not depend on f: it is given by ![]() at every point
at every point
![]() $b \in B$
.
$b \in B$
.
We may rewrite the definition of the Becker-Gottlieb transfer in terms of this functor ![]() as follows. Observe that for a
as follows. Observe that for a
![]() $\mathscr {C}$
-adjointable map
$\mathscr {C}$
-adjointable map
![]() $f\colon A \to B$
, the object
$f\colon A \to B$
, the object ![]() is dualizable by Proposition 4.33. Furthermore, the diagonal map
is dualizable by Proposition 4.33. Furthermore, the diagonal map
![]() $\Delta _A\colon A \to A \times _B A$
in
$\Delta _A\colon A \to A \times _B A$
in
![]() $\mathcal {S}_{/B}$
induces a map
$\mathcal {S}_{/B}$
induces a map
of which we can take the generalized trace.
Definition 6.2. Let
![]() $f\colon A \to B$
be a
$f\colon A \to B$
be a
![]() $\mathscr {C}$
-adjointable map of spaces. We define the Becker-Gottlieb pretransfer
$\mathscr {C}$
-adjointable map of spaces. We define the Becker-Gottlieb pretransfer
as the generalized trace in
![]() $\mathscr {C}^B$
of the diagonal map
$\mathscr {C}^B$
of the diagonal map ![]() .
.
We define the Becker-Gottlieb transfer ![]() as the composite
as the composite
obtained from the pretransfer
![]() $f^{!,\mathrm {pre}}$
by applying the colimit functor
$f^{!,\mathrm {pre}}$
by applying the colimit functor
![]() $B_!\colon \mathscr {C}^B \to \mathscr {C}$
.
$B_!\colon \mathscr {C}^B \to \mathscr {C}$
.
For completeness, we state and prove the main basic properties of Becker-Gottlieb transfers, which can be found for example in [Reference Dwyer25, Section 2] and [Reference Lewis, May and Steinberger47, p. 189].
Lemma 6.3.
-
(1) (Identity) The transfer for the identity
 $\mathrm {id}\colon B \to B$
is the identity
$\mathrm {id}\colon B \to B$
is the identity  ;
; -
(2) (Naturality) Consider a pullback square of spaces as on the left, where the maps f and
 $f'$
are
$f'$
are
 $\mathscr {C}$
-adjointable. Then there is a commutative diagram as on the right:
$\mathscr {C}$
-adjointable. Then there is a commutative diagram as on the right: 
-
(3) (Product) Let
 $f\colon A \to B$
and
$f\colon A \to B$
and
 $f'\colon A' \to B'$
be
$f'\colon A' \to B'$
be
 $\mathscr {C}$
-adjointable maps of spaces. Then the transfer map
$\mathscr {C}$
-adjointable maps of spaces. Then the transfer map  of the product map
of the product map
 $f \times f'\colon A \times A' \to B \times B'$
is equivalent to
$f \times f'\colon A \times A' \to B \times B'$
is equivalent to  .
.
Proof. Part (1) is obvious. For part (2), we will first relate the pretransfer of
![]() $f'$
with the pretransfer of f. Since
$f'$
with the pretransfer of f. Since
![]() $A'$
is a pullback of A along
$A'$
is a pullback of A along
![]() $\beta \colon B' \to B$
, we get an equivalence
$\beta \colon B' \to B$
, we get an equivalence ![]() in
in
![]() $\mathscr {C}^{B'}$
. Under this equivalence, the diagonal of
$\mathscr {C}^{B'}$
. Under this equivalence, the diagonal of ![]() is pulled back from the diagonal of
is pulled back from the diagonal of ![]() :
:
By symmetric monoidality, the functor
![]() $\beta ^*\colon \mathscr {C}^B \to \mathscr {C}^{B'}$
preserves generalized traces, and thus we get an equivalence
$\beta ^*\colon \mathscr {C}^B \to \mathscr {C}^{B'}$
preserves generalized traces, and thus we get an equivalence
![]() ${f'}^{!,\mathrm {pre}} \simeq \beta ^*{f}^{!,\mathrm {pre}}$
.
${f'}^{!,\mathrm {pre}} \simeq \beta ^*{f}^{!,\mathrm {pre}}$
.
Next, consider the following diagram:
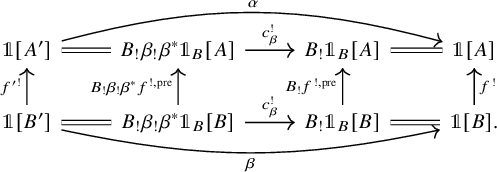
Here
![]() $c^!_{\beta }\colon \beta _!\beta ^* \to \mathrm {id}$
denotes the counit of the adjunction
$c^!_{\beta }\colon \beta _!\beta ^* \to \mathrm {id}$
denotes the counit of the adjunction
![]() $\beta _! \dashv \beta ^*$
. The right square commutes by definition, while the left square commutes by the description of the pretransfer of
$\beta _! \dashv \beta ^*$
. The right square commutes by definition, while the left square commutes by the description of the pretransfer of
![]() $f'$
in terms of the pretransfer of f. The middle square commutes by naturality. One checks that the top and bottom composites of the diagram are induced by
$f'$
in terms of the pretransfer of f. The middle square commutes by naturality. One checks that the top and bottom composites of the diagram are induced by
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
, respectively. This proves the claim.
$\beta $
, respectively. This proves the claim.
For part (3), we will again first describe the pretransfer of
![]() $f \times f'$
in terms of the pretransfers of f and
$f \times f'$
in terms of the pretransfers of f and
![]() $f'$
. Consider the external tensor product
$f'$
. Consider the external tensor product
![]() $- \boxtimes -\colon \mathscr {C}^B \times \mathscr {C}^{B'} \to \mathscr {C}^{B \times B'}$
, defined as the composite
$- \boxtimes -\colon \mathscr {C}^B \times \mathscr {C}^{B'} \to \mathscr {C}^{B \times B'}$
, defined as the composite
Informally, it sends a pair
![]() $(X,Y)$
to the family
$(X,Y)$
to the family
![]() $\{X_b \otimes Y_{b'}\}_{(b,b') \in B \times B'}$
. Observe that this is a symmetric monoidal functor, and that it preserves colimits in both variables. Furthermore, it is compatible with left Kan extension, in the sense that the following square commutes:
$\{X_b \otimes Y_{b'}\}_{(b,b') \in B \times B'}$
. Observe that this is a symmetric monoidal functor, and that it preserves colimits in both variables. Furthermore, it is compatible with left Kan extension, in the sense that the following square commutes:
It follows that the object ![]() is equivalent to the external tensor product of the objects
is equivalent to the external tensor product of the objects ![]() and
and ![]() , and that the diagonal of
, and that the diagonal of ![]() is obtained by taking the external tensor product of the diagonals of
is obtained by taking the external tensor product of the diagonals of ![]() and
and ![]() . Since symmetric monoidal functors preserve generalized traces, see Remark 2.7, we get that the pretransfer
. Since symmetric monoidal functors preserve generalized traces, see Remark 2.7, we get that the pretransfer
![]() $(f \times f')^{!,\mathrm {pre}}$
is equivalent to
$(f \times f')^{!,\mathrm {pre}}$
is equivalent to
![]() ${f^{!,\mathrm {pre}} \boxtimes {f'}^{!,\mathrm {pre}}}$
. The claim about Becker-Gottlieb transfers now follows from applying
${f^{!,\mathrm {pre}} \boxtimes {f'}^{!,\mathrm {pre}}}$
. The claim about Becker-Gottlieb transfers now follows from applying
![]() ${(B \times B')_!\colon \mathscr {C}^{B \times B'} \to \mathscr {C}}$
, using the above commutative diagram for the map
${(B \times B')_!\colon \mathscr {C}^{B \times B'} \to \mathscr {C}}$
, using the above commutative diagram for the map
![]() $B \times B' \to \mathrm {pt} \times \mathrm {pt}$
.
$B \times B' \to \mathrm {pt} \times \mathrm {pt}$
.
From the additivity of generalized traces, we may deduce additivity of Becker-Gottlieb transfers.
Lemma 6.4 (Additivity of Becker-Gottlieb transfers).
Let
![]() $f\colon A \to B$
be a map of spaces.
$f\colon A \to B$
be a map of spaces.
-
(1) Assume that
 $\mathscr {C}$
is a semiadditive
$\mathscr {C}$
is a semiadditive
 $\infty $
-category, and assume that A can be decomposed as a disjoint union
$\infty $
-category, and assume that A can be decomposed as a disjoint union
 $A = A_1 \sqcup A_2$
. For
$A = A_1 \sqcup A_2$
. For
 $i = 1,2$
, let
$i = 1,2$
, let
 $j_i\colon A_i \hookrightarrow A$
denote the inclusion and let
$j_i\colon A_i \hookrightarrow A$
denote the inclusion and let
 $f_i := f \circ j_i\colon A_i \to B$
. If the maps
$f_i := f \circ j_i\colon A_i \to B$
. If the maps
 $f_1$
and
$f_1$
and
 $f_2$
are
$f_2$
are
 $\mathscr {C}$
-adjointable, then f is also
$\mathscr {C}$
-adjointable, then f is also
 $\mathscr {C}$
-adjointable, and there is an equivalence
$\mathscr {C}$
-adjointable, and there is an equivalence 
-
(2) Assume that
 $\mathscr {C}$
is a stable
$\mathscr {C}$
is a stable
 $\infty $
-category, and assume that A is given as a pushout of the form Set
$\infty $
-category, and assume that A is given as a pushout of the form Set
 $j_3\colon A_3\to A$
to be the diagonal composite, and let
$j_3\colon A_3\to A$
to be the diagonal composite, and let
 $f_i := f \circ j_i\colon A_i \to B$
for
$f_i := f \circ j_i\colon A_i \to B$
for
 $i = 1,2,3$
. If each
$i = 1,2,3$
. If each
 $f_i$
is
$f_i$
is
 $\mathscr {C}$
-adjointable, then f is also
$\mathscr {C}$
-adjointable, then f is also
 $\mathscr {C}$
-adjointable, and there is an equivalence
$\mathscr {C}$
-adjointable, and there is an equivalence 
Proof. In part (1), the fact that f is
![]() $\mathscr {C}$
-adjointable follows from the fact that the diagonal functor
$\mathscr {C}$
-adjointable follows from the fact that the diagonal functor
![]() $\Delta \colon \mathscr {C} \to \mathscr {C} \times \mathscr {C}$
is an internal left adjoint, as semiadditivity implies that the left and right adjoint of
$\Delta \colon \mathscr {C} \to \mathscr {C} \times \mathscr {C}$
is an internal left adjoint, as semiadditivity implies that the left and right adjoint of
![]() $\Delta $
are equivalent. For the second part, we we will prove the stronger claim that there is an equivalence
$\Delta $
are equivalent. For the second part, we we will prove the stronger claim that there is an equivalence
in ![]() ; the desired claim will follow by applying
; the desired claim will follow by applying
![]() $B_!\colon \mathscr {C}^B \to \mathscr {C}$
. For
$B_!\colon \mathscr {C}^B \to \mathscr {C}$
. For
![]() $i = 1,2$
, we get from Remark 2.8 that the map
$i = 1,2$
, we get from Remark 2.8 that the map ![]() is the generalized trace in
is the generalized trace in
![]() $\mathscr {C}^B$
of the composite
$\mathscr {C}^B$
of the composite
induced by the map
![]() $(1,j_i)\colon A_i \to A_i \times _B A$
in
$(1,j_i)\colon A_i \to A_i \times _B A$
in
![]() $\mathcal {S}_{/B}$
. The direct sum of these two maps is the diagonal of
$\mathcal {S}_{/B}$
. The direct sum of these two maps is the diagonal of ![]() , hence the claim follows from Lemma 5.29.
, hence the claim follows from Lemma 5.29.
In part (2), the fact that f is
![]() $\mathscr {C}$
-adjointable follows from Lemma 4.28. For the second part, we will prove the stronger claim that there is an equivalence
$\mathscr {C}$
-adjointable follows from Lemma 4.28. For the second part, we will prove the stronger claim that there is an equivalence
in ![]() . As before, the desired claim follows by applying
. As before, the desired claim follows by applying
![]() $B_!\colon \mathscr {C}^B \to \mathscr {C}$
. We follow the proof of [Reference Lewis, May and Steinberger47, IV.2.9, p.184]. Since the functor
$B_!\colon \mathscr {C}^B \to \mathscr {C}$
. We follow the proof of [Reference Lewis, May and Steinberger47, IV.2.9, p.184]. Since the functor ![]() preserves colimits and
preserves colimits and
![]() $\mathscr {C}^B$
is an additive
$\mathscr {C}^B$
is an additive
![]() $\infty $
-category, we obtain a cofiber sequence
$\infty $
-category, we obtain a cofiber sequence
in
![]() $\mathscr {C}^B$
. Tensoring with
$\mathscr {C}^B$
. Tensoring with ![]() gives rise to a second cofiber sequence. Now consider the following morphism of cofiber sequences:
gives rise to a second cofiber sequence. Now consider the following morphism of cofiber sequences:
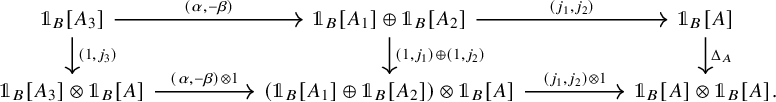
As in part (1), the generalized trace of the maps
is ![]() , and thus by Lemma 5.29 the generalized trace of the middle vertical map is the sum
, and thus by Lemma 5.29 the generalized trace of the middle vertical map is the sum
![]() $j_1 \circ {f}^{!,\mathrm {pre}}_1 + j_2 \circ {f}^{!,\mathrm {pre}}_1$
. The claim thus follows from additivity of generalized traces, Theorem 5.27.
$j_1 \circ {f}^{!,\mathrm {pre}}_1 + j_2 \circ {f}^{!,\mathrm {pre}}_1$
. The claim thus follows from additivity of generalized traces, Theorem 5.27.
Remark 6.5. When
![]() $\mathscr {C} = \mathrm {Sp}$
is the
$\mathscr {C} = \mathrm {Sp}$
is the
![]() $\infty $
-category of spectra, the four properties of the Becker-Gottlieb transfer listed above (naturality, identity, product and additivity) can be used to uniquely characterize the Becker-Gottlieb transfers on certain fiber bundles with compact fibers, see [Reference Becker and Schultz12]. In similar spirit is the result of [Reference Lewis46], where axioms are introduced to characterize the Becker-Gottlieb transfers on the level of cohomology.
$\infty $
-category of spectra, the four properties of the Becker-Gottlieb transfer listed above (naturality, identity, product and additivity) can be used to uniquely characterize the Becker-Gottlieb transfers on certain fiber bundles with compact fibers, see [Reference Becker and Schultz12]. In similar spirit is the result of [Reference Lewis46], where axioms are introduced to characterize the Becker-Gottlieb transfers on the level of cohomology.
6.2 Description in terms of the free loop transfer
Let
![]() $f\colon A \to B$
be a map of spaces with compact fibers. It was proved by Lind and Malkiewich [Reference Lind and Malkiewich48, Theorem 1.2] that the Becker-Gottlieb transfer
$f\colon A \to B$
be a map of spaces with compact fibers. It was proved by Lind and Malkiewich [Reference Lind and Malkiewich48, Theorem 1.2] that the Becker-Gottlieb transfer
![]() $f^!\colon \mathbb {S}[B] \to \mathbb {S}[A]$
can be obtained from the free loop transfer
$f^!\colon \mathbb {S}[B] \to \mathbb {S}[A]$
can be obtained from the free loop transfer
![]() $ {\mathrm {Tr}}_{\mathscr {C}}(f^*)\colon \mathbb {S}[LB] \to \mathbb {S}[LA]$
by precomposing with the constant loop map
$ {\mathrm {Tr}}_{\mathscr {C}}(f^*)\colon \mathbb {S}[LB] \to \mathbb {S}[LA]$
by precomposing with the constant loop map
![]() $c\colon \mathbb {S}[B] \to \mathbb {S}[LB]$
and postcomposing with the evaluation map
$c\colon \mathbb {S}[B] \to \mathbb {S}[LB]$
and postcomposing with the evaluation map
![]() $e\colon \mathbb {S}[LA] \to \mathbb {S}[A]$
. A proof of this statement for a smaller class of fibrations was given in [Reference Dorabiala and Johnson22] using the Becker-Schultz axiomatization of the Becker-Gottlieb transfer. The equivalence of these maps after composing with the projection
$e\colon \mathbb {S}[LA] \to \mathbb {S}[A]$
. A proof of this statement for a smaller class of fibrations was given in [Reference Dorabiala and Johnson22] using the Becker-Schultz axiomatization of the Becker-Gottlieb transfer. The equivalence of these maps after composing with the projection
![]() $\mathbb {S}[A] \to \mathbb {S}$
from A to the point was obtained by [Reference Douglas24].
$\mathbb {S}[A] \to \mathbb {S}$
from A to the point was obtained by [Reference Douglas24].
The result by Lind and Malkiewich admits a quick and elegant proof using the methods developed in this article, which works in the generality of an arbitrary presentably symmetric monoidal
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}$
. The main input is the simple but crucial observation that we can relate the Becker-Gottlieb transfer with the generalized character of a well-chosen map
$\mathscr {C}$
. The main input is the simple but crucial observation that we can relate the Becker-Gottlieb transfer with the generalized character of a well-chosen map
![]() $\delta (f)$
in
$\delta (f)$
in
![]() $\mathscr {C}^B$
.
$\mathscr {C}^B$
.
Definition 6.6. Let
![]() $f\colon A \to B$
be a map of spaces. We define the map
$f\colon A \to B$
be a map of spaces. We define the map
as the image under ![]() of the diagonal map
of the diagonal map
where we regard
![]() $A \times A$
as living over B via its first factor. Over a point
$A \times A$
as living over B via its first factor. Over a point
![]() $b \in B$
, it is given by the generalized endomorphism
$b \in B$
, it is given by the generalized endomorphism
where
![]() $\iota _b\colon A_b \to A$
is the inclusion of the fiber.
$\iota _b\colon A_b \to A$
is the inclusion of the fiber.
If
![]() $f\colon A \to B$
is
$f\colon A \to B$
is
![]() $\mathscr {C}$
-adjointable, then
$\mathscr {C}$
-adjointable, then ![]() is dualizable in
is dualizable in
![]() $\mathscr {C}^B$
(Proposition 4.33), and thus we obtain a generalized character map
$\mathscr {C}^B$
(Proposition 4.33), and thus we obtain a generalized character map
The Becker-Gottlieb transfer of f can be recovered from this character map as follows.
Proposition 6.7. For a
![]() $\mathscr {C}$
-adjointable map
$\mathscr {C}$
-adjointable map
![]() $f\colon A\to B$
, the following diagram commutes:
$f\colon A\to B$
, the following diagram commutes:
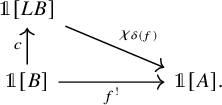
Proof. Observe that the map
![]() $\delta (f)$
can be written as the composite
$\delta (f)$
can be written as the composite
where
![]() $u_B$
denotes the map
$u_B$
denotes the map ![]() induced by the map
induced by the map
![]() $(1,f)\colon A \to A \times B$
over B. By Remark 2.8, it follows that the generalized trace of
$(1,f)\colon A \to A \times B$
over B. By Remark 2.8, it follows that the generalized trace of
![]() $\delta (f)$
in
$\delta (f)$
in
![]() $\mathscr {C}^B$
is given by the composite
$\mathscr {C}^B$
is given by the composite
which adjoints over to the map ![]() . The claim thus follows from Corollary 5.15.
. The claim thus follows from Corollary 5.15.
Our next aim is a better understanding of the character of
![]() $\delta (f)$
. We start with the case where f is the identity on a space A.
$\delta (f)$
. We start with the case where f is the identity on a space A.
Proposition 6.8. The character ![]() is the evaluation map
is the evaluation map ![]() .
.
Proof. The map
![]() $\delta (\mathrm {id}_A)$
is given by the A-indexed family of generalized traces
$\delta (\mathrm {id}_A)$
is given by the A-indexed family of generalized traces ![]() induced by the inclusions
induced by the inclusions
![]() $\iota _a\colon \{a\} \hookrightarrow A$
. By Example 2.3, the generalized character of this map is simply the map
$\iota _a\colon \{a\} \hookrightarrow A$
. By Example 2.3, the generalized character of this map is simply the map ![]() . It thus follows from the coherent character formula, Proposition 5.14, that the character
. It thus follows from the coherent character formula, Proposition 5.14, that the character ![]() is the mate of the map
is the mate of the map ![]() which sends a free loop
which sends a free loop
![]() $\gamma \in LA$
to the inclusion
$\gamma \in LA$
to the inclusion ![]() of the basepoint of
of the basepoint of
![]() $\gamma $
. The claim follows by adjunction.
$\gamma $
. The claim follows by adjunction.
To understand the character
![]() $\chi _{\delta (f)}$
for general maps
$\chi _{\delta (f)}$
for general maps
![]() $f\colon A \to B$
, we observe that for a second map
$f\colon A \to B$
, we observe that for a second map
![]() $g\colon B \to C$
the generalized endomorphisms
$g\colon B \to C$
the generalized endomorphisms
![]() $\delta (f)$
and
$\delta (f)$
and
![]() $\delta (gf)$
are closely related.
$\delta (gf)$
are closely related.
Proposition 6.9. Consider two composable maps of spaces
![]() $f \colon A \to B$
and
$f \colon A \to B$
and
![]() $g\colon B \to C$
. Then there is an equivalence of generalized endomorphisms
$g\colon B \to C$
. Then there is an equivalence of generalized endomorphisms
Proof. Spelling out the definitions, one observes that both maps are given by applying the functor ![]() to the diagonal map
to the diagonal map ![]() .
.
As a consequence, we obtain a description of the character
![]() $\chi _{\delta (gf)}$
in terms of the character
$\chi _{\delta (gf)}$
in terms of the character
![]() $\chi _{\delta (f)}$
and the free loop transfer of g:
$\chi _{\delta (f)}$
and the free loop transfer of g:
Corollary 6.10. Let
![]() $f\colon A\to B$
and
$f\colon A\to B$
and
![]() $g\colon B \to C$
be
$g\colon B \to C$
be
![]() $\mathscr {C}$
-adjointable maps of spaces. Then the following diagram commutes:
$\mathscr {C}$
-adjointable maps of spaces. Then the following diagram commutes:
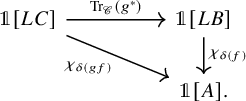
In particular, we obtain a description of the character
![]() $\chi _{\delta (f)}$
in terms of the free loop transfer of f:
$\chi _{\delta (f)}$
in terms of the free loop transfer of f:
Corollary 6.11. For a
![]() $\mathscr {C}$
-adjointable map of spaces
$\mathscr {C}$
-adjointable map of spaces
![]() $f\colon A\to B$
, the following diagram commutes:
$f\colon A\to B$
, the following diagram commutes:
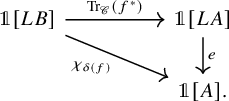
Proof. Applying Corollary 6.10 to the maps
![]() $\mathrm {id}_A\colon A \to A$
and
$\mathrm {id}_A\colon A \to A$
and
![]() $f\colon A \to B$
, this is immediate from the equivalence
$f\colon A \to B$
, this is immediate from the equivalence
![]() $\chi _{\delta (\mathrm {id}_A)} \simeq e$
of Proposition 6.8.
$\chi _{\delta (\mathrm {id}_A)} \simeq e$
of Proposition 6.8.
We thus obtain the main theorem of this section.
Theorem 6.12 (cf. Lind-Malkiewich [Reference Lind and Malkiewich48, Theorem 1.2]).
For a
![]() $\mathscr {C}$
-adjointable map of spaces
$\mathscr {C}$
-adjointable map of spaces
![]() $f\colon A \to B$
, the following diagram commutes:
$f\colon A \to B$
, the following diagram commutes:
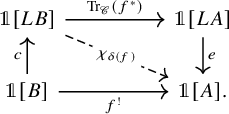
6.3 Composability of Becker-Gottlieb transfers
Consider two composable maps of spaces
![]() $f\colon A \to B$
and
$f\colon A \to B$
and
![]() $g\colon B \to C$
and assume both f and g are
$g\colon B \to C$
and assume both f and g are
![]() $\mathscr {C}$
-adjointable. Since the composite
$\mathscr {C}$
-adjointable. Since the composite
![]() $gf\colon A \to C$
is again
$gf\colon A \to C$
is again
![]() $\mathscr {C}$
-adjointable, we may form the Becker-Gottlieb transfers
$\mathscr {C}$
-adjointable, we may form the Becker-Gottlieb transfers ![]() ,
, ![]() and
and ![]() in
in
![]() $\mathscr {C}$
. It is natural to wonder how the map
$\mathscr {C}$
. It is natural to wonder how the map
![]() $(gf)^!$
relates to the composite
$(gf)^!$
relates to the composite
![]() $f^! \circ g^!$
.
$f^! \circ g^!$
.
Definition 6.13. We will say that f and g have composable Becker-Gottlieb transfers
Footnote
15
if the following triangle commutes in
![]() $\mathscr {C}$
:
$\mathscr {C}$
:
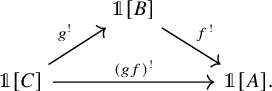
The naive guess that Becker-Gottlieb transfers are composable in full generality turns out to be incorrect.
Counterexample 6.14. Let
![]() $\mathscr {C} = \mathrm {Vect}_{\mathbb {Q}}$
be the category of rational vector spaces, and consider the maps
$\mathscr {C} = \mathrm {Vect}_{\mathbb {Q}}$
be the category of rational vector spaces, and consider the maps
![]() $f\colon \mathrm {pt} \to BH$
and
$f\colon \mathrm {pt} \to BH$
and
![]() $g\colon BH \to \mathrm {pt}$
, where H is a non-trivial finite group. By 1-semiadditivity of
$g\colon BH \to \mathrm {pt}$
, where H is a non-trivial finite group. By 1-semiadditivity of
![]() $\mathrm {Vect}_{\mathbb {Q}}$
, the maps f and g are
$\mathrm {Vect}_{\mathbb {Q}}$
, the maps f and g are
![]() $\mathscr {C}$
-adjointable, see Example 4.25. We claim that the composition
$\mathscr {C}$
-adjointable, see Example 4.25. We claim that the composition
![]() $f^! \circ g^!\colon \mathbb {Q} \to \mathbb {Q}$
is not given by the identity but rather by multiplication by the group order
$f^! \circ g^!\colon \mathbb {Q} \to \mathbb {Q}$
is not given by the identity but rather by multiplication by the group order
![]() $\lvert H \rvert $
of H. To see this, observe that the map g induces an equivalence
$\lvert H \rvert $
of H. To see this, observe that the map g induces an equivalence ![]() . Since this equivalence is compatible with the diagonal and with the evaluation and coevaluation, it follows that the composite
. Since this equivalence is compatible with the diagonal and with the evaluation and coevaluation, it follows that the composite ![]() is the identity. But note that the H-equivariant pretransfer
is the identity. But note that the H-equivariant pretransfer
![]() $\mathbb {Q} \to \mathbb {Q}[H]$
of f is given by
$\mathbb {Q} \to \mathbb {Q}[H]$
of f is given by
![]() $1 \mapsto \sum _{h \in H}h$
, so that passing to H-orbits gives a map
$1 \mapsto \sum _{h \in H}h$
, so that passing to H-orbits gives a map
![]() $f^!\colon \mathbb {Q}_H \to \mathbb {Q}$
which is
$f^!\colon \mathbb {Q}_H \to \mathbb {Q}$
which is
![]() $\lvert H \rvert $
times the map
$\lvert H \rvert $
times the map ![]() , proving the claim.
, proving the claim.
Warning 6.15. It is claimed in [Reference Klein and Malkiewich42] that when
![]() $\mathscr {C}$
is the
$\mathscr {C}$
is the
![]() $\infty $
-category of spectra and the maps f and g have compact fibers,Footnote
16
the Becker-Gottlieb transfers of f and g are composable. Unfortunately, the proof in [Reference Klein and Malkiewich42] contains a mistake: the diagram (13) on page 1135 does not commute, which renders the proof invalid. As this mistake appeared to be unfixable, Klein and Malkiewich have published a corrigendum [Reference Klein and Malkiewich43] retracting the main theorem of [Reference Klein and Malkiewich42]. To the best of our knowledge it is currently an open problem whether or not the Becker-Gottlieb transfers in spectra of maps with compact fibers are composable in full generality.
$\infty $
-category of spectra and the maps f and g have compact fibers,Footnote
16
the Becker-Gottlieb transfers of f and g are composable. Unfortunately, the proof in [Reference Klein and Malkiewich42] contains a mistake: the diagram (13) on page 1135 does not commute, which renders the proof invalid. As this mistake appeared to be unfixable, Klein and Malkiewich have published a corrigendum [Reference Klein and Malkiewich43] retracting the main theorem of [Reference Klein and Malkiewich42]. To the best of our knowledge it is currently an open problem whether or not the Becker-Gottlieb transfers in spectra of maps with compact fibers are composable in full generality.
To see the subtlety of this problem, we may use the description of Becker-Gottlieb transfers established in the previous section. Consider the following diagram:
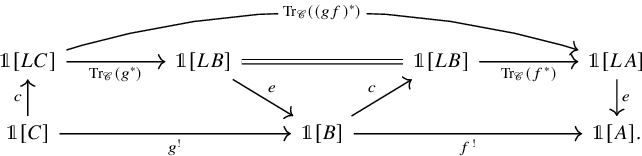
From Theorem 6.12 we obtain that the two trapezoids commute and that the composite along the top of the diagram is the Becker-Gottlieb transfer ![]() . The top part of the diagram commutes by functoriality of the
. The top part of the diagram commutes by functoriality of the
![]() $\mathscr {C}$
-linear trace. However, the middle triangle of the diagram does not commute: it replaces each free loop in B by the constant loop on its basepoint. Since the diagonal of the right square is the character
$\mathscr {C}$
-linear trace. However, the middle triangle of the diagram does not commute: it replaces each free loop in B by the constant loop on its basepoint. Since the diagonal of the right square is the character ![]() , we obtain the following two descriptions of
, we obtain the following two descriptions of
![]() $(gf)^!$
and
$(gf)^!$
and
![]() $f^!g^!$
:
$f^!g^!$
:
Corollary 6.16. Let
![]() $f\colon A\to B$
and
$f\colon A\to B$
and
![]() $g\colon B\to C$
be
$g\colon B\to C$
be
![]() $\mathscr {C}$
-adjointable maps of spaces. The Becker-Gottlieb transfer
$\mathscr {C}$
-adjointable maps of spaces. The Becker-Gottlieb transfer
![]() $(gf)^!$
of the composite
$(gf)^!$
of the composite
![]() $gf$
is homotopic to the following composite:
$gf$
is homotopic to the following composite:
On the other hand, the composite of the Becker-Gottlieb transfers
![]() $f^!$
and
$f^!$
and
![]() $g^!$
is given by the composite
$g^!$
is given by the composite
Corollary 6.16 gives us a concrete obstruction for composability of Becker-Gottlieb transfers. This has been used for instance by [Reference Klein, Malkiewich and Ramzi44] to prove composability for finitely dominated maps at the level of
![]() $\pi _0$
:
$\pi _0$
:
Proposition 6.17 [Reference Klein, Malkiewich and Ramzi44, Theorem B].
Let
![]() $f\colon A \to B$
and
$f\colon A \to B$
and
![]() $g\colon B \to C$
be maps of spaces with compact fibers. Then the Becker-Gottlieb transfers compose on
$g\colon B \to C$
be maps of spaces with compact fibers. Then the Becker-Gottlieb transfers compose on
![]() $\pi _0$
: the diagram
$\pi _0$
: the diagram
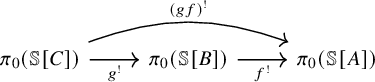
commutes.
In certain situations, the Becker-Gottlieb transfers of two maps are composable even before passing to
![]() $\pi _0$
. In the remainder of this subsection, we will give an overview of such results that were previously known in the literature, and provide various generalizations. The results are summarized in the following theorem:
$\pi _0$
. In the remainder of this subsection, we will give an overview of such results that were previously known in the literature, and provide various generalizations. The results are summarized in the following theorem:
Theorem 6.18 (cf. [Reference Lewis, May and Steinberger47], [Reference Williams65], [Reference Lind and Malkiewich48], [Reference Klein and Malkiewich43]).
Let
![]() $f\colon A \to B$
and
$f\colon A \to B$
and
![]() $g\colon B \to C$
be
$g\colon B \to C$
be
![]() $\mathscr {C}$
-adjointable morphisms of spaces. In the following situations, there is a homotopy
$\mathscr {C}$
-adjointable morphisms of spaces. In the following situations, there is a homotopy
![]() $f^! \circ g^! \simeq (g \circ f)^!$
of maps
$f^! \circ g^! \simeq (g \circ f)^!$
of maps ![]() :
:
-
(1) The map
 $f\colon A \to B$
is a base change of some map
$f\colon A \to B$
is a base change of some map
 $\mathscr {C}$
-adjointable map
$\mathscr {C}$
-adjointable map
 $B' \to C$
along
$B' \to C$
along
 $g\colon B \to C$
(Lemma 6.19);
$g\colon B \to C$
(Lemma 6.19); -
(1a) The map
 $f\colon A \to B$
is a projection
$f\colon A \to B$
is a projection
 $A_0 \times B \to B$
(Corollary 6.20);
$A_0 \times B \to B$
(Corollary 6.20); -
(2) The free loop transfer of g restricts to constant loops, in the sense of Definition 6.22 (Proposition 6.25);
-
(2a) The
 $\infty $
-category
$\infty $
-category
 $\mathscr {C}$
is stable and the map
$\mathscr {C}$
is stable and the map
 $g\colon B \to C$
is a smooth fiber bundle with closed manifold fibers (Corollary 6.28);
$g\colon B \to C$
is a smooth fiber bundle with closed manifold fibers (Corollary 6.28); -
(2b) The
 $\infty $
-category
$\infty $
-category
 $\mathscr {C}$
is semidadditive and the map
$\mathscr {C}$
is semidadditive and the map
 $g\colon B \to C$
is a finite covering map (Corollary 6.42);
$g\colon B \to C$
is a finite covering map (Corollary 6.42); -
(3) The space C is the classifying space of a compact Lie group G, and the map
 $g\colon B \to C$
is of the form
$g\colon B \to C$
is of the form
 $B^{\prime }_{hG} \to \mathrm {pt}_{hG} \simeq BG$
for some finite G-CW-complex
$B^{\prime }_{hG} \to \mathrm {pt}_{hG} \simeq BG$
for some finite G-CW-complex
 $B'$
(Corollary 6.34).
$B'$
(Corollary 6.34).
Let us comment about the history of these results. The case (1) seems to be a new observation. Its consequence (1a) has been obtained using different methods by [Reference Klein and Malkiewich43]. The case (2) was already observed by [Reference Lind and Malkiewich48]. The special case (2a) requires geometric input, which can be deduced from [Reference Williams65] but was reproved using different methods by [Reference Lind and Malkiewich48]. When
![]() $\mathscr {C}$
is stable, the special case (2b) follows from (2a), and was also proved using different methods by [Reference Klein and Malkiewich43]. The case in (2b) where
$\mathscr {C}$
is stable, the special case (2b) follows from (2a), and was also proved using different methods by [Reference Klein and Malkiewich43]. The case in (2b) where
![]() $\mathscr {C}$
is only assumed to be semiadditive seems to be new. The case (3) is a variant of a result proved by [Reference Lewis, May and Steinberger47], who worked in the setting of genuine G-spectra instead.
$\mathscr {C}$
is only assumed to be semiadditive seems to be new. The case (3) is a variant of a result proved by [Reference Lewis, May and Steinberger47], who worked in the setting of genuine G-spectra instead.
6.3.1 Trivial bundles
As a first example, we show that Becker-Gottlieb transfers compose when the map
![]() $f\colon A \to B$
is equivalent to a trivial bundle
$f\colon A \to B$
is equivalent to a trivial bundle
![]() $B \times A_0 \to B$
for some space
$B \times A_0 \to B$
for some space
![]() $A_0$
. More generally, we will show composability of Becker-Gottlieb transfers whenever f is obtained as a base change of some map along g. This seems to be a new observation.
$A_0$
. More generally, we will show composability of Becker-Gottlieb transfers whenever f is obtained as a base change of some map along g. This seems to be a new observation.
Lemma 6.19. Consider a pullback diagram of spaces
and assume that the maps f, g and h are
![]() $\mathscr {C}$
-adjointable. Then the Becker-Gottlieb transfers for f and g are composable:
$\mathscr {C}$
-adjointable. Then the Becker-Gottlieb transfers for f and g are composable:
![]() $f^! \circ g^! \simeq (g \circ f)^!$
$f^! \circ g^! \simeq (g \circ f)^!$
We may think of this lemma as an enhanced version of Lemma 6.3(3), parameterized over the space C. Indeed, for
![]() $C = \mathrm {pt}$
we have an equivalence
$C = \mathrm {pt}$
we have an equivalence
![]() $A \simeq B \times D$
, and the claim follows from Lemma 6.3(3). By naturality of Becker-Gottlieb transfers, we see that for general C the equivalence
$A \simeq B \times D$
, and the claim follows from Lemma 6.3(3). By naturality of Becker-Gottlieb transfers, we see that for general C the equivalence
![]() $f^!(g^!(c)) \simeq (g \circ f)^!(c)$
holds pointwise for all
$f^!(g^!(c)) \simeq (g \circ f)^!(c)$
holds pointwise for all
![]() $c \in C$
. The claim of Lemma 6.19 is that this works naturally in
$c \in C$
. The claim of Lemma 6.19 is that this works naturally in
![]() $c\in C$
.
$c\in C$
.
Proof. Spelling out the definition of the Becker-Gottlieb transfer in terms of the pretransfer, it will suffice to show that the following two maps in
![]() $\mathscr {C}^C$
are homotopic:
$\mathscr {C}^C$
are homotopic:
-
(1) the pretransfer
 of the composite
of the composite
 $gf\colon A \to C$
;
$gf\colon A \to C$
; -
(2) the composite
 of the pretransfers of g and f.
of the pretransfers of g and f.
We will show they are both homotopic to the following map:
-
(3) the tensor product
 of the pretransfers of h and g.
of the pretransfers of h and g.
We start by proving that (1) and (3) are homotopic. Since the objects ![]() and
and ![]() are dualizable in
are dualizable in
![]() $\mathscr {C}^C$
, so is their tensor product
$\mathscr {C}^C$
, so is their tensor product ![]() , and the duality data may be chosen to be the tensor product of the duality data for
, and the duality data may be chosen to be the tensor product of the duality data for ![]() and
and ![]() . It thus remains to show that the following square commutes:
. It thus remains to show that the following square commutes:

But this is clear, as both horizontal maps are induced by the diagonal of
![]() $A \simeq D \times _C B$
in
$A \simeq D \times _C B$
in
![]() $\mathcal {S}_{/C}$
.
$\mathcal {S}_{/C}$
.
Next we show that (2) and (3) are homotopic. For this, we rewrite (3) as a composite
As we saw in the proof of Lemma 6.3(2), under the equivalence ![]() the pretransfer of f is pulled back along g from the pretransfer of h, in the sense that the following diagram commutes:
the pretransfer of f is pulled back along g from the pretransfer of h, in the sense that the following diagram commutes:
Identifying ![]() with
with ![]() , the claim thus follows from the naturality of the projection formula:
, the claim thus follows from the naturality of the projection formula:
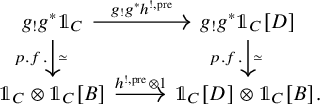
It follows that also the maps (1) and (2) are homotopic, finishing the proof.
From Lemma 6.19, we immediately obtain composability of Becker-Gottlieb transfers for trivial bundles.
Corollary 6.20. Let
![]() $f\colon A \to B$
and
$f\colon A \to B$
and
![]() $g\colon B \to C$
be
$g\colon B \to C$
be
![]() $\mathscr {C}$
-adjointable maps of spaces. Assume that f is equivalent to the trivial bundle
$\mathscr {C}$
-adjointable maps of spaces. Assume that f is equivalent to the trivial bundle
![]() $B \times A_0 \to B$
for some
$B \times A_0 \to B$
for some
![]() $\mathscr {C}$
-adjointable space
$\mathscr {C}$
-adjointable space
![]() $A_0$
. Then the Becker-Gottlieb transfers for f and g are composable:
$A_0$
. Then the Becker-Gottlieb transfers for f and g are composable:
![]() $f^! \circ g^! \simeq (g \circ f)^!$
.
$f^! \circ g^! \simeq (g \circ f)^!$
.
Proof. The map f fits in a pullback diagram of the form
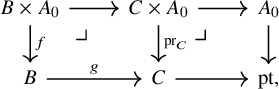
and thus this is a special case of Lemma 6.19.
Remark 6.21. When
![]() $\mathscr {C}$
is the
$\mathscr {C}$
is the
![]() $\infty $
-category of spectra, the result of Corollary 6.20 has also been obtained by [Reference Klein and Malkiewich43] via different methods.
$\infty $
-category of spectra, the result of Corollary 6.20 has also been obtained by [Reference Klein and Malkiewich43] via different methods.
6.3.2 The free loop transfer restricts to constant loops
As noted in [Reference Lind and Malkiewich48, Remark 8.10], the Becker-Gottlieb transfers of two
![]() $\mathscr {C}$
-adjointable maps
$\mathscr {C}$
-adjointable maps
![]() $f\colon A \to B$
and
$f\colon A \to B$
and
![]() $g\colon B \to C$
will always compose if g satisfies the property that its free loop transfer
$g\colon B \to C$
will always compose if g satisfies the property that its free loop transfer ![]() restricts to constant loops, the sense of the following definition:
restricts to constant loops, the sense of the following definition:
Definition 6.22. Let
![]() $g\colon B \to C$
be a
$g\colon B \to C$
be a
![]() $\mathscr {C}$
-adjointable map of spaces. We say that the free loop transfer of g restricts to constant loops if there exists a map
$\mathscr {C}$
-adjointable map of spaces. We say that the free loop transfer of g restricts to constant loops if there exists a map ![]() making the following diagram commute:
making the following diagram commute:
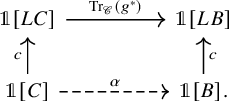
Remark 6.23. From functoriality and symmetric monoidality of the
![]() $\mathscr {C}$
-linear trace functor, maps of spaces whose free loop transfer restricts to constant loops are closed under composition and under cartesian products.
$\mathscr {C}$
-linear trace functor, maps of spaces whose free loop transfer restricts to constant loops are closed under composition and under cartesian products.
Although the map ![]() in the above definition can a priori be any map, it follows a posteriori that it must be the Becker-Gottlieb transfer of g.
in the above definition can a priori be any map, it follows a posteriori that it must be the Becker-Gottlieb transfer of g.
Lemma 6.24. Let
![]() $g\colon B \to C$
be a
$g\colon B \to C$
be a
![]() $\mathscr {C}$
-adjointable map of spaces, and assume that the free loop transfer of g restricts to some map
$\mathscr {C}$
-adjointable map of spaces, and assume that the free loop transfer of g restricts to some map ![]() on constant loops. Then there is a homotopy
on constant loops. Then there is a homotopy
![]() $\alpha \simeq g^!$
of maps
$\alpha \simeq g^!$
of maps ![]() . In particular, the following diagram commutes:
. In particular, the following diagram commutes:
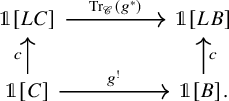
Proof. As the evaluation map
![]() $e\colon LB \to B$
is a retraction of the map
$e\colon LB \to B$
is a retraction of the map
![]() $c\colon B \to LB$
, the assumption implies
$c\colon B \to LB$
, the assumption implies
where the last equivalence is Theorem 6.12. The claim follows.
If the free loop transfer of g restricts to constant loops, composability of Becker-Gottlieb transfers is automatic.
Proposition 6.25. Let
![]() $f\colon A \to B$
and
$f\colon A \to B$
and
![]() $g\colon B \to C$
be a
$g\colon B \to C$
be a
![]() $\mathscr {C}$
-adjointable maps of spaces. Assume that the free loop transfer of g restricts to constant loops. Then the Becker-Gottlieb transfers for f and g are composable:
$\mathscr {C}$
-adjointable maps of spaces. Assume that the free loop transfer of g restricts to constant loops. Then the Becker-Gottlieb transfers for f and g are composable:
![]() $f^! \circ g^! \simeq (g \circ f)^!$
.
$f^! \circ g^! \simeq (g \circ f)^!$
.
Proof. Consider the following diagram:
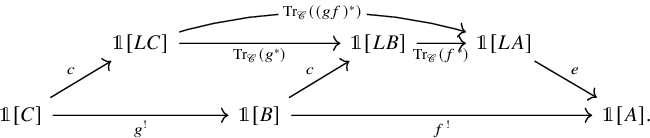
From Theorem 6.12 we obtain that the right trapezoid commutes and that the composite along the top of the diagram is the Becker-Gottlieb transfer ![]() . The left parallelogram commutes by Lemma 6.24. The top part of the diagram commutes by functoriality of the
. The left parallelogram commutes by Lemma 6.24. The top part of the diagram commutes by functoriality of the
![]() $\mathscr {C}$
-linear trace. Going around the diagram then gives the claim.
$\mathscr {C}$
-linear trace. Going around the diagram then gives the claim.
Because of Proposition 6.25, we are interested in maps of spaces
![]() $g\colon B \to C$
whose free loop transfer restricts to constant loops. When
$g\colon B \to C$
whose free loop transfer restricts to constant loops. When
![]() $\mathscr {C}$
is stable, it follows from the topological Riemann-Roch theorem [Reference Williams65, 2.7] that this holds whenever g is a smooth fiber bundle which has compact manifold fibers. This will be discussed below, see Proposition 6.27. The special case where g is a finite covering map also admits a completely formal proof, which will be given in Section 6.4.
$\mathscr {C}$
is stable, it follows from the topological Riemann-Roch theorem [Reference Williams65, 2.7] that this holds whenever g is a smooth fiber bundle which has compact manifold fibers. This will be discussed below, see Proposition 6.27. The special case where g is a finite covering map also admits a completely formal proof, which will be given in Section 6.4.
The question of whether or not the free loop transfer of an arbitrary map g restricts to constant loops is surprisingly subtle: as we will explain in the next remark, it is closely related to the Bass trace conjecture [Reference Bass7, Strong conjecture], an open conjecture in geometric group theory.
Remark 6.26 (Relation to Bass’ trace conjecture).
Let
![]() $\mathscr {C} = \mathrm {Sp}$
be the
$\mathscr {C} = \mathrm {Sp}$
be the
![]() $\infty $
-category of spectra and let
$\infty $
-category of spectra and let
![]() $C = \mathrm {pt}$
be the point. We may identify the free loop transfer
$C = \mathrm {pt}$
be the point. We may identify the free loop transfer
![]() $ {\mathrm {Tr}}_{\mathrm {Sp}}(B^*)\colon \mathbb {S} \to \mathbb {S}[LB]$
of B with a class in the 0-th stable homotopy group of
$ {\mathrm {Tr}}_{\mathrm {Sp}}(B^*)\colon \mathbb {S} \to \mathbb {S}[LB]$
of B with a class in the 0-th stable homotopy group of
![]() $LB$
:
$LB$
:
![]() $ {\mathrm {Tr}}_{\mathrm {Sp}}(B^*) \in \pi _0(\mathbb {S}[LB])$
. The condition that the free loop transfer restricts to constant loops is saying that this class is in the image of the constant loop map
$ {\mathrm {Tr}}_{\mathrm {Sp}}(B^*) \in \pi _0(\mathbb {S}[LB])$
. The condition that the free loop transfer restricts to constant loops is saying that this class is in the image of the constant loop map
This condition is closely related to the Bass trace conjecture [Reference Bass7, Strong conjecture], which states that for any group G the Hattori-Stallings trace
 $$ \begin{align*}K_0(\mathbb{Z}[G]) \to {\mathrm{HH}}_0(\mathbb{Z}[G]) \simeq \bigoplus_{G/{cong}} \mathbb{Z}\end{align*} $$
$$ \begin{align*}K_0(\mathbb{Z}[G]) \to {\mathrm{HH}}_0(\mathbb{Z}[G]) \simeq \bigoplus_{G/{cong}} \mathbb{Z}\end{align*} $$
lands in the direct summand indexed by the neutral element e of G. Concretely, the following two conditions are equivalent for a given finitely presented group G:
-
(1) The Bass trace conjecture holds for G;
-
(2) For every connected compact space B with
 $\pi _1(B)\simeq G$
, the free loop transfer
$\pi _1(B)\simeq G$
, the free loop transfer
 $ {\mathrm {Tr}}_{\mathrm {Sp}}(B^*) \in \pi _0(\mathbb {S}[LB])$
lies in the image of the constant loop map
$ {\mathrm {Tr}}_{\mathrm {Sp}}(B^*) \in \pi _0(\mathbb {S}[LB])$
lies in the image of the constant loop map
 $c_B\colon \pi _0(\mathbb {S}[B]) \hookrightarrow \pi _0(\mathbb {S}[LB])$
.
$c_B\colon \pi _0(\mathbb {S}[B]) \hookrightarrow \pi _0(\mathbb {S}[LB])$
.
See [Reference Klein and Malkiewich42, 1.1] for a related discussion.
6.3.3 Smooth fiber bundles
An important instance of a situation in which the commutativity of (5) is known is when
![]() $\mathscr {C}$
is the
$\mathscr {C}$
is the
![]() $\infty $
-category of spectra and
$\infty $
-category of spectra and
![]() $g\colon B \to C$
is a smooth fiber bundle with compact manifold fibers. This is a consequence of the topological Riemann-Roch theorem [Reference Williams65, 2.7], using the natural map from A-theory to topological Hochschild homology. A proof for closed manifold fibers, directly for topological Hochschild homology, was given by [Reference Lind and Malkiewich48, Corollary 1.9]. As the result for spectra in fact implies the result for an arbitrary stable presentably symmetric monoidal
$g\colon B \to C$
is a smooth fiber bundle with compact manifold fibers. This is a consequence of the topological Riemann-Roch theorem [Reference Williams65, 2.7], using the natural map from A-theory to topological Hochschild homology. A proof for closed manifold fibers, directly for topological Hochschild homology, was given by [Reference Lind and Malkiewich48, Corollary 1.9]. As the result for spectra in fact implies the result for an arbitrary stable presentably symmetric monoidal
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}$
, we will phrase the result in this generality.
$\mathscr {C}$
, we will phrase the result in this generality.
Proposition 6.27 [Reference Williams65, 2.7], [Reference Lind and Malkiewich48, Corollary 1.9].
Let
![]() $\mathscr {C}$
be stable, and let
$\mathscr {C}$
be stable, and let
![]() $g\colon B \to C$
be a smooth fiber bundle with compact manifold fibers, so that g is
$g\colon B \to C$
be a smooth fiber bundle with compact manifold fibers, so that g is
![]() $\mathscr {C}$
-adjointable by Example 4.27. Then the square
$\mathscr {C}$
-adjointable by Example 4.27. Then the square

commutes.
Proof. The case
![]() $\mathscr {C} = \mathrm {Sp}$
is [Reference Lind and Malkiewich48, Corollary 1.9]. The case for arbitrary
$\mathscr {C} = \mathrm {Sp}$
is [Reference Lind and Malkiewich48, Corollary 1.9]. The case for arbitrary
![]() $\mathscr {C}$
follows, as the unique colimit-preserving symmetric monoidal functor
$\mathscr {C}$
follows, as the unique colimit-preserving symmetric monoidal functor
![]() $F\colon \mathrm {Sp} \to \mathscr {C}$
preserves traces and categorical traces.
$F\colon \mathrm {Sp} \to \mathscr {C}$
preserves traces and categorical traces.
Corollary 6.28. Assume
![]() $\mathscr {C}$
is stable and let
$\mathscr {C}$
is stable and let
![]() $g\colon B \to C$
be a smooth fiber bundle with closed manifold fibers. Then for any other
$g\colon B \to C$
be a smooth fiber bundle with closed manifold fibers. Then for any other
![]() $\mathscr {C}$
-adjointable map
$\mathscr {C}$
-adjointable map
![]() $f\colon A \to B$
, the Becker-Gottlieb transfers for f and g are composable:
$f\colon A \to B$
, the Becker-Gottlieb transfers for f and g are composable:
![]() $f^! \circ g^! \simeq (g \circ f)^!$
.
$f^! \circ g^! \simeq (g \circ f)^!$
.
6.3.4 Via additivity of Becker-Gottlieb transfers
We may use the additivity of Becker-Gottlieb transfers (Lemma 6.4) to recursively obtain more cases of composability of Becker-Gottlieb transfers. Roughly speaking, the next two lemmas say that the collection of pairs of maps
![]() $f\colon A \to B$
and
$f\colon A \to B$
and
![]() $g\colon B \to C$
with composable Becker-Gottlieb transfers is closed under pushouts in A and B.
$g\colon B \to C$
with composable Becker-Gottlieb transfers is closed under pushouts in A and B.
Lemma 6.29. Let
![]() $\mathscr {C}$
be stable and let
$\mathscr {C}$
be stable and let
![]() $f\colon A \to B$
and
$f\colon A \to B$
and
![]() $g\colon B \to C$
be
$g\colon B \to C$
be
![]() $\mathscr {C}$
-adjointable maps of spaces. Assume that A is given as a pushout of the form
$\mathscr {C}$
-adjointable maps of spaces. Assume that A is given as a pushout of the form
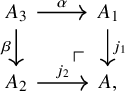
and let
![]() $j_3\colon A_3 \to A$
be the diagonal map. Assume further that each of the maps
$j_3\colon A_3 \to A$
be the diagonal map. Assume further that each of the maps
![]() $f_i := f \circ j_i\colon A_i \to B$
is
$f_i := f \circ j_i\colon A_i \to B$
is
![]() $\mathscr {C}$
-adjointable. If the Becker-Gottlieb transfer of g composes with that of
$\mathscr {C}$
-adjointable. If the Becker-Gottlieb transfer of g composes with that of
![]() $f_i$
for every
$f_i$
for every
![]() $i = 1,2,3$
, then also the Becker-Gottlieb transfers of g and f compose.
$i = 1,2,3$
, then also the Becker-Gottlieb transfers of g and f compose.
Proof. This follows immediately from additivity of Becker-Gottlieb transfers:
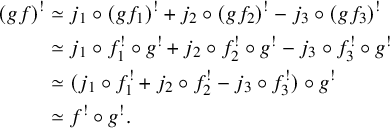 $$ \begin{align*} (gf)^! &\simeq j_1 \circ (gf_1)^! + j_2 \circ (gf_2)^! - j_3 \circ (gf_3)^! \\ &\simeq j_1 \circ f_1^! \circ g^! + j_2 \circ f_2^! \circ g^! - j_3 \circ f_3^! \circ g^! \\ &\simeq (j_1 \circ f_1^! + j_2 \circ f_2^! - j_3 \circ f_3^!) \circ g^! \\ &\simeq f^! \circ g^!.\\[-37pt] \end{align*} $$
$$ \begin{align*} (gf)^! &\simeq j_1 \circ (gf_1)^! + j_2 \circ (gf_2)^! - j_3 \circ (gf_3)^! \\ &\simeq j_1 \circ f_1^! \circ g^! + j_2 \circ f_2^! \circ g^! - j_3 \circ f_3^! \circ g^! \\ &\simeq (j_1 \circ f_1^! + j_2 \circ f_2^! - j_3 \circ f_3^!) \circ g^! \\ &\simeq f^! \circ g^!.\\[-37pt] \end{align*} $$
Lemma 6.30. Let
![]() $\mathscr {C}$
be stable and let
$\mathscr {C}$
be stable and let
![]() $f\colon A \to B$
and
$f\colon A \to B$
and
![]() $g\colon B \to C$
be
$g\colon B \to C$
be
![]() $\mathscr {C}$
-adjointable maps of spaces. Assume that B is given as a pushout of the form
$\mathscr {C}$
-adjointable maps of spaces. Assume that B is given as a pushout of the form
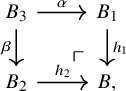
and let
![]() $h_3\colon B_3 \to B$
be the diagonal map. For every
$h_3\colon B_3 \to B$
be the diagonal map. For every
![]() $i=1,2,3$
, define the map
$i=1,2,3$
, define the map
![]() $f_i\colon A_i \to B_i$
via the following pullback square:
$f_i\colon A_i \to B_i$
via the following pullback square:
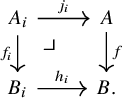
Assume further that each of the maps
![]() $g_i := g \circ h_i\colon B_i \to C$
is
$g_i := g \circ h_i\colon B_i \to C$
is
![]() $\mathscr {C}$
-adjointable. If the Becker-Gottlieb transfer of
$\mathscr {C}$
-adjointable. If the Becker-Gottlieb transfer of
![]() $g_i$
composes with that of
$g_i$
composes with that of
![]() $f_i$
for every
$f_i$
for every
![]() $i = 1,2,3$
, then also the Becker-Gottlieb transfers of g and f compose.
$i = 1,2,3$
, then also the Becker-Gottlieb transfers of g and f compose.
Proof. This follows immediately from additivity and naturality of Becker-Gottlieb transfers:
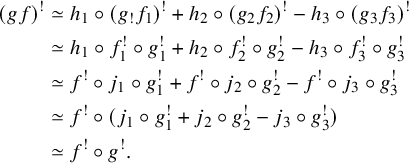 $$ \begin{align*} (gf)^! &\simeq h_1 \circ (g_!f_1)^! + h_2 \circ (g_2f_2)^! - h_3 \circ (g_3f_3)^! \\ &\simeq h_1 \circ f_1^! \circ g_1^! + h_2 \circ f_2^! \circ g_2^! - h_3 \circ f_3^! \circ g_3^! \\ &\simeq f^! \circ j_1 \circ g_1^! + f^! \circ j_2 \circ g_2^! - f^! \circ j_3 \circ g_3^! \\ &\simeq f^! \circ (j_1 \circ g_1^! + j_2 \circ g_2^! - j_3 \circ g_3^!) \\ &\simeq f^! \circ g^!.\\[-37pt] \end{align*} $$
$$ \begin{align*} (gf)^! &\simeq h_1 \circ (g_!f_1)^! + h_2 \circ (g_2f_2)^! - h_3 \circ (g_3f_3)^! \\ &\simeq h_1 \circ f_1^! \circ g_1^! + h_2 \circ f_2^! \circ g_2^! - h_3 \circ f_3^! \circ g_3^! \\ &\simeq f^! \circ j_1 \circ g_1^! + f^! \circ j_2 \circ g_2^! - f^! \circ j_3 \circ g_3^! \\ &\simeq f^! \circ (j_1 \circ g_1^! + j_2 \circ g_2^! - j_3 \circ g_3^!) \\ &\simeq f^! \circ g^!.\\[-37pt] \end{align*} $$
Lemma 6.30 has the following immediate corollary:
Corollary 6.31. Assume
![]() $\mathscr {C}$
is stable. Let C be a space, and let
$\mathscr {C}$
is stable. Let C be a space, and let
![]() $\mathcal {S}^{\mathrm {comp}}_{/C}$
the subcategory of
$\mathcal {S}^{\mathrm {comp}}_{/C}$
the subcategory of
![]() $\mathcal {S}_{/C}$
spanned by those
$\mathcal {S}_{/C}$
spanned by those
![]() $\mathscr {C}$
-adjointable morphisms
$\mathscr {C}$
-adjointable morphisms
![]() $g\colon B \to C$
such that for every other
$g\colon B \to C$
such that for every other
![]() $\mathscr {C}$
-adjointable morphism
$\mathscr {C}$
-adjointable morphism
![]() $f\colon A \to B$
the Becker-Gottlieb transfers of f and g are composable. Then
$f\colon A \to B$
the Becker-Gottlieb transfers of f and g are composable. Then
![]() $\mathcal {S}^{\mathrm {comp}}_{/C}$
is closed under finite colimits in
$\mathcal {S}^{\mathrm {comp}}_{/C}$
is closed under finite colimits in
![]() $\mathcal {S}_{/C}$
.
$\mathcal {S}_{/C}$
.
Proof. It is clear that
![]() $\mathcal {S}^{\mathrm {comp}}_{/C}$
contains the initial object
$\mathcal {S}^{\mathrm {comp}}_{/C}$
contains the initial object
![]() $\emptyset \to C$
, as any map
$\emptyset \to C$
, as any map
![]() $A \to \emptyset $
of spaces is an equivalence. It thus remains to show
$A \to \emptyset $
of spaces is an equivalence. It thus remains to show
![]() $\mathcal {S}^{\mathrm {comp}}_{/C}$
is closed under pushouts. By Lemma 4.28, the
$\mathcal {S}^{\mathrm {comp}}_{/C}$
is closed under pushouts. By Lemma 4.28, the
![]() $\mathscr {C}$
-adjointable morphisms
$\mathscr {C}$
-adjointable morphisms
![]() $B \to C$
are closed under finite colimits in
$B \to C$
are closed under finite colimits in
![]() $\mathcal {S}_{/C}$
. The result now follows directly from Lemma 6.30.
$\mathcal {S}_{/C}$
. The result now follows directly from Lemma 6.30.
For example, Corollary 6.28 shows that any smooth fiber bundle
![]() $g\colon B \to C$
with closed manifold fibers belongs to
$g\colon B \to C$
with closed manifold fibers belongs to
![]() $\mathcal {S}^{\mathrm {comp}}_{/C}$
.
$\mathcal {S}^{\mathrm {comp}}_{/C}$
.
6.3.5 Equivariant transfers
In [Reference Lewis, May and Steinberger47, Theorem IV.7.1], Lewis, May and Steinberger prove a result about composability of Becker-Gottlieb transfers in the setting of genuine equivariant homotopy theory for a compact Lie group G. This result has an analogue in the setting of spectra with G-action, which we will now discuss.
Definition 6.32. Let G be a compact Lie group and let
![]() $N \leqslant G$
be a closed normal subgroup. An orbit
$N \leqslant G$
be a closed normal subgroup. An orbit
![]() $G/H$
of G is called N-free if the action of N on
$G/H$
of G is called N-free if the action of N on
![]() $G/H$
is free, or equivalently if
$G/H$
is free, or equivalently if
![]() $N \cap H = e$
. A space with G-action
$N \cap H = e$
. A space with G-action
![]() $X \in \mathcal {S}^{BG}$
is called an N-free finite G-CW-complex if it is contained in the smallest subcategory of
$X \in \mathcal {S}^{BG}$
is called an N-free finite G-CW-complex if it is contained in the smallest subcategory of
![]() $\mathcal {S}^{BG}$
which contains the N-free orbits
$\mathcal {S}^{BG}$
which contains the N-free orbits
![]() $G/H$
and is closed under finite colimits.
$G/H$
and is closed under finite colimits.
Proposition 6.33 (cf. [Reference Lewis, May and Steinberger47, Theorem IV.7.1]).
Let
![]() $\mathscr {C}$
be a stable presentably symmetric monoidal
$\mathscr {C}$
be a stable presentably symmetric monoidal
![]() $\infty $
-category. Let G be a compact Lie group, let
$\infty $
-category. Let G be a compact Lie group, let
![]() $N \leqslant G$
be a closed normal subgroup, and let
$N \leqslant G$
be a closed normal subgroup, and let
![]() $J := G/N$
denote the quotient group. Let B be an N-free finite G-CW-complex, and let g be the composite
$J := G/N$
denote the quotient group. Let B be an N-free finite G-CW-complex, and let g be the composite
![]() $g\colon B_{hG} \to BG \to BJ$
.
$g\colon B_{hG} \to BG \to BJ$
.
-
(1) For any
 $\mathscr {C}$
-adjointable map
$\mathscr {C}$
-adjointable map
 $f\colon A \to B_{hG}$
, the Becker-Gottlieb transfers of f and g compose.
$f\colon A \to B_{hG}$
, the Becker-Gottlieb transfers of f and g compose. -
(2) If
 $f'\colon E \to B$
is a G-map with compact fibers, the induced map
$f'\colon E \to B$
is a G-map with compact fibers, the induced map
 $f := f^{\prime }_{hG}\colon E_{hG} \to B_{hG}$
on homotopy orbits is
$f := f^{\prime }_{hG}\colon E_{hG} \to B_{hG}$
on homotopy orbits is
 $\mathscr {C}$
-adjointable.
$\mathscr {C}$
-adjointable.
Proof. For part (1), we have to show that the map
![]() $g\colon B_{hG} \to BJ$
is contained in the subcategory
$g\colon B_{hG} \to BJ$
is contained in the subcategory
![]() $(\mathcal {S}_{/BJ})^{\mathrm {comp}} \subseteq \mathcal {S}_{/BJ}$
defined in Corollary 6.31. We will first prove the case where
$(\mathcal {S}_{/BJ})^{\mathrm {comp}} \subseteq \mathcal {S}_{/BJ}$
defined in Corollary 6.31. We will first prove the case where
![]() $B = G/H$
is an N-free orbit, i.e.
$B = G/H$
is an N-free orbit, i.e.
![]() $H \cap N = e$
. In this case, we have
$H \cap N = e$
. In this case, we have
![]() $B_{hG} = (G/H)_{hG} \simeq BH$
. Note that the assumption on H guarantees that the composite
$B_{hG} = (G/H)_{hG} \simeq BH$
. Note that the assumption on H guarantees that the composite
![]() $H \hookrightarrow G \twoheadrightarrow J$
is injective, allowing us to regard H as a subgroup of J. It follows that the map
$H \hookrightarrow G \twoheadrightarrow J$
is injective, allowing us to regard H as a subgroup of J. It follows that the map
![]() $BH \to BJ$
is a smooth fiber bundle with fiber given by the compact manifold
$BH \to BJ$
is a smooth fiber bundle with fiber given by the compact manifold
![]() $J/H$
. Consequently we deduce from Corollary 6.28 that the map
$J/H$
. Consequently we deduce from Corollary 6.28 that the map
![]() $BH \to BJ$
is in
$BH \to BJ$
is in
![]() $(\mathcal {S}_{/BJ})^{\mathrm {comp}}$
.
$(\mathcal {S}_{/BJ})^{\mathrm {comp}}$
.
The claim now follows for an arbitrary N-free finite G-CW-complex B, using Corollary 6.31 and the fact that the functor
![]() $(-)_{hG}\colon \mathcal {S}^{BG} \to \mathcal {S}$
preserves colimits. This finishes the proof of (1).
$(-)_{hG}\colon \mathcal {S}^{BG} \to \mathcal {S}$
preserves colimits. This finishes the proof of (1).
For part (2), it follows by descent that the map f fits in a pullback square

Since the fibers of
![]() $f'$
are compact, so are the fibers of f, and thus f is
$f'$
are compact, so are the fibers of f, and thus f is
![]() $\mathscr {C}$
-adjointable by Example 4.27.
$\mathscr {C}$
-adjointable by Example 4.27.
By letting N be the trivial subgroup of G, we obtain the following two immediate corollaries:
Corollary 6.34. Let G be a compact Lie group, let B be a finite G-CW-complex, and let
![]() $f'\colon E \to B$
be a G-map with compact fibers. Then the Becker-Gottlieb transfers for the maps
$f'\colon E \to B$
be a G-map with compact fibers. Then the Becker-Gottlieb transfers for the maps
compose.
Corollary 6.35. Let G be a compact Lie group and let
![]() $K \subseteq H \subseteq G$
be nested closed subgroups. Then the Becker-Gottlieb transfers for the maps
$K \subseteq H \subseteq G$
be nested closed subgroups. Then the Becker-Gottlieb transfers for the maps
compose.
6.4 The free loop transfer and relative free loops
Let
![]() $f\colon A \to B$
be a
$f\colon A \to B$
be a
![]() $\mathscr {C}$
-adjointable map of spaces. Because of Proposition 6.25, we are interested in a better understanding of the composite
$\mathscr {C}$
-adjointable map of spaces. Because of Proposition 6.25, we are interested in a better understanding of the composite
and in the question of whether or not it factors through the map ![]() . The goal of this subsection is to show that, at least under the stronger assumption that all fibers of f are
. The goal of this subsection is to show that, at least under the stronger assumption that all fibers of f are
![]() $\mathscr {C}$
-adjointable, cf. Lemma 4.21, this composite always canonically factors through the map
$\mathscr {C}$
-adjointable, cf. Lemma 4.21, this composite always canonically factors through the map ![]() . Here
. Here
![]() $LA \times _{LB} B$
is the space of ‘relative free loops’, i.e. those free loops in A which live in a single fiber of f. We will deduce this factorization formally from the functoriality of the free-loop space transfer in the fiberwise
$LA \times _{LB} B$
is the space of ‘relative free loops’, i.e. those free loops in A which live in a single fiber of f. We will deduce this factorization formally from the functoriality of the free-loop space transfer in the fiberwise
![]() $\mathscr {C}$
-adjointable map f. To set up this functoriality, we first need to assemble the fiberwise
$\mathscr {C}$
-adjointable map f. To set up this functoriality, we first need to assemble the fiberwise
![]() $\mathscr {C}$
-adjointable maps into a suitable
$\mathscr {C}$
-adjointable maps into a suitable
![]() $\infty $
-category.
$\infty $
-category.
Definition 6.36. Let
![]() $\mathcal {S}^{\mathrm {pb}}$
denote the (non-full) wide subcategory of the arrow category
$\mathcal {S}^{\mathrm {pb}}$
denote the (non-full) wide subcategory of the arrow category
![]() $\mathcal {S}^{[1]}$
containing all arrows as objects but only the pullback squares as morphisms. With
$\mathcal {S}^{[1]}$
containing all arrows as objects but only the pullback squares as morphisms. With
![]() $\mathscr {C}$
implicit in the notation, we let
$\mathscr {C}$
implicit in the notation, we let
![]() $\mathcal {S}^{\mathrm {pb}}_{\mathrm {adj}}$
denote the full subcategory of
$\mathcal {S}^{\mathrm {pb}}_{\mathrm {adj}}$
denote the full subcategory of
![]() $\mathcal {S}^{\mathrm {pb}}$
spanned by arrows whose fibers are
$\mathcal {S}^{\mathrm {pb}}$
spanned by arrows whose fibers are
![]() $\mathscr {C}$
-adjointable spaces. For
$\mathscr {C}$
-adjointable spaces. For
![]() $f\in \mathcal {S}^{\mathrm {pb}}$
, we denote its source by
$f\in \mathcal {S}^{\mathrm {pb}}$
, we denote its source by
![]() $A_f$
and its target by
$A_f$
and its target by
![]() $B_f$
.
$B_f$
.
Observe that the constructions
![]() $f\mapsto A_f$
and
$f\mapsto A_f$
and
![]() $f\mapsto B_f$
assemble into functors
$f\mapsto B_f$
assemble into functors
![]() $A_{(-)},B_{(-)}\colon \mathcal {S}^{\mathrm {pb}} \to \mathcal {S}$
, given by the following two compositions:
$A_{(-)},B_{(-)}\colon \mathcal {S}^{\mathrm {pb}} \to \mathcal {S}$
, given by the following two compositions:
In particular, we obtain functors ![]() and
and ![]() . We can now state and prove the naturality of the map
. We can now state and prove the naturality of the map ![]() in f.
in f.
Proposition 6.37. There is a natural transformation ![]() of functors
of functors
![]() $\mathcal {S}^{\mathrm {pb}}_{\mathrm {adj}} \to \mathscr {C}$
whose component at
$\mathcal {S}^{\mathrm {pb}}_{\mathrm {adj}} \to \mathscr {C}$
whose component at
![]() $f \in \mathcal {S}^{\mathrm {pb}}_{\mathrm {adj}}$
is the composition
$f \in \mathcal {S}^{\mathrm {pb}}_{\mathrm {adj}}$
is the composition
Proof. Observe first that the individual maps ![]() are the f-components of a natural transformation
are the f-components of a natural transformation ![]() . Indeed, this natural transformation is obtained from the natural transformation
. Indeed, this natural transformation is obtained from the natural transformation
![]() $c\colon \mathrm {id}_{\mathcal {S}} \to L$
by precomposing with
$c\colon \mathrm {id}_{\mathcal {S}} \to L$
by precomposing with
![]() $B_{(-)}\colon \mathcal {S}^{\mathrm {pb}}_{\mathrm {adj}} \to \mathcal {S}$
and post-composing with
$B_{(-)}\colon \mathcal {S}^{\mathrm {pb}}_{\mathrm {adj}} \to \mathcal {S}$
and post-composing with ![]() . Hence, it remains to assemble the free loop transfers
. Hence, it remains to assemble the free loop transfers ![]() into a natural transformation
into a natural transformation ![]() .
.
The functor
![]() $\mathscr {C}[-]\colon \mathcal {S} \to {\mathrm {Mod}}_{\mathscr {C}}$
induces a functor
$\mathscr {C}[-]\colon \mathcal {S} \to {\mathrm {Mod}}_{\mathscr {C}}$
induces a functor
![]() $\mathcal {S}^{[1]} \to {\mathrm {Mod}}_{\mathscr {C}}^{[1]}$
on arrow categories. By adjunction, we may regard the latter as a morphism in
$\mathcal {S}^{[1]} \to {\mathrm {Mod}}_{\mathscr {C}}^{[1]}$
on arrow categories. By adjunction, we may regard the latter as a morphism in
![]() $ {\mathrm {Fun}}(\mathcal {S}^{[1]}, {\mathrm {Mod}}_{\mathscr {C}})$
from
$ {\mathrm {Fun}}(\mathcal {S}^{[1]}, {\mathrm {Mod}}_{\mathscr {C}})$
from
![]() $f \mapsto \mathscr {C}[A_f]$
to
$f \mapsto \mathscr {C}[A_f]$
to
![]() $f\mapsto \mathscr {C}[B_f]$
which is pointwise given by
$f\mapsto \mathscr {C}[B_f]$
which is pointwise given by
![]() $f_!\colon \mathscr {C}[A_f] \to \mathscr {C}[B_f]$
. If we restrict this natural transformation to
$f_!\colon \mathscr {C}[A_f] \to \mathscr {C}[B_f]$
. If we restrict this natural transformation to
![]() $\mathcal {S}^{\mathrm {pb}}$
, then the naturality squares of this transformation are right adjointable by Proposition 4.11(1), and it follows from [Reference Haugseng33, Theorem 4.6] that this morphism admits a right adjoint in the
$\mathcal {S}^{\mathrm {pb}}$
, then the naturality squares of this transformation are right adjointable by Proposition 4.11(1), and it follows from [Reference Haugseng33, Theorem 4.6] that this morphism admits a right adjoint in the
![]() $(\infty ,2)$
-category
$(\infty ,2)$
-category
![]() $ {\mathrm {Fun}}(\mathcal {S}^{\mathrm {pb}}, {\mathrm {Mod}}_{\mathscr {C}})$
. Furthermore, this right adjoint is given pointwise by the adjoints
$ {\mathrm {Fun}}(\mathcal {S}^{\mathrm {pb}}, {\mathrm {Mod}}_{\mathscr {C}})$
. Furthermore, this right adjoint is given pointwise by the adjoints
![]() $f^*\colon \mathscr {C}[B] \to \mathscr {C}[A]$
. If we further restrict to
$f^*\colon \mathscr {C}[B] \to \mathscr {C}[A]$
. If we further restrict to
![]() $\mathcal {S}^{\mathrm {pb}}_{\mathrm {adj}}$
, this natural transformation is valued in the subcategory
$\mathcal {S}^{\mathrm {pb}}_{\mathrm {adj}}$
, this natural transformation is valued in the subcategory
![]() $ {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {dbl}} \subseteq {\mathrm {Mod}}_{\mathscr {C}}$
. Indeed, by definition, the functor
$ {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {dbl}} \subseteq {\mathrm {Mod}}_{\mathscr {C}}$
. Indeed, by definition, the functor
![]() $f^*\colon \mathscr {C}[B] \to \mathscr {C}[A]$
is an internal left adjoint for every
$f^*\colon \mathscr {C}[B] \to \mathscr {C}[A]$
is an internal left adjoint for every
![]() $\mathscr {C}$
-adjointable map
$\mathscr {C}$
-adjointable map
![]() $f\colon A \to B$
. Composing with
$f\colon A \to B$
. Composing with
![]() $ {\mathrm {Tr}}_{\mathscr {C}}\colon {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {dbl}} \to \mathscr {C}$
then gives the desired natural transformation
$ {\mathrm {Tr}}_{\mathscr {C}}\colon {\mathrm {Mod}}_{\mathscr {C}}^{\mathrm {dbl}} \to \mathscr {C}$
then gives the desired natural transformation ![]() .
.
Having established the functoriality of the map ![]() , we turn to deduce the main result of this section: the factorization of this map through the relative constant loops
, we turn to deduce the main result of this section: the factorization of this map through the relative constant loops ![]() . We shall deduce this factorization from the fact that, as we shall show next, the functor
. We shall deduce this factorization from the fact that, as we shall show next, the functor ![]() is colimit preserving. First, we show that its source admits all small colimits.
is colimit preserving. First, we show that its source admits all small colimits.
Lemma 6.38. The
![]() $\infty $
-category
$\infty $
-category
![]() $\mathcal {S}^{\mathrm {pb}}_{\mathrm {adj}}$
admits all colimits, and the inclusion
$\mathcal {S}^{\mathrm {pb}}_{\mathrm {adj}}$
admits all colimits, and the inclusion
![]() $\mathcal {S}^{\mathrm {pb}}_{\mathrm {adj}} \subseteq \mathcal {S}^{[1]}$
preserves colimits.
$\mathcal {S}^{\mathrm {pb}}_{\mathrm {adj}} \subseteq \mathcal {S}^{[1]}$
preserves colimits.
Proof. By definition, a morphism of spaces is fiberwise
![]() $\mathscr {C}$
-adjointable if and only if each of its fibers are
$\mathscr {C}$
-adjointable if and only if each of its fibers are
![]() $\mathscr {C}$
-adjointable, and thus the class of fiberwise
$\mathscr {C}$
-adjointable, and thus the class of fiberwise
![]() $\mathscr {C}$
-adjointable morphisms of spaces is a local class in the sense of [Reference Lurie49, Definition 6.1.3.8]. The result then follows from [Reference Lurie49, Theorem 6.1.3.5(3)].
$\mathscr {C}$
-adjointable morphisms of spaces is a local class in the sense of [Reference Lurie49, Definition 6.1.3.8]. The result then follows from [Reference Lurie49, Theorem 6.1.3.5(3)].
Corollary 6.39. The functor ![]() is colimit preserving.
is colimit preserving.
Proof. The functor
![]() $\mathcal {S}_{\mathrm {adj}}^{\mathrm {pb}} \to \mathcal {S}^{[1]}$
is colimit preserving by Lemma 6.38 above. Furthermore, the evaluation functor
$\mathcal {S}_{\mathrm {adj}}^{\mathrm {pb}} \to \mathcal {S}^{[1]}$
is colimit preserving by Lemma 6.38 above. Furthermore, the evaluation functor
![]() $\mathrm {ev}_1 \colon \mathcal {S}^{[1]} \to \mathcal {S}$
and the functor
$\mathrm {ev}_1 \colon \mathcal {S}^{[1]} \to \mathcal {S}$
and the functor ![]() are both colimit preserving. Composing these three functors we deduce that
are both colimit preserving. Composing these three functors we deduce that ![]() is colimit preserving as well.
is colimit preserving as well.
Proposition 6.40. Let
![]() $f\colon A \to B$
be a fiberwise
$f\colon A \to B$
be a fiberwise
![]() $\mathscr {C}$
-adjointable map of spaces. There exists a map
$\mathscr {C}$
-adjointable map of spaces. There exists a map ![]() making the following diagram commute:
making the following diagram commute:
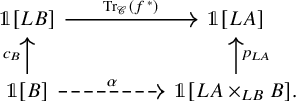
Proof. By descent, the object
![]() $(f\colon A \to B)$
of
$(f\colon A \to B)$
of
![]() $\mathcal {S}_{\mathrm {adj}}^{\mathrm {pb}}$
may be written as a colimit over B of the individual maps
$\mathcal {S}_{\mathrm {adj}}^{\mathrm {pb}}$
may be written as a colimit over B of the individual maps
![]() $f_b\colon A_b \to \{b\}$
, where
$f_b\colon A_b \to \{b\}$
, where
![]() $A_b$
denotes the fiber of f over
$A_b$
denotes the fiber of f over
![]() $b \in B$
. As the construction
$b \in B$
. As the construction
![]() $f \mapsto \eta _f$
is natural in f, we may consider the resulting assembly diagram
$f \mapsto \eta _f$
is natural in f, we may consider the resulting assembly diagram
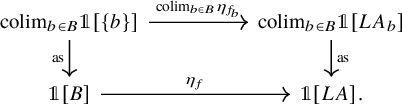
Since the functor ![]() preserves colimits, the left vertical map is an equivalence, and we deduce that the map
preserves colimits, the left vertical map is an equivalence, and we deduce that the map ![]() factors through the assembly map
factors through the assembly map ![]() . The claim thus follows from the observation that there is an equivalence
. The claim thus follows from the observation that there is an equivalence
![]() $ {\mathrm {colim}}_{b \in B} LA_b \simeq LA\times _{LB}B$
in
$ {\mathrm {colim}}_{b \in B} LA_b \simeq LA\times _{LB}B$
in
![]() $\mathcal {S}_{/LA}$
.
$\mathcal {S}_{/LA}$
.
Using Proposition 6.40, we obtain quick formal proofs of two strengthenings of Theorem 6.12, both already appearing in [Reference Lind and Malkiewich48] when
![]() $\mathscr {C} = \mathrm {Sp}$
. The first one shows that finite covering maps satisfy the criterion from Proposition 6.25, and thus always satisfy composability of Becker-Gottlieb transfers. In the stable setting, this is a special case of the more general statement for smooth fiber bundle with closed manifold fibers, see Proposition 6.27, but the proof for this special case is much simpler.
$\mathscr {C} = \mathrm {Sp}$
. The first one shows that finite covering maps satisfy the criterion from Proposition 6.25, and thus always satisfy composability of Becker-Gottlieb transfers. In the stable setting, this is a special case of the more general statement for smooth fiber bundle with closed manifold fibers, see Proposition 6.27, but the proof for this special case is much simpler.
Corollary 6.41. Let
![]() $\mathscr {C}$
be semiadditive, and let
$\mathscr {C}$
be semiadditive, and let
![]() $f\colon A \to B$
be a finite covering map, so that f is fiberwise
$f\colon A \to B$
be a finite covering map, so that f is fiberwise
![]() $\mathscr {C}$
-adjointable by Example 4.25. Then the following diagram commutes:
$\mathscr {C}$
-adjointable by Example 4.25. Then the following diagram commutes:
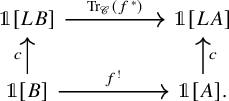
Proof. We will start by showing that there exists an equivalence
![]() $A \simeq LA \times _{LB} B$
. Indeed, we claim that the square
$A \simeq LA \times _{LB} B$
. Indeed, we claim that the square
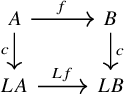
is a pullback square of spaces. To see this, it suffices to check that for every point
![]() $b \in B$
the induced map on horizontal fibers over b is an equivalence. This induced map is given by the inclusion
$b \in B$
the induced map on horizontal fibers over b is an equivalence. This induced map is given by the inclusion
![]() $c\colon A_b \to L(A_b)$
of the constant loops for the fiber
$c\colon A_b \to L(A_b)$
of the constant loops for the fiber
![]() $A_b$
. But since the map
$A_b$
. But since the map
![]() $f\colon A \to B$
is a finite covering, its fibers are discrete, and thus the map
$f\colon A \to B$
is a finite covering, its fibers are discrete, and thus the map
![]() $c\colon A_b \to L(A_b)$
is an equivalence. This proves that
$c\colon A_b \to L(A_b)$
is an equivalence. This proves that
![]() $A \simeq LA \times _{LB} B$
. Note that under this equivalence, the projection map
$A \simeq LA \times _{LB} B$
. Note that under this equivalence, the projection map
![]() $LA \times _{LB} B \to LA$
corresponds to the inclusion
$LA \times _{LB} B \to LA$
corresponds to the inclusion
![]() $c\colon A \to LA$
of constant loops.
$c\colon A \to LA$
of constant loops.
It thus follows from Proposition 6.40 that there exists a map ![]() making the following diagram commute:
making the following diagram commute:
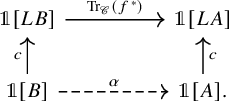
The desired claim is now an instance of Lemma 6.24.
Corollary 6.42. Assume
![]() $\mathscr {C}$
is semiadditive and let
$\mathscr {C}$
is semiadditive and let
![]() $g\colon B \to C$
be a finite covering map. Then for any other
$g\colon B \to C$
be a finite covering map. Then for any other
![]() $\mathscr {C}$
-adjointable map
$\mathscr {C}$
-adjointable map
![]() $f\colon A \to B$
, the Becker-Gottlieb transfers for f and g are composable:
$f\colon A \to B$
, the Becker-Gottlieb transfers for f and g are composable:
![]() $f^! \circ g^! \simeq (g \circ f)^!$
.
$f^! \circ g^! \simeq (g \circ f)^!$
.
For a fiberwise
![]() $\mathscr {C}$
-adjointable map
$\mathscr {C}$
-adjointable map
![]() $f\colon A \to B$
, the map
$f\colon A \to B$
, the map
![]() $ {\mathrm {Tr}}_{\mathscr {C}}(f^*) \circ c$
might not necessarily factor through
$ {\mathrm {Tr}}_{\mathscr {C}}(f^*) \circ c$
might not necessarily factor through ![]() . The following result, which appears as [Reference Lind and Malkiewich48, Theorem 7.10], says that at least it will factor through the map
. The following result, which appears as [Reference Lind and Malkiewich48, Theorem 7.10], says that at least it will factor through the map ![]() :
:
Lemma 6.43 (Lind-Malkiewich [Reference Lind and Malkiewich48, Theorem 7.10]).
Let
![]() $f\colon A\to B$
be a fiberwise
$f\colon A\to B$
be a fiberwise
![]() $\mathscr {C}$
-adjointable map of spaces. Then the following diagram commutes:
$\mathscr {C}$
-adjointable map of spaces. Then the following diagram commutes:
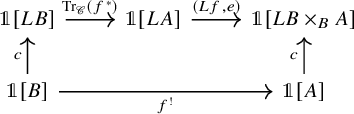
where the right vertical map is induced by the composite ![]() .
.
Proof. Consider the following commutative diagram:
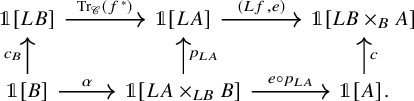
Here the left square is the commutative square from Proposition 6.40, and the right square commutes as it is induced from a commuting square on the level of spaces. (Note that
![]() $LA \times _{LB} B$
is in fact the pullback of the two maps
$LA \times _{LB} B$
is in fact the pullback of the two maps
![]() $(Lf,e)\colon LA \to LB \times _{B} A$
and
$(Lf,e)\colon LA \to LB \times _{B} A$
and
![]() $c\colon A \to LB \times _B A$
.)
$c\colon A \to LB \times _B A$
.)
Since the map
![]() $c \times _B A\colon A \to LB \times _B A$
admits a retraction
$c \times _B A\colon A \to LB \times _B A$
admits a retraction
![]() $p_A\colon LB \times _B A \to A$
, it follows from Theorem 6.12 that the bottom composite of this diagram must be
$p_A\colon LB \times _B A \to A$
, it follows from Theorem 6.12 that the bottom composite of this diagram must be ![]() , finishing the proof.
, finishing the proof.
7 Thom spectra
Given a presentably symmetric monoidal
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}$
, a pointed space A and a pointed map
$\mathscr {C}$
, a pointed space A and a pointed map
![]() $\xi \colon A \to \mathscr {C}$
, the Thom object
$\xi \colon A \to \mathscr {C}$
, the Thom object
![]() $\mathrm {Th}(\xi ) \in \mathscr {C}$
is, from a modern perspective, simply the colimit of
$\mathrm {Th}(\xi ) \in \mathscr {C}$
is, from a modern perspective, simply the colimit of
![]() $\xi $
. When A is connected, one can think of
$\xi $
. When A is connected, one can think of
![]() $\xi $
as encoding an action of the group
$\xi $
as encoding an action of the group
![]() $\Omega A$
on the monoidal unit
$\Omega A$
on the monoidal unit ![]() , and of
, and of
![]() $\mathrm {Th}(\xi )$
as the homotopy orbits of this action. The interest in this construction stems from the fact that if
$\mathrm {Th}(\xi )$
as the homotopy orbits of this action. The interest in this construction stems from the fact that if
![]() $A = G$
is an
$A = G$
is an
![]() $\mathbb {E}_n$
-groupFootnote
17
in
$\mathbb {E}_n$
-groupFootnote
17
in
![]() $\mathcal {S}$
(i.e. an n-fold loop space) and
$\mathcal {S}$
(i.e. an n-fold loop space) and
![]() $\xi $
is an
$\xi $
is an
![]() $\mathbb {E}_n$
-map with respect to the tensor product on
$\mathbb {E}_n$
-map with respect to the tensor product on
![]() $\mathscr {C}$
, then the object
$\mathscr {C}$
, then the object
![]() $\mathrm {Th}(\xi )$
inherits a canonical structure of an
$\mathrm {Th}(\xi )$
inherits a canonical structure of an
![]() $\mathbb {E}_n$
-algebra in
$\mathbb {E}_n$
-algebra in
![]() $\mathscr {C}$
. Several fundamental examples of
$\mathscr {C}$
. Several fundamental examples of
![]() $\mathbb {E}_n$
-ring spectra, including the cobordism rings
$\mathbb {E}_n$
-ring spectra, including the cobordism rings
![]() $MG$
(for
$MG$
(for
![]() $G = O,\, SO,\, U,\, \mathit {Sp},\, \mathit {Spin},...$
), arise in this way.
$G = O,\, SO,\, U,\, \mathit {Sp},\, \mathit {Spin},...$
), arise in this way.
Remark 7.1. for every
![]() $n\ge 0$
, an
$n\ge 0$
, an
![]() $\mathbb {E}_n$
-map
$\mathbb {E}_n$
-map
![]() $G \to \mathscr {C}$
factors uniquely through an
$G \to \mathscr {C}$
factors uniquely through an
![]() $\mathbb {E}_n$
-map
$\mathbb {E}_n$
-map
![]() $G \to {\mathrm {Pic}}(\mathscr {C})$
, where the latter denotes the
$G \to {\mathrm {Pic}}(\mathscr {C})$
, where the latter denotes the
![]() $\mathbb {E}_\infty $
-group of invertible objects in
$\mathbb {E}_\infty $
-group of invertible objects in
![]() $\mathscr {C}$
. Hence, it is usually the latter that is taken as the input to the Thom object construction. We shall use both perspectives interchangeably.
$\mathscr {C}$
. Hence, it is usually the latter that is taken as the input to the Thom object construction. We shall use both perspectives interchangeably.
For G an
![]() $\mathbb {E}_1$
-group, we may consider the Hochschild homology of the
$\mathbb {E}_1$
-group, we may consider the Hochschild homology of the
![]() $\mathbb {E}_1$
-algebra
$\mathbb {E}_1$
-algebra
![]() $\mathrm {Th}(\xi )$
,
$\mathrm {Th}(\xi )$
,
In the case where
![]() $\mathscr {C} = \mathrm {Sp}$
is the
$\mathscr {C} = \mathrm {Sp}$
is the
![]() $\infty $
-category of spectra, Blumberg, Cohen and Schlichtkrull [Reference Blumberg, Cohen and Schlichtkrull15] computed this object: they showed that it is itself the Thom spectrum (i.e. colimit) of a certain map
$\infty $
-category of spectra, Blumberg, Cohen and Schlichtkrull [Reference Blumberg, Cohen and Schlichtkrull15] computed this object: they showed that it is itself the Thom spectrum (i.e. colimit) of a certain map
![]() $LBG \longrightarrow \mathrm {Sp}$
associated with
$LBG \longrightarrow \mathrm {Sp}$
associated with
![]() $\xi $
. The goal of this section is to give an alternative proof of this theorem, generalizing it to an arbitrary presentably symmetric monoidal
$\xi $
. The goal of this section is to give an alternative proof of this theorem, generalizing it to an arbitrary presentably symmetric monoidal
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}$
.
$\mathscr {C}$
.
Theorem 7.2 (cf. [Reference Blumberg, Cohen and Schlichtkrull15, Theorem 1]).
Let G be an
![]() $\mathbb {E}_1$
-group in
$\mathbb {E}_1$
-group in
![]() $\mathcal {S}$
, and
$\mathcal {S}$
, and
![]() $\xi \colon G\to {\mathrm {Pic}}(\mathscr {C})$
be an
$\xi \colon G\to {\mathrm {Pic}}(\mathscr {C})$
be an
![]() $\mathbb {E}_1$
-group map. Then
$\mathbb {E}_1$
-group map. Then
![]() $ {\mathrm {HH}}_{\mathscr {C}}(\mathrm {Th}(\xi )) \in \mathscr {C}$
is the Thom object of the following composite:
$ {\mathrm {HH}}_{\mathscr {C}}(\mathrm {Th}(\xi )) \in \mathscr {C}$
is the Thom object of the following composite:
where
![]() $\eta \colon B {\mathrm {Pic}}(\mathscr {C}) \to {\mathrm {Pic}}(\mathscr {C})$
is the Hopf map.
$\eta \colon B {\mathrm {Pic}}(\mathscr {C}) \to {\mathrm {Pic}}(\mathscr {C})$
is the Hopf map.
Remark 7.3. The other main results of [Reference Blumberg, Cohen and Schlichtkrull15], namely Theorems 2 and 3, give a simplified formula for the Thom spectrum
![]() $\mathrm {Th}(\xi )$
, when
$\mathrm {Th}(\xi )$
, when
![]() $\xi $
is a map of
$\xi $
is a map of
![]() $\mathbb {E}_2$
- and
$\mathbb {E}_2$
- and
![]() $\mathbb {E}_3$
-groups respectively. These follow easily from [Reference Blumberg, Cohen and Schlichtkrull15, Theorem 1] by inspecting the decomposition
$\mathbb {E}_3$
-groups respectively. These follow easily from [Reference Blumberg, Cohen and Schlichtkrull15, Theorem 1] by inspecting the decomposition
![]() $LBG \simeq BG\times G$
, and in particular generalize verbatim to an arbitrary symmetric monoidal
$LBG \simeq BG\times G$
, and in particular generalize verbatim to an arbitrary symmetric monoidal
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}$
.
$\mathscr {C}$
.
Our proof differs from the one in [Reference Blumberg, Cohen and Schlichtkrull15], which relies on the cyclic bar construction model for Hochschild Homology. Instead, we show in Theorem 7.13 that the module category
![]() $ {\mathrm {RMod}}_{\mathrm {Th}(\xi )}(\mathscr {C})$
is the colimit of the composition
$ {\mathrm {RMod}}_{\mathrm {Th}(\xi )}(\mathscr {C})$
is the colimit of the composition
and apply the formula for the dimension of a colimit from Corollary 5.21. In other words, by treating Hochschild Homology as (categorified) monoidal dimension, it becomes amenable to (categorified) character theory.
There is, however, a mild technical difficulty arising from this categorification process, as it is convenient to work with presentable
![]() $\infty $
-categories throughout, but
$\infty $
-categories throughout, but
![]() $\mathrm {Pr}^{\text {L}}$
and hence
$\mathrm {Pr}^{\text {L}}$
and hence
![]() $ {\mathrm {Mod}}_{\mathscr {C}}(\mathrm {Pr}^{\text {L}})$
are not themselves presentable. We overcome this by adopting the solution of [Reference Lurie51, §5.3.2], replacing ‘presentable’ with ‘
$ {\mathrm {Mod}}_{\mathscr {C}}(\mathrm {Pr}^{\text {L}})$
are not themselves presentable. We overcome this by adopting the solution of [Reference Lurie51, §5.3.2], replacing ‘presentable’ with ‘
![]() $\kappa $
-compactly generated’ for a sufficiently large regular cardinal
$\kappa $
-compactly generated’ for a sufficiently large regular cardinal
![]() $\kappa $
. To make this transparent for the casual reader who does not wish to be bothered by set-theoretical technicalities, we employ the following notational convention:
$\kappa $
. To make this transparent for the casual reader who does not wish to be bothered by set-theoretical technicalities, we employ the following notational convention:
Convention 7.4. For every presentable
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}$
, there exists an uncountable regular cardinal
$\mathscr {C}$
, there exists an uncountable regular cardinal
![]() $\kappa $
such that
$\kappa $
such that
![]() $\mathscr {C}$
is
$\mathscr {C}$
is
![]() $\kappa $
-compactly generated. We shall always implicitly choose such
$\kappa $
-compactly generated. We shall always implicitly choose such
![]() $\kappa $
and treat
$\kappa $
and treat
![]() $\mathscr {C}$
as an object of the
$\mathscr {C}$
as an object of the
![]() $\infty $
-category
$\infty $
-category
![]() $\mathrm {Pr}^{\text {L}}_\kappa $
of
$\mathrm {Pr}^{\text {L}}_\kappa $
of
![]() $\kappa $
-compactly generated
$\kappa $
-compactly generated
![]() $\infty $
-categories, which is a presentably symmetric monoidal subcategory of
$\infty $
-categories, which is a presentably symmetric monoidal subcategory of
![]() $\mathrm {Pr}^{\text {L}}$
by [Reference Lurie51, Lemma 5.3.2.9 and Lemma 5.3.2.12]. If needed, we shall allow ourselves to implicitly replace
$\mathrm {Pr}^{\text {L}}$
by [Reference Lurie51, Lemma 5.3.2.9 and Lemma 5.3.2.12]. If needed, we shall allow ourselves to implicitly replace
![]() $\kappa $
by some larger
$\kappa $
by some larger
![]() $\kappa '$
using the canonical (non-full) inclusion
$\kappa '$
using the canonical (non-full) inclusion
![]() $\mathrm {Pr}^{\text {L}}_\kappa \hookrightarrow \mathrm {Pr}^{\text {L}}_{\kappa '}.$
If
$\mathrm {Pr}^{\text {L}}_\kappa \hookrightarrow \mathrm {Pr}^{\text {L}}_{\kappa '}.$
If
![]() $\mathscr {C}$
is furthermore presentably
$\mathscr {C}$
is furthermore presentably
![]() $\mathbb {E}_n$
-monoidal, we let
$\mathbb {E}_n$
-monoidal, we let
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
be the presentably
$ {\mathrm {Mod}}_{\mathscr {C}}$
be the presentably
![]() $\mathbb {E}_{n-1}$
-monoidal
$\mathbb {E}_{n-1}$
-monoidal
![]() $\infty $
-category
$\infty $
-category
![]() $ {\mathrm {Mod}}_{\mathscr {C}}(\mathrm {Pr}^{\text {L}}_\kappa )$
, for
$ {\mathrm {Mod}}_{\mathscr {C}}(\mathrm {Pr}^{\text {L}}_\kappa )$
, for
![]() $\kappa $
as in [Reference Lurie51, Lemma 5.3.2.12].
$\kappa $
as in [Reference Lurie51, Lemma 5.3.2.12].
Philosophically speaking, while
![]() $\mathrm {Pr}^{\text {L}}$
is not itself presentable, it is a (large) small-filtered colimit of the presentable
$\mathrm {Pr}^{\text {L}}$
is not itself presentable, it is a (large) small-filtered colimit of the presentable
![]() $\infty $
-categories
$\infty $
-categories
![]() $\mathrm {Pr}^{\text {L}}_\kappa $
in the
$\mathrm {Pr}^{\text {L}}_\kappa $
in the
![]() $\infty $
-category of large small-cocomplete
$\infty $
-category of large small-cocomplete
![]() $\infty $
-categories and small colimit preserving functors. Hence, every construction in
$\infty $
-categories and small colimit preserving functors. Hence, every construction in
![]() $\mathrm {Pr}^{\text {L}}$
(resp. property thereof) involving only a small amount of data, can be already carried out (resp. witnessed) in
$\mathrm {Pr}^{\text {L}}$
(resp. property thereof) involving only a small amount of data, can be already carried out (resp. witnessed) in
![]() $\mathrm {Pr}^{\text {L}}_\kappa $
for some, and hence all sufficiently large, regular cardinals
$\mathrm {Pr}^{\text {L}}_\kappa $
for some, and hence all sufficiently large, regular cardinals
![]() $\kappa $
.
$\kappa $
.
This section is organized as follows: in Section 7.1, we define Thom objects with their multiplicative structures, and prove that categories of modules over them can themselves be understood as (categorified) Thom objects; and in Section 7.2 we combine this with our formula for the trace of colimits to recover and generalize the result of [Reference Blumberg, Cohen and Schlichtkrull15] regarding the topological Hochschild homology of Thom spectra.
7.1 Thom objects and categorical group algebras
Let
![]() $\mathscr {C}$
be a presentably symmetric monoidal
$\mathscr {C}$
be a presentably symmetric monoidal
![]() $\infty $
-category. For every
$\infty $
-category. For every
![]() $\mathbb {E}_n$
-group G in
$\mathbb {E}_n$
-group G in
![]() $\mathcal {S}$
(i.e. an n-fold loop space), the
$\mathcal {S}$
(i.e. an n-fold loop space), the
![]() $\mathscr {C}$
-linear
$\mathscr {C}$
-linear
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}[G]$
inherits an
$\mathscr {C}[G]$
inherits an
![]() $\mathbb {E}_n$
-monoidal structure by symmetric monoidality of the functor
$\mathbb {E}_n$
-monoidal structure by symmetric monoidality of the functor
![]() $\mathscr {C}[-]\colon \mathcal {S} \to {\mathrm {Mod}}_{\mathscr {C}}$
. We refer to
$\mathscr {C}[-]\colon \mathcal {S} \to {\mathrm {Mod}}_{\mathscr {C}}$
. We refer to
![]() $\mathscr {C}[G]$
as the categorical group algebra. In this preliminary subsection, we collect some facts about
$\mathscr {C}[G]$
as the categorical group algebra. In this preliminary subsection, we collect some facts about
![]() $\mathscr {C}[G]$
and use them to describe the
$\mathscr {C}[G]$
and use them to describe the
![]() $\mathbb {E}_n$
-algebra structure on the Thom object
$\mathbb {E}_n$
-algebra structure on the Thom object
![]() $\mathrm {Th}(\xi )$
associated with an
$\mathrm {Th}(\xi )$
associated with an
![]() $\mathbb {E}_n$
-map
$\mathbb {E}_n$
-map
![]() $G \to \mathscr {C}$
.
$G \to \mathscr {C}$
.
7.1.1 Thom objects
Given an
![]() $\mathbb {E}_n$
-group G, the
$\mathbb {E}_n$
-group G, the
![]() $\mathbb {E}_n$
-group map
$\mathbb {E}_n$
-group map
![]() $G \to \mathrm {pt}$
induces an adjunction
$G \to \mathrm {pt}$
induces an adjunction
in which
![]() $G_!$
is
$G_!$
is
![]() $\mathbb {E}_n$
-monoidal and hence
$\mathbb {E}_n$
-monoidal and hence
![]() $G^*$
is lax
$G^*$
is lax
![]() $\mathbb {E}_n$
-monoidal.
$\mathbb {E}_n$
-monoidal.
Warning 7.5. While the underlying
![]() $\infty $
-category of
$\infty $
-category of
![]() $\mathscr {C}[G]$
is equivalent to the functor category
$\mathscr {C}[G]$
is equivalent to the functor category
![]() $\mathscr {C}^G$
, the
$\mathscr {C}^G$
, the
![]() $\mathbb {E}_n$
-monoidal structure on
$\mathbb {E}_n$
-monoidal structure on
![]() $\mathscr {C}[G]$
does not identify with the pointwise one on
$\mathscr {C}[G]$
does not identify with the pointwise one on
![]() $\mathscr {C}^G$
(for which it is
$\mathscr {C}^G$
(for which it is
![]() $G^*\colon \mathscr {C} \to \mathscr {C}^G$
which is strong
$G^*\colon \mathscr {C} \to \mathscr {C}^G$
which is strong
![]() $\mathbb {E}_n$
-monoidal while
$\mathbb {E}_n$
-monoidal while
![]() $G_!\colon \mathscr {C}^G \to \mathscr {C}$
is merely oplax
$G_!\colon \mathscr {C}^G \to \mathscr {C}$
is merely oplax
![]() $\mathbb {E}_n$
-monoidal). In fact, the
$\mathbb {E}_n$
-monoidal). In fact, the
![]() $\mathbb {E}_n$
-monoidal structure on
$\mathbb {E}_n$
-monoidal structure on
![]() $\mathscr {C}[G]$
corresponds to the Day convolution on
$\mathscr {C}[G]$
corresponds to the Day convolution on
![]() $\mathscr {C}^G = {\mathrm {Fun}}(G,\mathscr {C})$
, though we shall not use this fact.
$\mathscr {C}^G = {\mathrm {Fun}}(G,\mathscr {C})$
, though we shall not use this fact.
The
![]() $\mathbb {E}_n$
-monoidal adjunction
$\mathbb {E}_n$
-monoidal adjunction
![]() $G_! \dashv G^*$
allows for a simple description of the multiplicative structure on Thom objects.
$G_! \dashv G^*$
allows for a simple description of the multiplicative structure on Thom objects.
Definition 7.6. For
![]() $n\ge 0$
, the symmetric monoidal adjunction between
$n\ge 0$
, the symmetric monoidal adjunction between
![]() $\mathscr {C}[-]\colon \mathcal {S} \to {\mathrm {Mod}}_{\mathscr {C}}$
and the forgetful functor induces an adjunction on
$\mathscr {C}[-]\colon \mathcal {S} \to {\mathrm {Mod}}_{\mathscr {C}}$
and the forgetful functor induces an adjunction on
![]() $\mathbb {E}_n$
-algebras, hence any
$\mathbb {E}_n$
-algebras, hence any
![]() $\mathbb {E}_n$
-map
$\mathbb {E}_n$
-map
![]() $\xi \colon G \to \mathscr {C}$
induces an
$\xi \colon G \to \mathscr {C}$
induces an
![]() $\mathbb {E}_n$
-monoidal functor
$\mathbb {E}_n$
-monoidal functor
![]() $\xi _{\mathscr {C}} \colon \mathscr {C}[G] \to \mathscr {C}$
. The composite lax
$\xi _{\mathscr {C}} \colon \mathscr {C}[G] \to \mathscr {C}$
. The composite lax
![]() $\mathbb {E}_n$
-monoidal functor
$\mathbb {E}_n$
-monoidal functor
induces in turn a functor on
![]() $\mathbb {E}_n$
-algebras. We define
$\mathbb {E}_n$
-algebras. We define
This construction naturally promotes to a functor
We will drop the subscript
![]() $\mathscr {C}$
and write simply
$\mathscr {C}$
and write simply
![]() $\mathrm {Th}$
when it is harmless to do so.
$\mathrm {Th}$
when it is harmless to do so.
Note that by Corollary 4.12, the underlying object of
![]() $\mathrm {Th}_{\mathscr {C}}(\xi )$
is indeed simply
$\mathrm {Th}_{\mathscr {C}}(\xi )$
is indeed simply
![]() $ {\mathrm {colim}}_G \xi \in \mathscr {C}$
. Furthermore, the definition of
$ {\mathrm {colim}}_G \xi \in \mathscr {C}$
. Furthermore, the definition of
![]() $\mathrm {Th}_{\mathscr {C}}(\xi )$
is functorial in
$\mathrm {Th}_{\mathscr {C}}(\xi )$
is functorial in
![]() $\mathscr {C}$
in the following sense:
$\mathscr {C}$
in the following sense:
Lemma 7.7. Given a map
![]() $F\colon \mathscr {C} \to \mathscr {D}$
in
$F\colon \mathscr {C} \to \mathscr {D}$
in
![]() $ {\mathrm {CAlg}}(\mathrm {Pr}^{\text {L}})$
. For every n-monoidal
$ {\mathrm {CAlg}}(\mathrm {Pr}^{\text {L}})$
. For every n-monoidal
![]() $\xi \colon G \to \mathscr {C}$
, we have a natural isomorphism
$\xi \colon G \to \mathscr {C}$
, we have a natural isomorphism
Proof. Consider the diagram of lax n-monoidal functors
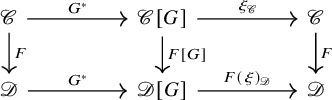
The left square commutes by naturality. For the right square, note that
![]() $F(\xi )_{\mathscr {D}}$
is the unique
$F(\xi )_{\mathscr {D}}$
is the unique
![]() $\mathscr {D}$
-linear functor whose restriction to G is given by
$\mathscr {D}$
-linear functor whose restriction to G is given by
![]() $F(\xi )\colon G \to \mathscr {D}$
. Restricting it to
$F(\xi )\colon G \to \mathscr {D}$
. Restricting it to
![]() $\mathscr {C}[G]$
will thus give a
$\mathscr {C}[G]$
will thus give a
![]() $\mathscr {C}$
-linear functor whose restriction to G is
$\mathscr {C}$
-linear functor whose restriction to G is
![]() $F(\xi )$
. Since
$F(\xi )$
. Since
![]() $F \circ \xi _{\mathscr {D}}$
is another such functor, we see that also the right square commutes. Comparing the two paths in the resulting diagram from the left upper corner to the bottom right corner gives the desired isomorphism.
$F \circ \xi _{\mathscr {D}}$
is another such functor, we see that also the right square commutes. Comparing the two paths in the resulting diagram from the left upper corner to the bottom right corner gives the desired isomorphism.
It is not immediately clear that our definition of the
![]() $\mathbb {E}_n$
-algebra structure on
$\mathbb {E}_n$
-algebra structure on
![]() $\mathrm {Th}_{\mathscr {C}}(\xi )$
agrees with other definitions in the literature, such as [Reference Ando, Blumberg and Gepner1], [Reference Antolín-Camarena and Barthel2] and [Reference Beardsley8]. We address this point by showing that every definition which is functorial in
$\mathrm {Th}_{\mathscr {C}}(\xi )$
agrees with other definitions in the literature, such as [Reference Ando, Blumberg and Gepner1], [Reference Antolín-Camarena and Barthel2] and [Reference Beardsley8]. We address this point by showing that every definition which is functorial in
![]() $\mathscr {C}$
, in the sense of the preceding lemma, is isomorphic to our definition.
$\mathscr {C}$
, in the sense of the preceding lemma, is isomorphic to our definition.
Proposition 7.8. Let G be an
![]() $\mathbb {E}_n$
-group and suppose that for every
$\mathbb {E}_n$
-group and suppose that for every
![]() $\mathscr {C} \in {\mathrm {CAlg}}(\mathrm {Pr}^{\text {L}})$
we have a functor
$\mathscr {C} \in {\mathrm {CAlg}}(\mathrm {Pr}^{\text {L}})$
we have a functor
lifting
![]() $ {\mathrm {colim}}_G$
along
$ {\mathrm {colim}}_G$
along
![]() $ {\mathrm {Alg}}_n(\mathscr {C}) \to \mathscr {C}$
, and such that for every n-monoidal functor
$ {\mathrm {Alg}}_n(\mathscr {C}) \to \mathscr {C}$
, and such that for every n-monoidal functor
![]() $\mathscr {C} \to \mathscr {D}$
we have a natural isomorphism
$\mathscr {C} \to \mathscr {D}$
we have a natural isomorphism
Then for every
![]() $\mathscr {C}$
we have an isomorphism of functors
$\mathscr {C}$
we have an isomorphism of functors
![]() $\mathrm {Th}^{\prime }_{\mathscr {C}} \simeq \mathrm {Th}_{\mathscr {C}}$
.
$\mathrm {Th}^{\prime }_{\mathscr {C}} \simeq \mathrm {Th}_{\mathscr {C}}$
.
Proof. We first use the functoriality in
![]() $\mathscr {C}$
to reduce to the universal case. Namely, every
$\mathscr {C}$
to reduce to the universal case. Namely, every
![]() $\xi \colon G \to \mathscr {C}$
factors essentially uniquely as
$\xi \colon G \to \mathscr {C}$
factors essentially uniquely as
where u is the adjunction unit map. Since
![]() $\xi _{\mathcal {S}}$
is an n-monoidal functor, we have a natural isomorphism
$\xi _{\mathcal {S}}$
is an n-monoidal functor, we have a natural isomorphism
Since by Lemma 7.7 the same holds for
![]() $\mathrm {Th}$
, it remains to show that there is an isomorphism
$\mathrm {Th}$
, it remains to show that there is an isomorphism
This in turn follows from the fact that the common underlying object
is terminal, and hence admits an essentially unique
![]() $\mathbb {E}_n$
-algebra structure.
$\mathbb {E}_n$
-algebra structure.
Remark 7.9. One can show that the individual functors
![]() $\mathrm {Th}_{\mathscr {C}}$
assemble into
$\mathrm {Th}_{\mathscr {C}}$
assemble into
where the target is the
![]() $\infty $
-category of pairs
$\infty $
-category of pairs
![]() $(\mathscr {C},R)$
with
$(\mathscr {C},R)$
with
![]() $\mathscr {C} \in {\mathrm {Alg}}_n(\mathrm {Pr}^{\text {L}})$
and
$\mathscr {C} \in {\mathrm {Alg}}_n(\mathrm {Pr}^{\text {L}})$
and
![]() $R\in {\mathrm {Alg}}_n(\mathscr {C})$
. The global functor
$R\in {\mathrm {Alg}}_n(\mathscr {C})$
. The global functor
![]() $\mathrm {Th}$
assigns to
$\mathrm {Th}$
assigns to
![]() $\xi \colon G \to \mathscr {C}$
the pair
$\xi \colon G \to \mathscr {C}$
the pair
![]() $(\mathscr {C}, \mathrm {Th}_{\mathscr {C}}(\xi ))$
. The functoriality of this formula is a coherent version of Lemma 7.7. Furthermore, the argument of Proposition 7.8 can be adopted to show that
$(\mathscr {C}, \mathrm {Th}_{\mathscr {C}}(\xi ))$
. The functoriality of this formula is a coherent version of Lemma 7.7. Furthermore, the argument of Proposition 7.8 can be adopted to show that
![]() $\mathrm {Th}$
is essentially uniquely characterized as a lift of the functor taking
$\mathrm {Th}$
is essentially uniquely characterized as a lift of the functor taking
![]() $\xi \colon G \to \mathscr {C}$
to
$\xi \colon G \to \mathscr {C}$
to
![]() $(\mathscr {C}, {\mathrm {colim}}_G \xi )$
along
$(\mathscr {C}, {\mathrm {colim}}_G \xi )$
along
![]() $\mathrm {Pr}{}^{\mathrm {L}, {\mathrm {Alg}}_n} \to \mathrm {Pr}{}^{\mathrm {L},\mathrm {Triv}}$
. We shall not prove nor use this.
$\mathrm {Pr}{}^{\mathrm {L}, {\mathrm {Alg}}_n} \to \mathrm {Pr}{}^{\mathrm {L},\mathrm {Triv}}$
. We shall not prove nor use this.
7.1.2 Projection formula
Considering the underlying
![]() $\mathbb {E}_1$
-monoidal structures, the monoidal adjunction
$\mathbb {E}_1$
-monoidal structures, the monoidal adjunction
![]() $G_! \dashv G^*$
is furthermore
$G_! \dashv G^*$
is furthermore
![]() $\mathscr {C}[G]$
-linear in the following sense:
$\mathscr {C}[G]$
-linear in the following sense:
Lemma 7.10. The monoidal adjunction
satisfies the projection formula. Namely, for every
![]() $X \in \mathscr {C}[G]$
and
$X \in \mathscr {C}[G]$
and
![]() $Y\in \mathscr {C}$
, the canonical map
$Y\in \mathscr {C}$
, the canonical map
is an isomorphism.
Proof. The
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}[G] \simeq \mathscr {C}^G$
is generated under colimits by the objects of the form
$\mathscr {C}[G] \simeq \mathscr {C}^G$
is generated under colimits by the objects of the form
![]() $g_! Z$
where
$g_! Z$
where
![]() $Z\in \mathscr {C}$
and
$Z\in \mathscr {C}$
and
![]() $g\colon \mathrm {pt} \to G$
(see [Reference Hopkins and Lurie36, Lemma 4.3.8]). Both the source and target of the projection formula map are colimit preserving and
$g\colon \mathrm {pt} \to G$
(see [Reference Hopkins and Lurie36, Lemma 4.3.8]). Both the source and target of the projection formula map are colimit preserving and
![]() $\mathscr {C}$
-linear in the variable X. By
$\mathscr {C}$
-linear in the variable X. By
![]() $\mathscr {C}$
-linearity of the functor
$\mathscr {C}$
-linearity of the functor
![]() $g_!$
, it thus suffices to show that the projection formula map is an isomorphism for
$g_!$
, it thus suffices to show that the projection formula map is an isomorphism for ![]() for every
for every
![]() $g \in G$
. The counit map
$g \in G$
. The counit map
![]() $G \to \mathscr {C}[G]^\times $
is a group homomorphism taking
$G \to \mathscr {C}[G]^\times $
is a group homomorphism taking
![]() $g \in G$
to
$g \in G$
to ![]() . Thus,
. Thus, ![]() is invertible and hence dualizable. Finally, by [Reference Fausk, Hu and May26, Proposition 3.12], the projection formula map is always an isomorphism when X is dualizable.
is invertible and hence dualizable. Finally, by [Reference Fausk, Hu and May26, Proposition 3.12], the projection formula map is always an isomorphism when X is dualizable.
Since
![]() $G^* \colon \mathscr {C} \to \mathscr {C}[G]$
is lax monoidal,
$G^* \colon \mathscr {C} \to \mathscr {C}[G]$
is lax monoidal, ![]() admits a canonical algebra structure. This is however not the unit of
admits a canonical algebra structure. This is however not the unit of
![]() $\mathscr {C}[G]$
. In fact, a
$\mathscr {C}[G]$
. In fact, a ![]() -module structure on an object of
-module structure on an object of
![]() $\mathscr {C}[G] \simeq \mathscr {C}^G$
exhibits it as “constant”, i.e. as lying in the image of the functor
$\mathscr {C}[G] \simeq \mathscr {C}^G$
exhibits it as “constant”, i.e. as lying in the image of the functor
![]() $G^*$
. More formally,
$G^*$
. More formally,
Lemma 7.11. The functor
![]() $G^*\colon \mathscr {C} \to \mathscr {C}[G]$
induces an equivalence
$G^*\colon \mathscr {C} \to \mathscr {C}[G]$
induces an equivalence
where
![]() $\mathscr {C}$
is a
$\mathscr {C}$
is a
![]() $\mathscr {C}[G]$
-linear
$\mathscr {C}[G]$
-linear
![]() $\infty $
-category via the symmetric monoidal left adjoint
$\infty $
-category via the symmetric monoidal left adjoint
![]() $G_!\colon \mathscr {C}[G] \to \mathscr {C}$
.
$G_!\colon \mathscr {C}[G] \to \mathscr {C}$
.
Proof. The adjunction
factors canonically as a composition of adjunctions
We shall show that the right adjunction is in fact an equivalence. The right adjoints in the above adjunctions fit into a commutative triangle:
The functor U is manifestly monadic with left adjoint given by ![]() . The functor
. The functor
![]() $G^*$
is conservative and preserves all colimits, as it admits a further right adjoint
$G^*$
is conservative and preserves all colimits, as it admits a further right adjoint
![]() $G_*$
. By [Reference Lurie51, Corollary 4.7.3.16], it suffices to check that the induced map of functors UF ! G
*
G
! is an isomorphism. Unwinding the definitions, for every
$G_*$
. By [Reference Lurie51, Corollary 4.7.3.16], it suffices to check that the induced map of functors UF ! G
*
G
! is an isomorphism. Unwinding the definitions, for every
![]() $X \in \mathscr {C}[G]$
, this map is the projection formula map
$X \in \mathscr {C}[G]$
, this map is the projection formula map
Thus, we are done by Lemma 7.10.
7.2 Hochschild Homology of Thom objects
In this subsection, we give the proof of Theorem 7.2, the computation of the Hochschild homology of the Thom object
![]() $\mathrm {Th}(\xi )$
of an
$\mathrm {Th}(\xi )$
of an
![]() $\mathbb {E}_1$
-group map
$\mathbb {E}_1$
-group map
![]() $\xi \colon G \to \mathscr {C}$
. We shift the perspective slightly in that we start with the pointed connected space
$\xi \colon G \to \mathscr {C}$
. We shift the perspective slightly in that we start with the pointed connected space
![]() $A := BG$
and a pointed map
$A := BG$
and a pointed map
![]() $\zeta := B\xi \colon A \to {\mathrm {Mod}}_{\mathscr {C}}$
, and identify the Thom object (i.e. colimit)
$\zeta := B\xi \colon A \to {\mathrm {Mod}}_{\mathscr {C}}$
, and identify the Thom object (i.e. colimit)
![]() $\mathrm {Th}(\zeta ) \in {\mathrm {Mod}}_{\mathscr {C}}$
with the
$\mathrm {Th}(\zeta ) \in {\mathrm {Mod}}_{\mathscr {C}}$
with the
![]() $\infty $
-category of modules over the Thom object
$\infty $
-category of modules over the Thom object
![]() $\mathrm {Th}(\Omega \zeta ) \in {\mathrm {Alg}}(\mathscr {C})$
.
$\mathrm {Th}(\Omega \zeta ) \in {\mathrm {Alg}}(\mathscr {C})$
.
7.2.1 Modules over Thom objects
The first part of our strategy is to show that the module category of a Thom object in
![]() $\mathscr {C}$
admits a description as a certain colimit in
$\mathscr {C}$
admits a description as a certain colimit in
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
. Let us denote by
$ {\mathrm {Mod}}_{\mathscr {C}}$
. Let us denote by
![]() $\mathscr {C}_{\Omega \zeta }$
the
$\mathscr {C}_{\Omega \zeta }$
the
![]() $\infty $
-category
$\infty $
-category
![]() $\mathscr {C}$
as an object of
$\mathscr {C}$
as an object of
![]() $( {\mathrm {Alg}}_{\mathscr {C}})_{\mathscr {C}[\Omega A]/}$
via the algebra map
$( {\mathrm {Alg}}_{\mathscr {C}})_{\mathscr {C}[\Omega A]/}$
via the algebra map
![]() $\mathscr {C}[\Omega A] \to \mathscr {C}$
associated with
$\mathscr {C}[\Omega A] \to \mathscr {C}$
associated with
![]() $\Omega \zeta $
. When
$\Omega \zeta $
. When
![]() $\zeta $
is the trivial map, we shall write simply
$\zeta $
is the trivial map, we shall write simply
![]() $\mathscr {C}$
. As an auxiliary step we establish the following formula for
$\mathscr {C}$
. As an auxiliary step we establish the following formula for
![]() $\mathrm {Th}(\zeta )$
:
$\mathrm {Th}(\zeta )$
:
Proposition 7.12. For every pointed map
![]() $\zeta \colon A \to {\mathrm {Mod}}_{\mathscr {C}}$
, there is an isomorphism
$\zeta \colon A \to {\mathrm {Mod}}_{\mathscr {C}}$
, there is an isomorphism
Proof. By definition, the object
![]() $\mathrm {Th}(\zeta ) \in {\mathrm {Mod}}_{\mathscr {C}}$
is given by the evaluation at
$\mathrm {Th}(\zeta ) \in {\mathrm {Mod}}_{\mathscr {C}}$
is given by the evaluation at
![]() $\mathscr {C} \in {\mathrm {Mod}}_{\mathscr {C}}$
of the composition
$\mathscr {C} \in {\mathrm {Mod}}_{\mathscr {C}}$
of the composition
Further, we have the following commutative diagram:

The middle vertical equivalence is the equivalence from Lemma 4.49, applied to the
![]() $\infty $
-category
$\infty $
-category
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
. The commutativity of the right square follows from Lemma 4.51 applied to the
$ {\mathrm {Mod}}_{\mathscr {C}}$
. The commutativity of the right square follows from Lemma 4.51 applied to the
![]() $\infty $
-category
$\infty $
-category
![]() $ {\mathrm {Mod}}_{\mathscr {C}}$
and the unit commutative algebra
$ {\mathrm {Mod}}_{\mathscr {C}}$
and the unit commutative algebra
![]() $\mathscr {C} \in {\mathrm {Mod}}_{\mathscr {C}}$
. The commutativity of the left square follows, by passing to right adjoints, from the commutativity of the right square in the special case where
$\mathscr {C} \in {\mathrm {Mod}}_{\mathscr {C}}$
. The commutativity of the left square follows, by passing to right adjoints, from the commutativity of the right square in the special case where
![]() $\zeta $
is trivial. The result follows by evaluating the composites of the two paths in the outer rectangle at the object
$\zeta $
is trivial. The result follows by evaluating the composites of the two paths in the outer rectangle at the object
![]() $\mathscr {C}\in {\mathrm {Mod}}_{\mathscr {C}}$
.
$\mathscr {C}\in {\mathrm {Mod}}_{\mathscr {C}}$
.
Theorem 7.13. Let A be a pointed connected space and let
![]() $\zeta \colon A \to {\mathrm {Mod}}_{\mathscr {C}}$
be a pointed map. There is an equivalence
$\zeta \colon A \to {\mathrm {Mod}}_{\mathscr {C}}$
be a pointed map. There is an equivalence
Proof. By Proposition 7.12 we have
Recall that by Lemma 7.11 we have
Let
![]() $(\Omega \zeta )_{\mathscr {C}} \colon \mathscr {C}[\Omega A] \to \mathscr {C}$
be the monoidal functor corresponding to
$(\Omega \zeta )_{\mathscr {C}} \colon \mathscr {C}[\Omega A] \to \mathscr {C}$
be the monoidal functor corresponding to
![]() $\Omega \zeta \colon \Omega A \to \mathscr {C}.$
By [Reference Lurie51, Theorem 4.8.4.6], we get
$\Omega \zeta \colon \Omega A \to \mathscr {C}.$
By [Reference Lurie51, Theorem 4.8.4.6], we get
By definition, we have an equality ![]() of algebra objects in
of algebra objects in
![]() $\mathscr {C}$
. Altogether, we obtain an equivalence
$\mathscr {C}$
. Altogether, we obtain an equivalence
finishing the proof.
7.2.2 Categorical character formula
Using the colimit presentation of Theorem 7.13, we have
where the first equivalence holds by Proposition 4.47. The map
![]() $\zeta $
is pointwise dualizable, as its value at each point is the unit
$\zeta $
is pointwise dualizable, as its value at each point is the unit
![]() $\mathscr {C} \in {\mathrm {Mod}}_{\mathscr {C}}$
. By Corollary 5.21 (cf. also Example 4.29 and Remark 4.30), we can compute the trace (i.e. dimension) of its colimit via the composition
$\mathscr {C} \in {\mathrm {Mod}}_{\mathscr {C}}$
. By Corollary 5.21 (cf. also Example 4.29 and Remark 4.30), we can compute the trace (i.e. dimension) of its colimit via the composition
We begin by analyzing the (categorified) free loop transfer
![]() $ {\mathrm {Tr}}_{ {\mathrm {Mod}}_{\mathscr {C}}}(A^*) \colon \mathscr {C} \to \mathscr {C}[LA]$
.
$ {\mathrm {Tr}}_{ {\mathrm {Mod}}_{\mathscr {C}}}(A^*) \colon \mathscr {C} \to \mathscr {C}[LA]$
.
Proposition 7.14. For every space A, we have
Proof. We shall make use of the fact that
![]() $ {\mathrm {Mod}}_{ {\mathrm {Mod}}_{\mathscr {C}}}$
is an
$ {\mathrm {Mod}}_{ {\mathrm {Mod}}_{\mathscr {C}}}$
is an
![]() $(\infty ,3)$
-category, and hence the trace functor
$(\infty ,3)$
-category, and hence the trace functor
is an
![]() $(\infty ,2)$
-functor. In particular it preserves the adjunction
$(\infty ,2)$
-functor. In particular it preserves the adjunction
![]() $A_! \dashv A^*$
. By Theorem 4.40 we have
$A_! \dashv A^*$
. By Theorem 4.40 we have
and thus the result follows from passing to right adjoints.
This implies a formula for
![]() $ {\mathrm {Tr}}_{\mathscr {C}}( {\mathrm {colim}}_A \zeta )$
for a general pointwise dualizable
$ {\mathrm {Tr}}_{\mathscr {C}}( {\mathrm {colim}}_A \zeta )$
for a general pointwise dualizable
![]() $\zeta \colon A\to {\mathrm {Mod}}_{\mathscr {C}}$
.
$\zeta \colon A\to {\mathrm {Mod}}_{\mathscr {C}}$
.
Corollary 7.15. For every space A and a pointwise dualizable map
![]() $\zeta \colon A \to {\mathrm {Mod}}_{\mathscr {C}}$
we get
$\zeta \colon A \to {\mathrm {Mod}}_{\mathscr {C}}$
we get
Next, to analyze the (categorified) character map
![]() $\chi _\zeta \colon LA \to \mathscr {C}$
, we consider the universal case.
$\chi _\zeta \colon LA \to \mathscr {C}$
, we consider the universal case.
Proposition 7.16. Let
![]() $\zeta \colon B {\mathrm {Pic}}(\mathscr {C}) \hookrightarrow {\mathrm {Mod}}_{\mathscr {C}}$
be the inclusion of the connected component of
$\zeta \colon B {\mathrm {Pic}}(\mathscr {C}) \hookrightarrow {\mathrm {Mod}}_{\mathscr {C}}$
be the inclusion of the connected component of
![]() $\mathscr {C}$
. The character map
$\mathscr {C}$
. The character map
![]() $\chi _\zeta \colon LB {\mathrm {Pic}}(\mathscr {C}) \to \mathscr {C}$
identifies with
$\chi _\zeta \colon LB {\mathrm {Pic}}(\mathscr {C}) \to \mathscr {C}$
identifies with
where
![]() $\eta $
is the Hopf map.
$\eta $
is the Hopf map.
Proof. Under the inclusion
![]() $B {\mathrm {Pic}}(\mathscr {C}) \hookrightarrow {\mathrm {Mod}}_{\mathscr {C}}$
, the isomorphism
$B {\mathrm {Pic}}(\mathscr {C}) \hookrightarrow {\mathrm {Mod}}_{\mathscr {C}}$
, the isomorphism
is given by
Since
![]() $\mathscr {C}$
-linear trace functor is symmetric monoidal (Remark 4.6), we have
$\mathscr {C}$
-linear trace functor is symmetric monoidal (Remark 4.6), we have
Thus, it suffices to observe that for
![]() $X \in {\mathrm {Pic}}(\mathscr {C})$
we have
$X \in {\mathrm {Pic}}(\mathscr {C})$
we have
and that
![]() $ {\mathrm {Tr}}_{\mathscr {C}} \colon B {\mathrm {Pic}}(\mathscr {C}) \to {\mathrm {Pic}}(\mathscr {C})$
is given by applying the Hopf map
$ {\mathrm {Tr}}_{\mathscr {C}} \colon B {\mathrm {Pic}}(\mathscr {C}) \to {\mathrm {Pic}}(\mathscr {C})$
is given by applying the Hopf map
![]() $\eta $
[Reference Carmeli, Schlank and Yanovski19, Proposition 3.20].
$\eta $
[Reference Carmeli, Schlank and Yanovski19, Proposition 3.20].
By combining the above results we obtain the desired description of the Hochschild homology of a Thom object.
Proof of Theorem 7.2.
By Theorem 7.13 and Corollary 7.15, we have
Now, by Proposition 7.16, the map
![]() $\chi _\zeta $
identifies with the composition
$\chi _\zeta $
identifies with the composition
and the claim follows.
Acknowledgements
We thank the anonymous referee for their valuable suggestions and corrections. We thank Merlin Christ for pointing out an oversight in our proof of Lemma 4.49. We would like to thank Alice Hedenlund for helpful discussions related to this work, as well as Cary Malkiewich and John Klein for valuable discussions related to the composability of Becker-Gottlieb transfers. We also thank Andrea Bianchi and Shai Keidar for many helpful comments on an earlier version of this article. S.C. and M.R. are supported by the Danish National Research Foundation through the Copenhagen Centre for Geometry and Topology (DNRF151). At the time of writing, B.C. was supported by the Max Planck Institute for Mathematics (MPIM) in Bonn. L.Y. wishes to thank the MPIM for its hospitality; part of this work was conducted during his stay there.
Competing interest
The authors have no competing interests to declare.
Data availability
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
Financial support
S.C. and M.R. were partially supported by the Danish National Research Foundation through the Copenhagen Centre for Geometry and Topology (DNRF151). B.C. is an associate member of the SFB 1085 ‘Higher Invariants’ at the University of Regensburg, funded by the DFG. L.Y. was supported by ISF1848/23.