Article contents
ANDRÉ–OORT CONJECTURE AND NONVANISHING OF CENTRAL 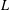 $L$ -VALUES OVER HILBERT CLASS FIELDS
$L$ -VALUES OVER HILBERT CLASS FIELDS
Published online by Cambridge University Press: 20 July 2016
Abstract
Let 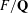 $F/\mathbf{Q}$ be a totally real field and
$F/\mathbf{Q}$ be a totally real field and 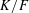 $K/F$ a complex multiplication (CM) quadratic extension. Let
$K/F$ a complex multiplication (CM) quadratic extension. Let 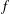 $f$ be a cuspidal Hilbert modular new form over
$f$ be a cuspidal Hilbert modular new form over 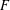 $F$ . Let
$F$ . Let  ${\it\lambda}$ be a Hecke character over
${\it\lambda}$ be a Hecke character over 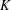 $K$ such that the Rankin–Selberg convolution
$K$ such that the Rankin–Selberg convolution 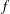 $f$ with the
$f$ with the 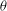 ${\it\theta}$ -series associated with
${\it\theta}$ -series associated with  ${\it\lambda}$ is self-dual with root number 1. We consider the nonvanishing of the family of central-critical Rankin–Selberg
${\it\lambda}$ is self-dual with root number 1. We consider the nonvanishing of the family of central-critical Rankin–Selberg 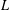 $L$ -values
$L$ -values 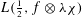 $L(\frac{1}{2},f\otimes {\it\lambda}{\it\chi})$ , as
$L(\frac{1}{2},f\otimes {\it\lambda}{\it\chi})$ , as  ${\it\chi}$ varies over the class group characters of
${\it\chi}$ varies over the class group characters of 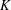 $K$ . Our approach is geometric, relying on the Zariski density of CM points in self-products of a Hilbert modular Shimura variety. We show that the number of class group characters
$K$ . Our approach is geometric, relying on the Zariski density of CM points in self-products of a Hilbert modular Shimura variety. We show that the number of class group characters  ${\it\chi}$ such that
${\it\chi}$ such that 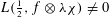 $L(\frac{1}{2},f\otimes {\it\lambda}{\it\chi})\neq 0$ increases with the absolute value of the discriminant of
$L(\frac{1}{2},f\otimes {\it\lambda}{\it\chi})\neq 0$ increases with the absolute value of the discriminant of 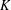 $K$ . We crucially rely on the André–Oort conjecture for arbitrary self-product of the Hilbert modular Shimura variety. In view of the recent results of Tsimerman, Yuan–Zhang and Andreatta–Goren–Howard–Pera, the results are now unconditional. We also consider a quaternionic version. Our approach is geometric, relying on the general theory of Shimura varieties and the geometric definition of nearly holomorphic modular forms. In particular, the approach avoids any use of a subconvex bound for the Rankin–Selberg
$K$ . We crucially rely on the André–Oort conjecture for arbitrary self-product of the Hilbert modular Shimura variety. In view of the recent results of Tsimerman, Yuan–Zhang and Andreatta–Goren–Howard–Pera, the results are now unconditional. We also consider a quaternionic version. Our approach is geometric, relying on the general theory of Shimura varieties and the geometric definition of nearly holomorphic modular forms. In particular, the approach avoids any use of a subconvex bound for the Rankin–Selberg 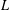 $L$ -values. The Waldspurger formula plays an underlying role.
$L$ -values. The Waldspurger formula plays an underlying role.
Information
- Type
- Research Article
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s) 2015
References
- 4
- Cited by


