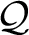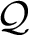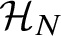1 Introduction
Many numerical integration methods for differential equations defined on Euclidean spaces have been understood and studied through the formalism of B-series introduced by John Butcher [Reference Butcher6, Reference Butcher7, Reference Butcher8, Reference Calvo and Sanz-Serna10, Reference Hairer and Wanner24]. Integration methods that can be formulated by B-series (so-called B-series methods) have been studied with an emphasis on algebraic structures defined on nonplanar rooted trees [Reference McLachlan, Modin, Munthe-Kaas and Verdier30]. Informally speaking, a B-series is a Taylor series with terms indexed by nonplanar rooted trees, together with an algebra morphism that maps the trees to a vector field and its derivatives. This formalism has been very successful in classifying properties of numerical integrators, and has led to results such as the order conditions for Runge–Kutta methods and classifications of structure-preserving methods [Reference Celledoni, McLachlan, Owren and Quispel13].
In his studies of Runge–Kutta methods on Lie groups [Reference Munthe-Kaas32, Reference Munthe-Kaas33], Munthe-Kaas defined the notion of Lie–Butcher series (LB-series). They play a role on homogeneous spaces, similar to that of Butcher’s B-series on Euclidean spaces. The study of LB-series methods emphasises algebraic structures defined on planar rooted trees [Reference Curry, Ebrahimi-Fard and Munthe-Kaas18, Reference Lundervold and Munthe-Kaas26, Reference Munthe-Kaas and Lundervold34, Reference Munthe-Kaas and Wright35]. A common theme for these algebraic structures is that they specialise to the corresponding structures for B-series methods, when planarity for the trees is removed. A nonplanar tree is a tree seen as a graph; a planar tree is a tree endowed with an embedding into the plane. The free pre-Lie algebra is one of the essential structures on nonplanar rooted trees. The planar generalisation of pre-Lie is the free post-Lie algebra, which is defined over formal Lie brackets of planar rooted trees.
It is of particular interest for the present paper to consider the notions of composition and substitution of LB-series. Connes and Kreimer [Reference Connes and Kreimer17] described the Hopf algebra that governs composition of B-series, by using the notion of admissible edge cuts in nonplanar rooted trees. The main idea of B-series composition is that the flow of a differential equation can be described by a B-series, and one aims to study the composition of flows as a composition of B-series. Munthe-Kaas and Wright [Reference Munthe-Kaas and Wright35] generalised this to the notion of admissible left edge cuts in planar rooted forests, with the goal of describing the Hopf algebra that governs composition of LB-series. Calaque, Ebrahimi-Fard and Manchon [Reference Calaque, Ebrahimi-Fard and Manchon9] described the so-called extraction-contraction bialgebra
![]() $\mathcal {H}$
that governs substitution of B-series, by using edge contractions in nonplanar rooted trees. They furthermore described a cointeraction of their bialgebra with the Hopf algebra of Connes and Kreimer. The idea behind B-series substitution is that a B-series, while being a sum over a vector field and its derivatives, can itself also describe a vector field. In this case, it makes sense to consider a B-series that has another B-series as its vector field, which we call substitution. A recursive formula for substitution in LB-series has been given by Lundervold and Munthe-Kaas [Reference Lundervold and Munthe-Kaas26]. The algebraic picture of a bialgebra cointeracting with the Hopf algebra of Munthe-Kaas and Wright is, however, not present. Substitution was also considered in [Reference Floystad and Munthe-Kaas20], where algebro-geometric methods were used to show that there is a bialgebraic description. That construction was, however, not made explicit.
$\mathcal {H}$
that governs substitution of B-series, by using edge contractions in nonplanar rooted trees. They furthermore described a cointeraction of their bialgebra with the Hopf algebra of Connes and Kreimer. The idea behind B-series substitution is that a B-series, while being a sum over a vector field and its derivatives, can itself also describe a vector field. In this case, it makes sense to consider a B-series that has another B-series as its vector field, which we call substitution. A recursive formula for substitution in LB-series has been given by Lundervold and Munthe-Kaas [Reference Lundervold and Munthe-Kaas26]. The algebraic picture of a bialgebra cointeracting with the Hopf algebra of Munthe-Kaas and Wright is, however, not present. Substitution was also considered in [Reference Floystad and Munthe-Kaas20], where algebro-geometric methods were used to show that there is a bialgebraic description. That construction was, however, not made explicit.
The paper at hand applies operadic methods to obtain a bialgebra of cosubstitution for LB-series. We use a construction by Foissy [Reference Foissy21], dualising operadic composition into a coproduct. We then show that applying this construction to the pre-Lie operad results in the bialgebra
![]() $\mathcal {H}$
that was used to describe substitution in B-series [Reference Calaque, Ebrahimi-Fard and Manchon9]. The pre-Lie operad is defined by replacing vertices in a nonplanar rooted tree by rooted trees, which is also how we think about concrete B-series substitution. This perspective motivates us to look at the post-Lie operad, which can be described by replacing vertices in planar rooted trees by Lie polynomials of planar rooted trees. Applying Foissy’s construction to the post-Lie operad gives us a bialgebra
$\mathcal {H}$
that was used to describe substitution in B-series [Reference Calaque, Ebrahimi-Fard and Manchon9]. The pre-Lie operad is defined by replacing vertices in a nonplanar rooted tree by rooted trees, which is also how we think about concrete B-series substitution. This perspective motivates us to look at the post-Lie operad, which can be described by replacing vertices in planar rooted trees by Lie polynomials of planar rooted trees. Applying Foissy’s construction to the post-Lie operad gives us a bialgebra
![]() $\mathcal {Q}$
defined over
$\mathcal {Q}$
defined over
![]() $S(Lie(\mathcal {PT}{\kern2.5pt}))$
, the symmetric algebra of Lie polynomials in planar rooted trees. Using the embedding into the space spanned by ordered forests
$S(Lie(\mathcal {PT}{\kern2.5pt}))$
, the symmetric algebra of Lie polynomials in planar rooted trees. Using the embedding into the space spanned by ordered forests
![]() $\mathcal {OF}$
of planar rooted trees,
$\mathcal {OF}$
of planar rooted trees,
![]() $Lie(\mathcal {PT}{\kern2.5pt}) \subset U(Lie(\mathcal {PT}{\kern2.5pt}))=\mathcal {OF}$
, we endow
$Lie(\mathcal {PT}{\kern2.5pt}) \subset U(Lie(\mathcal {PT}{\kern2.5pt}))=\mathcal {OF}$
, we endow
![]() $\mathcal {OF}$
with a module structure over the post-Lie operad, given by replacing vertices by Lie polynomials. As a matter of fact, replacing vertices by Lie polynomials is how we think about concrete
$\mathcal {OF}$
with a module structure over the post-Lie operad, given by replacing vertices by Lie polynomials. As a matter of fact, replacing vertices by Lie polynomials is how we think about concrete
![]() $LB$
-series substitution. By dualising in the same way as in Foissy’s construction, the module structure dualises to a coaction. The latter describes a cointeraction between the bialgebra
$LB$
-series substitution. By dualising in the same way as in Foissy’s construction, the module structure dualises to a coaction. The latter describes a cointeraction between the bialgebra
![]() $\mathcal {Q}$
and the Hopf algebra
$\mathcal {Q}$
and the Hopf algebra
![]() $\mathcal {H}_{N}$
of Munthe-Kaas and Wright [Reference Lundervold and Munthe-Kaas26]. We then show how substitution in
$\mathcal {H}_{N}$
of Munthe-Kaas and Wright [Reference Lundervold and Munthe-Kaas26]. We then show how substitution in
![]() $LB$
-series can be described and computed using this coaction.
$LB$
-series can be described and computed using this coaction.
The paper aims to further our understanding of the algebraic structures underlying the notion of LB-series, so that we can gain better insight into numerical methods for differential equations on manifolds. We would like to emphasise that the main results presented in this work are rather algebraic in nature. Therefore, we first define the relevant notions and notations required to understand those results.
Saying this, we outline the structure of the paper: In section 2, we summarise the definitions and results that the present paper builds upon. We also briefly indicate the links to numerical analysis. In section 3, we construct an operad over nonplanar rooted trees. We then prove that our construction provides an alternative description of the pre-Lie operad defined by Chapoton and Livernet in [Reference Chapoton and Livernet14]. The section is concluded by proving a duality between the pre-Lie operad and the extraction-contraction coproduct
![]() $\Delta _{\mathcal {H}}$
that is used to describe B-series substitution. In section 4, we construct an operad of Lie brackets over planar rooted trees in a way that is analogous to the operadic construction from section 3. In section 5, we extend the operadic composition from section 4 to let Lie brackets of planar rooted trees act on forests. We then dualise this to a coaction. In section 6, we prove that the coaction can be used to describe substitution in LB-series. In section 7, we provide a combinatorial picture.
$\Delta _{\mathcal {H}}$
that is used to describe B-series substitution. In section 4, we construct an operad of Lie brackets over planar rooted trees in a way that is analogous to the operadic construction from section 3. In section 5, we extend the operadic composition from section 4 to let Lie brackets of planar rooted trees act on forests. We then dualise this to a coaction. In section 6, we prove that the coaction can be used to describe substitution in LB-series. In section 7, we provide a combinatorial picture.
2 Preliminaries
We recall some definitions and fundamental results. All algebraic structures are assumed to be defined over some fixed field
![]() $\mathbb {K}$
of characteristic
$\mathbb {K}$
of characteristic
![]() $0$
.
$0$
.
2.1 Trees and forests
A nonplanar rooted tree is a directed graph with a distinguished vertex, called the root, such that every vertex except the root has exactly one incoming edge. The root has no incoming edges. Vertices without outgoing edges are called leaves. A planar rooted tree is a rooted tree endowed with an embedding into the plane. We will draw trees with the root at the top and edges oriented away from the root. Consider for example the two trees

They are isomorphic as graphs and hence equal as nonplanar rooted trees. However, as the embeddings into the plane are different, they are not equal as planar rooted trees. An unordered sequence of nonplanar rooted trees is called a forest. An ordered sequence of planar rooted trees is called an ordered forest. We denote the vector space spanned by all nonplanar rooted trees by
![]() $\mathcal {T}$
, the vector space spanned by all planar rooted trees by
$\mathcal {T}$
, the vector space spanned by all planar rooted trees by
![]() $\mathcal {PT}$
, the vector space spanned by all forests by
$\mathcal {PT}$
, the vector space spanned by all forests by
![]() $\mathcal {F}$
and the vector space spanned by all ordered forests by
$\mathcal {F}$
and the vector space spanned by all ordered forests by
![]() $\mathcal {OF}$
. The empty forest is denoted
$\mathcal {OF}$
. The empty forest is denoted
![]() $\emptyset $
.
$\emptyset $
.
We introduce the grafting operator
![]() $\curvearrowright : \mathcal {T} \otimes \mathcal {T} \to \mathcal {T}$
by defining
$\curvearrowright : \mathcal {T} \otimes \mathcal {T} \to \mathcal {T}$
by defining
![]() $\tau _{1} \curvearrowright \tau _{2}$
to be the sum over all ways of adding an edge from some vertex in
$\tau _{1} \curvearrowright \tau _{2}$
to be the sum over all ways of adding an edge from some vertex in
![]() $\tau _{2}$
to the root of
$\tau _{2}$
to the root of
![]() $\tau _{1}$
. For example:
$\tau _{1}$
. For example:

Endowing the space
![]() $\mathcal {T}$
with the grafting operator
$\mathcal {T}$
with the grafting operator
![]() $\curvearrowright $
produces a (left) pre-Lie algebra [Reference Burde5, Reference Cartier11, Reference Chapoton and Livernet14, Reference Livernet25, Reference Manchon28, Reference Oudom and Guin36], meaning that the so-called (left) pre-Lie identity
$\curvearrowright $
produces a (left) pre-Lie algebra [Reference Burde5, Reference Cartier11, Reference Chapoton and Livernet14, Reference Livernet25, Reference Manchon28, Reference Oudom and Guin36], meaning that the so-called (left) pre-Lie identity
is satisfied for all
![]() $\tau _{1},\tau _{2},\tau _{3} \in \mathcal {T}$
, which is equivalent to the nonplanarity of the trees.
$\tau _{1},\tau _{2},\tau _{3} \in \mathcal {T}$
, which is equivalent to the nonplanarity of the trees.
![]() $(\mathcal {T},\curvearrowright )$
is, in fact, the free pre-Lie algebra on one generator. The pre-Lie identity implies that for all
$(\mathcal {T},\curvearrowright )$
is, in fact, the free pre-Lie algebra on one generator. The pre-Lie identity implies that for all
![]() $\tau _{1},\tau _{2} \in \mathcal {T}$
, the commutator
$\tau _{1},\tau _{2} \in \mathcal {T}$
, the commutator
satisfies the Jacobi identity.
We furthermore define on planar rooted trees the left grafting operator
![]() $\operatorname {\mathrm {\triangleright }}: \mathcal {PT} \otimes \mathcal {PT} \to \mathcal {PT}$
by letting
$\operatorname {\mathrm {\triangleright }}: \mathcal {PT} \otimes \mathcal {PT} \to \mathcal {PT}$
by letting
![]() $\tau _{1} \operatorname {\mathrm {\triangleright }} \tau _{2}$
denote the sum over all ways of adding an edge from any vertex in
$\tau _{1} \operatorname {\mathrm {\triangleright }} \tau _{2}$
denote the sum over all ways of adding an edge from any vertex in
![]() $\tau _{2}$
to the root of
$\tau _{2}$
to the root of
![]() $\tau _{1}$
such that the added edge is leftmost on this vertex with respect to the planar embedding. Note that the left grafting operator is magmatic. Extending it to the free Lie algebra
$\tau _{1}$
such that the added edge is leftmost on this vertex with respect to the planar embedding. Note that the left grafting operator is magmatic. Extending it to the free Lie algebra
![]() $Lie(\mathcal {PT}{\kern2.5pt})$
generated by
$Lie(\mathcal {PT}{\kern2.5pt})$
generated by
![]() $\mathcal {PT}$
via the rules
$\mathcal {PT}$
via the rules
 $$ \begin{align*} \tau_{1} \operatorname{\mathrm{\triangleright}} [\tau_{2},\tau_{3}]&:=[\tau_{1} \operatorname{\mathrm{\triangleright}} \tau_{2},\tau_{3}] + [\tau_{2},\tau_{1} \operatorname{\mathrm{\triangleright}} \tau_{3}], \\ [\tau_{1},\tau_{2}] \operatorname{\mathrm{\triangleright}} \tau_{3} &:= \tau_{1} \operatorname{\mathrm{\triangleright}} (\tau_{2} \operatorname{\mathrm{\triangleright}} \tau_{3}) - (\tau_{1} \operatorname{\mathrm{\triangleright}} \tau_{2}) \operatorname{\mathrm{\triangleright}} \tau_{3} - \tau_{2} \operatorname{\mathrm{\triangleright}} (\tau_{1} \operatorname{\mathrm{\triangleright}} \tau_{3}) + (\tau_{2} \operatorname{\mathrm{\triangleright}} \tau_{1})\operatorname{\mathrm{\triangleright}} \tau_{3}, \\ \forall \tau_{1},\tau_{2},\tau_{3} &\in Lie(\mathcal{PT}{\kern2.5pt}) \end{align*} $$
$$ \begin{align*} \tau_{1} \operatorname{\mathrm{\triangleright}} [\tau_{2},\tau_{3}]&:=[\tau_{1} \operatorname{\mathrm{\triangleright}} \tau_{2},\tau_{3}] + [\tau_{2},\tau_{1} \operatorname{\mathrm{\triangleright}} \tau_{3}], \\ [\tau_{1},\tau_{2}] \operatorname{\mathrm{\triangleright}} \tau_{3} &:= \tau_{1} \operatorname{\mathrm{\triangleright}} (\tau_{2} \operatorname{\mathrm{\triangleright}} \tau_{3}) - (\tau_{1} \operatorname{\mathrm{\triangleright}} \tau_{2}) \operatorname{\mathrm{\triangleright}} \tau_{3} - \tau_{2} \operatorname{\mathrm{\triangleright}} (\tau_{1} \operatorname{\mathrm{\triangleright}} \tau_{3}) + (\tau_{2} \operatorname{\mathrm{\triangleright}} \tau_{1})\operatorname{\mathrm{\triangleright}} \tau_{3}, \\ \forall \tau_{1},\tau_{2},\tau_{3} &\in Lie(\mathcal{PT}{\kern2.5pt}) \end{align*} $$
produces the free post-Lie algebra [Reference Curry, Ebrahimi-Fard and Munthe-Kaas18, Reference Ebrahimi-Fard, Lundervold and Munthe-Kaas19, Reference Lundervold and Munthe-Kaas26, Reference Munthe-Kaas and Lundervold34, Reference Silva39]. For all
![]() $\tau _{1},\tau _{2} \in \mathcal {PT}$
, the commutator
$\tau _{1},\tau _{2} \in \mathcal {PT}$
, the commutator
![]() satisfies the Jacobi identity. Note that in general a post-Lie algebra with a vanishing Lie bracket reduces to a pre-Lie algebra.
satisfies the Jacobi identity. Note that in general a post-Lie algebra with a vanishing Lie bracket reduces to a pre-Lie algebra.
Defining the commutator
![]() $[\tau _{1},\tau _{2}]=\tau _{1}\tau _{2}-\tau _{2}\tau _{1}$
, one can identify the universal enveloping algebra of the free post-Lie algebra with
$[\tau _{1},\tau _{2}]=\tau _{1}\tau _{2}-\tau _{2}\tau _{1}$
, one can identify the universal enveloping algebra of the free post-Lie algebra with
![]() $\mathcal {OF}$
as vector space. The associative product becomes concatenation of ordered forests. We extend left grafting to
$\mathcal {OF}$
as vector space. The associative product becomes concatenation of ordered forests. We extend left grafting to
![]() $\mathcal {OF}$
by
$\mathcal {OF}$
by
 $$ \begin{align*} \tau_{1} \operatorname{\mathrm{\triangleright}} \tau_{2}\omega_{2}&:=\ (\tau_{1} \operatorname{\mathrm{\triangleright}} \tau_{2})\omega_{2} + \tau_{2}(\tau_{1} \operatorname{\mathrm{\triangleright}} \omega_{2}), \\ \tau_{1}\omega_{1} \operatorname{\mathrm{\triangleright}} \omega_{2}&:=\ \tau_{1} \operatorname{\mathrm{\triangleright}} (\omega_{1} \operatorname{\mathrm{\triangleright}} \omega_{2}) - (\tau_{1} \operatorname{\mathrm{\triangleright}} \omega_{1}) \operatorname{\mathrm{\triangleright}} \omega_{2}, \quad \forall \tau_{1},\tau_{2} \in \mathcal{PT}, \ \forall \omega_{1},\omega_{2} \in \mathcal{OF}. \end{align*} $$
$$ \begin{align*} \tau_{1} \operatorname{\mathrm{\triangleright}} \tau_{2}\omega_{2}&:=\ (\tau_{1} \operatorname{\mathrm{\triangleright}} \tau_{2})\omega_{2} + \tau_{2}(\tau_{1} \operatorname{\mathrm{\triangleright}} \omega_{2}), \\ \tau_{1}\omega_{1} \operatorname{\mathrm{\triangleright}} \omega_{2}&:=\ \tau_{1} \operatorname{\mathrm{\triangleright}} (\omega_{1} \operatorname{\mathrm{\triangleright}} \omega_{2}) - (\tau_{1} \operatorname{\mathrm{\triangleright}} \omega_{1}) \operatorname{\mathrm{\triangleright}} \omega_{2}, \quad \forall \tau_{1},\tau_{2} \in \mathcal{PT}, \ \forall \omega_{1},\omega_{2} \in \mathcal{OF}. \end{align*} $$
The vector space
![]() $\mathcal {OF}$
together with left grafting and concatenation is the free D-algebra generated by the single-vertex tree [Reference Munthe-Kaas and Wright35] (see Definition 1 in the next subsection).
$\mathcal {OF}$
together with left grafting and concatenation is the free D-algebra generated by the single-vertex tree [Reference Munthe-Kaas and Wright35] (see Definition 1 in the next subsection).
We define the function
![]() $B^{+}: \mathcal {OF} \to \mathcal {PT}$
given by
$B^{+}: \mathcal {OF} \to \mathcal {PT}$
given by
![]() $B^{+}(\omega )=\omega \operatorname {\mathrm {\triangleright }} \bullet $
, where
$B^{+}(\omega )=\omega \operatorname {\mathrm {\triangleright }} \bullet $
, where
![]() $\bullet $
is the single-vertex tree. For example:
$\bullet $
is the single-vertex tree. For example:

The inverse of
![]() $B^{+}$
, denoted
$B^{+}$
, denoted
![]() $B^{-}: \mathcal {PT} \to \mathcal {OF}$
, is given by removing the root together with its outgoing edges from the input tree. The operator
$B^{-}: \mathcal {PT} \to \mathcal {OF}$
, is given by removing the root together with its outgoing edges from the input tree. The operator
![]() $\diamond : \mathcal {OF} \times \mathcal {OF} \to \mathcal {OF}$
given by
$\diamond : \mathcal {OF} \times \mathcal {OF} \to \mathcal {OF}$
given by
is called the planar Grossman–Larson product. For example:

Let
![]() $\omega _{1},\omega _{2}$
be ordered forests; then we can write them as a sequence of trees:
$\omega _{1},\omega _{2}$
be ordered forests; then we can write them as a sequence of trees:
 $$ \begin{align*} \omega_{1}&= \tau_{1}^{1} \dotsm \tau_{1}^{n}, \\ \omega_{2}&= \tau_{2}^{1} \dotsm \tau_{2}^{m}. \end{align*} $$
$$ \begin{align*} \omega_{1}&= \tau_{1}^{1} \dotsm \tau_{1}^{n}, \\ \omega_{2}&= \tau_{2}^{1} \dotsm \tau_{2}^{m}. \end{align*} $$
We define the shuffle product
as the sum of all the ways to concatenate the trees
 $\tau _{1}^{1},\dotsc ,\tau _{1}^{n},\tau _{2}^{1},\dotsc ,\tau _{2}^{m}$
into a forest such that
$\tau _{1}^{1},\dotsc ,\tau _{1}^{n},\tau _{2}^{1},\dotsc ,\tau _{2}^{m}$
into a forest such that
![]() $\tau _{i}^{j}$
is to the left of
$\tau _{i}^{j}$
is to the left of
![]() $\tau _{k}^{\ell }$
if
$\tau _{k}^{\ell }$
if
![]() $i=k$
and
$i=k$
and
![]() $j \leq \ell $
. For example:
$j \leq \ell $
. For example:

The empty forest is the unit for the shuffle product,
. The shuffle coproduct
is defined by
being the sum of all
![]() $\omega _{1} \otimes \omega _{2}$
such that
$\omega _{1} \otimes \omega _{2}$
such that
contains the forest
![]() $\omega $
. For example:
$\omega $
. For example:

2.2 D-algebras
We now recall the definition of a D-algebra [Reference Lundervold and Munthe-Kaas26, Reference Munthe-Kaas and Lundervold34, Reference Munthe-Kaas and Wright35].
Definition 1. Let
![]() $(A,\cdot )$
be a unital associative algebra with unit
$(A,\cdot )$
be a unital associative algebra with unit
![]() $1$
. If A is furthermore equipped with a nonassociative product
$1$
. If A is furthermore equipped with a nonassociative product
![]() $\operatorname {\mathrm {\triangleright }}$
, denote by
$\operatorname {\mathrm {\triangleright }}$
, denote by
![]() $\mathcal {D}(A)=\{x \in A: x \operatorname {\mathrm {\triangleright }} (a \cdot b)= (x \operatorname {\mathrm {\triangleright }} a)\cdot b + a \cdot (x \operatorname {\mathrm {\triangleright }} b), \ \forall a,b\in A \}$
the set of derivations in A. The triple
$\mathcal {D}(A)=\{x \in A: x \operatorname {\mathrm {\triangleright }} (a \cdot b)= (x \operatorname {\mathrm {\triangleright }} a)\cdot b + a \cdot (x \operatorname {\mathrm {\triangleright }} b), \ \forall a,b\in A \}$
the set of derivations in A. The triple
![]() $(A,\cdot ,\operatorname {\mathrm {\triangleright }})$
is then called a D-algebra if the following identities hold:
$(A,\cdot ,\operatorname {\mathrm {\triangleright }})$
is then called a D-algebra if the following identities hold:
 $$ \begin{align*} 1 \operatorname{\mathrm{\triangleright}} a &= a, \\ a \operatorname{\mathrm{\triangleright}} x &\in \mathcal{D}(A), \\ x \operatorname{\mathrm{\triangleright}} (a \operatorname{\mathrm{\triangleright}} b) &= (x \cdot a)\operatorname{\mathrm{\triangleright}} b + (x \operatorname{\mathrm{\triangleright}} a) \operatorname{\mathrm{\triangleright}} b, \end{align*} $$
$$ \begin{align*} 1 \operatorname{\mathrm{\triangleright}} a &= a, \\ a \operatorname{\mathrm{\triangleright}} x &\in \mathcal{D}(A), \\ x \operatorname{\mathrm{\triangleright}} (a \operatorname{\mathrm{\triangleright}} b) &= (x \cdot a)\operatorname{\mathrm{\triangleright}} b + (x \operatorname{\mathrm{\triangleright}} a) \operatorname{\mathrm{\triangleright}} b, \end{align*} $$
for
![]() $a,b \in A$
and
$a,b \in A$
and
![]() $x \in \mathcal {D}(A)$
.
$x \in \mathcal {D}(A)$
.
A map
![]() $\phi : A \to A^{\prime }$
between two D-algebras A and
$\phi : A \to A^{\prime }$
between two D-algebras A and
![]() $A^{\prime }$
is called a D-algebra morphism if
$A^{\prime }$
is called a D-algebra morphism if
 $$ \begin{align*} \phi(a\cdot b)&= \phi(a) \cdot \phi(b), \\ \phi(a \operatorname{\mathrm{\triangleright}} b)&= \phi(a) \operatorname{\mathrm{\triangleright}} \phi(b), \\ \phi(\mathcal{D}(A)) &\subseteq \mathcal{D}(A^{\prime}) \end{align*} $$
$$ \begin{align*} \phi(a\cdot b)&= \phi(a) \cdot \phi(b), \\ \phi(a \operatorname{\mathrm{\triangleright}} b)&= \phi(a) \operatorname{\mathrm{\triangleright}} \phi(b), \\ \phi(\mathcal{D}(A)) &\subseteq \mathcal{D}(A^{\prime}) \end{align*} $$
for
![]() $a,b \in A$
. Note that in addition to the morphism property with respect to both products, we require that derivations be mapped to derivations.
$a,b \in A$
. Note that in addition to the morphism property with respect to both products, we require that derivations be mapped to derivations.
In [Reference Munthe-Kaas and Wright35] it was shown that
![]() $(\mathcal {OF},\cdot ,\operatorname {\mathrm {\triangleright }})$
is the free D-algebra and its derivations are exactly the Lie polynomials. These are the elements generated from planar trees
$(\mathcal {OF},\cdot ,\operatorname {\mathrm {\triangleright }})$
is the free D-algebra and its derivations are exactly the Lie polynomials. These are the elements generated from planar trees
![]() $\mathcal {PT} \subset \mathcal {OF}$
by the commutator bracket
$\mathcal {PT} \subset \mathcal {OF}$
by the commutator bracket
![]() $[\tau _{1},\tau _{2}]=\tau _{1}\tau _{2}-\tau _{2}\tau _{1}$
. The Lie polynomials are also exactly the elements that are primitive with respect to the shuffle coproduct, meaning those elements
$[\tau _{1},\tau _{2}]=\tau _{1}\tau _{2}-\tau _{2}\tau _{1}$
. The Lie polynomials are also exactly the elements that are primitive with respect to the shuffle coproduct, meaning those elements
![]() $\omega \in \mathcal {OF}$
satisfying
$\omega \in \mathcal {OF}$
satisfying
![]() .
.
Remark 1. The notion of a D-algebra has a geometric origin. Indeed, let M be a manifold. It is well-known that one can endow the space
![]() $\mathcal {X}M$
of vector fields over M with a post-Lie structure. The extension of this post-Lie structure to a D-algebra describes the differential operators. This is an important example, and details can be found, for example, in [Reference Lundervold and Munthe-Kaas26, Reference Munthe-Kaas and Lundervold34, Reference Munthe-Kaas and Wright35].
$\mathcal {X}M$
of vector fields over M with a post-Lie structure. The extension of this post-Lie structure to a D-algebra describes the differential operators. This is an important example, and details can be found, for example, in [Reference Lundervold and Munthe-Kaas26, Reference Munthe-Kaas and Lundervold34, Reference Munthe-Kaas and Wright35].
2.3 Operads and bialgebras
We recall the notion of an algebraic operad and its link to bialgebras. The reader is referred to [Reference Chapoton and Livernet14, Reference Foissy21, Reference Manchon27] for details.
A (symmetric) operad
![]() $\mathcal {P}=\oplus _{n=1}^{\infty }\mathcal {P}(n)$
consists of a sequence of vector spaces
$\mathcal {P}=\oplus _{n=1}^{\infty }\mathcal {P}(n)$
consists of a sequence of vector spaces
![]() $\mathcal {P}(n)$
together with an action of the symmetry group
$\mathcal {P}(n)$
together with an action of the symmetry group
![]() $\Sigma _{n} : \mathcal {P}(n) \to \mathcal {P}(n)$
and a map
$\Sigma _{n} : \mathcal {P}(n) \to \mathcal {P}(n)$
and a map
![]() $\circ : \oplus _{n \geq 1} \mathcal {P}^{\otimes n} \otimes \mathcal {P}(n) \to \mathcal {P}$
satisfying the following restrictions:
$\circ : \oplus _{n \geq 1} \mathcal {P}^{\otimes n} \otimes \mathcal {P}(n) \to \mathcal {P}$
satisfying the following restrictions:
-
∘
 $\circ : \mathcal {P}(i_{1}) \otimes \dotsb \otimes \mathcal {P}(i_{n}) \otimes \mathcal {P}(n) \to \mathcal {P}(i_{1} + \dotsb + i_{n})$
.
$\circ : \mathcal {P}(i_{1}) \otimes \dotsb \otimes \mathcal {P}(i_{n}) \otimes \mathcal {P}(n) \to \mathcal {P}(i_{1} + \dotsb + i_{n})$
. -
∘ There exists an identity element
 $1 \in \mathcal {P}(1)$
such that
$1 \in \mathcal {P}(1)$
such that
 $x \circ 1 =x$
and
$x \circ 1 =x$
and
 $1 \dotsm 1 \circ y = y$
for all
$1 \dotsm 1 \circ y = y$
for all
 $x,y \in \mathcal {P}$
.
$x,y \in \mathcal {P}$
. -
∘ The associativity relation
is satisfied. $$ \begin{align*} &\left(x_{1,1} \dotsm x_{1,n_{1}} \circ x_{1}\right) \dotsm \left(x_{m,1} \dotsm x_{m,n_{m}} \circ x_{m}\right) \circ x\\ &\qquad\qquad= x_{1,1} \dotsm x_{1,n_{1}} x_{2,1} \dotsm x_{2,n_{2}} x_{3,1} \dotsm x_{m,1} \dotsm x_{m,n_{m}} \circ (x_{1} \dotsm x_{m} \circ x) \end{align*} $$
$$ \begin{align*} &\left(x_{1,1} \dotsm x_{1,n_{1}} \circ x_{1}\right) \dotsm \left(x_{m,1} \dotsm x_{m,n_{m}} \circ x_{m}\right) \circ x\\ &\qquad\qquad= x_{1,1} \dotsm x_{1,n_{1}} x_{2,1} \dotsm x_{2,n_{2}} x_{3,1} \dotsm x_{m,1} \dotsm x_{m,n_{m}} \circ (x_{1} \dotsm x_{m} \circ x) \end{align*} $$
-
∘ The equivariance conditions
are satisfied. On the right side of the first equality, we interpret $$ \begin{align*} x_{\sigma^{-1}(1)} \dotsm x_{\sigma^{-1}(n)} \circ \sigma(x) &=\sigma(x_{1} \dotsm x_{n} \circ x), & \sigma &\in \Sigma_{n}, \\ \sigma_{1}(x_{1}) \dotsm \sigma_{n}(x_{n}) \circ x &= (\sigma_{1},\dotsc,\sigma_{n})(x_{1} \dotsm x_{n} \circ x), & \sigma_{i} &\in \Sigma_{\left\lvert x_{i}\right\rvert} \end{align*} $$
$$ \begin{align*} x_{\sigma^{-1}(1)} \dotsm x_{\sigma^{-1}(n)} \circ \sigma(x) &=\sigma(x_{1} \dotsm x_{n} \circ x), & \sigma &\in \Sigma_{n}, \\ \sigma_{1}(x_{1}) \dotsm \sigma_{n}(x_{n}) \circ x &= (\sigma_{1},\dotsc,\sigma_{n})(x_{1} \dotsm x_{n} \circ x), & \sigma_{i} &\in \Sigma_{\left\lvert x_{i}\right\rvert} \end{align*} $$
 $\sigma $
as acting on
$\sigma $
as acting on
 $\{1,2,\dotsc ,\lvert x_{1}\rvert +\dotsb +\lvert x_{n}\rvert \}$
by permuting the blocks
$\{1,2,\dotsc ,\lvert x_{1}\rvert +\dotsb +\lvert x_{n}\rvert \}$
by permuting the blocks
 $\{1,\dotsc ,\lvert x_{1}\rvert \}, \left \{\lvert x_{1}\rvert +\dotsb +\left \lvert x_{j}\right \rvert +1,\dotsc ,\lvert x_{1}\rvert +\dotsb +\left \lvert x_{j+1}\right \rvert \right \}, j=1,\dotsc ,n$
. In the second equality, we interpret
$\{1,\dotsc ,\lvert x_{1}\rvert \}, \left \{\lvert x_{1}\rvert +\dotsb +\left \lvert x_{j}\right \rvert +1,\dotsc ,\lvert x_{1}\rvert +\dotsb +\left \lvert x_{j+1}\right \rvert \right \}, j=1,\dotsc ,n$
. In the second equality, we interpret
 $(\sigma _{1},\dotsc ,\sigma _{n})$
as
$(\sigma _{1},\dotsc ,\sigma _{n})$
as
 $\sigma _{i}$
acting on the ith block.
$\sigma _{i}$
acting on the ith block.
A (right) module [Reference Fresse22]
![]() $\mathcal {M}=\oplus _{n=1}^{\infty }\mathcal {M}(n)$
over an operad
$\mathcal {M}=\oplus _{n=1}^{\infty }\mathcal {M}(n)$
over an operad
![]() $\mathcal {P}$
consists of a sequence of vector spaces
$\mathcal {P}$
consists of a sequence of vector spaces
![]() $\mathcal {M}(n)$
together with an action of the symmery group
$\mathcal {M}(n)$
together with an action of the symmery group
![]() $\Sigma _{n} : \mathcal {M}(n) \to \mathcal {M}(n)$
and a map
$\Sigma _{n} : \mathcal {M}(n) \to \mathcal {M}(n)$
and a map
![]() $\circ : \mathcal {M}(i_{1})\otimes \dotsb \otimes \mathcal {M}(i_{n}) \otimes \mathcal {P}(n) \to \mathcal {P}(i_{1} + \dotsb + i_{n})$
that satisfies associativity and equivariance.
$\circ : \mathcal {M}(i_{1})\otimes \dotsb \otimes \mathcal {M}(i_{n}) \otimes \mathcal {P}(n) \to \mathcal {P}(i_{1} + \dotsb + i_{n})$
that satisfies associativity and equivariance.
A bialgebra
![]() $(V,\cdot ,\Delta ,\eta ,\epsilon )$
is a vector space V together with an associative multiplication
$(V,\cdot ,\Delta ,\eta ,\epsilon )$
is a vector space V together with an associative multiplication
![]() $\cdot : V \otimes V \to V$
(
$\cdot : V \otimes V \to V$
(
![]() $x \cdot (y \cdot z)= (x \cdot y) \cdot z $
), a coassociative coproduct
$x \cdot (y \cdot z)= (x \cdot y) \cdot z $
), a coassociative coproduct
![]() $\Delta : V \to V \otimes V$
(
$\Delta : V \to V \otimes V$
(
![]() $(Id \otimes \Delta )\Delta =(\Delta \otimes Id)\Delta $
), a unit map
$(Id \otimes \Delta )\Delta =(\Delta \otimes Id)\Delta $
), a unit map
![]() $\eta : \mathbb {K} \to V$
(
$\eta : \mathbb {K} \to V$
(
![]() $\eta (1)\cdot x=x$
) and the counit
$\eta (1)\cdot x=x$
) and the counit
![]() $\epsilon : V \to \mathbb {K}$
(
$\epsilon : V \to \mathbb {K}$
(
![]() $(Id \otimes \epsilon )\Delta =Id=(\epsilon \otimes Id)\Delta $
), satisfying the following relations:
$(Id \otimes \epsilon )\Delta =Id=(\epsilon \otimes Id)\Delta $
), satisfying the following relations:
 $$ \begin{align*} \Delta(x \cdot y)&=\Delta(x) \cdot \Delta(y),\\ \epsilon(x)\epsilon(y)&=\epsilon(x \cdot y),\\ \Delta(\eta(x))&=(\eta \otimes \eta)(x),\\ Id_{\mathbb{K}} &= \epsilon \circ \eta. \end{align*} $$
$$ \begin{align*} \Delta(x \cdot y)&=\Delta(x) \cdot \Delta(y),\\ \epsilon(x)\epsilon(y)&=\epsilon(x \cdot y),\\ \Delta(\eta(x))&=(\eta \otimes \eta)(x),\\ Id_{\mathbb{K}} &= \epsilon \circ \eta. \end{align*} $$
A graded bialgebra is called connected if
![]() $\eta $
is an isomorphism between
$\eta $
is an isomorphism between
![]() $\mathbb {K}$
and the set of degree
$\mathbb {K}$
and the set of degree
![]() $0$
elements. A Hopf algebra is defined as a bialgebra equipped with an antihomomorphism
$0$
elements. A Hopf algebra is defined as a bialgebra equipped with an antihomomorphism
![]() $S: V \to V$
called the antipode, satisfying
$S: V \to V$
called the antipode, satisfying
A connected and graded bialgebra is a Hopf algebra.
Foissy [Reference Foissy21] describes how to construct bialgebras from operads. The following construction is especially relevant. Let
![]() $\mathcal {P}$
be an operad and consider the map
$\mathcal {P}$
be an operad and consider the map
![]() $\circ $
; the preimage of each vector space
$\circ $
; the preimage of each vector space
![]() $\mathcal {P}(n)$
under this map is
$\mathcal {P}(n)$
under this map is
 $$ \begin{align*} \circ^{-1}(\mathcal{P}(n)) =\bigoplus_{j=1}^{n} \bigoplus_{k_{1}+\dotsb+k_{j}=n} \mathcal{P}(k_{1}) \otimes \dotsb \otimes \mathcal{P}\left(k_{j}\right) \otimes \mathcal{P}(j). \end{align*} $$
$$ \begin{align*} \circ^{-1}(\mathcal{P}(n)) =\bigoplus_{j=1}^{n} \bigoplus_{k_{1}+\dotsb+k_{j}=n} \mathcal{P}(k_{1}) \otimes \dotsb \otimes \mathcal{P}\left(k_{j}\right) \otimes \mathcal{P}(j). \end{align*} $$
Furthermore, we identify the dual space
![]() $\mathcal {P}^{\ast }$
with
$\mathcal {P}^{\ast }$
with
![]() $\mathcal {P}$
by using the canonical dual pairing and consider the map
$\mathcal {P}$
by using the canonical dual pairing and consider the map
![]() $\Delta : \mathcal {P} \to T(\mathcal {P}) \otimes \mathcal {P}$
, where
$\Delta : \mathcal {P} \to T(\mathcal {P}) \otimes \mathcal {P}$
, where
![]() $T(\mathcal {P})$
is the tensor algebra over
$T(\mathcal {P})$
is the tensor algebra over
![]() $\mathcal {P}$
, defined by
$\mathcal {P}$
, defined by
Then
 $$ \begin{align*} \Delta(\mathcal{P}(n)) \subseteq \bigoplus_{j=1}^{n} \bigoplus_{k_{1}+\dotsb+k_{j}=n} \mathcal{P}(k_{1}) \dotsm \mathcal{P}\left(k_{j}\right) \otimes \mathcal{P}(j). \end{align*} $$
$$ \begin{align*} \Delta(\mathcal{P}(n)) \subseteq \bigoplus_{j=1}^{n} \bigoplus_{k_{1}+\dotsb+k_{j}=n} \mathcal{P}(k_{1}) \dotsm \mathcal{P}\left(k_{j}\right) \otimes \mathcal{P}(j). \end{align*} $$
Foissy showed that
![]() $(T(\mathcal {P}),m_{\mathrm {conc}},\Delta )$
is a graded bialgebra, where
$(T(\mathcal {P}),m_{\mathrm {conc}},\Delta )$
is a graded bialgebra, where
![]() $m_{\mathrm {conc}}$
is the concatenation product on
$m_{\mathrm {conc}}$
is the concatenation product on
![]() $T(\mathcal {P})$
and
$T(\mathcal {P})$
and
![]() $\Delta $
is multiplicatively extended to
$\Delta $
is multiplicatively extended to
![]() $T(\mathcal {P})$
with respect to this product.
$T(\mathcal {P})$
with respect to this product.
We conclude by recalling the important notion of bialgebras in cointeraction [Reference Calaque, Ebrahimi-Fard and Manchon9, Reference Foissy21, Reference Manchon29]:
Definition 2. We say that two bialgebras
![]() $(A,\cdot _{\scriptscriptstyle {A}},\Delta _{A},\epsilon _{A},\eta _{A})$
,
$(A,\cdot _{\scriptscriptstyle {A}},\Delta _{A},\epsilon _{A},\eta _{A})$
,
![]() $(B,\cdot _{\scriptscriptstyle {B}},\Delta _{B},\epsilon _{B},\eta _{B})$
are in cointeraction if B is coacting on A via a map
$(B,\cdot _{\scriptscriptstyle {B}},\Delta _{B},\epsilon _{B},\eta _{B})$
are in cointeraction if B is coacting on A via a map
![]() $\rho : A \to B \otimes A$
that satisfies
$\rho : A \to B \otimes A$
that satisfies
 $$ \begin{align*} \rho(1_{A})&=1_{B} \otimes 1_{A}, \\ \rho(x \cdot_{\scriptscriptstyle{A}} y)&=\rho(x) (\cdot_{\scriptscriptstyle{B}} \otimes \cdot_{\scriptscriptstyle{A}}) \rho(y), \\ (Id \otimes \epsilon_{A})\rho&=1_{B} \epsilon_{A}, \\ (Id \otimes \Delta_{A})\rho&=m_{\scriptscriptstyle{B}}^{1,3}(\rho \otimes \rho)\Delta_{A}, \end{align*} $$
$$ \begin{align*} \rho(1_{A})&=1_{B} \otimes 1_{A}, \\ \rho(x \cdot_{\scriptscriptstyle{A}} y)&=\rho(x) (\cdot_{\scriptscriptstyle{B}} \otimes \cdot_{\scriptscriptstyle{A}}) \rho(y), \\ (Id \otimes \epsilon_{A})\rho&=1_{B} \epsilon_{A}, \\ (Id \otimes \Delta_{A})\rho&=m_{\scriptscriptstyle{B}}^{1,3}(\rho \otimes \rho)\Delta_{A}, \end{align*} $$
where
 $$ \begin{align*} m_{\scriptscriptstyle{B}}^{1,3}(a \otimes b \otimes c \otimes d)=a \cdot_{\scriptscriptstyle{B}}c \otimes b \otimes d. \end{align*} $$
$$ \begin{align*} m_{\scriptscriptstyle{B}}^{1,3}(a \otimes b \otimes c \otimes d)=a \cdot_{\scriptscriptstyle{B}}c \otimes b \otimes d. \end{align*} $$
2.4 B-series
Let
![]() $(A,\cdot )$
denote an arbitrary pre-Lie algebra and introduce a fictitious unit
$(A,\cdot )$
denote an arbitrary pre-Lie algebra and introduce a fictitious unit
![]() $\mathbf {1}$
such that
$\mathbf {1}$
such that
![]() $\mathbf {1} \cdot a = a \cdot \mathbf {1} =a$
for any
$\mathbf {1} \cdot a = a \cdot \mathbf {1} =a$
for any
![]() $a \in A$
. As
$a \in A$
. As
![]() $(\mathcal {T},\curvearrowright )$
is the free pre-Lie algebra, there exists for any element
$(\mathcal {T},\curvearrowright )$
is the free pre-Lie algebra, there exists for any element
![]() $a \in A$
a unique pre-Lie morphism
$a \in A$
a unique pre-Lie morphism
![]() $F_{a}: \mathcal {T} \to A$
defined by
$F_{a}: \mathcal {T} \to A$
defined by
![]() $F_{a} (\bullet )=a$
. A B-series is then defined as a function
$F_{a} (\bullet )=a$
. A B-series is then defined as a function
 $$ \begin{align*} B(h,a,\alpha)=&\alpha(\emptyset)\mathbf{1}+\sum_{\tau \in \mathcal{T}}h^{v(\tau)}\frac{\alpha(\tau)}{\sigma(\tau)}F_{a}(\tau), \end{align*} $$
$$ \begin{align*} B(h,a,\alpha)=&\alpha(\emptyset)\mathbf{1}+\sum_{\tau \in \mathcal{T}}h^{v(\tau)}\frac{\alpha(\tau)}{\sigma(\tau)}F_{a}(\tau), \end{align*} $$
where
![]() $h \in \mathbb {K}$
is a constant,
$h \in \mathbb {K}$
is a constant,
![]() $v(\tau )$
denotes the function that counts the number of vertices of the input tree
$v(\tau )$
denotes the function that counts the number of vertices of the input tree
![]() $\tau \in \mathcal {T}$
,
$\tau \in \mathcal {T}$
,
![]() $\alpha : \mathcal {T}\oplus \mathbb {K}\emptyset \to \mathbb {K}$
is a linear function and
$\alpha : \mathcal {T}\oplus \mathbb {K}\emptyset \to \mathbb {K}$
is a linear function and
![]() $\sigma (\tau )$
is the number of symmetries of the tree
$\sigma (\tau )$
is the number of symmetries of the tree
![]() $\tau $
.
$\tau $
.
Remark 2 [Reference Chartier, Hairer and Vilmart15, Reference Chartier, Hairer and Vilmart16]
Let
![]() $f: \mathbb {R}^{n} \to \mathbb {R}^{n}$
be a vector field; then f and its derivatives form a pre-Lie algebra under composition. The typical B-series in numerical integration is going to map into this pre-Lie algebra via the pre-Lie algebra morphism given by
$f: \mathbb {R}^{n} \to \mathbb {R}^{n}$
be a vector field; then f and its derivatives form a pre-Lie algebra under composition. The typical B-series in numerical integration is going to map into this pre-Lie algebra via the pre-Lie algebra morphism given by
![]() $F_{f}(\bullet )=f$
. The map
$F_{f}(\bullet )=f$
. The map
![]() $F_{f}$
is called the elementary differential.
$F_{f}$
is called the elementary differential.
If the B-series
![]() $B(h,f,\alpha )$
is given by a linear map
$B(h,f,\alpha )$
is given by a linear map
![]() $\alpha $
with
$\alpha $
with
![]() $\alpha (\emptyset )=1$
, then
$\alpha (\emptyset )=1$
, then
![]() $B(h,f,\alpha )$
is close to the identity map and describes a flow
$B(h,f,\alpha )$
is close to the identity map and describes a flow

These flows can be composed, the result of which can surprisingly be described by a B-series. We call this composition of B-series.
If the B-series
![]() $B(h,f,\beta )$
is given by a linear map
$B(h,f,\beta )$
is given by a linear map
![]() $\beta $
with
$\beta $
with
![]() $\beta (\emptyset )=0$
, then
$\beta (\emptyset )=0$
, then
![]() $B(h,f,\beta )$
is close to f and describes a vector field. Since this B-series is a vector field, it then makes sense to consider something of the form
$B(h,f,\beta )$
is close to f and describes a vector field. Since this B-series is a vector field, it then makes sense to consider something of the form
![]() $B(h,B(h,f,\beta ),\alpha )$
. This is what we call substitution of B-series, and it turns out that this can be expressed again as a B-series in the vector field f.
$B(h,B(h,f,\beta ),\alpha )$
. This is what we call substitution of B-series, and it turns out that this can be expressed again as a B-series in the vector field f.
The results on composition and substitution of B-series come from finding appropriate bialgebra structures on the space of forests
![]() $\mathcal {F}$
: the Hopf algebra
$\mathcal {F}$
: the Hopf algebra
![]() $\mathcal {H}_{CK}=(\mathcal {F},\cdot ,\Delta _{CK})$
by Connes and Kreimer [Reference Connes and Kreimer17], as well as the extraction-contraction bialgebra
$\mathcal {H}_{CK}=(\mathcal {F},\cdot ,\Delta _{CK})$
by Connes and Kreimer [Reference Connes and Kreimer17], as well as the extraction-contraction bialgebra
![]() $\mathcal {H}=(\mathcal {F},\cdot ,\Delta _{\mathcal {H}})$
by Calaque, Ebrahimi-Fard and Manchon [Reference Calaque, Ebrahimi-Fard and Manchon9]. These are equal as algebras, both having the commutative concatenation product. The coproduct
$\mathcal {H}=(\mathcal {F},\cdot ,\Delta _{\mathcal {H}})$
by Calaque, Ebrahimi-Fard and Manchon [Reference Calaque, Ebrahimi-Fard and Manchon9]. These are equal as algebras, both having the commutative concatenation product. The coproduct
![]() $\Delta _{CK}$
is defined by admissible edge cuts. Let
$\Delta _{CK}$
is defined by admissible edge cuts. Let
![]() $\tau \in \mathcal {T}$
be a nonplanar rooted tree and let c be a (possibly empty) subset of edges in
$\tau \in \mathcal {T}$
be a nonplanar rooted tree and let c be a (possibly empty) subset of edges in
![]() $\tau $
. We say that c is an admissible edge cut if it contains at most one edge from each path in
$\tau $
. We say that c is an admissible edge cut if it contains at most one edge from each path in
![]() $\tau $
that starts in the root and ends in a leaf. Removing the edges in c from
$\tau $
that starts in the root and ends in a leaf. Removing the edges in c from
![]() $\tau $
produces several connected components; the connected component containing the root of
$\tau $
produces several connected components; the connected component containing the root of
![]() $\tau $
will be denoted by
$\tau $
will be denoted by
![]() $\mathrm {R}^{c}(\tau )$
. The concatenation of the remaining connected components will be denoted by
$\mathrm {R}^{c}(\tau )$
. The concatenation of the remaining connected components will be denoted by
![]() $\mathrm {P}^{c}(\tau )$
. The coproduct is then given by
$\mathrm {P}^{c}(\tau )$
. The coproduct is then given by
 $$ \begin{align*} \Delta_{CK}(\tau)=\sum_{c \text{ admissible cut}} \mathrm{P}^{c}(\tau) \otimes \mathrm{R}^{c}(\tau)+\tau \otimes \emptyset \end{align*} $$
$$ \begin{align*} \Delta_{CK}(\tau)=\sum_{c \text{ admissible cut}} \mathrm{P}^{c}(\tau) \otimes \mathrm{R}^{c}(\tau)+\tau \otimes \emptyset \end{align*} $$
on nonplanar rooted trees and extended to forests by
We illustrate this coproduct with a few examples:

The coproduct
![]() $\Delta _{\mathcal {H}}$
is defined by contractions of subtrees. Let
$\Delta _{\mathcal {H}}$
is defined by contractions of subtrees. Let
![]() $\tau \in \mathcal {T}$
be a nonplanar rooted tree and let
$\tau \in \mathcal {T}$
be a nonplanar rooted tree and let
![]() $(\tau _{1},\dotsc ,\tau _{n})$
be a spanning subforest of
$(\tau _{1},\dotsc ,\tau _{n})$
be a spanning subforest of
![]() $\tau $
– that is, each
$\tau $
– that is, each
![]() $\tau _{i}$
is a subtree of
$\tau _{i}$
is a subtree of
![]() $\tau $
and each vertex of
$\tau $
and each vertex of
![]() $\tau $
is contained in exactly one
$\tau $
is contained in exactly one
![]() $\tau _{i}$
. We denote by
$\tau _{i}$
. We denote by
![]() $\tau /\tau _{1}\dotsm \tau _{n}$
the tree obtained by contracting each subtree to a single vertex. The coproduct
$\tau /\tau _{1}\dotsm \tau _{n}$
the tree obtained by contracting each subtree to a single vertex. The coproduct
![]() $\Delta _{\mathcal {H}}$
is then given by
$\Delta _{\mathcal {H}}$
is then given by
 $$ \begin{align} \Delta_{\mathcal{H}}(\tau)=\sum_{\substack{\left(\tau_{1},\dotsc,\tau_{n}\right) \\ \text{spanning subforest}}} \tau_{1}\dotsm \tau_{n} \otimes \tau/\tau_{1} \dotsm \tau_{n} \end{align} $$
$$ \begin{align} \Delta_{\mathcal{H}}(\tau)=\sum_{\substack{\left(\tau_{1},\dotsc,\tau_{n}\right) \\ \text{spanning subforest}}} \tau_{1}\dotsm \tau_{n} \otimes \tau/\tau_{1} \dotsm \tau_{n} \end{align} $$
and extended to forests multiplicatively,
We illustrate the coproduct with a few examples:

The two bialgebras
![]() $\mathcal {H}_{CK}$
and
$\mathcal {H}_{CK}$
and
![]() $\mathcal {H}$
are in cointeraction [Reference Calaque, Ebrahimi-Fard and Manchon9]. We are now ready to recall two important theorems on B-series.
$\mathcal {H}$
are in cointeraction [Reference Calaque, Ebrahimi-Fard and Manchon9]. We are now ready to recall two important theorems on B-series.
Theorem 1. Let
![]() $\alpha ,\beta $
be characters of
$\alpha ,\beta $
be characters of
![]() $\mathcal {H}_{CK}$
. Let
$\mathcal {H}_{CK}$
. Let
![]() $m_{CK}$
denote the commutative concatenation product of
$m_{CK}$
denote the commutative concatenation product of
![]() $\mathcal {H}_{CK}$
; then the composition of B-series satisfies
$\mathcal {H}_{CK}$
; then the composition of B-series satisfies
where
![]() $\star _{CK}$
is the convolution product defined in terms of the coproduct of
$\star _{CK}$
is the convolution product defined in terms of the coproduct of
![]() $\mathcal {H}_{CK}$
, meaning
$\mathcal {H}_{CK}$
, meaning
Theorem 2. Let
![]() $\alpha ,\beta : \mathcal {T}\oplus \mathbb {K}\emptyset \to \mathbb {K}$
be linear maps satisfying
$\alpha ,\beta : \mathcal {T}\oplus \mathbb {K}\emptyset \to \mathbb {K}$
be linear maps satisfying
![]() $\alpha (\emptyset )=0$
. Extend
$\alpha (\emptyset )=0$
. Extend
![]() $\alpha $
to
$\alpha $
to
![]() $\mathcal {H}$
multiplicatively. Then the substitution of B-series satisfies
$\mathcal {H}$
multiplicatively. Then the substitution of B-series satisfies
 $$ \begin{align*} B\left(h,\frac{1}{h}B(h,a,\alpha),\beta \right)=B(h,a,\alpha \star_{\mathcal{H}} \beta), \end{align*} $$
$$ \begin{align*} B\left(h,\frac{1}{h}B(h,a,\alpha),\beta \right)=B(h,a,\alpha \star_{\mathcal{H}} \beta), \end{align*} $$
where
![]() $\star _{\mathcal {H}}$
is the convolution product defined in terms of the coproduct of
$\star _{\mathcal {H}}$
is the convolution product defined in terms of the coproduct of
![]() $\mathcal {H}$
.
$\mathcal {H}$
.
Remark 3. The characters of
![]() $\mathcal {H}_{CK}$
form a group under
$\mathcal {H}_{CK}$
form a group under
![]() $\star _{CK}$
. The linear maps
$\star _{CK}$
. The linear maps
![]() $\alpha $
with
$\alpha $
with
![]() $\alpha (\emptyset )=0$
act on this group by
$\alpha (\emptyset )=0$
act on this group by
![]() $\star _{\mathcal {H}}$
, meaning that the maps
$\star _{\mathcal {H}}$
, meaning that the maps
![]() $\alpha \star _{\mathcal {H}} : \mathcal {F}^{\ast } \to \mathcal {F}^{\ast }$
form a subgroup of the endomorphism group over characters of
$\alpha \star _{\mathcal {H}} : \mathcal {F}^{\ast } \to \mathcal {F}^{\ast }$
form a subgroup of the endomorphism group over characters of
![]() $\mathcal {H}_{CK}$
, where
$\mathcal {H}_{CK}$
, where
![]() $\mathcal {F}^{\ast }$
is the linear dual space of
$\mathcal {F}^{\ast }$
is the linear dual space of
![]() $\mathcal {F}$
. These maps are automorphisms when
$\mathcal {F}$
. These maps are automorphisms when
![]() $\alpha (\bullet )\neq 0$
. The cointeraction between
$\alpha (\bullet )\neq 0$
. The cointeraction between
![]() $\mathcal {H}_{CK}$
and
$\mathcal {H}_{CK}$
and
![]() $\mathcal {H}$
is vital for this action. This way of seeing a subgroup of the automorphism group over characters of
$\mathcal {H}$
is vital for this action. This way of seeing a subgroup of the automorphism group over characters of
![]() $\mathcal {H}_{CK}$
was used by Bruned, Hairer and Zambotti [Reference Bruned, Hairer and Zambotti3, Reference Bruned, Hairer and Zambotti4] to develop a theory of renormalisation of stochastic partial differential equations.
$\mathcal {H}_{CK}$
was used by Bruned, Hairer and Zambotti [Reference Bruned, Hairer and Zambotti3, Reference Bruned, Hairer and Zambotti4] to develop a theory of renormalisation of stochastic partial differential equations.
2.5 LB-series
Let
![]() $\mathbf {D}$
denote an arbitrary D-algebra and let
$\mathbf {D}$
denote an arbitrary D-algebra and let
![]() $a \in \mathcal {D}(\mathbf {D})$
be a derivation of
$a \in \mathcal {D}(\mathbf {D})$
be a derivation of
![]() $\mathbf {D}$
. By the freeness property of
$\mathbf {D}$
. By the freeness property of
![]() $(\mathcal {OF},\cdot ,\operatorname {\mathrm {\triangleright }})$
as a D-algebra, there is a unique D-algebra morphism defined by
$(\mathcal {OF},\cdot ,\operatorname {\mathrm {\triangleright }})$
as a D-algebra, there is a unique D-algebra morphism defined by
![]() $F_{a}(\bullet )=a$
. An LB-series is then defined as a formal sum
$F_{a}(\bullet )=a$
. An LB-series is then defined as a formal sum
 $$ \begin{align*} LB(a,\alpha)=\sum_{\omega \in \mathcal{OF}} \alpha(\omega)F_{a}(\omega), \end{align*} $$
$$ \begin{align*} LB(a,\alpha)=\sum_{\omega \in \mathcal{OF}} \alpha(\omega)F_{a}(\omega), \end{align*} $$
where
![]() $\alpha :\mathcal {OF} \to \mathbb {K}$
is a linear map. We say that
$\alpha :\mathcal {OF} \to \mathbb {K}$
is a linear map. We say that
![]() $LB(a,\alpha )$
, or just
$LB(a,\alpha )$
, or just
![]() $\alpha $
, is logarithmic if
$\alpha $
, is logarithmic if

for all nonempty
![]() $\omega _{1}, \omega _{2} \in \mathcal {OF}$
. We say that
$\omega _{1}, \omega _{2} \in \mathcal {OF}$
. We say that
![]() $LB(a,\beta )$
, or just
$LB(a,\beta )$
, or just
![]() $\beta $
, is exponential if
$\beta $
, is exponential if

for all
![]() $\omega _{1},\omega _{2} \in \mathcal {OF}$
.
$\omega _{1},\omega _{2} \in \mathcal {OF}$
.
Similar to how composition of B-series is understood with the help of the Hopf algebra by Connes and Kreimer, we capture composition of LB-series with the help of the Hopf algebra
![]() $\mathcal {H}_{N}$
introduced by Munthe-Kaas and Wright [Reference Munthe-Kaas and Wright35]. The Hopf algebra
$\mathcal {H}_{N}$
introduced by Munthe-Kaas and Wright [Reference Munthe-Kaas and Wright35]. The Hopf algebra
![]() $\mathcal {H}_{N}$
is defined over
$\mathcal {H}_{N}$
is defined over
![]() $\mathcal {OF}$
, its multiplication is the shuffle product
$\mathcal {OF}$
, its multiplication is the shuffle product
![]() and its coproduct
and its coproduct
![]() $\Delta _{N}$
is defined by planar left admissible edge cuts.
$\Delta _{N}$
is defined by planar left admissible edge cuts.
Let
![]() $\tau \in \mathcal {PT}$
be a planar rooted tree and let c be a (possibly empty) subset of edges in
$\tau \in \mathcal {PT}$
be a planar rooted tree and let c be a (possibly empty) subset of edges in
![]() $\tau $
. We say that c is an admissible planar left cut if it contains at most one edge from each path in
$\tau $
. We say that c is an admissible planar left cut if it contains at most one edge from each path in
![]() $\tau $
from the root to a leaf. Furthermore, if e is an edge in c, then every edge that is outgoing from the same vertex as e and that is to the left of e in the planar embedding is also in c. Removing the edges in c from
$\tau $
from the root to a leaf. Furthermore, if e is an edge in c, then every edge that is outgoing from the same vertex as e and that is to the left of e in the planar embedding is also in c. Removing the edges in c from
![]() $\tau $
produces several connected components; the one containing the root of
$\tau $
produces several connected components; the one containing the root of
![]() $\tau $
will be denoted by
$\tau $
will be denoted by
![]() $\mathrm {R}^{c}(\tau )$
. Connected components that are cut off from the same vertex will be concatenated to an ordered forest respecting the order, and then the resulting ordered forests will be shuffled, which is denoted by
$\mathrm {R}^{c}(\tau )$
. Connected components that are cut off from the same vertex will be concatenated to an ordered forest respecting the order, and then the resulting ordered forests will be shuffled, which is denoted by
![]() $\mathrm {P}^{c}(\tau )$
. The coproduct
$\mathrm {P}^{c}(\tau )$
. The coproduct
![]() $\Delta _{N}$
is defined by
$\Delta _{N}$
is defined by
 $$ \begin{align} \Delta_{N}(\tau)=\sum_{\substack{c \text{ planar left} \\ \text{admissible cut}}} \mathrm{P}^{c}(\tau) \otimes \mathrm{R}^{c}(\tau) + \tau \otimes \emptyset \end{align} $$
$$ \begin{align} \Delta_{N}(\tau)=\sum_{\substack{c \text{ planar left} \\ \text{admissible cut}}} \mathrm{P}^{c}(\tau) \otimes \mathrm{R}^{c}(\tau) + \tau \otimes \emptyset \end{align} $$
on planar rooted trees. It is extended to forests by
Note that this is dual to the planar Grossman–Larson product (1), meaning that it also satisfies
 $$ \begin{align} \Delta_{N}(\omega)=\sum_{\substack{\omega \text{ is a summand} \\ \text{in } \omega_{1} \diamond \omega_{2}}} \omega_{1} \otimes \omega_{2} \end{align} $$
$$ \begin{align} \Delta_{N}(\omega)=\sum_{\substack{\omega \text{ is a summand} \\ \text{in } \omega_{1} \diamond \omega_{2}}} \omega_{1} \otimes \omega_{2} \end{align} $$
for
![]() $\omega ,\omega _{1},\omega _{2}$
ordered forests.
$\omega ,\omega _{1},\omega _{2}$
ordered forests.
Remark 4. Note that the sum on the right-hand side of equation (4) could have been written running over
![]() $ \mathcal {OF}$
, using the natural pairing
$ \mathcal {OF}$
, using the natural pairing
![]() $\langle \omega _{1}, \omega _{2}\rangle =\delta _{\omega _{1}, \omega _{2}}$
in the summand. In fact, the duality to the Grossman–Larson product could have been taken as the definition of the coproduct, up to the identification that shuffle products appearing on the left-hand side must be evaluated (giving a linear combination of forests).
$\langle \omega _{1}, \omega _{2}\rangle =\delta _{\omega _{1}, \omega _{2}}$
in the summand. In fact, the duality to the Grossman–Larson product could have been taken as the definition of the coproduct, up to the identification that shuffle products appearing on the left-hand side must be evaluated (giving a linear combination of forests).
We illustrate the coproduct (4) with a few examples:

Before we move on to state the composition theorem for LB-series, we want to remark on D-algebras generated by vector fields over a manifold.
Remark 5. Typically in applications of LB-series in geometric integration over a manifold, the D-algebra morphism
![]() $F_{a}$
will map from ordered forests
$F_{a}$
will map from ordered forests
![]() $(\mathcal {OF},\cdot ,\operatorname {\mathrm {\triangleright }})$
into a D-algebra generated by vector fields over a manifold. In this case, logarithmic LB-series describe vector fields, which are the derivations in the target D-algebra. Exponential LB-series describe flows on the manifold. In this case, composition is understood as composition of flows, and this is what we mean concretely by composition of LB-series.
$(\mathcal {OF},\cdot ,\operatorname {\mathrm {\triangleright }})$
into a D-algebra generated by vector fields over a manifold. In this case, logarithmic LB-series describe vector fields, which are the derivations in the target D-algebra. Exponential LB-series describe flows on the manifold. In this case, composition is understood as composition of flows, and this is what we mean concretely by composition of LB-series.
Theorem 3 [Reference Munthe-Kaas and Wright35]
Let
![]() $\alpha ,\beta $
be characters of
$\alpha ,\beta $
be characters of
![]() $\mathcal {H}_{N}$
; then the composition of LB-series satisfies
$\mathcal {H}_{N}$
; then the composition of LB-series satisfies
where
![]() $\star _{N}$
is the convolution product defined in terms of the coproduct (4) of
$\star _{N}$
is the convolution product defined in terms of the coproduct (4) of
![]() $\mathcal {H}_{N}$
. This describes a group structure on the set of exponential LB-series.
$\mathcal {H}_{N}$
. This describes a group structure on the set of exponential LB-series.
By substituting an LB-series into another LB-series, we mean something of the form
![]() $LB(LB(a,\alpha ),\beta )$
–that is, replacing the derivation a in the target D-algebra by another LB-series expressed in a. This only makes sense if the LB-series
$LB(LB(a,\alpha ),\beta )$
–that is, replacing the derivation a in the target D-algebra by another LB-series expressed in a. This only makes sense if the LB-series
![]() $LB(a,\alpha )$
is again a derivation, which happens exactly when it is logarithmic. The aim of the sequel is now to find a Lie–Butcher version of Theorem 2 which describes substitution in B-series.
$LB(a,\alpha )$
is again a derivation, which happens exactly when it is logarithmic. The aim of the sequel is now to find a Lie–Butcher version of Theorem 2 which describes substitution in B-series.
2.6 B-series and LB-series in numerical analysis
The notion of B-series originated from Butcher’s seminal work on numerical methods [Reference Butcher6], and was originally used to find the order conditions of Runge–Kutta methods. Given a Runge–Kutta method expressed by a Butcher tableau, there is an explicit way to compute the corresponding B-series for the method [Reference Butcher8, Reference Hairer, Lubich and Wanner23]. One can, for example, find that the coefficient
 for the Runge–Kutta method given by the Butcher tableau parameters
for the Runge–Kutta method given by the Butcher tableau parameters
![]() $a_{ij},b_{k}$
is
$a_{ij},b_{k}$
is
 . From this construction, one finds the order conditions of Runge–Kutta methods by comparing the coefficients in the B-series expression of the method with the coefficients in the B-series expression for the exact solution.
. From this construction, one finds the order conditions of Runge–Kutta methods by comparing the coefficients in the B-series expression of the method with the coefficients in the B-series expression for the exact solution.
In more recent developments, following from the bialgebraic description of B-series substitution, structure-preservation properties of numerical methods have been studied using B-series and backwards error analysis. This has resulted in classifications of Hamiltonian methods and energy-preserving methods, based on the B-series description of those methods [Reference Celledoni, McLachlan, Owren and Quispel13].
As already indicated, LB-series methods are the natural generalisation of B-series methods in the context of numerical integration on manifolds. LB-series were originally constructed to describe Runge–Kutta–Munthe-Kaas methods for differential equations on Lie groups. Runge–Kutta methods on
![]() $\mathbb {R}^{d}$
rely on the linear structure of the space permitting the addition of vector fields. On Lie groups, on the other hand, this linear structure is not available. Instead, one has to consider the Lie algebra of the Lie group, which is a linear space. This is the reason why LB-series methods may include Lie brackets. Order conditions for LB-series methods have been studied in [Reference Berland, Owren and Skaflestad2, Reference Celledoni, Marthinsen and Owren12, Reference Munthe-Kaas33, Reference Owren37, Reference Owren and Marthinsen38]. Implementations of LB-series methods in Haskel were considered in [Reference Munthe-Kaas and Føllesdal31].
$\mathbb {R}^{d}$
rely on the linear structure of the space permitting the addition of vector fields. On Lie groups, on the other hand, this linear structure is not available. Instead, one has to consider the Lie algebra of the Lie group, which is a linear space. This is the reason why LB-series methods may include Lie brackets. Order conditions for LB-series methods have been studied in [Reference Berland, Owren and Skaflestad2, Reference Celledoni, Marthinsen and Owren12, Reference Munthe-Kaas33, Reference Owren37, Reference Owren and Marthinsen38]. Implementations of LB-series methods in Haskel were considered in [Reference Munthe-Kaas and Føllesdal31].
In this subsection, we shall discuss how LB-series can be used to approximate solutions to initial-value problems on manifolds by means of the notion of flow.
Let M be a manifold and let
![]() $\mathcal {X}M$
denote the vector fields on M. The flow of a vector field
$\mathcal {X}M$
denote the vector fields on M. The flow of a vector field
![]() $f:M \to TM$
is the diffeomorphism
$f:M \to TM$
is the diffeomorphism
![]() $\Phi _{t,f}: M \to M$
such that the following hold:
$\Phi _{t,f}: M \to M$
such that the following hold:
-
1.
 $\Phi _{s,f} \circ \Phi _{t,f} = \Phi _{s+t,f}$
.
$\Phi _{s,f} \circ \Phi _{t,f} = \Phi _{s+t,f}$
. -
2.
 $\Phi _{0,f}=Id$
.
$\Phi _{0,f}=Id$
. -
3.
 $\frac {\partial }{\partial t}\big \rvert _{t=0}\Phi _{t,f}(p)=f(p), \ \forall p \in M$
.
$\frac {\partial }{\partial t}\big \rvert _{t=0}\Phi _{t,f}(p)=f(p), \ \forall p \in M$
.
The fundamental assumption for LB-series methods is that there exists a Lie subalgebra
![]() $\mathfrak {g} \subset \mathcal {X}M$
that spans the tangent space
$\mathfrak {g} \subset \mathcal {X}M$
that spans the tangent space
![]() $T_{p}M$
at every point
$T_{p}M$
at every point
![]() $p \in M$
, and such that the flow
$p \in M$
, and such that the flow
![]() $\Phi _{t,g}$
can be computed exactly for every
$\Phi _{t,g}$
can be computed exactly for every
![]() $g \in \mathfrak {g}$
. The goal of numerical integration is to solve the differential equation
$g \in \mathfrak {g}$
. The goal of numerical integration is to solve the differential equation
by approximating the flow
![]() $\Phi _{t,f}(y_{0})$
in terms of flows
$\Phi _{t,f}(y_{0})$
in terms of flows
![]() $\Phi _{t,g}(y_{0})$
for
$\Phi _{t,g}(y_{0})$
for
![]() $g \in \mathfrak {g}$
.
$g \in \mathfrak {g}$
.
We are now going to construct a larger space of flows that can be computed exactly. Let
![]() $V \in \mathfrak {g}$
be a vector field. The Lie derivative of
$V \in \mathfrak {g}$
be a vector field. The Lie derivative of
![]() $\Psi \in C^{\infty }(M,\mathfrak {g})$
along V is defined by
$\Psi \in C^{\infty }(M,\mathfrak {g})$
along V is defined by
 $$ \begin{align*}V[\Psi](p)=\left.\frac{d}{dt}\right\rvert_{t=0}\Psi\left(\Phi_{t,V}(p)\right).\end{align*} $$
$$ \begin{align*}V[\Psi](p)=\left.\frac{d}{dt}\right\rvert_{t=0}\Psi\left(\Phi_{t,V}(p)\right).\end{align*} $$
The vector fields in
![]() $\mathfrak {g}$
are first-order differential operators acting on the space
$\mathfrak {g}$
are first-order differential operators acting on the space
![]() $C^{\infty }(M,\mathfrak {g})$
. We obtain higher-order differential operators by defining the concatenation product
$C^{\infty }(M,\mathfrak {g})$
. We obtain higher-order differential operators by defining the concatenation product
![]() $VW$
of two vector fields
$VW$
of two vector fields
![]() $V,W \in \mathfrak {g}$
as
$V,W \in \mathfrak {g}$
as
The space of differential operators in all orders, including the identity operator, is called the universal enveloping algebra
![]() $U(\mathfrak {g})$
. We extend the structure of the Lie derivative and the concatenation to the space
$U(\mathfrak {g})$
. We extend the structure of the Lie derivative and the concatenation to the space
![]() $C^{\infty }(M,U(\mathfrak {g}))$
by
$C^{\infty }(M,U(\mathfrak {g}))$
by
 $$ \begin{align*} g[h](p)&=(g(p)[h])(p),\\ (gh)(p)&=g(p)h(p) \end{align*} $$
$$ \begin{align*} g[h](p)&=(g(p)[h])(p),\\ (gh)(p)&=g(p)h(p) \end{align*} $$
for
![]() $g,h \in C^{\infty }(M,U(\mathfrak {g}))$
. This endows
$g,h \in C^{\infty }(M,U(\mathfrak {g}))$
. This endows
![]() $C^{\infty }(M,\mathfrak {g})$
with the structure of a D-algebra. Hence there exists a D-algebra morphism
$C^{\infty }(M,\mathfrak {g})$
with the structure of a D-algebra. Hence there exists a D-algebra morphism
![]() $F_{g}: \mathcal {OF} \to C^{\infty }(M,U(\mathfrak {g}))$
and the elements in
$F_{g}: \mathcal {OF} \to C^{\infty }(M,U(\mathfrak {g}))$
and the elements in
![]() $C^{\infty }(M,U(\mathfrak {g}))$
can be represented by LB-series. Now we use exponential LB-series to represent flows. Let
$C^{\infty }(M,U(\mathfrak {g}))$
can be represented by LB-series. Now we use exponential LB-series to represent flows. Let
![]() $LB(f,\alpha )$
represent the flow
$LB(f,\alpha )$
represent the flow
![]() $\Phi _{t,f}$
if
$\Phi _{t,f}$
if
for all
![]() $\Psi \in C^{\infty }(M,U(\mathfrak {g}))$
. Composition of LB-series in the sense of Theorem 3 corresponds to composition of flows. Numerical integration algorithms whose flows can be represented by LB-series are called LB-series methods.
$\Psi \in C^{\infty }(M,U(\mathfrak {g}))$
. Composition of LB-series in the sense of Theorem 3 corresponds to composition of flows. Numerical integration algorithms whose flows can be represented by LB-series are called LB-series methods.
Remark 6. Equation (6) should be thought of as being true for one specific t – for example,
![]() $t=h$
being the step size of the method. Different step sizes are obtained by a rescaling of f. If one sees f as a function of t by this rescaling, then equation (6) is true as functions of t.
$t=h$
being the step size of the method. Different step sizes are obtained by a rescaling of f. If one sees f as a function of t by this rescaling, then equation (6) is true as functions of t.
Remark 7. If
![]() $\Psi _{1},\dotsc ,\Psi _{d} \in C^{\infty }(M,\mathbb {R})\subset C^{\infty }(M,U(\mathfrak {g}))$
are the coordinate maps of some
$\Psi _{1},\dotsc ,\Psi _{d} \in C^{\infty }(M,\mathbb {R})\subset C^{\infty }(M,U(\mathfrak {g}))$
are the coordinate maps of some
![]() $\mathbb {R}^{d}$
-atlas for M, then equation (6) applied to the
$\mathbb {R}^{d}$
-atlas for M, then equation (6) applied to the
![]() $\Psi _{i}$
permits computation of the flow of an
$\Psi _{i}$
permits computation of the flow of an
![]() $LB$
-series method in terms of local coordinates.
$LB$
-series method in terms of local coordinates.
Expressing numerical integrators in terms of LB-series allows us to study the properties of the method. One example of this is backwards error analysis [Reference Hairer, Lubich and Wanner23]. Indeed, let
![]() $LB(f,\alpha )$
represent a numerical method for equation (5). Since
$LB(f,\alpha )$
represent a numerical method for equation (5). Since
![]() $LB(f,\alpha )$
represents a flow, there exists a modified vector field
$LB(f,\alpha )$
represents a flow, there exists a modified vector field
![]() $\tilde {f}$
such that the equation
$\tilde {f}$
such that the equation
is solved exactly by
![]() $LB(f,\alpha )$
. The modified vector field
$LB(f,\alpha )$
. The modified vector field
![]() $\tilde {f}$
can be written as a logarithmic LB-series
$\tilde {f}$
can be written as a logarithmic LB-series
![]() $\tilde {f}=LB(f,\beta )$
. Let
$\tilde {f}=LB(f,\beta )$
. Let
![]() $\alpha _{\mathrm {exact}}$
denote the character for the exact solution, which is given by
$\alpha _{\mathrm {exact}}$
denote the character for the exact solution, which is given by

Here we used the planar Grossman–Larson product defined in equation (1). Then we have the equality [Reference Lundervold and Munthe-Kaas26]
Finding the modified vector field
![]() $\tilde {f}=LB(f,\beta )$
is equivalent to finding
$\tilde {f}=LB(f,\beta )$
is equivalent to finding
![]() $\beta $
, given
$\beta $
, given
![]() $\alpha $
and
$\alpha $
and
![]() $\alpha _{\mathrm {exact}}$
. This is exactly described by the substitution problem.
$\alpha _{\mathrm {exact}}$
. This is exactly described by the substitution problem.
Backwards error analysis is of interest for studying structure-preserving properties of a method. The method
![]() $LB(f,\alpha )$
will preserve a structural property of f if and only if the modified vector field
$LB(f,\alpha )$
will preserve a structural property of f if and only if the modified vector field
![]() $\tilde {f}$
has the same structural property.
$\tilde {f}$
has the same structural property.
Example 4. The exponential Euler method applied to equation (5) is given by
where
![]() $c_{n}$
is the constant vector field that is everywhere equal to
$c_{n}$
is the constant vector field that is everywhere equal to
![]() $f(y_{n})$
. The
$f(y_{n})$
. The
![]() $LB$
-series for this method is given by [Reference Lundervold and Munthe-Kaas26]
$LB$
-series for this method is given by [Reference Lundervold and Munthe-Kaas26]
 $$ \begin{align*} \alpha_{\mathrm{euler}}=\emptyset + \bullet + \frac{1}{2!}\bullet \bullet + \frac{1}{3!}\bullet \bullet \bullet + \dotsb. \end{align*} $$
$$ \begin{align*} \alpha_{\mathrm{euler}}=\emptyset + \bullet + \frac{1}{2!}\bullet \bullet + \frac{1}{3!}\bullet \bullet \bullet + \dotsb. \end{align*} $$
To find the modified vector field
![]() $\tilde {f}$
for the exponential Euler method, we need to find the
$\tilde {f}$
for the exponential Euler method, we need to find the
![]() $\beta $
such that equation (7) is satisfied. We shall in the sequel see that the substitution in equation (7) can be rewritten as
$\beta $
such that equation (7) is satisfied. We shall in the sequel see that the substitution in equation (7) can be rewritten as
using a particular coaction
![]() $\rho $
. We will now compute coefficients
$\rho $
. We will now compute coefficients
![]() $\beta (\omega )$
for a few different
$\beta (\omega )$
for a few different
![]() $\omega $
by using the coaction. The computation
$\omega $
by using the coaction. The computation
tells us that
![]() $\alpha _{\mathrm {euler}}(\bullet )=\beta (\bullet )\alpha _{\mathrm {exact}}(\bullet )$
, so that
$\alpha _{\mathrm {euler}}(\bullet )=\beta (\bullet )\alpha _{\mathrm {exact}}(\bullet )$
, so that
![]() $\beta (\bullet )=1$
. The computation
$\beta (\bullet )=1$
. The computation

tells us that

Note that the combinatorial description of the coaction computation in equation (8) is the central part of this work, and will be unfolded in full generality further. Since we know that

we get from equation (9) that

This is in line with the computation of the modified vector field for the exponential Euler method given in [Reference Lundervold and Munthe-Kaas26, p. 184].
3 A substitution operad of nonplanar rooted trees
In this section we construct an operad of nonplanar rooted trees that is dual to the coproduct
![]() $\Delta _{\mathcal {H}}$
. We then see in Proposition 6 that this construction amounts to a different way of describing the pre-Lie operad defined by Chapoton and Livernet in [Reference Chapoton and Livernet14].
$\Delta _{\mathcal {H}}$
. We then see in Proposition 6 that this construction amounts to a different way of describing the pre-Lie operad defined by Chapoton and Livernet in [Reference Chapoton and Livernet14].
Let
![]() $\hat {\mathcal {T}}_{n}$
denote the vector space spanned by all nonplanar rooted trees with exactly n vertices, together with a bijection between the set
$\hat {\mathcal {T}}_{n}$
denote the vector space spanned by all nonplanar rooted trees with exactly n vertices, together with a bijection between the set
![]() $\{1,\dotsc ,n \}$
and the vertices of a tree in
$\{1,\dotsc ,n \}$
and the vertices of a tree in
![]() $\hat {\mathcal {T}}_{n}$
. We consider this bijection as a labelling of the vertices. In the sequel, we will use the hat notation as an indication for labelled vertices in other spaces also. Let the symmetric group
$\hat {\mathcal {T}}_{n}$
. We consider this bijection as a labelling of the vertices. In the sequel, we will use the hat notation as an indication for labelled vertices in other spaces also. Let the symmetric group
![]() $\Sigma _{n}$
act on
$\Sigma _{n}$
act on
![]() $\hat {\mathcal {T}}_{n}$
by permuting the labels of the vertices. Write
$\hat {\mathcal {T}}_{n}$
by permuting the labels of the vertices. Write
![]() $[x]$
for the orbit of
$[x]$
for the orbit of
![]() $x \in \hat {\mathcal {T}}_{n}$
under
$x \in \hat {\mathcal {T}}_{n}$
under
![]() $\Sigma _{n}$
. We consider this as an unlabelled tree. Define the equivalence relation
$\Sigma _{n}$
. We consider this as an unlabelled tree. Define the equivalence relation
![]() $x \sim y \iff [x]=[y]$
on
$x \sim y \iff [x]=[y]$
on
![]() $\hat {\mathcal {T}}_{n}$
. Let
$\hat {\mathcal {T}}_{n}$
. Let
 $\hat {\mathcal {T}}=\sum _{n=1}^{\infty }\hat {\mathcal {T}}_{n}$
; then
$\hat {\mathcal {T}}=\sum _{n=1}^{\infty }\hat {\mathcal {T}}_{n}$
; then
![]() $\hat {\mathcal {T}}/\sim $
can be identified with
$\hat {\mathcal {T}}/\sim $
can be identified with
![]() $\mathcal {T}$
. This identification is the bosonic Fock functor [Reference Aguiar and Mahajan1].
$\mathcal {T}$
. This identification is the bosonic Fock functor [Reference Aguiar and Mahajan1].
We will now define an operad over
![]() $\hat {\mathcal {T}}$
. Consider
$\hat {\mathcal {T}}$
. Consider
![]() $x \in \hat {\mathcal {T}}_{n}$
and
$x \in \hat {\mathcal {T}}_{n}$
and
![]() $x_{1},\dotsc ,x_{n} \in \hat {\mathcal {T}}$
. Each of the trees in
$x_{1},\dotsc ,x_{n} \in \hat {\mathcal {T}}$
. Each of the trees in
![]() $x,x_{1},\dotsc ,x_{n}$
has a factorisation in terms of the single-vertex tree and the grafting product in the free pre-Lie algebra. Define
$x,x_{1},\dotsc ,x_{n}$
has a factorisation in terms of the single-vertex tree and the grafting product in the free pre-Lie algebra. Define
to be the result of replacing each occurrence of the single-vertex tree corresponding to vertex number i in the factorisation of x by (the factorisation of)
![]() $x_{i}$
, for all
$x_{i}$
, for all
![]() $i=1,\dotsc ,n$
. The labels of the vertices in each
$i=1,\dotsc ,n$
. The labels of the vertices in each
![]() $x_{i}$
are shifted by the sum of the number of vertices in all
$x_{i}$
are shifted by the sum of the number of vertices in all
![]() $x_{j}$
with
$x_{j}$
with
![]() $j<i$
. This is well illustrated by an example:
$j<i$
. This is well illustrated by an example:
Example 5. Let

Then

The following proposition states that the combinatorial description of the operad is that of the pre-Lie operad:
Proposition 6. The expression
evaluates to the sum of all possible trees obtained by replacing vertex i in x by the tree
![]() $x_{i}$
, for all
$x_{i}$
, for all
![]() $i=1,\dotsc ,n$
. The incoming edge to vertex i becomes incoming to the root of
$i=1,\dotsc ,n$
. The incoming edge to vertex i becomes incoming to the root of
![]() $x_{i}$
. The edges outgoing from vertex i become outgoing from any vertex of
$x_{i}$
. The edges outgoing from vertex i become outgoing from any vertex of
![]() $x_{i}$
.
$x_{i}$
.
Proof. Recall the definition of the free pre-Lie product:
![]() $x_{i} \curvearrowright x_{j}$
is the sum of all trees obtained by adding an edge from any vertex in
$x_{i} \curvearrowright x_{j}$
is the sum of all trees obtained by adding an edge from any vertex in
![]() $x_{j}$
to the root of
$x_{j}$
to the root of
![]() $x_{i}$
. Furthermore, note that there is an edge from vertex j to vertex i in x if and only if vertex i is pre-Lie grafted onto a subtree of x that contains vertex j. Hence when vertex i is replaced by
$x_{i}$
. Furthermore, note that there is an edge from vertex j to vertex i in x if and only if vertex i is pre-Lie grafted onto a subtree of x that contains vertex j. Hence when vertex i is replaced by
![]() $x_{i}$
and vertex j is replaced by
$x_{i}$
and vertex j is replaced by
![]() $x_{j}$
, we get
$x_{j}$
, we get
![]() $x_{i}$
pre-Lie grafted onto
$x_{i}$
pre-Lie grafted onto
![]() $x_{j}$
.
$x_{j}$
.
We continue from Example 5 to illustrate the combinatorial picture:
Example 7. The expression

can be visualised by putting each input tree inside its respective vertex:

The four terms we see in Example 5 come from the four different ways of grafting the edges from
 onto some vertex of
onto some vertex of
![]() .
.
The visualisation in Example 7 illustrates a duality to the coproduct
![]() $\Delta _{\mathcal {H}}$
, which we make precise in the following proposition:
$\Delta _{\mathcal {H}}$
, which we make precise in the following proposition:
Proposition 8. Let
![]() $x \in \hat {\mathcal {T}}$
be a rooted tree; then
$x \in \hat {\mathcal {T}}$
be a rooted tree; then
 $$ \begin{align*} \Delta_{\mathcal{H}}([x])=&\sum_{\substack{[x] \text{ is a summand} \\ \text{in } \left[x_{1}\dotsm x_{n} \circ x^{\prime}\right]}} \frac{1}{n!} [x_{1}]\dotsm [x_{n}] \otimes [x^{\prime}] \end{align*} $$
$$ \begin{align*} \Delta_{\mathcal{H}}([x])=&\sum_{\substack{[x] \text{ is a summand} \\ \text{in } \left[x_{1}\dotsm x_{n} \circ x^{\prime}\right]}} \frac{1}{n!} [x_{1}]\dotsm [x_{n}] \otimes [x^{\prime}] \end{align*} $$
for
![]() $x_{1},\dotsc ,x_{n},x^{\prime }$
labeled trees.
$x_{1},\dotsc ,x_{n},x^{\prime }$
labeled trees.
Proof. If
![]() $[x]$
is a summand in
$[x]$
is a summand in
![]() $[x_{1}\dotsm x_{n} \circ x^{\prime }]$
, then
$[x_{1}\dotsm x_{n} \circ x^{\prime }]$
, then
![]() $[x_{1}] \dotsm [x_{n}]$
is a spanning subforest of
$[x_{1}] \dotsm [x_{n}]$
is a spanning subforest of
![]() $[x]$
. Furthermore,
$[x]$
. Furthermore,
![]() $[x]/[x_{1}] \dotsm [x_{n}] = [x^{\prime }]$
.
$[x]/[x_{1}] \dotsm [x_{n}] = [x^{\prime }]$
.
Conversely, let
![]() $[x_{1}] \dotsm [x_{n}]$
be an arbitrary spanning subforest of
$[x_{1}] \dotsm [x_{n}]$
be an arbitrary spanning subforest of
![]() $[x]$
. Then for any labelling of the vertex of
$[x]$
. Then for any labelling of the vertex of
![]() $[x]/[x_{1}] \dotsm [x_{n}]$
, there is an ordering of
$[x]/[x_{1}] \dotsm [x_{n}]$
, there is an ordering of
![]() $x_{1} \dotsm x_{n}$
such that the rooted tree that was contracted into vertex i is in position i, for
$x_{1} \dotsm x_{n}$
such that the rooted tree that was contracted into vertex i is in position i, for
![]() $i=1,\dotsc ,n$
. Then for any choice of labelling on each
$i=1,\dotsc ,n$
. Then for any choice of labelling on each
![]() $x_{i}$
, we have that
$x_{i}$
, we have that
![]() $[x_{1} \dotsm x_{n} \circ [x]/[x_{1}] \dotsm [x_{n}]]$
is the sum of all possible trees obtained by replacing each vertex in
$[x_{1} \dotsm x_{n} \circ [x]/[x_{1}] \dotsm [x_{n}]]$
is the sum of all possible trees obtained by replacing each vertex in
![]() $[x]/[x_{1}] \dotsm [x_{n}]$
by the rooted tree it was contracted from. In particular,
$[x]/[x_{1}] \dotsm [x_{n}]$
by the rooted tree it was contracted from. In particular,
![]() $[x]$
must be a summand in this sum.
$[x]$
must be a summand in this sum.
Finally, we note that each of the
![]() $n!$
different labellings of
$n!$
different labellings of
![]() $[x^{\prime }]$
gives us the same spanning subforest.
$[x^{\prime }]$
gives us the same spanning subforest.
Remark 8. One could consider the expression
![]() $x_{1}\dotsm x_{n} \circ x^{\prime }$
also for unlabelled trees, to mean the sum over all possible ways to pair vertices in
$x_{1}\dotsm x_{n} \circ x^{\prime }$
also for unlabelled trees, to mean the sum over all possible ways to pair vertices in
![]() $x^{\prime }$
with different
$x^{\prime }$
with different
![]() $x_{i}$
. In this setting, the coproduct
$x_{i}$
. In this setting, the coproduct
![]() $\Delta _{\mathcal {H}}$
is given as the dual to
$\Delta _{\mathcal {H}}$
is given as the dual to
![]() $\circ $
.
$\circ $
.
Remark 9. The coproduct construction in Proposition 8 is a symmetrisation of the bialgebra construction by Foissy that we discussed in section 2.3. The observation that the bialgebra
![]() $\mathcal {H}$
can be obtained this way was mentioned without proof by Foissy in [Reference Foissy21].
$\mathcal {H}$
can be obtained this way was mentioned without proof by Foissy in [Reference Foissy21].
4 A substitution operad of planar rooted trees
Motivated by the observation that the coproduct
![]() $\Delta _{\mathcal {H}}$
describing substitution in B-series can be seen as dual to a substitution operad of nonplanar trees, we shall in this section construct a substitution operad of Lie polynomials of planar rooted trees. Recall that substitution in LB-series is described by a map that sends the single-vertex tree to a Lie polynomial and then generates to be a D-algebra morphism. Furthermore, recall that the Lie polynomials are in bijection with the underlying free post-Lie algebra, which can be represented by formal Lie brackets on planar rooted trees.
$\Delta _{\mathcal {H}}$
describing substitution in B-series can be seen as dual to a substitution operad of nonplanar trees, we shall in this section construct a substitution operad of Lie polynomials of planar rooted trees. Recall that substitution in LB-series is described by a map that sends the single-vertex tree to a Lie polynomial and then generates to be a D-algebra morphism. Furthermore, recall that the Lie polynomials are in bijection with the underlying free post-Lie algebra, which can be represented by formal Lie brackets on planar rooted trees.
Let
 $\widehat {Lie(\mathcal {PT}{\kern2.5pt})}_{n}$
denote the vector space spanned by all Lie brackets over planar trees, such that there are in total exactly n vertices in the brackets, together with a bijection between the set
$\widehat {Lie(\mathcal {PT}{\kern2.5pt})}_{n}$
denote the vector space spanned by all Lie brackets over planar trees, such that there are in total exactly n vertices in the brackets, together with a bijection between the set
![]() $\{1,\dotsc ,n \}$
and the vertices. This bijection provides a labelling of the vertices. Let the symmetric group
$\{1,\dotsc ,n \}$
and the vertices. This bijection provides a labelling of the vertices. Let the symmetric group
![]() $\Sigma _{n}$
act on
$\Sigma _{n}$
act on
 $\widehat {Lie(\mathcal {PT}{\kern2.5pt})}_{n}$
by permuting the labels of the vertices. Write
$\widehat {Lie(\mathcal {PT}{\kern2.5pt})}_{n}$
by permuting the labels of the vertices. Write
![]() $[\omega ]$
for the orbit of
$[\omega ]$
for the orbit of
![]() $\omega $
under
$\omega $
under
![]() $\Sigma _{n}$
; we consider this as an unlabelled element. Define the equivalence relation
$\Sigma _{n}$
; we consider this as an unlabelled element. Define the equivalence relation
![]() $\omega _{1} \sim \omega _{2} \iff [\omega _{1}]=[\omega _{2}]$
on
$\omega _{1} \sim \omega _{2} \iff [\omega _{1}]=[\omega _{2}]$
on
 $\widehat {Lie(\mathcal {PT}{\kern2.5pt})}_{n}$
and let
$\widehat {Lie(\mathcal {PT}{\kern2.5pt})}_{n}$
and let
 $\widehat {Lie(\mathcal {PT}{\kern2.5pt})}=\sum _{n=1}^{\infty }\widehat {Lie(\mathcal {PT}{\kern2.5pt})}_{n}$
; then
$\widehat {Lie(\mathcal {PT}{\kern2.5pt})}=\sum _{n=1}^{\infty }\widehat {Lie(\mathcal {PT}{\kern2.5pt})}_{n}$
; then
 $\widehat {Lie(\mathcal {PT}{\kern2.5pt})}/\sim $
can be identified with
$\widehat {Lie(\mathcal {PT}{\kern2.5pt})}/\sim $
can be identified with
![]() $Lie(\mathcal {PT}{\kern2.5pt})$
.
$Lie(\mathcal {PT}{\kern2.5pt})$
.
We will now define an operad over
 $\widehat {Lie(\mathcal {PT}{\kern2.5pt})}$
. Consider
$\widehat {Lie(\mathcal {PT}{\kern2.5pt})}$
. Consider
 $\omega \in \widehat {Lie(\mathcal {PT}{\kern2.5pt})}_{n}$
and
$\omega \in \widehat {Lie(\mathcal {PT}{\kern2.5pt})}_{n}$
and
 $\omega _{1},\dotsc ,\omega _{n} \in \widehat {Lie(\mathcal {PT}{\kern2.5pt})}$
. Each element of
$\omega _{1},\dotsc ,\omega _{n} \in \widehat {Lie(\mathcal {PT}{\kern2.5pt})}$
. Each element of
![]() $\omega ,\omega _{1},\dotsc ,\omega _{n}$
can be expressed as a monomial in terms of the Lie bracket, the post-Lie grafting and the single-vertex tree. Define
$\omega ,\omega _{1},\dotsc ,\omega _{n}$
can be expressed as a monomial in terms of the Lie bracket, the post-Lie grafting and the single-vertex tree. Define
to be the result of replacing each occurrence of the single-vertex tree corresponding to vertex number i in the expression for
![]() $\omega $
by the expression for
$\omega $
by the expression for
![]() $\omega _{i}$
, for all
$\omega _{i}$
, for all
![]() $i=1,\dotsc ,n$
. Although the expressions for the
$i=1,\dotsc ,n$
. Although the expressions for the
![]() $\omega _{i}$
are not unique, this construction is still well defined, as we are working with free post-Lie algebras. The construction is well illustrated by an example:
$\omega _{i}$
are not unique, this construction is still well defined, as we are working with free post-Lie algebras. The construction is well illustrated by an example:
Example 9. Let

then
Proposition 10.
 $\left (\widehat {Lie(\mathcal {PT}{\kern2.5pt})},\circ \right )$
is an operad.
$\left (\widehat {Lie(\mathcal {PT}{\kern2.5pt})},\circ \right )$
is an operad.
Proof. It is clear that the single-vertex tree is an identity element. It remains to show associativity and equivariance.
We have that
is the expression obtained by replacing vertex i in
![]() $\omega $
by
$\omega $
by
![]() $\omega _{i,1} \dotsm \omega _{i,n_{i}} \circ \omega _{i}$
, for
$\omega _{i,1} \dotsm \omega _{i,n_{i}} \circ \omega _{i}$
, for
![]() $i=1,\dotsc ,l$
. Furthermore, we have that
$i=1,\dotsc ,l$
. Furthermore, we have that
is the expression obtained by first replacing vertex i in
![]() $\omega $
by
$\omega $
by
![]() $\omega _{i}$
and then replacing
$\omega _{i}$
and then replacing
![]() $\omega _{i}$
by
$\omega _{i}$
by
![]() $\omega _{i,1} \dots \omega _{i,n_{i}} \circ \omega _{i}$
, for
$\omega _{i,1} \dots \omega _{i,n_{i}} \circ \omega _{i}$
, for
![]() $i=1,\ldots ,l$
. Hence we have associativity.
$i=1,\ldots ,l$
. Hence we have associativity.
Equivariance follows from the observation that the resulting unlabelled elements depend only on a coupling between vertices and input elements.
We get the following combinatorial description of the operad:
Proposition 11. The expression
evaluates to the sum of all Lie brackets of planar trees obtained by replacing vertex i in
![]() $\omega $
by
$\omega $
by
![]() $\omega _{i}$
. Edges outgoing from vertex i becomes leftmost outgoing from any vertex of
$\omega _{i}$
. Edges outgoing from vertex i becomes leftmost outgoing from any vertex of
![]() $\omega _{i}$
, such that their left-to-right order is preserved when they are outgoing from the same vertex. Edges incoming to vertex j become incoming to the root of
$\omega _{i}$
, such that their left-to-right order is preserved when they are outgoing from the same vertex. Edges incoming to vertex j become incoming to the root of
![]() $\omega _{j}$
if
$\omega _{j}$
if
![]() $\omega _{j}$
is a tree. If
$\omega _{j}$
is a tree. If
![]() $\omega _{j}$
is a Lie bracket, we interpret the incoming edge as one edge per root and graft all trees in
$\omega _{j}$
is a Lie bracket, we interpret the incoming edge as one edge per root and graft all trees in
![]() $\omega _{j}$
onto the same vertex in all possible left-to-right orders prescribed by the interpretation
$\omega _{j}$
onto the same vertex in all possible left-to-right orders prescribed by the interpretation
![]() $[\omega _{a},\omega _{b}]=\omega _{a}\omega _{b}-\omega _{b}\omega _{a}$
.
$[\omega _{a},\omega _{b}]=\omega _{a}\omega _{b}-\omega _{b}\omega _{a}$
.
Proof. This is completely analogous to the statement and proof of Proposition 6. Note that there is now also a factor of planarity and that all grafting is done leftmost; note also that the identity
is used to deal with replacing a nonroot vertex by a Lie bracket.
Corollary 11.1. The operad
 $\left (\widehat {Lie(PT)},\circ \right )$
is the post-Lie operad.
$\left (\widehat {Lie(PT)},\circ \right )$
is the post-Lie operad.
Proof. In Proposition 11, we recovered the combinatorial description of the post-Lie operad from [Reference Silva39].
Motivated by Proposition 8, we are now going to define a coproduct as the dual of this substitution operad.
Definition 3. Let
![]() $S(Lie(\mathcal {PT}{\kern2.5pt}))$
denote the symmetric algebra over the vector space
$S(Lie(\mathcal {PT}{\kern2.5pt}))$
denote the symmetric algebra over the vector space
![]() $Lie(\mathcal {PT}{\kern2.5pt})$
, meaning that it is the vector space of all unordered sequences of Lie polynomials of ordered forests together with a commutative concatenation product. We denote the commutative concatenation of
$Lie(\mathcal {PT}{\kern2.5pt})$
, meaning that it is the vector space of all unordered sequences of Lie polynomials of ordered forests together with a commutative concatenation product. We denote the commutative concatenation of
![]() $\omega _{1}$
and
$\omega _{1}$
and
![]() $\omega _{2}$
by
$\omega _{2}$
by
![]() $\omega _{1}\centerdot \omega _{2}$
. We furthermore denote the identity element of this product by
$\omega _{1}\centerdot \omega _{2}$
. We furthermore denote the identity element of this product by
![]() $1$
.
$1$
.
Let
 $\omega \in \widehat {Lie(\mathcal {PT}{\kern2.5pt})}$
be a Lie polynomial. We define the coproduct
$\omega \in \widehat {Lie(\mathcal {PT}{\kern2.5pt})}$
be a Lie polynomial. We define the coproduct
![]() $\Delta _{\mathcal {Q}}: S(Lie(\mathcal {PT}{\kern2.5pt})) \to S(Lie(\mathcal {PT}{\kern2.5pt})) \otimes S(Lie(\mathcal {PT}{\kern2.5pt}))$
by
$\Delta _{\mathcal {Q}}: S(Lie(\mathcal {PT}{\kern2.5pt})) \to S(Lie(\mathcal {PT}{\kern2.5pt})) \otimes S(Lie(\mathcal {PT}{\kern2.5pt}))$
by
 $$ \begin{align*} \Delta_{\mathcal{Q}}([\omega])=\sum_{\substack{[\omega] \text{ is a summand in} \\ \left[\omega_{1} \dotsm \omega_{n} \circ \omega^{\prime}\right]}}\frac{1}{n!} [\omega_{1}]\centerdot \dotsb \centerdot[\omega_{n}] \otimes [\omega^{\prime}] \end{align*} $$
$$ \begin{align*} \Delta_{\mathcal{Q}}([\omega])=\sum_{\substack{[\omega] \text{ is a summand in} \\ \left[\omega_{1} \dotsm \omega_{n} \circ \omega^{\prime}\right]}}\frac{1}{n!} [\omega_{1}]\centerdot \dotsb \centerdot[\omega_{n}] \otimes [\omega^{\prime}] \end{align*} $$
for
![]() $\omega _{1},\dotsc ,\omega _{n},\omega ^{\prime }$
labelled Lie monomials. The coproduct is then extended to
$\omega _{1},\dotsc ,\omega _{n},\omega ^{\prime }$
labelled Lie monomials. The coproduct is then extended to
![]() $S(Lie(\mathcal {PT}{\kern2.5pt}))$
multiplicatively.
$S(Lie(\mathcal {PT}{\kern2.5pt}))$
multiplicatively.
We conclude the section with technical details.
Proposition 12. Let the linear map
![]() $\epsilon : S(Lie(\mathcal {PT}{\kern2.5pt})) \to \mathbb {K}$
be defined by
$\epsilon : S(Lie(\mathcal {PT}{\kern2.5pt})) \to \mathbb {K}$
be defined by
 $$ \begin{align*} \epsilon(\omega)=\begin{cases} 1 & \text{if }\omega=1\text{ or } \omega=\bullet, \\ 0 & \text{otherwise} \end{cases} \end{align*} $$
$$ \begin{align*} \epsilon(\omega)=\begin{cases} 1 & \text{if }\omega=1\text{ or } \omega=\bullet, \\ 0 & \text{otherwise} \end{cases} \end{align*} $$
for
![]() $\omega $
a Lie monomial, and extended to
$\omega $
a Lie monomial, and extended to
![]() $S(Lie(\mathcal {PT}{\kern2.5pt}))$
by
$S(Lie(\mathcal {PT}{\kern2.5pt}))$
by
Then
![]() $(S(Lie(\mathcal {PT}{\kern2.5pt})),\Delta _{\mathcal {Q}},\epsilon )$
is a coalgebra.
$(S(Lie(\mathcal {PT}{\kern2.5pt})),\Delta _{\mathcal {Q}},\epsilon )$
is a coalgebra.
Proof. The coassociativity of
![]() $\Delta _{\mathcal {Q}}$
follows immediately from the associativity of
$\Delta _{\mathcal {Q}}$
follows immediately from the associativity of
 $\left (\widehat {Lie(\mathcal {PT}{\kern2.5pt})},\circ \right )$
. It remains to show that
$\left (\widehat {Lie(\mathcal {PT}{\kern2.5pt})},\circ \right )$
. It remains to show that
![]() $\epsilon $
is a counit, meaning that it satisfies
$\epsilon $
is a counit, meaning that it satisfies
We have that
![]() $(Id \otimes \epsilon )\Delta _{\mathcal {Q}}(\omega _{1} \centerdot \dotsb \centerdot \omega _{n})$
is nonzero only on the unique term where every
$(Id \otimes \epsilon )\Delta _{\mathcal {Q}}(\omega _{1} \centerdot \dotsb \centerdot \omega _{n})$
is nonzero only on the unique term where every
![]() $\omega _{i}$
,
$\omega _{i}$
,
![]() $i=1,\dotsc ,n$
, is contracted into a single vertex. Hence this has to be the identity. Similarly, we have that
$i=1,\dotsc ,n$
, is contracted into a single vertex. Hence this has to be the identity. Similarly, we have that
![]() $(\epsilon \otimes Id)\Delta _{\mathcal {Q}}(\omega )$
is nonzero only on the unique term where every contracted subforest of
$(\epsilon \otimes Id)\Delta _{\mathcal {Q}}(\omega )$
is nonzero only on the unique term where every contracted subforest of
![]() $\omega $
consists of a single vertex. Hence this expression evaluates to
$\omega $
consists of a single vertex. Hence this expression evaluates to
![]() $\omega $
.
$\omega $
.
Proposition 13. Define the function
![]() $\lvert \cdot \rvert : Lie(\mathcal {PT}{\kern2.5pt}) \to \mathbb {N}$
by
$\lvert \cdot \rvert : Lie(\mathcal {PT}{\kern2.5pt}) \to \mathbb {N}$
by
![]() $\lvert \omega \rvert = \#\{\text {vertices in }\omega \}-1$
. Then
$\lvert \omega \rvert = \#\{\text {vertices in }\omega \}-1$
. Then
Proof. Since every vertex in
![]() $[\omega _{1} \dotsm \omega _{n} \circ \omega ]$
comes from a vertex in an
$[\omega _{1} \dotsm \omega _{n} \circ \omega ]$
comes from a vertex in an
![]() $\omega _{i}$
, we have
$\omega _{i}$
, we have
 $$ \begin{align*} \lvert[\omega_{1} \dotsm \omega_{n} \circ \omega ]\rvert+1&=(\lvert[\omega_{1}]\rvert+1) + \dotsb +(\lvert[\omega_{n}]\rvert+1) \\ &=(\lvert[\omega_{1}]\rvert + \dotsb +\lvert[\omega_{n}]\rvert+\lvert[\omega]\rvert)+n. \end{align*} $$
$$ \begin{align*} \lvert[\omega_{1} \dotsm \omega_{n} \circ \omega ]\rvert+1&=(\lvert[\omega_{1}]\rvert+1) + \dotsb +(\lvert[\omega_{n}]\rvert+1) \\ &=(\lvert[\omega_{1}]\rvert + \dotsb +\lvert[\omega_{n}]\rvert+\lvert[\omega]\rvert)+n. \end{align*} $$
Hence
 $$ \begin{align*} \lvert[\omega_{1} \dotsm \omega_{n} \circ \omega ]\rvert&=\lvert[\omega_{1}]\rvert + \dotsb +\lvert[\omega_{n}]\rvert+(n-1) \\ &=\lvert[\omega_{1}]\rvert + \dotsb +\lvert[\omega_{n}]\rvert+\lvert[\omega]\rvert. \end{align*} $$
$$ \begin{align*} \lvert[\omega_{1} \dotsm \omega_{n} \circ \omega ]\rvert&=\lvert[\omega_{1}]\rvert + \dotsb +\lvert[\omega_{n}]\rvert+(n-1) \\ &=\lvert[\omega_{1}]\rvert + \dotsb +\lvert[\omega_{n}]\rvert+\lvert[\omega]\rvert. \end{align*} $$
Corollary 13.1. The function
![]() $\lvert \cdot \rvert $
defined in Proposition 13 induces a grading on the bialgebra
$\lvert \cdot \rvert $
defined in Proposition 13 induces a grading on the bialgebra
![]() $\mathcal {Q}=(S(Lie(\mathcal {PT}{\kern2.5pt})),\centerdot ,\Delta _{\mathcal {Q}},1,\epsilon )$
.
$\mathcal {Q}=(S(Lie(\mathcal {PT}{\kern2.5pt})),\centerdot ,\Delta _{\mathcal {Q}},1,\epsilon )$
.
Proof. Let
![]() $\omega \in Lie(\mathcal {PT}{\kern2.5pt})$
and consider the term
$\omega \in Lie(\mathcal {PT}{\kern2.5pt})$
and consider the term
![]() $\omega _{1} \centerdot \dotsb \centerdot \omega _{n} \otimes \omega ^{\prime }$
in
$\omega _{1} \centerdot \dotsb \centerdot \omega _{n} \otimes \omega ^{\prime }$
in
![]() $\Delta _{\mathcal {Q}}(\omega )$
. By Proposition 13, we have that
$\Delta _{\mathcal {Q}}(\omega )$
. By Proposition 13, we have that
![]() $\lvert \omega _{1}\rvert + \dotsb +\lvert \omega _{n}\rvert +\lvert \omega ^{\prime }\rvert =\lvert \omega \rvert $
. Extend
$\lvert \omega _{1}\rvert + \dotsb +\lvert \omega _{n}\rvert +\lvert \omega ^{\prime }\rvert =\lvert \omega \rvert $
. Extend
![]() $\lvert \cdot \rvert $
to
$\lvert \cdot \rvert $
to
![]() $S(Lie(\mathcal {PT}{\kern2.5pt}))$
by
$S(Lie(\mathcal {PT}{\kern2.5pt}))$
by
![]() $\lvert \omega _{1} \centerdot \dotsb \centerdot \omega _{n}\rvert =\lvert \omega _{1}\rvert + \dotsb +\lvert \omega _{n}\rvert $
, then
$\lvert \omega _{1} \centerdot \dotsb \centerdot \omega _{n}\rvert =\lvert \omega _{1}\rvert + \dotsb +\lvert \omega _{n}\rvert $
, then
 $\lvert \omega \rvert =\left \lvert \omega _{(1)}\right \rvert +\left \lvert \omega _{(2)}\right \rvert $
and
$\lvert \omega \rvert =\left \lvert \omega _{(1)}\right \rvert +\left \lvert \omega _{(2)}\right \rvert $
and
![]() $S(Lie(\mathcal {PT}{\kern2.5pt}))=\oplus _{n=1}^{\infty } \{\omega \in S(Lie(\mathcal {PT}{\kern2.5pt})): \lvert \omega \rvert =n \}$
defines a grading.
$S(Lie(\mathcal {PT}{\kern2.5pt}))=\oplus _{n=1}^{\infty } \{\omega \in S(Lie(\mathcal {PT}{\kern2.5pt})): \lvert \omega \rvert =n \}$
defines a grading.
5 Two cointeracting bialgebras
In this section we are going to describe a cointeraction between the Munthe-Kaas–Wright Hopf algebra
![]() and the bialgebra
and the bialgebra
![]() $\mathcal {Q}$
defined in the previous section. This means that we will define a coaction
$\mathcal {Q}$
defined in the previous section. This means that we will define a coaction
![]() $\rho : \mathcal {H}_{N} \to \mathcal {Q} \otimes \mathcal {H}_{N}$
that satisfies the conditions of Definition 2. Informally, we want this coaction to be the opposite of substituting Lie polynomials into the vertices of forests.
$\rho : \mathcal {H}_{N} \to \mathcal {Q} \otimes \mathcal {H}_{N}$
that satisfies the conditions of Definition 2. Informally, we want this coaction to be the opposite of substituting Lie polynomials into the vertices of forests.
Remark 10. There exists an isomorphism [Reference Foissy20]
![]() . This means that our coproduct
. This means that our coproduct
![]() $\Delta _{\mathcal {Q}} : \mathcal {Q} \to \mathcal {Q} \otimes \mathcal {Q}$
can already be seen as a coaction
$\Delta _{\mathcal {Q}} : \mathcal {Q} \to \mathcal {Q} \otimes \mathcal {Q}$
can already be seen as a coaction
![]() $\mathcal {H}_{N} \to \mathcal {Q} \otimes \mathcal {H}_{N}$
via identification by this isomorphism. The isomorphism is, however, nontrivial. We will prefer to describe the coaction by using a module over an operad.
$\mathcal {H}_{N} \to \mathcal {Q} \otimes \mathcal {H}_{N}$
via identification by this isomorphism. The isomorphism is, however, nontrivial. We will prefer to describe the coaction by using a module over an operad.
Note that in the nonplanar case, we had an isomorphism between
![]() $\mathcal {H}_{CK}$
and
$\mathcal {H}_{CK}$
and
![]() $\mathcal {H}$
as algebras. This is now generalised also to the planar case.
$\mathcal {H}$
as algebras. This is now generalised also to the planar case.
Recall that
![]() $\mathcal {OF}$
is the universal enveloping algebra of
$\mathcal {OF}$
is the universal enveloping algebra of
![]() $Lie(\mathcal {PT}{\kern2.5pt})$
; hence there is an inclusion
$Lie(\mathcal {PT}{\kern2.5pt})$
; hence there is an inclusion
![]() $Lie(\mathcal {PT}{\kern2.5pt}) \subset \mathcal {OF}$
given by the commutator
$Lie(\mathcal {PT}{\kern2.5pt}) \subset \mathcal {OF}$
given by the commutator
![]() $[\tau _{1},\tau _{2}]=\tau _{1}\tau _{2} - \tau _{2}\tau _{1}$
. We will use this inclusion to define what it means to substitute elements of
$[\tau _{1},\tau _{2}]=\tau _{1}\tau _{2} - \tau _{2}\tau _{1}$
. We will use this inclusion to define what it means to substitute elements of
![]() $Lie(\mathcal {PT}{\kern2.5pt})$
into vertices of
$Lie(\mathcal {PT}{\kern2.5pt})$
into vertices of
![]() $\mathcal {OF}$
.
$\mathcal {OF}$
.
Let
![]() $\widehat {\mathcal {OF}}_{n}$
denote the vector space spanned by all ordered forests with exactly n vertices, together with a bijection between the set
$\widehat {\mathcal {OF}}_{n}$
denote the vector space spanned by all ordered forests with exactly n vertices, together with a bijection between the set
![]() $\{1,\dotsc ,n \}$
and the vertices of the forest. This bijection provides a labelling of the vertices. Let the symmetric group
$\{1,\dotsc ,n \}$
and the vertices of the forest. This bijection provides a labelling of the vertices. Let the symmetric group
![]() $\Sigma _{n}$
act on
$\Sigma _{n}$
act on
![]() $\widehat {\mathcal {OF}}_{n}$
by permuting the labels of the vertices. Write
$\widehat {\mathcal {OF}}_{n}$
by permuting the labels of the vertices. Write
![]() $[\omega ]$
for the orbit of
$[\omega ]$
for the orbit of
![]() $\omega $
under
$\omega $
under
![]() $\Sigma _{n}$
; we consider this as an unlabelled forest. Define the equivalence relation
$\Sigma _{n}$
; we consider this as an unlabelled forest. Define the equivalence relation
![]() $\omega _{1} \sim \omega _{2} \iff [\omega _{1}]=[\omega _{2}]$
on
$\omega _{1} \sim \omega _{2} \iff [\omega _{1}]=[\omega _{2}]$
on
![]() $\widehat {\mathcal {OF}}_{n}$
. Let
$\widehat {\mathcal {OF}}_{n}$
. Let
 $\widehat {\mathcal {OF}}=\sum _{n=1}^{\infty }\widehat {\mathcal {OF}}_{n}$
; then
$\widehat {\mathcal {OF}}=\sum _{n=1}^{\infty }\widehat {\mathcal {OF}}_{n}$
; then
![]() $\widehat {\mathcal {OF}}/\sim $
can be identified with
$\widehat {\mathcal {OF}}/\sim $
can be identified with
![]() $\mathcal {OF}$
. This identification is the bosonic Fock functor [Reference Aguiar and Mahajan1].
$\mathcal {OF}$
. This identification is the bosonic Fock functor [Reference Aguiar and Mahajan1].
We now define composition maps
 $\circ :\oplus _{n\geq 1} \widehat {Lie(\mathcal {PT}{\kern2.5pt})}^{\otimes n} \otimes \widehat {\mathcal {OF}}_{n} \to \widehat {\mathcal {OF}}$
. Set
$\circ :\oplus _{n\geq 1} \widehat {Lie(\mathcal {PT}{\kern2.5pt})}^{\otimes n} \otimes \widehat {\mathcal {OF}}_{n} \to \widehat {\mathcal {OF}}$
. Set
 $\omega _{1} \dotsm \omega _{n} \in \widehat {Lie(\mathcal {PT}{\kern2.5pt})}$
and
$\omega _{1} \dotsm \omega _{n} \in \widehat {Lie(\mathcal {PT}{\kern2.5pt})}$
and
![]() $\omega ^{\prime } \in \widehat {\mathcal {OF}}_{n}$
; then
$\omega ^{\prime } \in \widehat {\mathcal {OF}}_{n}$
; then
![]() $\omega ^{\prime }$
can be expressed in terms of the single-vertex tree, associative concatenation and the nonassociative D-algebra product
$\omega ^{\prime }$
can be expressed in terms of the single-vertex tree, associative concatenation and the nonassociative D-algebra product
![]() $\operatorname {\mathrm {\triangleright }}$
. Furthermore, all of
$\operatorname {\mathrm {\triangleright }}$
. Furthermore, all of
![]() $\omega _{1} \dotsm \omega _{n}$
can be expressed in the same way via the inclusion
$\omega _{1} \dotsm \omega _{n}$
can be expressed in the same way via the inclusion
 $\widehat {Lie(\mathcal {PT}{\kern2.5pt})} \subset \widehat {\mathcal {OF}}$
. By the composition
$\widehat {Lie(\mathcal {PT}{\kern2.5pt})} \subset \widehat {\mathcal {OF}}$
. By the composition
we will mean the expression obtained by replacing each occurence of vertex number i in the expression of
![]() $\omega ^{\prime }$
by the expression for
$\omega ^{\prime }$
by the expression for
![]() $\omega _{i}$
,
$\omega _{i}$
,
![]() $i=1,\dotsc ,n$
.
$i=1,\dotsc ,n$
.
Proposition 14. The composition turns
![]() $\widehat {\mathcal {OF}}$
into a (right) module over
$\widehat {\mathcal {OF}}$
into a (right) module over
 $\widehat {Lie(\mathcal {PT}{\kern2.5pt})}$
.
$\widehat {Lie(\mathcal {PT}{\kern2.5pt})}$
.
Proof. We first note that the composition is well defined, since expressing a forest
![]() $\omega ^{\prime }$
in terms of associative concatenation, the nonassociative product
$\omega ^{\prime }$
in terms of associative concatenation, the nonassociative product
![]() $\operatorname {\mathrm {\triangleright }}$
and the single-vertex tree is unique up to rewritings by the identities
$\operatorname {\mathrm {\triangleright }}$
and the single-vertex tree is unique up to rewritings by the identities
 $$ \begin{align*} \tau \operatorname{\mathrm{\triangleright}} (\omega_{1}\omega_{2})&=(\tau\operatorname{\mathrm{\triangleright}} \omega_{1})\omega_{2} + \omega_{1}(\tau \operatorname{\mathrm{\triangleright}} \omega_{2}), \\ \tau \operatorname{\mathrm{\triangleright}} (\omega_{1} \operatorname{\mathrm{\triangleright}} \omega_{2})&=(\tau \omega_{1})\operatorname{\mathrm{\triangleright}} \omega_{2} + (\tau \operatorname{\mathrm{\triangleright}} \omega_{1}) \operatorname{\mathrm{\triangleright}} \omega_{2} \end{align*} $$
$$ \begin{align*} \tau \operatorname{\mathrm{\triangleright}} (\omega_{1}\omega_{2})&=(\tau\operatorname{\mathrm{\triangleright}} \omega_{1})\omega_{2} + \omega_{1}(\tau \operatorname{\mathrm{\triangleright}} \omega_{2}), \\ \tau \operatorname{\mathrm{\triangleright}} (\omega_{1} \operatorname{\mathrm{\triangleright}} \omega_{2})&=(\tau \omega_{1})\operatorname{\mathrm{\triangleright}} \omega_{2} + (\tau \operatorname{\mathrm{\triangleright}} \omega_{1}) \operatorname{\mathrm{\triangleright}} \omega_{2} \end{align*} $$
for
![]() $\tau $
a derivation and
$\tau $
a derivation and
![]() $\omega _{1},\omega _{2}$
arbitrary. If
$\omega _{1},\omega _{2}$
arbitrary. If
![]() $\tau $
is a derivation, it is a Lie polynomial. Since Lie polynomials get mapped to Lie polynomials, these identities can be applied after substitution. Hence
$\tau $
is a derivation, it is a Lie polynomial. Since Lie polynomials get mapped to Lie polynomials, these identities can be applied after substitution. Hence
![]() $\circ $
commutes with rewriting and must be well defined.
$\circ $
commutes with rewriting and must be well defined.
Proving associativity and equivariance can be done in the same way as in Proposition 10.
Remark 11. Note that if we attempt to turn
![]() $\widehat {\mathcal {OF}}$
into an operad by replacing the single-vertex tree by an arbitrary forest, we are no longer mapping Lie polynomials to Lie polynomials. This means that computing
$\widehat {\mathcal {OF}}$
into an operad by replacing the single-vertex tree by an arbitrary forest, we are no longer mapping Lie polynomials to Lie polynomials. This means that computing
![]() $\omega _{1} \dotsm \omega _{n} \circ \omega ^{\prime }$
can give different results depending on how you choose to express
$\omega _{1} \dotsm \omega _{n} \circ \omega ^{\prime }$
can give different results depending on how you choose to express
![]() $\omega ^{\prime }$
.
$\omega ^{\prime }$
.
We get the following combinatorial picture.
Proposition 15. The expression
evaluates to the sum of all possible forests obtained by replacing vertex i in
![]() $\omega $
by the forest
$\omega $
by the forest
![]() $\omega _{i}$
, for all
$\omega _{i}$
, for all
![]() $i=1,\dotsc ,n$
. The incoming edge to vertex i becomes one incoming edge to each of the roots of
$i=1,\dotsc ,n$
. The incoming edge to vertex i becomes one incoming edge to each of the roots of
![]() $\omega _{i}$
. The edges outgoing from vertex i become leftmost outgoing from any vertex of
$\omega _{i}$
. The edges outgoing from vertex i become leftmost outgoing from any vertex of
![]() $\omega _{i}$
. The left-to-right ordering of edges outgoing from the same vertex i is preserved whenever the edges end up on the same vertex in
$\omega _{i}$
. The left-to-right ordering of edges outgoing from the same vertex i is preserved whenever the edges end up on the same vertex in
![]() $\omega _{i}$
.
$\omega _{i}$
.
Proof. Recall the definition of the nonassociative product in the free D-algebra;
![]() $\omega _{a} \operatorname {\mathrm {\triangleright }} \omega _{b}$
is the sum of all ways to add one edge incoming to each root of
$\omega _{a} \operatorname {\mathrm {\triangleright }} \omega _{b}$
is the sum of all ways to add one edge incoming to each root of
![]() $\omega _{a}$
that are outgoing in the leftmost position from any vertex of
$\omega _{a}$
that are outgoing in the leftmost position from any vertex of
![]() $\omega _{b}$
and such that if two trees from
$\omega _{b}$
and such that if two trees from
![]() $\omega _{a}$
are grafted on the same vertex of
$\omega _{a}$
are grafted on the same vertex of
![]() $\omega _{b}$
, their pairwise order in the planar embedding is preserved. Furthermore, note that there is an edge from vertex j to vertex i in
$\omega _{b}$
, their pairwise order in the planar embedding is preserved. Furthermore, note that there is an edge from vertex j to vertex i in
![]() $\omega $
if and only if vertex i is
$\omega $
if and only if vertex i is
![]() $\operatorname {\mathrm {\triangleright }}$
-grafted onto a subtree of
$\operatorname {\mathrm {\triangleright }}$
-grafted onto a subtree of
![]() $\omega $
that contains the vertex j. Hence when vertex i is replaced by
$\omega $
that contains the vertex j. Hence when vertex i is replaced by
![]() $\omega _{i}$
and vertex j is replaced by
$\omega _{i}$
and vertex j is replaced by
![]() $\omega _{j}$
, we get
$\omega _{j}$
, we get
![]() $\omega _{i}$
grafted onto
$\omega _{i}$
grafted onto
![]() $\omega _{j}$
by the product
$\omega _{j}$
by the product
![]() $\operatorname {\mathrm {\triangleright }}$
.
$\operatorname {\mathrm {\triangleright }}$
.
We are now ready to define the coaction. Let the coaction
![]() $\rho : \mathcal {H}_{N} \to \mathcal {Q} \otimes \mathcal {H}_{N}$
be defined by
$\rho : \mathcal {H}_{N} \to \mathcal {Q} \otimes \mathcal {H}_{N}$
be defined by
 $$ \begin{align*} \rho(\emptyset)&=1 \otimes \emptyset, \\ \rho([\omega])&=\sum_{\substack{[\omega] \text{ is a summand} \\ \text{in } \left[\omega_{1} \dotsm \omega_{n} \circ \omega^{\prime}\right]}}\frac{1}{n!} [\omega_{1}]\centerdot \dotsb \centerdot[\omega_{n}] \otimes [\omega^{\prime}] \end{align*} $$
$$ \begin{align*} \rho(\emptyset)&=1 \otimes \emptyset, \\ \rho([\omega])&=\sum_{\substack{[\omega] \text{ is a summand} \\ \text{in } \left[\omega_{1} \dotsm \omega_{n} \circ \omega^{\prime}\right]}}\frac{1}{n!} [\omega_{1}]\centerdot \dotsb \centerdot[\omega_{n}] \otimes [\omega^{\prime}] \end{align*} $$
for
![]() $\omega _{1},\dotsc ,\omega _{n}$
labelled Lie monomials and
$\omega _{1},\dotsc ,\omega _{n}$
labelled Lie monomials and
![]() $\omega ^{\prime }$
a labelled forest. We now want to give a few example computations of this coaction:
$\omega ^{\prime }$
a labelled forest. We now want to give a few example computations of this coaction:
Example 16.

Notation 1. We shall in the sequel write
![]() $\omega _{1} \dotsm \omega _{n} \circ \omega ^{\prime }$
also when the elements are unlabelled. In this case, we mean it as a sum over all ways to pair vertices in
$\omega _{1} \dotsm \omega _{n} \circ \omega ^{\prime }$
also when the elements are unlabelled. In this case, we mean it as a sum over all ways to pair vertices in
![]() $\omega ^{\prime }$
with input elements.
$\omega ^{\prime }$
with input elements.
Proposition 17. The coaction
![]() $\rho $
defines a cointeraction between
$\rho $
defines a cointeraction between
![]() $\mathcal {Q}$
and
$\mathcal {Q}$
and
![]() $\mathcal {H}_{N}$
.
$\mathcal {H}_{N}$
.
Proof. We first prove the identity
The identity is clear when
![]() $\omega = \emptyset $
. Suppose that
$\omega = \emptyset $
. Suppose that
![]() $\omega $
is a nonempty forest; then we have
$\omega $
is a nonempty forest; then we have
 $$ \begin{align*} (Id \otimes \Delta_{N})\rho(\omega)=\sum_{\substack{\omega \text{ is a summand} \\ \text{in } \omega_{1}\dotsm \omega_{n} \circ (\omega^{\prime} \diamond \omega^{\prime\prime})}} \omega_{1} \centerdot \dotsb \centerdot \omega_{n} \otimes \omega^{\prime} \otimes \omega^{\prime\prime}. \end{align*} $$
$$ \begin{align*} (Id \otimes \Delta_{N})\rho(\omega)=\sum_{\substack{\omega \text{ is a summand} \\ \text{in } \omega_{1}\dotsm \omega_{n} \circ (\omega^{\prime} \diamond \omega^{\prime\prime})}} \omega_{1} \centerdot \dotsb \centerdot \omega_{n} \otimes \omega^{\prime} \otimes \omega^{\prime\prime}. \end{align*} $$
Furthermore,
 $$ \begin{align*} &{m^{1,3}(\rho \otimes \rho)\Delta_{N}(\omega)}\\ &= m_{\centerdot}^{1,3}(\rho \otimes \rho) \sum_{\substack{\omega \text{ is a summand} \\ \text{in } \omega^{\prime} \diamond \omega^{\prime\prime}}} \omega^{\prime} \otimes \omega^{\prime\prime} \\ &= \sum_{\substack{\omega \text{ is a summand} \\ \text{in } \omega^{\prime} \diamond \omega^{\prime\prime}}} \sum_{\substack{\omega^{\prime} \text{ is a summand} \\ \text{in } \omega_{1}^{\prime} \cdots \omega_{k_{1}}^{\prime} \circ \bar{\omega}^{\prime}}}\sum_{\substack{\omega^{\prime\prime} \text{ is a summand} \\ \text{in } \omega_{1}^{\prime\prime} \cdots \omega_{k_{2}}^{\prime\prime} \circ \bar{\omega}^{\prime\prime}}} \omega_{1}^{\prime} \centerdot \dotsb \centerdot \omega_{k_{1}}^{\prime} \centerdot \omega_{1}^{\prime\prime} \centerdot \dotsb \centerdot \omega_{k_{2}}^{\prime\prime} \otimes \bar{\omega}^{\prime} \otimes \bar{\omega}^{\prime\prime} \\ &=\sum_{\substack{\omega \text{ is a summand} \\ \text{in } \left(\omega_{1}^{\prime} \dotsm \omega_{k_{1}}^{\prime} \circ \bar{\omega}^{\prime}\right) \diamond \left(\omega_{1}^{\prime\prime} \dotsm \omega_{k_{2}}^{\prime\prime} \circ \bar{\omega}^{\prime\prime}\right)}} \omega_{1}^{\prime} \centerdot \dotsb \centerdot \omega_{k_{1}}^{\prime} \centerdot \omega_{1}^{\prime\prime} \centerdot \dotsb \centerdot \omega_{k_{2}}^{\prime\prime} \otimes \bar{\omega}^{\prime} \otimes \bar{\omega}^{\prime} \\ &=\sum_{\substack{\omega \text{ is a summand} \\ \text{in } \omega_{1}\cdots \omega_{n} \circ (\omega^{\prime} \diamond \omega^{\prime\prime}) }} \omega_{1} \centerdot \dotsb \centerdot \omega_{n} \otimes \omega^{\prime} \otimes \omega^{\prime\prime}, \end{align*} $$
$$ \begin{align*} &{m^{1,3}(\rho \otimes \rho)\Delta_{N}(\omega)}\\ &= m_{\centerdot}^{1,3}(\rho \otimes \rho) \sum_{\substack{\omega \text{ is a summand} \\ \text{in } \omega^{\prime} \diamond \omega^{\prime\prime}}} \omega^{\prime} \otimes \omega^{\prime\prime} \\ &= \sum_{\substack{\omega \text{ is a summand} \\ \text{in } \omega^{\prime} \diamond \omega^{\prime\prime}}} \sum_{\substack{\omega^{\prime} \text{ is a summand} \\ \text{in } \omega_{1}^{\prime} \cdots \omega_{k_{1}}^{\prime} \circ \bar{\omega}^{\prime}}}\sum_{\substack{\omega^{\prime\prime} \text{ is a summand} \\ \text{in } \omega_{1}^{\prime\prime} \cdots \omega_{k_{2}}^{\prime\prime} \circ \bar{\omega}^{\prime\prime}}} \omega_{1}^{\prime} \centerdot \dotsb \centerdot \omega_{k_{1}}^{\prime} \centerdot \omega_{1}^{\prime\prime} \centerdot \dotsb \centerdot \omega_{k_{2}}^{\prime\prime} \otimes \bar{\omega}^{\prime} \otimes \bar{\omega}^{\prime\prime} \\ &=\sum_{\substack{\omega \text{ is a summand} \\ \text{in } \left(\omega_{1}^{\prime} \dotsm \omega_{k_{1}}^{\prime} \circ \bar{\omega}^{\prime}\right) \diamond \left(\omega_{1}^{\prime\prime} \dotsm \omega_{k_{2}}^{\prime\prime} \circ \bar{\omega}^{\prime\prime}\right)}} \omega_{1}^{\prime} \centerdot \dotsb \centerdot \omega_{k_{1}}^{\prime} \centerdot \omega_{1}^{\prime\prime} \centerdot \dotsb \centerdot \omega_{k_{2}}^{\prime\prime} \otimes \bar{\omega}^{\prime} \otimes \bar{\omega}^{\prime} \\ &=\sum_{\substack{\omega \text{ is a summand} \\ \text{in } \omega_{1}\cdots \omega_{n} \circ (\omega^{\prime} \diamond \omega^{\prime\prime}) }} \omega_{1} \centerdot \dotsb \centerdot \omega_{n} \otimes \omega^{\prime} \otimes \omega^{\prime\prime}, \end{align*} $$
which proves the identity.
Next we need to prove compatibility with the shuffle product – that is, the identity
Recall that using the natural identification
![]() $\langle \omega _{1},\omega _{2}\rangle =\delta _{\omega _{1},\omega _{2}}$
, we can write
$\langle \omega _{1},\omega _{2}\rangle =\delta _{\omega _{1},\omega _{2}}$
, we can write

We then have

where
![]() $\tau $
s are trees and we use the fact that the forests on the left-hand side of
$\tau $
s are trees and we use the fact that the forests on the left-hand side of
![]() $\rho $
are primitive to the coshuffle coproduct.
$\rho $
are primitive to the coshuffle coproduct.
The identity
is true by definition.
The identity
follows from the fact that both sides of the equation only evaluate to something nonzero on scalar multiples of the empty forest.
In conclusion, the bialgebras are in cointeraction.
Corollary 17.1. Let
![]() $S(Lie(\mathcal {PT}{\kern2.5pt}))^{\ast }$
and
$S(Lie(\mathcal {PT}{\kern2.5pt}))^{\ast }$
and
![]() $\mathcal {OF}^{\ast }$
denote the linear dual spaces of
$\mathcal {OF}^{\ast }$
denote the linear dual spaces of
![]() $S(Lie(\mathcal {PT}{\kern2.5pt}))$
and
$S(Lie(\mathcal {PT}{\kern2.5pt}))$
and
![]() $\mathcal {OF}$
, respectively. Define a map
$\mathcal {OF}$
, respectively. Define a map
![]() $\star : S(Lie(\mathcal {PT}{\kern2.5pt}))^{\ast } \otimes \mathcal {OF}^{\ast } \to \mathcal {OF}^{\ast }$
by
$\star : S(Lie(\mathcal {PT}{\kern2.5pt}))^{\ast } \otimes \mathcal {OF}^{\ast } \to \mathcal {OF}^{\ast }$
by
Now let
![]() $\alpha $
denote a character of
$\alpha $
denote a character of
![]() $\mathcal {Q}$
and let
$\mathcal {Q}$
and let
![]() $a,b \in \mathcal {OF}^{\ast }$
be arbitrary; then
$a,b \in \mathcal {OF}^{\ast }$
be arbitrary; then
where
![]() $\star _{N}$
is the convolution product in
$\star _{N}$
is the convolution product in
![]() $\mathcal {H}_{N}$
.
$\mathcal {H}_{N}$
.
Proof. We have
and
The statement now follows from Proposition 17 and the fact that
![]() $\alpha $
is a character with respect to the symmetric product on
$\alpha $
is a character with respect to the symmetric product on
![]() $\mathcal {Q}$
.
$\mathcal {Q}$
.
The following proposition states that the bialgebra
![]() $\mathcal {H}$
used for B-series substitution can be recovered from the bialgebra
$\mathcal {H}$
used for B-series substitution can be recovered from the bialgebra
![]() $\mathcal {Q}$
:
$\mathcal {Q}$
:
Proposition 18. Define a map
![]() $\pi : S(Lie(\mathcal {PT}{\kern2.5pt}))\to \mathcal {F}$
by
$\pi : S(Lie(\mathcal {PT}{\kern2.5pt}))\to \mathcal {F}$
by
![]() $\pi (\tau )$
being the unique nonplanar tree
$\pi (\tau )$
being the unique nonplanar tree
![]() $\tau ^{\prime }$
such that
$\tau ^{\prime }$
such that
![]() $\tau $
is a planar embedding of
$\tau $
is a planar embedding of
![]() $\tau ^{\prime }$
, whenever
$\tau ^{\prime }$
, whenever
![]() $\tau $
is a tree and extended by
$\tau $
is a tree and extended by
 $$ \begin{align*} \pi(1)&=\emptyset,\\ \pi([\tau_{1},\tau_{2}])&=0, \\ \pi(\tau_{1} \centerdot \tau_{2})&=\pi(\tau_{1})\pi(\tau_{2}). \end{align*} $$
$$ \begin{align*} \pi(1)&=\emptyset,\\ \pi([\tau_{1},\tau_{2}])&=0, \\ \pi(\tau_{1} \centerdot \tau_{2})&=\pi(\tau_{1})\pi(\tau_{2}). \end{align*} $$
Then
![]() $\pi : \mathcal {Q} \to \mathcal {H}$
is a surjective biagebra morphism. Hence
$\pi : \mathcal {Q} \to \mathcal {H}$
is a surjective biagebra morphism. Hence
![]() $\mathcal {Q}/\ker (\pi ) \simeq \mathcal {H}$
.
$\mathcal {Q}/\ker (\pi ) \simeq \mathcal {H}$
.
Proof. It is clear that
![]() $\pi $
is an algebra morphism by definition. It remains to show that
$\pi $
is an algebra morphism by definition. It remains to show that
![]() $\pi $
is a coalgebra morphism – that is, that
$\pi $
is a coalgebra morphism – that is, that
It is furthermore clear that both sides in this equation vanish on Lie brackets. Suppose that
![]() $\tau $
is a tree; then
$\tau $
is a tree; then
 $$ \begin{align*} (\pi \otimes \pi)\Delta_{\mathcal{Q}}(\tau)=\sum_{\substack{\tau \text{ is a summand} \\ \text{in } \tau_{1}\dotsm \tau_{n} \circ \tau^{\prime}}} \pi(\tau_{1})\dotsm\pi(\tau_{n}) \otimes \pi(\tau^{\prime}) \end{align*} $$
$$ \begin{align*} (\pi \otimes \pi)\Delta_{\mathcal{Q}}(\tau)=\sum_{\substack{\tau \text{ is a summand} \\ \text{in } \tau_{1}\dotsm \tau_{n} \circ \tau^{\prime}}} \pi(\tau_{1})\dotsm\pi(\tau_{n}) \otimes \pi(\tau^{\prime}) \end{align*} $$
and
 $$ \begin{align*} \Delta_{\mathcal{H}}(\pi(\tau))=\sum_{\substack{\pi(\tau) \text{ is a summand} \\ \text{in } \tau_{1} \dotsm \tau_{n} \circ \tau^{\prime}}} \tau_{1} \dotsm \tau_{n} \otimes \tau^{\prime}. \end{align*} $$
$$ \begin{align*} \Delta_{\mathcal{H}}(\pi(\tau))=\sum_{\substack{\pi(\tau) \text{ is a summand} \\ \text{in } \tau_{1} \dotsm \tau_{n} \circ \tau^{\prime}}} \tau_{1} \dotsm \tau_{n} \otimes \tau^{\prime}. \end{align*} $$
These have to be equal, since you get the expression of
![]() $\pi (\tau )$
in terms of the single-vertex tree and pre-Lie grafting from the expression of
$\pi (\tau )$
in terms of the single-vertex tree and pre-Lie grafting from the expression of
![]() $\tau $
in terms of the single-vertex tree and post-Lie grafting by replacing the post-Lie grafting product with the pre-Lie grafting product in the expression.
$\tau $
in terms of the single-vertex tree and post-Lie grafting by replacing the post-Lie grafting product with the pre-Lie grafting product in the expression.
6 Substitution in LB-series
Now consider the free D-algebra
![]() $\mathcal {OF}$
. It is graded by the number of vertices in a forest. Denote the completion of
$\mathcal {OF}$
. It is graded by the number of vertices in a forest. Denote the completion of
![]() $\mathcal {OF}$
, with respect to this grading, by
$\mathcal {OF}$
, with respect to this grading, by
![]() $\widetilde {\mathcal {OF}}$
. Denote its dual by
$\widetilde {\mathcal {OF}}$
. Denote its dual by
![]() $\mathcal {OF}^{\ast }$
; then there is a bijection
$\mathcal {OF}^{\ast }$
; then there is a bijection
![]() $\delta :\widetilde {\mathcal {OF}} \to \mathcal {OF}^{\ast }$
given by the dual basis. An LB-series can then be expressed as
$\delta :\widetilde {\mathcal {OF}} \to \mathcal {OF}^{\ast }$
given by the dual basis. An LB-series can then be expressed as
 $$ \begin{align*} LB(a,\alpha)=F_{a}\left(\delta^{-1}(\alpha)\right). \end{align*} $$
$$ \begin{align*} LB(a,\alpha)=F_{a}\left(\delta^{-1}(\alpha)\right). \end{align*} $$
We shall use this description in the sequel.
Lemma 19. Set
![]() $\alpha \in Lie(\mathcal {PT}{\kern2.5pt})^{\ast }$
. The map
$\alpha \in Lie(\mathcal {PT}{\kern2.5pt})^{\ast }$
. The map
![]() $B_{\alpha }:\mathcal {OF} \to \widetilde {\mathcal {OF}}$
given by
$B_{\alpha }:\mathcal {OF} \to \widetilde {\mathcal {OF}}$
given by
![]() $B_{\alpha }(\omega )=\delta ^{-1}(\alpha \star \delta (\omega ))$
is a D-algebra morphism.
$B_{\alpha }(\omega )=\delta ^{-1}(\alpha \star \delta (\omega ))$
is a D-algebra morphism.
Proof. Recall that
![]() $\Delta _{N}$
is dual to the planar Grossman–Larson product (1). Hence
$\Delta _{N}$
is dual to the planar Grossman–Larson product (1). Hence
Then we get
 $$ \begin{align*} B_{\alpha}(\omega_{1} \diamond \omega_{2})&=\delta^{-1}(\alpha \star \delta(\omega_{1} \diamond \omega_{2})) \\ &=\delta^{-1}(\alpha \star (\delta(\omega_{1}) \star_{N} \delta(\omega_{2}))) \\ &=\delta^{-1}( (\alpha \star \delta(\omega_{1})) \star_{N} (\alpha \star \delta(\omega_{2}) ) ) \\ &=\delta^{-1}(\alpha \star \delta(\omega_{1}) ) \diamond \delta^{-1}(\alpha \star \delta(\omega_{2})) \\ &=B_{\alpha}(\omega_{1}) \diamond B_{\alpha}(\omega_{2}). \end{align*} $$
$$ \begin{align*} B_{\alpha}(\omega_{1} \diamond \omega_{2})&=\delta^{-1}(\alpha \star \delta(\omega_{1} \diamond \omega_{2})) \\ &=\delta^{-1}(\alpha \star (\delta(\omega_{1}) \star_{N} \delta(\omega_{2}))) \\ &=\delta^{-1}( (\alpha \star \delta(\omega_{1})) \star_{N} (\alpha \star \delta(\omega_{2}) ) ) \\ &=\delta^{-1}(\alpha \star \delta(\omega_{1}) ) \diamond \delta^{-1}(\alpha \star \delta(\omega_{2})) \\ &=B_{\alpha}(\omega_{1}) \diamond B_{\alpha}(\omega_{2}). \end{align*} $$
Using Sweedler’s notation
![]() $\rho (\omega )=\omega _{(1)} \otimes \omega _{(2)}$
, we have that
$\rho (\omega )=\omega _{(1)} \otimes \omega _{(2)}$
, we have that
![]() $B_{\alpha }(\omega _{1} \omega _{2})$
is the sum over all forests
$B_{\alpha }(\omega _{1} \omega _{2})$
is the sum over all forests
![]() $\omega $
such that
$\omega $
such that
![]() $\omega _{(2)}$
contains
$\omega _{(2)}$
contains
![]() $\omega _{1}\omega _{2}$
, multiplied by the corresponding
$\omega _{1}\omega _{2}$
, multiplied by the corresponding
![]() $\alpha \left (\omega _{(1)}\right )$
. However,
$\alpha \left (\omega _{(1)}\right )$
. However,
![]() $\omega _{(1)}$
can be split into a part
$\omega _{(1)}$
can be split into a part
 $\omega ^{1}_{(1)}$
consisting of forests that got contracted into vertices in
$\omega ^{1}_{(1)}$
consisting of forests that got contracted into vertices in
![]() $\omega _{1}$
and a part
$\omega _{1}$
and a part
 $\omega ^{2}_{(1)}$
. Then
$\omega ^{2}_{(1)}$
. Then
 $\omega _{(1)}=\omega ^{1}_{(1)}\centerdot \omega ^{2}_{(2)}$
and
$\omega _{(1)}=\omega ^{1}_{(1)}\centerdot \omega ^{2}_{(2)}$
and
 $\alpha \left (\omega _{(1)}\right )=\alpha \left (\omega ^{1}_{(1)}\right )\alpha \left (\omega ^{2}_{(1)}\right )$
. Hence
$\alpha \left (\omega _{(1)}\right )=\alpha \left (\omega ^{1}_{(1)}\right )\alpha \left (\omega ^{2}_{(1)}\right )$
. Hence
This then implies
Lastly, we need to show that
![]() $B_{\alpha }$
maps derivations to derivations. This follows if we show that
$B_{\alpha }$
maps derivations to derivations. This follows if we show that
![]() $B_{\alpha }$
is a coshuffle morphism – that is, we have to show that
$B_{\alpha }$
is a coshuffle morphism – that is, we have to show that
Let
![]() $\tau $
be a tree; then
$\tau $
be a tree; then
 $$ \begin{align*} B_{\alpha}(\tau)&=B_{\alpha}(B^{-}(\tau) \operatorname{\mathrm{\triangleright}} \bullet) \\ &=B_{\alpha}(B^{-}(\tau)) \operatorname{\mathrm{\triangleright}} B_{\alpha}(\bullet) \\ &=B_{\alpha}(B^{-}(\tau))\operatorname{\mathrm{\triangleright}} \delta^{-1}(\alpha). \end{align*} $$
$$ \begin{align*} B_{\alpha}(\tau)&=B_{\alpha}(B^{-}(\tau) \operatorname{\mathrm{\triangleright}} \bullet) \\ &=B_{\alpha}(B^{-}(\tau)) \operatorname{\mathrm{\triangleright}} B_{\alpha}(\bullet) \\ &=B_{\alpha}(B^{-}(\tau))\operatorname{\mathrm{\triangleright}} \delta^{-1}(\alpha). \end{align*} $$
Recall from [Reference Ebrahimi-Fard, Lundervold and Munthe-Kaas19] the identity
Furthermore, recall that
![]() $\delta ^{-1}(\alpha )$
is a Lie polynomial. Hence
$\delta ^{-1}(\alpha )$
is a Lie polynomial. Hence

Now for an arbitrary forest, we get

Hence
![]() $B_{\alpha }$
is a coshuffle morphism and therefore maps derivations to derivations. In conclusion,
$B_{\alpha }$
is a coshuffle morphism and therefore maps derivations to derivations. In conclusion,
![]() $B_{\alpha }$
is a D-algebra morphism.
$B_{\alpha }$
is a D-algebra morphism.
Remark 12. Let
![]() $\alpha \in \mathcal {OF}^{\ast }$
be a logarithmic linear map; then it can be described by Lie polynomials in the dual basis – for example,
$\alpha \in \mathcal {OF}^{\ast }$
be a logarithmic linear map; then it can be described by Lie polynomials in the dual basis – for example,

is logarithmic. Then by the embedding
![]() $Lie(\mathcal {PT}{\kern2.5pt})\subset \mathcal {OF}$
, we can view
$Lie(\mathcal {PT}{\kern2.5pt})\subset \mathcal {OF}$
, we can view
![]() $\alpha $
as a linear map
$\alpha $
as a linear map
![]() $\hat {\alpha }\in Lie(\mathcal {PT}{\kern2.5pt})^{\ast }$
. For the example
$\hat {\alpha }\in Lie(\mathcal {PT}{\kern2.5pt})^{\ast }$
. For the example
![]() $\alpha $
in this remark, we would have
$\alpha $
in this remark, we would have

Theorem 20. Let
![]() $\alpha ,\beta $
be linear maps on
$\alpha ,\beta $
be linear maps on
![]() $\mathcal {OF}$
, with
$\mathcal {OF}$
, with
![]() $\alpha $
defining a logarithmic LB-series. Since
$\alpha $
defining a logarithmic LB-series. Since
![]() $\alpha $
is logarithmic, we can view it as a linear map
$\alpha $
is logarithmic, we can view it as a linear map
![]() $\hat {\alpha }\in Lie(\mathcal {PT}{\kern2.5pt})^{\ast }$
. Extend
$\hat {\alpha }\in Lie(\mathcal {PT}{\kern2.5pt})^{\ast }$
. Extend
![]() $\hat {\alpha }$
to be a character on
$\hat {\alpha }$
to be a character on
![]() $S(Lie(\mathcal {PT}{\kern2.5pt}))$
; then
$S(Lie(\mathcal {PT}{\kern2.5pt}))$
; then
Proof. Denote by
![]() $A_{\alpha }: \mathcal {OF} \to \mathcal {OF}^{\ast }$
the unique D-algebra morphism given by
$A_{\alpha }: \mathcal {OF} \to \mathcal {OF}^{\ast }$
the unique D-algebra morphism given by
![]() $A_{\alpha }(\bullet )=\delta ^{-1}(\alpha )$
. Extend
$A_{\alpha }(\bullet )=\delta ^{-1}(\alpha )$
. Extend
![]() $A_{\alpha }$
to be defined on
$A_{\alpha }$
to be defined on
![]() $\widetilde {\mathcal {OF}}$
. Then
$\widetilde {\mathcal {OF}}$
. Then
where
![]() $\circ $
means composition of functions, so that
$\circ $
means composition of functions, so that
 $$ \begin{align*} LB(LB(a,\alpha),\beta)=F_{a}\left(A_{\alpha}\left(\delta^{-1}(\beta)\right)\right). \end{align*} $$
$$ \begin{align*} LB(LB(a,\alpha),\beta)=F_{a}\left(A_{\alpha}\left(\delta^{-1}(\beta)\right)\right). \end{align*} $$
Furthermore,
 $$ \begin{align*} LB\left(a,\hat{\alpha} \star \beta\right)&=F_{a}\left(\delta^{-1}\left(\hat{\alpha} \star \beta\right)\right)\\ &=F_{a}\left(B_{\hat{\alpha}}\left(\delta^{-1}(\beta)\right)\right). \end{align*} $$
$$ \begin{align*} LB\left(a,\hat{\alpha} \star \beta\right)&=F_{a}\left(\delta^{-1}\left(\hat{\alpha} \star \beta\right)\right)\\ &=F_{a}\left(B_{\hat{\alpha}}\left(\delta^{-1}(\beta)\right)\right). \end{align*} $$
Now the theorem follows if
![]() $B_{\hat {\alpha }}=A_{\alpha }$
. However, it is clear that
$B_{\hat {\alpha }}=A_{\alpha }$
. However, it is clear that
![]() $B_{\hat {\alpha }}(\bullet )=A_{\alpha }(\bullet )$
. Then equality everywhere follows, as both maps are D-algebra morphisms.
$B_{\hat {\alpha }}(\bullet )=A_{\alpha }(\bullet )$
. Then equality everywhere follows, as both maps are D-algebra morphisms.
It is now worthwhile to relate the previous result with the recursive substitution formula from [Reference Lundervold and Munthe-Kaas26].
Remark 13. It is proved in [Reference Lundervold and Munthe-Kaas26] that
but no efficient method for evaluating
![]() $A_{\alpha }$
is given. Instead, the dual operator
$A_{\alpha }$
is given. Instead, the dual operator
![]() $A_{\alpha }^{\dagger }$
is defined by
$A_{\alpha }^{\dagger }$
is defined by
 $$ \begin{align*} \langle A_{\alpha}(\omega_{1}),\omega_{2} \rangle = \left\langle \omega_{1},A_{\alpha}^{\dagger}(\omega_{2}) \right\rangle. \end{align*} $$
$$ \begin{align*} \langle A_{\alpha}(\omega_{1}),\omega_{2} \rangle = \left\langle \omega_{1},A_{\alpha}^{\dagger}(\omega_{2}) \right\rangle. \end{align*} $$
Then a recursive formula for evaluating
![]() $A_{\alpha }^{\dagger }$
is shown. Now the observation that
$A_{\alpha }^{\dagger }$
is shown. Now the observation that
![]() $B_{\hat {\alpha }}=A_{\alpha }$
yields
$B_{\hat {\alpha }}=A_{\alpha }$
yields
 $$ \begin{align*} A_{\alpha}^{\dagger}(\omega)=\hat{\alpha}\left(\omega_{(1)}\right)\omega_{(2)}. \end{align*} $$
$$ \begin{align*} A_{\alpha}^{\dagger}(\omega)=\hat{\alpha}\left(\omega_{(1)}\right)\omega_{(2)}. \end{align*} $$
In particular, this means that the recursive formula given for
![]() $A_{\alpha }^{\dagger }$
can be used to evaluate
$A_{\alpha }^{\dagger }$
can be used to evaluate
![]() $\rho $
.
$\rho $
.
Proposition 21. Set
![]() $\hat {\alpha } \in Lie(\mathcal {PT}{\kern2.5pt})^{\ast }$
; then the map
$\hat {\alpha } \in Lie(\mathcal {PT}{\kern2.5pt})^{\ast }$
; then the map
![]() $\hat {\alpha } \star : \mathcal {OF}^{\ast } \to \mathcal {OF}^{\ast }$
is an endomorphism over the group of exponential linear maps.
$\hat {\alpha } \star : \mathcal {OF}^{\ast } \to \mathcal {OF}^{\ast }$
is an endomorphism over the group of exponential linear maps.
Proof. This follows from
![]() $B_{\hat {\alpha }}$
being a coshuffle morphism.
$B_{\hat {\alpha }}$
being a coshuffle morphism.
7 A coaction of ordered forest contractions
In this section we shall describe the combinatorial picture of the coaction
![]() $\rho $
.
$\rho $
.
Recall that the coaction
![]() $\rho $
is defined on ordered forests, as a sum over all the ways to obtain a forest
$\rho $
is defined on ordered forests, as a sum over all the ways to obtain a forest
![]() $\omega $
by inserting Lie polynomials
$\omega $
by inserting Lie polynomials
![]() $\omega _{1}, \dotsc , \omega _{n}$
into a forest
$\omega _{1}, \dotsc , \omega _{n}$
into a forest
![]() $\omega ^{\prime }$
. There is a bijection between vertices in
$\omega ^{\prime }$
. There is a bijection between vertices in
![]() $\omega $
and vertices in
$\omega $
and vertices in
![]() $\omega _{1}, \dotsc , \omega _{n}$
. We say that a partition of the vertices of a forest
$\omega _{1}, \dotsc , \omega _{n}$
. We say that a partition of the vertices of a forest
![]() $\omega $
into subforests
$\omega $
into subforests
![]() $\omega _{1}, \dotsc , \omega _{n}$
is an admissible partition if there exist a forest
$\omega _{1}, \dotsc , \omega _{n}$
is an admissible partition if there exist a forest
![]() $\omega ^{\prime }$
and a way to insert Lie brackets into each
$\omega ^{\prime }$
and a way to insert Lie brackets into each
![]() $\omega _{i}$
such that
$\omega _{i}$
such that
![]() $\omega $
is a summand in
$\omega $
is a summand in
![]() $\omega _{1} \dotsm \omega _{n} \circ \omega ^{\prime }$
. If
$\omega _{1} \dotsm \omega _{n} \circ \omega ^{\prime }$
. If
![]() $\omega _{1} \dotsm \omega _{n}$
is an admissible partition of
$\omega _{1} \dotsm \omega _{n}$
is an admissible partition of
![]() $\omega $
, we shall denote by
$\omega $
, we shall denote by
![]() $\omega /\omega _{1} \dotsm \omega _{n}$
the sum of all
$\omega /\omega _{1} \dotsm \omega _{n}$
the sum of all
![]() $\omega ^{\prime }$
such that
$\omega ^{\prime }$
such that
![]() $\omega $
is a summand in
$\omega $
is a summand in
![]() $\omega _{1} \dotsm \omega _{n} \circ \omega ^{\prime }$
. We illustrate this with an example.
$\omega _{1} \dotsm \omega _{n} \circ \omega ^{\prime }$
. We illustrate this with an example.
Example 22. The coaction
![]() $\rho $
maps the forest
$\rho $
maps the forest

to

corresponding to the following admissible partitions:

The right-hand side of the tensors is the corresponding
![]() $\omega ^{\prime }$
.
$\omega ^{\prime }$
.
Note that the purpose of the labelling of the vertices is to distinguish the different vertices in a partition. It does not relate to any operadic structure, as the coaction is defined over unlabelled forests.
Furthermore, note that the left-hand side of the tensors is in
![]() $S(Lie(\mathcal {PT}{\kern2.5pt}))$
, while the subforests in the admissible partitions are in
$S(Lie(\mathcal {PT}{\kern2.5pt}))$
, while the subforests in the admissible partitions are in
![]() $\mathcal {OF}$
.
$\mathcal {OF}$
.
We define a coaction
![]() $\Delta _{W}: \mathcal {OF} \to S\left ({{\mathcal{OF}}^{+}}\right ) \otimes \mathcal {OF}$
by
$\Delta _{W}: \mathcal {OF} \to S\left ({{\mathcal{OF}}^{+}}\right ) \otimes \mathcal {OF}$
by
 $$ \begin{align*} \Delta_{W}(\emptyset)&=1 \otimes \emptyset, \\ \Delta_{W}(\omega)&=\sum_{\omega_{1} \dotsm \omega_{n} \text{ admissible partition}} \omega_{1} \centerdot \dotsb \centerdot \omega_{n} \otimes \omega/\omega_{1}\dotsm \omega_{n}, \end{align*} $$
$$ \begin{align*} \Delta_{W}(\emptyset)&=1 \otimes \emptyset, \\ \Delta_{W}(\omega)&=\sum_{\omega_{1} \dotsm \omega_{n} \text{ admissible partition}} \omega_{1} \centerdot \dotsb \centerdot \omega_{n} \otimes \omega/\omega_{1}\dotsm \omega_{n}, \end{align*} $$
where
![]() $\left (S\left (\mathcal{OF}^{+}\right ),\centerdot \right )$
is the symmetric algebra of nonempty ordered forests. We can informally see this as the coaction obtained from
$\left (S\left (\mathcal{OF}^{+}\right ),\centerdot \right )$
is the symmetric algebra of nonempty ordered forests. We can informally see this as the coaction obtained from
![]() $\rho $
by ‘removing’ the Lie brackets, as shown by the following example:
$\rho $
by ‘removing’ the Lie brackets, as shown by the following example:
Example 23.

The reason we may want to consider
![]() $\Delta _{W}$
instead of
$\Delta _{W}$
instead of
![]() $\rho $
is that it eliminates the need to rewrite the logarithmic linear map
$\rho $
is that it eliminates the need to rewrite the logarithmic linear map
![]() $\alpha \in \mathcal {OF}^{\ast }$
into a map
$\alpha \in \mathcal {OF}^{\ast }$
into a map
![]() $\hat {\alpha }\in Lie(\mathcal {PT}{\kern2.5pt})^{\ast }$
, as shown in the following proposition:
$\hat {\alpha }\in Lie(\mathcal {PT}{\kern2.5pt})^{\ast }$
, as shown in the following proposition:
Proposition 24. Let
![]() $\alpha \in \mathcal {OF}^{\ast }$
be logarithmic and let
$\alpha \in \mathcal {OF}^{\ast }$
be logarithmic and let
![]() $\hat {\alpha }\in Lie(\mathcal {PT}{\kern2.5pt})^{\ast }$
be
$\hat {\alpha }\in Lie(\mathcal {PT}{\kern2.5pt})^{\ast }$
be
![]() $\alpha $
restricted to the Lie polynomials. Let
$\alpha $
restricted to the Lie polynomials. Let
![]() $\beta \in \mathcal {OF}^{\ast }$
be arbitrary. Define a map
$\beta \in \mathcal {OF}^{\ast }$
be arbitrary. Define a map
![]() $\star _{W} : S\left (\mathcal {OF}^{+}\right )^{\ast } \otimes \mathcal {OF}^{\ast } \to \mathcal {OF}^{\ast }$
by
$\star _{W} : S\left (\mathcal {OF}^{+}\right )^{\ast } \otimes \mathcal {OF}^{\ast } \to \mathcal {OF}^{\ast }$
by
Extend
![]() $\alpha ,\hat {\alpha }$
multiplicatively to
$\alpha ,\hat {\alpha }$
multiplicatively to
![]() $S\left (\mathcal {OF}^{+}\right )^{\ast }$
and
$S\left (\mathcal {OF}^{+}\right )^{\ast }$
and
![]() $S(Lie(\mathcal {PT}{\kern2.5pt}))^{\ast }$
, respectively; then
$S(Lie(\mathcal {PT}{\kern2.5pt}))^{\ast }$
, respectively; then
Proof. The coactions
![]() $\rho $
and
$\rho $
and
![]() $\Delta _{W}$
agree on every term where the left-hand side consists only of symmetric products of trees. The maps
$\Delta _{W}$
agree on every term where the left-hand side consists only of symmetric products of trees. The maps
![]() $\alpha $
and
$\alpha $
and
![]() $\hat {\alpha }$
agree on trees. Use the Jacobi identity and the antisymmetry of the Lie bracket to write all (nested) Lie brackets on the left-hand side of
$\hat {\alpha }$
agree on trees. Use the Jacobi identity and the antisymmetry of the Lie bracket to write all (nested) Lie brackets on the left-hand side of
![]() $\rho (\omega )$
in such a way that the left-to-right order of the trees in the Lie bracket agrees with the left-to-right order of the trees seen as subtrees in the planar embedding of
$\rho (\omega )$
in such a way that the left-to-right order of the trees in the Lie bracket agrees with the left-to-right order of the trees seen as subtrees in the planar embedding of
![]() $\omega $
. If the left-hand side of the coaction
$\omega $
. If the left-hand side of the coaction
![]() $\rho $
contains a term with a Lie bracket
$\rho $
contains a term with a Lie bracket
![]() $[\omega _{1},\omega _{2}]$
, then the corresponding term in
$[\omega _{1},\omega _{2}]$
, then the corresponding term in
![]() $\Delta _{W}$
contains instead a term
$\Delta _{W}$
contains instead a term
![]() $\omega _{1}\omega _{2}$
(iterate for nested brackets). If
$\omega _{1}\omega _{2}$
(iterate for nested brackets). If
![]() $\hat {\alpha }$
evaluates to
$\hat {\alpha }$
evaluates to
![]() $c\in \mathbb {K}$
on
$c\in \mathbb {K}$
on
![]() $[\omega _{1},\omega _{2}]$
, then
$[\omega _{1},\omega _{2}]$
, then
![]() $\alpha $
evaluates to c on
$\alpha $
evaluates to c on
![]() $\omega _{1}\omega _{2}$
and to
$\omega _{1}\omega _{2}$
and to
![]() $-c$
on
$-c$
on
![]() $\omega _{2}\omega _{1}$
. Every term in
$\omega _{2}\omega _{1}$
. Every term in
![]() $\rho $
and
$\rho $
and
![]() $\Delta _{W}$
agrees on the right side.
$\Delta _{W}$
agrees on the right side.
Corollary 24.1. Let
![]() $\alpha \in \mathcal {OF}^{\ast }$
be logarithmic. Extend
$\alpha \in \mathcal {OF}^{\ast }$
be logarithmic. Extend
![]() $\alpha $
multiplicatively to
$\alpha $
multiplicatively to
![]() $S\left (\mathcal {OF}^{+}\right )^{\ast }$
; then
$S\left (\mathcal {OF}^{+}\right )^{\ast }$
; then
Furthermore, the map
![]() $\alpha \star _{W} : \mathcal {OF}^{\ast } \to \mathcal {OF}^{\ast }$
is an endomorphism over the group of exponential linear maps.
$\alpha \star _{W} : \mathcal {OF}^{\ast } \to \mathcal {OF}^{\ast }$
is an endomorphism over the group of exponential linear maps.
We are now ready to formulate a combinatorial description of admissible partitions.
Proposition 25. Let
![]() $\omega $
be a forest and let
$\omega $
be a forest and let
![]() $\omega _{1} \dotsm \omega _{n}$
be a partition of the vertices of
$\omega _{1} \dotsm \omega _{n}$
be a partition of the vertices of
![]() $\omega $
into subforests. This partition is admissible if and only if the following conditions are met:
$\omega $
into subforests. This partition is admissible if and only if the following conditions are met:
-
1. Each root in the same
 $\omega _{i}$
are either roots of
$\omega _{i}$
are either roots of
 $\omega $
or grafted onto the same vertex of
$\omega $
or grafted onto the same vertex of
 $\omega $
. Furthermore, the roots of
$\omega $
. Furthermore, the roots of
 $\omega _{i}$
are adjacent in the planar embedding of
$\omega _{i}$
are adjacent in the planar embedding of
 $\omega $
.
$\omega $
. -
2. If e is an edge in an
 $\omega _{i}$
, then every edge
$\omega _{i}$
, then every edge
 $e^{\prime }$
in
$e^{\prime }$
in
 $\omega $
that is outgoing from the same vertex as e and is to the right of e in the planar embedding is also in
$\omega $
that is outgoing from the same vertex as e and is to the right of e in the planar embedding is also in
 $\omega _{i}$
.
$\omega _{i}$
.
Proof. First suppose that the partition is admissible. Then there exist some forest
![]() $\omega ^{\prime }$
and some way to insert Lie brackets into each
$\omega ^{\prime }$
and some way to insert Lie brackets into each
![]() $\omega _{i}$
such that
$\omega _{i}$
such that
![]() $\omega $
is a summand in
$\omega $
is a summand in
![]() $\omega _{1} \dotsm \omega _{n} \circ \omega ^{\prime }$
. If a vertex i is grafted on a vertex j in
$\omega _{1} \dotsm \omega _{n} \circ \omega ^{\prime }$
. If a vertex i is grafted on a vertex j in
![]() $\omega ^{\prime }$
, then this amounts to a Lie polynomial
$\omega ^{\prime }$
, then this amounts to a Lie polynomial
![]() $\omega _{i}$
being grafted onto a Lie polynomial
$\omega _{i}$
being grafted onto a Lie polynomial
![]() $\omega _{j}$
in
$\omega _{j}$
in
![]() $\omega _{1} \dotsm \omega _{n} \circ \omega ^{\prime }$
. However, since
$\omega _{1} \dotsm \omega _{n} \circ \omega ^{\prime }$
. However, since
![]() $\omega _{i}$
is a Lie polynomial, the terms where different roots of
$\omega _{i}$
is a Lie polynomial, the terms where different roots of
![]() $\omega _{i}$
go onto different vertices of
$\omega _{i}$
go onto different vertices of
![]() $\omega _{j}$
will cancel. Hence condition
$\omega _{j}$
will cancel. Hence condition
![]() $1$
is satisfied. Furthermore, the edges going from vertices in
$1$
is satisfied. Furthermore, the edges going from vertices in
![]() $\omega _{j}$
to vertices in
$\omega _{j}$
to vertices in
![]() $\omega _{i}$
must be to the left of edges going between vertices in
$\omega _{i}$
must be to the left of edges going between vertices in
![]() $\omega _{j}$
, since all grafting is done in the leftmost position. Hence condition
$\omega _{j}$
, since all grafting is done in the leftmost position. Hence condition
![]() $2$
is satisfied.
$2$
is satisfied.
Now suppose that
![]() $\omega _{1}\dotsm \omega _{n}$
is a partition that satisfies conditions
$\omega _{1}\dotsm \omega _{n}$
is a partition that satisfies conditions
![]() $1$
and
$1$
and
![]() $2$
. Let
$2$
. Let
![]() $\omega ^{\prime }$
denote the forest on n vertices obtained by adding an edge from vertex i to vertex j if there is an edge from
$\omega ^{\prime }$
denote the forest on n vertices obtained by adding an edge from vertex i to vertex j if there is an edge from
![]() $\omega _{i}$
to
$\omega _{i}$
to
![]() $\omega _{j}$
in
$\omega _{j}$
in
![]() $\omega $
. Condition
$\omega $
. Condition
![]() $1$
ensures that this is unambiguous. Now endow
$1$
ensures that this is unambiguous. Now endow
![]() $\omega ^{\prime }$
with a planar embedding such that vertex i is to the left of vertex j if
$\omega ^{\prime }$
with a planar embedding such that vertex i is to the left of vertex j if
![]() $\omega _{i}$
is to the left of
$\omega _{i}$
is to the left of
![]() $\omega _{j}$
in
$\omega _{j}$
in
![]() $\omega $
. The choice of planar embedding is not unique. Now turn each
$\omega $
. The choice of planar embedding is not unique. Now turn each
![]() $\omega _{i}$
into a Lie polynomial by insertion of Lie brackets and consider
$\omega _{i}$
into a Lie polynomial by insertion of Lie brackets and consider
![]() $\omega _{1} \dotsm \omega _{n} \circ \omega ^{\prime }$
. This results in a sum over all ways to graft
$\omega _{1} \dotsm \omega _{n} \circ \omega ^{\prime }$
. This results in a sum over all ways to graft
![]() $\omega _{i}$
onto
$\omega _{i}$
onto
![]() $\omega _{j}$
if there was an edge from
$\omega _{j}$
if there was an edge from
![]() $\omega _{i}$
to
$\omega _{i}$
to
![]() $\omega _{j}$
in
$\omega _{j}$
in
![]() $\omega $
. Because of condition
$\omega $
. Because of condition
![]() $2$
, the original placements of the edges from
$2$
, the original placements of the edges from
![]() $\omega $
will appear in this sum.
$\omega $
will appear in this sum.
Proposition 26. Let
![]() $\omega $
be a forest and let
$\omega $
be a forest and let
![]() $\omega _{1} \dotsm \omega _{n}$
be an admissible partition. Let
$\omega _{1} \dotsm \omega _{n}$
be an admissible partition. Let
![]() $\omega ^{\prime }$
denote the forest on n vertices obtained by adding an edge from vertex i to vertex j if there is an edge from
$\omega ^{\prime }$
denote the forest on n vertices obtained by adding an edge from vertex i to vertex j if there is an edge from
![]() $\omega _{i}$
to
$\omega _{i}$
to
![]() $\omega _{j}$
in
$\omega _{j}$
in
![]() $\omega $
. Then
$\omega $
. Then
![]() $\omega /\omega _{1}\dotsm \omega _{n}$
is the sum over all ways to endow the forest
$\omega /\omega _{1}\dotsm \omega _{n}$
is the sum over all ways to endow the forest
![]() $\omega ^{\prime }$
with a planar embedding such that vertex i is to the left of vertex j if
$\omega ^{\prime }$
with a planar embedding such that vertex i is to the left of vertex j if
![]() $\omega _{i}$
is to the left of
$\omega _{i}$
is to the left of
![]() $\omega _{j}$
.
$\omega _{j}$
.
Proof. It was shown in the proof of Proposition 25 that each such embedding is a summand in
![]() $\omega /\omega _{1} \dotsm \omega _{n}$
. Now suppose there exists an
$\omega /\omega _{1} \dotsm \omega _{n}$
. Now suppose there exists an
![]() $\omega ^{\prime \prime }$
such that
$\omega ^{\prime \prime }$
such that
![]() $\omega $
is a summand in
$\omega $
is a summand in
![]() $\omega _{1} \dotsm \omega _{n} \circ \omega ^{\prime \prime }$
but
$\omega _{1} \dotsm \omega _{n} \circ \omega ^{\prime \prime }$
but
![]() $\omega ^{\prime \prime }$
is not such a planar embedding of
$\omega ^{\prime \prime }$
is not such a planar embedding of
![]() $\omega ^{\prime }$
. If
$\omega ^{\prime }$
. If
![]() $\omega ^{\prime \prime }$
is a planar embedding of
$\omega ^{\prime \prime }$
is a planar embedding of
![]() $\omega ^{\prime }$
with vertex i to the right of vertex j but
$\omega ^{\prime }$
with vertex i to the right of vertex j but
![]() $\omega _{i}$
is to the left of
$\omega _{i}$
is to the left of
![]() $\omega _{j}$
, then it is clear that
$\omega _{j}$
, then it is clear that
![]() $\omega _{1} \dotsm \omega _{n} \circ \omega ^{\prime \prime }$
cannot produce the planar embedding of
$\omega _{1} \dotsm \omega _{n} \circ \omega ^{\prime \prime }$
cannot produce the planar embedding of
![]() $\omega $
. If
$\omega $
. If
![]() $\omega ^{\prime \prime }$
does not have an edge from vertex i to vertx j but
$\omega ^{\prime \prime }$
does not have an edge from vertex i to vertx j but
![]() $\omega $
has an edge from
$\omega $
has an edge from
![]() $\omega _{i}$
to
$\omega _{i}$
to
![]() $\omega _{j}$
, then it is also clear that
$\omega _{j}$
, then it is also clear that
![]() $\omega _{1} \dotsm \omega _{n} \circ \omega ^{\prime \prime }$
cannot produce
$\omega _{1} \dotsm \omega _{n} \circ \omega ^{\prime \prime }$
cannot produce
![]() $\omega $
.
$\omega $
.
Proposition 27. Extend
![]() $\Delta _{W}$
to be defined on symmetric products of forests,
$\Delta _{W}$
to be defined on symmetric products of forests,
![]() $\Delta _{W}: S\left ({\mathcal {OF}^{+}}\right ) \to S\left ({\mathcal {OF}^{+}}\right ) \otimes S\left ({\mathcal {OF}^{+}}\right )$
, by
$\Delta _{W}: S\left ({\mathcal {OF}^{+}}\right ) \to S\left ({\mathcal {OF}^{+}}\right ) \otimes S\left ({\mathcal {OF}^{+}}\right )$
, by
Then
![]() $\left (S\left (\mathcal {OF}^{+}\right ),\Delta _{W},\epsilon \right )$
is a coalgebra.
$\left (S\left (\mathcal {OF}^{+}\right ),\Delta _{W},\epsilon \right )$
is a coalgebra.
Proof. The only nontrivial thing to show is
This, however, follows from the fact that if
![]() $\omega _{1}, \dotsc , \omega _{n}$
is an admissible partition of
$\omega _{1}, \dotsc , \omega _{n}$
is an admissible partition of
![]() $\omega $
and
$\omega $
and
 $\omega _{i}^{1},\dotsc , \omega _{i}^{n_{i}}$
is an admissible partition of
$\omega _{i}^{1},\dotsc , \omega _{i}^{n_{i}}$
is an admissible partition of
![]() $\omega _{i}$
, for
$\omega _{i}$
, for
![]() $i=1,\dotsc ,n$
, then
$i=1,\dotsc ,n$
, then
 $\omega _{1}^{1},\dotsc ,\omega _{1}^{n_{1}},\omega _{2}^{2},\dotsc ,\omega _{n}^{n_{n}}$
is an admissible partition of
$\omega _{1}^{1},\dotsc ,\omega _{1}^{n_{1}},\omega _{2}^{2},\dotsc ,\omega _{n}^{n_{n}}$
is an admissible partition of
![]() $\omega $
.
$\omega $
.
Acknowledgements
The author is supported by the Research Council of Norway through project 302831 ‘Computational Dynamics and Stochastics on Manifolds’ (CODYSMA). This work was partially supported by the project Pure Mathematics in Norway, funded by the Trond Mohn Foundation and Tromsø Research Foundation.
The author thanks Kurusch Ebrahimi-Fard and Hans Munthe-Kaas for the helpful discussions. He furthermore thanks Dominique Manchon for reading the paper and for his suggestions.
Conflicts of Interest
None.