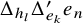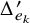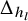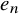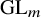1 Introduction
We prove the extended delta conjecture of Haglund, Remmel and Wilson [Reference Haglund, Remmel and Wilson14] by adapting methods from our work in [Reference Blasiak, Haiman, Morse, Pun and Seelinger2] on a generalized shuffle theorem and proving new results about the action of the elliptic Hall algebra on symmetric functions. As in [Reference Blasiak, Haiman, Morse, Pun and Seelinger2], we reformulate the conjecture as the polynomial truncation of an identity of infinite series of
![]() $\operatorname {\mathrm {GL}}_m$
characters, expressed in terms of LLT series. We then prove the stronger infinite series identity using a Cauchy identity for nonsymmetric Hall–Littlewood polynomials.
$\operatorname {\mathrm {GL}}_m$
characters, expressed in terms of LLT series. We then prove the stronger infinite series identity using a Cauchy identity for nonsymmetric Hall–Littlewood polynomials.
The conjecture stemmed from studies of the diagonal coinvariant algebra
![]() $\mathrm {DR}_n$
in two sets of n variables, whose character as a doubly graded
$\mathrm {DR}_n$
in two sets of n variables, whose character as a doubly graded
![]() $S_{n}$
module has remarkable links with both classical combinatorial enumeration and the theory of Macdonald polynomials. It was shown in [Reference Haiman17] that this character is neatly given by the formula
$S_{n}$
module has remarkable links with both classical combinatorial enumeration and the theory of Macdonald polynomials. It was shown in [Reference Haiman17] that this character is neatly given by the formula
![]() $\Delta ^{\prime }_{e_{n-1}} e_n$
, where
$\Delta ^{\prime }_{e_{n-1}} e_n$
, where
![]() $e_{n}$
is the n-th elementary symmetric function, and for any symmetric function f,
$e_{n}$
is the n-th elementary symmetric function, and for any symmetric function f,
![]() $\Delta ^{\prime }_{f}$
is a certain eigenoperator on Macdonald polynomials whose eigenvalues depend on f.
$\Delta ^{\prime }_{f}$
is a certain eigenoperator on Macdonald polynomials whose eigenvalues depend on f.
The shuffle theorem, conjectured in [Reference Haglund, Haiman, Loehr, Remmel and Ulyanov13] and proven by Carlsson and Mellit in [Reference Carlsson and Mellit4], gives a combinatorial expression for
![]() $\Delta ^{\prime }_{e_{n-1}}e_n$
in terms of Dyck paths—that is, lattice paths from
$\Delta ^{\prime }_{e_{n-1}}e_n$
in terms of Dyck paths—that is, lattice paths from
![]() $(0,n)$
to
$(0,n)$
to
![]() $(n,0)$
that lie weakly below the line segment connecting these two points.
$(n,0)$
that lie weakly below the line segment connecting these two points.
An expanded investigation led Haglund, Remmel and Wilson [Reference Haglund, Remmel and Wilson14] to the delta conjecture, a combinatorial prediction for
![]() $\Delta ^{\prime }_{e_{k}}e_n$
, for all
$\Delta ^{\prime }_{e_{k}}e_n$
, for all
![]() $0\leq k<n$
. This led to a flurry of activity (e.g., [Reference D’Adderio, Iraci and Vanden Wyngaerd6, Reference Garsia, Haglund, Remmel and Yoo11, Reference Haglund, Remmel and Wilson14, Reference Haglund, Rhoades and Shimozono15, Reference Haglund, Rhoades and Shimozono16, Reference Qiu and Wilson21, Reference Rhoades22, Reference Romero23, Reference Wilson26, Reference Zabrocki28]), including a conjecture by Zabrocki [Reference Zabrocki27] that
$0\leq k<n$
. This led to a flurry of activity (e.g., [Reference D’Adderio, Iraci and Vanden Wyngaerd6, Reference Garsia, Haglund, Remmel and Yoo11, Reference Haglund, Remmel and Wilson14, Reference Haglund, Rhoades and Shimozono15, Reference Haglund, Rhoades and Shimozono16, Reference Qiu and Wilson21, Reference Rhoades22, Reference Romero23, Reference Wilson26, Reference Zabrocki28]), including a conjecture by Zabrocki [Reference Zabrocki27] that
![]() $\Delta ^{\prime }_{e_{k}}e_n$
captures the character of the superdiagonal coinvariant ring
$\Delta ^{\prime }_{e_{k}}e_n$
captures the character of the superdiagonal coinvariant ring
![]() $\mathrm {SDR}_n$
, a deformation of
$\mathrm {SDR}_n$
, a deformation of
![]() $\mathrm {DR}_n$
involving the addition of a set of anticommuting variables.
$\mathrm {DR}_n$
involving the addition of a set of anticommuting variables.
The delta conjecture has been extended in two directions. One gives a compositional generalization, recently proved by D’Adderio and Mellit [Reference D’Adderio and Mellit7]. The other involves a second eigenoperator
![]() $\Delta _{h_l}$
, where
$\Delta _{h_l}$
, where
![]() $h_l$
is the l-th homogeneous symmetric function. The extended delta conjecture [Reference Haglund, Remmel and Wilson14, Conjecture 7.4] is, for
$h_l$
is the l-th homogeneous symmetric function. The extended delta conjecture [Reference Haglund, Remmel and Wilson14, Conjecture 7.4] is, for
![]() $l\geq 0$
and
$l\geq 0$
and
![]() $1\leq k\leq n$
,
$1\leq k\leq n$
,
 $$ \begin{align} \Delta_{h_l}\Delta^{\prime}_{e_{k-1}} e_n = \langle z^{n-k}\rangle \sum_{\substack{\lambda \in \mathbf {D}_{n+l}\\P\in{\mathbf {L}}_{n+l,l}(\lambda)}} q^{\operatorname{\mathrm{dinv}}(P)}t^{\operatorname{\mathrm{area}}(\lambda)} x^{\operatorname{\mathrm{wt}}_+(P)} \prod_{i\colon r_{i}(\lambda)=r_{i-1}(\lambda)+1} \left(1+ z\, t^{-r_i(\lambda)}\right), \end{align} $$
$$ \begin{align} \Delta_{h_l}\Delta^{\prime}_{e_{k-1}} e_n = \langle z^{n-k}\rangle \sum_{\substack{\lambda \in \mathbf {D}_{n+l}\\P\in{\mathbf {L}}_{n+l,l}(\lambda)}} q^{\operatorname{\mathrm{dinv}}(P)}t^{\operatorname{\mathrm{area}}(\lambda)} x^{\operatorname{\mathrm{wt}}_+(P)} \prod_{i\colon r_{i}(\lambda)=r_{i-1}(\lambda)+1} \left(1+ z\, t^{-r_i(\lambda)}\right), \end{align} $$
in which
![]() $\lambda $
is a Dyck path and P is a certain type of labelling of
$\lambda $
is a Dyck path and P is a certain type of labelling of
![]() $\lambda $
(see § 2 for full definitions). D’Adderio, Iraci and Wyngaerd proved the Schröder case and the
$\lambda $
(see § 2 for full definitions). D’Adderio, Iraci and Wyngaerd proved the Schröder case and the
![]() $t = 0$
specialization of the conjecture [Reference D’Adderio, Iraci and Vanden Wyngaerd5, Reference D’Adderio, Iraci and Vanden Wyngaerd6]; Qiu and Wilson [Reference Qiu and Wilson21] reformulated the conjecture and established the
$t = 0$
specialization of the conjecture [Reference D’Adderio, Iraci and Vanden Wyngaerd5, Reference D’Adderio, Iraci and Vanden Wyngaerd6]; Qiu and Wilson [Reference Qiu and Wilson21] reformulated the conjecture and established the
![]() $q=0$
specialization as well.
$q=0$
specialization as well.
Let us briefly outline the steps by which we prove equation (1).
Feigin–Tsymbaliuk [Reference Feigin and Tsymbaliuk8] and Schiffmann–Vasserot [Reference Schiffmann and Vasserot25] constructed an action of the elliptic Hall algebra
![]() ${\mathcal E} $
of Burban and Schiffmann [Reference Burban and Schiffmann3] on the algebra of symmetric functions. The operators
${\mathcal E} $
of Burban and Schiffmann [Reference Burban and Schiffmann3] on the algebra of symmetric functions. The operators
![]() $\Delta _{f}$
and
$\Delta _{f}$
and
![]() $\Delta ^{\prime }_{f}$
are part of the
$\Delta ^{\prime }_{f}$
are part of the
![]() ${\mathcal E}$
action. In Theorem 4.4.1, we use this to reformulate the left-hand side of equation (1) as the polynomial part of an explicit infinite series of virtual
${\mathcal E}$
action. In Theorem 4.4.1, we use this to reformulate the left-hand side of equation (1) as the polynomial part of an explicit infinite series of virtual
![]() $\operatorname {\mathrm {GL}}_{m}$
characters with coefficients in
$\operatorname {\mathrm {GL}}_{m}$
characters with coefficients in
![]() ${\mathbb Q} (q,t)$
. The proof of Theorem 4.4.1 relies on a symmetry (Proposition 4.3.3) between distinguished elements of
${\mathbb Q} (q,t)$
. The proof of Theorem 4.4.1 relies on a symmetry (Proposition 4.3.3) between distinguished elements of
![]() ${\mathcal E} $
introduced by Negut [Reference Negut19] and their transposes.
${\mathcal E} $
introduced by Negut [Reference Negut19] and their transposes.
In Theorem 5.1.1, we also reformulate the right-hand side of equation (1) as the polynomial part of an infinite series, in this case expressed in terms of the LLT series introduced by Grojnowski and Haiman in [Reference Grojnowski and Haiman12]. This given, we ultimately arrive at Theorem 6.3.6—an identity of infinite series of
![]() $\operatorname {\mathrm {GL}}_m$
characters which implies the extended delta conjecture by taking the polynomial part on each side.
$\operatorname {\mathrm {GL}}_m$
characters which implies the extended delta conjecture by taking the polynomial part on each side.
Although the extended delta conjecture and the compositional delta conjecture both imply the delta conjecture, they generalize it in different directions, and our methods are quite different from those of D’Adderio and Mellit. It would be interesting to know whether a common generalization is possible.
2 The extended delta conjecture
The extended delta conjecture equates a ‘symmetric function side,’ involving the action of a Macdonald operator on an elementary symmetric function, with a ‘combinatorial side.’ We begin by recalling the definitions of these two quantities.
2.1 Symmetric function side
Integer partitions are written
![]() $\lambda = (\lambda _{1}\geq \cdots \geq \lambda _{l})$
, sometimes with trailing zeroes allowed. We set
$\lambda = (\lambda _{1}\geq \cdots \geq \lambda _{l})$
, sometimes with trailing zeroes allowed. We set
![]() $|\lambda | = \lambda _{1}+\cdots +\lambda _{l}$
and let
$|\lambda | = \lambda _{1}+\cdots +\lambda _{l}$
and let
![]() $\ell (\lambda )$
be the number of nonzero parts. We identify a partition
$\ell (\lambda )$
be the number of nonzero parts. We identify a partition
![]() $\lambda $
with its French style Ferrers shape, the set of lattice squares (or boxes) with northeast corner in the set
$\lambda $
with its French style Ferrers shape, the set of lattice squares (or boxes) with northeast corner in the set
The shape generator of
![]() $\lambda $
is the polynomial
$\lambda $
is the polynomial
 $$ \begin{align} B_{\lambda }(q,t) = \sum _{(i,j)\in \lambda} q^{i-1}\, t^{j-1}. \end{align} $$
$$ \begin{align} B_{\lambda }(q,t) = \sum _{(i,j)\in \lambda} q^{i-1}\, t^{j-1}. \end{align} $$
Let
![]() $\Lambda = \Lambda _{{\mathbf k} }(X)$
be the algebra of symmetric functions in an infinite alphabet of variables
$\Lambda = \Lambda _{{\mathbf k} }(X)$
be the algebra of symmetric functions in an infinite alphabet of variables
![]() $X = x_{1},x_{2},\ldots $
, with coefficients in the field
$X = x_{1},x_{2},\ldots $
, with coefficients in the field
![]() ${\mathbf k} = {\mathbb Q} (q,t)$
. We follow the notation of Macdonald [Reference Macdonald18] for the graded bases of
${\mathbf k} = {\mathbb Q} (q,t)$
. We follow the notation of Macdonald [Reference Macdonald18] for the graded bases of
![]() $\Lambda $
. Basis elements are indexed by a partition
$\Lambda $
. Basis elements are indexed by a partition
![]() $\lambda $
and have homogeneous degree
$\lambda $
and have homogeneous degree
![]() $|\lambda |$
. Examples include the elementary symmetric functions
$|\lambda |$
. Examples include the elementary symmetric functions
![]() $e_{\lambda } = e_{\lambda _{1}}\cdots e_{\lambda _{k}}$
, complete homogeneous symmetric functions
$e_{\lambda } = e_{\lambda _{1}}\cdots e_{\lambda _{k}}$
, complete homogeneous symmetric functions
![]() $h_{\lambda } = h_{\lambda _{1}}\cdots h_{\lambda _{k}}$
, power-sums
$h_{\lambda } = h_{\lambda _{1}}\cdots h_{\lambda _{k}}$
, power-sums
![]() $p_{\lambda } = p_{\lambda _{1}}\cdots p_{\lambda _{k}}$
, monomial symmetric functions
$p_{\lambda } = p_{\lambda _{1}}\cdots p_{\lambda _{k}}$
, monomial symmetric functions
![]() $m_{\lambda }$
and Schur functions
$m_{\lambda }$
and Schur functions
![]() $s_{\lambda }$
.
$s_{\lambda }$
.
As is conventional,
![]() $\omega \colon \Lambda \rightarrow \Lambda $
denotes the
$\omega \colon \Lambda \rightarrow \Lambda $
denotes the
![]() ${\mathbf k} $
-algebra involution defined by
${\mathbf k} $
-algebra involution defined by
![]() $ \omega s_{\lambda } = s_{\lambda ^*}$
, where
$ \omega s_{\lambda } = s_{\lambda ^*}$
, where
![]() $\lambda ^{*}$
denotes the transpose of
$\lambda ^{*}$
denotes the transpose of
![]() $\lambda $
, and
$\lambda $
, and
![]() $\langle -, - \rangle $
denotes the symmetric bilinear inner product such that
$\langle -, - \rangle $
denotes the symmetric bilinear inner product such that
![]() $\langle s_{\lambda },s_{\mu } \rangle = \delta _{\lambda ,\mu }$
.
$\langle s_{\lambda },s_{\mu } \rangle = \delta _{\lambda ,\mu }$
.
The basis of modified Macdonald polynomials,
![]() $\tilde {H}_{\mu }(X;q,t)$
, is defined [Reference Garsia and Haiman9] from the integral form Macdonald polynomials
$\tilde {H}_{\mu }(X;q,t)$
, is defined [Reference Garsia and Haiman9] from the integral form Macdonald polynomials
![]() $J_{\mu }(X;q,t)$
of [Reference Macdonald18] using the device of plethystic evaluation. For an expression A in terms of indeterminates, such as a polynomial, rational function or formal series,
$J_{\mu }(X;q,t)$
of [Reference Macdonald18] using the device of plethystic evaluation. For an expression A in terms of indeterminates, such as a polynomial, rational function or formal series,
![]() $p_{k}[A]$
is defined to be the result of substituting
$p_{k}[A]$
is defined to be the result of substituting
![]() $a^{k}$
for every indeterminate a occurring in A. We define
$a^{k}$
for every indeterminate a occurring in A. We define
![]() $f[A]$
for any
$f[A]$
for any
![]() $f\in \Lambda $
by substituting
$f\in \Lambda $
by substituting
![]() $p_{k}[A]$
for
$p_{k}[A]$
for
![]() $p_{k}$
in the expression for f as a polynomial in the power-sums
$p_{k}$
in the expression for f as a polynomial in the power-sums
![]() $p_{k}$
so that
$p_{k}$
so that
![]() $f\mapsto f[A]$
is a homomorphism. The variables
$f\mapsto f[A]$
is a homomorphism. The variables
![]() $q, t$
from our ground field
$q, t$
from our ground field
![]() ${\mathbf k} $
count as indeterminates. The modified Macdonald polynomials are defined by
${\mathbf k} $
count as indeterminates. The modified Macdonald polynomials are defined by
 $$ \begin{align} \tilde{H} _{\mu }(X;q,t) = t^{n(\mu )} J_{\mu }\left[\frac{X}{1-t^{-1}};q,t^{-1}\right], \end{align} $$
$$ \begin{align} \tilde{H} _{\mu }(X;q,t) = t^{n(\mu )} J_{\mu }\left[\frac{X}{1-t^{-1}};q,t^{-1}\right], \end{align} $$
where
For any symmetric function
![]() $f\in \Lambda $
, let
$f\in \Lambda $
, let
![]() $f[B]$
denote the eigenoperator on the basis
$f[B]$
denote the eigenoperator on the basis
![]() $\{\tilde {H_{\mu }} \}$
of
$\{\tilde {H_{\mu }} \}$
of
![]() $\Lambda $
such that
$\Lambda $
such that
The left-hand side of equation (1) is expressed in the notation of [Reference Haglund, Remmel and Wilson14], where
![]() $\Delta _f=f[B]$
and
$\Delta _f=f[B]$
and
![]() $\Delta _f'=f[B-1]$
. Hence, the symmetric function side of the extended delta conjecture is
$\Delta _f'=f[B-1]$
. Hence, the symmetric function side of the extended delta conjecture is
2.2 The combinatorial side
The right-hand side of the extended delta conjecture (1) is a combinatorial generating function that counts labelled lattice paths.
Definition 2.2.1. A Dyck path is a south-east lattice path lying weakly below the line segment connecting the points
![]() $(0,N)$
and
$(0,N)$
and
![]() $(N,0)$
. The set of such paths is denoted
$(N,0)$
. The set of such paths is denoted
![]() $\mathbf {D}_N$
. The staircase path
$\mathbf {D}_N$
. The staircase path
![]() $\delta $
is the Dyck path alternating between south and east steps.
$\delta $
is the Dyck path alternating between south and east steps.
Each
![]() $\lambda \in \mathbf {D}_N$
has
$\lambda \in \mathbf {D}_N$
has
![]() $\operatorname {\mathrm {area}}(\lambda )=|\delta /\lambda |$
defined to be the number of lattice squares lying above
$\operatorname {\mathrm {area}}(\lambda )=|\delta /\lambda |$
defined to be the number of lattice squares lying above
![]() $\lambda $
and below
$\lambda $
and below
![]() $\delta $
. Let
$\delta $
. Let
![]() $r_i(\lambda )$
be the area contribution from squares in the i-th row, numbered from north to south; in other words,
$r_i(\lambda )$
be the area contribution from squares in the i-th row, numbered from north to south; in other words,
![]() $r_{i}$
is the distance from the i-th south step of
$r_{i}$
is the distance from the i-th south step of
![]() $\lambda $
to the i-th south step of
$\lambda $
to the i-th south step of
![]() $\delta $
. Note that
$\delta $
. Note that
 $$ \begin{align} r_1(\lambda)=0,\qquad r_i(\lambda)\leq r_{i-1}(\lambda)+1 \quad \text{for }i>1, \quad\text{and}\quad \sum_{i=1}^{N} r_i(\lambda)=|\delta/\lambda|\,. \end{align} $$
$$ \begin{align} r_1(\lambda)=0,\qquad r_i(\lambda)\leq r_{i-1}(\lambda)+1 \quad \text{for }i>1, \quad\text{and}\quad \sum_{i=1}^{N} r_i(\lambda)=|\delta/\lambda|\,. \end{align} $$
Definition 2.2.2. A labelling
![]() $P = (P_1,\dots ,P_N) \in {\mathbb N}^N$
attaches a label in
$P = (P_1,\dots ,P_N) \in {\mathbb N}^N$
attaches a label in
![]() ${\mathbb N}=\{0,1,\ldots \}$
to each south step of
${\mathbb N}=\{0,1,\ldots \}$
to each south step of
![]() $\lambda \in \mathbf {D}_N$
so that the labels increase from north to south along vertical runs of south steps, as shown in Figure 1. The set of labellings is denoted by
$\lambda \in \mathbf {D}_N$
so that the labels increase from north to south along vertical runs of south steps, as shown in Figure 1. The set of labellings is denoted by
![]() ${\mathbf {L}}_N(\lambda )$
, or simply
${\mathbf {L}}_N(\lambda )$
, or simply
![]() ${\mathbf {L}}(\lambda )$
. Given
${\mathbf {L}}(\lambda )$
. Given
![]() $0\leq l<N$
, a partial labelling of
$0\leq l<N$
, a partial labelling of
![]() $\lambda \in \mathbf {D}_{N}$
is a labelling where
$\lambda \in \mathbf {D}_{N}$
is a labelling where
![]() $0$
occurs exactly l times and never on the run at
$0$
occurs exactly l times and never on the run at
![]() $x=0$
. We denote the set of these partial labellings by
$x=0$
. We denote the set of these partial labellings by
![]() ${\mathbf {L}}_{N,l}(\lambda )$
.
${\mathbf {L}}_{N,l}(\lambda )$
.

Figure 1 A path
![]() $\lambda $
and partial labelling
$\lambda $
and partial labelling
![]() $P\in {\mathbf {L}}_{11,2}(\lambda )$
, with
$P\in {\mathbf {L}}_{11,2}(\lambda )$
, with
![]() $\operatorname {\mathrm {area}}(\lambda )=10$
,
$\operatorname {\mathrm {area}}(\lambda )=10$
,
![]() $\operatorname {\mathrm {dinv}}(P) = 15$
,
$\operatorname {\mathrm {dinv}}(P) = 15$
,
![]() $x^{\operatorname {\mathrm {wt}}_+(P)} = x_1^2 x_2 x_3^2 x_4^2 x_5 x_6$
and
$x^{\operatorname {\mathrm {wt}}_+(P)} = x_1^2 x_2 x_3^2 x_4^2 x_5 x_6$
and
![]() $x^{\operatorname {\mathrm {wt}}(P)} = x_0^2 x_1^2 x_2 x_3^2 x_4^2 x_5 x_6$
.
$x^{\operatorname {\mathrm {wt}}(P)} = x_0^2 x_1^2 x_2 x_3^2 x_4^2 x_5 x_6$
.
Each labelling
![]() $P \in {\mathbf {L}}(\lambda )$
is assigned a statistic
$P \in {\mathbf {L}}(\lambda )$
is assigned a statistic
![]() $\operatorname {\mathrm {dinv}}(P)$
, defined to be the number of pairs
$\operatorname {\mathrm {dinv}}(P)$
, defined to be the number of pairs
![]() $(i < j)$
such that either
$(i < j)$
such that either
 $$ \begin{align} \begin{cases} r_i(\lambda)=r_j(\lambda) \text{ and } P_i<P_j \;\;\mathrm{or}\\ r_i(\lambda)=r_j(\lambda)+1 \text{ and } P_i>P_j \,. \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} r_i(\lambda)=r_j(\lambda) \text{ and } P_i<P_j \;\;\mathrm{or}\\ r_i(\lambda)=r_j(\lambda)+1 \text{ and } P_i>P_j \,. \end{cases} \end{align} $$
The weight of a labelling P is defined so zero labels do not contribute by
This is equivalent to letting
![]() $x_0 = 1$
in
$x_0 = 1$
in
![]() $x^{\operatorname {\mathrm {wt}}(P)} := \prod _{i \in [N]} x_{P_i} $
.
$x^{\operatorname {\mathrm {wt}}(P)} := \prod _{i \in [N]} x_{P_i} $
.
The above defines the right-hand side of (1), with
![]() $\langle z^{n-k}\rangle $
denoting the coefficient of
$\langle z^{n-k}\rangle $
denoting the coefficient of
![]() $z^{n-k}$
.
$z^{n-k}$
.
Remark 2.2.3. In [Reference Haglund, Remmel and Wilson14], a Dyck path is a northeast lattice path lying weakly above the line segment connecting
![]() $(0,0)$
and
$(0,0)$
and
![]() $(N,N)$
, and labellings increase from south to north along vertical runs. After reflecting the picture about a horizontal line, our conventions on paths, labellings and the definition of
$(N,N)$
, and labellings increase from south to north along vertical runs. After reflecting the picture about a horizontal line, our conventions on paths, labellings and the definition of
![]() $\operatorname {\mathrm {dinv}} (P)$
match those in [Reference Haglund, Remmel and Wilson14]. Separately, [Reference Haglund, Haiman, Loehr, Remmel and Ulyanov13] uses the same conventions that we do for Dyck paths but defines labellings to increase from south to north and defines
$\operatorname {\mathrm {dinv}} (P)$
match those in [Reference Haglund, Remmel and Wilson14]. Separately, [Reference Haglund, Haiman, Loehr, Remmel and Ulyanov13] uses the same conventions that we do for Dyck paths but defines labellings to increase from south to north and defines
![]() $\operatorname {\mathrm {dinv}} (P)$
with the inequalities in equation (9) reversed. However, since the sum
$\operatorname {\mathrm {dinv}} (P)$
with the inequalities in equation (9) reversed. However, since the sum
is a symmetric function [Reference Haglund, Haiman, Loehr, Remmel and Ulyanov13], it is unchanged if we reverse the ordering on labels; after which, the conventions in [Reference Haglund, Haiman, Loehr, Remmel and Ulyanov13] agree with those used here.
We prefer another slight modification based on the following lemma which was mentioned in [Reference Haglund, Remmel and Wilson14] without details.
Lemma 2.2.4. For any Dyck path
![]() $\lambda \in \mathbf {D}_N$
, we have
$\lambda \in \mathbf {D}_N$
, we have
 $$ \begin{align} \prod_{\substack{1<i\leq N\\r_{i}(\lambda)=r_{i-1}(\lambda)+1}} (1+ z\, t^{-r_i(\lambda)}) = \prod_{\substack{1 <i \leq N \\ c_i(\lambda) = c_{i-1}(\lambda)+1}} (1+z\, t^{-c_i(\lambda)}) \,, \end{align} $$
$$ \begin{align} \prod_{\substack{1<i\leq N\\r_{i}(\lambda)=r_{i-1}(\lambda)+1}} (1+ z\, t^{-r_i(\lambda)}) = \prod_{\substack{1 <i \leq N \\ c_i(\lambda) = c_{i-1}(\lambda)+1}} (1+z\, t^{-c_i(\lambda)}) \,, \end{align} $$
where
![]() $c_i(\lambda )=r_i(\lambda ^*)$
is the contribution to
$c_i(\lambda )=r_i(\lambda ^*)$
is the contribution to
![]() $|\delta /\lambda |$
from boxes in the i-th column, numbered from right to left.
$|\delta /\lambda |$
from boxes in the i-th column, numbered from right to left.
Proof. The condition
![]() $r_{i}(\lambda )=r_{i-1}(\lambda )+1$
means that
$r_{i}(\lambda )=r_{i-1}(\lambda )+1$
means that
![]() $\lambda $
has consecutive south steps in rows
$\lambda $
has consecutive south steps in rows
![]() $i-1$
and i with no intervening east step. Similarly,
$i-1$
and i with no intervening east step. Similarly,
![]() $c_{i}(\lambda )=c_{i-1}(\lambda )+1$
if and only if
$c_{i}(\lambda )=c_{i-1}(\lambda )+1$
if and only if
![]() $\lambda $
has consecutive east steps in columns
$\lambda $
has consecutive east steps in columns
![]() $i-1$
and i (numbered right to left). Consider the word formed by listing the steps in
$i-1$
and i (numbered right to left). Consider the word formed by listing the steps in
![]() $\lambda $
in the south-east direction from
$\lambda $
in the south-east direction from
![]() $(0,N)$
to
$(0,N)$
to
![]() $(N,0)$
, as shown here for the example in Figure 1.
$(N,0)$
, as shown here for the example in Figure 1.
Treating south and east steps as left and right parentheses, each south step pairs with an east step to its right, and we have
![]() $r_{i}(\lambda ) = c_{j}(\lambda )$
if the i-th south step (numbered left to right) pairs with the j-th east step (numbered right to left). Furthermore, the leftmost member of each double south step pairs with the rightmost member of a double east step, as indicated in the word displayed above.
$r_{i}(\lambda ) = c_{j}(\lambda )$
if the i-th south step (numbered left to right) pairs with the j-th east step (numbered right to left). Furthermore, the leftmost member of each double south step pairs with the rightmost member of a double east step, as indicated in the word displayed above.
Since each index
![]() $i-1$
such that
$i-1$
such that
![]() $r_i(\lambda )= r_{i-1}(\lambda )+1$
pairs with an index
$r_i(\lambda )= r_{i-1}(\lambda )+1$
pairs with an index
![]() $j-1$
such that
$j-1$
such that
![]() $c_j(\lambda ) = c_{j-1}(\lambda )+1$
, we have
$c_j(\lambda ) = c_{j-1}(\lambda )+1$
, we have
 $$ \begin{align} \prod_{\substack{1 < i \leq N \\ r_i(\lambda) = r_{i-1}(\lambda)+1}} (1+z\, t^{-r_{i-1}(\lambda)-1}) \,\,\, = \!\!\! \prod_{\substack{1 < j \leq N \\ c_j(\lambda) = c_{j-1}(\lambda)+1}} (1+z\, t^{-c_{j-1}(\lambda)-1}) \,. \end{align} $$
$$ \begin{align} \prod_{\substack{1 < i \leq N \\ r_i(\lambda) = r_{i-1}(\lambda)+1}} (1+z\, t^{-r_{i-1}(\lambda)-1}) \,\,\, = \!\!\! \prod_{\substack{1 < j \leq N \\ c_j(\lambda) = c_{j-1}(\lambda)+1}} (1+z\, t^{-c_{j-1}(\lambda)-1}) \,. \end{align} $$
Now, equation (12) follows.
Setting
![]() $N=n+l$
and
$N=n+l$
and
![]() $m=k+l$
, the right-hand side of equation (1), or the combinatorial side of the extended delta conjecture, is equal to
$m=k+l$
, the right-hand side of equation (1), or the combinatorial side of the extended delta conjecture, is equal to
 $$ \begin{align} \langle z^{N-m} \rangle \sum_{\substack{\lambda\in\mathbf {D}_{N}\\ P\in{\mathbf {L}}_{N,l}(\lambda)}} t^{|\delta/\lambda|} \, q^{\operatorname{\mathrm{dinv}}(P)} \, x^{\operatorname{\mathrm{wt}}_+(P)} \prod_{\substack{1 <i \leq N \\ c_i(\lambda)= c_{i-1}(\lambda)+1}} (1+z\, t^{-c_i(\lambda)}) \,. \end{align} $$
$$ \begin{align} \langle z^{N-m} \rangle \sum_{\substack{\lambda\in\mathbf {D}_{N}\\ P\in{\mathbf {L}}_{N,l}(\lambda)}} t^{|\delta/\lambda|} \, q^{\operatorname{\mathrm{dinv}}(P)} \, x^{\operatorname{\mathrm{wt}}_+(P)} \prod_{\substack{1 <i \leq N \\ c_i(\lambda)= c_{i-1}(\lambda)+1}} (1+z\, t^{-c_i(\lambda)}) \,. \end{align} $$
3 Background on the Schiffmann algebra
 ${\mathcal E}$
${\mathcal E}$
From work of Feigin and Tsymbaliuk [Reference Feigin and Tsymbaliuk8] and Schiffmann and Vasserot [Reference Schiffmann and Vasserot25], we know that the operators
![]() $f[B]$
in equation (7) form part of an action of the elliptic Hall algebra
$f[B]$
in equation (7) form part of an action of the elliptic Hall algebra
![]() ${\mathcal E} $
of Burban and Schiffmann [Reference Burban and Schiffmann3, Reference Schiffmann24], or Schiffmann algebra for short, on the algebra of symmetric functions. In [Reference Blasiak, Haiman, Morse, Pun and Seelinger2], we used this action to express the symmetric function side of a generalized shuffle theorem as the polynomial part of an explicit infinite series of
${\mathcal E} $
of Burban and Schiffmann [Reference Burban and Schiffmann3, Reference Schiffmann24], or Schiffmann algebra for short, on the algebra of symmetric functions. In [Reference Blasiak, Haiman, Morse, Pun and Seelinger2], we used this action to express the symmetric function side of a generalized shuffle theorem as the polynomial part of an explicit infinite series of
![]() $\operatorname {\mathrm {GL}}_{l}$
characters. Here, we derive a similar expression (Theorem 4.4.1) for the symmetric function side (7) of the extended delta conjecture.
$\operatorname {\mathrm {GL}}_{l}$
characters. Here, we derive a similar expression (Theorem 4.4.1) for the symmetric function side (7) of the extended delta conjecture.
For this purpose, we need a deeper study of the Schiffmann algebra than we did in [Reference Blasiak, Haiman, Morse, Pun and Seelinger2], where a fragment of the theory was enough. We start with a largely self-contained description of
![]() ${\mathcal E} $
and its action on
${\mathcal E} $
and its action on
![]() $\Lambda $
, although we occasionally refer to [Reference Blasiak, Haiman, Morse, Pun and Seelinger2] for the restatements of results from [Reference Burban and Schiffmann3, Reference Schiffmann24, Reference Schiffmann and Vasserot25] in our notation and for some proofs. A precise translation between our notation and that of [Reference Burban and Schiffmann3, Reference Schiffmann24, Reference Schiffmann and Vasserot25] can be found in [Reference Blasiak, Haiman, Morse, Pun and Seelinger2, eq. (25)]. In the presentation of
$\Lambda $
, although we occasionally refer to [Reference Blasiak, Haiman, Morse, Pun and Seelinger2] for the restatements of results from [Reference Burban and Schiffmann3, Reference Schiffmann24, Reference Schiffmann and Vasserot25] in our notation and for some proofs. A precise translation between our notation and that of [Reference Burban and Schiffmann3, Reference Schiffmann24, Reference Schiffmann and Vasserot25] can be found in [Reference Blasiak, Haiman, Morse, Pun and Seelinger2, eq. (25)]. In the presentation of
![]() ${\mathcal E} $
and its action on
${\mathcal E} $
and its action on
![]() $\Lambda $
, we freely use plethystic substitution, defined in §2.1. Indeed, the ability to do so is a principal reason why we prefer the notation used here to that in the foundational papers on the Schiffmann algebra.
$\Lambda $
, we freely use plethystic substitution, defined in §2.1. Indeed, the ability to do so is a principal reason why we prefer the notation used here to that in the foundational papers on the Schiffmann algebra.
3.1 Description of
 ${\mathcal E}$
${\mathcal E}$
Let
![]() ${\mathbf k} = {\mathbb Q} (q,t)$
, as in §2. The Schiffmann algebra
${\mathbf k} = {\mathbb Q} (q,t)$
, as in §2. The Schiffmann algebra
![]() ${\mathcal E} $
is generated by a central Laurent polynomial subalgebra
${\mathcal E} $
is generated by a central Laurent polynomial subalgebra
![]() $F = {\mathbf k} [c_{1}^{\pm 1}, c_{2}^{\pm 1}]$
and a family of subalgebras
$F = {\mathbf k} [c_{1}^{\pm 1}, c_{2}^{\pm 1}]$
and a family of subalgebras
![]() $\Lambda _{F}(X^{m,n})$
isomorphic to the algebra of symmetric functions
$\Lambda _{F}(X^{m,n})$
isomorphic to the algebra of symmetric functions
![]() $\Lambda _{F}(X)$
over F, one for each pair of coprime integers
$\Lambda _{F}(X)$
over F, one for each pair of coprime integers
![]() $(m,n)$
. These are subject to defining relations spelled out below.
$(m,n)$
. These are subject to defining relations spelled out below.
For any algebra A containing a copy of
![]() $\Lambda $
, there is an adjoint action of
$\Lambda $
, there is an adjoint action of
![]() $\Lambda $
on A arising from the Hopf algebra structure of
$\Lambda $
on A arising from the Hopf algebra structure of
![]() $\Lambda $
. Using two formal alphabets X and Y to distinguish between the tensor factors in
$\Lambda $
. Using two formal alphabets X and Y to distinguish between the tensor factors in
![]() $\Lambda \otimes \Lambda \cong \Lambda (X) \Lambda (Y)$
, the coproduct and antipode for the Hopf algebra structure are given by the plethystic substitutions
$\Lambda \otimes \Lambda \cong \Lambda (X) \Lambda (Y)$
, the coproduct and antipode for the Hopf algebra structure are given by the plethystic substitutions
The adjoint action of
![]() $f\in \Lambda $
on
$f\in \Lambda $
on
![]() $\zeta \in A$
is then given by
$\zeta \in A$
is then given by
since the formula on the right is another way to write
![]() $(1\otimes S)\Delta f = \sum _{i} f_{i}\otimes g_{i}$
. More explicitly, we have
$(1\otimes S)\Delta f = \sum _{i} f_{i}\otimes g_{i}$
. More explicitly, we have
 $$ \begin{align} (\operatorname{\mathrm{Ad}} p_{n})\, \zeta =[p_{n},\zeta ]\quad \text{and} \quad (\operatorname{\mathrm{Ad}} h_{n})\, \zeta = \sum _{j+k=n} (-1)^{k} h_{j}\, \zeta \, e_{k}. \end{align} $$
$$ \begin{align} (\operatorname{\mathrm{Ad}} p_{n})\, \zeta =[p_{n},\zeta ]\quad \text{and} \quad (\operatorname{\mathrm{Ad}} h_{n})\, \zeta = \sum _{j+k=n} (-1)^{k} h_{j}\, \zeta \, e_{k}. \end{align} $$
The last formula can be expressed for all n at once as a generating function identity
where
 $$ \begin{align} \Omega (X) = \sum _{n = 0}^{\infty } h_{n}(X). \end{align} $$
$$ \begin{align} \Omega (X) = \sum _{n = 0}^{\infty } h_{n}(X). \end{align} $$
We fix notation for the quantities
which play a role in the presentation of
![]() ${\mathcal E} $
and will be referred to again later.
${\mathcal E} $
and will be referred to again later.
3.1.1 Basic structure and symmetries
The algebra
![]() ${\mathcal E}$
is
${\mathcal E}$
is
![]() ${\mathbb Z}^2$
graded with the central subalgebra F in degree
${\mathbb Z}^2$
graded with the central subalgebra F in degree
![]() $(0,0)$
and
$(0,0)$
and
![]() $f(X^{m,n})$
in degree
$f(X^{m,n})$
in degree
![]() $(dm,dn)$
for
$(dm,dn)$
for
![]() $f(X) $
of degree d in
$f(X) $
of degree d in
![]() $\Lambda (X)$
.
$\Lambda (X)$
.
The universal central extension
![]() $\widehat {\operatorname {\mathrm {SL}}_{2}({\mathbb Z} )}\rightarrow \operatorname {\mathrm {SL}} _{2}({\mathbb Z} )$
acts on the set of tuples
$\widehat {\operatorname {\mathrm {SL}}_{2}({\mathbb Z} )}\rightarrow \operatorname {\mathrm {SL}} _{2}({\mathbb Z} )$
acts on the set of tuples
lifting the
![]() $\operatorname {\mathrm {SL}} _{2}({\mathbb Z} )$
action on pairs
$\operatorname {\mathrm {SL}} _{2}({\mathbb Z} )$
action on pairs
![]() $(m,n)$
, with the central subgroup
$(m,n)$
, with the central subgroup
![]() ${\mathbb Z} $
generated by the ‘rotation by
${\mathbb Z} $
generated by the ‘rotation by
![]() $2\pi $
’ map
$2\pi $
’ map
![]() $(m,n,\theta )\mapsto (m,n,\theta +2\pi )$
. The group
$(m,n,\theta )\mapsto (m,n,\theta +2\pi )$
. The group
![]() $\widehat {\operatorname {\mathrm {SL}} _{2}({\mathbb Z} )}$
acts on
$\widehat {\operatorname {\mathrm {SL}} _{2}({\mathbb Z} )}$
acts on
![]() ${\mathcal E} $
by
${\mathcal E} $
by
![]() ${\mathbf k} $
-algebra automorphisms, compatibly with the action of
${\mathbf k} $
-algebra automorphisms, compatibly with the action of
![]() $\operatorname {\mathrm {SL}} _{2}({\mathbb Z} )$
on the grading group
$\operatorname {\mathrm {SL}} _{2}({\mathbb Z} )$
on the grading group
![]() ${\mathbb Z} ^{2}$
. Before giving the defining relations of
${\mathbb Z} ^{2}$
. Before giving the defining relations of
![]() ${\mathcal E} $
, we specify how
${\mathcal E} $
, we specify how
![]() $\widehat {\operatorname {\mathrm {SL}} _{2}({\mathbb Z} )}$
acts on the generators.
$\widehat {\operatorname {\mathrm {SL}} _{2}({\mathbb Z} )}$
acts on the generators.
For each pair of coprime integers
![]() $(m,n)$
, we introduce a family of alphabets
$(m,n)$
, we introduce a family of alphabets
![]() $X^{m,n}_{\theta }$
, one for each value
$X^{m,n}_{\theta }$
, one for each value
![]() $\theta $
of
$\theta $
of
![]() $\arg (m+in)$
, related by
$\arg (m+in)$
, related by
We make the convention that
![]() $X^{m,n}$
without a subscript means
$X^{m,n}$
without a subscript means
![]() $X^{m,n}_{\theta }$
with
$X^{m,n}_{\theta }$
with
![]() $\theta \in (-\pi ,\pi ]$
. For comparison, the implied convention in [Reference Blasiak, Haiman, Morse, Pun and Seelinger2] is
$\theta \in (-\pi ,\pi ]$
. For comparison, the implied convention in [Reference Blasiak, Haiman, Morse, Pun and Seelinger2] is
![]() $\theta \in [-\pi ,\pi )$
. The subalgebra
$\theta \in [-\pi ,\pi )$
. The subalgebra
![]() $\Lambda _{F}(X^{m,n}) = \Lambda _{F}(X^{m,n}_{\theta })$
only depends on
$\Lambda _{F}(X^{m,n}) = \Lambda _{F}(X^{m,n}_{\theta })$
only depends on
![]() $(m,n)$
and so does not depend on the choice of branch for the angle
$(m,n)$
and so does not depend on the choice of branch for the angle
![]() $\theta $
. When we refer to a subalgebra
$\theta $
. When we refer to a subalgebra
![]() $\Lambda _{{\mathbf k} } (X^{m,n})$
, which does depend on the branch, the convention
$\Lambda _{{\mathbf k} } (X^{m,n})$
, which does depend on the branch, the convention
![]() $\theta \in (-\pi ,\pi ]$
applies.
$\theta \in (-\pi ,\pi ]$
applies.
The
![]() $\widehat {\operatorname {\mathrm {SL}} _{2}({\mathbb Z} )}$
action is now given by
$\widehat {\operatorname {\mathrm {SL}} _{2}({\mathbb Z} )}$
action is now given by
![]() $\rho \cdot f(X^{m,n}_{\theta }) = f(X^{m',n'}_{\theta '})$
for
$\rho \cdot f(X^{m,n}_{\theta }) = f(X^{m',n'}_{\theta '})$
for
![]() $f(X)\in \Lambda _{{\mathbf k} }(X)$
, where
$f(X)\in \Lambda _{{\mathbf k} }(X)$
, where
![]() $\rho \in \widehat {\operatorname {\mathrm {SL}} _{2}({\mathbb Z} )}$
acts on the indexing data in equation (21) by
$\rho \in \widehat {\operatorname {\mathrm {SL}} _{2}({\mathbb Z} )}$
acts on the indexing data in equation (21) by
![]() $\rho \cdot (m,n,\theta ) = (m',n',\theta ')$
. Note that, if
$\rho \cdot (m,n,\theta ) = (m',n',\theta ')$
. Note that, if
![]() $m,n$
are coprime, then so are
$m,n$
are coprime, then so are
![]() $m',n'$
. The action on F factors through the action of
$m',n'$
. The action on F factors through the action of
![]() $\operatorname {\mathrm {SL}} _{2}({\mathbb Z} )$
on the group algebra
$\operatorname {\mathrm {SL}} _{2}({\mathbb Z} )$
on the group algebra
![]() ${\mathbf k} \cdot {\mathbb Z} ^{2}\cong F$
.
${\mathbf k} \cdot {\mathbb Z} ^{2}\cong F$
.
For instance, the ‘rotation by
![]() $2\pi $
’ element
$2\pi $
’ element
![]() $\rho \in \widehat {\operatorname {\mathrm {SL}} _{2}({\mathbb Z} )}$
fixes F and has
$\rho \in \widehat {\operatorname {\mathrm {SL}} _{2}({\mathbb Z} )}$
fixes F and has
![]() $\rho \cdot f(X_{\theta }^{m,n}) = f(X_{\theta +2\pi }^{m,n}) = f[c_{1}^{m} c_{2}^{n}X^{m,n}_{\theta }]$
. Thus,
$\rho \cdot f(X_{\theta }^{m,n}) = f(X_{\theta +2\pi }^{m,n}) = f[c_{1}^{m} c_{2}^{n}X^{m,n}_{\theta }]$
. Thus,
![]() $\rho $
coincides with multiplication by
$\rho $
coincides with multiplication by
![]() $c_{1}^{r} c_{2}^{s}$
in degree
$c_{1}^{r} c_{2}^{s}$
in degree
![]() $(r,s)$
and automatically preserves all relations that respect the
$(r,s)$
and automatically preserves all relations that respect the
![]() ${\mathbb Z} ^{2}$
grading.
${\mathbb Z} ^{2}$
grading.
We now turn to the defining relations of
![]() ${\mathcal E}$
. Apart from the relations implicit in
${\mathcal E}$
. Apart from the relations implicit in
![]() $F = {\mathbf k} [c_{1}^{\pm 1},c_{2}^{\pm 1}]$
being central and each
$F = {\mathbf k} [c_{1}^{\pm 1},c_{2}^{\pm 1}]$
being central and each
![]() $\Lambda _{F}(X^{m,n})$
being isomorphic to
$\Lambda _{F}(X^{m,n})$
being isomorphic to
![]() $\Lambda _{F}(X)$
, these fall into three families: Heisenberg relations, internal action relations and axis-crossing relations.
$\Lambda _{F}(X)$
, these fall into three families: Heisenberg relations, internal action relations and axis-crossing relations.
3.1.2 Heisenberg relations
Each pair of subalgebras
![]() $\Lambda _{F}(X^{m,n})$
and
$\Lambda _{F}(X^{m,n})$
and
![]() $\Lambda _{F}(X^{-m,-n})$
in degrees along opposite rays in
$\Lambda _{F}(X^{-m,-n})$
in degrees along opposite rays in
![]() ${\mathbb Z} ^{2}$
satisfy Heisenberg relations
${\mathbb Z} ^{2}$
satisfy Heisenberg relations
where
![]() $\widehat {M}$
is given by equation (20). As an exercise, the reader can check, using equation (22), that the relations in equation (23) are consistent with swapping the roles of
$\widehat {M}$
is given by equation (20). As an exercise, the reader can check, using equation (22), that the relations in equation (23) are consistent with swapping the roles of
![]() $\Lambda _{F} (X^{m,n})$
and
$\Lambda _{F} (X^{m,n})$
and
![]() $\Lambda _{F}(X^{-m,-n})$
.
$\Lambda _{F}(X^{-m,-n})$
.
3.1.3 Internal action relations
The internal action relations describe the adjoint action of each
![]() $\Lambda _{F}(X^{m,n})$
on
$\Lambda _{F}(X^{m,n})$
on
![]() ${\mathcal E} $
. For simplicity, we write these relations and also the axis-crossing relations below, with
${\mathcal E} $
. For simplicity, we write these relations and also the axis-crossing relations below, with
![]() $\Lambda _{F}(X^{1,0})$
distinguished. The full set of relations is understood to be given by closing the stated relations under the
$\Lambda _{F}(X^{1,0})$
distinguished. The full set of relations is understood to be given by closing the stated relations under the
![]() $\widehat {\operatorname {\mathrm {SL}} _{2}({\mathbb Z} )}$
action.
$\widehat {\operatorname {\mathrm {SL}} _{2}({\mathbb Z} )}$
action.
Bearing in mind that
![]() $X^{m,n}$
means
$X^{m,n}$
means
![]() $X^{m,n}_{\theta }$
with
$X^{m,n}_{\theta }$
with
![]() $\theta \in (-\pi ,\pi ]$
, the relations for the internal action of
$\theta \in (-\pi ,\pi ]$
, the relations for the internal action of
![]() $\Lambda _{F}(X^{1,0})$
are:
$\Lambda _{F}(X^{1,0})$
are:
 $$ \begin{align} \begin{aligned} (\operatorname{\mathrm{Ad}} f(X^{1,0}))\, p_1(X^{m,1}) & = (\omega f)[z] \Bigl| z^k \mapsto p_1(X^{m+ k,1})\\ (\operatorname{\mathrm{Ad}} f(X^{1,0}))\, p_1(X^{m,-1}) & = (\omega f)[-z] \Bigl| z^k \mapsto p_1(X^{m+ k,-1}). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} (\operatorname{\mathrm{Ad}} f(X^{1,0}))\, p_1(X^{m,1}) & = (\omega f)[z] \Bigl| z^k \mapsto p_1(X^{m+ k,1})\\ (\operatorname{\mathrm{Ad}} f(X^{1,0}))\, p_1(X^{m,-1}) & = (\omega f)[-z] \Bigl| z^k \mapsto p_1(X^{m+ k,-1}). \end{aligned} \end{align} $$
3.1.4 Axis-crossing relations
Again distinguishing
![]() $\Lambda _{F}(X^{1,0})$
and taking angles on the branch
$\Lambda _{F}(X^{1,0})$
and taking angles on the branch
![]() $\theta \in (-\pi ,\pi ]$
, the final set of relations is the closure under the
$\theta \in (-\pi ,\pi ]$
, the final set of relations is the closure under the
![]() $\widehat {\operatorname {\mathrm {SL}} _{2}({\mathbb Z} )}$
action of
$\widehat {\operatorname {\mathrm {SL}} _{2}({\mathbb Z} )}$
action of
 $$ \begin{align} [p_1(X^{b,-1}),\, p_1(X^{a,1})] = -\frac{e_{a+b}[-\widehat{M}X^{1,0}]}{\widehat{M}} \quad \text{for } a+b>0. \end{align} $$
$$ \begin{align} [p_1(X^{b,-1}),\, p_1(X^{a,1})] = -\frac{e_{a+b}[-\widehat{M}X^{1,0}]}{\widehat{M}} \quad \text{for } a+b>0. \end{align} $$
More generally, rotating this relation by
![]() $\pi $
determines
$\pi $
determines
![]() $[p_1(X^{b,-1}),\, p_1(X^{a,1})]$
for
$[p_1(X^{b,-1}),\, p_1(X^{a,1})]$
for
![]() $a + b < 0$
, and the Heisenberg relations determine it when
$a + b < 0$
, and the Heisenberg relations determine it when
![]() $a + b = 0$
. Combining these gives
$a + b = 0$
. Combining these gives
 $$ \begin{align} [p_1(X^{b,-1}),\, p_1(X^{a,1})] = -\frac{1}{\widehat{M}} \begin{cases} e_{a+b}[-\widehat{M}X^{1,0}] & a+b>0\\ 1-c_1^{-b}c_2 & a + b = 0\\ -c_1^{-b}c_2e_{-(a+b)}[-\widehat{M}X^{-1,0}] & a+b < 0\,.\\ \end{cases} \end{align} $$
$$ \begin{align} [p_1(X^{b,-1}),\, p_1(X^{a,1})] = -\frac{1}{\widehat{M}} \begin{cases} e_{a+b}[-\widehat{M}X^{1,0}] & a+b>0\\ 1-c_1^{-b}c_2 & a + b = 0\\ -c_1^{-b}c_2e_{-(a+b)}[-\widehat{M}X^{-1,0}] & a+b < 0\,.\\ \end{cases} \end{align} $$
3.1.5 Further remarks
Define upper and lower half subalgebras
![]() ${\mathcal E}^{* ,>0}, {\mathcal E} ^{*, <0} \subseteq {\mathcal E}$
to be generated by the
${\mathcal E}^{* ,>0}, {\mathcal E} ^{*, <0} \subseteq {\mathcal E}$
to be generated by the
![]() $\Lambda _{F}(X^{m,n})$
with
$\Lambda _{F}(X^{m,n})$
with
![]() $n> 0$
or
$n> 0$
or
![]() $n < 0$
, respectively. Using the
$n < 0$
, respectively. Using the
![]() $\widehat {\operatorname {\mathrm {SL}} _2({\mathbb Z} )}$
image of the relations in equation (25), one can express any
$\widehat {\operatorname {\mathrm {SL}} _2({\mathbb Z} )}$
image of the relations in equation (25), one can express any
![]() $e_{k}[-\widehat {M} X^{m,n}]$
for
$e_{k}[-\widehat {M} X^{m,n}]$
for
![]() $n>0$
in terms of iterated commutators of the elements
$n>0$
in terms of iterated commutators of the elements
![]() $p_{1}(X^{a,1})$
. This shows that
$p_{1}(X^{a,1})$
. This shows that
![]() $\{p_1(X^{a,1})\mid a \in {\mathbb Z}\}$
generates
$\{p_1(X^{a,1})\mid a \in {\mathbb Z}\}$
generates
![]() ${\mathcal E} ^{*,>0}$
as an F-algebra. Similarly,
${\mathcal E} ^{*,>0}$
as an F-algebra. Similarly,
![]() $\{p_1(X^{a,-1})\mid a \in {\mathbb Z}\}$
generates
$\{p_1(X^{a,-1})\mid a \in {\mathbb Z}\}$
generates
![]() ${\mathcal E} ^{*, <0}$
.
${\mathcal E} ^{*, <0}$
.
The internal action relations give the adjoint action of
![]() $\Lambda _{F}(X^{1,0})$
on the space spanned by
$\Lambda _{F}(X^{1,0})$
on the space spanned by
![]() $\{p_1(X^{a,\pm 1})\mid a \in {\mathbb Z}\}$
. Using the formula
$\{p_1(X^{a,\pm 1})\mid a \in {\mathbb Z}\}$
. Using the formula
![]() $(\operatorname {\mathrm {Ad}} f)(\zeta _{1}\zeta _{2}) = \sum ((\operatorname {\mathrm {Ad}} f_{(1)})\zeta _{1})((\operatorname {\mathrm {Ad}} f_{(2)})\zeta _{2})$
, where
$(\operatorname {\mathrm {Ad}} f)(\zeta _{1}\zeta _{2}) = \sum ((\operatorname {\mathrm {Ad}} f_{(1)})\zeta _{1})((\operatorname {\mathrm {Ad}} f_{(2)})\zeta _{2})$
, where
![]() $\Delta f = \sum f_{(1)}\otimes f_{(2)}$
in Sweedler notation, this determines the adjoint action of
$\Delta f = \sum f_{(1)}\otimes f_{(2)}$
in Sweedler notation, this determines the adjoint action of
![]() $\Lambda _{F}(X^{1,0})$
on
$\Lambda _{F}(X^{1,0})$
on
![]() ${\mathcal E} ^{*,>0}$
and
${\mathcal E} ^{*,>0}$
and
![]() ${\mathcal E} ^{*, <0}$
. The Heisenberg relations give the adjoint action of
${\mathcal E} ^{*, <0}$
. The Heisenberg relations give the adjoint action of
![]() $\Lambda _{F}(X^{1,0})$
on
$\Lambda _{F}(X^{1,0})$
on
![]() $\Lambda _{F}(X^{-1,0})$
, while
$\Lambda _{F}(X^{-1,0})$
, while
![]() $\Lambda _{F}(X^{1,0})$
acts trivially on itself, with
$\Lambda _{F}(X^{1,0})$
acts trivially on itself, with
![]() $(\operatorname {\mathrm {Ad}} f)\, g = f[1]\, g$
.
$(\operatorname {\mathrm {Ad}} f)\, g = f[1]\, g$
.
Together, these determine the adjoint action of
![]() $\Lambda _{F}(X^{1,0})$
on the whole algebra
$\Lambda _{F}(X^{1,0})$
on the whole algebra
![]() ${\mathcal E} $
. By symmetry, the same holds for the adjoint action of any
${\mathcal E} $
. By symmetry, the same holds for the adjoint action of any
![]() $\Lambda _{F}(X^{m,n})$
.
$\Lambda _{F}(X^{m,n})$
.
3.1.6 Anti-involution
One can check from the defining relations above that
![]() ${\mathcal E} $
has a further symmetry given by an involutory antiautomorphism (product reversing automorphism)
${\mathcal E} $
has a further symmetry given by an involutory antiautomorphism (product reversing automorphism)
 $$ \begin{align} \begin{gathered} \Phi \colon {\mathcal E} \rightarrow {\mathcal E} \\ \Phi (g(c_{1},c_{2})) = g(c_{2}^{-1},c_{1}^{-1}),\quad \Phi (f(X^{m,n}_{\theta })) = f(X^{n,m}_{\pi /2-\theta }). \end{gathered} \end{align} $$
$$ \begin{align} \begin{gathered} \Phi \colon {\mathcal E} \rightarrow {\mathcal E} \\ \Phi (g(c_{1},c_{2})) = g(c_{2}^{-1},c_{1}^{-1}),\quad \Phi (f(X^{m,n}_{\theta })) = f(X^{n,m}_{\pi /2-\theta }). \end{gathered} \end{align} $$
Note that
![]() $\Phi $
is compatible with reflecting degrees in
$\Phi $
is compatible with reflecting degrees in
![]() ${\mathbb Z} ^{2}$
about the line
${\mathbb Z} ^{2}$
about the line
![]() $x = y$
. Together with
$x = y$
. Together with
![]() $\widehat {\operatorname {\mathrm {SL}} _{2}({\mathbb Z} )}$
, it generates a
$\widehat {\operatorname {\mathrm {SL}} _{2}({\mathbb Z} )}$
, it generates a
![]() $\widehat {\operatorname {\mathrm {GL}} _{2}({\mathbb Z} )}$
action on
$\widehat {\operatorname {\mathrm {GL}} _{2}({\mathbb Z} )}$
action on
![]() ${\mathcal E} $
for which
${\mathcal E} $
for which
![]() $\rho \in \widehat {\operatorname {\mathrm {GL}} _{2}({\mathbb Z} )}$
is an anti-automorphism if
$\rho \in \widehat {\operatorname {\mathrm {GL}} _{2}({\mathbb Z} )}$
is an anti-automorphism if
![]() $\widehat {\operatorname {\mathrm {GL}} _{2}({\mathbb Z} )}\rightarrow \operatorname {\mathrm {GL}} _{2}({\mathbb Z} )\overset {\det }{\rightarrow }\{\pm 1 \}$
sends
$\widehat {\operatorname {\mathrm {GL}} _{2}({\mathbb Z} )}\rightarrow \operatorname {\mathrm {GL}} _{2}({\mathbb Z} )\overset {\det }{\rightarrow }\{\pm 1 \}$
sends
![]() $\rho $
to
$\rho $
to
![]() $-1$
.
$-1$
.
3.2 Action of
 ${\mathcal E} $
on
${\mathcal E} $
on
 $\Lambda $
$\Lambda $
We write
![]() $f^{\bullet }$
for the operator of multiplication by a function f to better distinguish between operator expressions such as
$f^{\bullet }$
for the operator of multiplication by a function f to better distinguish between operator expressions such as
![]() $(\omega f)^{\bullet }$
and
$(\omega f)^{\bullet }$
and
![]() $\omega \cdot f^{\bullet }$
. For f a symmetric function,
$\omega \cdot f^{\bullet }$
. For f a symmetric function,
![]() $f^{\perp }$
denotes the
$f^{\perp }$
denotes the
![]() $\langle -, - \rangle $
adjoint of
$\langle -, - \rangle $
adjoint of
![]() $f^{\bullet }$
.
$f^{\bullet }$
.
Here and again later on, we use an overbar to indicate inverting the variables in any expression; for example,
We extend the notation in equation (6) accordingly, setting
Proposition 3.2.1 [Reference Blasiak, Haiman, Morse, Pun and Seelinger2, Prop 3.3.1].
There is an action of
![]() ${\mathcal E} $
on
${\mathcal E} $
on
![]() $\Lambda $
characterized uniquely by the following properties.
$\Lambda $
characterized uniquely by the following properties.
-
(i) The central parameters
 $c_{1},c_{2}$
act as scalars (30)
$c_{1},c_{2}$
act as scalars (30) $$ \begin{align} c_{1}\mapsto 1,\quad c_{2}\mapsto (q\, t)^{-1}. \end{align} $$
$$ \begin{align} c_{1}\mapsto 1,\quad c_{2}\mapsto (q\, t)^{-1}. \end{align} $$
-
(ii) The subalgebras
 $\Lambda _{{\mathbf k} }(X^{\pm 1,0})$
act as (31)
$\Lambda _{{\mathbf k} }(X^{\pm 1,0})$
act as (31) $$ \begin{align} f(X^{1,0})\mapsto (\omega f)[B-1/M],\quad f(X^{-1,0})\mapsto (\omega f)[\overline{1/M-B}]. \end{align} $$
$$ \begin{align} f(X^{1,0})\mapsto (\omega f)[B-1/M],\quad f(X^{-1,0})\mapsto (\omega f)[\overline{1/M-B}]. \end{align} $$
-
(iii) The subalgebras
 $\Lambda _{{\mathbf k} }(X^{0,\pm 1})$
act as (32)
$\Lambda _{{\mathbf k} }(X^{0,\pm 1})$
act as (32) $$ \begin{align} f(X^{0,1})\mapsto f[-X/M]^{\bullet },\quad f(X^{0,-1})\mapsto f(X)^{\perp }. \end{align} $$
$$ \begin{align} f(X^{0,1})\mapsto f[-X/M]^{\bullet },\quad f(X^{0,-1})\mapsto f(X)^{\perp }. \end{align} $$
We will make particular use of operators representing the action on
![]() $\Lambda $
of elements
$\Lambda $
of elements
![]() $p_{1}(X^{a,1})$
and
$p_{1}(X^{a,1})$
and
![]() $p_{1}(X^{1,a})$
in
$p_{1}(X^{1,a})$
in
![]() ${\mathcal E} $
. For the first, we need the operator
${\mathcal E} $
. For the first, we need the operator
![]() $\nabla $
, defined in [Reference Bergeron, Garsia, Haiman and Tesler1] as an eigenoperator on the modified Macdonald basis by
$\nabla $
, defined in [Reference Bergeron, Garsia, Haiman and Tesler1] as an eigenoperator on the modified Macdonald basis by
where
![]() $n(\mu )$
is given by equation (5) and
$n(\mu )$
is given by equation (5) and
![]() $\mu ^{*}$
denotes the transpose partition.
$\mu ^{*}$
denotes the transpose partition.
For the second, we introduce the doubly infinite generating series
where
![]() $\Omega (X)$
is given by equation (19).
$\Omega (X)$
is given by equation (19).
Definition 3.2.2. For
![]() $a\in {\mathbb Z}$
, we define operators on
$a\in {\mathbb Z}$
, we define operators on
![]() $\Lambda = \Lambda _{{\mathbf k} }(X)$
:
$\Lambda = \Lambda _{{\mathbf k} }(X)$
:
The operators
![]() $D_a$
are the same as in [Reference Blasiak, Haiman, Morse, Pun and Seelinger2] and differ by a sign
$D_a$
are the same as in [Reference Blasiak, Haiman, Morse, Pun and Seelinger2] and differ by a sign
![]() $(-1)^{a}$
from those in [Reference Bergeron, Garsia, Haiman and Tesler1, Reference Garsia, Haiman and Tesler10].
$(-1)^{a}$
from those in [Reference Bergeron, Garsia, Haiman and Tesler1, Reference Garsia, Haiman and Tesler10].
Proposition 3.2.3. In the action of
![]() ${\mathcal E} $
on
${\mathcal E} $
on
![]() $\Lambda $
given by Proposition 3.2.1:
$\Lambda $
given by Proposition 3.2.1:
-
(i) The element
 $p_{1}[-M X^{1,a}] = -M p_{1}(X^{1,a})\in {\mathcal E} $
acts as the operator
$p_{1}[-M X^{1,a}] = -M p_{1}(X^{1,a})\in {\mathcal E} $
acts as the operator
 $D_{a}$
;
$D_{a}$
; -
(ii) The element
 $p_{1}[-M X^{a,1}] = -M p_{1}(X^{a,1})\in {\mathcal E} $
acts as the operator
$p_{1}[-M X^{a,1}] = -M p_{1}(X^{a,1})\in {\mathcal E} $
acts as the operator
 $E_a$
.
$E_a$
.
Proof. Part (i) is proven in [Reference Blasiak, Haiman, Morse, Pun and Seelinger2, Prop 3.3.4].
By equation (32),
![]() $p_1[-MX^{0,1}]$
acts on
$p_1[-MX^{0,1}]$
acts on
![]() $\Lambda $
as multiplication by
$\Lambda $
as multiplication by
![]() $p_1[X] = e_1(X)$
. It was shown in [Reference Blasiak, Haiman, Morse, Pun and Seelinger2, Lemma 3.4.1] that the action of
$p_1[X] = e_1(X)$
. It was shown in [Reference Blasiak, Haiman, Morse, Pun and Seelinger2, Lemma 3.4.1] that the action of
![]() ${\mathcal E} $
on
${\mathcal E} $
on
![]() $\Lambda $
satisfies the symmetry
$\Lambda $
satisfies the symmetry
![]() $\nabla f(X^{m,n}) \nabla ^{-1} = f(X^{m+n,n})$
. More generally, this implies
$\nabla f(X^{m,n}) \nabla ^{-1} = f(X^{m+n,n})$
. More generally, this implies
![]() $\nabla ^{a} f(X^{m,n}) \nabla ^{-a} = f(X^{m+an,n})$
for every integer a. Hence,
$\nabla ^{a} f(X^{m,n}) \nabla ^{-a} = f(X^{m+an,n})$
for every integer a. Hence,
![]() $p_{1}[-MX^{a,1}]$
acts as
$p_{1}[-MX^{a,1}]$
acts as
![]() $\nabla ^{a} p_{1}[-M X^{0,1}] \nabla ^{-a} = \nabla ^{a} e_{1}(X)^{\bullet }\, \nabla ^{-a}$
.
$\nabla ^{a} p_{1}[-M X^{0,1}] \nabla ^{-a} = \nabla ^{a} e_{1}(X)^{\bullet }\, \nabla ^{-a}$
.
3.3
 $\operatorname {\mathrm {GL}}_{l}$
characters and the shuffle algebra
$\operatorname {\mathrm {GL}}_{l}$
characters and the shuffle algebra
As usual, the weight lattice of
![]() $\operatorname {\mathrm {GL}} _{l}$
is
$\operatorname {\mathrm {GL}} _{l}$
is
![]() ${\mathbb Z} ^{l}$
, with Weyl group
${\mathbb Z} ^{l}$
, with Weyl group
![]() $W = S_{l}$
permuting the coordinates. A weight
$W = S_{l}$
permuting the coordinates. A weight
![]() $\lambda $
is dominant if
$\lambda $
is dominant if
![]() $\lambda _{1}\geq \cdots \geq \lambda _{l}$
. A polynomial weight is a dominant weight
$\lambda _{1}\geq \cdots \geq \lambda _{l}$
. A polynomial weight is a dominant weight
![]() $\lambda $
such that
$\lambda $
such that
![]() $\lambda _{l}\geq 0$
. In other words, polynomial weights of
$\lambda _{l}\geq 0$
. In other words, polynomial weights of
![]() $\operatorname {\mathrm {GL}} _{l}$
are integer partitions of length at most l.
$\operatorname {\mathrm {GL}} _{l}$
are integer partitions of length at most l.
As in [Reference Blasiak, Haiman, Morse, Pun and Seelinger2], §2.3, we identify the algebra of virtual
![]() $\operatorname {\mathrm {GL}} _{l}$
characters over
$\operatorname {\mathrm {GL}} _{l}$
characters over
![]() ${\mathbf k} $
with the algebra of symmetric Laurent polynomials
${\mathbf k} $
with the algebra of symmetric Laurent polynomials
![]() ${\mathbf k} [x_{1}^{\pm 1},\ldots ,x_{l}^{\pm 1}]^{S_{l}}$
. If
${\mathbf k} [x_{1}^{\pm 1},\ldots ,x_{l}^{\pm 1}]^{S_{l}}$
. If
![]() $\lambda $
is a polynomial weight, the irreducible character
$\lambda $
is a polynomial weight, the irreducible character
![]() $\chi _{\lambda }$
is equal to the Schur function
$\chi _{\lambda }$
is equal to the Schur function
![]() $s_{\lambda }(x_{1},\ldots ,x_{l})$
. Given a virtual
$s_{\lambda }(x_{1},\ldots ,x_{l})$
. Given a virtual
![]() $\operatorname {\mathrm {GL}} _{l}$
character
$\operatorname {\mathrm {GL}} _{l}$
character
![]() $f(x)= f(x_1,\dots ,x_l) = \sum _{\lambda }c_{\lambda }\chi _{\lambda }$
, the partial sum over polynomial weights
$f(x)= f(x_1,\dots ,x_l) = \sum _{\lambda }c_{\lambda }\chi _{\lambda }$
, the partial sum over polynomial weights
![]() $\lambda $
is a symmetric polynomial in l variables, which we denote by
$\lambda $
is a symmetric polynomial in l variables, which we denote by
![]() $f(x)_{\operatorname {\mathrm {pol}} }$
(this is different from the polynomial terms of
$f(x)_{\operatorname {\mathrm {pol}} }$
(this is different from the polynomial terms of
![]() $f(x)$
considered as a Laurent polynomial). We use the same notation for infinite formal sums
$f(x)$
considered as a Laurent polynomial). We use the same notation for infinite formal sums
![]() $f(x)$
of irreducible
$f(x)$
of irreducible
![]() $\operatorname {\mathrm {GL}} _{l}$
characters, in which case
$\operatorname {\mathrm {GL}} _{l}$
characters, in which case
![]() $f(x)_{\operatorname {\mathrm {pol}} }$
is a symmetric formal power series.
$f(x)_{\operatorname {\mathrm {pol}} }$
is a symmetric formal power series.
The Weyl symmetrization operator for
![]() $\operatorname {\mathrm {GL}} _{l}$
is
$\operatorname {\mathrm {GL}} _{l}$
is
 $$ \begin{align} {\boldsymbol \sigma } (\phi (x_{1},\ldots,x_{l})) = \sum _{w\in S_{l}} w\left(\frac{\phi (x)}{ \prod _{i<j} (1-x_{j}/x_{i})} \right). \end{align} $$
$$ \begin{align} {\boldsymbol \sigma } (\phi (x_{1},\ldots,x_{l})) = \sum _{w\in S_{l}} w\left(\frac{\phi (x)}{ \prod _{i<j} (1-x_{j}/x_{i})} \right). \end{align} $$
For dominant weights
![]() $\lambda $
, the Weyl character formula can be written
$\lambda $
, the Weyl character formula can be written
![]() $\chi _{\lambda } = {\boldsymbol \sigma } (x^{\lambda })$
. More generally, if
$\chi _{\lambda } = {\boldsymbol \sigma } (x^{\lambda })$
. More generally, if
![]() $\phi (x) = \phi (x_{1},\ldots ,x_{l})$
is a Laurent polynomial over any field
$\phi (x) = \phi (x_{1},\ldots ,x_{l})$
is a Laurent polynomial over any field
![]() ${\mathbf k} $
, then
${\mathbf k} $
, then
![]() ${\boldsymbol \sigma } (\phi (x))$
is a virtual
${\boldsymbol \sigma } (\phi (x))$
is a virtual
![]() $\operatorname {\mathrm {GL}}_{l}$
character over
$\operatorname {\mathrm {GL}}_{l}$
character over
![]() ${\mathbf k} $
.
${\mathbf k} $
.
The Hall–Littlewood symmetrization operator is defined by
 $$ \begin{align} {\mathbf H} ^{l}_q(\phi (x)) = {\boldsymbol \sigma } \left( \frac{\phi (x)}{ \prod _{i<j}(1-q\, x_{i}/x_{j})} \right). \end{align} $$
$$ \begin{align} {\mathbf H} ^{l}_q(\phi (x)) = {\boldsymbol \sigma } \left( \frac{\phi (x)}{ \prod _{i<j}(1-q\, x_{i}/x_{j})} \right). \end{align} $$
If
![]() $\phi (x) = \phi (x_{1},\ldots ,x_{l})$
is a rational function over a field
$\phi (x) = \phi (x_{1},\ldots ,x_{l})$
is a rational function over a field
![]() ${\mathbf k} $
containing
${\mathbf k} $
containing
![]() ${\mathbb Q} (q)$
, then
${\mathbb Q} (q)$
, then
![]() ${\mathbf H} ^{l}_{q}(\phi (x))$
is a symmetric rational function over
${\mathbf H} ^{l}_{q}(\phi (x))$
is a symmetric rational function over
![]() ${\mathbf k} $
. If
${\mathbf k} $
. If
![]() $\phi (x)$
is a Laurent polynomial, we can also regard
$\phi (x)$
is a Laurent polynomial, we can also regard
![]() ${\mathbf H} ^{l}_{q}(\phi (x))$
as an infinite formal sum of
${\mathbf H} ^{l}_{q}(\phi (x))$
as an infinite formal sum of
![]() $\operatorname {\mathrm {GL}} _{l}$
characters with coefficients in
$\operatorname {\mathrm {GL}} _{l}$
characters with coefficients in
![]() ${\mathbf k} $
, by interpreting the factors
${\mathbf k} $
, by interpreting the factors
![]() $1/(1-q\, x_{i}/x_{j})$
as geometric series
$1/(1-q\, x_{i}/x_{j})$
as geometric series
![]() $1+q\, x_{i}/x_{j}+(q\, x_{i}/x_{j})^2 + \cdots $
. We always understand
$1+q\, x_{i}/x_{j}+(q\, x_{i}/x_{j})^2 + \cdots $
. We always understand
![]() ${\mathbf H} ^{l}_{q}(\phi (x))$
in this sense when taking the polynomial part
${\mathbf H} ^{l}_{q}(\phi (x))$
in this sense when taking the polynomial part
![]() ${\mathbf H} ^{l}_{q}(\phi (x))_{\operatorname {\mathrm {pol}} }$
.
${\mathbf H} ^{l}_{q}(\phi (x))_{\operatorname {\mathrm {pol}} }$
.
We also use the two-parameter symmetrization operator
 $$ \begin{align} {\mathbf H}^{l}_{q,t}(\phi(x)) = {\mathbf H}^l_q\left(\phi(x) \prod_{i<j}\frac{ (1-q\,t\,x_{i}/x_{j})} {(1-t\, x_{i}/x_{j})} \right) = {\boldsymbol \sigma } \left(\frac{\phi (x)\prod _{i<j}(1-q\, t\, x_{i}/x_{j})}{\prod _{i<j}\bigl((1-q\, x_{i}/x_{j})(1-t\, x_{i}/x_{j})\bigr)} \right). \end{align} $$
$$ \begin{align} {\mathbf H}^{l}_{q,t}(\phi(x)) = {\mathbf H}^l_q\left(\phi(x) \prod_{i<j}\frac{ (1-q\,t\,x_{i}/x_{j})} {(1-t\, x_{i}/x_{j})} \right) = {\boldsymbol \sigma } \left(\frac{\phi (x)\prod _{i<j}(1-q\, t\, x_{i}/x_{j})}{\prod _{i<j}\bigl((1-q\, x_{i}/x_{j})(1-t\, x_{i}/x_{j})\bigr)} \right). \end{align} $$
Again, if
![]() $\phi (x)$
is a rational function over
$\phi (x)$
is a rational function over
![]() ${\mathbf k} ={\mathbb Q} (q,t)$
, then
${\mathbf k} ={\mathbb Q} (q,t)$
, then
![]() ${\mathbf H}^{l}_{q,t}(\phi (x))$
is a symmetric rational function over
${\mathbf H}^{l}_{q,t}(\phi (x))$
is a symmetric rational function over
![]() ${\mathbf k} $
, while if
${\mathbf k} $
, while if
![]() $\phi (x)$
is a Laurent polynomial, or more generally a Laurent polynomial times a rational function which has a power series expansion in the
$\phi (x)$
is a Laurent polynomial, or more generally a Laurent polynomial times a rational function which has a power series expansion in the
![]() $x_{i}/x_{j}$
for
$x_{i}/x_{j}$
for
![]() $i<j$
, we can also interpret
$i<j$
, we can also interpret
![]() ${\mathbf H}^{l}_{q,t}(\phi (x))$
as an infinite formal sum of
${\mathbf H}^{l}_{q,t}(\phi (x))$
as an infinite formal sum of
![]() $\operatorname {\mathrm {GL}} _l$
characters, similarly to equation (38). This series interpretation always applies when taking
$\operatorname {\mathrm {GL}} _l$
characters, similarly to equation (38). This series interpretation always applies when taking
![]() ${\mathbf H}^{l}_{q,t}(\phi (x))_{\operatorname {\mathrm {pol}} }$
.
${\mathbf H}^{l}_{q,t}(\phi (x))_{\operatorname {\mathrm {pol}} }$
.
Fixing
![]() ${\mathbf k} ={\mathbb Q} (q,t)$
once again, let
${\mathbf k} ={\mathbb Q} (q,t)$
once again, let
![]() $T = T({\mathbf k}[z^{\pm 1}])$
be the tensor algebra on the Laurent polynomial ring in one variable, that is, the noncommutative polynomial algebra with generators corresponding to the basis elements
$T = T({\mathbf k}[z^{\pm 1}])$
be the tensor algebra on the Laurent polynomial ring in one variable, that is, the noncommutative polynomial algebra with generators corresponding to the basis elements
![]() $z^{a}$
of
$z^{a}$
of
![]() ${\mathbf k} [z^{\pm 1}]$
as a vector space. Identifying
${\mathbf k} [z^{\pm 1}]$
as a vector space. Identifying
![]() $T^{m} = T^{m}({\mathbf k} [z^{\pm 1}])$
with
$T^{m} = T^{m}({\mathbf k} [z^{\pm 1}])$
with
![]() ${\mathbf k}[z_{1}^{\pm 1},\ldots ,z_{m}^{\pm 1}]$
, the product in T is given by ‘concatenation’,
${\mathbf k}[z_{1}^{\pm 1},\ldots ,z_{m}^{\pm 1}]$
, the product in T is given by ‘concatenation’,
The Feigin–Tsymbaliuk shuffle algebra [Reference Feigin and Tsymbaliuk8] is the quotient
![]() $S=T/I$
, where I is the graded two-sided ideal whose degree l component
$S=T/I$
, where I is the graded two-sided ideal whose degree l component
![]() $I^{l}\subseteq T^{l}$
is the kernel of the symmetrization operator
$I^{l}\subseteq T^{l}$
is the kernel of the symmetrization operator
![]() ${\mathbf H} ^{l}_{q,t}$
in variables
${\mathbf H} ^{l}_{q,t}$
in variables
![]() $z_{1},\ldots ,z_{l}$
, as explained further in [Reference Blasiak, Haiman, Morse, Pun and Seelinger2, §3.5].
$z_{1},\ldots ,z_{l}$
, as explained further in [Reference Blasiak, Haiman, Morse, Pun and Seelinger2, §3.5].
Let
![]() ${\mathcal E} ^{+} \subseteq {\mathcal E}$
be the subalgebra generated by the
${\mathcal E} ^{+} \subseteq {\mathcal E}$
be the subalgebra generated by the
![]() $\Lambda _{{\mathbf k} }(X^{m,n})$
for
$\Lambda _{{\mathbf k} }(X^{m,n})$
for
![]() $m>0$
. We leave out the central subalgebra F since the relations of
$m>0$
. We leave out the central subalgebra F since the relations of
![]() ${\mathcal E} ^{+}$
(as we will see in a moment) do not depend on the central parameters.
${\mathcal E} ^{+}$
(as we will see in a moment) do not depend on the central parameters.
The image of
![]() ${\mathcal E} ^{+}$
under the antiautomorphism
${\mathcal E} ^{+}$
under the antiautomorphism
![]() $\Phi $
in §3.1.6 is the subalgebra
$\Phi $
in §3.1.6 is the subalgebra
![]() $\Phi ({\mathcal E} ^{+})$
generated by the
$\Phi ({\mathcal E} ^{+})$
generated by the
![]() $\Lambda _{{\mathbf k} }(X^{m,n})$
for
$\Lambda _{{\mathbf k} }(X^{m,n})$
for
![]() $n>0$
. Note that our convention
$n>0$
. Note that our convention
![]() $\theta \in (-\pi ,\pi ]$
when the subscript is omitted yields
$\theta \in (-\pi ,\pi ]$
when the subscript is omitted yields
![]() $\Phi (f(X^{m,n})) = f(X^{n,m})$
for
$\Phi (f(X^{m,n})) = f(X^{n,m})$
for
![]() $\Lambda _{{\mathbf k} }(X^{m,n})\subseteq {\mathcal E} ^{+}$
since the branch cut is in the third quadrant.
$\Lambda _{{\mathbf k} }(X^{m,n})\subseteq {\mathcal E} ^{+}$
since the branch cut is in the third quadrant.
Schiffmann and Vasserot [Reference Schiffmann and Vasserot25] proved the following result. See [Reference Blasiak, Haiman, Morse, Pun and Seelinger2, §3.5] for more details on the translation of their theorem into our notation.
Proposition 3.3.1 [Reference Schiffmann and Vasserot25, Theorem 10.1].
There is an algebra isomorphism
![]() $\psi \colon S\rightarrow {\mathcal E} ^{+}$
and an anti-isomorphism
$\psi \colon S\rightarrow {\mathcal E} ^{+}$
and an anti-isomorphism
![]() $\psi ^{\operatorname {\mathrm {op}} } = \Phi \circ \psi \colon S\rightarrow \Phi ({\mathcal E} ^{+})$
, given on the generators by
$\psi ^{\operatorname {\mathrm {op}} } = \Phi \circ \psi \colon S\rightarrow \Phi ({\mathcal E} ^{+})$
, given on the generators by
![]() $\psi (z^{a}) = p_{1}[-MX^{1,a}]$
and
$\psi (z^{a}) = p_{1}[-MX^{1,a}]$
and
![]() $\psi ^{\operatorname {\mathrm {op}} } (z^{a}) = p_{1}[-MX^{a,1}]$
.
$\psi ^{\operatorname {\mathrm {op}} } (z^{a}) = p_{1}[-MX^{a,1}]$
.
To be clear, on monomials in m variables, representing elements of tensor degree m in S, the maps in Proposition 3.3.1 are given by
Later, we will need the following formula for the action of
![]() $\psi (\phi (z))$
on
$\psi (\phi (z))$
on
![]() $\Lambda (X)$
.
$\Lambda (X)$
.
Proposition 3.3.2 [Reference Blasiak, Haiman, Morse, Pun and Seelinger2, Proposition 3.5.2].
Let
![]() $\phi (z) = \phi (z_{1},\ldots ,z_{l})$
be a Laurent polynomial representing an element of tensor degree l in S, and let
$\phi (z) = \phi (z_{1},\ldots ,z_{l})$
be a Laurent polynomial representing an element of tensor degree l in S, and let
![]() $\zeta = \psi (\phi (z)) \in {\mathcal E} ^{+}$
be its image under the map in equation (41). With
$\zeta = \psi (\phi (z)) \in {\mathcal E} ^{+}$
be its image under the map in equation (41). With
![]() ${\mathcal E} $
acting on
${\mathcal E} $
acting on
![]() $\Lambda $
as in Proposition 3.2.1, we have
$\Lambda $
as in Proposition 3.2.1, we have
4 Schiffmann algebra reformulation of the symmetric function side
4.1 Distinguished elements
 $D_{{\mathbf b} }$
and
$D_{{\mathbf b} }$
and
 $E_{{\mathbf a} }$
$E_{{\mathbf a} }$
Negut [Reference Negut19] defined a family of distinguished elements
![]() $D_{{\mathbf b} }\in {\mathcal E} ^{+}$
, indexed by
$D_{{\mathbf b} }\in {\mathcal E} ^{+}$
, indexed by
![]() ${\mathbf b} \in {\mathbb Z} ^{l}$
, which in the case
${\mathbf b} \in {\mathbb Z} ^{l}$
, which in the case
![]() $l=1$
reduce to the elements in Proposition 3.2.3(i). Here, a remarkable symmetry between these elements and their images
$l=1$
reduce to the elements in Proposition 3.2.3(i). Here, a remarkable symmetry between these elements and their images
![]() $E_{{\mathbf a} }$
under the anti-involution
$E_{{\mathbf a} }$
under the anti-involution
![]() $\Phi $
will play a crucial role. After defining the Negut elements, we derive this symmetry in Proposition 4.3.3 with the help of a commutator formula of Negut [Reference Negut20].
$\Phi $
will play a crucial role. After defining the Negut elements, we derive this symmetry in Proposition 4.3.3 with the help of a commutator formula of Negut [Reference Negut20].
Definition 4.1.1 (see also [Reference Blasiak, Haiman, Morse, Pun and Seelinger2, §3.6]).
Given
![]() ${\mathbf b} = (b_1,\ldots ,b_l) \in {\mathbb Z}^l$
, set
${\mathbf b} = (b_1,\ldots ,b_l) \in {\mathbb Z}^l$
, set
 $$ \begin{align} \phi ({z}) = \frac{z_{1}^{b_1}\cdots z_{l}^{b_{l}}}{ \prod _{i=1}^{l-1}(1-q\, t\, z_{i}/z_{i+1})}, \end{align} $$
$$ \begin{align} \phi ({z}) = \frac{z_{1}^{b_1}\cdots z_{l}^{b_{l}}}{ \prod _{i=1}^{l-1}(1-q\, t\, z_{i}/z_{i+1})}, \end{align} $$
and let
![]() $\nu (z)=\nu (z_{1},\ldots ,z_{l})$
be a Laurent polynomial satisfying
$\nu (z)=\nu (z_{1},\ldots ,z_{l})$
be a Laurent polynomial satisfying
![]() ${\mathbf H}_{q,t}^l(\nu (z)) = {\mathbf H}_{q,t}^l(\phi (z))$
. Such a
${\mathbf H}_{q,t}^l(\nu (z)) = {\mathbf H}_{q,t}^l(\phi (z))$
. Such a
![]() $\nu (z)$
exists by [Reference Negut19, Proposition 6.1] and represents a well-defined element of the shuffle algebra S. The Negut element
$\nu (z)$
exists by [Reference Negut19, Proposition 6.1] and represents a well-defined element of the shuffle algebra S. The Negut element
![]() $D_{{\mathbf b} }$
and the transposed Negut element
$D_{{\mathbf b} }$
and the transposed Negut element
![]() $E_{{\mathbf a} }$
, where
$E_{{\mathbf a} }$
, where
![]() ${\mathbf a} = (b_{l},\ldots ,b_{1})$
is the reversed sequence of indices, are defined by
${\mathbf a} = (b_{l},\ldots ,b_{1})$
is the reversed sequence of indices, are defined by
We should point out that, strictly speaking, the Negut elements in the case
![]() $l=1$
are defined to be elements
$l=1$
are defined to be elements
![]() $D_{a} = p_{1}[-M X^{1,a}]$
and
$D_{a} = p_{1}[-M X^{1,a}]$
and
![]() $E_{a} = p_{1}[-M X^{a,1}]$
of
$E_{a} = p_{1}[-M X^{a,1}]$
of
![]() ${\mathcal E} $
, while in Definition 3.2.2, we used the notation
${\mathcal E} $
, while in Definition 3.2.2, we used the notation
![]() $D_{a}$
and
$D_{a}$
and
![]() $E_{a}$
for operators on
$E_{a}$
for operators on
![]() $\Lambda $
. However, by Proposition 3.2.3, these Negut elements act as the operators with the same name, so no confusion should ensue.
$\Lambda $
. However, by Proposition 3.2.3, these Negut elements act as the operators with the same name, so no confusion should ensue.
Later, we will use the following product formulas, which are immediate from Definition 4.1.1.
As noted in §3.1.5, the internal action relations determine the action of
![]() $\Lambda _{{\mathbf k} }(X^{0,1})$
on
$\Lambda _{{\mathbf k} }(X^{0,1})$
on
![]() $\Phi ( {\mathcal E} ^{+})$
. Using the anti-isomorphism between
$\Phi ( {\mathcal E} ^{+})$
. Using the anti-isomorphism between
![]() $\Phi ({\mathcal E} ^{+})$
and the shuffle algebra, we can make this more explicit.
$\Phi ({\mathcal E} ^{+})$
and the shuffle algebra, we can make this more explicit.
Lemma 4.1.2. Let
![]() $\phi (z)=\phi (z_{1},\ldots ,z_{n})$
be a Laurent polynomial representing an element of tensor degree n in S. Then
$\phi (z)=\phi (z_{1},\ldots ,z_{n})$
be a Laurent polynomial representing an element of tensor degree n in S. Then
As a particular consequence, we have
 $$ \begin{align} (\operatorname{\mathrm{Ad}} f(X^{1,0})) E_{a_{n},\ldots,a_{1}}= \psi^{\operatorname{\mathrm{op}}}\left( \frac{(\omega f)(z_{1},\ldots,z_{n})\cdot z_{1}^{a_{1}}\cdots z_{n}^{a_{n}}}{\prod_{i=1}^{n-1} (1-q\, t\, z_{i} / z_{i+1})}\right). \end{align} $$
$$ \begin{align} (\operatorname{\mathrm{Ad}} f(X^{1,0})) E_{a_{n},\ldots,a_{1}}= \psi^{\operatorname{\mathrm{op}}}\left( \frac{(\omega f)(z_{1},\ldots,z_{n})\cdot z_{1}^{a_{1}}\cdots z_{n}^{a_{n}}}{\prod_{i=1}^{n-1} (1-q\, t\, z_{i} / z_{i+1})}\right). \end{align} $$
Proof. This follows immediately from the rule in §3.1.5 for
![]() $\operatorname {\mathrm {Ad}} f$
acting on a product.
$\operatorname {\mathrm {Ad}} f$
acting on a product.
4.2 Commutator identity
We use a formula for the commutator of elements
![]() $D_{a}$
and
$D_{a}$
and
![]() $D_{{\mathbf b} }$
and a similar identity for
$D_{{\mathbf b} }$
and a similar identity for
![]() $E_{a}$
and
$E_{a}$
and
![]() $E_{{\mathbf b} }$
. This commutation relation was proved geometrically by Negut in [Reference Negut20], but to keep things self-contained, we provide an elementary algebraic proof. It is convenient to express the formula using the notation
$E_{{\mathbf b} }$
. This commutation relation was proved geometrically by Negut in [Reference Negut20], but to keep things self-contained, we provide an elementary algebraic proof. It is convenient to express the formula using the notation

As a mnemonic device, note that both cases can be interpreted as
![]() $\sum _{i = a}^{\infty } f_i - \sum _{i = b+1}^{\infty } f_i$
.
$\sum _{i = a}^{\infty } f_i - \sum _{i = b+1}^{\infty } f_i$
.
Proposition 4.2.1 [Reference Negut20, Proposition 4.7].
For any
![]() $a\in {\mathbb Z}$
and
$a\in {\mathbb Z}$
and
![]() $\mathbf {b} = (b_1,\ldots ,b_l) \in {\mathbb Z}^l$
, we have
$\mathbf {b} = (b_1,\ldots ,b_l) \in {\mathbb Z}^l$
, we have


We will need the following lemma for the proof. The notation
![]() $\Omega (X)$
is defined in equation (19). Since plethystic substitution into
$\Omega (X)$
is defined in equation (19). Since plethystic substitution into
![]() $\Omega (X)$
is characterized by
$\Omega (X)$
is characterized by
we have
Lemma 4.2.2. For any
![]() $f(z)=f(z_1,\ldots ,z_m)$
antisymmetric in
$f(z)=f(z_1,\ldots ,z_m)$
antisymmetric in
![]() $z_i$
and
$z_i$
and
![]() $z_{i+1}$
, we have
$z_{i+1}$
, we have
Proof. The definition of
![]() ${\mathbf H}^m_{q,t}$
and equation (55) imply that
${\mathbf H}^m_{q,t}$
and equation (55) imply that
 $$ \begin{align} {\mathbf H}^m_{q,t}\bigl(\Omega[M\, z_i/z_{i+1}]f(z)\bigr) = \sum_{w\in S_m} w\left( f(z)\prod_{j \neq k} \frac{1}{1-z_j/z_k}\prod_ {\substack{j<k \\ (j,k)\neq (i,i+1)}} \Omega[-M\, z_j/z_{k}] \right), \end{align} $$
$$ \begin{align} {\mathbf H}^m_{q,t}\bigl(\Omega[M\, z_i/z_{i+1}]f(z)\bigr) = \sum_{w\in S_m} w\left( f(z)\prod_{j \neq k} \frac{1}{1-z_j/z_k}\prod_ {\substack{j<k \\ (j,k)\neq (i,i+1)}} \Omega[-M\, z_j/z_{k}] \right), \end{align} $$
which vanishes since
![]() $f(z)$
is antisymmetric in
$f(z)$
is antisymmetric in
![]() $z_i$
and
$z_i$
and
![]() $z_{i+1}$
.
$z_{i+1}$
.
Proof of Proposition 4.2.1.
Identity (53) for
![]() $[E_{b_{l},\ldots ,b_{1}},\, E_{a}]$
follows from equation (52) by applying the antihomomorphism
$[E_{b_{l},\ldots ,b_{1}},\, E_{a}]$
follows from equation (52) by applying the antihomomorphism
![]() $\Phi $
, so we only prove equation (52), which can be written
$\Phi $
, so we only prove equation (52), which can be written

Using Definition 4.1.1 and the isomorphism
![]() $\psi \colon S\rightarrow {\mathcal E} ^{+}$
, we can prove equation (58) by showing that a rational function representing the left-hand side is in the kernel of the symmetrization operator
$\psi \colon S\rightarrow {\mathcal E} ^{+}$
, we can prove equation (58) by showing that a rational function representing the left-hand side is in the kernel of the symmetrization operator
![]() ${\mathbf H} ^{l+1}_{q,t}$
. For this, we can work directly with the rational functions
${\mathbf H} ^{l+1}_{q,t}$
. For this, we can work directly with the rational functions
![]() $\phi (z)$
in equation (44); there is no need to replace them explicitly with Laurent polynomials having the same symmetrization.
$\phi (z)$
in equation (44); there is no need to replace them explicitly with Laurent polynomials having the same symmetrization.
Let
![]() $\phi (z)$
be the function in equation (44) for
$\phi (z)$
be the function in equation (44) for
![]() $D_{{\mathbf b} }$
, and set
$D_{{\mathbf b} }$
, and set
 $$ \begin{align} \phi (\hat z_i) = \phi(z_1,\ldots,z_{i-1},z_{i+1},\ldots,z_{l+1}) = \dfrac{z_{1}^{ b_1}\cdots z_{i-1}^{b_{i-1}}z_{i+1}^{b_{i}}\cdots z_{l+1}^{b_{l} }}{ (1-q\, t\, z_{i-1}/z_{i+1})\prod\limits _ {\substack{1\leq j\leq l\\ j\neq i,i-1}} (1-q\, t\, z_{j}/z_{j+1})}\,. \end{align} $$
$$ \begin{align} \phi (\hat z_i) = \phi(z_1,\ldots,z_{i-1},z_{i+1},\ldots,z_{l+1}) = \dfrac{z_{1}^{ b_1}\cdots z_{i-1}^{b_{i-1}}z_{i+1}^{b_{i}}\cdots z_{l+1}^{b_{l} }}{ (1-q\, t\, z_{i-1}/z_{i+1})\prod\limits _ {\substack{1\leq j\leq l\\ j\neq i,i-1}} (1-q\, t\, z_{j}/z_{j+1})}\,. \end{align} $$
To prove equation (58), we want to show

Since
![]() $z_i^a\phi (\hat z_i) -\phi (\hat z_{i+1})z_{i+1}^a$
is antisymmetric in
$z_i^a\phi (\hat z_i) -\phi (\hat z_{i+1})z_{i+1}^a$
is antisymmetric in
![]() $z_i$
and
$z_i$
and
![]() $z_{i+1}$
, Lemma 4.2.2 implies
$z_{i+1}$
, Lemma 4.2.2 implies
 $$ \begin{align} \sum _{i=1}^{l} {\mathbf H}_{q,t}^{l+1} \biggl( \Omega [M\, z_{i}/z_{i+1}] (z_i^a\phi(\hat z_i) -\phi(\hat z_{i+1})z_{i+1}^a) \biggr) = 0. \end{align} $$
$$ \begin{align} \sum _{i=1}^{l} {\mathbf H}_{q,t}^{l+1} \biggl( \Omega [M\, z_{i}/z_{i+1}] (z_i^a\phi(\hat z_i) -\phi(\hat z_{i+1})z_{i+1}^a) \biggr) = 0. \end{align} $$
The first formula in equation (55) is algebraically the same as
After substituting this into equation (61), the linearity of
![]() ${\mathbf H}_{q,t}^{l+1}$
gives
${\mathbf H}_{q,t}^{l+1}$
gives
 $$ \begin{align} {\mathbf H}_{q,t}^{l+1}\bigg(\sum_{i = 1}^{l} \Big(z_i^a\phi(\hat{z_i}) -\phi(\hat{z_{i+1}})z_{i+1}^a -M \frac{z_i^a\phi(\hat{z_i}) -\phi(\hat{z_{i+1}})z_{i+1}^a}{(1-z_{i+1}/z_i)(1-q\, t\, z_i/z_{i+1})}\Big) \bigg)=0. \end{align} $$
$$ \begin{align} {\mathbf H}_{q,t}^{l+1}\bigg(\sum_{i = 1}^{l} \Big(z_i^a\phi(\hat{z_i}) -\phi(\hat{z_{i+1}})z_{i+1}^a -M \frac{z_i^a\phi(\hat{z_i}) -\phi(\hat{z_{i+1}})z_{i+1}^a}{(1-z_{i+1}/z_i)(1-q\, t\, z_i/z_{i+1})}\Big) \bigg)=0. \end{align} $$
The terms
![]() $z_i^a\phi (\hat {z_i}) -\phi (\hat {z_{i+1}})z_{i+1}^a$
telescope, reducing this to
$z_i^a\phi (\hat {z_i}) -\phi (\hat {z_{i+1}})z_{i+1}^a$
telescope, reducing this to
 $$ \begin{align} {\mathbf H}_{q,t}^{l+1}\bigg( z_1^a\phi(\hat{z_1 }) -\phi(\hat{z_{l+1}})z_{l+1}^a -M \sum_{i = 1}^{l} \frac{z_i^a\phi(\hat{z_i}) -\phi(\hat{z_{i+1}})z_{i+1}^a}{(1-z_{i+1}/z_i)(1-q\, t\, z_i/z_{i+1})}\bigg)=0. \end{align} $$
$$ \begin{align} {\mathbf H}_{q,t}^{l+1}\bigg( z_1^a\phi(\hat{z_1 }) -\phi(\hat{z_{l+1}})z_{l+1}^a -M \sum_{i = 1}^{l} \frac{z_i^a\phi(\hat{z_i}) -\phi(\hat{z_{i+1}})z_{i+1}^a}{(1-z_{i+1}/z_i)(1-q\, t\, z_i/z_{i+1})}\bigg)=0. \end{align} $$
If we use the convention
![]() $z_0=0$
and
$z_0=0$
and
![]() $z_{l+2}=\infty $
, collecting terms in
$z_{l+2}=\infty $
, collecting terms in
![]() $z_{i}^{a}\phi (\hat {z_{i}})$
and some further algebra manipulations give
$z_{i}^{a}\phi (\hat {z_{i}})$
and some further algebra manipulations give
 $$ \begin{align*} \sum _{i=1}^{l} \frac{z_i^a \phi(\hat{z_i}) - \phi(\hat{z_{i+1}}) z_{i+1}^a}{(1 - \frac{z_{i+1}}{z_{i}})(1 - q\, t \frac{z_{i}}{z_{i+1}})} & = \sum _{i=1}^{l+1} \left[\frac{1}{(1 - \frac{z_{i+1}}{z_{i}})(1 - q\, t\frac{z_{i}}{z_{i+1}})} - \frac{1}{(1 - \frac{z_{i}}{z_{i-1}})(1 - q\, t\frac{z_{i-1}}{z_{i}})}\right] z_i^a \phi(\hat{z_i}) \\ & = \sum _{i=1}^{l+1} \frac{z_i^a \phi(\hat{z_i}) (1 - q\, t \frac{z_{i-1}}{z_{i+1}})}{(1 - q\, t \frac{z_{i-1}}{z_{i}})(1 - q\, t \frac{z_{i}}{z_{i+1}})} \Big( \frac{1}{1 - \frac{z_{i+1}}{z_{i}}} - \frac{1}{1 - \frac{z_{i}}{z_{i-1}}}\Big)\\ & = \sum _{i=1}^{l+1} \frac{\dfrac{z_i^a \phi(\hat{z_i}) (1 - q\, t \frac{z_{i-1}}{z_{i+1}})}{(1 - q\, t \frac{z_{i-1}}{z_{i}})(1 - q\, t \frac{z_{i}}{z_{i+1}})} - \dfrac{z_{i+1}^a \phi(\hat{z_{i+1}}) (1 - q\, t \frac{z_{i}}{z_{i+2}})}{(1 - q\, t \frac{z_{i}}{z_{i+1}})(1 - q\, t \frac{z_{i+1}}{z_{i+2}})}}{1 - \frac{z_{i+1}}{z_i}}\,. \end{align*} $$
$$ \begin{align*} \sum _{i=1}^{l} \frac{z_i^a \phi(\hat{z_i}) - \phi(\hat{z_{i+1}}) z_{i+1}^a}{(1 - \frac{z_{i+1}}{z_{i}})(1 - q\, t \frac{z_{i}}{z_{i+1}})} & = \sum _{i=1}^{l+1} \left[\frac{1}{(1 - \frac{z_{i+1}}{z_{i}})(1 - q\, t\frac{z_{i}}{z_{i+1}})} - \frac{1}{(1 - \frac{z_{i}}{z_{i-1}})(1 - q\, t\frac{z_{i-1}}{z_{i}})}\right] z_i^a \phi(\hat{z_i}) \\ & = \sum _{i=1}^{l+1} \frac{z_i^a \phi(\hat{z_i}) (1 - q\, t \frac{z_{i-1}}{z_{i+1}})}{(1 - q\, t \frac{z_{i-1}}{z_{i}})(1 - q\, t \frac{z_{i}}{z_{i+1}})} \Big( \frac{1}{1 - \frac{z_{i+1}}{z_{i}}} - \frac{1}{1 - \frac{z_{i}}{z_{i-1}}}\Big)\\ & = \sum _{i=1}^{l+1} \frac{\dfrac{z_i^a \phi(\hat{z_i}) (1 - q\, t \frac{z_{i-1}}{z_{i+1}})}{(1 - q\, t \frac{z_{i-1}}{z_{i}})(1 - q\, t \frac{z_{i}}{z_{i+1}})} - \dfrac{z_{i+1}^a \phi(\hat{z_{i+1}}) (1 - q\, t \frac{z_{i}}{z_{i+2}})}{(1 - q\, t \frac{z_{i}}{z_{i+1}})(1 - q\, t \frac{z_{i+1}}{z_{i+2}})}}{1 - \frac{z_{i+1}}{z_i}}\,. \end{align*} $$
Expanding the definition (59) of
![]() $\phi (\hat {z_{i}})$
for each i yields
$\phi (\hat {z_{i}})$
for each i yields
 $$ \begin{align*} \frac{z_i^a \phi(\hat{z_i}) (1 -q\, t\, z_{i-1}/z_{i+1})}{(1 -q\, t\, z_{i-1} / z_{i}) (1- q\, t\, z_{i}/z_{i+1})} = \frac{z_1^{b_1}\cdots z_{i-1}^{b_{i-1}} z_i^a z_{i+1}^{b_i} \cdots z_{l+1}^{b_l}}{\prod_{j=1}^{l} (1 - q\, t\, z_j / z_{j+1})} \, \end{align*} $$
$$ \begin{align*} \frac{z_i^a \phi(\hat{z_i}) (1 -q\, t\, z_{i-1}/z_{i+1})}{(1 -q\, t\, z_{i-1} / z_{i}) (1- q\, t\, z_{i}/z_{i+1})} = \frac{z_1^{b_1}\cdots z_{i-1}^{b_{i-1}} z_i^a z_{i+1}^{b_i} \cdots z_{l+1}^{b_l}}{\prod_{j=1}^{l} (1 - q\, t\, z_j / z_{j+1})} \, \end{align*} $$
so that

Identity (60) follows by substituting this back into equation (63).
4.3 Symmetry identity for
 $D_{{\mathbf b} }$
and
$D_{{\mathbf b} }$
and
 $E_{{\mathbf a} }$
$E_{{\mathbf a} }$
Next, we will prove an identity between certain instances of the Negut elements
![]() $D_{{\mathbf b} }\in {\mathcal E} ^{+}$
and transposed Negut elements
$D_{{\mathbf b} }\in {\mathcal E} ^{+}$
and transposed Negut elements
![]() $E_{{\mathbf a} }\in \Phi ({\mathcal E} ^{+})$
. Before stating the identity, we need to describe how the indices
$E_{{\mathbf a} }\in \Phi ({\mathcal E} ^{+})$
. Before stating the identity, we need to describe how the indices
![]() ${\mathbf a} $
and
${\mathbf a} $
and
![]() ${\mathbf b} $
will correspond.
${\mathbf b} $
will correspond.
Definition 4.3.1. A south-east lattice path
![]() $\gamma $
from
$\gamma $
from
![]() $(0,n)$
to
$(0,n)$
to
![]() $(m,0)$
, for positive integers
$(m,0)$
, for positive integers
![]() $m, n$
, is admissible if it starts with a south step and ends with an east step; that is,
$m, n$
, is admissible if it starts with a south step and ends with an east step; that is,
![]() $\gamma $
has a step from
$\gamma $
has a step from
![]() $(0,n)$
to
$(0,n)$
to
![]() $(0,n-1)$
and one from
$(0,n-1)$
and one from
![]() $(m-1,0)$
to
$(m-1,0)$
to
![]() $(m,0)$
. Define
$(m,0)$
. Define
![]() $\mathbf {b}(\gamma ) = (b_1, \dots , b_m)$
by taking
$\mathbf {b}(\gamma ) = (b_1, \dots , b_m)$
by taking
![]() $b_i = ( \text {vertical run of } \gamma \text { at } x = i-1 )$
for
$b_i = ( \text {vertical run of } \gamma \text { at } x = i-1 )$
for
![]() $i = 1,\ldots , m$
and
$i = 1,\ldots , m$
and
![]() $\mathbf {a}(\gamma )=(a_n, \dots , a_1)$
with
$\mathbf {a}(\gamma )=(a_n, \dots , a_1)$
with
![]() $a_j = ( \text {horizontal run of } \gamma \text { at } y = j -1)$
for
$a_j = ( \text {horizontal run of } \gamma \text { at } y = j -1)$
for
![]() $j = 1,\ldots , n$
. Set
$j = 1,\ldots , n$
. Set
![]() $D_{\gamma }= D_{\mathbf {b}(\gamma )}$
and
$D_{\gamma }= D_{\mathbf {b}(\gamma )}$
and
![]() $E_{\gamma } = E_{\mathbf {a}(\gamma )}$
.
$E_{\gamma } = E_{\mathbf {a}(\gamma )}$
.
Note that, if
![]() $\gamma ^{*}$
is the transpose of an admissible path
$\gamma ^{*}$
is the transpose of an admissible path
![]() $\gamma $
with
$\gamma $
with
![]() ${\mathbf b} (\gamma ) = (b_1, \ldots , b_m)$
and
${\mathbf b} (\gamma ) = (b_1, \ldots , b_m)$
and
![]() ${\mathbf a} (\gamma ) = (a_n, \ldots , a_1)$
, as above, then
${\mathbf a} (\gamma ) = (a_n, \ldots , a_1)$
, as above, then
![]() ${\mathbf a} (\gamma ^{*}) = (b_m,\dots ,b_1) $
and
${\mathbf a} (\gamma ^{*}) = (b_m,\dots ,b_1) $
and
![]() ${\mathbf b} (\gamma ^{*}) = (a_1,\dots ,a_n)$
, and
${\mathbf b} (\gamma ^{*}) = (a_1,\dots ,a_n)$
, and
![]() $E_{\gamma } =\Phi (D_{\gamma ^*})$
.
$E_{\gamma } =\Phi (D_{\gamma ^*})$
.
Example 4.3.2. Paths
![]() $\gamma $
and
$\gamma $
and
![]() $\gamma ^*$
below are both admissible. Path
$\gamma ^*$
below are both admissible. Path
![]() $\gamma $
is from
$\gamma $
is from
![]() $(0,8)$
to
$(0,8)$
to
![]() $(4,0)$
with
$(4,0)$
with
![]() ${\mathbf b}(\gamma )=(2,1,3,2)$
and
${\mathbf b}(\gamma )=(2,1,3,2)$
and
![]() ${\mathbf a}(\gamma )=(0,1,1,0,0,1,0,1)$
, whereas
${\mathbf a}(\gamma )=(0,1,1,0,0,1,0,1)$
, whereas
![]() $\gamma ^*$
is from
$\gamma ^*$
is from
![]() $(0,4)$
to
$(0,4)$
to
![]() $(8,0)$
and has
$(8,0)$
and has
![]() ${\mathbf a}(\gamma ^*)=(2,3,1,2)$
and
${\mathbf a}(\gamma ^*)=(2,3,1,2)$
and
![]() ${\mathbf b}(\gamma ^*)=(1,0,1,0,0,1,1,0)$
.
${\mathbf b}(\gamma ^*)=(1,0,1,0,0,1,1,0)$
.

Proposition 4.3.3. For every admissible path
![]() $\gamma $
, we have
$\gamma $
, we have
![]() $D_{\gamma } = E_{\gamma } $
.
$D_{\gamma } = E_{\gamma } $
.
Proof. Let
![]() $\gamma $
be an admissible path
$\gamma $
be an admissible path
![]() $\gamma $
from
$\gamma $
from
![]() $(0,n)$
to
$(0,n)$
to
![]() $(m,0)$
, where
$(m,0)$
, where
![]() $m,n$
are positive integers.
$m,n$
are positive integers.
We first establish the case when
![]() $n = 1$
. In this case,
$n = 1$
. In this case,
![]() $E_{\gamma } = E_{m} = p_{1}[-M X^{m,1}]$
and
$E_{\gamma } = E_{m} = p_{1}[-M X^{m,1}]$
and
![]() $D_{\gamma } = D_{10^{m-1}}$
. If
$D_{\gamma } = D_{10^{m-1}}$
. If
![]() $m=1$
, these are
$m=1$
, these are
![]() $E_{1} = D_{1} = p_{1}[-M X^{1,1}]$
. In general, equation (24) implies
$E_{1} = D_{1} = p_{1}[-M X^{1,1}]$
. In general, equation (24) implies
![]() $E_{m}= p_1[-M X^{m,1}] = (\operatorname {\mathrm {Ad}} p_1(X^{1,0}))^{m-1} p_1[-M X^{1,1}] = (\operatorname {\mathrm {Ad}} p_1(X^{1,0}))^{m-1} D_{1}$
, while equation (17) and the commutator identity (52) imply
$E_{m}= p_1[-M X^{m,1}] = (\operatorname {\mathrm {Ad}} p_1(X^{1,0}))^{m-1} p_1[-M X^{1,1}] = (\operatorname {\mathrm {Ad}} p_1(X^{1,0}))^{m-1} D_{1}$
, while equation (17) and the commutator identity (52) imply
![]() $(\operatorname {\mathrm {Ad}} p_1(X^{1,0})) D_{10^k} = [p_1(X^{1,0}),\, D_{10^k}] = -(1/M)[D_0, D_{10^k}] = D_{10^{k+1}}$
, and therefore
$(\operatorname {\mathrm {Ad}} p_1(X^{1,0})) D_{10^k} = [p_1(X^{1,0}),\, D_{10^k}] = -(1/M)[D_0, D_{10^k}] = D_{10^{k+1}}$
, and therefore
![]() $(\operatorname {\mathrm {Ad}} p_{1}(X^{1,0}))^{m-1} D_{1} = D_{10^{m-1}}$
.
$(\operatorname {\mathrm {Ad}} p_{1}(X^{1,0}))^{m-1} D_{1} = D_{10^{m-1}}$
.
Using the involution
![]() $\Phi $
, we can deduce the
$\Phi $
, we can deduce the
![]() $m=1$
case from the
$m=1$
case from the
![]() $n=1$
case:
$n=1$
case:
For
![]() $m, n> 1$
, we proceed by induction, assuming that the result holds for paths from
$m, n> 1$
, we proceed by induction, assuming that the result holds for paths from
![]() $(0,n')$
to
$(0,n')$
to
![]() $(m',0)$
when
$(m',0)$
when
![]() $m'\leq m$
and
$m'\leq m$
and
![]() $n'\leq n$
and
$n'\leq n$
and
![]() $(m',n')\not =(m,n)$
.
$(m',n')\not =(m,n)$
.
For a given
![]() $m,n$
, there are finitely many admissible paths
$m,n$
, there are finitely many admissible paths
![]() $\gamma $
, and thus a finite-dimensional space V of linear combinations
$\gamma $
, and thus a finite-dimensional space V of linear combinations
![]() $\sum _{\gamma } c_{\gamma } D_{\gamma }$
involving these paths. Let
$\sum _{\gamma } c_{\gamma } D_{\gamma }$
involving these paths. Let
![]() $V'\subseteq V$
denote the subspace consisting of linear combinations which form the left-hand side of a valid instance of the identity
$V'\subseteq V$
denote the subspace consisting of linear combinations which form the left-hand side of a valid instance of the identity
Note that
![]() $V'=V$
if and only if
$V'=V$
if and only if
![]() $D_{\gamma } = E_{\gamma }$
for all the paths
$D_{\gamma } = E_{\gamma }$
for all the paths
![]() $\gamma $
in question.
$\gamma $
in question.
We will use the induction hypothesis to construct enough instances of equation (65) to reduce each
![]() $D_{\gamma }$
modulo
$D_{\gamma }$
modulo
![]() $V'$
to a scalar multiple of
$V'$
to a scalar multiple of
![]() $D_{\gamma _{0}}$
, where
$D_{\gamma _{0}}$
, where
![]() $\gamma _0$
is the path with a south run from
$\gamma _0$
is the path with a south run from
![]() $(0,n)$
to
$(0,n)$
to
![]() $(0,0)$
followed by an east run to
$(0,0)$
followed by an east run to
![]() $(m,0)$
. We will then prove one more instance of equation (65) for which the left-hand side reduces to a nonzero scalar multiple of
$(m,0)$
. We will then prove one more instance of equation (65) for which the left-hand side reduces to a nonzero scalar multiple of
![]() $D_{\gamma _{0}}$
, showing that
$D_{\gamma _{0}}$
, showing that
![]() $V' = V$
.
$V' = V$
.
Suppose now that
![]() $\gamma \not =\gamma _{0}$
. Then
$\gamma \not =\gamma _{0}$
. Then
![]() $\gamma $
contains an east step from
$\gamma $
contains an east step from
![]() $(m_1-1, n_2)$
to
$(m_1-1, n_2)$
to
![]() $(m_1, n_2)$
and a south step from
$(m_1, n_2)$
and a south step from
![]() $(m_1, n_2)$
to
$(m_1, n_2)$
to
![]() $(m_1, n_2-1)$
for some
$(m_1, n_2-1)$
for some
![]() $m_1+m_2=m$
and
$m_1+m_2=m$
and
![]() $n_1+n_2=n$
. In particular,
$n_1+n_2=n$
. In particular,
![]() $\gamma = \nu \cdot \eta $
for shorter admissible paths
$\gamma = \nu \cdot \eta $
for shorter admissible paths
![]() $\nu $
and
$\nu $
and
![]() $\eta $
, where
$\eta $
, where
![]() $\nu \cdot \eta $
is defined to be the lattice path obtained by placing
$\nu \cdot \eta $
is defined to be the lattice path obtained by placing
![]() $\nu $
and
$\nu $
and
![]() $\eta $
end to end; thus,
$\eta $
end to end; thus,
![]() $\nu \cdot \eta $
traces a copy of
$\nu \cdot \eta $
traces a copy of
![]() $\nu $
from
$\nu $
from
![]() $(0,n_1 + n_2)$
to
$(0,n_1 + n_2)$
to
![]() $(m_1,n_2) $
and then traces a copy of
$(m_1,n_2) $
and then traces a copy of
![]() $\eta $
from
$\eta $
from
![]() $(m_1, n_2)$
to
$(m_1, n_2)$
to
![]() $(m_1 + m_2,0)$
.
$(m_1 + m_2,0)$
.
Define
![]() $\gamma '=\nu \cdot ' \eta $
to be the admissible path obtained from
$\gamma '=\nu \cdot ' \eta $
to be the admissible path obtained from
![]() $\nu \cdot \eta $
by replacing the east-south corner at
$\nu \cdot \eta $
by replacing the east-south corner at
![]() $(m_1,n_2)$
with a south-east corner at
$(m_1,n_2)$
with a south-east corner at
![]() $(m_1-1,n_2 -1)$
;
$(m_1-1,n_2 -1)$
;
![]() $\gamma '$
contains a south step from
$\gamma '$
contains a south step from
![]() $(m_1-1, n_2)$
to
$(m_1-1, n_2)$
to
![]() $(m_1-1, n_2-1)$
and an east step from
$(m_1-1, n_2-1)$
and an east step from
![]() $(m_1 -1, n_2 -1)$
to
$(m_1 -1, n_2 -1)$
to
![]() $(m_1 , n_2-1)$
.
$(m_1 , n_2-1)$
.
The product formulas (47) and (48) imply that the elements corresponding to the paths constructed in this way satisfy
By induction,
![]() $D_{\nu }=E_{\nu }$
and
$D_{\nu }=E_{\nu }$
and
![]() $D_{\eta } =E_{\eta }$
, so equation (66) implies
$D_{\eta } =E_{\eta }$
, so equation (66) implies
![]() $D_{\gamma } - q\, t\, D_{\gamma '} = E_{\gamma } - q\, t\, E_{\gamma '}$
. In other words, in terms of the space
$D_{\gamma } - q\, t\, D_{\gamma '} = E_{\gamma } - q\, t\, E_{\gamma '}$
. In other words, in terms of the space
![]() $V'$
defined above, we have
$V'$
defined above, we have
![]() $D_{\gamma } \equiv q\, t\, D_{\gamma '} \pmod {V'}$
. Using this repeatedly, we obtain
$D_{\gamma } \equiv q\, t\, D_{\gamma '} \pmod {V'}$
. Using this repeatedly, we obtain
![]() $D_{\gamma }\equiv (q\, t)^{h(\gamma )} D_{\gamma _{0}}\pmod {V'}$
for every path
$D_{\gamma }\equiv (q\, t)^{h(\gamma )} D_{\gamma _{0}}\pmod {V'}$
for every path
![]() $\gamma $
, where
$\gamma $
, where
![]() $h(\gamma )$
is the area enclosed by the path
$h(\gamma )$
is the area enclosed by the path
![]() $\gamma $
and the x and y axes.
$\gamma $
and the x and y axes.
To complete the proof it suffices to establish one more identity of the form (65), for which the congruences
![]() $D_{\gamma }\equiv (q\, t)^{h(\gamma )} D_{\gamma _{0}}\pmod {V'}$
reduce the left-hand side to a nonzero scalar multiple of
$D_{\gamma }\equiv (q\, t)^{h(\gamma )} D_{\gamma _{0}}\pmod {V'}$
reduce the left-hand side to a nonzero scalar multiple of
![]() $D_{\gamma _{0}}$
.
$D_{\gamma _{0}}$
.
We can assume by induction that
![]() $D_{n,0^{m-2}} = E_{0^{n-1},m-1}$
since this case has the same n and a smaller m. Taking the commutator with
$D_{n,0^{m-2}} = E_{0^{n-1},m-1}$
since this case has the same n and a smaller m. Taking the commutator with
![]() $p_{1}(X^{1,0})$
on both sides gives
$p_{1}(X^{1,0})$
on both sides gives
Using equation (52) on the left-hand side and equation (50) on the right-hand side gives
 $$ \begin{align} \sum\limits_{k=0}^{n-1}D_{(n-k,k,0^{m-2})} = \sum\limits_{k = 0}^{n-1} E_{(0^{n-1},m-1)+\varepsilon_{n-k}}. \end{align} $$
$$ \begin{align} \sum\limits_{k=0}^{n-1}D_{(n-k,k,0^{m-2})} = \sum\limits_{k = 0}^{n-1} E_{(0^{n-1},m-1)+\varepsilon_{n-k}}. \end{align} $$
Now, for
![]() $1\leq k\leq n-1$
, we have
$1\leq k\leq n-1$
, we have
![]() $D_{(n-k,k,0^{m-2})} = D_{\gamma }$
and
$D_{(n-k,k,0^{m-2})} = D_{\gamma }$
and
![]() $E_{(0^{n-1}, m-1)+\varepsilon _{n-k}} = E_{\gamma }$
for an admissible path with
$E_{(0^{n-1}, m-1)+\varepsilon _{n-k}} = E_{\gamma }$
for an admissible path with
![]() $h(\gamma ) = k$
, as displayed below.
$h(\gamma ) = k$
, as displayed below.

This shows that equation (68) is an instance of equation (65). The previous congruences reduce the left-hand side of (68) to
![]() $(1+q\, t+\cdots +(q\, t)^{n-1}) D_{\gamma _{0}}$
. Since the coefficient is nonzero, we have now established a set of instances of equation (65) whose left-hand sides span V.
$(1+q\, t+\cdots +(q\, t)^{n-1}) D_{\gamma _{0}}$
. Since the coefficient is nonzero, we have now established a set of instances of equation (65) whose left-hand sides span V.
Corollary 4.3.4. For any indices
![]() $a_1, \dots , a_l$
, we have
$a_1, \dots , a_l$
, we have
Proof. To rephrase, we are to show that
![]() $E_{a_{l}, \ldots , a_{2}, a_{1}}\cdot 1$
does not depend on
$E_{a_{l}, \ldots , a_{2}, a_{1}}\cdot 1$
does not depend on
![]() $a_{1}$
. The symmetry
$a_{1}$
. The symmetry
![]() $f(X^{m,n})\mapsto f(X^{m+rn,n})$
of
$f(X^{m,n})\mapsto f(X^{m+rn,n})$
of
![]() $\Phi ({\mathcal E} ^{+})$
sends
$\Phi ({\mathcal E} ^{+})$
sends
![]() $E_{a_{l},\ldots ,a_{1}}$
to
$E_{a_{l},\ldots ,a_{1}}$
to
![]() $E_{a_{l}+r,\ldots ,a_{1}+r}$
. By [Reference Blasiak, Haiman, Morse, Pun and Seelinger2, Lemma 3.4.1], the action of
$E_{a_{l}+r,\ldots ,a_{1}+r}$
. By [Reference Blasiak, Haiman, Morse, Pun and Seelinger2, Lemma 3.4.1], the action of
![]() ${\mathcal E} $
on
${\mathcal E} $
on
![]() $\Lambda $
satisfies
$\Lambda $
satisfies
![]() $\nabla ^{r} f(X^{m,n}) \nabla ^{-r} = f(X^{m+rn,n})$
, and since
$\nabla ^{r} f(X^{m,n}) \nabla ^{-r} = f(X^{m+rn,n})$
, and since
![]() $\nabla (1) = 1$
, this gives
$\nabla (1) = 1$
, this gives
![]() $\nabla ^{r} E_{a_{l}, \ldots , a_{2}, a_{1}}\cdot 1 = E_{a_{l}+r, \ldots , a_{2}+r, a_{1}+r}\cdot 1$
. Hence, we can reduce to the case that
$\nabla ^{r} E_{a_{l}, \ldots , a_{2}, a_{1}}\cdot 1 = E_{a_{l}+r, \ldots , a_{2}+r, a_{1}+r}\cdot 1$
. Hence, we can reduce to the case that
![]() $a_{i}>0$
for all i.
$a_{i}>0$
for all i.
By [Reference Blasiak, Haiman, Morse, Pun and Seelinger2, Lemma 3.6.2], we have that
![]() $D_{b_{1},\ldots ,b_{n},0,\ldots ,0} \cdot 1$
is independent of the number of trailing zeroes. In the case that
$D_{b_{1},\ldots ,b_{n},0,\ldots ,0} \cdot 1$
is independent of the number of trailing zeroes. In the case that
![]() $b_{i}\geq 0$
for all i and
$b_{i}\geq 0$
for all i and
![]() $b_{1}>0$
, this and Proposition 4.3.3 imply that
$b_{1}>0$
, this and Proposition 4.3.3 imply that
![]() $E_{a_{l},\ldots ,a_{1}}\cdot 1$
is independent of
$E_{a_{l},\ldots ,a_{1}}\cdot 1$
is independent of
![]() $a_{1}$
, provided that
$a_{1}$
, provided that
![]() $a_{i}\geq 0$
for all i and
$a_{i}\geq 0$
for all i and
![]() $a_{1}>0$
. However, we already saw that this suffices.
$a_{1}>0$
. However, we already saw that this suffices.
4.4 Shuffling the symmetric function side of the extended delta conjecture
We can now give the promised reformulation of (7).
Theorem 4.4.1. For
![]() $0\leq l<m\leq N$
, we have
$0\leq l<m\leq N$
, we have
where
and
![]() $\overline {e_l(x_2,\ldots ,x_{m})} = e_l(x_2^{-1},\ldots ,x_{m}^{-1})$
by our convention on the use of the overbar.
$\overline {e_l(x_2,\ldots ,x_{m})} = e_l(x_2^{-1},\ldots ,x_{m}^{-1})$
by our convention on the use of the overbar.
Proof. For any symmetric function f set
![]() $g(X) = (\omega f)[X+1/M]$
; then equation (31) gives an identity in
$g(X) = (\omega f)[X+1/M]$
; then equation (31) gives an identity in
![]() $\Lambda $
for every
$\Lambda $
for every
![]() $\zeta \in {\mathcal E} $
$\zeta \in {\mathcal E} $
where
![]() $g[X+Y] = \sum g_{(1)}(X)g_{(2)}(Y)$
in Sweedler notation and we used the general formula
$g[X+Y] = \sum g_{(1)}(X)g_{(2)}(Y)$
in Sweedler notation and we used the general formula
![]() $g \,\zeta = \sum ((\operatorname {\mathrm {Ad}} g_{(1)}) \zeta )g_{(2)}$
. Since
$g \,\zeta = \sum ((\operatorname {\mathrm {Ad}} g_{(1)}) \zeta )g_{(2)}$
. Since
![]() $g[X+Y] = (\omega f)[X+Y+1/M]$
, and
$g[X+Y] = (\omega f)[X+Y+1/M]$
, and
![]() $h[B]\cdot 1 = h[0]\cdot 1$
for any
$h[B]\cdot 1 = h[0]\cdot 1$
for any
![]() $h(X)$
, the right-hand side of equation (72) is equal to
$h(X)$
, the right-hand side of equation (72) is equal to
 $$ \begin{align} \sum &((\operatorname{\mathrm{Ad}} \, (\omega f)_{(1)}(X^{1,0}))\, \zeta )\, (\omega f)_{(2)}[X^{1,0}+1/M] \cdot 1 \notag \\ &\qquad\qquad\qquad = \sum ((\operatorname{\mathrm{Ad}} \, (\omega f)_{(1)}(X^{1,0}))\, \zeta )\, (\omega f)_{(2)}[0] \cdot 1 = ((\operatorname{\mathrm{Ad}} \, (\omega f)(X^{1,0}))\, \zeta )\cdot 1. \end{align} $$
$$ \begin{align} \sum &((\operatorname{\mathrm{Ad}} \, (\omega f)_{(1)}(X^{1,0}))\, \zeta )\, (\omega f)_{(2)}[X^{1,0}+1/M] \cdot 1 \notag \\ &\qquad\qquad\qquad = \sum ((\operatorname{\mathrm{Ad}} \, (\omega f)_{(1)}(X^{1,0}))\, \zeta )\, (\omega f)_{(2)}[0] \cdot 1 = ((\operatorname{\mathrm{Ad}} \, (\omega f)(X^{1,0}))\, \zeta )\cdot 1. \end{align} $$
Let
![]() $n=N-l$
. Taking
$n=N-l$
. Taking
![]() $\zeta = E_{a_{n},\ldots ,a_{1}}$
and using equation (50), this gives
$\zeta = E_{a_{n},\ldots ,a_{1}}$
and using equation (50), this gives
By Corollary 4.3.4, the right-hand side is a function of
![]() $f(z_{n},\ldots ,z_{2},1)$
since the substitution for the monomial
$f(z_{n},\ldots ,z_{2},1)$
since the substitution for the monomial
![]() $z^{\mathbf {r}}$
does not depend on the exponent
$z^{\mathbf {r}}$
does not depend on the exponent
![]() $r_{1}$
. Expressing
$r_{1}$
. Expressing
![]() $f(z_{n},\ldots ,z_{2},1)$
as
$f(z_{n},\ldots ,z_{2},1)$
as
![]() $f[z_{n}+\cdots +z_{2}+1]$
and then substituting
$f[z_{n}+\cdots +z_{2}+1]$
and then substituting
![]() $f[X-1]$
for
$f[X-1]$
for
![]() $f(X)$
yields
$f(X)$
yields
By [Reference Negut19, Proposition 6.7],
![]() $E_{0^n} = \Phi (D_{0^n}) = \Phi (e_n[-MX^{1,0}]) = e_n[-MX^{0,1}]$
(see also [Reference Blasiak, Haiman, Morse, Pun and Seelinger2, Proposition 3.6.1]).
$E_{0^n} = \Phi (D_{0^n}) = \Phi (e_n[-MX^{1,0}]) = e_n[-MX^{0,1}]$
(see also [Reference Blasiak, Haiman, Morse, Pun and Seelinger2, Proposition 3.6.1]).
Using equation (75), we therefore obtain
 $$ \begin{align} e_{k-1}[B-1]e_n =e_{k-1} [z_n+\cdots+z_2] \mathbin{\Big|} z_n^{r_n}\cdots z_2^{r_2}&\mapsto E_{r_n, \ldots, r_2, 0} \cdot 1 \notag\\ &=\sum\limits_{|I|=k-1} E_{\varepsilon_I,0}\cdot 1 = \sum\limits_{|I|=k-1} E_{\varepsilon_I,1}\cdot 1\,, \end{align} $$
$$ \begin{align} e_{k-1}[B-1]e_n =e_{k-1} [z_n+\cdots+z_2] \mathbin{\Big|} z_n^{r_n}\cdots z_2^{r_2}&\mapsto E_{r_n, \ldots, r_2, 0} \cdot 1 \notag\\ &=\sum\limits_{|I|=k-1} E_{\varepsilon_I,0}\cdot 1 = \sum\limits_{|I|=k-1} E_{\varepsilon_I,1}\cdot 1\,, \end{align} $$
where the sum is over subsets
![]() $I\subseteq [n-1]$
and
$I\subseteq [n-1]$
and
![]() $\varepsilon _{I} = \sum _{i\in I}\varepsilon _{i}$
. The terms in the last sum are just
$\varepsilon _{I} = \sum _{i\in I}\varepsilon _{i}$
. The terms in the last sum are just
![]() $E_{{\mathbf a}(\nu )}\cdot 1$
for paths
$E_{{\mathbf a}(\nu )}\cdot 1$
for paths
![]() $\nu $
from
$\nu $
from
![]() $(0,n)$
to
$(0,n)$
to
![]() $(k,0)$
with single east steps on any
$(k,0)$
with single east steps on any
![]() $k-1$
chosen lines
$k-1$
chosen lines
![]() $y=j$
for
$y=j$
for
![]() $j\in [n-1]$
, and a final east step at
$j\in [n-1]$
, and a final east step at
![]() $y = 0$
. Denote the set of these admissible paths by
$y = 0$
. Denote the set of these admissible paths by
![]() $\mathcal P_{k,n}$
. For instance, with
$\mathcal P_{k,n}$
. For instance, with
![]() $n=8$
and
$n=8$
and
![]() $k=4$
, the path
$k=4$
, the path
![]() $\gamma $
in Example 4.3.2 corresponds to
$\gamma $
in Example 4.3.2 corresponds to
![]() $E_{\gamma } = E_{0,1,1,0,0,1,0,1}$
.
$E_{\gamma } = E_{0,1,1,0,0,1,0,1}$
.
By equation (74), applying
![]() $h_l[B]$
to equation (76) gives
$h_l[B]$
to equation (76) gives
 $$ \begin{align} h_l[B]e_{k-1}[B-1]e_n = \sum_{\nu\in\mathcal P_{k,n}} \; \sum_{\substack{{\mathbf r} \in\mathbb N^{n} \\ |{\mathbf r} |=l}} E_{{\mathbf r} +{\mathbf a}(\nu)}\cdot 1 \,. \end{align} $$
$$ \begin{align} h_l[B]e_{k-1}[B-1]e_n = \sum_{\nu\in\mathcal P_{k,n}} \; \sum_{\substack{{\mathbf r} \in\mathbb N^{n} \\ |{\mathbf r} |=l}} E_{{\mathbf r} +{\mathbf a}(\nu)}\cdot 1 \,. \end{align} $$
This last expression is the sum of
![]() $E_{\gamma }\cdot 1$
over admissible paths
$E_{\gamma }\cdot 1$
over admissible paths
![]() $\gamma $
from
$\gamma $
from
![]() $(0,n)$
to
$(0,n)$
to
![]() $(k+l,0)$
, together with a choice of
$(k+l,0)$
, together with a choice of
![]() $k-1$
indices
$k-1$
indices
![]() $j\in [n-1]$
for which
$j\in [n-1]$
for which
![]() $\gamma $
has at least one east step on the line
$\gamma $
has at least one east step on the line
![]() $y = j$
. We can consider these indices as distinguishing
$y = j$
. We can consider these indices as distinguishing
![]() $k-1$
east-south corners in
$k-1$
east-south corners in
![]() $\gamma $
. However, we can also distinguish these corners by their x coordinates, that is, by a set of
$\gamma $
. However, we can also distinguish these corners by their x coordinates, that is, by a set of
![]() $k-1$
indices
$k-1$
indices
![]() $i\in [k+l-1]$
for which
$i\in [k+l-1]$
for which
![]() $\gamma $
has at least one south step on the line
$\gamma $
has at least one south step on the line
![]() $x = i$
. Setting
$x = i$
. Setting
![]() $m = k+l$
and using Proposition 4.3.3, this yields the identity
$m = k+l$
and using Proposition 4.3.3, this yields the identity
 $$ \begin{align} h_l[B] e_{m-l-1}[B-1] e_n = \sum_{\substack{{\mathbf s} \in {\mathbb N}^{m}: |{\mathbf s} |=n-k \\ I\subseteq [2,m],|I|=l}} D_{{\mathbf s} + (1^{m})-\varepsilon_I}\cdot 1 \,. \end{align} $$
$$ \begin{align} h_l[B] e_{m-l-1}[B-1] e_n = \sum_{\substack{{\mathbf s} \in {\mathbb N}^{m}: |{\mathbf s} |=n-k \\ I\subseteq [2,m],|I|=l}} D_{{\mathbf s} + (1^{m})-\varepsilon_I}\cdot 1 \,. \end{align} $$
Now, since
 $$ \begin{align} \sum _{\substack{{\mathbf s} \in {\mathbb N} ^{m}: |{\mathbf s}|=n-k \\ I\subseteq [2,m],|I|=l}} {x^{{\mathbf s} + (1^{m}) - \varepsilon_I}} = x_1\, x_2 \cdots x_{m} h_{n-k}(x_1,\ldots, x_{m})\overline{e_l(x_2,\ldots,x_{m})}\,, \end{align} $$
$$ \begin{align} \sum _{\substack{{\mathbf s} \in {\mathbb N} ^{m}: |{\mathbf s}|=n-k \\ I\subseteq [2,m],|I|=l}} {x^{{\mathbf s} + (1^{m}) - \varepsilon_I}} = x_1\, x_2 \cdots x_{m} h_{n-k}(x_1,\ldots, x_{m})\overline{e_l(x_2,\ldots,x_{m})}\,, \end{align} $$
the definition of
![]() $D_{{\mathbf b} }$
and Proposition 3.3.2 imply that
$D_{{\mathbf b} }$
and Proposition 3.3.2 imply that
 $$ \begin{align} \omega \biggl(\, \, \sum_{\substack{{\mathbf s} \in {\mathbb N}^{m}: |{\mathbf s} |=n-k \\ I\subseteq [2,m],|I|=l}} D_{{\mathbf s} + (1^{m})-\varepsilon_I}\cdot 1 \biggr)(x_{1},\ldots,x_{m}) = {\mathbf H} ^{m}_{q,t}(\phi (x))_{\operatorname{\mathrm{pol}} } \end{align} $$
$$ \begin{align} \omega \biggl(\, \, \sum_{\substack{{\mathbf s} \in {\mathbb N}^{m}: |{\mathbf s} |=n-k \\ I\subseteq [2,m],|I|=l}} D_{{\mathbf s} + (1^{m})-\varepsilon_I}\cdot 1 \biggr)(x_{1},\ldots,x_{m}) = {\mathbf H} ^{m}_{q,t}(\phi (x))_{\operatorname{\mathrm{pol}} } \end{align} $$
with
![]() $\phi (x)$
given by equation (71).
$\phi (x)$
given by equation (71).
Remark 4.4.2. For any
![]() $\mathbf {b}\in {\mathbb Z}^m$
, [Reference Blasiak, Haiman, Morse, Pun and Seelinger2, Corollary 3.7.2] gives that the Schur expansion of
$\mathbf {b}\in {\mathbb Z}^m$
, [Reference Blasiak, Haiman, Morse, Pun and Seelinger2, Corollary 3.7.2] gives that the Schur expansion of
![]() $\omega (D_{\mathbf {b}}\cdot 1)$
involves only
$\omega (D_{\mathbf {b}}\cdot 1)$
involves only
![]() $s_{\lambda }(X)$
with
$s_{\lambda }(X)$
with
![]() $\ell (\lambda )\leq m$
. Hence, although Theorem 4.4.1 is a statement in m variables, it determines
$\ell (\lambda )\leq m$
. Hence, although Theorem 4.4.1 is a statement in m variables, it determines
![]() $\omega ( h_l[B]e_{m-l-1}[B-1] e_{N-l})$
by equation (78).
$\omega ( h_l[B]e_{m-l-1}[B-1] e_{N-l})$
by equation (78).
5 Reformulation of the combinatorial side
5.1 Statement of the reformulation
We reformulate (14) by explicitly extracting the coefficient of
![]() $z^{N-m}$
. The most natural form of the resulting expression involves a generating function
$z^{N-m}$
. The most natural form of the resulting expression involves a generating function
![]() $N_{\beta /\alpha }$
for q-weighted tableaux rather than partially labelled paths. For now, we work only with the tableau description of
$N_{\beta /\alpha }$
for q-weighted tableaux rather than partially labelled paths. For now, we work only with the tableau description of
![]() $N_{\beta /\alpha }$
, but in §6.2, we will see that
$N_{\beta /\alpha }$
, but in §6.2, we will see that
![]() $N_{\beta /\alpha }$
is a truncation of an LLT series introduced by Grojnowski and Haiman in [Reference Grojnowski and Haiman12].
$N_{\beta /\alpha }$
is a truncation of an LLT series introduced by Grojnowski and Haiman in [Reference Grojnowski and Haiman12].
The q-weight in our reformulation involves two auxiliary statistics: for
![]() $\eta ,\tau \in {\mathbb N}^m$
, define
$\eta ,\tau \in {\mathbb N}^m$
, define
 $$ \begin{align} d(\eta,\tau) = \sum_{1 \leq j < r \leq m} \big| [\eta_{j},\eta_{j}+\tau_j] \cap [\eta_{r},\eta_{r}+\tau_r-1] \big| \,, \end{align} $$
$$ \begin{align} d(\eta,\tau) = \sum_{1 \leq j < r \leq m} \big| [\eta_{j},\eta_{j}+\tau_j] \cap [\eta_{r},\eta_{r}+\tau_r-1] \big| \,, \end{align} $$
with
![]() $[a,b]=\{a,\ldots ,b\}$
and
$[a,b]=\{a,\ldots ,b\}$
and
![]() $[b]=[1,b]$
, and for a vector
$[b]=[1,b]$
, and for a vector
![]() $\eta $
of length n and
$\eta $
of length n and
![]() $I\subseteq [n]$
, define
$I\subseteq [n]$
, define
where
![]() $(r<s)$
denotes a pair of positions
$(r<s)$
denotes a pair of positions
![]() $(r,s)$
in
$(r,s)$
in
![]() $\eta $
with
$\eta $
with
![]() $1\leq r<s\leq n$
.
$1\leq r<s\leq n$
.
Our reformulation of (14) is stated in the following theorem, proven at the end of this section.
Theorem 5.1.1. For
![]() $0\leq l < m\leq N$
, we have
$0\leq l < m\leq N$
, we have
 $$ \begin{align} \langle z^{N-m}\rangle & \sum_{\substack{\lambda\in\mathbf {D}_{N}\\ P\in{\mathbf {L}}_{N,l}(\lambda)}} t^{|\delta/\lambda|}\,\prod_{\substack{1<i\leq N\\ c_i(\lambda)=c_{i-1}(\lambda)+1}} (1+z\,t^{-c_i(\lambda)})\ q^{\mathrm{dinv}(P)}x^{\operatorname{\mathrm{wt}}_+(P)} \notag \\&\qquad\qquad = \sum_{\substack{J \subseteq [m-1]\\ |J|=l}} \, \sum_{\substack{\tau,(0,{\mathbf a})\in \mathbb N^{m}\\ |\tau|=N-m}} t^{|{\mathbf a}|} q^{d((0,{\mathbf a}),\tau)+h_J({\mathbf a})} N_{((0,{\mathbf a})+(1^{m})+\tau )/(({\mathbf a},0)+\varepsilon_J)}(X;q)\,, \end{align} $$
$$ \begin{align} \langle z^{N-m}\rangle & \sum_{\substack{\lambda\in\mathbf {D}_{N}\\ P\in{\mathbf {L}}_{N,l}(\lambda)}} t^{|\delta/\lambda|}\,\prod_{\substack{1<i\leq N\\ c_i(\lambda)=c_{i-1}(\lambda)+1}} (1+z\,t^{-c_i(\lambda)})\ q^{\mathrm{dinv}(P)}x^{\operatorname{\mathrm{wt}}_+(P)} \notag \\&\qquad\qquad = \sum_{\substack{J \subseteq [m-1]\\ |J|=l}} \, \sum_{\substack{\tau,(0,{\mathbf a})\in \mathbb N^{m}\\ |\tau|=N-m}} t^{|{\mathbf a}|} q^{d((0,{\mathbf a}),\tau)+h_J({\mathbf a})} N_{((0,{\mathbf a})+(1^{m})+\tau )/(({\mathbf a},0)+\varepsilon_J)}(X;q)\,, \end{align} $$
where
![]() $N_{\beta /\alpha }$
is given by Definition 5.2.1 below.
$N_{\beta /\alpha }$
is given by Definition 5.2.1 below.
5.2 Definition of
 $N_{\beta /\alpha }$
$N_{\beta /\alpha }$
For
![]() $\alpha ,\beta \in {\mathbb Z} ^{l}$
such that
$\alpha ,\beta \in {\mathbb Z} ^{l}$
such that
![]() $\alpha _{j}\leq \beta _{j}$
for all j, define
$\alpha _{j}\leq \beta _{j}$
for all j, define
![]() $\beta /\alpha $
to be the tuple of single row skew shapes
$\beta /\alpha $
to be the tuple of single row skew shapes
![]() $(\beta _{j})/(\alpha _{j})$
such that the x coordinates of the right edges of boxes a in the j-th row are the integers
$(\beta _{j})/(\alpha _{j})$
such that the x coordinates of the right edges of boxes a in the j-th row are the integers
![]() $\alpha _{j}+1,\ldots ,\beta _{j}$
. The boxes just outside the j-th row, adjacent to the left and right ends of the row, then have x coordinates
$\alpha _{j}+1,\ldots ,\beta _{j}$
. The boxes just outside the j-th row, adjacent to the left and right ends of the row, then have x coordinates
![]() $\alpha _{j}$
and
$\alpha _{j}$
and
![]() $\beta _{j}+1$
. We consider these two boxes to be adjacent to the ends of an empty row, with
$\beta _{j}+1$
. We consider these two boxes to be adjacent to the ends of an empty row, with
![]() $\alpha _{j} = \beta _{j}$
, as well.
$\alpha _{j} = \beta _{j}$
, as well.
Given a tuple of skew row shapes
![]() $\beta /\alpha $
, three boxes
$\beta /\alpha $
, three boxes
![]() $(u,v,w)$
form a
$(u,v,w)$
form a
![]() $w_0$
-triple when box v is in row r of
$w_0$
-triple when box v is in row r of
![]() $\beta /\alpha $
, boxes u and w are in or adjacent to a row j with
$\beta /\alpha $
, boxes u and w are in or adjacent to a row j with
![]() $j>r$
and the x-coordinates
$j>r$
and the x-coordinates
![]() $i_u, i_v, i_w$
of these boxes satisfy
$i_u, i_v, i_w$
of these boxes satisfy
![]() $i_u=i_{v}$
and
$i_u=i_{v}$
and
![]() $i_w=i_v+1$
. These triples are a special case of
$i_w=i_v+1$
. These triples are a special case of
![]() $\sigma $
-triples defined for any
$\sigma $
-triples defined for any
![]() $\sigma \in S_l$
in [Reference Blasiak, Haiman, Morse, Pun and Seelinger2]. We denote the number of
$\sigma \in S_l$
in [Reference Blasiak, Haiman, Morse, Pun and Seelinger2]. We denote the number of
![]() $w_0$
-triples in
$w_0$
-triples in
![]() $\beta /\alpha $
by
$\beta /\alpha $
by
![]() $h_{w_0}(\beta /\alpha )$
. The reader can verify that
$h_{w_0}(\beta /\alpha )$
. The reader can verify that
For a totally ordered alphabet
![]() ${\mathcal A}$
, a row strict tableau of shape
${\mathcal A}$
, a row strict tableau of shape
![]() $\beta /\alpha $
is a map
$\beta /\alpha $
is a map
![]() $S \colon \beta /\alpha \to {\mathcal A}$
that is strictly increasing on each row. The set of these maps is denoted by
$S \colon \beta /\alpha \to {\mathcal A}$
that is strictly increasing on each row. The set of these maps is denoted by
![]() $\operatorname {\mathrm {RST}}(\beta /\alpha ,{\mathcal A})$
. For convenience, given
$\operatorname {\mathrm {RST}}(\beta /\alpha ,{\mathcal A})$
. For convenience, given
![]() $\alpha ,\beta \in {\mathbb Z} ^{l}$
with some
$\alpha ,\beta \in {\mathbb Z} ^{l}$
with some
![]() $\alpha _{j}> \beta _{j}$
, we set
$\alpha _{j}> \beta _{j}$
, we set
![]() $\operatorname {\mathrm {RST}}(\beta /\alpha ,{\mathcal A}) = \varnothing $
.
$\operatorname {\mathrm {RST}}(\beta /\alpha ,{\mathcal A}) = \varnothing $
.
A
![]() $w_0$
-triple
$w_0$
-triple
![]() $(u,v,w)$
is an increasing
$(u,v,w)$
is an increasing
![]() $w_0$
-triple in S if
$w_0$
-triple in S if
![]() $S(u) < S(v) < S(w)$
, with the convention that
$S(u) < S(v) < S(w)$
, with the convention that
![]() $S(u) = -\infty $
if u is adjacent to the left end of a row of
$S(u) = -\infty $
if u is adjacent to the left end of a row of
![]() $\beta /\alpha $
and
$\beta /\alpha $
and
![]() $S(w) = \infty $
if w is adjacent to the right end of a row. Let
$S(w) = \infty $
if w is adjacent to the right end of a row. Let
![]() $h_{w_0}(S)$
be the number of increasing
$h_{w_0}(S)$
be the number of increasing
![]() $w_0$
-triples in S.
$w_0$
-triples in S.
For
![]() $S \in \operatorname {\mathrm {RST}}(\beta /\alpha ,{\mathbb N})$
, define
$S \in \operatorname {\mathrm {RST}}(\beta /\alpha ,{\mathbb N})$
, define
 $$ \begin{align} x^{\operatorname{\mathrm{wt}}_+(S)} = \prod_{u \in \beta/\alpha, \, S(u) \neq 0} x_{S(u)}\qquad\text{and}\qquad x^{\operatorname{\mathrm{wt}}(S)} = \prod_{u \in \beta/\alpha} x_{S(u)}\,. \end{align} $$
$$ \begin{align} x^{\operatorname{\mathrm{wt}}_+(S)} = \prod_{u \in \beta/\alpha, \, S(u) \neq 0} x_{S(u)}\qquad\text{and}\qquad x^{\operatorname{\mathrm{wt}}(S)} = \prod_{u \in \beta/\alpha} x_{S(u)}\,. \end{align} $$
Definition 5.2.1. For
![]() $\alpha ,\beta \in {\mathbb N}^{m}$
, define
$\alpha ,\beta \in {\mathbb N}^{m}$
, define
 $$ \begin{align} N_{\beta/\alpha} = N_{\beta/\alpha}(X;q) = \sum_{S \in \operatorname{\mathrm{RST}}(\beta/\alpha, {\mathbb Z} _{>0} )} q^{h_{w_0}(S)} x^{\operatorname{\mathrm{wt}}(S)}\,. \end{align} $$
$$ \begin{align} N_{\beta/\alpha} = N_{\beta/\alpha}(X;q) = \sum_{S \in \operatorname{\mathrm{RST}}(\beta/\alpha, {\mathbb Z} _{>0} )} q^{h_{w_0}(S)} x^{\operatorname{\mathrm{wt}}(S)}\,. \end{align} $$
Note that, if
![]() $\alpha _{j}> \beta _{j}$
for any j, then
$\alpha _{j}> \beta _{j}$
for any j, then
![]() $N_{\beta /\alpha }=0$
by our convention that
$N_{\beta /\alpha }=0$
by our convention that
![]() $\operatorname {\mathrm {RST}}(\beta /\alpha ,{\mathcal A}) = \varnothing $
.
$\operatorname {\mathrm {RST}}(\beta /\alpha ,{\mathcal A}) = \varnothing $
.
Remark 5.2.2. It is shown in [Reference Blasiak, Haiman, Morse, Pun and Seelinger2, Proposition 4.5.2] and its proof that, for
![]() $\alpha ,\beta \in {\mathbb N}^{m}$
,
$\alpha ,\beta \in {\mathbb N}^{m}$
,
![]() $\omega N_{\beta /\alpha }$
is a symmetric function whose Schur expansion involves only
$\omega N_{\beta /\alpha }$
is a symmetric function whose Schur expansion involves only
![]() $s_{\lambda }$
where
$s_{\lambda }$
where
![]() $\ell (\lambda )\leq m$
.
$\ell (\lambda )\leq m$
.
5.3 Transforming the combinatorial side
To prove equation (83), we first associate each Dyck path with a tuple of row shapes recording vertical runs.
Definition 5.3.1. The LLT data associated to a path
![]() $\lambda \in \mathbf {D}_N$
are
$\lambda \in \mathbf {D}_N$
are
where
![]() $c_{i}(\lambda )$
counts lattice squares between
$c_{i}(\lambda )$
counts lattice squares between
![]() $\lambda $
and the line segment connecting
$\lambda $
and the line segment connecting
![]() $(0,N)$
to
$(0,N)$
to
![]() $(N,0)$
in column i, numbered from right to left, as in Lemma 2.2.4.
$(N,0)$
in column i, numbered from right to left, as in Lemma 2.2.4.
Figure 2 shows the LLT data
![]() $\beta ,\alpha $
associated to the path
$\beta ,\alpha $
associated to the path
![]() $\lambda $
in Figure 1. Note that
$\lambda $
in Figure 1. Note that
![]() $\beta _i$
(resp.
$\beta _i$
(resp.
![]() $\alpha _i$
) is the furthest (resp. closest) distance from the diagonal to the path
$\alpha _i$
) is the furthest (resp. closest) distance from the diagonal to the path
![]() $\lambda $
on the line
$\lambda $
on the line
![]() $x = N-i$
so that
$x = N-i$
so that
![]() $\beta _i-\alpha _i$
is the number of south steps of
$\beta _i-\alpha _i$
is the number of south steps of
![]() $\lambda $
on that line.
$\lambda $
on that line.

Figure 2 For
![]() $\beta =(12211123233)$
,
$\beta =(12211123233)$
,
![]() $\alpha =(11000121220)$
, there are
$\alpha =(11000121220)$
, there are
![]() $h_{w_0}(\beta /\alpha )=29 \ w_0$
-triples in
$h_{w_0}(\beta /\alpha )=29 \ w_0$
-triples in
![]() $\beta /\alpha $
. The row strict tableau S of shape
$\beta /\alpha $
. The row strict tableau S of shape
![]() $\beta /\alpha $
has
$\beta /\alpha $
has
![]() $h_{w_0}(S)=15$
increasing
$h_{w_0}(S)=15$
increasing
![]() $w_0$
-triples,
$w_0$
-triples,
![]() $x^{\operatorname {\mathrm {wt}}_+(S)} \!= x_1^2 x_2 x_3^2 x_4^2 x_5 x_6$
, and
$x^{\operatorname {\mathrm {wt}}_+(S)} \!= x_1^2 x_2 x_3^2 x_4^2 x_5 x_6$
, and
![]() $x^{\operatorname {\mathrm {wt}}(S)} = x_0^2 x_1^2 x_2 x_3^2 x_4^2 x_5 x_6$
.
$x^{\operatorname {\mathrm {wt}}(S)} = x_0^2 x_1^2 x_2 x_3^2 x_4^2 x_5 x_6$
.
This association allows us to relate q-weighted sums over partial labellings to the
![]() $N_{\beta /\alpha }$
.
$N_{\beta /\alpha }$
.
Lemma 5.3.2. For
![]() $\lambda \in \mathbf {D}_{N}$
and its associated LLT data
$\lambda \in \mathbf {D}_{N}$
and its associated LLT data
![]() $\alpha ,\beta $
, we have
$\alpha ,\beta $
, we have
 $$ \begin{align} \sum_{P\in{\mathbf {L}}_{N,l}(\lambda)} q^{\operatorname{\mathrm{dinv}}(P)} x^{\operatorname{\mathrm{wt}}_+(P)} = \sum_{\substack{I\subseteq [N-1] \\ |I|=l}} q^{h_I(\alpha)} N_{\beta/(\alpha+\varepsilon_I)}(X;q)\,. \end{align} $$
$$ \begin{align} \sum_{P\in{\mathbf {L}}_{N,l}(\lambda)} q^{\operatorname{\mathrm{dinv}}(P)} x^{\operatorname{\mathrm{wt}}_+(P)} = \sum_{\substack{I\subseteq [N-1] \\ |I|=l}} q^{h_I(\alpha)} N_{\beta/(\alpha+\varepsilon_I)}(X;q)\,. \end{align} $$
Proof. There is a natural weight-preserving bijection mapping
![]() $P \in {\mathbf {L}}_N(\lambda )$
to
$P \in {\mathbf {L}}_N(\lambda )$
to
![]() $S \in \operatorname {\mathrm {RST}}(\beta /\alpha ,{\mathbb N})$
, where the labels of column
$S \in \operatorname {\mathrm {RST}}(\beta /\alpha ,{\mathbb N})$
, where the labels of column
![]() $x=i$
of P, read north to south, are placed into row
$x=i$
of P, read north to south, are placed into row
![]() $N-i$
of
$N-i$
of
![]() $\beta /\alpha $
, west to east. See Figures 1 and 2. Moreover,
$\beta /\alpha $
, west to east. See Figures 1 and 2. Moreover,
![]() $\operatorname {\mathrm {dinv}}(P) = h_{w_0}(S)$
. To see this, let
$\operatorname {\mathrm {dinv}}(P) = h_{w_0}(S)$
. To see this, let
![]() $\hat P$
be the same labelling as P but with the ordering on letters taken to be
$\hat P$
be the same labelling as P but with the ordering on letters taken to be
![]() $0>1>2\cdots $
. It is proven in [Reference Blasiak, Haiman, Morse, Pun and Seelinger2, Proposition 6.1.1] that
$0>1>2\cdots $
. It is proven in [Reference Blasiak, Haiman, Morse, Pun and Seelinger2, Proposition 6.1.1] that
![]() $\operatorname {\mathrm {dinv}}_1(\hat P) = h_{w_0}(S)$
, where
$\operatorname {\mathrm {dinv}}_1(\hat P) = h_{w_0}(S)$
, where
![]() $\operatorname {\mathrm {dinv}}_1(\hat P)$
was introduced in [Reference Haglund, Haiman, Loehr, Remmel and Ulyanov13] and matches
$\operatorname {\mathrm {dinv}}_1(\hat P)$
was introduced in [Reference Haglund, Haiman, Loehr, Remmel and Ulyanov13] and matches
![]() $\operatorname {\mathrm {dinv}}(P)$
as discussed in Remark 2.2.3. The bijection restricts to a bijection from
$\operatorname {\mathrm {dinv}}(P)$
as discussed in Remark 2.2.3. The bijection restricts to a bijection from
![]() ${\mathbf {L}}_{N,l}(\lambda )$
to the subset of tableaux
${\mathbf {L}}_{N,l}(\lambda )$
to the subset of tableaux
![]() $S \in \operatorname {\mathrm {RST}}(\beta /\alpha ,{\mathbb N})$
with exactly l 0’s, none in row N. This gives
$S \in \operatorname {\mathrm {RST}}(\beta /\alpha ,{\mathbb N})$
with exactly l 0’s, none in row N. This gives
 $$ \begin{align} \sum_{P\in{\mathbf {L}}_{N,l}(\lambda)} q^{\operatorname{\mathrm{dinv}}(P)} x^{\operatorname{\mathrm{wt}}_+(P)} = \sum_{\substack{I\subseteq [N-1]\\ |I|=l }} \sum_{\substack{S\in\operatorname{\mathrm{RST}}(\beta/\alpha, {\mathbb N})\\ 0\text{ in rows }i\in I}} q^{h_{w_0}(S)} x^{\operatorname{\mathrm{wt}}_+(S)} \,. \end{align} $$
$$ \begin{align} \sum_{P\in{\mathbf {L}}_{N,l}(\lambda)} q^{\operatorname{\mathrm{dinv}}(P)} x^{\operatorname{\mathrm{wt}}_+(P)} = \sum_{\substack{I\subseteq [N-1]\\ |I|=l }} \sum_{\substack{S\in\operatorname{\mathrm{RST}}(\beta/\alpha, {\mathbb N})\\ 0\text{ in rows }i\in I}} q^{h_{w_0}(S)} x^{\operatorname{\mathrm{wt}}_+(S)} \,. \end{align} $$
The claim then follows from Definition 5.2.1 and the following Lemma.
Lemma 5.3.3. For
![]() $\alpha ,\beta \in {\mathbb N}^{N}$
and
$\alpha ,\beta \in {\mathbb N}^{N}$
and
![]() $S \in \operatorname {\mathrm {RST}}(\beta /\alpha ,{\mathbb N})$
, let
$S \in \operatorname {\mathrm {RST}}(\beta /\alpha ,{\mathbb N})$
, let
![]() $I\subseteq [N]$
be the rows of S containing a zero and let T be the tableau in
$I\subseteq [N]$
be the rows of S containing a zero and let T be the tableau in
![]() $\operatorname {\mathrm {RST}}(\beta /(\alpha +\varepsilon _I), {\mathbb Z} _{>0} )$
obtained by deleting all zeros from S. Then
$\operatorname {\mathrm {RST}}(\beta /(\alpha +\varepsilon _I), {\mathbb Z} _{>0} )$
obtained by deleting all zeros from S. Then
where
![]() $h_I(\alpha )$
is defined in equation (82).
$h_I(\alpha )$
is defined in equation (82).
Proof. Consider an increasing
![]() $w_0$
-triple
$w_0$
-triple
![]() $(u,v,w)$
of S; the entries satisfy
$(u,v,w)$
of S; the entries satisfy
![]() $S(u)<S(v)<S(w)$
, v lies in some row r and both u and w lie in a row
$S(u)<S(v)<S(w)$
, v lies in some row r and both u and w lie in a row
![]() $j>r$
. When
$j>r$
. When
![]() $r\not \in I$
, either
$r\not \in I$
, either
![]() $j\not \in I$
so that
$j\not \in I$
so that
![]() $(u,v,w)$
is an increasing
$(u,v,w)$
is an increasing
![]() $w_0$
-triple of T with the same entries as S, or
$w_0$
-triple of T with the same entries as S, or
![]() $j\in I$
and
$j\in I$
and
![]() $S(u)=0$
changes to
$S(u)=0$
changes to
![]() $T(u)=-\infty $
where still
$T(u)=-\infty $
where still
![]() $(u,v,w)$
is an increasing
$(u,v,w)$
is an increasing
![]() $w_0$
-triple of T. However, if
$w_0$
-triple of T. However, if
![]() $r\in I$
,
$r\in I$
,
![]() $S(v)=0$
changes to
$S(v)=0$
changes to
![]() $T(v)=-\infty $
and thus
$T(v)=-\infty $
and thus
![]() $(u,v,w)$
is not an increasing
$(u,v,w)$
is not an increasing
![]() $w_0$
-triple of T. Note the increasing condition implies that this happens only when
$w_0$
-triple of T. Note the increasing condition implies that this happens only when
![]() $j\not \in I$
and
$j\not \in I$
and
![]() $\alpha _r=\alpha _j-1$
since
$\alpha _r=\alpha _j-1$
since
![]() $S(u)<0<S(w)$
. Thus (89) follows.
$S(u)<0<S(w)$
. Thus (89) follows.
Definition 5.3.4. Given
![]() ${\mathbf a}=(a_1,\ldots ,a_{m-1})\in {\mathbb N}^{m-1}$
and
${\mathbf a}=(a_1,\ldots ,a_{m-1})\in {\mathbb N}^{m-1}$
and
![]() $\tau = (\tau _1,\ldots ,\tau _{m}) \in {\mathbb N}^{m}$
, we define two sequences
$\tau = (\tau _1,\ldots ,\tau _{m}) \in {\mathbb N}^{m}$
, we define two sequences
![]() $\beta _{{\mathbf a} \tau }$
and
$\beta _{{\mathbf a} \tau }$
and
![]() $\alpha _{{\mathbf a} \tau }$
of length
$\alpha _{{\mathbf a} \tau }$
of length
![]() $|\tau |+m$
as follows.
$|\tau |+m$
as follows.
The sequence
![]() $\beta _{{\mathbf a} \tau }$
is the concatenation of sequences
$\beta _{{\mathbf a} \tau }$
is the concatenation of sequences
![]() $(1,2,\ldots ,\tau _{1}+1)$
and
$(1,2,\ldots ,\tau _{1}+1)$
and
![]() $(a_{i-1}+1, a_{i-1}+2, \ldots , a_{i-1}+\tau _{i}+1)$
for
$(a_{i-1}+1, a_{i-1}+2, \ldots , a_{i-1}+\tau _{i}+1)$
for
![]() $i=2,\ldots ,m$
. The sequence
$i=2,\ldots ,m$
. The sequence
![]() $\alpha _{{\mathbf a} \tau }$
is the same as
$\alpha _{{\mathbf a} \tau }$
is the same as
![]() $\beta _{{\mathbf a} \tau }$
except in the positions corresponding to the ends of the concatenated subsequences. In these positions, we change the entries
$\beta _{{\mathbf a} \tau }$
except in the positions corresponding to the ends of the concatenated subsequences. In these positions, we change the entries
![]() $\tau _{1}+1, a_{1}+\tau _{2}+1 ,\ldots ,a_{m-1}+\tau _{m}+1 $
in
$\tau _{1}+1, a_{1}+\tau _{2}+1 ,\ldots ,a_{m-1}+\tau _{m}+1 $
in
![]() $\beta _{{\mathbf a} \tau }$
to
$\beta _{{\mathbf a} \tau }$
to
![]() $a_{1}, a_{2},\ldots , a_{m-1}, 0$
. Equivalently,
$a_{1}, a_{2},\ldots , a_{m-1}, 0$
. Equivalently,
![]() $\alpha _{{\mathbf a} \tau }$
is the same as the sequence obtained by subtracting
$\alpha _{{\mathbf a} \tau }$
is the same as the sequence obtained by subtracting
![]() $1$
from all entries of
$1$
from all entries of
![]() $\beta _{{\mathbf a} \tau }$
and shifting one place to the left, deleting the first entry and adding a zero at the end.
$\beta _{{\mathbf a} \tau }$
and shifting one place to the left, deleting the first entry and adding a zero at the end.
Example 5.3.5. For
![]() ${\mathbf a}=(130012)$
and
${\mathbf a}=(130012)$
and
![]() $\tau = (2311022)$
,
$\tau = (2311022)$
,

The wider spaces show the division into blocks of size
![]() $\tau _i+1$
. The last entry of
$\tau _i+1$
. The last entry of
![]() $\alpha _{{\mathbf a} \tau }$
in each block is
$\alpha _{{\mathbf a} \tau }$
in each block is
![]() $a_i$
, and the next block in
$a_i$
, and the next block in
![]() $\alpha _{{\mathbf a} \tau }$
and
$\alpha _{{\mathbf a} \tau }$
and
![]() $\beta _{{\mathbf a} \tau }$
starts with
$\beta _{{\mathbf a} \tau }$
starts with
![]() $a_i+1$
.
$a_i+1$
.
Lemma 5.3.6. For
![]() $0\leq l<m\le N$
,
$0\leq l<m\le N$
,
 $$ \begin{align} \langle z^{N-m}\rangle\!\!\! \sum_{\substack{\lambda\in \mathbf {D} _{N}\\ P\in{\mathbf {L}}_{N,l}(\lambda)}} t^{|\delta/\lambda|} &\prod_{\substack{1 <i \leq N \\ c_i(\lambda) = c_{i-1}(\lambda)+1}} (1+z\,t^{-c_i(\lambda)})\, q^{\operatorname{\mathrm{dinv}}(P)} x^{\operatorname{\mathrm{wt}}_+(P)} \notag \\ &\qquad\qquad= \sum_{\substack{I\subseteq [N-1]\\ |I|=l}} \, \sum_{\substack{\tau, \, (0,{\mathbf a})\, \in \, {\mathbb N}^{m}\\ |\tau|=N-m}} t^{|{\mathbf a}|} q^{h_I(\alpha_{{\mathbf a}\tau})} N_{\beta_{{\mathbf a}\tau}/(\alpha_{{\mathbf a}\tau}+\varepsilon_I)}(X;q)\,. \end{align} $$
$$ \begin{align} \langle z^{N-m}\rangle\!\!\! \sum_{\substack{\lambda\in \mathbf {D} _{N}\\ P\in{\mathbf {L}}_{N,l}(\lambda)}} t^{|\delta/\lambda|} &\prod_{\substack{1 <i \leq N \\ c_i(\lambda) = c_{i-1}(\lambda)+1}} (1+z\,t^{-c_i(\lambda)})\, q^{\operatorname{\mathrm{dinv}}(P)} x^{\operatorname{\mathrm{wt}}_+(P)} \notag \\ &\qquad\qquad= \sum_{\substack{I\subseteq [N-1]\\ |I|=l}} \, \sum_{\substack{\tau, \, (0,{\mathbf a})\, \in \, {\mathbb N}^{m}\\ |\tau|=N-m}} t^{|{\mathbf a}|} q^{h_I(\alpha_{{\mathbf a}\tau})} N_{\beta_{{\mathbf a}\tau}/(\alpha_{{\mathbf a}\tau}+\varepsilon_I)}(X;q)\,. \end{align} $$
Proof. Use Lemma 5.3.2 to rewrite the left-hand side of equation (91) as
 $$ \begin{align} \langle z^{N-m}\rangle \sum_{\lambda\in\mathbf {D}_{N}} t^{|\delta/\lambda|} \prod_{\substack{1 <i \leq N \\ c_i(\lambda) = c_{i-1}(\lambda)+1}} (1+z\,t^{-c_i(\lambda)}) \sum_{\substack{I\subseteq [N-1]\\ |I|=l}} q^{h_I(\alpha)}N_{\beta/(\alpha+\varepsilon_I),} \end{align} $$
$$ \begin{align} \langle z^{N-m}\rangle \sum_{\lambda\in\mathbf {D}_{N}} t^{|\delta/\lambda|} \prod_{\substack{1 <i \leq N \\ c_i(\lambda) = c_{i-1}(\lambda)+1}} (1+z\,t^{-c_i(\lambda)}) \sum_{\substack{I\subseteq [N-1]\\ |I|=l}} q^{h_I(\alpha)}N_{\beta/(\alpha+\varepsilon_I),} \end{align} $$
where
![]() $\beta = (1^{N})+(0,c_2(\lambda ),\ldots ,c_{N}(\lambda ))$
,
$\beta = (1^{N})+(0,c_2(\lambda ),\ldots ,c_{N}(\lambda ))$
,
![]() $\alpha = (c_2(\lambda ),\ldots ,c_{N}(\lambda ),0)$
are the LLT data for
$\alpha = (c_2(\lambda ),\ldots ,c_{N}(\lambda ),0)$
are the LLT data for
![]() $\lambda $
. Note that a tuple
$\lambda $
. Note that a tuple
![]() $\mathbf c=(c_1,c_2,\ldots ,c_{N}) \in {\mathbb N}^N$
is the sequence of column heights
$\mathbf c=(c_1,c_2,\ldots ,c_{N}) \in {\mathbb N}^N$
is the sequence of column heights
![]() $c_{i}(\lambda )$
of a path
$c_{i}(\lambda )$
of a path
![]() $\lambda \in \mathbf {D}_{N}$
if and only if
$\lambda \in \mathbf {D}_{N}$
if and only if
![]() $c_s\leq c_{s-1}+1$
for all
$c_s\leq c_{s-1}+1$
for all
![]() $s>1$
and
$s>1$
and
![]() $c_1=0$
; in this case,
$c_1=0$
; in this case,
![]() $|\delta /\lambda |=|\mathbf c|$
. Replace
$|\delta /\lambda |=|\mathbf c|$
. Replace
![]() $\mathbf {D}_{N}$
in equation (92) by these tuples, and expand the product to obtain
$\mathbf {D}_{N}$
in equation (92) by these tuples, and expand the product to obtain
 $$ \begin{align} \langle z^{N-m}\rangle \sum_{A\subseteq [N]\setminus \{1\}}\,\, &\sum_{\substack{c_i \leq c_{i-1}+1 \ \forall i \\ c_i = c_{i-1}+1 \ \forall i \in A}} \!\!\! t^{|\mathbf c|-\sum_{i\in A}c_i} \, z^{|A|} \sum _{\substack{I\subseteq [N-1]\\ |I|=l}} q^{h_I(\alpha)}\,N_{\beta/(\alpha+\varepsilon_I)} \notag\\ &\qquad\qquad\quad = \sum_{\substack{\{1\} \subseteq J\subseteq [N] \\ |J| = m}} \,\, \sum_{c_j = c_{j-1}+1 \ \forall j \notin J } \!\! t^{\sum_{j\in J}c_j} \sum_{\substack{I\subseteq [N-1]\\ |I|=l}} q^{h_I(\alpha)}\,N_{\beta/(\alpha+\varepsilon_I)}\,, \end{align} $$
$$ \begin{align} \langle z^{N-m}\rangle \sum_{A\subseteq [N]\setminus \{1\}}\,\, &\sum_{\substack{c_i \leq c_{i-1}+1 \ \forall i \\ c_i = c_{i-1}+1 \ \forall i \in A}} \!\!\! t^{|\mathbf c|-\sum_{i\in A}c_i} \, z^{|A|} \sum _{\substack{I\subseteq [N-1]\\ |I|=l}} q^{h_I(\alpha)}\,N_{\beta/(\alpha+\varepsilon_I)} \notag\\ &\qquad\qquad\quad = \sum_{\substack{\{1\} \subseteq J\subseteq [N] \\ |J| = m}} \,\, \sum_{c_j = c_{j-1}+1 \ \forall j \notin J } \!\! t^{\sum_{j\in J}c_j} \sum_{\substack{I\subseteq [N-1]\\ |I|=l}} q^{h_I(\alpha)}\,N_{\beta/(\alpha+\varepsilon_I)}\,, \end{align} $$
where the equality comes from reindexing with
![]() $J = [N]\setminus A$
and noting that we can drop the condition
$J = [N]\setminus A$
and noting that we can drop the condition
![]() $c_j \leq c_{j-1}+1 \ \forall j\in J$
because
$c_j \leq c_{j-1}+1 \ \forall j\in J$
because
![]() $N_{\beta /(\alpha +\varepsilon _I)}=0$
if any
$N_{\beta /(\alpha +\varepsilon _I)}=0$
if any
![]() $(\alpha +\varepsilon _I)_j\geq \alpha _j>\beta _j$
.
$(\alpha +\varepsilon _I)_j\geq \alpha _j>\beta _j$
.
If we replace the sum over J by a sum over
![]() $\{\tau \in {\mathbb N}^m : |\tau |=N-m\}$
using
$\{\tau \in {\mathbb N}^m : |\tau |=N-m\}$
using
![]() $J= \{1,\tau _1+2,\tau _1+\tau _2+3,\ldots ,\tau _1+\cdots +\tau _{m-1}+m\}$
, then, for fixed J (or fixed
$J= \{1,\tau _1+2,\tau _1+\tau _2+3,\ldots ,\tau _1+\cdots +\tau _{m-1}+m\}$
, then, for fixed J (or fixed
![]() $\tau $
), the sum over
$\tau $
), the sum over
![]() $\mathbf {c}$
can be replaced by a sum over
$\mathbf {c}$
can be replaced by a sum over
for
![]() $\mathbf a$
ranging over
$\mathbf a$
ranging over
![]() ${\mathbb N}^{m-1}$
. Note that
${\mathbb N}^{m-1}$
. Note that
![]() $\sum _{j\in J} c_j = |{\mathbf a}|$
. With this encoding of
$\sum _{j\in J} c_j = |{\mathbf a}|$
. With this encoding of
![]() $\mathbf {c}$
, we have
$\mathbf {c}$
, we have
![]() $\beta /\alpha = \beta _{{\mathbf a}\tau }/\alpha _{{\mathbf a}\tau }$
in the notation of Definition 5.3.4, and the quantity in equation (93) becomes the right-hand side of equation (91).
$\beta /\alpha = \beta _{{\mathbf a}\tau }/\alpha _{{\mathbf a}\tau }$
in the notation of Definition 5.3.4, and the quantity in equation (93) becomes the right-hand side of equation (91).
We make a final adjustment to the right-hand side of equation (91). This sum runs over tuples
![]() $\beta _{{\mathbf a}\tau }/(\alpha _{{\mathbf a}\tau }+\varepsilon _I)$
with
$\beta _{{\mathbf a}\tau }/(\alpha _{{\mathbf a}\tau }+\varepsilon _I)$
with
![]() $|\tau |$
necessarily empty rows which can be removed at the cost of a q factor. We introduce some notation depending on a given
$|\tau |$
necessarily empty rows which can be removed at the cost of a q factor. We introduce some notation depending on a given
![]() ${\mathbf a}\in {\mathbb N}^{m-1}$
,
${\mathbf a}\in {\mathbb N}^{m-1}$
,
![]() $\tau =(\tau _1,\ldots ,\tau _{m})\in {\mathbb N}^{m}$
, and the associated
$\tau =(\tau _1,\ldots ,\tau _{m})\in {\mathbb N}^{m}$
, and the associated
![]() $\beta _{{\mathbf a}\tau }/\alpha _{{\mathbf a}\tau }$
from Definition 5.3.4. First, we set
$\beta _{{\mathbf a}\tau }/\alpha _{{\mathbf a}\tau }$
from Definition 5.3.4. First, we set
![]() $j_{\uparrow }=j+\sum _{x\leq j}\tau _x$
for
$j_{\uparrow }=j+\sum _{x\leq j}\tau _x$
for
![]() $j\in [m]$
, so the entry of
$j\in [m]$
, so the entry of
![]() $\beta _{{\mathbf a} \tau }$
in position
$\beta _{{\mathbf a} \tau }$
in position
![]() $j_{\uparrow }$
is
$j_{\uparrow }$
is
![]() $a_{j-1}+\tau _{j}+1$
, or
$a_{j-1}+\tau _{j}+1$
, or
![]() $\tau _{1}+1$
if
$\tau _{1}+1$
if
![]() $j = 1$
, and the entry of
$j = 1$
, and the entry of
![]() $\alpha _{{\mathbf a} \tau }$
in the same position is
$\alpha _{{\mathbf a} \tau }$
in the same position is
![]() $a_{j}$
or
$a_{j}$
or
![]() $0$
if
$0$
if
![]() $j = m$
. For a subset
$j = m$
. For a subset
![]() $J\subseteq [m]$
, we set
$J\subseteq [m]$
, we set
![]() $J_{\uparrow } = \{j_{\uparrow }: j\in J\}$
. In positions
$J_{\uparrow } = \{j_{\uparrow }: j\in J\}$
. In positions
![]() $i\not \in [m]_{\uparrow }$
, the sequences
$i\not \in [m]_{\uparrow }$
, the sequences
![]() $\beta _{{\mathbf a} \tau }$
and
$\beta _{{\mathbf a} \tau }$
and
![]() $ \alpha _{{\mathbf a} \tau }$
agree, so row i is empty in
$ \alpha _{{\mathbf a} \tau }$
agree, so row i is empty in
![]() $\beta _{{\mathbf a}\tau } /\alpha _{{\mathbf a}\tau } $
. The tuple of row shapes obtained by deleting these empty rows from
$\beta _{{\mathbf a}\tau } /\alpha _{{\mathbf a}\tau } $
. The tuple of row shapes obtained by deleting these empty rows from
![]() $\beta _{{\mathbf a} \tau }/\alpha _{{\mathbf a} \tau }$
is
$\beta _{{\mathbf a} \tau }/\alpha _{{\mathbf a} \tau }$
is
![]() $((0,{\mathbf a})+(1^m)+\tau )/({\mathbf a},0)$
, where row
$((0,{\mathbf a})+(1^m)+\tau )/({\mathbf a},0)$
, where row
![]() $j\in [m]$
corresponds to row
$j\in [m]$
corresponds to row
![]() $j_{\uparrow }$
of
$j_{\uparrow }$
of
![]() $\beta _{{\mathbf a} \tau }/\alpha _{{\mathbf a} \tau }$
; note that rows
$\beta _{{\mathbf a} \tau }/\alpha _{{\mathbf a} \tau }$
; note that rows
![]() $(j-1)_{\uparrow }$
and
$(j-1)_{\uparrow }$
and
![]() $j_{\uparrow }$
are separated by
$j_{\uparrow }$
are separated by
![]() $\tau _j$
empty rows. See Figure 3.
$\tau _j$
empty rows. See Figure 3.

Figure 3 Comparing the tuples of rows
![]() $\beta _{{\mathbf a} \tau }/\alpha _{{\mathbf a} \tau }$
and
$\beta _{{\mathbf a} \tau }/\alpha _{{\mathbf a} \tau }$
and
![]() $((0,{\mathbf a})+(1^m)+\tau )/({\mathbf a},0)$
for
$((0,{\mathbf a})+(1^m)+\tau )/({\mathbf a},0)$
for
![]() ${\mathbf a} \in {\mathbb N}^{m-1}$
and
${\mathbf a} \in {\mathbb N}^{m-1}$
and
![]() $\tau \in {\mathbb N}^m$
. Here,
$\tau \in {\mathbb N}^m$
. Here,
![]() $a_j=2$
,
$a_j=2$
,
![]() $a_{r-1} = 0, a_r = 3$
and
$a_{r-1} = 0, a_r = 3$
and
![]() $\tau _r = 5$
.
$\tau _r = 5$
.
Lemma 5.3.7. For
![]() $J\subseteq [m]$
,
$J\subseteq [m]$
,
![]() ${\mathbf a}\in {\mathbb N}^{m-1}$
and
${\mathbf a}\in {\mathbb N}^{m-1}$
and
![]() $\tau \in {\mathbb N}^m$
, let
$\tau \in {\mathbb N}^m$
, let
![]() $I=J_{\uparrow }$
. Then
$I=J_{\uparrow }$
. Then
where
![]() $h^{\prime }_J({\mathbf a},\tau )=\left |\{(j<r): j\in J, r\in [m],a_j\in [a_{r-1},a_{r-1}+\tau _r-1]\}\right |$
with
$h^{\prime }_J({\mathbf a},\tau )=\left |\{(j<r): j\in J, r\in [m],a_j\in [a_{r-1},a_{r-1}+\tau _r-1]\}\right |$
with
![]() $a_0=0$
, and
$a_0=0$
, and
![]() $d((0,{\mathbf a}),\tau )$
is defined by equation (81).
$d((0,{\mathbf a}),\tau )$
is defined by equation (81).
Proof. Set
![]() $a_0=0$
. We can assume
$a_0=0$
. We can assume
![]() $a_j+(\varepsilon _J)_j \leq a_{j-1}+\tau _j+1$
for all
$a_j+(\varepsilon _J)_j \leq a_{j-1}+\tau _j+1$
for all
![]() $j\in [m]$
since otherwise both sides of equation (95) vanish by Definition 5.2.1. Hence, each side is a q-generating function for row strict tableaux on tuples of single row skew shapes; rows of
$j\in [m]$
since otherwise both sides of equation (95) vanish by Definition 5.2.1. Hence, each side is a q-generating function for row strict tableaux on tuples of single row skew shapes; rows of
![]() $\beta _{{\mathbf a}\tau }/(\alpha _{{\mathbf a}\tau }+\varepsilon _I)$
on the left-hand side differ from the right-hand side only by the removal of empty rows
$\beta _{{\mathbf a}\tau }/(\alpha _{{\mathbf a}\tau }+\varepsilon _I)$
on the left-hand side differ from the right-hand side only by the removal of empty rows
![]() $r\not \in [m]_{\uparrow }$
. Thus, the two sides agree up to a factor
$r\not \in [m]_{\uparrow }$
. Thus, the two sides agree up to a factor
![]() $q^{d}$
, where d counts
$q^{d}$
, where d counts
![]() $w_0$
-triples of
$w_0$
-triples of
![]() $\beta _{{\mathbf a}\tau }/(\alpha _{{\mathbf a}\tau }+\varepsilon _I)$
involving one of these empty rows.
$\beta _{{\mathbf a}\tau }/(\alpha _{{\mathbf a}\tau }+\varepsilon _I)$
involving one of these empty rows.
To evaluate d, consider such an empty row
![]() $(b)/(b)$
, coming from
$(b)/(b)$
, coming from
![]() $b\in \{a_{r-1}+1,\ldots ,a_{r-1}+\tau _r\}$
for some
$b\in \{a_{r-1}+1,\ldots ,a_{r-1}+\tau _r\}$
for some
![]() $r\in [m]$
. The adjacent boxes on the left and right of this empty row form a
$r\in [m]$
. The adjacent boxes on the left and right of this empty row form a
![]() $w_{0}$
-triple, increasing in every tableau, with one box in each nonempty lower row
$w_{0}$
-triple, increasing in every tableau, with one box in each nonempty lower row
![]() $j_{\uparrow }$
, of the form
$j_{\uparrow }$
, of the form
![]() $(a_{j-1}+\tau _j+1)/(a_j+(\varepsilon _J)_j)$
, such that
$(a_{j-1}+\tau _j+1)/(a_j+(\varepsilon _J)_j)$
, such that
![]() $b\in [a_j+(\varepsilon _J)_j +1,a_{j-1}+\tau _j+1]$
. Hence,
$b\in [a_j+(\varepsilon _J)_j +1,a_{j-1}+\tau _j+1]$
. Hence,
 $$ \begin{align*} d & = \sum_{1\leq j<r\leq m} \big| [a_j+(\varepsilon_J)_j ,a_{j-1}+\tau_j] \cap [a_{r-1},a_{r-1}+\tau_r-1] \big| \\ & = \sum_{1\leq j<r\leq m} \big| [a_j,a_{j-1}+\tau_j] \cap [a_{r-1},a_{r-1}+\tau_r-1] \big| - \sum_{\substack{1\leq j<r\leq m \\ j\in J}} \big|\{a_j\}\cap [a_{r-1},a_{r-1}+\tau_r-1] \big|. \end{align*} $$
$$ \begin{align*} d & = \sum_{1\leq j<r\leq m} \big| [a_j+(\varepsilon_J)_j ,a_{j-1}+\tau_j] \cap [a_{r-1},a_{r-1}+\tau_r-1] \big| \\ & = \sum_{1\leq j<r\leq m} \big| [a_j,a_{j-1}+\tau_j] \cap [a_{r-1},a_{r-1}+\tau_r-1] \big| - \sum_{\substack{1\leq j<r\leq m \\ j\in J}} \big|\{a_j\}\cap [a_{r-1},a_{r-1}+\tau_r-1] \big|. \end{align*} $$
The sum after the minus sign is
![]() $h_J'({\mathbf a},\tau )$
. To prove that the remaining sum is
$h_J'({\mathbf a},\tau )$
. To prove that the remaining sum is
![]() $d((0,{\mathbf a}),\tau )$
, first rewrite it as
$d((0,{\mathbf a}),\tau )$
, first rewrite it as
 $$ \begin{align} \! \sum_{1\leq j<r \leq m} \!\!\! \left( \big| [a_j,\infty) \cap [a_{r-1},a_{r-1}+\tau_r-1] \big|- \big| [a_{j-1}+\tau_j+1,\infty) \cap [a_{r-1},a_{r-1}+\tau_r-1] \big|\right),\! \end{align} $$
$$ \begin{align} \! \sum_{1\leq j<r \leq m} \!\!\! \left( \big| [a_j,\infty) \cap [a_{r-1},a_{r-1}+\tau_r-1] \big|- \big| [a_{j-1}+\tau_j+1,\infty) \cap [a_{r-1},a_{r-1}+\tau_r-1] \big|\right),\! \end{align} $$
using the fact that
![]() $a_{j}\leq a_{j-1}+\tau _{j}+1$
by assumption. Next, observe that since
$a_{j}\leq a_{j-1}+\tau _{j}+1$
by assumption. Next, observe that since
![]() $a_{0} = 0\leq a_{r-1}$
,
$a_{0} = 0\leq a_{r-1}$
,
Adding
![]() $\sum _{1<j<r} \big | [a_{j-1},\infty ) \cap [a_{r-1},a_{r-1}+\tau _r-1] \big |$
to both sides, it follows that
$\sum _{1<j<r} \big | [a_{j-1},\infty ) \cap [a_{r-1},a_{r-1}+\tau _r-1] \big |$
to both sides, it follows that
 $$ \begin{align*} \sum_{1\leq j<r} \big| [a_{j},\infty) \cap [a_{r-1},a_{r-1}+\tau_r-1] \big| = \sum_{1\leq j<r} \big| [a_{j-1},\infty) \cap [a_{r-1},a_{r-1}+\tau_r-1] \big|. \end{align*} $$
$$ \begin{align*} \sum_{1\leq j<r} \big| [a_{j},\infty) \cap [a_{r-1},a_{r-1}+\tau_r-1] \big| = \sum_{1\leq j<r} \big| [a_{j-1},\infty) \cap [a_{r-1},a_{r-1}+\tau_r-1] \big|. \end{align*} $$
Hence, formula (96) is unchanged upon replacing
![]() $[a_j,\infty )$
with
$[a_j,\infty )$
with
![]() $[a_{j-1},\infty )$
and is thus equal to
$[a_{j-1},\infty )$
and is thus equal to
 $$ \begin{align*} \sum_{1\leq j<r\leq m} \big|[a_{j-1},a_{j-1}+\tau_j]\cap [a_{r-1},a_{r-1}+\tau_r-1]\big| = d((0,{\mathbf a}),\tau).\\[-46pt] \end{align*} $$
$$ \begin{align*} \sum_{1\leq j<r\leq m} \big|[a_{j-1},a_{j-1}+\tau_j]\cap [a_{r-1},a_{r-1}+\tau_r-1]\big| = d((0,{\mathbf a}),\tau).\\[-46pt] \end{align*} $$
Proof of Theorem 5.1.1.
Consider a summand
![]() $t^{|{\mathbf a}|} q^{h_I(\alpha _{{\mathbf a}\tau })} N_{\beta _{{\mathbf a}\tau }/(\alpha _{{\mathbf a}\tau }+\varepsilon _I)}$
on the right-hand side of identity (91) for
$t^{|{\mathbf a}|} q^{h_I(\alpha _{{\mathbf a}\tau })} N_{\beta _{{\mathbf a}\tau }/(\alpha _{{\mathbf a}\tau }+\varepsilon _I)}$
on the right-hand side of identity (91) for
![]() $I\subseteq [N-1]$
,
$I\subseteq [N-1]$
,
![]() ${\mathbf a}\in {\mathbb N}^{m-1}$
,
${\mathbf a}\in {\mathbb N}^{m-1}$
,
![]() $\tau \in {\mathbb N}^m$
. It vanishes unless
$\tau \in {\mathbb N}^m$
. It vanishes unless
![]() $I=J_{\uparrow }$
for some
$I=J_{\uparrow }$
for some
![]() $J\subseteq [m-1]$
since
$J\subseteq [m-1]$
since
![]() $N_{\beta /(\alpha +\varepsilon _I)}=0$
when
$N_{\beta /(\alpha +\varepsilon _I)}=0$
when
![]() $(\alpha +\varepsilon _I)_i>\beta _i$
for some index i. For
$(\alpha +\varepsilon _I)_i>\beta _i$
for some index i. For
![]() $I=J_{\uparrow }$
, we can use Lemma 5.3.7 to replace this summand with
$I=J_{\uparrow }$
, we can use Lemma 5.3.7 to replace this summand with
![]() $t^{|{\mathbf a}|} q^{d((0,{\mathbf a}),\tau ) + h_{I}(\alpha _{{\mathbf a}\tau }) - h^{\prime }_J({\mathbf a},\tau )} N_{((0,{\mathbf a}) + (1^{m})+\tau ) / (({\mathbf a},0)+\varepsilon _J)}$
.
$t^{|{\mathbf a}|} q^{d((0,{\mathbf a}),\tau ) + h_{I}(\alpha _{{\mathbf a}\tau }) - h^{\prime }_J({\mathbf a},\tau )} N_{((0,{\mathbf a}) + (1^{m})+\tau ) / (({\mathbf a},0)+\varepsilon _J)}$
.
It now suffices to prove that, for
![]() $\alpha =\alpha _{{\mathbf a}\tau }$
,
$\alpha =\alpha _{{\mathbf a}\tau }$
,
We recall that
![]() $N=m_{\uparrow }$
and note that
$N=m_{\uparrow }$
and note that
![]() $[N]\setminus I =([N]\setminus [m]_{\uparrow } )\sqcup ([m]_{\uparrow }\setminus I) =([N]\setminus [m]_{\uparrow }) \sqcup ([m]\setminus J)_{\uparrow }$
. Hence,
$[N]\setminus I =([N]\setminus [m]_{\uparrow } )\sqcup ([m]_{\uparrow }\setminus I) =([N]\setminus [m]_{\uparrow }) \sqcup ([m]\setminus J)_{\uparrow }$
. Hence,
![]() $h_I(\alpha )=\left | \{(x<y): x\in I, y\in [N]\setminus I,\alpha _y=\alpha _x+1\} \right | =\left |S_1\right |+\left |S_2\right |$
for
$h_I(\alpha )=\left | \{(x<y): x\in I, y\in [N]\setminus I,\alpha _y=\alpha _x+1\} \right | =\left |S_1\right |+\left |S_2\right |$
for
 $$ \begin{align*} S_1 & = \{(x<y): x\in J_{\uparrow},\, y \in [N]\setminus [m]_{\uparrow},\, \alpha_y=\alpha_x+1\}\, ,\\ S_2 & = \{(x<y): x\in J_{\uparrow},\, y\in ([m]\setminus J)_{\uparrow},\, \alpha_y=\alpha_x+1\}\,. \end{align*} $$
$$ \begin{align*} S_1 & = \{(x<y): x\in J_{\uparrow},\, y \in [N]\setminus [m]_{\uparrow},\, \alpha_y=\alpha_x+1\}\, ,\\ S_2 & = \{(x<y): x\in J_{\uparrow},\, y\in ([m]\setminus J)_{\uparrow},\, \alpha_y=\alpha_x+1\}\,. \end{align*} $$
Since
![]() $\alpha _{m_{\uparrow }}=0$
implies
$\alpha _{m_{\uparrow }}=0$
implies
![]() $(x<m_{\uparrow })\not \in S_2$
for all
$(x<m_{\uparrow })\not \in S_2$
for all
![]() $x<m_{\uparrow }$
, we use that
$x<m_{\uparrow }$
, we use that
![]() $a_u=\alpha _{u_{\uparrow }}$
for every
$a_u=\alpha _{u_{\uparrow }}$
for every
![]() $u\in [m-1]$
to see that
$u\in [m-1]$
to see that
Furthermore,
![]() $\{(j<r):j\in J, r\in [m],a_{r-1}+1\leq a_j+1\leq a_{r-1}+\tau _r\}$
and
$\{(j<r):j\in J, r\in [m],a_{r-1}+1\leq a_j+1\leq a_{r-1}+\tau _r\}$
and
![]() $S_1$
are equinumerous, as we can see by letting a pair
$S_1$
are equinumerous, as we can see by letting a pair
![]() $(j<r)$
in the first set correspond to the pair
$(j<r)$
in the first set correspond to the pair
![]() $(j_{\uparrow }<y)$
in
$(j_{\uparrow }<y)$
in
![]() $S_{1}$
, where y is the unique row index in the range
$S_{1}$
, where y is the unique row index in the range
![]() $(r-1)_{\uparrow }<y<r_{\uparrow }$
such that
$(r-1)_{\uparrow }<y<r_{\uparrow }$
such that
![]() $\alpha _{y} = \alpha _{j_{\uparrow }} +1 = a_j+1$
, as illustrated in Figure 3.
$\alpha _{y} = \alpha _{j_{\uparrow }} +1 = a_j+1$
, as illustrated in Figure 3.
6 Stable unstraightened extended delta theorem
6.1 Overview
By Theorems 4.4.1 and 5.1.1, the extended delta conjecture is equivalent to
 $$ \begin{align} {\mathbf H}^{m}_q &\left( \frac{\prod _{i+1<j\leq m} (1 - q\, t\, x_i/x_j)}{\prod _{i< j\leq m} (1 - t\, x_i/x_j)} x_1\cdots x_{m} h_{N-m}(x_1,\ldots,x_{m}) \overline{e_l(x_2,\ldots,x_{m})} \right)_{\mathrm{pol}}\notag\\ &\qquad\qquad\qquad\qquad= \sum_{\substack{J \subseteq [m-1]\\ |J|=l}} \ \sum_{\substack{(0,{\mathbf a}),\tau\in \mathbb N^{m} \\ |\tau|=N-m}} t^{|{\mathbf a}|} q^{d((0,{\mathbf a}),\tau)+h_J({\mathbf a})} \; \left(\omega N_{\beta/\alpha}\right)(x_1,\ldots,x_{m};q) \,, \end{align} $$
$$ \begin{align} {\mathbf H}^{m}_q &\left( \frac{\prod _{i+1<j\leq m} (1 - q\, t\, x_i/x_j)}{\prod _{i< j\leq m} (1 - t\, x_i/x_j)} x_1\cdots x_{m} h_{N-m}(x_1,\ldots,x_{m}) \overline{e_l(x_2,\ldots,x_{m})} \right)_{\mathrm{pol}}\notag\\ &\qquad\qquad\qquad\qquad= \sum_{\substack{J \subseteq [m-1]\\ |J|=l}} \ \sum_{\substack{(0,{\mathbf a}),\tau\in \mathbb N^{m} \\ |\tau|=N-m}} t^{|{\mathbf a}|} q^{d((0,{\mathbf a}),\tau)+h_J({\mathbf a})} \; \left(\omega N_{\beta/\alpha}\right)(x_1,\ldots,x_{m};q) \,, \end{align} $$
where
![]() $\beta = (0,{\mathbf a})+(1^{m})+\tau $
,
$\beta = (0,{\mathbf a})+(1^{m})+\tau $
,
![]() $\alpha =({\mathbf a},0)+\varepsilon _J$
and
$\alpha =({\mathbf a},0)+\varepsilon _J$
and
![]() $\left (\omega N_{\beta /\alpha }\right )(x_1,\ldots ,x_{m};q)$
is
$\left (\omega N_{\beta /\alpha }\right )(x_1,\ldots ,x_{m};q)$
is
![]() $\omega N_{\beta /\alpha }(X;q)$
evaluated in m variables.
$\omega N_{\beta /\alpha }(X;q)$
evaluated in m variables.
Although this is an identity in only m variables, it does amount to the extended delta conjecture by Remarks 4.4.2 and 5.2.2: Both
![]() $\omega ( h_l[B]e_{m-l-1}[B-1] e_{N-l})$
and
$\omega ( h_l[B]e_{m-l-1}[B-1] e_{N-l})$
and
![]() $\omega N_{\beta /\alpha }(X;q)$
for the
$\omega N_{\beta /\alpha }(X;q)$
for the
![]() $\alpha ,\beta $
arising in equation (99) are linear combinations of Schur functions
$\alpha ,\beta $
arising in equation (99) are linear combinations of Schur functions
![]() $s_{\lambda }$
with
$s_{\lambda }$
with
![]() $\ell (\lambda )\leq m$
.
$\ell (\lambda )\leq m$
.
By Proposition 6.2.2 (below, proven in [Reference Blasiak, Haiman, Morse, Pun and Seelinger2]), the functions
![]() $\omega N_{\beta /\alpha }$
on the right-hand side of equation (99) are the polynomial parts of the ‘LLT series’ introduced in [Reference Grojnowski and Haiman12], making each side of equation (99) the polynomial part of an infinite series of
$\omega N_{\beta /\alpha }$
on the right-hand side of equation (99) are the polynomial parts of the ‘LLT series’ introduced in [Reference Grojnowski and Haiman12], making each side of equation (99) the polynomial part of an infinite series of
![]() $\operatorname {\mathrm {GL}}_m$
characters. We then prove equation (99) as a consequence of a stronger identity between these infinite series.
$\operatorname {\mathrm {GL}}_m$
characters. We then prove equation (99) as a consequence of a stronger identity between these infinite series.
Hereafter, we use x to abbreviate the alphabet
![]() $x_1,\ldots ,x_m$
.
$x_1,\ldots ,x_m$
.
6.2 LLT series
We will work with the (twisted) nonsymmetric Hall–Littlewood polynomials as in [Reference Blasiak, Haiman, Morse, Pun and Seelinger2]. For a
![]() $\operatorname {\mathrm {GL}} _{m}$
weight
$\operatorname {\mathrm {GL}} _{m}$
weight
![]() $\lambda \in {\mathbb Z} ^{m}$
and
$\lambda \in {\mathbb Z} ^{m}$
and
![]() $\sigma \in S_m$
, the twisted nonsymmetric Hall–Littlewood polynomial
$\sigma \in S_m$
, the twisted nonsymmetric Hall–Littlewood polynomial
![]() $E^{\sigma }_{\lambda }(x;q)$
is an element of
$E^{\sigma }_{\lambda }(x;q)$
is an element of
![]() ${\mathbb Z}[q^{\pm 1}][x_1^{\pm 1}, \dots , x_m^{\pm 1}]$
defined using an action of the Hecke algebra on this ring; we refer the reader to [Reference Blasiak, Haiman, Morse, Pun and Seelinger2, §4.3] for the precise definition, citing properties as needed. We also have their variants
${\mathbb Z}[q^{\pm 1}][x_1^{\pm 1}, \dots , x_m^{\pm 1}]$
defined using an action of the Hecke algebra on this ring; we refer the reader to [Reference Blasiak, Haiman, Morse, Pun and Seelinger2, §4.3] for the precise definition, citing properties as needed. We also have their variants
recalling that
![]() $\overline {f(x_1,\ldots ,x_m;q)}=f(x_1^{-1},\ldots ,x_m^{-1};q^{-1})$
.
$\overline {f(x_1,\ldots ,x_m;q)}=f(x_1^{-1},\ldots ,x_m^{-1};q^{-1})$
.
For any weights
![]() $\alpha ,\beta \in {\mathbb Z} ^{m}$
and a permutation
$\alpha ,\beta \in {\mathbb Z} ^{m}$
and a permutation
![]() $\sigma \in S_{m}$
, the LLT series
$\sigma \in S_{m}$
, the LLT series
![]() ${\mathcal L}^{\sigma } _{\beta /\alpha }(x;q) ={\mathcal L}^{\sigma } _{\beta /\alpha }(x_{1},\ldots ,x_{m};q)$
is defined in [Reference Blasiak, Haiman, Morse, Pun and Seelinger2, §4.4] by
${\mathcal L}^{\sigma } _{\beta /\alpha }(x;q) ={\mathcal L}^{\sigma } _{\beta /\alpha }(x_{1},\ldots ,x_{m};q)$
is defined in [Reference Blasiak, Haiman, Morse, Pun and Seelinger2, §4.4] by
Alternatively, [Reference Blasiak, Haiman, Morse, Pun and Seelinger2, Proposition 4.4.2] gives the following expression in terms of the Hall–Littlewood symmetrization operator in equation (38):
where
![]() $w_0$
denotes the permutation of maximum length here and after. We will only need the LLT series for
$w_0$
denotes the permutation of maximum length here and after. We will only need the LLT series for
![]() $\sigma =w_0$
and
$\sigma =w_0$
and
![]() $\sigma = id$
, although most of what follows can be generalized to any
$\sigma = id$
, although most of what follows can be generalized to any
![]() $\sigma $
.
$\sigma $
.
In addition to the above formulas, we have the following combinatorial expressions for the polynomial truncations of LLT series as tableau generating functions with q weights that count triples. As usual, a semistandard tableau on a tuple of skew row shapes
![]() $\nu =\beta /\alpha $
is a map
$\nu =\beta /\alpha $
is a map
![]() $T \colon \nu \to [m]$
which is weakly increasing on rows. Let
$T \colon \nu \to [m]$
which is weakly increasing on rows. Let
![]() $\operatorname {\mathrm {SSYT}}(\nu )$
denote the set of these, and define
$\operatorname {\mathrm {SSYT}}(\nu )$
denote the set of these, and define
![]() $x^{\operatorname {\mathrm {wt}}(T)}=\prod _{b\in \nu }x_{T(b)}$
.
$x^{\operatorname {\mathrm {wt}}(T)}=\prod _{b\in \nu }x_{T(b)}$
.
Proposition 6.2.1 [Reference Blasiak, Haiman, Morse, Pun and Seelinger2, Remark 4.5.5 and Corollary 4.5.7].
If
![]() $\alpha _i \leq \beta _i$
for all i, then
$\alpha _i \leq \beta _i$
for all i, then
 $$ \begin{align} {\mathcal L}^{w_0}_{\beta/\alpha}(x;q)_{\operatorname{\mathrm{pol}}} = \sum_{T \in \operatorname{\mathrm{SSYT}}(\beta/\alpha)} q^{h^{\prime}_{w_0}(T)} x^{\operatorname{\mathrm{wt}}(T)} \,, \end{align} $$
$$ \begin{align} {\mathcal L}^{w_0}_{\beta/\alpha}(x;q)_{\operatorname{\mathrm{pol}}} = \sum_{T \in \operatorname{\mathrm{SSYT}}(\beta/\alpha)} q^{h^{\prime}_{w_0}(T)} x^{\operatorname{\mathrm{wt}}(T)} \,, \end{align} $$
where
![]() $h^{\prime }_{w_0}(T)$
is the number of
$h^{\prime }_{w_0}(T)$
is the number of
![]() $w_0$
-triples
$w_0$
-triples
![]() $(u,v,w)$
of
$(u,v,w)$
of
![]() $\beta /\alpha $
such that
$\beta /\alpha $
such that
![]() $T(u) \leq T(v) \leq T(w)$
.
$T(u) \leq T(v) \leq T(w)$
.
Proposition 6.2.2 [Reference Blasiak, Haiman, Morse, Pun and Seelinger2, Proposition 4.5.2].
For any
![]() $\alpha , \beta \in {\mathbb Z}^m$
,
$\alpha , \beta \in {\mathbb Z}^m$
,
6.3 Extended delta theorem
We now give several lemmas on nonsymmetric Hall–Littlewood polynomials, then conclude by using the Cauchy formula for these polynomials to prove Theorem 6.3.6, below, yielding the stronger series identity that implies equation (99).
Lemma 6.3.1. For
![]() ${\mathbf a}\in \mathbb N^{m-1}$
and
${\mathbf a}\in \mathbb N^{m-1}$
and
![]() $w_0\in S_m$
and
$w_0\in S_m$
and
![]() $\tilde w_0\in S_{m-1}$
the permutations of maximum length, we have
$\tilde w_0\in S_{m-1}$
the permutations of maximum length, we have
Proof. By [Reference Blasiak, Haiman, Morse, Pun and Seelinger2, Lemma 4.3.4], we have
![]() $E_{({\mathbf a},0)}^{w_0}(x_1,\ldots ,x_m;q) = E_{{\mathbf a}}^{\tilde w_0}(x_1,\ldots ,x_{m-1};q) E_{(0)}^{id}(x_m;q)$
and
$E_{({\mathbf a},0)}^{w_0}(x_1,\ldots ,x_m;q) = E_{{\mathbf a}}^{\tilde w_0}(x_1,\ldots ,x_{m-1};q) E_{(0)}^{id}(x_m;q)$
and
![]() $E_{(0,-{\mathbf a})}^{id}(x_1,\ldots ,x_m;q) = E_{(0)}^{id}(x_1;q) E_{-{\mathbf a}}^{id}(x_2,\ldots ,x_m;q)$
. The claim then follows from the definition
$E_{(0,-{\mathbf a})}^{id}(x_1,\ldots ,x_m;q) = E_{(0)}^{id}(x_1;q) E_{-{\mathbf a}}^{id}(x_2,\ldots ,x_m;q)$
. The claim then follows from the definition
![]() $F_{\mathbf a}^{\sigma }=\overline {E_{-{\mathbf a}}^{w_0\sigma }}$
and noting that
$F_{\mathbf a}^{\sigma }=\overline {E_{-{\mathbf a}}^{w_0\sigma }}$
and noting that
![]() $E_{(0)}^{id}(x_{m};q)=1= F^{id}_{(0)}(x_1;q)$
.
$E_{(0)}^{id}(x_{m};q)=1= F^{id}_{(0)}(x_1;q)$
.
Inverting all variables and specializing
![]() $\sigma = w_0$
in [Reference Blasiak, Haiman, Morse, Pun and Seelinger2, Lemma 4.5.1] yields the following lemma.
$\sigma = w_0$
in [Reference Blasiak, Haiman, Morse, Pun and Seelinger2, Lemma 4.5.1] yields the following lemma.
Lemma 6.3.2. For
![]() $l\leq m$
,
$l\leq m$
,
![]() ${\mathbf a} \in {\mathbb Z}^m$
, we have
${\mathbf a} \in {\mathbb Z}^m$
, we have
where
![]() $ h_I({\mathbf a}) = \left | \{( i<j) \mid a_j=a_i+1,i\in I, j \notin I\} \right |$
, as defined in equation (82).
$ h_I({\mathbf a}) = \left | \{( i<j) \mid a_j=a_i+1,i\in I, j \notin I\} \right |$
, as defined in equation (82).
Lemma 6.3.3. For every
![]() $\lambda \in {\mathbb Z} ^{m}$
and
$\lambda \in {\mathbb Z} ^{m}$
and
![]() $\sigma \in S_{m}$
, we have
$\sigma \in S_{m}$
, we have
Proof. The desired identity follows from
by applying
![]() $w_{0}$
to both sides; substituting
$w_{0}$
to both sides; substituting
![]() $\sigma \mapsto \sigma w_{0}$
,
$\sigma \mapsto \sigma w_{0}$
,
![]() $\lambda \mapsto -\lambda $
and
$\lambda \mapsto -\lambda $
and
![]() $q\mapsto q^{-1}$
and using the definition of
$q\mapsto q^{-1}$
and using the definition of
![]() $F^{\sigma }_{\lambda }$
.
$F^{\sigma }_{\lambda }$
.
To prove equation (109), we use the characterization of
![]() $E^{\sigma }_{\lambda }(x;q)$
by the recurrence [Reference Blasiak, Haiman, Morse, Pun and Seelinger2, (77)] and initial condition
$E^{\sigma }_{\lambda }(x;q)$
by the recurrence [Reference Blasiak, Haiman, Morse, Pun and Seelinger2, (77)] and initial condition
![]() $E^{\sigma }_{\lambda } = x^{\lambda }$
for
$E^{\sigma }_{\lambda } = x^{\lambda }$
for
![]() $\lambda $
dominant. The change of variables
$\lambda $
dominant. The change of variables
![]() $x^{\mu }\mapsto x^{-w_{0}(\mu )}$
replaces the Hecke algebra operator
$x^{\mu }\mapsto x^{-w_{0}(\mu )}$
replaces the Hecke algebra operator
![]() $T_{i} = T_{s_{i}}$
in the recurrence with
$T_{i} = T_{s_{i}}$
in the recurrence with
![]() $T_{w_{0}s_{i}w_{0}}$
, giving a modified recurrence satisfied by the left-hand side of (109). It is straightforward to verify that the right-hand side of equation (109) satisfies the same modified recurrence. Since both sides reduce to
$T_{w_{0}s_{i}w_{0}}$
, giving a modified recurrence satisfied by the left-hand side of (109). It is straightforward to verify that the right-hand side of equation (109) satisfies the same modified recurrence. Since both sides reduce to
![]() $x^{-w_{0}(\lambda )}$
for
$x^{-w_{0}(\lambda )}$
for
![]() $\lambda $
dominant, equation (109) holds.
$\lambda $
dominant, equation (109) holds.
Lemma 6.3.4. Given
![]() $\alpha ,\beta \in {\mathbb Z} ^{m}$
and a symmetric Laurent polynomial
$\alpha ,\beta \in {\mathbb Z} ^{m}$
and a symmetric Laurent polynomial
![]() $f(x_{1},\ldots ,x_{m})$
, we have, for any
$f(x_{1},\ldots ,x_{m})$
, we have, for any
![]() $\sigma \in S_{m}$
,
$\sigma \in S_{m}$
,
Proof. In fact, we will show that
even if we do not assume that
![]() $f(x)$
is symmetric. By Lemma 6.3.3, the right-hand side of equation (111) is equal to
$f(x)$
is symmetric. By Lemma 6.3.3, the right-hand side of equation (111) is equal to
By [Reference Blasiak, Haiman, Morse, Pun and Seelinger2, Proposition 4.3.2], the functions
![]() $E^{\sigma }_{\lambda }(x;q)$
and
$E^{\sigma }_{\lambda }(x;q)$
and
![]() $E^{\sigma w_{0}}_{-\lambda }(x;q)$
are dual bases with respect to to the inner product
$E^{\sigma w_{0}}_{-\lambda }(x;q)$
are dual bases with respect to to the inner product
![]() $\langle - , - \rangle _{q}$
defined there. Moreover, it is immediate from the construction of the inner product that multiplication by any
$\langle - , - \rangle _{q}$
defined there. Moreover, it is immediate from the construction of the inner product that multiplication by any
![]() $f(x)$
is self-adjoint. This gives
$f(x)$
is self-adjoint. This gives
in which the left-hand side is equal to the left-hand side of equation (111), and the right-hand side is equal to equation (112).
Lemma 6.3.5. For
![]() $w_0$
the maximum length permutation in
$w_0$
the maximum length permutation in
![]() $S_m$
and
$S_m$
and
![]() $\eta \in \mathbb N^m$
, we have
$\eta \in \mathbb N^m$
, we have
 $$ \begin{align} h_l(x) F_{\eta}^{w_0}(x;q) = \sum_{\substack{\tau\in\mathbb N^m\\ |\tau|=l}} q^{d(\eta,\tau)} F_{\eta+\tau}^{w_0}(x;q)\,, \end{align} $$
$$ \begin{align} h_l(x) F_{\eta}^{w_0}(x;q) = \sum_{\substack{\tau\in\mathbb N^m\\ |\tau|=l}} q^{d(\eta,\tau)} F_{\eta+\tau}^{w_0}(x;q)\,, \end{align} $$
recalling from equation (81) that
![]() $d(\eta ,\tau ) = \sum _{j < r} \big | [\eta _{j},\eta _{j}+\tau _j] \cap [\eta _{r},\eta _{r}+\tau _r-1] \big |$
.
$d(\eta ,\tau ) = \sum _{j < r} \big | [\eta _{j},\eta _{j}+\tau _j] \cap [\eta _{r},\eta _{r}+\tau _r-1] \big |$
.
Proof. Set
![]() $\alpha = -\eta -\tau $
and
$\alpha = -\eta -\tau $
and
![]() $\beta = -\eta $
. By equation (101) and Lemma 6.3.4 (with
$\beta = -\eta $
. By equation (101) and Lemma 6.3.4 (with
![]() $\sigma =w_{0}$
), we have
$\sigma =w_{0}$
), we have
By specializing all but one variable in equation (103) to zero, Proposition 6.2.1 implies that the coefficient of
![]() $h_l$
in
$h_l$
in
![]() ${\mathcal L}^{w_0}_{w_0(\beta /\alpha )}(x;q)_{\operatorname {\mathrm {pol}}}$
is
${\mathcal L}^{w_0}_{w_0(\beta /\alpha )}(x;q)_{\operatorname {\mathrm {pol}}}$
is
![]() $q^{h^{\prime }_{w_0}(T)}$
for T the semistandard tableau of shape
$q^{h^{\prime }_{w_0}(T)}$
for T the semistandard tableau of shape
![]() $w_0(\beta /\alpha )$
filled with a single letter, where
$w_0(\beta /\alpha )$
filled with a single letter, where
![]() $h^{\prime }_{w_0}(T)$
is the number of
$h^{\prime }_{w_0}(T)$
is the number of
![]() $w_0$
-triples of
$w_0$
-triples of
![]() $w_0(\beta /\alpha )=w_0(-\eta /(-\eta -\tau ))$
. By equation (84), this number is
$w_0(\beta /\alpha )=w_0(-\eta /(-\eta -\tau ))$
. By equation (84), this number is
![]() $d(\eta ,\tau )$
.
$d(\eta ,\tau )$
.
Theorem 6.3.6. For
![]() $0\leq l<m\leq N$
and
$0\leq l<m\leq N$
and
![]() $w_0\in S_{m}$
the maximum length permutation, we have
$w_0\in S_{m}$
the maximum length permutation, we have
 $$ \begin{align*} & \frac{\prod_{i+1<j\le m}(1-qtx_i/x_j)} {\prod_{i < j\le m} (1-tx_i/x_j)} x_1 \cdots x_{m} h_{N-m}(x_1,\ldots,x_{m}) \overline{e_l(x_2,\ldots,x_{m})} \\[1ex] &\ =\!\!\!\! \sum_{\substack{(0,{\mathbf a}), \tau \in\mathbb N^{m}\\ I\subseteq [m-1]\\ |\tau|=N-m, |I|=l}} t^{|{\mathbf a}|} q^{d((0,{\mathbf a}),\tau)+h_I({\mathbf a})}\; w_0 \bigl( F^{w_0}_{(0,{\mathbf a})+\tau+(1^{m})}(x_1,\ldots,x_{m};q) \overline{E^{w_0}_{({\mathbf a},0)+\varepsilon_I}(x_1,\ldots,x_{m};q)}\bigr). \end{align*} $$
$$ \begin{align*} & \frac{\prod_{i+1<j\le m}(1-qtx_i/x_j)} {\prod_{i < j\le m} (1-tx_i/x_j)} x_1 \cdots x_{m} h_{N-m}(x_1,\ldots,x_{m}) \overline{e_l(x_2,\ldots,x_{m})} \\[1ex] &\ =\!\!\!\! \sum_{\substack{(0,{\mathbf a}), \tau \in\mathbb N^{m}\\ I\subseteq [m-1]\\ |\tau|=N-m, |I|=l}} t^{|{\mathbf a}|} q^{d((0,{\mathbf a}),\tau)+h_I({\mathbf a})}\; w_0 \bigl( F^{w_0}_{(0,{\mathbf a})+\tau+(1^{m})}(x_1,\ldots,x_{m};q) \overline{E^{w_0}_{({\mathbf a},0)+\varepsilon_I}(x_1,\ldots,x_{m};q)}\bigr). \end{align*} $$
Proof. Our starting point is the Cauchy formula [Reference Blasiak, Haiman, Morse, Pun and Seelinger2, Theorem 5.1.1] for the twisted nonsymmetric Hall–Littlewood polynomials associated to any
![]() $\tilde \sigma \in S_{m-1}$
:
$\tilde \sigma \in S_{m-1}$
:
 $$ \begin{align} \frac{\prod _{i<j< m} (1 - q\, t\, x_{i} \, y_{j})}{\prod _{i\leq j < m} (1 - t\, x_{i}\, y_{j})} = \sum _{{\mathbf a}\in\mathbb N^{m-1}} t^{|{\mathbf a} |}\, E^{\tilde \sigma }_{{\mathbf a} }(x_{1},\ldots,x_{m-1};q^{-1}) \, F^{\tilde\sigma }_{{\mathbf a} }(y_{1},\ldots,y_{m-1};q)\,. \end{align} $$
$$ \begin{align} \frac{\prod _{i<j< m} (1 - q\, t\, x_{i} \, y_{j})}{\prod _{i\leq j < m} (1 - t\, x_{i}\, y_{j})} = \sum _{{\mathbf a}\in\mathbb N^{m-1}} t^{|{\mathbf a} |}\, E^{\tilde \sigma }_{{\mathbf a} }(x_{1},\ldots,x_{m-1};q^{-1}) \, F^{\tilde\sigma }_{{\mathbf a} }(y_{1},\ldots,y_{m-1};q)\,. \end{align} $$
Take
![]() $\tilde \sigma = \tilde w_0$
the maximum length permutation in
$\tilde \sigma = \tilde w_0$
the maximum length permutation in
![]() $S_{m-1}$
, replace
$S_{m-1}$
, replace
![]() $x_i$
by
$x_i$
by
![]() $x_i^{-1}$
and then let
$x_i^{-1}$
and then let
![]() $y_j=x_{j+1}$
to get
$y_j=x_{j+1}$
to get
 $$ \begin{align} \frac{\prod _{i+1<j\leq m}(1 - q\, t\, x_{j}/x_{i})}{\prod _{i<j\leq m}(1 - t\, x_{j}/x_{i})} = \sum_{{\mathbf a}\in{\mathbb N}^{m-1}} t^{|{\mathbf a} |} F^{\tilde w_0}_{ {\mathbf a}}(x_2,\ldots,x_{m};q) \overline{E^{\tilde w_0}_{{\mathbf a}}(x_1,\ldots,x_{m-1};q)}\,. \end{align} $$
$$ \begin{align} \frac{\prod _{i+1<j\leq m}(1 - q\, t\, x_{j}/x_{i})}{\prod _{i<j\leq m}(1 - t\, x_{j}/x_{i})} = \sum_{{\mathbf a}\in{\mathbb N}^{m-1}} t^{|{\mathbf a} |} F^{\tilde w_0}_{ {\mathbf a}}(x_2,\ldots,x_{m};q) \overline{E^{\tilde w_0}_{{\mathbf a}}(x_1,\ldots,x_{m-1};q)}\,. \end{align} $$
By equation (106) and the definition of
![]() $F^{\sigma }$
,
$F^{\sigma }$
,
for
![]() $w_0\in S_{m}$
. Hence,
$w_0\in S_{m}$
. Hence,
 $$ \begin{align*} &\frac{\prod _{i+1<j\leq m}(1 - q\, t\, x_{j}/x_{i})}{\prod _{i<j\leq m}(1 - t\, x_{j}/x_{i})} (x_1\cdots x_{m}) \notag\\ &\qquad\qquad\qquad\qquad = \sum_{{\mathbf a}\in{\mathbb N}^{m-1}} t^{|{\mathbf a} |} F^{w_0}_{ (0,{\mathbf a})+(1^{m})}(x_1,\ldots,x_{m};q) \overline{E^{\tilde w_0}_{{\mathbf a}}(x_1,\ldots,x_{m-1};q)}\,. \end{align*} $$
$$ \begin{align*} &\frac{\prod _{i+1<j\leq m}(1 - q\, t\, x_{j}/x_{i})}{\prod _{i<j\leq m}(1 - t\, x_{j}/x_{i})} (x_1\cdots x_{m}) \notag\\ &\qquad\qquad\qquad\qquad = \sum_{{\mathbf a}\in{\mathbb N}^{m-1}} t^{|{\mathbf a} |} F^{w_0}_{ (0,{\mathbf a})+(1^{m})}(x_1,\ldots,x_{m};q) \overline{E^{\tilde w_0}_{{\mathbf a}}(x_1,\ldots,x_{m-1};q)}\,. \end{align*} $$
Multiplying by
![]() $h_{N-m}(x_1,\ldots ,x_{m})$
with the help of Lemma 6.3.5 yields
$h_{N-m}(x_1,\ldots ,x_{m})$
with the help of Lemma 6.3.5 yields
 $$ \begin{align*} &\frac{\prod _{i+1<j\le m}(1 - q\, t\, x_{j}/x_{i})}{\prod _{i<j\le m}(1 - t\, x_{j}/x_{i})} (x_1\cdots x_{m}) h_{N-m}(x_1,\ldots,x_{m}) \notag\\ &\qquad\qquad\qquad\qquad= \sum_{\substack{(0,{\mathbf a}), \tau\in{\mathbb N}^{m}\\|\tau|=N-m}} t^{|{\mathbf a} |} q^{d((0,{\mathbf a}),\tau)} F^{w_0}_{\eta +\tau}(x_1,\ldots,x_{m};q) \overline{E^{\tilde w_0}_{{\mathbf a}}(x_1,\ldots,x_{m-1};q)}\,, \end{align*} $$
$$ \begin{align*} &\frac{\prod _{i+1<j\le m}(1 - q\, t\, x_{j}/x_{i})}{\prod _{i<j\le m}(1 - t\, x_{j}/x_{i})} (x_1\cdots x_{m}) h_{N-m}(x_1,\ldots,x_{m}) \notag\\ &\qquad\qquad\qquad\qquad= \sum_{\substack{(0,{\mathbf a}), \tau\in{\mathbb N}^{m}\\|\tau|=N-m}} t^{|{\mathbf a} |} q^{d((0,{\mathbf a}),\tau)} F^{w_0}_{\eta +\tau}(x_1,\ldots,x_{m};q) \overline{E^{\tilde w_0}_{{\mathbf a}}(x_1,\ldots,x_{m-1};q)}\,, \end{align*} $$
where
![]() $\eta =(1^{m})+(0,{\mathbf a})$
and we have used that
$\eta =(1^{m})+(0,{\mathbf a})$
and we have used that
![]() $d(\eta ,\tau )=d((0,{\mathbf a}),\tau )$
by equation (81). Now, multiply by
$d(\eta ,\tau )=d((0,{\mathbf a}),\tau )$
by equation (81). Now, multiply by
![]() $\overline { e_l(x_1,\ldots ,x_{m-1})}$
and apply equation (107) to get
$\overline { e_l(x_1,\ldots ,x_{m-1})}$
and apply equation (107) to get
 $$ \begin{align} &\frac{\prod _{i+1<j\le m}(1 - q\, t\, x_{j}/x_i)}{\prod _{i<j\le m}(1 - t\, x_{j}/x_{i})} (x_1\cdots x_{m}) \overline{ e_l(x_1,\ldots,x_{m-1})} h_{N-m}(x_1,\ldots,x_{m}) \notag\\ &\qquad\qquad= \sum_{\substack{(0,{\mathbf a}),\tau\,\in\mathbb N^{m}\\ |\tau|=N-m}} \, \sum_{|I|=l} t^{|{\mathbf a} |} q^{d((0,{\mathbf a}),\tau)+h_I({\mathbf a})} F^{w_0}_{\eta +\tau}(x_1,\ldots,x_{m};q) \overline{E^{\tilde w_0}_{{\mathbf a}+\varepsilon_I}(x_1,\ldots,x_{m-1};q)}\,, \end{align} $$
$$ \begin{align} &\frac{\prod _{i+1<j\le m}(1 - q\, t\, x_{j}/x_i)}{\prod _{i<j\le m}(1 - t\, x_{j}/x_{i})} (x_1\cdots x_{m}) \overline{ e_l(x_1,\ldots,x_{m-1})} h_{N-m}(x_1,\ldots,x_{m}) \notag\\ &\qquad\qquad= \sum_{\substack{(0,{\mathbf a}),\tau\,\in\mathbb N^{m}\\ |\tau|=N-m}} \, \sum_{|I|=l} t^{|{\mathbf a} |} q^{d((0,{\mathbf a}),\tau)+h_I({\mathbf a})} F^{w_0}_{\eta +\tau}(x_1,\ldots,x_{m};q) \overline{E^{\tilde w_0}_{{\mathbf a}+\varepsilon_I}(x_1,\ldots,x_{m-1};q)}\,, \end{align} $$
where
![]() $I\subseteq [m-1]$
. The result then follows by using equation (105) on the right-hand side and applying
$I\subseteq [m-1]$
. The result then follows by using equation (105) on the right-hand side and applying
![]() $w_0\in S_{m}$
to both sides, noting that
$w_0\in S_{m}$
to both sides, noting that
![]() $w_0(\overline { e_l(x_2,\ldots ,x_{m})})= \overline { e_l(x_1,\ldots ,x_{m-1})}$
.
$w_0(\overline { e_l(x_2,\ldots ,x_{m})})= \overline { e_l(x_1,\ldots ,x_{m-1})}$
.
Acknowledgments
JB was supported by NSF grant DMS-1855784 and 2154282. JM was supported by Simons Foundation grant 821999 and NSF grant DMS-2154281. JM and GS were supported by NSF grant DMS-1855804.
Conflict of Interest
The authors have no conflict of interest to declare.