Impact Statement
Laminar-flow control seeks to reduce the drag on aircraft by delaying the laminar-to-turbulent transition in the viscous boundary-layer flow on aerodynamic surfaces. This reduction in drag translates directly to a reduction in fuel burn and ![]() ${\rm CO}_2$ emissions.
${\rm CO}_2$ emissions.
To achieve extended laminar flow, the aerodynamic surfaces are designed to suppress the growth of naturally occurring flow instabilities that trigger transition. These instabilities are also sensitive to surface imperfections (such as steps and gaps), which can result from the manufacturing of the aircraft. Since the minimization or avoidance of surface imperfections can result in costly constraints on the manufacturing process, high-fidelity models are needed to predict the impact of these imperfections. This paper provides qualitative and quantitative descriptions for the underlying mechanisms that can lead to a loss in laminar flow due to surface gaps. This systematic characterization of gap effects can help facilitate the trades necessary to support commercial applications.
1. Introduction
The transition location on air vehicles can have a significant impact on the overall vehicle performance. An extended region of laminar flow results in lower friction drag, and can also influence other contributors to drag such as wave drag and spanloading. Under quiet-flow conditions characteristic of flight, the onset of transition is linked to the growth and nonlinear breakdown of naturally occurring instabilities. One of the most effective methods for predicting the transition location is to link the linear growth of instabilities ![]() $n= \ln (A/ A_0)$ to the transition onset using a critical growth-factor value
$n= \ln (A/ A_0)$ to the transition onset using a critical growth-factor value ![]() $N$, where
$N$, where ![]() $A_0$ is an initial amplitude (Reference Smith and GamberoniSmith & Gamberoni, 1956; Reference Van IngenVan Ingen, 1956). In this approach, when the instability amplification reaches
$A_0$ is an initial amplitude (Reference Smith and GamberoniSmith & Gamberoni, 1956; Reference Van IngenVan Ingen, 1956). In this approach, when the instability amplification reaches ![]() $n=N$, the disturbance amplitudes
$n=N$, the disturbance amplitudes ![]() $A$ are estimated to be sufficient to cause transition.
$A$ are estimated to be sufficient to cause transition.
For many flows of interest (e.g. over low-sweep wings, nacelles and axisymmetric bodies) the dominant mode of instability is the Tollmien–Schlichting (TS) wave. The TS instability is sensitive to pressure gradient and Reynolds number – being more stable in favourable pressure gradients (![]() ${\rm d} P/{{\rm d}\,x}<0$) and less stable in adverse gradients (
${\rm d} P/{{\rm d}\,x}<0$) and less stable in adverse gradients (![]() ${\rm d} P/{{\rm d}\,x}>0$). Thus, for a typical aerodynamic surface, the TS waves are damped near the leading edge and then go unstable near the pressure minimum, ultimately transitioning to turbulence farther downstream. In practice, surface irregularities such as steps and gaps alter the growth characteristics and can move transition forward relative to an idealized smooth surface. Accounting for these effects is essential for realistic transition predictions on air vehicles to support laminar-flow applications.
${\rm d} P/{{\rm d}\,x}>0$). Thus, for a typical aerodynamic surface, the TS waves are damped near the leading edge and then go unstable near the pressure minimum, ultimately transitioning to turbulence farther downstream. In practice, surface irregularities such as steps and gaps alter the growth characteristics and can move transition forward relative to an idealized smooth surface. Accounting for these effects is essential for realistic transition predictions on air vehicles to support laminar-flow applications.
The influence of steps on transition has been considered in several studies, as described in the summaries of Reference Eppink, Wlezien, King and ChoudhariEppink, Wlezien, King, and Choudhari (Reference Eppink, Wlezien, King and Choudhari2019), Reference Tufts, Reed, Crawford, Duncan and SaricTufts, Reed, Crawford, Duncan, and Saric (Reference Tufts, Reed, Crawford, Duncan and Saric2017), Reference Crouch and KosoryginCrouch and Kosorygin (Reference Crouch and Kosorygin2020) and Reference Perraud, Arnal and KuehnPerraud, Arnal, and Kuehn (Reference Perraud, Arnal and Kuehn2014). In TS-dominated boundary layers, studies show that moderate step heights result in a forward movement of transition relative to the smooth surface. For sufficiently large step heights, the transition location moves all the way to the step location. The forward movement of transition for moderate step heights is linked to a destabilization effect on the TS waves in the neighbourhood of the step (Reference Klebanoff and TidstromKlebanoff & Tidstrom, 1972). This enhanced growth has been investigated numerically for different flow conditions (see for example Reference Edelmann and RistEdelmann & Rist, 2015; Reference Hildebrand, Choudhari and ParedesHildebrand, Choudhari, & Paredes, 2020; Reference NayfehNayfeh, 1992; Reference Perraud and SéraudiePerraud & Séraudie, 2000). The calculated change in the linear growth factor ![]() $n(x)$ at some downstream position (where transition is observed or assumed to occur) can be correlated to the transition movement. Alternatively, an experimentally observed change in transition location due to a step can be correlated with a change in the value of the critical growth factor
$n(x)$ at some downstream position (where transition is observed or assumed to occur) can be correlated to the transition movement. Alternatively, an experimentally observed change in transition location due to a step can be correlated with a change in the value of the critical growth factor ![]() $N$ (Reference Crouch and KosoryginCrouch & Kosorygin, 2020; Reference Crouch, Kosorygin and NgCrouch, Kosorygin, & Ng, 2006; Wang & Gaster, Reference Wang and Gaster2005). In this variable
$N$ (Reference Crouch and KosoryginCrouch & Kosorygin, 2020; Reference Crouch, Kosorygin and NgCrouch, Kosorygin, & Ng, 2006; Wang & Gaster, Reference Wang and Gaster2005). In this variable ![]() $N$-factor approach, the growth factor
$N$-factor approach, the growth factor ![]() $n(x)$ is calculated in the absence of the step, but the threshold value for transition onset varies with the step characteristics.
$n(x)$ is calculated in the absence of the step, but the threshold value for transition onset varies with the step characteristics.
The influence of surface gaps on transition has received less attention. Early work of Reference Nenni and GluyasNenni and Gluyas (Reference Nenni and Gluyas1966) investigated gap effects on transition in flight and proposed a threshold free-stream Reynolds number of 15 000, based on gap width, to identify significant forward movement of transition. The work of Reference Sinha, Gupta and OberaiSinha, Gupta, and Oberai (Reference Sinha, Gupta and Oberai1982) provided a qualitative classification of gaps based on experimentally observed flow patterns inside the gap cavity. However, these qualitative distinctions regarding the base flow do not appear to be linked to differences in the instability growth characteristics, or to the transition location.
Measurements of Reference Olive and BlanchardOlive and Blanchard (Reference Olive and Blanchard1982), and supplemental experiments of Reference SéraudieSéraudie (Reference Séraudie2010) and Reference GentiliGentili (Reference Gentili2012) (see Reference Beguet, Perraud, Forte and BrazierBeguet, Perraud, Forte, and Brazier (Reference Beguet, Perraud, Forte and Brazier2017) for a summary of these Office National d'Études et de Recherches Aérospatiales – ONERA test results) characterize the threshold effects of gaps, where transition moves forward to the gap location. The threshold behaviour is expressed in terms of ![]() $w / \delta ^*$ and
$w / \delta ^*$ and ![]() $d / \delta ^*$ boundaries, where
$d / \delta ^*$ boundaries, where ![]() $w$ is the width and
$w$ is the width and ![]() $d$ is the depth, and
$d$ is the depth, and ![]() $\delta ^*$ is the boundary-layer displacement thickness at the gap location (for the smooth surface). Gaps with
$\delta ^*$ is the boundary-layer displacement thickness at the gap location (for the smooth surface). Gaps with ![]() $w/ \delta ^* \geq 18$ and
$w/ \delta ^* \geq 18$ and ![]() $d/ \delta ^* \geq 2$ are likely to result in transition at the gap location.
$d/ \delta ^* \geq 2$ are likely to result in transition at the gap location.
A numerically based approach to characterizing the transition movement was presented by Reference Perraud, Arnal and KuehnPerraud et al. (Reference Perraud, Arnal and Kuehn2014) based on linear stability theory. A peak in the growth factor ![]() $n(x)$, which occurs near the gap location, is linked to the potential transition at the gap. A far-field change in the growth factor
$n(x)$, which occurs near the gap location, is linked to the potential transition at the gap. A far-field change in the growth factor ![]() ${\rm \Delta} n$, compared with the smooth surface, is linked to potential movements of the transition location farther downstream.
${\rm \Delta} n$, compared with the smooth surface, is linked to potential movements of the transition location farther downstream.
Reference Beguet, Perraud, Forte and BrazierBeguet et al. (Reference Beguet, Perraud, Forte and Brazier2017) provide a survey of several studies conducted at ONERA, and introduce modelling to characterize the effects of gaps on transition. The models capture the localized peak in the growth factor and the far-field change in the growth factor as a function of the gap width and location using two local Reynolds number parameters, ![]() $Re_w$ and
$Re_w$ and ![]() $Re_{\theta }$;
$Re_{\theta }$; ![]() $Re_w$ is based on the gap width and
$Re_w$ is based on the gap width and ![]() $Re_{\theta }$ is based on the (smooth-surface) boundary-layer momentum thickness at the gap location. The model does not take into account gap depth or any potential influence of pressure gradients. Experiments confirm the negligible effect of gap depth on transition over the range
$Re_{\theta }$ is based on the (smooth-surface) boundary-layer momentum thickness at the gap location. The model does not take into account gap depth or any potential influence of pressure gradients. Experiments confirm the negligible effect of gap depth on transition over the range ![]() $0.2 < d/w < 0.7$. Reference Beguet, Perraud, Forte and BrazierBeguet et al. (Reference Beguet, Perraud, Forte and Brazier2017) suggest the need to further investigate the effects of pressure gradient, compressibility and larger gap depths.
$0.2 < d/w < 0.7$. Reference Beguet, Perraud, Forte and BrazierBeguet et al. (Reference Beguet, Perraud, Forte and Brazier2017) suggest the need to further investigate the effects of pressure gradient, compressibility and larger gap depths.
Reference Zahn and RistZahn and Rist (Reference Zahn and Rist2016) used direct numerical simulation to study deep-gap effects on transition for ![]() $d/w > 5$ in compressible flow, and provided a simple model for estimation. The gaps are analysed on a flat plate with zero pressure gradient. They observed that deep gaps have an effect on transition farther downstream, characterized by a change in amplification of
$d/w > 5$ in compressible flow, and provided a simple model for estimation. The gaps are analysed on a flat plate with zero pressure gradient. They observed that deep gaps have an effect on transition farther downstream, characterized by a change in amplification of ![]() ${\rm \Delta} n$ between 0 and 0.5, varying non-monotonically with gap depth. Their observation suggests that the
${\rm \Delta} n$ between 0 and 0.5, varying non-monotonically with gap depth. Their observation suggests that the ![]() ${\rm \Delta} n$ variation results from an acoustic feedback within the gap cavity. This dependence on gap depth is in contrast to the models introduced by Reference Beguet, Perraud, Forte and BrazierBeguet et al. (Reference Beguet, Perraud, Forte and Brazier2017) that suggest no dependency of transition on gap depth for shallower gaps. Reference Zahn and RistZahn and Rist (Reference Zahn and Rist2016) also show that the presence of a gap in combination with a step can reduce the level of
${\rm \Delta} n$ variation results from an acoustic feedback within the gap cavity. This dependence on gap depth is in contrast to the models introduced by Reference Beguet, Perraud, Forte and BrazierBeguet et al. (Reference Beguet, Perraud, Forte and Brazier2017) that suggest no dependency of transition on gap depth for shallower gaps. Reference Zahn and RistZahn and Rist (Reference Zahn and Rist2016) also show that the presence of a gap in combination with a step can reduce the level of ![]() ${\rm \Delta} n$ compared with an isolated step.
${\rm \Delta} n$ compared with an isolated step.
For shallow gaps, ![]() $d/w < 0.02$, Reference Crouch and KosoryginCrouch and Kosorygin (Reference Crouch and Kosorygin2020) provide a gap
$d/w < 0.02$, Reference Crouch and KosoryginCrouch and Kosorygin (Reference Crouch and Kosorygin2020) provide a gap ![]() ${\rm \Delta} N$ based on a superposition of steps. Their results show that shallow gaps produce the same effects on TS-wave growth as an isolated backward-facing step – without any discernible effect from the forward-facing step at the downstream edge of the gap. This is in contrast to a rectangular protrusion, where both the initial forward-facing step and the following backward-facing step contribute to the altered TS-wave growth.
${\rm \Delta} N$ based on a superposition of steps. Their results show that shallow gaps produce the same effects on TS-wave growth as an isolated backward-facing step – without any discernible effect from the forward-facing step at the downstream edge of the gap. This is in contrast to a rectangular protrusion, where both the initial forward-facing step and the following backward-facing step contribute to the altered TS-wave growth.
The occurrence of transition at the gap location is investigated using global stability analysis by Reference Mathias and MedeirosMathias and Medeiros (Reference Mathias and Medeiros2019). Their results suggest that the observed transition at the gap location is a form of bypass transition, independent of the TS instability. The bypass mechanism is driven by the instability of the shear layer over the gap, with acoustic feedback due to scattering of the shear-layer instability at the downstream edge of the gap (Reference RossiterRossiter, 1964).
In this paper, we use a combination of experiments and linear stability theory to investigate the effects of gaps on the transition process. A series of wind-tunnel tests provides a large database with varied gap characteristics yielding a wide range of effects on transition. In extreme cases, the gaps cause a rapid transition just downstream of the gap. In other cases, the transition exhibits a more gradual change resulting in a transition location between the smooth-surface transition location and the gap location.
2. Experimental set-up and flow characteristics
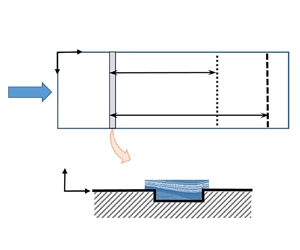
The flow field used for this investigation is based on a typical airfoil pressure distribution, with a favourable pressure gradient near the leading edge followed by a mild adverse pressure gradient downstream. To enable a systematic investigation of many gap geometries, the measurements are conducted on a flat plate with the pressure gradient imposed by contouring the opposing wind-tunnel wall. Figure 1 provides a schematic description of the test set-up, showing a top-down view on the test plate with a rectangular gap running spanwise across the plate surface. The gap is characterized by its streamwise position ![]() $x_G$ (measured from the plate leading edge to the gap leading edge), width
$x_G$ (measured from the plate leading edge to the gap leading edge), width ![]() $w$ and depth
$w$ and depth ![]() $d$. The gaps are created by interchangeable inserts, resulting in sharp-corner rectangular cavities. Measurements show the width and depth are uniform across the span to within
$d$. The gaps are created by interchangeable inserts, resulting in sharp-corner rectangular cavities. Measurements show the width and depth are uniform across the span to within ![]() $\pm$0.1 mm and
$\pm$0.1 mm and ![]() $\pm$0.01 mm, respectively.
$\pm$0.01 mm, respectively.

Figure 1. Schematic showing top-down view of the test model, parameters contributing to the normalized transition length ![]() $\xi$ and gap characteristics.
$\xi$ and gap characteristics.
The effect of the gap on transition is primarily assessed by the change in transition location ![]() $x_T$ relative to the smooth-surface transition location
$x_T$ relative to the smooth-surface transition location ![]() $x_{T0}$. This transition movement is expressed in terms of the normalized transition length
$x_{T0}$. This transition movement is expressed in terms of the normalized transition length ![]() $\xi = (x_T - x_G )/( x_{T0} - x_G )$.
$\xi = (x_T - x_G )/( x_{T0} - x_G )$.
The experiments are conducted in the T-324 low-turbulence wind tunnel at the Khristianovich Institute of Theoretical and Applied Mechanics. Two test plates are used, each is 2050 mm long and 996 mm wide spanning the width of the test section. A trailing-edge flap is used to position the stagnation line on the upper quarter of a semi-circular plate leading edge. Measured coefficient of pressure Cp distributions are given in figure 2 for both gap positions that are considered, ![]() $x_G =127$ and
$x_G =127$ and ![]() $x_G =450$ mm. The small differences in the pressure (visible on the expanded scale of the inset) are the result of using different leading-edge lengths to position the gap, and some small inaccuracies in the plate mounting. These differences in
$x_G =450$ mm. The small differences in the pressure (visible on the expanded scale of the inset) are the result of using different leading-edge lengths to position the gap, and some small inaccuracies in the plate mounting. These differences in ![]() $Cp$ are accounted for in the analysis of § 3. The first measured points downstream of
$Cp$ are accounted for in the analysis of § 3. The first measured points downstream of ![]() $x \approx 0$ show there is a small suction peak on the upper (working) surface of the plate. Apart from the local variation at the leading edge, the upstream pressure distribution has a favourable gradient up to approximately
$x \approx 0$ show there is a small suction peak on the upper (working) surface of the plate. Apart from the local variation at the leading edge, the upstream pressure distribution has a favourable gradient up to approximately ![]() $x \approx 200$ mm. This is followed by a mild adverse gradient that extends downstream beyond the transition location. Thus, the gap at
$x \approx 200$ mm. This is followed by a mild adverse gradient that extends downstream beyond the transition location. Thus, the gap at ![]() $x_G =127$ mm is in a favourable pressure gradient, and the gap at
$x_G =127$ mm is in a favourable pressure gradient, and the gap at ![]() $x_G = 450$ mm is in an adverse pressure gradient.
$x_G = 450$ mm is in an adverse pressure gradient.

Figure 2. Pressure distribution, ![]() $Cp$, for the
$Cp$, for the ![]() $x_G =$ 127 and
$x_G =$ 127 and ![]() $x_G=$ 450 mm configurations.
$x_G=$ 450 mm configurations.
The study focuses on low Mach numbers, ![]() $M< 0.1$, similar to earlier investigations on steps (Crouch & Kosorygin, Reference Crouch and Kosorygin2020). Measurements are conducted using four different flow velocities, referred to as U18, U20, U22 and U27, with actual velocities, 18.3, 20.6, 22.6 and 27.5 m s
$M< 0.1$, similar to earlier investigations on steps (Crouch & Kosorygin, Reference Crouch and Kosorygin2020). Measurements are conducted using four different flow velocities, referred to as U18, U20, U22 and U27, with actual velocities, 18.3, 20.6, 22.6 and 27.5 m s![]() $^{-1}$, respectively. For this range of tunnel velocities, the free-stream turbulence (measured with the model in place) varies between
$^{-1}$, respectively. For this range of tunnel velocities, the free-stream turbulence (measured with the model in place) varies between ![]() $Tu=0.028\,\%$ and
$Tu=0.028\,\%$ and ![]() $Tu=0.039\,\%$ (bandwidth
$Tu=0.039\,\%$ (bandwidth ![]() $2\text {--}4 \times 10^3$ Hz). A representative turbulence spectrum for this facility is provided in Reference Crouch, Ng, Kachanov, Borodulin and IvanovCrouch, Ng, Kachanov, Borodulin, and Ivanov (Reference Crouch, Ng, Kachanov, Borodulin and Ivanov2015). Average values (over multiple tests entries) for the unit Reynolds number and the displacement thickness at the gap locations are provided in table 1. These displacement thickness values are from measurements on the smooth surface that are used to non-dimensionalize the gap width and depth in the results below.
$2\text {--}4 \times 10^3$ Hz). A representative turbulence spectrum for this facility is provided in Reference Crouch, Ng, Kachanov, Borodulin and IvanovCrouch, Ng, Kachanov, Borodulin, and Ivanov (Reference Crouch, Ng, Kachanov, Borodulin and Ivanov2015). Average values (over multiple tests entries) for the unit Reynolds number and the displacement thickness at the gap locations are provided in table 1. These displacement thickness values are from measurements on the smooth surface that are used to non-dimensionalize the gap width and depth in the results below.
Table 1. Overview of test parameters.

The transition location is determined using a 1 mm diameter Preston tube to measure the total pressure near the plate surface, as described in the earlier study on surface-step effects (Reference Crouch and KosoryginCrouch & Kosorygin, 2020). The transition onset is here defined based on the mean-flow profile rather than the unsteady fluctuations, since the mean flow is the essential quantity for most applications. The dynamic pressure drops with increasing ![]() $x$ distance, due to viscous thickening of the boundary layer. At the onset of transition, the dynamic pressure begins to rise – similar to the friction coefficient
$x$ distance, due to viscous thickening of the boundary layer. At the onset of transition, the dynamic pressure begins to rise – similar to the friction coefficient ![]() $C_f$. The transition-onset location
$C_f$. The transition-onset location ![]() $x_T$ is estimated based on the minimum in the dynamic pressure. Repeat runs (between 10 to 20 cases for each of the smooth-surface reference conditions) show the estimated transition location varies with a standard deviation of approximately
$x_T$ is estimated based on the minimum in the dynamic pressure. Repeat runs (between 10 to 20 cases for each of the smooth-surface reference conditions) show the estimated transition location varies with a standard deviation of approximately ![]() $\pm$15 mm. This variation includes flow-condition uncertainty as well as transition-measurement uncertainty. A direct determination of the transition-measurement uncertainty based on various fits through the data gives an estimated value of
$\pm$15 mm. This variation includes flow-condition uncertainty as well as transition-measurement uncertainty. A direct determination of the transition-measurement uncertainty based on various fits through the data gives an estimated value of ![]() ${\rm \Delta} x_T \pm 10$ mm.
${\rm \Delta} x_T \pm 10$ mm.
3. Linear stability analysis
Linear stability analysis is used to assess the effects of the gaps on the transition location. The experimental ![]() $Cp$ distributions from figure 2 are used to create edge conditions for calculating the boundary-layer flow for the stability analysis. Earlier studies have shown very good agreement between the measured and calculated mean profiles for this flow (Reference Kosorygin, Crouch, Ng and SchlatterKosorygin, Crouch, & Ng, 2010). Calculated values for
$Cp$ distributions from figure 2 are used to create edge conditions for calculating the boundary-layer flow for the stability analysis. Earlier studies have shown very good agreement between the measured and calculated mean profiles for this flow (Reference Kosorygin, Crouch, Ng and SchlatterKosorygin, Crouch, & Ng, 2010). Calculated values for ![]() $\delta ^*$ are within
$\delta ^*$ are within ![]() $\pm$0.01 mm of the experimental values of table 1. Following quasi-parallel theory, the amplification of TS instabilities is described by the spatial growth rate
$\pm$0.01 mm of the experimental values of table 1. Following quasi-parallel theory, the amplification of TS instabilities is described by the spatial growth rate ![]() $\gamma (x; \omega, \beta )$, which is determined from the Orr–Sommerfeld equation for the frequency
$\gamma (x; \omega, \beta )$, which is determined from the Orr–Sommerfeld equation for the frequency ![]() $\omega = 2 {\rm \pi}f$ and spanwise wavenumber
$\omega = 2 {\rm \pi}f$ and spanwise wavenumber ![]() $\beta = 2 {\rm \pi}/ \lambda _z$. A physical mode of instability with fixed frequency
$\beta = 2 {\rm \pi}/ \lambda _z$. A physical mode of instability with fixed frequency ![]() $f$ and spanwise wavelength
$f$ and spanwise wavelength ![]() $\lambda _z$ can be characterized by its amplification factor
$\lambda _z$ can be characterized by its amplification factor ![]() $m$, defined as the natural log of the amplitude ratio
$m$, defined as the natural log of the amplitude ratio
In the ![]() $e^N$ method, when the amplification factor for any given mode reaches a critical value
$e^N$ method, when the amplification factor for any given mode reaches a critical value ![]() $N$, transition is assumed to occur. This is tracked using the
$N$, transition is assumed to occur. This is tracked using the ![]() $n$-factor envelope of the physical growth curves,
$n$-factor envelope of the physical growth curves,
such that the transition location is estimated from the occurrence where ![]() $n$ reaches the critical value
$n$ reaches the critical value ![]() $N$.
$N$.
In the variable ![]() $N$-factor approach, the threshold value
$N$-factor approach, the threshold value ![]() $N$ is defined as a function of key parameters that can alter the linear amplitude of the instability through either receptivity or enhanced amplification (Reference Crouch and SherwinCrouch, 2021). This is equivalent to a linear-amplitude method that correlates the transition onset to the amplitude
$N$ is defined as a function of key parameters that can alter the linear amplitude of the instability through either receptivity or enhanced amplification (Reference Crouch and SherwinCrouch, 2021). This is equivalent to a linear-amplitude method that correlates the transition onset to the amplitude ![]() $A$ reaching some threshold value
$A$ reaching some threshold value ![]() $A_T$. Rather than tracking an increase in the physical amplitude relative to
$A_T$. Rather than tracking an increase in the physical amplitude relative to ![]() $A_T$, the variable
$A_T$, the variable ![]() $N$-factor approach tracks a reduction in the critical value
$N$-factor approach tracks a reduction in the critical value ![]() $N$ relative to a reference condition with
$N$ relative to a reference condition with ![]() $N_0$,
$N_0$, ![]() $N= N_0 - {\rm \Delta} N$ (Reference Crouch and SherwinCrouch, 2021). The amplification factors
$N= N_0 - {\rm \Delta} N$ (Reference Crouch and SherwinCrouch, 2021). The amplification factors ![]() $m$ or
$m$ or ![]() $n$ are calculated the same as for the standard
$n$ are calculated the same as for the standard ![]() $e^N$ method, with only the critical value
$e^N$ method, with only the critical value ![]() $N$ changing as a function of receptivity or growth modifiers.
$N$ changing as a function of receptivity or growth modifiers.
Amplification curves ![]() $m(x; \omega, \beta )$ for the
$m(x; \omega, \beta )$ for the ![]() $U18$
$U18$ ![]() $x_G = 450$ mm configuration are shown in figure 3 for a frequency range
$x_G = 450$ mm configuration are shown in figure 3 for a frequency range ![]() $100$ Hz
$100$ Hz ![]() $\leq f \leq 520$ Hz. For these conditions, the smooth surface transition location is
$\leq f \leq 520$ Hz. For these conditions, the smooth surface transition location is ![]() $x_{T0} = 980$ mm. The dominant mode at this location is highlighted in red, and corresponds to
$x_{T0} = 980$ mm. The dominant mode at this location is highlighted in red, and corresponds to ![]() $f=180$ Hz. This yields a non-dimensional frequency
$f=180$ Hz. This yields a non-dimensional frequency ![]() $F = 10^6 \omega \nu / U^2 =51$. These growth characteristics are consistent with TS instability being the mechanism for transition. As is typical for an airfoil pressure distribution, the same physical mode is dominant over an extended streamwise distance. Thus, any modest movement in transition is likely to be linked to a change in amplitude for this mode.
$F = 10^6 \omega \nu / U^2 =51$. These growth characteristics are consistent with TS instability being the mechanism for transition. As is typical for an airfoil pressure distribution, the same physical mode is dominant over an extended streamwise distance. Thus, any modest movement in transition is likely to be linked to a change in amplitude for this mode.

Figure 3. Instability amplification factors ![]() $m(x; \omega, \beta )$, for different frequencies
$m(x; \omega, \beta )$, for different frequencies ![]() $f =\omega / \textit{2} {\rm \pi}$, based on the
$f =\omega / \textit{2} {\rm \pi}$, based on the ![]() $x_G=$ 450 mm
$x_G=$ 450 mm ![]() $Cp$ distribution and the U18 velocity. The thick red line corresponds to
$Cp$ distribution and the U18 velocity. The thick red line corresponds to ![]() $f=$ 180 Hz.
$f=$ 180 Hz.
The ![]() $n$-factor envelopes for the various conditions tested are given in figure 4 (focusing on the frequency range relevant to transition). The solid red line in figure 4 is the envelope corresponding to figure 3. The dashed lines show the envelopes for the
$n$-factor envelopes for the various conditions tested are given in figure 4 (focusing on the frequency range relevant to transition). The solid red line in figure 4 is the envelope corresponding to figure 3. The dashed lines show the envelopes for the ![]() $x_G = 127$ mm configuration. The small differences in pressure distribution shown in figure 2 result in a slight destabilization of the
$x_G = 127$ mm configuration. The small differences in pressure distribution shown in figure 2 result in a slight destabilization of the ![]() $x_G=127$ mm configuration compared with
$x_G=127$ mm configuration compared with ![]() $x_G=450$ mm. However, the
$x_G=450$ mm. However, the ![]() $n$-factor differences between the two configurations remain less than
$n$-factor differences between the two configurations remain less than ![]() $0.3$. For all flow conditions considered, the gap at
$0.3$. For all flow conditions considered, the gap at ![]() $x_G = 127$ mm is upstream of the instability neutral point, and the gap at
$x_G = 127$ mm is upstream of the instability neutral point, and the gap at ![]() $x_G =450$ mm is downstream of the instability neutral point for all modes influencing transition.
$x_G =450$ mm is downstream of the instability neutral point for all modes influencing transition.

Figure 4. Instability amplification-factor envelopes ![]() $n(x)$, for different velocities
$n(x)$, for different velocities ![]() $U$, based on the
$U$, based on the ![]() $x_G =$ 127 mm and
$x_G =$ 127 mm and ![]() $x_G=$ 450 mm
$x_G=$ 450 mm ![]() $Cp$ distributions.
$Cp$ distributions.
4. Experimental results on gap effects
For the reference conditions on a smooth plate, the transition location varies between ![]() $780\,{\rm mm} \leq x_{T0} \leq 980\,{\rm mm}$, changing primarily due to velocity. The associated smooth-plate transition
$780\,{\rm mm} \leq x_{T0} \leq 980\,{\rm mm}$, changing primarily due to velocity. The associated smooth-plate transition ![]() $N$-factors are between
$N$-factors are between ![]() $8.9$ and
$8.9$ and ![]() $9.8$, and dominated by two-dimensional modes. The transition location varies weakly in the spanwise direction, with
$9.8$, and dominated by two-dimensional modes. The transition location varies weakly in the spanwise direction, with ![]() ${\rm \Delta} x_T \pm 5$ mm over
${\rm \Delta} x_T \pm 5$ mm over ![]() ${\rm \Delta} z = 100$ mm, both for the smooth surface and with the spanwise-uniform gaps. The experimental data consider a wide range of gap widths and depths – expressed non-dimensionally by
${\rm \Delta} z = 100$ mm, both for the smooth surface and with the spanwise-uniform gaps. The experimental data consider a wide range of gap widths and depths – expressed non-dimensionally by ![]() $0 < w / \delta ^* < 110$ and
$0 < w / \delta ^* < 110$ and ![]() $0 < d / \delta ^* < 11$. Uncertainties in these non-dimensional values are dominated by the small
$0 < d / \delta ^* < 11$. Uncertainties in these non-dimensional values are dominated by the small ![]() $\delta ^*$ variations, and are estimated to be less than
$\delta ^*$ variations, and are estimated to be less than ![]() $\pm 2\,\%$. For the smallest values of
$\pm 2\,\%$. For the smallest values of ![]() $w$ and
$w$ and ![]() $d$, the uncertainties are set by the gap-measurement uncertainties of
$d$, the uncertainties are set by the gap-measurement uncertainties of ![]() $\pm$0.1 and
$\pm$0.1 and ![]() $\pm$0.01 mm, respectively.
$\pm$0.01 mm, respectively.
A scatter plot of the various test points is given in figure 5. Each symbol represents a transition measurement, and the different symbol types show the normalized transition length ![]() $\xi$. The small black open symbols correspond to large transition lengths
$\xi$. The small black open symbols correspond to large transition lengths ![]() $\xi > 90\,\%$, with relatively little movement of transition due to the gap. The intermediate black open symbols correspond to
$\xi > 90\,\%$, with relatively little movement of transition due to the gap. The intermediate black open symbols correspond to ![]() $\xi$ between 50 % and 90 %. The large red open symbols (for larger
$\xi$ between 50 % and 90 %. The large red open symbols (for larger ![]() $w / \delta ^*$ values) are associated with larger movements of transition toward the gap, with
$w / \delta ^*$ values) are associated with larger movements of transition toward the gap, with ![]() $\xi$ between 10 % and 50 %. Finally, the solid red symbols show conditions resulting in transition near, or at, the gap location. These cases of abrupt transition at the gap location appear to be the result of a bypass mechanism, not related to TS instability. For larger values of
$\xi$ between 10 % and 50 %. Finally, the solid red symbols show conditions resulting in transition near, or at, the gap location. These cases of abrupt transition at the gap location appear to be the result of a bypass mechanism, not related to TS instability. For larger values of ![]() $d/ \delta ^*$, the experimental data suggest a threshold value of
$d/ \delta ^*$, the experimental data suggest a threshold value of ![]() $w / \delta ^* > 19$ for bypass transition. The dashed lines in figure 5 (for
$w / \delta ^* > 19$ for bypass transition. The dashed lines in figure 5 (for ![]() $d / \delta ^* =2$ and
$d / \delta ^* =2$ and ![]() $w/ \delta ^* =18$) are taken from Reference Beguet, Perraud, Forte and BrazierBeguet et al. (Reference Beguet, Perraud, Forte and Brazier2017). These lines show the boundary for gap characteristics leading to rapid transition at the gap location based on several experiments conducted at ONERA. The boundary between the open symbols and the solid symbols is in good agreement with these earlier experiments. To compare with the
$w/ \delta ^* =18$) are taken from Reference Beguet, Perraud, Forte and BrazierBeguet et al. (Reference Beguet, Perraud, Forte and Brazier2017). These lines show the boundary for gap characteristics leading to rapid transition at the gap location based on several experiments conducted at ONERA. The boundary between the open symbols and the solid symbols is in good agreement with these earlier experiments. To compare with the ![]() $Re_w =15\,000$ threshold criterion from Reference Nenni and GluyasNenni and Gluyas (Reference Nenni and Gluyas1966), we recast the observed threshold boundary at
$Re_w =15\,000$ threshold criterion from Reference Nenni and GluyasNenni and Gluyas (Reference Nenni and Gluyas1966), we recast the observed threshold boundary at ![]() $w/ \delta ^* =19$ into
$w/ \delta ^* =19$ into ![]() $Re_w$ values. This yields a range of
$Re_w$ values. This yields a range of ![]() $Re_w$ values from approximately 12 000 up to approximately 33 000. While
$Re_w$ values from approximately 12 000 up to approximately 33 000. While ![]() $Re_w = 15\,000$ is within this range, it does not provide a clear demarcation of the threshold. Note that the conditions studied in the work of Reference Zahn and RistZahn and Rist (Reference Zahn and Rist2016) are along the
$Re_w = 15\,000$ is within this range, it does not provide a clear demarcation of the threshold. Note that the conditions studied in the work of Reference Zahn and RistZahn and Rist (Reference Zahn and Rist2016) are along the ![]() $d / \delta ^*$ axis, outside the range of the current results.
$d / \delta ^*$ axis, outside the range of the current results.

Figure 5. Scatter plot of experimental points in terms of gap width and gap depth, with symbols corresponding to the transition length ![]() $\xi$. (a) Full data set (both
$\xi$. (a) Full data set (both ![]() $x_G =$127 and
$x_G =$127 and ![]() $x_G=$ 450 mm), with dashed line showing the threshold boundary for bypass from Reference Beguet, Perraud, Forte and BrazierBeguet et al. (Reference Beguet, Perraud, Forte and Brazier2017), (b) Expanded view for smaller values of width and depth.
$x_G=$ 450 mm), with dashed line showing the threshold boundary for bypass from Reference Beguet, Perraud, Forte and BrazierBeguet et al. (Reference Beguet, Perraud, Forte and Brazier2017), (b) Expanded view for smaller values of width and depth.
Figure 5(b) provides an expanded view of the results for smaller values of ![]() $w/ \delta ^*$ and
$w/ \delta ^*$ and ![]() $d/ \delta ^*$. For
$d/ \delta ^*$. For ![]() $d/ \delta ^* < 3.7$, the boundary for bypass transition shifts toward larger
$d/ \delta ^* < 3.7$, the boundary for bypass transition shifts toward larger ![]() $w/ \delta ^*$. At
$w/ \delta ^*$. At ![]() $d/ \delta ^* \approx 1.8$, the threshold value for bypass is estimated as
$d/ \delta ^* \approx 1.8$, the threshold value for bypass is estimated as ![]() $w/ \delta ^* \approx 35$ based on the trend below
$w/ \delta ^* \approx 35$ based on the trend below ![]() $d/ \delta ^* \approx 3.7$. Values of
$d/ \delta ^* \approx 3.7$. Values of ![]() $d/ \delta ^*$ below
$d/ \delta ^*$ below ![]() $1.8$ do not result in bypass transition, even for large values of
$1.8$ do not result in bypass transition, even for large values of ![]() $w/ \delta ^*$.
$w/ \delta ^*$.
Streamwise disturbance amplitudes measured for three different flow conditions from figure 5 are presented in figure 6. The gap position is shown schematically on the ![]() $x$ axis. The amplitudes are measured using a hot-wire at a varying height above the surface corresponding to
$x$ axis. The amplitudes are measured using a hot-wire at a varying height above the surface corresponding to ![]() $U/Ue_G = 0.4$, where
$U/Ue_G = 0.4$, where ![]() $U$ is the boundary-layer mean velocity and
$U$ is the boundary-layer mean velocity and ![]() $Ue_G$ is the edge velocity measured at the gap location
$Ue_G$ is the edge velocity measured at the gap location ![]() $x_G =450$ mm. The root-mean-square amplitude is obtained by band pass filtering the
$x_G =450$ mm. The root-mean-square amplitude is obtained by band pass filtering the ![]() $u'$ signal over a narrow frequency band of
$u'$ signal over a narrow frequency band of ![]() $1.5\,\%$ of the central value. The target frequencies are selected to match the dominant frequency just prior to breakdown, as observed in measured spectra. In all cases, transition occurs due to ‘natural’ background forcing, without any direct excitation.
$1.5\,\%$ of the central value. The target frequencies are selected to match the dominant frequency just prior to breakdown, as observed in measured spectra. In all cases, transition occurs due to ‘natural’ background forcing, without any direct excitation.

Figure 6. Streamwise variation of the disturbance amplitude for four different conditions with ![]() $x_G=\textit{450}$ mm: smooth plate at U18,
$x_G=\textit{450}$ mm: smooth plate at U18, ![]() $f=\textit{178}$ Hz; case A(
$f=\textit{178}$ Hz; case A(![]() $w/ \delta ^* =\textit{27}$,
$w/ \delta ^* =\textit{27}$, ![]() $d/ \delta ^* =\textit{2.60}$) at U18,
$d/ \delta ^* =\textit{2.60}$) at U18, ![]() $f=\textit{175}$ Hz; case B(
$f=\textit{175}$ Hz; case B(![]() $w/ \delta ^* =\textit{18}$,
$w/ \delta ^* =\textit{18}$, ![]() $d/ \delta ^* =\textit{3.45}$) at U18,
$d/ \delta ^* =\textit{3.45}$) at U18, ![]() $f=\textit{183}$ Hz; case C(
$f=\textit{183}$ Hz; case C(![]() $w/ \delta ^* =\textit{20}$,
$w/ \delta ^* =\textit{20}$, ![]() $d/ \delta ^* =\textit{3.83}$) at U22,
$d/ \delta ^* =\textit{3.83}$) at U22, ![]() $f=\textit{830}$ Hz. Symbols are measurements and thin lines are linear theory for U18. Rectangles show the measured transition locations.
$f=\textit{830}$ Hz. Symbols are measurements and thin lines are linear theory for U18. Rectangles show the measured transition locations.
The black circular symbols are for measurements on the smooth plate for the U18 condition, and are provided for reference. The disturbance frequency for this case is ![]() $178$ Hz, which corresponds to a non-dimensional frequency of
$178$ Hz, which corresponds to a non-dimensional frequency of ![]() $F=10^6 \times 2 {\rm \pi}f \nu /U^2 = 53$. The solid line running through the data is derived from the calculated growth factor
$F=10^6 \times 2 {\rm \pi}f \nu /U^2 = 53$. The solid line running through the data is derived from the calculated growth factor ![]() $m$ from (3.1) for
$m$ from (3.1) for ![]() $f=180$ Hz. The amplitude variation is given by
$f=180$ Hz. The amplitude variation is given by ![]() $e^m$, and the initial amplitude
$e^m$, and the initial amplitude ![]() $A_0$ is chosen to provide a good fit to the data in the neighbourhood of
$A_0$ is chosen to provide a good fit to the data in the neighbourhood of ![]() $x \approx 700$ mm. As shown in figure 3, this mode is predicted to be dominant at transition. This overall agreement with the quasi-parallel theory suggests that the non-parallel effects are small over this part of the amplification curve. The black rectangle at
$x \approx 700$ mm. As shown in figure 3, this mode is predicted to be dominant at transition. This overall agreement with the quasi-parallel theory suggests that the non-parallel effects are small over this part of the amplification curve. The black rectangle at ![]() $x=980$ mm shows the measured transition location for this smooth-plate condition, and the associated linear threshold amplitude at transition is approximately 0.5 %.
$x=980$ mm shows the measured transition location for this smooth-plate condition, and the associated linear threshold amplitude at transition is approximately 0.5 %.
The three amplitude curves identified as A, B and C are measured in the presence of surface gaps at ![]() $x_G=450$ mm. For cases A (
$x_G=450$ mm. For cases A (![]() $w/ \delta ^* =27$,
$w/ \delta ^* =27$, ![]() $d/ \delta ^* =2.6$) and B (
$d/ \delta ^* =2.6$) and B (![]() $w/ \delta ^* =18$,
$w/ \delta ^* =18$, ![]() $d/ \delta ^* =3.45$), the free-stream conditions are the same as for the smooth-surface reference case, U18. Case C (
$d/ \delta ^* =3.45$), the free-stream conditions are the same as for the smooth-surface reference case, U18. Case C (![]() $w/ \delta ^* =20$,
$w/ \delta ^* =20$, ![]() $d/ \delta ^* =3.83$) is measured at condition U22. The measured frequency for cases A and B is
$d/ \delta ^* =3.83$) is measured at condition U22. The measured frequency for cases A and B is ![]() $f=175$ and
$f=175$ and ![]() $f=183$ Hz, respectively. These are essentially the same as the smooth-plate frequency. The calculated linear-amplitude curve for
$f=183$ Hz, respectively. These are essentially the same as the smooth-plate frequency. The calculated linear-amplitude curve for ![]() $f=180$ Hz is overlaid on the experimental data for these cases. Similar to the smooth-plate comparison, the initial amplitude level was chosen to provide a match to the data in the neighbourhood of
$f=180$ Hz is overlaid on the experimental data for these cases. Similar to the smooth-plate comparison, the initial amplitude level was chosen to provide a match to the data in the neighbourhood of ![]() $x \approx 700$ mm. The good agreement between theory and experiment for the pre-transition amplitude variation shows that the primary effect of the gap is to locally destabilize the TS wave, resulting in a larger amplitude. Assuming the same linear threshold amplitude for transition as for the smooth plate 0.5 % (using the current
$x \approx 700$ mm. The good agreement between theory and experiment for the pre-transition amplitude variation shows that the primary effect of the gap is to locally destabilize the TS wave, resulting in a larger amplitude. Assuming the same linear threshold amplitude for transition as for the smooth plate 0.5 % (using the current ![]() $u'$ amplitude definition), the shifted linear-amplitude curves for A and B provide a good prediction for the transition onset as shown by the rectangles for these cases. This provides support for using a linear-amplitude method, or the simplified variant of a variable
$u'$ amplitude definition), the shifted linear-amplitude curves for A and B provide a good prediction for the transition onset as shown by the rectangles for these cases. This provides support for using a linear-amplitude method, or the simplified variant of a variable ![]() $N$-factor method, for predicting the transition movement due to gaps.
$N$-factor method, for predicting the transition movement due to gaps.
The amplitude variation for case C is qualitatively different from cases A and B. The amplification at the gap location is much greater, and this leads to a more rapid transition – essentially at the gap location. In this case, there is no sign of any TS-wave growth. In addition, the frequency for case C is ![]() $f=830$ Hz (or
$f=830$ Hz (or ![]() $F=163$), which is well outside the expected range for TS-wave transition. This case can be characterized as a bypass to the underlying linear transition mechanism. This supports the observation that the threshold boundary in figure 5 is associated with bypass transition. Further evidence for this is provided by the recent global stability analysis of Reference Mathias and MedeirosMathias and Medeiros (Reference Mathias and Medeiros2019).
$F=163$), which is well outside the expected range for TS-wave transition. This case can be characterized as a bypass to the underlying linear transition mechanism. This supports the observation that the threshold boundary in figure 5 is associated with bypass transition. Further evidence for this is provided by the recent global stability analysis of Reference Mathias and MedeirosMathias and Medeiros (Reference Mathias and Medeiros2019).
5. Analysis of gap effects for TS transition
Linear stability analysis and the variable ![]() $N$-factor formulation are used to investigate the linkage between the gap effects on TS waves and the observed transition movement presented in figure 5. For a given gap and flow condition, a smooth-surface amplification envelope from figure 4 is used to determine the critical
$N$-factor formulation are used to investigate the linkage between the gap effects on TS waves and the observed transition movement presented in figure 5. For a given gap and flow condition, a smooth-surface amplification envelope from figure 4 is used to determine the critical ![]() $N$-factor
$N$-factor ![]() $N$ at the measured transition location
$N$ at the measured transition location ![]() $x_T$. For the same flow condition, the smooth-surface transition location
$x_T$. For the same flow condition, the smooth-surface transition location ![]() $x_{T0}$ is used to determine the reference
$x_{T0}$ is used to determine the reference ![]() $N$-factor
$N$-factor ![]() $N_0$. This provides a
$N_0$. This provides a ![]() ${\rm \Delta} N = N_0 - N$ as a function of the gap characteristics
${\rm \Delta} N = N_0 - N$ as a function of the gap characteristics ![]() $w/ \delta ^*$,
$w/ \delta ^*$, ![]() $d/ \delta ^*$.
$d/ \delta ^*$.
There are two primary factors contributing to the uncertainty in the calculated ![]() ${\rm \Delta} N$. The first is the uncertainty in the measured transition location
${\rm \Delta} N$. The first is the uncertainty in the measured transition location ![]() $x_T$ or
$x_T$ or ![]() $x_{T0}$, which, as noted above, is
$x_{T0}$, which, as noted above, is ![]() $\pm$10 mm. Using the steepest envelope curve from figure 4, this translates to an
$\pm$10 mm. Using the steepest envelope curve from figure 4, this translates to an ![]() $N$-factor uncertainty of
$N$-factor uncertainty of ![]() $\pm$0.17. The other source of uncertainty is a
$\pm$0.17. The other source of uncertainty is a ![]() $3 \times (10)^4\,{\rm m}^{-1}$ standard deviation in unit Reynolds number for the range of test points corresponding to a given test condition in table 1. This results in an
$3 \times (10)^4\,{\rm m}^{-1}$ standard deviation in unit Reynolds number for the range of test points corresponding to a given test condition in table 1. This results in an ![]() $N$-factor uncertainty of
$N$-factor uncertainty of ![]() ${\pm }0.12$. The cumulative uncertainty for a given
${\pm }0.12$. The cumulative uncertainty for a given ![]() $N$-factor calculation is
$N$-factor calculation is ![]() ${\pm }0.21$, and the associated uncertainty for
${\pm }0.21$, and the associated uncertainty for ![]() ${\rm \Delta} N$ is
${\rm \Delta} N$ is ![]() ${\pm }0.3$. Note that a larger transition uncertainty of
${\pm }0.3$. Note that a larger transition uncertainty of ![]() ${\pm }15$ mm would result in a cumulative
${\pm }15$ mm would result in a cumulative ![]() ${\rm \Delta} N$ uncertainty of
${\rm \Delta} N$ uncertainty of ![]() ${\pm }0.4$.
${\pm }0.4$.
Figure 7 shows the calculated ![]() ${\rm \Delta} N$ for all of the gap measurements with
${\rm \Delta} N$ for all of the gap measurements with ![]() $x_G =450$ mm as a function of the gap depth and gap width. The different symbols correspond to the gap-width bins that are used to organize the data. The solid line in figure 7(a) shows the
$x_G =450$ mm as a function of the gap depth and gap width. The different symbols correspond to the gap-width bins that are used to organize the data. The solid line in figure 7(a) shows the ![]() ${\rm \Delta} N =4.4 d/ \delta ^*$ variation for a backward-facing step from Reference Crouch, Kosorygin and NgCrouch et al. (Reference Crouch, Kosorygin and Ng2006). All of the data are bounded by the backward-facing step trend line, showing that the gap effects on TS waves are no worse than a backward-facing step of height
${\rm \Delta} N =4.4 d/ \delta ^*$ variation for a backward-facing step from Reference Crouch, Kosorygin and NgCrouch et al. (Reference Crouch, Kosorygin and Ng2006). All of the data are bounded by the backward-facing step trend line, showing that the gap effects on TS waves are no worse than a backward-facing step of height ![]() $d / \delta ^*$. The results show that the
$d / \delta ^*$. The results show that the ![]() ${\rm \Delta} N$ initially increases with
${\rm \Delta} N$ initially increases with ![]() $d/ \delta ^*$ similar to a backward-facing step but then
$d/ \delta ^*$ similar to a backward-facing step but then ![]() ${\rm \Delta} N$ plateaus to a nearly constant value, which depends on the gap width. The points in the grey band between
${\rm \Delta} N$ plateaus to a nearly constant value, which depends on the gap width. The points in the grey band between ![]() $6 < {\rm \Delta} N <7.5$ correspond to transition occurring at the gap location, and are likely the result of bypass transition as discussed above.
$6 < {\rm \Delta} N <7.5$ correspond to transition occurring at the gap location, and are likely the result of bypass transition as discussed above.

Figure 7. Variation of ![]() ${\rm \Delta} N$ as a function of (a) gap depth and (b) gap width for gaps at
${\rm \Delta} N$ as a function of (a) gap depth and (b) gap width for gaps at ![]() $x_G=\textit{450}$ mm, in an adverse pressure gradient. Dashed lines show the mean slope (
$x_G=\textit{450}$ mm, in an adverse pressure gradient. Dashed lines show the mean slope (![]() $\textit{0.1} w/ \delta ^*$) and
$\textit{0.1} w/ \delta ^*$) and ![]() $\pm$ one standard deviation.
$\pm$ one standard deviation.
Figure 7(b) shows the same data plotted as a function of gap width ![]() $w/ \delta ^*$. The thick dashed line through the data (
$w/ \delta ^*$. The thick dashed line through the data (![]() $0.1 w/ \delta ^*$) shows the mean value calculated from
$0.1 w/ \delta ^*$) shows the mean value calculated from ![]() ${\rm \Delta} N /(w/ \delta ^*)$ for data in the range
${\rm \Delta} N /(w/ \delta ^*)$ for data in the range ![]() $7 \leq w/ \delta ^* \leq 30$; smaller values of
$7 \leq w/ \delta ^* \leq 30$; smaller values of ![]() $w/ \delta ^*$ overly amplify data scatter, and larger values are potentially influenced by bypass transition. The thin dashed lines in figure 7(b) show the mean slope plus or minus one standard deviation. The mean plus one standard deviation provides a good bounding curve for the data.
$w/ \delta ^*$ overly amplify data scatter, and larger values are potentially influenced by bypass transition. The thin dashed lines in figure 7(b) show the mean slope plus or minus one standard deviation. The mean plus one standard deviation provides a good bounding curve for the data.
The non-bypass results of figure 7 show two distinct trends in the ![]() ${\rm \Delta} N$ variation. For small values of
${\rm \Delta} N$ variation. For small values of ![]() $d/ \delta ^*$, the
$d/ \delta ^*$, the ![]() ${\rm \Delta} N$ varies with
${\rm \Delta} N$ varies with ![]() $d/ \delta ^*$ similar to a backward-facing step. This variation is independent of the gap width
$d/ \delta ^*$ similar to a backward-facing step. This variation is independent of the gap width ![]() $w/ \delta ^*$, as long as the width is sufficiently large compared with the depth. Qualitatively, this is a shallow gap that is dominated by the upstream backward-facing step, with minimal influence from the downstream forward-facing step. For larger values of
$w/ \delta ^*$, as long as the width is sufficiently large compared with the depth. Qualitatively, this is a shallow gap that is dominated by the upstream backward-facing step, with minimal influence from the downstream forward-facing step. For larger values of ![]() $d/ \delta ^*$, the
$d/ \delta ^*$, the ![]() ${\rm \Delta} N$ approaches a constant value that depends on the gap width. In this deep-gap limiting case, the value of
${\rm \Delta} N$ approaches a constant value that depends on the gap width. In this deep-gap limiting case, the value of ![]() ${\rm \Delta} N$ is independent of the depth.
${\rm \Delta} N$ is independent of the depth.
Based on the slope for the average ![]() $w/ \delta ^*$ dependence from figure 7(b), the overall
$w/ \delta ^*$ dependence from figure 7(b), the overall ![]() ${\rm \Delta} N$ variation is given by
${\rm \Delta} N$ variation is given by
The boundary between the shallow-gap and deep-gap behaviour is determined by equating ![]() ${\rm \Delta} N$ from the two expressions. A deep-gap behaviour is also seen in the study of Reference Beguet, Perraud, Forte and BrazierBeguet et al. (Reference Beguet, Perraud, Forte and Brazier2017) based on the change in the far-field growth factor
${\rm \Delta} N$ from the two expressions. A deep-gap behaviour is also seen in the study of Reference Beguet, Perraud, Forte and BrazierBeguet et al. (Reference Beguet, Perraud, Forte and Brazier2017) based on the change in the far-field growth factor ![]() ${\rm \Delta} n_{far}$. When applied to the current test conditions for
${\rm \Delta} n_{far}$. When applied to the current test conditions for ![]() $x_G=450$ mm, their
$x_G=450$ mm, their ![]() ${\rm \Delta} n_{far}$ variation slopes are between
${\rm \Delta} n_{far}$ variation slopes are between ![]() $0.07 w/ \delta ^*$ and
$0.07 w/ \delta ^*$ and ![]() $0.08 w/ \delta ^*$, which is at the lower end of the range of slopes from figure 7(b).
$0.08 w/ \delta ^*$, which is at the lower end of the range of slopes from figure 7(b).
The limiting behaviours of (5.1) are shown schematically by the solid and dashed straight lines in figure 8. A simple model that smoothly transitions between the shallow-gap and deep-gap behaviour, based on the average slope of ![]() ${\rm \Delta} N$ versus
${\rm \Delta} N$ versus ![]() $w/ \delta ^*$, is
$w/ \delta ^*$, is
This model variation is shown by the red dashed curve in figure 8, in relation to the limiting behaviours.

Figure 8. Schematic showing the ![]() ${\rm \Delta} N$ variation with gap depth for a fixed gap width. For shallow gaps the
${\rm \Delta} N$ variation with gap depth for a fixed gap width. For shallow gaps the ![]() ${\rm \Delta} N$ varies like a backward-facing step, and for deep gaps the
${\rm \Delta} N$ varies like a backward-facing step, and for deep gaps the ![]() ${\rm \Delta} N$ takes on a constant value that depends on the width.
${\rm \Delta} N$ takes on a constant value that depends on the width.
Due to the data scatter of figure 7, the ![]() $d/w$ value differentiating shallow-gap behaviour from deep-gap behaviour is not well defined, but is in the range
$d/w$ value differentiating shallow-gap behaviour from deep-gap behaviour is not well defined, but is in the range ![]() $0.017 < d/w < 0.028$ (or,
$0.017 < d/w < 0.028$ (or, ![]() $36 < w/d < 59$), based on using the slopes of the two thin dashed lines from figure 7(b). To conservatively account for this data scatter, an alternative expression for
$36 < w/d < 59$), based on using the slopes of the two thin dashed lines from figure 7(b). To conservatively account for this data scatter, an alternative expression for ![]() ${\rm \Delta} N$ is given by
${\rm \Delta} N$ is given by
This provides an approximate bounding curve for the results (Crouch, Kosorygin, & Sutanto, Reference Crouch, Kosorygin and Sutanto2020) – essentially one sigma above the average in figure 7(b). This study did not include detailed investigation of the gap flow, but the shallow-gap/deep-gap boundary is thought to be linked to the flow-reattachment distance within the gap. For the shallow gap, the recirculation length is set by the gap depth, but for the deep gap it is limited by the gap width.
Comparisons between the model expressions of (5.2) and (5.3) and the experimental data are provided in figure 9, which essentially combines figures 7 and 8. Similar to figure 7, the grey bands at larger ![]() ${\rm \Delta} N$ show points that have transition at the gap location, and are likely bypass transition. The thicker dashed lines are for the average behaviour of (5.2), and the thin dashed lines are for the bounding case of (5.3). Figure 9(a) shows the results for
${\rm \Delta} N$ show points that have transition at the gap location, and are likely bypass transition. The thicker dashed lines are for the average behaviour of (5.2), and the thin dashed lines are for the bounding case of (5.3). Figure 9(a) shows the results for ![]() $x_G=450$ mm, with the gap in the adverse pressure gradient. This is from the same data set shown in figure 7, and used to develop the model. Figure 9(b) shows results for
$x_G=450$ mm, with the gap in the adverse pressure gradient. This is from the same data set shown in figure 7, and used to develop the model. Figure 9(b) shows results for ![]() $x_G=127$ mm, with the gap in the favourable pressure gradient. These data also show good agreement with the model, although biased towards smaller
$x_G=127$ mm, with the gap in the favourable pressure gradient. These data also show good agreement with the model, although biased towards smaller ![]() ${\rm \Delta} N$ values, similar to earlier step results (Reference Crouch, Kosorygin and NgCrouch et al., 2006). Even though the TS-instabilities are nominally damped at
${\rm \Delta} N$ values, similar to earlier step results (Reference Crouch, Kosorygin and NgCrouch et al., 2006). Even though the TS-instabilities are nominally damped at ![]() $x=127$ mm, this location is relatively close to the neutral points for the critical modes. In this case, the destabilizing effects of the gaps are still significant.
$x=127$ mm, this location is relatively close to the neutral points for the critical modes. In this case, the destabilizing effects of the gaps are still significant.
To provide a general characterization of the gap effects, the model of (5.2) is used to recast the transition length results of figure 5 into ![]() ${\rm \Delta} N$ contours. Figure 10 shows the
${\rm \Delta} N$ contours. Figure 10 shows the ![]() ${\rm \Delta} N$ resulting from different gap widths and depths. The cross-hatch area shows the region where bypass transition occurs, which is independent of the TS-wave amplification.
${\rm \Delta} N$ resulting from different gap widths and depths. The cross-hatch area shows the region where bypass transition occurs, which is independent of the TS-wave amplification.
(i) For gap depths greater than
 $d/ \delta ^* \approx 3.7$, bypass transition occurs for gap widths
$d/ \delta ^* \approx 3.7$, bypass transition occurs for gap widths  $w/ \delta ^* > 19$; for narrower widths,
$w/ \delta ^* > 19$; for narrower widths,  $w/ \delta ^* < 19$, the maximum
$w/ \delta ^* < 19$, the maximum  ${\rm \Delta} N$ is less than 2. For this range of gap depths, the reduction in the critical
${\rm \Delta} N$ is less than 2. For this range of gap depths, the reduction in the critical  $N$-factor results in a relatively small movement in transition compared with bypass.
$N$-factor results in a relatively small movement in transition compared with bypass.(ii) For depths in the range
 $1.8 < d/ \delta ^* < 3.7$, the reduction in critical
$1.8 < d/ \delta ^* < 3.7$, the reduction in critical  $N$-factor can be as large as 3.5.
$N$-factor can be as large as 3.5.(iii) For depths below
 $d/ \delta ^* \approx 1.8$, the transition movements result from changes in the TS-wave critical
$d/ \delta ^* \approx 1.8$, the transition movements result from changes in the TS-wave critical  $N$-factor. In this range of depths, the transition movement is a function of both the gap width and depth.
$N$-factor. In this range of depths, the transition movement is a function of both the gap width and depth.

Figure 10. The TS-wave ![]() ${\rm \Delta} N$ contours and bypass-transition region as a function of the gap width
${\rm \Delta} N$ contours and bypass-transition region as a function of the gap width ![]() $w/ \delta ^*$ and depth
$w/ \delta ^*$ and depth ![]() $d/ \delta ^*$ based on low Mach number data (
$d/ \delta ^*$ based on low Mach number data (![]() $M<\textit{0.1}$) for nominally two-dimensional boundary layers.
$M<\textit{0.1}$) for nominally two-dimensional boundary layers.
6. Conclusions and recommendations
Linear stability analysis in conjunction with detailed boundary-layer transition experiments have been used to characterize the effects of spanwise-running gaps on transition in nominally two-dimensional boundary layers. Similar to earlier studies, the gap effects are expressed in terms of the non-dimensional gap width ![]() $w/ \delta ^*$ and depth
$w/ \delta ^*$ and depth ![]() $d/ \delta ^*$ for a rectangular cross-section gap. A variable
$d/ \delta ^*$ for a rectangular cross-section gap. A variable ![]() $N$-factor model has been developed to capture the movement in transition due to enhanced amplification of TS waves. Results show two limiting behaviours for the effects on TS waves: a shallow-gap limit where the incremental amplification is independent of the gap width, and a deep-gap limit where the incremental amplification is independent of the gap depth. The model is shown to be in good agreement with the experimental data for gaps placed upstream of the instability neutral point (in a favourable pressure gradient) and downstream of the instability neutral point (in an adverse pressure gradient).
$N$-factor model has been developed to capture the movement in transition due to enhanced amplification of TS waves. Results show two limiting behaviours for the effects on TS waves: a shallow-gap limit where the incremental amplification is independent of the gap width, and a deep-gap limit where the incremental amplification is independent of the gap depth. The model is shown to be in good agreement with the experimental data for gaps placed upstream of the instability neutral point (in a favourable pressure gradient) and downstream of the instability neutral point (in an adverse pressure gradient).
Transition movements observed in the experiments that are not correlated to changes in TS-wave amplification are shown to result from some form of bypass transition, with a significantly higher characteristic frequency. The boundary for bypass transition is in good agreement with earlier experiments. The variable ![]() $N$-factor results, in combination with the bypass-transition boundary, provide a full description for the potential transition movement due to gaps for nominally two-dimensional boundary layers.
$N$-factor results, in combination with the bypass-transition boundary, provide a full description for the potential transition movement due to gaps for nominally two-dimensional boundary layers.
Even though these results are based on low-speed test conditions, the basic methodology and gap characterization extends to higher-speed flows typical for commercial transport aircraft. Future studies are needed to assess the quantitative effects of Mach number to enable the full generalization of the current findings. In addition, the current results have focused on nominally two-dimensional flows where the smooth-surface transition is dominated by TS waves. For swept flows that are dominated by cross-flow instability, additional investigations are needed. In these cases, the TS-wave variable ![]() $N$-factor results are not applicable, but the bypass boundary is likely to be similar to the current findings.
$N$-factor results are not applicable, but the bypass boundary is likely to be similar to the current findings.
Acknowledgements
Elements of this work have been presented earlier as AIAA paper 2020-3075.
Declaration of Interests
The authors report no conflict of interest.
Author Contributions
J.D.C. and V.S.K. created the research plan and designed the experiments, V.S.K. conducted the experiments and J.D.C., M.I.S. and G.D.M. carried out the analysis and model development.
Data Availability Statement
Further details on underlying data are available from the corresponding author (J.D.C.).
Ethical Standards
The research meets all ethical guidelines, including adherence to the legal requirements of the study country.