1. Introduction and main results
In this paper, we are concerned with the study of an age-dependent epidemic model with nonlocal diffusion in space, motivated by [Reference Ducrot6], where the first author studied a similar problem with random diffusion in space. Our aim is to study a classical SI model from the point of view of the spatial spread of an epidemic. Here,
![]() $a\in (0, a^+)$
denotes the physiological age and
$a\in (0, a^+)$
denotes the physiological age and
![]() $a^+\in (0, \infty )$
is the maximum age of an individual;
$a^+\in (0, \infty )$
is the maximum age of an individual;
![]() $t\gt 0$
denotes the time and
$t\gt 0$
denotes the time and
![]() $x\in \mathbb{R}$
is the spatial position of an individual. The population can be split into two sub-populations: the susceptible and the infective populations. We denote by
$x\in \mathbb{R}$
is the spatial position of an individual. The population can be split into two sub-populations: the susceptible and the infective populations. We denote by
![]() $S(t, a, x)$
and
$S(t, a, x)$
and
![]() $I(t,a,x)$
the age distribution of the susceptible individuals, respectively, at time
$I(t,a,x)$
the age distribution of the susceptible individuals, respectively, at time
![]() $t$
and spatial location
$t$
and spatial location
![]() $x\in \mathbb{R}$
. With these notations, the model that we consider reads as follows:
$x\in \mathbb{R}$
. With these notations, the model that we consider reads as follows:
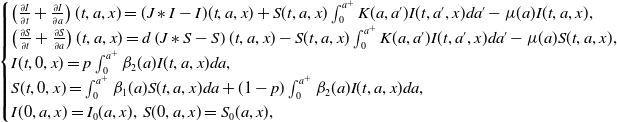 \begin{equation} \begin{cases} \left (\frac{\partial I}{\partial t}+\frac{\partial I}{\partial a}\right )(t, a, x)=(J\ast I-I)(t, a, x)+S(t, a, x)\int _0^{a^+}K(a, a')I(t, a', x)da'-\mu (a)I(t, a, x),\\ \left (\frac{\partial S}{\partial t}+\frac{\partial S}{\partial a}\right )(t, a, x)=d\left (J\ast S-S\right )(t, a, x)-S(t, a, x)\int _0^{a^+}K(a, a')I(t, a', x)da'-\mu (a)S(t, a, x),\\ I(t, 0, x)=p\int _0^{a^+}\beta _2(a)I(t, a, x)da,\\ S(t, 0, x)=\int _0^{a^+}\beta _1(a)S(t, a, x)da+(1-p)\int _0^{a^+}\beta _2(a)I(t, a, x)da,\\ I(0, a, x)=I_0(a, x),\;S(0, a, x)=S_0(a, x), \end{cases} \end{equation}
\begin{equation} \begin{cases} \left (\frac{\partial I}{\partial t}+\frac{\partial I}{\partial a}\right )(t, a, x)=(J\ast I-I)(t, a, x)+S(t, a, x)\int _0^{a^+}K(a, a')I(t, a', x)da'-\mu (a)I(t, a, x),\\ \left (\frac{\partial S}{\partial t}+\frac{\partial S}{\partial a}\right )(t, a, x)=d\left (J\ast S-S\right )(t, a, x)-S(t, a, x)\int _0^{a^+}K(a, a')I(t, a', x)da'-\mu (a)S(t, a, x),\\ I(t, 0, x)=p\int _0^{a^+}\beta _2(a)I(t, a, x)da,\\ S(t, 0, x)=\int _0^{a^+}\beta _1(a)S(t, a, x)da+(1-p)\int _0^{a^+}\beta _2(a)I(t, a, x)da,\\ I(0, a, x)=I_0(a, x),\;S(0, a, x)=S_0(a, x), \end{cases} \end{equation}
wherein we have set
for some continuous convolution kernel
![]() $J\;:\;\mathbb{R}\to \mathbb{R}$
, whose specific properties will be presented in Assumption 1.1 below, while
$J\;:\;\mathbb{R}\to \mathbb{R}$
, whose specific properties will be presented in Assumption 1.1 below, while
![]() $C_b(\mathbb{R})$
denotes the space of bounded and continuous functions. Here, the function
$C_b(\mathbb{R})$
denotes the space of bounded and continuous functions. Here, the function
![]() $K(a, a')$
denotes the rate of the disease transmission from infective individuals of age
$K(a, a')$
denotes the rate of the disease transmission from infective individuals of age
![]() $a'$
to susceptible individuals of age
$a'$
to susceptible individuals of age
![]() $a$
. In addition, the function
$a$
. In addition, the function
![]() $\mu$
denotes the age-specific death rate for both the infective and susceptible individuals,
$\mu$
denotes the age-specific death rate for both the infective and susceptible individuals,
![]() $\beta _1$
and
$\beta _1$
and
![]() $\beta _2$
denote the age-specific birth rate for the susceptible and infective ones, respectively. Moreover, we assume that these birth rates are identical, that is
$\beta _2$
denote the age-specific birth rate for the susceptible and infective ones, respectively. Moreover, we assume that these birth rates are identical, that is
![]() $\beta _1\equiv \beta _2=\beta$
. The constant
$\beta _1\equiv \beta _2=\beta$
. The constant
![]() $p\in [0, 1]$
denotes the proportion of the vertical transmission, that is the proportion of the infective newborns inherited from their infective parents. Further, we assume that
$p\in [0, 1]$
denotes the proportion of the vertical transmission, that is the proportion of the infective newborns inherited from their infective parents. Further, we assume that
![]() $S$
and
$S$
and
![]() $I$
have the same diffusion coefficient, that is
$I$
have the same diffusion coefficient, that is
![]() $d=1$
. This assumption combined with no additional death rate due to the disease allows us to reduce the system to a single scalar equation. We would like to mention that the existence of travelling wave of age-structured
$d=1$
. This assumption combined with no additional death rate due to the disease allows us to reduce the system to a single scalar equation. We would like to mention that the existence of travelling wave of age-structured
![]() $SI$
system with random diffusion has been obtained by Ducrot and Magal [Reference Ducrot and Magal11, Reference Ducrot and Magal12] with/without external supply and Ducrot et al. [Reference Ducrot, Magal and Ruan13] in a multigroup framework, respectively.
$SI$
system with random diffusion has been obtained by Ducrot and Magal [Reference Ducrot and Magal11, Reference Ducrot and Magal12] with/without external supply and Ducrot et al. [Reference Ducrot, Magal and Ruan13] in a multigroup framework, respectively.
In this work, we consider that the total population has a demographic equilibrium, meaning that birth and death equilibrate the population. This prevents the population from going to extinction and from exploding as time increases. The total population stabilises to a steady state as
![]() $t\to \infty$
. Mathematically speaking, this assumption can be written as the following condition on the demographic functions
$t\to \infty$
. Mathematically speaking, this assumption can be written as the following condition on the demographic functions
![]() $\beta$
and
$\beta$
and
![]() $\mu$
:
$\mu$
:
This condition may imply that multiple steady states exist for the total population
![]() $I+S$
when
$I+S$
when
![]() $d=1$
(see Webb [Reference Webb27] for some discussions on this condition). Next, we are looking for heteroclinic solutions of system (1.1) with the following behaviour for
$d=1$
(see Webb [Reference Webb27] for some discussions on this condition). Next, we are looking for heteroclinic solutions of system (1.1) with the following behaviour for
![]() $x\to \pm \infty$
:
$x\to \pm \infty$
:
These conditions mean that at
![]() $x=+\infty$
, the population is only composed of the susceptible, whereas at
$x=+\infty$
, the population is only composed of the susceptible, whereas at
![]() $x=-\infty$
, the population is only composed of infected individuals.
$x=-\infty$
, the population is only composed of infected individuals.
Now when
![]() $d=1$
, adding-up the first two equations in (1.1), the nonlinear terms cancel and one obtains using (1.3), that
$d=1$
, adding-up the first two equations in (1.1), the nonlinear terms cancel and one obtains using (1.3), that
As a consequence, system (1.1)–(1.3) reduces to the scalar equation for the unknown function
![]() $I$
$I$
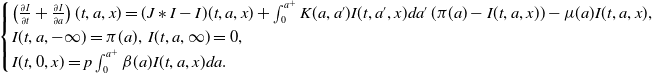 \begin{equation} \begin{cases} \left (\frac{\partial I}{\partial t}+\frac{\partial I}{\partial a}\right )(t, a, x)=(J\ast I-I)(t, a, x)+\int _0^{a^+}K(a, a')I(t, a', x)da'\,(\pi (a)-I(t, a, x))-\mu (a)I(t, a, x),\\ I(t, a, -\infty )=\pi (a),\; I(t, a, \infty )=0,\\ I(t, 0, x)=p\int _0^{a^+}\beta (a)I(t, a, x)da. \end{cases} \end{equation}
\begin{equation} \begin{cases} \left (\frac{\partial I}{\partial t}+\frac{\partial I}{\partial a}\right )(t, a, x)=(J\ast I-I)(t, a, x)+\int _0^{a^+}K(a, a')I(t, a', x)da'\,(\pi (a)-I(t, a, x))-\mu (a)I(t, a, x),\\ I(t, a, -\infty )=\pi (a),\; I(t, a, \infty )=0,\\ I(t, 0, x)=p\int _0^{a^+}\beta (a)I(t, a, x)da. \end{cases} \end{equation}
We rewrite this problem with the new unknown function
![]() $u(t, a, x)$
defined by
$u(t, a, x)$
defined by
and we obtain the following equation for the function
![]() $u$
:
$u$
:
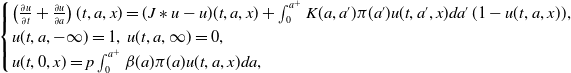 \begin{equation} \begin{cases} \left (\frac{\partial u}{\partial t}+\frac{\partial u}{\partial a}\right )(t, a, x)=(J\ast u-u)(t, a, x)+\int _0^{a^+}K(a, a')\pi (a')u(t, a', x)da'\,(1-u(t, a, x)),\\ u(t, a, -\infty )=1,\; u(t, a, \infty )=0,\\ u(t, 0, x)=p\int _0^{a^+}\beta (a)\pi (a)u(t, a, x)da, \end{cases} \end{equation}
\begin{equation} \begin{cases} \left (\frac{\partial u}{\partial t}+\frac{\partial u}{\partial a}\right )(t, a, x)=(J\ast u-u)(t, a, x)+\int _0^{a^+}K(a, a')\pi (a')u(t, a', x)da'\,(1-u(t, a, x)),\\ u(t, a, -\infty )=1,\; u(t, a, \infty )=0,\\ u(t, 0, x)=p\int _0^{a^+}\beta (a)\pi (a)u(t, a, x)da, \end{cases} \end{equation}
Note that
![]() $u$
may not be zero at
$u$
may not be zero at
![]() $a=a^+$
. Now we set
$a=a^+$
. Now we set
and recalling condition (1.2), we impose the following assumptions.
Assumption 1.1 We assume that the following properties hold true:
-
(i) the function
 $\gamma$
is continuous and non-negative in
$\gamma$
is continuous and non-negative in
 $[0, a^+]$
and satisfies
$[0, a^+]$
and satisfies
 $\int _0^{a^+}\gamma (a)da=1$
;
$\int _0^{a^+}\gamma (a)da=1$
; -
(ii) the function
 $\pi$
is continuous, positive in
$\pi$
is continuous, positive in
 $[0, a^+)$
and the function
$[0, a^+)$
and the function
 $\gamma \pi$
does not identically vanish on
$\gamma \pi$
does not identically vanish on
 $(0, a^+)$
;
$(0, a^+)$
; -
(iii) the kernel
 $J$
is continuous and non-negative with
$J$
is continuous and non-negative with
 $\int _{\mathbb{R}} J(x)dx=1, J(0)\gt 0$
and
$\int _{\mathbb{R}} J(x)dx=1, J(0)\gt 0$
and
 $J(-x)=J(x), \forall x\in \mathbb{R}$
. Moreover,
$J(-x)=J(x), \forall x\in \mathbb{R}$
. Moreover,
 $\int _{\mathbb{R}} J(x)e^{l x}dx\lt \infty$
for any
$\int _{\mathbb{R}} J(x)e^{l x}dx\lt \infty$
for any
 $l\gt 0$
;
$l\gt 0$
; -
(iv) the transmission rate
 $K(\cdot, \,\cdot )$
is continuous and positive in
$K(\cdot, \,\cdot )$
is continuous and positive in
 $[0, a^+]\times [0, a^+]$
.
$[0, a^+]\times [0, a^+]$
.
We are now interested in the existence of the traveling wave solutions of the form
![]() $U(a, \xi )=u(a, x-ct)$
with
$U(a, \xi )=u(a, x-ct)$
with
![]() $\xi =x-ct$
. Here,
$\xi =x-ct$
. Here,
![]() $c$
is an unknown real number, which should be found together with the unknown function
$c$
is an unknown real number, which should be found together with the unknown function
![]() $U$
. Before proceeding, we set the rate of vertical transmission to be one, i.e.
$U$
. Before proceeding, we set the rate of vertical transmission to be one, i.e.
![]() $p=1$
. This setting is kind of technical mathematically, since
$p=1$
. This setting is kind of technical mathematically, since
![]() $p=1$
is used to guarantee that (1) the limiting equation (2.4) has only two solutions
$p=1$
is used to guarantee that (1) the limiting equation (2.4) has only two solutions
![]() $0$
and
$0$
and
![]() $1$
, see Section 2.2; (2) the hair-trigger effect holds, see Lemma 4.1. Next, using the moving frame, that is the variable
$1$
, see Section 2.2; (2) the hair-trigger effect holds, see Lemma 4.1. Next, using the moving frame, that is the variable
![]() $\xi =x-ct$
, the equation for the profile function
$\xi =x-ct$
, the equation for the profile function
![]() $U$
becomes for
$U$
becomes for
![]() $\xi \in \mathbb{R}$
and
$\xi \in \mathbb{R}$
and
![]() $a\in [0,a^+]$
:
$a\in [0,a^+]$
:
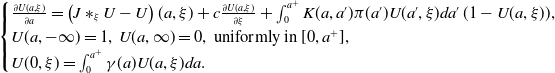 \begin{equation} \begin{cases} \frac{\partial U(a, \xi )}{\partial a}=\left (J\ast _\xi U-U\right )(a, \xi )+c\frac{\partial U(a, \xi )}{\partial \xi }+\int _0^{a^+}K(a, a')\pi (a')U(a', \xi )da'\,(1-U(a, \xi )),\\ U(a, -\infty )=1,\; U(a, \infty )=0, \text{ uniformly in $[0, a^+]$},\\ U(0, \xi )=\int _0^{a^+}\gamma (a)U(a, \xi )da. \end{cases} \end{equation}
\begin{equation} \begin{cases} \frac{\partial U(a, \xi )}{\partial a}=\left (J\ast _\xi U-U\right )(a, \xi )+c\frac{\partial U(a, \xi )}{\partial \xi }+\int _0^{a^+}K(a, a')\pi (a')U(a', \xi )da'\,(1-U(a, \xi )),\\ U(a, -\infty )=1,\; U(a, \infty )=0, \text{ uniformly in $[0, a^+]$},\\ U(0, \xi )=\int _0^{a^+}\gamma (a)U(a, \xi )da. \end{cases} \end{equation}
When the age-specific demographic and epidemic functions are ignored, this equation reduces to a monostable equation with nonlocal diffusion, which has been well studied by many researchers, see, for example, Coville et al. [Reference Coville, Dávila and Martínez2–Reference Coville and Dupaigne5], Fang and Zhao [Reference Fang and Zhao14], Li et al. [Reference Li, Sun and Wang17, Reference Sun, Li and Wang24] and Shen et al. [Reference Shen and Shen22, Reference Shen and Zhang23] and the references therein. In addition, we mention that the global dynamics of (1.4) with spatially dependent coefficients on the bounded domain can be studied using the sign of the spectral bound of a linearised operator at zero, the interested readers can refer to Ducrot et al. [Reference Ducrot, Kang and Ruan9, Reference Ducrot, Kang and Ruan10] and Kang and Ruan [Reference Kang and Ruan16] for more details.
Next, we solve (1.6) formally along characteristic lines. Define the characteristic line
![]() $h(a, \xi )$
as the solution of the following equation:
$h(a, \xi )$
as the solution of the following equation:
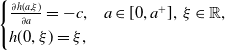 \begin{equation} \begin{cases} \frac{\partial h(a, \xi )}{\partial a}=-c, &a\in [0, a^+],\;\xi \in \mathbb{R},\\ h(0, \xi )=\xi, \end{cases} \end{equation}
\begin{equation} \begin{cases} \frac{\partial h(a, \xi )}{\partial a}=-c, &a\in [0, a^+],\;\xi \in \mathbb{R},\\ h(0, \xi )=\xi, \end{cases} \end{equation}
that reads as
![]() $h(a, \xi )=\xi -ca$
, which implies that
$h(a, \xi )=\xi -ca$
, which implies that
![]() $\partial _\xi h(a, \xi )=1$
. Next, solving (1.6) along the characteristic line
$\partial _\xi h(a, \xi )=1$
. Next, solving (1.6) along the characteristic line
![]() $h(a, \xi )$
, one obtains that the function
$h(a, \xi )$
, one obtains that the function
satisfies the following equation,
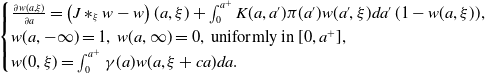 \begin{equation} \begin{cases} \frac{\partial w(a, \xi )}{\partial a}=\left (J\ast _\xi w-w\right )(a, \xi )+\int _0^{a^+}K(a, a')\pi (a')w(a', \xi )da'\,(1-w(a, \xi )),\\ w(a, -\infty )=1,\; w(a, \infty )=0,\text{ uniformly in $[0, a^+]$},\\ w(0, \xi )=\int _0^{a^+}\gamma (a)w(a, \xi +ca)da. \end{cases} \end{equation}
\begin{equation} \begin{cases} \frac{\partial w(a, \xi )}{\partial a}=\left (J\ast _\xi w-w\right )(a, \xi )+\int _0^{a^+}K(a, a')\pi (a')w(a', \xi )da'\,(1-w(a, \xi )),\\ w(a, -\infty )=1,\; w(a, \infty )=0,\text{ uniformly in $[0, a^+]$},\\ w(0, \xi )=\int _0^{a^+}\gamma (a)w(a, \xi +ca)da. \end{cases} \end{equation}
The above reformulation using the characteristic lines allows us to avoid the term
![]() $\frac{\partial U}{\partial \xi }$
appearing in (1.6). We now give the definition of a travelling wave solution of (1.5) as follows.
$\frac{\partial U}{\partial \xi }$
appearing in (1.6). We now give the definition of a travelling wave solution of (1.5) as follows.
Definition 1.2
A function
![]() $w=w(a,\xi )$
is said to be a travelling wave solution of (
1.5
) if
$w=w(a,\xi )$
is said to be a travelling wave solution of (
1.5
) if
![]() $w\in C([0, a^+]\times \mathbb{R})$
is a bounded solution of (
1.9
) such that for any
$w\in C([0, a^+]\times \mathbb{R})$
is a bounded solution of (
1.9
) such that for any
![]() $a\in (0, a^+)$
the map
$a\in (0, a^+)$
the map
![]() $\xi \mapsto w(a, \xi )$
is globally Lipschitz continuous and for any
$\xi \mapsto w(a, \xi )$
is globally Lipschitz continuous and for any
![]() $\xi \in \mathbb{R}$
,
$\xi \in \mathbb{R}$
,
![]() $a\mapsto w(a, \xi )\in W^{1, 1}(0, a^+)$
.
$a\mapsto w(a, \xi )\in W^{1, 1}(0, a^+)$
.
The first aim of this paper is to prove the existence of travelling wave solutions for (1.5).
Theorem 1.3
Let Assumption 1.1 be satisfied. Then there exists
![]() $c^*\gt 0$
such that for any
$c^*\gt 0$
such that for any
![]() $c\ge c^*$
, system (
1.5
) has a travelling wave solution. Moreover, any travelling wave solution
$c\ge c^*$
, system (
1.5
) has a travelling wave solution. Moreover, any travelling wave solution
![]() $w=w(a,\xi )$
is nonincreasing with respect to
$w=w(a,\xi )$
is nonincreasing with respect to
![]() $\xi \in \mathbb{R}$
and
$\xi \in \mathbb{R}$
and
![]() $c^*$
is given as follows:
$c^*$
is given as follows:
where
![]() $\lambda _0$
is the principal eigenvalue of the following age-structured problem:
$\lambda _0$
is the principal eigenvalue of the following age-structured problem:
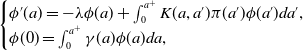 \begin{equation} \begin{cases} \phi '(a)=-\lambda \phi (a)+\int _0^{a^+}K(a, a')\pi (a')\phi (a')da',\\ \phi (0)=\int _0^{a^+}\gamma (a)\phi (a)da, \end{cases} \end{equation}
\begin{equation} \begin{cases} \phi '(a)=-\lambda \phi (a)+\int _0^{a^+}K(a, a')\pi (a')\phi (a')da',\\ \phi (0)=\int _0^{a^+}\gamma (a)\phi (a)da, \end{cases} \end{equation}
This theorem provides the existence of travelling wave solutions for Equation (1.4). Indeed we have the following theorem:
Theorem 1.4
Let Assumption 1.1 be satisfied. Then there exists
![]() $c^*\gt 0$
such that Equation (
1.4
) has a travelling wave solution for any wave speed
$c^*\gt 0$
such that Equation (
1.4
) has a travelling wave solution for any wave speed
![]() $c\ge c^*$
and there is no travelling wave solution of Equation (
1.4
) if
$c\ge c^*$
and there is no travelling wave solution of Equation (
1.4
) if
![]() $c\lt c^*$
. Moreover, the obtained travelling wave for
$c\lt c^*$
. Moreover, the obtained travelling wave for
![]() $c\ge c^*$
vanishes at the maximum age, that is at
$c\ge c^*$
vanishes at the maximum age, that is at
![]() $a=a^+$
.
$a=a^+$
.
The proofs of these results are based on the comparison principle to construct suitable super- and sub-solutions for Equation (1.9), motivated by Ducrot [Reference Ducrot6]. An important difference between this work and [Reference Ducrot6] (dealing with the corresponding equation with random diffusion) is that the solution map for (1.9) has no compactness property, thus the Schauder fixed point theorem may not directly be applied. However, (1.9) preserves the monotonicity and thus a monotone iteration method still works and allows us to overcome the lack of smoothing effect for nonlocal diffusion equation. In addition, we establish the required regularity of travelling wave solutions with respect to the variable
![]() $\xi$
in Definition 1.2 using suitable comparison arguments. Thus, this regularity will make the term
$\xi$
in Definition 1.2 using suitable comparison arguments. Thus, this regularity will make the term
![]() $\frac{\partial U}{\partial \xi }$
, appearing in (1.6), to be well-defined at least almost everywhere.
$\frac{\partial U}{\partial \xi }$
, appearing in (1.6), to be well-defined at least almost everywhere.
Our second aim in this work is to study the spreading speeds of the solutions of the Cauchy problem, that is of the following initial value problem associated with (1.5)
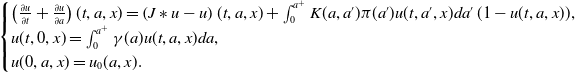 \begin{equation} \begin{cases} \left (\frac{\partial u}{\partial t}+\frac{\partial u}{\partial a}\right )(t, a, x)=\left (J\ast u-u\right )(t, a, x)+\int _0^{a^+}K(a, a')\pi (a')u(t, a', x)da'\,(1-u(t, a, x)),\\ u(t, 0, x)=\int _0^{a^+}\gamma (a)u(t, a, x)da,\\ u(0, a, x)=u_0(a, x). \end{cases} \end{equation}
\begin{equation} \begin{cases} \left (\frac{\partial u}{\partial t}+\frac{\partial u}{\partial a}\right )(t, a, x)=\left (J\ast u-u\right )(t, a, x)+\int _0^{a^+}K(a, a')\pi (a')u(t, a', x)da'\,(1-u(t, a, x)),\\ u(t, 0, x)=\int _0^{a^+}\gamma (a)u(t, a, x)da,\\ u(0, a, x)=u_0(a, x). \end{cases} \end{equation}
Then our result reads as follows.
Theorem 1.5
Let Assumption 1.1 be satisfied and assume that the initial data
![]() $u_0\in C([0, a^+]\times \mathbb{R})$
with
$u_0\in C([0, a^+]\times \mathbb{R})$
with
![]() $u_0\le 1$
are compactly supported, that is,
$u_0\le 1$
are compactly supported, that is,
![]() $\textrm{supp}(u_0)\subset [0, a^+]\times [-R, R]$
for some
$\textrm{supp}(u_0)\subset [0, a^+]\times [-R, R]$
for some
![]() $R\gt 0$
. Recalling that
$R\gt 0$
. Recalling that
![]() $c^*$
is defined in Theorem
1.3
, the solution
$c^*$
is defined in Theorem
1.3
, the solution
![]() $u=u(t, a, x)$
of problem (
1.11
) enjoys the following properties
$u=u(t, a, x)$
of problem (
1.11
) enjoys the following properties
-
(i) For all
 $c\gt c^*$
, it holds that
$c\gt c^*$
, it holds that
 \begin{equation*} \lim \limits _{t\to \infty }\sup _{|x|\ge ct, 0\lt a\lt a^+}u(t, a, x)=0. \end{equation*}
\begin{equation*} \lim \limits _{t\to \infty }\sup _{|x|\ge ct, 0\lt a\lt a^+}u(t, a, x)=0. \end{equation*}
-
(ii) For all
 $0\le c\lt c^*$
, it holds that
$0\le c\lt c^*$
, it holds that
 \begin{equation*} \lim \limits _{t\to \infty }\inf _{|x|\le ct, 0\lt a\lt a^+}u(t, a, x)=1. \end{equation*}
\begin{equation*} \lim \limits _{t\to \infty }\inf _{|x|\le ct, 0\lt a\lt a^+}u(t, a, x)=1. \end{equation*}
Remark 1.6
The non-existence of travelling wave solution of (
1.1
) for
![]() $c\lt c^*$
is a direct consequence of the above spreading property (Theorem
1.5
). In fact, if there exists
$c\lt c^*$
is a direct consequence of the above spreading property (Theorem
1.5
). In fact, if there exists
![]() $c\gt 0$
such that travelling wave solution exists and
$c\gt 0$
such that travelling wave solution exists and
![]() $c_0\gt 0$
such that
$c_0\gt 0$
such that
![]() $\liminf _{t\to \infty }U(a, c_0t-ct)=u(t, a, c_0t)\gt 0$
, then due to
$\liminf _{t\to \infty }U(a, c_0t-ct)=u(t, a, c_0t)\gt 0$
, then due to
![]() $U(a, -\infty )=1$
, there holds
$U(a, -\infty )=1$
, there holds
![]() $c_0\le c$
. Thus (ii) in Theorem
1.5
provides a lower bound for the admissible speed for which travelling wave solution exists.
$c_0\le c$
. Thus (ii) in Theorem
1.5
provides a lower bound for the admissible speed for which travelling wave solution exists.
Since the functions
![]() $\pi$
and
$\pi$
and
![]() $\gamma$
do not depend on the spatial variable
$\gamma$
do not depend on the spatial variable
![]() $x$
, the above spreading speed results are established by comparing the solutions of (1.11) with whose of the nonlocal diffusion problem with constant demographic functions. More precisely, for outer spreading, namely
$x$
, the above spreading speed results are established by comparing the solutions of (1.11) with whose of the nonlocal diffusion problem with constant demographic functions. More precisely, for outer spreading, namely
![]() $c\gt c^*$
, we can use the classical super-solution based on the travelling wave profile, while for inner spreading, namely
$c\gt c^*$
, we can use the classical super-solution based on the travelling wave profile, while for inner spreading, namely
![]() $c\lt c^*$
, we construct sub-solutions with suitable wave speed using a Fisher-KPP equation with nonlocal diffusion.
$c\lt c^*$
, we construct sub-solutions with suitable wave speed using a Fisher-KPP equation with nonlocal diffusion.
The paper is organised as follows. In Section 2, we discuss the well-posedness of (1.11) and construct suitable super-/sub-solutions for Equation (1.9). In Section 3, we prove the existence of travelling wave solutions via monotone iteration method and derive regularity estimates for travelling wave solutions. In Section 4, we study the spreading speed for some solutions of (1.11) and complete the proof of Theorem1.5.
2. Preliminaries
2.1 Well-posedness of (1.11)
In this section, we first study the well-posedness of (1.11). To this aim, we introduce some functional framework and we define
wherein
![]() $0_X$
denotes the zero element in
$0_X$
denotes the zero element in
![]() $X$
. These spaces become Bamach spaces when they are endowed with the usual product norms and we also introduce their positive cones as follows
$X$
. These spaces become Bamach spaces when they are endowed with the usual product norms and we also introduce their positive cones as follows
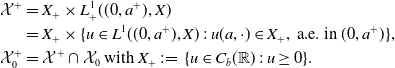 \begin{align*} \mathcal{X}^+&=X_+\times L^1_+((0, a^+), X)\\ &=X_+\times \{u\in L^1((0, a^+), X)\;:\; u(a, \cdot )\in X_+,\; \text{a.e. in }(0, a^+)\},\\ \mathcal{X}^+_0&=\mathcal{X}^+\cap \mathcal{X}_0\text{ with } X_+\;:\!=\;\{u\in C_b(\mathbb{R})\;:\; u\ge 0\}. \end{align*}
\begin{align*} \mathcal{X}^+&=X_+\times L^1_+((0, a^+), X)\\ &=X_+\times \{u\in L^1((0, a^+), X)\;:\; u(a, \cdot )\in X_+,\; \text{a.e. in }(0, a^+)\},\\ \mathcal{X}^+_0&=\mathcal{X}^+\cap \mathcal{X}_0\text{ with } X_+\;:\!=\;\{u\in C_b(\mathbb{R})\;:\; u\ge 0\}. \end{align*}
We also define the linear positive and bounded convolution operator
![]() $T\in \mathcal L(X)$
by
$T\in \mathcal L(X)$
by
Note that due to Assumption 1.1, (iii) one has
Next, define the operator
![]() $\mathcal B\;:\; dom(\mathcal B)\subset \mathcal X\to \mathcal X$
by
$\mathcal B\;:\; dom(\mathcal B)\subset \mathcal X\to \mathcal X$
by
Note that
![]() $\mathcal B$
is a closed Hille-Yosida operator. Moreover, define the nonlinear operator
$\mathcal B$
is a closed Hille-Yosida operator. Moreover, define the nonlinear operator
![]() $\mathcal C$
from
$\mathcal C$
from
![]() $\mathcal X_0$
to
$\mathcal X_0$
to
![]() $\mathcal X$
as follows:
$\mathcal X$
as follows:
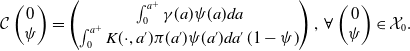 \begin{equation*} \mathcal C\begin {pmatrix} 0\\ \psi \end {pmatrix}=\begin {pmatrix}\int _{0}^{a^+}\gamma (a)\psi (a)da\\ \int _0^{a^+}K(\cdot, a')\pi (a')\psi (a')da'\,(1-\psi )\end {pmatrix},\;\forall \begin {pmatrix} 0\\ \psi \end {pmatrix}\in \mathcal X_0. \end{equation*}
\begin{equation*} \mathcal C\begin {pmatrix} 0\\ \psi \end {pmatrix}=\begin {pmatrix}\int _{0}^{a^+}\gamma (a)\psi (a)da\\ \int _0^{a^+}K(\cdot, a')\pi (a')\psi (a')da'\,(1-\psi )\end {pmatrix},\;\forall \begin {pmatrix} 0\\ \psi \end {pmatrix}\in \mathcal X_0. \end{equation*}
Then by identifying
![]() $U(t)=\begin{pmatrix} 0\\ u(t) \end{pmatrix}$
, problem (1.11) rewrites as the following abstract Cauchy problem:
$U(t)=\begin{pmatrix} 0\\ u(t) \end{pmatrix}$
, problem (1.11) rewrites as the following abstract Cauchy problem:
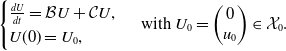 \begin{equation} \begin{cases} \frac{dU}{dt}=\mathcal{B}U+\mathcal CU,\\ U(0)=U_0, \end{cases}\text{ with }U_0=\begin{pmatrix} 0\\ u_0 \end{pmatrix}\in \mathcal{X}_0. \end{equation}
\begin{equation} \begin{cases} \frac{dU}{dt}=\mathcal{B}U+\mathcal CU,\\ U(0)=U_0, \end{cases}\text{ with }U_0=\begin{pmatrix} 0\\ u_0 \end{pmatrix}\in \mathcal{X}_0. \end{equation}
Based on the Lipshcitz property of
![]() $\mathcal C$
, by Thieme [Reference Thieme25, Reference Thieme26] or Magal and Ruan [Reference Magal and Ruan18], the existence and uniqueness of a mild solution for (2.3) are guaranteed. Next, recalling the definition of
$\mathcal C$
, by Thieme [Reference Thieme25, Reference Thieme26] or Magal and Ruan [Reference Magal and Ruan18], the existence and uniqueness of a mild solution for (2.3) are guaranteed. Next, recalling the definition of
![]() $\mathcal{B}$
, one may observe that
$\mathcal{B}$
, one may observe that
![]() $\mathcal{B}$
is resolvent positive. Moreover, there exists some constant
$\mathcal{B}$
is resolvent positive. Moreover, there exists some constant
![]() $L\gt 0$
such that the operator
$L\gt 0$
such that the operator
![]() $\mathcal C+LId_X$
is monotone on the subset
$\mathcal C+LId_X$
is monotone on the subset
![]() $\mathcal S_0\subset \mathcal X_0$
given by:
$\mathcal S_0\subset \mathcal X_0$
given by:
which means that for all
![]() $(U,V)\in \mathcal S_0$
, one has
$(U,V)\in \mathcal S_0$
, one has
where the partial order
![]() $\le$
in
$\le$
in
![]() $\mathcal X_0$
and
$\mathcal X_0$
and
![]() $\mathcal X$
is induced by the positive cones
$\mathcal X$
is induced by the positive cones
![]() $\mathcal{X}_0^+$
and
$\mathcal{X}_0^+$
and
![]() $\mathcal{X}^+$
, respectively. To see this, let us observe that for any
$\mathcal{X}^+$
, respectively. To see this, let us observe that for any
![]() $k\gt 0$
, if
$k\gt 0$
, if
![]() $L\gt k$
, then the function
$L\gt k$
, then the function
![]() $(v,u)\mapsto v(1-u)+Lu$
is increasing with respect to both variables
$(v,u)\mapsto v(1-u)+Lu$
is increasing with respect to both variables
![]() $(v,u)\in (-\infty, k]\times (-\infty, 1]$
. Due to the above monotonicity property, one also obtains that
$(v,u)\in (-\infty, k]\times (-\infty, 1]$
. Due to the above monotonicity property, one also obtains that
![]() $\mathcal CU+LU\in \mathcal X^+$
for all
$\mathcal CU+LU\in \mathcal X^+$
for all
![]() $U\in \mathcal X_0^+\cap \mathcal S_0$
. Hence, the result by Magal et al. [Reference Magal, Seydi and Wang19, Theorem 4.5] applies and ensures that Problem (2.3) is well posed in
$U\in \mathcal X_0^+\cap \mathcal S_0$
. Hence, the result by Magal et al. [Reference Magal, Seydi and Wang19, Theorem 4.5] applies and ensures that Problem (2.3) is well posed in
![]() $\mathcal X_0^+\cap \mathcal S_0$
, which is forward invariant and the comparison principle holds for (2.3) in
$\mathcal X_0^+\cap \mathcal S_0$
, which is forward invariant and the comparison principle holds for (2.3) in
![]() $\mathcal S_0$
. The latter result can be written as follows.
$\mathcal S_0$
. The latter result can be written as follows.
Lemma 2.1 (Comparison Principle). Assume that
![]() $U_0, V_0\in \mathcal{S}_0$
and
$U_0, V_0\in \mathcal{S}_0$
and
![]() $U_0\leq V_0$
, then the mild solutions
$U_0\leq V_0$
, then the mild solutions
![]() $U(t)$
and
$U(t)$
and
![]() $V(t)$
to (
2.3
) with initial data
$V(t)$
to (
2.3
) with initial data
![]() $U_0$
and
$U_0$
and
![]() $V_0$
, respectively, satisfy
$V_0$
, respectively, satisfy
![]() $U(t)\leq V(t)$
for any
$U(t)\leq V(t)$
for any
![]() $t\ge 0$
.
$t\ge 0$
.
It follows that the comparison principle also holds for (1.11).
2.2 Limiting behaviour
In this subsection, we consider the steady state Equation (2.4) below. The study of the problem will be used in the sequel to investigate the limit behaviour of travelling wave solutions.
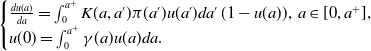 \begin{equation} \begin{cases} \frac{d u(a)}{d a}=\int _0^{a^+}K(a, a')\pi (a')u(a')da'\,(1-u(a)),\; a\in [0, a^+],\\ u(0)=\int _0^{a^+}\gamma (a)u(a)da. \end{cases} \end{equation}
\begin{equation} \begin{cases} \frac{d u(a)}{d a}=\int _0^{a^+}K(a, a')\pi (a')u(a')da'\,(1-u(a)),\; a\in [0, a^+],\\ u(0)=\int _0^{a^+}\gamma (a)u(a)da. \end{cases} \end{equation}
Due to Assumption 1.1
![]() $(i)$
, let us observe that (2.4) has constant solutions:
$(i)$
, let us observe that (2.4) has constant solutions:
![]() $a\mapsto 0$
and
$a\mapsto 0$
and
![]() $a\mapsto 1$
. We will show that (2.4) only has these two solutions with values into
$a\mapsto 1$
. We will show that (2.4) only has these two solutions with values into
![]() $[0, 1]$
. More specifically, we have the following result.
$[0, 1]$
. More specifically, we have the following result.
Lemma 2.2
Problem (
2.4
) only has the two solutions
![]() $u\in W^{1,1}(0,a^+)$
such that
$u\in W^{1,1}(0,a^+)$
such that
![]() $0\leq u\leq 1$
:
$0\leq u\leq 1$
:
![]() $u\equiv 0$
and
$u\equiv 0$
and
![]() $u\equiv 1$
.
$u\equiv 1$
.
Proof. To prove the above lemma, we argue by contradiction by assuming that there exists a function
![]() $u^*\in W^{1, 1}(0, a^+)$
with
$u^*\in W^{1, 1}(0, a^+)$
with
![]() $u^*\not \equiv 0, 1$
, which is another solution of (2.4) satisfying
$u^*\not \equiv 0, 1$
, which is another solution of (2.4) satisfying
![]() $0\le u^*(a)\le 1$
for all
$0\le u^*(a)\le 1$
for all
![]() $a\in [0,a^+]$
. Observe that since
$a\in [0,a^+]$
. Observe that since
![]() $K$
is continuous and
$K$
is continuous and
![]() $u^*$
is continuous by Sobolev embedding, then
$u^*$
is continuous by Sobolev embedding, then
![]() $a\mapsto u^*(a)$
is of class
$a\mapsto u^*(a)$
is of class
![]() $C^1$
on
$C^1$
on
![]() $[0,a^+]$
.
$[0,a^+]$
.
First we claim that
![]() $0\lt u^*(a)\lt 1$
holds for all
$0\lt u^*(a)\lt 1$
holds for all
![]() $a\in [0, a^+]$
. To prove this claim, first note that if
$a\in [0, a^+]$
. To prove this claim, first note that if
![]() $u^*$
touches
$u^*$
touches
![]() $1$
at some
$1$
at some
![]() $a_0\in [0, a^+]$
, then by the Cauchy Lipschitz theorem for ODE, one has
$a_0\in [0, a^+]$
, then by the Cauchy Lipschitz theorem for ODE, one has
![]() $u^*\equiv 1$
, which is a contradiction. Next if
$u^*\equiv 1$
, which is a contradiction. Next if
![]() $u^*$
touches
$u^*$
touches
![]() $0$
at some point
$0$
at some point
![]() $a_0\in [0, a^+]$
, namely
$a_0\in [0, a^+]$
, namely
![]() $u^*(a_0)=0$
, then two cases may appear: either
$u^*(a_0)=0$
, then two cases may appear: either
![]() $a_0=0$
or
$a_0=0$
or
![]() $a_0\in (0, a^+]$
. If
$a_0\in (0, a^+]$
. If
![]() $a_0=0$
, then the boundary condition at
$a_0=0$
, then the boundary condition at
![]() $a=0$
yields
$a=0$
yields
But since
![]() $\gamma \not \equiv 0$
, there exists
$\gamma \not \equiv 0$
, there exists
![]() $a_1\in (0,a^+)$
such that
$a_1\in (0,a^+)$
such that
![]() $u^*(a_1)=0$
. Therefore, it is sufficient to consider the case where there exists
$u^*(a_1)=0$
. Therefore, it is sufficient to consider the case where there exists
![]() $a_0\in (0,a^+]$
such that
$a_0\in (0,a^+]$
such that
![]() $u^*(a_0)=0$
. Now to reach a contradiction, recalling
$u^*(a_0)=0$
. Now to reach a contradiction, recalling
![]() $u^*\geq 0$
, there holds
$u^*\geq 0$
, there holds
![]() $u(a_0)=0$
with
$u(a_0)=0$
with
![]() $a_0\in (0,a^+]$
, which ensures that
$a_0\in (0,a^+]$
, which ensures that
Plugging this information together with
![]() $u^*(a_0)=0$
into (2.4) yields
$u^*(a_0)=0$
into (2.4) yields
which by the positivity of
![]() $K$
and
$K$
and
![]() $\pi$
implies that
$\pi$
implies that
![]() $u^*(a)\equiv 0$
, which is a contradiction again. Thus, we have obtained that
$u^*(a)\equiv 0$
, which is a contradiction again. Thus, we have obtained that
![]() $0\lt u^*(a)\lt 1$
for all
$0\lt u^*(a)\lt 1$
for all
![]() $a\in [0,a^+]$
.
$a\in [0,a^+]$
.
Now to complete the proof of the lemma, let us obtain a contradiction with the existence of
![]() $u^*$
. To that aim, let us show that one has
$u^*$
. To that aim, let us show that one has
![]() $u^*(a)\geq 1$
for all
$u^*(a)\geq 1$
for all
![]() $a\in [0,a^+]$
so that
$a\in [0,a^+]$
so that
![]() $u^*\equiv 1$
, a contradiction with
$u^*\equiv 1$
, a contradiction with
![]() $u^*\not \equiv 1$
. To reach this issue, let us define
$u^*\not \equiv 1$
. To reach this issue, let us define
![]() $\kappa ^*$
by
$\kappa ^*$
by
Note that
![]() $\kappa ^*$
is well-defined. Let us show that
$\kappa ^*$
is well-defined. Let us show that
![]() $\kappa ^*\leq 1$
by a contradiction argument and assuming that
$\kappa ^*\leq 1$
by a contradiction argument and assuming that
![]() $\kappa ^*\gt 1$
. Since
$\kappa ^*\gt 1$
. Since
![]() $\kappa ^*u^*(a)\ge 1$
for all
$\kappa ^*u^*(a)\ge 1$
for all
![]() $a\in [0,a^+]$
, we consider two cases: (i)
$a\in [0,a^+]$
, we consider two cases: (i)
![]() $\kappa ^*u^*\ge 1$
and
$\kappa ^*u^*\ge 1$
and
![]() $\kappa ^*u^*\not \equiv 1$
and (ii)
$\kappa ^*u^*\not \equiv 1$
and (ii)
![]() $\kappa ^*u^*\equiv 1$
.
$\kappa ^*u^*\equiv 1$
.
Case (i)
![]() $\kappa ^*u^*\ge 1, \kappa ^*u^*\not \equiv 1$
. Set
$\kappa ^*u^*\ge 1, \kappa ^*u^*\not \equiv 1$
. Set
![]() $v^*(a)=\kappa ^* u^*(a)$
that satisfies the problem
$v^*(a)=\kappa ^* u^*(a)$
that satisfies the problem
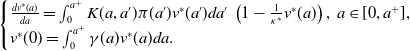 \begin{equation} \begin{cases} \frac{d v^*(a)}{d a}=\int _0^{a^+}K(a, a')\pi (a')v^*(a')da'\,\left (1-\frac{1}{\kappa ^*}v^*(a)\right ),\; a\in [0, a^+],\\ v^*(0)=\int _0^{a^+}\gamma (a)v^*(a)da. \end{cases} \end{equation}
\begin{equation} \begin{cases} \frac{d v^*(a)}{d a}=\int _0^{a^+}K(a, a')\pi (a')v^*(a')da'\,\left (1-\frac{1}{\kappa ^*}v^*(a)\right ),\; a\in [0, a^+],\\ v^*(0)=\int _0^{a^+}\gamma (a)v^*(a)da. \end{cases} \end{equation}
Note that from the definition of
![]() $\kappa ^*$
, there exists
$\kappa ^*$
, there exists
![]() $a_0\in [0,a^+]$
such that
$a_0\in [0,a^+]$
such that
![]() $v^*(a_0)=1$
. Due to the condition
$v^*(a_0)=1$
. Due to the condition
as above, the boundary condition ensures that one can choose
![]() $a_0\in (0,a^+]$
. Hence, we have
$a_0\in (0,a^+]$
. Hence, we have
so that
Since
![]() $\kappa ^*\gt 1$
and
$\kappa ^*\gt 1$
and
![]() $K\gt 0$
, this yields
$K\gt 0$
, this yields
![]() $v^*\equiv 0$
, a contradiction with
$v^*\equiv 0$
, a contradiction with
![]() $0\lt u^*\lt 1$
, which proves
$0\lt u^*\lt 1$
, which proves
![]() $\kappa ^*\leq 1$
in the first case (i).
$\kappa ^*\leq 1$
in the first case (i).
Case (ii)
![]() $\kappa ^*u^*=v^*\equiv 1$
. In that case (2.5) yields for all
$\kappa ^*u^*=v^*\equiv 1$
. In that case (2.5) yields for all
![]() $a\in (0,a^+)$
$a\in (0,a^+)$
which is a contradiction again, since
![]() $\kappa ^*\gt 1$
and thus the right hand side is positive. Thus, we still have
$\kappa ^*\gt 1$
and thus the right hand side is positive. Thus, we still have
![]() $\kappa ^*\leq 1$
. To sum-up, we have proved that
$\kappa ^*\leq 1$
. To sum-up, we have proved that
![]() $u^*(a)\ge 1$
for all
$u^*(a)\ge 1$
for all
![]() $a\in [0,a^+]$
. We also have
$a\in [0,a^+]$
. We also have
![]() $1\ge u^*$
. This proves that
$1\ge u^*$
. This proves that
![]() $1$
is the unique positive solution of (2.4) and completes the proof of the lemma.
$1$
is the unique positive solution of (2.4) and completes the proof of the lemma.
2.3 Construction of sub- and super-solutions
In this section, we will construct exponentially bounded sub- and super-solutions for problem (1.9). Exponential bound is used to define the convolution with the kernel
![]() $J$
. As explained above, these functions will be of particular importance to derive our existence result.
$J$
. As explained above, these functions will be of particular importance to derive our existence result.
2.3.1 Super-solution
We start with the construction of a super-solution. We are looking for an exponentially bounded function
![]() $\overline{U}=\overline{U}(a,\xi )\gt 0$
satisfying
$\overline{U}=\overline{U}(a,\xi )\gt 0$
satisfying
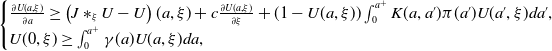 \begin{equation} \begin{cases} \frac{\partial U(a, \xi )}{\partial a}\geq \left (J\ast _\xi U-U\right )(a, \xi )+c\frac{\partial U(a, \xi )}{\partial \xi }+(1-U(a,\xi ))\int _0^{a^+}K(a, a')\pi (a')U(a', \xi )da',\\ U(0, \xi )\geq \int _0^{a^+}\gamma (a)U(a, \xi )da, \end{cases} \end{equation}
\begin{equation} \begin{cases} \frac{\partial U(a, \xi )}{\partial a}\geq \left (J\ast _\xi U-U\right )(a, \xi )+c\frac{\partial U(a, \xi )}{\partial \xi }+(1-U(a,\xi ))\int _0^{a^+}K(a, a')\pi (a')U(a', \xi )da',\\ U(0, \xi )\geq \int _0^{a^+}\gamma (a)U(a, \xi )da, \end{cases} \end{equation}
for some speed
![]() $c\gt 0$
to be specified latter.
$c\gt 0$
to be specified latter.
Since
![]() $\overline U\gt 0$
, it is sufficient to construct
$\overline U\gt 0$
, it is sufficient to construct
![]() $\overline U$
as a solution of the following linear problem
$\overline U$
as a solution of the following linear problem
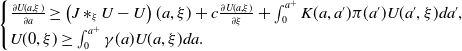 \begin{equation} \begin{cases} \frac{\partial U(a, \xi )}{\partial a}\ge \left (J\ast _\xi U-U\right )(a, \xi )+c\frac{\partial U(a, \xi )}{\partial \xi }+\int _0^{a^+}K(a, a')\pi (a')U(a', \xi )da',\\ U(0, \xi )\ge \int _0^{a^+}\gamma (a)U(a, \xi )da. \end{cases} \end{equation}
\begin{equation} \begin{cases} \frac{\partial U(a, \xi )}{\partial a}\ge \left (J\ast _\xi U-U\right )(a, \xi )+c\frac{\partial U(a, \xi )}{\partial \xi }+\int _0^{a^+}K(a, a')\pi (a')U(a', \xi )da',\\ U(0, \xi )\ge \int _0^{a^+}\gamma (a)U(a, \xi )da. \end{cases} \end{equation}
We now construct such a super-solution by looking for it with the following form:
with
![]() $\lambda \gt 0$
and
$\lambda \gt 0$
and
![]() $\phi (a)\gt 0$
. Due to the differential inequality (2.7), we are looking for
$\phi (a)\gt 0$
. Due to the differential inequality (2.7), we are looking for
![]() $\lambda \gt 0$
and
$\lambda \gt 0$
and
![]() $\phi \gt 0$
such that
$\phi \gt 0$
such that
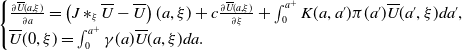 \begin{equation} \begin{cases} \frac{\partial \overline{U}(a, \xi )}{\partial a}=\left (J\ast _\xi \overline{U}-\overline{U}\right )(a, \xi )+c\frac{\partial \overline{U}(a, \xi )}{\partial \xi }+\int _0^{a^+}K(a, a')\pi (a')\overline{U}(a', \xi )da',\\ \overline{U}(0, \xi )=\int _0^{a^+}\gamma (a)\overline{U}(a, \xi )da. \end{cases} \end{equation}
\begin{equation} \begin{cases} \frac{\partial \overline{U}(a, \xi )}{\partial a}=\left (J\ast _\xi \overline{U}-\overline{U}\right )(a, \xi )+c\frac{\partial \overline{U}(a, \xi )}{\partial \xi }+\int _0^{a^+}K(a, a')\pi (a')\overline{U}(a', \xi )da',\\ \overline{U}(0, \xi )=\int _0^{a^+}\gamma (a)\overline{U}(a, \xi )da. \end{cases} \end{equation}
To solve this problem, we end-up with the following equation for
![]() $\lambda \gt 0, c\in \mathbb{R}$
and
$\lambda \gt 0, c\in \mathbb{R}$
and
![]() $\phi =\phi (a)\gt 0$
.
$\phi =\phi (a)\gt 0$
.
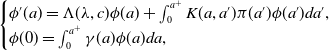 \begin{equation} \begin{cases} \phi '(a)=\Lambda (\lambda, c)\phi (a)+\int _0^{a^+}K(a, a')\pi (a')\phi (a')da',\\ \phi (0)=\int _0^{a^+}\gamma (a)\phi (a)da, \end{cases} \end{equation}
\begin{equation} \begin{cases} \phi '(a)=\Lambda (\lambda, c)\phi (a)+\int _0^{a^+}K(a, a')\pi (a')\phi (a')da',\\ \phi (0)=\int _0^{a^+}\gamma (a)\phi (a)da, \end{cases} \end{equation}
wherein we have set
Setting
![]() $s=\Lambda (\lambda, c)$
, the above problem is equivalent to find
$s=\Lambda (\lambda, c)$
, the above problem is equivalent to find
![]() $s\in \mathbb{R}$
and
$s\in \mathbb{R}$
and
![]() $\phi =\phi (a)\gt 0$
such that
$\phi =\phi (a)\gt 0$
such that
Define the linear operator
![]() $L_s\in \mathcal L(L^1(0, a^+))$
for any parameter
$L_s\in \mathcal L(L^1(0, a^+))$
for any parameter
![]() $s\in \mathbb{R}$
and
$s\in \mathbb{R}$
and
![]() $\phi \in L^1(0, a^+)$
as follows:
$\phi \in L^1(0, a^+)$
as follows:
We claim now that
![]() $L_s$
enjoys the following properties:
$L_s$
enjoys the following properties:
-
(1)
 $L_s$
is a positive operator, that is
$L_s$
is a positive operator, that is
 $L_s\left (L^1_+(0,a^+)\right )\subset L^1_+(0,a^+)$
;
$L_s\left (L^1_+(0,a^+)\right )\subset L^1_+(0,a^+)$
; -
(2)
 $L_s$
is a compact operator;
$L_s$
is a compact operator; -
(3)
 $L_s$
is a non-supporting operator.
$L_s$
is a non-supporting operator.
Note that (1) is true due to Assumption 1.1-(i), (ii) and (iv). Next, applying Fréchet–Kolmogorov–Riesz compactness theorem to
![]() $L_s$
yields (2). To prove (3), by taking the dual product between
$L_s$
yields (2). To prove (3), by taking the dual product between
![]() $L_s\phi$
with
$L_s\phi$
with
![]() $\phi \in L^1_+(0, a^+)\setminus \{0\}$
and any
$\phi \in L^1_+(0, a^+)\setminus \{0\}$
and any
![]() $\psi \in L^\infty _+(0, a^+)\setminus \{0\}$
, we obtain
$\psi \in L^\infty _+(0, a^+)\setminus \{0\}$
, we obtain
Recalling Assumption 1.1-(ii) and (iv), one can see that the second term of the above equality is positive. Thus (3) is proved.
Hence by Krein–Rutman theorem, the spectral radius
![]() $\rho (L_s)$
is the principal eigenvalue of
$\rho (L_s)$
is the principal eigenvalue of
![]() $L_s$
(see Sawashima [Reference Sawashima21]) and moreover the map
$L_s$
(see Sawashima [Reference Sawashima21]) and moreover the map
![]() $s\to \rho (L_s)$
is continuous and strictly increasing (see Marek [Reference Marek20]). In addition, notice that
$s\to \rho (L_s)$
is continuous and strictly increasing (see Marek [Reference Marek20]). In addition, notice that
![]() $\rho (L_s)\to 0$
as
$\rho (L_s)\to 0$
as
![]() $s\to -\infty$
.
$s\to -\infty$
.
On the other hand, for
![]() $s=0$
, applying the constant function
$s=0$
, applying the constant function
![]() $a\mapsto 1$
to
$a\mapsto 1$
to
![]() $L_0$
yields, due to Assumption 1.1-(i),
$L_0$
yields, due to Assumption 1.1-(i),
so that
![]() $\rho (L_0)\gt 1$
. It follows that there exists a unique
$\rho (L_0)\gt 1$
. It follows that there exists a unique
![]() $s_0\lt 0$
such that
$s_0\lt 0$
such that
![]() $\rho (L_{s_0})=1$
. We now consider the equation
$\rho (L_{s_0})=1$
. We now consider the equation
![]() $\Lambda (\lambda, c)=s_0$
that reads as
$\Lambda (\lambda, c)=s_0$
that reads as
Thus, we have the following lemma:
Lemma 2.3
There exists
![]() $c^*\gt 0$
such that Equation (
2.12
) with respect to the unknown
$c^*\gt 0$
such that Equation (
2.12
) with respect to the unknown
![]() $\lambda$
has no positive solution when
$\lambda$
has no positive solution when
![]() $c\lt c^*$
, only one solution for
$c\lt c^*$
, only one solution for
![]() $c=c^*$
, and exactly two solutions for
$c=c^*$
, and exactly two solutions for
![]() $c\gt c^*$
. In addition for
$c\gt c^*$
. In addition for
![]() $c\gt c^*$
, these two solutions
$c\gt c^*$
, these two solutions
![]() $\lambda _1$
and
$\lambda _1$
and
![]() $\lambda _2$
are such that
$\lambda _2$
are such that
where
![]() $\lambda (c)$
is the unique root of the following equation:
$\lambda (c)$
is the unique root of the following equation:
We will see in the proof of the lemma that the critical value
![]() $c^*$
is implicitly given by the equation
$c^*$
is implicitly given by the equation
which uniquely provides the value of
![]() $c^*\gt 0$
.
$c^*\gt 0$
.
Proof of Lemma 2.3. First, observe that
and
As a consequence, for any
![]() $c\gt 0$
, the function
$c\gt 0$
, the function
![]() $\lambda \mapsto \frac{\partial \Lambda (\lambda, c)}{\partial \lambda }$
is non-decreasing from
$\lambda \mapsto \frac{\partial \Lambda (\lambda, c)}{\partial \lambda }$
is non-decreasing from
![]() $-\infty$
to
$-\infty$
to
![]() $\infty$
and, using again the symmetry of
$\infty$
and, using again the symmetry of
![]() $J$
, satisfies
$J$
, satisfies
Hence for any
![]() $c\gt 0$
, there exists a unique
$c\gt 0$
, there exists a unique
![]() $\lambda (c)\gt 0$
such that
$\lambda (c)\gt 0$
such that
![]() $\int _{\mathbb{R}} J(y)e^{\lambda y}ydy-c\lt 0$
(resp.
$\int _{\mathbb{R}} J(y)e^{\lambda y}ydy-c\lt 0$
(resp.
![]() $\gt 0$
) for all
$\gt 0$
) for all
![]() $\lambda \lt \lambda (c)$
(resp. for all
$\lambda \lt \lambda (c)$
(resp. for all
![]() $\lambda \gt \lambda (c)$
). We also deduce that for any
$\lambda \gt \lambda (c)$
). We also deduce that for any
![]() $c\gt 0$
, the function
$c\gt 0$
, the function
![]() $\lambda \to \Lambda (\lambda, c)$
is decreasing on
$\lambda \to \Lambda (\lambda, c)$
is decreasing on
![]() $(0, \lambda (c))$
and increasing on
$(0, \lambda (c))$
and increasing on
![]() $(\lambda (c), \infty )$
.
$(\lambda (c), \infty )$
.
As a consequence of the above analysis, the solution of (2.12) relies on the position of its minimum over
![]() $[0,\infty )$
, i.e.
$[0,\infty )$
, i.e.
![]() $\Lambda (\lambda (c), c)$
, with respect to
$\Lambda (\lambda (c), c)$
, with respect to
![]() $s_0$
. This quantity is given by the formula
$s_0$
. This quantity is given by the formula
To study the equation
![]() $\Lambda (\lambda (c), c)=s_0$
, let us note that the implicit function theorem ensures that the map
$\Lambda (\lambda (c), c)=s_0$
, let us note that the implicit function theorem ensures that the map
![]() $c\mapsto \lambda (c)$
is of class
$c\mapsto \lambda (c)$
is of class
![]() $C^1$
with respect to
$C^1$
with respect to
![]() $c\in (0,\infty )$
, so is the function
$c\in (0,\infty )$
, so is the function
![]() $c\mapsto \Lambda (\lambda (c), c)$
and we have:
$c\mapsto \Lambda (\lambda (c), c)$
and we have:
The above expression implies that
![]() $c\mapsto \Lambda (\lambda (c), c)$
is monotonically decreasing with respect to
$c\mapsto \Lambda (\lambda (c), c)$
is monotonically decreasing with respect to
![]() $c$
. Furthermore, this function takes the value
$c$
. Furthermore, this function takes the value
![]() $0$
for
$0$
for
![]() $c=0$
and tends to
$c=0$
and tends to
![]() $-\infty$
as
$-\infty$
as
![]() $c\to \infty$
. Indeed since
$c\to \infty$
. Indeed since
![]() $J$
is symmetric and has a unit mass, we have
$J$
is symmetric and has a unit mass, we have
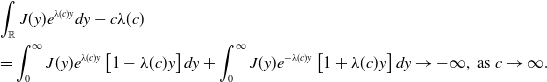 \begin{align*} &\int _{\mathbb{R}} J(y)e^{\lambda (c)y}dy-c\lambda (c)\\ &=\int _0^\infty J(y)e^{\lambda (c)y}\left [1-\lambda (c)y\right ]dy+\int _0^\infty J(y)e^{-\lambda (c)y}\left [1+\lambda (c)y\right ]dy\to -\infty, \text{ as }c\to \infty . \end{align*}
\begin{align*} &\int _{\mathbb{R}} J(y)e^{\lambda (c)y}dy-c\lambda (c)\\ &=\int _0^\infty J(y)e^{\lambda (c)y}\left [1-\lambda (c)y\right ]dy+\int _0^\infty J(y)e^{-\lambda (c)y}\left [1+\lambda (c)y\right ]dy\to -\infty, \text{ as }c\to \infty . \end{align*}
Recalling that
![]() $s_0\lt 0$
, this proves there exists a unique
$s_0\lt 0$
, this proves there exists a unique
![]() $c^*\gt 0$
such that
$c^*\gt 0$
such that
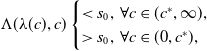 \begin{equation*} \Lambda (\lambda (c), c)\begin {cases} \lt s_0,\;\forall c\in (c^*,\infty ),\\ \gt s_0,\;\forall c\in (0,c^*), \end {cases} \end{equation*}
\begin{equation*} \Lambda (\lambda (c), c)\begin {cases} \lt s_0,\;\forall c\in (c^*,\infty ),\\ \gt s_0,\;\forall c\in (0,c^*), \end {cases} \end{equation*}
that concludes the proof of the lemma.
To sum-up for all
![]() $c\gt c^*$
, the function
$c\gt c^*$
, the function
![]() $\overline{U}(a,\xi )=e^{-\lambda \xi }\phi (a)$
, where
$\overline{U}(a,\xi )=e^{-\lambda \xi }\phi (a)$
, where
![]() $\lambda$
is a solution of (2.12), is a super-solution that satisfies (2.6). Note also that the constant function
$\lambda$
is a solution of (2.12), is a super-solution that satisfies (2.6). Note also that the constant function
![]() $(a,\xi )\mapsto 1$
is also a super-solution.
$(a,\xi )\mapsto 1$
is also a super-solution.
2.3.2 Sub-solution
In this subsection, we construct a suitable sub-solution. Let
![]() $c\gt c^*$
be fixed and let
$c\gt c^*$
be fixed and let
![]() $\lambda \gt 0$
be the smallest solution of (2.12). Moreover, let
$\lambda \gt 0$
be the smallest solution of (2.12). Moreover, let
![]() $\phi =\phi (a)$
be defined as in (2.10) with
$\phi =\phi (a)$
be defined as in (2.10) with
![]() $s=s_0$
. Observe that the function
$s=s_0$
. Observe that the function
![]() $a\mapsto \phi (a)$
is continuous and
$a\mapsto \phi (a)$
is continuous and
![]() $\phi (a)\gt 0$
for any
$\phi (a)\gt 0$
for any
![]() $a\in [0, a^+]$
.
$a\in [0, a^+]$
.
Now our aim is to construct an exponentially bounded sub-solution with the speed
![]() $c$
that is a solution
$c$
that is a solution
![]() $\underline{U}=\underline{U}(a,\xi )$
such that
$\underline{U}=\underline{U}(a,\xi )$
such that
and satisfying the following differential inequality
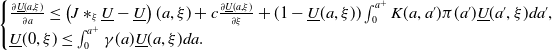 \begin{equation} \begin{cases} \frac{\partial \underline{U}(a, \xi )}{\partial a}\leq \left (J\ast _\xi \underline{U}-\underline{U}\right )(a, \xi )+c\frac{\partial \underline{U}(a, \xi )}{\partial \xi }+(1-\underline{U}(a,\xi ))\int _0^{a^+}K(a, a')\pi (a')\underline{U}(a', \xi )da',\\ \underline{U}(0, \xi )\leq \int _0^{a^+}\gamma (a)\underline{U}(a, \xi )da. \end{cases} \end{equation}
\begin{equation} \begin{cases} \frac{\partial \underline{U}(a, \xi )}{\partial a}\leq \left (J\ast _\xi \underline{U}-\underline{U}\right )(a, \xi )+c\frac{\partial \underline{U}(a, \xi )}{\partial \xi }+(1-\underline{U}(a,\xi ))\int _0^{a^+}K(a, a')\pi (a')\underline{U}(a', \xi )da',\\ \underline{U}(0, \xi )\leq \int _0^{a^+}\gamma (a)\underline{U}(a, \xi )da. \end{cases} \end{equation}
Note that we have
for some sufficiently large constant
![]() $\alpha \gt 0$
and where the superscript ‘
$\alpha \gt 0$
and where the superscript ‘
![]() $+$
’ denotes the positive part. Hence, it is sufficient to look for an exponentially bounded function
$+$
’ denotes the positive part. Hence, it is sufficient to look for an exponentially bounded function
![]() $\underline{U}$
satisfying
$\underline{U}$
satisfying
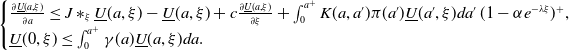 \begin{equation} \begin{cases} \frac{\partial \underline{U}(a,\xi )}{\partial a}\le J\ast _\xi \underline{U}(a,\xi )-\underline{U}(a,\xi )+c\frac{\partial \underline{U}(a,\xi )}{\partial \xi }+\int _0^{a^+}K(a, a')\pi (a')\underline{U}(a',\xi )da'\,(1-\alpha e^{-\lambda \xi })^+,\\ \underline{U}(0, \xi )\leq \int _0^{a^+}\gamma (a)\underline{U}(a, \xi )da. \end{cases} \end{equation}
\begin{equation} \begin{cases} \frac{\partial \underline{U}(a,\xi )}{\partial a}\le J\ast _\xi \underline{U}(a,\xi )-\underline{U}(a,\xi )+c\frac{\partial \underline{U}(a,\xi )}{\partial \xi }+\int _0^{a^+}K(a, a')\pi (a')\underline{U}(a',\xi )da'\,(1-\alpha e^{-\lambda \xi })^+,\\ \underline{U}(0, \xi )\leq \int _0^{a^+}\gamma (a)\underline{U}(a, \xi )da. \end{cases} \end{equation}
We look for such a function
![]() $\underline{U}$
of the form
$\underline{U}$
of the form
where the function
![]() $\phi$
is defined in (2.10) with
$\phi$
is defined in (2.10) with
![]() $s=s_0$
, while
$s=s_0$
, while
![]() $k\gt 0$
and
$k\gt 0$
and
![]() $\eta \gt 0$
have to be determined. We split our analysis into two regions:
$\eta \gt 0$
have to be determined. We split our analysis into two regions:
![]() $1-\alpha e^{-\lambda \xi }\gt 0$
and
$1-\alpha e^{-\lambda \xi }\gt 0$
and
![]() $\left (1-\alpha e^{-\lambda \xi }\right )^{+}=0$
. We define
$\left (1-\alpha e^{-\lambda \xi }\right )^{+}=0$
. We define
![]() $\xi _M$
by
$\xi _M$
by
so that the two above regions become
![]() $\{\xi \gt \xi _M\}$
and
$\{\xi \gt \xi _M\}$
and
![]() $\{\xi \leq \xi _M\}$
.
$\{\xi \leq \xi _M\}$
.
Case 1 :
![]() $\xi \gt \xi _M$
. First simple computations show that
$\xi \gt \xi _M$
. First simple computations show that
![]() $\underline{U}$
satisfies the differential inequality (2.15) for
$\underline{U}$
satisfies the differential inequality (2.15) for
![]() $\xi \gt \xi _M$
if and only if we have for all
$\xi \gt \xi _M$
if and only if we have for all
![]() $\xi \gt \frac{1}{\lambda }\log \alpha$
and all
$\xi \gt \frac{1}{\lambda }\log \alpha$
and all
![]() $a\in (0, a^+)$
,
$a\in (0, a^+)$
,
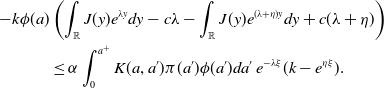 \begin{align} -k\phi (a)&\left (\int _{\mathbb{R}} J(y)e^{\lambda y}dy-c\lambda -\int _{\mathbb{R}} J(y)e^{(\lambda +\eta )y}dy+c(\lambda +\eta )\right )\nonumber \\ &\leq \alpha \int _0^{a^+}K(a, a')\pi (a')\phi (a')da'\, e^{-\lambda \xi }(k-e^{\eta \xi }). \end{align}
\begin{align} -k\phi (a)&\left (\int _{\mathbb{R}} J(y)e^{\lambda y}dy-c\lambda -\int _{\mathbb{R}} J(y)e^{(\lambda +\eta )y}dy+c(\lambda +\eta )\right )\nonumber \\ &\leq \alpha \int _0^{a^+}K(a, a')\pi (a')\phi (a')da'\, e^{-\lambda \xi }(k-e^{\eta \xi }). \end{align}
Then if we set
the above inequality becomes for all
![]() $\xi \gt \frac{1}{\lambda }\log \alpha$
and all
$\xi \gt \frac{1}{\lambda }\log \alpha$
and all
![]() $a\in (0, a^+)$
,
$a\in (0, a^+)$
,
Recalling that
![]() $\lambda \lt \lambda (c)$
, function satisfies
$\lambda \lt \lambda (c)$
, function satisfies
![]() $p(0)=0$
and
$p(0)=0$
and
![]() $p'(0)\gt 0$
. Therefore for any sufficiently small and non-negative
$p'(0)\gt 0$
. Therefore for any sufficiently small and non-negative
![]() $\eta$
, we have
$\eta$
, we have
![]() $p(\eta )\gt 0$
. Next, for
$p(\eta )\gt 0$
. Next, for
![]() $k$
sufficiently large and
$k$
sufficiently large and
![]() $\eta$
small enough, due to
$\eta$
small enough, due to
![]() $\inf _{a\in [0, a^+]}\phi (a)\gt 0$
, it is sufficient to have for any
$\inf _{a\in [0, a^+]}\phi (a)\gt 0$
, it is sufficient to have for any
![]() $\xi \gt \xi _M$
:
$\xi \gt \xi _M$
:
Therefore, with such a choice of parameters
![]() $k$
and
$k$
and
![]() $\eta$
, inequality (2.17) is satisfied for any
$\eta$
, inequality (2.17) is satisfied for any
![]() $\xi \gt \xi _M$
, which completes Case 1.
$\xi \gt \xi _M$
, which completes Case 1.
Case 2 :
![]() $\xi \leq \xi _M$
. For
$\xi \leq \xi _M$
. For
![]() $\xi \leq \xi _M$
,
$\xi \leq \xi _M$
,
![]() $\underline{U}$
satisfies (2.15) if and only if the following inequality holds:
$\underline{U}$
satisfies (2.15) if and only if the following inequality holds:
In order to reach this inequality, it is sufficient to have
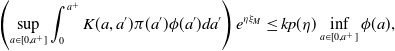 \begin{equation*} \left (\sup _{a\in [0,a^+]}\int _0^{a^+}K(a, a')\pi (a')\phi (a')da'\right ) e^{\eta \xi _M}\le kp(\eta )\inf _{a\in [0,a^+]}\phi (a), \end{equation*}
\begin{equation*} \left (\sup _{a\in [0,a^+]}\int _0^{a^+}K(a, a')\pi (a')\phi (a')da'\right ) e^{\eta \xi _M}\le kp(\eta )\inf _{a\in [0,a^+]}\phi (a), \end{equation*}
which is satisfied for sufficiently large values of
![]() $k$
, since
$k$
, since
![]() $p(\eta )\gt 0$
. This completes the Case 2. In summary, we have proved that
$p(\eta )\gt 0$
. This completes the Case 2. In summary, we have proved that
![]() $\underline U$
satisfies (2.15) for all
$\underline U$
satisfies (2.15) for all
![]() $\xi \in \mathbb{R}$
as soon as
$\xi \in \mathbb{R}$
as soon as
![]() $\eta \gt 0$
is small enough and
$\eta \gt 0$
is small enough and
![]() $k\gt 0$
is chosen large enough.
$k\gt 0$
is chosen large enough.
Next, define the functions
so that
![]() $\underline{w}\leq \overline{w}$
. These functions will be used in the next section for the construction of wave solutions and to derive our existence result.
$\underline{w}\leq \overline{w}$
. These functions will be used in the next section for the construction of wave solutions and to derive our existence result.
3. Travelling wave solution
In this section, we prove Theorems1.3 and 1.4.
3.1 Existence
In this subsection, we will employ a monotone iteration method to derive an existence result for travelling wave solutions. To this aim, we study the following nonlinear problem with
![]() $c\in \mathbb{R}$
.
$c\in \mathbb{R}$
.
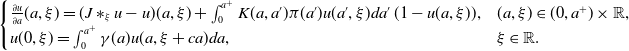 \begin{equation} \begin{cases} \frac{\partial u}{\partial a}(a, \xi )=(J\ast _\xi u-u)(a, \xi )+\int _0^{a^+}K(a, a')\pi (a')u(a', \xi )da'\, (1-u(a, \xi )),&(a, \xi )\in (0, a^+)\times \mathbb{R},\\ u(0, \xi )=\int _0^{a^+}\gamma (a)u(a, \xi +ca)da, &\xi \in \mathbb{R}. \end{cases} \end{equation}
\begin{equation} \begin{cases} \frac{\partial u}{\partial a}(a, \xi )=(J\ast _\xi u-u)(a, \xi )+\int _0^{a^+}K(a, a')\pi (a')u(a', \xi )da'\, (1-u(a, \xi )),&(a, \xi )\in (0, a^+)\times \mathbb{R},\\ u(0, \xi )=\int _0^{a^+}\gamma (a)u(a, \xi +ca)da, &\xi \in \mathbb{R}. \end{cases} \end{equation}
Definition 3.1
We say that a function
![]() $\overline{u}\in W^{1, 1}((0, a^+), C(\mathbb{R}))$
satisfying
$\overline{u}\in W^{1, 1}((0, a^+), C(\mathbb{R}))$
satisfying
is a super-solution of ( 3.1 ), if it satisfies that
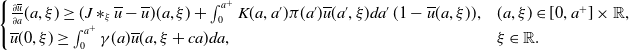 \begin{equation} \begin{cases} \frac{\partial \overline{u}}{\partial a}(a, \xi )\ge (J\ast _\xi \overline{u}-\overline{u})(a, \xi )+\int _0^{a^+}K(a, a')\pi (a')\overline u(a', \xi )da'\, (1-\overline u(a, \xi )),&(a, \xi )\in [0, a^+]\times \mathbb{R},\\ \overline{u}(0, \xi )\ge \int _0^{a^+}\gamma (a)\overline{u}(a, \xi +ca)da, &\xi \in \mathbb{R}. \end{cases} \end{equation}
\begin{equation} \begin{cases} \frac{\partial \overline{u}}{\partial a}(a, \xi )\ge (J\ast _\xi \overline{u}-\overline{u})(a, \xi )+\int _0^{a^+}K(a, a')\pi (a')\overline u(a', \xi )da'\, (1-\overline u(a, \xi )),&(a, \xi )\in [0, a^+]\times \mathbb{R},\\ \overline{u}(0, \xi )\ge \int _0^{a^+}\gamma (a)\overline{u}(a, \xi +ca)da, &\xi \in \mathbb{R}. \end{cases} \end{equation}
Similarly, we define a sub-solution by interchanging the inequalities. Here, (
3.2
) is used to guarantee the convolution
![]() $J\ast \overline u$
to be well-defined.
$J\ast \overline u$
to be well-defined.
Proposition 3.2
Assume that there exists a pair of sub/super-solution of (
3.1
) such that
![]() $0\le \underline{u}\le \overline{u}\le 1$
, then there exist a minimal solution
$0\le \underline{u}\le \overline{u}\le 1$
, then there exist a minimal solution
![]() $u_*$
and a maximal solution
$u_*$
and a maximal solution
![]() $u^*$
of (
3.1
), in the sense that for any other solution
$u^*$
of (
3.1
), in the sense that for any other solution
![]() $u\in \{v\in W^{1, 1}((0, a^+), L^1_{loc}(\mathbb{R}))\;:\; \underline{u}\le v\le \overline{u}\}$
, it holds that
$u\in \{v\in W^{1, 1}((0, a^+), L^1_{loc}(\mathbb{R}))\;:\; \underline{u}\le v\le \overline{u}\}$
, it holds that
Proof. Define
![]() $M\gt 0$
as follows:
$M\gt 0$
as follows:
and define the sequence of the functions
![]() $(u_n)_{n\geq 0}$
as
$(u_n)_{n\geq 0}$
as
![]() $u_0=\underline{u}$
and for
$u_0=\underline{u}$
and for
![]() $n\ge 1$
, for
$n\ge 1$
, for
![]() $(a,\xi )\in [0,a^+]\times \mathbb{R}$
by
$(a,\xi )\in [0,a^+]\times \mathbb{R}$
by
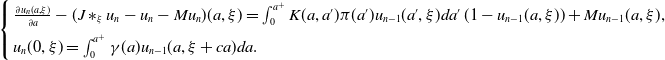 \begin{equation} \left\{\begin{array}{l}\frac{\partial u_n(a, \xi )}{\partial a}- (J\ast _\xi u_n-u_n-Mu_n)(a, \xi )=\int _0^{a^+}K(a, a')\pi (a')u_{n-1}(a', \xi )da'\, (1-u_{n-1}(a, \xi ))+Mu_{n-1}(a, \xi ),\\[5pt] u_n(0, \xi )= \int _0^{a^+}\gamma (a)u_{n-1}(a, \xi +ca)da. \end{array}\right. \end{equation}
\begin{equation} \left\{\begin{array}{l}\frac{\partial u_n(a, \xi )}{\partial a}- (J\ast _\xi u_n-u_n-Mu_n)(a, \xi )=\int _0^{a^+}K(a, a')\pi (a')u_{n-1}(a', \xi )da'\, (1-u_{n-1}(a, \xi ))+Mu_{n-1}(a, \xi ),\\[5pt] u_n(0, \xi )= \int _0^{a^+}\gamma (a)u_{n-1}(a, \xi +ca)da. \end{array}\right. \end{equation}
Next, set
![]() $u^0=\overline{u}$
and define
$u^0=\overline{u}$
and define
![]() $u^n$
with
$u^n$
with
![]() $n\ge 1$
, for
$n\ge 1$
, for
![]() $(a,\xi )\in [0,a^+]\times \mathbb{R}$
, by the resolution of the problem
$(a,\xi )\in [0,a^+]\times \mathbb{R}$
, by the resolution of the problem
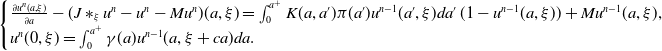 \begin{equation} \begin{cases} \frac{\partial u^n(a, \xi )}{\partial a}- (J\ast _\xi u^n-u^n-Mu^n)(a, \xi )=\int _0^{a^+}K(a, a')\pi (a')u^{n-1}(a', \xi )da'\, (1-u^{n-1}(a, \xi ))+Mu^{n-1}(a, \xi ),\\ u^n(0, \xi )= \int _0^{a^+}\gamma (a)u^{n-1}(a, \xi +ca)da. \end{cases} \end{equation}
\begin{equation} \begin{cases} \frac{\partial u^n(a, \xi )}{\partial a}- (J\ast _\xi u^n-u^n-Mu^n)(a, \xi )=\int _0^{a^+}K(a, a')\pi (a')u^{n-1}(a', \xi )da'\, (1-u^{n-1}(a, \xi ))+Mu^{n-1}(a, \xi ),\\ u^n(0, \xi )= \int _0^{a^+}\gamma (a)u^{n-1}(a, \xi +ca)da. \end{cases} \end{equation}
First, we show that
![]() $u_n\in W^{1, 1}((0, a^+), C(\mathbb{R}))$
is well-defined. Note that
$u_n\in W^{1, 1}((0, a^+), C(\mathbb{R}))$
is well-defined. Note that
so that
![]() $u_1$
is well-defined by the linear nonlocal diffusion equations. Analogously, by induction, we get that
$u_1$
is well-defined by the linear nonlocal diffusion equations. Analogously, by induction, we get that
![]() $u_n$
is well-defined. Similarly, the existence of
$u_n$
is well-defined. Similarly, the existence of
![]() $u^n$
follows the same induction arguments.
$u^n$
follows the same induction arguments.
We will show that the sequence
![]() $u_n$
(respectively
$u_n$
(respectively
![]() $u^n$
) is increasing (respectively decreasing) in the sense that
$u^n$
) is increasing (respectively decreasing) in the sense that
Indeed, taking
![]() $w\;:\!=\;u_1-u_0$
, it satisfies
$w\;:\!=\;u_1-u_0$
, it satisfies
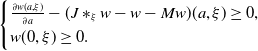 \begin{equation*} \begin {cases} \frac {\partial w(a, \xi )}{\partial a}- (J\ast _\xi w-w-Mw)(a, \xi ) \ge 0, \\ w(0, \xi )\ge 0. \end {cases} \end{equation*}
\begin{equation*} \begin {cases} \frac {\partial w(a, \xi )}{\partial a}- (J\ast _\xi w-w-Mw)(a, \xi ) \ge 0, \\ w(0, \xi )\ge 0. \end {cases} \end{equation*}
Using the comparison principle of nonlocal diffusion problems, we conclude that
![]() $w\ge 0$
, i.e.
$w\ge 0$
, i.e.
![]() $\underline{u}=u_0\le u_1$
. Now assume that
$\underline{u}=u_0\le u_1$
. Now assume that
![]() $u_{n-1}\le u_n$
. Observe that
$u_{n-1}\le u_n$
. Observe that
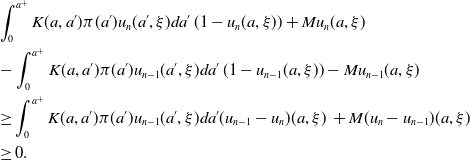 \begin{align*} &\int _0^{a^+}K(a, a')\pi (a')u_n(a', \xi )da'\,(1-u_n(a, \xi ))+Mu_n(a, \xi )\\ &-\int _0^{a^+}K(a, a')\pi (a')u_{n-1}(a', \xi )da'\,(1-u_{n-1}(a, \xi ))-Mu_{n-1}(a, \xi )\\ &\ge \int _0^{a^+}K(a, a')\pi (a')u_{n-1}(a', \xi )da'(u_{n-1}-u_n)(a, \xi )\,+M(u_n-u_{n-1})(a, \xi )\\ &\ge 0. \end{align*}
\begin{align*} &\int _0^{a^+}K(a, a')\pi (a')u_n(a', \xi )da'\,(1-u_n(a, \xi ))+Mu_n(a, \xi )\\ &-\int _0^{a^+}K(a, a')\pi (a')u_{n-1}(a', \xi )da'\,(1-u_{n-1}(a, \xi ))-Mu_{n-1}(a, \xi )\\ &\ge \int _0^{a^+}K(a, a')\pi (a')u_{n-1}(a', \xi )da'(u_{n-1}-u_n)(a, \xi )\,+M(u_n-u_{n-1})(a, \xi )\\ &\ge 0. \end{align*}
Then
![]() $w\;:\!=\;u_{n+1}-u_n$
satisfies
$w\;:\!=\;u_{n+1}-u_n$
satisfies
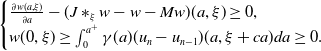 \begin{equation*} \begin {cases} \frac {\partial w(a, \xi )}{\partial a}- (J\ast _\xi w-w-Mw)(a, \xi )\ge 0,\\ w(0, \xi )\ge \int _0^{a^+}\gamma (a)(u_n-u_{n-1})(a, \xi +ca)da\ge 0. \end {cases} \end{equation*}
\begin{equation*} \begin {cases} \frac {\partial w(a, \xi )}{\partial a}- (J\ast _\xi w-w-Mw)(a, \xi )\ge 0,\\ w(0, \xi )\ge \int _0^{a^+}\gamma (a)(u_n-u_{n-1})(a, \xi +ca)da\ge 0. \end {cases} \end{equation*}
Again the comparison principle shows that
![]() $u_n\le u_{n+1}$
. The rest of the inequalities in (3.7) can be proved similarly.
$u_n\le u_{n+1}$
. The rest of the inequalities in (3.7) can be proved similarly.
Next, for all
![]() $(a, \xi )\in (0, a^+)\times \mathbb{R}$
,
$(a, \xi )\in (0, a^+)\times \mathbb{R}$
,
![]() $u_n(a, \xi )$
has a limit as
$u_n(a, \xi )$
has a limit as
![]() $n\to \infty$
by monotone convergence theorem, denoted by
$n\to \infty$
by monotone convergence theorem, denoted by
![]() $u_*(a, \xi )$
; that is
$u_*(a, \xi )$
; that is
![]() $u_n(a, \xi )\to u_*(a, \xi )$
for all
$u_n(a, \xi )\to u_*(a, \xi )$
for all
![]() $(0, a^+)\times \mathbb{R}$
. Thus, one has that for all
$(0, a^+)\times \mathbb{R}$
. Thus, one has that for all
![]() $\xi \in \mathbb{R}$
,
$\xi \in \mathbb{R}$
,
In addition, one has
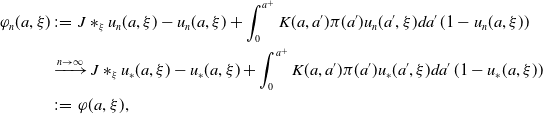 \begin{align*} \varphi _n(a, \xi )&\;:\!=\;J\ast _\xi u_n(a, \xi )-u_n(a, \xi )+\int _0^{a^+}K(a, a')\pi (a')u_n(a', \xi )da'\, (1-u_n(a, \xi ))\\ &\xrightarrow{n\to \infty } J\ast _\xi u_*(a, \xi )-u_*(a, \xi )+\int _0^{a^+}K(a, a')\pi (a')u_*(a', \xi )da'\, (1-u_*(a, \xi ))\\ &\;:\!=\;\varphi (a, \xi ), \end{align*}
\begin{align*} \varphi _n(a, \xi )&\;:\!=\;J\ast _\xi u_n(a, \xi )-u_n(a, \xi )+\int _0^{a^+}K(a, a')\pi (a')u_n(a', \xi )da'\, (1-u_n(a, \xi ))\\ &\xrightarrow{n\to \infty } J\ast _\xi u_*(a, \xi )-u_*(a, \xi )+\int _0^{a^+}K(a, a')\pi (a')u_*(a', \xi )da'\, (1-u_*(a, \xi ))\\ &\;:\!=\;\varphi (a, \xi ), \end{align*}
in
![]() $(0, a^+)\times \mathbb{R}$
and in
$(0, a^+)\times \mathbb{R}$
and in
![]() $L^1((0, a^+), L^1_{loc}(\mathbb{R}))$
. Hence, for all
$L^1((0, a^+), L^1_{loc}(\mathbb{R}))$
. Hence, for all
![]() $\xi \in \mathbb{R}$
and
$\xi \in \mathbb{R}$
and
![]() $(\eta, \theta )\subset (0, a^+)$
, one has
$(\eta, \theta )\subset (0, a^+)$
, one has
which implies by letting
![]() $n\to \infty$
that
$n\to \infty$
that
Since
![]() $\varphi \in L^1((0, a^+), L^1_{loc}(\mathbb{R}))$
, it follows that
$\varphi \in L^1((0, a^+), L^1_{loc}(\mathbb{R}))$
, it follows that
![]() $u_*\in W^{1, 1}((0, a^+), L^1_{loc}(\mathbb{R}))$
satisfies the first equation of (3.1) with
$u_*\in W^{1, 1}((0, a^+), L^1_{loc}(\mathbb{R}))$
satisfies the first equation of (3.1) with
![]() $\partial _au_*=\varphi$
a.e. in
$\partial _au_*=\varphi$
a.e. in
![]() $(0, a^+)\times \mathbb{R}$
. Further,
$(0, a^+)\times \mathbb{R}$
. Further,
![]() $u_*(\cdot, \xi )$
is continuous in
$u_*(\cdot, \xi )$
is continuous in
![]() $[0, a^+]$
for all
$[0, a^+]$
for all
![]() $\xi \in \mathbb{R}$
. Thus, one has
$\xi \in \mathbb{R}$
. Thus, one has
![]() $u_n(0, \xi )\to u_*(0, \xi )$
as
$u_n(0, \xi )\to u_*(0, \xi )$
as
![]() $n\to \infty$
in
$n\to \infty$
in
![]() $\mathbb{R}$
, which by (3.8) implies that
$\mathbb{R}$
, which by (3.8) implies that
It follows that
![]() $u_*\in W^{1, 1}((0, a^+), L^1_{loc}(\mathbb{R}))$
satisfies the Equation (3.1).
$u_*\in W^{1, 1}((0, a^+), L^1_{loc}(\mathbb{R}))$
satisfies the Equation (3.1).
We now claim that
![]() $u_*$
is the minimal solution of (3.1). Indeed, if
$u_*$
is the minimal solution of (3.1). Indeed, if
![]() $u$
is a solution of (3.1) such that
$u$
is a solution of (3.1) such that
![]() $u\in [\underline{u}, \overline{u}]$
, it can be shown that the sequence
$u\in [\underline{u}, \overline{u}]$
, it can be shown that the sequence
![]() $u_n$
built in (3.5) satisfies that
$u_n$
built in (3.5) satisfies that
![]() $\underline{u}\le u_n\le u$
. Hence,
$\underline{u}\le u_n\le u$
. Hence,
![]() $u_n\uparrow u_*\le u$
. We can argue similarly with the sequence
$u_n\uparrow u_*\le u$
. We can argue similarly with the sequence
![]() $u^n$
and conclude
$u^n$
and conclude
![]() $u^*$
is maximal. This completes the proof.
$u^*$
is maximal. This completes the proof.
Now define
By the constructions proposed in Section 2.3,
![]() $\underline u$
and
$\underline u$
and
![]() $\overline u$
are indeed the sub- and super-solutions of (3.1), respectively. Next, due to
$\overline u$
are indeed the sub- and super-solutions of (3.1), respectively. Next, due to
![]() $u^0=\overline u\le 1$
and recalling
$u^0=\overline u\le 1$
and recalling
![]() $M$
defined in (3.4), Proposition 3.2 applies to the system (1.9) and one concludes to the existence of a maximal solution
$M$
defined in (3.4), Proposition 3.2 applies to the system (1.9) and one concludes to the existence of a maximal solution
![]() $w\in W^{1, 1}((0, a^+), L^1_{loc}(\mathbb{R}))$
satisfying
$w\in W^{1, 1}((0, a^+), L^1_{loc}(\mathbb{R}))$
satisfying
It follows that
![]() $w(a, \xi )\to 0$
as
$w(a, \xi )\to 0$
as
![]() $\xi \to \infty$
uniformly in
$\xi \to \infty$
uniformly in
![]() $a\in [0, a^+]$
. Hence to complete the proof of Theorem1.3, it remains to study the behaviour of
$a\in [0, a^+]$
. Hence to complete the proof of Theorem1.3, it remains to study the behaviour of
![]() $w$
as
$w$
as
![]() $\xi \to -\infty$
. Note that the function
$\xi \to -\infty$
. Note that the function
![]() $\xi \to \overline w(a, \xi )$
is nonincreasing on
$\xi \to \overline w(a, \xi )$
is nonincreasing on
![]() $\mathbb{R}$
, then the limit function
$\mathbb{R}$
, then the limit function
![]() $\xi \to w(a, \xi )$
is also nonincreasing on
$\xi \to w(a, \xi )$
is also nonincreasing on
![]() $\mathbb{R}$
for a.e.
$\mathbb{R}$
for a.e.
![]() $a\in (0, a^+)$
.
$a\in (0, a^+)$
.
On the other hand, recalling the definition of
![]() $\underline w$
in (2.16), there exists
$\underline w$
in (2.16), there exists
![]() $\xi _0$
large enough such that
$\xi _0$
large enough such that
Hence due to the monotonicity of
![]() $w$
with respect to
$w$
with respect to
![]() $\xi$
, it follows that
$\xi$
, it follows that
Moreover, the monotonicity of
![]() $\xi \mapsto w(a, \xi )$
, for any
$\xi \mapsto w(a, \xi )$
, for any
![]() $a\in [0, a^+]$
, ensures that the limit
$a\in [0, a^+]$
, ensures that the limit
![]() $w^-(a)\;:\!=\;\lim \limits _{\xi \to -\infty }w(a, \xi )$
does exist for any
$w^-(a)\;:\!=\;\lim \limits _{\xi \to -\infty }w(a, \xi )$
does exist for any
![]() $a\in [0,a^+]$
. Hence, since
$a\in [0,a^+]$
. Hence, since
![]() $0\leq w(a,\xi )\leq 1$
for all
$0\leq w(a,\xi )\leq 1$
for all
![]() $(a, \xi )\in [0, a^+]\times \mathbb{R}$
, the Lebesgue convergence theorem yields
$(a, \xi )\in [0, a^+]\times \mathbb{R}$
, the Lebesgue convergence theorem yields
As a consequence,
![]() $w^-$
satisfies (2.4). Now recall that (2.4) has a unique positive solution, the constant function
$w^-$
satisfies (2.4). Now recall that (2.4) has a unique positive solution, the constant function
![]() $a\mapsto 1$
, which is shown in Section 2.2, thus we have
$a\mapsto 1$
, which is shown in Section 2.2, thus we have
the convergence being in fact uniform for
![]() $a\in [0,a^+]$
since
$a\in [0,a^+]$
since
![]() $\partial _a w(a,\xi )$
is globally bounded.
$\partial _a w(a,\xi )$
is globally bounded.
3.2 Regularity
At last, we show the regularity of
![]() $w$
with respect to
$w$
with respect to
![]() $\xi$
. To this aim, let us fix
$\xi$
. To this aim, let us fix
![]() $\lambda \gt 0$
as the smallest solution of (2.12). We now summarise some Lipschitz regularity estimates in the following lemma, motivated by Shen and Shen [Reference Shen and Shen22] and Ducrot and Jin [Reference Ducrot and Jin7].
$\lambda \gt 0$
as the smallest solution of (2.12). We now summarise some Lipschitz regularity estimates in the following lemma, motivated by Shen and Shen [Reference Shen and Shen22] and Ducrot and Jin [Reference Ducrot and Jin7].
Lemma 3.3
For the sequence
![]() $\{u^n\}_{n\ge 1}$
defined in (
3.6
), there exists some constant
$\{u^n\}_{n\ge 1}$
defined in (
3.6
), there exists some constant
![]() $m\ge \lambda$
large enough such that for all
$m\ge \lambda$
large enough such that for all
![]() $n\ge 1$
, one has
$n\ge 1$
, one has
Proof. In the following, we prove it for
![]() $h\gt 0$
. The case for
$h\gt 0$
. The case for
![]() $h\lt 0$
can be proved similarly.
$h\lt 0$
can be proved similarly.
Recall that
![]() $u^0(a, \xi )=\overline{u}(a, \xi )$
defined in (3.9) is given as follows:
$u^0(a, \xi )=\overline{u}(a, \xi )$
defined in (3.9) is given as follows:
 \begin{equation*} u^0(a, \xi )=\begin {cases} e^{-\lambda (\xi -ca)}\phi (a), &\text { if }\xi \ge ca+\frac {1}{\lambda }\ln \phi (a),\\ 1, &\text { if }\xi \lt ca+\frac {1}{\lambda }\ln \phi (a), \end {cases} \end{equation*}
\begin{equation*} u^0(a, \xi )=\begin {cases} e^{-\lambda (\xi -ca)}\phi (a), &\text { if }\xi \ge ca+\frac {1}{\lambda }\ln \phi (a),\\ 1, &\text { if }\xi \lt ca+\frac {1}{\lambda }\ln \phi (a), \end {cases} \end{equation*}
while for
![]() $h\gt 0$
, one has
$h\gt 0$
, one has
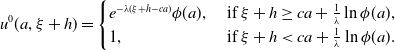 \begin{equation*} u^0(a, \xi +h)=\begin {cases} e^{-\lambda (\xi +h-ca)}\phi (a), &\text { if }\xi +h\ge ca+\frac {1}{\lambda }\ln \phi (a),\\ 1, &\text { if }\xi +h\lt ca+\frac {1}{\lambda }\ln \phi (a). \end {cases} \end{equation*}
\begin{equation*} u^0(a, \xi +h)=\begin {cases} e^{-\lambda (\xi +h-ca)}\phi (a), &\text { if }\xi +h\ge ca+\frac {1}{\lambda }\ln \phi (a),\\ 1, &\text { if }\xi +h\lt ca+\frac {1}{\lambda }\ln \phi (a). \end {cases} \end{equation*}
Then we infer from these formulas that,
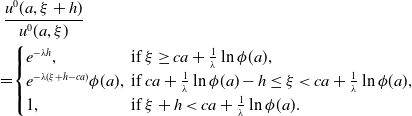 \begin{align*} &\frac{u^0(a, \xi +h)}{u^0(a, \xi )}\\ &\!\!=\!\begin{cases} e^{-\lambda h}, \!\!\!\!&\text{ if }\xi \ge ca+\frac{1}{\lambda }\ln \phi (a),\\ e^{-\lambda (\xi +h-ca)}\phi (a), \!\!\!\!&\text{ if }ca+\frac{1}{\lambda }\ln \phi (a)-h\le \xi \lt ca+\frac{1}{\lambda }\ln \phi (a),\\ 1, \!\!\!\!&\text{ if }\xi +h\lt ca+\frac{1}{\lambda }\ln \phi (a). \end{cases} \end{align*}
\begin{align*} &\frac{u^0(a, \xi +h)}{u^0(a, \xi )}\\ &\!\!=\!\begin{cases} e^{-\lambda h}, \!\!\!\!&\text{ if }\xi \ge ca+\frac{1}{\lambda }\ln \phi (a),\\ e^{-\lambda (\xi +h-ca)}\phi (a), \!\!\!\!&\text{ if }ca+\frac{1}{\lambda }\ln \phi (a)-h\le \xi \lt ca+\frac{1}{\lambda }\ln \phi (a),\\ 1, \!\!\!\!&\text{ if }\xi +h\lt ca+\frac{1}{\lambda }\ln \phi (a). \end{cases} \end{align*}
Hence, one can choose
![]() $m\gt \lambda$
large enough such that
$m\gt \lambda$
large enough such that
Now consider the functions
![]() $v_{n, h}=v_{n, h}(a, \xi ), n\ge 0$
given by
$v_{n, h}=v_{n, h}(a, \xi ), n\ge 0$
given by
Next, we choose
![]() $M\gt 0$
a little bit different from (3.4), since now
$M\gt 0$
a little bit different from (3.4), since now
![]() $v_{n, h}$
could be larger than
$v_{n, h}$
could be larger than
![]() $1$
. Observe that
$1$
. Observe that
![]() $v_{n, h}\le e^{mh}$
for all
$v_{n, h}\le e^{mh}$
for all
![]() $n\ge 0$
, so set
$n\ge 0$
, so set
For any
![]() $0\le v\le 1$
and
$0\le v\le 1$
and
![]() $v\le u\le e^{mh}$
, direct computations yield
$v\le u\le e^{mh}$
, direct computations yield
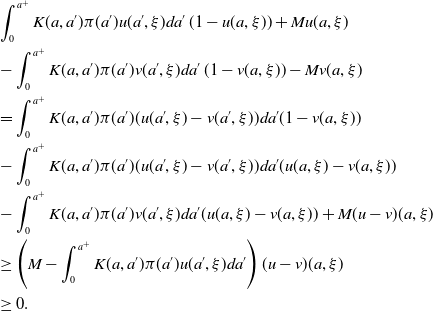 \begin{align} &\int _0^{a^+}K(a, a')\pi (a')u(a', \xi )da'\,(1-u(a, \xi ))+Mu(a, \xi )\nonumber \\ &-\int _0^{a^+}K(a, a')\pi (a')v(a', \xi )da'\,(1-v(a, \xi ))-Mv(a, \xi )\nonumber \\ &=\int _0^{a^+}K(a, a')\pi (a')(u(a', \xi )-v(a', \xi ))da'(1-v(a, \xi ))\nonumber \\ &-\int _0^{a^+}K(a, a')\pi (a')(u(a', \xi )-v(a', \xi ))da'(u(a, \xi )-v(a, \xi ))\nonumber \\ &-\int _0^{a^+}K(a, a')\pi (a')v(a', \xi )da'(u(a, \xi )-v(a, \xi ))+M(u-v)(a, \xi )\nonumber \\ &\ge \left (M-\int _0^{a^+}K(a, a')\pi (a')u(a', \xi )da'\right )(u-v)(a, \xi )\nonumber \\ &\ge 0. \end{align}
\begin{align} &\int _0^{a^+}K(a, a')\pi (a')u(a', \xi )da'\,(1-u(a, \xi ))+Mu(a, \xi )\nonumber \\ &-\int _0^{a^+}K(a, a')\pi (a')v(a', \xi )da'\,(1-v(a, \xi ))-Mv(a, \xi )\nonumber \\ &=\int _0^{a^+}K(a, a')\pi (a')(u(a', \xi )-v(a', \xi ))da'(1-v(a, \xi ))\nonumber \\ &-\int _0^{a^+}K(a, a')\pi (a')(u(a', \xi )-v(a', \xi ))da'(u(a, \xi )-v(a, \xi ))\nonumber \\ &-\int _0^{a^+}K(a, a')\pi (a')v(a', \xi )da'(u(a, \xi )-v(a, \xi ))+M(u-v)(a, \xi )\nonumber \\ &\ge \left (M-\int _0^{a^+}K(a, a')\pi (a')u(a', \xi )da'\right )(u-v)(a, \xi )\nonumber \\ &\ge 0. \end{align}
First, let us consider
![]() $n=1$
. Observe that
$n=1$
. Observe that
![]() $v_{1, h}$
satisfies the following equation,
$v_{1, h}$
satisfies the following equation,
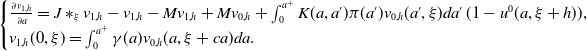 \begin{equation*} \begin {cases} \frac {\partial v_{1, h}}{\partial a}=J\ast _\xi v_{1, h}-v_{1, h}-Mv_{1, h}+Mv_{0, h}+\int _0^{a^+}K(a, a')\pi (a')v_{0, h}(a', \xi )da'\,(1-u^{0}(a, \xi +h)),\\ v_{1, h}(0, \xi )=\int _0^{a^+}\gamma (a)v_{0, h}(a, \xi +ca)da. \end {cases} \end{equation*}
\begin{equation*} \begin {cases} \frac {\partial v_{1, h}}{\partial a}=J\ast _\xi v_{1, h}-v_{1, h}-Mv_{1, h}+Mv_{0, h}+\int _0^{a^+}K(a, a')\pi (a')v_{0, h}(a', \xi )da'\,(1-u^{0}(a, \xi +h)),\\ v_{1, h}(0, \xi )=\int _0^{a^+}\gamma (a)v_{0, h}(a, \xi +ca)da. \end {cases} \end{equation*}
It follows from
![]() $v_{0, h}(a, \xi )\ge u^0(a, \xi +h)$
that
$v_{0, h}(a, \xi )\ge u^0(a, \xi +h)$
that
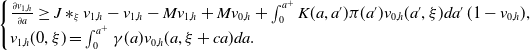 \begin{equation*} \begin {cases} \frac {\partial v_{1, h}}{\partial a}\ge J\ast _\xi v_{1, h}-v_{1, h}-Mv_{1, h}+Mv_{0, h}+\int _0^{a^+}K(a, a')\pi (a')v_{0, h}(a', \xi )da'\,(1-v_{0, h}),\\ v_{1, h}(0, \xi )=\int _0^{a^+}\gamma (a)v_{0, h}(a, \xi +ca)da. \end {cases} \end{equation*}
\begin{equation*} \begin {cases} \frac {\partial v_{1, h}}{\partial a}\ge J\ast _\xi v_{1, h}-v_{1, h}-Mv_{1, h}+Mv_{0, h}+\int _0^{a^+}K(a, a')\pi (a')v_{0, h}(a', \xi )da'\,(1-v_{0, h}),\\ v_{1, h}(0, \xi )=\int _0^{a^+}\gamma (a)v_{0, h}(a, \xi +ca)da. \end {cases} \end{equation*}
On the other hand, recall that
![]() $u^1$
satisfies (3.6), thus due to the monotonicity (3.11) and
$u^1$
satisfies (3.6), thus due to the monotonicity (3.11) and
![]() $v_{0, h}\ge u^0$
, we have
$v_{0, h}\ge u^0$
, we have
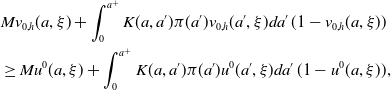 \begin{align*} &Mv_{0, h}(a, \xi )+\int _0^{a^+}K(a, a')\pi (a')v_{0, h}(a', \xi )da'\,(1-v_{0, h}(a, \xi ))\\ &\ge Mu^{0}(a, \xi )+\int _0^{a^+}K(a, a')\pi (a')u^{0}(a', \xi )da'\, (1-u^{0}(a, \xi )), \end{align*}
\begin{align*} &Mv_{0, h}(a, \xi )+\int _0^{a^+}K(a, a')\pi (a')v_{0, h}(a', \xi )da'\,(1-v_{0, h}(a, \xi ))\\ &\ge Mu^{0}(a, \xi )+\int _0^{a^+}K(a, a')\pi (a')u^{0}(a', \xi )da'\, (1-u^{0}(a, \xi )), \end{align*}
and the initial data satisfies,
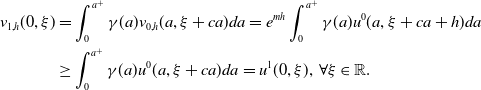 \begin{align*} v_{1, h}(0, \xi )&=\int _0^{a^+}\gamma (a)v_{0, h}(a, \xi +ca)da=e^{m h}\int _0^{a^+}\gamma (a)u^0(a, \xi +ca+h)da\\ &\ge \int _0^{a^+}\gamma (a)u^0(a, \xi +ca)da=u^1(0, \xi ), \;\forall \xi \in \mathbb{R}. \end{align*}
\begin{align*} v_{1, h}(0, \xi )&=\int _0^{a^+}\gamma (a)v_{0, h}(a, \xi +ca)da=e^{m h}\int _0^{a^+}\gamma (a)u^0(a, \xi +ca+h)da\\ &\ge \int _0^{a^+}\gamma (a)u^0(a, \xi +ca)da=u^1(0, \xi ), \;\forall \xi \in \mathbb{R}. \end{align*}
The comparison principle applies and provides
Now since for all
![]() $a\in [0, a^+]$
the function
$a\in [0, a^+]$
the function
![]() $\xi \to u^1(a, \xi )$
is nonincreasing (whose proof is exactly the same with the one to show
$\xi \to u^1(a, \xi )$
is nonincreasing (whose proof is exactly the same with the one to show
![]() $u_n\le u_{n+1}$
provided
$u_n\le u_{n+1}$
provided
![]() $u_{n-1}\le u_n$
in Proposition 3.2), for all
$u_{n-1}\le u_n$
in Proposition 3.2), for all
![]() $a\in [0, a^+]$
and
$a\in [0, a^+]$
and
![]() $\xi \in \mathbb{R}$
, we get
$\xi \in \mathbb{R}$
, we get
Next, let us prove the result (3.12) for any
![]() $n\gt 1$
by induction. Assume that
$n\gt 1$
by induction. Assume that
![]() $v_{n, h}(a, \xi )\ge u^n(a, \xi )$
for any
$v_{n, h}(a, \xi )\ge u^n(a, \xi )$
for any
![]() $(a, \xi )\in [0, a^+]\times \mathbb{R}$
. Observe that
$(a, \xi )\in [0, a^+]\times \mathbb{R}$
. Observe that
![]() $v_{n+1, h}$
satisfies the following equation,
$v_{n+1, h}$
satisfies the following equation,
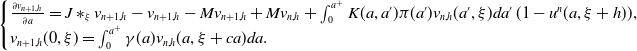 \begin{equation*} \begin {cases} \frac {\partial v_{n+1, h}}{\partial a}=J\ast _\xi v_{n+1, h}-v_{n+1, h}-Mv_{n+1, h}+Mv_{n, h}+\int _0^{a^+}K(a, a')\pi (a')v_{n, h}(a', \xi )da'\,(1-u^{n}(a, \xi +h)),\\ v_{n+1, h}(0, \xi )=\int _0^{a^+}\gamma (a)v_{n, h}(a, \xi +ca)da. \end {cases} \end{equation*}
\begin{equation*} \begin {cases} \frac {\partial v_{n+1, h}}{\partial a}=J\ast _\xi v_{n+1, h}-v_{n+1, h}-Mv_{n+1, h}+Mv_{n, h}+\int _0^{a^+}K(a, a')\pi (a')v_{n, h}(a', \xi )da'\,(1-u^{n}(a, \xi +h)),\\ v_{n+1, h}(0, \xi )=\int _0^{a^+}\gamma (a)v_{n, h}(a, \xi +ca)da. \end {cases} \end{equation*}
By
![]() $v_{n,h}(a, \xi )\ge u^n(a, \xi +h)$
due to (3.10), it follows that
$v_{n,h}(a, \xi )\ge u^n(a, \xi +h)$
due to (3.10), it follows that
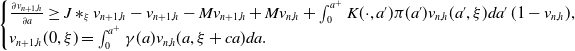 \begin{equation*} \begin {cases} \frac {\partial v_{n+1, h}}{\partial a}\ge J\ast _\xi v_{n+1, h}-v_{n+1, h}-Mv_{n+1, h}+Mv_{n, h}+\int _0^{a^+}K(\cdot, a')\pi (a')v_{n, h}(a', \xi )da'\,(1-v_{n, h}),\\ v_{n+1, h}(0, \xi )=\int _0^{a^+}\gamma (a)v_{n, h}(a, \xi +ca)da. \end {cases} \end{equation*}
\begin{equation*} \begin {cases} \frac {\partial v_{n+1, h}}{\partial a}\ge J\ast _\xi v_{n+1, h}-v_{n+1, h}-Mv_{n+1, h}+Mv_{n, h}+\int _0^{a^+}K(\cdot, a')\pi (a')v_{n, h}(a', \xi )da'\,(1-v_{n, h}),\\ v_{n+1, h}(0, \xi )=\int _0^{a^+}\gamma (a)v_{n, h}(a, \xi +ca)da. \end {cases} \end{equation*}
On the other hand, recalling that
![]() $u^{n+1}$
satisfies (3.6) and due to the monotonicity (3.11) again along with
$u^{n+1}$
satisfies (3.6) and due to the monotonicity (3.11) again along with
![]() $v_{n, h}\ge u^n$
, we have
$v_{n, h}\ge u^n$
, we have
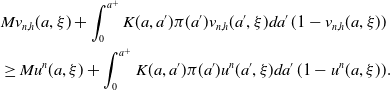 \begin{align*} &Mv_{n, h}(a, \xi )+\int _0^{a^+}K(a, a')\pi (a')v_{n, h}(a', \xi )da'\,(1-v_{n, h}(a, \xi ))\\ &\ge Mu^{n}(a, \xi )+\int _0^{a^+}K(a, a')\pi (a')u^{n}(a', \xi )da'\,(1-u^{n}(a, \xi )). \end{align*}
\begin{align*} &Mv_{n, h}(a, \xi )+\int _0^{a^+}K(a, a')\pi (a')v_{n, h}(a', \xi )da'\,(1-v_{n, h}(a, \xi ))\\ &\ge Mu^{n}(a, \xi )+\int _0^{a^+}K(a, a')\pi (a')u^{n}(a', \xi )da'\,(1-u^{n}(a, \xi )). \end{align*}
As the initial data satisfies,
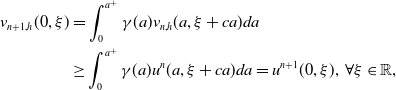 \begin{align*} v_{n+1, h}(0, \xi )&=\int _0^{a^+}\gamma (a)v_{n, h}(a, \xi +ca)da\\ &\ge \int _0^{a^+}\gamma (a)u^n(a, \xi +ca)da=u^{n+1}(0, \xi ), \;\forall \xi \in \mathbb{R}, \end{align*}
\begin{align*} v_{n+1, h}(0, \xi )&=\int _0^{a^+}\gamma (a)v_{n, h}(a, \xi +ca)da\\ &\ge \int _0^{a^+}\gamma (a)u^n(a, \xi +ca)da=u^{n+1}(0, \xi ), \;\forall \xi \in \mathbb{R}, \end{align*}
the comparison principle applies and provides
Now since for all
![]() $a\in [0, a^+]$
the function
$a\in [0, a^+]$
the function
![]() $\xi \to u^{n+1}(a, \xi )$
is nonincreasing, for all
$\xi \to u^{n+1}(a, \xi )$
is nonincreasing, for all
![]() $a\in [0, a^+]$
and
$a\in [0, a^+]$
and
![]() $\xi \in \mathbb{R}$
, we get
$\xi \in \mathbb{R}$
, we get
Hence, we have obtained that for all
![]() $n\ge 1$
and for all
$n\ge 1$
and for all
![]() $h\gt 0$
$h\gt 0$
As mentioned before, the case
![]() $h\lt 0$
can be handled similarly and thus the result is desired.
$h\lt 0$
can be handled similarly and thus the result is desired.
Now the estimates provided in Lemma 3.3 allows us to conclude that the limit
![]() $w$
obtained in Section 3.1 is globally Lipschitz continuous. This completes the desired regularity of
$w$
obtained in Section 3.1 is globally Lipschitz continuous. This completes the desired regularity of
![]() $w$
with respect to
$w$
with respect to
![]() $\xi$
as needed in Definition 1.2. Thus, we have obtained a continuous and bounded solution
$\xi$
as needed in Definition 1.2. Thus, we have obtained a continuous and bounded solution
![]() $w$
satisfying (1.9), which is a travelling wave solution of (1.5). This completes the proof of Theorem1.3 for
$w$
satisfying (1.9), which is a travelling wave solution of (1.5). This completes the proof of Theorem1.3 for
![]() $c\gt c^*$
.
$c\gt c^*$
.
Next, let us prove the existence of travelling waves for the critical wave speed
![]() $c=c^*$
. To this aim, assume that
$c=c^*$
. To this aim, assume that
![]() $\{c_l\}_{l\in \mathbb{N}}\in (c^*, c^*+1)$
is a decreasing sequence satisfying
$\{c_l\}_{l\in \mathbb{N}}\in (c^*, c^*+1)$
is a decreasing sequence satisfying
![]() $\lim \limits _{l\to \infty }c_l=c^*$
. Following the argument after Proposition 3.2, for each
$\lim \limits _{l\to \infty }c_l=c^*$
. Following the argument after Proposition 3.2, for each
![]() $c_l$
, there exists a travelling wave solution satisfying (1.9), denoted by
$c_l$
, there exists a travelling wave solution satisfying (1.9), denoted by
![]() $w_l$
. Since
$w_l$
. Since
![]() $w_l(a, \cdot +\eta )$
is also a solution of (1.9) for any
$w_l(a, \cdot +\eta )$
is also a solution of (1.9) for any
![]() $\eta \in \mathbb{R}$
, we can assume that
$\eta \in \mathbb{R}$
, we can assume that
![]() $w_l(0, 0)=\frac{1}{2}$
. Recalling Lemma 2.3, for any
$w_l(0, 0)=\frac{1}{2}$
. Recalling Lemma 2.3, for any
![]() $c_l$
, there exists
$c_l$
, there exists
![]() $\lambda _l$
satisfying (2.12). Observe that
$\lambda _l$
satisfying (2.12). Observe that
![]() $c_l\to \lambda _l=\lambda _l(c_l)$
is continuous due to (2.12). It follows that
$c_l\to \lambda _l=\lambda _l(c_l)$
is continuous due to (2.12). It follows that
![]() $\{\lambda _l\}_{l\in \mathbb{N}}$
is bounded due to
$\{\lambda _l\}_{l\in \mathbb{N}}$
is bounded due to
![]() $\{c_l\}_{l\in \mathbb{N}}\in (c^*, c^*+1)$
and thus we can choose
$\{c_l\}_{l\in \mathbb{N}}\in (c^*, c^*+1)$
and thus we can choose
![]() $m\gt 0$
large enough such that
$m\gt 0$
large enough such that
![]() $m\gt \{\lambda _l\}_{l\in \mathbb{N}}$
. Applying the argument in Lemma 3.3 to
$m\gt \{\lambda _l\}_{l\in \mathbb{N}}$
. Applying the argument in Lemma 3.3 to
![]() $\{w_l\}_{l\in \mathbb{N}}$
, we obtain that
$\{w_l\}_{l\in \mathbb{N}}$
, we obtain that
![]() $\{w_l\}_{l\in \mathbb{N}}$
is equi-continuous with respect to
$\{w_l\}_{l\in \mathbb{N}}$
is equi-continuous with respect to
![]() $\xi$
. Due to
$\xi$
. Due to
![]() $\{w_l\}_{l\in \mathbb{N}}\in [0, 1]$
, one see from the equation that
$\{w_l\}_{l\in \mathbb{N}}\in [0, 1]$
, one see from the equation that
![]() $\{w_l\}_{l\in \mathbb{N}}$
is equi-continuous with respect to
$\{w_l\}_{l\in \mathbb{N}}$
is equi-continuous with respect to
![]() $a$
. Now by Arzelà–Ascoli Theorem, there exists a subsequence of
$a$
. Now by Arzelà–Ascoli Theorem, there exists a subsequence of
![]() $\{w_l\}_{l\in \mathbb{N}}$
, again denoted by
$\{w_l\}_{l\in \mathbb{N}}$
, again denoted by
![]() $\{w_l\}_{l\in \mathbb{N}}$
satisfying
$\{w_l\}_{l\in \mathbb{N}}$
satisfying
![]() $w_l\to w^*$
as
$w_l\to w^*$
as
![]() $l\to \infty$
and that
$l\to \infty$
and that
![]() $\xi \to w^*(a, \xi )$
is globally Lipschitz continuous for any
$\xi \to w^*(a, \xi )$
is globally Lipschitz continuous for any
![]() $a\in [0, a^+]$
and that
$a\in [0, a^+]$
and that
![]() $a\to w^*(a, \xi )\in W^{1, 1}(0, a^+)$
for any
$a\to w^*(a, \xi )\in W^{1, 1}(0, a^+)$
for any
![]() $\xi \in \mathbb{R}$
. It is clear that
$\xi \in \mathbb{R}$
. It is clear that
![]() $w^*(0, 0)=\frac{1}{2}$
. In addition, by the same argument in Proposition 3.2,
$w^*(0, 0)=\frac{1}{2}$
. In addition, by the same argument in Proposition 3.2,
![]() $w^*$
satisfies the following equation:
$w^*$
satisfies the following equation:
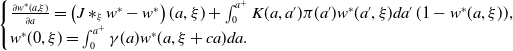 \begin{equation} \begin{cases} \frac{\partial w^*(a, \xi )}{\partial a}=\left (J\ast _\xi w^*-w^*\right )(a, \xi )+\int _0^{a^+}K(a, a')\pi (a')w^*(a', \xi )da'\,(1-w^*(a, \xi )),\\ w^*(0, \xi )=\int _0^{a^+}\gamma (a)w^*(a, \xi +ca)da. \end{cases} \end{equation}
\begin{equation} \begin{cases} \frac{\partial w^*(a, \xi )}{\partial a}=\left (J\ast _\xi w^*-w^*\right )(a, \xi )+\int _0^{a^+}K(a, a')\pi (a')w^*(a', \xi )da'\,(1-w^*(a, \xi )),\\ w^*(0, \xi )=\int _0^{a^+}\gamma (a)w^*(a, \xi +ca)da. \end{cases} \end{equation}
On the other hand,
![]() $0\le w^*\le 1$
and
$0\le w^*\le 1$
and
![]() $\xi \to w^*(a, \xi )$
, being nonincreasing for any
$\xi \to w^*(a, \xi )$
, being nonincreasing for any
![]() $a\in [0, a^+]$
, imply that the limits
$a\in [0, a^+]$
, imply that the limits
![]() $w^*(a, \pm \infty )=w^\pm (a)$
exist for any
$w^*(a, \pm \infty )=w^\pm (a)$
exist for any
![]() $a\in [0, a^+]$
. Moreover, the limits satisfy the Equation (2.4), together with the condition
$a\in [0, a^+]$
. Moreover, the limits satisfy the Equation (2.4), together with the condition
Hence, Lemma 2.2 applies and ensures that
![]() $w^*(a, -\infty )=1$
and
$w^*(a, -\infty )=1$
and
![]() $w^*(a, \infty )=0$
uniformly in
$w^*(a, \infty )=0$
uniformly in
![]() $[0, a^+]$
. Hence, the existence for
$[0, a^+]$
. Hence, the existence for
![]() $c=c^*$
is complete.
$c=c^*$
is complete.
Now we set
![]() $I=\pi (a)u$
and then obtain that it is a travelling wave solution of (1.4) with speed
$I=\pi (a)u$
and then obtain that it is a travelling wave solution of (1.4) with speed
![]() $c$
. Finally, let us notice that
$c$
. Finally, let us notice that
![]() $\pi (a^+)=0$
and
$\pi (a^+)=0$
and
![]() $u$
being bounded implies that function
$u$
being bounded implies that function
![]() $I$
vanishes at
$I$
vanishes at
![]() $a=a^+$
. Hence, Theorem1.4 is complete.
$a=a^+$
. Hence, Theorem1.4 is complete.
4. Spreading speeds
In this section, we shall prove Theorem1.5.
4.1 Outer spreading
For Theorem1.5-(i), let
![]() $c\gt c^*$
be given and fixed. We now look for a super-solution of (1.11) with the form
$c\gt c^*$
be given and fixed. We now look for a super-solution of (1.11) with the form
![]() $v(t, a, x)=v_0e^{-\lambda (x-ct)}\phi (a)$
for some positive constant
$v(t, a, x)=v_0e^{-\lambda (x-ct)}\phi (a)$
for some positive constant
![]() $v_0$
to be chosen later and
$v_0$
to be chosen later and
![]() $\lambda \gt 0$
satisfying (2.12). Here,
$\lambda \gt 0$
satisfying (2.12). Here,
![]() $\phi$
is defined in (2.10) with
$\phi$
is defined in (2.10) with
![]() $s=s_0$
, where
$s=s_0$
, where
![]() $s_0$
is defined in Section 2.3. Note that, for all
$s_0$
is defined in Section 2.3. Note that, for all
![]() $t\in \mathbb{R}, a\in (0, a^+)$
and
$t\in \mathbb{R}, a\in (0, a^+)$
and
![]() $x\in \mathbb{R}$
, one has
$x\in \mathbb{R}$
, one has
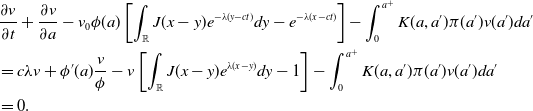 \begin{align*} &\frac{\partial v}{\partial t}+\frac{\partial v}{\partial a}-v_0\phi (a)\left [\int _{\mathbb{R}} J(x-y)e^{-\lambda (y-ct)}dy-e^{-\lambda (x-ct)}\right ]-\int _0^{a^+}K(a, a')\pi (a')v(a')da'\\ &=c\lambda v+\phi '(a)\frac{v}{\phi }-v\left [\int _{\mathbb{R}} J(x-y)e^{\lambda (x-y)}dy-1\right ]-\int _0^{a^+}K(a, a')\pi (a')v(a')da'\\ &=0. \end{align*}
\begin{align*} &\frac{\partial v}{\partial t}+\frac{\partial v}{\partial a}-v_0\phi (a)\left [\int _{\mathbb{R}} J(x-y)e^{-\lambda (y-ct)}dy-e^{-\lambda (x-ct)}\right ]-\int _0^{a^+}K(a, a')\pi (a')v(a')da'\\ &=c\lambda v+\phi '(a)\frac{v}{\phi }-v\left [\int _{\mathbb{R}} J(x-y)e^{\lambda (x-y)}dy-1\right ]-\int _0^{a^+}K(a, a')\pi (a')v(a')da'\\ &=0. \end{align*}
Besides, again by (2.10), one has
On the other hand, we know from (1.11) that
Finally, since
![]() $u_0$
is compactly supported and
$u_0$
is compactly supported and
![]() $\inf _{a\in [0, a^+]}\phi (a)\gt 0$
, we can choose
$\inf _{a\in [0, a^+]}\phi (a)\gt 0$
, we can choose
![]() $v_0$
large enough such that
$v_0$
large enough such that
which implies that
![]() $v$
is a super-solution of (1.11). Hence we end-up with the following estimate due to Lemma 2.1
$v$
is a super-solution of (1.11). Hence we end-up with the following estimate due to Lemma 2.1
Now let
![]() $c_1$
be any real number such that
$c_1$
be any real number such that
![]() $c_1\gt c\gt c^*$
. Then, we have
$c_1\gt c\gt c^*$
. Then, we have
therefore as
![]() $c\gt c^*$
can be chosen arbitrary close to
$c\gt c^*$
can be chosen arbitrary close to
![]() $c^*$
, Theorem1.5-(i) holds true in the case
$c^*$
, Theorem1.5-(i) holds true in the case
![]() $x\ge ct$
and consequently for
$x\ge ct$
and consequently for
![]() $|x|\ge ct$
as well. This concludes the proof of Theorem1.5-(i).
$|x|\ge ct$
as well. This concludes the proof of Theorem1.5-(i).
4.2 Hair-trigger effects
In order to prove Theorem1.5-(ii), we first investigate the so-called hair-trigger effect of (1.11) that roughly speaking indicates the ability of the solutions of the system to become uniformly positive whatever the smallness of the non-zero and non-negative initial data.
Lemma 4.1
Let
![]() $u=u(t, a, x)$
be the solution of (
1.11
) with the initial data
$u=u(t, a, x)$
be the solution of (
1.11
) with the initial data
![]() $u_0=u_0(a, x)$
. If there exist two constants
$u_0=u_0(a, x)$
. If there exist two constants
![]() $x_0\in \mathbb{R}$
and
$x_0\in \mathbb{R}$
and
![]() $\rho _0\in (0, 1)$
such that
$\rho _0\in (0, 1)$
such that
then for any
![]() $\rho \in (0, 1)$
, there exists
$\rho \in (0, 1)$
, there exists
![]() $T_{\rho _0}^\rho \ge 0$
, which is independent of
$T_{\rho _0}^\rho \ge 0$
, which is independent of
![]() $x_0$
such that
$x_0$
such that
Proof. We consider the following auxiliary problem
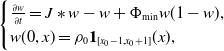 \begin{equation} \begin{cases} \frac{\partial w}{\partial t}=J\ast w-w+\Phi _{\min }w(1-w), \\ w(0, x)=\rho _0\mathbf{1}_{[x_0-1,x_0+1]}(x), \end{cases} \end{equation}
\begin{equation} \begin{cases} \frac{\partial w}{\partial t}=J\ast w-w+\Phi _{\min }w(1-w), \\ w(0, x)=\rho _0\mathbf{1}_{[x_0-1,x_0+1]}(x), \end{cases} \end{equation}
where
and
![]() $\mathbf{1}_S$
denotes the indicator function of the set
$\mathbf{1}_S$
denotes the indicator function of the set
![]() $S$
. Then, it is easy to see that the solution
$S$
. Then, it is easy to see that the solution
![]() $w$
of (4.2) is a sub-solution of (1.11) with
$w$
of (4.2) is a sub-solution of (1.11) with
![]() $u_0(a, x)\ge \rho _0\mathbf{1}_{B_1(x_0)}(x)$
.
$u_0(a, x)\ge \rho _0\mathbf{1}_{B_1(x_0)}(x)$
.
However, recall Xu et al. [Reference Xu, Li and Ruan28, Lemma 4.1] (see also Alfaro [Reference Alfaro1, Theorem 2.6] or Finkelschtein and Tkachov [Reference Finkelshtein and Tkachov15, Theorems 2.5 and 2.7]), the Equation (4.2) exhibits the hair-trigger effect that is there exists
![]() $T_{\rho _0}^\rho \ge 0$
, which is independent of
$T_{\rho _0}^\rho \ge 0$
, which is independent of
![]() $x_0$
such that
$x_0$
such that
Finally, the comparison principle applies to conclude the desired result (4.1).
Corollary 4.2
Let
![]() $u=u(t, a, x)$
be the solution of (
1.11
) with non-negative initial data
$u=u(t, a, x)$
be the solution of (
1.11
) with non-negative initial data
![]() $u_0=u_0(a, x)\in C([0,a^+]\times \mathbb{R})\setminus \{0\}$
. Then one has for each
$u_0=u_0(a, x)\in C([0,a^+]\times \mathbb{R})\setminus \{0\}$
. Then one has for each
![]() $t\ge a^+$
and for any
$t\ge a^+$
and for any
![]() $x\in \mathbb{R}$
,
$x\in \mathbb{R}$
,
Due to the above property, Lemma 4.1 implies that if in addition
![]() $u_0\leq 1$
, then
$u_0\leq 1$
, then
Proof. First, we define an operator
![]() $\mathcal K\;:\; L^1((0, a^+), X)\to L^1((0, a^+), X)$
as follows:
$\mathcal K\;:\; L^1((0, a^+), X)\to L^1((0, a^+), X)$
as follows:
Next, solving the problem (1.11) along the characteristic line
![]() $a-t=c$
, where
$a-t=c$
, where
![]() $c\in \mathbb{R}$
, we now derive the formula for a solution to (1.1). For fixed
$c\in \mathbb{R}$
, we now derive the formula for a solution to (1.1). For fixed
![]() $c\in \mathbb{R}$
, we set
$c\in \mathbb{R}$
, we set
![]() $w(t)=u(t, t+c)$
for
$w(t)=u(t, t+c)$
for
![]() $t\in [\max (-c, 0), \infty )$
. With
$t\in [\max (-c, 0), \infty )$
. With
![]() $a=t+c$
, one obtains for
$a=t+c$
, one obtains for
![]() $t\in [\max (-c, 0), \infty )$
the equation
$t\in [\max (-c, 0), \infty )$
the equation
where
![]() $T$
is defined in (2.1). We first study the case
$T$
is defined in (2.1). We first study the case
![]() $c\ge 0$
. Clearly,
$c\ge 0$
. Clearly,
![]() $w(0)=u(0, c)=u(0, a-t)=u_0(a-t)$
. Considering the equation (4.4) with initial data
$w(0)=u(0, c)=u(0, a-t)=u_0(a-t)$
. Considering the equation (4.4) with initial data
![]() $w(0)\ge 0$
and
$w(0)\ge 0$
and
![]() $w(0)\not \equiv 0$
, we have
$w(0)\not \equiv 0$
, we have
![]() $w(t)\gt 0$
for
$w(t)\gt 0$
for
![]() $t\gt 0$
by the strong comparison principle of the nonlinear nonlocal diffusion problem, due to
$t\gt 0$
by the strong comparison principle of the nonlinear nonlocal diffusion problem, due to
![]() $J(0)\gt 0$
in Assumption 1.1-(iii). It follows that
$J(0)\gt 0$
in Assumption 1.1-(iii). It follows that
![]() $u(t, a)\gt 0$
for
$u(t, a)\gt 0$
for
![]() $a\ge t$
. On the other hand, integrating (4.4) from
$a\ge t$
. On the other hand, integrating (4.4) from
![]() $0$
to
$0$
to
![]() $t$
, one obtains
$t$
, one obtains
and thus
Next, we consider the case
![]() $c\lt 0$
. Integrating (4.4) from
$c\lt 0$
. Integrating (4.4) from
![]() $-c$
to
$-c$
to
![]() $t$
, one gets
$t$
, one gets
and thus
Thus, the solution to (1.1) reads as follows:
 \begin{equation} u(t, a)= \begin{cases} e^{(T-I)t}u_0(a-t)+\int _0^{t}e^{(T-I)(t-s)}[\mathcal K(u(s))](s+a-t)ds, &a\ge t,\\ e^{(T-I)a}u(t-a, 0)+\int _{t-a}^te^{(T-I)(t-s)}[\mathcal K(u(s))](s+a-t)ds, &a\lt t. \end{cases} \end{equation}
\begin{equation} u(t, a)= \begin{cases} e^{(T-I)t}u_0(a-t)+\int _0^{t}e^{(T-I)(t-s)}[\mathcal K(u(s))](s+a-t)ds, &a\ge t,\\ e^{(T-I)a}u(t-a, 0)+\int _{t-a}^te^{(T-I)(t-s)}[\mathcal K(u(s))](s+a-t)ds, &a\lt t. \end{cases} \end{equation}
Next, we plug the explicit formula (4.5) into
![]() $u(t, 0)$
to obtain
$u(t, 0)$
to obtain
 \begin{align} u(t, 0)&=&\int _0^{t}\chi (a)\gamma (a)\left [e^{(T-I)a}u(t-a, 0)+\int _{t-a}^te^{(T-I)(t-s)}[\mathcal K(u(s))](s+a-t)ds\right ]da\nonumber \\ &&+\int _t^{a^+}\chi (a)\gamma (a)\left [e^{(T-I)t}u_0(a-t)+\int _0^{t}e^{(T-I)(t-s)}[\mathcal K(u(s))](s+a-t)ds\right ]da, \end{align}
\begin{align} u(t, 0)&=&\int _0^{t}\chi (a)\gamma (a)\left [e^{(T-I)a}u(t-a, 0)+\int _{t-a}^te^{(T-I)(t-s)}[\mathcal K(u(s))](s+a-t)ds\right ]da\nonumber \\ &&+\int _t^{a^+}\chi (a)\gamma (a)\left [e^{(T-I)t}u_0(a-t)+\int _0^{t}e^{(T-I)(t-s)}[\mathcal K(u(s))](s+a-t)ds\right ]da, \end{align}
where
![]() $\chi (a)$
is the cut-off function satisfying
$\chi (a)$
is the cut-off function satisfying
![]() $\chi (a)=1$
when
$\chi (a)=1$
when
![]() $a\in (0, a^+)$
otherwise
$a\in (0, a^+)$
otherwise
![]() $\chi (a)=0$
. Now we consider two cases.
$\chi (a)=0$
. Now we consider two cases.
Case 1. If
![]() $t\lt a^+$
, (4.6) is written as follows:
$t\lt a^+$
, (4.6) is written as follows:
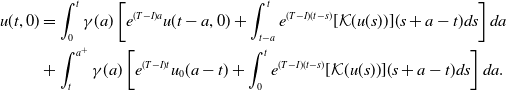 \begin{align} u(t, 0)&=\int _0^{t}\gamma (a)\left [e^{(T-I)a}u(t-a, 0)+\int _{t-a}^te^{(T-I)(t-s)}[\mathcal K(u(s))](s+a-t)ds\right ]da\\ &+\int _t^{a^+}\gamma (a)\left [e^{(T-I)t}u_0(a-t)+\int _0^{t}e^{(T-I)(t-s)}[\mathcal K(u(s))](s+a-t)ds\right ]da.\nonumber \end{align}
\begin{align} u(t, 0)&=\int _0^{t}\gamma (a)\left [e^{(T-I)a}u(t-a, 0)+\int _{t-a}^te^{(T-I)(t-s)}[\mathcal K(u(s))](s+a-t)ds\right ]da\\ &+\int _t^{a^+}\gamma (a)\left [e^{(T-I)t}u_0(a-t)+\int _0^{t}e^{(T-I)(t-s)}[\mathcal K(u(s))](s+a-t)ds\right ]da.\nonumber \end{align}
Since
![]() $e^{(T-I)t}u_0(a-t)\gt 0$
for
$e^{(T-I)t}u_0(a-t)\gt 0$
for
![]() $a\ge t$
and
$a\ge t$
and
![]() $\gamma \ge 0$
for any
$\gamma \ge 0$
for any
![]() $a\in [0, a^+]$
by Assumption 1.1-(i), the second term on the right hand of (4.7) must be positive. Thus we have
$a\in [0, a^+]$
by Assumption 1.1-(i), the second term on the right hand of (4.7) must be positive. Thus we have
![]() $u(t, 0)\gt 0$
, which implies
$u(t, 0)\gt 0$
, which implies
![]() $u(t, a)\gt 0$
for
$u(t, a)\gt 0$
for
![]() $a\lt t$
via (4.5).
$a\lt t$
via (4.5).
Case 2. If
![]() $t\ge a^+$
, (4.6) is written as follows:
$t\ge a^+$
, (4.6) is written as follows:
Let us claim that
![]() $u(t, 0, x)\;:\!=\;[u(t, 0)](x)\gt 0$
in
$u(t, 0, x)\;:\!=\;[u(t, 0)](x)\gt 0$
in
![]() $[a^+, \infty )\times \mathbb{R}$
. By contradiction, suppose that there exists
$[a^+, \infty )\times \mathbb{R}$
. By contradiction, suppose that there exists
![]() $(t_0, x_0)\in [a^+, \infty )\times \mathbb{R}$
such that
$(t_0, x_0)\in [a^+, \infty )\times \mathbb{R}$
such that
![]() $u(t_0, 0, x_0)=0$
. Thus, one obtains
$u(t_0, 0, x_0)=0$
. Thus, one obtains
where we used the fact that
![]() $e^{-a}$
and
$e^{-a}$
and
![]() $e^{Ta}$
are commuting. By Assumption 1.1-(i) on
$e^{Ta}$
are commuting. By Assumption 1.1-(i) on
![]() $\gamma$
, we can find one point
$\gamma$
, we can find one point
![]() $b_0\in (0, a^+]$
such that
$b_0\in (0, a^+]$
such that
![]() $e^{Tb_0}u(t_0-b_0, 0, x_0)=0$
. By definition, one has
$e^{Tb_0}u(t_0-b_0, 0, x_0)=0$
. By definition, one has
where
![]() $J^{*n}$
denotes the
$J^{*n}$
denotes the
![]() $n$
-fold convolution of
$n$
-fold convolution of
![]() $K$
; that is
$K$
; that is
![]() $J^{*n}=J\ast \cdots \ast J$
,
$J^{*n}=J\ast \cdots \ast J$
,
![]() $n$
times. It follows that for each
$n$
times. It follows that for each
![]() $n\in \mathbb{N}$
,
$n\in \mathbb{N}$
,
However, by Assumption 1.1-(iii) on
![]() $J$
, one has
$J$
, one has
![]() $J\gt 0$
in
$J\gt 0$
in
![]() $(-r, r)$
for some
$(-r, r)$
for some
![]() $r\gt 0$
, which implies that
$r\gt 0$
, which implies that
Since
![]() $\mathbb{R}=\sum _{n=0}^\infty (x_0-nr, x_0+nr)$
, we have
$\mathbb{R}=\sum _{n=0}^\infty (x_0-nr, x_0+nr)$
, we have
![]() $u(t_0-b_0, 0, \cdot )\equiv 0$
in
$u(t_0-b_0, 0, \cdot )\equiv 0$
in
![]() $\mathbb{R}$
.
$\mathbb{R}$
.
Next, replace
![]() $t_0$
by
$t_0$
by
![]() $t_0-b_0$
in (4.6). If
$t_0-b_0$
in (4.6). If
![]() $t_0-b_0$
falls in
$t_0-b_0$
falls in
![]() $[0, a^+]$
, by the argument as Case 1, one has
$[0, a^+]$
, by the argument as Case 1, one has
![]() $u(t_0-b_0, 0)\gt 0$
, which is a contradiction. Hence,
$u(t_0-b_0, 0)\gt 0$
, which is a contradiction. Hence,
![]() $t_0-b_0$
must fall in
$t_0-b_0$
must fall in
![]() $(a^+, \infty )$
. Then by the same argument as Case 2, one can find
$(a^+, \infty )$
. Then by the same argument as Case 2, one can find
![]() $b_1\in (0, a^+]$
such that
$b_1\in (0, a^+]$
such that
![]() $u(t_0-b_0-b_1, 0)=0$
. Now, repeating the above process by induction, one can find a sequence
$u(t_0-b_0-b_1, 0)=0$
. Now, repeating the above process by induction, one can find a sequence
![]() $\{b_i\}_{i\ge 0}$
such that
$\{b_i\}_{i\ge 0}$
such that
![]() $u(t_0-\sum _{i=0}^{\widehat M} b_i, 0)=0$
for any
$u(t_0-\sum _{i=0}^{\widehat M} b_i, 0)=0$
for any
![]() $\widehat M\ge 0$
. But we know every
$\widehat M\ge 0$
. But we know every
![]() $b_i$
is in
$b_i$
is in
![]() $(0, a^+]$
, then there always exists a minimal
$(0, a^+]$
, then there always exists a minimal
![]() $M_0\gt 0$
such that
$M_0\gt 0$
such that
![]() $t_0-\sum _{i=0}^{M_0} b_i\lt a^+$
. Then, by Case 1, one has
$t_0-\sum _{i=0}^{M_0} b_i\lt a^+$
. Then, by Case 1, one has
![]() $u(t_0-\sum _{i=0}^{M_0} b_i, 0)\gt 0$
.
$u(t_0-\sum _{i=0}^{M_0} b_i, 0)\gt 0$
.
Now consider (4.8) at
![]() $t=t_0-\sum _{i=0}^{M_0-1}b_i$
, which is larger than or equal to
$t=t_0-\sum _{i=0}^{M_0-1}b_i$
, which is larger than or equal to
![]() $a^+$
, we get a contradiction, since now the left hand side of (4.8) equals to zero, while the right hand side of (4.8) is larger than zero.
$a^+$
, we get a contradiction, since now the left hand side of (4.8) equals to zero, while the right hand side of (4.8) is larger than zero.
In summary, we cannot have
![]() $(t, x)\in (0, \infty )\times \mathbb{R}$
such that
$(t, x)\in (0, \infty )\times \mathbb{R}$
such that
![]() $u(t, 0, x)=0$
, which implies that
$u(t, 0, x)=0$
, which implies that
![]() $u(t, 0, x)\gt 0$
and thus
$u(t, 0, x)\gt 0$
and thus
![]() $u(t, a)\gt 0$
by (4.5). Hence, the proof is complete.
$u(t, a)\gt 0$
by (4.5). Hence, the proof is complete.
4.3 Inner spreading
In this section, we prove the inner spreading. To this aim, we consider the following auxiliary equation
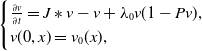 \begin{equation} \begin{cases} \frac{\partial v}{\partial t}=J\ast v-v+\lambda _0v(1-Pv),\\ v(0, x)=v_0(x), \end{cases} \end{equation}
\begin{equation} \begin{cases} \frac{\partial v}{\partial t}=J\ast v-v+\lambda _0v(1-Pv),\\ v(0, x)=v_0(x), \end{cases} \end{equation}
where
![]() $v_0$
denotes a Lipschitz continuous in
$v_0$
denotes a Lipschitz continuous in
![]() $\mathbb{R}$
with compact support satisfying
$\mathbb{R}$
with compact support satisfying
and, recalling the definition of the function
![]() $\phi$
in (2.10) with
$\phi$
in (2.10) with
![]() $s=s_0\lt 0$
,
$s=s_0\lt 0$
,
![]() $P$
and
$P$
and
![]() $\lambda _0$
are the positive constants given by
$\lambda _0$
are the positive constants given by
Recall that
![]() $u_0=u_0(a,x)\in C^0([0,a^+]\times \mathbb{R})\setminus \{0\}$
is non-negative,
$u_0=u_0(a,x)\in C^0([0,a^+]\times \mathbb{R})\setminus \{0\}$
is non-negative,
![]() $u_0\leq 1$
and
$u_0\leq 1$
and
![]() $\textrm{supp}(u_0)$
is compact in
$\textrm{supp}(u_0)$
is compact in
![]() $[0,a^+]\times \mathbb{R}$
. Hence, according to Corollary 4.2, one has there exists
$[0,a^+]\times \mathbb{R}$
. Hence, according to Corollary 4.2, one has there exists
![]() $\rho \gt 0$
such that
$\rho \gt 0$
such that
Next, we fix
![]() $v_0\;:\;\mathbb{R}\to \mathbb{R}^+$
Lipschitz continuous such that
$v_0\;:\;\mathbb{R}\to \mathbb{R}^+$
Lipschitz continuous such that
so that the function
![]() $\underline{\textbf{u}}_0\in C([0, a^+]\times \mathbb{R})$
given by
$\underline{\textbf{u}}_0\in C([0, a^+]\times \mathbb{R})$
given by
satisfies
Next, set
![]() $\underline{\textbf{u}}(t, a, x)=\phi (a)v(t, x)$
, where
$\underline{\textbf{u}}(t, a, x)=\phi (a)v(t, x)$
, where
![]() $v=v(t, x)$
is the solution of (4.10) with the initial data
$v=v(t, x)$
is the solution of (4.10) with the initial data
![]() $v_0$
. Next, we verify that
$v_0$
. Next, we verify that
![]() $\underline{\textbf{u}}$
is a sub-solution of (1.11). Indeed, we have
$\underline{\textbf{u}}$
is a sub-solution of (1.11). Indeed, we have
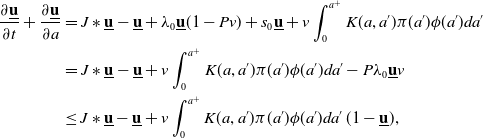 \begin{align} \frac{\partial \underline{\textbf{u}}}{\partial t}+\frac{\partial \underline{\textbf{u}}}{\partial a}&=J\ast \underline{\textbf{u}}-\underline{\textbf u}+\lambda _0\underline{\textbf u}(1-Pv)+s_0\underline{\textbf u}+v\int _0^{a^+}K(a, a')\pi (a')\phi (a')da'\,\nonumber\\ &=J\ast \underline{\textbf{u}}-\underline{\textbf{u}}+v\int _0^{a^+}K(a, a')\pi (a')\phi (a')da'-P\lambda _0\underline{\textbf{u}}v\nonumber\\ &\le J\ast \underline{\textbf{u}}-\underline{\textbf{u}}+v\int _0^{a^+}K(a, a')\pi (a')\phi (a')da'\, (1-\underline{\textbf{u}}), \end{align}
\begin{align} \frac{\partial \underline{\textbf{u}}}{\partial t}+\frac{\partial \underline{\textbf{u}}}{\partial a}&=J\ast \underline{\textbf{u}}-\underline{\textbf u}+\lambda _0\underline{\textbf u}(1-Pv)+s_0\underline{\textbf u}+v\int _0^{a^+}K(a, a')\pi (a')\phi (a')da'\,\nonumber\\ &=J\ast \underline{\textbf{u}}-\underline{\textbf{u}}+v\int _0^{a^+}K(a, a')\pi (a')\phi (a')da'-P\lambda _0\underline{\textbf{u}}v\nonumber\\ &\le J\ast \underline{\textbf{u}}-\underline{\textbf{u}}+v\int _0^{a^+}K(a, a')\pi (a')\phi (a')da'\, (1-\underline{\textbf{u}}), \end{align}
and by (2.8) and the choice of
![]() $v_0$
, one has
$v_0$
, one has
 \begin{align*} &\underline{\textbf{u}}(t, 0, x)=\phi (0)v(t, x)=\int _0^{a^+}\gamma (a)\phi (a)da\,v(t, x)=\int _0^{a^+}\gamma (a)\underline{\textbf{u}}(t, a, x)da,\\ &\underline{\textbf{u}}(0, a, x)=\phi (a)v_0(x)\le \tilde u_0(a, x). \end{align*}
\begin{align*} &\underline{\textbf{u}}(t, 0, x)=\phi (0)v(t, x)=\int _0^{a^+}\gamma (a)\phi (a)da\,v(t, x)=\int _0^{a^+}\gamma (a)\underline{\textbf{u}}(t, a, x)da,\\ &\underline{\textbf{u}}(0, a, x)=\phi (a)v_0(x)\le \tilde u_0(a, x). \end{align*}
Now define
Note that
![]() $c_0\gt 0$
since
$c_0\gt 0$
since
![]() $J$
is symmetric. Then, let us recall a spreading result for Equation (4.10), from Ducrot and Jin [Reference Ducrot and Jin8, Lemma 1.27].
$J$
is symmetric. Then, let us recall a spreading result for Equation (4.10), from Ducrot and Jin [Reference Ducrot and Jin8, Lemma 1.27].
Lemma 4.3
Let
![]() $v=v(t, x)$
be the solution of (4.10) supplemented with a continuous initial data
$v=v(t, x)$
be the solution of (4.10) supplemented with a continuous initial data
![]() $0\le v_0(\cdot )\le \frac{1}{P}$
and
$0\le v_0(\cdot )\le \frac{1}{P}$
and
![]() $v_0\not \equiv 0$
with compact support. Let us further assume that
$v_0\not \equiv 0$
with compact support. Let us further assume that
![]() $v$
is uniformly continuous for all
$v$
is uniformly continuous for all
![]() $t\ge 0, x\in \mathbb{R}$
. Then one has
$t\ge 0, x\in \mathbb{R}$
. Then one has
Here, let us mention that the condition
![]() $v_0\le \frac{1}{P}$
is not necessary to reach the same conclusion. It is only used for the sake of simplicity and to cite directly the above existing result. For more general compactly supported initial data, one can also obtain a similar result by a suitable application of the comparison principles.
$v_0\le \frac{1}{P}$
is not necessary to reach the same conclusion. It is only used for the sake of simplicity and to cite directly the above existing result. For more general compactly supported initial data, one can also obtain a similar result by a suitable application of the comparison principles.
Next, let us show
![]() $c_0=c^*$
. Define the function
$c_0=c^*$
. Define the function
![]() $H(\lambda ), \lambda \gt 0$
as follows:
$H(\lambda ), \lambda \gt 0$
as follows:
Differentiating
![]() $H$
with respect to
$H$
with respect to
![]() $\lambda$
and setting
$\lambda$
and setting
![]() $\lambda ^*=\lambda (c^*)$
, one obtains by (2.13)
$\lambda ^*=\lambda (c^*)$
, one obtains by (2.13)
Next, when
![]() $H'(\lambda )=0$
, one obtains that
$H'(\lambda )=0$
, one obtains that
![]() $\lambda$
satisfies
$\lambda$
satisfies
which implies
![]() $\lambda =\lambda ^*$
due to the monotonicity of
$\lambda =\lambda ^*$
due to the monotonicity of
![]() $\int _{\mathbb{R}}J(y)e^{\lambda y}(\lambda y-1)dy$
with respect to
$\int _{\mathbb{R}}J(y)e^{\lambda y}(\lambda y-1)dy$
with respect to
![]() $\lambda$
and thus
$\lambda$
and thus
![]() $c_0=c^*$
. Hence now for any
$c_0=c^*$
. Hence now for any
![]() $0\leq c\lt c^*$
we have
$0\leq c\lt c^*$
we have
Moreover, one may assume that
![]() $\rho _0\lt 1$
. Thus, (4.11) implies that for any
$\rho _0\lt 1$
. Thus, (4.11) implies that for any
![]() $c\in [0,c^*)$
, there exists
$c\in [0,c^*)$
, there exists
![]() $T\gt 0$
such that
$T\gt 0$
such that
Now, for any
![]() $\rho \in (0, 1)$
, applying Lemma 4.1 to (1.11) yields that there exists
$\rho \in (0, 1)$
, applying Lemma 4.1 to (1.11) yields that there exists
![]() $T_{\rho _0}^\rho \gt 0$
such that
$T_{\rho _0}^\rho \gt 0$
such that
which implies that
For any
![]() $\epsilon \in (0, c)$
, there exists a constant
$\epsilon \in (0, c)$
, there exists a constant
![]() $T'\ge T_{\rho _0}^\rho$
such that
$T'\ge T_{\rho _0}^\rho$
such that
![]() $\epsilon T'\ge cT_{\rho _0}^\rho$
. Then, we have that
$\epsilon T'\ge cT_{\rho _0}^\rho$
. Then, we have that
![]() $ct-cT_{\rho _0}^\rho \ge (c-\epsilon )t$
and
$ct-cT_{\rho _0}^\rho \ge (c-\epsilon )t$
and
Now, since
![]() $\rho \in (0, 1)$
is arbitrary close to
$\rho \in (0, 1)$
is arbitrary close to
![]() $1$
, we obtain
$1$
, we obtain
Due to the arbitrariness of
![]() $\epsilon$
, hence we have the following result.
$\epsilon$
, hence we have the following result.
Theorem 4.4
Let
![]() $u=u(t, a, x)$
be the solution of (
1.11
) supplemented with a continuous initial data
$u=u(t, a, x)$
be the solution of (
1.11
) supplemented with a continuous initial data
![]() $0\le u_0\le 1$
and
$0\le u_0\le 1$
and
![]() $u_0\not \equiv 0$
with
$u_0\not \equiv 0$
with
![]() $u_0$
being compactly supported in
$u_0$
being compactly supported in
![]() $[0, a^+]\times \mathbb{R}$
, then one has
$[0, a^+]\times \mathbb{R}$
, then one has
This proves Theorem1.5-(ii).
Acknowledgements
We thank the anonymous reviewers for their helpful comments and suggestions.
Funding statement
Research was partially supported by the National Natural Science Foundation of China (No. 12301259, and No. 12371169).
Competing interest
None.


