Article contents
Spatial dynamics of a nonlocal model with periodic delay and competition
Published online by Cambridge University Press: 06 January 2020
Abstract
Each species is subject to various biotic and abiotic factors during growth. This paper formulates a deterministic model with the consideration of various factors regulating population growth such as age-dependent birth and death rates, spatial movements, seasonal variations, intra-specific competition and time-varying maturation simultaneously. The model takes the form of two coupled reaction–diffusion equations with time-dependent delays, which bring novel challenges to the theoretical analysis. Then, the model is analysed when competition among immatures is neglected, in which situation one equation for the adult population density is decoupled. The basic reproduction number  $\mathcal{R}_0$ is defined and shown to determine the global attractivity of either the zero equilibrium (when
$\mathcal{R}_0$ is defined and shown to determine the global attractivity of either the zero equilibrium (when 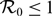 $\mathcal{R}_0\leq 1$) or a positive periodic solution (
$\mathcal{R}_0\leq 1$) or a positive periodic solution (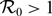 $\mathcal{R}_0\gt1$) by using the dynamical system approach on an appropriate phase space. When the immature intra-specific competition is included and the immature diffusion rate is neglected, the model is neither cooperative nor reducible to a single equation. In this case, the threshold dynamics about the population extinction and uniform persistence are established by using the newly defined basic reproduction number
$\mathcal{R}_0\gt1$) by using the dynamical system approach on an appropriate phase space. When the immature intra-specific competition is included and the immature diffusion rate is neglected, the model is neither cooperative nor reducible to a single equation. In this case, the threshold dynamics about the population extinction and uniform persistence are established by using the newly defined basic reproduction number  $\widetilde{\mathcal{R}}_0$ as a threshold index. Furthermore, numerical simulations are implemented on the population growth of two different species for two different cases to validate the analytic results.
$\widetilde{\mathcal{R}}_0$ as a threshold index. Furthermore, numerical simulations are implemented on the population growth of two different species for two different cases to validate the analytic results.
MSC classification
Information
- Type
- Papers
- Information
- Copyright
- © The Author(s) 2020. Published by Cambridge University Press
Footnotes
The work of YL and KL is supported in part by the Research Grants Council of Hong Kong (PolyU 153277/16P) and the Research Grants of Jiangsu University (4111190009). ZW and LZ are supported by NNSF of China (11371179 and 11701242) and the Fundamental Research Funds for the Central Universities (lzujbky-2017-ot09, lzujbky-2017-27 and lzujbky-2019-79).
References
- 1
- Cited by


