Article contents
Entire solutions of the Fisher–KPP equation on the half line
Published online by Cambridge University Press: 26 March 2019
Abstract
In this paper, we study the entire solutions of the Fisher–KPP (Kolmogorov–Petrovsky–Piskunov) equation ut = uxx + f(u) on the half line [0, ∞) with Dirichlet boundary condition at x = 0. (1) For any 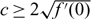 $c \ge 2\sqrt {f'(0)} $, we show the existence of an entire solution
$c \ge 2\sqrt {f'(0)} $, we show the existence of an entire solution 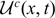 ${{\cal U}^c}(x,t)$ which connects the traveling wave solution φc(x + ct) at t = −∞ and the unique positive stationary solution V(x) at t = +∞; (2) We also construct an entire solution
${{\cal U}^c}(x,t)$ which connects the traveling wave solution φc(x + ct) at t = −∞ and the unique positive stationary solution V(x) at t = +∞; (2) We also construct an entire solution 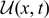 ${{\cal U}}(x,t)$ which connects the solution of ηt = f(η) at t = −∞ and V(x) at t = +∞.
${{\cal U}}(x,t)$ which connects the solution of ηt = f(η) at t = −∞ and V(x) at t = +∞.
MSC classification
Information
- Type
- Papers
- Information
- Copyright
- © Cambridge University Press 2019
Footnotes
This research was partly supported by the NSFC (No. 11671262) and JSPS KAKENHI Grant Number, 18H01139, 26247013 and JST CREST Grant Number JPMJCR14D3.
References
- 4
- Cited by

