Article contents
Semimartingale decomposition of convex functions of continuoussemimartingales by Brownian perturbation
Published online by Cambridge University Press: 17 May 2013
Abstract
In this note we prove that the local martingale part of a convex functionf of a d-dimensional semimartingaleX = M + A can be written in terms ofan Itô stochastic integral∫H(X)dM, whereH(x) is some particular measurable choice ofsubgradient \hbox{$\sub$}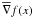 ∇f(x) off at x, and M is the martingale partof X. This result was first proved by Bouleau in [N. Bouleau, C.R. Acad. Sci. Paris Sér. I Math. 292 (1981) 87–90]. Here wepresent a new treatment of the problem. We first prove the result for\hbox{$\widetilde{X}=X+\epsilon B$}
∇f(x) off at x, and M is the martingale partof X. This result was first proved by Bouleau in [N. Bouleau, C.R. Acad. Sci. Paris Sér. I Math. 292 (1981) 87–90]. Here wepresent a new treatment of the problem. We first prove the result for\hbox{$\widetilde{X}=X+\epsilon B$}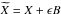 X=X+ϵB,ϵ > 0, where B is a standardBrownian motion, and then pass to the limit as ϵ → 0, using results in[M.T. Barlow and P. Protter, On convergence of semimartingales. In Séminaire deProbabilités, XXIV, 1988/89, Lect. Notes Math., vol. 1426.Springer, Berlin (1990) 188–193; E. Carlen and P. Protter, Illinois J. Math.36 (1992) 420–427]. The former paper concerns convergence ofsemimartingale decompositions of semimartingales, while the latter studies a special caseof converging convex functions of semimartingales.
X=X+ϵB,ϵ > 0, where B is a standardBrownian motion, and then pass to the limit as ϵ → 0, using results in[M.T. Barlow and P. Protter, On convergence of semimartingales. In Séminaire deProbabilités, XXIV, 1988/89, Lect. Notes Math., vol. 1426.Springer, Berlin (1990) 188–193; E. Carlen and P. Protter, Illinois J. Math.36 (1992) 420–427]. The former paper concerns convergence ofsemimartingale decompositions of semimartingales, while the latter studies a special caseof converging convex functions of semimartingales.
Information
- Type
- Research Article
- Information
- Copyright
- © EDP Sciences, SMAI, 2013
References
- 3
- Cited by

