Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Comte, Fabienne
and
Merlevède, Florence
2002.
Adaptive estimation of the stationary density of discrete and continuous time mixing processes.
ESAIM: Probability and Statistics,
Vol. 6,
Issue. ,
p.
211.
Blanke, Delphine
2003.
Estimation adaptative de la densité avec données échantillonnées.
Comptes Rendus. Mathématique,
Vol. 337,
Issue. 10,
p.
675.
Klemelä, Jussi
and
Tsybakov, Alexandre B.
2004.
Exact constants for pointwise adaptive estimation under the Riesz transform.
Probability Theory and Related Fields,
Vol. 129,
Issue. 3,
p.
441.
Butucea, Cristina
and
Matias, Catherine
2005.
Minimax estimation of the noise level and of the deconvolution density in a semiparametric convolution model.
Bernoulli,
Vol. 11,
Issue. 2,
Klemelä, Jussi
2006.
Sharp adaptive estimation of quadratic functionals.
Probability Theory and Related Fields,
Vol. 134,
Issue. 4,
p.
539.
Blanke, Delphine
2006.
Adaptive sampling schemes for density estimation.
Journal of Statistical Planning and Inference,
Vol. 136,
Issue. 9,
p.
2898.
Butucea, C.
and
Comte, F.
2009.
Adaptive estimation of linear functionals in the convolution model and applications.
Bernoulli,
Vol. 15,
Issue. 1,
Plancade, S.
2009.
Estimation of the density of regression errors by pointwise model selection.
Mathematical Methods of Statistics,
Vol. 18,
Issue. 4,
p.
341.
Giné, Evarist
and
Nickl, Richard
2009.
An exponential inequality for the distribution function of the kernel density estimator, with applications to adaptive estimation.
Probability Theory and Related Fields,
Vol. 143,
Issue. 3-4,
p.
569.
Comte, F.
and
Genon-Catalot, V.
2012.
Convolution power kernels for density estimation.
Journal of Statistical Planning and Inference,
Vol. 142,
Issue. 7,
p.
1698.
Bec, Mélina
and
Lacour, Claire
2015.
Adaptive pointwise estimation for pure jump Lévy processes.
Statistical Inference for Stochastic Processes,
Vol. 18,
Issue. 3,
p.
229.
Strauch, Claudia
2016.
Exact adaptive pointwise drift estimation for multidimensional ergodic diffusions.
Probability Theory and Related Fields,
Vol. 164,
Issue. 1-2,
p.
361.
Patschkowski, Tim
and
Rohde, Angelika
2016.
Adaptation to lowest density regions with application to support recovery.
The Annals of Statistics,
Vol. 44,
Issue. 1,
Bertin, Karine
and
Klutchnikoff, Nicolas
2017.
Pointwise adaptive estimation of the marginal density of a weakly dependent process.
Journal of Statistical Planning and Inference,
Vol. 187,
Issue. ,
p.
115.
Butucea, Cristina
Delmas, Jean-François
Dutfoy, Anne
and
Fischer, Richard
2018.
Fast adaptive estimation of log-additive exponential models in Kullback-Leibler divergence.
Electronic Journal of Statistics,
Vol. 12,
Issue. 1,
Bertin, Karine
El Kolei, Salima
and
Klutchnikoff, Nicolas
2019.
Adaptive density estimation on bounded domains.
Annales de l'Institut Henri Poincaré, Probabilités et Statistiques,
Vol. 55,
Issue. 4,
Liu, Youming
and
Wu, Cong
2019.
Point-wise estimation for anisotropic densities.
Journal of Multivariate Analysis,
Vol. 171,
Issue. ,
p.
112.
Liu, Youming
and
Wu, Cong
2020.
Point-Wise Wavelet Estimation in the Convolution Structure Density Model.
Journal of Fourier Analysis and Applications,
Vol. 26,
Issue. 6,
Kroll, Martin
2021.
On density estimation at a fixed point under local differential privacy.
Electronic Journal of Statistics,
Vol. 15,
Issue. 1,
Wu, Cong
Zeng, Xiaochen
and
Mi, Na
2021.
Adaptive and optimal pointwise deconvolution density estimations by wavelets.
Advances in Computational Mathematics,
Vol. 47,
Issue. 1,
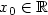 , over the densityfunctions that belong to the Sobolev class Wn(β,L). We consider theadaptive problem setup, where the regularity parameter β is unknownand varies in a given set B n . A sharp adaptive estimator is obtained,and the explicit asymptotical constant, associated to its rate ofconvergence is found.
, over the densityfunctions that belong to the Sobolev class Wn(β,L). We consider theadaptive problem setup, where the regularity parameter β is unknownand varies in a given set B n . A sharp adaptive estimator is obtained,and the explicit asymptotical constant, associated to its rate ofconvergence is found.