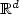Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Luschgy, Harald
and
Pagès, Gilles
2007.
High-resolution product quantization for Gaussian processes under sup-norm distortion.
Bernoulli,
Vol. 13,
Issue. 3,
Pagès, Gilles
and
Printems, Jacques
2009.
Special Volume: Mathematical Modeling and Numerical Methods in Finance.
Vol. 15,
Issue. ,
p.
595.
Sellami, Afef
2010.
Quantization Based Filtering Method Using First Order Approximation.
SIAM Journal on Numerical Analysis,
Vol. 47,
Issue. 6,
p.
4711.
BARDOU, OLIVIER
BOUTHEMY, SANDRINE
and
PAGÈS, GILLES
2010.
WHEN ARE SWING OPTIONS BANG-BANG?.
International Journal of Theoretical and Applied Finance,
Vol. 13,
Issue. 06,
p.
867.
Pagès, Gilles
and
Sellami, Afef
2011.
Séminaire de Probabilités XLIII.
Vol. 2006,
Issue. ,
p.
269.
Junglen, Stefan
2011.
Quantization Balls and Asymptotics of Quantization Radii for Probability Distributions with Radial Exponential Tails.
Electronic Communications in Probability,
Vol. 16,
Issue. none,
Graf, Siegfried
Luschgy, Harald
and
Pagès, Gilles
2012.
The local quantization behavior of absolutely continuous probabilities.
The Annals of Probability,
Vol. 40,
Issue. 4,
Pagès, Gilles
and
Sagna, Abass
2012.
Asymptotics of the maximal radius of an Lr-optimal sequence of quantizers.
Bernoulli,
Vol. 18,
Issue. 1,
Bronstein, Anne Laure
Pagès, Gilles
and
Portès, Jacques
2013.
Multi-asset American Options and Parallel Quantization.
Methodology and Computing in Applied Probability,
Vol. 15,
Issue. 3,
p.
547.
Zhu, Sanguo
2013.
A characterization of the optimal sets for self-similar measures with respect to the geometric mean error.
Acta Mathematica Hungarica,
Vol. 138,
Issue. 3,
p.
201.
Corlay, Sylvain
Lebovits, Joachim
and
Véhel, Jacques Lévy
2014.
MULTIFRACTIONAL STOCHASTIC VOLATILITY MODELS.
Mathematical Finance,
Vol. 24,
Issue. 2,
p.
364.
Luschgy, Harald
and
Pagès, Gilles
2015.
Greedy vector quantization.
Journal of Approximation Theory,
Vol. 198,
Issue. ,
p.
111.
Pagès, Gilles
and
Sagna, Abass
2018.
Improved error bounds for quantization based numerical schemes for BSDE and nonlinear filtering.
Stochastic Processes and their Applications,
Vol. 128,
Issue. 3,
p.
847.
Zhu, San Guo
2019.
On the Asymptotic Uniformity of the Quantization Error for Moran Measures on ℝ1.
Acta Mathematica Sinica, English Series,
Vol. 35,
Issue. 9,
p.
1520.
Guo, Gaoyue
and
Obłój, Jan
2019.
Computational methods for martingale optimal transport problems.
The Annals of Applied Probability,
Vol. 29,
Issue. 6,
Zhu, Sanguo
2020.
Asymptotic uniformity of the quantization error for the Ahlfors-David probability measures.
Science China Mathematics,
Vol. 63,
Issue. 6,
p.
1039.
Lemaire, Vincent
Montes, Thibaut
and
Pagès, Gilles
2020.
New weak error bounds and expansions for optimal quantization.
Journal of Computational and Applied Mathematics,
Vol. 371,
Issue. ,
p.
112670.
Zhu, Sanguo
and
Zhou, Youming
2021.
On the optimal Voronoi partitions for Ahlfors-David measures with respect to the geometric mean error.
Journal of Mathematical Analysis and Applications,
Vol. 498,
Issue. 2,
p.
124897.
El Nmeir, Rancy
Luschgy, Harald
and
Pagès, Gilles
2022.
New approach to greedy vector quantization.
Bernoulli,
Vol. 28,
Issue. 1,
Zhu, Sanguo
2023.
Asymptotics of the quantization errors for some Markov-type measures with complete overlaps.
Journal of Mathematical Analysis and Applications,
Vol. 528,
Issue. 2,
p.
127585.