Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ricci, Valeria
and
Wennberg, Bernt
2004.
On the derivation of a linear Boltzmann equation from a periodic lattice gas.
Stochastic Processes and their Applications,
Vol. 111,
Issue. 2,
p.
281.
Marklof, Jens
and
Strömbergsson, Andreas
2008.
Kinetic transport in the two-dimensional periodic Lorentz gas.
Nonlinearity,
Vol. 21,
Issue. 7,
p.
1413.
Sanders, David P.
2008.
Normal diffusion in crystal structures and higher-dimensional billiard models with gaps.
Physical Review E,
Vol. 78,
Issue. 6,
Caglioti, Emanuele
and
Golse, François
2008.
The Boltzmann–Grad limit of the periodic Lorentz gas in two space dimensions.
Comptes Rendus. Mathématique,
Vol. 346,
Issue. 7-8,
p.
477.
Golse, François
2009.
On the Periodic Lorentz Gas and the Lorentz Kinetic Equation.
Annales de la Faculté des sciences de Toulouse : Mathématiques,
Vol. 17,
Issue. 4,
p.
735.
Caglioti, Emanuele
and
Golse, François
2010.
On the Boltzmann-Grad Limit for the Two Dimensional Periodic Lorentz Gas.
Journal of Statistical Physics,
Vol. 141,
Issue. 2,
p.
264.
Bernard, Etienne
Caglioti, Emanuele
and
Golse, François
2010.
Homogenization of the Linear Boltzmann Equation in a Domain with a Periodic Distribution of Holes.
SIAM Journal on Mathematical Analysis,
Vol. 42,
Issue. 5,
p.
2082.
Marklof, Jens
and
Strömbergsson, Andreas
2010.
The distribution of free path lengths in the periodic Lorentz gas and related lattice point problems.
Annals of Mathematics,
Vol. 172,
Issue. 3,
p.
1949.
Marklof, Jens
and
Strömbergsson, Andreas
2011.
The Periodic Lorentz Gas in The Boltzmann–Grad Limit: Asymptotic Estimates.
Geometric and Functional Analysis,
Vol. 21,
Issue. 3,
p.
560.
Marklof, Jens
and
Strömbergsson, Andreas
2011.
The Boltzmann-Grad limit of the periodic Lorentz gas.
Annals of Mathematics,
Vol. 174,
Issue. 1,
p.
225.
Wennberg, Bernt
2012.
Free Path Lengths in Quasi Crystals.
Journal of Statistical Physics,
Vol. 147,
Issue. 5,
p.
981.
Golse, François
2012.
Nonlinear Partial Differential Equations.
p.
39.
Marklof, Jens
and
Strömbergsson, Andreas
2014.
Free Path Lengths in Quasicrystals.
Communications in Mathematical Physics,
Vol. 330,
Issue. 2,
p.
723.
Marklof, Jens
and
Strömbergsson, Andreas
2014.
Power-Law Distributions for the Free Path Length in Lorentz Gases.
Journal of Statistical Physics,
Vol. 155,
Issue. 6,
p.
1072.
Nándori, Péter
Szász, Domokos
and
Varjú, Tamás
2014.
Tail Asymptotics of Free Path Lengths for the Periodic Lorentz Process: On Dettmann’s Geometric Conjectures.
Communications in Mathematical Physics,
Vol. 331,
Issue. 1,
p.
111.
Hening, Alexandru
Rizzolo, Douglas
and
Wayman, Eric
2016.
The free path in a high velocity random flight process associated to a Lorentz gas in an external field.
Transactions of the American Mathematical Society, Series B,
Vol. 3,
Issue. 2,
p.
27.
Kraemer, Atahualpa S
Kryukov, Nikolay
and
Sanders, David P
2016.
Efficient algorithms for general periodic Lorentz gases in two and three dimensions.
Journal of Physics A: Mathematical and Theoretical,
Vol. 49,
Issue. 2,
p.
025001.
Marklof, Jens
and
Tóth, Bálint
2016.
Superdiffusion in the Periodic Lorentz Gas.
Communications in Mathematical Physics,
Vol. 347,
Issue. 3,
p.
933.
Holmin, Samuel
Kurlberg, Pär
and
Månsson, Daniel
2018.
On the free path length distribution for linear motion in an n-dimensional box.
Journal of Physics A: Mathematical and Theoretical,
Vol. 51,
Issue. 46,
p.
465201.
Marklof, Jens
and
Strömbergsson, Andreas
2024.
Kinetic Theory for the Low-Density Lorentz Gas.
Memoirs of the American Mathematical Society,
Vol. 294,
Issue. 1464,
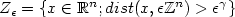 and let the free path length be defined as $\tau_\epsilon(x,v)=\inf\{t> 0 ; x-tv\in Z_\epsilon\}.$
and let the free path length be defined as $\tau_\epsilon(x,v)=\inf\{t> 0 ; x-tv\in Z_\epsilon\}.$ 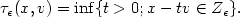 In the Boltzmann-Grad scaling corresponding to $\gamma=\frac{n}{n-1}$
In the Boltzmann-Grad scaling corresponding to $\gamma=\frac{n}{n-1}$ 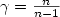 , it is shownthat the limiting distribution $\phi_\epsilon$
, it is shownthat the limiting distribution $\phi_\epsilon$ 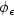 of $\tau_\epsilon$
of $\tau_\epsilon$ 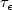 is bounded from belowby an expression of the form C/t, for some C> 0. A numerical study seems toindicate that asymptotically for large t, $\phi_\epsilon\sim C/t$
is bounded from belowby an expression of the form C/t, for some C> 0. A numerical study seems toindicate that asymptotically for large t, $\phi_\epsilon\sim C/t$ 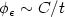 .This is an extension of a previous work [J. Bourgain et al., Comm. Math. Phys.190 (1998) 491-508]. As aconsequence, it is proved that the linear Boltzmann type transport equation is inappropriate to describethe Boltzmann-Grad limit of the periodic Lorentz gas, at variance with the usualcase of a Poisson distribution of scatterers treated in [G. Gallavotti (1972)].
.This is an extension of a previous work [J. Bourgain et al., Comm. Math. Phys.190 (1998) 491-508]. As aconsequence, it is proved that the linear Boltzmann type transport equation is inappropriate to describethe Boltzmann-Grad limit of the periodic Lorentz gas, at variance with the usualcase of a Poisson distribution of scatterers treated in [G. Gallavotti (1972)].
