Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kulshreshtha, Kshitij
Nataraj, Neela
and
Jung, Michael
2004.
Performance of a parallel mixed finite element implementation for fourth order clamped anisotropic plate bending problems in distributed memory environments.
Applied Mathematics and Computation,
Vol. 155,
Issue. 3,
p.
753.
Nataraj, Neela
2004.
A Mixed Finite Element Method for Fourth Order Eigenvalue Problems.
PAMM,
Vol. 4,
Issue. 1,
p.
358.
Kulshreshtha, Kshitij
and
Nataraj, Neela
2005.
A parallel mixed finite element implementation for approximation of eigenvalues and eigenvectors of fourth-order eigenvalue problems.
Journal of Sound and Vibration,
Vol. 285,
Issue. 4-5,
p.
1242.
Nataraj, Neela
2009.
A mixed finite element method for fourth order eigenvalue problems.
Applied Mathematics and Computation,
Vol. 213,
Issue. 1,
p.
60.
Gudi, Thirupathi
Gupta, Hari Shanker
and
Nataraj, Neela
2013.
Analysis of an Interior Penalty Method for Fourth Order Problems on Polygonal Domains.
Journal of Scientific Computing,
Vol. 54,
Issue. 1,
p.
177.
Doss, L. Jones Tarcius
and
Nandini, A. P.
2019.
A fourth‐order H1‐Galerkin mixed finite element method for Kuramoto–Sivashinsky equation.
Numerical Methods for Partial Differential Equations,
Vol. 35,
Issue. 2,
p.
445.
Song, Shicang
and
Liu, Zhixin
2021.
A second‐order isoparametric element method to solve plane linear elastic problem.
Numerical Methods for Partial Differential Equations,
Vol. 37,
Issue. 2,
p.
1535.
Liu, Zhixin
and
Song, Shicang
2021.
An isoparametric mixed finite element method for approximating a class of fourth-order elliptic problem.
Computers & Mathematics with Applications,
Vol. 96,
Issue. ,
p.
77.
Li, Yu
Xie, Manting
and
Xiong, Chunguang
2022.
A New Family of Mixed Method for the Biharmonic Eigenvalue Problem Based on the First Order Equations of Hellan–Herrmann–Johnson Type.
Journal of Scientific Computing,
Vol. 93,
Issue. 3,
Liu, Zhixin
Song, Minghui
and
Liang, Hui
2024.
An Isoparametric Finite Element Method for Time-fractional Parabolic Equation on 2D Curved Domain.
Journal of Scientific Computing,
Vol. 99,
Issue. 3,
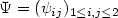 anddisplacement field `u', have been developed.
anddisplacement field `u', have been developed.