Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Sarghini, F.
Coppola, G.
and
de Felice, G.
2002.
A new high‐order finite volume element method with spectral‐like resolution.
International Journal for Numerical Methods in Fluids,
Vol. 40,
Issue. 3-4,
p.
487.
Croisille, Jean‐Pierre
and
Greff, Isabelle
2002.
Some nonconforming mixed box schemes for elliptic problems.
Numerical Methods for Partial Differential Equations,
Vol. 18,
Issue. 3,
p.
355.
Chatzipantelidis, P.
Makridakis, Ch.
and
Plexousakis, M.
2003.
A-posteriori error estimates for a finite volume method for the Stokes problem in two dimensions.
Applied Numerical Mathematics,
Vol. 46,
Issue. 1,
p.
45.
El Alaoui, Linda
and
Ern, Alexandre
2004.
Residual and hierarchicalaposteriorierror estimates for nonconforming mixed finite element methods.
ESAIM: Mathematical Modelling and Numerical Analysis,
Vol. 38,
Issue. 6,
p.
903.
Croisille, Jean-Pierre
and
Greff, Isabelle
2005.
An efficient box-scheme for convection–diffusion equations with sharp contrast in the diffusion coefficients.
Computers & Fluids,
Vol. 34,
Issue. 4-5,
p.
461.
Kim, Kwang Y.
2006.
New mixed finite volume methods for second order eliptic problems.
ESAIM: Mathematical Modelling and Numerical Analysis,
Vol. 40,
Issue. 1,
p.
123.
El Alaoui, Linda
and
Ern, Alexandre
2006.
Nonconforming finite element methods with subgrid viscosity applied to advection‐diffusion‐reaction equations.
Numerical Methods for Partial Differential Equations,
Vol. 22,
Issue. 5,
p.
1106.
Croisille, J.-P.
2006.
A Hermitian Box-scheme for One-dimensional Elliptic Equations – Application to Problems with High Contrasts in the Ellipticity.
Computing,
Vol. 78,
Issue. 4,
p.
329.
Ern, Alexandre
and
Guermond, Jean-Luc
2006.
Evaluation of the condition number in linear systems arising in finite element approximations.
ESAIM: Mathematical Modelling and Numerical Analysis,
Vol. 40,
Issue. 1,
p.
29.
Droniou, Jérôme
and
Eymard, Robert
2006.
A mixed finite volume scheme for anisotropic diffusion problems on any grid.
Numerische Mathematik,
Vol. 105,
Issue. 1,
p.
35.
Mishev, Ilya D.
and
Chen, Qian‐Yong
2007.
A mixed finite volume method for elliptic problems.
Numerical Methods for Partial Differential Equations,
Vol. 23,
Issue. 5,
p.
1122.
Tabatabaei, Amir Hossein A.E.
Shakour, Elham
and
Dehghan, Mehdi
2007.
Some implicit methods for the numerical solution of Burgers’ equation.
Applied Mathematics and Computation,
Vol. 191,
Issue. 2,
p.
560.
Perot, J.B.
and
Subramanian, V.
2007.
A discrete calculus analysis of the Keller Box scheme and a generalization of the method to arbitrary meshes.
Journal of Computational Physics,
Vol. 226,
Issue. 1,
p.
494.
Greff, Isabelle
2007.
Nonconforming Box‐Schemes for Elliptic Problems on Rectangular Grids.
SIAM Journal on Numerical Analysis,
Vol. 45,
Issue. 3,
p.
946.
El Alaoui, Linda
2009.
An adaptive finite volume box scheme for solving a class of nonlinear parabolic equations.
Applied Mathematics Letters,
Vol. 22,
Issue. 3,
p.
291.
Ju, Lili
and
Du, Qiang
2009.
A finite volume method on general surfaces and its error estimates.
Journal of Mathematical Analysis and Applications,
Vol. 352,
Issue. 2,
p.
645.
Dhawan, S.
Kapoor, S.
Kumar, S.
and
Rawat, S.
2012.
Contemporary review of techniques for the solution of nonlinear Burgers equation.
Journal of Computational Science,
Vol. 3,
Issue. 5,
p.
405.
Kwak, Do Y.
2012.
A New Class of Higher Order Mixed Finite Volume Methods for Elliptic Problems.
SIAM Journal on Numerical Analysis,
Vol. 50,
Issue. 4,
p.
1941.
Ranjan, R.
and
Pantano, C.
2013.
A collocated method for the incompressible Navier–Stokes equations inspired by the Box scheme.
Journal of Computational Physics,
Vol. 232,
Issue. 1,
p.
346.
Liu, Huipo
Wang, Shuanghu
and
Han, Hongbin
2016.
Error Analysis and Adaptive Methods of Least Squares Nonconforming Finite Element for the Transport Equations.
Advances in Applied Mathematics and Mechanics,
Vol. 8,
Issue. 5,
p.
871.
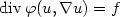 . The first scheme, which has been introduced in [CITE], is a generalization in two dimensions of Keller's box-scheme. The second scheme is the dual of the first one, and is a cell-centeredscheme for u and the flux φ. For the first scheme, the two trial finite element spaces are the nonconforming space of Crouzeix-Raviartfor the primal unknown u and the div-conformingspace of Raviart-Thomas for the flux φ. The two test spaces are the functions constant per cell both for the conservative and for the fluxequations.We prove an optimal second order error estimate for the box scheme and we emphasize the link between this scheme and the post-processing of Arnold and Brezzi of the classical mixed method.
. The first scheme, which has been introduced in [CITE], is a generalization in two dimensions of Keller's box-scheme. The second scheme is the dual of the first one, and is a cell-centeredscheme for u and the flux φ. For the first scheme, the two trial finite element spaces are the nonconforming space of Crouzeix-Raviartfor the primal unknown u and the div-conformingspace of Raviart-Thomas for the flux φ. The two test spaces are the functions constant per cell both for the conservative and for the fluxequations.We prove an optimal second order error estimate for the box scheme and we emphasize the link between this scheme and the post-processing of Arnold and Brezzi of the classical mixed method.
