Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kevrekidis, Ioannis G.
and
Samaey, Giovanni
2009.
Equation-Free Multiscale Computation: Algorithms and Applications.
Annual Review of Physical Chemistry,
Vol. 60,
Issue. 1,
p.
321.
Härdin, Hanna M.
Zagaris, Antonios
Krab, Klaas
and
Westerhoff, Hans V.
2009.
Simplified yet highly accurate enzyme kinetics for cases of low substrate concentrations.
The FEBS Journal,
Vol. 276,
Issue. 19,
p.
5491.
Lebiedz, Dirk
Reinhardt, Volkmar
and
Siehr, Jochen
2010.
Minimal curvature trajectories: Riemannian geometry concepts for slow manifold computation in chemical kinetics.
Journal of Computational Physics,
Vol. 229,
Issue. 18,
p.
6512.
Lebiedz, Dirk
2010.
Entropy-Related Extremum Principles for Model Reduction of Dissipative Dynamical Systems.
Entropy,
Vol. 12,
Issue. 4,
p.
706.
Lebiedz, Dirk
Siehr, Jochen
and
Unger, Jonas
2011.
A Variational Principle for Computing Slow Invariant Manifolds in Dissipative Dynamical Systems.
SIAM Journal on Scientific Computing,
Vol. 33,
Issue. 2,
p.
703.
Vanderhoydonc, Y.
and
Vanroose, W.
2011.
Lifting in hybrid lattice Boltzmann and PDE models.
Computing and Visualization in Science,
Vol. 14,
Issue. 2,
p.
67.
Zagaris, Antonios
Vandekerckhove, Christophe
William Gear, C.
J. Kaper, Tasso
and
G. Kevrekidis, Ioannis
2012.
Stability and stabilization of the constrained runs schemes for equation-free projection to a slow manifold.
Discrete & Continuous Dynamical Systems - A,
Vol. 32,
Issue. 8,
p.
2759.
Ariel, G.
Sanz-Serna, J. M.
and
Tsai, R.
2012.
A Multiscale Technique for Finding Slow Manifolds of Stiff Mechanical Systems.
Multiscale Modeling & Simulation,
Vol. 10,
Issue. 4,
p.
1180.
Mazzi, Giacomo
De Decker, Yannick
and
Samaey, Giovanni
2012.
Towards an efficient multiscale modeling of low-dimensional reactive systems: Study of numerical closure procedures.
The Journal of Chemical Physics,
Vol. 137,
Issue. 20,
Kan, Xingye
Duan, Jinqiao
Kevrekidis, Ioannis G.
and
Roberts, Anthony J.
2013.
Simulating Stochastic Inertial Manifolds by a Backward-Forward Approach.
SIAM Journal on Applied Dynamical Systems,
Vol. 12,
Issue. 1,
p.
487.
Siettos, Constantinos
2014.
Equation-free computation of coarse-grained center manifolds of microscopic simulators.
Journal of Computational Dynamics,
Vol. 1,
Issue. 2,
p.
377.
Marschler, Christian
Sieber, Jan
Berkemer, Rainer
Kawamoto, Atsushi
and
Starke, Jens
2014.
Implicit Methods for Equation-Free Analysis: Convergence Results and Analysis of Emergent Waves in Microscopic Traffic Models.
SIAM Journal on Applied Dynamical Systems,
Vol. 13,
Issue. 3,
p.
1202.
Härdin, Hanna M.
Zagaris, Antonios
Willms, Allan R.
and
Westerhoff, Hans V.
2014.
Clusters of reaction rates and concentrations in protein networks such as the phosphotransferase system.
The FEBS Journal,
Vol. 281,
Issue. 2,
p.
531.
Kristiansen, K. U.
Brøns, M.
and
Starke, J.
2014.
An Iterative Method for the Approximation of Fibers in Slow-Fast Systems.
SIAM Journal on Applied Dynamical Systems,
Vol. 13,
Issue. 2,
p.
861.
Marschler, Christian
Sieber, Jan
Hjorth, Poul G.
and
Starke, Jens
2015.
Traffic and Granular Flow '13.
p.
423.
Benoît, Eric
Brøns, Morten
Desroches, Mathieu
and
Krupa, Martin
2015.
Extending the zero-derivative principle for slow–fast dynamical systems.
Zeitschrift für angewandte Mathematik und Physik,
Vol. 66,
Issue. 5,
p.
2255.
Maclean, John
and
Gottwald, Georg A.
2015.
On convergence of higher order schemes for the projective integration method for stiff ordinary differential equations.
Journal of Computational and Applied Mathematics,
Vol. 288,
Issue. ,
p.
44.
Scheibe, Timothy D.
Murphy, Ellyn M.
Chen, Xingyuan
Rice, Amy K.
Carroll, Kenneth C.
Palmer, Bruce J.
Tartakovsky, Alexandre M.
Battiato, Ilenia
and
Wood, Brian D.
2015.
An Analysis Platform for Multiscale Hydrogeologic Modeling with Emphasis on Hybrid Multiscale Methods.
Groundwater,
Vol. 53,
Issue. 1,
p.
38.
Kristiansen, K. U.
2015.
Computation of Saddle-Type Slow Manifolds Using Iterative Methods.
SIAM Journal on Applied Dynamical Systems,
Vol. 14,
Issue. 2,
p.
1189.
Kuehn, Christian
2015.
Multiple Time Scale Dynamics.
Vol. 191,
Issue. ,
p.
327.
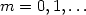 )finds iterativelyan approximationof the appropriate zeroof the (m+1)st time derivativeof the remaining variablesanduses this rootto approximate the locationof the pointon the slow manifoldcorresponding to these valuesof the observables.This articleis the firstof two articlesin whichthe accuracy and convergenceof the iterative algorithmsare analyzed.Here,we work directlywith fast-slow systems,in which there isan explicit small parameter, ε,measuring the separationof time scales.We show that,for each $m = 0, 1, \ldots$
)finds iterativelyan approximationof the appropriate zeroof the (m+1)st time derivativeof the remaining variablesanduses this rootto approximate the locationof the pointon the slow manifoldcorresponding to these valuesof the observables.This articleis the firstof two articlesin whichthe accuracy and convergenceof the iterative algorithmsare analyzed.Here,we work directlywith fast-slow systems,in which there isan explicit small parameter, ε,measuring the separationof time scales.We show that,for each $m = 0, 1, \ldots$ 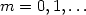 ,the fixed pointof the iterative algorithmapproximates the slow manifoldup to and includingterms of ${\mathcal O}(\varepsilon^m)$
,the fixed pointof the iterative algorithmapproximates the slow manifoldup to and includingterms of ${\mathcal O}(\varepsilon^m)$ 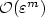 .Moreover,for each m,we identify explicitlythe conditionsunder whichthe mth iterative algorithmconverges to this fixed point.Finally,we show thatwhenthe iterationis unstable(orconverges slowly)it may be stabilized(orits convergencemay be accelerated)by applicationof the Recursive Projection Method.Alternatively,the Newton-KrylovGeneralized Minimal Residual Methodmay be used.In the subsequent article,we will considerthe accuracy and convergenceof the iterative algorithmsfor a broader classof systems – in whichthere need not bean explicitsmall parameter – to whichthe algorithms also apply.
.Moreover,for each m,we identify explicitlythe conditionsunder whichthe mth iterative algorithmconverges to this fixed point.Finally,we show thatwhenthe iterationis unstable(orconverges slowly)it may be stabilized(orits convergencemay be accelerated)by applicationof the Recursive Projection Method.Alternatively,the Newton-KrylovGeneralized Minimal Residual Methodmay be used.In the subsequent article,we will considerthe accuracy and convergenceof the iterative algorithmsfor a broader classof systems – in whichthere need not bean explicitsmall parameter – to whichthe algorithms also apply.
